Análise dos Sistemas Produtivos

Os conceitos apresentados sobre o Controle Estatístico do Processo levam às análises estatísticas de processos, à aplicação de médias, desvios e outros parâmetros de controle de processos visando à sua qualidade, mas também são fundamentais na avaliação da capacidade de um processo.

Os gráficos de controle utilizados na avaliação da estabilidade de um processo são de grande valia na garantia da qualidade de um processo, mas, mesmo um processo estável e previsível, pode apresentar defeitos. Dessa forma, não é suficiente colocar e manter um processo sob controle, é essencial avaliar se é capaz de atender às especificações fixadas. Essa avaliação constitui o estudo da capacidade do processo (MONTGOMERY, 2009). É interessante lembrar que qualquer projeto de produto fornece, além das medidas que o produto deve ter, também o intervalo de medidas possíveis. Tais valores especificados no projeto são:

• Valor Nominal (\(VN\)): valor que determinada a “medida” que o produto deve ter;
• Limite Superior da Especificação (\(LSE\)): limite superior que o intervalo de valores pode apresentar;
• Limite Inferior de Especificação (\(LIE\)): limite inferior que o intervalo pode apresentar.

A diferença entre o \(LSE\) e o \(LIE\) é conhecida como tolerância do projeto, mas

não há relação matemática ou estatística entre limite de controle e limite de especificação, os limites de controle são função da variabilidade do processo, medida pelo desvio padrão. Os limites de especificação são estabelecidos no projeto por engenheiros, técnicos ou pelo cliente (VIEIRA, 2012, p. 181).

Vale lembrar também que qualquer novo processo necessita de melhorias. Quando as causas especiais de variação de um processo estão sob controle, ou seja, quando a variabilidade ocorre apenas devido a causas comuns, pode-se dizer que o processo atingiu o nível de controle estatístico. Ainda segundo a autora, a capacidade do processo é definida a partir da faixa:

\[Intervalo = μ ±3σ\]

O intervalo, denominado faixa característica do processo, vai do limite natural de tolerância inferior (\(LNTI\)), ou \(μ – 3σ\), até o limite natural de tolerância superior (\(LNTS\)), ou \(μ + 3σ\), e tem como variação de intervalo um valor de \(6σ\). Nesse caso específico, se o processo estiver sob controle e normalizado, 99,73% dos valores da variável de interesse devem pertencer ao intervalo. Para estudar a capacidade do processo, deve-se, portanto, definir o intervalo \(6σ\) e comparar essa faixa com as especificações estabelecidas.

De forma conceitual, pode-se definir o intervalo entre \(μ - 3σ\) (\(LNTI\)) e \(μ + 3σ\) (\(LNTS\)) como a Capacidade do Processo, ou seja:

Capacidade do Processo = 6σ

Os valores de \(μ\) (média) e \(σ\) (desvio) são encontrados por meio de dados amostrais e utilizados na avaliação da capacidade do processo. A média \(μ\) pode ser aproximada pela média amostral, enquanto que \(σ\) pode ser aproximado por \(s\). Uma das maneiras de se avaliar a capacidade de um processo é por meio de procedimentos gráficos, com o uso de histogramas. A análise gráfica da capacidade de um processo corresponde à comparação de histogramas e gráficos sequenciais, construídos para o parâmetro de qualidade avaliado com os limites de especificação.

Segundo Pedroza (2019, p. 192), para estudar a capacidade do processo, é preciso executar a elaboração de um histograma, que segue os seguintes passos:

• colete uma amostra de pelo menos 100 itens produzidos e meça a característica da qualidade que se deseja analisar;
• calcule a média e o desvio padrão;
• calcule os limites naturais de tolerância e a capacidade do processo;
• organize uma tabela de distribuição de frequências e desenhe um histograma.

Uma vez elaborado o histograma, com base nas informações disponíveis, é possível analisar a capacidade de um processo. É interessante lembrar que o histograma é mais um facilitador da análise do que propriamente uma obrigação no procedimento, como se vê a seguir. De acordo com Pedroza (2019, p. 192-193), os passos a serem executados para isso são os seguintes:

• verifique se a média global coincide ou tem valor próximo ao valor nominal;
• compare a capacidade do processo (6σ) com a tolerância do projeto (\(LSE\) – \(LIE\));
• analise o histograma quanto à forma e à disposição;
• veja se os dados estão distribuídos entre os limites de especificação.

Novamente, é válido lembrar que o procedimento de análise de capacidade de um processo se relaciona à comparação dos limites de especificação (\(LIE\) e \(LSE\)) com os limites naturais (\(LNTI\) e \(LNTS\)), procedendo ao comparativo do que foi projetado com o que foi verificado. A seguir está um exemplo da aplicação desse tipo de abordagem para se verificar a capacidade de um processo, utilizado também por Vieira (2012). Considere, inicialmente, a tabela apresentada a seguir.

Nesse exemplo, foram tomadas cinco amostras de peças a cada hora, em um dia de trabalho, e um deles está representado acima. O mesmo elemento característico de qualidade foi medido nas cinco amostras (\(m = 5\)), em cada uma das quatro peças (\(n = 4\)).

Suponha que o valor nominal, limite superior da especificação e o limite inferior de especificação sejam:

\[VN = 81,5\]

\[LSE = 88\]

\[LIE = 75\]

O próximo passo para se averiguar a capacidade de processo é analisar o histograma referente ao caso. Nele, os dados são apresentados em intervalos específicos, aos quais é demarcada a frequência de ocorrência dessa faixa de valores:

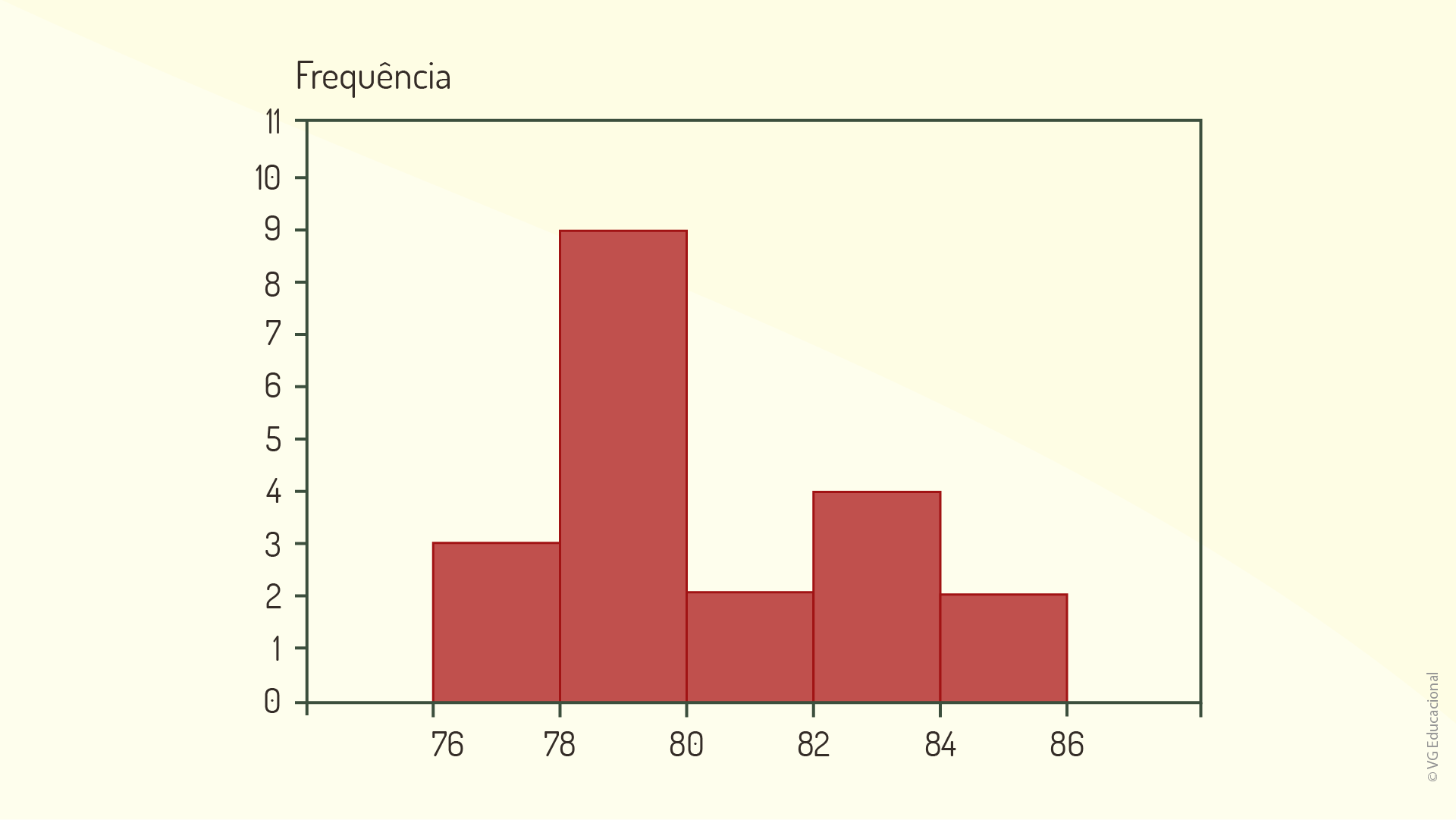
Optou-se, aqui, por dividir os dados em intervalos de amplitude igual a 2. Percebe-se uma forte tendência para que os valores estejam entre 78 e 80. Agora, podem-se calcular a média e o desvio para esse conjunto de dados. As equações utilizadas para essa determinação em relação ao histograma são diferentes das regularmente utilizadas para um conjunto de dados:

\[\underline{x}=\frac{\underline{x}_1+\underline{x}_2+...+\underline{x}_n}{m}\]

\[σ = \underline{R}/d2\]

Em que cada \(\underline{x}_i\) é a média de um intervalo, \(m\) é o número de amostras, \(σ\) é o desvio padrão, \(\underline{R}\) é a média das amplitudes das amostras e \(d2\) é um parâmetro estatístico tabelado, próprio da aplicação desse tipo de análise:

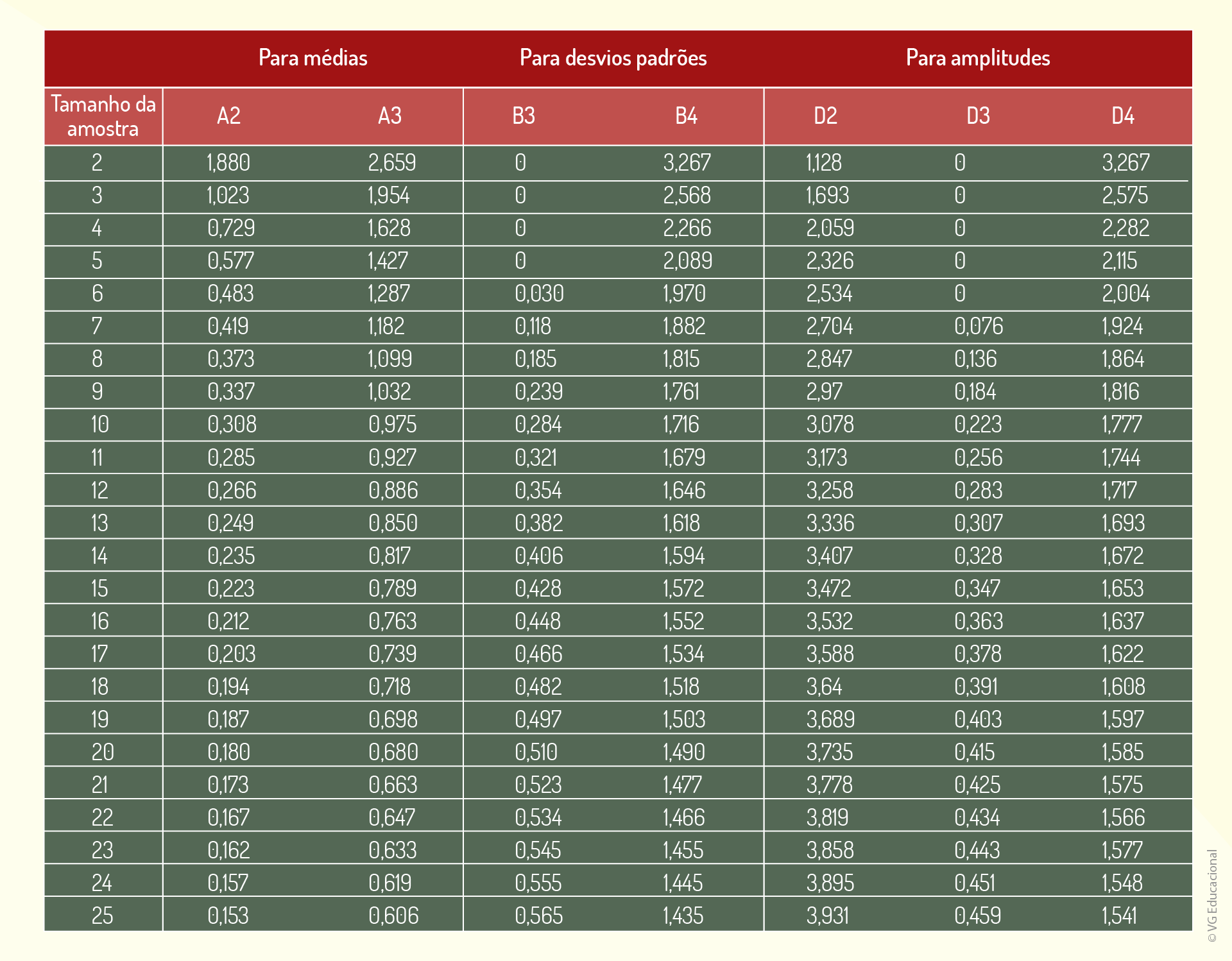
O uso de tabelas como essas é útil no trabalho com dados estatísticos que estão apresentados na forma de intervalos de valores, o que costuma ser verificado na maioria das tomadas de dados de um processo.

Retornando para os dados apresentados, é possível calcular os valores das médias dos intervalos, bem como encontrar as amplitudes de cada uma. Dessa forma, podem-se calcular a média e o desvio padrão (\(d_2\) = 2,059).

\[\underline{x}= (79 + 81 + 83 + 79 + 78)/5 = 80\]

\[\underline{R}= (5 + 3 + 7 + 4 + 3)/5 = 4,4\]

\[σ = /d_2 = 4,4/2,059 = 2,317\]

Sendo assim, a capacidade desse processo pode ser estimada, correspondendo, como dito anteriormente, a seis vezes o valor obtido para o desvio padrão das amostras verificadas no exemplo:

\[Capacidade = 6σ = 6.2,317 = 12,822\]

De posse dessas informações, pode-se afirmar que os dados medidos estão entre os limites de especificação (LIE = 75 e LSE = 88), no entanto, os valores mínimos (76) e máximos (86) estão muito próximos. Vieira (2012) afirma que isso implica um processo com poucas folgas.

Já no que diz respeito à média, que é igual a 80, ela está abaixo do valor nominal. Sendo assim, segundo a autora, temos um histograma assimétrico (como fica visivelmente claro), com um processo não centrado. A capacidade do processo, definida como 12,882 nesse exemplo específico, está muito próxima da tolerância definida para o projeto (LSE – LIE = 13), novamente indicando pouca folga, o que é indesejável para um processo. Nesse sentido, Vieira (2012) define que é necessário ajustar a média do processo para um valor mais próximo ao VN e, também, diminuir a variabilidade do processo.