Como se sabe, produtos e serviços são criados e prestados a todo momento, e uma das características mais valorizadas por empresas e indústrias, além de pelos próprios consumidores, é a qualidade desses produtos e serviços.
Nesse contexto, o Controle Estatístico de Processos (CEP) surge como uma ferramenta necessária para a avaliação dos parâmetros de qualidade, verificados a partir de dados, tabelas e gráficos, que, por sua vez, traduzem, em números, as informações dos processos, produtos e serviços.
Nesta unidade, serão abordados os conceitos básicos que definem essa área de atuação, os conceitos de estatística utilizados em CEP e o uso da distribuição de probabilidade. Por fim, serão avaliadas as variabilidades dos processos, tanto as causas comuns como as específicas envolvidas.
O Controle Estatístico de Processos (CEP) é, sem dúvida, uma das melhores metodologias desenvolvidas com o intuito de auxiliar o controle da qualidade de processos. O CEP tem sido utilizado, de maneira ampla, desde a Segunda Guerra Mundial.
Ramos (2000) afirma que foi apenas quando o Japão surgiu como líder em qualidade que os demais países começaram, verdadeiramente, a dar importância à obtenção de produtos por meio de processos estáveis e capazes de atender aos clientes, ou seja, processos estatisticamente padronizados. De acordo com Montgomery (2009), o CEP pode ser entendido como um conjunto de técnicas baseadas na análise de informações contidas em uma amostra, análise esta que, posteriormente, será aplicada na tomada de decisão de um processo.
Como o próprio nome indica, no CEP, as ferramentas estatísticas desempenham um papel crucial na melhoria da qualidade, uma vez que fornecem os meios pelos quais os produtos (bens e serviços) podem ser categorizados, selecionados, testados e avaliados. O conjunto de dados obtido nesse procedimento pode, então, ser utilizado para controlar e otimizar o processo de produção.
Para Ribeiro e Caten (2012), um dos principais objetivos do CEP é permitir um controle adequado e eficaz da qualidade. Tal procedimento, aumenta o comprometimento com a qualidade e, uma vez que é executado pelos próprios operadores, libera os gestores para outras tarefas. Segundo os autores, outra característica do CEP é possibilitar o monitoramento das características de interesse, ressaltando-se que é importante detectar os defeitos o mais cedo possível, para evitar a continuidade de processos com problemas e a produção de produtos com defeitos. Assim, o CEP também pode ser aplicado para aumentar a capacidade dos processos, reduzindo o refugo, o retrabalho e o custo.
Segundo Ribeiro e Caten (2012), considera-se que a origem do controle de qualidade teve início na década de 1920, nos Estados Unidos. Essa área se desenvolveu graças aos avanços das tecnologias de mediação e aplicação das cartas de controle, desenvolvidas pelo Dr. Walter A. Stewart, da empresa de telefonia Bell Telephone Laboratories. Shewhart propôs a utilização de cartas de controle com o intuito de analisar os dados provenientes de amostras, substituindo a detecção e a correção de itens com defeitos pelo estudo e pela prevenção de todos os problemas relacionados à qualidade (RIBEIRO; CATEN, 2012).
Ainda de acordo com os autores, posteriormente, o controle da qualidade foi adotado na Inglaterra, sendo que, na década de 1930, os trabalhos do estatístico E. S. Pearson foram usados como fundamento dos padrões normativos britânicos. A partir da década de 1950, os japoneses começaram a perceber que o controle da qualidade era afetado por inúmeros fatores, como humanos e culturais. Ribeiro e Caten (2012) indicam que, por meio dessa percepção, foi desenvolvido um novo método para o controle da qualidade, que, por sua vez, deu origem ao controle da qualidade total, o qual envolvia todos os setores da organização.
Mas quais são os elementos ou os principais aspectos, no contexto da qualidade, inerentes ao CEP? A qualidade tem dois aspectos a serem destacados: a qualidade do projeto e a qualidade de conformação. Para Vieira (2012, p. 2):
Os projetos têm diferentes graus de qualidade. Essa variação é intencional. Em princípio, um automóvel é simples meio de transporte, mas existem grandes diferenças de tamanho, desempenho e aparência entre eles. Essas diferenças são determinadas pela qualidade do projeto. É a qualidade do projeto que faz o produto ser ‘de luxo’ ou ‘popular’, ‘executivo’ ou ‘turista’, ‘5 estrelas’ ou ‘3 estrelas’ etc. Toda melhoria na qualidade do projeto aumenta o custo de produção e, consequentemente, o preço do produto. A qualidade de conformação mostra se o produto atende às especificações do projeto. Todo projeto estabelece especificações. Por exemplo, a embalagem de qualquer produto comercializado obedece às especificações quanto ao material que deverá ser utilizado, ao formato, às medidas, à cor etc.
O CEP corresponde à união de ferramentas voltadas à resolução de problemas, objetivando a estabilidade de processos e a melhoria da produção, por meio da diminuição das variabilidades, as quais podem ser comuns ou específicas. O CEP tem, em seu arcabouço, algumas ferramentas, todas elas relacionadas à gestão da qualidade (PEDROZA, 2019):
Segundo Pedroza (2019), as sete ferramentas englobam os aspectos técnicos básicos do controle estatístico de processos, todavia, quando aplicadas isoladamente, elas não conseguem alcançar os mesmos resultados que são verificados quando elas são aplicadas em conjunto. Ainda segundo Pedroza (2019), o desenvolvimento de um ambiente de melhoria contínua é dependente de um envolvimento da alta administração, uma vez que, nas organizações, essa cultura é incorporada de “cima para baixo”.
Compreender e buscar a melhoria da qualidade de bens e serviços são fatores decisivos e que conduzem as organizações e empresas ao sucesso, ao crescimento e a uma posição de competitividade em relação aos seus concorrentes. Além disso, o uso da qualidade como elemento integrante da estratégia de uma organização produz retorno sobre o investimento, uma vez que o cliente busca um produto que tenha comprado ou contratado anteriormente se ele satisfizer suas necessidades. A qualidade, na visão de Torelli e Ferreira (1995), também é parte crucial do ambiente produtivo e se correlaciona com as várias áreas e subáreas dos processos de uma organização, como apresentado na figura a seguir:
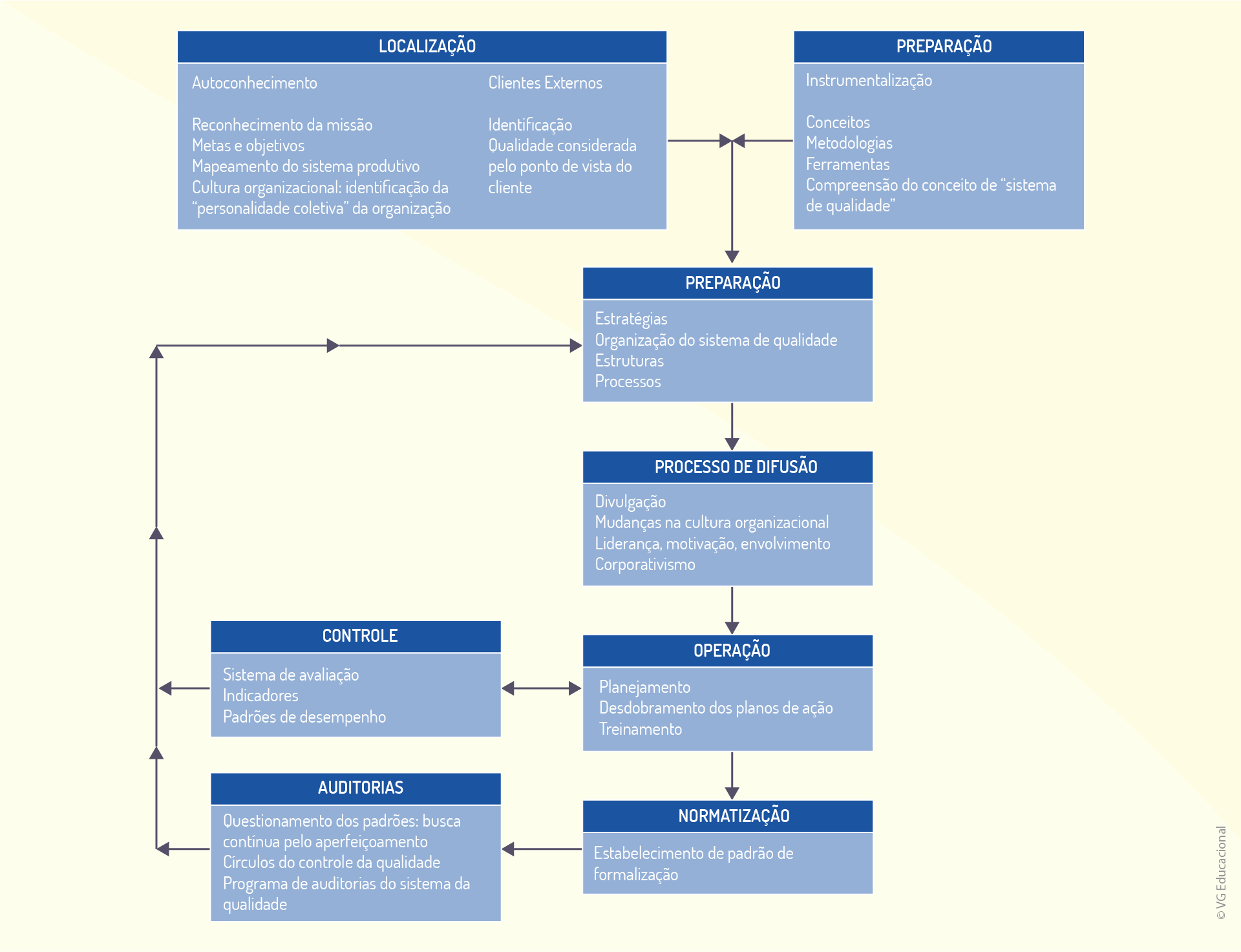
Ao se avaliar a atualidade do CEP, engana-se quem acredita que essa ferramenta é ultrapassada. Na verdade, ela apenas ressalta que o CEP tornou-se crucial, tendo um papel cada vez mais decisivo nas organizações, uma vez que a qualidade tem se tornado um dos principais objetivos no âmbito produtivo. Vale ressaltar, ainda, que o CEP foi um dos primeiros métodos analíticos com uso de recursos matemáticos (estatística) aplicados na produção (PALADINI, 2012; NETTO, 2017).
Mas qual seria a definição de qualidade?
Costumeiramente, considera-se que os produtos têm qualidade quando, em geral, são adequados para o uso. Para Vieira (2012), o consumidor percebe a qualidade do produto por meio de características que variam conforme o tipo de produto. De maneira sintética, as características relacionadas à qualidade de um produto são descritas no quadro a seguir.
Quadro 1.1 – Características da qualidade
Fonte: Adaptado de Vieira (2012), Montgomery (2009) e Garvin (1987).
Ainda no que se refere aos elementos inerentes à qualidade de um produto, segundo Montgomery (2009) e Netto (2017), há indicadores de qualidade que podem se dividir em características:
Nesse contexto, dos diversos fatores que impactam a qualidade de um produto e das formas de elencá-los e categorizá-los, surgiram, inclusive, abordagens de gestão focadas na qualidade. Um exemplo a ser citado é a Gestão da Qualidade Total (GQT) (do inglês, Total Quality Management), em que a qualidade está presente na gestão organizacional.
A GQT é uma estratégia que se iniciou nos anos 1980, com as filosofias de Deming e Juran como fundamento principal, e evoluiu para um espectro mais abrangente, “envolvendo organizações participativas e cultura organizacional, foco no cliente, melhoria da qualidade de fornecedores, integração do sistema de qualidade com os objetivos da empresa, em torno da melhoria da qualidade” (PEDROZA, 2019, p. 21).
A implantação de programas organizacionais pautados na qualidade total é afetada por peculiaridades e especificidades da organização e do ambiente no qual ela está inserida. No artigo a seguir, os autores apresentam uma forma de implantação de um programa de qualidade total. Artigo disponível em: https://www.scielo.br/pdf/gp/v2n3/a04v2n3.pdf. Acesso em: 09 nov. 2020.

Quanto à motivação para o uso do CEP, diversas são as vantagens para as operações de uma empresa. Provavelmente, as mais importantes são (RAMOS, 2000, p. 8-9):
Determinar o tipo de ação requerida (local ou no sistema) e, consequentemente, estabelecer a responsabilidade pela sua adoção (operação ou administração); Reduzir a variabilidade das características críticas dos produtos de forma a obter-se uma maior uniformidade e segurança dos itens produzidos; Permitir a determinação da real viabilidade de atender às especificações do produto ou às necessidades dos clientes, em condições normais de operação; Implantar soluções técnicas e administrativas que permitam a melhoria da qualidade e (principalmente) aumento da produtividade; Possibilitar o combate às causas dos problemas ao invés de seus efeitos, de modo a erradicá-los definitivamente do sistema de trabalho.
Também é importante aliar procedimentos estatísticos com outras ferramentas, que, em conjunto, permitam uma produção de qualidade, buscando a melhoria contínua da qualidade e da produtividade.
Sendo o CEP uma poderosa ferramenta para o controle de qualidade de um processo, seria possível garantir a qualidade da produção sem o uso de procedimentos matemáticos de análise? Reflita sobre o assunto.

Uma vez entendido o papel do CEP na realidade dos processos, cabe, agora, analisar quais são os conceitos essenciais relacionados a ele, procurando entender como o próprio CEP constitui-se.
A qualidade, como foco principal do Controle Estatístico de Processos (CEP), apresenta-se por características definidas, as quais são comumente percebidas e julgadas pelo consumidor. Tais características podem ser entendidas por dois elementos: a qual aspecto do produto ela se relaciona e a situação típica a qual ela está vinculada. Considerando esse tema, avalie as alternativas a seguir e assinale aquela em que as características analisadas e sua descrição são condizentes.
Desempenho (falhas do produto): consumidores analisam se as características do produto estão em conformidade com o padrão.
Incorreta. Para a característica desempenho, que se relaciona ao fato de o produto cumprir o que promete, os consumidores analisam se as informações fornecidas por propagandas ou vendedores são verdadeiras.
Confiabilidade (reputação do produto): consumidores avaliam benefícios extras ao se consumir o produto.
Incorreta. Na característica confiabilidade, que se relaciona à quantidade de falhas que o produto apresenta, os consumidores avaliam com que frequência é necessário realizar reparos no produto.
Estética (beleza do produto): consumidores analisam aspectos como estilo, cor e forma do produto.
Correta. A característica estética está ligada aos fatores visuais do produto, avaliados pelos consumidores por meio da análise de forma, cor, maleabilidade, estilo, dentre outras características.
Durabilidade (duração do produto): consumidores avaliam o produto de acordo com características consideradas essenciais.
Incorreta. A característica durabilidade de um produto está associada ao tempo de duração dele. Para esse fator, os consumidores costumam avaliar o tempo que o produto durará até que um novo ou similar precise ser comprado.
Qualidade observada (produto padronizado): consumidores avaliam o produto de acordo com a durabilidade dele.
Incorreta. A qualidade observada está mais ligada à reputação de um produto, ou seja, sua fama no mercado, e os consumidores a avaliam levando em consideração sua própria experiência.
Alguns elementos são básicos para que se entenda o papel do CEP no contexto de um processo, e o primeiro deles é o próprio processo. Entender o que é um processo é crucial para entender a importância do CEP.
Todas as atividades realizadas em uma organização, empresa ou indústria podem ser encaradas como um processo, ou seja, um conjunto de tarefas realizadas com determinado propósito. De forma geral, um processo corresponde à combinação de pessoas, equipamentos, ferramentas, insumos e métodos, cuja finalidade é a produção de um bem ou serviço. A figura a seguir ilustra a relação entre tais elementos.
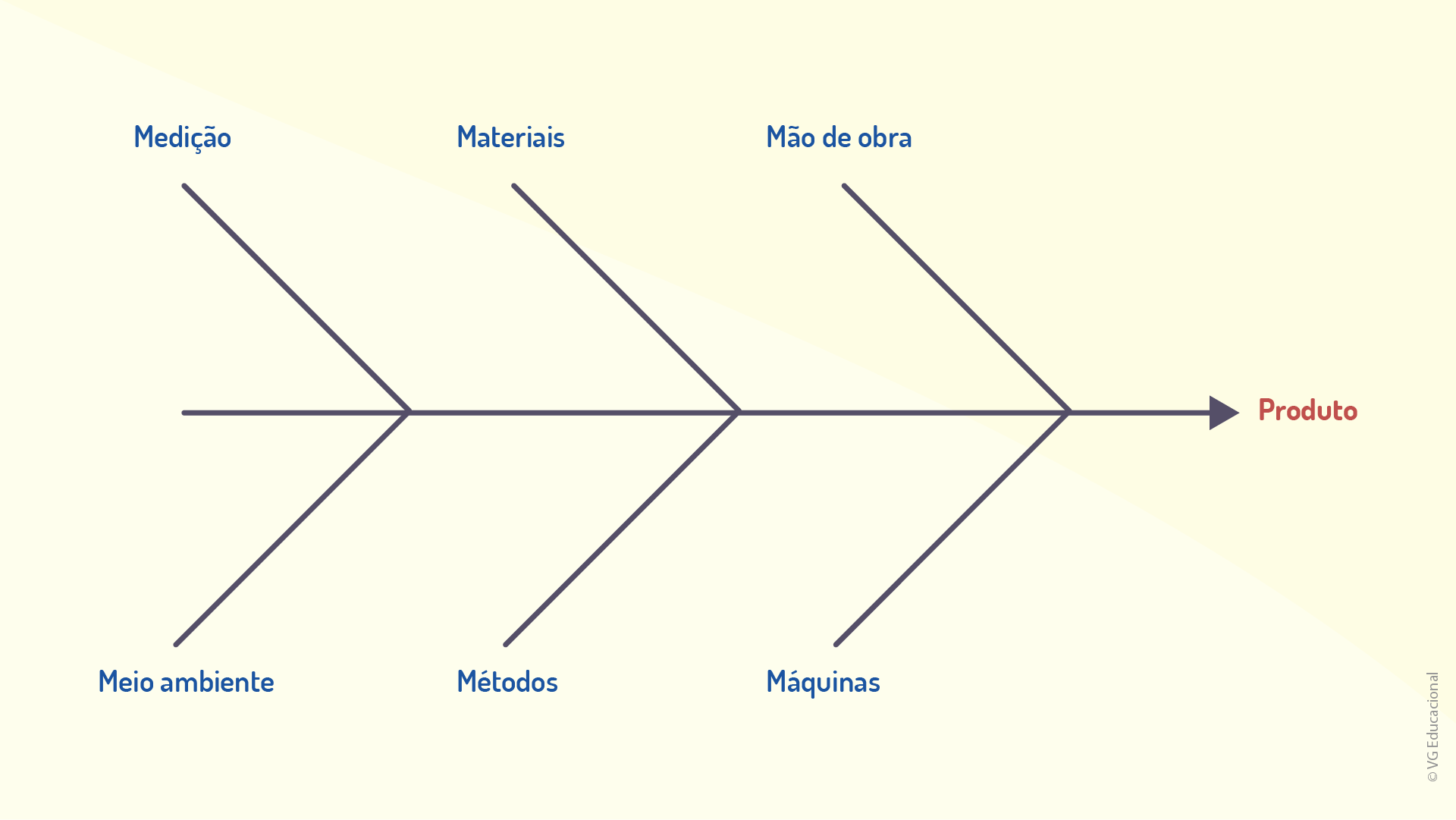
Ramos (2000) indica que, em todas as organizações, há um número enorme de processos, que podem ser produtivos ou administrativos, porém, apenas alguns deles são responsáveis por um maior impacto no resultado final. Inclusive, essa é a principal premissa da utilização do gráfico de Pareto para a análise de processos.
Ainda de acordo com Ramos (2000, p. 3), todos os processos têm cinco componentes essenciais:
A figura a seguir representa a forma genérica de um processo com os cinco elementos apresentados anteriormente e traz, ainda, outros dois elementos, que não são consumidos no processo, mas que são necessários para que ele ocorra adequadamente: o controle (para garantir a qualidade e a estabilidade) e os recursos (insumos gerais).
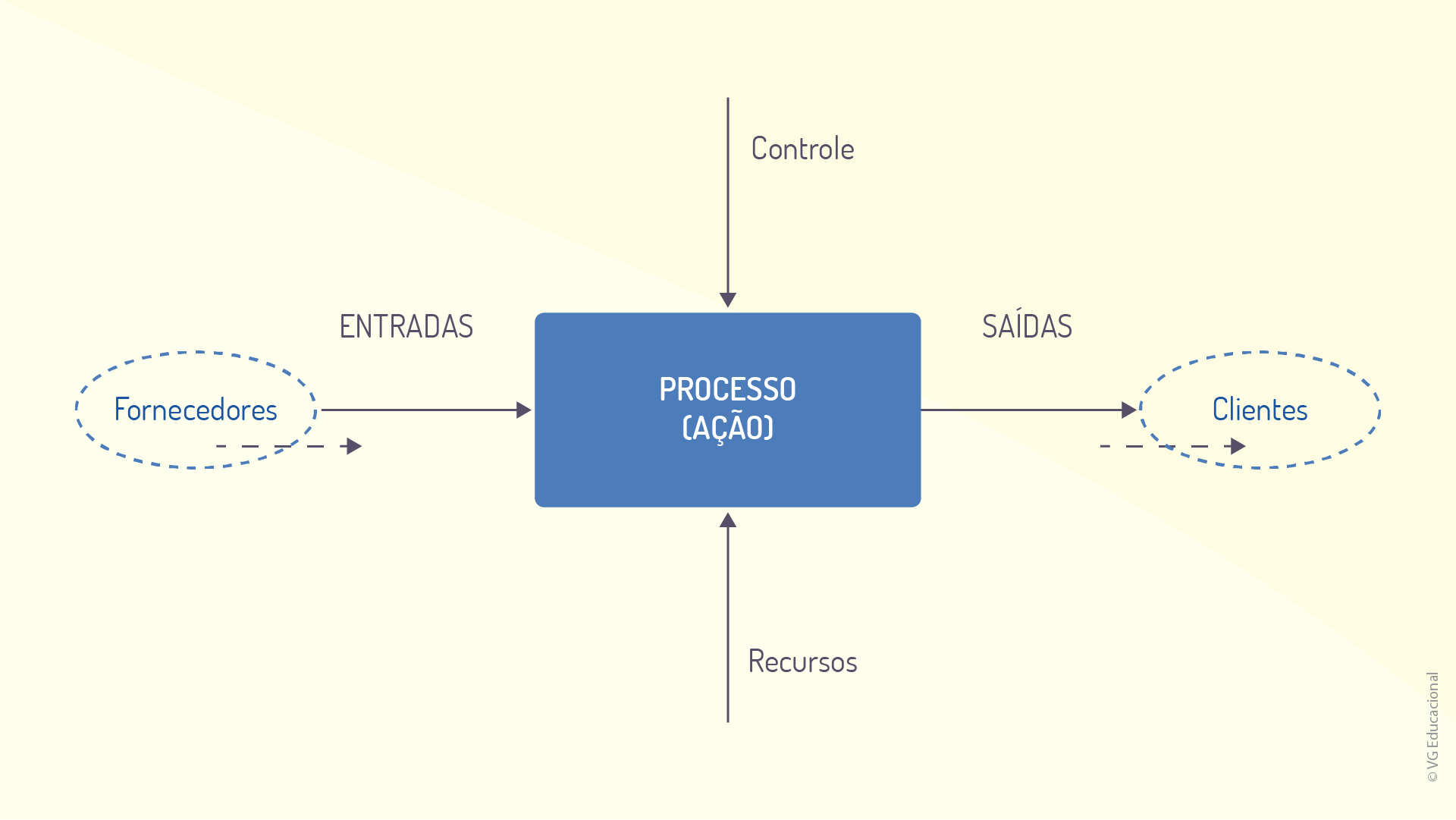
Essa representação, apesar de simples, é útil para se determinar os elementos essenciais de um processo. No quadro a seguir, são apresentados dois exemplos de processos, um produtivo e outro administrativo.
Quadro 1.2 – Exemplos de processos
Fonte: Adaptado de Ramos (2000, p. 4).
Percebe-se, no quadro apresentado, que, apesar de totalmente distintos, ambos os processos compartilham uma estrutura geral, com fornecedores, entradas, processos (processamentos ou métodos), saídas e clientes. Portanto, sendo a qualidade, como argumentado anteriormente, correspondente ao atendimento das necessidades dos clientes, o CEP pode auxiliar grandemente, uma vez que permite que os processos gerem produtos de qualidade garantida.
Existem certas categorias nas quais os diferentes processos podem ser categorizados: produção em massa, produção intermitente (repetitiva ou sob encomenda), produção enxuta, processo contínuo e processo em batelada (RAMOS, 2000).
Segundo Ramos (2000), a produção em massa se caracteriza por produzir uma quantidade limitada de produtos, com pequena diferenciação e em grandes quantidades. Normalmente, nesses casos, adota-se um arranjo físico linear (linha de montagem), com pouca flexibilidade.
A produção intermitente (repetitiva ou sob encomenda) está presente na maior parte das indústrias brasileiras; nesse modelo, há maior diversidade e uma linha própria de produtos.
A produção enxuta, por sua vez, caracteriza-se por apresentar baixos estoques, equipamentos mais versáteis e flexibilidade considerável para a modificação de volumes e tipos de bens/serviços.
Por fim, o processo contínuo ou em batelada, representado pelas indústrias químicas e petroquímicas, dentre outras, é aquele em que não há unidades individuais de produto ao longo do processo.
De acordo com o modelo de processo, principalmente no que se refere ao fato de ele ser discreto ou contínuo, os elementos principais que o compõem podem se diferenciar. Essas diferenças estão apresentadas no quadro a seguir.
Quadro 1.3 – Particularidades de processos
Fonte: Adaptado de Ramos (2000, p. 11).
Nessa perspectiva, percebe-se que, de acordo com as características do processo, seus elementos se distinguem e, assim, o próprio controle é modificado e, do mesmo modo, a forma de coletar as informações para o controle do processo. Essas particularidades devem ser levadas em consideração ao se implementar o CEP em qualquer organização.
Como ferramenta da qualidade ligada à estatística, o CEP é afetado diretamente pela quantidade e pelo volume de dados obtidos a partir do processo. Como varia a quantidade de dados nos diferentes tipos de processos discutidos aqui? Reflita a respeito.

O segundo conceito básico relacionado ao CEP refere-se à própria terminologia da ferramenta. Afinal, o que é controle?

O termo controle pode se referir tanto à fiscalização, ou seja, ao ato de vigiar algo para evitar um comportamento indesejado, como ao auxílio prestado para que seja obtido um melhor desempenho. O CEP se encaixa nessa última definição.
De maneira bastante abrangente, o controle, em seu ciclo de funcionamento, tem algumas etapas básicas (RAMOS, 2000, p. 4-5):
Esses passos, quando representados de maneira gráfica, esquematizam o ciclo de controle, que pode ser observado na figura a seguir.
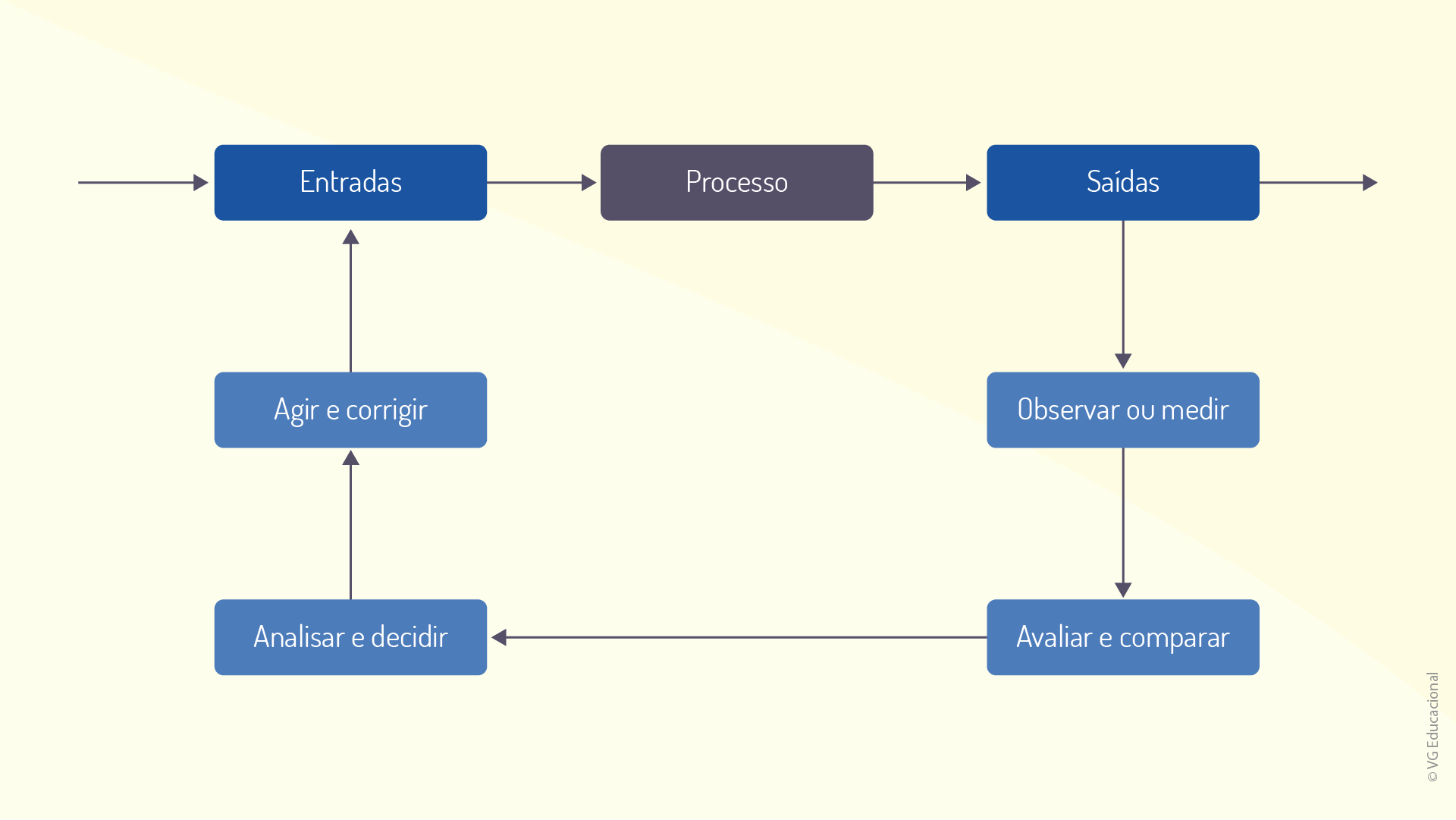
É interessante notar que o ciclo finaliza com a tomada de decisão em relação às entradas, dessa forma, a ação ocorre sobre a produção, sobre o processo, e não sobre os produtos. Isso delimita uma das características mais importantes do controle, em especial, o Controle Estatístico de Processos (CEP), e evidencia como se dá a relação CEP X processo produtivo/administrativo. De maneira resumida:
[...] o CEP prega o controle da qualidade conduzido simultaneamente com a manufatura (controle do processo), ao invés da inspeção após a produção, em que se separa os produtos bons daqueles que são defeituosos (controle do produto). Seu enfoque está na prevenção de defeitos ou erros. É muito mais fácil e barato fazer certo na primeira vez, do que depender de seleção e retrabalho de itens que não sejam perfeitos (RAMOS, 2000, p. 5).
É possível, por fim, distinguir a diferença entre o controle de processos e o controle de produtos, como indicado no quadro a seguir.
Quadro 1.4 – Distinção entre os tipos de controle
Fonte: Adaptado de Ramos (2000, p. 5).
Já para Ribeiro e Caten (2012 apud NETTO, 2017, p. 36), o controle da qualidade depende de alguns elementos essenciais, que compreendem um sistema de controle do processo. São eles:
O processo em si é uma combinação de equipamentos, insumos, métodos, procedimentos e pessoas, tendo como objetivo a fabricação de um bem ou o fornecimento de um serviço (efeito); As informações sobre o desempenho de um processo são obtidas a partir do estudo cruzado dos itens a seguir: qualidade das características do produto final; qualidade das características intermediárias; ajuste dos parâmetros do processo; A coleta de dados e as ações ao longo do processo são orientadas para o futuro, pois permitem detectar o defeito assim que ele é gerado, possibilitando a atuação sobre o processo no momento e local adequados; Ações sobre o produto final: as inspeções sobre o produto final são orientadas para o passado, pois elas permitem apenas separar o produto conforme o produto não conforme (refugo), que pode eventualmente ser retrabalhado (RIBEIRO; CATEN, 2012 apud NETTO, 2017, p. 36).
O controle de qualidade de um processo, como se pode perceber, é um procedimento metódico, que exige cuidado e, principalmente, dedicação e conhecimento.
A implementação do CEP no contexto de uma instituição implica o envolvimento de diversas equipes, cada uma atuando da forma que lhe cabe. Gerenciar essa implementação exige cuidado e uma gestão eficaz e comprometida com a qualidade. Fique por dentro do tema acessando o link disponível em: https://youtu.be/x8lTNB2YaHE. Acesso em: 10 nov. 2020.

O próximo elemento básico relacionado ao CEP é a qualidade, que passou por uma evolução ao longo da história. Conforme Barçante (1998), os processos de qualidade evoluíram, passando por 4 períodos (eras) bem distintos:
A figura a seguir apresenta, de forma complementar, mais características de cada uma das eras da qualidade.
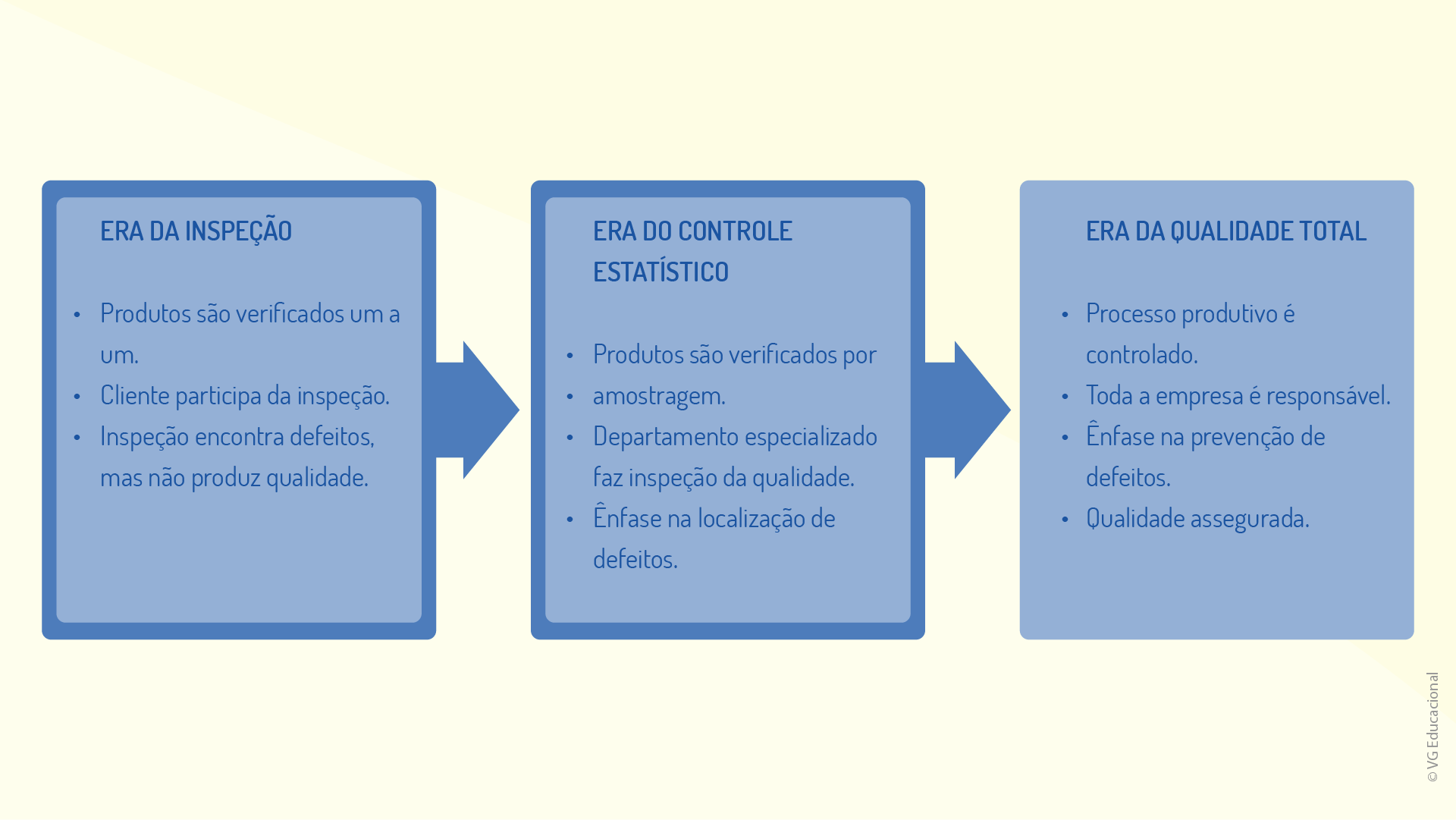
O seguinte questionamento pode surgir após a observação dessa figura: se o controle estatístico está posicionado, historicamente, em uma era anterior à da qualidade total, ele ainda pode ser considerado uma ferramenta útil?
A resposta é sim, pois, apesar de existir uma nova era, focada na qualidade total, a mudança está no enfoque, e não nas ferramentas utilizadas. Todo o aporte estatístico e todas as ferramentas inerentes ao CEP continuam atuais, o que ocorre é que, atualmente, a preocupação vai além de se garantir um processo ou um sistema de qualidade, o CEP tem como objetivo garantir alta qualidade ao negócio.
Assim, finalizamos a discussão sobre os elementos básicos relacionados ao CEP, no entanto, pelo fato de ele ser embasado em procedimentos estatísticos, cabe agora analisar os elementos estatísticos que merecem destaque no estudo dessa importante ferramenta.
No contexto do CEP, o controle da qualidade se dá por meio de um sistema de controle do processo, que é formado por elementos distintos. Esses elementos, quatro, no total, são fundamentais para o procedimento de controle em qualquer processo. Sobre os elementos citados, assinale a alternativa correta.
Um dos elementos é o processo, que é composto apenas por equipamentos e pessoas e corresponde ao núcleo da produção.
Incorreta. O processo é a combinação de equipamentos, insumos, métodos, procedimentos e pessoas e tem como objetivo a fabricação de um bem ou o fornecimento de um serviço.
As informações sobre o desempenho do processo são obtidas a partir da análise de características intermediárias e do produto final, assim como do processo.
Correta. As informações sobre o desempenho de um processo são obtidas a partir do estudo cruzado da qualidade das características do produto final, da qualidade das características intermediárias e do ajuste dos parâmetros do processo.
A coleta de dados e as ações ao longo do processo são orientadas para a revisão de atividades que já foram realizadas.
Incorreta. A coleta de informações e as ações ao longo do processo se preocupam com o futuro do processo, pois permitem detectar um defeito quando ele é gerado, o que possibilita a atuação sobre o processo no momento pertinente.
A coleta de dados e as ações ao longo do processo são orientadas para o acompanhamento de atividades que estão sendo realizadas atualmente.
Incorreta. A coleta de dados e as ações ao longo do processo são pautadas em atividades do futuro, uma vez que permitem que o defeito seja detectado assim que ele ocorre, possibilitando a atuação sobre o processo de maneira adequada.
As ações sobre o produto final são importantes para o controle do processo produtivo, apesar de não terem nenhuma vantagem prática.
Incorreta. As inspeções têm certas vantagens, pois impedem que o cliente adquira produtos defeituosos, embora não sejam uma forma eficiente de ação, impedem que novas peças defeituosas sejam produzidas.
Dentre os inúmeros conceitos existentes na estatística, alguns são muito recorrentes e úteis para processos e procedimentos envolvendo o CEP. Um dos primeiros que devem ser compreendidos é a probabilidade.
A probabilidade pode ser entendida como a chance de algo ocorrer. Por exemplo, considere n eventos, mutuamente exclusivos, com iguais chances de acontecer. Um determinado conjunto desses eventos, e que possui uma certa característica, é chamado de m (VIEIRA, 2012; PEDROZA, 2019). Nessa perspectiva, a probabilidade de m ser verificado ou de m ocorrer seria:
\[P(m) = m/n\]
Suponha, agora, a seguinte situação: durante um teste, 100 itens foram produzidos; 40 deles têm mais do que 50 centímetros de largura (L) e 60 têm menos do que 50 centímetros de largura. Assim, escolhendo um item ao acaso:
\(P(L>50)=60/100=0,60=60%\)
\(P(L<50)=40/100=0,40=40%\)
Ou seja, a probabilidade de se escolher, ao acaso, um item com mais do que 50 centímetros é de 60%, enquanto a probabilidade de se escolher, ao acaso, um item com menos do que 50 centímetros é de 40%.
Esse exemplo deixa claro que, quanto maior a quantidade de itens, de características e de fatores a serem avaliados, mais complexa é a análise. Uma variante da probabilidade comum é a probabilidade condicional, caracterizada quando determinado evento pode ocorrer, mas apenas sob uma determinada condição. Indica-se a probabilidade de ocorrer um evento \(A\) sob a condição de ter ocorrido \(B\). Temos, nesse caso, a seguinte notação: \(P (A/B)\), que se lê “probabilidade de \(A\) dado \(B\)”.
Como exemplo, pode-se retomar a situação anterior. Considere que, dentre os itens com mais de 50 centímetros de largura, apenas 10 foram maiores do que 52 centímetros.
Nesse caso:
\(A\) – chance de um item ter \(L\) > 52 cm
\(B\) – chance de um item ter \(L\) > 50 cm
Assim, dado que um item tem mais do que 50 centímetros, qual a probabilidade de se escolher, ao acaso, um item maior do que 52 centímetros?
\(P(A/B)=10/40=0,25=25%\)
Nesse caso, a resposta seria de 25%.
Existem, ainda, regras e leis que correlacionam as probabilidades, como visto a seguir (PEDROZA, 2019):
Para calcular a probabilidade de dois eventos independentes ocorrerem, P(A⋂B), aplica-se o teorema do produto, que é dado por:
\[P(A⋂B) = P(A).P(B)\]
Já para se verificar a ocorrência de um ou outro evento, ou seja, A ou B, simbolizado por P(A⋃B), aplica-se o teorema da soma, que é dado por:
\[P(A⋃B) = P(A) + P(B)\]
Segundo Netto (2017) e Oliveira et al. (2013), alguns outros parâmetros estatísticos que devem ser considerados no CEP são:
\[A = x_{máximo} - x_{mínimo}\]
\[\sigma =\sqrt{\frac{{{\sum\nolimits_{1}^{n}{({{x}_{i-\underline{x}}})}}^{2}}}{n-1}}\]
\[\underline{x}=\frac{\sum _{i}^{n}{{x}_{i}}}{n}\]
Essas informações são essenciais para a avaliação estatística de qualquer amostra, ou seja, são fundamentais para o CEP, e traduzem numericamente a variabilidade e a estabilidade do processo.
Considere, agora o exemplo a seguir: uma determinada empresa, ao averiguar a massa de seus produtos alimentícios industrializados, retirou uma amostra com dez medidas, em quilogramas, a saber:
Nesse caso, pode-se analisar a amplitude, a média, a mediana e o desvio-padrão da amostra.
A média será:
\[\underset{\scriptscriptstyle-}{x} = (1,01+1,00+0,98+0,99+0,99+1,00+1,00+1,02+1,01+1,00)/10\]
\[\underset{\scriptscriptstyle-}{x} = 10/10 = 1\]
O desvio será:
\(σ=\sqrt{\frac{(1,01-1)²+(1,00-1)²+(0,98-1)²+(0,99-1)²+(0,99-1)²+(1,00-1)²+(1,00-1)²+(1,02-1)²+(1,01-1)²+(1,00-1)²}{10-1}}\)
\(σ=\sqrt{\frac{(0,01)²+0+(-0,02)²+(-0,01)²+(-0,01)²+0+0+(0,02)²+(0,01)²+0)}{9}}=\sqrt{\frac{(0,0001+0,0004+0,0001+0,0001+0,0004+0,0001}{9}}\)
\[\sqrt{\frac{0,0012}{9}}=0,0115\]
A amplitude será:
\[A = 1,02 - 0,98 = 0,04\]
E a mediana será:
\(\widehat{x}\) = 1,00
Vale ressaltar que apenas aplicar as ferramentas estatísticas não é suficiente para se analisar um processo. É necessária uma equipe que avalie tais dados, além do compromisso da gestão em utilizar o CEP e suas ferramentas.
A estatística é um ramo vasto dentro da matemática e, por vezes, apesar de extremamente útil, não faz parte do aporte de conhecimentos dos futuros profissionais. Para se aprofundar um pouco mais nesse tema, acesse os links disponíveis em: http://periodicos.ifsul.edu.br/index.php/thema/article/download/1033/953 e
https://drive.google.com/file/d/105s7Wv_BJYR07iXdLov7ixYFfXQOL0v-/view?usp=sharing
Acesso em: 10 nov. 2020.

Conforme as avaliações das probabilidades de um certo evento ocorrer ou de certo parâmetro ser verificado são aprofundadas, o número de amostras aumenta. Considere, por exemplo, a massa de um certo produto. A massa, assim como algumas outras características de um produto, é uma variável aleatória, uma vez que seus valores exatos só podem ser determinados após se escolher uma amostra aleatória dentro de um grupo (PEDROZA, 2019; VIEIRA, 2012).
De maneira geral, os valores que podem ser encontrados por uma variável aleatória (nesse caso, da massa do produto) e suas correspondentes probabilidades constituem uma distribuição de probabilidades.
No eixo horizontal de histogramas (representação dos dados em colunas) e distribuição de probabilidades, são avaliados os valores verificados nas análises ou os valores identificados nas amostras. Tal eixo pode, ainda, indicar a média, a mediana e o desvio-padrão da amostra. No eixo vertical, é representada a possibilidade de se encontrar determinada situação ou evento. Observe o histograma apresentado a seguir.

Nesse exemplo, há uma representação genérica das probabilidades. Nele, a probabilidade de se verificar um x = 33 é de 0,03 ou, ainda, 3%, bem como a probabilidade de se encontrar um x = 50 é ligeiramente maior do que 0,01, ou seja, de 1%. Segundo Ribeiro e Caten (2012), uma distribuição de probabilidades é caracterizada por três parâmetros:
A seguir, são apresentados alguns exemplos visuais de cada um desses casos.
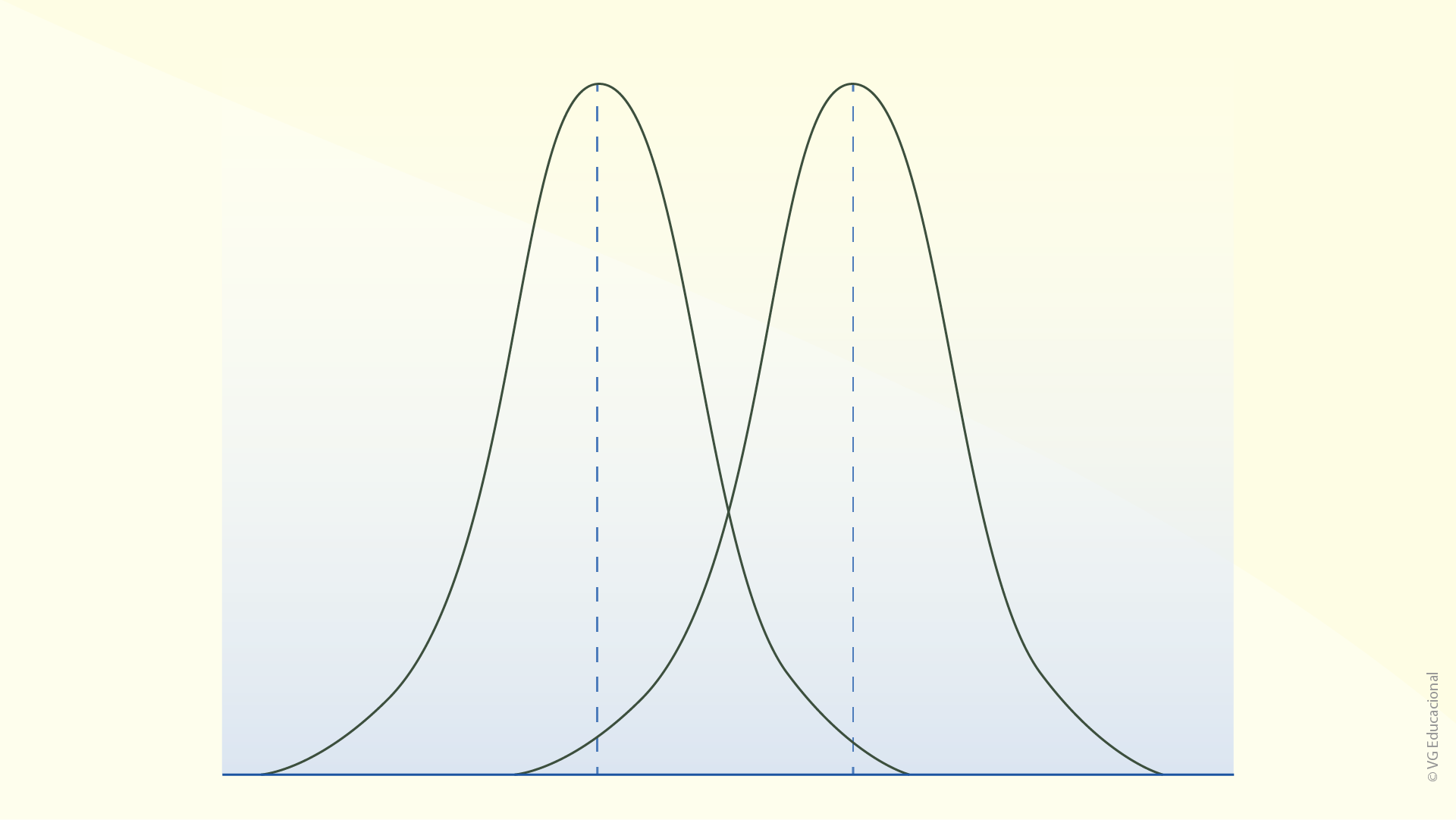
Nota-se, na figura apresentada anteriormente, que o aspecto geral das curvas de probabilidade é idêntico, o que as diferencia são as posições centrais (parâmetro de localização), ou seja, as médias obtidas para cada conjunto.
Quanto ao parâmetro de dispersão, observe a figura a seguir.
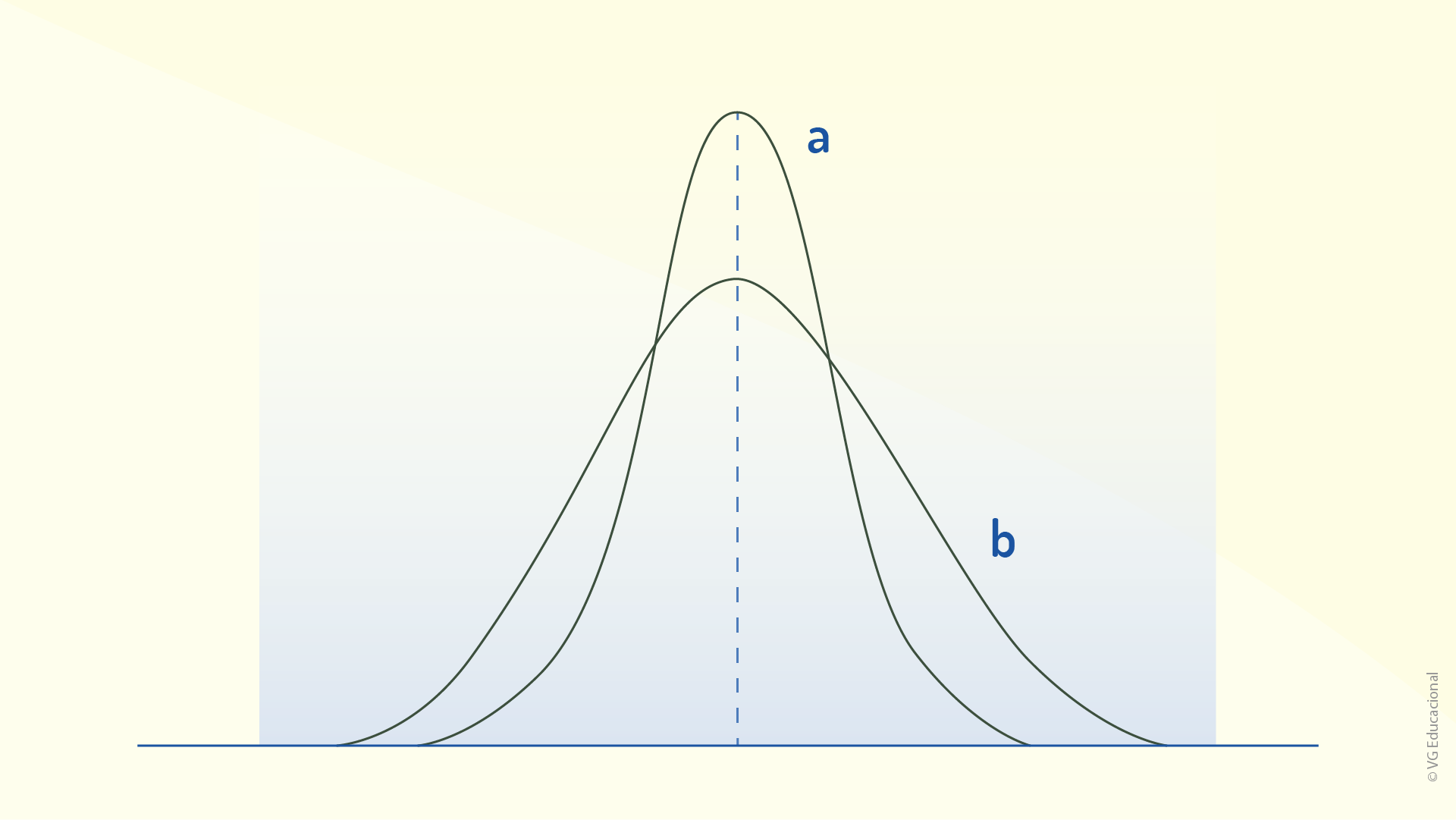
Nessa figura, é possível observar dois casos, os quais têm amostras com a mesma média, no entanto, o modo como os eventos/ocorrências se comportam em relação à média é diferente. No caso a, a probabilidade de se verificar uma situação próxima à média é bem maior do que no caso b.
Por fim, as distribuições de probabilidades podem ser simétricas ou assimétricas, em que a forma indica que as probabilidades maiores acabam não sendo máximas para valores iguais à média, como se pode verificar na figura a seguir.

Nesses três casos, verifica-se que, dependendo da relação entre a média e a mediana, tem-se curvas diferentes para se descrever a probabilidade de um evento ocorrer. Vale a pena ressaltar que a assimetria se refere à forma da curva, e não à posição da maior probabilidade. Quando as três possibilidades de simetria de distribuição de probabilidade são comparadas, pode-se utilizar também as nomenclaturas “nominal é melhor” (A), “menor é melhor” (B) e “maior é melhor” (C) (RIBEIRO; CATEN, 2012):
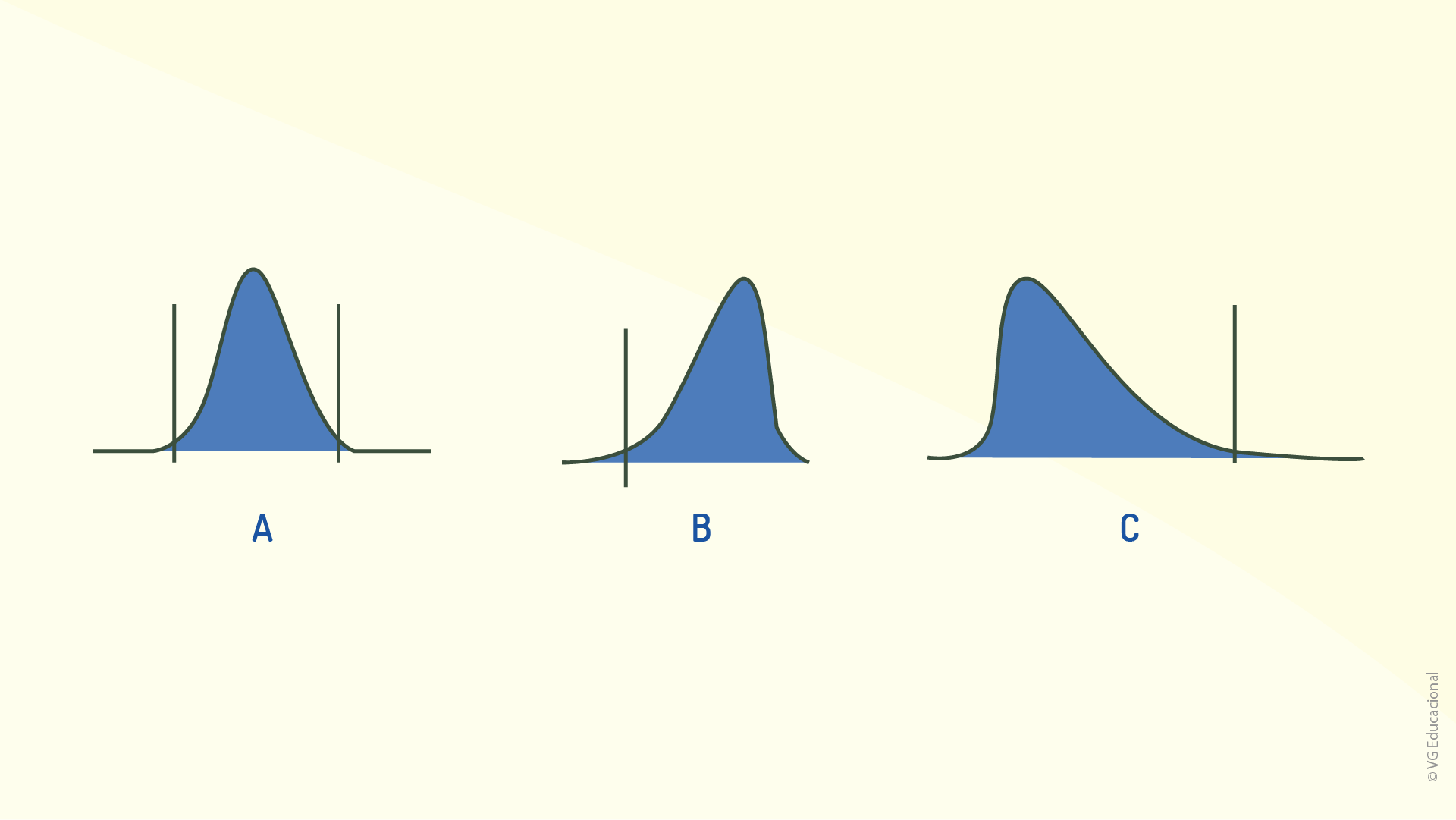
Segundo Ribeiro e Caten (2012), as distribuições do tipo “nominal é melhor” são típicas de situações que envolvem características dimensionais e, além disso, são simétricas, apresentando, também, limites superiores e inferiores evidentes. As distribuições do tipo “maior é melhor”, que são típicas de problemas envolvendo a resistência mecânica de produtos, são assimétricas à esquerda. Já as distribuições do tipo “menor é melhor” (por exemplo, nível de ruído) tendem a apresentar uma distribuição de probabilidade assimétrica à direita. Tanto os casos “maior é melhor” quanto “menor é melhor” costumam ocorrer devido a limitações físicas, que modificam a estrutura da distribuição.
Todas as formas de representação de uma distribuição de probabilidade dizem quais as características evidentes para os elementos analisados em uma amostra. No CEP, qual seria a importância de se conhecer a distribuição de probabilidades?

Os conhecimentos estatísticos são essenciais para os procedimentos típicos do CEP, por isso, definições, conceitos, procedimentos de cálculo e outros elementos devem estar sempre à mão de um profissional que trabalha com essa ferramenta da qualidade. Mas qual a causa da aleatoriedade das características de um produto?
As variabilidades são as causas dessas modificações e elas serão abordadas no tópico a seguir.
Os conhecimentos de probabilidade estão no coração do controle estatístico de processos e são essenciais para a determinação de parâmetros centrais e intervalos de valores, sendo os conceitos de média, mediana, desvio e amplitude de grande valia nesses procedimentos. Considere o quadro de valores a seguir, que apresenta a massa, em gramas, de certo produto. Para essa amostra, assinale a alternativa que apresenta corretamente os valores de média, mediana, desvio-padrão e amplitude.
Fonte: Elaborada pelo autor.
Média = 150; mediana = 150; desvio-padrão = 1,12; amplitude = 148-152.
Incorreta.
Cálculos:
Média: \(\underset{\scriptscriptstyle-}{x}=\frac{\sum\nolimits_{i}^{20}{{{x}_{i}}}}{n}=\frac{3002}{20}=150,1\)
Mediana: 148-148-149-149-149-150-150-150-150-150-150-150-150-151-151-151-151-151-152-152
Desvio-padrão:
\[\sigma =\sqrt{\frac{\sum\nolimits_{1}^{20}{{{({{x}_{i-\underset{\scriptscriptstyle-}{x}}})}^{2}}}}{n-1}}=\sqrt{\frac{23,8}{19}}=1,12\]
Amplitude: Mínimo: 148 / Máximo 152.
Média = 150,1; mediana = 149; desvio-padrão = 1,10; amplitude = 148-152.
Incorreta.
Cálculos:
Média: \(\underset{\scriptscriptstyle-}{x}=\frac{\sum\nolimits_{i}^{20}{{{x}_{i}}}}{n}=\frac{3002}{20}=150,1\)
Mediana: 148-148-149-149-149-150-150-150-150-150-150-150-150-151-151-151-151-151-152-152
Desvio-padrão:
\[\sigma =\sqrt{\frac{\sum\nolimits_{1}^{20}{{{({{x}_{i-\underset{\scriptscriptstyle-}{x}}})}^{2}}}}{n-1}}=\sqrt{\frac{23,8}{19}}=1,12\]
Amplitude: Mínimo: 148 / Máximo 152.
Média = 150; mediana = 150; desvio-padrão = 1,12; amplitude = 148-151.
Incorreta.
Cálculos:
Média: \(\underset{\scriptscriptstyle-}{x}=\frac{\sum\nolimits_{i}^{20}{{{x}_{i}}}}{n}=\frac{3002}{20}=150,1\)
Mediana: 148-148-149-149-149-150-150-150-150-150-150-150-150-151-151-151-151-151-152-152
Desvio-padrão:
\[\sigma =\sqrt{\frac{\sum\nolimits_{1}^{20}{{{({{x}_{i-\underset{\scriptscriptstyle-}{x}}})}^{2}}}}{n-1}}=\sqrt{\frac{23,8}{19}}=1,12\]
Amplitude: Mínimo: 148 / Máximo 152.
Média = 150,1; mediana = 150; desvio-padrão = 1,12; amplitude = 148-152.
Correta.
Cálculos:
Média: \(\underset{\scriptscriptstyle-}{x}=\frac{\sum\nolimits_{i}^{20}{{{x}_{i}}}}{n}=\frac{3002}{20}=150,1\)
Mediana: 148-148-149-149-149-150-150-150-150-150-150-150-150-151-151-151-151-151-152-152
Desvio-padrão:
\[\sigma =\sqrt{\frac{\sum\nolimits_{1}^{20}{{{({{x}_{i-\underset{\scriptscriptstyle-}{x}}})}^{2}}}}{n-1}}=\sqrt{\frac{23,8}{19}=1,12~Desvio~-~padr\tilde{a}o}:=1,21\]
Amplitude: Mínimo: 148 / Máximo 152.
Média = 150,1; mediana = 150; desvio padrão = 1,10; amplitude = 149-152.
Incorreta.
Cálculos:
Média: \(\underset{\scriptscriptstyle-}{x}=\frac{\sum\nolimits_{i}^{20}{{{x}_{i}}}}{n}=\frac{3002}{20}=150,1\)
Mediana: 148-148-149-149-149-150-150-150-150-150-150-150-150-151-151-151-151-151-152-152
Desvio-padrão:
\[\sigma =\sqrt{\frac{\sum\nolimits_{1}^{20}{{{({{x}_{i-\underset{\scriptscriptstyle-}{x}}})}^{2}}}}{n-1}}=\sqrt{\frac{23,8}{19}}=1,12\]
Amplitude: Mínimo: 148 / Máximo 152.
Na área da qualidade, considera-se que ela é inversamente proporcional à variabilidade do processo. Considerando essa definição, conforme se diminui a variabilidade de um processo, maximiza-se a qualidade e, além disso, obtém-se menor desperdício. Um exemplo de que isso é um fato, no contexto das organizações, é o caso de “um fabricante de tampas plásticas para indústrias de água e refrigerantes: o diâmetro da tampa tem valor especificado. Se essa característica, que é crítica, apresentar grande variabilidade, muitas tampas serão descartadas. Está caracterizado o desperdício” (VIEIRA, 2012, p. 3).
Para Ferreira e Caten (2012), a variabilidade é um elemento sempre presente em processos produtivos (bens ou serviços). E essa variabilidade não depende da qualidade do projeto e da operabilidade. Ocorre que, na prática, é praticamente impossível produzir dois itens exatamente iguais, uma vez que, por menor que seja, sempre há alguma diferenciação. Segundo Ribeiro e Caten (2012, p. 9):
[...] a diferença entre peças pode ser grande, provocando o aparecimento de produtos defeituosos, ou pode ser praticamente imperceptível. Além disso, as fontes de variabilidade podem agir de forma diferente sobre o processo. Conforme a fonte de variabilidade, o resultado pode ser: a) pequenas diferenças peça-a-peça (habilidade do operador, diferenças na matéria-prima etc.), b) alteração gradual no processo (desgaste de ferramentas, temperatura do dia etc.) e c) alteração brusca no processo (mudança de procedimento, queda de corrente, troca de set up etc.).
Assim, para que um processo seja gerido e controlado, é necessário reduzir a variabilidade e investigar as causas dessas variabilidades no processo. O primeiro passo que se pode dar para promover essa análise é diferenciar as causas comuns e as causas especiais de variabilidade.
Causas comuns
As causas comuns são as que ocorrem com mais frequência em um processo e, de certa forma, são até mesmo esperadas durante a produção e a realização de tarefas e atividades. De acordo com Netto (2017, p. 39):
As causas comuns podem ser geradas por diversas fontes, ou também por diversas causas, que podem gerar variação no objeto observado, mas que principalmente atuam de forma aleatória no processo, gerando assim uma variabilidade inerente ao processo analisado. Quando analisamos a variabilidade gerada pelas causas comuns, verificamos um padrão natural do processo, pois é resultante de pequenas fontes de variabilidade (causas) que acontecem cotidianamente devido ao processo estar trabalhando sob condições normais de operação.
É interessante notar que processos que apresentam apenas causas comuns de variabilidade são considerados estáveis ou mesmo “sob controle”, uma vez que apresentam variabilidade constante ao longo do tempo (MONTGOMERY, 2009). Montgomery (2009) destaca que, nesses casos, as medidas individuais de cada característica dos produtos dentro dos processos podem diferir entre si, mas o agrupamento das análises mostra um padrão estatístico. Nas figuras a seguir, é possível entender como isso ocorre.
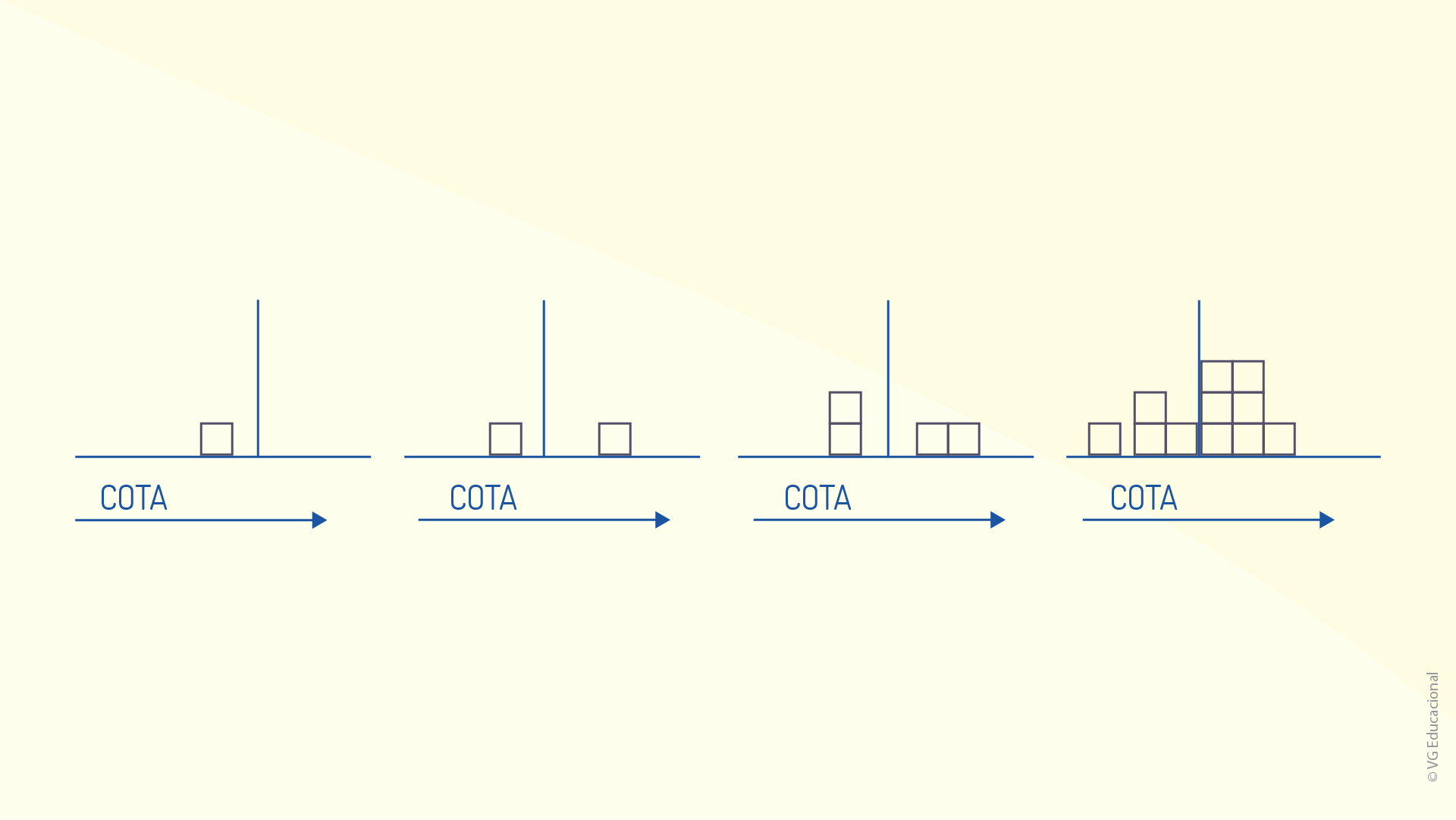
Na figura anterior, percebe-se que, quando analisados individualmente, é, de fato, impossível notar qualquer padrão que possa ser descrito e atribuído ao processo. No entanto, com o acúmulo de informações, as análises começam a exibir certo padrão, como é possível perceber na figura a seguir.
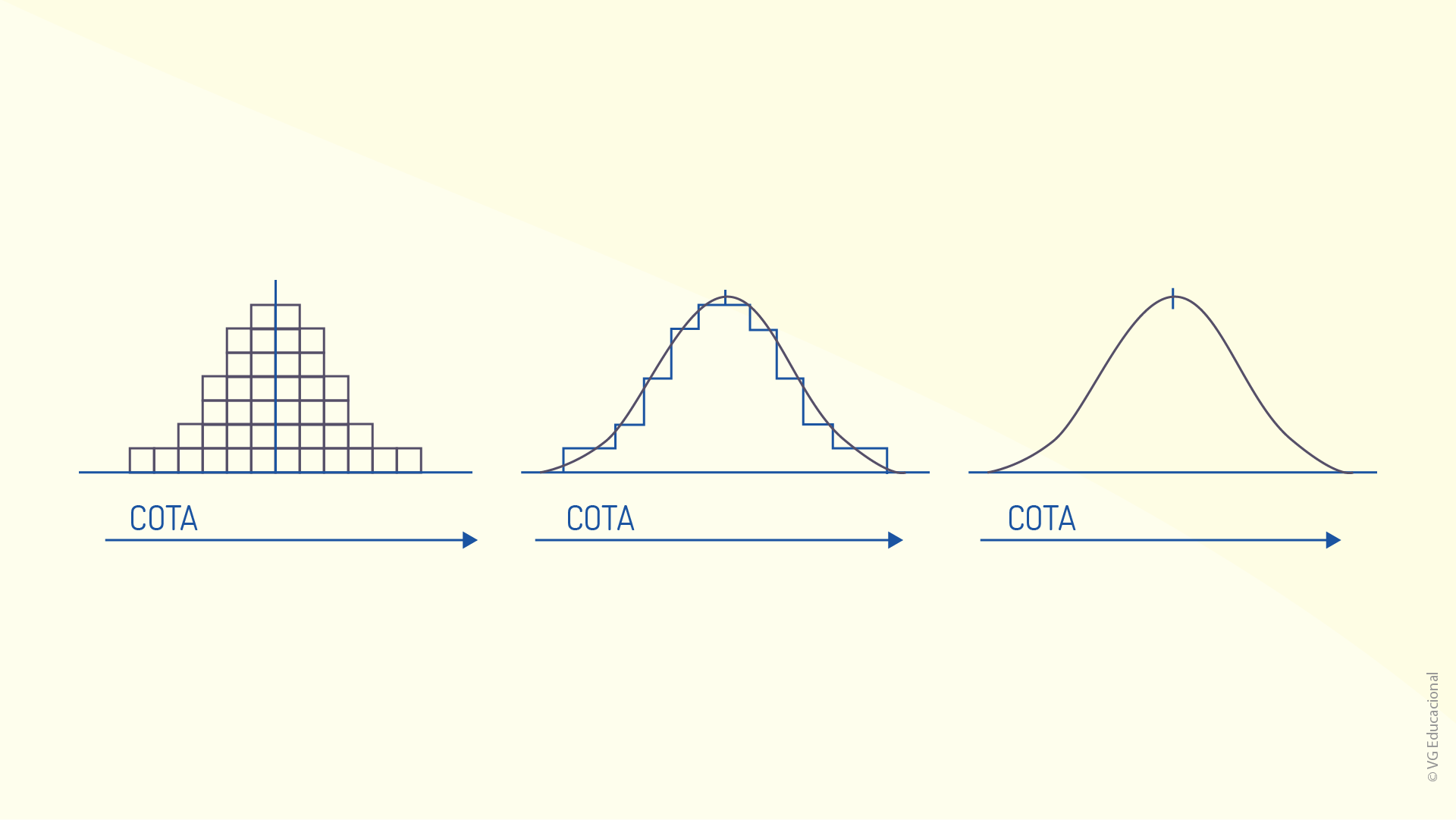
Agora fica claro que após, avaliado um grande número de amostras, o perfil de uma distribuição de probabilidades é encontrado, apresentando bastante simetria, nesse caso, justificada pela existência de causas comuns de variabilidade. Dessa forma, é possível, então, descrever os dados por meio de uma distribuição simétrica, como a apresentada na figura a seguir.
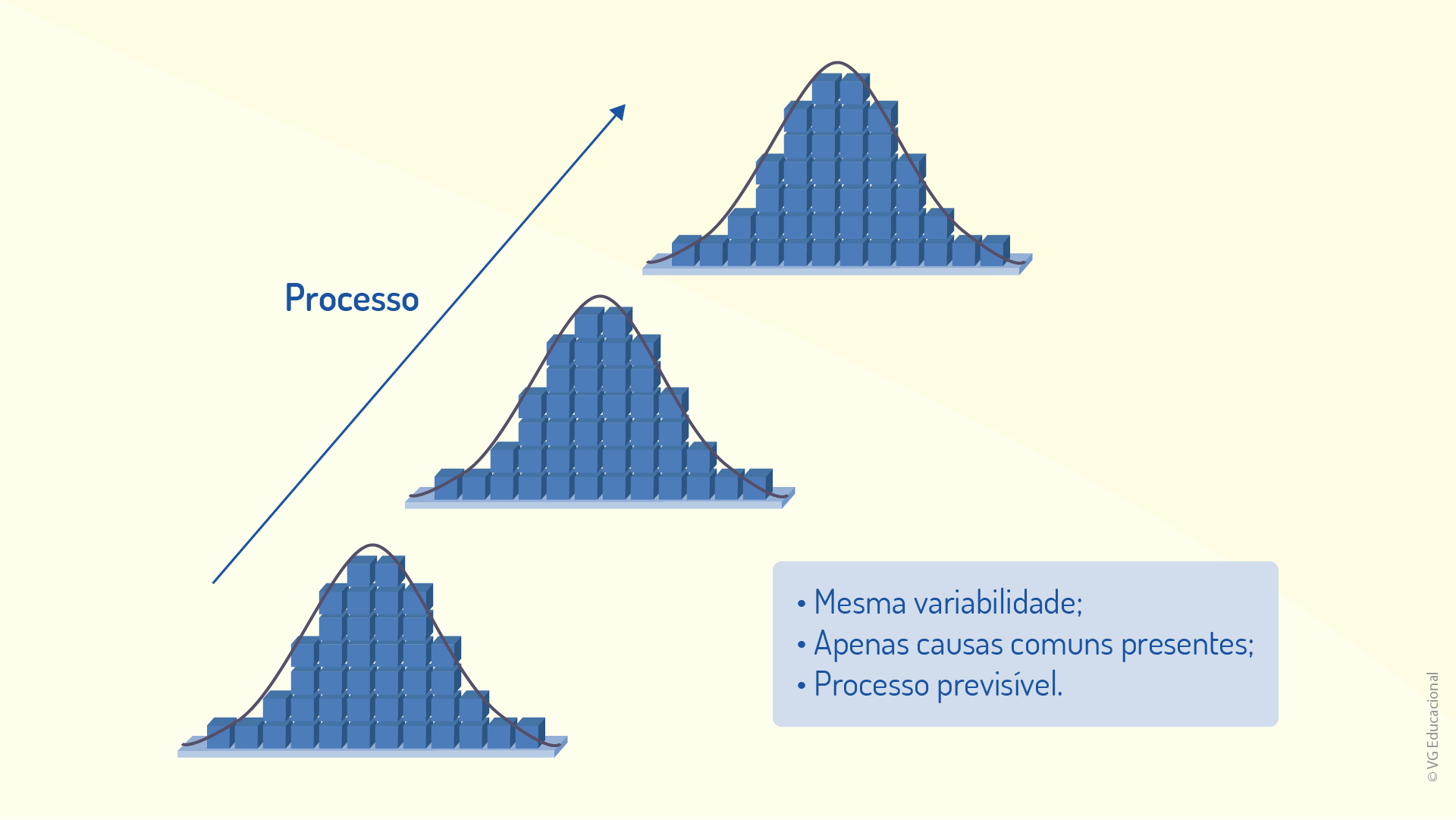
Essas causas de variação são, de certa forma, esperadas nos processos, mas existe um segundo tipo: as causas especiais.
Causas especiais
Essas causas de variação, diferentemente das comuns, não seguem um perfil aleatório, mas o que, de acordo com Netto (2017), poderia ser definido como ocasional. Tais causas podem ser decorrentes de diversos fatores, como “problemas devido à matéria-prima com propriedades diferentes das projetadas, erros de setup do ferramental ou equipamentos” (NETTO, 2017, p. 40). Por esse motivo, segundo o autor, essas causas podem ser conhecidas, também, como causas assinaláveis, pois são específicas, ocorrendo de forma não estatística, podendo ser falhas de operação. Dessa maneira, essas causas acarretam modificações na distribuição da tendência central do processo ou geram variabilidade da qualidade, como é possível verificar na figura a seguir.
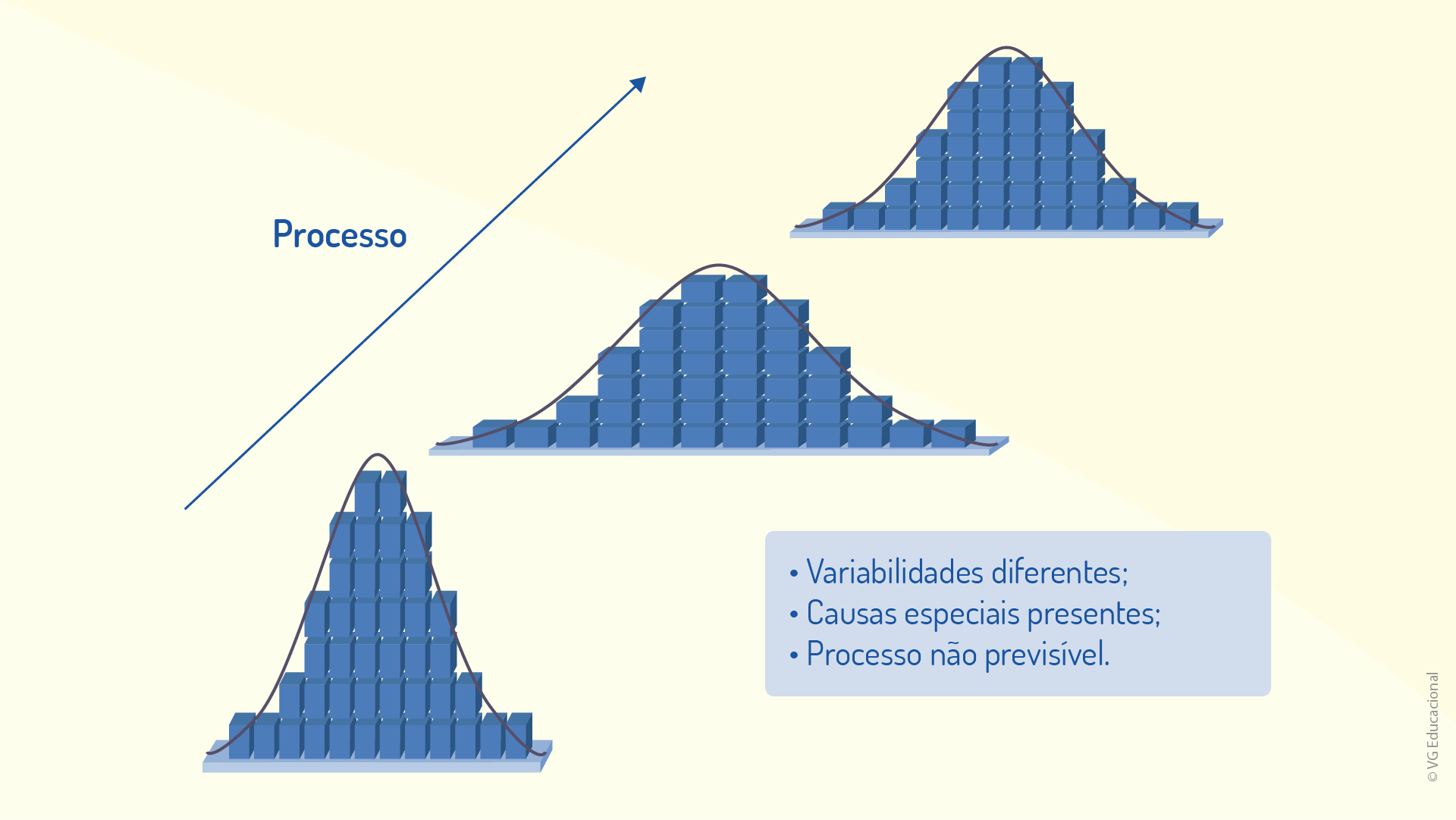
Nota-se, na imagem anterior, que, nesse processo, há uma grande distorção da distribuição das probabilidades, dificultando a definição de intervalos fixos de características de produtos, o que afeta, diretamente, a qualidade.
É possível, após esse entendimento, avaliar esses dois tipos de causa em contraste, com o intuito de analisar as principais distinções decorrentes da natureza (comum ou especial) das variabilidades. Tais distinções podem ser verificadas no quadro a seguir.
Quadro 1.5 – Distinção entre os tipos de causas de variabilidade
Fonte: Adaptado de Netto (2017, p. 11).
Por meio dessa análise, Netto (2017) destaca que as causas comuns são mais claramente notadas e requerem, de forma geral, menor investimento e mobilização da empresa/organização como um todo. Já a ocorrência das causas especiais é mais difícil de se verificar, e os dados e análises requeridos são de natureza complexa, portanto, demandam bastante tempo e recursos para serem entendidos, além disso, a própria gerência deve estar envolvida, para que a variabilidade decorrente dessas causas seja mitigada.
O controle da variabilidade de processos dentro do CEP é uma poderosa ferramenta para organizações que buscam processos e negócios de qualidade, pois se traduz na estabilidade de um processo, portanto, faz com que ele tenha um padrão, que pode ser alinhado a um padrão de qualidade. Para conhecer um exemplo de aplicação de controle de variabilidade acesse o link disponível em: https://is.gd/lweyNS. Acesso em: 10 nov. 2020.

Assim, pode-se perceber que existe uma “evolução” nos processos, de forma que um processo que tenha tanto causas comuns como especiais deve ser modificado, melhorado, para passar a ser um processo que tenha apenas causas comuns de variabilidade, que, embora sejam aleatórias, seguem um padrão estatístico. A figura a seguir indica como seria essa transição.

Nessa perspectiva, o processo é considerado instável quando apresenta distribuições não padronizadas das características do produto. Isso seria verificado por inconstância da média, mudança de valores das medianas ou, ainda, valores muito diferentes de desvio, indicando amplitudes variáveis de dados. Por outro lado, uma vez que as causas especiais sejam mitigadas, tem-se um processo sujeito apenas a causas comuns de variabilidade, em que médias, medianas, desvios e amplitudes não variam de análise para análise.
Sendo a variabilidade das características do processo um fator importante na averiguação da qualidade, como a variabilidade pode ser descrita em relação aos parâmetros estatísticos mais recorrentes? Reflita a respeito.

Assim, finalizamos a primeira unidade sobre o Controle Estatístico de Processos (CEP), que apresentou a definição e a importância desse processo, bem como seus elementos mais marcantes.
A variabilidade de um processo está vinculada a ocorrências (problemas) dentro do processo produtivo e está relacionada ao que, em CEP, é chamado de causa. Essas causas podem ser comuns ou especiais e afetam diretamente a qualidade do processo. Avalie, a seguir, as distribuições de probabilidade (a), (b), (c) e (d).
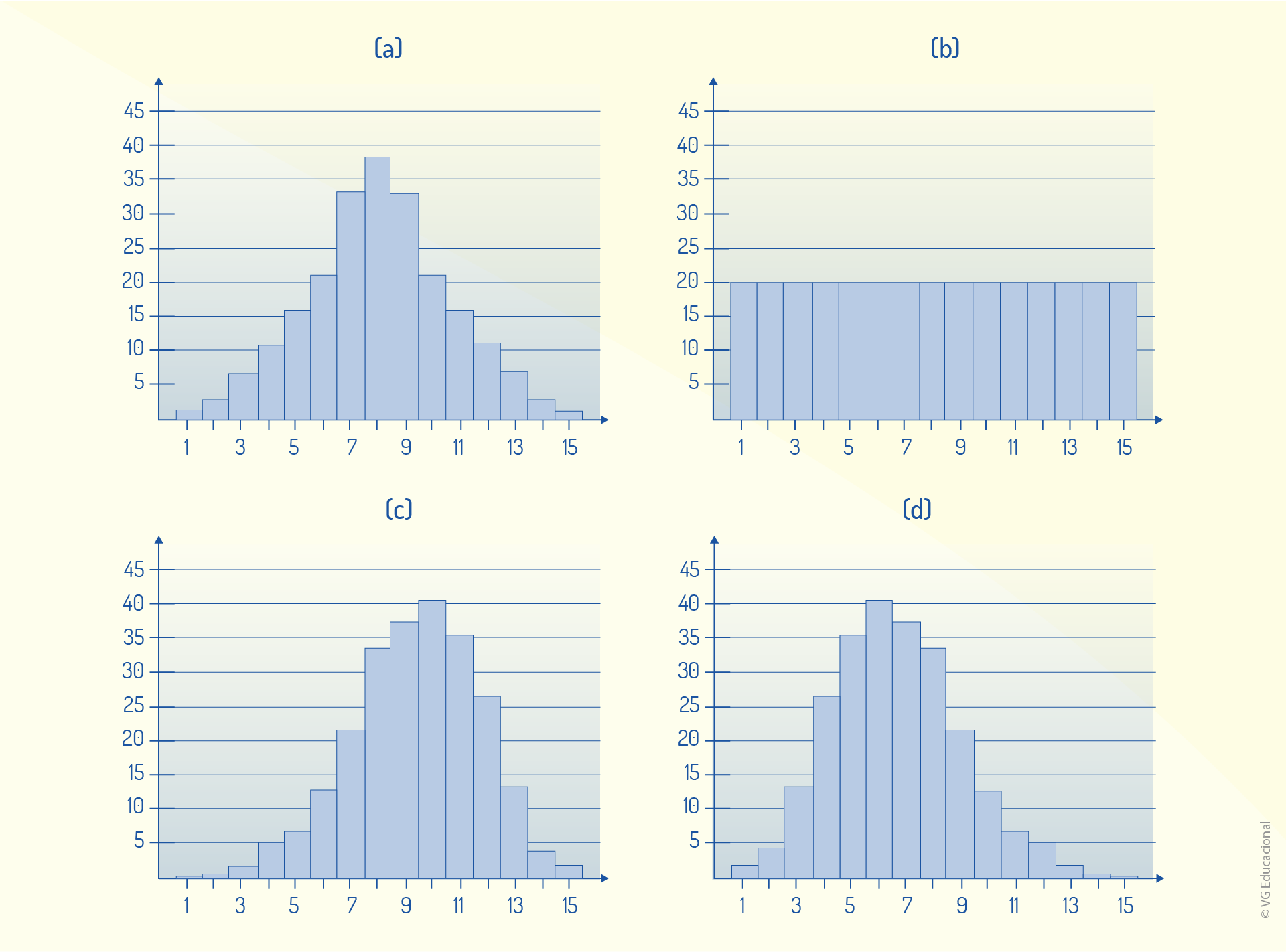
Com base no que foi apresentado, assinale a alternativa correta.
Em um processo em que se verifica apenas distribuições do tipo (a), com mesma tendência central e mesma variabilidade, pode-se considerar que há apenas causas comuns de variabilidade.
Correta. Considerando que, para esse tipo de distribuição (simétrica), verifica-se mesma tendência central (média e mediana) e mesma variabilidade (amplitude e desvio padrão), o processo é estável e tem apenas causas comuns.
Em um processo em que se verifica apenas distribuições do tipo (a), com mesma tendência central e amplitudes que variam regularmente, pode-se considerar que há apenas causas comuns de variabilidade.
Incorreta. Como as amplitudes variam, mesmo se tratando de uma distribuição simétrica e tendo sempre uma mesma tendência central, a variabilidade causa instabilidade no processo, o que denota a presença de causas especiais.
Em um processo em que se verifica apenas distribuições do tipo (a), com tendências centrais que se modificam e variabilidade constante, pode-se considerar que há apenas causas comuns de variabilidade.
Incorreta. Ainda que se trate de uma distribuição simétrica e possuindo variabilidade constante, como as tendências centrais mudam, há instabilidade no processo, implicando na existência de causas especiais de variabilidade.
Os casos (c) e (d) são considerados distribuições assimétricas, ou seja, os parâmetros de variabilidade (média, mediana e moda) têm os mesmos valores, indicando uma uniformidade dos dados.
Incorreta. Esses dois casos são considerados distribuições assimétricas de probabilidade, pois os valores de média, mediana e moda são consideravelmente diferentes.
Em casos como (b), tem-se uma distribuição uniforme de probabilidades, em que o desvio-padrão (um dos parâmetros de variabilidade) é zero, garantindo, assim, que os dados sejam todos iguais.
Incorreta. Apesar de se tratar de uma distribuição uniforme de probabilidades, o que se garante é a constância na probabilidade, e não o fato de o desvio-padrão ser zero (existe apenas um valor medido para todas as amostras).
Editora: Elsevier.
Autor: Edson Pacheco Paladini.
ISBN: 9788535248876.
Comentário: O livro apresenta a evolução da qualidade, bem como as tendências para o futuro da área. A obra permite a ampliação do horizonte do leitor a respeito do tema, mostrando o impacto da gestão da qualidade em bens e serviços.

Nome do filme: O homem que mudou o jogo (Moneyball)
Gênero: Drama.
Ano: 2012.
Elenco principal: Brad Pitt, Jonah Hill e Philip Seymour Hoffman.
Comentário: O filme aborda como métodos estatísticos podem melhorar a qualidade de qualquer organização, até mesmo de um time esportivo, em que o sucesso é garantido não apenas pelo empenho, mas pela gestão e pelo controle das atividades.
