A qualidade, como foco principal do Controle Estatístico de Processos (CEP), apresenta-se por características definidas, as quais são comumente percebidas e julgadas pelo consumidor. Tais características podem ser entendidas por dois elementos: a qual aspecto do produto ela se relaciona e a situação típica a qual ela está vinculada. Considerando esse tema, avalie as alternativas a seguir e assinale aquela em que as características analisadas e sua descrição são condizentes.
Desempenho (falhas do produto): consumidores analisam se as características do produto estão em conformidade com o padrão.
Incorreta. Para a característica desempenho, que se relaciona ao fato de o produto cumprir o que promete, os consumidores analisam se as informações fornecidas por propagandas ou vendedores são verdadeiras.
Confiabilidade (reputação do produto): consumidores avaliam benefícios extras ao se consumir o produto.
Incorreta. Na característica confiabilidade, que se relaciona à quantidade de falhas que o produto apresenta, os consumidores avaliam com que frequência é necessário realizar reparos no produto.
Estética (beleza do produto): consumidores analisam aspectos como estilo, cor e forma do produto.
Correta. A característica estética está ligada aos fatores visuais do produto, avaliados pelos consumidores por meio da análise de forma, cor, maleabilidade, estilo, dentre outras características.
Durabilidade (duração do produto): consumidores avaliam o produto de acordo com características consideradas essenciais.
Incorreta. A característica durabilidade de um produto está associada ao tempo de duração dele. Para esse fator, os consumidores costumam avaliar o tempo que o produto durará até que um novo ou similar precise ser comprado.
Qualidade observada (produto padronizado): consumidores avaliam o produto de acordo com a durabilidade dele.
Incorreta. A qualidade observada está mais ligada à reputação de um produto, ou seja, sua fama no mercado, e os consumidores a avaliam levando em consideração sua própria experiência.
No contexto do CEP, o controle da qualidade se dá por meio de um sistema de controle do processo, que é formado por elementos distintos. Esses elementos, quatro, no total, são fundamentais para o procedimento de controle em qualquer processo. Sobre os elementos citados, assinale a alternativa correta.
Um dos elementos é o processo, que é composto apenas por equipamentos e pessoas e corresponde ao núcleo da produção.
Incorreta. O processo é a combinação de equipamentos, insumos, métodos, procedimentos e pessoas e tem como objetivo a fabricação de um bem ou o fornecimento de um serviço.
As informações sobre o desempenho do processo são obtidas a partir da análise de características intermediárias e do produto final, assim como do processo.
Correta. As informações sobre o desempenho de um processo são obtidas a partir do estudo cruzado da qualidade das características do produto final, da qualidade das características intermediárias e do ajuste dos parâmetros do processo.
A coleta de dados e as ações ao longo do processo são orientadas para a revisão de atividades que já foram realizadas.
Incorreta. A coleta de informações e as ações ao longo do processo se preocupam com o futuro do processo, pois permitem detectar um defeito quando ele é gerado, o que possibilita a atuação sobre o processo no momento pertinente.
A coleta de dados e as ações ao longo do processo são orientadas para o acompanhamento de atividades que estão sendo realizadas atualmente.
Incorreta. A coleta de dados e as ações ao longo do processo são pautadas em atividades do futuro, uma vez que permitem que o defeito seja detectado assim que ele ocorre, possibilitando a atuação sobre o processo de maneira adequada.
As ações sobre o produto final são importantes para o controle do processo produtivo, apesar de não terem nenhuma vantagem prática.
Incorreta. As inspeções têm certas vantagens, pois impedem que o cliente adquira produtos defeituosos, embora não sejam uma forma eficiente de ação, impedem que novas peças defeituosas sejam produzidas.
Os conhecimentos de probabilidade estão no coração do controle estatístico de processos e são essenciais para a determinação de parâmetros centrais e intervalos de valores, sendo os conceitos de média, mediana, desvio e amplitude de grande valia nesses procedimentos. Considere o quadro de valores a seguir, que apresenta a massa, em gramas, de certo produto. Para essa amostra, assinale a alternativa que apresenta corretamente os valores de média, mediana, desvio-padrão e amplitude.
Fonte: Elaborada pelo autor.
Média = 150; mediana = 150; desvio-padrão = 1,12; amplitude = 148-152.
Incorreta.
Cálculos:
Média: \(\underset{\scriptscriptstyle-}{x}=\frac{\sum\nolimits_{i}^{20}{{{x}_{i}}}}{n}=\frac{3002}{20}=150,1\)
Mediana: 148-148-149-149-149-150-150-150-150-150-150-150-150-151-151-151-151-151-152-152
Desvio-padrão:
\[\sigma =\sqrt{\frac{\sum\nolimits_{1}^{20}{{{({{x}_{i-\underset{\scriptscriptstyle-}{x}}})}^{2}}}}{n-1}}=\sqrt{\frac{23,8}{19}}=1,12\]
Amplitude: Mínimo: 148 / Máximo 152.
Média = 150,1; mediana = 149; desvio-padrão = 1,10; amplitude = 148-152.
Incorreta.
Cálculos:
Média: \(\underset{\scriptscriptstyle-}{x}=\frac{\sum\nolimits_{i}^{20}{{{x}_{i}}}}{n}=\frac{3002}{20}=150,1\)
Mediana: 148-148-149-149-149-150-150-150-150-150-150-150-150-151-151-151-151-151-152-152
Desvio-padrão:
\[\sigma =\sqrt{\frac{\sum\nolimits_{1}^{20}{{{({{x}_{i-\underset{\scriptscriptstyle-}{x}}})}^{2}}}}{n-1}}=\sqrt{\frac{23,8}{19}}=1,12\]
Amplitude: Mínimo: 148 / Máximo 152.
Média = 150; mediana = 150; desvio-padrão = 1,12; amplitude = 148-151.
Incorreta.
Cálculos:
Média: \(\underset{\scriptscriptstyle-}{x}=\frac{\sum\nolimits_{i}^{20}{{{x}_{i}}}}{n}=\frac{3002}{20}=150,1\)
Mediana: 148-148-149-149-149-150-150-150-150-150-150-150-150-151-151-151-151-151-152-152
Desvio-padrão:
\[\sigma =\sqrt{\frac{\sum\nolimits_{1}^{20}{{{({{x}_{i-\underset{\scriptscriptstyle-}{x}}})}^{2}}}}{n-1}}=\sqrt{\frac{23,8}{19}}=1,12\]
Amplitude: Mínimo: 148 / Máximo 152.
Média = 150,1; mediana = 150; desvio-padrão = 1,12; amplitude = 148-152.
Correta.
Cálculos:
Média: \(\underset{\scriptscriptstyle-}{x}=\frac{\sum\nolimits_{i}^{20}{{{x}_{i}}}}{n}=\frac{3002}{20}=150,1\)
Mediana: 148-148-149-149-149-150-150-150-150-150-150-150-150-151-151-151-151-151-152-152
Desvio-padrão:
\[\sigma =\sqrt{\frac{\sum\nolimits_{1}^{20}{{{({{x}_{i-\underset{\scriptscriptstyle-}{x}}})}^{2}}}}{n-1}}=\sqrt{\frac{23,8}{19}=1,12~Desvio~-~padr\tilde{a}o}:=1,21\]
Amplitude: Mínimo: 148 / Máximo 152.
Média = 150,1; mediana = 150; desvio padrão = 1,10; amplitude = 149-152.
Incorreta.
Cálculos:
Média: \(\underset{\scriptscriptstyle-}{x}=\frac{\sum\nolimits_{i}^{20}{{{x}_{i}}}}{n}=\frac{3002}{20}=150,1\)
Mediana: 148-148-149-149-149-150-150-150-150-150-150-150-150-151-151-151-151-151-152-152
Desvio-padrão:
\[\sigma =\sqrt{\frac{\sum\nolimits_{1}^{20}{{{({{x}_{i-\underset{\scriptscriptstyle-}{x}}})}^{2}}}}{n-1}}=\sqrt{\frac{23,8}{19}}=1,12\]
Amplitude: Mínimo: 148 / Máximo 152.
A variabilidade de um processo está vinculada a ocorrências (problemas) dentro do processo produtivo e está relacionada ao que, em CEP, é chamado de causa. Essas causas podem ser comuns ou especiais e afetam diretamente a qualidade do processo. Avalie, a seguir, as distribuições de probabilidade (a), (b), (c) e (d).
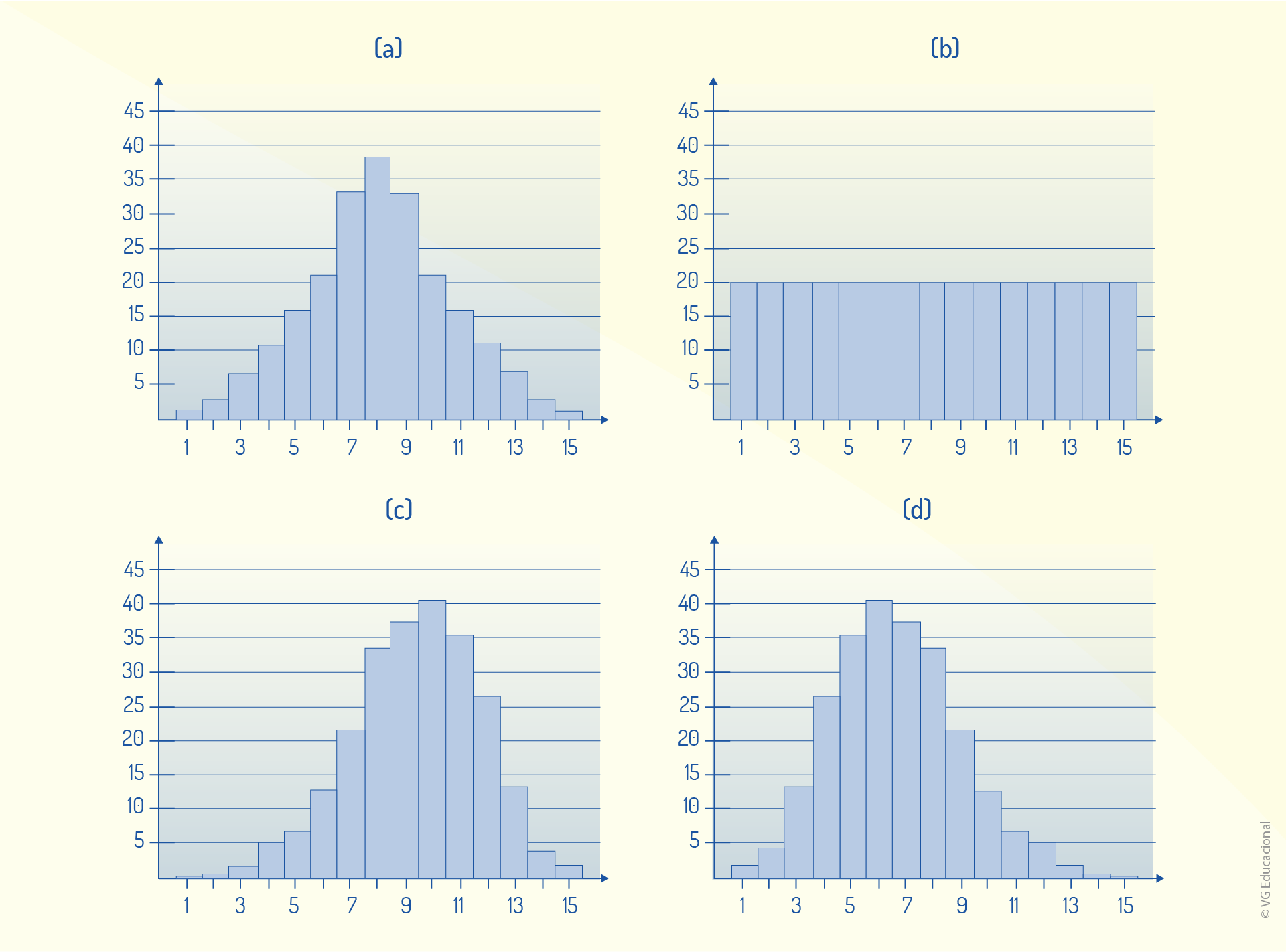
Com base no que foi apresentado, assinale a alternativa correta.
Em um processo em que se verifica apenas distribuições do tipo (a), com mesma tendência central e mesma variabilidade, pode-se considerar que há apenas causas comuns de variabilidade.
Correta. Considerando que, para esse tipo de distribuição (simétrica), verifica-se mesma tendência central (média e mediana) e mesma variabilidade (amplitude e desvio padrão), o processo é estável e tem apenas causas comuns.
Em um processo em que se verifica apenas distribuições do tipo (a), com mesma tendência central e amplitudes que variam regularmente, pode-se considerar que há apenas causas comuns de variabilidade.
Incorreta. Como as amplitudes variam, mesmo se tratando de uma distribuição simétrica e tendo sempre uma mesma tendência central, a variabilidade causa instabilidade no processo, o que denota a presença de causas especiais.
Em um processo em que se verifica apenas distribuições do tipo (a), com tendências centrais que se modificam e variabilidade constante, pode-se considerar que há apenas causas comuns de variabilidade.
Incorreta. Ainda que se trate de uma distribuição simétrica e possuindo variabilidade constante, como as tendências centrais mudam, há instabilidade no processo, implicando na existência de causas especiais de variabilidade.
Os casos (c) e (d) são considerados distribuições assimétricas, ou seja, os parâmetros de variabilidade (média, mediana e moda) têm os mesmos valores, indicando uma uniformidade dos dados.
Incorreta. Esses dois casos são considerados distribuições assimétricas de probabilidade, pois os valores de média, mediana e moda são consideravelmente diferentes.
Em casos como (b), tem-se uma distribuição uniforme de probabilidades, em que o desvio-padrão (um dos parâmetros de variabilidade) é zero, garantindo, assim, que os dados sejam todos iguais.
Incorreta. Apesar de se tratar de uma distribuição uniforme de probabilidades, o que se garante é a constância na probabilidade, e não o fato de o desvio-padrão ser zero (existe apenas um valor medido para todas as amostras).
Considere que um dado processo analisado em uma indústria reflete um conjunto de dados em distribuição normal, com uma distribuição de médias amostrais com \(n\) = 50, sendo o valor da média \(μ\) = 25 e o desvio-padrão igual a \(σ\) = 1,5. Assinale a alternativa correta com relação à análise desse cenário prático.
Como se trata de uma distribuição normal populacional, cujo conjunto de dados amostral é pequeno, a média amostral deve ser calculada.
Incorreta. Pelo teorema do limite central, sendo \(n≥30\), é possível afirmar que a seguinte relação é válida: \(μ = μ_{\underline{x}}\) (ou seja, na prática, as médias populacional e amostral são iguais).
Sendo a média populacional igual a 25, como apresentado no enunciado, é correto afirmar que a média amostral também é 25.
Correta. Como o número de amostras é 50, pelo teorema do limite central, sendo \(n≥30\), é possível afirmar que \(μ = μ_{\underline{x}}\), ou seja, as médias populacional e amostral são iguais.
Como a amostra da população é suficientemente grande, é possível afirmar que os desvios-padrão populacional e amostral são os mesmos.
Incorreta. Mesmo sendo válido utilizar o teorema do limite central, ele estabelece, na prática, que o desvio amostral é calculado a partir do populacional (\(σ\)), pela seguinte relação: \(σ_{\underline{x}}=\frac{σ}{\sqrt{n}}\), em que n é o número de amostras.
Os escores-x, nesse caso, são calculados pela tabela de distribuição normal padrão, a partir da curva estabelecida nesse caso.
Incorreta. De fato, é utilizada a tabela de distribuição normal padrão, pois, no enunciado, afirma-se que, nesse caso, trata-se de uma distribuição desse tipo, entretanto, o correto é escores-z.
O valor do desvio-padrão populacional estabelecido como 1,5 pode ser facilmente obtido na tabela de distribuição normal padrão.
Incorreta. Pois o valor de desvio-padrão populacional de 1,5 é escolhido ou adotado a partir dos dados analisados, dependendo do que mais se aproxima ou das escolhas do responsável pela análise.
Como você pôde ver ao longo de seu estudo, a distribuição normal será utilizada como base para o desenvolvimento de um gráfico de controle, e sabe-se, ainda, que tal uso é justificado como base para o controle de processos. Com relação aos gráficos de controle, é correto afirmar que:
normalmente, os gráficos de controle utilizam três desvios-padrão com relação à média e intervalo de confiança de 93,73%.
Correta. Como proposto por Shewhart, em 1931, o valor de três desvios-padrão a mais ou a menos com relação à média é efetivo para boa parte das análises práticas e, além disso, o intervalo de confiança correspondente é de 93,73%.
normalmente, os gráficos de controle utilizam um desvio-padrão com relação à média e intervalo de confiança de 6,27%.
Incorreta. Normalmente, são utilizados três desvios-padrão, conforme propostos por Shewhart. Além disso, 6,27% representam, no intervalo de confiança normalmente adotado, a chance de erro.
o LSC corresponde ao limiar superior de correlação, ao passo que LIC é o inferior de correlação.
Incorreta. Em um gráfico de controle (carta de controle), as medidas de limiares de controle são representadas por LSC e LIC, sendo o limite superior e o inferior, respectivamente.
a média em um gráfico de controle representa a quantidade de erros médios do sistema de controle analisado.
Incorreta. Na verdade, a média representa a média dos dados amostrados e, no gráfico de controle, é a linha central para traçá-lo, junto com os limiares de controle.
as causas comuns associadas a um gráfico de controle normalmente representarão problemas inerentes e que surgem de forma previsível.
Incorreta. Um problema decorrente de causas comuns, obtidas a partir de um gráfico de controle, será geralmente de origem aleatória, além de, normalmente, ser inerente ao processo.
Apesar de haver muitas orientações na literatura e o responsável pela análise da carta de controle poder contar, também, com sua própria expertise, observa-se, na prática, que, embora encontrar pontos fora dos limites seja fácil, encontrar padrões não aleatórios pode ser bastante difícil. Com base nesse tema, assinale a alternativa correta sobre a análise de cartas de controle.
Os pontos fora dos limites de controle podem ser facilmente identificados a partir da inspeção com instrumentos de medição, como réguas.
Incorreta. Geralmente, na maior parte dos casos de análise de gráficos de controle, os pontos que excederem os limites de controle podem ser facilmente visualizados na ferramenta gráfica.
Assim como configurações não aleatórias, sequências de pontos também são menos triviais para identificação, mas se sabe que elas dizem respeito a causas comuns.
Incorreta. Pois sequências de pontos no gráfico de controle geralmente se estabelecem por conta de causas especiais, sendo necessário analisar, em vários casos, se elas poderão melhorar ou prejudicar o processo.
A periodicidade é outro exemplo de padrão normalmente identificável em gráficos de controle, a partir de análises de curto prazo.
Incorreta. O padrão de periodicidade em gráficos de controle está diretamente relacionado a configurações geralmente detectáveis em análises de longo prazo.
A tendência, outro possível padrão identificável no gráfico de controle, pode estar relacionada a duas classes distintas: tendências claras ou ocultas.
Incorreta. Pois a tendência em um gráfico de controle, normalmente, denota dois tipos principais: a tendência de pontos ascendentes ou a de pontos descendentes (normalmente 7 ou mais pontos).
A aproximação dos limites de controle é outro tipo de padrão a ser detectado, em certos casos, no gráfico de controle, geralmente de dois ou mais pontos.
Correta. De fato, nas análises, considera-se pelo menos dois pontos nos limites de controle, sendo que tais aproximações, normalmente, são vistas tipicamente em grandes ajustes nos processos.
Tomando como exemplo um gráfico de controle (carta de controle), sabe-se que existirão ferramentas mais indicadas, ou não, dependendo do cenário analisado ao qual se refere o processo, como o caso de ferramentas indicadas para trabalhar com o número médio de não conformidades na amostra. Com relação a esse tema, aponte, dentre as alternativas apresentadas, qual é esse gráfico.
Gráfico \(p\).
Incorreta. Embora esse seja um exemplo de gráfico de controle para atributos, os gráficos \(p\) são mais indicados para medir a fração de produtos defeituosos ou não conformes.
Gráfico de controle \(u\).
Correta. Esse tipo de gráfico é mais indicado para processos sujeitos a atributos, nos quais se utiliza o número médio de não conformidades visto na amostra analisada dos dados.
Gráfico \(np\).
Incorreta. Embora esse seja um exemplo de gráfico de controle para atributos, os gráficos \(np\) são mais indicados para medir a fração de defeituosos ou não conformes, mas no caso de amostras de tamanho constante.
Gráfico de controle de desvio.
Incorreta. Esse é um tipo de gráfico ou carta de controle utilizado em casos em que o processo de amostragem trata de variáveis contínuas e análises de variabilidade.
Gráfico de moda.
Incorreta. Esse não é um tipo de gráfico ou carta de controle existente. Dentre os gráficos de controle de atributos, por exemplo, é possível citar os gráficos pelo \(np\).
Em determinada empresa, foram realizadas verificações da característica da massa de um conjunto de itens e os valores verificados foram representados na tabela a seguir, em que foram aferidas 4 medidas em 4 amostras. Sabe-se que, para esse produto, \(LIE\) = 158, \(VN\) = 150 e \(LSC\) = 152. Além disso, para que os cálculos de desvio padrão possa ser aplicado, considere \(d_2\) = 2,059.
Fonte: Elaborada pelo autor.
Levando essas informações em consideração, indique a alternativa correta.
Para esse conjunto de dados, a média dos intervalos é de 150.
Incorreta. \(\underline{x}_1 = (150+150+151+150)/4 = 150,25;\underline{x}_2 = (151+152+151+152)/4 = 151,5; \underline{x}_3 = \)
\( (149+150+150+151)/4 = 150; \underline{x}_4 = (149+149+150+149)/4 = 149,25\).
\(\underline{x}= (150,25 + 151,50 + 150,00 + 149,25)/4 = 150,25\)
Para esse conjunto de dados, o desvio dos valores é de 0,550.
Incorreta. \(σ =\underline{R}/d_2 = 1,25/2,059 = 0,607\)
Para esse conjunto de dados, a média das amplitudes é de 1,5.
Incorreta. \(\underline{x}= (1 + 1 + 2 + 1)/4 = 1,25\)
A capacidade do processo é igual a, aproximadamente, 2,85.
Incorreta. Capacidade = \(6σ = 3,64\)
O índice \(PCR\) para esse processo é de, aproximadamente, 1,1.
Correta. \(PCR = (LSE – LIE)/6σ = (152 – 148)/3,54 = 1,1\).
Considere que, em determinada empresa que produz peças metálicas, as dimensões de um certo item devam ser iguais a 20 cm (valor nominal ou meta). Sabe-se que, em casos em que essa especificação varie mais do que 2 cm, é necessário realizar um conserto a um custo de R$ 1,00. Considere também que, durante análises, percebeu-se que as peças estavam sendo produzidas com 20,5 cm.
Levando essas informações em consideração e utilizando a função de perda quadrática, assinale a alternativa correta.
Nesse caso, tem-se que o parâmetro k = 0,50 R$/cm.
Incorreta. Para a determinação de \(k\), utilizamos a equação a seguir:
\[k = A_0/Δ² = 1/(2)² = 1/4 = 0,25\]
Para esse caso, o parâmetro \(Δ\) é 20 cm.
Incorreta. O parâmetro em questão equivale ao tamanho do intervalo de tolerância para valores, ou seja, \(Δ = 22 – 20 = 2\)
Para esse caso, o parâmetro m é 4 cm.
Incorreta. Esse parâmetro equivale à meta, ou ao valor nominal da peça, que nesse caso corresponde a 20 cm.
Para esse caso, o custo associado às peças de 20,5 cm é R$ 0,25.
Correta. \(L_i = k(y_i – m)² = 0,25(20,5 – 20)² = 0,25(0,5)² = 0,25.0,25 = 0,06\)
Para esse caso, o custo associado às peças de 20,5 cm é R$ 0,06.
Incorreta. \(L_i = k(y_i – m)² = 0,25(20 – 20,5)² = 0,25(0,5)² = 0,25.0,25 = 0,06\)
Determinada organização está preocupada com a estabilidade e a acurácia de seu processo produtivo. Para poder analisar alguns parâmetros dentro de seu processo que possam dizer respeito sobre esses dois fatores, foram tomadas algumas amostras da massa de produtos, e os resultados (em gramas) foram apresentados na tabela a seguir. Considere \(d_2\) = 2,326 e que a meta é de 500 gramas.
Fonte: Elaborada pelo autor.
Em relação ao apresentado, assinale a alternativa correta.
O valor das médias de todos os intervalos é menor do que 500.
Incorreta. Como apresentado a seguir, uma das médias é maior do que 500.
O processo possui grande instabilidade devido às grandes variações das médias.
Incorreta. Como as médias são próximas entre si (não variam mais do que 1,2 uma da outra), então o processo é consideravelmente estável
O processo apresenta uma leve tendência para valores menores do que a meta.
Correta. A média global dos intervalos é calculada em 499,48 gramas.
\((499+500,2+499+499,8+499,4)/5 = 499,48\).
Esse valor é levemente menor do 500, então a tendência é levemente menor.
O processo apresenta precisão muito baixa, devido ao desvio maior do que 5.
Incorreta. \(σ = \underline{R}/d_2 ⇒ \underline{R}= (4+3+4+5+5)/5 = 4,2 ⇒ σ = 4,2/2,326 = 1,81\).
O processo possui desvio menor do que 1.
Incorreta. \(σ = 4,2/2,326 = 1,81\).
Uma certa empresa iniciou o processo de implementação do CEP há algum tempo. Primeiramente, ela se planejou, buscando engajar gestores e supervisores no programa, depois promoveu reuniões e levantamentos, e listou os recursos necessários. Quando partiu para as primeiras análises, percebeu que, para o índice PCR, foi obtido o valor 1,05. Sendo assim, assinale a alternativa que indica o que a empresa deve fazer agora.
A empresa deve providenciar o aumento de controle de processo, dando enfoque a inspeções, avaliando também a estabilidade que o processo possui.
Correta. Esse é o procedimento mais indicado a ser realizado pela organização, uma vez que o índice PCR está muito próximo do valor 1,00, ou seja, um processo sem folga, que precisa de um controle mais intensivo.
A empresa deve se dedicar à estratégia de treinamento dos operadores e funcionários, além das necessidades financeiras.
Incorreta. Ao analisarmos os passos a serem seguidos pelas organizações, verifica-se que essa é a segunda etapa do programa de implementação do CEP, um passo de gestão que não atende à necessidade de aumento de controle do processo.
A empresa deve acionar a equipe de melhoria, buscando traçar meios de se eliminar causas especiais de variação no processo.
Incorreta. Equivale a uma ação da terceira etapa do programa de implementação do CEP. No caso da empresa em questão, o que é preciso fazer é aumentar o nível de controle do processo e dar enfoque a inspeções.
A empresa deve proceder a uma quantidade de inspeções reduzidas e utilizar apenas cartas de controle nas verificações.
Incorreta. Tal procedimento é aplicável nos casos em que o índice de PCR é próximo ao valor de 1,33, onde se tem um processo com mais folga, cujo controle não precisa ser intensificado, devido ao bom índice.
A empresa deve proceder a uma verificação pontual do processo e utilizar cartas de controle para avaliar os comportamentos do processo.
Incorreta. Esse procedimento diz respeito a um processo cujo índice PCR está próximo de 1,63, que corresponde a um processo bem controlado, com pequena variabilidade e que necessita apenas de procedimentos de verificação leve.
Como já levantado ao longo do estudo acerca do Lean Manufacturing, os princípios do Lean Thinking englobam, na prática nas organizações, diversos pontos genéricos, conforme previsto pelo próprio Lean Institute Brasil, tanto no processo de estruturação quanto na possível reestruturação da metodologia.
Assim, com base nisso, assinale a alternativa que apresenta corretamente algum desses princípios.
Geração de valor.
Incorreta. Normalmente, o que se faz é especificar o valor, tratando-se do que é valorizado pelo cliente nessa etapa inicial de análise. Define-se então o que é o valor e pode-se prosseguir para as demais etapas.
Especificação de valor.
Correta. O processo de especificação de valor é o passo inicial nesse tipo de abordagem e envolverá, basicamente, compreender as principais necessidades estabelecidas pelo cliente.
Criação do fluxo de valor.
Incorreta. O que se faz, nesse caso, em um segundo momento, é identificar o fluxo de valor. Levando a passos como o dissecamento da cadeia produtiva e a separação dos processos em alguns tipos distintos.
Criação do fluxo de caixa.
Incorreta. Como mencionado, tem-se num segundo momento a identificação do fluxo de valor. Levando a passos como o dissecamento da cadeia produtiva e separação dos processos em alguns tipos distintos.
Finalização de fluxos contínuos.
Incorreta. O que se faz, nesses casos, em um terceiro momento, é criar fluxos contínuos para gerar fluidez aos processos e às atividades que restarem na análise a esse ponto do processo.
Pensando na construção de um novo modelo integrando Lean e Seis Sigma, deve-se considerar, conforme diversos autores apontam, alguns fatores principais para análise: o modelo estar focado em processos, mas aproveitando as vantagens do Lean e do Seis Sigma simultaneamente; a existência de equilíbrio entre a complexidade e sua sustentabilidade; e a estruturação do modelo acerca do problema real.
Acerca desse processo de integração na prática, demonstrando como muitas vezes o Seis Sigma é usado, é correto afirmar que:
nesse tipo de integração, o Lean será capaz de modificar a filosofia da estrutura.
Incorreta. O que o Lean faz, na verdade, é reforçar a priorização pelo uso de um modelo estruturado no processo de integração com a metodologia Seis Sigma.
dentro da integração, o Lean é capaz de fornecer o direcionamento estratégico para melhoria.
Correta. Ao reforçar a filosofia de estrutura do modelo, o Lean, na prática, permitirá, em conjunto, um direcionamento estratégico para possíveis melhorias no processo.
no processo de integração, o Seis Sigma é responsável por orientar a dinâmica geral do sistema.
Incorreta. Na integração Lean Manufacturing e Seis Sigma, o Lean é que será o responsável por direcionar a dinâmica geral do sistema em análise.
para a identificação de pontos críticos, utiliza-se o Seis Sigma no foco para as melhorias.
Incorreta. O Seis Sigma é de fato utilizado na prática, na integração, para o foco nas melhorias necessárias. Entretanto, isso é feito após o processo de identificação dos pontos críticos.
após analisar a integração, embora haja vantagens, conclui-se que o Seis Sigma é preferencial.
Incorreta. O uso do Lean Manufacturing e do Seis Sigma de forma integrada, mostra ainda mais que essas metodologias são complementares entre si e trazem resultados de maneira conjunta.
Como você pôde ver ao longo de seu estudo até o momento, a distribuição normal será utilizada como base para o desenvolvimento de um gráfico de controle. Esse uso é justificado pela base para o controle de processos. Com relação aos gráficos de controle, é correto afirmar que:
Normalmente, os gráficos de controle utilizam três desvios padrão com relação à média, e intervalo de confiança de 93,73%.
Correta. Como proposto por Shewhart, em 1931, o valor de três desvios padrão a mais ou a menos com relação à média é efetivo para boa parte das análises práticas. Além disso, o intervalo de confiança correspondente é de 93,73%.
Normalmente, os gráficos de controle utilizam um desvio padrão com relação à média, e intervalo de confiança de 6,27%.
Incorreta. Normalmente, são utilizados três desvios padrão, propostos por Shewhart e utilizados até hoje. Além disso, 6,27% representa, no intervalo de confiança normalmente adotado, a chance de erro.
O LSC corresponde ao limiar superior de correlação, ao passo que o LIC é o inferior de correlação.
Incorreta. Em um gráfico de controle (carta de controle), as medidas de limiares de controle são representadas por LSC e LIC, representando o limite superior e o inferior, respectivamente.
A média em um gráfico de controle representa a quantidade de erros médios do sistema de controle analisado.
Incorreta. Na verdade, refere-se à média dos dados amostrados. No gráfico de controle, é a linha central para traçá-lo, junto com os limiares de controle utilizados para a carta.
As causas comuns associadas a um gráfico de controle normalmente representarão problemas inerentes, que surgem de forma previsível.
Incorreta. Um problema decorrente de causas comuns, obtidas a partir de um gráfico de controle, será geralmente de origem aleatória, além de normalmente ser inerente ao processo.