A forma como os dados obtidos em processos industriais, máquinas, sistemas etc. comportam-se pode ser analisada mediante características de distribuição estatística e probabilística dos próprios dados e das informações relacionadas a eles. Além disso, a partir desse conhecimento diretamente estatístico, é possível obter ferramentas técnicas que podem ser utilizadas para a implementação do controle estatístico de processos, como as cartas de controle.
Nesta unidade, você verá os principais aspectos sobre a distribuição normal e a distribuição normal padrão, para que possa compreender como são desenvolvidas, utilizadas e analisadas as cartas de controle (ou gráficos de controle, como também são conhecidas).
Sabe-se que o controle estatístico de variáveis é realizado por meio do monitoramento simultâneo de duas cartas de controle. Adicionalmente, sabe-se que, para compreender a razão de se monitorar, de forma simultânea, a tendência central, bem como a questão da variabilidade do processo, será necessário compreender o papel da distribuição de probabilidade.
Tipicamente, observa-se que as variáveis poderão seguir um dado tipo de distribuição de probabilidade. Dentre elas, tem-se as distribuições: simétrica, assimétricas (para a direita ou para a esquerda), uniforme, exponencial e bimodal. Além disso, aponta-se que a distribuição normal é a mais comum delas, para o contexto apresentado. Assim, estudaremos como esse tipo de distribuição se estabelece e veremos suas principais características e análises pertinentes.
Ademais, do ponto de vista específico da área, Kume (1993) destaca que, no caso em que a variação de uma característica qualquer da qualidade é gerada, por diversos fatores, pela soma de vários erros infinitesimais independentes, a distribuição de característica da qualidade será, exatamente, ou muito próxima, de uma distribuição normal.
Antes de analisarmos especificamente como essas distribuições se estabelecem, é fundamental recordar o que são variáveis aleatórias discretas e contínuas. Sabe-se que uma variável aleatória contínua terá um número infinito de possíveis valores, que poderão ser representados, na prática, por meio de um intervalo em uma reta numérica. Por outro lado, as variáveis aleatórias discretas estão associadas a um número finito desses possíveis valores ou, ainda, a um número infinito enumerável. À distribuição das variáveis aleatórias contínuas, dá-se o nome de distribuição contínua de probabilidade, sendo que uma das principais distribuições contínuas é, de fato, a distribuição normal.
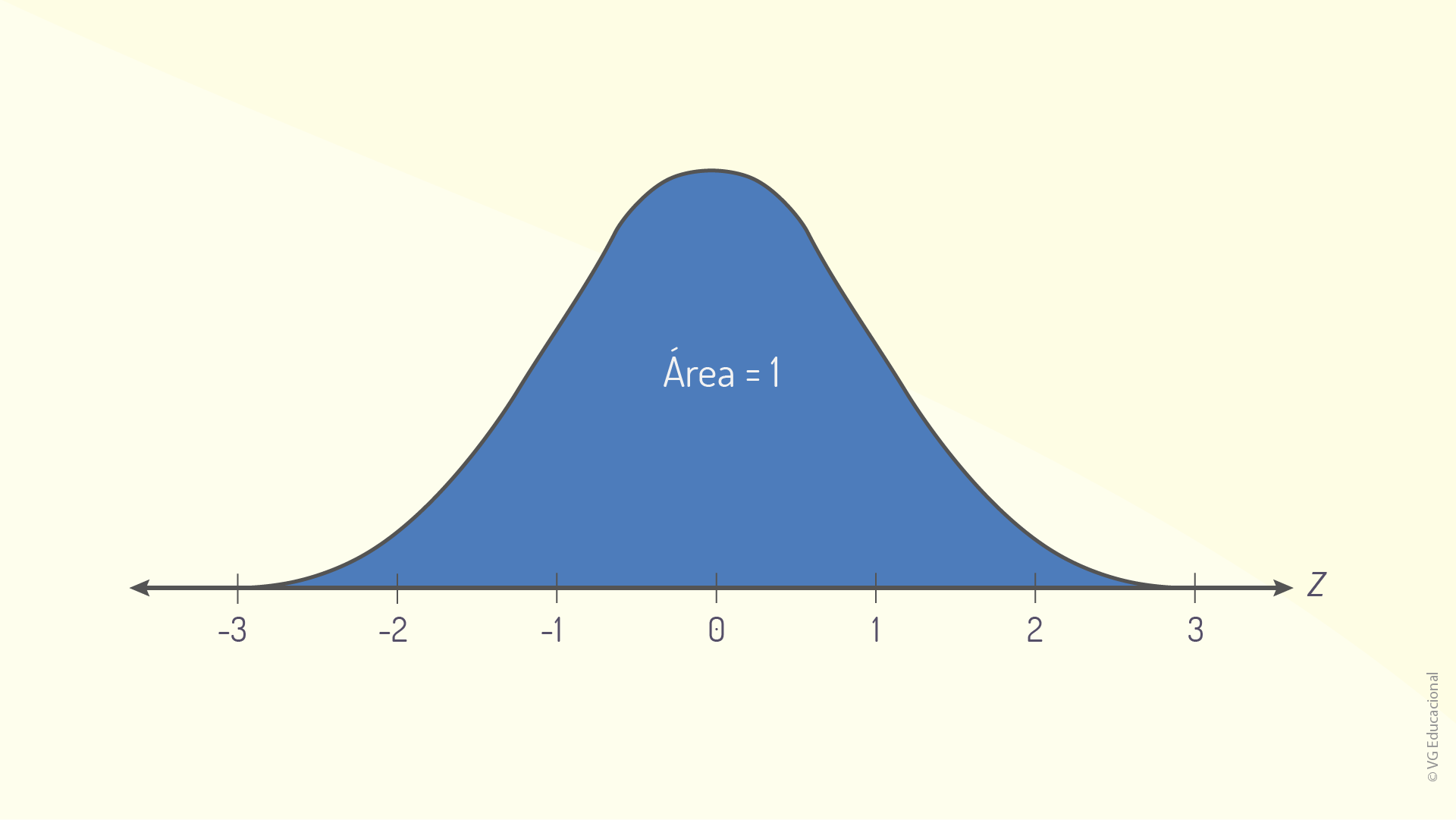
As distribuições normais poderão ser utilizadas para a modelagem de diversos dados da natureza, da indústria e de negócios, visto que, na prática, grande parte dessas variáveis associadas será de variáveis aleatórias normalmente distribuídas. Tem-se, então, a definição, conforme Larson e Farber (2015, p. 218), de que “uma distribuição normal é uma distribuição de probabilidade contínua para uma variável aleatória \(x\), cujo gráfico é chamado de curva normal”. O gráfico de uma curva normal típica é apresentado na figura a seguir.

Sabe-se, tipicamente, que, nesse tipo de distribuição, a média (\(μ\)), a mediana e a moda são iguais. Esse tipo de curva tem a “forma de sino” e, em torno da média dos dados, é simétrica; a área total sob a curva pode ser calculada e é tipicamente igual a 1. Além disso, quanto mais distante um ponto dessa curva está da média, percebe-se que a tendência é que ele esteja mais próximo do eixo \(x\), visto que, à medida que a curva se distancia da média, esta tende a decair e a se aproximar indefinidamente do eixo \(x\). Por último, sabe-se, ainda, que, entre os pontos \(μ-σ\) e \(μ+σ\) (área central da curva), o gráfico apresenta concavidade para baixo, sendo \(σ\) o desvio-padrão e, a partir de \(μ-σ\) e de \(μ+σ\), à esquerda e à direita deles, respectivamente, o gráfico apresenta concavidade para cima (LARSON; FARBER, 2015). Esses pontos são denominados pontos de inflexão, como marcado na figura anterior.
Assim, em casos de distribuição contínua de probabilidade, é possível utilizar uma função de densidade de probabilidade (fdp), que deverá, na prática, satisfazer a duas condições principais:
Para a função de densidade de probabilidade normal, tem-se:
\[y = \frac{1}{\sigma\sqrt{2\pi }}e^{-(x-μ)^2/(2σ^2)}~~~~~~~~~~(1)\]
Considerando, ainda, que \(e\) = 2,718 e \(π\) = 3,14, lembre-se de que o valor dependerá completamente dos valores da média e do desvio e que eles determinarão o formato da curva normal, em que a média traz a localização da linha de simetria, e o desvio apresenta a dispersão dos dados analisados. Adicionalmente, denomina-se distribuição normal padrão a distribuição normal cuja média é igual a 0 e o desvio-padrão é unitário, sendo que, na escala horizontal, haverá o parâmetro escore-z, uma medida de posição que indica o número de desvios-padrão a partir da média, para medição do deslocamento (LARSON; FARBER, 2015). Um valor \(x\) pode ser transformado em um escore-z a partir da relação expressa na Equação 2.
\[z=\frac{valor - média}{desvio-padrão}=\frac{x - μ}{σ}~~~~~~~~~~(2)\]
Na prática, arredonda-se o valor obtido na Equação 2 para o valor centesimal mais próximo. O quadro a seguir apresenta, de forma resumida, a diferença entre \(x\) e \(z\).
Quadro 2.1 - Comparativo entre \(x\) e \(z\)
Fonte: Elaborado pela autora.
A figura a seguir apresenta a curva normal correspondente à distribuição normal padrão, um tipo especial de distribuição normal que tem, como você verá adiante, algumas características predeterminadas, comuns a qualquer tipo de dado.
Assim, como propriedades de uma distribuição normal padrão, destacam-se as seguintes observações, acerca da área sob a curva, válidas para qualquer tipo de dado, desde que eles estejam distribuídos dessa forma:
Além disso, observa-se que, como a distribuição normal é, de fato, uma distribuição contínua de probabilidade, a área sob a curva normal padrão, à esquerda de um dado escore-z, trará a informação de o quanto é provável que a variável z seja menor que esse escore-z, por exemplo (LARSON; FARBER, 2015).
A seguir, você entenderá melhor como é estabelecido o conceito de probabilidade na distribuição normal, compreendendo como encontrar probabilidades para variáveis normalmente distribuídas, por meio do uso de tabelas e tecnologias.
Para o cálculo da área acumulada sob o gráfico da curva normal padrão, referente a esse tipo de distribuição, utiliza-se a tabela normal padrão. Essa tabela pode ser facilmente acessada em qualquer livro de estatística, por ser utilizada em diversas áreas, mas você também pode acessá-la no link disponível em: http://wiki.icmc.usp.br/images/f/f9/Tabela_Normal.pdf. Acesso em: 25 out. 2020.

Sabe-se que, quando uma variável aleatória \(x\) é normalmente distribuída, é possível determinar a probabilidade de \(x\) estar em um dado intervalo, a partir do cálculo da área sob a curva normal no intervalo analisado (LARSON; FARBER, 2015). Para que isso possa ser feito, são considerados os seguintes passos:
Lembrando que o gráfico poderá ser um esboço, para auxiliar a resolução do problema. Para entender como ele é feito na prática, considere o exemplo a seguir. Suponha que uma dada pesquisa indica que, normalmente, as pessoas adquirem uma nova calça jeans, caso as que possuem não apresentem nenhum defeito, a cada um ano e meio. O desvio-padrão é de 0,25 ao ano, e a seleção de uma das pessoas que participaram da pesquisa foi feita de forma aleatória. Assim, deseja-se calcular qual a probabilidade de essa pessoa comprar uma nova calça jeans em menos de um ano, considerando, ainda, que as durações de tempo indicadas na pesquisa são distribuídas de forma normal e apresentadas pela variável aleatória \(x\). O gráfico apresentado na figura a seguir representa a situação prática do problema.
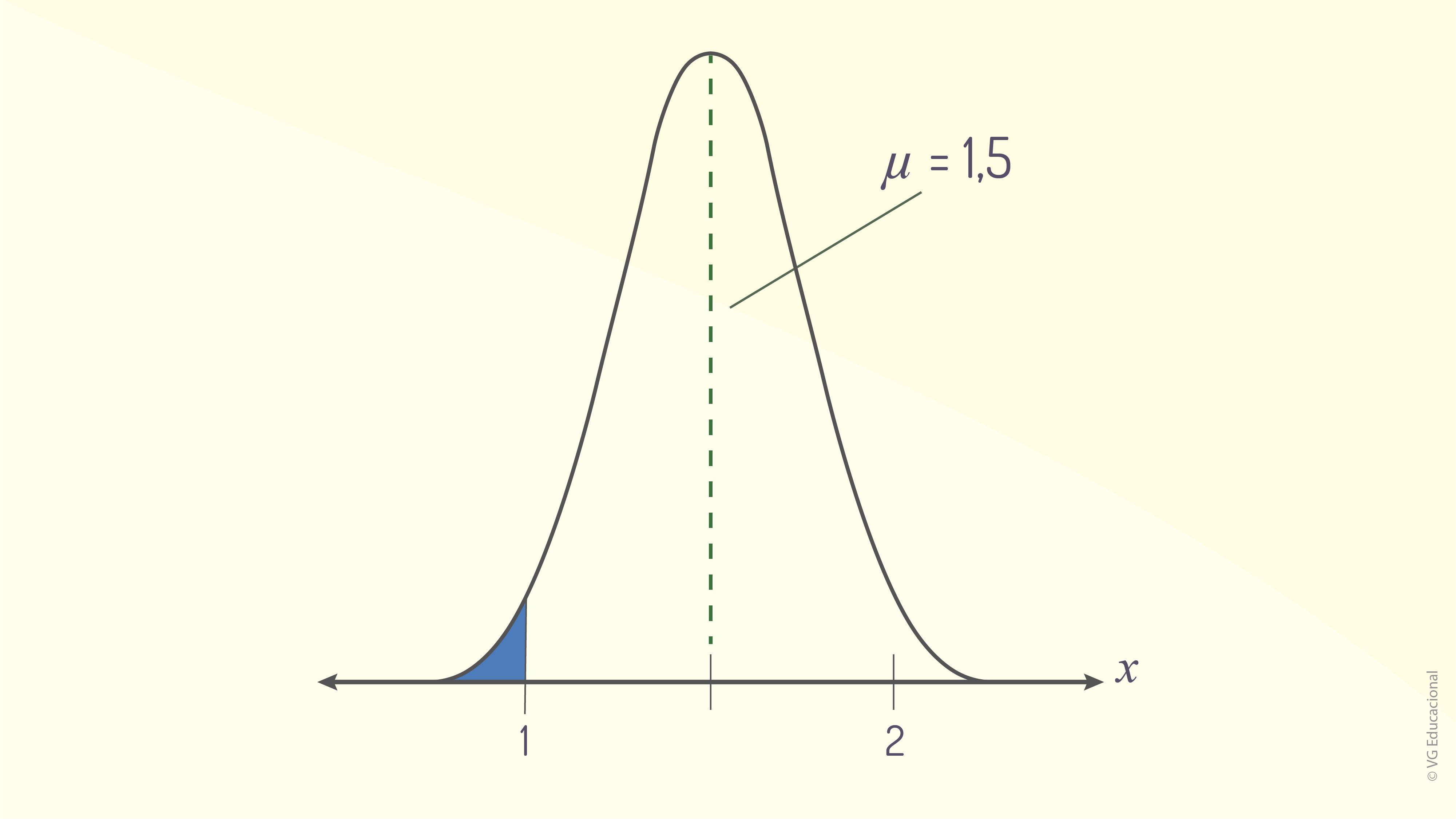
Iniciando-se o cálculo pelo escore-x, sabe-se, então, que:
\[z = \frac{1 - 1,5}{0,25}= -2\]
Pela tabela normal padrão (consultar Anexo 1), tem-se que \(P(z < -2) = 0,0228\) (busca-se, na linha, \(z = -2\) e \(z = 0\)). Logo, interpreta-se que: cerca de 2,28% das pessoas comprarão uma nova calça jeans em menos de 1 ano; e, como essa probabilidade é menor que 5%, trata-se de um evento incomum dentro da situação analisada.
Caso o problema envolva um intervalo com duas probabilidades, deve-se calculá-lo como indicado no próximo exemplo. Assim, considere, agora, que, em uma outra pesquisa, analisou-se o tempo gasto por operários na execução de uma tarefa da linha de produção de uma empresa. Esses dados representam uma distribuição normal, e pode ser de interesse da análise calcular qual a probabilidade de um operário, selecionado de forma aleatória, gastar entre a minutos e b minutos nessa tarefa, por exemplo. Para isso, tem-se:
\[P(a < x < b) = P(z_a< z < z_b) = P(z < z_b) - P(z < z_a)~~~~~~~~~~(3)\]
Em que \(z_a\) e \(z_b\) representam os escores-z de a e b, respectivamente. Suponha que os valores do intervalo sejam \(z = -1,5\) e \(z = 1,25\). Isso levaria à probabilidade final \(P(-1,5 < z < 1,25)\) que, assim, é de 0,8276 (conforme nos mostra a tabela, considerando os valores tabelados (ver Anexo 1) e o cálculo da Equação 3.
Existem ferramentas e softwares, como o Minitab, o Excel ou o TI-84 Plus, que têm recursos suficientes para determinar a área sob a curva na análise de uma distribuição normal, sem a necessidade de se obter os escores-z diretamente. O Minitab, por exemplo, pode ser baixado, na versão gratuita, no link disponível em: https://www.minitab.com/pt-br/products/minitab/free-trial/. Acesso em: 17 nov. 2020.

A seguir, você verá como encontrar os valores de escores-z a partir da área de um intervalo sob a curva normal, como transformar o valor do escore-z em um valor \(x\) e quais são os passos necessários para o cálculo de um valor específico de uma variável aleatória com distribuição normal, considerando a probabilidade.
É possível se deparar com algumas situações para encontrar o valor do escore-z. Uma delas é calculá-lo a partir do valor da área. Para entender como isso pode ser feito, considere o exemplo a seguir. Tomando como exemplo a determinação do escore-z, a partir da informação de que a área acumulada é de 0,3632, tem-se os valores de linha e coluna da tabela -0,3 e 0,05, respectivamente, o que dá um escore-z de -0,35. Além disso, considerando, ainda, que há um intervalo que representa 10,75% da área da distribuição à direita, tem-se, então, 0,1075, e a área acumulada é 1 - 0,1075 = 0,8925. Correspondente a esse valor de área tem-se, para a linha, 1,2, conforme a tabela, e 0,04, para a coluna, o que resulta em 1,24 de escore-z. Lembrando que todos esses valores foram retirados da tabela normal padrão no Anexo 1.
Outra possibilidade prática é ter a determinação do escore-z condicionada ao valor de um dado percentil e, para entender como esse cálculo é feito, é necessário relembrar que os 99 percentis dividirão um dado conjunto de dados em 100 partes iguais (LARSON; FARBER, 2015). Considerando, então, um percentil de 5%, ou seja, \(P_5\), deve-se determinar o escore-z que corresponda a uma área de 0,05 à esquerda de \(z\). Localizando 0,05 na tabela normal padrão, percebe-se que os valores mais próximos são 0,0495 e 0,0505, cujos valores são \(z = -1,65\) e \(z = -1,64\), respectivamente. Fazendo a média, obtém-se \(z = -1,645\).
Por outro lado, pode ser desejável transformar um escore-z em um valor \(x\), o que é possível pela relação a seguir, obtida a partir da Equação 2, apresentada anteriormente.
\[x = μ + zσ~~~~~~~~~~(4)\]
Ademais, será possível, ainda, determinar um valor específico, a partir de uma dada probabilidade, com base na tabela. Adiante, você verá a relação entre uma média da população e as médias das amostras aleatórias obtidas a partir dessa população, para entender o papel das relações amostrais na distribuição normal, além disso, conhecerá uma importante ferramenta: o teorema do limite central.
Uma distribuição amostral é definida como a distribuição de probabilidade de uma estatística amostral, a partir de amostras de tamanho n obtidas da população (LARSON; FARBER, 2015). Caso o processo envolvido seja a média, tem-se a distribuição amostral das médias, por exemplo, e, com relação a ela, têm-se as seguintes propriedades (LARSON; FARBER, 2015):
O teorema do limite central irá estabelecer a relação entre a distribuição amostral das médias e a população correspondente, de onde são retiradas tais amostras. Assim, com relação ao teorema, há duas proposições principais (LARSON; FARBER, 2015):
Perceba que, quanto maior o tamanho do conjunto de amostras, melhor será a aproximação, mas, também, que as relações expressas pelas propriedades da distribuição amostral das médias são válidas. A figura a seguir resume os possíveis cenários no painel apresentado, partindo de populações distribuídas normalmente ou não.
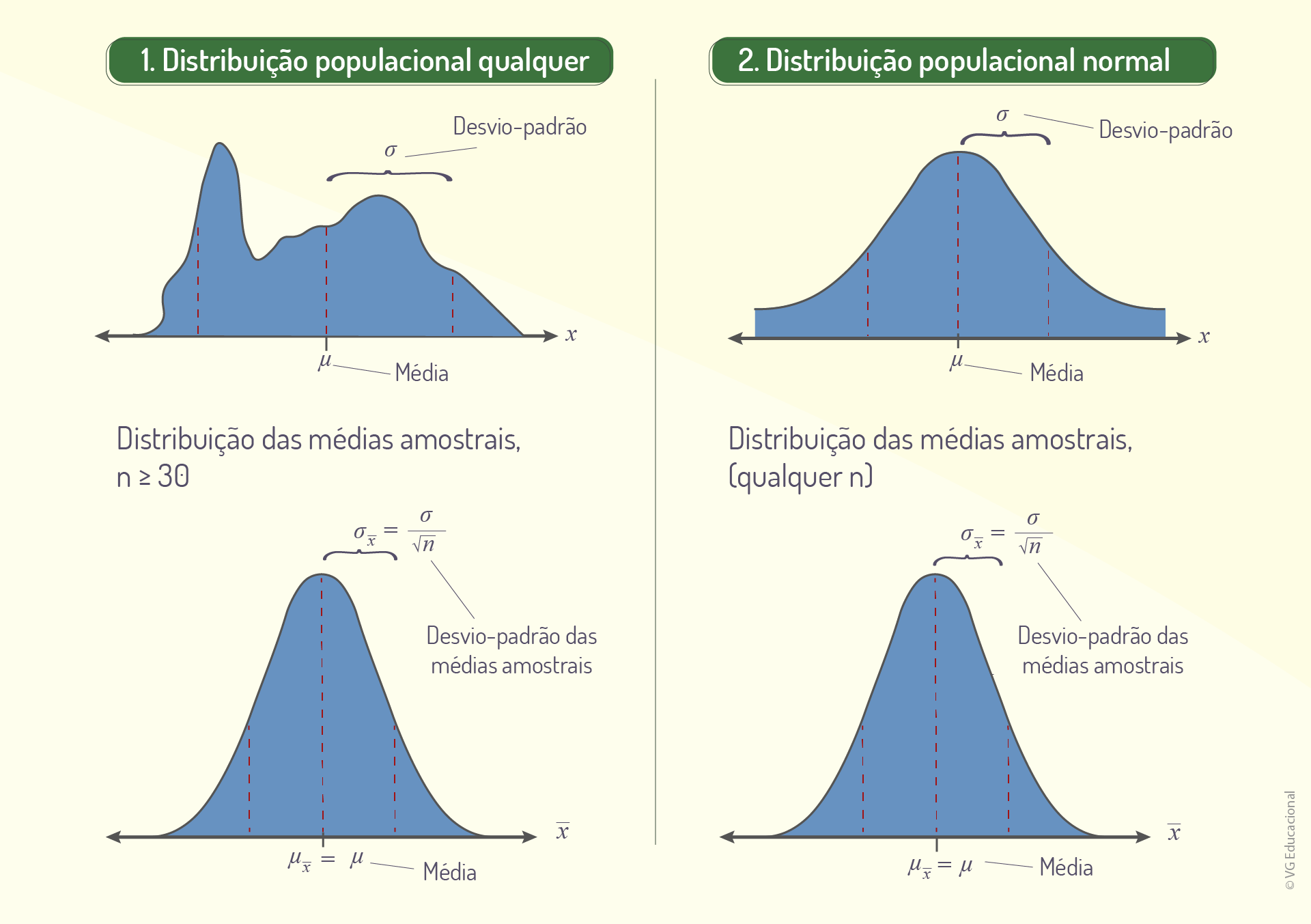
Observe, então, na Figura 2.4, que existem dois possíveis cenários: a amostra, no primeiro caso, não é suficiente, apresentando um padrão diferente da distribuição normal; entretanto, é possível utilizar a distribuição normal padrão com um valor de erro. Por outro lado, no segundo caso, o número de amostras é suficiente para se aproximar da distribuição normal padrão. Para calcular a probabilidade a partir do teorema do limite central, tem-se a seguinte expressão de transformação do valor de \(\underline{x}\) em escore-z:
\[z=\frac{\underline{x}-{{\mu }_{\underline{x}}}}{{{\sigma }_{\underline{x}}}}=\frac{\underline{x}-\mu }{\sigma /\sqrt{n}}~~~~~~~~~~(5)\]
Uma dica prática de cálculo é: antes de encontrar as probabilidades correspondentes para intervalos da média amostral \(\underline{x}\), deve-se utilizar o teorema para a determinação da média e do desvio-padrão da distribuição amostral das médias. Além disso, o teorema também pode ser utilizado para a investigação de eventos incomuns (LARSON; FARBER, 2015). Suponha que um dado processo avaliado apresenta, na medição entre suas 50 amostras, um valor a ser analisado, de 24,7 segundos, sendo que a média apresentada para esses dados foi de 25 segundos e o desvio-padrão considerado, nesse caso, é de 1,5. Dessa forma, a partir da Equação 5, tem-se o seguinte escore-z associado:
\[z=\frac{24,7-25}{1,5/\sqrt{50}}≈-1,41\]
A seguir, será apresentada a aproximação normal para distribuições binomiais, além da relação de correção de continuidade e da aproximação de probabilidades binomiais.
Outra importante estratégia prática é determinar a aproximação de uma distribuição normal de uma distribuição binomial, tanto para facilitar os cálculos quanto pelo uso de padronizações em tabela (LARSON; FARBER, 2015).

Uma distribuição binomial é definida como a distribuição de probabilidades discretas de números de sucessos, sendo que as n tentativas envolvidas serão definidas tal que (LARSON; FARBER, 2015):
Abordando, inicialmente, a aproximação normal para uma distribuição binomial, tem-se que a média é dada por:
\[μ = np~~~~~~~~~~(6)\]
E o desvio-padrão é dado por:
\[σ = \sqrt{npq}~~~~~~~~~~(7)\]
Para a correção de continuidade, realiza-se a correção necessária baseando-se no fato de que uma distribuição binomial é discreta e pode ser representada em um histograma de probabilidade. Assim, conforme Larson e Farber (2015, p. 260), “quando você usa uma distribuição normal contínua para aproximar uma probabilidade binomial, você precisa mover 0,5 unidade para a esquerda e para a direita do ponto médio, para incluir todos os possíveis valores de x no intervalo”. A figura a seguir apresenta essa relação.
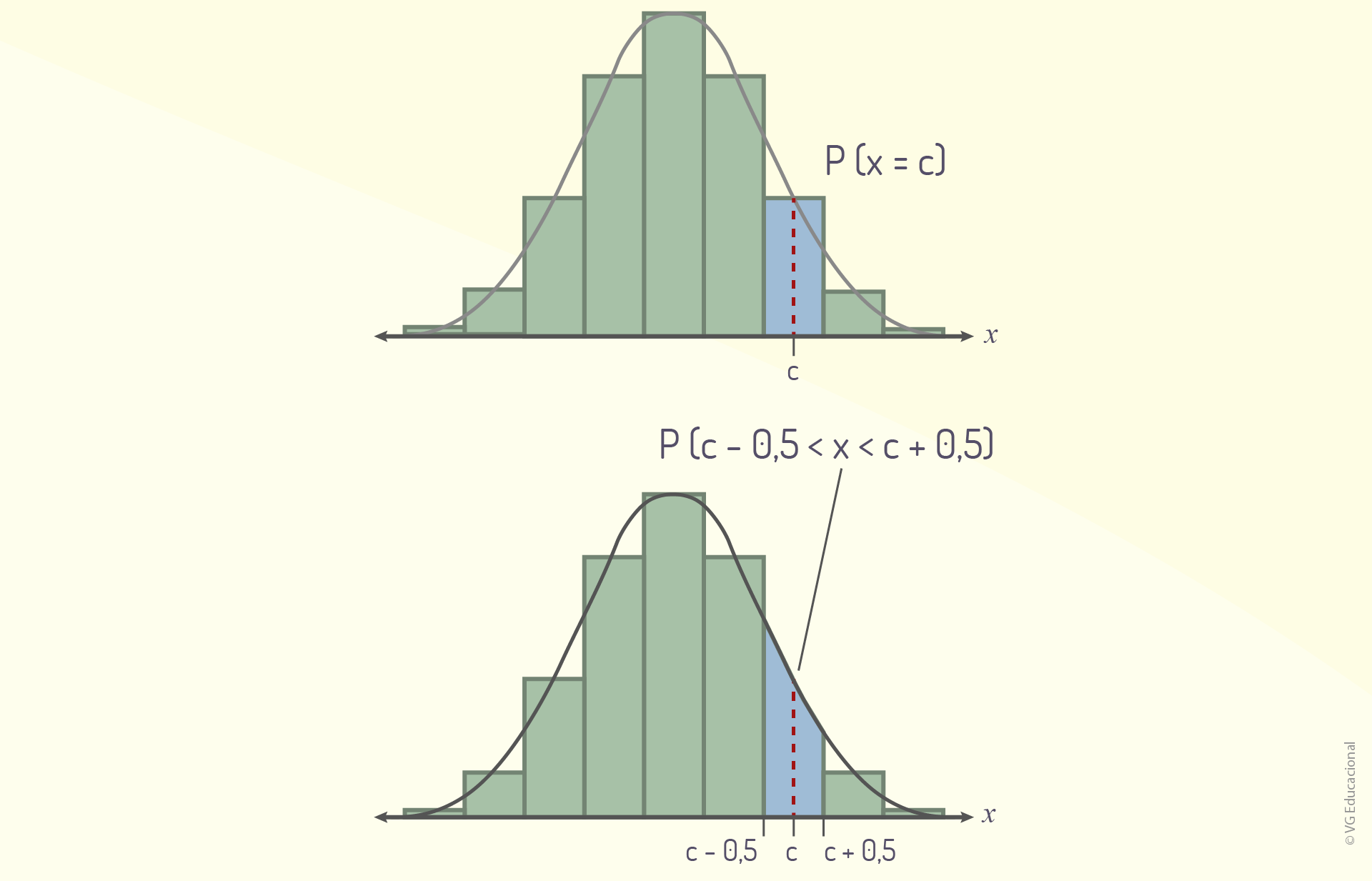
Por último, existem algumas relações básicas, comuns a qualquer caso analisado, para aproximar uma probabilidade binomial a partir de uma normal, como sugere o quadro a seguir.
Quadro 2.2 - Aproximação de probabilidades binomiais
Fonte: Elaborado pela autora.
Agora, vamos entender, na prática, como pode ocorrer tal aproximação de probabilidades binomiais com o apoio da Quadro 2.2. Assim, considere uma pesquisa feita com usuários frequentes de mídia, nos Estados Unidos, que têm entre 8 e 18 anos. Esses usuários foram indagados sobre quais são as notas que costumam obter em seus estudos. Dentre eles, 47% afirmaram que tiram notas regulares ou até ruins. Caso sejam selecionados, de forma aleatória, 45 usuários desse grupo, e seja feita a mesma pergunta anterior, deseja-se saber qual a probabilidade de menos de 20 responderem que têm notas regulares ou ruins (LARSON; FARBER, 2015, p. 261). Assim, sendo que, nesse experimento binomial, \(n= 45\), \(p = 0,47\) e \(q = 0,53\), isso nos leva a \(np = 45\cdot0,47 = 21,15\) e \(nq = 45\cdot0,53 = 23,85\). Sendo que, tanto \(np\) quanto \(nq\), são maiores do que 5, sugere-se usar uma distribuição normal, tal que a média seja atribuída a \(np\) e o desvio a \(npq\). Assim:
\(μ=np=21,15\) e \(σ=\sqrt{npq}=\sqrt{45\cdot0,47\cdot0,53}≈3,35\)
Além disso, é necessário lembrar que a correção de continuidade para o valor de \(x\) deve ser aplicada e que, em uma distribuição binomial, tem-se 17, 18 e 19 como possíveis pontos médios. Para utilizar a distribuição normal, faz-se, pela correção, \(x\) = 19,5 e, aplicando a Equação 5, obtém-se, aproximadamente, -0,49. Pela tabela normal padrão, do Anexo 1, a probabilidade será de 31,21%.
No próximo tópico, veremos uma introdução às cartas de controle, com uma visão geral de como as relações estatísticas mencionadas se estabelecem no controle estatístico de processos.
Considere que um dado processo analisado em uma indústria reflete um conjunto de dados em distribuição normal, com uma distribuição de médias amostrais com \(n\) = 50, sendo o valor da média \(μ\) = 25 e o desvio-padrão igual a \(σ\) = 1,5. Assinale a alternativa correta com relação à análise desse cenário prático.
Como se trata de uma distribuição normal populacional, cujo conjunto de dados amostral é pequeno, a média amostral deve ser calculada.
Incorreta. Pelo teorema do limite central, sendo \(n≥30\), é possível afirmar que a seguinte relação é válida: \(μ = μ_{\underline{x}}\) (ou seja, na prática, as médias populacional e amostral são iguais).
Sendo a média populacional igual a 25, como apresentado no enunciado, é correto afirmar que a média amostral também é 25.
Correta. Como o número de amostras é 50, pelo teorema do limite central, sendo \(n≥30\), é possível afirmar que \(μ = μ_{\underline{x}}\), ou seja, as médias populacional e amostral são iguais.
Como a amostra da população é suficientemente grande, é possível afirmar que os desvios-padrão populacional e amostral são os mesmos.
Incorreta. Mesmo sendo válido utilizar o teorema do limite central, ele estabelece, na prática, que o desvio amostral é calculado a partir do populacional (\(σ\)), pela seguinte relação: \(σ_{\underline{x}}=\frac{σ}{\sqrt{n}}\), em que n é o número de amostras.
Os escores-x, nesse caso, são calculados pela tabela de distribuição normal padrão, a partir da curva estabelecida nesse caso.
Incorreta. De fato, é utilizada a tabela de distribuição normal padrão, pois, no enunciado, afirma-se que, nesse caso, trata-se de uma distribuição desse tipo, entretanto, o correto é escores-z.
O valor do desvio-padrão populacional estabelecido como 1,5 pode ser facilmente obtido na tabela de distribuição normal padrão.
Incorreta. Pois o valor de desvio-padrão populacional de 1,5 é escolhido ou adotado a partir dos dados analisados, dependendo do que mais se aproxima ou das escolhas do responsável pela análise.
A seguir, estudaremos a teoria básica por trás dos gráficos de controle, importantes elementos do controle estatístico de processos. Observa-se que esse tipo de gráfico é usado para o monitoramento da conformidade de características de produtos e/ou processos, sendo aplicado para a identificação rápida de possíveis alterações inusitadas, em pontos estratégicos da linha de produção, por exemplo (SAMOHYL, 2009). Assim, é possível observar que se trata de uma ferramenta estatística visual e que, com o monitoramento de um processo feito a partir de um gráfico de controle, tem-se meios mais eficientes para a busca de melhorias contínuas, sendo possível melhorar a qualidade da produção e minimizar custos em boa parte dos casos.
Para entender a importância do gráfico de controle, considere o exemplo a seguir, representado pelo esquema da Figura 2.6, de monitoramento do processo e inspeção de peças em uma dada indústria em análise.
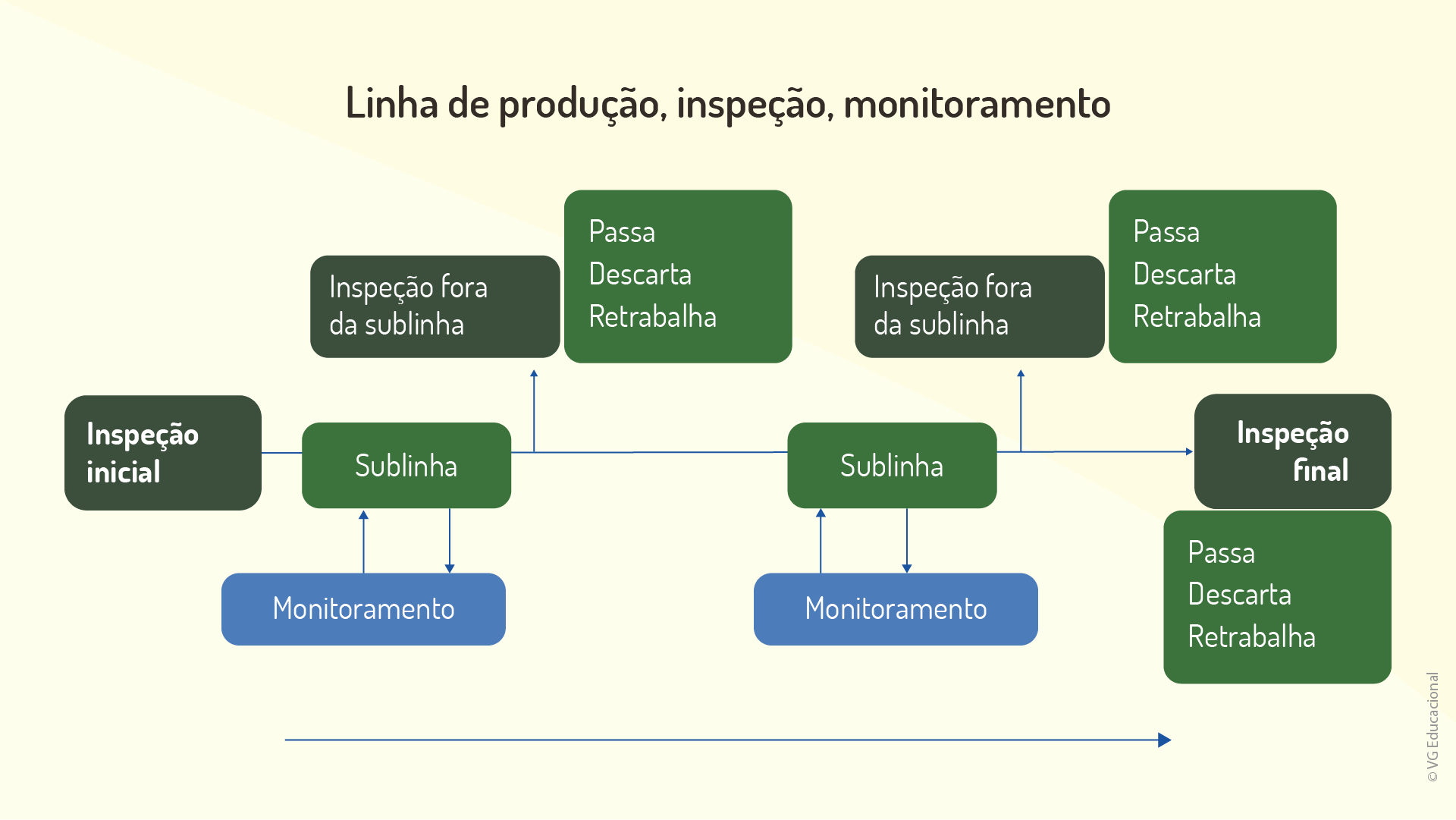
Além disso, é importante salientar que o uso de cartas de controle (como também são chamados esses gráficos) envolverá dados, como as dimensões de uma peça usinada e a quantidade de defeitos em um dado produto, dentre vários outros parâmetros acerca do produto ou do processo produtivo. A coleta dos dados é feita em uma determinada frequência e tem tamanho de amostra definido mediante a expertise dos responsáveis pela análise ou das características do próprio processo/produto analisado, sendo a frequência sempre compatível com as principais causas de variabilidade que podem ser observadas no sistema analisado. Em seguida, calcula-se a média, o desvio-padrão e os limites de controle que estão associados diretamente às causas comuns de variabilidade no cenário analisado. Na prática, eles representarão limiares estabelecidos acerca de dados do problema, superiores e inferiores. Além disso, a partir do momento que se define esses limites, os dados continuarão sendo coletados e, após, plotados no gráfico.
A estabilidade do processo também pode ser analisada a partir desse tipo de ferramenta gráfica, como mostra a figura a seguir, que apresenta as relações entre as possíveis distribuições, os limites de controle estabelecidos e as questões de dimensão. Lembre-se de que, na parte central da distribuição, concentram-se causas mais comuns, ao passo que, nas extremidades, tem-se causas especiais.
Note que o processo estável (sob controle) permitirá a eliminação de possíveis causas especiais na análise, ao passo que, da forma como são estabelecidos nos limites, os processos instáveis contarão com o possível surgimento dessas causas menos frequentes.
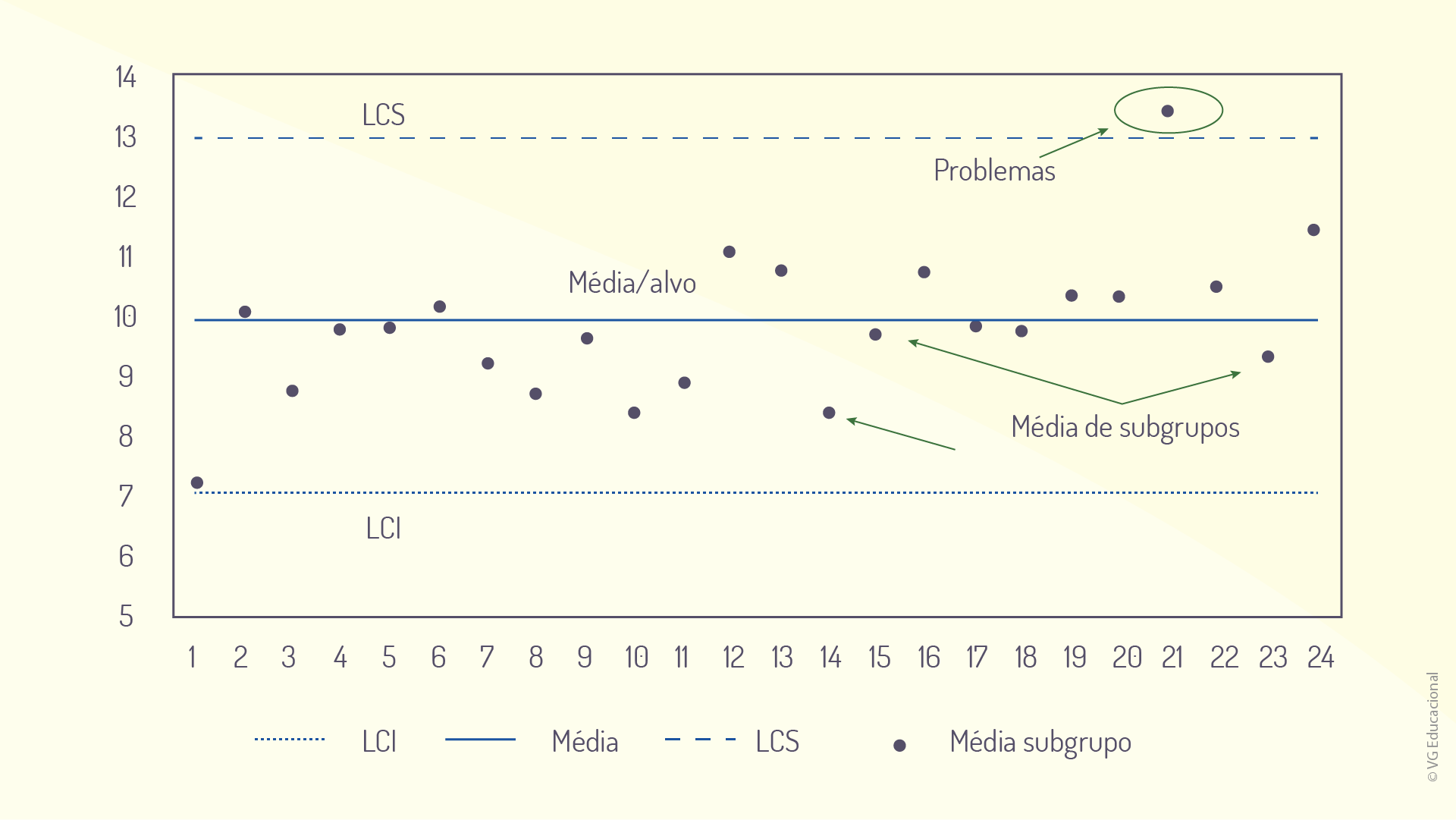
Assim, de forma sucinta, sabe-se que o gráfico de controle é obtido a partir da plotagem de três linhas, que representarão os limites de controle e a média ou o alvo do processo, além dos pontos que representarão as médias de amostras (também chamadas, nesse caso, de subgrupos racionais) (SAMOHYL, 2009). Como já visto, a mensuração poderá ser estabelecida a partir de conhecimentos prévios do cenário analisado, estabelecendo-se a periodicidade a partir desses pressupostos, por exemplo, ao passo que os possíveis defeitos poderão ser analisados considerando-se graus diferentes de severidade e, na prática, refletindo-se em atribuições distintas de pesos. As características amostrais dos subgrupos, por sua vez, são escolhidas de forma a esclarecer qualidades importantes da linha de produção, por exemplo, sendo importante ressaltar que, normalmente, a orientação para os limites de controle é que eles estejam a uma distância de três desvios-padrão da média (ou alvo), como estabelecido por Shewhart (1931), sendo esse alvo referente às amostras e podendo ser obtido a partir dos dados da população, como visto anteriormente. A figura a seguir apresenta o gráfico de controle referente ao exemplo apresentado, anteriormente, na Figura 2.6.

A partir do gráfico anterior, é possível perceber, inclusive, a probabilidade de alarmes falsos ocorrerem. Para isso, são medidos os limites de controle em três desvios da linha central, como mostram as linhas \(LCI\) e \(LCS\) (limites inferior e superior). É possível perceber que a probabilidade de um alarme falso ocorrer é de 27 a cada 10000 subgrupos, o que resulta em 0,27%. Lembre-se de que a amostragem poderá acarretar alarmes falsos, por isso, é importante analisar tal probabilidade, entretanto, torna-se perceptível que, quanto melhor a amostragem, menor a probabilidade de esse tipo de ocorrência, porém, o processo de amostragem pode ser uma tarefa bastante dispendiosa, como ficará mais claro ao longo da unidade.
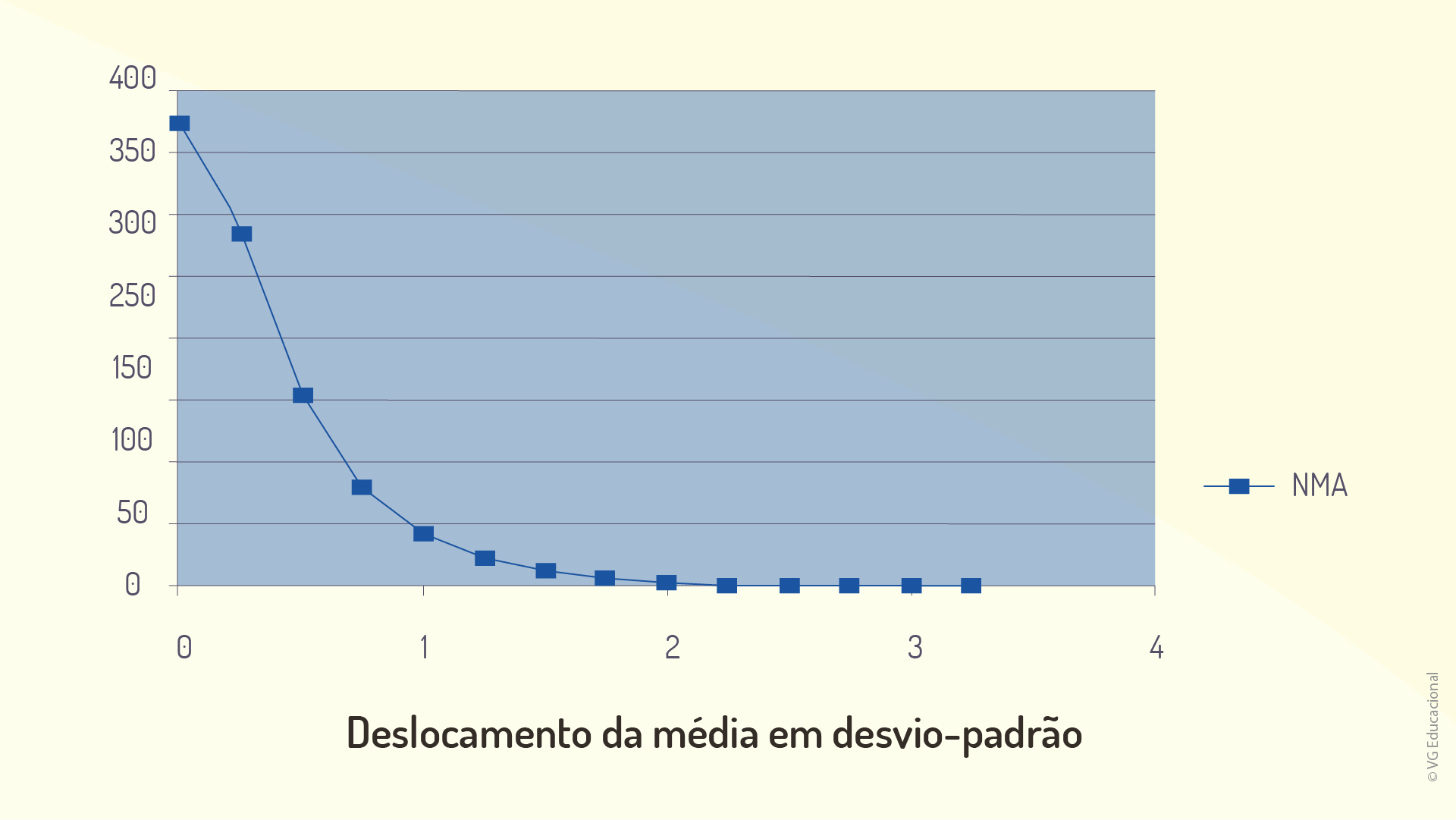
Dado o cenário, é possível definir, ainda, outro parâmetro, o \(NMA\) (Número Médio de Amostras até o alarme), sendo \(NMA_0\) análogo a \(H_0\), no caso de alarmes falsos, e \(NMA_1\) com \(H_1\), para os verdadeiros. O \(NMA_1\) poderá ser proveniente da severidade do deslocamento da média do processo, sendo possível defini-lo a partir do deslocamento da média do processo. Caso o processo sofra uma causa especial forte, e a média do processo se desloque a uma distância de vários desvios-padrão, o \(NMA_1\) será pequeno e o gráfico detectará rapidamente a presença da causa. Por outro lado, no caso de deslocamentos pequenos da média do processo, sabe-se que eles dificilmente serão detectados rapidamente quanto desejável (SAMOHYL, 2009; ROSA, 2016). No caso do problema utilizado como exemplo, tem-se que o \(NMA_1\) é de 6,3 subgrupos (como pode ser visto na próxima tabela) e, assim, é possível interpretar que a detecção da mudança de dois desvios-padrão desse processo gastará 6 períodos, em média, podendo ser mais ou menos que isso. A tabela a seguir apresenta os possíveis valores com relação a alarmes verdadeiros e falsos, para o problema analisado, para análise de probabilidade.
Tabela 2.1 - Resultados do \(NMA_0\) e do \(NMA_1\) para a situação problema apresentada
Fonte: Adaptada de Samohyl (2009, p. 105).
A partir da tabela, tem-se, ainda, a visualização gráfica dessa relação do \(NMA_1\), como mostra a figura a seguir.
Entretanto, é de fundamental importância destacar que, de maneira geral, normalmente alarmes falsos representam, na prática, um erro significativo a ser considerado. A hipótese nula, nesses casos, considerará que o processo é estável, o que indica que a média do processo e a variabilidade são constantes. Por outro lado, é importante observar que um processo perturbado pela ocorrência de causas especiais exibirá, em seu gráfico de controle, pontos fora dos limites de controle e, ainda, limites possivelmente muito distantes da média (alvo) estabelecida para esse processo. Esse tipo de ocorrência ocasiona, na prática, possíveis alarmes não disparados, outro problema diretamente relacionado ao processo bastante importante de ser considerado. Além disso, sabe-se que, na prática, quando o desvio-padrão do processo é relativamente pequeno, possíveis variações no processo, aquém dos limites de controle, são toleráveis, já que a estabilidade relativa é critério suficiente, pois é assegurada a produção dentro dos conformes (SAMOHYL, 2009).
Dessa forma, ressalta-se que a estimação de limites de controle será válida, na prática, para processos estáveis ou de estabilidade relativa, nos quais mantém-se constante a média e o desvio-padrão, o que implica, ainda, que um processo seja considerado de fato estável, no momento em que uma possível causa especial no contexto é revelada. Considerando, adicionalmente, a amostra e os limites de controle, é possível utilizar a seguinte relação, expressa no esquema da figura a seguir.
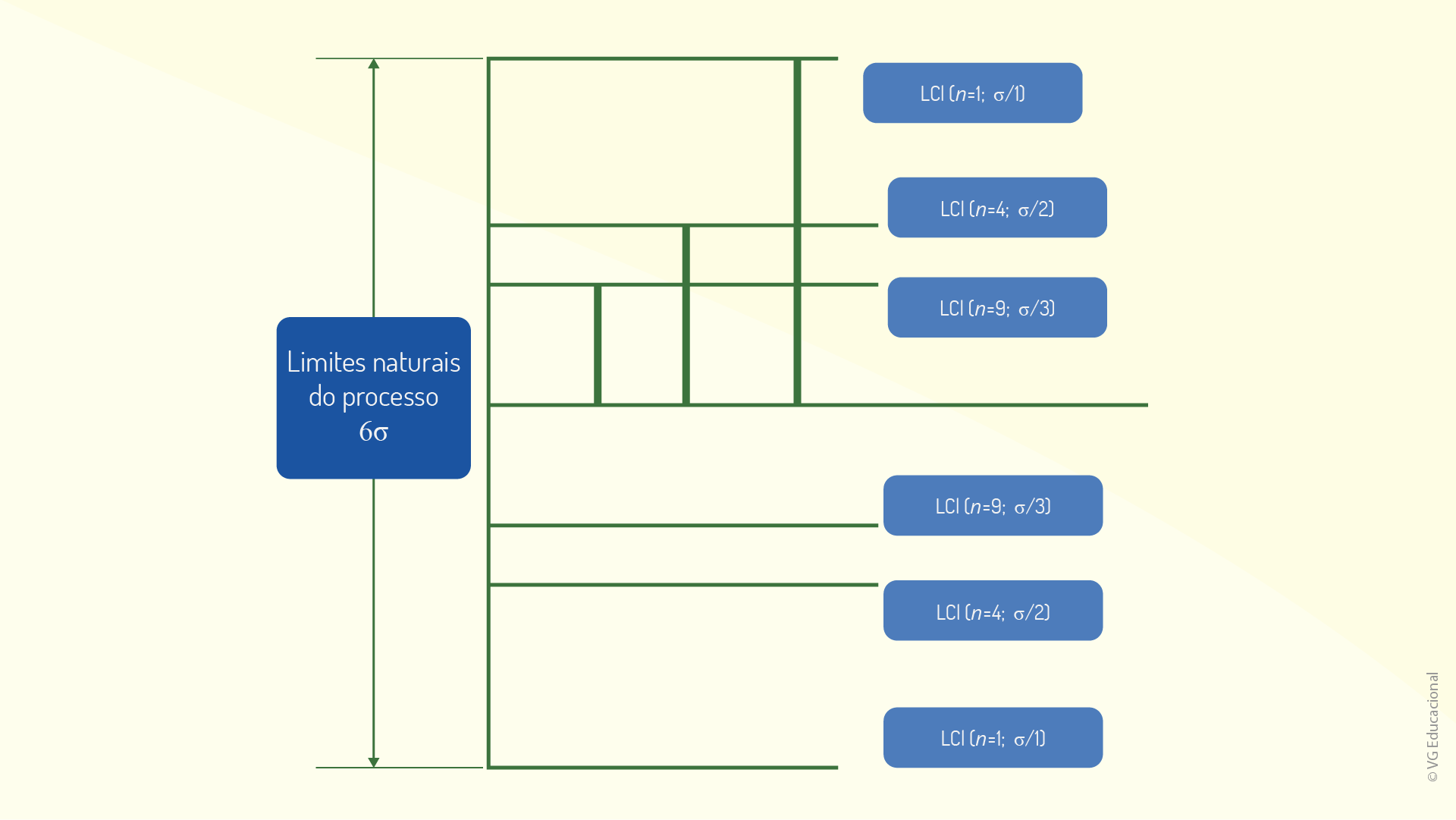
Com essa relação, é possível, ainda, concluir que, geralmente, a definição do tamanho da amostra estará diretamente relacionada a aspectos técnicos e financeiros, e não, necessariamente, estatísticos. Amostras maiores, por sua vez, serão, de fato, sempre melhores e mais vantajosas, quando comparadas com as amostras menores de um mesmo processo, pois aumentarão a probabilidade de detecção de alterações no processo. Por outro lado, é importante lembrar que o tamanho aumentado da amostra também estará diretamente relacionado à maior replicação de erros durante a mensuração.
Agora, vamos analisar outro aspecto prático com relação ao uso dos gráficos de controle em geral: a operacionalidade. Assim, a primeira fase engloba a montagem do gráfico, na qual os dados serão levantados, além do cálculo de parâmetros estatísticos, como a média e o desvio-padrão. Adicionalmente, define-se uma segunda e última fase distinta, em que se tem o monitoramento do processo, na qual utiliza-se o gráfico, e os novos dados poderão, ainda, ser levantados no decorrer do dia, além de possíveis novos pontos calculados e inseridos no gráfico (SAMOHYL, 2009).
Outro ponto importante é a presença de certos padrões de pontos dentro dos gráficos de controle. Esses padrões também são responsáveis, na prática, por demonstrar a existência de possíveis causas especiais no processo analisado. Alguns exemplos desses padrões são (SAMOHYL, 2009, p. 108):
Além disso, observa-se que poderão existir, ainda, outros tipos de padrões preestabelecidos para alerta, entretanto, o uso de padrões deverá ser minimizado, pois eles, frequentemente, estarão associados a alarmes falsos. Para calcular a probabilidade de alarme falso na presença de vários padrões, tem-se: em que \(P_{alarme}\) é a probabilidade de alarme falso, e k o número de padrões usados:
\[P(alarme~falso,~k) = 1 - (1 - P_{alarme})^k~~~~~~~~~~(8)\]
Ademais, é possível concluir que, para a garantia de bom funcionamento dos gráficos de controle, bem como para o estabelecimento de processos de alto desempenho e mínimo custo possível, algumas premissas e ações são necessárias. Embora haja uma repartição de conceitos estatísticos, no monitoramento do processo e na inspeção de peças, para encontrar não conformidades, há diferenças enormes entre eles. Além disso, sabe-se que, na realidade, haverá erros de monitoramento inevitáveis, mas que, com o uso de gráficos de controle, passarão, em grande parte, a serem mensuráveis e controláveis.
Por último, observa-se que as amostras extremamente pequenas, quando comparadas com o tamanho da população (que pode ser um lote da produção, por exemplo), são adequadas para monitorar o processo como um todo e também alguns possíveis padrões de pontos que possam surgir nos gráficos de controle e que possam estar associados a alarmes. Entretanto, sobretudo considerando essa associação a alarmes, lembre-se de que o número de padrões usados deve ser mínimo, a fim de evitar falsos alarmes (SAMOHYL, 2009; ROSA, 2016). No próximo tópico, você verá pontos importantes acerca da análise dos gráficos de controle (cartas de controle), além de entender a principal distinção entre esse tipo de ferramenta e os gráficos destinados a variáveis e a atributos.
Como você pôde ver ao longo de seu estudo, a distribuição normal será utilizada como base para o desenvolvimento de um gráfico de controle, e sabe-se, ainda, que tal uso é justificado como base para o controle de processos. Com relação aos gráficos de controle, é correto afirmar que:
normalmente, os gráficos de controle utilizam três desvios-padrão com relação à média e intervalo de confiança de 93,73%.
Correta. Como proposto por Shewhart, em 1931, o valor de três desvios-padrão a mais ou a menos com relação à média é efetivo para boa parte das análises práticas e, além disso, o intervalo de confiança correspondente é de 93,73%.
normalmente, os gráficos de controle utilizam um desvio-padrão com relação à média e intervalo de confiança de 6,27%.
Incorreta. Normalmente, são utilizados três desvios-padrão, conforme propostos por Shewhart. Além disso, 6,27% representam, no intervalo de confiança normalmente adotado, a chance de erro.
o LSC corresponde ao limiar superior de correlação, ao passo que LIC é o inferior de correlação.
Incorreta. Em um gráfico de controle (carta de controle), as medidas de limiares de controle são representadas por LSC e LIC, sendo o limite superior e o inferior, respectivamente.
a média em um gráfico de controle representa a quantidade de erros médios do sistema de controle analisado.
Incorreta. Na verdade, a média representa a média dos dados amostrados e, no gráfico de controle, é a linha central para traçá-lo, junto com os limiares de controle.
as causas comuns associadas a um gráfico de controle normalmente representarão problemas inerentes e que surgem de forma previsível.
Incorreta. Um problema decorrente de causas comuns, obtidas a partir de um gráfico de controle, será geralmente de origem aleatória, além de, normalmente, ser inerente ao processo.
Para compreender a construção e a análise de um gráfico de controle qualquer, você verá o passo a passo do processo de construção de um gráfico simples. Assim, o objetivo principal, nesse caso, será compreender o funcionamento de uma empresa de telemarketing, a partir das ligações ativas de vendas. Identificou-se, na ocasião, que são feitas 43 ligações a cada 4 horas de um turno de trabalho, com uma variação, de mais ou menos, 8 ligações nesse período. Além disso, o mês analisado foi de 22 dias de trabalho e considerando cinco funcionários, representados de X1 até X5. A partir desses dados, obteve-se a seguinte tabela.
Tabela 2.2 - Dados sobre o cenário analisado de telemarketing
Fonte: Adaptada de Netto (2017, p. 55).
Note que, nesse caso, a média é de 43, o mínimo é 35 e o máximo 51. Agora, tomando como exemplo o trabalhador representado por X1, sendo os dias do mês trabalhados representados pelo eixo das abscissas e as quantidades de ligações pelo das ordenadas, obtém-se o gráfico de controle apresentado na figura a seguir.
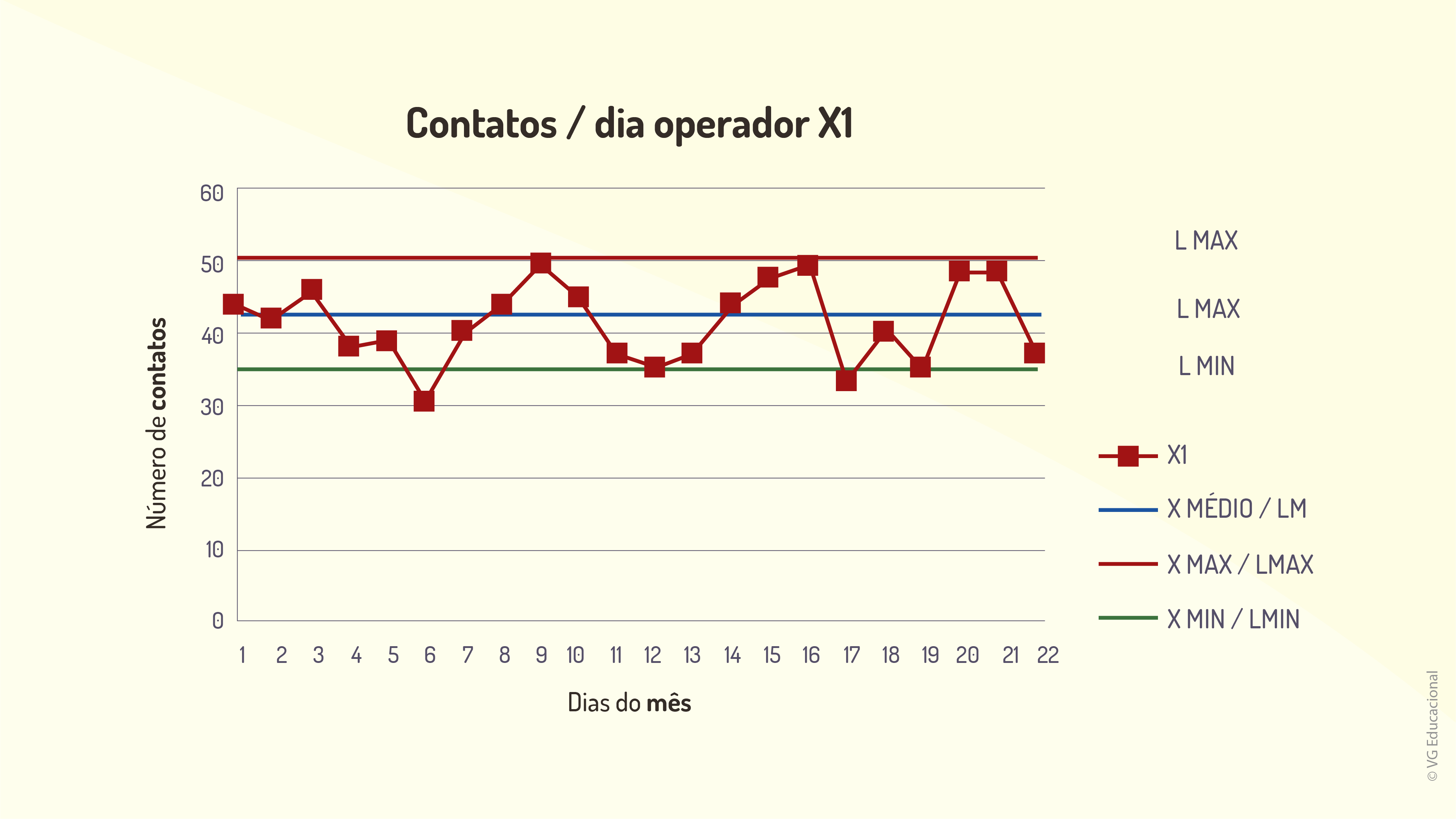
Por outro lado, é possível perceber facilmente que o gráfico poderá, ainda, ser representado de forma otimizada, alterando-se a escala para valores mais próximos do limite mínimo, o que poderá facilitar a interpretação de um possível usuário do sistema, por exemplo. Além disso, note que, mesmo sendo uma ferramenta simples, especialmente para o problema apresentado, o gráfico de controle poderá trazer para os gestores, nesse caso específico, estratégias mais claras de melhoria de performance dos operadores, por exemplo.
Adicionalmente, é importante reforçar que o Controle Estatístico de Processos (CEP), por meio das cartas de controle, é utilizado com alguns possíveis objetivos principais (MONTGOMERY, 2004):
Sem dúvida alguma esse último objetivo reforça ainda mais o uso de gráficos de controle. Ademais, reforça-se que todo tipo de processo pode ser estudado e analisado a partir de cartas de controle, embora esse tipo de ferramenta possa exercer mais ou menos possíveis melhorias para o controle do processo, dependendo de aspectos importantes, como a expertise do profissional e características do próprio sistema analisado, por exemplo.
Assim, é possível sugerir alguns passos básicos e gerais para a análise de cartas de controle (WERKEMA, 1995, p. 209):
Caso o passo 2 seja verdadeiro, ou seja, ambas as condições sejam satisfeitas, é possível afirmar que o processo está sob controle estatístico, assim, é sugerido avaliar a capacidade do processo. Além disso, caso haja pontos fora e/ou configuração não aleatória, é possível concluir que o processo está fora do estado de controle estatístico, assim, sugere-se a verificação de possíveis causas especiais por trás de tais efeitos, em cada ponto identificado nesse caso e/ou padrão fora do esperado. Por outro lado, é importante ressaltar que, caso os passos mencionados sejam executados de forma contínua, é possível diminuir, de forma significativa, a representatividade do processo, devido à baixa quantidade de pontos nesses casos e, caso isso ocorra, orienta-se coletar novas amostras e reiniciar as análises (WERKEMA, 1995).
Por fim, dentre possíveis padrões indesejados a serem analisados, como já visto brevemente no tópico anterior, tem-se: pontos fora dos limites de controle, grandes sequências de pontos, periodicidades, tendências e aproximações, tanto dos limites de controle quanto da média. Todos eles poderão ser indícios de possíveis causas especiais, refletindo-se em situações indesejadas, na prática. No próximo e último tópico, você estudará as cartas de controle relacionadas às variáveis e aos atributos, as principais classes dessas ferramentas.
Apesar de haver muitas orientações na literatura e o responsável pela análise da carta de controle poder contar, também, com sua própria expertise, observa-se, na prática, que, embora encontrar pontos fora dos limites seja fácil, encontrar padrões não aleatórios pode ser bastante difícil. Com base nesse tema, assinale a alternativa correta sobre a análise de cartas de controle.
Os pontos fora dos limites de controle podem ser facilmente identificados a partir da inspeção com instrumentos de medição, como réguas.
Incorreta. Geralmente, na maior parte dos casos de análise de gráficos de controle, os pontos que excederem os limites de controle podem ser facilmente visualizados na ferramenta gráfica.
Assim como configurações não aleatórias, sequências de pontos também são menos triviais para identificação, mas se sabe que elas dizem respeito a causas comuns.
Incorreta. Pois sequências de pontos no gráfico de controle geralmente se estabelecem por conta de causas especiais, sendo necessário analisar, em vários casos, se elas poderão melhorar ou prejudicar o processo.
A periodicidade é outro exemplo de padrão normalmente identificável em gráficos de controle, a partir de análises de curto prazo.
Incorreta. O padrão de periodicidade em gráficos de controle está diretamente relacionado a configurações geralmente detectáveis em análises de longo prazo.
A tendência, outro possível padrão identificável no gráfico de controle, pode estar relacionada a duas classes distintas: tendências claras ou ocultas.
Incorreta. Pois a tendência em um gráfico de controle, normalmente, denota dois tipos principais: a tendência de pontos ascendentes ou a de pontos descendentes (normalmente 7 ou mais pontos).
A aproximação dos limites de controle é outro tipo de padrão a ser detectado, em certos casos, no gráfico de controle, geralmente de dois ou mais pontos.
Correta. De fato, nas análises, considera-se pelo menos dois pontos nos limites de controle, sendo que tais aproximações, normalmente, são vistas tipicamente em grandes ajustes nos processos.
Antes de analisarmos cada tipo de gráfico, é importante salientar que existem alguns passos básicos relacionados ao desenvolvimento de qualquer carta de controle, bem como à utilização dela na prática, como apontam Montgomery (2004), Paladini (2012), Ribeiro e Caten (2012) e Oliveira et al. (2013):
Sabe-se que as cartas de controle são divididas conforme o tipo de medição realizada, sendo compostas por dois grandes grupos, como indica o quadro a seguir.
Quadro 2.3 - Tipos de cartas de controle
Fonte: Adaptado de Montgomery (2004).
No caso dos gráficos de controle contínuos, sabe-se, ainda, que, para o gráfico de média e amplitude, tem-se, normalmente, que \(3≤n≤9\) e, para o de média e desvio, sugere-se \(n>9\). Além disso, para entender qual tipo de gráfico de controle deverá ser utilizado, é possível utilizar como referência, para boa parte dos casos, o fluxograma apresentado na figura a seguir.

A seguir veremos, em cada subtópico, os principais conceitos para obtenção e análise de um gráfico de controle por variáveis e, adiante, por atributos.
As cartas de controle que utilizam variável, por conta de maior precisão nos dados, e as medições contínuas, cujas dimensões provêm de medições que poderão variar de forma contínua, necessitam que o controle seja mantido, normalmente, com base em duas situações: analisando-se a média das medições e a variabilidade do processo em si. Com isso, é comum observar a implementação do controle da média do processo e, então, utiliza-se uma carta de controle para médias (\(\underline{x}\)), embora também seja possível utilizar uma carta de controle para valores individuais, nos casos em que não ocorrerem medidas replicadas nos subgrupos. Além disso, como mencionado, a segunda situação será estabelecida em relação à variabilidade do processo, e, com isso, observa-se que as cartas geradas devem ser trabalhadas e analisadas de forma conjunta (ROSA, 2016). Adicionalmente, é importante compreender que, na prática, características como a variabilidade do processo poderão ser tanto monitoradas como controladas pelo uso de um gráfico de controle para amplitudes (\(R\)) e/ou por meio do uso conjunto ou individual, em certos casos, da carta de controle para desvios-padrão (\(s\)). Sem medidas replicadas nos subgrupos, tem-se, ainda, a opção de usar o gráfico de amplitudes móveis (AM ou MR).
Outra observação importante é que, para se optar pelo uso de gráficos de controle por variáveis, o especialista deverá observar que a distribuição das medidas a serem controladas deve ter a forma normal. Assim, geralmente, testa-se a normalidade dos resultados, nos dados de medidas individuais e de médias destes. Adiante, veremos como isso pode ser feito. Então, tomando como exemplo a carta de controle de médias e amplitude, sendo \(μ\) a média e \(σ\) o desvio-padrão, ambos conhecidos, com n amostras dessa população, todas as observações feitas anteriormente, acerca do teorema do limite central, são válidas. Geralmente, as distribuições das amplitudes e dos desvios-padrão não são normais, embora sejam tomadas como aproximadamente normais, na estimação das constantes para o cálculo dos limites de controle. Outra consideração comum nesse tipo de análise é supor que a variabilidade das medidas é constante e aceitável, demandando a implementação conjunta de gráficos de amplitude e desvio-padrão. Além disso, sabe-se que as cartas de controle de médias e amplitudes são usadas normalmente para casos de subgrupos com 2 ou até, no máximo, 9 replicatas (sendo mais comum, ainda, entre 4 e 6 replicatas). Isso é feito devido ao efeito visto, de que, à medida que o tamanho do subgrupo aumenta, a sensibilidade apresentada pela amplitude, como estimador do desvio-padrão do processo, irá diminuir (OLIVEIRA et al., 2013).
Para calcular os valores dos limites de controle na carta de controle de médias e amplitude, tem-se duas situações principais: contando-se os valores de referência ou sem eles. Supondo-se m subgrupos de medições com n replicatas, (\(X_1\)) até (\(X_m\)), e os valores das m médias das replicatas de cada subgrupo, é possível definir um estimador de média do processo (\(μ\) ou \(\underline{\underline{X}}\)) correspondente à linha de controle (LC), tal que (ROSA, 2016):
\[\mu =\underline{\underline{X}}=\frac{\underline{{{X}_{1}}}+...+\underline{{{X}_{m}}}}{m}~~~~~~~~~~(9)\]
A amplitude \(R\) é correspondente a \(X_{m\acute{a}x} - X_{m\acute{i}n}\) e um bom estimador é dado por:
\[\underline{R}=\frac{R_1+...+R_m}{m}~~~~~~~~~~(10)\]
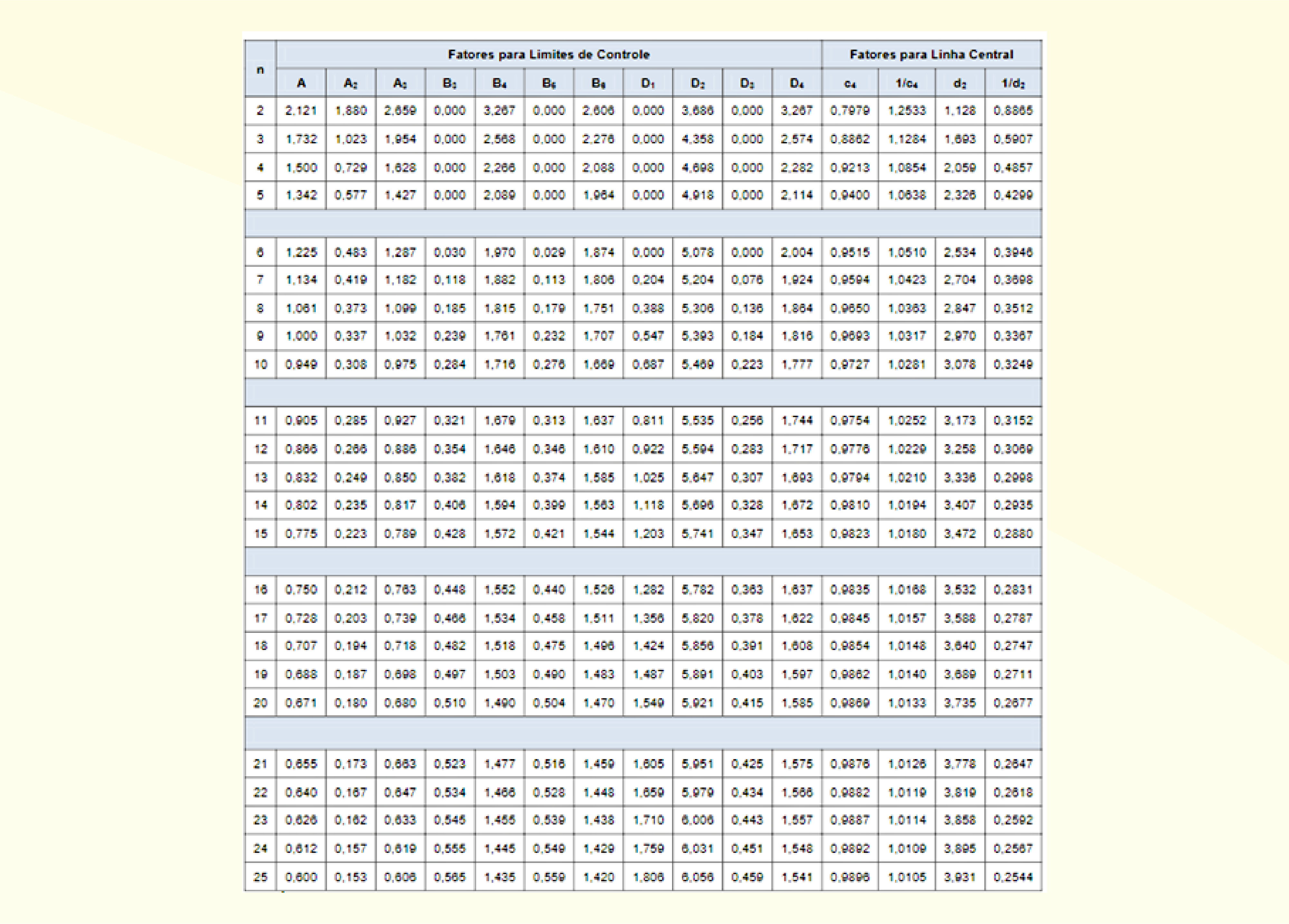
Em que \(\underline{R} = LC\). Para definir os limites superior e inferior, complementarmente, estabelece-se o parâmetro \(d_2\), dado pela norma técnica ISO 8258, tal que \(LCS\) e \(LCI\) são, respectivamente:
\[LCS = μ+3 \frac{σ}{\sqrt{n}}=\underline{\underline{X}}+3\frac{\underline{R}}{d_2\sqrt{n}}~~~~~~~~~~(11.1)\]
\[LCI = μ-3 \frac{σ}{\sqrt{n}}=\underline{\underline{X}}-3\frac{\underline{R}}{d_2\sqrt{n}}~~~~~~~~~~(11.2)\]
Além disso, é possível expressar esses limites em função da estimativa da amplitude média, definindo-se as constantes também tabeladas \(D_3\) e \(D_4\), que resultam em \(LCS = D_4\underline{R}\) e \(LCI = D_3\underline{R}\). Além disso, ressalta-se que o desvio-padrão de \(R\) é dado por \(d_3\frac{\underline{R}}{d_2}\) e que \(d_3\) também é um valor tabelado, sendo que \(D_3\) e \(D_4\) são dados como \(D_3 = 1-3\frac{d_3}{d_2}\) e \(D_4 = 1+3\frac{d_3}{d_2}\), respectivamente. Esses valores são vistos nas tabelas do Anexo 2. Por outro lado, caso os valores de referência sejam conhecidos, é mais fácil elaborar o gráfico e obter tais limites, visto que se conhece a média e o desvio-padrão, não sendo necessário estimá-los. Para isso, utilizam-se as seguintes equações, no caso de uma carta de controle de médias (ROSA, 2016):
\[LC = μ~~~~~~~~~~(12.1)\]
\[LCS = μ + 3 \frac{ρ}{\sqrt{n}}~~~~~~~~~~(12.2)\]
\[LCI = μ - 3 \frac{ρ}{\sqrt{n}}~~~~~~~~~~(12.3)\]
Nas equações anteriores, tem-se, também, o estabelecimento da constante \(A\), tal que \(A = \frac{3}{\sqrt{n}}\), sendo este um valor tabelado, como no caso anterior, sem as referências. Para se estabelecer, então, os limites com relação ao número \(n\) de replicatas, é possível estipular os valores de \(D_1\) e \(D_2\), também tabeláveis (Anexo 2), tal que obtém-se os limites anteriores expressos como:
\[LC = d_2σ~~~~~~~~~~(13.1)\]
\[LCS = D_2σ~~~~~~~~~~(13.2)\]
\[LCI = D_1σ~~~~~~~~~~(13.3)\]
Mais informações sobre a ISO 8258, norma técnica base da área de controle estatístico de processos, também válida internacionalmente, podem ser vistas no link a seguir, como referência para o cálculo dos limites de controle, por exemplo, para todos os tipos de cartas de controle. Fique por dentro acessando o link disponível em: https://www.iso.org/standard/15366.html. Acesso em: 26 out. 2020.

Com relação aos gráficos de controle de média e desvio, tem-se a seguinte possibilidade, quando os valores de referência não são conhecidos, como mostra a equação adiante, para estimação do desvio, que é igual a LC (limite de controle) (ROSA, 2016):
\[\underline{s} = {S_1 + ...+ S_m}{m}~~~~~~~~~~(14)\]
Para o gráfico de média, estabelece-se o uso da constante \(c_4\), que também pode ser expressa a partir do valor de outra, em função de \(n\), como \(A_3 = 3/c_4\sqrt{n}\):
\[LC = μ = \underline{\underline{X}}~~~~~~~~~~(15.1)\]
\[LCS = μ + 3\frac{σ}{\sqrt{n}}=\underline{\underline{X}}+3\frac{\underline{s}}{c_4\sqrt{n}}~~~~~~~~~~(15.2)\]
\[LCS = μ + 3\frac{σ}{\sqrt{n}}=\underline{\underline{X}}+3\frac{\underline{s}}{c_4\sqrt{n}}~~~~~~~~~~(15.3)\]
Estabelecendo-se, em função das constantes \(B_3\) e \(B_4\), também obtidas em tabela (Anexo 2), tem-se que elas são, respectivamente \(1 + 3\sqrt{1-c_4^2}/c_4\) e \(1 - 3\sqrt{1-c_4^2}/c_4\).
Sendo os valores conhecidos, estabelece-se, para o gráfico de média:
\[LC = μ~~~~~~~~~~(16.1)\]
\[LCS = μ + Aσ~~~~~~~~~~(16.2)\]
\[LCI = μ - Aσ~~~~~~~~~~(16.3)\]
E para o de desvio:
\[LC = c_4σ~~~~~~~~~~(17.1)\]
\[LCS = c_4σ+3σ\sqrt{1-c_4^2}~~~~~~~~~~(17.2)\]
\[LCI = c_4σ-3σ\sqrt{1-c_4^2}~~~~~~~~~~(17.3)\]
Ou, ainda, utilizando-se os parâmetros tabelados \(B_5 = c_4-3\sqrt{1-c_4^2}\) e \(B_6 = c_4+3\sqrt{1-c_4^2}\) (Anexo 2).
Na Figura 2.13, a seguir, tem-se um exemplo de gráfico de controle por variáveis, que apresenta um exemplo prático de gráfico de controle para médias (carta \(\underline{x}\)) de uma empresa que produz ração para gatos e cachorros.

Lembre-se de que o estabelecimento de todas as constantes para o cálculo dos limites de controle é fundamental, visto que existirão valores preestabelecidos mediante parâmetros do processo e tipo de carta de controle, como estabelecido na norma ISO 8258, embora seja possível ainda, mesmo que menos comum, estabelecer valores para esses limites de forma empírica ou baseando-se em conhecimentos específicos do processo ou sistema.
Os gráficos de controle por atributos são utilizados, principalmente, em processos sujeitos à produção de itens defeituosos, sujeitos à produção de itens com pequenos defeitos corrigidos ao longo do processo, ou não, no controle da qualidade de serviços, dentre outros (MONTGOMERY, 2004). Além disso, tem-se que os atributos se dividem em:
Iniciando pelos gráficos da proporção de itens defeituosos (geralmente os gráficos p e np), tem-se que o gráfico \(p\) medirá a fração de produtos defeituosos ou produtos que são não conformes em uma dada amostra, sendo que \(p\) (fração de defeituosos ou não conformes) é dado por \(n\) (número de itens inspecionados) e \(d\) (número de itens defeituosos ou não conformes) (SAMOHYL, 2009; ROSA, 2016):
\[p=\frac{d}{n}~~~~~~~~~~(18)\]
Além disso, a estimativa será dada pela Equação 19, sendo \(k\) o número de subgrupos analisados:
\[\underline{p} = \frac{d_1+...+ d_k}{n_1+...+ n_k}~~~~~~~~~~(19)\]
E, assim, de forma similar ao que já foi visto, os limites de controle serão dados pelas próximas equações, em que i se refere ao i-ésimo grupo:
\[LC = ▁p~~~~~~~~~~(20.1)\]
\[LCS = \underline{p}+3σ_{pi}~~~~~~~~~~(20.2)\]
\[LCI = \underline{p}-3σ_{pi}~~~~~~~~~~(20.3)\]
O desvio geralmente é calculado como:
\[σ_p=\frac{\sqrt{\underline{p}(1 - \underline{p})}}{\sqrt{n}}~~~~~~~~~~(21)\]
Para a carta de controle np, por outro lado, tem-se algumas condições similares, sendo, nesse caso, o cálculo de estimação:
\[n\underline{p} = \frac{d_1 + ...+ d_k}{k}~~~~~~~~~~(22)\]
E o desvio:
\[σ_{np}=\sqrt{n\underline{p}(1-\underline{p}}~~~~~~~~~~(23)\]
Com isso, os limites de controle serão dados por:
\[LC = n▁p~~~~~~~~~~(24.1)\]
\[LCS = n\underline{p} + 3σ_{np}~~~~~~~~~~(24.2)\]
\[LCI = n\underline{p} - 3σ_{np}~~~~~~~~~~(24.3)\]
Por último, analisando o caso da carta c, para números de não conformidades (defeitos), estabelece-se a seguinte estimativa
\[\underline{c} = \frac{c_1 + ...+ c_k}{k}~~~~~~~~~~(25)\]
Com desvio de:
\[σ_c=\sqrt{\underline{c}}~~~~~~~~~~(26)\]
E, assim, os limites de controle podem ser calculados como:
\[LC = \sqrt{\underline{c}}~~~~~~~~~~(27.1)\]
\[LCS = \underline{c} + 3σ_c~~~~~~~~~~(27.2)\]
\[LCI = \underline{c} - 3σ_c~~~~~~~~~~(27.3)\]
Na Figura 2.14, é apresentado um exemplo de gráfico de atributos, como a carta de controle a seguir, para controle de defeitos vistos em uma linha de produção, por exemplo.

Ademais, percebe, com esses conceitos, que, de fato, os gráficos de controle obtidos a partir de atributos fornecem outra opção importante para a implementação de estratégias de controle estatístico de processos, pois, em muitos casos, talvez não será possível realizar medições do processo, ou, ainda, não será o desejável, em razão de uma série de fatores. Além dos tipos de gráficos de atributos mencionados, há, ainda, o gráfico u, baseado em não conformidades.
Tomando como exemplo um gráfico de controle (carta de controle), sabe-se que existirão ferramentas mais indicadas, ou não, dependendo do cenário analisado ao qual se refere o processo, como o caso de ferramentas indicadas para trabalhar com o número médio de não conformidades na amostra. Com relação a esse tema, aponte, dentre as alternativas apresentadas, qual é esse gráfico.
Gráfico \(p\).
Incorreta. Embora esse seja um exemplo de gráfico de controle para atributos, os gráficos \(p\) são mais indicados para medir a fração de produtos defeituosos ou não conformes.
Gráfico de controle \(u\).
Correta. Esse tipo de gráfico é mais indicado para processos sujeitos a atributos, nos quais se utiliza o número médio de não conformidades visto na amostra analisada dos dados.
Gráfico \(np\).
Incorreta. Embora esse seja um exemplo de gráfico de controle para atributos, os gráficos \(np\) são mais indicados para medir a fração de defeituosos ou não conformes, mas no caso de amostras de tamanho constante.
Gráfico de controle de desvio.
Incorreta. Esse é um tipo de gráfico ou carta de controle utilizado em casos em que o processo de amostragem trata de variáveis contínuas e análises de variabilidade.
Gráfico de moda.
Incorreta. Esse não é um tipo de gráfico ou carta de controle existente. Dentre os gráficos de controle de atributos, por exemplo, é possível citar os gráficos pelo \(np\).
Título do artigo: Controle estatístico de processos: uma aplicação em características sensoriais
Periódico: Iberoamerican Journal of Industrial Engineering.
Autor: Elisa Henning et al.
ISSNe: 2175-8018.
Comentário: Nesse artigo, é possível ver a aplicação de estratégias de Controle Estatístico de Processos (CEP) na prática, tomando como exemplo o processo de controle de qualidade em produtos alimentícios, mais especificamente com relação às suas características sensoriais.