Uma das grandes constatações no sistema de ensino vigente atual é que a maior parte dos alunos tem dificuldade para compreender os conceitos matemáticos. Eles até aprendem a realizar operações matemáticas, porém acabam executando estes processos de forma mecânica, decorando as fórmulas. Ou seja, os alunos conhecem o algoritmo, entretanto, não conseguem entender os conceitos envolvidos por trás dos números e, como consequência, não estabelecem uma ligação entre a teoria matemática e a prática do mundo real que os circunda. Percebe-se, ainda, que toda a revisão dos conteúdos básicos feita no começo de cada ano não traz qualquer resultado adicional.
Vale considerar que o ensino da matemática se encaixa no processo de educação ao qual nos situamos: aquele em que o docente apresenta o conteúdo e, em seguida, os alunos simplesmente resolvem uma sequência de exercícios. No entanto, tal método é ineficaz e pouco produtivo, já que nele não se constrói um conhecimento verdadeiro sobre o que a aritmética trata.
Sendo assim, esta unidade visa fazer essa ponte entre os conceitos teóricos e a prática em si, unindo os dois aprendizados e trazendo à tona os grandes estudiosos da matemática, além de suas descobertas. Dessa forma, será possível ter um conhecimento mais aprofundado sobre os fundamentos da aritmética. Tudo isso para que o aprendizado seja mais eficaz e proveitoso.
As equações polinomiais, também conhecidas como “equações algébricas”, são indispensáveis em nosso dia a dia, principalmente para a modelagem e resolução de problemas. Dada a sua importância, é comum que nos perguntemos sobre a existência de fórmulas capazes de resolver equações de grau maior do que 2.
Desde o século XIX, sabe-se que, além das equações de 2°grau, apenas as de 3° e 4° graus podem ser resolvidas por fórmulas que envolvem os radicais e os coeficientes das equações. No entanto, isso não quer dizer que seja impossível conhecer as raízes de equações algébricas de grau maior do que 4.
Definem-se como monômios as expressões algébricas representadas por apenas um só termo. Por exemplo, a sentença: 2x; 10y; 25ab;√2x, etc.
A parte numérica dos monômios é denominada “coeficiente”. Na unidade 2x2, por exemplo, o algarismo 2 é o coeficiente, ou seja, todas as representações numéricas.
Em algumas situações, ou problemas, o coeficiente aparecerá em forma de letras, como no caso de ax², sendo que o elemento “a” pode ser considerado coeficiente de x². A parte composta por letras em um monômio é denominada “parte literal”.
Exemplificando:
10 k³ corresponde à parte literal.
Em \(80m^100\), \(m^100\) corresponde à parte literal.
Dadas essas informações, podemos nos perguntar: afinal qual é a definição de polinômio?
Um polinômio, ou função polinomial, pode ser definido de várias maneiras. Para nossos propósitos, vamos nos concentrar em apenas uma delas. Chama-se “polinômio” a soma algébrica de vários monômios, ou “função polinomial”, na variável complexa x, toda função definida por:
\[P(x)=an{{x}^{n}}+an-1{{x}^{(n-1)}}+an-2{{x}^{(n-2)}}+...+a2{{x}^{2}}+a1{{x}^{1}}+a0\]
Esta é a expressão para todo x C, sendo n N, e an, an-1,an-2,...,a2,a1 e a0 sendo os coeficientes do polinômio P(X). Os monômios \(an{{x}^{n}},an-1{{x}^{(n-1)}}^{,}an-2{{x}^{(n-2)}},a2{{x}^{2}}ea1{{x}^{1}}\) são os termos do polinômio, sendo que a0 é o termo independente de x.
Exemplificando:
\(P(x)= 5x^4+3x^2-10ix +4\)
Os elementos 5, 3, -10i e 4 são os coeficientes de P(x), considerando que 4 é o termo independente deste polinômio.
Agora veja:
\(Q(x)=-x^5+x +10\)
Veja que os termos \(x^4,x^3 e x^2\) não constam no polinômio Q(x). Isso mostra que os coeficientes desses elementos são todos iguais a zero. Assim, teremos:
\(Q(x)=-5x^5+0x^4+0x^3+0x^2+x+10\)
Ao tirar seus coeficientes, fica: -5, 0, 0, 0, 1 e 10.
H(x) = 100
Perceba que o polinômio H(x) é denominado “polinômio constante”, pois ele é formado por apenas um número complexo (em particular, um número real).
R(x) = 0
O polinômio R(x) também é constante, porém todos os seus coeficientes são iguais a zero. Dessa forma, R(x) é chamado de polinômio nulo e pode ser representado por:
\(R(x)= 0x^n+ 0x^{n-1}+0x^{n-2}+...+0x^2+0x^1+0\)
Considere o polinômio \(P(x)=anx^n+an-1x^{n-1}+an-2x^{n-2}+...+a2x^2+a1x^1+a0\) sendo um polinômio não nulo. O grau de P(x) é o maior valor numérico do expoente que acompanha a variável x dentre todos os monômios com coeficientes diferentes de zero.
Exemplificando:
\(Q(x)= 2400x^2+2000x +1100\) tem grau 2.
\(H(x)= 10x^10+5x^7+x^5\) tem grau 10.
\(P(x)=0x^3+0x^2+10x\) tem grau 1.
Nota: Todo polinômio constante tem grau 0.
Vale ressaltar que não se define grau para o polinômio nulo. Esta é uma observação que precisamos ficar atentos.
O valor numérico de um polinômio nada mais é do que o valor que ele irá assumir em um ponto específico de seu domínio.
Como a função \(P(x)=anx^n+an-1x^{n-1}+an-2x^{n-2}+...+a2x^2+a1x^1+a0\) assume valores em quaisquer pontos de seu domínio C, neste caso, tem-se:
\(P(z)= anz^n+ an-1z^{n-1}+an-2z^{n-2}+...+a2z^2+a1z^1+a0\) , para todo z E C.
Exemplificando:
Para o polinômio \(P(x) =10x^2- 20x^1-50\), calcule P (1).
P (1) = 10 *(1) ² - 20 *(1) -50 = 10-20 -50 = -60.
P (i) = 10 (i) ²-20 (i) -50.
Dado um número z E C, tal que P(z) = 0, sendo que, para um polinômio qualquer P: C -> C, dizemos que z é a raiz do polinômio P(x).
Exemplificando:
\(P(x)= 10x^10+ 5x^7+x^5\).
Veja que, se x = 0, temos:
\(P(0) = 10 (0)^10+ 5(0)^7+(0)^5= 0\).
Assim, dizemos que x = 0 é raiz do polinômio P(x).
Agora, observe que x = 1, sendo:
\(P(1) = 10(1)^10+ 5(1)^7+(1)^5= 10+5+1=16\)
Ou seja, x = 1 não é raiz de P(x).
\(Q(x) = x^3+ 2x^2-x^1-2\).
Para x = -2, tem-se:
\(Q(-2) =(-2)^3+ 2(-2)^2-(2)^1-2 = 0\).
Ou seja, x = -2 é raiz do polinômio Q(x).
Considere dois polinômios P, Q: C -> C. Eles são similares em caso de assumirem valores numéricos semelhantes para quaisquer valores em comum designados à variável. Ou seja, P(x) = Q (x), x E C. Assim, denota-se que P(x) ≡ Q(x).
Nota: Para que P(x) e Q(x) sejam iguais, basta que os coeficientes de P(x) e Q(x) sejam iguais.
Exemplo:
Para que \(P(x) = ax^3+ bx^2+cx^1+d\) e \(Q(x)= 100x^3- 2x^2+20x^1+400\) sejam iguais, basta que: a = 100, b = -2, c =20 e d= 400.
Em um primeiro momento, vamos efetuar as operações conhecidas entre polinômios, como adição, subtração e multiplicação. Logo em seguida, estudaremos detalhadamente a divisão entre polinômios.
Dado dois polinômios P(x) e H(x), obtemos a soma adicionando os coeficientes dos termos correspondentes de P(x) e H(x).
Exemplo:
Sendo \(P(x)= 10x^3+ 5x^2+4x^1+1 e H(x)= 6x^2-3x^1+9\), temos que:
\(P(x)+ H(x)= (10x^3+ 5x^2+4x^1+1) +( 0x^3+6x^2-3x^1+9)\)
\(= (10+0)x^3+( 5+6)x^2+(4-3)x^1+(1+9) = 10x^3+ 11x^2+1x^1+10 \)
Já a subtração entre os polinômios P(x) e H(x) é realizada de modo similar à adição entre eles, porém fazemos a adição do primeiro com o oposto do segundo, ou seja, P(x) + (- Q (x)) = P(x) – Q(x).
Exemplo:
\(P(x) - Q(x) = (10x^3+ 5x^2+4x^1+1) - ( 0x^3+6x^2-3x^1+9) = \)
\((10- 0)x^3+( 5-6)x^2+(4+3)x^1+(1- 9) = 10x^3- 1x^2+7x^1- 8 \)
Nota: De forma geral, o grau do polinômio P(x) + Q(x) é, no máximo, igual ao maior dos graus entre P(x) e Q(x) e, no mínimo, zero.
O produto de dois polinômios P(x) e Q(x) é feito por meio da multiplicação de cada termo de P(x) por todos os termos de Q(x), diminuindo os termos semelhantes.
Exemplo:
Para \(P1(x) = 2x^2+4 e P2(x)= 5x^1+10\), obtém-se:
\(C(x)= P1(x) ∙ P2(x) \)
\(C(x) = (2x^2+4)∙ (5x^1+10) \)
\(C(x) = 10x^3+20x^2+20x^1+40\)
Para \(P1(x) = 2x^2+4\), obtém-se:
\(D(x)= P1(x) ∙ P1(x) \)
\(D(x) = (2x^2+4)∙ (2x^2+4)\)
\(D(x) = 4x^4+8x^2+8x^2 +16\)
\(D(x) = 4x^4+16x^2 +16 \)
Nota: O grau do polinômio P(x) ∙ Q(x) é dado pela soma do grau de P(x) com o grau de Q(x). Desse modo, gr(P∙Q) = gr(P)+gr(Q).
Considere dois polinômios P(x) e D(x), com D(x) não nulo. Dividir P(x), o dividendo, por D(x), o divisor, possui o sentido em definir os polinômios Q(x) e R(x), sendo esses, respectivamente, o quociente e o resto que satisfaz duas condições:
P(x) = Q(x)∙D(x) + R(x)
Gr (R) < gr (D) ou R(x) = 0
Observe que:
P(x) | D(x)
R(x) Q(x)
Para realizar a divisão entre dois polinômios, podemos utilizar a mesma ideia da divisão entre números naturais, usando o método da chave.
Exemplo: Divida \(P(x) = x^3-6x^2-x^1 +12\) por \(D(x) = x^1 - 2\)
Etapa 1: Escreva ordenadamente o dividendo e o divisor, seguindo as potências decrescentes do polinômio. Sendo assim:
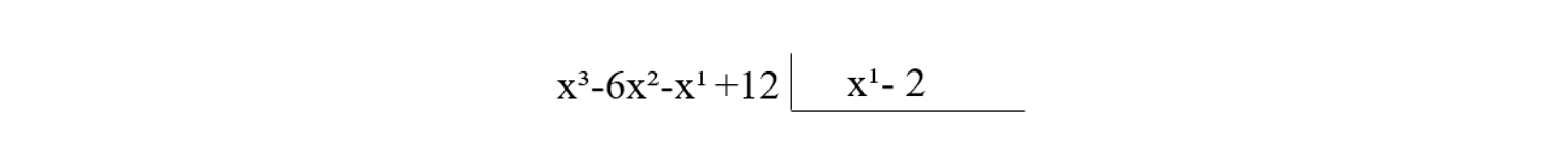
Etapa 2: Separamos o elemento com o grau mais superior de P(x) pelo termo de grau superior de D(x) (x³ : x¹), obtendo x², termo de Q(x).
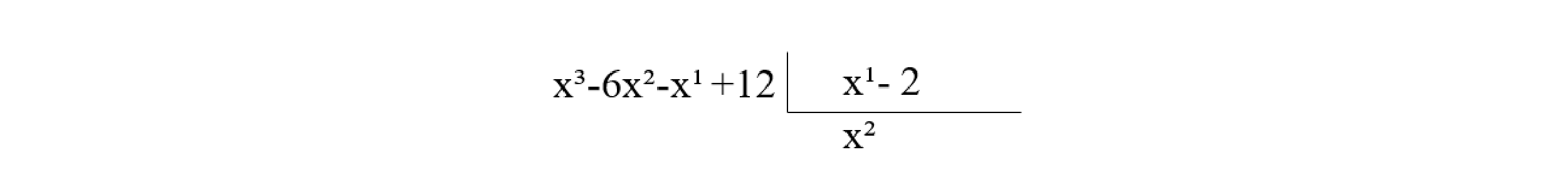
Etapa 3: Multiplicamos o termo x² do quociente pelo divisor, subtraímos do dividendo o resultado (x² + 2x²) e encontramos um resto parcial (-4x² - x + 12).
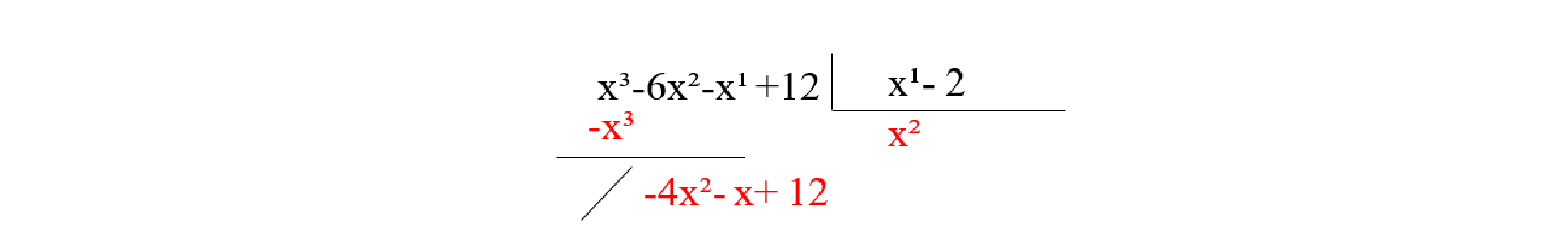
Etapa 4: Realizamos o processo da divisão com o termo que possui o maior grau do dividendo sobre o termo de grau mais elevado do divisor (-4x²: x), obtendo -4x. Assim:
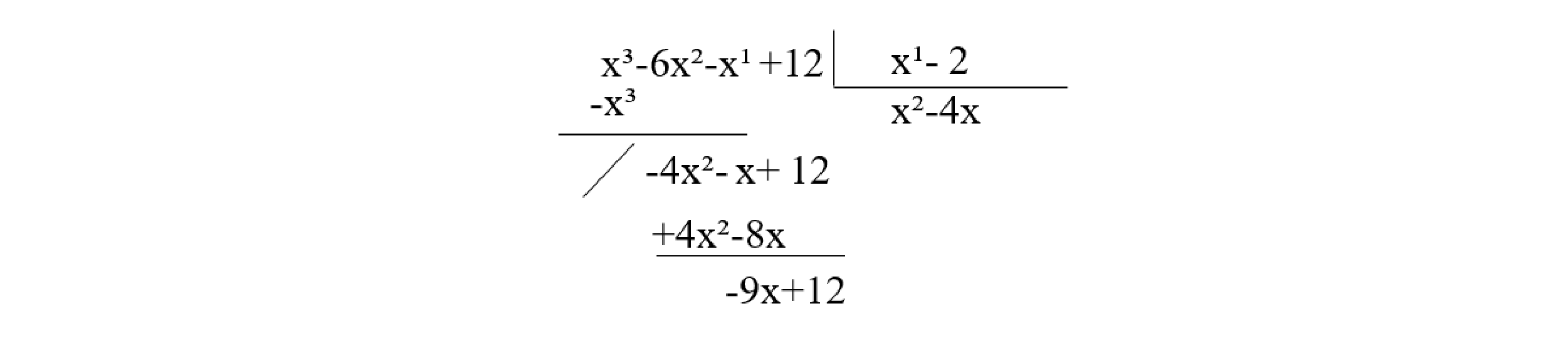
Etapa 5: Replicaremos a mesma ideia da etapa anterior, realizando a divisão com o termo de maior grau do dividendo sobre o termo de maior grau do divisor (-9x : x), obtendo -9. Logo:
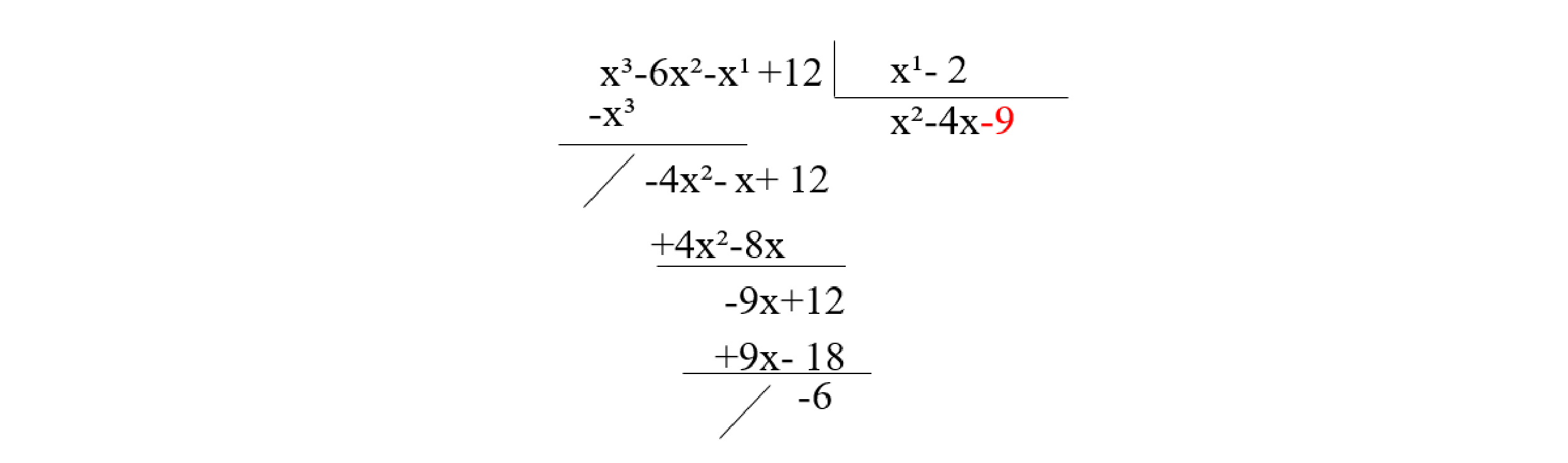
Etapa 6: A divisão se encerra quando o grau do resto for menor que o grau do divisor (neste caso menor que 1) ou quando obtemos o resto zero.
Portanto, P(x) : Q(x) = x² -4x - 9 e com resto R(x) = 6.
Assim, para P(x) = Q(x)∙D(x) + R(x), temos que P(x) = (x - 2) ∙ ( x² - 4x - 9) + 6.
Observe que gr(Q) = gr(P) – gr(D) e que o maior grau possível para R(x) = gr(D) -1.
Nota: Quando R(x) = 0, dizemos que o polinômio P(x) é divisível por D(x), ou, ainda, que a divisão é exata.
O método de Descartes consiste em determinar os coeficientes dos polinômios quociente e divisor, baseando-se na relação já vista anteriormente, em que:
P(x) = Q(x) ∙ D(x) + R(x)
Exemplo: Dividir \(f = 3x^4-2x^3+7x^1+2\) por \(g = 3x^3-2x^2+4x^1-1\).
Temos: r(Q) = gr(f) - gr(g) = 4 -3 = 1.
Dessa forma, o polinômio Q(x) é do 1° grau, ou seja, é do tipo Q(x) = ax +b. Quanto ao resto, seu grau não pode exceder a 3 (grau do polinômio divisor). Assim, gr(R) < 3.
Na situação menos favorável, vamos considerar que o grau do resto seja 2.
Logo, \(R(x) = cx^2+dx^1+e \)
Aplicando o teorema P(x) = Q(x) ∙ D(x) + R(x), temos que:
f = Q(x) ∙ g + R(x)
\(3x^4-2x^3+7x^1+2 = (ax +b) ∙(3x^3-2x^2+4x^1-1 ) + cx^2+dx^1+e\)
Desenvolvendo essa expressão, chegamos a:
\(3ax^4+(3b-2a)x^3+(4a-2b+c)x^2+(4b-a+d)x^1+(e-b) = 3x^4-2x^3+7x^1+2\)
Por igualdade de polinômios, temos:
3a = 3 -> a = 1
3b – 2a = -2 -> 3b = -2 + 2(1) = 0 -> b =0
4a -2b+c = 0 -> c = 2b -4a -> c = -4
4b – a +d = 7 -> d =a – 4b +7 -> d = 8
e – b = 2 -> e = b +2 -> r = 2
Resposta: Q(x) = x e \(R(x) = -4x^2- 8x^1 + 2\)
A divisão de um polinômio P(x) por um binômio do tipo B(x) = x – a merece especial atenção.
Observe que o número a é raiz do binômio, pois B(a) = 0.
Como o binômio possui grau 1, o resto da divisão de P(x), com gr(P) ≥ 1, por B(x) necessariamente terá que ser um polinômio constante (ou de grau zero).
Exemplificando:
Efetuaremos a divisão entre \(P(x) = x^3-2x^2+x^1-10\) por \(Q(x) = x-3\) e vamos calcular P(3).
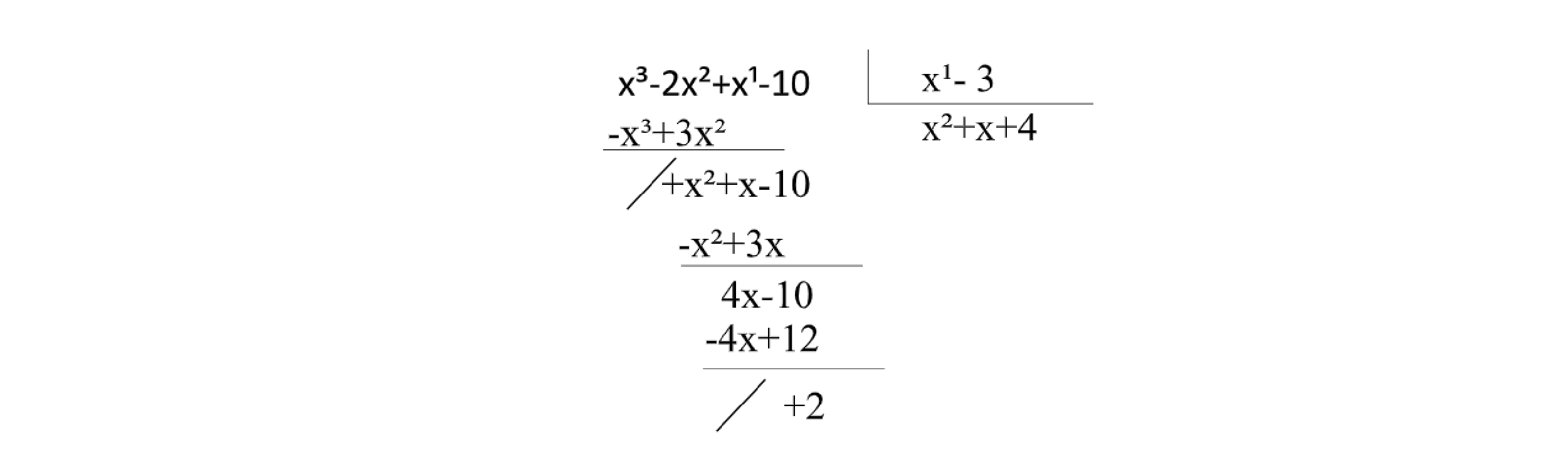
Agora, para o cálculo de \(P(3) =(3)^3-2(3)^2+(3)^1-10 = 2\).
Observe que o valor obtido em P(3) é o mesmo que o resto da divisão de P(x) por x-3.
Dado um polinômio P(x) com grau qualquer, o resto da divisão de P(x) por x-a é igual a P(a).
Exemplos: Na divisão de P(x) por x-a, temos: P(x) = Q(x) ∙ (x-a) + R(x), com R(x) = R, e R E C, ∀ x∈ C. Substituindo x por a, temos que: P(a) = Q(a) ∙ (a-a) + R = 0 + R-> P(a) = R.
Este método utiliza apenas os coeficientes do dividendo P(x) e o valor de a, que é a raiz do divisor x-a.
Exemplificando:
Iremos determinar o quociente e o resto da divisão entre \(P(x) = 2x^3-4x^1+1\) por \(x-4\), utilizando Briot-Ruffini.
Para isso, vamos reescrever o polinômio da seguinte forma:
\(P(x) = 2x^3+0x^2-4x^1+1\)
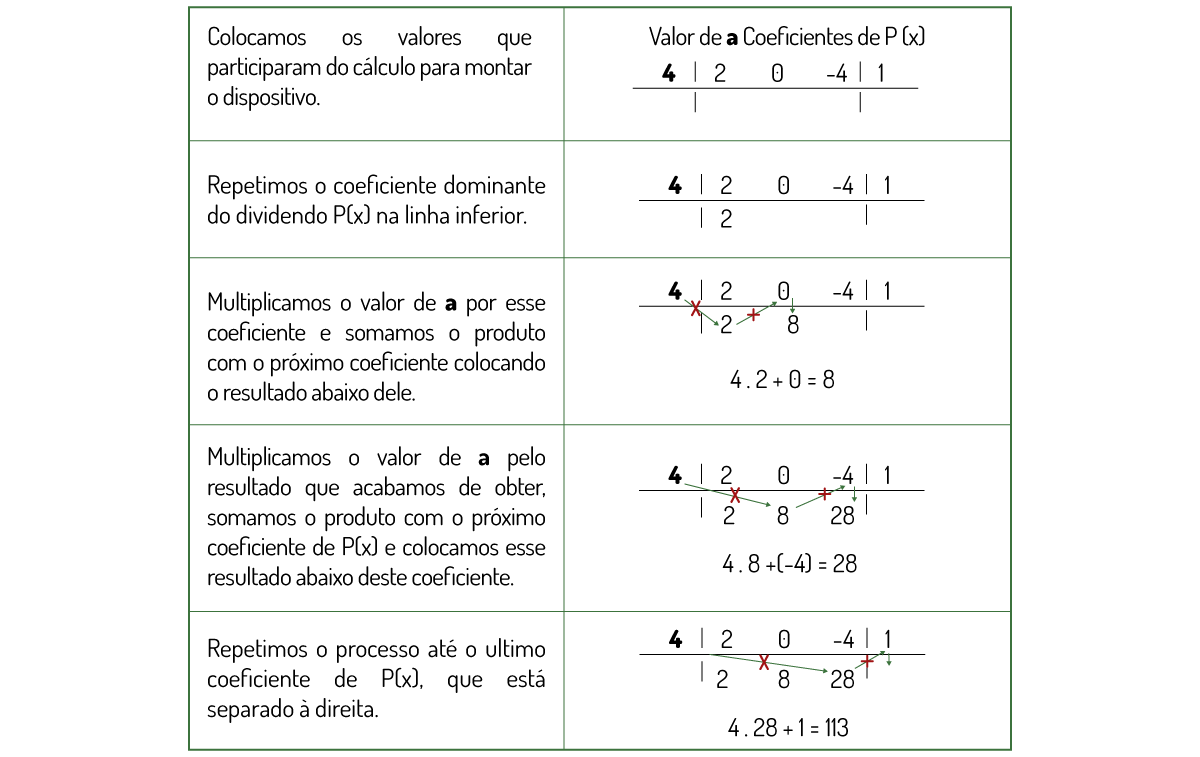
O último valor obtido é o resto da divisão e os demais são os coeficientes do quociente, dispostos ordenadamente de acordo com as potências de x.
Dessa forma, \(Q(x) = 2x^2+8x^1+28\) e o resto é R(x)=113.
Um polinômio é divisível por (x-a) e, também, por (x-b), com a ≠ b, se P(x) também for divisível pelo produto de (x-a) (x-b).
Exemplo: Se P(x) = x3 + x2 − 10x + 8, determine P(x) para x = 3, x = 2 e x = 0. A seguir, escreva P(x) como produto de dois fatores (DANTE, 2009, p. 449).
Solução:
Como P(2) = 0, então x−2 é um fator de P(x).
Agora, vamos realizar a aplicação do dispositivo prático feito por Briot-Ruffini, considerando q(x) = x2 + 3x − 4:
P(x) = (x−2) (x2+3x−4)
Exemplo: Iremos verificar se = x3 -3x2 − 6x + 8 é divisível por (x+2) (x-4) sem efetuar divisão. Temos:
\(P(-2)= (-2)^3-3(-2)^2-6(-2)^1+8 = 0\)
\(P(4) = (4)^3-3(4)^2-6(4)^1+8 = 0\)
Como P(-2) = 0, sabe-se que P(x) é divisível por (x+2). O polinômio também é divisível por (x-4), porque P(4) = 0.
Assim, o polinômio P(x) se divide por (x+2) (x-4).
A fatoração é a operação inversa da multiplicação, isto é, fatorar um polinômio significa escrevê-lo como produto de polinômios menores, geralmente como produto entre monômios e binômios.
Exemplo: (x+3)(x+4)= x²+7x¹+12
Veja que realizar o processo de fatoração \(x^2+7x^1+12\) corresponde a simplesmente encontrar os polinômios que resultaram nele próprio.
Ocorre quando todos os termos do polinômio têm, pelo menos, um fator comum.
O fator que se põe em evidência é obtido da seguinte forma:
Exemplificando:
4x²+8x³
O MDC entre os coeficientes 4 e 8 é 4. A variável comum é \x^2. Logo, coloca-se em evidência o termo 4x^2. Dessa forma:
4x²+8x³ = 4x² (1 + 2x)
Trata-se da fatoração que ocorre quando o polinômio tem fatores comuns, mas não a todos os termos.
Exemplo: ab + ac+ db+ dc
Põe-se em evidência a, nos dois primeiros termos, e d, nos dois últimos. Assim: a (b+c) + d(b+c) e depois (b+c). Desse modo, (a+d) (b+c).
Exemplo: x³+2x² - x¹-2
Põe-se em evidência x² nos dois primeiros termos e -1 nos dois últimos, x²(x+2) -1(x+2). Agora, coloca-se x+2 em evidência.
Assim, temos que: (x+2)(x^2-1)
A diferença de dois quadrados resulta no produto da soma e diferença (produtos notáveis).
a² - b² = (a+b) (a-b)
Exemplos:
x²- y² = (x+y) (x-y)
a² - 9= (a+3) (a-3)
\(16a^4- 4b^2= (4a^2+2b) (4a^2-2b)\)
É o caso do quadrado da soma e diferença (produtos notáveis).
Para fatorar, extrai-se a raiz quadrada dos coeficientes e das variáveis que são quadrados perfeitos. Depois, é verificado se o dobro do produto do primeiro pelo segundo é o terceiro termo do polinômio. Convém lembrar que:
\((a+b)^2= a^2 + 2ab+b^2\)
\((a-b)^2= a^2 - 2ab+b^2\)
Exemplos: \(x^2+4x +4 = (x+2)^2\)
O produto 2 ∙x ∙2 = 4x
\(x^2+4xy +4y² = (x+2y)^2\)
O produto 2 ∙x ∙2y = 4xy.
A fatoração do trinômio de segundo grau que pode ser decomposto no produto de dois binômios.
Consideramos o produto:
\((x+a)(x+b)= x^2 + 2(a+b)+a ∙b\)
Chama-se:
S = a +b (soma)
P = a ∙ b (produto)
Exemplo: \(x^2+5x +6\)
Assim, temos: S = 5, e P = 6.
Dessa forma, precisamos encontrar dois números a e b, cujo produto é 6 e, a soma, 5.
Como o produto é positivo, conclui-se que os dois números têm sinais iguais e podem ser:
2 e 3 ou -2 e -3 -> soma ±5
1 e 6 ou -1 e -6 -> soma ±7
Já que a somatória é positiva, os dois números devem ser positivos e resultar em 5. Logo, só podem ser 2 e 3. Portanto, \(x^2+5x +6 = (x+2)(x+3)\)
Exemplo: \(x^2-2x -24\)
Temos soma S = -2 e produto P = -24
Como o produto é negativo, conclui-se que os números possuem sinais diferentes. Assim:
-1 e 24 ou 1 e -24 -> soma ± 23
-2 e 12 ou 2 e -12 -> soma ± 10
-3 e 8 ou 3 e -8 -> soma ± 5
-4 e 6 ou 4 e -6 -> soma ± 2
As únicas das possibilidades em que a soma é -2 e o produto -24 são os números -4 e 6.
1. Vamos considerar o polinômio:
\[P(X)=4x^4+3x^3-2x^2+x+k\]
Sabendo que P(1) = 2, qual será o valor de P(3) e qual o grau do polinômio, respectivamente?
a) 386 e 4.
Correta. Para encontrar o resultado, é necessário resolver a equação de polinômio.
Como P(1) = 2, temos:
P(1) = 4.1 + 3.1 – 2.1 + 1 + k = 2
4 + 3 – 2 + 1 + k = 2
6 + k = 2
k = 2 – 6
k = – 4
O polinômio será P(x) = 4x4 + 3x³ - 2x² + x - 4
Calculando P(3):
P (x) = 4x4 + 3x³ - 2x² + x - 4
P (3) = 4.34 + 3.3³ - 2.3² + 3 - 4
P (3) = 4.81 + 3.27 - 2.9 + 3 - 4
P (3) = 324 + 81 - 18 + 3 - 4
P (3) = 386.
O maior expoente do polinômio que acompanha a variável independente x é o 4, como observa-se no exercício. Portanto, este é o grau do polinômio.
b) 405 e 4.
Incorreta. Embora 4 seja o grau do polinômio, P(3) = 386 e, não, 405, como afirma a alternativa.
c) 324 e 2.
Incorreta. O grau do polinômio assume o valor do maior expoente que acompanha a variável independente x, e vale 4. Além disso, P(3) = 386 e, não, 324.
d) 81 e 10.
Incorreta. O valor de P(3) é 386 e, não, 81. Além disso, o grau do polinômio é igual ao valor do maior expoente que acompanha a variável independente x e não igual a soma de todos os expoentes, nesse caso, 10.
e) 368 e 5.
Incorreta. O valor de P(3) é 386 e, não, 368, como afirma a questão. Além disso, o grau do polinômio é 4 e, não, 5.
Na matemática, a teoria dos grupos é responsável por estudar as estruturas algébricas que são denominadas “grupos”. Tal conceito é de extrema importância para a álgebra abstrata, pois muitas outras áreas algébricas de que se tem conhecimento, como anéis, campos, espaços e axiomas, podem ser olhadas como grupos.
Os grupos estão presentes em todas as partes da aritmética e seus métodos e processos influenciaram diversos outros ramos da álgebra. Vale dizer que um dos mais importantes avanços da matemática no século XX foi o esforço de colaboração, responsável por um grande espaço nas páginas de periódicos publicados em todo o século passado, a maioria entre as décadas de 1960 e 1980, resultando na organização dos grupos simples finitos.
Grupos são utilizados para capturar a igualdade interna de uma estrutura no formato de automorfismos de grupo. Esta igualdade, ou simetria, geralmente está associada a alguma propriedade que não varia e o conjunto de mudanças que sustenta este invariante, juntamente com a operação de compor essas transformações, forma um grupo de simetria.
A ideia essencial por trás da teoria dos grupos se dá em pegar dois elementos de um determinado conjunto e, de alguma forma, combiná-los a um outro elemento deste mesmo conjunto. É justamente essa a função das operações binárias. Desse modo, seja então G um conjunto não vazio, uma operação binária sobre G torna-se uma função ∗, que conecta a cada par ordenado (a, b) ∈ G × G um elemento a ∗ b ∈ G.
Denotamos, assim, uma operação binária sobre G da seguinte forma:
∗ : G × G → G
(a, b) 7→ a ∗ b
Veja que a ∗ b (lê-se: a estrela b) é uma outra maneira de se apontar a função ∗ (a, b), e que uma operação binária irá propor uma combinação entre dois elementos, apenas. Tirando isso, quando houver qualquer operação ∗ definida sobre G, seja binária ou não, dizemos que G é um conjunto carregado da operação ∗.
De modo particular, se ∗ é binário sobre G, assim, podemos concluir que G é fechado em relação à operação ∗.
Primeira Definição:
Consideramos N como o conjunto dos números naturais, incluindo o elemento 0; Z é o conjunto dos inteiros; Q representa os números racionais; R os números reais; e C os números complexos. Assim:
A soma e o produto de matrizes são operações binárias em relação ao conjunto Mn (R) de todas as matrizes quadradas n×n com entradas em R. Do mesmo modo sobre Mn (Q) e Mn (C), respectivamente, os conjuntos das matrizes quadradas n×n com entradas racionais e complexos.
A soma de vetores em um ambiente vetorial V é uma operação binária, já que:
+ : V × V → V
(u, v) 7→ u + v
Porém o produto por escala não é considerado uma operação binária, já que a multiplicação se define como:
·: R × V → V
(k, v) 7→ k · v
Segunda definição:
Considere um conjunto G, não vazio, carregado de uma operação ∗. Concluímos que G é um grupo que está de acordo com operação ∗ se as afirmações a seguir acontecerem:
Observe que, nesta definição, o item I aponta que G precisa ser fechado, relacionando-se à operação ∗. Isto é, da operação ∗ pelos membros de G continuarão resultando um elemento de G. Já o item II pede que ∗ seja uma operação que se associe, ou seja, a operação ∗ deverá oferecer permissão para agir em mais de dois números sem ter a necessidade de utilizar os parênteses, estando ciente que qualquer comunhão entre os elementos proporciona o mesmo resultado final. Por exemplo:
a ∗ b ∗ c ∗ d = (a ∗ b) ∗ (c ∗ d) = a ∗ (b ∗ (c ∗ d)) = a ∗ ((b ∗ c) ∗ d) = · · ·
Em seguida, o terceiro item indica que é preciso existir um elemento especial e ∈ G, voltado à operação ∗, descrito como elemento neutro. Por fim, o item IV ordena a garantia de que todos os elementos a ∈ G tenham, com relação à operação ∗, um inverso a −1 ∈ G.
Perceba que, para criar um grupo, será preciso ter um par de objetos: um conjunto G não vazio e uma operação ∗ que deve ser definida sobre ele. Assim, teremos uma notação intuitiva para o grupo (G, ∗) a ser usada diversas vezes, entretanto, para simplificar, dizemos simplesmente que G é um grupo ou, então, a nomenclatura de grupo G, o que obviamente já pressupõe que a operação exista. Vale lembrar que, quando mencionamos um grupo G mais específico, temos que ter clareza de qual operação está ligada a ele.
Exemplificando:
Considere um conjunto Z com a operação comum de soma (+). Já que a operação + é binária associativa sobre Z, teremos:
Assim, (Z, +) é um grupo.
De forma parecida ao item anterior, (Q, +), (R, +) e (C, +) também são grupos que possuem suas operações de adição, de modo que, em todos os problemas, o 0 será neutro e o inverso de x é –x.
O conjunto Z suportado pela subtração (-) não possui características de um grupo. Assim, apesar de a operação ser binária e associativa, -Z não tem qualquer elemento neutro com relação ao símbolo negativo (-). Isso ocorre pois não há um elemento e ∈ Z, de modo que, em todo x ∈ Z, terá: e − x = x.
Agora, considere Q ∗, conjunto dos números racionais excluindo-se o zero, trazido pela multiplicação usual em Q. Dizemos que (Q, ·) é um grupo, como observado a seguir:
∀a, b ∈ Q ∗ ⇒ a 6= 0 e b 6= 0 ⇒ a · b 6= 0 ⇒ a · b ∈ Q ∗
Já sabemos que (·) trata-se de uma operação binária associativa, isto é, para todo a, b, c ∈ Q ∗, tem-se: a · (b · c) = (a · b) · c.
Q ∗ contempla o 1 como número neutro da multiplicação, já que em todo a ∈ Q ∗ teremos: 1 · a = a.
Assim, (Q ∗, ·) se caracteriza como grupo.
Similar ao item 4, (R ∗ , ·) e (C ∗ , ·) são grupos com suas comuns operações de multiplicação, sendo que, na totalidade das ocorrências, o 1 é o número neutro e o inverso de x é 1/x
O conjunto R ∗ composto da operação divisão (÷) não se considera como grupo. Realmente, a operação de divisibilidade é binária, mas não é associativa, já que:
(48 ÷ 12) ÷ 4 = 4 ÷ 4 = 1
48 ÷ (12 ÷ 4) = 48 ÷ 3 = 16
Assim: (48 ÷ 12) ÷ 4 6= 48 ÷ (12 ÷ 4).
Considere G = {1, −1}. Vamos dizer que G é um grupo com a operação de multiplicação comum dos números reais. Sempre houver possibilidade, e também por simplicidade, omitiremos a partir de agora o (·), que denota a multiplicação usual.
Desse modo, G é um grupo multiplicativo.
O conjunto N composto pela operação de potenciação, dada por a, b = a b, não corresponde a um grupo?
Correto, N é fechado, mas a operação não é associativa. Sendo assim, para os números 2, 3, 4 ∈ N, temos:
(2 * 3) * 4 = 2³ * 4 = (2³) 4 = 2³.4 = 2¹²
2 *(3 * 4) = 2 * 34 = 2(34) = 281
Portanto, (2 * 3) * 4 ≠ 2 * (3 * 4) e (N, *) não é um grupo.
O conjunto Mn(R) que inclui a operação de multiplicação usual das matrizes não se considera como um grupo. Assim, sendo In ∈ Mn (R) a matriz identidade, temos:
Entretanto, não é toda matriz A ∈ Mn (R) que tem um inverso, já que algumas não possuem matriz quadrada e, sim, um determinante não nulo.
Desse modo, Mn(R) não é um grupo, tendo a operação de multiplicação usual das suas matrizes.
Considere um grupo G e, H, seu subgrupo, não vazio. Apontamos que H é um subgrupo a partir de G e descrevemos essa relação como H ≤ G, se o elemento H se formar como operação binária de G. Perceba que {e} e G serão, em todos os casos, subgrupos a partir de G, denominados “triviais”.
Entendemos que H é um subgrupo próprio de G e descrevemos essa expressão por H < G, se H é um subgrupo de G, com H 6= G e H 6= {e}.
É simples observar que:
Z < Q < R em relação à operação usual de soma.
Q ∗ < R ∗ e R + < R ∗ em relação à operação usual de produto.
O grupo formado pelos números pares infinitos, a saber 2Z = {2k | k ∈ Z}, é um subgrupo de (Z, +).
A seguir, mostramos maneiras de realizar uma verificação se um determinado subconjunto H de G é um subgrupo de G, sem a necessidade de que exibir que ele mesmo é um grupo com a operação de G.
Considerando H como subconjunto de (G, ∗), teremos H sendo subgrupo apenas se as seguintes condições acontecerem:
Exemplificando:
Vamos supor que H ≤ G e consideraremos que as restrições I II e III foram cumpridas. Se eh é o membro neutro de H, portanto, eh ∗ eh = eh. Além disso, eh ∈ H ⊆ G, consequentemente, se e é elemento neutro de G, vamos ter e ∗ eh = eh. Entre essas igualdades, decidimos que e ∗ eh = eh ∗ eh. Assim, mostra-se que e = eh ∈ H, o que comprova a condição I.
Sendo (H, ∗) um grupo, temos H sendo fechado em relação à operação ∗, isto é, em todo a, b ∈ H temos a ∗ b ∈ H. Ainda assim, para todo a ∈ H haverá o oposto de a em H, ou seja, a −1 ∈ H. Desse modo, se verificam-se as condições II e III.
Agora vamos supor que os critérios I, II e III são satisfeitos e que H é um subgrupo de G, isto é, vamos provar que (H, ∗) é um grupo. Realmente, em I, temos que H 6?= ∅ e contém um número neutro, já que e ∈ H. No critério III, diz-se que H é fechado em relação à operação ∗. Como a operação ∗ é a operação igual sobre o grupo G, segue de modo imediato que ∗ é uma operação associativa sobre H. Por fim, o critério II traz que todo elemento de H possui oposto, por isso, podemos concluir que H é um grupo.
Dá-se o nome de “grupos cíclicos” para aqueles grupos que têm um dos elementos Î. Neste caso, G é considerado como gerador do grupo (G, *). Portanto, para ser um grupo cíclico, é necessário que existam os elementos Î G, a fim de formar a expressão m’ = a*m.
Outra definição mais resumida é que todo grupo (G, *), criado por um elemento único deste G, é cíclico, gerado por a. Este grupo cíclico, desenvolvido pelo a, é denotado como <a>.
Se a Î (G, *), então H = {am, m Î Z} é o grupo cíclico de G, originado por a. Sendo assim:
<a> = {am | m Î Z}
Devemos lembrar que am = a*a*a....
Em um grupo multiplicativo, am = a.a.a... e <a> é o conjunto das potências de a.
Em um grupo aditivo am = a + a + a + ..., que se descreve m.a, o conjunto <a> é denotado como conjunto dos múltiplos de a.
Exemplificando:
Precisamos demonstrar que (H, *) é um grupo (subgrupo de G).
De acordo com as condições mostradas, H = {am, a Î G e m Î Z) é um grupo e, de acordo com a definição, H é o grupo cíclico gerado por a.
Demonstração 1
(Z, +) é cíclico, pois, para cada m Î Z, m = m.1. Logo, Z = {m.1 | m Î Z} = <1>.
Demonstração 2
(2Z, +) é um grupo (na verdade, subgrupo) de Z, criado pelo número inteiro 2. Isto é: 2Z = {2m | m Î Z} = <2>.
Demonstração 3
O conjunto C’ = {im, i = Ö-1 e m Î N} é um grupo cíclico para a operação multiplicação C’ = <i>.
Demonstração 4
Considere Z4 = {0, 1, 2, 3}. Assim, o Z4 é cíclico e 1 e 3 são criadores de Z4, isto é < 1 >=< 3 >= Z4, levando em conta a operação adição.
Observe:
1 + 0 = 1, 1 + 1 = 2, 1 + 2 = 3 e 1 + 3 = 0 . Desse modo, todos os membros de Z4 são encontrados a partir do 1.
3 + 0 = 3, 3 + 1 = 0, 3 + 2 = 1, 3 + 3 = 2. Todos os membros de Z4 são encontrados a partir do elemento 3.
Veja que qualquer elemento de Z4 é seu gerador, levando em conta a operação adição.
Demonstração 5
Para a multiplicação, Z4 – {0} é um grupo cíclico em que 1 e 3 são iniciadores. Porém 2 não é.
Demonstração 6
O grupo {1, i, -1, -i} é cíclico e considerado como originário i ou –i, utilizando a operação de multiplicação.
Demonstração 7
Dá-se o grupo (Z, +). Determinaremos < 3 >. Neste grupo, a notação é aditiva e < 3 > deverá possuir:
3, 3 + 3 = 6, 3 + 3 + 3 = 9, e assim progressivamente...
0, -3, -3 + (-3) = -6, -3 + (-3) + (-3) = -9, e assim progressivamente...
Em outras palavras, o subgrupo cíclico originado por 3 é composto pelos múltiplos de 3, sejam eles positivos, negativos ou nulos. Dessa maneira, <3> = 3Z. De modo parecido, demonstra que kZ é o grupo cíclico <k> de Z. Veja que 6Z Ì 3Z.
Exemplificando:
Considere G = {im | i = Ö-1 e m Î N} = < i >
A ordenação de G é finita, pois " m Î N, im = ir, sendo que m = 4k + r, com k e r Î N. Ou seja, r é o resto da divisão de m por 4. Desse modo, tem-se: r = 0, 1, 2, 3.
Outras definições de grupos cíclicos:
Definição 1: Dado o grupo G e a Î G, dizemos que G foi criado por “a” e tem ordenação infinita, caso os elementos a0, a, a2, ... sejam todos diferentes. Neste caso, utiliza-se a denotação O (G) = ¥.
Exemplificando:
Considere um grupo cíclico G =< a > finito. Pela proposição passada, há inteiros positivos r e s diferentes, tais que ar = as. Assim, r < s ou r > s. Sem haver perda de generalidade, podemos concluir que r < s, sendo que s - r > 0. De ar = as, conclui-se que as - r = n. Logo, existe um natural k, tal que ak = n e A = {n Î N | ak = n} ¹ Æ. Por N ser, em parte, ordenado, o conjunto A possui elemento primário e tem-se a = n.
Agora, vamos provar que < a > = {n, a, . . ., ag-1}. É evidente que {n, a, . . ., ag-1} Í < a >. Assim, a’ Î < a >.
Considere p > g. Tem-se, então, p = gq + r, sendo que r Î {0, . . . g - 1} e q Î N.
Ficamos, portanto, com ap = aq + r = (ag)qar = nar = ar Î {n, a, . . . , ag-1}. Então, < a > Í {n, a, . . ., ag-1}.
Assim, G = {n, a, . . ., ag-1}.
Definição 2: A ordenação de um grupo G originado por a Î G é igual ao inteiro inferior positivo de k, de modo que ak = n.
A exibição decorre de maneira direta das proposições passadas e da definição da ordenação de um membro. Assim, observamos que a ordenação de i é igual a 4, pois i0 = i4 = 1, e 4 é o menor número natural que corresponde à condição i4 = n. Da proposição demonstrada, tem-se que se < a > é finito, O (G) = 4.
Conclui-se que todo subgrupo de um grupo cíclico é cíclico.
Exemplificando:
Considere um subgrupo H, partido do grupo cíclico G = < a >. Caso H = {n}, então H = < n > é cíclico. Vamos supor que H = {n}, assim, H = < n > é cíclico. Se H ¹ {n}, seja am um dos membros de H, de expoente positivo mínimo. Então, dado arbitrariamente ak Î H e considerando k = mq + r, com 0 < r < m, teremos ar = ak-mq = ak.(am)-q Î H, pelo que r = 0. Assim, ak = amq = (am) q. Ou simplificando, H =< am >.
O resultado deste teorema é que se H ¹ {n} é um subgrupo de G = < a >, então H = < am >, sendo que m é o menor inteiro positivo, tal que am Î H. Entretanto, se H ¹ {n} é um subgrupo de um grupo cíclico G, H é finito ou infinito se G for finito ou infinito.
2. Analise as afirmações a seguir e escolha a única alternativa verdadeira entre elas:
a) Um grupo não pode ter mais de um elemento neutro.
Incorreta. Um grupo pode ter diversos elementos neutros, conforme a regra, e até mesmo nos subgrupos.
b) O conjunto vazio pode ser um grupo, independentemente da operação escolhida.
Incorreta. Mesmo não possuindo elementos, um conjunto pode ser um grupo, isso quando a ele está atrelada alguma operação. Porém, quando vazio, sem nenhuma operação, não pode ser um grupo.
c) Se um grupo tem uma quantidade finita de elementos, então ele é abeliano (comutativo).
Correta. Em caso de o grupo não ser infinito, ele será abeliano comutativo, como descreve a regra.
d) Uma equação da forma a ∗ x ∗ b = c sempre tem uma única solução x em um grupo.
Incorreta. A equação, da forma proposta, terá mais que uma única solução x em um grupo.
e) O conjunto dos números inteiros Z é um grupo com a operação de multiplicação usual.
Incorreta. Os inteiros Z são um grupo caracterizado pela multiplicação usual.
Os grupos abelianos possuem suas particularidades e, obviamente, sua importância na área dos grupos. Portanto, neste tópico, vamos defini-los e escrevê-los de forma aditiva.
Considere um grupo G como sendo abeliano, levando em conta g e h como subgrupos, ou elementos a partir de G, com ordenação semelhante a n e m. Nesse momento, considere l = mmc {m, n}. Dessa forma, l(g ± h) = lg ± lh = 0, isto é, g ± h também irá ter uma ordenação finita. É certo que o conjunto G[n] está composto, basicamente, pelos elementos do subgrupo g e do grupo G, sendo que ng = 0 é um subgrupo de G. Fica explícito, também, que o conjunto T = S n∈N G[n] torna-se um dos subgrupos do principal (G). Isso sem contar o conjunto Gp = S n∈N G[p n ], sendo mais um dos subgrupos, tendo para todos os primos, denotados p, a denominação p-componente primária de G.
Exemplificando:
Tendo x ∈ T em uma ordem n, iremos escrever n como o resultado de multiplicação das potências de primos, ou seja, n = p k1 1 … pkr r, com p1, ..., pn primos, em pares diferentes.
Considere ni = n/pki i, em cada i ∈ {1, ..., r}. Veja o mdc {n1, ..., nr} = 1. Dessa forma, possuem l1, ..., lr ∈ Z, tais que l1n1 + ... + lrnr = 1. Então, x = (l1n1 + ... + lrnr) x = l1n1x + ... + lrnrx. Pondo xi = nix para cada i ∈ {1, ..., r}, teremos |xi | = p ki i, isto é, xi ∈ Gpi .
Dessa forma, T está contido na somatória dos componentes iniciais de G. Essa soma será direta, seguindo o fato de que Gp ∩ Gq = {1}, se p 6 = q, e que G é abeliano. Como, evidentemente Drp ∈ P Gp 6 T, o resultado continua. Assim, T está contido na soma das componentes primárias de G. Essa soma é direta, pois Gp ∩ Gq = {1}, se p 6= q, e G é abeliano. Como claramente Drp∈P Gp 6 T, o resultado segue. Seja g um membro de G e m um inteiro positivo, dizemos que g é divisível por m se existe h ∈ G, tal que g = mh.
Definição 1: Um grupo abeliano G é dito ser divisível se todos os membros de G também forem divisíveis por qualquer inteiro positivo. Uma demonstração de grupo divisível é o conjunto dos racionais carregados com a operação de adição.
Outra classe relevante de grupos abelianos é a dos grupos que possuem a propriedade injetiva, que definiremos a seguir.
Um grupo abeliano G é dito injetivo se tiver µ: H → K, um monomorfismo de grupos abelianos, e α: H → G, um homomorfismo de grupos. Assim, existirá um homomorfismo β : K → G, tal que α = µβ.
Perceba que, na definição 1, por ser µ um monomorfismo, tem-se H Im (µ) 6? K. Dessa forma, é simples observar que um grupo abeliano G é injetivo se, para qualquer grupo abeliano K, todo homomorfismo α: H → G, com H 6 K, pode ser ampliado a um homomorfismo β: K → G. Possui-se uma relação entre grupos divisíveis e grupos injetivos, como demonstra o teorema de Baer, dizendo que um grupo abeliano G é injetivo se ele for divisível.
Uma das questões mais relevantes a respeito da ordenação de um subgrupo é que se G é um grupo finito e H é um subgrupo de G, então [H] divide [G], ou seja, a ordem (número de membros) de H divide a de G. O resultado disso é compreendido como Teorema de Lagrange.
Dessa forma, um grupo G de 8 elementos, por exemplo, só irá englobar subgrupos de 1, 2, 4 ou 18 membros, mantendo, porém, a possibilidade de G ainda ter inúmeros subgrupos. Para entender melhor o Teorema de Lagrange, vamos descrever o conceito de classes laterais.
Considerando (G, *) um grupo e H um subgrupo de G. Para cada elemento a Î G, será definida uma classe lateral direita de H, determinada por a, como sendo o conjunto H*a = {h*a | h Î H}.
De forma parecida, irá se definir a*H = {a*h | h Î H} como a classe lateral esquerda de H, determinada por a. Da definição de classe lateral, conclui-se que a*H = H*a, "a Î G, se G for um grupo abeliano.
Definição 1: Se pegarmos G, e considerarmos como um grupo e H um subgrupo de G, denotaremos por G/H ou G : H o conjunto das classes laterais H. O conjunto G/H é denominado de grupo quociente.
No exemplo anterior, G/Hd = Z12 /H = {H, H + 1, H + 2}, ou seja, G/H = { {0, 3, 6, 9}, {1, 4, 7, 10}, {2, 6, 8, 11} }.
Teorema 1: se (G, *) é um grupo e H, um subgrupo "a, b Î G, se b Î H*a. Assim, teremos: H*b = H*a.
Exemplificando:
Vamos supor que b Î H*a. Por conceito de H*a, b = h*a para qualquer h Î H.
Teremos b*a-1 = h*a*a-1 Þ b*a-1 = h Þ h = b*a-1, descontando b*a-1 Î H.
Teorema 2: se duas classes laterais do lado direito em um subgrupo H de G são semelhantes ou disjuntas. Ou seja, "a, b Î G, H*a = H*b ou H*a Ç H*b = Æ.
Em particular, H*a = H Û a Î H.
Exemplificando:
Dois conjuntos são disjuntos ou não. Vamos supor, então, que H*a e H*b não são disjuntas.
Logo, existe x Î G, tal que x Î H*a Ç H*b. Então, x = h*a = h’*b, para certos membros h e h’ de H.
Teremos que: a*b-1 = h-1*h’. Assim, a*b-1 Î H.
Teorema 3: considerando G finito, a junção de todas as classes laterais direitas de H é resultante em G.
Simbolicamente: \(\bigcup\limits_{a\in G}{H*a=G}\)
Exemplificando:
De acordo com o conceito de classe lateral, para cada elemento x de G, temos que xÎH*x.
Dessa forma: \(\bigcup\limits_{a\in G}{H*a=G}\)
Em contrapartida, x*H Ì G, para cada x de G.
Assim: \(\bigcup\limits_{a\in G}{H*x\subset G}\)
Portanto: \(\bigcup\limits_{a\in G}{H*a=G}\)
Vemos repetidamente as classes laterais em que (G, *) = (Z12, +) e H = <3> = {0, 3, 6, 9}.
É possível analisar de forma imediata, visto que [H + a] = [H] = 4, "a Î Z12 e que duas classes laterais H + a e H + b, com a e b em Z12, são semelhantes iguais ou disjuntas.
Veja, por exemplo, que H + 0 = H + 3 = H + 6 = H + 9 = H, já que 0, 3, 6 e 9 são os membros de H.
Entretanto, já haveria a possibilidade de se prever que H + 1 = H + 4, pois 1 - 4 = -3 º 9 ÎH. De forma, pode-se dizer que H + 11 = H + 5, pois 11 - 5 = 6 Î H.
Acontece também que, como H +1 = {1, 4, 7, 10}, temos então H +1 = H +4 = H + 7 = H + 10.
Teorema 4 (Teorema de Lagrange): considerando um grupo G finito, H um subgrupo de G e G/H o junção das classes laterais direitas.
Temos que |H| divide |G|. Ou, de forma mais precisa, |G/H| = |G|/|H|.
Observação: o símbolo |G/H|, que representa o número de classes laterais de H em G, também pode ser indicado por |G : H|.
Exemplificando:
Considerando G um grupo finito, temos a existência de um número finito de classes laterais direitas em H, já que a união de todas elas é igual a G, Podemos supor, dessa forma, que há s classes laterais direitas de H, sendo s > 1, em pares diferentes. Isto é, G/H = {H*x1, H*x2, . . ., H*xs} para determinados membros x1, x2, . . . , xs de G, sendo as classes H*x1, H*x2, . . ., H*xs diferentes entre elas.
Como classes laterais, mesmo diferentes, são também disjuntas, teremos: G = H*x1 È H*x2 È . . . È H*xs.
Além disso: |G| = |H*x1| + |H*x2 | + . . .+ |H*xs|.
Sendo, porém, |H*xk| = |H|, para cada k, 1 < k < s, resulta |G| = |H| + |H| + ...+ |H| = s.|H|.
Dessa forma: |G|/|H| = s = |G/H|.
3. Considerando o grupo abeliano G = (Z8, +) e H um subgrupo de G, podemos afirmar que:
a) A ordem de H é igual a 4, obrigatoriamente.
Incorreta. A ordem de H pode ser de outros membros além do 4.
b) H pode ter ordem 6.
Incorreta. Nesta expressão, não seria possível o subgrupo H possuir ordem 6.
c) Devemos ter (G: H) = 4, obrigatoriamente.
Incorreta. H é subgrupo de G, que possui os elementos finitos de Z.
d) G não pertence a H.
Incorreta. O grupo H é subgrupo de G, como o próprio enunciado diz.
e) H ▹ G.
Correta. Aqui se põe H como dependente e originário de G, o que é verdadeiro, já que H é subgrupo de G e foi criado a partir dele.
Na área da matemática mais abstrata, a teoria do homomorfismo é conhecida, também, como teorema holomórfico fundamental. Como já visto anteriormente, tem como objetivo principal relacionar dois objetos entre os quais há um homomorfismo, considerando o núcleo e a imagem de ambos. O teorema holomórfico é utilizado, basicamente, para se constatar teoremas do isomorfismo.
Considerando E, F ELCs Hausdorff e u ∈ L (E, F), dizemos que u é um homomorfismo se dado U aberto em E, então u (U) é aberto em u (E). De forma equivalente, u é um homomorfismo se a aplicação u: E/ ker u → F, induzida por u, define um isomorfismo topológico entre E/ ker u e u (E).
Se E, F são ELCs Hausdorff e se u ∈ L (E, F), então: (ker u)0 = tu (F´), fecho em σ(E´ , E).
Basta fazer a verificação em que tu (F´)0 = ker u (teorema do bipolar). Uma vez que tu (F´)0 = {f ◦ u: f ∈ F 0} segue que x ∈t u (F´)0 se, e somente se, f (u (x)) = para todo f ∈ F´, que é equivalente a u (x) = 0 (teorema de Hahn-Banach). Valem também as igualdades, quaisquer que sejam, A ⊂ E B ⊂ F´: u (A)0 = (tu) −1 (A0), tu (B)0= u −1 (B0).
Nesta variação do teorema, se E, F são ELCs Hausdorff, e se u ∈ L (E, F), então u será um homomorfismo se as duas propriedades seguintes forem válidas:
Assumimos que u é um homomorfismo e considere x0´ como pertencente ao fecho de tu (F´) em σ(E´ , E). Então, por (B) teremos que x0´ se anula sobre o kernel de u. Fica então bem definida a aplicação linear.
l: u(E) → K, l (u(x)) = x0´ (x).
Podemos provar que l não se encerra, quando u (E) é carregada da topologia induzida por F. De fato, seja ε > 0. Então U = {x ∈ E: |h x0´, x| ≤ ε} é uma vizinhança de 0 em E e, portanto, u (U) é uma vizinhança de zero em u (E) e | ≤ ε em u (U). Pelo teorema de Hahn-Banach, o funcional l se estende a um elemento y´0 ∈ F0. Agora tu (y´0) = y´0 ◦ u = l ◦ u = x0´ e, portanto, x0´ ∈ tu (F´). Assim, vale (1). Tome agora M como em (2) e seja V ∈ ΦE (0) tal que M ⊂ V o. Como u é um homomorfismo, existe um tonel W ∈ ΦF (0), tal que W ∩ u (E) ⊂ u (V). Logo, V + ker u = u −1 (u (V)) ⊃ u −1 (W ∩ u (E)) = u −1 (W) =tu (Wo) o, já que W é um tonel. Então,
M ⊂t u (F´) ∩ Vo= (ker u) o ∩ Vo ⊂ (ker u + V) o ⊂t u (Wo) oo.
Por fim, com Wo é muito pouco compactado em F´ (Teorema de Banach Alaoglu-Bourbaki) segue que tu (Wo) é fracamente compacto e, portanto, fracamente fechado em E´. Consequentemente, tu (Wo)00 = tu (W0) e (2) fica provada, com N = W0.
É preciso demonstrar, nesse momento, que (1) + (2) implicam que u é um homomorfismo. Para isso, precisamos mostrar que dada V1 ∈ Φe (0) existe W ∈ Φf (0), tal que W ∩ u (E) ⊂ u (V1). Considerando a aplicação canônica Π: E → E/ ker u, existe um tonel V2 ∈ Φe/ ker u (0) tal que V2 ⊂ Π (V1). Logo, V.= Π−1 (V2) ∈ Φe (0) é um tonel em E que contém ker u. Se mostrarmos que existe W ∈ Φf (0) tal que W ∩ u (E) ⊂ u (V), então: W ∩ u (E) ⊂ u (V) ⊂ u (V1).
Já que é dado x ∈ V, existe y ∈ V1 com x − y ∈ ker u.
Considere M.= Vo. Então, M é equicontínuo em E´ e, também, M ⊂ (ker u)0 = tu (F´) por (1). Por (2), existe N equicontínuo, tal que V0 ⊂ tu (N). Seja W ∈ Φf (0) um tonel, tal que N ⊂ W0. Então, W ⊂ No. Assim: u −1 (W) ⊂ u −1 (No) = tu (N) o ⊂ V.
Ao usar (C) e o teorema do bipolar, teremos:
W ∩ u (E) ⊂ u (V)
Assim, o teorema está demonstrado.
4. Analise as afirmações e escolha a alternativa correta entre as seguintes:
a) Existem inteiros m > 2 e n > 2, tais que o grupo de permutações (S m, ◦) é isomorfo ao grupo de classes de restos (Zn, +).
Incorreta. Este grupo não pode ser isomorfo.
b) O grupo de permutações (S 5, ◦) é isomorfo ao grupo de classes de restos (Z120, +) . J.
Incorreta. Este grupo não pode ser isomorfo.
c) Dados inteiros m > 2 e n > 2, o grupo de permutações (S m, ◦) não é isomorfo ao grupo de classes de restos (Zn, +) . J.
Correta. Considerando estes inteiros, esse grupo não é isomorfo, comprovando-se ainda mais com restos sendo os inteiros positivos.
d) O grupo de permutações (S 4, ◦) é isomorfo ao grupo de classes de restos (Z4, +).
Incorreta. Este grupo não pode ser isomorfo.
e) O grupo de permutações (S 4, ◦) é isomorfo a algum subgrupo do grupo de classes de restos (Z24, +).
Incorreta. Este grupo não pode ser isomorfo.
Quando imaginamos a matemática e suas mais diversas áreas, nos atentamos sobre o quão complexa e intrigante ela pode ser. Se pensarmos de uma maneira mais amplificada, somos privilegiados por poder viver, hoje, os resultados de séculos de pesquisas e descobertas matemáticas. Entretanto, esse processo histórico não está chegando em sua conclusão, pois ainda há muito a ser feito. Cada um de nós pode fazer a diferença para construir mais páginas de teorias, equações, esquemas e processos, seja de modo racional ou abstrato.
Para aprofundar seus conhecimentos, acesse o artigo a seguir:
ALTOÉ, T. J. Grupos e Corpos com aplicações em GAP Volta Redonda. 2007. 74 f. Trabalho de Conclusão de Curso (Graduação) – Universidade Federal Fluminense, Volta Redonda, 2007. Disponível em: <https://app.uff.br/riuff/bitstream/1/4175/1/TulioJoaquimAltoe%202016-2.PDF>. Acesso em: 26 fev. 2019.

“A matemática, vista corretamente, possui não apenas verdade, mas também suprema beleza - uma beleza fria e austera, como a da escultura” – (Bertrand Russell).

Livro: Fundamentos da matemática.
Editora: LTC; Edição: 1ª, Obra Nova.
Autor: Waldemar de Maio.
ISBN: 8521617054.
Neste livro, você terá uma base de todos os conceitos e fórmulas matemáticas de forma resumida e simplificada, tratando especificamente das áreas abstratas, como grupos e subgrupos.

Filme: Sob o domínio do medo.
Gênero: Suspense / Drama.
Ano: 1971.
Elenco Principal: Dustin Hoffman, Susan George e Peter Vaughan.
O filme apresenta a história de um professor de matemática que se refugia no interior da Inglaterra e começa a ser hostilizado, tornando-se um vingador calculista para sobreviver.
