Adquirir o conhecimento da ciência matemática é, para muitos, um processo complicado e traumático, visto que a álgebra é uma das matérias mais temidas pelos alunos, fundamentalmente, para os que frequentam o ensino fundamental, que ao se depararem com fórmulas, contas, e o aprofundamento matemático, se assustam, pois estavam acostumados com uma linguagem numérica diferente e mais figurativa. Para Garcia (2003), esse contato introdutório com a álgebra causa uma grande separação entre a matemática "concreta" da aritmética, e envolve o aluno em uma matemática "abstrata" da álgebra. No processo educacional, as crianças que frequentam as escolas, em sua grande maioria, não estão prontas para essa nova abordagem no estudo da álgebra e os professores não se atentam ao processo de transição de conhecimento e abordagem e acabam, assim, pulando etapas, espalhando os conteúdos e, dessa forma, os alunos não só perdem o interesse pela matemática, como, muitas vezes, ficam assustados, passando a temer pelo resto da caminhada escolar a matéria.
O âmbito algébrico, ou o linguajar matemático, são apresentados inúmeras vezes sem conexão e com ausência de sentido. Como uma ciência, a matemática deve ser compreendida e precisa ser o mais cativante possível para o estudante se apaixonar e a decifrar sem medo, sem ser obrigado a apenas tirar sua nota para passar de ano letivo, mas para carregá-la pela vida e sentir cada experiência prática que a álgebra pode explicar e promover.
O objetivo central deste guia visa exemplificar conceitos aritméticos de forma mais contundente e eficaz no sentido de criar uma relação mais aprofundada e íntima do aluno com os números.
Os números estão presentes na história da humanidade desde os tempos mais remotos. Segundo Caraça (1998), existem evidências arqueológicas de que o homem, há 50.000 anos, era capaz de contar.
A humanidade cresceu e se desenvolveu juntamente com a ciência matemática, pois a necessidade do ser humano de contar objetos fez com que as civilizações criassem seus próprios símbolos para a representação dos números e para realizar operações.
Com o passar do tempo, o homem foi sendo desafiado a desenvolver contagens mais complexas, dessa forma, foi se desenvolvendo sistemas numéricos, que podem ser conceituados como métodos de se realizar grandes contagens seguindo uma forma sistematizada.
Essencialmente, estes métodos de contagem se baseavam em definir um determinado algarismo, N, e, a partir dele, atribuir nomes aos seguintes (1,2,3,4..., N). Os números formados nada mais eram do que uma combinação com a base N. Por exemplo, atualmente utilizamos o conjunto numérico decimal (0,1,2,3,4,5,6,7,8,9) sendo que esses algarismos são conhecidos como indo-arábicos. Observa-se que, este sistema de numeração é composto por 10 números. O número 1 representa simplesmente ele mesmo multiplicado por 100 que resulta em uma unidade. Já o número 111 é dado a partir de uma multiplicação de (1X102) +(1X101) + (1X100) = (1X100) + (1X10) + (1X1) = 111.
Dessa forma, cada povo desenvolveu seu próprio sistema de contagem. Os egípcios apresentavam diversos complexos numéricos, entre eles o chamado sistema de base 10. Os babilônios já se firmaram no sistema sexagesimal, de base 60. Os gregos utilizavam um sistema baseado na representação alfabética. Na Índia utilizava-se um sistema muito bem estruturado com figurações para os mais variados dígitos, incluindo o zero.
Com o passar dos anos, o homem desenvolveu equações matemáticas e foi aos poucos percebendo a existência de outros tipos de número. Na Babilônia já existia um algoritmo que realizava o cálculo de raízes quadradas. Os gregos perceberam que a existência dos números irracionais, embora não tenha criado esses “novos números”, criou uma teoria para tentar explicá-los.
Tempos depois, o escocês John Napier inventou os logaritmos, que desenvolveu bastante a compreensão numérica. Assim, com o passar dos séculos, o homem foi descobrindo sua própria personalidade e junto a isso, desvendou a essência dos algarismos até compreendê-los e enxergá-los da maneira que conhecemos em nossa época, favorecendo nossa compreensão numérica.
Números relativos são aqueles que estão acompanhados de um sinal + (mais) ou de - (menos). A única exceção é o zero, pois não é acompanhado de sinal algum, denominado número neutro.
Exemplificando: (+8), (-4), (-100), 0.
Toma-se uma reta qualquer orientada em um determinado sentido, no qual denomina-se eixo orientado. Assim, em um ponto aleatório dessa reta, coloca-se o número zero, ponto este que é chamado de origem.
__________________________|0____________________________>
A partir do zero no sentido da flecha, coloca-se os números acompanhados do sinal de +, ou seja, os números positivos.
__________________________|0___|+1__|+2__|+3__|+4___|+5____>
Obs.: Os números que não estão acompanhados com o sinal de mais subentendem-se que são positivos também 8 = +8.
A partir do zero, escreve-se, no sentido oposto da flecha, os números acompanhados do sinal de – (negativos).
___________-4|__-3_|_-2|_-1__|0___|+1__|+2__|+3__|+4___|+5____>
Obs.: Os números sempre crescem no sentido da flecha.
Assim:
1>-12
-9>-20
4<8
Isto é, os números positivos crescem conforme se afastam da origem e os números negativos decrescem conforme se afastam da origem.
Módulo, ou valor absoluto, é o valor do número sem considerar seu sinal.
Exemplo: módulo de +8 é 8 e o módulo de -8 é 8. Geralmente representa-se o módulo através de duas barras.
Exemplificando:
O módulo de -2 representa-se por |-2| = 2.
Números simétricos não são apenas os iguais ou parecidos. Esse conceito se estende também aos que são opostos um do outro, ou seja, são números que em uma reta possuem a mesma distância do ponto zero, o ponto inicial. O aparecimento desses números opostos está ligado de modo direto ao desenvolvimento dos números inteiros. No conjunto dos inteiros, cada elemento positivo também possui um valor correspondente negativo, sendo, portanto, simétricos. Quando são ordenados a partir da reta numérica, os números inteiros são designados da seguinte forma:
Exemplo: +2 e -2 têm o mesmo módulo |+2|=|-2|=2, porém apresentam sinais opostos.
Se quisermos simplificar este conceito, podemos identificar o oposto ou simétrico de qualquer número apenas colocando o sinal de – (negativo) antes do número. Observe os exemplos:
Na matemática existem diferentes grupos representando os diferentes tipos de números que se tem conhecimento, aos quais chamamos de Conjuntos Numéricos. Cada conjunto é como se fosse uma comunidade única de algarismos, que foram, então, separadas de acordo com suas características em comum, conforme listado a seguir:
Os números naturais são aqueles que usamos cotidianamente para realizar contagens. Seu objetivo foi justamente esse. Atualmente, além de realizar contas, utiliza-se esse conjunto de algarismos para compor dígitos, por exemplo, identificar os números do celular de uma pessoa, ou demonstrar o horário em um relógio digital.
Os números naturais são representados pela letra N, como mostrado abaixo:
N = {0,1,2,3,4,5,6,7, ...}
Quando a representação excluir o número zero, então adiciona-se um asterisco (*) e é dada por:
N*= {1,2,3,4,5,6,7...}
Acrescentando os números negativos aos números naturais, forma-se o conjunto dos inteiros. Sendo, então, todos os naturais positivos e os negativos e o zero.
O conjunto dos números inteiros é representado por:
Z= {..., -2, -1,0,1,2,3...}
Ao excluir o zero deste conjunto, obtém-se:
Z* = {..., -2, -1,1,2,3,4,5...}
Neste conjunto, qualquer algarismo que pode ser descrito no formato de razão do tipo \(\frac{a}{b}\), com a Є (pertence) ao conjunto Z e b Є Z*, fazem parte do conjunto dos números racionais.
Exemplos: \(\frac{8}{25};-2=-\frac{2}{1};0,3333=\frac{1}{3}\)
Nota: Q*, assim como nos exemplos anteriores, aparece com o símbolo (*), que denota a ausência do zero.
Q+ é a representação do conjunto dos números racionais não-negativos.
Q- é a representação do conjunto dos números racionais não-positivos.
Aqueles elementos os quais sua escrita não pode ser feita como divisão entre dois inteiros, pois são infinitos e não periódicos, chamam-se de números irracionais. Este conjunto representa-se pela letra I.
Exemplo: I = {...√2, π= 3,141592, ϕ = 1,618033, e=2,718281,...}
Todas as raízes não exatas são exemplos de número irracional. No exemplo acima, respectivamente, aparecem: a raiz quadrada de 2, o número Pi, o número de Ouro e o número de Euler.
Os números reais são aqueles compostos pela junção dos conjuntos dos números racionais e dos irracionais, sendo que os números naturais, inteiros são subconjuntos dos números reais. A representação dos reais se dá por:
R = {...-10, - π, -2, -1.12, 0, 1,2.45, 5...}
R* é a representação dos números reais com exceção do zero.
R+ representa, evidentemente, todos os reais não-negativos.
R- é a representação dos números reais com não-positivos.
A grosso modo, os números reais são todos aqueles que conhecemos, exceto os números complexos.
Quando se relaciona um elemento qualquer a um conjunto utiliza-se o símbolo de pertence (Є).
Exemplificando:
O número 2 Є R, ou seja, o número 2 faz parte e está inserido no conjunto dos números reais.
Quando se relaciona um conjunto com outro utiliza-se o símbolo de contido (C). Partindo dessa premissa, concluímos que o conjunto dos Racionais (Q) está contido nos números reais (R)
Nota: Os símbolos ȼ e EɆ, significam, respectivamente, não contido e não pertence.
Assim, para termos a dimensão dessas inclusões de um conjunto para o outro, é mostrado conforme a Figura 1.1
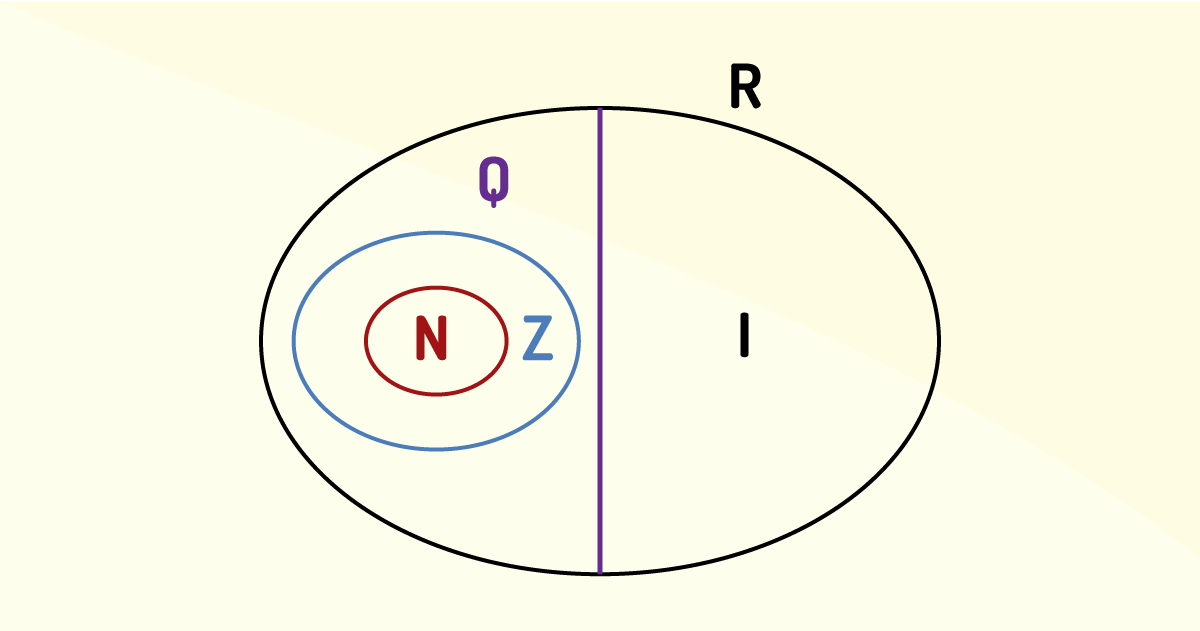
Note que ao unir os conjuntos de números racionais e irracionais, o resultado obtido é, na verdade, o conjunto dos números reais.
Considerando o conjunto dos números naturais visto anteriormente, sendo ele:
N = {0,1,2,3,4,5,6,7, ...}
Multiplica-se o número 5 por todos os elementos que pertencem aos naturais, como demonstrado abaixo:
5 x 0 = 0
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
Representemos por M5 o grupo dos números múltiplos de 5.
Assim, M5 = {0,5,10,15,20,25,30...}
Dessa maneira, conclui-se que para se encontrar os múltiplos de um determinado número, basta multiplicá-lo por um conjunto qualquer, seja ele, o conjunto dos números naturais, racionais, irracionais, inteiros, reais ou complexos.
Outros exemplos:
M6 = {0,6,12,18,24, 30...}
M8 = {0,8,16,24, 32,}
Nos exemplos analisados acima, vemos que os múltiplos de um número podem ser infinitos. Também se sabe que o múltiplo de um elemento é o produto deste com um outro número qualquer.
Nota: O zero só tem um múltiplo que é ele mesmo. O zero, portanto, é múltiplo de qualquer número.
Também, qualquer algarismo é múltiplo de 1. Sendo que todos os números são além de tudo, múltiplos deles mesmos.
Observa-se abaixo, um conjunto de elementos múltiplos de 5.
M5 = {0,5,10,15,20,25, ...}
Veja que 20 é múltiplo de 5, logo 5 é divisor de 20.
Quando um número é múltiplo do outro, denomina-se então de divisor do primeiro. Portanto 5 é divisor, submúltiplo ou fator de 20.
Exemplificando:
Encontre os divisores de 20:
20 -> 1x 20 = 20
20 -> 2 x 10 = 20
20 -> 4 x 5 = 20
D20 = {1,2,4,5,10,20}
Mais exemplos:
D8 = {1,2,4,8}
D10= {1,2,5,10}
D30= {1,2,3,5,6,10,15,30}
Dos exemplos acima, pode-se observar que o 1 é divisor em comum de qualquer número.
0:1 = 0; 1:1 = 1; 2:1 = 2.
Todo número (diferente de zero) é divisível por si mesmo.
Exemplo: 4:4 = 1; 6:6 = 1; 10:10 = 1.
Nenhum número é divisível por zero.
Exemplo: 2:0 = impossível.
Nota: O conjunto dos divisores de um número é finito.
Veja que:
M6 = {1,2,3,6}
M10 = {1,2,5,10}
Estes dois conjuntos acimas são finitos.
Se considerarmos um conjunto A, tendo seus elementos os múltiplos de 2, teremos este conjunto representado por:
A = {0,2,4,6,8,10,12,14,16,18,20, ...}
Agora, colocando um conjunto, B, como sendo o conjunto de números múltiplos de 3, teremos:
B = {0,3,6,9,12,15,18,21...}
Colocando estes conjuntos de múltiplos de 2 e 3 acionamos um novo conjunto C.
C = {0,6,12, ...}
Exemplo: Determinemos o conjunto dos múltiplos comuns de 2 e de 5.
A = {0,2,4,6,8,10,12,14,16,18,20...}
B = {0,5,10,15,20,25,30, ...}
C = {0, 10, 20...}
Seja A o grupo algébrico dos divisores de 36, dado por:
A = {1,2,3,4,6,9,12,18, 36}
B sendo o conjunto dos divisores de 54.
B = {1,2,3,6,9,18,27, 54}
C é o conjunto dos divisores comuns de 36 e de 54.
C é o conjunto intersecção de A e B.
Assim, os números que dividem ao mesmo tempo tanto 36 como 54 são:
C = {1,2,3,6,9,18}
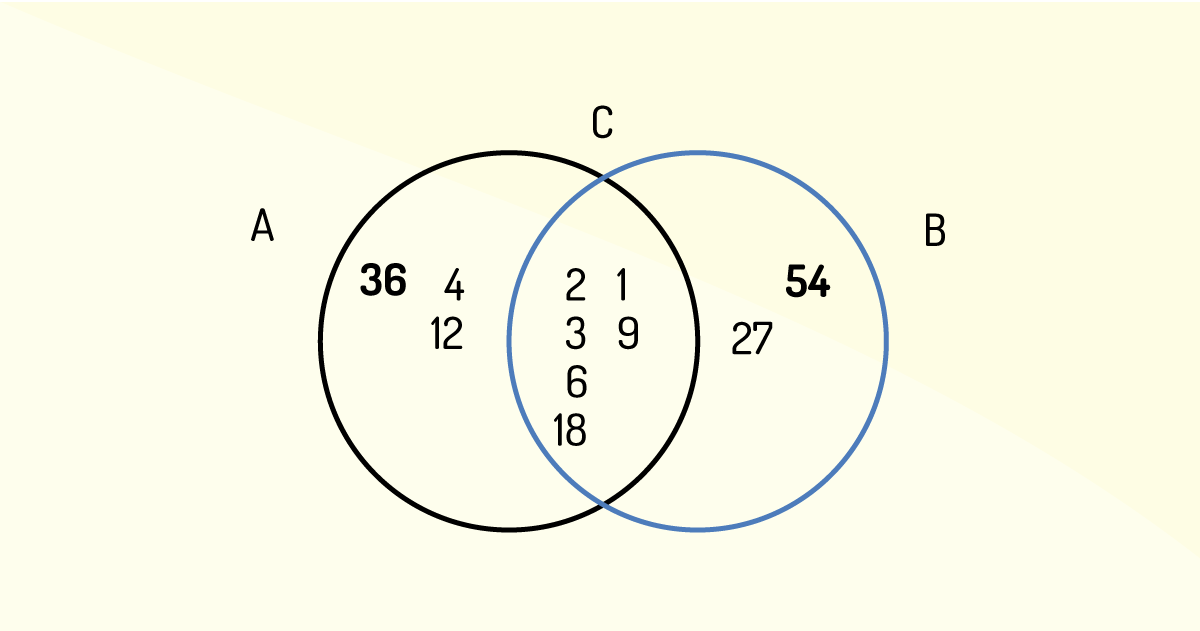
Nota: Conforme a Figura 1.2 conclui-se que o divisor em comum entre 36 e 54 são {1,2,3,6,9,18}.
1- Um matemático, ao mencionar a Teoria dos Conjuntos, em uma certa turma, realizou uma pesquisa sobre as preferências das pessoas por seleções de vôlei, de seus n alunos, obtido o seguinte resultado:
Se designarmos por A o conjunto dos admiradores do Brasil, por B o conjunto dos admiradores da Alemanha e por C o conjunto dos admiradores da França, todos da referida turma, teremos, evidentemente, A ∩ B = Ø. Concluímos que o número n de alunos dessa turma é:
a) 95.
Incorreta.
Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.
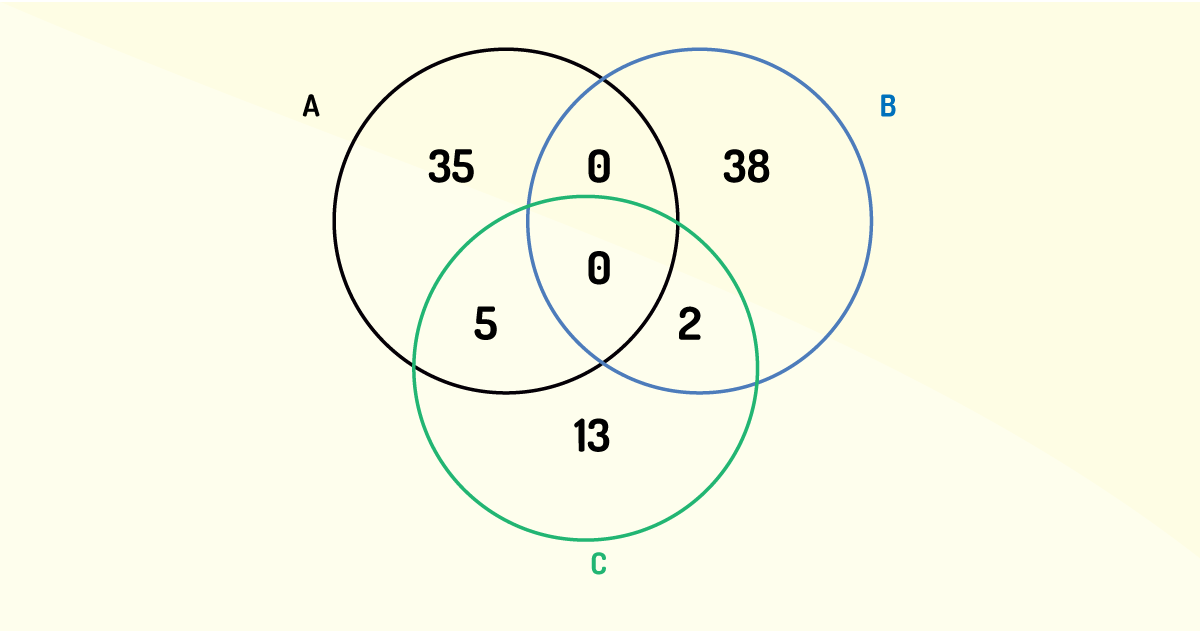
Efetuando a adição, temos que: 35+38+5+2+13 = 93 =
O número n de alunos dessa turma é 93 e não 95.
b) 93.
Correta.
RESOLUÇÃO
Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.

Efetuando a adição, temos que: 35+38+5+2+13 = 93 =
O número n de alunos dessa turma é 93. A resposta dessa questão é a alternativa “b”.
c) 86.
Incorreta.
Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.

Efetuando a adição, temos que: 35+38+5+2+13 = 93 =
O número n de alunos dessa turma é 93 e não 86.
d) 92.
Incorreta.
Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.

Efetuando a adição, temos que: 35+38+5+2+13 = 93 =
O número n de alunos dessa turma é 93 e não 92.
e) 83
Incorreta.
Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.

Efetuando a adição, temos que: 35+38+5+2+13 = 93 =
O número n de alunos dessa turma é 93 e não 83.
Todos os tipos de estudos ou ciências naturais lidam em seus processos com um procedimento denominado de indução empírica. Essa indução, serve, primordialmente, para a formulação de regras ou leis que apontam fenômenos, baseados em uma quantidade de observações exclusivas, selecionadas atentamente pelos estudiosos. Esse processo não é pelo ponto de vista da lógica o mais correto a ser utilizado, entretanto, seus resultados são altamente satisfatórios. Por exemplo, não há como duvidar do fato de que quando um corpo é solto no vácuo, considerando seu próprio peso, cairá na posição vertical local.
Porém um teorema matemático, para ser válido, deve se estabelecer de modo totalmente diferente. Basicamente se for verificado que certo fato ou afirmação é verdadeiro em uma grande quantidade de casos, no ramo matemático, ainda não seria possível concluir que tal fato é verdadeiro em todos os casos. Por esse motivo, o princípio da indução no âmbito da matemática é definido como uma metodologia de demonstração baseado no princípio da indução finita, que é muito utilizado quando se tem que provar que certos elementos são válidos para todos os números naturais.
Considerando todos os algarismos já criados pelo ser humano até os dias atuais, os números naturais foram os primeiros a serem descobertos, no primeiro momento, com o objetivo principal e único de se contar as coisas, principalmente, elementos da natureza. Mesmo sendo os mais simples, o conjunto dos números naturais não são compreendidos em sua totalidade, existindo ainda um campo de descoberta a ser desvendado.
Visto isso, podemos nos perguntar, afinal de contas, o que realmente são os números naturais representados pelo conjunto N? Por já termos adquirido um conhecimento primário, podemos descrever seus algarismos em forma de números reais, como segue abaixo:
1, 2 = 1+ 1, 3 = 2+ 1 = (1+ 1) + 1, 4 = 3+ 1 = (1+ 1+ 1) + 1, · · ·
A grande dificuldade, entretanto, se dá quando temos que provar as propriedades elementares destes números. Nesse ponto, não podemos mais apenas contar com essa descrição simplista, pois apesar de termos consciência de quais são esses algarismos, ainda assim, teríamos grandes problemas em descrevê-los de modo mais abrangente e explícito. Uma saída para tal problema seria dar a esses números propriedades que faça as suas características se tornarem mais inequívocas ao conjunto dos números naturais, isso, já o vendo dentro dos reais. De modo inicial, consideraremos um subconjunto S dos números reais, que possuem as propriedades a seguir:
Em suma, podemos explicar as propriedades acima, dizendo que o item (3) coloca o fato de que S possui efetivamente as propriedades anteriores, e se o subconjunto S 0 pertence a S, este último, obrigatoriamente, contém as propriedades (1) e (2), então, S 0 é igual ao S.
Provaremos que, se existe de fato um subconjunto S dos números reais, aos quais satisfaça exatamente as três condições postas acima, então, este conjunto será único. Se S1 e S2 são, na verdade, dois subconjuntos, temos que S1 ∩ S2, contemplam as propriedades (1) e (2), e pela terceira segue que:
\[S1 = S1 ∩ S2 = S2\]
Neste estágio inicial ainda não é possível provar que o conjunto S de fato existe. Porém admitamos a existência do seguinte axioma: há um subconjunto dos números reais o qual possui todas as três propriedades listadas. A este subconjunto excepcional, denominaremos de conjunto dos números naturais e será representado pela letra N. A terceira propriedade é o que chamamos de Princípio da Indução matemática, que se define mais precisamente a partir do conceito em que um subconjunto S dos números naturais é dado de tal modo que o número 1 pertence a S e de acordo com as propriedades sempre que o 1 pertencer a S o n+1 também pertencerá, tendo por indução S = N.
A propriedade, então, nos traz um dos mais fortes e poderosos métodos matemáticos, a de demonstração por indução.
Suponhamos que seja apresentada uma sentença matemática chamada de P (n), a qual se necessite de uma variável natural n, podendo ser confirmada ou desmentida dependendo de qual elemento n a substituímos. Estas sentenças serão chamadas de sentenças abertas, definidas apenas sobre os conjuntos dos números naturais. (N).
Abaixo, daremos alguns exemplos sobre as sentenças abertas, todas definidas sobre N:
a) P (n): n é par.
Aqui, obviamente a afirmação P (1) não é verdadeira, já que coloca o número 1 como par. A partir disso, os elementos P (3), P (5) e P (9) também são falsos, já que afirmam que 3, 5 e 9 são números pares também. Entretanto fica evidente que P (2), P (4), P (8) e P (22) são autênticos, pois 2, 4, 8 e 22 são sim pares.
b) P (n) : n é múltiplo de 3.
Nesse item, teremos, por exemplo, P (1), P (2), P (4) e P (5) sendo falsos, em contrapartida P (3) e P (6) são confiáveis, seguindo a mesma lógica do item a).
c) P (n): 1 + 3 + 5 + 7 + · · · + (2n − 1) = n 2.
Agora, os elementos, P (1), P (2), P (3), P (4), . . ., P (10) são autênticos. Define-se aqui de forma precisa o significado do axioma aberto P (n). Ela representa o valor total dos n primeiros números ímpares que são iguais a n 2. Você consegue enxergar algum número natural m de modo que P (m) seja falso? Pois bem, se prosseguirmos a busca e realizarmos algumas outras tentativas, você se certificará de que esta fórmula tem enormes probabilidades de ser correta para todo o conjunto dos números naturais n; ou seja, P (n) é aplicável para todo n ∈ N.
d) P (n): n 2 − n + 41 é um primo, para todo n ∈ N.
De forma simples, é possível verificar que os elementos P (1), P (2), P (3) são autênticos. Se formos prolongar um pouco, com algum trabalho, será possível ir mais adiante, comprovando também que P (4), P (5), . . ., P (35) são igualmente corretas. Portanto é de se considerar que tenhamos encontrado um polinômio os quais seus valores nos números inteiros serão sempre números primos.
Por fim, podemos aplicar mais testes e confirmar as suspeitas? Evidentemente sim. Os elementos P (36), P (37), P (38) e P (40) são legítimos.
Podemos encerrar as hipóteses e finalizar satisfeitos por nossa descoberta? Para aqueles que ainda insistirem em contrariar essa teoria, realizaremos um último teste com a proporção n = 41.
Perceba que 412 − 41 + 41 = 412 não é primo. Assim, para a nossa decepção, P (41) é ilegítima! Para saber se é possível provar que não há qualquer polinômio em uma variável com coeficientes inteiros cujos valores nos naturais representam sempre algarismos primos, não havia, então, a princípio qualquer probabilidade de P (n) ser autêntico para todo número natural n.
Como justificar, portanto, que um axioma aberto que se define sobre os naturais é sempre legítimo? Primeiramente, você entra de acordo com o fato de ser impossível testar um por um os elementos, ou seja, todos os números naturais, já que são infinitos. Desse modo, será preciso buscar algum método alternativo.
Iremos, abaixo, exibir esse método, demonstrando por indução matemática a forma que resolverá a nossa questão.
Considerando P (n) uma sentença aberta em relação aos naturais e denotado pela letra V o seu conjunto verdade em N, ou seja, um subconjunto de N, que se expressa como:
V = {n ∈ N; P (n) é verdadeira}.
Para se comprovar que P (n) é legítima para todo caso n ∈ N, é necessário demonstrar que V = N. Isso pode ser executado usando o Princípio de Indução Matemática.
Considere, para isto, demonstrar que o número 1 pertence a V e que n + 1 está em V, sempre que n pertence a V. Assim, nós provamos o seguinte teorema, descrito abaixo:
Teorema (Prova por Indução Matemática). Seja P (n) um axioma aberto sobre N. Presuma que:
Portanto P (n) é sim autêntico em todo n ∈ N. Utilizaremos agora, esta estratégia para demonstrar que é válido em todo conjunto natural n, da seguinte expressão:
1 + 3 + · · · + (2n − 1) = n 2.
Veja que P (1) é legítima, pois a fórmula é corriqueiramente válida para n = 1. Imagine agora que, para qualquer n natural, P (n) seja autêntico. Esperamos provar que P (n+ 1) é legítima. Se somarmos 2n+ 1, sendo ele o elemento ímpar mais próximo depois de 2n−1, nos dois lados da igualdade acima, teremos essa igualdade também aceita:
1 + 3 + · · · + (2n − 1) + (2n + 1) = n 2 + (2n + 1) = (n + 1)2.
Isso evidencia que, de fato P (n+ 1) é autêntica, sempre que P (n) também for. De acordo com o teorema, essa fórmula é aceita para qualquer algarismo natural n.
Historicamente, essa demonstração realizada foi elaborada pela primeira vez em 1575, de acordo com os registros do estudioso Francesco Maurolycos. Perceba que nesta demonstração, pode-se dar a impressão de que estamos utilizando o argumento de P (n) ser sempre verdadeira para impor e concluir que a expressão P (n + 1) também seja autêntica. Mas na prática, o que realmente está acontecendo? Estamos utilizando essa tese para provar o teorema?
Na verdade, não! Preste bem atenção, pois esse estágio é o mais delicado de todo o teorema. Tendo um número natural n, haverá duas possibilidades:
A segunda hipótese do Teorema coloca que não é necessário assumirmos de maneira absoluta que P (n) é autêntico nos casos de n ∈ N, podendo em algumas circunstâncias ser falsa em determinados valores de n, ou quem sabe até, para todos os valores de n. O que esse item está exigindo é que todas as vezes em que n pertença ao item (a) acima, n + 1 também possa se enquadrar a essa mesma categoria; não exigindo nada quando n pertencer à categoria (b).
De forma exemplificada, o axioma aberto P (n): n = n + 1 cumpre (por vacuidade) a segunda hipótese do Teorema, já que nenhum n ∈ N está na categoria (a). O que causa uma imperfeição, no sentido que o Teorema já não nos garanta que P (n) é legítima para todo n, e, portanto, a primeira hipótese não é verificada, já que P (1): 1 = 2 é falsa!
É necessário ter a percepção de que o princípio da Indução Matemática é distinto da indução empírica das ciências naturais, onde se é comum, depois de um razoável número, finito, por necessidade, de testes, já considerar leis gerais que predominaram e reinaram aquele campo de estudo. Tais leis são tomadas como verdades absolutas, até que algum outro estudioso, prove ao contrário. Na aritmética não existe espaço para se lidar com informações verdadeiras até que se prove outra coisa. A Prova por Indução Matemática visa justamente comprovar e estabelecer que aquele determinado axioma aberto, sobre os elementos naturais, será sempre autêntico, em todos os casos, sem haver margem para oposição.
Para se ter uma compreensão completa sobre as definições e os teoremas que circundam todas as teorias da aritmética, é preciso, primordialmente, se habituar na utilização de uma linguagem diferenciada, mais rigorosa e técnica em relação a que usamos em nosso cotidiano. Adquirir este costume pode ser tornar mais fácil quando se utiliza os recursos de alguns símbolos e noções da lógica matemática, dos quais falaremos um pouco neste item. Entretanto é importante destacar que a lógica matemática possui atualmente aplicações diversas e de extrema importância nas mais diferentes áreas, sendo uma das principais e com mais destaque, o ramo tecnológico.
A linguagem utilizada na aritmética, assim como qualquer outra, possui suas designações, seus termos próprios e nomes, além, claro, das proposições características dessa área. Essa especificação serve, principalmente, para indicar aspectos matemáticos: algarismos, pontos, funções, conjuntos, operações, figuras geométricas etc. No caso das proposições, é essencialmente usada para determinar se as afirmações são verdadeiras ou não. Para exemplificar essas designações específicas podemos citar a seguinte:
1: 7, 3 + 4, 2 − √ π 7, 2 + 3i, N, R.
Veja que nessas duas primeiras designações, existe um mesmo objeto em comum, ou seja, são equivalentes. Portanto o símbolo que se usa para salientar que as designações a e b são sinônimas é o sinal de igual (=), deste modo, teríamos no linguajar matemático a = b. Em relação às proposições (verdadeira ou falsa) indica-se:
7 = 3 + 4, 4 ≤ 4, 2 + 3i = 3 + 2i, 2 + 1 < 1 + 2.
Sendo uma proposição, precisa ser obrigatoriamente verdadeira ou falsa, porém, jamais uma coisa e outra. Na primeira hipótese, deverá ter um valor lógico de 1 e consequentemente na segunda o valor de 0. Assim, os símbolos (1 e 0) servem para classificar verdade ou falsidade.
No caso de ambas as proposições obtiverem um mesmo valor lógico, serão, então, chamadas de equivalentes:
7 ≤ 0 e (−2)5 = 2 x (-5)
Neste caso, a indicação se dá pelos símbolos p e q. Na linguagem matemática escreve-se p ⇐⇒ q.
Quando temos duas proposições demarcadas, como visto antes pelos símbolos p e q, escrevemos p∧q (ler “p e q”), que serão consideradas verdadeiras ou autênticas quando ambas assim forem, e se tornarão falsas, no caso de pelo menos uma delas ser falsa.
Por exemplo, se considerarmos duas proposições, sendo a primeira “4 é um número par” e a segunda “4 é um divisor de 10”, teremos uma proposição falsa, pois a hipótese número 2 não é verdadeira.
Oposto a isso, temos a disjunção, ou comumente escrita na linguagem matemática p ∨ q, (“p ou q”), que se baseia em constatar o fato de ao menos uma das proposições ser verdade. Nessa regra, p v q só será considerada falsa quando as duas forem falsas, e não apenas uma como no exemplo acima.
Nota: A conjunção e a disjunção podem ser definidas de forma completamente parecidas, caso se tenha mais de duas proposições. Para exemplificar isso, podemos considerar um conjunto de proposições p, q e r. Se afirmarmos que todas são autênticas, ela por completo será verdadeira. Se tornará falsa se uma delas, e apenas uma, também for falsa.
Agora se p é uma proposição, a negação de p, se tornaria uma nova, sendo escrita pelo símbolo ∼ p ou simplesmente dizendo não p. Teríamos, então, que a proposição ∼ p é autêntica e 2p falsa. Se somarmos ambos os valores lógicos dessas proposições, serão iguais a unidade, portanto se evidencia que toda proposição p, teremos:
∼ (∼ p) ⇐⇒ p.
De forma mais simples, são verificadas as propriedades a seguir, conhecidas como as primeiras leis de De Morgan, se relacionando às três operações lógicas, representadas pelos símbolos ∨, ∧ e ∼:
∼ (p ∧ q) ⇐⇒ (∼ p) ∨ (∼ q)
∼ (p ∨ q) ⇐⇒ (∼ p) ∧ (∼ q)
Podemos descrever essa linguagem dizendo que as proposições p e q estão sendo negadas, ou seja, não são legítimas, o que é similar a dizer que no mínimo uma delas é falsa. Outro ponto importante é a implicação, que se designa pelo símbolo p =⇒ q (que pode ler-se “p implica q” ou “se p, então q”) uma nova proposição que permite dizer, se p é legítima, q também será. Essa implicação p =⇒ q só será, então, falsa, no caso de p ser verdadeira e q falsa, ou seja, se o valor lógico de p for superior. Como no exemplo das proposições abaixo:
2 ≥ 2 =⇒ 3 > 2 + 1,
3 = 2 =⇒ 5 < 0,
3 = 2 =⇒ 5 ≥ 0,
(1000!)2 > 2 20000 =⇒ 1000! > 2 1000
Apenas a primeira não é verdadeira. É evidente que quando se analisa essas implicações de forma conjunta p =⇒ q e q =⇒ p, as proposições p e q são equivalentes; simbolicamente:
[ (p =⇒ q) ∧ (q =⇒ p) ] ⇐⇒ (p ⇐⇒ q).
Além desses termos e das proposições que consideramos no tópico anterior, a linguagem matemática utiliza diversas vezes expressões que fazem mediações com variáveis, ou seja, adiciona em seu vocabulário diversos símbolos, a maioria das vezes, letras que podem substituir designações a partir de regras determinadas. Como na expressão abaixo:
x, (x − y) 2 , x 2 − 2xy + y 2
Essas designações se converterão de letras para números reais, isso se forem substituídas de acordo com as regras estabelecidas. Por exemplo, se trocarmos as letras x pelo algarismo 1 e o y por 0, teremos a expressão acima convertida em designação do número 1. Já as expressões que possuírem variáveis, também se transformarão quando as suas figuras e símbolos forem adequadamente substituídos de forma conveniente a elas. Essas chamaremos de expressões designatórias, como a que se segue abaixo:
√ x − 1, cotg x, y x.
É preciso frisar, no entanto, que para as últimas expressões se converterem em números é preciso mais que simples substituições destas variáveis. De forma prática, por exemplo, de nada adiantaria substituir o x pelo 0, já que não iria resultar em nenhum número real, independentemente do valor que fosse posto ao y, portanto duas expressões designatórias que estiverem em uma mesma variável x, serão equivalentes se no caso os valores de todos os x se convertam a uma designação e a partir dela, converta a outra também. Nesse sentido, as expressões x e √3 x 3, por exemplo, são equivalentes, pois uma converte a outra, diferentemente das expressões p |x| e √ x, que se trocarmos o x por −1, por exemplo, a primeira se transformará em uma designação do número 1 e a segunda ficará sendo um símbolo sem significado. Obviamente, essa definição de equivalência é similar no caso de se ter expressões designatórias com mais de uma variável. Assim, torna-se equivalentes as expressões designatórias:
(x − y) 2 e x 2 − 2xy + y 2
Suponhamos que x e y têm em seu domínio o conjunto R. Consideremos agora a seguinte expressão:
x 2 > 0, 2 x = x 2 , x 2 − y 2 = 0, x − y > y − z.
Em ambos os casos, se formos trocar todas as variáveis por designações de números reais, teremos, a partir daí, não mais designações, mas sim proposições e como já visto, terão que ser classificadas em autênticas ou falsas.
Nesse caso, quando podem se tornar proposição, as expressões chamam-se de proposicionais ou de condições. Elas podem também se combinar por meio de operações lógicas, similares ao que consideramos nas proposições. Por exemplo, p (x) e q (x), expressões proposicionais que possuem uma variável apenas. A conjunção p (x) ∧ q (x) se converte para proposição legítima no caso de serem atribuídos valores a x que a torne verdadeira em ambas condições. P (x) e q (x).
Agora, a disjunção p (x) ∨ q (x) é uma condição que será falsa para os valores da variável que tornam p (x) e q (x) ambas falsas.
A negação de p (x) é a condição ∼ p (x), que apenas se tornará verdadeira para os valores de x que se converterão p (x) em uma proposição falsa.
Em relação a implicação, p (x) =⇒ q (x), também se converterá em uma proposição falsa, no caso de atribuição a x os valores nos quais p (x) forem verdadeiros e em contrapartida, q (x) falsa. Por fim, a equivalência p (x) ⇐⇒ q (x) é o conjunto das implicações p (x) =⇒ q (x) e q (x) =⇒ p (x).
Abaixo, alguns exemplos de equivalências verdadeiras, independentemente dos valores reais que forem atribuídos às variáveis.
[ (x > 3) ∨ (x = 3) ] ⇐⇒ x ≥ 3,
[ (x < 3) ∧ (x ≥ 2) ] ⇐⇒ 2 ≤ x < 3,
∼ (x < 1) ⇐⇒ x ≥ 1, x 2 > 0 ⇐⇒ x 6= 0.
Serão, também, verdadeiras em todos os casos:
x < 1 =⇒ x < 3,
[ (x < y) ∧ (y < z) ] =⇒ x < z,
Se formos supor que x se designa agora a uma variável ao qual o domínio é o conjunto N, dos números naturais, temos:
∼ (x é par) ⇐⇒ x é ímpar
x é múltiplo de 6 =⇒ x é múltiplo de 3,
[ (x é múltiplo de 2) ∧ (x é múltiplo de 3) ] ⇐⇒ (x é múltiplo de 6).
Se no caso for dada uma condição p (x), e nela for atribuída a variável x, valores referentes ao seu domínio, teremos como visto, uma conversão para proposição. Contudo em aritmética, tem-se outra forma de extrema relevância para se obter proposições através desta condição p (x). Chama-se quantificadores e são descritos na linguagem própria da matemática pelos símbolos, ∀x ou ∃x.
Essa proposição ∀x p (x) pode ser lida da seguinte forma “qualquer que seja x, p (x) ” ou então “para todo o x, tem-se p (x) ”. Além disso, será verdadeira ao atribuir qualquer valor de x do seu domínio. Já a proposição ∃x p (x), que se lê “existe um x tal que p (x) ” ou “para algum x, tem-se p (x) ”, não é legítima, portanto é falsa, isso também se converter seus valores atribuídos a x, com um valor de seu domínio, da mesma forma que o anterior.
Por exemplo, considerando x uma variável real, são verdadeiras as proposições:
∀x x 2 + 1 > 0, ∃x x 4 ≤ 0 e ∃x x 2 − 3 = 0.
No caso das proposições que tiverem mais de uma variável, o uso de quantificadores torna-se bem similar. Se considerarmos, por exemplo, variáveis x e y a proposição ∀x∃y y < x poderá ser interpretada como “qualquer que seja x existe um y tal que y < x” e se assemelha, a dizer que “não existe um número real que seja menor do que todos os outros”. Obviamente, essa proposição é legítima, mas não seria caso o domínio de x e y fosse o conjunto dos reais ao invés dos naturais. Como não é o caso, então torna-se verdadeira.
A proposição ∃y∀x y < x, que traz à tona a existência de um número real ser menor do que os outros quaisquer é evidentemente falsa. É interessante ressaltar também que, ao trocar a posição dos quantificadores se obterá, a partir daí, uma proposição não equivalente. Entretanto os quantificadores do mesmo tipo inclinarão sempre para uma proposição equivalente, como é fácil de se imaginar a essa altura, como os exemplos abaixo, de proposições equivalentes.
∀x∀y [x 3 = y 3 ⇐⇒ x = y]
∀y∀x [x 3 = y 3 ⇐⇒ x = y]
De forma abreviada, tornam-se:
∀x, y [x 3 = y 3 ⇐⇒ x = y].
Se formos dar duas condições — p (x, y) e q (x, y) por exemplo — diremos que a primeira implicará formalmente a segunda, se é verdadeira a proposição:
∀x, y p (x, y) =⇒ q (x, y)
Por exemplo, no conjunto dos reais, x = y 2 implica formalmente x 2 = y 4, mas já a implicação:
x > y =⇒ x 2 > y 2 não é formal.
Veja que na linguagem da aritmética utiliza-se apenas a palavra “implica”, no sentido formal, ou até mesmo pode-se utilizar o recurso dos símbolos da forma p (x) =⇒ q (x), em lugar de ∀x p (x) =⇒ q (x). São nada mais do que “abusos de linguagem”, ou o popular “gastar vocabulário”, onde geralmente não influencia e não traz nenhum inconveniente para o contexto matemático, visto que tanto uma forma como outra, ainda permite reconhecer e identificar os quantificadores.
De forma parecida, dizemos que as condições p (x, y) e q (x, y) são formalmente equivalentes (ou apenas equivalentes) se tiver:
∀x, y p (x, y) ⇐⇒ q (x, y),
É importante ressaltar que a implicação formal p (x, y) =⇒ q (x, y) pode também se manifestar dizendo que “p (x, y) é condição suficiente para q (x, y) ” ou que “q (x, y) é condição indispensável para p (x, y) ”. Já no caso de equivalência formal, é comum também dizer-se que “p (x, y) é condição necessária e suficiente para q (x, y) ”.
É de suma e fundamental relevância as seguintes leis, que foram também designadas a partir de De Morgan, que indicam o processo de se negar proposições com quantificadores:
∼ ∀x p (x) ⇐⇒ ∃x ∼ p (x),
∼ ∃x p (x) ⇐⇒ ∀x ∼ p (x).
Para declarar esta última, podemos dizer que “não havendo qualquer valor de x que faça com que p (x) seja verdadeira, todos os valores de x farão essa proposição falsa, e reciprocamente”. Por exemplo:
∼ ∀x x 2 > 0 ⇐⇒ ∃x x 2 ≤ 0,
∼ ∀x,y∃z x = yz ⇐⇒ ∃x,y∀z x 6= yz
O conceito de raciocínio é que tal ação faz o cérebro partir de um estado de premissa, ou suposição, até uma conclusão, uma definição sobre algo. Com esse embasamento podemos argumentar que o raciocínio é um tipo de conhecimento indireto e mediato, isto é, não depende apenas de nós mesmos, e nem de um ou outro fator, mas é intermediado por uma série de questões. Portanto raciocínio é o oposto de intuição.
Raciocinar, ou argumentar, é quando colocamos as informações de modo organizado e as evidenciamos de uma maneira que nos faça chegar a alguma conclusão sobre determinado assunto. Esse processo nos faz ter uma ligação entre aquilo que já conhecemos e aquilo que ainda desconhecemos, que através do raciocínio bem elaborado passaremos a desbravar. Em suma, portanto, são meios de se construir novos conhecimentos, a partir de uma prévia que já existia. Resumidamente, existem dois processos aos quais organizamos nosso modo de pensar e raciocinar que são a dedução e a indução.
Deduzir significa alcançar a verdade específica, com base em outra que geralmente é maior e mais abrangente. Deste modo, quando colocamos um fato específico dentro de outro mais generalizado, estamos raciocinando por meio da dedução, como no exemplo a seguir:
Partimos agora para um exemplo que envolva e se aplica no âmbito da matemática:
Ou seja, 2 x 162 + 1 = 325.
No processo da indução, fazemos o oposto da dedução. Ao induzir, buscamos situações isoladas, particulares e entre elas procuramos algo em comum, algum padrão ou norma geral que possa se aplicar a todos os casos isolados ou parecidos observados, como se segue no exemplo:
Partimos para uma exemplificação numérica:
No âmbito das ciências experimentais, induzir é um processo natural, como a biologia e a química. Mesmo não sendo o padrão da matemática, que se compreende muito mais como uma ciência de exatidão, alguns ramos que estão em desenvolvimento baseiam suas respostas por meio do método de indução.
É preciso considerar que, os resultados alcançados sob essa técnica, necessitam ser postos à prova, se deparando com outros critérios mais independentes, já que o processo de indução pode acarretar conclusões erradas, pois obter premissas verdadeiras não significa que as conclusões também serão verdadeiras.
Analisamos dois exemplos:
Aqui, a generalização da premissa verdadeira resultou em uma conclusão falsa ou incorreta.
Seguimos para um outro exemplo:
Analisando esse exemplo, podemos encontrar conclusões autênticas para ≤n ?? 40; entretanto, a expressão, f (41) = 41² - 41 + 41 = 41², não é primo! Resumidamente, podemos dizer que o fato de se generalizar as 41 premissas, resultaram em uma conclusão equivocada.
Esses exemplos trazem à tona um pensamento relevante. Afinal, até que ponto deve-se testar a validade de uma hipótese? Uma outra questão é: como assegurar essa conclusão alcançada?
Há, na verdade, dois métodos para resolver essas questões. A primeira é uma abordagem experimental, onde o cientista buscaria a resolução do problema, na base do experimento em si, e após testar inúmeras possibilidades, descobriria e concluiria que a fórmula fracassa quando chega no n = 41. A questão é que a hipótese poderia cair apenas em um n muito grande, o que levaria muito tempo para descobrir e seria descoberto após muito trabalho, isso ainda considerando a fórmula que poderia ser verdadeira. Após algumas centenas de testes, o cientista concluiria que há inúmeras evidências para que a expressão realmente gere todos os primos superiores a 40. Entretanto jamais teria absoluta certeza de que isto é autêntico, pois poderia existir algum elemento não testado que derrubaria sua tese, afinal, existem infinitos números naturais e só é possível explorar uma pequena parte deles, então, neste método, o pesquisador teria que conviver com o fato de que sua tese poderia ser quebrada a qualquer momento.
Um segundo método é a abordagem matemática, onde o cientista buscará resolver esses problemas a partir de um raciocínio sistemático e lógico, a qual a solução seria única, indiscutível, correta e permaneceria pela eternidade.
Quadro 1.1 – Dedução x Indução
Fonte: Ângela Maria (2011).
No quadro acima, comparamos as duas formas de raciocínio, apontando duas diferenças relevantes, a respeito das características de cada uma, tanto na forma dedutiva como indutiva. Visualizamos, então, as diferenças básicas destas formas de pensamento, aos quais estamos em constante contato.
Voltando um pouco, o método da indução finita corresponde a um processo aritmético criado para provar proposições que são autênticas em uma determinada sequência de objetos. Esse conceito é muito usado em áreas da matemática como a teoria dos números, geometria, análise combinatória etc. Entretanto a indução pode também aparecer em qualquer outro ramo da aritmética e por essa razão existem duas formas de se descrever esse princípio.
a) Princípio da Indução Finita - 1ª forma
Consideramos P (n) como um enunciado que descreve uma propriedade sobre um algarismo natural n maior ou igual a um número natural n0 fixado.
Definição (PIF 1ª forma). Caso precisemos provar que as duas condições abaixo são válidas:
C1: P (n0) é autêntica (ou seja, vale a propriedade para n0);
C2: é autêntica a implicação P (n) → P (n + 1) isso para todo n ≥ n0.
Portanto podemos dizer que a propriedade P (n) é verdadeira e autêntica para todo n ≥ n0.
Na prática, para conseguirmos confirmar um teorema por indução finita, precisamos demonstrar que essas duas condições dadas pelo princípio estão sendo satisfeitas. Isso é fundamental, pois é o que vai basear nossa garantia da propriedade em toda a infinidade de casos existentes. Especificamente na segunda condição, como apenas uma única implicação será falsa, se a sua premissa for autêntica e a conclusão falsa, só é preciso eliminar essa possibilidade para termos, então, a validação da implicação que deseja.
Dessa forma, o que se faz comumente é tornar um k qualquer valor maior ou igual a n0, isso admitindo que P (k) seja legítimo, e provar que essencialmente P (k + 1) também precisa ser autêntico. Além de tudo isso, é realizada também a prova de que é válida a propriedade para n0 (primeiro natural), a indução nos garante em todas as afirmações a validação da propriedade.
Exemplificando:
Considerando que 2^4 = 16 e 4! = 4.3.2.1 = 24, logo vale que 2^4 < 4! E dessa maneira, a (C1), primeira condição do P IF, foi alcançada. Assumindo que 2?k = k! (∗) para um k genérico maior do que 4, como:
• 2 k+1 = 2.2 k • (k + 1)! = (k + 1) k! • (k + 1) > 2, se k > 4
A partir da desigualdade (*) teremos:
2 k+1 = 2.2 k < 2.k! < (k + 1). k! = (k + 1)!
Fica, então, consolidada a validação de (C2), a segunda condição do P IF. Desse modo, o princípio da indução finita garante que vale 2? n < n!, para todo n > 4.
b) Princípio da Indução Finita - 2ª forma
Considerando P (n) uma pronúncia que descreve uma propriedade sobre um número natural n maior ou igual a um número natural n0 fixado.
Definição (PIF 2ª forma). Se conseguirmos provar que valem as duas condições abaixo:
CC1: P (n0) é autêntica (ou seja, vale a propriedade para n0);
CC2: para todo n ≥ n0, é verdadeira a implicação P (n0) ∧ P (n0 + 1) ∧ ... ∧ P (n − 1) ∧ P (n) → P (n + 1).
Podemos concluir, a partir dessas condições, que a propriedade P (n) é autêntica para todo n ≥ n0.
Na execução, para se provar uma propriedade, baseado na segunda forma de indução, é preciso provar que esta propriedade P tenha validade para n0, e em seguida, seja dado um n aleatório superior ao n0 admitindo que P vale para todos os elementos entre o n0 e ele mesmo (n), é preciso provar também que P valerá para n + 1. Ou resumidamente, comprovar a seguinte afirmação:
P (k) verdadeira para n0 ≤ k ≤ n → P (n) verdadeira.
Esta forma pode ser fundamental e essencial em algumas oportunidades, como no Teorema fundamental da Aritmética, que veremos a seguir.
Exemplificando:
O primeiro algarismo é o 2, que é número primo. Como 2 é igual a 2, concluímos que 2 admite uma "fatoração"/ única em primos. E, desse modo (CC1) está satisfeita. Assumimos agora que todos os números entre 2 e n, incluindo eles mesmos, permitem uma fatoração em números primos, única a menos da ordem dos fatores. Consideremos o número n + 1, haverá duas opções:
Já que as fatorações de p e q são exclusivas a menos da ordem dos fatores, é preciso ainda provar que, no caso de haver outro elementos primos que realizassem a fatoração encontrada, teríamos também fatorações diversas para p e q, o que é impossível por hipótese.
Existem na matemática clássica alguns axiomas que consideram objetos que não podem ser desenvolvidos, nem como algoritmo finito, nem infinito. Podemos ver isso como um lado mais abstrato da aritmética, mas de toda forma, essa abstração toda não traz muitas consequências produtivas ao desenvolvimento matemático. Não se tem nenhum relato de existência de algum resultado verdadeiramente prático e relevante, decorrente dessas práticas e teorias que envolvem o abstrato. A matemática construtiva, portanto, não faz parte e não contribui para esse método.
Um dos exemplos mais clássicos que se tem desse modo de enxergar a aritmética é o princípio da Boa ordem. Juntamente com outros exemplos, esses princípios podem ser nomeados de teoremas sem serem admitidos também como axiomas. Se fossem axiomas, passariam a reger o que é e o que não é uma verdade absoluta e exata, o que complicaria muito a matemática.
Em suma, o Princípio da Boa ordem, diz que todo conjunto aritmético pode ser bem ordenado, ou seja, cada conjunto x, por exemplo, possui uma relação de ordem, representado por R (pode-se pensar na relação de ordem <= da aritmética dos números inteiros, como exemplo) de modo que (X, R) é completamente ordenado (i.e., para todos x, y em X, xRy ou yRx) e todo subconjunto Y de X contém um elemento minimizante b (i.e., bRx para todo elemento x de Y).
Podemos ver isso na prática, se colocarmos, por exemplo, o conjunto dos números naturais N= {0,1,2,3, …}. Ele é extremamente bem ordenado pela relação de ordem <=, menor ou igual. O conjunto N é limitado inferiormente, então todo subconjunto de N terá elemento mínimo, que é, então, um elemento minimizante.
Em conjuntos com cardinalidade elevada, é interessante observar como se concentra a relação de ordem. Em alguns casos, pode acontecer de não existir algoritmo ou algarismo finito ou não para estabelecer essa relação ordenada, além disso se considerarmos conjuntos dos números inteiros Z, com cardinalidade alefe 0, e o operador P, construía-se o conjunto P (Z) com cardinalidade alefe um, o conjunto P (P (Z)) com cardinalidade alefe dois, o conjunto P (P (… (P (Z)) …), n vezes, com cardinalidade alefe n, e assim sucessivamente.
Consideramos S um subconjunto de N, podemos afirmar que um número natural a é o elemento mais inferior de S, isso no caso de possuírem as propriedades que seguem: i) a ∈ S, ii) a ≤ n, para todo n ∈ S. Logo de cara, verificamos que se o conjunto S possui um elemento menor, se torna único. Concluímos isso, pela lógica em que se o elemento a e a0 são os menores de S, então, a ≤ a 0, ou seja, a = a0. Essa denotação quando ocorre é dada por minS. Essa informação é importante, pois nem sempre é fácil provar aquilo que é óbvio, muitas vezes, quando afirmamos isso, dá-se a impressão de que qualquer um poderia resolver sem grande esforço.
Mas iremos agora, de forma efetiva, mostrar o que parece óbvio, isto é, todo subconjunto não vazio N, possui um elemento menor.
Exemplificando:
Considere S sendo um subconjunto não vazio de N. Imaginemos que este conjunto S não tenha nenhum menor elemento. Demonstraremos que S é vazio, levando a uma contradição. Imagine um conjunto T, que seja um complementar de S em N, isto é, o conjunto dos naturais pertencentes a S. Queremos demonstrar, portanto, que T = N, ou para se utilizar outra linguagem simbólica S = ∅. Defina o conjunto:
In = {k ∈ N; k ≤ n}, e considere a sentença aberta
P (n): In ⊂ T.
Já que 1 ≤ n, para todo n ∈ N, tem-se, portanto, que 1 ∈ T, pois, se fosse o oposto, 1 seria um menor elemento de S. Desse modo, P (1) é verdadeira.
Considere agora que P (n) seja autêntico, para qualquer n. Se n + 1 ∈ S, como não há elemento de In pertencente a em S, obteríamos n + 1 que é um menor elemento de S, fato, como visto, que não é permitido. Assim, n + 1 ∈ T, onde se segue que In+1 = In ∪ {n + 1} ⊂ T, provando que, para todo n, temos que In ⊂ T; portanto, N ⊂ T ⊂ N e, consequentemente, T = N.
2) Tendo em vista o raciocínio dedutivo e suas especificidades na matemática, assinale V para verdadeiro e F para falso, em relação às afirmações a seguir.
I - É uma técnica de raciocínio dedutivo, usada para provar alguma ideia obtida com um raciocínio indutivo.
II- Ao utilizar a indução para provar resultados, podemos assumir que “P(k) é V” para forçar o resultado esperado, tranquilamente.
III- Todo subconjunto não-vazio do conjunto dos inteiros positivos tem um elemento mínimo.
IV- Indução matemática é um método de prova matemática utilizado para demonstrar a verdade de um número finito de proposições.
Está correto o que se afirma em:
a) I apenas.
Apesar da afirmativa I ser correta, a III também está. Um subconjunto não vazio precisa ter um elemento mínimo.
b) II apenas.
É falso, pode-se assumir sim P (k), porém, não tranquilamente, é preciso ter cuidado e cautela, para tal proposição não forçar demais o resultado.) As afirmativas I e III são as corretas.
c) I e II apenas.
Apesar da afirmativa I ser correta, a II não está. Pode-se assumir sim P (k), porém, não tranquilamente, é preciso ter cuidado e cautela, para tal proposição não forçar demais o resultado).
d) I e III apenas.
De fato, as afirmativas I e III estão corretas. A Indução corresponde a uma técnica considerando o raciocínio de dedução como da indução e como visto no decorrer dos tópicos um subconjunto não vazio precisa ter um elemento mínimo.
e) II, III e IV apenas.
Apesar da afirmativa III ser correta, a II e a IV não estão. Pode-se assumir sim P (k), porém, não tranquilamente, é preciso ter cuidado e cautela, para tal proposição não forçar demais o resultado. E a indução matemática é um método utilizado para demonstrar um número INFINITO de proposições e não apenas finito.
No entendimento dos gregos sobre matemática, os algarismos eram magnitudes geométricas. Assim, este termo, para eles, pode ser compreendido como uma sequência finita e ordenada de regras ou passos, em um esquema de processamento, que possibilita a realização de uma determinada função - resolução de problemas, cálculos etc.
Algoritmo, então, é uma palavra latinizada, que tem origem do nome Al Khowarizmi, que foi um matemático árabe do século nono. Surgiu, a partir, de uma necessidade em se realizar cálculos sem o auxílio de recursos como os dedos ou os ábacos. Antes disso, a estruturação de cálculo era muito associada às ferramentas que se dispunham à mão, como pedras, varetas, calculadora à manivela etc. Os utensílios que temos à disposição, atualmente, levaram séculos para se desenvolverem e foram criados a partir de muito estudo.
Após a realização de cálculos mais práticos, foi possível se criar operações. A divisão juntamente com adição, subtração e multiplicação correspondem ao que chamamos de quatro operações básicas. A divisão é muito temida, principalmente entre os alunos das séries iniciais, do ensino fundamental e é tida como a mais difícil por muitos, entretanto, o diferencial da divisão é que possui um algoritmo diferenciado em relação às outras três.
Para entendermos bem este algoritmo é preciso que relembremos todos os elementos que de fato compõem uma operação de divisão, e consequentemente comporão seu algoritmo. Abaixo segue a descrição de cada um:
Dividendo (D): número que será dividido
Divisor (d): número que se divide
Quociente (q): resultado da divisão
Resto (r): diversas vezes, ao finalizar a divisão, sobra uma quantidade que não pode ser dividida mais. Essa quantidade recebe o nome de resto.
Seguindo esses elementos, a operação da divisão define-se dentro da seguinte fórmula: D= d.q+r.
A resolução da divisão se dá então em D: d, em que procuraremos um número q, que será multiplicado por d, e aí será encontrado D como resultado ou, no mínimo, muito próximo a ele. O resto r se formará, quando de fato sobrar, na subtração D – d.q. Se esse resultado for 0, então não há resto evidente.
Essa técnica é usada para se dividir algarismos próximos aos presentes nas tabuadas de 1 ao 10. Por exemplo, ao se dividir 80:9, procura-se um número q, que ao ser multiplicado por 9, tenha como resultado 80 ou, no mínimo, próximo a isso. Sabemos que 9.8 = 72, assim, podemos realizar a subtração 80-72 = 8, portanto temos todos os elementos encontrados.
D= d.q+r
80= 9.8 + 8
Este algoritmo da divisão compreende um método fácil e prático na realização das divisões de algarismos a algarismos, da mesma maneira que as outras operações. Na linguagem escolar, esse algoritmo tem sido chamado de forma geral como “método chave”, pois é representado da seguinte forma:
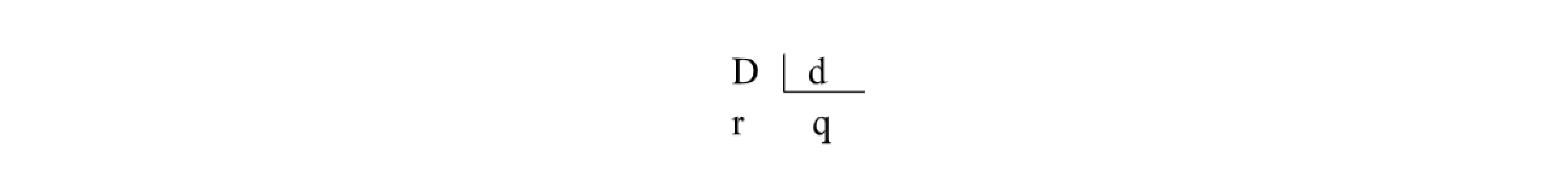
Da mesma maneira, é preciso encontrar um número q, que ao ser multiplicado por d, tenha o resultado D. Caso não seja possível o resultado exato, deve-se encontrar um valor aproximado e anotar as sobras nas posições descritas acima. O método chave auxilia nessa visualização.
Exemplificando:
Exemplo 1: Veja como é feita a divisão de 9 por 3:
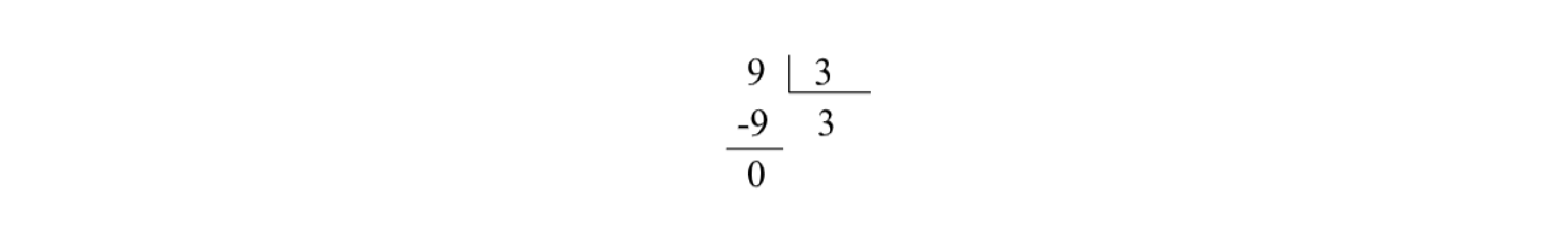
Nesse exemplo, percebemos que: dividendo = 9, divisor = 3, quociente = 3 e resto = 0. Se o resultado (r) foi 0, portanto, não há resto. (r).
Exemplo 2: Analise agora a divisão de 92 por 2. Em um primeiro passo, divida 9 por 2 e anote o resto 1. Perceba que 4·2 +1 = 9, então colocaremos 4 no quociente, o resultado de 4·2 abaixo do 9 (que é o algarismo o qual estamos dividindo nessa primeira etapa) e subtraímos 9 por esse resultado. Temos, então, que o resto é 1.
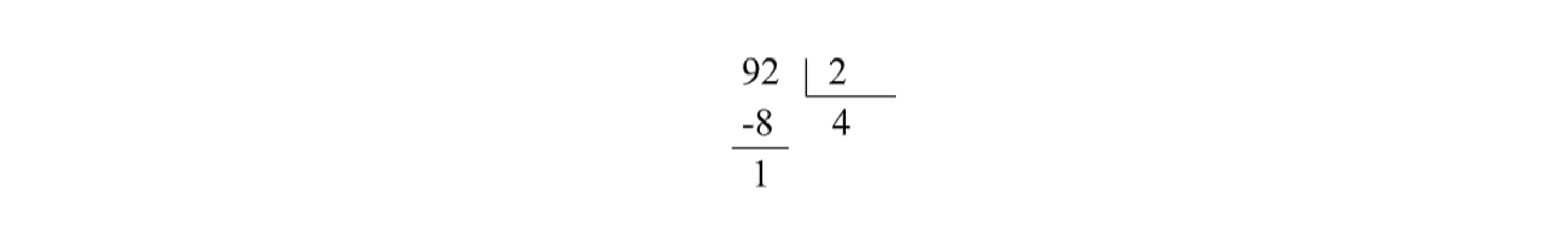
Ao lado do resto 1, “puxe” o próximo algarismo do dividendo:
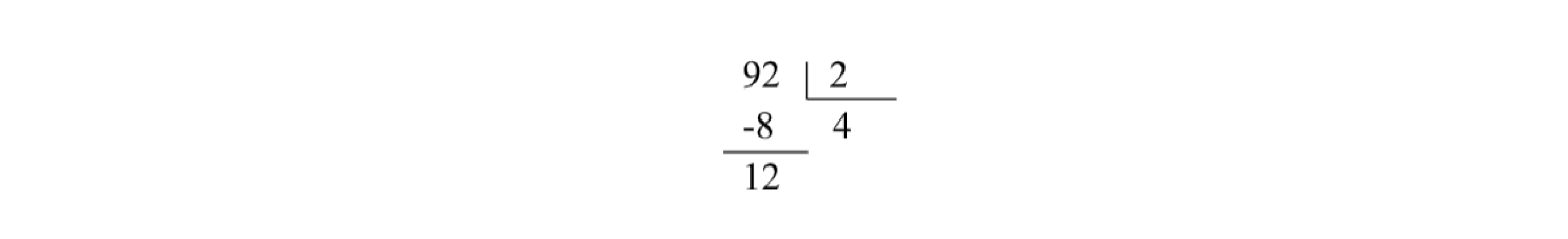
Em seguida, repita o procedimento para o número 12, composto agora pelo resto e pelo próximo número do dividendo inicial:
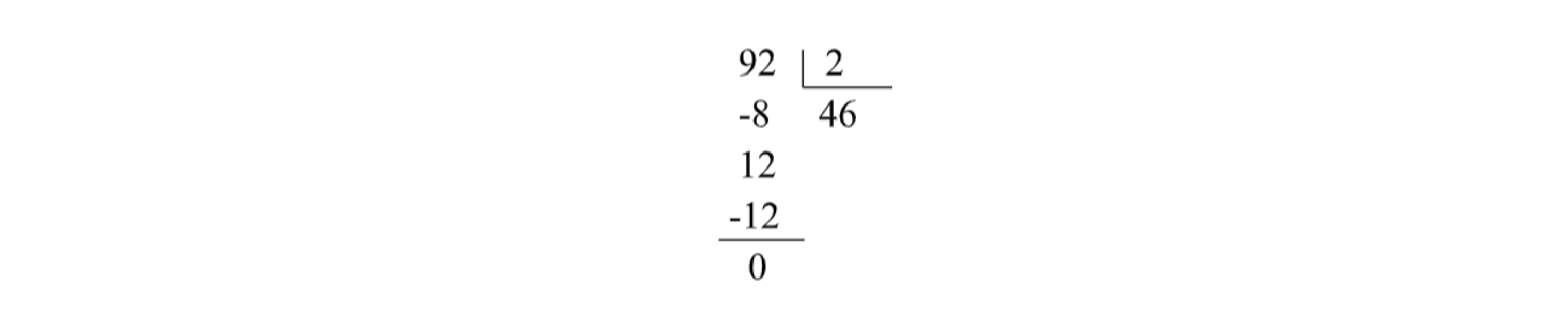
Enfim, chegamos ao resultado da divisão: 46. Escrevemos, portanto, a expressão que segue:
r+ q·d = D
0 + 46·2 = 92
Em aritmética, o Algoritmo de Euclides corresponde a um processo simples e muito eficaz para se encontrar o máximo divisor comum entre dois ou mais números inteiros, isso, se forem diferentes de zero. Este algoritmo é um dos mais antigos da história da matemática, sendo conhecido desde o surgimento nos livros VII e X da grande obra “Elementos de Euclides”, aproximadamente nos anos 300 a.C. Este algoritmo não exige que se fatore os elementos.
O máximo divisor comum, ou MDC corresponde ao maior número inteiro que se possa dividir ambos elementos, sem deixar nenhum resto. Podemos citar de exemplo o número 21, que é o MDC de 252 e 105. (252 = 21x12; 105= 21x5). Agora observe que 252 – 105 = 147, por essa razão o MDC de 147 e 105 também será 21 e assim sucessivamente, os números diminuirão até se alcançar o zero.
Se formos fazer o oposto e reverter os passos do algoritmo de Euclides, o MDC passará a ser expresso como a soma dos dois algarismos originais, onde cada um deles será multiplicado por um valor inteiro, positivo ou negativo, por exemplo, 21 = 5x105 + (-2) x 252. Essa propriedade é denominada de Bézout.
O algoritmo original de Euclides foi elaborado apenas para números naturais e comprimentos geométricos, entretanto, no século XIX, foi generalizado para diversas outras classes matemáticas como os inteiros gaussianos e os polinômios.
O cálculo do algoritmo baseia-se na ideia de que dois números naturais sempre terão divisores em comum. Por exemplo, os números 12 e 18 possuem 1,2,3 e 6 como divisores iguais, sendo que o 6 é o maior. Então, neste caso, o 6 será chamado de máximo divisor comum de 12 e 18, e indicado como m.d.c (12,18) = 6
Exemplificando:
mdc(6,12)=6
mdc(12,20)=4
mdc(20,24)=4
mdc(12,20,24)=4
mdc (6,12,15) = 3
Uma das maneiras de se aplicar o algoritmo de Euclides e calculá-lo a fim de se encontrar o m.d.c, é utilizando a decomposição em fatores primos. Acompanhe, por exemplo, o cálculo do m.d.c entre os elementos 36 e 90:
36 = 2 x 2 x 3 x 3
90 = 2 x 3 x 3 x 5
O m.d.c. será sempre o produto dos fatores primos em comuns, que nesse caso se dará por:
m.d.c.(36,90)= 2x3x3
Enfim, m.d.c.(36,90) = 18.
Se escrevêssemos essa fatoração em forma de potência, teríamos os seguintes números:
36=2² x 3²
90= 2 x 3² x 5
Ou seja, m.d.c.(36,90) = 2 x 3² = 18
Um outro método que pode ser utilizado na resolução do m.d.c é o processo da divisão sucessiva. Esse método consiste basicamente em dividir dois ou mais números simultaneamente pelo menor fator primo que se encontre. Caso o número ainda não seja divisível pelo menor primo, então deverá ser repetido.
Ao final das divisões, o m.d.c se tornará o produto dos diferentes fatores primos encontrados.
Exemplificando:
Encontre o MDC entre 90 e 54.
Primeiro, monta-se uma tabela contendo os números, depois realiza-se a divisão dos números pelo menor fator primo e em seguida multiplica-se pelos fatores primos diferentes encontrados. Esses passos estão devidamente exemplificados na imagem abaixo:
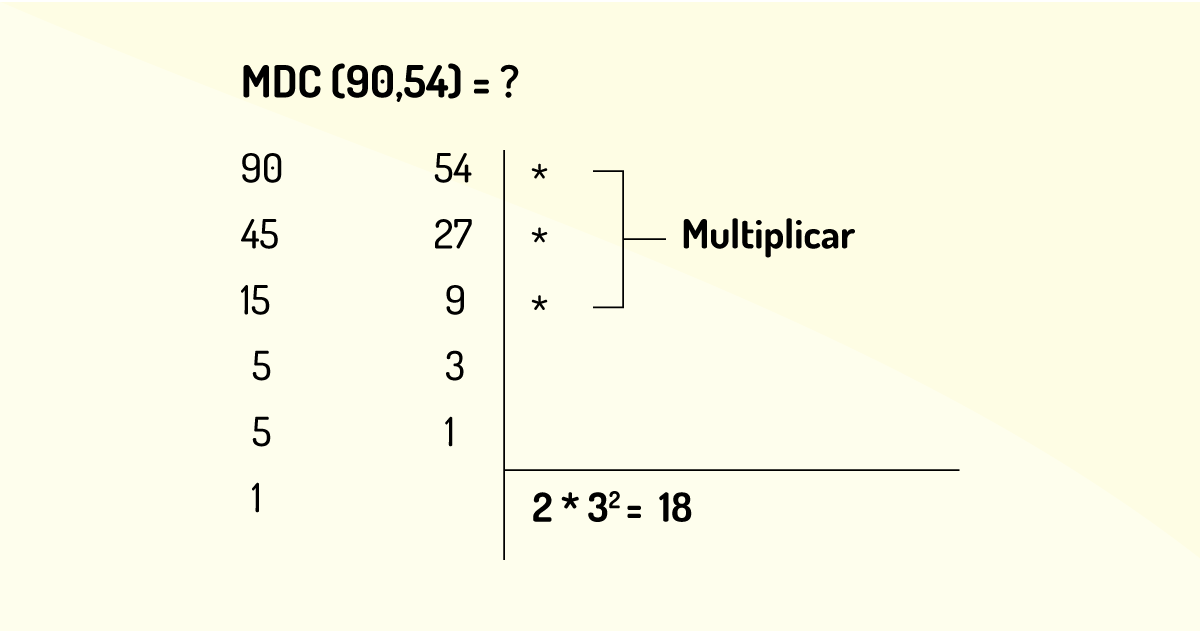
Portanto temos:
MDC (90, 54) = 2 x 3² = 18.
Observação: Veja que 2 e 3 foram os menores fatores primos que dividiram simultaneamente os algarismos 90 e 54. Portanto o produto entre eles é o m.d.c entre os números em questão.
Os números considerados primos são aqueles naturais que possuem apenas dois divisores diferentes, e não mais que isso. Esses divisores são o 1 e eles próprios.
Exemplificando:
Curiosamente o número 1 não é primo, pois possui, nesse caso, apenas um divisor, ele próprio.
Já o número 2 é o único número primo que é par.
Todos os números naturais que possuírem mais de dois divisores não são primos e são chamados de compostos, por exemplo, o número 15, que tem mais do que apenas dois divisores. Assim, 15 é um número composto. Para se comprovar e conferir que um número é primo, basta executarmos a divisão dele por outros primos 2, 3, 5, 7, 11 etc., até que nós tenhamos:
Outra maneira é multiplicar dois números primos. O resultado será um número composto, ou seja, um número composto é resultado do produto de dois números primos, conforme: 2 x 5 = 10, 2 e 5 são primos e o produto entre eles é o número composto: 10.
Exemplificando:
1) O número 203:
2) O número 137:
Um cientista da aritmética chamado Eratóstenes (285-194 a.C) desenvolveu um simples sistema, de forma objetiva para desvendar se um número é ou não primo. Esse conceito foi denominado crivo de Eratóstenes. Para fazer a representação do crivo, consideremos uma tabela simples, com os 100 primeiros números naturais de 1 a 100:
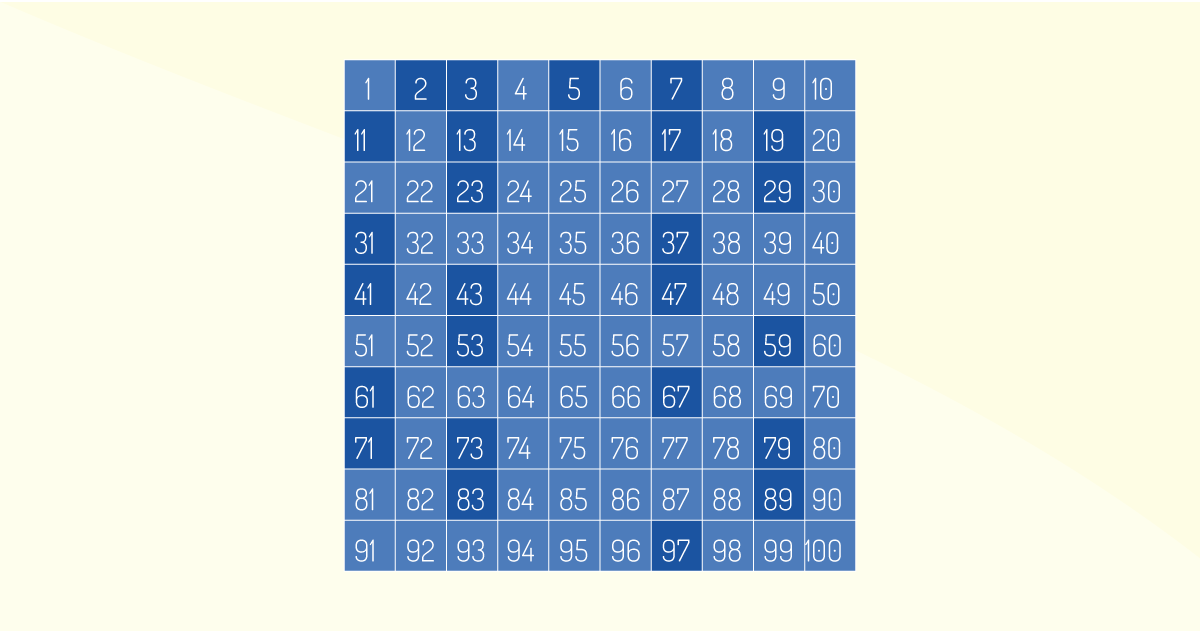
Na tabela representada pela Figura 1.5, destaca-se a lista dos 100 primeiros números naturais, com ênfase em roxo nos números primos entre 1 e 100. São eles: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
3 – Como foi visto, o número primo é um tipo de número que é divisível por 1 ou por ele mesmo. Então, tendo como base a unidade estudada, qual das opções abaixo representa um número primo?
a) 2002
Não é primo, pois pode ser divisível por outros valores que não apenas o 1 ou ele mesmo, por exemplo por 2, que daria 1001.
b) 1950
Não é primo, pois pode ser divisível por outros valores que não apenas o 1 ou ele mesmo, por exemplo por 2, que daria 975.
c) 1943
Não representa primo, pois é divisível por mais números além de 1 e ele mesmo, diferentemente dos outros.
d) 1917
Não é primo, pois pode ser divisível por outros valores que não apenas o 1 ou ele mesmo, por exemplo por 3, que daria 639.
e) 647
Este é primo, pois só pode ser dividido igualmente por 1 ou por ele mesmo. É, portanto, a alternativa correta.
Sabemos que toda matéria é composta e formada por pequenas partículas chamadas de átomos. Os primeiros a saberem de tal afirmação foram os gregos antigos, especificamente, o filósofo Demócrito (que viveu entre 546 a 460 a.C.), que deu o nome dessas partículas de átomos (do grego a: não; tomo: divisão), pois de fato se acreditava que não poderiam ser divididas, ou seja, um átomo seria indivisível. Entretanto, nos dias atuais, sabe-se que cada partícula de átomo pode sim ser dividida em outras mais pequenas, porém, a ideia em que a matéria exista em mínimas unidades ainda persiste.
Na aritmética também existe esse conceito de unidades mínimas, mas no lugar dos átomos, essa função é realizada pelos números primos.
Aqui se baseia o teorema fundamental da matemática, ou da aritmética, o TFA. Os descendentes de Pitágoras (Pitagóricos, 500 a 300 a.C.) foram os primeiros a tentarem desmistificar as propriedades gerais desses números, mas diferentemente das partículas atômicas, os números primos seguem em pleno funcionamento, como um conjunto numérico de extrema relevância, sendo atribuída a eles, até mesmo a responsabilidade em se criar absolutamente todos os números naturais diferentes de 0 e 1.
O TFA garante que um número natural que seja diferente de 0 e de 1, é sim, um número primo ou, no mínimo pode ser escrito como um produto de números primos, conforme mostra a Figura 1.5.
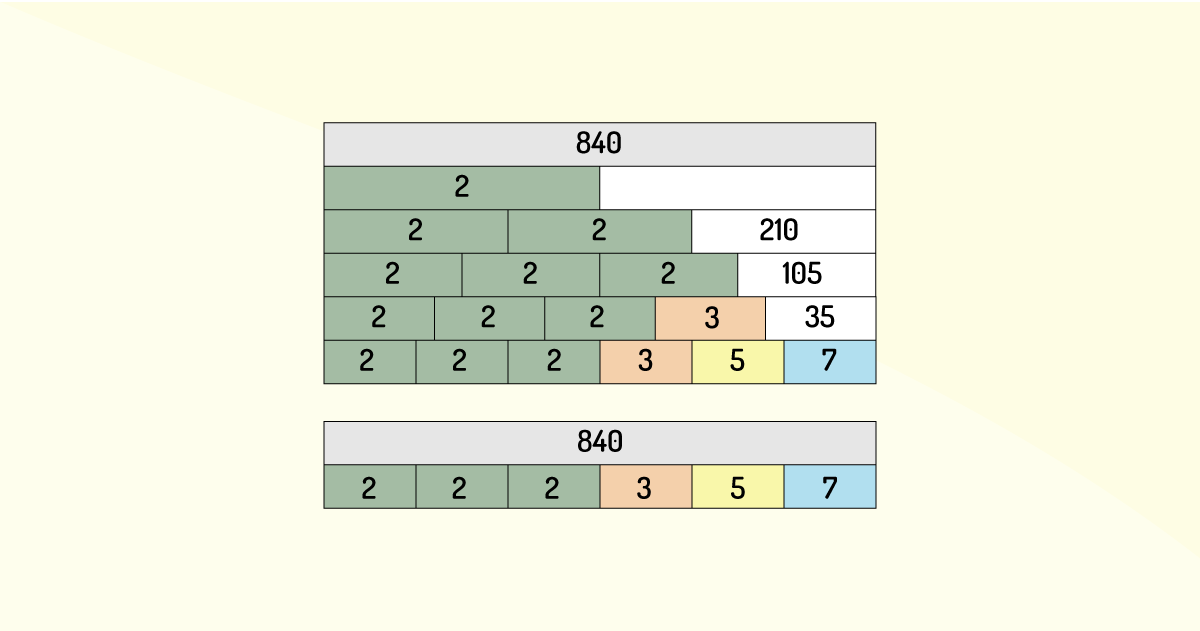
No exemplo acima percebe-se que o valor 840 não é primo, ou seja, é divisível por outros valores que não 1 ou ele mesmo, porém, quando se faz a fatoração, aparece em seu produto números primos, nisto é que se baseia o TFA.
Na linguagem matemática, especificamente no meio dos números naturais, as palavras divisor, divide e divisível são similares. Em termos gerais, podemos explicá-las como a e b números naturais sendo que: “a é um divisor de b” significando que há um número c, de modo ac = b; “a divide b” já mostra que “existe um número natural c tal que ac = b; Se dissermos que “b é divisível por a”, significa, neste caso, que “existe um número natural c tal que ac = b;
Como este teorema garante que todo algarismo natural superior a 1 ( n > 1) pode ser escrito como um produto de números primos e essa decomposição de primos é única, isso permite que se use uma notação para a fatoração.
Exemplo: 1512 = 2×2×2×2×3×3×7 = Fatoração de (1512) = 2 3×3 2×7.
Como já vimos no tópico anterior, este segundo método de se escrever, por meio da fatoração, é um exemplo de escrita exponencial da decomposição em primos. É preferível que se descreva sempre a decomposição em primos na ordem crescente, pois permite uma referência aos expoentes mais facilmente. No caso do exemplo acima, os expoentes seriam 3, 2 e 1.
Para se fatorar um número natural n, n>1, existem alguns passos que podem ser seguidos formalmente, sendo os seguintes:
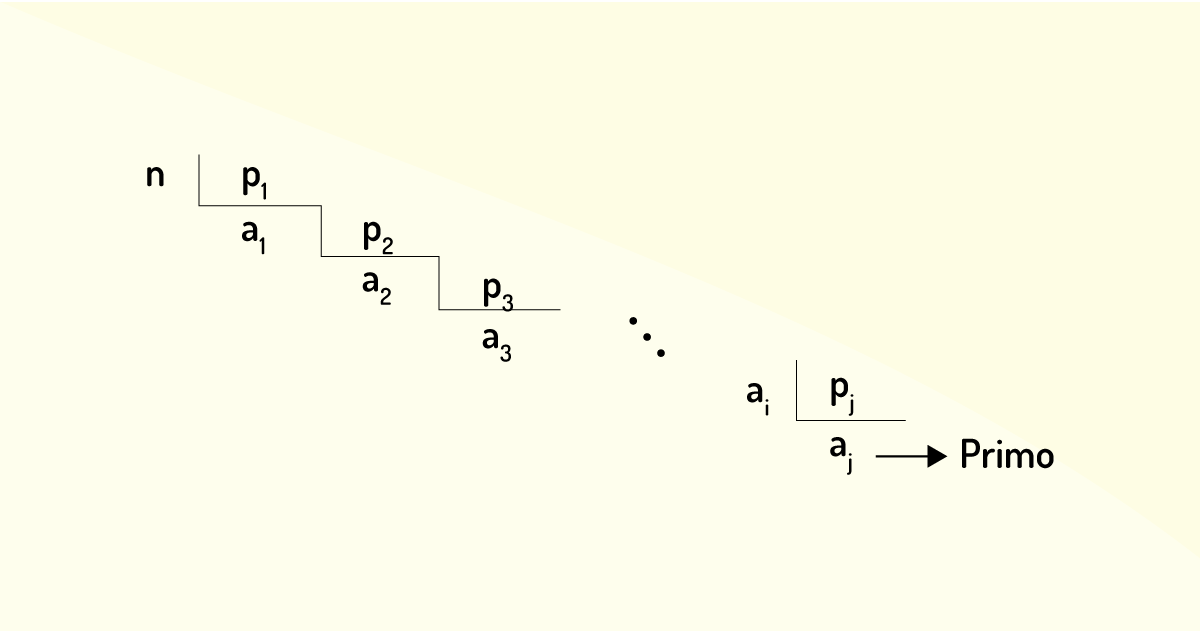
Observa-se que todas as vezes que um fator primo pj é achado, a partir de um divisor aj de n, um novo procedimento se abre e novos passos são executados. Este processo abre uma sequência decrescente, a1>a2>a3>⋯ de divisores de n. Por essa sequência, ter um número finito de termos, podemos concluir que o processo terá um fim, em algum momento. Muito provavelmente, este final se dará quando se encontrar um número primo.
O processo sucessivo por primos, quando aplicada no processo de fatoração ou decomposição, podem ser representadas, ou escritas das mais variadas maneiras. Para ficar no âmbito numérico, vejamos a decomposição de 60 em três maneiras diferentes:
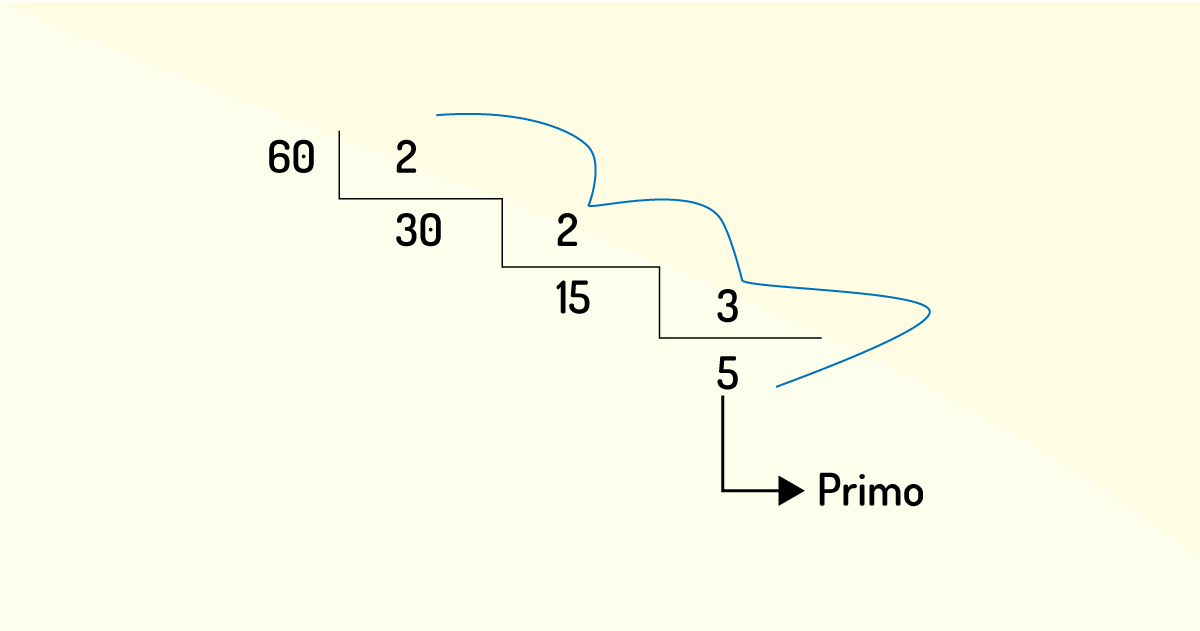
Baseando-se nessa lógica, é necessário conhecer os números primos menores ou iguais a n√n, se quisermos realizar a decomposição de um número natural n, superior a 1.
O TFA aparece vinculado à obra Elementos de Euclides, entretanto, sua primeira demonstração correta foi feita por Gauss e publicada em 1801, na obra Disquisitiones Arithmeticae.
Podemos conceituar o teorema a partir de duas abordagens. A primeira, conceitua que qualquer número natural maior que 1 ou é primo ou poderá ser escrito como fator de primo, como citado já anteriormente. Para este conceito, existe uma justificativa que se segue:
Justificativa - Se n é um número natural, ou seja, n>1, ele sendo um número primo, já não haverá nada para ser demonstrado. Partimos então, de que n seja um número composto. Como n tem divisores diferentes de 1, chama-se p1 o menor dentre esses divisores distintos de 1. Assim, existe um número natural n1 tal que: n=p1⋅n1. (i)
Se na primeira forma, a regra coloca que todo número maior que 1 pode ser primo ou produto primo, nesta segunda forma de se ver o teorema os algarismos maiores que 1 ou são primos, podem ser escritos de forma única.
Aqui, baseia-se de forma teórica o exemplo visto acima, portanto, o TFA defende essa ideia central de que qualquer número pode ser fatorado e seus produtos serem transformados em números primos, ou que ele próprio seja primo, sendo divisível apenas por 1 ou ele mesmo.
Assim, o teorema aritmético apresenta um resultado que além de assegurar a representatividade de um número natural maior do que 1, como produto de seus divisores primos, também confirma que essa representação será única. Além de outros benefícios, este resultado nos faz iniciar um processo de divisores de forma segura, pelo primo que nos for mais conveniente, dependendo da situação que apareça.
Já a segunda maneira é mais simbólica. Se n representa um número natural, n>1, então existirão números primos, p1, p2, p3...pr, com r ≥ 1, sendo que n=p1, p2, p3…pr.…, essa representação também é única.
4- Um dos princípios do teorema fundamental da aritmética é sobre os restos da divisão. Se considerarmos o número \(6^{2015}\) e o dividirmos por 10, qual seria o valor correspondente ao seu resto?
a) 4.
Falsa, pois podemos presumir que, em qualquer potência de 6, o resultado terá como algarismo final o próprio número 6.
b) 5.
Falsa, pois podemos presumir que, em qualquer potência de 6, o resultado terá como algarismo final o próprio número 6.
c) 6.
Correta,
Resolução: Para resolver esse exercício, não é necessário calcular 62015, mas somente descobrir qual é o último algarismo dessa potência. Para tanto, observe as seguintes potências:
\(6^2\) = 36
\(6^3\) = 216
\(6^4\) = 1296
\(6^5\) = 7776
Dessa forma, podemos presumir que, em qualquer potência de 6, o resultado terá como algarismo final o próprio número 6. Isso é verdade, pois 6·6 = 36; ao multiplicar 36 por 6, teremos novamente, no algarismo final, o número 6. Seguindo esse raciocínio, qualquer potência de base 6 terá como último algarismo o próprio 6.
Por outro lado, considerando os dois últimos algarismos de uma potência de base 6, teremos uma dezena terminada em 6. Suponha que essa dezena seja 36:
\[36 = 10·3 + 6\]
36 é dividendo, 10 é divisor, 3 é quociente e 6 é resto. Observe que, independentemente do número que ocupe a posição das dezenas, ele será divisível por 10 e deixará resto 6. Portanto o resto da divisão de \(6^{2015}\) por 10 é igual a 6.
d) 8.
Falsa, pois podemos presumir que, em qualquer potência de 6, o resultado terá como algarismo final o próprio número 6.
e) 9.
Falsa, pois podemos presumir que, em qualquer potência de 6, o resultado terá como algarismo final o próprio número 6.
Em nosso cotidiano, quando estamos em alguma situação relacionada à matemática, dificilmente lembramos das aulas que vimos e dos assuntos que lemos. Porém a matemática elementar, como vimos nesta unidade, se faz presente em diversas tarefas do nosso dia a dia. É preciso estar atento e compreender que a matemática envolve interação com o mundo a nossa volta.
Para aprofundar seus conhecimentos leia o artigo: Múltiplos e divisores: importantes ferramentas no ensino médio, disponível em: <http://uenf.br/posgraduacao/matematica/wp-content/uploads/sites/14/2017/09/11072014Bruno-Franca-Marques-da-Silva.pdf> e o site: <https://pt.khanacademy.org/math/pre-algebra/pre-algebra-factors-multiples/pre-algebra-factors-mult/a/factors-and-multiples-review>.

Estou vendo a matemática como fonte de estudo primordial para minha vida? Ou a quero simplesmente como meio de tirar nota? Que importância eu dou a ela?

Livro: Manual da Indução matemática
Editora: Interciência; Edição: 1ª (1 de janeiro de 1999)
Autor: Luis Lopes
ISBN: 8571930139
Este livro possui uma sistematização muito bem ordenada sobre a indução matemática e outros conteúdos algébricos. Sua grande vantagem é que possui muitas fórmulas, explicações e diversos exemplos e exercícios muito úteis para o aprendizado.

Filme: PI
Gênero: Suspense, Ficção científica
Ano: 1998
Elenco Principal: Sean Gullette, Mark Margolis, Ben Shenkman
O filme PI conta a história de Max, que construiu um supercomputador capaz de descobrir o número completo do Pi e compreender a existência da vida na Terra, adivinhando, dessa forma, os acontecimentos no mercado da bolsa de valores e, por isso, ser requisitado por representantes de Wall Street e também por uma seita que busca decifrar os mistérios da matemática. Vale a pena assisti-lo!
