Olá, aluno(a)! Bem-vindo(a) à terceira unidade de nosso material. A partir de agora estudaremos a respeito da congruência ou congruência módulo m, que é uma importante ferramenta da teoria elementar dos números. Esse fundamental conceito matemático tem diversas aplicações e foi desenvolvida, essencialmente, pelo matemático alemão Carl Friedrich Gauss (1777-1855). O matemático nomeou m como congruência, com base no fato de que o elemento a daria sempre o mesmo resto de b, quando dividido pelo m.
Quando estudamos alguns aspectos do conjunto dos números inteiros, deparamo-nos com o problema da divisão euclidiana (divisão com restos), conforme discutimos nas unidades anteriores. Tais conteúdos devem ser introduzidos já no Ensino Fundamental, assim como a congruência. Buscaremos apresentar algumas aplicações e propriedades básicas dessa área aritmética.
Exemplificando:
Dada a expressão:
27 31 (mod 4),
teremos o (mod 4), pois, se utilizarmos os princípios da teoria euclidiana de divisibilidade, nesse contexto, teremos tanto o 27 quanto o 31 deixando em suas divisões um resto 3, quando divididos por 4.
O conteúdo relativo à álgebra modular pode ser estudado introduzindo relações de congruências a partir do conjunto dos números inteiros, que se encaixam, também, nas operações do anel dos inteiros, abrangendo três das operações básicas da matemática: a adição, subtração e multiplicação. De forma mais concreta, dizemos que um inteiro positivo chamado n terá dois elementos, que denominaremos a e b, ditos aqui como congruentes ou côngruos, escrito como módulo n ou em uma formula organizada:
a = b (mod n)
Quando a diferença entre a - b for um inteiro múltiplo de n, chamaremos o elemento n de modelo da congruência. Observe o exemplo abaixo:
Exemplificando:
38 = 2 (mod 12), pois 38 - 2 = 36, que é múltiplo de 12.
Podemos aplicar essa mesma regra, em relação aos números negativos:
-8 = 7 (mod 5)
2 = -3 (mod 5)
-3 = -8 (mod 5)
Caso os elementos a e b sejam ambos positivos ou ambos negativos, teremos a = b (mod n). Essa afirmação pode ser considerada se a/n e b/n possuir o mesmo resto. Colocando em números poderemos observar melhor, por exemplo, 38 = 14 (mod 12), em que os dois valores 38/12 e 14/12, possuem o mesmo resto, isto é, 2.
Veja, também, que 38 - 14 = 24, portanto, o resultado é um inteiro múltiplo de 12, o que entra em concordância com a definição inicial de relação em congruência.
Vale destacar que é muito comum a congruência possuir várias relações simultâneas com diferentes módulos e esses módulos são incorporados na notação. Mesmo se essa notação tiver quatro elementos, ainda assim a relação será fixada como binária. Isso precisa estar esclarecido se a notação \(a ≡_n b\) for utilizada, ao invés da tradicional.
As propriedades existentes nessa relação de congruência são as seguintes:
se, \(a_1 = b_1 (mod n)\) e \(a_2 = b_2 (mod n)\)
então:
\(a_1 + a_2 = b_1 + b_2 (mod n)\)
\(a_1 - a_2 = b_1 - b_2 (mod n)\)
Observe que as propriedades descritas acima serão válidas se expandirmos a teoria e incluir nela os números reais.
Você deve estar se perguntando, mas onde está a operação de divisão, em todo esse processo da congruência? Pois bem, em congruências não se aplica divisões. Em seu lugar realiza-se uma multiplicação, em ambos os elementos, por algum número que não seja conveniente. Como qualquer número, na divisão por 1 deve restar 0, então, não é interessante, nem recomendado, utilizar o módulo 1, já que para qualquer a e b inteiro sempre existirá a = b = 0 (mod1).
Todas as vezes em que houver uma relação de equivalência em um conjunto X, será possível definir uma parte P sobre esse mesmo X. Várias partes de P, que podemos chamar de subconjuntos X, é denominada (a coleção) de partição de X, evidentemente, se todos os elementos dessa coleção participarem de ambos conjuntos X e P. Os elementos de P são postos em pares e quando se unem formam, novamente, o conjunto X.
Já para se elaborar uma partição de Z, utilizando o método da congruência de módulo m, primeiramente será preciso definir para cada número inteiro a sua classe de equivalência, como se dá na expressão abaixo:
\([a]_m\) = {x e Z; x = a (mod m)}
Em casos que o número inteiro m já estiver subentendido sua presença, na expressão será utilizado apenas [a], que denota \([a]_m\). Com esses termos, o quociente do conjunto Z se dará pela relação = (mod m) e a partição escrita por:
\(Z/=_{(mod m)} = {[a]_m; a~e~Z}\)
Simplificando a expressão, podemos descrever \(Z/=_{(mod m)}\) apenas como \(Z_m\). Para conseguirmos enxergar essa partição de Z, podemos visualizar uma linha, em que são marcados todos os números inteiros, separando-os pela mesma distância. Logo após, para se ter a representação de \(Z_m\), imagine essa linha sendo enrolada em volta de uma circunferência (infinitas vezes, já que esse é um exercício de imaginação, pois os números inteiros são infinitos). O zero será posto de forma que ocupe a mesma posição dos inteiros: … -2n, -n, n, 2n, 3n, .... Posteriormente à conclusão, poderemos pensar nos elementos \(Z_n\) como sendo os n pontos distribuídos sobre a circunferência que se formou. Veja o esquema a seguir, que ajuda nessa visualização:
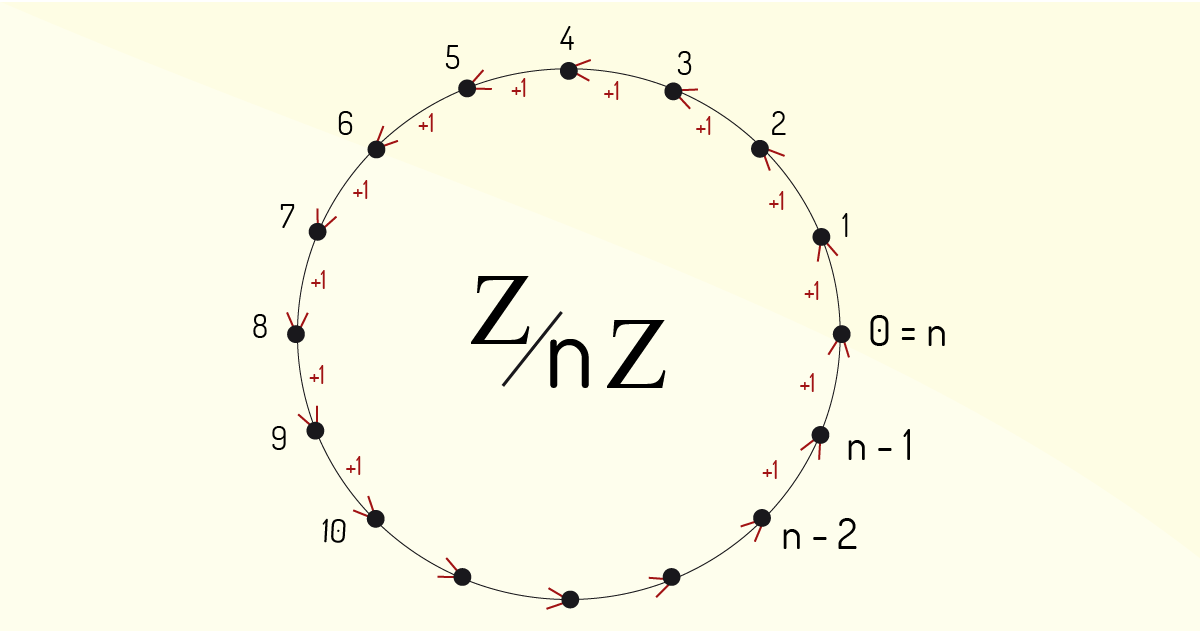
Conforme representado anteriormente, cada ponto da circunferência representa uma equivalência de módulo n, isto é, são classes que ilustram o conjunto dos inteiros que estão sobrepostos naqueles pontos, dentro da circunferência criada. Agora, o que há de tão atrativo na participação dos números inteiros?
Bem, a grande vantagem de se dividir os números inteiros em classes de congruência que se tem, é a consequência que essas classes terão em ser mais compatíveis com as operações de adição e de multiplicação. Se essas classes forem compatíveis será possível definirmos em cada \(Z_m\) ainda mais operações de adição e multiplicação, ou seja, criar mais e novas operações. Para isso, devemos seguir o procedimento a seguir:
Quando fixado um inteiro m e dadas as classes [a] e [b], definimos:
[a] + [b] = [a + b]
[a] x [b] = [a x b] ou, para simplificar, ([a] [b] = [ab]).
Em outras palavras, temos a soma do produto das classes de congruência, elementos inteiros a e b, que é a classe da sua própria soma dos produtos. É essencial notar, também, de que forma a compatibilidade da congruência com as operações nos subconjuntos Z é usada. Podemos dar duas classes de equivalência: A = [a] = [a´] e B = [b] = [b´], que será similar a expressão [A] + [B], resultando em [a + b], [a´ + b], [a + b´] ou [a´ + b´]. Nesse caso, todas essas classes são equivalentes. Mais do que isso, definindo essas operações, os elementos (\(z_m\), +, x) também se tornam um anel com unidade, ou seja, passam a valer as propriedades a seguir:
Z = {0, + ou - 1, + ou - 2, + ou - 3...} e Zm = {mZ + 0, mZ + 1, ..., mZ + (m - 1) }
1) Com base nos estudos desta unidade e de seus conhecimentos adquiridos ao longo dessa trajetória, faça o que se pede:
A partir da propriedade MOD, ao observar três números que, somados a 16, tornam o resultado divisível por 6, podemos dizer que:
a) Os três números são 4, 10 e 20.
Falsa. Veja que o número 10 não torna o 16 divisível por 6. Observe, ainda, que 16 + 10, utilizando o Mod16, que é 4 e, utilizando mod6, temos: 4 + 4 + 6 ≡4 + 4 + 0 ≡ 8, ou seja, não tem resto nulo, logo, não é múltiplo de 6.
b) Os três números são 2, 8 e 14.
Verdadeira. Veja que:
16 + 2 = 18;
16 + 8 = 24;
16 + 14 = 30;
Utilizando a propriedade (Mod) podemos reescrever essas expressões da seguinte forma:
16 + 2 -> 4 + 2 ≡ 0;
16 + 8 -> 4 + 2 + 6 ≡ 0;
16 + 14 -> 4 + 2 + 6 + 6 ≡ 0.
Desse modo, o MOD de 16 é 4. Fatorou-se os demais números.
Como se trabalha com Mod6 e todas as operações são congruentes a 2 (mod6), elas têm por resultado o zero. Grosso modo, equivale dizer que como todas elas são divisíveis por 6, porque o resto será sempre nulo.
c) Os três números são 4, 6 e 8.
Falsa. Veja que o número 6 não torna o 16 divisível por 6. Observe, ainda, que 16 + 6, utilizando o Mod16, que é 4, e utilizando mod6 temos: 4 + 6≡4 + 0 + 0 ≡ 4, ou seja, não tem resto nulo, logo não é múltiplo de 6.
d) Os três números são 2, 10 e 12.
Falsa. Veja que o número 12 não torna o 16 divisível por 6. Observe, ainda, que 16 + 12, utilizando o Mod16, que é 4 e, utilizando mod6, temos: 4 + 6 + 6 ≡4 + 0 + 0 ≡ 4, ou seja, não tem resto nulo, logo não é múltiplo de 6.
e) Os três números são 4, 8 e 10.
Falsa. Veja que o número 10 não torna o 16 divisível por 6. Observe, ainda, que 16 + 10, utilizando o Mod16, que é 4 e, utilizando mod6, temos: 4 + 4 + 6 ≡4 + 4 + 0 ≡ 8, ou seja, não tem resto nulo, logo não é múltiplo de 6.
Nos estudos voltados para a matemática do último século, as questões algébricas e numéricas, que tanto a marcavam, diminuíram, passando a se dedicar mais, de forma tendenciosa, para aquilo que é abstrato. Entre essa área, denominada de álgebra moderna, chama-se a atenção para a teoria dos anéis e dos ideais, pois são completamente abstratas, desde a sua origem. Trata-se de um conteúdo impensável na antiguidade, já que é totalmente moderno. Se pesquisarmos a fundo, encontraremos a maior parte dos estudos que se relacionam com os anéis desenvolvidos nos últimos 80 e 90 anos. Portanto, essa é, de fato, uma área que vem se desenvolvendo muito recentemente.
Em contrapartida, a teoria dos anéis teve sua origem em meados do século XIX, tendo, na verdade, poucos autores dedicados em estudar essa teoria moderna. O primeiro a iniciar os estudos foi Richard Dedekind (1831-1916), que foi o responsável por introduzir, em 1871, as noções de ideais, a fim de generalizar o teorema fundamental da matemática a um patamar mais abstrato. Em seguida, David Hilbert (1862-1945), Edmund Lasker (1868-1941) e Francis Sowerby Macaulay (1862-1927) contribuíram para o desenvolvimento de anéis e polinômios.
No entanto, quem, de fato, criou a teoria dos anéis foi Adolf Fraenkel (1891-1965), em seu trabalho, denominado “On the divisors of zero and the decomposition of rings” (Divisores de zero e a decomposição dos anéis). Nesse estudo, Fraenkel desenvolveu a primeira caracterização para as noções de anel que conhecemos e estudamos atualmente.
Vale ressaltar que essas noções postas por ele, hoje servem apenas como critério histórico e não são mais estudadas, no entanto, naquele momento, foram muito importantes para o desenvolvimento dessa teoria. Seu real objetivo era de generalizar e amplificar os estudos dos corpos, a fim de obter uma teoria para ser aplicada aos módulos inteiros n e a desenvolver os sistemas conhecidos como números hipercomplexos.
A definição de anéis que embasa os estudos atuais teria surgido no século XX, mais precisamente em 1917, com o matemático japonês Masazo Sono, em sua obra “On congruences” (Em congruências).
Se falarmos em contribuição, quem mais fez pelo avanço das questões abstratas da matemática e da teoria dos anéis foi Emmy Noether (1882-1935). Seu artigo, “Ideal theory in rings” (Teoria ideal em Anéis), publicado em 1921, deu origem a teoria abstrata dos anéis. Nesse trabalho, a autora e matemática estende ainda mais os trabalhos de Hilbert, Lasker e Macaulay sobre os anéis de polinômios e, na sequência, ainda evolui conceitos de anel abstrato que Dedekind havia realizado para anéis de números algébricos.
Essa revolução em trabalhar com os modos abstratos da aritmética nas áreas dos anéis e ideais levou a um contexto de estudo da fatoração prima e acabou, por consequência, criando o que hoje chamamos de álgebra comutativa. Na década de 30, todas essas ideias foram organizadas e postas à disposição da nova geração de pesquisadores, estudiosos e matemáticos que vinham pela frente, a fim de desvendarem e evoluírem esse lado abstrato.
Questões fundamentais como, por que (-1) + (-1) = 1 e a · 0 = 0, são pontos relevantes e objetos centrais de estudo que fazem parte da justificação dessas áreas abstratas de estudo, conduzindo aos conceitos de anel e domínio de integridade.
Quando pensamos na teoria dos números vemos que a matemática faz parte de toda nossa vida e está ligada diretamente ao nosso cotidiano, seja ele qual for, desde o início dos tempos. Recorremos aos números para descrevermos e planejarmos boa parte das ocorrências de nosso dia.
Quando realizamos uma conta simples, utilizamo-nos, por exemplo, de números naturais. Quando cortamos um bolo fazemos uso de frações ou números racionais, medimos distâncias, tamanhos, contabilizamos prejuízos, enfim, se prestarmos atenção estamos mais que familiarizados com os diversos conjuntos numéricos existentes. Podemos então, relacionar os conjuntos, da seguinte maneira:
N ⊂ Z ⊂ Q ⊂ R ⊂ C.
Enfatizamos que, conforme vimos anteriormente, já estamos acostumados, em nosso dia a dia, a lidar com esses números e conjuntos. Ainda que não saibamos seus conceitos, não são estranhos para nós e temos condições de perceber que cada um desses conjuntos numéricos estão inseridas em operações de adição e de multiplicação, possuindo diversas propriedades.
Diante disso, no próximo tópico introduziremos o estudo de estruturas algébricas, baseando-se nos conceitos sobre a teoria dos anéis e seus domínios.
Podemos definir anel (A, +, ·), como um conjunto A, que tem duas operações binárias, em que as denotaremos de + e ·, sendo que esse anel pode ser descrito da seguinte forma:
(1) (A, +) é um grupo abeliano
(2) é associativa; isto é,
(a · b) · c = a · (b · c), para quaisquer a, b, c ∈ A
(3) é distributiva relativamente a +; ou seja,
a · (b + c) = a · b + a · c, e,
(b + c) · a = b · a + c · a, para quaisquer a, b, c ∈ A.
Utilizaremos a denotação A, simplesmente para falar sobre um anel arbitrário (A, +, ·). Se observarmos esse anel A, considerando-o como comutativo, então, juntamente com o elemento ·, devemos chamá-lo de anel com identidade ou, também, de anel unitário. Mostraremos no quadro a seguir algumas notações adicionais:
Quadro 3.1 – Notações de anéis
Fonte: Adaptado de Waerden (1931).
Apresentaremos, a partir de agora, a composição algébrica de anel e, também, a exemplificaremos.
Temos conhecimento de diversos tipos de conjuntos, todos variáveis, certo? Internamente a cada conjunto, estão definidas as operações de adição e de multiplicação entre seus membros. Essas operações apresentam, também, propriedades únicas. Vamos relembrar algumas delas a seguir:
Os conjuntos dos números inteiros, racionais e reais podem ser equiparados, também, com uma relação com ordem ≤. Observemos que nas operações de adição e de multiplicação, a ordenação e suas propriedades relacionam-se com as características gerais dos números inteiros.
Retomando a definição que fizemos no início deste tópico, um anel A é um conjunto que tem operações de adição (+) e de multiplicação (·). Essas operações apresentam as seguintes propriedades:
Exemplificando:
Consideremos um intervalo I = (-1, 1), sendo F (I) o conjunto de todas as funções de I em R, ou seja:
F (I) = {f: I - → R | f é uma função}
Para qualquer elemento de f, g ∈ F (I), as operações comuns de adição e de multiplicação de funções são determinadas por:
(f + g) (x) = f(x) + g(x), para todo x ∈ I e
(f · g) (x) = f(x) · g(x), para todo x ∈ I
Dadas essas operações, podemos concluir que F (I) é um anel.
Como algumas propriedades elementares dos anéis, tem-se a unicidade de um elemento neutro aditivo, além do simétrico e, também, casos em que se tenha o elemento neutro multiplicativo.
Então, considerando um anel A, teremos as opções:
Exemplificando:
(i) No primeiro caso, consideramos θ e θ′ como elementos neutros aditivos do anel A. Portanto, descreveremos:
θ = θ′ + θ = θ′
Observamos a primeira igualdade originada do fato de θ′ ser um elemento neutro da adição e, na sequência, a segunda proveniente de θ ser um neutro da adição. Desse modo, temos a conclusão de que θ = θ′ e o elemento neutro aditivo é único.
(ii) No segundo caso, daremos um anel A, com unidades e e e′. Teremos, então:
e = e′ · e = e′
Aqui, a primeira igualdade deve-se ao fato de e´ ser uma unidade, assim como a segunda. Temos, portanto, e = e′ e o elemento neutro multiplicativo é único.
(iii) No terceiro caso, veremos a′ ∈ A e a′′ ∈ A simétricos de a ∈ A. Assim, teremos:
(θ = a + a′′, θ = a′ + a) e (a ′ = a ′ + θ = a ′ + (a + a ′′) = (a ′ + a) + a ′′ = θ + a ′′ = a ′′)
Com isso, a terceira igualdade terá uma associação da adição. Então, a simetria dessa expressão será única.
Desse modo, a partir da unicidade do elemento neutro aditivo, do simétrico e do neutro multiplicativo, quando ele aparece, denotaremos daqui pra frente um anel A, com propriedades elementares, sendo:
Além disso, devemos descrever a expressão, a - b = a + (-b) e a nomearemos de subtração.
Podemos definir domínio de integridade como um próprio anel de integridade ou comutativo, com unidade e sem divisores de zero. Um anel Z tem propriedades que, de maneira geral, um anel comum não tem.
Considerando um elemento não nulo “a”, em um anel comutativo A, é chamado um divisor de zero caso exista um elemento não nulo “b” em A, de modo que ab = 0.
Dessa maneira, quanto tiver um anel comutativo, com unidade, será chamado de domínio integral ou, de forma mais simples, apenas de domínio, caso não tenha nenhum divisor de zero. Assim, um domínio integral pode ser representado pela expressão: ab = 0 ⇔ a = 0 ou b = 0.
2 - Após o estudo da Teoria dos Anéis e os conhecimentos adquiridos ao longo dessa trajetória, analise as alternativas e julgue a única correta.
a) O conjunto dos números inteiros (Z) não é Anel.
Falsa. O conjunto Z é um anel.
b) O conjunto dos números inteiros (Z) é Anel.
Verdadeira.
Para mostrar que o conjunto dos inteiros Z é um anel, verificamos, primeiramente, alguns pontos:
Notação (Z,+,*).
Verificando as operações de soma e de multiplicação de dois elementos internos a e b dentro do conjunto, temos que:
+: Z x Z -> Z (a+b) -> a+b
*: Z x Z -> Z (a*b) -> a*b
Observe que tanto a soma quanto a multiplicação de dois inteiros gera outro número inteiro que, por sua vez, pertence ao conjunto dos números inteiros.
Em um segundo momento, avalia-se se as propriedades de associatividade, comutatividade, elemento neutro e elemento simetrizável são válidas.
Para a operação (+), tem-se que:
associatividade: (a+b)+c | a+(b+c) ->
a+b+c | a+b+c.
A operação (+) em Z admite associatividade.
Veja que a propriedade é válida.
Comutatividade: (a+b) = (b+a), válida, também, tratando-se dos números inteiros.
A operação (+) em Z admite comutatividade.
Elemento neutro: sendo a, e E Z
a+e = e+a = a; logo, o elemento neutro (e) só pode ser zero.
e = 0.
A operação (+) em Z admite elemento neutro.
Elemento simetrizável: sendo a, a`E Z:
a+a´= 0, logo a´= -a.
A operação (+) em Z admite elemento simetrizável.
Verificando, agora, as mesmas propriedades para a operação (*), temos que:
Associatividade: (a*b)*c | a*(b*c) ->
a*b*c | a*b*c.
A operação (*) em Z admite associatividade.
Distributiva: a(b+c) = (b+c)a
a(b+c) | (b+c)a
ab+ca | ba+ca
A operação (*) em Z admite a propriedade distributiva.
Elemento neutro: sendo a, e1, e2 E Z
a*e1 = e1*a = a;
a*e2 = e2*a = a;
se e1 e e2 são elementos neutros na equação, então:
e1*e2 = e1| e1*e2 = e2
Logo, e1 = e2; então, e1 = e2/e2 = 1 => e2 = e1/e1 = 1.
A operação (*) em Z admite elemento neutro.
c) 12≡5(mod3), pois 12 - 5 = 7. Então, dizemos que 12 é côngruo a 5.
Falsa. 12≡5(mod3), pois 12 - 5 = 7. Então, dizemos que 12 não é côngruo a 5.
d) 11≡ 5(mod3), pois 11 - 5 = 6 = 2*3. Então, dizemos que 11 não é côngruo a 5.
Falsa. 11≡ 5(mod3), pois 11 - 5 = 6 = 2*3. Então, dizemos que 11 é côngruo a 5.
e) 7≡15(mod2), pois 7 - 15 = -8 = 2*-4. Então, dizemos que 7 não é côngruo a 15.
Falsa. 7≡ 15(mod2), pois 7 - 15 = -8 = 2*-4. Então, dizemos que 7 é côngruo a 15.
Podemos definir os anéis Z e Q como domínios de integridade ou anéis de integridade. Entretanto, enquanto no anel dos inteiros apenas os elementos 1 e -1 são simétricos e multiplicativos, nos anéis de números racionais todos os elementos que não sejam nulos podem admitir a simetria e a multiplicação. Portanto, podemos definir um anel K, comutativo com unidade, como corpo, isso se todos os elementos não nulos desse conjunto K também admitirem ser simétricos multiplicativos, isto é:
∀ a ∈ K, a ≠ 0, ∃ b ∈ K; a * b = 1
Nota: O b que aparece na definição de corpo também é chamado de oposto de a e descrito como a-1. Em um anel com unidade, indicaremos a denotação U (A) como subconjunto de A, elaborado pelos membros que possuem simétrico multiplicativo (inverso). Damos o nome a esses elementos de invisíveis. Desse modo, um corpo definido por K é, de fato, um anel comutativo com unidade, de modo que U (K) = K∗ = K - {0K}.
Exemplificando:
As letras Q, R e C são os exemplos mais conhecidos de corpos. O teorema que explicitaremos diz que, se for finito, corpos e domínios passam a ser os mesmos, ou seja, se D for um domínio do tipo finito, D também se tornará um corpo.
Se D é um domínio, logo D será um anel comutativo com unidade. Dessa forma, só resta provar que todos os elementos não nulos também podem ser invertidos. Portanto, seja a ≠ 0 um dos elementos de D, sendo esse conjunto finito, a sequência de a, a2, a3, a4... irá se repetir, ou seja, existe um i > j, tal que a i = a j. Assim, pela lei do cancelamento, a j (a i - j - 1) = 0 e como a ≠ 0, temos que a i - j = 1. Se i - j = 1, a = 1 e, portanto, se inverte.
Consideramos K como um conjunto qualquer e, nele estão definidas operações binárias, adição e multiplicação, denotadas com os símbolos ++ e xx, respectivamente. Dizemos que KK, inserida a essas operações, constituirá um corpo quando se tiver as seguintes propriedades:
(1) Propriedades da adição:
(2) Propriedades da multiplicação:
(3) Propriedade (distributiva) de ligação:
Exemplificando:
Um dos exemplos mais comuns de corpos é o conjunto RR, dos números reais, com as operações comuns de adição e de multiplicação. Também é um corpo o conjunto QQ, dos números racionais, com operações habituais. E, por fim, o conjunto CC, dos números complexos, com operações habituais.
Quando dizemos que serão considerados corpos apenas os números reais, subentende-se que serão observadas somente as operações usuais, mas nelas se incluem os números racionais e complexos, já que estamos falando dos reais.
Porém, é possível definir inúmeros outros corpos. Poderíamos elaborar um corpo, por exemplo, a partir do conjunto K = {0, 1, 2} K = {0, 1, 2}, estabelecendo as duas operações de adição e de multiplicação, a partir das figuras apresentadas:
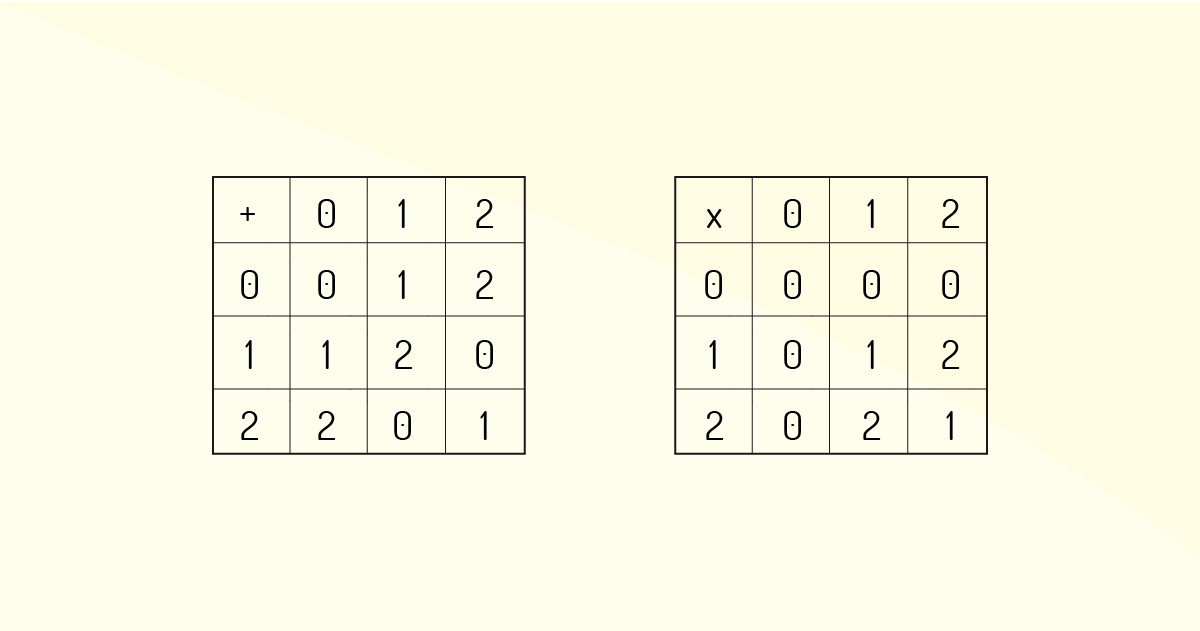
A propriedade 2 - c, conforme definição vista anteriormente, demonstra que um corpo só será, de fato, corpo, se tiver, no mínimo, dois elementos diferentes. Mas, vemos que, mesmo com um conjunto simples de dois elementos, será possível a construção de um corpo, sendo K = {0, 1} K = {0, 1}. Para esse exemplo, observemos as seguintes figuras:
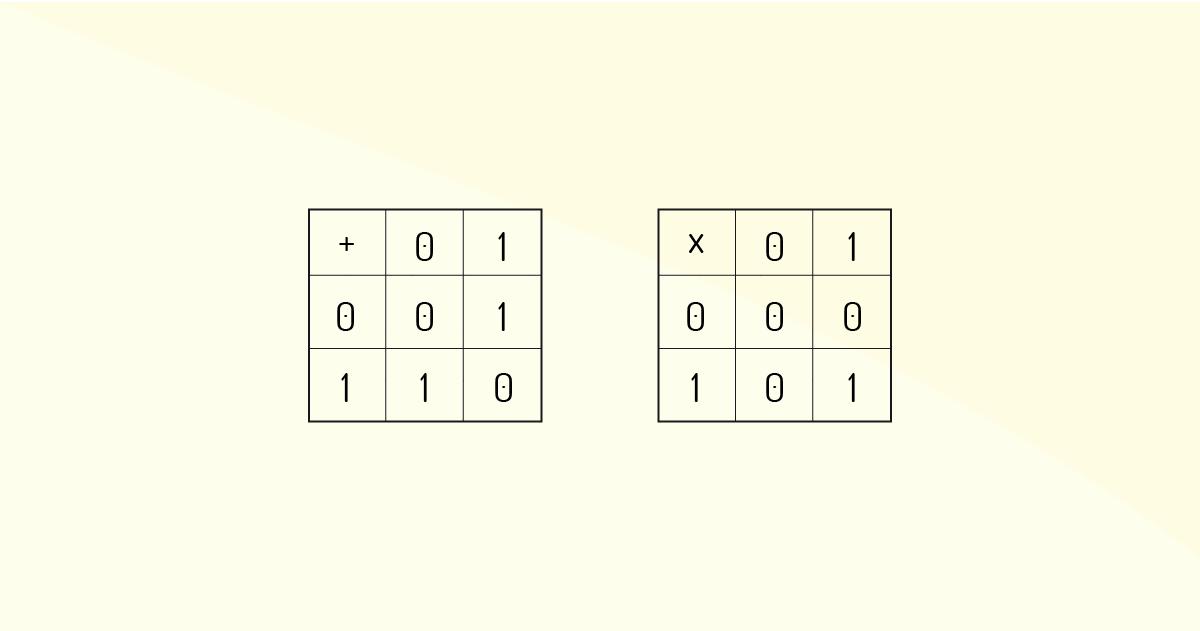
Veja que na figura 3.3 temos a construção do corpo, primeiramente, pela propriedade da adição e, em seguida, pela propriedade da multiplicação. Observe que ambas as propriedades apresentam dois elementos distintos, ou seja, encontramos nas duas figuras os números zero e um.
A seguir, veremos os subanéis.
Resumidamente, podemos definir um subanel (de acordo com o nome sub) como um subconjunto não vazio denominado S, baseado em um anel (R, +, ·). Dizemos que R pode ser um subanel se nas operações induzidas pelas operações de R (restrições) existir o subanel S que, nesse caso, seria um anel também.
Em suma, a partir desse teorema, um subconjunto S ≠ Ø de um anel (R, +, ·) será um subanel de R se as seguintes afirmações forem contempladas:
(→) Se S ⊆ R é um subanel, logo em todos os elementos a, b ϵ S, teremos -b ϵ S e a ϵ S. Então, a - b ϵ S, pois + é uma operação binária em S e, a · b ϵ S, pois · é uma operação em S.
(←) Sejam + |S: S × S → R e · |S: S × S → R, como restrições de + e · à S, a condição (ii) implica que → · |S: S ×S → S, i · é, · | S é uma operação em S., porém, ainda teria:
Como a associação de +, a comutação de + e a associação e distribuição valem em R, teremos, também, essas propriedades ativas em S, que é seu subconjunto. Desse modo, (S, +, ·) torna-se um anel, provando que S é subanel de R.
Exemplificando:
É certo que, para todo a, b ϵ n Z → a = nk1, b = nk2, com k1, k2 ϵ Z. Assim, a - b = n (k1 - k2) ϵ n Z e a · b = n (k1 k2 n) ϵ n Z. Se analisarmos R = Z6, teremos:
S1 = {0, 2, 4} e S2 = {0, 3} são subanéis de Z6, pois 2 · 4 = 2, -2 = 4;
3 = -3, 3 · 3 = 3.
Veja que 1R = 1, 1S1 = 4, 1S2 = 3. Dessa forma, Si ⊆ R são subanéis com 1, tais que:
1Si ≠ 1R, para i = 1, 2.
{0} e R são sempre subanéis de R, denominados como subanéis triviais.
Z ⊆ Q ⊆ R⊆ C é, portanto, uma fileira de subanéis.
Outra propriedade dos subanéis é que a unidade de um anel não necessariamente é a do subanel. Vejamos, por exemplo, o anel Z12 e seu subconjunto B = ﴾0; 3; 6; 9﴿. Verificamos, de forma simples, que para cada x ϵ B e cada y ϵ B, tem-se um x - y ϵ B e um x. y ϵ B. Portanto, B é um subanel de Z12.
Veja, agora, que 9 . 3 = 3, 9 . 6 = 6 e 9 . 9 = 9. Então, se denotarmos 1B = 9, teremos 1B . x = x, ∀ x ϵ B. Como esse caso é comutativo, teremos que 1B = 9 é um elemento de unidade da multiplicação em B. Assim, B torna-se um subanel comutativo com unidade, mesmo que seu elemento unidade não seja a mesma que o anel Z12.
Considerando (A, +, ·) e S, ∅ um subconjunto de A, S será um subanel de A somente se S for fechado com relação a subtração e a multiplicação de A. Ou seja, somente se x - y ∈ S e x · y ∈ S para quaisquer x, y ∈ S .
Dentro da teoria dos anéis e dos subanéis é possível identificarmos sete axiomas. A seguir, demonstraremos a definição de cada um deles:
3) Em relação aos grupos, corpos e subanéis, assinale a alternativa correta.
a) um grupo tem duas propriedades fundamentais, Associatividade e Elemento Neutro.
Falsa. Entre outras propriedades, um grupo tem três propriedades fundamentais, Associatividade, Elemento Neutro e Inversos.
b) Podemos definir subanel como um subconjunto vazio denominado S.
Falsa. Podemos definir subanel como um subconjunto não vazio denominado S.
c) A essência por trás da Teoria dos Grupos é tomar dois elementos de um conjunto, combinar eles de alguma maneira e retornar um terceiro elemento do mesmo conjunto e é esse o papel das operações binárias.
Falsa. O objetivo principal dessa teoria é fazer com que dois elementos de um conjunto combinem-se.
d) As letras Q, R e S são os exemplos mais conhecidos de corpos.
Falsa. Os exemplos mais conhecidos são Q, R e C, ao invés de S.
e) Na teoria dos anéis e subanéis existem até sete axiomas.
Verdadeira. Dentro da teoria existem sete axiomas.
Os ideais foram propostos, primeiramente, por Dedekind, em 1876, de forma generalizada, pois, um matemático chamado Ernst Kummer, já havia contemplado algo sobre essa área. Alguns anos mais tarde, essa teoria foi ainda mais expandida por David Hilbert e Emmy Noether.
Na teoria dos anéis, ramo já abordado nos tópicos anteriores, um ideal é, na verdade, um subconjunto diferenciado de um anel. O conceito amplia, de forma apropriada, algumas propriedades muito importantes dos números inteiros, como “número par” e “múltiplo de 3”.
Por exemplo, na teoria dos anéis, os ideais são estudados como primos. Ao invés de números primos, em que se definem ideais coprimos como uma generalização dos algarismos coprimos e, também, pode-se provar um teorema de resto para ideais. Dedekind criou seus domínios e foi considerado uma importante classe dos anéis. Os ideais poderiam até mesmo imitar esses domínios, originando uma versão atualizada do teorema fundamental da aritmética. Nesses anéis, todos os ideais não nulos, podendo ser descritos como produtos únicos de ideais primos.
Um ideal também pode ser utilizado na construção de um anel quociente, da mesma maneira que um subgrupo normal é utilizado na elaboração de um grupo quociente.
Assim, podemos definir ideal a partir da lógica em que seja o conjunto R um anel com (R, +) e, sendo o grupo abeliano desse anel um subconjunto I de R, é chamado ideal à direita se cumprirem tais afirmações:
Igualmente, será reconhecido e nomeado como ideal à esquerda se:
Se observarmos, os ideais que estão à esquerda em R são os mesmos que estão à direita do anel oposto Rop e vice-versa. Concluímos, desse modo, que quando R for um anel comutativo, as noções de ideal à esquerda e à direita coincidirão e, se o ideal for bilateral, não precisaremos nomeá-lo esquerda ou direita, apenas chamá-lo de ideal.
Os subconjuntos {0} e R de um anel R são ideais.
Chamamos de ideal próprio, se o conjunto de R também for próprio. Por sua vez, será chamado de Ideal gerado, caso A seja um conjunto qualquer de R.
O ideal estará bem definido quando a interseção dele com os conjuntos (não vazia, porque {\displaystyle A\subset R\,}) de todos os ideais que estão em A (que na interseção seja descrito por <A> ou (A)), for compreendido com todas as somatórias finitas da forma apresentada a seguir:
r1a1 + ··· + rnan
com cada ri em R respectivamente e cada ai em A.
Os ideais são importantes, pois aparecem como centros dos homomorfismos (que veremos mais à frente) e, também, permitem definir os anéis quocientes. Existem diversos tipos de ideais analisados, uma vez que cada tipo gera distintos anéis quocientes. A seguir, veremos alguns deles:
Veremos, na sequência, um pouco mais sobre alguns deles.
Dado um ideal M 6 = A, o anel A denomina-se maximal se, em qualquer ideal I de A, a propriedade M ⊆ I implicar I = M ou I = A.
Exemplificando:
Aplicado no anel dos inteiros Z, (0) e (10) não são maximais:
(0) ⊂ (10) ⊂ (5) ⊂ Z.
Em contrapartida, (5) é maximal:
(5) ⊆ (m) ⊆ Z ⇔ m|5 ⇒ m = 1 ou m = 5 ⇔ (m) = Z ou (m) = (5).
Por fim, teremos: o elemento A como um anel comutativo com identidade e I um ideal de A.
Logo:
(a) A/I é um domínio de integridade se e, só se, I for primo.
(b) A/I é um corpo se e, só se, I for maximal.
(c) Todo o ideal maximal de A é primo.
O ideal primo define-se por ser um subconjunto de um anel que tem inúmeras propriedades em comum com as de um valor primo dos anéis inteiros. Para esses anéis inteiros, os ideais primos são conjuntos que apresentam todos os múltiplos de qualquer elemento primo dado, juntamente com o nulo.
Em suma, podemos afirmar que os ideais primitivos são primos e ideais primos são simultaneamente primários, além de se enquadrarem como semiprimos.
Exemplificando:
Cabe informar, também, que a utilidade prática dos ideais primos dá-se na área da geometria algébrica, em que as variedades são determinadas como conjuntos nulos de ideais em anéis de polinômios.
Em uma abordagem moderna, que se prega o abstratismo, inicia-se com um anel comutativo arbitrário e, a partir dele, transforma-se em um conjunto de seus ideais primos, também denominado de seu espectro. A partir disso, define-se uma série de generalizações e de variações, que são chamadas de esquemas, sendo aplicadas não somente na geometria ou nesses conteúdos abstratos, mas, também, na teoria dos números.
A entrada desses ideais primos, na teoria da álgebra, foi um avanço grandioso. Naquele momento, percebeu-se que a propriedade da fatoração única expressada no teorema fundamental da matemática não se aplicava em todo anel de inteiros algébricos, mas foi encontrado seu substituto à altura, quando Dedekind trocou elementos por esses ideais primos.
Podemos definir um ideal principal como aquele que é gerado por um elemento. Esse ideal apresenta três denominações distintas:
No caso comutativo, o principal dá-se por um conjunto na representação aR = aR / r E R. Em Z, é simples demonstrar que todo ideal, na verdade, também é principal, mas isso não se valida em todos os casos. Podemos perceber isso ao analisar quando um ideal é criado por {2, x} no domínio de integridade {\displaystyle \mathbb {Z} [x]\,}Z [x] dos polinômios de coeficientes inteiros.
A partir de agora, estudaremos a definição de homomorfismos. Esse conceito matemático diz respeito a aplicações, com o intuito de fazer comparações de estruturas algébricas de mesma origem. Os termos utilizados no homomorfismo são, em sua base, muito parecidos com os utilizados na teoria dos grupos. Tem-se um núcleo, uma imagem, além dos teoremas de isomorfismos, entre outras propriedades.
Podemos descobrir muitas informações e dados sobre anéis observando sua interação com outros anéis. No entanto, isso só é possível através dos homomorfismos. O homomorfismo é, portanto, uma ferramenta que preserva as operações soma e multiplicação dos anéis.
Definição: um homomorfismo representado por φ, de um anel R, em um anel S, é uma aplicação de R em S, que preserva, como dito, as operações de um anel. Ou seja:
Φ (a + b) = φ (a) + φ (b)
Φ (ab) = φ (a) · φ (b)
Quando se tem um homomorfismo de anéis injetivo e sobrejetivo, ele passa a ser denominado isomorfismo de anéis. Nesse caso, podemos dizer que R e S são isomorfos. Veja que na definição apresentada anteriormente, as operações do lado esquerdo do sinal igualitário são as de R, já as do lado direito são de S. Quando se tem um isomorfismo φ : R → S isso mostra que R e S são, em linguagem algébrica, idênticos e similares.
Exemplificando:
De forma geral, se I é um ideal de um anel R, a ferramenta que faz a associação para cada elemento r de R a sua classe r + I, chama-se homomorfismo de anéis ou, nesse caso, homomorfismo canônico.
Seja φ: R [x] → R, que se associa a f (x) 7- → f (1), então φ é um homomorfismo sobrejetivo, já que:
Φ (f + g) = (f + g) (1) = f (1) + g (1) = φ (f) + φ (g)
Φ (f · g) = (f · g) (1) = f(1) · g (1) = φ (f) · φ (g)
Para todo a ∈ R, a = f (1), em que f (x) = a ∈ R [x]. Isso prova, definitivamente, que φ é sobrejetivo.
Considerando φ um homomorfismo de um anel R sobre um anel S, então, teremos as seguintes propriedades:
Exemplificando:
Na área da álgebra abstrata, a definição de isomorfismo apresenta-se como um homomorfismo bijetivo. Ou seja, duas estruturas algébricas são denominadas isomorfos, se houver, entre elas, um mapeamento bijetivo.
Outra maneira de se conceituar isomorfismo é pensar em dois objetos que, essencialmente, devem ser indistinguíveis, isto é, que não podem ser distinguidos. Essa área algébrica realizará o levantamento sobre esses elementos, mostrando, assim, um relacionamento entre as propriedades ou as operações.
Os isomorfismos são estudados para que se possa estender os conhecimentos a respeito de uns fenômenos para outros. Por exemplo, se dois objetos forem isomorfos, então, todas as propriedades deles podem ser mantidas por um isomorfismo e o que for válido para um dos objetos também será válido para o outro.
Caso um dos isomorfismos seja encontrado em alguma área ou parte do ensino matemático (em que inúmeros teoremas já foram desbravados e muitos processos estão disponíveis para encontrar a resolução), a função isomorfa pode ser utilizada para mapear as questões dessa área desconhecida, para um ambiente em que os problemas serão melhor entendidos e, dessa forma, para melhor trabalhar com eles.
Na álgebra abstrata, dois isomorfismos principais e básicos são considerados. Definimos cada um deles a seguir:
Do mesmo modo que os automorfismos de uma sustentação algébrica formam um grupo, os isomorfismos entre dois elementos que partilham entre si a mesma estrutura também formam uma unidade.
Existem diversos exemplos de isomorfismo entre os teoremas e teorias algébricas. A teoria de Laplace é um isomorfismo que mapeia e transforma equações complicadas em equações mais fáceis. Na teoria das categorias, se considerarmos uma categoria C, em que se consiste em duas classes, uma de objetos distintos e outra de morfismos, passaremos a ter uma definição geral de isomorfismo que ultrapassa a anterior, sendo todo isomorfismo um morfismo.
Dessa forma, temos: ƒ: a → b, que tem uma inversa i.e., existindo um morfismo g: b → a, com g: b → a e gƒ = 1a. Como exemplo, podemos citar um mapa linear bijetor, que corresponde a um isomorfismo constituído a partir de espaços vetoriais, de maneira que a função seguirá bijetora, uma vez que a inversa é, também, contínua. Trata-se, portanto, de um isomorfismo sob espaços topológicos, chamada homeomorfismo.
Já no teorema dos grafos, um isomorfismo sob dois grafos, G e H, é um mapa bijetor f de um vértice de G para um vértice de H, que sustenta os “pilares de arestas”, no sentido de que há uma aresta de um vértice u para outro v em G, se houver uma aresta de f (u) para f (v) em H.
Em análise aritmética, um isomorfismo entre dois espaços de Hilbert é uma bijeção que mantém a adição, a multiplicação escalar e o produto interno. Logo, nas teorias primárias do atomismo lógico, o convívio formal entre fatos e proposições legítimas foi desenvolvido por Bertrand Russel e Ludwig Wittgenstein para ser isomórfico. Um modelo dessa forma de pensar pode ser visto na Introdução à Filosofia da Matemática de Russell.
4) A partir da função ƒ: G → J, assinale a alternativa que apresenta expressões que correspondem a um homomorfismo.
a) G = (Z, +), J = (Z, +), ƒ (x) = 7x.
Correta. Para quaisquer x, y E Z, temos ƒ (x + y) = 7 (x + y) = 7x + 7y = ƒ (x) + ƒ (y). Logo, ƒ é um homomorfismo de Z em Z.
b) G = (Z, +), J = (Z, +), ƒ (x) = 7x + 1.
Falsa. Nesse caso, temos que ƒ (1) = 8, ƒ (2) = 15, ƒ (1 + 2) = ƒ (3) = 22 e ƒ (1) + ƒ (2) = 23. Logo, ƒ (1 + 2) ≠ ƒ (1) + ƒ (2). Com isso, ƒ não é um homomorfismo.
c) G = (Z, +), J = (Z, +), ƒ (x) = 7 x 2.
Falsa. Por exemplo, ƒ (1) = 7, ƒ (3) = 63, ƒ (1 + 3) = ƒ (4) = 112 e ƒ (1) + ƒ (3) = 70. Logo, ƒ (1 + 3) ≠ ƒ (1) + ƒ (3) e, assim, temos que ƒ não é um homomorfismo de grupos.
d) G = (R, +), J = (Z, +), ƒ (x) = IxI.
Falsa. Por exemplo, ƒ (-2) = 2, ƒ (2) = 2, ƒ (-2 + 2) = ƒ (0) = 0 e ƒ (-2) + ƒ (2) = 4. Logo, ƒ (-2 + 2) ≠ ƒ (-2) + ƒ (2), ƒ não é um homomorfismo.
e) G = (Z, +), J = (Z, +), ƒ (x) = 8x + 1.
Falsa. Nesse caso, temos que ƒ (1) = 9, ƒ (2) = 17, ƒ (1 + 2) = ƒ (3) = 25 e ƒ (1) + ƒ (2) = 26. Logo, ƒ (1 + 2) ≠ ƒ (1) + ƒ (2). Logo, ƒ não é um homomorfismo.
Essa terceira unidade distanciou-se um pouco da álgebra tradicional e trouxe estudos relacionado ao abstrato. Trata-se de uma área mais recente na matemática, que enaltece conceitos como anéis e homomorfismos, relativamente mais complexos que os estudos tradicionais, pois não possuem uma lógica tão concreta quanto aos números em si. É interessante observar a importância de se adquirir novos conhecimentos e sair de nossa zona de conforto, estimulando nossa mente para o novo e buscando raciocínios diferentes, para sabermos resolver os mais diversos e complexos tipos de problemas.
Para aprofundar seus conhecimentos, recomendamos a leitura do artigo: “Aneis Euclidianos no contexto das Equações Diofantinas”, disponível em: <https://www.ime.unicamp.br/~ftorres/ENSINO/MONOGRAFIAS/yuri.pdf> e do site: <http://www.uel.br/projetos/matessencial/superior/algebra/corpos.htm>.

“A Matemática apresenta invenções tão sutis que poderão servir não só para satisfazer os curiosos como, também para auxiliar as artes e poupar trabalho aos homens” (DESCARTES, século XVII).

Nome do Livro: Álgebra Moderna
Editora: Saraiva
Edição: 5ª (8 de dezembro de 2017)
Autor: Hygino H. Domingues
ISBN: 8547223053
Neste livro, o autor apresenta os principais elementos da álgebra moderna e descreve, de forma simples, e com uma linguagem acessível, as teorias e os teoremas, fundamentais para ampliar nosso horizonte matemático.

Filme: Quebrando a banca
Gênero: Policial
Ano: 2008
Elenco Principal: Kevin Spacey, Jim Sturgess, Kate Bosworth, Jeff Ma, Laurence Fishburne
O filme Quebrando a banca apresenta a história de Ben Campbell, um jovem que, para custear a faculdade, participa de jogos de cartas, em Las Vegas, com uma identidade falsa, todos os fins de semana. O grupo que ele integra é liderado por um professor de matemática e gênio em estatística, com quem consegue montar um código infalível. Contando cartas e usando um complexo sistema de sinais, eles conseguem quebrar diversos cassinos. Vale a pena assistir!
