Como visto na unidade anterior, é possível encontrar divisores em comum entre dois ou até mais números. Chamamos de máximo divisor comum aquele número que for o maior dos divisores entre os dois números naturais comparados.
É isso que veremos nesta unidade intitulada de Divisores e Múltiplos Comuns nos tópicos Máximo Divisor Comum (MDC), Mínimo Múltiplo Comum (MMC), Equações diofantinas lineares e Aplicações da teoria dos números no ensino básico.
Vamos lá, então?
A fórmula e o procedimento para realizar essa determinação de encontrar o máximo divisor comum é muito simples, como veremos a seguir:
Nota: dois números naturais possuem sempre divisores em comum.
Na unidade anterior, vimos a decomposição por fatores primos e por meio dela podemos calcular o MDC entre dois números. Para a realização deste cálculo são necessárias três etapas descritas abaixo:
Exemplificando:
Encontre o MDC entre 36 e 90.
1ª etapa: é preciso decompor 36 e 90, a partir dos fatores primos, podendo escrevê-los em forma exponencial também.
36 = 2 x 2 x 3 x 3 = 2² x 3²
90 = 2 x 3 x 3 x 5 = 2 x 3² x 5
2ª etapa: entre eles, selecionamos os fatores primos de menores expoentes que se repetem em ambos os casos.
Neste exemplo, os números 2 e 3² se repetem nos dois casos e possuem menores expoentes.
3ª etapa: realiza-se a multiplicação dos fatores primos, e encontra-se o resultado final.
Portanto o MDC entre 36 e 90 que é igual MDC (36,90) = 3² x 2 = 18.
1- Utilizando os conhecimentos adquiridos até o presente momento desta unidade, calcule o MDC entre os números 12 e 32.
a) (32, 12) = 2 * 2 = 2
Incorreta.
Solução:
Para resolver este problema, você deve conhecer o método da decomposição em fatores primos para a determinação do MDC. Veja a parte 1 sobre MDC.
Assim, decompondo simultaneamente 32 e 12 temos que:
12, 32, | 2
6, 16, | 2
3, 8, | 2
3, 4, | 2
3, 2, | 2
3, 1, | 2
3, 1, | 3
1, 1, |
Logo, o MDC (32, 12) = 2 * 2 = 4, e não (32, 12) = 2 * 2 = 2
b) (32, 12) = 2 * 2 = 4
Correta.
Solução:
Para resolver este problema, você deve conhecer o método da decomposição em fatores primos para a determinação do MDC. Veja a parte 1 sobre MDC.
Assim, decompondo simultaneamente 32 e 12 temos que:
12, 32, | 2
6, 16, | 2
3, 8, | 2
3, 4, | 2
3, 2, | 2
3, 1, | 2
3, 1, | 3
1, 1, |
Logo, o MDC (32, 12) = 2 * 2 = 4.
c) (32, 12) = 2 * 2 = 7
Incorreta.
Solução:
Para resolver este problema, você deve conhecer o método da decomposição em fatores primos para a determinação do MDC. Veja a parte 1 sobre MDC.
Assim, decompondo simultaneamente 32 e 12 temos que:
12, 32, | 2
6, 16, | 2
3, 8, | 2
3, 4, | 2
3, 2, | 2
3, 1, | 2
3, 1, | 3
1, 1, |
Logo, o MDC (32, 12) = 2 * 2 = 4, e não (32, 12) = 2 * 2 = 7
d) (32, 12) = 2 * 2 = 8
Incorreta.
Solução:
Para resolver este problema, você deve conhecer o método da decomposição em fatores primos para a determinação do MDC. Veja a parte 1 sobre MDC.
Assim, decompondo simultaneamente 32 e 12 temos que:
12, 32, | 2
6, 16, | 2
3, 8, | 2
3, 4, | 2
3, 2, | 2
3, 1, | 2
3, 1, | 3
1, 1, |
Logo, o MDC (32, 12) = 2 * 2 = 4, e não (32, 12) = 2 * 2 = 8
e) (32, 12) = 2 * 2 = 3
Incorreta.
Solução:
Para resolver este problema, você deve conhecer o método da decomposição em fatores primos para a determinação do MDC. Veja a parte 1 sobre MDC.
Assim, decompondo simultaneamente 32 e 12 temos que:
12, 32, | 2
6, 16, | 2
3, 8, | 2
3, 4, | 2
3, 2, | 2
3, 1, | 2
3, 1, | 3
1, 1, |
Logo, o MDC (32, 12) = 2 * 2 = 4, e não (32, 12) = 2 * 2 = 3
O mínimo múltiplo comum (MMC) corresponde à operação para encontrar o menor múltiplo que seja diferente de zero, visto que é múltiplo comum entre todos os números fornecidos.
Pode ser bem observado em situações em que encontramos o denominador comum entre frações, por exemplo, e para encontrá-lo, assim como o MDC, também é muito simples e pode-se repetir o processo da decomposição por fatores primos, ou a decomposição simultânea.
Vale ressaltar que para se localizar os múltiplos de determinado número, basta multiplicá-lo pela sequência dos naturais. O zero, por exemplo, será múltiplo de todos os números, já que a sequência dos naturais parte dele.
Agora, como saber se números são ou não múltiplo um do outro? Para responder essa pergunta, é primordial descobrir se este número é divisível pelo outro. Como exemplo, podemos afirmar que 25 é múltiplo de 5, já que é divisível por 5.
Nesse sentido, podemos afirmar que o cálculo do MMC pode ser realizado pela comparação da tabuada desses números.
Exemplificando:

Para termos clareza com relação a este exemplo, descobriremos qual o MMC de 2 e 3. Veja na imagem da tabuada, que o menor valor que multiplica estes dois números é 6, portanto, de forma fácil, sem contas, e apenas na visualização da tabuada, encontramos o mínimo múltiplo comum entre esses dois elementos, que é o número 6.
O único problema dessa fórmula prática e direta é quando nos deparamos com números maiores. Nesse caso, essa técnica não será tão eficiente, já que é mais difícil se ter uma tabuada com números extensos. Nesses casos, a dica será utilizar o método da fatoração, isto é, decompor os números em fatores primos. Por esse método, já conhecido por nós, veja como acontece o cálculo do MMC entre 12 e 45.
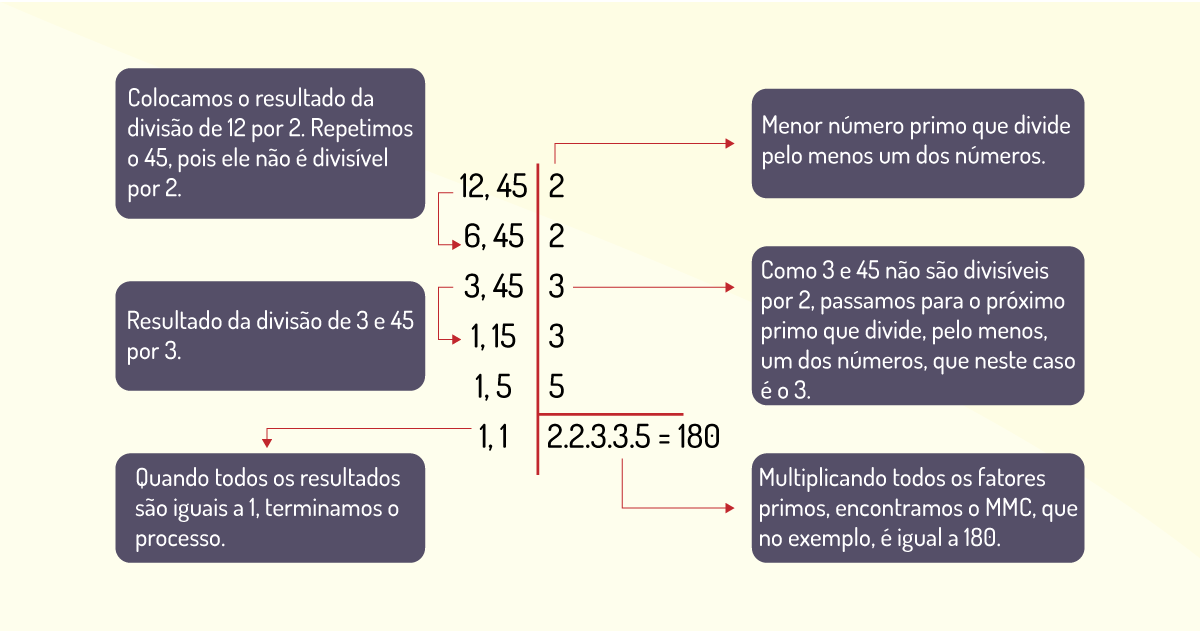
Perceba que nesse sistema, vamos dividindo os dois elementos por números primos, ou seja, os números naturais que são divisíveis por 1 e eles mesmos apenas. Ao fim da decomposição multiplica-se esses números primos, encontrando, assim, o mínimo múltiplo comum, que no exemplo acima é 180. Daremos abaixo um exemplo contendo três elementos, veja:
Exemplificando:
Calcule o MMC entre os números 4, 6 e 12.
Observe que os números 4, 6 e 12 podem ser escritos como fatores de números primos. Desse modo, realizamos as três etapas, já conhecidas por nós:
1ª etapa: fatora-se o número em fatores primos.
4 = 2 x 2 = 2²
6 = 2 X 3
12 = 2 x 2 x 3 = 2² x 3
2ª etapa: entre todos os números primos do exemplo acima, seleciona-se apenas os fatores primos distintos de maiores expoentes.
Neste caso, os fatores primos distintos de maiores expoentes são o 2² e o 3¹.
3ª etapa: realiza-se a multiplicação dos fatores primos.
Logo, 2² x 3 = 4 x 3 = 12.
Logo, o MMC entre 2,6 e 12 ou o MMC (2;6;12) é 12.
O processo de se encontrar o MMC também é muito utilizado em operações com frações, que para a grande maioria dos alunos, é motivo de medo e complicação, porém, mostraremos que é mais simples do que se pensa.
Pela matemática básica, ainda nas séries iniciais, aprendemos que para somar ou subtrair frações, é necessário que ambas tenham denominadores em comum. Desse modo, entre frações, podemos calcular o MMC entre os denominadores, e, a partir daí, o resultado passará a ser o novo denominador das frações.
Exemplificando: 2/5+ 2/6
Aqui vemos que os denominadores são distintos, 5 e 6, portanto o primeiro passo é encontrar o MMC entre eles. Assim temos:
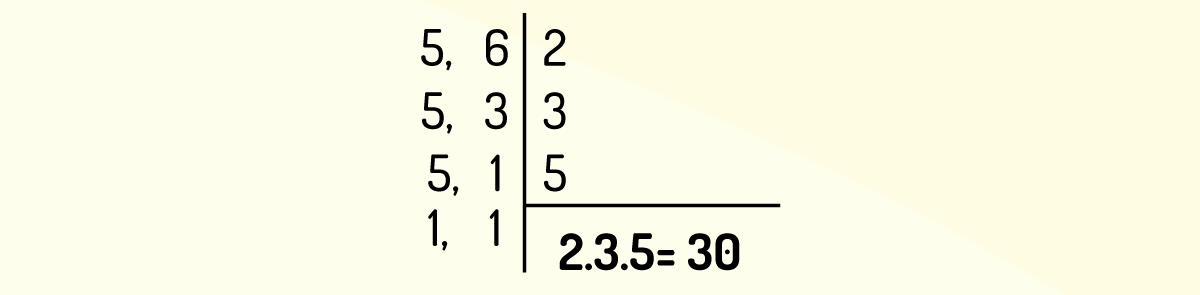
Agora que encontramos o MMC entre 5 e 6, que é 30, podemos realizar a soma das frações, pois agora o 30 passará a ser o denominador em comum. Essa adição se dá através do esquema abaixo:
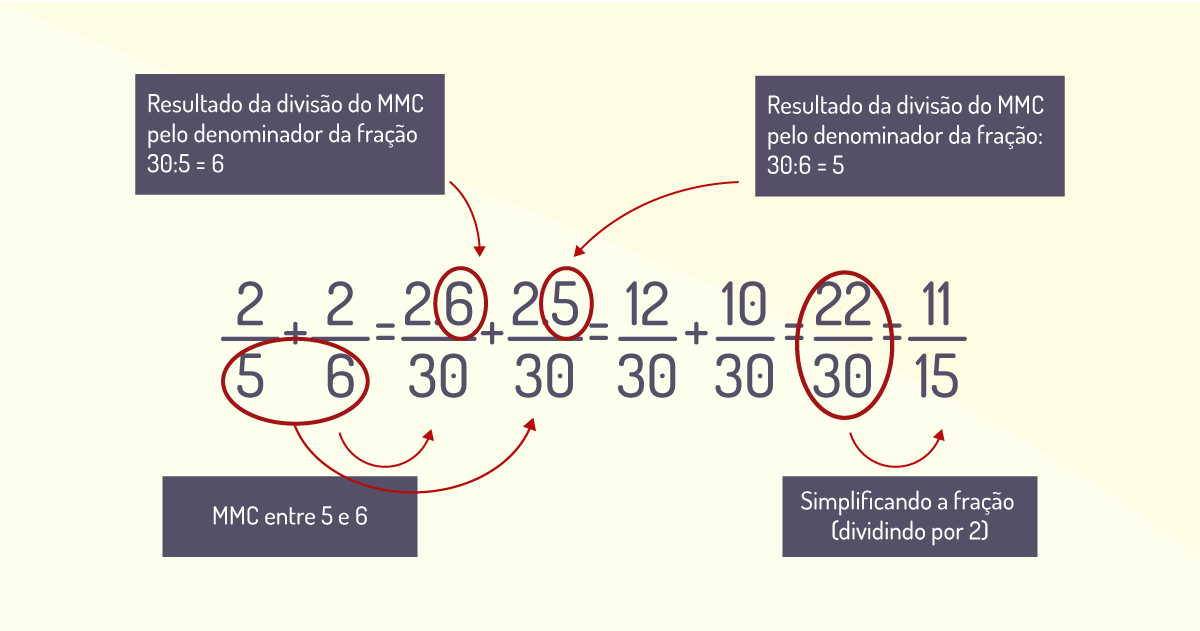
Soma-se as frações conforme o esquema acima, igualando os denominadores encontrados pelo MMC e depois dividindo o resultado pelo denominador, simplificando, então, a fração e executando a soma. No caso de subtração, realiza-se o mesmo procedimento.
Um outro método, muito simples e útil para o cálculo do MMC, é a decomposição simultânea.
Essa técnica consiste em realizar a divisão de todos os números encontrados na questão pelo menor fator primo correspondente a eles. A partir daí, o MMC será encontrado pela multiplicação de todos esses fatores usados na decomposição.
Exemplificando: Calcule o MMC entre 80, 60 e 30.
Para isso, a exemplo do MDC, montaremos uma tabela contendo os números e realizaremos a divisão em fatores primos, para assim, multiplicarmos e encontrarmos o MMC entre esses valores, conforme a Figura 2.4:
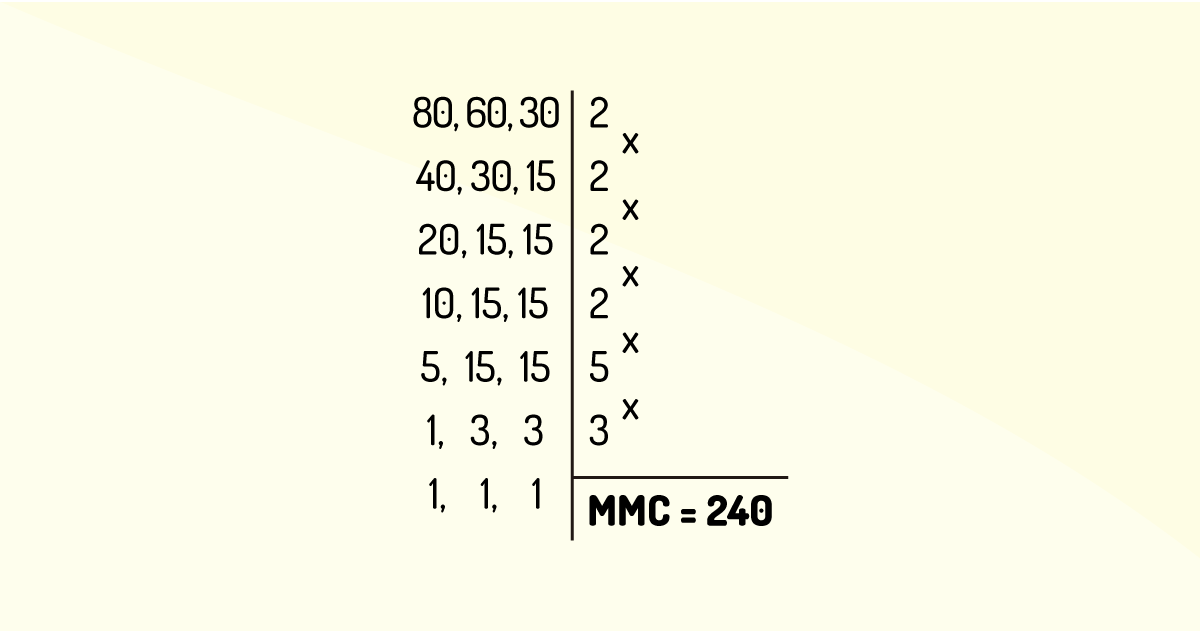
O resultado, então, é o MMC (80,60 e 30) = 2 x 2 x 2 x 2 x 5 x 3 = 240.
Essa técnica é a melhor entre todas, quando se tem muitos elementos.
O mínimo múltiplo comum possui duas propriedades as quais descreveremos abaixo:
1ª propriedade: o MMC entre dois algarismos primos entre si será o produto entre esses dois.
Ex: como já foi visto, 4 e 15, por exemplo, são primos entre si, então o MMC entre eles será 4 x 15 = 60.
2ª propriedade: se for dado dois ou até mais números e se um deles for múltiplo de todos os outros, então também será o m.m.c. dos números dados.
Ex: perceba que 30 é múltiplo de 6 e consequentemente múltiplo de 3. Assim, o MMC (3;6;30) = 30.
2 – Considere os números 30, 60 e 90. Baseado no aprendizado sobre MDC e MMC, assinale a partir das afirmações a alternativa correta.
I - 3 é o único divisor positivo ímpar de 60.
II - A soma dos números primos positivos que são simultaneamente divisores de 30 e de 60 é igual a 5.
III - A soma dos divisores positivos primos do número 30 é igual a 10.
IV - O mínimo múltiplo comum entre 30 e 60 é 2700.
V- O máximo divisor comum entre 30, 60 e 90 é 6.
Qual das afirmações é verdadeira? Assinale a alternativa correta.
a) III e V.
Correta.
Veja que os divisores primos de 30 são os números 2 ,3 e 5:
30,60,90 | 2
15,30,45 | 2
15,15,45 | 3
5, 5, 9 | 3
5, 5, 3 | 3
5, 5, 1 | 5
1, 1, 1 |
Logo, somando-se 2+3+5 = 10.
Já na alternativa V, temos que o MDC entre 30, 60 e 90 é dado por:
30,60,90 | 2
15,30,45 | 2
15,15,45 | 3
5, 5, 9 | 3
5, 5, 3 | 3
5, 5, 1 | 5
1, 1, 1 |
Observe que os números que dividem simultaneamente 30, 60 e 90 são os números 2 e 3. Portanto MDC (30,60,90) = 2 * 3 = 6.
b) II, III e IV.
Falsa.
Os números primos que dividem simultaneamente 30 e 60 são 2,3 e 5. Como observa-se:
30,60,90 | 2
15,30,45 | 2
15,15,45 | 3
5, 5, 9 | 3
5, 5, 3 | 3
5, 5, 1 | 5
1, 1, 1 |
Assim, somando 2 + 3 + 5 =10.
Já o MMC entre 30 e 60 é dado por:
30,60, | 2
15,30, | 2
15,15, | 3
5, 5, | 5
1, 1, |
MMC (30,60) = 2 * 2 * 3 * 5 = 60. Veja que o MMC é 60 e não 2700.
c) I e V.
Falsa.
Embora a alternativa V esteja correta a alternativa I é falsa.
d) I e II.
Falsa.
Ambas as alternativas estão incorretas. A alternativa I está incorreta, já que 5 também é um divisor ímpar de 60. Na alternativa 2 a soma dos divisores primos é 10 e não 5 como já visto.
e) Todas estão corretas.
Falsa.
As opções I, II e IV estão incorretas, portanto não são todas as corretas evidentemente.
O matemático Diofanto foi um dos responsáveis pelo grande crescimento e evolução da álgebra no mundo, e a partir deles, outros inúmeros matemáticos se inspiraram e se dedicaram aos estudos da teoria dos números. A maioria dos historiadores colocam Diofanto como pertencente ao século III d. C. Além do fato de que seus estudos e carreira terem sidos baseados na região de Alexandria, nada mais se sabe de grande relevância sobre o grego.
Entre seus principais trabalhos, Diofanto foi cultor da aritmética, números poligonais e Porisma. Entre eles, porém, o que mais destaca-se é a aritmética, já que é a obra mais intacta e mais completa do matemático, sendo seis livros de todos os treze que já escreveu.
Nesta obra da aritmética citada, Diofanto faz uma abordagem complexa em relação à teoria dos números, se dedicando, principalmente, na resolução de 130 problemas que ocorrem entre as equações. A obra possui tanta importância no meio matemático que os problemas algébricos que tem resultados indeterminados, encontrando-se apenas soluções racionais, foram batizados como “problemas diofantinos”, e esse termo designa até hoje as soluções que não são inteiras.
Uma das técnicas de Diofanto era de realizar simplificações, por meio de abreviações. A palavra aritmética em si é uma conjunção entre arithmos (número) e techne (ciência). O autor utilizou essa palavra em grego para denotar alguns de seus símbolos e abreviações como no caso arithmos, em que colocou α e ρ, e com o passar dos anos se desenvolveu para um sinal sigma grego ϛ.
Existe também uma teoria, apesar de ainda haver dúvidas quanto a ela, de que a notação para potência se indicaria pelas letras da palavra grega dunamis (NAMI∑) que na tradução significa “potência” e “incógnita ao cubo”.
Compreendendo isso facilmente, podemos explicar os símbolos das potências seguintes da incógnita (quadrado-quadrado), (quadrado-cubo) e (cubo-cubo).
Para a expressão “menos”, Diofanto utiliza um símbolo que se assemelha a um V inverso com a bissetriz traçada nele. Também teria se originado a partir da palavra grega leipis (ᴧEIΨI∑), que significa “menos”. Todos os elementos negativos eram associados e antes de se escreverem eram denotados com o sinal de menos.
As equações Diofantinas compõem uma teoria em que estão inseridas na teoria dos números e tem como objetivo central investigar se as soluções das equações são inteiras ou racionais, por exemplo, a equação, 2x + 4y = 5, y² - x³ = -2 ou x² + y² = z². Em relação a nomenclatura, obviamente, equações Diofantinas, faz uma homenagem a um dos maiores estudiosos de álgebra que já existiu, Diophantus de Alexandria, que foi o responsável por descobrir, desenvolver e formular inúmeras equações. Como já citado, serviu de grande inspiração para outros matemáticos brilhantes, como o francês Pierre de Fermat (1601-1665).
Fermat tinha um cargo, na época, de conselheiro, e uma de suas responsabilidades estava interligada com a condenação de pessoas para serem mortas na fogueira, por essa razão, não devia ter muitas amizades. Quando tinha tempo livre, Pierre se dedicava ao estudo da aritmética e ganhou até um apelido de “Príncipe dos Amadores”, pois nesses momentos de estudo acabou descobrindo os conceitos de probabilidade, fundamentos do cálculo e complexos teoremas sobre os números inteiros. Fermat, porém, ganhou interesse pela matemática graças a uma obra de um escritor chamado Bachet, Arithmetica de Diophantus, livro que consolidou as ideias de Diofanto.
A partir daí, Fermat iniciou um novo ciclo da área da teoria dos números, tendo entre elas a análise diofantina, sendo responsável por formular os mais famosos problemas da matemática, desafiando estudiosos por diversas gerações. Podemos afirmar que Pierre Fermat influenciou praticamente todas as áreas da aritmética, afirmando até mesmo que possuía demonstrações para as Ternas Pitagóricas: se n≥3, a equação xⁿ + yⁿ = zⁿ, não admite soluções inteiras não-nulas.
Foi nessa demonstração que criou a conhecida “demonstração de Fermat”, que por muitos anos foi considerada o desafio mais complicado e famoso da matemática, justamente por parecer muito simples, mas nenhum matemático antes de 1994 conseguiu desvendar.
Fermat adorava provocar situações embaraçosas com outros matemáticos, principalmente os ingleses, porém, o destino fez com que justamente um inglês chamado Andrew Wiles fosse o iluminado para desvendar o “último teorema de Fermat”. Na época (1994), tal feito chegou a ser comparado com a descoberta dos átomos e o descobrimento das estruturas do DNA.
Wiles conta que desde criança tinha obsessão por esse teorema e se propôs de todas as maneiras tentar resolvê-lo. É considerado uma das conquistas mais importantes da história da matemática, e tudo se originou das ideias de Diofanto, ainda no século III. Podemos perceber assim, a importância e relevância que o matemático possui em toda a história.
As equações diofantinas costumam aparecer em problemas, cuja característica principal é de agrupamento, como nos casos abaixo:
Exemplo 1: Um laboratório médico tem a seu dispor 2 máquinas de raio x. Uma delas examina 15 imagens por vez, já a outra 25 imagens. Quantas vezes essas máquinas devem ser ligadas para examinar 2 mil imagens?
Exemplo 2: Quantos campos de futebol e quantos campos de queimada são necessários para que 80 alunos joguem simultaneamente? E se forem 77 alunos?
Exemplo 3: Para agrupar 13 aviões em filas de 3 ou de 5, quantas filas serão formadas de cada tipo?
Para se resolver esses problemas, precisamos buscar soluções inteiras e positivas, sendo assim, não se permite números negativos nesses casos. Dessa forma, podemos organizar o raciocínio pela equação diofantina:
\[ax~+~b~y~=~c\]
Observando os casos acima descritos e entendendo a fórmula dada, o problema do laboratório médico pode ser descrito através de: 15x+25y = 2000.
Na questão dos campos, uma equação é 10l0x+12y=80, que demonstra 2 soluções x = 2 e y = 5 ou x = 8 e y = 0, enquanto a outra questão baseia-se no mesmo método e é representada pela equação l0x + 12y = 77, não possuindo soluções (que sejam pares de números inteiros).
Em relação aos aviões (que pode ser usado como figura de linguagem e ser, portanto, apresentado desde as fases iniciais da escola), a equação 3x+5y=13 apresenta uma única solução (pares de números inteiros e positivos) x = 1 , y=2.
Ao se elaborar e colocar em prática qualquer um dos problemas, é preciso zelar na escolha dos coeficientes a, b e c, pois não determinarão apenas o nível de dificuldade do problema, mas também controlarão a quantidade de soluções possíveis que existirá, desde que sejam, como visto, inteiros ou inteiros positivos.
Quando estudamos qualquer problema matemático, é interessante termos algum processo para seguir, pois assim, para qualquer problema, teremos já na cabeça a forma de resolução e também identificaremos se possui ou não soluções, e se possui, saber quantas são.
Podemos citar como exemplo a equação de segundo grau abaixo:
\[ax^2 + bx + c = 0\] ,
Essa equação só terá soluções reais se os seus elementos forem maiores que zero.
\[b^2 - 4ac~0\] .
Quando isso ocorrer,vas soluções reais x1 e x2 serão dadas por:
\({{x}_{1}}=(-b+\sqrt{{{b}^{2}}-4ac})/2ª\) e \({{x}_{2}}=(-b+\sqrt{{{b}^{2}}-4ac})/2ª\)
Quando estudamos as equações Diofantinas, ax + by = c, com a,b e c sendo números inteiros, é necessário saber se existe um critério predeterminado que permita afirmar que aquela equação, originada de um problema, possui solução e também um método para achar tais soluções, caso existam de fato. No caso das diofantinas, nosso único interesse é colocar soluções inteiras de ax + by = c.
Há, realmente, um critério único, que nos faz decidir se a equação padrão de ax + by = c possui ou não soluções inteiras. Esse critério está descrito a seguir:
Tendo, portanto, identificado a resolução da equação diofantina sendo ela:
\[ax + by = c\],
Ou seja, sendo a, b e c como números inteiros, devemos, então, procurar as soluções x e y, para que se forme um par ordenado de números inteiros.
Para isso, deveremos usar propriedades de divisibilidade, que descreveremos abaixo, sendo que as duas primeiras possuem conotação de verificação imediata e a terceira sendo responsável por prova. Essas propriedades foram retiradas da Revista Professor de Matematica (RPM):
Propriedade 1 - Se d divide a, então dividirá am, para qualquer inteiro m;
Propriedade 2 - Se d divide a e divide b, então dividirá a + b;
Propriedade 3 - Se d é o máximo divisor comum de a e b, então existem inteiros r e s tais que ar + bs = d.
Vemos que, com base nas duas primeiras propriedades, caso o problema apareça da forma ax + by = c, e, a partir dele, houver solução com x0 e y0 inteiros, sendo d um divisor comum, de a e b, então deverá dividir o elemento c. Portanto temos já, uma condição para que se exista uma solução inteira na equação.
Segundo a terceira propriedade, essa condição já é suficiente para comprovar que há solução, não precisando de outros elementos. Entretanto no caso de d, além de divisor comum, for o máximo divisor, então c = dm, a partir daí, segundo essa propriedade três, existirão inteiros r e s tais que ar + bs = d. Assim, multiplicando-se os membros desta igualdade pelo inteiro m, teremos a (rm) + b (sm) = c, sendo que x = rm e y = sm será a solução procurada.
Concluímos dessa forma, que uma equação diofantina ax + by = c, possui solução inteira, se o MDC de a e b puder dividir c.
Exemplificando:
Aplicando-se o teorema 1, podemos perceber que uma equação diofantina com os elementos 4x + 6y = 9, não possui solução, pois o máximo divisor comum (4 e 6) é 2 e o número 2 não pode dividir 9. O número 4x + 6y, com x e y, sendo inteiros, sempre serão pares, evidentemente, que jamais chegaram a ser 9, não importando a divisão que se faça.
De todo modo, se formos pensar na expressão 8x + 12y = 36, haverá solução, já que o MDC entre 8 e 12 é 4, e 4 divide 36.
Nota: Se o MDC entre o elemento a e b forem primos, então, pode-se afirmar que a equação diofantina sempre tem soluções inteiras, independentemente de qual seja o valor de c.
Observamos, então, no tópico anterior, que para a busca de soluções inteiras de uma equação diofantina, podemos tomar o MDC de a e b como algum elemento primo, preferencialmente o 1, e que ao encontrar as soluções inteiras também se compara com encontrar valores inteiros para r e s tais que ar + bs = 1. Entretanto não é construtiva a prova que temos para se chegar a esses elementos r e s.
Um dos métodos que podemos utilizar, para se alcançar tais números, é aplicar o algoritmo de Euclides, que já conhecemos, ou então realizar o processo das divisões sucessivas para calcular o MDC de a e b. Esse algoritmo será autêntico quando estiver de acordo com as observações abaixo:
O oposto também é válido, se o elemento g divide b e r, como a = bq + r, segue-se que g divide a e b.
Agora, demonstraremos, através de exemplo, como encontrar os inteiros r e s, sendo eles ar + bs = 1, citado anteriormente. Para que isso aconteça, consideremos dois números, 32 e 9. Ao aplicarmos o algoritmo de Euclides, no cálculo do máximo divisor comum entre eles, teremos o seguinte resultado:
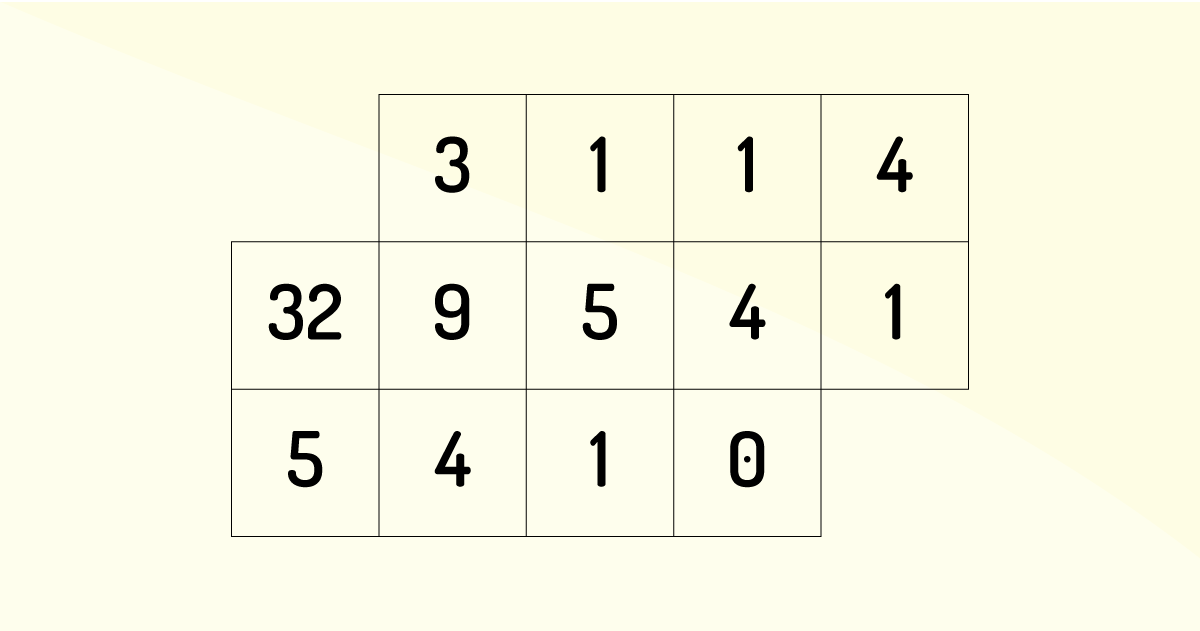
Pelo algoritmo, podemos resumir as divisões, a partir do esquema abaixo:
32 = 3 x 9 + 5 (A)
9 = 1 x 5 + 4 (B)
5 = 1 x 4 + 1 (C)
e, a partir, da análise da segunda tabela, concluímos que:
mdc (32,9) = mdc (9,5) = mdc (5,4) = mdc (4,1) = 1.
O próximo passo é combinar de forma que fique conveniente as três expressões (A), (B), (C) e aí, encontraremos os inteiros r e s, sendo que teremos 32r + 9s = 1. Desse modo, nós tiramos da expressão (C), a afirmação 5 1 x 4=1. De (B), resultou o axioma 4 = 9 1 x 5 que, se jogarmos na expressão acima, ficaria:
5 l x (9 l x 5) = l ou 5 1 x 9 + 1 x 5 = 1 ou, ainda, de forma mais direta, 2 x 5 1 x 9 = 1.
Por fim, da expressão (A), obtemos 5 = 32 3 x 9 que, assim como na (B), incluiremos na expressão acima, chegando então a:
2 x (32 3 x 9) 1 x 9 =1 ou 2 x 32 7 x 9 = 1
Finalmente, os números que procuramos se fazem presentes, e são o 2 e o 7.
Tendo os coeficientes x0, y0, obteremos uma solução inteira a partir da equação diofantina se a e b forem relativamente inteiros. Portanto a expressão deverá ficar ax0+by0 = c. Veja agora que, se, no primeiro elemento, somarmos e subtrairmos o mesmo número, essa igualdade continuará em vigor. Se quisermos colocar a e b em evidência, deveremos exigir que o número a ser acrescentado seja múltiplo de ab, ou seja teríamos uma escrita na forma abk, sendo o k um elemento inteiro. A partir daí, teríamos que:
Essa expressão, prova que o par (x0 + bk, y0 ak) continua sendo uma equação diofantina. Perceba também que até este momento ainda não utilizamos a hipótese de o máximo divisor comum a e b ser igual a 1.
A pergunta fundamental agora é: será que estas opções são todas as soluções inteiras existentes? Ou poderão existir outras? Para responder isso, faremos uma suposição de que (x0, y0) e (x1, y1) são soluções inteiras da equação, agora sim incluindo o MDC de a e b = 1. Assim teremos:
ax0 + by0 = c e ax1 + by1 = c.
O que resulta em:
a (x1 x0) = b(y0 y1).
Primeiro caso: Se o a = 1, chamaremos de k; o inteiro que resultar em y0 y1 e teremos x0 x1 = bk, isto é, x1 = x0 + bk, sendo que y0 y1 = k, ou seja, y1 = y0 k, que é igual a y1 = y0 ak, pois a = 1. Então, neste caso, qualquer solução (x1,y1) é da forma (x0 + bk, y0 ak), com k inteiro.
Segundo caso: Se o a 1, a não dividirá b, isso porque a e b são primos. Então, a divide y0 y1, ou seja, existe k; inteiro tal que y0 y1 = ak, sendo que y1 = y0 ak. Mas então a( x1 x0 ) = bak, e, como a 0, vem que x1 x0 = bk, ou seja, x1=x0+bk.
Assim, exibimos um teorema que diz se o par ordenado (x0, y0) de fato for uma solução da equação diofantina ax + by = c, com regra mdc (a, b) = 1, então (x1, y1) será consequentemente solução da equação se, e somente se, existir um inteiro k tal que x1 = x0 + bk e y1 = y0 ak.
Preste atenção que a condição de a e b serem primos, não é necessária aqui, para que o x1 e y1 tornem-se soluções da equação diofantina, entretanto, essa regra ainda é importante para garantir que essas sejam todas as soluções da equação proposta.
Exemplificando:
Dada a equação diofantina 143x + 17y = 132, buscaremos as soluções inteiras para ela. De início, colocamos o máximo divisor comum entre (143,17) = 1, portanto, já podemos estabelecer que essa equação terá soluções inteiras. Para se achar, ao menos uma delas, veja que:
143 = 8 x 17 + 7, 17 = 2 x 7 + 3, 7 = 2 x 3 + 1. Logo temos:
l = 7 2 x 3 = 7 2 x [17 2 x 7] = 5 x 7 2 x 17 =
= 5 x [143 8 x 17] 2 x 17 = 5 x 143 42 x 17.
Em que descrevemos:
143 x [5 x 132] + 17 x [ 42 x 132] = 132,
Isto é a solução da equação que se dá por: (x0, y0) = (660, 5544), portanto, todas as demais soluções ainda não encontradas, se darão da mesma forma: x = 660 + 17k e y = 5544 143k , em que k é um inteiro arbitrário.
De forma conceitual, para se resolver uma equação diofantina, é necessário encontrar valores correspondentes para as variáveis x e y, que precisam necessariamente ser números inteiros. Uma solução padrão é mais fácil de ser encontrada do que uma integral, exigindo, de quem faz, um processo de inúmeras etapas. Antes de tudo, é preciso encontrar o MDC dos coeficientes dados no problema. Se, caso, conseguir encontrar uma solução integral, de uma equação linear, será mais fácil aplicar a ela um padrão e, assim, identificar inúmeras outras soluções possíveis. A seguir, colocaremos três métodos de resolução das equações, dando a cada um deles, o passo a passo necessário.
Método 1: Preparando a Equação
a) Escreva-a em formato padrão – para uma equação ser linear, não deve ter nenhum expoente maior que 1, em qualquer uma de suas variáveis. O primeiro passo para solucioná-la é escrevê-la de forma padronizada, representada no estilo diofantino ax + bx = c, sendo que a, b e c sempre serão valores inteiros. Em muitos problemas, a equação já estará neste padrão, porém, caso não esteja, é preciso utilizar-se das regras de álgebra para executar essa ordenação, ou partir para uma combinação de termos. Se o problema der, por exemplo, 23x + 4y – 7x = -3y + 15, você pode simplificar essa equação combinando elementos similares até chegar em 16x + 7y = 15.
b) Se possível reduza a equação – após sua equação estar dentro do formato padrão, observe bem os termos de a, b e c. Caso haja, entre eles, algum fator comum, busque uni-los a fim de reduzir a equação. Após reduzir igualmente os três termos, as soluções encontradas também serão válidas para a descrição original. Se os três forem elementos pares, por exemplo, poderá dividi-los e simplificá-los por 2, como segue a demonstração abaixo:
c) Determine a impossibilidade de uma solução – para algumas equações, será possível determinar se existe ou não solução possível. Se houver, algum múltiplo comum do lado esquerdo da expressão que não convém com o lado direito, pode ser, neste caso, que a solução não exista. Se a e b forem pares, a soma de ambos os lados também precisa ser par, se não for, é possível também que não se tenha resultados. Por outro lado, se o elemento c for ímpar, aí não existirá solução inteira.
Método 2 – Utilizando o algoritmo euclidiano
a) Reaprenda o algoritmo euclidiano – esse sistema consiste em divisões repetidas, em que será usado cada resto como divisor de uma nova conta. O último divisor utilizado será o MDC entre os valores analisados. Os passos, descritos abaixo, demonstram o uso do algoritmo euclidiano na determinação do MDC entre 272 e 36:
b) Aplique o algoritmo euclidiano aos coeficientes a{\displaystyle {\text{a}}} e b{\displaystyle {\text{b}}} – se a equação já estiver em formato padrão, identifique os coeficientes a e b e realize o cálculo do MDC, pelo algoritmo euclidiano entre esses elementos. A partir daí, determine soluções integrais para a equação linear. Por exemplo 87x + 64y = 3. Os passos a seguir mostrarão como isso ocorre:
87 = 1 x 64 + 23
64 = 2 x 23 + 18
23 = 1 x 18 + 5
18 = 3 x 5 + 3
5 = 1 x 3 + 2
3 = 1 x 2 + 1
2 = 2 x 1 + 0
c) Identifique o máximo divisor comum (MDC) – se o algoritmo euclidiano se suceder para esse par ordenado até a divisão chegar a 1, então, concluiremos, que o MDC entre 87 e 64 é 1. Ou simplesmente dizemos que ambos os números são primos entre si mesmos.
d) Interprete o resultado – após o complemento do algoritmo e a determinação do MDC entre a e b, deveremos comparar os resultados com o valor de c, dado na equação. Se o MDC entre esses dois valores também for divisor, então, essa equação linear terá uma solução integral. Se não for, então, não haverá solução possível. Voltando ao 87x + 64y =3, essa equação terá solução integral, já que seu MDC pode ser igualmente dividido pelo elemento c (3). Se supormos que o MDC fosse 5, aí não poderia haver essa divisão, então, não obteríamos soluções integrais, evidentemente.
Método 3 – Renomeando o MDC para encontrar a solução.
a) Rotule os passos da redução do MDC – neste método, para se encontrar a solução de uma equação linear, será preciso utilizar o trabalho feito no algoritmo euclidiano como suporte em um processo de repetição, sendo que o objetivo é renomear e simplificar os valores. De início, numere os passos da redução do algoritmo para ter um caminho referencial, após isso terá a lógica que se exemplifica abaixo:
Passo 1: 87 = (1 x 64) + 23
Passo 2: 64 = (2 x 23) + 18
Passo 3: 23 = (1 x 18) + 5
Passo 4: 18 = (3 x 5) + 3
Passo 5: 5 = (1 x 3) + 2
Passo 6: 3 = (1 x 2) + 1
Passo 7: 2 = (2 x 1) + 0
{\displaystyle 87x-64y=3}
b) Comece com o último passo contendo um resto – reescreva a equação, para que siga o restante das informações dadas na expressão. Nesse problema, o passo 6 é o último a ter um resto que é o próprio 1. Nesse caso, poderá ser reescrito da seguinte forma:
1 = 3 – (1 x 2).
c) Isole o resto do passo anterior – esse processo pode ser considerado um passo a passo de como ir elevando cada etapa. Todas as vezes, você deverá rever o lado direito da equação e focar nos valores da etapa acima. É possível reavaliar o passo 5, para isolar o resto que se segue, como demonstrado abaixo:
2 = 5 – (1 x 3) ou 2 = 5 -3
d) Faça uma substituição e simplifique – observe que a revisão do sexto passo possui o número 2, e a revisão do quinto passo também é igual a 2. Então teremos que substituir ?a igual? dado do passo 5 para que entre no lugar do 2 no passo 6, como abaixo:
1 = 3 – (1 x 2) – Essa é a revisão do passo 6.
1 = 3 – (5 x 3) – Faça a substituição no lugar do valor 2.
1 = 3 – (5 + 3) – Distribuição do sinal negativo.
1 = 2 (3) – 5 – Simplifique.
e) Repita o processo de substituição e simplificação – caminhando pelos passos do algoritmo euclidiano, inverte-se a forma e repete-se o mesmo procedimento. Após cada etapa, reveja a anterior e substitua o valor do último resultado encontrado. Se a última foi o passo 5, agora refaça o quarto passo, e siga isolando o resto:
3 = 18 – (3 x 5)
Substitua o valor no lugar do 3{\displaystyle 3} na última etapa e simplifique:
1= 2 (18 – 3 x 5) – 5
1= 2 (18) – 6(5) – 5
1= 2 (18) – 7(5)
f) Continue repetindo os passos de substituição e simplificação – esse procedimento seguirá se repetindo, até que se chegue novamente a etapa original do algoritmo euclidiano. O objetivo central, deste processo, é determinar uma equação que seja baseada nos termos 87 e 64, que são os coeficientes originais do problema que estamos exemplificando.
Esse processo se repetirá, passo a passo, até chegar novamente à etapa original do algoritmo euclidiano. A finalidade desse procedimento é determinar uma equação que seja escrita em termos de {\displaystyle 87} 87 e 64{\displaystyle 64}, os coeficientes originais do problema a serem resolvidos. Desse modo, os próximos passos a se seguir são:
1 = 2(18) – 7(5)
1 = 2(18) – 7(23 – 18) – Substituição do passo 3
1 = 2(18) – 7(23) + 7(18)
1 = 9(18) – 7(23)
1= 9(64 – 2 x 23) – 7(23) – Substituição do passo 2
1= 9(64) – 18(23) – 7(23)
1= 9(64) – 25(23)
1= 9(64) – 25(87 – 64) – Substituição do passo 1
1= 9(64) – 25(87) + 25(64)
1= 34(64) – 25(87)
g) Reescreva o resultado em termos dos coeficientes originais – ao voltar para o início, no primeiro passo, do algoritmo euclidiano, perceba que os coeficientes do problema original também retornam. Então, recoloque os números para que se alinhem junto com a primeira equação. Desse modo, a expressão inicial para se resolver é 87x – 64y = 3. Assim, é possível remarcar a última etapa do processo a fim de deixar todos os termos padronizados. É preciso aqui, ter uma atenção especial, principalmente ao 64. Veja que na equação original, é subtraído, entretanto, o algoritmo euclidiano o trata como sendo positivo. Só será possível considerar a subtração, transformando o 34 em um valor negativo. Ficando, então, da seguinte forma nossa equação:
87 -25) – 64(-34) = 1
h) Multiplique o fator necessário para determinar as soluções – veja que o MDC do problema era 1, de tal forma que essa foi a solução exigida. Mas essa solução não representa a real solução do problema proposto, pois originalmente a equação é 87x – 64y = 3. É preciso então, uma multiplicação dos termos da última equação por esse termo, para se chegar a uma real solução, ficando:
87 (-25 x 3) – 64( -34x 3) = 1 x 3
87(-75) – 64(-102) = 3
i) Identifique a solução integral da equação – os elementos que serão multiplicados pelos coeficientes originais representam a solução x e y do nosso problema. Podemos identificar como um par ordenado, (x,y) = (-75, -102).
3) Tendo como base nossos estudos acerca das Equações Diofantinas, analise as assertivas a seguir:
I - Antes de se resolver uma equação diofantina, é preciso ordenar e padronizar os elementos da equação, mas não se faz necessário tirar o MDC dos coeficientes.
II - Uma equação diofantina possui apenas um padrão e todas possuem uma ou mais soluções.
III - Para se resolver uma equação diofantina, é necessário encontrar valores correspondentes para as variáveis x e y.
IV - As Equações Diofantinas são equações algébricas que apresentam solução no conjunto dos números inteiros.
Está correto o que se afirma em:
a) I apenas.
Realmente é preciso ordenar os elementos, mas para saber se há solução, é preciso tirar o MDC entre os coeficientes. As afirmativas corretas são a III e IV.
b) II apenas.
Uma equação diofantina pode ser de primeiro e segundo grau, e também nem todas têm soluções e podem haver equações sem solução racional. As afirmativas corretas são a III e a IV.
c) I, II e III apenas.
Apesar da afirmativa III ser correta, a I e a II não estão. Realmente, é preciso ordenar os elementos, mas para saber se há solução, é preciso tirar o MDC entre os coeficientes. Uma Equação Diofantina pode ser de primeiro e segundo grau, e também nem todas têm soluções, podem haver equações sem solução racional.
d) II e IV apenas.
Apesar da afirmativa IV ser correta, a II não está. Uma Equação Diofantina pode ser de primeiro e segundo grau, e também nem todas têm soluções, podem haver equações sem solução racional.
e) III e IV apenas.
De fato, as afirmativas III e IV estão corretas. É preciso encontrar valores para x e y para se resolver uma Equação Diofantina. A definição de que as Equações Diofantinas são equações algébricas que apresentam solução no conjunto dos números inteiros está correta, pois apresentam soluções considerando apenas números inteiros.
Chama-se de teoria dos números o ramo de estudos sobre todos os números naturais ou inteiros positivos (1,2,3,4 ...), considerando todas as suas propriedades. O matemático Leopold Kronecker disse certa vez que, em relação aos números, Deus criou todos os naturais, e suas derivações foram criadas pelo homem que se evoluiu e desenvolveu. Entretanto os inteiros positivos foram, sem dúvida, a primeira criação matemática dos seres humanos e é até impossível pensar a humanidade sem o contato com os números, mesmo que de forma inconsciente e sem o domínio total, pode-se concluir que em toda história o homem possuía uma relação com os algarismos.
Apesar de o conjunto dos números naturais formar o principal sistema da matemática, estudar suas propriedades e derivações tem chamado muita atenção dos matemáticos desde sempre.
No antigo Egito, guardado junto ao enorme tesouro ali pertencente, foi encontrou o papiro Rhind, que descreve a aritmética praticada ali, há pelo menos 2000 anos a.C., provando que essas curiosidades e relações numéricas não vem de hoje. No fim do terceiro milênio a. C., tábuas cuneiformes da Mesopotâmia já mostravam uma matemática avançada e bem aplicada desses povos.
Desde a antiguidade, os números são utilizados em transações comerciais, e desde desse período, já se tem pensado em aprofundar os estudos sobre eles. A princípio, se tem notícia de uma primeira teoria oficial dos números no ano 600 a. C. com Pitágoras e seus discípulos, que foram responsáveis por classificar os inteiros das mais diversas maneiras, como pares, ímpares, primos e assim por diante.
A teoria dos números, a partir daí, foi se desenvolvendo e é a área da matemática que tem o objetivo de descobrir e aprofundar as relações dos números entre si. Por exemplo, consideremos um conjunto dos quadrados de 1, 4, 9, 16, 25,... Se pegarmos a somatória de dois desses quadrados, eventualmente, teremos como resultado um outro número quadrado.
Outro fascínio que envolve os números inteiros são as ternas de Pitágoras, como (3, 4, 5), (5, 12, 13), (20, 21, 29). Veja que 2²+4²= 5², o mesmo acontece para: 5² + 12²= 13² e 20² + 21² = 29². Em contrapartida, se colocarmos por exemplo (2,3,4) ao quadrado 2² + 3² = 4², não dará um resultado quadrado. Então, será que existiram ou não ternas infinitas? E se existir, há uma fórmula padrão para descrevê-las? Estas questões são exemplos sobre em que se baseia a teoria dos números.
Dentro dessa teoria, há uma grande variedade de objetos investigados: primos, quadrados, ímpares, conjuntos, números racionais, algébricos, funções, códigos e muitos outros.
Já na antiguidade, Pitágoras mencionava que os números são quem, na verdade, governam e ditam o ritmo do mundo. O significado dessa frase é grandiosa e impactante e coloca a matemática como o centro de nossa vida cotidiana.
Ao longo da história, o ser humano administrou a matemática como uma ferramenta de organização de processos e estruturação de várias atividades, desde contar frutos colhidos no campo, até calcular distâncias e dimensões e assim se localizar melhor no planeta Terra.
A matemática sustenta-se, portanto, pelas relações que fazemos dela com as coisas. O sistema decimal, por exemplo, foi concebido a partir da condição em que temos dez dedos nas mãos e nos pés, o que comprova que usamos essa ciência como relacionamentos a nossa volta. A aplicação matemática se dá também em provar a existência ou não de alguma situação, como se comprovar ou não a existência de um triângulo, em que suas medidas não podem ser aleatórias e que cada parte deve ter o mesmo tamanho sendo que um dos lados deve ser maior que a diferença dos outros dois.
Assim como em outras ciências exatas, para que um argumento matemático seja autêntico, é preciso que seja provado. Esse questionamento será comprovado ou não a partir de axiomas, teoremas, hipóteses, testes, observações e deduções.
Atualmente, outra importância da aplicação fundamental da matemática é a respeito do indivíduo, pois aquele que a domina e a compreende é considerado muito mais capaz de planejar e executar as funções sociais do que aquele que tem dificuldade. Portanto podemos concluir que a matemática é um meio de inclusão nos grupos sociais e pessoais, possuindo os seguintes objetivos:
Além dessas qualificações, muitas outras podem ser apontadas, como benefícios do conhecimento e domínio matemático.
Na parte teórica, de conteúdos em si, a aritmética pode apresentar, inúmeras divisões distintas, sendo classificada, principalmente, a partir de quatro grandes grupos, listados a seguir:
1 - Espaço e forma: Estuda-se e analisa-se diversas formas e estruturas geométricas, aprendendo a realizar os cálculos de tamanho e distâncias, por exemplo. Podemos nomeá-los como:
2 - Grandezas e medidas: Essa área da matemática é utilizada para descrever padrões como velocidade, tempo, capacidade, densidade, volume, entre outros. Nesse sentido, temos os seguintes conteúdos abrangidos:
3 - Número e operações / álgebra e funções: a matemática se relaciona de forma mais direta com a álgebra, os cálculos e os números em si. Destaca-se os seguintes conteúdos:
4 - Tratamento da informação: Usa-se o tratamento da informação para fazer padrões de análise e compará-los a outros ou não. Os conteúdos deste grupo são os seguintes:
Uma das metodologias de ensino e aprendizagem para a teoria dos números é a aplicação de jogos matemáticos, que estimulem o pensamento e a criação. Se o jogo for proposto com argumentos e objetivos bem explícitos, que quando posto em prática, realmente fará o educando aplicar seus conhecimentos matemáticos, então, é uma ótima opção.
Em um primeiro momento, os jogos devem ser apresentados e depois relacionados com os conhecimentos já pré-adquiridos, sempre com relação à teoria dos números. Ao final, é feita uma conexão entre a prática elaborada e executada e a teoria estudada. A seguir, colocaremos dois exemplos de jogos, retirados do livro Os desafios das escolas públicas paranaenses, de Nunes (2014, p. 12-13) referenciado no final desta apostila.
Quadro 2.1: Exemplos de jogos
Fonte: Nunes (2014, p. 12-13).
Como visto, os jogos matemáticos são uma forma de estimular o pensamento lógico, a criatividade e o raciocínio. Vale a pena sua utilização para aplicar conhecimentos matemáticos adquiridos!
4 - Sobre a teoria dos Números, assinale qual alternativa está correta.
a) Possui três grandes áreas de estudo.
Incorreta.
A matemática se divide em quatro grandes áreas.
b) Tem se desenvolvido a partir dos tempos modernos.
Incorreta.
Desde o início dos tempos, o homem já se relaciona com a matemática e os números.
c) Foi inventada por Pitágoras.
Incorreta.
Pitágoras estudou e aprofundou a teoria dos números, mas não há indícios exatos de como ou quando ela foi criada, apenas relatos de que desde o início das civilizações o homem já se relaciona com ela.
d) Sua aplicação pode se dar em qualquer área de nossas vidas.
Correta.
A matemática está inserida em todos os lugares que vamos.
e) Os jogos matemáticos não podem se relacionar de forma direta, no estudo da teoria dos números.
Incorreta.
Os jogos são dinâmicas eficientes e importantes para garantir o aprendizado numérico.
Nesta unidade, vivenciamos diversas evoluções de pensamento. A jornada de uma ideia, desde a sua percepção até seus ajustes finais deve ser modelada de acordo com a realidade em que se vive. O aumento das necessidades do ser humano faz com que o conhecimento abra cada vez mais as portas. Por mais que inúmeras vezes, as propriedades trabalhadas aqui, como os múltiplos, os divisores, as equações, as teorias, entre outras áreas, sejam assustadoras vistas de longe, é preciso ter cautela e determinação, já que sem seus estudos e vivências não teríamos um chão seguro para pisar.
Para aprofundar seus conhecimentos, acesse o artigo: Equações Diofantinas Lineares: Um desafio motivador para os alunos do ensino médio. Disponível em: <https://sapientia.pucsp.br/bitstream/handle/11292/1/Wagner%20Marcelo%20Pommer.pdf>. Veja mais pelo site: <https://www.somatematica.com.br/coluna/gisele/25052001.php>.

Estou completamente envolvido com minha formação educacional? Em que esses conhecimentos podem me ajudar? Pense a respeito!

Nome do livro: Princípios da Matemática para concursos vol 1: Múltiplos e divisores
Nome do autor: Jamerson Fernando Confort Martins
Editora: Ciência Moderna
ISBN: 9788539904556
Para aqueles que pensam em prestar concurso, fica a indicação dos princípios da matemática. Mesmo que você não realize concursos, mas quer se aprofundar em múltiplos e divisores, este livro, possui uma aprendizagem sólida, organizado de forma clara e precisa.

Filme: O quarto de Fermat
Gênero: Suspense
Ano: 2007
Elenco Principal: Alejo Sauras, Elena Ballesteros, Lluís Homar e Pascal Santi Millán
A obra O quarto de Fermat apresenta uma história sobre quatro matemáticos que vão passar um fim de semana em um lugar da Espanha tentando solucionar desafios intelectuais, mas aos poucos o enigma fica ainda mais difícil, e coisas estranhas começam a acontecer, como paredes que começam a se mexer, a porta que é trancada e a sala encolhendo-se pouco a pouco.
