1- Um matemático, ao mencionar a Teoria dos Conjuntos, em uma certa turma, realizou uma pesquisa sobre as preferências das pessoas por seleções de vôlei, de seus n alunos, obtido o seguinte resultado:
Se designarmos por A o conjunto dos admiradores do Brasil, por B o conjunto dos admiradores da Alemanha e por C o conjunto dos admiradores da França, todos da referida turma, teremos, evidentemente, A ∩ B = Ø. Concluímos que o número n de alunos dessa turma é:
a) 95.
Incorreta.
Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.
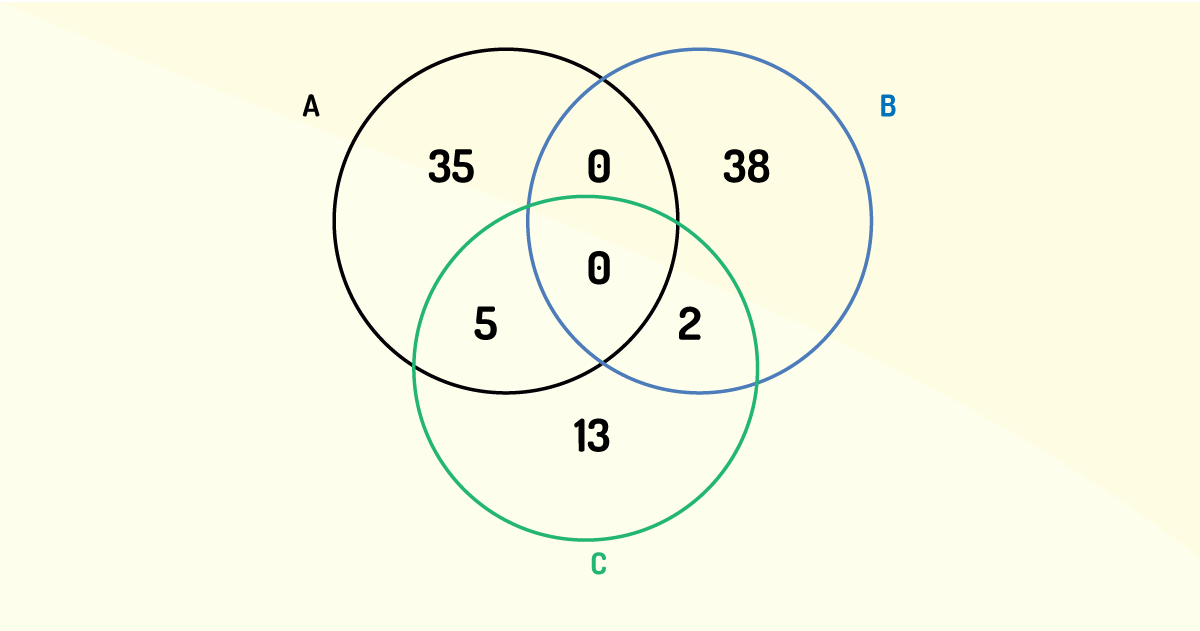
Efetuando a adição, temos que: 35+38+5+2+13 = 93 =
O número n de alunos dessa turma é 93 e não 95.
b) 93.
Correta.
RESOLUÇÃO
Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.

Efetuando a adição, temos que: 35+38+5+2+13 = 93 =
O número n de alunos dessa turma é 93. A resposta dessa questão é a alternativa “b”.
c) 86.
Incorreta.
Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.

Efetuando a adição, temos que: 35+38+5+2+13 = 93 =
O número n de alunos dessa turma é 93 e não 86.
d) 92.
Incorreta.
Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.

Efetuando a adição, temos que: 35+38+5+2+13 = 93 =
O número n de alunos dessa turma é 93 e não 92.
e) 83
Incorreta.
Para resolver essa questão, devemos desenhar os diagramas de todos os conjuntos descritos no enunciado, destacando a sua intersecção.

Efetuando a adição, temos que: 35+38+5+2+13 = 93 =
O número n de alunos dessa turma é 93 e não 83.
2) Tendo em vista o raciocínio dedutivo e suas especificidades na matemática, assinale V para verdadeiro e F para falso, em relação às afirmações a seguir.
I - É uma técnica de raciocínio dedutivo, usada para provar alguma ideia obtida com um raciocínio indutivo.
II- Ao utilizar a indução para provar resultados, podemos assumir que “P(k) é V” para forçar o resultado esperado, tranquilamente.
III- Todo subconjunto não-vazio do conjunto dos inteiros positivos tem um elemento mínimo.
IV- Indução matemática é um método de prova matemática utilizado para demonstrar a verdade de um número finito de proposições.
Está correto o que se afirma em:
a) I apenas.
Apesar da afirmativa I ser correta, a III também está. Um subconjunto não vazio precisa ter um elemento mínimo.
b) II apenas.
É falso, pode-se assumir sim P (k), porém, não tranquilamente, é preciso ter cuidado e cautela, para tal proposição não forçar demais o resultado.) As afirmativas I e III são as corretas.
c) I e II apenas.
Apesar da afirmativa I ser correta, a II não está. Pode-se assumir sim P (k), porém, não tranquilamente, é preciso ter cuidado e cautela, para tal proposição não forçar demais o resultado).
d) I e III apenas.
De fato, as afirmativas I e III estão corretas. A Indução corresponde a uma técnica considerando o raciocínio de dedução como da indução e como visto no decorrer dos tópicos um subconjunto não vazio precisa ter um elemento mínimo.
e) II, III e IV apenas.
Apesar da afirmativa III ser correta, a II e a IV não estão. Pode-se assumir sim P (k), porém, não tranquilamente, é preciso ter cuidado e cautela, para tal proposição não forçar demais o resultado. E a indução matemática é um método utilizado para demonstrar um número INFINITO de proposições e não apenas finito.
3 – Como foi visto, o número primo é um tipo de número que é divisível por 1 ou por ele mesmo. Então, tendo como base a unidade estudada, qual das opções abaixo representa um número primo?
a) 2002
Não é primo, pois pode ser divisível por outros valores que não apenas o 1 ou ele mesmo, por exemplo por 2, que daria 1001.
b) 1950
Não é primo, pois pode ser divisível por outros valores que não apenas o 1 ou ele mesmo, por exemplo por 2, que daria 975.
c) 1943
Não representa primo, pois é divisível por mais números além de 1 e ele mesmo, diferentemente dos outros.
d) 1917
Não é primo, pois pode ser divisível por outros valores que não apenas o 1 ou ele mesmo, por exemplo por 3, que daria 639.
e) 647
Este é primo, pois só pode ser dividido igualmente por 1 ou por ele mesmo. É, portanto, a alternativa correta.
4- Um dos princípios do teorema fundamental da aritmética é sobre os restos da divisão. Se considerarmos o número \(6^{2015}\) e o dividirmos por 10, qual seria o valor correspondente ao seu resto?
a) 4.
Falsa, pois podemos presumir que, em qualquer potência de 6, o resultado terá como algarismo final o próprio número 6.
b) 5.
Falsa, pois podemos presumir que, em qualquer potência de 6, o resultado terá como algarismo final o próprio número 6.
c) 6.
Correta,
Resolução: Para resolver esse exercício, não é necessário calcular 62015, mas somente descobrir qual é o último algarismo dessa potência. Para tanto, observe as seguintes potências:
\(6^2\) = 36
\(6^3\) = 216
\(6^4\) = 1296
\(6^5\) = 7776
Dessa forma, podemos presumir que, em qualquer potência de 6, o resultado terá como algarismo final o próprio número 6. Isso é verdade, pois 6·6 = 36; ao multiplicar 36 por 6, teremos novamente, no algarismo final, o número 6. Seguindo esse raciocínio, qualquer potência de base 6 terá como último algarismo o próprio 6.
Por outro lado, considerando os dois últimos algarismos de uma potência de base 6, teremos uma dezena terminada em 6. Suponha que essa dezena seja 36:
\[36 = 10·3 + 6\]
36 é dividendo, 10 é divisor, 3 é quociente e 6 é resto. Observe que, independentemente do número que ocupe a posição das dezenas, ele será divisível por 10 e deixará resto 6. Portanto o resto da divisão de \(6^{2015}\) por 10 é igual a 6.
d) 8.
Falsa, pois podemos presumir que, em qualquer potência de 6, o resultado terá como algarismo final o próprio número 6.
e) 9.
Falsa, pois podemos presumir que, em qualquer potência de 6, o resultado terá como algarismo final o próprio número 6.
1- Utilizando os conhecimentos adquiridos até o presente momento desta unidade, calcule o MDC entre os números 12 e 32.
a) (32, 12) = 2 * 2 = 2
Incorreta.
Solução:
Para resolver este problema, você deve conhecer o método da decomposição em fatores primos para a determinação do MDC. Veja a parte 1 sobre MDC.
Assim, decompondo simultaneamente 32 e 12 temos que:
12, 32, | 2
6, 16, | 2
3, 8, | 2
3, 4, | 2
3, 2, | 2
3, 1, | 2
3, 1, | 3
1, 1, |
Logo, o MDC (32, 12) = 2 * 2 = 4, e não (32, 12) = 2 * 2 = 2
b) (32, 12) = 2 * 2 = 4
Correta.
Solução:
Para resolver este problema, você deve conhecer o método da decomposição em fatores primos para a determinação do MDC. Veja a parte 1 sobre MDC.
Assim, decompondo simultaneamente 32 e 12 temos que:
12, 32, | 2
6, 16, | 2
3, 8, | 2
3, 4, | 2
3, 2, | 2
3, 1, | 2
3, 1, | 3
1, 1, |
Logo, o MDC (32, 12) = 2 * 2 = 4.
c) (32, 12) = 2 * 2 = 7
Incorreta.
Solução:
Para resolver este problema, você deve conhecer o método da decomposição em fatores primos para a determinação do MDC. Veja a parte 1 sobre MDC.
Assim, decompondo simultaneamente 32 e 12 temos que:
12, 32, | 2
6, 16, | 2
3, 8, | 2
3, 4, | 2
3, 2, | 2
3, 1, | 2
3, 1, | 3
1, 1, |
Logo, o MDC (32, 12) = 2 * 2 = 4, e não (32, 12) = 2 * 2 = 7
d) (32, 12) = 2 * 2 = 8
Incorreta.
Solução:
Para resolver este problema, você deve conhecer o método da decomposição em fatores primos para a determinação do MDC. Veja a parte 1 sobre MDC.
Assim, decompondo simultaneamente 32 e 12 temos que:
12, 32, | 2
6, 16, | 2
3, 8, | 2
3, 4, | 2
3, 2, | 2
3, 1, | 2
3, 1, | 3
1, 1, |
Logo, o MDC (32, 12) = 2 * 2 = 4, e não (32, 12) = 2 * 2 = 8
e) (32, 12) = 2 * 2 = 3
Incorreta.
Solução:
Para resolver este problema, você deve conhecer o método da decomposição em fatores primos para a determinação do MDC. Veja a parte 1 sobre MDC.
Assim, decompondo simultaneamente 32 e 12 temos que:
12, 32, | 2
6, 16, | 2
3, 8, | 2
3, 4, | 2
3, 2, | 2
3, 1, | 2
3, 1, | 3
1, 1, |
Logo, o MDC (32, 12) = 2 * 2 = 4, e não (32, 12) = 2 * 2 = 3
2 – Considere os números 30, 60 e 90. Baseado no aprendizado sobre MDC e MMC, assinale a partir das afirmações a alternativa correta.
I - 3 é o único divisor positivo ímpar de 60.
II - A soma dos números primos positivos que são simultaneamente divisores de 30 e de 60 é igual a 5.
III - A soma dos divisores positivos primos do número 30 é igual a 10.
IV - O mínimo múltiplo comum entre 30 e 60 é 2700.
V- O máximo divisor comum entre 30, 60 e 90 é 6.
Qual das afirmações é verdadeira? Assinale a alternativa correta.
a) III e V.
Correta.
Veja que os divisores primos de 30 são os números 2 ,3 e 5:
30,60,90 | 2
15,30,45 | 2
15,15,45 | 3
5, 5, 9 | 3
5, 5, 3 | 3
5, 5, 1 | 5
1, 1, 1 |
Logo, somando-se 2+3+5 = 10.
Já na alternativa V, temos que o MDC entre 30, 60 e 90 é dado por:
30,60,90 | 2
15,30,45 | 2
15,15,45 | 3
5, 5, 9 | 3
5, 5, 3 | 3
5, 5, 1 | 5
1, 1, 1 |
Observe que os números que dividem simultaneamente 30, 60 e 90 são os números 2 e 3. Portanto MDC (30,60,90) = 2 * 3 = 6.
b) II, III e IV.
Falsa.
Os números primos que dividem simultaneamente 30 e 60 são 2,3 e 5. Como observa-se:
30,60,90 | 2
15,30,45 | 2
15,15,45 | 3
5, 5, 9 | 3
5, 5, 3 | 3
5, 5, 1 | 5
1, 1, 1 |
Assim, somando 2 + 3 + 5 =10.
Já o MMC entre 30 e 60 é dado por:
30,60, | 2
15,30, | 2
15,15, | 3
5, 5, | 5
1, 1, |
MMC (30,60) = 2 * 2 * 3 * 5 = 60. Veja que o MMC é 60 e não 2700.
c) I e V.
Falsa.
Embora a alternativa V esteja correta a alternativa I é falsa.
d) I e II.
Falsa.
Ambas as alternativas estão incorretas. A alternativa I está incorreta, já que 5 também é um divisor ímpar de 60. Na alternativa 2 a soma dos divisores primos é 10 e não 5 como já visto.
e) Todas estão corretas.
Falsa.
As opções I, II e IV estão incorretas, portanto não são todas as corretas evidentemente.
3) Tendo como base nossos estudos acerca das Equações Diofantinas, analise as assertivas a seguir:
I - Antes de se resolver uma equação diofantina, é preciso ordenar e padronizar os elementos da equação, mas não se faz necessário tirar o MDC dos coeficientes.
II - Uma equação diofantina possui apenas um padrão e todas possuem uma ou mais soluções.
III - Para se resolver uma equação diofantina, é necessário encontrar valores correspondentes para as variáveis x e y.
IV - As Equações Diofantinas são equações algébricas que apresentam solução no conjunto dos números inteiros.
Está correto o que se afirma em:
a) I apenas.
Realmente é preciso ordenar os elementos, mas para saber se há solução, é preciso tirar o MDC entre os coeficientes. As afirmativas corretas são a III e IV.
b) II apenas.
Uma equação diofantina pode ser de primeiro e segundo grau, e também nem todas têm soluções e podem haver equações sem solução racional. As afirmativas corretas são a III e a IV.
c) I, II e III apenas.
Apesar da afirmativa III ser correta, a I e a II não estão. Realmente, é preciso ordenar os elementos, mas para saber se há solução, é preciso tirar o MDC entre os coeficientes. Uma Equação Diofantina pode ser de primeiro e segundo grau, e também nem todas têm soluções, podem haver equações sem solução racional.
d) II e IV apenas.
Apesar da afirmativa IV ser correta, a II não está. Uma Equação Diofantina pode ser de primeiro e segundo grau, e também nem todas têm soluções, podem haver equações sem solução racional.
e) III e IV apenas.
De fato, as afirmativas III e IV estão corretas. É preciso encontrar valores para x e y para se resolver uma Equação Diofantina. A definição de que as Equações Diofantinas são equações algébricas que apresentam solução no conjunto dos números inteiros está correta, pois apresentam soluções considerando apenas números inteiros.
4 - Sobre a teoria dos Números, assinale qual alternativa está correta.
a) Possui três grandes áreas de estudo.
Incorreta.
A matemática se divide em quatro grandes áreas.
b) Tem se desenvolvido a partir dos tempos modernos.
Incorreta.
Desde o início dos tempos, o homem já se relaciona com a matemática e os números.
c) Foi inventada por Pitágoras.
Incorreta.
Pitágoras estudou e aprofundou a teoria dos números, mas não há indícios exatos de como ou quando ela foi criada, apenas relatos de que desde o início das civilizações o homem já se relaciona com ela.
d) Sua aplicação pode se dar em qualquer área de nossas vidas.
Correta.
A matemática está inserida em todos os lugares que vamos.
e) Os jogos matemáticos não podem se relacionar de forma direta, no estudo da teoria dos números.
Incorreta.
Os jogos são dinâmicas eficientes e importantes para garantir o aprendizado numérico.
1) Com base nos estudos desta unidade e de seus conhecimentos adquiridos ao longo dessa trajetória, faça o que se pede:
A partir da propriedade MOD, ao observar três números que, somados a 16, tornam o resultado divisível por 6, podemos dizer que:
a) Os três números são 4, 10 e 20.
Falsa. Veja que o número 10 não torna o 16 divisível por 6. Observe, ainda, que 16 + 10, utilizando o Mod16, que é 4 e, utilizando mod6, temos: 4 + 4 + 6 ≡4 + 4 + 0 ≡ 8, ou seja, não tem resto nulo, logo, não é múltiplo de 6.
b) Os três números são 2, 8 e 14.
Verdadeira. Veja que:
16 + 2 = 18;
16 + 8 = 24;
16 + 14 = 30;
Utilizando a propriedade (Mod) podemos reescrever essas expressões da seguinte forma:
16 + 2 -> 4 + 2 ≡ 0;
16 + 8 -> 4 + 2 + 6 ≡ 0;
16 + 14 -> 4 + 2 + 6 + 6 ≡ 0.
Desse modo, o MOD de 16 é 4. Fatorou-se os demais números.
Como se trabalha com Mod6 e todas as operações são congruentes a 2 (mod6), elas têm por resultado o zero. Grosso modo, equivale dizer que como todas elas são divisíveis por 6, porque o resto será sempre nulo.
c) Os três números são 4, 6 e 8.
Falsa. Veja que o número 6 não torna o 16 divisível por 6. Observe, ainda, que 16 + 6, utilizando o Mod16, que é 4, e utilizando mod6 temos: 4 + 6≡4 + 0 + 0 ≡ 4, ou seja, não tem resto nulo, logo não é múltiplo de 6.
d) Os três números são 2, 10 e 12.
Falsa. Veja que o número 12 não torna o 16 divisível por 6. Observe, ainda, que 16 + 12, utilizando o Mod16, que é 4 e, utilizando mod6, temos: 4 + 6 + 6 ≡4 + 0 + 0 ≡ 4, ou seja, não tem resto nulo, logo não é múltiplo de 6.
e) Os três números são 4, 8 e 10.
Falsa. Veja que o número 10 não torna o 16 divisível por 6. Observe, ainda, que 16 + 10, utilizando o Mod16, que é 4 e, utilizando mod6, temos: 4 + 4 + 6 ≡4 + 4 + 0 ≡ 8, ou seja, não tem resto nulo, logo não é múltiplo de 6.
2 - Após o estudo da Teoria dos Anéis e os conhecimentos adquiridos ao longo dessa trajetória, analise as alternativas e julgue a única correta.
a) O conjunto dos números inteiros (Z) não é Anel.
Falsa. O conjunto Z é um anel.
b) O conjunto dos números inteiros (Z) é Anel.
Verdadeira.
Para mostrar que o conjunto dos inteiros Z é um anel, verificamos, primeiramente, alguns pontos:
Notação (Z,+,*).
Verificando as operações de soma e de multiplicação de dois elementos internos a e b dentro do conjunto, temos que:
+: Z x Z -> Z (a+b) -> a+b
*: Z x Z -> Z (a*b) -> a*b
Observe que tanto a soma quanto a multiplicação de dois inteiros gera outro número inteiro que, por sua vez, pertence ao conjunto dos números inteiros.
Em um segundo momento, avalia-se se as propriedades de associatividade, comutatividade, elemento neutro e elemento simetrizável são válidas.
Para a operação (+), tem-se que:
associatividade: (a+b)+c | a+(b+c) ->
a+b+c | a+b+c.
A operação (+) em Z admite associatividade.
Veja que a propriedade é válida.
Comutatividade: (a+b) = (b+a), válida, também, tratando-se dos números inteiros.
A operação (+) em Z admite comutatividade.
Elemento neutro: sendo a, e E Z
a+e = e+a = a; logo, o elemento neutro (e) só pode ser zero.
e = 0.
A operação (+) em Z admite elemento neutro.
Elemento simetrizável: sendo a, a`E Z:
a+a´= 0, logo a´= -a.
A operação (+) em Z admite elemento simetrizável.
Verificando, agora, as mesmas propriedades para a operação (*), temos que:
Associatividade: (a*b)*c | a*(b*c) ->
a*b*c | a*b*c.
A operação (*) em Z admite associatividade.
Distributiva: a(b+c) = (b+c)a
a(b+c) | (b+c)a
ab+ca | ba+ca
A operação (*) em Z admite a propriedade distributiva.
Elemento neutro: sendo a, e1, e2 E Z
a*e1 = e1*a = a;
a*e2 = e2*a = a;
se e1 e e2 são elementos neutros na equação, então:
e1*e2 = e1| e1*e2 = e2
Logo, e1 = e2; então, e1 = e2/e2 = 1 => e2 = e1/e1 = 1.
A operação (*) em Z admite elemento neutro.
c) 12≡5(mod3), pois 12 - 5 = 7. Então, dizemos que 12 é côngruo a 5.
Falsa. 12≡5(mod3), pois 12 - 5 = 7. Então, dizemos que 12 não é côngruo a 5.
d) 11≡ 5(mod3), pois 11 - 5 = 6 = 2*3. Então, dizemos que 11 não é côngruo a 5.
Falsa. 11≡ 5(mod3), pois 11 - 5 = 6 = 2*3. Então, dizemos que 11 é côngruo a 5.
e) 7≡15(mod2), pois 7 - 15 = -8 = 2*-4. Então, dizemos que 7 não é côngruo a 15.
Falsa. 7≡ 15(mod2), pois 7 - 15 = -8 = 2*-4. Então, dizemos que 7 é côngruo a 15.
3) Em relação aos grupos, corpos e subanéis, assinale a alternativa correta.
a) um grupo tem duas propriedades fundamentais, Associatividade e Elemento Neutro.
Falsa. Entre outras propriedades, um grupo tem três propriedades fundamentais, Associatividade, Elemento Neutro e Inversos.
b) Podemos definir subanel como um subconjunto vazio denominado S.
Falsa. Podemos definir subanel como um subconjunto não vazio denominado S.
c) A essência por trás da Teoria dos Grupos é tomar dois elementos de um conjunto, combinar eles de alguma maneira e retornar um terceiro elemento do mesmo conjunto e é esse o papel das operações binárias.
Falsa. O objetivo principal dessa teoria é fazer com que dois elementos de um conjunto combinem-se.
d) As letras Q, R e S são os exemplos mais conhecidos de corpos.
Falsa. Os exemplos mais conhecidos são Q, R e C, ao invés de S.
e) Na teoria dos anéis e subanéis existem até sete axiomas.
Verdadeira. Dentro da teoria existem sete axiomas.
4) A partir da função ƒ: G → J, assinale a alternativa que apresenta expressões que correspondem a um homomorfismo.
a) G = (Z, +), J = (Z, +), ƒ (x) = 7x.
Correta. Para quaisquer x, y E Z, temos ƒ (x + y) = 7 (x + y) = 7x + 7y = ƒ (x) + ƒ (y). Logo, ƒ é um homomorfismo de Z em Z.
b) G = (Z, +), J = (Z, +), ƒ (x) = 7x + 1.
Falsa. Nesse caso, temos que ƒ (1) = 8, ƒ (2) = 15, ƒ (1 + 2) = ƒ (3) = 22 e ƒ (1) + ƒ (2) = 23. Logo, ƒ (1 + 2) ≠ ƒ (1) + ƒ (2). Com isso, ƒ não é um homomorfismo.
c) G = (Z, +), J = (Z, +), ƒ (x) = 7 x 2.
Falsa. Por exemplo, ƒ (1) = 7, ƒ (3) = 63, ƒ (1 + 3) = ƒ (4) = 112 e ƒ (1) + ƒ (3) = 70. Logo, ƒ (1 + 3) ≠ ƒ (1) + ƒ (3) e, assim, temos que ƒ não é um homomorfismo de grupos.
d) G = (R, +), J = (Z, +), ƒ (x) = IxI.
Falsa. Por exemplo, ƒ (-2) = 2, ƒ (2) = 2, ƒ (-2 + 2) = ƒ (0) = 0 e ƒ (-2) + ƒ (2) = 4. Logo, ƒ (-2 + 2) ≠ ƒ (-2) + ƒ (2), ƒ não é um homomorfismo.
e) G = (Z, +), J = (Z, +), ƒ (x) = 8x + 1.
Falsa. Nesse caso, temos que ƒ (1) = 9, ƒ (2) = 17, ƒ (1 + 2) = ƒ (3) = 25 e ƒ (1) + ƒ (2) = 26. Logo, ƒ (1 + 2) ≠ ƒ (1) + ƒ (2). Logo, ƒ não é um homomorfismo.
1. Vamos considerar o polinômio:
\[P(X)=4x^4+3x^3-2x^2+x+k\]
Sabendo que P(1) = 2, qual será o valor de P(3) e qual o grau do polinômio, respectivamente?
a) 386 e 4.
Correta. Para encontrar o resultado, é necessário resolver a equação de polinômio.
Como P(1) = 2, temos:
P(1) = 4.1 + 3.1 – 2.1 + 1 + k = 2
4 + 3 – 2 + 1 + k = 2
6 + k = 2
k = 2 – 6
k = – 4
O polinômio será P(x) = 4x4 + 3x³ - 2x² + x - 4
Calculando P(3):
P (x) = 4x4 + 3x³ - 2x² + x - 4
P (3) = 4.34 + 3.3³ - 2.3² + 3 - 4
P (3) = 4.81 + 3.27 - 2.9 + 3 - 4
P (3) = 324 + 81 - 18 + 3 - 4
P (3) = 386.
O maior expoente do polinômio que acompanha a variável independente x é o 4, como observa-se no exercício. Portanto, este é o grau do polinômio.
b) 405 e 4.
Incorreta. Embora 4 seja o grau do polinômio, P(3) = 386 e, não, 405, como afirma a alternativa.
c) 324 e 2.
Incorreta. O grau do polinômio assume o valor do maior expoente que acompanha a variável independente x, e vale 4. Além disso, P(3) = 386 e, não, 324.
d) 81 e 10.
Incorreta. O valor de P(3) é 386 e, não, 81. Além disso, o grau do polinômio é igual ao valor do maior expoente que acompanha a variável independente x e não igual a soma de todos os expoentes, nesse caso, 10.
e) 368 e 5.
Incorreta. O valor de P(3) é 386 e, não, 368, como afirma a questão. Além disso, o grau do polinômio é 4 e, não, 5.
2. Analise as afirmações a seguir e escolha a única alternativa verdadeira entre elas:
a) Um grupo não pode ter mais de um elemento neutro.
Incorreta. Um grupo pode ter diversos elementos neutros, conforme a regra, e até mesmo nos subgrupos.
b) O conjunto vazio pode ser um grupo, independentemente da operação escolhida.
Incorreta. Mesmo não possuindo elementos, um conjunto pode ser um grupo, isso quando a ele está atrelada alguma operação. Porém, quando vazio, sem nenhuma operação, não pode ser um grupo.
c) Se um grupo tem uma quantidade finita de elementos, então ele é abeliano (comutativo).
Correta. Em caso de o grupo não ser infinito, ele será abeliano comutativo, como descreve a regra.
d) Uma equação da forma a ∗ x ∗ b = c sempre tem uma única solução x em um grupo.
Incorreta. A equação, da forma proposta, terá mais que uma única solução x em um grupo.
e) O conjunto dos números inteiros Z é um grupo com a operação de multiplicação usual.
Incorreta. Os inteiros Z são um grupo caracterizado pela multiplicação usual.
3. Considerando o grupo abeliano G = (Z8, +) e H um subgrupo de G, podemos afirmar que:
a) A ordem de H é igual a 4, obrigatoriamente.
Incorreta. A ordem de H pode ser de outros membros além do 4.
b) H pode ter ordem 6.
Incorreta. Nesta expressão, não seria possível o subgrupo H possuir ordem 6.
c) Devemos ter (G: H) = 4, obrigatoriamente.
Incorreta. H é subgrupo de G, que possui os elementos finitos de Z.
d) G não pertence a H.
Incorreta. O grupo H é subgrupo de G, como o próprio enunciado diz.
e) H ▹ G.
Correta. Aqui se põe H como dependente e originário de G, o que é verdadeiro, já que H é subgrupo de G e foi criado a partir dele.
4. Analise as afirmações e escolha a alternativa correta entre as seguintes:
a) Existem inteiros m > 2 e n > 2, tais que o grupo de permutações (S m, ◦) é isomorfo ao grupo de classes de restos (Zn, +).
Incorreta. Este grupo não pode ser isomorfo.
b) O grupo de permutações (S 5, ◦) é isomorfo ao grupo de classes de restos (Z120, +) . J.
Incorreta. Este grupo não pode ser isomorfo.
c) Dados inteiros m > 2 e n > 2, o grupo de permutações (S m, ◦) não é isomorfo ao grupo de classes de restos (Zn, +) . J.
Correta. Considerando estes inteiros, esse grupo não é isomorfo, comprovando-se ainda mais com restos sendo os inteiros positivos.
d) O grupo de permutações (S 4, ◦) é isomorfo ao grupo de classes de restos (Z4, +).
Incorreta. Este grupo não pode ser isomorfo.
e) O grupo de permutações (S 4, ◦) é isomorfo a algum subgrupo do grupo de classes de restos (Z24, +).
Incorreta. Este grupo não pode ser isomorfo.