Finalizando o assunto de Cálculo 2, caro(a) aluno(a), chegou o momento de aprender como lidar com problemas de integrais de funções de mais de uma variável. Você verá que, apesar de aparentar ser uma teoria extremamente complexa, a prática dessas integrais não é muito mais complexa que aquela vista nas integrais de funções de uma única variável. Sendo assim, a presente Unidade se inicia com a descrição do problema das integrais duplas. Será feita uma analogia com o desenvolvimento da integral de funções de única variável, para depois levar o assunto para integrais triplas. Além disso, como as regiões de integração podem ser realmente complexas, as mudanças de variáveis típicas para o assunto também serão apresentadas.
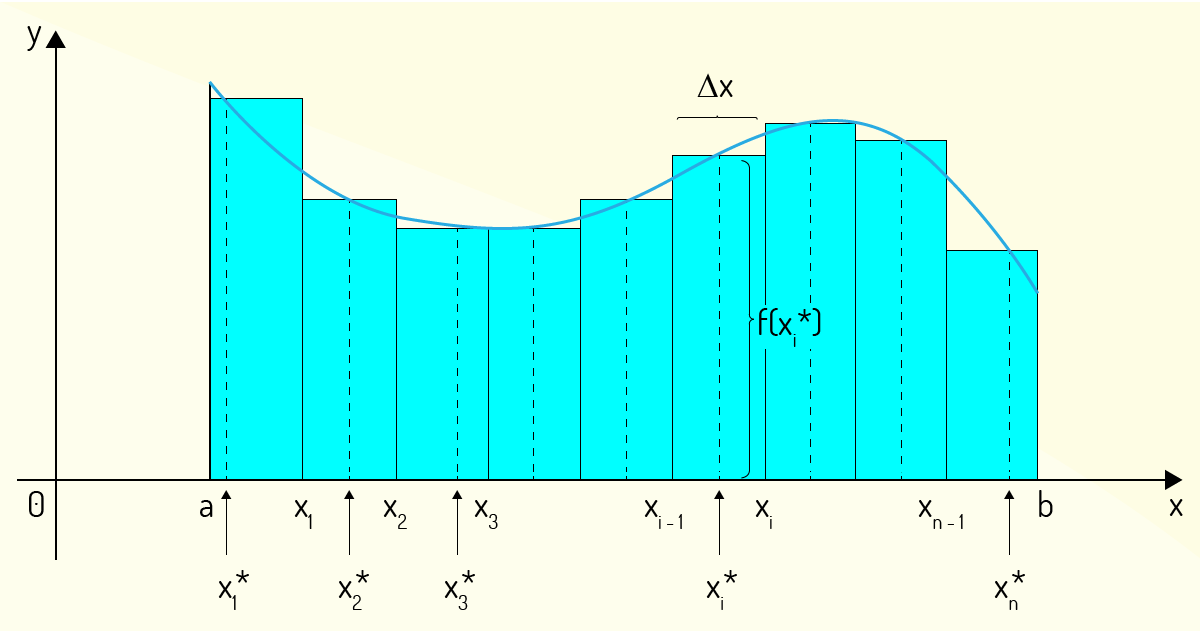
Stewart (2017b) retoma que um dos primeiros métodos apresentados ao se iniciar os estudos de integrais é aquele no qual, para se calcular a área sob a curva, faz-se o uso de diversos retângulos. Um procedimento semelhante também pode ser utilizado para o caso de integrais de funções com duas variáveis.
Para facilitar a compreensão do assunto, o referido teórico sugere que, antes de iniciarmos os nossos estudos de integrais duplas, revisemos rapidamente o conceito de integrais definidas para uma função de uma variável. Seja, então, uma função \(f\left( x \right)\) definida no intervalo fechado \(\left[ a,b \right]\), para o qual \(a\le x\le b\). Se você substituir esse intervalo \(\left[ a,b \right]\) em \(n\) subintervalos \(\left[ {{x}_{i-1}},{{x}_{i}} \right]\), todos com um mesmo comprimento \(\Delta x=\left( b-a \right)/n\), e escolher pontos de amostragem \(x_{i}^{*}\) em cada um desses intervalos, você pode formar a soma de Riemann:
\[\underset{i=1}{\overset{n}{\mathop \sum }}\,f\left( x_{i}^{*} \right)\Delta x~~~~(1)\]
Agora, se você criar infinitos subintervalos, ou seja, tomando-se o limite quando \(n\to \infty \), você tem a integral definida de \(f\left( x \right)\) no intervalo \(\left[ a,b \right]\):
\[\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx=\underset{n\to \infty }{\mathop{lim}}\,\underset{i=1}{\overset{n}{\mathop \sum }}\,f\left( x_{i}^{*} \right)\Delta x~~~~(2)\]
Assim, no caso especial em que \(f\left( x \right)\ge 0\), Stewart (2017b) indica que a soma de Riemann pode simplesmente ser interpretada como a soma dos infinitos retângulos aproximadores sob a curva, delimitada por valores de \(x\) que vão de \(a\) até \(b\), como mostra a Figura 4.1.
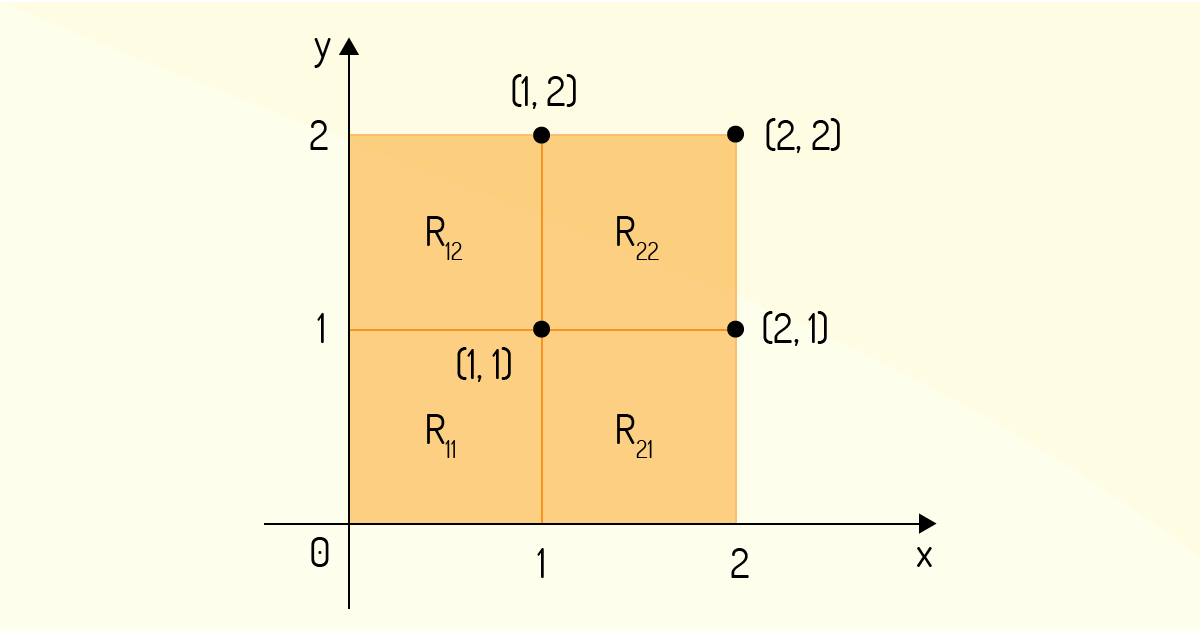
Esse mesmo pensamento pode ser expandido para o caso de uma função de duas variáveis, segundo Thomas Jr (2016), visto que retângulos são uma das mais simples construções planares para manipulação matemática. Sendo assim, considere uma função \(z=f\left( x,y \right)\), a qual é definida em uma região retangular \(R=\left[ a,b \right]\times \left[ c,d \right]=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}~|~a\le x\le b,~c\le y\le d \right\}\). A fim de simplificar a compreensão, Stewart (2017b) ainda diz para se considerar \(z\ge 0\), pois, assim, tem-se a formação de um sólido \(S\), delimitado pela base retangular \(R\) e por \(f\left( x,y \right)\), representado por \(S=\left\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}~|~0\le z\le f\left( x,y \right),~\left( x,y \right)\in {{\mathbb{R}}^{2}} \right\}\). A Figura 4.2 evidencia a representação gráfica desse sólido \(S\).
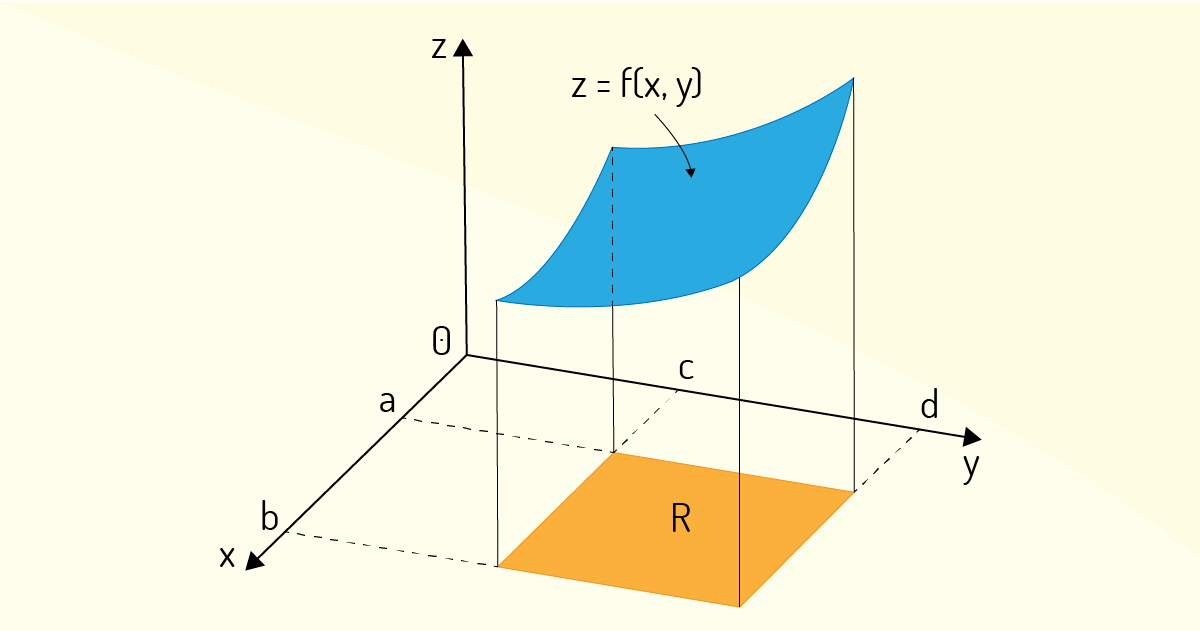
Portanto, Thomas Jr. (2016) e Stewart (2017b) indicam que o objetivo para se determinar uma integral dupla simplesmente será avaliar o volume desse sólido \(S\). Entretanto como se pode realizar tal tarefa? Basicamente, da mesma forma descrita anteriormente para a definição de integral definida de uma função de única variável, ainda de acordo com Thomas Jr. (2016) e Stewart (2017b). Logo, a primeira coisa a ser feita é subdividir o retângulo \(R\) em outros retângulos menores, da seguinte forma: o intervalo \(\left[ a,b \right]\) pode ser dividido em \(m\) subintervalos \(\left[ {{x}_{i-1}},{{x}_{i}} \right]\), todos com um mesmo comprimento \(\Delta x=\left( b-a \right)/m\), e o intervalo \(\left[ c,d \right]\) pode ser dividido em \(n\) subintervalos \(\left[ {{y}_{j-1}},{{y}_{j}} \right]\), todos com um mesmo comprimento \(\Delta y=\left( b-a \right)/n\). Com isso, o retângulo \(R\) apresentará diversos retângulos menores de área \(\Delta A=\Delta x\Delta y\), sendo esses retângulos menores representados por
\[{{R}_{ij}}=\left[ {{x}_{i-1}},{{x}_{i}} \right]\times \left[ {{y}_{j-1}},{{y}_{j}} \right]=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}~|~{{x}_{i-1}}\le x\le {{x}_{i}},~{{y}_{j-1}}\le y\le {{y}_{j}} \right\}\]
A Figura 4.3 representa essa divisão do retângulo \(R\).
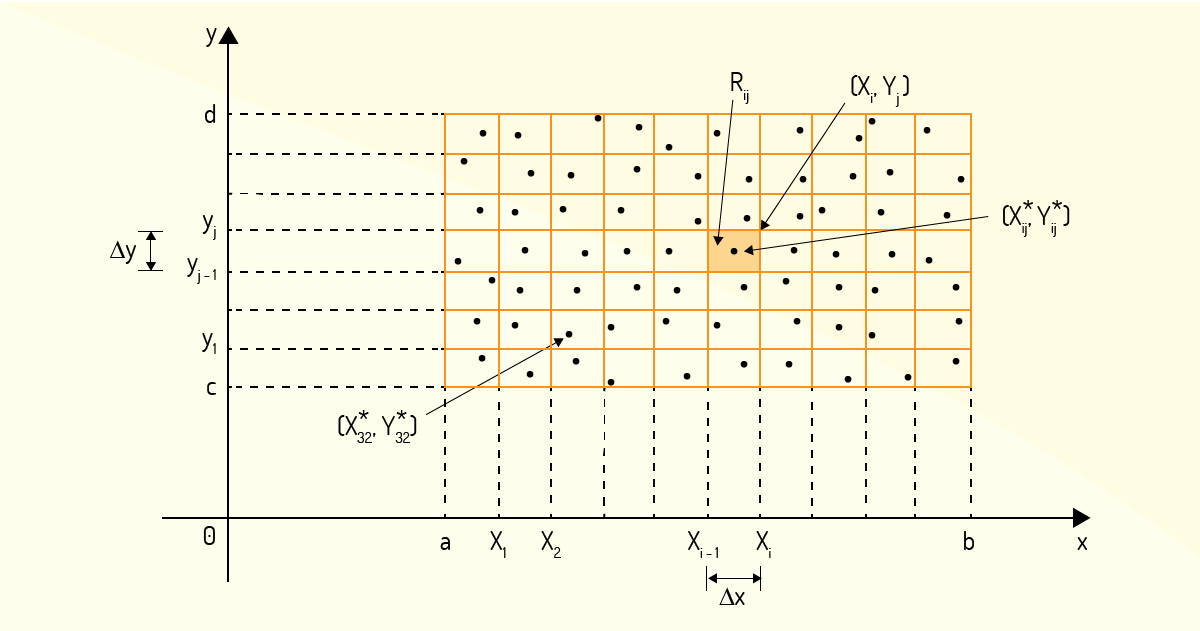
Mantendo a semelhança do que foi feito no caso da integração de funções de uma única variável, você deve escolher, agora, pontos aleatórios dentro dos retângulos \({{R}_{ij}}\), sendo esses pontos chamados de pontos de amostragem \(\left( x_{ij}^{*},y_{ij}^{*} \right)\), segundo Stewart (2017b). Na Figura 4.3, os pontos de amostragem estão representados como pequenos pontos dentro de cada retângulo. A escolha desses pontos permitirá que você aproxime a região do sólido \(S\) que se encontra acima de cada retângulos \({{R}_{ij}}\) com um pequeno bloco retangular de base \(\Delta A\) e altura \(f\left( x_{ij}^{*},y_{ij}^{*} \right)\), ou seja, um pequeno bloco retangular de volume \({{V}_{ij}}=\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)\). Logo, ao avaliar os volumes de cada um dos retângulos \({{R}_{ij}}\) obtidos e somar todos esses volumes \({{V}_{ij}}\), você encontrará uma aproximação para o volume \(V\) de \(S\), ou seja:
\[V=\underset{i=1}{\overset{m}{\mathop \sum }}\,\underset{j=1}{\overset{n}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)~~~~~~(3)\]
A Figura 4.4 mostra um desses retângulos \({{R}_{ij}}\), sendo ele comparado à curva de \(f\left( x,y \right)\), assim como também se vê todos os blocos retangulares usados para aproximar o volume de \(S\).
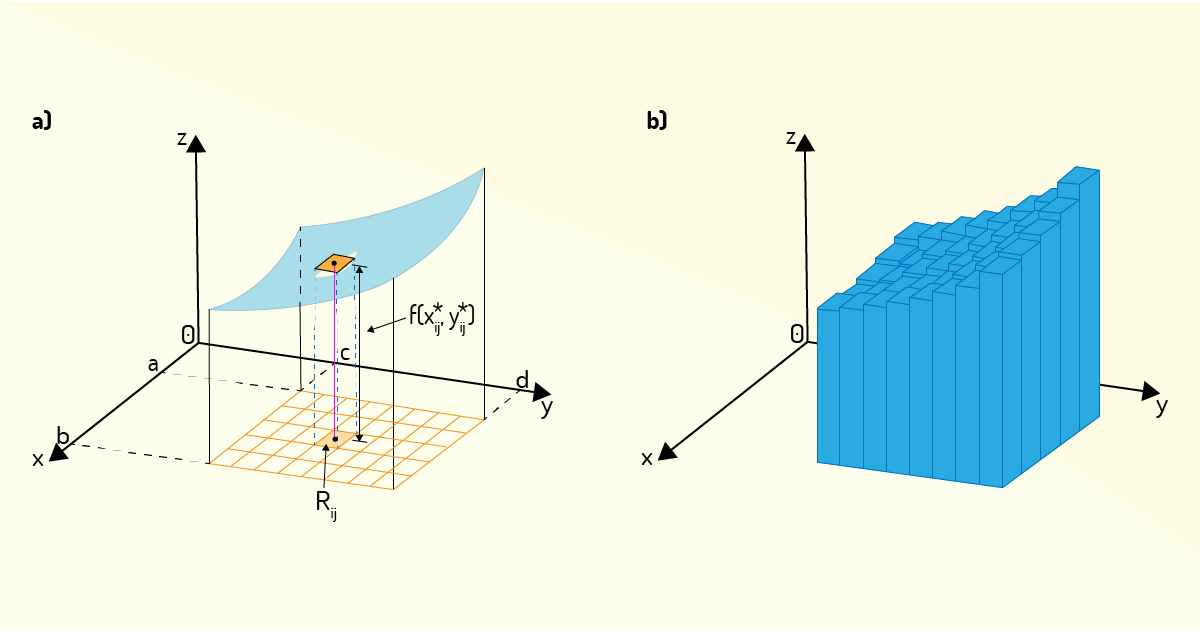
Como fica evidente pela análise da Figura 4.4 b), apenas alguns blocos retangulares, certamente, não irão gerar uma aproximação tão boa do sólido \(S\). Uma forma que existe e permite melhorar essa aproximação, segundo Stewart (2017b), é utilizar o máximo de blocos retangulares possíveis, ou seja:
\[V=\underset{m,n\to \infty }{\mathop{lim}}\,\underset{i=1}{\overset{m}{\mathop \sum }}\,\underset{j=1}{\overset{n}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)~~~~~~(4)\]
Como esse limite apresentado em (4) é muito recorrente, inclusive para situações em que \(f\left( x,y \right)\) não é positiva, assim como quando não se está exatamente calculando o volume de um sólido, convém empregar a seguinte definição:
Definição 1: A integral dupla de uma função \(f\left( x,y \right)\), em um espaço retangular \(R\), é definida como
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{m,n\to \infty }{\mathop{lim}}\,\underset{i=1}{\overset{m}{\mathop \sum }}\,\underset{j=1}{\overset{n}{\mathop \sum }}\,f\left( x_{ij}^{*},y_{ij}^{*} \right)\Delta A~~~~~~(5)\]
Se o limite acima existir.
Flemming e Gonçalves (2005) apresentam algumas considerações a respeito do que foi comentado até aqui:
Stewart (2017b) ainda relata que o significado preciso do limite apresentado em (5) é que, para qualquer \(\varepsilon >0\), existirá um número inteiro \(N\), tal que:
\[\left| \underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA-\underset{i=1}{\overset{m}{\mathop \sum }}\,\underset{j=1}{\overset{n}{\mathop \sum }}\,f\left( x_{ij}^{*},y_{ij}^{*} \right)\Delta A \right|<\varepsilon ~~~~(6)\]
Note que (6) é válida para todos os inteiros \(m\) e \(n\) maiores que \(N\) e para qualquer ponto de amostragem em \({{R}_{ij}}\).
Outro ponto destacado por Stewart (2017b) é relacionado à escolha dos pontos de amostragem. Os pontos \(x_{ij}^{*}\) e \(y_{ij}^{*}\) podem ser escolhidos em qualquer local dentro dos limites de \({{R}_{ij}}\), mas, caso sejam escolhidos apenas os pontos do canto superior de \({{R}_{ij}}\), ou seja, \({{x}_{i}}\) e \({{y}_{i}}\), de acordo com a Figura 4.3, a equação (5) se reduz a
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{m,n\to \infty }{\mathop{lim}}\,\underset{i=1}{\overset{m}{\mathop \sum }}\,\underset{j=1}{\overset{n}{\mathop \sum }}\,f\left( {{x}_{i}},{{y}_{i}} \right)\Delta A~~~~~~(7)\]
Dito isso, uma função \(f\left( x,y \right)\) será considerada integrável se o limite proposto em (5) existir. De uma forma mais geral, cursos avançados de cálculo mostram que todas as funções contínuas são integráveis (STEWART, 2017b).
Exemplo 1.1: Estime o volume do sólido que se encontra acima da região \(R=\left[ 0,2 \right]\times \left[ 0,2 \right]\) e abaixo do paraboloide definido pela função \(z=9-2{{x}^{2}}-{{y}^{2}}\). Para isso, divida \(R\) em quatro regiões iguais e escolha os pontos de amostragem nos cantos superiores direitos de cada quadrado \({{R}_{ij}}\).
Solução
Na Figura 4.5, tem-se uma representação de \(R\) no plano cartesiano, destacando-se também os quatro pontos de amostragem pedidos no enunciado.
Analisando a Figura 4.5, percebe-se que a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=1\cdot 1=1\). Como \(R\) foi dividida em quatro regiões iguais, tem-se também que \(m=n=2\). Basta, então, aplicar a equação (3), pois o volume de um sólido pode ser aproximado por uma soma de Riemann:
\[V=\underset{i=1}{\overset{2}{\mathop \sum }}\,\underset{j=1}{\overset{2}{\mathop \sum }}\,\Delta A\cdot f\left( {{x}_{i}},{{y}_{i}} \right)\]
\[=f\left( 1,1 \right)\cdot \Delta A+f\left( 2,1 \right)\cdot \Delta A+f\left( 1,2 \right)\cdot \Delta A+f\left( 2,2 \right)\cdot \Delta A\]
\[=f\left( 1,1 \right)\cdot 1+f\left( 2,1 \right)\cdot 1+f\left( 1,2 \right)\cdot 1+f\left( 2,2 \right)\cdot 1\]
\[=\left( 9-2\cdot {{1}^{2}}-{{1}^{2}} \right)+\left( 9-2\cdot {{2}^{2}}-{{1}^{2}} \right)+\left( 9-2\cdot {{1}^{2}}-{{2}^{2}} \right)+\left( 9-2\cdot {{2}^{2}}-{{2}^{2}} \right)\]
\[=6+0+3+\left( -3 \right)=6\]
Veja que, conforme você aumenta a quantidade de quadrados para calcular esse volume, o resultado irá se alterando. Por exemplo, se você repetir o procedimento dividindo \(R\) em oito regiões iguais, o que resulta em 16 pontos, você deverá encontrar \(V=13,5\); já com o uso de dezesseis regiões iguais, o que resulta em 64 pontos, você deverá encontrar \(V=16,875\); finalmente, com a divisão de \(R\) em 32 regiões iguais, resultando em 256 pontos, você encontrará \(V=18,4688\). Caso aumente ainda mais a divisão da região \(R\), mais você se aproximará do valor real desse volume, que é igual a 20.
Leithold (1994) e Flemming e Gonçalves (2005) apresentam algumas propriedades úteis para o trabalho com integrais duplas. Antes de analisarmos essas propriedades, é preciso considerar que a fronteira da região de integração \(R\) será formada por uma quantidade finita de arcos com curvas suaves, assim como as funções \(f\left( x,y \right)\) e \(g\left( x,y \right)\) são contínuas em \(R\). Com isso, garante-se que as integrais duplas, apresentadas a seguir, existem.
Vejamos, então, essas propriedades das integrais duplas apresentadas por Leithold (1994) e Flemming e Gonçalves (2005):
A prova de todas essas propriedades é semelhante às provas realizadas para as propriedades semelhantes das integrais de funções de uma única variável. Então, as provas das seis propriedades apresentadas anteriormente podem ser feitas simplesmente com a definição dada para integral dupla e com as propriedades de limite. Então, caro(a) aluno(a), caso deseje praticar um pouco a análise matemática e relembrar os conceitos de limite, um bom exercício é provar as cinco propriedades listadas acima.
Considere o sólido delimitado acima da região \(R=\left[ 0,4 \right]\times \left[ 0,4 \right]\) e abaixo da curva da função \(z=\sqrt{36-{{x}^{2}}-{{y}^{2}}}\). Visando, então, a fixação prática do cálculo de volume de sólidos, assinale a alternativa correta. Note que \(u~=\) unidade de comprimento genérica.
Estime o volume do sólido que se encontra acima da região \(R\) e abaixo do paraboloide definido pela função \(z\). Para isso, divida \(R\) em quatro regiões iguais e escolha os pontos de amostragem nos cantos superiores direitos de cada quadrado \({{R}_{ij}}\).
Ao se dividir \(R\) nas duas regiões iguais \({{R}_{11}}=\left[ 0,4 \right]\times \left[ 2,4 \right]\) e \({{R}_{21}}=\left[ 2,4 \right]\times \left[ 4,4 \right]\), considerando os pontos de amostragem como aqueles no canto superior direito, o volume estimado do sólido será \(96~{{u}^{2}}\).
Justificativa: Com os dados indicados, a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=2\cdot 4=8\). Tem-se também que \(m=2\) e \(n=1\). Aplicando a equação (3):
\[V=\underset{i=1}{\overset{2}{\mathop \sum }}\,\underset{j=1}{\overset{1}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)\]
\[=f\left( 2,4 \right)\cdot \Delta A+f\left( 4,4 \right)\cdot \Delta A=8\cdot \left[ f\left( 2,4 \right)+f\left( 4,4 \right) \right]=8\cdot \left( 4+2 \right)=48~{{u}^{2}}\]
Ao se dividir \(R\) em oito regiões iguais, dividindo o lado \(x\) em quatro e o lado \(y\) em dois, considerando os pontos de amostragem como aqueles no centro de cada \({{R}_{ij}}\), o volume estimado do sólido será aproximadamente \(80,6~{{u}^{2}}\).
Justificativa correta: Com os dados indicados, a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=1\cdot 2=2\). Tem-se também que \(m=4\) e \(n=2\). Aplicando a equação (3):
\[V=\underset{i=1}{\overset{4}{\mathop \sum }}\,\underset{j=1}{\overset{2}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)\]
\[\Delta A\cdot \left[ f\left( 0.5,1 \right)+f\left( 0.5,3 \right)+f\left( 1.5,1 \right)+f\left( 1.5,3 \right)+f\left( 2.5,1 \right)+f\left( 2.5,3 \right)+f\left( 3.5,1 \right)+f\left( 2.5,3 \right) \right]\]
\[=2\cdot \left[ 5,57+4,36+5,29+4,00+4,80+3,32+4,00+2,00 \right]=2\cdot \left( 33,3 \right)=80,6~{{u}^{2}}\]
Ao se dividir \(R\) em quatro regiões iguais, considerando os pontos de amostragem como aqueles no canto superior direito de cada \({{R}_{ij}}\), o volume estimado do sólido será aproximadamente \(79,0~{{u}^{2}}\).
Justificativa: Com os dados indicados, a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=2\cdot 2=4\). Tem-se também que \(m=n=2\). Aplicando a equação (3):
\[V=\underset{i=1}{\overset{2}{\mathop \sum }}\,\underset{j=1}{\overset{2}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)=\Delta A\cdot \left[ f\left( 2,2 \right)+f\left( 2,4 \right)+f\left( 4,2 \right)+f\left( 4,4 \right) \right]\]
\[=4\cdot \left[ 5,29+4,00+4,00+2,00 \right]=4\cdot \left( 15,3 \right)=61,2~{{u}^{2}}\]
Ao se dividir \(R\) em oito regiões iguais, dividindo o lado \(x\) em quatro e o lado \(y\) em dois, considerando os pontos de amostragem como aqueles no canto superior direito de cada \({{R}_{ij}}\), o volume estimado do sólido será aproximadamente \(81,1~{{u}^{2}}\).
Justificativa: Com os dados indicados, a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=1\cdot 2=2\). Tem-se também que \(m=4\) e \(n=2\). Aplicando a equação (3):
\[V=\underset{i=1}{\overset{4}{\mathop \sum }}\,\underset{j=1}{\overset{2}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)\]
\[=\Delta A\cdot \left[ f\left( 1,2 \right)+f\left( 1,4 \right)+f\left( 2,2 \right)+f\left( 2,4 \right)+f\left( 3,2 \right)+f\left( 3,4 \right)+f\left( 4,2 \right)+f\left( 4,4 \right) \right]\]
\[=2\cdot \left[ 5,57+4,36+5,29+4,00+4,80+3,32+4,00+2,00 \right]=2\cdot \left( 33,3 \right)=66,7~{{u}^{2}}\]
Ao se dividir \(R\) em quatro regiões iguais, considerando os pontos de amostragem como aqueles no centro de cada \({{R}_{ij}}\), o volume estimado do sólido será aproximadamente \(61,2~{{u}^{2}}\).
Justificativa: Com os dados indicados, a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=2\cdot 2=4\). Tem-se também que \(m=n=2\). Aplicando a equação (3):
\[V=\underset{i=1}{\overset{2}{\mathop \sum }}\,\underset{j=1}{\overset{2}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)=\Delta A\cdot \left[ f\left( 1,1 \right)+f\left( 1,3 \right)+f\left( 3,1 \right)+f\left( 3,3 \right) \right]\]
\[=4\cdot \left[ 5,83+5,10+5,10+4,24 \right]=4\cdot \left( 20,3 \right)=81,1~{{u}^{2}}\]
Tendo em mãos os conceitos básicos de integral dupla e suas respectivas propriedades, agora, devemos analisar o assunto dando um enfoque mais prático. Até o momento, o cálculo das integrais duplas era feito de forma iterativa, o que se mostra uma tarefa consideravelmente trabalhosa. Será avaliada, então, a possibilidade de existir uma maneira mais prática de calcular a integral dupla de uma função. Em seguida, as aplicações desse conceito serão brevemente discutidas e analisadas.
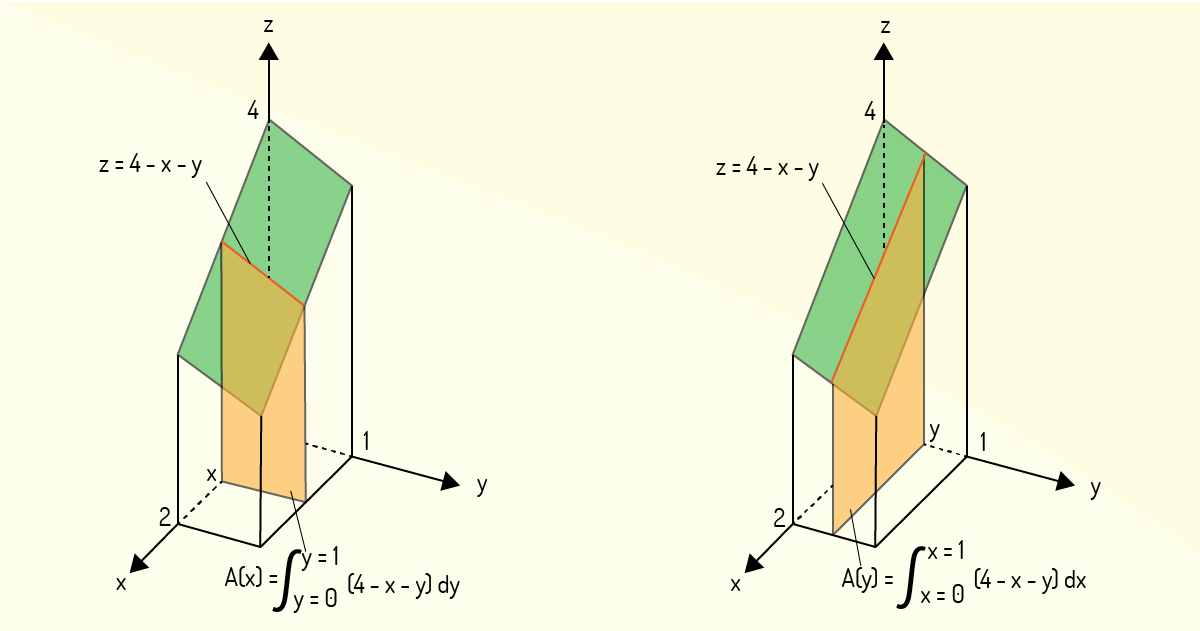
Thomas Jr. (2016) apresenta o seguinte problema: considere que se deseja calcular o volume do sólido limitado pela função \(z=4-x-y\) e acima da região retangular \(R=\left[ 0,2 \right]\times \left[ 0,1 \right]\) no plano \(xy\). Esse problema pode ser resolvido utilizando-se o método das seções transversais, que considera seções perpendiculares ao eixo \(x\). Então, sendo \(A\left( x \right)\) a área de seção transversal em \(x\), o volume desse sólido será
\[V=\underset{x=0}{\overset{x=2}{\mathop \int }}\,A\left( x \right)dx~~~~~~(8)\]
Com esse método, para cada valor de \(x\), essa área \(A\left( x \right)\) pode ser calculada pela seguinte integral
\[A\left( x \right)=\underset{y=0}{\overset{y=1}{\mathop \int }}\,\left( 4-x-y \right)dy~~~~~~(9)\]
Note que (8) nada mais é do que a área sob a curva de \(z\) no plano da seção transversal em \(x\). Então, ao calcular \(A\left( x \right)\), \(x\) será fixado e a integração será feita apenas em relação a \(y\). Combinando, então, as equação (8) e (9), percebe-se que o volume do sólido pode ser avaliado como:
\[V=\underset{x=0}{\overset{x=2}{\mathop \int }}\,\left[ \underset{y=0}{\overset{y=1}{\mathop \int }}\,\left( 4-x-y \right)dy \right]dx=\underset{x=0}{\overset{x=2}{\mathop \int }}\,\left( 4y-xy-\frac{{{y}^{2}}}{2} \right)_{y=0}^{y=1}dx\]
\[=\underset{x=0}{\overset{x=2}{\mathop \int }}\,\left( \frac{7-2x}{2} \right)dx=\left( \frac{7x-{{x}^{2}}}{2} \right)_{x=0}^{x=2}=5\]
Ou seja, vimos que o volume do sólido pôde ser avaliado pela seguinte equação:
\[V=\underset{x=0}{\overset{x=2}{\mathop \int }}\,\underset{y=0}{\overset{y=1}{\mathop \int }}\,\left( 4-x-y \right)dydx~~~~~~(10)\]
A expressão da direita em (10) é conhecida como integral repetida ou integral iterada. Stewart (2017b) destaca que esse método foi realizado mantendo-se uma das variáveis fixas, nesse caso, a variável \(x\), enquanto a função era integrada para a outra variável, nesse caso, a variável \(y\), de uma forma muito semelhante àquela que foi vista para os processos de derivação parcial. Assim, esse processo de integração também pode ser conhecido como integração parcial.
Perceba que você pode realizar esse processo fixando inicialmente a variável \(y\) enquanto a função \(f\left( x,y \right)\) é integrada em relação à \(x\). Assim, para o problema proposto no início desta seção, teriam-se duas equações semelhantes às equações (8) e (9):
\[V=\underset{y=0}{\overset{y=1}{\mathop \int }}\,A\left( y \right)dy~~~~~~(11)\]
\[A\left( y \right)=\underset{x=0}{\overset{x=2}{\mathop \int }}\,\left( 4-x-y \right)dx~~~~~~(12)\]
Resolvendo, então, o problema com essa abordagem, pela combinação das equações (11) e (12):
\[V=\underset{y=0}{\overset{y=1}{\mathop \int }}\,\left[ \underset{x=0}{\overset{x=2}{\mathop \int }}\,\left( 4-x-y \right)dx \right]dy=\underset{y=0}{\overset{y=1}{\mathop \int }}\,\left( 4x-\frac{{{x}^{2}}}{2}-xy \right)_{x=0}^{x=2}dy\]
\[=\underset{y=0}{\overset{y=1}{\mathop \int }}\,\left( 6-2y \right)dy=\left( 6y-{{y}^{2}} \right)_{y=0}^{y=1}=5\]
Note que o resultado encontrado aqui é igual àquele encontrado anteriormente. Esse resultado é esperado, visto que a integral dupla simplesmente mede o volume de uma mesma região, segundo Thomas Jr. (2016). De fato, um teorema publicado em 1907 pelo matemático italiano Guido Fubini expõe que toda integral dupla de qualquer função contínua em uma região retangular pode ser calculada como uma integral iterada em qualquer sequência de integração:
Teorema 1 - O Teorema de Fubini na primeira forma: Seja uma função \(f\left( x,y \right)\) contínua em um espaço retangular \(R=\left[ a,b \right]\times \left[ c,d \right]\), então, suas integrais duplas obedecem à seguinte relação:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=V=\underset{c}{\overset{d}{\mathop \int }}\,\underset{a}{\overset{b}{\mathop \int }}\,f\left( x,y \right)dxdy=\underset{a}{\overset{b}{\mathop \int }}\,\underset{c}{\overset{d}{\mathop \int }}\,f\left( x,y \right)dydx\]
A Figura 4.7 apresenta graficamente o desenvolvimento desse método. Em tal figura, a área de seção transversal, na qual se mantém uma variável fixa enquanto a outra é usada na integração, encontra-se destacada.
Exemplo 2.1: Calcule a integral dupla da função \(z=f\left( x,y \right)=9-2{{x}^{2}}-{{y}^{2}}\) apresentada no Exemplo 1.1 para a região \(R=\left[ 0,2 \right]\times \left[ 0,2 \right]\). Em seguida, compare o resultado encontrado com aqueles mostrados no Exemplo 1.1.
Solução
Aplicando o Teorema de Fubini para a função dada:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{y=0}{\overset{y=2}{\mathop \int }}\,\underset{x=0}{\overset{x=2}{\mathop \int }}\,f\left( x,y \right)dxdy=\underset{x=0}{\overset{x=2}{\mathop \int }}\,\underset{y=0}{\overset{y=2}{\mathop \int }}\,f\left( x,y \right)dydx\]
Escolhendo a primeira forma para resolver:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{y=0}{\overset{y=2}{\mathop \int }}\,\left[ \underset{x=0}{\overset{x=2}{\mathop \int }}\,\left( 9-2{{x}^{2}}-{{y}^{2}} \right)dx \right]dy\]
\[=\underset{y=0}{\overset{y=2}{\mathop \int }}\,\left[ \left( 9x-\frac{2}{3}{{x}^{3}}-x{{y}^{2}} \right)_{x=0}^{x=2} \right]dy=\underset{y=0}{\overset{y=2}{\mathop \int }}\,\left( \frac{38-6{{y}^{2}}}{3} \right)dy\]
\[=\left( \frac{38y}{3}-\frac{2{{y}^{3}}}{3} \right)_{y=0}^{y=2}=20\]
Note que, avaliando essa integral dupla de forma reversa, o mesmo resultado é encontrado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{x=0}{\overset{x=2}{\mathop \int }}\,\left[ \underset{y=0}{\overset{y=2}{\mathop \int }}\,\left( 9-2{{x}^{2}}-{{y}^{2}} \right)dy \right]dx\]
\[=\underset{x=0}{\overset{x=2}{\mathop \int }}\,\left[ \left( 9y-2{{x}^{2}}y-\frac{{{y}^{3}}}{3} \right)_{y=0}^{y=2} \right]dy=\underset{x=0}{\overset{x=2}{\mathop \int }}\,\left( \frac{46-12{{x}^{2}}}{3} \right)dx\]
\[=\left( \frac{46x}{3}-\frac{4{{x}^{3}}}{3} \right)_{x=0}^{x=2}=20\]
Veja que, ao usar apenas quatro regiões para a aproximação, você encontrou 6 como resultado da integral dupla. Aumentando a quantidade de regiões utilizadas no cálculo, o resultado encontrado foi 16,875 para dezesseis regiões e 18,4688 para 32 regiões iguais. Ou seja, conforme a quantidade de prismas retos usados no cálculo aumentou, o resultado se aproximou do valor teórico, que é 20.
Pode-se expandir o que foi exposto até aqui. Note que nem sempre a região na qual iremos avaliar a integral dupla será retangular. Assim, Flemming e Gonçalves (2005) indicam que pode ser que se tenha um dos seguintes tipos de região para avaliar a integral dupla:
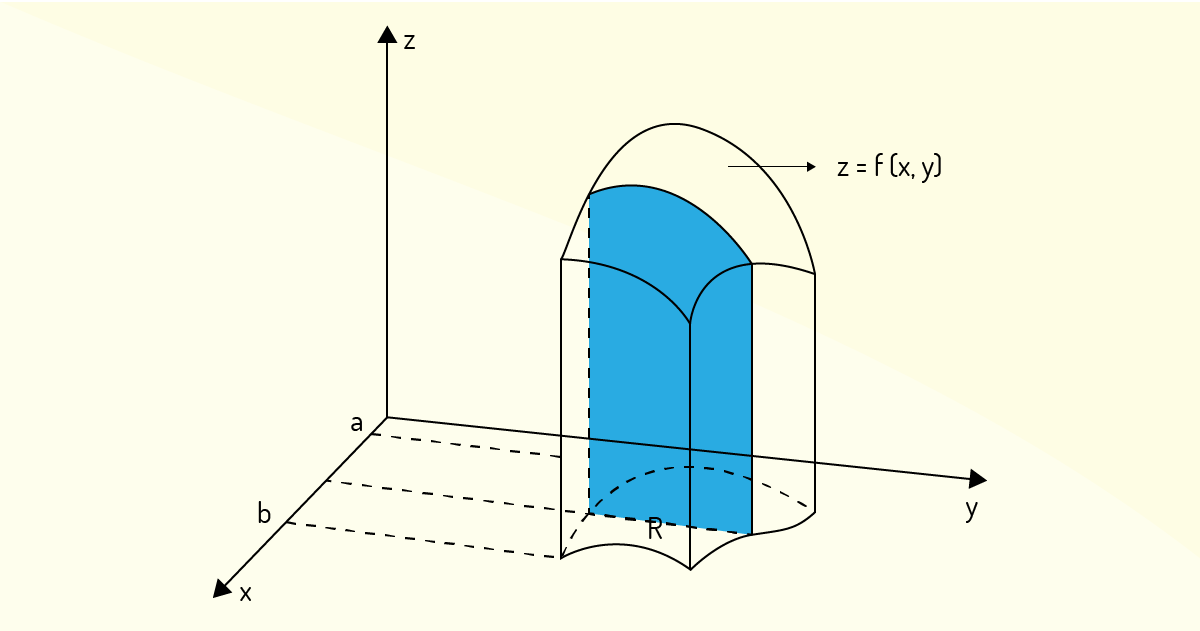
No caso de uma integral dupla do tipo 1, tem-se uma região delimitada de acordo com o que se vê na Figura 4.8.
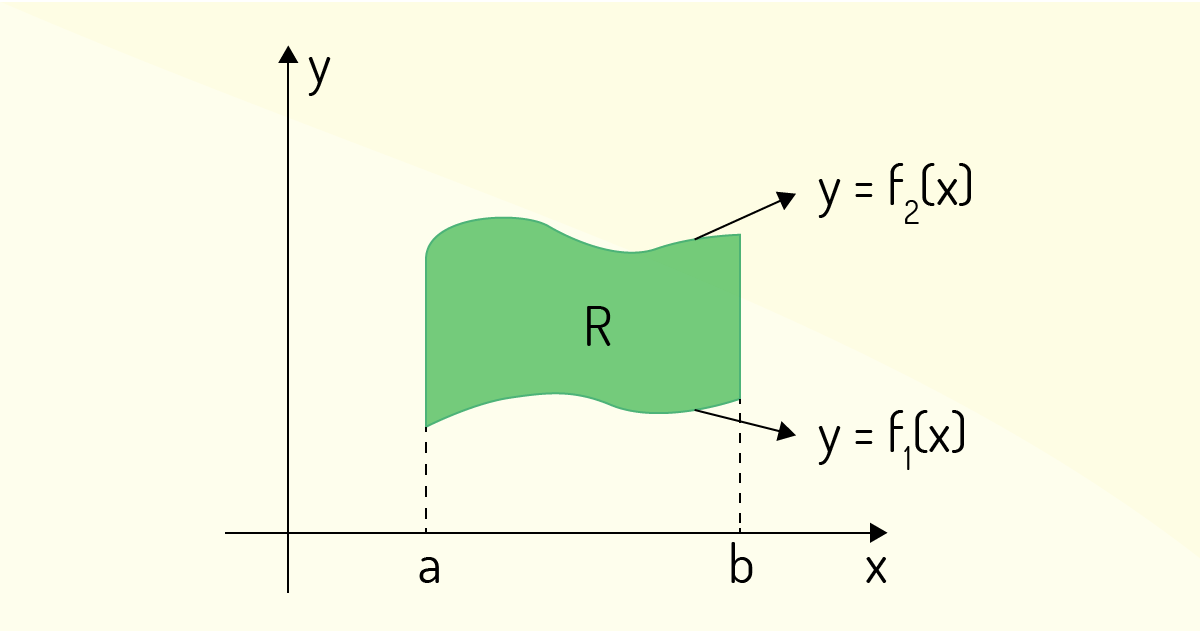
Para tal situação, a integral dupla de uma função \(f\left( x,y \right)\) será calculada da seguinte maneira:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{a}{\overset{b}{\mathop \int }}\,\underset{{{f}_{1}}\left( x \right)}{\overset{{{f}_{2}}\left( x \right)}{\mathop \int }}\,f\left( x,y \right)dydx~~~~~~(13)\]
Geometricamente, a integral interna de (13), ou seja
\[\underset{{{f}_{1}}\left( x \right)}{\overset{{{f}_{2}}\left( x \right)}{\mathop \int }}\,f\left( x,y \right)dy~~~~~~(14)\]
pode ser interpretada como uma área de seção transversal perpendicular ao eixo \(x\) do sólido cujo volume se deseja calcular, como é mostrado na Figura 4.9.
Essa integral (14) pode, ainda, ser representada como \(A\left( x \right)\):
\[A\left( x \right)=\underset{{{f}_{1}}\left( x \right)}{\overset{{{f}_{2}}\left( x \right)}{\mathop \int }}\,f\left( x,y \right)dy~~~~~~(15)\]
De forma que (13) pode ser reescrita como:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{a}{\overset{b}{\mathop \int }}\,A\left( x \right)dx~~~~~~(16)\]
Para uma integral dupla do tipo 2, um pensamento semelhante pode ser desenvolvido. Aqui, tem-se uma região delimitada de acordo com a Figura 4.10.
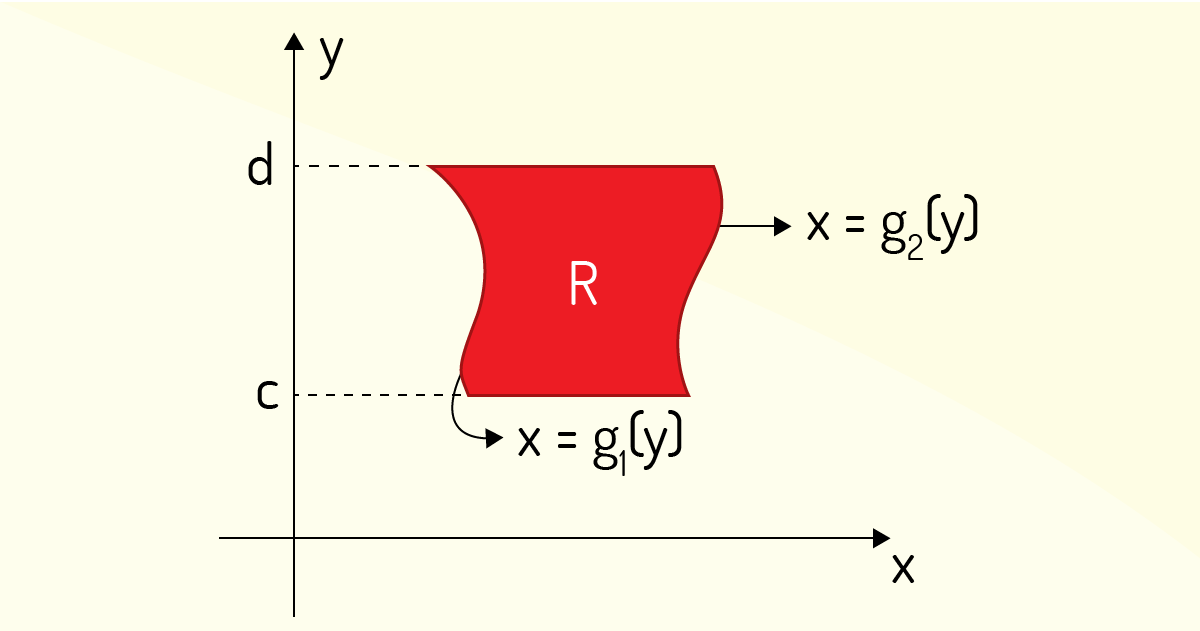
Para esse tipo de problema, a integral dupla de uma função \(f\left( x,y \right)\) será calculada da seguinte maneira:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{c}{\overset{d}{\mathop \int }}\,\underset{{{g}_{1}}\left( y \right)}{\overset{{{g}_{2}}\left( y \right)}{\mathop \int }}\,f\left( x,y \right)dxdy~~~~~~(17)\]
Exemplo 2.2: Calcule o volume do sólido delimitado superiormente pela função \(z=f\left( x,y \right)=4-x-y\) e inferiormente pela região \(R\), na qual \(0\le x\le 2\) e pela reta que passa pelos pontos \(y=0\) e \(y=x\).
Solução
Esta é uma integral dupla do tipo 1 descrita anteriormente. Logo, o volume desse sólido poderá ser avaliado utilizando-se a equação (13):
\[V=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{a}{\overset{b}{\mathop \int }}\,\underset{{{f}_{1}}\left( x \right)}{\overset{{{f}_{2}}\left( x \right)}{\mathop \int }}\,f\left( x,y \right)dydx\]
Os pontos \(a\) e \(b\) já estão determinados, então, deve-se avaliar agora os limites \({{f}_{1}}\left( x \right)\) e \({{f}_{2}}\left( x \right)\). Como foi dito ser uma reta, os limites de \(y\) podem ser definidos como \(0\le y\le x\). Resolvendo, então, a integral dupla apresentada:
\[V=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{0}{\overset{2}{\mathop \int }}\,\left[ \underset{0}{\overset{x}{\mathop \int }}\,\left( 4-x-y \right)dy \right]dx\]
\[=\underset{0}{\overset{2}{\mathop \int }}\,\left[ \left( 4y-xy-\frac{{{y}^{2}}}{2} \right)_{y=0}^{y=x} \right]dx=\underset{0}{\overset{2}{\mathop \int }}\,\left( 4x-\frac{3{{x}^{2}}}{2} \right)dx\]
\[=\left( 2{{x}^{2}}-\frac{{{x}^{3}}}{2} \right)_{x=0}^{x=2}=4\]
Exemplo 2.3: Calcule a integral dupla da função \(z=f\left( x,y \right)=x+y\), delimitada pela região \(R\), definida entre \(y=2{{x}^{2}}\) e \(y=4x\).
Solução
A região de integração se encontra entre uma reta e uma parábola, como se evidencia na Figura 4.11.
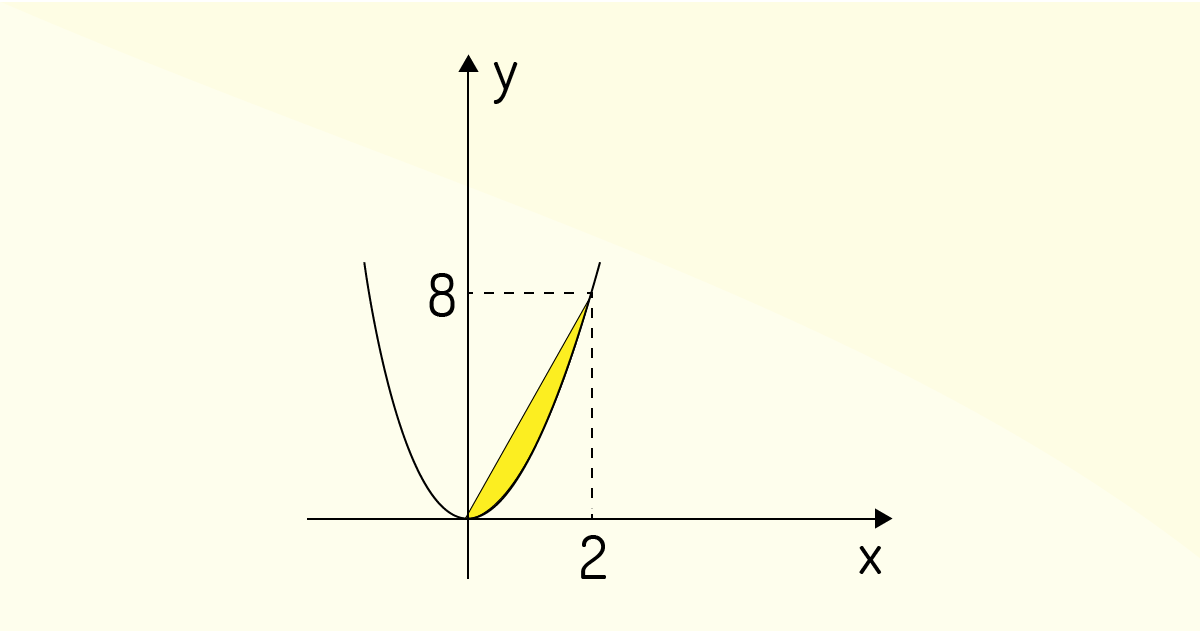
Com isso, pode-se notar que essa integral dupla pode ser tanto do tipo 1 quanto do tipo 2, pois a região \(R\) pode ser descrita como:
\[R=\left\{ \begin{matrix} 2{{x}^{2}}\ll y\ll 4x \\ 0\ll x\ll 2 \\ \end{matrix}~~~~ou~~~~R= \right.\left\{ \begin{matrix} y/4\ll x\ll \sqrt{y/2} \\ 0\ll y\ll 8 \\ \end{matrix} \right.\]
Calculando, então, essa integral considerando-a como sendo do tipo 1:
\[V=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{0}{\overset{2}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{4x}{\mathop \int }}\,\left( x+y \right)dydx\]
\[=\underset{0}{\overset{2}{\mathop \int }}\,\left[ \left( xy+\frac{{{y}^{2}}}{2} \right)_{y=2{{x}^{2}}}^{y=4x} \right]dx=\underset{0}{\overset{2}{\mathop \int }}\,\left( 12{{x}^{2}}-2{{x}^{3}}-2{{x}^{4}} \right)dx\]
\[=\left( 4{{x}^{3}}-\frac{{{x}^{4}}}{2}-\frac{2{{x}^{5}}}{5} \right)_{x=0}^{x=2}=\frac{56}{5}\]
E calculando-a considerando como uma integral dupla do tipo 2:
\[V=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{0}{\overset{8}{\mathop \int }}\,\underset{y/4}{\overset{\sqrt{y/2}}{\mathop \int }}\,\left( x+y \right)dxdy\]
\[=\underset{0}{\overset{8}{\mathop \int }}\,\left[ \left( xy+\frac{{{x}^{2}}}{2} \right)_{x=y/4}^{x=\sqrt{y/2}} \right]dy=\underset{0}{\overset{2}{\mathop \int }}\,\left( \frac{1}{2}y\sqrt{2}\sqrt{y}+\frac{1}{4}y-\frac{9}{32}{{y}^{2}} \right)dy\]
\[=\left( \frac{\sqrt{2}}{5}{{y}^{2}}\sqrt{y}+\frac{1}{8}{{y}^{2}}-\frac{3}{32}{{y}^{3}} \right)_{y=0}^{y=8}=\frac{56}{5}\]
Note que, apesar dos resultados serem os mesmos, o segundo cálculo pode ser visto como ligeiramente mais complexo. Logo, uma boa escolha do tipo de integral dupla a ser avaliado pode facilitar muito o seu trabalho.
Quando se tem um caso de uma integral de uma função de única variável se mostrar muito complexa, pode-se mudar as variáveis dessa função, buscando-se uma maneira mais simples de avaliar tal integral, segundo Flemming e Gonçalves (2005). Nesse caso:
\[\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx=\underset{c}{\overset{d}{\mathop \int }}\,f\left( g\left( t \right) \right)g'\left( t \right)dt\]
sendo \(a=g\left( c \right)\) e \(b=g\left( d \right)\). Assim, pode-se notar que a mudança das variáveis na integração definida faz com que os limites de integração também se alterem.
Como muito do que foi visto e trabalhado até o momento para o cálculo com funções de duas variáveis, um método semelhante pode ser proposto para as integrais duplas. Assim, Flemming e Gonçalves (2005) indicam que, por meio da seguinte mudança de variáveis
\[x=x\left( u,v \right)~~~~e ~~~~y=y\left( u,v \right)~~~~~~(18)\]
a integral dupla sobre uma região \(R\) localizada no plano \(xy\) pode ser avaliada em uma região \(R'\) localizada no plano \(uv\).
Geometricamente, Flemming e Gonçalves (2005) relatam que as mudanças de variáveis citadas simplesmente definem uma aplicação ou transformação que faz os pontos de \(uv\) a pontos de \(xy\), da mesma forma que se tem na definição de uma função. Assim, a região \(uv\) pode ser aplicada na região \(xy\). Disso, tem-se que, se a transformação proposta leva pontos distintos de \(R'\) a um único ponto de \(R\), tem-se uma transformação um para um ou bijetora, o que garante que a transformação reversa também é possível:
\[u=u\left( x,y \right)~~~~e~~~~v=v\left( x,y \right)~~~~~~(19)\]
Se as funções (18) e (19) forem contínuas e apresentarem derivadas parciais contínuas em \(R'\) e \(R\), respectivamente, então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dxdy=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R'}{\overset{{}}{\mathop \int }}\,f\left( x\left( u,v \right),y\left( u,v \right) \right)\left| \frac{\partial \left( x,y \right)}{\partial \left( u,v \right)} \right|dudv~~~~(20)\]
Note que, em (20), o termo \(\left| \frac{\partial \left( x,y \right)}{\partial \left( u,v \right)} \right|\) é o jacobiano de \(x\) e \(y\) em relação às novas variáveis \(u\) e \(v\), o qual é dado por:
\[\frac{\partial (x,y)}{\partial (u,v)}=\left| \begin{matrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ \end{matrix} \right|\]
Flemming e Gonçalves (2005) ainda destacam alguns pontos sobre esse assunto:
Suponha que você se depare com um problema no qual tenha que calcular a integral dupla de uma função em uma região \(R\) em uma das formas a seguir.
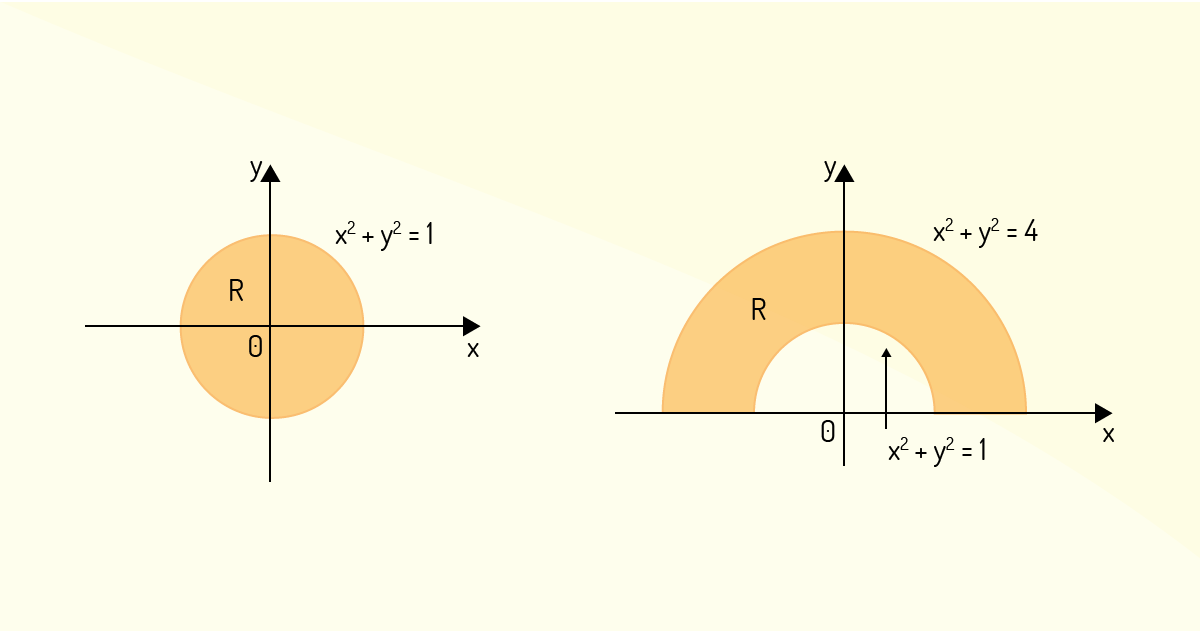
Veja que é complexo descrever essas duas regiões \(R\) em coordenadas retangulares. No entanto, fazendo-se o uso de coordenadas polares, o trabalho fica consideravelmente mais simples. Para as regiões acima, tem-se, respectivamente,
\[R=\left\{ \left( r,\theta \right)~|~0\le r\le 1,~0\le \theta \le 2\pi \right\}~~~~e~~~~R=\left\{ \left( r,\theta \right)~|~1\le r\le 2,~0\le \theta \le \pi \right\}\]
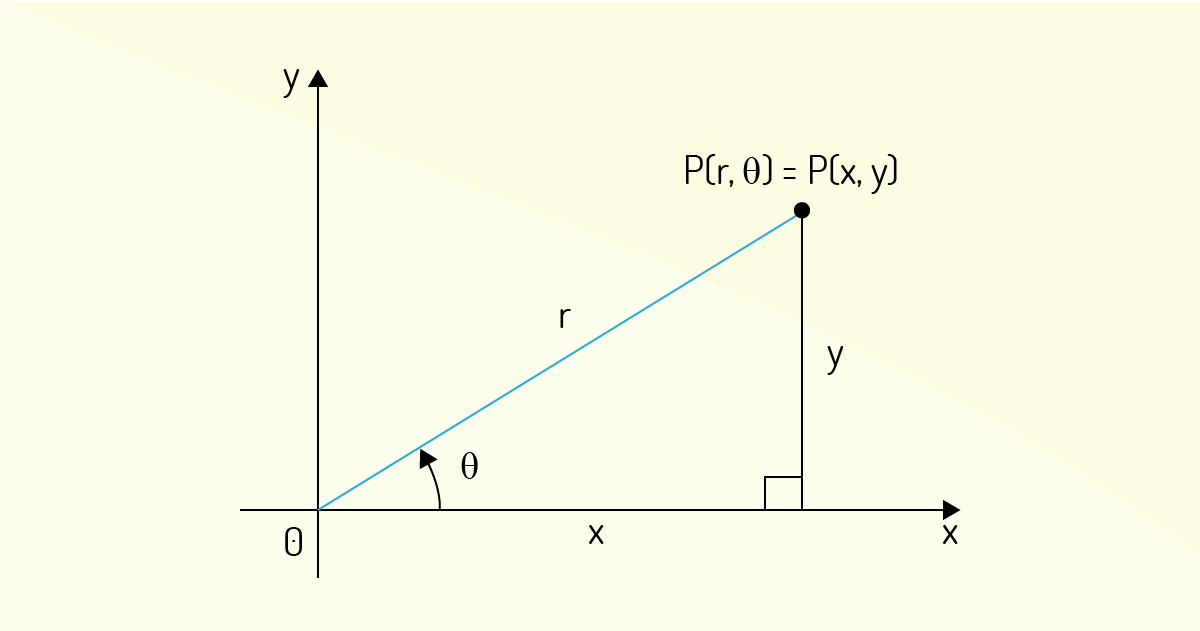
Segundo Stewart (2017b), as coordenadas polares \(\left( r,\theta \right)\) de um ponto se relacionam com as coordenadas retangulares \(\left( x,y \right)\) da seguinte forma, como se pode confirmar pela Figura 4.13.
\[{{r}^{2}}={{x}^{2}}+{{y}^{2}}~~~~x=rcos\theta ~~~~y=rsen\theta \]
Assim, Stewart (2017b) diz que, com essas transformações, as regiões expostas na Figura 4.12 nada mais são do que casos especiais de um retângulo polar, ou seja:
\[R=\left\{ \left( r,\theta \right)~|~a\le r\le b,~\alpha \le \theta \le \beta \right\}\]
Esse retângulo polar é evidenciado na Figura 4.14 a). Então, para avaliar a integral dupla de uma função em uma região que é um retângulo polar, divide-se o intervalo fechado \(\left[ a,b \right]\) em \(m\) subintervalos \(\left[ {{r}_{i-1}},{{r}_{i}} \right]\), sendo que todos esses subintervalos apresentam a mesma largura \(\Delta r=\left( b-a \right)/m\), e o intervalo fechado \(\left[ \alpha ,\beta \right]\) em \(n\) subintervalos \(\left[ {{\theta }_{j-1}},{{\theta }_{j}} \right]\), também com a mesma largura \(\Delta \theta =\left( \beta -\alpha \right)/n\). Com isso, círculos \(r={{r}_{i}}\) e os raios \(\theta ={{\theta }_{j}}\) irão dividir \(R\) em retângulos polares menores \({{R}_{ij}}\), como mostra a Figura 4.14 b).
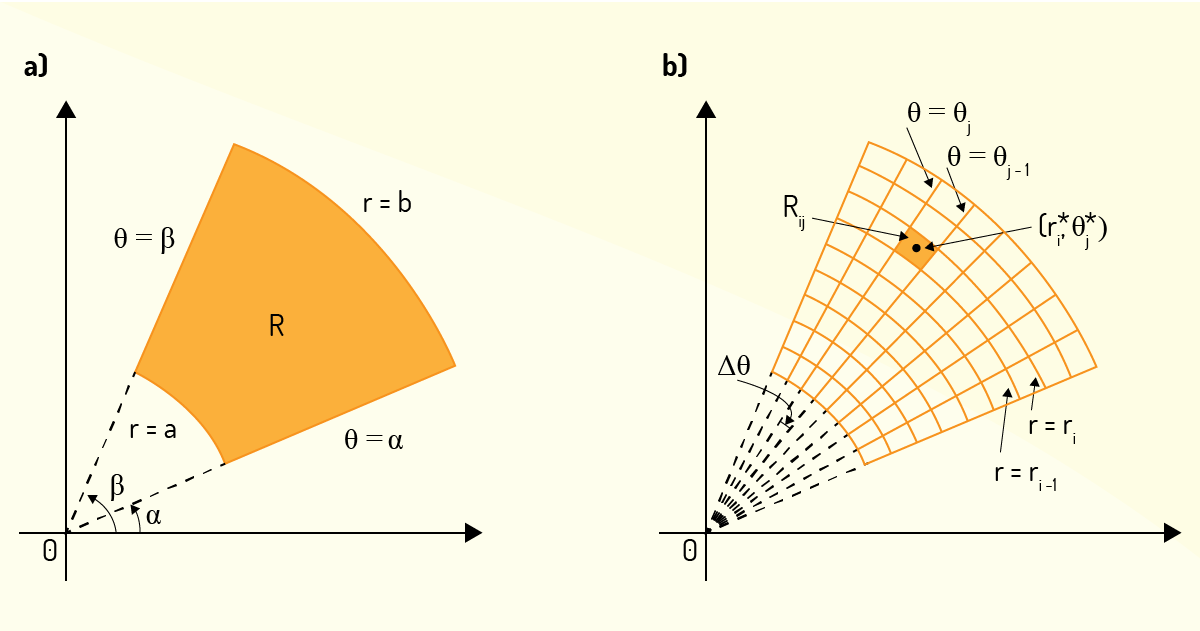
Com isso, o centro de um desses retângulos polares menores descritos por \(R=\left\{ \left( r,\theta \right)~|~{{r}_{i-1}}\le r\le {{r}_{i}},~{{\theta }_{j-1}}\le \theta \le {{\theta }_{j}} \right\}\) deverá apresentar como coordenadas:
\[r_{i}^{*}=\frac{1}{2}\left( {{r}_{i-1}}+{{r}_{i}} \right)~~~~e~~~~\theta _{j}^{*}=\frac{1}{2}\left( {{\theta }_{j-1}}+{{\theta }_{j}} \right)\]
Agora, é preciso identificar como determinar a área de cada retângulo \({{R}_{ij}}\). Segundo Stewart (2017b), isso pode ser feito considerando-se que a área de um setor de círculo de raio igual a \(r\) e ângulo central \(\theta \) deve ser \(\frac{1}{2}{{r}^{2}}\theta \). Fazendo, então, a subtração das áreas de dois desses setores cujo ângulo central é \(\Delta \theta ={{\theta }_{j}}-{{\theta }_{j-1}}\), descobre-se a área:
\[\Delta {{A}_{i}}=\frac{1}{2}{{r}_{i}}^{2}\Delta \theta -\frac{1}{2}{{r}_{i-1}}^{2}\Delta \theta =\frac{1}{2}\left( {{r}_{i}}^{2}-{{r}_{i-1}}^{2} \right)\Delta \theta \]
\[=\frac{1}{2}\left( {{r}_{i}}-{{r}_{i-1}} \right)\left( {{r}_{i}}-{{r}_{i-1}} \right)\Delta \theta =r_{i}^{*}\Delta r\Delta \theta \]
Então, com o que foi exposto até aqui, pode-se expressar a soma de Riemann para um retângulo polar. Sendo as coordenadas retangulares do centro de um \({{R}_{ij}}\) \(\left( r_{i}^{*}cos~\theta _{j}^{*},r_{i}^{*}sen~\theta _{j}^{*} \right)\), a soma de Riemann para esse caso se torna:
\[\underset{i=1}{\overset{m}{\mathop \sum }}\,\underset{j=1}{\overset{n}{\mathop \sum }}\,\Delta {{A}_{i}}\cdot f\left( r_{i}^{*}cos~\theta _{j}^{*},r_{i}^{*}sen~\theta _{j}^{*} \right)=\underset{i=1}{\overset{m}{\mathop \sum }}\,\underset{j=1}{\overset{n}{\mathop \sum }}\,f\left( r_{i}^{*}cos~\theta _{j}^{*},r_{i}^{*}sen~\theta _{j}^{*} \right)\cdot r_{i}^{*}\Delta r\Delta \theta ~~~~(21)\]
Você pode tornar (21) ainda mais parecida com a soma de Riemann do caso das coordenadas retangulares, fazendo a consideração
\[g\left( r,\theta \right)=rf\left( rcos~\theta ,rsen~\theta \right)\]
Com isso, a soma de Riemann fica:
\[\underset{i=1}{\overset{m}{\mathop \sum }}\,\underset{j=1}{\overset{n}{\mathop \sum }}\,g\left( r_{i}^{*},\theta _{j}^{*} \right)\cdot \Delta r\Delta \theta~~~~~~(22)\]
Para a qual se tem a integral dupla ao tomar o limite com \(m,n\to \infty \):
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{m,n\to \infty }{\mathop{lim}}\,\underset{i=1}{\overset{m}{\mathop \sum }}\,\underset{j=1}{\overset{n}{\mathop \sum }}\,\Delta {{A}_{i}}\cdot f\left( r_{i}^{*}cos~\theta _{j}^{*},r_{i}^{*}sen~\theta _{j}^{*} \right)\]
\[=\underset{m,n\to \infty }{\mathop{lim}}\,\underset{i=1}{\overset{m}{\mathop \sum }}\,\underset{j=1}{\overset{n}{\mathop \sum }}\,g\left( r_{i}^{*},\theta _{j}^{*} \right)\cdot \Delta r\Delta \theta =\underset{\alpha }{\overset{\beta }{\mathop \int }}\,\underset{a}{\overset{b}{\mathop \int }}\,g\left( r,\theta \right)drd\theta \]
\[=\underset{\alpha }{\overset{\beta }{\mathop \int }}\,\underset{a}{\overset{b}{\mathop \int }}\,f\left( rcos~\theta ,rsen~\theta \right)rdrd\theta ~~~~(23)\]
Exemplo 2.4: Calcule a integral dupla da função \(z=f\left( x,y \right)=3{{x}^{2}}+4y\), em que a região \(R\) é a região no semiplano superior definida pelos círculos \({{x}^{2}}+{{y}^{2}}=1\) e \({{x}^{2}}+{{y}^{2}}=4\).
Solução
A região \(R\) pode ser descrita como \(R=\left\{ \left( x,y \right)~|~y\ge 0,~1\le {{x}^{2}}+{{y}^{2}}\le 4 \right\}\). Essa região é idêntica ao anel mostrado na Figura 4.12, sendo fácil verificar por essa figura que, em coordenadas polares, tem-se \(1\le r\le 2\) e \(0\le \theta \le \pi \). Portanto, aplicando as mudanças de coordenadas \(x=rcos~\theta \) e \(y=rsen~\theta \) e a equação (23):
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,\left( 3{{x}^{2}}+4y \right)dA=\underset{0}{\overset{\pi }{\mathop \int }}\,\underset{1}{\overset{2}{\mathop \int }}\,\left( 3{{r}^{2}}co{{s}^{2}}~\theta +4rsen~\theta \right)rdrd\theta \]
\[=\underset{0}{\overset{\pi }{\mathop \int }}\,\underset{1}{\overset{2}{\mathop \int }}\,\left( 3{{r}^{3}}co{{s}^{2}}~\theta +4{{r}^{2}}sen~\theta \right)drd\theta =\underset{0}{\overset{\pi }{\mathop \int }}\,\left[ \left( \frac{3}{4}{{r}^{4}}co{{s}^{2}}~\theta +\frac{4}{3}{{r}^{3}}sen~\theta \right)_{r=1}^{r=2} \right]d\theta \]
\[=\underset{0}{\overset{\pi }{\mathop \int }}\,\left( \frac{45}{4}co{{s}^{2}}~\theta +\frac{28}{3}sen~\theta \right)d\theta =\left( \frac{45}{16}sen~2\theta +\frac{45}{8}\theta +\frac{28}{3}cos~\theta \right)_{\theta =0}^{\theta =\pi }\]
\[=\frac{45}{8}\pi +\frac{56}{3}\]
Exemplo 2.5: Determine o volume do sólido delimitado pelo plano \(z=0\) e pelo paraboloide \(z=f\left( x,y \right)=4-{{x}^{2}}-{{y}^{2}}\).
Solução
Tomando \(z=0\) na função dada, tem-se que \({{x}^{2}}+{{y}^{2}}=4\). Então, o plano intercepta o paraboloide no círculo \({{x}^{2}}+{{y}^{2}}=4\), sendo que o sólido se encontra acima desse círculo. Tem-se, então, em coordenadas polares, que essa região é descrita por \(0\le r\le 2\) e \(0\le \theta \le 2\pi \). Portanto, aplicando as mudanças de coordenadas \(x=rcos~\theta \) e \(y=rsen~\theta \) e a equação (23):
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,\left( 4-{{x}^{2}}-{{y}^{2}} \right)dA=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{2}{\mathop \int }}\,\left( 4-{{r}^{2}}co{{s}^{2}}~\theta -{{r}^{2}}se{{n}^{2}}~\theta \right)rdrd\theta \]
\[=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{2}{\mathop \int }}\,\left[ 4-{{r}^{2}}\left( co{{s}^{2}}~\theta +se{{n}^{2}}~\theta \right) \right]rdrd\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{2}{\mathop \int }}\,\left( 4-{{r}^{2}} \right)rdrd\theta \]
\[=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{2}{\mathop \int }}\,\left( 4r-{{r}^{3}} \right)drd\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( 2{{r}^{2}}-\frac{1}{4}{{r}^{4}} \right)_{r=0}^{r=2}d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,4d\theta \]
\[=\left( 4\theta \right)_{\theta =0}^{\theta =2\pi }=8\pi \]
As integrais duplas apresentam uma série de aplicações, nas mais diversas áreas. Uma das mais comuns, como foi visto em praticamente todo o desenvolvimento do assunto, é para o cálculo do volume.
Além disso, Flemming e Gonçalves (2005) ainda indicam que as integrais duplas podem ser empregadas para avaliar áreas de regiões planas. Isso acontece caso a função \(f\left( x,y \right)\) seja igual a 1. Nesse caso:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,dA\]
Assim, por exemplo, se a região \(R\) for do tipo 1, tem-se:
\[A=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,dA=\underset{a}{\overset{b}{\mathop \int }}\,\underset{{{f}_{1}}\left( x \right)}{\overset{{{f}_{2}}\left( x \right)}{\mathop \int }}\,dydx=\underset{a}{\overset{b}{\mathop \int }}\,\left( y \right)_{{{f}_{1}}\left( x \right)}^{{{f}_{2}}\left( x \right)}dx\]
\[=\underset{a}{\overset{b}{\mathop \int }}\,\left[ {{f}_{2}}\left( x \right)-{{f}_{1}}\left( x \right) \right]dx~~~~(24)\]
Exemplo 2.6 (Flemming e Gonçalves, 2005): Determine a área da região \(R\) delimitada por \(x={{y}^{2}}+1\) e \(y=3-x\).
Solução
Essa região é evidenciada na Figura 4.15.
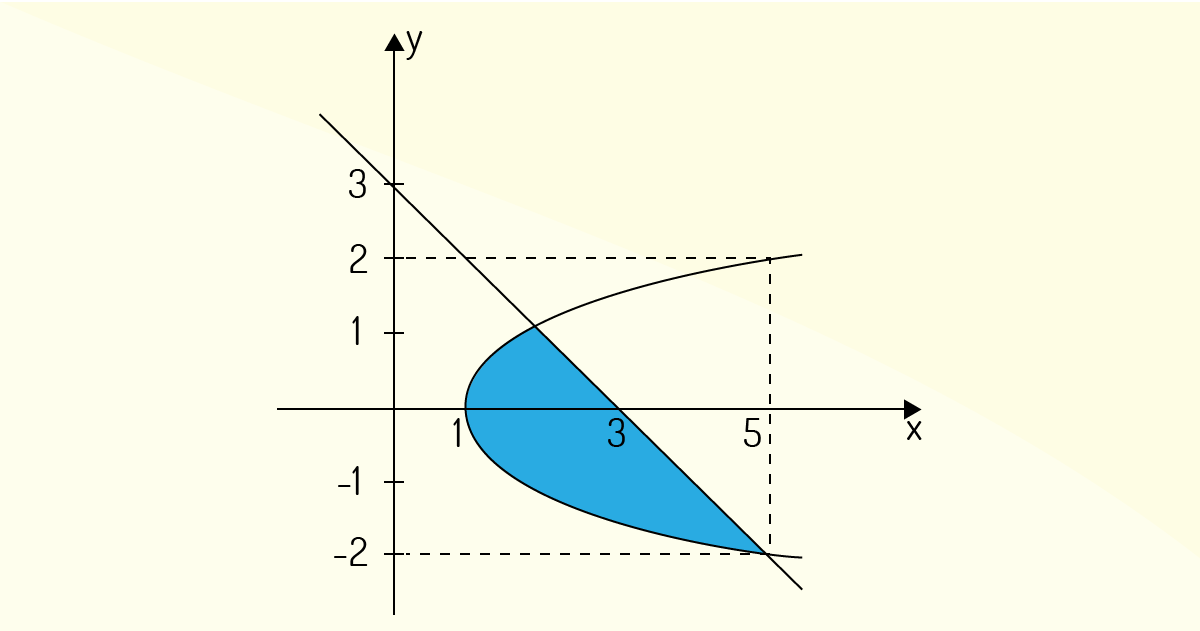
Aplicando a equação (24):
\[A=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,dA=\underset{-2}{\overset{1}{\mathop \int }}\,\underset{{{y}^{2}}+1}{\overset{3-y}{\mathop \int }}\,dxdy=\underset{-2}{\overset{1}{\mathop \int }}\,\left( x \right)_{{{y}^{2}}+1}^{3-y}dy\]
\[\underset{-2}{\overset{1}{\mathop \int }}\,\left( 2-y-{{y}^{2}} \right)dy=\left( 2y-\frac{1}{2}{{y}^{2}}-\frac{1}{3}{{y}^{3}} \right)_{y=-2}^{y=1}=9/2\]
Além de áreas e volumes, as integrais duplas podem ser também empregadas em diversos tópicos de física, como no cálculo da massa, do centro da massa e do momento de inércia.
Visando a prática de cálculo de integrais duplas em coordenadas modificadas, calcule a integral dupla da função \(f\left( x,y \right)={{x}^{2}}+2y\) em uma região \(D\) que é delimitada pelas parábolas \(y=2{{x}^{2}}\) e \(y=1+{{x}^{2}}\). Assinale, então, a alternativa correta.
A integral dupla em questão é avaliada em uma região tipo 1, cujo resultado é igual a 32/5.
Justificativa: A região delimitada apresentará dois pontos de encontro, determinados onde \(2{{x}^{2}}=1+{{x}^{2}}\), ou seja, em \(x=\pm 1\). Assim, esta é uma região do tipo 1 descrita como:
\[D=\left\{ \left( x,y \right)~|~-1\le x\le 1,~2{{x}^{2}}\le y\le 1+{{x}^{2}} \right\}\]
Então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{-1}{\overset{1}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{1+{{x}^{2}}}{\mathop \int }}\,\left( {{x}^{2}}+2y \right)~dydx=\underset{-1}{\overset{1}{\mathop \int }}\,\left[ \left( {{x}^{2}}y+{{y}^{2}} \right)_{2{{x}^{2}}}^{1+{{x}^{2}}} \right]dx=\underset{-1}{\overset{1}{\mathop \int }}\,\left( 1+3{{x}^{2}}-4{{x}^{4}} \right)dx=\left( x+{{x}^{3}}-\frac{4}{5}{{x}^{5}} \right)_{-1}^{1}=\frac{12}{5}\]
A integral dupla em questão é avaliada em uma região tipo 1, cujo resultado é igual a 12/5.
Justificativa: A região delimitada apresentará dois pontos de encontro, determinados onde \(2{{x}^{2}}=1+{{x}^{2}}\) ou seja, em \(x=\pm 1\). Assim, esta é uma região do tipo 1 descrita como:
\[D=\left\{ \left( x,y \right)~|~-1\le x\le 1,~2{{x}^{2}}\le y\le 1+{{x}^{2}} \right\}\]
Então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{-1}{\overset{1}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{1+{{x}^{2}}}{\mathop \int }}\,\left( {{x}^{2}}+2y \right)~dydx=\underset{-1}{\overset{1}{\mathop \int }}\,\left[ \left( {{x}^{2}}y+{{y}^{2}} \right)_{2{{x}^{2}}}^{1+{{x}^{2}}} \right]dx=\underset{-1}{\overset{1}{\mathop \int }}\,\left( 1+3{{x}^{2}}-4{{x}^{4}} \right)dx=\left( x+{{x}^{3}}-\frac{4}{5}{{x}^{5}} \right)_{-1}^{1}=\frac{12}{5}\]
A integral dupla em questão é avaliada em uma região tipo 2, cujo resultado é igual a 12/5.
Justificativa: A região delimitada apresentará dois pontos de encontro, determinados onde \(2{{x}^{2}}=1+{{x}^{2}}\), ou seja, em $x=\pm 1$. Assim, esta é uma região do tipo 1 descrita como:
\[D=\left\{ \left( x,y \right)~|~-1\le x\le 1,~2{{x}^{2}}\le y\le 1+{{x}^{2}} \right\}\]
Então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{-1}{\overset{1}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{1+{{x}^{2}}}{\mathop \int }}\,\left( {{x}^{2}}+2y \right)~dydx=\underset{-1}{\overset{1}{\mathop \int }}\,\left[ \left( {{x}^{2}}y+{{y}^{2}} \right)_{2{{x}^{2}}}^{1+{{x}^{2}}} \right]dx=\underset{-1}{\overset{1}{\mathop \int }}\,\left( 1+3{{x}^{2}}-4{{x}^{4}} \right)dx=\left( x+{{x}^{3}}-\frac{4}{5}{{x}^{5}} \right)_{-1}^{1}=\frac{12}{5}\]
A integral dupla em questão é avaliada em uma região tipo 2, cujo resultado é igual a 32/5.
Justificativa: A região delimitada apresentará dois pontos de encontro, determinados onde \(2{{x}^{2}}=1+{{x}^{2}}\), ou seja, em \(x=\pm 1\). Assim, esta é uma região do tipo 1 descrita como:
\[D=\left\{ \left( x,y \right)~|~-1\le x\le 1,~2{{x}^{2}}\le y\le 1+{{x}^{2}} \right\}\]
Então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{-1}{\overset{1}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{1+{{x}^{2}}}{\mathop \int }}\,\left( {{x}^{2}}+2y \right)~dydx=\underset{-1}{\overset{1}{\mathop \int }}\,\left[ \left( {{x}^{2}}y+{{y}^{2}} \right)_{2{{x}^{2}}}^{1+{{x}^{2}}} \right]dx=\underset{-1}{\overset{1}{\mathop \int }}\,\left( 1+3{{x}^{2}}-4{{x}^{4}} \right)dx=\left( x+{{x}^{3}}-\frac{4}{5}{{x}^{5}} \right)_{-1}^{1}=\frac{12}{5}\]
A integral dupla em questão é avaliada em uma região tipo 1, cujo resultado é igual a 4/5.
Justificativa: A região delimitada apresentará dois pontos de encontro, determinados onde \(2{{x}^{2}}=1+{{x}^{2}}\), ou seja, em \(x=\pm 1\). Assim, esta é uma região do tipo 1 descrita como:
\[D=\left\{ \left( x,y \right)~|~-1\le x\le 1,~2{{x}^{2}}\le y\le 1+{{x}^{2}} \right\}\]
Então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{-1}{\overset{1}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{1+{{x}^{2}}}{\mathop \int }}\,\left( {{x}^{2}}+2y \right)~dydx=\underset{-1}{\overset{1}{\mathop \int }}\,\left[ \left( {{x}^{2}}y+{{y}^{2}} \right)_{2{{x}^{2}}}^{1+{{x}^{2}}} \right]dx=\underset{-1}{\overset{1}{\mathop \int }}\,\left( 1+3{{x}^{2}}-4{{x}^{4}} \right)dx=\left( x+{{x}^{3}}-\frac{4}{5}{{x}^{5}} \right)_{-1}^{1}=\frac{12}{5}\]
Vamos, agora, caro(a) aluno(a), expandir tudo o que foi visto até aqui para outro caso de integração: o caso da integral tripla. Stewart (2017b) indica que o processo para determinar esse tipo de integral pode ser avaliado de forma semelhante ao que foi descrito para as integrais duplas. No entanto, no caso das integrais triplas, a região onde a integral tripla é avaliada já é tridimensional, acarretando a falta de uma analogia geométrica mais simples de se realizar.
Então, iniciaremos os estudos considerando uma das mais simples formas de região tridimensional: uma caixa retangular. Essa construção tridimensional pode ser representada da seguinte forma:
\[B=\left[ a,b \right]\times \left[ c,d \right]\times \left[ r,s \right]=\left\{ \left( x,y,z \right)~|~a\le x\le b,~c\le y\le d,~r\le z\le s \right\}~~~~~~(25)\]
Essa região \(R\) pode ser subdividida em \(B\) caixas menores, fazendo o intervalo \(\left[ a,b \right]\) ser dividido em \(l\) subintervalos \(\left[ {{x}_{i-1}},{{x}_{i}} \right]\), todos com o mesmo comprimento \(\Delta x=\left( b-a \right)/l\), o intervalo \(\left[ c,d \right]\) ser dividido em \(m\) subintervalos \(\left[ {{y}_{j-1}},{{y}_{j}} \right]\), todos com o mesmo comprimento \(\Delta y=\left( b-a \right)/m\) e o intervalo \(\left[ r,s \right]\) ser dividido em \(n\) subintervalos \(\left[ {{z}_{k-1}},{{z}_{k}} \right]\) de mesmo comprimento \(\Delta z=\left( s-r \right)/n\). Com isso, cada uma dessas caixas menores é descrita como:
\[{{B}_{ijk}}=\left[ {{x}_{i-1}},{{x}_{i}} \right]\times \left[ {{y}_{j-1}},{{y}_{j}} \right]\times \left[ {{z}_{k-1}},{{z}_{k}} \right]~~~~~~(26)\]
Esse procedimento está ilustrado na Figura 4.16.
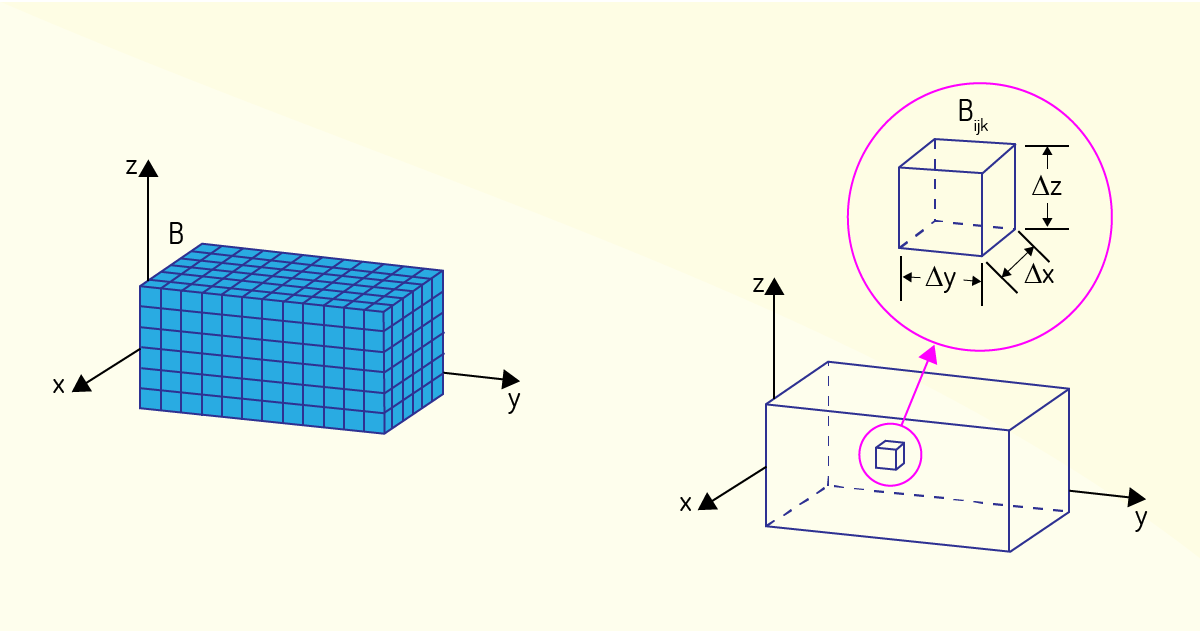
Note que o volume de cada uma dessas caixas \({{B}_{ijk}}\) é \(\Delta V=\Delta x\Delta y\Delta z\). Pode-se propor a soma tripla de Riemann para esse caso:
\[\underset{i=1}{\overset{l}{\mathop \sum }}\,\underset{j=1}{\overset{m}{\mathop \sum }}\,\underset{k=1}{\overset{n}{\mathop \sum }}\,f\left( x_{ijk}^{*},y_{ijk}^{*},z_{ijk}^{*} \right)\cdot \Delta V~~~~~~(27)\]
sendo que \(\left( x_{ijk}^{*},y_{ijk}^{*},z_{ijk}^{*} \right)\) simplesmente é um ponto de amostragem localizado em algum ponto das caixas \({{B}_{ijk}}\). Então, por analogia ao caso da integral dupla, pode-se definir a integral tripla como o limite de \(l,m,n\to \infty \) da soma tripla de Riemann, caso esse limite exista:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{B}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{l,m,n\to \infty }{\mathop{lim}}\,\underset{i=1}{\overset{l}{\mathop \sum }}\,\underset{j=1}{\overset{m}{\mathop \sum }}\,\underset{k=1}{\overset{n}{\mathop \sum }}\,f\left( x_{ijk}^{*},y_{ijk}^{*},z_{ijk}^{*} \right)\cdot \Delta V~~~~~~(28)\]
De forma análoga também, pode-se propor uma extensão do Teorema de Fubini para as integrais triplas.
Teorema 2 - O Teorema de Fubini para integral tripla: Seja uma função \(f\left( x,y,z \right)\) contínua em um espaço retangular \(B=\left[ a,b \right]\times \left[ c,d \right]\times \left[ r,s \right]\), então, as integrais triplas obedecem à seguinte relação:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{B}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{r}{\overset{s}{\mathop \int }}\,\underset{c}{\overset{d}{\mathop \int }}\,\underset{a}{\overset{b}{\mathop \int }}\,f\left( x,y,z \right)dxdydz~~~~~~(29)\]
Ou seja, de acordo com esse teorema, mantém-se \(y\) e \(z\) constantes e integra-se em relação a \(x\). Em seguida, mantém-se \(z\) constante e integra-se em relação a \(y\). E, finalmente, integra-se o resultado em relação à \(z\). Note que é possível alterar a ordem de integração, assim como se faz no caso da integral dupla.
Exemplo 3.1: Avalie a integral tripla da função \(f\left( x,y,z \right)=xyz\) na região \(B=\left[ 0,1 \right]\times \left[ 0,2 \right]\times \left[ 0,3 \right]\).
Solução
Basta aplicar a equação (29):
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{B}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{0}{\overset{3}{\mathop \int }}\,\underset{0}{\overset{2}{\mathop \int }}\,\underset{0}{\overset{1}{\mathop \int }}\,xyz~dxdydz=\underset{0}{\overset{3}{\mathop \int }}\,\underset{0}{\overset{2}{\mathop \int }}\,\left( \frac{1}{2}{{x}^{2}}yz \right)_{x=0}^{x=1}~dydz\]
\[=\underset{0}{\overset{3}{\mathop \int }}\,\underset{0}{\overset{2}{\mathop \int }}\,\frac{1}{2}yz~dydz=\underset{0}{\overset{3}{\mathop \int }}\,\left( \frac{1}{4}{{y}^{2}}z \right)_{y=0}^{y=2}~dz=\underset{0}{\overset{3}{\mathop \int }}\,z~dz=\]
\[\left( \frac{1}{2}{{z}^{2}} \right)_{z=0}^{z=3}=9/2\]
Stewart (2017b) destaca que, essencialmente, as integrais triplas apresentam as mesmas propriedades que as integrais duplas, de modo que as propriedades discutidas na seção 1.2 podem ser estendidas sem problemas para os casos nos quais se busca avaliar uma integral tripla. O mesmo se tem para as aplicações das integrais duplas: todas as aplicações das integrais duplas podem ser estendidas para as integrais triplas, de modo a ser possível lidar com casos mais complexos.
Retornando para a sequência empregada no caso de integrais duplas, Stewart (2017b) expõe que se deve considerar, agora, o caso de avaliar uma integral tripla em uma região qualquer, não apenas em uma região que seja uma caixa retangular. Por exemplo, considere a região genérica \(E\) exposta na Figura 4.17.
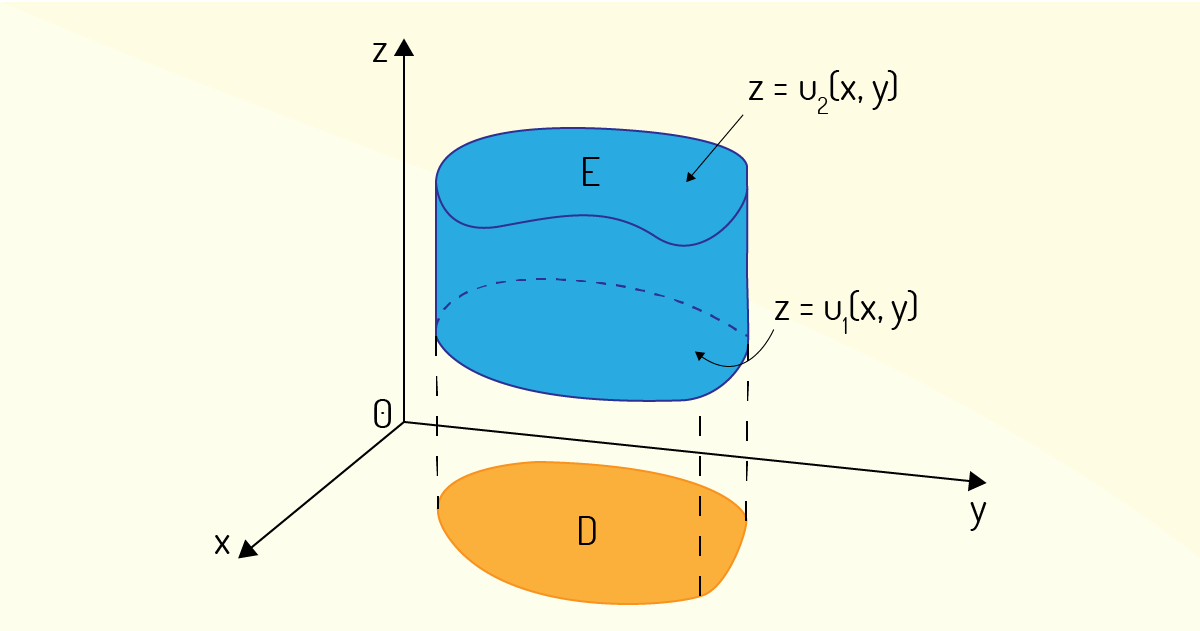
Supondo que essa região \(E\) seja limitada, ela pode se encontrar contida em uma região cúbica, semelhante àquela descrita por (25). Considerando esse passo, pode-se definir uma função \(F\), de modo que \(F\) coincida com a função original \(f\) na região \(E\) e seja igual a zero nos demais pontos fora da região \(E\). Ou seja:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{B}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,F\left( x,y,z \right)dV~~~~~~(30)\]
Para continuarmos as análises, iremos nos restringir a funções que sejam contínuas e a determinados tipos de regiões. O primeiro tipo a ser estudado é aquele no qual a região \(E\) está contida entre os gráficos de duas funções contínuas de \(x\) e \(y\). Então, sendo \(D\) a projeção do sólido \(E\) sobre o plano \(xy\), como mostra a Figura 4.17, esse caso é dito tipo 1 e pode ser representado como
\[E=\left\{ \left( x,y,z \right)~|~\left( x,y \right)\in D,~{{u}_{1}}\left( x,y \right)\le z\le {{u}_{2}}\left( x,y \right) \right\}~~~~~~(31)\]
Assim, tem-se
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{{{u}_{1}}\left( x,y \right)}{\overset{{{u}_{2}}\left( x,y \right)}{\mathop \int }}\,f\left( x,y,z \right)dz \right]dA~~~~~~(32)\]
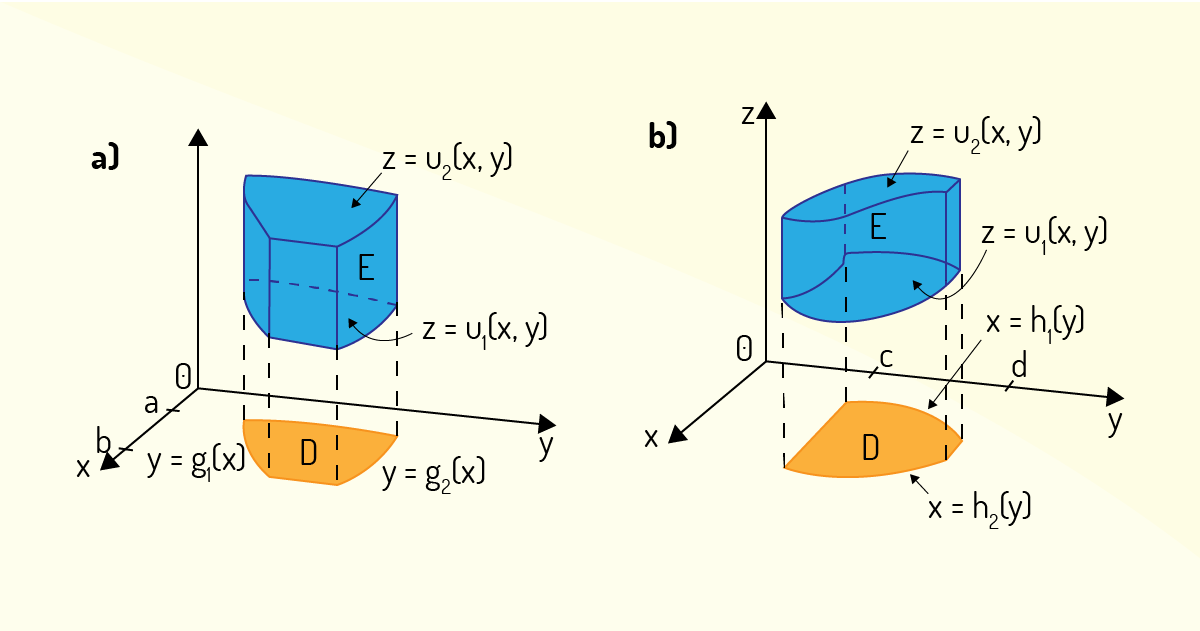
Para esse caso de integral tripla, se a projeção \(D\) for uma região do tipo 1 para o caso da integral dupla, como mostra a Figura 4.18 a), então, o que se tem é:
\[E=\left\{ \left( x,y,z \right)~|~a\le x\le b,~{{g}_{1}}\left( x \right)\le y\le {{g}_{2}}\left( x \right),~{{u}_{1}}\left( x,y \right)\le z\le {{u}_{2}}\left( x,y \right) \right\}~~~~~~(33)\]
Com isso, a equação (32) se torna:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{a}{\overset{b}{\mathop \int }}\,\underset{{{g}_{1}}\left( x \right)}{\overset{{{g}_{2}}\left( x \right)}{\mathop \int }}\,\underset{{{u}_{1}}\left( x,y \right)}{\overset{{{u}_{2}}\left( x,y \right)}{\mathop \int }}\,f\left( x,y,z \right)dzdydx~~~~~~(34)\]
Agora, se a projeção \(D\) for uma região do tipo 2 para o caso da integral dupla, como mostra a Figura 4.18 b), então, o que se tem é:
\[E=\left\{ \left( x,y,z \right)~|~{{h}_{1}}\left( x \right)\le x\le {{h}_{2}}\left( x \right),~c\le y\le d,~{{u}_{1}}\left( x,y \right)\le z\le {{u}_{2}}\left( x,y \right) \right\}~~~~~~(35)\]
Com isso, a equação (32) se torna:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{c}{\overset{d}{\mathop \int }}\,\underset{{{h}_{1}}\left( x \right)}{\overset{{{h}_{2}}\left( x \right)}{\mathop \int }}\,\underset{{{u}_{1}}\left( x,y \right)}{\overset{{{u}_{2}}\left( x,y \right)}{\mathop \int }}\,f\left( x,y,z \right)dzdxdy~~~~~~(36)\]
A Figura 4.19 apresenta os outros dois tipos de regiões sólidas a serem considerados nos estudos de integrais triplas.
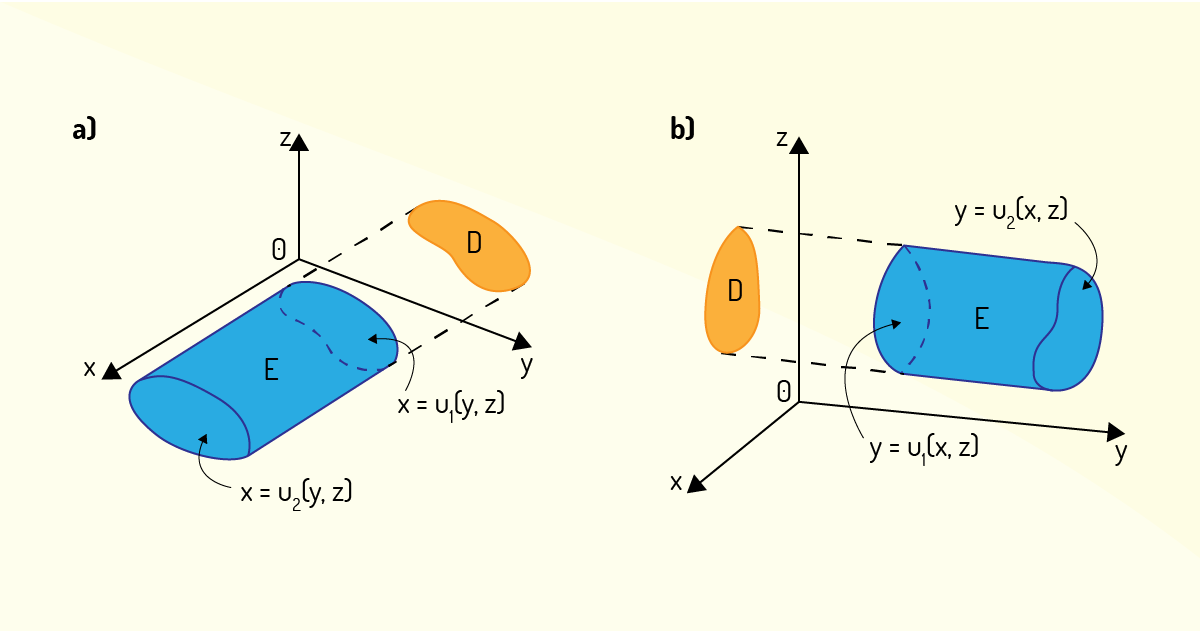
O segundo tipo a ser estudado é aquele no qual a projeção do sólido \(E\) se dá sobre o plano \(yz\), como mostra a Figura 4.19 a). Nesse caso, dito tipo 2, a superfície traseira é \(x={{u}_{1}}\left( y,z \right)\) e a superfície frontal é \(x={{u}_{2}}\left( y,z \right)\). Assim, tem-se:
\[E=\left\{ \left( x,y,z \right)~|~\left( y,z \right)\in D,~{{u}_{1}}\left( y,z \right)\le x\le {{u}_{2}}\left( y,z \right) \right\}~~~~~~(37)\]
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{{{u}_{1}}\left( y,z \right)}{\overset{{{u}_{2}}\left( y,z \right)}{\mathop \int }}\,f\left( x,y,z \right)dx \right]dA~~~~~~(38)\]
Finalmente, o terceiro tipo é aquele no qual a projeção do sólido \(E\) se dá sobre o plano \(xz\), como mostra a Figura 4.19 b). Nesse caso, dito tipo 3, a superfície esquerda é \(y={{u}_{1}}\left( x,z \right)\) e a superfície direita é \(y={{u}_{2}}\left( x,z \right)\). Assim, tem-se:
\[E=\left\{ \left( x,y,z \right)~|~\left( x,z \right)\in D,~{{u}_{1}}\left( x,z \right)\le y\le {{u}_{2}}\left( x,z \right) \right\}~~~~~~(39)\]
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{{{u}_{1}}\left( x,z \right)}{\overset{{{u}_{2}}\left( x,z \right)}{\mathop \int }}\,f\left( x,y,z \right)dy \right]dA~~~~~~(40)\]
Um ponto que facilita o desenvolvimento dos conceitos de integrais duplas é visualizar o problema como caso de calcular o volume de um sólido. Agora, no caso da integral tripla, um sólido tridimensional já é a região de integração, dificultando a visualização do resultado de uma integral tripla. No entanto uma expansão dos conceitos geométricos pode ser feita aqui: se você for capaz de pensar em quatro dimensões, você pode imaginar o cálculo de uma integral tripla como um caso de “volume” de um hipercilindro ou outra forma geométrica mais complexa. Esses elementos geométricos são muito úteis em áreas de ciência avançada.
Você pode saber mais a respeito desse assunto acessando o link disponível em: <http://nautilus.fis.uc.pt/gazeta/revistas/29_4/vol29_4_Art01.pdf>. Acesso em: 29 abr. 2019.

Visando à prática de cálculo de integrais triplas, calcule a integral tripla da função \(f\left( x,y,z \right)=2x\) em uma região \(B\) que é delimitada pelos planos coordenados e pelo plano \(\frac{x}{3}+\frac{y}{2}+z=1\). Assinale, então, a alternativa correta.
A região onde se deve avaliar essa integral tripla é claramente uma região exclusivamente do tipo 2.
Justificativa: A região \(B\) descrita pode se encaixar facilmente em qualquer um dos tipos descritos - 1, 2 ou 3.
Avaliando a integral tripla pedida, o resultado será 3/2.
Justificativa: A região \(B\) proposta é um tetraedro, para o qual se tem \(0\le x\le 3\), \(0\le y\le 2\) e \(0\le z\le 1\). Considerando essa região como tipo 1, a projeção de \(B\) sobre o plano \(xy\) será o triângulo \(R\) evidenciado a seguir:
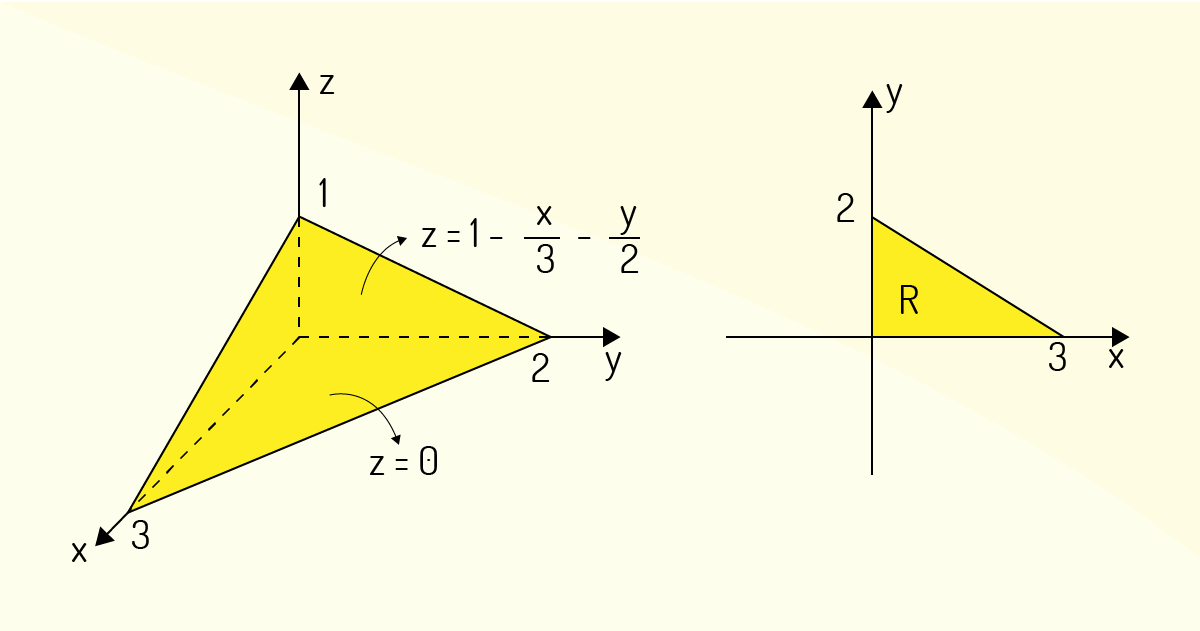
Ou seja, \(0\le x\le 3\) e \(0\le y\le 2-\frac{2}{3}x\). Assim, usando (32):
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{{{u}_{1}}\left( x,y \right)}{\overset{{{u}_{2}}\left( x,y \right)}{\mathop \int }}\,f\left( x,y,z \right)dz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{0}{\overset{1-\frac{x}{3}-\frac{y}{2}}{\mathop \int }}\,2xdz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( 2xz \right)_{0}^{1-\frac{x}{3}-\frac{y}{2}}dydx\]
\[=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\underset{0}{\overset{2-\frac{2}{3}x}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\left( \frac{2}{9}{{x}^{3}}-\frac{4}{3}{{x}^{2}}+2x \right)dx=\frac{3}{2}\]
Avaliando a integral tripla pedida, o resultado será 1/2.
Justificativa: A região \(B\) proposta é um tetraedro, para o qual se tem \(0\le x\le 3\), \(0\le y\le 2\) e \(0\le z\le 1\). Considerando essa região como tipo 1, a projeção de \(B\) sobre o plano \(xy\) será o triângulo \(R\) evidenciado a seguir:
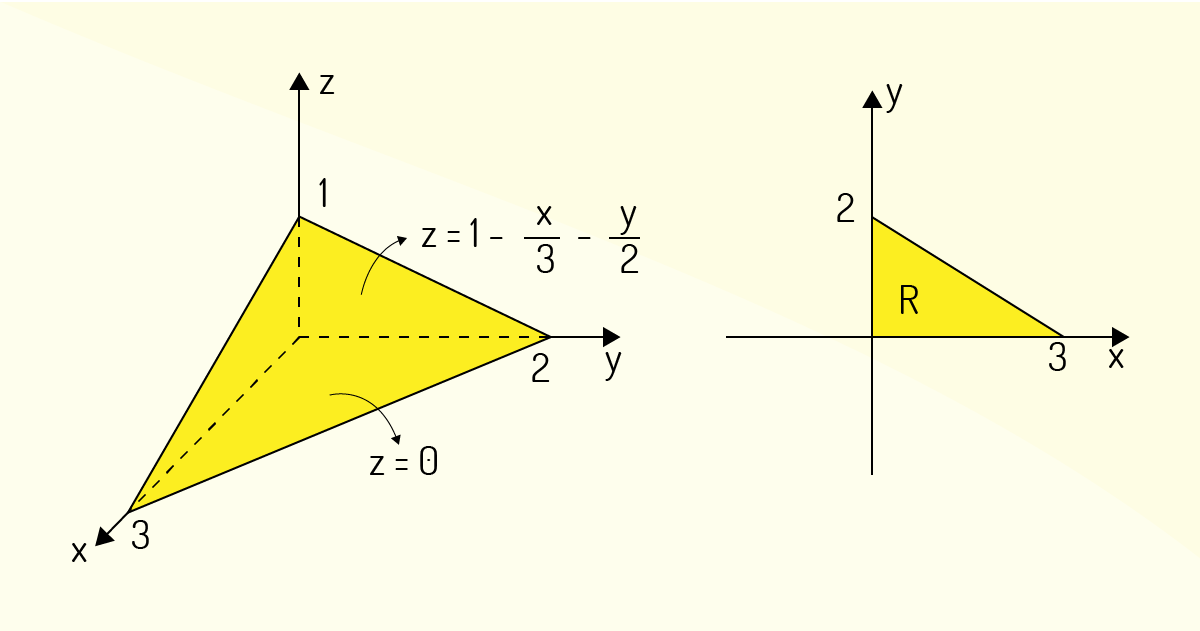
Ou seja, \(0\le x\le 3\) e \(0\le y\le 2-\frac{2}{3}x\). Assim, usando (32):
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{{{u}_{1}}\left( x,y \right)}{\overset{{{u}_{2}}\left( x,y \right)}{\mathop \int }}\,f\left( x,y,z \right)dz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{0}{\overset{1-\frac{x}{3}-\frac{y}{2}}{\mathop \int }}\,2xdz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( 2xz \right)_{0}^{1-\frac{x}{3}-\frac{y}{2}}dydx\]
\[=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\underset{0}{\overset{2-\frac{2}{3}x}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\left( \frac{2}{9}{{x}^{3}}-\frac{4}{3}{{x}^{2}}+2x \right)dx=\frac{3}{2}\]
A região de integração apresentada, caso seja considerada uma região de tipo 3, apresentará como limites \(0\le y\le 1-\frac{x}{3}-z\) , \(0\le x\le 1-\frac{1}{3}x\) e \(0\le z\le 1\).
Justificativa: A região de integração e a projeção no plano\(xz\) são evidenciadas a seguir:
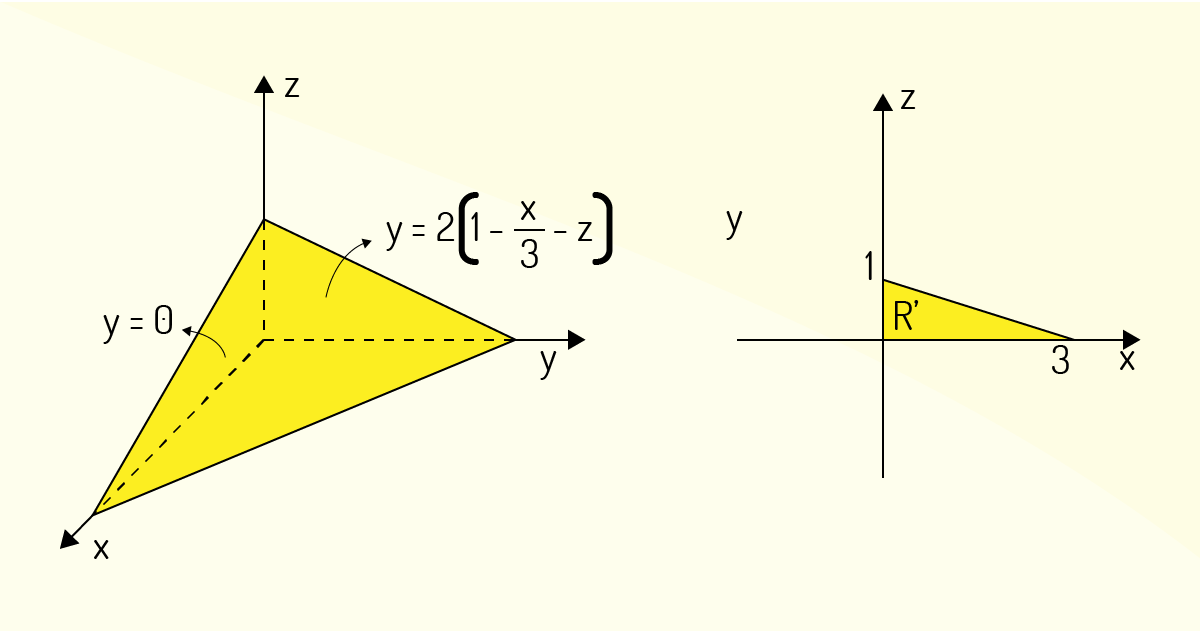
Analisando-as, nota-se que \(0\le y\le 2\left( 1-\frac{x}{3}-z \right)\), que é a descrição em relação a \(y\), \(0\le x\le 1-\frac{1}{3}x\), que define \(z=g\left( x \right)\), e \(0\le z\le 1\).
Avaliando a integral tripla pedida, o resultado será 5/2.
Justificativa: A região \(B\) proposta é um tetraedro, para o qual se tem \(0\le x\le 3\), \(0\le y\le 2\) e \(0\le z\le 1\). Considerando essa região como tipo 1, a projeção de \(B\) sobre o plano \(xy\) será o triângulo \(R\) evidenciado a seguir:

Ou seja, \(0\le x\le 3\) e \(0\le y\le 2-\frac{2}{3}x\). Assim, usando (32):
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{{{u}_{1}}\left( x,y \right)}{\overset{{{u}_{2}}\left( x,y \right)}{\mathop \int }}\,f\left( x,y,z \right)dz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{0}{\overset{1-\frac{x}{3}-\frac{y}{2}}{\mathop \int }}\,2xdz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( 2xz \right)_{0}^{1-\frac{x}{3}-\frac{y}{2}}dydx\]
\[=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\underset{0}{\overset{2-\frac{2}{3}x}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\left( \frac{2}{9}{{x}^{3}}-\frac{4}{3}{{x}^{2}}+2x \right)dx=\frac{3}{2}\]
Vimos que, na geometria plana, é mais prático utilizar coordenadas polares quando se trabalha com regiões curvas. Já no caso tridimensional, existe mais de uma forma prática de se realizar mudança de variável: nessa situação, geralmente se trabalha com coordenadas cilíndricas e esféricas, como veremos a seguir.
Em um sistema de coordenadas cilíndricas, um ponto \(P\) qualquer deve ser representado pela tripla ordenada \(\left( r,\theta ,z \right)\). Dessas coordenadas, \(r\) e \(\theta \) são coordenadas polares da projeção desse ponto \(P\) no plano \(xy\), enquanto a coordenada \(z\) é a distância orientada entre \(P\) e \(xy\), como mostra a Figura 4.20 (STEWART, 2017b).
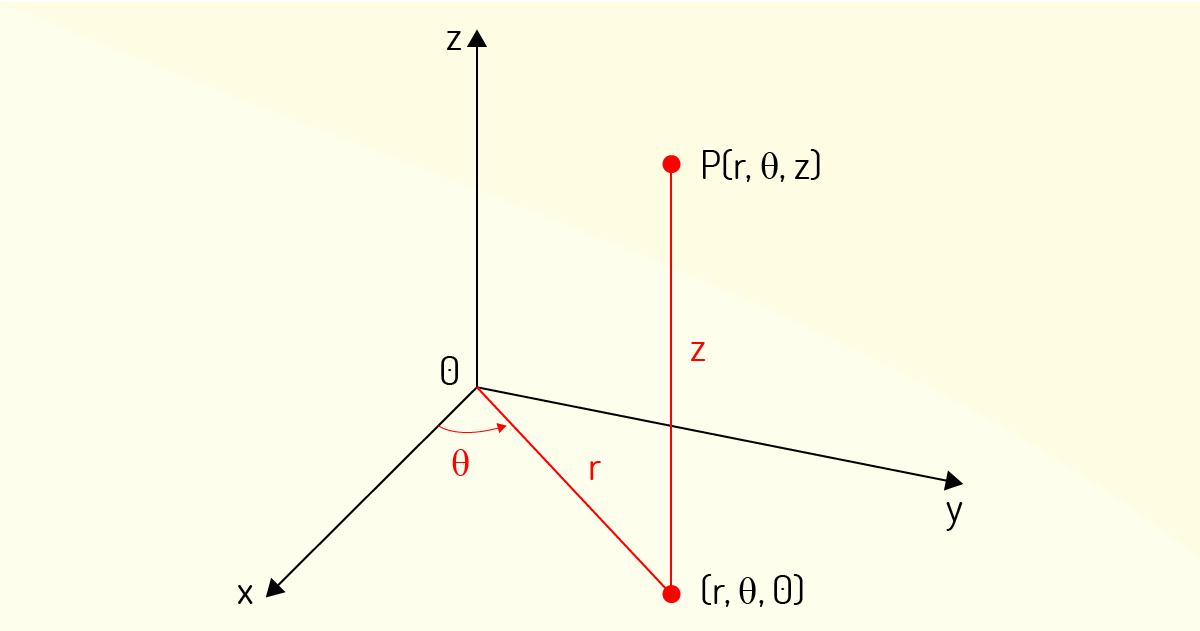
Segundo Stewart (2017b), a mudança das coordenadas cilíndricas para as retangulares pode ser feita mediante as seguintes equações:
\[x=rcos~\theta ~~~~y=rsen~\theta ~~~~z=z~~~~~~(41)\]
Já a conversão de coordenadas retangulares para coordenadas cilíndricas, ocorre da seguinte forma:
\[{{r}^{2}}={{x}^{2}}+{{y}^{2}}~~~~tg~\theta =\frac{y}{x}~~~~z=z~~~~~~(42)\]
Esse tipo de coordenadas é muito útil para lidar com problemas em que se tem algum tipo de simetria em torno do eixo \(z\).
Primeiramente, suponha que a região de integração \(E\) seja uma região do tipo 1, para a qual a projeção no plano \(xy\) seja feita simplesmente em coordenadas polares, como mostra a Figura 4.21.
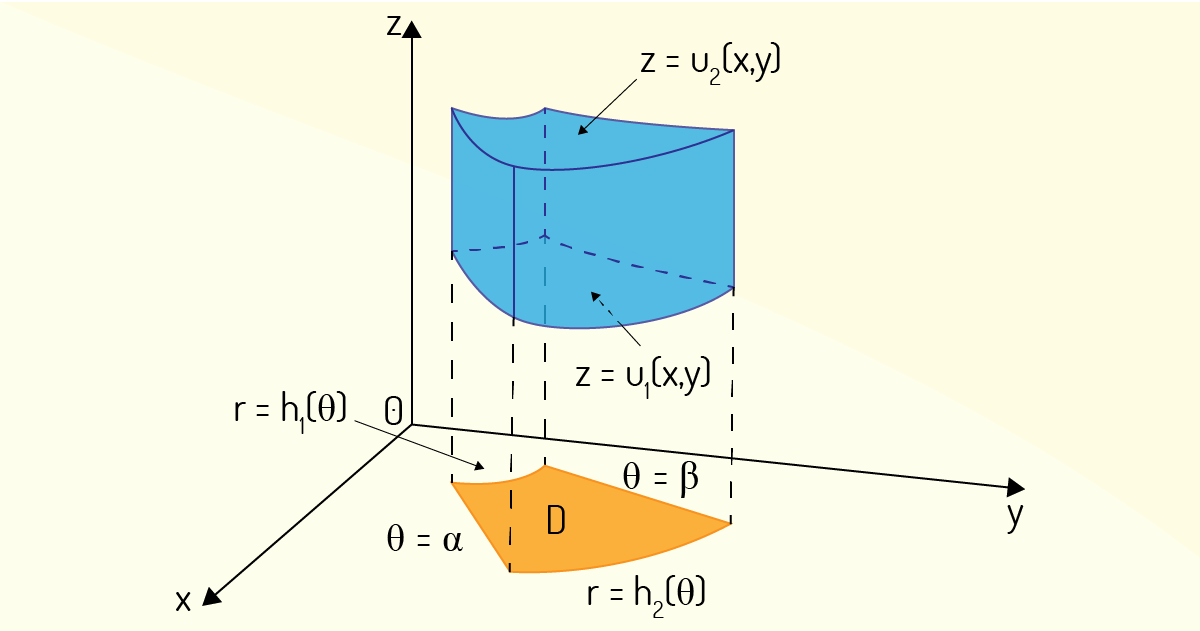
Sendo a função \(f\)contínua e a região \(E\) definida como
\[E=\left\{ \left( x,y,z \right)~|~\left( x,y \right)\in D,~{{u}_{1}}\left( x,y \right)\le z\le {{u}_{2}}\left( x,y \right) \right\}\]
sabe-se como é possível avaliar a integral tripla com essas condições: basta aplicar a equação (32). No entanto já foi visto como avaliar uma integral dupla em coordenadas polares. Aplicando, então, o mesmo raciocínio empregado no caso das integrais duplas, a equação (32) pode ser avaliada, em coordenadas cilíndricas, da seguinte forma:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{\alpha }{\overset{\beta }{\mathop \int }}\,\underset{{{h}_{1}}\left( \theta \right)}{\overset{{{h}_{2}}\left( \theta \right)}{\mathop \int }}\,\underset{{{u}_{1}}\left( rcos~\theta ,rsen~\theta \right)}{\overset{{{u}_{2}}\left( rcos~\theta ,rsen~\theta \right)}{\mathop \int }}\,f\left( rcos~\theta ,rsen~\theta ,z \right)rdzdrd\theta ~~~~~~(43)\]
A equação (43) é conhecida como fórmula de integração tripla para coordenadas cilíndricas. Essa fórmula, segundo Stewart (2017b), deve ser empregada para os casos em que a região \(E\) apresenta uma descrição em coordenadas cilíndricas mais simples. Além disso, um caso que geralmente pede o uso desse tipo de integração tripla é quando se tem \(f\left( x,y,z \right)\) envolvendo a expressão \({{x}^{2}}+{{y}^{2}}\).
Quando se tem uma região de integração de forma cônica ou esférica, o uso de coordenadas cilíndricas pode ser tão complexo quanto o uso de coordenadas retangulares. Para esses tipos de problemas, é aconselhável o uso de coordenadas esféricas.
No sistema de coordenadas esféricas, um ponto \(P\) qualquer deve ser representado pela tripla ordenada \(\left( \rho ,\theta ,\phi \right)\). A Figura 4.22 apresenta como localizar um ponto \(P\) nesse sistema de coordenadas. Note que a coordenada \(\rho \) nada mais é do que \(\left| OP \right|\), ou seja, a distância do ponto \(P\) à origem. Já a coordenada \(\theta \) é a mesma definida nas coordenadas cilíndricas. Finalmente, a coordenada \(\phi \) indica o ângulo entre o eixo \(z\) positivo e o segmento de reta \(OP\). Dito isso, note que \(\rho \ge 0\) e \(0\le \phi \le \pi \) (STEWART, 2017b).
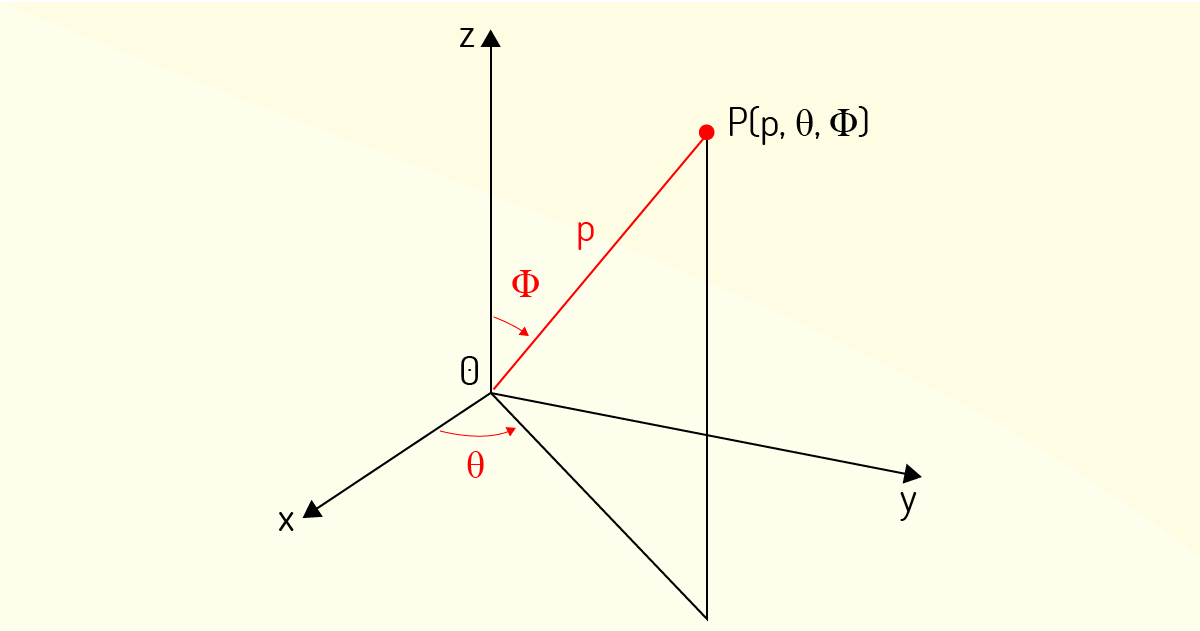
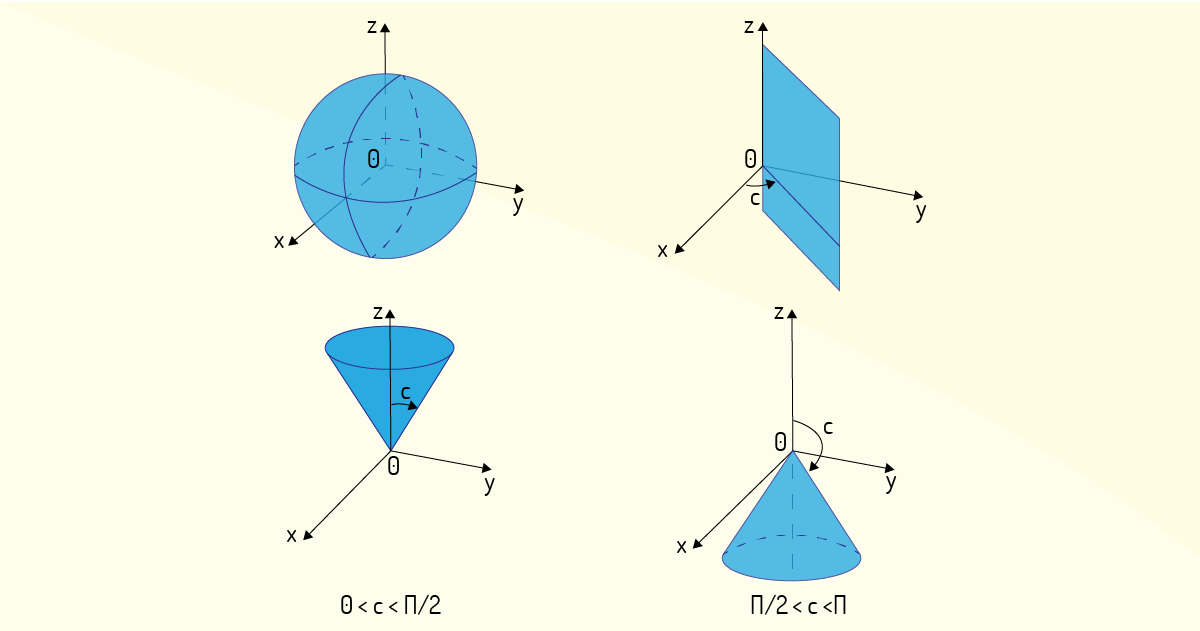
Esse tipo de coordenadas, além de ser útil para avaliar integrais triplas em regiões esféricas e cônicas, mostra-se muito prático quando se tem problemas com algum tipo de simetria ao redor de um ponto, que deve ser considerado como a origem na análise do problema. Por exemplo, sendo \(c\) um valor real, nas coordenadas esféricas, se \(\rho =c\), essas coordenadas descrevem uma esfera de raio \(c\); se \(\theta =c\), tem-se um semiplano vertical localizado no ângulo \(c\); e se \(\phi =c\), a região descrita é um semicone cujo eixo se encontra no eixo \(z\) (STEWART, 2017b). Esses casos são exemplificados na Figura 4.23.
Agora, é preciso determinar como coordenadas retangulares são representadas na forma de coordenadas esféricas. Para isso, a Figura 4.24 apresenta informações úteis para essa mudança.
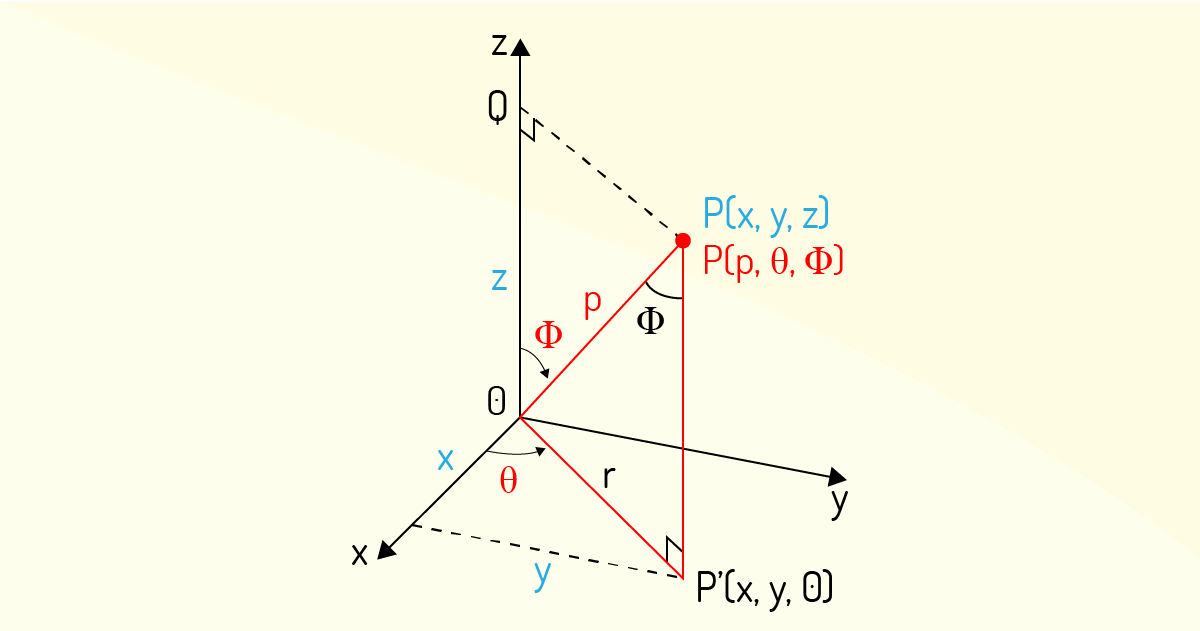
Pela análise dos triângulos \(OPQ\) e \(OPP'\), da trigonometria, encontra-se que \(z=\rho cos~\phi \) e \(r=\rho sen~\phi \). No entanto tem-se que \(x=rcos~\theta \) e \(y=rsen~\theta \). Então, para converter coordenadas esféricas para coordenadas retangulares, faz-se o uso das seguintes equações:x
\[x=\rho sen~\phi ~cos~\theta ~~~~y=\rho sen~\phi ~sen~\theta ~~~~z=\rho cos~\phi ~~~~~~(44)\]
Além disso, convém destacar que:
\[{{\rho }^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}~~~~~~(45)\]
Quando se trabalha com o sistema de coordenadas esféricas, o elemento geométrico correspondente à caixa retangular é a cunha esférica, como mostra a Figura 4.25.
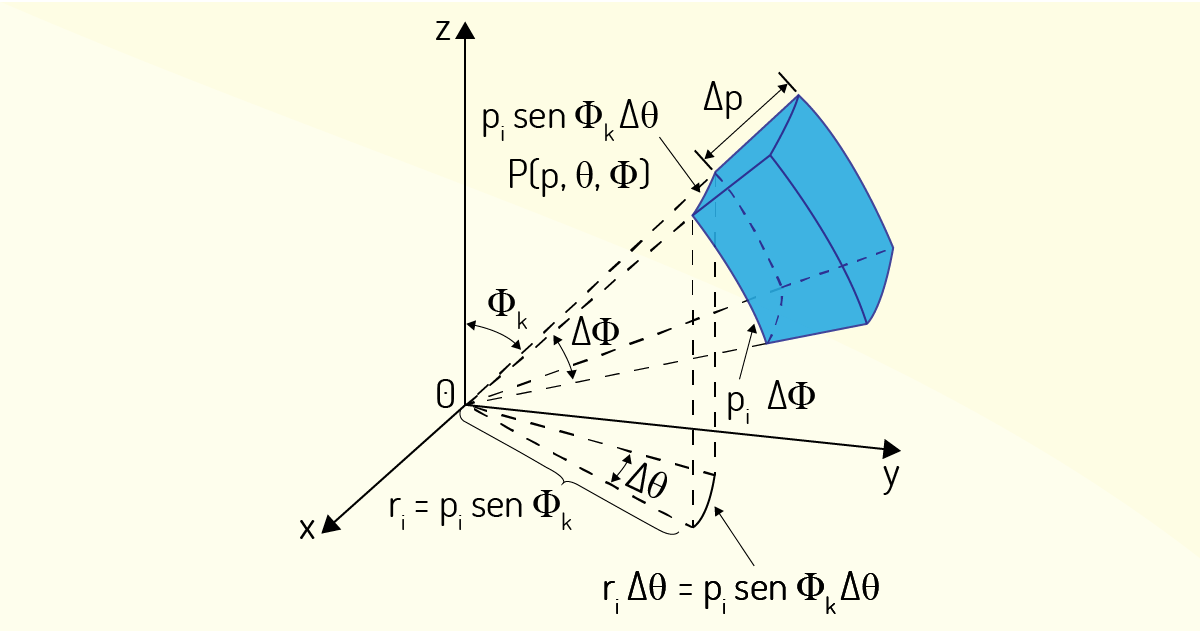
Essa cunha é definida como
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~a\le \rho \le b,~\alpha \le \theta \le \beta ,~c\le \phi \le d \right\}\]
onde \(a\ge 0\), \(\beta -\alpha \le 2\pi \) e \(d-c\le \pi \). Mesmo que anteriormente as integrais triplas tenham sido avaliadas em regiões divididas em pequenas caixas, Stewart (2017b) relata que não há problemas em usar cunhas para tal tarefa.
Dividindo, então, a região \(E\) em pequenas cunhas esféricas \({{E}_{ijk}}\), com pequenas esferas igualmente espaçadas \(\rho ={{\rho }_{i}}\), semiplanos \(\theta ={{\theta }_{j}}\) e semicones \(\phi ={{\phi }_{k}}\), o resultado que se tem é aquele evidenciado na Figura 4.25, uma caixa quase retangular cujas dimensões são \(\Delta \rho \), \({{\rho }_{i}}\Delta \phi \) e \({{\rho }_{i}}sen{{\phi }_{k}}\Delta \theta \). Com isso, Stewart (2017b) indica que uma aproximação para o volume desse elemento \({{E}_{ijk}}\) pode ser
\[{{V}_{ijk}}\approx \left( \Delta \rho \right)\left( {{\rho }_{i}}\Delta \phi \right)\left( {{\rho }_{i}}sen{{\phi }_{k}}\Delta \theta \right)={{\rho }_{i}}^{2}sen{{\phi }_{k}}\Delta \rho \Delta \phi \Delta \theta ~~~~~~(46)\]
Usando o Teorema do Valor Médio, Stewart (2017b) ainda diz que o volume exato do elemento \({{E}_{ijk}}\) é
\[{{V}_{ijk}}={{\underset{\scriptscriptstyle-}{\rho }}_{i}}^{2}sen{{\underset{\scriptscriptstyle-}{\phi }}_{k}}\Delta \rho \Delta \phi \Delta \theta ~~~~~~(47)\]
onde \(\left( {{{\underset{\scriptscriptstyle-}{\rho }}}_{i}},{{{\underset{\scriptscriptstyle-}{\theta }}}_{j}},{{{\underset{\scriptscriptstyle-}{\phi }}}_{k}} \right)\) é um ponto qualquer dentro de \({{E}_{ijk}}\). Se a coordenada retangular desse ponto for \(\left( x_{ijk}^{*},y_{ijk}^{*},z_{ijk}^{*} \right)\), então \(\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{l,m,n\to \infty }{\mathop{lim}}\,\underset{i=1}{\overset{l}{\mathop \sum }}\,\underset{j=1}{\overset{m}{\mathop \sum }}\,\underset{k=1}{\overset{n}{\mathop \sum }}\,f\left( x_{ijk}^{*},y_{ijk}^{*},z_{ijk}^{*} \right)\cdot \Delta {{V}_{ijk}}\).
\[=\underset{l,m,n\to \infty }{\mathop{lim}}\,\underset{i=1}{\overset{l}{\mathop \sum }}\,\underset{j=1}{\overset{m}{\mathop \sum }}\,\underset{k=1}{\overset{n}{\mathop \sum }}\,f\left( {{{\underset{\scriptscriptstyle-}{\rho }}}_{i}}sen~{{{\underset{\scriptscriptstyle-}{\phi }}}_{k}}~cos~{{{\underset{\scriptscriptstyle-}{\theta }}}_{j}},{{{\underset{\scriptscriptstyle-}{\rho }}}_{i}}sen~{{{\underset{\scriptscriptstyle-}{\phi }}}_{k}}~sen~{{{\underset{\scriptscriptstyle-}{\theta }}}_{j}},{{{\underset{\scriptscriptstyle-}{\rho }}}_{i}}cos~{{{\underset{\scriptscriptstyle-}{\phi }}}_{k}} \right){{\underset{\scriptscriptstyle-}{\rho }}_{i}}^{2}sen{{\underset{\scriptscriptstyle-}{\phi }}_{k}}\Delta \rho \Delta \phi \Delta \theta \]
Como essa soma é uma soma de Riemann para uma função
\[f\left( \rho ,\theta ,\phi \right)=f\left( \rho sen~\phi ~cos~\theta ,\rho sen~\phi ~sen~\theta ,\rho cos~\phi \right){{\rho }^{2}}sen~\phi \]
Então, a fórmula para integração tripla em coordenadas esféricas é:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{c}{\overset{d}{\mathop \int }}\,\underset{\alpha }{\overset{\beta }{\mathop \int }}\,\underset{a}{\overset{b}{\mathop \int }}\,f\left( \rho sen~\phi ~cos~\theta ,\rho sen~\phi ~sen~\theta ,\rho cos~\phi \right){{\rho }^{2}}sen~\phi d\rho d\theta d\phi ~~~~~~(48)\]
As mudanças de variáveis são muito práticas para trabalhos manuais, tornando o cálculo de algumas integrais um processo consideravelmente mais simples. Computacionalmente, você acha que mudanças de variáveis podem ser úteis, pensando em nível de processamento?

Visando a prática de cálculo de integrais triplas em coordenadas modificadas, calcule o volume do sólido delimitado pelo cone \(z=\sqrt{{{x}^{2}}+{{y}^{2}}}\) e pela esfera \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}=z\), como evidencia a figura a seguir.
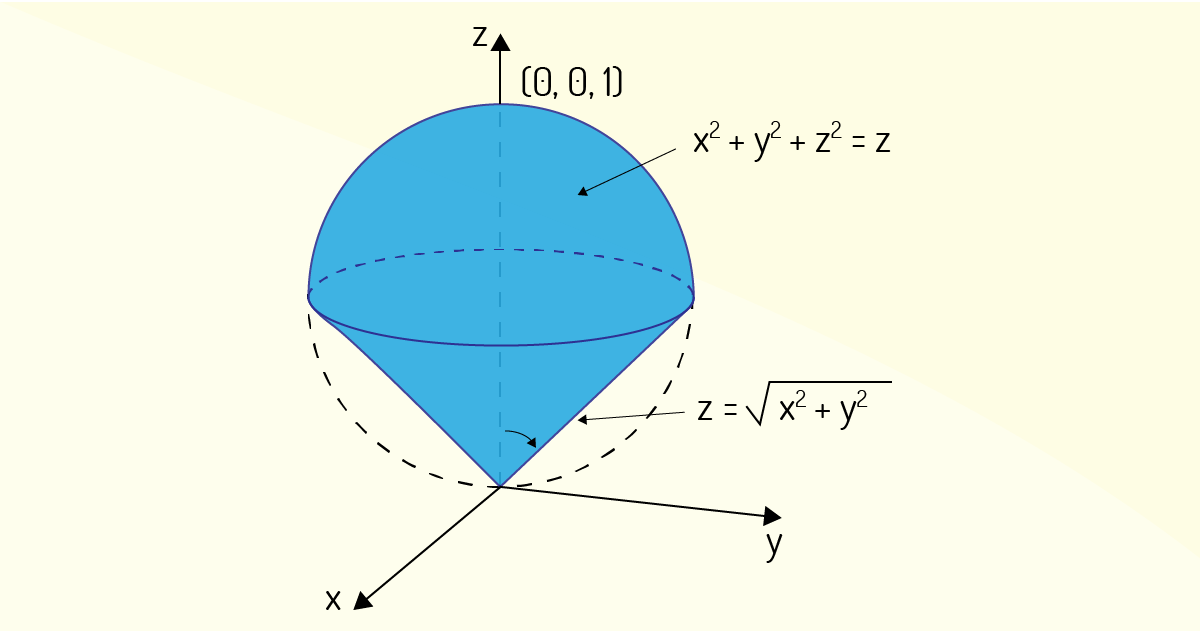
O volume será igual a \(1/8\).
Justificativa: Veja que a esfera definida passa pela origem e tem seu centro no ponto \(\left( 0,0,1/2 \right)\). Para a esfera, tem-se que ela pode ser escrita em coordenadas esféricas como \({{\rho }^{2}}=\rho cos~\phi ~\to ~\rho =cos~\phi \) Já escrevendo a equação do cone em coordenadas esféricas, deve-se encontrar que \(\rho cos~\phi =\rho sen~\phi \). Como isso só é possível para \(phi =\pi /4\), a descrição do sólido em coordenadas esféricas deve ser
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~0\le \theta \le 2\pi ,~0\le \phi \le \pi /4,~0\le \rho \le cos~\phi \right\}\]
Assim, o volume desse sólido pode ser avaliado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,dV=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\underset{0}{\overset{cos~\phi }{\mathop \int }}\,\left( {{\rho }^{2}}sen~\phi \right)d\rho d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\left( \frac{co{{s}^{3}}~\phi ~sen\phi }{3} \right)d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( \frac{1}{16} \right)d\theta =\frac{\pi }{8}\]
O volume será igual a \(\pi /8\).
Justificativa correta: Veja que a esfera definida passa pela origem e tem seu centro no ponto \(\left( 0,0,1/2 \right)\). Para a esfera, tem-se que ela pode ser escrita em coordenadas esféricas como \({{\rho }^{2}}=\rho cos~\phi ~\to ~\rho =cos~\phi \). Já escrevendo a equação do cone em coordenadas esféricas, deve-se encontrar que \(\rho cos~\phi =\rho sen~\phi \). Como isso só é possível para\(\phi =\pi /4\), a descrição do sólido em coordenadas esféricas deve ser
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~0\le \theta \le 2\pi ,~0\le \phi \le \pi /4,~0\le \rho \le cos~\phi \right\}\]
Assim, o volume desse sólido pode ser avaliado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,dV=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\underset{0}{\overset{cos~\phi }{\mathop \int }}\,\left( {{\rho }^{2}}sen~\phi \right)d\rho d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\left( \frac{co{{s}^{3}}~\phi ~sen\phi }{3} \right)d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( \frac{1}{16} \right)d\theta =\frac{\pi }{8}\]
O volume será igual a \(\pi /4\).
Justificativa: Veja que a esfera definida passa pela origem e tem seu centro no ponto \(\left( 0,0,1/2 \right)\). Para a esfera, tem-se que ela pode ser escrita em coordenadas esféricas como \({{\rho }^{2}}=\rho cos~\phi ~\to ~\rho =cos~\phi \). Já escrevendo a equação do cone em coordenadas esféricas, deve-se encontrar que \(\rho cos~\phi =\rho sen~\phi \). Como isso só é possível para \(\phi =\pi /4\), a descrição do sólido em coordenadas esféricas deve ser
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~0\le \theta \le 2\pi ,~0\le \phi \le \pi /4,~0\le \rho \le cos~\phi \right\}\]
Assim, o volume desse sólido pode ser avaliado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,dV=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\underset{0}{\overset{cos~\phi }{\mathop \int }}\,\left( {{\rho }^{2}}sen~\phi \right)d\rho d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\left( \frac{co{{s}^{3}}~\phi ~sen\phi }{3} \right)d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( \frac{1}{16} \right)d\theta =\frac{\pi }{8}\]
O volume será igual a \(1/4\).
Justificativa: Veja que a esfera definida passa pela origem e tem seu centro no ponto \(\left( 0,0,1/2 \right)\). Para a esfera, tem-se que ela pode ser escrita em coordenadas esféricas como \({{\rho }^{2}}=\rho cos~\phi ~\to ~\rho =cos~\phi \). Já escrevendo a equação do cone em coordenadas esféricas, deve-se encontrar que \(\rho cos~\phi =\rho sen~\phi \). Como isso só é possível para \(\phi =\pi /4\), a descrição do sólido em coordenadas esféricas deve ser
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~0\le \theta \le 2\pi ,~0\le \phi \le \pi /4,~0\le \rho \le cos~\phi \right\}\]
Assim, o volume desse sólido pode ser avaliado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,dV=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\underset{0}{\overset{cos~\phi }{\mathop \int }}\,\left( {{\rho }^{2}}sen~\phi \right)d\rho d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\left( \frac{co{{s}^{3}}~\phi ~sen\phi }{3} \right)d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( \frac{1}{16} \right)d\theta =\frac{\pi }{8}\]
O volume será igual a \(\pi /2\).
Justificativa: Veja que a esfera definida passa pela origem e tem seu centro no ponto \(\left( 0,0,1/2 \right)\). Para a esfera, tem-se que ela pode ser escrita em coordenadas esféricas como \({{\rho }^{2}}=\rho cos~\phi ~\to ~\rho =cos~\phi \). Já escrevendo a equação do cone em coordenadas esféricas, deve-se encontrar que \(\rho cos~\phi =\rho sen~\phi \). Como isso só é possível para \(\phi =\pi /4\), a descrição do sólido em coordenadas esféricas deve ser
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~0\le \theta \le 2\pi ,~0\le \phi \le \pi /4,~0\le \rho \le cos~\phi \right\}\]
Assim, o volume desse sólido pode ser avaliado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,dV=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\underset{0}{\overset{cos~\phi }{\mathop \int }}\,\left( {{\rho }^{2}}sen~\phi \right)d\rho d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\left( \frac{co{{s}^{3}}~\phi ~sen\phi }{3} \right)d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( \frac{1}{16} \right)d\theta =\frac{\pi }{8}\]
Nome do livro: Cálculo: Volume 2
Editora: Pearson
Autor: George B. Thomas, Maurice D. Weir e Joel Hass
ISBN: 8581430872
Comentário: Esse livro de Cálculo contém uma boa quantidade de exemplos e gráficos de funções de duas variáveis, facilitando a compreensão dos assuntos, os quais são abordados em uma linguagem simples e didática. É um excelente material para aprimorar e exercitar os seus conhecimentos.
