O estudo de funções de uma única variável pode ser expandido e aplicado para casos de funções de mais de uma variável. Portanto, na presente Unidade, vamos ampliar as aplicações de derivadas para a análise de funções de duas variáveis. Inicialmente, discutiremos a respeito dos máximos e mínimos de funções com mais de uma variável, iniciando os estudos com um embasamento teórico, partindo, então, para a aplicação do conceito de derivadas para auxiliar na determinação de pontos críticos para, então, aprender a determinar quais pontos críticos são pontos extremantes e quais são pontos de sela. Fundamentada a teoria de determinação dos tipos de pontos críticos de uma função, estudaremos a aplicação desses conceitos com alguns exemplos.
Assim como você estudou nos casos de funções com apenas uma variável, uma das principais aplicações das derivadas de 1ª ordem se encontra na análise de uma função, permitindo a você identificar os valores máximos e mínimos de uma função. Como você já deve ter percebido, a derivada parcial de 1ª ordem para funções com duas ou mais variáveis também pode ser utilizada com esta finalidade (STEWART, 2017). Logo, a presente unidade será dedicada a esse tipo de aplicação das derivadas parciais.
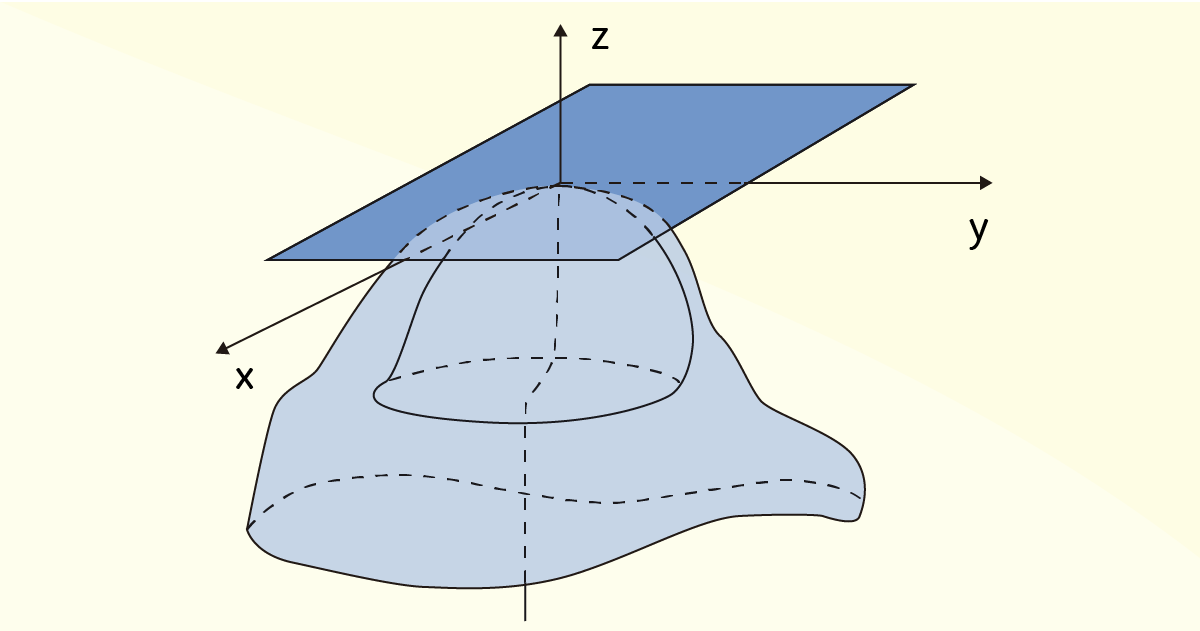
Os valores de máximo e mínimo de uma função podem ocorrer tanto nas regiões fronteiriças quanto nas regiões internas da representação gráfica de uma função. Inicialmente, será desenvolvida a análise desses pontos dentro de uma região. Para ilustrar esses casos de pontos de mínimo e máximo de uma função, considere a função genérica \(z=f\left( x,y \right)\) e o conjunto de pontos \(A\), representados geometricamente conforme mostra a Figura 3.1 a seguir:
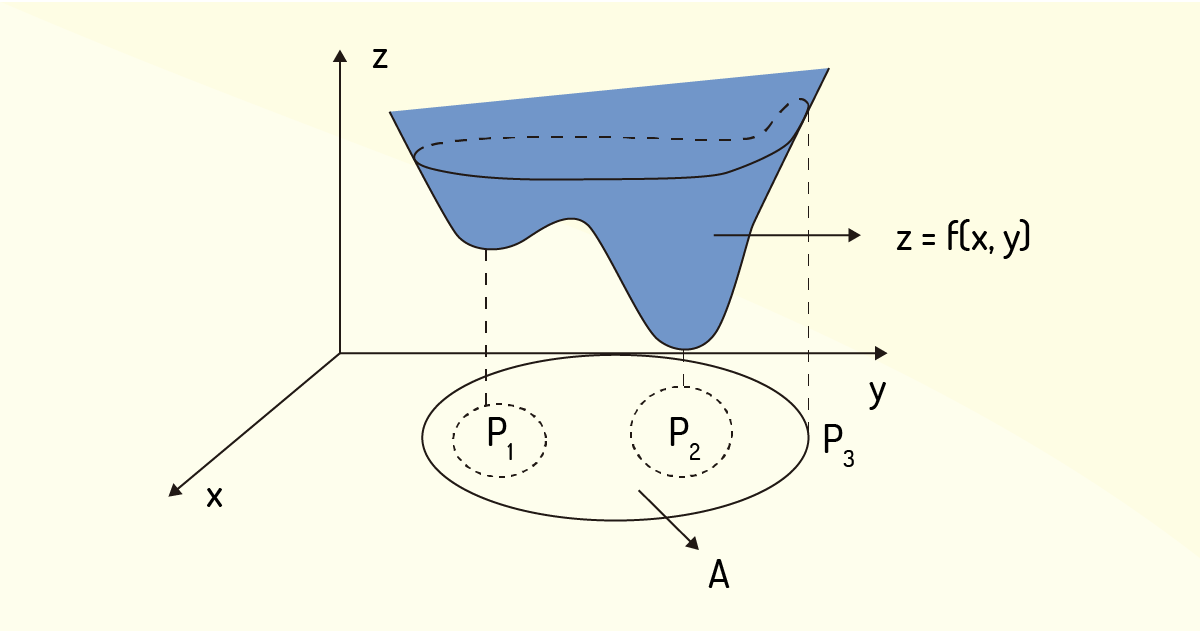
Observando os pontos \(\left( x,y \right)\) delimitados pela região \(A\), é possível notar que, nos pontos \({{P}_{1}}\) e \({{P}_{2}}\), a função \(z\) apresentará valores mínimos. Já o ponto \({{P}_{3}}\), que se encontra na fronteira desse conjunto \(A\), é um ponto de máximo. Dessa imagem e breve análise, Flemming e Gonçalves (2005) propõem as seguintes definições:
Definição 1 - máximo global ou absoluto: seja uma função \(z=f\left( x,y \right)\) qualquer, cujo domínio seja \({{D}_{f}}\). Então, o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in {{D}_{f}}\) é um ponto de máximo global ou absoluto se, para qualquer outro ponto \(\left( x,y \right)\in {{D}_{f}}\), tem-se que \(f\left( x,y \right)\le f\left( {{x}_{0}},{{y}_{0}} \right)\). Logo, pode-se afirmar que \(f\left( {{x}_{0}},{{y}_{0}} \right)\) é o valor máximo de \(f\).
Definição 2 - mínimo global ou absoluto: seja uma função \(z=f\left( x,y \right)\) qualquer, cujo domínio seja \({{D}_{f}}\). Então, o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in {{D}_{f}}\) é um ponto de mínimo global ou absoluto se, para qualquer outro ponto \(\left( x,y \right)\in {{D}_{f}}\), tem-se que \(f\left( x,y \right)\ge f\left( {{x}_{0}},{{y}_{0}} \right)\). Logo, pode-se afirmar que \(f\left( {{x}_{0}},{{y}_{0}} \right)\) é o valor mínimo de \(f\).
Exemplo 1.1: Considere o paraboloide definido pela função \(z=9-{{x}^{2}}-{{y}^{2}}\). Qual deverá ser o máximo absoluto dessa função?
Solução
A representação gráfica desse paraboloide, conforme na Figura 3.2, provavelmente já é familiar a você.
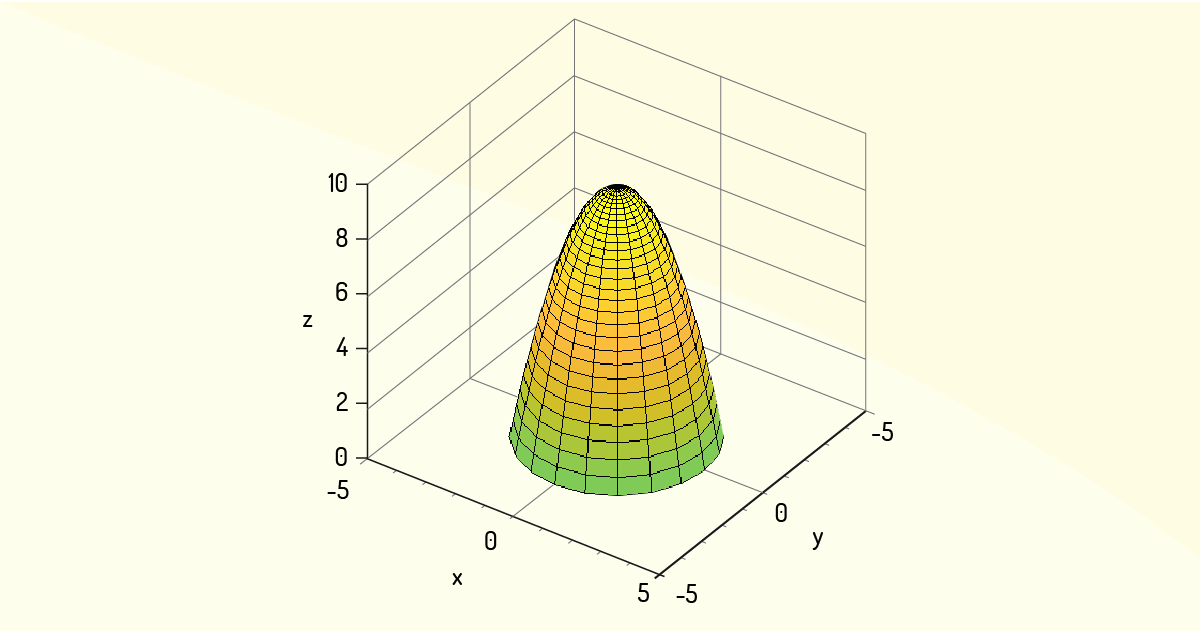
Analisando tal gráfico, fica simples deduzir que o valor máximo absoluto dessa função irá ocorrer no ponto \(\left( 0,0 \right)\), para o qual se tem que \(z=9\). Isso pode ser comprovado pela Definição 1, pois, para qualquer \(\left( x,y \right)\in {{D}_{z}}\), tem-se que \(f\left( x,y \right)\le 9\). Em outra notação:
\[\forall \left( x,y \right)\in {{D}_{z}},f\left( x,y \right)\le f\left( 0,0 \right)\]
Exemplo 1.2: Considere o paraboloide definido pela função \(z=4+{{x}^{2}}+{{y}^{2}}\). Qual deverá ser o máximo absoluto dessa função?
Solução
Esse paraboloide está representado na Figura 3.3.
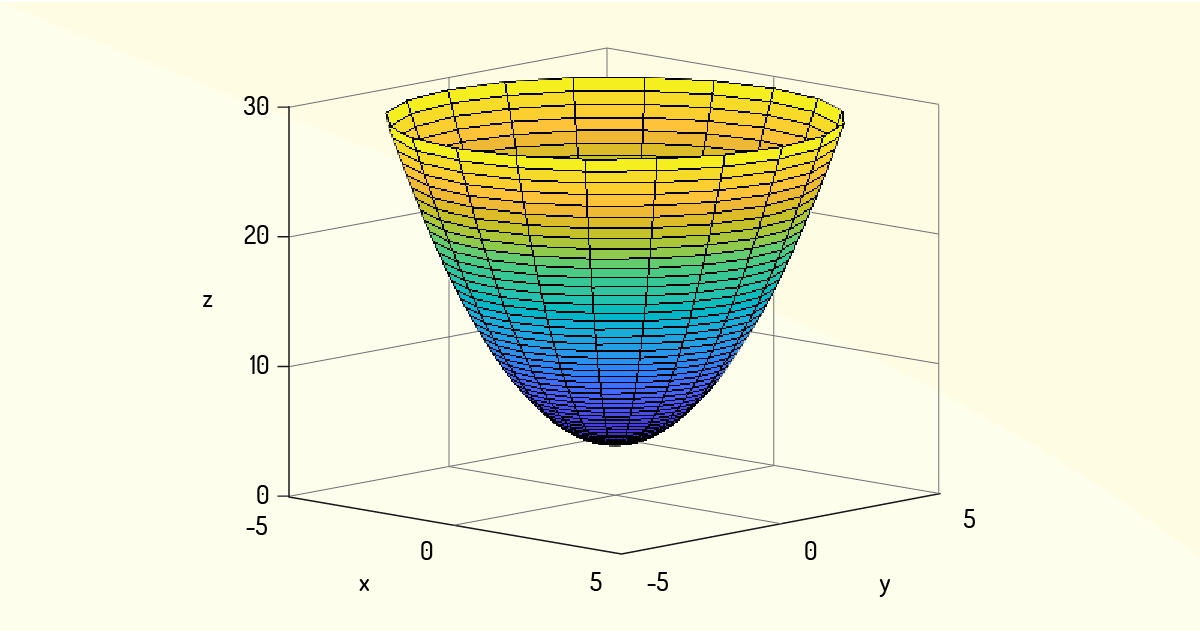
Analisando tal gráfico, fica simples deduzir que o valor máximo absoluto dessa função também irá ocorrer no ponto \(\left( 0,0 \right)\), para o qual se tem que \(z=4\). Isso pode ser comprovado pela Definição 2, pois, para qualquer \(\left( x,y \right)\in {{D}_{z}}\), tem-se que \(f\left( x,y \right)\ge 9\). Em outra notação:
\[\forall \left( x,y \right)\in {{D}_{z}},f\left( x,y \right)\ge f\left( 0,0 \right)\]
Além dos máximos e mínimos absolutos, Flemming e Gonçalves (2005) ainda apresentam a definição dos máximos e mínimos locais, da mesma forma que se tem para funções de uma única variável.
Definição 3 - máximo local ou relativo: seja uma função \(z=f\left( x,y \right)\) qualquer, cujo domínio seja \({{D}_{f}}\). Então, o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in {{D}_{f}}\) será um ponto de máximo local ou relativo se existir uma bola aberta \(B\left( \left( {{x}_{0}},{{y}_{0}} \right);r \right)\in {{D}_{f}}\) para a qual se tem que, para qualquer ponto \(\left( x,y \right)\in B\), tem-se que \(f\left( x,y \right)\le f\left( {{x}_{0}},{{y}_{0}} \right)\).
Definição 4 - mínimo local ou relativo: seja uma função \(z=f\left( x,y \right)\) qualquer, cujo domínio seja \({{D}_{f}}\). Então, o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in {{D}_{f}}\) será um ponto de mínimo local ou relativo se existir uma bola aberta \(B\left( \left( {{x}_{0}},{{y}_{0}} \right);r \right)\in {{D}_{f}}\) para a qual se tem que, para qualquer ponto \(\left( x,y \right)\in B\), tem-se que \(f\left( x,y \right)\ge f\left( {{x}_{0}},{{y}_{0}} \right)\).
Exemplo 1.3: Considere a função \(z=se{{n}^{2}}~x+\frac{1}{2}{{y}^{2}}\). Existem mínimos locais nessa função?
Solução
A representação gráfica dessa função é mostrada na Figura 3.4.
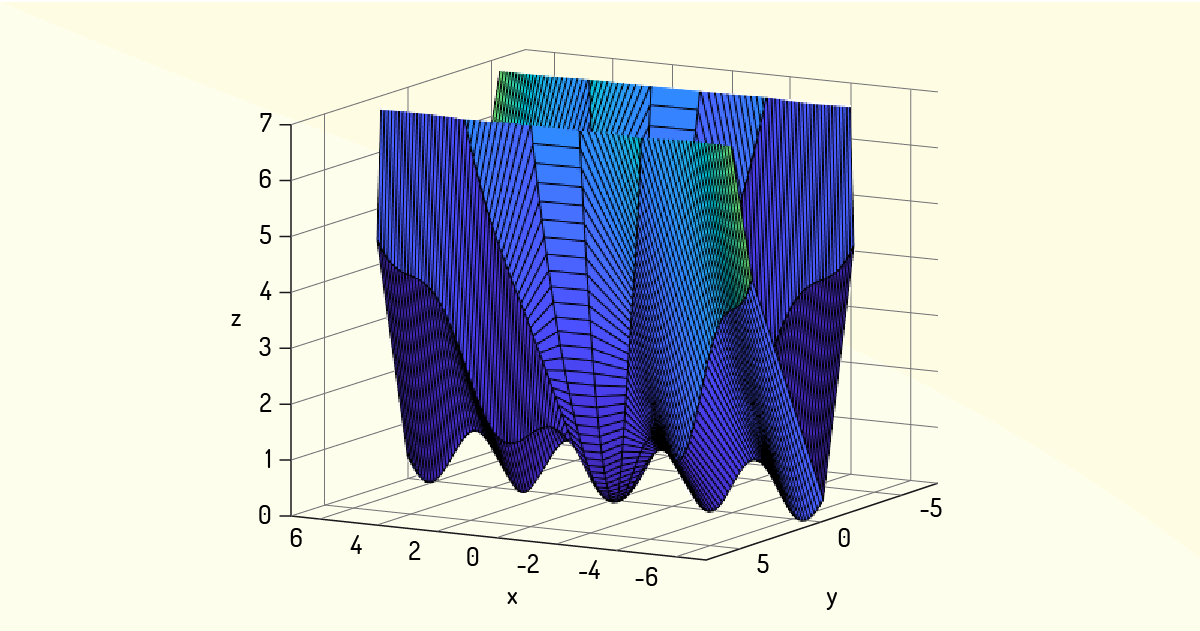
Como você pode ver na Figura 3.4, a função \(z\) definida tem como valor mínimo \(z=0\). Analisando o gráfico, é possível ver que ele apresenta diversos pontos de mínimo local, pois periodicamente se tem que \(z=0\).
Verificando, então, essa função, pode-se concluir que os mínimos irão ocorrer quando se tem que \(se{{n}^{2}}~x=0\) e \(\frac{1}{2}{{y}^{2}}=0\). Assim, toda vez que se tem \(x=k\pi \), em que \(k\in Z\) e \(y=0\), a função apresentará um mínimo local.
Segundo Flemming e Gonçalves (2005), os pontos de máximo e mínimo também podem ser encontrados na literatura como pontos extremantes, tanto no caso dos globais como dos locais. Além disso, você deve imaginar que é possível que exista uma metodologia diferenciada e mais simples para que esses pontos extremantes sejam identificados, fazendo uso de conceitos de cálculo desenvolvidos até aqui. Tal metodologia será discutida na próxima seção.
Quando se lida com funções de uma única variável, a análise da representação gráfica é uma excelente forma de buscar máximos e mínimos. Você acha que essa prática para a análise de funções de duas variáveis é tão útil e simples quanto no caso de funções de uma única variável?

Uma das análises mais corriqueiras que se faz de uma função é identificar a existência dos pontos de máximo e mínimo das funções. Visando desenvolver essa habilidade e praticar os conceitos de máximos e mínimos de uma função, analise as alternativas a seguir e assinale a correta.
Uma função definida como \(z=a+{{x}^{2}}+{{y}^{2}}\) tem o ponto \(\left( 0,0 \right)\) como ponto de máximo global.
Justificativa: Essa função é um paraboloide positivo. Para essa função, o ponto \(\left( 0,0 \right)\) indica um ponto de mínimo global.
Todas as funções com mais de uma variável apresentam um valor de máximo e um valor de mínimo global.
Justificativa correta: Isso não é válido para todas as funções com mais de uma variável, como se vê nos casos de funções com uma variável. Inúmeras funções vão apresentar tendência ao infinito positivo ou negativo e, como infinito não é um número, essas funções não apresentarão pontos de máximo ou mínimo. Por exemplo, um paraboloide \(z=a+{{x}^{2}}+{{y}^{2}}\) não apresenta valor de máximo global.
Para valores de \(x\) entre \(-2\) e \(2\) e para valores de \(y\) entre \(-1\) e \(1\), a função definida como \(z=a-{{x}^{2}}-{{y}^{2}}\) tem três pontos como pontos de máximo locais.
Justificativa: A região delimitada pelos valores de \(x\) e \(y\) indicados apresenta um único valor de mínimo local. Observe que essa função é um paraboloide e seu máximo ocorre em \(\left( 0,0 \right)\).
A função \(z=co{{s}^{2}}~x+{{y}^{2}}\) apresentará mínimos locais sempre que \(y=0\) e \(x=k\pi \), em que \(k\in Z\).
Justificativa: A condição indicada para \(x\) indica valores para os quais se tem que \(co{{s}^{2}}~x=1\). Para os mínimos locais, é preciso encontrar os valores para os quais se tem que \(co{{s}^{2}}~x=0\).
A única forma para se identificar máximos e mínimos locais de uma função com duas variáveis é pela análise gráfica da função.
Justificativa: A análise da representação gráfica é muito útil para identificar esses pontos de máximo e mínimo locais, mas não é a única forma. A análise matemática da função também pode identificar os pontos de máximo e mínimo.
Assim como mencionado anteriormente, encontrar os pontos extremantes de uma função de duas variáveis dependendo apenas da análise gráfica dessa variável ou da análise da função pode não ser uma prática tão simples, sendo necessário o uso de softwares para visualização da representação gráfica da função ou uma extensa e, por vezes, trabalhosa análise matemática. É nesse momento que o cálculo surge para facilitar o trabalho de localizar os pontos: assim como nos casos de análise de funções de uma única variável, podemos fazer uso do ferramental fornecido pelo cálculo para esse tipo de análise.
Para aplicarmos o cálculo na análise de pontos extremantes de uma função, considere a função de duas variáveis \(z=f\left( x,y \right)\), a qual é definida em um conjunto aberto \(A\subset {{\mathbb{R}}^{2}}\).
Segundo Flemming e Gonçalves (2005), um ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in A\) será chamado de ponto crítico de \(f\) se as derivadas parciais \(\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)\) e \(\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)\) forem iguais a zero ou se a função \(f\) não for diferenciável no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in A\). Ou seja, pensando de forma geométrica, os pontos críticos de uma função são aqueles pontos em que o gráfico não apresenta um plano tangente ou, quando apresentar esse plano tangente, ele será horizontal.
Flemming e Gonçalves (2005) ainda destacam que os pontos extremantes de \(f\) se encontram entre os pontos críticos de tal função. No entanto, Thomas Júnior (2016) afirma que nem todos os pontos críticos encontrados serão pontos extremantes. Disso, tem-se que um ponto crítico que não é um ponto extremante será denominado ponto de sela.
Exemplo 2.1: Verifique se o ponto \(\left( 0,0 \right)\) é um ponto crítico de alguma das seguintes funções:
\[f\left( x,y \right)=2{{x}^{2}}+{{y}^{2}}\]
\[f\left( x,y \right)=\sqrt{3{{x}^{2}}+2{{y}^{3}}}\]
Solução
Para identificar se um dado ponto é um ponto crítico de uma função com duas variáveis, devemos verificar se as derivadas parciais em tal ponto são iguais a zero ou se a função não é diferenciável no ponto indicado. Então:
a. Para \(f\left( x,y \right)=2{{x}^{2}}+{{y}^{2}}\), tem-se que:
\[\frac{\partial f}{\partial x}\left( 0,0 \right)=4x=0~~~~e~~~~\frac{\partial f}{\partial y}\left( 0,0 \right)=2y=0\]
Então, como ambas derivadas parciais no ponto \(\left( 0,0 \right)\) são iguais a zero, tem-se que o ponto \(\left( 0,0 \right)\) é um ponto crítico para essa função. A Figura 3.5 ilustra o gráfico dessa função e o plano tangente ao ponto \(\left( 0,0 \right)\).
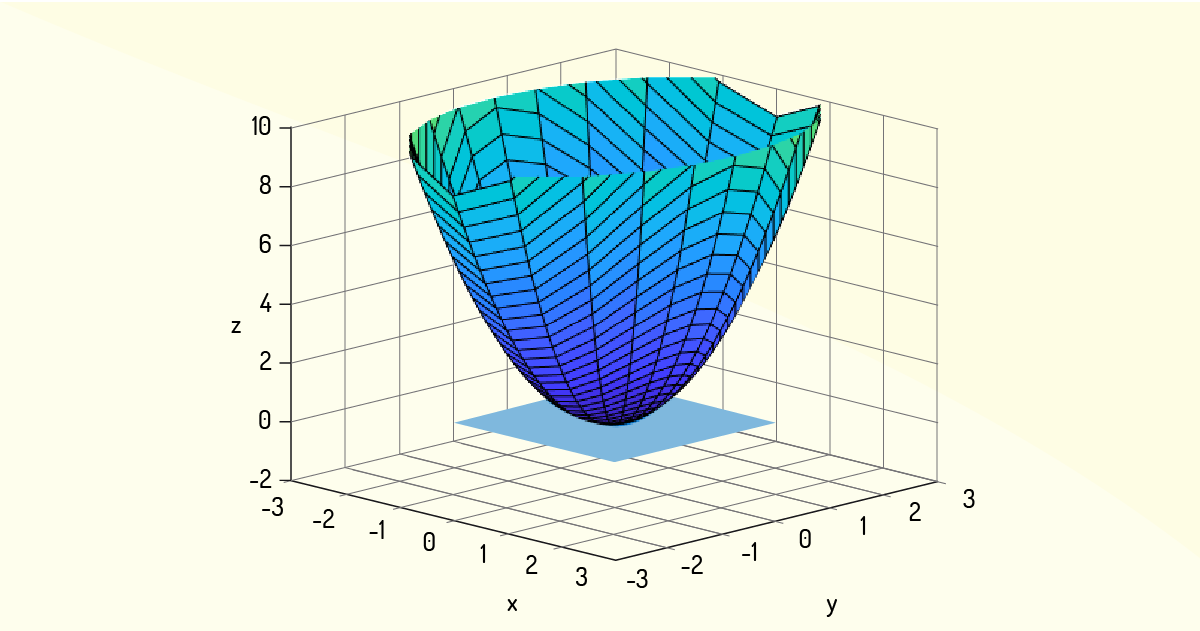
b. Já para a função \(f\left( x,y \right)=\sqrt{3{{x}^{2}}+2{{y}^{3}}}\), tem-se que:
\[\frac{\partial f}{\partial x}=\frac{3x\sqrt{3{{x}^{2}}+2{{y}^{3}}}}{3{{x}^{2}}+2{{y}^{3}}}~~~~e~~~~\frac{\partial f}{\partial y}=\frac{3{{y}^{2}}\sqrt{3{{x}^{2}}+2{{y}^{3}}}}{3{{x}^{2}}+2{{y}^{3}}}\]
Note que as derivadas parciais no ponto \(\left( 0,0 \right)\) não existem. Então, em tal ponto, a função não apresenta plano tangente. Na Figura 3.6 é mostrada uma representação gráfica dessa função. Note que no ponto \(\left( 0,0 \right)\) existe um “bico”, o que indica que não existe derivada em tal ponto.
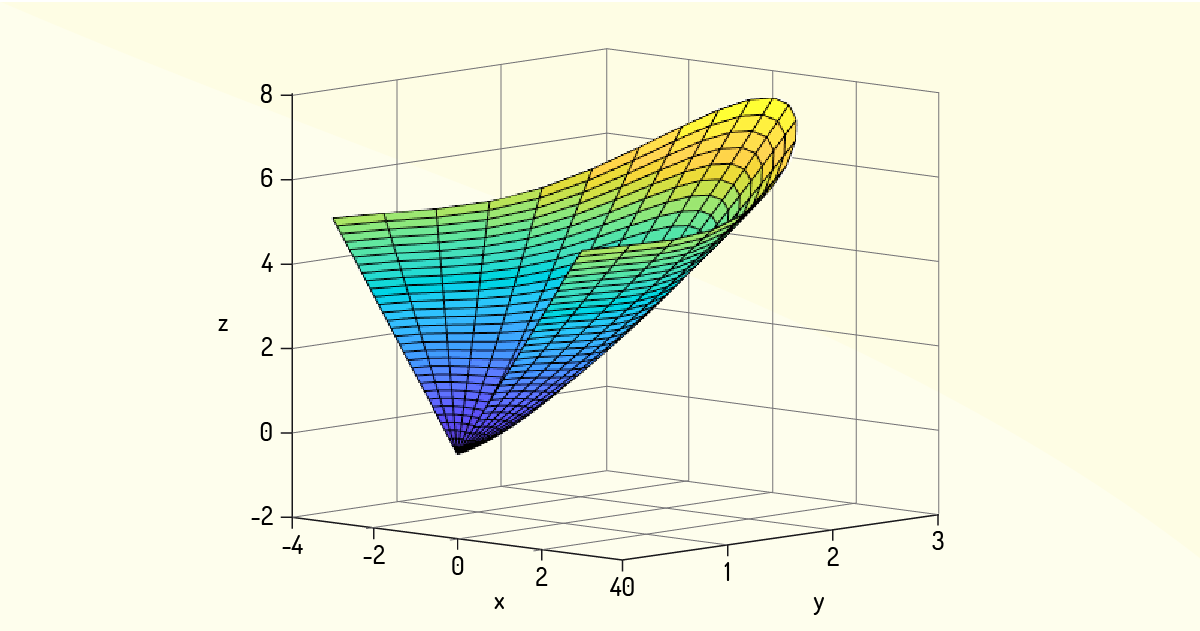
A seguir veremos a condição requisitada para a existência de pontos extremantes. Vamos lá?!
Seja a função de duas variáveis \(z=f\left( x,y \right)\) diferenciável em um conjunto aberto \(A\subset {{\mathbb{R}}^{2}}\). Para garantir que um ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in A\) é um ponto extremante, quer de máximo ou mínimo local, então \(\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)=0\) e \(\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)=0\). Ou seja, o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\) deve ser um ponto crítico de \(f\), segundo Flemming e Gonçalves (2005).
A prova disso pode ser feita de maneira relativamente simples, de acordo com Flemming e Gonçalves (2005). Suponha que o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in A\) é um ponto de máximo local da função \(f\). Então, deve existir uma bola aberta \(B=B\left( \left( {{x}_{0}},{{y}_{0}} \right),r \right)\) na qual, para todos os pontos \(\left( x,y \right)\in B\), tem-se que \(f\left( x,y \right)\le f\left( {{x}_{0}},{{y}_{0}} \right)\).
Considere, agora, a função de uma variável \(h\), definida como \(h:I\subset \mathbb{R}\to \mathbb{R}\), em que \(h\left( x \right)=f\left( x,{{y}_{0}} \right)\) e \(I\) é um intervalo aberto que contém o valor \({{x}_{0}}\), tal que se tem \(\left( x,{{y}_{0}} \right)\in B\) para todo \(x\in I\). Isso pode ser visualizado na Figura 3.7 a seguir.
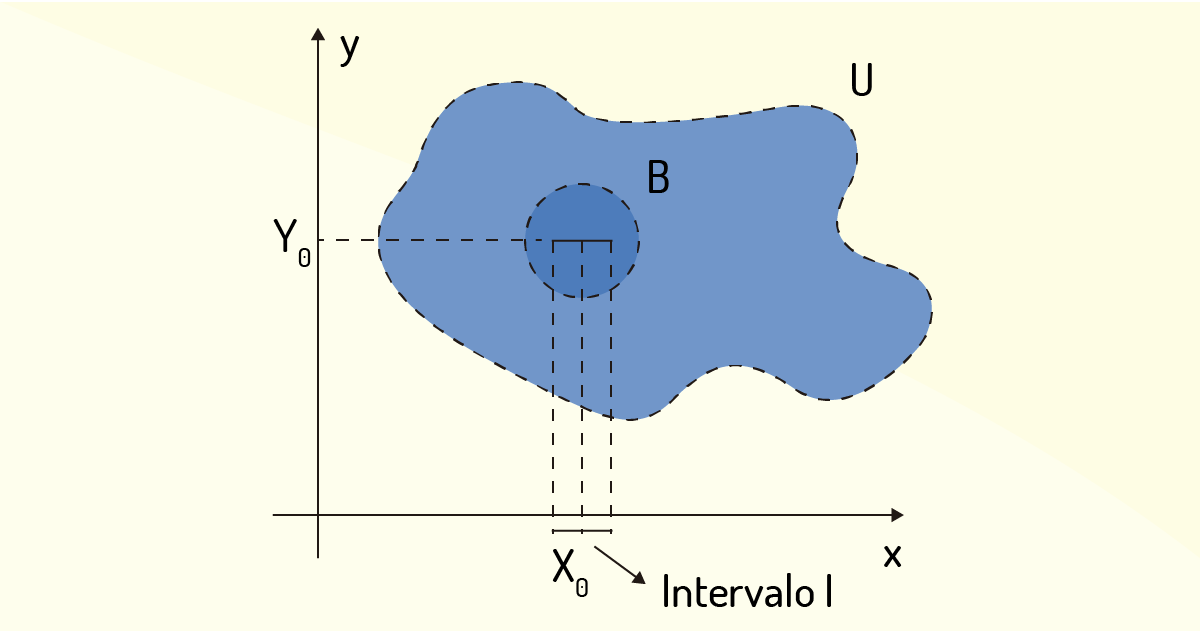
Tem-se, então, que \(h\left( x \right)\) é derivável no ponto \({{x}_{0}}\), tal que \(h'\left( {{x}_{0}} \right)=\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)\). Além disso, \({{x}_{0}}\) é um ponto interior de \(I\), assim como também é um ponto de máximo local da função \(h\left( x \right)\). Com isso, Flemming e Gonçalves (2005) indicam que podemos encontrar diversos pontos que sejam candidatos a pontos extremantes.
Exemplo 2.2: Encontre os pontos críticos da função \(f\left( x,y \right)=2{{x}^{2}}y+3{{x}^{2}}-2y\).
Solução
A função \(f\left( x,y \right)\) é polinomial, o que acarreta na existência de derivadas parciais para todos os pontos \(\left( x,y \right)\in {{\mathbb{R}}^{2}}\). Basta, então, que avaliemos as derivadas parciais \(\frac{\partial f}{\partial x}\) e \(\frac{\partial f}{\partial y}\) dessa função e identificar em quais pontos as duas derivadas serão simultaneamente iguais a zero. Avaliando as derivadas parciais da função $f$ dada, tem-se que:
\[\frac{\partial f}{\partial x}=4xy+6x\]
\[\frac{\partial f}{\partial y}=2{{x}^{2}}-2\]
Agora, deve-se resolver o sistema:
\[\left\{\begin{matrix} 4xy+6x=0 \\ 2{{x}^{2}}-2=0 \\ \end{matrix} \right.\]
Da segunda equação do sistema, tem-se que \({{x}^{2}}=1\), ou seja, \(x=\pm 1\). Agora, para a primeira equação, convém evidenciar o termo \(x\), ou seja, a derivada \(\frac{\partial f}{\partial x}\) pode ser reescrita como \(4xy+6x=2x\left( 2y+3 \right)\). Então, é preciso identificar onde \(2x\left( 2y+3 \right)=0\). Da análise de \(\frac{\partial f}{\partial y}\), já sabemos que \(x=\pm 1\), logo, é preciso que \(2y+3\) seja igual a 0. Então, encontra-se que \(y=-3/2\).
Com isso, podemos inferir que a função dada apresentará dois pontos críticos, que serão os pontos \(\left( 1,-\frac{3}{2} \right)\) e \(\left( -1,-\frac{3}{2} \right)\).
Exemplo 2.3: Encontre os pontos críticos da função \(f\left( x,y \right)=2{{x}^{2}}y+2{{y}^{2}}-8y\).
Solução
Novamente, a função \(f\left( x,y \right)\) é polinomial, o que acarreta na existência de derivadas parciais para todos os pontos \(\left( x,y \right)\in {{\mathbb{R}}^{2}}\). Basta avaliar as derivadas parciais \(\frac{\partial f}{\partial x}\) e \(\frac{\partial f}{\partial y}\) dessa função e identificar em quais pontos as duas derivadas serão simultaneamente iguais a zero. Tem-se, então:
\[\frac{\partial f}{\partial x}=4xy\]
\[\frac{\partial f}{\partial y}=2{{x}^{2}}+4y-8\]
Agora, deve-se resolver o sistema:
\[\left\{ \begin{matrix} 4xy=0 \\ 2{{x}^{2}}+4y-8=0 \\ \end{matrix} \right.\]
De \(4xy=0\), tem-se que \(x=0\) ou \(y=0\). Deve-se partir disso para analisar a outra equação. Assim, se \(x=0\), de \(2{{x}^{2}}+4y-8=0\), tem-se que \(4y-8=0\), ou seja, se \(x=0\), então \(y=2\). Logo, o ponto \(\left( 0,2 \right)\) é um ponto crítico da função dada. Agora, se se \(y=0\), de \(2{{x}^{2}}+4y-8=0\), tem-se que \(2{{x}^{2}}-8=0\), ou seja, se \(y=0\), então \(x=\pm 2\). Disso, tem-se que os pontos \(\left( 2,0 \right)\) e \(\left( -2,0 \right)\) também serão pontos críticos de \(f\). Então, mostrou-se que a função dada apresentará três pontos críticos.
Exemplo 2.4: Mostre que os pontos da reta \(y=x-k\pi \), em que \(k\in Z\), são pontos críticos da função \(f\left( x,y \right)=2cos\left( x-y \right)\).
Solução
Avaliando as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=-2sen\left( x-y \right)\]
\[\frac{\partial f}{\partial y}=2sen\left( x-y \right)\]
Agora, deve-se resolver o sistema:
\[\left\{ \begin{matrix} -2sen(x-y)=0 \\ 2sen(x-y)=0 \\ \end{matrix} \right.\]
Antes de buscar a resolução direta do sistema dado acima, perceba que tal sistema pode ser reescrito como:
\[\left\{ \begin{matrix} sen(x-y)=0 \\ sen(x-y)=0 \\ \end{matrix} \right.\]
Ou seja, basta avaliar onde \(sen\left( x-y \right)=0\) para identificar os pontos críticos. Lembrando-se da função seno, sabe-se que ela será igual a zero de forma periódica da seguinte forma: \(sen\left( k\pi \right)=0\), em que \(k\) é um número inteiro, ou seja, \(k\in Z\). Logo, da equação que se tem, é preciso que:
\[x-y=k\pi ~\to y=x-k\pi ~\]
Note que essa equação é uma equação de reta. Portanto, qualquer ponto \(\left( x,x-k\pi \right)\) será um ponto crítico da função \(f\) dada.
Como visto anteriormente, um ponto crítico de uma função pode ser visto geometricamente como aqueles pontos nos quais não se encontra um plano tangente ou o plano tangente é horizontal. Com isso, pode-se identificar, segundo Flemming e Gonçalves (2005), qual paraboloide mais se aproxima do gráfico da função nas proximidades de um ponto crítico \(\left( {{x}_{0}},{{y}_{0}} \right)\).
Na Figura 3.8 a seguir, é apresentado o gráfico de uma função \(z=f\left( x,y \right)\) hipotética e o plano horizontal tangente em um de seus pontos críticos. Nessa mesma figura pode-se ver que existe um paraboloide que aproxima de forma adequada a região gráfica da função \(z\).
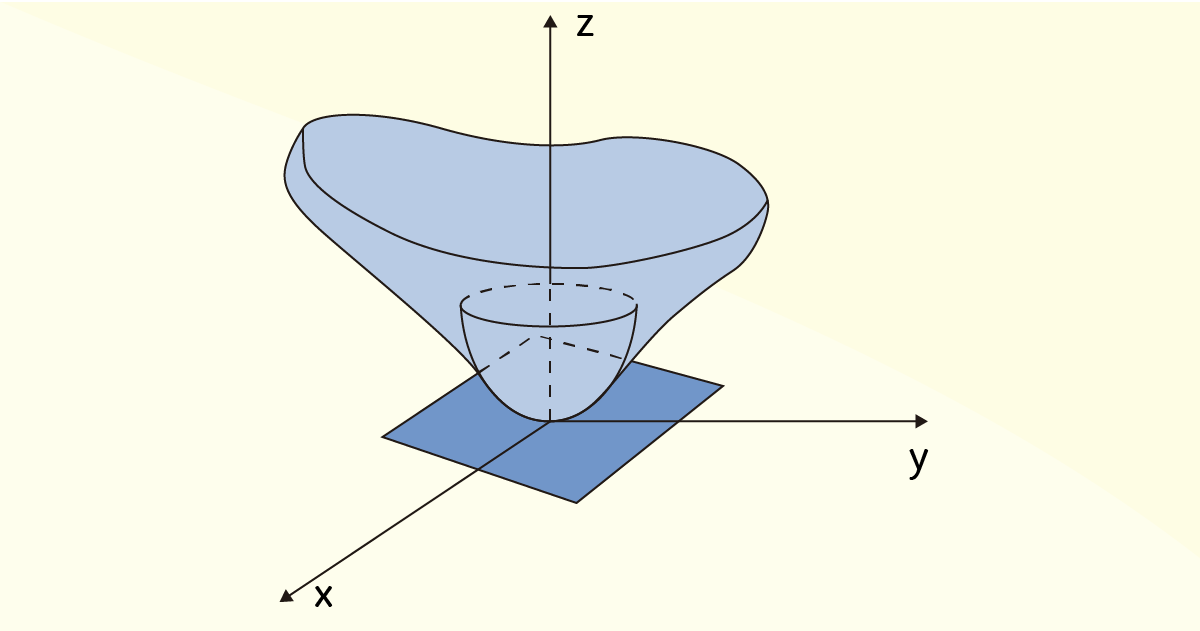
Veja que o paraboloide na Figura 3.8 apresenta concavidade voltada para cima. Isso, segundo Flemming e Gonçalves (2005), é um indicativo de que o ponto crítico em questão é um ponto de mínimo. Na Figura 3.9 a seguir, é apresentado um caso semelhante ao que acabamos de descrever, mas o paraboloide encontrado tem concavidade voltada para baixo, o que indica que o ponto crítico em questão é um ponto de máximo.
De acordo com Flemming e Gonçalves (2005), essa noção geométrica apresentará uma condição suficiente para identificar se um ponto crítico é um ponto extremante local. Para isso, considere que a função \(z=f\left( x,y \right)\) apresenta derivadas parciais de primeira e segunda ordem contínuas em um conjunto aberto \(A\), o qual contém o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\) – ponto crítico de \(f\). Então, considere o determinante \(H\left( x,y \right)\), definido a seguir:
\[H(x,y)=\left| \begin{matrix} \frac{{{\partial }^{2}}}{\partial {{x}^{2}}}f(x,y)~~~~~~~~~\frac{{{\partial }^{2}}}{\partial y\partial x}f(x,y) \\ \frac{{{\partial }^{2}}}{\partial x\partial y}f(x,y)~~~~~~~~~\frac{{{\partial }^{2}}}{\partial {{y}^{2}}}f(x,y) \\ \end{matrix} \right|\]
Da análise desse determinante, pode-se chegar a quatro conclusões:
Flemming e Gonçalves (2005) ainda destacam que a matriz que origina o determinante acima é comum no cálculo, recebendo um nome específico para a designar: matriz hessiana. A seguir tem-se a matriz hessiana:
\[\left[ \begin{matrix} \frac{{{\partial }^{2}}}{\partial {{x}^{2}}}f(x,y)~~~~~~~~~\frac{{{\partial }^{2}}}{\partial y\partial x}f(x,y) \\ \frac{{{\partial }^{2}}}{\partial x\partial y}f(x,y)~~~~~~~~~\frac{{{\partial }^{2}}}{\partial {{y}^{2}}}f(x,y) \\ \end{matrix} \right]\]
Dito isso, o determinante mostrado acima é chamado hessiano da função \(z\).
A prova do que foi proposto aqui é consideravelmente complexa, mas a ideia fundamental reside no uso de derivadas parciais de segunda ordem da função em questão para determinar qual é o tipo de paraboloide que mais se aproxima da região do ponto crítico. Esse paraboloide pode ser representado de forma genérica como:
\[P\left( x,y \right)=\frac{1}{2}A{{x}^{2}}+Bxy+\frac{1}{2}C{{y}^{2}}+Dx+Fy+G\]
Para essa forma genérica, tem-se que um paraboloide que satisfaça às seguintes cinco condições
\[\frac{\partial P}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)=\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)\]
\[\frac{\partial P}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)=\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)\]
\[\frac{{{\partial }^{2}}P}{\partial {{x}^{2}}}\left( {{x}_{0}},{{y}_{0}} \right)=\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}\left( {{x}_{0}},{{y}_{0}} \right)\]
\[\frac{{{\partial }^{2}}P}{\partial {{y}^{2}}}\left( {{x}_{0}},{{y}_{0}} \right)=\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}\left( {{x}_{0}},{{y}_{0}} \right)\]
\[\frac{{{\partial }^{2}}P}{\partial x\partial y}\left( {{x}_{0}},{{y}_{0}} \right)=\frac{{{\partial }^{2}}f}{\partial x\partial y}\left( {{x}_{0}},{{y}_{0}} \right)\]
apresentará o mesmo plano tangente que o gráfico da função \(f\) no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\). Note que as cinco condições apresentadas acima podem ser reescritas como:
\[A{{x}_{0}}+B{{y}_{0}}+D=\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)\]
\[B{{x}_{0}}+C{{y}_{0}}+F=\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)\]
\[A=\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}\left( {{x}_{0}},{{y}_{0}} \right)\]
\[C=\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}\left( {{x}_{0}},{{y}_{0}} \right)\]
\[B=\frac{{{\partial }^{2}}f}{\partial x\partial y}\left( {{x}_{0}},{{y}_{0}} \right)\]
Ou seja, os termos \(A\), \(B\) e \(C\) do paraboloide devem ser iguais às derivadas parciais de segunda ordem da função \(f\).
Com essas definições, você também é capaz de determinar as curvas de nível do paraboloide que realiza a aproximação no ponto crítico: basta igualar a equação do paraboloide a uma constante \(k\) qualquer:
\[\frac{1}{2}A{{x}^{2}}+Bxy+\frac{1}{2}C{{y}^{2}}+Dx+Fy+G=k\]
Essa equação pode representar alguns tipos pré-específicos de curvas, da seguinte forma:
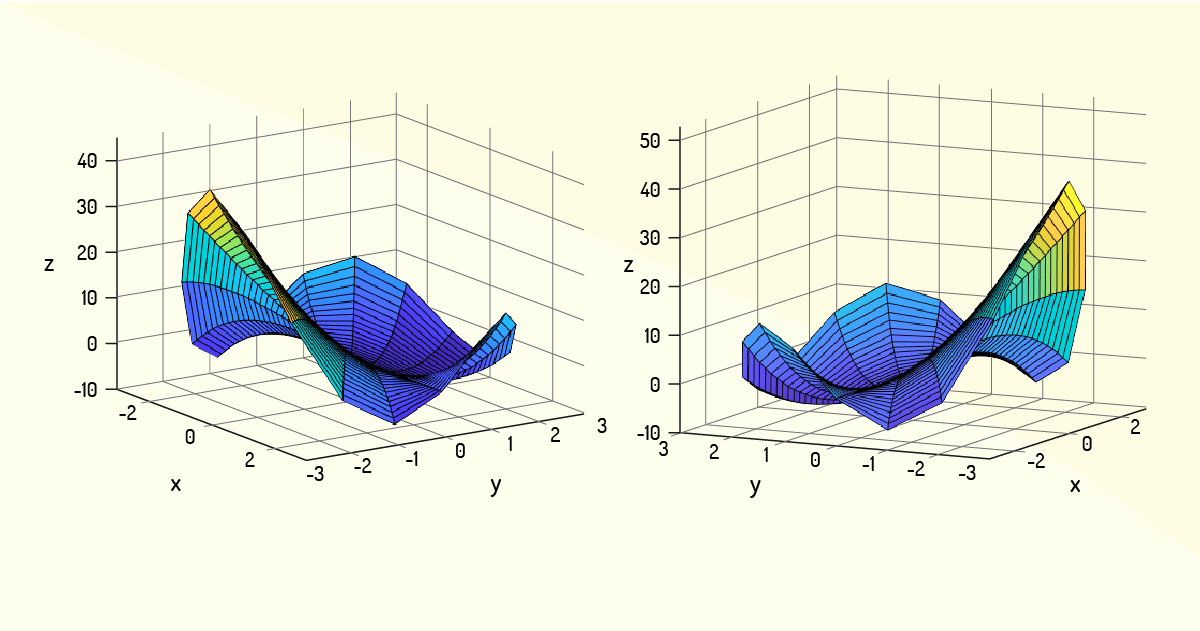
Exemplo 2.5: Classifique os pontos críticos da função \(f\left( x,y \right)=2{{x}^{2}}y+2{{y}^{2}}-8y\).
Solução
Os pontos críticos dessa função foram determinados anteriormente, no Exemplo 2.3. Tais pontos críticos são \(\left( 0,2 \right)\), \(\left( 2,0 \right)\) e \(\left( -2,0 \right)\). Para classificar esses pontos, fazemos uso do hessiano da função. Assim, as seguintes derivadas parciais para tal função são:
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=4y~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=4~\]
\[\frac{{{\partial }^{2}}f}{\partial x\partial y}=4x~~~~\frac{{{\partial }^{2}}f}{\partial y\partial x}=4x\]
Com isso, tem-se o seguinte hessiano:
\[H(x,y)=\left| \begin{matrix} 4y~~~~~~4x \\ 4x~~~~~~~~4 \\\end{matrix} \right|\]
Para o qual se tem, então:
\[H\left( x,y \right)=16y-16{{x}^{2}}\]
Agora, pode-se fazer a análise:
Finaliza-se, assim, a análise desses pontos. A Figura 3.10 apresenta a função em sua forma gráfica.
Exemplo 2.6: Mostre que a função \(f\left( x,y \right)=2{{x}^{2}}+xy+{{y}^{2}}+\frac{5}{x}+\frac{3}{y}+4\) tem um mínimo local no ponto \(\left( 1,1 \right)\).
Solução
Inicialmente, deve-se provar que o ponto em questão é um ponto crítico. Para isso, precisa-se avaliar as derivadas parciais de 1ª ordem da função:
\[\frac{\partial f}{\partial x}=4x+y-\frac{5}{{{x}^{2}}}\]
\[\frac{\partial f}{\partial y}=2y+x-\frac{3}{{{y}^{2}}}\]
Como \(\frac{\partial f}{\partial x}\left( 1,1 \right)=4+1-5=0\) e \(\frac{\partial f}{\partial y}\left( 1,1 \right)=2+1-3=0\), então o ponto \(\left( 1,1 \right)\) é um ponto crítico dessa função. Agora, devemos avaliar o hessiano. Para tal, é preciso avaliar as derivadas parciais de segunda ordem:
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=4+\frac{10}{{{x}^{3}}}~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=2+\frac{6}{{{y}^{3}}}~~~~\frac{{{\partial }^{2}}f}{\partial x\partial y}=1~~~~\frac{{{\partial }^{2}}f}{\partial y\partial x}=1\]
Com isso, tem-se o seguinte hessiano:
\[H(x,y)=\left| \begin{matrix} 4+\frac{10}{{{x}^{3}}} & 1 \\ 1 & 2+\frac{6}{{{x}^{3}}} \\ \end{matrix} \right|\]
Resolvendo esse determinante, você encontra:
\[H\left( x,y \right)=\left( 4+\frac{10}{{{x}^{3}}} \right)\left( 2+\frac{6}{{{y}^{3}}} \right)-1\]
Agora, você deve analisar esse determinante. Para o ponto dado, \(\left( 1,1 \right)\), tem-se \(H\left( 1,1 \right)=\left( 4+10 \right)\left( 2+6 \right)-1=111\). Ou seja, \(H\left( 1,1 \right)>0\). Apenas esse resultado não basta para chegar a alguma conclusão; é preciso checar a derivada parcial de segunda ordem \(\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}\) para esse ponto:
\[\frac{{{\partial }^{2}}}{\partial {{x}^{2}}}f\left( 1,1 \right)=4+\frac{10}{1}=14\]
Como \(H\left( 1,1 \right)>0\) e \(\frac{{{\partial }^{2}}}{\partial {{x}^{2}}}f\left( 1,1 \right)>0\), então o ponto \(\left( 1,1 \right)\) é realmente um ponto de mínimo da função \(f\).
Os conceitos de derivadas parciais são muito úteis para a verificação de pontos extremantes de funções. Buscando praticar essa aplicação de derivadas, analise a função e as alternativas dadas a seguir, assinalando a correta.
\[f\left( x,y \right)=3{{x}^{2}}-2{{x}^{3}}-3{{y}^{2}}+6xy\]
O ponto \(\left( 0,2 \right)\) é um ponto crítico dessa função \(f\).
Avaliando, então, as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=6x-6{{x}^{2}}+6y~~~~~~\frac{\partial f}{\partial y}=6x-6y\]
Agora, deve-se resolver o sistema:
\[\left\{ \begin{matrix} 6x-6{{x}^{2}}+6y=0 \\ 6x-6y=0 \\ \end{matrix} \right.\]
Da segunda equação desse sistema, tem-se que \(x=y\). Com isso, reescrevendo a primeira equação, tem-se \(6x-6{{x}^{2}}+6x=x\left( 2-x \right)=0\), para a qual se encontra que \(x=0\) ou \(*x=2\). Com isso, a função dada apresentará dois pontos críticos: \(\left( 0,0 \right)\) e \(\left( 2,2 \right)\).
O ponto \(\left( 0,0 \right)\) é um ponto de sela para essa função.
Justificativa correta: Avaliando, então, as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=6x-6{{x}^{2}}+6y~~~~\frac{\partial f}{\partial y}=6x-6y\]
Como \(\frac{\partial f}{\partial x}\left( 0,0 \right)=\frac{\partial f}{\partial y}\left( 0,0 \right)=0\), o ponto \(\left( 0,0 \right)\) é um ponto crítico de \(f\). Agora, devemos avaliar o hessiano. Para tal, é preciso avaliar as derivadas parciais de segunda ordem:
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=6-12x~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=-6~~~~\frac{{{\partial }^{2}}f}{\partial x\partial y}=6~~~~\frac{{{\partial }^{2}}f}{\partial y\partial x}=6\]
Com isso, tem-se o seguinte hessiano:
\[H(x,y)=\left| \begin{matrix} 6-12x & 6 \\ 6 & -6 \\ \end{matrix} \right|\]
Resolvendo esse determinante, você encontra \(H\left( x,y \right)=-36+72x-36=72\left( x-1 \right)\). Para o ponto \(\left( 0,0 \right)\), tem-se \(H\left( 0,0 \right)=72\left( 0-1 \right)=-72\). Ou seja, \(H\left( 0,0 \right)<0\), então o ponto \(\left( 0,0 \right)\) é um ponto de sela de \(f\).
A função \(f\) apresentará quatro pontos críticos: \(\left( 0,0 \right)\), \(\left( 0,2 \right)\), \(\left( 2,0 \right)\) e \(\left( 2,2 \right)\).
Justificativa: Avaliando, então, as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=6x-6{{x}^{2}}+6y~~~~\frac{\partial f}{\partial y}=6x-6y\]
Agora, deve-se resolver o sistema:
\[\left\{ \begin{matrix} 6x-6{{x}^{2}}+6y=0 \\ 6x-6y=0 \\ \end{matrix} \right.\]
Da segunda equação desse sistema, tem-se que \(x=y\). Com isso, reescrevendo a primeira equação, tem-se \(6x-6{{x}^{2}}+6x=x\left( 2-x \right)=0\), para a qual se encontra que \(x=0\) ou \(x=2\). Com isso, a função dada apresentará dois pontos críticos: \(\left( 0,0 \right)\) e \(\left( 2,2 \right)\).
O ponto \(\left( 0,0 \right)\) é um ponto de mínimo para essa função.
Justificativa: Avaliando, então, as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=6x-6{{x}^{2}}+6y~~~~\frac{\partial f}{\partial y}=6x-6y\]
Como \(\frac{\partial f}{\partial x}\left( 0,0 \right)=\frac{\partial f}{\partial y}\left( 0,0 \right)=0\), o ponto \(\left( 0,0 \right)\) é um ponto crítico de \(f\). Agora, devemos avaliar o hessiano. Para tal, é preciso avaliar as derivadas parciais de segunda ordem:
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=6-12x~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=-6~~~~\frac{{{\partial }^{2}}f}{\partial x\partial y}=6~~~~\frac{{{\partial }^{2}}f}{\partial y\partial x}=6\]
Com isso, tem-se o seguinte hessiano:
\[H(x,y)=\left| \begin{matrix} 6-12x & 6 \\ 6 & -6 \\ \end{matrix} \right|\]
Resolvendo esse determinante, você encontra \(H\left( x,y \right)=-36+72x-36=72\left( x-1 \right)\). Para o ponto \(\left( 0,0 \right)\), tem-se \(H\left( 0,0 \right)=72\left( 0-1 \right)=-72\). Ou seja, \(H\left( 0,0 \right)<0\), então o ponto \(\left( 0,0 \right)\) é um ponto de sela de \(f\).
O ponto \(\left( 2,2 \right)\) é um ponto de mínimo para essa função.
Justificativa: Avaliando, então, as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=6x-6{{x}^{2}}+6y~~~~\frac{\partial f}{\partial y}=6x-6y\]
Como \(\frac{\partial f}{\partial x}\left( 2,2 \right)=\frac{\partial f}{\partial y}\left( 2,2 \right)=0\), o ponto \(\left( 2,2 \right)\) é um ponto crítico de \(f\). Agora, devemos avaliar o hessiano. Para tal, é preciso avaliar as derivadas parciais de segunda ordem:
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=6-12x~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=-6~~~~\frac{{{\partial }^{2}}f}{\partial x\partial y}=6~~~~\frac{{{\partial }^{2}}f}{\partial y\partial x}=6\]
Com isso, tem-se o seguinte hessiano:
\[H(x,y)=\left| \begin{matrix} 6-12x & 6 \\ 6 & -6 \\ \end{matrix} \right|\]
Resolvendo esse determinante, você encontra \(H\left( x,y \right)=-36+72x-36=72\left( x-1 \right)\). Para o ponto \(\left( 2,2 \right)\), tem-se \(H\left( 2,2 \right)=72\left( 2-1 \right)=72\). Ou seja, como \(H\left( 0,0 \right)>0\), é preciso avaliar a derivada parcial de segunda ordem \(\frac{{{\partial }^{2}}}{\partial {{x}^{2}}}f\left( 2,2 \right)=6-12\left( 2 \right)=-18\). Como \(H\left( 2,2 \right)>0\) e \(\frac{{{\partial }^{2}}}{\partial {{x}^{2}}}f\left( 2,2 \right)<0\), então o ponto \(\left( 2,2 \right)\) é um ponto de máximo local de \(f\).
Nos estudos de máximos e mínimos de funções, você irá se deparar com um teorema muito útil e importante: o Teorema de Weierstrass ou Teorema do Valor Extremo. Segundo Stewart (2017), sendo \(f\) uma função de uma única variável, o Teorema de Weierstrass diz que, sendo essa função \(f\) contínua em um intervalo fechado \(\left[ a,b \right]\), então essa função \(f\) apresentará um valor de máximo absoluto e um valor de mínimo absoluto.
No entanto, não é exatamente o caso de funções com uma única variável que nos interessa. Então, veremos o caso de funções com duas variáveis, que é nosso objetivo. Considere, então, a função \(f:A\subset {{\mathbb{R}}^{2}}\to \mathbb{R}\) e \(z=f\left( x,y \right)\), a qual é contínua no conjunto fechado e limitado \(A\). Então, de acordo com Flemming e Gonçalves (2005), existem \({{P}_{1}},{{P}_{2}}\in A\) tais que, para qualquer \(P\in A\), tem-se \(f\left( {{P}_{1}} \right)\le f\left( P \right)\le f\left( {{P}_{2}} \right)\).
A prova desse Teorema de Weierstrass não será feita no presente material. Para encontrar a prova, você pode buscar materiais de análise matemática.
Esse Teorema é de grande importância, principalmente para a resolução de problemas práticos, nos quais é necessário que os pontos extremos estejam localizados na fronteira de um conjunto: tal Teorema garante a existência de um ponto de máximo e de um ponto de mínimo para uma função que seja contínua e com domínio fechado e limitado. Vejamos alguns exemplos que aplicam esse Teorema.
Exemplo 3.1: Seja a função \(f\left( x,y \right)=2{{x}^{2}}+2{{y}^{2}}-4x-4y\). Determine o valor máximo e o valor mínimo dessa função no conjunto B, delimitado pelo triângulo MNP da Figura 3.11.
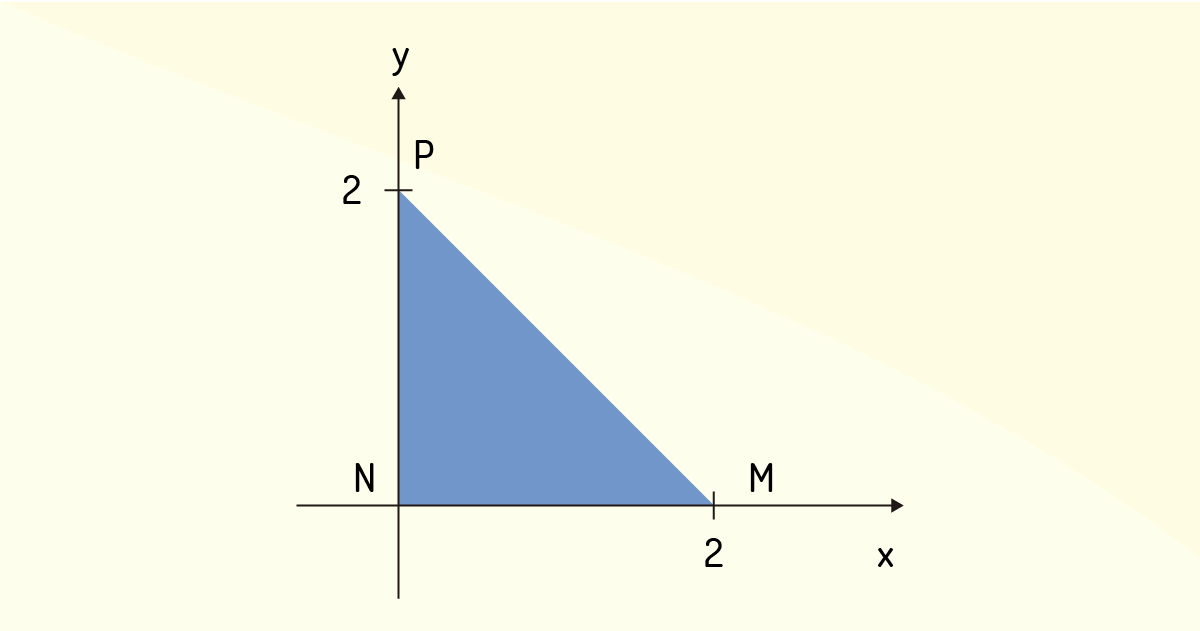
O Teorema de Weierstrass garante que existem \({{P}_{1}},{{P}_{2}}\in A\) tais que se tem \(f\left( {{P}_{1}} \right)\le f\left( P \right)\le f\left( {{P}_{2}} \right)\) para qualquer \(P\in A\). Precisamos, então, analisar todos os pontos de \(B\), ou seja, devemos buscar \({{P}_{1}}\) e \({{P}_{2}}\) que sejam os pontos de máximo e mínimo de \(f\) no conjunto \(B\).
Façamos uma análise dos pontos pertencentes a \(B\) entã. Inicialmente, é útil verificar a existência de pontos críticos dentro desse conjunto. Então:
\[\frac{\partial f}{\partial x}=4x-4=4\left( x-1 \right)~~~~\frac{\partial f}{\partial y}=4y-4=4\left( y-1 \right)\]
Agora, deve-se resolver o sistema:
\[\left\{ \begin{matrix} 4(x-1)=0 \\ 4(y-1)=0 \\ \end{matrix} \right.\]
Esse sistema é de simples resolução: de forma direta, pode-se encontrar que \(x=y=1\). Então, o único ponto crítico dessa função é \(\left( 1,1 \right)\), o qual se encontra dentro do conjunto \(B\). Agora, para identificar qual o tipo de ponto, devemos avaliar o hessiano. Para tal, é preciso avaliar as derivadas parciais de segunda ordem:
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=4~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=4~~~~\frac{{{\partial }^{2}}f}{\partial x\partial y}=0~~~~\frac{{{\partial }^{2}}f}{\partial y\partial x}=0\]
Com isso, tem-se o seguinte hessiano:
\[H(x,y)=\left| \begin{matrix} 4 & 0 \\ 0 & 4 \\ \end{matrix} \right|\]
Resolvendo esse determinante, você encontra \(H\left( x,y \right)=16\), ou seja, \(H\left( 1,1 \right)>0\). Como a derivada parcial de segunda ordem \(\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}\left( 1,1 \right)=4\), tem-se \(H\left( 1,1 \right)>0\) e \(\frac{{{\partial }^{2}}}{\partial {{x}^{2}}}f\left( 1,1 \right)>0\), acarretando que o ponto \(\left( 1,1 \right)\) é um ponto de mínimo local da função \(f\).
Agora precisamos analisar a região fronteiriça de \(B\). Para tal, convém separar triângulo em três segmentos: \(\underline{MN}\), \(\underline{NP}\) e \(\underline{PM}\). Assim:
Pode-se, então, compilar todos os resultados obtidos dessa análise em uma tabela:
Tabela 3.1 - Dados da análise da função em B
Fonte: Elaborada pelo autor.
Logo, nota-se que o máximo dessa função \(f\left( x,y \right)\) em \(B\) será 0 e o mínimo será -4.
Um dos grandes focos que se tem para a aplicação de análise de máximos e mínimos de funções reside na otimização de processos. Em teoria, todo processo ou fenômeno pode ser traduzido em linguagem matemática na forma de uma função conhecida como modelo, via uma técnica conhecida como modelagem. Por exemplo, uma fábrica de produtos químicos cujos processos estejam bem modelados é capaz de identificar e melhorar pontos do processo, via análise matemática do modelo. Logo, a análise de máximos e mínimos de funções, principalmente em conjuntos fechados, é extremamente importante, sendo o profissional que domina essa habilidade mais requisitado pelo mercado atualmente.
Saiba mais acessando o link: <https://novida.com.br/blog/otimizacao-de-processos-industriais/>. Acesso em: 29 abr. 2019.

O Teorema de Weierstrass é muito útil para a análise de máximos e mínimos de funções, até porque diversos casos práticos exigem a análise de uma função em um conjunto fechado. Visando fixar os conceitos e a aplicação desse teorema e considerando a função e o conjunto retangular \(D\) dados, analise as alternativas a seguir e assinale a correta.
\[f\left( x,y \right)={{x}^{2}}-4xy+8y~~~~D=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}|0\le x\le 3,0\le y\le 2 \right\}\]
A função dada não apresentará nenhum ponto extremante no conjunto delimitado.
Justificativa: O Teorema de Weierstrass garante exatamente o oposto do que é proposto aqui: em um conjunto fechado, a função irá certamente apresentar um ponto de máximo e um mínimo.
O máximo de \(f\) em \(D\) ocorre no ponto \(\left( 0,2 \right)\), em que se tem \(f\left( 0,2 \right)=16\).
Justificativa correta: Para a base horizontal inferior, tem-se \(f\left( x,0 \right)={{x}^{2}}\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 9. Já para a base horizontal superior, tem-se \(f\left( x,2 \right)={{x}^{2}}-8x+16\) ou \(f\left( x,2 \right)={{\left( x-4 \right)}^{2}}\). Essa função, no conjunto \(D\) apresentado, apresentará um máximo em \(x=0\), para o qual se tem \(f\left( 0,2 \right)=16\).
Para o lado vertical esquerdo, tem-se \(f\left( 0,y \right)=8y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 16. Já para o lado vertical direito, tem-se \(f\left( 3,y \right)=9-4y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 1 e 9.
Essa função tem como ponto crítico \(\left( 2,1 \right)\), para o qual se tem \(f\left( 2,1 \right)=4\).
Essa função apresenta um ponto crítico, mas este se encontra fora de \(D\).
Justificativa: Vejamos:
\[\frac{\partial f}{\partial x}=2x-4y~~~~\frac{\partial f}{\partial y}=8-4x\]
Igualando essas derivadas a zero e resolvendo-as simultaneamente, você encontrará que \(x=2\) e \(y=1\). Logo, a função apresenta realmente um único ponto crítico, que é \(\left( 2,1 \right)\), mas este se encontra dentro de \(D\).
O máximo de \(f\) na fronteira de \(D\) ocorrerá no ponto \(\left( 3,2 \right)\).
Justificativa: Para a base horizontal inferior, tem-se \(f\left( x,0 \right)={{x}^{2}}\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 9. Já para a base horizontal superior, tem-se \(f\left( x,2 \right)={{x}^{2}}-8x+16\) ou \(f\left( x,2 \right)={{\left( x-4 \right)}^{2}}\). Essa função, no conjunto \(D\) apresentado, apresentará um máximo em \(x=0\), para o qual se tem \(f\left( 0,2 \right)=16\).
Para o lado vertical esquerdo, tem-se \(f\left( 0,y \right)=8y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 16. Já para o lado vertical direito, tem-se \(f\left( 3,y \right)=9-4y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 1 e 9. No ponto \(\left( 3,2 \right)\), tem-se \(f=1\), o que não é o ponto de máximo das fronteiras.
O mínimo de \(f\) na fronteira de \(D\) ocorrerá no ponto \(\left( 2,2 \right)\)
Justificativa: Para a base horizontal inferior, tem-se \(f\left( x,0 \right)={{x}^{2}}\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 9. Já para a base horizontal superior, tem-se \(f\left( x,2 \right)={{x}^{2}}-8x+16\) ou \(f\left( x,2 \right)={{\left( x-4 \right)}^{2}}\). Essa função, no conjunto \(D\) apresentado, apresentará um máximo em \(x=0\), para o qual se tem \(f\left( 0,2 \right)=16\) No ponto \(\left( 2,2 \right)\), tem-se \(f=4\), o que não é o ponto de mínimo das fronteiras.
Para o lado vertical esquerdo, tem-se \(f\left( 0,y \right)=8y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 16. Já para o lado vertical direito, tem-se \(f\left( 3,y \right)=9-4y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 1 e 9.
Maximizar ou minimizar funções é um tipo de atividade corriqueira em várias áreas, fazendo com que aplicações dos conceitos abordados nesta unidade sejam amplamente empregados em diversas áreas da ciência. Problemas geométricos, físicos, químicos, industriais, econômicos e de planejamento são apenas alguns exemplos simples de uso da maximização e minimização de funções. Logo, nesta seção faremos uma breve introdução às aplicações práticas do que foi discutido até o momento.
De forma geral, quando se deseja avaliar o máximo de uma função \(f\), a operação pode ser representada como \(max~f\). De forma análoga, quando se deseja buscar o mínimo de uma função \(f\), representa-se por \(min~f\). A busca desses máximos e mínimos de uma função é um processo conhecido como otimização de funções, no qual a função sendo maximizada ou minimizada é chamada função objetivo. Essa abordagem de análise de funções leva a uma otimização irrestrita, para a qual basta aplicar as metodologias vistas até o momento, sendo este resultado conhecido como máximo ou mínimo livre (FLEMMING; GONÇALVES, 2005).
No entanto Flemming e Gonçalves (2005) destacam que esse procedimento de otimização irrestrita não é algo muito comum na prática. Você irá notar que casos reais de otimização apresentarão algum tipo de restrição, ou seja, nem todos os máximos e mínimos encontrados para uma função que represente algo real são praticáveis.
Por exemplo, considere que você trabalhe em uma empresa e deseja prever qual será o máximo lucro que ela pode obter com a venda de dois produtos diferentes. Sendo \(x\) e \(y\) a quantidade de vendas desses produtos, você pode propor uma função lucro na forma \(L\left( x,y \right)\), de modo que seu problema se reduz a avaliar \(max~L\). No entanto, você sabe que a quantidade de vendas está fadada a ser algo maior ou igual a zero, ou seja, ou você vende alguma quantidade, ou você não vende nada. Logo, você deverá buscar \(max~L\), sujeito à condição de \(x,y\ge 0\).
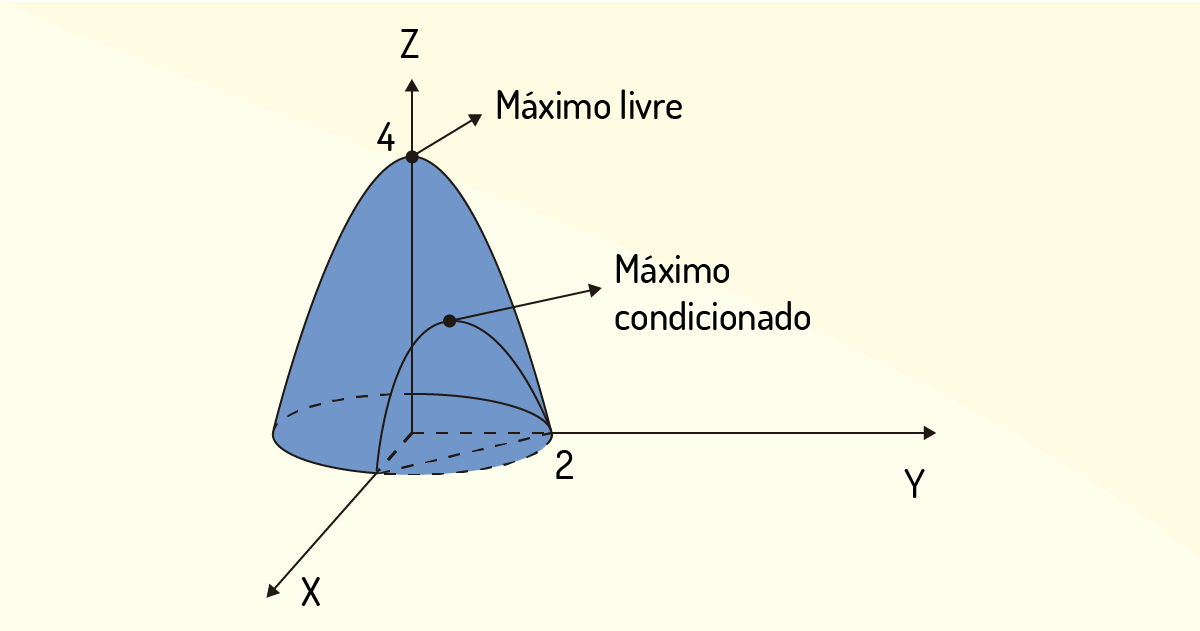
Quando se tem alguma condição restritiva ou algum vínculo para a otimização de uma função, Flemming e Gonçalves (2005) dizem que se tem um problema de otimização restrita. Simbolicamente, as restrições ou vínculos de uma otimização restrita são indicadas pelo símbolo \(s.a.\). Assim, voltando ao exemplo dado acima sobre a maximização do lucro, você pode representar como \(max~L,~s.a.~x,y\ge 0\). Essa abordagem de otimização restrita leva a um ponto de máximo ou mínimo condicionado. Na Figura 3.12 tem-se a exemplificação gráfica da um máximo condicionado do problema de otimização \(max~f\left( x,y \right)=4-{{x}^{2}}-{{y}^{2}},~s.a.~x+y=2\).
Exemplo 4.1: Considere a caixa apresentada na Figura 3.13. Quais dimensões deve apresentar essa caixa retangular sem a tampa para que seu volume seja \(32~{{m}^{3}}\) e sua área superficial seja a menor possível?
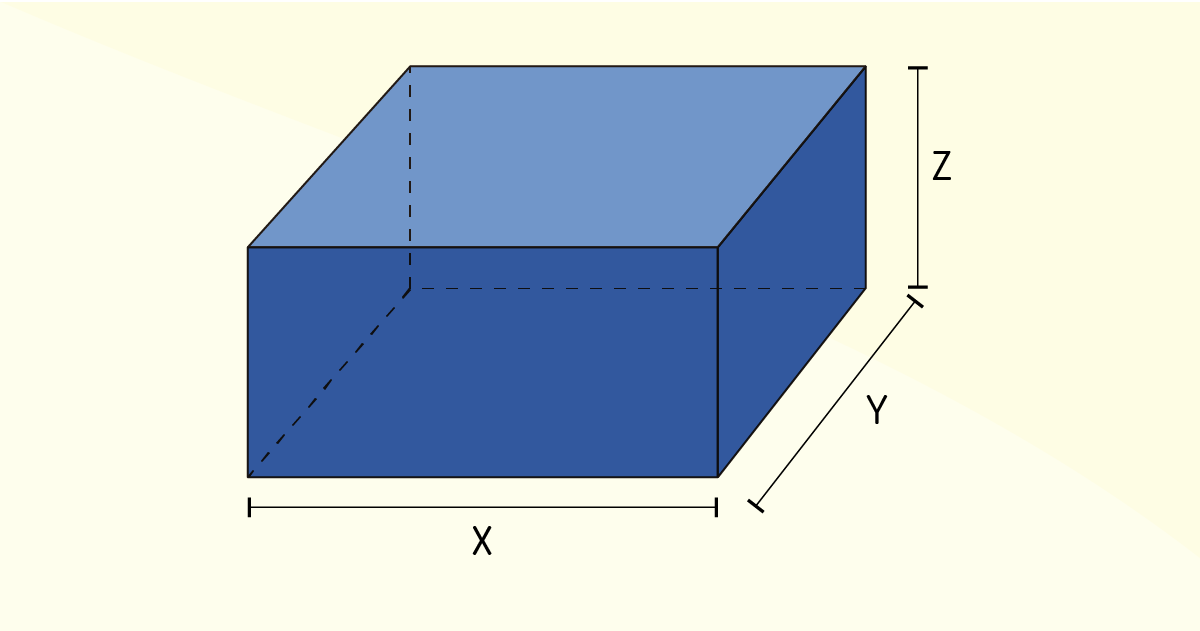
Solução
Da geometria básica, sabe-se que o volume dessa caixa pode ser calculado como \(V=xyz\) e sua área de superfície será \(S=2xz+2yz+xy\). Logo, esse problema consiste em minimizar a função \(S\), sabendo que \(xyz=32\) e que \(x\), \(y\) e \(z\) devem ser não nulos. Simbolicamente:
\[min~S~=2xz+2yz+xy,~s.a.~xyz=32~e~x,y,z>0\]
Usando a restrição dada para o volume, pode-se isolar a variável \(z\), fazendo com que \(S\) seja representada como uma função de duas variáveis:
\[z=\frac{32}{xy}~~~~~~~\to ~~~~~~~S=2x\frac{32}{xy}+2y\frac{32}{xy}+xy=\frac{64}{y}+\frac{64}{x}+xy\]
Com essa restrição modificada, nosso problema se reduz agora a:
\[min~S~=\frac{64}{y}+\frac{64}{x}+xy,~s.a.~x,y,z>0\]
Agora, basta encontrar o ponto de mínimo para a função. Assim:
\[\frac{\partial S}{\partial x}=-\frac{64}{{{x}^{2}}}+y~~~~\frac{\partial S}{\partial y}=-\frac{64}{{{y}^{2}}}+x\]
Resolvendo o seguinte sistema:
\[\left\{ \begin{matrix} -\frac{64}{{{x}^{2}}}+y=0 \\ -\frac{64}{{{y}^{2}}}+x=0 \\ \end{matrix} \right.\]
Da primeira equação, encontra-se que \(y=\frac{64}{{{x}^{2}}}\). Assim, reescrevendo a segunda equação, você encontrará:
\[x-\frac{64}{{{\left( \frac{64}{{{x}^{2}}} \right)}^{2}}}=0~~~~~~~\to ~~~~~~~\frac{64x-{{x}^{4}}}{64}=0\]
\[x\left( 64-{{x}^{3}} \right)=0\]
Tem-se, então, que \(x=0\) ou \(x=4\). Devido à restrição, o único desses valores de \(x\) que pode ser usado é \(x=4\). Então, tem-se que \(y=4\). Logo, o ponto \(\left( 4,4 \right)\) é um ponto crítico que pode ser utilizado. Para verificar se esse ponto é realmente um ponto de mínimo, avalia-se o hessiano.
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=\frac{128}{{{x}^{3}}}~~~~\to ~~~~\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}\left( 4,4 \right)=2~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=\frac{128}{{{y}^{3}}}~~~~\to ~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}\left( 4,4 \right)=2\]
\[\frac{{{\partial }^{2}}f}{\partial x\partial y}=1~~~~\frac{{{\partial }^{2}}f}{\partial y\partial x}=1\]
\[H(4,4)=\left| \begin{matrix} 2 & 1 \\ 1 & 2 \\ \end{matrix} \right|=4-1=3\]
Como \(H\left( 4,4 \right)>0\) e \(\frac{{{\partial }^{2}}}{\partial {{x}^{2}}}f\left( 4,4 \right)>0\), o ponto \(\left( 4,4 \right)\) é realmente um ponto de mínimo local da função \(S\). Então, as dimensões que a caixa deve apresentar para satisfazer às condições determinadas são:
\[x=4~m$ $y=4~m~~~~z=\frac{32}{xy}=\frac{32}{4\cdot 4}=2~m\]
Infelizmente, nem todos os problemas de máximos e mínimos condicionados são tão simples de serem resolvidos quanto o mostrado no Exemplo 4.1. Um método que permite a resolução desse tipo de problema de forma mais geral é o método dos multiplicadores de Lagrange. Ao aplicar esse método em um problema de otimização restrita que apresente \(n\) variáveis e \(m\) restrições de igualdade, o problema pode ser resolvido como um caso de otimização irrestrita de \(n+m\) variáveis (FLEMMING; GONÇALVES, 2005).
Por exemplo, considere o problema \(max~f\left( x,y \right),~s.a.~g\left( x,y \right)=0\). Das propriedades do vetor gradiente, Flemming e Gonçalves (2005) dizem que é possível ter uma visão gráfica do método dos multiplicadores de Lagrange, permitindo a determinação dos pontos de mínimo e máximo condicionados de \(f\). Esse método consiste em desenhar o gráfico de \(g\left( x,y \right)=0\) e várias curvas de nível da função objetivo, ou seja, \(f\left( x,y \right)=k\), observando seu comportamento crescente da constante \(k\). Então, o valor máximo de \(f\left( x,y \right)\) irá coincidir com a maior constante \(k\) tal que a curva de nível intercepte a curva de \(g\left( x,y \right)=0\). Esse evento ocorre em um ponto \({{P}_{0}}\), no qual ambas curvas têm a mesma reta tangente \(t\), como mostra a Figura 3.14.
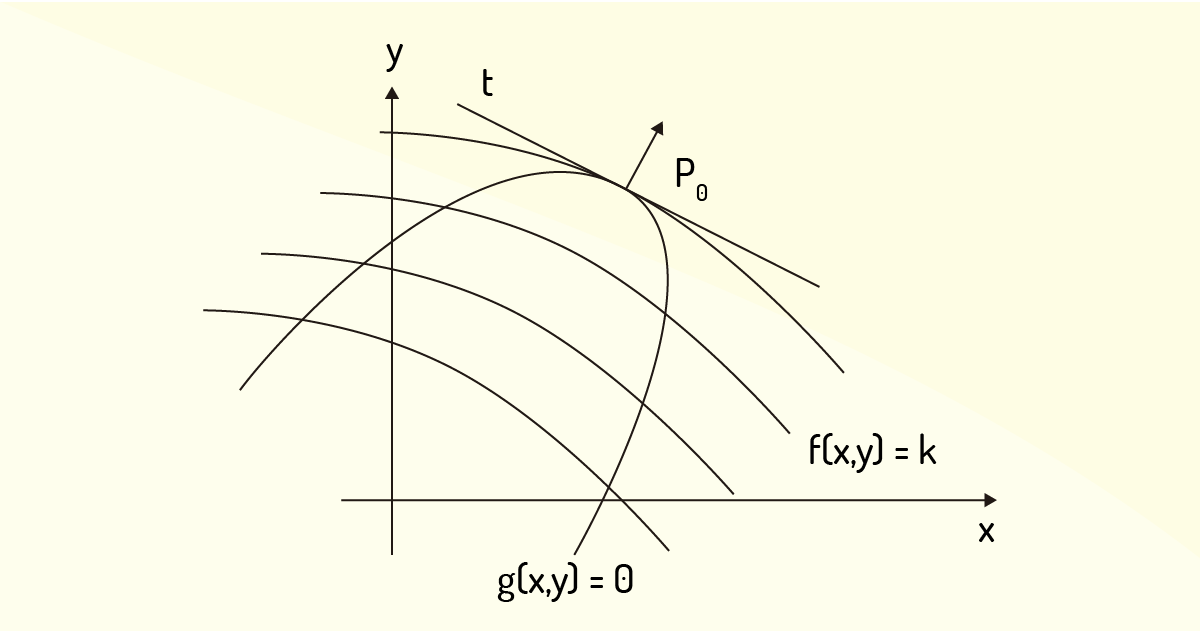
De acordo com Flemming e Gonçalves (2005), essa representação geométrica leva à seguinte proposição: considere a função \(f\left( x,y \right)\), diferenciável em um conjunto aberto \(A\), e função \(g\left( x,y \right),\) cujas derivadas parciais sejam contínuas em \(A\), de tal forma que \(\nabla g\left( x,y \right)\ne \left( 0,0 \right),~\forall ~\left( x,y \right)\in B\), no qual \(B=\left\{ \left( x,y \right)\in A|g\left( x,y \right)=0 \right\}\). Para que o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in B\) seja um ponto extremante local da função \(f\) em \(B\), uma condição necessária é que, para um \(\lambda \) real:
\[\nabla f\left( {{x}_{0}},{{y}_{0}} \right)=\lambda \nabla g\left( {{x}_{0}},{{y}_{0}} \right)~~~~(1)~\]
A demonstração dessa proposição não será feita, pois não condiz com o objetivo desse material. No entanto, dado o que foi proposto no parágrafo acima, Flemming e Gonçalves (2005) dizem que os pontos extremantes condicionados da função $f$ deverão satisfazer às seguintes equações para um $\lambda $ real:
\[\frac{\partial f}{\partial x}=\lambda \frac{\partial g}{\partial x}~~~~~~\frac{\partial f}{\partial y}=\lambda \frac{\partial y}{\partial x}~~~~~~g\left( x,y \right)=0~~~~~~(2)\]
O número \(\lambda \) real que satisfaça às equações de (2) é chamado multiplicador de Lagrange. Logo, esse método consiste basicamente em encontrar a seguinte função de três variáveis:
\[L\left( x,y,\lambda \right)=f\left( x,y \right)-\lambda g\left( x,y \right)~~~~(3)\]
enquanto se observa o fato de que as três equações de (2) simplesmente equivalem a \(\nabla L=0\), ou simplesmente
\[\frac{\partial L}{\partial x}=0~~~~\frac{\partial L}{\partial y}=0~~~~\frac{\partial L}{\partial \lambda }=0~~~~(4)\]
Flemming e Gonçalves (2005) atentam para o fato de que deve-se tomar cuidado por esse método simplesmente ajudar a identificar os potenciais pontos extremantes da função dadas as restrições. A classificação desses pontos deverá ser feita por outra forma. Vejamos um exemplo que os mesmos autores apresentam sobre o método.
Exemplo 4.2: Um galpão retangular deverá ser construído em um terreno de forma triangular, como mostra a Figura 3.15. Encontre a área máxima que esse galpão poderá apresentar.
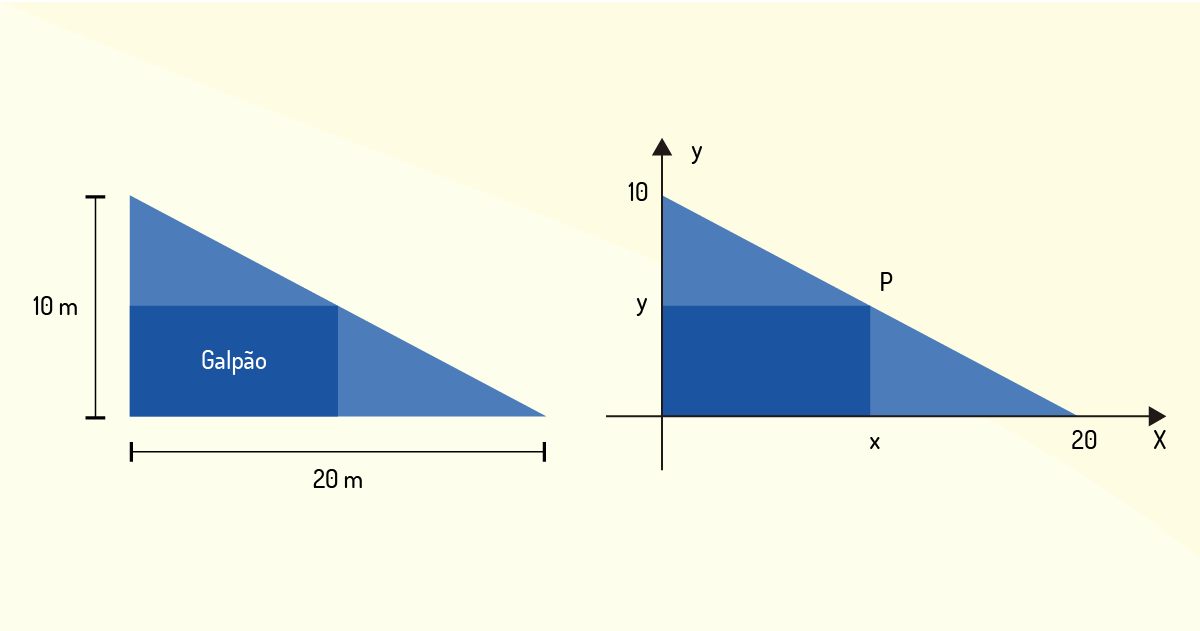
Solução
A representação cartesiana do terreno facilita a manipulação matemática para a resolução desse problema. Da Figura 3.15, pode-se concluir que a área do galpão será \(A\left( x,y \right)=x\cdot y\), assim como o ponto \(P\), que é uma das quinas do retângulo, deverá se encontrar sobre a reta \(x+2y=20\). Formulado isso, tem-se o seguinte problema a ser resolvido:
\[max~A~=xy,~s.a.~x+y=20\]
Para aplicar o método do multiplicador de Lagrange, deve-se reescrever a restrição desse problema, igualando-a a zero. Assim, a restrição será \(x+2y-20=0\). Logo, a função lagrangeana será:
\[L\left( x,y,\lambda \right)=xy-\lambda \left( x+2y-20 \right)\]
Da equação (4), nota-se que é preciso avaliar as derivadas parciais da função lagrangeana. Então:
\[\frac{\partial L}{\partial x}=y-\lambda~~~~~~\frac{\partial L}{\partial y}=x-2\lambda ~~~~~~\frac{\partial L}{\partial \lambda }=-\left( x+2y-20 \right)\]
Como essas três derivadas devem ser iguais a zero, encontra-se o seguinte sistema:
\[\left\{ \begin{matrix} y-\lambda =0 \\ x-2\lambda =0 \\ 20-x-y=0 \\ \end{matrix} \right.\]
Resolvendo esse sistema, você deve encontrar que \(x=10\), \(y=5\) e \(\lambda =5\). Note que o valor encontrado para \(\lambda \) simplesmente serve para a resolução da função lagrangeana, não sendo efetivamente importante para a solução final do problema.
Com as dimensões que foram encontradas por esse método, a área do galpão deverá ser \(A=\left( 10~m \right)\cdot \left( 5~m \right)=50~{{m}^{2}}\). Veja que o método que utilizamos aqui para a resolução do problema não classifica o ponto \(\left( 10,5 \right)\) que encontramos. No entanto, você pode verificar de forma relativamente simples, com alguns poucos testes, se necessário, que o valor encontrado é um máximo para essa função.
Existem ainda outras maneiras de avaliar máximos e mínimos condicionados. No entanto, dada a vasta quantidade de técnicas disponíveis para tais procedimentos, existe uma área da ciência que se dedica exclusivamente aos estudos de problemas deste tipo – a área de otimização. Como o foco do presente material reside no estudo do Cálculo, outras técnicas de otimização não serão aqui discutidas.
Uma empresa de entregas aceita apenas caixas cuja soma do comprimento mais perímetro não exceda 405 cm, conforme ilustra a figura a seguir. Assinale a alternativa correta.
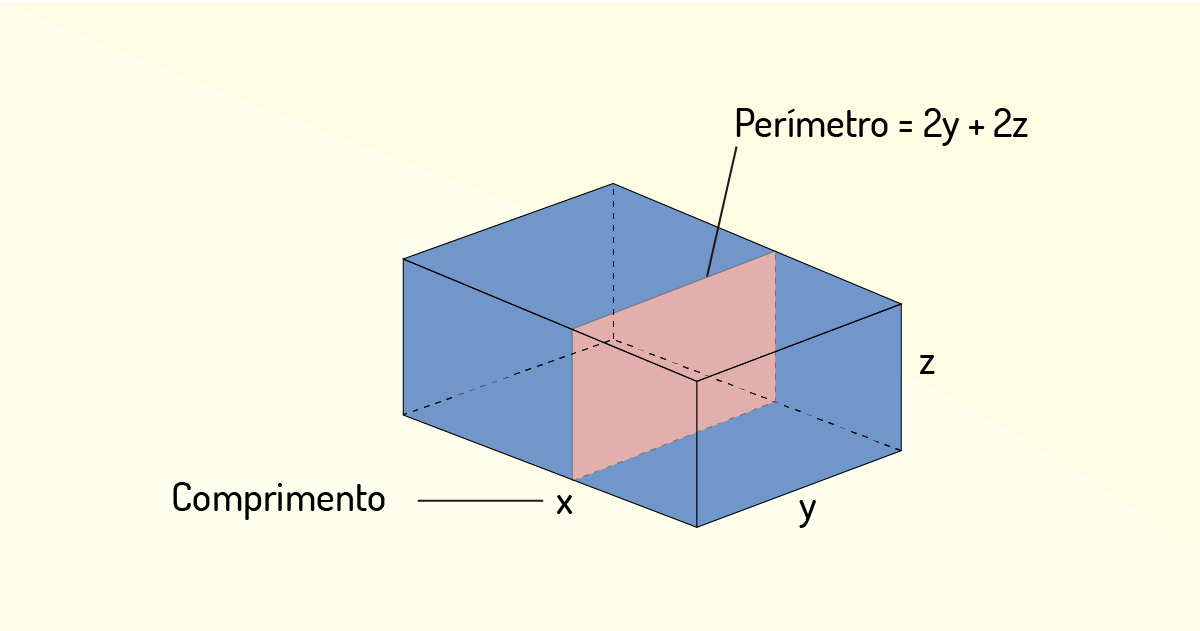
Figura 3.16 - Dimensões da caixa
Fonte: Adaptado de Thomas Júnior (2016, p. 856).
As dimensões que maximizam o volume dessa caixa são \(x=105~cm\) e \(y=z=75~cm\).
Justificativa: É pedido que se maximize o volume \(V=xyz\) tal que \(x+2y+2z=405\) (maiores dimensões admitidas pela companhia), ou seja, o problema é
\[max~V=xyz,~s.a.~x+2y+2z=405\]
Reescrevendo a restrição, encontra-se uma nova forma para representar \(x\), o que permite reescrever \(V\) como uma função de duas variáveis, na forma \(V=\left( 405-2y-2z \right)yz\). Para tal, tem-se as seguintes derivadas parciais de primeira ordem:
\[{{V}_{y}}=405z-4yz-2{{z}^{2}}=\left( 405-4y-2z \right)z~~~~e~~~~{{V}_{z}}=405y-2{{y}^{2}}-4zy=\left( 405-2y-4z \right)y\]
Igualando essas duas derivadas parciais a zero e resolvendo-as simultaneamente, você encontra rapidamente que dois valores possíveis para \(y\) e \(z\) é 0. Fazendo, então, \(y=0\), você encontrará que \(z=202,5\) assim como, com \(z=0\), você encontrará que \(y=202,5\). A outra possibilidade é que os termos entre parênteses em \({{V}_{y}}\) e \({{V}_{z}}\) sejam iguais a zero. Assim, de \({{V}_{z}}\), você pode analisar o termo entre parênteses fazendo \(y=202,5-2z\), e, do termo entre parênteses de \({{V}_{y}}\), você encontra que \(z=67,5\), acarretando em \(y=67,5\). Então, existem quatro pontos críticos para a função: \(\left( 0,0 \right)\), \(\left( 0,135 \right)\), \(\left( 135,0 \right)\) e \(\left( 67,5,67,5 \right)\). Note que se qualquer dimensão do volume for zero, então \(V=0\). Com isso, o único ponto crítico que nos interessa é \(\left( 67,5,67,5 \right)\). Para verificar se esse ponto é realmente um ponto de máximo, avalia-se o hessiano.
\[{{V}_{yy}}=-4z~~~~{{V}_{zz}}=-4y~~~~{{V}_{yy}}\left( 67,5,67,5 \right)={{V}_{zz}}\left( 67,5,67,5 \right)=-270\]
\[{{V}_{yz}}=405-4y-4z~~~~{{V}_{zy}}=405-4y-4z~~~~{{V}_{yz}}\left( 67,5,67,5 \right)={{V}_{zy}}\left( 67,5,67,5 \right)=-135\]
\[H(67,5,67,5)=\left| \begin{matrix} -270 & -135 \\ -135 & -270 \\ \end{matrix} \right|\]
Como \(H\left( 67,5,67,5 \right)=54675\), ou seja, \(H\left( 67,5,67,5 \right)>0\) e \({{V}_{yy}}\left( 67,5,67,5 \right)<0\), o ponto \(\left( 67,5,67,5 \right)\) é um ponto de máximo local da função \(V\). Logo, pode-se encontrar que:
\[x=405-2y-2z=405-2\left( 67,5 \right)-2\left( 67,5 \right)=135\]
Portanto, as dimensões que maximizam o volume da caixa são \(x=135~cm\) e \(y=z=67,5~cm\).
O volume máximo de uma caixa que essa transportadora aceita é de aproximadamente 615,1 L.
Justificativa correta: É pedido que se maximize o volume \(V=xyz\) tal que \(x+2y+2z=405\) (maiores dimensões admitidas pela companhia), ou seja, o problema é
\[max~V=xyz,~s.a.~x+2y+2z=405\]
Reescrevendo a restrição, encontra-se uma nova forma para representar \(x\), o que permite reescrever \(V\) como uma função de duas variáveis, na forma \(V=\left( 405-2y-2z \right)yz\). Para tal, tem-se as seguintes derivadas parciais de primeira ordem:
\[{{V}_{y}}=405z-4yz-2{{z}^{2}}=\left( 405-4y-2z \right)z~~~~e~~~~{{V}_{z}}=405y-2{{y}^{2}}-4zy=\left( 405-2y-4z \right)y\]
Igualando essas duas derivadas parciais a zero e resolvendo-as simultaneamente, você encontra rapidamente que dois valores possíveis para \(y\) e \(z\) é 0. Fazendo, então, \(y=0\), você encontrará que \(z=202,5\) assim como, com \(z=0\), você encontrará que \(y=202,5\). A outra possibilidade é que os termos entre parênteses em \({{V}_{y}}\) e \({{V}_{z}}\) sejam iguais a zero. Assim, de \({{V}_{z}}\), você pode analisar o termo entre parênteses fazendo \(y=202,5-2z\), e, do termo entre parênteses de \({{V}_{y}}\), você encontra que \(z=67,5\), acarretando em \(y=67,5\). Então, existem quatro pontos críticos para a função: \(\left( 0,0 \right)\), \(\left( 0,135 \right)\), \(\left( 135,0 \right)\) e \(\left( 67,5,67,5 \right)\). Note que se qualquer dimensão do volume for zero, então \(V=0\). Com isso, o único ponto crítico que nos interessa é \(\left( 67,5,67,5 \right)\). Para verificar se esse ponto é realmente um ponto de máximo, avalia-se o hessiano.
\[{{V}_{yy}}=-4z~~~~{{V}_{zz}}=-4y~~~~{{V}_{yy}}\left( 67,5,67,5 \right)={{V}_{zz}}\left( 67,5,67,5 \right)=-270\]
\[{{V}_{yz}}=405-4y-4z~~~~{{V}_{zy}}=405-4y-4z~~~~{{V}_{yz}}\left( 67,5,67,5 \right)={{V}_{zy}}\left( 67,5,67,5 \right)=-135\]
\[H(67,5,67,5)=\left| \begin{matrix} -270 & -135 \\ -135 & -270 \\ \end{matrix} \right|\]
Como \(H\left( 67,5,67,5 \right)=54675\), ou seja, \(H\left( 67,5,67,5 \right)>0\) e \({{V}_{yy}}\left( 67,5,67,5 \right)<0\), o ponto \(\left( 67,5,67,5 \right)\) é um ponto de máximo local da função \(V\). Logo, pode-se encontrar que
\[x=405-2y-2z=405-2\left( 67,5 \right)-2\left( 67,5 \right)=135\]
Portanto, o volume máximo da caixa é \(V=xyz=615.093,75~c{{m}^{3}}\) ou aproximadamente \(615,1~L\).
O volume máximo de uma caixa que essa transportadora aceita é aproximadamente 307,5 L.
Justificativa: É pedido que se maximize o volume \(V=xyz\) tal que \(x+2y+2z=405\) (maiores dimensões admitidas pela companhia), ou seja, o problema é:
\[max~V=xyz,~s.a.~x+2y+2z=405\]
Reescrevendo a restrição, encontra-se uma nova forma para representar \(x\), o que permite reescrever \(V\) como uma função de duas variáveis, na forma \(V=\left( 405-2y-2z \right)yz\). Para tal, tem-se as seguintes derivadas parciais de primeira ordem:
\[{{V}_{y}}=405z-4yz-2{{z}^{2}}=\left( 405-4y-2z \right)z~~~~e~~~~{{V}_{z}}=405y-2{{y}^{2}}-4zy=\left( 405-2y-4z \right)y\]
Igualando essas duas derivadas parciais a zero e resolvendo-as simultaneamente, você encontra rapidamente que dois valores possíveis para \(y\) e \(z\) é 0. Fazendo, então, \(y=0\), você encontrará que \(z=202,5\) assim como, com \(z=0\), você encontrará que \(y=202,5\). A outra possibilidade é que os termos entre parênteses em \({{V}_{y}}\) e \({{V}_{z}}\) sejam iguais a zero. Assim, de \({{V}_{z}}\), você pode analisar o termo entre parênteses fazendo \(y=202,5-2z\), e, do termo entre parênteses de \({{V}_{y}}\), você encontra que \(z=67,5\), acarretando em \(y=67,5\). Então, existem quatro pontos críticos para a função: \(\left( 0,0 \right)\), \(\left( 0,135 \right)\), \(\left( 135,0 \right)\) e \(\left( 67,5,67,5 \right)\). Note que se qualquer dimensão do volume for zero, então \(V=0\). Com isso, o único ponto crítico que nos interessa é \(\left( 67,5,67,5 \right)\). Para verificar se esse ponto é realmente um ponto de máximo, avalia-se o hessiano.
\[{{V}_{yy}}=-4z~~~~{{V}_{zz}}=-4y~~~~{{V}_{yy}}\left( 67,5,67,5 \right)={{V}_{zz}}\left( 67,5,67,5 \right)=-270\]
\[{{V}_{yz}}=405-4y-4z~~~~{{V}_{zy}}=405-4y-4z~~~~{{V}_{yz}}\left( 67,5,67,5 \right)={{V}_{zy}}\left( 67,5,67,5 \right)=-135\]
\[H(67,5,67,5)=\left| \begin{matrix} -270 & -135 \\ -135 & -270 \\ \end{matrix} \right|\]
Como \(H\left( 67,5,67,5 \right)=54675\), ou seja, \(H\left( 67,5,67,5 \right)>0\) e \({{V}_{yy}}\left( 67,5,67,5 \right)<0\), o ponto \(\left( 67,5,67,5 \right)\) é um ponto de máximo local da função \(V\). Logo, pode-se encontrar que:
\[x=405-2y-2z=405-2\left( 67,5 \right)-2\left( 67,5 \right)=135\]
Portanto, o volume máximo da caixa é \(V=xyz=615.093,75~c{{m}^{3}}\) ou cerca de \(615,09375~L\).
As que maximizam o volume dessa caixa são \(x=y=z=81~cm\).
É pedido que se maximize o volume \(V=xyz\) tal que \(x+2y+2z=405\) (maiores dimensões admitidas pela companhia), ou seja, o problema é:
\[max~V=xyz,~s.a.~x+2y+2z=405\]
Reescrevendo a restrição, encontra-se uma nova forma para representar \(x\), o que permite reescrever \(V\) como uma função de duas variáveis, na forma \(V=\left( 405-2y-2z \right)yz\). Para tal, tem-se as seguintes derivadas parciais de primeira ordem:
\[{{V}_{y}}=405z-4yz-2{{z}^{2}}=\left( 405-4y-2z \right)z~~~~e~~~~{{V}_{z}}=405y-2{{y}^{2}}-4zy=\left( 405-2y-4z \right)y\]
Igualando essas duas derivadas parciais a zero e resolvendo-as simultaneamente, você encontra rapidamente que dois valores possíveis para \(y\) e \(z\) é 0. Fazendo, então, \(y=0\), você encontrará que \(z=202,5\) assim como, com \(z=0\), você encontrará que \(y=202,5\). A outra possibilidade é que os termos entre parênteses em \({{V}_{y}}\) e \({{V}_{z}}\) sejam iguais a zero. Assim, de \({{V}_{z}}\), você pode analisar o termo entre parênteses fazendo \(y=202,5-2z\), e, do termo entre parênteses de \({{V}_{y}}\), você encontra que \(z=67,5\), acarretando em \(y=67,5\). Então, existem quatro pontos críticos para a função: \(\left( 0,0 \right)\), \(\left( 0,135 \right)\), \(\left( 135,0 \right)\)e \(\left( 67,5,67,5 \right)\). Note que se qualquer dimensão do volume for zero, então \(V=0\). Com isso, o único ponto crítico que nos interessa é \(\left( 67,5,67,5 \right)\). Para verificar se esse ponto é realmente um ponto de máximo, avalia-se o hessiano.
\[{{V}_{yy}}=-4z~~~~{{V}_{zz}}=-4y~~~~{{V}_{yy}}\left( 67,5,67,5 \right)={{V}_{zz}}\left( 67,5,67,5 \right)=-270\]
\[{{V}_{yz}}=405-4y-4z~~~~{{V}_{zy}}=405-4y-4z~~~~{{V}_{yz}}\left( 67,5,67,5 \right)={{V}_{zy}}\left( 67,5,67,5 \right)=-135\]
\[H(67,5,67,5)=\left| \begin{matrix} -270 & -135 \\ -135 & -270 \\ \end{matrix} \right|\]
Como \(H\left( 67,5,67,5 \right)=54675\), ou seja, \(H\left( 67,5,67,5 \right)>0\) e \({{V}_{yy}}\left( 67,5,67,5 \right)<0\), o ponto \(\left( 67,5,67,5 \right)\) é um ponto de máximo local da função \(V\). Logo, pode-se encontrar que
$x=405-2y-2z=405-2\left( 67,5 \right)-2\left( 67,5 \right)=135$
Portanto, as dimensões que maximizam o volume da caixa são \(x=135~cm\) e \(y=z=67,5~cm\).
O volume máximo de uma caixa que essa transportadora aceita é aproximadamente 531,4 L.
Justificativa: É pedido que se maximize o volume \(V=xyz\) tal que \(x+2y+2z=405\) (maiores dimensões admitidas pela companhia), ou seja, o problema é:
\[max~V=xyz,~s.a.~x+2y+2z=405\]
Reescrevendo a restrição, encontra-se uma nova forma para representar \(x\), o que permite reescrever \(V\) como uma função de duas variáveis, na forma \(V=\left( 405-2y-2z \right)yz\). Para tal, tem-se as seguintes derivadas parciais de primeira ordem:
\[{{V}_{y}}=405z-4yz-2{{z}^{2}}=\left( 405-4y-2z \right)z~~~~e~~~~{{V}_{z}}=405y-2{{y}^{2}}-4zy=\left( 405-2y-4z \right)y\]
Igualando essas duas derivadas parciais a zero e resolvendo-as simultaneamente, você encontra rapidamente que dois valores possíveis para \(y\) e \(z\) é 0. Fazendo, então, \(y=0\), você encontrará que \(z=202,5\) assim como, com \(z=0\), você encontrará que \(y=202,5\). A outra possibilidade é que os termos entre parênteses em \({{V}_{y}}\) e \({{V}_{z}}\) sejam iguais a zero. Assim, de \({{V}_{z}}\), você pode analisar o termo entre parênteses fazendo \(y=202,5-2z\), e, do termo entre parênteses de \({{V}_{y}}\), você encontra que \(z=67,5\), acarretando em \(y=67,5\). Então, existem quatro pontos críticos para a função: \(\left( 0,0 \right)\), \(\left( 0,135 \right)\), \(\left( 135,0 \right)\) e \(\left( 67,5,67,5 \right)\). Note que se qualquer dimensão do volume for zero, então \(V=0\). Com isso, o único ponto crítico que nos interessa é \(\left( 67,5,67,5 \right)\). Para verificar se esse ponto é realmente um ponto de máximo, avalia-se o hessiano.
\[{{V}_{yy}}=-4z~~~~{{V}_{zz}}=-4y~~~~{{V}_{yy}}\left( 67,5,67,5 \right)={{V}_{zz}}\left( 67,5,67,5 \right)=-270\]
\[{{V}_{yz}}=405-4y-4z~~~~{{V}_{zy}}=405-4y-4z~~~~{{V}_{yz}}\left( 67,5,67,5 \right)={{V}_{zy}}\left( 67,5,67,5 \right)=-135\]
\[H(67,5,67,5)=\left| \begin{matrix} -270 & -135 \\ -135 & -270 \\ \end{matrix} \right|\]
Como \(H\left( 67,5,67,5 \right)=54675\), ou seja, \(H\left( 67,5,67,5 \right)>0\) e \({{V}_{yy}}\left( 67,5,67,5 \right)<0\), o ponto \(\left( 67,5,67,5 \right)\) é um ponto de máximo local da função \(V\). Logo, pode-se encontrar que
\[x=405-2y-2z=405-2\left( 67,5 \right)-2\left( 67,5 \right)=135\]
Portanto, o volume máximo da caixa é \(V=xyz=615.093,75~c{{m}^{3}}\) ou cerca de \(615,09375~L\).
Nome do livro: Cálculo: volume 2
Editora: Pearson
Autor: James Stewart
ISBN: 9788522125845
Comentário: Um livro de cálculo extremamente didático, com inúmeras figuras que facilitam consideravelmente a compreensão dos tópicos estudados. Apresenta também uma boa quantidade de exemplos e exercícios, facilitando a absorção do conteúdo.
