Após fixar os conceitos básicos sobre funções com mais de uma variável e fundamentar o conceito de limite para esse tipo de função, chegou o momento de expandirmos os conceitos para as derivadas. Na presente Unidade, iremos estudar as variações instantâneas de uma função com mais de uma variável. Você verá que a base deste tópico é semelhante àquela utilizada no estudo de derivadas de funções com uma única variável. Sendo assim, as duas primeiras seções se dedicam à definição das derivadas parciais e da diferencial de uma função com mais de uma variável, fundando as bases desta Unidade. Após isso, estudaremos o caso da regra da cadeia para esse tipo de função, as derivadas de ordem superior e a derivação implícita, completando o objetivo de estudo da presente Unidade.
Existindo funções com mais de uma variável, é natural que você se veja em situações nas quais você deverá analisar como ocorrem as variações instantâneas nessas funções. Ou seja, você certamente será confrontado com problemas que exigem o cálculo de derivadas de funções com mais de uma variável.
Thomas Júnior (2016) destaca que o cálculo aplicado em funções com mais de uma variável será muito parecido com o cálculo para funções de uma única variável. No caso do cálculo aplicado em funções de múltiplas variáveis, o que se deve fazer é aplicar os conceitos do cálculo para funções de uma única variável em uma variável de cada vez.
Então, de acordo Leithold (1994), os estudos sobre derivação de uma função com n variáveis acaba se mostrando um caso unidimensional, pois a função será considerada uma função de apenas uma variável, sendo cada uma de suas n variáveis individualmente. Esse conceito de derivada aplicada apenas a uma variável por vez é o que se chama de derivada parcial.
Considere uma função de duas variáveis \(z=f\left( x,y \right)\) e o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in {{\mathbb{R}}^{2}}\). Com essas informações básicas, a seguinte definição de derivada parcial é dada por Flemming e Gonçalves (2005):
Definição 1: Ao fixar a variável \(y\) em um valor \({{y}_{0}}\), a função \(z\) irá se tornar uma função de variável única, ou seja, você está lidando com a função \(g=f\left( x,{{y}_{0}} \right)\). Então, a derivada parcial de \(f\) em relação a \(x\) no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\) é definida da seguinte maneira:
\[\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{lim}}\,\frac{g\left( x \right)-g\left( {{x}_{0}} \right)}{x-{{x}_{0}}}=\underset{x\to {{x}_{0}}}{\mathop{lim}}\,\frac{f\left( x,{{y}_{0}} \right)-f\left( {{x}_{0}},{{y}_{0}} \right)}{x-{{x}_{0}}}~~~~(1)\]
Isso se o limite acima existir. De maneira semelhante, se você fixar \(x\) em um valor \({{x}_{0}}\), você estará lidando com a função \(h=f\left( {{x}_{0}},y \right)\) e a derivada parcial de \(f\) em relação a \(y\) no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\) é:
\[\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)=\underset{y\to {{y}_{0}}}{\mathop{lim}}\,\frac{h\left( y \right)-h\left( {{y}_{0}} \right)}{y-{{y}_{0}}}=\underset{y\to {{y}_{0}}}{\mathop{lim}}\,\frac{f\left( {{x}_{0}},y \right)-f\left( {{x}_{0}},y \right)}{y-{{y}_{0}}}~~~~(2)\]
Thomas Júnior (2016) e Stewart (2017) apresentam algumas formas comuns de representar as derivadas parciais de uma função \(z=f\left( x,y \right)\) tomada em um ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\), as quais podem ser encontradas em diferentes literaturas da área:
\[\frac{\partial f}{\partial x}=\frac{\partial }{\partial x}f\left( {{x}_{0}},{{y}_{0}} \right)={{f}_{x}}={{f}_{x}}\left( {{x}_{0}},{{y}_{0}} \right)=\frac{\partial z}{\partial x}{{|}_{x={{x}_{0}}}}={{z}_{x}}\left( {{x}_{0}},{{y}_{0}} \right)={{D}_{1}}f={{D}_{x}}f\]
\[\frac{\partial f}{\partial y}=\frac{\partial }{\partial y}f\left( {{x}_{0}},{{y}_{0}} \right)={{f}_{y}}={{f}_{y}}\left( {{x}_{0}},{{y}_{0}} \right)=\frac{\partial z}{\partial y}{{|}_{y={{y}_{0}}}}={{z}_{y}}\left( {{x}_{0}},{{y}_{0}} \right)={{D}_{2}}f={{D}_{y}}f\]
Visando tornar essa definição mais próxima da que você certamente está acostumado(a) para a derivada de uma função de uma variável, Flemming e Gonçalves (2005) sugerem usar o \(\Delta \). Assim, fazendo \(\Delta x=x-{{x}_{0}}\) e \(\Delta y=y-{{y}_{0}}\) em (1) e (2), você terá:
\[\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)=\underset{\Delta x\to 0}{\mathop{lim}}\,\frac{f\left( {{x}_{0}}+\Delta x,{{y}_{0}} \right)-f\left( {{x}_{0}},{{y}_{0}} \right)}{\Delta x}~~~~(3)\]
\[\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)=\underset{\Delta y\to 0}{\mathop{lim}}\,\frac{f\left( {{x}_{0}},{{y}_{0}}+\Delta y \right)-f\left( {{x}_{0}},{{y}_{0}} \right)}{\Delta y}~~~~(4)\]
Exemplo 1.1: Considere o paraboloide definido pela função \(z=9-{{x}^{2}}-{{y}^{2}}\). Tomando o plano \(y=1\), encontre a curva \(c\) resultante da interseção de \(z\) e desse plano e, em seguida, avalie a derivada parcial \({{f}_{x}}\) no ponto \(\left( 1,1 \right)\).
Solução
Lembrando do gráfico dessa função, ela deve cruzar o eixo \(z\) em \(z=9\) e sua projeção no eixo \(xy\) deve ser uma circunferência de raio \(\sqrt{9}=3\). A Figura 2.1 ilustra o gráfico dessa função e o plano \(y=1\).
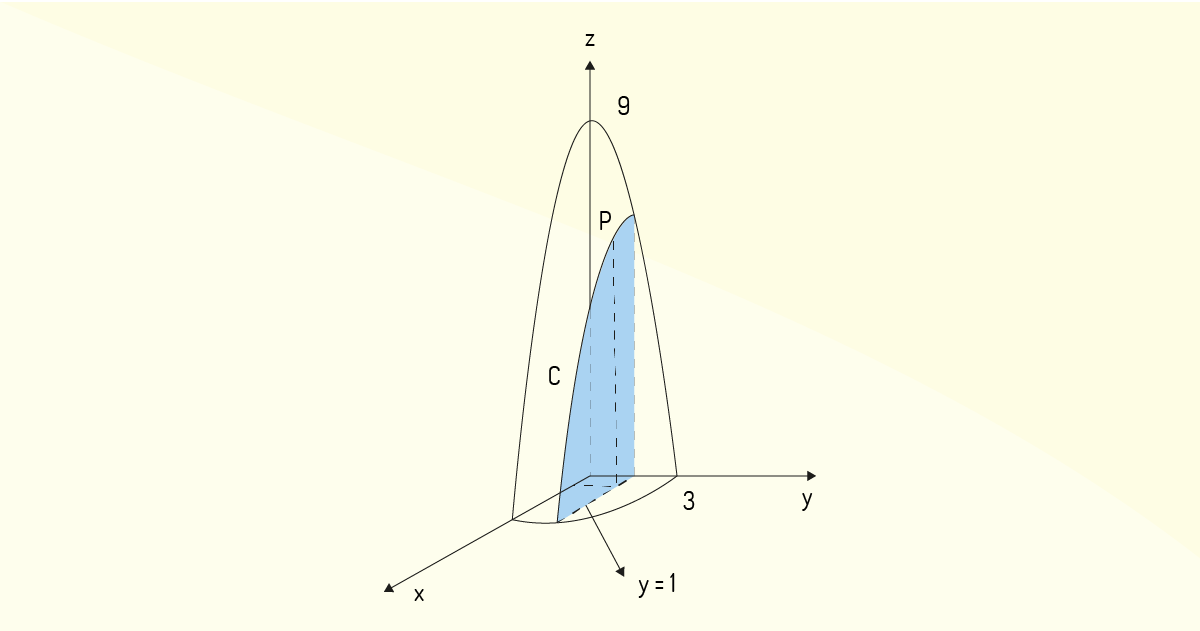
Para encontrar a curva \(c\) resultante da interseção de \(z\) com o plano \(y=1\), basta avaliar \(z\left( x,1 \right)\), pois tal curva representa a fixação do valor de \(y\) em 1. Assim:
\[c=z\left( x,1 \right)=9-{{x}^{2}}-{{\left( 1 \right)}^{2}}=8-{{x}^{2}}\]
Ou seja, pode-se dizer que \(c=g\left( x \right)=z\left( x,1 \right)\). Agora, a inclinação da reta tangente a \(c\) no ponto \(\left( 1,1 \right)\) simplesmente é \(g'\left( 1 \right)\) ou \(\frac{\partial f}{\partial x}\left( 1,1 \right)\). Aplicando, então, a Definição 1:
\[\frac{\partial f}{\partial x}\left( 1,1 \right)=\underset{x\to 1}{\mathop{lim}}\,\frac{g\left( x \right)-g\left( 1 \right)}{x-1}=\underset{x\to 1}{\mathop{lim}}\,\frac{8-{{x}^{2}}-\left[ 8-{{\left( 1 \right)}^{2}} \right]}{x-1}=\underset{x\to 1}{\mathop{lim}}\,\frac{8-{{x}^{2}}-8+1}{x-1}\]
\[=\underset{x\to 1}{\mathop{lim}}\,\frac{1-{{x}^{2}}}{x-1}=\underset{x\to 1}{\mathop{lim}}\,\frac{-\left( x+1 \right)\left( x-1 \right)}{x-1}=\underset{x\to 1}{\mathop{lim}}\,-\left( x+1 \right)=-2\]
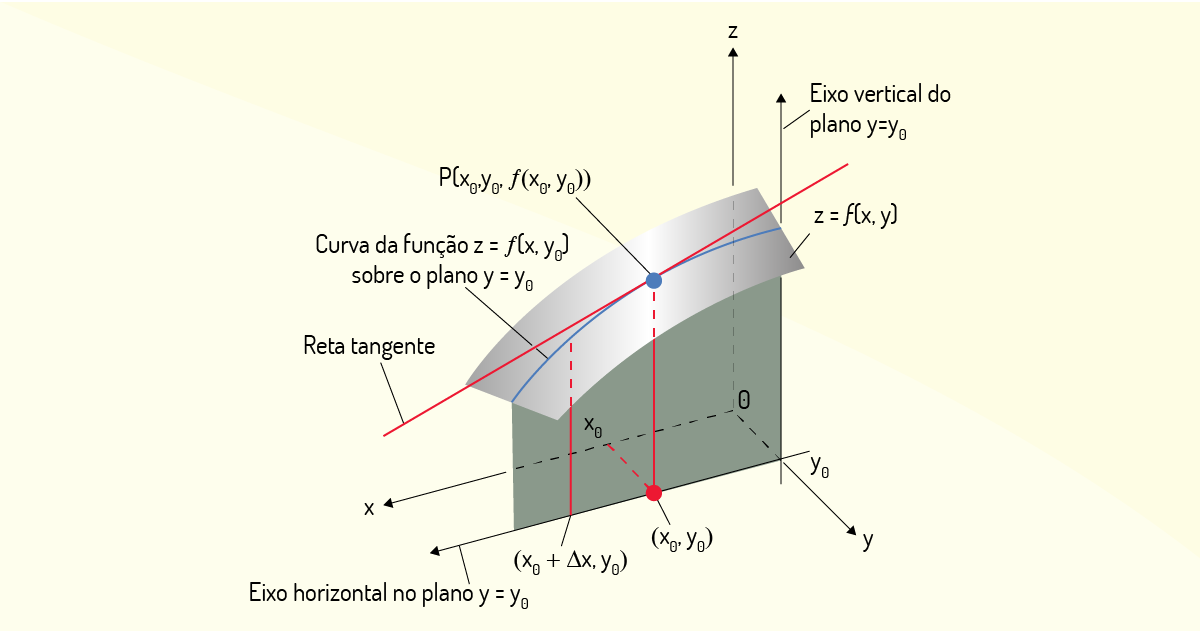
Partindo também da Definição 1, Flemming e Gonçalves (2005) e Thomas Júnior (2016) realizam uma análise geométrica das derivadas parciais. Considere a função \(z=f\left( x,y \right)\) e um conjunto \(A\in {{\mathbb{R}}^{2}}\), sendo que tal função admite derivada parcial no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in A\). Se você considerar que a variável \(y\) apresenta um valor constante igual a \({{y}_{0}}\), a função \(z\) se tornará uma função de uma única variável \(z=f\left( x,{{y}_{0}} \right)\), sendo essa curva contida na interseção do plano \(y={{y}_{0}}\) com a superfície de \(z=f\left( x,y \right)\). Agora, a derivada parcial dessa função avaliada em um ponto \(P=\left( {{x}_{0}},{{y}_{0}},f\left( {{x}_{0}},{{y}_{0}} \right) \right)\) pertencente à curva \(z=f\left( x,{{y}_{0}} \right)\) será a inclinação de uma reta tangente à curva \(z=f\left( x,{{y}_{0}} \right)\) no ponto \(P\). Na Figura 2.2, tem-se a representação geométrica dessa derivada parcial em relação a \(x\) no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\).
De modo a tornar mais clara a visão da inclinação da tangente ou o seu coeficiente angular, a Figura 2.3 ilustra um ângulo distinto da Figura 2.2, em que podemos identificar o ângulo \(\alpha \) que mede tal valor.
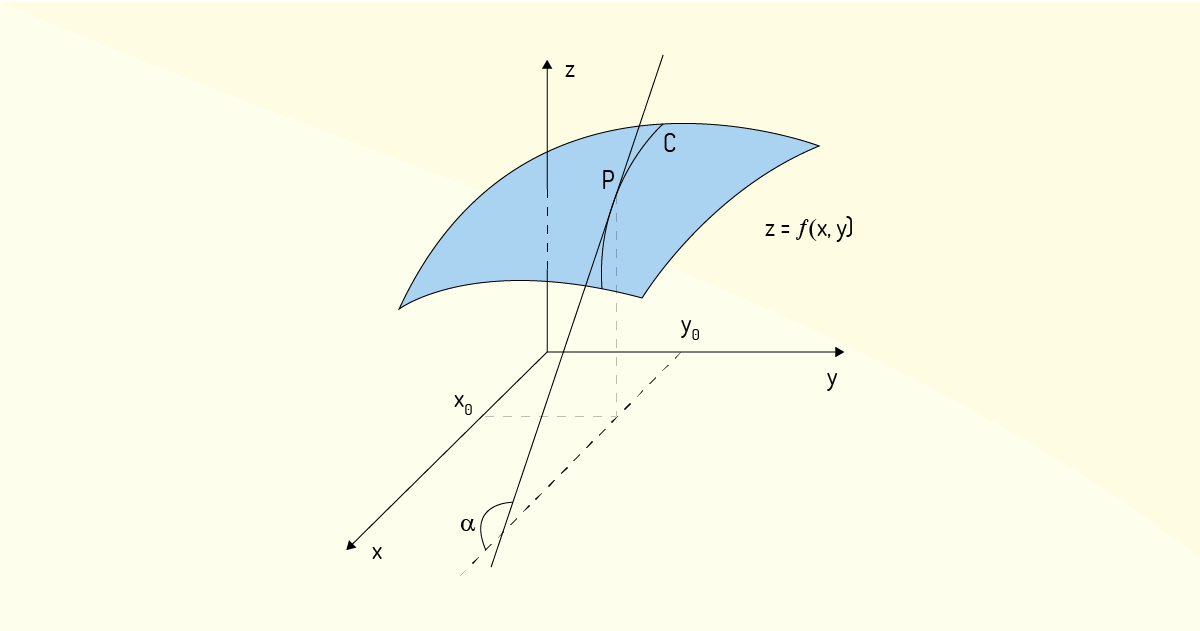
Ainda segundo Flemming e Gonçalves (2005), esse ângulo \(\alpha \) pode ser avaliado da seguinte forma:
\[tg\left( \alpha \right)=\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)~~~~(5)\]
Para a derivada parcial dessa mesma função \(z=f\left( x,y \right)\) com relação a \(y\), pode-se realizar uma análise análoga. Considerando, agora, que a variável \(x\) apresenta um valor constante igual a \({{x}_{0}}\), a função \(z\) se tornará uma função de uma única variável \(z=f\left( {{x}_{0}},y \right)\), sendo essa curva contida na interseção do plano \(x={{x}_{0}}\) com a superfície de \(z=f\left( x,y \right)\). Agora, a derivada parcial dessa função avaliada em um ponto \(P=\left( {{x}_{0}},{{y}_{0}},f\left( {{x}_{0}},{{y}_{0}} \right) \right)\) pertencente à curva \(z=f\left( {{x}_{0}},y \right)\) será a inclinação de uma reta tangente à curva \(z=f\left( {{x}_{0}},y \right)\) no ponto \(P\). Na Figura 2.4, tem-se a representação geométrica dessa derivada parcial em relação a \(y\) no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\).
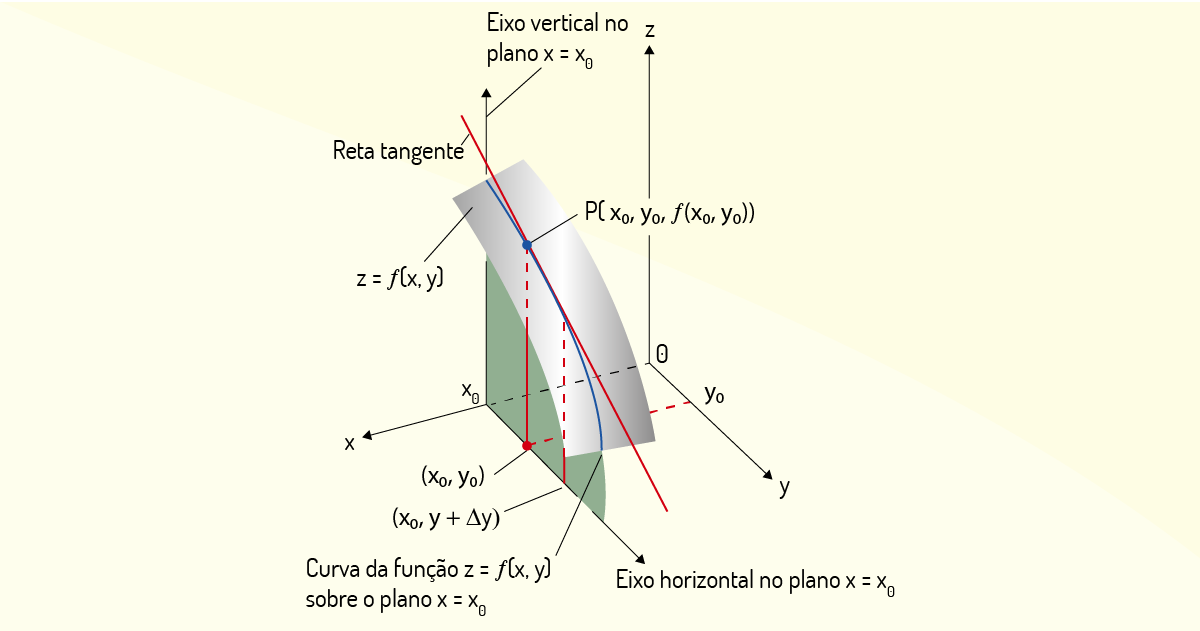
Assim como no caso anterior, podemos avaliar a inclinação \(\beta \) dessa tangente. A Figura 2.5 ilustra um ângulo distinto da Figura 2.4, facilitando a identificação do ângulo \(\beta \).
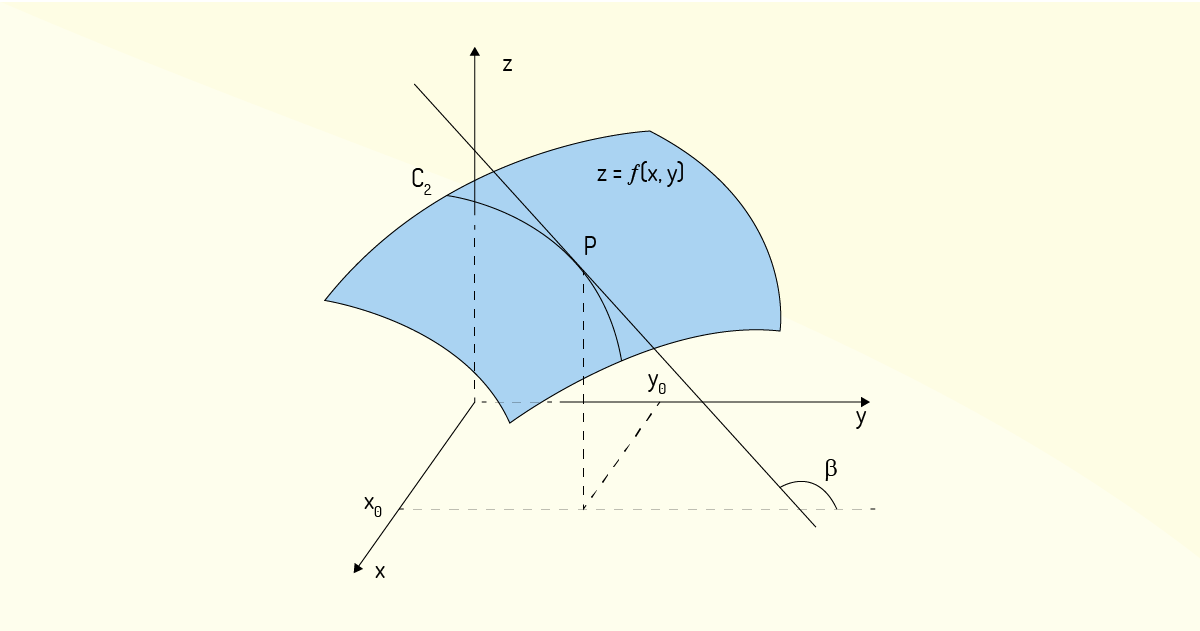
Este ângulo \(\beta \) pode ser avaliado da seguinte forma:
\[tg\left( \beta \right)=\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)~~~~(6)\]
Exemplo 1.2: Sendo a função \(f\left( x,y \right)=9-{{x}^{2}}-{{y}^{2}}\), encontre a derivada parcial de \(f\) em relação a \(x\) e \(y\) no ponto \(\left( 1,1 \right)\) e interprete esses números.
Solução
Analisando a função fornecida, tem-se um paraboloide com valor máximo em \(z=9\).
Iniciando a análise pela derivada parcial \({{f}_{x}}\), tem-se uma parábola descrita como \(g\left( x \right)=8-{{x}^{2}}\), resultante da interceptação do plano \(y=1\) com a superfície descrita por \(f\left( x,y,z \right)\). Tal qual visto no Exemplo 1.1, essa derivada parcial deve ser \({{f}_{x}}\left( 1,1 \right)=~-2\). Ou seja, essa derivada parcial simplesmente é a inclinação da reta tangente que toca o ponto \(x=1\) da parábola \(g\left( x \right)\). Na Figura 2.6, temos a representação tridimensional dessa função e do plano \(y=1\) e a visão bidimensional da parábola com a reta tangente.
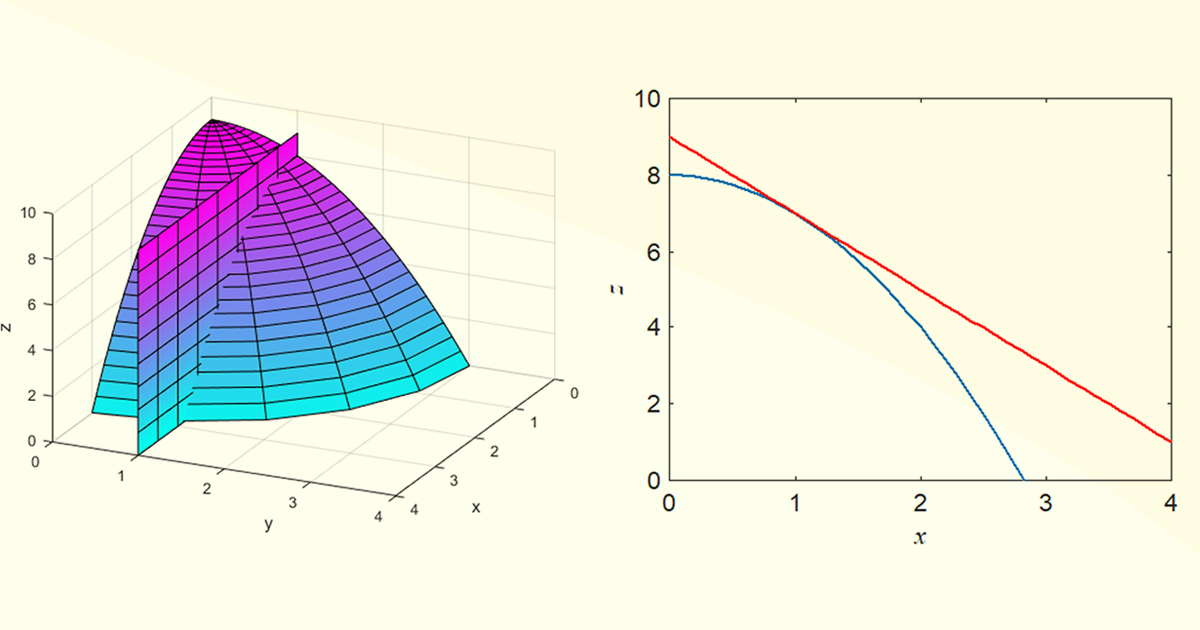
Ou seja, \(tg~\alpha =-2\).
Analisando agora a derivada parcial \({{f}_{y}}\), você encontrará uma parábola descrita como \(h\left( y \right)=8-{{y}^{2}}\), resultante da interceptação do plano \(x=1\) com a superfície descrita por \(f\left( x,y,z \right)\). Da mesma forma que foi realizado no Exemplo 1.1, você deve encontrar que essa derivada parcial também deve ser igual a \(-2\). Assim, essa derivada parcial também será a inclinação da reta tangente que toca o ponto \(y=1\) da parábola \(h\left( x \right)\). Na Figura 2.7, temos a representação tridimensional da função mais o plano \(x=1\) e a visão bidimensional da parábola como a reta tangente.
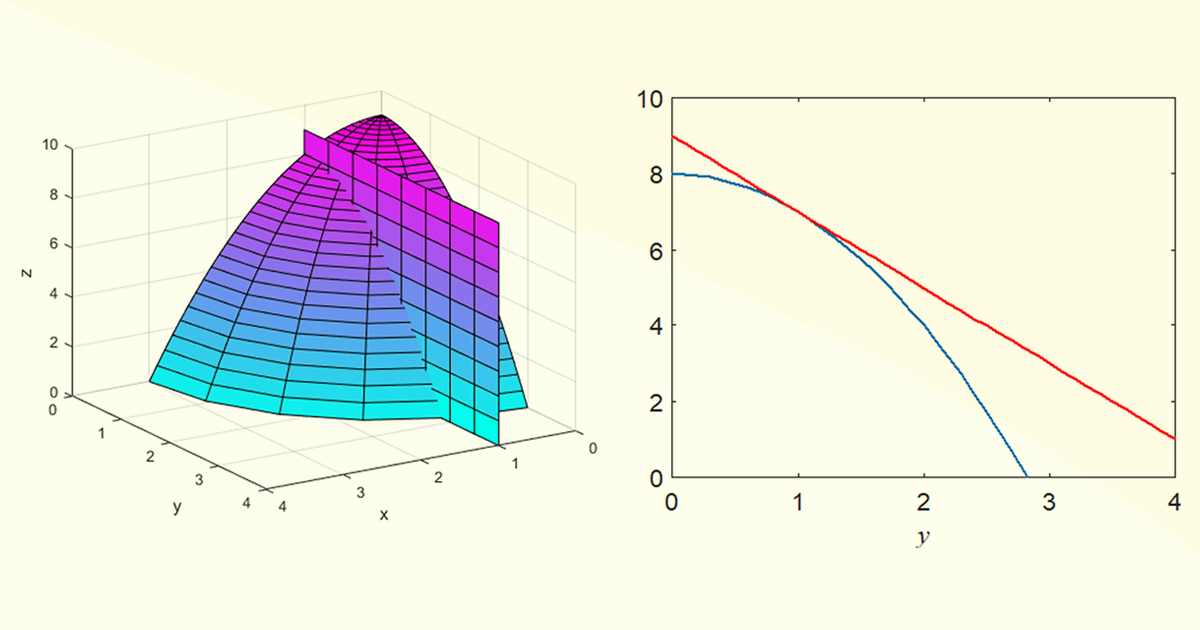
Ou seja, \(tg~\beta =-2\).
Se você comparar a Definição 1 com a definição da derivada de uma função de uma única variável, você perceberá que a derivada parcial da função\(f\left( x,y \right)\) em relação a \(x\) apresentada pela definição 1 é a derivada de uma função \(g\left( x \right)=f\left( x,{{y}_{0}} \right)\). Ou seja, fixando o valor de \(y\) em uma constante \({{y}_{0}}\), a função \(f\left( x,y \right)\) se reduz a uma função de uma única variável \(g\left( x \right)\). Então, avaliando a derivada \(g'\left( x \right)\), temos a derivada parcial de \(f\left( x,y \right)\) em relação a \(x\). Analogamente, para a derivada parcial de uma função \(f\left( x,y \right)\) em relação a \(y\), fixando o valor de \(x\) em uma constante \({{x}_{0}}\), a função \(f\left( x,y \right)\) se reduz a uma função de uma única variável \(h\left( y \right)\). Então, avaliando a derivada \(g'\left( y \right)\), temos a derivada parcial de \(f\left( x,y \right)\) em relação a \(y\) (LEITHOLD, 1994).
Essa abordagem para o cálculo de derivadas parciais é bem mais simples que a mostrada na Definição 1, pois não há necessidade de calcular um limite que pode se mostrar complexo às vezes. Note que essa metodologia pode ser aplicada para funções com n variáveis: se você quer avaliar a derivada parcial em relação a uma variável, basta fixar o valor das demais variáveis, fazendo com que seu problema se reduza ao cálculo da derivada de uma função de uma única variável (LEITHOLD, 1994).
Exemplo 1.3: Sendo a função \(f\left( x,y \right)=2{{x}^{3}}+2xy+{{y}^{2}}+2\), encontre a derivada parcial de \(f\) em relação a \(x\) e \(y\) no ponto \(\left( 3,-4 \right)\).
Solução
Para avaliar a derivada parcial em relação a \(x\), basta considerar que \(y\) é uma constante \({{y}_{0}}\), o que reduz a função \(f\left( x,y \right)\) a uma função \(g\left( x \right)=f\left( x,{{y}_{0}} \right)\). Então:
\[g\left( x \right)=f\left( x,{{y}_{0}} \right)~~\to ~~g\left( x \right)=2{{x}^{3}}+2x{{y}_{0}}+{{y}_{0}}^{2}+2\]
Agora, basta avaliar a derivada de primeira ordem de \(g\left( x \right)\):
\[~g'\left( x \right)=\frac{d}{dx}g\left( x \right)=6{{x}^{2}}+2{{y}_{0}}\]
Finalmente, você deve substituir os valores do ponto estabelecido:
\[\frac{\partial f}{\partial x}\left( 3,-4 \right)=6{{\left( 3 \right)}^{2}}+2\left( -4 \right)=54-8=46\]
Para avaliar a derivada parcial em relação a \(y\), basta considerar agora que \(x\) é uma constante \({{x}_{0}}\), o que reduz a função \(f\left( x,y \right)\) a uma função \(h\left( y \right)=f\left( x,{{y}_{0}} \right)\). Então:
\[h\left( y \right)=f\left( {{x}_{0}},y \right)~~\to ~~h\left( y \right)=2{{x}_{0}}^{3}+2{{x}_{0}}y+{{y}^{2}}+2\]
Agora, basta avaliar a derivada de primeira ordem de \(h\left( y \right)\):
\[~h'\left( y \right)=\frac{d}{dy}g\left( y \right)=2{{x}_{0}}+2y\]
Finalmente, você deve substituir os valores do ponto estabelecido:
\[\frac{\partial f}{\partial y}\left( 3,-4 \right)=2\left( 3 \right)+2\left( -4 \right)=6-8=-2\]
Leithold (1994) expande a Definição 1 para avaliar a derivada parcial de uma função de duas variáveis em todo o domínio da função \(f\left( x,y \right)\), o que é uma situação mais corriqueira no Cálculo. Então, segundo Leithold (1994):
Definição 2: a derivada parcial de uma função \(f\left( x,y \right)\) em relação a \(x\) é definida, para qualquer ponto do domínio de \(f\), como:
\[\frac{\partial f}{\partial x}\left( x,y \right)=\underset{\Delta x\to 0}{\mathop{lim}}\,\frac{f\left( x+\Delta x,y \right)-f\left( x,y \right)}{\Delta x}~~~~(5)\]
E de modo semelhante para \(y\):
\[\frac{\partial f}{\partial y}\left( x,y \right)=\underset{\Delta y\to 0}{\mathop{lim}}\,\frac{f\left( x,y+\Delta y \right)-f\left( x,y \right)}{\Delta y}~~~~~(6)\]
Essa Definição 2, dada por Leithold, é de aplicação mais comum, chamada derivada parcial de 1ª ordem de \(f\). A seguir, serão apresentados alguns exemplos de avaliação de derivadas parciais para todo o domínio de funções.
Exemplo 1.4: Aplique a definição de derivada parcial para encontrar as derivadas parciais de 1ª ordem para a seguinte função \(f\left( x,y \right)=2{{x}^{2}}-4xy+{{y}^{2}}\).
Solução
Dada a Definição 2, basta que apliquemos as equações (5) e (6) para avaliar as derivadas parciais pedidas. Então, aplicando a equação (5) para \(\partial f/\partial x\):
\[\frac{\partial f}{\partial x}\left( x,y \right)=\underset{\Delta x\to 0}{\mathop{lim}}\,\frac{f\left( x+\Delta x,y \right)-f\left( x,y \right)}{\Delta x}=\underset{\Delta x\to 0}{\mathop{lim}}\,\frac{2{{\left( x+\Delta x \right)}^{2}}-4\left( x+\Delta x \right)\left( y \right)+{{\left( y \right)}^{2}}-2{{x}^{2}}+4xy-{{y}^{2}}}{\Delta x}\]
\[=\underset{\Delta x\to 0}{\mathop{lim}}\,\frac{2\left( {{x}^{2}}+2x\Delta x+\Delta {{x}^{2}} \right)-4xy-4y\Delta x+{{y}^{2}}-2{{x}^{2}}+4xy-{{y}^{2}}}{\Delta x}\]
\[=\underset{\Delta x\to 0}{\mathop{lim}}\,\frac{2{{x}^{2}}+4x\Delta x+2\Delta {{x}^{2}}-4xy-4y\Delta x+{{y}^{2}}-2{{x}^{2}}+4xy-{{y}^{2}}}{\Delta x}\]
\[=\underset{\Delta x\to 0}{\mathop{lim}}\,\frac{4x\Delta x+2\Delta {{x}^{2}}-4y\Delta x}{\Delta x}=\underset{\Delta x\to 0}{\mathop{lim}}\,\frac{\Delta x\left( 4x+2\Delta x-4y \right)}{\Delta x}=\underset{\Delta x\to 0}{\mathop{lim}}\,\left( 4x+2\Delta x-4y \right)\]
\[=4x-4y\]
Agora, aplicando a equação (6) para \(\partial f/\partial y\):
\[\frac{\partial f}{\partial y}\left( x,y \right)=\underset{\Delta y\to 0}{\mathop{lim}}\,\frac{f\left( x,y+\Delta y \right)-f\left( x,y \right)}{\Delta y}=\underset{\Delta y\to 0}{\mathop{lim}}\,\frac{2{{x}^{2}}-4\left( x \right)\left( y+\Delta y \right)+{{\left( y+\Delta y \right)}^{2}}-2{{x}^{2}}+4xy-{{y}^{2}}}{\Delta y}\]
\[=\underset{\Delta y\to 0}{\mathop{lim}}\,\frac{2{{x}^{2}}-4xy-4x\Delta y+{{y}^{2}}+2y\Delta y+\Delta {{y}^{2}}-2{{x}^{2}}+4xy-{{y}^{2}}}{\Delta y}\]
\[=\underset{\Delta y\to 0}{\mathop{lim}}\,\frac{-4x\Delta y+2y\Delta y+\Delta {{y}^{2}}}{\Delta y}=\underset{\Delta y\to 0}{\mathop{lim}}\,\frac{\Delta y\left( -4x+2y+\Delta y \right)}{\Delta y}=\underset{\Delta y\to 0}{\mathop{lim}}\,\left( -4x+2y+\Delta y \right)\]
\[=2y-4x\]
Certamente você está se perguntando se a maneira simplificada apresentada no final do tópico 1.1 também não pode ser aplicada nestas situações. Para a nossa sorte, a resposta é sim. O exemplo anterior foi realizado de modo a demonstrar a resolução de uma derivada parcial utilizando sua definição. Então, para avaliar a derivada parcial de uma função \(f\left( x,y \right)\) em relação a \(x\) em todo o seu domínio, transforme a função \(f\left( x,y \right)\) em uma função de única variável \(g\left( x \right)=f\left( x,{{y}_{0}} \right)\) fixando \(y\) em um valor constante \({{y}_{0}}\). Avaliando, então, a derivada \(g'\left( x \right)\) irá fornecer a derivada parcial de \({{f}_{x}}\left( x,y \right)\). Utilizando essa mesma linha de raciocínio, mas fixando \(x\) em um valor constante \({{x}_{0}}\), você é capaz de reduzir a função \(f\left( x,y \right)\) a uma função de única variável \(h\left( y \right)=f\left( {{x}_{0}},y \right)\). Então, avaliando a derivada \(g'\left( y \right)\), temos a derivada parcial de \(f\left( x,y \right)\) em relação a \(y\) (LEITHOLD, 1994).
Exemplo 1.5: Encontre as derivadas parciais de 1ª ordem para a função \(f\left( x,y \right)=2{{x}^{2}}-4xy+{{y}^{2}}\).
Solução
Para encontrarmos a derivada parcial de uma função utilizando a forma simplificada, basta considerar todas as variáveis como constantes, exceto aquela na qual se quer avaliar a derivada. Então, para avaliar \(\partial f/\partial x\), basta considerar que \(y\) é uma constante \({{y}_{0}}\). Assim, você terá a seguinte função:
\[f\left( x,{{y}_{0}} \right)=g\left( x \right)=2{{x}^{2}}-4x{{y}_{0}}+{{y}_{0}}^{2}\]
Agora, basta avaliar \(g'\left( x \right)\). Note que \(4{{y}_{0}}\) é uma constante, o que resulta em:
\[g'\left( x \right)=2\cdot 2{{x}^{1}}-1\cdot 4{{y}_{0}}\cdot {{x}^{0}}+0\]
\[g'\left( x \right)=\frac{\partial f}{\partial x}=4x-4y\]
Perceba que no resultado final é indiferente você representar \(y\) ou \({{y}_{0}}\). Basta lembrar que ele é um valor constante. Agora, para \(\partial f/\partial y\), considerando que \(x\) é uma constante \({{x}_{0}}\), então:
\[f\left( {{x}_{0}},y \right)=h\left( y \right)=2{{x}_{0}}^{2}-4{{x}_{0}}y+{{y}^{2}}\]
Como \(4{{x}_{0}}\) é uma constante, então:
\[h'\left( y \right)=0-1\cdot 4{{x}_{0}}\cdot {{y}^{0}}+2\cdot {{y}^{1}}\]
\[h'\left( y \right)=\frac{\partial f}{\partial y}=-4x+2y\]
Exemplo 1.6: Verifique se a função \(f\left( x,y \right)=x+y+ln\left( xy \right)\) satisfaz a seguinte equação:
\[x\frac{\partial f}{\partial x}-y\frac{\partial f}{\partial y}=x-y\]
Solução
Primeiro, você precisa avaliar as derivadas parciais de 1ª ordem indicadas, caso elas existam. Para tal, você se verá com o caso de avaliar a derivada de \(ln\left( xy \right)\) em que terá uma das variáveis como constante de cada vez. Isso significa que terá de aplicar a regra da cadeia, pois tem a derivada de uma função composta, como \(g\circ h=g\left( h\left( x \right) \right)\), em que \(g\left( x \right)=ln~x\) e \(h\left( x \right)=xy\). Por exemplo, no caso de \(y\) ser considerada constante:
\[\frac{d}{dx}\left[ g\left( h\left( x \right) \right) \right]=g'\left( h\left( x \right) \right)\cdot h'\left( x \right)~~\to ~~~\frac{\partial }{\partial x}\left[ ln\left( xy \right) \right]=\frac{1}{xy}\cdot y\]
O mesmo é feito quando se considera \(x\) como constante.
Agora, dando continuidade à resolução do exemplo, vamos avaliar a derivada parcial em relação a \(x\):
\[\frac{\partial }{\partial x}f\left( x,y \right)=1+\frac{1}{xy}\cdot y=1+\frac{1}{x}\]
E a derivada parcial em relação a \(y\):
\[\frac{\partial }{\partial y}f\left( x,y \right)=1+\frac{1}{xy}\cdot x=1+\frac{1}{y}\]
Finalmente, deve-se avaliar o que é proposto no enunciado:
\[x\frac{\partial f}{\partial x}-y\frac{\partial f}{\partial y}=x-y~~\to ~~x\left( 1+\frac{1}{x} \right)-y\left( 1+\frac{1}{y} \right)=x-y\]
\[x+\frac{x}{x}-y-\frac{y}{y}=x+1-y-1=x-y\]
Logo, a função indicada satisfaz a equação dada.
É importante ressaltar que tudo o que foi visto até aqui é aplicável para funções com mais de duas variáveis, como dito ao final do tópico 1.1.
Exemplo 1.7: Encontre as derivadas parciais de 1ª ordem da função a seguir.
\[f\left( x,y,z,w \right)=xyz\cdot ln\left( {{x}^{3}}+{{z}^{2}}+{{w}^{2}} \right)\]
Solução
Perceba que a função indicada apresenta quatro variáveis. Assim, as derivadas parciais de primeira ordem dessa função devem ser \(\partial f/\partial x\), \(\partial f/\partial y\), \(\partial f/\partial z\) e \(\partial f/\partial w\). Começando com \(\partial f/\partial x\), devemos considerar \(y,z\) e \(w\) como constantes. Você precisará da regra do produto e da regra da cadeia para resolver essa derivada, pois está lidando com a diferencial de uma função \(F\left( x \right)={{c}_{1}}x\cdot ln\left( {{c}_{2}}+{{x}^{3}} \right)\), em que \({{c}_{1}}=yz\) e \({{c}_{2}}={{z}^{2}}+{{w}^{2}}\). A regra do produto para duas funções \(g\left( x \right)\cdot h\left( x \right)\) é:
\[\frac{d}{dx}\left[ g\left( x \right)\cdot h\left( x \right) \right]=g\left( x \right)\cdot h'\left( x \right)+g'\left( x \right)\cdot h\left( x \right)\]
Fazendo \(g\left( x \right)=xyz\), então \(g'\left( x \right)=yz\) e, se \(h\left( x \right)=ln\left( {{x}^{3}}+{{z}^{2}}+{{w}^{2}} \right)\), então, pela regra da cadeia, revisada no Exemplo 1.6, \(h'\left( x \right)=3{{x}^{2}}/\left( {{x}^{3}}+{{z}^{2}}+{{w}^{2}} \right)\). Logo, a derivada parcial de 1ª ordem de \(f\) em relação a \(x\) será:
\[\frac{\partial }{\partial x}f\left( x,y,z,w \right)=\frac{d}{dx}F\left( x \right)=xyz\cdot \frac{3{{x}^{2}}}{{{x}^{3}}+{{z}^{2}}+{{w}^{2}}}+yz\cdot ln\left( {{x}^{3}}+{{z}^{2}}+{{w}^{2}} \right)\]
\[\frac{\partial }{\partial x}f\left( x,y,z,w \right)=\frac{3{{x}^{3}}yz}{{{x}^{3}}+{{z}^{2}}+{{w}^{2}}}+yz\cdot ln\left( {{x}^{3}}+{{z}^{2}}+{{w}^{2}} \right)\]
Para as demais derivadas parciais, você deve proceder de forma análoga à apresentada acima. Para \(\partial f/\partial y\), note que todo o termo do logaritmo será constante; assim:
\[\frac{\partial f}{\partial y}\left( x,y,z,t \right)=xz\cdot ln\left( {{x}^{3}}+{{z}^{2}}+{{w}^{2}} \right)\]
Para \(\partial f/\partial z\), o caso será mais parecido com \(\partial f/\partial x\), pois serão necessárias as regras do produto e da cadeia novamente. Sendo \(g\left( z \right)=xyz\), então \(g'\left( z \right)=xy\) e, se \(h\left( z \right)=ln\left( {{x}^{3}}+{{z}^{2}}+{{w}^{2}} \right)\), então \(h'\left( z \right)=2z/\left( {{x}^{3}}+{{z}^{2}}+{{w}^{2}} \right)\). Logo:
\[\frac{\partial }{\partial z}f\left( x,y,z,w \right)=\frac{2xy{{z}^{2}}}{{{x}^{3}}+{{z}^{2}}+{{w}^{2}}}+xy\cdot ln\left( {{x}^{3}}+{{z}^{2}}+{{w}^{2}} \right)\]
E, finalmente, para \(\partial f/\partial w\), em que se tem \(xyz\) igual a uma constante:
\[\frac{\partial f}{\partial w}\left( x,y,z,t \right)=xyz\cdot \frac{1}{{{x}^{3}}+{{z}^{2}}+{{w}^{2}}}\cdot 2w\]
\[\frac{\partial f}{\partial w}\left( x,y,z,t \right)=\frac{2xyzw}{{{x}^{3}}+{{z}^{2}}+{{w}^{2}}}\]
Como esperado, as derivadas parciais apresentam diversos usos em várias outras disciplinas mais avançadas. Afinal, o cálculo é a base ferramental para diversas outras áreas da ciência que o empregam largamente. Visando apresentar um exemplo simples da aplicação dos conceitos de derivadas parciais, a seguir é indicado um artigo no qual os autores fazem uso de derivadas parciais para melhorar os dados de levantamentos topográficos, ou seja, uma aplicação voltada para a engenharia civil e geografia.
Link: <https://bit.ly/2PLOIPf>. Acesso em: 22 abr. 2019.

Um dos tópicos centrais do Cálculo reside na avaliação de derivadas de funções. Como problemas com mais de uma variável são muito comuns, visando sua prática de resoluções de derivadas de funções com mais de uma variável, considere as três funções indicadas a seguir, analise as alternativas e assinale a que apresenta derivada parcial indicada de forma correta.
\[f\left( x,y \right)={{x}^{2}}{{y}^{2}}\cdot ln\left( {{x}^{2}}+{{y}^{2}} \right)~~~~g\left( x,y,z \right)=xyz\cdot ln~{{\left( y+z \right)}^{2}}~~~~h\left( x,y \right)={{e}^{y/x}}\cdot ln~\left( \frac{{{x}^{2}}}{{{y}^{2}}} \right)\]
A derivada parcial de 1ª ordem de \(f\) em relação a \(x\) é igual a
\[{{f}_{x}}=2{{x}^{2}}{{y}^{2}}\left[ \frac{x}{{{x}^{2}}+{{y}^{2}}}+ln\left( {{x}^{2}}+{{y}^{2}} \right) \right]\]
Justificativa: Considerando $y$ uma constante e aplicando as regras do produto e da cadeia, então \(g\left( x \right)={{x}^{2}}{{y}^{2}}\to g'\left( x \right)=2x{{y}^{2}}\) e \(h\left( x \right)=ln\left( {{x}^{2}}+{{y}^{2}} \right)\to h'\left( x \right)=2x/\left( {{x}^{2}}+{{y}^{2}} \right)\). Logo:
\[{{f}_{x}}={{x}^{2}}{{y}^{2}}\frac{2x}{{{x}^{2}}+{{y}^{2}}}+2x{{y}^{2}}\cdot ln\left( {{x}^{2}}+{{y}^{2}} \right)~\to ~{{f}_{x}}=2x{{y}^{2}}\left[ \frac{{{x}^{2}}}{{{x}^{2}}+{{y}^{2}}}+ln\left( {{x}^{2}}+{{y}^{2}} \right) \right]\]
A derivada parcial de 1ª ordem de \(g\) em relação a \(y\) é igual a
\[{{f}_{y}}=xz\left[ \frac{2}{y+z}+ln~{{\left( y+z \right)}^{2}} \right]\]
Justificativa correta: Considerando \(y\) uma constante e aplicando as regras do produto e da cadeia, então \(f\left( y \right)=xyz\to f'\left( y \right)=xz\) e \(h\left( x \right)=ln~{{\left( y+z \right)}^{2}}\to h'\left( x \right)=2\left( y+z \right)/{{\left( y+z \right)}^{2}}=2/\left( y+z \right)\). Logo:
\[{{f}_{y}}=xyz\frac{2}{y+z}+xz\cdot ln~{{\left( y+z \right)}^{2}}~\to ~{{f}_{x}}=xz\left[ \frac{2}{y+z}+ln{{\left( y+z \right)}^{2}} \right]\]
Para a função \(g\) dada, tem-se que \({{f}_{x}}={{f}_{z}}\).
Justificativa: Para a derivada parcial de 1ª ordem de \(g\), o termo logaritmo é uma constante. Logo, \({{f}_{x}}=yz\cdot ln~{{\left( y+z \right)}^{2}}\). Para \({{f}_{z}}\), você deve considerar a variável \(z\) uma constante; aplicando as regras do produto e da cadeia, você encontrará \(f\left( z \right)=xyz\to f'\left( z \right)=xy\) e \(h\left( z \right)=ln~{{\left( y+z \right)}^{2}}\to h'\left( z \right)=2\left( y+z \right)/{{\left( y+z \right)}^{2}}=2/\left( y+z \right)\). Logo:
\[{{f}_{z}}=xyz\frac{2}{y+z}+xy\cdot ln~{{\left( y+z \right)}^{2}}~\to ~{{f}_{x}}=xy\left[ \frac{2}{y+z}+ln{{\left( y+z \right)}^{2}} \right]\]
Com isso, observa-se que \({{f}_{x}}\ne {{f}_{z}}\).
A derivada parcial de 1ª ordem de \(h\) em relação a \(x\) é igual a
\[{{f}_{x}}=\frac{{{e}^{y/x}}}{x}\left[ 2-y\cdot ln\left( \frac{{{x}^{2}}}{{{y}^{2}}} \right) \right]\]
Justificativa: Considerando \(y\) uma constante e aplicando as regras do produto e da cadeia, então \(f\left( x \right)={{e}^{y/x}}\to f'\left( x \right)=-\frac{y}{{{x}^{2}}}{{e}^{y/x}}\) e \(g\left( x \right)=ln\left( {{x}^{2}}/{{y}^{2}} \right)\to g'\left( x \right)=\frac{{{y}^{2}}}{{{x}^{2}}}\frac{2x}{{{y}^{2}}}=2/x\). Logo:
\[{{f}_{x}}={{e}^{y/x}}\cdot \frac{2}{x}+\left( -\frac{y}{{{x}^{2}}}{{e}^{y/x}} \right)\cdot ln\left( {{x}^{2}}/{{y}^{2}} \right)~\to ~{{f}_{x}}=\frac{{{e}^{y/x}}}{x}\left[ 2-\frac{y}{x}ln\left( {{x}^{2}}/{{y}^{2}} \right) \right]\]
A derivada parcial de 1ª ordem de \(h\) em relação a \(y\) é igual a
\[{{f}_{y}}=\frac{{{e}^{y/x}}}{y}\left[ 2+\frac{y}{x}\cdot ln\left( \frac{{{x}^{2}}}{{{y}^{2}}} \right) \right]\]
Justificativa: Considerando \(y\) uma constante e aplicando as regras do produto e da cadeia, então \(f\left( y \right)={{e}^{y/x}}\to f'\left( y \right)=\frac{{{e}^{y/x}}}{x}\) e \(g\left( y \right)=ln\left( {{x}^{2}}/{{y}^{2}} \right)\to g'\left( y \right)=\frac{{{y}^{2}}}{{{x}^{2}}}\frac{-2{{x}^{2}}}{{{y}^{3}}}=-2/y\). Logo:
\[{{f}_{y}}={{e}^{y/x}}\cdot \frac{-2}{y}+\frac{{{e}^{y/x}}}{x}\cdot ln\left( {{x}^{2}}/{{y}^{2}} \right)~\to ~{{f}_{y}}=\frac{{{e}^{y/x}}}{y}\left[ -2+\frac{y}{x}\cdot ln\left( {{x}^{2}}/{{y}^{2}} \right) \right]\]
Após estudar as derivadas parciais no tópico anterior, agora vamos expandir nosso conhecimento a respeito de outros assuntos das derivadas de funções com única variável para casos de funções com duas variáveis.
Agora devemos estender o conceito de diferenciabilidade do caso de funções de uma única variável para funções com duas variáveis. Quando você estudou diferenciais de funções com uma única variável, você viu que era fácil identificar graficamente onde uma função é derivável: basta encontrar pontos angulosos. Ou seja, uma função cuja curva se apresente suave terá que cada um de seus pontos apresenta uma reta tangente única (FLEMMING; GONÇALVES, 2005).
Devemos, então, buscar expandir esse conceito para funções com duas variáveis. Flemming e Gonçalves (2005) afirmam que, para uma função \(f\left( x,y \right)\), cada ponto \(\left( {{x}_{0}},{{y}_{0}},f\left( {{x}_{0}},{{y}_{0}} \right) \right)\) em seu gráfico deverá apresentar um único plano tangente que represente uma aproximação decente de \(f\) nos arredores do ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\).
Novamente caímos em um conceito aparente abstrato. Afinal, o que seria a aproximação decente dita no parágrafo acima? Esse conceito pode ser exemplificado, de acordo com Leithold (1994), utilizando uma função \(y=f\left( x \right)\). Se essa função \(y\) é derivável em um ponto \({{x}_{0}}\), sua derivada será dada por:
\[\frac{dy}{dx}=f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{lim}}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}=\underset{\Delta x\to 0}{\mathop{lim}}\,\frac{\Delta y}{\Delta x}~~~~~~(7)\]
Em (7), os valores \(\Delta x\) e \(\Delta y\) são chamados de incrementos de \(x\) e \(y\). Leithold (1994) ainda destaca que \(\Delta y=f\left( x+\Delta x \right)-f\left( x \right)\).
Agora, se o módulo do incremento de \(x\) for pequeno, mas nunca igual a zero, Leithold (1994) diz que a razão \(\Delta y/\Delta x\) irá diferir da derivada \(f'\left( x \right)\) por um número muito pequeno, dependente de \(\Delta x\). Tal número, sendo denotado por \(\epsilon \), é definido, para \(\Delta x\ne 0\) como:
\[\epsilon =\frac{\Delta y}{\Delta x}-f'\left( x \right)~~~~(8)\]
A equação (8) ainda pode ser reescrita como:
\[\Delta y=f'\left( x \right)\Delta x+\epsilon \Delta x~~~~(9)\]
Note que \(\epsilon \) é uma função de \(\Delta x\), sendo que, se \(\Delta x\to 0\), então \(\epsilon \to 0\), ou seja, \(\underset{\Delta x\to 0}{\mathop{lim}}\,\epsilon =0\). Disso, tem-se que, se a função \(f\) for derivável em um ponto \({{x}_{0}}\), então, o incremento de \(f\) nesse ponto \({{x}_{0}}\), \(\Delta f\left( {{x}_{0}} \right)\) será:
\[\Delta f\left( {{x}_{0}} \right)=f'\left( {{x}_{0}} \right)\Delta x+\epsilon \Delta x~~~~(10)\]
Outra forma de ver essa aproximação decente pode ser encontrada, segundo Flemming e Gonçalves (2005), a partir da definição da derivada de uma função \(f\left( x \right)\), que é:
\[f'\left( {{x}_{0}} \right)=\underset{x\to {{x}_{0}}}{\mathop{lim}}\,\frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}\]
Essa definição pode ser reescrita como:
\[0=\underset{x\to {{x}_{0}}}{\mathop{lim}}\,\left[ \frac{f\left( x \right)-f\left( {{x}_{0}} \right)}{x-{{x}_{0}}}-f'\left( {{x}_{0}} \right) \right]~~\to ~~0=\underset{x\to {{x}_{0}}}{\mathop{lim}}\,\left\{ \frac{f\left( x \right)-\left[ f\left( {{x}_{0}} \right)+f'\left( {{x}_{0}} \right)\left( x-{{x}_{0}} \right) \right]}{x-{{x}_{0}}} \right\}\]
A expressão \(y=f\left( {{x}_{0}} \right)+f'\left( {{x}_{0}} \right)\left( x-{{x}_{0}} \right)\) é a reta tangente ao gráfico da função \(f\left( x \right)\) no ponto \(\left( {{x}_{0}},f\left( {{x}_{0}} \right) \right)\). Essa função \(y\) é considerada uma aproximação boa ou decente para \(f\) próximo de \({{x}_{0}}\). Disso, Flemming e Gonçalves (2005) destacam que, quando \(x\) se aproxima de \({{x}_{0}}\), a diferença entre \(y\) e \(f\left( x \right)\) irá se aproximar de zero de maneira mais rápida, como mostra a Figura 2.8.
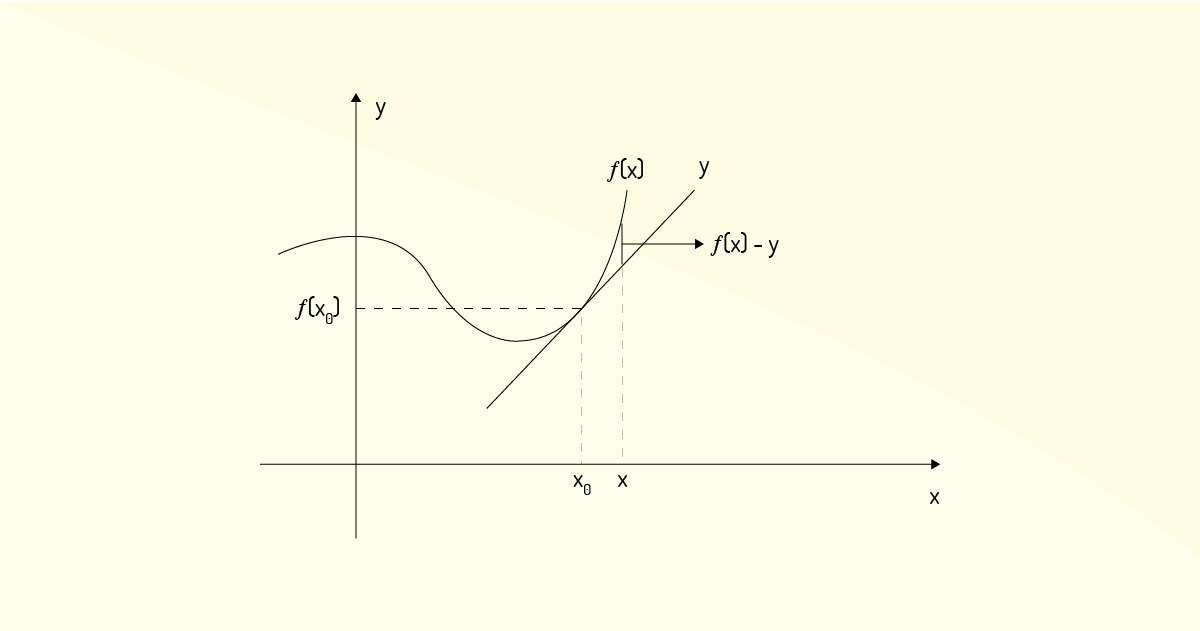
Agora podemos fazer a expansão dessa definição feita para funções de uma única variável para o caso de funções com duas variáveis. Das definições de derivadas parciais, foi visto que \({{f}_{x}}\) é o coeficiente angular da reta tangente à curva de interseção da superfície de \(f\left( x,y \right)\) com o plano \(y={{y}_{0}}\), no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\). Uma interpretação análoga pode ser proposta para \({{f}_{y}}\), que é o coeficiente angular da reta tangente à curva de interseção da superfície de \(f\left( x,y \right)\) com o plano \(x={{x}_{0}}\), no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\). Flemming e Gonçalves (2005) destacam que é intuitivo que essas duas retas tangentes pertençam a um mesmo plano, como ilustra a Figura 2.9.
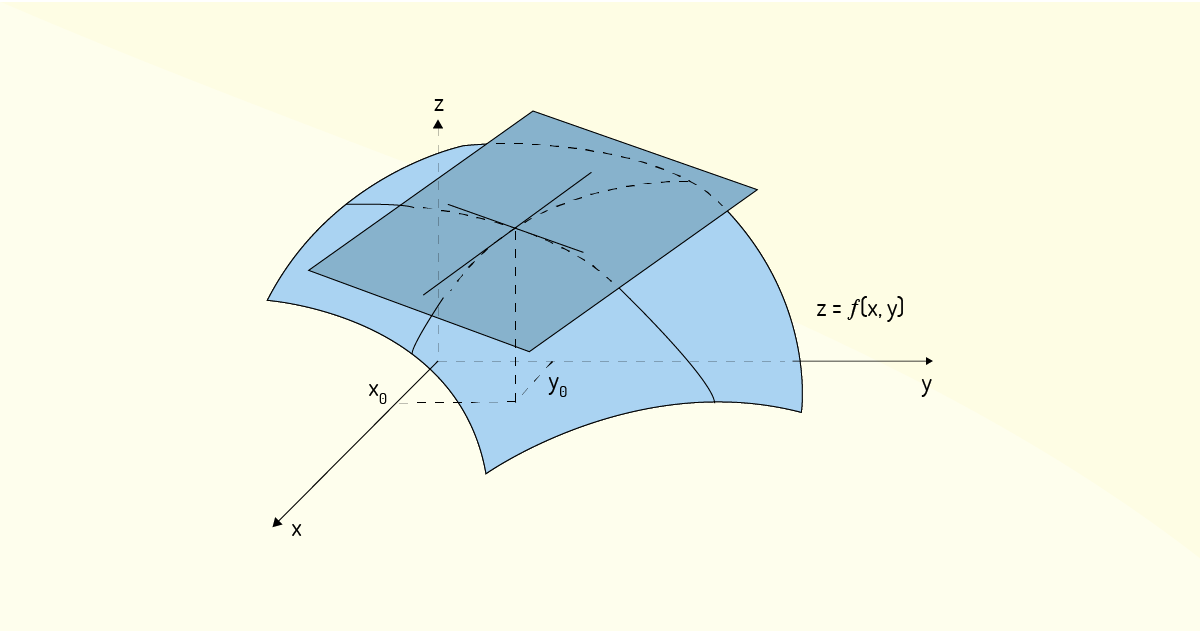
Com isso, pode-se propor a seguinte equação para o plano tangente a \(z=f\left( x,y \right)\), em um ponto \(\left( {{x}_{0}},{{y}_{0}},f\left( {{x}_{0}},{{y}_{0}} \right) \right)\):
\[h\left( x,y \right)=ax+by+c~~~~(11).\]
Partindo de (11), sendo a, b e c constantes, Flemming e Gonçalves (2005) destacam que você deve conseguir identificar que:
Substituindo (12) e (13) em (11):
\[h\left( x,y \right)=x\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)+y\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)+c~~~~(15)\]
Agora, avaliando (15) para o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\):
\[h\left( x,y \right)=f\left( {{x}_{0}},{{y}_{0}} \right)={{x}_{0}}\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)+{{y}_{0}}\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)+c\]
\[c=f\left( {{x}_{0}},{{y}_{0}} \right)-{{x}_{0}}\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)-{{y}_{0}}\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)~~~~(16)\]
Finalmente, substituindo agora (16) em (15):
\[h\left( x,y \right)=f\left( {{x}_{0}},{{y}_{0}} \right)+\left( x-{{x}_{0}} \right)\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)+\left( y-{{y}_{0}} \right)\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)~~~~(17)\]
A Equação (17) é a equação do plano tangente ao gráfico da função \(z=f\left( x,y \right)\) no ponto \(\left( {{x}_{0}},{{y}_{0}},f\left( {{x}_{0}},{{y}_{0}} \right) \right)\), caso esse plano exista. Disso, pode-se propor, então, a definição de uma função diferenciável. De acordo com Flemming e Gonçalves (2005):
Definição 3: Uma função \(z=f\left( x,y \right)\) será diferenciável no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\) caso suas duas derivadas parciais \(\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)\) e \(\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)\) existam e se
\[\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,\frac{f\left( x,y \right)-\left[ f\left( {{x}_{0}},{{y}_{0}} \right)+\left( x-{{x}_{0}} \right)\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)+\left( y-{{y}_{0}} \right)\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right) \right]}{\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}}=0~~~~(18)\]
Note que o denominador de (18) é a distância dos pontos \(\left( x,y \right)\) e \(\left( {{x}_{0}},{{y}_{0}} \right)\). Assim, da Definição 3, Flemming e Gonçalves (2005) indicam que \(z\) será diferenciável em um conjunto \(A\subset {{D}_{z}}\), em que \({{D}_{z}}\) é o domínio de \(z\), se esta função for diferenciável em todos os pontos de \(A\).
Veja que, para provar que uma função \(z\) é diferenciável em um conjunto de pontos \(\left( x,y \right)\), as derivadas parciais de todas as combinações \(\left( x,y \right)\) possíveis para esse conjunto devem existir e o limite indicado por (18) deve existir. Se apenas um desses pontos não for verificado verdadeiro, então \(z\) não é diferenciável em um ponto e, por consequência, não é diferenciável em todo o conjunto de pontos em questão.
Exemplo 2.1: Verifique se a função \(f\left( x,y \right)=2{{x}^{2}}+2{{y}^{2}}\) é diferenciável em \({{\mathbb{R}}^{2}}\).
Solução
Dada a Definição 3, precisamos checar se a função dada apresenta derivadas parciais para quaisquer pontos de \({{\mathbb{R}}^{2}}\). Então, para qualquer ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in {{\mathbb{R}}^{2}}\), você terá:
\(\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)=4{{x}_{0}}\) e \(\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)=4{{y}_{0}}\)
Veja que as derivadas parciais de 1ª ordem existem para quaisquer pontos \(\left( {{x}_{0}},{{y}_{0}} \right)\in {{\mathbb{R}}^{2}}\). Agora, deve-se verificar o limite proposto em (18):
\[\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,\frac{f\left( x,y \right)-\left[ f\left( {{x}_{0}},{{y}_{0}} \right)+\left( x-{{x}_{0}} \right)\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)+\left( y-{{y}_{0}} \right)\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right) \right]}{\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}}=0\]
\[\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,\frac{2{{x}^{2}}+2{{y}^{2}}-\left[ 2{{x}_{0}}^{2}+2{{y}_{0}}^{2}+\left( x-{{x}_{0}} \right)\left( 4{{x}_{0}} \right)+\left( y-{{y}_{0}} \right)\left( 4{{y}_{0}} \right) \right]}{\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}}=0\]
\[=\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,\frac{2{{x}^{2}}+2{{y}^{2}}+2{{x}_{0}}^{2}-4x{{x}_{0}}+2{{y}_{0}}^{2}-4y{{y}_{0}}}{\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}}=\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,\frac{2{{\left( x-{{x}_{0}} \right)}^{2}}+2{{\left( y-{{y}_{0}} \right)}^{2}}}{\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}}\]
\[=2\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,\frac{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}{\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}}\]
\[=2\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,\frac{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}{\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}}\frac{\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}}{\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}}\]
\[=2\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}=2\cdot 0=0\]
Como tanto o limite quanto as derivadas parciais de primeira ordem existem, então, a função \(f\left( x,y \right)\) é diferenciável em \({{\mathbb{R}}^{2}}\).
Exemplo 2.2: Verifique se a função a seguir é diferenciável na origem.
\[f(x,y)=\left\{ \frac{{{y}^{3}}}{\begin{matrix} {{x}^{2}}+{{y}^{2}} \\ 0 \\ \end{matrix}} \right.\begin{matrix} {} \\ ~~,se~x~\ne ~0 \\ ~~,se~x~=~0 \\\end{matrix}\]
Solução
O primeiro passo é checar se as derivadas parciais existem na origem. Note que, para essa função, é mais fácil avaliar a derivada parcial utilizando a definição com limite, dado pela Equação (1):
\[\frac{\partial f}{\partial x}\left( 0,0 \right)=\underset{x\to 0}{\mathop{lim}}\,\frac{f\left( x,0 \right)-f\left( 0,0 \right)}{x-0}=\underset{x\to 0}{\mathop{lim}}\,\frac{\frac{0}{{{x}^{2}}+0}-0}{x-0}=\underset{x\to 0}{\mathop{lim}}\,\frac{0-0}{x}=0\]
\[\frac{\partial f}{\partial y}\left( 0,0 \right)=\underset{y\to 0}{\mathop{lim}}\,\frac{f\left( y,0 \right)-f\left( 0,0 \right)}{y-0}=\underset{y\to 0}{\mathop{lim}}\,\frac{\frac{{{y}^{3}}}{0+{{y}^{2}}}-0}{y-0}=\underset{y\to 0}{\mathop{lim}}\,\frac{y-0}{y}=1\]
Agora, deve-se verificar o limite proposto em (18):
\[\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{lim}}\,\frac{f\left( x,y \right)-\left[ f\left( 0,0 \right)+\left( x-0 \right)\frac{\partial f}{\partial x}\left( 0,0 \right)+\left( y-0 \right)\frac{\partial f}{\partial y}\left( 0,0 \right) \right]}{\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}}}=0\]
\[\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{lim}}\,\frac{\frac{{{y}^{3}}}{{{x}^{2}}+{{y}^{2}}}-\left[ 0+\left( x-0 \right)\left( 0 \right)+\left( y-0 \right)\left( 1 \right) \right]}{\sqrt{{{x}^{2}}+{{y}^{2}}}}=\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{lim}}\,\frac{\frac{{{y}^{3}}}{{{x}^{2}}+{{y}^{2}}}-y}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\]
\[=\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{lim}}\,\frac{\frac{{{y}^{3}}-y\left( {{x}^{2}}+{{y}^{2}} \right)}{{{x}^{2}}+{{y}^{2}}}}{\sqrt{{{x}^{2}}+{{y}^{2}}}}=\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{lim}}\,\frac{\frac{-{{x}^{2}}y}{{{x}^{2}}+{{y}^{2}}}}{\sqrt{{{x}^{2}}+{{y}^{2}}}}=\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{lim}}\,\frac{-{{x}^{2}}y}{{{\left( {{x}^{2}}+{{y}^{2}} \right)}^{3/2}}}\]
Para avaliar o limite, faça a análise da aproximação para \(\left( 0,0 \right)\) em cada eixo. Assim, fixando \(y=0\), analisamos o caso de \(x\to 0\):
\[\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{lim}}\,\frac{-{{x}^{2}}\cdot 0}{{{\left( {{x}^{2}}+0 \right)}^{3/2}}}=\underset{x\to 0}{\mathop{lim}}\,\frac{0}{{{\left( {{x}^{2}} \right)}^{3/2}}}=\underset{x\to 0}{\mathop{lim}}\,0=0\]
Agora, analisando \(\left( x,y \right)\to 0\) pela semirreta \(y=x\) para valores \(x>0\):
\[\underset{\left( x,y \right)\to \left( {{0}^{+}},x \right)}{\mathop{lim}}\,\frac{-{{x}^{2}}\cdot {{y}^{3}}}{{{\left( {{x}^{2}}+{{y}^{2}} \right)}^{3/2}}}=\underset{\left( x,y \right)\to \left( {{0}^{+}},x \right)}{\mathop{lim}}\,\frac{-{{x}^{3}}}{{{\left( {{x}^{2}}+{{x}^{2}} \right)}^{3/2}}}=\underset{\left( x,y \right)\to \left( {{0}^{+}},x \right)}{\mathop{lim}}\,\frac{-{{x}^{3}}}{{{\left( 2{{x}^{2}} \right)}^{3/2}}}=\underset{\left( x,y \right)\to \left( {{0}^{+}},x \right)}{\mathop{lim}}\,\frac{-{{x}^{3}}}{2\sqrt{2}{{x}^{3}}}\]
\[=\underset{\left( x,y \right)\to \left( {{0}^{+}},x \right)}{\mathop{lim}}\,\frac{-1}{2\sqrt{2}}=\frac{-\sqrt{2}}{4}\]
Como o limite não existe, pois aproximações diferentes levam a resultados diferentes, então a função dada não é diferenciável na origem.
Antes de continuarmos com esse assunto, você já deve ter percebido que não é muito simples provar a diferenciabilidade de uma função. Mais adiante, será apresentado um critério que facilita identificar funções diferenciáveis. Mas antes de ver tal critério, Leithold (1994) ainda propõe uma relação entre a diferenciabilidade de uma função com a continuidade desta: uma função \(f\left( x,y \right)\) que é diferenciável em um ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\) também será contínua nesse ponto, ou seja:
\[\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,f\left( x,y \right)=f\left( {{x}_{0}},{{y}_{0}} \right)\]
Agora pode-se enunciar a condição que Flemming e Gonçalves (2005) afirmam como suficiente para a diferenciabilidade de uma função de duas variáveis: seja a função \(f\left( x,y \right)\) e o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in {{D}_{f}}\), contido em um conjunto aberto \(A\). Se a função \(f\left( x,y \right)\) tiver as duas derivadas parciais de 1ª ordem \(\partial f/\partial x\) e \(\partial f/\partial y\) em \(A\) e se essas derivadas parciais forem contínuas no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\), então pode-se dizer que \(f\left( x,y \right)\) é diferenciável em \(\left( {{x}_{0}},{{y}_{0}} \right)\).
Exemplo 2.3: Verifique se a função \(f\left( x,y \right)=2x{{y}^{2}}+4{{x}^{2}}y+3xy\) é diferenciável em \({{\mathbb{R}}^{2}}\).
Solução
De acordo com a proposição de Flemming e Gonçalves (2005), precisamos verificar se as derivadas parciais de 1ª ordem existem e se são contínuas em \({{\mathbb{R}}^{2}}\). Então, para qualquer ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\in {{\mathbb{R}}^{2}}\):
\[\frac{\partial f}{\partial x}\left( x,y \right)=2{{y}^{2}}+8xy+3y~~~~\to ~~~~\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)=2{{y}_{0}}^{2}+8{{x}_{0}}{{y}_{0}}+3{{y}_{0}}\]
\[\frac{\partial f}{\partial y}\left( x,y \right)=4xy+4{{x}^{2}}+3x~~~~\to ~~~~\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)=4{{x}_{0}}^{2}+4{{x}_{0}}{{y}_{0}}+3{{x}_{0}}\]
Observe que as derivadas parciais são polinômios com domínio igual a \({{\mathbb{R}}^{2}}\). Logo, ambas as derivadas parciais são contínuas em todo o \({{\mathbb{R}}^{2}}\). Com isso, tem-se que a função \(f\) indicada é diferenciável em \({{\mathbb{R}}^{2}}\).
Flemming e Gonçalves (2005) apresentam uma informação interessante sobre o plano tangente descrito pela equação (17): nem sempre o plano definido pela equação (17) irá existir e, mesmo que exista, pode não ser tangente à função \(f\left( x,y \right)\).
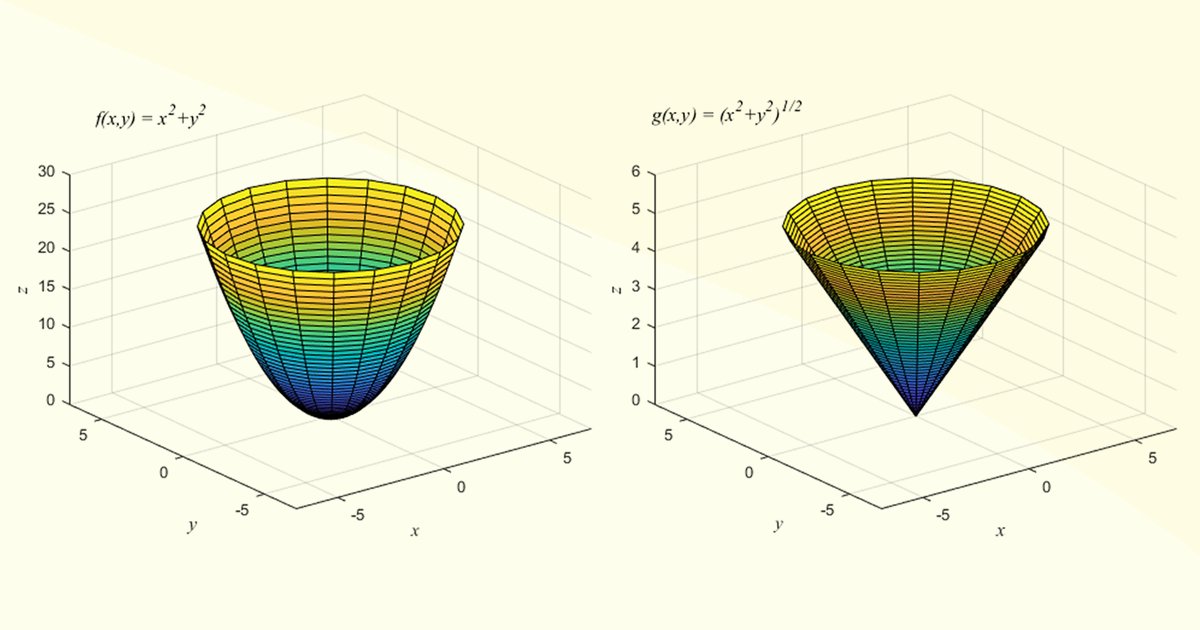
Funções que apresentam um gráfico suave, como os paraboloides, apresentam um plano tangente em todos os seus pontos. No entanto, funções que apresentam no gráfico alguma região angulosa, como o gráfico da função de um cone, não admitem o plano tangente nessas regiões angulosas. Na Figura 2.10 são mostrados os gráficos das funções \(f\left( x,y \right)={{x}^{2}}+{{y}^{2}}\) e \(g\left( x,y \right)=\sqrt{{{x}^{2}}+{{y}^{2}}}\). Observe que claramente a função \(g\left( x,y \right)\) não apresentará nenhum plano tangente em sua origem, diferente do que se tem com a função \(f\left( x,y \right)\).
Com isso, Flemming e Gonçalves (2005) apresentam a seguinte definição para o plano tangente ao gráfico de uma função de duas variáveis:
Definição 4: considere uma função \(f\left( x,y \right)\in {{\mathbb{R}}^{2}}\) que seja diferenciável em um ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\). O plano tangente ao gráfico dessa função em um ponto \(\left( {{x}_{0}},{{y}_{0}},f\left( {{x}_{0}},{{y}_{0}} \right) \right)\) é aquele plano definido pela seguinte equação:
\[z-f\left( {{x}_{0}},{{y}_{0}} \right)=\left( x-{{x}_{0}} \right)\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)+\left( y-{{y}_{0}} \right)\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)~~~~(19)\]
Portanto, basicamente, para que o plano definido pela Equação (19) exista, é necessário, além de satisfazer a Equação (19), que a função apresente derivadas parciais no ponto em questão. Por exemplo, considerando o paraboloide definido como \(f\left( x,y \right)={{x}^{2}}+{{y}^{2}}\), você tem as seguintes derivadas parciais de 1ª ordem:
\(\frac{\partial f}{\partial x}=2x\) e \(\frac{\partial f}{\partial y}=2y\)
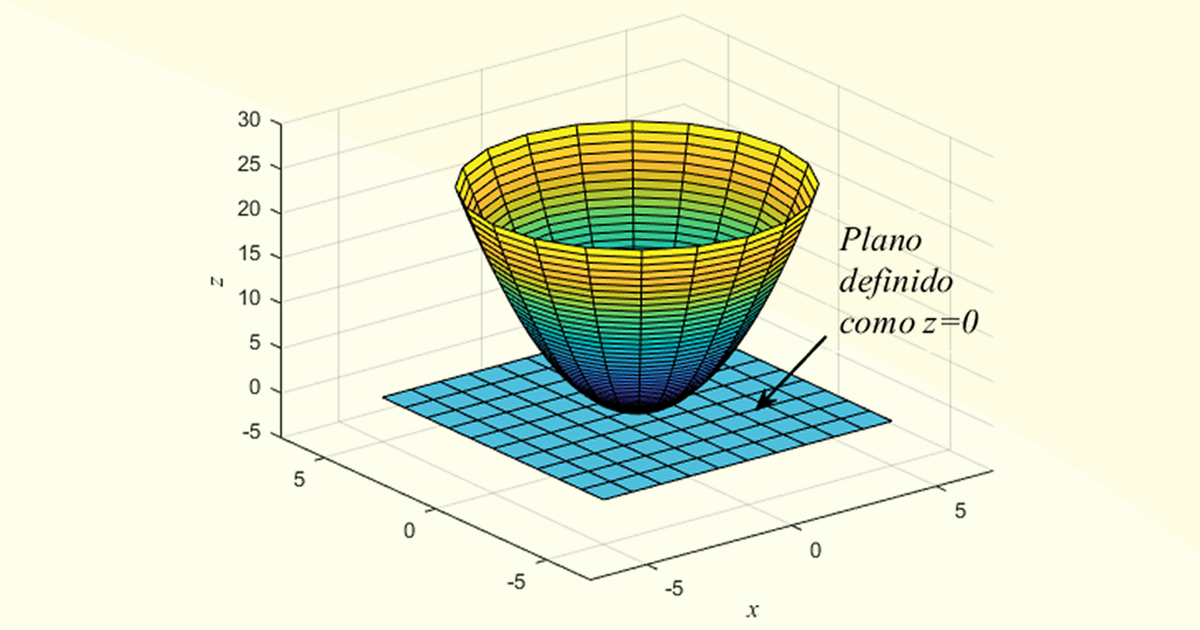
Veja que, para o ponto \(\left( 0,0 \right)\), ou seja, a origem, a Equação (19) se reduz a:
\[z-0=\left( x-0 \right)\cdot 2\cdot 0+\left( y-0 \right)\cdot 2\cdot 0~~~~\to ~~~~z=0\]
Ou seja, o plano definido pelos eixos \(xy\) em \(z=0\) é o plano tangente à origem nesse gráfico, como se pode ver na Figura 2.11.
Se você verificar para a função cone \(f\left( x,y \right)=\sqrt{{{x}^{2}}+{{y}^{2}}}\), verá que as derivadas parciais de 1ª ordem existem e são as seguintes:
\(\frac{\partial f}{\partial x}=\frac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\) e \(\frac{\partial f}{\partial y}=\frac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\)
No entanto, não é possível avaliar \({{f}_{x}}\left( 0,0 \right)\) e \({{f}_{y}}\left( 0,0 \right)\), que são necessárias para avaliar a Equação (19). Logo, realmente não existe o plano tangente na origem do gráfico cone indicado.
Flemming e Gonçalves (2005) fazem um destaque muito interessante sobre as derivadas parciais \(\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)\) e \(\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)\). Quando essas derivadas parciais são organizadas de certa forma, elas formam um vetor, representado por \(\left( \frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right),\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right) \right)\).
Tal vetor é muito comum no cálculo e em disciplinas que fazem uso do Cálculo. Esse vetor apresenta uma série de propriedades interessantes e a seguir será discutida uma breve apresentação sobre algumas dessas propriedades, mas esse assunto não será tratado muito profundamente neste material. Uma das definições mais importantes desse vetor é o gradiente, definido por Flemming e Gonçalves (2005) da seguinte maneira:
Definição 5: considere uma função \(f\left( x,y \right)\), que admite derivadas parciais de 1ª ordem em um ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\). O gradiente dessa função em tal ponto, denotada como \(grad~f\left( {{x}_{0}},{{y}_{0}} \right)\) ou \(\nabla ~f\left( {{x}_{0}},{{y}_{0}} \right)\), é o vetor cujas componentes são as derivadas parciais de 1ª ordem da função no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\). Assim:
\[\nabla ~f\left( {{x}_{0}},{{y}_{0}} \right)=\left( \frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right),\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right) \right)~~~~(20)\]
Esse vetor gradiente pode ser aplicado a um ponto genérico \(\left( x,y \right)\) do domínio da função. Essa aplicação genérica é a mais usual que se tem para o gradiente:
\[\nabla ~f=\left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right)\]
Observe que essa definição pode ser ampliada para funções com mais de duas variáveis, seguindo a mesma linha de raciocínio apresentada. Assim, para uma função \(w=f\left( x,y,z \right)\), tem-se o seguinte gradiente:
\[\nabla ~w=\left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} \right)\]
Exemplo 2.4: Determinar o vetor gradiente da função \(w=2x{{y}^{2}}+3xyz\).
Solução
Para encontrar o vetor gradiente, é necessário avaliar as derivadas parciais de 1ª ordem da função dada. Assim:
\[\frac{\partial w}{\partial x}=2{{y}^{2}}+3yz\]
\[\frac{\partial w}{\partial y}=2xy+3xz\]
\[\frac{\partial w}{\partial z}=3xy\]
Logo, o vetor gradiente para tal função será:
\[\nabla ~w=\left( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} \right)~~~~\to ~~~~\nabla ~w=\left( 2{{y}^{2}}+3yz,2xy+3xz,3xy \right)\]
Flemming e Gonçalves (2005) fazem destaque de outro ponto a respeito de propriedades dos gradientes. Uma das mais importantes propriedades do gradiente de uma função é que ele é perpendicular às curvas de nível dessa função. Ou seja, considere uma função \(f\left( x,y \right)\) e o ponto \({{P}_{0}}=\left( {{x}_{0}},{{y}_{0}} \right)\), pelo qual passa uma curva de nível \({{C}_{k}}\). Então, se \(\nabla ~f\left( {{x}_{0}},{{y}_{0}} \right)\) não for nulo, ele será perpendicular à curva \({{C}_{k}}\) em \({{P}_{0}}\), ou seja, ele será perpendicular à reta tangente a \({{C}_{k}}\) no ponto \({{P}_{0}}\). A Figura 2.12 ilustra essa propriedade.
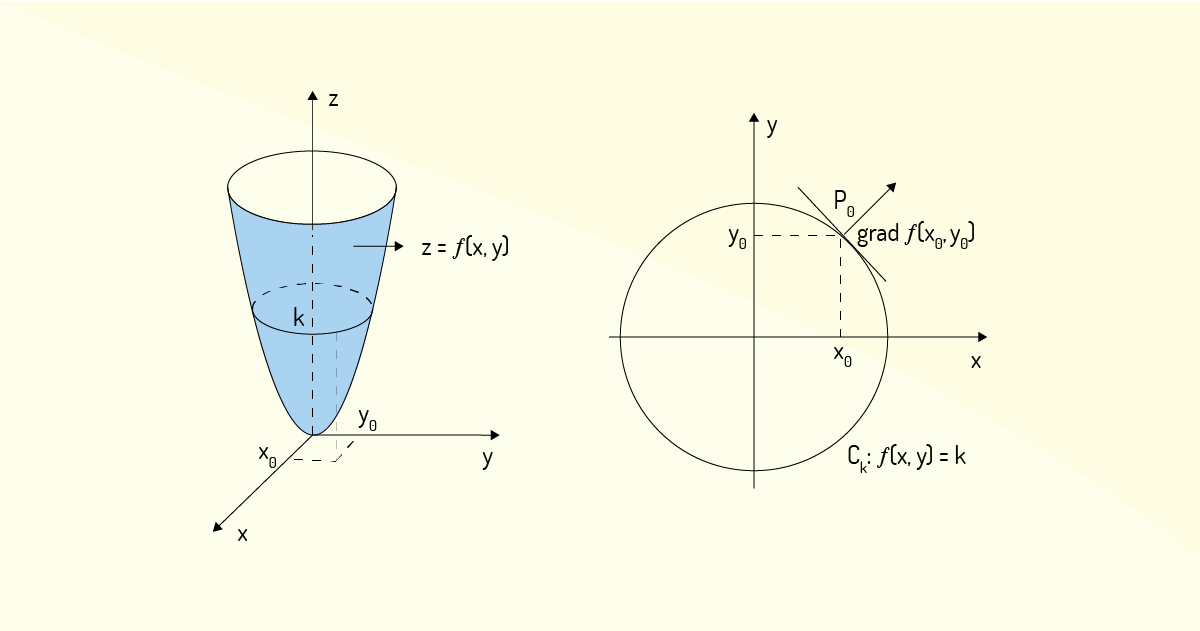
Observe que o gradiente se encontra no plano \(xy\), que é o domínio da função dada.
Até o momento, analisamos basicamente o plano tangente à superfície de uma função \(f\left( x,y \right)\). Agora analisaremos o diferencial de uma função. Para funções de uma única variável \(y=f\left( x \right)\), a diferencial pode ser aproximada a um acréscimo \(\Delta y\) de sua variável dependente. Analogamente, para uma função \(z=f\left( x,y \right)\), a diferencial deverá ser uma transformação linear que aproxime um acréscimo \(\Delta z\) de \(z\). Com isso, Flemming e Gonçalves (2005) enunciam a seguinte definição:
Definição 6: considere uma função \(f\left( x,y \right)\), que é diferenciável no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\). A diferencial dessa função no ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\) será definida pela seguinte transformação linear \(T:{{\mathbb{R}}^{2}}\to \mathbb{R}\):
\[T\left( x-{{x}_{0}},y-{{y}_{0}} \right)=\left( x-{{x}_{0}} \right)\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)+\left( y-{{y}_{0}} \right)\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)~~~~(21)\]
Fazendo \(h=x-{{x}_{0}}\) e \(k=y-{{y}_{0}}\), (21) pode ser reescrita com:
\[T\left( h,k \right)=h\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)+k\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)~~~~(22)\]
Veja que as equações (21) e (22) são parecidas com a equação (19), a equação do plano tangente à superfície de \(z=f\left( x,y \right)\). A transformada linear \(T\) irá fornecer, de acordo com Flemming e Gonçalves (2005), uma aproximação para o acréscimo \(\Delta z\) sofrido pela função, quando se passa de \(\left( {{x}_{0}},{{y}_{0}} \right)\) para \(\left( x,y \right)\). Então:
\[\Delta z=f\left( x,y \right)-f\left( {{x}_{0}},{{y}_{0}} \right)\cong h\frac{\partial f}{\partial x}\left( {{x}_{0}},{{y}_{0}} \right)+k\frac{\partial f}{\partial y}\left( {{x}_{0}},{{y}_{0}} \right)~~~~(23)\]
Flemming e Gonçalves (2005) ainda indicam que é comum usar a notação \(\Delta x=h=x-{{x}_{0}}\) e \(\Delta y=k=y-{{y}_{0}}\) na diferencial apresentada em (23), de modo a deixar mais claro que se tem a diferencial de \(z=f\left( x,y \right)\) em \(\left( {{x}_{0}},{{y}_{0}} \right)\) relativa a acréscimos \(\Delta x\) e \(\Delta y\). Tomando uma notação ainda mais clássica, pode-se fazer os acréscimos \(\Delta x\) e \(\Delta y\) serem muito pequenos de forma que o operador \(\Delta \) se torne uma derivada, ou seja, \(\Delta x=dx\) e \(\Delta y=dy\). Com isso, pode-se encontrar a diferencial total da função \(z=f\left( x,y \right)\):
\[dz=\frac{\partial f}{\partial x}\left( x,y \right)dx+\frac{\partial f}{\partial y}\left( x,y \right)dy~~~~(24)\]
Exemplo 2.5: Calcule a diferencial da função \(f\left( x,y \right)={{x}^{2}}y+\sqrt{xy}\) no ponto \(\left( 1,1 \right)\).
Solução
Primeiro, deve-se avaliar as derivadas parciais de tal função:
\[\frac{\partial f}{\partial x}=2xy+\frac{\sqrt{y}}{2\sqrt{x}}~~~~\to ~~~~\frac{\partial f}{\partial x}\left( 1,1 \right)=2\cdot 1\cdot 1+\frac{\sqrt{1}}{2\sqrt{1}}=2+\frac{1}{2}=\frac{5}{2}\]
\[\frac{\partial f}{\partial y}={{x}^{2}}+\frac{\sqrt{x}}{2\sqrt{y}}~~~~\to ~~~~\frac{\partial f}{\partial y}\left( 1,1 \right)={{1}^{2}}+\frac{\sqrt{1}}{2\sqrt{1}}=1+\frac{1}{2}=\frac{3}{2}\]
Agora, basta usar a equação (21):
\[T\left( x-1,y-1 \right)=\left( x-1 \right)\frac{\partial f}{\partial x}\left( 1,1 \right)+\left( y-1 \right)\frac{\partial f}{\partial y}\left( 1,1 \right)\]
\[T\left( x-1,y-1 \right)=\left( x-1 \right)\frac{5}{2}+\left( y-1 \right)\frac{3}{2}\]
Você ainda pode utilizar a notação clássica para representar essa diferencial, usando a Equação (24):
\[df=\frac{5}{2}dx+\frac{3}{2}dy\]
As diferenciais de uma função são úteis para se calcular aproximações. A seguir é mostrado um exemplo dessa aplicação das diferenciais, em que esta é aplicada para estimar variações na área de polígonos.
Exemplo 2.6: Seja um retângulo de lados iguais a 5 e 2 cm, respectivamente. Qual será a variação da área, aproximadamente, se os lados forem modificados para 5,02 e 2,005 cm?
Solução
Considerando que um retângulo genérico tem lados de tamanho \(x\) e \(y\), respectivamente, então sua área será \(A=xy\). Para tal função, tem-se as seguintes derivadas parciais:
\(\frac{\partial A}{\partial x}=y\) e \(\frac{\partial A}{\partial y}=x\)
Agora, para estimar a variação da área quando se modificam as dimensões do retângulo, você pode utilizar a Equação (24), ou seja, a diferencial total da função:
\[dA=\frac{\partial A}{\partial x}dx+\frac{\partial A}{\partial y}dy=ydx+xdy\]
Considerando \(x=5\), então tem-se que \(y=2\). Logo, pode-se dizer que, de forma aproximada, \(dx=5,02-5=0,02\) cm e \(dy=2,005-2=0,005\) cm. Assim, pode-se estimar a variação da área:
\[dA=2\cdot 0,02+5\cdot 0,005=0,065~c{{m}^{2}}\]
Ou seja, quando as dimensões do retângulo variam de 5 para 5,02 cm e de 2 para 2,005 cm, a área desse retângulo deve sofrer um acréscimo de aproximadamente 0,65 cm2.
Analisar a diferencial de uma função é algo que lhe fornecerá uma estimativa de como uma função irá se comportar com pequenas alterações de suas variáveis. Sendo assim, visando fixar este conceito, considere que uma empresa fabrica caixas cilíndricas, sendo que o custo de matéria-prima para essa caixa é de R$ 0,07 cada 10 cm². Analise as alternativas a seguir e assinale a correta.
Se as dimensões da caixa variarem um pouco, você pode estimar o custo aproximado da nova caixa utilizando a equação \(dC=0,007\left[ \left( 2\pi h+2\pi r \right)dr+\left( 2\pi r \right)dh \right]\).
Justificativa: A área da caixa é calculada somando-se a área lateral com as áreas das duas bases circulares, ou seja, \(A=2\pi rh+2\pi {{r}^{2}}\). Já o custo é \(C=0,07A=0,07\left( 2\pi rh+2\pi {{r}^{2}} \right)\). Para estimar o custo com a diferencial dessa função, avalie as variáveis parciais:
\[\frac{\partial C}{\partial r}=0,007\left( 2\pi h+4\pi r \right)~~~~e~~~~\frac{\partial C}{\partial h}=0,007\left( 2\pi r \right)\]
Agora, basta aplicar a Equação (24):
\[dC=\frac{\partial C}{\partial r}dr+\frac{\partial C}{\partial h}dh=0,007\left[ \left( 2\pi h+4\pi r \right)dr+\left( 2\pi r \right)dh \right]\]
Para uma caixa com \(r=5~cm\) e \(h=10~cm\), se o raio aumentar 2% e a altura aumentar 5%, o aumento do custo da nova caixa será de aproximadamente R$ 0,20.
Justificativa correta: A área da caixa é calculada somando-se a área lateral com as áreas das duas bases circulares, ou seja, \(A=2\pi rh+2\pi {{r}^{2}}\). Já o custo é \(C=0,07A=0,07\left( 2\pi rh+2\pi {{r}^{2}} \right)\). Para estimar o custo com a diferencial dessa função, avalie as variáveis parciais:
\[\frac{\partial C}{\partial r}=0,007\left( 2\pi h+4\pi r \right)~~~~e~~~~\frac{\partial C}{\partial h}=0,007\left( 2\pi r \right)\]
Agora, basta aplicar a Equação (24):
\[dC=\frac{\partial C}{\partial r}dr+\frac{\partial C}{\partial h}dh=0,007\left[ \left( 2\pi h+4\pi r \right)dr+\left( 2\pi r \right)dh \right]\]
Para um aumento de 2%, o raio será 5,1 cm, o que gera um \(\Delta r=5,1-5=0,1\) cm e, se a altura aumentar 5%, será 10,5 cm, o que gera um \(\Delta h=10,5-10=0,5\) cm. Assim, tem-se:
\[dC=0,007\left[ \left( 2\pi \cdot 10+4\pi \cdot 5 \right)\cdot 0,1+\left( 2\pi 5 \right)\cdot 0,5 \right]=0,19792\simeq 0,20\]
Para uma caixa com \(r=5~cm\) e \(h=10~cm\), se o raio aumentar 2% e a altura aumentar 5%, o aumento do custo da nova caixa será de aproximadamente R$ 0,10.
Justificativa: A área da caixa é calculada somando-se a área lateral com as áreas das duas bases circulares, ou seja, \(A=2\pi rh+2\pi {{r}^{2}}\). Já o custo é \(C=0,07A=0,07\left( 2\pi rh+2\pi {{r}^{2}} \right)\). Para estimar o custo com a diferencial dessa função, avalie as variáveis parciais:
\[\frac{\partial C}{\partial r}=0,007\left( 2\pi h+4\pi r \right)~~~~e~~~~\frac{\partial C}{\partial h}=0,007\left( 2\pi r \right)\]
Agora, basta aplicar a Equação (24):
\[dC=\frac{\partial C}{\partial r}dr+\frac{\partial C}{\partial h}dh=0,007\left[ \left( 2\pi h+4\pi r \right)dr+\left( 2\pi r \right)dh \right]\]
Para um aumento de 2%, o raio será 5,1 cm, o que gera um \(\Delta r=5,1-5=0,1\) cm e, se a altura aumentar 5%, será 10,5 cm, o que gera um \(\Delta h=10,5-10=0,5\) cm. Assim, tem-se:
\[dC=0,007\left[ \left( 2\pi \cdot 10+4\pi \cdot 5 \right)\cdot 0,1+\left( 2\pi 5 \right)\cdot 0,5 \right]=0,19792\simeq 0,20\]
Para uma caixa com \(r=2~cm\) e \(h=5~cm\), se o raio aumentar 5% e a altura aumentar 2%, o custo da nova caixa será de aproximadamente R$ 0,20.
Justificativa: A área da caixa é calculada somando-se a área lateral com as áreas das duas bases circulares, ou seja, \(A=2\pi rh+2\pi {{r}^{2}}\). Já o custo é \(C=0,07A=0,07\left( 2\pi rh+2\pi {{r}^{2}} \right)\). Para estimar o custo com a diferencial dessa função, avalie as variáveis parciais:
\[\frac{\partial C}{\partial r}=0,007\left( 2\pi h+4\pi r \right)~~~~e~~~~\frac{\partial C}{\partial h}=0,007\left( 2\pi r \right)\]
Agora, basta aplicar a Equação (24):
\[dC=\frac{\partial C}{\partial r}dr+\frac{\partial C}{\partial h}dh=0,007\left[ \left( 2\pi h+4\pi r \right)dr+\left( 2\pi r \right)dh \right]\]
Para um aumento de 5%, o raio será 5,25 cm, o que gera um $\Delta r=5,25-5=0,25$ cm e, se a altura aumentar 2%, será 10,2 cm, o que gera um \(\Delta h=10,2-10=0,2\) cm. Assim, tem-se:
\[dC=0,007\left[ \left( 2\pi \cdot 10+4\pi \cdot 5 \right)\cdot 0,25+\left( 2\pi 5 \right)\cdot 0,2 \right]=0,2639\simeq 0,26\]
Se as dimensões da caixa variarem um pouco, você pode estimar o custo aproximado da nova caixa utilizando a equação \(dC=0,07\left[ \left( 2\pi h \right)dr+\left( 2\pi r \right)dh \right]\).
Justificativa: A área da caixa é calculada somando-se a área lateral com as áreas das duas bases circulares, ou seja, \(A=2\pi rh+2\pi {{r}^{2}}\). Já o custo é \(C=0,07A=0,07\left( 2\pi rh+2\pi {{r}^{2}} \right)\). Para estimar o custo com a diferencial dessa função, avalie as variáveis parciais:
\[\frac{\partial C}{\partial r}=0,007\left( 2\pi h+4\pi r \right)~~~~e~~~~\frac{\partial C}{\partial h}=0,007\left( 2\pi r \right)\]
Agora, basta aplicar a Equação (24):
\[dC=\frac{\partial C}{\partial r}dr+\frac{\partial C}{\partial h}dh=0,007\left[ \left( 2\pi h+4\pi r \right)dr+\left( 2\pi r \right)dh \right]\]
Assim como você já estudou para casos de funções de uma única variável, você também verá casos de funções compostas em funções de mais de uma variável, sendo que é possível se ver com a necessidade de avaliar a derivada dessa função. Por exemplo, sendo a função \(y=f\left( x \right)\) uma função diferenciável de \(x\) e \(x=g\left( t \right)\) uma função diferenciável de \(t\), então a função \(y\) é diferenciável em relação a \(t\), sendo, segundo Thomas Júnior (2016), essa derivada avaliada pela regra da cadeia, da seguinte forma:
\[\frac{dy}{dt}=\frac{dy}{dx}\frac{dx}{dt}\]
Você pode pensar na função \(y\) como \(y=f\left( g\left( t \right) \right)\), ou seja, a variável \(x\) pode ser vista como uma variável intermediária, visto que \(x\) depende de \(t\).
Para introduzir, agora, a ideia da regra da cadeia para funções com mais de uma variável, Morettin, Hazzan e Bussab (2016) apresentam o seguinte exemplo. Considere que a produção de uma empresa pode ser representada pela seguinte função:
\[P\left( x,y \right)=6{{x}^{1/2}}{{y}^{1/2}}\]
Em que \(x\) representa o capital e \(y\) representa o trabalho investido. Tanto o capital quanto o trabalho podem ser representados como funções do tempo, na forma \(x=f\left( t \right)=0,16t\) e \(y=g\left( t \right)=0,09t\). Assim, a função produção também pode ser reescrita como uma função do tempo:
\[P\left( t \right)=6{{\left( 0,16t \right)}^{1/2}}{{\left( 0,09t \right)}^{1/2}}=0,72{{\left( {{t}^{2}} \right)}^{1/2}}=0,72t\]
Note que a derivada de \(P\left( t \right)\) pode ser encontrada diretamente, sendo \(P'\left( t \right)=0,72\). No entanto, nem sempre essa substituição poderá ser feita de forma simples, sendo prático que você saiba como avaliar a derivada de uma função composta de forma direta, sem precisar reescrever a função em questão. Para tal, usaremos também a regra da cadeia.
Vejamos, então, como pode-se aplicar a regra da cadeia para funções com mais de uma variável. Stewart (2017b) indica que existem diversas versões da regra da cadeia para funções com mais de uma variável. Estudaremos alguns desses casos, sendo o primeiro deles aquele em que a função \(z=f\left( x,y \right)\) apresenta ambas variáveis como funções de outra mesma variável, ou seja, \(x=g\left( t \right)\) e \(y=h\left( t \right)\). Assim, conforme descrito anteriormente, a função \(z\) é indiretamente função de \(t\), sendo \(x\) e \(y\) variáveis intermediárias. Pode-se, então, escrever a função \(z\) como sendo \(z=f\left( g\left( t \right),h\left( t \right) \right)\). Nesse caso, Flemming e Gonçalves (2005) e Stewart (2017b) propõem a seguinte definição:
Definição 7: considere os conjuntos \(A\in {{\mathbb{R}}^{2}}\) e \(B\in \mathbb{R}\), ambos abertos. Se, então, a função \(z=f\left( x,y \right)\) admite derivadas parciais de 1ª ordem contínuas em \(A\), ou seja, \(z\) é diferenciável em relação a \(x\) e \(y\), e se essas variáveis \(x\) e \(y\) são funções de \(t\) diferenciáveis em \(B\), ou seja, em relação a \(t\), então, para qualquer \(t\in B\), tem-se que \(\left( x\left( t \right),y\left( t \right) \right)\in A\). Logo, \(z\) será diferenciável para qualquer \(t\in B\) e:
\[\frac{dz}{dt}=\frac{\partial f}{\partial x}\cdot \frac{dx}{dt}+\frac{\partial f}{\partial y}\cdot \frac{dy}{dt}~~~~(25)\]
Exemplo 3.1: Seja a função \(z=f\left( x,y \right)={{x}^{2}}y+x\), para a qual se tem que \(x\left( t \right)=t\) e \(y\left( t \right)=t+2\). Verifique a fórmula da regra da cadeia para esse caso.
Solução
Verificar a fórmula simplesmente é verificar que a Equação (25) é verdadeira. Assim, primeiro vamos avaliar \(z\left( t \right)\):
\[z\left( t \right)={{\left( t \right)}^{2}}\left( t+2 \right)+\left( t \right)={{t}^{3}}+2{{t}^{2}}+t={{t}^{3}}+3t\]
Avaliando a derivada de \(z\) em relação a \(t\):
\[\frac{dz}{dt}=3{{t}^{2}}+4t+1\]
Agora, avaliando as demais derivadas que são apresentadas em (25):
\[\frac{\partial f}{\partial x}=2xy+1~~~~e~~~~\frac{dx}{dt}=1\]
\[\frac{\partial f}{\partial y}={{x}^{2}}~~~~ e ~~~~\frac{dy}{dt}=1\]
Disso, tem-se que:
\[\frac{\partial f}{\partial x}\cdot \frac{dx}{dt}+\frac{\partial f}{\partial y}\cdot \frac{dy}{dt}=\left( 2xy+1 \right)\cdot \left( 1 \right)+\left( {{x}^{2}} \right)\cdot \left( 1 \right)\]
\[=2xy+1+{{x}^{2}}\]
Como \(x\left( t \right)=t\) e \(y\left( t \right)=t+2\), então:
\[2xy+1+{{x}^{2}}=2\cdot \left( t \right)\cdot \left( t+2 \right)+1+{{\left( t \right)}^{2}}\]
\[=2{{t}^{2}}+4t+{{t}^{2}}+1=3{{t}^{2}}+4t+1\]
Então, como mostramos que:
\[\frac{dz}{dt}=\frac{\partial f}{\partial x}\cdot \frac{dx}{dt}+\frac{\partial f}{\partial y}\cdot \frac{dy}{dt}\]
Podemos afirmar que verificamos a regra da cadeia.
Exemplo 3.2: Seja a função \(z=f\left( x,y \right)=xy+ln~{{x}^{2}}{{y}^{2}}\), para a qual se tem que \(x\left( t \right)={{t}^{2}}\) e \(y\left( t \right)=t\), encontre \(dz/dt\) utilizando a regra da cadeia.
Solução
Para encontrar tal derivada utilizando a regra da cadeia, basta aplicar a Equação (25). Assim, avaliando as derivadas necessárias:
\[\frac{\partial f}{\partial x}=y+\frac{2}{x}~~~~e~~~~\frac{dx}{dt}=2t\]
\[\frac{\partial f}{\partial y}=x+\frac{2}{y}~~~~e~~~~\frac{dy}{dt}=1\]
Agora, basta resolver a Equação (25):
\[\frac{dz}{dt}=\frac{\partial f}{\partial x}\cdot \frac{dx}{dt}+\frac{\partial f}{\partial y}\cdot \frac{dy}{dt}=\left( y+\frac{2}{x} \right)\cdot \left( 2t \right)+\left( x+\frac{2}{y} \right)\cdot \left( 1 \right)\]
\[=2ty+\frac{4t}{x}+x+\frac{2}{y}=\frac{4t+{{x}^{2}}}{x}+\frac{2t{{y}^{2}}+2}{y}\]
\[=\frac{4ty+{{x}^{2}}y+2tx{{y}^{2}}+2x}{xy}=\frac{t\left( 4y+2x{{y}^{2}} \right)+x\left( xy+2 \right)}{xy}\]
Como \(x\left( t \right)={{t}^{2}}\) e \(y\left( t \right)=t\), então:
\[\frac{dz}{dt}=\frac{t\left( 4t+2{{t}^{2}}{{t}^{2}} \right)+{{t}^{2}}\left( {{t}^{2}}t+2 \right)}{{{t}^{2}}t}\]
\[=\frac{4{{t}^{2}}+2{{t}^{5}}+{{t}^{2}}\left( {{t}^{3}}+2 \right)}{{{t}^{2}}t}=\frac{4+2{{t}^{3}}+{{t}^{3}}+2}{t}=\frac{3{{t}^{3}}+6}{t}\]
O segundo caso é aquele no qual a função \(z=f\left( x,y \right)\) apresenta ambas variáveis como funções de outras duas variáveis, ou seja, \(x=g\left( s,t \right)\) e \(y=h\left( s,t \right)\). Assim, a função \(z\) é indiretamente função de \(s\) e \(t\), sendo \(x\) e \(y\) variáveis intermediárias. Pode-se, então, escrever a função \(z\) como sendo \(z=f\left( g\left( s,t \right),h\left( s,t \right) \right)\). Para esse caso, Flemming e Gonçalves (2005) e Stewart (2017b) propõem a seguinte definição:
Definição 8: considere os conjuntos \(A,B\in {{\mathbb{R}}^{2}}\), ambos abertos. Se, então, a função \(z=f\left( u,v \right)\) admite derivadas parciais de 1ª ordem contínuas em \(A\), ou seja, \(z\) é diferenciável em relação a \(u=u\left( x,y \right)\) e \(v=v\left( x,y \right)\), e se essas variáveis \(u\) e \(v\) são diferenciáveis em \(B\) tais que, para qualquer \(\left( x,y \right)\in B\), tem-se que \(\left( u\left( x,y \right),v\left( x,y \right) \right)\in A\). Logo, \(z\) será diferenciável para qualquer \(\left( x,y \right)\in B\) e:
\[\frac{\partial z}{\partial x}=\frac{\partial f}{\partial u}\cdot \frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\cdot \frac{\partial v}{\partial x}~~~~(26)\]
\[\frac{\partial z}{\partial y}=\frac{\partial f}{\partial u}\cdot \frac{\partial u}{\partial y}+\frac{\partial f}{\partial v}\cdot \frac{\partial v}{\partial y}~~~~(27)\]
Exemplo 3.3: Seja a função \(z=f\left( u,v \right)={{v}^{2}}+u-v\), para a qual se tem que \(u\left( x,y \right)=x+2y\) e \(v\left( y,x \right)={{x}^{2}}{{y}^{2}}\). Verifique a fórmula da regra da cadeia para esse caso.
Solução
Verificar a fórmula simplesmente é verificar que as equações (26) e (27) são verdadeiras. Assim, primeiro vamos avaliar \(z\left( x,y \right)\):
\[z\left( x,y \right)={{\left( {{x}^{2}}{{y}^{2}} \right)}^{2}}+\left( x+2y \right)-\left( {{x}^{2}}{{y}^{2}} \right)\]
\[={{x}^{4}}{{y}^{4}}+x+2y-{{x}^{2}}{{y}^{2}}\]
Avaliando a derivada parcial de \(z\) em relação a \(x\):
\[\frac{\partial z}{\partial x}=4{{x}^{3}}{{y}^{4}}+1-2x{{y}^{2}}\]
E agora a derivada parcial de \(z\) em relação a \(y\):
\[\frac{\partial z}{\partial y}=4{{x}^{4}}{{y}^{3}}+2-2{{x}^{2}}y\]
Agora, avaliando as demais derivadas que são apresentadas nas equações (26) e (27):
\[\frac{\partial f}{\partial u}=1~~~~~~\frac{du}{dx}=1~~~~~~\frac{dv}{dx}=2x{{y}^{2}}\]
\[\frac{\partial f}{\partial v}=2v-1=2{{x}^{2}}{{y}^{2}}-1~~~~\frac{du}{dy}=2~~~~\frac{dv}{dy}=2{{x}^{2}}y\]
Aplicando-as no lado direito de (26):
\[\frac{\partial f}{\partial u}\cdot \frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\cdot \frac{\partial v}{\partial x}=\left( 1 \right)\cdot \left( 1 \right)+\left( 2{{x}^{2}}{{y}^{2}}-1 \right)\cdot \left( 2x{{y}^{2}} \right)\]
\[=1+4{{x}^{3}}{{y}^{4}}-2x{{y}^{2}}\]
E no lado direito de (27):
\[\frac{\partial f}{\partial u}\cdot \frac{\partial u}{\partial y}+\frac{\partial f}{\partial v}\cdot \frac{\partial v}{\partial y}=\left( 1 \right)\cdot \left( 2 \right)+\left( 2{{x}^{2}}{{y}^{2}}-1 \right)\cdot \left( 2{{x}^{2}}y \right)\]
\[=2+4{{x}^{4}}{{y}^{3}}-2{{x}^{2}}y\]
Então, comparando os resultados encontrados, mostramos que:
\[\frac{\partial z}{\partial x}=\frac{\partial f}{\partial u}\cdot \frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\cdot \frac{\partial v}{\partial x}~~~~e~~~~\frac{\partial z}{\partial y}=\frac{\partial f}{\partial u}\cdot \frac{\partial u}{\partial y}+\frac{\partial f}{\partial v}\cdot \frac{\partial v}{\partial y}\]
Exemplo 3.4: Seja a função \(z=f\left( u,v \right)={{e}^{u}}cos~v\), para a qual se tem que \(u\left( x,y \right)=x{{y}^{2}}\) e \(v\left( x,y \right)={{x}^{2}}y\), com a regra da cadeia, encontre \(\partial z/\partial x\) e \(\partial z/\partial y\).
Solução
Para encontrar \(\partial z/\partial x\) utilizando a regra da cadeia, basta usar a Equação (26). Assim, avaliando as derivadas necessárias:
\[\frac{\partial f}{\partial u}={{e}^{u}}cos~v={{e}^{x{{y}^{2}}}}cos~{{x}^{2}}y~~~~~~e~~~~~~\frac{\partial f}{\partial v}=-{{e}^{u}}sen~v=-{{e}^{x{{y}^{2}}}}sen~{{x}^{2}}y\]
\[\frac{du}{dx}={{y}^{2}}~~~~\frac{dv}{dx}=2xy\]
Resolvendo a Equação (26):
\[\frac{\partial z}{\partial x}=\frac{\partial f}{\partial u}\cdot \frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\cdot \frac{\partial v}{\partial x}=\left( {{e}^{x{{y}^{2}}}}cos~{{x}^{2}}y \right)\cdot \left( {{y}^{2}} \right)+\left( -{{e}^{x{{y}^{2}}}}sen~{{x}^{2}}y \right)\cdot \left( 2xy \right)\]
\[\frac{\partial z}{\partial x}={{y}^{2}}{{e}^{x{{y}^{2}}}}cos~{{x}^{2}}y-2xy{{e}^{x{{y}^{2}}}}sen~{{x}^{2}}y\]
\[\frac{\partial z}{\partial x}=y{{e}^{x{{y}^{2}}}}\left( y~cos~{{x}^{2}}y-2x~sen~{{x}^{2}}y \right)\]
Para encontrar $\partial z/\partial y$ utilizando a regra da cadeia, basta usar a equação (27). Assim, avaliando as demais derivadas necessárias:
\[\frac{du}{dy}=2xy~~~~~~\frac{dv}{dy}={{x}^{2}}\]
Resolvendo a equação (27):
\[\frac{\partial z}{\partial y}=\frac{\partial f}{\partial u}\cdot \frac{\partial u}{\partial y}+\frac{\partial f}{\partial v}\cdot \frac{\partial v}{\partial y}=\left( {{e}^{x{{y}^{2}}}}cos~{{x}^{2}}y \right)\cdot \left( 2xy \right)+\left( -{{e}^{x{{y}^{2}}}}sen~{{x}^{2}}y \right)\cdot \left( {{x}^{2}} \right)\]
\[\frac{\partial z}{\partial y}=2xy{{e}^{x{{y}^{2}}}}cos~{{x}^{2}}y-{{x}^{2}}{{e}^{x{{y}^{2}}}}sen~{{x}^{2}}y\]
\[\frac{\partial z}{\partial y}=x{{e}^{x{{y}^{2}}}}\left( 2y~cos~{{x}^{2}}y-x~sen~{{x}^{2}}y \right)\]
Após termos estudado esses dois casos, pode-se apresentar uma generalização para a regra da cadeia. Para esse caso generalizado, Stewart (2017b) propõe a seguinte definição:
Definição 9: considere que \(z\) seja uma função diferenciável de \(n\) variáveis \({{x}_{1}},{{x}_{2}},...,{{x}_{n}}\), para a qual se tem que cada variável \({{x}_{j}}\) seja uma função diferenciável de \(m\) variáveis \({{t}_{1}},{{t}_{2}},...,{{t}_{m}}\). Tem-se então que \(z\) também é uma função de \({{t}_{1}},{{t}_{2}},...,{{t}_{m}}\) para a qual se tem que a derivada parcial em relação à i-ésima variável \({{t}_{i}}\) será encontrada por:
\[\frac{\partial z}{\partial {{t}_{i}}}=\frac{\partial z}{\partial {{x}_{1}}}\cdot \frac{\partial {{x}_{1}}}{\partial {{t}_{i}}}+\frac{\partial z}{\partial {{x}_{2}}}\cdot \frac{\partial {{x}_{2}}}{\partial {{t}_{i}}}+...+\frac{\partial z}{\partial {{x}_{n}}}\cdot \frac{\partial {{x}_{n}}}{\partial {{t}_{i}}}~~~~(28)\]
Para a qual \(i=1,2,...,n\).
Exemplo 3.5: Escreve a regra da cadeia para uma função \(z=f\left( x,y,w,s \right)\), para a qual se tem que \(x=x\left( u,v,r \right)\), \(y=y\left( u,v,r \right)\), \(w=w\left( u,v,r \right)\) e \(t=t\left( u,v,r \right)\).
Solução
Para esse caso, temos uma equação \(z\) com quatro variáveis, sendo que cada uma dessas variáveis é uma função de outras três variáveis. Então, de acordo com o que foi enunciado na definição 9, tem-se \(n=4\) e \(m=3\), as quais podem ser identificadas como \({{x}_{1}}=x\), \({{x}_{2}}=y\), \({{x}_{3}}=w\) e \({{x}_{4}}=s\) e \({{t}_{1}}=u$, ${{t}_{2}}=v\) e \({{t}_{3}}=r\).
Precisamos, então, encontrar \(\partial z/\partial u\), \(\partial z/\partial v\) e \(\partial z/\partial r\) utilizando a Equação (28). Para a primeira variável, ou seja, para \(u\), tem-se:
\[\frac{\partial z}{\partial u}=\frac{\partial z}{\partial x}\cdot \frac{\partial x}{\partial u}+\frac{\partial z}{\partial y}\cdot \frac{\partial y}{\partial u}+\frac{\partial z}{\partial w}\cdot \frac{\partial w}{\partial u}+\frac{\partial z}{\partial s}\cdot \frac{\partial s}{\partial u}\]
E para a segunda variável, ou seja, para \(v\):
\[\frac{\partial z}{\partial v}=\frac{\partial z}{\partial x}\cdot \frac{\partial x}{\partial v}+\frac{\partial z}{\partial y}\cdot \frac{\partial y}{\partial v}+\frac{\partial z}{\partial w}\cdot \frac{\partial w}{\partial v}+\frac{\partial z}{\partial s}\cdot \frac{\partial s}{\partial v}\]
E, finalmente, para a terceira variável, ou seja, para \(r\):
\[\frac{\partial z}{\partial r}=\frac{\partial z}{\partial x}\cdot \frac{\partial x}{\partial r}+\frac{\partial z}{\partial y}\cdot \frac{\partial y}{\partial r}+\frac{\partial z}{\partial w}\cdot \frac{\partial w}{\partial r}+\frac{\partial z}{\partial s}\cdot \frac{\partial s}{\partial r}\]
Exemplo 3.6: Seja a função \(w={{x}^{2}}+{{y}^{2}}+z\), para a qual se tem que \(x=r\cdot sen~\theta \), \(y=r\cdot cos~\gamma \) e \(z=r\theta \gamma \), encontre as derivadas parciais de \(z\).
Solução
Para esse caso, temos uma equação \(z\) com três variáveis, sendo que cada uma é uma função de outras três variáveis. Então, de acordo com o que foi enunciado na definição 8, tem-se \(n=m=3\), as quais podem ser identificadas como \({{x}_{1}}=x\), \({{x}_{2}}=y\) e \({{x}_{3}}=z\) e \({{t}_{1}}=r\), \({{t}_{2}}=\theta \) e \({{t}_{3}}=\gamma \).
Precisamos, então, encontrar \(\partial w/\partial r\), \(\partial w/\partial \theta \) e \(\partial w/\partial \gamma \) utilizando a equação (28). Para \(r\), tem-se:
\[\frac{\partial w}{\partial r}=\frac{\partial w}{\partial x}\cdot \frac{\partial x}{\partial r}+\frac{\partial w}{\partial y}\cdot \frac{\partial y}{\partial r}+\frac{\partial w}{\partial z}\cdot \frac{\partial z}{\partial r}\]
Para \(\theta \):
\[\frac{\partial w}{\partial \theta }=\frac{\partial w}{\partial x}\cdot \frac{\partial x}{\partial \theta }+\frac{\partial w}{\partial y}\cdot \frac{\partial y}{\partial \theta }+\frac{\partial w}{\partial z}\cdot \frac{\partial z}{\partial \theta }\]
E para \(\gamma \):
\[\frac{\partial w}{\partial \gamma }=\frac{\partial w}{\partial x}\cdot \frac{\partial x}{\partial \gamma }+\frac{\partial w}{\partial y}\cdot \frac{\partial y}{\partial \gamma }+\frac{\partial w}{\partial z}\cdot \frac{\partial z}{\partial \gamma }\]
Temos, então, todas as três derivadas parciais para a função indicada. Agora, podemos avaliá-las. Para facilitar, vamos avaliar, antes, as derivadas parciais que aparecem nas equações que encontramos.
\[\frac{\partial w}{\partial x}=2x=2r\cdot sen~\theta ~~~~\frac{\partial w}{\partial y}=2y=2r\cdot cos~\gamma ~~~~\frac{\partial w}{\partial z}=1\]
\[\frac{\partial x}{\partial r}=sen~\theta ~~~~~~\frac{\partial x}{\partial \theta }=r\cdot cos~\theta ~~~~~~\frac{\partial x}{\partial \gamma }=0\]
\[\frac{\partial y}{\partial r}=cos~\gamma ~~~~~~\frac{\partial y}{\partial \theta }=0~~~~~~\frac{\partial y}{\partial \gamma }=-r\cdot sen~\gamma \]
\[\frac{\partial z}{\partial r}=\theta \gamma ~~~~~~\frac{\partial z}{\partial \theta }=r\gamma ~~~~~~\frac{\partial z}{\partial \gamma }=r\theta \]
Basta, então, substituir as derivadas acima nas equações encontradas. Para \(\partial w/\partial r\):
\[\frac{\partial w}{\partial r}=\frac{\partial w}{\partial x}\cdot \frac{\partial x}{\partial r}+\frac{\partial w}{\partial y}\cdot \frac{\partial y}{\partial r}+\frac{\partial w}{\partial z}\cdot \frac{\partial z}{\partial r}\]
\[\frac{\partial w}{\partial r}=\left( 2r\cdot sen~\theta \right)\cdot \left( sen~\theta \right)+\left( 2r\cdot cos~\gamma \right)\cdot \left( cos~\gamma \right)+\left( 1 \right)\cdot \left( \theta \gamma \right)\]
\[\frac{\partial w}{\partial r}=2r\cdot {{\left( sen~\theta \right)}^{2}}+2r\cdot {{\left( cos~\gamma \right)}^{2}}+\theta \gamma \]
Para \(\partial w/\partial \theta \):
\[\frac{\partial w}{\partial \theta }=\frac{\partial w}{\partial x}\cdot \frac{\partial x}{\partial \theta }+\frac{\partial w}{\partial y}\cdot \frac{\partial y}{\partial \theta }+\frac{\partial w}{\partial z}\cdot \frac{\partial z}{\partial \theta }\]
\[\frac{\partial w}{\partial \theta }=\left( 2r\cdot sen~\theta \right)\cdot \left( r\cdot cos~\theta \right)+\left( 2r\cdot cos~\gamma \right)\cdot \left( 0 \right)+\left( 1 \right)\cdot \left( r\gamma \right)\]
\[\frac{\partial w}{\partial \theta }=2{{r}^{2}}\cdot sen~\theta \cdot cos~\gamma +r\gamma \]
Para \(\partial w/\partial \gamma \):
\[\frac{\partial w}{\partial \gamma }=\frac{\partial w}{\partial x}\cdot \frac{\partial x}{\partial \gamma }+\frac{\partial w}{\partial y}\cdot \frac{\partial y}{\partial \gamma }+\frac{\partial w}{\partial z}\cdot \frac{\partial z}{\partial \gamma }\]
\[\frac{\partial w}{\partial \gamma }=\left( 2r\cdot sen~\theta \right)\cdot \left( 0 \right)+\left( 2r\cdot cos~\gamma \right)\cdot \left( -r\cdot sen~\gamma \right)+\left( 1 \right)\cdot \left( r\theta \right)\]
\[\frac{\partial w}{\partial \gamma }=-2{{r}^{2}}\cdot sen~\gamma \cdot cos~\gamma +r\theta \]
A regra da cadeia pode parecer um processo complexo e de dificuldade considerável para se avaliar derivadas de funções compostas, visto que você pode reescrever a função substituindo suas variáveis intermediárias. Qual, então, é o sentido em desenvolver toda essa teoria sobre a regra da cadeia?

Você foi convidado para analisar a pressão \(P\) de um gás ideal em um experimento laboratorial, cuja reação ocorre em um recipiente esférico de volume \(V=\frac{4}{3}\pi {{r}^{3}}\). Para tal, você identificou que a temperatura da reação varia com o tempo de reação \(t\), a posição radial no recipiente $r$ de acordo com a relação \(T=70-t\cdot ln~r\) e o número de mols na reação depende linearmente do tempo de reação de acordo com a relação \(n=0,2t\). Sabendo que a pressão de um gás ideal se comporta de acordo com a equação dos gases ideais, apresentada a seguir, analise as alternativas e assinale a correta. O valor \(R\) é uma constante.
Essa função \(P\) pode ser completamente analisada com no mínimo 3 derivadas parciais.
Justificativa: Essa função apresenta três variáveis intermediárias (\(n\), \(T\) e \(V\)), que são funções apenas de \(t\) e \(r\). Logo, essa função pode ser reescrita apresentando apenas duas variáveis, o que faz com que ela possa ser analisada com um mínimo de 2 derivadas parciais.
A derivada parcial de \(P\) em relação ao tempo é:
\[\frac{\partial P}{\partial t}=\frac{3R}{2\pi {{r}^{3}}}\left[ 7-0,2t\cdot ln~r \right]\]
Justificativa correta: Para encontrar essa derivada, aplicando a definição 8, você encontrará que:
\[\frac{\partial P}{\partial t}=\frac{\partial P}{\partial n}\cdot \frac{\partial n}{\partial t}+\frac{\partial P}{\partial T}\cdot \frac{\partial T}{\partial t}+\frac{\partial P}{\partial V}\cdot \frac{\partial V}{\partial t}\]
Pelas informações dadas, você tem:
\[\frac{\partial P}{\partial n}=\frac{RT}{V}~~~~\frac{\partial P}{\partial T}=\frac{nR}{V}~~~~\frac{\partial P}{\partial V}=\frac{-nRT}{{{V}^{2}}}~~~~\frac{\partial n}{\partial t}=0,2~~~~\frac{\partial T}{\partial t}=-ln~r~~~~\frac{\partial V}{\partial t}=0~\]
Logo:
\[\frac{\partial P}{\partial t}=\left( \frac{RT}{V} \right)\cdot \left( 0,2 \right)+\left( \frac{nR}{V} \right)\cdot \left( -ln~r \right)+\left( \frac{-nRT}{{{V}^{2}}} \right)\cdot \left( 0 \right)=\frac{R}{V}\left( 0,2T-n\cdot ln~r \right)\]
\[=\frac{3R}{4\pi {{r}^{3}}}\left[ 14-0,2t\cdot ln~r-0,2t\cdot ln~r \right]=\frac{3R}{2\pi {{r}^{3}}}\left[ 7-0,2t\cdot ln~r \right]\]
A derivada parcial de \(P\) em relação ao tempo \(t\) é \(\frac{\partial P}{\partial t}=\frac{21R}{2\pi {{r}^{3}}}\)
Justificativa: Para encontrar essa derivada, aplicando a definição 8, você encontrará que:
\[\frac{\partial P}{\partial t}=\frac{\partial P}{\partial n}\cdot \frac{\partial n}{\partial t}+\frac{\partial P}{\partial T}\cdot \frac{\partial T}{\partial t}+\frac{\partial P}{\partial V}\cdot \frac{\partial V}{\partial t}\]
Pelas informações dadas, você tem:
\[\frac{\partial P}{\partial n}=\frac{RT}{V}~~~~\frac{\partial P}{\partial T}=\frac{nR}{V}~~~~\frac{\partial P}{\partial V}=\frac{-nRT}{{{V}^{2}}}~~~~\frac{\partial n}{\partial t}=0,2~~~~\frac{\partial T}{\partial t}=-ln~r~~~~\frac{\partial V}{\partial t}=0\]
Logo:
\[\frac{\partial P}{\partial t}=\left( \frac{RT}{V} \right)\cdot \left( 0,2 \right)+\left( \frac{nR}{V} \right)\cdot \left( -ln~r \right)+\left( \frac{-nRT}{{{V}^{2}}} \right)\cdot \left( 0 \right)=\frac{R}{V}\left( 0,2T-n\cdot ln~r \right)\]
\[=\frac{3R}{4\pi {{r}^{3}}}\left[ 14-0,2t\cdot ln~r-0,2t\cdot ln~r \right]=\frac{3R}{2\pi {{r}^{3}}}\left[ 7-0,2t\cdot ln~r \right]\]
A derivada parcial de \(P\) em relação ao raio \(r\) é:
\[\frac{\partial P}{\partial r}=-\frac{3Rt}{20\pi {{r}^{4}}}\left[ t\left( 1-ln~r \right)+210 \right]\]
Justificativa: Para encontrar essa derivada, aplicando a definição 8, você encontrará que:
\[\frac{\partial P}{\partial r}=\frac{\partial P}{\partial n}\cdot \frac{\partial n}{\partial r}+\frac{\partial P}{\partial T}\cdot \frac{\partial T}{\partial r}+\frac{\partial P}{\partial V}\cdot \frac{\partial V}{\partial r}\]
Pelas informações dadas, você tem:
\[\frac{\partial P}{\partial n}=\frac{RT}{V}~~~~\frac{\partial P}{\partial T}=\frac{nR}{V}~~~~\frac{\partial P}{\partial V}=\frac{-nRT}{{{V}^{2}}}~~~~\frac{\partial n}{\partial r}=0~~~~\frac{\partial T}{\partial r}=-\frac{t}{r}~~~~\frac{\partial V}{\partial r}=4\pi {{r}^{2}}\]
Logo:
\[\frac{\partial P}{\partial r}=\left( \frac{RT}{V} \right)\cdot \left( 0 \right)+\left( \frac{nR}{V} \right)\cdot \left( -\frac{t}{r} \right)+\left( \frac{-nRT}{{{V}^{2}}} \right)\cdot \left( 4\pi {{r}^{2}} \right)=-\frac{nRt}{Vr}-\frac{4\pi nRT{{r}^{3}}}{{{V}^{2}}}=-\frac{nR}{r{{V}^{2}}}\left( tV+4\pi {{r}^{3}}T \right)\]
\[=-\frac{9Rt}{80{{\pi }^{2}}{{r}^{7}}}\left[ t\frac{4}{3}\pi {{r}^{3}}+4\pi {{r}^{3}}\left( 70-tln~r \right) \right]=-\frac{9Rt}{20\pi {{r}^{4}}}\left[ \frac{t}{3}+\left( 70-tln~r \right) \right]=-\frac{3Rt}{20\pi {{r}^{4}}}\left[ t\left( 1-3ln~r \right)+210 \right]\]
A função \(P\) dada apresenta duas variáveis intermediárias que são funções de três variáveis.
Justificativa: É o oposto: a função \(P\) dada apresenta três variáveis intermediárias, que são funções de duas variáveis.
Agora é o momento de concluirmos os estudos de derivadas de funções com mais de uma variável. Portanto, agora, vamos estudar a derivação implícita de funções com mais de uma variável e, em seguida, aprenderemos como avaliar derivadas parciais de ordem superior.
Ao estudar funções com uma única variável, você se deparou com casos em que uma função \(y=f\left( x \right)\)pode ser expressa de maneira implícita, ou seja, em uma forma \(F\left( x,y \right)=0\). Note que, nessa definição, substituindo \(y=f\left( x \right)\), fará com que você tenha uma identidade (FLEMMING; GONÇALVES, 2005).
Assim, de forma análoga a esta, Flemming e Gonçalves (2005) dizem que uma função \(z=f\left( x,y \right)\) também pode ser representada de forma implícita como \(F\left( x,y,z \right)=0\). Novamente, a substituição de \(z\) por \(f\left( x,y \right)\) faz com que se tenha uma identidade. Um exemplo disso, uma função \(z=\sqrt{{{x}^{3}}+2{{y}^{2}}}\) pode ser escrita implicitamente como \({{x}^{3}}+2{{y}^{2}}-{{z}^{2}}=0\).
Outros casos de funções com mais de uma variável definidas implicitamente mostrados por Flemming e Gonçalves (2005) são o de um sistema de duas equações. O primeiro desses casos é aquele em que se tem duas equações simultâneas, como:
\[\left\{ \begin{matrix} F(x,y,z)=0 \\ G(x,y,z)=0 \\ \end{matrix} \right.\]
Note que esse sistema pode definir implicitamente duas funções de uma variável, \(y=y\left( x \right)\) e \(z=z\left( x \right)\). Já o sistema
\[\left\{ \begin{matrix} F(x,y,u,v)=0 \\ G(x,y,u,v)=0 \\ \end{matrix} \right.\]
pode definir de forma implícita duas funções com duas variáveis, ou seja, \(x=x\left( u,v \right)\) e \(y=y\left( u,v \right)\).
Veja que é possível que funções de mais de uma variável sejam expressas de forma implícita, mas nem sempre é possível escrever uma função implícita de forma explícita. Então, devemos analisar como encontrar derivadas de funções nesse caso. Vejamos os quatro casos de funções implícitas descritas acima.
Iniciaremos nosso estudo com o caso da função $y=f\left( x \right)$, que pode ser definida implicitamente pela função:
\[F\left( x,y \right)=0~~~~~~(29)\]
Se \(f\) e \(F\) forem funções diferenciáveis e no ponto \(\left( x,f\left( x \right) \right)\) tem-se que \(\partial F/\partial y~\ne ~0\), Flemming e Gonçalves (2005) dizem que a derivada \(dy/dx\) pode ser encontrada derivando-se (29) em relação a \(x\) fazendo uso da regra da cadeia:
\[\frac{\partial F}{\partial x}\cdot \frac{dx}{dx}+\frac{\partial F}{\partial y}\cdot \frac{dy}{dx}=0~~~~\to ~~~\frac{\partial F}{\partial x}\cdot 1+\frac{\partial F}{\partial y}\cdot \frac{dy}{dx}=0\]
\[~\frac{dy}{dx}=\frac{-~\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}~~~~(30)\]
Exemplo 4.1: Seja a função de uma circunferência de raio 1 e centro na origem apresentada a seguir, encontre a derivada parcial \(dy/dx\).
\[{{x}^{2}}+{{y}^{2}}=1\]
Solução
Essa função da circunferência é uma função implícita na forma \(F\left( x,y \right)=0\), para a qual se tem \(F\left( x,y \right)={{x}^{2}}+{{y}^{2}}-1\). Apesar de essa função poder ser representada na forma explícita como \(y=\pm \sqrt{1-{{x}^{2}}}\), vamos considerar encontrar a derivada utilizando a técnica de derivação implícita, ou seja, usaremos a Equação (30). Para tal, precisamos de algumas derivadas parciais da função \(F\left( x,y \right)\):
\[\frac{\partial F}{\partial x}=2x~~~~\frac{\partial F}{\partial y}=2y\]
Agora, usando, então, a Equação (30):
\[\frac{dy}{dx}=-\frac{\partial F/\partial x}{\partial F/\partial y}=-\frac{2x}{2y}=-\frac{x}{y}\]
Observe que esse resultado só é válido para \(y~\ne ~0\). Caso deseje comprovar esse resultado, derive a função \(y\) escrita explicitamente acima e compare o resultado encontrado.
Para uma função \(z=f\left( x,y \right)\), definida implicitamente pela função:
\[F\left( x,y,z \right)=0~~~~~~(31)\]
Se \(f\) e \(F\) forem funções diferenciáveis e no ponto \(\left( x,y,f\left( x,y \right) \right)\), tem-se, então, que \(\partial F/\partial z~\ne ~0\). Disso, Flemming e Gonçalves (2005) dizem que as derivadas parciais \(\partial z/\partial x\) e \(\partial z/\partial y\) podem ser encontradas com a regra da cadeia. Assim, derivando (31) em relação a \(x\):
\[\frac{\partial F}{\partial x}\cdot \frac{\partial x}{\partial x}+\frac{\partial F}{\partial y}\cdot \frac{\partial y}{\partial x}+\frac{\partial F}{\partial z}\cdot \frac{\partial z}{\partial x}=0~~~~\to ~~~\frac{\partial F}{\partial x}\cdot 1+\frac{\partial F}{\partial y}\cdot 0+\frac{\partial F}{\partial z}\cdot \frac{\partial z}{\partial x}=0\]
\[\frac{\partial z}{\partial x}=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}}~~~~(32)\]
E derivando (30) em relação a \(x\):
\[\frac{\partial F}{\partial x}\cdot \frac{\partial x}{\partial y}+\frac{\partial F}{\partial y}\cdot \frac{\partial y}{\partial y}+\frac{\partial F}{\partial z}\cdot \frac{\partial z}{\partial y}=0~~~~\to ~~~\frac{\partial F}{\partial x}\cdot 0+\frac{\partial F}{\partial y}\cdot 1+\frac{\partial F}{\partial z}\cdot \frac{\partial z}{\partial y}=0\]
\[\frac{\partial z}{\partial y}=-\frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial z}}~~~~~~(33)\]
Exemplo 4.2: Seja a função \(z=f\left( x,y \right)\) diferenciável e definida pela equação a seguir, encontre as derivadas parciais de \(z\).
\[{{x}^{3}}y+2{{y}^{2}}+{{z}^{3}}+3z=6\]
Solução
Note que essa função \(z\) está definida implicitamente na forma \(F\left( x,y,z \right)=0\), para a qual se tem \(F\left( x,y,z \right)={{x}^{3}}y+2{{y}^{2}}+{{z}^{3}}+3z-6\). Logo, a função \(z\) apresentará as derivadas parciais \(\partial z/\partial x\) e \(\partial z/\partial y\). Para essa função \(F\left( x,y,z \right)\), observe que:
\[\frac{\partial F}{\partial x}=3{{x}^{2}}y~~~~\frac{\partial F}{\partial y}={{x}^{3}}+4y~~~~\frac{\partial F}{\partial z}=3{{z}^{2}}+3\]
Veja que apenas as equações (32) e (33) são necessárias para encontrarmos as derivadas parciais de uma função na forma implícita. Assim, de (32):
\[\frac{\partial z}{\partial x}=-\frac{\partial F/\partial x}{\partial F/\partial z}=-\frac{3{{x}^{2}}y}{3{{z}^{2}}+3}=-\frac{{{x}^{2}}y}{{{z}^{2}}+1}\]
E, de (33):
\[\frac{\partial z}{\partial y}=-\frac{\partial F/\partial y}{\partial F/\partial z}=-\frac{{{x}^{3}}+4y}{3{{z}^{2}}+3}=-\frac{{{x}^{3}}+4y}{3\left( {{z}^{2}}+1 \right)}\]
\[\left\{ \begin{matrix} F(x,y,z)=0 \\ G(x,y,z)=0 \\ \end{matrix} \right.\]
Vejamos o caso de duas funções \(y=y\left( x \right)\) e \(z=z\left( x \right)\) serem definidas de forma implícita por um sistema de duas equações como:
\[\left\{ \begin{matrix} F(x,y,z)=0 \\ G(x,y,z)=0 \\ \end{matrix} \right.~~~~(34)\]
Se \(F\) e \(G\) forem funções diferenciáveis, as derivadas parciais \(dy/dx\) e \(dz/dx\) podem ser encontradas simplesmente derivando (34) em relação a $x$ usando a regra da cadeia. Dessa forma:
\[\left\{ \begin{matrix} \frac{\partial F}{\partial x}.\frac{dx}{dx}+\frac{\partial F}{\partial y}.\frac{dy}{dx}+\frac{\partial F}{\partial z}.\frac{dz}{dx}=0 \\ \frac{\partial G}{\partial x}.\frac{dx}{dx}+\frac{\partial G}{\partial y}.\frac{dy}{dx}+\frac{\partial G}{\partial z}.\frac{dz}{dx}=0 \\ \end{matrix} \right.\]
\[\left\{ \begin{matrix} \frac{\partial F}{\partial y}.\frac{dy}{dx}+\frac{\partial F}{\partial z}.\frac{dz}{dx}=-\frac{\partial F}{\partial x} \\ \frac{\partial G}{\partial y}.\frac{dy}{dx}+\frac{\partial G}{\partial z}.\frac{dz}{dx}=-\frac{\partial G}{\partial x} \\ \end{matrix} \right.~~~~ (35)\]
Observe que o sistema apresentado em (35) é um sistema linear com incógnitas iguais a \(dy/dx\) e \(dz/dx\). De acordo com Flemming e Gonçalves (2005), você pode fazer uso da regra de Cramer para encontrar a solução desse sistema. Com isso, deve encontrar:
\[\frac{dy}{dx}=\frac{\left| \begin{matrix} -\frac{\partial F}{\partial x}~~~~\frac{\partial F}{\partial z} \\ -\frac{\partial G}{\partial x}~~~~\frac{\partial G}{\partial z} \\ \end{matrix} \right|}{\left| \begin{matrix} \frac{\partial F}{\partial y}~~~~\frac{\partial F}{\partial z} \\ \frac{\partial G}{\partial y}~~~~\frac{\partial G}{\partial z} \\ \end{matrix} \right|}=-\frac{\left| \begin{matrix} \frac{\partial F}{\partial x}~~~~\frac{\partial F}{\partial z} \\ \frac{\partial G}{\partial x}~~~~\frac{\partial G}{\partial z} \\ \end{matrix} \right|}{\left| \begin{matrix} \frac{\partial F}{\partial y}~~~~\frac{\partial F}{\partial z} \\ \frac{\partial G}{\partial y}~~~~\frac{\partial G}{\partial z} \\ \end{matrix} \right|}~~~~~~(36)\]
e
\[\frac{dz}{dx}=\frac{\left| \begin{matrix} \frac{\partial F}{\partial y}~~~~-\frac{\partial F}{\partial x} \\ \frac{\partial G}{\partial y}~~~~-\frac{\partial G}{\partial x} \\ \end{matrix} \right|}{\left| \begin{matrix} \frac{\partial F}{\partial y}~~~~\frac{\partial F}{\partial z} \\ \frac{\partial G}{\partial y}~~~~\frac{\partial G}{\partial z} \\ \end{matrix} \right|}=-\frac{\left| \begin{matrix} \frac{\partial F}{\partial y}~~~~\frac{\partial F}{\partial x} \\ \frac{\partial G}{\partial y}~~~~\frac{\partial G}{\partial x} \\ \end{matrix} \right|}{\left| \begin{matrix} \frac{\partial F}{\partial y}~~~~\frac{\partial F}{\partial z} \\ \frac{\partial G}{\partial y}~~~~\frac{\partial G}{\partial z} \\ \end{matrix} \right|}~~~~(37)\]
Os termos entre as barras indicam o determinante da matriz, sendo que os determinantes em (36) e (37) são conhecidos como jacobianos, segundo Flemming e Gonçalves (2005), e você certamente lidará com jacobianos em outros assuntos mais avançados que fazem uso do cálculo.
Exemplo 4.3: Sejam as funções \(y=y\left( x \right)\) e \(z=z\left( x \right)\), em que \(z>0\), diferenciáveis e definidas pelo sistema a seguir. Encontre as derivadas \(dy/dx\) e \(dz/dx\).
\[\left\{ \begin{matrix} {{x}^{2}}+{{y}^{2}}={{z}^{2}} \\ x+y=4 \\ \end{matrix} \right.\]
Solução
Temos um caso semelhante ao descrito pela equação (34), para o qual se tem \(F\left( x,y,z \right)={{x}^{2}}+{{y}^{2}}-{{z}^{2}}\) e \(G\left( x,y,z \right)=x+y-4\). Assim, pode-se avaliar as derivadas pedidas com as equações (36) e (37). Para isso, precisamos de algumas derivadas parciais das funções:
\[\frac{\partial F}{\partial x}=2x~~~~\frac{\partial F}{\partial y}=2y~~~~\frac{\partial F}{\partial z}=-2z\]
\[\frac{\partial G}{\partial x}=1~~~~\frac{\partial G}{\partial y}=1~~~~\frac{\partial G}{\partial z}=0\]
Então, para \(dy/dx\):
\[\frac{dy}{dx}=\frac{\left| \begin{matrix} 2x~~~~-2x \\ 1~~~~~~~~~0 \\ \end{matrix} \right|}{\left| \begin{matrix} 2y~~~~-2z \\ 1~~~~~~~~~0 \\ \end{matrix} \right|}=-1\]
E, para \(dz/dx\):
\[\frac{dy}{dx}=\frac{\left| \begin{matrix} 2x~~~~-2x \\ 1~~~~~~~~~0 \\ \end{matrix} \right|}{\left| \begin{matrix} 2y~~~~-2z \\ 1~~~~~~~~~0 \\ \end{matrix} \right|}=-\frac{2y-2x}{2z}=\frac{x-y}{z}\]
Esta situação é ligeiramente semelhante àquela discutida na seção anterior. Nesse caso, considere que as funções \(x=x\left( u,v \right)\) e \(y=y\left( u,v \right)\) são definidas implicitamente pelo sistema apresentado em (38):
\[\left\{ \begin{matrix} F(x,y,u,v)=0 \\ G(x,y,u,v)=0 \\ \end{matrix} \right.~~~~(38)\]
Se as funções \(F\) e \(G\) forem diferenciáveis, as derivadas parciais \(\partial x/\partial u\), \(\partial x/\partial v\), \(\partial y/\partial u\) e \(\partial y/\partial v\) podem ser encontradas aplicando a regra da cadeia em (38). Então, mantendo a variável \(v\) como uma constante e tomando a derivada em relação a \(u\):
\[\left\{ \begin{matrix} \frac{\partial F}{\partial x}.\frac{\partial x}{\partial u}+\frac{\partial F}{\partial y}.\frac{\partial y}{\partial u}+\frac{\partial F}{\partial u}.\frac{\partial u}{\partial u}+\frac{\partial F}{\partial v}.\frac{\partial v}{\partial u}=0 \\ \frac{\partial G}{\partial x}.\frac{\partial x}{\partial u}+\frac{\partial G}{\partial y}.\frac{\partial y}{\partial u}+\frac{\partial G}{\partial u}.\frac{\partial u}{\partial u}+\frac{\partial G}{\partial v}.\frac{\partial v}{\partial u}=0 \\ \end{matrix} \right.\]
Note que no sistema acima tem-se \(\partial u/\partial u=1\) e \(\partial v/\partial u=0\). Então:
\[\left\{ \begin{matrix} \frac{\partial F}{\partial x}.\frac{\partial x}{\partial u}+\frac{\partial F}{\partial y}.\frac{\partial y}{\partial u}=-\frac{\partial F}{\partial u} \\ \frac{\partial G}{\partial x}.\frac{\partial x}{\partial u}+\frac{\partial G}{\partial y}.\frac{\partial y}{\partial u}=-\frac{\partial G}{\partial u} \\ \end{matrix} \right. ~~~~(39)\]
Novamente, o sistema apresentado em (39) é um sistema linear com incógnitas iguais a \(\partial x/\partial u\) e \(\partial y/\partial u\). Usando, então, a regra de Cramer:
\[\frac{\partial x}{\partial u}=-\frac{\left| \begin{matrix} \frac{\partial F}{\partial u}~~~~\frac{\partial F}{\partial y} \\ \frac{\partial G}{\partial u}~~~~\frac{\partial G}{\partial y} \\\end{matrix} \right|}{\left| \begin{matrix} \frac{\partial F}{\partial x}~~~~\frac{\partial F}{\partial y} \\ \frac{\partial G}{\partial x}~~~~\frac{\partial G}{\partial y} \\ \end{matrix} \right|}~~~~e~~~~\frac{\partial y}{\partial u}=-\frac{\left| \begin{matrix} \frac{\partial F}{\partial x}~~~~\frac{\partial F}{\partial u} \\ \frac{\partial G}{\partial x}~~~~\frac{\partial G}{\partial u} \\ \end{matrix} \right|}{\left| \begin{matrix} \frac{\partial F}{\partial x}~~~~\frac{\partial F}{\partial y} \\ \frac{\partial G}{\partial x}~~~~\frac{\partial G}{\partial y} \\ \end{matrix} \right|}~~~~(40)\]
Lembre-se que (40) é válida para numeradores não nulos. Tanto quanto no caso da seção "Derivando as Funções", temos um jacobiano como resultado. Fazendo um processo análogo a este, mas mantendo agora a variável \(u\) constante, você encontrará:
\[\frac{\partial x}{\partial v}=-\frac{\left| \begin{matrix} \frac{\partial F}{\partial v}~~~~\frac{\partial F}{\partial y} \\ \frac{\partial G}{\partial v}~~~~\frac{\partial G}{\partial y} \\ \end{matrix} \right|}{\left| \begin{matrix} \frac{\partial F}{\partial x}~~~~\frac{\partial F}{\partial y} \\ \frac{\partial G}{\partial x}~~~~\frac{\partial G}{\partial y} \\\end{matrix} \right|}~~~~e~~~~\frac{\partial y}{\partial u}=-\frac{\left| \begin{matrix} \frac{\partial F}{\partial x}~~~~\frac{\partial F}{\partial v} \\ \frac{\partial G}{\partial x}~~~~\frac{\partial G}{\partial v} \\ \end{matrix} \right|}{\left| \begin{matrix} \frac{\partial F}{\partial x}~~~~\frac{\partial F}{\partial y} \\ \frac{\partial G}{\partial x}~~~~\frac{\partial G}{\partial y} \\ \end{matrix} \right|}~~~~(41)\]
Exemplo 4.4: Sejam as funções \(x=x\left( u,v \right)\) e \(y=y\left( u,v \right)\) diferenciáveis, definidas pelo sistema a seguir, encontre as derivadas parciais de \(x\) e \(y\) em relação a \(u\) e \(v\).
\[\left\{ \begin{matrix} {{x}^{2}}-2u-2v=0 \\ y-2u+v=0 \\ \end{matrix} \right.\]
Solução
Para esse sistema, tem-se que \(F\left( x,y,u,v \right)={{x}^{2}}-2u-2v\) e \(G\left( x,y,u,v \right)=y-2u+v\). As derivadas pedidas podem ser encontradas com as equações (40) e (41). Para isso, precisamos de algumas derivadas parciais das funções:
\[\frac{\partial F}{\partial x}=2x~~~~\frac{\partial F}{\partial y}=0~~~~\frac{\partial F}{\partial u}=-2~~~~\frac{\partial F}{\partial v}=-2\]
\[\frac{\partial G}{\partial x}=0~~~~\frac{\partial G}{\partial y}=1~~~~\frac{\partial G}{\partial u}=-2~~~~\frac{\partial G}{\partial v}=1\]
Então, para \(\partial x/\partial u\) e \(\partial y/\partial u\), de (40):
\[\frac{\partial x}{\partial u}=\frac{\left| \begin{matrix} -2~~~~0 \\ -2~~~~1 \\ \end{matrix} \right|}{\left| \begin{matrix} 2x~~~~0 \\ 0~~~~~~1 \\ \end{matrix} \right|}=-\frac{-2-0}{2x-0}=\frac{1}{x}~~~~e~~~~\frac{\partial y}{\partial u}=-\frac{\left| \begin{matrix} 2x~~~~-2 \\ 0~~~~~~-2 \\ \end{matrix} \right|}{\left| \begin{matrix} 2x~~~~0 \\ 0~~~~~~1 \\ \end{matrix} \right|}=-\frac{-4x-0}{2x-0}=2\]
Agora, para \(\partial x/\partial v\) e \(\partial y/\partial v\), de (41):
\[\frac{\partial x}{\partial v}=\frac{\left| \begin{matrix} -2~~~~0 \\ ~~1~~~~~~1 \\ \end{matrix} \right|}{\left| \begin{matrix} 2x~~~~0 \\ 0~~~~~~1 \\ \end{matrix} \right|}=-\frac{-2-0}{2x-0}=\frac{1}{x}~~~~e~~~~\frac{\partial y}{\partial v}=-\frac{\left| \begin{matrix} 2x~~~~-2 \\ 0~~~~~~1 \\ \end{matrix} \right|}{\left| \begin{matrix} 2x~~~~0 \\ 0~~~~~~1 \\ \end{matrix} \right|}=-\frac{2x-0}{2x-0}=1\]
Após todo o desenvolvimento teórico sobre as derivadas de primeira ordem, você certamente estudou o caso de tomar a derivada de uma função mais de uma vez, gerando derivadas de ordens superiores. Esse procedimento também pode ser expandido para o caso das funções com mais de uma variável.
Segundo Stewart (2017b), se uma função \(z=f\left( x,y \right)\) é diferenciável, então, suas derivadas parciais de 1ª ordem também devem ser funções de duas variáveis, ou seja, \(\partial f/\partial x={{f}_{x}}\left( x,y \right)\) e \(\partial f/\partial y={{f}_{y}}\left( x,y \right)\). Logo, nada nos impede de tomar uma nova derivada dessas funções em relação a uma de suas variáveis. Essa derivada parcial de uma derivada parcial de 1ª ordem é chamada derivada parcial de 2ª ordem.
Para uma função \(z=f\left( x,y \right)\), pode-se ter quatro derivadas parciais de 2ª ordem, pois as derivadas parciais de 1ª ordem podem ser derivadas em relação a qualquer uma de suas variáveis, ou seja, pode-se derivar \(\partial f/\partial x\) em relação a \(x\) ou \(y\), assim como \(\partial f/\partial y\) também pode ser derivada em relação a \(x\) ou \(y\). Essas derivadas de 2ª ordem podem ser representadas das seguintes formas:
\[\frac{\partial }{\partial x}\left( \frac{\partial f}{\partial x} \right)=\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=\frac{{{\partial }^{2}}z}{\partial {{x}^{2}}}={{\left( {{f}_{x}} \right)}_{x}}={{f}_{xx}}={{f}_{11}}\]
\[\frac{\partial }{\partial y}\left( \frac{\partial f}{\partial x} \right)=\frac{{{\partial }^{2}}f}{\partial y\partial x}=\frac{{{\partial }^{2}}z}{\partial y\partial x}={{\left( {{f}_{x}} \right)}_{y}}={{f}_{xy}}={{f}_{12}}\]
\[\frac{\partial }{\partial y}\left( \frac{\partial f}{\partial y} \right)=\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=\frac{{{\partial }^{2}}z}{\partial {{y}^{2}}}={{\left( {{f}_{y}} \right)}_{y}}={{f}_{yy}}={{f}_{22}}\]
\[\frac{\partial }{\partial x}\left( \frac{\partial f}{\partial y} \right)=\frac{{{\partial }^{2}}f}{\partial x\partial y}=\frac{{{\partial }^{2}}z}{\partial x\partial y}={{\left( {{f}_{y}} \right)}_{x}}={{f}_{yx}}={{f}_{21}}\]
Nessas notações, observe que \({{f}_{xy}}\) significa que você deve derivar primeiro em relação à variável \(x\) e, depois, em relação à variável \(y\). De modo análogo, para a notação \({{f}_{yx}}\), significa que você deve derivar, primeiro, em relação à variável \(y\), e, depois, em relação à variável \(x\).
Exemplo 4.5: Determine as derivadas parciais de 2ª ordem da função a seguir.
\(f\left( x,y \right)=2{{x}^{4}}y-{{x}^{3}}{{y}^{2}}+x{{y}^{3}}\)
Solução
Primeiro, você deve avaliar as derivadas parciais de 1ª ordem da função indicada:
\[\frac{\partial f}{\partial x}=8{{x}^{3}}y-3{{x}^{2}}{{y}^{2}}+{{y}^{3}}\]
\[\frac{\partial f}{\partial y}=2{{x}^{4}}-2{{x}^{3}}y+3x{{y}^{2}}\]
Agora, podemos encontrar as derivadas de 2ª ordem. Derivando \(\partial f/\partial x\) em relação a \(x\):
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=\frac{\partial }{\partial x}\left( 8{{x}^{3}}y-3{{x}^{2}}{{y}^{2}}+{{y}^{3}} \right)=24{{x}^{2}}y-6x{{y}^{2}}\]
E em relação a \(y\):
\[\frac{{{\partial }^{2}}f}{\partial y\partial x}=\frac{\partial }{\partial y}\left( 8{{x}^{3}}y-3{{x}^{2}}{{y}^{2}}+{{y}^{3}} \right)=8{{x}^{3}}-6{{x}^{2}}y+3{{y}^{2}}\]
Finalmente, derivando \(\partial f/\partial y\) em relação a \(x\):
\[\frac{{{\partial }^{2}}f}{\partial x\partial y}=\frac{\partial }{\partial x}\left( 2{{x}^{4}}-2{{x}^{3}}y+3x{{y}^{2}} \right)=8{{x}^{3}}-6{{x}^{2}}y+3{{y}^{2}}\]
E em relação a \(y\):
\[\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=\frac{\partial }{\partial y}\left( 2{{x}^{4}}-2{{x}^{3}}y+3x{{y}^{2}} \right)=-2{{x}^{3}}+6xy\]
Note que, no Exemplo 4.5, as derivadas \({{f}_{xy}}\) e \({{f}_{yx}}\) são iguais. Segundo Stewart (2017b), isso não é simples coincidência, é algo corriqueiro para diversas funções. O matemático francês Alexis Clairaut (1713-1765) enunciou um teorema que fornece condições para identificar se as derivadas \({{f}_{xy}}\) e \({{f}_{yx}}\) serão iguais em uma função:
Teorema de Clairaut: seja a função \(f\) definida em uma bola aberta \(A\), que contenha o ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\). Se as funções \({{f}_{xy}}\) e \({{f}_{yx}}\) forem contínuas em \(D\), então \({{f}_{xy}}\left( {{x}_{0}},{{y}_{0}} \right)={{f}_{yx}}\left( {{x}_{0}},{{y}_{0}} \right)\)(STEWART, 2017b).
Flemming e Gonçalves (2005) apresentam uma definição semelhante a essa, conhecida como teorema de Schwarz, que leva à mesma conclusão do teorema de Clairaut. Também é comum que esse teorema seja enunciado como teorema de Clairaut-Schwarz.
Cabe dizer, também, que você pode continuar derivando funções quantas vezes você quiser, obtendo, assim, derivadas parciais de ordem superior. O procedimento para se encontrar essas derivadas parciais de ordem superior é o mesmo descrito para se encontrar as derivadas parciais de 2ª ordem.
A derivação implícita é um tipo de derivação que algumas pessoas apresentam certa dificuldade em lidar. Visando praticar esse assunto e melhor fixá-lo, considere as funções a seguir, e analise as alternativas e assinale a correta.
\[{{x}^{2}}{{y}^{2}}+ln~xy+{{z}^{3}}=8\]
\[6{{x}^{3}}+2{{y}^{4}}=36\]
\[{{x}^{2}}z+ln~{{x}^{4}}y+xy{{z}^{2}}=0\]
A derivada parcial \(\partial z/\partial x\) da função I é igual a \(-\frac{2{{x}^{2}}y+1/x}{3{{z}^{2}}}\).
Justificativa: A função I pode ser escrita como \(F\left( x,y,z\right)={{x}^{2}}{{y}^{2}}+ln~xy+{{z}^{3}}-8\), para a qual se tem que \(\partial F/\partial x=2x{{y}^{2}}+1/x\) e \(\partial F/\partial z=3{{z}^{2}}\). Logo, porser uma função implícita, a derivada \(\partial z/\partial x\) será igual a:
\[\frac{\partial z}{\partial x}=-\frac{\partial F/\partial x}{\partial F/\partial z}=-\frac{2x{{y}^{2}}+1/x}{3{{z}^{2}}}\]
A derivada parcial \(\partial z/\partial x\) da função III é igual a \(-\frac{2xz+y{{z}^{2}}+4/x}{{{x}^{2}}+xyz}\).
Justificativa correta: A função III pode ser escrita como \(F\left( x,y,z \right)={{x}^{2}}z+ln~{{x}^{4}}y+xy{{z}^{2}}\), para a qual se tem que \(\partial F/\partial x=2xz+y{{z}^{2}}+4/x\) e \(\partial F/\partial z={{x}^{2}}+xyz\). Logo, por ser uma função implícita, a derivada \(\partial z/\partial x\) será igual a:
\[\frac{\partial z}{\partial x}=-\frac{\partial F/\partial y}{\partial F/\partial z}=-\frac{2xz+y{{z}^{2}}+4/x}{{{x}^{2}}+xyz}\]
A derivada parcial \(\partial z/\partial y\) da função I é igual a \(-\frac{2x{{y}^{2}}+1/y}{3{{z}^{2}}}\).
Justificativa: A função I pode ser escrita como \(F\left( x,y,z \right)={{x}^{2}}{{y}^{2}}+ln~xy+{{z}^{3}}-8\), para a qual se tem que \(\partial F/\partial y=2{{x}^{2}}y+1/y\) e \(\partial F/\partial z=3{{z}^{2}}\). Logo, por ser uma função implícita, a derivada \(\partial z/\partial y\) será igual a:
\[\frac{\partial z}{\partial x}=-\frac{\partial F/\partial y}{\partial F/\partial z}=-\frac{2{{x}^{2}}y+1/y}{3{{z}^{2}}}\]
A derivada parcial \(dy/dx\) da função II é igual a \(-\frac{9{{x}^{2}}}{8{{z}^{3}}}\).
Justificativa: A função II pode ser escrita como \(F\left( x,y \right)=6{{x}^{3}}+2{{y}^{4}}-36\), para a qual se tem que \(\partial F/\partial x=18{{x}^{2}}\) e \(\partial F/\partial y=8{{y}^{3}}\). Logo, por ser uma função implícita, a derivada \(dy/dx\) será igual a:
\[\frac{dy}{dx}=-\frac{\partial F/\partial x}{\partial F/\partial y}=-\frac{18{{x}^{2}}}{8{{y}^{3}}}=-\frac{9{{x}^{2}}}{4{{y}^{3}}}\]
A derivada parcial \(\partial z/\partial y\) da função III é igual a \(-\frac{x{{z}^{2}}+1/{{y}^{2}}}{{{x}^{2}}+xyz}\).
Justificativa: A função III pode ser escrita como \(F\left( x,y,z \right)={{x}^{2}}z+ln~{{x}^{4}}y+xy{{z}^{2}}\), para a qual se tem que \(\partial F/\partial y=x{{z}^{2}}+1/y\) e \(\partial F/\partial z={{x}^{2}}+xyz\). Logo, por ser uma função implícita, a derivada \(\partial z/\partial y\) será igual a:
\[\frac{\partial z}{\partial x}=-\frac{\partial F/\partial y}{\partial F/\partial z}=-\frac{x{{z}^{2}}+1/y}{{{x}^{2}}+xyz}\]
Nome do livro: Cálculo B: funções de várias variáveis, integrais múltiplas, integrais curvilíneas e de superfície
Editora: Makron Books
Autor: FLEMMING, D. M.; GONÇALVES, M. B.
ISBN: 9788576051169
Comentário: O livro apresenta explicações extremamente benfeitas e com diversos exemplos, inclusive gráficos. Livro de apoio muito bom e focado no estudo de funções de mais de uma variável.
