O objeto central de estudos do Cálculo são as funções. Ao iniciar seus estudos de Cálculo, você, caro(a) aluno(a), certamente você já estudou o que são funções com uma única variável, quais suas características e como aplicá-las de forma adequada nos mais diferentes tipos de problemas.
Mas as funções de uma variável têm um uso limitado, sendo muito comum que você, estudante, precise lidar com funções mais complexas, que apresentam mais de uma variável. Sendo assim, a presente Unidade visa fundamentar as bases que você precisará para trabalhar com tais funções de várias variáveis. Logo, inicialmente será apresentada uma base sobre os espaços dimensionais antes de comentarmos sobre as funções de n variáveis, o que facilitará sua compreensão sobre as funções mais complexas. Após essa base ser firmada, partiremos para o estudo do Cálculo, efetivamente, em que veremos limites e continuidade dessas funções de n variáveis.
Ao iniciar seus estudos em Cálculo, você, estudante, certamente foi apresentado a determinadas grandezas conhecidas como variáveis, sendo, inclusive, um dos focos do Cálculo, realizar análises de como uma variável irá se relacionar com outra variável. Cabe aqui, então, realizar uma nova abordagem desses conceitos, de modo a expandirmos esses conhecimentos prévios que você já apresenta.
Primeiramente, considere apenas uma variável \(x\) qualquer. Uma variável qualquer simplesmente indica um valor qualquer, segundo Thomas Júnior (2016). Assim, quando temos apenas uma variável em mãos, pouco podemos fazer, além de observar os valores, visto que com apenas um conjunto de números, não podemos relacionar estes com nada. Assim, como cada variável pode ser representada simplesmente como um ponto, podemos dizer que o conjunto de valores de uma variável é um espaço unidimensional, de modo que um valor de uma variável pode ser representado simplesmente como um valor, por exemplo, \(x\) (MORETTIN; HAZZAN; BUSSAB, 2016).
O estudo de variáveis solitárias não é de interesse prático para diversas áreas da ciência. Durante seus estudos de Cálculo, você se deparou com situações e problemas de funções, que, segundo Stewart (2017a), são uma lei que associa um único elemento \(y\) a cada elemento \(x\) de um determinado conjunto, chamado domínio da função. Ou seja, uma função é uma regra que associa as variáveis \(x\) do domínio com um único valor \(y\), sendo o conjunto de todos os valores possíveis de \(y\) chamado de imagem. De forma geral, as variáveis \(x\) do domínio são chamadas variáveis independentes e as variáveis \(y\) da imagem são chamadas variáveis dependentes.
Assim, os problemas com os quais você lidou ao estudar Cálculo eram do tipo \(y=f\left( x \right)\). Resolvendo problemas desse tipo, uma das maneiras para representar a resposta obtida é na forma de um par ordenado \(\left( x,y \right)\). Note que, ao trabalharmos com uma função \(y=f\left( x \right)\), estamos, de fato, lidando com a observação simultânea de duas variáveis, conforme Morettin, Hazzan e Bussab (2016). Por isso, tais problemas podem ser tratados como a análise de um espaço bidimensional.
No entanto, você certamente já deve ter imaginado que os estudos de uma função não devem se limitar ao caso da observação simultânea de apenas duas variáveis. Granville, Smith e Longley (1986) indicam exemplos simples de funções com mais de uma variável, tirados da geometria espacial, como:
a. ao avaliar o volume de um cilindro, você utiliza a função \(V_{cil}=\pi{r}^{2}h\), ou seja, o volume é função tanto da altura quanto do raio do objeto;
b. a área de um triângulo ABC qualquer pode ser calculada em função do seno de um de seus ângulos segundo a função. \(A=\frac{1}{2}ab~sen~\alpha\) , em que a e b são dois lados do triângulo e α é o ângulo entre estes lados. Logo, a função área de um triângulo pode ser expressa como uma função de três variáveis.
Além disso, funções podem ser empregadas na modelagem matemática de fenômenos. Logo, você já deve ter percebido que os estudos de uma função não devem se limitar ao caso da observação simultânea de apenas duas variáveis. Certamente, você consegue imaginar que fenômenos mais complexos podem apresentar mais de uma variável independente.
Agora é o momento de estudarmos casos de funções com mais de uma variável. Antes de partirmos para o estudo das funções mais complexas, iremos, primeiramente, trabalhar um pouco com as dimensões de diferentes espaços.
Segundo Leithold (1994), o conjunto de todos os números inteiros, racionais e irracionais é conhecido como conjunto dos números reais, sendo representado pelo símbolo \(\Re\) ou ℝ. Esse conjunto será o foco do desenvolvimento desta unidade.
Quando tomamos dois números reais e os representamos em uma ordem pertinente, temos um par ordenado. Assim, sendo \(x\) e \(y\) números reais, o par \(\left( x,y \right)\) representa um par ordenado real. É imprescindível que você note a importância da ordem em que se representa os elementos num par ordenado: o par \(\left( x,y \right)\) é diferente do par \(\left( y,x \right)\), mesmo que ambos pares sejam formados pelos mesmos números reais (MORETTIN; HAZZAN; BUSSAB, 2016).
Agora, assim como foi feito com os números reais, você também pode considerar todos os pares ordenados reais arranjados em um conjunto. Tal conjunto formado por todos os pares ordenados reais é conhecido como espaço bidimensional. Como um par ordenado real contém dois elementos do conjunto dos números reais, o espaço bidimensional pode ser representado por ℝ x ℝ. ou simplesmente por ℝ². Numa notação matemática mais correta, esse conjunto é representado da seguinte maneira:
\[{{\mathbb{R}}^{2}}=\left\{ \left( a,b \right)|a,b\in \mathbb{R} \right\}~~~~~~~~(1)\]
Morettin, Hazzan e Bussab (2016) indicam que os elementos do espaço bidimensional também podem ser representados geometricamente, com o uso do plano cartesiano. Em tal representação, o primeiro elemento do par ordenado indica um valor da abscissa, ou seja, do eixo horizontal do plano cartesiano, enquanto o segundo elemento do par ordenado indica um valor do eixo das ordenadas, ou seja, do eixo vertical do plano cartesiano. Logo, um par ordenado pode ser visto simplesmente como a determinação de um ponto no plano cartesiano, tal qual a Figura 1.1 ilustra.
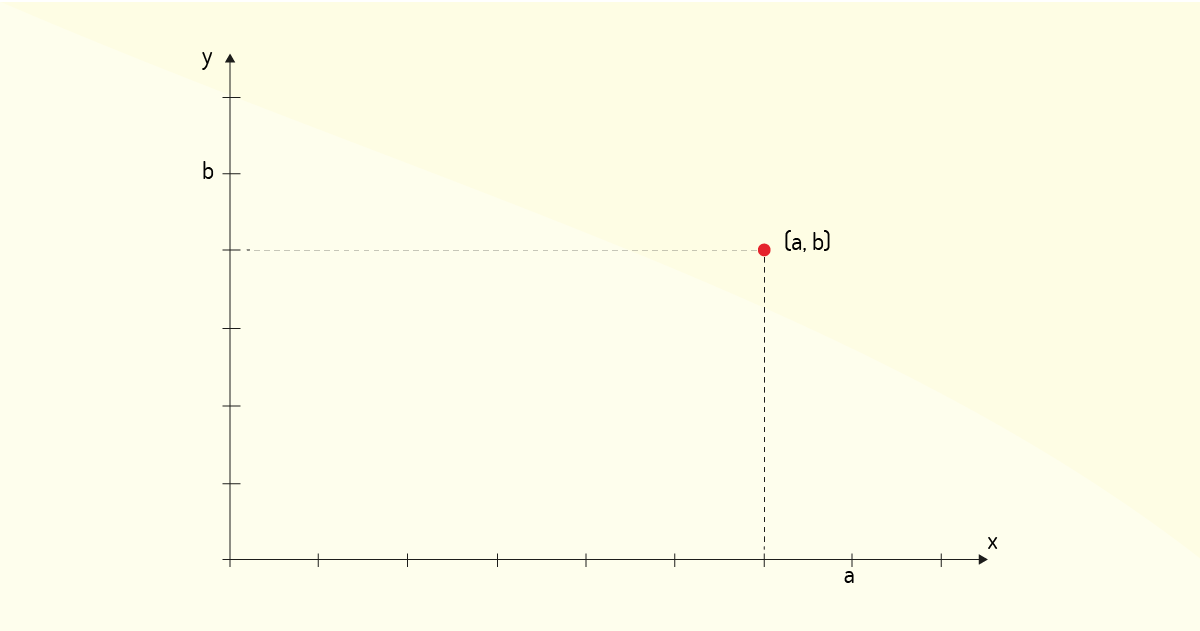
Logo, como foi apresentado na Figura 1.1, a convenção de representação de um par ordenado indica, primeiro, a abcissa, depois, apresenta o valor das ordenadas.
Outro destaque de Morettin, Hazzan e Bussab (2016) se dá ao fato de que uma função pode ser facilmente representada na forma de um conjunto de pares ordenados. Ou seja, uma função pode ser representada por um subconjunto de ℝ\(^2\) por meio de uma relação binária ou relação no ℝ\(^2\). Por exemplo, a função \(y=f\left( x \right)=x+2\) pode ser representada pelo conjunto de pares ordenados na forma \(\left( x,x+2 \right)\), para qualquer valor de \(x\in \mathbb{R}\). Ou seja, a função \(y=f\left( x \right)\) indicada pode ser representada por um conjunto \(Y=\left\{ \left( x,y \right)\in \mathbb{R}|y=x+2 \right\}\), sendo \(Y\) um subconjunto do espaço bidimensional. Geometricamente, este subconjunto \(Y\) é apresentado na Figura 1.2, em que se pode ver três pontos destacados.
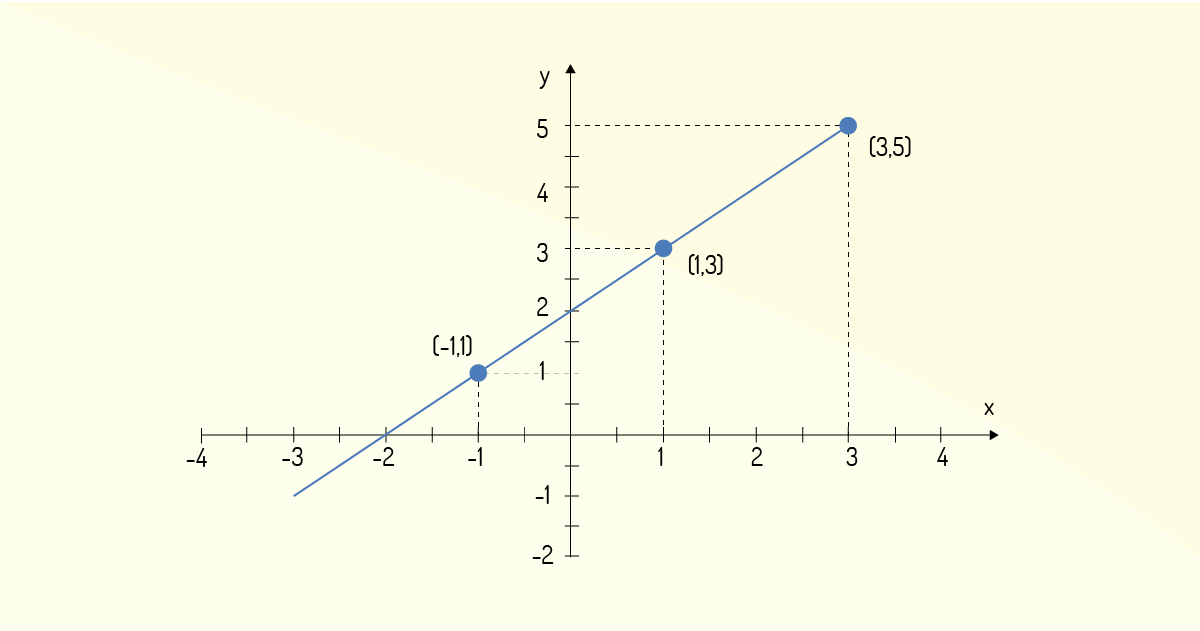
Morettin, Hazzan e Bussab (2016) ainda apresentam a seguinte conclusão: seja a função definida por \(Y=\left\{ \left( x,y \right)\in \mathbb{R}|y=f\left( x \right) \right\}\) e seja um ponto descrito pelo par ordenado \(\left( a,b \right)\), no qual \(a\) pertence ao domínio da função. Para qualquer ponto no qual \(b>y\), tem-se que o ponto encontrar-se-á acima da curva obtida pela união dos pares ordenados que satisfazem a função \(y=f\left( x \right)\). Já para o caso de \(b<y\), o ponto estará abaixo da curva obtida pela união dos pares ordenados que satisfazem a função \(y=f\left( x \right)\).
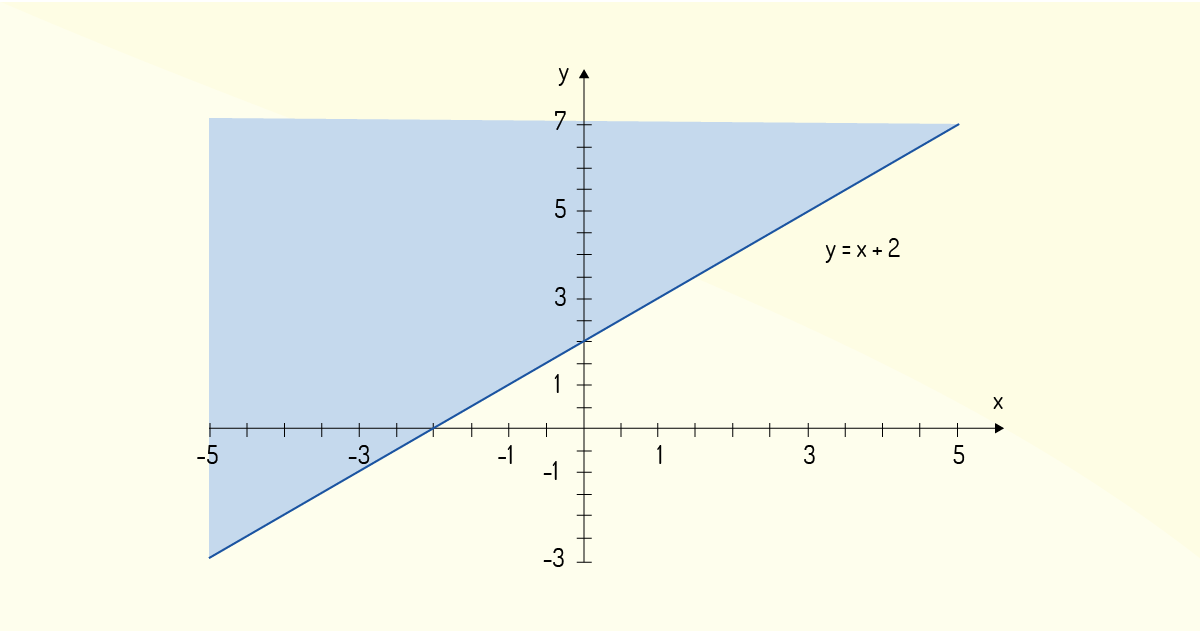
Essa análise geométrica binária pode ser estendida para tipos especiais de funções. Por exemplo, quando se tem uma inequação, o resultado geométrico é um semiplano, que pode estar tanto acima quanto abaixo da curva apresentada. Tome como exemplo a inequação \(y~≥~x~+~2\). Tem-se que o conjunto de pares ordenados que a representa é \(A~=~{(x, y)~∈~ℝ|y~≥~x~+~2}\), ou seja, qualquer valor de \(y\) maior ou igual à \(x~+~2\) satisfaz a inequação dada. Assim, na Figura 1.3, a área destacada acima da curva representa um semiplano do qual pares ordenados que satisfazem a inequação podem ser encontrados.
Um outro exemplo de semiplano formado pelo conjunto de todos os pares ordenados que satisfazem uma inequação é no caso da inequação que define um círculo. Retomando a função que descreve uma circunferência, você deve se lembrar que tal função é implícita, sendo escrita na forma \(y^{2}~+~x^{2}~=~r^{2}\). Considere como exemplo, então, o conjunto \(C=\left\{ \left( x,y \right)\in \mathbb{R}|{{y}^{2}}+{{x}^{2}}\le 1 \right\}\). Nele, temos uma função implícita que define uma circunferência de raio , sendo que o conjunto irá conter todos os pares ordenados que satisfazem a função \({{y}^{2}}+{{x}^{2}}=1\) e todos os pontos contidos dentro da circunferência descrita por tal curva. Na Figura 1.4, são mostradas a representação geométrica da função \({{y}^{2}}+{{x}^{2}}=1\) e a área, que está destacada, indicando os pontos contidos no conjunto .
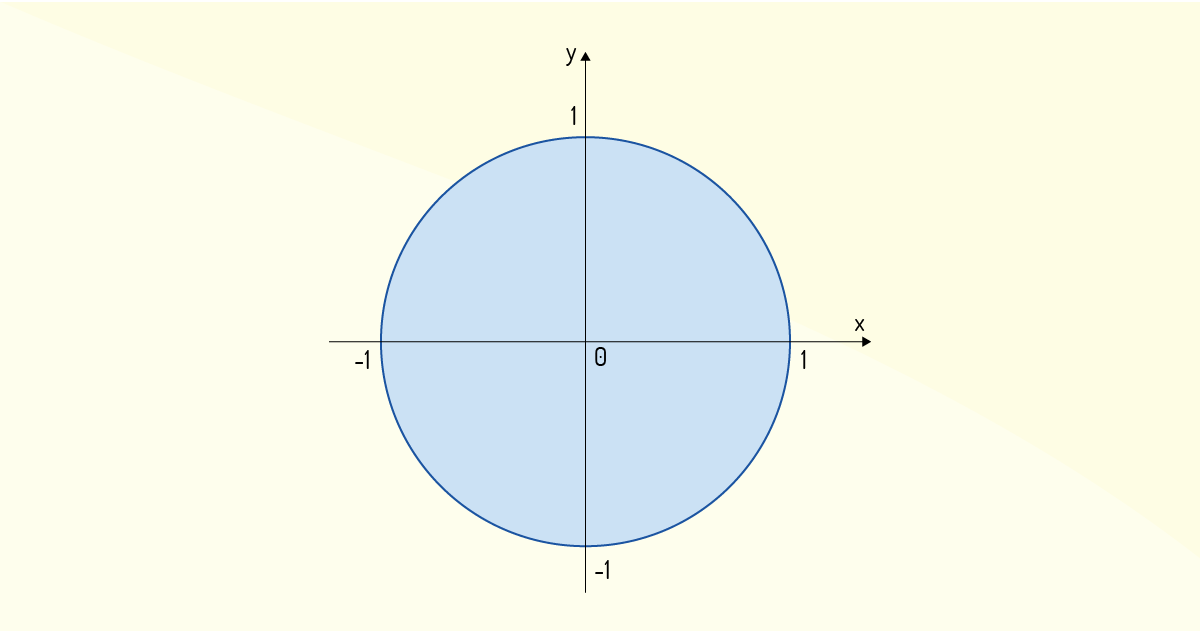
Note que caso o conjunto fosse \(C'~=~\left\{\left(x,~y\right)\in\mathbb{R}~|~{{y}^{2}}~+~{{x}^{2}}\ge 1 \right\}\), os pontos a serem considerados seriam aqueles fora da circunferência. Lembre-se também que os sinais e incluem os pontos da curva. Caso o sinal de desigualdade usado fosse > ou <, os pontos sobre a curva não seriam considerados como parte do conjunto de pares ordenados que satisfazem a relação indicada.
Morettin, Hazzan e Bussab (2016) ainda indicam que, no plano cartesiano, também somos capazes de avaliar qual a distância entre dois pontos de forma relativamente simples. Considere os pontos \(A=\left({{x}_{1}},{{y}_{1}}\right)\) e \(B=\left({{x}_{2}},{{y}_{2}}\right)\), sendo \(A,B\in\mathbb{R}\). Geometricamente, esses pontos são representados tal qual nos mostra a Figura 1.5.
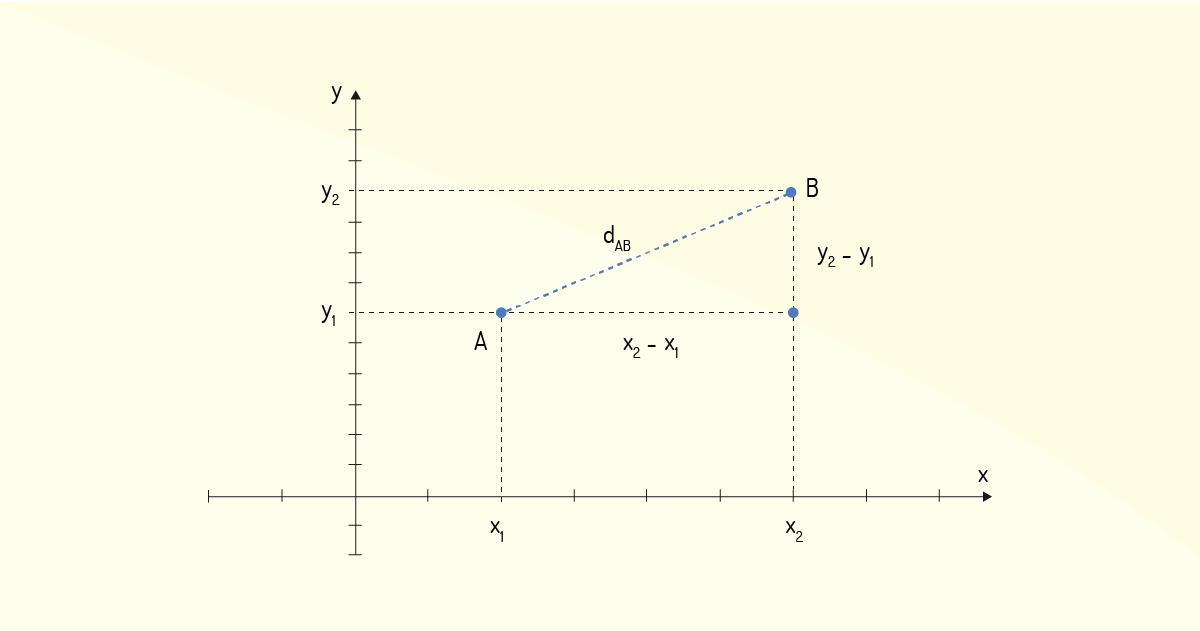
Observe que os dois pontos formam um triângulo retângulo quando se usa um ponto auxiliar \(V\left( {{x}_{2}},{{y}_{1}} \right)\), para o qual se tem os lados \(AV={{x}_{2}}-{{x}_{1}}\) e \(BV={{y}_{2}}-{{y}_{1}}\), além da hipotenusa ${{d}_{AB}}$, que é a distância entre os pontos $A$ e $B$. Logo, da trigonometria, tem-se que:
\[d_{AB}^{2}=A{{V}^{2}}+B{{V}^{2}}\to d_{AB}^{2}={{\left({{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}\]
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}~~~~~~(2)\]
Exemplo 1.1: Considere os pontos \(A=\left(2,6 \right)\), \(B=\left( 4,3 \right)\). e \(C=\left( 0,0 \right)\). Calcule, então, as distâncias \({{d}_{AB}}\), \({{d}_{AC}}\) e \({{d}_{BC}}\).
Solução
Na Figura 1.6, podemos ver geometricamente a posição de cada um dos três pontos apresentados:
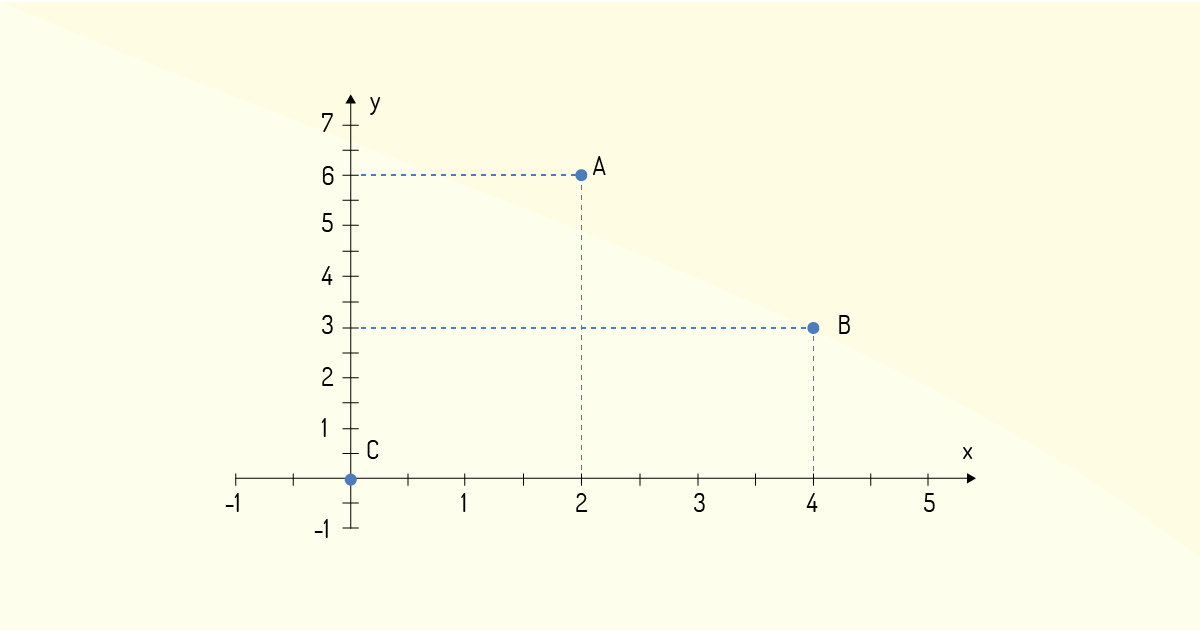
Utilizando o raciocínio trigonométrico apresentado anteriormente, as distâncias entre os pontos pedidos poderão ser calculadas utilizando a Equação (2) nas seguintes formas:
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{B}}-{{x}_{A}} \right)}^{2}}+{{\left( {{y}_{B}}-{{y}_{A}} \right)}^{2}}}\]
\[{{d}_{AC}}=\sqrt{{{\left( {{x}_{A}}-{{x}_{C}} \right)}^{2}}+{{\left( {{y}_{A}}-{{y}_{C}} \right)}^{2}}}\]
\[{{d}_{BC}}=\sqrt{{{\left( {{x}_{B}}-{{x}_{C}} \right)}^{2}}+{{\left( {{y}_{B}}-{{y}_{C}} \right)}^{2}}}\]
Então:
\[{{d}_{AB}}=\sqrt{{{\left( 4-2 \right)}^{2}}+{{\left( 6-3 \right)}^{2}}}=\sqrt{4+9}=\sqrt{13}\]
\[{{d}_{AC}}=\sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( 6-0 \right)}^{2}}}=\sqrt{4+36}=\sqrt{40}=2\sqrt{10}\]
\[{{d}_{BC}}=\sqrt{{{\left( 4-0 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}}=\sqrt{16+9}=\sqrt{25}=5\]
De forma semelhante ao caso dos pares ordenados, Morettin, Hazzan e Bussab (2016) dizem que se tomamos três números reais e os representamos em uma ordem pertinente, temos uma tripla ordenada. Assim, sendo x, y e z números reais, a tripla (x, y, z) representa uma tripla ordenada real. Considerando, então, todas as triplas ordenadas reais em um conjunto, você obtém um conjunto conhecido como espaço tridimensional. Cada tripla ordenada real contém três elementos do conjunto dos números reais, fazendo com que o espaço tridimensional possa ser representado por ℝ x ℝ x ℝ ou ℝ\(^3\). Na notação matemática de conjuntos, tem-se:
\[{{\mathbb{R}}^{3}}=\left\{ \left( a,b,c \right)|a,b,c\in \mathbb{R} \right\}~~~~~~(3)\]
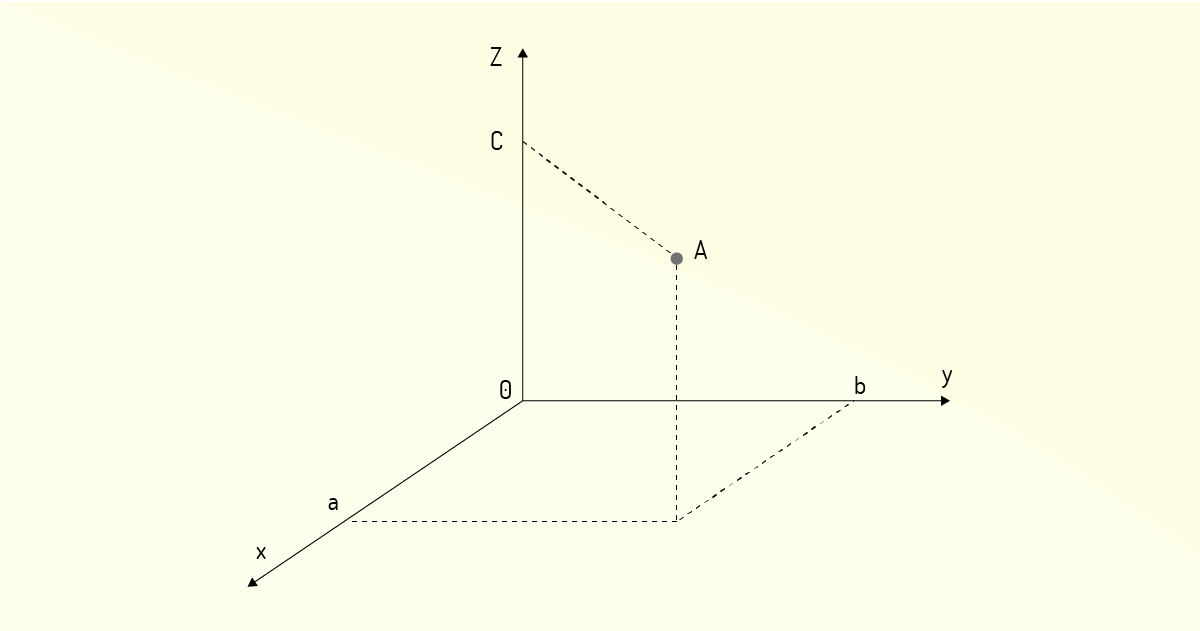
Tal qual os pares ordenados, as triplas ordenadas também podem ser representadas geometricamente como pontos, mas não no plano cartesiano. Os elementos de ℝ\(^3\) precisam de um terceiro eixo para serem representados. A Figura 1.7 exemplifica a representação geométrica de um ponto \(A=\left( a,b,c \right)\).
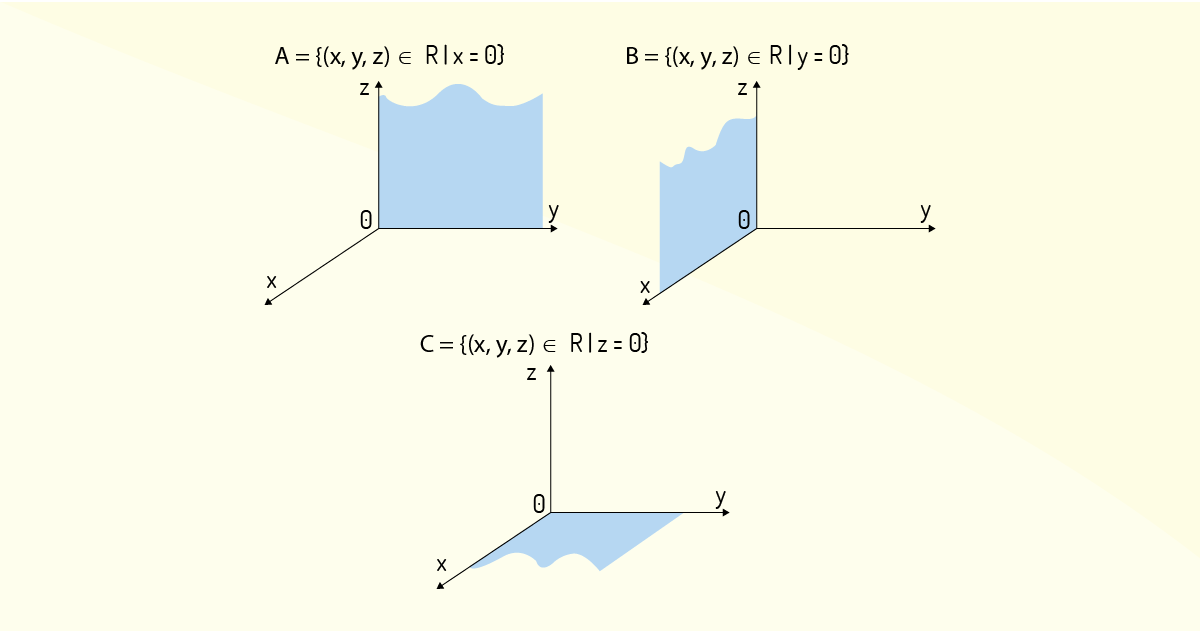
Segundo Morettin, Hazzan e Bussab (2016), é importante estar atento ao trabalhar com triplas ordenadas na forma geométrica, pois se uma das coordenadas for igual a zero, o conjunto de pares ordenados que irá representar a tripla é um plano determinado pelos demais eixos. Assim, o conjunto A = {(x, y, z) ∈ ℝ | x = 0} consiste de todos os pontos do plano formado pelos eixos 0\(_y\) e 0\(_z\); para um conjunto B = {(x, y, z) ∈ ℝ | y = 0}, seriam todos os pontos do plano formado pelos eixos 0\(_x\) e 0\(_z\); e, para um conjunto C = {(x, y, z) ∈ ℝ | z = 0}, seriam todos os pontos do plano formado pelos eixos 0\(_x\) e 0\(_y\). Na Figura 1.8 são mostrados esses conjuntos.
Em um exemplo semelhante ao discutido anteriormente, caso uma das coordenadas da tripla ordenada seja um outro inteiro diferente de zero, o resultado geométrico é semelhante ao mostrado na Figura 1.8. A única diferença consistirá em que o plano formado será deslocado de acordo com a necessidade. Por exemplo, o conjunto C' = {(x, y, z) ∈ ℝ | z = 1} possui representação geométrica idêntica à do conjunto C = {(x, y, z) ∈ ℝ | z = 0}; a diferença é que o plano deverá se encontrar deslocando 1 unidade no sentido positivo do eixo z, como mostra a Figura 1.9.
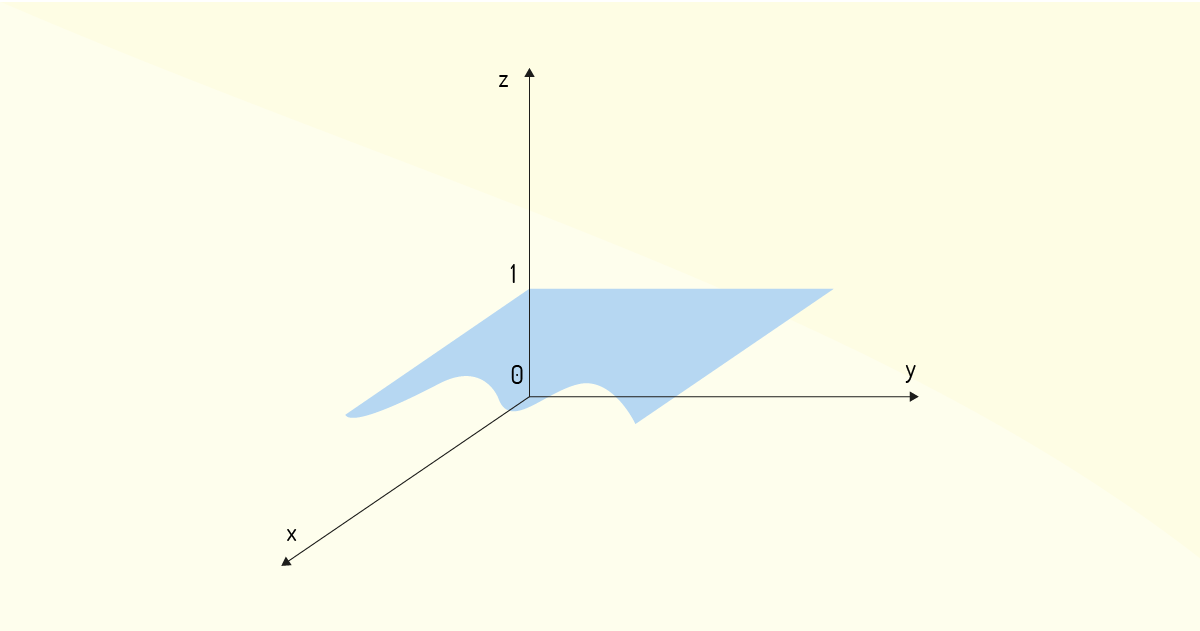
Concluindo o estudo sobre espaço tridimensional, de acordo com Morettin, Hazzan e Bussab (2016), a distância entre dois pontos também pode ser facilmente avaliada com técnicas de trigonometria, como se fosse a diagonal de um cubo, partindo de uma linha de raciocínio semelhante àquela usada para o caso da distância entre dois pontos no plano. Na Figura 1.10 tem-se os pontos \(A\left({{x}_{1}},~{{y}_{1}},~{{z}_{1}}\right)\) e \(B\left( {{x}_{2}},~{{y}_{2}},~{{z}_{2}}\right)\), sendo que eles se localizam em pontos diagonais opostos de um cubo imaginário.
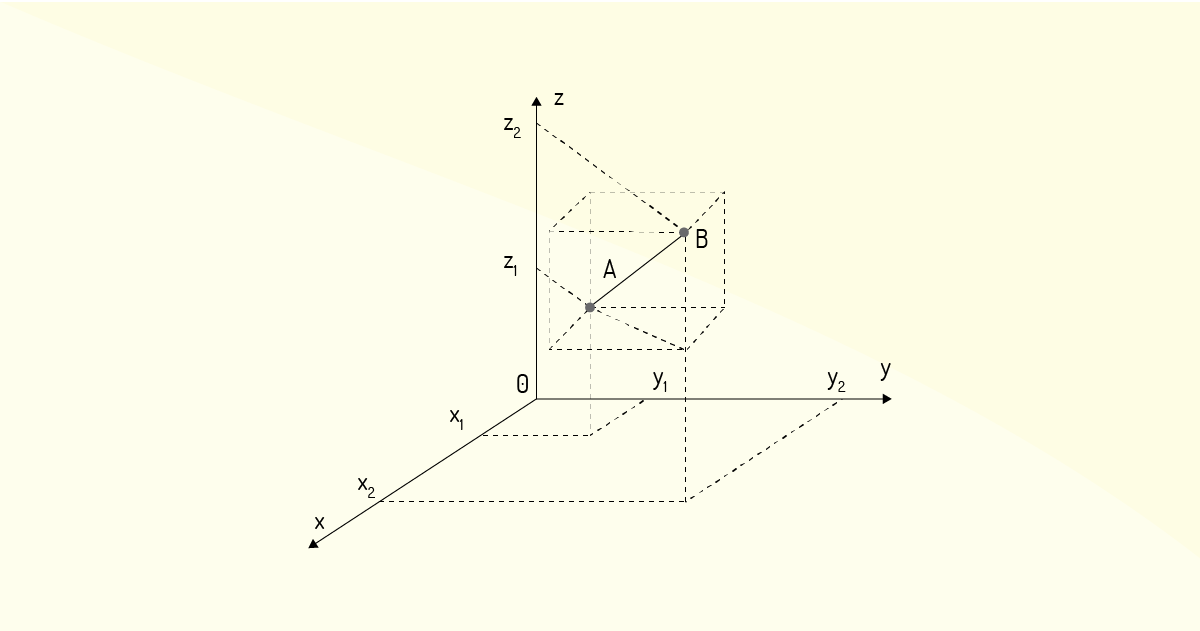
Logo, a distância ${{d}_{AB}}$ entre os pontos pode ser avaliada da seguinte maneira:
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}~~~~~~(4)\]
Chegando a este ponto, você, estudante, deve ter percebido que podemos formar sequências de quantos números reais quisermos, de modo a encontrarmos n-uplas ordenadas reais, para as quais o conjunto contendo todas essas n-uplas ordenadas é chamado espaço n-dimensional. Morettin, Hazzan e Bussab (2016) destacam que esse espaço n-dimensional pode ser representado por ℝ\(^n\). Na notação matemática de conjuntos, tem-se:
\[{{\mathbb{R}}^{n}}=\left\{ \left( {{a}_{1}},{{a}_{2}},...,{{a}_{n}} \right)|{{a}_{1}},{{a}_{2}},...,{{a}_{n}}\in \mathbb{R} \right\}~~~~~~(5)\]
Perceba que a definição dada acima por Morettin, Hazzan e Bussab (2016) corrobora o que já vimos anteriormente sobre espaços bi e tridimensionais. Na verdade, se você substituir \(n~=~1,~2\) ou \(3\), você terá o conjunto dos números reais, um espaço bidimensional e um espaço tridimensional, como descrito anteriormente. Faça essas substituições em (5) e compare com o que é mostrado em (1) e (3).
Um ponto interessante sobre o espaço n-dimensional mostrado por Morettin, Hazzan e Bussab (2016) é o fato de que apenas n-uplas ordenadas de \(n\le 3\) admitem representação geométrica. Logo, espaços quadridimensionais ou de dimensões superiores não poderão ser representadas na forma gráfica. No entanto, mesmo com essa limitação, ainda podemos avaliar qual a distância entre dois pontos para qualquer que seja o valor de $n$. Morettin, Hazzan e Bussab (2016) afirmam que, para qualquer ponto \(A=\left( {{a}_{1}},{{a}_{2}},...,{{a}_{n}} \right)\) e \(B=\left( {{b}_{1}},{{b}_{2}},...,{{b}_{n}} \right)\) pertencentes a ℝ\(^n\), a distância \({{d}_{AB}}\) pode ser avaliada da seguinte forma:
\[{{d}_{AB}}=\sqrt{{{\left( {{a}_{1}}-{{b}_{1}} \right)}^{2}}+{{\left( {{a}_{2}}-{{b}_{2}} \right)}^{2}}+...+{{\left( {{a}_{n}}-{{b}_{n}} \right)}^{2}}}~~~~~~(6)\]
A questão de espaços com mais de três dimensões é algo que muitos estudantes têm dificuldade de visualizar e mesmo imaginar, até porque somente somos capazes de representar geometricamente dimensões de n ≤ 3. Você consegue imaginar, então, qual o sentido de estudarmos tais casos de dimensões maiores que três e como diferentes áreas da ciência podem se beneficiar de dimensões mais complexas?

Um dos pontos-chave de se estudar pontos no espaço ℝ\(^n\) é saber identificar qual a distância de um ponto a outro, o que se mostrará uma habilidade importante para definições futuras na presente disciplina. Visando à prática deste tópico, analise as alternativas a seguir: apenas uma delas indica uma distância entre pontos calculada erroneamente. Assinale aquela em que a distância apresentada é correta.
A distância entre os pontos \(A=\left( -2,5 \right)\) e \(B=\left( 4,3 \right)\) é igual a \(4\sqrt{10}\) unidades de comprimento.
Justificativa: Como os pontos \(A\) e \(B\) pertencem a ℝ\(^2\) , a distância entre eles é avaliada da seguinte forma:
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}=\sqrt{{{\left( 4+2 \right)}^{2}}+{{\left( 3-5 \right)}^{2}}}=\sqrt{36+4}=\sqrt{40}=\sqrt{2\cdot 2\cdot 10}=2\sqrt{10}\]
Logo, a distância apresentada está certa, tornando essa alternativa falsa.
A distância entre os pontos \(C=\left( 1,1,1,1 \right)\) e \(D=\left( 2,3,3,1 \right)\) é igual a 3 unidades de comprimento.
Justificativa correta: Como os pontos \(C\) e \(D\) pertencem a ℝ\(^4\) , a distância entre eles é avaliada da seguinte forma:
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}+{{\left( {{w}_{2}}-{{w}_{1}} \right)}^{2}}}=\sqrt{{{\left( 2-1 \right)}^{2}}+{{\left( 3-1 \right)}^{2}}+{{\left( 3-1 \right)}^{2}}+{{\left( 1-1 \right)}^{2}}}=\]
\[=\sqrt{1+4+4+0}=\sqrt{9}=3\]
Logo, essa alternativa encontra-se correta.
A distância entre os pontos\(E=\left( -2,-1,3 \right)\) e \(F=\left( 0,3,-1 \right)\) é igual a \(2\) unidades de comprimento.
Justificativa: Como os pontos \(E\) e \(F\) pertencem a ℝ\(^3\) , a distância entre eles é avaliada da seguinte forma:
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}=\sqrt{{{\left( 0+2 \right)}^{2}}+{{\left( 3+1 \right)}^{2}}+{{\left( -1-3 \right)}^{2}}}=\]
\[=\sqrt{4+16+16}=\sqrt{36}=6\]
Logo, a distância apresentada está certa, tornando essa alternativa falsa.
A distância entre os pontos \(A=\left( -2,5 \right)\) e \(F=\left( 0,3,-1 \right)\) é igual a 5 .
Justificativa: Como o ponto \(A$\) pertence a ℝ\(^2\) e o ponto \(F\) pertence a ℝ\(^3\), não podemos avaliar a distância entre eles. Ou seja, pontos pertencentes a espaços dimensionais diferentes não podem ter a distância entre si avaliadas.
A distância entre os pontos \(G=\left( -2,-3,-3 \right)\) e \(H=\left( 4,3,0 \right)\) é igual a \(3\sqrt{5}\) unidades de comprimento.
Justificativa: Como os pontos \(G\) e \(H\) pertencem a ℝ\(^3\) , a distância entre eles é avaliada da seguinte forma:
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}=\sqrt{{{\left( 4+2 \right)}^{2}}+{{\left( 3+3 \right)}^{2}}+{{\left( 0+3 \right)}^{2}}}=\]
\[=\sqrt{36+36+9}=\sqrt{81}=9\]
Logo, a distância apresentada está certa, tornando essa alternativa falsa.
Agora que fizemos uma breve revisão a respeito das dimensões dos espaços, voltaremos nossos estudos de forma mais direta e aplicada para o Cálculo. Faremos isso expandindo o conceito de função com o qual você já está acostumado.
Como já foi dito no início da presente Unidade, existem inúmeras funções que apresentam mais de uma variável independente. Como Thomas Júnior (2016) e Stewart (2017b) afirmam, essa situação de funções com mais de uma variável independente são corriqueiras no mundo real, sendo possível apresentar uma gama de exemplos simples de tal situação.
Já no início desta unidade, foram apresentados dois exemplos geométricos de funções com mais de uma variável independente, mas tal lista pode ser expandida, apresentando exemplos mais abrangentes e de diferentes áreas. Por exemplo:
a. a velocidade do som se propagando na água do mar, \({{v}_{\acute{a}gua}}\), é uma função que pode ser escrita de forma simplificada como uma função da concentração de sais na água, \({{C}_{S}}\), e sua temperatura, \(T\). Então, pode-se escrever que \({{v}_{\acute{a}gua}}=f\left( {{C}_{S}},T \right)\).
b. para se avaliar a área externa do corpo de um ser humano, \({{A}_{ex}}\), pode ser proposta uma função que leva em consideração tanto a altura $h$ do indivíduo quanto seu peso \(w\), ou seja, \({{A}_{ex}}=f\left(h,w \right)\).
c. na química e na física, você pode ser confrontado constantemente com o problema de avaliar a pressão de um gás ideal. Para tal, você deve usar a equação de estado \(P=\left( nRT \right)/V\), na qual se tem que \(P\) é a pressão do gás, \(n\) é o número de mols do gás, \(R\) é a constante universal dos gases ideais, \(T\) é a temperatura que o gás se encontra e \(V\) é o volume no qual o gás está contido. Ou seja, tem-se que \(P\) é uma função de \(n\), \(T\) e \(V\), visto que \(R\) é uma constante. Ou seja, para este caso, tem-se que \(P=f\left( n,T,V \right)\)
Logo, agora vamos expandir as definições e conceitos desenvolvidos para funções com uma única variável independente para os casos em que se tem mais de uma variável independente.
Como visto anteriormente, o espaço n-dimensional ℝ\(^n\) contém todas as n-uplas de números reais possíveis, sendo que cada n-upla \(\left( {{a}_{1}},{{a}_{2}},...,{{a}_{n}} \right)\) é um ponto no espaço n-dimensional. Partindo disso, Leithold (1994) apresenta as seguintes definições:
Definição 1: seja \(P=\left( {{a}_{1}},{{a}_{2}},...,{{a}_{n}} \right)\) um ponto no espaço n-dimensional e o número real \(w\). Então, o conjunto de pares ordenados \(\left(P, w \right)\) no qual dois pares distintos não apresentam os primeiros elementos iguais determinam uma função de n variáveis;
Definição 2: o conjunto que contém todos os valores que são possíveis para o ponto \(P\) da Definição 1 é conhecido como domínio da função;
Definição 3: o conjunto que contém todos os valores que são possíveis para o valor real \(w\) da Definição 1 é conhecido como imagem da função.
Das Definições 2 e 3, podemos inferir que o domínio de uma função de n variáveis será um conjunto de ℝ\(^n\), enquanto a imagem da função será apenas um conjunto de números reais, ou seja, um conjunto de ℝ. Conferindo, também, a Definição 1, note que quando se tem n = 1, então \(P\) se reduz a um único valor real. Logo, o par ordenado indicado contém dois elementos reais, ou seja, é exatamente o caso de uma função com uma única variável. Veja ainda que o domínio da função neste caso será um conjunto de ℝ, tal qual a definição de uma função de uma variável indica. Ou seja, de acordo com Leithold (1994), uma função de uma variável é o caso particular da Definição 1, em que n = 1.
Após a situação mais simples de uma função, que é o caso de uma única variável, temos, então, o caso de uma função com duas variáveis. Esse tipo de função, segundo Thomas Júnior (2016) e Stewart (2017b), frequentemente é representado como \(z=f\left( x,y \right)\), tem como domínio um subconjunto de ℝ² e, como imagem, um subconjunto de ℝ e será o foco principal dos nossos estudos de funções de mais de uma variável, inclusive por ser um caso-limite de capacidade de representação geométrica. Assim como você estudou nos casos de funções de uma única variável, uma função com duas variáveis também pode ser representada por meio de um diagrama de setas. Observe, na Figura 1.11, a ilustração dessa representação.
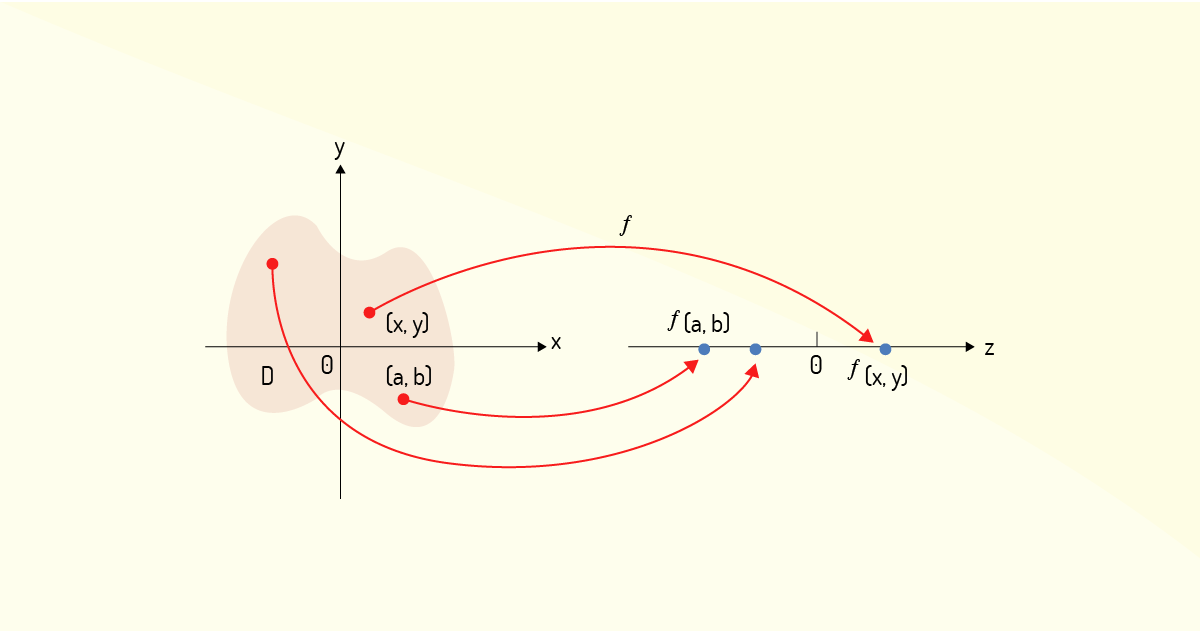
Note que o domínio \(D\) da função está destacado à esquerda na Figura 1.11. Do domínio, cada par ordenado \(P=\left( {{p}_{1}},{{p}_{2}} \right)\) está associado a um único elemento real igual à \(f\left(P \right)=f\left( {{p}_{1}},{{p}_{2}} \right)\), tal qual é dada a definição de uma função.
Stewart (2017b) ainda traz um fato importante a respeito das funções. Caso uma função \(f\) de n variáveis estiver bem definida por uma fórmula, mas não apresentar um domínio especificado, subentende-se que o domínio dela será o conjunto de todos os pontos \(P=\left( {{a}_{1}},{{a}_{2}},...,{{a}_{n}} \right)\) para o qual a função retornar um valor real bem definido.
Exemplo 2.1: Considere a função \(z\) definida por \(z\left( x,y \right)=2{{x}^{2}}-3y\). Encontre, então, \(z\left( 0,3 \right)\), \(z\left( 3a,-5b \right)\) e \(z\left( {{x}^{2}},{{y}^{2}} \right)\).
Solução
Assim como no caso de uma função de uma única variável, basta substituir os valores de acordo com o apresentado nos pares ordenados. Portanto:
\[z\left( x,y \right)=2{{x}^{2}}-3y\to z\left( 0,3 \right)=2{{\left( 0 \right)}^{2}}-3\left( 3 \right)\]
\[z\left( 0,3 \right)=0-9=-9\]
Mesmo quando se tem incógnitas, o procedimento é o mesmo:
\[z\left( x,y \right)=2{{x}^{2}}-3y\to z\left( 3a,-5b \right)=2{{\left( 3a \right)}^{2}}-3\left( -5b \right)\]
\[z\left( 3a,-5b \right)=2\cdot 9{{a}^{2}}+15b=18{{a}^{2}}+15b\]
Observe que você ainda pode colocar o resultado encontrado acima em evidência:
\[z\left( 3a,-5b \right)=3\left( 6{{a}^{2}}+5b \right)\]
Finalizando, o último resultado deverá ser:
\[z\left( x,y \right)=2{{x}^{2}}-3y\to z\left( {{x}^{2}},{{y}^{2}} \right)=2{{\left( {{x}^{2}} \right)}^{2}}-3\left( {{y}^{2}} \right)\]
\[z\left( {{x}^{2}},{{y}^{2}} \right)=2{{x}^{4}}-3{{y}^{2}}\]
Ainda a respeito das funções de duas variáveis, Leithold (1994) define o caso das funções compostas, comumente expressas como \(f\circ g\):
Definição 4: sejam as funções \(f\) e \(g\), sendo \(f\) uma função de uma variável e \(g\) uma função de duas variáveis. Então, a função composta \(f\circ g\) será uma função de duas variáveis, sendo esta função definida como:
\[\left( f\circ g \right)\left( x,y \right)=f\left( g\left( x,y \right) \right)\]
Para tal função composta, tem-se que o domínio será o conjunto de todos os pontos \(\left( x,y \right)\) no domínio da função \(g\), para os quais se tem que \(g\left( x,y \right)\) está no domínio de \(f\).
Observe que essa definição de função composta pode ser estendida para casos em que a função \(g\) apresenta n variáveis. Assim, sendo \(f\) uma função de uma variável e \(g\) uma função de n variáveis, a função composta \(f\circ g\) também será uma função de n variáveis, com a função composta definida como:
\[\left( f\circ g \right)\left( {{a}_{1}},{{a}_{2}},...,{{a}_{n}} \right)=f\left( g\left( {{a}_{1}},{{a}_{2}},...,{{a}_{n}} \right) \right)\]
Para tal função composta, também se tem como domínio o conjunto de todos os pontos \(\left( {{a}_{1}},{{a}_{2}},...,{{a}_{n}} \right)\) no domínio da função $g$, para os quais se tem que \(g\left( {{a}_{1}},{{a}_{2}},...,{{a}_{n}} \right)\) está no domínio de \(f\) (LEITHOLD, 1994).
Exemplo 2.2: Considere as funções \(f\left( t \right)=ln~t~+2t\) e \(g\left( x,y \right)=x+{{y}^{2}}\). Encontre, então, a função composta \(f\circ g\) e seu domínio.
Solução
Da Definição 4, tem-se que uma função composta \(f\circ g\) é obtida da seguinte forma:
\[\left( f\circ g \right)\left( x,y \right)=f\left( g\left( x,y \right) \right)\]
Então, utilizando as funções informadas:
\[\left( f\circ g \right)\left( x,y \right)=f\left( g\left( x,y \right) \right)=ln~\left( g\left( x,y \right) \right)~+2\left( g\left( x,y \right) \right)\]
\[\left( f\circ g \right)\left( x,y \right)=ln~\left( x+{{y}^{2}} \right)~+2\left( x+{{y}^{2}} \right)\]
Para o domínio da função composta, note que \(g\left( x,y \right)\) é definida para todos os pares ordenados reais. No entanto, a função \(f\left( t \right)\) só está definida para os casos em que \(t>0\), pois o logaritmo natural de um número só está definido para valores maiores que zero. Portanto, o domínio dessa função composta será o conjunto \(D=\left\{ \left( x,y \right)\left| x+{{y}^{2}} \right\rangle 0 \right\}\).
Um dos tipos mais comuns de funções que se têm são as funções polinomiais. No caso das funções com duas variáveis, Leithold (1994) considera que uma função polinomial com duas variáveis é simplesmente a soma de r termos \(c{{x}^{n}}{{y}^{m}}\), sendo \(c\) um número real e \(m\) e \(n\) inteiros não negativos. Para uma função polinomial com duas variáveis, tem-se que o grau do polinômio será determinado pelo maior valor de uma soma \(m+n\) de termos que apresentem \(c\ne 0\).
Ilustrando uma função polinomial, considere a função polinomial \(f\left( x,y \right)=2{{x}^{3}}+3{{x}^{2}}{{y}^{3}}+y\); o grau desse polinômio será igual a 5, pois é o maior valor de soma \(m+n\). Agora, se a função fosse \(f\left( x,y \right)={{x}^{6}}+2{{x}^{3}}{{y}^{2}}+{{y}^{3}}\), o grau do polinômio seria igual a 6 – lembre-se que o zero é considerado um número inteiro, logo, \({{x}^{6}}={{x}^{6}}\cdot {{y}^{0}}\), então \(m+n=6\).
Quando temos em mãos apenas uma variável real, esta pode ser representada geometricamente (ou graficamente) apenas com o uso de uma reta, a reta numérica real. Tal reta é uma forma de representar o conjunto de todos os números reais (STEWART, 2017a).
Durante os estudos de funções com uma única variável, a representação geométrica passou a ser feita no plano cartesiano, que é duas retas numéricas reais perpendiculares, sendo uma reta horizontal, conhecida como eixo das abscissas, e uma reta vertical, o eixo das ordenadas. Tais retas se cruzam na origem O, como nos mostra a Figura 1.12.
Ainda de acordo com Stewart (2017a), a representação geométrica de uma função com uma variável \(f\left( x \right)\) consiste simplesmente em representar no plano cartesiano o conjunto de pares ordenados \(\left( x,f\left( x \right) \right)\) para todo o domínio de uma função, ou seja, apresentar em forma gráfica o conjunto \(\left\{ \left( x,f\left( x \right) \right)|x\in D \right\}\) ou \(\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}|y=f\left( x \right)~e~x\in \mathbb{R} \right\}\).
Para o nosso caso de interesse no momento, que são funções com duas variáveis, a definição da representação geométrica pode ser análoga à descrita acima, com a ressalva de que os pontos de uma função com duas variáveis são pertencentes a ℝ\(^3\). Então, tal qual define Leithold (1994):
Definição 5: o gráfico de uma função \(f\) de duas variáveis será o conjunto de todos os pontos \(\left( x,y,z \right)\) pertencentes a ℝ\(^3\) para os quais se têm que \(\left( x,y \right)\) são pontos do domínio de \(f\) e \(z=f\left( x,y \right)\).
Então, o gráfico de uma função de duas variáveis é simplesmente a representação no espaço tridimensional do conjunto de triplas ordenadas \(\left( x,y,f\left( x,y \right) \right)\) para todo o domínio de uma função. Para a representação gráfica de funções com duas variáveis, você pode fazer uso de uma versão adaptada do plano cartesiano na qual se adiciona uma terceira reta numérica representando o eixo \(z\), como mostra a Figura 1.13.
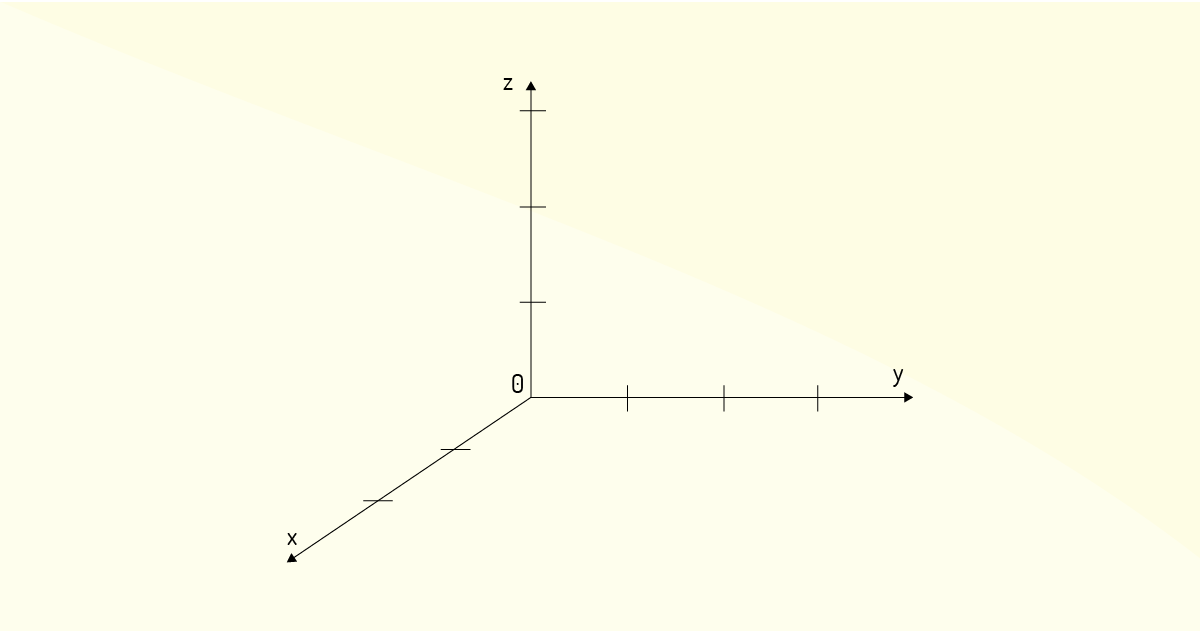
Note que a Figura 1.13 não apresenta a única forma de representarmos um eixo tridimensional! Existem diferentes formas, sendo que a escolha de qual você deve usar depende simplesmente de você e do que deseja enfatizar graficamente.
Como os gráficos tridimensionais nem sempre são simples de se construir manualmente, a seguir serão indicados alguns exemplos de representações gráficas de algumas funções com duas variáveis comuns.
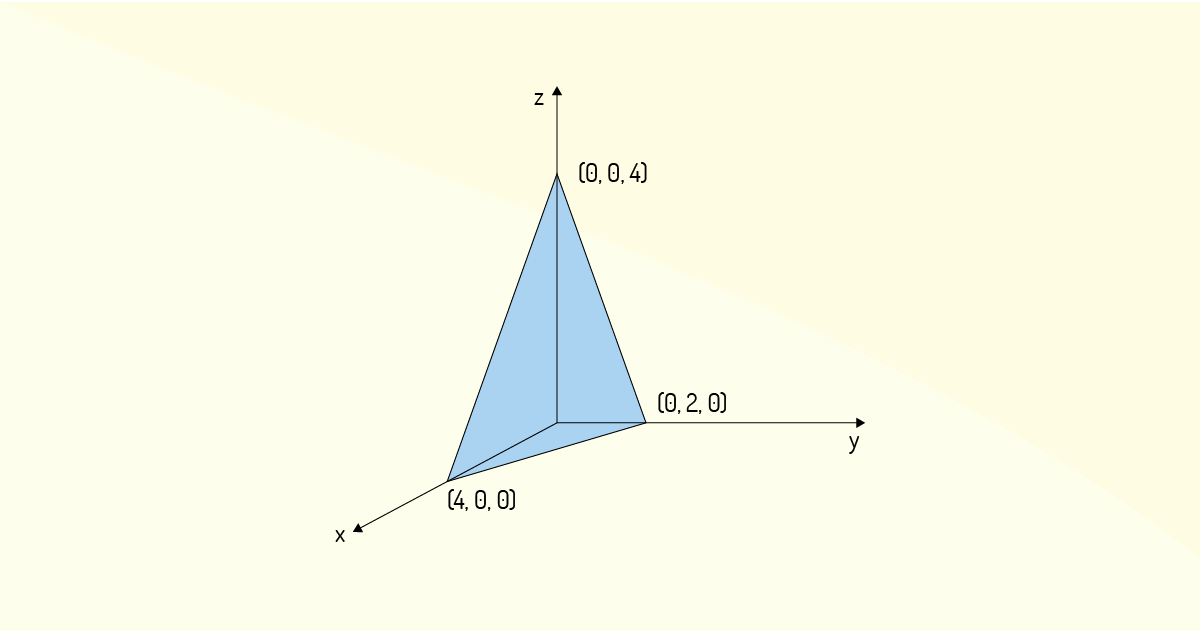
Exemplo 2.3: Considere a função \(z=f\left( x,y \right)=4-x-2y\). Para representá-la graficamente, o primeiro passo é identificar as interseções com os eixos. Isso é encontrado avaliando \(f\left( 0,0 \right)\), para a interseção em \(z\); fazendo \(y=z=0\) para a interseção em \(x\); e fazendo \(x=z=0\) para a interseção em \(y\). Com isso, encontra-se que a interseção em \(z\) será em 4, a interseção em \(x\) será em 4 e a interseção em \(y\) será em 2. Fazendo, então, cada uma das variáveis ser igual a zero, você encontrará os traços do gráfico dessa função. Assim, quando \(y=0\), \(z=4-x\); quando \(x=0\), \(z=4-2y\); e quando \(z=0\), \(x=4-2y\). Veja que todos os traços são lineares. Basta, então, unir os pontos linearmente, como mostra a Figura 1.14.
Exemplo 2.4: Considere a função \(z=f\left( x,y \right)=\sqrt{{{r}^{2}}-{{x}^{2}}-{{y}^{2}}}\). Veja que essa função pode ser elevada ao quadrado, resultando em \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{r}^{2}}\), que é a equação de uma esfera. No entanto, como a função indicada irá retornar apenas valores positivos para \(z\), ela representa apenas o hemisfério superior de uma esfera com um raio de \(r\) unidades de comprimento, centrado na origem do espaço tridimensional e que toca o plano \(xy\). A Figura 1.15 mostra o gráfico de uma função desse tipo.
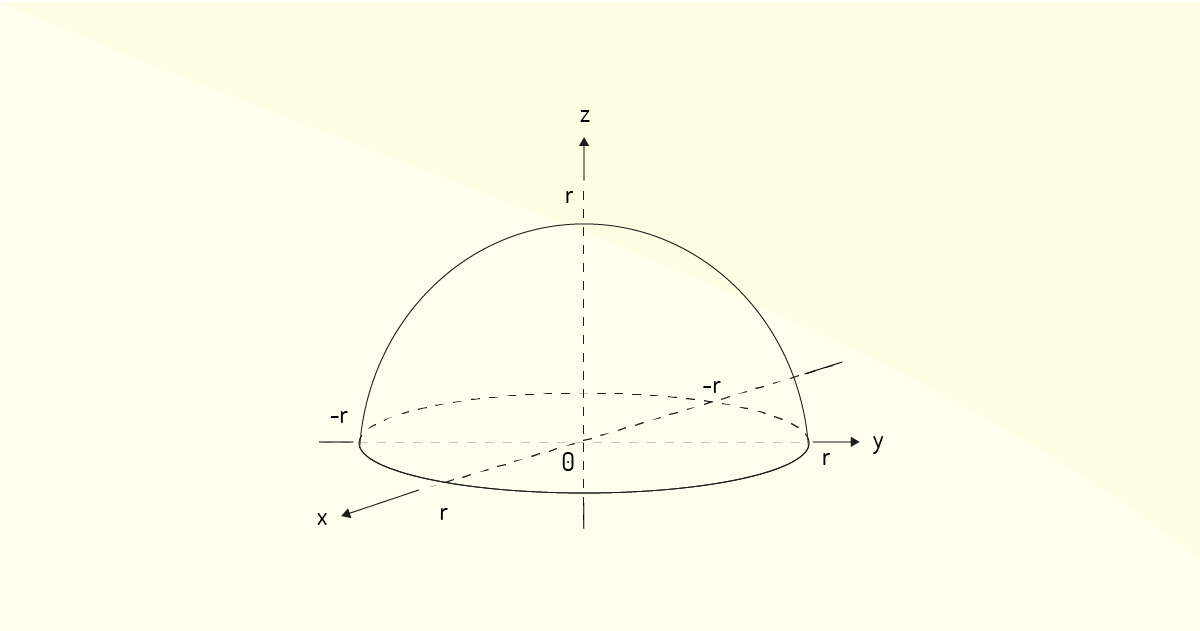
Note que você não será capaz de representar uma esfera graficamente apenas com uma função de \(x\) e \(y\). Para a representação do hemisfério superior, você usa a função \(z=\sqrt{{{r}^{2}}-{{x}^{2}}-{{y}^{2}}}\). Para o hemisfério inferior, você deve utilizar a função \(z=-\sqrt{{{r}^{2}}-{{x}^{2}}-{{y}^{2}}}\).
Ainda, caso você queira uma esfera que não apresente seu centro na origem do espaço tridimensional, você deverá adicionar a coordenada desejada do centro como um ponto \(\left( {{x}_{0}},{{y}_{0}},{{z}_{0}} \right)\) à equação da seguinte forma:
\[{{r}^{2}}={{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}+{{\left( z-{{z}_{0}} \right)}^{2}}\]
Exemplo 2.5: Considere a função \(z=f\left( x,y \right)={{x}^{2}}+{{y}^{2}}\). Para esboçá-la graficamente, precisamos identificar eventuais interseções. Note que não haverá valores negativos em \(z\) para essa função, logo, seu gráfico estará totalmente acima da origem. O valor mínimo para ela é facilmente obtível – será \(f\left( 0,0 \right)=0\). Agora, para os traços dessa função, veja que quando \(y=0\), \(z={{x}^{2}}\), quando \(x=0\), \(z={{y}^{2}}\) e quando \(z=0\), \({{y}^{2}}=-{{x}^{2}}\). Se você analisar o caso de \(z=0\), verá que o traço resultante é \({{x}^{2}}+{{y}^{2}}=0\), que é semelhante à equação da circunferência. Logo, se olharmos o gráfico dessa função “do topo” do eixo $z$, visão esta que seria a do plano \(xy\), veríamos um gráfico circular de raio é igual a \(\sqrt{z}\). Já quando se tem \(x=0\) ou \(y=0\), os traços serão parábolas. Logo, unindo essas informações, pode-se esboçar o gráfico da função dada, como mostra a Figura 1.16.
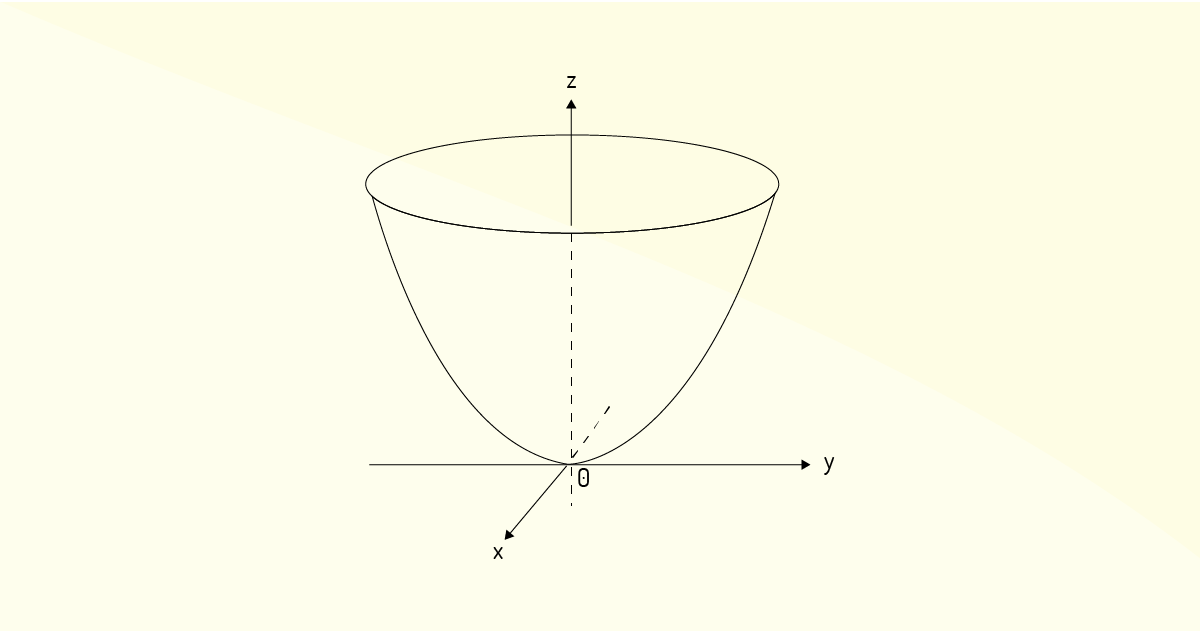
Você também pode exercitar um pouco de sua imaginação com este gráfico. Como seus traços laterais são parábolas e a visão do eixo \(z\) em direção ao plano \(xy\) consiste de um círculo de raio \(\sqrt{z}\), para encontrar este gráfico, basta que você tome uma das parábolas dos traços e faça ela “girar” ao redor do eixo \(z\).
Ainda sobre esta função, escrevendo-a na forma \(z=a+{{x}^{2}}+{{y}^{2}}\), o valor \(a\) irá indicar o mínimo da função, ou seja, o ponto mais baixo que o gráfico deverá atingir no eixo \(z\).
Apesar dos exemplos vistos anteriormente serem relativamente simples, existem vários casos mais complexos de gráficos de funções com mais de uma variável, para os quais a visualização pode, inclusive, ser prejudicada. Nesse caso, pode ser útil que busquemos uma outra forma de representarmos graficamente as funções de duas variáveis.
Da forma como apresentamos o eixo \(z\) na representação de um espaço tridimensional e também na definição de uma função com duas variáveis, somos capazes de determinar uma maneira diferente de visualizarmos tais gráficos. Tal método é semelhante ao método de representar uma paisagem tridimensional com um mapa topológico (LEITHOLD, 1994).
Seja o gráfico de uma função \(z=f\left( x,y \right)\) qualquer. Considere, agora, um plano paralelo ao plano \(xy\). Esse plano, que é ortogonal ao eixo \(z\), representa um valor constante da função, ou seja, delimita uma região em que se tem \(z=f\left( x,y \right)=c\). Essa região do espaço, em que se terá sempre pontos \(\left( x,y,c \right)\), é chamada curva de nível da função (LEITHOLD, 1994).
Como exemplo, para ilustrarmos o que é uma curva de nível, considere a função \(z=f\left( x,y \right)=100-{{x}^{2}}-{{y}^{2}}\). Observe que essa função é semelhante à mostrada no Exemplo 2.5, diferindo nos sinais das variáveis e apresentando uma constante, a qual indica o valor máximo positivo dessa função. Já os sinais negativos em \({{x}^{2}}\) e \({{y}^{2}}\) indicam que as parábolas dos traços serão opostas àquelas mostradas na Figura 1.16. Logo, o gráfico esperado para a função \(z=100-{{x}^{2}}-{{y}^{2}}\) é basicamente oposto ao mostrado na Figura 1.16.
Considere, agora, um plano \(\alpha \) localizado em \(z=75\) no gráfico da função \(z\) indicada no parágrafo anterior. Esse plano delimita uma região em que todos os pontos do gráfico apresentam valor igual a 75, ou seja, tem-se que, em tal plano, \(75=100-{{x}^{2}}-{{y}^{2}}\). Reescrevendo essa função, você encontrará a função \({{x}^{2}}+{{y}^{2}}=25\), que descreve uma circunferência de raio igual a \(\sqrt{25}=5\), localizada na origem do plano cartesiano. Assim, como a função \(z\) foi descrita num plano \(\alpha\), ela é uma bidimensional; logo, podemos projetar essa função no plano \(xy\), de modo que encontramos todos os pares ordenados \(\left( x,y \right)\) que satisfazem a condição de \(z=75\) estabelecida inicialmente, ou seja, podemos projetar no plano \(xy\) a curva de nível de \(z\) em que se tem \(z=75\). Na Figura 1.17, podemos ver todo esse desenvolvimento para encontrar tal curva de nível no gráfico da função.
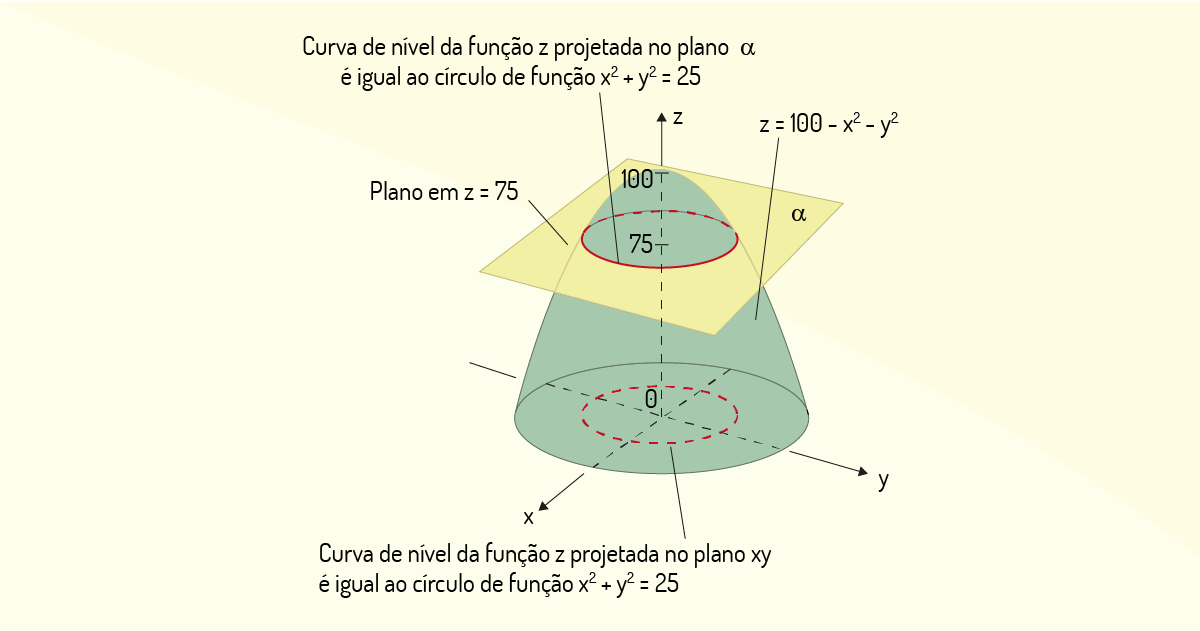
Agora podemos representar uma função com duas variáveis de forma bidimensional. Se você tomar diferentes curvas de nível em diferentes valores de $z$, você terá diversas curvas representadas no plano cartesiano, para as quais se tem $z$ igual a uma constante determinada previamente.
Exemplo 2.6: Considerando ainda a função \(z=100-{{x}^{2}}-{{y}^{2}}\), esboce as projeções das curvas de nível para \(z=0\), \(z=36\), \(z=51\), \(z=75\), \(z=91\) e \(z=99\).
Solução
Como cada curva de nível apresenta um valor constante para \(z\), basta que a função seja reescrita para que encontremos a curva de nível em cada caso. Assim:
Como já analisamos anteriormente a projeção de uma curva de nível no plano \(xy\), sabemos que cada uma dessas projeções deve ser um círculo. Analisando as funções obtidas acima:
A projeção dessas curvas de nível é apresentada na Figura 1.18.
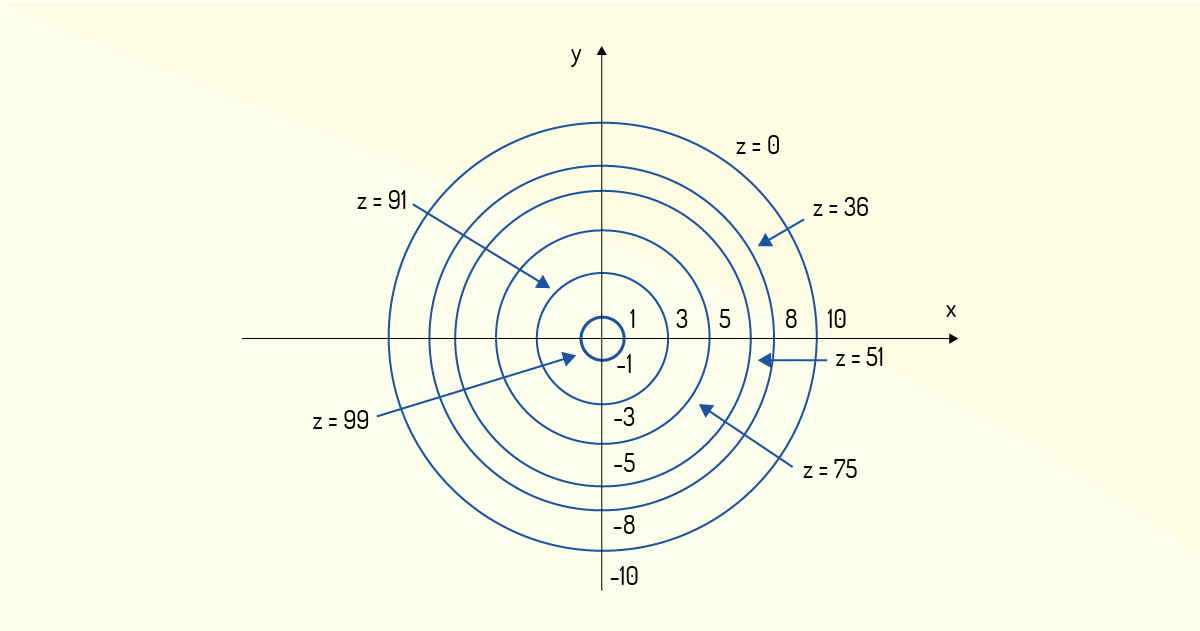
Assim, cada círculo da Figura 1.18 apresenta todos os pares ordenados \((x, y)\) que, quando aplicados na função dada, geram um resultado igual à constante que se arbitrou como valor de \(z\).
Trabalhar com gráficos de funções com mais de uma variável pode não ser uma tarefa tão simples de se realizar manualmente. No entanto, temos diversos softwares que podem ser utilizados para a produção de gráficos. Logo, caso você necessite trabalhar com gráficos de funções com mais de uma variável que não se mostrem tão simples de visualizar ou desenhar, busque tais softwares e pratique seu manuseio. Você verá que o manuseio e a visualização de problemas desse tipo se tornarão bem mais simples. Sugestões de softwares:

Finalizando a análise gráfica de funções com mais de uma variável, Flemming e Gonçalves (2005) ainda ressaltam que as curvas de nível podem ser empregadas para se esboçar o gráfico de uma função de duas variáveis. Como cada curva de nível faz parte de um plano paralelo ao plano \(xy\), indicando uma região em que a função \(z\) apresenta um valor constante igual a \(c\), você pode empilhar uma série de curvas de nível em diferentes alturas do eixo \(z\), unindo, em seguida, as bordas dessas curvas de nível, sempre respeitando o traço dos eixos \(x\) e \(y\).
Funções com mais de uma variável são comuns quando se usa o cálculo para estudos de fenômenos mais complexos. Visando fixar seu aprendizado sobre as funções com mais de uma variável, analise as alternativas a seguir e assinale a correta.
Analisando a função de estado de um gás ideal, \(PV=nRT\), ao dobrar a temperatura \(T\) e o volume \(V\) se mantendo \(n\) constante, a pressão \(P\) irá quadruplicar.
Justificativa: Note que \(P\) é diretamente proporcional à \(T\) e inversamente proporcional ao \(V\). Logo, duplicar a temperatura também duplicaria a pressão, mas duplicar o volume faz com que a pressão caia à metade. Logo, \(P\) se mantém inalterado neste caso.
As curvas de nível da função \(z=3-6x-3y\) serão funções lineares do tipo \(y=\frac{\left( 3-z \right)}{3}-2x\).
Justificativa correta: Para determinar uma curva de nível, basta fornecer um valor constante para \(z\). Assim, considerando que \(z\) é constante, pode-se reescrever a equação indicada como:
\(3y=3-6x-z\)
Agrupando as constantes 3 e \(z\) e, em seguida, dividindo toda a equação por 3:
\[3y=\left( 3-z \right)-6x~~\to ~~y=\frac{\left( 3-z \right)}{3}-2x\]
O domínio e a imagem da função \(f\left( x,y,x \right)=\frac{1}{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}+3}\) são ℝ\(^3\).
Justificativa: Esta função, sendo um quociente, não pode apresentar um denominador igual a zero. Logo, seu domínio será o conjunto \(\left\{ x,y,z\in \mathbb{R}|{{x}^{2}}+{{y}^{2}}+{{z}^{2}}+3\ne 0 \right\}\). Por exemplo, nos pontos \(\left( \pm 1,\pm 1,\pm 1 \right),\) essa função não está definida. Já a imagem dessa função contém apenas valores positivos, o que já invalida a informação dada.
A função \(w=4-{{r}^{2}}-{{t}^{2}}\) apresenta como máximo em \(w\) o valor 4 e sua curva de nível em \(w=0\) é uma circunferência de raio igual a 4 e centro na origem do eixo \(rt\).
Justificativa: O máximo da função no eixo \(w\) ocorre quando \(r\) e \(t\) são iguais a zero, ou seja, seu máximo em \(w\) realmente é 4. Já sua curva de nível quando \(w=0\) é:
\[{{r}^{2}}+{{t}^{2}}=4\]
Que indica uma circunferência de raio igual a \(\sqrt{4}=2\).
O domínio e a imagem da função \(f\left( x,y \right)=ln\left( 5-\sqrt{{{x}^{2}}+{{y}^{2}}} \right)\) são o conjunto \(\left\{ x,y\in \mathbb{R}|{{x}^{2}}+{{y}^{2}}\le 25 \right\}\).
Justificativa: Esta função, sendo um logaritmo natural, não pode existir para valores negativos ou iguais a zero. Assim, \(5-\sqrt{{{x}^{2}}+{{y}^{2}}}>0\), ou seja, \(\sqrt{{{x}^{2}}+{{y}^{2}}}<5\), o que implica que \({{x}^{2}}+{{y}^{2}}<25\). Logo, o domínio será \(\left\{ x,y\in \mathbb{R}|{{x}^{2}}+{{y}^{2}}<25 \right\}\).
Agora, podemos, finalmente, direcionar nossos estudos para o Cálculo. Após analisar os conceitos de funções com mais de uma variável, iremos estudar a respeito do limite de uma função com mais de uma variável.
Segundo Morettin, Hazzan e Bussab (2016), todas as mesmas noções de limite vistas para o caso de funções com uma variável também são válidas para o caso de funções com mais de uma variável. Logo, convém propor inicialmente uma definição intuitiva para o limite no caso de funções com duas variáveis.
Assim, Morettin, Hazzan e Bussab (2016) afirmam que se o valor da função \(z=f\left( x,y \right)\) tender a um determinado valor \(L\) quando o par ordenado \(\left( x,y \right)\) se aproxima arbitrariamente de um ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\), mas jamais sendo igual a \(\left( {{x}_{0}},{{y}_{0}} \right)\), esse valor \(L\) é considerado o limite da função quando \(\left( x,y \right)\) tende a \(\left( {{x}_{0}},{{y}_{0}} \right)\). Note que os valores do par ordenado devem sempre pertencer ao domínio da função. Simbolicamente, isso pode ser representado da seguinte forma:
\[\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,f\left( x,y \right)=L~~~~~~(7)\]
Essa ideia de “se aproxima arbitrariamente de um ponto, sem jamais ser igual a esse ponto” é algo que alguns podem ter dificuldade em compreender. Flemming e Gonçalves (2005) consideram que essa frase pode ser representada matematicamente da seguinte forma:
\[\left| f\left( x,y \right)-L \right|<\varepsilon~~~~~~(8)\]
O valor \(\varepsilon \) indicado é sempre um número positivo, sendo ele tão pequeno quanto você puder imaginar.
Note que, dada essa definição mais informal, você é capaz de avaliar numericamente os limites de uma função de mais de uma variável assim como se faz com as funções de uma única variável. Ou seja, basta ir aproximando as variáveis por diferentes combinações.
Para chegarmos a uma definição mais acurada matematicamente do limite de uma função com duas variáveis, Leithold (1994) parte da definição da distância entre dois pontos. Retomando o que foi visto no início desta Unidade, sendo os pontos \(P=\left( {{x}_{1}},{{x}_{2}}...,{{x}_{n}} \right)\) e \(A=\left( {{a}_{1}},{{a}_{2}}...,{{a}_{n}} \right)\), ambos pertencentes a ℝ\(^n\), a distância \({{d}_{PA}}\) pode ser avaliada utilizando a Equação (6), de modo que você encontrará que:
\[{{d}_{PA}}=\sqrt{{{\left( {{x}_{1}}-{{a}_{1}} \right)}^{2}}+{{\left( {{x}_{2}}-{{a}_{2}} \right)}^{2}}+...+{{\left( {{x}_{n}}-{{a}_{n}} \right)}^{2}}}~~~~~~(9)\]
Note que \({{d}_{PA}}\), também representado como \(\left| \left| P-A \right| \right|\), sempre será um número positivo, visto que ele avalia uma distância. Da distância entre dois pontos, Leithold (1994) apresenta duas definições:
Definição 6: sendo A um ponto de ℝ\(^n\) e \(r\) um número qualquer real e positivo, o conjunto de todos os pontos \(P\in {{\mathbb{R}}^{n}}\), tais que se tenha \(\left| \left| P-A \right| \right|<r\), é chamado bola aberta \(B\left( A;r \right)\);
Definição 7: sendo A um ponto de ℝ\(^n\) e \(r\) um número qualquer real e positivo, o conjunto de todos os pontos \(P\in {{\mathbb{R}}^{n}}\), tais que se tenha \(\left| \left| P-A \right| \right|\le r\), é chamado bola fechada \(B\left[ A;r \right]\).
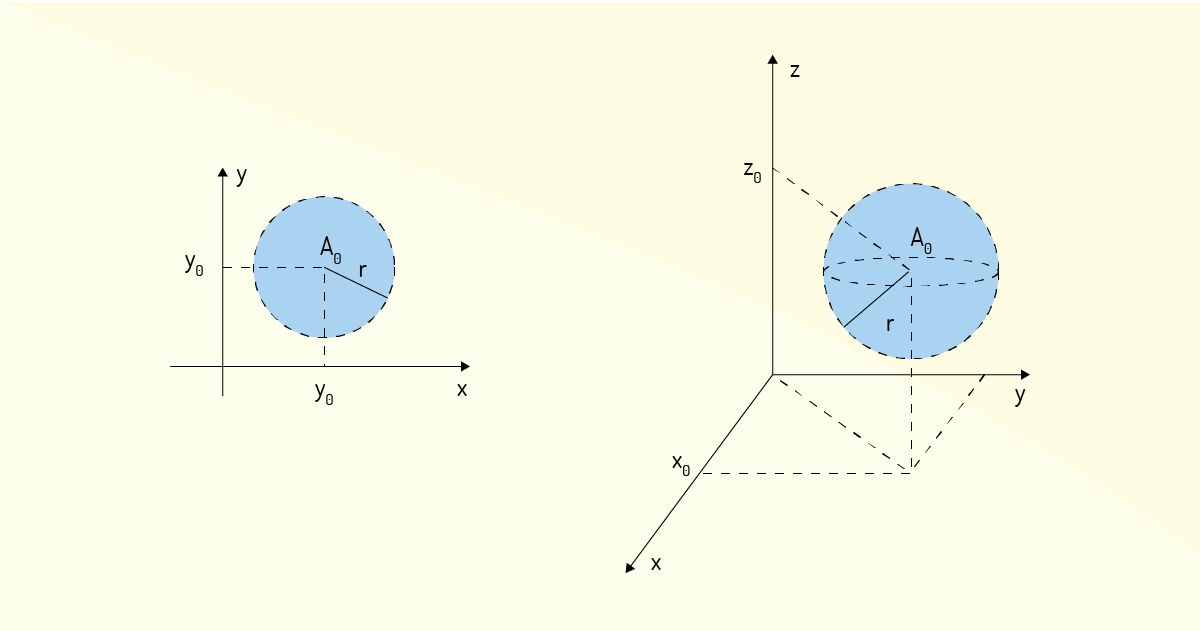
Mas por que a denominação de bola para essas distâncias? Flemming e Gonçalves (2005) dizem que isso deriva da forma geométrica das representações das definições 6 e 7. Por exemplo, se \(A\in {{\mathbb{R}}^{2}}\), então a bola aberta \(B\left( A;r \right)\):
\[B\left( A;r \right)=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}|\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}<r \right\}~~~~~~(10)\]
Note que (10) pode ser reescrita da seguinte forma:
\[B\left( A;r \right)=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}|{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}<{{r}^{2}} \right\}~~~~~~(11)\]
Veja que a condição indicada em (11) é a equação de uma circunferência de raio $r$ e centro em um ponto ~\({{A}_{0}}=\left( {{x}_{0}},{{y}_{0}} \right)\). Ou seja, a bola aberta \(B\left( A;r \right)\) para \(A\in {{\mathbb{R}}^{2}}\) é o conjunto de todos os pontos contidos no interior da circunferência de raio \(r\) e centro em um ponto \({{A}_{0}}=\left( {{x}_{0}},{{y}_{0}} \right)\), descartando os pontos que delimitam a circunferência.
Já para o caso de \(A\in {{\mathbb{R}}^{3}}\), você encontrará
\[B\left( A;r \right)=\left\{ \left( x,y,z \right)\in {{\mathbb{R}}^{2}}|\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}+{{\left( z-{{z}_{0}} \right)}^{2}}}<r \right\}~~~~~~(12)\]
ou:
\[B\left( A;r \right)=\left\{ \left( x,y,z \right)\in {{\mathbb{R}}^{2}}|{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}+{{\left( z-{{z}_{0}} \right)}^{2}}<{{r}^{2}} \right\}~~~~~~(13)\]
Assim, a condição mostrada em (13) não descreve uma esfera de raio \(r\) e centro em um ponto \({{A}_{0}}=\left( {{x}_{0}},{{y}_{0}},{{z}_{0}} \right)\). Logo, a bola aberta \(B\left( A;r \right)\) para \(A\in {{\mathbb{R}}^{3}}\) indica todos os pontos contidos no interior de uma esfera de raio \(r\) e centro em um ponto \({{A}_{0}}=\left( {{x}_{0}},{{y}_{0}},{{z}_{0}} \right)\), descartando os pontos que delimitam a esfera. A Figura 1.19 ilustra esses casos.
O mesmo pode ser estendido para o conceito de bola fechada, com a diferença que os pontos que delimitam a circunferência ou a esfera são incluídos.
Essa definição de bola aberta e bola fechada remete à definição de intervalos abertos e intervalos fechados. Para ilustrar essa semelhança, Leithold (1994) considera o espaço unidimensional ℝ. A bola aberta \(B\left( a;r \right)\) apresenta o conjunto de todos os valores \(x\) para os quais se tem que \(\left| x-a \right|<r\). Ou seja, a distância \(\left| x-a \right|\) pode ser tomada infinitesimalmente próxima a um valor \(r\), mas jamais pode ser igual a \(r\). Logo, a bola aberta \(B\left( a;r \right)\) é um intervalo aberto. De forma análoga, a bola fechada \(B\left[ A;r \right]\) apresenta o conjunto de todos os valores \(x\) para os quais se tem que \(\left| x-a \right|\le r\), de modo que a distância \(\left| x-a \right|\) pode ser igual a \(r\), o que caracteriza a bola fechada como um intervalo fechado.
Uma outra definição que se mostrará útil adiante, dada por Flemming e Gonçalves (2005), é a de ponto interior. Tal definição será aplicada apenas a conjuntos pertinentes a ℝ\(^2\) e ℝ\(^3\).
Definição 8: seja, então, \(A\) um conjunto pertencente a um desses espaços. Um ponto \(P\in A\) será dito ponto interior do conjunto \(A\) se existir uma bola aberta centrada em \(P\) e contida no conjunto \(A\). Agora, se todos os pontos \(P\in A\) são pontos interiores de \(A\), o conjunto \(A\) é, então, denominado aberto.
É interessante notar que um conjunto aberto no plano ou no espaço simplesmente é o domínio de uma função. Na Figura 1.20 são mostrados exemplos de pontos interiores e conjuntos abertos no plano e no espaço.
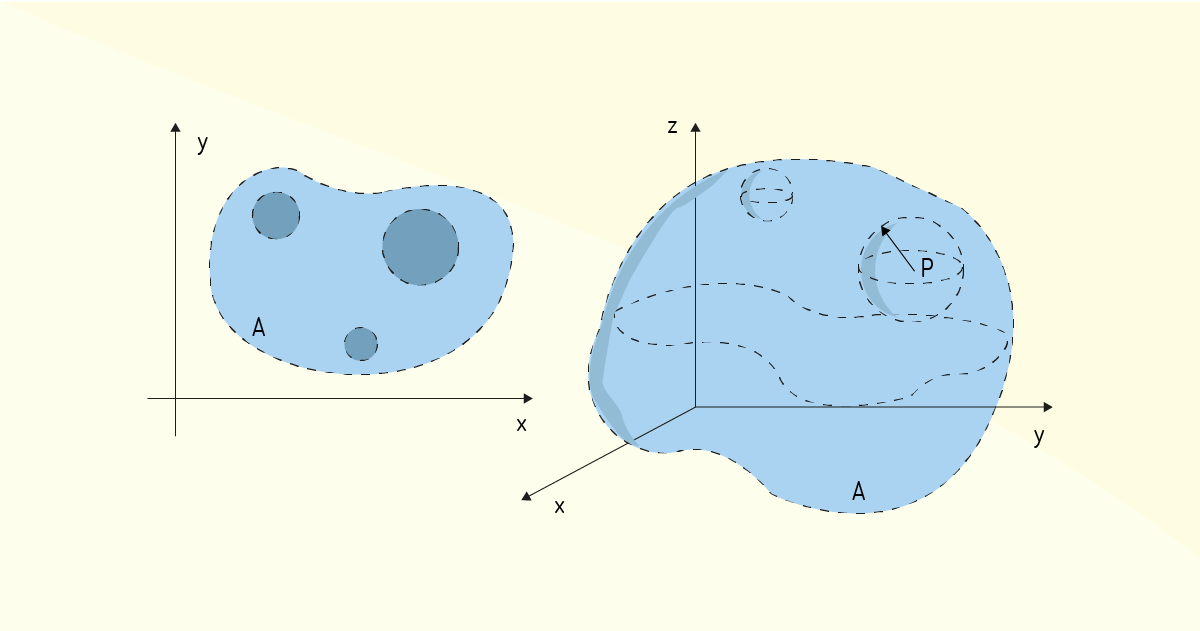
Aproveitando a mesma definição do ponto \(P\in A\) usada para pontos interiores, sendo o conjunto \(A\subset {{\mathbb{R}}^{2}}\), então, quando uma bola aberta centrada em \(P\) contiver pontos que pertencem a \(A\) e pontos que não pertencem a \(A\), o ponto \(P\) é chamado ponto de fronteira de \(A\). Juntando todos os pontos de fronteira desse conjunto \(A\), tem-se a fronteira de \(A\) (FLEMMING; GONÇALVES, 2005).
Leithold (1994) usa a definição de bola aberta para uma definição mais formal do limite de funções com n variáveis:
Definição 9: considere a função de n variáveis \(f\) como sendo definida em uma bola aberta \(B\left( A;r \right)\), exceto possivelmente no próprio ponto \(A\). Diz-se, então, que o limite de \(f\left( P \right)\) quando \(P\) tende a \(A\) será igual ao valor \(L\), ou seja, \(\underset{P\to A}{\mathop{lim}}\,f\left( P \right)=L\), se, para todo \(\varepsilon >0\), existir um \(\delta >0\) tal que, se
\[0<\left| \left| P-A \right| \right|<\delta \]
então \(\left| f\left( P \right)-L \right|<\varepsilon \).
Note que a Definição 9 pode ser facilmente reduzida ao caso de uma função de uma variável, pois, em tal caso, tem-se que \(P~=~x\) e \(A~=~a\), resultando que, se \(f\) for definida em qualquer intervalo aberto cujo centro seja o ponto \(a\), exceto possivelmente nesse ponto \(a\), então o limite de \(f\left( x \right)\) quando \(x\) tende a \(a\) será igual ao valor \(L\), ou seja, \(\underset{x\to a}{\mathop{lim}}\,f\left( x \right)=L\), se, para todo \(\varepsilon >0\), existir um \(\delta >0\) tal que, se
\[0<\left| x-a \right|<\delta \],
então $\left| f\left( x \right)-L \right|<\varepsilon $.
A Definição 9 pode ser, agora, aplicada ao caso de nosso interesse, que é a função com duas variáveis. De acordo com Leithold (1994):
Definição 10: seja o par ordenado \(A=\left( {{x}_{0}},{{y}_{0}} \right)\) e a função de 2 variáveis \(f\) definida em uma bola aberta \(B\left( A;r \right)\), exceto possivelmente no próprio ponto \(A\). Diz-se, então, que o limite de \(f\left( x,y \right)\), quando o par ordenado \(\left( x,y \right)\) tende a \(A=\left( {{x}_{0}},{{y}_{0}} \right)\), será igual ao valor \(L\), ou seja, \(\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,f\left( x,y \right)=L\), se, para todo \(\varepsilon >0\), existir um \(\delta >0\) tal que, se
\[0<\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}<\delta,\]
então \(\left| f\left( x,y \right)-L \right|<\varepsilon\).
É interessante destacar que pelas definições de limites dadas aqui, não é necessário que a função esteja definida no ponto \(A\) para que o limite exista; basta que a função esteja definida para valores próximos desse ponto.
Exemplo 3.1: Usando a definição de limite de funções de duas variáveis apresentada, mostre que
\[\underset{\left( x,y \right)\to \left( 1,1 \right)}{\mathop{lim}}\,\left( 2x+5y \right)=7\]
Solução
Partindo da Definição 9, que temos para o limite de uma função com duas variáveis, para mostrar que o limite existe, é preciso mostrar que para todo \(\varepsilon >0\) irá existir um \(\delta >0\) tal que \(\left| f\left( x,y \right)-7 \right|<\varepsilon\) sempre que
\[0<\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}}<\delta\]
Da mesma forma que você deve ter desenvolvido quando trabalhou com o caso de limites de funções com uma única variável, pode-se buscar pistas para encontrar \(\delta \) a partir da desigualdade de \(\varepsilon\). Assim, substituindo a função \(f\left( x,y \right)\) dada, encontra-se:
\[|f\left( x,y \right)-7\left| \left\langle \varepsilon ~\to ~ \right|2x+5y-7 \right|\]
\[=\left| 2x-2+5y-5\left| = \right|2\left( x-1 \right)+5\left( y-1 \right) \right|\]
\[=2\left| x-1 \right|+5\left| y-1 \right|\]
Então, tem-se que \(~\left| 2x+5y-7 \right|\le 2\left| x-1 \right|+5\left| y-1 \right|\). Note agora que:
\[\left| x-1 \right|\le \sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}}\]
\[\left| y-1 \right|\le \sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}}\]
Logo, se \(0<\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}}<\delta\), então \(2\left| x-1 \right|+5\left| y-1 \right|<2\delta +5\delta \). Portanto, tem-se que uma escolha adequada para \(\delta \) será \(7\delta =\varepsilon \), ou seja, \(\delta =\frac{1}{7}\varepsilon \). Utilizando, então, este valor de \(\delta\) em \(0<\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}}<\delta \), tem-se que:
\[~\left| 2x+5y-7 \right|\le 2\left| x-1 \right|+5\left| y-1 \right|<2\delta +5\delta \]
\[~\left| 2x+5y-7\left| \le \right|2\left( x-1 \right)+5\left( y-1 \right) \right|<2\frac{1}{7}\varepsilon +5\frac{1}{7}\varepsilon \]
\[\left| 2\left( x-1 \right)+5\left( y-1 \right) \right|<\frac{2}{7}\varepsilon +\frac{5}{7}\varepsilon \]
\[\left| 2\left( x-1 \right)+5\left( y-1 \right) \right|<\varepsilon \]
Então, tendo \(~\left| 2x+5y-7 \right|<\varepsilon\), demonstramos que para todo \(\varepsilon >0\), ao escolher um \(\delta =\frac{1}{7}\varepsilon \), a Definição 9 será verdadeira. Provou-se, então, que o limite indicado no início é verdadeiro.
Ainda sobre a Definição 9, podemos encontrar uma distância entre \(f\left( x,~y \right)\) e \(L\) tão pequena quanto desejarmos, desde que a distância do par ordenado \(\left( x,~y \right)\) seja suficientemente pequena do ponto \(\left( {{x}_{0}},~{{y}_{0}} \right)\), mas nunca nula. Ou seja, conforme Stewart (2017b) indica, essa é uma definição baseada apenas na distância entre pontos, não indicando nada sobre o sentido que devemos tomar para realizar essa aproximação. Assim, no caso do limite lateral de uma função de uma única variável, para que o limite de uma função exista, é preciso que a aproximação de \(\left( x,~y \right)\) no sentido do ponto \(\left( {{x}_{0}},~{{y}_{0}} \right)\) leve sempre ao mesmo resultado \(L\), independente de qual for o sentido utilizado para realizar a aproximação dos pontos. Caso usando aproximações de diferentes formas o limite estimado não seja o mesmo, então, entende-se que o limite da função em questão, quando \(\left( x,~y \right)\) tende ao ponto \(\left( {{x}_{0}},~{{y}_{0}} \right)\), não existe.
Exemplo 3.2: Mostre que o limite indicado a seguir não existe.
\[\underset{\left( x,y \right)\to \left( 0,0 \right)}{\mathop{lim}}\,\left( \frac{{{x}^{3}}-{{y}^{3}}}{{{x}^{3}}+{{y}^{3}}} \right)\]
Solução
Para realizar a prova pedida, podemos partir da noção que temos de limites laterais. Assim, vamos analisar como se dá a aproximação da função ao ponto \(\left( 0,0 \right)\). Isso pode ser feito analisando a aproximação em cada coordenada separadamente, deixando a outra coordenada fixa.
Por exemplo, iniciemos analisando o que ocorre com os valores da função dada ao longo do eixo \(x\). Escolha um valor para manter a coordenada \(y\) fixa, até mesmo o valor do ponto no qual se deseja calcular o limite; então, fazendo \(y=0\), veja que, para qualquer valor de \(x\), você terá:
\[\frac{{{x}^{3}}-{{y}^{3}}}{{{x}^{3}}+{{y}^{3}}}=\frac{{{x}^{3}}-{{0}^{3}}}{{{x}^{3}}+{{0}^{3}}}=\frac{{{x}^{3}}}{{{x}^{3}}}=1\]
Ou seja, aproximando a função ao longo do eixo $x$, para todos os valores reais diferentes de zero, a função irá tender a 1. Logo, podemos dizer que $f\left( x,y \right)\to 1$ quando $\left( x,y \right)\to \left( 0,0 \right)$ ao longo do eixo $x$.
Repetindo o mesmo procedimento, mas agora fixando o valor da coordenada $x$ em zero, você encontrará:
\[\frac{{{x}^{3}}-{{y}^{3}}}{{{x}^{3}}+{{y}^{3}}}=\frac{{{0}^{3}}-{{y}^{3}}}{{{0}^{3}}+{{y}^{3}}}=\frac{-{{y}^{3}}}{{{y}^{3}}}=-1\]
Veja que ao aproximar a função ao longo do eixo \(y\), para todos os valores reais diferentes de zero, a função dada irá tender à -1, ou seja, \(f\left( x,y \right)\to -1\) quando \(\left( x,y \right)\to \left( 0,0 \right)\) ao longo do eixo \(y\).
Como as aproximações do ponto \(\left( 0,0 \right)\) feitas para a dada função não levam ao mesmo valor, então podemos concluir que o limite informado não existe.
Também é possível formalizar esse cálculo de limite lateral para funções com mais de uma variável, como indicam Leithold (1994) e Flemming e Gonçalves (2005). Para tal, é necessário mais uma definição ser enunciada, a de ponto de acumulação:
Definição 11: seja o conjunto \(A\subset {{\mathbb{R}}^{n}}\) e o ponto \({{P}_{0}}\). O ponto \({{P}_{0}}\) será chamado de ponto de acumulação se toda bola aberta centrada em \({{P}_{0}}\) conter uma infinidade de pontos de \(A\).
Como exemplo de pontos de acumulação, considere o conjunto \(A\) que consiste de todos os pontos do 1º e 4º quadrantes, ou seja, todos os pontos do plano para \(x\ge 0\). A bola aberta centrada na origem do plano cartesiano \(B\left( O;r \right)\) será um ponto acumulação, mesmo que apenas metade da circunferência esteja localizada em $A$, pois é possível identificar uma infinidade de pontos de \(A\) dentro de \(B\left( O;r \right)\) (LEITHOLD, 1994).
Outro exemplo de ponto de acumulação, dado por Flemming e Gonçalves (2005), é o seguinte: seja o conjunto \(A=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}|0<\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}}<1 \right\}\), ou seja, \(A\) é uma circunferência de origem \(\left( 1,2 \right)\) e raio 1. Note que todos os pontos de \(A\), incluindo os que delimitam a circunferência, são pontos de acumulação. Mesmo a origem \(\left( 1,2 \right)\), que não pertence a \(A\), também é um ponto de acumulação de \(A\). Apenas pontos externos ao conjunto não serão pontos de acumulação, como se pode ver na Figura 1.21.
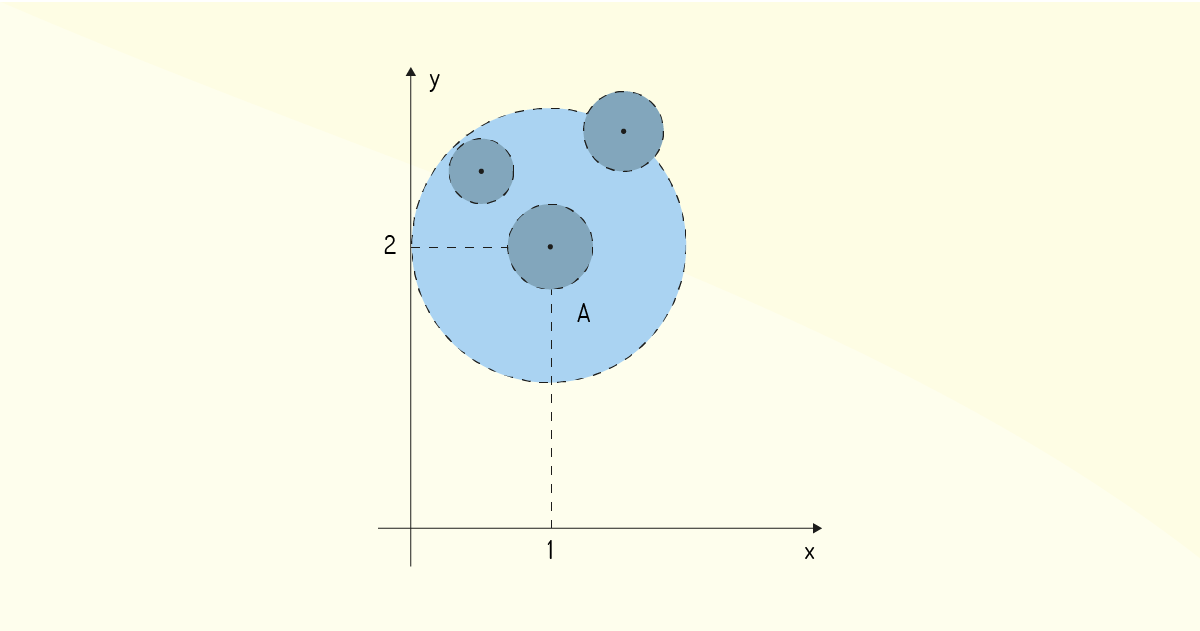
Agora, com essas definições formalizadas, Leithold (1994) enuncia a seguinte definição, relativa a limites laterais para funções de duas variáveis:
Definição 12: seja a função \(f\) definida no conjunto \(A\subset {{\mathbb{R}}^{2}}\) e o ponto de acumulação de \(A\), \({{P}_{0}}=\left( {{x}_{0}},{{y}_{0}} \right)\), então o limite de \(f\left( x,y \right)\), quando \(\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)\) em \(A\), será o número real \(L\) se, para todo \(\varepsilon >0\), existir um \(\delta >0\) tal que, se
\[0<\sqrt{{{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}}<\delta,\]
então \(\left| f\left( x,y \right)-L \right|<\varepsilon \) e \(\left( x,y \right)\) pertence a \(A\).
Partindo da Definição 12, pode ser possível que o limite a ser calculado se torne o limite de uma função de uma única variável. Leithold (1994) indica os seguintes exemplos; considerando \(\underset{\left( x,~y \right)\to \left( 0,0 \right)}{\mathop{lim}}\,f\left( x,y \right)\), então:
Assim, se a função $f\left( x,y \right)$ apresentar diferentes limites quando \(\left( x,y \right)\to \left( {{x}_{0}},~{{y}_{0}} \right)\) por meio de dois conjuntos distintos que contenham o ponto de acumulação \(\left( {{x}_{0}},~{{y}_{0}} \right)\), então, Leithold (1994) diz que o limite \(\underset{\left(x,~y \right)\to \left({{x}_{0}},~{{y}_{0}} \right)}{\mathop{lim}}\,f\left( x,y \right)\) não irá existir.
Nem sempre é uma tarefa simples identificar os conjuntos adequados para checar se um dado limite existe. Logo, um pouco de prática é necessário para identificar tais pontos de forma simples e dinâmica.
A definição de limites exige um bom domínio de conceitos, como a identificação de um conjunto como bola aberta, que consiste em encontrar uma equação da circunferência para \({{\mathbb{R}}^{2}}\) ou de uma esfera para \({{\mathbb{R}}^{3}}\). Sendo assim, buscando fixar essas definições mais básicas, úteis para a definição de um limite, analise as alternativas a seguir e assinale a correta.
O conjunto \(A=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}|{{x}^{2}}+{{y}^{2}}-4y<8 \right\}\) é bola aberta com centro em \(\left( 0,2 \right)\) e raio 4.
Justificativa: Reescreva \({{x}^{2}}+{{y}^{2}}-4y<8\) buscando uma equação de circunferência. Para tal, veja que o termo \({{y}^{2}}-4y\) pode derivar de um termo \({{\left( y-{{y}_{0}} \right)}^{2}}~\to ~{{\left( y-2 \right)}^{2}}\). Assim:
\[{{x}^{2}}+{{y}^{2}}-4y<8~~\to ~~{{\left( x-0 \right)}^{2}}+{{\left( y-2 \right)}^{2}}<8\]
Mas, como \({{\left( y-2 \right)}^{2}}={{y}^{2}}-4y+4\), deve-se reajustar a equação dada, adicionando-se -4 a ambos os lados:
\[~{{\left( x+0 \right)}^{2}}+{{\left( y-2 \right)}^{2}}<4\]
Logo, o conjunto dado é bola aberta, com centro em \(\left( 0,2 \right)\) e raio \(\sqrt{4}=2\).
O conjunto \(A=\left\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}|{{x}^{2}}+{{y}^{2}}+{{z}^{2}}+8z<25 \right\}\) é uma bola aberta com centro em \(\left( 0,0,-4 \right)\) para \({{\mathbb{R}}^{3}}\) e raio 3.
Justificativa correta: Reescreva \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}+8z<8\) buscando uma equação de circunferência. Para tal, veja que o termo \({{z}^{2}}+8z\) pode derivar de um termo \({{\left( z-{{z}_{0}} \right)}^{2}}~\to ~{{\left( z+4 \right)}^{2}}\).
\[~{{x}^{2}}+{{y}^{2}}+{{z}^{2}}+8z<25~~\to ~~{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}+{{\left( z+4 \right)}^{2}}<25\]
Mas, como \({{\left( z+4 \right)}^{2}}={{z}^{2}}+8z+16\), deve-se reajustar a equação dada adicionando-se -16 a ambos os lados:
\[~{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}+{{\left( z+4 \right)}^{2}}<25~~\to ~~~{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}+{{\left( z+4 \right)}^{2}}<25-16\]
Portanto, a equação de esfera deve ficar:
\[~{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}+{{\left( z+4 \right)}^{2}}<9\]
Logo, o conjunto dado é bola aberta, com centro em \(\left( 0,0,-4 \right)\) e raio \(\sqrt{9}=3\).
O conjunto \(A=\left\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}|{{x}^{2}}+{{y}^{2}}-{{z}^{2}}<0 \right\}\) é uma bola aberta com centro em \(\left( 0,0,0 \right)\) para \({{\mathbb{R}}^{3}}\).
Justificativa: Não é possível encontrar uma equação da esfera para o conjunto dado, pois o sinal do termo \({{z}^{2}}\) difere dos sinais de \({{x}^{2}}\) e \({{y}^{2}}\). Logo, pode-se presumir que esse conjunto não é uma bola aberta.
O conjunto \(A=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{3}}\left| {{x}^{2}}+{{y}^{2}}-4 \right\rangle 0 \right\}\) é uma bola aberta com centro em \(\left( 0,1 \right)\) para \({{\mathbb{R}}^{2}}\).
Justificativa: Reescreva \({{x}^{2}}+{{y}^{2}}-4>0\) buscando uma equação de circunferência. Para tal, basta adicionar +4 a ambos os lados:
\[{{x}^{2}}+{{y}^{2}}>4\]
Perceba que a equação encontrada não condiz com os elementos internos de uma circunferência, mas com os elementos externos. Logo, o conjunto dado não é bola aberta.
O conjunto \(A=\left\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}|{{x}^{2}}+{{y}^{2}}+z<16 \right\}\) é uma bola aberta com centro em \(\left( 0,0,0 \right)\) para \({{\mathbb{R}}^{3}}\) e raio igual a 4.
Justificativa: Não é possível encontrar uma equação da esfera para o conjunto dado, pois o termo \(z\) está em potência 1. Logo, pode-se presumir que esse conjunto não é uma bola aberta.
Aprimorando, agora, o estudo de limites com mais de uma variável, veremos uma série de propriedades, não tão novas, que podem facilitar seu trabalho. Todas as propriedades apresentadas para limites de funções com uma única variável também são válidas para os limites de funções com mais de uma variável. Thomas Júnior (2016) apresenta, então, um resumo de todas as propriedades para limites de funções com mais de uma variável. Para que tais propriedades sejam apresentadas, considere os números reais \(L\), \(M\) e \(k\) e que os limites \(\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,f\left( x,y \right)=L\) e \(\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,g\left( x,y \right)=M\) existem.
Observe que, na regra da raiz, caso $n$ seja par, assume-se que o valor de $L$ é par. Também deve-se ficar atento que, no caso de $n$ ser par, é necessário que $f\left( x,y \right)$ também seja maior ou igual a zero.
Assim como nos casos de limites de funções de uma única variável, você deve tomar cuidado em relação a casos de indeterminações. Por exemplo, considere as funções de duas variáveis \(f\) e \(g\), tais que:
\[\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,f\left( x,y \right)=\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,g\left( x,y \right)=0\]
Se você aplicasse de forma direta a regra do quociente, você se veria incapaz de determinar o limite de \(h=f/g\) quando \(\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)\). Em tal situação, Flemming e Gonçalves (2005) afirmam que, dependendo de como sejam as funções \(f\) e \(g\), você poderá encontrar que o limite de \(h=f/g\) quando \(\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)\) for um número real ou até confirmar que esse limite não existe. Para exemplificar melhor esse caso de indeterminação, Flemming e Gonçalves (2005) apresenta o seguinte exemplo.
Exemplo 4.1: Calcule o limite a seguir.
\[\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( \frac{{{x}^{3}}+{{x}^{2}}y-2xy-2{{x}^{2}}-2x+4}{xy+x-2y-2} \right)\]
Solução
Vamos verificar, primeiro, o limite do numerador e do denominador individualmente:
\[\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( {{x}^{3}}+{{x}^{2}}y-2xy-2{{x}^{2}}-2x+4 \right)=8+4-4-8-4+4=0\]
\[\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( xy+x-2y-2 \right)=2+2-2-2=0\]
Agora, se aplicarmos a regra do quociente à função dada, encontraremos a indeterminação \(0/0\). Da definição de tal regra, já sabíamos que não seria possível aplicá-la, pois o denominador seria 0.
Para lidar com tal limite, no entanto, você pode realizar uma manipulação matemática nas funções. Por exemplo, você pode reescrever a primeira expressão como:
\[x\left( {{x}^{2}}+xy-2 \right)-2\left( {{x}^{2}}+xy-2 \right)=\left( x-2 \right)\left( {{x}^{2}}+xy-2 \right),\]
e a segunda como:
\[x\left( y+1 \right)-2\left( y+1 \right)=\left( x-2 \right)\left( y+1 \right)\]
Agora, reescrevendo o limite:
\[\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( \frac{{{x}^{3}}+{{x}^{2}}y-2xy-2{{x}^{2}}-2x+4}{xy+x-2y-2} \right)=\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( \frac{\left( x-2 \right)\left( {{x}^{2}}+xy-2 \right)}{\left( x-2 \right)\left( y+1 \right)} \right)\]
\[=\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( \frac{\left( {{x}^{2}}+xy-2 \right)}{\left( y+1 \right)} \right)\]
Verificando, novamente, o limite do numerador e do denominador:
\[\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( {{x}^{2}}+xy-2 \right)=4+2-2=4\]
\[\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( y+1 \right)=1+1=2\]
Agora, podemos aplicar a regra do quociente:
\[\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( \frac{{{x}^{3}}+{{x}^{2}}y-2xy-2{{x}^{2}}-2x+4}{xy+x-2y-2} \right)=\frac{\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( {{x}^{2}}+xy-2 \right)}{\underset{\left( x,y \right)\to \left( 2,1 \right)}{\mathop{lim}}\,\left( y+1 \right)}=\frac{4}{2}=2\]
Finalmente, após expandirmos os conceitos de limites de funções de uma única variável já conhecidos para casos de funções com mais de uma variável, chegamos no momento final desta unidade, que visa definir para funções de várias variáveis um conceito muito importante a respeito das funções: a continuidade.
Thomas Júnior (2016) nos diz que o conceito de uma função de uma única variável também é válido aqui para uma função com n variáveis. Logo, tanto quanto no caso das funções de variável única, a continuidade de funções de n variáveis também será definida em termos do limite. Para esse assunto, Thomas Júnior (2016) enuncia a seguinte definição:
Definição 13: a função \(f\left( x,y \right)\) será dita contínua num ponto \(\left( {{x}_{0}},{{y}_{0}} \right)\) se:
Essa definição de continuidade e de um ponto pode, ainda, ser estendida para a continuidade da função como um todo: se uma função for contínua em todos os pontos de seu domínio, tal função é dita contínua.
Ainda segundo Thomas Júnior (2016), qualquer combinação algébrica de funções contínuas também resultará em uma função contínua. Ou seja, a soma, a diferença e a multiplicação por constante, produtos, quocientes e potenciação de funções contínuas também irão produzir funções contínuas em seus domínios.
Sobre alguns tipos comuns de funções contínuas, Stewart (2017b) nos diz que as funções polinomiais de duas variáveis são sempre contínuas em \({{\mathbb{R}}^{2}}\), o que acaba por se estender às funções racionais, que são contínuas em seu domínio. Logo, em tais tipos de funções, o cálculo do limite pode ser feito facilmente pela substituição direta.
Com respeito à continuidade de funções, Flemming e Gonçalves (2005) enunciam uma outra propriedade de limites de funções. Considere \(f\) uma função de uma variável e \(g\) uma função de duas variáveis, contínua em \(\left( {{x}_{0}},{{y}_{0}} \right)\); então, a função composta \(\left( f\circ g \right)\) também será contínua em \(\left( {{x}_{0}},{{y}_{0}} \right)\). Se essa mesma função \(f\) for contínua num ponto \(a\) e a função \(g\) for tal que seu limite \(\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,g\left( x,y \right)=a\), então:
\[~\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,\left( f\circ g \right)\left( x,y \right)=f\left( a \right)\]
ou
\[~\underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,f\left( g\left( x,y \right) \right)=f\left( \underset{\left( x,y \right)\to \left( {{x}_{0}},{{y}_{0}} \right)}{\mathop{lim}}\,g\left( x,y \right) \right)\]
Saber identificar se uma função é contínua ou não é importante para auxiliar na resolução de exercícios de Cálculo. Logo, buscando aprimorar sua habilidade nesse processo de identificação, analise as alternativas a seguir e assinale a correta.
A função \(f\left( x,y \right)=ln\left( {{x}^{2}}+{{y}^{2}}-9 \right)\) é contínua em \(\left( 3,3 \right)\).
Justificativa: Note que a função não existe no ponto indicado. Logo, essa função não pode ser contínua em \(\left( 3,3 \right)\)
A função \(f\left( x,y \right)=\frac{4-x}{{{x}^{2}}+3{{y}^{2}}+2}\) é contínua para todos os valores de \(x\) e \(y\) pertencentes a \({{\mathbb{R}}^{2}}\).
Justificativa correta: Observe que o denominador dessa função jamais será menor que 2. Como para qualquer valor de \(x\) e \(y\), essa função estará definida, é uma função racional e será contínua em todo o seu domínio, que é \({{\mathbb{R}}^{2}}\).
A função \(f\left( x,y \right)=\frac{x-y}{2{{x}^{2}}+3{{y}^{2}}}\) é contínua para todos os valores de \(x\) e \(y\) pertencentes a \({{\mathbb{R}}^{2}}\).
Justificativa: Note que essa função não está definida no ponto \(\left( 0,0 \right)\). Logo, ela não será contínua em todo \({{\mathbb{R}}^{2}}\).
A função \(f\left( x,y \right)=arctan\left( \frac{2x}{y} \right)\) é contínua para todos os valores de \(x\) e \(y\) pertencentes a \({{\mathbb{R}}^{2}}\).
Justificativa: Aqui tem-se uma função composta. Note que \(2x/y\) é uma função racional, o que significa que será contínua para todo seu domínio. Logo, \(2x/y\) é contínua para todo \({{\mathbb{R}}^{2}}\) exceto em \(y=0\). Como a função \(arctan~t\) é contínua para todo \(\mathbb{R}\), a função \(f\left( x,y \right)\) dada será contínua para todo \({{\mathbb{R}}^{2}}\) exceto em \(y=0\).
A função \(f\left( x,y \right)=\frac{2{{x}^{2}}}{{{x}^{2}}+{{x}^{2}}{{y}^{2}}}\) não é contínua em \(\left( 0,0 \right)\).
Justificativa: A função dada pode ser simplificada para:
\[f\left( x,y \right)=\frac{2{{x}^{2}}}{{{x}^{2}}+{{x}^{2}}{{y}^{2}}}=\frac{2{{x}^{2}}}{{{x}^{2}}\left( 1+{{y}^{2}} \right)}=\frac{2}{1+{{y}^{2}}}\]
Logo, essa função está definida em \(\left( 0,0 \right)\). Como se tem uma função racional, ela é contínua em todo seu domínio. Logo, a função dada é contínua em \(\left( 0,0 \right)\).
Nome do livro: Cálculo – funções de uma e várias variáveis.
Editora: Saraiva
Autor: MORETTIN, P. A.; HAZZAN, S.; BUSSAB, W. O.
ISBN: 8547201106
Comentário: O livro indicado apresenta conteúdos introdutórios de forma muito prática e foi escrito em uma linguagem simples. Há vários exercícios, o que facilita a fixação dos conteúdos estudados.
