Um dos pontos-chave de se estudar pontos no espaço ℝ\(^n\) é saber identificar qual a distância de um ponto a outro, o que se mostrará uma habilidade importante para definições futuras na presente disciplina. Visando à prática deste tópico, analise as alternativas a seguir: apenas uma delas indica uma distância entre pontos calculada erroneamente. Assinale aquela em que a distância apresentada é correta.
A distância entre os pontos \(A=\left( -2,5 \right)\) e \(B=\left( 4,3 \right)\) é igual a \(4\sqrt{10}\) unidades de comprimento.
Justificativa: Como os pontos \(A\) e \(B\) pertencem a ℝ\(^2\) , a distância entre eles é avaliada da seguinte forma:
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}=\sqrt{{{\left( 4+2 \right)}^{2}}+{{\left( 3-5 \right)}^{2}}}=\sqrt{36+4}=\sqrt{40}=\sqrt{2\cdot 2\cdot 10}=2\sqrt{10}\]
Logo, a distância apresentada está certa, tornando essa alternativa falsa.
A distância entre os pontos \(C=\left( 1,1,1,1 \right)\) e \(D=\left( 2,3,3,1 \right)\) é igual a 3 unidades de comprimento.
Justificativa correta: Como os pontos \(C\) e \(D\) pertencem a ℝ\(^4\) , a distância entre eles é avaliada da seguinte forma:
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}+{{\left( {{w}_{2}}-{{w}_{1}} \right)}^{2}}}=\sqrt{{{\left( 2-1 \right)}^{2}}+{{\left( 3-1 \right)}^{2}}+{{\left( 3-1 \right)}^{2}}+{{\left( 1-1 \right)}^{2}}}=\]
\[=\sqrt{1+4+4+0}=\sqrt{9}=3\]
Logo, essa alternativa encontra-se correta.
A distância entre os pontos\(E=\left( -2,-1,3 \right)\) e \(F=\left( 0,3,-1 \right)\) é igual a \(2\) unidades de comprimento.
Justificativa: Como os pontos \(E\) e \(F\) pertencem a ℝ\(^3\) , a distância entre eles é avaliada da seguinte forma:
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}=\sqrt{{{\left( 0+2 \right)}^{2}}+{{\left( 3+1 \right)}^{2}}+{{\left( -1-3 \right)}^{2}}}=\]
\[=\sqrt{4+16+16}=\sqrt{36}=6\]
Logo, a distância apresentada está certa, tornando essa alternativa falsa.
A distância entre os pontos \(A=\left( -2,5 \right)\) e \(F=\left( 0,3,-1 \right)\) é igual a 5 .
Justificativa: Como o ponto \(A$\) pertence a ℝ\(^2\) e o ponto \(F\) pertence a ℝ\(^3\), não podemos avaliar a distância entre eles. Ou seja, pontos pertencentes a espaços dimensionais diferentes não podem ter a distância entre si avaliadas.
A distância entre os pontos \(G=\left( -2,-3,-3 \right)\) e \(H=\left( 4,3,0 \right)\) é igual a \(3\sqrt{5}\) unidades de comprimento.
Justificativa: Como os pontos \(G\) e \(H\) pertencem a ℝ\(^3\) , a distância entre eles é avaliada da seguinte forma:
\[{{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}=\sqrt{{{\left( 4+2 \right)}^{2}}+{{\left( 3+3 \right)}^{2}}+{{\left( 0+3 \right)}^{2}}}=\]
\[=\sqrt{36+36+9}=\sqrt{81}=9\]
Logo, a distância apresentada está certa, tornando essa alternativa falsa.
Funções com mais de uma variável são comuns quando se usa o cálculo para estudos de fenômenos mais complexos. Visando fixar seu aprendizado sobre as funções com mais de uma variável, analise as alternativas a seguir e assinale a correta.
Analisando a função de estado de um gás ideal, \(PV=nRT\), ao dobrar a temperatura \(T\) e o volume \(V\) se mantendo \(n\) constante, a pressão \(P\) irá quadruplicar.
Justificativa: Note que \(P\) é diretamente proporcional à \(T\) e inversamente proporcional ao \(V\). Logo, duplicar a temperatura também duplicaria a pressão, mas duplicar o volume faz com que a pressão caia à metade. Logo, \(P\) se mantém inalterado neste caso.
As curvas de nível da função \(z=3-6x-3y\) serão funções lineares do tipo \(y=\frac{\left( 3-z \right)}{3}-2x\).
Justificativa correta: Para determinar uma curva de nível, basta fornecer um valor constante para \(z\). Assim, considerando que \(z\) é constante, pode-se reescrever a equação indicada como:
\(3y=3-6x-z\)
Agrupando as constantes 3 e \(z\) e, em seguida, dividindo toda a equação por 3:
\[3y=\left( 3-z \right)-6x~~\to ~~y=\frac{\left( 3-z \right)}{3}-2x\]
O domínio e a imagem da função \(f\left( x,y,x \right)=\frac{1}{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}+3}\) são ℝ\(^3\).
Justificativa: Esta função, sendo um quociente, não pode apresentar um denominador igual a zero. Logo, seu domínio será o conjunto \(\left\{ x,y,z\in \mathbb{R}|{{x}^{2}}+{{y}^{2}}+{{z}^{2}}+3\ne 0 \right\}\). Por exemplo, nos pontos \(\left( \pm 1,\pm 1,\pm 1 \right),\) essa função não está definida. Já a imagem dessa função contém apenas valores positivos, o que já invalida a informação dada.
A função \(w=4-{{r}^{2}}-{{t}^{2}}\) apresenta como máximo em \(w\) o valor 4 e sua curva de nível em \(w=0\) é uma circunferência de raio igual a 4 e centro na origem do eixo \(rt\).
Justificativa: O máximo da função no eixo \(w\) ocorre quando \(r\) e \(t\) são iguais a zero, ou seja, seu máximo em \(w\) realmente é 4. Já sua curva de nível quando \(w=0\) é:
\[{{r}^{2}}+{{t}^{2}}=4\]
Que indica uma circunferência de raio igual a \(\sqrt{4}=2\).
O domínio e a imagem da função \(f\left( x,y \right)=ln\left( 5-\sqrt{{{x}^{2}}+{{y}^{2}}} \right)\) são o conjunto \(\left\{ x,y\in \mathbb{R}|{{x}^{2}}+{{y}^{2}}\le 25 \right\}\).
Justificativa: Esta função, sendo um logaritmo natural, não pode existir para valores negativos ou iguais a zero. Assim, \(5-\sqrt{{{x}^{2}}+{{y}^{2}}}>0\), ou seja, \(\sqrt{{{x}^{2}}+{{y}^{2}}}<5\), o que implica que \({{x}^{2}}+{{y}^{2}}<25\). Logo, o domínio será \(\left\{ x,y\in \mathbb{R}|{{x}^{2}}+{{y}^{2}}<25 \right\}\).
A definição de limites exige um bom domínio de conceitos, como a identificação de um conjunto como bola aberta, que consiste em encontrar uma equação da circunferência para \({{\mathbb{R}}^{2}}\) ou de uma esfera para \({{\mathbb{R}}^{3}}\). Sendo assim, buscando fixar essas definições mais básicas, úteis para a definição de um limite, analise as alternativas a seguir e assinale a correta.
O conjunto \(A=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}|{{x}^{2}}+{{y}^{2}}-4y<8 \right\}\) é bola aberta com centro em \(\left( 0,2 \right)\) e raio 4.
Justificativa: Reescreva \({{x}^{2}}+{{y}^{2}}-4y<8\) buscando uma equação de circunferência. Para tal, veja que o termo \({{y}^{2}}-4y\) pode derivar de um termo \({{\left( y-{{y}_{0}} \right)}^{2}}~\to ~{{\left( y-2 \right)}^{2}}\). Assim:
\[{{x}^{2}}+{{y}^{2}}-4y<8~~\to ~~{{\left( x-0 \right)}^{2}}+{{\left( y-2 \right)}^{2}}<8\]
Mas, como \({{\left( y-2 \right)}^{2}}={{y}^{2}}-4y+4\), deve-se reajustar a equação dada, adicionando-se -4 a ambos os lados:
\[~{{\left( x+0 \right)}^{2}}+{{\left( y-2 \right)}^{2}}<4\]
Logo, o conjunto dado é bola aberta, com centro em \(\left( 0,2 \right)\) e raio \(\sqrt{4}=2\).
O conjunto \(A=\left\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}|{{x}^{2}}+{{y}^{2}}+{{z}^{2}}+8z<25 \right\}\) é uma bola aberta com centro em \(\left( 0,0,-4 \right)\) para \({{\mathbb{R}}^{3}}\) e raio 3.
Justificativa correta: Reescreva \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}+8z<8\) buscando uma equação de circunferência. Para tal, veja que o termo \({{z}^{2}}+8z\) pode derivar de um termo \({{\left( z-{{z}_{0}} \right)}^{2}}~\to ~{{\left( z+4 \right)}^{2}}\).
\[~{{x}^{2}}+{{y}^{2}}+{{z}^{2}}+8z<25~~\to ~~{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}+{{\left( z+4 \right)}^{2}}<25\]
Mas, como \({{\left( z+4 \right)}^{2}}={{z}^{2}}+8z+16\), deve-se reajustar a equação dada adicionando-se -16 a ambos os lados:
\[~{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}+{{\left( z+4 \right)}^{2}}<25~~\to ~~~{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}+{{\left( z+4 \right)}^{2}}<25-16\]
Portanto, a equação de esfera deve ficar:
\[~{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}+{{\left( z+4 \right)}^{2}}<9\]
Logo, o conjunto dado é bola aberta, com centro em \(\left( 0,0,-4 \right)\) e raio \(\sqrt{9}=3\).
O conjunto \(A=\left\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}|{{x}^{2}}+{{y}^{2}}-{{z}^{2}}<0 \right\}\) é uma bola aberta com centro em \(\left( 0,0,0 \right)\) para \({{\mathbb{R}}^{3}}\).
Justificativa: Não é possível encontrar uma equação da esfera para o conjunto dado, pois o sinal do termo \({{z}^{2}}\) difere dos sinais de \({{x}^{2}}\) e \({{y}^{2}}\). Logo, pode-se presumir que esse conjunto não é uma bola aberta.
O conjunto \(A=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{3}}\left| {{x}^{2}}+{{y}^{2}}-4 \right\rangle 0 \right\}\) é uma bola aberta com centro em \(\left( 0,1 \right)\) para \({{\mathbb{R}}^{2}}\).
Justificativa: Reescreva \({{x}^{2}}+{{y}^{2}}-4>0\) buscando uma equação de circunferência. Para tal, basta adicionar +4 a ambos os lados:
\[{{x}^{2}}+{{y}^{2}}>4\]
Perceba que a equação encontrada não condiz com os elementos internos de uma circunferência, mas com os elementos externos. Logo, o conjunto dado não é bola aberta.
O conjunto \(A=\left\{ \left( x,y,z \right)\in {{\mathbb{R}}^{3}}|{{x}^{2}}+{{y}^{2}}+z<16 \right\}\) é uma bola aberta com centro em \(\left( 0,0,0 \right)\) para \({{\mathbb{R}}^{3}}\) e raio igual a 4.
Justificativa: Não é possível encontrar uma equação da esfera para o conjunto dado, pois o termo \(z\) está em potência 1. Logo, pode-se presumir que esse conjunto não é uma bola aberta.
Saber identificar se uma função é contínua ou não é importante para auxiliar na resolução de exercícios de Cálculo. Logo, buscando aprimorar sua habilidade nesse processo de identificação, analise as alternativas a seguir e assinale a correta.
A função \(f\left( x,y \right)=ln\left( {{x}^{2}}+{{y}^{2}}-9 \right)\) é contínua em \(\left( 3,3 \right)\).
Justificativa: Note que a função não existe no ponto indicado. Logo, essa função não pode ser contínua em \(\left( 3,3 \right)\)
A função \(f\left( x,y \right)=\frac{4-x}{{{x}^{2}}+3{{y}^{2}}+2}\) é contínua para todos os valores de \(x\) e \(y\) pertencentes a \({{\mathbb{R}}^{2}}\).
Justificativa correta: Observe que o denominador dessa função jamais será menor que 2. Como para qualquer valor de \(x\) e \(y\), essa função estará definida, é uma função racional e será contínua em todo o seu domínio, que é \({{\mathbb{R}}^{2}}\).
A função \(f\left( x,y \right)=\frac{x-y}{2{{x}^{2}}+3{{y}^{2}}}\) é contínua para todos os valores de \(x\) e \(y\) pertencentes a \({{\mathbb{R}}^{2}}\).
Justificativa: Note que essa função não está definida no ponto \(\left( 0,0 \right)\). Logo, ela não será contínua em todo \({{\mathbb{R}}^{2}}\).
A função \(f\left( x,y \right)=arctan\left( \frac{2x}{y} \right)\) é contínua para todos os valores de \(x\) e \(y\) pertencentes a \({{\mathbb{R}}^{2}}\).
Justificativa: Aqui tem-se uma função composta. Note que \(2x/y\) é uma função racional, o que significa que será contínua para todo seu domínio. Logo, \(2x/y\) é contínua para todo \({{\mathbb{R}}^{2}}\) exceto em \(y=0\). Como a função \(arctan~t\) é contínua para todo \(\mathbb{R}\), a função \(f\left( x,y \right)\) dada será contínua para todo \({{\mathbb{R}}^{2}}\) exceto em \(y=0\).
A função \(f\left( x,y \right)=\frac{2{{x}^{2}}}{{{x}^{2}}+{{x}^{2}}{{y}^{2}}}\) não é contínua em \(\left( 0,0 \right)\).
Justificativa: A função dada pode ser simplificada para:
\[f\left( x,y \right)=\frac{2{{x}^{2}}}{{{x}^{2}}+{{x}^{2}}{{y}^{2}}}=\frac{2{{x}^{2}}}{{{x}^{2}}\left( 1+{{y}^{2}} \right)}=\frac{2}{1+{{y}^{2}}}\]
Logo, essa função está definida em \(\left( 0,0 \right)\). Como se tem uma função racional, ela é contínua em todo seu domínio. Logo, a função dada é contínua em \(\left( 0,0 \right)\).
Um dos tópicos centrais do Cálculo reside na avaliação de derivadas de funções. Como problemas com mais de uma variável são muito comuns, visando sua prática de resoluções de derivadas de funções com mais de uma variável, considere as três funções indicadas a seguir, analise as alternativas e assinale a que apresenta derivada parcial indicada de forma correta.
\[f\left( x,y \right)={{x}^{2}}{{y}^{2}}\cdot ln\left( {{x}^{2}}+{{y}^{2}} \right)~~~~g\left( x,y,z \right)=xyz\cdot ln~{{\left( y+z \right)}^{2}}~~~~h\left( x,y \right)={{e}^{y/x}}\cdot ln~\left( \frac{{{x}^{2}}}{{{y}^{2}}} \right)\]
A derivada parcial de 1ª ordem de \(f\) em relação a \(x\) é igual a
\[{{f}_{x}}=2{{x}^{2}}{{y}^{2}}\left[ \frac{x}{{{x}^{2}}+{{y}^{2}}}+ln\left( {{x}^{2}}+{{y}^{2}} \right) \right]\]
Justificativa: Considerando $y$ uma constante e aplicando as regras do produto e da cadeia, então \(g\left( x \right)={{x}^{2}}{{y}^{2}}\to g'\left( x \right)=2x{{y}^{2}}\) e \(h\left( x \right)=ln\left( {{x}^{2}}+{{y}^{2}} \right)\to h'\left( x \right)=2x/\left( {{x}^{2}}+{{y}^{2}} \right)\). Logo:
\[{{f}_{x}}={{x}^{2}}{{y}^{2}}\frac{2x}{{{x}^{2}}+{{y}^{2}}}+2x{{y}^{2}}\cdot ln\left( {{x}^{2}}+{{y}^{2}} \right)~\to ~{{f}_{x}}=2x{{y}^{2}}\left[ \frac{{{x}^{2}}}{{{x}^{2}}+{{y}^{2}}}+ln\left( {{x}^{2}}+{{y}^{2}} \right) \right]\]
A derivada parcial de 1ª ordem de \(g\) em relação a \(y\) é igual a
\[{{f}_{y}}=xz\left[ \frac{2}{y+z}+ln~{{\left( y+z \right)}^{2}} \right]\]
Justificativa correta: Considerando \(y\) uma constante e aplicando as regras do produto e da cadeia, então \(f\left( y \right)=xyz\to f'\left( y \right)=xz\) e \(h\left( x \right)=ln~{{\left( y+z \right)}^{2}}\to h'\left( x \right)=2\left( y+z \right)/{{\left( y+z \right)}^{2}}=2/\left( y+z \right)\). Logo:
\[{{f}_{y}}=xyz\frac{2}{y+z}+xz\cdot ln~{{\left( y+z \right)}^{2}}~\to ~{{f}_{x}}=xz\left[ \frac{2}{y+z}+ln{{\left( y+z \right)}^{2}} \right]\]
Para a função \(g\) dada, tem-se que \({{f}_{x}}={{f}_{z}}\).
Justificativa: Para a derivada parcial de 1ª ordem de \(g\), o termo logaritmo é uma constante. Logo, \({{f}_{x}}=yz\cdot ln~{{\left( y+z \right)}^{2}}\). Para \({{f}_{z}}\), você deve considerar a variável \(z\) uma constante; aplicando as regras do produto e da cadeia, você encontrará \(f\left( z \right)=xyz\to f'\left( z \right)=xy\) e \(h\left( z \right)=ln~{{\left( y+z \right)}^{2}}\to h'\left( z \right)=2\left( y+z \right)/{{\left( y+z \right)}^{2}}=2/\left( y+z \right)\). Logo:
\[{{f}_{z}}=xyz\frac{2}{y+z}+xy\cdot ln~{{\left( y+z \right)}^{2}}~\to ~{{f}_{x}}=xy\left[ \frac{2}{y+z}+ln{{\left( y+z \right)}^{2}} \right]\]
Com isso, observa-se que \({{f}_{x}}\ne {{f}_{z}}\).
A derivada parcial de 1ª ordem de \(h\) em relação a \(x\) é igual a
\[{{f}_{x}}=\frac{{{e}^{y/x}}}{x}\left[ 2-y\cdot ln\left( \frac{{{x}^{2}}}{{{y}^{2}}} \right) \right]\]
Justificativa: Considerando \(y\) uma constante e aplicando as regras do produto e da cadeia, então \(f\left( x \right)={{e}^{y/x}}\to f'\left( x \right)=-\frac{y}{{{x}^{2}}}{{e}^{y/x}}\) e \(g\left( x \right)=ln\left( {{x}^{2}}/{{y}^{2}} \right)\to g'\left( x \right)=\frac{{{y}^{2}}}{{{x}^{2}}}\frac{2x}{{{y}^{2}}}=2/x\). Logo:
\[{{f}_{x}}={{e}^{y/x}}\cdot \frac{2}{x}+\left( -\frac{y}{{{x}^{2}}}{{e}^{y/x}} \right)\cdot ln\left( {{x}^{2}}/{{y}^{2}} \right)~\to ~{{f}_{x}}=\frac{{{e}^{y/x}}}{x}\left[ 2-\frac{y}{x}ln\left( {{x}^{2}}/{{y}^{2}} \right) \right]\]
A derivada parcial de 1ª ordem de \(h\) em relação a \(y\) é igual a
\[{{f}_{y}}=\frac{{{e}^{y/x}}}{y}\left[ 2+\frac{y}{x}\cdot ln\left( \frac{{{x}^{2}}}{{{y}^{2}}} \right) \right]\]
Justificativa: Considerando \(y\) uma constante e aplicando as regras do produto e da cadeia, então \(f\left( y \right)={{e}^{y/x}}\to f'\left( y \right)=\frac{{{e}^{y/x}}}{x}\) e \(g\left( y \right)=ln\left( {{x}^{2}}/{{y}^{2}} \right)\to g'\left( y \right)=\frac{{{y}^{2}}}{{{x}^{2}}}\frac{-2{{x}^{2}}}{{{y}^{3}}}=-2/y\). Logo:
\[{{f}_{y}}={{e}^{y/x}}\cdot \frac{-2}{y}+\frac{{{e}^{y/x}}}{x}\cdot ln\left( {{x}^{2}}/{{y}^{2}} \right)~\to ~{{f}_{y}}=\frac{{{e}^{y/x}}}{y}\left[ -2+\frac{y}{x}\cdot ln\left( {{x}^{2}}/{{y}^{2}} \right) \right]\]
Analisar a diferencial de uma função é algo que lhe fornecerá uma estimativa de como uma função irá se comportar com pequenas alterações de suas variáveis. Sendo assim, visando fixar este conceito, considere que uma empresa fabrica caixas cilíndricas, sendo que o custo de matéria-prima para essa caixa é de R$ 0,07 cada 10 cm². Analise as alternativas a seguir e assinale a correta.
Se as dimensões da caixa variarem um pouco, você pode estimar o custo aproximado da nova caixa utilizando a equação \(dC=0,007\left[ \left( 2\pi h+2\pi r \right)dr+\left( 2\pi r \right)dh \right]\).
Justificativa: A área da caixa é calculada somando-se a área lateral com as áreas das duas bases circulares, ou seja, \(A=2\pi rh+2\pi {{r}^{2}}\). Já o custo é \(C=0,07A=0,07\left( 2\pi rh+2\pi {{r}^{2}} \right)\). Para estimar o custo com a diferencial dessa função, avalie as variáveis parciais:
\[\frac{\partial C}{\partial r}=0,007\left( 2\pi h+4\pi r \right)~~~~e~~~~\frac{\partial C}{\partial h}=0,007\left( 2\pi r \right)\]
Agora, basta aplicar a Equação (24):
\[dC=\frac{\partial C}{\partial r}dr+\frac{\partial C}{\partial h}dh=0,007\left[ \left( 2\pi h+4\pi r \right)dr+\left( 2\pi r \right)dh \right]\]
Para uma caixa com \(r=5~cm\) e \(h=10~cm\), se o raio aumentar 2% e a altura aumentar 5%, o aumento do custo da nova caixa será de aproximadamente R$ 0,20.
Justificativa correta: A área da caixa é calculada somando-se a área lateral com as áreas das duas bases circulares, ou seja, \(A=2\pi rh+2\pi {{r}^{2}}\). Já o custo é \(C=0,07A=0,07\left( 2\pi rh+2\pi {{r}^{2}} \right)\). Para estimar o custo com a diferencial dessa função, avalie as variáveis parciais:
\[\frac{\partial C}{\partial r}=0,007\left( 2\pi h+4\pi r \right)~~~~e~~~~\frac{\partial C}{\partial h}=0,007\left( 2\pi r \right)\]
Agora, basta aplicar a Equação (24):
\[dC=\frac{\partial C}{\partial r}dr+\frac{\partial C}{\partial h}dh=0,007\left[ \left( 2\pi h+4\pi r \right)dr+\left( 2\pi r \right)dh \right]\]
Para um aumento de 2%, o raio será 5,1 cm, o que gera um \(\Delta r=5,1-5=0,1\) cm e, se a altura aumentar 5%, será 10,5 cm, o que gera um \(\Delta h=10,5-10=0,5\) cm. Assim, tem-se:
\[dC=0,007\left[ \left( 2\pi \cdot 10+4\pi \cdot 5 \right)\cdot 0,1+\left( 2\pi 5 \right)\cdot 0,5 \right]=0,19792\simeq 0,20\]
Para uma caixa com \(r=5~cm\) e \(h=10~cm\), se o raio aumentar 2% e a altura aumentar 5%, o aumento do custo da nova caixa será de aproximadamente R$ 0,10.
Justificativa: A área da caixa é calculada somando-se a área lateral com as áreas das duas bases circulares, ou seja, \(A=2\pi rh+2\pi {{r}^{2}}\). Já o custo é \(C=0,07A=0,07\left( 2\pi rh+2\pi {{r}^{2}} \right)\). Para estimar o custo com a diferencial dessa função, avalie as variáveis parciais:
\[\frac{\partial C}{\partial r}=0,007\left( 2\pi h+4\pi r \right)~~~~e~~~~\frac{\partial C}{\partial h}=0,007\left( 2\pi r \right)\]
Agora, basta aplicar a Equação (24):
\[dC=\frac{\partial C}{\partial r}dr+\frac{\partial C}{\partial h}dh=0,007\left[ \left( 2\pi h+4\pi r \right)dr+\left( 2\pi r \right)dh \right]\]
Para um aumento de 2%, o raio será 5,1 cm, o que gera um \(\Delta r=5,1-5=0,1\) cm e, se a altura aumentar 5%, será 10,5 cm, o que gera um \(\Delta h=10,5-10=0,5\) cm. Assim, tem-se:
\[dC=0,007\left[ \left( 2\pi \cdot 10+4\pi \cdot 5 \right)\cdot 0,1+\left( 2\pi 5 \right)\cdot 0,5 \right]=0,19792\simeq 0,20\]
Para uma caixa com \(r=2~cm\) e \(h=5~cm\), se o raio aumentar 5% e a altura aumentar 2%, o custo da nova caixa será de aproximadamente R$ 0,20.
Justificativa: A área da caixa é calculada somando-se a área lateral com as áreas das duas bases circulares, ou seja, \(A=2\pi rh+2\pi {{r}^{2}}\). Já o custo é \(C=0,07A=0,07\left( 2\pi rh+2\pi {{r}^{2}} \right)\). Para estimar o custo com a diferencial dessa função, avalie as variáveis parciais:
\[\frac{\partial C}{\partial r}=0,007\left( 2\pi h+4\pi r \right)~~~~e~~~~\frac{\partial C}{\partial h}=0,007\left( 2\pi r \right)\]
Agora, basta aplicar a Equação (24):
\[dC=\frac{\partial C}{\partial r}dr+\frac{\partial C}{\partial h}dh=0,007\left[ \left( 2\pi h+4\pi r \right)dr+\left( 2\pi r \right)dh \right]\]
Para um aumento de 5%, o raio será 5,25 cm, o que gera um $\Delta r=5,25-5=0,25$ cm e, se a altura aumentar 2%, será 10,2 cm, o que gera um \(\Delta h=10,2-10=0,2\) cm. Assim, tem-se:
\[dC=0,007\left[ \left( 2\pi \cdot 10+4\pi \cdot 5 \right)\cdot 0,25+\left( 2\pi 5 \right)\cdot 0,2 \right]=0,2639\simeq 0,26\]
Se as dimensões da caixa variarem um pouco, você pode estimar o custo aproximado da nova caixa utilizando a equação \(dC=0,07\left[ \left( 2\pi h \right)dr+\left( 2\pi r \right)dh \right]\).
Justificativa: A área da caixa é calculada somando-se a área lateral com as áreas das duas bases circulares, ou seja, \(A=2\pi rh+2\pi {{r}^{2}}\). Já o custo é \(C=0,07A=0,07\left( 2\pi rh+2\pi {{r}^{2}} \right)\). Para estimar o custo com a diferencial dessa função, avalie as variáveis parciais:
\[\frac{\partial C}{\partial r}=0,007\left( 2\pi h+4\pi r \right)~~~~e~~~~\frac{\partial C}{\partial h}=0,007\left( 2\pi r \right)\]
Agora, basta aplicar a Equação (24):
\[dC=\frac{\partial C}{\partial r}dr+\frac{\partial C}{\partial h}dh=0,007\left[ \left( 2\pi h+4\pi r \right)dr+\left( 2\pi r \right)dh \right]\]
Você foi convidado para analisar a pressão \(P\) de um gás ideal em um experimento laboratorial, cuja reação ocorre em um recipiente esférico de volume \(V=\frac{4}{3}\pi {{r}^{3}}\). Para tal, você identificou que a temperatura da reação varia com o tempo de reação \(t\), a posição radial no recipiente $r$ de acordo com a relação \(T=70-t\cdot ln~r\) e o número de mols na reação depende linearmente do tempo de reação de acordo com a relação \(n=0,2t\). Sabendo que a pressão de um gás ideal se comporta de acordo com a equação dos gases ideais, apresentada a seguir, analise as alternativas e assinale a correta. O valor \(R\) é uma constante.
Essa função \(P\) pode ser completamente analisada com no mínimo 3 derivadas parciais.
Justificativa: Essa função apresenta três variáveis intermediárias (\(n\), \(T\) e \(V\)), que são funções apenas de \(t\) e \(r\). Logo, essa função pode ser reescrita apresentando apenas duas variáveis, o que faz com que ela possa ser analisada com um mínimo de 2 derivadas parciais.
A derivada parcial de \(P\) em relação ao tempo é:
\[\frac{\partial P}{\partial t}=\frac{3R}{2\pi {{r}^{3}}}\left[ 7-0,2t\cdot ln~r \right]\]
Justificativa correta: Para encontrar essa derivada, aplicando a definição 8, você encontrará que:
\[\frac{\partial P}{\partial t}=\frac{\partial P}{\partial n}\cdot \frac{\partial n}{\partial t}+\frac{\partial P}{\partial T}\cdot \frac{\partial T}{\partial t}+\frac{\partial P}{\partial V}\cdot \frac{\partial V}{\partial t}\]
Pelas informações dadas, você tem:
\[\frac{\partial P}{\partial n}=\frac{RT}{V}~~~~\frac{\partial P}{\partial T}=\frac{nR}{V}~~~~\frac{\partial P}{\partial V}=\frac{-nRT}{{{V}^{2}}}~~~~\frac{\partial n}{\partial t}=0,2~~~~\frac{\partial T}{\partial t}=-ln~r~~~~\frac{\partial V}{\partial t}=0~\]
Logo:
\[\frac{\partial P}{\partial t}=\left( \frac{RT}{V} \right)\cdot \left( 0,2 \right)+\left( \frac{nR}{V} \right)\cdot \left( -ln~r \right)+\left( \frac{-nRT}{{{V}^{2}}} \right)\cdot \left( 0 \right)=\frac{R}{V}\left( 0,2T-n\cdot ln~r \right)\]
\[=\frac{3R}{4\pi {{r}^{3}}}\left[ 14-0,2t\cdot ln~r-0,2t\cdot ln~r \right]=\frac{3R}{2\pi {{r}^{3}}}\left[ 7-0,2t\cdot ln~r \right]\]
A derivada parcial de \(P\) em relação ao tempo \(t\) é \(\frac{\partial P}{\partial t}=\frac{21R}{2\pi {{r}^{3}}}\)
Justificativa: Para encontrar essa derivada, aplicando a definição 8, você encontrará que:
\[\frac{\partial P}{\partial t}=\frac{\partial P}{\partial n}\cdot \frac{\partial n}{\partial t}+\frac{\partial P}{\partial T}\cdot \frac{\partial T}{\partial t}+\frac{\partial P}{\partial V}\cdot \frac{\partial V}{\partial t}\]
Pelas informações dadas, você tem:
\[\frac{\partial P}{\partial n}=\frac{RT}{V}~~~~\frac{\partial P}{\partial T}=\frac{nR}{V}~~~~\frac{\partial P}{\partial V}=\frac{-nRT}{{{V}^{2}}}~~~~\frac{\partial n}{\partial t}=0,2~~~~\frac{\partial T}{\partial t}=-ln~r~~~~\frac{\partial V}{\partial t}=0\]
Logo:
\[\frac{\partial P}{\partial t}=\left( \frac{RT}{V} \right)\cdot \left( 0,2 \right)+\left( \frac{nR}{V} \right)\cdot \left( -ln~r \right)+\left( \frac{-nRT}{{{V}^{2}}} \right)\cdot \left( 0 \right)=\frac{R}{V}\left( 0,2T-n\cdot ln~r \right)\]
\[=\frac{3R}{4\pi {{r}^{3}}}\left[ 14-0,2t\cdot ln~r-0,2t\cdot ln~r \right]=\frac{3R}{2\pi {{r}^{3}}}\left[ 7-0,2t\cdot ln~r \right]\]
A derivada parcial de \(P\) em relação ao raio \(r\) é:
\[\frac{\partial P}{\partial r}=-\frac{3Rt}{20\pi {{r}^{4}}}\left[ t\left( 1-ln~r \right)+210 \right]\]
Justificativa: Para encontrar essa derivada, aplicando a definição 8, você encontrará que:
\[\frac{\partial P}{\partial r}=\frac{\partial P}{\partial n}\cdot \frac{\partial n}{\partial r}+\frac{\partial P}{\partial T}\cdot \frac{\partial T}{\partial r}+\frac{\partial P}{\partial V}\cdot \frac{\partial V}{\partial r}\]
Pelas informações dadas, você tem:
\[\frac{\partial P}{\partial n}=\frac{RT}{V}~~~~\frac{\partial P}{\partial T}=\frac{nR}{V}~~~~\frac{\partial P}{\partial V}=\frac{-nRT}{{{V}^{2}}}~~~~\frac{\partial n}{\partial r}=0~~~~\frac{\partial T}{\partial r}=-\frac{t}{r}~~~~\frac{\partial V}{\partial r}=4\pi {{r}^{2}}\]
Logo:
\[\frac{\partial P}{\partial r}=\left( \frac{RT}{V} \right)\cdot \left( 0 \right)+\left( \frac{nR}{V} \right)\cdot \left( -\frac{t}{r} \right)+\left( \frac{-nRT}{{{V}^{2}}} \right)\cdot \left( 4\pi {{r}^{2}} \right)=-\frac{nRt}{Vr}-\frac{4\pi nRT{{r}^{3}}}{{{V}^{2}}}=-\frac{nR}{r{{V}^{2}}}\left( tV+4\pi {{r}^{3}}T \right)\]
\[=-\frac{9Rt}{80{{\pi }^{2}}{{r}^{7}}}\left[ t\frac{4}{3}\pi {{r}^{3}}+4\pi {{r}^{3}}\left( 70-tln~r \right) \right]=-\frac{9Rt}{20\pi {{r}^{4}}}\left[ \frac{t}{3}+\left( 70-tln~r \right) \right]=-\frac{3Rt}{20\pi {{r}^{4}}}\left[ t\left( 1-3ln~r \right)+210 \right]\]
A função \(P\) dada apresenta duas variáveis intermediárias que são funções de três variáveis.
Justificativa: É o oposto: a função \(P\) dada apresenta três variáveis intermediárias, que são funções de duas variáveis.
A derivação implícita é um tipo de derivação que algumas pessoas apresentam certa dificuldade em lidar. Visando praticar esse assunto e melhor fixá-lo, considere as funções a seguir, e analise as alternativas e assinale a correta.
\[{{x}^{2}}{{y}^{2}}+ln~xy+{{z}^{3}}=8\]
\[6{{x}^{3}}+2{{y}^{4}}=36\]
\[{{x}^{2}}z+ln~{{x}^{4}}y+xy{{z}^{2}}=0\]
A derivada parcial \(\partial z/\partial x\) da função I é igual a \(-\frac{2{{x}^{2}}y+1/x}{3{{z}^{2}}}\).
Justificativa: A função I pode ser escrita como \(F\left( x,y,z\right)={{x}^{2}}{{y}^{2}}+ln~xy+{{z}^{3}}-8\), para a qual se tem que \(\partial F/\partial x=2x{{y}^{2}}+1/x\) e \(\partial F/\partial z=3{{z}^{2}}\). Logo, porser uma função implícita, a derivada \(\partial z/\partial x\) será igual a:
\[\frac{\partial z}{\partial x}=-\frac{\partial F/\partial x}{\partial F/\partial z}=-\frac{2x{{y}^{2}}+1/x}{3{{z}^{2}}}\]
A derivada parcial \(\partial z/\partial x\) da função III é igual a \(-\frac{2xz+y{{z}^{2}}+4/x}{{{x}^{2}}+xyz}\).
Justificativa correta: A função III pode ser escrita como \(F\left( x,y,z \right)={{x}^{2}}z+ln~{{x}^{4}}y+xy{{z}^{2}}\), para a qual se tem que \(\partial F/\partial x=2xz+y{{z}^{2}}+4/x\) e \(\partial F/\partial z={{x}^{2}}+xyz\). Logo, por ser uma função implícita, a derivada \(\partial z/\partial x\) será igual a:
\[\frac{\partial z}{\partial x}=-\frac{\partial F/\partial y}{\partial F/\partial z}=-\frac{2xz+y{{z}^{2}}+4/x}{{{x}^{2}}+xyz}\]
A derivada parcial \(\partial z/\partial y\) da função I é igual a \(-\frac{2x{{y}^{2}}+1/y}{3{{z}^{2}}}\).
Justificativa: A função I pode ser escrita como \(F\left( x,y,z \right)={{x}^{2}}{{y}^{2}}+ln~xy+{{z}^{3}}-8\), para a qual se tem que \(\partial F/\partial y=2{{x}^{2}}y+1/y\) e \(\partial F/\partial z=3{{z}^{2}}\). Logo, por ser uma função implícita, a derivada \(\partial z/\partial y\) será igual a:
\[\frac{\partial z}{\partial x}=-\frac{\partial F/\partial y}{\partial F/\partial z}=-\frac{2{{x}^{2}}y+1/y}{3{{z}^{2}}}\]
A derivada parcial \(dy/dx\) da função II é igual a \(-\frac{9{{x}^{2}}}{8{{z}^{3}}}\).
Justificativa: A função II pode ser escrita como \(F\left( x,y \right)=6{{x}^{3}}+2{{y}^{4}}-36\), para a qual se tem que \(\partial F/\partial x=18{{x}^{2}}\) e \(\partial F/\partial y=8{{y}^{3}}\). Logo, por ser uma função implícita, a derivada \(dy/dx\) será igual a:
\[\frac{dy}{dx}=-\frac{\partial F/\partial x}{\partial F/\partial y}=-\frac{18{{x}^{2}}}{8{{y}^{3}}}=-\frac{9{{x}^{2}}}{4{{y}^{3}}}\]
A derivada parcial \(\partial z/\partial y\) da função III é igual a \(-\frac{x{{z}^{2}}+1/{{y}^{2}}}{{{x}^{2}}+xyz}\).
Justificativa: A função III pode ser escrita como \(F\left( x,y,z \right)={{x}^{2}}z+ln~{{x}^{4}}y+xy{{z}^{2}}\), para a qual se tem que \(\partial F/\partial y=x{{z}^{2}}+1/y\) e \(\partial F/\partial z={{x}^{2}}+xyz\). Logo, por ser uma função implícita, a derivada \(\partial z/\partial y\) será igual a:
\[\frac{\partial z}{\partial x}=-\frac{\partial F/\partial y}{\partial F/\partial z}=-\frac{x{{z}^{2}}+1/y}{{{x}^{2}}+xyz}\]
Uma das análises mais corriqueiras que se faz de uma função é identificar a existência dos pontos de máximo e mínimo das funções. Visando desenvolver essa habilidade e praticar os conceitos de máximos e mínimos de uma função, analise as alternativas a seguir e assinale a correta.
Uma função definida como \(z=a+{{x}^{2}}+{{y}^{2}}\) tem o ponto \(\left( 0,0 \right)\) como ponto de máximo global.
Justificativa: Essa função é um paraboloide positivo. Para essa função, o ponto \(\left( 0,0 \right)\) indica um ponto de mínimo global.
Todas as funções com mais de uma variável apresentam um valor de máximo e um valor de mínimo global.
Justificativa correta: Isso não é válido para todas as funções com mais de uma variável, como se vê nos casos de funções com uma variável. Inúmeras funções vão apresentar tendência ao infinito positivo ou negativo e, como infinito não é um número, essas funções não apresentarão pontos de máximo ou mínimo. Por exemplo, um paraboloide \(z=a+{{x}^{2}}+{{y}^{2}}\) não apresenta valor de máximo global.
Para valores de \(x\) entre \(-2\) e \(2\) e para valores de \(y\) entre \(-1\) e \(1\), a função definida como \(z=a-{{x}^{2}}-{{y}^{2}}\) tem três pontos como pontos de máximo locais.
Justificativa: A região delimitada pelos valores de \(x\) e \(y\) indicados apresenta um único valor de mínimo local. Observe que essa função é um paraboloide e seu máximo ocorre em \(\left( 0,0 \right)\).
A função \(z=co{{s}^{2}}~x+{{y}^{2}}\) apresentará mínimos locais sempre que \(y=0\) e \(x=k\pi \), em que \(k\in Z\).
Justificativa: A condição indicada para \(x\) indica valores para os quais se tem que \(co{{s}^{2}}~x=1\). Para os mínimos locais, é preciso encontrar os valores para os quais se tem que \(co{{s}^{2}}~x=0\).
A única forma para se identificar máximos e mínimos locais de uma função com duas variáveis é pela análise gráfica da função.
Justificativa: A análise da representação gráfica é muito útil para identificar esses pontos de máximo e mínimo locais, mas não é a única forma. A análise matemática da função também pode identificar os pontos de máximo e mínimo.
Os conceitos de derivadas parciais são muito úteis para a verificação de pontos extremantes de funções. Buscando praticar essa aplicação de derivadas, analise a função e as alternativas dadas a seguir, assinalando a correta.
\[f\left( x,y \right)=3{{x}^{2}}-2{{x}^{3}}-3{{y}^{2}}+6xy\]
O ponto \(\left( 0,2 \right)\) é um ponto crítico dessa função \(f\).
Avaliando, então, as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=6x-6{{x}^{2}}+6y~~~~~~\frac{\partial f}{\partial y}=6x-6y\]
Agora, deve-se resolver o sistema:
\[\left\{ \begin{matrix} 6x-6{{x}^{2}}+6y=0 \\ 6x-6y=0 \\ \end{matrix} \right.\]
Da segunda equação desse sistema, tem-se que \(x=y\). Com isso, reescrevendo a primeira equação, tem-se \(6x-6{{x}^{2}}+6x=x\left( 2-x \right)=0\), para a qual se encontra que \(x=0\) ou \(*x=2\). Com isso, a função dada apresentará dois pontos críticos: \(\left( 0,0 \right)\) e \(\left( 2,2 \right)\).
O ponto \(\left( 0,0 \right)\) é um ponto de sela para essa função.
Justificativa correta: Avaliando, então, as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=6x-6{{x}^{2}}+6y~~~~\frac{\partial f}{\partial y}=6x-6y\]
Como \(\frac{\partial f}{\partial x}\left( 0,0 \right)=\frac{\partial f}{\partial y}\left( 0,0 \right)=0\), o ponto \(\left( 0,0 \right)\) é um ponto crítico de \(f\). Agora, devemos avaliar o hessiano. Para tal, é preciso avaliar as derivadas parciais de segunda ordem:
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=6-12x~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=-6~~~~\frac{{{\partial }^{2}}f}{\partial x\partial y}=6~~~~\frac{{{\partial }^{2}}f}{\partial y\partial x}=6\]
Com isso, tem-se o seguinte hessiano:
\[H(x,y)=\left| \begin{matrix} 6-12x & 6 \\ 6 & -6 \\ \end{matrix} \right|\]
Resolvendo esse determinante, você encontra \(H\left( x,y \right)=-36+72x-36=72\left( x-1 \right)\). Para o ponto \(\left( 0,0 \right)\), tem-se \(H\left( 0,0 \right)=72\left( 0-1 \right)=-72\). Ou seja, \(H\left( 0,0 \right)<0\), então o ponto \(\left( 0,0 \right)\) é um ponto de sela de \(f\).
A função \(f\) apresentará quatro pontos críticos: \(\left( 0,0 \right)\), \(\left( 0,2 \right)\), \(\left( 2,0 \right)\) e \(\left( 2,2 \right)\).
Justificativa: Avaliando, então, as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=6x-6{{x}^{2}}+6y~~~~\frac{\partial f}{\partial y}=6x-6y\]
Agora, deve-se resolver o sistema:
\[\left\{ \begin{matrix} 6x-6{{x}^{2}}+6y=0 \\ 6x-6y=0 \\ \end{matrix} \right.\]
Da segunda equação desse sistema, tem-se que \(x=y\). Com isso, reescrevendo a primeira equação, tem-se \(6x-6{{x}^{2}}+6x=x\left( 2-x \right)=0\), para a qual se encontra que \(x=0\) ou \(x=2\). Com isso, a função dada apresentará dois pontos críticos: \(\left( 0,0 \right)\) e \(\left( 2,2 \right)\).
O ponto \(\left( 0,0 \right)\) é um ponto de mínimo para essa função.
Justificativa: Avaliando, então, as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=6x-6{{x}^{2}}+6y~~~~\frac{\partial f}{\partial y}=6x-6y\]
Como \(\frac{\partial f}{\partial x}\left( 0,0 \right)=\frac{\partial f}{\partial y}\left( 0,0 \right)=0\), o ponto \(\left( 0,0 \right)\) é um ponto crítico de \(f\). Agora, devemos avaliar o hessiano. Para tal, é preciso avaliar as derivadas parciais de segunda ordem:
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=6-12x~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=-6~~~~\frac{{{\partial }^{2}}f}{\partial x\partial y}=6~~~~\frac{{{\partial }^{2}}f}{\partial y\partial x}=6\]
Com isso, tem-se o seguinte hessiano:
\[H(x,y)=\left| \begin{matrix} 6-12x & 6 \\ 6 & -6 \\ \end{matrix} \right|\]
Resolvendo esse determinante, você encontra \(H\left( x,y \right)=-36+72x-36=72\left( x-1 \right)\). Para o ponto \(\left( 0,0 \right)\), tem-se \(H\left( 0,0 \right)=72\left( 0-1 \right)=-72\). Ou seja, \(H\left( 0,0 \right)<0\), então o ponto \(\left( 0,0 \right)\) é um ponto de sela de \(f\).
O ponto \(\left( 2,2 \right)\) é um ponto de mínimo para essa função.
Justificativa: Avaliando, então, as derivadas parciais da função \(f\) dada:
\[\frac{\partial f}{\partial x}=6x-6{{x}^{2}}+6y~~~~\frac{\partial f}{\partial y}=6x-6y\]
Como \(\frac{\partial f}{\partial x}\left( 2,2 \right)=\frac{\partial f}{\partial y}\left( 2,2 \right)=0\), o ponto \(\left( 2,2 \right)\) é um ponto crítico de \(f\). Agora, devemos avaliar o hessiano. Para tal, é preciso avaliar as derivadas parciais de segunda ordem:
\[\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=6-12x~~~~\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=-6~~~~\frac{{{\partial }^{2}}f}{\partial x\partial y}=6~~~~\frac{{{\partial }^{2}}f}{\partial y\partial x}=6\]
Com isso, tem-se o seguinte hessiano:
\[H(x,y)=\left| \begin{matrix} 6-12x & 6 \\ 6 & -6 \\ \end{matrix} \right|\]
Resolvendo esse determinante, você encontra \(H\left( x,y \right)=-36+72x-36=72\left( x-1 \right)\). Para o ponto \(\left( 2,2 \right)\), tem-se \(H\left( 2,2 \right)=72\left( 2-1 \right)=72\). Ou seja, como \(H\left( 0,0 \right)>0\), é preciso avaliar a derivada parcial de segunda ordem \(\frac{{{\partial }^{2}}}{\partial {{x}^{2}}}f\left( 2,2 \right)=6-12\left( 2 \right)=-18\). Como \(H\left( 2,2 \right)>0\) e \(\frac{{{\partial }^{2}}}{\partial {{x}^{2}}}f\left( 2,2 \right)<0\), então o ponto \(\left( 2,2 \right)\) é um ponto de máximo local de \(f\).
O Teorema de Weierstrass é muito útil para a análise de máximos e mínimos de funções, até porque diversos casos práticos exigem a análise de uma função em um conjunto fechado. Visando fixar os conceitos e a aplicação desse teorema e considerando a função e o conjunto retangular \(D\) dados, analise as alternativas a seguir e assinale a correta.
\[f\left( x,y \right)={{x}^{2}}-4xy+8y~~~~D=\left\{ \left( x,y \right)\in {{\mathbb{R}}^{2}}|0\le x\le 3,0\le y\le 2 \right\}\]
A função dada não apresentará nenhum ponto extremante no conjunto delimitado.
Justificativa: O Teorema de Weierstrass garante exatamente o oposto do que é proposto aqui: em um conjunto fechado, a função irá certamente apresentar um ponto de máximo e um mínimo.
O máximo de \(f\) em \(D\) ocorre no ponto \(\left( 0,2 \right)\), em que se tem \(f\left( 0,2 \right)=16\).
Justificativa correta: Para a base horizontal inferior, tem-se \(f\left( x,0 \right)={{x}^{2}}\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 9. Já para a base horizontal superior, tem-se \(f\left( x,2 \right)={{x}^{2}}-8x+16\) ou \(f\left( x,2 \right)={{\left( x-4 \right)}^{2}}\). Essa função, no conjunto \(D\) apresentado, apresentará um máximo em \(x=0\), para o qual se tem \(f\left( 0,2 \right)=16\).
Para o lado vertical esquerdo, tem-se \(f\left( 0,y \right)=8y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 16. Já para o lado vertical direito, tem-se \(f\left( 3,y \right)=9-4y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 1 e 9.
Essa função tem como ponto crítico \(\left( 2,1 \right)\), para o qual se tem \(f\left( 2,1 \right)=4\).
Essa função apresenta um ponto crítico, mas este se encontra fora de \(D\).
Justificativa: Vejamos:
\[\frac{\partial f}{\partial x}=2x-4y~~~~\frac{\partial f}{\partial y}=8-4x\]
Igualando essas derivadas a zero e resolvendo-as simultaneamente, você encontrará que \(x=2\) e \(y=1\). Logo, a função apresenta realmente um único ponto crítico, que é \(\left( 2,1 \right)\), mas este se encontra dentro de \(D\).
O máximo de \(f\) na fronteira de \(D\) ocorrerá no ponto \(\left( 3,2 \right)\).
Justificativa: Para a base horizontal inferior, tem-se \(f\left( x,0 \right)={{x}^{2}}\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 9. Já para a base horizontal superior, tem-se \(f\left( x,2 \right)={{x}^{2}}-8x+16\) ou \(f\left( x,2 \right)={{\left( x-4 \right)}^{2}}\). Essa função, no conjunto \(D\) apresentado, apresentará um máximo em \(x=0\), para o qual se tem \(f\left( 0,2 \right)=16\).
Para o lado vertical esquerdo, tem-se \(f\left( 0,y \right)=8y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 16. Já para o lado vertical direito, tem-se \(f\left( 3,y \right)=9-4y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 1 e 9. No ponto \(\left( 3,2 \right)\), tem-se \(f=1\), o que não é o ponto de máximo das fronteiras.
O mínimo de \(f\) na fronteira de \(D\) ocorrerá no ponto \(\left( 2,2 \right)\)
Justificativa: Para a base horizontal inferior, tem-se \(f\left( x,0 \right)={{x}^{2}}\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 9. Já para a base horizontal superior, tem-se \(f\left( x,2 \right)={{x}^{2}}-8x+16\) ou \(f\left( x,2 \right)={{\left( x-4 \right)}^{2}}\). Essa função, no conjunto \(D\) apresentado, apresentará um máximo em \(x=0\), para o qual se tem \(f\left( 0,2 \right)=16\) No ponto \(\left( 2,2 \right)\), tem-se \(f=4\), o que não é o ponto de mínimo das fronteiras.
Para o lado vertical esquerdo, tem-se \(f\left( 0,y \right)=8y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 0 e 16. Já para o lado vertical direito, tem-se \(f\left( 3,y \right)=9-4y\). Logo, em \(D\), esse lado conterá valores de \(f\) entre 1 e 9.
Uma empresa de entregas aceita apenas caixas cuja soma do comprimento mais perímetro não exceda 405 cm, conforme ilustra a figura a seguir. Assinale a alternativa correta.
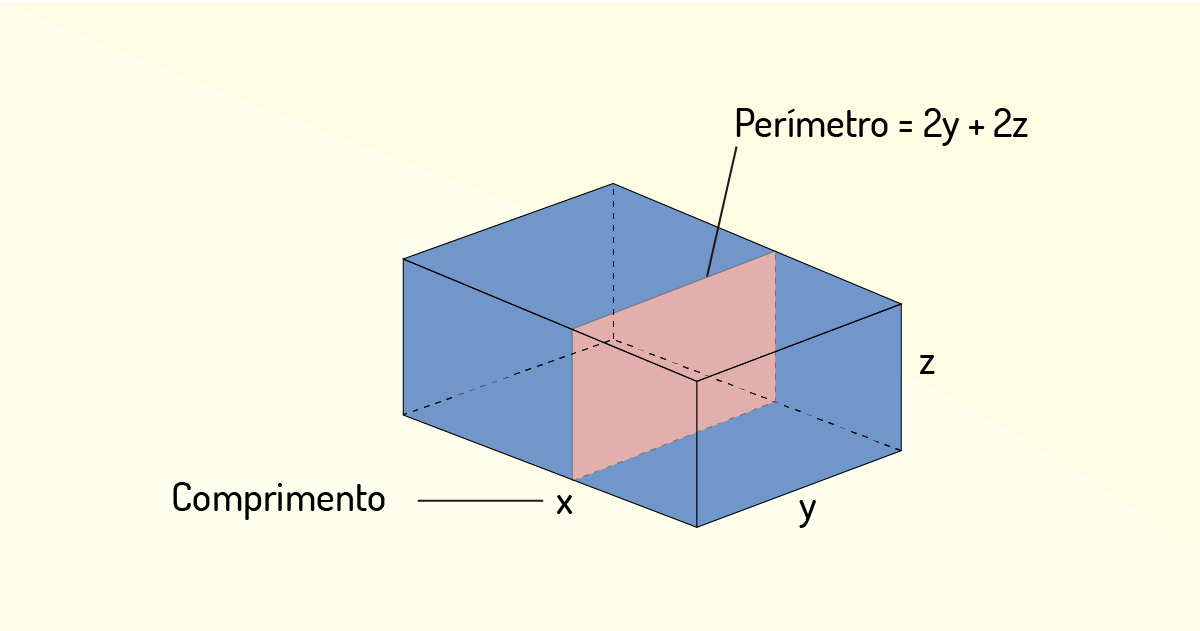
Figura 3.16 - Dimensões da caixa
Fonte: Adaptado de Thomas Júnior (2016, p. 856).
As dimensões que maximizam o volume dessa caixa são \(x=105~cm\) e \(y=z=75~cm\).
Justificativa: É pedido que se maximize o volume \(V=xyz\) tal que \(x+2y+2z=405\) (maiores dimensões admitidas pela companhia), ou seja, o problema é
\[max~V=xyz,~s.a.~x+2y+2z=405\]
Reescrevendo a restrição, encontra-se uma nova forma para representar \(x\), o que permite reescrever \(V\) como uma função de duas variáveis, na forma \(V=\left( 405-2y-2z \right)yz\). Para tal, tem-se as seguintes derivadas parciais de primeira ordem:
\[{{V}_{y}}=405z-4yz-2{{z}^{2}}=\left( 405-4y-2z \right)z~~~~e~~~~{{V}_{z}}=405y-2{{y}^{2}}-4zy=\left( 405-2y-4z \right)y\]
Igualando essas duas derivadas parciais a zero e resolvendo-as simultaneamente, você encontra rapidamente que dois valores possíveis para \(y\) e \(z\) é 0. Fazendo, então, \(y=0\), você encontrará que \(z=202,5\) assim como, com \(z=0\), você encontrará que \(y=202,5\). A outra possibilidade é que os termos entre parênteses em \({{V}_{y}}\) e \({{V}_{z}}\) sejam iguais a zero. Assim, de \({{V}_{z}}\), você pode analisar o termo entre parênteses fazendo \(y=202,5-2z\), e, do termo entre parênteses de \({{V}_{y}}\), você encontra que \(z=67,5\), acarretando em \(y=67,5\). Então, existem quatro pontos críticos para a função: \(\left( 0,0 \right)\), \(\left( 0,135 \right)\), \(\left( 135,0 \right)\) e \(\left( 67,5,67,5 \right)\). Note que se qualquer dimensão do volume for zero, então \(V=0\). Com isso, o único ponto crítico que nos interessa é \(\left( 67,5,67,5 \right)\). Para verificar se esse ponto é realmente um ponto de máximo, avalia-se o hessiano.
\[{{V}_{yy}}=-4z~~~~{{V}_{zz}}=-4y~~~~{{V}_{yy}}\left( 67,5,67,5 \right)={{V}_{zz}}\left( 67,5,67,5 \right)=-270\]
\[{{V}_{yz}}=405-4y-4z~~~~{{V}_{zy}}=405-4y-4z~~~~{{V}_{yz}}\left( 67,5,67,5 \right)={{V}_{zy}}\left( 67,5,67,5 \right)=-135\]
\[H(67,5,67,5)=\left| \begin{matrix} -270 & -135 \\ -135 & -270 \\ \end{matrix} \right|\]
Como \(H\left( 67,5,67,5 \right)=54675\), ou seja, \(H\left( 67,5,67,5 \right)>0\) e \({{V}_{yy}}\left( 67,5,67,5 \right)<0\), o ponto \(\left( 67,5,67,5 \right)\) é um ponto de máximo local da função \(V\). Logo, pode-se encontrar que:
\[x=405-2y-2z=405-2\left( 67,5 \right)-2\left( 67,5 \right)=135\]
Portanto, as dimensões que maximizam o volume da caixa são \(x=135~cm\) e \(y=z=67,5~cm\).
O volume máximo de uma caixa que essa transportadora aceita é de aproximadamente 615,1 L.
Justificativa correta: É pedido que se maximize o volume \(V=xyz\) tal que \(x+2y+2z=405\) (maiores dimensões admitidas pela companhia), ou seja, o problema é
\[max~V=xyz,~s.a.~x+2y+2z=405\]
Reescrevendo a restrição, encontra-se uma nova forma para representar \(x\), o que permite reescrever \(V\) como uma função de duas variáveis, na forma \(V=\left( 405-2y-2z \right)yz\). Para tal, tem-se as seguintes derivadas parciais de primeira ordem:
\[{{V}_{y}}=405z-4yz-2{{z}^{2}}=\left( 405-4y-2z \right)z~~~~e~~~~{{V}_{z}}=405y-2{{y}^{2}}-4zy=\left( 405-2y-4z \right)y\]
Igualando essas duas derivadas parciais a zero e resolvendo-as simultaneamente, você encontra rapidamente que dois valores possíveis para \(y\) e \(z\) é 0. Fazendo, então, \(y=0\), você encontrará que \(z=202,5\) assim como, com \(z=0\), você encontrará que \(y=202,5\). A outra possibilidade é que os termos entre parênteses em \({{V}_{y}}\) e \({{V}_{z}}\) sejam iguais a zero. Assim, de \({{V}_{z}}\), você pode analisar o termo entre parênteses fazendo \(y=202,5-2z\), e, do termo entre parênteses de \({{V}_{y}}\), você encontra que \(z=67,5\), acarretando em \(y=67,5\). Então, existem quatro pontos críticos para a função: \(\left( 0,0 \right)\), \(\left( 0,135 \right)\), \(\left( 135,0 \right)\) e \(\left( 67,5,67,5 \right)\). Note que se qualquer dimensão do volume for zero, então \(V=0\). Com isso, o único ponto crítico que nos interessa é \(\left( 67,5,67,5 \right)\). Para verificar se esse ponto é realmente um ponto de máximo, avalia-se o hessiano.
\[{{V}_{yy}}=-4z~~~~{{V}_{zz}}=-4y~~~~{{V}_{yy}}\left( 67,5,67,5 \right)={{V}_{zz}}\left( 67,5,67,5 \right)=-270\]
\[{{V}_{yz}}=405-4y-4z~~~~{{V}_{zy}}=405-4y-4z~~~~{{V}_{yz}}\left( 67,5,67,5 \right)={{V}_{zy}}\left( 67,5,67,5 \right)=-135\]
\[H(67,5,67,5)=\left| \begin{matrix} -270 & -135 \\ -135 & -270 \\ \end{matrix} \right|\]
Como \(H\left( 67,5,67,5 \right)=54675\), ou seja, \(H\left( 67,5,67,5 \right)>0\) e \({{V}_{yy}}\left( 67,5,67,5 \right)<0\), o ponto \(\left( 67,5,67,5 \right)\) é um ponto de máximo local da função \(V\). Logo, pode-se encontrar que
\[x=405-2y-2z=405-2\left( 67,5 \right)-2\left( 67,5 \right)=135\]
Portanto, o volume máximo da caixa é \(V=xyz=615.093,75~c{{m}^{3}}\) ou aproximadamente \(615,1~L\).
O volume máximo de uma caixa que essa transportadora aceita é aproximadamente 307,5 L.
Justificativa: É pedido que se maximize o volume \(V=xyz\) tal que \(x+2y+2z=405\) (maiores dimensões admitidas pela companhia), ou seja, o problema é:
\[max~V=xyz,~s.a.~x+2y+2z=405\]
Reescrevendo a restrição, encontra-se uma nova forma para representar \(x\), o que permite reescrever \(V\) como uma função de duas variáveis, na forma \(V=\left( 405-2y-2z \right)yz\). Para tal, tem-se as seguintes derivadas parciais de primeira ordem:
\[{{V}_{y}}=405z-4yz-2{{z}^{2}}=\left( 405-4y-2z \right)z~~~~e~~~~{{V}_{z}}=405y-2{{y}^{2}}-4zy=\left( 405-2y-4z \right)y\]
Igualando essas duas derivadas parciais a zero e resolvendo-as simultaneamente, você encontra rapidamente que dois valores possíveis para \(y\) e \(z\) é 0. Fazendo, então, \(y=0\), você encontrará que \(z=202,5\) assim como, com \(z=0\), você encontrará que \(y=202,5\). A outra possibilidade é que os termos entre parênteses em \({{V}_{y}}\) e \({{V}_{z}}\) sejam iguais a zero. Assim, de \({{V}_{z}}\), você pode analisar o termo entre parênteses fazendo \(y=202,5-2z\), e, do termo entre parênteses de \({{V}_{y}}\), você encontra que \(z=67,5\), acarretando em \(y=67,5\). Então, existem quatro pontos críticos para a função: \(\left( 0,0 \right)\), \(\left( 0,135 \right)\), \(\left( 135,0 \right)\) e \(\left( 67,5,67,5 \right)\). Note que se qualquer dimensão do volume for zero, então \(V=0\). Com isso, o único ponto crítico que nos interessa é \(\left( 67,5,67,5 \right)\). Para verificar se esse ponto é realmente um ponto de máximo, avalia-se o hessiano.
\[{{V}_{yy}}=-4z~~~~{{V}_{zz}}=-4y~~~~{{V}_{yy}}\left( 67,5,67,5 \right)={{V}_{zz}}\left( 67,5,67,5 \right)=-270\]
\[{{V}_{yz}}=405-4y-4z~~~~{{V}_{zy}}=405-4y-4z~~~~{{V}_{yz}}\left( 67,5,67,5 \right)={{V}_{zy}}\left( 67,5,67,5 \right)=-135\]
\[H(67,5,67,5)=\left| \begin{matrix} -270 & -135 \\ -135 & -270 \\ \end{matrix} \right|\]
Como \(H\left( 67,5,67,5 \right)=54675\), ou seja, \(H\left( 67,5,67,5 \right)>0\) e \({{V}_{yy}}\left( 67,5,67,5 \right)<0\), o ponto \(\left( 67,5,67,5 \right)\) é um ponto de máximo local da função \(V\). Logo, pode-se encontrar que:
\[x=405-2y-2z=405-2\left( 67,5 \right)-2\left( 67,5 \right)=135\]
Portanto, o volume máximo da caixa é \(V=xyz=615.093,75~c{{m}^{3}}\) ou cerca de \(615,09375~L\).
As que maximizam o volume dessa caixa são \(x=y=z=81~cm\).
É pedido que se maximize o volume \(V=xyz\) tal que \(x+2y+2z=405\) (maiores dimensões admitidas pela companhia), ou seja, o problema é:
\[max~V=xyz,~s.a.~x+2y+2z=405\]
Reescrevendo a restrição, encontra-se uma nova forma para representar \(x\), o que permite reescrever \(V\) como uma função de duas variáveis, na forma \(V=\left( 405-2y-2z \right)yz\). Para tal, tem-se as seguintes derivadas parciais de primeira ordem:
\[{{V}_{y}}=405z-4yz-2{{z}^{2}}=\left( 405-4y-2z \right)z~~~~e~~~~{{V}_{z}}=405y-2{{y}^{2}}-4zy=\left( 405-2y-4z \right)y\]
Igualando essas duas derivadas parciais a zero e resolvendo-as simultaneamente, você encontra rapidamente que dois valores possíveis para \(y\) e \(z\) é 0. Fazendo, então, \(y=0\), você encontrará que \(z=202,5\) assim como, com \(z=0\), você encontrará que \(y=202,5\). A outra possibilidade é que os termos entre parênteses em \({{V}_{y}}\) e \({{V}_{z}}\) sejam iguais a zero. Assim, de \({{V}_{z}}\), você pode analisar o termo entre parênteses fazendo \(y=202,5-2z\), e, do termo entre parênteses de \({{V}_{y}}\), você encontra que \(z=67,5\), acarretando em \(y=67,5\). Então, existem quatro pontos críticos para a função: \(\left( 0,0 \right)\), \(\left( 0,135 \right)\), \(\left( 135,0 \right)\)e \(\left( 67,5,67,5 \right)\). Note que se qualquer dimensão do volume for zero, então \(V=0\). Com isso, o único ponto crítico que nos interessa é \(\left( 67,5,67,5 \right)\). Para verificar se esse ponto é realmente um ponto de máximo, avalia-se o hessiano.
\[{{V}_{yy}}=-4z~~~~{{V}_{zz}}=-4y~~~~{{V}_{yy}}\left( 67,5,67,5 \right)={{V}_{zz}}\left( 67,5,67,5 \right)=-270\]
\[{{V}_{yz}}=405-4y-4z~~~~{{V}_{zy}}=405-4y-4z~~~~{{V}_{yz}}\left( 67,5,67,5 \right)={{V}_{zy}}\left( 67,5,67,5 \right)=-135\]
\[H(67,5,67,5)=\left| \begin{matrix} -270 & -135 \\ -135 & -270 \\ \end{matrix} \right|\]
Como \(H\left( 67,5,67,5 \right)=54675\), ou seja, \(H\left( 67,5,67,5 \right)>0\) e \({{V}_{yy}}\left( 67,5,67,5 \right)<0\), o ponto \(\left( 67,5,67,5 \right)\) é um ponto de máximo local da função \(V\). Logo, pode-se encontrar que
$x=405-2y-2z=405-2\left( 67,5 \right)-2\left( 67,5 \right)=135$
Portanto, as dimensões que maximizam o volume da caixa são \(x=135~cm\) e \(y=z=67,5~cm\).
O volume máximo de uma caixa que essa transportadora aceita é aproximadamente 531,4 L.
Justificativa: É pedido que se maximize o volume \(V=xyz\) tal que \(x+2y+2z=405\) (maiores dimensões admitidas pela companhia), ou seja, o problema é:
\[max~V=xyz,~s.a.~x+2y+2z=405\]
Reescrevendo a restrição, encontra-se uma nova forma para representar \(x\), o que permite reescrever \(V\) como uma função de duas variáveis, na forma \(V=\left( 405-2y-2z \right)yz\). Para tal, tem-se as seguintes derivadas parciais de primeira ordem:
\[{{V}_{y}}=405z-4yz-2{{z}^{2}}=\left( 405-4y-2z \right)z~~~~e~~~~{{V}_{z}}=405y-2{{y}^{2}}-4zy=\left( 405-2y-4z \right)y\]
Igualando essas duas derivadas parciais a zero e resolvendo-as simultaneamente, você encontra rapidamente que dois valores possíveis para \(y\) e \(z\) é 0. Fazendo, então, \(y=0\), você encontrará que \(z=202,5\) assim como, com \(z=0\), você encontrará que \(y=202,5\). A outra possibilidade é que os termos entre parênteses em \({{V}_{y}}\) e \({{V}_{z}}\) sejam iguais a zero. Assim, de \({{V}_{z}}\), você pode analisar o termo entre parênteses fazendo \(y=202,5-2z\), e, do termo entre parênteses de \({{V}_{y}}\), você encontra que \(z=67,5\), acarretando em \(y=67,5\). Então, existem quatro pontos críticos para a função: \(\left( 0,0 \right)\), \(\left( 0,135 \right)\), \(\left( 135,0 \right)\) e \(\left( 67,5,67,5 \right)\). Note que se qualquer dimensão do volume for zero, então \(V=0\). Com isso, o único ponto crítico que nos interessa é \(\left( 67,5,67,5 \right)\). Para verificar se esse ponto é realmente um ponto de máximo, avalia-se o hessiano.
\[{{V}_{yy}}=-4z~~~~{{V}_{zz}}=-4y~~~~{{V}_{yy}}\left( 67,5,67,5 \right)={{V}_{zz}}\left( 67,5,67,5 \right)=-270\]
\[{{V}_{yz}}=405-4y-4z~~~~{{V}_{zy}}=405-4y-4z~~~~{{V}_{yz}}\left( 67,5,67,5 \right)={{V}_{zy}}\left( 67,5,67,5 \right)=-135\]
\[H(67,5,67,5)=\left| \begin{matrix} -270 & -135 \\ -135 & -270 \\ \end{matrix} \right|\]
Como \(H\left( 67,5,67,5 \right)=54675\), ou seja, \(H\left( 67,5,67,5 \right)>0\) e \({{V}_{yy}}\left( 67,5,67,5 \right)<0\), o ponto \(\left( 67,5,67,5 \right)\) é um ponto de máximo local da função \(V\). Logo, pode-se encontrar que
\[x=405-2y-2z=405-2\left( 67,5 \right)-2\left( 67,5 \right)=135\]
Portanto, o volume máximo da caixa é \(V=xyz=615.093,75~c{{m}^{3}}\) ou cerca de \(615,09375~L\).
Considere o sólido delimitado acima da região \(R=\left[ 0,4 \right]\times \left[ 0,4 \right]\) e abaixo da curva da função \(z=\sqrt{36-{{x}^{2}}-{{y}^{2}}}\). Visando, então, a fixação prática do cálculo de volume de sólidos, assinale a alternativa correta. Note que \(u~=\) unidade de comprimento genérica.
Estime o volume do sólido que se encontra acima da região \(R\) e abaixo do paraboloide definido pela função \(z\). Para isso, divida \(R\) em quatro regiões iguais e escolha os pontos de amostragem nos cantos superiores direitos de cada quadrado \({{R}_{ij}}\).
Ao se dividir \(R\) nas duas regiões iguais \({{R}_{11}}=\left[ 0,4 \right]\times \left[ 2,4 \right]\) e \({{R}_{21}}=\left[ 2,4 \right]\times \left[ 4,4 \right]\), considerando os pontos de amostragem como aqueles no canto superior direito, o volume estimado do sólido será \(96~{{u}^{2}}\).
Justificativa: Com os dados indicados, a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=2\cdot 4=8\). Tem-se também que \(m=2\) e \(n=1\). Aplicando a equação (3):
\[V=\underset{i=1}{\overset{2}{\mathop \sum }}\,\underset{j=1}{\overset{1}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)\]
\[=f\left( 2,4 \right)\cdot \Delta A+f\left( 4,4 \right)\cdot \Delta A=8\cdot \left[ f\left( 2,4 \right)+f\left( 4,4 \right) \right]=8\cdot \left( 4+2 \right)=48~{{u}^{2}}\]
Ao se dividir \(R\) em oito regiões iguais, dividindo o lado \(x\) em quatro e o lado \(y\) em dois, considerando os pontos de amostragem como aqueles no centro de cada \({{R}_{ij}}\), o volume estimado do sólido será aproximadamente \(80,6~{{u}^{2}}\).
Justificativa correta: Com os dados indicados, a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=1\cdot 2=2\). Tem-se também que \(m=4\) e \(n=2\). Aplicando a equação (3):
\[V=\underset{i=1}{\overset{4}{\mathop \sum }}\,\underset{j=1}{\overset{2}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)\]
\[\Delta A\cdot \left[ f\left( 0.5,1 \right)+f\left( 0.5,3 \right)+f\left( 1.5,1 \right)+f\left( 1.5,3 \right)+f\left( 2.5,1 \right)+f\left( 2.5,3 \right)+f\left( 3.5,1 \right)+f\left( 2.5,3 \right) \right]\]
\[=2\cdot \left[ 5,57+4,36+5,29+4,00+4,80+3,32+4,00+2,00 \right]=2\cdot \left( 33,3 \right)=80,6~{{u}^{2}}\]
Ao se dividir \(R\) em quatro regiões iguais, considerando os pontos de amostragem como aqueles no canto superior direito de cada \({{R}_{ij}}\), o volume estimado do sólido será aproximadamente \(79,0~{{u}^{2}}\).
Justificativa: Com os dados indicados, a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=2\cdot 2=4\). Tem-se também que \(m=n=2\). Aplicando a equação (3):
\[V=\underset{i=1}{\overset{2}{\mathop \sum }}\,\underset{j=1}{\overset{2}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)=\Delta A\cdot \left[ f\left( 2,2 \right)+f\left( 2,4 \right)+f\left( 4,2 \right)+f\left( 4,4 \right) \right]\]
\[=4\cdot \left[ 5,29+4,00+4,00+2,00 \right]=4\cdot \left( 15,3 \right)=61,2~{{u}^{2}}\]
Ao se dividir \(R\) em oito regiões iguais, dividindo o lado \(x\) em quatro e o lado \(y\) em dois, considerando os pontos de amostragem como aqueles no canto superior direito de cada \({{R}_{ij}}\), o volume estimado do sólido será aproximadamente \(81,1~{{u}^{2}}\).
Justificativa: Com os dados indicados, a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=1\cdot 2=2\). Tem-se também que \(m=4\) e \(n=2\). Aplicando a equação (3):
\[V=\underset{i=1}{\overset{4}{\mathop \sum }}\,\underset{j=1}{\overset{2}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)\]
\[=\Delta A\cdot \left[ f\left( 1,2 \right)+f\left( 1,4 \right)+f\left( 2,2 \right)+f\left( 2,4 \right)+f\left( 3,2 \right)+f\left( 3,4 \right)+f\left( 4,2 \right)+f\left( 4,4 \right) \right]\]
\[=2\cdot \left[ 5,57+4,36+5,29+4,00+4,80+3,32+4,00+2,00 \right]=2\cdot \left( 33,3 \right)=66,7~{{u}^{2}}\]
Ao se dividir \(R\) em quatro regiões iguais, considerando os pontos de amostragem como aqueles no centro de cada \({{R}_{ij}}\), o volume estimado do sólido será aproximadamente \(61,2~{{u}^{2}}\).
Justificativa: Com os dados indicados, a área de cada quadrado \({{R}_{ij}}\) será \(\Delta A=\Delta x\Delta y=2\cdot 2=4\). Tem-se também que \(m=n=2\). Aplicando a equação (3):
\[V=\underset{i=1}{\overset{2}{\mathop \sum }}\,\underset{j=1}{\overset{2}{\mathop \sum }}\,\Delta A\cdot f\left( x_{ij}^{*},y_{ij}^{*} \right)=\Delta A\cdot \left[ f\left( 1,1 \right)+f\left( 1,3 \right)+f\left( 3,1 \right)+f\left( 3,3 \right) \right]\]
\[=4\cdot \left[ 5,83+5,10+5,10+4,24 \right]=4\cdot \left( 20,3 \right)=81,1~{{u}^{2}}\]
Visando a prática de cálculo de integrais duplas em coordenadas modificadas, calcule a integral dupla da função \(f\left( x,y \right)={{x}^{2}}+2y\) em uma região \(D\) que é delimitada pelas parábolas \(y=2{{x}^{2}}\) e \(y=1+{{x}^{2}}\). Assinale, então, a alternativa correta.
A integral dupla em questão é avaliada em uma região tipo 1, cujo resultado é igual a 32/5.
Justificativa: A região delimitada apresentará dois pontos de encontro, determinados onde \(2{{x}^{2}}=1+{{x}^{2}}\), ou seja, em \(x=\pm 1\). Assim, esta é uma região do tipo 1 descrita como:
\[D=\left\{ \left( x,y \right)~|~-1\le x\le 1,~2{{x}^{2}}\le y\le 1+{{x}^{2}} \right\}\]
Então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{-1}{\overset{1}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{1+{{x}^{2}}}{\mathop \int }}\,\left( {{x}^{2}}+2y \right)~dydx=\underset{-1}{\overset{1}{\mathop \int }}\,\left[ \left( {{x}^{2}}y+{{y}^{2}} \right)_{2{{x}^{2}}}^{1+{{x}^{2}}} \right]dx=\underset{-1}{\overset{1}{\mathop \int }}\,\left( 1+3{{x}^{2}}-4{{x}^{4}} \right)dx=\left( x+{{x}^{3}}-\frac{4}{5}{{x}^{5}} \right)_{-1}^{1}=\frac{12}{5}\]
A integral dupla em questão é avaliada em uma região tipo 1, cujo resultado é igual a 12/5.
Justificativa: A região delimitada apresentará dois pontos de encontro, determinados onde \(2{{x}^{2}}=1+{{x}^{2}}\) ou seja, em \(x=\pm 1\). Assim, esta é uma região do tipo 1 descrita como:
\[D=\left\{ \left( x,y \right)~|~-1\le x\le 1,~2{{x}^{2}}\le y\le 1+{{x}^{2}} \right\}\]
Então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{-1}{\overset{1}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{1+{{x}^{2}}}{\mathop \int }}\,\left( {{x}^{2}}+2y \right)~dydx=\underset{-1}{\overset{1}{\mathop \int }}\,\left[ \left( {{x}^{2}}y+{{y}^{2}} \right)_{2{{x}^{2}}}^{1+{{x}^{2}}} \right]dx=\underset{-1}{\overset{1}{\mathop \int }}\,\left( 1+3{{x}^{2}}-4{{x}^{4}} \right)dx=\left( x+{{x}^{3}}-\frac{4}{5}{{x}^{5}} \right)_{-1}^{1}=\frac{12}{5}\]
A integral dupla em questão é avaliada em uma região tipo 2, cujo resultado é igual a 12/5.
Justificativa: A região delimitada apresentará dois pontos de encontro, determinados onde \(2{{x}^{2}}=1+{{x}^{2}}\), ou seja, em $x=\pm 1$. Assim, esta é uma região do tipo 1 descrita como:
\[D=\left\{ \left( x,y \right)~|~-1\le x\le 1,~2{{x}^{2}}\le y\le 1+{{x}^{2}} \right\}\]
Então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{-1}{\overset{1}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{1+{{x}^{2}}}{\mathop \int }}\,\left( {{x}^{2}}+2y \right)~dydx=\underset{-1}{\overset{1}{\mathop \int }}\,\left[ \left( {{x}^{2}}y+{{y}^{2}} \right)_{2{{x}^{2}}}^{1+{{x}^{2}}} \right]dx=\underset{-1}{\overset{1}{\mathop \int }}\,\left( 1+3{{x}^{2}}-4{{x}^{4}} \right)dx=\left( x+{{x}^{3}}-\frac{4}{5}{{x}^{5}} \right)_{-1}^{1}=\frac{12}{5}\]
A integral dupla em questão é avaliada em uma região tipo 2, cujo resultado é igual a 32/5.
Justificativa: A região delimitada apresentará dois pontos de encontro, determinados onde \(2{{x}^{2}}=1+{{x}^{2}}\), ou seja, em \(x=\pm 1\). Assim, esta é uma região do tipo 1 descrita como:
\[D=\left\{ \left( x,y \right)~|~-1\le x\le 1,~2{{x}^{2}}\le y\le 1+{{x}^{2}} \right\}\]
Então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{-1}{\overset{1}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{1+{{x}^{2}}}{\mathop \int }}\,\left( {{x}^{2}}+2y \right)~dydx=\underset{-1}{\overset{1}{\mathop \int }}\,\left[ \left( {{x}^{2}}y+{{y}^{2}} \right)_{2{{x}^{2}}}^{1+{{x}^{2}}} \right]dx=\underset{-1}{\overset{1}{\mathop \int }}\,\left( 1+3{{x}^{2}}-4{{x}^{4}} \right)dx=\left( x+{{x}^{3}}-\frac{4}{5}{{x}^{5}} \right)_{-1}^{1}=\frac{12}{5}\]
A integral dupla em questão é avaliada em uma região tipo 1, cujo resultado é igual a 4/5.
Justificativa: A região delimitada apresentará dois pontos de encontro, determinados onde \(2{{x}^{2}}=1+{{x}^{2}}\), ou seja, em \(x=\pm 1\). Assim, esta é uma região do tipo 1 descrita como:
\[D=\left\{ \left( x,y \right)~|~-1\le x\le 1,~2{{x}^{2}}\le y\le 1+{{x}^{2}} \right\}\]
Então:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{R}{\overset{{}}{\mathop \int }}\,f\left( x,y \right)dA=\underset{-1}{\overset{1}{\mathop \int }}\,\underset{2{{x}^{2}}}{\overset{1+{{x}^{2}}}{\mathop \int }}\,\left( {{x}^{2}}+2y \right)~dydx=\underset{-1}{\overset{1}{\mathop \int }}\,\left[ \left( {{x}^{2}}y+{{y}^{2}} \right)_{2{{x}^{2}}}^{1+{{x}^{2}}} \right]dx=\underset{-1}{\overset{1}{\mathop \int }}\,\left( 1+3{{x}^{2}}-4{{x}^{4}} \right)dx=\left( x+{{x}^{3}}-\frac{4}{5}{{x}^{5}} \right)_{-1}^{1}=\frac{12}{5}\]
Visando à prática de cálculo de integrais triplas, calcule a integral tripla da função \(f\left( x,y,z \right)=2x\) em uma região \(B\) que é delimitada pelos planos coordenados e pelo plano \(\frac{x}{3}+\frac{y}{2}+z=1\). Assinale, então, a alternativa correta.
A região onde se deve avaliar essa integral tripla é claramente uma região exclusivamente do tipo 2.
Justificativa: A região \(B\) descrita pode se encaixar facilmente em qualquer um dos tipos descritos - 1, 2 ou 3.
Avaliando a integral tripla pedida, o resultado será 3/2.
Justificativa: A região \(B\) proposta é um tetraedro, para o qual se tem \(0\le x\le 3\), \(0\le y\le 2\) e \(0\le z\le 1\). Considerando essa região como tipo 1, a projeção de \(B\) sobre o plano \(xy\) será o triângulo \(R\) evidenciado a seguir:
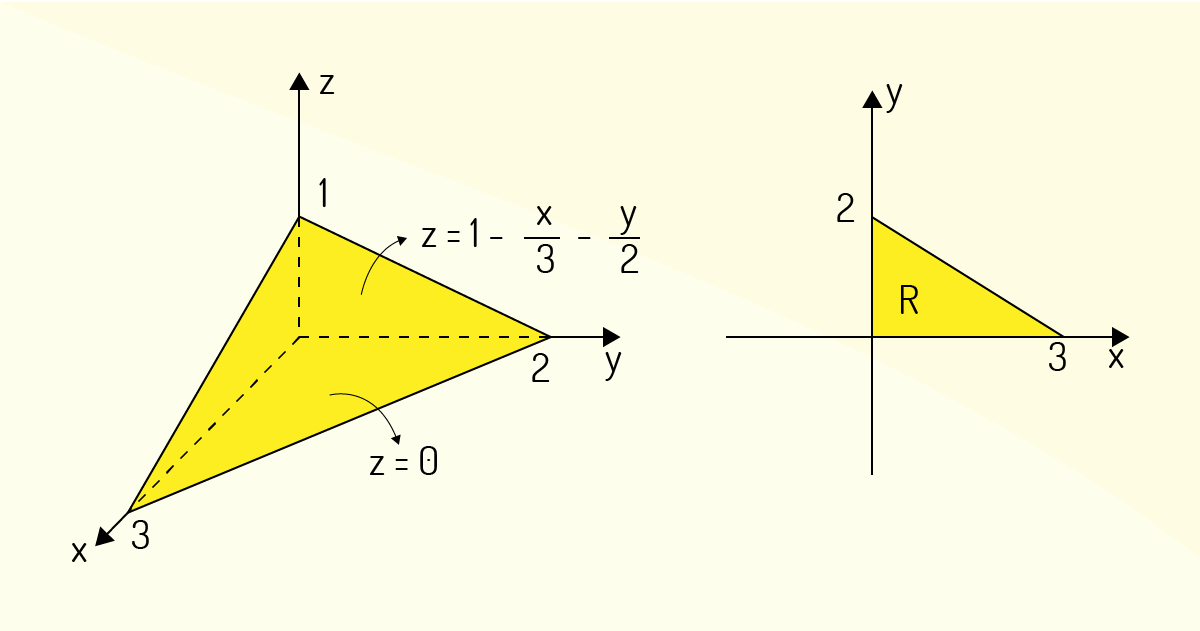
Ou seja, \(0\le x\le 3\) e \(0\le y\le 2-\frac{2}{3}x\). Assim, usando (32):
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{{{u}_{1}}\left( x,y \right)}{\overset{{{u}_{2}}\left( x,y \right)}{\mathop \int }}\,f\left( x,y,z \right)dz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{0}{\overset{1-\frac{x}{3}-\frac{y}{2}}{\mathop \int }}\,2xdz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( 2xz \right)_{0}^{1-\frac{x}{3}-\frac{y}{2}}dydx\]
\[=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\underset{0}{\overset{2-\frac{2}{3}x}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\left( \frac{2}{9}{{x}^{3}}-\frac{4}{3}{{x}^{2}}+2x \right)dx=\frac{3}{2}\]
Avaliando a integral tripla pedida, o resultado será 1/2.
Justificativa: A região \(B\) proposta é um tetraedro, para o qual se tem \(0\le x\le 3\), \(0\le y\le 2\) e \(0\le z\le 1\). Considerando essa região como tipo 1, a projeção de \(B\) sobre o plano \(xy\) será o triângulo \(R\) evidenciado a seguir:
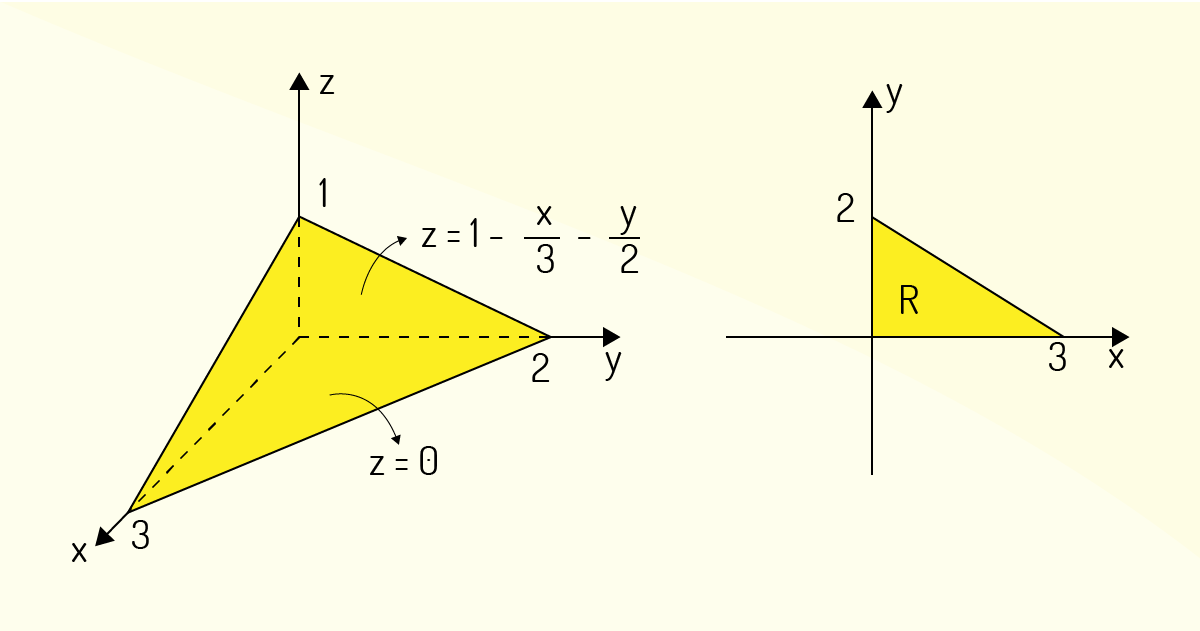
Ou seja, \(0\le x\le 3\) e \(0\le y\le 2-\frac{2}{3}x\). Assim, usando (32):
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{{{u}_{1}}\left( x,y \right)}{\overset{{{u}_{2}}\left( x,y \right)}{\mathop \int }}\,f\left( x,y,z \right)dz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{0}{\overset{1-\frac{x}{3}-\frac{y}{2}}{\mathop \int }}\,2xdz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( 2xz \right)_{0}^{1-\frac{x}{3}-\frac{y}{2}}dydx\]
\[=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\underset{0}{\overset{2-\frac{2}{3}x}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\left( \frac{2}{9}{{x}^{3}}-\frac{4}{3}{{x}^{2}}+2x \right)dx=\frac{3}{2}\]
A região de integração apresentada, caso seja considerada uma região de tipo 3, apresentará como limites \(0\le y\le 1-\frac{x}{3}-z\) , \(0\le x\le 1-\frac{1}{3}x\) e \(0\le z\le 1\).
Justificativa: A região de integração e a projeção no plano\(xz\) são evidenciadas a seguir:
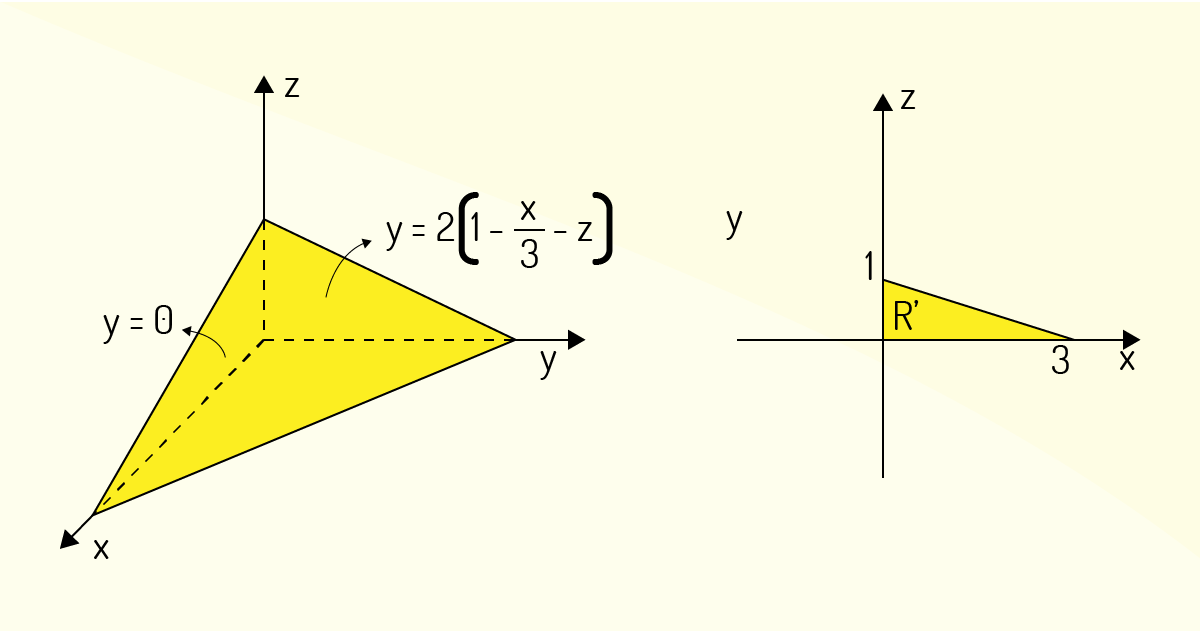
Analisando-as, nota-se que \(0\le y\le 2\left( 1-\frac{x}{3}-z \right)\), que é a descrição em relação a \(y\), \(0\le x\le 1-\frac{1}{3}x\), que define \(z=g\left( x \right)\), e \(0\le z\le 1\).
Avaliando a integral tripla pedida, o resultado será 5/2.
Justificativa: A região \(B\) proposta é um tetraedro, para o qual se tem \(0\le x\le 3\), \(0\le y\le 2\) e \(0\le z\le 1\). Considerando essa região como tipo 1, a projeção de \(B\) sobre o plano \(xy\) será o triângulo \(R\) evidenciado a seguir:

Ou seja, \(0\le x\le 3\) e \(0\le y\le 2-\frac{2}{3}x\). Assim, usando (32):
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,f\left( x,y,z \right)dV=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{{{u}_{1}}\left( x,y \right)}{\overset{{{u}_{2}}\left( x,y \right)}{\mathop \int }}\,f\left( x,y,z \right)dz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left[ \underset{0}{\overset{1-\frac{x}{3}-\frac{y}{2}}{\mathop \int }}\,2xdz \right]dydx=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( 2xz \right)_{0}^{1-\frac{x}{3}-\frac{y}{2}}dydx\]
\[=\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{D}{\overset{{}}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\underset{0}{\overset{2-\frac{2}{3}x}{\mathop \int }}\,\left( -\frac{2}{3}{{x}^{2}}-xy+2x \right)dydx=\underset{0}{\overset{3}{\mathop \int }}\,\left( \frac{2}{9}{{x}^{3}}-\frac{4}{3}{{x}^{2}}+2x \right)dx=\frac{3}{2}\]
Visando a prática de cálculo de integrais triplas em coordenadas modificadas, calcule o volume do sólido delimitado pelo cone \(z=\sqrt{{{x}^{2}}+{{y}^{2}}}\) e pela esfera \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}=z\), como evidencia a figura a seguir.
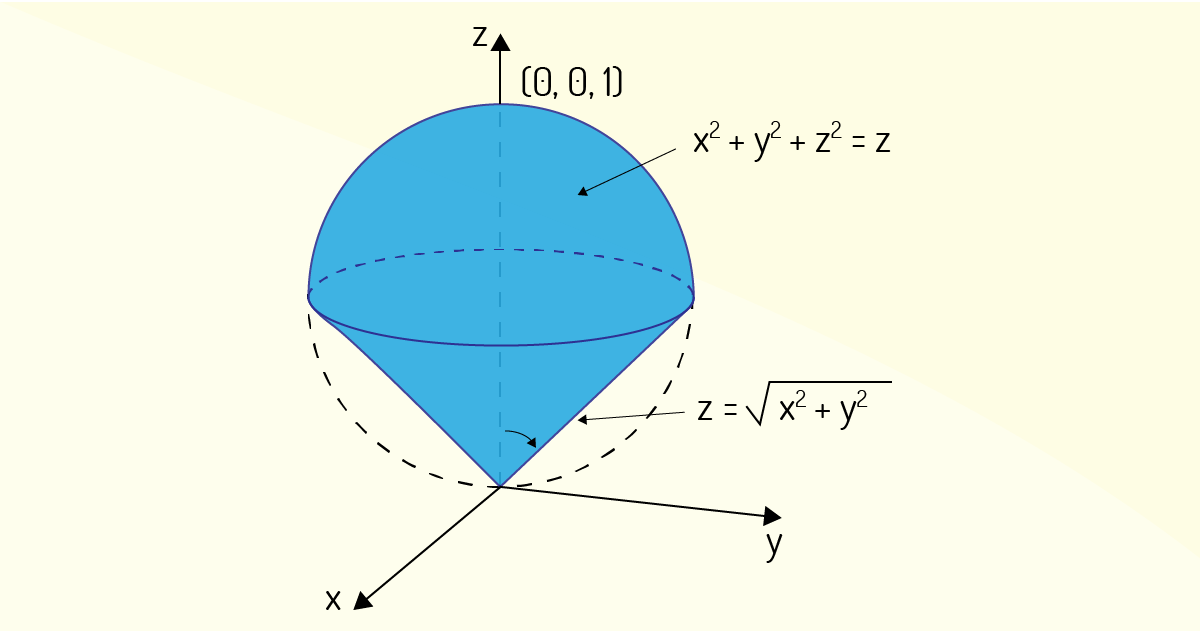
O volume será igual a \(1/8\).
Justificativa: Veja que a esfera definida passa pela origem e tem seu centro no ponto \(\left( 0,0,1/2 \right)\). Para a esfera, tem-se que ela pode ser escrita em coordenadas esféricas como \({{\rho }^{2}}=\rho cos~\phi ~\to ~\rho =cos~\phi \) Já escrevendo a equação do cone em coordenadas esféricas, deve-se encontrar que \(\rho cos~\phi =\rho sen~\phi \). Como isso só é possível para \(phi =\pi /4\), a descrição do sólido em coordenadas esféricas deve ser
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~0\le \theta \le 2\pi ,~0\le \phi \le \pi /4,~0\le \rho \le cos~\phi \right\}\]
Assim, o volume desse sólido pode ser avaliado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,dV=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\underset{0}{\overset{cos~\phi }{\mathop \int }}\,\left( {{\rho }^{2}}sen~\phi \right)d\rho d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\left( \frac{co{{s}^{3}}~\phi ~sen\phi }{3} \right)d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( \frac{1}{16} \right)d\theta =\frac{\pi }{8}\]
O volume será igual a \(\pi /8\).
Justificativa correta: Veja que a esfera definida passa pela origem e tem seu centro no ponto \(\left( 0,0,1/2 \right)\). Para a esfera, tem-se que ela pode ser escrita em coordenadas esféricas como \({{\rho }^{2}}=\rho cos~\phi ~\to ~\rho =cos~\phi \). Já escrevendo a equação do cone em coordenadas esféricas, deve-se encontrar que \(\rho cos~\phi =\rho sen~\phi \). Como isso só é possível para\(\phi =\pi /4\), a descrição do sólido em coordenadas esféricas deve ser
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~0\le \theta \le 2\pi ,~0\le \phi \le \pi /4,~0\le \rho \le cos~\phi \right\}\]
Assim, o volume desse sólido pode ser avaliado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,dV=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\underset{0}{\overset{cos~\phi }{\mathop \int }}\,\left( {{\rho }^{2}}sen~\phi \right)d\rho d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\left( \frac{co{{s}^{3}}~\phi ~sen\phi }{3} \right)d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( \frac{1}{16} \right)d\theta =\frac{\pi }{8}\]
O volume será igual a \(\pi /4\).
Justificativa: Veja que a esfera definida passa pela origem e tem seu centro no ponto \(\left( 0,0,1/2 \right)\). Para a esfera, tem-se que ela pode ser escrita em coordenadas esféricas como \({{\rho }^{2}}=\rho cos~\phi ~\to ~\rho =cos~\phi \). Já escrevendo a equação do cone em coordenadas esféricas, deve-se encontrar que \(\rho cos~\phi =\rho sen~\phi \). Como isso só é possível para \(\phi =\pi /4\), a descrição do sólido em coordenadas esféricas deve ser
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~0\le \theta \le 2\pi ,~0\le \phi \le \pi /4,~0\le \rho \le cos~\phi \right\}\]
Assim, o volume desse sólido pode ser avaliado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,dV=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\underset{0}{\overset{cos~\phi }{\mathop \int }}\,\left( {{\rho }^{2}}sen~\phi \right)d\rho d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\left( \frac{co{{s}^{3}}~\phi ~sen\phi }{3} \right)d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( \frac{1}{16} \right)d\theta =\frac{\pi }{8}\]
O volume será igual a \(1/4\).
Justificativa: Veja que a esfera definida passa pela origem e tem seu centro no ponto \(\left( 0,0,1/2 \right)\). Para a esfera, tem-se que ela pode ser escrita em coordenadas esféricas como \({{\rho }^{2}}=\rho cos~\phi ~\to ~\rho =cos~\phi \). Já escrevendo a equação do cone em coordenadas esféricas, deve-se encontrar que \(\rho cos~\phi =\rho sen~\phi \). Como isso só é possível para \(\phi =\pi /4\), a descrição do sólido em coordenadas esféricas deve ser
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~0\le \theta \le 2\pi ,~0\le \phi \le \pi /4,~0\le \rho \le cos~\phi \right\}\]
Assim, o volume desse sólido pode ser avaliado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,dV=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\underset{0}{\overset{cos~\phi }{\mathop \int }}\,\left( {{\rho }^{2}}sen~\phi \right)d\rho d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\left( \frac{co{{s}^{3}}~\phi ~sen\phi }{3} \right)d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( \frac{1}{16} \right)d\theta =\frac{\pi }{8}\]
O volume será igual a \(\pi /2\).
Justificativa: Veja que a esfera definida passa pela origem e tem seu centro no ponto \(\left( 0,0,1/2 \right)\). Para a esfera, tem-se que ela pode ser escrita em coordenadas esféricas como \({{\rho }^{2}}=\rho cos~\phi ~\to ~\rho =cos~\phi \). Já escrevendo a equação do cone em coordenadas esféricas, deve-se encontrar que \(\rho cos~\phi =\rho sen~\phi \). Como isso só é possível para \(\phi =\pi /4\), a descrição do sólido em coordenadas esféricas deve ser
\[E=\left\{ \left( \rho ,\theta ,\phi \right)~|~0\le \theta \le 2\pi ,~0\le \phi \le \pi /4,~0\le \rho \le cos~\phi \right\}\]
Assim, o volume desse sólido pode ser avaliado:
\[\underset{{}}{\overset{{}}{\mathop \int }}\,\underset{E}{\overset{{}}{\mathop \int }}\,\underset{{}}{\overset{{}}{\mathop \int }}\,dV=\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\underset{0}{\overset{cos~\phi }{\mathop \int }}\,\left( {{\rho }^{2}}sen~\phi \right)d\rho d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\underset{0}{\overset{\pi /4}{\mathop \int }}\,\left( \frac{co{{s}^{3}}~\phi ~sen\phi }{3} \right)d\phi d\theta =\underset{0}{\overset{2\pi }{\mathop \int }}\,\left( \frac{1}{16} \right)d\theta =\frac{\pi }{8}\]