A presente unidade é um fechamento para os estudos de Álgebra Linear. Nela, iremos desenvolver os conceitos a respeito de transformações lineares e entender como esses podem nos ser úteis. Em seguida, iremos focar nosso trabalho em autovalores e autovetores, um conceito que tornará extremamente prático o nosso trabalho para outras áreas, como a resolução de sistemas lineares. Após formalizar os conceitos de autovetores e autovalores, veremos que os encontrar via definição pode não ser algo muito prático. Iremos, então, desenvolver um outro método para lidar com isso, que se mostra muito mais prático e rápido de se aplicar - a diagonalização de matrizes.
Um dos tipos mais comuns e simples que temos de funções são as funções lineares, que definem de uma maneira direta como uma função y depende de uma variável x:
\[y=ax+b~~~~~~~~~~(1)\]
A função y é mostrada como \(f\left( x \right)=y\) em diversos casos. Esse tipo de função apresenta-se graficamente como um reta, de modo que visualizar funções lineares também não é algo muito trabalhoso (BOLDRINI, 1980).
Boldrini (1980) nos dá um exemplo desse tipo de função. A extração de óleo de soja feita da soja pode ser expressa linearmente. Sendo y a quantidade de litros de óleo de soja extraídos (em litros) e x a massa de soja (em quilogramas), podemos estimar a quantidade de óleo extraído pela seguinte relação:
\[y=0,2x~~~~~~~~~~(2)\]
De (2), conseguimos deduzir que, a cada quilograma de soja utilizado no processo de extração, conseguiremos extrair 0,2 L de óleo. Para isso, basta que façamos a substituição do valor de x para encontrarmos f(1):
\[y=f\left( 1 \right)=0,2\cdot 1=0,2\]
Podemos, assim, encontrar a quantidade de óleo que conseguiremos extrair a partir de qualquer quantidade de grãos de soja. Essas quantidades podem ser encontradas mais facilmente se usarmos um gráfico, visto que funções lineares são de simples visualização; logo, graficamente, essa função pode ser vista como:
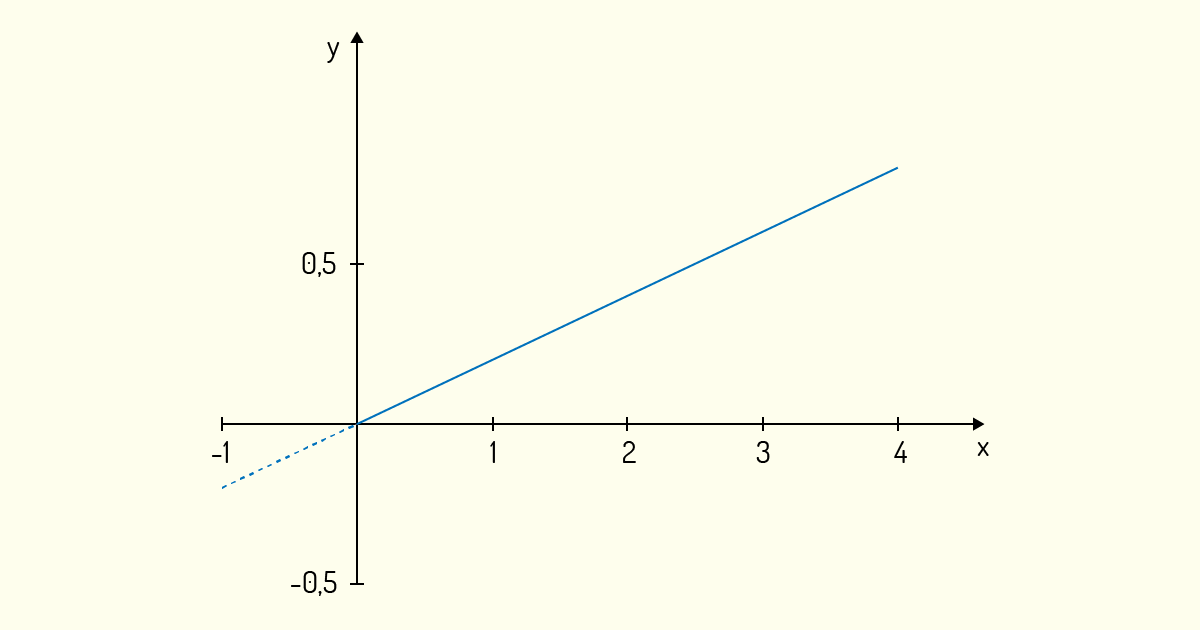
Note que podemos desenhar o gráfico para valores de x menores que zero, mas tais valores não nos apresentam valor prático de informação, pois não podemos utilizar uma massa negativa de soja para extrair óleo. Logo, na Figura 4.1, o pontilhado no gráfico da função apresenta esses valores irreais.
Façamos, agora, uma breve análise dessa função:
Essas duas análises feitas serão úteis na caracterização do que viremos a chamar de transformação linear.
Você já deve saber que podemos também usar matrizes e vetores para lidarmos com funções lineares. Para refrescar tais conceitos, vejamos um exemplo: uma cooperativa de extração de óleo de vegetais sabe que, ao processar 1 kg de soja e 1 kg de milho, ela produzirá 0,26 L de óleo. Já no caso de ela processar apenas 3 kg de milho, irá produzir apenas 0,18 L de óleo. Chamando a massa de soja de s e a massa de milho de m, podemos escrever o seguinte sistema:
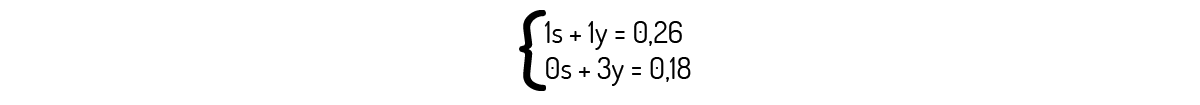
Tal qual você deve se lembrar, esse sistema pode ser escrito na forma do produto de uma matriz por um vetor, resultando em um vetor:
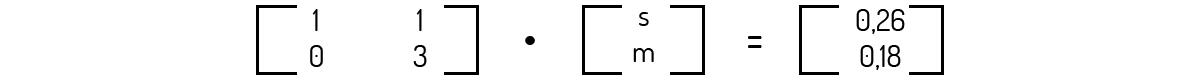
Podemos resolver, então, o problema de forma simples. Encontraremos que m=0,06 e s=0,2.
No entanto, não temos mais o interesse apenas na resolução de sistemas assim. Nosso foco agora é outro. Do problema acima, podemos gerar um caso genérico no qual podemos ter qualquer valor de algum cereal sendo processado, representado por \({{x}_{i}}\), e uma quantidade qualquer de óleo total \({{y}_{i}}\) sendo produzido. Assim, para um caso genérico, o sistema acima pode ser representado por:
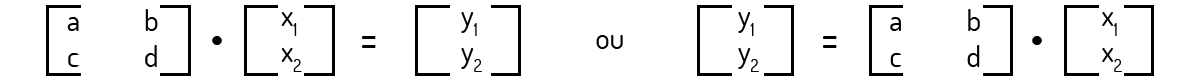
Poole (2004) nos diz que a forma mostrada à direita em (3) pode ser representada de forma mais geral como:
\[y=F\cdot x ~~~~~~~~~~(4)\]
Observe que a forma descrita em (4) é muito parecida com (1). Ou seja, podemos fazer uma analogia de (4) com uma função, onde o vetor y seria a variável dependente, o vetor x seria a variável independente e F identificaria a função.
Podemos analisar o problema acima de uma outra forma também, segundo Poole (2004). De um modo geral, vemos que a matriz F irá transformar um vetor de dimensão 2 em outro vetor de dimensão 2. Isso pode ser representado como \(F:{{\Re }^{2}}\to {{\Re }^{2}}\). Mas podemos ter casos diferentes do que foi exemplificado acima. Por exemplo, se tivermos a função A e o vetor arbitrário v das variáveis independentes como mostrado a seguir:

Encontramos a seguinte função:
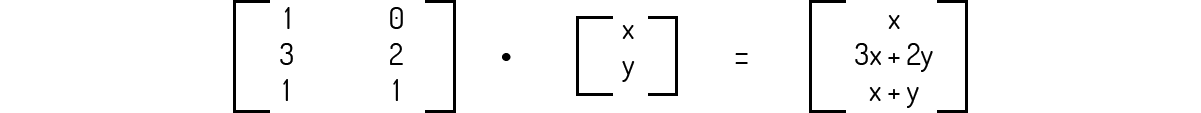
Ou seja, temos uma forma de mostrar que A transforma o vetor v de \({{\Re }^{2}}\) em um vetor de \({{\Re }^{3}}\). Poole (2004) ainda nos indica uma forma diferente para representarmos essa transformação \({{T}_{A}}\):
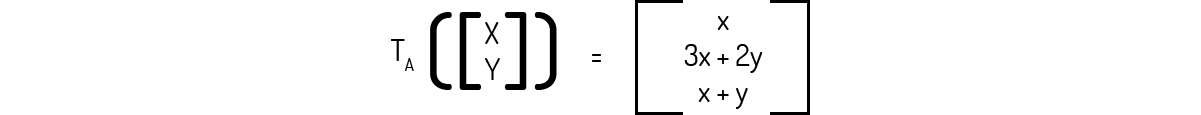
Ainda com esse exemplo em mente, Poole (2004) propõe uma terminologia:
I. A transformação T de \({{\Re }^{n}}\) em \({{\Re }^{m}}\) nada mais é do que uma regra que atribui a cada vetor v de \({{\Re }^{n}}\) um único vetor T(v) em \({{\Re }^{n}}\) .
II. \({{\Re }^{n}}\) é chamado de domínio de T e \({{\Re }^{n}}\) é o codomínio, sendo isso indicado por \(T:{{\Re }^{n}}\to {{\Re }^{m}}\).
III. O vetor T(v) no codomínio é chamado imagem do vetor v sob A. Já o conjunto de todas as imagens de vetores é chamado de imagem de T.
IV. Se n=m, ou seja, se \(T:{{\Re }^{n}}\to {{\Re }^{n}}\), temos que a transformação linear T é chamada de operador linear em \({{\Re }^{n}}\).
Com essas terminologias, para o exemplo acima teremos: o domínio é \({{\Re }^{2}}\) e o codomínio é \({{\Re }^{3}}\), sendo a transformação indicada por \({{T}_{A}}:{{\Re }^{2}}\to {{\Re }^{3}}\).
Exemplo 1.1: Para os vetores u=(1,1) e v=(3,2), determine a imagem usando a transformação indicada por (5).
Solução
Para tal, basta que façamos a substituição de x e y adequadamente. Para u:
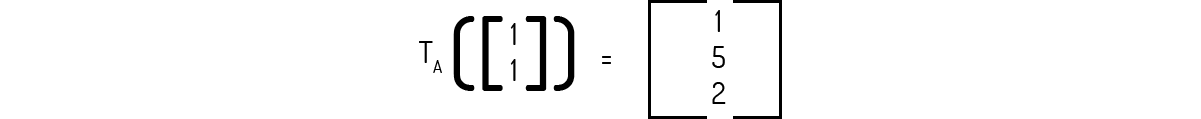
E para v:
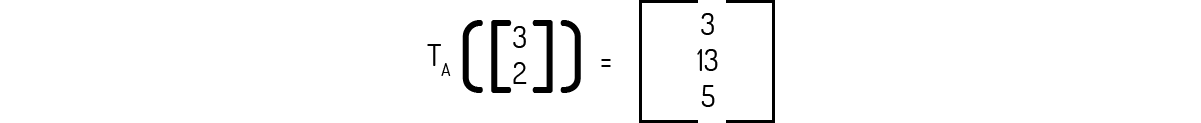
Agora, iremos dar uma definição formal para transformações lineares, um tópico de extrema importância para a matemática e diversas outras áreas das ciências.
Definição 1: Uma transformação linear \(T:{{\Re }^{n}}\to {{\Re }^{m}}\) é uma função que irá associar cada vetor u de \({{\Re }^{n}}\) a um único vetor T(u) em \({{\Re }^{m}}\) tal que:
1. T(u+v)=T(u)+T(v) para todos os vetores u e v de \({{\Re }^{n}}\).
2. T(ku)=kT(u) para todo vetor u de \({{\Re }^{n}}\) e escalar k.
Exemplo 1.2: Comprove que a transformação \(T:{{\Re }^{2}}\to {{\Re }^{3}}\) definida a seguir é uma transformação linear.
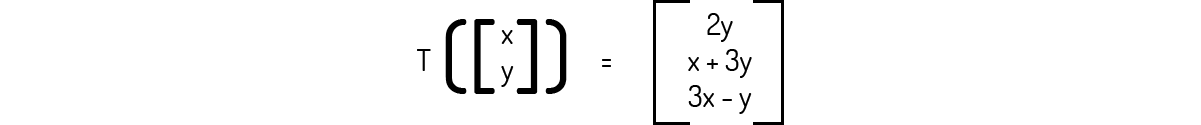
Solução
Precisamos provar os dois axiomas da Definição 1 para atestar que a transformação dada é uma transformação linear. Para isso, consideremos o escalar k e os seguintes vetores aleatórios:
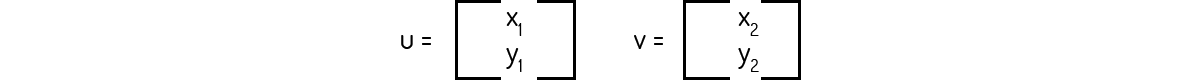
Então, para o axioma 1:
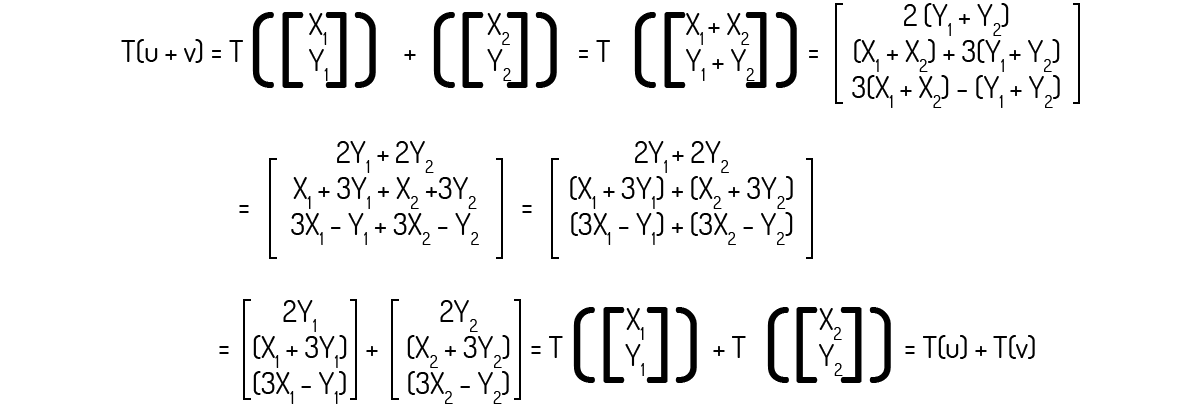
Agora, para o axioma 2:
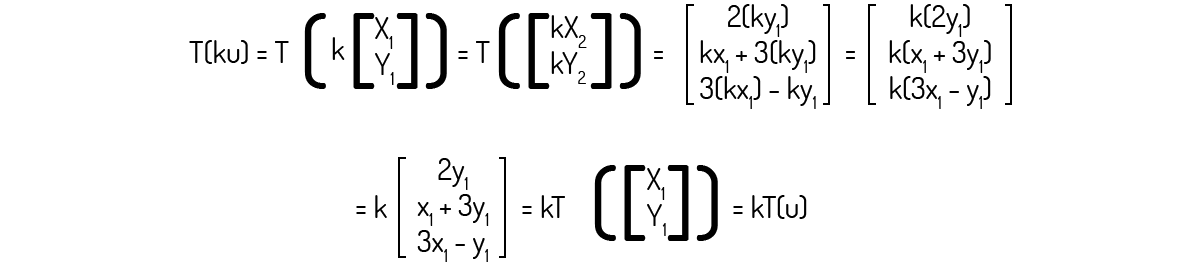
Como ambos axiomas foram provados, podemos afirmar que a transformação \(T:{{\Re }^{2}}\to {{\Re }^{3}}\) é uma transformação linear.
Exemplo 1.3: Comprove que a transformação \(T:{{\Re }^{3}}\to {{\Re }^{2}}\) definida como \(T\left( \left[ x~y~z \right] \right)=\left[ x~y \right]\) é uma transformação linear.
Solução
Para efetuarmos essa prova, é necessário que verifiquemos a validade dos dois axiomas apresentados na Definição 1. Para isso, consideremos o escalar k e os seguintes vetores aleatórios:

Então, para o axioma 1:
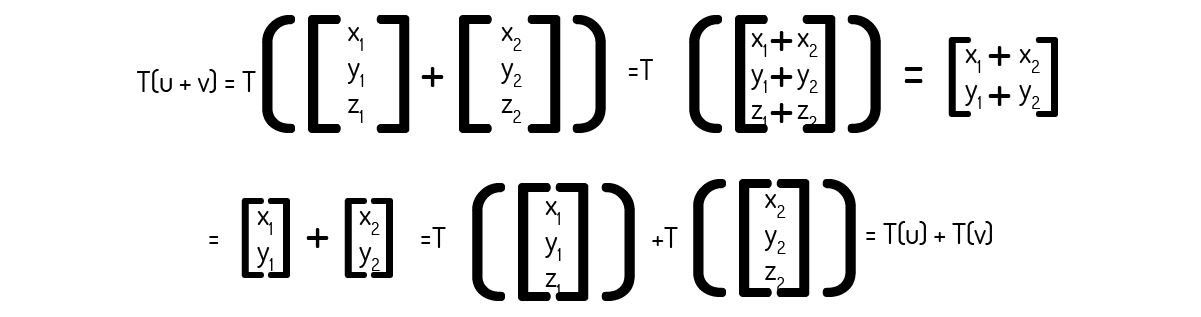
Agora, para o axioma 2:

Como ambos axiomas foram provados, podemos afirmar que a transformação \(T:{{\Re }^{3}}\to {{\Re }^{2}}\) é uma transformação linear. Inclusive, como nos informa Kolman (1999), essa transformação é chamada de projeção, pois ela projeta um vetor tridimensional no plano cartesiano. A Figura 4.2 nos mostra o vetor v=(x,y), imagem da projeção de um vetor u=(x,y,z) no qual foi aplicada esta transformada linear.
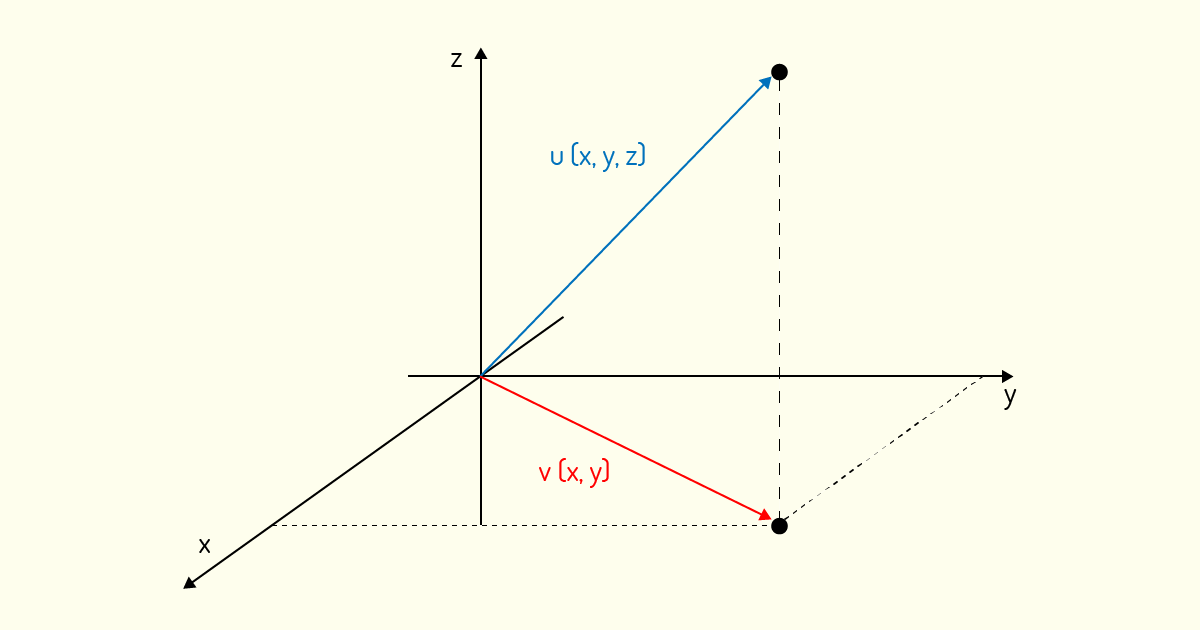
Exemplo 1.4: Comprove que a transformação \(T:{{\Re }^{2}}\to {{\Re }^{2}}\) definida como T(v)=av, onde a é um número real qualquer, é uma transformação linear.
Solução
Para efetuarmos essa prova, é necessário que verifiquemos a validade dos dois axiomas apresentados na Definição 1. Para isso, consideremos o escalar k e os seguintes vetores aleatórios:

Então, para o axioma 1:
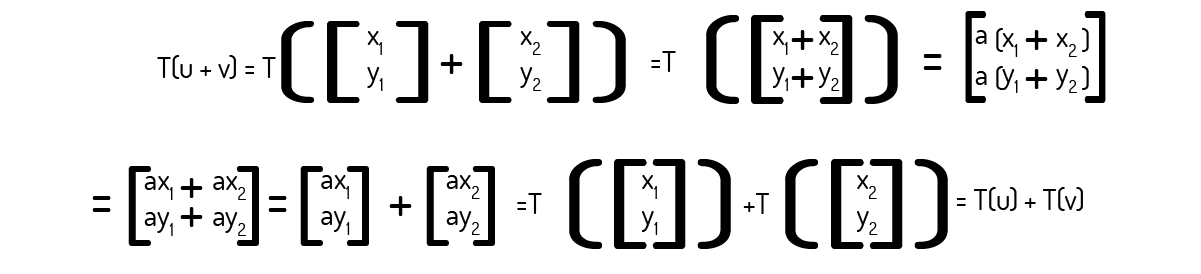
Agora, para o axioma 2:
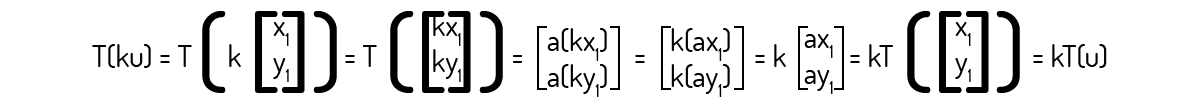
Como ambos axiomas foram provados, podemos afirmar que a transformação \(T:{{\Re }^{2}}\to {{\Re }^{2}}\) é uma transformação linear. Inclusive, como nos informa Boldrini (1980), esse tipo de transformação pode ser chamada de contração quando temos \(0<a<1\) ou expansão quando \(a>1\).
Poole (2004) mostra que a Definição 1 ainda pode ser resumida e agrupada em único axioma, no qual tem-se que a transformação linear \(T:{{\Re }^{n}}\to {{\Re }^{m}}\) é uma função que irá associar cada vetor u de \({{\Re }^{n}}\) a um único vetor \(T(u)\) em \({{\Re }^{m}}\) tal que:
1. \(T({{k}_{1}}u+{{k}_{2}}v)={{k}_{1}}T(u)+{{k}_{2}}T(v)\) para todos os vetores u e v de \({{\Re }^{n}}\) e escalares \({{k}_{1}}\) e \({{k}_{2}}\).
Também devemos destacar que é importante que, dada uma transformação, sejamos capazes de encontrar a matriz que gera a transformação. Por exemplo, se tomarmos a transformação mostrada no Exemplo 1.2:
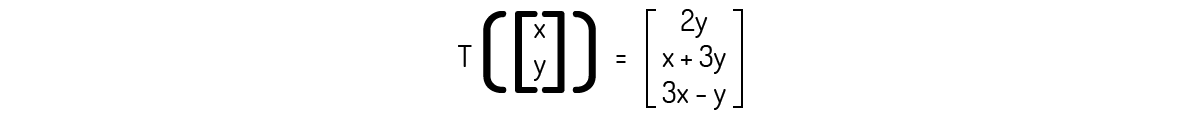
Somos capazes de usar engenharia reversa e encontrar facilmente a matriz: note que existem duas variáveis. Logo, podemos desmembrar o vetor resultante na adição de dois vetores multiplicados por escalares e, em seguida, na multiplicação de duas matrizes:
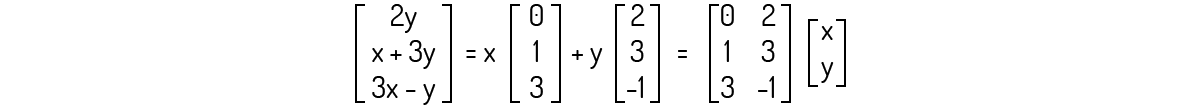
Poole (2004) indica que transformações como as obtidas anteriormente são efetivamente chamadas de transformações matriciais, ou seja:
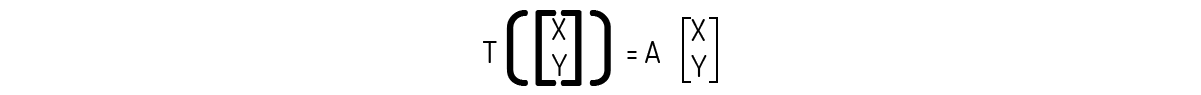
No entanto, ele enuncia um teorema que liga as transformações lineares com as transformações matriciais:
Teorema 1: Seja a matriz \(A\) uma matriz \(m\times n\). Então, a transformação \({{T}_{A}}:{{\Re }^{n}}\to {{\Re }^{m}}\) definida como \({{T}_{A}}(x)=A\)x para todo vetor x de \({{\Re }^{n}}\) também será uma transformação linear.
Ainda sobre as transformações matriciais, Poole (2004) destaca que, ao multiplicarmos uma matriz por um vetor \({{e}_{i}}\) que seja um componente da base canônica do espaço vetorial em questão, iremos sempre obter uma das colunas da matriz. Por exemplo:

Isso nos leva a um novo teorema, de acordo com Poole (2004):
Teorema 2: Seja a transformação linear \(T:{{\Re }^{n}}\to {{\Re }^{m}}\). Podemos afirmar, então, que T é uma transformação matricial T_A tal que, sendo A uma matriz m×n:
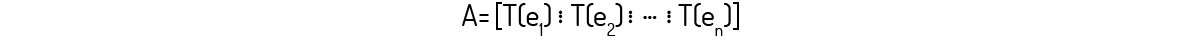
Essa matriz A é chamada de matriz padrão da transformação linear T.
Vejamos alguns exemplos de como podemos utilizar isso na identificação de transformações lineares agora.
Exemplo 1.5: Comprove que a transformação \(F:{{\Re }^{2}}\to {{\Re }^{2}}\) definida como a reflexão de cada ponto no eixo x é uma transformação linear.
Solução
A reflexão de um ponto (x,y) no eixo x nada mais é do que encontrar o ponto (x,-y), ou seja, mantemos o ponto fixo no eixo x e o giramos ao redor desse eixo. A Figura 4.3 nos mostra o ponto \(P'\), que é a reflexão de um ponto P(x,y) no eixo x.
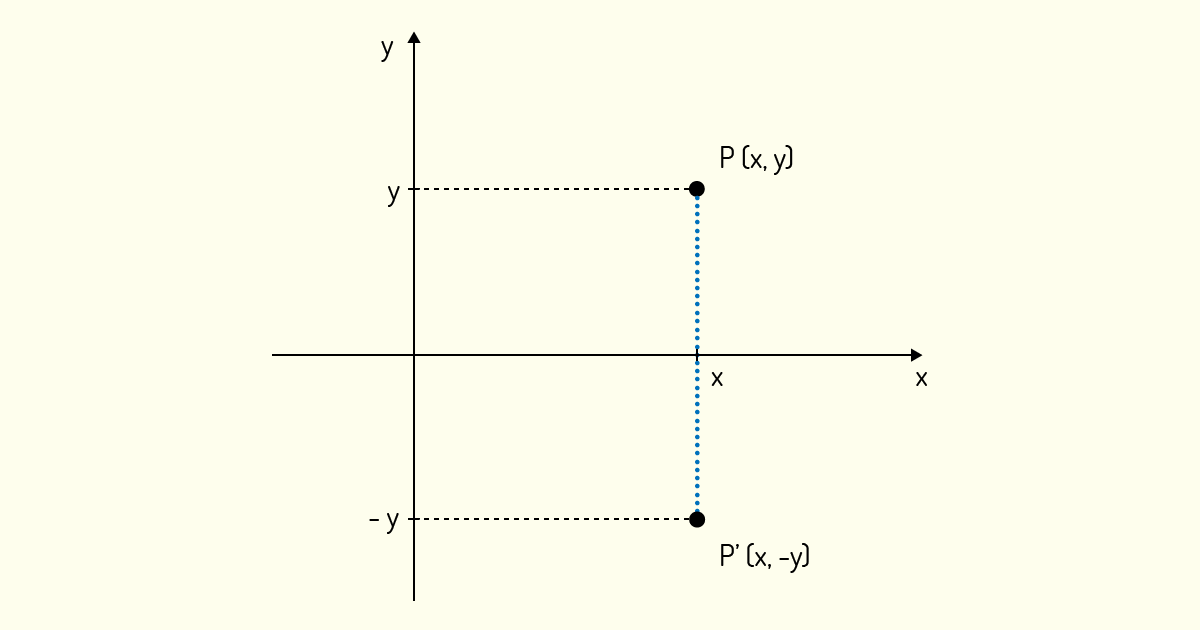
Logo, podemos definir essa transformação como:
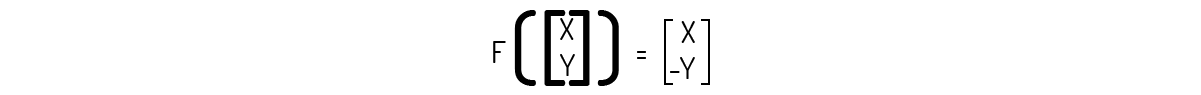
O mais correto para provarmos que essa transformação é uma transformação linear seria pelo mesmo procedimento do Exemplo 1.2. No entanto, veja que:
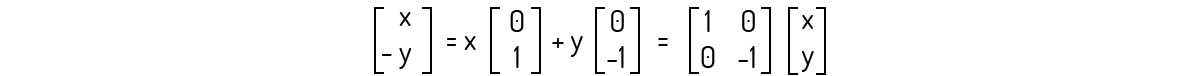
Ou seja, encontramos que
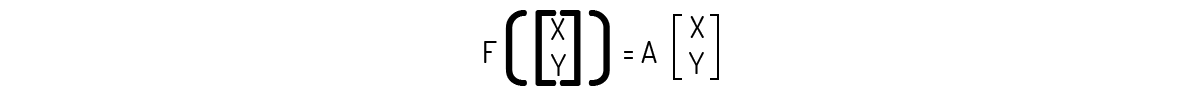
Logo, pelo Teorema 1, podemos afirmar que F é uma transformação linear. Uma transformação linear semelhante a essa também pode ser aplicada em relação ao eixo y, ou seja, podemos rotacionar um ponto ao longo do eixo y, mantendo fixo sua coordenada y e encontrando uma nova coordenada -x para sua coordenada inicial x. Outra transformação semelhante a essa é a reflexão na origem, onde giramos o vetor deixando sua origem fixada. Assim, um vetor u=(x,y) seria transformado em um vetor v=(-x,-y). Buscando sua prática nesse assunto, prove que essas transformações são transformações lineares.
Exemplo 1.6: Comprove que a transformação \(T:{{\Re }^{3}}\to {{\Re }^{2}}\) definida como \(T\left( \left[ x~y~z \right] \right)=\left[ x~y \right]\) é uma transformação linear.
Solução
Logo, podemos definir essa transformação como:

O mais correto para provarmos que essa transformação é uma transformação linear seria pelo mesmo procedimento do Exemplo 1.2. No entanto, veja que:
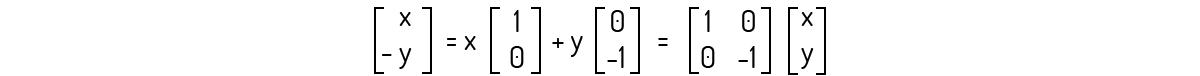
Ou seja, encontramos que
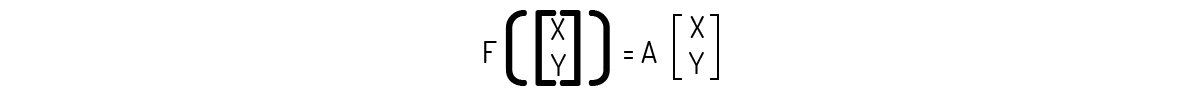
Logo, pelo Teorema 1, podemos afirmar que F é uma transformação linear.
Após termos estudado os conceitos mais básicos das transformadas lineares, iremos nos aprofundar um pouco mais no assunto das transformadas lineares, definindo novos conceitos e ampliando aqueles que já estudamos.
A partir de agora, iremos tratar as transformações em qualquer espaço vetorial, propondo uma nova definição mais generalista, conforme Lipschutz (1994) propõe:
Definição 2: Sejam V e W dois espaços vetoriais. Assim, uma transformação linear \(T:V\to W\) é uma função que irá associar cada vetor u de V a um único vetor T(u) em W tal que:
Para essa nova definição, Poole (2004) mostra que podemos incluir o Teorema 1 também, ou seja, sendo a matriz A uma matriz m×n, então a transformação \({{T}_{A}}:{{\Re }^{n}}\to {{\Re }^{m}}\) definida como \({{T}_{A}}(x)=A\)x para todo vetor x de \({{\Re }^{n}}\) também será uma transformação linear.
Em conjunto com essa definição geral, Kolman (1999) e Poole (2004) enunciam um teorema contendo propriedades das transformações lineares:
Teorema 3: Seja a transformação \(T:V\to W\) uma transformação linear. Então:
a) \(T(0_V\))=\)\(0_W\), sendo \(0_V\) e \(0_W\) os vetores os vetores nulos de V e W, respectivamente
b) \(T(-u)=-T(u)\) para todo vetor u de V.
c) \(T(u-v)=T(u)-T(v)\) para todos os vetores u e v de V.
Complementando a Definição 2 e o Teorema 3, Lipschutz (1994) e Poole (2004) destacam duas transformações lineares especiais:
Agora que temos uma definição mais geral das transformadas lineares, podemos também partir para uma visão mais geral da imagem de uma transformada linear. Lipschutz (1994) nos dá a seguinte definição para imagem:
Definição 2: Considere a transformação linear \(T:V\to W\). A imagem de T, simbolizada ImT ou imagem(T), é o conjunto de pontos obtidos pela aplicação de T em todos os vetores de V, ou seja:
\(ImT=\{u\in W/T(v)=\)u para algum v\(\in V\}\)
Para pensarmos um pouco sobre o tamanho da imagem de uma transformação linear, Kolman (1999) pede que retomemos os nossos conhecimentos de funções. Uma função f é uma lei que associa cada um dos valores de um conjunto V para um único elemento noutro conjunto W. No entanto, também podemos representar f numa forma tabular, onde ao lado de cada elemento de V colocaremos seu elemento associado de W. Já sabemos que podemos ver uma função como uma transformação linear. Agora, sabendo disso pode parecer impossível descrevermos uma transformação linear \(T:V\to W\), visto que diversos conjuntos V podem ser infinitos. Para contornar esse problema, Kolman (1999) enuncia um teorema que nos diz que, conhecendo os valores de T em uma base de V, teremos T completamente determinada, o que torna possível descrever T partindo-se apenas da imagem de um pequeno conjunto de vetores de V:
Teorema 4: Seja a transformação \(T:V\to W\) uma transformação linear de um espaço vetorial V de dimensão n num espaço vetorial W. Considerando a base \(S=\{~v1,v2,...vn\}\) como uma base para o espaço V e u um vetor arbitrário de V, então a determinação completa de T(u) é dada por \(\{T(~v1),T(v2),...,T(vn)\}\).
Além da imagem de uma transformação linear, dada a importância do espaço nulo, é útil que saibamos também qual é o núcleo da transformação linear. Lipschutz (1994) nos dá a seguinte definição:
Definição 3: Considere a transformação linear \(T:V\to W\). O núcleo de T, simbolizado Ker T ou ker(T), é o conjunto de vetores de V que são transformados em vetores nulos de W. Ou seja:
\(ker\left( T \right)=\{v\in V/T(v)=0\}\)
Além disso, Kolman (1999) nos diz que se \(T:V\to W\) é uma transformação linear, então ker(T) será um subespaço de V. Isso é facilmente checado pelo fato do núcleo de uma transformada linear ser um conjunto não nulo. Quando uma transformada linear apresenta como núcleo apenas o vetor nulo, seu núcleo é chamado de subespaço trivial {0}.
Essas definições possibilitam que estudemos alguns tipos especiais de transformações lineares: as transformações injetoras e sobrejetoras. Sobre tais transformações, Kolman (1999) nos dá a seguinte definição:
Definição 4: Uma transformação linear \(T:V\to W\) será dita injetora se, para quaisquer vetores \(v_1\),\(v_2\),...\(v_n\) de \(V\), tenhamos \(T(v1)~\ne ~T(v2)~\ne ~...T(vn)\). Ou seja, \(T\) é injetora se \(T(vi)~\ne ~T(vj)\) sempre que vi ≠ vj.
Definição 5: Uma transformação linear \(T:V\to W\) será dita sobrejetora se \(ImT=W\).
Kolman (1999) nos diz que, se \(T:V\to W\) é uma transformação linear, então \(ImT\) será um subespaço de \(W\). Ele também enuncia que uma transformação linear \(T:V\to W\) será injetora se, e somente se, \(ker\left( T \right)=\{0V\}\). Finalizando esse assunto, ele ainda enuncia um teorema:
Teorema 5: Seja a transformação \(T:V\to W\) uma transformação linear de um espaço vetorial V de dimensão n num espaço vetorial W. Então
\(dim\left( ker\left( T \right) \right)+dim\left( ImT \right)=dim~V\)
Sendo que \(dim\left( ker\left( T \right) \right)\) também é chamada de nulidade de \(T\) e \(dim\left( ImT \right)\) é chamada de posto de \(T\).
Exemplo 1.7: Verifique se a transformação \(T:{{\Re }^{2}}\to {{\Re }^{2}}\) definida como \(T\left( \left[ x~y \right] \right)=\left[ x+y~~x-y \right]\) é injetora.
Solução
Para isso, consideremos dois vetores aleatórios: u\(=\left( {{x}_{1}},{{y}_{1}} \right)\) e v\(=\left( {{x}_{2}},{{y}_{2}} \right)\). Para que esta transformação seja injetora, precisamos verificar se \(T(u)=T(v)\). Como a transformada gera um vetor de dimensão dois, precisamos checar a possibilidade de igualdade dos dois elementos que o compõem. Assim, o primeiro termo nos diz que:
\({{x}_{1}}+{{y}_{1}}={{x}_{2}}+{{y}_{2}}\)
E o segundo:
\({{x}_{1}}-{{y}_{1}}={{x}_{2}}-{{y}_{2}}\)
Ou seja, temos um sistema. Se somarmos as duas equações que encontramos, teremos que:
\({{x}_{1}}+{{y}_{1}}+{{x}_{1}}-{{y}_{1}}={{x}_{2}}+{{y}_{2}}+{{x}_{2}}-{{y}_{2}}\)
\(2{{x}_{1}}=2{{x}_{2}}\to {{x}_{1}}={{x}_{2}}\)
Essa igualdade implica que tenhamos \({{y}_{1}}={{y}_{2}}\). Logo, podemos concluir que \(T(u)=T(v)\) apenas para um vetor u\(=\left( {{x}_{1}},{{y}_{1}} \right)\), o que nos leva a crer que a transformada é injetora.
Exemplo 1.8: Encontre o núcleo da transformação apresentada no Exemplo 1.7.
Solução
O núcleo de uma transformação nada mais é do que o conjunto de vetores de um espaço para os quais temos T(u)=0. Portanto, para encontrarmos o núcleo dessa transformação, precisamos resolver o sistema linear gerado pelos elementos de T(u):
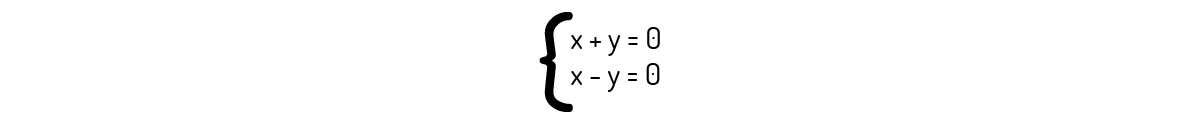
Se somarmos as duas equações, encontramos que x=0. Logo, também temos que y=0. Logo, a única solução para esse caso é u=0, ou seja, ker(T)=0.
Tal qual ocorre em funções, é possível que tenhamos casos de uma transformada linear de uma transformada linear. Por exemplo, se \(T:V\to W\) e \(S:W\to P\) são transformadas lineares, então, a composta de \(S\) com \(T\) será definida como:
\[\left( S\circ T \right)(u)=S(T(u))\]
sendo u um vetor de \(V\)
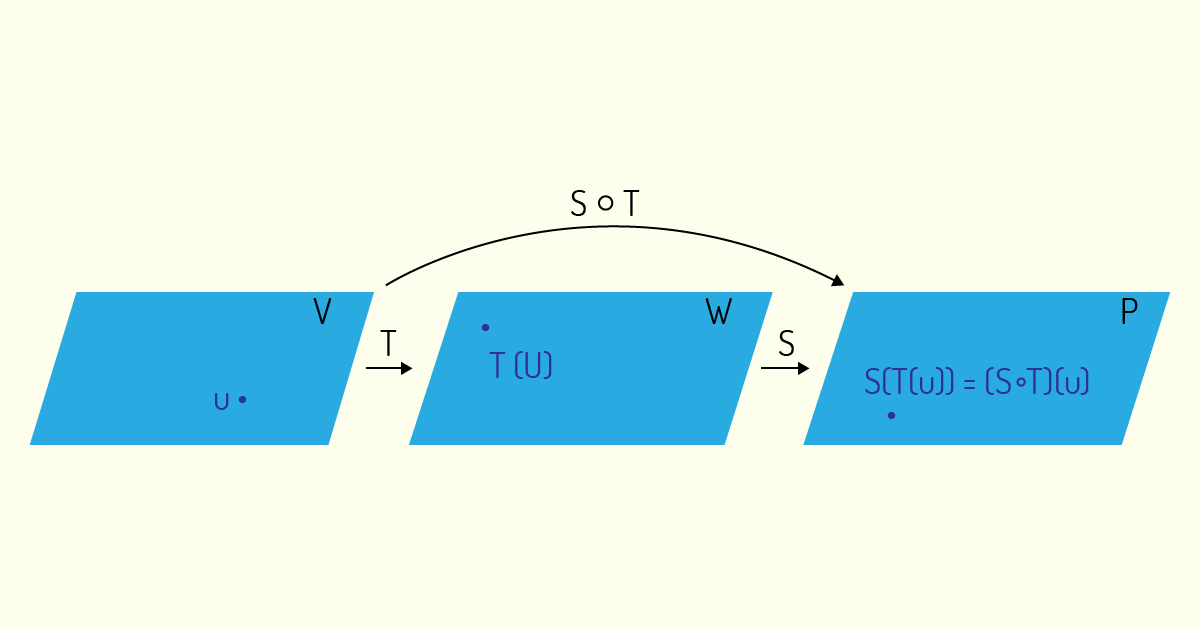
Partindo dessa definição, Poole (2004) ainda afirma que, se \(T:V\to W\) e \(S:W\to P\) são transformadas lineares, então \(S\circ T:V\to P\) também é uma transformada linear.
Agora que temos domínio de toda a base teórica acerca das transformações lineares, iremos estudar alguns casos especiais de aplicação das transformadas lineares. Primeiramente, pensemos no seguinte problema: dada uma transformação linear \(T:V\to V\), quais vetores são levados a um múltiplo de si mesmo?
Boldrini (1980) nos diz que esse problema consiste em buscarmos um vetor v pertencente ao um espaço vetorial V e um escalar λ∈R tal que
\[T(v)=\lambda \]v
Note que o problema acima pode ser solucionado para qualquer v usando-se o vetor nulo, v=0, o que se mostra uma solução trivial. Logo, estamos realmente interessados em encontrar um v que seja não nulo. Nesse caso, o escalar λ será chamado de autovalor ou valor característico de T, enquanto o vetor v será chamado de autovetor ou vetor característico de T.
Vamos formalizar isso. A partir de agora, a transformação \(T:V\to V\), ou seja, de um espaço para ele mesmo, será chamada de operador linear. Assim, de acordo com Boldrini (1980):
Definição 6: Seja o operador linear \(T:V\to V\). Caso exista um vetor v∈V sendo v≠0 e um escalar λ∈R tal que T(v)=λv, então λ é um autovalor de T e o vetor v é um autovetor de T que é associado à λ.
Kolman (1999) ainda sugere uma definição para autovetores e autovalores utilizando matrizes:
Definição 7: Seja A uma matriz quadrada n×n. Um escalar λ∈R será chamado de autovalor de A se existir um vetor v não nulo em \({{\Re }^{n}}\) tal que:
\[Ax=\lambda \]x
Assim, todos os vetores x que satisfizerem a relação acima serão chamados de autovetores de A associado à λ.
Vejamos um exemplo de como podemos encontrar autovalores e autovetores.
Exemplo 1.9: Encontre os autovalores e autovetores do operador linear \(T:{{\Re }^{n}}\to {{\Re }^{n}}\) definido como \(T(u)={{I}_{n}}\)u.
Solução
\({{I}_{n}}\) é a matriz identidade. Para essa matriz, seu único autovalor é 1 por definição. Logo, qualquer vetor u não nulo de \({{\Re }^{n}}\) pode ser um autovetor associado ao autovalor λ=1.
Exemplo 1.10: Encontre os autovalores e autovetores do operador linear \(T:{{\Re }^{2}}\to {{\Re }^{2}}\) definido como T(u)=2u.
Solução
Note que da definição do próprio operador linear conseguimos encontrar o autovalor de T como sendo 2. Agora, para encontrarmos o autovetor, consideremos o vetor genérico u=(x,y). Esse operador linear pode ser escrito como:
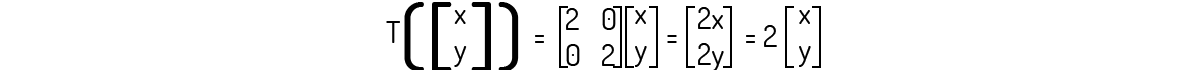
Note que qualquer vetor na forma de u e não nulo satisfaz às condições para ser um autovetor.
Partindo do Exemplo 1.10, Boldrini (1980) afirma que as transformações semelhantes à utilizada em tal exemplo, ou seja, \(T:{{\Re }^{2}}\to {{\Re }^{2}}\) definido como T(u)=ku, apresentam de forma direta seu autovalor como sendo igual a k e seus autovetores são na forma u=(x,y). Um caso interessante que podemos encontrar desse exemplo genérico é para o caso de k=1, onde temos que T gera a identidade do vetor u.
Ele também enuncia o seguinte teorema:
Teorema 6: Seja a transformação \(T:V\to V\) e um autovetor u associado a um autovalor λ. Logo, qualquer vetor w=ku, sendo k ≠ 0também é um autovetor associado a λ.
Os autovalores e autovetores apresentam uma vasta gama de aplicações em diversos tipos de problemas, sendo muito conhecidos pelo seu uso na resolução de sistemas. Pensando computacionalmente agora, qual seria o método mais prático para empregarmos em um software visando à resolução de sistemas lineares?

Nos exemplos que fizemos anteriormente, buscamos os autovalores e autovetores nos baseando na definição de autovetores e autovalores. No entanto, esse método pode ser muito complexo de se efetuar. Assim, Boldrini (1980) sugere que busquemos um método mais prático para encontrarmos os autovalores e autovetores de uma matriz A uma quadrada de ordem n.
Para desenvolvermos essa metodologia diferente, consideremos o caso de uma matriz de ordem 3. Em tal situação, procuramos vetores v\(\in {{\Re }^{3}}\) e escalares λ∈R tais que
\[Av=\lambda ~~~~~~~~~~v(6)\]
Boldrini (1980) destaca que, sendo \({{I}_{3}}\) a matriz identidade de ordem 3, então podemos reescrever (6) como
\[Av=\left( \lambda {{I}_{3}} \right)~~~~~~~~~~v(7)\]
ou ainda
\[\left( A-\lambda {{I}_{3}} \right)v=~~~~~~~~~~0(8)\]
Considerando a matriz genérica e o vetor v a seguir:
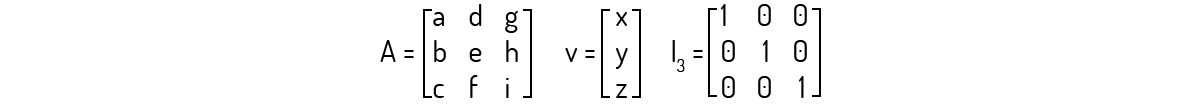
Podemos reescrever (8) então:
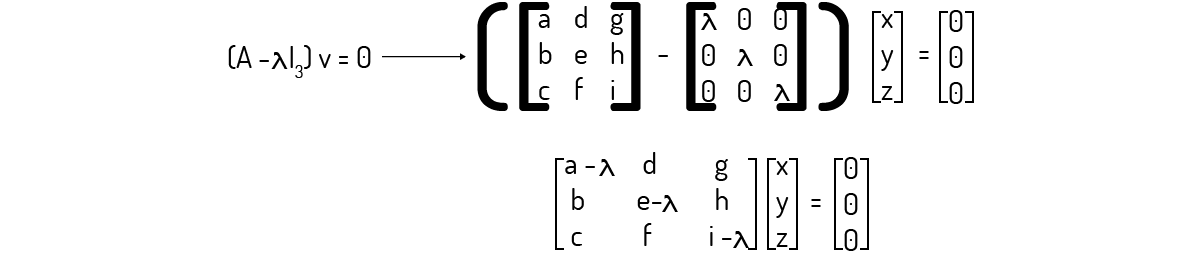
Escrevendo o sistema representado por essa operação resulta num caso com três equações e três incógnitas. Logo, como Boldrini (1980) nos diz, se o determinante da matriz dos coeficientes for diferente de zero, esse sistema irá apresentar uma solução única, que é a solução trivial, ou seja, x=y=z=0. Como nosso interesse aqui é o cálculo de autovetores e autovalores, buscamos vetores v que sejam diferentes do vetor nulo. Isso implica que \(\left( A-\lambda {{I}_{3}} \right)\) deverá ser igual a zero. Logo, devemos encontrar:
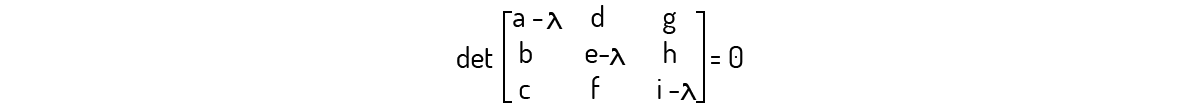
Lembrando-se da definição de determinante, vemos que o determinante acima será um polinômio de λ. Esse polinômio é chamado de polinômio característico de A, de acordo com Kolman (1999). Resolvendo esse polinômio, iremos, então, encontrar os autovalores para a matriz A. Para encontrar os autovetores, basta substituir os autovalores e resolver o sistema obtido a partir de (6).
Até o momento, desenvolvemos uma linha de pensamento para o caso de uma matriz de ordem 3. Mas, como Kolman (1999) nos mostra, podemos expandir o que fizemos até aqui para matrizes de ordem n. Dessa forma, a equação (8) nos levaria à seguinte situação:
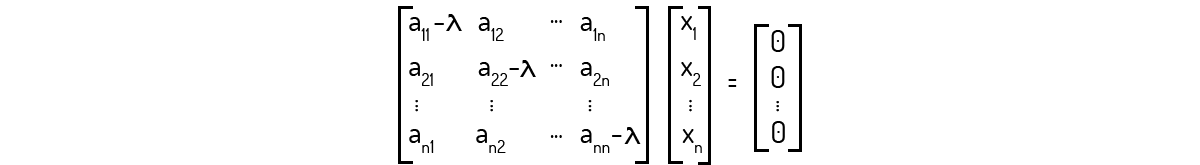
Exemplo 1.11: Encontre os autovalores e autovetores para a matriz A abaixo.
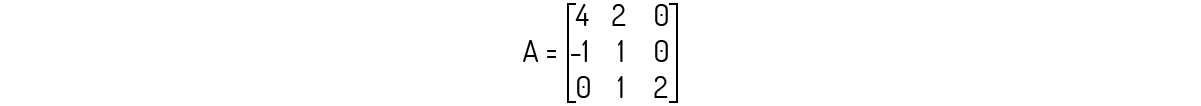
Solução
Tal qual desenvolvemos, precisamos avaliar \(det\left( A-\lambda {{I}_{3}} \right)=0\) para essa matriz. Assim:
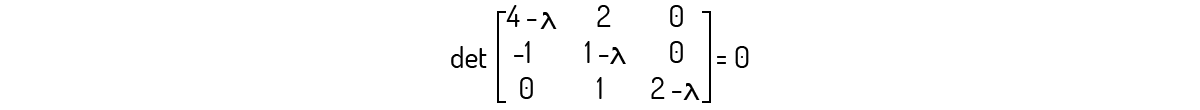
Avaliando esse determinante, você encontrará o seguinte polinômio:
\[-{{\lambda }^{3}}+7{{\lambda }^{2}}-16\lambda +12=0\]
Note que esse polinômio pode ser reescrito como:
\[\left( \lambda -3 \right){{\left( \lambda -2 \right)}^{2}}=0\]
De onde conseguimos facilmente as raízes, ou seja, λ=2 e λ=3. Agora, devemos analisar os dois casos para encontrarmos os autovetores. Primeiro, para λ=2:
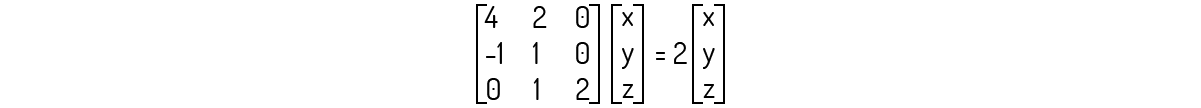
Que nos leva ao seguinte sistema:
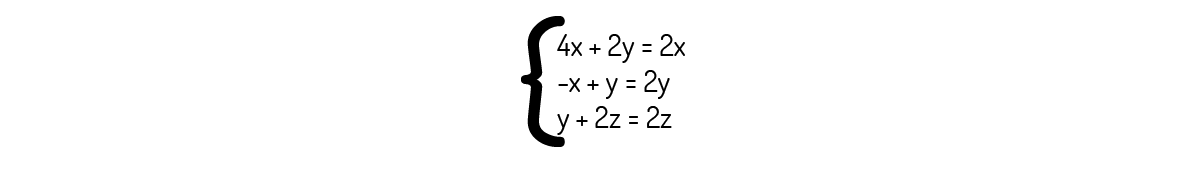
Analisando a terceira equação, encontramos que y=0. Logo, conseguimos também verificar, tanto pela primeira quanto pela segunda equação, que x=0 também. Fora isso, vemos que não existe nenhuma restrição para a coordenada z. Com isso, concluímos que os autovetores associados a λ=2 são os vetores de forma (0,0,z).
Agora, para λ=3:
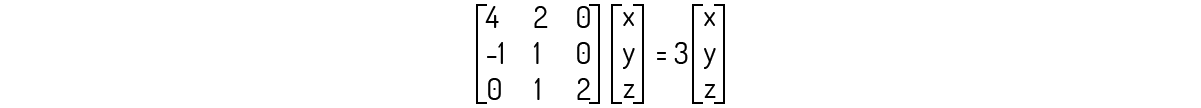
Que nos leva ao seguinte sistema:
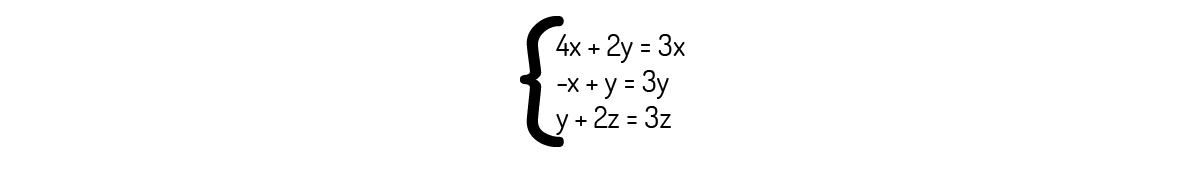
Analisando a primeira e a segunda equação, encontramos que x=-2y. Analisando a terceira, encontramos que z=y. Ou seja, temos duas coordenadas em função de uma terceira. Disso, podemos concluir que os autovetores associados a λ=3 são os vetores de forma (-2y,y,y).
Kolman (1999) também nos diz que as matrizes que apresentam o 0 como único autovalor são chamadas de matrizes singulares.
Autovalores e autovetores têm uma especial importância na resolução de problemas que envolvem equações diferenciais, um dos objetos centrais do estudo de cálculo e de inúmeras outras disciplinas que fazem uso desse tipo de equações. Problemas desse tipo podem ser complexos para lidar, mas um bom domínio sobre as formas de encontrarmos autovalores e autovetores pode ser de grande valia para a simplificação do processo.
Link: revistas.utfpr.edu.br

Agora, iremos aplicar nossos conhecimentos desenvolvidos até aqui para encontrarmos uma base de um espaço vetorial onde a matriz de um determinado operador linear seja o mais simples possível. Boldrini (1980) nos diz que o caso mais simples para isso é quando encontramos uma matriz diagonal associada a um operador.
Visando esse objetivo, Boldrini (1980) enuncia que, se um espaço vetorial V de dimensão n e um operador linear \(T:V\to V\) apresentam n autovalores distintos, então B possui uma base cujos vetores são todos autovetores de T. Ou seja, se formos capazes de encontrar tantos autovalores distintos quanto à dimensão do espaço, podemos garantir que existe uma base de autovetores.
Buscando encontrar a tal base diagonal, vamos agora desenvolver uma outra formulação para descrever problemas de autovalores e autovetores. Para isso, precisamos do conceito de matrizes semelhantes, tal qual é definida por Kolman (1999):
Definição 8: Uma matriz B será dita uma matriz semelhante de uma matriz A se existir uma matriz P que seja invertível, tal que:
\[B={{P}^{-1}}AP\]
Kolman (1999) ainda destaca que essas matrizes semelhantes apresentam as seguintes propriedades:
Exemplo 1.12: Encontre a matriz B que seja semelhante à matriz A dada a seguir, utilizando a matriz P indicada.
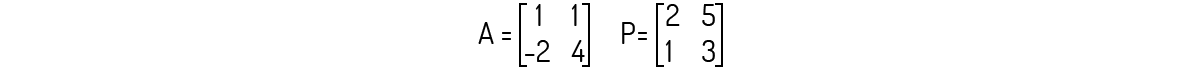
Solução
Checando primeiramente se a matriz P apresenta uma inversa, encontramos que det(P)=1. Logo, ela é invertível. Agora, calculando a inversa de P, você deve encontrar:
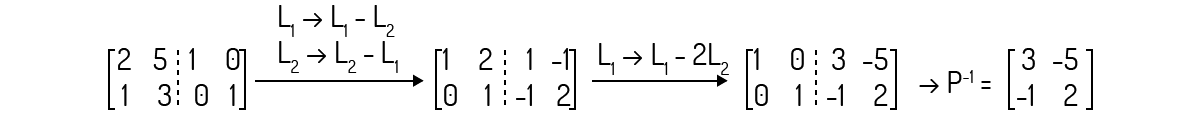
Agora, aplicando a definição de uma matriz semelhante:
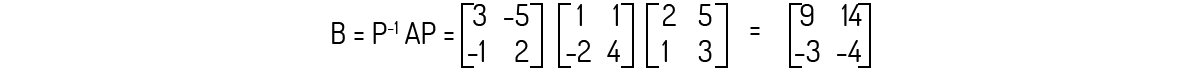
Agora, sabendo o que é uma matriz semelhante, Kolman (1999) e Leon (1999) definem um novo tipo de matriz:
Definição 9: Uma matriz A será dita uma matriz diagonalizável se ela for semelhante a uma matriz diagonal. Nessa situação, dizemos que A pode ser diagonalizada.
Kolman (1999) ainda enuncia um teorema sobre matrizes diagonalizáveis:
Teorema 7: Uma matriz quadrada A de ordem n será diagonalizável se, e somente se, apresentar n autovetores linearmente independentes, caso para o qual tem-se que A será semelhante a uma matriz diagonal D. Ou seja, teremos \({{P}^{-1}}AP=D\), sendo que os elementos não nulos de D são os autovalores de A, enquanto P será uma matriz cujas colunas são os respectivos autovetores linearmente independentes de A. Deve-se notar que a ordem dos elementos de P irá ditar a ordem dos elementos de D.
Exemplo 1.13: Considere a mesma matriz A indicada no Exemplo 1.12. Verifique se A é diagonalizável.
Solução
Primeiramente, devemos avaliar \(det\left( A-\lambda {{I}_{2}} \right)=0\) para essa matriz. Assim:
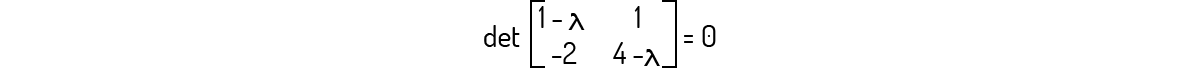
Avaliando esse determinante, você encontrará o seguinte polinômio:
\[{{\lambda }^{2}}-5\lambda +6=0\]
As raízes para este polinômio são λ=2 e λ=3. Devemos analisar os dois casos para encontrarmos os autovetores. Primeiro, para λ=2:
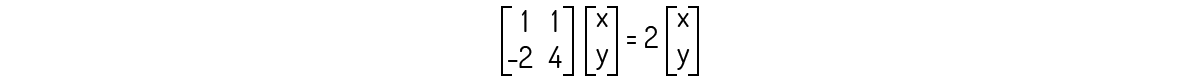
Que nos leva ao seguinte sistema:
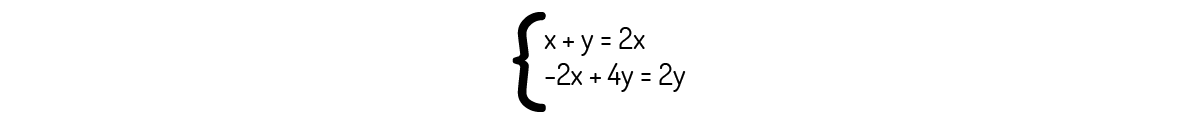
Analisando a primeira equação, encontramos que y=x. Então, os autovetores associados a λ=2 são os vetores de forma (x,x). Agora, para λ=3:
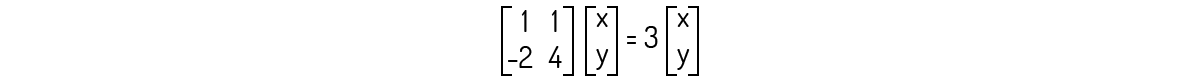
Que nos leva ao seguinte sistema:
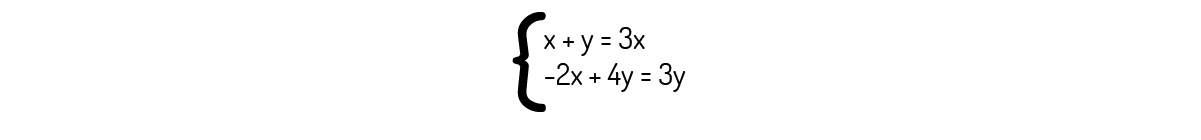
Analisando a primeira equação, encontramos que y=2x. Então, os autovetores associados a λ=3 são os vetores de forma (x,2x). Podemos dizer que esses autovetores pertencem ao subespaço u=(1,1) e v=(1,2), respectivamente. Os vetores u e v são linearmente independentes (comprove como um exercício). Então, A é diagonalizável.
Podemos confirmar o Teorema 7 agora. Para os autovalores e autovetores que encontramos, teremos:

É fácil confirmar que P é invertível e sua inversa é igual a:
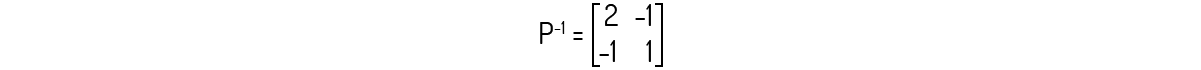
Avaliando agora \({{P}^{-1}}AP\):
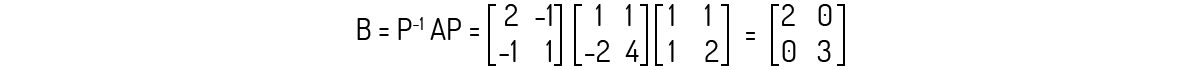
Kolman (1999) ainda destaca outro teorema sobre esse assunto:
Teorema 8: Uma matriz será diagonalizável se todas as raízes de seu polinômio característico forem distintas e reais.
Como você já deve ter imaginado, nem todos os operadores são diagonalizáveis. Boldrini (1980) cita, por exemplo, que temos casos de operadores cujo polinômio característico não apresentará raízes reais, o que o leva a não possuir autovalores nem autovetores. Esse caso pode ser resolvido se o espaço vetorial em consideração for um espaço complexo, o que fará com que o polinômio característico venha a apresentar raízes complexas.
No entanto, Boldrini (1980) ainda destaca que, mesmo considerando espaços complexos, não garantimos que todos os operadores serão diagonalizáveis. Para situações onde \(T:V\to V\) for um operador linear não diagonalizável e V for um espaço vetorial complexo, Boldrini (1980) e Kolman (1999) dizem que podemos achar uma base desse espaço, tal que essa base apresente uma forma especial conhecida como forma canônica de Jordan. De acordo com Lipschutz (1994), essa forma apresenta-se como uma diagonal por blocos, como mostrado a seguir:

Nessa forma, o bloco diagonal é chamado de bloco de Jordan.
Nome do livro: Álgebra
Editora: Atual Editora
Autor: John K. Baumgart
ISBN: 8570564546
Comentário: Esse livro é muito interessante, pois visa a um conhecimento histórico de conceitos que foram trabalhados no presente material. Esse tipo de abordagem é importante para estudiosos da área compreenderem melhor sobre o desenvolvimento de conceitos.

Nome do livro: Álgebra Linear
Editora: Pearson
Autores: Alfredo Steinbruch e Paulo Winterle
ISBN: 0074504126
Comentário: Esse livro usa uma linguagem simplificada e com diversos exemplos, focando na maximização dos conceitos teóricos sendo desenvolvidos. É um bom material de apoio para o aprendizado e prática da Álgebra Linear.
