A presente unidade irá finalizar o básico necessário para o manuseio de matrizes, apresentando uma forma alternativa de calcularmos o determinante de matrizes e também apresentando o conceito de matriz inversa.
Fechado o tópico de matrizes, chegou o momento de iniciarmos nossos estudos num dos tópicos centrais da Álgebra Linear: os sistemas lineares. Iremos definir primeiramente o que são estes sistemas lineares, mostrando os tipos genéricos de solução que estes podem apresentar e também como podemos utilizar as matrizes para trabalharmos com sistemas lineares.
Em seguida, discutiremos métodos práticos de resolução de sistemas lineares, sendo o principal foco o escalonamento de sistemas. Uma série de exemplos também será apresentada em cada tópico, visando uma melhor compreensão do desenvolvimento desses métodos.
Tendo a base de matrizes sido estudadas, vamos agora nos aprofundar um pouco mais em alguns tópicos de matrizes, antes de iniciarmos os nossos estudos de sistemas lineares.
Você deve se lembrar que estudamos como realizar as operações básicas com matrizes, como a adição, a multiplicação por escalar e a transposição. Em seguida, analisamos como se dá a multiplicação entre matrizes e, finalmente, vimos como proceder o cálculo de determinantes, principalmente focando em matrizes de ordem 2 e 3.
Agora, iremos verificar algumas formas mais gerais de avaliarmos o determinante de matrizes de qualquer tamanho. Em seguida, iremos ver como podemos encontrar a inversa de uma matriz, um conceito útil sempre que lidamos com matemática.
Você certamente se lembra que a forma que vimos para calcular o determinante de matrizes pode ser complicada, principalmente para casos de matrizes de ordem maior que 2. Agora, veremos alguns métodos alternativos visando facilitar o cálculo de determinantes.
No primeiro método, veremos como podemos calcular o determinante de uma matriz de ordem n utilizando matrizes de ordem n – 1. Assim, podemos, por exemplo, calcular o determinante de uma matriz de ordem 3 utilizando matrizes de ordem 2 (KOLMAN, 1999). Esse método, segundo Boldrini (1980), é conhecido como desenvolvimento (ou expansão) de Laplace.
Vejamos como este método funciona. Considere a matriz A a seguir:

Para encontrar o determinante dessa matriz A, utilizamos a seguinte equação:
\[det\left( A \right)={{a}_{11}}{{a}_{22}}{{a}_{33}}+{{a}_{12}}{{a}_{23}}{{a}_{31}}+{{a}_{13}}{{a}_{21}}{{a}_{32}}-{{a}_{11}}{{a}_{23}}{{a}_{32}}-{{a}_{12}}{{a}_{21}}{{a}_{33}}-{{a}_{13}}{{a}_{22}}{{a}_{31}}~~~~~~~~~~(1)\]
Note que, na soma apresentada em (1), podemos colocar em evidência os termos comuns em alguns produtos. Assim, podemos reescrever (1) da seguinte forma:
\[det\left( A \right)={{a}_{11}}\left( {{a}_{22}}{{a}_{33}}-{{a}_{23}}{{a}_{32}} \right)-{{a}_{12}}\left( {{a}_{21}}{{a}_{33}}-{{a}_{23}}{{a}_{31}} \right)+{{a}_{13}}\left( {{a}_{21}}{{a}_{32}}-{{a}_{22}}{{a}_{31}} \right)~~~~~~~~~~(2)\]
Vamos, agora, analisar os termos entre parênteses na equação (2). Neles, temos a multiplicação de dois elementos sendo subtraídos pelo produto de outros dois elementos. Ou seja, numa forma genérica:
\[a\cdot b-c\cdot d~~~~~~~~~~(3)\]
Se compararmos essa equação (3) com o cálculo do determinante de uma matriz B de ordem 2:

\[det\left( B \right)={{b}_{11}}b-{{b}_{12}}{{b}_{21}}~~~~~~~~~~(4)\]
...veremos que (3) e (4) são equivalentes.
Com isso, podemos enxergar a equação (2) de uma forma diferente. Sejam as seguintes matrizes de ordem 2, derivadas da matriz A descrita acima:

É possível, então, reescrever (2) como:
\[det\left( A \right)={{a}_{11}}\cdot det\left( {{A}_{1}} \right)-{{a}_{12}}\cdot det\left( {{A}_{2}} \right)+{{a}_{13}}\cdot det\left( {{A}_{3}} \right)~~~~~~~~~~(5)\]
Ou seja, vimos que é possível calcular a determinante de uma matriz de ordem três, utilizando apenas matrizes de ordem dois. Essa Equação (5) também pode ser expressa da seguinte forma, como destaca Boldrini (1980):
\[det\left( A \right)={{a}_{11}}\cdot det\left( {{A}_{11}} \right)-{{a}_{12}}\cdot det\left( {{A}_{12}} \right)+{{a}_{13}}\cdot det\left( {{A}_{13}} \right)~~~~~~~~~~(6)\]
Essa forma mostrada na Equação (6) apresenta o termo \({{A}_{ij}}\), que é conhecido como submatriz da inicial, da qual se retirou a i-ésima linha e a j-ésima coluna. Poole (2004) destaca que essa submatriz também pode ser chamada de cofator-(i, j) de A, sendo utilizada uma das seguintes notações para sua representação:
\[{{\Delta }_{ij}}={{C}_{ij}}={{\left( -1 \right)}^{i+j}}\cdot det\left( {{A}_{ij}} \right)~~~~~~~~~~(7)\]
Combinando as Equações (6) e (7) e aplicando para o caso genérico de uma matriz A de ordem n, temos:
\[det\left( A \right)={{a}_{i1}}\cdot {{\Delta }_{i1}}+{{a}_{i2}}\cdot {{\Delta }_{i2}}+...+{{a}_{in}}\cdot {{\Delta }_{in}}\)
\[det\left( A \right)=\underset{j=1}{\overset{n}{\mathop \sum }}\,{{a}_{ij}}\cdot {{\Delta }_{ij}}~~~~~~~~~~(8)\]
De forma análoga ao que foi desenvolvido para a i-ésima linha, Poole (2004) mostra que podemos repetir o procedimento para a j-ésima coluna, chegando à seguinte Equação:
\[det\left( A \right)=\underset{i=1}{\overset{n}{\mathop \sum }}\,{{a}_{ij}}\cdot {{\Delta }_{ij}}~~~~~~~~~~(9)\]
Agora vamos formalizar esse procedimento de cálculo do determinante de uma matriz de ordem n utilizando matrizes de ordem n - 1, de acordo com o que Poole (2004) nos diz:
Definição 1 – Desenvolvimento de Laplace: O determinante de uma matriz quadrada A de ordem n, sendo n ≥ 2, pode ser avaliado utilizando-se a Equação (8), chamada de expansão por cofatores ao longo da i-ésima linha, ou a Equação (9), chamada de expansão por cofatores ao longo da i-ésima coluna.
Visando facilitar a identificação do sinal a ser utilizado no cofator, Poole (2004) nos mostra que uma forma rápida de nos lembrarmos do sinal é nos recordarmos que os sinais formam um padrão semelhante a um tabuleiro de xadrez:

Além disso, destacamos aqui uma nova forma de indicarmos o cálculo do determinante de uma matriz. Tal qual nos mostra Poole (2004), podemos indicar o cálculo do determinante de uma matriz A das seguintes formas:
\[det\left( A \right)=\left| A \right|\]
Assim, se, em uma operação com matrizes apresentarmos os elementos de uma matriz utilizando barras, para delimitarmos tais elementos, estamos indicando o cálculo do determinante. Por exemplo, seja a matriz:

Então:
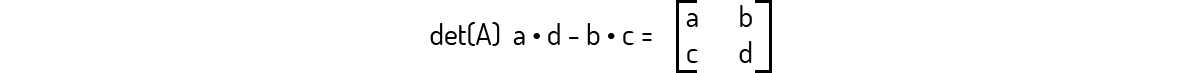
Exemplo 2.1 - Calcule o determinante da matriz abaixo, utilizando o desenvolvimento de Laplace com expansão por cofatores ao longo da terceira linha e depois, a expansão por cofatores, ao longo da segunda coluna.

Solução
Apliquemos as expansões indicadas. Primeiramente, realizaremos a expansão por cofatores ao longo da terceira linha, ou seja, i = 3. Utilizando a Equação (8), teremos:
\[det\left( A \right)=\underset{j=1}{\overset{n}{\mathop \sum }}\,{{a}_{ij}}\cdot {{\Delta }_{ij}}={{a}_{31}}\cdot {{\Delta }_{31}}+{{a}_{32}}\cdot {{\Delta }_{32}}+{{a}_{33}}\cdot {{\Delta }_{33}}\]

\[=3\cdot \left( -8 \right)+\left( 11 \right)+2\cdot \left( 2 \right)=-24+11+4=-9\]
Veja que as submatrizes \({{\Delta }_{3j}}\) são obtidas da matriz original, excluindo-se a linha 3 e a coluna j indicada.
Agora, vamos aplicar a expansão ao longo da coluna j = 2. Da Equação (9):
\[det\left( A \right)=\underset{i=1}{\overset{n}{\mathop \sum }}\,{{a}_{ij}}\cdot {{\Delta }_{ij}}={{a}_{12}}\cdot {{\Delta }_{12}}+{{a}_{22}}\cdot {{\Delta }_{22}}+{{a}_{32}}\cdot {{\Delta }_{32}}\]

\[=2\cdot \left( -10 \right)+0+\left( 11 \right)=-20+11=-9\]
Veja que, como esperado, ambos os resultados dos determinantes são iguais, apesar das diferentes formas empregadas no cálculo. Vale notar, também, que na segunda vez que realizamos este cálculo, foi necessário avaliarmos um determinante a menos, pois \({{a}_{22}}=0\). Assim, fica uma dica para o uso da expansão de Laplace: busque a expansão por cofatores, de modo a minimizar o número de determinantes a ser calculado.
Além do método da expansão de Laplace, temos alguns outros métodos para calcularmos o determinante de uma matriz. Um método que você provavelmente já viu no Ensino Médio, e que já vimos quando iniciamos as nossas discussões, foi o método de Sarrus, apresentado por Kolman (1999), onde repetimos as duas primeiras colunas, de uma matriz de ordem três, para calcular o determinante e multiplicamos cada elemento cortado por uma mesma seta, somando os produtos cujas setas apontam para a direita e subtraindo os que as setas apontam para a esquerda:

\[det\left( A \right)={{a}_{11}}{{a}_{22}}{{a}_{33}}+{{a}_{12}}{{a}_{23}}{{a}_{31}}+{{a}_{13}}{{a}_{21}}{{a}_{32}}-{{a}_{11}}{{a}_{23}}{{a}_{32}}-{{a}_{12}}{{a}_{21}}{{a}_{33}}-{{a}_{13}}{{a}_{22}}{{a}_{31}}\]
Agora iremos avaliar a possibilidade da existência de uma matriz que possamos corresponder ao inverso de um número real, que seja diferente de zero. Matematicamente falando, o inverso multiplicativo de um número x será o número y tal que o produto \(x\cdot y=y\cdot x=1\), sendo simples inferir que, neste caso, \(y=1/x={{x}^{-1}}\).
No caso de matrizes, também é possível que tenhamos matrizes inversas. No entanto, encontrar tais inversas pode não ser algo tão intuitivo quando trabalhamos com números reais.
Para desenvolvermos o pensamento da inversa de uma matriz, iremos lidar apenas com matrizes quadradas de ordem n. Kolman (1999) nos mostra a seguinte definição:
Definição 2 – Inversibilidade: Uma matriz A de ordem n será invertível se existir uma matriz B de ordem n para a qual:
\[A\cdot B=B\cdot A={{I}_{n}}\]
Sendo I_n uma matriz identidade de ordem n. Nesse caso, a matriz B é chamada de inversa de A. Caso não exista uma matriz que satisfaça essa condição, então A é chamada de singular ou não-invertível.
Dada essa definição da possibilidade de invertermos uma matriz, você deve ficar atento ao fato destacado por Kolman (1999): se uma matriz possui uma inversa, essa inversa é única. Hoffman & Kunze (1976) nos mostram uma prova disso: suponha que a matriz A possui uma matriz inversa à esquerda B, ou seja:
\[B\cdot A={{I}_{n}}\]
Se essa mesma matriz A também possui uma matriz inversa à direita C então:
\[A\cdot C={{I}_{n}}\]
Aplicando, então, as propriedades da multiplicação de matrizes e das matrizes identidade:
\[B=B\cdot {{I}_{n}}=B\cdot \left( A\cdot C \right)=\left( B\cdot A \right)\cdot C={{I}_{n}}\cdot C=C\]
A partir de agora, também utilizaremos uma notação específica para nos referirmos às matrizes inversas. Tal qual Kolman (1999) propõe, se uma matriz apresentar inversa, sua inversa será indicada pela mesma letra da matriz original com o sobrescrito -1. Assim, se uma matriz A possui inversa, esta inversa será representada por \({{A}^{-1}}\).
Boldrini (1980) também destaca dois pontos interessantes sobre as matrizes inversíveis. Primeiramente, se duas matrizes A e B, de mesma ordem n forem inversíveis, então o produto A ⋅ B também será inversível, sendo o resultado igual a \({{A}^{-1}}\cdot {{B}^{-1}}\). Isso pode ser mostrado de forma semelhante ao que foi feito para indicar que uma matriz, se inversível, apresenta uma única inversa:
\[\left( A\cdot B \right)\cdot \left( {{A}^{-1}}\cdot {{B}^{-1}} \right)=A\cdot \left( B\cdot {{B}^{-1}} \right)\cdot {{A}^{-1}}=A\cdot {{I}_{n}}\cdot {{A}^{-1}}=A\cdot {{A}^{-1}}={{I}_{n}}\]
ou:
\[\left( B\cdot A \right)\cdot \left( {{B}^{-1}}\cdot {{A}^{-1}} \right)=B\cdot \left( A\cdot {{A}^{-1}} \right)\cdot {{B}^{-1}}=B\cdot {{I}_{n}}\cdot {{B}^{-1}}=B\cdot {{B}^{-1}}={{I}_{n}}\]
Depois disso, Boldrini destaca outro ponto extremamente importante para esse assunto: nem todas as matrizes possuem uma inversa.
Exemplo 2.2 - Seja a matriz A dada abaixo, encontre a sua inversa \({{A}^{-1}}\), se existir.

Solução
Para encontrarmos a inversa de uma matriz, basta aplicarmos a definição dada para uma matriz inversa. Assim, dada uma matriz A, precisamos encontrar uma matriz B tal que:
\[A\cdot B={{I}_{n}}\]
Como A é uma matriz de ordem 2, esperamos que B também seja. Logo, como não sabemos quais os elementos que a matriz B deve apresentar, representaremos tais elementos como as variáveis a, b, c e d, ou seja:
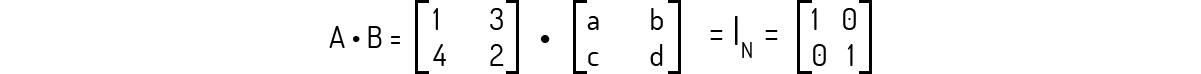
Resolvendo a multiplicação das matrizes, temos que:
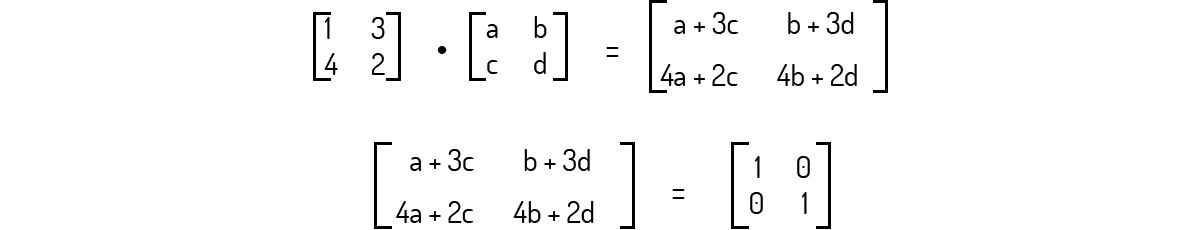
Devemos, agora, igualar os elementos correspondentes das duas matrizes:
\[a+3c=1\]
\[b+3d=0\]
\[4a+2c=0\]
\[4b+2d=1\]
Precisamos resolver simultaneamente essas quatro equações. Da primeira e terceira:
\[4a=-2c\to a=-c/2\]
\[a+3c=1\to \left( -c/2 \right)+3c=5c/2=1\]
\[c=2/5\]
Logo, \(a=-1/5\). Da segunda e quarta:
\[b=-3d\]
\[4b+2d=1\to 4\left( -3d \right)+2d=-10d=1\]
\[d=-1/10\]
Logo, b=3/10. Temos, então, que a matriz inversa de A será:
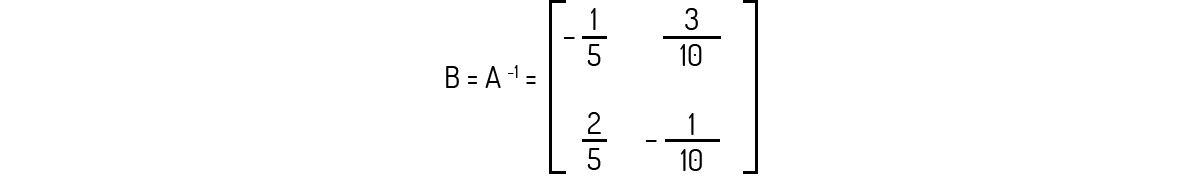
Kolman (1999) ainda destaca três propriedades das inversas de matrizes:
Boldrini (1980) também nos mostra uma relação interessante entre o determinante de uma matriz e a inversibilidade desta. Aplicando o determinante na definição de matriz inversa, temos que:
\[det\left( A\cdot {{A}^{-1}} \right)=det\left( {{I}_{n}} \right)\]
\[det\left( A \right)\cdot det\left( {{A}^{-1}} \right)=1\]
\[det\left( {{A}^{-1}} \right)=\frac{1}{det\left( A \right)}\]
Essa relação é interessante pelo seguinte motivo: se det(A) for igual a zero, então, \(det\left( {{A}^{-1}} \right)\) não existirá; logo, \({{A}^{-1}}\) não existirá. Com isso, temos que uma matriz irá ser invertível se, e somente se, det(A) ≠ 0.
Voltando agora para o cálculo de matrizes inversas, você certamente notou que o cálculo destas pode não ser algo tão simples. Kolman nos mostra uma outra forma de encontrarmos a inversa de uma matriz seguindo três passos:
O passo mais complexo deste método talvez seja as operações elementares nas linhas. Como diz Kolman (1999), estas operações nada mais são do que você realizar o produto de k por todos os elementos de uma linha ou a adição do produto k de uma linha a outra linha, sendo k um real qualquer.
Essa metodologia é útil com matrizes maiores que as de ordem 2, casos onde teríamos em mãos um sistema com, ao menos seis equações para ser resolvido. Para facilitar o entendimento deste método, vejamos um exemplo.
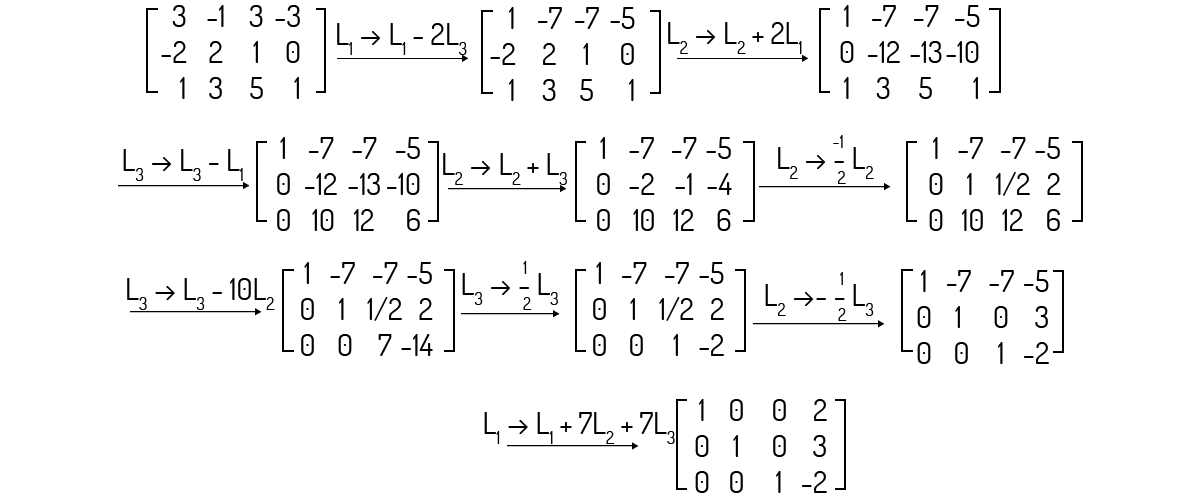
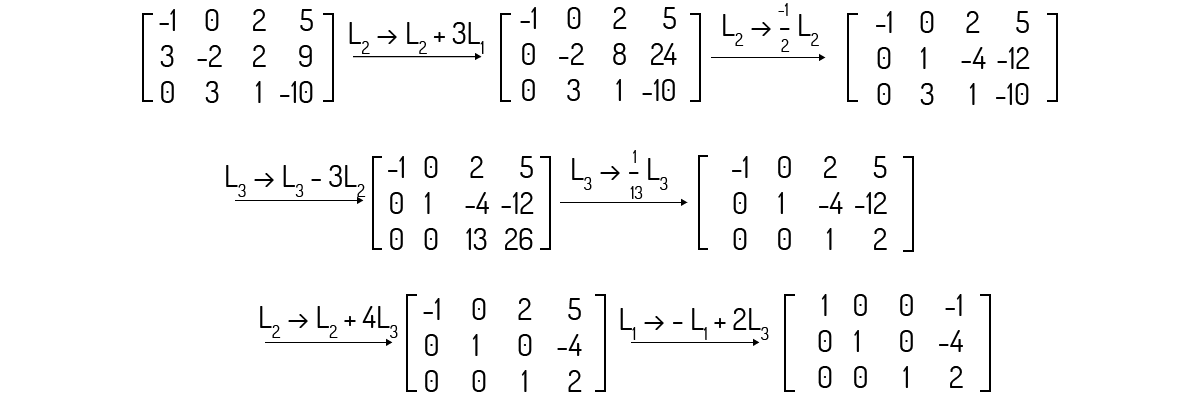
Exemplo 2.3 - Seja a matriz A dada a seguir, encontre a sua inversa \({{A}^{-1}}\), se existir.
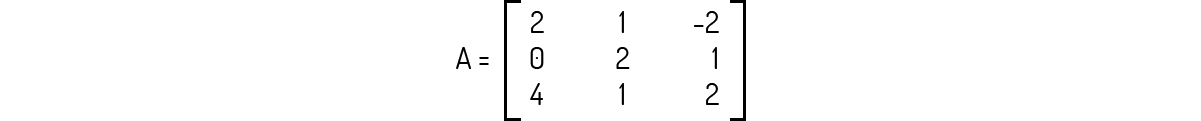
Solução
Pela nova metodologia indicada, primeiramente devemos construir a matriz \(\left[ A|{{I}_{n}} \right]\):

Devemos tornar o lado esquerdo da matriz acima o mais próximo possível de uma matriz identidade. Note que isso nem sempre é feito em um único passo, pois, pode ser que várias operações devam ser feitas aqui, para encontrarmos nosso objetivo. Comecemos então multiplicando a linha 1 da matriz por ½; com isso, nossa matriz ficará:

Multiplicando também a linha 2 da matriz por ½:

Multiplicando agora a linha 1 dessa matriz por -4 e somando à linha 3:

Somando a linha 2 dessa matriz à linha 3:

Multiplicando a linha 3 dessa matriz por 2/13:
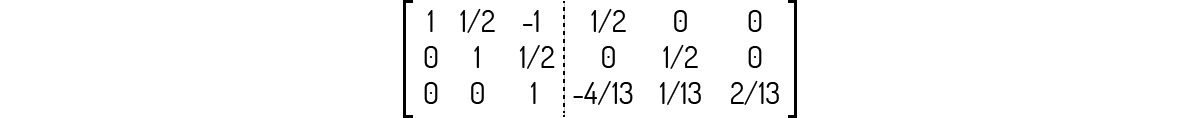
Multiplicando agora a linha 3 dessa matriz por -1/2 e somando à linha 2:
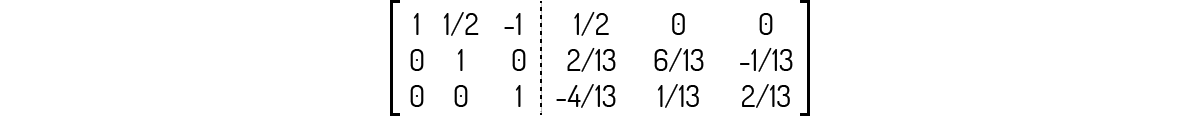
Somando a linha 3 dessa matriz à linha 1:
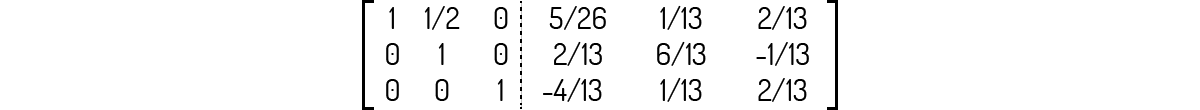
Multiplicando agora a linha 2 dessa matriz por -1/2 e somando à linha 1:
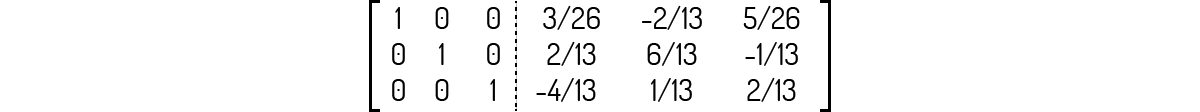
Veja que o lado esquerdo da matriz é igual à identidade de ordem 3, ou seja, \(C={{I}_{3}}\). Logo, podemos dizer que a inversa de A será igual à:
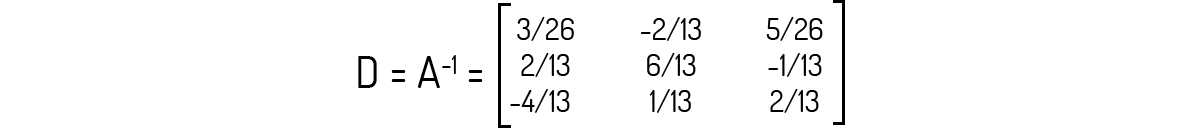
Agora que sabemos sobre determinantes e matrizes inversas, temos um exemplo interessante para a aplicação destes assuntos: a criptografia, como exemplifica Leon (1999). Mensagens criptografadas são aquelas que fazem uso de um código para inviabilizar a compreensão de sua leitura por parte de pessoas indesejadas, sendo usadas desde tempos remotos.
Em períodos de guerra, por exemplo, criptografar mensagens é algo vital para ambos os lados envolvidos, pois a transmissão de planos de combate não pode parar e seus oponentes não devem compreender quais serão seus próximos passos.
Atualmente, com uma alta transmissão de dados por programas de mensagens e redes sociais, uma forma que existe de proteger os usuários de terem seus dados revelados é, também, pelo uso de criptografias.
Dando sequência à esse tipo de aplicação, vejamos como Leon (1999) desenvolve o assunto. Seja A uma matriz cujos elementos são inteiros e det(A)=±1. Se estas condições forem obedecidas, você terá que \({{A}^{-1}}\) será uma matriz composta também por elementos inteiros. Uma matriz A que obedeça a estes quesitos pode ser utilizada como elemento de criptografia.
Por exemplo, suponha que você deseje mandar a mensagem MANDE FOTO criptografada para alguém. Você primeiramente deverá atribuir à cada letra da mensagem um número aleatório, por exemplo:
M=7, A=4, N=12, D=8, E=3, F=2, O=1, T=5
Ou seja, nossa mensagem codificada seria 7, 4, 12, 8, 3, 2, 1, 5, 1. Agora, organizando este código numérico e escrevendo a mensagem como uma matriz B de ordem 3, encontramos:

Uma matriz A que cumpra os requisitos ditos acima é:

De modo que:

Se realizarmos o produto A ⋅ B, encontramos uma nova matriz, que fornecerá a mensagem que temos que enviar:

Assim, a mensagem que você deverá enviar será 24, 15, 17, 57, 38, 37, 40, 27, 32. Para que a pessoa desejada possa decodificar essa mensagem, ela deve multiplicar o produto A ⋅ B pela inversa de A. Veja:

Perceba que as operações de cálculo do determinante e da inversa de A foram omitidos aqui, assim como o passo a passo da multiplicação das matrizes. Agora, faça você a conferência desses passos!
Diferentemente do que temos com os números reais, as matrizes nem sempre irão apresentar um inverso matemático. Visando praticar o assunto da inversa de matrizes, analise as matrizes abaixo e as alternativas a seguir, assinalando a alternativa correta.

A inversa da matriz A abaixo é:
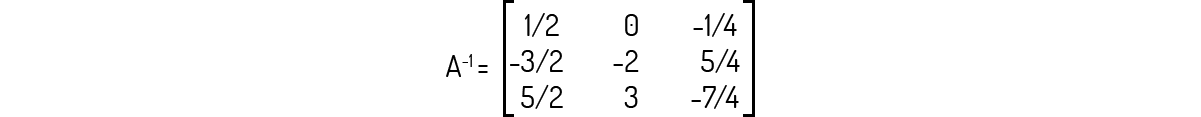
A primeira coisa antes de buscar a inversa de uma matriz é checar se esta apresenta uma inversa. Logo, avalie primeiramente o determinante da matriz. Neste caso, temos que det(A)=0 pois a linha 3 nada mais é do que duas vezes a linha 1.
A inversa da matriz C é:

Verificando primeiro que o determinante de C é diferente de zero:
\(det\left( C \right)={{c}_{11}}{{c}_{22}}{{c}_{33}}+{{c}_{12}}{{c}_{23}}{{c}_{31}}+{{c}_{13}}{{c}_{21}}{{c}_{32}}-{{c}_{11}}{{c}_{23}}{{c}_{32}}-{{c}_{12}}{{c}_{21}}{{c}_{33}}-{{c}_{13}}{{c}_{22}}{{c}_{31}}\)
\(=0+18+0-0-2-0=18-2=16\)
Agora, podemos calcular a inversa desejada. As operações realizadas para obter a forma escada podem ser:
i) Adicionar a linha 2 à linha 1; ii) Subtrair a linha 1 da linha 2;
iii) Somar a linha 2 à linha 1; iv) Somar a linha 2 à linha 3;
v) Multiplicar a linha 2 por -1/2; vi) Multiplicar a linha 1 por -3 e adicionar à linha 3;
vii) Multiplicar a linha 3 por -1/8; viii) Multiplicar a linha 3 por -3 e adicionar à linha 1.
Com isso, você deve encontrar a seguinte matriz:
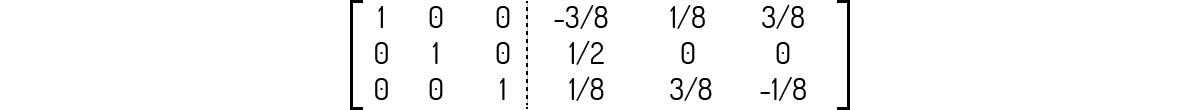
Todas as três matrizes acima apresentam inversa.
Para checar se uma matriz apresenta inversa devemos avaliar primeiramente o determinante desta matriz. Neste caso, temos que det(A)=0 pois a linha 3 nada mais é do que duas vezes a linha 1; det(B)=5; e det(C)=16. Logo, A não apresenta inversa.
\(det\left( B \right)={{b}_{11}}{{b}_{22}}{{b}_{33}}+{{b}_{12}}{{b}_{23}}{{b}_{31}}+{{b}_{13}}{{b}_{21}}{{b}_{32}}-{{b}_{11}}{{b}_{23}}{{b}_{32}}-{{b}_{12}}{{b}_{21}}{{b}_{33}}-{{b}_{13}}{{b}_{22}}{{b}_{31}}\)
\(=1+6+0-0-\left( -4 \right)-6=7-2=5\)
\(det\left( C \right)={{c}_{11}}{{c}_{22}}{{c}_{33}}+{{c}_{12}}{{c}_{23}}{{c}_{31}}+{{c}_{13}}{{c}_{21}}{{c}_{32}}-{{c}_{11}}{{c}_{23}}{{c}_{32}}-{{c}_{12}}{{c}_{21}}{{c}_{33}}-{{c}_{13}}{{c}_{22}}{{c}_{31}}\)
\(=0+18+0-0-2-0=18-2=16\)
Apenas a matriz C acima não apresenta inversa.
A primeira coisa antes de buscar a inversa de uma matriz é checar se esta apresenta uma inversa. Logo, avalie primeiramente o determinante da matriz. Das matrizes acima, temos que det(A)=0 pois a linha 3 nada mais é do que duas vezes a linha 1; det(B)=5; e det(C)=16. Logo, apenas A não apresenta inversa das matrizes acima.
\(det\left( B \right)={{b}_{11}}{{b}_{22}}{{b}_{33}}+{{b}_{12}}{{b}_{23}}{{b}_{31}}+{{b}_{13}}{{b}_{21}}{{b}_{32}}-{{b}_{11}}{{b}_{23}}{{b}_{32}}-{{b}_{12}}{{b}_{21}}{{b}_{33}}-{{b}_{13}}{{b}_{22}}{{b}_{31}}\)
\(=1+ 6 + 0 - 0 - (-4) - 6 = 7 - 2 = 5\)
\(det\left( C \right)={{c}_{11}}{{c}_{22}}{{c}_{33}}+{{c}_{12}}{{c}_{23}}{{c}_{31}}+{{c}_{13}}{{c}_{21}}{{c}_{32}}-{{c}_{11}}{{c}_{23}}{{c}_{32}}-{{c}_{12}}{{c}_{21}}{{c}_{33}}-{{c}_{13}}{{c}_{22}}{{c}_{31}}\)
\(=0+18+0-0-2-0=18-2=16\)
Para encontrar a inversa de uma matriz, basta inverter cada um de seus elementos. Logo, matrizes que apresentem 0 como um elemento, como é o caso de B e C, não apresentam inversa.
Não podemos confundir a definição de inverso matemático de um número real com o inverso de uma matriz. Logo, tal afirmação é incorreta.
Um problema muito comum que encontramos ao aplicar a matemática em diversas áreas é aquele onde temos a necessidade de resolver mais de uma equação simultaneamente, sendo que, se tais equações forem lineares, teremos um sistema de equações lineares (LEON, 1999). Com um pouco de prática, você certamente verá que podemos reduzir diversos problemas complexos para um conjunto de equações lineares, o que pode facilitar muito o seu trabalho.
Portanto, antes de darmos continuidade ao assunto, retomemos um pouco sobre o assunto de equações lineares. Se você se lembrar do assunto funções, certamente recordará do caso de uma equação linear, ou seja, uma equação do tipo:
\[y=a+bx~~~~~~~~~~(10)\]
Você ainda deve recordar que essa equação é comumente chamada de equação da reta, pois o gráfico de equações desse tipo são retas. Destacamos que, em (10), x e y são chamados de variáveis, enquanto a e b são constantes. Poole (2004) expande essa equação para a seguinte forma:
\[{{a}_{1}}y+{{a}_{2}}x=b~~~~~~~~~~(11)\]
Sendo que \({{a}_{1}}\), \({{a}_{2}}\) e b são constantes.
Poole (2004) mostra que podemos expandir ainda mais a Equação (11), para um caso onde temos n constantes e n variáveis:
\[{{a}_{1}}{{x}_{1}}+{{a}_{2}}{{x}_{2}}+...+{{a}_{n}}{{x}_{n}}=b~~~~~~~~~~(12)\]
Assim, usamos a Equação (12) para definirmos uma equação linear de n variáveis, onde as constantes \({{a}_{1}}\), \({{a}_{2}}\), …, \({{a}_{n}}\) são chamadas de coeficientes.
Poole (2004) também nos diz que, ao resolvermos uma equação linear encontraremos um vetor \(\left[ {{s}_{1}}~{{s}_{2}}~...~{{s}_{n}} \right]\) como solução. Ou seja, o vetor solução apresenta valores \({{s}_{i}}\) que iremos substituir no \({{x}_{i}}\) correspondente da equação linear, tal qual a equação seja verdadeira. Por exemplo, o vetor \(\left[ 3~-5~-2 \right]\), que nos diz que \({{x}_{1}}=3\), \({{x}_{2}}=-5\) e \({{x}_{3}}=-2\), é um vetor solução da seguinte equação linear:
\[4{{x}_{1}}+2{{x}_{2}}-3{{x}_{3}}=8\]
Uma vez que:
\[4\cdot 3+2\cdot \left( -5 \right)-3\cdot \left( -2 \right)=8\]
Mas, note que o vetor indicado não é a única solução para a equação linear dada. Existem outras combinações que também satisfazem a equação dada, como [0 4 0] e [2 -3 -2].
Agora, quando temos um conjunto de m equações lineares, estaremos lidando com um sistema linear de m equações com n incógnitas:
\[{{a}_{11}}{{x}_{1}}+{{a}_{12}}{{x}_{2}}+...+{{a}_{1n}}{{x}_{n}}={{b}_{1}}\]
\[{{a}_{21}}{{x}_{1}}+{{a}_{22}}{{x}_{2}}+...+{{a}_{2n}}{{x}_{n}}={{b}_{2}}\]
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\)
\[{{a}_{m1}}{{x}_{1}}+{{a}_{m2}}{{x}_{2}}+...+{{a}_{mn}}{{x}_{n}}={{b}_{m}}~~~~~~~~~~(12)\]
Para um sistema linear, Poole (2004) diz que o vetor solução é aquele que seja solução de todas as m equações simultaneamente.
Kolman (1999) chama a atenção para o uso da forma semelhante à que usamos com matrizes para identificarmos os elementos. Note que cada coeficiente de (12) pode ser representado por \({{a}_{ij}}\), onde i indica qual equação estamos considerando e j nos indica a qual variável o elemento está associado.
Ainda com semelhanças ao caso de matrizes, Leon (1999) sugere que façamos referência a um sistema linear de forma semelhante ao que fazemos com matrizes, ou seja, os sistemas lineares são de ordem m × n. Com isso, sabemos que o vetor solução deverá apresentar sempre n elementos.
Quanto ao vetor solução de um sistema linear, Leon (1999) destaca que nem todos os sistemas lineares irão apresentar uma solução. Um sistema linear que não tenha solução é chamado de incompatível ou impossível. Logo, a solução de um sistema impossível é um conjunto vazio. Poole (2004) amplia a classificação de sistemas lineares, mostrando três tipos de sistemas lineares:
Poole (2004) ainda define um sistema linear equivalente: sistemas lineares que apresentem o mesmo vetor solução, são ditos equivalentes. Com isso, temos definido o que são sistemas lineares e quais os tipos de sistemas lineares que temos.
O manuseio de sistemas lineares pode ser feito de uma maneira mais prática se escrevermos o sistema numa forma matricial. Como Boldrini (1980) nos mostra, podemos reescrever (12) como uma multiplicação de matrizes:

Ou seja, o que temos acima nada mais é do que A ⋅ X = B, sendo a matriz A a matriz dos coeficientes, X a matriz das incógnitas ou variáveis e B a matriz dos termos independentes. Por exemplo, para o sistema:
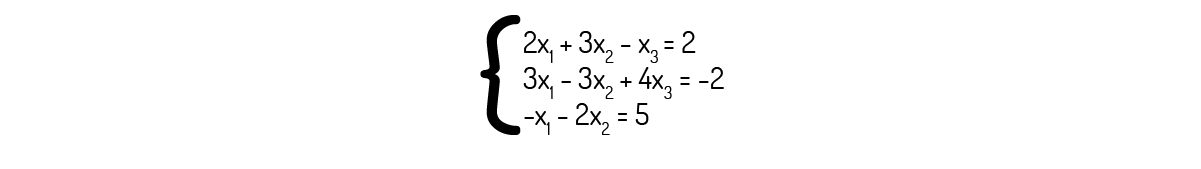
Temos que:
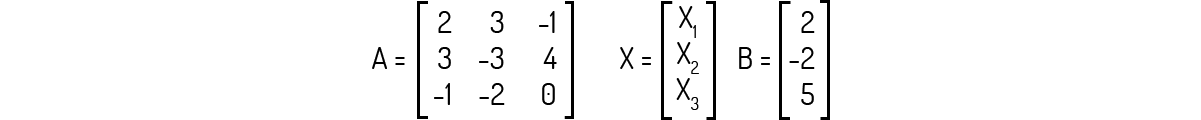
Kolman (1999) dá uma nomenclatura especial para os sistemas cuja matriz dos termos independentes contém apenas elementos nulos, ou seja, temos que A ⋅ X = 0. Esse tipo de matriz é conhecido como sistema linear homogêneo. Num sistema linear homogêneo, podemos ter como resposta um vetor nulo, caso que é conhecido como solução trivial. Caso a solução deste tipo de sistema linear homogêneo for um vetor não nulo, temos uma solução não trivial. Kolman (1999) destaca que um sistema linear homogêneo cujo número de incógnitas é maior que o número de equações sempre apresentará uma solução não trivial.
Outra matriz que é útil nos trabalhos com sistemas lineares é a matriz composta pela matriz dos coeficientes e pela matriz dos termos independentes, da seguinte forma:
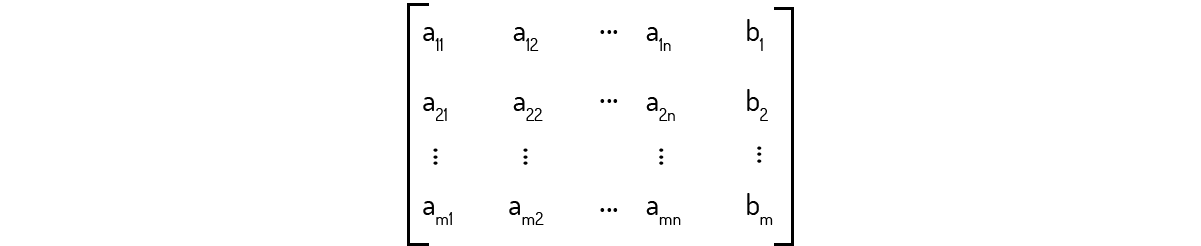
Essa matriz, segundo Boldrini (1980), é conhecida como matriz ampliada do sistema, onde cada linha da matriz representa, de forma abreviada, uma equação do sistema. Por exemplo, para o sistema:
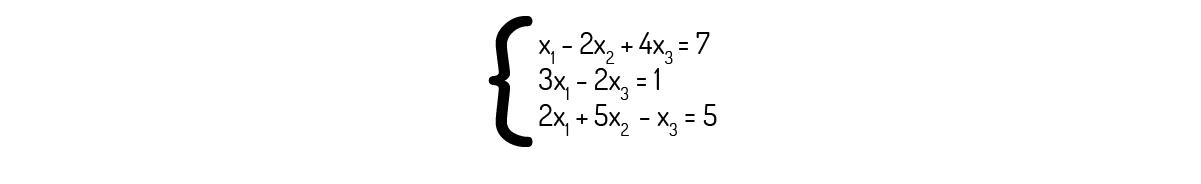
Temos que a matriz ampliada do sistema será:
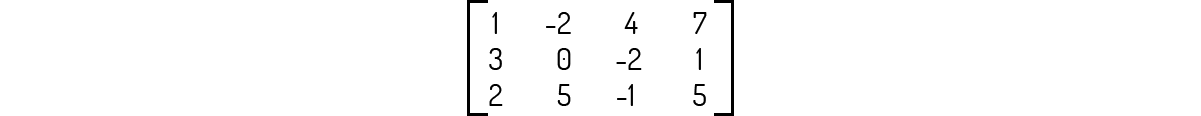
Note que pode ser muito mais comum você encontrar as incógnitas de um sistema linear representadas por letras diferentes e não por \({{x}_{n}}\). Assim, você certamente irá se deparar com o uso de x, y, z e assim por diante, no trabalho com sistemas lineares.
Veremos agora um dos métodos mais simples que temos para resolver um sistema linear, o método da eliminação. Você certamente já utilizou este método para resolver algum sistema linear, mesmo durante o ensino médio. Kolman (1999) nos diz que esse método consiste de eliminarmos incógnitas através da manipulação das equações que temos disponíveis, de forma semelhante ao processo que utilizamos para encontrar a inversa de uma matriz pelo método de operações elementares por linhas.
Essa manipulação das equações pode ser feita pelo que Boldrini (1980) chama de operações elementares. São três as operações elementares que podemos realizar com as linhas de uma matriz ou sistema linear:
I. Permuta entre uma i-ésima e uma j-ésima linha, ou seja, trocarmos de lugar duas linhas, representado por \({{L}_{i}}\leftrightarrow {{L}_{j}}\). Exemplo: \({{L}_{1}}\leftrightarrow {{L}_{3}}\):

II. Multiplicação da i-ésima linha por um escalar k que seja não nulo, representado por \({{L}_{i}}\leftrightarrow k{{L}_{j}}\). Exemplo: \({{L}_{2}}\leftrightarrow 3{{L}_{2}}\):

III. Substituição da i-ésima linha pela i-ésima linha mais k vezes uma j-ésima linha, representado por \({{L}_{i}}\leftrightarrow {{L}_{i}}+k{{L}_{j}}\). Exemplo: \({{L}_{1}}\leftrightarrow {{L}_{1}}+2{{L}_{3}}\):

Quando conseguimos encontrar uma matriz B partindo de uma matriz A utilizando uma quantidade finita de operações elementares, Boldrini (1980) diz que podemos chamar B de linha equivalente de A.
Vejamos agora alguns exemplos de resolução de sistemas, utilizando o método da eliminação.
Exemplo 2.4 - Encontre uma solução para o seguinte sistema linear, utilizando o método da eliminação.
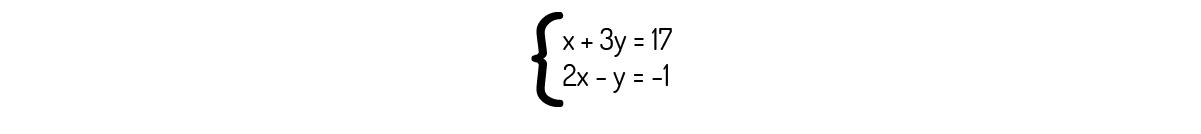
Solução
Nosso objetivo com este método é ir eliminando incógnitas para encontrarmos o vetor solução. Assim, se fizermos \({{L}_{2}}\leftrightarrow {{L}_{2}}-2{{L}_{1}}\) no sistema:
\[2x-y-2\left( x+3y \right)=-1-2\cdot \left( 17 \right)\to 2x-y-2x-6y=-35\to -7y=-35\]
\[y=5\]
Agora que sabemos o valor de y, podemos encontrar x utilizando qualquer uma das duas equações do sistema fornecido. Utilizando a primeira:
\[x+3y=17\to x+3\cdot 5=17\to x+15=17\]
\[x=2\]
Faça a prova real destes valores que encontramos com as duas equações do sistema linear fornecido. Logo, o vetor [2 5] é o vetor solução para este sistema.
Também podemos encontrar, graficamente, a solução para sistemas lineares com duas equações e duas incógnitas, como nos mostra Boldrini (1980). Para isso, devemos converter as equações dadas na forma de uma equação da reta, como mostrado na Equação (10). Por exemplo, reorganizando as equações dadas no Exemplo 2.4, encontramos:
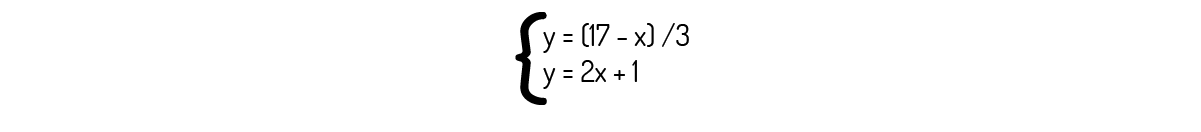
Agora, chamando a primeira equação de (1) e a segunda de (2) e fazendo os gráficos das retas:
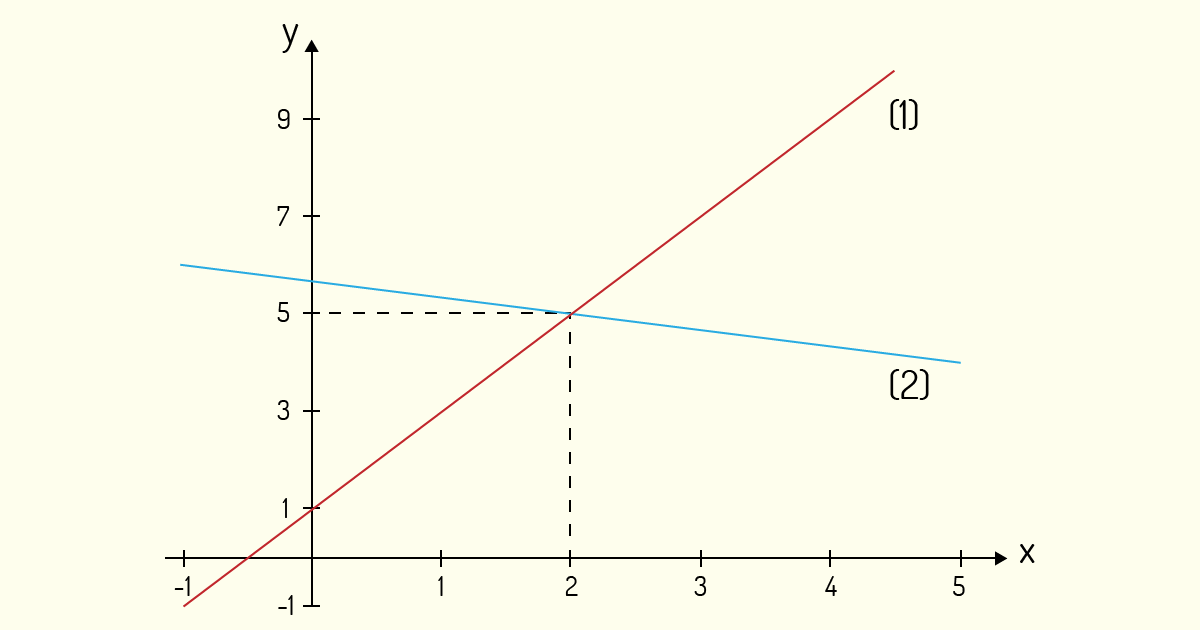
Note que elas se cruzam em um único ponto, (2,5). Observe que esse ponto contém o mesmo resultado que encontramos anteriormente, pelo método da eliminação.
Exemplo 2.5 - Encontre uma solução para o seguinte sistema linear:
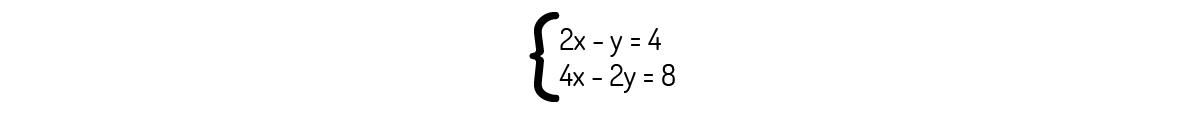
Solução
Antes de prosseguirmos com a eliminação de alguma das variáveis, analise as equações que compõem o sistema linear dado. Se você multiplicar a primeira equação por 2, você encontrará:
\[4x-2y=8\]
Que é igual à segunda equação do sistema linear. Quando ocorre essa situação de termos uma equação sendo múltiplo de outra, num sistema linear com duas equações, o sistema que temos em mãos é possível e indeterminado, pois admite infinitas soluções.
Esse caso é mais facilmente visualizado graficamente. Se você converter as equações dadas para a forma de equação da reta, encontrará duas equações iguais:
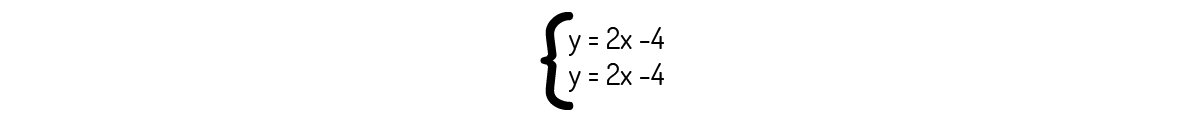
Ou seja, graficamente, o sistema é representado por uma única reta:

Sendo assim, qualquer ponto dessa reta é uma solução para o sistema linear dado.
Exemplo 2.6 - Encontre uma solução para o seguinte sistema linear:
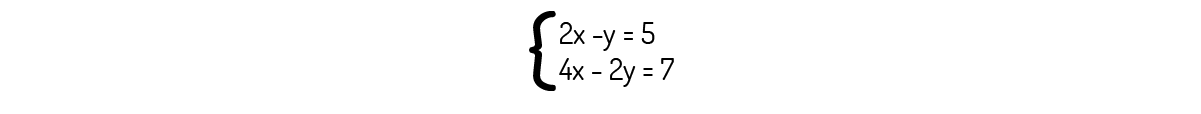
Solução
Tentaremos eliminar incógnitas para encontrar o vetor solução. Assim, se fizermos \({{L}_{2}}\leftrightarrow {{L}_{2}}-2{{L}_{1}}\) nesse sistema:
\[4x-2y-2\left( 2x-y \right)=7-2\cdot \left( 5 \right)\to 4x-2y-2x-2y=-3\]
\[0=-3\]
Note que é impossível este resultado encontrado. Se você tentar outra eliminação chegará em resultados semelhantes. Isso é um indicativo de que o sistema é impossível, ou seja, não apresenta solução.
Vejamos graficamente como esse sistema se comporta. Convertendo as equações dadas para a forma de equação da reta, encontrará:
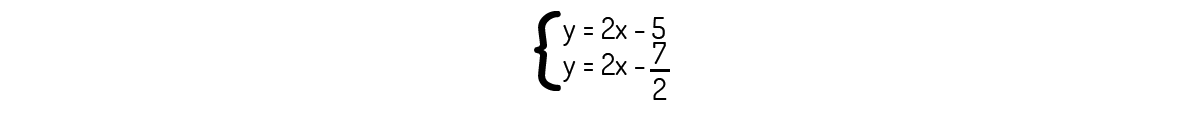
Graficamente, esse sistema é representado por duas retas paralelas, sendo a primeira equação (1) e a segunda (2):
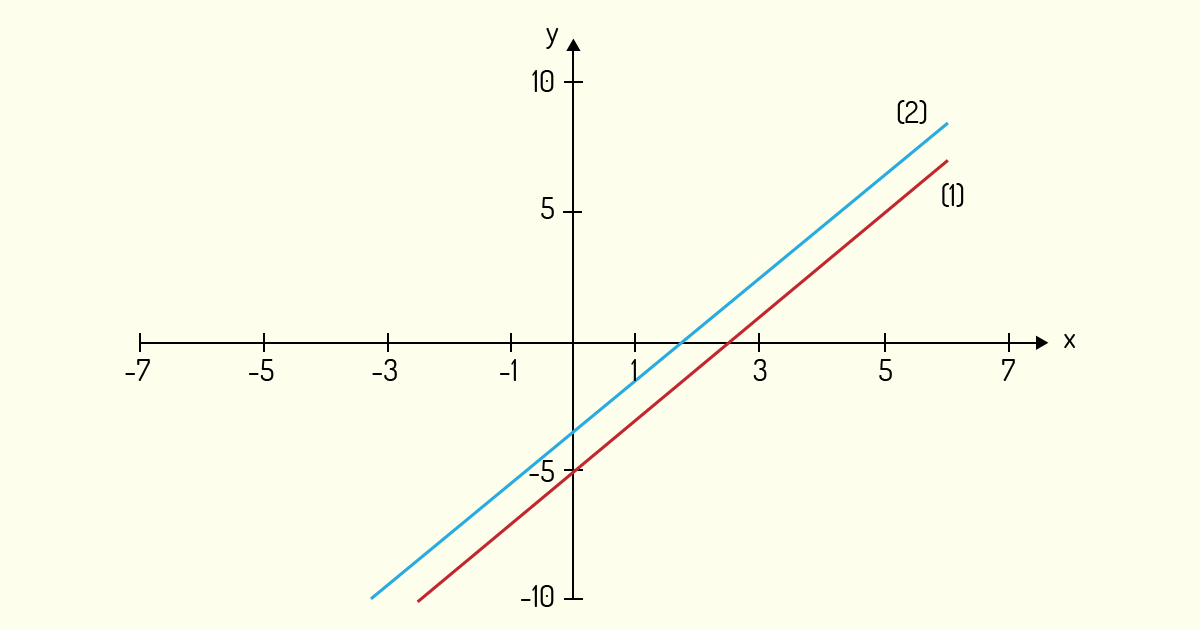
Sendo assim, não há nenhuma interseção das retas. Logo, não existe nenhuma solução para o sistema dado, ou seja, o sistema realmente é impossível.
Buscando fundamentar a identificação e possibilidade de resolução de sistemas lineares, um dos mais importantes tópicos da álgebra, analise as alternativas abaixo e assinale a que for correta.
O sistema abaixo é um sistema linear.
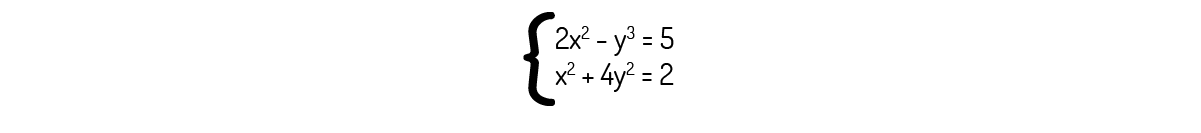
O sistema indicado é um sistema não linear. Note a presença das potências nas incógnitas, algo que não temos em sistemas lineares. Logo, o sistema informado é não linear.
O sistema abaixo é um sistema possível e determinado, sendo o vetor [1 0,5] sua solução.
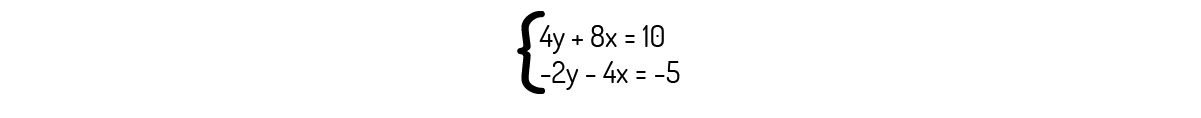
Analisando o sistema informado, temos que a segunda equação é igual à primeira multiplicada por -½. Logo, o sistema linear dado é possível, mas indeterminado e o vetor informado é uma das infinitas soluções deste sistema.
Graficamente, o sistema abaixo apresenta-se como duas retas paralelas, o que garante que esse sistema tenha infinitas soluções.
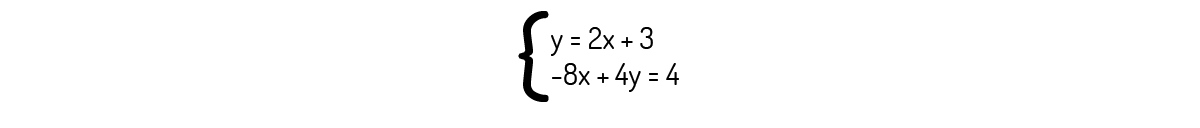
Se você reorganizar a segunda equação, encontrará y=2x+1. Logo, sabemos que, graficamente, este sistema se apresentará como duas retas paralelas. No entanto, isso acarreta que o sistema não possua nenhuma solução.
O sistema abaixo é um sistema possível e determinado, sendo o x=3 e y=1 sua solução.
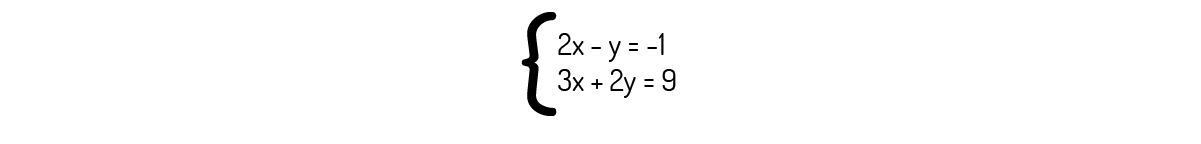
Utilizando o método da eliminação, fazendo L_2→L_2+2L_1:
\(3x+2y+2\left( 2x-y \right)=9+2\cdot \left( -1 \right)\to 3x+2y+4x-2y=7\to 7x=7\)
\(x=1\)
Logo, substituindo esse valor de x na primeira equação, encontramos que:
\(y=2\cdot 1+1=3\)
O sistema abaixo é um sistema possível e indeterminado, apresentando infinitas soluções.
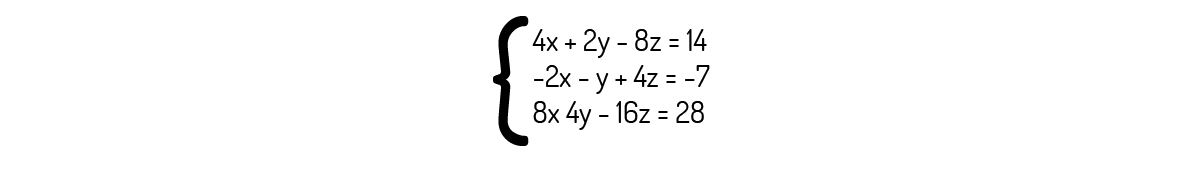
Veja que todas as equações podem ser escritas como um múltiplo da primeira equação do sistema. Logo, o sistema é realmente possível e indeterminado.
Um grande problema que vários alunos, sejam do ensino fundamental ou superior, enfrentam, ao estudar diversos assuntos da matemática é visualizar a aplicabilidade dos assuntos complexos estudados. No caso dos sistemas lineares, eles são facilmente empregados em inúmeras áreas de conhecimento e, quando você adquirir prática no manuseio e emprego destes sistemas, certamente conseguirá lidar melhor com inúmeros problemas.
Link: www.ppgedmat.ufop.br. Acesso em: 20 nov. 2018.

Tendo definido os sistemas lineares, agora iremos nos aprofundar mais no uso de matrizes para resolução e análise de tais sistemas.
Uma das formas mais práticas que temos para resolver sistemas lineares é obter a forma escada, reduzida por linhas, ou forma triangular da matriz ampliada do sistema, ou mesmo forma escalonada. Leon (1999) e Kolman (1999) definem essa forma matricial da seguinte maneira:
Definição 3 – Forma escada: Uma matriz A de ordem n encontra-se na forma escada se:
Assim, uma matriz que cumpra as quatro condições acima irá encontrar-se na forma escada reduzida, de forma que os primeiros elementos não nulos dessas matrizes formam uma “escada”. A seguir, apresentaremos alguns exemplos, analisando se as matrizes se encontram ou não na forma escada.
Exemplo 2.7 - Verifique se as matrizes a seguir encontram-se na forma escada.
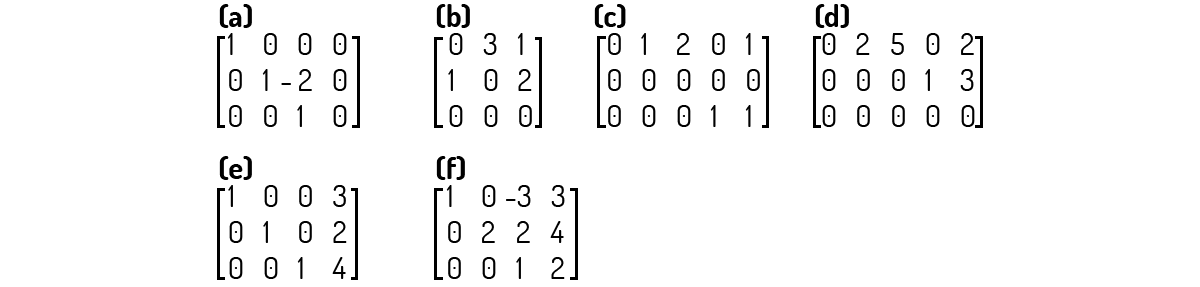
Solução
A matriz a) não encontra-se na forma escada porque a condição III não foi cumprida - vide a coluna 3.
A matriz b) não encontra-se na forma escada porque as condições I e IV não foram cumpridas - vide as linhas 1 e 2.
A matriz c) não encontra-se na forma escada porque a condição II não foi cumprida - vide a linha 2.
A matriz d) não encontra-se na forma escada porque a condição I não foi cumprida - vide a linha 1.
A matriz e) encontra-se na forma escada.
A matriz f) não encontra-se na forma escada porque a condição I e a condição III não foram cumpridas - vide a linha 2 e coluna 3.
Transformar matrizes e sistemas na forma escada é muito útil na resolução de sistemas. Note que um sistema representado pela matriz e) do Exemplo 2.7 nos fornece uma solução direta para um sistema. Como este método geralmente utiliza contas mais simples, praticá-lo é uma excelente forma de dominar a resolução de sistemas.
Boldrini (1980) nos diz que toda matriz \({{A}_{m\times n}}\) é linha equivalente de uma única matriz \({{B}_{m\times n}}\) na forma escada. Para encontrarmos essa matriz \({{B}_{m\times n}}\), basta que utilizemos operações elementares na matriz até que esta cumpra as condições necessárias.
Outro método parecido com o que vimos até aqui para a resolução de matrizes é o método de Gauss. O método de Gauss difere do escalonamento apenas no ponto III da definição da forma escada, sendo, para este método:
III’) Cada coluna contendo o primeiro elemento não nulo de uma linha terá todos os demais elementos abaixo desta linha nulos.
Logo, pelo método de Gauss não temos a solução direta do sistema; conseguimos isso realizando substituições.
Ainda dessa relação de \({{A}_{m\times n}}\) com sua linha equivalente escada \({{B}_{m\times n}}\), podemos encontrar o posto e a nulidade da matriz A. Boldrini (1980) define o posto p de A como sendo o número de linhas não nulas em B e a nulidade de A como sendo n - p.
Exemplo 2.8 - Encontre o posto e a nulidade da matriz A abaixo.

Solução
Para encontrar o posto de uma matriz precisamos analisar sua linha equivalente escada. Analisando rapidamente esta matriz, vemos que ela não se encontra na forma escada. Vamos, então, realizar uma série de operações para encontrar a matriz linha equivalente de A na forma escada:
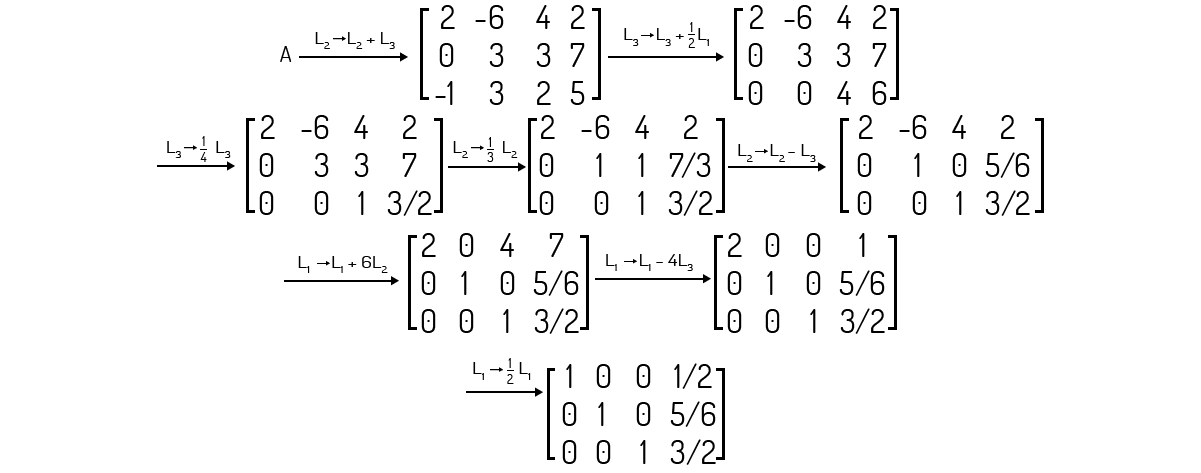
Agora que encontramos a matriz linha equivalente de A. Note que ela não apresenta nenhuma linha nula; logo, seu posto deve ser igual a 3. Agora, para a nulidade desta matriz, devemos substituir o seu número de colunas do posto, ou seja, a nulidade desta matriz será 4 - 3 = 1.
O posto de uma matriz também pode ser ligado à um termo muito familiar no estudo de sistemas lineares. Ou seja, o posto de uma matriz nos indica o número de equações “independentes” e “dependentes” do sistema. Cada linha nula num sistema é uma linha dependente, ou seja, é uma equação que pode ser obtida de outra. É comum, como destaca Boldrini (1980), chamarmos as linhas dependentes de combinação linear das demais linhas.
O posto de uma matriz também pode ser usado para determinar o tipo de sistema com o qual lidamos. Para essa análise, usamos o posto da matriz dos coeficientes de um sistema linear e o posto da matriz ampliada do sistema linear; o posto da matriz dos coeficientes será representado por p_c e o posto da matriz ampliada será representado por \({{p}_{a}}\), como sugere Boldrini (1980). Caso \({{p}_{a}}={{p}_{c}}\), iremos nos referir simplesmente ao posto da matriz, representado por p. Assim:
Exemplo 2.9 - Analise e resolva o sistema a seguir, se possível.
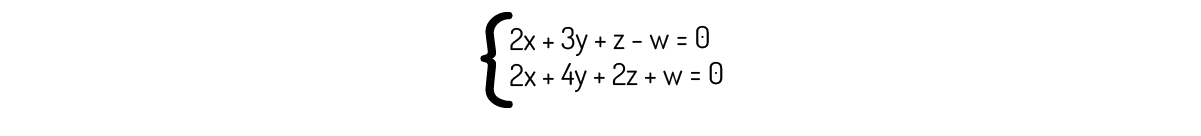
Solução
Antes de mais nada, vemos que o sistema dado apresenta o matriz dos termos independentes nula, logo, este sistema é homogêneo. Para tal, sabemos que o vetor nulo [0 0 0 0] é uma solução trivial.
Partindo para uma análise mais a fundo, o sistema pode ser representado pela seguinte matriz ampliada:
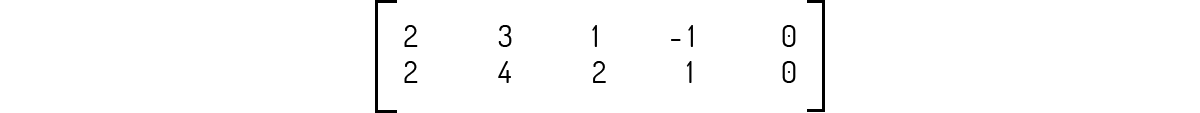
Encontrando a matriz na forma escada:
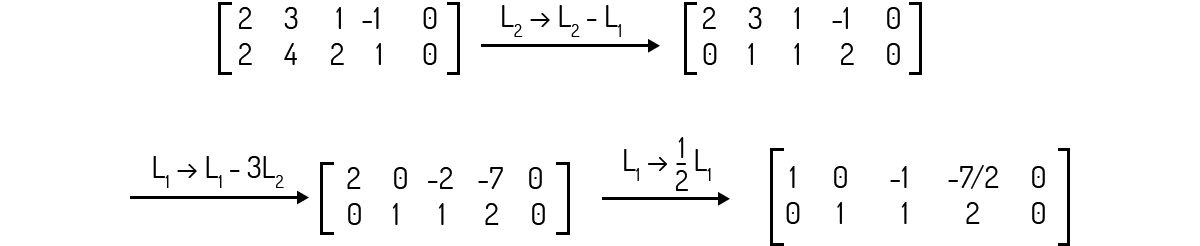
Da qual temos que a matriz linha equivalente dos coeficientes será:
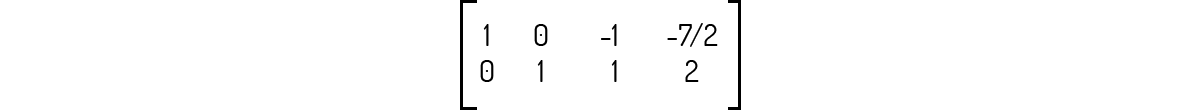
Vejamos agora as informações deste sistema, que apresenta m = 2 equações e n = 4 variáveis. Da matriz escada ampliada, vemos que \({{p}_{a}}=2\) e da matriz escada dos coeficientes, vemos que \({{p}_{c}}=2\) também, ou seja, p = 2. Logo, essa matriz apresenta solução, como dita a condição A acima.
Como temos que p < n, o sistema apresenta grau de liberdade n - p = 4 - 2 = 2. Isso quer dizer, na prática, que o sistema só conseguirá ter uma solução em função de duas de suas incógnitas, o que faz com que ele admita infinitas soluções. Então, devemos escolher duas incógnitas para definirmos as demais em função destas.
Se chamarmos z de \({{\lambda }_{1}}\) e \(w\) de \({{\lambda }_{2}}\), conseguiremos encontrar solução para este sistema. Da matriz na forma escada ampliada, encontraremos a seguinte solução para o sistema:
\[x={{\lambda }_{1}}+\frac{7}{2}{{\lambda }_{2}}\]
\[y=-{{\lambda }_{1}}-2{{\lambda }_{2}}\]
\[z={{\lambda }_{1}}\]
\[w={{\lambda }_{2}}\]
Logo, para encontrar uma solução para este sistema, basta escolher valores aleatórios para as incógnitas z e w que, com as relações acima, você encontrará automaticamente os valores de x e y.
Veja que a escolha dessas variáveis é completamente aleatória. Você poderia, por exemplo, escolher chamar x de \({{\lambda }_{1}}\) e y de \({{\lambda }_{2}}\) ou qualquer outra combinação de duas variáveis para resolver esse sistema. A escolha que fizemos acima se mostra mais simples pelas equações que dispunhamos neste sistema. Por exemplo, fazendo \(y={{\lambda }_{1}}\) e \(w={{\lambda }_{2}}\), encontraremos a seguinte solução para o sistema:
\[x=-{{\lambda }_{1}}-2{{\lambda }_{2}}+\frac{7}{2}{{\lambda }_{2}}=-{{\lambda }_{1}}+\frac{3}{2}{{\lambda }_{2}}\]
\[y={{\lambda }_{1}}\]
\[z=-{{\lambda }_{1}}-2{{\lambda }_{2}}\]
\[w={{\lambda }_{2}}\]
A resolução e análise de sistemas lineares apresenta diversos métodos, sendo o escalonamento, o método de Gauss e análise do posto muito importantes para este fim. Sobre esses métodos, analise os sistemas abaixo e depois as alternativas a seguir. Então assinale a alternativa que se encontra correta.
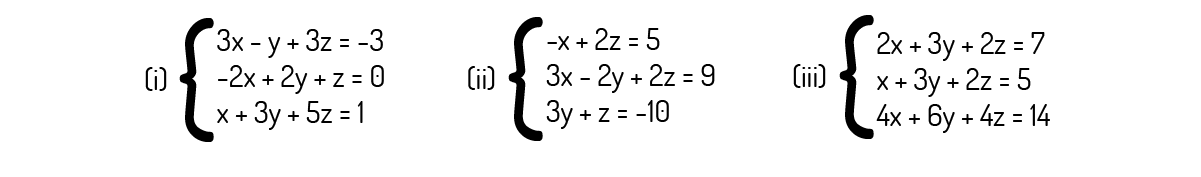
O sistema (iii) é possível e determinado, pois apresenta p=n=3.
Analisemos o posto da matriz ampliada deste sistema:
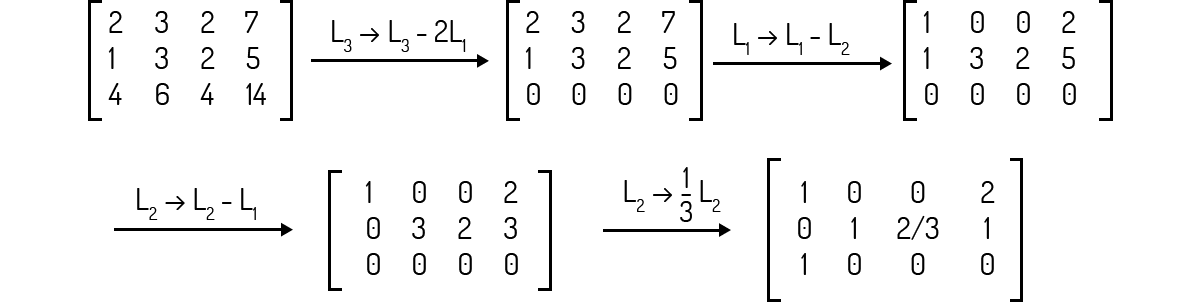
Note que existe uma linha nula na matriz escada. Logo, como o posto da matriz aumentada e da matriz dos coeficientes será o mesmo, temos p=2. Como n=3, p<n, fazendo com que o sistema seja indeterminado.
A solução do sistema (i) é representada pela seguinte matriz:

Escalonando a matriz ampliada deste sistema:
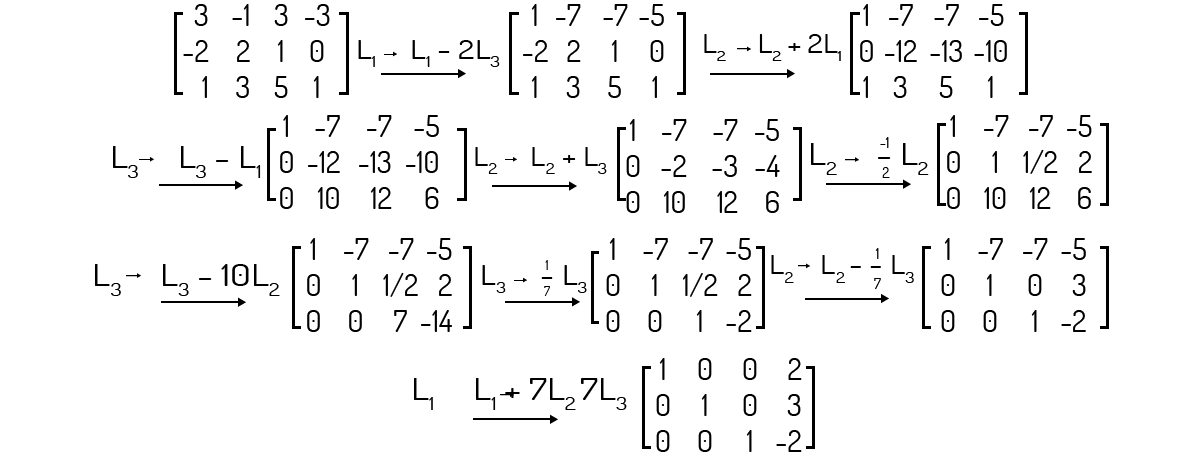
O posto do sistema (ii) é 2, tornando este sistema indeterminado.
Analisemos o posto da matriz ampliada deste sistema:
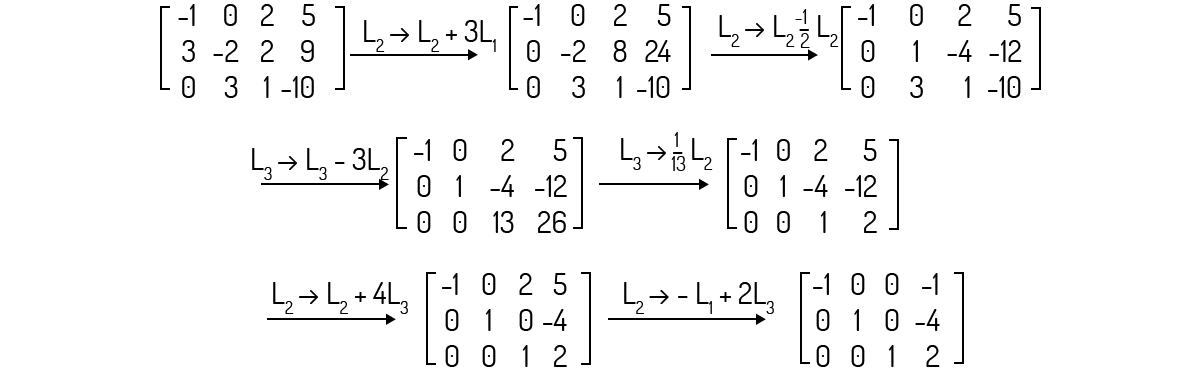
Note que não existe linha nula na matriz escada. O posto da matriz aumentada e da matriz dos coeficientes será o mesmo, ou seja, p=3. Como n=3, p=n, e o sistema é determinado.
O sistema (i) apresenta um grau de liberdade.
Analisemos o posto da matriz ampliada deste sistema:
Note que não existe linha nula na matriz escada. O posto da matriz aumentada e da matriz dos coeficientes será o mesmo, ou seja, p=3. Como n=3, p=n, e o sistema não possui grau de liberdade.
A solução do sistema (ii) é apresentada pela seguinte matriz:

Escalonando a matriz ampliada deste sistema:
Logo, a solução informada encontrava-se errada.
No início desta Unidade, vimos como podemos calcular a inversa de matriz. Veremos agora, tal qual Kolman (1999) nos diz, um método no qual podemos resolver sistemas lineares de n equações e n incógnitas, utilizando a inversa da matriz de coeficientes.
Boldrini (1980) e Kolman (1999) alertam que este método só pode ser usado para os casos de sistemas lineares que apresentam o mesmo número de equações e incógnitas. Ou seja, poderemos aplicar este método para os sistemas da seguinte forma:
\[{{a}_{11}}{{x}_{1}}+{{a}_{12}}{{x}_{2}}+...+{{a}_{1n}}{{x}_{n}}={{b}_{1}}\]
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\)
\[{{a}_{n1}}{{x}_{1}}+{{a}_{n2}}{{x}_{2}}+...+{{a}_{nn}}{{x}_{n}}={{b}_{n}}~~~~~~~~~~(13)\]
Sendo que podemos representar este sistema pelo produto da matriz dos coeficientes A pela matriz das incógnitas X, produto que será igual à matriz dos termos independentes B. Ou seja, A ⋅ X = B.
Para desenvolvermos esse método, Boldrini (1980) diz que devemos supor que det(A) ≠ 0, resultando no fato de A apresentar uma inversa \({{A}^{-1}}\), como já foi discutido anteriormente. Se multiplicarmos o produto de matrizes que representa o sistema mostrado em (13) em ambos os lados pela inversa \({{A}^{-1}}\):
\[{{A}^{-1}}\cdot \left( A\cdot X \right)={{A}^{-1}}\cdot B\]
\[\left( {{A}^{-1}}\cdot A \right)\cdot X={{A}^{-1}}\cdot B\to {{I}_{n}}\cdot X={{A}^{-1}}\cdot B\]
\[X={{A}^{-1}}\cdot B~~~~~~~~~~(14)\]
Ou, na forma matricial:

Para uma matriz \(C\) qualquer, já vimos que o cofator \({{\Delta }_{ij}}\) de um elemento \({{c}_{ij}}\) qualquer é \({{\left( -1 \right)}^{i+j}}\cdot det\left( {{C}_{ij}} \right)\), sendo \({{C}_{ij}}\) a submatriz de \(C\), a qual obtemos pela extração da \(i\)-ésima linha e \(j\)-ésima coluna. Se unirmos todos os cofatores dessa matriz \(C\), temos a matriz dos cofatores de \(C\), \(\overline{C}=\left[{{\Delta }_{ij}} \right]\) (BOLDRINI, 1980).
Tomando a transposta da matriz dos cofatores de C, teremos a matriz adjunta de C, \(adj~C={{\overline{C}}^{T}}\). Partindo disso, Boldrini (1980) enuncia que:
\[C\cdot{{\overline{C}}^{T}}=C\cdot (adj~C)=\det (C)\cdot {{I}_{n}}\]
Disso, podemos chegar a:
\[{{C}^{-1}}=\frac{1}{dec(C)}\cdot(adj~C)\]
Usando essa relação em (14):
\[X=\frac{1}{det\left( A \right)}\cdot adj\left( A \right)\cdot B~~~~~~~~~~(14)\]
Na forma matricial:

Com isso, temos que:
\[{{x}_{1}}=\frac{{{b}_{1}}{{\Delta }_{11}}+...+{{b}_{n}}{{\Delta }_{n1}}}{det~\left( A \right)}\]
O que podemos expandir para qualquer x_i:
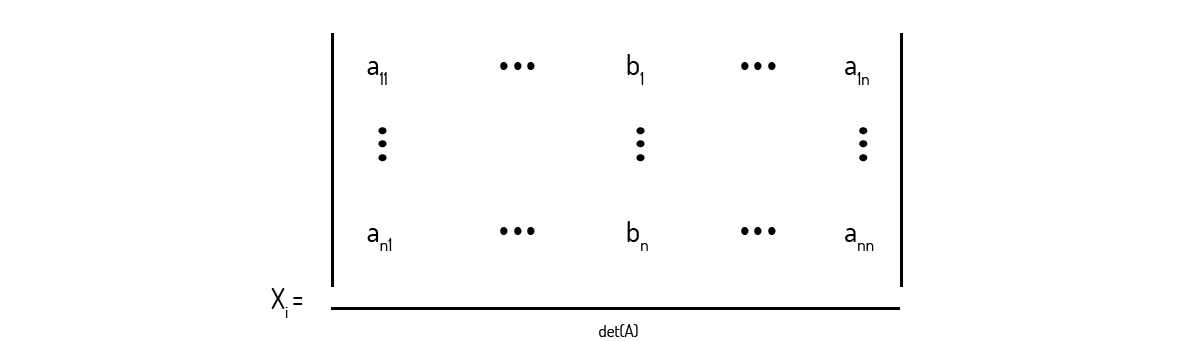
Ou seja, basicamente, ao aplicarmos a Regra de Cramer para a resolução de um sistema, o que iremos fazer é:
I. Calcular o determinante da matriz dos coeficientes det (A) e checar se det (A)≠0. Caso isso seja verificado, podemos seguir com o uso do método.
II. Para cada incógnita \({{x}_{i}}\), iremos alocar a matriz dos termos independentes na i-ésima coluna da matriz dos coeficientes, no lugar dos elementos originais desta coluna. Por exemplo, para \({{x}_{1}}\):
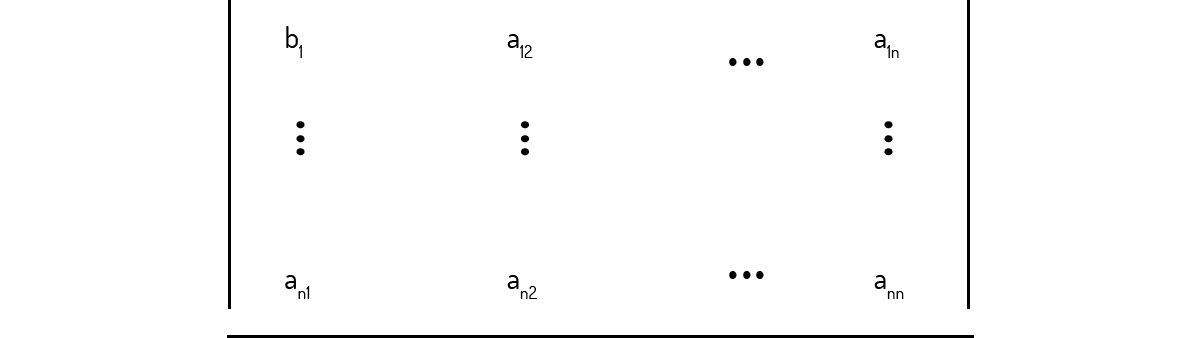
E para \({{x}_{2}}\):
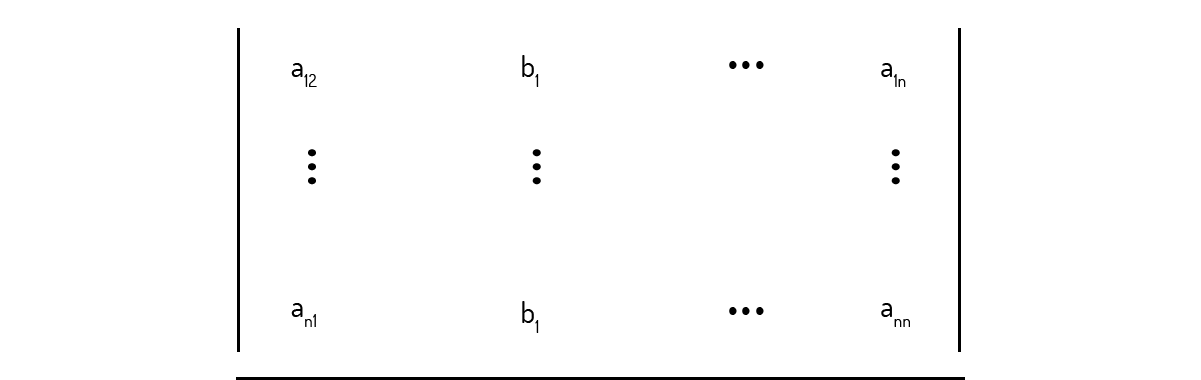
E assim por diante.
III. Para encontrar a incógnita \({{x}_{i}}\), calculamos o determinante da respectiva matriz obtida em II e dividimos esse valor pelo determinante da matriz dos coeficientes det (A).
Vejamos agora, na prática, como funciona o uso da Regra de Cramer para a resolução de sistemas.
Exemplo 2.10 - Resolva o sistema abaixo pela Regra de Cramer, se possível.
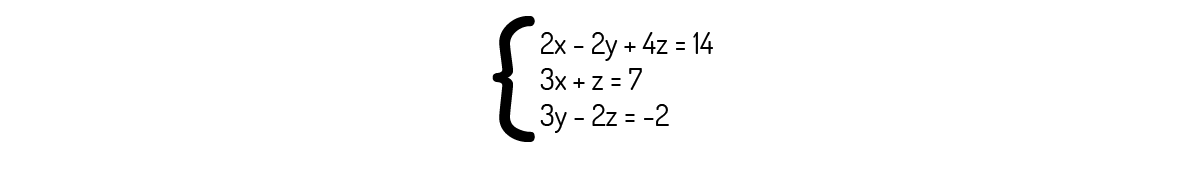
Solução
O primeiro passo para usarmos a Regra de Cramer é o determinante da matriz dos coeficientes do sistema ser diferente de zero. Assim, calculando o determinante:
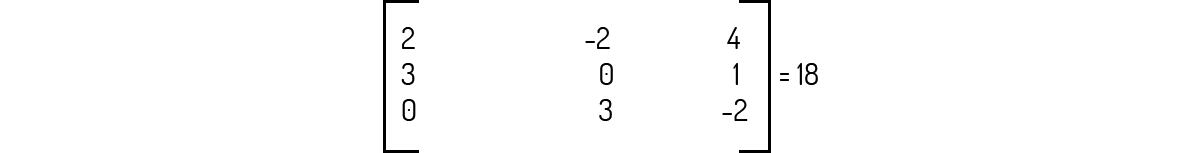
O determinante da matriz dos coeficientes é 18, sendo diferente de zero. Podemos, então, utilizar a Regra de Cramer. Fazendo \({{x}_{1}}=x\), \({{x}_{2}}=y\) e \({{x}_{3}}=z\):
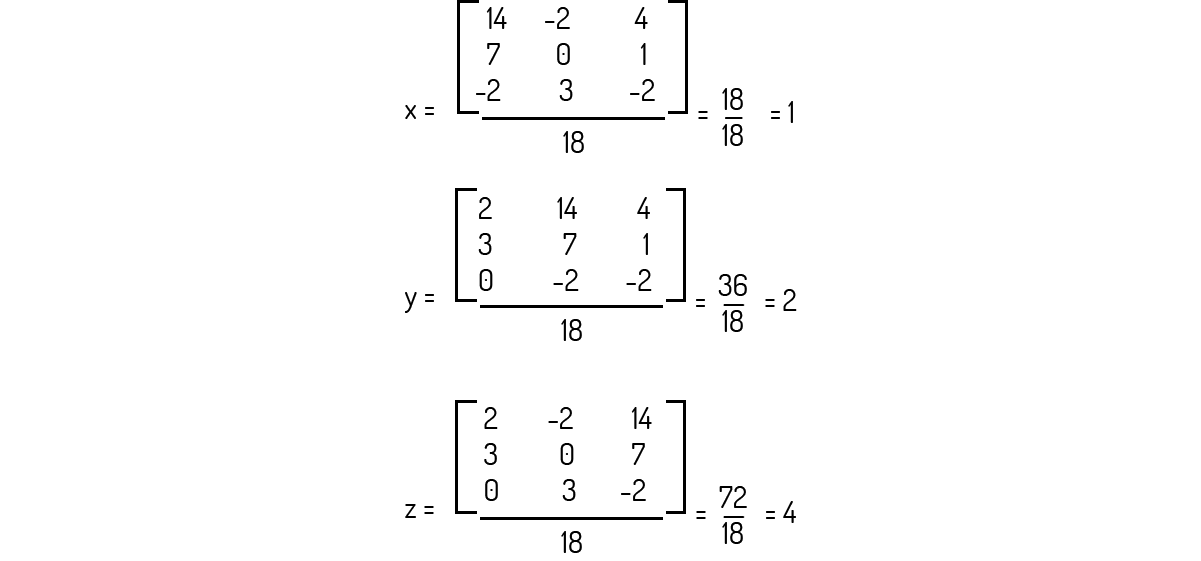
Com respeito à Regra de Cramer para a resolução de sistemas, um método direto para o cálculo da solução de um sistema, analise as seguintes alternativas, assinalando aquela que se encontra correta.
O sistema abaixo pode ser resolvido pela regra de Cramer.
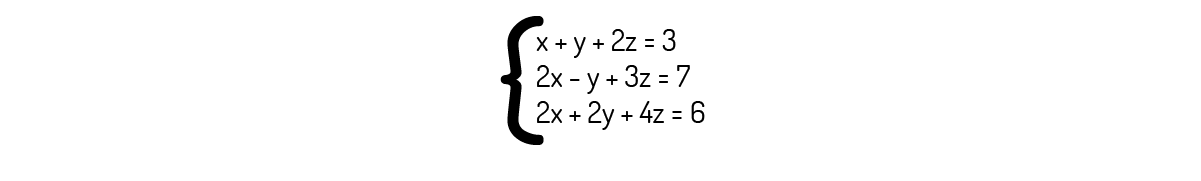
Se você observar a primeira e a terceira equação deste sistema, verá que a terceira é simplesmente a primeira multiplicada por 2. Logo, o determinante da matriz dos coeficientes será igual à 0, impossibilitando o uso da Regra de Cramer.
Podemos utilizar a regra de Cramer para resolver qualquer sistema linear.
A regra de Cramer só pode ser usada nos sistemas que apresentem o mesmo número de equações e incógnitas, além de ser necessário que o determinante da matriz dos coeficientes seja diferente de zero.
Um sistema cujo determinante da matriz dos coeficientes seja menor que 0 não pode ser resolvido pela regra de Cramer.
A restrição quanto ao determinante para uso da regra de Cramer é apenas que o determinante não seja igual a zero. Logo, um sistema cujo determinante da matriz dos coeficientes seja menor que zero, pode ser resolvido pela regra de Cramer.
Para o sistema abaixo, podemos usar a regra de Cramer, com a qual encontramos y=7.
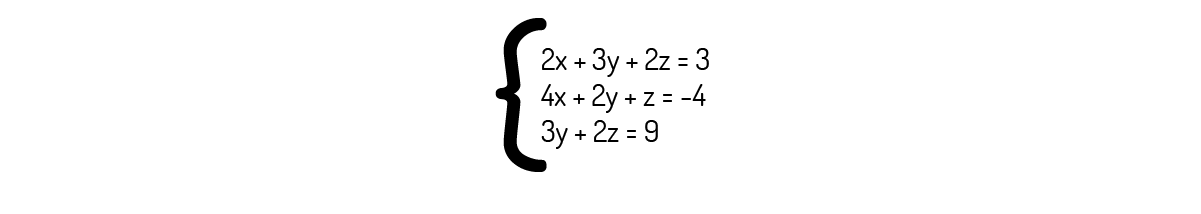
Primeiramente, devemos calcular o determinante da matriz dos coeficientes deste sistema:

Agora, como o determinante é diferente de 0, podemos calcular y:
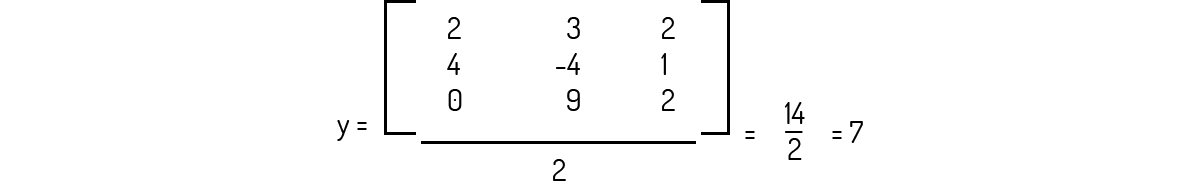
Para o sistema abaixo, podemos usar a regra de Cramer, com a qual encontramos que z=2.
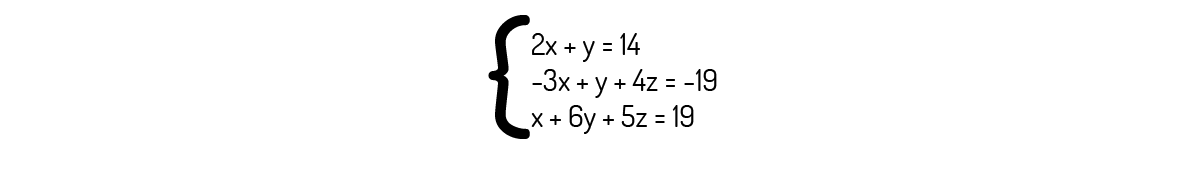
Calculando o determinante da matriz dos coeficientes desse sistema:
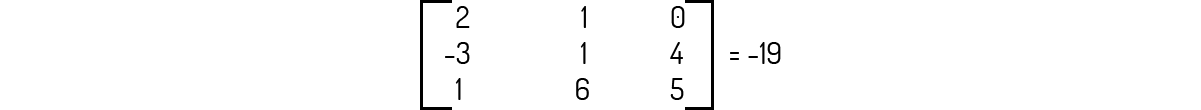
Agora podemos usar a regra de Cramer para avaliarmos z, já que o determinante é diferente de 0:

Apesar de ser simples para sistemas pequenos, a Regra de Cramer acaba não sendo muito utilizada em sistemas com muitas incógnitas. Existem diversos casos de problemas de biologia, economia e engenharia onde é comum ter um número de variáveis maior que 100. Você consegue imaginar o porquê de não fazermos uso mais extensivo da Regra de Cramer?

Nome do livro: Álgebra Linear (Coleção Schaum)
Editora: Bookman
Autor: Seymour Lipschutz & Marc Lipson
ISBN: 9788577808335
Um livro excelente para fixação de conteúdo, repleto de exercícios e exemplos resolvidos. É um material que certamente lhe auxiliará a fixar melhor e a praticar todos os tópicos de álgebra.

Nome do livro: Introdução à Álgebra Linear com Aplicações
Editora: LTC
Autor: Bernard Kolman
ISBN: 852161196X
Livro com linguagem simples e vários exemplos. Um grande diferencial que apresenta são exemplos na linguagem MATLAB, que é um software muito bom e prático para se trabalhar com matrizes.
