Unidade III

Vetores

Enquanto você cursava o ensino médio, durante os estudos da disciplina de Física certamente estudou o conceito de força que atua sobre um corpo qualquer. Para que essa força ficasse bem estabelecida, você deveria determinar qual era o valor numérico (módulo) dela, sua direção e o sentido que ela atuava. Além da força, outras grandezas, como velocidade e aceleração, também precisam dessa definição mais detalhada para serem bem definidas. A esse tipo de grandeza era dado o nome de grandeza vetorial, sendo a grandeza definida em si chamada de vetor (BOLDRINI, 1980).

Agora, você deve estar se perguntando: qual o sentido de estudarmos tais vetores na Álgebra Linear? Relembremos uma definição dada por Kolman (1999) sobre os diferentes tipos de matrizes: aquelas cujo tamanho sejam 1 × n e n × 1, ou seja, matrizes linha ou coluna, podem ser chamadas de vetores de dimensão n. Assim, veremos que é possível estudar vetores fazendo uso da Álgebra Linear.

Novamente tomando lembrança dos tipos de grandeza, as quantidades que podem ser caracterizadas apenas por um valor numérico são chamadas de escalares. Assim, para facilitar o entendimento dos símbolos que serão utilizados no presente material, os vetores serão representados utilizando uma letra minúscula e negrita, por exemplo, u, v e w. Já os escalares serão representados por letras minúsculas e itálicas, como a, b e c (KOLMAN, 1999).

Definindo vetores

Inicialmente, vamos nos restringir a vetores no plano cartesiano. Esse sistema já deve ser familiar para você: consiste em duas retas ortogonais, geralmente identificadas por x e y. No espaço definido por essas retas, podemos encontrar infinitos pontos, sendo cada um deles definido por um par de números reais $\left( {{x}_{i}},{{y}_{i}} \right)$, chamados de coordenadas do ponto, segundo Boldrini (1980). Assim, o ponto onde as duas retas x e y se cruzam é chamado de origem e tem, por definição, as coordenadas (0,0), sendo tal ponto representado pela letra O ou O=(0,0) (BOLDRINI, 1980).

Kolman (1999) ainda nos informa que, no plano cartesiano, assumimos que os valores à esquerda de O no eixo x serão negativos, enquanto os valores à direita serão positivos. Já no eixo y, os valores abaixo de O no eixo x serão negativos, enquanto os valores acima serão positivos.

Ainda visando bem definirmos o plano cartesiano, precisamos determinar um certo comprimento a ser definido como a unidade básica de comprimento, ou seja, qual comprimento equivale a 1. Com a distância unitária bem definida nas retas que compõem o plano cartesiano, podemos determinar qualquer comprimento (KOLMAN, 1999).

Agora, sejam dois pontos $A=\left( {{x}_{A}},{{y}_{A}} \right)$ e $B=\left( {{x}_{B}},{{y}_{B}} \right)$ contidos nesse plano. Pontos pertencentes a um mesmo plano são ditos coplanares. Conforme nos explica Kolman (1999), a união de dois pontos utilizando a menor distância possível entre esses é obtida com um segmento de reta, como nos mostra a Figura 3.1.

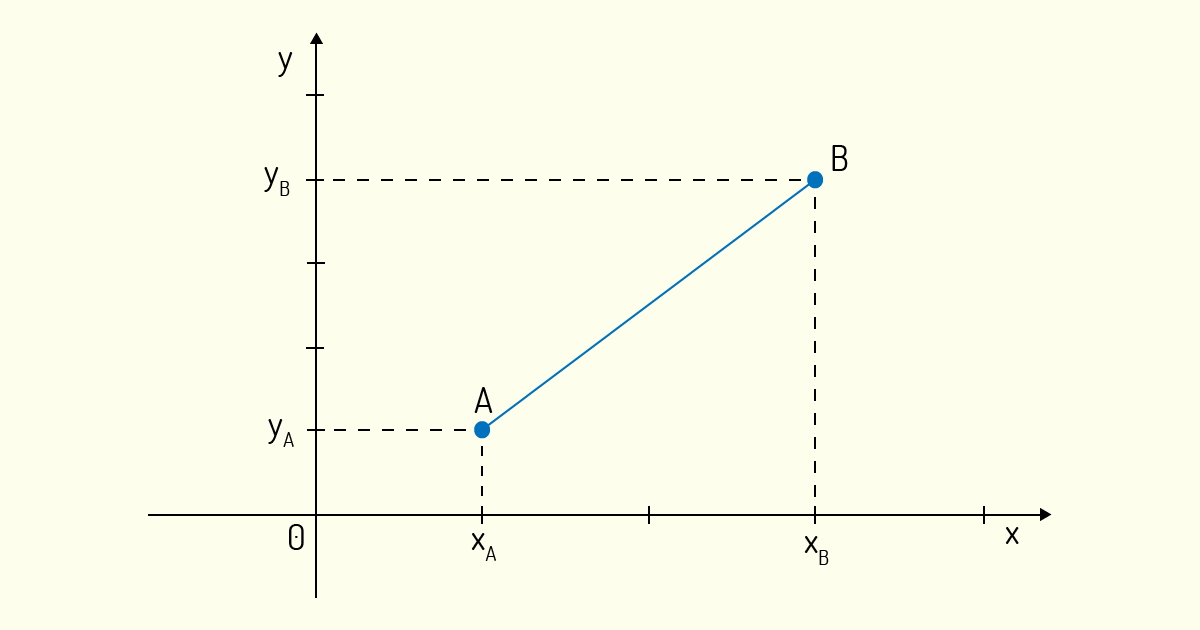
Lembre-se de que uma reta é infinita. A partir do momento em que delimitamos o ponto inicial e o ponto final de uma reta, temos um segmento de reta (BOLDRINI, 1980).

Agora vem um aspecto importante: qual ponto será o inicial e qual será o final no segmento de reta acima? Como Boldrini (1980) diz, independente de qual ponto for escolhido como inicial e final, o comprimento do segmento de reta será o mesmo. Ou seja, se escolhermos o ponto A como inicial, teremos o segmento de reta $\overrightarrow{AB}$; mas, se escolhermos o ponto B como inicial, teremos o segmento de reta $\overrightarrow{BA}$. No entanto, o sentido do segmento $\overrightarrow{AB}$ será oposto ao do segmento $\overrightarrow{BA}$. Observe a diferença na notação: a ordem dos pontos indica qual é o inicial e qual é o final, assim como a seta acima dos pontos.

Kolman (1999) nos diz que, em um segmento de reta, quando definimos a direção, que é reta contendo o segmento, e o sentido, que é de onde para onde vai o segmento, temos um segmento de reta orientado. Falta definirmos o tamanho desse segmento de reta, o qual será dado pelo comprimento do segmento. Com todas essas três características definidas, temos um vetor bidimensional.

Poole (2004) mostra uma classe específica de vetores do plano cartesiano: aqueles cuja origem se encontra na origem do plano, ou seja, em O. Assim, a cada ponto A, temos um vetor $a =$ $\overrightarrow{OA}$ . Por exemplo, se A=(1,3), então o vetor a pode ser descrito por uma das seguintes matrizes:

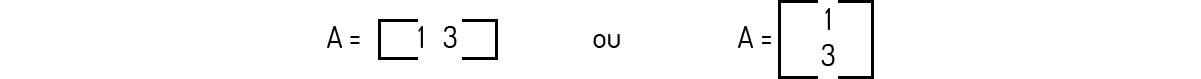
A esses vetores, Boldrini (1980) dá o nome de vetores no plano. Partindo disso, Kolman (1999) e Poole (2004) mostram que podemos propor uma definição para vetores no plano:

Definição 1: Um vetor bidimensional é um vetor que se encontra no plano, podendo ser representado na forma matricial como

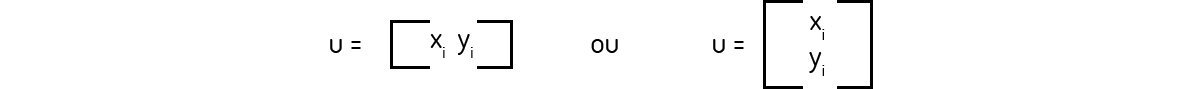
de modo que ${{x}_{i}}$ e ${{y}_{i}}$ são chamados de componentes de u. Iremos nos referir a um vetor bidimensional apenas como vetor.

Boldrini (1980) e Poole (2004) ainda acrescentam uma outra notação para vetores, semelhante à da matriz linha. O vetor u pode ser representado também como $u=\left( {{x}_{i}},{{y}_{i}} \right)$. O ponto $O=\left( 0,0 \right)$ também é conhecido como vetor nulo, mesmo que seja apenas um ponto.

Com essa definição de vetores no plano, Boldrini (1980) destaca que todos os pontos do plano $P=\left( x,y \right)$ apresentarão um vetor correspondente p$=$ $\overrightarrow{OP}$. Esse tipo de correspondência é chamada de biunívoca. Ele ainda destaca a definição de vetores opostos: um vetor u será oposto de um vetor v se, e somente se, u e v apresentarem o mesmo tamanho e direção, mas sentidos opostos. Ou seja, se $u=\left( a,b \right)$, então, $v=-u=\left( -a,-b \right)$.

Poole (2004) ainda nos dá uma definição interessante: o conjunto de todos os vetores que apresentem dois componentes reais é representado por ${{\Re }^{2}}$, sendo que R denota que seus componentes são números reais e o número 2 indica a quantidade de números reais necessários para caracterizar o vetor.

Também dada a definição de vetores na forma de matriz, temos que dois vetores serão iguais se, e apenas se, todos os seus respectivos componentes forem iguais, tal qual definimos a igualdade de matrizes (KOLMAN, 1999).

Exemplo 1.1: Verifique se os vetores u = (3,2) e v = (1,2) são iguais

Solução

Simplesmente, devemos olhar os componentes de cada vetor: veja que o primeiro componente de u é igual a 3, enquanto que o primeiro componente de v é igual a 1. Logo, mesmo que o segundo componente dos vetores u e v seja iguais, podemos afirmar que esses vetores não são iguais.

É claro que não lidamos apenas com vetores de origem em O. É muito comum que você encontre casos nos quais a origem do vetor será um outro ponto. Por exemplo, consideremos um vetor $u =$ $\overrightarrow{PQ}$, como indica Kolman (1999), sendo que $P=\left( {{x}_{1}},{{y}_{1}} \right)$ e $Q=\left( {{x}_{2}},{{y}_{2}} \right)$. Nesse caso, os componentes desse vetor serão ${{x}_{2}}-{{x}_{1}}$ e ${{y}_{2}}-{{y}_{1}}$. Ou seja:

\[u=\left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}} \right)~~~~~~~~~(1)\]

É interessante que possamos representar esse vetor u também como um vetor com origem O. Basta fazer com que as coordenadas do ponto final sejam iguais a $\left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}} \right)$. Ou seja, teremos na prática um vetor com ponto inicial $O=\left( 0,0 \right)$ e um ponto final $P'=\left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}} \right)$.

Exemplo 1.2: Sejam os pontos $P=\left( 2,3 \right)$, $Q=\left( 5,2 \right)$, $R=\left( 0,0 \right)$, $S=\left( 3,-1 \right)$, $A=\left( -2,1 \right)$ e $B=\left( 1,0 \right)$. Análise uma eventual igualdade entre os vetores $u =$ $\overrightarrow{PQ}$, $v =$ $\overrightarrow{RS}$ e $w =$ $\overrightarrow{AB}$.

Solução

Para que vetores sejam iguais, seus componentes devem ser iguais. Se os três vetores indicados tivessem a origem como ponto inicial, isso seria simples de ser avaliado. No entanto, apenas o vetor $v =$ $\overrightarrow{AB}$ apresenta como ponto inicial (0,0). Logo, rapidamente identificamos que v = (3,-1).

Agora, para encontrarmos a forma matricial dos demais vetores, usaremos a equação (1) para determinar os componentes de u e w. Assim:

\[u= \overrightarrow{PQ} =\left( {{x}_{Q}}-{{x}_{P}},{{y}_{Q}}-{{y}_{P}} \right)=\left( 5-2,2-3 \right)=\left( 3,-1 \right)\]

\[w= \overrightarrow{AB} =\left( {{x}_{B}}-{{x}_{A}},{{y}_{B}}-{{y}_{A}} \right)=\left( 1-\left( -2 \right),0-1 \right)=\left( 3,-1 \right)\]

Como v = (3,-1), u = (3,-1) e w = 3,-1), então podemos afirmar que os três vetores são iguais. Vejamos na Figura 3.2 esses três vetores.

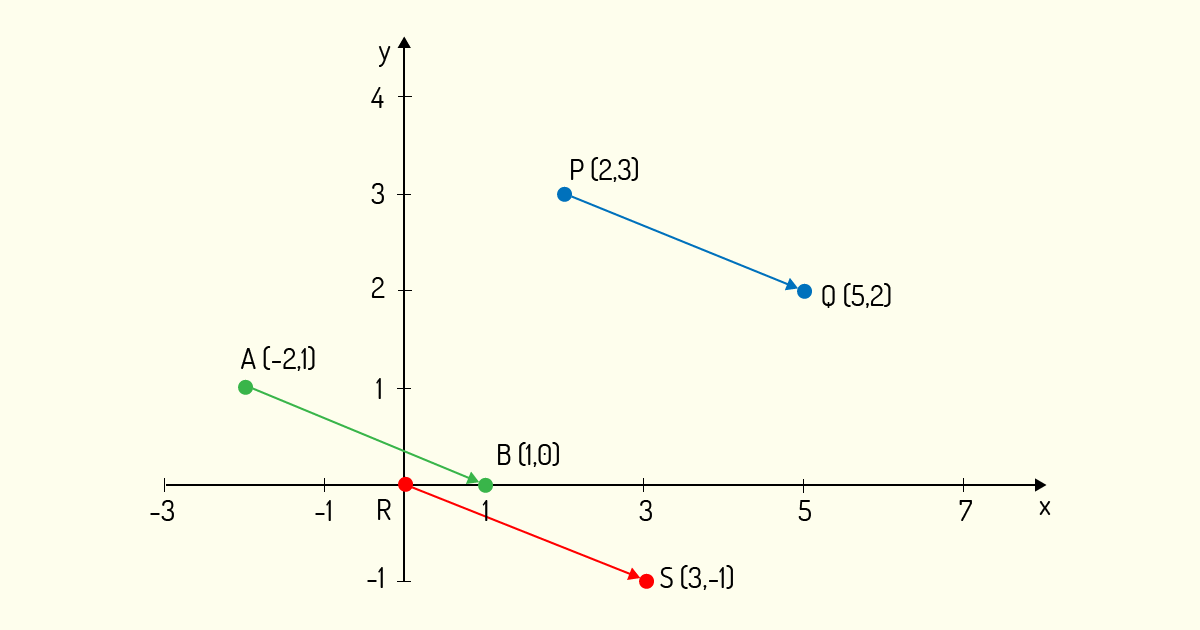
Note que realmente os vetores são todos iguais. A única diferença entre eles é a posição em que se encontram dispersos no plano.

Exemplo 1.3: Seja o vetor u = (4,3). Para que o vetor v = $\overrightarrow{PQ}$, sendo P = (-1,5), seja igual a u, quais devem ser as coordenadas de Q?

Solução

Como sabemos, dois vetores serão iguais se, e somente se, seus componentes forem respectivamente iguais. Vemos que o ponto P não é localizado na origem. Assim, se considerarmos as coordenadas do ponto Q como (a,b), na forma matricial, teremos o vetor v como:

\[v= \overrightarrow{PQ} =\left( a-\left( -1 \right),b-5 \right)=\left( a+1,b-5 \right)\]

Logo, dada a condição de igualdade, temos que o primeiro elemento do vetor v deve ser igual a 4 e o segundo elemento de v deve ser igual a 3. Então:

\[a+1=4\to a=3\]

\[b-5=3\to b=8\]

Portanto, caro(a) aluno(a), o ponto Q para que tenhamos u = v deverá ter coordenadas (3,8).

Operações com vetores

Chegou o momento de averiguarmos como podemos proceder ao lidarmos com operações envolvendo vetores. Iremos constatar que existe uma semelhança gigantesca com as operações feitas com matrizes.

i. Tamanho de um vetor

A primeira operação com vetores que estudaremos é como determinar o tamanho (ou comprimento ou norma ou magnitude) de um vetor, como define Kolman (1999). Seja o vetor u$=$ $\overrightarrow{OP}$ $=\left( {{x}_{i}},{{y}_{i}} \right)$, veja pela Figura 3.3 que podemos utilizar o teorema de Pitágoras para calcularmos o comprimento do vetor, pois o tamanho do vetor se mostra como a hipotenusa de um triângulo retângulo de base ${{x}_{i}}$ e altura ${{y}_{i}}$.

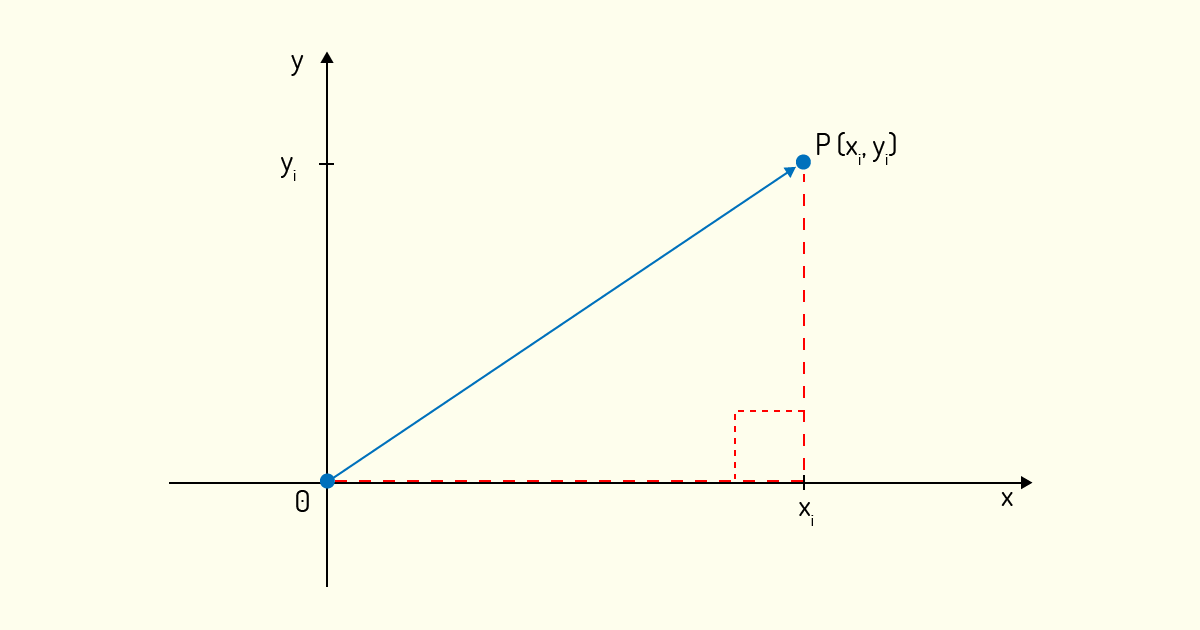
Assim, temos que o comprimento ||u|| do vetor será calculado da seguinte forma:

\[||u|| = \sqrt{x_{i}^{2}+y_{i}^{2}} ~~~~~~~~~(2)\]

Veja que podemos aplicar o mesmo raciocínio para casos de vetores cuja origem não seja o ponto inicial, ou seja, podemos usar o teorema de Pitágoras para determinar a distância entre dois pontos no plano. Sejam os pontos $P=\left( {{x}_{1}},{{y}_{1}} \right)$ e $Q=\left( {{x}_{2}},{{y}_{2}} \right)$, o comprimento do vetor u que une esses dois pontos pode ser obtido aplicando o teorema de Pitágoras de acordo com a Figura 3.4:

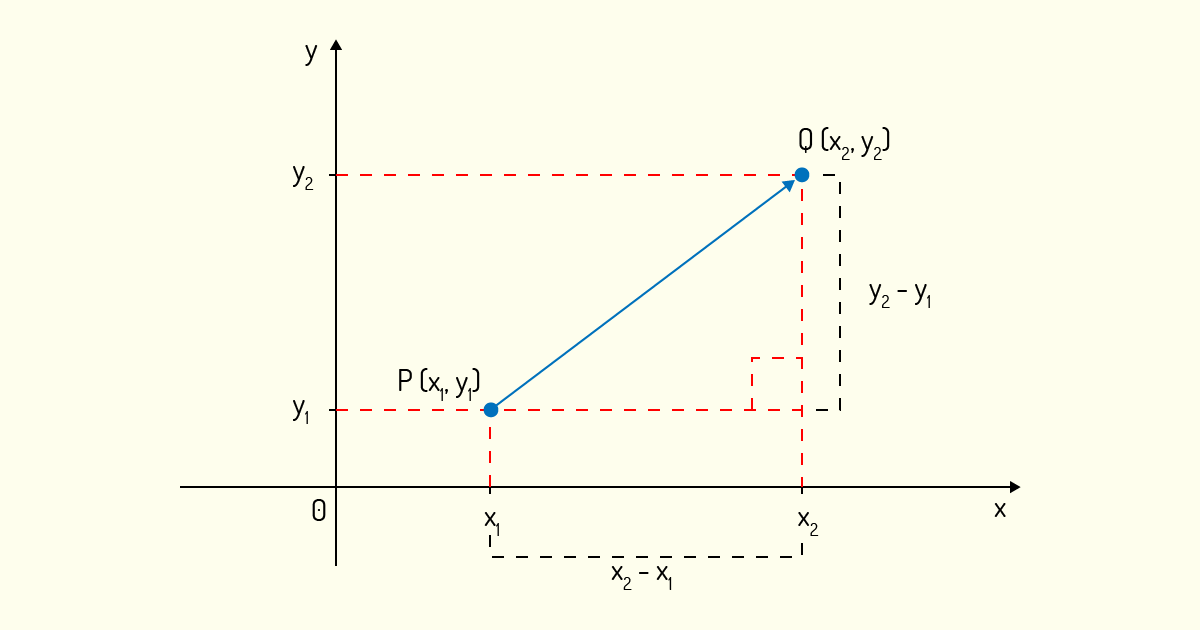
Analisando a Figura 3.4, temos um triângulo retângulo cuja base é igual a ${{x}_{2}}-{{x}_{1}}$ e a altura é igual a ${{y}_{2}}-{{y}_{1}}$. Assim, aplicando o teorema de Pitágoras:

\[||u||=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}~~~~~~~~~(3)\]

É importante que você note que o tamanho de um vetor deve ser sempre um valor positivo: não existe distância negativa. O uso das duas barras, inclusive, serve para que você se lembre disso, visto a semelhança dessa simbologia com aquela usada para determinar o valor absoluto (KOLMAN, 1999).

Exemplo 1.4: Qual o tamanho do vetor $u=\left( 1,4 \right)$? E do vetor $v=$$\overrightarrow{PQ}$ , sendo os pontos $P=\left( 1,1 \right)$ e $Q=\left( 3,2 \right)$?

Solução

Para o vetor u, basta aplicar a Equação (2):

\[||u|| = \sqrt{x_{i}^{2}+y_{i}^{2}}=\sqrt{{{1}^{2}}+{{4}^{2}}}=\sqrt{17}\]

Agora, para o vetor v, temos de usar a Equação (3):

\[||v||=\sqrt{{{\left( 3-1 \right)}^{2}}+{{\left( 2-1 \right)}^{2}}}=\sqrt{{{2}^{2}}+{{1}^{2}}}=\sqrt{5}\]

Logo, podemos afirmar que o vetor u apresenta tamanho (ou comprimento) igual a $\sqrt{17}$ e o vetor v apresenta tamanho (ou comprimento) igual a $\sqrt{5}$.

ii. Multiplicação por escalar

Seja k um escalar real qualquer. Boldrini (1980) diz que podemos multiplicar um vetor u qualquer por esse k, obtendo um novo vetor definido como

\[w=ku~~~~~~~~~(4)\]

Se nessa multiplicação temos $k>0$, então w terá a mesma direção e sentido de u, mas o tamanho de w será igual a $k$ vezes o tamanho de u, ou seja:

\[||w||=k ||u||~~~~~~~~~(5)\]

Para o caso onde $k<0$, então w terá a mesma direção de u, mas o sentido de w será oposto ao de u. O tamanho de w pode ser obtido pela Equação (5). Já para o caso onde $k=0$, o resultado será sempre um vetor nulo.

Em termos matriciais, para realizarmos essa operação, basta que nos lembremos da multiplicação por escalar. Assim, se u = (a,b), ao aplicarmos a Equação (4), teremos

\[w=ku=\left( k\cdot a,~k\cdot b \right)~~~~~~~~~(6)\]

Exemplo 1.5: Seja o vetor u$=\left( 2,5 \right)$, determine os vetores $w =3u$, $v=-2u$ e $t=5w$.

Solução

Para encontrarmos os vetores desejados, basta que apliquemos a Equação (6). Para w, temos k = 3, assim:

\[w = 3u = \left( 3\cdot 2,~3\cdot 5 \right)=\left( 6,15 \right)\]

Para v, temos k =-2, assim:

\[v =-2u = ((-2)\cdot 2,~( -2)\cdot 5)= ( -4,-10)\]

Finalmente, para t, temos k = 5. No entanto, devemos multiplicar w por esse escalar:

\[t=5w =\left( 5\cdot 6,~5\cdot 15 \right)=\left( 30,75 \right)\]

iii. Adição de vetores

Sejam dois vetores $u=\left( {{x}_{1}},{{y}_{1}} \right)$ e $v =\left( {{x}_{2}},{{y}_{2}} \right)$. Kolman (1999) diz que esses dois vetores podem ser somados, gerando um terceiro vetor w da seguinte forma:

\[w = u + v =\left( {{x}_{1}}+{{x}_{2}},{{y}_{1}}+{{y}_{2}} \right~~~~~~~~~(7))\].

Ou seja, ao somarmos vetores, fazemos a soma elemento a elemento, da mesma forma que realizamos a adição de matrizes. Com isso, Boldrini (1980) já adianta que a adição de vetores irá herdar as propriedades da adição de matrizes. Assim, dessas propriedades, podemos inferir que a soma de vetores opostos irá resultar no vetor nulo, ou seja:

\[w = u + (u) = \left( x-x,y-y \right)=\left( 0,0 \right)~~~~~~~~~(8)\]

Essa soma de vetores pode ser visualizada graficamente, facilitando nossa compreensão. Para esse fim, Boldrini (1980) pede que pensemos no vetor força que atua sobre um corpo. Esse vetor pode ser representado apresentando a direção e o sentido que atua a força, sendo seu comprimento igual à intensidade da força atuante. A origem do sistema deve ser posicionada no ponto onde a força atua.

Sendo assim, se duas forças ${{F}_{1}}$ e ${{F}_{2}}$ atuam num certo corpo, como podemos determinar a força resultante ${{F}_{R}}$ da atuação dessas duas forças? Isso nada mais é do que obter a soma dos vetores ${{F}_{1}}$ e ${{F}_{2}}$. Se as forças atuantes forem ${{F}_{1}}=\left( a,b \right)$ e ${{F}_{2}}=\left( c,d \right)$, graficamente iremos encontrar o seguinte:

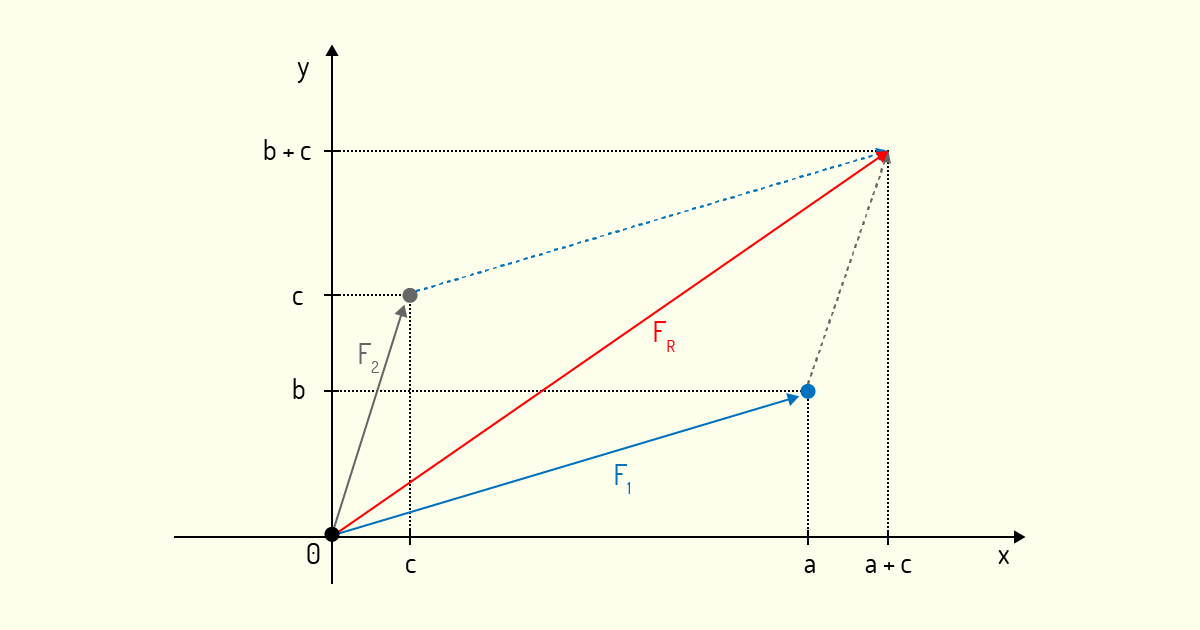
Caro(a) aluno(a), analisando melhor a Figura 3.5, vemos que ${{F}_{R}}$ nada mais é do que a diagonal do paralelogramo construído utilizando os vetores ${{F}_{1}}$ e ${{F}_{2}}$. Inclusive, como nos diz Boldrini (1980), pela congruência de triângulos, podemos provar que as coordenadas de ${{F}_{R}}$ são $\left( a+c,b+d \right)$.

Da adição de vetores, podemos encontrar também a diferença de vetores. Essa diferença é simbolizada por u – v, e o vetor resultante é obtido da mesma forma que apresentado na Figura 3.5, com a diferença que usamos o vetor oposto de v para construir o paralelogramo, conforme nos diz Kolman (1999). Algebricamente, essa operação pode ser realizada primeiramente realizando a multiplicação de v pelo escalar –1 e, em seguida, realizando a adição de u a este vetor –v, ou seja

\[w = u + [( -1)v)]= u + (-v)=({x}_{1}-{x}_{2},{y}_{1}-{y}_{2})~~~~~~~~~(9)\]

Exemplo 1.6: Sejam os vetores u = (1,6) e v = (3,4). Determine os vetores $w = u + v, t = u - v$ e $z = 2u + 3v$.

Solução

Para encontrarmos w, basta aplicarmos a Equação (7):

\[w = u + v = (1 + 3, 6 + 4) = (4,10)\]

Para encontrarmos t, usaremos a Equação (9). Mas antes avaliamos o oposto de v:

\[–v = –1 ⋅ (3,4) = (-3,-4)\]

Agora, da Equação (9):

\[t = u + (–v) = (1,6) + (–3,-4) = (1 – 3, 6 – 4) = (–2,2)\]

Finalmente, para z, precisamos realizar antes da adição dos vetores a multiplicação de u pelo escalar 2 e v pelo escalar 3. Disso encontramos:

\[2u = (2 ⋅ 1, 2 ⋅ 6) = (2,12)\]

\[3v = (3 ⋅ 3, 3 ⋅ 4) = (9,12)\]

Finalmente:

\[z = 2u + 3v = (2 + 9, 12 + 12) = (11,24)\]

Vetores no espaço

De forma semelhante ao que desenvolvemos para o plano cartesiano, também podemos considerar o caso de vetores que se encontram no espaço. Nesse caso, tal qual Boldrini (1980) nos diz, teremos um sistema coordenado composto por três retas, ao invés de apenas duas.

Essas três retas devem ser perpendiculares duas a duas e geralmente são representadas por x, y e z. Agora, para definirmos a localização de um ponto, precisamos definir as três coordenadas. Logo, os pontos definidos no espaço terão simbologia como P(x, y, z) (BOLDRINI, 1980).

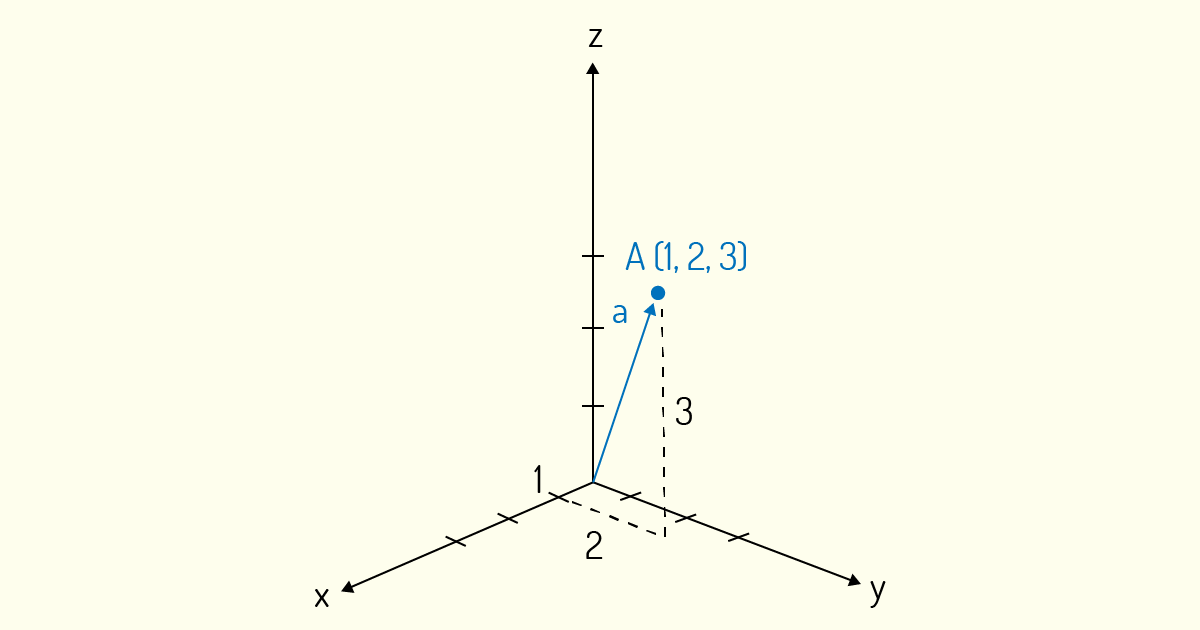
Tal qual no caso do plano cartesiano, também se define a interseção das três retas como a origem do espaço ou o ponto O(0,0,0). De forma semelhante ao que Poole (2004) comentou sobre os vetores no plano, temos também que o conjunto de todos os vetores no espaço é representado por ${{\Re }^{3}}$, sendo que $\Re $ denota que seus componentes são números reais e o número 3 indica a quantidade de números reais necessários para caracterizar o vetor. A Figura 3.6 nos mostra a representação de um vetor A = (1, 2, 3) no plano tridimensional.

Kolman (1999) vai ainda além do espaço, definindo vetores de dimensão n. Com isso, ele nos mostra que não estamos limitados à existência de vetores apenas com duas ou três dimensões, mas com quantas dimensões forem necessárias. Ou seja, vetores podem apresentar n dimensões e o conjunto de todos os vetores de n dimensões é representado por ${{\Re }^{n}}$. Ele ainda destaca que, independente da dimensão de um vetor, todos os elementos de um vetor devem ser números reais.

Com essa generalização, devemos propor uma generalização para as operações com vetores de qualquer dimensão. Para o caso da adição, considere os dois vetores u=$\left( {{u}_{1}},{{u}_{2}},...,{{u}_{n}} \right)$ e v$=\left( {{v}_{2}},{{v}_{2}},...{{v}_{n}} \right)$. Kolman (1999) diz que esses dois vetores podem ser somados de forma semelhante à que vimos na Equação (7), quando definimos essa operação para vetores bidimensionais, gerando um terceiro vetor w da seguinte forma:

\[w = u + v = ({u}_{1} + {v}_{1}, {u}_{2} + {v}_{2}, ...,{u}_{n} + {v}_{n}~~~~~~~~~(10)\]

O mesmo podemos estender para a multiplicação por escalar de um vetor de dimensão n. Seja o vetor $u=\left( {{u}_{1}},{{u}_{2}},...,{{u}_{n}} \right)$ e o escalar k, podemos multiplicar o vetor u por esse escalar, encontrando um vetor w que será igual a:

\[w = ku = (k\cdot {u}_{1}, k\cdot {u}_{2}, ...,k\cdot {u}_{n})~~~~~~~~~(11)\]

Boldrini (1980) e Kolman (1999) enumeram uma série de propriedades para os vetores pertencentes à ${{\Re }^{n}}$. Para averiguarmos tais propriedades, considere os vetores arbitrários u e v em ${{\Re }^{n}}$ e os escalares a e b. Então:

A adição u+v também será um vetor em ${{\Re }^{n}}$.

A adição u+v também será um vetor em ${{\Re }^{n}}$.
u + v = v + u.
u + (v + w) = (u + v) + w.
Existe um vetor nulo, representado por 0, em ${{\Re }^{n}}$ tal que, para qualquer vetor u em ${{\Re }^{n}}$, teremos u+0=0+u=u.
Para qualquer vetor u em ${{\Re }^{n}}$ existe um vetor -u em ${{\Re }^{n}}$ tal que u+(-u)=0. Esse vetor -u é chamado de simétrico de u.
O produto por escalar au também será um vetor em ${{\Re }^{n}}$.
a(u + v) = au + av.
(a + b)u = au + bu.
(a ⋅ b)u = a ⋅ (bu).
1u = u.

Kolman (1999) mostra que o tamanho de um vetor de dimensão n pode ser calculado de forma semelhante à apresentada também na Equação (2). Seja um vetor $u = (u_1,u_2,...,u_n )$ em ${{\Re }^{n}}$, seu tamanho pode ser obtido por:

\[||u||=\sqrt{u_{1}^{2}+u_{2}^{2}+...u_{n}^{2}}~~~~~~~~~(12)\]

Atividade

Os vetores são uma unidade fundamental da Álgebra Linear. É esperado que você seja capaz de lidar sem problemas com as operações que envolvem vetores. Visando sua prática em tal assunto, considere os vetores a seguir, analise as alternativas e assinale a correta.

\[u = (2,0,1) v = (1,3,1) z = (1,2,3,1) t = (-1,-2,3,-1)\]

Podemos afirmar que w = u + 2v = (6,6,4).

Antes da soma, realizamos a multiplicação por escalar de v:

$2v = (2,6,2)$

Agora, realizando a adição dos vetores:

$w = u + 2v = (4,6,3)$

Temos que w = v + z = (2,5,4,1).

Não podemos realizar a adição de vetores que apresentam quantidades diferentes de elementos, como no caso de matrizes.

Temos que w = u + 2v = (2,0,1,1,3,1).

A adição de vetores deve ser realizada termo a termo. O vetor que resulta da soma de dois vetores deve apresentar a mesma quantidade de elementos que seus vetores genitores.

Não existe um vetor w = u + z.

Alternativa correta. Tal qual a adição de matrizes, não podemos somar vetores que apresentem quantidade de elementos diferentes.

Temos que w = 2z - t = (1,2,9,1)

Antes da soma, realizamos a multiplicação por escalar de v:

2z = (2,4,6,2)

Agora, realizando a adição dos vetores:

w = 2z - t = (3,6,3,3)

Espaços Vetoriais

Anteriormente, caro(a) aluno(a), vimos de maneira simplificada o espaço ${{\Re }^{n}}$, tendo, inclusive, analisado algumas de suas propriedades básicas. Agora, vamos estudar a estrutura desses espaços vetoriais de maneira mais cuidadosa.

Definindo os espaços vetoriais

Antes de mais nada, vamos definir o que é um espaço vetorial. A definição passa pelas propriedades que foram definidas sobre as operações de soma e produto por escalar de vetores de dimensão n, como você verá. Um espaço vetorial será representado de forma genérica por uma letra maiúscula itálica no presente material, como V. Isso está de acordo com Boldrini (1980) e Kolman (1999):

Definição 2: Um espaço vetorial é um conjunto V não vazio, cujos elementos são chamados de vetores onde as operações de soma e multiplicação por escalar são fechados, ou seja, para quaisquer vetores u, v, w, t ∈ V e a, b ∈ ${{\Re}}$, os seguintes axiomas são válidos:

A. O vetor w = u + v pertence a V (isso significa ser fechado em relação à soma).

u + v = v + u.
u + (v + w) = (u + v) + w.
u + 0 = 0 + u = u.
Todo vetor u ∈ V apresenta o vetor simétrico –u.

B. O vetor t = au pertence a V (isso significa ser fechado em relação à multiplicação por escalar).

a(u + v) = au+av.
(a + b)u = au + bu.
(a ⋅ b)u = a ⋅ (bu).
1u = u para todo vetor u ∈ V.

Boldrini (1980) diz também que essa definição de espaço vetorial pode ser modificada para o caso de usarmos números complexos no lugar de números reais nas operações com escalares. Nesse caso, chamamos o espaço vetorial de espaço vetorial complexo. No entanto, o presente material não abordará esse tipo de espaço vetorial.

Vejamos alguns exemplos de espaços vetoriais agora. Como já definimos no item 1.3 da presente unidade, para qualquer n ≥ 1 todas as n-uplas ${{\Re }^{n}}$ de números reais constituem um espaço vetorial. Outro exemplo de espaço vetorial que temos é o conjunto de matrizes reais m × n.

Exemplo 1.7: Considere ${{P}_{2}}$ o conjunto de todos os polinômios de ordem 2 ou menor cujos coeficientes sejam números reais. Veja se esse conjunto é um espaço vetorial.

Solução

Para tal, consideremos que ${{a}_{i}}$ e ${{b}_{i}}$ sejam números reais. Sejam os seguintes polinômios pertencentes à ${{P}_{2}}$:

\[p\left( x \right)={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}\]

\[q\left( x \right)={{b}_{0}}+{{b}_{1}}x+{{b}_{2}}{{x}^{2}}\]

Temos que a soma desses dois polinômios é igual a:

\[p\left( x \right)+q\left( x \right)={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+{{b}_{0}}+{{b}_{1}}x+{{b}_{2}}{{x}^{2}}\]

Agrupando os termos semelhantes:

\[p\left( x \right)+q\left( x \right)=\left( {{a}_{0}}+{{b}_{0}} \right)+\left( {{a}_{1}}+{{b}_{1}} \right)x+\left( {{a}_{2}}+{{b}_{2}} \right){{x}^{2}}\]

Note que para qualquer valor real de a_i e b_i teremos que o maior grau do polinômio $p(x) + q (x)$ será 2. Portanto, vemos que a soma está fechada para esse conjunto, ou seja, $p\left( x \right)+q\left( x \right)\in {{P}_{2}}$.

Agora, seja o número real c, ou seja, c é um escalar. Se multiplicarmos $p(x)$ por c:

\[cp\left( x \right)=c\cdot {{a}_{0}}+c\cdot {{a}_{1}}x+c\cdot {{a}_{2}}{{x}^{2}}\]

Como c é um número real, novamente temos que o maior grau do polinômio $cp(x)$ será 2. Portanto, vemos que a multiplicação por escalar está fechada para esse conjunto, ou seja, $cp\left( x \right)\in {{P}_{2}}$. Com isso, verificamos os axiomas A e B citados anteriormente.

Para esse conjunto de polinômios, temos que o vetor nulo $p_0 (x)$ é igual a

\[p\left( x \right)=0+0\cdot x+0\cdot {{x}^{2}}=0\]

O elemento simétrico de um polinômio $p(x)$ é $-p\left( x \right)=-{{a}_{0}}-{{a}_{1}}x-{{a}_{2}}{{x}^{2}}$. Vamos verificar agora os demais axiomas da adição:

Para mostrar que p(x)+q(x)=q(x)+p(x), vamos desenvolver o termo da direita, já que temos o termo da esquerda:

$q\left( x \right)+p\left( x \right)={{b}_{0}}+{{b}_{1}}x+{{b}_{2}}{{x}^{2}}+{{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}} \\=\left( {{b}_{0}}+{{a}_{0}} \right)+\left( {{b}_{1}}+{{a}_{1}} \right)x+\left( {{b}_{2}}+{{a}_{2}} \right){{x}^{2}} \\=\left( {{a}_{0}}+{{b}_{0}} \right)+\left( {{a}_{1}}+{{b}_{1}} \right)x+\left( {{a}_{2}}+{{b}_{2}} \right){{x}^{2}}=p\left( x \right)+q\left( x \right)$
Esse axioma apresenta um prova semelhante ao axioma a).
Vamos verificar o vetor nulo:
‍
$p\left( x \right)+{{p}_{0}}\left( x \right)={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+0={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}=p\left( x \right)$
Vamos verificar o elemento simétrico:

$p\left( x \right)+\left( -p\left( x \right) \right)={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+\left( -{{a}_{0}}-{{a}_{1}}x-{{a}_{2}}{{x}^{2}} \right)=0={{p}_{0}}\left( x \right)$

Vamos verificar, agora, os demais axiomas da multiplicação por escalar. Para tal, consideremos os escalares k e m, ambos reais:

$k\left( p\left( x \right)+q\left( x \right) \right)=k\left[ {{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+{{b}_{0}}+{{b}_{1}}x+{{b}_{2}}{{x}^{2}}\right]$ $=k{{a}_{0}}+k{{a}_{1}}x+k{{a}_{2}}{{x}^{2}}+k{{b}_{0}}+k{{b}_{1}}x+k{{b}_{2}}{{x}^{2}}$ $=k\left( {{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}} \right)+k\left( {{b}_{0}}+{{b}_{1}}x+{{b}_{2}}{{x}^{2}} \right)=kp\left( x \right)+kq\left( x \right)$
$\left( k+m \right)p\left( x \right)=\left( k+m \right)\left( {{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}} \right)$ $=\left( k+m \right){{a}_{0}}+\left( k+m \right){{a}_{1}}x+\left( k+m \right){{a}_{2}}{{x}^{2}}$ $=k{{a}_{0}}+k{{a}_{1}}x+k{{a}_{2}}{{x}^{2}}+m{{a}_{0}}+m{{a}_{1}}x+m{{a}_{2}}{{x}^{2}}$ $=k\left( {{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}} \right)+m\left( {{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}} \right)=kp\left( x \right)+mp\left( x \right)$
$\left( k\cdot m \right)p\left( x \right)=\left( k\cdot m \right)\left( {{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}} \right)$ $=km{{a}_{0}}+km{{a}_{1}}x+km{{a}_{2}}{{x}^{2}}=k\left( m{{a}_{0}}+m{{a}_{1}}x+m{{a}_{2}}{{x}^{2}} \right)$ $=k\left[ m\left( {{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}} \right) \right]=k\left[ mp\left( x \right) \right]$
Vamos mostrar que $1p(x)=p(x)$ para todo $p(x)∈V:$

$1⋅\left( {{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}} \right)=1\cdot {{a}_{0}}+1\cdot {{a}_{1}}x+1\cdot {{a}_{2}}{{x}^{2}}\\ ={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}=p\left( x \right)$

Veja que conseguimos provar todos os oito axiomas. Logo, provamos que o conjunto ${{P}_{2}}$ é um espaço vetorial.

Como Kolman (1999) adianta, o Exemplo 1.7 descreve o passo a passo para determinarmos se um conjunto constitui um espaço vetorial: a primeira coisa que devemos fazer é avaliar a validade dos axiomas A e B. Se esses dois axiomas forem verificados como verdadeiros, então você deve prosseguir para avaliar os demais axiomas.

Tal exemplo nos mostra a extrema versatilidade da Definição 2. Tal definição foi proposta pensando apenas em conjuntos de vetores como segmentos de reta orientados, mas veja que ela pode ser facilmente aplicada a matrizes que não sejam linha ou coluna, polinômios e até mesmo funções. Assim, estabelecemos uma quebra de costumes aqui: vetores não precisam estar necessariamente associados a segmentos de reta orientados (KOLMAN, 1999).

O Exemplo 1.7 também pode ser visto como interessante para a análise de polinômios como espaços vetoriais. Na verdade, Poole (2004) diz que podemos expandir esse conceito ainda mais. Seja o seguinte polinômio de grau n:

\[p\left( x \right)={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+...+{{a}_{n-1}}{{x}^{n-1}}+{{a}_{n}}{{x}^{n}}\]

Podemos, então, seguir um procedimento semelhante ao mostrado no Exemplo 1.7 para provar que o conjunto ${{P}_{n}}$ composto pelos polinômios de grau n ≥ 1 é um espaço vetorial.

Exemplo 1.8: Considere F como o conjunto de todas as funções que apresentam valor real definido para um intervalo real. Veja se esse conjunto é um espaço vetorial.

Solução

Para tal, consideremos que f e g sejam funções pertencentes à F. Das definições de funções reais, sabemos que:

\[\left( f+g \right)\left( x \right)=f\left( x \right)+g\left( x \right)\]

Ou seja, sabemos que a função definida como a soma de duas funções é igual à soma dessas duas funções. Com isso, o axioma A está provado.

Sendo c um escalar, então, também das definições de funções reais, sabemos que:

\[\left( cf \right)\left( x \right)=cf\left( x \right)\]

Ou seja, a multiplicação da função por um escalar avaliado em x é igual à função avaliada em x multiplicada pelo escalar c. Com isso, o axioma B está provado.

Os demais axiomas podem ser facilmente provados partindo desses dois. Assim, como uma prática para você, avalie a validade dos demais oito axiomas.

Exemplo 1.9: Considere V = M(m × n) como o conjunto de todas as matrizes reais. Tal conjunto é um espaço vetorial?

Solução

Considere as matrizes A, B ∈ V e c ∈ ${{\Re}}$. Se realizarmos a adição C = A + B, temos que C também será uma matriz pertencente ao conjunto V. De forma semelhante, a multiplicação por escalar de uma matriz que pertença à V resultará numa matriz de mesma ordem que a original. Sendo assim, os axiomas A e B estão provados.

Os demais axiomas podem ser facilmente provados partindo desses dois e dos seus conhecimentos de matrizes. Assim, como uma prática para você, avalie a validade dos demais oito axiomas.

Agora, antes de passarmos para o próximo passo na análise de espaço vetoriais, Poole (2004) enuncia uma série de propriedades através de um teorema:

Teorema 1: Sendo V um espaço vetorial, u um dos vetores pertencentes à V e a ∈ ${{\Re}}$ um escalar, então:

0u = 0.
a0 = 0.
(-1)u = –u.
Ao se deparar com au = 0, então você tem que a = 0 ou u = 0.

Subespaços vetoriais

Você já deve ter percebido que ao estudarmos ${{\Re }^{n}}$ temos uma situação onde existem espaços vetoriais dentro de espaços vetoriais. Por exemplo, ${{\Re }^{2}}$ está contido em ${{\Re }^{4}}$ e ${{\Re }^{3}}$ está contido em ${{\Re }^{7}}$. Ou seja, podemos encontrar subconjuntos W dentro de um espaço vetorial V que sejam espaços vetoriais menores em relação às operações de V. Nessa situação, chamamos W de subespaço vetorial de V (BOLDRINI, 1980; KOLMAN, 1999).

Um exemplo simples que temos de um subespaço vetorial é dado por Boldrini (1980): uma reta que passa pela origem do plano cartesiano. Ou seja, temos o espaço $V={{\Re }^{2}}$ e o subespaço W, que é a reta que passa pela origem do plano cartesiano. Mas por que essa reta é um subespaço?

Veja que funciona como um pequeno espaço vetorial contido dentro de V: se somarmos dois vetores contidos em W, o vetor resultante ainda estará em W; se multiplicarmos algum vetor de W por um escalar, o vetor resultante também estará dentro de W. Ou seja, W é fechado para a adição e para a multiplicação por escalar. A Figura 3.7 irá ajudar a visualização do que foi dito:

Vamos, então, definir, de acordo com Boldrini (1980), o que é um subespaço vetorial.

Definição 3: Sendo V um espaço vetorial, o subconjunto W contido em V de será um subespaço de V se:

Para quaisquer vetores u, v ∈ W, tem-se que u + v ∈ W.
Para qualquer a ∈ ${{\Re}}$ e u ∈ W, tem-se que au ∈ W.

Boldrini (1980) ainda diz que as duas condições anteriores são o suficiente para garantir que, ao operarmos em W, iremos obter apenas vetores dentro de W. Também não precisamos provar os demais oito axiomas de um espaço vetorial, pois sua prova já está contida na validade de V, que contém W.

Kolman (1999) também nos alerta para o fato de todos os subespaços vetoriais precisarem conter o vetor nulo. Disso, temos que todos os espaços vetoriais irão admitir sempre ao menos dois subespaços vetoriais: um conjunto formado apenas pelo vetor nulo e o próprio espaço vetorial. Boldrini (1980) chama esses dois subespaços vetoriais que sempre existem de subespaços triviais. No entanto, deve-se tomar o cuidado de não pensar que todo conjunto que apresenta o vetor nulo será um subespaço.

Exemplo 1.10: Considere V = M(n × n) como o conjunto de todas as matrizes quadradas. O subconjunto W constituído de todas as matrizes triangulares inferiores é um subespaço de V?

Solução

Para checarmos isso, caro(a) aluno(a), devemos verificar os dois axiomas da Definição 3. Uma matriz triangular inferior é representada genericamente por:

Logo, veja que, se somarmos uma matriz triangular inferior A com outra matriz triangular inferior B, a matriz resultante C = A + B ainda será uma matriz triangular inferior, pois sempre teremos que todos os elementos acima da diagonal principal serão nulos. Com isso, o axioma a) está provado.

Se realizarmos a multiplicação por escalar de uma matriz desse tipo, também teremos uma matriz triangular inferior como resultado, pois qualquer escalar multiplicado por zero é igual a zero. Então, o axioma b) está provado. Logo, podemos afirmar que o W é um subespaço de V.

Exemplo 1.11: Uma situação interessante sobre subespaços vetoriais ocorre quando encontramos o conjunto solução de um sistema linear homogêneo W, que pode ser considerada um subespaço de ${{\Re }^{n}}$. Verifique isso considerando um sistema linear homogêneo genérico:

Solução

Um sistema linear homogêneo genérico é mostrado abaixo, sendo A a matriz m × n dos coeficientes, X a matriz das incógnitas e 0 é a matriz dos termos independentes, cujos elementos são todos nulos:

\[AX = 0\]

Veja que o conjunto de todas as matrizes incógnitas para esse caso nada mais é do que ${{\Re }^{n}}$, ou seja, esse é o nosso espaço vetorial. Agora, precisamos verificar se W prova os axiomas dados na Definição 3. Seja x, y ∈ W, ou seja, os dois vetores são solução do sistema. Isso implica que Ax = 0 e Ay = 0. Vejamos agora o que temos de A(x + y):

\[A(x+y) = Ax + Ay = 0 + 0 = 0\]

Assim, comprovamos que W está fechado para a soma. Vejamos agora para o caso de multiplicação por escalar; seja c ∈ R, então:

\[A(cx) = c(Ax) =c ⋅ 0 = 0\]

Ou seja, cx é uma solução também, ou seja, W está fechado para a multiplicação por escalar também. Logo, podemos afirmar que o W é um subespaço de ${{\Re }^{n}}$. Esse subespaço é, geralmente, chamado de espaço solução sistema linear homogêneo ou núcleo da matriz A, como nos diz Kolman (1999).

Finalizando o assunto de subespaços vetoriais, Boldrini (1980) enuncia dois teoremas interessantes:

Teorema 2 - Intersecção de subespaços: Se ${{W}_{1}}$ e ${{W}_{2}}$ são subespaços de um espaço vetorial V, então, a intersecção entre ${{W}_{1}}$ e ${{W}_{2}}$, representada por ${{W}_{1}}~\cap ~{{W}_{2}}$, também será um subespaço de V.

Teorema 3 - Soma de subespaços: Se ${{W}_{1}}$ e ${{W}_{2}}$ são subespaços de um espaço vetorial V, então o conjunto

\[{{W}_{1}}+{{W}_{2}}=\{v\in V;v=w1+w, w1\in {{W}_{1}} e w2\in {{W}_{2}}\}\]

também será subespaço de V.

Atividade

Os espaços e subespaços vetoriais são muito importantes para nosso trabalho com vetores, sendo interessante que tenhamos um bom conhecimento sobre suas propriedades. Desse modo, analise as seguintes alternativas e assinale a correta.

Se V é um espaço vetorial e o vetor u ∈ V, na multiplicação por escalar a ⋅ u = 0 só é possível se u for um vetor nulo.

Isso também pode ocorrer caso o escalar a seja igual a zero também.

Se $V={{\Re }^{2}}$, uma reta que não passe pela origem do plano cartesiano não será um subespaço W de V.

Se tal reta não passa pela origem, o vetor nulo não pertencerá à W. Logo, essa reta não será um subespaço de V.

É possível que, se v + u = v + z, u ≠ z, caso u, v, z ∈ V.

Isso não é possível. Se os vetores pertencem a V, eles devem ser fechados na soma. Logo, a igualdade acima só é possível se u = z.

O conjunto solução de sistemas lineares não homogêneos pode ser considerado um subespaço.

Nem sempre a soma de dois vetores solução de um sistema linear não homogêneo resultará num vetor solução. Logo, não temos um subespaço.

Sendo Z o conjunto dos números inteiros, podemos dizer que Z é um espaço vetorial.

Se tal conjunto engloba apenas os números inteiros, podemos afirmar que não será um espaço vetorial por um simples motivo: a multiplicação por escalar pode ser feita com não inteiros, o que resultaria num elemento não pertencente à Z.

Dependência e independência linear

Agora que sabemos o que é um espaço vetorial, você deve estar imaginando a infinidade de vetores que um espaço pode apresentar. No entanto, um número tão grande de vetores para descrever um conjunto não é algo tão prático. Logo, é melhor que sejamos capazes de definir um espaço vetorial com o mínimo possível de vetores.

A identificação de quais vetores são realmente úteis para se descrever um espaço vetorial é feita verificando se um dado vetor pode ser escrito como uma combinação de outros vetores, ou seja, se um dado vetor é uma combinação linear de outros vetores do espaço vetorial. Tais vetores são desnecessários para a definição de um espaço vetorial. Veremos como podemos identificar quais vetores são indispensáveis para descrevermos um espaço vetorial.

Combinação linear

Como já vimos ao estudar vetores, podemos sempre encontrar novos vetores a partir de outros vetores conhecidos. Agora, veremos isso em espaços vetoriais. Boldrini (1980) e Kolman (1999) definem essa forma de obtenção de novos vetores como combinação linear:

Definição 4: Considere o espaço vetorial V. Sejam v_1, v_2, v_3,...,v_n vetores pertencentes a tal espaço vetorial e ${{a}_{1}},{{a}_{2}},{{a}_{3}},...,{{a}_{n}}$ números reais. Então, um vetor

\[v={{a}_{1}}v1+{{a}_{2}}v2+{{a}_{3}}v3 … +{{a}_{n}}vn\]

também será elemento de V, sendo esse vetor v uma combinação linear de v_1, v_2, v_3,...,v_n. Note que, se pegarmos o conjunto W que contém todas as combinações lineares do espaço vetorial V, teremos um subespaço vetorial.

Exemplo 1.12: Verifique se o vetor v = (1,2,4) é uma combinação linear dos vetores v_1 = (1,1,2), v_2 = (2,0,1) e v_3=(1,1,0).

Solução

Para realizarmos tal verificação, consideremos os escalares a_1, a_2 e a_3. Precisamos verificar se existem números reais que satisfaçam

\[v = {{a}_{1}}v1+{{a}_{2}}v2+{{a}_{3}}v3\]

Substituindo os vetores:

\[\left( 1,1,5 \right)={{a}_{1}}\left( 1,1,2 \right)+{{a}_{2}}\left( 2,0,1 \right)+{{a}_{3}}\left( 1,1,0 \right)\]

Se realizarmos as operações anteriores, conseguimos encontrar o seguinte sistema linear:

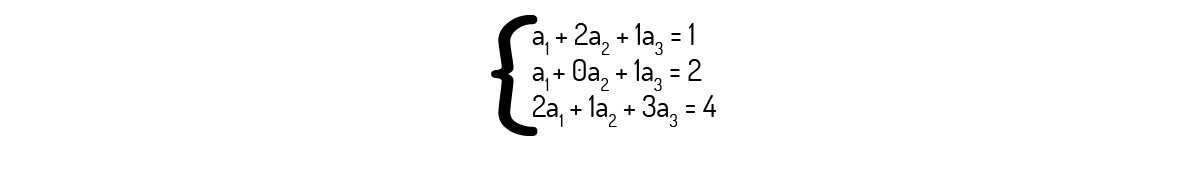
Resolvendo tal sistema, você deve encontrar a seguinte solução: ${{a}_{1}}=9/4$, ${{a}_{2}}=-1/2$ e ${{a}_{3}}=-1/4$. Como encontramos valores reais para os escalares, podemos afirmar que v é uma combinação linear de v_1, v_2 e v_3 na seguinte forma:

\[v=\frac{9}{4}v1-\frac{1}{2}v2-\frac{1}{4}v3\]

Independência linear

Em seus estudos de Álgebra Linear, é fundamental ser capaz de identificar se um vetor é uma combinação linear de outros vetores. Como adiantado no início desse tópico, ao estudarmos espaços vetoriais, é possível visualizar espaços vetoriais que irão conter uma infinidade de vetores. No entanto, os vetores que são combinação linear são vistos como supérfluos para a descrição de tal espaço. Iremos, então, mostrar que, em sua maioria, os espaços vetoriais irão apresentar um número finito de vetores que podem descrever completamente o espaço vetorial (KOLMAN, 1999).

Para isso, precisamos definir dependência e independência linear. Boldrini (1980) define tais termos como:

Definição 5: Considere o espaço vetorial V para o qual v_1, v_2, ...,v_n sejam vetores pertencentes a $V$. Um conjunto $v1,v2,...,vn$ será dito linearmente independente (ou LI) se a seguinte equação

\[{{a}_{1}}v_1 + {{a}_{2}} v_2 +...+{{a}_{n}}v_n = 0\]

implica que ${{a}_{1}}={{a}_{2}}=...={{a}_{n}}=0$. Caso exista um único ${{a}_{i}}\ne 0$, então o conjunto $\{$v_1, v_2, ..., v_n\) é linearmente dependente (ou LD).

Agora que sabemos identificar um conjunto de vetores como LD ou LI, podemos verificar se um pequeno conjunto de vetores é capaz de gerar um espaço vetorial. Ou seja, dizemos que um conjunto de vetores S = {v_1, v_2, ..., v_n} irá gerar um espaço vetorial V se todos os demais vetores desse espaço forem uma combinação linear dos vetores desse conjunto. Assim, conforme explica Kolman (1999), dizemos que S gera V.

O procedimento necessário para identificarmos se um conjunto de vetores S gera um espaço vetorial V é constituído de dois passos, de acordo com Kolman (1999):

escolha um vetor arbitrário v de V;
verifique se o vetor arbitrário escolhido em a) é uma combinação linear dos vetores de S; caso positivo, S gera V; caso negativo, S não gera o espaço V.

Vejamos na prática como isso é feito.

Exemplo 1.13: Considerando o espaço vetorial $V={{\Re }^{3}}$, verifique se o conjunto $S=\{v1=\left( 1,3,2 \right),v2=\left( 0,2,1 \right)v3=\left( 3,1,3 \right)\}$ .gera tal espaço vetorial

Solução

Para averiguarmos se o conjunto dado gera o espaço vetorial V em questão, devemos verificar os dois passos citados anteriormente. Consideremos o vetor arbitrário v = (a, b, c), onde a, b e c são números reais. Vejamos se existem constantes ${{a}_{1}}$, ${{a}_{2}}$ e ${{a}_{3}}$ tal que:

\[{{a}_{1}} v_1 +{{a}_{2}} v_2 + {{a}_{3}}v_3=v\]

Substituindo os vetores de S:

\[{{a}_{1}}\left( 1,3,2 \right)+{{a}_{2}}\left( 0,2,1 \right)+{{a}_{3}}\left( 3,1,3 \right)=\left( a,b,c \right)\]

De onde encontramos o seguinte sistema:

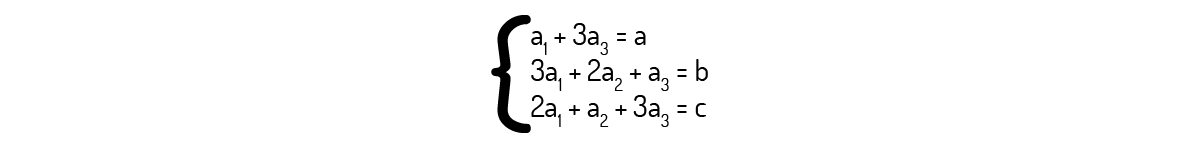
Resolvendo esse sistema, você deverá encontrar:

\[{{a}_{1}}=\frac{5a+3b-6c}{2}\]

\[{{a}_{2}}=-\frac{7a+3b-8c}{2}\]

\[{{a}_{3}}=-\frac{a+b-2c}{2}\]

Veja que conseguimos uma solução para qualquer valor de a, b e c. Logo, podemos concluir que S gera V.

Atividade

A capacidade de determinar se um conjunto de vetores é capaz de gerar um espaço vetorial é importante para que sejamos capazes de determinar as propriedades desse espaço. Focando na geração de espaços vetoriais, analise as alternativas a seguir e assinale qual dos conjuntos de vetores dados se mostra incapaz de gerar ${{\Re }^{2}}$.

$v_1 = \left( 0,0 \right)$ e $v_2 = \left(0,1 \right)$.

Para averiguarmos se o conjunto dado gera o espaço vetorial em questão, consideremos o vetor arbitrário v=(a,b), onde a e b são números reais. Vejamos se existem constantes $a_{1}$ e $a_{2}$ tal que:

$a_1v_1+a_2v_2=v$

Substituindo os vetores:

${{a}_{1}}\left( 0,0 \right)+{{a}_{2}}\left( 0,1 \right)=\left( a,b \right)$

De onde encontramos o seguinte sistema:

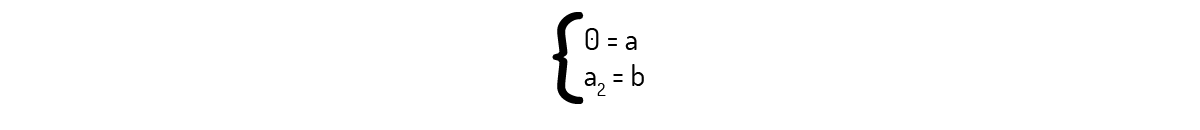
Como a pode ser qualquer real, temos uma impossibilidade no sistema acima, que força a = 0. Logo, o conjunto de vetores não gera ${{\Re }^{2}}$.

$v_1=\left(1,2 \right) e v_2=\left( -1,1 \right)$

$a_1v_1+a_2v_2 = v$

Substituindo os vetores:

${{a}_{1}}\left( 1,2 \right)+{{a}_{2}}\left( -1,1 \right)=\left( a,b \right)$

De onde encontramos o seguinte sistema:

Resolvendo esse sistema, você deverá encontrar:

${{a}_{1}}=\frac{a+b}{3}$ e ${{a}_{2}}=-\frac{2a-b}{3}$

Veja que conseguimos uma solução para qualquer valor de a e b. Logo, esses vetores geram ${{\Re }^{2}}$.

$v_1=\left( 3,1 \right)$ e $v_2 = \left( -2,2 \right)$

$a_1v_1+a_2v_2 = v$

Substituindo os vetores:

${{a}_{1}}\left( 3,1 \right)+{{a}_{2}}\left( -2,2 \right)=\left( a,b \right)$

De onde encontramos o seguinte sistema:

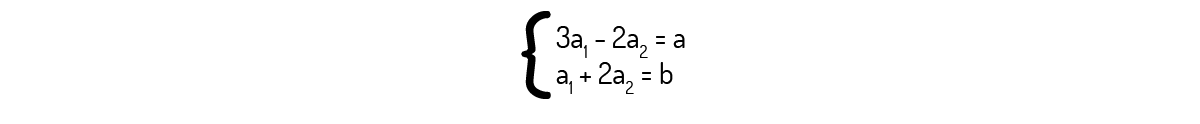
Resolvendo esse sistema, você deverá encontrar:

${{a}_{1}}=\frac{3a+3b}{12}$ e ${{a}_{2}}=-\frac{a-3b}{8}$

Veja que conseguimos uma solução para qualquer valor de a e b. Logo, esses vetores geram ${{\Re }^{2}}$.

$v_1 = \left( -1,-2 \right) e v_2 = \left(4,2 \right)$

$a_1v_1+a_2v_2=v$

Substituindo os vetores:

${{a}_{1}}\left( -1,2 \right)+{{a}_{2}}\left( -1,1 \right)=\left( a,b \right)$

De onde encontramos o seguinte sistema:

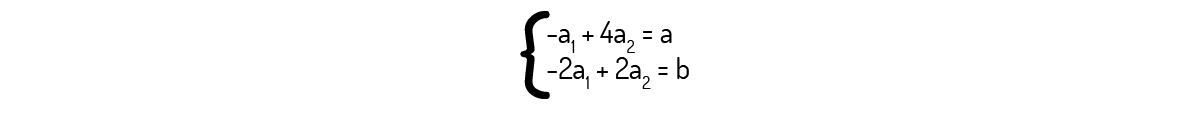
Resolvendo esse sistema, você deverá encontrar:

${{a}_{1}}=\frac{a-2b}{3}$ e ${{a}_{2}}=\frac{2a-b}{6}$

Veja que conseguimos uma solução para qualquer valor de a e b. Logo, esses vetores geram ${{\Re }^{2}}$.

$v_1=\left(0,1 \right) e v_2 = \left( 1,0 \right)$

$a_1v_1+a_2v_2=v$

Substituindo os vetores:

${{a}_{1}}\left( 0,1 \right)+{{a}_{2}}\left( 1,0 \right)=\left( a,b \right)$

Encontramos diretamente

${{a}_{1}}=b$ e ${{a}_{2}}=a$

Veja que conseguimos uma solução para qualquer valor de a e b. Logo, esses vetores geram ${{\Re }^{2}}$.

Base de um espaço vetorial

Sabemos que um espaço vetorial V pode ser descrito tomando como base um número finito de vetores dentre os diversos vetores que compõem um espaço vetorial. Chegou o momento de determinarmos agora um conjunto mínimo de vetores de V que possam gerar todos os demais vetores de V (BOLDRINI, 1980).

Kolman (1999) chama esse conjunto mínimo de vetores que geram um espaço vetorial V de base de um espaço vetorial. Boldrini (1980) e Kolman (1999) definem uma base como:

Definição 6: Um conjunto de vetores ${v_1, v_2, ..., v_n}$ pertencentes ao espaço vetorial V será uma base desse espaço vetorial se todos os vetores ${v_1, v_2, ..., v_n}$ forem LI e se V for completamente gerado por ${v_1, v_2, ..., v_n}$.

Kolman (1999) destaca que, para que os vetores que compõem o conjunto ${v_1, v_2, ..., v_n}$ formem uma base de V, é necessário que tais vetores sejam distintos e não nulos.

Um dos exemplos mais simples que temos de base nos é dado por Boldrini (1980), que é o conjunto formado por $v_1 = (1,0)$ e $v_2 = (0,1)$ para o ${\Re }$. Esse par ${v_1,v_2}$ também é conhecido como base canônica ou base natural para o $R^2$. Bases canônicas são as bases mais intuitivas para cada espaço vetorial.

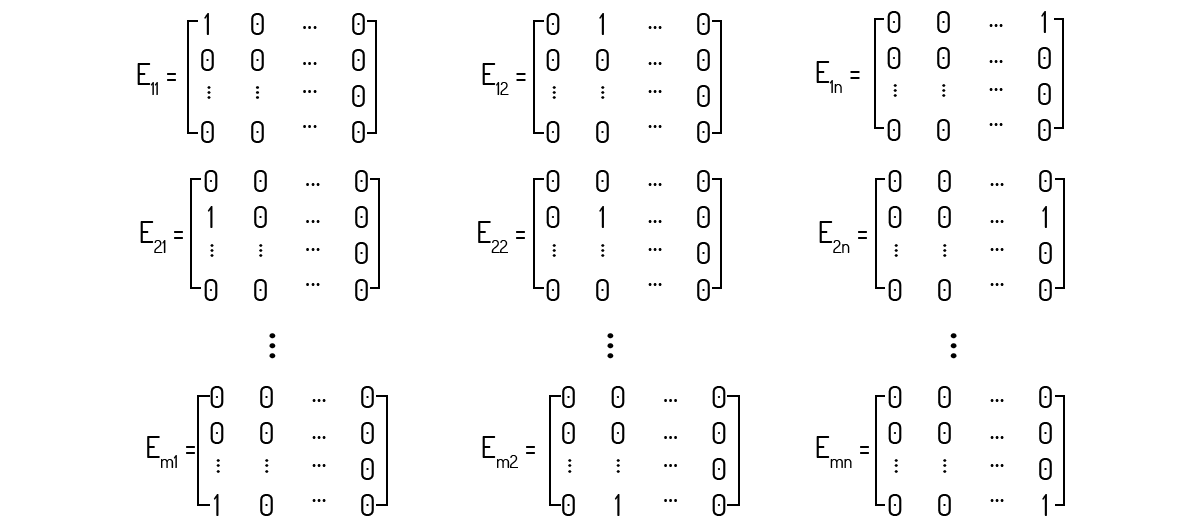
Outros exemplos de bases canônicas de espaços vetoriais muito comuns são dados por Poole (2004), por exemplo, o conjunto ${1, x, x^2, x^3,. .., x^n }$ para o espaço $P_n$ dos polinômios de grau n. Já o conjunto

\[E={E_{11}, ...,E_{1n}, E_{21}, E_{2n}, ...E_{m1}, ...E_{mn}}\]

é a base canônica para o conjunto das matrizes de ordem m×n. Os vetores dessa base são encontrados da seguinte maneira:

Boldrini (1980) destaca um outro ponto muito importante sobre bases: existem espaços vetoriais que não apresentam uma base finita. Esse caso é muito comum de ocorrer no espaço de funções. Logo, situações como essa exigem que tenhamos um conjunto infinito de vetores para gerar o espaço vetorial. No entanto, o presente material irá lidar apenas com bases finitas.

Boldrini (1980) e Kolman (1999) também enunciam um conjunto de teoremas que são úteis para obtermos as propriedades da base de um espaço vetorial.

Teorema 4: Se o conjunto de vetores ${v_1,v_2,...,v_n}$ for não nulo e gerar um espaço vetorial V, então podemos extrair uma base para V desse conjunto de vetores

Teorema 5: Se um espaço vetorial V apresenta como base um conjunto finito de n vetores, qualquer conjunto que apresente mais do que n vetores será LD. Ou seja, o máximo de vetores que essa base finita suporta para ser LI é n.

Teorema 6: Qualquer conjunto de vetores LI em um espaço vetorial V pode ser completado para gerar uma base V.

Do Teorema 5, Boldrini (1980) mostra uma conclusão interessante: qualquer base de um espaço vetorial deve sempre apresentar o mesmo número de vetores. Tal número é chamado de dimensão do espaço V, sendo representado por dim V. Logo, se soubermos a dimensão de um espaço vetorial, podemos determinar quantos vetores são necessários para gerar uma base para tal espaço.

Boldrini (1980) prova isso da seguinte forma: sejam os conjuntos $v={v_1, v_2, ..., v_n}$ e $u = {u_1, u_2, ..., u_m}$ duas bases distintas de V. Como v gera V e os vetores do conjunto u devem ser LI para ser uma base de V, concluímos pelo Teorema 5 que m ≤ n. Analisando de outra forma, u gera V e os vetores do conjunto v devem ser LI para ser uma base de V, o que nos leva, pelo que nos diz o Teorema 5, a n ≤ m. Dessas duas análises, chegamos a um caso limite: a única forma que temos dessas duas condições serem reais é que m = n.

Mudança de base

Várias áreas das ciências exatas e tecnológicas apresentam problemas nos quais um referencial adequado significa muito menos trabalho na hora de serem solucionados. Por exemplo, ao analisarmos um reator cilíndrico, é muito mais simples usarmos um sistema que seja descrito com características mais comuns de um cilindro.

Mas como fazemos para escolher esse novo referencial? Após escolhermos o novo referencial, como podemos relacionar as coordenadas dos pontos no referencial original com as coordenadas do novo referencial?

Quanto à primeira pergunta feita acima, Boldrini (1980) diz que sua resposta é bem complicada. A escolha de um novo referencial, devido à sua complexidade, é abordada por outras disciplinas, não sendo abordada nesta. Já a segunda pergunta é aquela em que iremos nos focar em responder agora.

Até o momento, não nos preocupamos com a ordem dos vetores em uma base: o que vimos até agora é que um espaço vetorial V de dimensão n irá apresentar uma base S com n vetores, como nos diz Kolman (1999). Se o conjunto $S = {v_1, v_2, ...,v_n}$ é uma base ordenada para V, então o conjunto $S' = {v_2, v_1, ..., v_n}$ é uma base ordenada diferente para V. Ou seja, tal qual Hoffman e Kunze (1976):

Definição 7: Uma base ordenada de um espaço vetorial V nada mais é do que um conjunto com coordenação fixa de seus vetores. Logo, é conveniente representarmos os elementos vi de uma base ordenada com i crescente.

Logo, considerando a base ordenada $S = {v_1, v_2, ..., v_n}$ como a geradora de um espaço vetorial V, qualquer vetor desse espaço vetorial poderá ser escrito como

\[v = a_1v_1 + a_2v_2 + a_3v_3 … + a_nv_n\]

onde a_i indicam números reais. Como afirma Kolman (1999), podemos nos referir a esse vetor genérico numa forma matricial:

sendo essa matriz chamada de vetor de coordenadas de v em relação à base ordenada S. Essa matriz é única, sendo seus elementos, como podemos ver, as coordenadas de v em relação à S.

Exemplo 1.14: Considerando S a base canônica para ${{\Re }^{3}}$, calcule o vetor de coordenadas do vetor v = (-2,2,3) em relação à S.

Solução

A base canônica de ${{\Re }^{3}}$ é composta pelos vetores $v_1 = (1,0,0)$, $v_2 = (0,1,0)$ e $v_3 = (0,0,1)$. Logo, para encontrarmos o vetor indicado, precisamos encontrar os escalares $a_1$, $a_2$ e $a_3$ tal que:

\[a_1v_1 + a_2v_2 + a_3v_3 = v\]

Substituindo os vetores de S:

\[a_1 (1,0,0) + a_2 (0,1,0) + a_3 (0,0,1) = (-2,2,3)\]

Dada a simplicidade da base canônica, conseguimos identificar que $a_1 = -2$, $a_2 = 2$ e $a_3 = 3$. Logo:

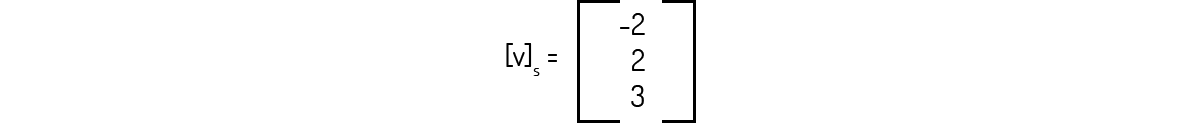
Exemplo 1.15: Seja o espaço vetorial P_1 composto por todos os polinômios de ordem igual ou menor a 1. Se $S = {v_1,v_2}$ e $T = {w_1,w_2}$, onde $v_1 = (t)$, $v_2 = (1)$, $w_1 = (t + 1)$ e $w_2 = (t - 1)$, para o vetor $v = 3t + 4$ calcule $[v]_S$ e $[v]_T$.

Solução

Encontrar $[v]_S$ é relativamente simples, visto que S é a base canônica de $P_1$. Precisamos encontrar os escalares a_1 e a_2 tal que:

\[a_1v1+a_2v2=v\]

Conseguimos identificar rapidamente que $a_1 = 3$ e $a_2 = 4$. Assim:

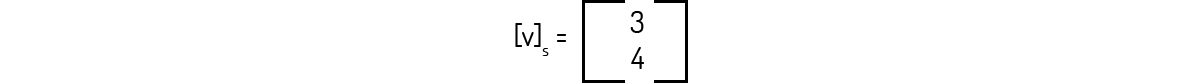
Agora, para encontrar $[v]_T$ precisaremos realizar um pouco mais de cálculos, pois precisamos escrever v como uma combinação linear de $w_1$ e $w_2$. Ou seja:

\[b_1w_1 + b_2w_2 = v → b_1 (t + 1) + b_2 (t - 1) = 3t + 4\]

Reescrevendo a relação acima:

\[b_1 t + b_1 + b_2 t - b_2 = 3t + 4\]

\[t(b_1 + b_1 ) + (b_1 - b_2 ) = 3t + 4\]

Podemos concluir que $(b_1 + b_1 ) = 3 e (b_1 - b_2 ) = 4$. Ou seja, temos em nossas mãos um sistema linear:

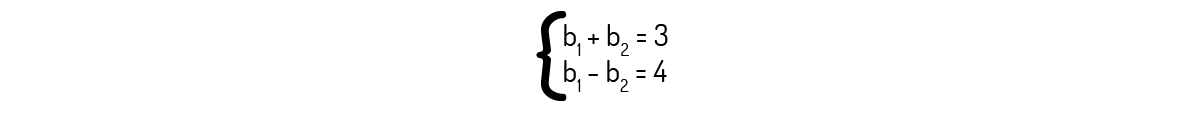
Resolvendo esse sistema, você deve encontrar que $b_1=7/2$ e $b_1=-1/2$. Então:

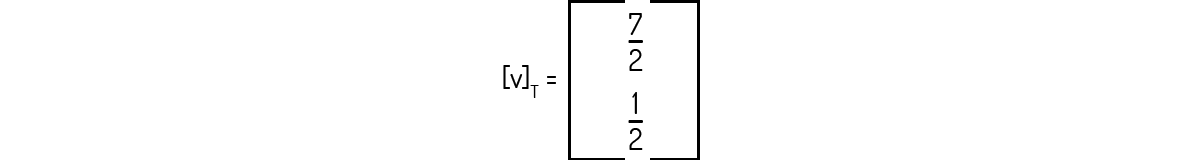
Como vimos com o Exemplo 1.15, para um mesmo espaço vetorial podemos encontrar dois vetores de coordenadas de um vetor v em relação a diferentes bases ordenadas - no caso do exemplo, encontramos em relação à S e a T.

Kolman (1999) também cita que os vetores de coordenadas dos elementos de um espaço vetorial têm um comportamento algébrico semelhante a vetores. Com isso, temos que, sendo S uma base para um espaço V cuja dimensão é n, os vetores v e w pertencentes à V e o escalar c:

\[[v + w]_S = [v]_S + [w]_S~~~~~~~~~(13)\]

\[[cv]_S=c[v]_S~~~~~~~~~(14)\]

O que nos leva ao fato de que o vetor coordenada de uma soma de dois vetores é igual à soma dos vetores de coordenadas de cada um. As relações (13) e (14) ainda podem ser tratadas de forma genérica:

\[[c_1v~_1+c_2v_2+...+c_nv_n]_S=c_1 [v_1]_S+c_2 [v_2]_S+...c_nv_n~~~~~~(15)\]

Partindo disso, considere $S={v_1, v_2, ..., v_n}$ e $T = {w_1, w_2 ..., w_n}$ como bases para um espaço vetorial V, cuja dimensão seja n. Um vetor v ∈ Virá apresentar vetores de coordenadas $[v]_S$ e $[v]_T$ e, segundo Kolman (1999), podemos analisar a relação entre esses dois vetores de coordenadas.

Para analisarmos essa relação, Kolman (1999) pede que consideremos um vetor arbitrário v∈V. Sabemos que esse vetor pode ser representado por

\[v = a_1w_1 + a_2w_2 + ... + a_nw_n~~~~~~~~~(16)\]

o que nos leva a

Como S também é uma base para V, então:

\[[v]_S = [a_1w_1 + a_2w_2 + ... + a_nw_n]_S\]

Podemos trabalhar a relação acima com as Equações (13) a (15) para chegarmos a:

\[v=[a_1w_1]_S + [a_2w_2]_S + ... + [a_nw_n]_S\]

\[v = a_1 [w_1]_S + a_2 [w_2]_S + ... + a_n [w_n]_S\]

O vetor de coordenadas w_j em relação à S pode ser escrito como

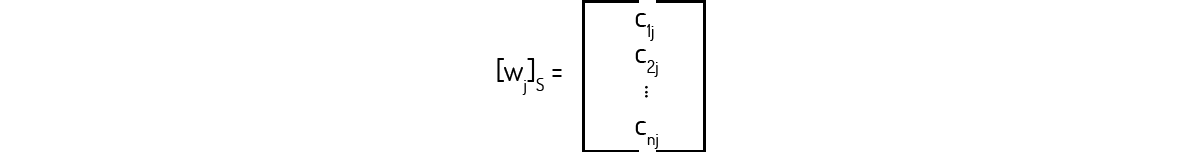
Então:

ou:

\[[v]_S = P_{S ← T} [v]_T~~~~~~~~~(17)\]

sendo

A matriz $P_{S ← T}$ é chamada de matriz de mudança de uma base T para uma base S, segundo Kolman (1999). Para encontrarmos essa matriz, precisamos seguir um procedimento de duas etapas. Para vermos tais etapas, consideremos $S = {v_1, v_2, ..., v_n}$ e $T = {w_1, w_2 ..., w_n}$ como bases para um espaço vetorial V. A primeira consiste em encontrarmos o vetor de coordenadas $w_j$, com j variando de 1 a n em relação à base S, ou seja, devemos escrever wj como uma combinação linear de vetores em S:

\[a_{1j}v_1 + a_{2j}v_2 + ... + a_{nj}v_n = w_j\]

Resolvemos esse problema pela transformação da matriz aumentada do sistema em sua forma escada reduzida. A matriz de mudança $P_{(S←T)}$ de uma base T para S é encontrada pegando $[wj]_S$ como a j-ésima coluna da matriz de mudança. Vejamos um exemplos desse método.

Exemplo 1.16: Seja o espaço vetorial ${{\Re }^{3}}$. Se $S = {v_1, v_2, v_3}$ e $T = {w_1, w_2, w_3}$, onde $v_1 = (1,0,2)$, $v_2 = (0,2,1)$, $v_3 = (1,1,1)$, $w_1 = (12,12,6)$, $w_2 = (12,3,6)$ e $w_3 = (9,9,3)$, calcule a matriz mudança de base da base T para a base S.

Solução

Para que encontremos $P_{S←T}$, primeiramente devemos encontrar os escalares $a_1$, $a_2$, $a_3$, $b_1$, $b_2$, $b_3$, $c_1$, $c_2$ e $c_3$ tal que:

\[a_1v_1+a_2v_2+a_3v_3=w_1\]

\[b_1v_1 + b_2v_2 + b_3v_3 = w_2\]

\[c_1v_1 + c_2v_2 + c_3v_3 = w_3\]

Cada uma das equações vetoriais acima irá nos levar a um sistema linear que apresentará três equações e três incógnitas da seguinte forma:

Destes três sistemas, encontramos as seguintes matrizes aumentadas:

Devemos resolver os três sistemas acima, encontrando a forma escada de cada um deles. Seria algo muito trabalhoso de ser feito, mas note que a matriz dos coeficientes de cada um dos sistemas acima é igual. Com isso, podemos combinar todos as matrizes aumentadas dos três sistemas, formando uma matriz dita particionada:

Um sistema representado por esse tipo de matriz pode ser resolvido por escalonamento normalmente. Basta realizarmos as operações elementares, buscando deixar a matriz dos coeficientes na forma escada e, assim, encontrando a forma escada da matriz acima:

Se você resolver individualmente cada um dos sistemas, deverá encontrar as mesmas respostas mostradas na matriz particionada acima. Com tal matriz, encontramos a matriz mudança de base da base T para a base S utilizando os vetores solução que encontramos:

Atividade

O conhecimento sobre bases vetoriais é imprescindível para poupar o estudante de trabalhar com enormes conjuntos vetoriais, visto que uma base vetorial indica o mínimo de vetores necessários para caracterizar um espaço vetorial. Focando nesse assunto, analise as seguintes alternativas e assinale a correta.

Se ${{e}_{i}}$ é a $i-$ésima coluna de uma matriz identidade $n\times n$, o conjunto $S=\left\{ {{e}_{1}},~{{e}_{2}},...{{e}_{n}} \right\}$, então $S$ não é uma base de ${{\Re }^{n}}$.

Não só S é uma base, como é a base canônica de ${{\Re }^{n}}$.

O conjunto $S=\left\{ \left( 1,0 \right),\left( 0,1 \right),\left( 2,1 \right) \right\}$ é uma base de ${{\Re }^{2}}$.

Claramente vemos que o terceiro vetor de $S$ é uma combinação linear dos dois primeiros: $\left( 2,1 \right)=2\left( 1,0 \right)+\left( 0,1 \right)$. Logo, tal conjunto não é uma base porque é um conjunto LD.

O conjunto $S=\left\{ \left( 1,0,1 \right),\left( 2,0,0 \right) \right\}$ não é uma base de ${{\Re }^{3}}$.

Alternativa correta. Tomando um vetor $\left( a,b,c \right)$ aleatório de ${{\Re }^{3}}$ e dois escalares $\alpha $ e $\beta $:

$\left( a,b,c \right)=\alpha \left( 1,0,1 \right)+\beta \left( 2,0,0 \right)$

Encontramos o seguinte sistema:

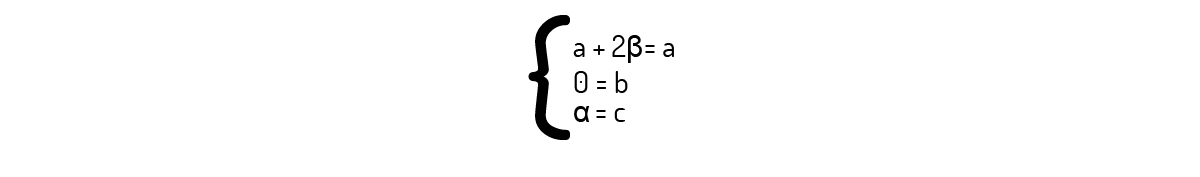
Dele, vemos que existe uma restrição na segunda equação, que faz com que tais vetores geram apenas vetores na forma $\left( a,0,c \right)$ e não todo ${{\Re }^{3}}$.

A base canônica do conjunto ${{P}_{n}}$ apresenta dimensão $n$.

Como os polinômios apresentam um termo real que não multiplica a variável, então a base do conjunto de polinômios ${{P}_{n}}$ deve ter dimensão $n+1$.

O conjunto $S=\left\{ \left( 1,0,0 \right),\left( 1,0,1 \right),\left( 0,0,1 \right) \right\}$ é uma base de ${{\Re }^{2}}$.

Claramente vemos que o terceiro vetor de $S$ é uma combinação linear dos dois primeiros: $\left( 0,0,1 \right)=\left( 1,0,1 \right)-\left( 1,0,0 \right)$. Logo, tal conjunto não é uma base porque é um conjunto LD.

Espaços Vetoriais

Introdução

Vetores

Definindo vetores

Operações com vetores

Vetores no espaço

Atividade

REFLITA

Espaços Vetoriais

Definindo os espaços vetoriais

Subespaços vetoriais

Atividade

FIQUE POR DENTRO

Dependência e independência linear

Combinação linear

Independência linear

Atividade

Base de um espaço vetorial

Mudança de base

Atividade

indicação de leitura

indicação de leitura