Visando fixar melhor os tipos de matrizes que você usará durante os estudos de álgebra, analise as alternativas abaixo e assinale aquela que se encontra correta.
Uma matriz diagonal também é uma matriz simétrica.
Uma matriz diagonal apresenta todos os elementos fora da diagonal principal iguais a zero. Já uma matriz simétrica é uma matriz quadrada onde os elementos \({{a}_{ij}}={{a}_{ji}}\). Logo, uma matriz diagonal é uma matriz simétrica.
A matriz A abaixo é uma matriz diagonal porque apresenta todos os elementos da diagonal principal com o mesmo valor.

Uma matriz diagonal apresenta todos os elementos fora da diagonal principal iguais a zero. O fato de todos os elementos da diagonal principal da matriz serem iguais não quer dizer nada especial.
Uma matriz triangular superior é uma matriz onde todos os elementos acima da diagonal principal são nulos.
Uma matriz triangular superior é aquela cujos elementos abaixo da diagonal principal são nulos.
A matriz A abaixo pode ser considerada uma matriz triangular inferior.
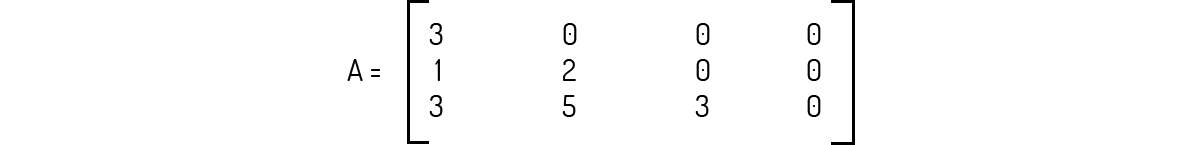
A matriz em questão não é uma matriz quadrada. Logo, ela não apresenta uma diagonal principal e não pode ser considerada uma matriz triangular superior.
A matriz A abaixo não pode ser considerada uma matriz triangular superior porque apresenta um elemento nulo acima da diagonal principal.

Apresentar um elemento nulo acima da diagonal principal não exclui uma matriz do tipo triangular superior. Para que uma matriz seja triangular superior, basta que ela seja quadrada e que apresente todos os elementos abaixo da diagonal principal como nulos.
Sejam as seguintes matrizes dadas abaixo. Nas alternativas a seguir são mostrados os resultados de algumas operações. Avalie tais resultados e assinale a alternativa correta.

A+B é uma operação possível e é igual a
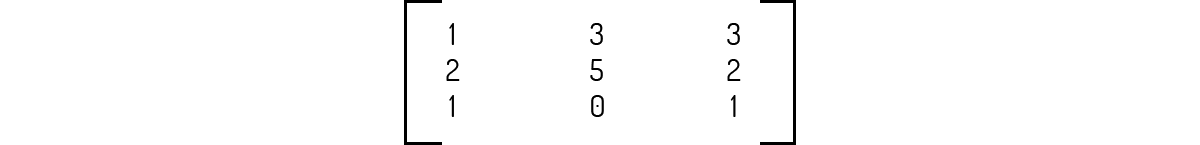
A adição de matrizes só é possível se as duas matrizes apresentarem o mesmo tamanho, o que não ocorre com A e B.
B-2D é uma operação possível e é igual a

Essa operação pode ser vista como a adição B+(-2)D. Realizando a multiplicação por escalar indicada:

Em seguida à adição dos elementos correspondentes, encontramos como resultado:

\(C+{{D}^{T}}\) é uma operação possível e é igual a
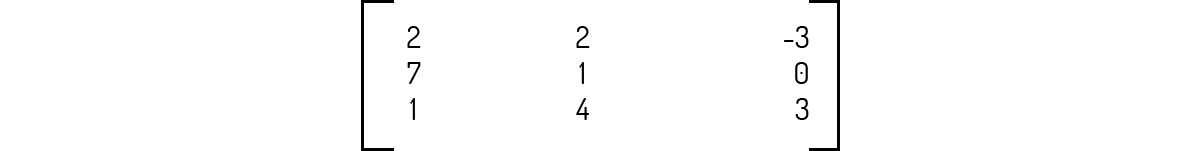
A matriz \({{D}^{T}}\) é uma matriz 2×3. Como a adição de matrizes só é possível se as duas matrizes apresentarem o mesmo tamanho, a operação destacada não é factível.
\(3{{A}^{T}}-{{C}^{T}}\) é uma operação possível e é igual a:

Avaliando cada uma das transpostas, você deve encontrar:

Agora, realizando a multiplicação por escalar em \({{A}^{T}}\) e, em seguida a subtração, você deve encontrar:

\(2{{B}^{T}}+2{{D}^{T}}\) é uma operação possível e é igual a:

Avaliando cada uma das transpostas, você deve encontrar:

Agora, realizando as multiplicações por escalar em \({{B}^{T}}\) e \({{D}^{T}}\) e, em seguida a adição, você deve encontrar:
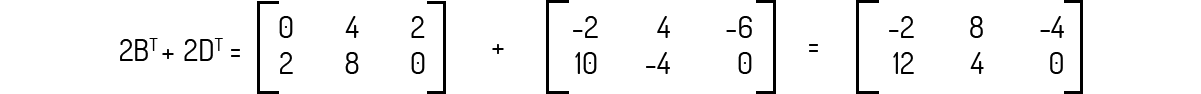
Sejam as seguintes matrizes apresentadas abaixo. Visando fixar a operação de multiplicação de matrizes, analise as seguintes alternativas e assinale a que for correta.

A multiplicação B⋅A é igual a:
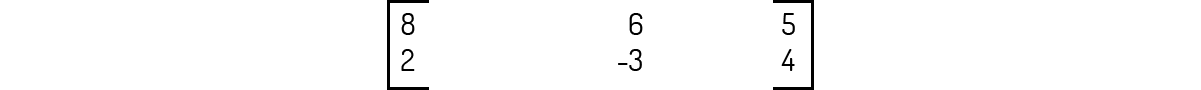
A multiplicação B⋅A não é possível porque a ordem de B é 3×3 e a ordem de A é 2×3. Como o número de colunas de B é diferente do número de linhas de A, essa multiplicação não é possível.
A multiplicação C⋅A é igual a:

A multiplicação C⋅A não é possível porque a ordem de C é 3×1 e a ordem de A é 2×3. Como o número de colunas de C é diferente do número de linhas de A, essa multiplicação não é possível.
A multiplicação B⋅C é igual a:

Como o tamanho de B é 3×3 e o tamanho de C é 3×1, então podemos prosseguir com a multiplicação informada, que será igual à:
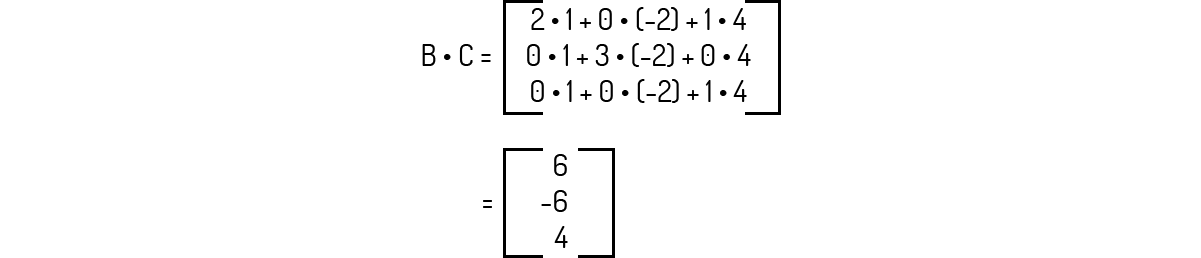
A multiplicação A⋅C é igual a:

Como o tamanho de A é 2×3 e o tamanho de C é 3×1, então podemos prosseguir com a multiplicação informada, que será igual à:
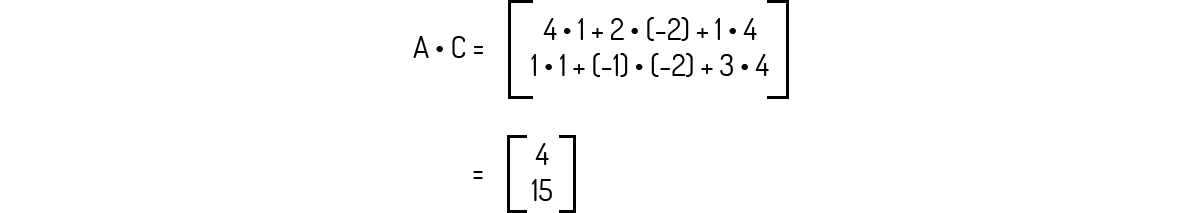
A multiplicação A⋅B é igual a:
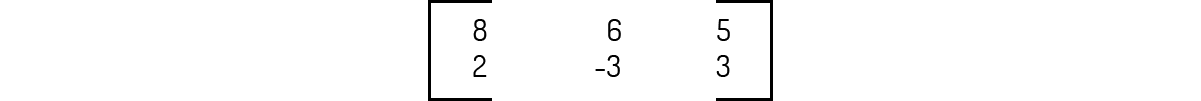
Como o tamanho de A é 2×3 e o tamanho de B é 3×3, então podemos prosseguir com a multiplicação informada, que será igual à:
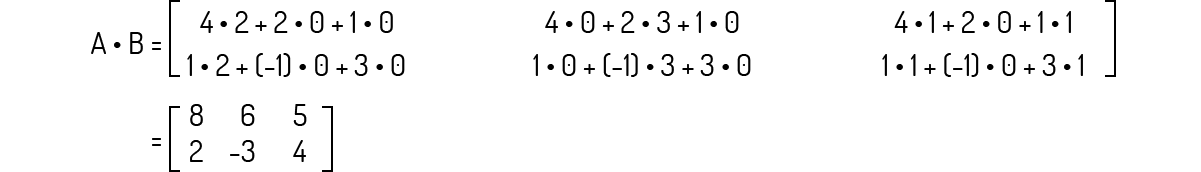
O tema determinantes tem uma teoria relativamente densa, de modo que é útil ter um bom domínio das bases deste assunto. Englobando todo o assunto de determinantes visto até o momento, analise as alternativas abaixo e assinale a correta.
Dadas as matrizes A e B abaixo, sabemos de antemão que o determinante delas serão iguais.
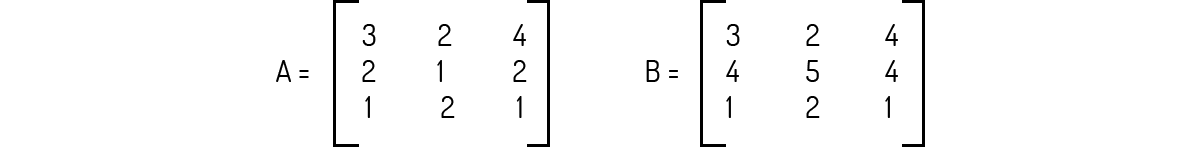
Pelo Teorema 6 sabemos disso, pois a linha 2 de B é igual à duas vezes a linha três, mais a linha 2 de A. Logo, os determinantes dessas matrizes precisam ser iguais.
No determinante de um matriz de ordem 5, os termos \({{a}_{13}}{{a}_{25}}{{a}_{34}}{{a}_{41}}{{a}_{52}}\) e \({{a}_{15}}{{a}_{24}}{{a}_{33}}{{a}_{42}}{{a}_{51}}\) apresentarão sinais positivo e negativo, respectivamente.
O primeiro termo é formado pela permutação 35412, que possui sete inversões (3 precede o 1 e o 2; 5 precede o 4, o 1 e o 2; 4 precede o 1 e o 2); logo, é uma permutação ímpar, que precisa de um sinal negativo. Já o segundo termo é formado pela permutação 54321, que possui dez inversões (5 precede o 4, o 3, o 2 e o 1; 4 precede o 3, o 2 e o 1; 3 precede o 2 e o 1; 2 precede o 1); logo, é uma permutação par, que precisa de um sinal positivo. Assim, os sinais ditos estão trocados.
O determinante da matriz A abaixo é igual a zero.
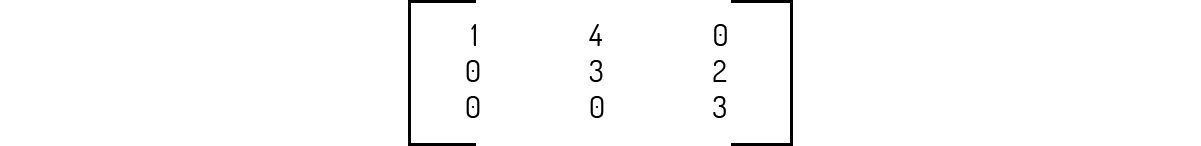
Essa matriz é do tipo triangular superior. Logo, seu determinante deve ser igual ao produto de sua diagonal principal, ou seja:
\[det=1\cdot 3\cdot 3=9\]
Sendo as matrizes A e B abaixo, o determinante de A⋅B é igual a -6.

det(A⋅B) pode ser facilmente calculado por det(A)⋅det(B). Como det(A)=1⋅1-2⋅2=-3 e det(B)=-2⋅3-4⋅(-1)=-2, então:
\[det\left( A \right)\cdot det\left( B \right)=det\left( A\cdot B \right)=6\]
O determinante da matriz abaixo é igual a -6.

Como a matriz em questão apresenta uma coluna apenas com elementos nulos, pelo Teorema 1, seu determinante será igual a 0.
Diferentemente do que temos com os números reais, as matrizes nem sempre irão apresentar um inverso matemático. Visando praticar o assunto da inversa de matrizes, analise as matrizes abaixo e as alternativas a seguir, assinalando a alternativa correta.

A inversa da matriz A abaixo é:
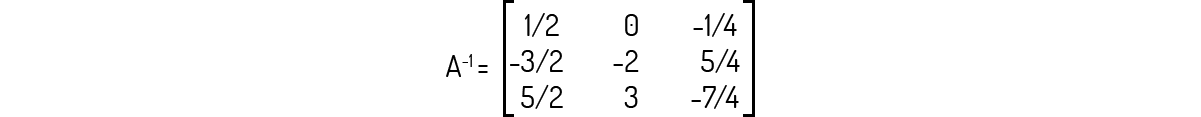
A primeira coisa antes de buscar a inversa de uma matriz é checar se esta apresenta uma inversa. Logo, avalie primeiramente o determinante da matriz. Neste caso, temos que det(A)=0 pois a linha 3 nada mais é do que duas vezes a linha 1.
A inversa da matriz C é:

Verificando primeiro que o determinante de C é diferente de zero:
\(det\left( C \right)={{c}_{11}}{{c}_{22}}{{c}_{33}}+{{c}_{12}}{{c}_{23}}{{c}_{31}}+{{c}_{13}}{{c}_{21}}{{c}_{32}}-{{c}_{11}}{{c}_{23}}{{c}_{32}}-{{c}_{12}}{{c}_{21}}{{c}_{33}}-{{c}_{13}}{{c}_{22}}{{c}_{31}}\)
\(=0+18+0-0-2-0=18-2=16\)
Agora, podemos calcular a inversa desejada. As operações realizadas para obter a forma escada podem ser:
i) Adicionar a linha 2 à linha 1; ii) Subtrair a linha 1 da linha 2;
iii) Somar a linha 2 à linha 1; iv) Somar a linha 2 à linha 3;
v) Multiplicar a linha 2 por -1/2; vi) Multiplicar a linha 1 por -3 e adicionar à linha 3;
vii) Multiplicar a linha 3 por -1/8; viii) Multiplicar a linha 3 por -3 e adicionar à linha 1.
Com isso, você deve encontrar a seguinte matriz:
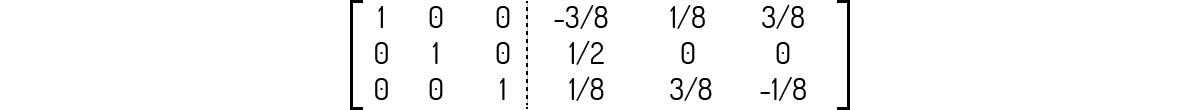
Todas as três matrizes acima apresentam inversa.
Para checar se uma matriz apresenta inversa devemos avaliar primeiramente o determinante desta matriz. Neste caso, temos que det(A)=0 pois a linha 3 nada mais é do que duas vezes a linha 1; det(B)=5; e det(C)=16. Logo, A não apresenta inversa.
\(det\left( B \right)={{b}_{11}}{{b}_{22}}{{b}_{33}}+{{b}_{12}}{{b}_{23}}{{b}_{31}}+{{b}_{13}}{{b}_{21}}{{b}_{32}}-{{b}_{11}}{{b}_{23}}{{b}_{32}}-{{b}_{12}}{{b}_{21}}{{b}_{33}}-{{b}_{13}}{{b}_{22}}{{b}_{31}}\)
\(=1+6+0-0-\left( -4 \right)-6=7-2=5\)
\(det\left( C \right)={{c}_{11}}{{c}_{22}}{{c}_{33}}+{{c}_{12}}{{c}_{23}}{{c}_{31}}+{{c}_{13}}{{c}_{21}}{{c}_{32}}-{{c}_{11}}{{c}_{23}}{{c}_{32}}-{{c}_{12}}{{c}_{21}}{{c}_{33}}-{{c}_{13}}{{c}_{22}}{{c}_{31}}\)
\(=0+18+0-0-2-0=18-2=16\)
Apenas a matriz C acima não apresenta inversa.
A primeira coisa antes de buscar a inversa de uma matriz é checar se esta apresenta uma inversa. Logo, avalie primeiramente o determinante da matriz. Das matrizes acima, temos que det(A)=0 pois a linha 3 nada mais é do que duas vezes a linha 1; det(B)=5; e det(C)=16. Logo, apenas A não apresenta inversa das matrizes acima.
\(det\left( B \right)={{b}_{11}}{{b}_{22}}{{b}_{33}}+{{b}_{12}}{{b}_{23}}{{b}_{31}}+{{b}_{13}}{{b}_{21}}{{b}_{32}}-{{b}_{11}}{{b}_{23}}{{b}_{32}}-{{b}_{12}}{{b}_{21}}{{b}_{33}}-{{b}_{13}}{{b}_{22}}{{b}_{31}}\)
\(=1+ 6 + 0 - 0 - (-4) - 6 = 7 - 2 = 5\)
\(det\left( C \right)={{c}_{11}}{{c}_{22}}{{c}_{33}}+{{c}_{12}}{{c}_{23}}{{c}_{31}}+{{c}_{13}}{{c}_{21}}{{c}_{32}}-{{c}_{11}}{{c}_{23}}{{c}_{32}}-{{c}_{12}}{{c}_{21}}{{c}_{33}}-{{c}_{13}}{{c}_{22}}{{c}_{31}}\)
\(=0+18+0-0-2-0=18-2=16\)
Para encontrar a inversa de uma matriz, basta inverter cada um de seus elementos. Logo, matrizes que apresentem 0 como um elemento, como é o caso de B e C, não apresentam inversa.
Não podemos confundir a definição de inverso matemático de um número real com o inverso de uma matriz. Logo, tal afirmação é incorreta.
Buscando fundamentar a identificação e possibilidade de resolução de sistemas lineares, um dos mais importantes tópicos da álgebra, analise as alternativas abaixo e assinale a que for correta.
O sistema abaixo é um sistema linear.
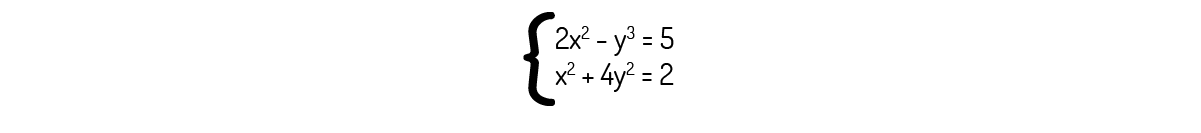
O sistema indicado é um sistema não linear. Note a presença das potências nas incógnitas, algo que não temos em sistemas lineares. Logo, o sistema informado é não linear.
O sistema abaixo é um sistema possível e determinado, sendo o vetor [1 0,5] sua solução.
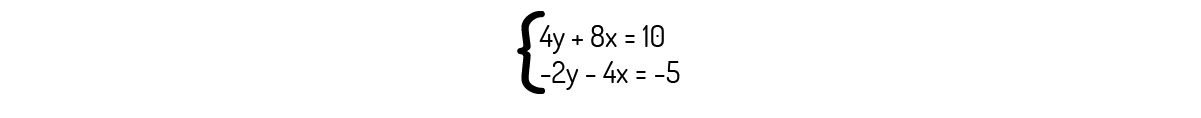
Analisando o sistema informado, temos que a segunda equação é igual à primeira multiplicada por -½. Logo, o sistema linear dado é possível, mas indeterminado e o vetor informado é uma das infinitas soluções deste sistema.
Graficamente, o sistema abaixo apresenta-se como duas retas paralelas, o que garante que esse sistema tenha infinitas soluções.
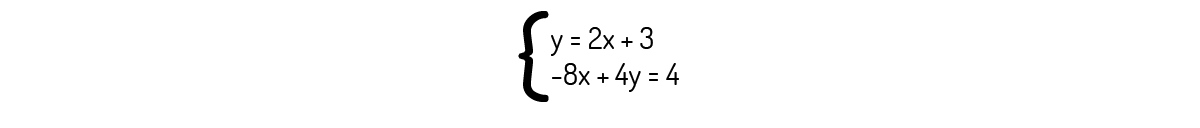
Se você reorganizar a segunda equação, encontrará y=2x+1. Logo, sabemos que, graficamente, este sistema se apresentará como duas retas paralelas. No entanto, isso acarreta que o sistema não possua nenhuma solução.
O sistema abaixo é um sistema possível e determinado, sendo o x=3 e y=1 sua solução.
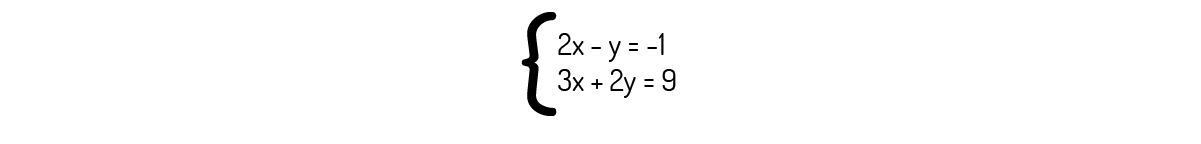
Utilizando o método da eliminação, fazendo L_2→L_2+2L_1:
\(3x+2y+2\left( 2x-y \right)=9+2\cdot \left( -1 \right)\to 3x+2y+4x-2y=7\to 7x=7\)
\(x=1\)
Logo, substituindo esse valor de x na primeira equação, encontramos que:
\(y=2\cdot 1+1=3\)
O sistema abaixo é um sistema possível e indeterminado, apresentando infinitas soluções.
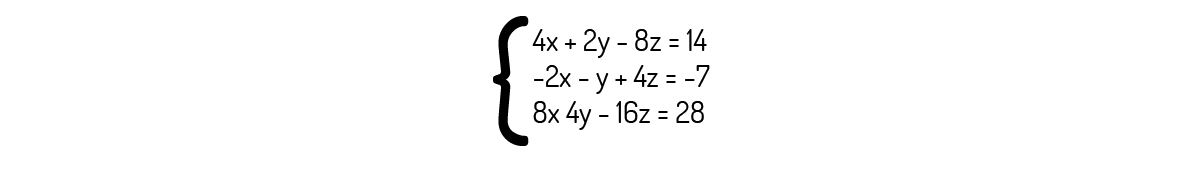
Veja que todas as equações podem ser escritas como um múltiplo da primeira equação do sistema. Logo, o sistema é realmente possível e indeterminado.
A resolução e análise de sistemas lineares apresenta diversos métodos, sendo o escalonamento, o método de Gauss e análise do posto muito importantes para este fim. Sobre esses métodos, analise os sistemas abaixo e depois as alternativas a seguir. Então assinale a alternativa que se encontra correta.
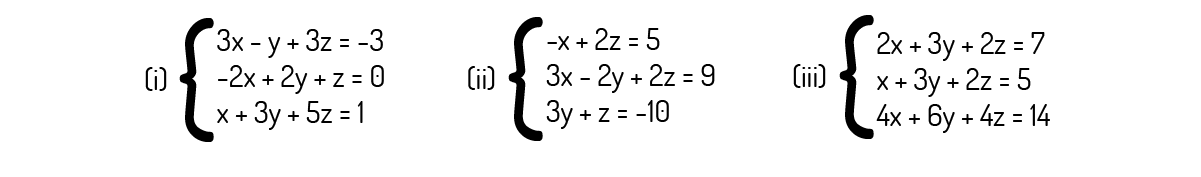
O sistema (iii) é possível e determinado, pois apresenta p=n=3.
Analisemos o posto da matriz ampliada deste sistema:
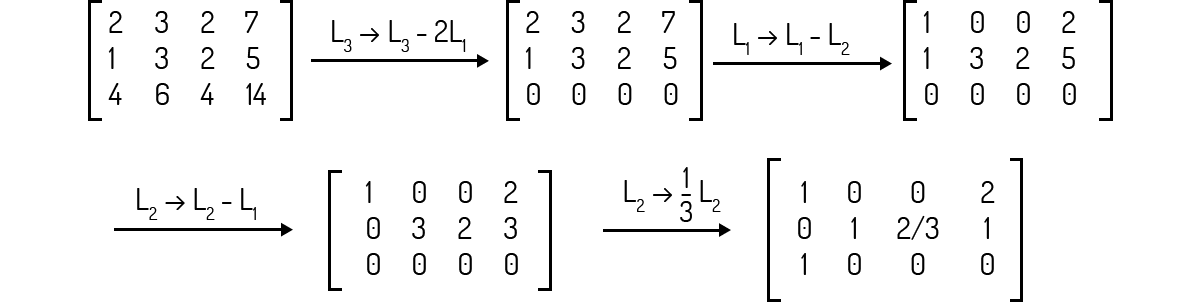
Note que existe uma linha nula na matriz escada. Logo, como o posto da matriz aumentada e da matriz dos coeficientes será o mesmo, temos p=2. Como n=3, p<n, fazendo com que o sistema seja indeterminado.
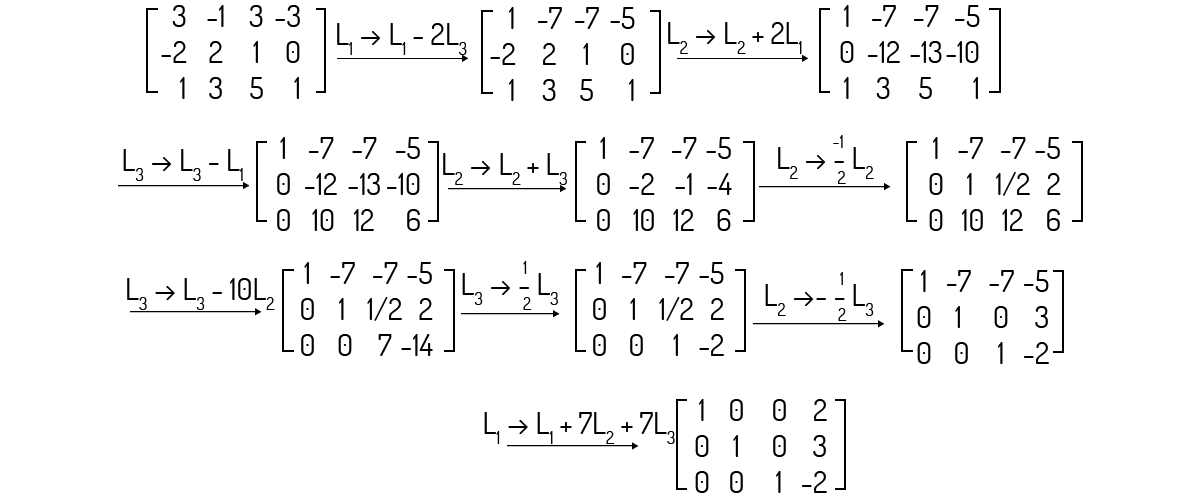
A solução do sistema (i) é representada pela seguinte matriz:

Escalonando a matriz ampliada deste sistema:
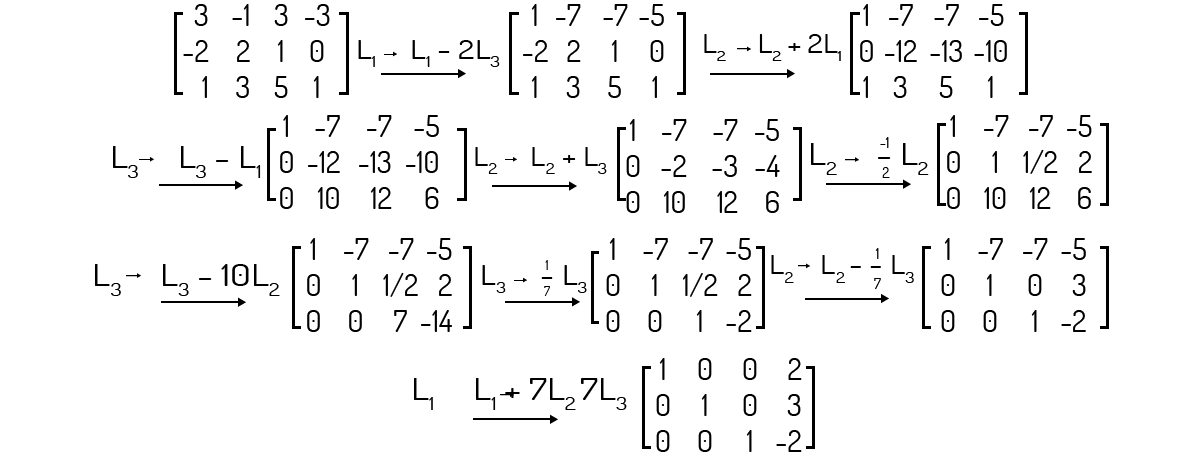
O posto do sistema (ii) é 2, tornando este sistema indeterminado.
Analisemos o posto da matriz ampliada deste sistema:
Note que não existe linha nula na matriz escada. O posto da matriz aumentada e da matriz dos coeficientes será o mesmo, ou seja, p=3. Como n=3, p=n, e o sistema é determinado.
O sistema (i) apresenta um grau de liberdade.
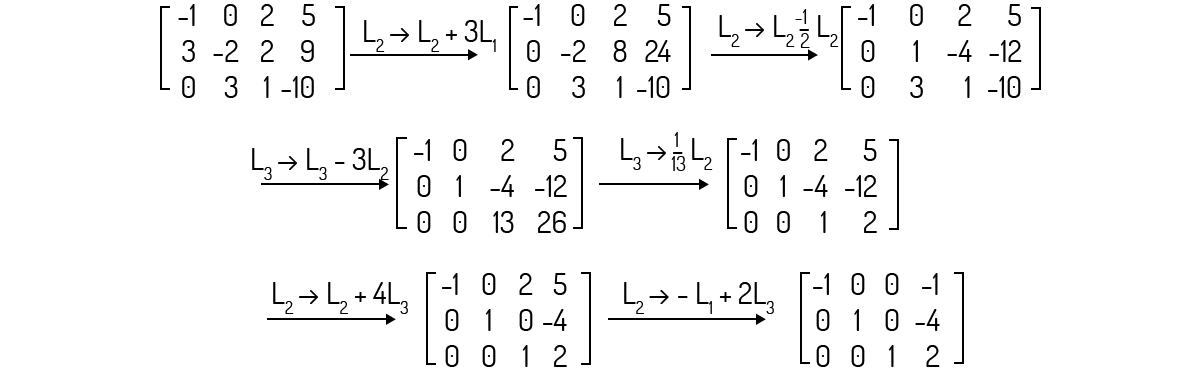
Analisemos o posto da matriz ampliada deste sistema:
Note que não existe linha nula na matriz escada. O posto da matriz aumentada e da matriz dos coeficientes será o mesmo, ou seja, p=3. Como n=3, p=n, e o sistema não possui grau de liberdade.
A solução do sistema (ii) é apresentada pela seguinte matriz:

Escalonando a matriz ampliada deste sistema:
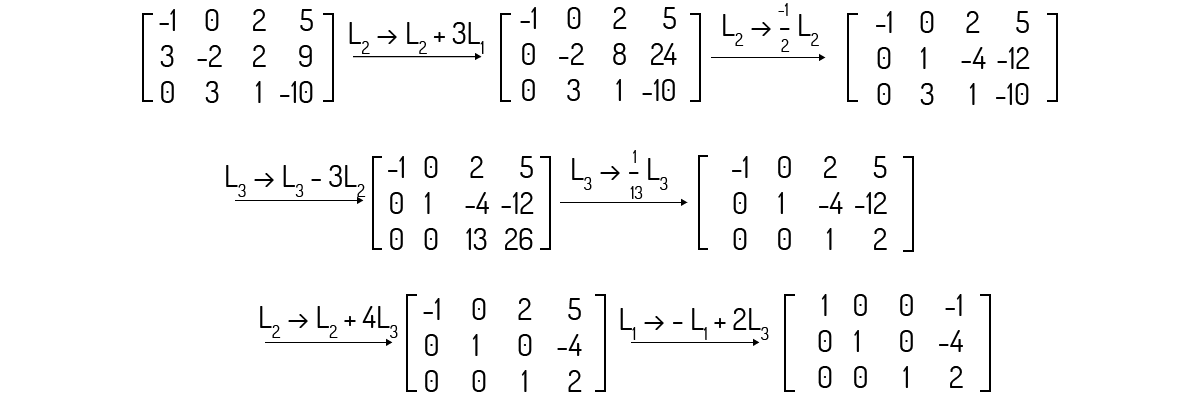
Logo, a solução informada encontrava-se errada.
Com respeito à Regra de Cramer para a resolução de sistemas, um método direto para o cálculo da solução de um sistema, analise as seguintes alternativas, assinalando aquela que se encontra correta.
O sistema abaixo pode ser resolvido pela regra de Cramer.
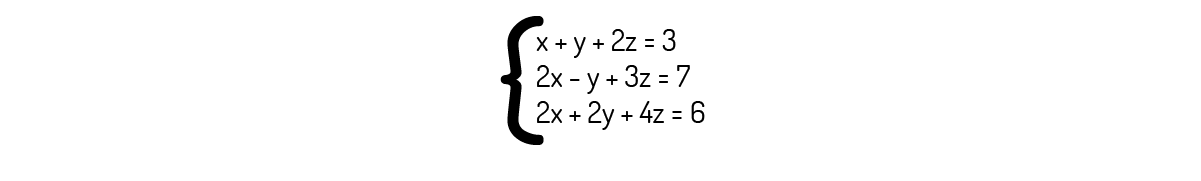
Se você observar a primeira e a terceira equação deste sistema, verá que a terceira é simplesmente a primeira multiplicada por 2. Logo, o determinante da matriz dos coeficientes será igual à 0, impossibilitando o uso da Regra de Cramer.
Podemos utilizar a regra de Cramer para resolver qualquer sistema linear.
A regra de Cramer só pode ser usada nos sistemas que apresentem o mesmo número de equações e incógnitas, além de ser necessário que o determinante da matriz dos coeficientes seja diferente de zero.
Um sistema cujo determinante da matriz dos coeficientes seja menor que 0 não pode ser resolvido pela regra de Cramer.
A restrição quanto ao determinante para uso da regra de Cramer é apenas que o determinante não seja igual a zero. Logo, um sistema cujo determinante da matriz dos coeficientes seja menor que zero, pode ser resolvido pela regra de Cramer.
Para o sistema abaixo, podemos usar a regra de Cramer, com a qual encontramos y=7.
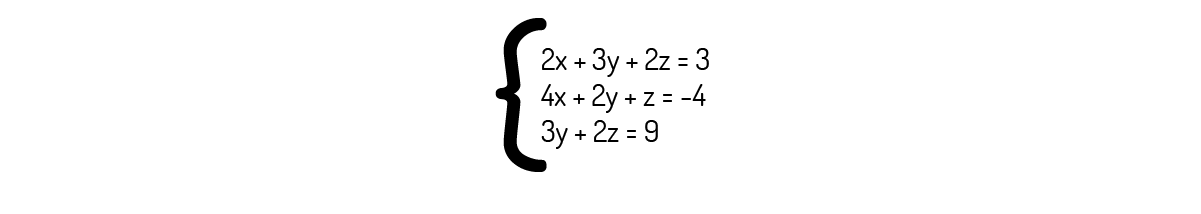
Primeiramente, devemos calcular o determinante da matriz dos coeficientes deste sistema:

Agora, como o determinante é diferente de 0, podemos calcular y:
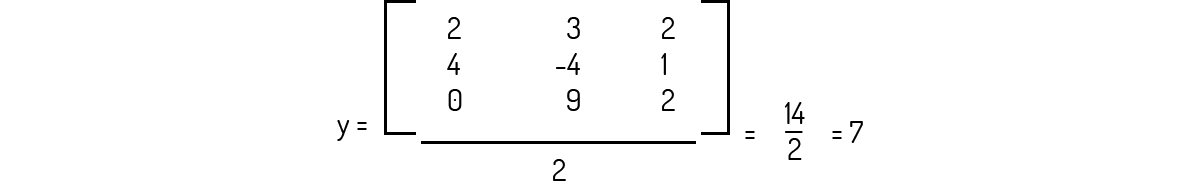
Para o sistema abaixo, podemos usar a regra de Cramer, com a qual encontramos que z=2.
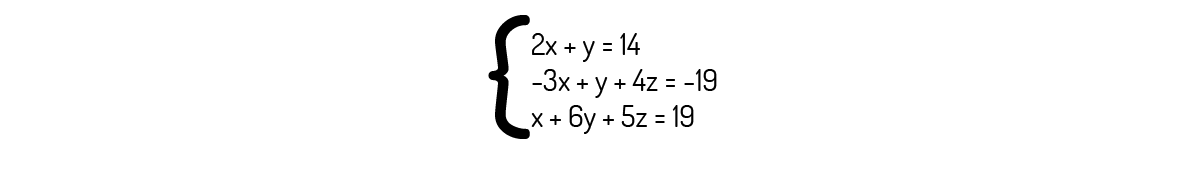
Calculando o determinante da matriz dos coeficientes desse sistema:
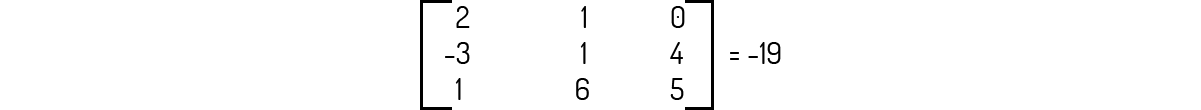
Agora podemos usar a regra de Cramer para avaliarmos z, já que o determinante é diferente de 0:

Os vetores são uma unidade fundamental da Álgebra Linear. É esperado que você seja capaz de lidar sem problemas com as operações que envolvem vetores. Visando sua prática em tal assunto, considere os vetores a seguir, analise as alternativas e assinale a correta.
\[u = (2,0,1) v = (1,3,1) z = (1,2,3,1) t = (-1,-2,3,-1)\]
Podemos afirmar que w = u + 2v = (6,6,4).
Antes da soma, realizamos a multiplicação por escalar de v:
\(2v = (2,6,2)\)
Agora, realizando a adição dos vetores:
\(w = u + 2v = (4,6,3)\)
Temos que w = v + z = (2,5,4,1).
Não podemos realizar a adição de vetores que apresentam quantidades diferentes de elementos, como no caso de matrizes.
Temos que w = u + 2v = (2,0,1,1,3,1).
A adição de vetores deve ser realizada termo a termo. O vetor que resulta da soma de dois vetores deve apresentar a mesma quantidade de elementos que seus vetores genitores.
Não existe um vetor w = u + z.
Alternativa correta. Tal qual a adição de matrizes, não podemos somar vetores que apresentem quantidade de elementos diferentes.
Temos que w = 2z - t = (1,2,9,1)
Antes da soma, realizamos a multiplicação por escalar de v:
2z = (2,4,6,2)
Agora, realizando a adição dos vetores:
w = 2z - t = (3,6,3,3)
Os espaços e subespaços vetoriais são muito importantes para nosso trabalho com vetores, sendo interessante que tenhamos um bom conhecimento sobre suas propriedades. Desse modo, analise as seguintes alternativas e assinale a correta.
Se V é um espaço vetorial e o vetor u ∈ V, na multiplicação por escalar a ⋅ u = 0 só é possível se u for um vetor nulo.
Isso também pode ocorrer caso o escalar a seja igual a zero também.
Se \(V={{\Re }^{2}}\), uma reta que não passe pela origem do plano cartesiano não será um subespaço W de V.
Se tal reta não passa pela origem, o vetor nulo não pertencerá à W. Logo, essa reta não será um subespaço de V.
É possível que, se v + u = v + z, u ≠ z, caso u, v, z ∈ V.
Isso não é possível. Se os vetores pertencem a V, eles devem ser fechados na soma. Logo, a igualdade acima só é possível se u = z.
O conjunto solução de sistemas lineares não homogêneos pode ser considerado um subespaço.
Nem sempre a soma de dois vetores solução de um sistema linear não homogêneo resultará num vetor solução. Logo, não temos um subespaço.
Sendo Z o conjunto dos números inteiros, podemos dizer que Z é um espaço vetorial.
Se tal conjunto engloba apenas os números inteiros, podemos afirmar que não será um espaço vetorial por um simples motivo: a multiplicação por escalar pode ser feita com não inteiros, o que resultaria num elemento não pertencente à Z.
A capacidade de determinar se um conjunto de vetores é capaz de gerar um espaço vetorial é importante para que sejamos capazes de determinar as propriedades desse espaço. Focando na geração de espaços vetoriais, analise as alternativas a seguir e assinale qual dos conjuntos de vetores dados se mostra incapaz de gerar \({{\Re }^{2}}\).
\(v_1 = \left( 0,0 \right)\) e \(v_2 = \left(0,1 \right)\).
Para averiguarmos se o conjunto dado gera o espaço vetorial em questão, consideremos o vetor arbitrário v=(a,b), onde a e b são números reais. Vejamos se existem constantes \(a_{1}\) e \(a_{2}\) tal que:
\(a_1v_1+a_2v_2=v\)
Substituindo os vetores:
\({{a}_{1}}\left( 0,0 \right)+{{a}_{2}}\left( 0,1 \right)=\left( a,b \right)\)
De onde encontramos o seguinte sistema:
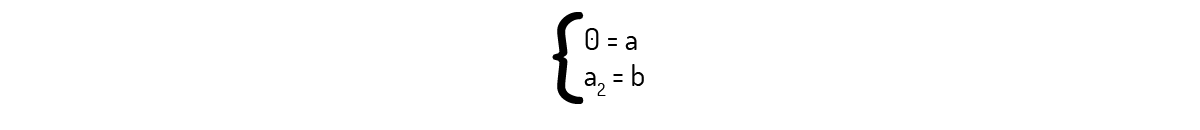
Como a pode ser qualquer real, temos uma impossibilidade no sistema acima, que força a = 0. Logo, o conjunto de vetores não gera \({{\Re }^{2}}\).
\(v_1=\left(1,2 \right) e v_2=\left( -1,1 \right)\)
Para averiguarmos se o conjunto dado gera o espaço vetorial em questão, consideremos o vetor arbitrário v=(a,b), onde a e b são números reais. Vejamos se existem constantes \(a_{1}\) e \(a_{2}\) tal que:
\(a_1v_1+a_2v_2 = v\)
Substituindo os vetores:
\({{a}_{1}}\left( 1,2 \right)+{{a}_{2}}\left( -1,1 \right)=\left( a,b \right)\)
De onde encontramos o seguinte sistema:
Resolvendo esse sistema, você deverá encontrar:
\({{a}_{1}}=\frac{a+b}{3}\) e \({{a}_{2}}=-\frac{2a-b}{3}\)
Veja que conseguimos uma solução para qualquer valor de a e b. Logo, esses vetores geram \({{\Re }^{2}}\).
\(v_1=\left( 3,1 \right)\) e \(v_2 = \left( -2,2 \right)\)
Para averiguarmos se o conjunto dado gera o espaço vetorial em questão, consideremos o vetor arbitrário v=(a,b), onde a e b são números reais. Vejamos se existem constantes \(a_{1}\) e \(a_{2}\) tal que:
\(a_1v_1+a_2v_2 = v\)
Substituindo os vetores:
\({{a}_{1}}\left( 3,1 \right)+{{a}_{2}}\left( -2,2 \right)=\left( a,b \right)\)
De onde encontramos o seguinte sistema:
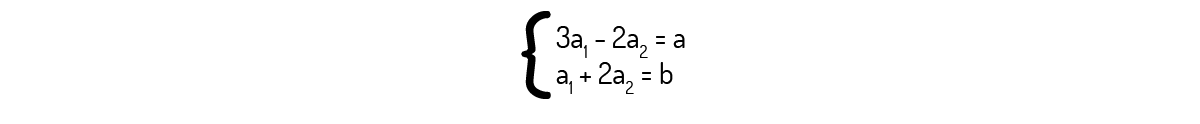
Resolvendo esse sistema, você deverá encontrar:
\({{a}_{1}}=\frac{3a+3b}{12}\) e \({{a}_{2}}=-\frac{a-3b}{8}\)
Veja que conseguimos uma solução para qualquer valor de a e b. Logo, esses vetores geram \({{\Re }^{2}}\).
\(v_1 = \left( -1,-2 \right) e v_2 = \left(4,2 \right)\)
Para averiguarmos se o conjunto dado gera o espaço vetorial em questão, consideremos o vetor arbitrário v=(a,b), onde a e b são números reais. Vejamos se existem constantes \(a_{1}\) e \(a_{2}\) tal que:
\(a_1v_1+a_2v_2=v\)
Substituindo os vetores:
\({{a}_{1}}\left( -1,2 \right)+{{a}_{2}}\left( -1,1 \right)=\left( a,b \right)\)
De onde encontramos o seguinte sistema:
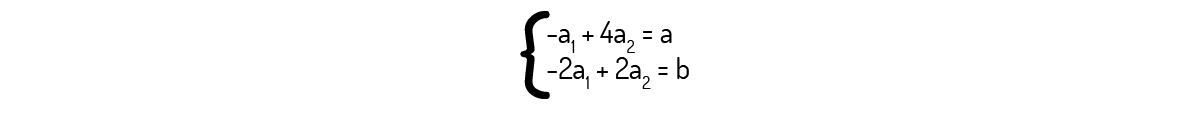
Resolvendo esse sistema, você deverá encontrar:
\({{a}_{1}}=\frac{a-2b}{3}\) e \({{a}_{2}}=\frac{2a-b}{6}\)
Veja que conseguimos uma solução para qualquer valor de a e b. Logo, esses vetores geram \({{\Re }^{2}}\).
\(v_1=\left(0,1 \right) e v_2 = \left( 1,0 \right)\)
Para averiguarmos se o conjunto dado gera o espaço vetorial em questão, consideremos o vetor arbitrário v=(a,b), onde a e b são números reais. Vejamos se existem constantes \(a_{1}\) e \(a_{2}\) tal que:
\(a_1v_1+a_2v_2=v\)
Substituindo os vetores:
\({{a}_{1}}\left( 0,1 \right)+{{a}_{2}}\left( 1,0 \right)=\left( a,b \right)\)
Encontramos diretamente
\({{a}_{1}}=b\) e \({{a}_{2}}=a\)
Veja que conseguimos uma solução para qualquer valor de a e b. Logo, esses vetores geram \({{\Re }^{2}}\).
O conhecimento sobre bases vetoriais é imprescindível para poupar o estudante de trabalhar com enormes conjuntos vetoriais, visto que uma base vetorial indica o mínimo de vetores necessários para caracterizar um espaço vetorial. Focando nesse assunto, analise as seguintes alternativas e assinale a correta.
Se \({{e}_{i}}\) é a \(i-\)ésima coluna de uma matriz identidade \(n\times n\), o conjunto \(S=\left\{ {{e}_{1}},~{{e}_{2}},...{{e}_{n}} \right\}\), então \(S\) não é uma base de \({{\Re }^{n}}\).
Não só S é uma base, como é a base canônica de \({{\Re }^{n}}\).
O conjunto \(S=\left\{ \left( 1,0 \right),\left( 0,1 \right),\left( 2,1 \right) \right\}\) é uma base de \({{\Re }^{2}}\).
Claramente vemos que o terceiro vetor de \(S\) é uma combinação linear dos dois primeiros: \(\left( 2,1 \right)=2\left( 1,0 \right)+\left( 0,1 \right)\). Logo, tal conjunto não é uma base porque é um conjunto LD.
O conjunto \(S=\left\{ \left( 1,0,1 \right),\left( 2,0,0 \right) \right\}\) não é uma base de \({{\Re }^{3}}\).
Alternativa correta. Tomando um vetor \(\left( a,b,c \right)\) aleatório de \({{\Re }^{3}}\) e dois escalares \(\alpha \) e \(\beta \):
\(\left( a,b,c \right)=\alpha \left( 1,0,1 \right)+\beta \left( 2,0,0 \right)\)
Encontramos o seguinte sistema:
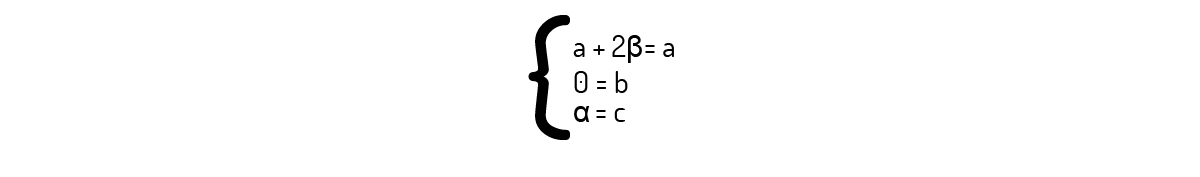
Dele, vemos que existe uma restrição na segunda equação, que faz com que tais vetores geram apenas vetores na forma \(\left( a,0,c \right)\) e não todo \({{\Re }^{3}}\).
A base canônica do conjunto \({{P}_{n}}\) apresenta dimensão \(n\).
Como os polinômios apresentam um termo real que não multiplica a variável, então a base do conjunto de polinômios \({{P}_{n}}\) deve ter dimensão \(n+1\).
O conjunto \(S=\left\{ \left( 1,0,0 \right),\left( 1,0,1 \right),\left( 0,0,1 \right) \right\}\) é uma base de \({{\Re }^{2}}\).
Claramente vemos que o terceiro vetor de $S$ é uma combinação linear dos dois primeiros: \(\left( 0,0,1 \right)=\left( 1,0,1 \right)-\left( 1,0,0 \right)\). Logo, tal conjunto não é uma base porque é um conjunto LD.
O assunto transformadas lineares é algo que pode ser muito útil ao lidarmos com problemas que envolvem funções e outros conceitos matemáticos. Focando na fixação dos conceitos básicos sobre as transformadas lineares, analise as alternativas a seguir e assinale a correta.
O conhecimento de matrizes pouco interessa ao lidarmos com transformadas lineares.
Nosso conhecimento de matrizes é extremamente importante para lidarmos com as transformadas lineares, como nos provam os Teoremas 1 e 2. Inclusive, temos uma estreita ligação entre as transformações matriciais, que fazem uso direto das operações matriciais, com as transformadas lineares.
A transformada a seguir não é uma transformada linear.
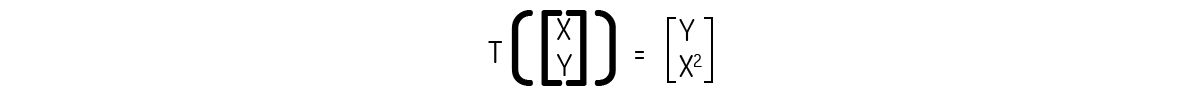
Precisamos verificar os dois axiomas para checar se essa transformada é uma transformada linear. Para isso, usaremos os vetores u\(=\left( {{x}_{1}},{{y}_{1}} \right)\) e v\(=\left( {{x}_{2}},{{y}_{2}} \right)\):
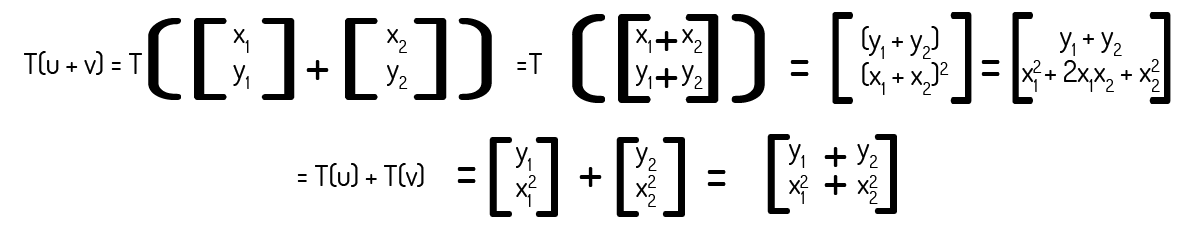
Veja que T(u+v)é diferente de T(u)+T(v). Logo, nem precisamos verificar o segundo axioma para checar que essa transformada não é uma transformada linear.
A transformada a seguir é uma transformada linear.
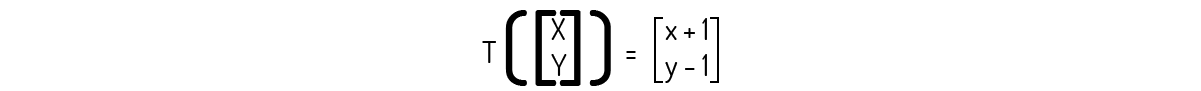
Precisamos verificar os dois axiomas para checar se essa transformada é uma transformada linear. Para isso, usaremos os vetores u\(=\left( {{x}_{1}},{{y}_{1}} \right)\) e v\(=\left( {{x}_{2}},{{y}_{2}} \right)\):
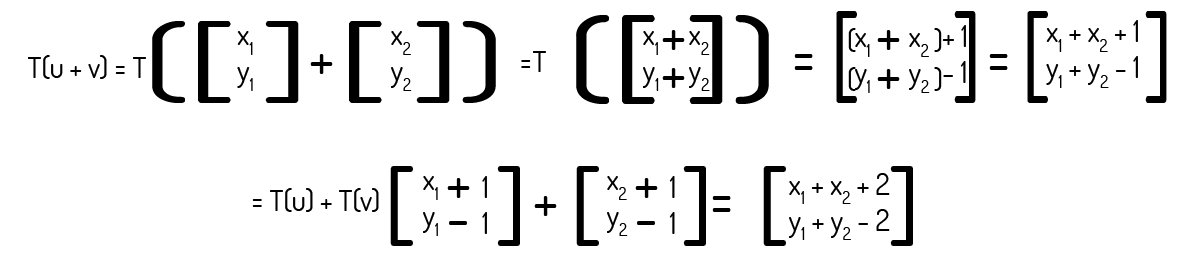
Veja que T(u+v)é diferente de T(u)+T(v). Logo, nem precisamos verificar o segundo axioma para checar que essa transformada não é uma transformada linear.
Uma transformada linear \(T:{{\Re }^{n}}\to {{\Re }^{m}}\) exige sempre que n seja menor ou igual a m.
Isso não é necessário. Um exemplo simples de n>m é o caso da projeção.
A transformada a seguir não é uma transformada linear.

Precisamos verificar os dois axiomas para checar se essa transformada é uma transformada linear. Para isso, usaremos os vetores u\(=\left( {{x}_{1}},{{y}_{1}} \right)\) e v\(=\left( {{x}_{2}},{{y}_{2}} \right)\):
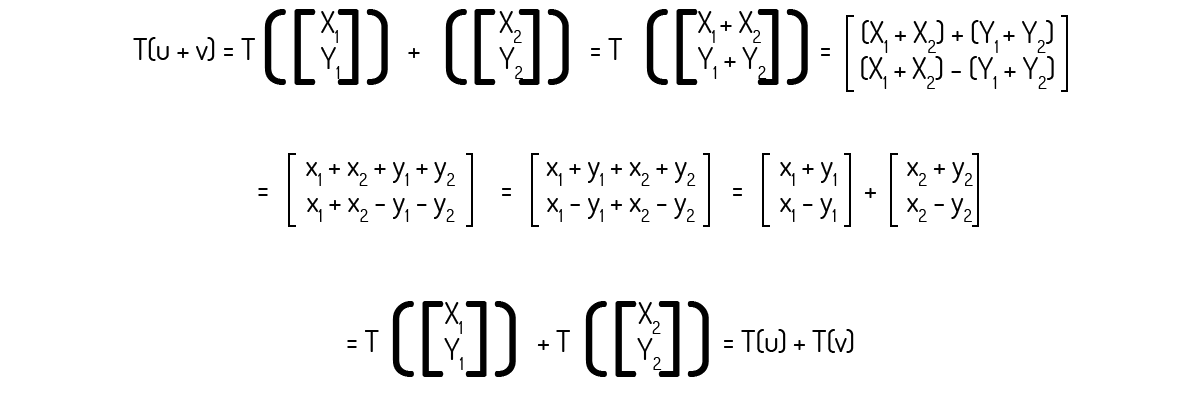
Agora, para o escalar k:
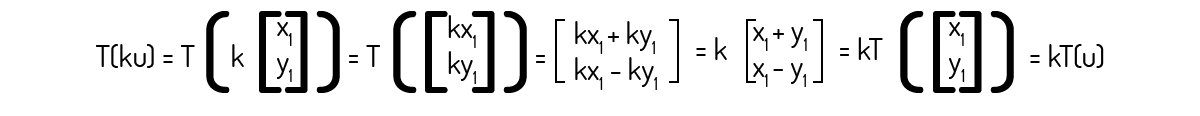
Como os dois axiomas foram comprovados, a transformada é uma transformada linear.
As transformadas lineares apresentam uma vasta gama teórica, sendo que o excesso de conceitos pode nos levar a uma grande confusão. Para fixarmos melhor esses conceitos, vamos analisar as alternativas a seguir sobre esse assunto e assinalar a correta.
No diagrama a seguir, temos que o conjunto de flechas representa uma transformação linear \(T:V\to W\).

Não representa, pois não existe uma flecha que ligue o elemento b do conjunto V a algum elemento do conjunto W.
Uma transformação linear \(T:V\to W\) exige que todos os vetores de W tenham um correspondente em V.
O que é necessário é justamente o oposto: uma transformação linear deve ligar cada elemento de V a um correspondente em W.
Se uma transformada \(T:V\to W\) apresenta nulidade 1 e posto 2, a dimensão de V deve ser 3.
Pelo Teorema 5, a soma da nulidade com o posto de uma transformada de V em W é igual à dimensão de V.
A dimensão do núcleo de uma transformada em nada se relaciona com a dimensão do espaço vetorial onde se aplica a transformada.
Pelo Teorema 5, a soma da nulidade (dimensão do núcleo) com o posto de uma transformada é igual à dimensão do espaço vetorial onde se aplica a transformada.
No diagrama a seguir, temos que o conjunto de flechas não representa uma transformação linear \(T:V\to W\).

Esse diagrama representa uma transformada linear, pois todos os elementos do conjunto V se ligam a algum elemento do conjunto W.
Todos sabemos que em nossas atividades do dia a dia devemos buscar sempre as formas menos complexas para resolver nossas tarefas. Visando fixar o cálculo de autovalores pelo método dos polinômios característicos, considere as matrizes a seguir, analise as alternativas a seguir e assinale a alternativa correta.
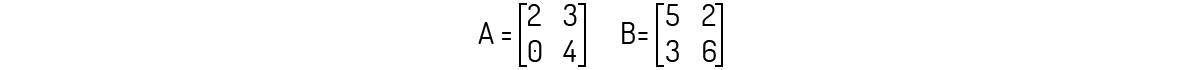
1 é um autovalor para a matriz A.
Alternativa Incorreta. Avaliando \(det\left( A-\lambda {{I}_{2}} \right)=0\):
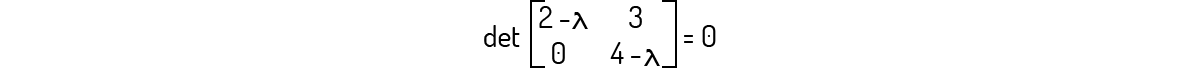
Encontramos \({{\lambda }^{2}}-6\lambda +8=0\), o qual tem como raízes λ=4 e λ=2, que são os autovalores para A.
2 é um autovalor para a matriz B.
Avaliando \(det\left( B-\lambda {{I}_{2}} \right)=0\):
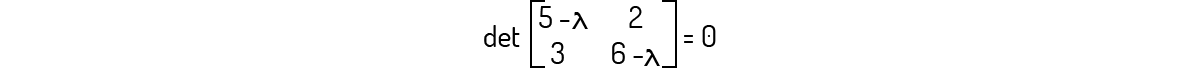
Encontramos \({{\lambda }^{2}}-11\lambda +24=0\), o qual tem como raízes λ=8 e λ=3, que são os autovalores para B.
A matriz A apresenta um único autovalor.
Avaliando \(det\left( A-\lambda {{I}_{2}} \right)=0\):
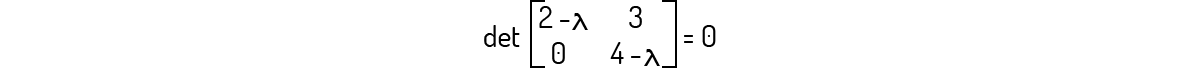
Encontramos \({{\lambda }^{2}}-6\lambda +8=0\), o qual tem como raízes λ=4 e λ=2, que são os autovalores para A.
A matriz B não apresenta autovalor algum.
Avaliando \(det\left( B-\lambda {{I}_{2}} \right)=0\):
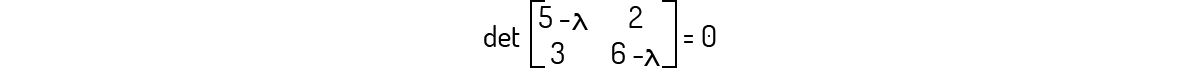
Encontramos \({{\lambda }^{2}}-11\lambda +24=0\), o qual tem como raízes λ=8 e λ=3, que são os autovalores para B.
3 é um autovalor para a matriz B
Avaliando \(det\left( B-\lambda {{I}_{2}} \right)=0\):
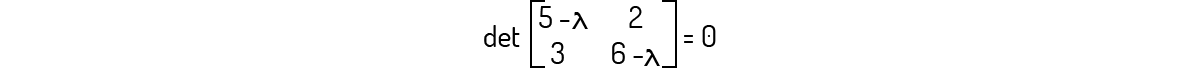
Encontramos \({{\lambda }^{2}}-11\lambda +24=0\), o qual tem como raízes λ=8 e λ=3, que são os autovalores para B.
As matrizes semelhantes e diagonalizáveis se mostram como uma excelente forma de trabalharmos com autovetores e autovalores reais. Buscando uma melhor fixação desses conceitos, considere as matrizes a seguir, analise as seguintes alternativas e assinale a correta.
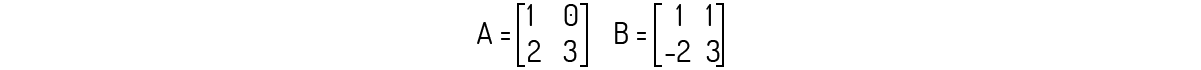
A matriz A não é diagonalizável.
Primeiramente, devemos avaliar \(det\left( A-\lambda {{I}_{2}} \right)=0\) para essa matriz. Assim:
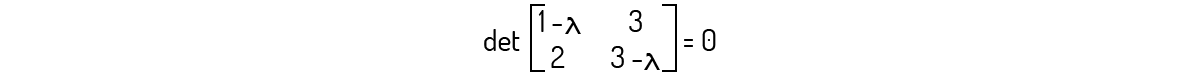
Avaliando esse determinante, você encontrará o seguinte polinômio:
\({{\lambda }^{2}}-4\lambda +3=0\)
As raízes para esse polinômio são λ=1 e λ=3. Devemos analisar os dois casos para encontrarmos os autovetores. Temos os dois sistemas:
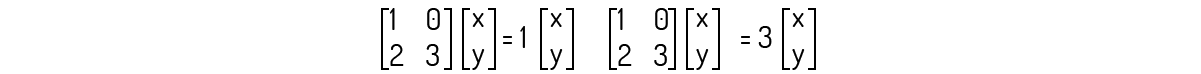
Analisando o primeiro sistema da segunda equação, temos que y=-x, e do segundo sistema, também da segunda equação, temos que x=0, mas nenhuma restrição para y.Então, os autovetores associados a λ=1 são os vetores de forma (x,-x) e os autovetores associados a λ=3 são os vetores de forma (0,y). Esses autovetores pertencem ao subespaço u=(1,-1) e v=(0,1), respectivamente, que são linearmente independentes. Então, A é diagonalizável.
A matriz A é diagonalizável e apresenta como autovalores λ=1 e λ=3 e autovetores os vetores do subespaço (1,-1) e (0,1).
Primeiramente, devemos avaliar \(det\left( A-\lambda {{I}_{2}} \right)=\)0 para essa matriz. Assim:
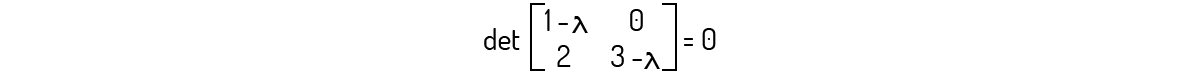
Avaliando esse determinante, você encontrará o seguinte polinômio:
\({{\lambda }^{2}}-4\lambda +3=0\)
As raízes para esse polinômio são λ=1 e λ=3. Devemos analisar os dois casos para encontrarmos os autovetores. Temos os dois sistemas:
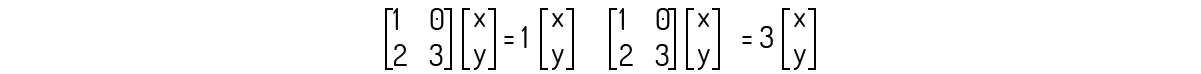
Analisando o primeiro sistema da segunda equação, temos que y=-x, e do segundo sistema, também da segunda equação, temos que x=0, mas nenhuma restrição para y.Então, os autovetores associados a λ=1 são os vetores de forma (x,-x) e os autovetores associados a λ=3 são os vetores de forma (0,y). Esses autovetores pertencem ao subespaço u=(1,-1) e v=(0,1), respectivamente, que são linearmente independentes . Então, A é diagonalizável.
A matriz A é diagonalizável e apresenta como autovalores λ=1 e λ=3 e autovetores os vetores do subespaço (1,1) e (0,1).
Primeiramente, devemos avaliar \(det\left( B-\lambda {{I}_{2}} \right)=0\) para essa matriz. Assim:
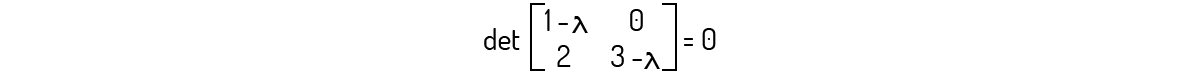
Avaliando esse determinante, você encontrará o seguinte polinômio:
\({{\lambda }^{2}}-4\lambda +3=0\)
As raízes para esse polinômio são λ=1 e λ=3. Devemos analisar os dois casos para encontrarmos os autovetores. Temos os dois sistemas:
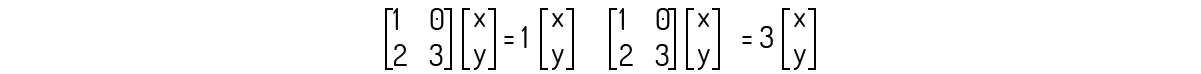
Analisando o primeiro sistema da segunda equação, temos que y=-x, e do segundo sistema, também da segunda equação, temos que x=0, mas nenhuma restrição para y.Então, os autovetores associados a λ=1 são os vetores de forma (x,-x) e os autovetores associados a λ=3 são os vetores de forma (0,y). Esses autovetores pertencem ao subespaço u=(1,-1) e v=(0,1), respectivamente, que são linearmente independentes. Então, A é diagonalizável.
A matriz B é diagonalizável.
Primeiramente, devemos avaliar \(det\left( B-\lambda {{I}_{2}} \right)=0\) para essa matriz. Assim:
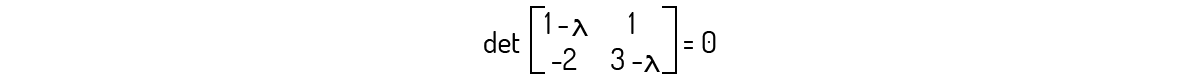
Avaliando esse determinante, você encontrará o seguinte polinômio:
\({{\lambda }^{2}}-4\lambda +5=0\)
Esse polinômio não apresenta raízes. Logo, ele não apresenta autovalores, não sendo diagonalizável.
A matriz B é diagonalizável e apresenta como autovalores λ=1 e λ=3 e autovetores os vetores do subespaço (1,-1) e (0,1).
Primeiramente, devemos avaliar \(det\left( B-\lambda {{I}_{2}} \right)=0\) para essa matriz. Assim:
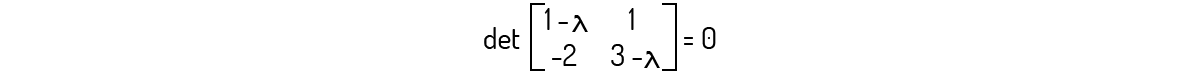
Avaliando esse determinante, você encontrará o seguinte polinômio:
\({{\lambda }^{2}}-4\lambda +5=0\)
Esse polinômio não apresenta raízes; logo, ele não apresenta autovalores, não sendo diagonalizável.