Na presente unidade iremos discutir sobre uma unidade fundamental da álgebra: as matrizes. Veremos que as matrizes tem um arranjo retangular semelhante àquele que vemos nas tabelas, mas, ao contrário destas, podemos utilizar as matrizes para diferentes operações, cada uma delas com suas próprias características e propriedades.
Logo, vamos iniciar esta unidade definindo o que são exatamente as matrizes e então, analisaremos brevemente os tipos mais comuns de matrizes com as quais iremos lidar. Tendo essa parte conceitual sido bem definida, partiremos para a análise das operações que podemos fazer utilizando as matrizes, como a adição, e a multiplicação por escalar.
Finalizando esta unidade, iremos apresentar algumas noções de determinantes, que será útil futuramente nesta disciplina.
Na presente unidade iremos discutir os conceitos básicos de matrizes. As matrizes se mostrarão úteis em diversos problemas: podemos usar matrizes para ordenar e simplificar problemas, o que facilita a compreensão destes, e também, ao fazer uso das matrizes, teremos em mãos diferentes métodos de resolução de problemas.
Uma forma simples de você visualizar uma matriz, conforme nos diz Boldrini et al. (1980), é como uma tabela, onde temos elementos dispostos em linhas e colunas. Por exemplo, considere que você tenha em mãos uma tabela contendo dados de altura, peso e idade de três pessoas diferentes, como a Tabela 1.1.
Tabela 1.1 - Dados físicos de três indivíduos
Fonte: Elaborada pelo autor.
Se reescrevermos os dados desta tabela, abstraindo o significado das linhas e colunas, teremos uma matriz na seguinte forma:
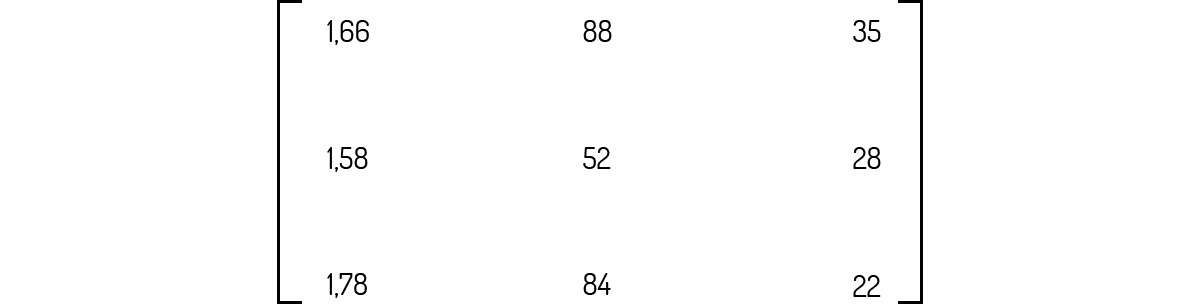
Ou seja, como resume Leon (1999), uma matriz nada mais é do que um arranjo retangular de números em m linhas e n colunas, a qual representaremos, a partir deste ponto por uma letra maiúscula, podendo também acrescentar o subscrito m×n à direita. Esse subscrito é lido como “m por n”. Por exemplo, podemos chamar a matriz que obtivemos da Tabela 1.1 de \(T\) ou \({{T}_{3\times 3}}\), pois ela apresenta 3 linhas e 3 colunas:

Note que, até o momento, fizemos o uso de colchetes para delimitar uma matriz. No entanto, em diferentes materiais, você poderá encontrar outros símbolos com tal finalidade, como os parênteses ou duas barras:
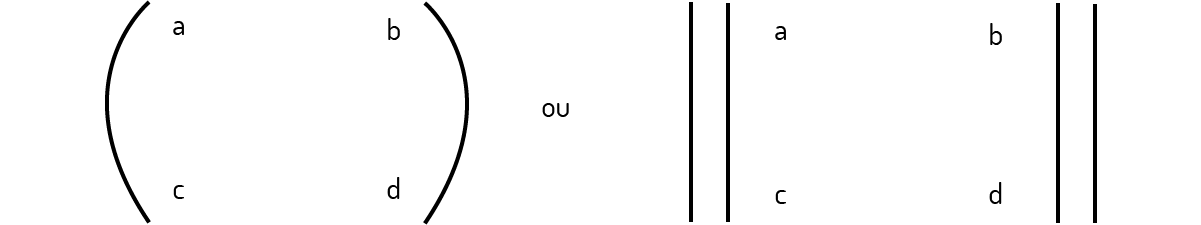
Para facilitar a compreensão, este material sempre usará colchetes para o fim de delimitar matrizes (BOLDRINI et al., 1980).
Como não existe limite para o número de elementos dentro de uma matriz, é melhor que tenhamos uma forma simplificada para designarmos cada um dos termos da matriz. Para isso, conforme Boldrini et al. (1980) indica, iremos usar a mesma letra usada para designar a matriz, mas na versão minúscula, e com índice duplo i e j, sendo que o i indica a i-ésima linha e j a j-ésima coluna, onde o elemento se encontra. Note que, como Lima (2000) destaca, \(1<i<m\) e \(1<j<n\).
Partindo dessa definição, para a matriz gerada a partir da Tabela 1.1, usaremos a notação \({{t}_{ij}}\) para identificar os elementos da matriz. Logo, temos que \({{t}_{11}}\) remete ao elemento situado na linha 1 e coluna 1 da matriz \({{T}_{3\times 3}}\), ou seja, \({{t}_{11}}=1,66\); \({{t}_{32}}\) remete ao elemento situado na linha 3 e coluna 2 da matriz \({{T}_{3\times 3}}\), ou seja, \({{t}_{32}}=84\).
Com o que foi dito até o momento, podemos agora apresentar uma notação para uma matriz genérica de qualquer tamanho:
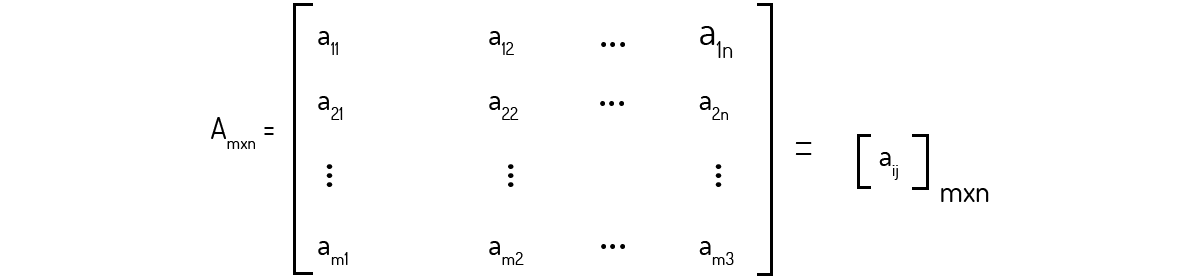
E também podemos citar uma definição mais formal do que é uma matriz:
Definição 1: Uma matriz é um arranjo retangular de números, que são chamados de entradas ou elementos. O tamanho de uma matriz é uma descrição da quantidade de linhas m e colunas n que ela apresenta (POOLE, 2004).
No presente material, iremos considerar que os elementos que compõem a matriz são números reais. Agora que definimos o que é uma matriz e determinamos uma forma simples de identificar cada elemento desta matriz, podemos desenvolver nosso trabalho com elas.
O manuseio de matrizes é indispensável para inúmeros profissionais na atual década. Áreas, como a genética, análises econômicas e desenvolvimento de inúmeras tecnologias precisam lidar com matrizes, geralmente de tamanhos imensos, o que faz com que a tecnologia computacional simples, que temos disponível atualmente, não seja suficiente para as análises requeridas de forma direta. Sabendo disso, você seria capaz de pensar em como lidar em tais situações?

Durante o uso de matrizes na resolução de problemas, você certamente irá se deparar com alguns tipos de matrizes que apresentam características comuns. Agora iremos discutir essas matrizes especiais.
Primeiramente, iremos definir a igualdade entre matrizes. Sejam duas matrizes, \({{A}_{m\times n}}\) e \({{B}_{r\times s}}\). De acordo com Boldrini et al. (1980) e Poole (2004), essas duas matrizes serão iguais se, e somente se, elas possuírem o mesmo número de linhas, o mesmo número de colunas e, se cada elemento correspondente for igual. Ou seja, para essas duas matrizes serem iguais, é necessário que \(m=r\), \(n=s\) e \({{a}_{ij}}={{b}_{ij}}\).
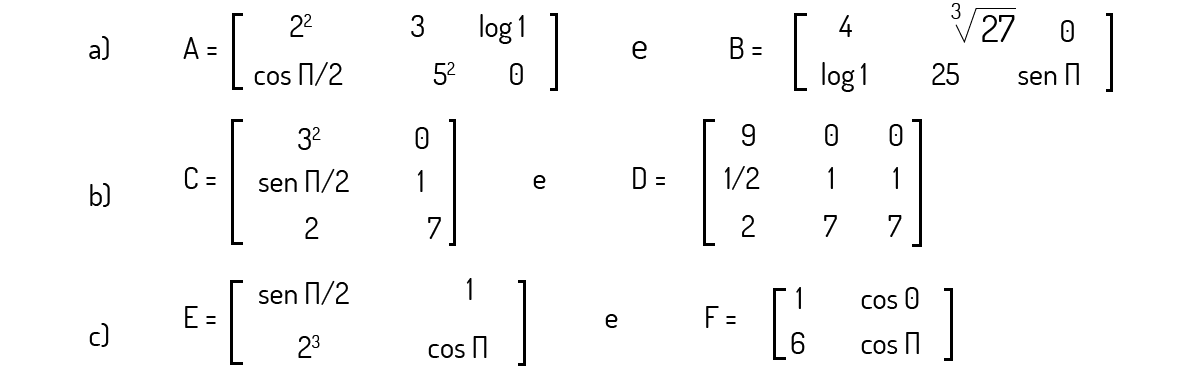
Exemplo 1.1: Verifique se as matrizes dadas a seguir são iguais:
Solução
a) Para avaliarmos a igualdade das matrizes, precisamos analisar os três pontos indicados. Primeiramente, devemos comparar quantas linhas A e B possuem: como ambas as matrizes apresentam duas linhas, passamos para a comparação do número de colunas. Facilmente identificamos que tanto A quanto B apresentam três colunas. Como os números de linhas e colunas são iguais nas duas matrizes, devemos, finalmente, realizar uma avaliação termo a termo das duas matrizes:
i. \({{a}_{11}}={{2}^{2}}=4\); \({{b}_{11}}=4\); logo, \({{a}_{11}}={{b}_{11}}\).
ii. \({{a}_{21}}=cos~\pi /2=0\); \({{b}_{21}}=log~1=0\); logo, \({{a}_{21}}={{b}_{21}}\).
iii. \({{a}_{12}}=3\); \({{b}_{12}}=\sqrt[3]{27}=3\); logo, \({{a}_{12}}={{b}_{12}}\).
iv. \({{a}_{22}}={{5}^{2}}=25\); \({{b}_{22}}=5\); logo, \({{a}_{22}}={{b}_{22}}\).
v. \({{a}_{13}}=log~1=0\); \({{b}_{13}}=0\); logo, \({{a}_{13}}={{b}_{13}}\).
vi. \({{a}_{23}}=0\); \({{b}_{23}}=sen~\pi \); logo, \({{a}_{23}}={{b}_{23}}\).
Verificamos que cada um dos termos é igual, ou seja, \({{a}_{ij}}={{b}_{ij}}\). Então, podemos concluir agora que A=B.
b) Seguimos os mesmos passos realizados em a). Então, comparemos quantas linhas C e D possuem: ambas as matrizes apresentam três linhas. Agora, verifiquemos o número de colunas: identificamos que C apresenta duas colunas, enquanto D apresenta três colunas. Como os números de colunas não são iguais nas duas matrizes, não é preciso analisar os termos das matrizes: já podemos afirmar que C ≠ D.
c) Seguimos os mesmos passos realizados em a). Comparando quantas linhas E e F possuem: ambas as matrizes apresentam duas linhas. Em seguida, identificamos que tanto E quanto F apresentam duas colunas. Como os números de linhas e colunas são iguais nas duas matrizes, devemos, finalmente, realizar uma avaliação termo a termo das duas matrizes:
i. \({{e}_{11}}=sen~\pi /2=1\); \({{f}_{11}}=1\); logo, \({{e}_{11}}={{f}_{11}}\).
ii. \({{e}_{21}}={{2}^{3}}=8\); \({{f}_{21}}=6\); logo, \({{e}_{21}}\ne {{f}_{21}}\).
iii. \({{e}_{12}}=1\); \({{f}_{12}}=cos~0=1\); logo, \({{e}_{21}}={{f}_{21}}\).
iv. \({{e}_{22}}=cos~\pi =-1\); \({{f}_{22}}=cos~\pi =-1\); logo, \({{e}_{22}}={{f}_{22}}\).
Verificamos que nem todos os termos são iguais, ou seja, \({{e}_{ij}}\ne {{f}_{ij}}\). Então, podemos concluir agora que E ≠ F.
Além das matrizes iguais, Boldrini et al. (1980) e Poole (2004) ainda mencionam a existência de dez tipos especiais de matrizes com o qual você irá se deparar com uma boa frequência em seus estudos. Estas matrizes especiais serão discutidas a seguir.
O primeiro tipo de matriz especial consiste naquelas matrizes onde temos que o número de linhas é igual ao número de colunas, ou seja, matrizes onde m = n. As matrizes com essa característica são chamadas de matrizes quadradas. Abaixo são mostrados alguns exemplos de matrizes quadradas.
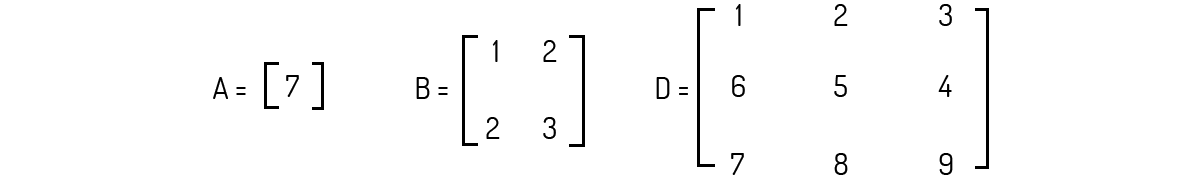
Geralmente, dizemos que uma matriz quadrada de ordem m é aquela que apresenta m colunas e m linhas. Logo, uma matriz de ordem 2 nada mais é do que uma matriz 2 × 2.
Kolman (1999) nos mostra que os elementos \({{a}_{ij}}\) para i=j compõem a diagonal principal da matriz. Por exemplo, numa matriz A de ordem 2, os elementos \({{a}_{11}}~e~{{a}_{22}}~\)são a diagonal desta matriz. Já numa matriz B de ordem 5, os elementos \({{a}_{11}},~{{a}_{22}},~{{a}_{33}},~{{a}_{44}}~e~{{a}_{55}}\) serão a diagonal de B.
O segundo tipo de matriz que comumente aparece é aquela onde todos os elementos são nulos, ou seja, \({{a}_{ij}}=0\) para todo i e j. Essas matrizes são chamadas de matrizes nulas. Abaixo são mostrados alguns exemplos de matrizes nulas.
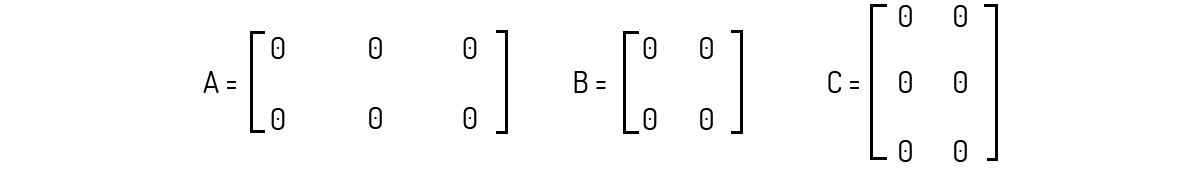
Alguns autores, como Boldrini (1980) e Poole (2004), costumam denotar uma matriz nula por 0 ou \({{0}_{m\times n}}\). Sinta-se livre para usar essa notação, apenas tome o cuidado de não se confundir com o tamanho da matriz nula com a qual você está trabalhando.
O terceiro tipo especial de matriz é aquele onde temos uma única coluna, ou seja, são matrizes onde se tem que n = 1. Essas matrizes são chamadas de matrizes coluna, com alguns exemplos apresentados abaixo.

De modo semelhante, quando temos matrizes onde m = 1, ou seja, matrizes que consistem de uma única linha, temos uma matriz linha. Este é o quarto tipo especial de matriz.
Lipschutz (1994) indica uma nomenclatura diferenciada para as matrizes coluna e matrizes linha: esses tipos de matrizes também podem ser encontradas na literatura como vetor coluna e vetor linha, respectivamente.
O quinto tipo de matriz especial que você deve conhecer é a matriz diagonal. Esse tipo de matriz é sempre uma matriz quadrada onde \({{a}_{ij}}=0\) quando i ≠ j. Simplificando, uma matriz diagonal é aquela onde todos os elementos que não se encontram na “diagonal” são nulos. A seguir são mostrados alguns exemplos de matrizes diagonais.

Um caso especial de matriz diagonal destacado pr Boldrini (1980) é aquele onde todos os elementos da diagonal principal são iguais a 1, ou seja, onde \({{a}_{ii}}=1\) e \({{a}_{ij}}=0\) \(j\ne i\). Uma matriz deste tipo é dita matriz identidade quadrada.

Outro caso especial que temos de uma matriz diagonal, destacado por Kolman (1999) e Poole (2004) é quando todos os elementos da diagonal principal são iguais a uma constante c, isto é, uma matriz onde \({{a}_{ii}}=c\) e \({{a}_{ij}}\)=0 para j ≠ i. Uma matriz que se encaixa nesta definição é chamada de matriz escalar.

O oitavo e o nono tipo de matriz especial são parecidos entre si: são matrizes quadradas onde todos os elementos acima ou abaixo da diagonal principal são nulos. Numa matriz triangular superior, todos os elementos abaixo da diagonal principal são nulos, ou seja, quando \(i>j\), \({{a}_{ij}}=0\).
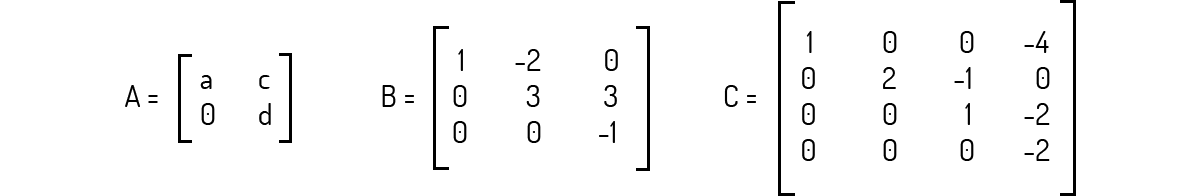
Note que podem existir elementos nulos acima da diagonal principal. O que não ocorre neste tipo de matriz é ter todos os elementos acima e abaixo da diagonal principal como nulos. Já numa matriz triangular inferior, todos os elementos acima da diagonal principal são nulos, ou seja, quando \(i<j\), \({{a}_{ij}}=0\).
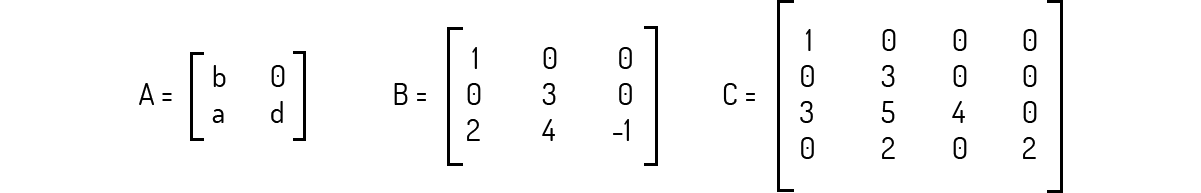
De forma semelhante ao que foi dito para uma matriz triangular superior, não há necessidade de todos os elementos abaixo da diagonal principal serem não-nulos numa matriz triangular inferior. Para que a matriz seja classificada neste tipo, basta que todos os elementos acima da diagonal principal sejam nulos e que haja, ao menos, um elemento que não seja nulo abaixo da diagonal principal.
Finalmente, o último tipo especial de matriz que você deve encontrar em seus estudos são as matrizes simétricas. Este tipo de matriz é aquela matriz quadrada onde o elemento \({{a}_{ij}}={{a}_{ji}}\), ou seja, a parte inferior desse tipo de matriz é uma reflexão da parte superior em relação à diagonal.

Visando fixar melhor os tipos de matrizes que você usará durante os estudos de álgebra, analise as alternativas abaixo e assinale aquela que se encontra correta.
Uma matriz diagonal também é uma matriz simétrica.
Uma matriz diagonal apresenta todos os elementos fora da diagonal principal iguais a zero. Já uma matriz simétrica é uma matriz quadrada onde os elementos \({{a}_{ij}}={{a}_{ji}}\). Logo, uma matriz diagonal é uma matriz simétrica.
A matriz A abaixo é uma matriz diagonal porque apresenta todos os elementos da diagonal principal com o mesmo valor.

Uma matriz diagonal apresenta todos os elementos fora da diagonal principal iguais a zero. O fato de todos os elementos da diagonal principal da matriz serem iguais não quer dizer nada especial.
Uma matriz triangular superior é uma matriz onde todos os elementos acima da diagonal principal são nulos.
Uma matriz triangular superior é aquela cujos elementos abaixo da diagonal principal são nulos.
A matriz A abaixo pode ser considerada uma matriz triangular inferior.
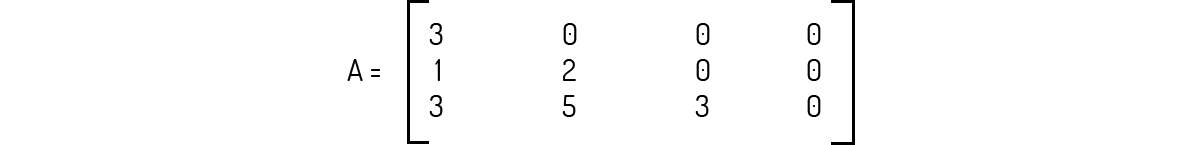
A matriz em questão não é uma matriz quadrada. Logo, ela não apresenta uma diagonal principal e não pode ser considerada uma matriz triangular superior.
A matriz A abaixo não pode ser considerada uma matriz triangular superior porque apresenta um elemento nulo acima da diagonal principal.

Apresentar um elemento nulo acima da diagonal principal não exclui uma matriz do tipo triangular superior. Para que uma matriz seja triangular superior, basta que ela seja quadrada e que apresente todos os elementos abaixo da diagonal principal como nulos.
Tendo você se familiarizado com matrizes, devemos agora definir como iremos trabalhar com elas. Ou seja, devemos definir e formalizar agora como realizamos operações com matrizes, de modo a encontrar novas matrizes a partir de matrizes conhecidas.
A primeira operação que discutiremos primeiramente é a adição de matrizes. Nessa operação, partiremos de, no mínimo, duas matrizes diferentes para encontrar uma nova matriz. A adição de matrizes é semelhante à adição de números reais.
Definição 2 – Adição de matrizes: Sejam \(A=\left[ {{a}_{ij}} \right]\) e \(B=\left[ {{b}_{ij}} \right]\) duas matrizes de mesma ordem m×n, a adição destas matrizes, denotada por A+B, será a matriz C, cujos elementos c_ij serão iguais à soma dos elementos correspondentes, ou seja, \({{a}_{ij}}+{{b}_{ij}}\) (KOLMAN, 1999).
Exemplo 2.1: Sendo as matrizes A e B dadas abaixo, calcule a matriz C = A + B, se possível.

Solução
Antes de efetuarmos a soma, devemos verificar os tamanhos das matrizes. Neste caso, tanto A quanto B são matrizes 3 × 2. Para encontrarmos a matriz C, então, basta que somemos os elementos correspondentes das duas matrizes dadas:
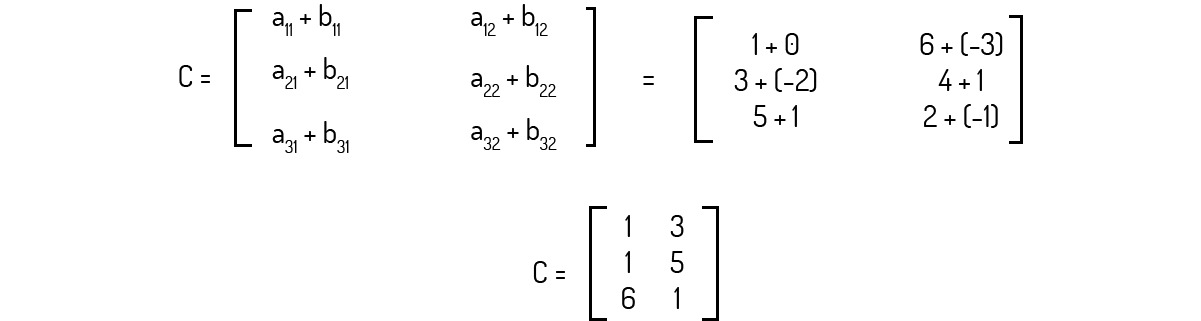
Exemplo 2.2 - Sendo as matrizes A, B e C dadas abaixo, calcule as somas A + B, A + C e B + C, se possível.
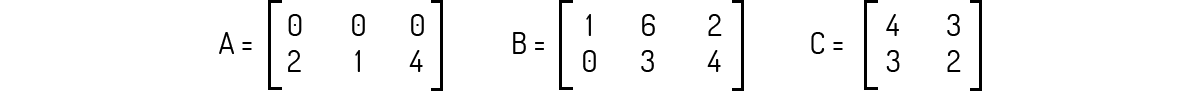
Solução
Antes de efetuarmos qualquer operação de adição de matrizes, devemos verificar os tamanhos das matrizes que serão usadas na operação. Neste exemplo, tanto A quanto B são matrizes 2 × 3, mas C é uma matriz 2 × 2. Com essa informação, já sabemos que não é possível calcularmos A + C nem B + C.
Efetuaremos, então, a única adição possível das requisitadas:

A Definição 2 nos diz apenas da adição de duas matrizes, mas ela é facilmente expansível para inúmeras matrizes a serem adicionadas. Também é importante notar que, por essa definição, só podemos somar matrizes do mesmo tamanho. Boldrini (1980) também destaca que a adição de matrizes também irá apresentar as mesmas propriedades da operação adição, realizada entre números reais.
Para averiguarmos essas propriedades da adição de números reais e já as aplicarmos à adição de matrizes, consideremos três matrizes, A, B e C, sendo essas três matrizes de um mesmo tamanho m × n. Elas estarão sujeitas às seguintes três propriedades, de acordo com Boldrini (1980):
I. Comutatividade: a propriedade da comutatividade da soma nos diz que a ordem que realizamos a adição não altera o resultado final, ou seja:
\(A+B=B+A\)
II. Associatividade: a propriedade da associatividade da soma nos diz que independentemente da forma que realizarmos a soma de parcelas, o resultado será o mesmo, ou seja:
\(A+\left( B+C \right)=\left( A+B \right)+C=\left( A+C \right)+B\)
III. Elemento neutro: a propriedade do elemento neutro nos diz que existe uma matriz nula 0 de tamanho m×n que pode ser somada a uma matriz sem alterar seus elementos, ou seja:
\[A+0=A\]
\[B+0=B\]
\[C+0=C\]
A segunda operação a ser vista é a multiplicação de uma matriz por um número, chamada de multiplicação por escalar. Neste material, iremos nos ater à multiplicação por um escalar real, mas saiba que esta operação também contempla a multiplicação de matrizes por números complexos (BOLDRINI, 1980).
Definição 3 – Multiplicação por escalar: Sejam \(A=\left[ {{a}_{ij}} \right]\) uma matriz de ordem m × n, e k um número real, então o produto escalar k ⋅ A, também chamado de kA, será uma matriz B de ordem m × n onde cada elemento é igual ao produto de k por cada um dos elementos de A, ou seja, é igual a \(\left[ k{{a}_{ij}} \right]\) (POOLE, 2004).
Exemplo 2.3 - Sejam as matrizes A, B e C dadas abaixo e os escalares k = 2 e c = -1. Calcule kA, cB, cC e kA + cA.
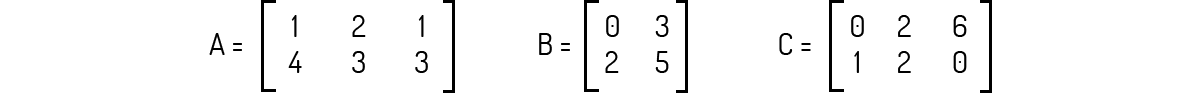
Solução
As primeiras três matrizes que nos é pedida para calcular são simples aplicação da multiplicação por escalar. Vejamos:
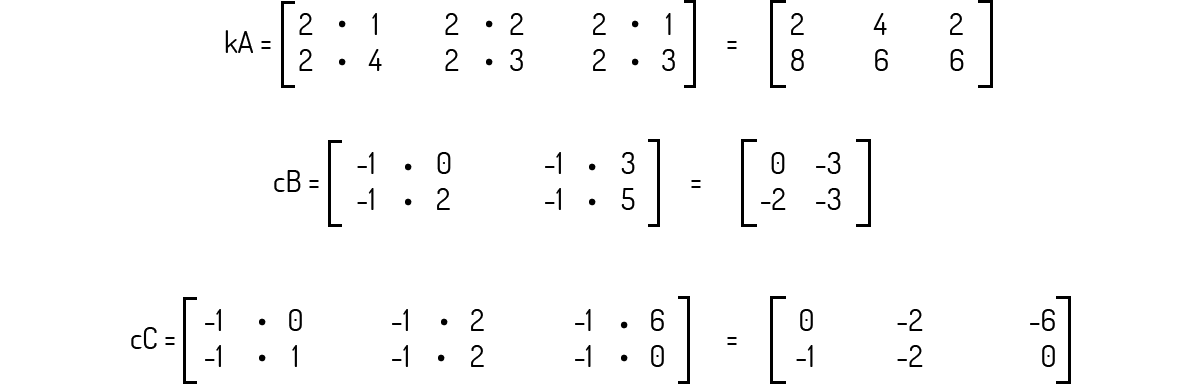
Agora vamos combinar a multiplicação por escalar com a adição e calcular a última matriz desejada:
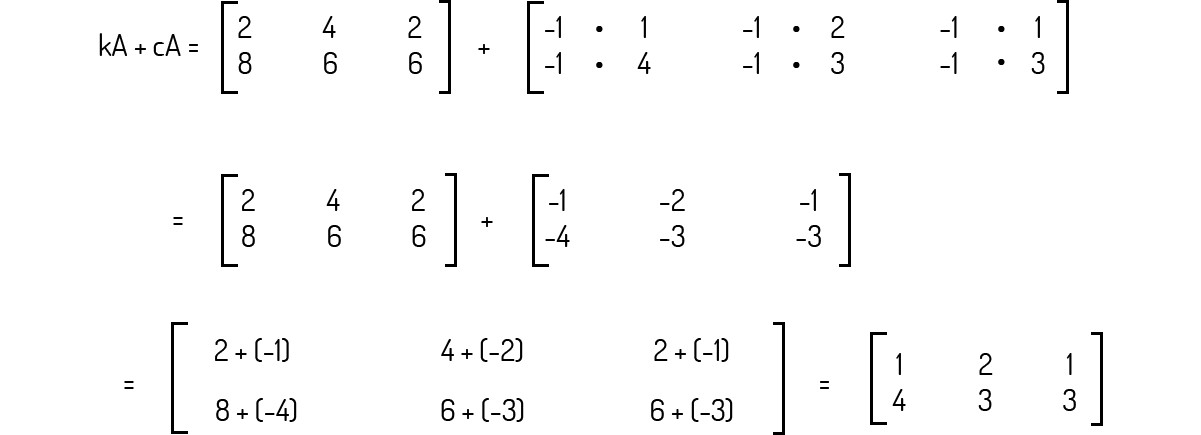
O Exemplo 2.3 nos traz um caso interessante no final. Note que, efetivamente, calculamos kA - A. Isto é, a subtração de matrizes pode ser realizada combinando as operações de adição e multiplicação por escalar, usando o escalar -1 para tal. Assim, sendo as matrizes \(A=\left[ {{a}_{ij}} \right]\) e \(B=\left[ {{b}_{ij}} \right]\), a subtração de matrizes A - B pode ser escrita como A + (-1) ⋅ B. Lipschutz (1994), com essa definição da subtração de matrizes, adiciona uma outra propriedade à adição de matrizes:
IV. Elemento inverso: a propriedade do elemento inverso na adição de matrizes nos diz que, para qualquer matriz A de tamanho m × n existe uma matriz B = (-1) ⋅ A também de tamanho m × n para a qual a soma A + B será uma matriz nula:
\[A+B=A-A=0\]
A operação de multiplicação por escalar de matrizes também apresenta uma série de propriedades. De acordo com Boldrini (1980), a operação de multiplicação por escalar está sujeita às seguintes propriedades listadas abaixo. Sejam A e B matrizes de mesmo tamanho m×n e \(k\), \({{k}_{1}}\) e \({{k}_{2}}\) números reais:
I. Distributividade em relação à matrizes: a multiplicação por escalar de uma soma de matrizes é igual à soma das matrizes multiplicadas pelo escalar:
\[k\left( A+B \right)=kA+kB\]
II. Distributividade em relação ao escalar: a multiplicação de uma matriz pela soma de dois números reais é igual à soma das multiplicações pelos escalares:
\[\left( {{k}_{1}}+{{k}_{2}} \right)A={{k}_{1}}A+{{k}_{2}}A\]
III. Associatividade: a multiplicação por escalar de uma matriz que já é obtida pela multiplicação de um escalar é igual à multiplicação da matriz pela multiplicação dos reais:
\[\left( {{k}_{1}} \right)\cdot {{k}_{2}}A=\left( {{k}_{1}}\cdot {{k}_{2}} \right)A\]
IV. Elemento nulo: a propriedade do elemento neutro nos diz que existe o número 0 que pode ser multiplicado a uma matriz, resultando numa matriz nula:
\[0\cdot A=0\]
\[0\cdot B=0\]
Existirão diversos casos em que você precisará considerar os elementos das linhas de uma matriz como sendo os elementos das colunas da matriz. Essa é a terceira operação que veremos em nosso estudo, chamada de Transposição de matrizes (BOLDRINI, 1980).
Definição 4 – Transposição: seja a matriz \(A=\left[ {{a}_{ij}} \right]\) uma matriz de tamanho m × n. Podemos obter uma nova matriz a partir desta, onde as linhas são as colunas de A, sendo esta nova matriz, a matriz transposta de A, representada por \(A'\) ou \({{A}^{T}}\) (KOLMAN, 1999).
Segundo essa definição, temos que a matriz \({{A}^{T}}\) será composta por elementos \(a_{ij}^{T}={{a}_{ji}}\) (BOLDRINI, 1980). O Exemplo 2.4 tornará mais clara essa definição.
Exemplo 2.4 - Sejam as matrizes A, B e C dadas abaixo. Obtenha as matrizes transpostas de cada uma delas.

Solução
Para obtermos a transposta de uma matriz, devemos substituir as linhas pelas colunas. Assim, tomando primeiramente a matriz A, que possui apenas uma linha, em sua transposta teremos apenas uma coluna, pois a única linha desta matriz será a coluna na transposta:
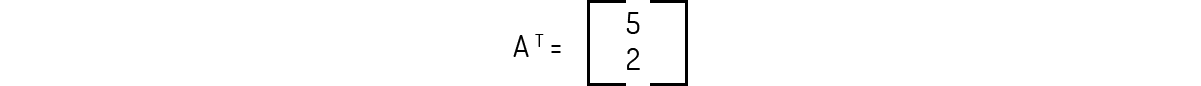
Repetindo o processo para a matriz B, tornando cada uma de suas três linhas em colunas, encontramos:

Finalmente, para a matriz C:

A operação de transposição de matrizes também apresenta uma série de propriedades que você deve conhecer. Boldrini (1980) lista as seguintes propriedades para a transposição:
I. Uma matriz será chamada de simétrica se, e somente se, ela for igual à sua transposta:
\[A={{A}^{T}}\]
II. A transposta de uma matriz transposta é igual à matriz original:
\[{{A}^{TT}}=A\]
III. A transposta de uma soma de matrizes é igual à soma de suas respectivas transpostas:
\[{{\left( A+B \right)}^{T}}={{A}^{T}}+{{B}^{T}}\]
IV. Uma matriz multiplicada por escalar e transposta é igual à multiplicação por escalar da matriz transposta originalmente:
\[{{\left( kA \right)}^{T}}=k{{A}^{T}}\]
Sejam as seguintes matrizes dadas abaixo. Nas alternativas a seguir são mostrados os resultados de algumas operações. Avalie tais resultados e assinale a alternativa correta.

A+B é uma operação possível e é igual a
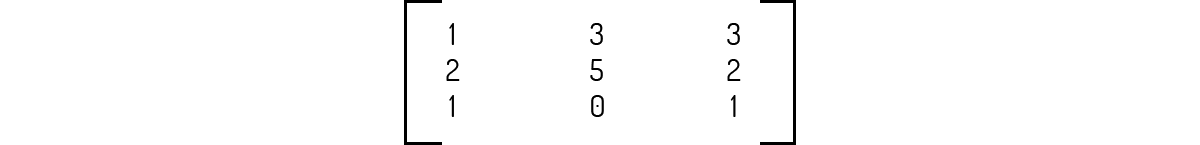
A adição de matrizes só é possível se as duas matrizes apresentarem o mesmo tamanho, o que não ocorre com A e B.
B-2D é uma operação possível e é igual a

Essa operação pode ser vista como a adição B+(-2)D. Realizando a multiplicação por escalar indicada:

Em seguida à adição dos elementos correspondentes, encontramos como resultado:

\(C+{{D}^{T}}\) é uma operação possível e é igual a
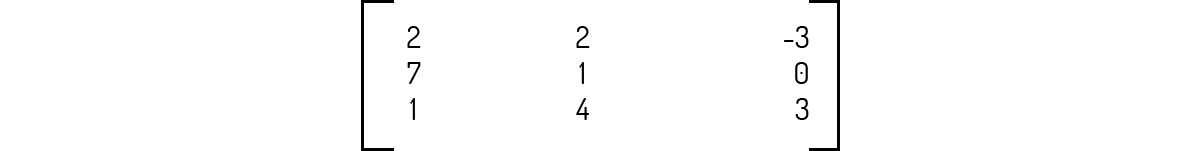
A matriz \({{D}^{T}}\) é uma matriz 2×3. Como a adição de matrizes só é possível se as duas matrizes apresentarem o mesmo tamanho, a operação destacada não é factível.
\(3{{A}^{T}}-{{C}^{T}}\) é uma operação possível e é igual a:

Avaliando cada uma das transpostas, você deve encontrar:

Agora, realizando a multiplicação por escalar em \({{A}^{T}}\) e, em seguida a subtração, você deve encontrar:

\(2{{B}^{T}}+2{{D}^{T}}\) é uma operação possível e é igual a:

Avaliando cada uma das transpostas, você deve encontrar:

Agora, realizando as multiplicações por escalar em \({{B}^{T}}\) e \({{D}^{T}}\) e, em seguida a adição, você deve encontrar:
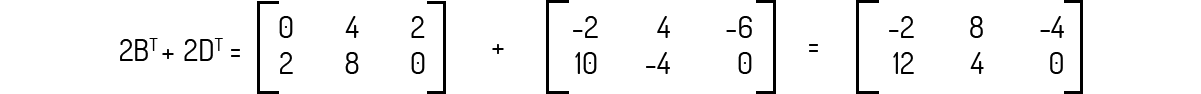
Agora que vimos as operações mais básicas utilizando matrizes, chegou o momento de lidarmos com uma outra operação, ligeiramente mais complexa, mas indispensável para lidarmos com matrizes: a multiplicação de matrizes.
Diferentemente do que vimos até o momento, essa operação não é tão intuitiva quanto a adição ou multiplicação por escalar, apresentando algumas propriedades diferentes destas operações também (KOLMAN, 1999).
Talvez, a principal diferença dessa operação, conforme nos diz Poole (2004), seja o fato de que ela não é realizada simplesmente elemento por elemento, como as vistas anteriormente, apesar de ser possível uma definição desta operação para tal condição. Tal definição, elemento a elemento, no entanto, acaba sendo inviável pela pouca aplicabilidade.
Para tentarmos compreender melhor como é feita esta operação, façamos um exemplo prático aqui, tal qual proposto por Boldrini (1980). Suponha que você tenha em mãos a tabela nutricional de dois alimentos, indicando a composição de fibras, vitamina C e de cálcio para uma certa unidade de consumo destes alimentos, como nos mostra a Tabela 1.2, a seguir.
Tabela 1.2 - Tabela nutricional de alimentos
Fonte: Elaborada pelo autor.
Se consumirmos 2 unidades de alface e 1 unidade de tomate, quanto iremos ingerir de cada componente da tabela acima? Para tal, basta que resolvamos a seguinte conta:
\[Fibras=2\cdot 2+1\cdot 1=4+1=5~g\]
\[Vitamina~C=2\cdot 0+1\cdot 22=0+22=22~mg\]
\[C\acute{a}lcio=2\cdot 28+1\cdot 7=56+7=63~mg\]
Resolvemos o problema dado de uma forma manual. Mas, como já sabemos, podemos transformar qualquer tabela em uma matriz. Assim, podemos fazer com que a tabela seja representada pela seguinte matriz A:

As quantidades de consumo também podem ser representadas na forma matricial com a matriz linha B:
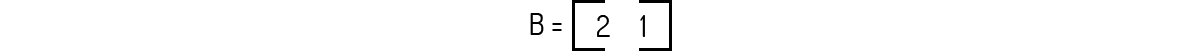
Finalmente, o total de componentes ingeridos também pode ser representado na forma matricial como a matriz C:
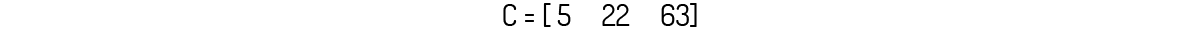
O cálculo manual que realizamos anteriormente é o que chamamos efetivamente de multiplicação de matrizes, ou seja, temos que o produto A ⋅ B será igual a C, ou seja:

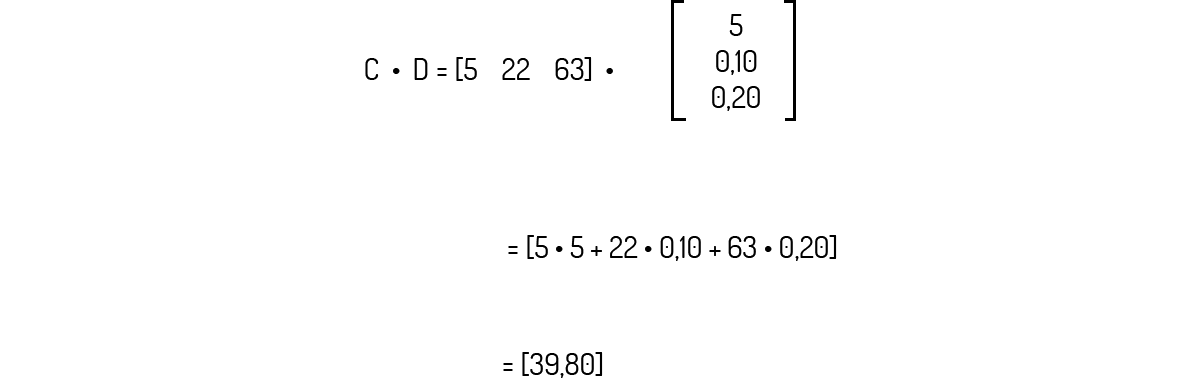
Agora, suponha você deseja substituir esses componentes nutricionais por uma pílula manipulada. Ao ir até um centro de manipulação, você é informado que os custos dessas vitaminas são R$ 5 para cada g de fibra, R$ 0,10 para cada mg de vitamina C e R$ 0,20 para cada mg de cálcio. Assim, o preço de uma pílula que contenha todos esses componentes será:
\[Preço=5\cdot 5+22\cdot 0,10+63\cdot 0,20=25+2,20+12,60=R\$~39,80\]
Essa operação também pode ser transcrita para a forma de matrizes. Os custos dos componentes pode ser transformado na matriz D:

E o preço da pílula também pode ser obtido por uma multiplicação matricial, ou seja, C⋅D:
Note que os “produtos” que encontramos nas multiplicações não são simplesmente a multiplicação dos elementos das matrizes. O resultado destes “produtos” é obtido utilizando os elementos da coluna de uma das matrizes e os elementos da linha da outra matriz.
Boldrini (1980) explicita que, com isso, podemos encontrar uma relação dos tamanhos das matrizes com essa operação. Veja:
\[{{B}_{1\times 2}}\cdot {{A}_{2\times 3}}={{C}_{1\times 3}}\]
\[{{C}_{1\times 3}}\cdot {{D}_{3\times 1}}={{E}_{1\times 1}}\]
Na primeira operação, temos o produto de uma matriz 2 × 3 por uma matriz 1 × 2. O número de linhas de A é o mesmo número de colunas de B. Já a matriz C, que resulta dessa multiplicação, possui o mesmo número de linhas que B e o mesmo número de colunas de A. Na segunda operação, temos o mesmo esquema: a matriz D possui 3 linhas, que é o mesmo número de colunas apresentado por C, e uma coluna, que é o mesmo número de linhas da matriz C. A matriz E, resultado desta multiplicação, apresenta uma linha e uma coluna, ou seja, o mesmo número de linhas de C e o mesmo número de colunas de D.
Assim, acabamos de mostrar como funciona a multiplicação de matrizes envolvendo uma matriz linha e uma matriz coluna. Partindo do que vimos até o momento, podemos partir, então, para uma definição geral da multiplicação de matrizes.
Definição 5 – Multiplicação de matrizes: Seja \(A=\left[ {{a}_{ij}} \right]\) uma matriz de tamanho m × n e \(B=\left[ {{b}_{ij}} \right]\) uma matriz de tamanho n×r. De acordo com Poole (2004), podemos obter uma nova matriz \(C=\left[ {{c}_{ij}} \right]\) a partir destas matrizes, realizando a multiplicação A ⋅ B, sendo o tamanho de C igual a m × r. Cada elemento da nova matriz será igual a:
\[{{c}_{ij}}=\underset{k=1}{\overset{n}{\mathop \sum }}\,{{a}_{ik}}\cdot {{b}_{kj}}={{a}_{i1}}\cdot {{b}_{1j}}+{{a}_{i2}}\cdot {{b}_{2j}}+...+{{a}_{in}}\cdot {{b}_{nj}}\]
Note que, diferente da adição, as matrizes A e B não precisam ser do mesmo tamanho. Basta que o número de colunas de A seja igual ao número de linhas de B.

Essa forma como calculamos o produto de duas matrizes nos diz que o elemento i, j-ésimo de C é simplesmente o produto escalar da i-ésima linha de A com a j-ésima coluna de B.

Exemplo 2.5: Sejam as matrizes A e B. Encontre a matriz C = A ⋅ B.

Solução
Para avaliarmos uma multiplicação de matrizes, primeiramente devemos checar o tamanho das matrizes. A é uma matriz de tamanho 2 × 3 e B é uma matriz de tamanho 3 × 2. Como o número de colunas de A é igual ao número de linhas de B, essa multiplicação é possível e sabemos que a matriz resultante dessa multiplicação será do tamanho 2 × 2, ou seja, o mesmo número de linhas de A e o mesmo número de colunas de B. Agora, basta efetuarmos a operação desejada:
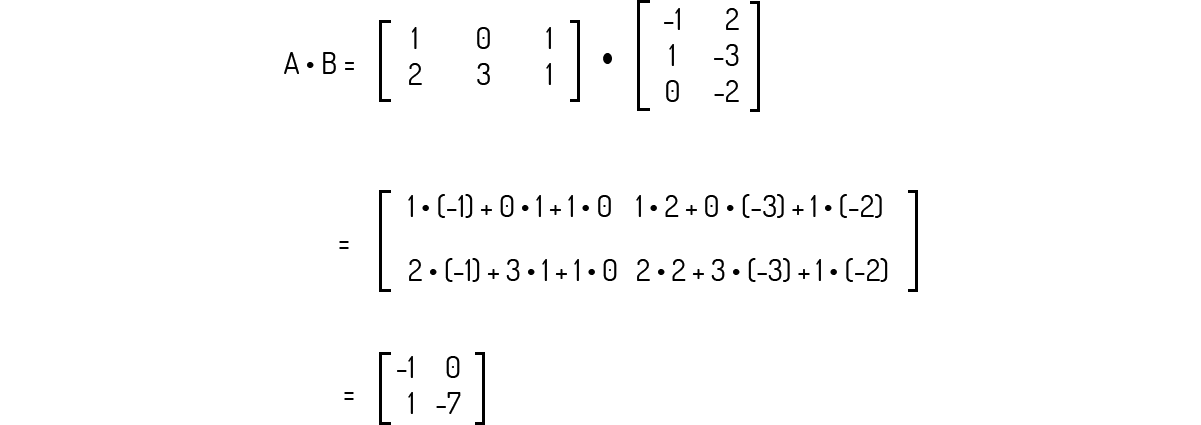
Exemplo 2.6 - Sejam as matrizes A e B. Encontre a matriz C = A ⋅ B.
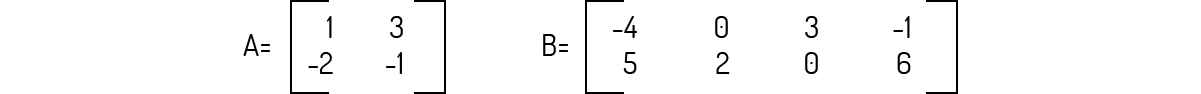
Solução
Verifiquemos o tamanho das matrizes. A é uma matriz de tamanho 2 × 2 e B é uma matriz de tamanho 2 × 4. Como o número de colunas de A é igual ao número de linhas de B, essa multiplicação é possível e sabemos que a matriz resultante dessa multiplicação será do tamanho 2 × 4, ou seja, o mesmo número de linhas de A e o mesmo número de colunas de B. Agora, efetuando a operação desejada:
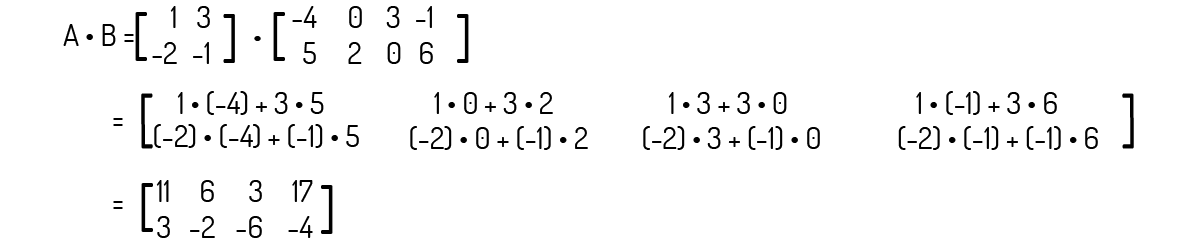
Essa operação de multiplicação de matrizes apresenta algumas propriedades. De acordo com Boldrini (1980), tem-se as seguintes propriedades:
I. Comutatividade: A ⋅ B quase sempre será diferente de B ⋅ A, sendo, inclusive, possível que uma dessas operações seja possível e a outra não. Ou seja, a multiplicação de matrizes não é comutativa. Por exemplo, sejam as seguintes matrizes:

Então:

II. Matriz identidade: seja a matriz I uma matriz identidade quadrada de ordem m e A uma matriz qualquer de ordem m também. Então:
\[A\cdot I=I\cdot A=A\]
III. Distributividade à esquerda: a seguinte distributiva é válida para a multiplicação de matrizes:
\]A\cdot \left( B+C \right)=A\cdot B+A\cdot C\]
IV. Distributividade à direita: a seguinte distributiva também é válida para a multiplicação de matrizes:
\[\left( A+B \right)\cdot C=A\cdot C+B\cdot C\]
V. Associatividade: a associatividade é válida para a multiplicação de matrizes na seguinte forma:
\[\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)\]
VI. Transposta: a transposta de uma matriz que é o produto de $A\cdot B$ é igual à multiplicação das transpostas em ordem inversa:
\[{{\left( A\cdot B \right)}^{T}}={{B}^{T}}\cdot {{A}^{T}}\]
Fique atento à ordem das matrizes ao utilizar esta propriedade!
VII. Matriz nula: a multiplicação de uma matriz por uma matriz nula de tamanho adequado sempre é igual a uma matriz nula:
\[0\cdot A=A\cdot 0=0\]
Sejam as seguintes matrizes apresentadas abaixo. Visando fixar a operação de multiplicação de matrizes, analise as seguintes alternativas e assinale a que for correta.

A multiplicação B⋅A é igual a:
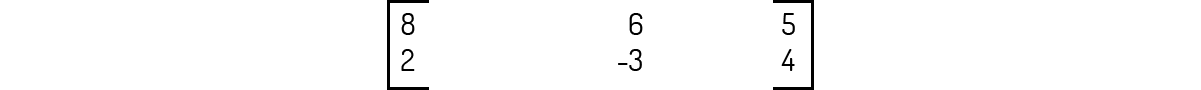
A multiplicação B⋅A não é possível porque a ordem de B é 3×3 e a ordem de A é 2×3. Como o número de colunas de B é diferente do número de linhas de A, essa multiplicação não é possível.
A multiplicação C⋅A é igual a:

A multiplicação C⋅A não é possível porque a ordem de C é 3×1 e a ordem de A é 2×3. Como o número de colunas de C é diferente do número de linhas de A, essa multiplicação não é possível.
A multiplicação B⋅C é igual a:

Como o tamanho de B é 3×3 e o tamanho de C é 3×1, então podemos prosseguir com a multiplicação informada, que será igual à:
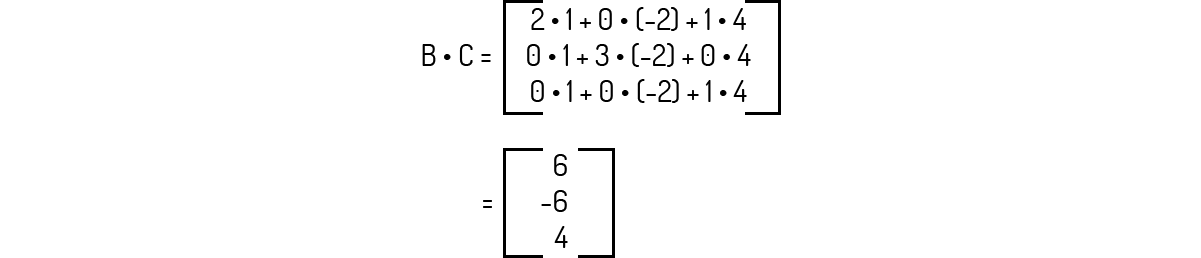
A multiplicação A⋅C é igual a:

Como o tamanho de A é 2×3 e o tamanho de C é 3×1, então podemos prosseguir com a multiplicação informada, que será igual à:
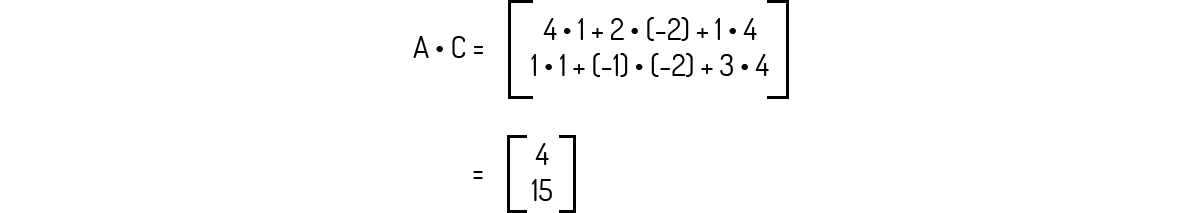
A multiplicação A⋅B é igual a:
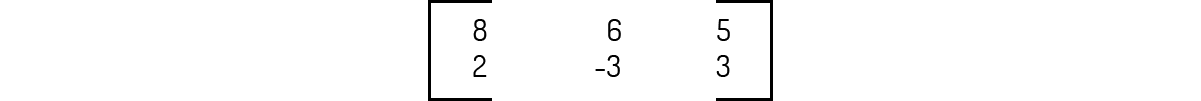
Como o tamanho de A é 2×3 e o tamanho de B é 3×3, então podemos prosseguir com a multiplicação informada, que será igual à:
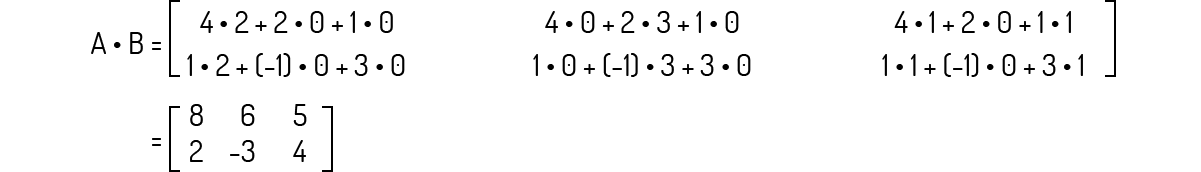
Acabamos vendo diversas operações utilizando matrizes, como a adição, subtração e os dois tipos de multiplicação envolvendo matrizes, a multiplicação por escalar e a multiplicação entre matrizes. Mas, e a divisão de matrizes? É possível realizar esta operação? Se sim, como você realizaria esta operação?

Tendo fundamentado as operações possíveis com matrizes, iremos expandir um pouco os conceitos úteis agora. Chegou o momento de discutirmos sobre as determinantes das matrizes.
O conceito de determinantes é algo muito antigo, existindo registros sobre tal assunto datando de 250 a.C. em livros chineses, segundo Boldrini (1980). Poole (2004) destaca que o conceito de determinantes precede em cerca de duzentos anos o conceito de matrizes, o que pode ser visto com uma certa estranheza atualmente, pois sempre que se estuda tal tópico, iniciamos por matrizes. Poole (2004) ainda cita que esse desenvolvimento do uso de determinantes se deu para a resolução de inúmeros problemas práticos.
Kolman (1999) adianta que podemos usar as determinantes de matrizes na resolução de problemas de diversas áreas da álgebra, como resolução de sistemas lineares e determinação da possibilidade de inverter uma matriz. Assim, iremos desenvolver aqui os conceitos básicos para trabalharmos com determinantes.
Segundo Leon (1999), toda matriz quadrada pode ser associada a um número real, sendo este número chamado de determinante da matriz. Esse escalar será representado por det(A) ou |A|. Essa segunda notação demanda um certo cuidado para não ser confundida com o valor absoluto de A. Com isso, no presente material optou-se pelo uso de det(A).
Um dos conceitos necessários para o entendimento das determinantes é a permutação. Kolman (1999) nos apresenta uma definição deste conceito:
Definição 6 – Permutação: Seja S = {1,2,...,n} um conjunto com todos os números inteiros de 1 a n, devidamente ordenados de forma crescente. Então, qualquer outra ordem \({{j}_{1}},~{{j}_{2}},...{{j}_{n}}\) que coloquemos esses elementos é chamada de permutação de S.
Kolman (1999) diz que é mais fácil denotarmos os conjuntos S utilizando o n subscrito. Assim, \({{S}_{n}}\) indica um conjunto de n números, \({{S}_{1}}\) indica o conjunto de \(1\) número \({{S}_{1}}=\left\{ 1 \right\}\), \({{S}_{2}}\) indica um conjunto de \(2\) números \({{S}_{2}}=\left\{ 1,2 \right\}\), \({{S}_{3}}\) indica um conjunto de \(3\) números \({{S}_{3}}=\left\{ 1,2,3 \right\}\) e assim por diante.
De modo a demonstrar essa definição, considere o conjunto \({{S}_{4}}\). Temos, então, que 1,3,2,4 e 4,3,1,2 são permutações de \({{S}_{4}}\). Assim, podemos colocar qualquer elemento de S na primeira posição, qualquer dos n - 1 elementos restantes na segunda posição, qualquer dos n - 2 elementos restantes na terceira posição e assim por diante, até a n-ésima posição conter o último dos elementos. Como Kolman (1999) confirma, podemos calcular quantas permutações um conjunto S pode apresentar; representando este valor máximo por \({{S}_{m}}\), teremos:
\[{{S}_{m}}=n\cdot \left( n-1 \right)\cdot \left( n-2 \right)\cdot ...\cdot 2\cdot 1~~~~~~~~~~~~(1)\]
Note que (1) nada mais é do que a equação utilizada para avaliar o fatorial do número n, ou seja, n!.
Agora, dada uma permutação de S, dizemos que ela apresentará uma inversão se um inteiro j preceder um inteiro menor \({{j}_{s}}\) (KOLMAN, 1999). Por exemplo, analisemos as permutações do conjunto \({{S}_{3}}\):
Podemos, como outro exemplo, analisar algumas das 24 permutações de \({{S}_{4}}\). A combinação 3214, por exemplo, apresenta três inversões (o 3 precede o 2 e o 1; o 2 precede o 1) e a combinação 4132 apresenta quatro inversões (o 4 precede o 1, o 3 e 2; o 3 precede o 2).
Se o número total de inversões possíveis em um conjunto for par, dizemos que a permutação também é par. De modo semelhante, se o número total de inversões em um conjunto for ímpar, a permutação é chamada de ímpar. E, se n ≥ 2, é possível mostrarmos também que o conjunto S apresentará n!/2 permutações pares e um número igual de permutações ímpares (KOLMAN, 1999).
Para comprovar isso, analise as permutações de \({{S}_{3}}\) que vimos: teremos três permutações pares (123, 231 e 312) e três permutações ímpares (132, 213 e 321). Já em \({{S}_{2}}\), onde temos 2 permutações, uma delas é par (12, que não apresenta inversão) e a outra é ímpar (21, que apresenta uma inversão).
Tendo em mãos essa definição de permutação e inversão, podemos então dar uma definição formal para o que é determinante.
Definição 7 – Determinante: Seja A uma matriz de tamanho m × n. O determinante det(A) dessa matriz A será
\[det\left( A \right)=\underset{{}}{\overset{{}}{\mathop \sum }}\,\pm {{a}_{1{{j}_{1}}}}{{a}_{2{{j}_{2}}}}...{{a}_{n{{j}_{n}}}}~~~~~~~~~~~~(2)\]
Sendo o somatório tomado sobre todas as permutações possíveis j, \({{j}_{1}}\),... \({{j}_{n}}\) do conjunto \({{S}_{n}}\). O sinal ± será + se a permutação for par e - se a permutação for ímpar (KOLMAN, 1999).
Visando fixar e compreender melhor esta definição, vejamos como procedemos para calcular o determinante de uma matriz de ordem 2. Genericamente, esta matriz pode ser representada da seguinte forma:

Para obter o determinante, sendo nosso n = 2, teremos um total de duas permutações. Logo, a somatória (2) será composta por dois termos:
\[det\left( A \right)=\pm {{a}_{1-}}{{a}_{2-}}\pm {{a}_{1-}}{{a}_{2-}}\]
Os espaços vazios deixados devem ser preenchidos com as permutações de \({{S}_{2}}\), ou seja, 1 e 2 depois 2 e 1. Então:
\[det\left( A \right)=\pm {{a}_{11}}{{a}_{22}}\pm {{a}_{12}}{{a}_{21}}\]
Como já vimos anteriormente, a permutação 12 é par e a permutação 21 é ímpar. Então, \({{a}_{11}}{{a}_{22}}\) tem sinal positivo e \({{a}_{12}}{{a}_{21}}\) tem sinal negativo. Logo:
\[det\left( A \right)={{a}_{11}}{{a}_{22}}-{{a}_{12}}{{a}_{21}}\]
Exemplo 2.7 - Encontre o determinante de uma matriz de ordem 3.
Solução
Uma matriz genérica de ordem 3 é representada da seguinte forma:
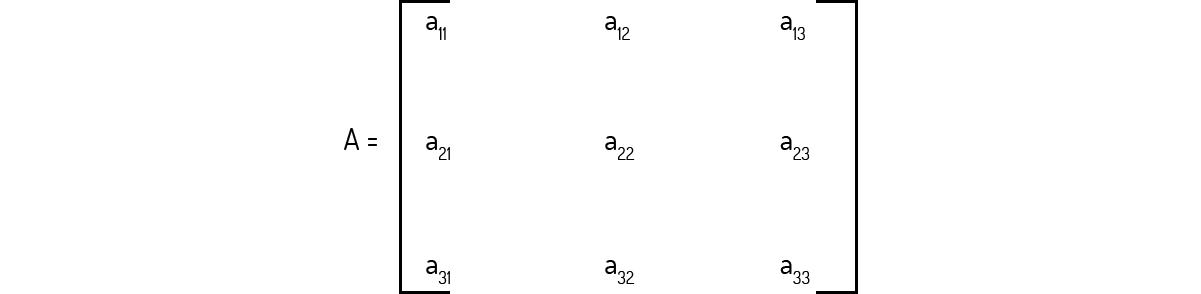
Para obter o determinante, sendo n = 3, sabemos que existe um total de seis permutações, pois 3! = 3 ⋅ 2 ⋅ 1 = 6. Logo, a somatória (2) será composta por seis termos:
\[det\left( A \right)=\pm {{a}_{1-}}{{a}_{2-}}{{a}_{3-}}\pm {{a}_{1-}}{{a}_{2-}}{{a}_{3-}}\pm {{a}_{1-}}{{a}_{2-}}{{a}_{3-}}\pm {{a}_{1-}}{{a}_{2-}}{{a}_{3-}}\pm {{a}_{1-}}{{a}_{2-}}{{a}_{3-}}\pm {{a}_{1-}}{{a}_{2-}}{{a}_{3-}}\]
Os espaços vazios deixados devem ser preenchidos com as permutações de \({{S}_{3}}\): 123, 132, 213, 231, 312 e 321. Logo:
\[det\left( A \right)=\pm {{a}_{11}}{{a}_{22}}{{a}_{33}}\pm {{a}_{11}}{{a}_{23}}{{a}_{32}}\pm {{a}_{12}}{{a}_{21}}{{a}_{33}}\pm {{a}_{12}}{{a}_{23}}{{a}_{31}}\pm {{a}_{13}}{{a}_{21}}{{a}_{32}}\pm {{a}_{13}}{{a}_{22}}{{a}_{31}}\]
Já analisamos anteriormente as permutações de \({{S}_{3}}\): 123, 231 e 312 são pares e 132, 213 e 321 são ímpares. Então:
\[det\left( A \right)={{a}_{11}}{{a}_{22}}{{a}_{33}}-{{a}_{11}}{{a}_{23}}{{a}_{32}}-{{a}_{12}}{{a}_{21}}{{a}_{33}}+{{a}_{12}}{{a}_{23}}{{a}_{31}}+{{a}_{13}}{{a}_{21}}{{a}_{32}}-{{a}_{13}}{{a}_{22}}{{a}_{31}}\]
\[={{a}_{11}}{{a}_{22}}{{a}_{33}}+{{a}_{12}}{{a}_{23}}{{a}_{31}}+{{a}_{13}}{{a}_{21}}{{a}_{32}}-{{a}_{11}}{{a}_{23}}{{a}_{32}}-{{a}_{12}}{{a}_{21}}{{a}_{33}}-{{a}_{13}}{{a}_{22}}{{a}_{31}}\]
Existe uma outra forma de obtermos o determinante de uma matriz de ordem três, provavelmente mais simples que o método que exige a resolução da somatória (2). Neste método alternativo, você deve repetir as duas primeiras colunas da matriz, como mostrado abaixo:
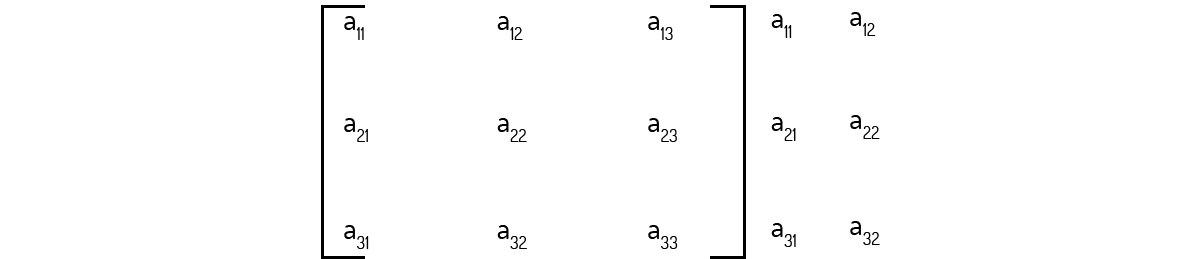
Agora, trace setas nas diagonais formadas da direita para a esquerda e da esquerda para a direita:
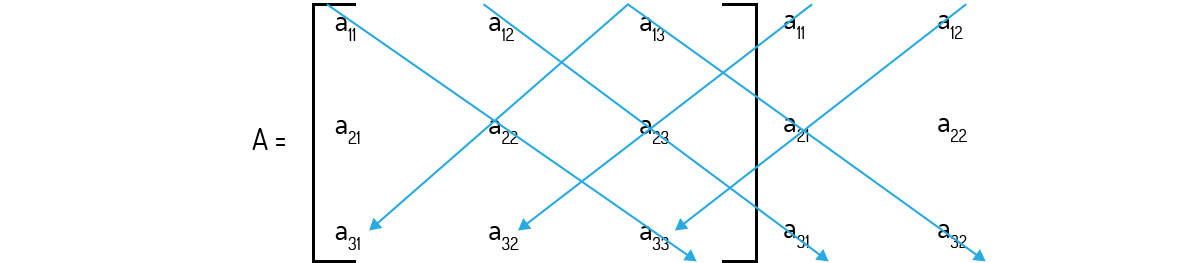
Os elementos que são cortados por uma mesma seta formam uma sequência de produto de três elementos. Aqueles que são cortados por setas que vão da esquerda para a direita, são positivos; logo, temos os seguintes produtos positivos:
\[{{a}_{11}}{{a}_{22}}{{a}_{33}}, {{a}_{12}}{{a}_{23}}{{a}_{31}} e {{a}_{13}}{{a}_{21}}{{a}_{32}}\]
Os que são cortados por setas que vão da direita para a esquerda são negativos; logo, os seguintes termos serão produtos negativos:
\[{{a}_{12}}{{a}_{21}}{{a}_{33}}, {{a}_{11}}{{a}_{23}}{{a}_{32}} e {{a}_{13}}{{a}_{22}}{{a}_{31}}\]
Você já deve ter percebido que, qualquer que seja a forma, o cálculo de determinantes é extremamente trabalhoso, principalmente se pensarmos em valores de n maiores que 3.
O trabalho manual com matrizes pode ser algo cansativo e até complexo de se realizar. Após ter o domínio teórico da base, pode ser útil que você também domine o uso de alguns softwares que facilitem o manuseio de grandes matrizes. Dentre os softwares úteis para esse uso, destacam-se o MATLAB®️, o SciLab e o GNU Octave, sendo os dois últimos softwares livres. O mundo atual exige um bom conhecimento e manuseio da tecnologia, então, é útil que você seja apto a utilizar algum destes softwares ao menos de forma básica.
Links: www.scilab.org

Boldrini (1980) e Kolman (1999) apresentam uma série de teoremas que ditam as propriedades dos determinantes de matrizes. Vejamos tais teoremas:
Teorema 1: Se uma matriz apresenta todos os elementos de uma linha ou coluna como nulos, então det(A) = 0 (BOLDRINI, 1980).
Isso se dá pelo fato de que em cada um dos termos usados no cálculo do determinante, teremos um elemento da linha ou coluna nula realizando uma multiplicação. Logo, como qualquer valor multiplicado por zero é igual a zero, teremos um determinante nulo também.
Teorema 2: Os determinantes de uma matriz e de sua respectiva matriz transposta são iguais, ou seja, \(det\left( A \right)=det\left( {{A}^{T}} \right)\) (KOLMAN, 1999).
Para a prova deste Teorema 2, lembre-se que, se \(A=\left[ {{a}_{ij}} \right]\), então \({{A}^{T}}=\left[ {{b}_{ij}} \right]\), onde \({{b}_{ij}}={{a}_{ji}}\). Utilizando, então, (2):
\[det\left( {{A}^{T}} \right)=\underset{{}}{\overset{{}}{\mathop \sum }}\,\pm {{b}_{1{{j}_{1}}}}{{b}_{2{{j}_{2}}}}...{{b}_{n{{j}_{n}}}}=\underset{{}}{\overset{{}}{\mathop \sum }}\,\pm {{a}_{{{j}_{1}}1}}{{a}_{{{j}_{2}}2}}...{{a}_{{{j}_{n}}n}}\]
Podemos arrumar os fatores \({{a}_{{{j}_{1}}1}},~{{a}_{{{j}_{2}}2}}...{{a}_{{{j}_{n}}n}}\) de modo que os índices das linhas fiquem em sua ordem natural. Então:
\[{{a}_{{{j}_{1}}1}}{{a}_{{{j}_{2}}2}}...{{a}_{{{j}_{n}}n}}={{a}_{1{{j}_{1}}}}{{a}_{2{{j}_{2}}}}...{{a}_{n{{j}_{n}}}}\]
Vejamos como exemplo o seguinte caso:

\[det\left( A \right)={{a}_{11}}{{a}_{22}}-{{a}_{12}}{{a}_{21}}=2\cdot 2-3\cdot 1=4-3=1\]
\[det\left( {{A}^{T}} \right)={{b}_{11}}{{b}_{22}}-{{b}_{12}}{{b}_{21}}=2\cdot 2-1\cdot 3=4-3=1\]
Teorema 3: Se trocarmos a posição de duas linhas de uma matriz, o sinal do determinante irá mudar (KOLMAN, 1999).
A razão de termos isso acontecendo é que, ao trocarmos duas linhas de uma matriz também iremos alterar a paridade do número de inversões dos índices, o que acarreta na troca de sinal dos termos.
Vejamos um exemplo simples deste teorema. Sejam as matrizes A e B abaixo:

Então:
\[det\left( A \right)={{a}_{11}}{{a}_{22}}-{{a}_{12}}{{a}_{21}}=2\cdot 3-4\cdot 1=6-4=2\]
\[det\left( B \right)={{b}_{11}}{{b}_{22}}-{{b}_{12}}{{b}_{21}}=1\cdot 4-3\cdot 2=4-6=-2\]
Teorema 4: Se uma matriz apresenta duas linhas ou colunas iguais, seu determinante será zero (KOLMAN, 1999).
Vejamos uma demonstração simples deste teorema. Sejam as linhas 1 e 3 de uma matriz A_(3 × 3) iguais. Se trocarmos essas duas linhas de lugar, formando uma nova matriz B, pelo Teorema 3, teremos que det(B)=-det(A). No entanto, como as linhas trocadas são iguais, temos que B = A, o que acarreta que det(B) = det(A). Dessas duas observações, chegamos a conclusão que det(A) = -det(A) e o único número que satisfaz essa condição é o zero.
Teorema 5: Se uma matriz B é obtida de uma matriz A onde multiplicamos uma linha ou coluna por uma constante k, então tem-se que det(B) = k ⋅ det(A) (KOLMAN, 1999).
A justificativa deste Teorema é semelhante à do Teorema 1. Como em cada termo usado no cálculo do determinante de uma matriz temos um elemento de cada linha ou coluna, temos que em cada elemento teremos um elemento multiplicado por k, de modo que podemos deixar essa constante em evidência, multiplicando o determinante da matriz original.
Teorema 6: Se uma matriz B é obtida de uma matriz A onde somamos a cada elemento de uma r-ésima linha (ou coluna) uma constante k vezes o elemento correspondente da s-ésima linha (ou coluna) de A, sendo r ≠ s, então \(det\left( B \right)=det\left( A \right)\) (KOLMAN, 1999).
Assim, se temos as seguintes matrizes:

Note que a r-ésima linha de B nada mais é do que a r-ésima linha de A adicionada de k multiplicado pelos respectivos elementos da s-ésima linha de A. Então:
\[det\left( B \right)=det\left( A \right)\]
Teorema 7: Para matrizes triangulares superiores ou inferiores, o determinante simplesmente é o produto dos elementos da diagonal principal da matriz (KOLMAN, 1999).
Fora da multiplicação dos elementos da diagonal principal, o cálculo do determinante de uma matriz envolve a multiplicação de elementos que estão na região de nulos desses tipos de matrizes, fazendo com que todos os demais termos do cálculo de determinante sejam nulos. Por exemplo, vejamos a seguinte matriz:

Tem-se que:
\[det\left( A \right)={{a}_{11}}{{a}_{22}}{{a}_{33}}+{{a}_{12}}{{a}_{23}}{{a}_{31}}+{{a}_{13}}{{a}_{21}}{{a}_{32}}-{{a}_{11}}{{a}_{23}}{{a}_{32}}-{{a}_{12}}{{a}_{21}}{{a}_{33}}-{{a}_{13}}{{a}_{22}}{{a}_{31}}\]
\[det\left( A \right)=1\cdot 2\cdot 1+0\cdot 0\cdot 2+0\cdot 1\cdot 3-1\cdot 0\cdot 3-0\cdot 1\cdot 1-0\cdot 2\cdot 2\]
\[det\left( A \right)=2+0+0-0-0-0=2\]
Teorema 8: O determinante de um produto de matrizes é igual ao produto de seus determinantes, ou seja, \(det\left( A\cdot B \right)=det\left( A \right)\cdot det\left( B \right)\) (BOLDRINI, 1980).
A prova deste Teorema é um pouco complexa, mas podemos demonstrá-lo com um exemplo. Sejam as matrizes abaixo:

Temos que:
\[det\left( A \right)={{a}_{11}}{{a}_{22}}-{{a}_{12}}{{a}_{21}}=1\cdot 2-3\cdot 5=2-15=-13\]
\[det\left( B \right)={{b}_{11}}{{b}_{22}}-{{b}_{12}}{{b}_{21}}=4\cdot 6-3\cdot 1=24-3=21\]
Se multiplicarmos A por B, encontramos:
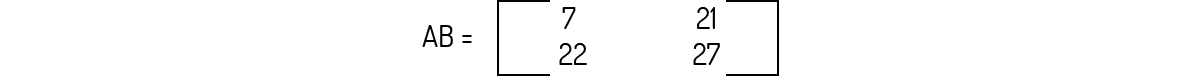
Para a qual:
\[det\left( AB \right)=a{{b}_{11}}a{{b}_{22}}-a{{b}_{12}}a{{b}_{21}}=7\cdot 27-21\cdot 22=189-462=-273\]
Comparando os resultados:
\[det\left( AB \right)=-273\]
\[det\left( A \right)\cdot det\left( B \right)=-13\cdot 21=-273\]
O tema determinantes tem uma teoria relativamente densa, de modo que é útil ter um bom domínio das bases deste assunto. Englobando todo o assunto de determinantes visto até o momento, analise as alternativas abaixo e assinale a correta.
Dadas as matrizes A e B abaixo, sabemos de antemão que o determinante delas serão iguais.
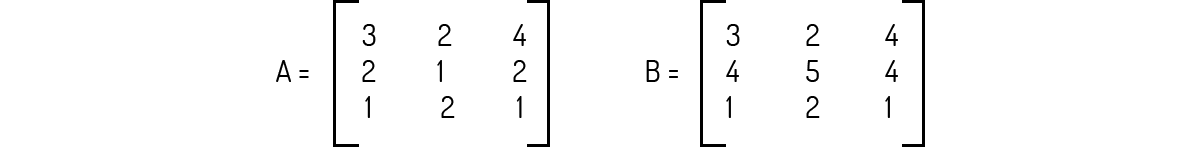
Pelo Teorema 6 sabemos disso, pois a linha 2 de B é igual à duas vezes a linha três, mais a linha 2 de A. Logo, os determinantes dessas matrizes precisam ser iguais.
No determinante de um matriz de ordem 5, os termos \({{a}_{13}}{{a}_{25}}{{a}_{34}}{{a}_{41}}{{a}_{52}}\) e \({{a}_{15}}{{a}_{24}}{{a}_{33}}{{a}_{42}}{{a}_{51}}\) apresentarão sinais positivo e negativo, respectivamente.
O primeiro termo é formado pela permutação 35412, que possui sete inversões (3 precede o 1 e o 2; 5 precede o 4, o 1 e o 2; 4 precede o 1 e o 2); logo, é uma permutação ímpar, que precisa de um sinal negativo. Já o segundo termo é formado pela permutação 54321, que possui dez inversões (5 precede o 4, o 3, o 2 e o 1; 4 precede o 3, o 2 e o 1; 3 precede o 2 e o 1; 2 precede o 1); logo, é uma permutação par, que precisa de um sinal positivo. Assim, os sinais ditos estão trocados.
O determinante da matriz A abaixo é igual a zero.
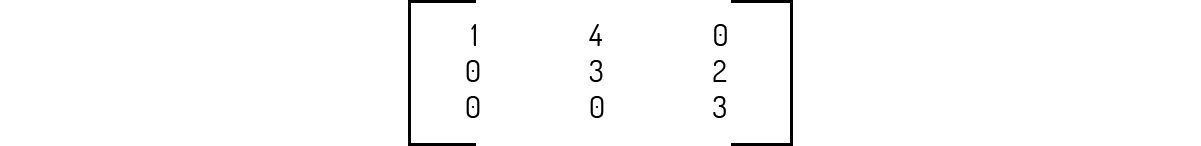
Essa matriz é do tipo triangular superior. Logo, seu determinante deve ser igual ao produto de sua diagonal principal, ou seja:
\[det=1\cdot 3\cdot 3=9\]
Sendo as matrizes A e B abaixo, o determinante de A⋅B é igual a -6.

det(A⋅B) pode ser facilmente calculado por det(A)⋅det(B). Como det(A)=1⋅1-2⋅2=-3 e det(B)=-2⋅3-4⋅(-1)=-2, então:
\[det\left( A \right)\cdot det\left( B \right)=det\left( A\cdot B \right)=6\]
O determinante da matriz abaixo é igual a -6.

Como a matriz em questão apresenta uma coluna apenas com elementos nulos, pelo Teorema 1, seu determinante será igual a 0.
Nome do livro: Álgebra Linear
Editora: Harper & Row do Brasil
Autor: BOLDRINI, J. L. et al.
ISBN: 8529402022
Um livro contendo vários exemplos e linguagem facilitada para o aprendizado. Deve ser mantido quase como uma companhia constante no estudo desta disciplina.

Nome do livro: Álgebra Linear
Editora: Cengage CTP
Autor: POOLE, D.
ISBN: 852212390X
Este livro apresenta uma linguagem simples e fácil de fixar, apresentando o conteúdo em conjunto com diversos exemplos, facilitando assim, a compreensão de cada tópico tratado.
