Nesta unidade, abordaremos, como temática principal, a configuração e especificação de controladores programáveis, explicitando os sistemas numéricos: decimal, binário, octal e hexadecimal, além de abordar o funcionamento dos circuitos lógicos, dos circuitos combinacionais e dos circuitos sequenciais. Por conseguinte, abordaremos os controladores lógicos, as linguagens de programação e os comandos de automação.
Os sistemas numéricos são representações de conjuntos de números. Um conjunto de cinquenta e duas maçãs, por exemplo, pode ser representado pelos algarismos:
Isso ocorre, porque a linguagem computacional empregada nos controladores e dispositivos eletrônicos precisa comunicar-se por meio de conjuntos numéricos (CAPELLI, 2007).
Estamos acostumados a um só sistema, todavia os controladores, computadores e circuitos lógicos utilizam os sistemas decimal, octal, binário e hexadecimal. Como estamos tratando de bases numéricas, temos, como base principal, o binário, que é fundamentalmente empregado em praticamente todos os sistemas numéricos, ou seja, controladores, circuitos lógicos, máquinas industriais, computadores etc.
Temos, também, o octal e o hexadecimal, que são dois sistemas bastante empregados, pelo fato de utilizarem bases que são potências de 2 (\(2^3\)= 8 e \(2^4\) = 16). Os sistemas numéricos possuem características em comum na representação dos números (FIALHO, 2014). A partir da compreensão dessas regras simples, torna-se bem mais simples converter números de uma base para outra. A partir de um número XYZ, ABC qualquer, em um sistema numérico com base n qualquer, temos as seguintes regras:
Podemos verificar a potência passando de positiva, na parte inteira do respectivo número, para negativa, na parte fracionária após a vírgula. Como exemplo, temos, na base 10, o número 431.975. Faremos a decomposição deste, em que cada algarismo que faz parte do número terá uma potência, como pode-se ver no exemplo abaixo.
Tabela 3.1 - Conversão de base numérica - Parte 1
Fonte: Elaborada pelo autor.
Ou, então, aplicando as potências:
Tabela 3.2 - Conversão de base numérica - Parte 2
Fonte: Elaborada pelo autor.
Para um número binário que usa a base 2, teremos, similarmente, a regra anteriormente aplicada. A decomposição do número 110,111 ficaria:
Tabela 3.3 - Decomposição de bases
Fonte: Elaborada pelo autor.
Dessa forma, o número 110,111 é representado por: (4+2) = 6, na parte inteira, e (1/2+1/4+1/8) = 0,875, na parte fracionária. Assim, 110,111 em binário (base 2) é o mesmo que 6,875 em decimal (base 10).
No sistema decimal, temos 10 algarismos diferentes para representar os números (0 a 9). Este é o sistema que costumamos ver com maior clareza no dia a dia. Já o sistema binário utiliza 2 algarismos diferentes para representar os números 0 e 1 (MONTEIRO, 2007).
Ambos são empregados em controladores, máquinas industriais e computadores, mas o sistema numérico é mais utilizado nas linguagens de máquina, que é composto por dois estados (aberto e fechado, ligado e desligado, sim e não etc.), sendo representado, respectivamente, por 0 e 1. Em outras representações, poderemos ter a base subscrita após o número binário, por exemplo, \(110101_2\) (base 2) ou \(110101_{bin}\).
Já o sistema octal utiliza 8 algarismos diferentes para representar os números de 0 a 7. Este é muito utilizado para representar números binários de forma mais compacta, tendo em vista que, a cada dígito octal, temos a representação de três bits. Muitas vezes, números do sistema octal são representados com um pequeno "o". Exemplo: \(4701_o\) ou \(4701_{oct}\),; \(1572_o\) ou \(1572_{oct}\),; \(1057_o\) ou \(1057_{oct}\),; \(721_o\) ou \(721_{oct}\).
O sistema hexadecimal, que utiliza a base 16, apresenta 16 algarismos diferentes, os quais representam números. No caso, então, não temos algarismos que representam números maiores que nove, logo, precisamos utilizar letras do alfabeto (NATALE, 2007).
No hexadecimal, temos letras que representam os números acima de nove até o quinze, respectivamente, sendo A, B, C, D, E e F. Na base 16, temos a precedência do “0x”, que representa um número na base 16, por exemplo, 0xFA. Se desejamos converter um dado número decimal para binário, realizamos a decomposição do número da base 10 em potência de 2. Assim, temos que um número decimal X poderá ser decomposto em uma soma de potências de 2; com isso, X será igual a \(x_1\) x \(2^0\) + \(x_2\) x \(2^1\) + \(x_3\) x \(2^2\) + \(x_4\) x \(2^3\) etc. Exemplo: 567, 2043, 57283 e 12839696.
Nesse sentido, \(x_i\) é sempre zero ou um. Exemplo: a decomposição do número 486 é realizada da seguinte maneira:
A partir da decomposição, temos o número no sistema binário a seguir.
Tabela 3.4 - Decomposição para sistema binário de potência 2
Fonte: Elaborada pelo autor.
O número decimal (base 10) 48, convertido em binário (base 2), portanto, é 111100110.
Já a conversão de octal (base 8) para binário (base 2) dá-se a partir da tradução de cada algarismo em octal para um conjunto de três bits (\(2^3\) = 8 possibilidades), começando sempre pela direita (THOMAZINI; ALBUQUERQUE, 2005). Desse modo, o número 25173 em octal pode ser convertido em binário.
Como material complementar, indicamos explorar mais o conteúdo por meio do vídeo “Resumão: Conversão de Bases”, disponível em:
<https://www.youtube.com/watch?v=KNCS8OwiEmE>. Acesso em: 21 out. 2019.

Tabela 3.5 - Decomposição de base octal
Fonte: Elaborada pelo autor.
Vemos que 25173 (Octal) é 010101001111011 (Binário). O contrário também será verdadeiro, isto é, um binário poderá ser separado de três em três bits, para ser convertido em octal, da direita para a esquerda. O número 010101001111011 está em binário e será convertido para octal, como exemplo apresentado na sequência.
Tabela 3.6 - Composição de base binária para octal
Fonte: Elaborada pelo autor.
Da mesma forma, podemos converter hexadecimal para binário por meio de um conjunto de 4 bits (\(2^4\) = 16 possibilidades). Dessa forma, o número ADC02 poderá ser convertido em binário, com cada posição em hexadecimal, conforme podemos ver a seguir.
Tabela 3.7 - Conversão de base hexadecimal para binário
Fonte: Elaborada pelo autor.
Por continuação, o número AFC02 em hexadecimal é convertido em 10101111110000000010. Em hexadecimal, a conversão inversa pode ser utilizada para cada 4 algarismos binários, então teremos a conversão para o seu respectivo algarismo hexadecimal. Temos, também, que as conversões de decimal para octal são simples, caso utilizemos o sistema binário para intermediar, ou seja, esta é a melhor maneira de converter o número decimal em binário e de binário para octal.
Agora, iremos converter o número 3289 em decimal para octal. Decompondo o número 3289 em potências de 2, temos que 3289 = 2048 + 1024 + 128 + 64 + 16 + 8 + 1, ou seja, 3289 em binário é igual a:
Tabela 3.8 - Decomposição de base para binário
Fonte: Elaborada pelo autor.
Dessa vez, converteremos de binário para octal. Os bits serão agrupados de três em três, da direita para a esquerda, do número 110011011001.
Tabela 3.9 - Conversão de base binária para octal
Fonte: Elaborada pelo autor.
Por conseguinte, o número 3289, em decimal, é representado pelo número 6331, em octal; a conversão de decimal (base 10) para hexadecimal (base 16). O número 861, em decimal, pode ser, então, convertido em hexadecimal:
§ 861 = 512 + 256 + 64 + 16 + 8 + 4 + 1 = 1101011101;
Separando o número binário de quatro em quatro bits, sempre começando pela direita, temos:
Tabela 3.10 - Conversão de binário para hexadecimal
Fonte: Elaborada pelo autor.
Podemos perceber, com isso, que o número decimal 861 é igual a 35D em hexadecimal. As conversões de octal para decimal e hexadecimal para decimal são triviais, quando utilizamos o sistema binário como intermediário. Por exemplo, vamos converter 634 octal e 9FA para decimal:
Tabela 3.11 - Conversão de base octal para binário
Fonte: Elaborada pelo autor.
Para converter de binário para decimal, basta somar as potências de 2.
Tabela 3.12 - Decomposição para base binária
Fonte: Elaborada pelo autor.
Temos, então, que 110011100 (binário) em decimal é igual a \(2^8\) + \(2^7\) + \(2^4\) + \(2^3\) + \(2^2\) = 256 128 + 16 + 8 + 4 = 412. Logo, o número 634, em octal, é 412, em decimal.

Ao converter o número hexadecimal 1FA em binário, temos:
Tabela 3.13 - Conversão de base hexadecimal para binário
Fonte: Elaborada pelo autor.
Para converter de binário para decimal, basta somar as potências de 2.
Tabela 3.14 - Decomposição de base para binário
Fonte: Elaborada pelo autor.
O número 9FA, em hexadecimal, é igual a 100111111010, em binário, que, por sua vez, é igual ao número em decimal \(2^11\) + \(2^8\) + \(2^7\) + \(2^6\) + \(2^5\) +\(2^4\) + \(2^3\) + \(2^1\) = 2048 + 256 + 128 + 64 + 32 + 16 + 8 + 2 = 2554.
A conversão do sistema de numeração binário para o sistema de numeração hexadecimal é bastante empregada nas representações computacionais que trabalham com um conjunto de 4 bits. Diante disso, converta 11001111 na base binária para seu respectivo correspondente na base hexadecimal e assinale a alternativa correta.
AC.
Incorreta. Transformar 11001111 da base binária para a base hexadecimal é bem simples, basta agrupar em conjuntos de 4 bits o nosso conjunto de 0 e 1. Logo, teremos: 1010 = A e 1100 =C.
CF.
Correta. Transformar 11001111 da base binária para a base hexadecimal é bem simples, basta agrupar em conjuntos de 4 bits o nosso conjunto de 0 e 1. Logo, teremos: 1100 = C e 1111 = F na base hexadecimal.
FC.
Incorreta. Transformar 11001111 da base binária para a base hexadecimal é bem simples, basta agrupar em conjuntos de 4 bits o nosso conjunto de 0 e 1. Logo, teremos: 1111 = F e 1100 =C.
AD.
Incorreta. Transformar 11001111 da base binária para a base hexadecimal é bem simples, basta agrupar em conjuntos de 4 bits o nosso conjunto de 0 e 1. Logo, teremos: 1010 = A e 1101 = D.
DF.
Incorreta. Transformar 11001111 da base binária para a base hexadecimal é bem simples, basta agrupar em conjuntos de 4 bits o nosso conjunto de 0 e 1. Logo, teremos: 1101 = D e 1111 = F.
Em 1854, foi apresentado um sistema de análise lógica, pelo matemático George Boole, conhecido como álgebra de Boole. A álgebra de Boole foi utilizada ao longo do tempo para implementar os circuitos lógicos. Nas funções lógicas, temos apenas dois estados: Estado 0 e Estado 1.
No caso, então, o Estado 0 representará, por exemplo: portão fechado, aparelho desligado, ausência de tensão e chave aberta. O Estado 1 representará: portão aberto, aparelho ligado, presença de tensão, chave fechada etc. Em 1938, o Engenheiro Claude Shannon, por meio das teorias de Boole, encontra a solução de problemas de circuitos de telefonia com relés - interruptores comandados com sinais elétricos - e que podiam, portanto, ligar ou desligar circuitos muito rapidamente. Até hoje, os relés são empregados. Aqui, começou a implementação das funções lógicas que compõem os circuitos lógicos (E, OU, NÃO E, NOU etc.).
Os circuitos lógicos derivam da álgebra de Boole, sendo as variáveis e expressões chamadas de variáveis e expressões booleanas. Nossa primeira função é o E (AND). Para demonstrar seu funcionamento em um circuito lógico, nada melhor do que apresentar um circuito lógico que utiliza a função E.
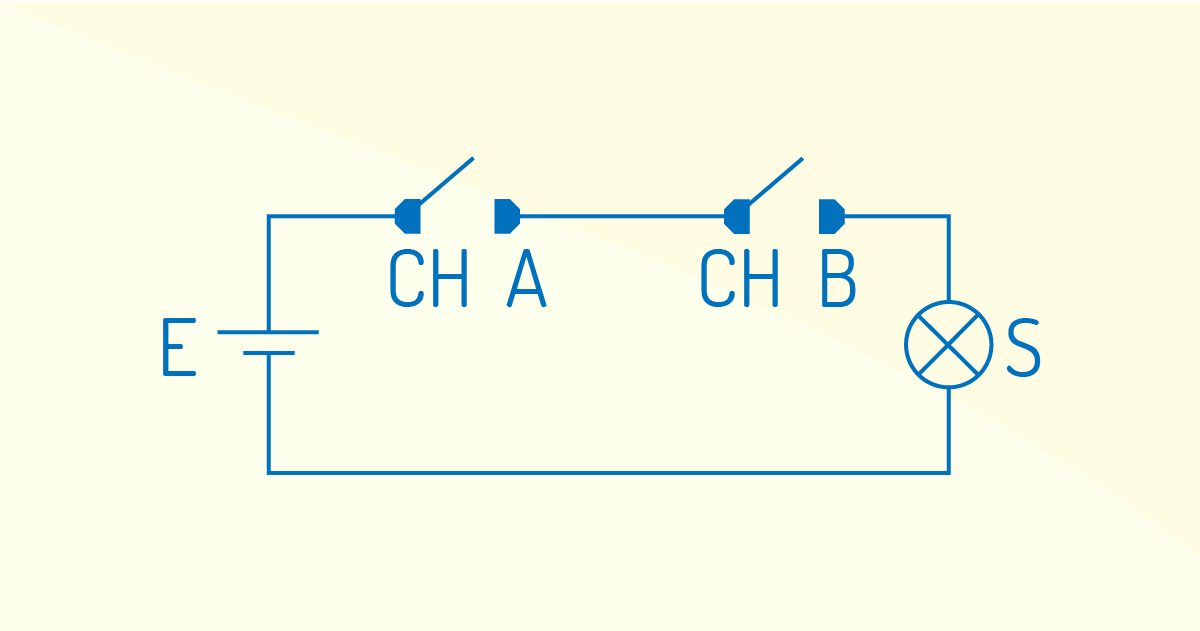
O circuito apresentado Figura 3.1 demonstra que a lâmpada
somente acenderá SOMENTE SE ambas as chaves estiverem fechadas e, seguindo a convenção, tem-se: CH A=1, CH B=1, resulta em S=1.Pode-se, desta forma, escrever todas as possíveis combinações de operação das chaves na chamada Tabela da Verdade, um mapa onde se depositam todas as possíveis situações de entrada com seus respectivos resultados de saída, logo podemos verificar que o números de possíveis combinações é \(2^n\), onde n é o número de variáveis de entrada (CAPELLI, 2007, p. 135).
As portas lógicas são representadas na lógica de Boole, respectivamente, pelos símbolos a seguir.
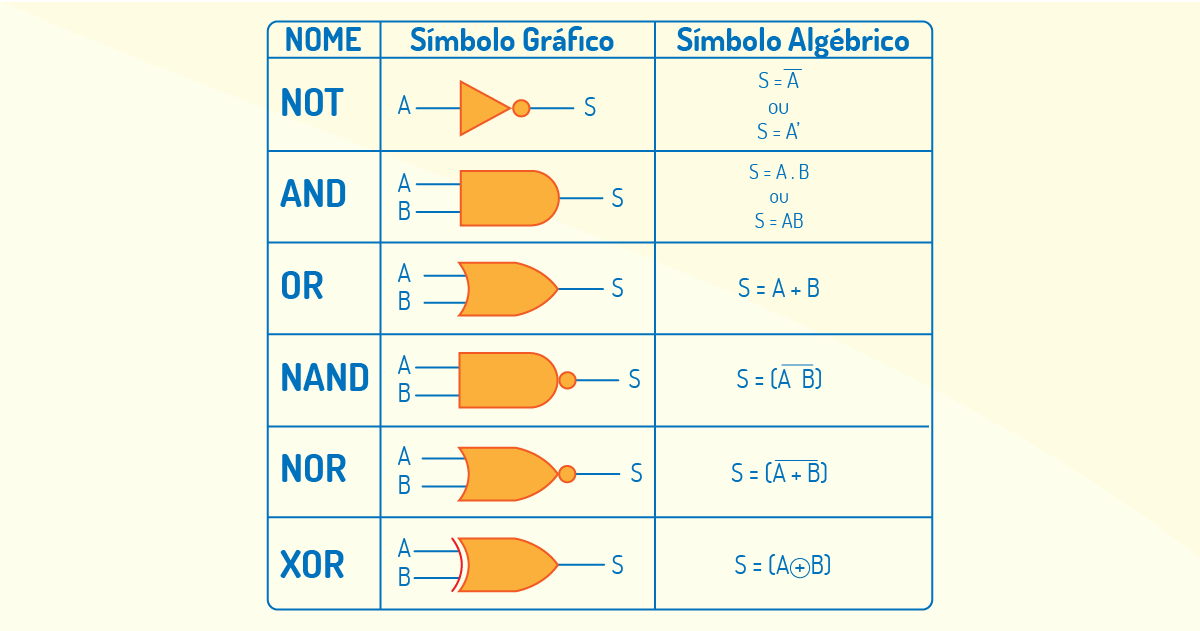
Temos, também, a função OU (OR), que determina dois possíveis caminhos para o fluxo de um circuito lógico. No circuito lógico apresentado na sequência, o sinal de saída irá para nível lógico 1, se qualquer uma das entradas estiver em nível lógico 1 (THOMAZINI; ALBUQUERQUE, 2005).
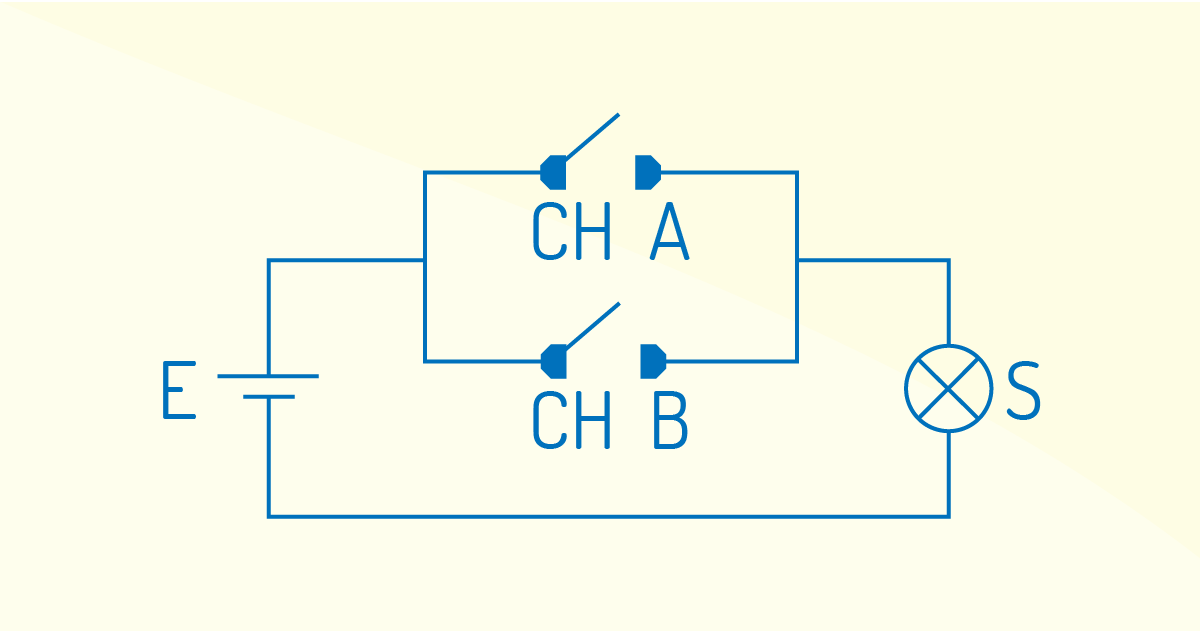
Dessa forma, temos o circuito demonstrado na Figura 3.3, que apresenta a lâmpada acendendo, quando qualquer uma das chaves estiver fechada, e permanece apagada, se ambas estiverem abertas, ou seja, CH A=0, CH B=0 resulta em S=0.
Temos, também, a função NÃO (NOT) ou função inversora. No circuito lógico a seguir, o sinal de saída irá para o nível lógico 1, se a entrada for 0 e vice-versa.
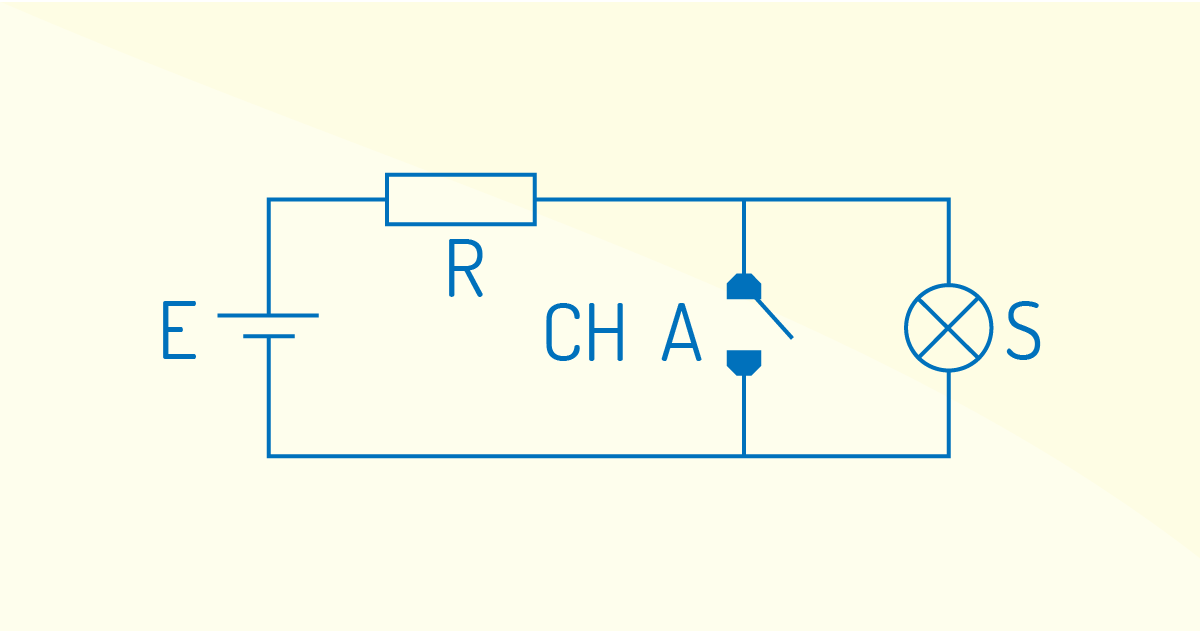
Podemos verificar, ao observar os circuitos, que a lâmpada estará acesa somente se a chave estiver aberta (CH A=0, S=1). Quando a chave fecha, a corrente desvia por ela e a lâmpada apaga (CH A=1, S=0). O inversor é o bloco lógico que executa a função NÃO.
Temos, também, a função NÃO E (NAND), que é a combinação da função NÃO e da função E. No circuito lógico a seguir, o sinal de saída irá para o nível lógico 1, se, pelo menos, uma das entradas estiver em nível lógico 0.
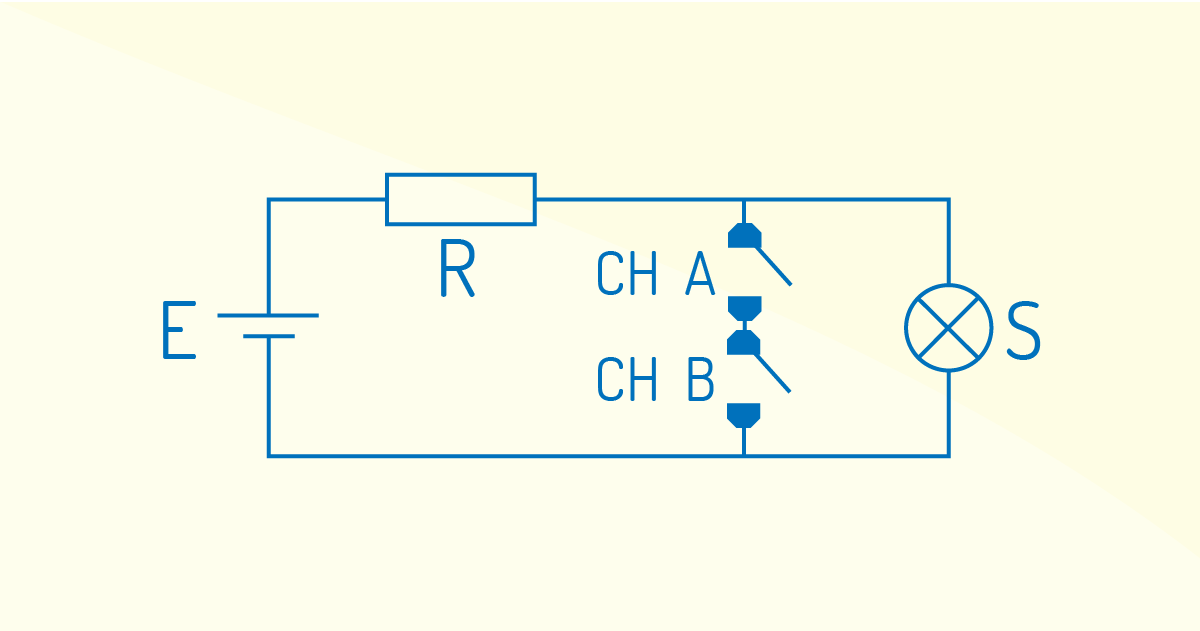
Observa-se que a lâmpada apaga somente quando ambas as chaves são fechadas, ou seja, CH A=1, CH B=1 implica em S=0.
Temos, também, a função NÃO OU (NOR), que é a combinação de uma porta NÃO e de uma OU. No circuito demonstrado na Figura 3.6, temos que o sinal de saída irá para o nível lógico 1, SOMENTE SE as entradas estiverem em nível lógico 0.
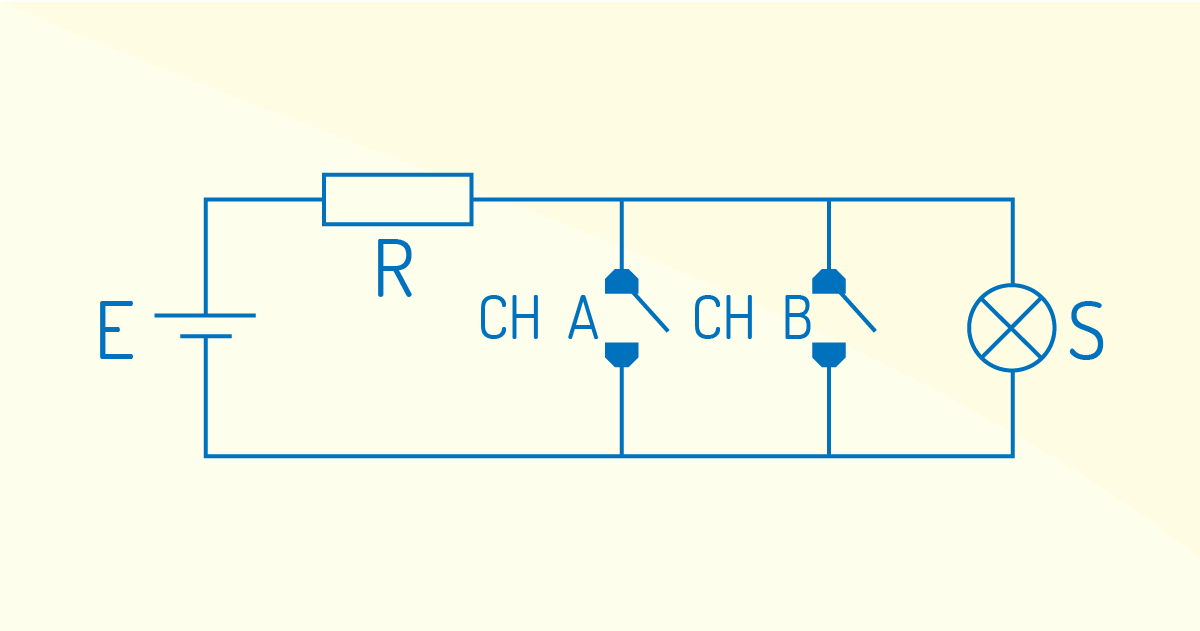
Ao analisar este circuito, é possível concluir que a lâmpada fica acesa somente quando as duas chaves estão abertas. Assim, CH A=0, CHB=0 resulta em S=1.
Ademais, tem-se a função OU EXCLUSIVO (XOR), que é a combinação das portas E e OU e Inversoras. No circuito lógico a seguir, o sinal de saída irá para o nível lógico 1, SOMENTE SE as entradas forem diferentes.
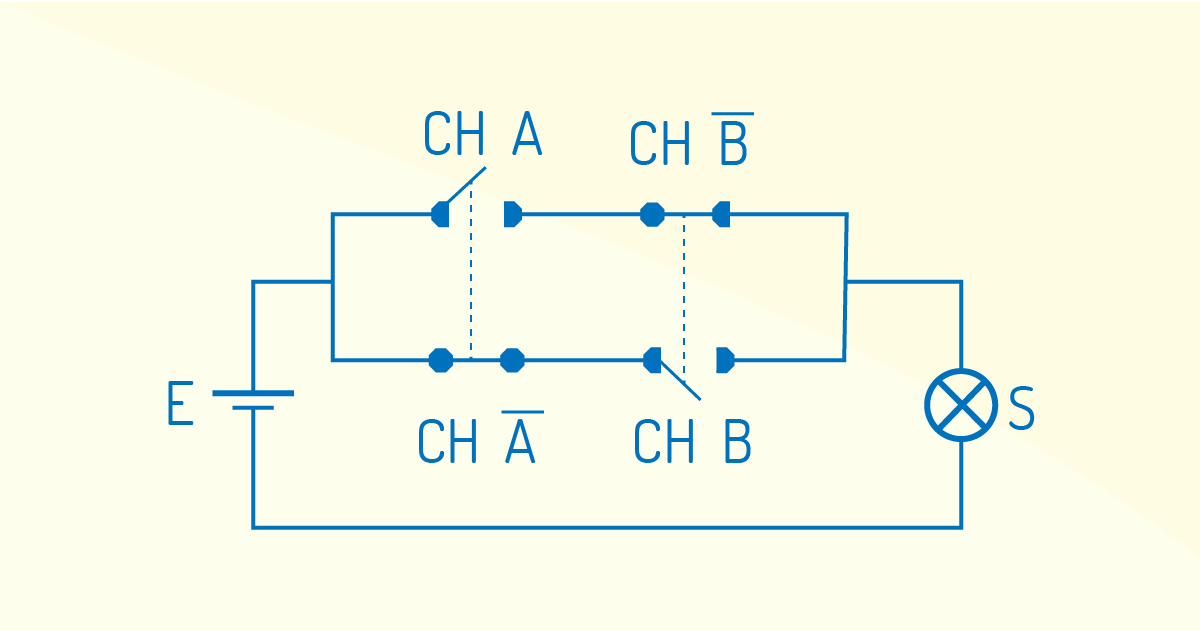
Podemos verificar que as chaves CH A_ e CH B_ estão abertas (há caminho para a corrente circular e a lâmpada não acende; a respectiva lâmpada continua apagada, quando as chaves CH A e CH B estão fechadas, pois quando estão abertas, interrompem o fluxo de corrente).
Por fim, temos a função NÃO OU EXCLUSIVO, conhecida, também, como função coincidência, que é uma combinação das funções E e OU e INVERSORAS. No circuito lógico a seguir, podemos identificá-la.
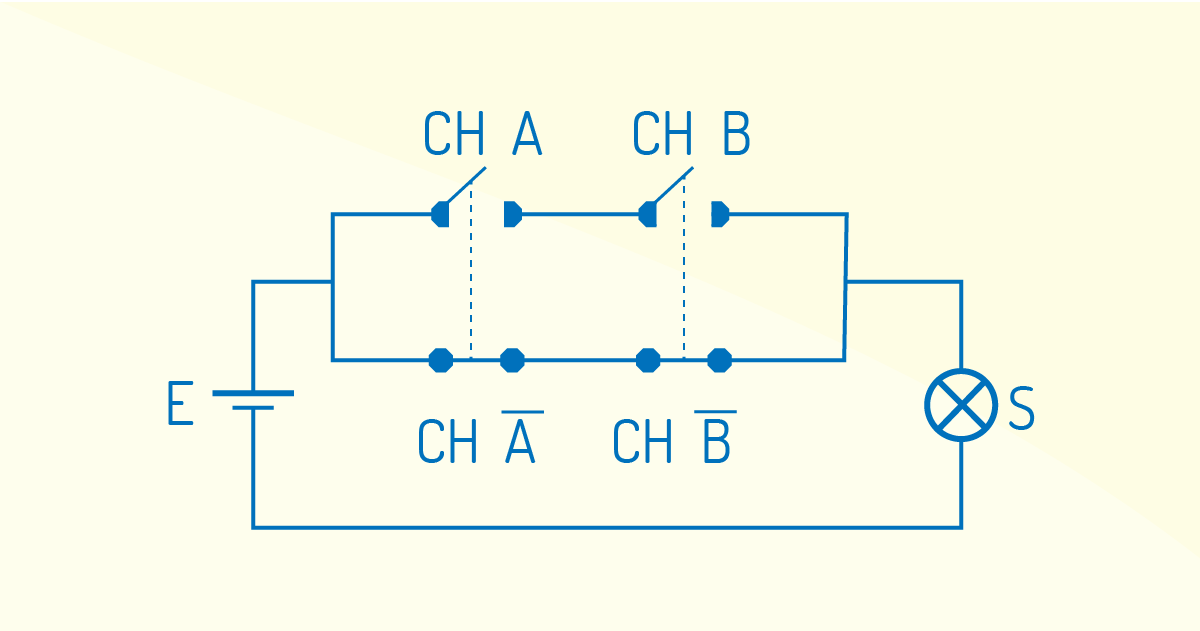
Quando as chaves CH A_ e CH B_ estão abertas na linha superior, e estão fechadas na linha inferior do circuito, a corrente circula pela lâmpada, que será acesa.
Observe a figura a seguir.
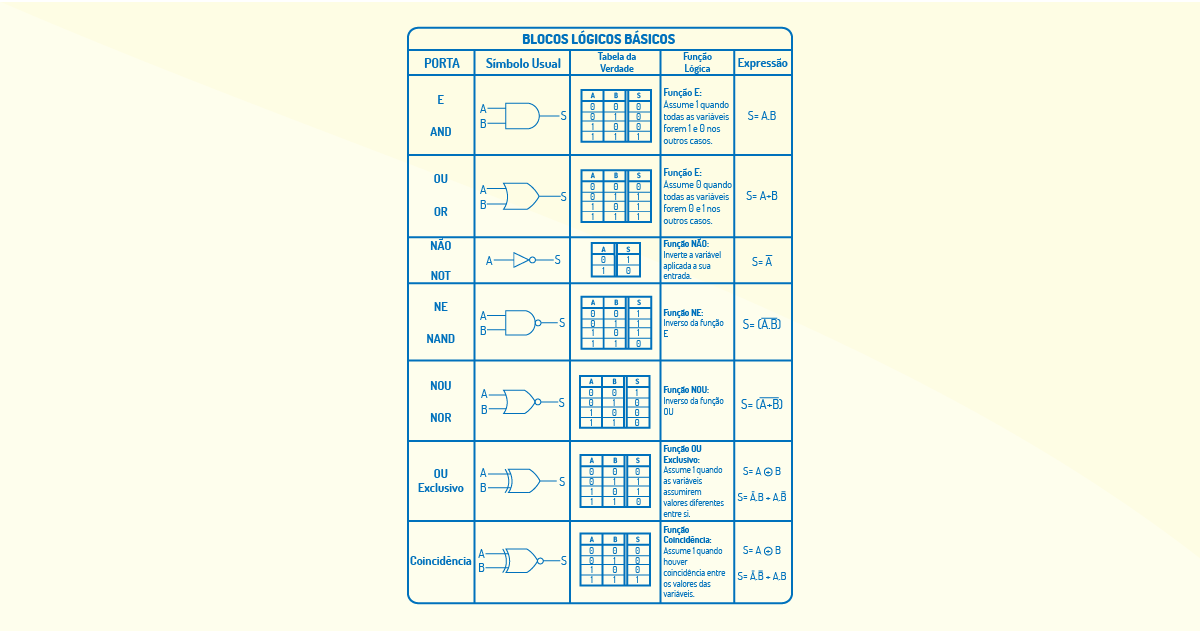
Temos, então, os seguintes blocos lógicos básicos nos circuitos lógicos, como apresentado na Figura 3.9.
As funções de um circuito lógico são responsáveis por implementarem o desenho para a solução que o circuito visa representar. Assinale qual expressão matemática apresenta as respectivas funções lógicas: OR.
S = A + B
Correta. A função lógica OR é representada pela expressão S = A + B.
S = A . B
Incorreta. A função lógica AND é representada pela expressão S = A . B.
S = A > B
Incorreta. Não existe representação com esta expressão.
S = A < B
Incorreta. Não existe representação com esta expressão.
S = (- A.B)
Incorreta. A expressão (-A.B) é a representação da função NAND, que é a inversão da função AND.
Podemos dividir os circuitos lógicos em: circuitos combinacionais ou circuitos sequenciais.
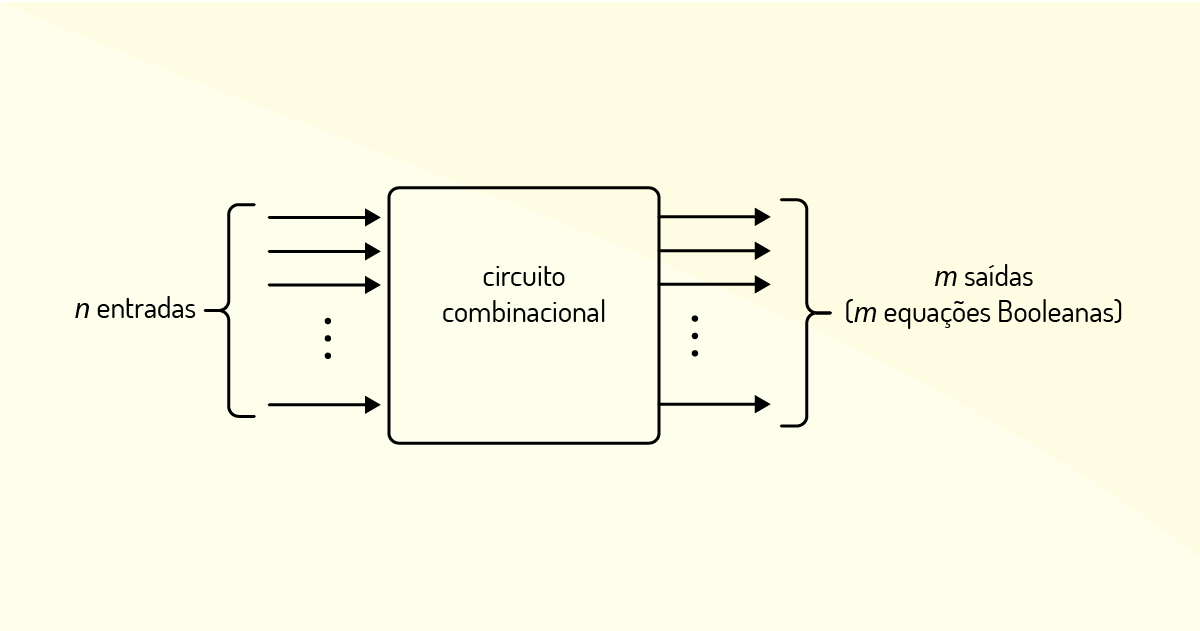
Um circuito combinacional é a representação de um aglomerado de portas lógicas, as quais determinam os valores de saídas a partir dos valores de entrada. Cada combinação booleana de valores na entrada gerará uma determinada saída, conforme mostrado a seguir.
Já um circuito sequencial consistirá em elementos de armazenamento conhecidos como flip-flops e portas lógicas. Os valores das saídas do circuito dependem dos valores das entradas e dos estados dos latches ou flip-flops utilizados. Como os estados dos latches e flip-flops são funções dos valores anteriores das entradas, diz-se que as saídas de um circuito sequencial dependem dos valores das entradas e do histórico do próprio circuito. Logo, o comportamento de um circuito sequencial é especificado pela sequência temporal das entradas e de seus estados internos. Assim, o comportamento do circuito sequencial está diretamente ligado à sequência temporal das entradas e de seus estados internos. Dentre os exemplos de circuitos sequenciais, temos um circuito de um relógio que informa e quadra dados da hora, como um cronômetro, enquanto um circuito combinacional não guarda dados, logo, pode ser somente o circuito de um relógio, que apenas mostra as horas.
Um circuito sequencial é composto por um circuito combinacional e elementos de memória. As entradas e saídas do circuito sequencial estão conectadas somente ao circuito combinacional. Um exemplo comum é o seu emprego em sistemas com portas lógicas, como elevadores que abrem e fecham suas portas por meio de sensores de presença ou de temporizadores.
A informação armazenada nos elementos de memória em um dado instante determina o estado em que se encontra o circuito sequencial. O circuito sequencial recebe informação binária das entradas que, juntamente com a informação do estado atual, determina os valores das saídas e os valores do próximo estado.
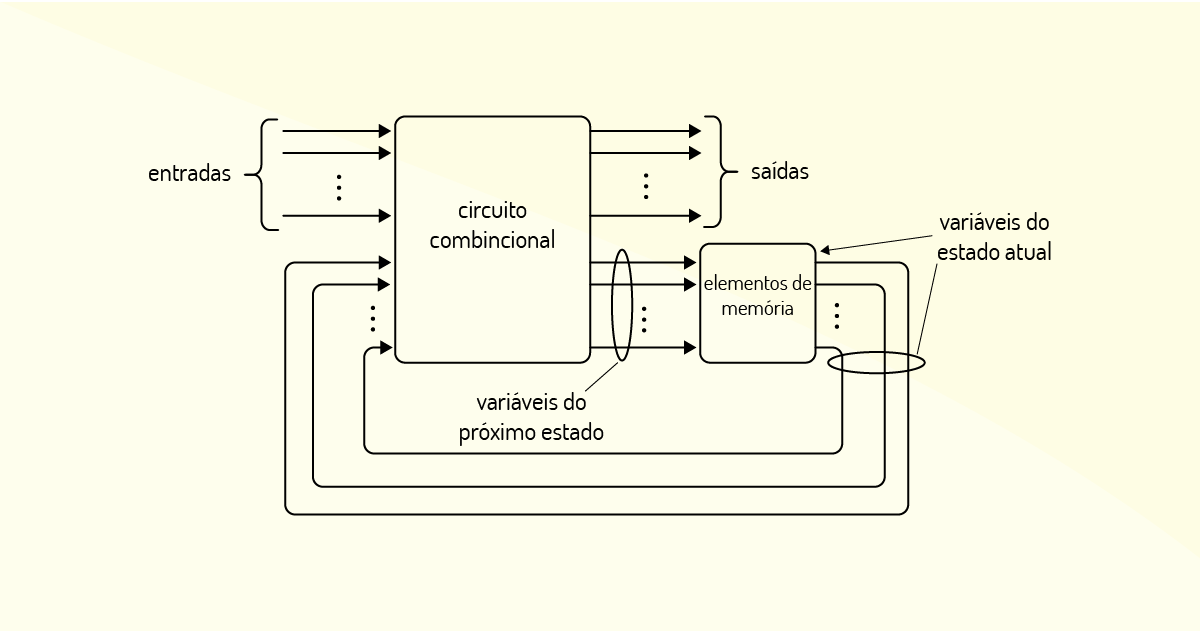
Os circuitos sequenciais podem ser divididos em dois tipos, conforme o comportamento temporal de seus sinais: síncronos e assíncronos.
Um circuito assíncrono é dependente da ordem em que as entradas mudam e o estado do circuito pode alterar-se a qualquer tempo, como consequência de uma mudança de suas entradas. Os elementos de memória utilizados nos circuitos sequenciais assíncronos apresentam uma capacidade de armazenamento que está associada diretamente ao atraso de propagação dos circuitos que os compõem. Os circuitos assíncronos têm, também, as portas lógicas, que provêm de um atraso de propagação, com valor adequado para o funcionamento do circuito. Então, um circuito sequencial assíncrono pode ser visto como um circuito combinacional com realimentação.
A principal dificuldade provém do fato de que os componentes apresentam atrasos não fixos, podendo ser diferentes mesmo para exemplares com mesma função e de um mesmo fabricante. Dessa forma, os circuitos sequenciais assíncronos têm sido evitados, sempre que possível, em favor do uso de circuitos sequenciais síncronos.
Os circuitos sequenciais síncronos utilizam um sinal denominado relógio (clock, em inglês), o qual tem a função de cadenciar uma eventual troca de estado. O tempo que decorre para o sinal repetir-se é denominado período e é representado por T. Por exemplo, o tempo entre duas bordas de subida sucessivas é igual a T. Da mesma forma, o tempo entre duas bordas de descida sucessivas é igual a T J. Exemplos comuns de sistemas síncronos são as transmissões de dados. Quando é ao vivo, temos sistemas síncronos atuando com o envio e recebimento de dados; já quando acessamos uma transmissão gravada, temos sistemas assíncronos atuando, pois não temos, nesse caso, necessidade de sincronização no tempo.
Os circuitos lógicos podem ser divididos em circuitos sequenciais e circuitos combinacionais. Os circuitos sequenciais também podem ser divididos em dois tipos, conforme o comportamento temporal dos seus sinais, que são:
digital e analógico.
Incorreta. A dotação para tempo, que divide os circuitos em dois tipos, é síncrono e assíncrono. Não existe para tempo a dotação digital e analógico; essa dotação é utilizada quanto ao sinal processado pelo circuito lógico.
aberto e semiaberto.
Incorreta. A dotação para tempo, que divide os circuitos em dois tipos, é síncrono e assíncrono. Não existe para tempo a dotação aberto e semiaberto.
síncrono e assíncrono.
Correta. A dotação para tempo, que divide os circuitos em dois tipos, é síncrono e assíncrono.
temporal e atemporal.
Incorreta. A dotação para tempo, que divide os circuitos em dois tipos, é síncrono e assíncrono. Não existe para tempo a dotação temporal e atemporal.
completo e incompleto.
Incorreta. A dotação para tempo, que divide os circuitos em dois tipos, é síncrono e assíncrono. Não existe para tempo a dotação completo e incompleto.
Originado em 1968, o Controlador Lógico Programável (CLP) é derivado do nome do seu primeiro fabricante, Modular Digital Controller, com o nome de MODICON, idealizado e criado por Richard Morley. Sua ideia inicial era projetar um equipamento mais robusto, adaptável, confiável e de fácil manuseio e modificação (BEGA, 2006).
Os CLPs são componentes amplamente difundidos nos sistemas dinâmicos industriais. São dispositivos que permitem o comando de máquinas e equipamentos de maneira simples e flexível, de forma a possibilitar alterações rápidas no modo de operá-los, por meio de aplicação de programas dedicados e armazenados em memória EPROM (MAMEDE, 2017).
Os CLPs podem substituir, com grandes vantagens, os tradicionais comandos de máquinas e equipamentos industriais, tais como botoeiras, chaves comutadoras, contadores e relés. Existe, no mercado, uma grande diversidade de CLPs destinados a diferentes níveis de automação e controle, em conformidade com a complexidade de cada aplicação (FIALHO, 2014).
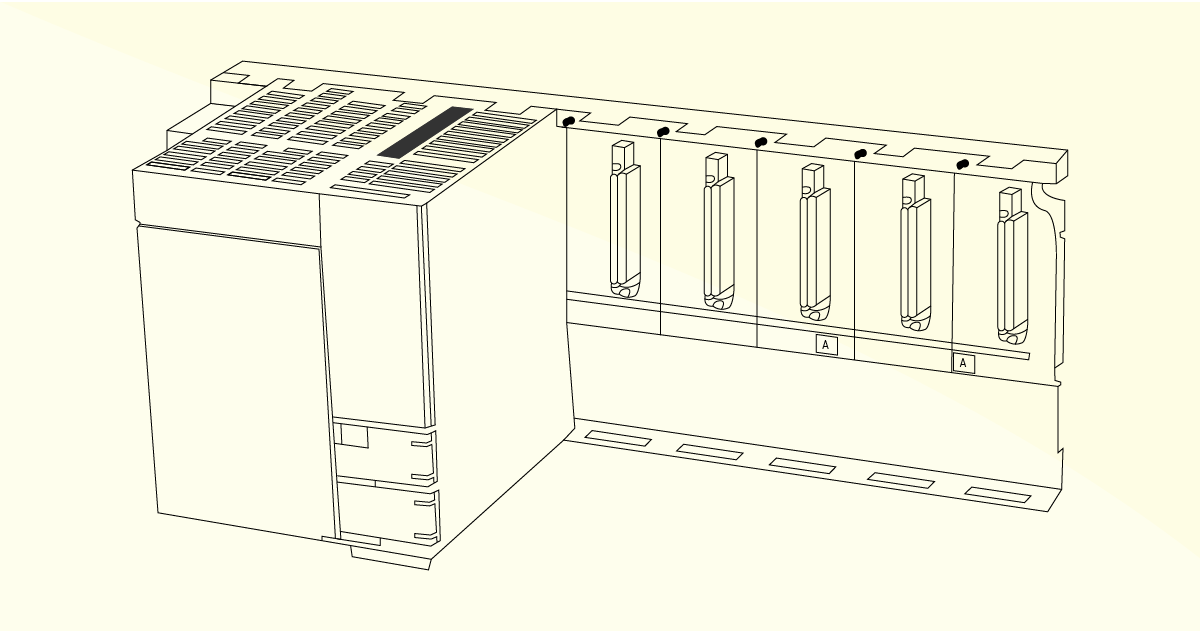
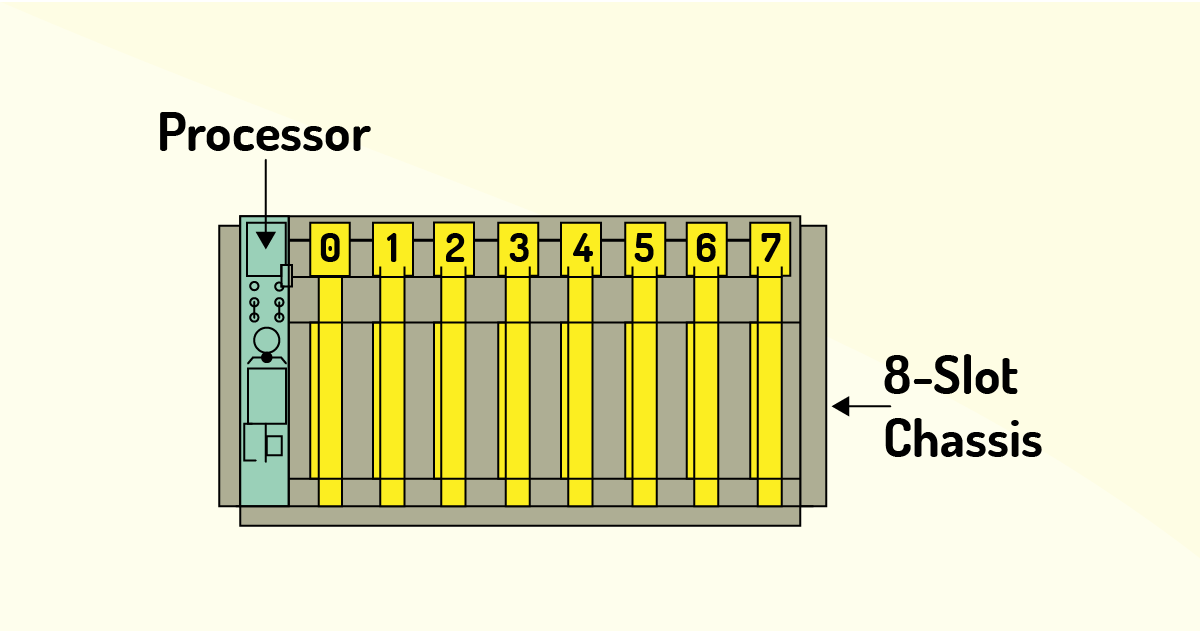
Os CLPs são constituídos por um gabinete contendo um determinado número de cartões, cada um desempenhando funções específicas, ou seja:
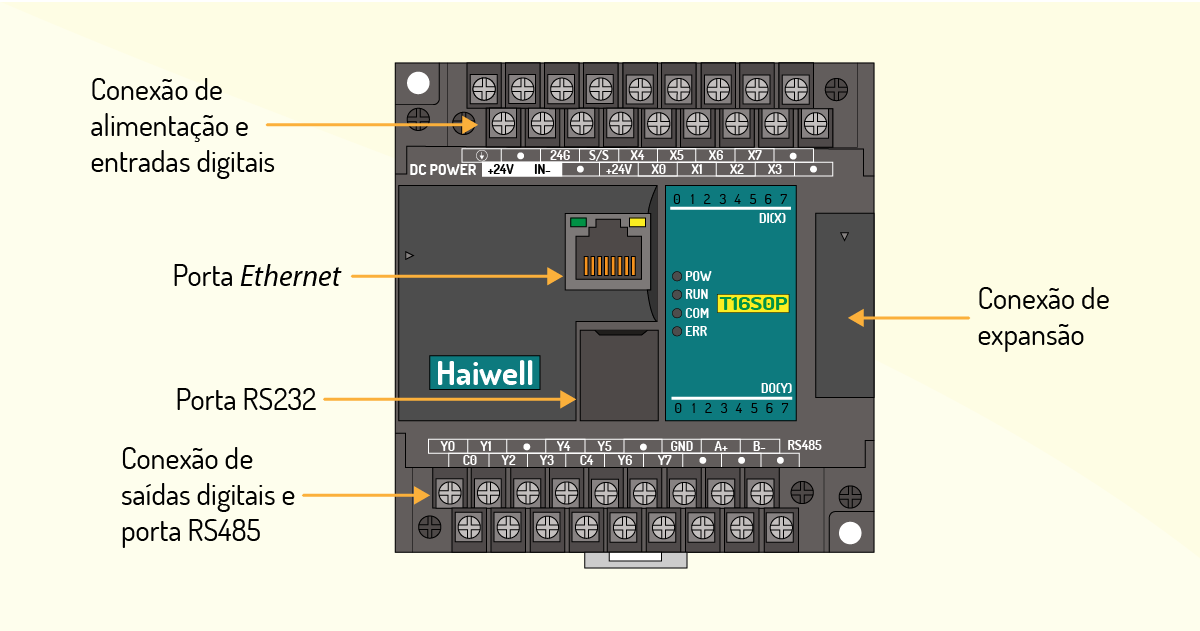
Cada CLP tem uma quantidade determinada de terminais de entrada e saída, que dependem da capacidade, conforme a função da máquina ou do próprio componente industrial. Cada terminal costuma, também, ter um LED, o qual é utilizado para o monitoramento do sinal lógico (THOMAZINI; ALBUQUERQUE, 2005). Os sinais de saída utilizados para a comutação de cargas indutivas são compostos de dispositivos, como diodos e varistores, que são protegidos por fusíveis.
Os CLPs (Controladores Lógicos Programáveis) são utilizados em vários tipos de aplicações industriais, sendo possível a sua utilização sozinha ou acoplada a outras unidades. Nos projetos em áreas muito extensas, como esteiras rolantes, utilizadas no transporte de minérios, com processos de carga e descarga de materiais, é fundamental a utilização de inúmeros CLPs acoplados, para sincronizar todo o processo de controle (NATALE, 2007).
Nesta situação, a arquitetura da automação é descentralizada e divide-se a responsabilidade com várias unidades de CLPs, que estão localizadas em vários pontos estratégicos.
Ao intercâmbio de informações entre CLPs dá-se o nome de acoplamento, sendo que a hierarquia é gerenciada por software dedicados, em que os CLPs ficam dedicados.
Dessa forma, caso um CLP de processo necessite realizar intercomunicação com outro CLP, a comunicação parará pelo CLP mestre. É possível, também, implementar configurações de acoplamento de CLPs, a depender da solução atribuída ao processo. Com as facilidades obtidas com o acoplamento, podemos utilizar estações remotas, com distância de cerca de 1.000 m, sem o emprego de um modem específico, lembrando que, com o emprego do modem, não temos limite de distância (CAPELLI, 2007). O acoplamento também permite a implementação de uma arquitetura de sistema funcional e distribuída. Na indústria, empregamos os CLPs para:
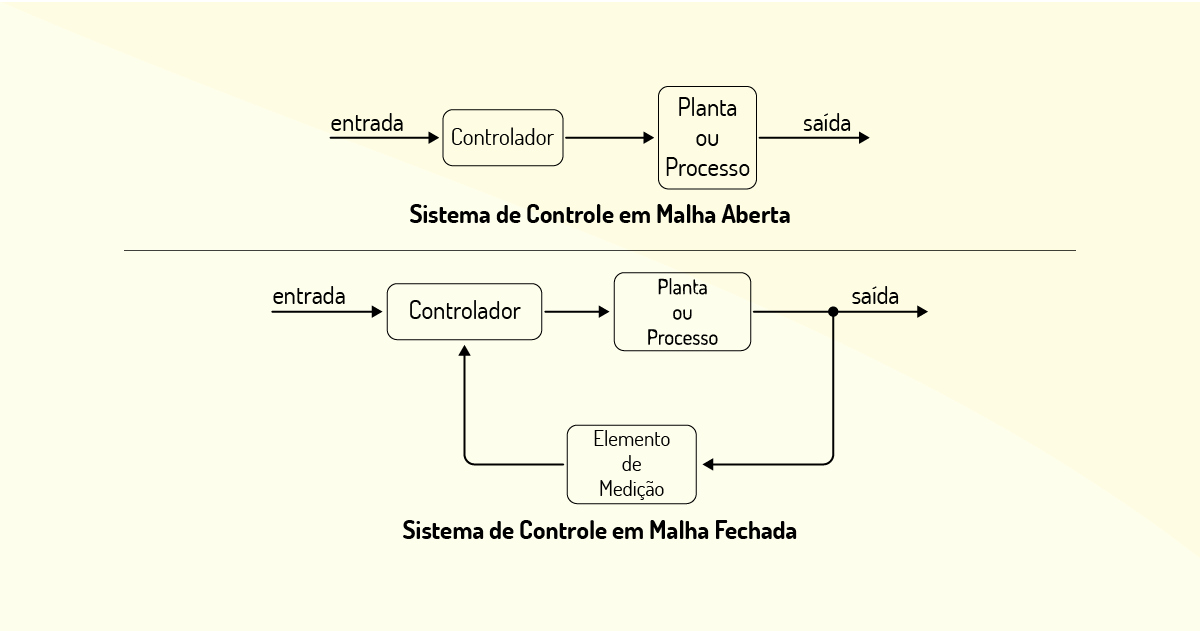
Temos o controle de malha aberta, que é utilizado nos processos de produção que não têm necessidade de comparar a variável controlada com os valores de referência pré-ajustados. Por exemplo, caso quiséssemos comparar a variável controlada com um outro valor de referência, nesse caso, a ideia é identificar um processo industrial de verificação automática de engarrafamento de bebida. A condição assumida é, então, engarrafada ou não engarrafada. Ou seja, temos uma variável digital: sim e não. A verificação de qualidade de enchimento da garrafa, ou seja, se a garrafa está 50% cheia ou 100% cheia, deve-se ocorrer em outra malha de produção. Já o controle de malha fechada é utilizado nos processos de produção. Nestes, a variável de controle é constantemente comparada a um valor de referência. No caso, temos uma correspondência biunívoca entre a variável controlada e o sistema de controle.
O controle da malha fechada implica na utilização de interfaces de sinais analógicos ou conversores analógicos/digitais e digitais/analógicos. Podemos, ainda, para melhorar a compreensão, dividir dois tipos básicos: controle de malha fechada em máquina operatriz e controle de malha fecha em processo.
No controle de malha fechada em máquinas operatrizes, utilizam-se dispositivos de alta sensibilidade para controle dimensional do produto, fazendo as correções necessárias, de forma a manter, dentro de uma faixa de precisão já definida, as dimensões do produto final. No controle de malha fechada, uma quantidade de sensores posicionados ao longo do processo retroalimenta o sistema de controle, com sinais analógicos transformados em variáveis controladas. Esses sinais são permanentemente comparados a um padrão de referência, gerando um sinal de desvio que atua sobre os dispositivos de controle do processo, reconduzindo as variáveis controladas aos valores predefinidos, estabelecendo-se, assim, um controle em malha fechada.
Trataremos, agora, sobre linguagem de programação e comandos de automação. Inicialmente, precisamos compreender o que é a linguagem de programação, que nada mais é que o emprego da lógica computacional sob uma determinada linguagem. Para que isso funcione e tenhamos comandos de automação, é necessária uma sequência de ações para alcançar um determinado objetivo.
Descrito o contexto, podemos conhecer os comandos de linguagem de programação que realizam a automação de tarefas por meio de instruções computacionais (MONTEIRO, 2007).
Comando de automação: decisão e repetição.
As estruturas de seleção ou decisão são empregadas para interferir na sequência lógica das instruções, conforme podemos verificar a seguir:
Temos, também, além do “Se/Então”, a estrutura de decisão case ou múltipla escolha, em que são testadas condições de decisão:
Temos, também, as estruturas de repetição, que são muito utilizadas para automatizar processos computacionais e industriais. Essas estruturas são utilizadas quando se deseja que um determinado conjunto de instruções ou comandos sejam executados mais de uma vez, conforme podemos ver a seguir.
No primeiro tipo de estrutura de repetição, realiza-se um teste antes de executar qualquer instrução dentro de seu bloco. Temos, também, a repetição com variáveis de controle While Do.
Podemos ter outras estruturas mais complexas para automatizar cenários mais arrojados, como a recursividade. Entretanto, dentro dos cenários de automação comum, estas são as instruções de controles mais comuns. Destacam-se, também, as linguagens Ladder e Grafcet, como exemplos de linguagens específicas para a implementação de instruções em CLPs. A Ladder foi a primeira linguagem a ser desenvolvida para CLPS e é similar aos diagramas utilizados para lógica de relés, baseando-se em interruptores a bobinas, a fim de orquestrar circuitos lógicos. A seguir, temos um exemplo simples de acionamento de motor, em que um CLP acionando o motor, com um botão de partida, respectivamente, tem-se outra chave que, quando acionada, desliga o motor, com base na linguagem Ladder.
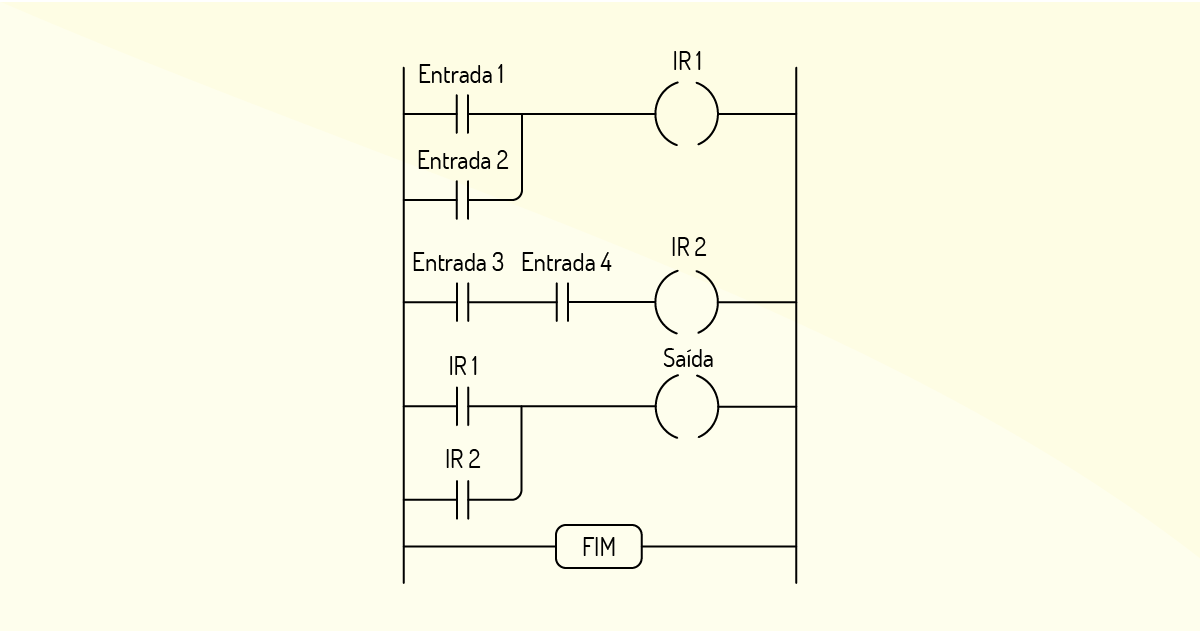
Já a linguagem Grafect tem a mesma finalidade de trabalho com CLPs da linguagem Ladder, a fim de ilustrar circuitos lógicos. Todavia esta foi pensada para a criação de processos com várias etapas simultâneas, utilizando linguagens comuns de programação, sendo, então, uma linguagem de modelagem de sistemas sequenciais.
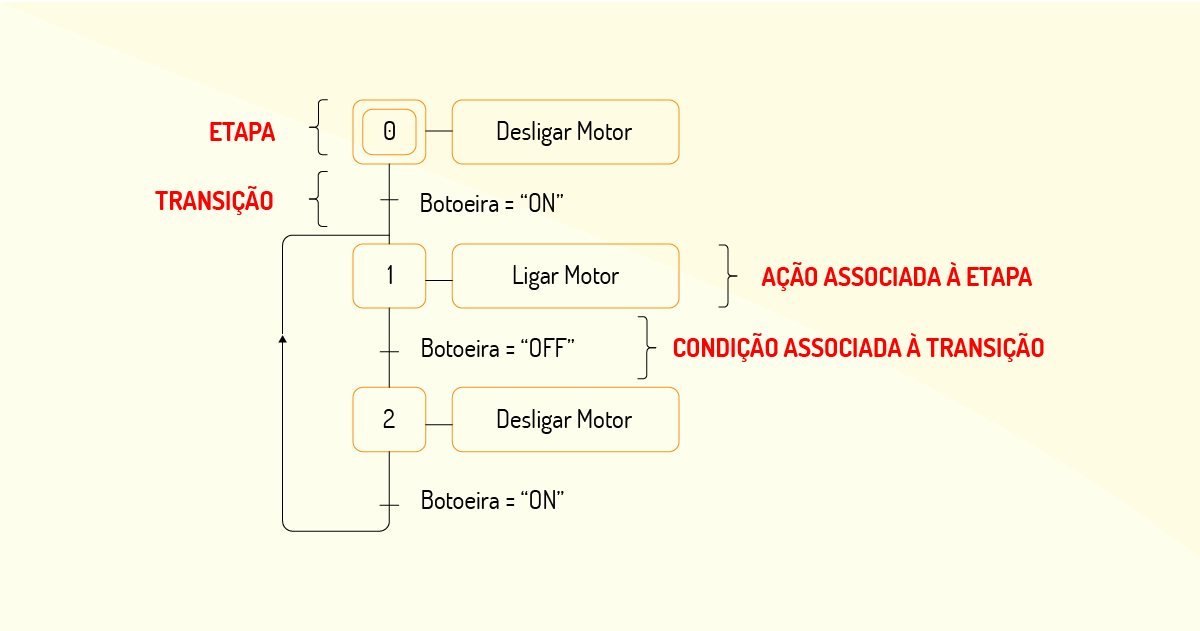
O Grafect apresenta três estruturas: etapas (ações), transições (condições) e ligações orientadas (conexões entre etapas e transições). Se, por exemplo, quisermos acionar um motor e, respectivamente, desligar o motor, teremos a modelagem com Grafect, exibida na Figura 3.17.
As estruturas de seleção são utilizadas para interferir na lógica sequencial que está sendo executada. Além destas, temos, também, as estruturas de repetição. Assim, assinale a alternativa que utiliza a sintaxe correta para automação.
Enquanto, então.
Incorreta. A estrutura lógica de repetição utiliza a sintaxe para automação: enquanto, faça. Não temos enquanto, então.
Se, faça.
Incorreta. A estrutura lógica de repetição utiliza a sintaxe para automação: enquanto, faça. Não temos se, faça.
Selecione, caso.
Incorreta. A estrutura lógica de selecione, caso é a sintaxe da estrutura de decisão.
Se, então.
Incorreta. A estrutura lógica de se, então é a sintaxe da estrutura de decisão.
Enquanto, faça.
Correta. A estrutura lógica de repetição utiliza a sintaxe para automação.
Editora: LTC
Autor: J. Mamede Filho.
ISBN: 978-85-216-3372-3 1
O livro é referência em todo o mundo sobre projetos industriais envolvendo instalações elétricas.
