A partir do estudo da resistência dos materiais, é possível conhecer as propriedades mecânicas de sólidos reais, para fins de projetos, modelagem e cálculo de estruturas, de modo que, aliada à mecânica do sólidos, podemos dizer que essa viabiliza uma melhor compreensão de grandezas, como a tensão e a deformação de materiais, além das relações entre as cargas externas aplicadas ao corpo deformável e as forças internas que atuam dentro dele. Complementar a esses conteúdos, podemos citar o estudo de sua estabilidade quando submetida a solicitações externas (HIBBELER, 2004). Diante disso, nesta unidade, trataremos de deformação, cargas axiais, torção e cisalhamento.
Precisamos discutir alguns conceitos em resistência dos materiais essenciais para nosso entendimento dessa ciência como um todo. Sendo assim, começaremos com algumas propriedades mecânicas dos materiais, como:
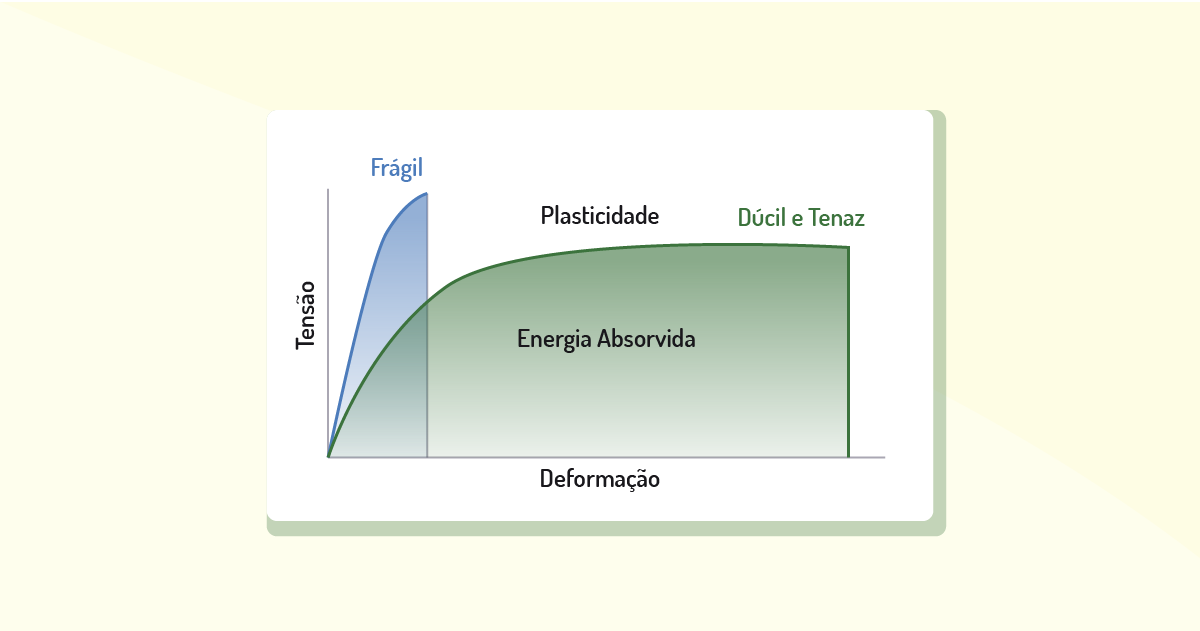
Esse tipo de mudança na forma do material é resultante de uma força tanto interna quanto externa, e pode ser do tipo extensiva ou compressiva, a partir da variação da pressão, temperatura ou mudança estrutural; e medida, segundo a mudança no comprimento do material.
Quando a deformação é resultado de um alongamento ou contração em um pequeno intervalo por unidade de comprimento \(\left( \Delta S~e~\Delta S' \right)\), a chamamos de deformação normal \({{\varepsilon }_{m\acute{e}d}}\).
A deformação normal pode ser calculada a partir de \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\).
Todavia, quando esses intervalos são retas perpendiculares e sofrem uma variação na angulação, temos a deformação por cisalhamento \({{\gamma }_{nt}}\), ou seja, em se tratando de materiais, podemos dizer que há certa variação no ângulo \({\theta }'\) de uma fibra, por exemplo, em relação a um plano. A deformação por cisalhamento pode ser calculada a partir de \({{\gamma }_{nt}}=\frac{\pi }{2}-\theta '\).
Vale lembrar que a deformação é medida com precisão por meio de sensor específico (geralmente do tipo metálico e de junção), o qual varia sua resistência elétrica de maneira proporcional à deformação mecânica, ou seja, por meio de comparação, identifica as mudanças ocorridas no comprimento da amostra quando certa carga é aplicada a ela. Tal medida é mais precisa em materiais homogêneos, visto que os não homogêneos podem apresentar diversas complicações durante as medições, fornecendo medidas de deformação imprecisas.
Além do conceito de deformação, é importante que o estudante seja íntimo do conceito de tensão \(\sigma \), o qual indica a intensidade das forças, as quais podem produzir dilatação, compressão ou torção no material, dada por \(\sigma =\frac{P}{A}\), ou seja, descreve a força P por unidade de área.
Vale lembrar que se o material tem comportamentos do tipo linear e plástico, podemos aplicar a ele a Lei de Hook, dada por \(\sigma =E\varepsilon \), de modo que haja uma relação proporcional entre a deformação e tensão dada por \(\varepsilon =\frac{\theta }{E}=\frac{P}{A}\frac{1}{E}=\frac{P}{EA}\).
Para melhor compreender os conceitos de deformação, você pode recorrer a diversos materiais disponíveis na internet, como a Aula 4 sobre deformações e propriedades mecânicas, dos materiais do Instituto Federal de Educação, Ciência e Tecnologia de São Paulo, do professor Luiz Eduardo Miranda, disponível em: http://www.engbrasil.eng.br/pp/res/aula4.pdf. Acesso em: 08 jan. 2020.

Vale lembrar que a deformação mecânica não pode ser encarada como uma tragédia a ser evitada na engenharia, ela pode ser bastante útil quando usada adequadamente, por meio da conformação de materiais. Em busca da aplicação de seu conhecimento, faça uma breve pesquisa sobre os principais processos de conformação: forjamento, laminação, trefilação e extrusão.

A deformação na forma do material é resultante de uma força tanto interna quanto externa, e pode ser do tipo extensiva ou compressiva, a partir da variação da pressão, temperatura ou mudança estrutural; e medida, segundo a mudança no comprimento do material. Assim, é correto afirmar que a deformação normal na direção y sofrida por uma chapa de comprimento inicial 5,656854 polegadas e comprimento final de 5,660399 polegadas tem valor, em porcentagem, de:
\(6,3667\times 10\wedge -2\).
Incorreta. O cálculo correto é dado por \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\), logo seria \({{\varepsilon }_{m\acute{e}d}}=\frac{\left( 5,660399-5,656854 \right)}{5,656854}=6,2667\times 10\wedge -4\), em porcentagem, faremos esse valor x100, logo \(6,2667\times 10\wedge -2\).
\(6,2628\times 10\wedge -4\).
Incorreta. O cálculo correto é dado por \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\), logo seria \({{\varepsilon }_{m\acute{e}d}}=\frac{\left( 5,660399-5,656854 \right)}{5,656854}=6,2667\times 10\wedge -4\), em porcentagem, faremos esse valor x100, logo \(6,2667\times 10\wedge -2\).
\(5,66\times 10\wedge -4\).
Incorreta. O cálculo correto é dado por \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\), logo seria \({{\varepsilon }_{m\acute{e}d}}=\frac{\left( 5,660399-5,656854 \right)}{5,656854}=6,2667\times 10\wedge -4\), em porcentagem, faremos esse valor x100, logo \(6,2667\times 10\wedge -2\).
\(6,2667\times 10\wedge -2\).
Correta. O cálculo correto é dado por \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\), logo seria \({{\varepsilon }_{m\acute{e}d}}=\frac{\left( 5,660399-5,656854 \right)}{5,656854}=6,2667\times 10\wedge -4\), em porcentagem, faremos esse valor x100, logo \(6,2667\times 10\wedge -2\).
\(2,06\times 10\wedge -2\).
Incorreta. O cálculo correto é dado por \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\), logo seria \({{\varepsilon }_{m\acute{e}d}}=\frac{\left( 5,660399-5,656854 \right)}{5,656854}=6,2667\times 10\wedge -4\), em porcentagem, faremos esse valor x100, logo \(6,2667\times 10\wedge -2\).
Percebemos que os materiais podem ser expostos a diversas propriedades que alterarão sua dinâmica e estrutura, dos quais podemos citar a aplicação de uma força devido a uma carga axial, ou seja, aplicação de uma carga e força dissipadas ao longo do eixo central, como uma carga aplicada na mesma direção (vertical) de um pilar.
Para estudarmos as diferentes formas de aplicação de uma carga em um material ou estrutura, começaremos com o Princípio de Saint-Venant, que, além do caso citado anterior, permite analisar situações nas quais a carga se encontre concentrada, considerando uma distribuição uniforme das tensões à medida que nos afastamos da região de aplicação dela e desconsiderando a distribuição das tensões nas regiões mais próximas ao ponto de aplicação, pois, para essas condições, seriam necessários métodos matemáticos avançados, os quais não cabem aos nossos estudos atuais, o que nos permite concluir que as tensões que se encontram mais próximas à carga tenderão a uma distribuição mais variável em dada seção transversal. Ainda, considerando um corpo sob ação de uma carga como um corpo situado entre duas placas, de modo que sobre elas haja uma tensão uniforme, podemos afirmar que tal tensão também será distribuída ao longo de todas as seções transversais e extensão do corpo, desde que sejam seguidas as condições de distanciamento mínimo do ponto de aplicação da carga concentrada.
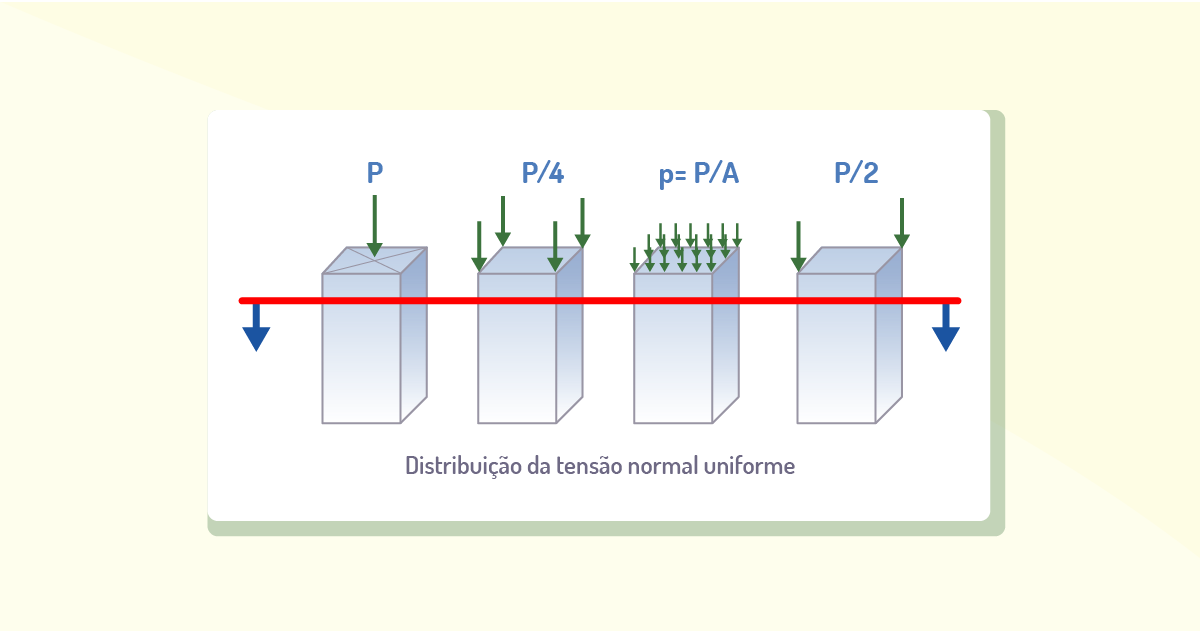
Portanto, considerando o princípio de Saint-Venant, percebemos que efeitos concentrados resultantes de qualquer carga atuante no corpo tendem a se dissipar ou se ajustar às regiões distantes dela. As tensões resultantes de qualquer outra carga estaticamente similar aplicada ao corpo de mesma área serão equivalentes à tensão resultante na área distante de aplicação da carga. De modo que não se faz necessário ponderar as distribuições de tensões complexas atuantes nos pontos de aplicação da carga ou apoios, desde que estejam distantes desses pontos.
Partindo das definições vistas anteriormente sobre tensão, deformação e lei de Hooke, podemos determinar a deformação elástica de um corpo submetido a cargas axiais a partir do estudo de uma barra com área de seção transversal variável progressivamente ao longo do comprimento L, como mostra a Figura 4.3. Aplicando a essa barra uma carga concentrada em suas extremidades e uma carga externa variável por toda extensão longitudinal de seu comprimento, podemos determinar o deslocamento relativo δ (delta) de uma extremidade da barra no que se refere à outra, segundo essa carga. Lembre-se que desprezaremos as deformações concentradas em pontos de carregamento e em seções transversais variáveis, de modo que a deformação ocorrerá uniformemente, distribuindo da mesma forma a tensão normal na seção transversal da barra.
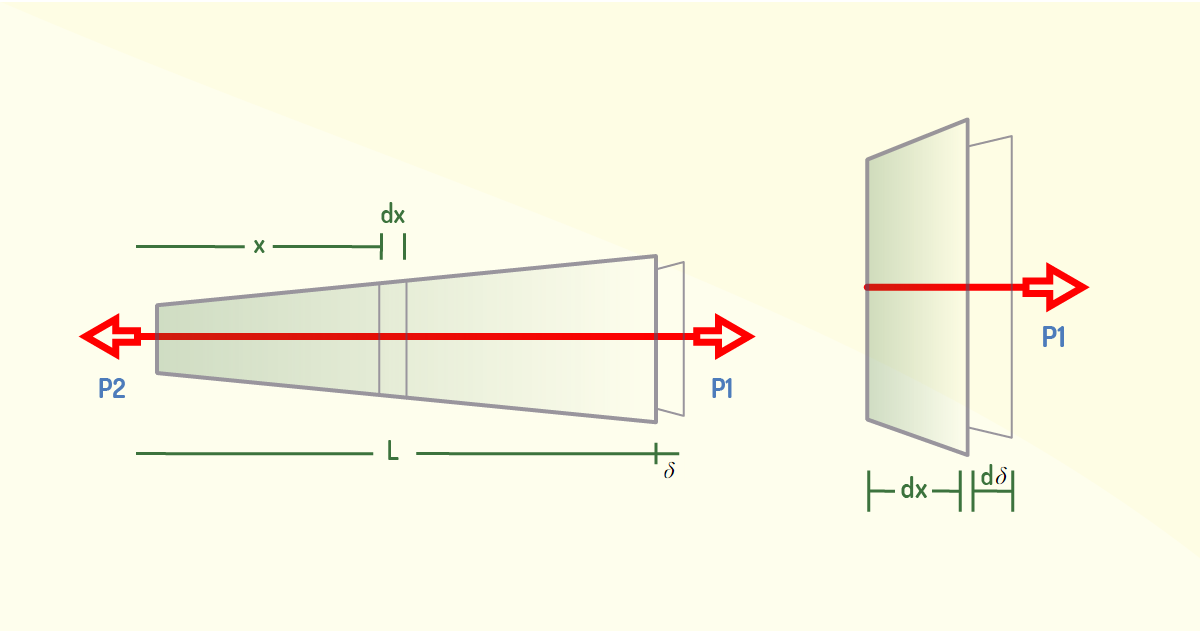
Partindo agora do diagrama de força da Figura 4.3 e do método das seções, isolaremos um pequeno elemento da barra com comprimento dx e área de seção transversal A (x) em uma posição x. De modo que a força axial interna resultante será P (x), variável ao longo do comprimento da barra, de modo que cause deformação no elemento escolhido, cujo deslocamento será dδ.
Lembrando que tensão \(\sigma =\frac{P\left( x \right)}{A\left( x \right)}\), a deformação é \(\varepsilon =\frac{d\delta }{dx}\) nesse elemento, então poderemos aplicar a lei de Hooke vista anteriormente, de modo que \(\sigma =E\varepsilon \Rightarrow \frac{P\left( x \right)}{A\left( x \right)}=E\left( \frac{d\delta }{dx} \right)\Rightarrow d\delta =\frac{P\left( x \right)dx}{A\left( x \right)E}\).
Para o comprimento total da barra L, devemos integrar essa expressão para determinar o deslocamento da extremidade exigido de modo que \(\delta =\mathop{\int }_{0}^{L}\frac{P\left( x \right)dx}{A\left( x \right)E}\) e \(d\delta =\frac{P\left( x \right)dx}{A\left( x \right)E}\), em que δ é o deslocamento de um ponto na barra relativo a outro; L, a distância original entre os pontos; P(x), a força axial interna na seção, localizada a distância x de uma extremidade; A(x), a área da seção transversal da barra, expressa em função de x; e E, o módulo de elasticidade para o material.
Para o caso de uma carga constante, teremos que, se a força externa, aplicada a cada extremidade da barra, também for constante, podemos dizer que em todo o comprimento da barra essa força interna P também será constante; assim, chegamos à conclusão de que \(\delta =\mathop{\int }_{0}^{L}\frac{P\left( x \right)dx}{A\left( x \right)E}=\frac{PL}{AE}\). Essa equação poderá ser aplicada se:
Para todos esses casos, teremos que o deslocamento de uma extremidade da barra em relação à outra será determinado pela adição de deslocamentos das extremidades de cada segmento, ou seja, \(\delta =\mathop{\sum }_{{}}^{{}}\frac{PL}{AE}\), sendo convencional adotar sinal positivo, para o caso da força axial interna e deslocamento de uma extremidade em relação à outra acarretarem em tração e alongamento; e sinal negativo, para o caso de acarretarem compressão e contração (HIBBELER, 2010).
Em alguns casos, determinar a tensão ou o deslocamento pontual de um corpo sujeito a um carregamento complexo não é uma tarefa trivial, sendo necessária a subdivisão das cargas em elementos distintos para que seja possível determinar tensão ou deslocamento provocados pela carga em questão, cuja componente individual atuará separadamente sobre o corpo. A essa suposição, damos o nome de princípio da superposição. Perceberemos que a tensão ou o deslocamento resultante serão determinados a partir da somatória das contribuições das componentes individuais. E, para que isso seja verdadeiro, é preciso que:
Suponhamos uma barra fixa em uma de suas extremidades sob ação de uma carga axial, para que seja possível a determinação da reação de apoio fixo, é preciso e suficiente que a equação de equilíbrio da força aplicada ao longo do eixo da barra seja conhecida e estritamente possível de se determinar. Temos aqui um exemplo de uma barra estaticamente determinada, será a partir dela que discutiremos a condição para que ela seja indeterminada.
Suponhamos agora que a barra se encontra fixa em suas duas extremidades, nesse momento, é possível perceber que haverá sobre ela, duas reações axiais inéditas, de modo que teremos \(+\uparrow \Sigma F=0~\) como equação de equilíbrio da força, o que nos permite chegar a \({{F}_{B}}+{{F}_{A}}-P={{0}_{{}}}\), ou seja, um sistema insuficiente para sua solução, portanto uma barra estaticamente indeterminada.
Para ser solúvel esse problema, deve contar com uma condição de compatibilidade ou cinemática, a qual tem origem na geometria da deformação, ou seja, uma outra equação que especifique as condições do deslocamento.
Uma condição usual de compatibilidade é considerar o deslocamento relativo de uma extremidade da barra em relação à outra, nulo, visto que os apoios das extremidades são fixos. Assim, temos \({{\delta }_{A/B}}=0\), a qual pode ser expressa em termos das cargas aplicadas, caso usemos a relação carga-deslocamento, dependente do material.
Além da condição de compatibilidade, é possível resolver um problema estaticamente indeterminado a partir do método da flexibilidade ou métodos das forças, o qual permite escrever a equação de compatibilidade com a superposição das forças. Vamos supor novamente uma barra fixa nas duas extremidades, de modo que, para escrevermos a equação de compatibilidade, temos que:
Percebemos que os resultados obtidos são similares aos obtidos conforme já vimos anteriormente, diferenciando-se dele apenas na aplicação da condição de compatibilidade e, depois, na da condição de equilíbrio. Além disso, é possível perceber a aplicabilidade do princípio da superposição nesse caso, pois deslocamento e carga são relacionados linearmente, indicando comportamento linear- elástico do material em questão (ONOUYE, 2015).
Em geral, a alteração na temperatura de um material gera mudanças em suas dimensões, de forma que para um aumento da temperatura haja expansão do material, enquanto para uma diminuição da temperatura haja contração dele. Vale lembrar que a variação de temperatura está linearmente relacionada à contração do material.
Para um material homogêneo e isotrópico (propriedades físicas constantes), é possível a determinação da deformação de um elemento com comprimento L, experimentalmente a partir de \({{\delta }_{T}}=\alpha \Delta TL\), em que α é o coeficiente linear de expansão térmica; ΔT é a variação de temperatura; L o comprimento inicial do elemento, δT a variação no comprimento do elemento.
Caso α ou a variação de temperatura ocorra em todo o comprimento do elemento (ΔT= ΔT(x)), teremos que \({{\delta }_{T}}=\mathop{\int }_{0}^{L}\alpha \Delta Tdx\) como resultado da \({{\delta }_{T}}=\alpha \Delta TL\) aplicada em cada segmento do comprimento.
Percebemos que a mudança no comprimento de um elemento estaticamente determinado pode ser calculada também a partir de \({{\delta }_{T}}=\alpha \Delta TL\), pois tal elemento encontra-se livre para contrair ou expandir diante da ΔT, o que não ocorre para os casos de elementos estaticamente indeterminados, os quais são limitados pelos apoios, produzindo tensões térmicas significativas no projeto.
Para o caso de uma estrutura não isostática, cuja variação de comprimento provocada pela temperatura seja livre, não surgirão tensões causadas pela variação de temperatura.
Para o caso de uma estrutura hiperestática, a variação de comprimento da barra provocada pela temperatura será bloqueada e aparecerão tensões térmicas. Essas tensões podem chegar a valores muito altos, causando danos à estrutura, como sua ruptura. Por esse motivo, há juntas de dilatação, em estruturas de grande porte, como pontes, para possibilitar a livre movimentação térmica da estrutura.
Para a resolução desse tipo de problema, é possível considerar a reação do apoio como reação redundante e aplicar o princípio da superposição, conforme Figura 4.4.
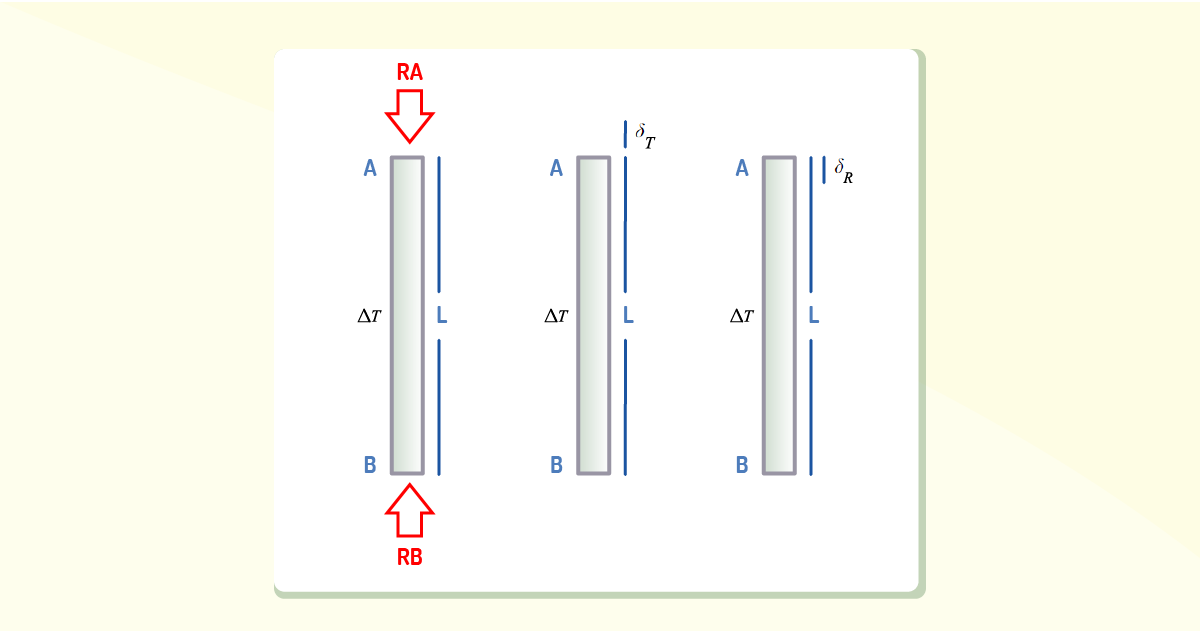
Desse modo, teremos que:
Assim, RA-RB=0, ou, ainda, RA= RB.
Dada uma haste de aço com diâmetro de 5 mm presa a uma parede fixa em seu segmento A, temos que, antes de ser carregada com uma carga específica, esta possui uma folga de 1 mm entre o ponto B’(parede) e ela. Determine as reações em A e B’ a partir da descrição anterior para quando a haste for submetida a uma força axial P = 20 kN. Lembre-se de desprezar o tamanho do colar em Ce, considere Eaço = 200 GPa.
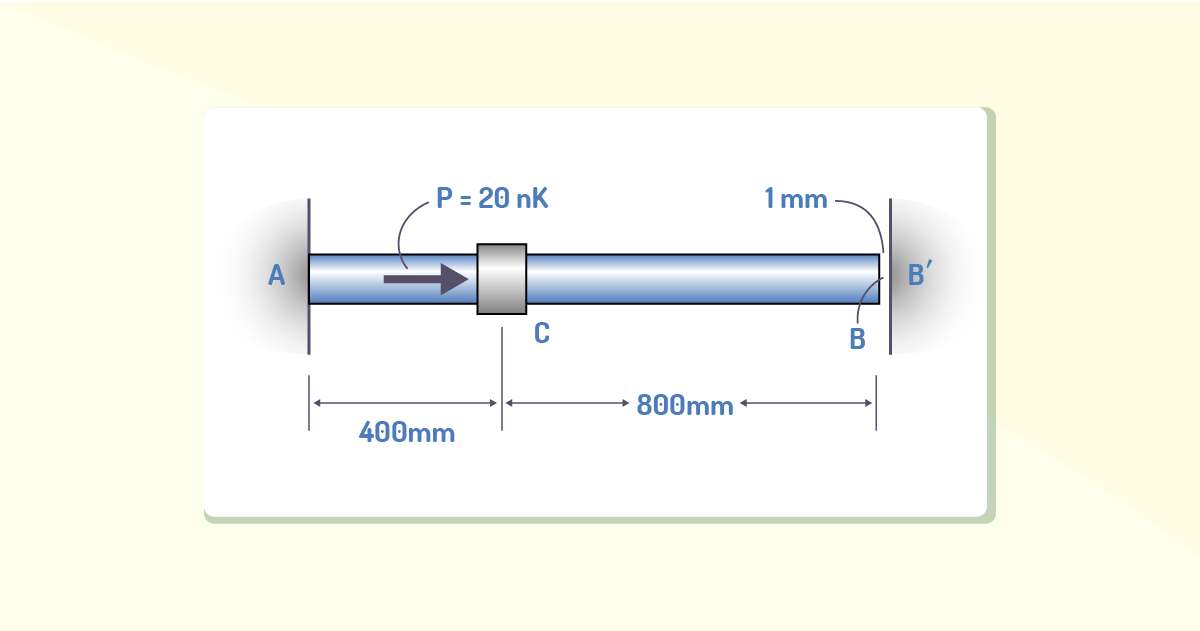
Fonte: Adaptada de Hibbeler (2010, p. 117).
A força em A será de FA= 18,6 kN.
Incorreta. Visto que -FA - FB + 20x10^3 = 0 e que 400 FA- 800 FB = 3,93x10^6 N.mm, então, teremos que o valor de FA = 16,6 kN.
A força em B será de FB = 3,36 kN.
Correta. Dado que -FA-FB+20x10^3=0 e que 400 FA- 800 FB= 3,93x10^6 N.mm, então, teremos que FB= 3,36kN, como descrito na alternativa.
A condição de compatibilidade para a haste é δAB = 1m.
Incorreta. O valor de δAB é de 1mm.
O equilíbrio da haste será dado por FA-FB-20x10^3=0.
Incorreta. O equilíbrio da haste será dado por -FA-FB+20x10^3=0.
A força em A será de 16,6N.
Incorreta. Visto que -FA-FB+20x10^3=0 e que 400 FA- 800 FB= 3,93x10^6 N.mm, então, teremos que o valor de FA= 16,6 kN.
Agora, consideraremos um eixo ou um tubo, ou seja, um elemento linear longo, cuja seção transversal é circular, de modo que estudaremos os efeitos da aplicação de esforços torcionais sobre ele.
Quando um material sofre uma torcedura em torno de seu eixo longitudinal, dizemos que houve um torque nesse material. Suponhamos que um torque seja aplicado a um eixo cujo material seja borrachoso, ou seja, altamente deformável. Imaginemos que a esse eixo cilíndrico faremos diversos cortes: na horizontal, formando discos; e na vertical, formando uma grelha, conforme Figura 4.5.
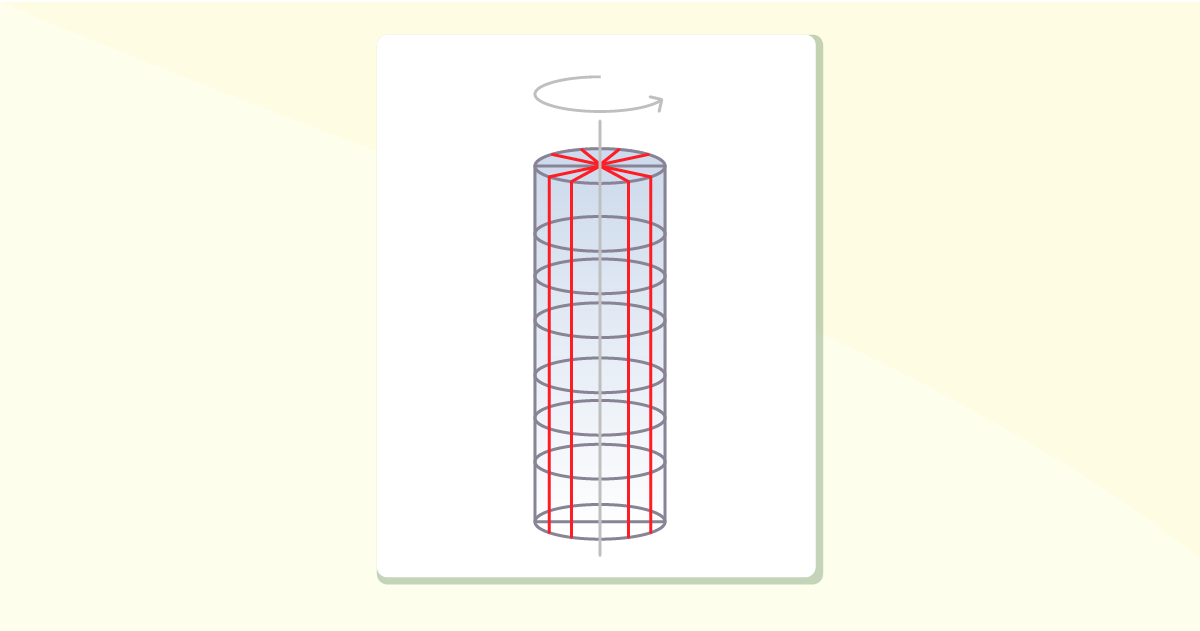
Em reação ao torque:
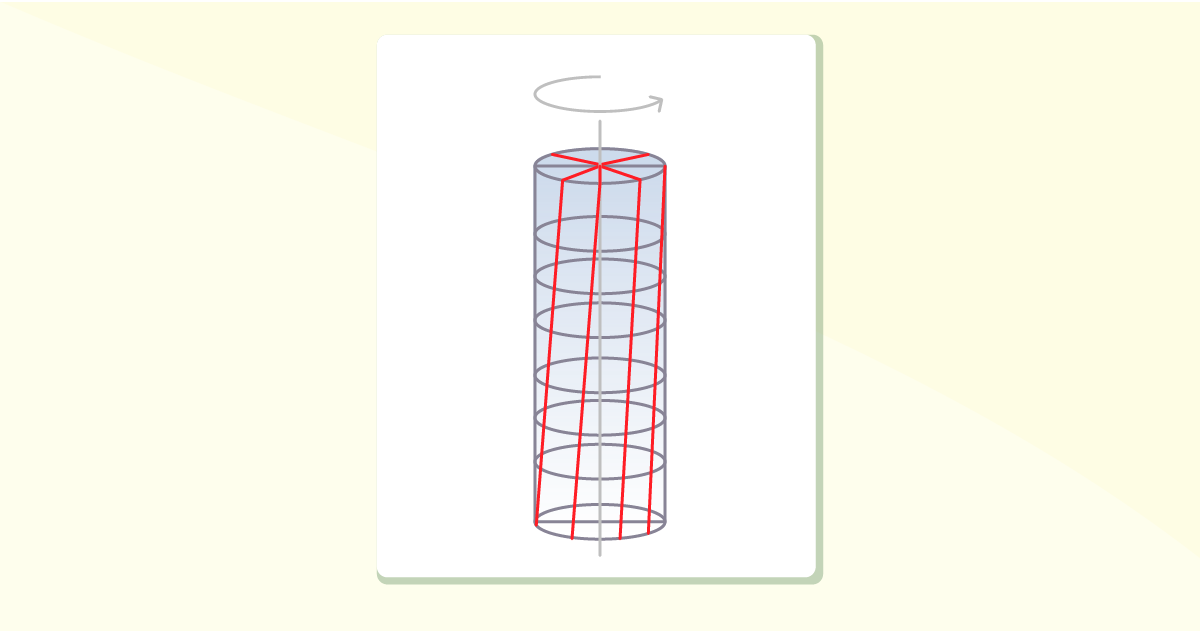
Para o caso de usarmos o mesmo eixo citado anteriormente, mas agora prendendo uma de suas extremidades, teremos que, ao aplicarmos um torque à extremidade livre, o plano desse será distorcido e se manifestará em uma forma oblíqua, formando ângulo agudo. Perceberemos que uma linha radial presente na seção transversal a uma distância x da extremidade fixa do eixo terá rotação com angulação Φ(x), ou seja, ângulo de torção, o qual é dependente da posição x e variável longitudinalmente.
Nesse momento, se isolarmos um pequeno elemento a uma distância radial σ do eixo central, veremos que as faces desse elemento sofrerão rotação devido à deformação. Nessa conformação, teremos que a face posterior rotacionará por Φ (x) e a face anterior por Φ (x) + ΔΦ, resultando em uma deformação por cisalhamento do elemento, quando tivermos a diferença entre as rotações ΔΦ, a qual pode ser calculada a partir de \(\gamma =\frac{\pi }{2}\begin{matrix} {} \\ -\lim \,\theta '\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ \begin{align} & \ C\to A\,along\,C\,A \\ & \ B\to A\,along\,B\,A \\ \end{align} \\ \end{matrix}\), em que \(\gamma \) é relacionado ao Δx e à ΔΦ. AC e AB são bordas do cilindro inicial, cuja angulação entre elas era de 90º, e após a deformação, as bordas do elemento são AD e AC, cuja angulação é ϴ’.
Ao admitirmos Δx→dx e ΔΦ→dΦ, teremos que \(BD=\rho d\phi =dx\gamma \), logo \(\gamma =\rho \frac{d\phi }{dx}\). Aqui, percebemos que dx e dΦ são os mesmos em todos os elementos da seção transversal, de modo que a razão entre eles é constante, indicando que a intensidade da deformação por cisalhamento de qualquer um desses elementos variará com a distância radial ρ que parte da linha central do eixo. Ou, ainda, podemos afirmar que a deformação por cisalhamento no interior do eixo é variável linearmente ao longo da reta radial, de zero na linha central do eixo a um máximo \(\gamma \) máx em seu limite externo, resultando em \(\gamma =\left( \frac{\rho }{c} \right){{\gamma }_{m\acute{a}x}}\), desde que \(\frac{d\phi }{dx}=\frac{\gamma }{\rho }=\frac{{{\gamma }_{m\acute{a}x}}}{c}~\) (HIBBELER, 2010).
A quantidade de rotação ou torção é limitante em um projeto de eixos quando esses estão submetidos a torques, sendo necessário o conhecimento do ângulo de torção para que seja possível analisar as reações em eixos estaticamente indeterminados.
Quando um eixo fica submetido a um torque externo, há um torque também interno no interior do eixo, sendo possível e necessário relacioná-lo à distribuição de tensões de cisalhamento na seção transversal do eixo ou tubo circular.
Supondo novamente que o elemento seja formado por material linear e elástico, podemos:
Nessa conformidade, temos:
Vale lembrar que, até aqui, o cálculo da tensão é feito para material homogêneo e cujo eixo é circular, indicando que a tensão de cisalhamento é proporcional à deformação de cisalhamento.
Para o caso de um eixo sólido, teremos que:
Para o caso de um eixo tubular (eixo vazado), teremos que:
Elementos com seção transversal circular, como tubos e eixos, transmitem potência gerada por máquinas, de modo que, submetidos a torques, dependem dessa potência e da velocidade angular do eixo.
Dado que a potência é a razão entre trabalho realizado e tempo, e o trabalho transmitido por um eixo rotativo é o produto entre o torque aplicado e ângulo de rotação, podemos entender que, para um pequeno diferencial de tempo, o torque T fará o eixo rotacionar em dϴ, então, teremos que a potência, a qual chamaremos de instantânea, será dada por P= Tdϴ/dt, na qual, se considerarmos ω= dϴ/dt, medido em rad/s, teremos P= Tω , expressa em watts, de modo que 1W= 1Nm/s.
Além da potência e do torque em uma máquina, outra grandeza essencial é a frequência de rotação de um eixo, dada por f, a qual representa o número de ciclos ou revoluções que o eixo realiza por segundo, no qual 1 ciclo corresponde a 2π rad, sendo possível reescrever ω como sendo ω=2πf e P como P=2πf T.
Quando pensamos em termos do projeto de um eixo, saber a potência transmitida por ele e sua frequência é essencial para determinarmos o torque desenvolvido por ele. Sabendo, então, o torque e a tensão de cisalhamento suportável pelo material, \({{\tau }_{adm}}\), é possível conhecermos a área da seção transversal, sob a condição de que esse material seja linear-elástico, em que o projeto ou parâmetro geométrico (J/c) é dado por \(\frac{J}{c}=\frac{T}{{{\tau }_{adm}}}\).
A partir da relação J/c, podemos compreender e calcular o único valor do raio para um eixo maciço: \(J=\left( \frac{\pi }{2} \right){{c}^{4}}\). Para o caso de um eixo tubular, o projeto pode considerar diversas maneiras de ser empregado, pois é possível escolher arbitrariamente tanto co como ci, chegando à equação \(J=\left( \frac{\pi }{2} \right)\left( c_{o}^{4}-c_{i}^{4} \right)\).
Sabemos que o projeto de um eixo é dependente da quantidade de rotação ou torção ocorridos ao eixo sob torque, além de sabermos o ângulo de torção (Φ), é extremamente importante que saibamos analisar as reações em eixos estaticamente indeterminados. Para isso, vamos supor que:
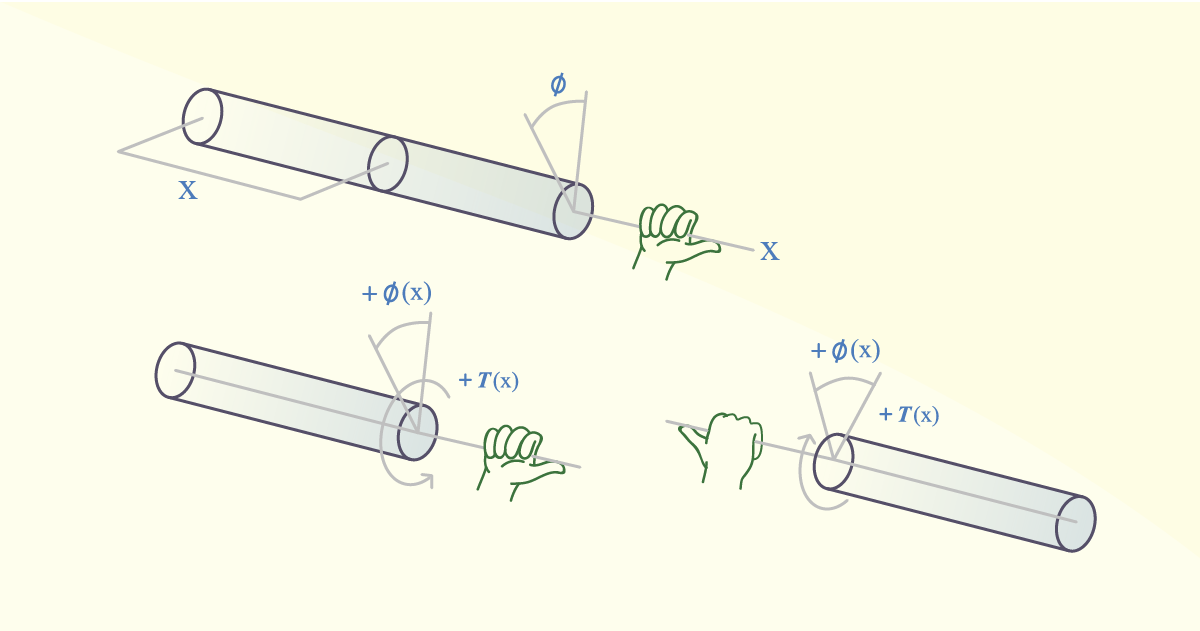
Assim, torque e ângulo de torção terão valores positivos se a direção indicada pelo polegar tiver o sentido de afastamento do eixo (BOTELHO, 1998).
Um eixo carregado por torque será considerado estaticamente indeterminado quando a equação do momento na condição de equilíbrio em torno de sua linha central não for suficiente para determinar os torques desconhecidos atuantes sobre ela.
A partir do diagrama de corpos livre, para a situação descrita anteriormente, podemos encontrar \(\Sigma {{M}_{x}}=0\) e T- TA- TB= 0, a partir da qual percebemos que o número de incógnitas é maior do que o número de equações, corroborando com a indeterminação estática do sistema. Para que seja possível, devemos considerar que a condição cinemática ou condição de compatibilidade necessárias requerem que o ângulo de torção de uma extremidade até a outra seja nulo, já que os pontos de apoio das extremidades se encontram fixos, logo, \({{\phi }_{A/B}}=0\). E mais, supondo que o material mantenha o comportamento linear-elástico, em que \(\phi =\frac{TL}{JG}\), teremos em termos dos torques desconhecidos que \(\frac{{{T}_{A}}{{L}_{AC}}}{JG}-\frac{{{T}_{B}}{{L}_{BC}}}{JG}=0\).
Supondo que JG seja constante e \(L={{L}_{AC}}+{{L}_{BC}}\), teremos que \({{T}_{A}}=T\left( \frac{{{L}_{BC}}}{L} \right)\) e \({{T}_{B}}=T\left( \frac{{{L}_{AC}}}{L} \right)\), os quais aumentarão ou diminuirão linearmente de acordo com a localização de LAC e LBC.
Elementos com seção transversal circular, como tubos e eixos, transmitem potência gerada por máquinas, de modo que, submetidos a torques, dependem dessa potência e da velocidade angular do eixo. Sabendo que um eixo tubular de diâmetro interno de 30mm e diâmetro externo de 42 mm é usado para transmitir 90kW de potência, assinale a alternativa correta, sabendo que a tensão de cisalhamento não excede 50 MPa.
O momento de inércia J terá valor de 3,29x10^-6 m^4.
Incorreta. Visto que \(J=\left( \frac{\pi }{2} \right)\left( c_{O}^{4}-c_{i}^{4} \right)\), logo J= π ((0,021^4)- (0,015^4))/2, então J= 2,2597 x10^-7 m^4.
O Torque T terá valor de 538 Nm.
Correta. Sabendo que \({{T}_{m\acute{a}x}}=\frac{{{T}_{c}}}{J}\), então T= (50x10^6.2,2597 x 10^-7)/0,021, logo T= 538, como descrito na alternativa.
O momento de inércia será nulo.
Incorreta. Visto que \(J=\left( \frac{\pi }{2} \right)\left( c_{O}^{4}-c_{i}^{4} \right)\), logo J= π ((0,021^4)- (0,015^4))/2, então J= 2,2597 x10^-7 m^4.
A frequência de rotação terá valor de 27,7 Hz.
Incorreta. Visto que P=2⋅π⋅ f⋅T, então f= 90x10^3/(2⋅π⋅538), logo f= 26,6Hz.
O valor do torque será 540 Nm.
Incorreta. Sabendo que \({{T}_{m\acute{a}x}}=\frac{{{T}_{c}}}{J}\), então T= (50x10^6.2,2597 x 10^-7)/0,021, logo T= 538, como descrito na alternativa.
Discutiremos as deformações que ocorrem em uma viga prismática feita de material homogêneo e borrachoso, submetida a uma flexão.
Faremos um exemplo similar ao analisado no tópico de “Deformação por torção de um eixo circular”, de modo que particionaremos a viga, como mostrado na Figura 4.8, e aplicaremos nela um momento fletor, que tenderá a distorcer as retas longitudinais, tornando-as curvas, e as retas transversais permanecerão retas, porém rotacionadas.
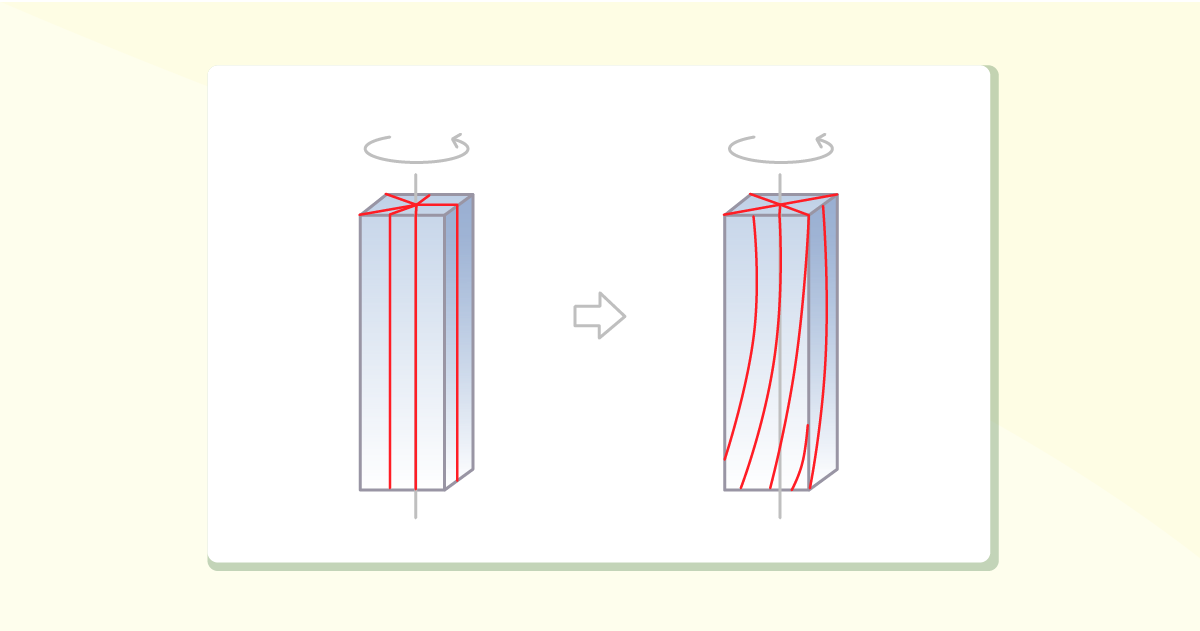
O comportamento da barra ao ser deformada, devido ao momento fletor, permite que a parte superior da barra fique comprimida, enquanto a parte inferior estica-se, mudando o padrão, como descrito na Figura 4.9. Em contrapartida, entre essas duas regiões há uma superfície, chamada neutra, na qual as fibras longitudinais do material não se alteram no comprimento.
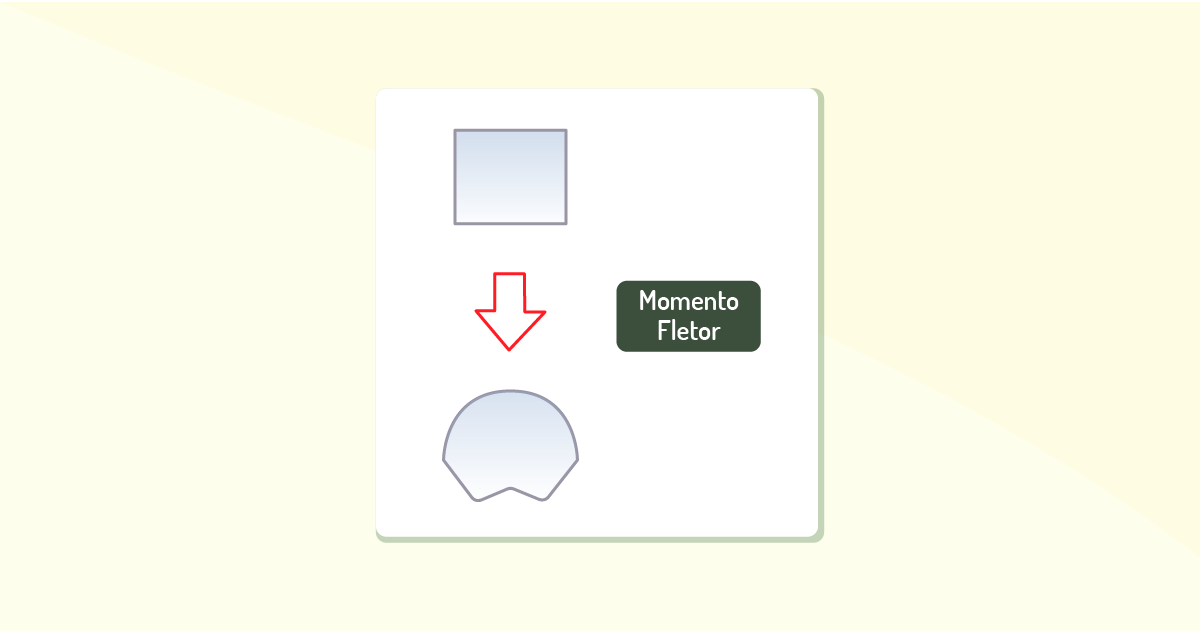
A partir disso, podemos supor sobre o modo de deformação do material em resposta à tensão:
A fim de corroborar com as hipóteses, admitiremos um pequeno elemento da viga, localizado a uma distância x e de espessura Δx, a partir do qual podemos observar que, quando localizado na superfície neutra da viga, não tem seu comprimento alterado. Por outro lado, quando um elemento é localizado em y, o qual chamaremos de ΔS, teremos que, diante da deformação, ΔS contrair-se-á, de modo que \(\epsilon =\underset{\Delta s\to 0}{\mathop{lim}}\,\frac{\Delta s'-\Delta s}{\Delta s}\). Em que, para ΔS= Δx= ρ Δ ϴ e ΔS’= (ρ-y) Δ ϴ, teremos \(\epsilon =-\frac{y}{\rho }\). O que nos permite concluir que para qualquer seção transversal específica, a deformação normal longitudinal variará linearmente com y a partir do eixo neutro.
A deformação máxima, \({{\epsilon }_{m\acute{a}x}}\), ocorrerá na fibra externa da viga, localizada a uma distância c do eixo neutro, de modo que \(\frac{\epsilon }{{{\epsilon }_{m\acute{a}x}}}=\frac{\frac{-y}{\rho }}{\frac{c}{\rho }}\) ou \(\epsilon =-\left( \frac{y}{c} \right){{\epsilon }_{m\acute{a}x}}\) (HIBBLER, 2010).
Agora, tentaremos relacionar a distribuição da tensão longitudinal de uma viga ao momento fletor resultante interno que atua sobre ela em sua seção transversal. Supondo novamente um material que se comporta de maneira linear-elástica, temos que a ele é aplicável a lei de Hooke e também haverá uma variação linear da deformação normal, a qual é consequência da variação linear da tensão, de modo que podemos calcular a tensão sobre a área da seção transversal a partir da equação, \(\sigma =-\left( \frac{y}{c} \right){{\sigma }_{m\acute{a}x}}\).
Para o caso do momento fletor positivo atuante na direção z+, teremos que os valores positivos de y resultarão em valores negativos para σ, decorridos a uma tensão de compressão, já que essa atua na direção negativa de x. Concomitantemente, teremos que os valores negativos de y resultarão em valores positivos ou de tração para cima.
Ao selecionarmos um elemento de volume desse material em um ponto específico de sua seção transversal, observaremos que apenas as tensões normais de tração ou compressão atuarão sobre ele. E saberemos sua localização no eixo neutro da seção transversal respeitando a condição de que a força resultante produzida pela distribuição dessa atenção sobre a seção transversal é igual a zero, de modo que a encontraremos a partir da força resultante, dada pela somatória das forças em x: FR= ∑ Fx, daí teremos que \(0=\mathop{\int }_{A}^{{}}dF=\mathop{\int }_{A}^{{}}\sigma dA=\mathop{\int }_{A}^{{}}-\left( \frac{y}{c} \right){{\sigma }_{m\acute{a}x}}dA=\frac{-{{\sigma }_{m\acute{a}x}}}{c}\mathop{\int }_{A}^{{}}ydA\), em que dF= σ dA e σmáx/c, logo \(\mathop{\int }_{A}^{{}}ydA=0\).
A equação anterior nos mostra que o primeiro momento da área de seção transversal do elemento precisa ser nulo. Essa condição só será satisfatória se o eixo neutro for coincidente ao eixo horizontal de simetria da seção transversal, de modo que momento de dF em torno do eixo neutro será dado por dM = y dF, o qual é positivo, visto que o polegar está direcionado ao sentido positivo do eixo Z, como visto na regra da mão direita. O que nos permite chegar à equação \(M=\frac{{{\sigma }_{m\acute{a}x}}}{c}\mathop{\int }_{A}^{{}}{{y}^{2}}dA\).
Essa integral representará o momento de inércia da área de seção transversal calculada em torno do eixo neutro, a qual, em termos de σmáx, pode ser escrita como \({{\sigma }_{m\acute{a}x}}=\frac{Mc}{I}\), em que σ máx é a tensão normal máxima no elemento localizada no ponto da área da seção transversal mais infestada do eixo neutro; M é o momento interno resultante obtido a partir do método das seções e das equações de equilíbrio, calculado em torno do eixo neutro da seção transversal; I é o momento de inércia da área de seção transversal em torno do eixo dado por \(I=\frac{1}{12}b{{h}^{3}}\); c é a distância perpendicular do eixo neutro ao ponto mais longínquo desse eixo, na qual a máxima atua.
Lembrando que \(\frac{{{\sigma }_{m\acute{a}x}}}{c}=-\frac{{{\sigma }_{{}}}}{y}\), temos que tensão normal na distância intermediária y pode ser determinada por \({{\sigma }_{{}}}=-\frac{My}{I}\), a partir da qual podemos observar que o sinal negativo é extremamente necessário para corroborar com o estabelecido para os eixos x, y e z; de modo que, pela regra da mão direita, teremos M positivo ao longo do eixo z+; y positivo para cima, e σ negativo devido à compressão atuante na direção negativa de x.
Tanto \({{\sigma }_{m\acute{a}x}}=-\frac{Mc}{I}\) quanto \({{\sigma }_{{}}}=-\frac{My}{I}\) nos dizem respeito da fórmula de flexão, usada para determinar a tensão normal em um membro reto cuja seção transversal é simétrica em relação ao eixo e no qual o momento seja aplicado no sentido perpendicular a ele. Além de ser aplicada a seções retas, a fórmula da flexão pode ser usada na maioria dos projetos de engenharia para determinar, também, a tensão normal nos membros que tenham pequena conicidade.
Percebemos que as vigas, em geral, suportam tanto cargas de cisalhamento quanto de momento fletor, de modo que o cisalhamento é o resultado de uma distribuição de tensão de cisalhamento transversal, o qual atua sobre a seção transversal da viga. As tensões de cisalhamento longitudinais associadas à propriedade complementar de cisalhamento também atuam ao longo dos planos longitudinais da viga.
Mais uma vez, usaremos como exemplo um elemento típico retirado do interior da seção transversal, o qual estará sujeito a tensões de cisalhamento transversais e longitudinais.
Resultante da tensão de cisalhamento, temos que haverá deformações de cisalhamento no elemento citado de modo que distorceram a seção transversal de maneira mais complexa. Para isso, consideraremos uma barra feita de material altamente deformável e marcada como uma grade de linhas horizontais e verticais.
Ao aplicarmos uma força de cisalhamento V nessa barra, verificaremos a deformação das linhas, conforme o padrão mostrado na Figura 4.10, a qual nos indica que a distribuição não uniforme da tensão de cisalhamento sobre essa seção provoca a distorção dela. Em (a), encontram-se tábuas sem acoplamento, e em (b), encontram-se tábuas com acoplamentos.
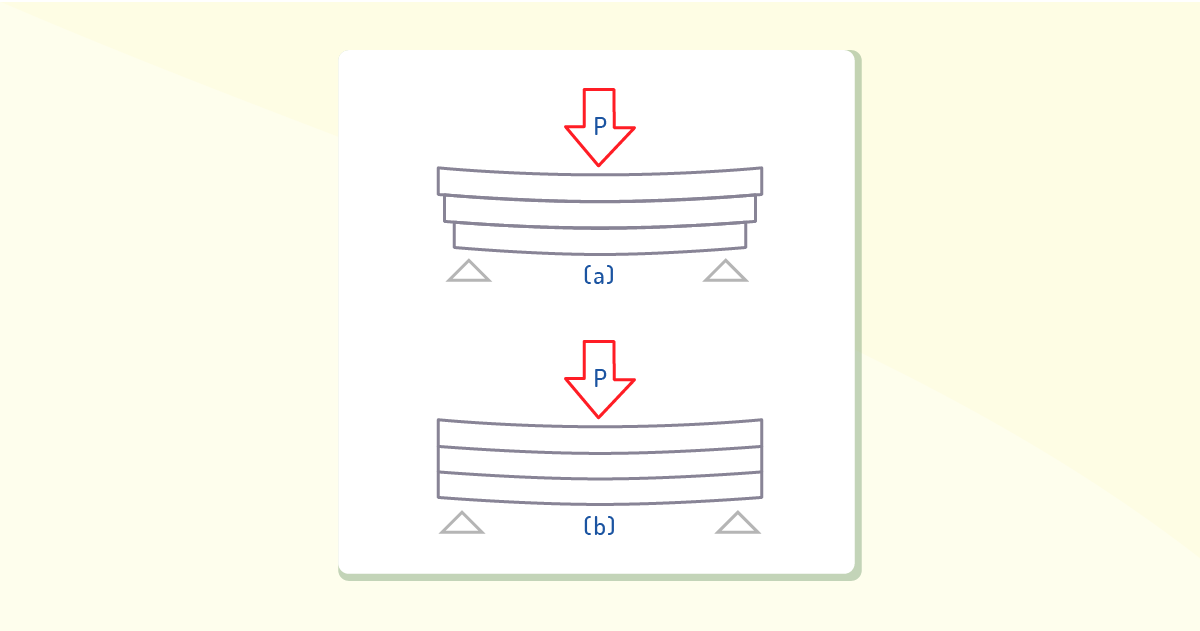
Para desenvolvermos a fórmula de flexão, partimos do pressuposto de que as seções transversais tinham de permanecer planas e perpendiculares ao eixo longitudinal da viga mesmo após a deformação. Entretanto, no caso citado anteriormente, essa condição é violada quando viga está submetida a uma flexão e cisalhamento, o que nos permite supor que a distorção ocorrida na seção transversal é insignificante e pequena, podendo assim ser desprezada. Essa hipótese é utilizada para análise da viga do tipo esbelta, a qual possui uma largura extremamente pequena em relação ao seu comprimento.
A relação existente entre a distribuição da tensão de cisalhamento que atua sobre a seção transversal de uma viga e a força cortante ou força de cisalhamento resultante nessa seção é fundamentada no estudo da tensão de cisalhamento longitudinal. Para isso, relacionaremos o equilíbrio da força horizontal de uma parte do elemento retirado da viga, a partir do qual é possível esquematizar o diagrama de corpo livre, que nos mostra somente a distribuição da tensão normal atuante sobre ele, o qual nos diz que a distribuição é resultado dos momentos fletores M e M + dm. Por outro lado, o diagrama de corpo livre sobre os efeitos de V não será incluído aqui, pois essas cargas estão sendo aplicadas na vertical. Sendo assim, o elemento descrito satisfará o somatório das forças em x, o qual deve ser nulo, visto que a distribuição de tensão em cada lado forma apenas um conjugado e, portanto, uma força resultante nula, conforme Figura 4.11.
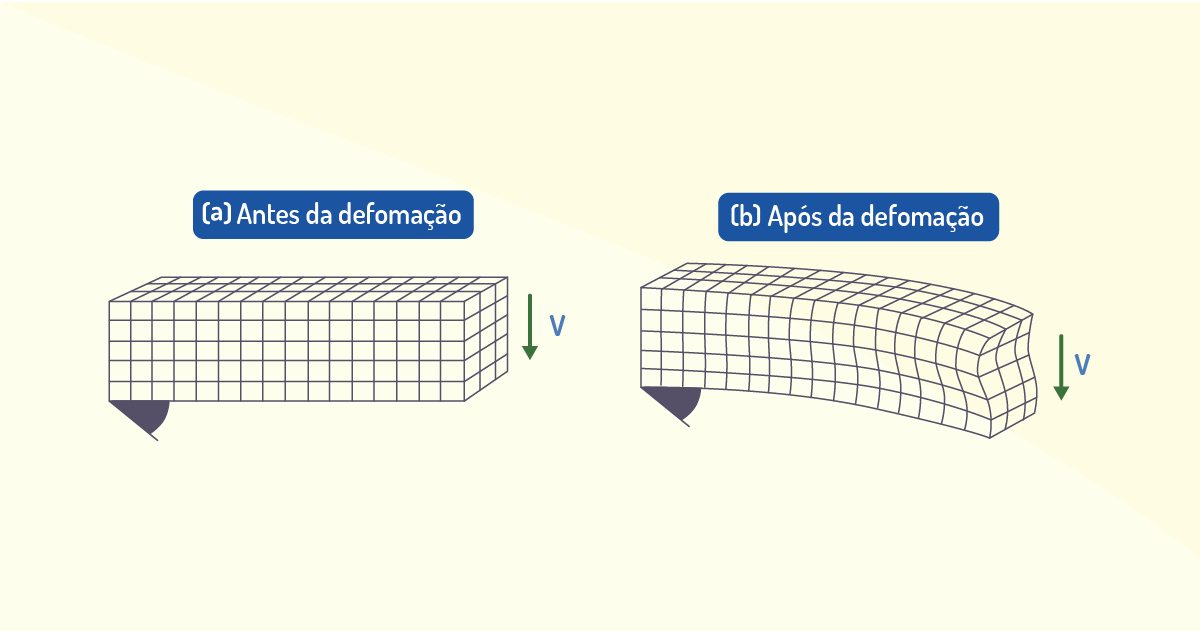
Ao admitir o segmento superior do elemento selecionado a uma distância y' do eixo neutro, cuja largura é t na seção e cada lado dela possui área A', uma vez que os momentos resultantes de cada lado do elemento diferem por dm, percebemos que o somatório das forças em x não será igual a 0, a menos que a tensão de cisalhamento longitudinal atue sobre a face inferior do segmento. Sendo assim, supomos que essa tensão de cisalhamento será constante em toda a largura t da face inferior e atuante sobre a área t dx.
Segundo as equações de equilíbrio das forças horizontais e flexão, teremos que \(\mathop{\int }_{A'}^{{}}\sigma 'dA-\mathop{\int }_{A'}^{{}}\sigma 'dA-\tau \left( t~dx \right)=0\), logo, em termos de \(\tau \), \(\tau =\frac{1}{It}\left( \frac{dM}{dx} \right)\mathop{\int }_{A'}^{{}}ydA\).
Sendo \(\underset{\scriptscriptstyle-}{y}'=\mathop{\int }_{A'}^{{}}ydA/A'\), podemos reescrever a equação como \(Q=\mathop{\int }_{A'}^{{}}ydA=\underset{\scriptscriptstyle-}{y}'A'\), em que A’ é a parte superior ou inferior da área da seção transversal do elemento definido a partir da sessão, em que t é medido, e y’ é a distância entre o centroide de A’ medida a partir do eixo neutro.
Ainda podemos relacionar \(\tau =\frac{VQ}{It}\), chamada de fórmula de cisalhamento, em que \(\tau \) é a tensão de cisalhamento no ponto localizado a uma distância y' do eixo neutro do elemento, a qual é constante e, portanto, média ao longo da largura t do membro; V é a força cortante resultante interna determinada a partir do método das seções e pelas equações de equilíbrio; I é o momento de inércia de toda área da seção transversal em torno do eixo neutro; t é largura da área de seção transversal do elemento no ponto \(\tau \).
Vale lembrar que a fórmula do cisalhamento pode ser aplicada igualmente para se determinar a tensão de cisalhamento transversal da área da seção transversal, visto que o cisalhamento transversal e longitudinal tem valores de tensões complementares e numericamente iguais.
A tensão de cisalhamento em elementos compostos, ou seja, nos quais as seções transversais possuem materiais diferentes, também é obtida a partir da fórmula de cisalhamento, sendo necessário calcular Q e I a partir da seção transformada do elemento, em que a largura t da seção transversal se mantém para o ponto \(\tau \) a ser determinado (SILVA, 2013).
A partir da fórmula do cisalhamento, poderemos estudar as distribuições da tensão de cisalhamento em alguns tipos comuns de seções transversais de vigas. Para uma seção transversal retangular, devemos considerar que a viga possui seção transversal retangular de largura b e altura h, conforme Figura 4.12.
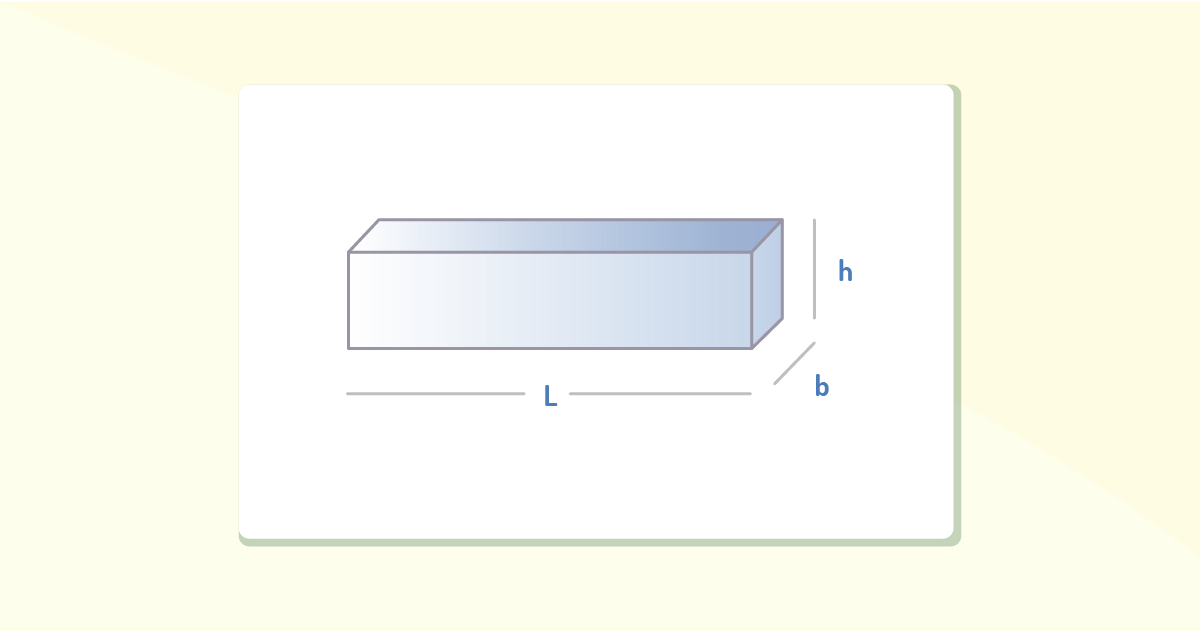
Percebemos que, ao longo de toda a seção transversal, a distribuição da tensão de cisalhamento, a qual pode ser calculada a partir de uma altura arbitrária y do eixo neutro, será r \(Q=\underset{\scriptscriptstyle-}{y}'A'=\left[ y+\frac{1}{2}\left( \frac{h}{2}-y \right) \right]\left( \frac{h}{2}-y \right)b=\frac{1}{2}\left( \frac{{{h}^{2}}}{4}-{{y}^{2}} \right)b\), de modo que, combinada à fórmula do cisalhamento, será dada por \(\tau =\frac{VQ}{It}=\frac{V\left( \frac{1}{2} \right)\left[ \left( \frac{{{h}^{2}}}{4} \right)-{{y}^{2}} \right]b}{\left( \frac{1}{12}b{{h}^{3}} \right)b}\) ou \(\tau =\frac{6V}{b{{h}^{3}}}\left( \frac{{{h}^{2}}}{4}-{{y}^{2}} \right)\).
Essa equação nos indica que a distribuição da tensão de cisalhamento sobre a seção transversal é parabólica, e a intensidade varia de 0 nas partes superior e inferior para y=h/2, ao valor máximo no eixo neutro para y = 0.
Sabendo que A=b.h, teremos que para y=0, \({{\tau }_{m\acute{a}x}}=1,5\frac{V}{A}\). O mesmo poderia ser verificado para a equação \(\tau =\frac{VQ}{It}\), pois \({{\tau }_{m\acute{a}x}}\) ocorre onde Q tem valor máximo, para área acima ou abaixo do eixo neutro, visto que A’= bh/2; ӯ= h/4; V e I são constantes, comprovando que \({{\tau }_{m\acute{a}x}}=\frac{VQ}{It}=\frac{V\left( \frac{h}{4} \right)\left( \frac{bh}{2} \right)}{\left[ \frac{1}{12}b{{h}^{3}} \right]b}=1,5\frac{V}{A}\).
Percebemos que a \({{\tau }_{m\acute{a}x}}\) é 50% maior quando comparada à \({{\tau }_{m\acute{e}d}}\), dada por V/A, vista anteriormente.
Além disso, é possível ver que para cada \({{\tau }_{{}}}\) atuante sobre a área de seção transversal, haverá um correspondente atuando no sentido longitudinal ao longo da veia de modo que, se essa viga foi cortada por um plano longitudinal através do seu eixo neutro, podemos observar que a tensão de cisalhamento máxima atuará nesse plano formado.
É exatamente essa tensão que provoca a falha de uma viga feita de madeira, por exemplo, como já discutido anteriormente. Quando a distribuição da tensão de cisalhamento é integrada ao domínio da seção transversal, é produzido o cisalhamento resultante V; de modo que, se escolhemos uma tira infinitesimal de área dA= bdy e \({{\tau }_{{}}}\), na qual atua uniformemente em toda ela, teremos \(\mathop{\int }_{A}^{{}}\tau dA=\mathop{\int }_{-h/2}^{h/2}\frac{6V}{b{{h}^{3}}}\left( \frac{{{h}^{2}}}{4}-{{y}^{2}} \right)b~dy=\frac{6V}{{{h}^{3}}}\left[ \frac{{{h}^{2}}}{4}y-\frac{1}{3}{{y}^{3}} \right]_{-h/2}^{h/2}=\frac{6V}{{{h}^{3}}}\left[ \frac{{{h}^{2}}}{4}\left( \frac{h}{2}+\frac{h}{2} \right)-\frac{1}{3}\left( \frac{{{h}^{3}}}{8}+\frac{{{h}^{3}}}{8} \right) \right]=V\).
Para o caso de uma viga de abas largas, a qual é formada por 2 abas e uma ‘alma’, de acordo com Figura 4.13, temos que:
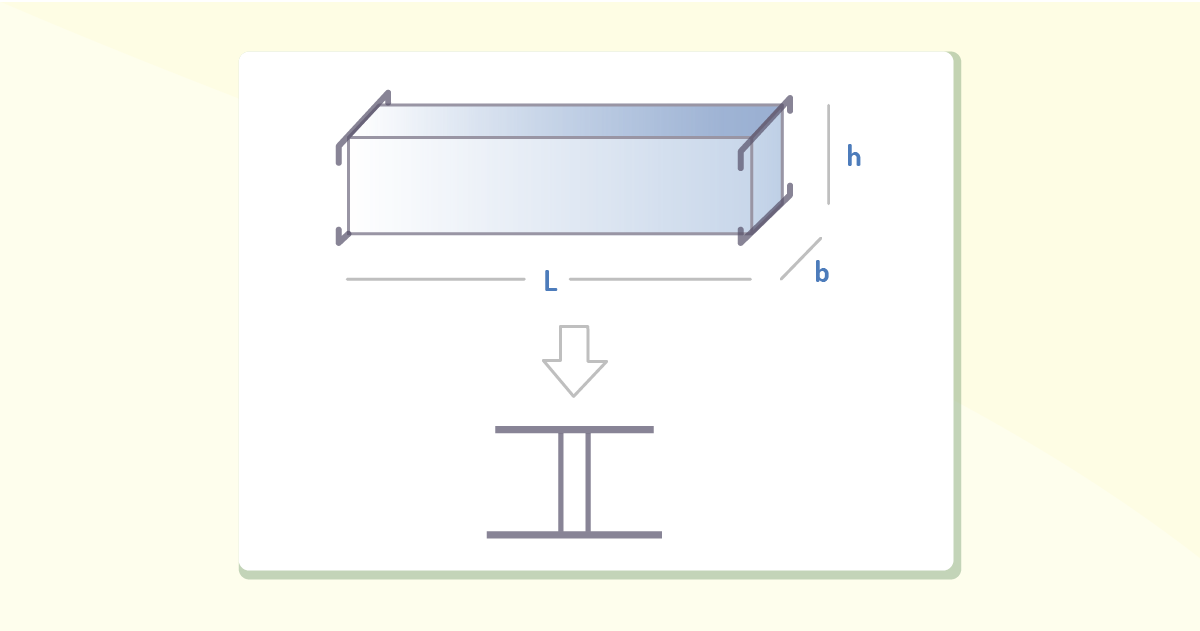
Assim como no exemplo anterior, determinaremos a distribuição da tensão de cisalhamento que atua sobre a seção transversal de uma viga a partir de sua seção retangular e tensão de cisalhamento, a qual é variável parabolicamente ao longo da altura da viga, visto que sua seção transversal pode ser tratada como uma seção retangular, a qual, inicialmente, tem largura da aba superior, B, e, depois, com espessura da ‘alma’, Tw, por fim, a largura da aba inferior, B.
A tensão de cisalhamento variará sutilmente ao longo da ‘alma’, e a tensão de cisalhamento saltará na junção da aba com a ‘alma’, visto que sua espessura muda nesse ponto da seção transversal. Fazendo um comparativo, podemos dizer que ‘alma’ suportará significativamente mais força cortante do que as abas. Algumas limitações ao uso da fórmula de cisalhamento serão discutidas a seguir.
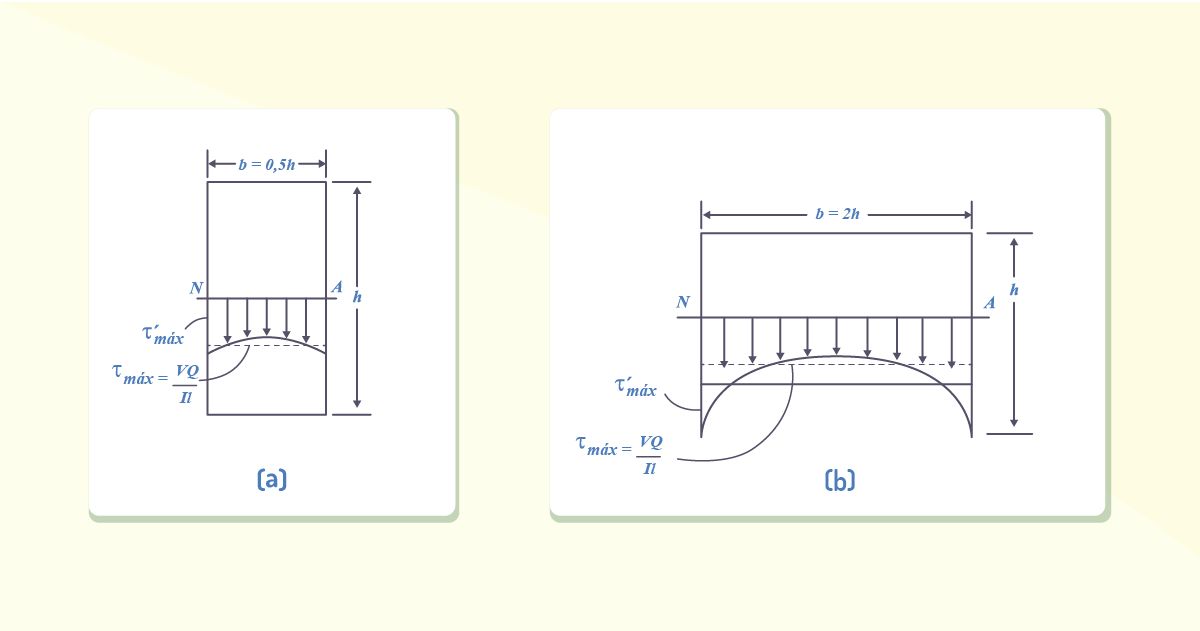
Tratando-se de uma distribuição uniforme da tensão de cisalhamento sobre a largura de uma sessão, podemos afirmar que a tensão de cisalhamento média é calculada ao longo de sua largura. Isso é possível comparando-a à uma análise matemática mais exata fundamentada na teoria da elasticidade. Sendo assim, se a seção transversal da viga for retangular, a distribuição real da tensão de cisalhamento ao longo do eixo neutro variará de acordo com a teoria da elasticidade.
Podemos perceber que o valor máximo \(\tau {{'}_{m\acute{a}x}}\) ocorrerá nas bordas da seção transversal, e sua intensidade dependerá da relação largura por comprimento, de modo que, para seções com relação b/h= 0,5, \(\tau {{'}_{m\acute{a}x}}\) , terá valor de 3% maior quando comparada à calculada pela fórmula do cisalhamento. Porém, para seções cuja relação b/h=2, ou seja, para seções largas, temos \(\tau {{'}_{m\acute{a}x}}\), que apresentará valor 40% maior quando comparada à calculada pela fórmula do cisalhamento.
À medida que a seção se torna mais larga ou a relação b/h aumenta, percebemos que o erro também aumenta, de modo que essa ordem é intolerável, caso a fórmula de cisalhamento seja usada para determinar a tensão de cisalhamento na aba de uma viga de abas largas.
Vale lembrar que a fórmula de cisalhamento não oferece resultados precisos quando usada para determinação de tensão de cisalhamento na junção aba e ‘alma’ de uma viga de abas largas, já que se trata de um ponto de mudança súbita na seção transversal, onde ocorrem concentração de tensão. Além disso, a tensão de cisalhamento nos limites deve ser nula, ou seja, em regiões internas das abas, nas quais as superfícies são livres, é possível que a tensão de cisalhamento também seja nula. Porém, quando tratadas na prática, essas limitações citadas anteriormente são desprezadas nos projetos de engenharia, como citado anteriormente.
Quando tratamos de uma viga com seção irregular ou contorno não retangular, percebemos que a aplicação da fórmula de cisalhamento para determinar a tensão de cisalhamento média ao longo da reta AB será orientada, conforme Figura 4.14.
Admitindo um elemento do material retirado do ponto b da superfície, de modo que uma de suas faces encontra-se na superfície externa da viga, percebemos que a tensão de cisalhamento calculada na face frontal do elemento pode ser desdobrada nos componentes de \(\tau {{'}_{{}}}\) e \(\tau ''\).
Admitindo ainda que a componente \(\tau '\) deve ser igual a zero, dada sua componente longitudinal que atua na superfície do contorno livre de tensão, temos que essa também deve ser nula. Nessa condição, a tensão de cisalhamento que atua sobre o elemento de contorno deve ser tangente ao contorno, de modo que, ao longo da reta AB, deve ser orientada, pois a maior inclinação das tensões de cisalhamento é dada exatamente em A e B, na qual a tensão de cisalhamento máxima também é acordada nesses pontos, que podem ser obtidos por meio dos princípios da teoria da elasticidade. Assim, podemos aplicar a fórmula do cisalhamento para obter a tensão de cisalhamento atuante em cada linha descrita na Figura 4.14.
Aplicando a fórmula de cisalhamento para obter a tensão de cisalhamento que atua em cada linha das retas que interceptam as tangentes ao contorno da seção transversal em ângulos retos, percebemos que elas são verticais e constantes. Portanto, a fórmula de cisalhamento não oferece resultados precisos quando aplicada a elementos com seção transversal curta ou larga, ou a pontos em que a sessão muda subitamente. Desse modo, ela é viável de ser determinada por meio de métodos mais avançados baseados na teoria da elasticidade (HIBBELER, 2010; BOTELHO, 1998).
Considere uma viga cuja seção transversal é retangular e seu momento interno é 2,88 kN para a seção transversal de 60x120mm. Agora, determine o cálculo advindo dessa situação.
O momento de inércia dessa viga terá valor de 5,64x10^4 mm^4.
Incorreta. Visto que \(I=\frac{b{{h}^{3}}}{12}\), então I= (60.120)/12, logo I= 864x10^4 mm^4.
O momento de inércia dessa viga terá valor de 8,64x10^4mm^4.
Incorreta. Visto que \(I=\frac{b{{h}^{3}}}{12}\), então I= (60.120)/12, logo I= 864x10^4 mm^4.
A tensão máxima sobre a viga será de 12 N/mm^2.
Incorreta. Como vimos, \({{\sigma }_{m\acute{a}x}}=\frac{Mc}{I}\), então \({{\sigma }_{m\acute{a}x}}=\) (2,88x10^6. 60)/ 864x10^4, logo \({{\sigma }_{m\acute{a}x}}=\) 20 N/mm^2 ou 20 MPa, o que não condiz com a alternativa apresentada.
O momento de inércia dessa viga terá valor de 864x10^4 mm^4 e tensão máxima de 15 MPa.
Incorreta. Visto que \(I=\frac{b{{h}^{3}}}{12}\), então I= (60.120)/12, logo I= 864x10^4 mm^4 e \({{\sigma }_{m\acute{a}x}}=\frac{Mc}{I}\), então \({{\sigma }_{m\acute{a}x}}=\) (2,88x10^6. 60)/ 864x10^4, logo \({{\sigma }_{m\acute{a}x}}=\) 20 N/mm^2 ou 20 MPa.
A tensão máxima sobre a viga será de 20 MPa.
Correta. \({{\sigma }_{m\acute{a}x}}=\frac{Mc}{I}\), então \({{\sigma }_{m\acute{a}x}}=\) (2,88x10^6. 60)/ 864x10^4, logo \({{\sigma }_{m\acute{a}x}}=\) 20 N/mm^2 ou 20 MPa, como descrito na alternativa.
Nome do livro: Resistência dos materiais - uma abordagem sintética
Editora: Elsevier
Autor: Marceo Greco e Daniel Nelson Maciel
ISBN: 8535274588
O livro relaciona capacidade de resistência dos materiais usados em estruturas com as aplicações específicas para engenharias, além de ações usuais em problemas práticos de engenharia e cálculo para equilíbrio de corpos, esforços solicitantes, tensões, dentre outros, sendo bastante pertinente para complementação do conhecimento do estudante.
