A mecânica é um ramo da física presente na maior parte das engenharias. O objetivo central e fundamental de compreender um pouco mais sobre a mecânica na engenharia é poder desenvolver a capacidade de prever os efeitos de forças e movimentos, quando houver, ao desempenhar as funções criativas de um projeto.
Nesse contexto, esta disciplina aborda conceitos importantes do ramo da mecânica, em especial, sobre a estática. A estática é o estudo dos corpos em repouso ou movimento retilíneo e uniforme, e para que o corpo esteja em um desses estados, algumas condições devem ser satisfeitas, as quais vamos estudar nesta unidade.
No tópico I, serão abordados conceitos de grandezas física e unidades de medidas. No tópico II, vamos fazer uma breve revisão sobre vetores e o estudo sobre equilíbrio de um ponto material. Além da definição de ponto material, também buscamos explorar as condições de equilíbrio. No tópico III, será introduzido o conceito de corpos rígidos, as definições sobre forças interna e externa, o princípio da transmissibilidade e o teorema de Virignon, além dos conceitos de momento angular sobre um ponto P. No tópico IV, será tratado sobre o equilíbrio de corpos rígidos em duas e três dimensões.
Neste tópico, trataremos do sistema de unidades a ser utilizado na magnitude das grandezas físicas dos processos mecânicos. Diversos sistemas de unidades são utilizados para expressar dimensões, logo há a necessidade de se definir corretamente os processos numéricos de conversão de unidades.
Em virtude dos diversos sistemas de unidades que são utilizados em ambientes industriais, comerciais, laboratoriais, residenciais, dentre outros, utiliza-se o sistema definido internacionalmente pela Conferência Geral de Pesos e Medidas: o Sistema Internacional de Unidades, representado pela sigla SI. Nesse sistema, temos as seguintes unidades básicas:
a) comprimento em metro [m];
b) massa em quilograma [kg];
c) tempo em segundos [s];
d) temperatura em Kelvin [K];
e) corrente em Ampère [A];
f) quantidade de matéria em mole [mol];
g) intensidade luminosa em candela [cd].
As demais unidades podem ser obtidas por meio dessas unidades de medidas, e são classificadas como unidades derivadas, por exemplo, trabalho em Joule [J], potência em Watt [W] etc.
Na física, definimos como dimensão a quantidade física utilizada para qualificar uma propriedade que pode ser medida ou observada, por exemplo, comprimento, massa, tempo, temperatura, corrente, quantidade de matéria, intensidade luminosa etc. Já as unidades são definidas por nomes arbitrários, atribuídos às dimensões e acompanhados por valores numéricos, por exemplo, metro, quilograma, segundos, Kelvin, Ampère, mole, candela etc. No Quadro 1.1, estão apresentadas algumas grandezas físicas e as unidades derivadas no sistema internacional de unidades (SI).
Quadro 1.1 - Grandezas físicas e as unidades derivadas no sistema internacional de unidades (SI)
Fonte: Adaptado de Inmetro (BRASIL, on-line).
Em algumas situações, como aplicações industriais e comerciais, utilizam-se diferentes sistemas de unidades, conhecidas por Unidades de Engenharia. No Quadro 1.2, são apresentados exemplos de Unidades de Engenharia e sua correspondência com o SI.
Quadro 1.2 - Exemplos de Unidades de Engenharia e sua correspondência com o SI
Fonte: Adaptado de Inmetro (BRASIL, on-line).
Um sistema de unidades muito utilizado na área da mecânica é o CGS. Este se baseia em três dimensões e suas unidades básicas: dimensões em centímetro; massa em grama; tempo em segundo. Já no setor automobilístico, utiliza-se o Sistema Inglês de Unidades, com diferenças de unidades de acordo com cada país que o emprega, por exemplo, o pé inglês é maior que o pé americano. Logo, para melhor compreensão dessas unidades e uma eficiente comunicação, encontra-se, na Tabela 1.1, uma relação de coeficientes de conversão para diversas grandezas físicas.
Outro aspecto fundamental, utilizado na escrita de grandezas físicas com magnitudes muito grandes, é o uso de prefixos de unidades, os quais designam múltiplos e submúltiplos de uma determinada magnitude. Veja na tabela a seguir os prefixos, simbologias e fator multiplicador.
Tabela 1.1 - Prefixos, simbologias e fator multiplicador
Fonte: Adaptado de IPEM-SP (SÃO PAULO, on-line).
Compreender as grandezas físicas bem como as respectivas unidades de grandeza e saber relacioná-las com as unidades do SI (Sistema Internacional de Medidas) são de grande importância para o conteúdo que vem a seguir.
Qualquer número usado para descrever quantitativamente um fenômeno físico é uma grandeza física. Ao medir uma grandeza, sempre a comparamos com um padrão de referência. Tal padrão define uma unidade de grandeza, como, por exemplo, o metro, que é uma unidade de distância, e segundo, que é uma unidade de tempo. No mundo, as medidas de referência seguem o Sistema Internacional, ou SI (das iniciais do francês Systèm Internacional). Nesse contexto, assinale a alternativa correta.
A unidade de temperatura no Sistema Internacional é o ºC (graus Celsius).
Incorreta. No SI, a unidade de temperatura é o Kelvin, ou K.
Usando a definição de que 1 milha = 1,61 km, no SI, 5 milhas é igual a, aproximadamente, 8 km.
Incorreta. A unidade de comprimento no SI é o metros.
Para controlar o seu consumo de bebida alcoólica, você resolveu beber 0,04 m³ de vinho durante um ano. Supondo o ano tendo 365 dias, você não poderá beber mais que 110cm³/dia.
Correta. Basta fazer as mudanças de unidade de tal forma a chegar até cm³/dia.
Newtons por metro cúbico, ou seja, força sobre volume é unidade de pressão.
Incorreta. A unidade de pressão é força sobre área, ou seja, N/m².
O fluxo sanguíneo de um homem adulto é, em média, 2 litros por minuto, ou seja, uma ordem de 10³ litros por dia.
Incorreta. Alternativa sobre ordem de grandeza. 20 litros por minuto equivale a 1200 L por hora, 28000 L por dia, o mesmo que 2,8 . 10\(^4\) L.
Antes de adentrarmos nos conceitos físicos sobre estática, uma revisão bastante sólida sobre vetores é necessária. Faremos operações com vetores, analisando sentido e direção da força resultante etc.
Para dar início ao estudo sobre vetores e utilizando nossos conhecimentos básicos de física, vejamos um exemplo.
Pai e filho, sentados em uma lanchonete, falam sobre a física e o movimento dos corpos, quando o pai pergunta para o filho:
O filho, bastante atento às suas aulas de física, percebe que está faltando informação fornecida pelo seu pai, uma vez que não sabemos em que sentido e em que direção os carros estão se movimentando. É exatamente nesse ponto que encontramos uma das muitas aplicações sobre vetores.
Um vetor possui:
Também conhecidos como versores, os vetores unitários são caracterizados por apresentarem comprimento, ou módulo, igual a uma unidade. Esse vetor tem como principal objetivo indicar o sentido e a direção de uma grandeza vetorial. Por exemplo, ao associar ao eixo x um vetor unitário î, que representa a mesma orientação do eixo, assim como para o eixo y um vetor unitário j (“jota” chapéu), componentes de um vetor projetado em x e y, respectivamente, como na Figura 1.1.
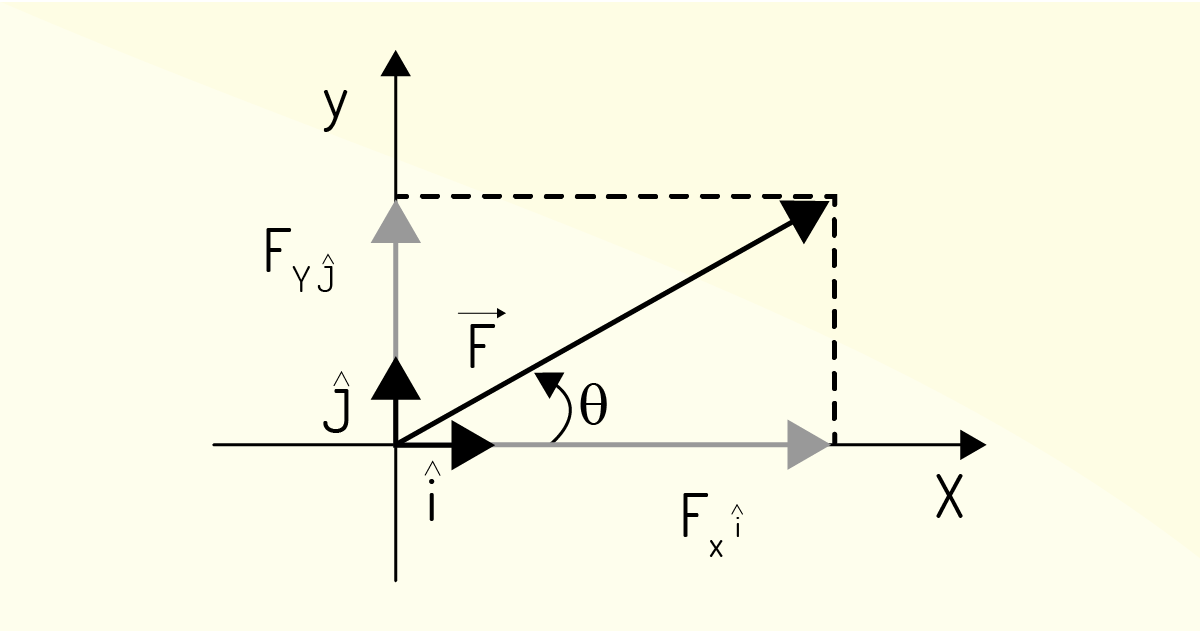
Agora, vamos associar os vetores unitários a suas respectivas componentes vetoriais, conforme descrito a seguir:
\[\overrightarrow{{{\text{F}}_{\text{x}}}}\,=\,{{\text{F}}_{{\hat{i}}}}\]
\[\overrightarrow{{{\text{F}}_{\text{y}}}}\,=\,{{\text{F}}_{{\hat{j}}}}\]
Muitas vezes, nos deparamos com vetores que não estão sobre os eixos, x e y, no caso R², vetores que estão no plano xy. Nesse caso, é necessário fazer uso de uma técnica bastante simples. Esse é o método das componentes vetoriais, que são encontradas a partir da decomposição de um vetor, ou seja, encontrando as projeções sobre os eixos x e y.
Para encontrar as componentes de um vetor F, primeiramente, é preciso utilizar um sistema de coordenadas (sistema cartesiano, por exemplo) e esboçar o vetor, como na Figura 1.2.
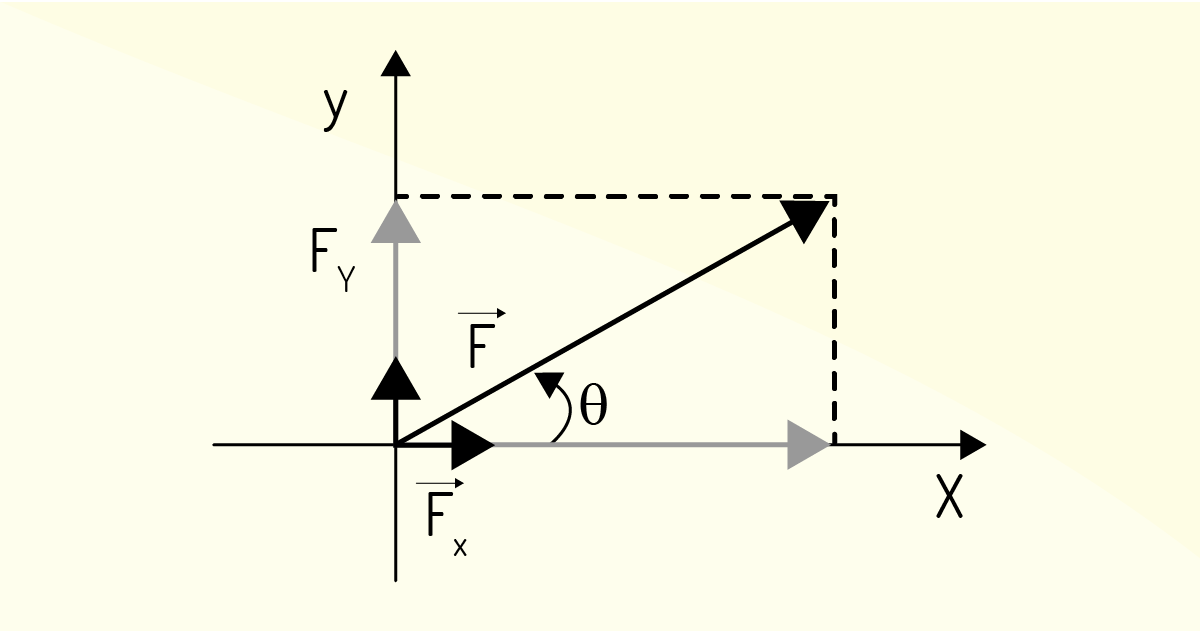
Os vetores \({{F}_{X}}\) e \({{F}_{Y}}\) são denominados de componentes do vetor F sobre os respectivos eixos ou projeção do vetor F sobre os eixos. A relação entre os vetores F e suas projeções pode ser expressa da seguinte forma:
\[\overrightarrow{\text{F}}\,\,\text{=}\,\,\overrightarrow{{{\text{F}}_{\text{x}}}}\,\text{+}\,\,\overrightarrow{{{\text{F}}_{\text{y}}}}\]
A direção de cada componente do vetor F é dada pela direção do eixo de coordenadas. Com isso, basta um número para descrever cada componente e os vetores i e j, vetores unitários indicando a direção e o sentido.
\[\overrightarrow{\text{F}}\,\,\text{=}\,\,{{\text{F}}_{\text{x}}}\,\hat{i}\,\text{+}\,\,{{\text{F}}_{\text{y}}}\,\hat{j}\]
Os números \({{F}_{X}}\) e \({{F}_{Y}}\) são as intensidades das projeções sobre os eixos x e y, ou seja, um número. Na representação anterior, eles não são vetores.
Agora, vamos dar um passo a mais, descrevendo as componentes em relação ao ângulo que o vetor resultante faz com a horizontal. Como mostrado na Figura 1.2, o eixo x é o eixo de referência, e o ângulo que o vetor F faz com o sentido positivo do eixo de referência é θ. Usando conceitos de trigonometria, supondo uma rotação no sentido do eixo x para o eixo y para o ângulo θ, encontramos as equações a seguir:
\[\frac{{{F}_{x}}}{F}=cos~\theta \]
\[\frac{{{F}_{y}}}{F}=sen~\theta \]
Agora, ao escrevermos as componentes \({{F}_{X}}\) e \({{F}_{Y}}\) em função do vetor F e do ângulo θ, encontramos:
\[{{F}_{x}}=Fcos~\theta \]
\[{{F}_{y}}=Fsen~\theta \]
Fique ligado(a)! As equações encontradas anteriormente são válidas quando levamos em conta o ângulo mencionado. Se o ângulo do vetor resultante for medido considerando o eixo de referência e outro sentido de rotação, as relações podem ser diferentes.
Veja um exemplo para fixação: Um carro se desloca por 5 km na direção nordeste. A reta que liga a origem até o ponto de destino faz um ângulo de 30º com a horizontal. Dessa forma, determine qual foi o deslocamento relativo entre o eixo x e y.
Solução: basta calcular as componentes x e y do vetor deslocamento. O ângulo formado entre o vetor D e sentido positivo do eixo x é 30º, com isso, montamos as equações a seguir:
\[{{D}_{x}}=D~cos~\theta ~\]
\[{{D}_{y}}=D~sen~\theta \]
Substituindo os valores na expressão, obtemos:
\[{{D}_{x}}=5~cos~30{}^\text{o}\]
\[{{D}_{y}}=5~sen~30{}^\text{o}\]
Logo, \({{D}_{X}}=~4,3Km\) e \({{D}_{X}}=~2,5~Km\)
Agora, nos deparamos com uma situação inversa, escrever um vetor F desconhecido a partir das componentes sobre os eixos x e y. Para isso, basta usar a regra do paralelogramo, na qual a diagonal é o vetor resultante. Projetando a componente \({{F}_{Y}}\), nos deparamos com um triângulo retângulo onde os catetos são as componentes x e y, e a hipotenusa é o próprio vetor F. A imagem pode ser vista na Figura 1.3.
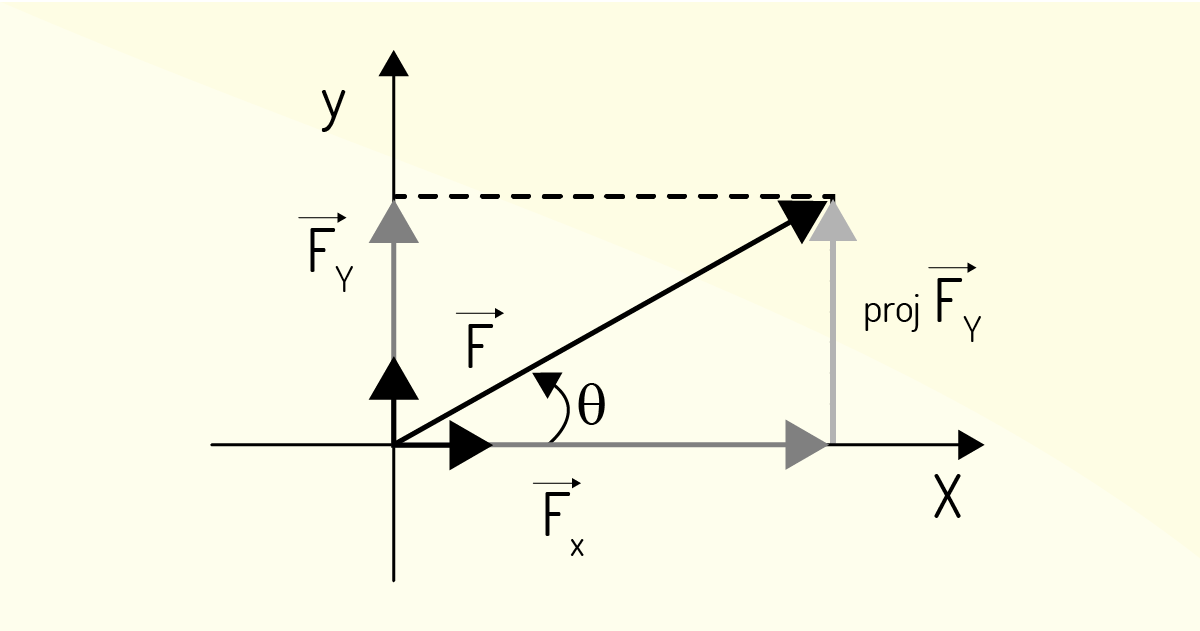
Aplicando o teorema de Pitágoras, obtemos o módulo do vetor F da seguinte forma:
\[F=\sqrt{F_{x}^{2}+F{{_{y}^{2}}_{{}}}}\]
Como estamos procurando apenas o módulo, a intensidade do vetor F, devemos considerar apenas o sinal positivo da raiz, pois um comprimento negativo não faz sentido fisicamente.
Depois de obter o módulo de F, vamos encontrar as outras informações que estão faltando do vetor, a direção e o sentido. A direção e o sentido podem ser facilmente encontradas utilizando a definição da tangente do ângulo, como na equação a seguir.
\[tan~\theta =\frac{{{F}_{y}}}{{{F}_{x}}}\]
Para o ângulo θ, basta encontrar o arco tangente da razão \({{F}_{Y}}\) / \({{F}_{X}}\). Agora, temos todas as informações sobre o vetor, seu tamanho e para onde a seta aponta, ou seja, o ângulo em relação ao eixo x (eixo de referência).
Como o próprio nome sugere, estática é uma área da física que se preocupa em estudar as propriedades associadas ao equilíbrio de corpos. O estudo de equilíbrio dos corpos é de grande relevância para as engenharias, haja vista que as estruturas construídas devam ser seguras. Tomando a engenharia civil como exemplo, um engenheiro projetista deve identificar todas as forças e torques externos que possam atuar sobre a estrutura. A partir daí, fazer uma boa e adequada escolha dos materiais, a fim de garantir que a estrutura resista às cargas nela aplicadas. Tais análises são necessárias para garantir que um edifício não irá desabar, que uma ponte não cairá sob a ação de fortes ventos e do intenso tráfego de veículos, que um trem de pouso de uma aeronave suporte os choques de uma aterrissagem mal executada etc.
Alguns objetos apresentam dimensões que podem ser desprezadas em relação às intensidades das forças que atuam sobre eles. Nesse caso, o objeto é denominado de ponto material (ou partícula). Ao recorrer a segunda lei de Newton, escrita como segue,
\[\mathop{\sum }_{{}}^{{}}F~=~m.a\]
Um ponto material estará em equilíbrio, ou seja, a aceleração resultante sob uma partícula é zero, em um sistema de referencial, quando a soma vetorial de todas as forças que atuam sobre a partícula é igual a zero, como pode ser visto na equação:
\[\mathop{\sum }_{{}}^{{}}F~=~0\]
A equação é suficiente para garantir o equilíbrio de um ponto material. Logo, como o conjunto de forças satisfaz a condição anterior, a expressão m.a = 0 é verificada e, portanto, a aceleração do ponto material precisa ser igual a zero. Resumindo, o equilíbrio de um ponto material é observado nos casos em que ele encontra-se em repouso ou movendo-se com velocidade constante (MRU). Um passo importante para ter êxito nos cálculos é realizar uma boa ilustração das forças aplicadas sobre o corpo ou um diagrama de corpo livre.
Entender o que é um diagrama de corpo livre é bastante simples. Tomando um ponto material como a representação de um corpo, já discutido anteriormente, devemos considerar todas as forças que estão agindo sobre esse corpo. O diagrama é apenas um esboço que ilustra o ponto material livre de seu entorno com todas as forças que atuam sobre ele e, para construir o diagrama de corpo livre, basta seguir alguns passos: i) desenhar o contorno do ponto material a ser estudado, imaginando-o isolado; ii) indicar nesse esboço todas as forças que atuam sobre o ponto material; iii) as forças já conhecidas devem ser indicadas com suas intensidades (quando houver), sentido e direção. Veja um exemplo indicado na Figura 1.4.
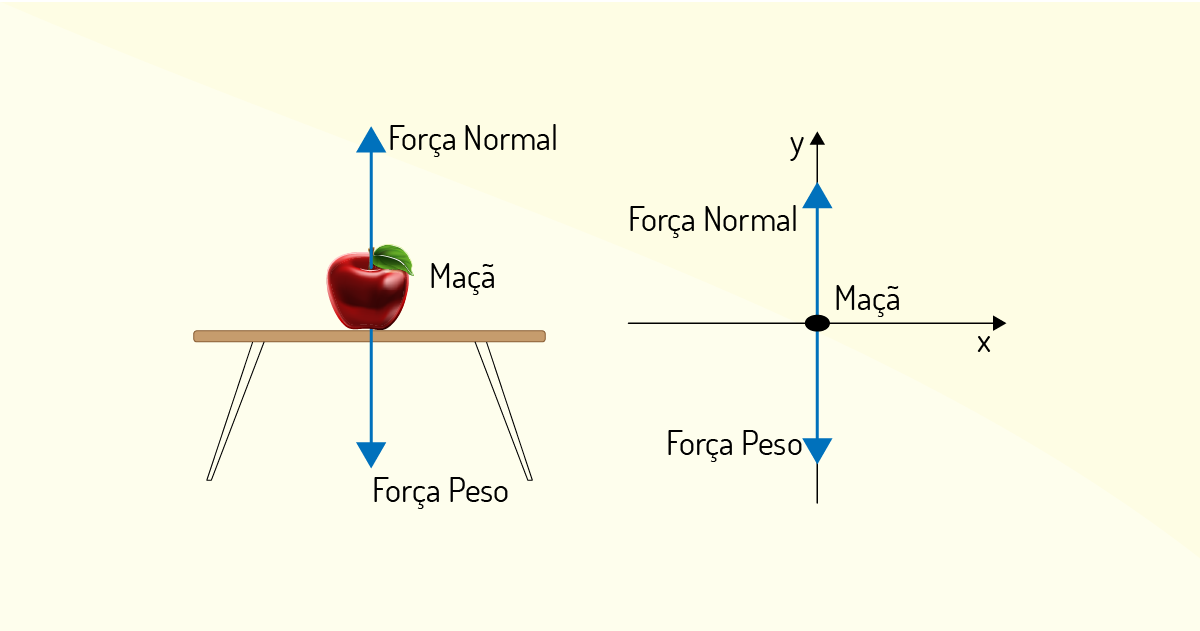
Após uma revisão sobre vetores e a sintetização de conceitos sobre as condições de equilíbrio de um ponto material e o uso do diagrama de corpos livres, podemos aplicar tudo isso em um mesmo contexto.
Veja um exemplo para fixação. Na Figura 1.5, o motor de um carro, de massa igual a 380 kg, é pendurado e encontra-se em equilíbrio. Determine as trações nas cordas AB e AD.

O primeiro passo para resolver um problema como esse é ilustrar o diagrama de forças livres:
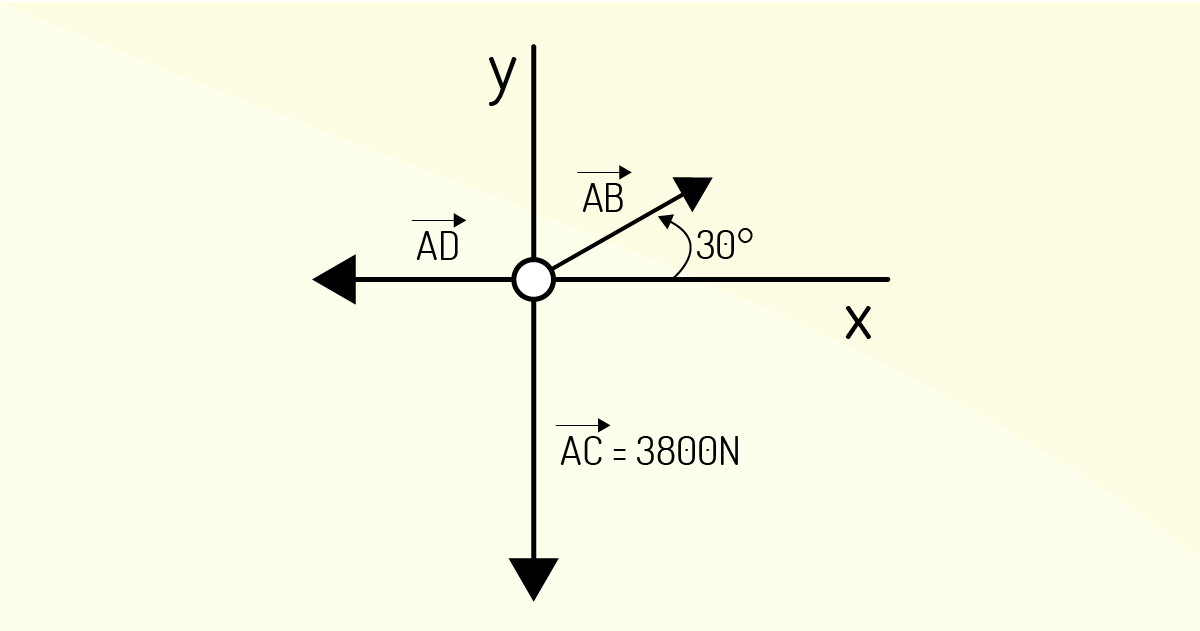
As duas incógnitas AB e AD são encontradas aplicando a condição de equilíbrio para um ponto material:
\[\mathop{\sum }_{{}}^{{}}{{F}_{X}}=~0~e~\mathop{\sum }_{{}}^{{}}{{F}_{Y}}=~0\]
Da somatória das forças para o eixo x, obtemos:
\[\mathop{\sum }_{{}}^{{}}{{F}_{X}}=~0~\Rightarrow {{T}_{AD}}~-~~{{T}_{AB~}}\left( componente~x \right)~=~0\]
\[{{T}_{AD}}~-~~{{T}_{AB}}cos~30{}^\text{o}~=~0\]
\[{{T}_{AD}}~=~0,86~{{T}_{AB}}\]
Agora, para a somatória das forças sobre o eixo y, teremos:
\[\mathop{\sum }_{{}}^{{}}{{F}_{y}}=~0~\Rightarrow {{T}_{AC}}~-~~{{T}_{AB~}}\left( componente~y \right)~=~0\]
\[{{T}_{AC}}~-~~{{T}_{AB}}sen~30{}^\text{o}~=~0\]
Substituindo o valor de \({{T}_{AC}}\), obtemos:
\[3800~=~0,5{{T}_{AB}}\]
Logo, \({{T}_{AB}}~=~7200 N\).
Substituindo \({{T}_{AB}}\) para encontrar o valor de \({{T}_{AD}}\):
\[{{T}_{AD}}~=~0,86~\left( 7200 \right)\]
\[{{T}_{AD}}~=~6235,4~N\]
Fundamentado no princípio da inércia (1ª Lei de Newton), podemos concluir que uma partícula em equilíbrio pode se encontrar em duas situações: em repouso (equilíbrio estático) ou em movimento retilíneo e uniforme (equilíbrio dinâmico).
Vejamos outro exemplo.
Ana, Bianca, Camila e Daniela estão brincando de cabo de guerra com um pneu, como ilustrado na Figura 1.7. Sabe-se que a força de Ana \(({{F}_{A}}_{{}})\) é de 120 N e de Camila (\({{F}_{C}}\)) é de 40 N. (Dados sen θ = 0,60 e cos θ = 0,80). Se o sistema está em equilíbrio, qual o valor das forças da Bianca e da Daniela, respectivamente.
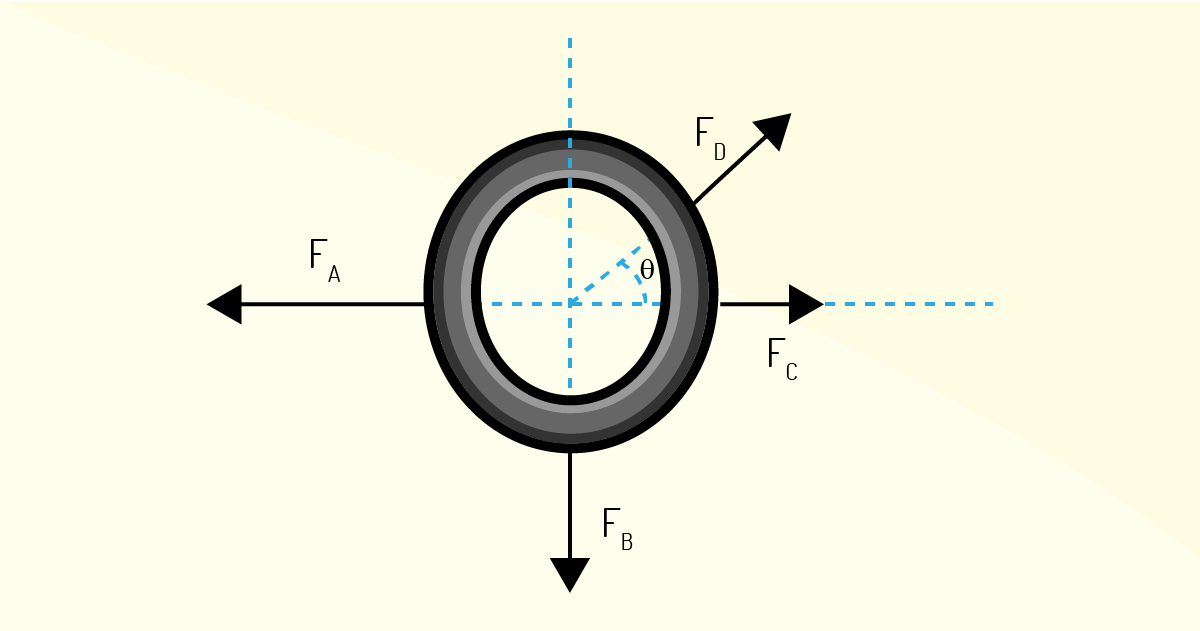
O modo de resolver esse exercício é bastante similar ao anterior, basta aplicar as condições de equilíbrio estático de um ponto material, assim, temos:
\[\mathop{\sum }_{{}}^{{}}{{F}_{X}}=~0~e ~\mathop{\sum }_{{}}^{{}}{{F}_{Y}}=~0\]
Em seguida, decompor a força de Daniela sobre os eixos x e y, ficando da seguinte forma as componentes dessa força em x e y:
\[{{F}_{X}}~=~{{F}_{D}}cos\theta \]
\[{{F}_{X}}~=~{{F}_{D}}cos\theta \]
Agora, podemos escrever as equações de equilíbrio para os eixos x e y. Para o eixo x,
\[{{F}_{A}}={{F}_{C}}~+~{{F}_{D}}cos\theta \]
e para o eixo y,
\[{{F}_{B}}=~{{F}_{D}}sen\theta ~\]
Da primeira, encontramos o valor de \({{F}_{D}}~\) e, substituindo na segunda, entramos com o valor de \({{F}_{B}}\). Assim, a força da Bianca é de 60 e a da Daniela é de 100N.
Quando falamos de força, logo imaginamos a situação de empurrar ou puxar um objeto. Conceitualmente, a força nos fornece o grau de interação entre dois corpos ou entre o corpo e o meio, ou seja, uma descrição quantitativa da interação.
Existem duas classificações para forças: forças de contato e forças de campo. As forças de contato são aquelas que envolvem o contato direto entre os corpos, por exemplo, quando você precisa empurrar um carro que ficou atolado na lama. Para empurrar o carro, você precisa exercer uma força sobre ele. Um cabo de aço sustenta um elevador para que este não caia.
Já as forças de campo, também conhecidas como forças de longo alcance, são aquelas que não envolvem contato direto entre os corpos, sendo assim, atuam mesmo quando os corpos estão afastados. A força da gravidade é um exemplo de força de longo alcance, haja vista que, para manter a Terra em órbita, o sol exerce uma força de atração sobre a Terra, chamada de força gravitacional. Você já deve ter se deparado com outra força de campo bastante conhecida e nem se deu conta dela. Ao brincar com dois ímãs, você está diante de uma força de longo alcance, por exemplo.
Discutimos brevemente sobre como podemos classificar as forças quanto à interação entre os corpos, porém não dizemos nada sobre como as forças podem afetar o movimento. A força é a causa e o movimento, a consequência. Se um corpo está em repouso, ele tende a permanecer em repouso, a menos que uma força externa aja sobre ele.
Se um corpo está em movimento retilíneo e uniforme (MRU), ele tende a permanecer, a menos que uma força externa aja sobre ele.

Isaac Newton (1647 - 1727) é considerado o pai da física clássica devido às suas enormes contribuições em diversas áreas da física, em particular na mecânica. As leis de Newton são partes fundamentais da dinâmica, haja vista que toda a dinâmica “gira” em torno das leis propostas por Newton.
Ao dirigir, use o cinto de segurança. O cinto de segurança é um dos meios mais eficaz de reduzir possíveis riscos de ferimentos graves e até a morte. Como já estudamos, a primeira lei de Newton propõe que corpos tendem a permanecer em movimento (uniforme) a menos que uma força externa aja sobre ele. Nos casos de acidentes com vítima sem cinto de segurança, a força externa que age sobre essa vítima será a força de colisão contra o volante ou para-brisa.

Um corpo de 500N encontra-se suspenso, como mostra a figura a seguir. Os fios que mantêm o corpo suspenso e em equilíbrio estático são ideais e têm pesos desprezíveis. A tração na corda AB, em N, é de:
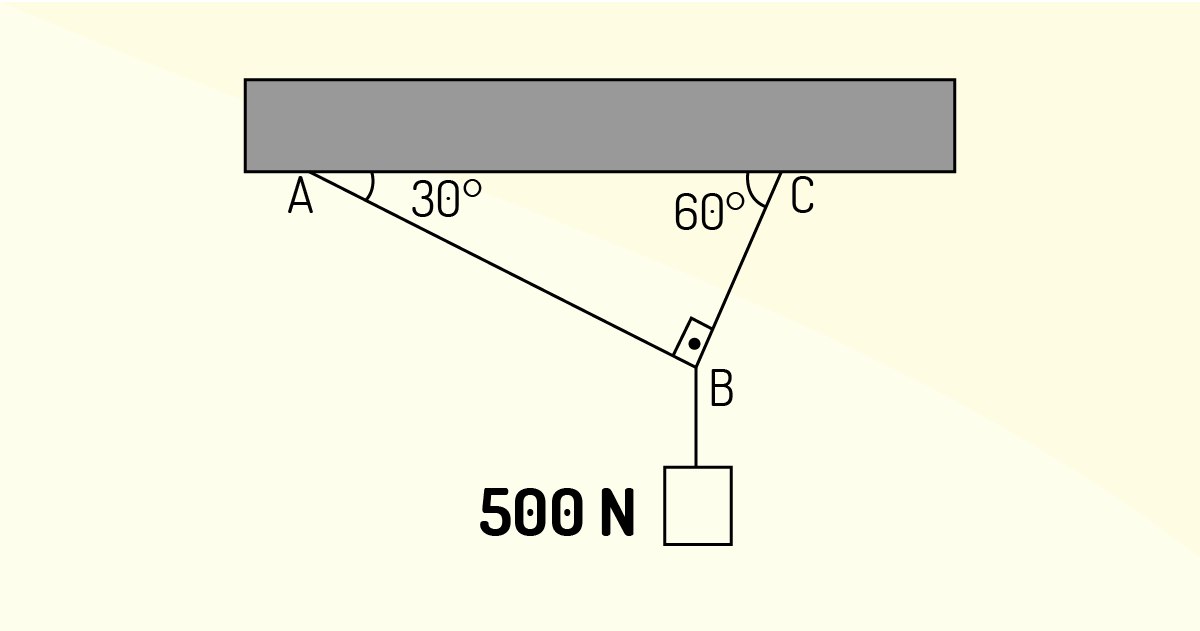
Fonte: Elaborada pelo autor.
250 N.
Correta. Nesse exercício, é preciso decompor os vetores \({{T}_{AB}}\) e \({{T}_{BC}}\) em suas componentes x e y. Feito isso, basta aplicar as condições de equilíbrio para um ponto material. Você vai obter duas equações e terá duas incógnitas. Sistema determinado.
300 N.
Incorreta. Nesse exercício, é preciso decompor os vetores \({{T}_{AB}}\) e \({{T}_{BC}}\) em suas componentes x e y. Feito isso, basta aplicar as condições de equilíbrio para um ponto material. Você vai obter duas equações e terá duas incógnitas. Sistema determinado.
325 N.
Incorreta. Nesse exercício, é preciso decompor os vetores \({{T}_{AB}}\) e \({{T}_{BC}}\) em suas componentes x e y. Feito isso, basta aplicar as condições de equilíbrio para um ponto material. Você vai obter duas equações e terá duas incógnitas. Sistema determinado.
350 N.
Incorreta. Nesse exercício, é preciso decompor os vetores \({{T}_{AB}}\) e \({{T}_{BC}}\) em suas componentes x e y. Feito isso, basta aplicar as condições de equilíbrio para um ponto material. Você vai obter duas equações e terá duas incógnitas. Sistema determinado.
375 N.
Incorreta. Nesse exercício, é preciso decompor os vetores \({{T}_{AB}}\) e \({{T}_{BC}}\) em suas componentes x e y. Feito isso, basta aplicar as condições de equilíbrio para um ponto material. Você vai obter duas equações e terá duas incógnitas. Sistema determinado.
Corpo rígido pode ser entendido como sendo resultado da combinação de um grande número de partículas com distâncias invariantes, mesmo submetida à ação de forças externas. Entenda o corpo rígido como um modelo ideal no estudo da mecânica.
Força pode ser entendida como a interação entre dois corpos. As forças que atuam em um corpo rígido podem ser classificadas como sendo forças externas e internas, diferenciadas pelo local da sua ação. Enquanto as forças internas são aquelas que mantêm a forma dos corpos rígidos, ou seja, as forças que mantêm unidas as várias partes de uma estrutura; as forças externas representam a ação de outros corpos sobre o corpo rígido.
A ação de uma força não se altera mesmo quando essa for aplicada em diferentes pontos ao longo da linha de ação do corpo rígido, facilmente compreendida pela Figura 1.9.
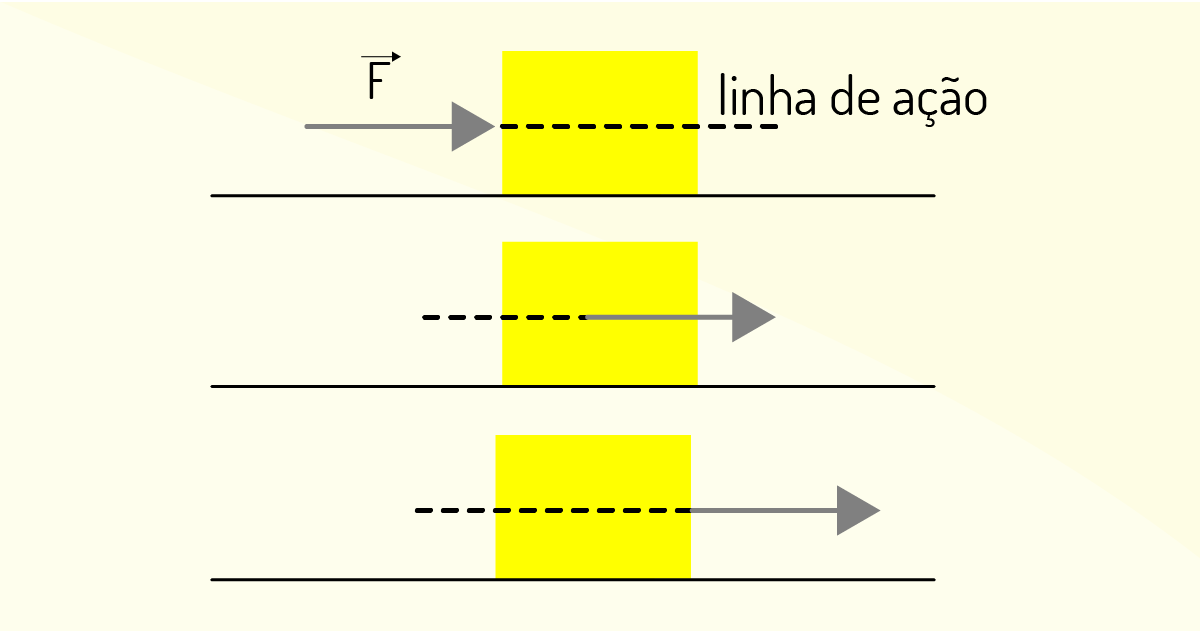
Dessa forma, o princípio da transmissibilidade pode ser assim enunciado: uma força de intensidade F aplicada em um ponto P pode ser substituída por uma nova força F’, de mesma intensidade, mesma direção e mesmo sentido aplicada em um novo ponto P’. Se os pontos P e P’ estiverem na mesma linha de ação, ambas as forças são equivalentes para as condições de movimento e equilíbrio do corpo.
Ao realizar ações, como a troca de um pneu, brincar de gangorra ou até abrir a maçaneta de uma porta, as extremidades da abertura ficam em posição oposta, ou seja, há o ponto de giro da porta.
Tudo isso tem a ver com a capacidade que os corpos possuem em girar em torno de um ponto. Para entender um pouco mais sobre isso, vamos estudar o momento de uma força em relação a um ponto de equilíbrio.
O momento de uma força pode ser entendido como a tendência que um determinado corpo adquire em girar em torno de um ponto que não esteja na mesma linha de atuação da força, como pode ser visto na Figura 1.10.
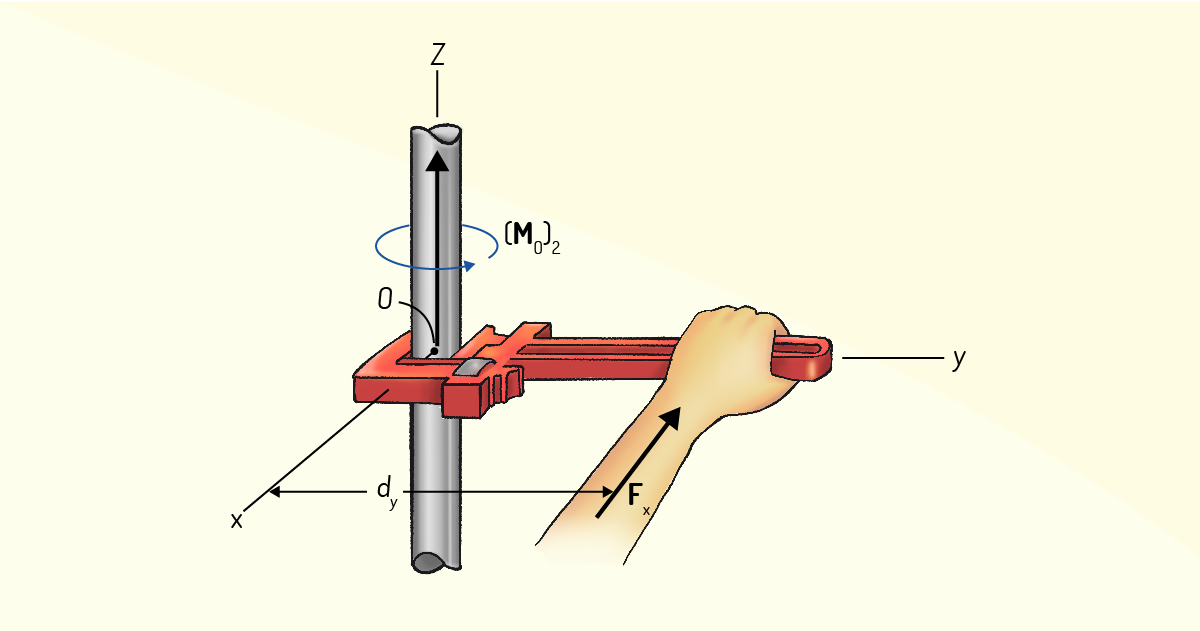
Essa tendência em girar recebe, usualmente, dois nomes: torque ou momento de uma força, ou simplesmente momento. Matematicamente, a expressão para o momento é dada pelo produto vetorial entre a força F e a distância d que essa faz com um ponto P. Veja a expressão a seguir:
\[\text{M = F x d}\]
Pela definição de produto vetorial, M é um vetor e o seu módulo pode ser encontrado da seguinte forma:
\[\text{M} = F~d~senθ\]
Logo, o momento será máximo para \(θ = 90º\), pois \(sen90º = 1\), ou seja, o maior valor para o momento angular se dá quando a força aplicada for perpendicular ao eixo da distância até o ponto P sobre a qual tende a girar. O momento angular é zero nos casos em que a força aplicada é paralela ao eixo que liga ao ponto P, fazendo um ângulo de \(θ = 0º\), com isso, o \(sen0º = 0\).
Como o momento angular é entendido como a tendência em girar em torno de um ponto, nos casos bidimensionais, podemos adotar uma regra de sinal para o giro. Isso é apenas uma convenção.
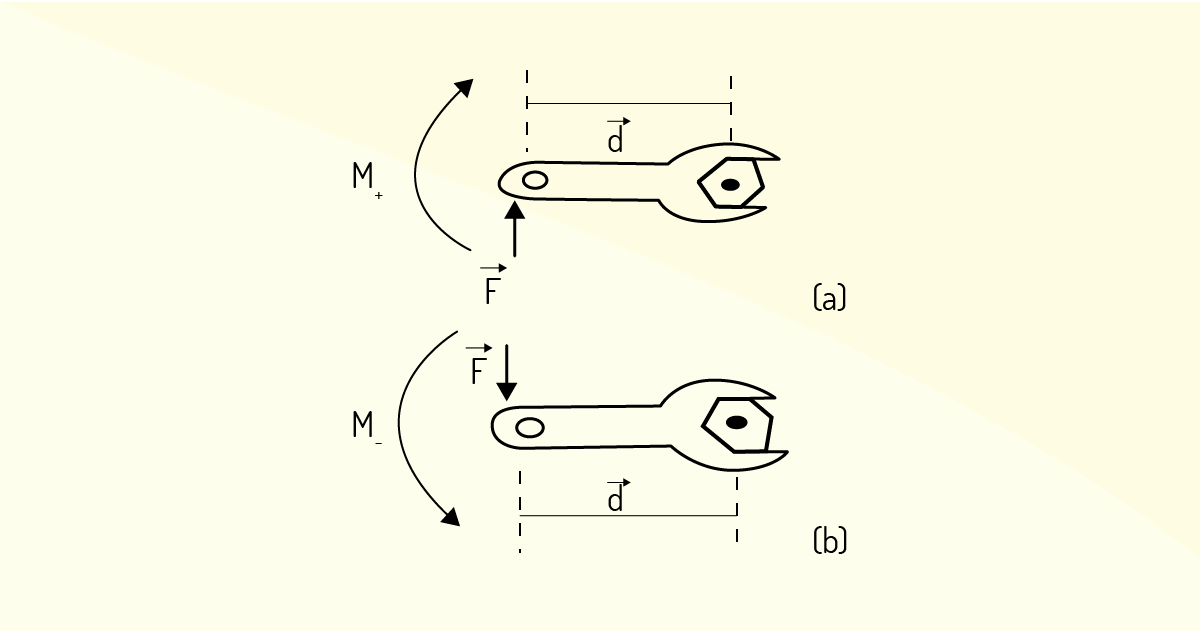
Veja mais um exemplo para nos ajudar na compreensão e fixação:
Um bombeiro hidráulico, incapaz de afrouxar a conexão de um tubo, encaixa um pedaço de sucata (uma alavanca) sobre a haste da chave de grifa. A seguir ele usa seu peso de 900 N para ficar em pé na extremidade da alavanca. A distância entre o centro da conexão e o ponto onde o peso atua é igual a 0.80 m, e o eixo da alavanca faz um ângulo de 19° com a horizontal (YOUNG; FREEDMAN, 2006, p. 290).
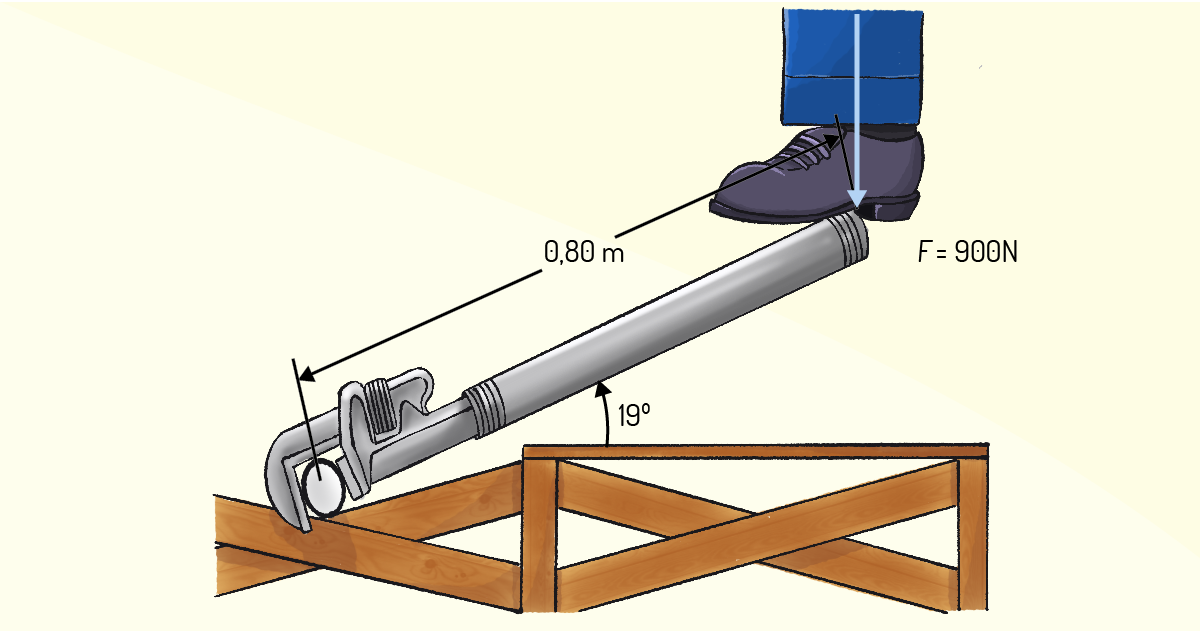
O primeiro passo é fazer o diagrama de forças, como indicado na Figura 1.13.
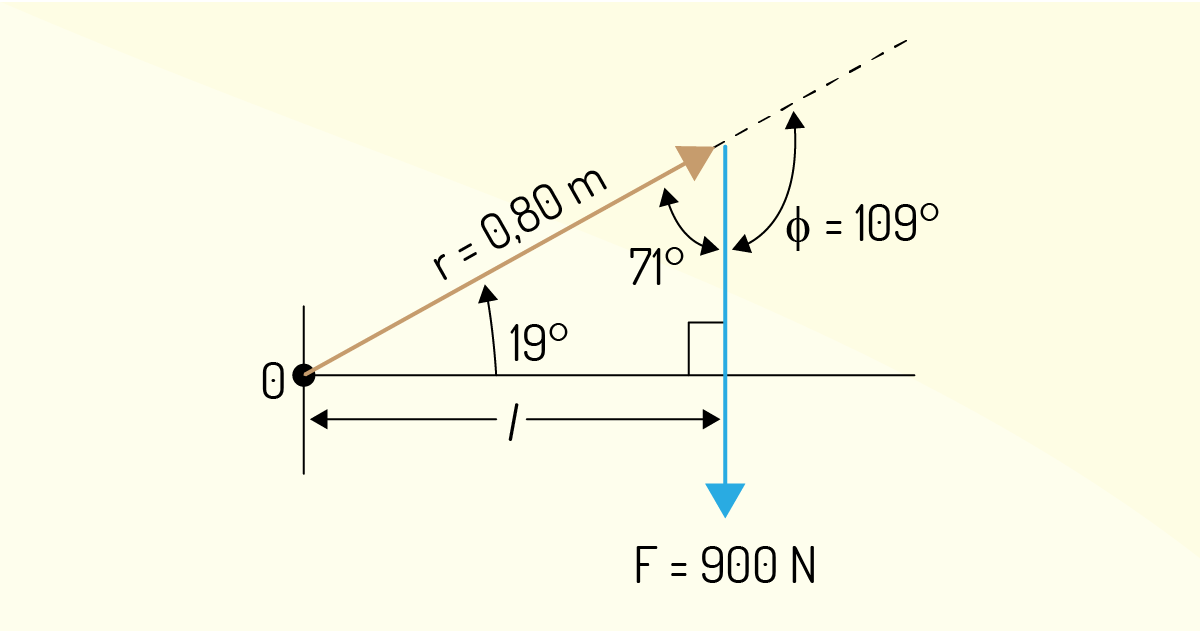
Tome muito cuidado com as análises angulares agora!
É preciso identificar o ângulo formado entre a força F e o vetor distância d. Usando as propriedades trigonométricas do triângulo retângulo, o ângulo formado entre F e d é 109º ou 71º, haja vista que o seno é uma função ímpar, com isso, a expressão fica da seguinte forma:
\[\text{M} = F~d~senθ\]
\[\text{M} = 900.(0,8) sen 109º = 900.(0,8)sen 71º\]
\[\text{M} = 680 N.m\]
Como o momento é positivo, o sentido do giro é horário.
Veja outro exemplo.
Uma força horizontal de 250 N é aplicada na extremidade de uma alavanca fixa em um ponto O, como segue a Figura 1.14. Qual o momento da força no ponto O.
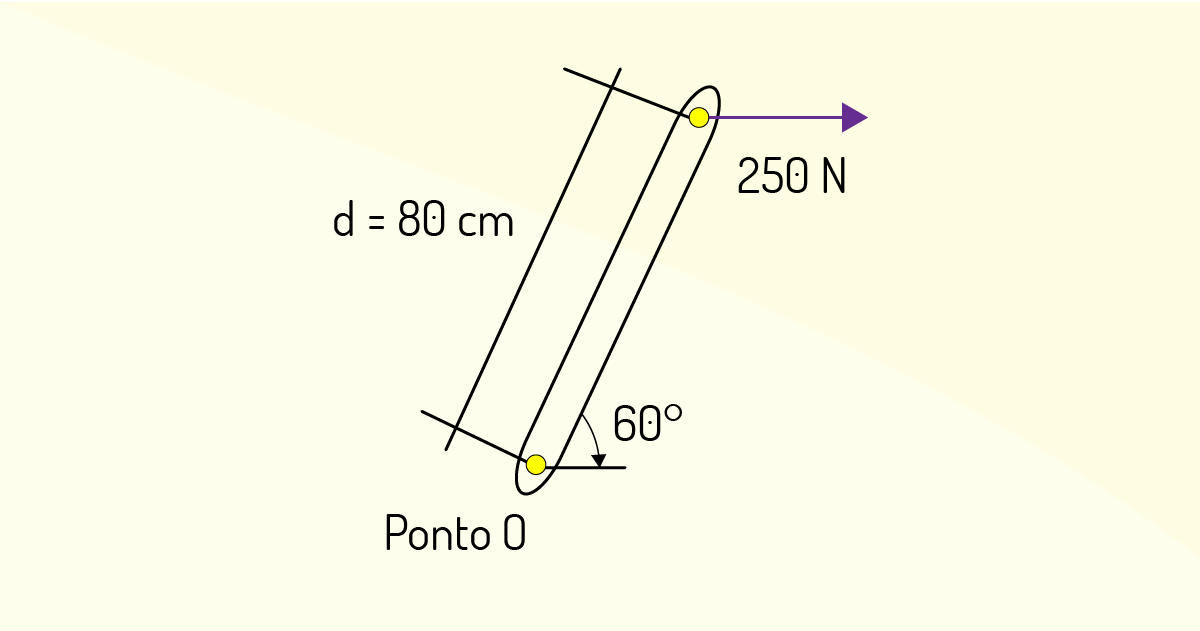
A força F gera um momento no sentido horário e seguindo a fórmula já conhecida, a expressão do momento é:
\[\text{M} = F~d~senθ\]
\[\text{M} = 250.~0,8~sen60\]
\[\text{M} = 173,2 N.m\]
A ação de duas ou mais forças concorrentes sobre um ponto P gera um momento resultante e esse pode ser calculado somando vetorialmente os momentos individuais gerados por cada força, isoladamente. A esse teorema, damos o nome de teorema de Varignon. Em outras palavras, podemos dizer que em um sistema de duas ou mais forças, a força resultante deve gerar um momento de mesma intensidade que a somatória de todos os momentos gerados por todas as forças.
\[{{M}_{R}}~=~{{F}_{R}}.d~=~\mathop{\sum }_{n}^{{}}{{F}_{n}}~x {{d}_{{{n}_{{}}}}}\]
Como o momento angular é uma grandeza vetorial, o momento resultante pode ser expressado pela soma dos momentos nas direções x e y, para o caso bidimensional. A mesma análise pode ser estendida para o caso em que temos momento nas três direções, x, y e z.
\[\overrightarrow{\text{M}}_{R}\,\,\text{=}\,\,{{\text{M}}_{\text{x}}}\,\hat{i}\,\text{+}\,\,{{\text{M}}_{\text{y}}}\,\hat{j}\]
Duas forças de intensidade 500 N e 800 N atuam sobre um ponto A localizado sobre um suporte de metal, conforme ilustra a Figura 1.15. Determine o momento resultante em relação ao ponto P.

Solução: Usaremos a ideia proposta no teorema de Varignon, o qual nos diz que o momento resultante é igual à soma dos momentos independentes.
Analisando a figura, a força \({{F}_{2}}\) realiza momento girando em torno do eixo x e, pelo princípio da transmissibilidade, o ponto de ação da força dista 0,6 m do ponto P. A força \({{F}_{1}}\), por sua vez, realiza um momento girando ao redor do eixo y, da mesma forma, o ponto de ação da força dista 1,2 metros do ponto P. Com isso, podemos montar a equação do momento da seguinte forma:
\[{{M}_{R}}~=~{{F}_{R}}.d~=~\mathop{\sum }_{n}^{{}}{{F}_{n}}~x {{d}_{{{n}_{{}}}}}\]
O módulo do momento angular pode ser escrito:
\[{{M}_{R}}={{F}_{1}}.~{{d}_{1}}-{{F}_{2}}.~{{d}_{2}}\]
O sinal negativo do momento gerado pela força \({{F}_{2}}\) é devido ao sentido da rotação, uma vez que a força \({{F}_{1}}\) gera um momento no sentido horário, e a força \({{F}_{2}}\) gera um momento no sentido anti-horário. Agora, vamos substituir os valores. Assim:
\[{{M}_{R}}~=~500.\left( 1,2 \right)~-~800.\left( 0,6 \right)~~\]
\[{{M}_{R}}~=~600-~480~\]
\[{{M}_{R}}~=~120$N.m\]
O resultado nos mostra que haverá uma tendência em girar no sentido horário com a intensidade de 120 N.m.
Para soltar o pneu furado do seu caminhão, Pedro utiliza uma chave de rodas no formado de uma cruz, como ilustrado na figura a seguir.

Fonte: Serezniy / 123RF.
Sabendo que a distância de duas extremidades opostas é de 60 cm, qual é a força aplicada sobre as duas extremidades para soltar um parafuso apertado com um torque de 60 N.m?
50 N.
Incorreta. Utilizando conceitos do princípio da transmissibilidade, esboçando o diagrama de forças e aplicando o somatório dos momentos sobre o ponto central, obtemos que a força necessária seja de 100 N.m.
100 N.
Correta. Utilizando conceitos do princípio da transmissibilidade, esboçando o diagrama de forças e aplicando o somatório dos momentos sobre o ponto central, obtemos que a força necessária seja de 100 N.m.
150 N.
Incorreta. Utilizando conceitos do princípio da transmissibilidade, esboçando o diagrama de forças e aplicando o somatório dos momentos sobre o ponto central, obtemos que a força necessária seja de 100 N.m.
200 N.
Incorreta. Utilizando conceitos do princípio da transmissibilidade, esboçando o diagrama de forças e aplicando o somatório dos momentos sobre o ponto central, obtemos que a força necessária seja de 100 N.m.
250 N.
Incorreta. Utilizando conceitos do princípio da transmissibilidade, esboçando o diagrama de forças e aplicando o somatório dos momentos sobre o ponto central, obtemos que a força necessária seja de 100 N.m.
Um ponto material está em equilíbrio quando a somatória de todas as forças que atuam sobre ele for nula. Normalmente, esse enunciado é conhecido como a primeira condição de equilíbrio. Todavia, para situações em que envolvam corpos rígidos, essa condição não é o suficiente. Agora, quando forças atuam em pontos diferentes em um corpo que tenha uma distribuição de massa ao longo de seu comprimento, uma outra condição também precisa ser satisfeita para que esse esteja em equilíbrio: a soma dos torques em relação a qualquer ponto deve ser igual a zero. Garantir que o corpo não possa girar.
Um corpo rígido que, dentro de um sistema inercial, não gira em torno de um ponto específico e pré-estabelecido possui momento angular igual a zero em torno desse ponto. Resumindo, um corpo rígido que se encontra em equilíbrio não pode girar em torno de nenhum ponto, de tal forma que a soma dos torques deve ser igual a zero em relação a qualquer um dos pontos. Esta é conhecida como a segunda condição de equilíbrio. Matematicamente, a segunda condição de equilíbrio pode ser expressa da seguinte forma:
\[\mathop{\sum }_{{}}^{{}}\tau ~=~0 ~ou~ \mathop{\sum }_{{}}^{{}}M~=~0\]
Atenção! Ao escolher um ponto de referência de forma arbitrária, esse deve ser mantido para calcular todos os torques sobre o corpo.
Uma estrutura submetida a um conjunto de forças estará em equilíbrio estático quando não houver movimento translacional e rotacional. No plano, um sistema bidimensional, uma estrutura estará em equilíbrio estático quando as equações a seguir são satisfeitas.
\[\mathop{\sum }_{{}}^{{}}{{F}_{x}}=~0\]
\[\mathop{\sum }_{{}}^{{}}{{F}_{y}}=~0\]
\[\mathop{\sum }_{{}}^{{}}M=~0\]
Com isso, podemos afirmar que, em um sistema bidimensional, há apenas três graus de liberdade. No espaço, um sistema tridimensional, uma estrutura espacial estará em equilíbrio estático quando as equações a seguir são satisfeitas.
\[\mathop{\sum }_{{}}^{{}}{{F}_{x}}=~0\]
\[\mathop{\sum }_{{}}^{{}}{{F}_{y}}=~0\]
\[\mathop{\sum }_{{}}^{{}}{{F}_{Z}}=~0\]
\[\mathop{\sum }_{{}}^{{}}{{M}_{x}}=~0\]
\[\mathop{\sum }_{{}}^{{}}{{M}_{Y}}=~0\]
\[\mathop{\sum }_{{}}^{{}}{{M}_{Z}}=~0\]
A fim de eliminar todo e qualquer movimento, além das possíveis rotações, algumas restrições precisam ser feitas. Essas restrições são dadas por meio de esforços reativos de dispositivos mecânicos que recebem o nome de apoio ou vínculos.
As reações de apoio são responsáveis pelo vínculo da estrutura, seja qual for, de tal modo que assegura a sua não mobilidade e não rotação, garantindo, assim, o equilíbrio da estrutura. Sendo assim, a função básica das reações de apoio é de restringir os graus de liberdade de uma estrutura ao gerar reações opostas ao sentido do movimento ou rotação.
As reações de apoio, ou vínculos, são classificadas de acordo com o número de movimentos impedidos. Nos casos de estruturas planas, estruturas bidimensionais, os vínculos podem ser de três tipos.
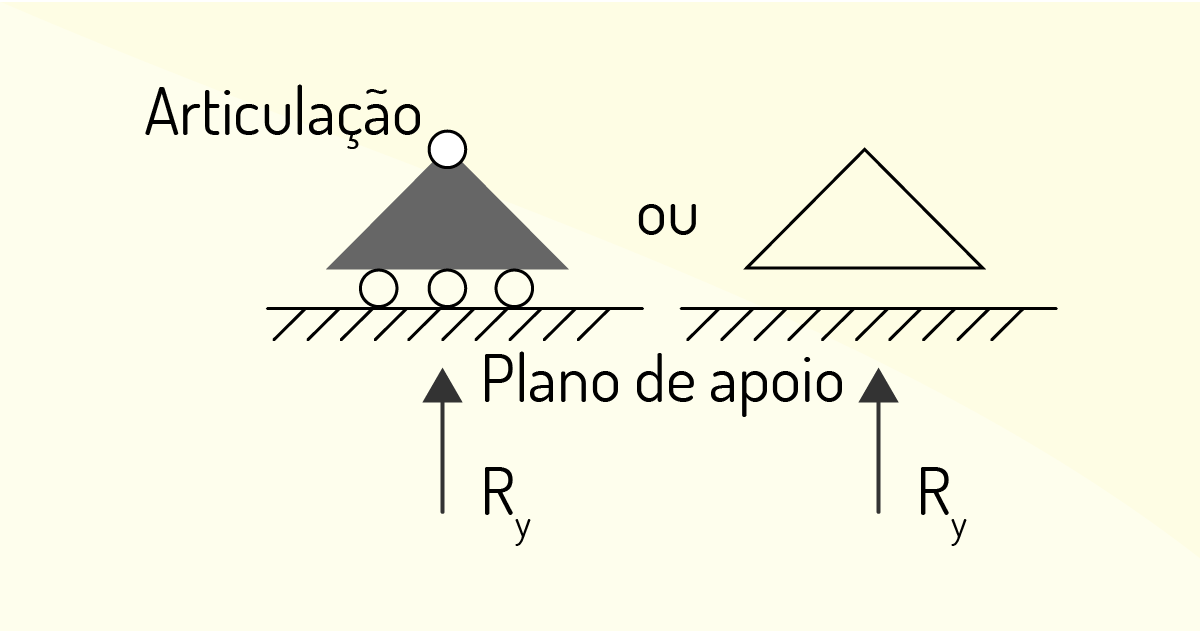
Vínculo de primeira ordem: são aqueles vínculos que permitem dois graus de liberdade à estrutura plana, ou seja, impedem o movimento somente em uma única direção. Resumindo, os vínculos de primeira ordem oferecem apenas uma restrição e, com isso, permitem dois graus de liberdade (movimento em outra direção e a rotação).
São exemplos de vínculo de primeira ordem: os roletes, superfícies lisas, hastes curtas e cabos, cursores e pinos deslizantes. A representação de um apoio de primeira ordem é dada da seguinte forma:
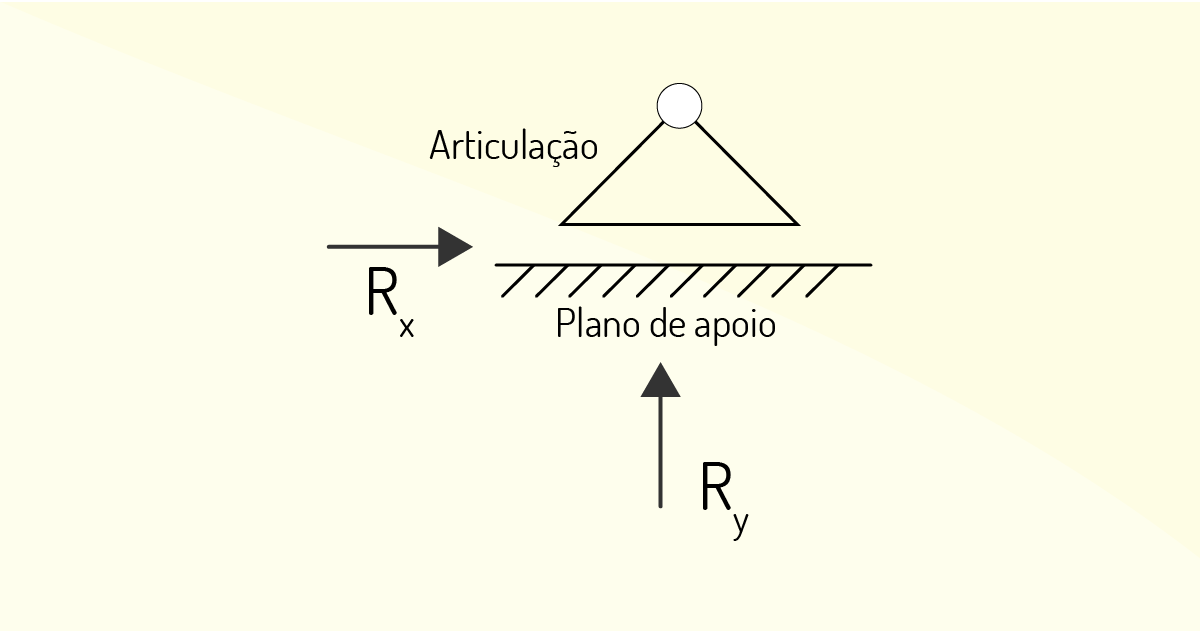
Vínculo de segunda ordem: são aqueles que permitem um único grau de liberdade para a estrutura plana, ou seja, impedem o movimento nas direções x e y. Mesmo restringindo o corpo de se mover, isso não impede que ele rotacione em torno de um ponto. Resumindo, os vínculos de primeira ordem oferecem duas restrições, restrições ao movimento em x e y, e, com isso, permitem a rotação em torno de um ponto. São exemplos de vínculo de segunda ordem: os pinos polidos em orifícios ajustados, articulações e superfícies rugosas. A representação de um apoio de segunda ordem é dada da seguinte forma:
Vínculo de terceira ordem: são aqueles que não permitem grau de liberdade para uma estrutura plana, ou seja, impedem o movimento nas direções x e y, e a rotação sobre um ponto.
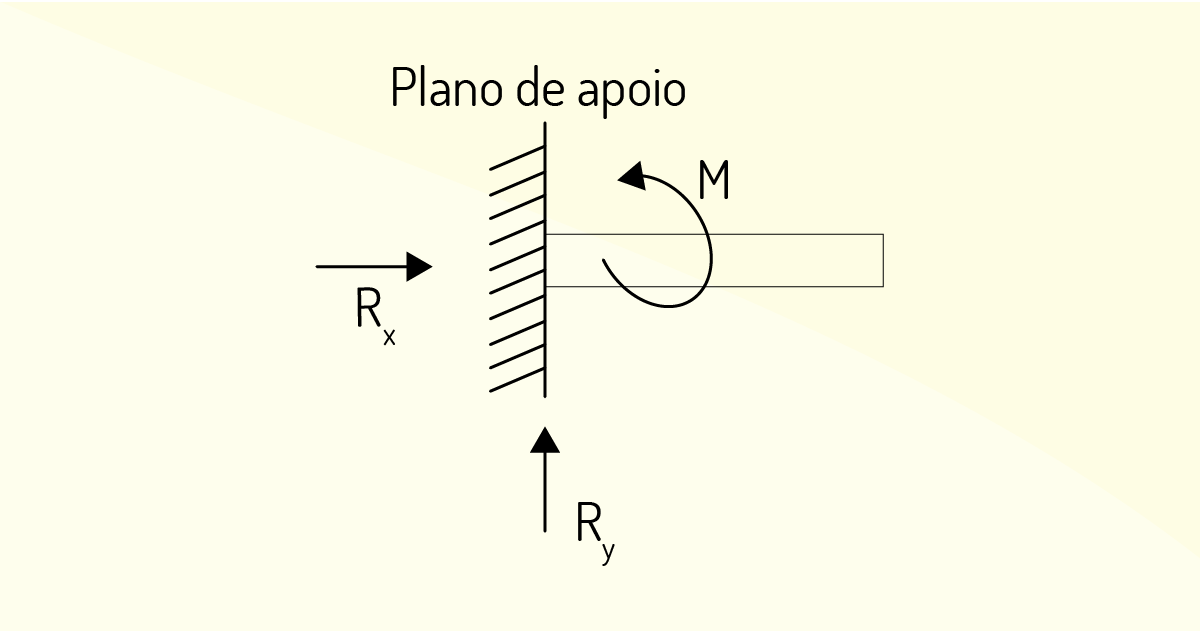
Resumindo, os vínculos de terceira ordem impedem o movimento e a rotação.
Agora, traremos exemplos de equilíbrio em um sistema de forças bidimensionais.
Exemplo para fixar o conteúdo: uma viga com comprimento de 8 m encontra-se apoiada nas duas extremidades e sustenta três cargas concentradas atuantes, como observado na Figura 1.19.

Uma representação esquemática das forças atuantes sobre a viga pode ser ilustrada como na Figura 1.20.
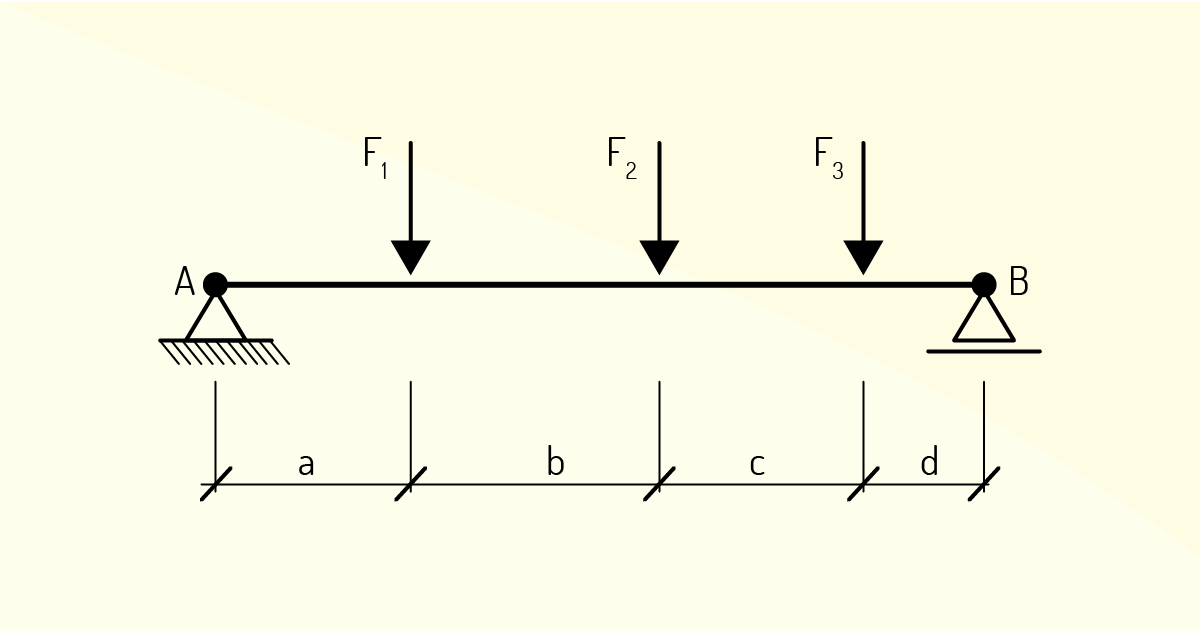
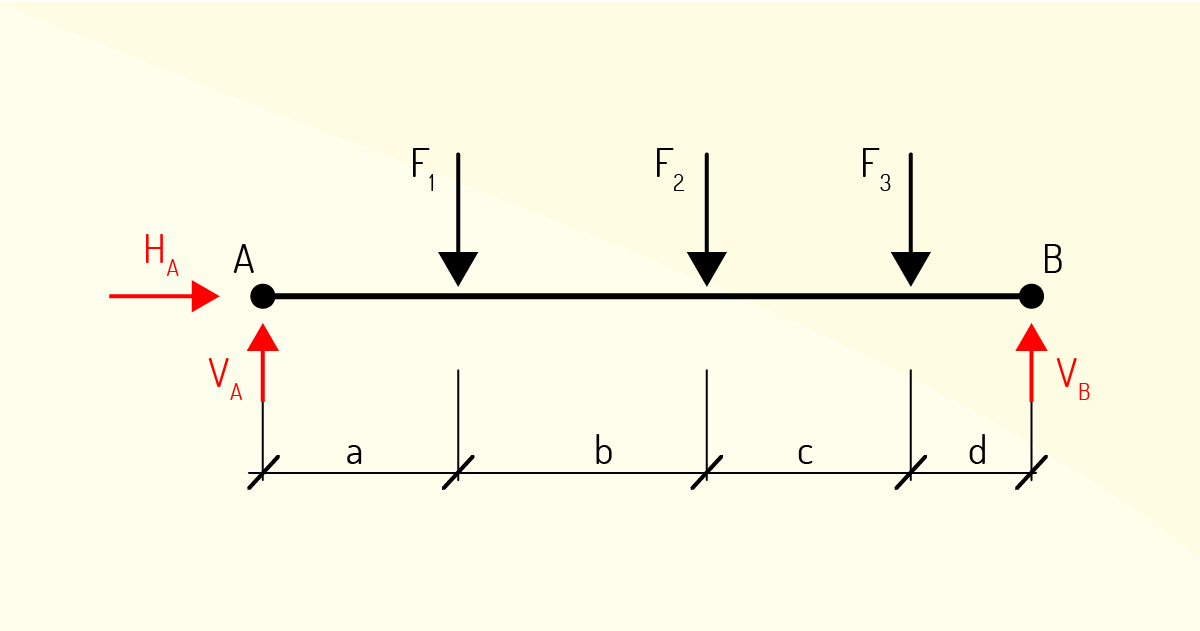
Como você pôde perceber, o valor de nenhuma força foi fornecido ainda. Para resolver um problema como esse, o primeiro passo é esboçar o diagrama de esforços ou diagrama de corpo livre.
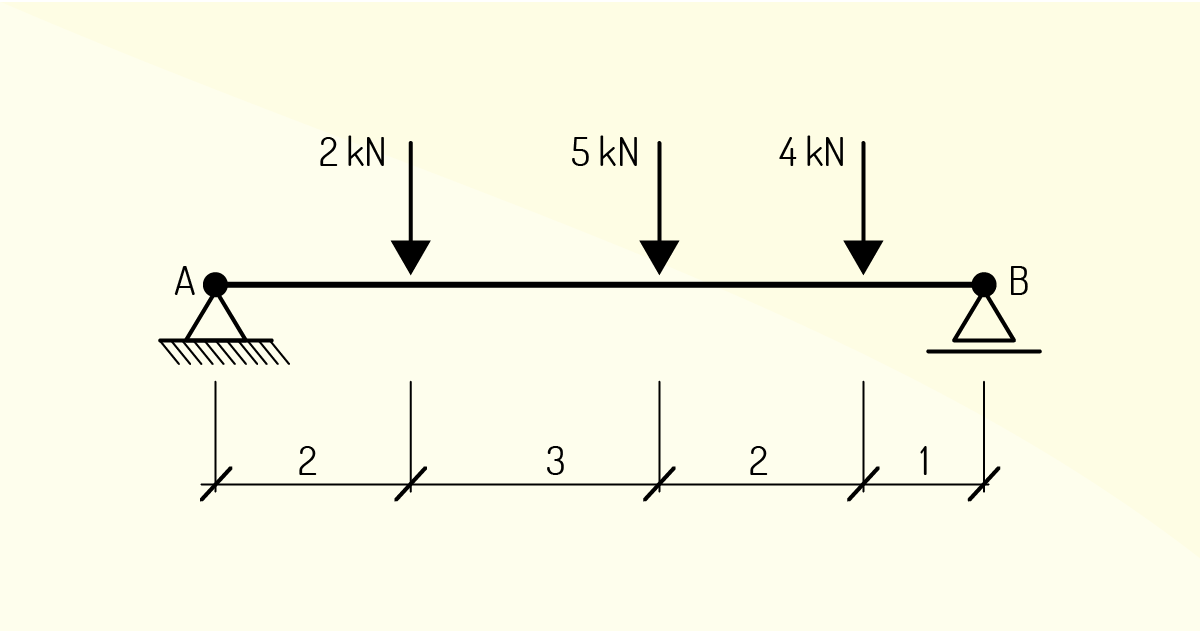
Como se trata de um exemplo de fixação, vamos designar valores para as forças e as respectivas distâncias, como na Figura 1.22, e a partir daí desenvolver os cálculos.
Nosso objetivo é encontrar as reações de apoio \({{V}_{A}}\) (Reação vertical no ponto A), \({{H}_{A}}\) (Reação horizontal no ponto A) e \({{V}_{B}}\) (Reação vertical no ponto B). Veja que no ponto A temos um apoio de segunda ordem, com isso, teremos duas reações de apoio. Já no ponto B, temos um apoio de primeira ordem, logo teremos apenas uma reação de apoio. Aplicando agora as condições de equilíbrio para um corpo rígido em duas dimensões, teremos:
\[\mathop{\sum }_{{}}^{{}}{{F}_{x~}}=~0~\Rightarrow {{H}_{A}}~=~{{0}_{{}}}\]
Como era de se esperar, a reação horizontal no ponto A é igual a zero, pois não há força externa alguma sobre o eixo x.
Agora, vamos analisar as outras duas condições de equilíbrio, primeiro, a somatória das forças em y.
\[\mathop{\sum }_{{}}^{{}}{{F}_{y~}}=~0~\Rightarrow {{V}_{A}}+{{V}_{B}}~=~~{{F}_{1}}+{{F}_{2}}+{{F}_{3}}~\]
\[{{V}_{A}}+{{V}_{B}}~=~~2000~+~5000~+~{{4000}_{{}}}~\]
\[{{V}_{A}}+{{V}_{B}}~=~11000N\]
Agora, obtemos uma equação com duas incógnitas que não é possível resolver, em princípio. Utilizando a somatória dos momentos em relação ao ponto A, obtemos a seguinte expressão:
\[\mathop{\sum }_{{}}^{{}}{{M}_{~}}=~0~\Rightarrow {{F}_{1}}{{d}_{1}}+{{F}_{2}}{{d}_{2}}+{{F}_{3}}{{d}_{3}}~-{{V}_{B}}d~=~0~\]
\[{{F}_{1}}{{d}_{1}}+{{F}_{2}}{{d}_{2}}+{{F}_{3}}{{d}_{3}}~={{V}_{B}}d~\]
\[2000.\left( 2 \right)+5000.\left( 5 \right)+4000.\left( 7 \right)~={{V}_{B}}\left( 8 \right)~\]
\[{{V}_{B}}=~7125~N\]
Substituindo o valor de \({{V}_{B}}\) encontrado na expressão \({{V}_{A}}+{{V}_{B}}~=~11000 N\), obtemos:
\[{{V}_{A}}~=~11000 N - 7125 N\]
\[{{V}_{A}}~=~3875 N\]
Na mecânica, muitos problemas exigem análises mais apuradas e em três dimensões. Dessa forma, é conveniente escrever todas as forças em função das componentes x, y e z.
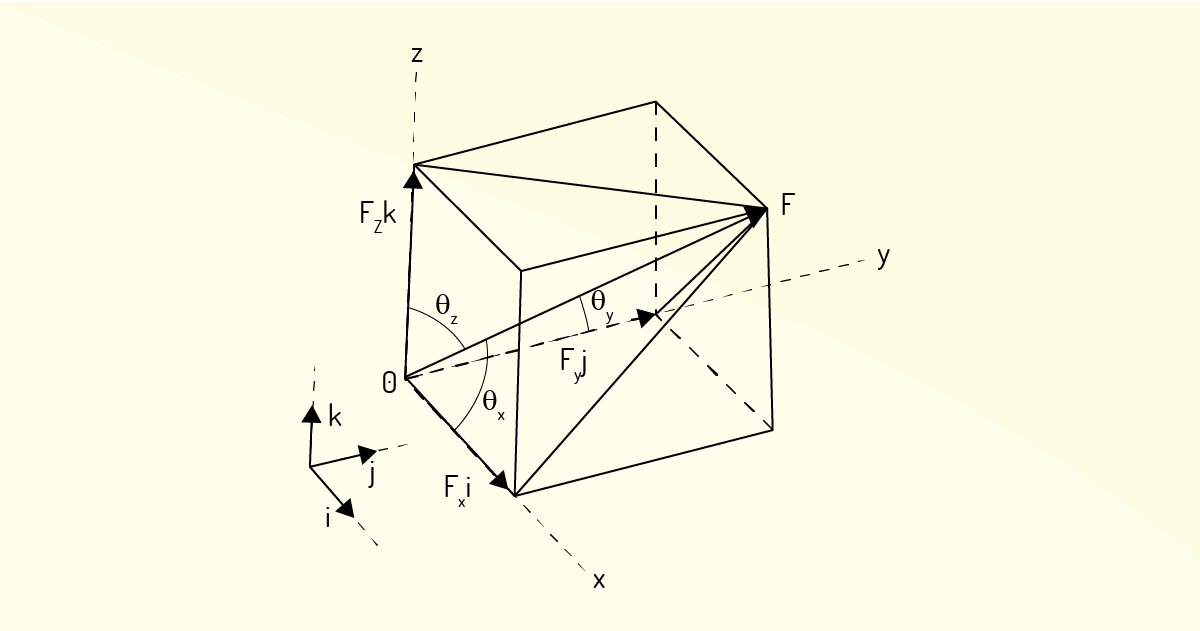
Para um vetor F no espaço, vamos escolher os ângulos \({{\theta }_{x}},~{{\theta }_{y}}~e~\theta {{z}_{{}}}\) como sendo os ângulos entre o vetor F e os eixos x, y e z, respectivamente. Para escrever as projeções \({{F}_{x}}\), \({{F}_{Y}}\) e \({{F}_{Z}}\) de um vetor F sobre os eixos de um sistema espacial, vamos adotar as seguintes expressões:
\[\overrightarrow{\text{F}}\,\,\text{=}\,\,{{\text{F}}_{\text{x}}}\,\hat{i}\,\text{+}\,\,{{\text{F}}_{\text{y}}}\,\hat{j}\,\text{+}\,\,{{\text{F}}_{\text{z}}}\,\hat{k}\]
\[F=\sqrt{F_{x}^{2}+F_{y}^{2}+F_{z}^{2}}\]
\[{{F}_{x}}=Fcos~{{\theta }_{x}}\]
\[{{F}_{y}}=Fcos~{{\theta }_{y}}\]
\[{{F}_{z}}=Fcos~{{\theta }_{z}}\]
Aplicando as condições de equilíbrio para uma estrutura em três dimensões, podemos calcular as reações de apoio.
Com as ferramentas que foram dadas, vamos resolver, juntos, um exercício que nos ajudará na fixação do conteúdo: a barra AB está sujeita a uma força de 200 N sobre o ponto C, como ilustrado na Figura 1.24. Determine a reação no ponto A e as tensões nas cordas BE e BD.
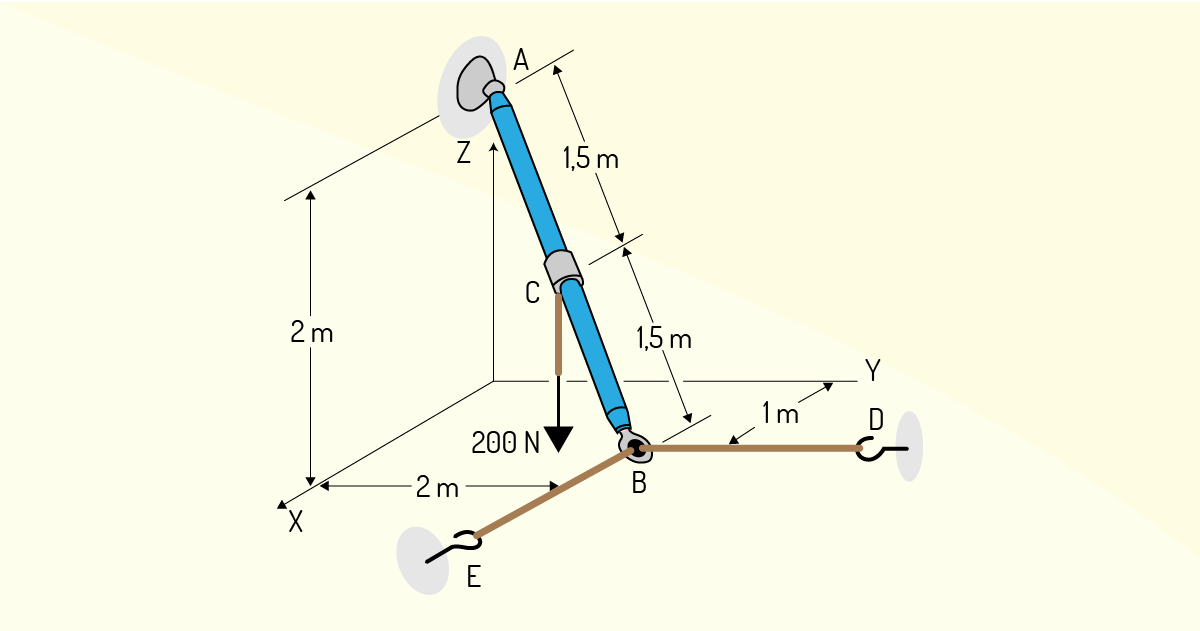
Como já vimos, para que esse sistema permaneça em equilíbrio, as seis condições, três para a somatória das forças e três para a somatória dos momentos, precisam ser satisfeitas. O ponto de partida é expressar todas as forças envolvidas sobre os seus respectivos eixos, como na Figura 1.25.

As forças \({{A}_{X}},~{{A}_{y~}}e~{{A}_{z}}\) são as reações no ponto A. As Atrações \({{T}_{BE}}\) e \({{T}_{BD}}\) são as forças nos cabos. Agora, o próximo passo é aplicar as condições de equilíbrio para as forças, assim, ficaremos com:
\[\mathop{\sum }_{{}}^{{}}{{F}_{x}}=~0~\Rightarrow ~{{A}_{x}}={{T}_{BE}}~\]
\[\mathop{\sum }_{{}}^{{}}{{F}_{y}}=~0~\Rightarrow ~{{A}_{y}}={{T}_{BD}}~\]
\[\mathop{\sum }_{{}}^{{}}{{F}_{Z}}=~0~\Rightarrow ~{{A}_{Z}}=200~N~\]
Verifique que ainda nos falta descobrir o valor de 4 incógnitas e, para encontrá-las, utilizaremos a somatória dos momentos. A escolha do ponto onde iremos analisar o momento sobre ele é de grande importância, devemos escolher de tal forma a eliminar o maior número de forças possíveis e, com isso, o maior número de incógnitas.
Agora, vamos encontrar as coordenadas cartesianas dos pontos A, B e C da seguinte forma:
\[\text{A(0;0;2)}\]
\[\text{B(1;2;0)}\]
\[\text{C(½;1;1)}\]
Para você que ficou na dúvida de como encontrar as coordenadas de um ponto no espaço, em três dimensões, o link a seguir pode te ajudar com algumas orientações importantes: https://www.youtube.com/watch?v=YkKN9AJmKJg. Acesso em: 06 jan. 2020.

Uma vez que o ponto C está no ponto médio entre A e B, a expressão do momento genérico fica:
\[M~=~{{d}_{AB}}x ~{{T}_{BE}}~+ ~{{d}_{AB}}x ~{{T}_{BD}}~+ ~{{d}_{AC}}x ~{{F}_{{}}}\]
O passo a seguir requer um pouco de álgebra linear, em que é preciso encontrar o vetor distância \({{d}_{AB}}\) e \(~{{d}_{AC}}\), ou a distância entre dois pontos, assim, encontraremos:
\({{d}_{AB}}\)= (1î, 2j(“chapéu”), -2(chapéu”))
\({{d}_{AC}}\) = (1/2î, 1j(“chapéu”), -1(chapéu”))
Veja que é necessário calcular três produtos vetoriais, calculando o determinante da matriz formada pelas componentes dos vetores, aqui, resolveremos apenas um deles.
\(~{{d}_{AB}}x~{{T}_{BE}}\)= \(\left| \left. \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\ 1 &2 & -1 \\ {{\text{F}}_{\text{BE}}} & 0 & 0 \\ \end{matrix} \right| \right.\) \(det = - 2\) \({{F}_{BE}}j\left(''chap\acute{e}u'' \right)~-~2{{F}_{BE}}k\left( ''chap\acute{e}u'' \right)\)
Fazendoo mesmo procedimento para os demais produtos vetoriais.
\(~{{d}_{AB}}x~{{T}_{BD}}\)= \(\left| \left. \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\ 1 &2 & -1 \\ \text{0} & {{\text{F}}_{\text{BD}}} & 0 \\ \end{matrix} \right| \right.\) \(det =\) \({{F}_{BD}}k\left(''chap\acute{e}u'' \right)~+2{{F}_{BD}}\hat{i}\)
\(~{{d}_{AC}}x ~{{F}_{{}}}= \left| \left.\begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\ 1/2& 1 & -1 \\ \text{0} & \text{0} & -200 \\ \end{matrix} \right| \right. det = -200\hat{i}~+~100~j\left(''chap\acute{e}u \right)\)
Agora, vamos juntar todas os produtos vetoriais na expressão do momento:
\(\text{M} = [- 2 {{F}_{BE}}j\left( ''chap\acute{e}u'' \right)~-~2{{F}_{BE}}k\left( ''chap\acute{e}u'' \right)] + [{{F}_{BD}}k\left( ''chap\acute{e}u'' \right)~+2{{F}_{BD}}\hat{i}] + [-200\hat{i}~+~100~j\left( ''chap\acute{e}u \right)]\)
Juntando todas as expressões que estão na mesma direção:
\(\text{M} = [2{{F}_{BD}}-200]î + [100~-~2{{F}_{BE}}] j(“chapéu”) +[{{F}_{BD}} - 2{{F}_{BE}}] k(“chapéu”)\)
Como o momento deve ser igual a zero em todas as direções, ou seja:
\[{{M}_{x}}=~0\]
\[{{M}_{Y}}=~0\]
\[{{M}_{Z}}=~0\]
em x, temos que: \(2{{F}_{BD}}-200=~0~\Rightarrow {{F}_{BD}}=~100~N~\)
em y: \(100~-~2{{F}_{BE}}=~0~\Rightarrow {{F}_{BE}}=~50~N~\)
O momento em z serve para validar as forças já encontradas.
Depois de encontrar as forças \({{F}_{BE}}\) e \({{F}_{BD}}\), vamos achar as reações no ponto A.
\[~{{A}_{x}}={{T}_{BE}}~\Rightarrow ~~{{A}_{x~}}=~{{F}_{BE}}=~50~N~~\]
\[~{{A}_{y}}={{T}_{BD~}}\Rightarrow ~{{A}_{y}}~{{F}_{BD}}=~100~N~~\]
\[{{A}_{Z}}=200~N~\]
Pedro e Paulo estão carregando um bloco de concreto que pesa 1000 N, suspenso em uma barra extremamente rígida AB de 200 N e 3,0 m de comprimento, cujas extremidades apoiam-se nos respectivos ombros, pontos A e B. O cofre está a 0,5 m da extremidade A. A força aplicada pela extremidade A ao ombro de Pedro será de, aproximadamente:
450 N.
Incorreta. Faça o diagrama de forças sobre a barra rígida, distribua as distâncias e aplique as condições de equilíbrio para as forças e momentos. Escolha um dos pontos A ou B para ser o ponto, aconselho escolher o ponto B, pois a incógnita pedida é encontrada logo no início.
500 N.
Incorreta. Faça o diagrama de forças sobre a barra rígida, distribua as distâncias e aplique as condições de equilíbrio para as forças e momentos. Escolha um dos pontos A ou B para ser o ponto, aconselho escolher o ponto B, pois a incógnita pedida é encontrada logo no início.
867 N.
Incorreta. Faça o diagrama de forças sobre a barra rígida, distribua as distâncias e aplique as condições de equilíbrio para as forças e momentos. Escolha um dos pontos A ou B para ser o ponto, aconselho escolher o ponto B, pois a incógnita pedida é encontrada logo no início.
933 N.
Correta. Faça o diagrama de forças sobre a barra rígida, distribua as distâncias e aplique as condições de equilíbrio para as forças e momentos. Escolha um dos pontos A ou B para ser o ponto, aconselho escolher o ponto B, pois a incógnita pedida é encontrada logo no início.
1028 N.
Incorreta. Faça o diagrama de forças sobre a barra rígida, distribua as distâncias e aplique as condições de equilíbrio para as forças e momentos. Escolha um dos pontos A ou B para ser o ponto, aconselho escolher o ponto B, pois a incógnita pedida é encontrada logo no início.
Nome do livro: Mecânica para engenharia
Editora: LTC
Autor: J. L. Meriam e L. G. Kraige
ISBN: 9788521617181
O livro “Mecânica para engenharia” traz uma abordagem mais ampla sobre a mecânica aplicada às engenharias. A partir das leis de Newton e conceitos básicos de vetores até sistemas complexos para aplicação equações fundamentais da dinâmica e estática.

Nome do livro: Geometria análitica - um tratemento vetorial
Editora: Pearson Universidades
Autor: P. Boulos e I. Camargo
ISBN: 978-8587918918
O produto vetorial entre dois vetores pode até parecer difícil. Se você sentir que tem dificuldade, aconselho acompanhar os conteúdos do livro “Geometria Analítica - um tratamento vetorial”, que faz uma abordagem bem detalhada sobre o conteúdo citado.

Nome do livro: Álgebra linear
Editora: Harbra
Autor: José Luiz Boldrini
ISBN: 978-8529402024
O livro “Álgebra linear”, de José Luiz Boldrini, trata, dentre outros temas, do determinante de uma matriz, que pode ser facilmente calculado utilizando a regra de Sarrus. É muito importante para quem estuda essa área do conhecimento, portanto, indicado para o conteúdo tratado nesta unidade.
