A mecânica e a resistência de materiais tiveram seu desenvolvimento ampliado a partir dos estudos realizados por Leonardo da Vinci e Galileu Galilei, no que diz respeito à geometria das estruturas, entre elas, das vigas, que, aliadas ao comportamento dos materiais, deram origem à compreensão e à resistência dos materiais como ciência.
A análise estrutural é parte fundamental para o desenvolvimento de um projeto de engenharia de estruturas, visto que se refere aos efeitos das cargas sobre essas estruturas físicas e seus componentes (vigas, treliças e cabos), correlacionando a mecânica e a matemática aplicadas à ciência dos materiais, calculando a deformação, força interna, tensão, reação de apoio e estabilidade da estrutura. A partir dessas relações, é possível verificar a disposição de uma estrutura para seu uso (HIBBELER, 2010).
Sabemos que uma estrutura é o conjunto de partes resistentes, ou seja, um corpo ou sistema de partes que suportam uma carga e certificam a estabilidade de um elemento do projeto de modo que sua análise permite a simplificação desses projetos em modelos estruturais, cujos principais fatores para sua elaboração são:
Admitindo que os sistemas estruturais são modelos em reposta à análise estrutural, os quais podemos classificá-los quanto à sua dimensão ou geometria, temos:
Para que esse sistema estrutural não se mova em determinados pontos na peça (rotação ou translação), são utilizados elementos chamados de vínculos, os quais podem ser classificados em:
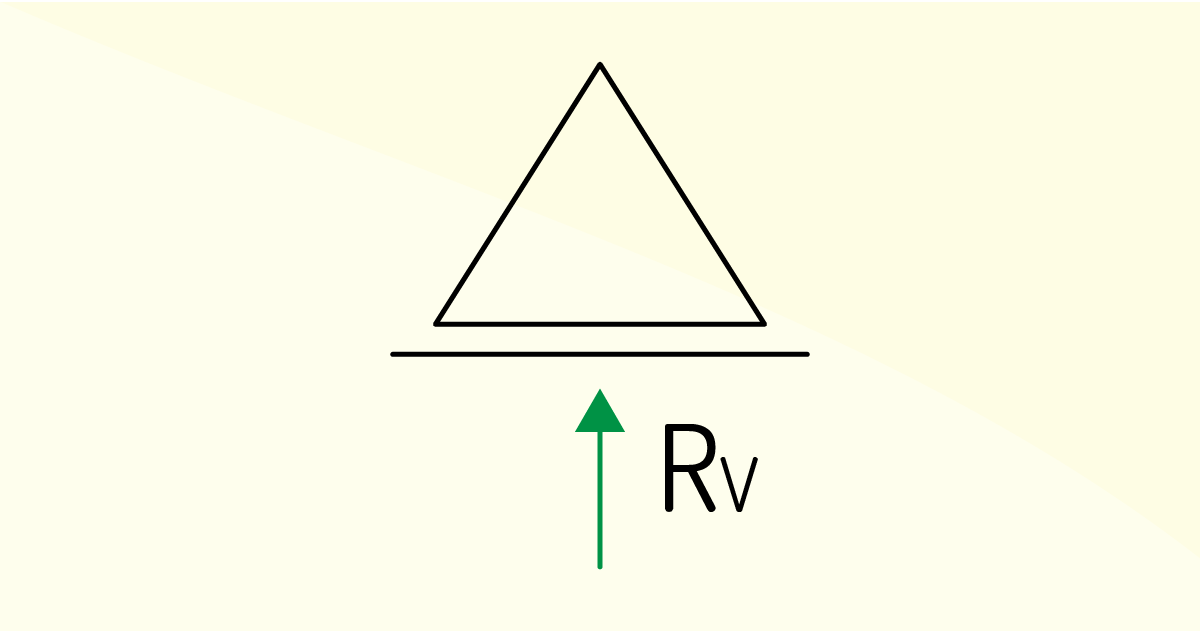
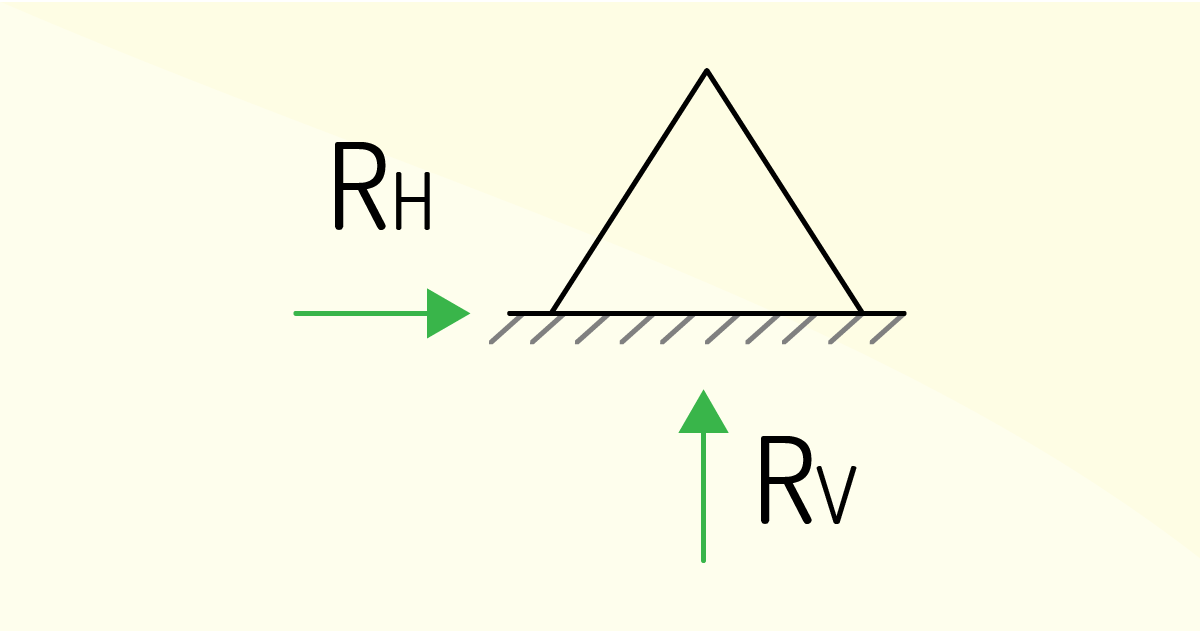
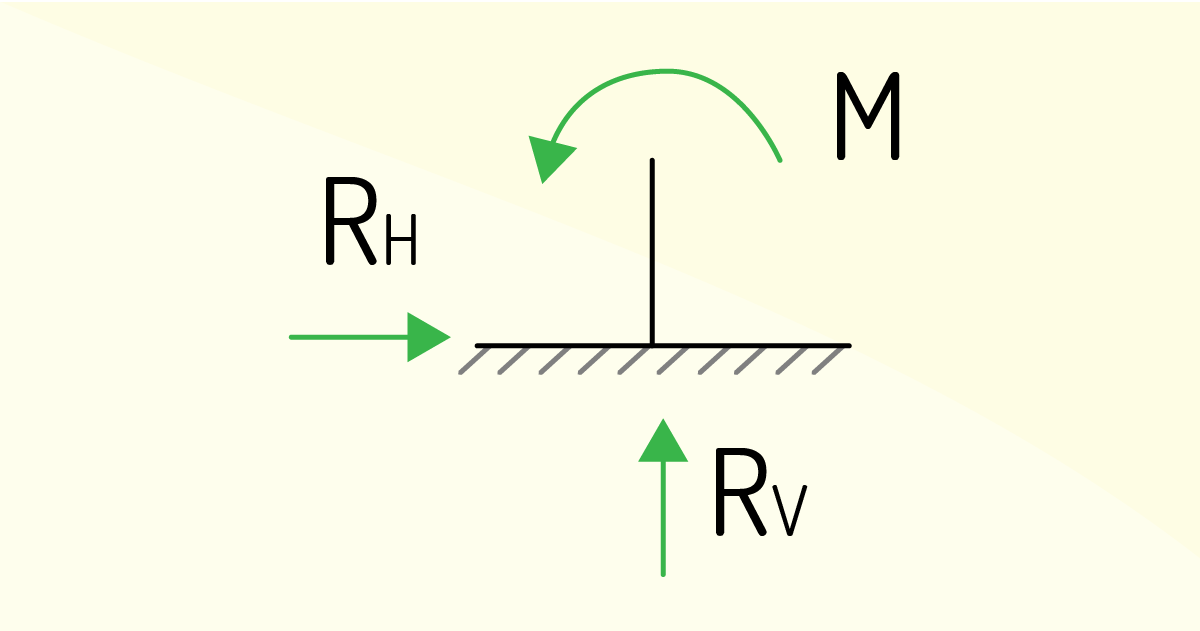
São tipos de vínculos o cabo, a ligação esbelta, os roletes, as rótulas, a luva com articulação, a articulação, o apoio deslizante, a luva rígida e o apoio rígido.
Quando uma estrutura possui vínculos suficientes para impedir sua rotação e translação, dizemos que essa estrutura está restringida, nos permitindo entender sobre sua estaticidade e estabilidade. Lembrando que temos duas condições para o equilíbrio estático de uma estrutura:
A partir disso é possível entender que:
a) se uma estrutura tem restrição e tem mesmo número de incógnitas e equações de equilíbrio, então dizemos que essa estrutura é do tipo isostática, ou seja, o número de reações de apoio é igual ao número de equações de equilíbrio disponíveis (sistema determinado);
b) se a estrutura tem restrição e o número de equações de equilíbrio menor do que o número de incógnitas, então dizemos que essa estrutura é do tipo hiperestática, ou seja, o número de reações de apoio é maior do que o número de equações de equilíbrio disponíveis (sistema indeterminado);
c) se a estrutura não tem restrição, então dizemos que essa estrutura é do tipo hipoestática, ou seja, o número de reações de apoio é menor do que o número de equações de equilíbrio disponíveis (sistema instável).
Cuidado para não equiparar os conceitos de equilíbrio e deformações. Uma estrutura pode estar em equilíbrio e, ainda assim, apresentar deformações. Como, por exemplo, um galho de uma árvore que se dobra/verga ante o efeito de um vento e, mesmo assim, está em equilíbrio, enquanto não sair do local.

Podemos descobrir se uma estrutura é restringida ou não a partir do seu grau de estaticidade ou hiperestaticidade (gh), Equação 1:
\[gh = C1 + 2 . C2 + 3 . C3 – 3 . m (1)\]
Em que C1 é o número de vínculos de 1º gênero; C2 é o número de vínculos de 2º gênero; C3 é o número de vínculos de 3º gênero; m é o número de hastes presentes na estrutura.
Ainda sobre o grau de hiperestaticidade, temos a Equação 2:
\[gh = ge + gi, (2)\]
Em que ge é o grau de hiperestaticidade externa e gi é o grau de hiperestaticidade interna.
Conhecer e identificar os mais diversos tipos de vínculos é essencial para sua aplicação em estruturas. Sendo assim, complemente seu estudo sobre os tipos de vínculo observando a Tabela 1.1, disponível na página 17, da 7ª edição do livro Resistência dos Materiais, de R. C. Hibbeler, disponível em:
<http://souexatas.eng.br/livro-em-pdf-de-resistencia-dos-materiais-resistencia-dos-materiais-r-c-hibbeler-setima-edicao-7ed-pearson/>. Acesso em: 30 jan. 2020.

Uma estrutura é o conjunto de partes resistentes, ou seja, um corpo ou sistema de partes que suportam uma carga e certificam a estabilidade de um elemento do projeto de modo que sua análise permite a simplificação desses projetos em modelos estruturais. Sobre estruturas com vínculos, ou seja, estruturas com apoios, observe a figura a seguir.
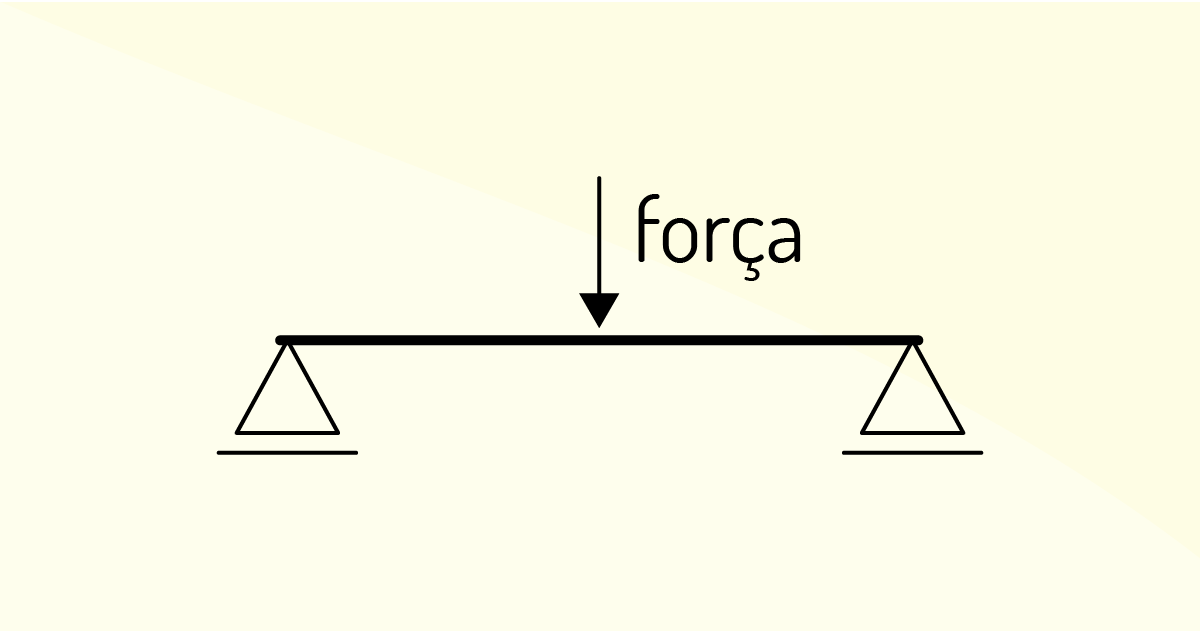
É verdadeiro o que se afirma em:
Podemos perceber que essa estrutura possui 2 vínculos de 2º gênero.
Incorreta. Visto que se trata de uma estrutura com 2 vínculos de 1º gênero.
Trata-se de uma estrutura hiperestática.
Incorreta. Pois o grau de estaticidade é igual a -1, indicando que o número de reações de apoio é menor do que o número de equações de equilíbrio disponíveis.
O grau de estaticidade dessa estrutura é -1.
Correta. O grau de estaticidade é dado por: gh = C1 + 2 . C2 + 3 . C3 - 3 . m
Então gh = (2) + 2 . (0) + 3 . (0) - 3 . (1), logo gh = 2 - 3 e, portanto, gh = - 1.
Por se tratar de uma estrutura isostática, essa é restringida.
Incorreta. Pois não se trata de uma estrutura isostática. Como possui gh=-1 é tida como hipoestática.
Estrutura desse tipo possui apoio de 3º gênero, tendo movimentos restritos tanto de rotação quanto de translação.
Incorreta. Pois não se trata de uma estrutura com apoio de 3º gênero, e sim com 2 apoios de 1º gênero.
Pensando em estrutura isostática, podemos citar as vigas, “elementos lineares em que a flexão é preponderante” (ABNT, 2004), de modo que os esforços predominantes são conhecidos como momento fletor e força cortante.
Ainda podemos entender as vigas como elementos estruturais com direção horizontal, as quais transferem as cargas ao longo de seu comprimento para os suportes (nesses pontos, as cargas são transformadas em forças verticais), de modo que resistam além das cargas verticais, às forças de cisalhamento e momento de flexão.
As vigas são fabricadas em diversos materiais, como aço, ferro fundido, concreto armado, concreto protendido, madeira e alumínio, tendo as mais variadas aplicações nas construções. Tendo como referência os suportes, podemos tipificar as vigas.





No que diz respeito à aplicação das vigas, podemos tipificá-las em:
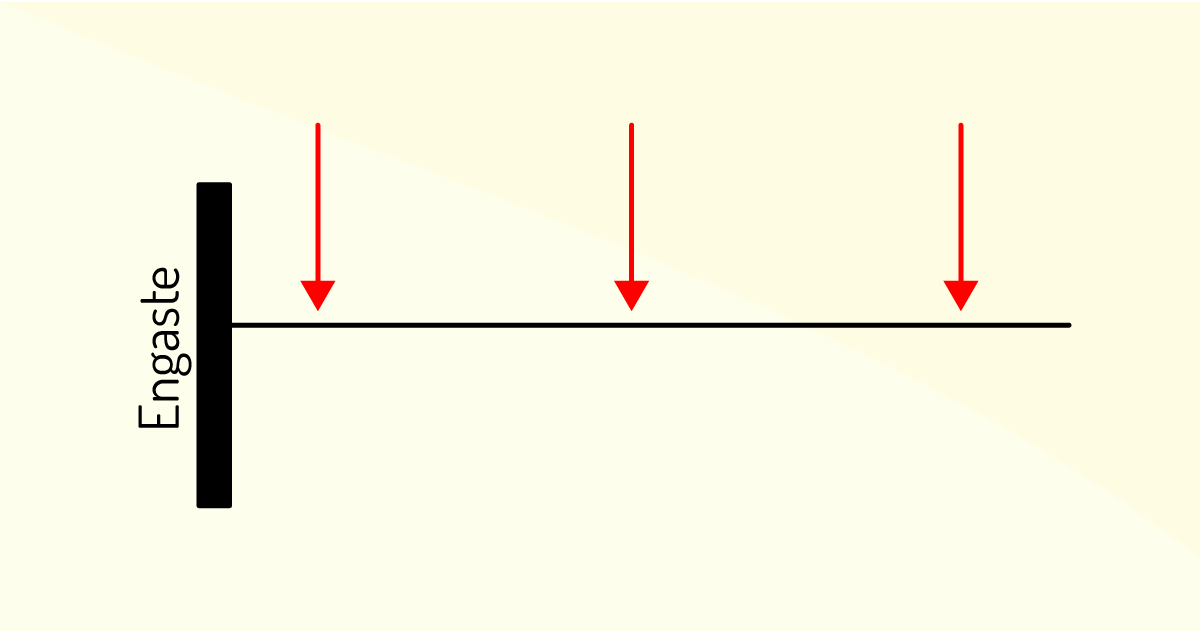
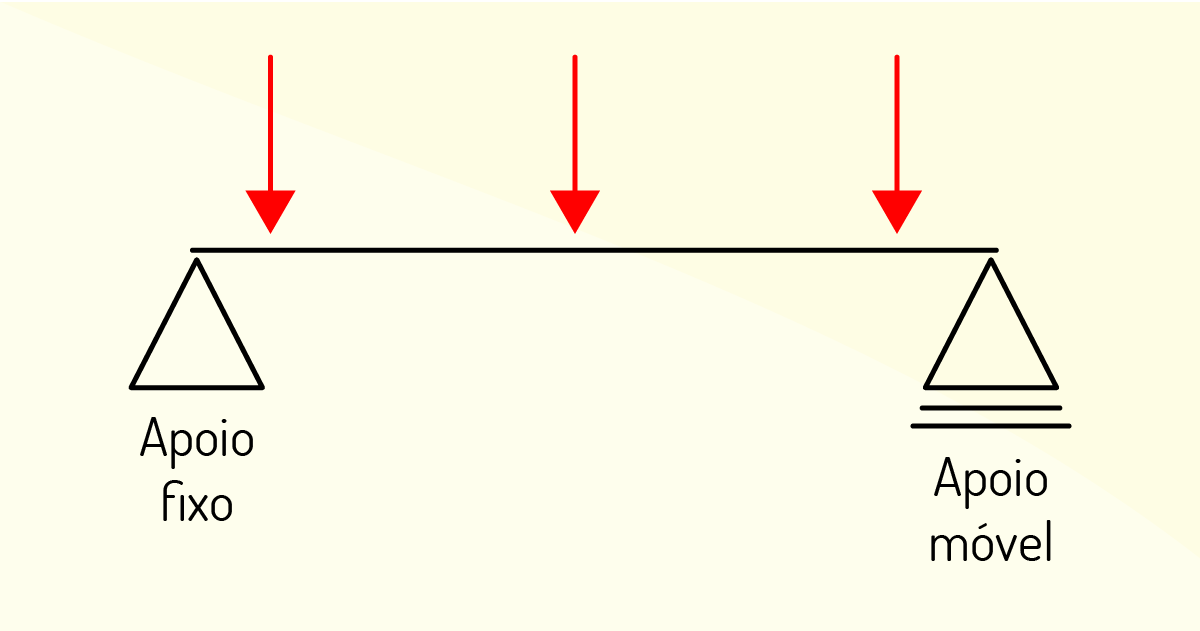
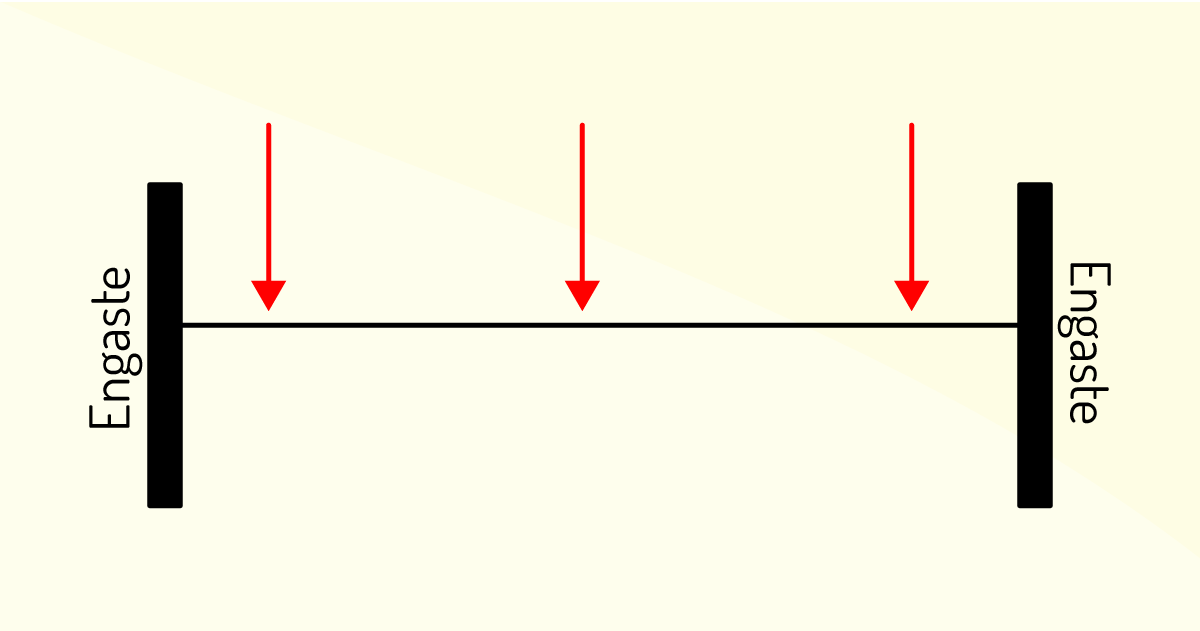
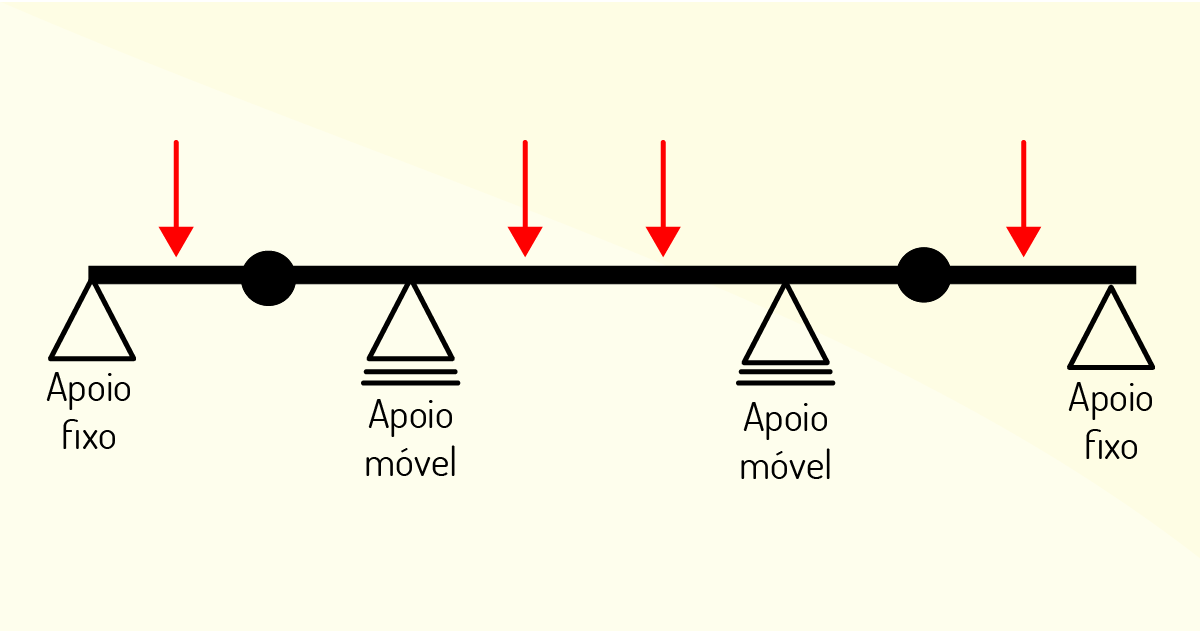
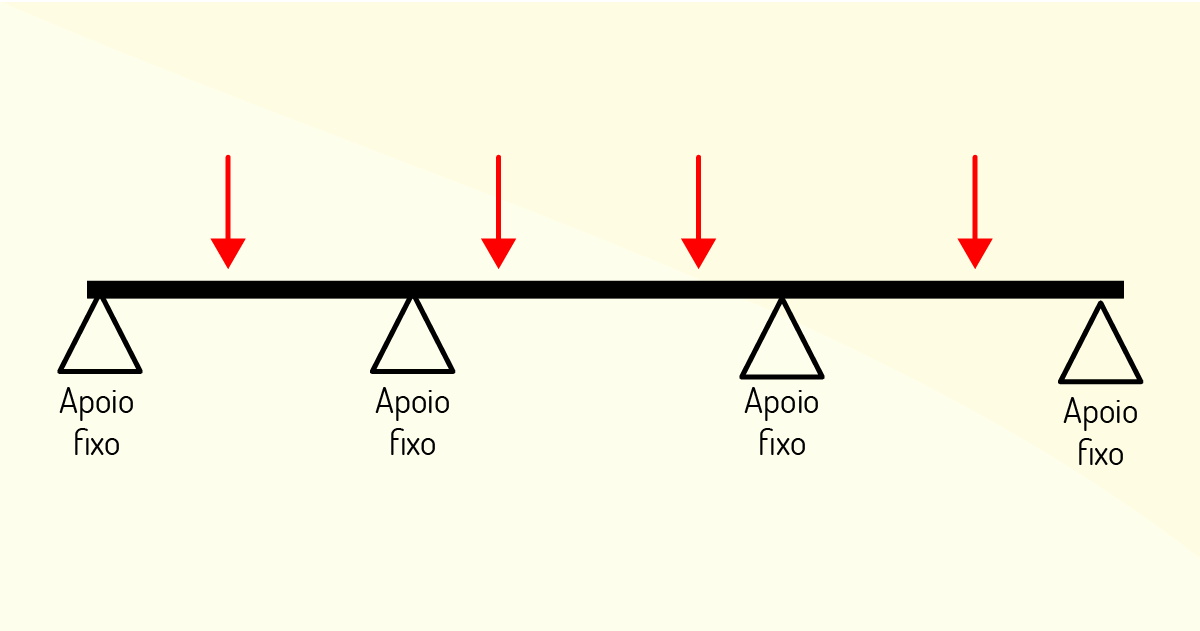
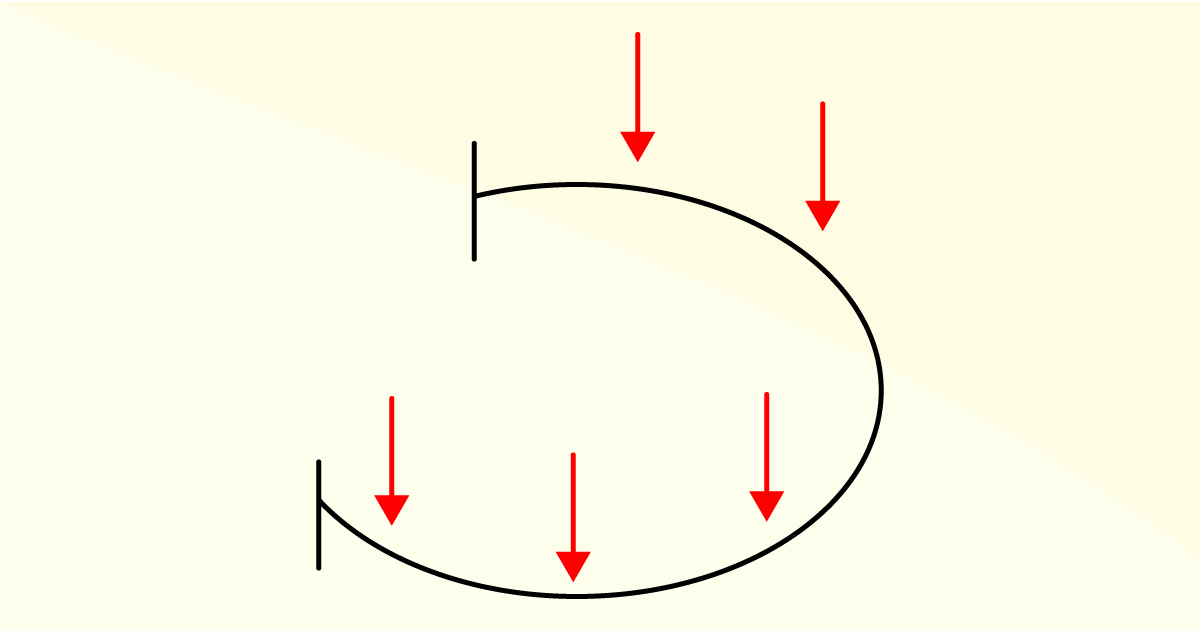
Conhecer e identificar os mais diversos tipos de vigas é essencial para sua aplicação em estruturas. Sendo assim, complemente seu estudo sobre os tipos de vigas com o material de “Estabilidade das construções”, disponível em: https://docente.ifrn.edu.br/edilbertoborja/estabilidade-das-construcoes/estabilidade-das-construcoes-superior-2/apostila-completa-vigas-isostaticas/vigas-isostaticas-apostila-completa-em-pdf. Acesso em: 08 jan. 2020.

Agora que conhecemos os tipos de vigas e suas estruturas, podemos estudar seu comportamento estrutural. Sendo assim, pensando em uma viga sob ação de um esforço de momento fletor, podemos pensar simplificadamente em sua flexão. A flexão em uma viga é um tipo de tensão normal na direção axial da viga, logo o momento fletor gera tensões normais nessa estrutura.
Sendo os efeitos de compressão máximos e de tração concentrados nas partes externas da seção da viga, podemos afirmar que haverá maior concentração de material nessas áreas, pois qualquer material em um ponto intermediário a essas partes será menos requisitado, por conseguinte, utilizado de forma ineficiente. Desse modo, se for possível concentrar esse material nas bordas e a área dessa borda satisfizer a resistência, a compressão e a resistência à tração, temos que todo o material seria solicitado na sua máxima capacidade, implicando em uma seção mais eficiente e econômica. Porém as situações de carregamento nas vigas são as mais diversas, entre elas, podemos citar a força cortante ou força de cisalhamento, de modo que a utilização de áreas externas não é suficiente para haver melhorias na resistência ao esforço cortante.
O esforço cortante gera tensões de cisalhamento existente tanto vertical quanto horizontalmente ao longo da viga (HIBBELER, 2010).
A viga em uma construção estará submetida a diversas cargas, como às cargas concentradas, às cargas distribuídas ou à combinação delas.
As cargas distribuídas podem ser trocadas por uma carga concentrada, a qual atuaria no centro gravitacional do carregamento, de modo que essa ação facilitaria seu cálculo. Sendo assim:
Seções transversais (também conhecidas como seções planas ou retas) são a intersecção de um corpo no espaço em três dimensões com um plano. Dependendo do material, há tipos de seções transversais mais usuais na construção de vigas, as quais são consideradas de acordo com sua eficácia. Vigas confeccionadas em aço ou alumínio possibilitam maior inércia à flexão, pois afastam as áreas do centro de gravidade, resultando na redução da intensidade de tensão normal e de cisalhamento na viga. O uso de metais na construção de viga possibilita a formação de seções com espessuras reduzidas a partir de elementos delgados, gerando maior economia de material, e isso só é possível devido à sua resistência, ao módulo de elasticidade, que é elevado, e à sua homogeneidade. Nesse caso, é possível fazer a ligação de seus elementos ainda na fabricação por meio da solda, dentre outras.
No caso de seções em madeiras, estas não devem ser construídas com a mesma ordem de dimensão, pois, comparadas aos metais, possuem menor resistência e módulo de elasticidade; desse modo, é pertinente que as ligações sejam realizadas por meio de ligações coladas, pregos e parafusos, cuidando para que haja a menor deformação possível dessa ligação, a qual afetará a resistência e a inércia para a flexão da viga.
As seções confeccionadas em concreto possuem mais dimensões quando comparadas às de madeira e metal, isso se deve exatamente às dimensões dos componentes do concreto, como armaduras, no caso do concreto armado ou protendido; e aos agregados, comparados às dimensões dos elementos de seção delgada.
A Casa, de Vinícius de Moraes
Era uma casa
Muito engraçada
Não tinha teto
Não tinha nada
Ninguém podia
Entrar nela, não
Porque na casa
Não tinha chão
Ninguém podia
Dormir na rede
Porque na casa
Não tinha parede
Ninguém podia
Fazer pipi
Porque penico
Não tinha ali
Mas era feita
Com muito esmero
Na Rua dos Bobos
Número Zero (MORAES, on-line).

Assim, vigas construídas de aço ou alumínio, cujos elementos são delgados, possuem espessuras medianas, quando usadas em madeiras; e robustas, quando usadas em concreto armado.
A seguir, verificaremos as seções mais utilizadas na construção civil.
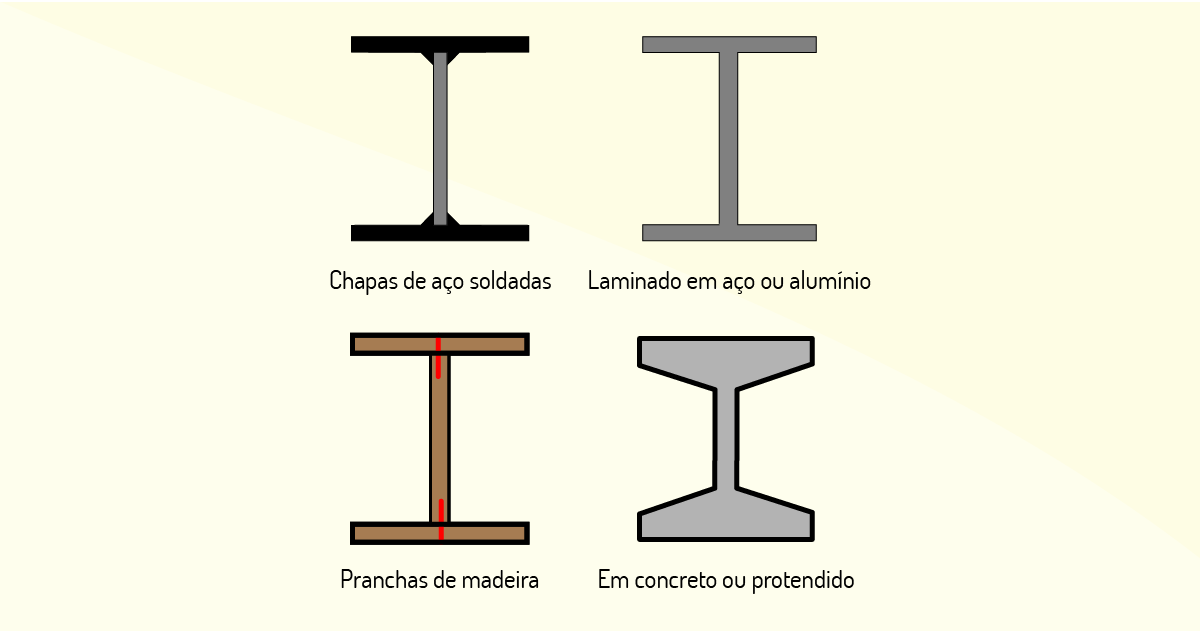
Percebemos que o tipo de material deve ser condizente com o tipo de estrutura que se deseja utilizar em uma construção, pois os projetos devem considerar além da logística estrutural, o custo e, até mesmo, a beleza da construção.
Sabemos que as vigas são elementos estruturais usados para distribuir as cargas aplicadas a elas ao longo do seu comprimento, sendo confeccionadas de madeira, metal ou concreto. Sendo assim, assinale a alternativa correta.
Podemos classificar as vigas por meio dos materiais dos quais são confeccionadas, sendo a viga universal e a treliçada exemplos desse tipo de classificação. A classificação das vigas é feita exclusivamente por meio de sua matéria-prima e beleza a ser exibida no projeto.
Incorreta. Visto que uma das classificações de vigas é feita a partir dos suportes que as complementam, sendo exemplos a viga universal e a treliçada.
São exemplos de vigas, de acordo com sua aplicação, biengastada, Gerber e em balanço.
Correta. Pois a viga biengastada é aquela em que as duas extremidades encontram-se engastadas, ou seja, assentadas ou encaixadas. A viga Gerber é aquela apoiada em mais de dois suportes ou apoios. E a viga em balanço é aquela na qual apenas uma de suas extremidades se encontra suportada ou encaixada. Diante dessas definições, é possível saber a aplicabilidade e a tipologia das vigas, como descrito na alternativa.
O momento fletor em uma viga é oriundo da ação de um esforço de relaxação da viga.
Incorreta. Pois o momento fletor está relacionado à flexão da viga, ou seja, uma tensão normal aplicada na direção axial da viga.
O esforço cortante em uma viga gera tensões de cisalhamento em apenas uma direção da viga, no caso, a horizontal.
Incorreta. Pois o esforço cortante gera tensões ao longo da viga, ou seja, nas duas direções: na vertical e na horizontal.
A viga em uma construção está submetida somente a um tipo de carga, a concentrada, ou seja, carga aplicada em um único ponto da estrutura.
Incorreta. Pois uma viga está sujeita a cargas concentradas, distribuídas, ou a uma combinação entre elas.
A projeção e a utilização de uma viga em um projeto devem seguir alguns requisitos iniciais em relação:
Após os dados iniciais, precisamos considerar a estaticidade, os vãos e as dimensões ou proporções das seções transversais, respeitando:
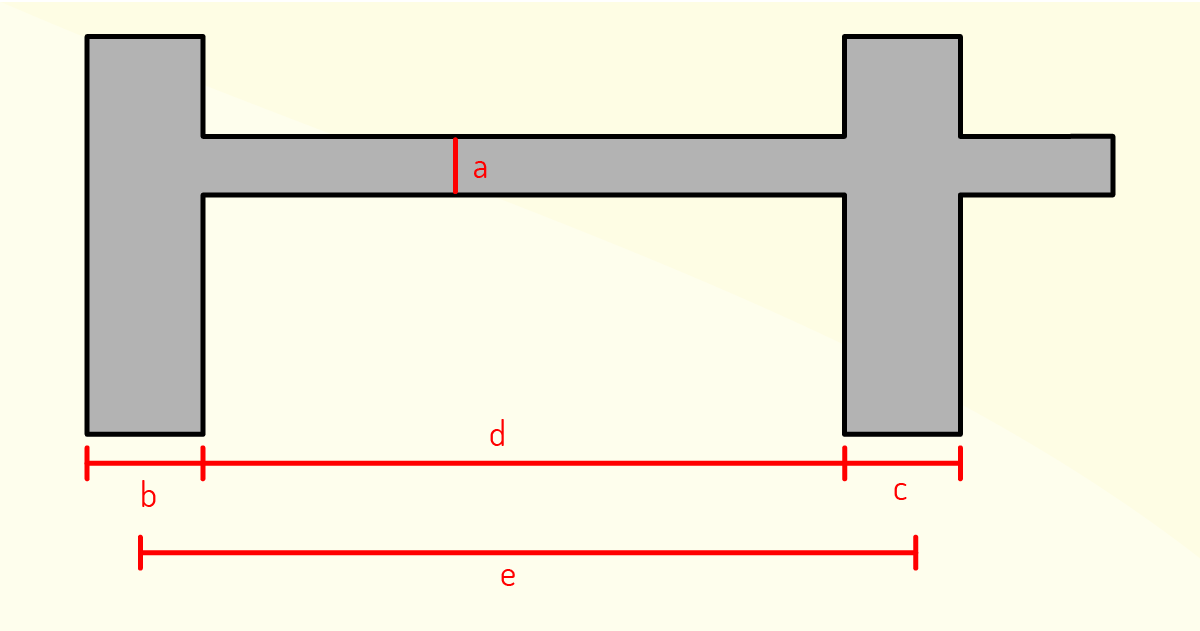
Analisando a Figura 2.16, nota-se que a corresponde à altura da viga (h); b e c correspondem aos apoios da viga (t1 e t2); d corresponde ao vão livre (l0) e e corresponde ao vão efetivo (lef), de modo que o vão efetivo pode ser calculado por meio de lef = lo + a1 + a2; em que a1 é igual ao menor valor entre t1 / 2 e 0,3h e a2 igual a t2 / 2.
Além disso, é importante fazer uma pré-análise das dimensões das vigas antes de se iniciar o projeto, pois não é permitido que elas apresentem largura inferior a 12 centímetros. A exceção acontece para uma largura L na qual 10<L<12, de modo que o projeto respeite o item 13.2.2 da NBR 6118 (ABNT, 2004), na qual são citados:
Vale lembrar que a largura da viga é calculada de modo que essa fique embutida na estrutura da parede onde será colocada, sendo adotadas larguras maiores para os casos de grandes vãos ou de tramos muito carregados, de modo que o impacto na arquitetura e estrutura da construção seja amenizado. Além disso, as vigas não devem interferir nos espaços de portas (as quais possuem 2,20 metros de altura) e janelas, de modo que o cimbramento deve ser considerado de acordo com a padronização das alturas das vigas, não sendo comum o uso de duas alturas distintas, o que pode acarretar na necessidade de aplicação de uma armadura dupla em alguns pontos da estrutura. Em se tratando dos tramos carregados e maiores vãos, há necessidade de verificação constante de suas flechas, que são deformações ao longo do eixo longitudinal da viga.
Geralmente, as cargas existentes em uma viga são provenientes do seu próprio peso, das reações de apoio das lajes e do peso das paredes relacionadas a elas. Porém essas três situações não são únicas quando tratamos de cargas em uma viga. Além delas, podemos citar as cargas provenientes de pilares em vigas de transição ou vigas de fundação, de modo que as demais cargas que possam sobrecarregar a viga são uniformemente distribuídas por ela.
Entendemos como esforços internos as ligações internas de tensões em uma estrutura, ou seja, as tensões ao longo de sua seção transversal. Esses esforços representam o efeito de forças e momentos entre duas frações de uma estrutura reticulada dada pelo corte em uma seção transversal, de modo que esses são iguais e contrários, correspondendo a uma ação e reação.
O esforço interno, conhecido como esforço cortante (Q), é resultante de forças de uma parte isolada sobre a outra na direção transversal ao eixo da barra na seção transversal de corte. O esforço cortante é representado pelo efeito de força cisalhante presente na seção transversal da viga.
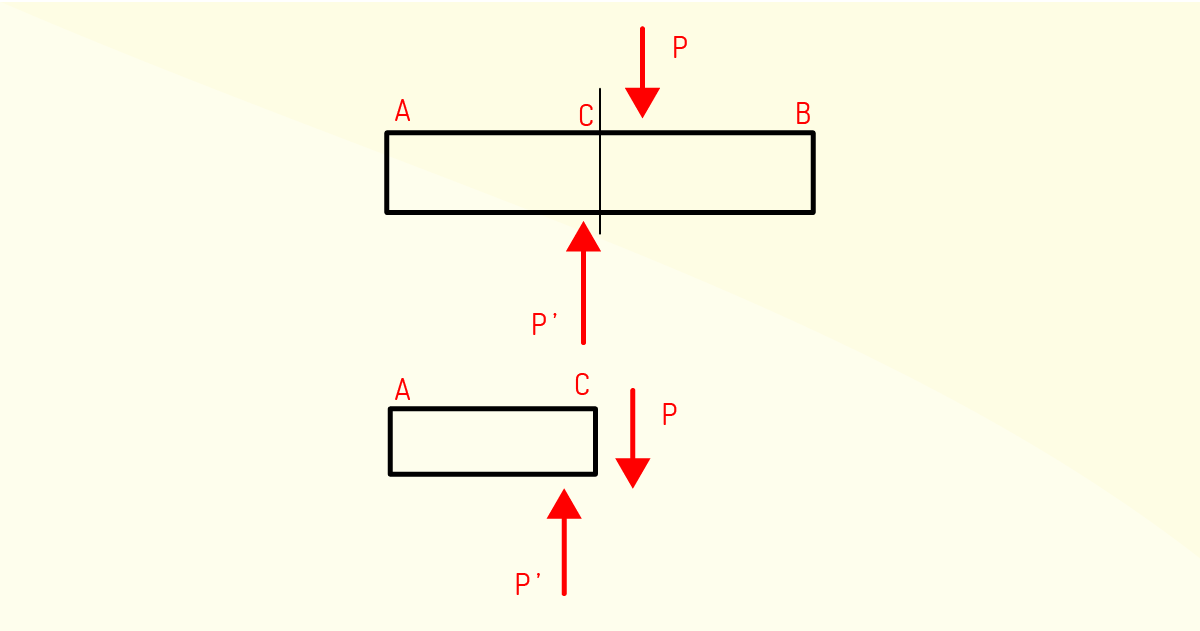
A máxima força cortante VSd, na face do apoio, não deve ultrapassar a força cortante última VRd2, relativa à ruína das bielas comprimidas de concreto (item 17.4.2.2 da NBR 6118 – ABNT, 2004), de modo que:
\[{{V}_{Rd2}}=0,27~{{\alpha }_{v2~~}}{{f}_{cd}}~{{b}_{w~}}d\]
\[onde~{{\alpha }_{v2}}=\left( 1-{{f}_{ck}}/250 \right),~{{f}_{ck~}}em~MPa\]
\[ou~{{\alpha }_{v2}}=\left( 1-{{f}_{ck}}/25 \right),~{{f}_{ck}}~em~kN/c{{m}^{2}}\]
Ainda, fcd é dada pela resistência de cálculo do concreto; bw é dada pela menor largura da seção, compreendida ao longo da altura útil; e d é a altura útil da seção, ou seja, é igual à medida da borda comprimida ao centro de gravidade da armadura de tração.
Os esforços cortantes são dados como positivos quando as forças à esquerda de uma seção transversal estiverem entrando e a resultante das forças na direção transversal apresentar o sentido para cima; ainda, quando forças à direita de uma seção transversal estiverem entrando e a resultante das forças na direção transversal apresentar o sentido para baixo. Se o esforço for contrário ao indicado, dizemos que esse é negativo.
A variação dos esforços cortantes por toda a extensão longitudinal da seção transversal de uma estrutura é melhor representada a partir de um diagrama de esforços cortantes. De modo que, convencionalmente, o desenho é elaborado de modo que os valores positivos cortantes são traçados ao lado das fibras superiores da barra/viga e negativos, do outro lado. Quando se trata de uma viga do tipo biapoiada, cuja carga é centralizada, determinamos o seu diagrama a partir das situações (1) e (2).
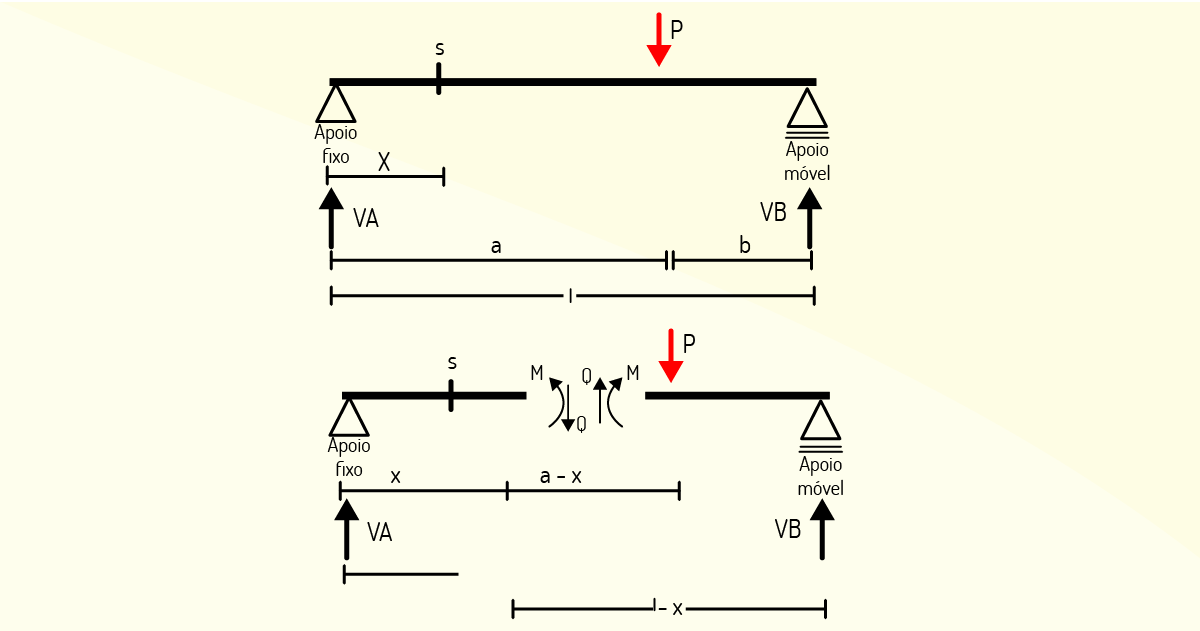
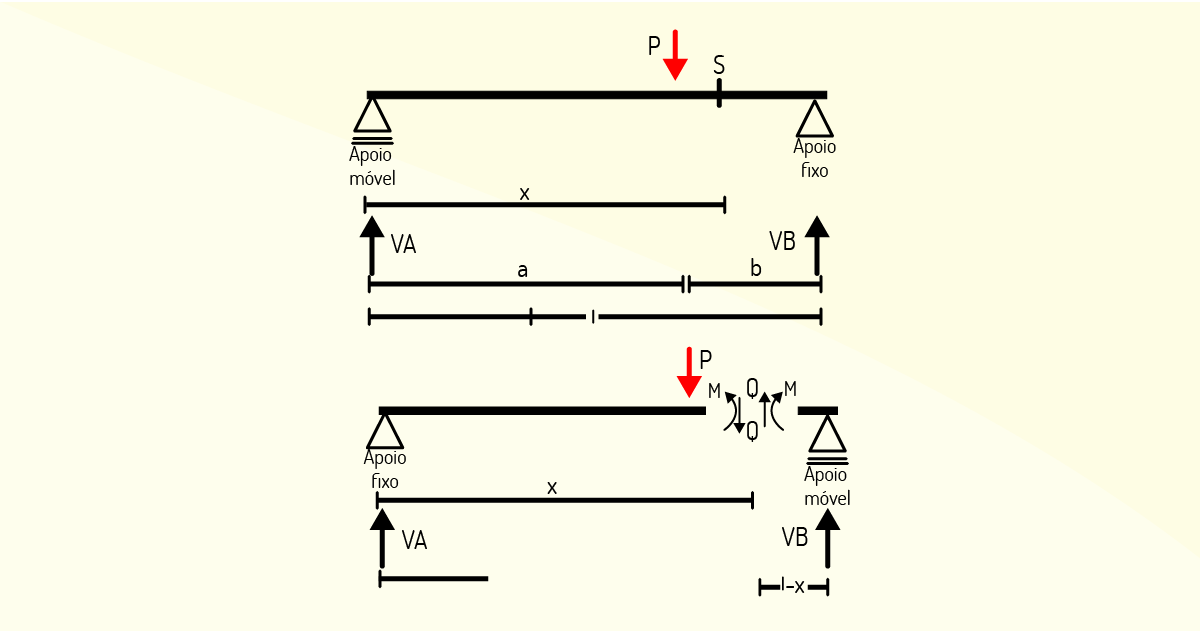
O diagrama de esforços cortantes resultará em descontinuidade sob o ponto de aplicação da carga, como você pode ver na Figura 2.20.
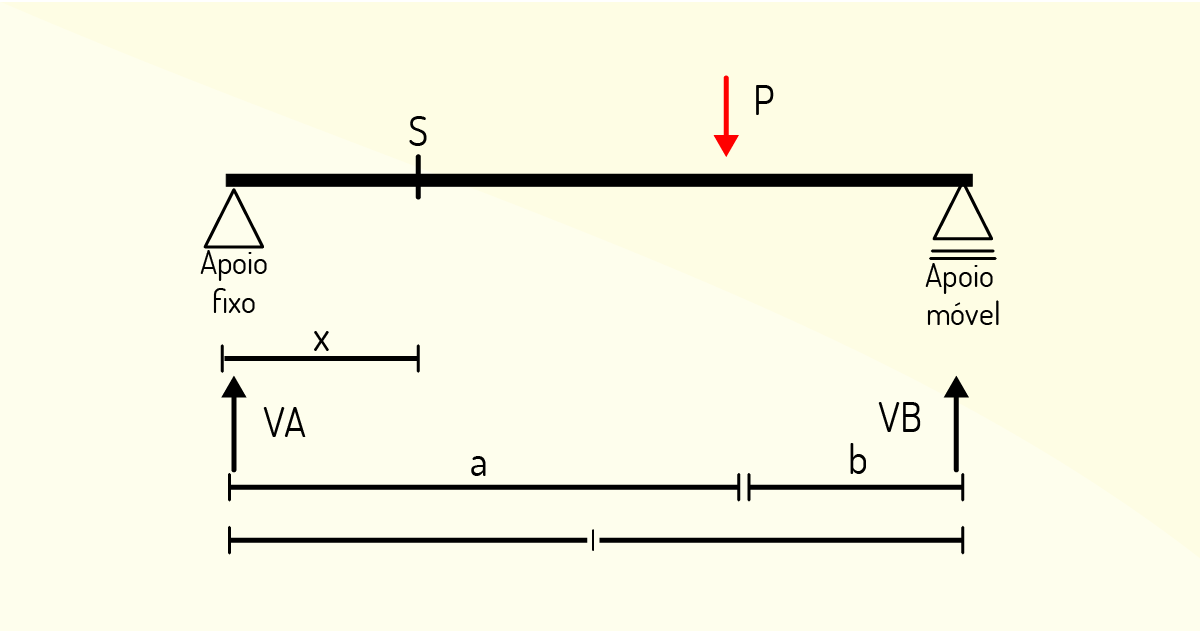
Podemos observar que o valor da descontinuidade do diagrama condiz com o valor da carga concentrada P aplicada (BOTELHO, 1998).
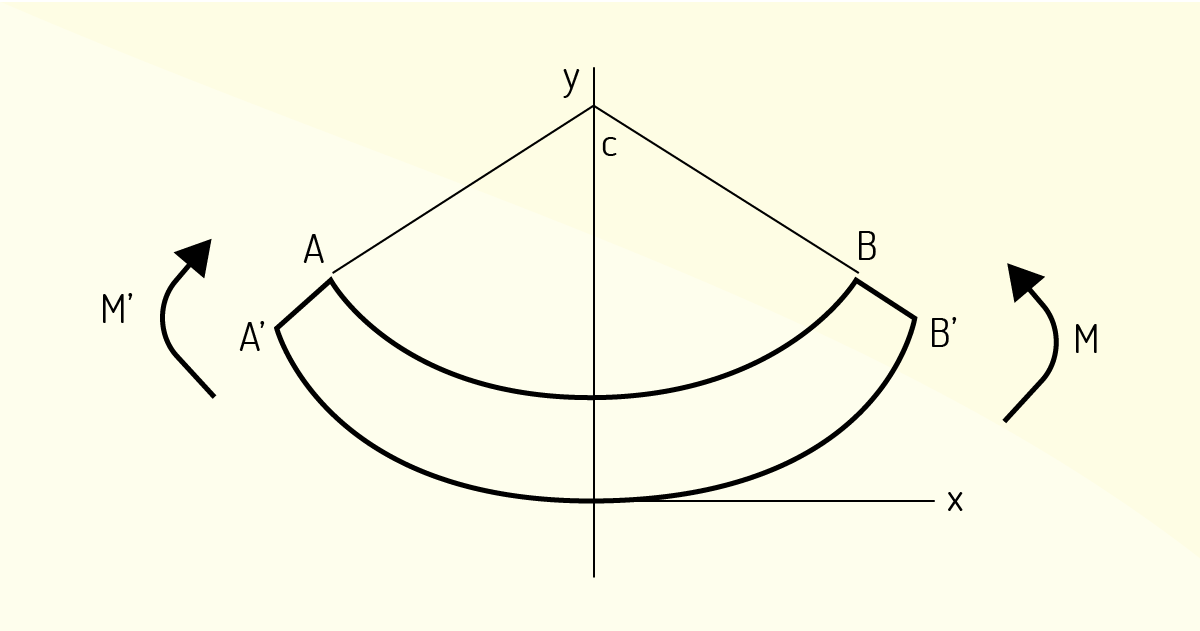
Momento fletor (M) é conhecido como o momento resultante de todas as forças presentes na viga juntamente com os momentos de uma parte isolada sobre a outra na direção transversal ao eixo da viga na seção transversal de corte, ou seja, representa a capacidade de flexionar ou dobrar em uma seção transversal de uma viga.
O momento limite para armadura simples é dado por \({{M}_{d,lim}}=\frac{b.{{d}^{2}}}{{{K}_{c,lim}}}\), em que \({{K}_{c,lim}}\) é valor de kc correspondente ao limite entre os domínios 3 e 4 (ver Tabela 2.1). Verificamos que \({{M}_{d,lim}}=\frac{b.{{d}^{2}}}{{{K}_{c,lim}}}\) explana o momento limite para a armação, na qual kc tem seu valor correspondente entre os domínios 3 e 4 verificáveis na Tabela 2.1.
Tabela 2.1 - Valores de flexão simples para seções retangulares
Fonte: Adaptada de Moreira e Pinheiro (1993, p. 1).
Para o valor de Md,máx ≤ Md,lim podemos utilizar armadura simples; para o valor Md,máx até uma ordem de 1,2 ⋅Md,lim podemos utilizar armadura dupla (para o caso de aço do tipo CA-50). Quando os valores de Md,máx forem máximos, poderemos ou aumentar a seção da viga ou utilizaremos uma seção T como alternativa. Podemos, ainda, reduzir o momento fletor a partir da alteração da vinculação, do vão ou da carga; ou aumentar a resistência do concreto, processo menos viável, pois, geralmente, adotamos a mesma resistência do concreto para todos os elementos estruturais.
Os valores dos momentos fletores serão positivos quando a entrada das forças e momentos à esquerda de uma seção transversal tiverem como resultante de momento na seção o sentido horário. E momentos fletores serão positivos quando a entrada das forças e momentos à direita seção transversal também tiverem como resultante de momento na seção o sentido anti-horário. Para o contrário ao indicado, o momento fletor será negativo.
O diagrama de momentos fletores é uma forma de representar graficamente a variação dos momentos fletores ao longo das seções transversais da estrutura. De modo que, convencionalmente, o desenho é elaborado de maneira que os valores positivos de momentos fletores são traçados ao lado das fibras inferiores da barra/viga e negativos do outro lado. Quando se trata de viga do tipo biapoiada, cuja carga é centralizada, determinamos o seu diagrama a partir das situações (1) e (2) vista em esforços cortantes.
Os cálculos a serem realizados sobre esforço cortante e momento fletor podem gerar bastante dúvidas. Sendo assim, complemente seu estudo assistindo à videoaula “Diagrama de esforços cortantes e momento fletor exercícios resolvidos (passo a passo)”, disponível em: https://www.youtube.com/watch?v=2ECOqeZDGLQ. Acesso em: 08 jan. 2020.

O diagrama de momentos fletores é contínuo, ou seja, com resultados das situações (1), e (2) condizem na seção do ponto de aplicação da carga concentrada P.
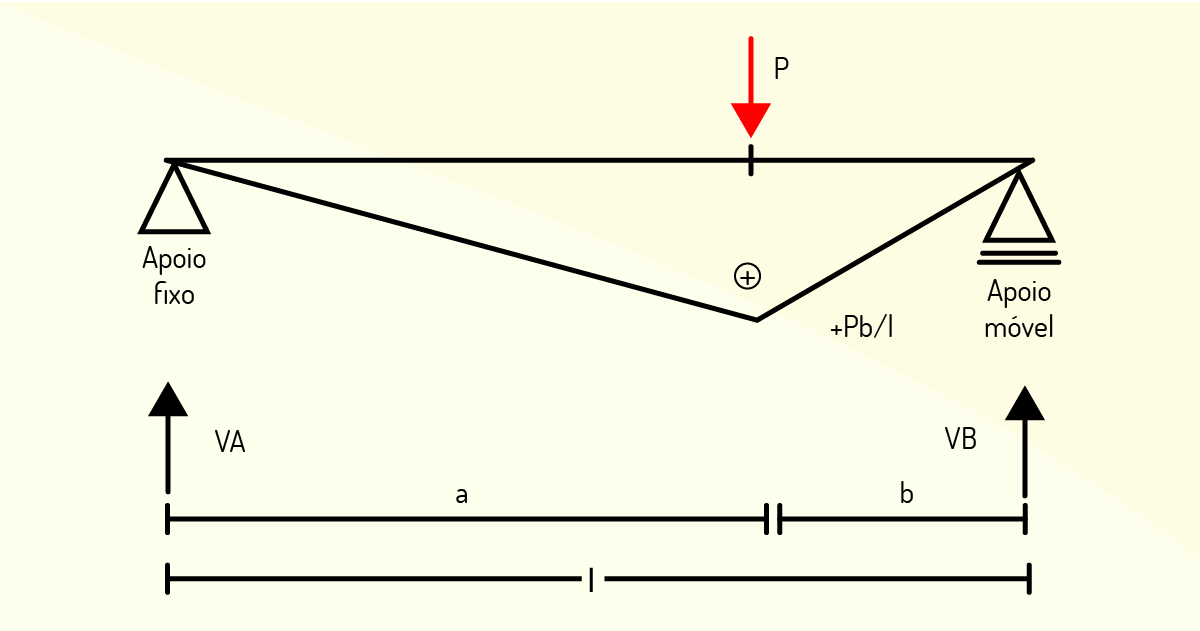
A partir daí, podemos observar também que o diagrama apresenta uma protuberância no ponto de aplicação de P, de modo que o valor máximo de momento fletor para essa seção é dado quando Mmáx = +Pab/l.
Considerando um pequeno elemento distante dx em uma viga, teremos que, diante de uma pequena carga, o momento fletor e o esforço cortante variarão na ordem de x, apresentando valores distintos em relação ao lado direito e esquerdo.
Desse modo, ao estabelecermos o equilíbrio entre as forças presentes nesse segmento da viga, obteremos que sua somatória será descrita por \(\Sigma ~{{F}_{y}}=0\uparrow \oplus \), de modo que \(V-q.dx-\left( V+dV \right)=0\). Logo, podemos deduzir que \(dV=~-q.~dx\) e, portanto, \(\frac{dV}{dx}=-q\). O que nos permite inferir que a taxa de variação do esforço cortante em relação a x terá o valor de -q. E para q com valor de zero, teremos que V apresentará um valor constante.
Em relação à somatória dos momentos, teremos \(\sum{M{{|}_{face\,\,esq.}}=\,0\,\,\oplus}\), de modo que \(-M+\left( M+dM \right)-\left( V+dV \right)-q.dx.\left( \frac{dx}{2} \right)=0\) ou \(-dM+V.dx-dV.dx-q\frac{{{\left( dx \right)}^{2}}}{2}=0\).
Sabendo que os produtos diferenciais são desprezíveis, podemos chegar à seguinte conclusão \(\frac{dM}{dx}=V\), ou seja, verificamos que a taxa de variação do momento fletor em relação a x deverá ser igual ao esforço cortante V para uma carga concentrada atuante na viga.
Logo, fazendo as operações necessárias, podemos chegar à conclusão de que
\(\frac{d}{dx}\left( \frac{dM}{dx} \right)=~-q\) ou \(\frac{d{{~}^{2}}M}{dx{{~}^{2}}}=~-q\). Desse modo, ao considerarmos que o momento máximo ocorrerá para \(\frac{dM}{tdx}=0\), eremos que V = 0.
Considerando agora, uma carga distribuída de modo que a seja maior do que zero e que seu sentido seja positivo quando estiver para baixo \(\downarrow \oplus \), teremos que o esforço cortante será dado por \(V=\frac{a.L}{2}-a.x~\) e \(\frac{dV}{dx}=~-a\). A somatória dos momentos é dada por \(\sum{M{{|}_{5}}}=\,\,0\,\,\,\oplus\), ou seja, \(\frac{a,L}{2}.~x+a\frac{{{x}^{2}}_{{}}}{2}+{{M}_{5}}=0\). , portanto, para \(X=0\to {{M}_{5}}=0,~X=l\to {{M}_{5}}=0~~\) e \(x=\frac{L}{2}\to {{M}_{5}}=\frac{a.~{{L}^{2}}}{8}.\) Vale lembrar que:
“Estudar não é fácil nem tão difícil assim, somente precisamos ser otimistas em encarar tal realidade” – Nelson Ty Napildy.

Um bom material de apoio para melhor entendimento do conteúdo estudado é o livro “Introdução à isostática”, de Eloy Ferraz Machado Junior. O livro está disponível em: http://sinop.unemat.br/site_antigo/prof/foto_p_downloads/fot_8354intboduyyo_y_isostytica_-_eesc_usp_-_eloy_febbaz_machado_juniob_pdf.pdf. Acesso em: 08 jan. 2020.

A seguir, traremos alguns exercícios comentados, a fim de que possam auxiliar no conteúdo que tratamos até aqui. Vamos lá?
Dadas as estruturas a seguir, determine suas reações de apoio.
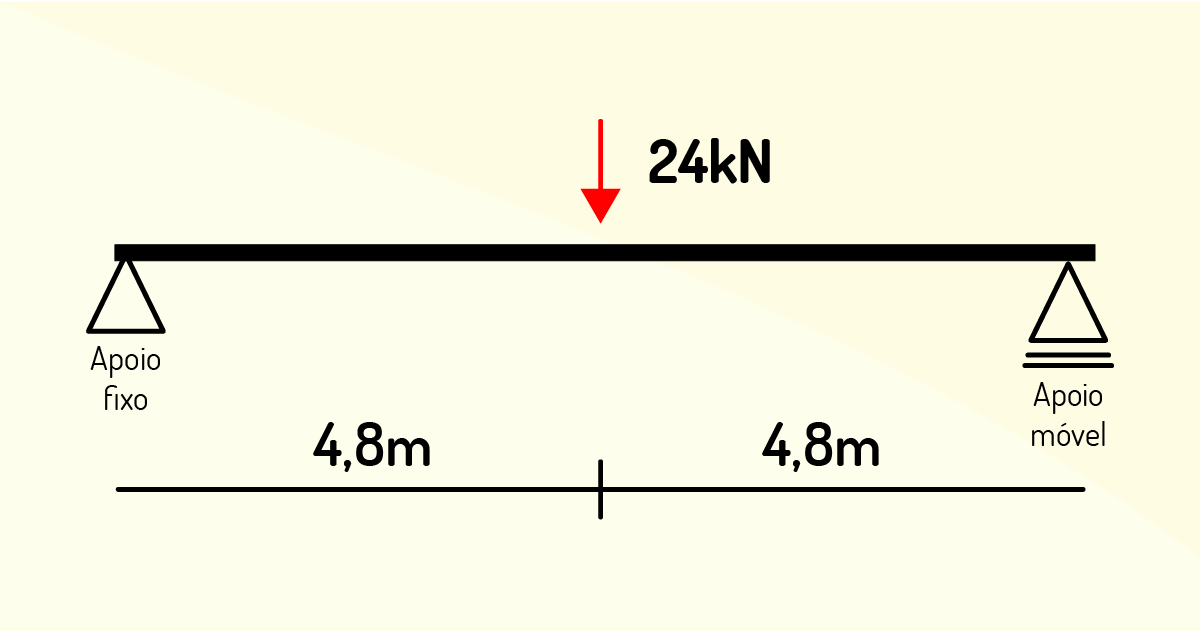
Iniciaremos o exercício indicando as forças e identificando apoios de 1º e 2º gênero, os quais nos darão 2 reações (A\(_x\) e A\(_y\)) e 1 reação (B\(_y\)), respectivamente.
Teremos que encontrar a somatória das forças em x, em y e dos momentos, lembrando que todos são iguais a zero.
Desse momento, em y teremos:
\[Σ Fy = 0, logo, A_y + B_y -24 = 0\]
De modo que \(A_y + B_y = 24\)
Em x, teremos que:
\[Σ F_x = 0, logo, A_x = 0\]
E em termos do momento no ponto A, admitiremos o sentido horário para o giro, e momento como sendo o produto entre a força e o braço de alavanca, temos:
\[Σ MA = 0, logo, 24. 4,8- By.9,6=0\]
De modo que \(B_y = = 12 kN\)
Voltando à equação \(A_y + B_y = 24\)
Teremos que \(A_y + 12 = 24 kN\)
Logo, \(A_y = 12 kN\)
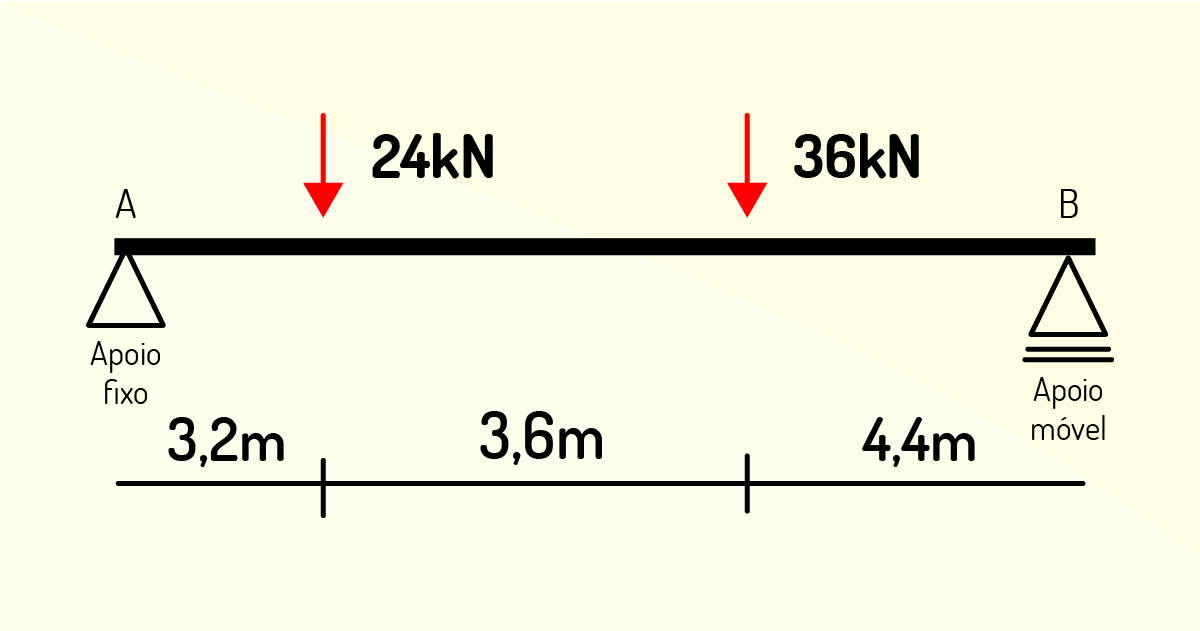
Iniciaremos o exercício indicando as forças e identificando apoios de 1º e 2º gênero, os quais nos darão 2 reações (A\(_x\) e A\(_y\)) e 1 reação (B\(_y\)), respectivamente.
Teremos que encontrar a somatória das forças em x, em y e dos momentos, lembrando que todos são iguais a zero.
Desse momento, em y teremos:
\[Σ F_y = 0, logo, A_y + B_y-24-36=0\]
De modo que \(A_y + B_y= 24+36\)
Logo, \(A_y +B_y= 60\)
Em x, teremos que:
\[Σ F_x = 0, logo, A_x = 0\]
E em termos do momento no ponto A, admitiremos o sentido horário para o giro, e momento como sendo o produto entre a força e o braço de alavanca, temos:
\[Σ MA = 0, logo, 24. 3,2+ 36. (3,2+3,6)- B_y. (3,2+3,6+4,4)=0\]
\(76,8+244,8- By. 11,2=0\)
De modo que \(B_y= = 28,71 kN\)
Voltando à equação \(A_y + B_y = 60\)
Teremos que \(A_y + 28,71 = 60 kN\)
Logo, \(A_y = 31,29 kN\)
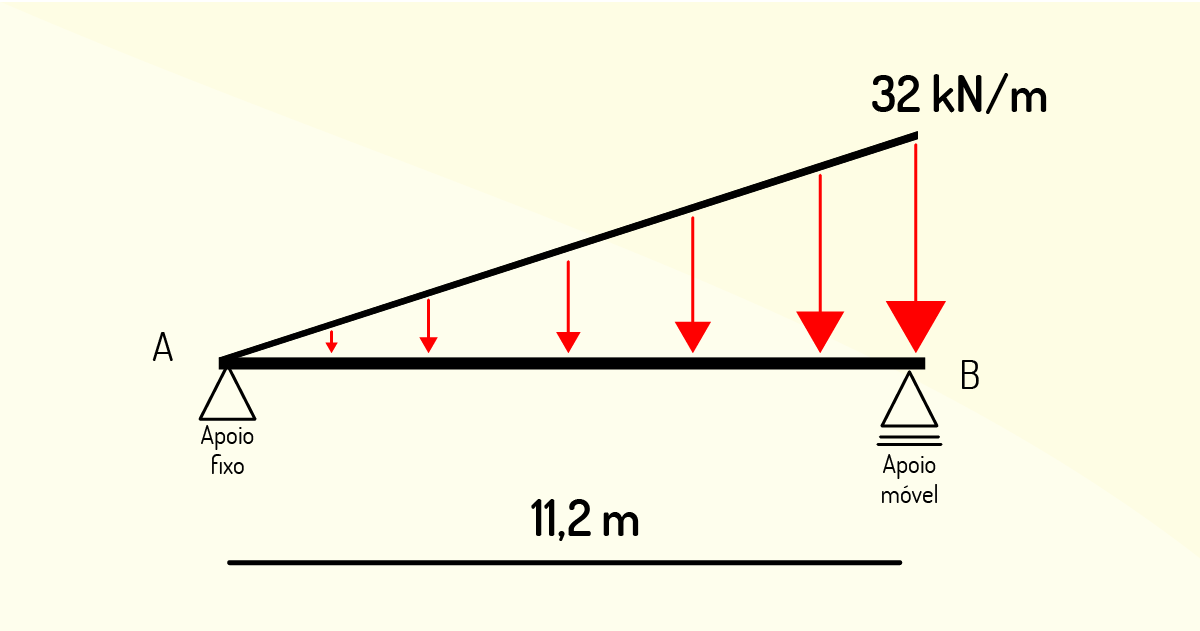
Observando aqui uma carga distribuída triangular com dois apoios, temos que, inicialmente, indicaremos as forças e identificaremos os apoios de 1º e 2º gêneros, os quais nos darão 2 reações (A\(_x\) e A\(_y\)) e 1 reação (B\(_y\)), respectivamente.
Em seguida, devemos decompor a carga triangular em uma força encontrando a área do triângulo evidente: \(A= = =179,2 kN\), a qual será aplicada a 1/3 do lado maior dela.
De modo que = . L, então = . 11,2
Logo = 3,73 m
Vemos que essa será a distância do apoio B na qual a carga estará mais concentrada, sendo assim, podemos tratar o problema como um de carga distribuída simples.
Refazendo os esquemas, teremos que:
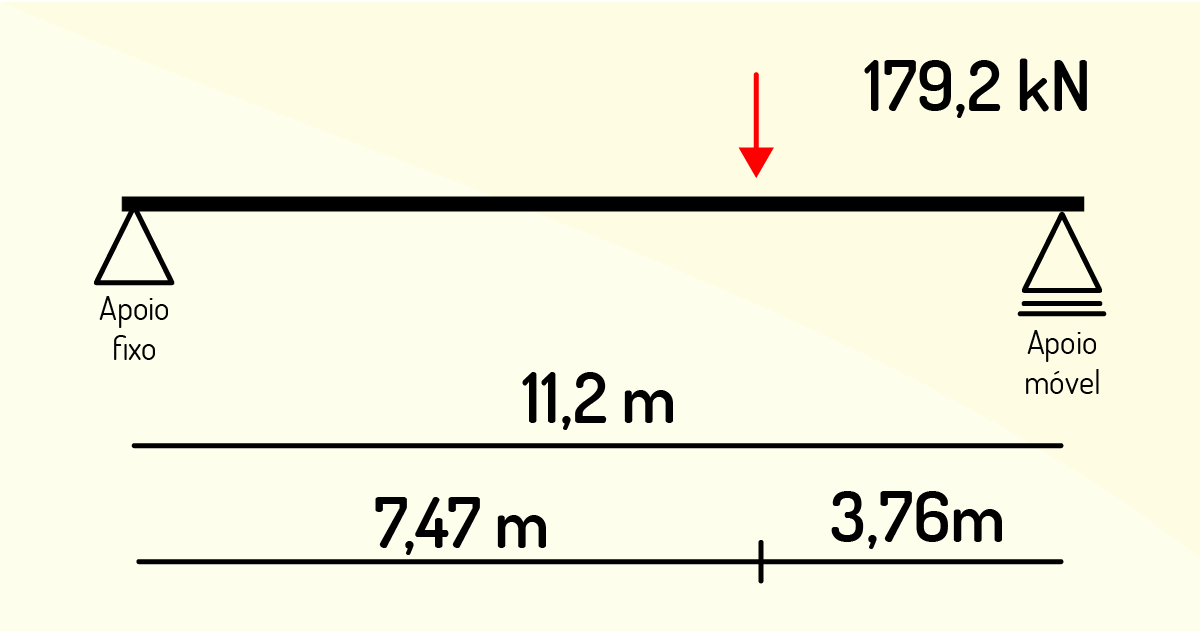
Trataremos de 2 reações (A\(_x\) e A\(_y\)) e 1 reação (B\(_y\)), respectivamente.
Teremos que encontrar a somatória das forças em x, em y e dos momentos. Lembrando que todos são iguais a zero.
Desse momento, em y, teremos:
\[Σ F_y = 0, então, A_y + B_y-179,2 = 0\]
Logo \(A_y + B_y = 179,2 kN\)
Em x, teremos que:
\[Σ F_x = 0, logo, A_x = 0\]
E em termos do momento no ponto A, admitiremos o sentido horário para o giro, e momento como sendo o produto entre a força e o braço de alavanca, assim temos:
\[Σ MA = 0, logo, 179,2. 7,47- B_y .11,2 = 0\]
\(1.338,624- By. 11,2 = 0\)
De modo que \(B_y= = 119,52 kN\)
Voltando à equação \(A_y + B_y = 60\)
Teremos que \(A_y + 119,52 = 179,2 kN\)
Logo, \(A_y = 59,68 kN\)
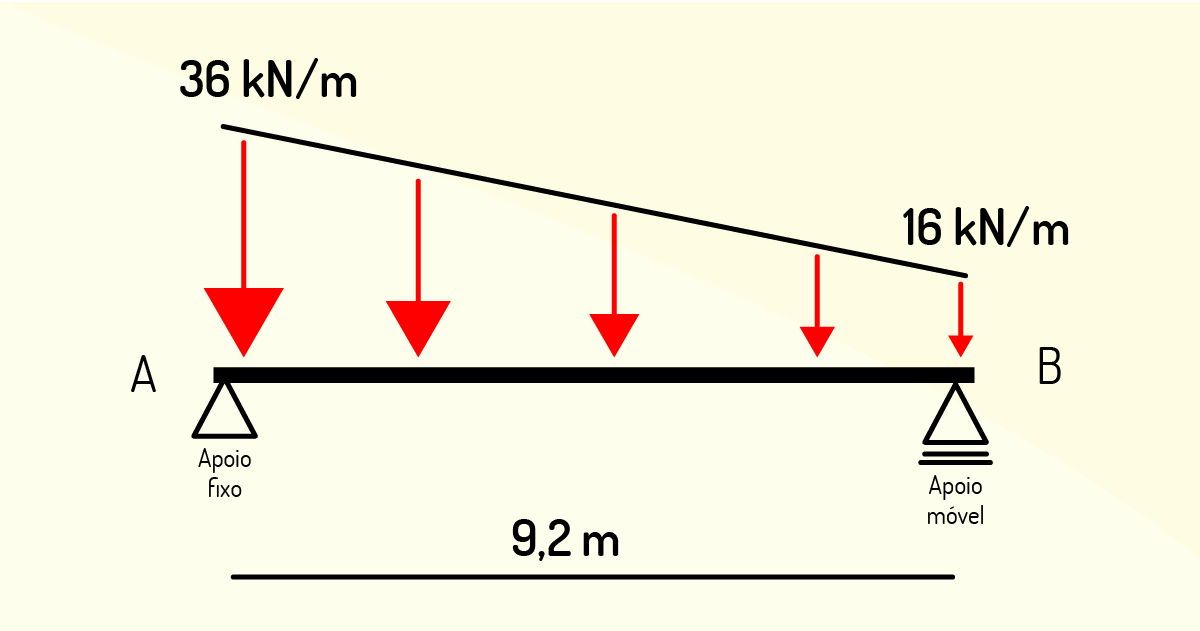
Iniciaremos o exercício dividindo o trapézio em um triângulo e um retângulo (traçar uma linha imaginária na horizontal do trapézio), em seguida, encontraremos as áreas das novas figuras geométricas.
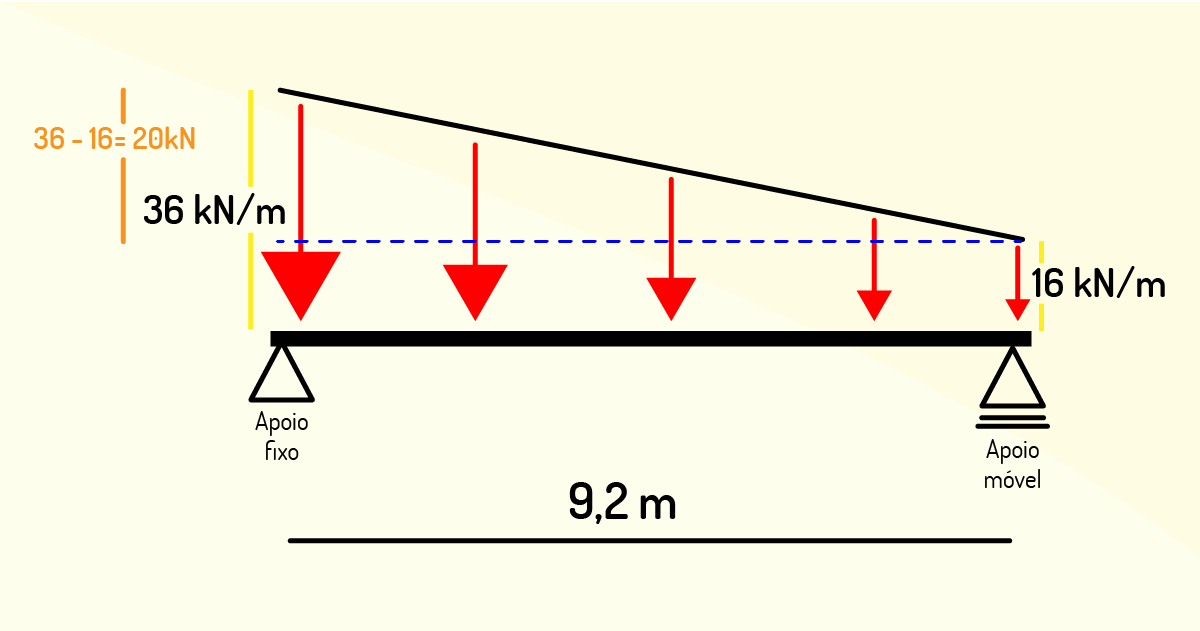
A área do retângulo é dada por \(A = b.h\), de modo que \(A = 9,2.16 = 147,2 kN\) (valor da força concentrada no retângulo considerado).
A área do triângulo é \(A= = = 92 kN\) (valor da força concentrada no triângulo considerado).
Agora, encontraremos as posições nas quais aplicaremos essas forças.
No triângulo, teremos que = . L, então = . 9,2
Logo = 3,06 m
No retângulo, teremos . L, então = . 9,2
Logo = 4,6 m
Refazendo os esquemas, teremos que:
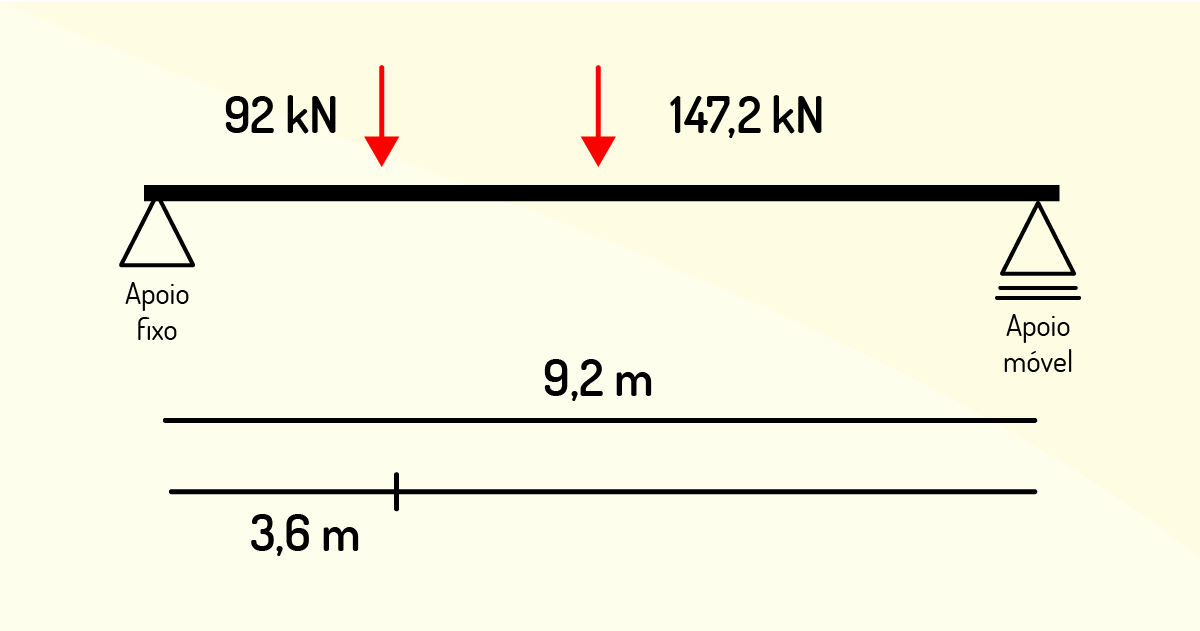
Trataremos de 2 reações (A\(_x\) e A\(_y\)) e de 1 reação (B\(_y\)), respectivamente.
Teremos que encontrar a somatória das forças em x, em y e dos momentos, lembrando que todos são iguais a zero.
Desse momento, em y, teremos:
\[Σ F_y = 0, então, A_y + B_y-147,2-92=0\]
Logo, \(A_y + B_y= 239,2 kN\)
Em x, teremos que:
\[Σ F_x = 0, logo, A_x = 0\]
E em termos do momento no ponto A, admitiremos o sentido horário para o giro e momento como sendo o produto entre a força e o braço de alavanca, temos:
\[Σ MA = 0, logo, 92. 3,06+ 147,2. 4,6- B_y .9,2=0\]
\(958,64 - B_y. 9,2=0)
De modo que \(B_y= = 104,2 kN\)
Voltando à equação \(A_y + B_y = 239,2\)
Sabe-se que \(A_y + 104,2 = 239,2 kN\)
Logo, \(A_y = 135 kN\)
Considere uma viga com 13 m de comprimento, com um apoio móvel e um apoio fixo (em suas extremidades). Agora, assinale a alternativa correta sobre esforço cortante e momento fletor da viga para o caso dela estar submetida a uma carga distribuída de 1 tonelada de força por metro.
A reação Ay será de 4,5 toneladas força e a reação By também será de 4,5 toneladas força.
Incorreta. Visto que, como se trata de dois apoios, a carga será dividida por dois, logo Ay terá uma carga de 6,5 toneladas força e By também terá uma carga de 6,5 toneladas força, já que a carga concentrada inicial era de 1.13 = 13 toneladas força.
A força cortante V para x = 13m terá valor de - 6,5 N.
Correta. Dado que a somatória das forças em y é igual a zero, teremos que V + x - 6,5 = 0, logo, considerando x = 13, teremos que V = - 6,5 N.
A somatória das forças em x será igual a 10 N.
Incorreta. Pois não há nenhuma força em x, logo a normal neste caso será zero.
O momento fletor para x = 13 m terá valor de 21 N.m.
Incorreta. Pois a soma dos momentos será igual a zero, assim M + x . X/2 - 6,5.x = 0, logo M = (-x/2)²+ 6,5x, em que, para x = 13, temos M = 0 N.m.
Como o momento é dado por M + x . X/2 - 6,5 . x = 0, teremos que sua representação será uma parábola côncava para baixo.
Incorreta. Pois, ao desenharmos o diagrama de momento fletor, é necessário que se faça a troca de sinais, de modo que a parábola M + x . X/2 - 6,5 . x = 0 ficará côncava para cima.
Cabos são elementos estruturais extensos, delgados e flexíveis em toda sua extensão, ou seja, articulados; projetados para suportar cargas axiais. A principal diferença entre um cabo e um fio está na área de secção transversal (a região determinada pela intersecção do cilindro com um plano paralelo às bases), de modo que os cabos a apresentam maior e por isso são capazes de suportar maiores cargas.
Existem duas categorias para os cabos, as quais estão de acordo com o seu carregamento:
Ao analisarmos como as cargas se comportam nos cabos, percebemos que, no caso de estarem distribuídas, as linhas de pequena flecha integradas à suspensão parabólica se comportam como se as cargas se distribuíssem uniformemente ao longo do vão, o que na realidade não acontece, visto que são distribuídas ao longo do fio. No caso dos cabos utilizados em pontes suspensas, julgamos que estão carregados, pois seu peso é muito pequeno comparado com o peso do tabuleiro. Sendo assim, para melhor entendermos essa dinâmica das cargas, faz-se necessário o estudo das forças nesses cabos.
Analisando a Figura 2.30, percebemos que se trata de um cabo flexível, cuja resistência à flexão pode ser desprezada, preso a dois pontos fixos A e B, e sujeito a três cargas concentradas verticais Q1, Q2 e Q3. O peso do cabo é desprezível diante das cargas que suporta. De modo que as forças internas em qualquer ponto do cabo são reduzidas a uma força de tração cuja direção é tangencial ao cabo nesse ponto.
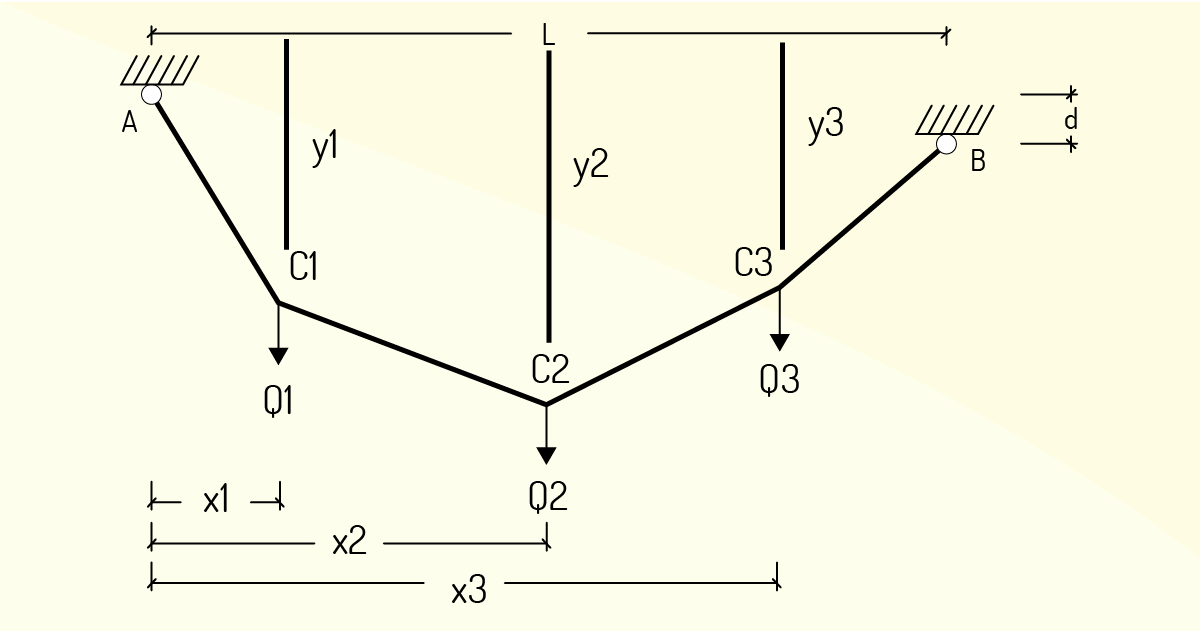
Acima temos que L é o comprimento do vão, d é o desnivelamento vertical entre os apoios; x1, x2 e x3 são as distâncias existentes entre as forças e os apoios; e x e y posições de um qualquer ponto P, a partir dos quais é possível calcular outras grandezas, como VA, HA, VB e HB, as quais são as reações de apoio; y1, y2 e y3, os quais são configurações do cabo e até mesmo o comprimento total do cabo.
Um bom material de apoio para melhor entendimento deste conteúdo é a dissertação de mestrado “Análise de tensões e deformações em fios de cabos condutores de linhas de transmissão”, de Eduardo Luis Souza de Athayde Nunes Filho, disponível em: http://repositorio.unb.br/bitstream/10482/21494/1/2016_EduardoLuisSouzadeAthaydeNunesFilho.pdf. Acesso em: 08 jan. 2020.

Na Figura 2.31, podemos observar o diagrama de corpo livre no qual são evidenciadas as forças para todo cabo.
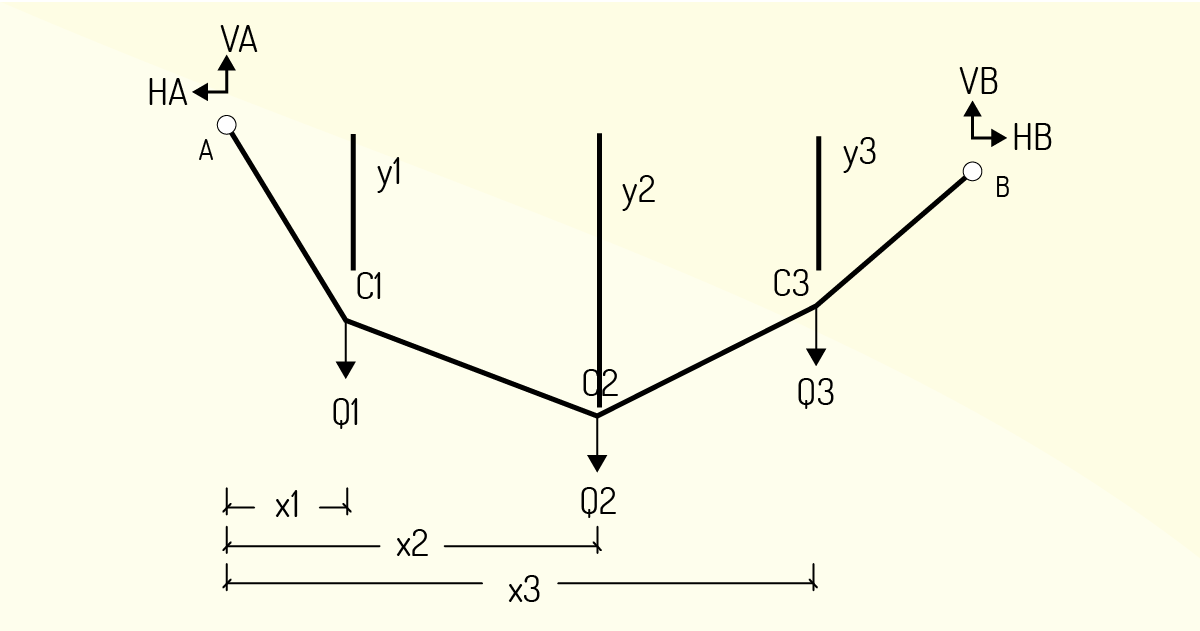
A partir do diagrama de corpo livre de todo o cabo, podemos inferir que:
\(∑MA = 0 ou ∑MB = 0,\)
\(∑Fx = 0 e ∑Fy = 0 \)
Na Figura 2.32, podemos observar o diagrama de corpo livre no qual ficam evidenciadas as forças para o trecho de A até o ponto P.
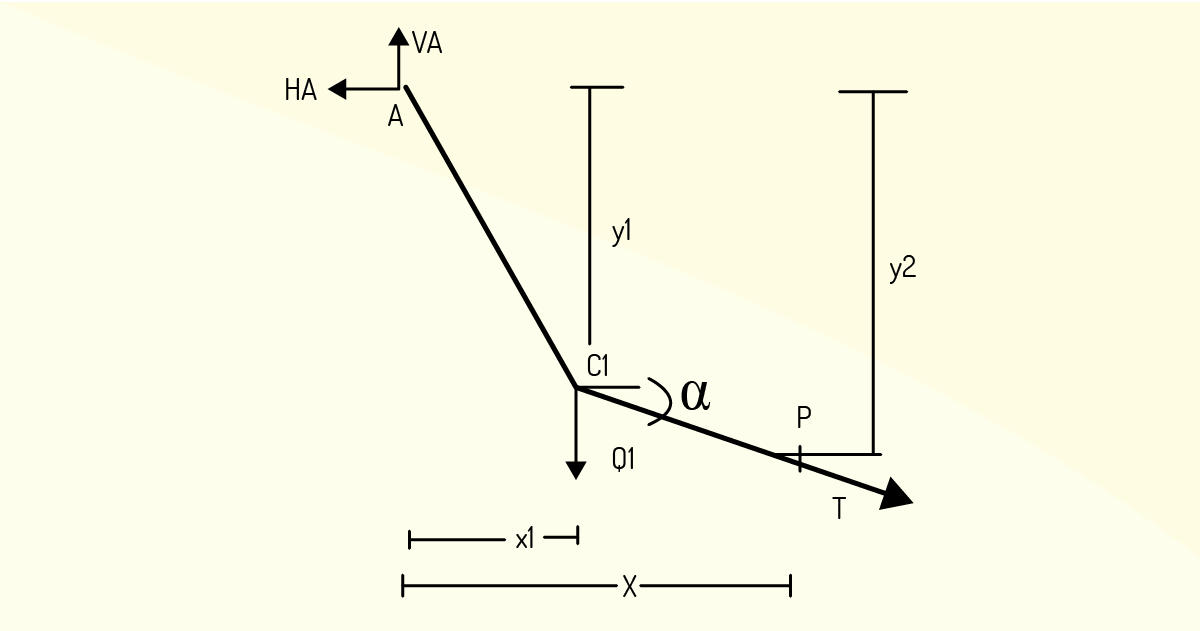
A partir do diagrama de corpo livre do trecho AP, podemos concluir que ∑MP = 0.
A partir das conclusões explanadas nas Figuras 2.31 e 2.32, podemos calcular as reações de apoio para o cabo em questão, de modo que, para calcularmos cada uma das ordenadas y1, y2 e y3 dos pontos C1, C2 e C3, precisamos considerar:
No diagrama de corpo livre de um trecho qualquer do cabo, teremos que a equação ∑Fx = 0 conduzirá à T cos α = HA = HB, ou seja, a componente horizontal da força de tração terá o mesmo valor em qualquer ponto do cabo. Desse modo, podemos concluir que a força de tração T será máxima e cos α será mínimo, portanto, o trecho de maior inclinação será aquele adjacente a um dos dois apoios.
Um cabo flexível preso às duas extremidades (A e B), ao estar sujeito a uma carga distribuída, apresenta uma configuração curvilínea e força interna em dado ponto igual à força de tração, cuja direção é tangencial à curva.
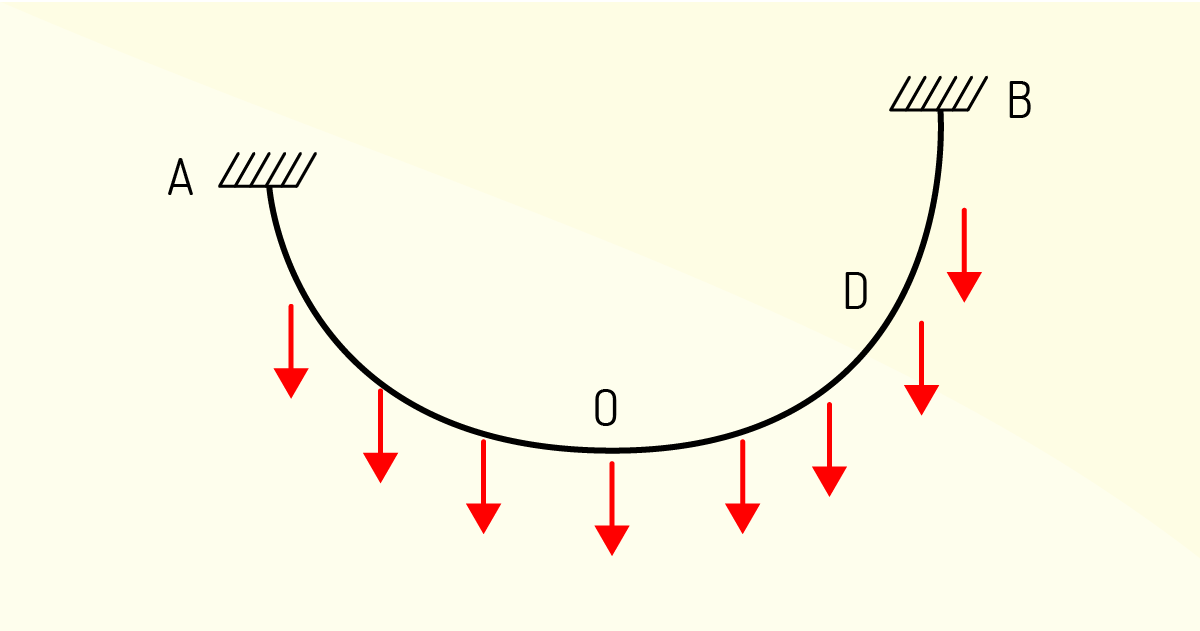
Ao analisarmos o intervalo do ponto mais baixo do cabo ao ponto D por meio do diagrama de corpo livre, percebemos que há forças de tração T para horizontal (To) e tangencial à curva D (T), além da presença da força resultante P devido à carga distribuída suportada pelo trecho OD.
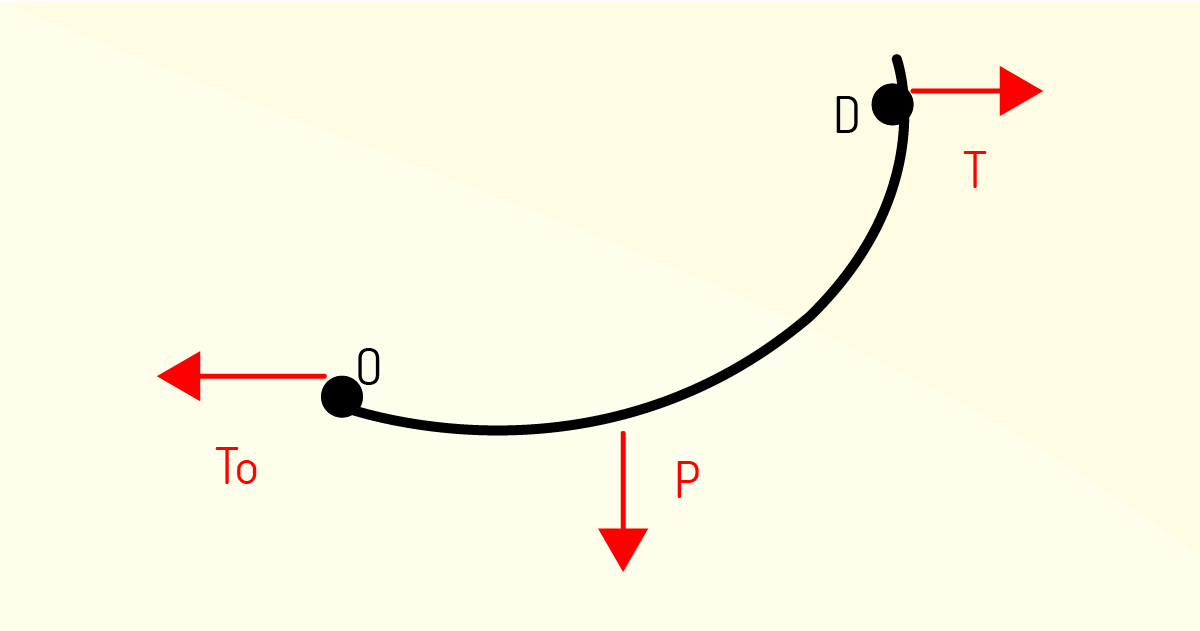
Sabendo que o sistema está em equilíbrio e encontrando por meio do Teorema de Pitágoras a relação poligonal para os vetores, chegamos às seguintes relações:
\[Tcos~\theta ={{T}_{0}}\]
\[Tsen~\theta =P\]
\[T{{\left( T_{0}^{2}+{{P}^{2}} \right)}^{\frac{1}{2}}}^{{}}\]
\[tg~\theta =\frac{P}{{{T}_{0}}}\]
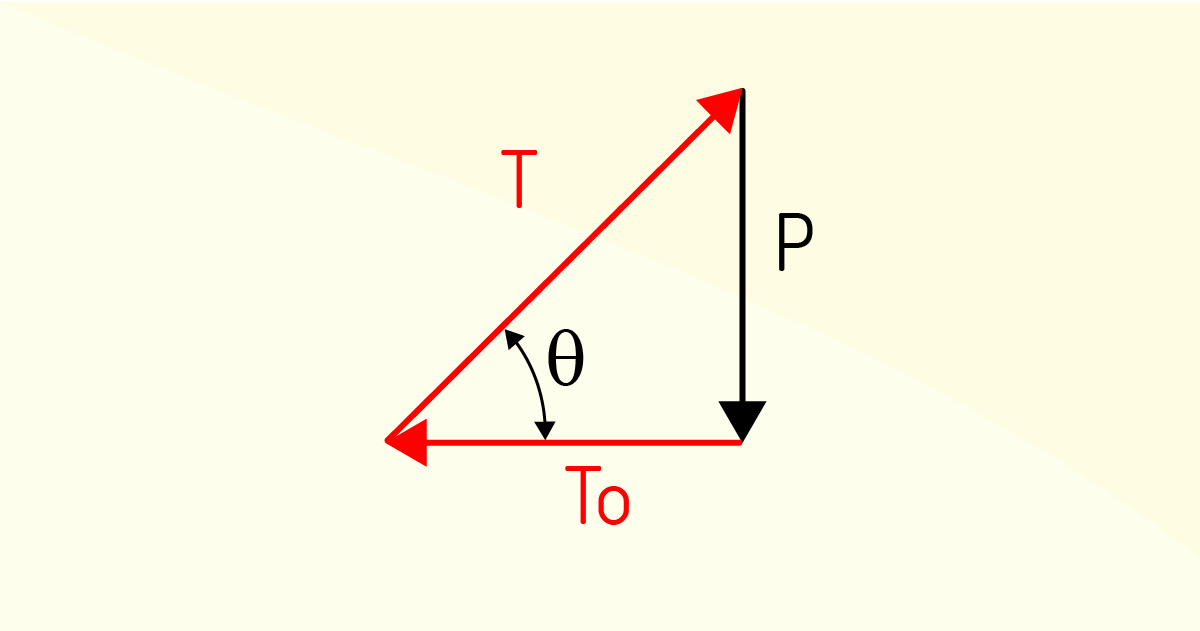
A partir do que foi visto até então, podemos concluir que o componente horizontal da força de tração será o mesmo em qualquer ponto do cabo; a tração mínima está exatamente no ponto mais baixo do cabo no qual θ = 0 tende a cos θ = 1, e a força de tração máxima encontra-se em um dos pontos fixos do cabo.
Calcular as grandezas de tração mínima e máxima em um cabo e seu comprimento não são tarefas fáceis. Confira as dicas de conteúdo e exercícios resolvidos dos slides sobre cabos flexíveis dos professores Leonardo Goliatt e Alexandre Curry, para a disciplina de Resistência dos Materiais, disponível em: http://www.ufjf.br/mac015/files/2015/02/cabos-2.pdf. Acesso em: 08 jan. 2020.

Supondo uma nova situação ilustrada na Figura 2.36, percebemos que o cabo AB suporta uma carga uniformemente distribuída chamada de p, ao longo da direção horizontal.
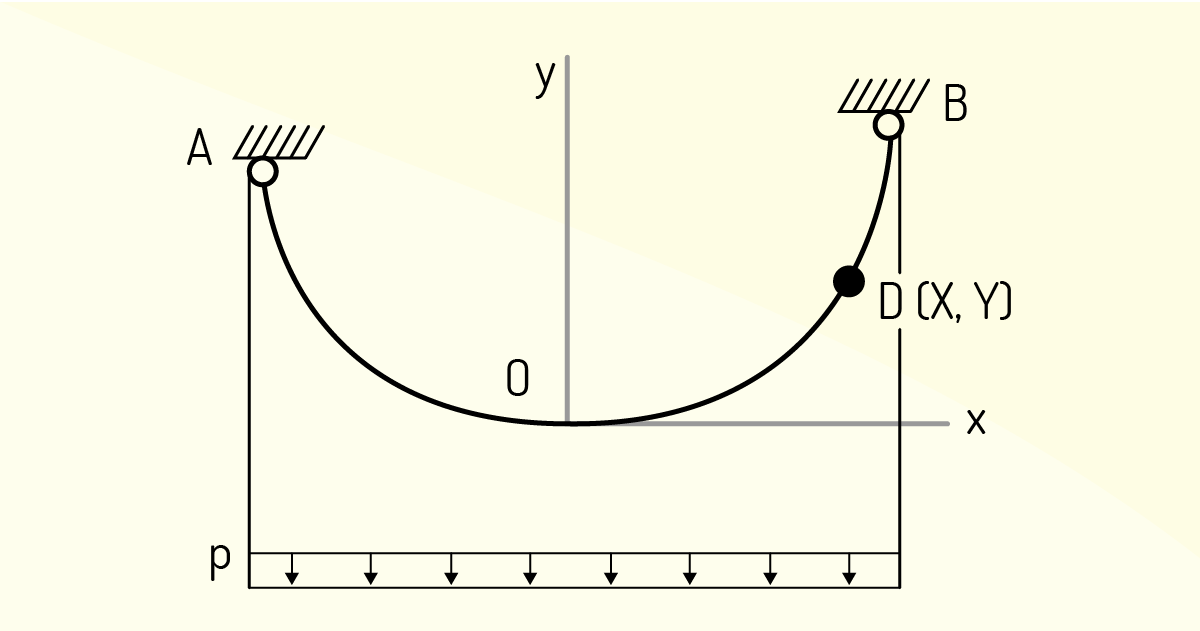
De modo que seu diagrama de corpo livre é ilustrado na Figura 2.37, do intervalo entre o ponto mais baixo O e um outro ponto qualquer chamado de D.
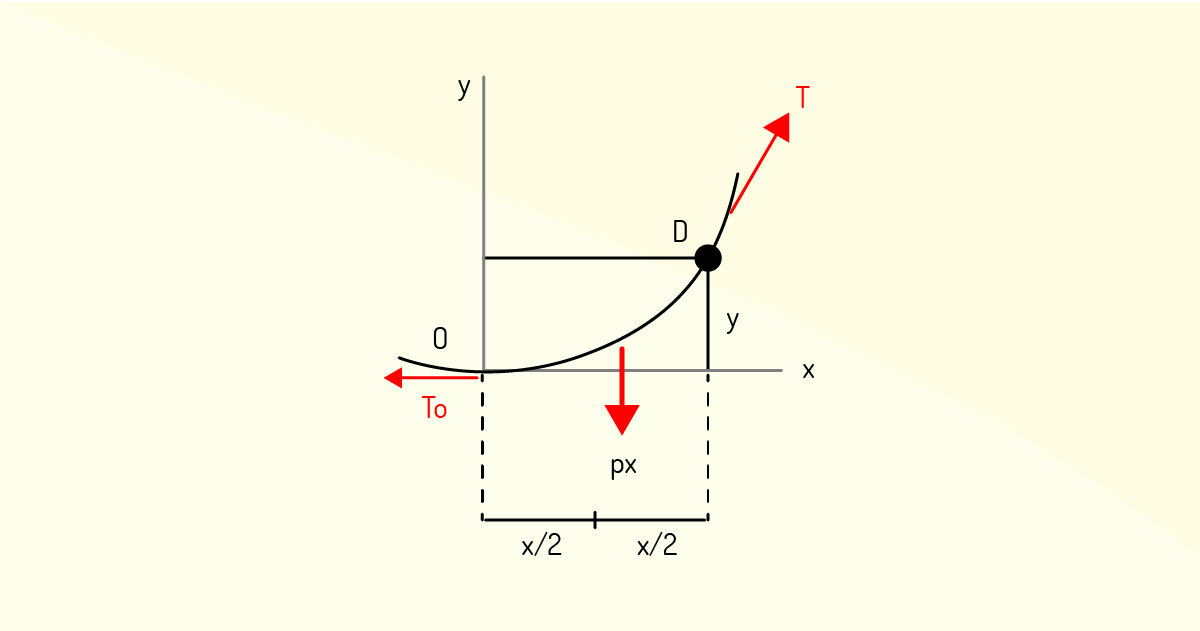
Lembrando que ∑M D = 0, então, teremos \(px~\frac{x}{2}-{{T}_{0}}~y=0\), de modo que \(y=p\frac{{{x}^{2}}}{2}{{T}_{0}}\), a qual descreve uma parábola com eixo vertical e vértice na origem das coordenadas.
A partir da análise da Figura 2.38, podemos concluir que o vão é dado pela distância horizontal L entre os apoios do cabo, e a flecha é dada pela projeção vertical da distância adotada h desde os apoios ao ponto mais baixo do cabo. De modo que podemos calcular o comprimento do cabo desde o seu ponto mais baixo O até o apoio B por meio da série: \({{S}_{B}}={{X}_{B}}\left[ 1+\frac{2}{3}{{\left( \frac{{{Y}_{B}}}{{{X}_{B}}} \right)}^{2}}-\frac{2}{5}~{{\left( \frac{{{Y}_{B}}}{{{X}_{B}}} \right)}^{4}}+.... \right]\), de maneira que, para valores de yB/xB menores do que 0,5, seja necessário calcular apenas os dois primeiros termos da série.
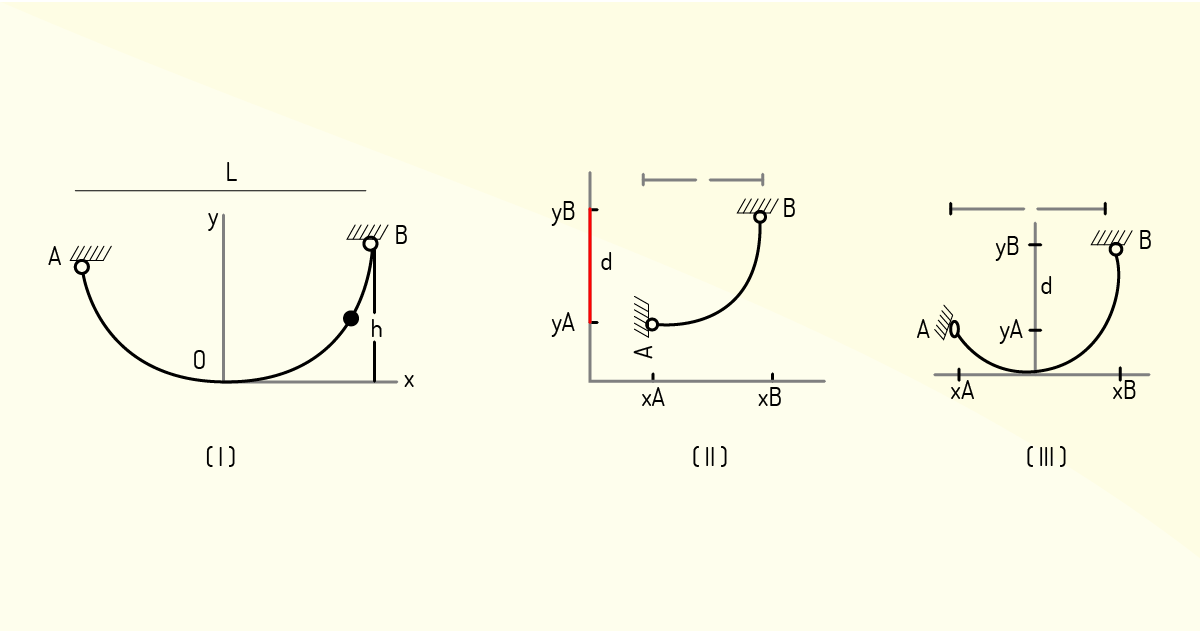
Resumindo:
“Você nunca será a pessoa que você pode ser se a pressão, tensão e disciplina forem tiradas da sua vida” – James Bilkey.

Para saber mais sobre a análise estrutural I e conhecer os parâmetros que influenciam a concepção de sistemas estruturais, os esforços internos em estruturas isostáticas (treliças, vigas, pórticos, dentre outros) e o estudo de cargas móveis em estruturas isostáticas; além de exercícios resolvidos, acesse o material a seguir, do Departamento de Engenharia Civil da Universidade Federal de Santa Catarina, dos autores Ângela do Valle, Henriette Lebre La Rovere e Nora Maria De Patta Pillar. Disponível em: http://pet.ecv.ufsc.br/arquivos/apoio-didatico/ECV5219%20-%20An%C3%A1lise%20Estrutural%20I.pdf. Acesso em: 08 jan. 2020.

Considere que um cabo de luz pode suportar uma massa de 10 kg por metro linear, e que este se encontra suspenso nos pontos A e B, no mesmo nível, separados a 200 m de distância, e que a flecha no meio do vão é 30m. Agora, assinale a alternativa correta a respeito desse cabo.
A carga por comprimento linear será de 110 N/m.
Incorreta. Pois o valor da carga por comprimento linear será o valor da massa vezes a aceleração da gravidade na Terra, logo será 10.9,8 = 98 N/m.
A tração máxima no cabo terá valor de 28 kN.
Incorreta. Visto que a tração máxima é dada pela raiz quadrada de T0² + (wl)², temos Tmáx= ((16.333,33²)+ ((98. 100)²))^(½)= 362.817.66 N ou 36,28 kN.
A tração máxima ocorrerá somente no cabo de sustentação A.
Incorreta. Visto que, por se tratar de um cabo simétrico, teremos que a tração máxima ocorrerá tanto no cabo A quanto no cabo B.
O comprimento do cabo será de 215 m.
Incorreta. Pois, como a razão h/l= 0,3, ou seja, < 05, temos que o comprimento do cabo pode ser calculado a partir da série: S = l (1+ ⅔. (h/)l² - ⅖ (h/l)\(^4\) + ..., de modo que S = 100 (1 + ⅔. (30/100)² - ⅖ (30/100)\(^4\) = 100.(1,06-3,24x10\(^{-3}\)) = 100 . 105676 =105,676 m., e como o comprimento do cabo é igual a 2.S, temos que S = 211,352 m.
A tração mínima desse cabo será igual a 16,33 kN.
Correta. Sabendo que a tração mínima é dada por T0 = (w.L²)/ 2.h, temos que T0 = (98.(100²))/2.30 = 16.333, 33 N, ou 16,33 kN, como descrito na alternativa.
Nome do livro: Resistência dos materiais
Editora: Pearson
Autor: Russel C. Hibbeler
ISBN: 9788587918673
Livro bastante completo e importante referência no estudo de resistência dos materiais, aborda os temas estudados nesta unidade e muito outros, extremamente relevantes para sua formação, trazendo conteúdo de ótima qualidade, ilustrações de fácil entendimento e exercícios que instigam o aprendizado.

Nome do filme: A Travessia
Gênero: biografia, drama, aventura
Ano: 2015
O filme trata da vida do equilibrista Philippe Petit e suas aventuras para esticar um cabo de aço nos mais variados lugares, como a capela de Notre Dame e as torres gêmeas do World Trade Center. Nele, podemos verificar a força de tração em um cabo de aço, o uso de algumas estruturas em construções, além de enriquecer nosso conhecimento cultural.
