Caro(a) aluno(a), nesta unidade, iremos nos deparar com sistemas contendo uma distribuição de carga ao longo de um comprimento, área ou volume. No tópico I, serão propostos conceitos sobre centroide ou baricentro, determinação do centro de gravidade de uma figura plana, por exemplo, além dos casos que envolvam um conjunto de massas. No tópico II, serão introduzidos conceitos da utilização de integrais para determinar o centro de gravidade de determinadas figuras planas e espaciais. Já no tópico III, serão desenvolvidos mecanismos para determinar o momento de inércias para essas figuras. Aqui, será introduzido o teorema dos eixos paralelos, além de proposto um exemplo sobre sistemas que envolvam mudanças de coordenadas para coordenadas polares. No último tópico, chegaremos aos casos que envolvam momento de inércia de corpos volumétricos.
Centroides têm como definição o centro geométrico de uma figura. O centro geométrico coincide com o centro de massa de um corpo quando a forma geométrica for homogênea. Baricentro, por sua vez, pode ser entendido como o ponto em que há um equilíbrio de forças sobre ele.
Durante uma aula de física, um aluno começa a brincar com seu livro tentando equilibrar apenas com um dedo. Depois de muitas tentativas, ele consegue. Ao encontrar o ponto de equilíbrio, ou seja, o ponto onde o peso resultante do corpo está localizado, o aluno conseguiu equilibrar o livro em seu dedo na vertical, como visto na Figura 3.1. A esse ponto, damos o nome de centro de gravidade, centro de massa ou centroide.

Sobre centro de gravidade, alguns autores propuseram definições importantes. Para Lehmkuhl e Smith (1989), centro de gravidade é o único ponto de um corpo onde as partículas ao redor estão igualmente distribuídas. Já para Watkin (2001), centro de gravidade é um ponto por meio do qual a linha de ação do peso de um objeto atua, independentemente da posição dele. Por fim, Okuno e Fratin (2003, p. 93) propõem que centro de gravidade seja o local em um corpo onde é aplicada a resultante das forças-peso, como se toda a massa do corpo estivesse concentrada nesse ponto.
Depois das definições propostas, centro de gravidade (CG) é o ponto onde pode ser considerada a ação das forças de atração gravitacional, a força peso, como podemos ver na Figura 3.2.
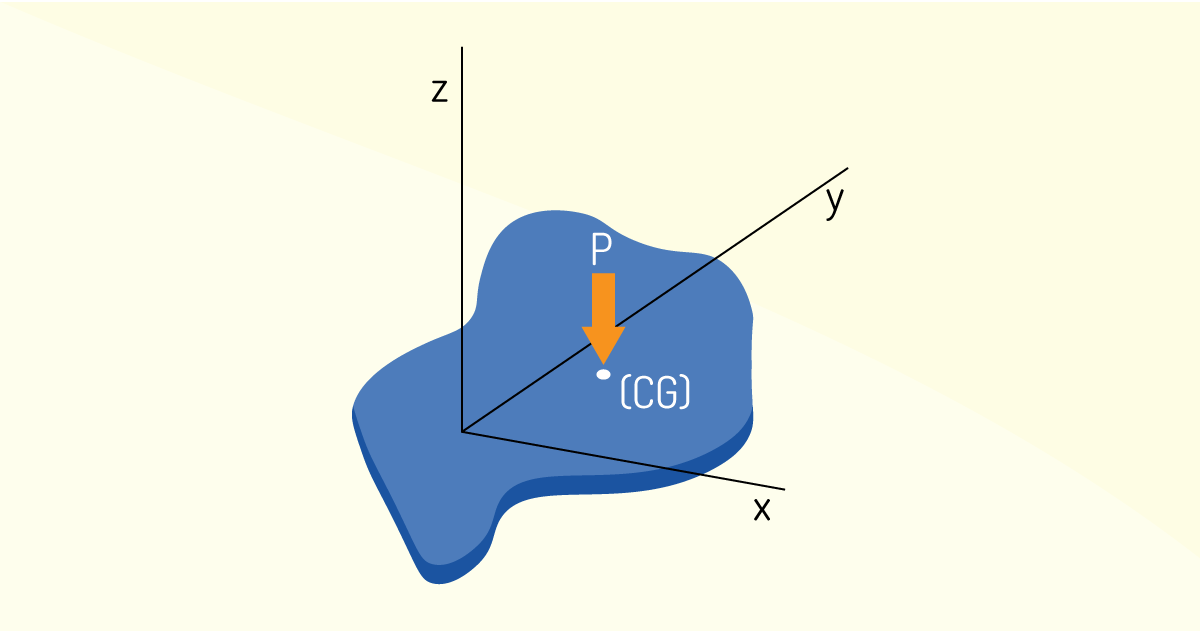
A determinação do centro de gravidade para um sistema de uma ou duas dimensões pode ser feita, como podemos ver a seguir.
Um sistema contendo três partículas, como mostra a Figura 3.3, está em equilíbrio.

Quanto maior o peso da partícula, como no caso da partícula 3, maior será a influência desta na determinação do centro de gravidade do sistema. Na Figura 3.4, temos uma ilustração das partículas e suas respectivas distâncias até o centro de gravidade. Como é possível notar, a posição de equilíbrio, ou seja, o centro de gravidade, estará mais próxima da partícula de maior massa, como era de se esperar.
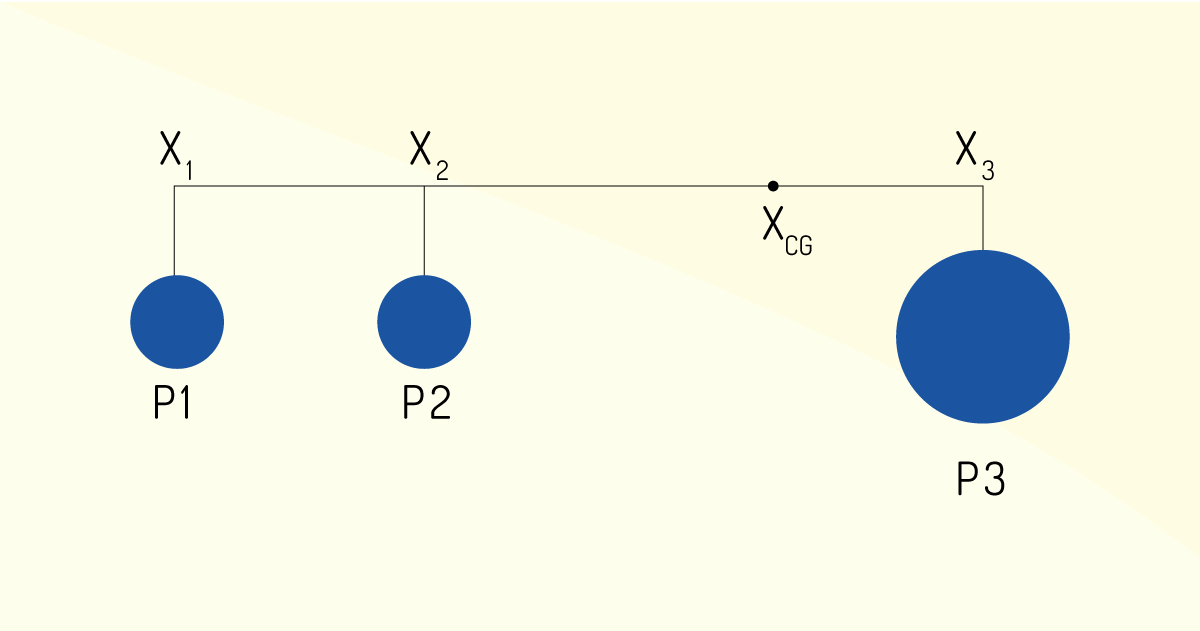
Matematicamente, a coordenada do centro de gravidade pode ser determinada por uma média ponderada em função dos pesos de cada uma das partículas, como a seguir:
\[~{{X}_{CG}}=\frac{{{P}_{1}}.{{X}_{1}}+~{{P}_{2}}.{{X}_{2}}~+~{{P}_{3}}.{{X}_{3}}}{{{P}_{1}}+{{P}_{2}}+{{P}_{3}}}\]
Um sistema composto por uma figura geométrica não regular pode ser dividido em pequenas figuras regulares, como na Figura 3.5.
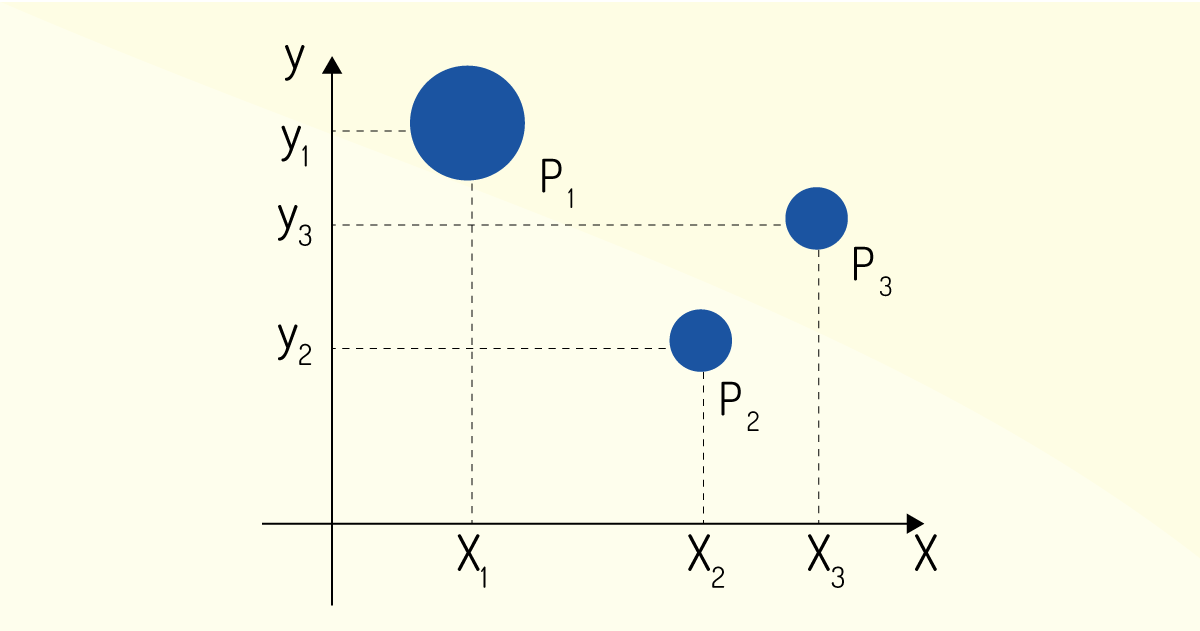
Após a divisão, a determinação do centro de gravidade pode ser encontrada ao considerar um novo sistema de várias partículas.
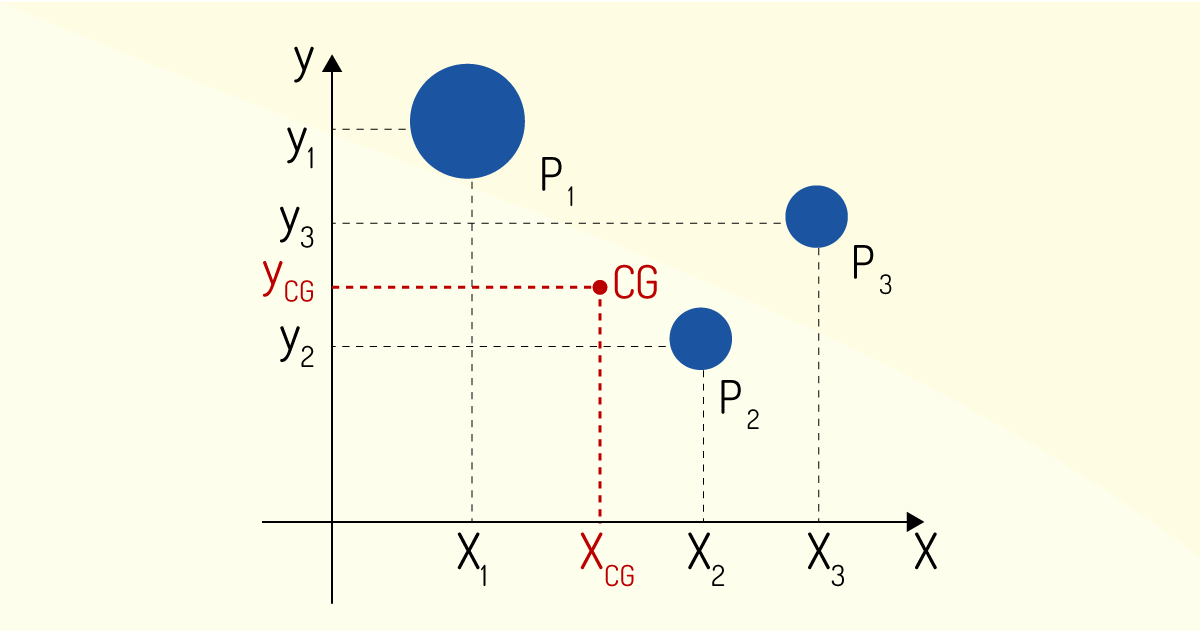
Matematicamente, o centro de gravidade do sistema apresenta coordenadas em x e y, e pode ser encontrado, como podemos ver a seguir:
\[~{{X}_{CG}}=\frac{{{P}_{1}}.{{X}_{1}}+~{{P}_{2}}.{{X}_{2}}~+~{{P}_{3}}.{{X}_{3}}}{{{P}_{1}}+{{P}_{2}}+{{P}_{3}}}\]
\[~{{Y}_{CG}}=\frac{{{P}_{1}}.{{y}_{1}}+~{{P}_{2}}.{{y}_{2}}~+~{{P}_{3}}.{{y}_{3}}}{{{P}_{1}}+{{P}_{2}}+{{P}_{3}}}\]
Corpo homogêneo: possuir a mesma natureza ou a mesma substância em qualquer parte do corpo.
Corpo isotrópico: possuir as mesmas propriedades físicas em qualquer parte do corpo.
A determinação do centro de gravidade de figuras planas, como na Figura 3.7, pode ser feita da seguinte forma: o primeiro passo para se determinar o centroide e o baricentro de uma figura é projetá-la em um plano cartesiano e orientá-la a partir do plano.

Ao orientar a figura no plano cartesiano, é possível dividir a figura geométrica em pequenas figuras regulares de áreas conhecidas. Depois de dividi-las em pequenas áreas, é possível determinar o centro de gravidade de cada figura individualmente, como visto na Figura 3.8.
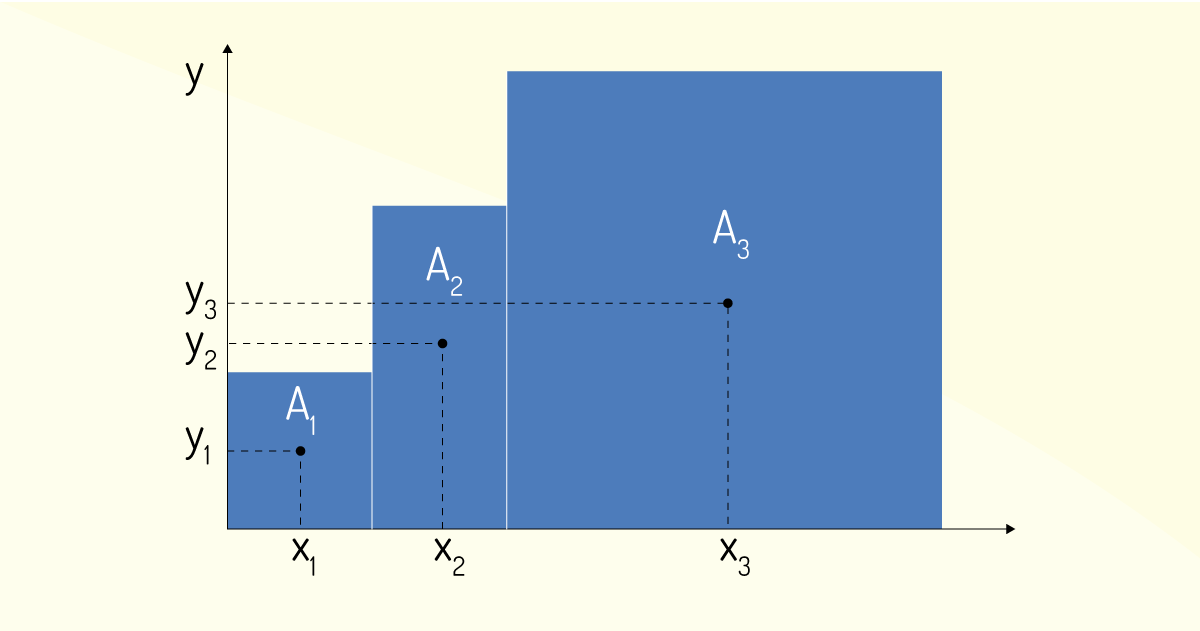
Matematicamente a expressão que nos dá o centro de gravidade de uma figura geométrica anterior é a seguinte:
\[~{{x}_{CG}}=\frac{{{A}_{1}}.{{x}_{1}}+~{{A}_{2}}.{{x}_{2}}~+~{{A}_{3}}.{{x}_{3}}}{A+{{A}_{2}}+{{A}_{3}}}\]
\[~{{y}_{CG}}=\frac{{{A}_{1}}.{{y}_{1}}+~{{A}_{2}}.{{y}_{2}}~+~{{A}_{3}}.{{y}_{3}}}{{{A}_{1}}+{{A}_{2}}+{{A}_{3}}}\]
O centro de gravidade é destacado na Figura 3.9, em que \(~{{x}_{CG}}\) é a localização em x do centro de gravidade, e \({{y}_{CG}}\) é a localização em y dele.
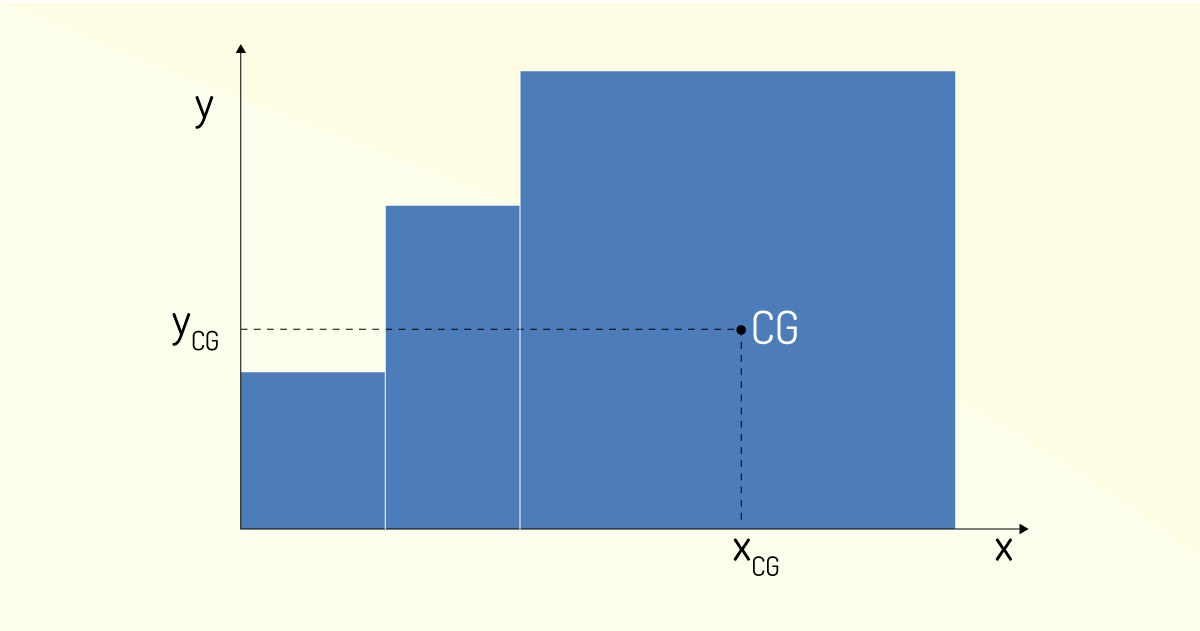
A coordenada do centro de gravidade é dada por (\({{x}_{CG}}, ~{{y}_{CG}}\)). Uma observação importante que vale a pena ressaltar é que o centro de gravidade nem sempre coincide com o centro de massa.
Além das figuras regulares, temos aquelas figuras irregulares e as circulares e os centroides, bem como os momentos de inércia em relação aos eixos x e y, respectivamente, são evidenciados na Figura 3.10.

Mais discussões sobre centro de gravidade e momento de inércia de figuras irregulares, circulares e curvilíneas serão realizadas posteriormente.
O conhecimento a respeito de centro de gravidade é de grande importância em muitos esportes, como o judô. Para derrubar o adversário, será preciso deslocar o centro de gravidade, fazendo com que este perca o equilíbrio, o que facilita a queda. No Jiu Jitsu, é válida a mesma proposta, quando a luta se desenvolve no chão, os competidores procuram deslocar o centro de gravidade do seu oponente em todo momento.

Uma chapa de metal é construída de forma homogênea, como segue na figura a seguir. Supondo a gravidade constante em todos os pontos, a coordenada do centro de gravidade é:
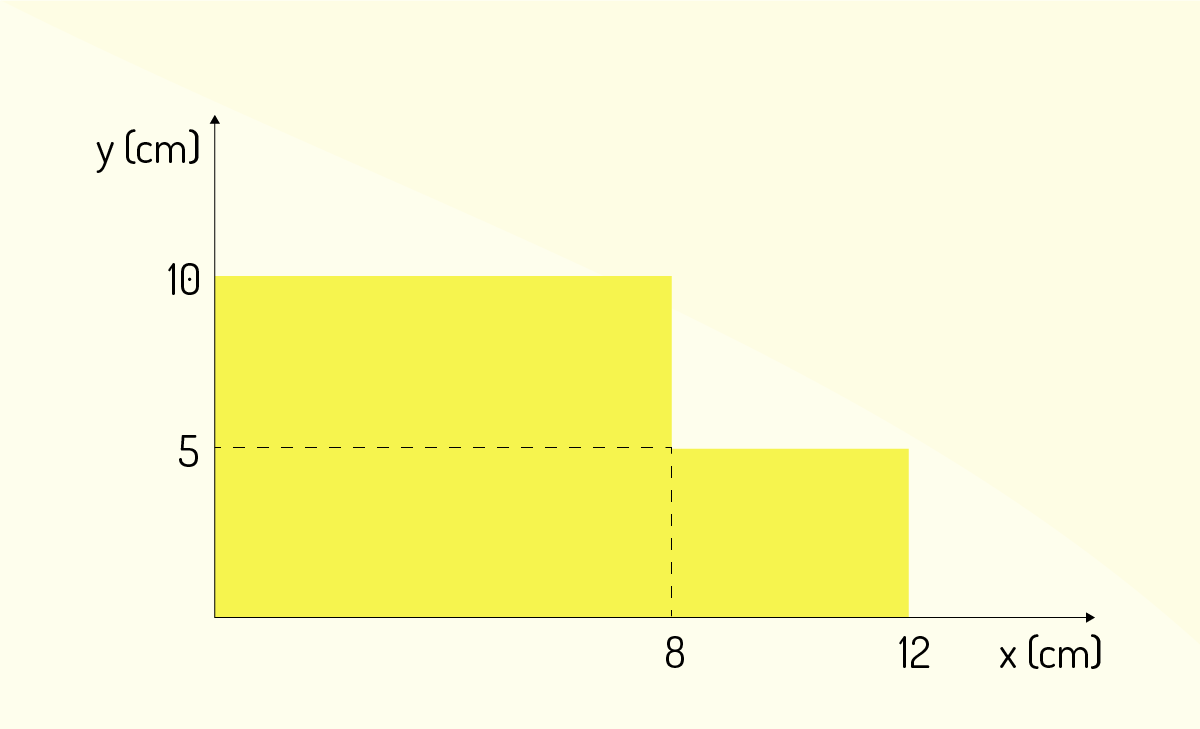
Fonte: Elaborada pelo autor.
\({{P}_{CG}}\) (10,8;9).
Incorreta. Utilizando a equação para determinar o centro geométrico de uma figura plana. A posição x1 e x2 são as coordenadas em x do centro de gravidade das figuras 1 e 2. Da mesma forma, y1 e y2 são as coordenadas em y do centro de gravidade. Calculando as áreas das figuras separadamente e substituindo na equação, obtém-se o valor do centro de gravidade, que é \({{P}_{CG}}\)(5,4;4,5).
\({{P}_{CG}}\)(2,7;3,1).
Incorreta. Utilizando a equação para determinar o centro geométrico de uma figura plana. A posição x1 e x2 são as coordenadas em x do centro de gravidade das figuras 1 e 2. Da mesma forma, y1 e y2 são as coordenadas em y do centro de gravidade. Calculando as áreas das figuras separadamente e substituindo na equação, obtém-se o valor do centro de gravidade, que é \({{P}_{CG}}\)(5,4;4,5).
\({{P}_{CG}}\)(5,4;4,5).
Correta. Utilizando a equação para determinar o centro geométrico de uma figura plana. A posição x1 e x2 são as coordenadas em x do centro de gravidade das figuras 1 e 2. Da mesma forma, y1 e y2 são as coordenadas em y do centro de gravidade. Calculando as áreas das figuras separadamente e substituindo na equação, obtém-se o valor do centro de gravidade, que é \({{P}_{CG}}\)(5,4;4,5).
\({{P}_{CG}}\)(6;5).
Incorreta. Utilizando a equação para determinar o centro geométrico de uma figura plana. A posição x1 e x2 são as coordenadas em x do centro de gravidade das figuras 1 e 2. Da mesma forma, y1 e y2 são as coordenadas em y do centro de gravidade. Calculando as áreas das figuras separadamente e substituindo na equação, obtém-se o valor do centro de gravidade, que é \({{P}_{CG}}\)(5,4;4,5).
\({{P}_{CG}}\) (3;2,5).
Incorreta. Utilizando a equação para determinar o centro geométrico de uma figura plana. A posição x1 e x2 são as coordenadas em x do centro de gravidade das figuras 1 e 2. Da mesma forma, y1 e y2 são as coordenadas em y do centro de gravidade. Calculando as áreas das figuras separadamente e substituindo na equação, obtém-se o valor do centro de gravidade, que é \({{P}_{CG}}\)(5,4;4,5).
Neste momento, trataremos de figuras geométricas irregulares e do método para determinação do centro de gravidade ou centroide; nos casos em que a ação da gravidade é constante, é o método é realizado por integração. A essas integrais, chamamos de momentos de primeira ordem em relação aos eixos x e y, respectivamente, como indicado a seguir:
\[{{M}_{x}}=\mathop{\int }_{{}}^{{}}ydA\]
\[{{M}_{x}}={{y}_{CM}}A\]
\[My~=\mathop{\int }_{{}}^{{}}xdA\]
\[{{M}_{y}}={{x}_{CM}}A\]
Os momentos de primeira ordem de uma seção de uma barra, por exemplo, são muito utilizados para se determinar a tensão de cisalhamento em resistência dos materiais.
Podemos afirmar que a centroide coincide com o centro gravitacional nos casos em que a ação da gravidade é constante. Dada uma figura irregular, como podemos ver na Figura 3.11, devemos identificar as coordenadas do seu centro de gravidade.
Assim como nos casos que já vimos, o nosso ponto de partida é projetar a figura em um plano cartesiano e orientá-la a partir do plano. O segundo passo é identificar um elemento de área dA, de coordenadas \({{x}_{EL}}~\) e \({{y}_{EL}}~\). Os valores das coordenadas \({{x}_{EL}}~\) e \({{y}_{EL}}~\) são as coordenadas em x e y, respectivamente, para o elemento dA.
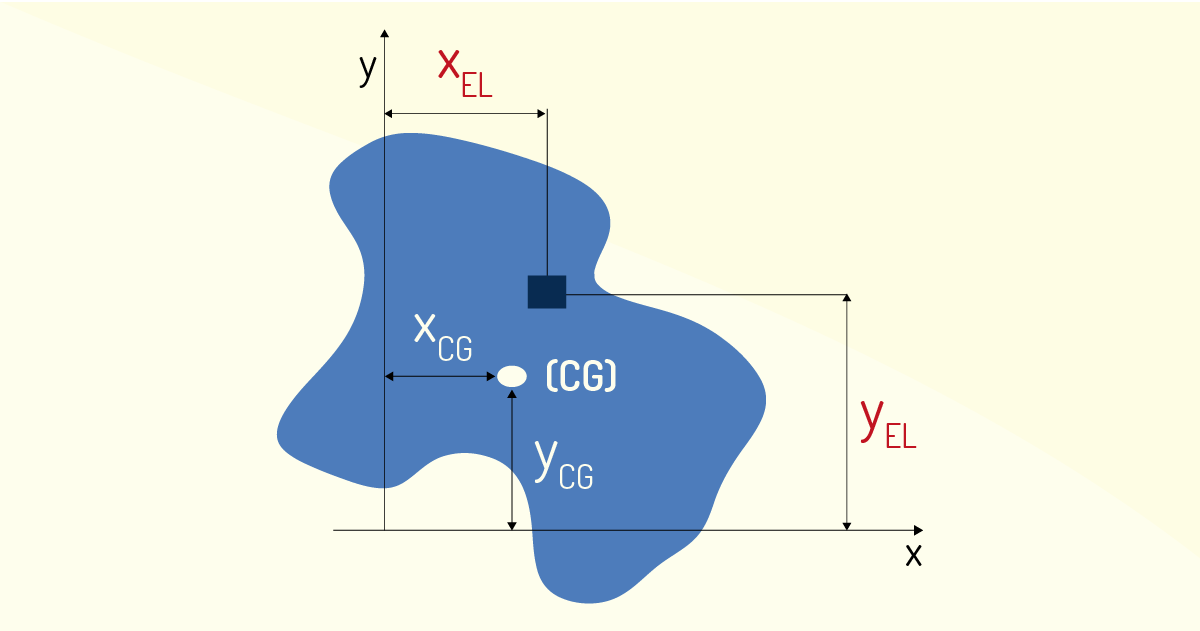
Partindo de (\({{x}_{EL}}; ~{{y}_{EL}}~\)) e integrando sobre toda a área, o centro de gravidade pode ser encontrado matematicamente da seguinte forma:
\[{{x}_{CM}}=~\frac{\mathop{\int }_{{}}^{{}}{{x}_{EL}}\times dA}{\mathop{\int }_{{}}^{{}}dA}\]
\[{{y}_{CM}}=~\frac{\mathop{\int }_{{}}^{{}}{{y}_{EL}}\times dA}{\mathop{\int }_{{}}^{{}}dA}\]
A integral \(\mathop{\int }_{{}}^{{}}{{x}_{EL}}\times dA\) é o momento angular estático de área ou de primeira ordem em relação ao eixo y. Da mesma forma, \(\mathop{\int }_{{}}^{{}}{{y}_{EL}}\times dA~\) é o momento angular estático de primeira ordem em relação ao eixo x. Já a integral \(\mathop{\int }_{{}}^{{}}dA\) fornece a área total da figura geométrica.
Vejamos o exemplo a seguir.
Determine o centro de gravidade da Figura 3.13 limitada pela função x².
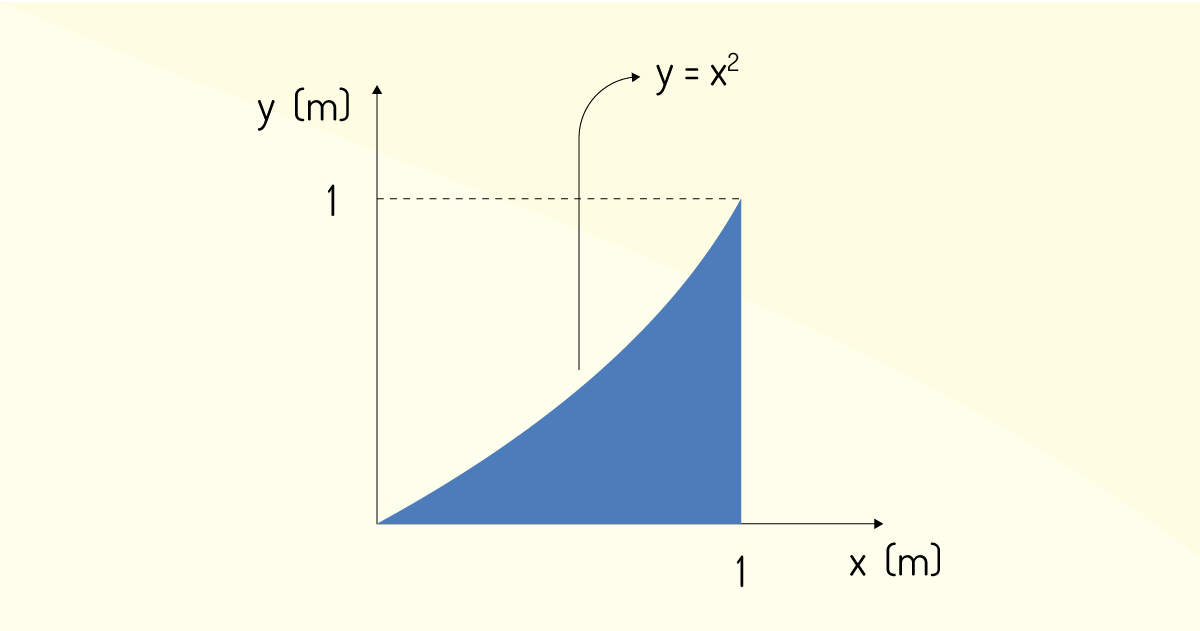
Para determinar o centro de gravidade da Figura 3.13, vamos utilizar as equações:
\[{{x}_{CM}}=~\frac{\mathop{\int }_{{}}^{{}}{{x}_{EL}}\times dA}{\mathop{\int }_{{}}^{{}}dA}\]
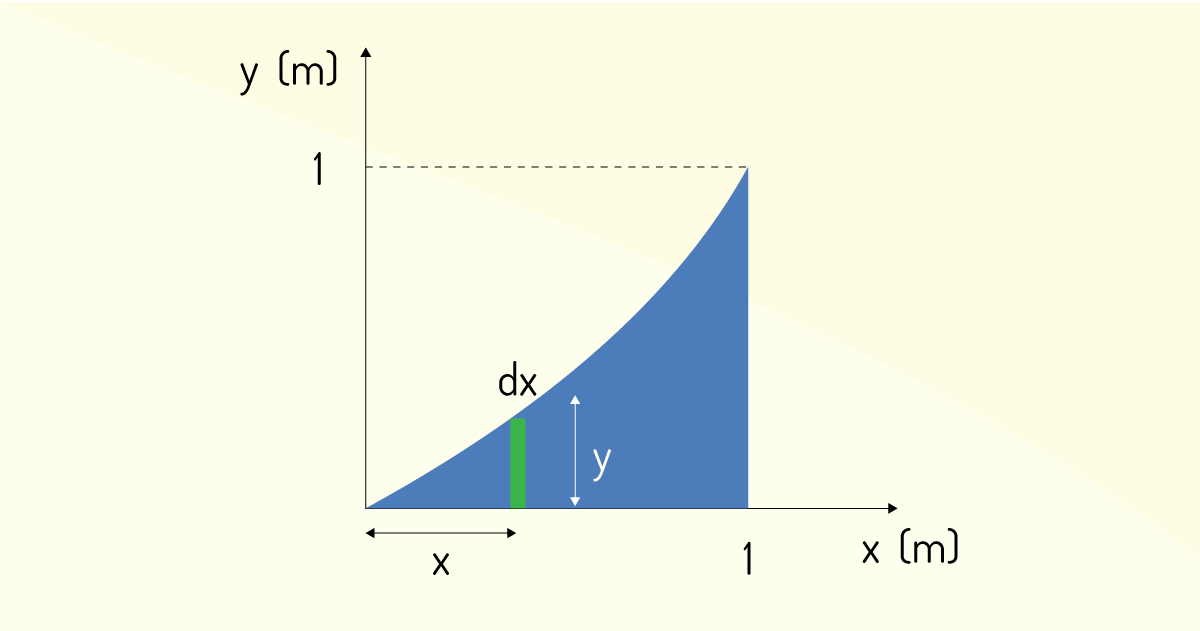
\({{x}_{EL}}\) é o centroide da figura de espessura infinitesimal dx, e podemos assumir que \({{x}_{EL}}=~x\). Da mesma forma, \({{y}_{EL}}\) é o centroide da espessura infinitesimal dx e altura y, assim, temos que \({{y}_{EL}}=~\frac{y}{2}\). O elemento dA é a área do retângulo, calculado multiplicando a base pela a sua altura, logo, temos que dA = y.dx. Utilizando todas essas informações na integral \({{x}_{CM}}=~\frac{\mathop{\int }_{{}}^{{}}{{x}_{EL}}\times dA}{\mathop{\int }_{{}}^{{}}dA}\), temos:
\[{{x}_{CM}}=~\frac{\mathop{\int }_{{}}^{{}}x\times y\times dx}{\mathop{\int }_{{}}^{{}}y\times dx}\]
Olhando para a figura, é preciso determinar uma relação entre y e x, haja vista que a variável de integração é a variável x. Como informado, y = x², basta substituir na integral anterior, e assim obtemos:
\[{{x}_{CM}}=~\frac{\mathop{\int }_{{}}^{{}}x\times {{x}^{2}}\times dx}{\mathop{\int }_{{}}^{{}}{{x}^{2}}\times dx}\]
realizando o produto no numerador,
\[{{x}_{CM}}=~\frac{\mathop{\int }_{{}}^{{}}{{x}^{3}}\times dx}{\mathop{\int }_{{}}^{{}}{{x}^{2}}\times dx}\]
Como a variável de integração é o x e ele varia de 0 a 1, substituímos o limite na integral:
\[{{x}_{CM}}=~\frac{\mathop{\int }_{0}^{1}{{x}^{3}}\times dx}{\mathop{\int }_{0}^{1}{{x}^{2}}\times dx}\]
O resultado da integral:
\[{{x}_{CM}}=~\frac{\frac{{{x}^{4}}}{4}}{\frac{{{x}^{3}}}{3}}\]
Utilizando nossos conhecimentos de matemática básica, mais precisamente propriedades de frações, podemos simplificar o resultado anterior da seguinte forma:
\[{{x}_{CM}}=\frac{{{x}^{4}}}{4}~\frac{3}{{{x}^{3}}}=\frac{3}{4}x\]
Agora, enfim, basta substituir os valores do limite de integração e vamos obter que:
\[{{x}_{CM}}=\frac{3}{4}\]
De forma análoga, o procedimento é realizado para o retângulo de espessura infinitesimal dy, como mostra a Figura 3.15.
\[{{y}_{CM}}=\frac{\mathop{\int }_{{}}^{{}}{{y}_{EL}}\times dA}{\mathop{\int }_{{}}^{{}}dA}~\]
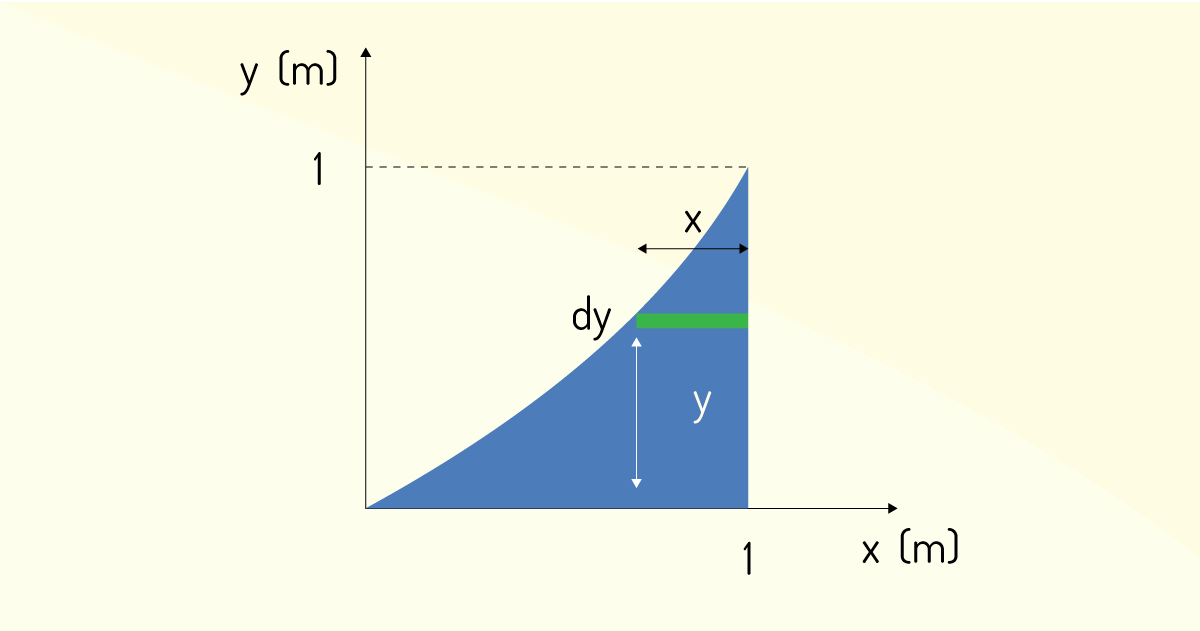
\({{y}_{EL}}\) é o centroide da figura de espessura infinitesimal dy, e podemos assumir que \({{y}_{EL}}=~y\). Da mesma forma, \({{x}_{EL}}\) é o centroide da espessura infinitesimal dy e altura y, assim temos que \({{x}_{EL}}=~\frac{\left( 1-x \right)}{2}~+~x\). O elemento dA é a área do retângulo, calculado multiplicando a base pela a sua altura, logo, temos que dA = x.dy.
\[{{y}_{CM}}=\frac{\mathop{\int }_{{}}^{{}}y\times \left( 1-x \right)\times dy}{\mathop{\int }_{{}}^{{}}\left( 1-x \right)\times dy}~\]
Para determinar a coordenada y do centro de massa, é preciso resolver a integral anterior. A integral é feita sobre a coordenada y, logo, é preciso encontrar uma relação entre as coordenadas x e y, ou seja, escrever a coordenada x em função da coordenada y. A relação é a seguinte:
\[\sqrt{y}=x\]
substituindo na integral, obtemos:
\[{{y}_{CM}}=\frac{\mathop{\int }_{{}}^{{}}y\times \left( 1-\sqrt{y} \right)\times dy}{\mathop{\int }_{{}}^{{}}\left( 1-\sqrt{y} \right)\times dy}~\]
Fazendo o produto no numerador e adicionando os limites de integração, as integrais ficam:
\[{{y}_{CM}}=\frac{\mathop{\int }_{0}^{1}\left( y-{{y}^{\frac{3}{2}}} \right)\times dy}{\mathop{\int }_{0}^{1}\left( 1-{{y}^{\frac{1}{2}}} \right)\times dy}~\]
Resolvemos separadamente as integrais. A integral do numerador, separamos em duas, como segue:
\[\mathop{\int }_{0}^{1}\left( y-{{y}^{\frac{3}{2}}} \right)\times dy=\mathop{\int }_{0}^{1}y\times dy-\mathop{\int }_{0}^{1}{{y}^{\frac{3}{2}}}\times dy=\]
Ao utilizar a regra da potencial para a integral, ficamos com:
\[\mathop{\int }_{0}^{1}\left( y-{{y}^{\frac{3}{2}}} \right)\times dy=\frac{{{y}^{2}}}{2}-\frac{{{y}^{\frac{5}{2}}}}{\frac{5}{2}}=\]
Ao utilizar propriedades de frações, podemos escrever:
\[\mathop{\int }_{0}^{1}\left( 1-{{y}^{\frac{3}{2}}} \right)\times dy=y-\frac{2}{3}{{y}^{\frac{3}{2}}}=\]
Ao realizar o mesmo procedimento para integral do denominador, separando em duas integrais, vamos obter:
\[\mathop{\int }_{0}^{1}\left( 1-{{y}^{\frac{3}{2}}} \right)\times dy=\mathop{\int }_{0}^{1}y\times dy-\mathop{\int }_{0}^{1}{{y}^{\frac{3}{2}}}\times dy=\]
Ao resolver a integral da mesma forma, temos que:
\[\mathop{\int }_{0}^{1}\left( 1-{{y}^{\frac{3}{2}}} \right)\times dy=y-\frac{{{y}^{\frac{3}{2}}}}{\frac{3}{2}}\]
Ao ajustar o resultado e utilizar os mesmos conceitos de fração, obtemos:
\[\mathop{\int }_{0}^{1}\left( 1-{{y}^{\frac{3}{2}}} \right)\times dy=y-\frac{2}{3}{{y}^{\frac{3}{2}}}\]
Ao substituir os limites de integração da resposta da integral do numerador, ficamos com:
\[\frac{{{y}^{2}}}{2}-\frac{2}{5}{{y}^{\frac{5}{2}}}=\frac{1}{2}-\frac{2}{5}=\frac{5-4}{10}=\frac{1}{10}\]
Da mesma forma, ao substituir os limites de integração para as integrais do denominador:
\[y-\frac{2}{3}{{y}^{\frac{3}{2}}}=1-\frac{2}{3}=\frac{3-2}{3}=\frac{1}{3}\]
A resposta final da coordenada y do centro de gravidade da figura dada é:
\[{{y}_{CM}}=\frac{3}{10}\]
De forma análoga ao que foi feito para uma figura plana, o centro de gravidade para uma figura volumétrica ou tridimensional pode ser determinado matematicamente da seguinte forma:
\[{{x}_{CM}}=\frac{\mathop{\int }_{{}}^{{}}{{x}_{EL}}\times dV}{\mathop{\int }_{{}}^{{}}dV}\]
\[{{y}_{CM}}=\frac{\mathop{\int }_{{}}^{{}}{{y}_{EL}}\times dV}{\mathop{\int }_{{}}^{{}}dV}\]
\[{{z}_{CM}}=\frac{\mathop{\int }_{{}}^{{}}{{z}_{EL}}\times dV}{\mathop{\int }_{{}}^{{}}dV}\]
Da mesma forma, a integral \(\mathop{\int }_{{}}^{{}}{{x}_{EL}}\times dV\) é o momento angular estático ou momento angular de primeira ordem de volume em relação ao plano yz. A integral \(\mathop{\int }_{{}}^{{}}{{y}_{EL}}\times dV\) é o momento angular estático ou momento angular de primeira ordem de volume em relação ao plano xz. Já a integral \(\mathop{\int }_{{}}^{{}}{{z}_{EL}}\times dV\) é o momento angular estático ou momento angular de primeira ordem de volume em relação ao plano xy. Por fim, a integral \(\mathop{\int }_{{}}^{{}}dV\) fornece o volume total da figura.
No link a seguir, você terá o passo a passo de como identificar o centro de gravidade de figuras geométricas irregulares utilizando integrais. Este é material base para melhor compreensão do conteúdo estudado. Veja mais em: https://www.youtube.com/watch?v=O4NtwxwB5cM. Acesso em: 08 jan. 2020.

Considerando as figuras geométricas irregulares e o método para determinação do centro de gravidade ou centroide, nos casos em que a ação da gravidade é constante, o método é feito por integração. Dada a figura a seguir, as coordenadas do centro de gravidade da chapa homogênea limitada pelas curvas \(y =\frac{{{x}^{4}}}{3}~e~x~=~\frac{{{y}^{2}}}{2}\) são de:
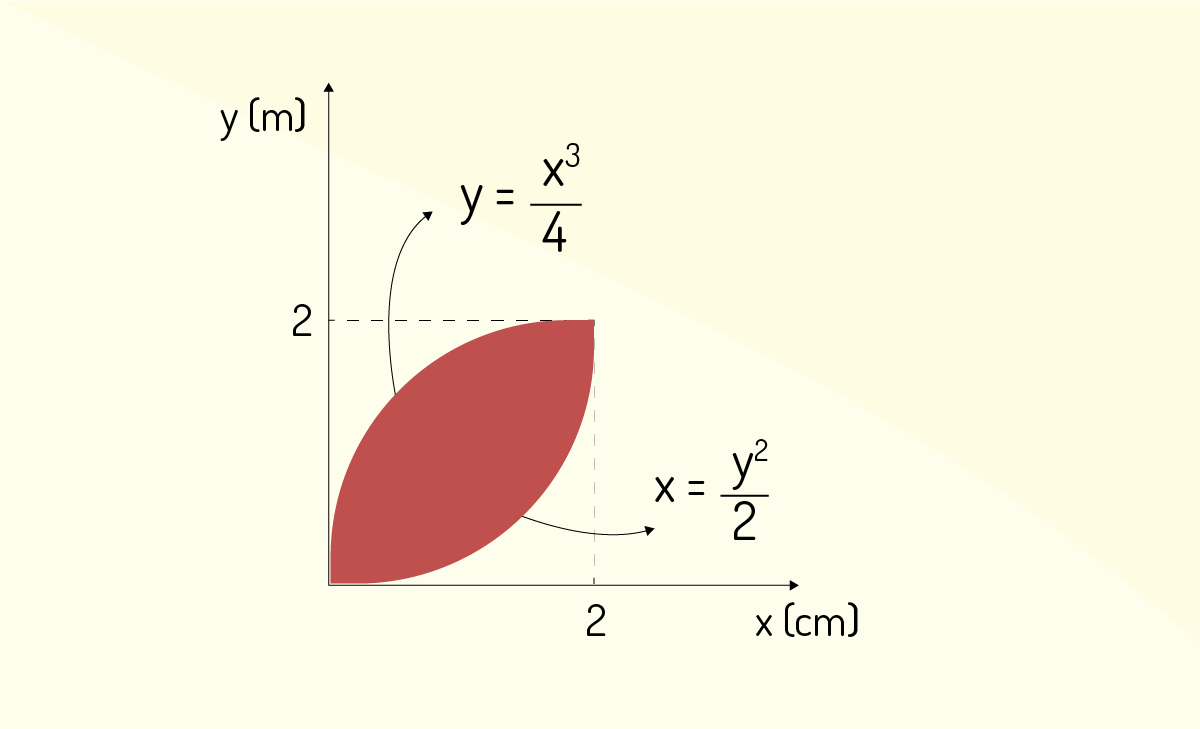
Fonte: Elaborada pelo autor.
\({{P}_{CG}}\)(15/8;3/4).
Incorreta. Dividindo a figura de área desconhecida em retângulos horizontais e verticais de espessura infinitesimal. As integrais \({{x}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{24}{25}\) e \({{y}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \frac{\sqrt{2x}+\frac{{{x}^{3}}}{4}}{2} \right)\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{6}{7}\) são facilmente calculadas utilizando regra de potência para as integrais.
\({{P}_{CG}}\) (20/9;3/4).
Incorreta. Dividindo a figura de área desconhecida em retângulos horizontais e verticais de espessura infinitesimal. As integrais \({{x}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{24}{25}\) e \({{y}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \frac{\sqrt{2x}+\frac{{{x}^{3}}}{4}}{2} \right)\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{6}{7}\) são facilmente calculadas utilizando regra de potência para as integrais.
\({{P}_{CG}}\) (24/25;8/9).
Incorreta. Dividindo a figura de área desconhecida em retângulos horizontais e verticais de espessura infinitesimal. As integrais \({{x}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{24}{25}\) e \({{y}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \frac{\sqrt{2x}+\frac{{{x}^{3}}}{4}}{2} \right)\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{6}{7}\) são facilmente calculadas utilizando regra de potência para as integrais.
\({{P}_{CG}}\) (6/7;3/4).
Incorreta. Dividindo a figura de área desconhecida em retângulos horizontais e verticais de espessura infinitesimal. As integrais \({{x}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{24}{25}\) e \({{y}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \frac{\sqrt{2x}+\frac{{{x}^{3}}}{4}}{2} \right)\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{6}{7}\) são facilmente calculadas utilizando regra de potência para as integrais.
\({{P}_{CG}}\) (24/25;6/7).
Correta. Dividindo a figura de área desconhecida em retângulos horizontais e verticais de espessura infinitesimal. As integrais \({{x}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{24}{25}\) e \({{y}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \frac{\sqrt{2x}+\frac{{{x}^{3}}}{4}}{2} \right)\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{6}{7}\) são facilmente calculadas utilizando regra de potência para as integrais.
Como já visto anteriormente, momento de inércia mede quantitativamente a capacidade dos corpos girar em torno de um ponto de referência. Agora, vamos abordar a capacidade que alguns corpos apresentam em girar em torno de um eixo, momento de inércia de superfície ou uma figura plana. Na Figura 3.16, há o momento de inércia de figuras geométricas simples.
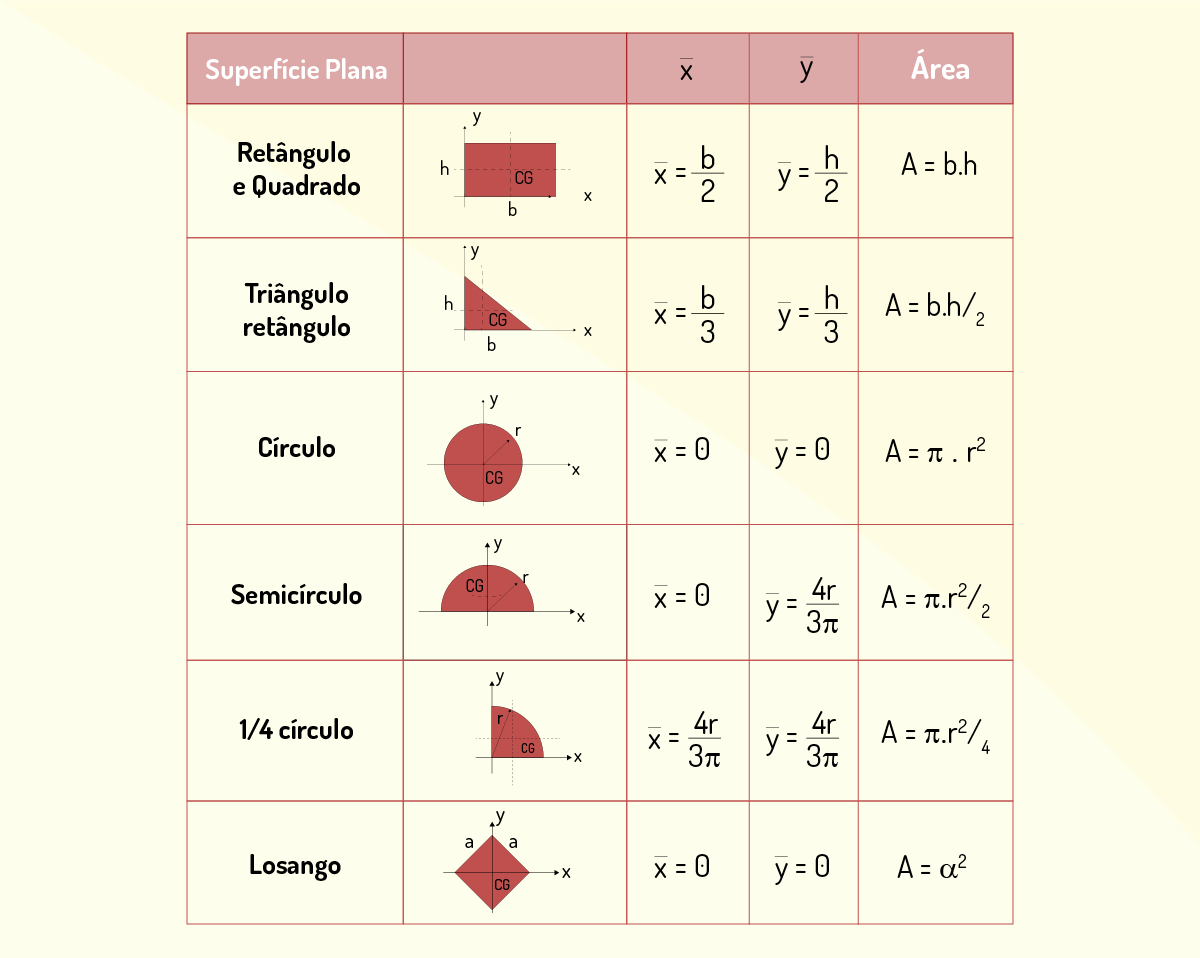
A Figura 3.16 oferece um giro em torno do eixo x e do eixo y, e a expressão matemática é dada a seguir:
\[{{M}_{x}}=\mathop{\int }_{{}}^{{}}{{y}^{2}}dA\]
\[{{M}_{y}}=\mathop{\int }_{{}}^{{}}{{x}^{2}}dA\]
O elemento dA é o segmento de área da figura, x é a distância do elemento de área até o eixo x, e y é a distância do elemento de área até o eixo y. Na Figura 3.17, os elementos são representados por \({{x}_{EL}}~\) e \({{y}_{EL}}~\), coordenada x do elemento de área e coordenada y do elemento de área, respectivamente. A escolha do elemento de área é de grande importância visando facilitar os cálculos com a integrais.
Vejamos um exemplo para a aplicação das fórmulas citadas anteriormente.
Uma chapa de metal ilustrada sobre o eixo x e y, como na Figura 3.18. Determine o momento em relação aos eixos x e y.
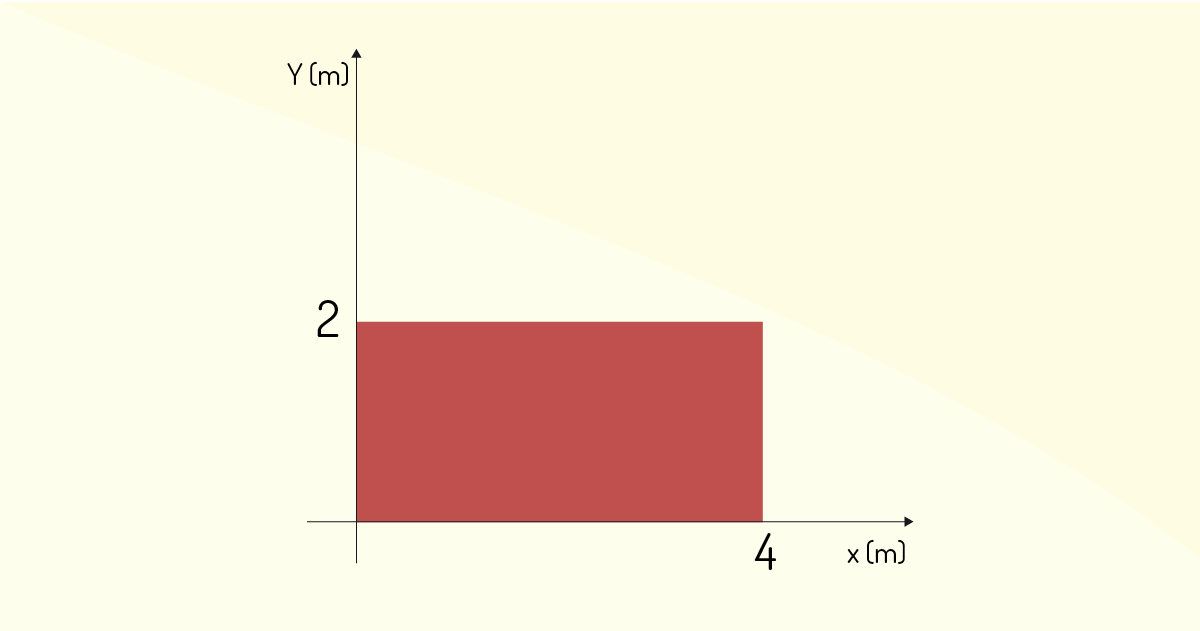
As equações são:
\[{{M}_{x}}=\mathop{\int }_{{}}^{{}}{{y}^{2}}dA~~~~{{M}_{y}}=\mathop{\int }_{{}}^{{}}{{x}^{2}}dA\]
Primeiro, vamos encontrar o momento em x.
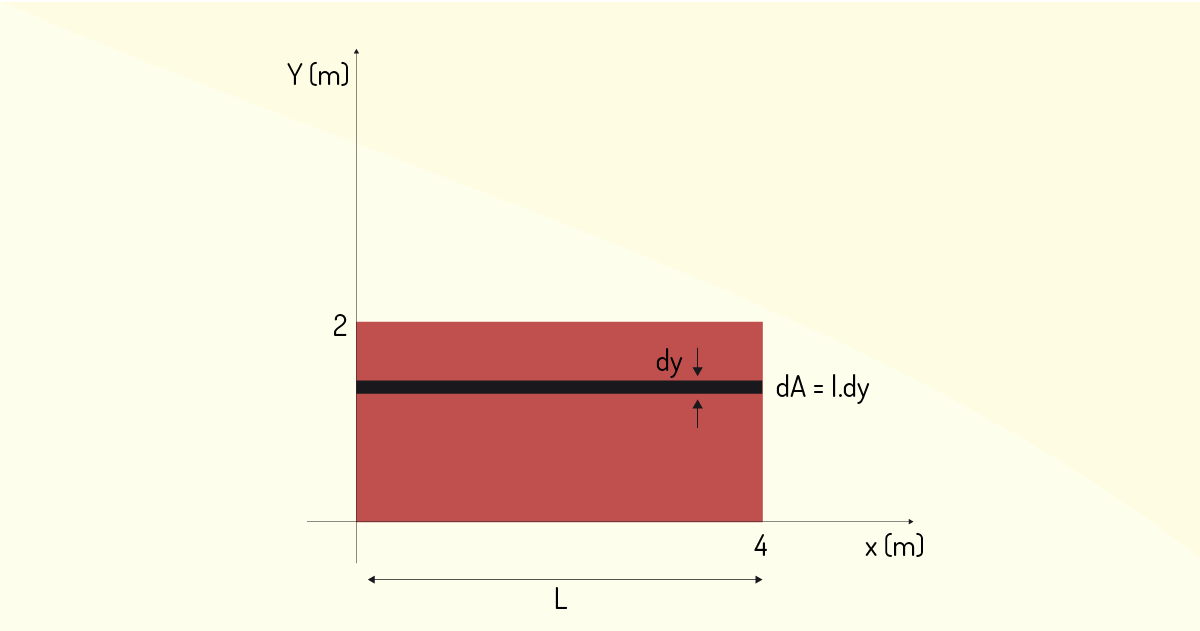
Assumimos que:
\[dA=l\times dy\]
em que l é o comprimento da barra, nesse caso, l = 4 m e, substituindo na integral do momento em x, obtemos:
\[{{M}_{x}}=\mathop{\int }_{{}}^{{}}{{y}^{2}}\times l\times dA\]
Tirando a constante h para fora da integral e incluindo os limites de integração, temos:
\[{{M}_{x}}=l\mathop{\int }_{0}^{2}{{y}^{2}}\times dy\]
Ao resolver a integral, uma integral simples, ficamos com:
\[{{M}_{x}}=l\frac{{{y}^{3}}}{3}\]
em que y varia de 0 a 2, largura da barra. Ao substituir os limites de integração e o valor de l = 4 m, o momento em \({{M}_{x}}=\frac{32}{3}N.m~~\)
O procedimento é análogo para o momento em torno do eixo y.
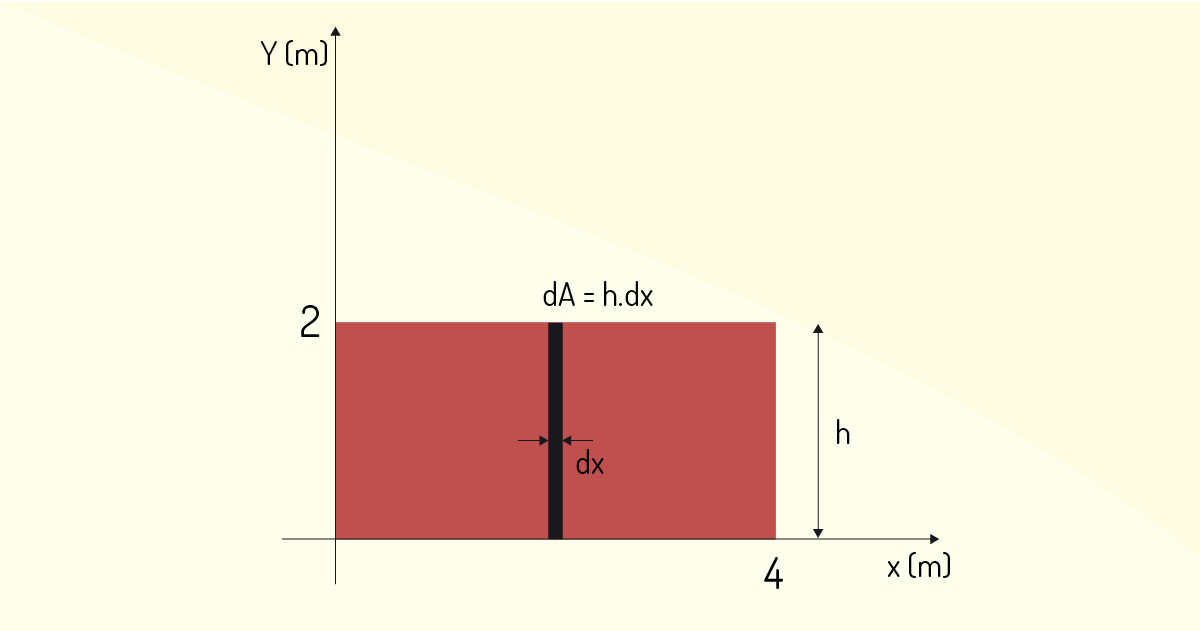
Assumimos que:
\[dA=h\times dx\]
em que l é a largura da barra, nesse caso, l = 4. Ao fazer da mesma forma, substituímos a expressão anterior na integral.
\[{{M}_{y}}=\mathop{\int }_{{}}^{{}}{{x}^{2}}\times h\times dx\]
tirando a constante l para fora de integral e adicionando os limites de integração, ficamos com:
\[{{M}_{y}}=h\mathop{\int }_{0}^{4}{{x}^{2}}\times dx\]
Ao resolver a integral, obtemos:
\[{{M}_{y}}=h\frac{{{x}^{3}}}{3}\]
em que x varia de 0 a 4. Substituindo o valor de h = 2 no resultado da integral anterior, o momento em relação ao eixo y é de \({{M}_{y}}=\frac{128}{3}N.m~\).
O teorema dos eixos paralelos nos dirá que, se conhecemos o momento de um corpo em relação a um eixo passando pelo centro de gravidade, é possível determinar facilmente o momento em relação a qualquer outro eixo paralelo a esse. Veja a Figura 3.21.
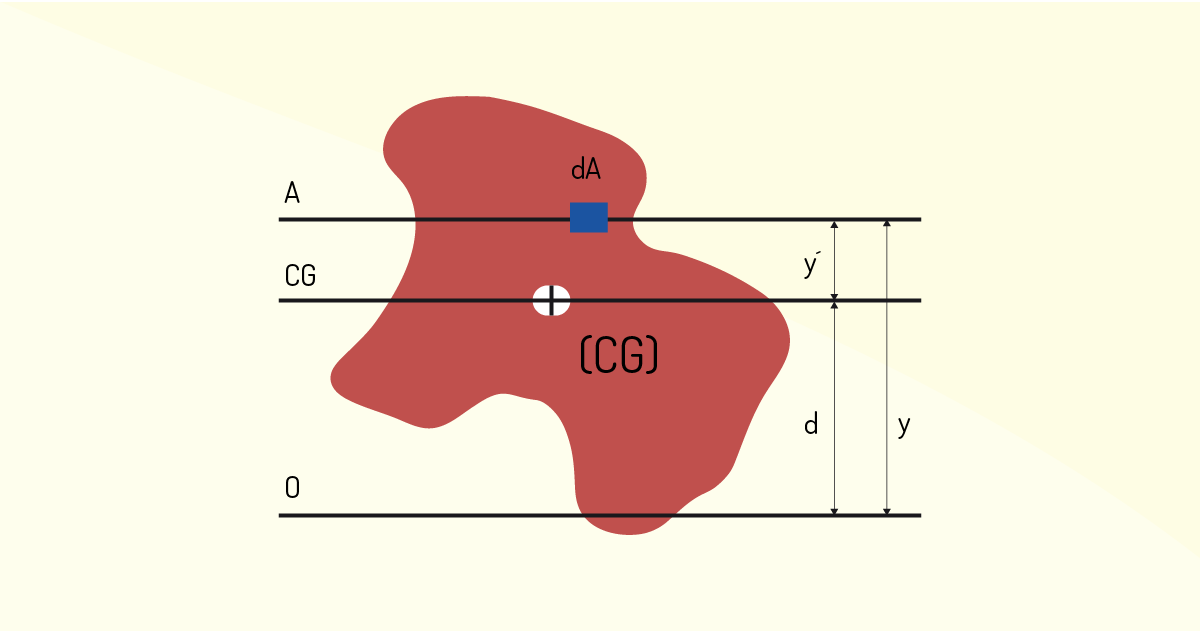
O momento sobre o eixo O pode ser calculado da seguinte forma:
\[{{M}_{O}}=\mathop{\int }_{{}}^{{}}{{y}^{2}}dA\]
substituindo y² por \({{\left( {y}'+d \right)}^{2}}\), obtemos:
\[{{M}_{O}}=\mathop{\int }_{{}}^{{}}{{\left( {y}'+d \right)}^{2}}~dA\]
Ao desenvolver o quadrado e separar em três integrais, como segue abaixo:
\[{{M}_{O}}=\mathop{\int }_{{}}^{{}}{{y}^{'~2}}d\Lambda +\mathop{\int }_{{}}^{{}}{{y}^{'~2}}dd\Lambda +\mathop{\int }_{{}}^{{}}{{d}^{2}}d\Lambda \]
A primeira integral já é conhecida.
\[{{M}_{O}}=\mathop{\int }_{{}}^{{}}{{y}^{'~2}}dA\]
A segunda integral, vindo do produto misto, é zero, pois se refere ao centro de gravidade.
\[2d=\mathop{\int }_{{}}^{{}}{{y}^{'~2}}dA=0\]
A última integral, obtemos da seguinte maneira:
\[\mathop{\int }_{{}}^{{}}{{d}^{2}}dA={{d}^{2}}\times A\]
Portanto,
\[{{M}_{xA}}=\mathop{\int }_{{}}^{{}}{{y}^{'~2}}dA+{{d}^{2}}\times A\]
Substituindo a integral pelo momento já conhecido, obtemos:
\[{{M}_{xA}}={{M}_{xCG}}+{{d}^{2}}\times A\]
Da mesma forma, é válido para o momento em relação ao eixo y, ficando com:
\[{{M}_{yA}}=\mathop{\int }_{{}}^{{}}{{x}^{'~2}}dA+{{d}^{2}}\times A\]
e
\[{{M}_{xA}}={{M}_{yCG}}+{{d}^{2}}\times A\]
Outro tipo de material que merece ser analisado são aqueles com geometria circular. Nesse caso, é preciso utilizar coordenadas polares para determinar o momento angular desses materiais em relação a um eixo.
No link a seguir, há um exemplo de como calcular o momento de inércia em relação a um ponto de uma figura circular utilizando coordenadas polares. Nesse exemplo, é necessário compreensão de mudanças de coordenadas, de coordenadas cartesianas para polares. Assista em: https://www.youtube.com/watch?v=z2XBqJDkgHk. Acesso em: 08 jan. 2020.

No link a seguir, você pode ver um exemplo no qual é resolvido e determinado o momento de inércia de um cilindro de raio R e massa m ao redor do eixo z. A solução desse exemplo pode ser usada para ajudar na solução da atividade proposta nesta unidade. Assista em: https://www.youtube.com/watch?v=cfGDmchY9wE. Acesso em: 08 jan. 2020.

Um cilindro homogêneo de massa 25 g e raio de 0,5 cm, que se encontra ao longo do eixo z, tende a girar em torno desse mesmo eixo. O momento de inércia em torno do eixo z para o cilindro é de:
312 \(\mu N.m\).
Incorreta. O momento de inércia de um cilindro ao longo de um eixo não depende do comprimento, dependendo somente da massa e do raio do cilindro. Basta substituir os valores fornecidos no problema, mas deve-se ter cuidado com as unidades, resultando em 0,31 \(\mu N.m\)
31,2 \(\mu N.m\).
Incorreta. O momento de inércia de um cilindro ao longo de um eixo não depende do comprimento, dependendo somente da massa e do raio do cilindro. Basta substituir os valores fornecidos no problema, mas deve-se ter cuidado com as unidades, resultando em 0,31 \(\mu N.m\).
3,1 \(\mu N.m\).
Incorreta. O momento de inércia de um cilindro ao longo de um eixo não depende do comprimento, dependendo somente da massa e do raio do cilindro. Basta substituir os valores fornecidos no problema, mas deve-se ter cuidado com as unidades, resultando em 0,31 \(\mu N.m\).
0,31 \(\mu N.m\).
Correta. O momento de inércia de um cilindro ao longo de um eixo não depende do comprimento, dependendo somente da massa e do raio do cilindro. Basta substituir os valores fornecidos no problema, mas deve-se ter cuidado com as unidades, resultando em 0,31 \(\mu N.m\).
0,03 \(\mu N.m\).
Incorreta. O momento de inércia de um cilindro ao longo de um eixo não depende do comprimento, dependendo somente da massa e do raio do cilindro. Basta substituir os valores fornecidos no problema, mas deve-se ter cuidado com as unidades, resultando em 0,31 \(\mu N.m\).
Aqui, você verá conceitos e exemplos de como calcular o momento de inércia de corpos volumétricos ao redor de um eixo. Algumas definições sobre momento já foram trazidas ao longo da unidade, e nada melhor para entender um pouco mais do que a resolução de exemplos.
Imaginemos um corpo de massa m posto para girar em torno de um eixo. O corpo de massa m pode ser dividido em vários elementos infinitesimais de massa dm. O momento de inércia do corpo pode ser calculado da seguinte forma:
\[M=\mathop{\int }_{{}}^{{}}{{r}^{2}}dm\]
em que r é a distância do elemento dm até o eixo.
O momento de inércia escrito matematicamente acima pode ser expresso em relação a um eixo de coordenadas x, y, z do elemento dm, como ilustrado na Figura 3.22.
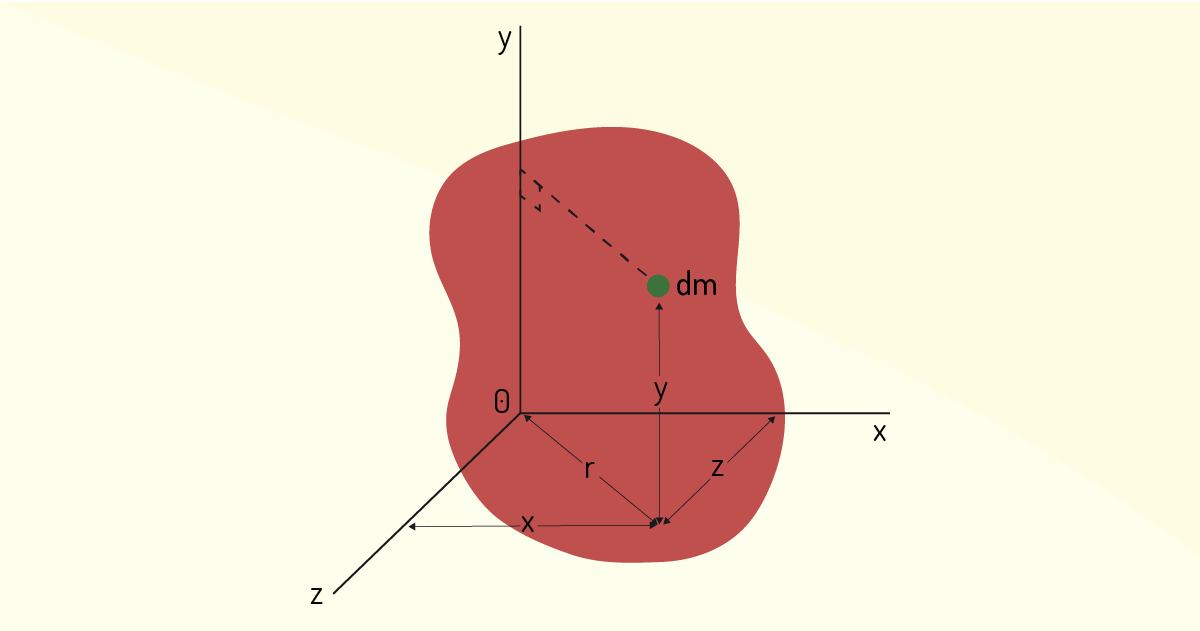
A partir da primeira equação, podemos escrever outras três equações para os momentos de inércia em relação aos eixos x, y e z.
\[{{M}_{x}}=\mathop{\int }_{{}}^{{}}\left( {{y}^{2}}+{{z}^{2}} \right)dm\]
\[{{M}_{y}}=\mathop{\int }_{{}}^{{}}\left( {{x}^{2}}+{{z}^{2}} \right)dm\]
\[{{M}_{z}}=\mathop{\int }_{{}}^{{}}\left( {{x}^{2}}+{{y}^{2}} \right)dm\]
Veja a Figura 3.23 com o momento de inércia de figuras geométricas conhecidas.
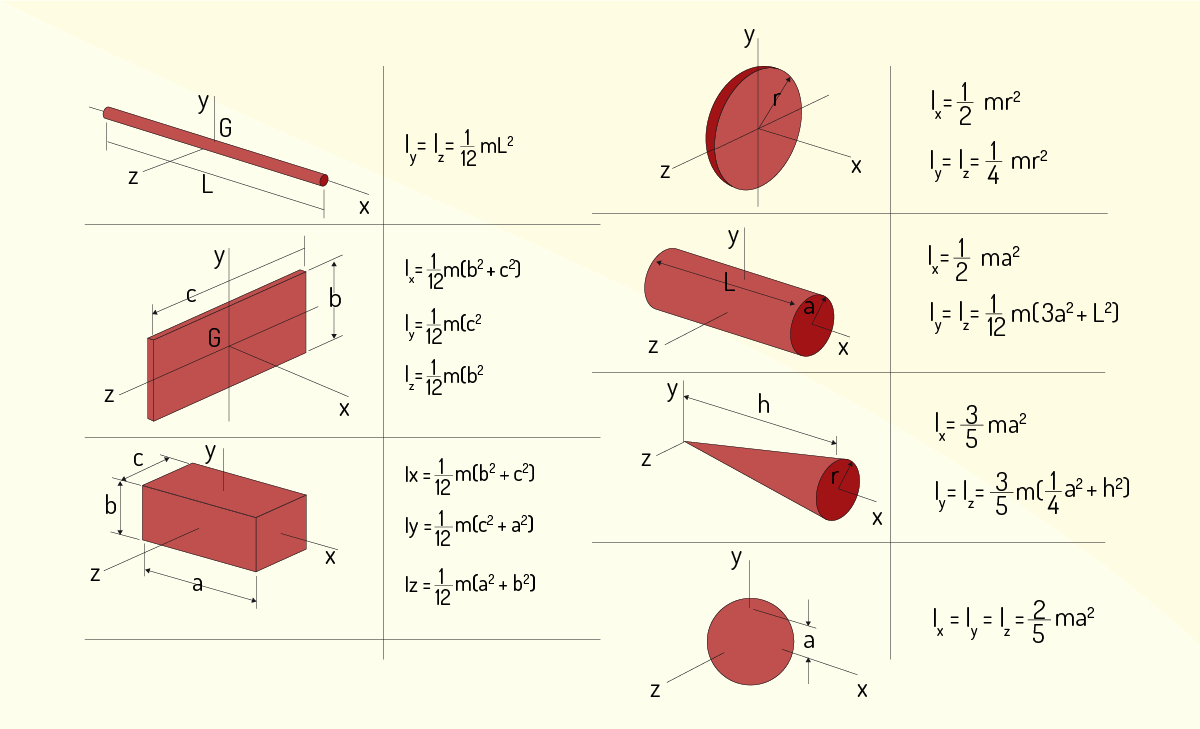
Na Figura 3.23, o momento de inércia é trazido com a letra I, bastante comum em alguns materiais. Em nosso material, padronizamos o momento como a letra M.
Outro exemplo: determine o momento de inércia de uma barra homogênea de massa m em relação a um eixo perpendicular a ela:
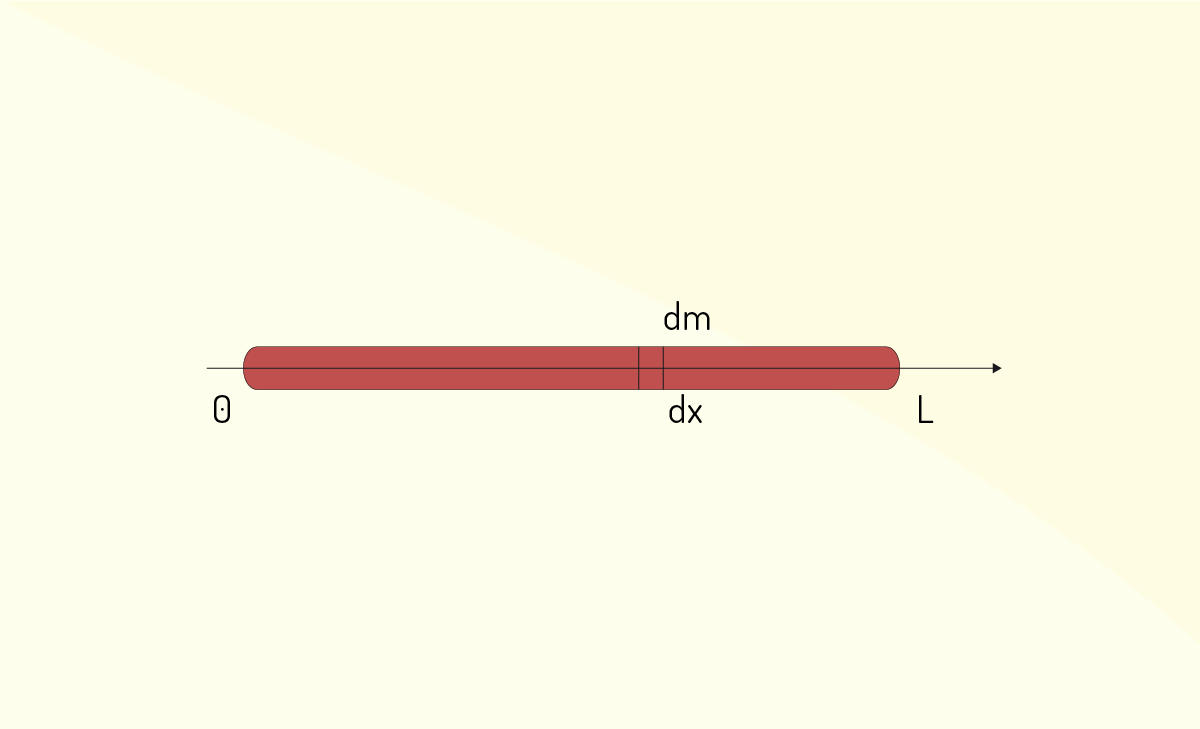
O segmento de comprimento dx tem massa dm, e a relação abaixo pode ser estabelecida:
\[\frac{dm}{m}=\frac{dx}{L}\]
isolando a massa do elemento infinitesimal,
\[dm=\left( \frac{m}{L} \right)dx\]
A integral para determinar o momento de inércia pode ser escrita como segue:
\[\mathop{\int }_{{}}^{{}}{{x}^{2}}dm\]
Substituindo dm na integral anterior,
\[\mathop{\int }_{{}}^{{}}{{x}^{2}}\left( \frac{m}{L} \right)dx\]
tirando a constante para fora da integral e substituindo os limites de integração, que é o próprio comprimento da barra:
\[\left( \frac{m}{L} \right)\mathop{\int }_{0}^{L}{{x}^{2}}dx\]
Ao resolver a integral definida, temos:
\[\left( \frac{m}{L} \right)\mathop{\int }_{0}^{L}{{x}^{2}}dx=\left( \frac{m}{L} \right)\frac{{{L}^{3}}}{3}\]
E o momento de inércia é:
\[M=m\frac{{{L}^{2}}}{3}\]
Vejamos o próximo caso.
Dado um prisma como segue, de dimensões, determine o momento de inércia em relação ao eixo z.
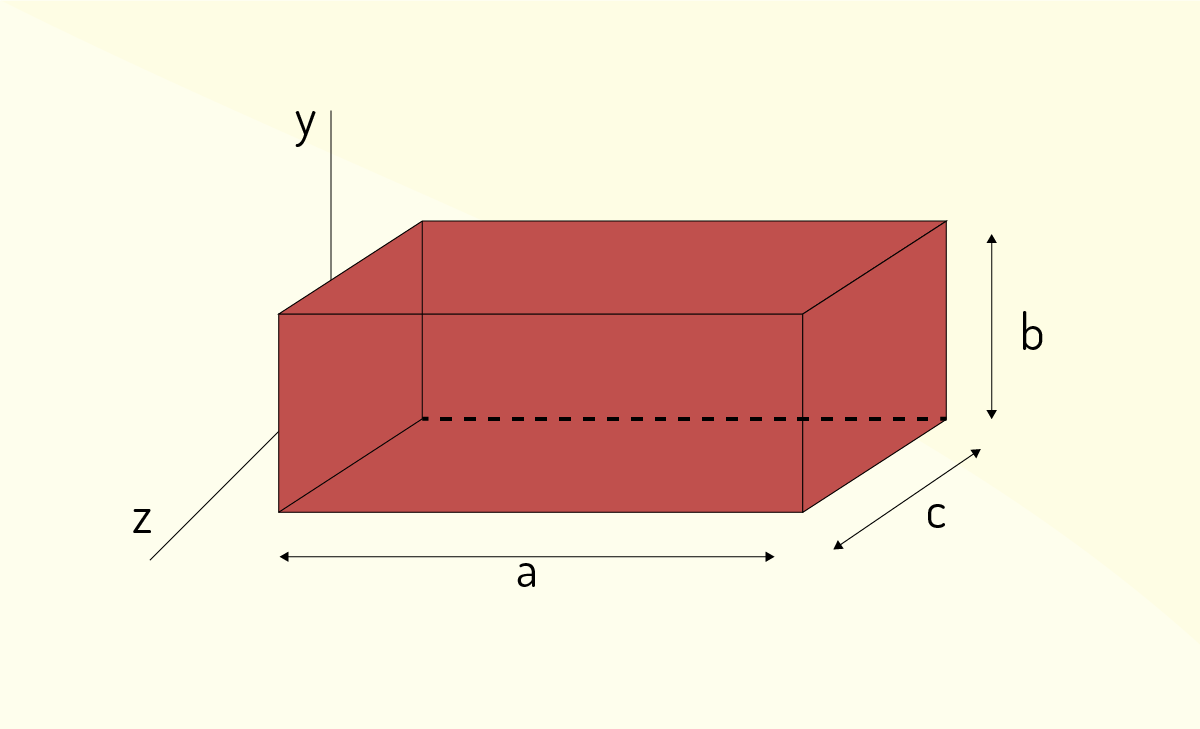
Supondo o prisma retangular de densidade homogênea,
\[\rho =\frac{m}{V}\]
A expressão da massa em função do volume é dada por:
\[m=\rho \times V\]
As dimensões são a x b x c, e o volume é calculado pelo produto entre os lados da figura, chegando à seguinte equação:
\[m=\rho abc\]
Do prisma retangular, pegamos um elemento infinitesimal de comprimento dx, como na Figura 3.26.
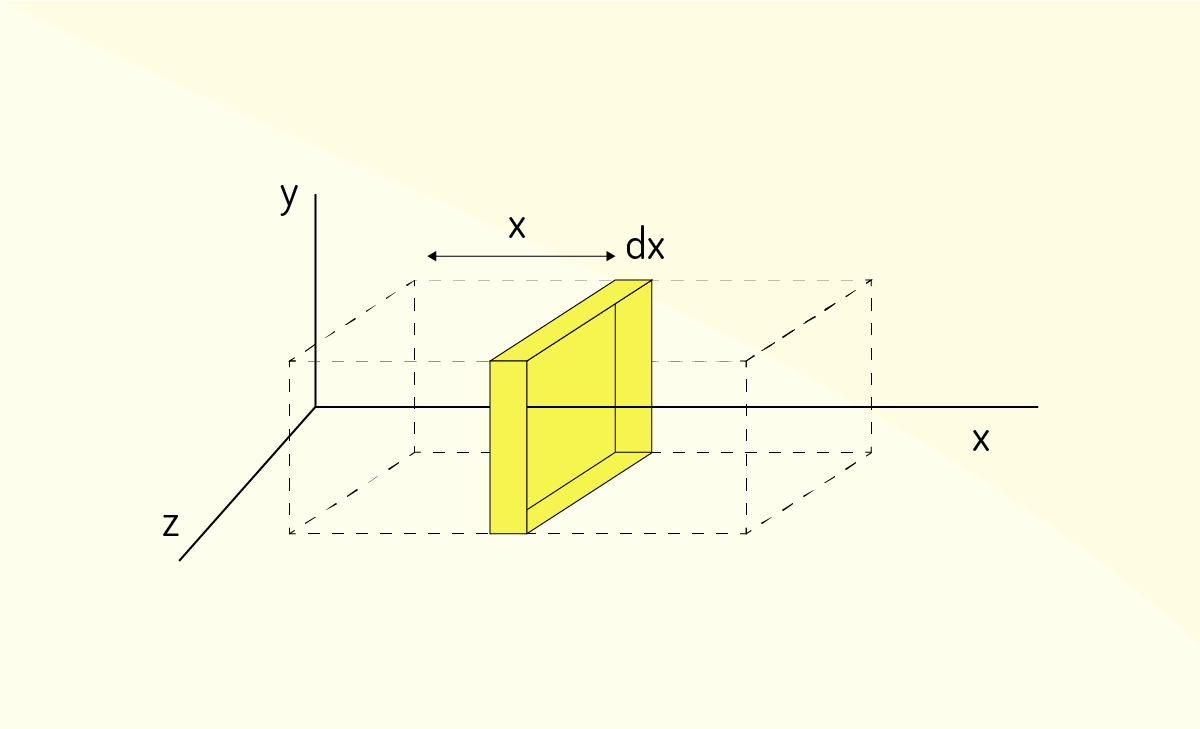
O elemento de massa desse elemento é:
\[dm=\rho bcdx\]
O momento de uma placa de espessura infinitesimal ao longo do eixo z é dado na tabela e tem valor de:
\[{{M}_{z~'}}=\frac{1}{12}m{{b}^{2}}^{{}}\]
Como estamos olhando apenas para um elemento de massa dm, o momento em relação ao eixo z desse elemento é:
\[d{{M}_{z~'}}=\frac{1}{12}{{b}^{2}}dm\]
Ao recordar o teorema dos eixos paralelos visto anteriormente e supor a gravidade constante ao longo de todo o material, podemos substituir a área pelo valor da massa. Sendo assim, a expressão para o momento é:
\[{{M}_{z}}={{M}_{z~!}}+{{x}^{2}}\times m\]
Então, o momento de uma pequena porção de massa do prisma pode ser escrito:
\[d{{M}_{z}}=d{{M}_{z!}}+{{x}^{2}}\times dm\]
Substituindo o valor do momento sobre a pequena porção de massa,
\[d{{M}_{z}}=\frac{1}{12}{{b}^{2}}dm+{{x}^{2}}\times dm\]
isolando as massas e colocando em evidência, temos:
\[d{{M}_{z}}=\left( \frac{1}{12}{{b}^{2}}+{{x}^{2}} \right)\times dm\]
Ao substituir o elemento de massa:
\[d{{M}_{z}}=\left( \frac{1}{12}{{b}^{2}}+{{x}^{2}} \right)\rho bcdx\]
podemos reescrever a expressão acima da seguinte anterior:
\[d{{M}_{z}}=\rho bc\left( \frac{1}{12}{{b}^{2}}+{{x}^{2}} \right)dx\]
A integral do momento em torno do eixo z pode ser escrita como sendo a integral de todos os pequenos elementos:
\[{{M}_{z}}=\mathop{\int }_{{}}^{{}}d{{M}_{z}}\]
Substituindo:
\[\mathop{\int }_{{}}^{{}}d{{M}_{z}}=\mathop{\int }_{{}}^{{}}\rho bc\left( \frac{1}{12}{{b}^{2}}+{{x}^{2}} \right)dx\]
Separando em duas integrais e incluindo os limites de integração, em que x vai de zero até a.
\[\mathop{\int }_{{}}^{{}}d{{M}_{z}}=\rho bc\left( \mathop{\int }_{0}^{a}\frac{1}{12}{{b}^{2}}dx+\mathop{\int }_{0}^{a}{{x}^{2}}dx \right)\]
Resolvendo a integral já conhecida e utilizando o método da potencial para as integrais, obtemos que o momento:
\[{{M}_{z}}=\rho bc\left( \frac{1}{12}{{b}^{2}}a+\frac{{{a}^{3}}}{3} \right)\]
Como aparece a constante a em ambos os termos, podemos colocar em evidência:
\[{{M}_{z}}=\rho bc\left( \frac{1}{12}{{b}^{2}}+\frac{{{a}^{3}}}{3} \right)\]
Ao substituir as constantes pela massa, a expressão para o momento em torno do eixo z para a figura dada é a seguinte:
\[{{M}_{z}}=m\left( \frac{1}{12}{{b}^{2}}+\frac{{{a}^{3}}}{3} \right)\]
O resultado é o momento de inércia para o prisma retangular em torno do eixo z. Com o cálculo feito acima, é possível resolver a atividade proposta da unidade.
Supondo que o material do exemplo acima seja uma pequena barra de ouro de 77,28 g, de dimensões 4,0 cm x 2,0 cm x 0,5 cm, sendo comprimento, largura e espessura, respectivamente, o momento dessa barra em torno do eixo z será de:
7,3 kN.m.
Incorreta. Substituindo os valores da massa, comprimento e espessura, lembrando que as unidades precisam estar no SI, ou seja, massa em kg e centímetro em metro, o resultado obtido é de 73,4 µN.m.
734 N.m.
Incorreta. Substituindo os valores da massa, comprimento e espessura, lembrando que as unidades precisam estar no SI, ou seja, massa em kg e centímetro em metro, o resultado obtido é de 73,4 µN.m.
73,4 N.m.
Incorreta. Substituindo os valores da massa, comprimento e espessura, lembrando que as unidades precisam estar no SI, ou seja, massa em kg e centímetro em metro, o resultado obtido é de 73,4 µN.m.
73,4 mN.m.
Incorreta. Substituindo os valores da massa, comprimento e espessura, lembrando que as unidades precisam estar no SI, ou seja, massa em kg e centímetro em metro, o resultado obtido é de 73,4 µN.m.
73,4 µN.m.
Correta. Substituindo os valores da massa, comprimento e espessura, lembrando que as unidades precisam estar no SI, ou seja, massa em kg e centímetro em metro, o resultado obtido é de 73,4 µN.m.
Nome do livro: Mecânica vetorial para engenharia
Editora: AMGH Editora LTDA
Autor: Ferdinand Pierre Beer e Elwood Russell Johnston
ISBN: 978-85-8055-144-0
Para complementar os conteúdos estudados, este livro deve ser usado como material-base para quem deseja ter sucesso na disciplina. Determinação do centro de gravidade, momento de inércia por meio de somatório e de integrais, para somas infinitesimais.
