Qualquer número usado para descrever quantitativamente um fenômeno físico é uma grandeza física. Ao medir uma grandeza, sempre a comparamos com um padrão de referência. Tal padrão define uma unidade de grandeza, como, por exemplo, o metro, que é uma unidade de distância, e segundo, que é uma unidade de tempo. No mundo, as medidas de referência seguem o Sistema Internacional, ou SI (das iniciais do francês Systèm Internacional). Nesse contexto, assinale a alternativa correta.
A unidade de temperatura no Sistema Internacional é o ºC (graus Celsius).
Incorreta. No SI, a unidade de temperatura é o Kelvin, ou K.
Usando a definição de que 1 milha = 1,61 km, no SI, 5 milhas é igual a, aproximadamente, 8 km.
Incorreta. A unidade de comprimento no SI é o metros.
Para controlar o seu consumo de bebida alcoólica, você resolveu beber 0,04 m³ de vinho durante um ano. Supondo o ano tendo 365 dias, você não poderá beber mais que 110cm³/dia.
Correta. Basta fazer as mudanças de unidade de tal forma a chegar até cm³/dia.
Newtons por metro cúbico, ou seja, força sobre volume é unidade de pressão.
Incorreta. A unidade de pressão é força sobre área, ou seja, N/m².
O fluxo sanguíneo de um homem adulto é, em média, 2 litros por minuto, ou seja, uma ordem de 10³ litros por dia.
Incorreta. Alternativa sobre ordem de grandeza. 20 litros por minuto equivale a 1200 L por hora, 28000 L por dia, o mesmo que 2,8 . 10\(^4\) L.
Um corpo de 500N encontra-se suspenso, como mostra a figura a seguir. Os fios que mantêm o corpo suspenso e em equilíbrio estático são ideais e têm pesos desprezíveis. A tração na corda AB, em N, é de:
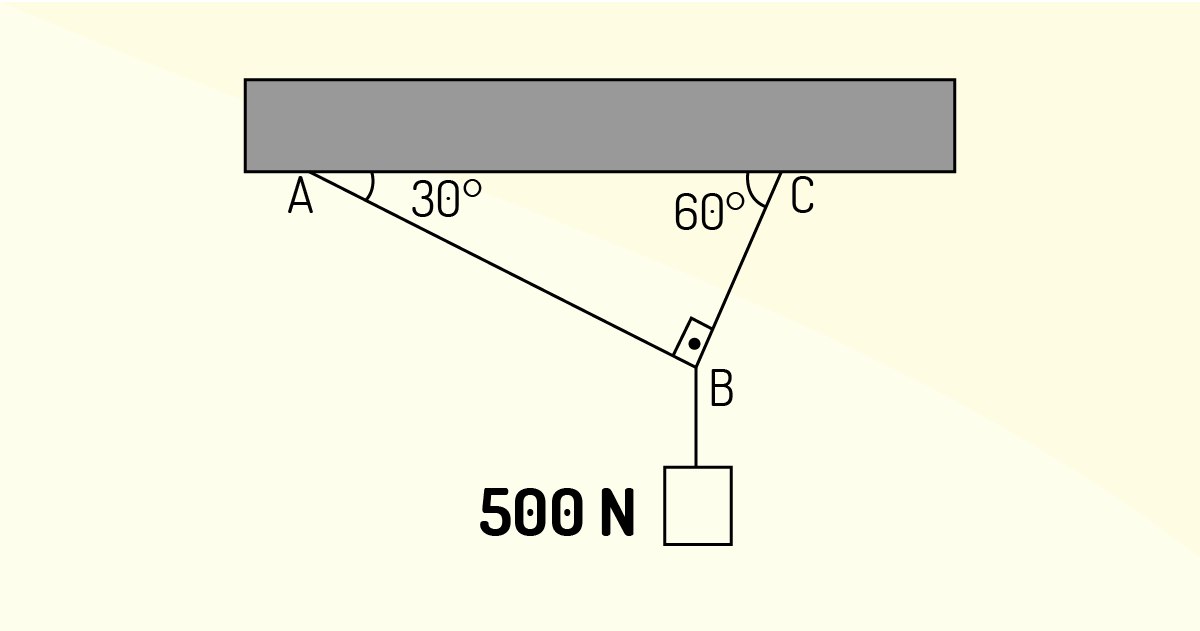
Fonte: Elaborada pelo autor.
250 N.
Correta. Nesse exercício, é preciso decompor os vetores \({{T}_{AB}}\) e \({{T}_{BC}}\) em suas componentes x e y. Feito isso, basta aplicar as condições de equilíbrio para um ponto material. Você vai obter duas equações e terá duas incógnitas. Sistema determinado.
300 N.
Incorreta. Nesse exercício, é preciso decompor os vetores \({{T}_{AB}}\) e \({{T}_{BC}}\) em suas componentes x e y. Feito isso, basta aplicar as condições de equilíbrio para um ponto material. Você vai obter duas equações e terá duas incógnitas. Sistema determinado.
325 N.
Incorreta. Nesse exercício, é preciso decompor os vetores \({{T}_{AB}}\) e \({{T}_{BC}}\) em suas componentes x e y. Feito isso, basta aplicar as condições de equilíbrio para um ponto material. Você vai obter duas equações e terá duas incógnitas. Sistema determinado.
350 N.
Incorreta. Nesse exercício, é preciso decompor os vetores \({{T}_{AB}}\) e \({{T}_{BC}}\) em suas componentes x e y. Feito isso, basta aplicar as condições de equilíbrio para um ponto material. Você vai obter duas equações e terá duas incógnitas. Sistema determinado.
375 N.
Incorreta. Nesse exercício, é preciso decompor os vetores \({{T}_{AB}}\) e \({{T}_{BC}}\) em suas componentes x e y. Feito isso, basta aplicar as condições de equilíbrio para um ponto material. Você vai obter duas equações e terá duas incógnitas. Sistema determinado.
Para soltar o pneu furado do seu caminhão, Pedro utiliza uma chave de rodas no formado de uma cruz, como ilustrado na figura a seguir.

Fonte: Serezniy / 123RF.
Sabendo que a distância de duas extremidades opostas é de 60 cm, qual é a força aplicada sobre as duas extremidades para soltar um parafuso apertado com um torque de 60 N.m?
50 N.
Incorreta. Utilizando conceitos do princípio da transmissibilidade, esboçando o diagrama de forças e aplicando o somatório dos momentos sobre o ponto central, obtemos que a força necessária seja de 100 N.m.
100 N.
Correta. Utilizando conceitos do princípio da transmissibilidade, esboçando o diagrama de forças e aplicando o somatório dos momentos sobre o ponto central, obtemos que a força necessária seja de 100 N.m.
150 N.
Incorreta. Utilizando conceitos do princípio da transmissibilidade, esboçando o diagrama de forças e aplicando o somatório dos momentos sobre o ponto central, obtemos que a força necessária seja de 100 N.m.
200 N.
Incorreta. Utilizando conceitos do princípio da transmissibilidade, esboçando o diagrama de forças e aplicando o somatório dos momentos sobre o ponto central, obtemos que a força necessária seja de 100 N.m.
250 N.
Incorreta. Utilizando conceitos do princípio da transmissibilidade, esboçando o diagrama de forças e aplicando o somatório dos momentos sobre o ponto central, obtemos que a força necessária seja de 100 N.m.
Pedro e Paulo estão carregando um bloco de concreto que pesa 1000 N, suspenso em uma barra extremamente rígida AB de 200 N e 3,0 m de comprimento, cujas extremidades apoiam-se nos respectivos ombros, pontos A e B. O cofre está a 0,5 m da extremidade A. A força aplicada pela extremidade A ao ombro de Pedro será de, aproximadamente:
450 N.
Incorreta. Faça o diagrama de forças sobre a barra rígida, distribua as distâncias e aplique as condições de equilíbrio para as forças e momentos. Escolha um dos pontos A ou B para ser o ponto, aconselho escolher o ponto B, pois a incógnita pedida é encontrada logo no início.
500 N.
Incorreta. Faça o diagrama de forças sobre a barra rígida, distribua as distâncias e aplique as condições de equilíbrio para as forças e momentos. Escolha um dos pontos A ou B para ser o ponto, aconselho escolher o ponto B, pois a incógnita pedida é encontrada logo no início.
867 N.
Incorreta. Faça o diagrama de forças sobre a barra rígida, distribua as distâncias e aplique as condições de equilíbrio para as forças e momentos. Escolha um dos pontos A ou B para ser o ponto, aconselho escolher o ponto B, pois a incógnita pedida é encontrada logo no início.
933 N.
Correta. Faça o diagrama de forças sobre a barra rígida, distribua as distâncias e aplique as condições de equilíbrio para as forças e momentos. Escolha um dos pontos A ou B para ser o ponto, aconselho escolher o ponto B, pois a incógnita pedida é encontrada logo no início.
1028 N.
Incorreta. Faça o diagrama de forças sobre a barra rígida, distribua as distâncias e aplique as condições de equilíbrio para as forças e momentos. Escolha um dos pontos A ou B para ser o ponto, aconselho escolher o ponto B, pois a incógnita pedida é encontrada logo no início.
Uma estrutura é o conjunto de partes resistentes, ou seja, um corpo ou sistema de partes que suportam uma carga e certificam a estabilidade de um elemento do projeto de modo que sua análise permite a simplificação desses projetos em modelos estruturais. Sobre estruturas com vínculos, ou seja, estruturas com apoios, observe a figura a seguir.
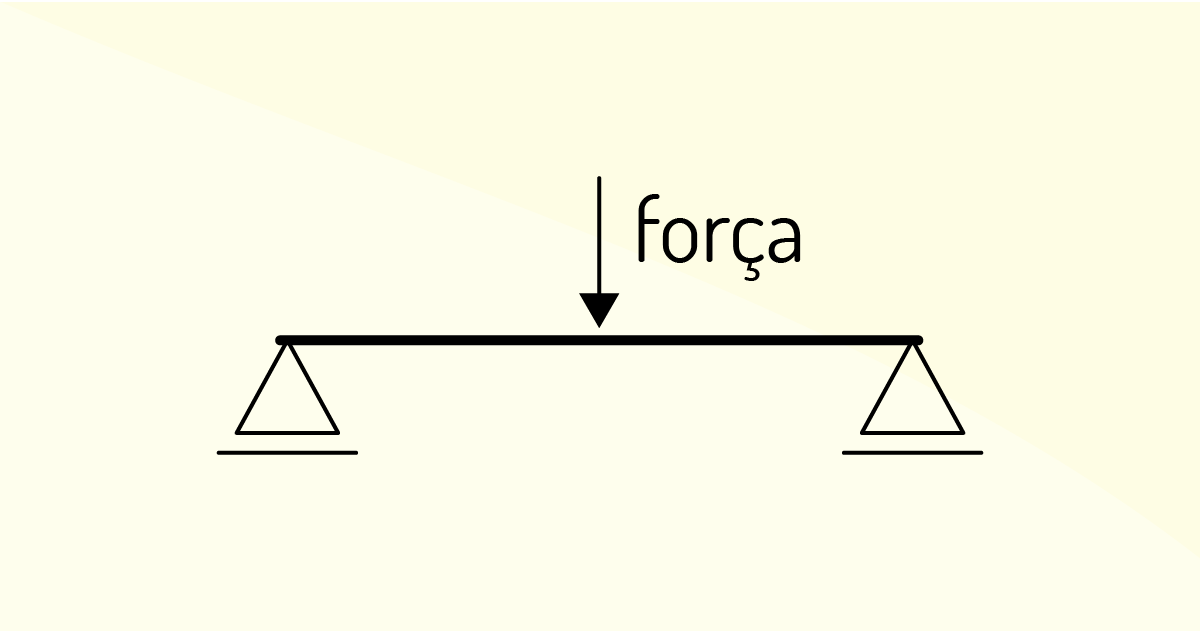
É verdadeiro o que se afirma em:
Podemos perceber que essa estrutura possui 2 vínculos de 2º gênero.
Incorreta. Visto que se trata de uma estrutura com 2 vínculos de 1º gênero.
Trata-se de uma estrutura hiperestática.
Incorreta. Pois o grau de estaticidade é igual a -1, indicando que o número de reações de apoio é menor do que o número de equações de equilíbrio disponíveis.
O grau de estaticidade dessa estrutura é -1.
Correta. O grau de estaticidade é dado por: gh = C1 + 2 . C2 + 3 . C3 - 3 . m
Então gh = (2) + 2 . (0) + 3 . (0) - 3 . (1), logo gh = 2 - 3 e, portanto, gh = - 1.
Por se tratar de uma estrutura isostática, essa é restringida.
Incorreta. Pois não se trata de uma estrutura isostática. Como possui gh=-1 é tida como hipoestática.
Estrutura desse tipo possui apoio de 3º gênero, tendo movimentos restritos tanto de rotação quanto de translação.
Incorreta. Pois não se trata de uma estrutura com apoio de 3º gênero, e sim com 2 apoios de 1º gênero.
Sabemos que as vigas são elementos estruturais usados para distribuir as cargas aplicadas a elas ao longo do seu comprimento, sendo confeccionadas de madeira, metal ou concreto. Sendo assim, assinale a alternativa correta.
Podemos classificar as vigas por meio dos materiais dos quais são confeccionadas, sendo a viga universal e a treliçada exemplos desse tipo de classificação. A classificação das vigas é feita exclusivamente por meio de sua matéria-prima e beleza a ser exibida no projeto.
Incorreta. Visto que uma das classificações de vigas é feita a partir dos suportes que as complementam, sendo exemplos a viga universal e a treliçada.
São exemplos de vigas, de acordo com sua aplicação, biengastada, Gerber e em balanço.
Correta. Pois a viga biengastada é aquela em que as duas extremidades encontram-se engastadas, ou seja, assentadas ou encaixadas. A viga Gerber é aquela apoiada em mais de dois suportes ou apoios. E a viga em balanço é aquela na qual apenas uma de suas extremidades se encontra suportada ou encaixada. Diante dessas definições, é possível saber a aplicabilidade e a tipologia das vigas, como descrito na alternativa.
O momento fletor em uma viga é oriundo da ação de um esforço de relaxação da viga.
Incorreta. Pois o momento fletor está relacionado à flexão da viga, ou seja, uma tensão normal aplicada na direção axial da viga.
O esforço cortante em uma viga gera tensões de cisalhamento em apenas uma direção da viga, no caso, a horizontal.
Incorreta. Pois o esforço cortante gera tensões ao longo da viga, ou seja, nas duas direções: na vertical e na horizontal.
A viga em uma construção está submetida somente a um tipo de carga, a concentrada, ou seja, carga aplicada em um único ponto da estrutura.
Incorreta. Pois uma viga está sujeita a cargas concentradas, distribuídas, ou a uma combinação entre elas.
Considere uma viga com 13 m de comprimento, com um apoio móvel e um apoio fixo (em suas extremidades). Agora, assinale a alternativa correta sobre esforço cortante e momento fletor da viga para o caso dela estar submetida a uma carga distribuída de 1 tonelada de força por metro.
A reação Ay será de 4,5 toneladas força e a reação By também será de 4,5 toneladas força.
Incorreta. Visto que, como se trata de dois apoios, a carga será dividida por dois, logo Ay terá uma carga de 6,5 toneladas força e By também terá uma carga de 6,5 toneladas força, já que a carga concentrada inicial era de 1.13 = 13 toneladas força.
A força cortante V para x = 13m terá valor de - 6,5 N.
Correta. Dado que a somatória das forças em y é igual a zero, teremos que V + x - 6,5 = 0, logo, considerando x = 13, teremos que V = - 6,5 N.
A somatória das forças em x será igual a 10 N.
Incorreta. Pois não há nenhuma força em x, logo a normal neste caso será zero.
O momento fletor para x = 13 m terá valor de 21 N.m.
Incorreta. Pois a soma dos momentos será igual a zero, assim M + x . X/2 - 6,5.x = 0, logo M = (-x/2)²+ 6,5x, em que, para x = 13, temos M = 0 N.m.
Como o momento é dado por M + x . X/2 - 6,5 . x = 0, teremos que sua representação será uma parábola côncava para baixo.
Incorreta. Pois, ao desenharmos o diagrama de momento fletor, é necessário que se faça a troca de sinais, de modo que a parábola M + x . X/2 - 6,5 . x = 0 ficará côncava para cima.
Considere que um cabo de luz pode suportar uma massa de 10 kg por metro linear, e que este se encontra suspenso nos pontos A e B, no mesmo nível, separados a 200 m de distância, e que a flecha no meio do vão é 30m. Agora, assinale a alternativa correta a respeito desse cabo.
A carga por comprimento linear será de 110 N/m.
Incorreta. Pois o valor da carga por comprimento linear será o valor da massa vezes a aceleração da gravidade na Terra, logo será 10.9,8 = 98 N/m.
A tração máxima no cabo terá valor de 28 kN.
Incorreta. Visto que a tração máxima é dada pela raiz quadrada de T0² + (wl)², temos Tmáx= ((16.333,33²)+ ((98. 100)²))^(½)= 362.817.66 N ou 36,28 kN.
A tração máxima ocorrerá somente no cabo de sustentação A.
Incorreta. Visto que, por se tratar de um cabo simétrico, teremos que a tração máxima ocorrerá tanto no cabo A quanto no cabo B.
O comprimento do cabo será de 215 m.
Incorreta. Pois, como a razão h/l= 0,3, ou seja, < 05, temos que o comprimento do cabo pode ser calculado a partir da série: S = l (1+ ⅔. (h/)l² - ⅖ (h/l)\(^4\) + ..., de modo que S = 100 (1 + ⅔. (30/100)² - ⅖ (30/100)\(^4\) = 100.(1,06-3,24x10\(^{-3}\)) = 100 . 105676 =105,676 m., e como o comprimento do cabo é igual a 2.S, temos que S = 211,352 m.
A tração mínima desse cabo será igual a 16,33 kN.
Correta. Sabendo que a tração mínima é dada por T0 = (w.L²)/ 2.h, temos que T0 = (98.(100²))/2.30 = 16.333, 33 N, ou 16,33 kN, como descrito na alternativa.
Uma chapa de metal é construída de forma homogênea, como segue na figura a seguir. Supondo a gravidade constante em todos os pontos, a coordenada do centro de gravidade é:
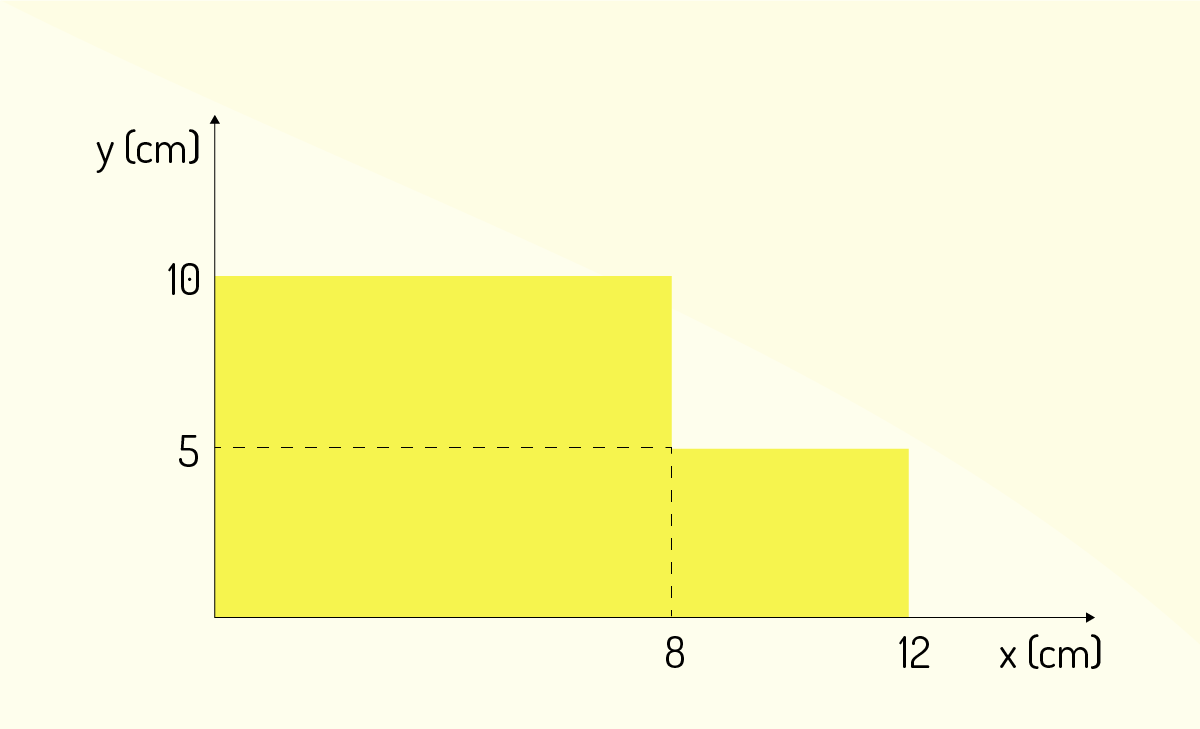
Fonte: Elaborada pelo autor.
\({{P}_{CG}}\) (10,8;9).
Incorreta. Utilizando a equação para determinar o centro geométrico de uma figura plana. A posição x1 e x2 são as coordenadas em x do centro de gravidade das figuras 1 e 2. Da mesma forma, y1 e y2 são as coordenadas em y do centro de gravidade. Calculando as áreas das figuras separadamente e substituindo na equação, obtém-se o valor do centro de gravidade, que é \({{P}_{CG}}\)(5,4;4,5).
\({{P}_{CG}}\)(2,7;3,1).
Incorreta. Utilizando a equação para determinar o centro geométrico de uma figura plana. A posição x1 e x2 são as coordenadas em x do centro de gravidade das figuras 1 e 2. Da mesma forma, y1 e y2 são as coordenadas em y do centro de gravidade. Calculando as áreas das figuras separadamente e substituindo na equação, obtém-se o valor do centro de gravidade, que é \({{P}_{CG}}\)(5,4;4,5).
\({{P}_{CG}}\)(5,4;4,5).
Correta. Utilizando a equação para determinar o centro geométrico de uma figura plana. A posição x1 e x2 são as coordenadas em x do centro de gravidade das figuras 1 e 2. Da mesma forma, y1 e y2 são as coordenadas em y do centro de gravidade. Calculando as áreas das figuras separadamente e substituindo na equação, obtém-se o valor do centro de gravidade, que é \({{P}_{CG}}\)(5,4;4,5).
\({{P}_{CG}}\)(6;5).
Incorreta. Utilizando a equação para determinar o centro geométrico de uma figura plana. A posição x1 e x2 são as coordenadas em x do centro de gravidade das figuras 1 e 2. Da mesma forma, y1 e y2 são as coordenadas em y do centro de gravidade. Calculando as áreas das figuras separadamente e substituindo na equação, obtém-se o valor do centro de gravidade, que é \({{P}_{CG}}\)(5,4;4,5).
\({{P}_{CG}}\) (3;2,5).
Incorreta. Utilizando a equação para determinar o centro geométrico de uma figura plana. A posição x1 e x2 são as coordenadas em x do centro de gravidade das figuras 1 e 2. Da mesma forma, y1 e y2 são as coordenadas em y do centro de gravidade. Calculando as áreas das figuras separadamente e substituindo na equação, obtém-se o valor do centro de gravidade, que é \({{P}_{CG}}\)(5,4;4,5).
Considerando as figuras geométricas irregulares e o método para determinação do centro de gravidade ou centroide, nos casos em que a ação da gravidade é constante, o método é feito por integração. Dada a figura a seguir, as coordenadas do centro de gravidade da chapa homogênea limitada pelas curvas \(y =\frac{{{x}^{4}}}{3}~e~x~=~\frac{{{y}^{2}}}{2}\) são de:
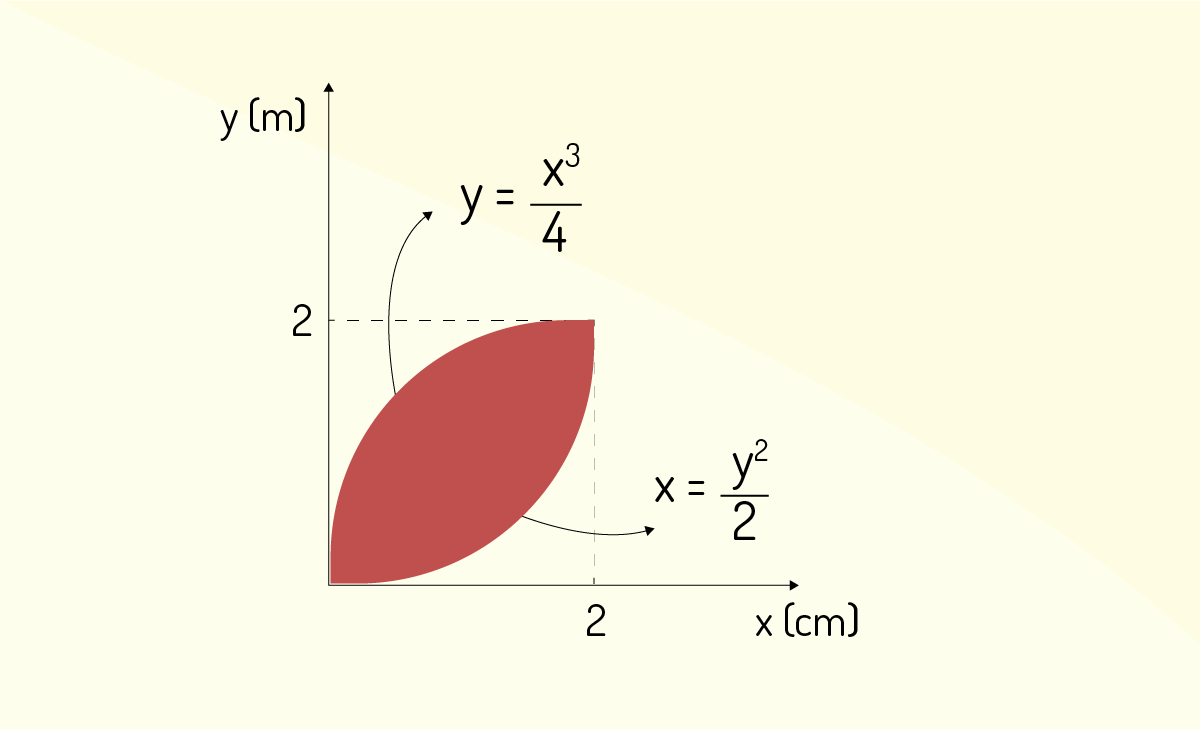
Fonte: Elaborada pelo autor.
\({{P}_{CG}}\)(15/8;3/4).
Incorreta. Dividindo a figura de área desconhecida em retângulos horizontais e verticais de espessura infinitesimal. As integrais \({{x}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{24}{25}\) e \({{y}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \frac{\sqrt{2x}+\frac{{{x}^{3}}}{4}}{2} \right)\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{6}{7}\) são facilmente calculadas utilizando regra de potência para as integrais.
\({{P}_{CG}}\) (20/9;3/4).
Incorreta. Dividindo a figura de área desconhecida em retângulos horizontais e verticais de espessura infinitesimal. As integrais \({{x}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{24}{25}\) e \({{y}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \frac{\sqrt{2x}+\frac{{{x}^{3}}}{4}}{2} \right)\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{6}{7}\) são facilmente calculadas utilizando regra de potência para as integrais.
\({{P}_{CG}}\) (24/25;8/9).
Incorreta. Dividindo a figura de área desconhecida em retângulos horizontais e verticais de espessura infinitesimal. As integrais \({{x}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{24}{25}\) e \({{y}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \frac{\sqrt{2x}+\frac{{{x}^{3}}}{4}}{2} \right)\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{6}{7}\) são facilmente calculadas utilizando regra de potência para as integrais.
\({{P}_{CG}}\) (6/7;3/4).
Incorreta. Dividindo a figura de área desconhecida em retângulos horizontais e verticais de espessura infinitesimal. As integrais \({{x}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{24}{25}\) e \({{y}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \frac{\sqrt{2x}+\frac{{{x}^{3}}}{4}}{2} \right)\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{6}{7}\) são facilmente calculadas utilizando regra de potência para as integrais.
\({{P}_{CG}}\) (24/25;6/7).
Correta. Dividindo a figura de área desconhecida em retângulos horizontais e verticais de espessura infinitesimal. As integrais \({{x}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{24}{25}\) e \({{y}_{CM}}=\frac{\mathop{\int }_{0}^{2}\left( \frac{\sqrt{2x}+\frac{{{x}^{3}}}{4}}{2} \right)\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}{\mathop{\int }_{0}^{2}\left( \sqrt{2x}-\frac{{{x}^{3}}}{4} \right)dx}=\frac{6}{7}\) são facilmente calculadas utilizando regra de potência para as integrais.
Um cilindro homogêneo de massa 25 g e raio de 0,5 cm, que se encontra ao longo do eixo z, tende a girar em torno desse mesmo eixo. O momento de inércia em torno do eixo z para o cilindro é de:
312 \(\mu N.m\).
Incorreta. O momento de inércia de um cilindro ao longo de um eixo não depende do comprimento, dependendo somente da massa e do raio do cilindro. Basta substituir os valores fornecidos no problema, mas deve-se ter cuidado com as unidades, resultando em 0,31 \(\mu N.m\)
31,2 \(\mu N.m\).
Incorreta. O momento de inércia de um cilindro ao longo de um eixo não depende do comprimento, dependendo somente da massa e do raio do cilindro. Basta substituir os valores fornecidos no problema, mas deve-se ter cuidado com as unidades, resultando em 0,31 \(\mu N.m\).
3,1 \(\mu N.m\).
Incorreta. O momento de inércia de um cilindro ao longo de um eixo não depende do comprimento, dependendo somente da massa e do raio do cilindro. Basta substituir os valores fornecidos no problema, mas deve-se ter cuidado com as unidades, resultando em 0,31 \(\mu N.m\).
0,31 \(\mu N.m\).
Correta. O momento de inércia de um cilindro ao longo de um eixo não depende do comprimento, dependendo somente da massa e do raio do cilindro. Basta substituir os valores fornecidos no problema, mas deve-se ter cuidado com as unidades, resultando em 0,31 \(\mu N.m\).
0,03 \(\mu N.m\).
Incorreta. O momento de inércia de um cilindro ao longo de um eixo não depende do comprimento, dependendo somente da massa e do raio do cilindro. Basta substituir os valores fornecidos no problema, mas deve-se ter cuidado com as unidades, resultando em 0,31 \(\mu N.m\).
Supondo que o material do exemplo acima seja uma pequena barra de ouro de 77,28 g, de dimensões 4,0 cm x 2,0 cm x 0,5 cm, sendo comprimento, largura e espessura, respectivamente, o momento dessa barra em torno do eixo z será de:
7,3 kN.m.
Incorreta. Substituindo os valores da massa, comprimento e espessura, lembrando que as unidades precisam estar no SI, ou seja, massa em kg e centímetro em metro, o resultado obtido é de 73,4 µN.m.
734 N.m.
Incorreta. Substituindo os valores da massa, comprimento e espessura, lembrando que as unidades precisam estar no SI, ou seja, massa em kg e centímetro em metro, o resultado obtido é de 73,4 µN.m.
73,4 N.m.
Incorreta. Substituindo os valores da massa, comprimento e espessura, lembrando que as unidades precisam estar no SI, ou seja, massa em kg e centímetro em metro, o resultado obtido é de 73,4 µN.m.
73,4 mN.m.
Incorreta. Substituindo os valores da massa, comprimento e espessura, lembrando que as unidades precisam estar no SI, ou seja, massa em kg e centímetro em metro, o resultado obtido é de 73,4 µN.m.
73,4 µN.m.
Correta. Substituindo os valores da massa, comprimento e espessura, lembrando que as unidades precisam estar no SI, ou seja, massa em kg e centímetro em metro, o resultado obtido é de 73,4 µN.m.
A deformação na forma do material é resultante de uma força tanto interna quanto externa, e pode ser do tipo extensiva ou compressiva, a partir da variação da pressão, temperatura ou mudança estrutural; e medida, segundo a mudança no comprimento do material. Assim, é correto afirmar que a deformação normal na direção y sofrida por uma chapa de comprimento inicial 5,656854 polegadas e comprimento final de 5,660399 polegadas tem valor, em porcentagem, de:
\(6,3667\times 10\wedge -2\).
Incorreta. O cálculo correto é dado por \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\), logo seria \({{\varepsilon }_{m\acute{e}d}}=\frac{\left( 5,660399-5,656854 \right)}{5,656854}=6,2667\times 10\wedge -4\), em porcentagem, faremos esse valor x100, logo \(6,2667\times 10\wedge -2\).
\(6,2628\times 10\wedge -4\).
Incorreta. O cálculo correto é dado por \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\), logo seria \({{\varepsilon }_{m\acute{e}d}}=\frac{\left( 5,660399-5,656854 \right)}{5,656854}=6,2667\times 10\wedge -4\), em porcentagem, faremos esse valor x100, logo \(6,2667\times 10\wedge -2\).
\(5,66\times 10\wedge -4\).
Incorreta. O cálculo correto é dado por \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\), logo seria \({{\varepsilon }_{m\acute{e}d}}=\frac{\left( 5,660399-5,656854 \right)}{5,656854}=6,2667\times 10\wedge -4\), em porcentagem, faremos esse valor x100, logo \(6,2667\times 10\wedge -2\).
\(6,2667\times 10\wedge -2\).
Correta. O cálculo correto é dado por \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\), logo seria \({{\varepsilon }_{m\acute{e}d}}=\frac{\left( 5,660399-5,656854 \right)}{5,656854}=6,2667\times 10\wedge -4\), em porcentagem, faremos esse valor x100, logo \(6,2667\times 10\wedge -2\).
\(2,06\times 10\wedge -2\).
Incorreta. O cálculo correto é dado por \({{\varepsilon }_{m\acute{e}d}}=\frac{\Delta S'-\Delta S}{\Delta S}\), logo seria \({{\varepsilon }_{m\acute{e}d}}=\frac{\left( 5,660399-5,656854 \right)}{5,656854}=6,2667\times 10\wedge -4\), em porcentagem, faremos esse valor x100, logo \(6,2667\times 10\wedge -2\).
Dada uma haste de aço com diâmetro de 5 mm presa a uma parede fixa em seu segmento A, temos que, antes de ser carregada com uma carga específica, esta possui uma folga de 1 mm entre o ponto B’(parede) e ela. Determine as reações em A e B’ a partir da descrição anterior para quando a haste for submetida a uma força axial P = 20 kN. Lembre-se de desprezar o tamanho do colar em Ce, considere Eaço = 200 GPa.
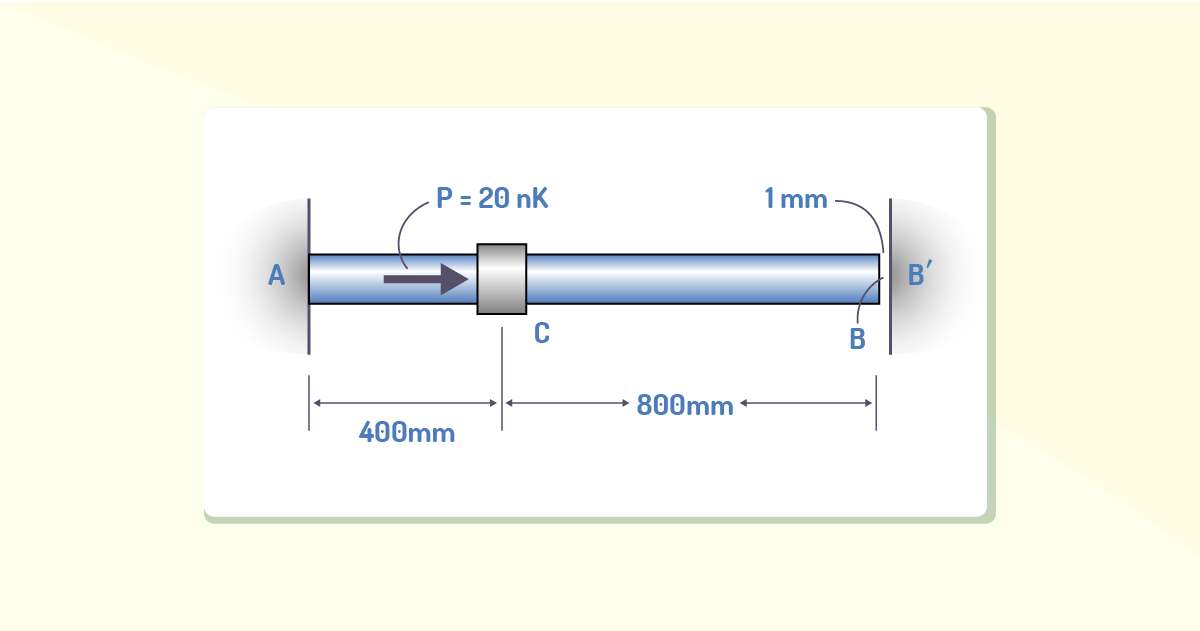
Fonte: Adaptada de Hibbeler (2010, p. 117).
A força em A será de FA= 18,6 kN.
Incorreta. Visto que -FA - FB + 20x10^3 = 0 e que 400 FA- 800 FB = 3,93x10^6 N.mm, então, teremos que o valor de FA = 16,6 kN.
A força em B será de FB = 3,36 kN.
Correta. Dado que -FA-FB+20x10^3=0 e que 400 FA- 800 FB= 3,93x10^6 N.mm, então, teremos que FB= 3,36kN, como descrito na alternativa.
A condição de compatibilidade para a haste é δAB = 1m.
Incorreta. O valor de δAB é de 1mm.
O equilíbrio da haste será dado por FA-FB-20x10^3=0.
Incorreta. O equilíbrio da haste será dado por -FA-FB+20x10^3=0.
A força em A será de 16,6N.
Incorreta. Visto que -FA-FB+20x10^3=0 e que 400 FA- 800 FB= 3,93x10^6 N.mm, então, teremos que o valor de FA= 16,6 kN.
Elementos com seção transversal circular, como tubos e eixos, transmitem potência gerada por máquinas, de modo que, submetidos a torques, dependem dessa potência e da velocidade angular do eixo. Sabendo que um eixo tubular de diâmetro interno de 30mm e diâmetro externo de 42 mm é usado para transmitir 90kW de potência, assinale a alternativa correta, sabendo que a tensão de cisalhamento não excede 50 MPa.
O momento de inércia J terá valor de 3,29x10^-6 m^4.
Incorreta. Visto que \(J=\left( \frac{\pi }{2} \right)\left( c_{O}^{4}-c_{i}^{4} \right)\), logo J= π ((0,021^4)- (0,015^4))/2, então J= 2,2597 x10^-7 m^4.
O Torque T terá valor de 538 Nm.
Correta. Sabendo que \({{T}_{m\acute{a}x}}=\frac{{{T}_{c}}}{J}\), então T= (50x10^6.2,2597 x 10^-7)/0,021, logo T= 538, como descrito na alternativa.
O momento de inércia será nulo.
Incorreta. Visto que \(J=\left( \frac{\pi }{2} \right)\left( c_{O}^{4}-c_{i}^{4} \right)\), logo J= π ((0,021^4)- (0,015^4))/2, então J= 2,2597 x10^-7 m^4.
A frequência de rotação terá valor de 27,7 Hz.
Incorreta. Visto que P=2⋅π⋅ f⋅T, então f= 90x10^3/(2⋅π⋅538), logo f= 26,6Hz.
O valor do torque será 540 Nm.
Incorreta. Sabendo que \({{T}_{m\acute{a}x}}=\frac{{{T}_{c}}}{J}\), então T= (50x10^6.2,2597 x 10^-7)/0,021, logo T= 538, como descrito na alternativa.
Considere uma viga cuja seção transversal é retangular e seu momento interno é 2,88 kN para a seção transversal de 60x120mm. Agora, determine o cálculo advindo dessa situação.
O momento de inércia dessa viga terá valor de 5,64x10^4 mm^4.
Incorreta. Visto que \(I=\frac{b{{h}^{3}}}{12}\), então I= (60.120)/12, logo I= 864x10^4 mm^4.
O momento de inércia dessa viga terá valor de 8,64x10^4mm^4.
Incorreta. Visto que \(I=\frac{b{{h}^{3}}}{12}\), então I= (60.120)/12, logo I= 864x10^4 mm^4.
A tensão máxima sobre a viga será de 12 N/mm^2.
Incorreta. Como vimos, \({{\sigma }_{m\acute{a}x}}=\frac{Mc}{I}\), então \({{\sigma }_{m\acute{a}x}}=\) (2,88x10^6. 60)/ 864x10^4, logo \({{\sigma }_{m\acute{a}x}}=\) 20 N/mm^2 ou 20 MPa, o que não condiz com a alternativa apresentada.
O momento de inércia dessa viga terá valor de 864x10^4 mm^4 e tensão máxima de 15 MPa.
Incorreta. Visto que \(I=\frac{b{{h}^{3}}}{12}\), então I= (60.120)/12, logo I= 864x10^4 mm^4 e \({{\sigma }_{m\acute{a}x}}=\frac{Mc}{I}\), então \({{\sigma }_{m\acute{a}x}}=\) (2,88x10^6. 60)/ 864x10^4, logo \({{\sigma }_{m\acute{a}x}}=\) 20 N/mm^2 ou 20 MPa.
A tensão máxima sobre a viga será de 20 MPa.
Correta. \({{\sigma }_{m\acute{a}x}}=\frac{Mc}{I}\), então \({{\sigma }_{m\acute{a}x}}=\) (2,88x10^6. 60)/ 864x10^4, logo \({{\sigma }_{m\acute{a}x}}=\) 20 N/mm^2 ou 20 MPa, como descrito na alternativa.