A cinemática é a descrição precisa do movimento e é essencial para entender a biomecânica do movimento humano. A cinemática pode variar de descrições anatômicas de rotações articulares a medidas matemáticas precisas de movimentos musculoesqueléticos. Ela se divide de acordo com os tipos de medidas usadas, lineares ou angulares.
Qualquer que seja a forma de medição, os estudos biomecânicos da cinemática de intérpretes qualificados fornecem informações valiosas sobre a técnica de movimento desejável. A biomecânica tem uma longa história de medições cinemáticas do movimento humano. Medições cinemáticas exatas são algumas vezes usadas para o cálculo de variáveis cinéticas mais complexas. Nesta unidade você irá conhecer a importância da cinemática linear e angular nas ciências do movimento.
Bons estudos!
Esta parte da unidade vai mostrar a você, aluno(a), o estudo da mecânica do movimento humano com uma discussão sobre quantidades cinemáticas lineares e movimento de projéteis.
Cinemática é a geometria, padrão ou forma de movimento em relação ao tempo. A cinemática, que descreve a aparência do movimento, distingue-se da cinética, as forças associadas ao movimento. Cinemática Linear envolve a forma, o padrão e o sequenciamento do movimento linear por meio do tempo, sem referência particular às forças que causam ou resultado do movimento.
Análises cinemáticas cuidadosas do desempenho são inestimáveis para os médicos, professores de atividade física, treinadores e demais profissionais que buscam a análise do movimento. Quando as pessoas aprendem uma nova habilidade motora, uma modificação progressiva dos reflexos cinemáticos do movimento são itens que compõem o processo de aprendizagem.
Isto é particularmente verdadeiro para as crianças pequenas, cujos movimentos da cinemática mudam com as mudanças normais na antropometria e coordenação neuromuscular que acompanham o crescimento. Da mesma forma, quando um paciente reabilita uma articulação lesada, o terapeuta ou o clínico procura o retorno gradual da cinemática da articulação normal.
A cinemática abrange as formas qualitativa e quantitativa de análise. Por exemplo, descrevendo qualitativamente a cinemática de um chute de futebol implica identificar as principais ações conjuntas, incluindo plantiflexão e, possivelmente, flexão plantar no tornozelo.
Uma análise qualitativa mais detalhada é a análise da cinemática. A análise cinemática também pode descrever o sequenciamento preciso e o tempo dos movimentos do segmento do corpo, o que se traduz no grau de habilidade evidente por parte do jogador.
Embora a maioria das avaliações de movimento é realizada qualitativamente mediante a observação visual, a análise quantitativa também é, por vezes, apropriada. Fisioterapeutas, por exemplo, frequentemente medem a amplitude de movimento de uma articulação lesada e ajuda a determinar em que medida os exercícios de amplitude de movimento podem ser necessários.
Quando um treinador mede o desempenho de um atleta no tiro ou salto em comprimento, isso também é uma avaliação quantitativa. Biomecânicos do esporte muitas vezes estudam quantitativamente os fatores cinemáticos que caracterizam um desempenho de elite ou os fatores biomecânicos que pode limitar o desempenho de um determinado atleta.
Pesquisadores descobriram que os velocistas de elite, por exemplo, desenvolvem velocidade vertical saindo dos blocos de partida, em comparação com velocistas não elites. Durante a abordagem para o pico de salto no voleibol e a decolagem no salto de esqui são as sutilezas na abordagem cinemática que influenciam a altura do pico do salto e o comprimento do salto de esqui.
A maioria dos estudos biomecânicos da cinemática humana, no entanto, é realizada em atletas não elíticos. A pesquisa cinemática tem mostrado que crianças exibem diferentes estratégias na caminhada do que os adultos, exibindo variabilidade e comportamento exploratório em comparação aos adultos.
Em colaboração com especialistas adaptados em educação física, biomecânicos documentaram os padrões cinemáticos característicos associados a condições incapacitantes relativamente comuns, como paralisia cerebral, Síndrome de Down e acidente vascular cerebral.
Os biomecânicos que estudam a propulsão de cadeira de rodas mostraram que, para impulsionar uma cadeira de rodas, os paraplégicos aumentam o tronco para a frente magra e empregaram frequência de curso aumentada juntamente com a diminuição da velocidade de braçada.
Unidades de distância e deslocamento são unidades de comprimento. No sistema métrico, a unidade mais comumente utilizada de distância e deslocamento é o metro (m). Um quilômetro (km) é de 1000 m, um centímetro (cm) é \(\frac{1}{1000}\).mm, e um milímetro (mm) é \(\frac{1}{1000}\).m. No sistema inglês, unidades comuns de comprimento são a polegada, o pé (0,30 m), o pátio (0,91 m) e a milha (1,61 km).
Distância e deslocamento são avaliados de forma diferente. Distância é medida ao longo do caminho do movimento. Quando um corredor completa 1 1⁄2 voltas ao redor uma pista de 400 metros, a distância que o corredor cobriu é igual a 600 (400 + 200) metros.
O deslocamento linear é medido em uma linha reta posição 1 para a posição 2, ou da posição inicial para a posição final. No fim de 1 1⁄2 voltas ao redor da pista, o deslocamento do corredor é o comprimento da linha imaginária reta que atravessa o campo, conectando o corredor da posição inicial para a posição final do corredor na metade da pista.
Na conclusão de 2 voltas ao redor da pista, a distância percorrida é de 800 metros. Pelo fato das posições inicial e final serem as mesmas, no entanto, o deslocamento do corredor é zero. Quando um skatista se movimenta em uma pista, a distância percorrida pelo skatista pode ser medida ao longo dos trilhos deixados pelos patins. O deslocamento do patinador é medido ao longo de uma reta linha da posição inicial até a final no gelo.
Outra diferença é que a distância é uma grandeza escalar durante o deslocamento é uma quantidade vetorial. Consequentemente, o deslocamento inclui mais que apenas o comprimento da linha entre duas posições. De igual importância é a direção na qual o deslocamento ocorre.
A direção de um deslocamento relaciona a posição final com a posição inicial. Por exemplo, o deslocamento de um iate que navegou 900 metros para o sul seria identificado como 900 metros ao sul.
A direção de um deslocamento pode ser indicada em várias formas igualmente aceitáveis. Direções de bússola como Sul e Noroeste e os termos esquerda/direita, cima/baixo e positivo/negativo são todos apropriados rótulos.
A direção positiva é tipicamente definida como ascendente e/ou direito, com negativo considerado como para baixo e/ou para a esquerda. Isso permite indicação de direção usando sinais de mais e menos.
O mais importante é ser consistente em usar o sistema ou convenção adotada para indicar a direção em um determinado contexto. Seria confuso descrever um deslocamento a 500 metros Norte seguido por 300 metros à direita.
Qualquer distância ou deslocamento pode ser a quantidade mais importante de interesse dependendo da situação. Muitos hipódromos de 5 km e 10 km são configurados de maneira correta para promoverem melhor desempenho do atleta.
Os participantes dessas corridas, geralmente, estão interessados no número de quilômetros de distância que percorreram ou na quantidade que falta para finalizar a corrida. Por isso, esses ambientes necessitam estar sinalizados com as distâncias.
O conhecimento do deslocamento não é particularmente valioso durante este tipo de evento. Em outras situações, no entanto, o deslocamento é mais importante. Por exemplo, as competições de triatlo podem envolver um mergulho em um lago.
Porque nadar em uma perfeitamente reta linha por meio de um lago é praticamente impossível, a distância real de um nadador cobre é sempre um pouco maior do que a largura do lago.
No entanto, o curso é configurado para que o comprimento identificado do curso de natação é o comprimento do deslocamento entre a entrada e pontos de saída no lago.
A magnitude do deslocamento e a distância percorrida podem ser idênticas. Quando um esquiador de fundo percorre um caminho reto pela floresta, a distância percorrida e o deslocamento são iguais. No entanto, a qualquer momento o caminho de movimento não é retilíneo, a distância percorrida e o tamanho do deslocamento serão diferentes.
Duas grandezas que paralela distância e deslocamento linear são rapidez e velocidade linear. Estes termos são frequentemente usados como sinônimos em geral conversa, mas na mecânica, eles têm significados precisos e diferentes.
A velocidade, uma grandeza escalar, é definida como a distância percorrida e o tempo gasto para cobri-lo:
\[rapidez~=\frac{comprimento~\left( ou~dist\hat{a}ncia \right)}{mudana~no~tempo}\]
Velocidade (v) é a mudança de posição, ou deslocamento, que ocorre durante um determinado período de tempo:
\[velocidade~=\frac{mudana~de~posi\tilde{a}o~\left( ou~deslocamento \right)}{mudana~no~tempo}\]
Porque a letra maiúscula grega delta (Δ) é comumente usada em matemática expressões para significar "mudar em", uma versão abreviada do relacionamento expresso a seguir, com t representando a quantidade de tempo decorrido durante a avaliação de velocidade:
\[velocidade~=\frac{mudana~de~posi\tilde{a}o~\left( ou~deslocamento \right)}{mudana~no~tempo}\]
Porque a letra maiúscula grega delta (Δ) é comumente usada em matemática expressões para significar "mudar em", uma versão abreviada do relacionamento expresso a seguir, com t representando a quantidade de tempo decorrido durante a avaliação de velocidade:
\[velocidade~=\frac{\Delta ~posi\tilde{a}o}{\Delta ~tempo}=~\frac{d}{\Delta t}\]
Outra maneira de expressar a mudança de posição é posição² _ posção¹, em qual posição¹ representa a posição do corpo em um ponto no tempo e posição² representa a posição do corpo em um momento posterior:
\[velocidade~=\frac{posi\tilde{a}o{}^\text{2}~-~posi\tilde{a}o{}^\text{1}}{tempo{}^\text{2}~-~tempo{}^\text{1}}\]
Como a velocidade é baseada no deslocamento, também é uma grandeza vetorial. Consequentemente, a descrição da velocidade deve incluir uma indicação da direção e a magnitude do movimento.
Se a direção do movimento é positiva, a velocidade é positiva; se a direção for negativa, a velocidade é negativa. Uma mudança na velocidade de um corpo pode representar uma mudança em sua velocidade, direção do movimento ou ambos.
Sempre que duas ou mais velocidades atuam, as leis da álgebra vetorial governam a velocidade e direção finais do movimento resultante. Por exemplo, o caminho realmente tomado por um nadador atravessando um rio é determinado pela soma vetorial da velocidade do nadador na direção desejada e da velocidade da corrente do rio.
Unidades de rapidez e velocidade são unidades de comprimento divididas por unidades de tempo. No sistema métrico, as unidades comuns para velocidade são metros por segundo (m/s) e quilômetros por hora (km/h). No entanto, qualquer unidade de comprimento dividido por qualquer unidade de tempo produz uma unidade aceitável de velocidade.
Por exemplo, uma velocidade de 5 m/s também pode ser expressa como 5000 mm/s ou 18.000 m/h. Geralmente, é mais prático selecionar unidades que resultarão em expressão da quantidade na forma menor e mais manejável. Para a marcha humana, a velocidade é o produto do comprimento da passada e da frequência da passada.
Caro(a) aluno(a), nos últimos anos, a biomecânica apresenta inúmeras contribuições para o esporte, dentre essas, podemos citar a análise e a melhoria da técnica desportiva, o desenvolvimento de equipamentos esportivos, a prevenção de lesões etc. Como você pode ver, o uso da biomecânica no seu dia a dia? Reflita!

Durante a corrida, uma variável cinemática, como o comprimento da passada, não é simplesmente uma função da altura do corpo do corredor, mas também é influenciada pelo músculo composição de fiéis, calçados, nível de fadiga, histórico de lesões e inclinação (grau) e rigidez da superfície de corrida.
Corredores viajando a um ritmo lento tendem a aumentar a velocidade principalmente aumentando o comprimento da passada. Em velocidades de corrida mais rápidas, os corredores recreativos confiam mais aumentando a frequência da passada para aumentar a velocidade.
Em esqui cross-country, à medida que a velocidade aumenta, a velocidade da passada aumenta e o comprimento da passada tende a diminuir. Overstriding, ou usando um comprimento de passada muito longo, deve ser evitado tanto na corrida quanto no esqui, já que é um fator de risco para as estirpes de isquiotibiais.
Aqueles que correm regularmente para o exercício geralmente preferem um determinado passo frequência ao longo de um intervalo de velocidades de funcionamento lento a moderado. Uma razão para isso pode estar relacionada à economia de corrida - o consumo de oxigênio necessário para executar uma determinada tarefa.
A maioria dos corredores tende a escolher o custo fisiológico da corrida. Como já sabemos, muitas espécies de animais fazem a mesma coisa. Correndo em superfícies de descidas e subidas tende a aumentar e diminuir, respectivamente, a velocidade de corrida, diferenças principalmente em função do aumento e diminuição do comprimento da passada. A presença de fadiga, como seria de esperar perto do final de uma maratona, tende a resultar em aumento da frequência de passada e comprimento diminuído da passada.
Como maximizar a velocidade é o objetivo de todos os eventos de corrida, o esporte biomecânico se concentra nas características cinemáticas que parecem acompanhar performances rápidas em corrida, esqui, patinação, ciclismo, eventos de natação e remo.
Pesquisas mostram que corredores de elite de 1500 metros distinguem-se de outros artistas qualificados no evento por cinemática do quadril, sugerindo um uso mais eficiente dos quadris durante a corrida.
No esqui cross-country, o uso da técnica de duplo impulso é superior a outras técnicas para a velocidade de patinação em subida em que envolve comprimentos de ciclo mais longos, uma taxa de ciclo mais baixa e uma recuperação mais longa.
Quando as performances de corrida são analisadas, as comparações são geralmente com base no ritmo, em vez de velocidade. O ritmo é o inverso da velocidade. Em vez de unidades de distância divididas por unidades de tempo, o ritmo é apresentado como unidades de tempo divididas por unidades de distância. Ritmo é o tempo necessário para cobrir uma determinada distância e é comumente quantificado como minutos por km ou minutos por milha.
Estamos bem conscientes de que a consequência de pressionar ou desistir o acelerador pedal de um automóvel é geralmente uma mudança na velocidade do automóvel. A aceleração linear (a) é definida como a taxa de mudança na velocidade, ou a mudança na velocidade que ocorre durante um dado intervalo de tempo (t):
\[a~=\frac{mudana~de~velocidade}{mudana~de~tempo}~=\frac{\Delta ~v}{\Delta t}\]
Outra maneira de expressar a mudança na velocidade é v2 - v1, onde v1 representa a velocidade em um ponto no tempo e v2 representa a velocidade em um ponto posterior:
\[a~=\frac{v2~-~v1}{\Delta t}\]
Unidades de aceleração são unidades de velocidade divididas por unidades de tempo. Se um carro aumenta sua velocidade em 1 km/h a cada segundo, sua aceleração é de 1 km/h/s.
Se um esquiador aumenta a velocidade em 1 m/s por segundo, a aceleração é 1 m/s/s. Em termos matemáticos, é mais simples expressar a aceleração do esquiador como 1 m/s ao quadrado (1 m/s²). Uma unidade comum de aceleração no sistema métrico é m/s².
Aceleração é a taxa de mudança na velocidade, ou o grau com o qual a velocidade está mudando em relação ao tempo. Por exemplo, um corpo acelerando em uma direção positiva a uma taxa constante de 2 m/s² está aumentando sua velocidade por 2 m/s por segundo.
Se a velocidade inicial do corpo fosse zero, um segundo depois sua velocidade seria 2 m/s, um segundo depois disso sua velocidade seria 4 m/s, e um segundo depois disso sua velocidade seria 6 m/s.
No uso geral, o termo aceleração significa acelerar ou aumentar em velocidade. Se v2 é maior que v1, a aceleração é um número positivo, e o corpo em movimento pode ter acelerado durante o período em questão.
No entanto, porque às vezes é apropriado rotular a direção de movimento como positivo ou negativo, um valor positivo de aceleração pode não significar que o corpo está acelerando. Se a direção do movimento é descrita em termos diferentes de positivo ou negativo, um valor positivo de aceleração indica que o corpo que está sendo analisado acelerou.
Por exemplo, se a velocidade de um velocista é de 3 m/s deixando os blocos e é 5 m/s um segundo depois, no cálculo da aceleração ocorreu um número positivo. Porque v1 = 3 m/s, v2 = 5 m/s, e t = 1 s:
\[a=\frac{v2~-~v1}{\Delta ~t}\]
\[=\frac{5~m/s~-~3~m/s}{1~s}\]
\[=~2~m/s{}^\text{2}\]
Sempre que a direção do movimento é descrita em termos diferentes de positivo ou negativo, e v2 é maior que v1, o valor da aceleração será um número positivo e o objeto em questão está acelerando.
A aceleração também pode assumir um valor negativo. Enquanto a direção do movimento é descrita em termos diferentes de positivo ou negativo, negativo aceleração indica que o corpo em movimento está diminuindo, ou que sua velocidade está diminuindo.
Por exemplo, quando um corredor base desliza para uma parada na home plate, a aceleração é negativa. Se a velocidade de um corredor base é 4 m/s ao entrar em uma corrediça de 0,5 s que interrompe o movimento, v1 = 4 m/s, v2 = o, e t = 0.5 s. A aceleração pode ser calculada da seguinte forma:
\[a=\frac{v2~-~v1}{~t}\]
\[=\frac{0~-~4~m/s}{0.5~s}\]
\[=~-8~m/s{}^\text{2}\]
Sempre que v1 for maior que v2 nesse tipo de situação, a aceleração será negativa. Entender a aceleração é mais complicado quando uma direção é designada como positivo e a direção oposta é designada como negativa. Nesta situação, um valor positivo de aceleração pode indicar que o objeto está acelerando em uma direção positiva ou que está desacelerando para baixo em uma direção negativa.
Considere o caso de uma bola cair de uma mão. Como a bola cai mais rápido por causa da influência da gravidade, está ganhando velocidade, por exemplo, 0,3 m/s a 0,5 m/s a 0,8 m/s. Porque a direção descendente é considerada como a direção negativa, a velocidade da bola é realmente –0,3 m/s a –0,5 m/s a –0,8 m/s. Se v1 = - 0,3 m/s, v2 = - 0,5 m/s e t = 0,02 s. A aceleração é calculada da seguinte forma:
\[a=\frac{v2~-~v1}{~t}\]
\[\frac{-0.5~m/s~-~\left( -0.3~~m/s \right)}{0.02~s}\]
\[=~-10~m/s{}^\text{2}\]
Nesta situação, a bola está acelerando, mas sua aceleração é negativa porque está acelerando em uma direção negativa. Se a aceleração for negativa, a velocidade pode estar aumentando em uma direção negativa ou diminuindo direção positiva.
Alternativamente, se a aceleração for positiva, a velocidade pode ser que seja aumentada em uma direção positiva ou diminuída em uma direção negativa. A terceira alternativa é a aceleração ser igual a zero.
Aceleração é zero sempre que a velocidade é constante, isto é, quando v1 e v2 são os mesmos. No meio de uma corrida de 100 metros, a aceleração de um sprinter deve ser perto de zero, porque nesse ponto o corredor deve estar correndo em uma velocidade constante, quase máxima.
Aceleração e desaceleração (o prazo para aceleração negativa) tem implicações para a lesão do corpo humano, já que a mudança de velocidade resulta da aplicação da força. O cruzado anterior ligamento, que restringe o deslizamento para a frente do fêmur no nervo tibial planaltos durante a expiração do joelho, é frequentemente ferido quando um atleta que está correndo desacelera rapidamente ou muda de direção rapidamente.
É importante lembrar que, como a aceleração é uma grandeza vetorial, mudando de direção, mesmo mantendo uma velocidade constante, representam uma mudança na aceleração. As forças associadas com mudança na aceleração com base na mudança de direção devem ser compensadas por esquiadores e ciclistas de velódromo, em particular.
Geralmente é interessante determinar a velocidade de aceleração de um objeto ou segmento do corpo em um determinado momento. Por exemplo, o instantâneo velocidade de um tiro ou de um disco no momento em que o atleta o libera afeta a distância que o implemento irá percorrer. Às vezes, é suficiente para quantificar a velocidade média ou a velocidade de todo o desempenho.
Quando a velocidade e velocidade linear são calculadas, os procedimentos dependem se o valor médio ou instantâneo é a quantidade de interesse. A velocidade média é calculada como o deslocamento final dividido pelo tempo total. A aceleração média é calculada como a diferença no final e velocidades iniciais divididas por todo o intervalo de tempo.
Cálculo de valores instantâneos podem ser aproximados dividindo as diferenças entre velocidades durante um intervalo de tempo extremamente pequeno. Com cálculo, a velocidade pode ser calculada como a derivada do deslocamento, e aceleração como a derivada da velocidade.
A seleção do intervalo de tempo em que a velocidade é quantificada é importante ao analisar o desempenho de atletas em eventos de corrida. Muitos atletas podem manter recordes mundiais pela primeira metade ou três quartos do evento, mas lento durante a última etapa por causa da fadiga.
Alternativamente, alguns atletas podem realizar intencionalmente ritmo durante os segmentos anteriores de uma corrida e, em seguida, atingir a velocidade máxima no fim. Quanto mais longo for o evento, mais informações serão potencialmente perdidas ou ocultado quando apenas o tempo final ou a velocidade média é reportada.
Existem muitos usos da análise cinemática. Os cientistas e treinadores esportivos costumam usar a cinemática para caracterizar o desempenho da elite, por exemplo, analisando um padrão de movimento e a velocidade da cabeça do taco de golfe. Nesse sentido, escolha a alternativa correta em relação a cinemática do movimento humano.
A cinemática é a área de estudo que examina as forças que agem sobre o corpo humano.
Incorreta. Cinemática é a geometria, padrão ou forma de movimento em relação ao tempo.
A cinemática corresponde tanto às análises qualitativas quanto as quantitativas do movimento.
Correta. A cinemática abrange as formas qualitativa e quantitativa de análise. Cinemática é o ramo da física que se ocupa da descrição dos movimentos dos corpos, sem se preocupar com a análise de suas causas.
A posição inicial com a posição final está relacionada com a direção de deslocamento.
Incorreta. A direção de um deslocamento relaciona a posição final com a posição inicial.
São avaliados de formas iguais a distância e o deslocamento.
Incorreta. Distância e deslocamento são avaliados de forma diferente.
Unidades de distância e deslocamento são unidades de largura.
Incorreta. Unidades de distância e deslocamento são unidades de comprimento.
Corpos projetados no ar são projéteis. Uma bola de basquete, um disco, um saltador alto e um mergulhador do céu são todos projéteis, desde que eles se movam as quantidades cinemáticas são de interesse.
O deslocamento horizontal resultante do projétil determina o vencedor do concurso em campo de eventos como arremesso de peso, arremesso de disco e arremesso de dardo. Saltadores altos e volteadores de vara maximizam o deslocamento vertical para vencer eventos.
Os saltadores de paraquedas manipulam componentes horizontais e verticais de velocidade para pousar o mais próximo possível de alvos no chão. No entanto, nem todos os objetos que voam pelo ar são projéteis.
Um projétil é um corpo em queda livre que está sujeito apenas às forças da gravidade e a resistência do ar. Portanto, objetos como aviões e foguetes não são qualificados como projéteis, porque eles também são influenciados pelas forças geradas por seus motores.
Assim como é mais conveniente analisar o movimento geral em termos de componentes lineares e angulares, é geralmente mais significativo analisar os componentes horizontais e verticais do movimento do projétil separadamente. Isto é verdade por duas razões.
Primeiro, o componente vertical é influenciado por gravidade, ao passo que nenhuma força (negligenciando a resistência do ar) afeta a componente. Em segundo lugar, o componente horizontal do movimento refere-se à distância percorrida pelo projétil e a componente vertical à altura máxima alcançada pelo projétil.
Uma vez que um corpo tenha sido projetado no ar, sua velocidade geral (resultante) está mudando constantemente por causa das forças que agem sobre ele. Quando examinados separadamente, no entanto, os componentes horizontais e verticais da mudança de velocidade do projétil previsivelmente. Componentes horizontais e verticais do movimento do projétil são independentes de cada um.
Um fator importante que influencia o componente vertical, mas não o horizontal de movimento de projétil é a força da gravidade, que acelera os corpos em uma direção vertical em direção à superfície da terra.
Ao contrário dos fatores aerodinâmicos que podem variar com a velocidade do vento, a gravitacional força é uma força constante e imutável que produz uma constante para baixo da aceleração vertical. Usando a convenção de que para cima é positivo e negativo é negativo, a aceleração da gravidade é tratada como negativa em quantidade (- 9,81 m/s²).
Esta aceleração permanece constante independentemente do tamanho, forma ou peso do projétil. O componente vertical da velocidade inicial de projeção determina o deslocamento vertical máximo alcançado por um corpo projetado a partir de uma determinada altura de projeção relativa.
Se um objeto foi projetado em um vácuo (sem resistência do ar), a horizontal componente de sua velocidade permaneceria exatamente a mesma ao longo do voo. No entanto, na maioria das situações da vida real, a resistência do ar afeta o componente horizontal da velocidade do projétil.
Uma bola jogada com uma dada velocidade inicial em uma área ao ar livre viajará muito mais longe se for lançada com um vento de cauda ao invés de um vento de proa. Porque os efeitos do ar e a resistência são variáveis, no entanto, é costume desconsiderar a resistência do ar ao discutir e resolver problemas relacionados com o movimento de projéteis, uma vez que isso permite tratar o componente horizontal do movimento do projétil como uma quantidade imutável (constante).
Quando um projétil cai verticalmente no ar em uma vida real típica situação, sua velocidade em qualquer ponto também está relacionada à resistência do ar. Um céu a velocidade do mergulhador, por exemplo, é muito menor após a abertura do paraquedas do que antes de sua abertura.
Três fatores influenciam a trajetória (trajetória de voo) de um projétil:
(a) Ângulo de projeção.
(b) A velocidade de projeção.
(c) A altura relativa da projeção.
Entender como esses fatores interagem é útil no contexto do esporte, tanto para determinar como melhor projeto das bolas e outros implementos e para prever a melhor forma de pegar ou golpear bolas projetadas.
O ângulo de projeção e os efeitos da resistência do ar governam a forma da trajetória de um projétil. Mudanças na velocidade de projeção influenciam o tamanho da trajetória, mas o formato da trajetória depende apenas da projeção ângulo.
Na ausência de resistência do ar, a trajetória de um projétil assume uma das três formas gerais, dependendo do ângulo de projeção. Se o ângulo de projeção é perfeitamente vertical, a trajetória também é perfeitamente vertical, com o projétil seguindo o mesmo caminho para cima e depois para baixo novamente.
Se o ângulo de projeção é oblíquo (em algum ângulo entre 0° e 90°), a trajetória é parabólica, ou em forma de parábola. Uma parábola é simétrica, então suas metades direita e esquerda são imagens espelhadas de cada um.
Um corpo projetado perfeitamente horizontalmente (em um ângulo de 0°) seguirá uma trajetória parecida com a metade de uma parábola. Uma bola lançada para cima em um ângulo de projeção de 80° para a horizontal segue um ângulo relativamente alto e estreito da trajetória, alcançando mais altura que a distância horizontal. Uma bola projetada para cima em um ângulo de 10° em relação à horizontal segue uma trajetória que é plana e longa em forma.
O ângulo de projeção tem implicações diretas para o sucesso no esporte de basquete, já que um ângulo quase vertical de entrada na cesta permite uma margem de erro um pouco maior do que um ângulo de entrada mais horizontal.
Dentro de 4,57 metros da cesta, os ângulos de liberação do arremesso são de cerca de 52 a 55°, proporcionando um ângulo de entrada relativamente vertical, enquanto 6,40 metros tendem a ser liberados a 48-50°, permitindo uma liberação mínima da velocidade, mas um ângulo de entrada menos vertical.
Ao fotografar em close proximidade de um defensor, os jogadores tendem a soltar a bola de uma forma mais vertical o ângulo de liberação e de uma altura maior do que é o caso quando o jogador está aberto. Embora a estratégia por trás disso seja tipicamente impedir que a foto seja bloqueada, ela também pode resultar em tiroteio.
Em situações de projeção em um campo, a resistência do ar pode, na realidade, criar irregularidades na forma da trajetória de um projétil. Uma modificação típica na trajetória causada pela resistência do ar é exibida na Figura 3.1.
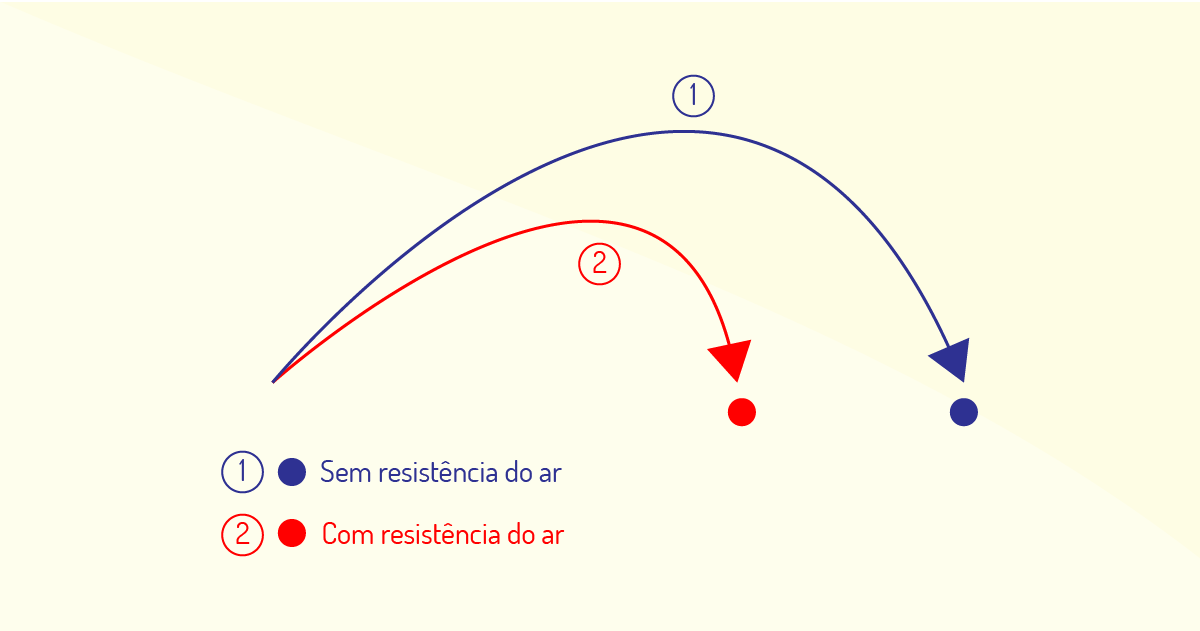
A seguir, veremos a velocidade de projeção.
Quando o ângulo de projeção e outros fatores são constantes, a velocidade de projeção define a duração ou até mesmo o tamanho da trajetória de um projétil. Por exemplo, quando um corpo é projetado verticalmente para cima, a velocidade inicial do projétil define a altura do ápice da trajetória. Para um corpo que é projetado em um ângulo oblíquo, a velocidade de projeção define a altura e o comprimento horizontal da trajetória.
O desempenho na execução de um salto vertical em uma superfície plana é inteiramente dependente da velocidade de decolagem; isto é, quanto maior a velocidade vertical na decolagem, maior o salto, e quanto maior o salto, maior a quantidade de tempo que o saltador está no ar.
Os jogadores de vôlei de praia de elite podem pular mais alto e permanecer no ar por mais tempo ao decolar de uma superfície sólida do que da areia, porque a instabilidade da areia produz uma redução na velocidade de decolagem.
O tempo necessário para a execução de um salto vertical pode ser uma essencial questão para coreógrafos de dança. A incorporação de saltos verticais em um desempenho deve ser planejada com atenção e cuidado.
Se o ritmo da música necessita que os saltos verticais sejam realizados dentro de um terço de segundo, a altura dos saltos é restrita a aproximadamente 12 cm. O coreógrafo deve estar ciente de que, nessas situações, grande parte dos dançarinos não têm folga suficiente para apontar seus dedos durante a execução do salto.
O terceiro fator principal que influencia a trajetória do projétil é a altura relativa da projeção. Quando um disco é lançado por um lançador de uma altura de 1½ metro acima do solo, a altura de projeção relativa é 1 ½ metro, porque a projeção altura é 1 ½ metro maior do que a altura do campo entre o disco e a terra.
Se uma bola de golfe acionada se aloja em uma árvore, a projeção relativa da altura é negativa, porque a altura de pouso é maior que a projeção altura. Quando a velocidade de projeção é constante, a maior projeção relativa da altura traduz-se em mais tempo de voo e maior deslocamento do projétil.
No esporte do mergulho, a altura de projeção relativa é a altura do trampolim ou plataforma acima da água. Se o centro de gravidade de um mergulhador elevada 1,5 metro acima do trampolim no ápice da trajetória, o tempo do voo é de cerca de 1,2 segundos de uma placa de 1 metro e 1,4 segundos de uma placa de 3 metros. Isso fornece tempo suficiente para um mergulhador qualificado completar 3 cambalhotas a partir de 1 metro bordo e 3 ½ cambalhotas de uma placa de 3 metros.
A implicação é que um mergulhador tentando aprender um mergulho de salto mortal de 3 ½ a partir do trampolim de 3 metros deve primeiro ser capaz de executar facilmente um mergulho de salto mortal de 2 ½ da prancha de 1 metro.
2.4.4 Condições ótimas de projeção
Em eventos esportivos baseados em atingir o deslocamento horizontal máximo ou deslocamento vertical máximo de um projétil, o principal objetivo é maximizar a velocidade de projeção. Nos eventos de arremesso, outro objetivo é maximizar a altura de lançamento, porque maior a altura da projeção produz maior tempo de voo e, consequentemente, deslocamento horizontal do projétil.
No entanto, geralmente não é prudente para um lançador sacrificar a velocidade de liberação para maior altura de liberação. O fator que mais varia, com o evento e o performer, é o ângulo ideal de projeção.
Quando a altura de projeção relativa é zero, o ângulo de projeção que produz o deslocamento horizontal máximo é de 45°. Como a altura de projeção relativa aumenta, o ângulo ideal de projeção diminui, e à medida que a altura da projeção relativa diminui, o ângulo aumenta.
É importante reconhecer que existem relações entre a projeção velocidade, altura e ângulo, de modo que quando se é deslocado para mais perto do que seria teoricamente, ser ótimo, outro se afasta do ótimo. Isto é porque os humanos não são máquinas, e a anatomia humana dita certas restrições. Reflita!

Pesquisas mostraram, por exemplo, que as relações entre velocidade de lançamento, altura e ângulo de desempenho no arremesso de peso são tais essa velocidade de liberação alcançável que diminui com o aumento do ângulo de 1,7 (m/s)/rad e diminui com o aumento da altura de liberação a 0,8 (m/s)/m.
Tanto para o arremesso quanto para o disco, no entanto, os biomecânicos encontraram que o ângulo ideal de liberação é específico do atleta, variando de 35 a 44 graus entre os artistas de elite por causa das diferenças individuais na diminuição da velocidade de projeção com o aumento do ângulo de liberação.
Da mesma forma, quando o corpo humano é o projétil durante um salto, a velocidade de decolagem serve para restringir o ângulo de projeção que pode ser alcançado. No desempenho do salto em distância, por exemplo, porque a decolagem e as alturas de aterrissagem são as mesmas, o ângulo teoricamente ideal da decolagem é de 45° em relação à horizontal. No entanto, foi estimado que para obter este ângulo de decolagem teoricamente ótimo, jumpers longos diminuiriam a velocidade horizontal que poderiam obter em aproximadamente 50%.
Estudos mostram que o sucesso no salto em distância, salto em altura e salto com vara está relacionado à capacidade do atleta de maximizar a velocidade horizontal indo para a decolagem. A decolagem real dos ângulos empregados pelos saltadores de elite varia de aproximadamente 18° para 27º.
Ângulos de decolagem durante as três fases do salto triplo são ainda menor para os artistas de elite do que aqueles usados no salto em distância. O desempenho no salto triplo é complicado pelo fato de que existe uma troca direta entre velocidade horizontal e velocidade vertical durante os saltos.
No salto de esqui, onde os atletas têm a vantagem de uma grande altura relativa entre decolagem e pouso, os ângulos de decolagem são pequenos como 4,6–6,2°. Em um evento como o salto em altura, em que o objetivo é maximizar o deslocamento vertical, ângulos de decolagem entre os jumpers estilo Fosbury Flop variam de 40° a 48°.
Como a velocidade é uma grandeza vetorial, a velocidade inicial de um projétil incorpora a velocidade inicial (magnitude) e o ângulo de projeção (direção) em uma única quantidade. Quando a velocidade inicial de um projétil é resolvida em componentes horizontais e verticais, o horizontal componente tem uma certa velocidade ou magnitude em uma direção horizontal, e o componente vertical tem uma velocidade ou magnitude na direção vertical.
As magnitudes dos componentes horizontais e verticais são sempre quantificadas, de modo que, se fossem adicionados juntos ao processo de composição vetorial, o vetor de velocidade resultante seria igual em magnitude e direção ao vetor de velocidade inicial original.
Os componentes horizontal e vertical da velocidade inicial podem ser quantificados ambos graficamente e trigonometricamente. Para fins de análise do movimento de projéteis, será assumido que o componente horizontal da velocidade do projétil é constante ao longo da trajetória e que o componente vertical da velocidade do projétil está mudando constantemente por causa da influência da gravidade (Figura 3.2).
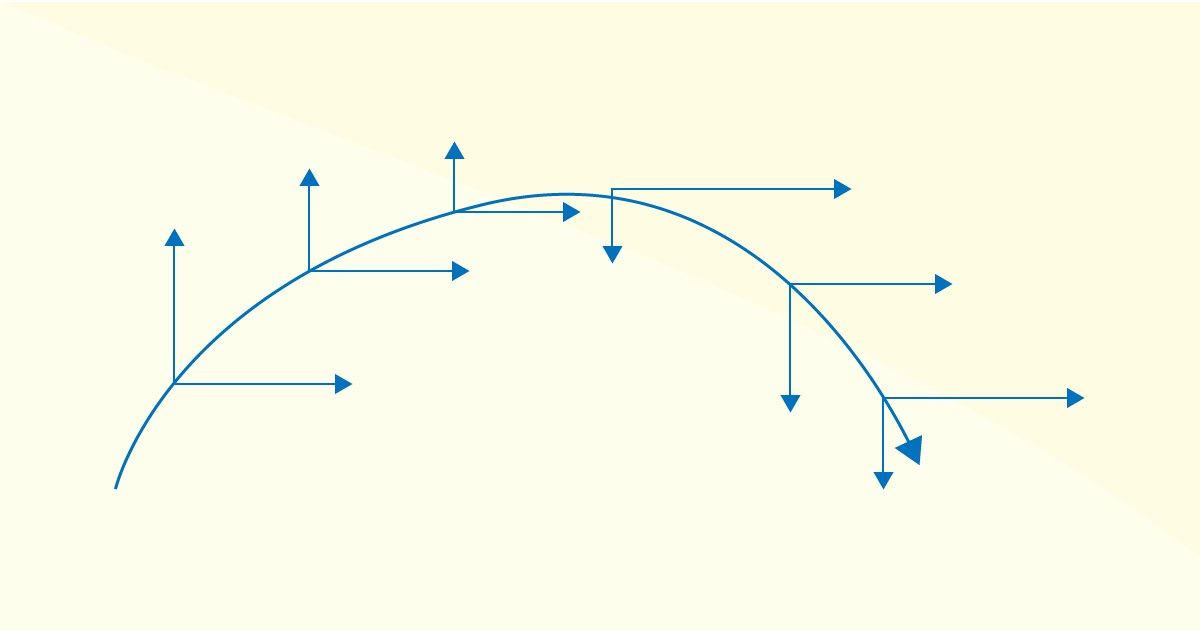
Como a velocidade do projétil horizontal é constante, a aceleração horizontal é igual à constante de zero ao longo da trajetória. A aceleração vertical de um projétil é igual à constante -9,81 m/s².
Quando um corpo está se movendo com uma aceleração constante (positivo, negativo ou igual a zero), certas inter-relações estão presentes entre a cinemática quantidades associadas ao movimento do corpo.
Essas inter-relações podem ser expressas usando três equações matemáticas originalmente derivadas Galileo, que são conhecidas como as leis da aceleração constante, ou as leis de movimento uniformemente acelerado.
Usando os símbolos de variáveis d, v, a e t (representando deslocamento, velocidade, aceleração e tempo, respectivamente) e com os índices 1 e 2 (representando primeiro ou segundo pontos no tempo), as equações são as seguintes:
\[v2~=~v1~+~at\]
\[d~=~v1t~+~\frac{1}{2}at{}^\text{2}\]
\[v\frac{2}{2}~=~v\frac{2}{1}~+~2ad\]
Observe que cada uma das equações contém uma combinação única de três das quatro quantidades cinemáticas: deslocamento, velocidade, aceleração e tempo. Isto proporciona considerável flexibilidade para resolver problemas nos quais duas das quantidades são conhecidas e o objetivo é resolver por um terço.
É instrutivo examinar essas relações quando aplicadas na horizontal componente do movimento do projétil em que a = 0. Neste caso, cada termo contendo aceleração pode ser removido da equação. As equações aparecem como as seguintes:
\[v2~=~v1\]
\[d~=~v1t\]
\[v\frac{2}{2}~=~v\frac{2}{1}\]
As equações 1 e 3 reafirmam que no componente horizontal do projétil a velocidade é uma constante. A equação 2 indica que o deslocamento horizontal é igual ao produto da velocidade horizontal e do tempo.
Quando as relações de aceleração constante são aplicadas à vertical componente do movimento do projétil, a aceleração é igual a –9,81 m/s², e as equações não podem ser simplificadas pela supressão da aceleração prazo. No entanto, na análise do componente vertical do movimento do projétil, a velocidade inicial (v1) é igual a zero em certos casos.
Por exemplo, quando um objeto é retirado de uma posição estacionária, a velocidade inicial do objeto é zero. Quando este é o caso, as equações de aceleração constante podem ser expressas da seguinte forma:
\[v2~=~at$\]
\[d~=~\frac{1~}{2~}at²\]
\[v\frac{2}{2}~=~2~ad\]
Quando um objeto é descartado, a primeira equação relata que a velocidade do objeto em qualquer instante é o produto da aceleração gravitacional e da quantidade de tempo que o objeto esteve em queda livre.
A segunda equação indica que a distância vertical por meio da qual o objeto caiu pode ser calculado a partir da aceleração gravitacional e da quantidade de tempo que o objeto foi caindo. A terceira equação expressa a relação entre a velocidade do objeto e o deslocamento vertical em um determinado tempo e aceleração gravitacional.
É útil na análise de movimento de projétil para lembrar que no ápice da trajetória de um projétil, o componente vertical da velocidade é zero. Se o objetivo é determinar a altura máxima alcançada por um projétil, v2 na equação 3 pode ser igual a zero:
\[0~=~v\frac{1}{2}+~2ad\]
Um exemplo desse uso da equação 3A é mostrado no Exemplo de Problema 10,6. Se o problema é determinar o tempo total de voo, uma abordagem é calcular o tempo que leva para chegar ao ápice, que é metade do tempo total de voo se a projeção e a altura de pouso forem iguais. Neste caso, v2 na equação 1 para o componente vertical do movimento pode ser igual a zero porque a velocidade vertical é zero no ápice:
\[0~=~v1+~at\]
Ao usar as equações de aceleração constante, é importante lembrar que eles podem ser aplicados ao componente horizontal do projétil movimento ou para o componente vertical do movimento do projétil, mas não para o movimento resultante do projétil.
Se o componente horizontal de movimento está sendo analisado, um 5 0, mas se o componente vertical está sendo analisada, a = 5 -9,81 m/s².
Caro(a) aluno(a), chegamos ao final do estudo da forma ou sequenciamento do movimento linear em relação ao tempo. As grandezas cinemáticas lineares incluem as grandezas escalares de distância e velocidade, e as quantidades vetoriais de deslocamento, velocidade e aceleração. Dependendo do movimento que está sendo analisado, uma quantidade vetorial ou seu equivalente escalar e uma quantidade instantânea ou média podem ser de interesse.
Foi possível entender que um projétil é um corpo em queda livre que é afetado apenas pela gravidade e pela resistência do ar. O movimento dos projéteis é analisado em termos de seus componentes horizontais e verticais.
Os dois componentes são independentes um do outro e somente o componente vertical é influenciado pela força gravitacional. Fatores que determinam a altura e distância que o projétil atinge são o ângulo de projeção, a velocidade de projeção e a altura relativa da projeção e as equações de aceleração constante podem ser usadas para analisar quantitativamente o movimento de projétil, com aceleração vertical de -9,81 m/s e ² horizontal aceleração sendo zero.
Entender o movimento angular é particularmente importante para o(a) estudante de movimento humano, porque a maioria dos movimentos humanos volitivos envolvem rotação de um ou mais segmentos do corpo em torno das articulações em que articular.
A tradução do corpo como um todo durante a marcha ocorre por virtude de movimentos rotacionais que ocorrem no quadril, joelho e tornozelo em torno do imaginário eixos médio-laterais de rotação.
Durante o desempenho do salto de macacos, ambos os braços e as pernas giram em torno do anteroposterior imaginário, passando pelas articulações do ombro e quadril.
O movimento angular de implementos esportivos, como tacos de golfe, bastões de beisebol e tacos de hóquei, bem como ferramentas domésticas e de jardim, também é frequentemente de interesse.
Profissionais clínicos, treinadores e professores de atividades rotineiramente analisam o movimento humano com base na observação visual. O que é realmente observado em tais situações é a cinemática angular do movimento humano.
Baseado na observação do tempo e amplitude de movimento de ações conjuntas, o analista experiente pode fazer inferências sobre a coordenação da atividade muscular produzindo as ações conjuntas e as forças resultantes dessas ações conjuntas.
Um ângulo é composto de dois lados que se cruzam em um vértice. A análise cinemática quantitativa pode ser obtida projetando-se filmagens do corpo humano em um pedaço de papel, com junta centros, em seguida, marcando com pontos e os pontos conectados com linhas que representam os eixos longitudinais dos segmentos do corpo.
Um transferidor pode ser usado para fazer medições manuais de ângulos de interesse a partir desta representação, com os centros conjuntos formando os vértices dos ângulos entre os segmentos adjacentes do corpo.
Vídeos e filmes de movimento humano também podem ser analisados usando este mesmo procedimento básico de avaliar os ângulos presentes nas articulações do corpo humano e das orientações angulares dos segmentos corporais. As avaliações de ângulo são geralmente feitas com software de computador a partir de representações de figuras do corpo humano construído na memória do computador.
Avaliar o ângulo em uma articulação envolve medir o ângulo de um corpo segmento em relação ao outro segmento do corpo articulado na articulação. O ângulo relativo no joelho é o ângulo formado entre o eixo longitudinal da coxa e o eixo longitudinal da perna inferior (Figura 3.3).
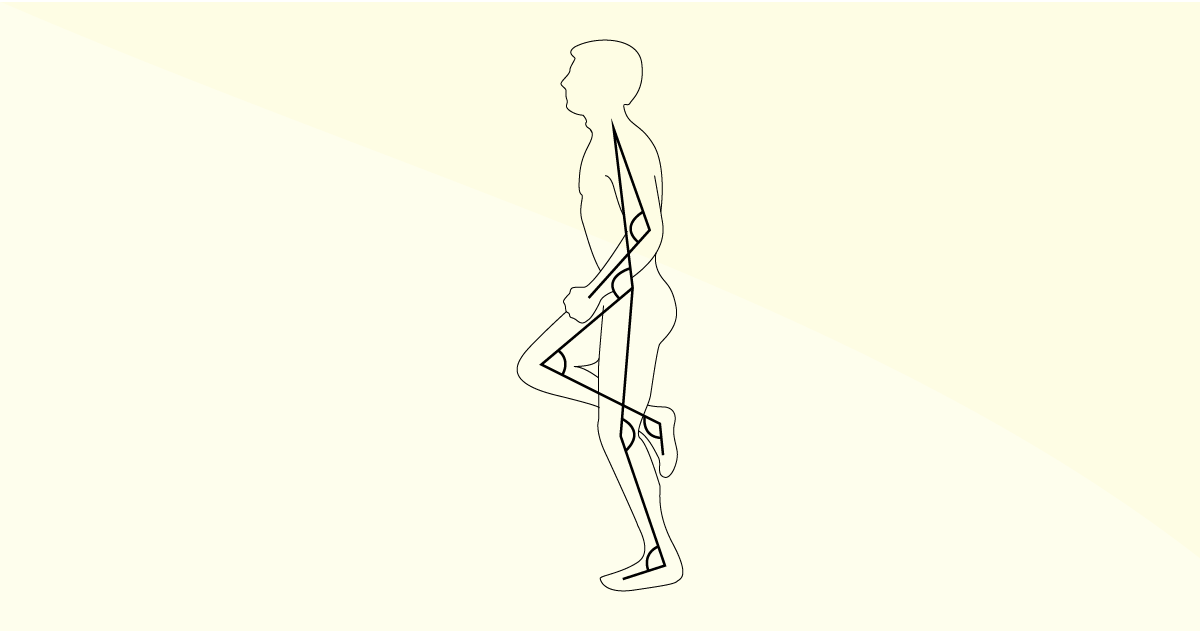
Quando a convenção usada para medir os ângulos articulares relativos é a anatômica posição de referência, todos os ângulos de articulação estão em 0°. O movimento articular é, então, medido direcionalmente.
Por exemplo, quando o braço estendido é elevado 30° na frente do corpo no plano sagital, o braço está em 30° de flexão no ombro. Quando a perna é abduzida no quadril, a amplitude de movimento em abdução também é medida a partir de 0° em referência anatômica da posição.
Outros ângulos de interesse são frequentemente as orientações dos segmentos corporais de si mesmos. Quando um indivíduo está em um ângulo de inclinação do tronco quando vai pegar algum objeto no porta-malas de um carro, afeta diretamente a quantidade de força que deve ser gerada pelos músculos extensores do tronco para apoiar o tronco na posição assumida.
O ângulo de inclinação de um segmento do corpo, referido como o seu ângulo absoluto, é medido em relação a uma referência absoluta linha, geralmente horizontal ou vertical.
Os goniômetros (Figura 3.4) são comumente usados pelos clínicos para mensurar diretamente ângulos conjuntos relativos a um ser humano.
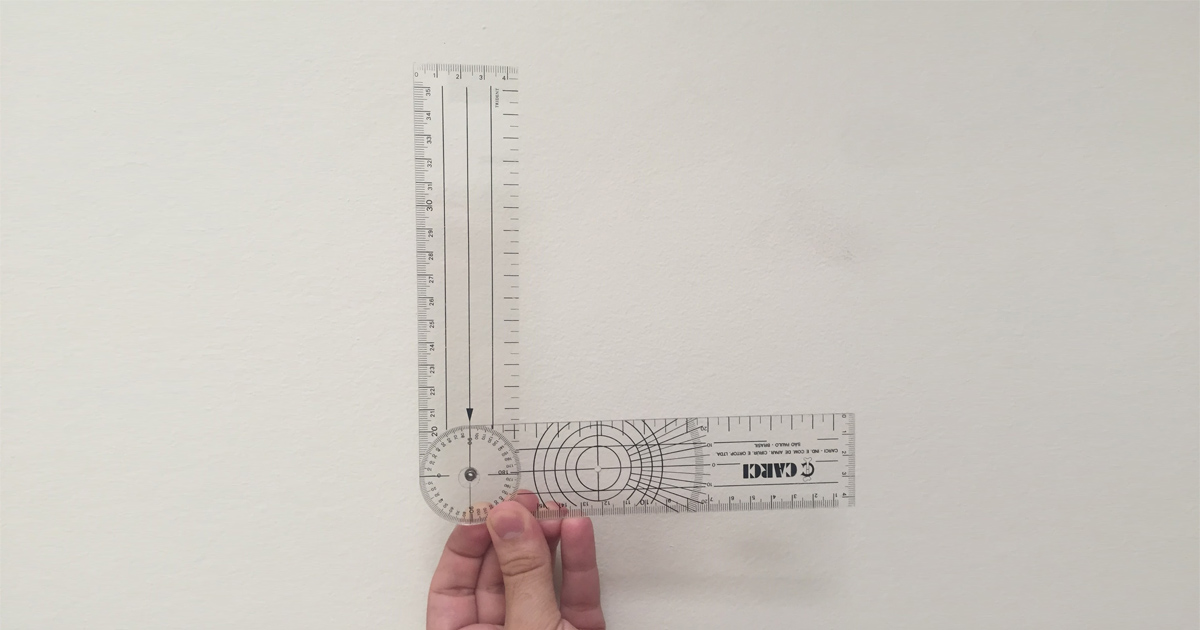
Um goniômetro é essencialmente um transferidor com dois braços longos ligados. Um braço é fixado para que se estende do transferidor em um ângulo de 0°. O outro braço se estende do centro do transferidor e está livre para girar.
A goniometria é a medida da amplitude de movimento em uma articulação. A técnica pode ser utilizada como uma medida de diagnóstico ou terapêutica para determinar o estado funcional de um indivíduo com uma alteração musculoesquelética. Veja um vídeo que vai mostrar na prática como realizar a goniometria nos segmentos corporais no link a seguir: <https://www.youtube.com/watch?v=Bd9JRSdZae0>. Acesso em: 09 jul. 2019.

O centro do transferidor está alinhado sobre o centro da articulação, e os dois braços estão alinhados sobre os eixos longitudinais dos dois segmentos do corpo que se conectam na articulação. O ângulo na articulação é então lido na interseção do braço rotativo livre e da escala do transferidor.
A precisão da leitura depende da precisão do posicionamento do goniômetro. O conhecimento do subjacente e a anatomia da articulação são essenciais para a localização adequada do centro articular de rotação.
Colocar marcas na pele para identificar a localização do centro de rotação na articulação e nos eixos longitudinais dos segmentos do corpo antes de alinhar o goniômetro às vezes é útil, especialmente se as medições repetidas estão sendo feitas na mesma articulação.
A quantificação de ângulos articulares é complexa devido ao movimento articular ser frequentemente acompanhado pelo deslocamento de um osso em relação a articulação.
Esse fenômeno é ocasionado por assimetrias nas formas das superfícies ósseas articuladas. Um exemplo é a articulação tibiofemoral, onde a rotação medial e o deslocamento anterior do fêmur acompanham a flexão.
Como resultado, a localização do centro exato de rotação na articulação altera levemente quando o ângulo da articulação também altera. O centro de rotação em uma específica articulação do ângulo, ou em um certo instante no tempo durante um movimento dinâmico é denominado de centro instantâneo.
A localização exata do centro instantâneo para uma dada articulação pode ser determinada mediante medições feitas a partir de radiografias (Raios-X), que são geralmente tomadas em intervalos de 10° ao longo da amplitude de movimento da articulação. O centro instantâneo na articulação tibiofemoral do joelho muda durante o movimento angular no joelho, devido às formas elipsoides os côndilos femorais.
As inter-relações entre as grandezas cinemáticas angulares são semelhantes àquelas para grandezas lineares cinemáticas. Vamos conhecer um pouco mais a seguir sobre as principais relações cinéticas angulares na biomecânica.
Considere um pêndulo balançando para frente e para trás a partir de um ponto de apoio. O pêndulo está girando em torno de um eixo passando por seu ponto de apoio perpendicular ao plano de movimento. Se o pêndulo balançar por meio de um arco de 60°, oscilou mediante uma distância angular de 60°.
Se o pêndulo em seguida, volta a 60° para a sua posição original, tem viajado uma distância angular, totalizando 120° (60° + 60°). A distância angular é medida como a soma de todas as alterações angulares sofridas por um corpo em rotação.
O mesmo procedimento pode ser usado para quantificar as distâncias angulares por meio do qual os segmentos do corpo humano se movem. Se o ângulo nas alterações da articulação do cotovelo de 90° a 160° durante a fase de exérese de um antebraço exercício de ondulação, a distância angular coberta é de 70°.
Se a fase de extensão da curva retorna o cotovelo para sua posição original de 90°, 70° foram cobertos, resultando em uma distância angular total de 140° para a onda completa. Se forem feitos 10 cachos, a distância angular transcrita no cotovelo é 1400° (10 x 140°).
Assim como com sua contraparte linear, o deslocamento angular é avaliado como a diferença nas posições inicial e final do corpo em movimento. Se o ângulo no joelho da perna de apoio mudar de 5° para 12° durante a fase de apoio inicial de uma passada em corrida, a distância angular e o deslocamento angular no joelho é de 7°.
Se a extensão ocorrer no joelho, retornando a articulação para sua posição original de 5°, a distância angular totaliza 14° (7° + 7°), mas o deslocamento angular é 0°, porque é o final. A posição da articulação é a mesma que a sua posição original.
Como o deslocamento linear, o deslocamento angular é definido por ambos magnitude e direção. Como a rotação observada de uma vista lateral ocorre no sentido horário ou anti-horário, a direção do angular deslocamento pode ser indicada usando estes termos.
O sentido anti-horário de direção é convencionalmente designada como positiva (+), e o sentido horário como negativo (-). Com o corpo humano, também é apropriado indicar a direção do deslocamento angular com terminologia relacionada à articulação, como flexão ou abdução.
No entanto, não há relação definida entre a direção positiva (sentido anti-horário) e flexão ou extensão ou qualquer outro movimento em uma articulação. Este é porque quando visto de um lado, flexão em uma determinada articulação, como o quadril é positivo, mas quando visto do lado oposto é negativo.
Quando biomecânicos fazem estudos de captura de movimento com computador e câmeras, o software quantifica movimentos conjuntos em direções positivas ou negativas. O pesquisador deve, então, traduzir esses valores na flexão/extensão ou outros movimentos articulares, dependendo da visão da câmera.
Pacotes de software mais sofisticados farão essa tradução com contribuição apropriada do pesquisador. Três unidades de medida são comumente usadas para representar a distância angular e deslocamento angular. A mais familiar dessas unidades é o grau.
Um círculo completo de rotação transcreve um arco de 360°, um arco de 180° subtende uma linha reta e 90° forma um ângulo reto entre a linha perpendicular e as linhas. Outra unidade de medida angular por vezes utilizada em biomecânica análises é o radiano. Uma linha conectando o centro de um círculo a qualquer ponto na circunferência do círculo é um raio.
Um radiano é definido como o tamanho do ângulo subentendido no centro de um círculo por um arco de comprimento igual ao raio do círculo. Um círculo completo é um arco de 2π radianos ou 360°. Porque 360° dividido por 2_π é 57,3°, um radiano é equivalente a 57,3°. Pelo fato do radiano ser muito maior que um grau, é uma unidade mais conveniente para a representação de angular extremamente a grandes distâncias ou deslocamentos. Os radianos são frequentemente quantificados em múltiplos de pi (π).
A terceira unidade usada às vezes para quantificar a distância angular ou o deslocamento é a revolução. Uma revolução transcreve um arco igual a um círculo. Mergulhos e algumas habilidades de ginástica são frequentemente descritas pelo número de revoluções que o corpo humano sofre durante a sua execução.
O salto para trás é um exemplo descritivo. A Figura 3.5 ilustra a maneira em que graus, radianos e revoluções se comparam como unidades angulares a medida.
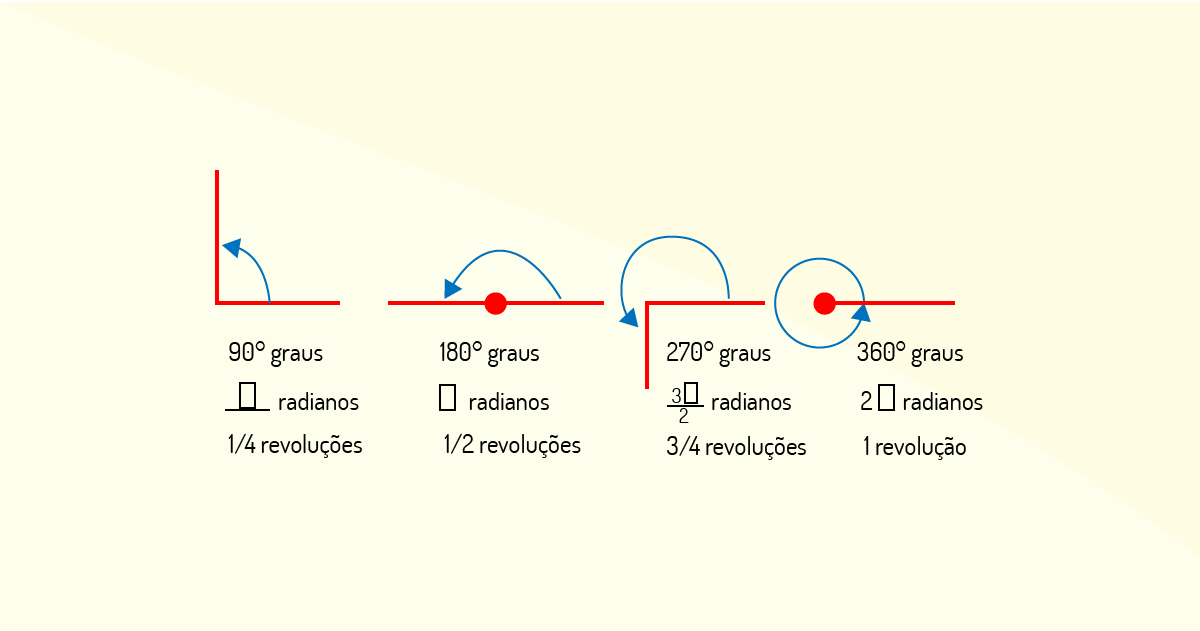
A seguir, veremos a velocidade angular.
A velocidade angular é uma grandeza escalar e é definida como a distância angular coberta dividido pelo intervalo de tempo durante o qual a moção ocorreu:
\[velocidade~angular~=~\frac{dist\hat{a}ncia~\hat{a}ngular}{Mudana~de~tempo}\]
\[\sigma ~=\frac{\phi }{\Delta t}~\]
A letra grega maiúscula sigma (σ) refere-se à velocidade angular, a minúscula A letra grega phi (ϕ) significa a distância angular e t represe-se ao tempo.
A velocidade angular é calculada como a alteração na posição angular, ou o deslocamento angular, que acontece durante um determinado período de tempo:
\[velocidade~angular~=~\frac{mudana~na~posi\tilde{a}o~angular}{mudana~no~tempo}\]
\[\omega ~=~\frac{\Delta ~posi\tilde{a}o~angular}{\Delta ~tempo}\]
\[velocidade~angular~=~\frac{deslocamento~angular}{mudana~no~tempo}\]
\[\omega ~=~\frac{\theta }{\Delta ~t}\]
A letra grega ômega (ω) representa a velocidade angular, a maiúscula A letra grega theta (θ) representa o deslocamento angular e t representa o tempo decorrido durante a avaliação da velocidade. Outra maneira da mudança expressa na posição angular é a posição angular2 - posição angular1, em que posição angular1 representa a posição do corpo em um ponto no tempo e a posição angular2 representa a posição do corpo em um ponto posterior:
\[\omega =\frac{posi\tilde{a}o~angular2~-~posi\tilde{a}o~angular1}{tempo2~-~tempo1}\]
A velocidade angular deve incluir uma identificação da direção (sentido horário ou anti-horário, negativo ou positivo) em que ocorreu o deslocamento angular em que se baseia.
Unidades de velocidade angular são unidades de distância angular ou deslocamento angular dividido por unidades de tempo. A unidade do tempo mais comumente usada é o segundo. Unidades de velocidade angular são graus por segundo (graus/s), radianos por segundo (rad/s), revoluções por segundo (rev/s) e revoluções por minuto (rpm).
Mover os segmentos do corpo a uma alta taxa de velocidade angular é uma característica de desempenho qualificado em muitos esportes. Foi evidenciado em tenistas masculinos e femininos de classe mundial uma rotação sequencial de rotações segmentais. Quando o corpo humano se torna um projétil durante a execução de um salto, a altura do salto determina a quantidade de tempo que o corpo está no ar.
A aceleração angular é representada pela taxa de mudança na velocidade angular, ou a alteração na velocidade angular que acontece durante um dado tempo. O convencional símbolo para aceleração angular é representado pela letra grega minúscula alpha (α):
\[acelera\tilde{a}o~angular~=~\frac{mudana~na~velocidade~angular}{mudana~no~tempo}\]
\[\alpha ~=~\frac{\Delta \omega }{\Delta t}\]
A fórmula de cálculo para aceleração angular é, portanto, a seguinte:
\[\alpha ~=~\frac{\omega 2~-~\omega 1}{t2~-~t1}\]
Nesta fórmula, ω1 refere-se à velocidade angular em um ponto inicial no tempo, ω2 exemplifica a velocidade angular em um segundo ou último ponto no tempo e t1 e t2 são considerados como os tempos em que a velocidade foi avaliada.
Assim como na aceleração linear, a aceleração angular pode ser positiva, negativa ou zero. Quando a aceleração angular é zero, a velocidade angular é constante. Assim como na aceleração linear, a aceleração angular positiva pode indicar o aumento da velocidade angular na direção positiva ou diminuindo a velocidade angular na direção negativa.
Da mesma forma, um negativo valor da aceleração angular pode representar um decréscimo angular da velocidade na direção positiva ou aumentando a velocidade angular na direção negativa.
Unidades de aceleração angular são consideradas unidades de velocidade angular que são separadas por unidades de tempo. Exemplos comuns são graus por segundo ao quadrado (graus/s²), radianos por segundo ao quadrado (rad/s²) ou até mesmo revoluções por segundo ao quadrado (rev/s²).
Os vetores de movimento angular são representados com vetores retos convencionais, usando o que é chamado de regra da mão direita.
De acordo com essa regra, quando os dedos da mão direita estão enrolados a direção de um movimento angular, o vetor usado para representar o movimento é orientado perpendicularmente ao plano de rotação, na direção dos pontos de polegar estendidos. A magnitude da quantidade pode ser indicada por meio da proporcionalidade com o comprimento do vetor.
Velocidade angular, rapidez e aceleração podem ser calculadas como valores médios ou instantâneas, dependendo da duração do intervalo de tempo que foi selecionado.
Por exemplo, a velocidade angular instantânea de um taco de beisebol no instante de contato com uma bola apresenta tipicamente de maior interesse do que a velocidade angular média do balanço.
Entender a cinemática do movimento humano é um valor básico e aplicado no esporte. A medição do movimento pode ser usada para avaliar o desempenho funcional dos membros em condições normais e anormais. O conhecimento cinemático também é essencial para o diagnóstico adequado e o tratamento cirúrgico da doença articular e o projeto de dispositivos protéticos para restaurar a função. Em relação à cinemática do movimento, escolha a alternativa correta.
A velocidade da decolagem interfere na execução de um salto horizontal.
Incorreta. O desempenho na execução de um salto vertical em uma superfície plana é inteiramente dependente da velocidade de decolagem.
O tamanho da trajetória é influenciado pelas mudanças na velocidade de projeção.
Correta. Mudanças na velocidade de projeção influenciam o tamanho da trajetória, mas o formato da trajetória depende apenas da projeção do ângulo.
Os fatores que interferem a trajetória de um projétil é o ângulo de projeção, a corrida de projeção e a largura relativa da projeção.
Incorreta. Três fatores influenciam a trajetória de um projétil: o ângulo de projeção, a velocidade de projeção e a altura relativa da projeção.
A força de gravidade é um fator que influencia o componente horizontal de movimento do projétil.
Incorreta. Um fator importante que influencia o componente vertical, mas não o horizontal de movimento do projétil é a força da gravidade, que acelera os corpos em uma direção vertical rumo à superfície da terra.
O deslocamento vertical máximo alcançado por um projétil é determinado pelo componente horizontal da velocidade.
Incorreta. O componente vertical da velocidade inicial de projeção determina o deslocamento vertical máximo alcançado por um corpo projetado a partir de uma determinada altura da projeção relativa.
Nesta parte da disciplina, você vai conhecer qual é a relação do movimento linear com o angular. É essencial conhecermos este conteúdo, pois vai dar suporte na hora de pensarmos alguns gestos esportivos no dia a dia.
Quanto maior o raio entre um ponto de um corpo em rotação e o eixo de rotação, maior será a distância linear percorrida por esse ponto ao longo de um movimento angular. Esta análise é expressa na forma de uma equação simples.
A distância curvilínea explorada pelo ponto de interesse s é o produto de r, o raio de rotação do ponto, e ϕ, a distância angular por meio de que o corpo em rotação se move, onde é quantificado em radianos.
Para esta relação ser válida, duas condições devem ser atendidas:
(a) distância linear e o raio de rotação devem ser quantificados na mesma unidade de comprimento;
(b) distância angular deve ser expressa em radianos.
Embora as unidades de medida sejam normalmente equilibradas em lados opostos de um sinal de igual quando uma relação válida é expressa (este não é o caso aqui). Quando o raio de rotação (expresso em metros) é multiplicado por deslocamento angular em radianos, o resultado é o deslocamento linear metros.
Radianos desaparecem no lado direito da equação neste caso porque, como pode ser observado a partir da definição do radiano, ele serve como um fator de conversão entre medições lineares e angulares.
O mesmo tipo de relação existe entre a velocidade angular de um corpo girando e a velocidade linear de um ponto do corpo em um dado instante no tempo. O relacionamento é expresso da seguinte maneira:
\[v~=~r\omega \]
A velocidade linear (tangencial) do ponto de interesse é v, r é o raio de rotação para esse ponto, e ωé a velocidade angular da rotação corpo. Para que a equação seja válida, a velocidade angular deve ser expressa em unidades baseadas em radianos (normalmente rad/s), e a velocidade deve ser expressa nas unidades do raio de rotação dividido pelas unidades de tempo apropriadas.
Os radianos são novamente usados como um fator de conversão linear-angular e não são equilibrados em lados opostos do sinal de igual:
\[m/s~=~\left( m \right)~\left( rad/s \right)\]
Durante várias atividades esportivas, uma meta imediata de desempenho é direcionar um objeto como bola, peteca ou disco de hóquei com precisão, ao transmitir uma quantidade relativamente grande de velocidade a ele com um bastão, raquete ou vara.
Nas rebatidas de baseball, o início do balanço e da velocidade angular do balanço deve ser cronometrada precisamente para fazer contato com a bola e direcioná-la para o solo. Um campo de 40 m/s atinge o bater 0,41 s depois de deixar a mão do lançador.
Estima-se que uma diferença de 0,001s no tempo de início do swing pode determinar se a bola é direcionada para o centro ou para baixo da linha de falta, e que um swing iniciado 0,003s, muito cedo ou muito tarde, não resultará em contato com a bola.
Da mesma forma, há uma janela muito pequena de tempo durante a qual ginastas na barra alta podem liberar a partir do bar para executar um hábil desmontar. Para finalistas de alto nível nos Jogos Olímpicos de 2000 em Sydney, a janela de lançamento foi uma média de 0,055s.
Com todos os outros fatores mantidos constantes, quanto maior o raio de rotação em que um instrumento de balanço bate em uma bola, quanto maior a velocidade linear comunicada à bola. No entanto, a magnitude da velocidade angular é tão grande quanto o comprimento do raio de rotação na determinação da velocidade linear de um ponto em um implemento oscilante.
É importante reconhecer que a velocidade linear de uma bola atingida por um morcego, raquete ou taco não é idêntico à velocidade linear do contato ponto no implemento de oscilação.
Outros fatores, como a franqueza do impacto e a elasticidade do impacto, também influenciam a velocidade da bola. Reflita!

A aceleração de um corpo em movimento angular pode ser resolvida em dois componentes de aceleração linear perpendiculares. Esses componentes são dirigidos ao longo e perpendicular ao caminho do movimento angular em qualquer ponto no tempo (Figura 3.6).
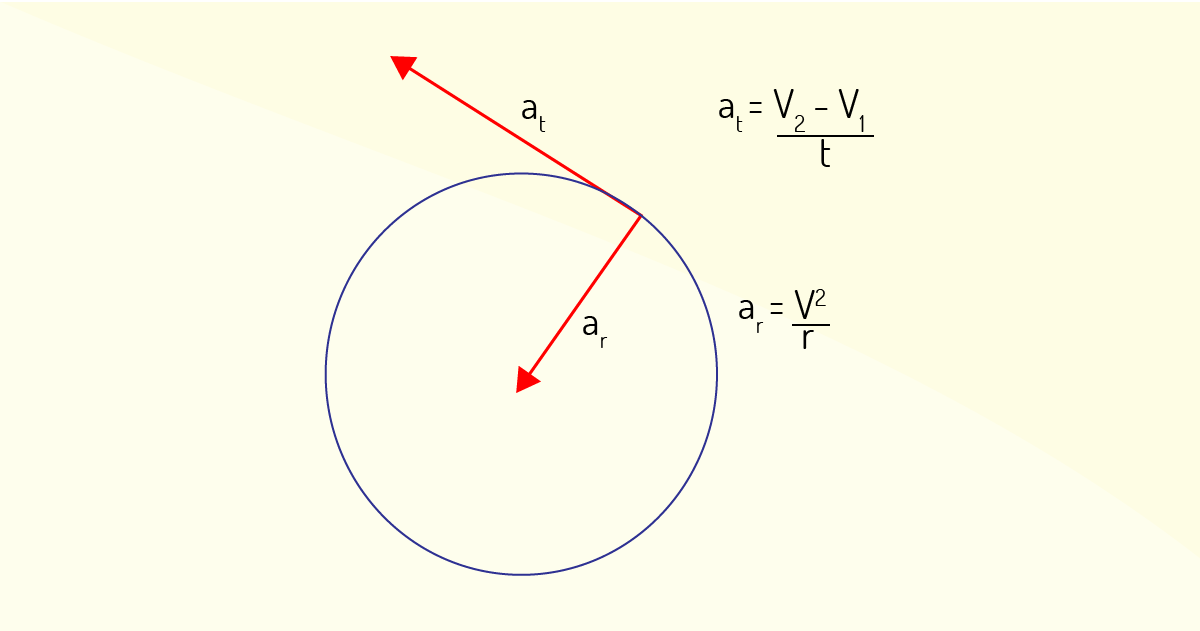
O componente dirigido ao longo do caminho do movimento angular leva seu nome do termo tangente. Uma tangente é uma linha que toca, mas não cruza, uma curva em um único ponto. O componente tangencial, conhecido como aceleração tangencial, representa a mudança na velocidade linear para um corpo viajando em um caminho curvo.
A fórmula para aceleração tangencial é a seguinte:
\[at~=~\frac{v2~-~v1}{t}\]
A aceleração tangencial está em: v1 é a velocidade linear tangencial do movimento corpo em um tempo inicial, v2 é a velocidade linear tangencial do movimento corpo em uma segunda vez, e t é o intervalo de tempo sobre o qual as velocidades são avaliadas.
Quando uma bola é lançada, a bola segue um caminho curvo à medida que é acelerada pelos músculos do ombro, cotovelo e punho. O componente tangencial de aceleração da bola representa a taxa de mudança na velocidade linear da bola.
Porque a velocidade da projeção afeta muito o alcance de um projétil da velocidade tangencial que deve ser máxima antes da liberação da bola se o objetivo é jogar a bola rápido ou longe. Uma vez que a liberação da bola ocorre, tangencial a aceleração é zero, porque o lançador não está mais aplicando uma força.
A relação entre a aceleração tangencial e aceleração angular é expresso da seguinte forma:
\[at~=~r~\alpha \]
A aceleração linear é at, r é o raio de rotação e α é aceleração angular. As unidades de aceleração linear e o raio de rotação devem ser compatíveis, e a aceleração angular deve ser expressa em base radiana das unidades para que o relacionamento seja preciso.
Embora a velocidade linear de um objeto viajando ao longo de um caminho curvo não muda, sua direção de movimento está mudando constantemente. O segundo componente de aceleração angular representa a taxa de mudança na direção de um corpo em movimento angular.
Esse componente é chamado de aceleração radial e é sempre direcionado para o centro da curvatura. A aceleração radial pode ser quantificada usando a seguinte fórmula:
\[ar~=~\frac{v{}^\text{2}}{r}\]
A aceleração radial é ar, v é a velocidade linear tangencial do movimento corpo, e r é o raio de rotação. Um aumento na velocidade linear ou diminuição no raio de curvatura aumenta a aceleração radial. Então, quanto menor o raio de curvatura (quanto mais apertada a curva), mais difícil é para um ciclista realizar a curva em alta velocidade.
Durante a execução de um lançamento de bola, ela segue um caminho curvo porque o braço e a mão do lançador o restringem. Esta força de restrição causa aceleração radial em direção ao centro de curvatura ao longo do movimento.
Quando o lançador solta a bola, a aceleração radial não existe mais e o implemento segue o caminho da tangente à curva naquele instante. O momento da liberação é, portanto, crítico: se a liberação ocorrer também cedo ou tarde, a bola será direcionada para a esquerda ou para a direita, em vez de ir direto em frente.
Os componentes tangenciais e radiais do movimento podem contribuir para a velocidade linear resultante de um projétil na liberação. Por exemplo, durante cambalhota desmonta da barra alta em rotinas de ginástica, embora a principal contribuição para a velocidade linear do centro de gravidade do corpo é geralmente de aceleração tangencial, o componente radial pode contribuir até 50% da velocidade resultante. O tamanho da contribuição do componente radial, e se a contribuição é positiva ou negativa, varia de acordo com a técnica do artista.
As rotações do segmento do corpo se combinam para produzir movimento linear de todo o corpo ou de um ponto específico em um segmento do corpo. Para ciclistas, isso ocorre porque as rotações da articulação criam forças nos pedais, as forças nos pedais giram as engrenagens que giram as rodas e a rotação das rodas resulta em movimento linear do ciclista. Em relação ao movimento linear, escolha a alternativa correta.
Cinco componentes de aceleração linear perpendiculares podem ser resolvidos a partir da aceleração de um corpo em movimento linear.
Incorreta. A aceleração de um corpo em movimento angular pode ser resolvida em dois componentes de aceleração linear perpendiculares.
A maior distância linear percorrida é resultado do maior raio entre um determinado ponto de um corpo em rotação e o eixo de rotação.
Correta. Quanto maior o raio entre um determinado ponto de um corpo em rotação e o eixo de rotação, maior é a distância linear percorrida por esse ponto durante um movimento angular.
A distância linear deve ser expressa em radianos.
Incorreta. É a distância angular que deve ser expressa em radianos.
Os componentes tangenciais e radiais do movimento podem contribuir para a velocidade angular resultante de um projétil na liberação.
Incorreta. A velocidade que pode ser favorecida pelos componentes tangenciais e radiais do movimento é a velocidade linear.
A distância angular deve ser quantificada na mesma unidade de comprimento.
Incorreta. É a distância linear e o raio de rotação que devem ser quantificados na mesma unidade de comprimento.
Lesões musculares são comuns, sendo a maioria relativamente menor. Felizmente, o músculo esquelético saudável possui considerável capacidade de autorreparo.
As deformações musculares resultam do alongamento excessivo do tecido muscular. Normalmente, um músculo ativo está sobrecarregado, com a magnitude da lesão relacionada ao tamanho da sobrecarga e à taxa de sobrecarga. Os estiramentos podem ser leves, moderados ou graves.
Os estiramentos leves envolvem danos estruturais mínimos e são caracterizadas por uma sensação de aperto ou tensão no músculo. Os estiramentos de segundo grau envolvem uma ruptura parcial no tecido muscular, com sintomas de dor, fraqueza e alguma perda de função. Com estiramentos de terceiro grau, há ruptura grave do músculo, perda funcional, hemorragia e inchaço.
Os isquiotibiais são os músculos mais frequentemente tensos no corpo humano. Os estiramentos de isquiotibiais são particularmente problemáticas para os atletas, porque demoram a cicatrizar e têm quase um terço de incidência de recorrência no primeiro ano após o retorno à participação esportiva.
Contusões são causadas por forças compressivas sofridas durante os impactos. Eles consistem em hematomas dentro do tecido muscular. Uma séria contusão muscular, ou uma contusão que é repetidamente afetada, pode levar ao desenvolvimento de uma condição muito mais séria, conhecida como miosite óssea.
Miosite consiste na presença de uma massa calcificada dentro do músculo. Aparentemente, os fibroblastos recrutados durante o processo de cicatrização começam a se diferenciar em osteoblastos, com a calcificação se tornando visível em uma radiografia após três ou quatro semanas. Após seis ou sete semanas, a reabsorção da massa calcificada geralmente começa, embora algumas vezes uma lesão óssea no músculo permaneça.
A etiologia das cãibras musculares não é bem compreendida, com possíveis fatores causais, incluindo desequilíbrios eletrolíticos, deficiências de cálcio e magnésio e desidratação. Cãibras também podem ocorrer secundárias a impactos diretos. Cãibras podem envolver espasmos musculares moderados a graves, com níveis proporcionais de dor acompanhante.
Dor muscular geralmente ocorre depois de algum período de tempo após o exercício desacostumado. A dor muscular de início tardio surge 24-72 horas após a participação em um exercício longo ou extenuante de exercício e é caracterizada por dor, inchaço e os mesmos tipos de alterações histológicas que acompanham a inflamação aguda. Microlesões do tecido muscular estão envolvidas com sintomas de dor, rigidez e restrita amplitude de movimento.
Existe a hipótese de que o aumento da rigidez articular pode servir como um mecanismo de proteção que ajuda a prevenir danos adicionais e dor. Reflita!

Hemorragia ou edema dentro de um compartimento muscular podem resultar de lesão ou esforço muscular excessivo. A pressão aumenta dentro do compartimento e danos severos às estruturas neurais e vasculares dentro do compartimento seguem na ausência de liberação de pressão. Inchaço, descoloração, diminuição do pulso distal, perda de sensibilidade e perda da função motora são todos sintomas progressivamente aparentes.
Caro(a) aluno(a), chegamos ao final desta unidade e foi possível compreender que o movimento angular é uma parte importante do estudo de biomecânica, porque a maior parte do movimento volitivo do corpo humano envolve a rotação dos ossos em torno dos eixos imaginários de rotação passando pela articulação central nos quais os ossos se articulam.
As quantidades cinemáticas angulares do deslocamento angular, da velocidade angular e aceleração angular possuem as mesmas inter-relações que suas contrapartes lineares, com deslocamento angular representando mudança na posição angular, velocidade angular definida como a taxa de mudança na posição angular e aceleração angular indicando a taxa de mudança na velocidade angular durante um determinado tempo.
Dependendo da seleção do intervalo de tempo, valores médios ou instantâneos de velocidade e aceleração angular podem ser quantificadas. Variáveis cinemáticas angulares podem ser quantificadas para o ângulo relativo formado pelos eixos longitudinais de dois segmentos do corpo articulados, ou para a orientação angular absoluta de um único segmento do corpo em relação a uma linha de referência fixa. Diferentes instrumentos estão disponíveis para medição direta de ângulos em um sujeito humano.
Bons estudos e até a próxima unidade!
O exercício físico é uma abordagem de promover a saúde e qualidade de vida do indivíduo, mas às vezes o praticante pode se machucar enquanto prática. Acidentes, más práticas de treinamento ou equipamentos inadequados podem causar estas lesões. Escolha a alternativa correta sobre as lesões musculares mais comuns que acontecem no esporte.
Contusões são causadas por forças compressivas sofridas durante os impactos e os hematomas presentes estão fora do tecido muscular.
Incorreta. Os hematomas presentes nas contusões são dentro do tecido muscular.
A miosite óssea pode ser desenvolvida após uma séria contusão muscular.
Correta: Alternativa correta. Uma séria contusão muscular, ou uma contusão que é repetidamente afetada, pode levar ao desenvolvimento de uma condição muito mais séria, conhecida como miosite óssea.
Após a participação de uma pessoa em um exercício longo ou extenuante a dor muscular de início tardio surge antes de 24 horas.
Incorreta. A dor muscular de início tardio surge 24 a 72 horas após a participação em um exercício longo ou extenuante de exercício.
A síndrome compartimental diminui a pressão dentro do compartimento.
Incorreta. A pressão na síndrome compartimental é aumentada dentro do compartimento.
Miosite consiste na presença de uma massa calcificada fora do músculo.
Incorreta. A massa calcificada que está presenta na miosite está localizada dentro do músculo.
Nome do livro: Bases biomecânicas do movimento humano
Editora: Manole
Edição: 4ª
Autores: Joseph Hamill, Kathleen M. Knutzen e Timothy R. Derrick
ISBN: 978-8520446706
Neste livro você vai conhecer a importância da biomecânica de forma quantitativa e alguns exemplos numéricos significativos que desmistificam a motricidade da biomecânica. Além disso, ele vai dar um suporte teórico e prático sobre alguns temas de forma mais aprofundada como a anatomia funcional, física, cálculo e fisiologia.

Nome do filme: Forrest Gump
Gênero: Drama/Comédia dramática
Ano: 1994
Elenco principal: Tom Hanks, Robin Wright, Gary Sinise, Sally Field e Mykelti Williamson.
Este filme é considerado um clássico do cinema americano. Forrest é uma pessoa que participa de grandes eventos sociais e políticos das décadas de 60 e 70, sempre contando com a corrida como uma virtude fundamental. Ele sempre teve um raciocínio lento, mas nunca se sentiu desfavorecido. Com o apoio da sua mãe, ele teve uma vida normal e desde a infância praticou esportes e se tornou um astro do esporte e neste filme você vai ver como ocorre uma preparação de um atleta e como é importante ter profissionais que vão orientar a maneira correta de se preparar.
