O termo população refere-se a qualquer grupo de indivíduos da mesma espécie que ocupam um determinado espaço e que funcionam como parte da comunidade biótica. Cada população evolui e se adapta ao meio de formas diferentes. Assim, as populações surgem, crescem e se estabilizam, havendo ainda aquelas que declinam e se extinguem.
No estudo das populações, veremos que elas estão em contínua mudança com o passar do tempo, devido a propriedades como natalidade, mortalidade e movimentos de indivíduos (emigração e imigração), bem como distribuição etária, dispersão e formas de crescimento.
Além dessas propriedades, também veremos que existem alguns fatores que podem alterar o número de indivíduos em uma população, como o suprimento de alimento, a taxa de predação, a disponibilidade de lugar para ninho etc.
Já estudamos que a população diz respeito ao grupo de indivíduos da mesma espécie, que ocupam um determinado espaço. Atente-se que, em qualquer momento do tempo, um ser vivo ocupa apenas um local do espaço e tem um determinado tamanho e idade. Já os membros da população distribuem-se no espaço e diferem em tamanho e idade (SADAVA et al., 2009).
De acordo com Odum e Barrett (2007), uma população tem propriedades únicas do grupo, como densidade, natalidade (taxa de nascimento), mortalidade (taxa de morte), distribuição etária, potencial biótico, dispersão e formas de crescimento r e k selecionadas. Além disso, as populações possuem características genéticas que estão relacionadas a suas ecologias. Em outras palavras: capacidade de adaptação, sucesso reprodutivo e persistência.
A densidade populacional refere-se ao tamanho de uma população em relação a unidade do espaço que ocupa. A densidade pode ser expressa como o número de indivíduos por área ou também expressa como a biomassa da população por área ou volume. Exemplos: 50 leões por hectare, um milhão de algas por metro cúbico de água etc.
Caro(a) aluno(a), atente-se que o número de indivíduos de uma população pode variar de acordo com alguns fatores ecológicos, entre eles: suprimentos alimentares, taxas de predação e disponibilidade de sítios de aninhamento.
Odum e Barret (2007) diferenciam a densidade em densidade bruta (número ou biomassa, por unidade do espaço total) e densidade ecológica (número ou biomassa, por unidade do espaço do habitat, ou seja, área ou volume disponível que pode ser colonizado pela população).
Já no contexto da densidade populacional humana, denominada de densidade demográfica, esta é calculada com base em levantamentos periódicos (censos demográficos). À título ilustrativo, o Instituto Brasileiro de Geografia e Estatística (IBGE) realiza censos, e a estimativa para o ano de 2017 no Brasil foi de 207.660.929 de pessoas distribuídas pelos 8,5 milhões de quilômetros quadrados de superfície do território nacional. Dessa forma, a densidade demográfica no Brasil em 2017 foi de aproximadamente 24,43 hab.km². No entanto, ressalta-se que a densidade demográfica apresenta aspectos gerais da população brasileira, visto que existem áreas mais densamente povoadas, como as cidades grandes, e outras menos habitadas, como a floresta amazônica.
Caro(a) aluno(a), para determinar o tamanho de uma população deve-se contar todos os indivíduos, e isso só é possível para espécies pouco numerosas, de grande tamanho corporal e isoladas. No entanto, para a maioria das espécies existentes isso é quase impossível, de modo que os ecólogos determinaram alguns métodos para estimar o tamanho da população.
O índice de Lincoln é um método utilizado para estimar a densidade da população total (número de organismos de uma espécie) em uma determinada área. O método baseia-se na captura e marcação de parte da população total e no uso dessa fração para a estimativa da densidade da população total.
Utiliza-se a equação abaixo para a estimativa da população total:
\[\frac{Estimativa~da~populaç\tilde{a}o~\left(x \right)}{N\acute{u}mero~de~animais~capturados~e~marcados~na~amostra~S1~no~tempo~t{{1}_{{}}}}=\]
\[\frac{N\acute{u}mero~de~animais~capturados~na~amostra~S1~no~tempo~t2}{N\acute{u}mero~de~animais~marcados~encontrados~na~amostra~S2~no~tempo~t2}\]
Segundo Odum e Barrett (2007), a validade desse método depende de algumas suposições. São elas:
Além desse método, pode-se citar outros como (ODUM e BARRETT, 2007):
Não existe um tipo único de marcação de espécies. As aves são marcadas com anéis coloridos nas pernas; as borboletas através de manchas coloridas nas asas; as abelhas por identificação numerada no corpo; os mamíferos através de etiquetas ou tingimentos no pêlo; as plantas através de etiquetas amarradas nos galhos etc. (SADAVA et al., 2009).

A natalidade representa a capacidade de uma população crescer por meio da reprodução. O termo cobre a produção de novos indivíduos de qualquer organismo por unidade de tempo, tenha esse indivíduo nascido, sido chocado, germinado ou surgido por divisão.
A natalidade máxima diz respeito à produção máxima teórica de novos indivíduos sob condições ideais (sem fatores limitantes) e é uma constante em uma dada população. Já a natalidade ecológica refere-se ao crescimento populacional sob uma condição ambiental de campo específica ou real, e que pode variar com a composição do tamanho e da idade da população e com as condições físicas e ambientais (ODUM e BARRETT, 2007).
A taxa de natalidade absoluta é expressa como a taxa determinada pela divisão do número de novos indivíduos produzidos pela unidade específica de tempo. Já a taxa de natalidade específica é expressa dividindo-se o número de novos indivíduos por unidade de tempo por uma unidade de população.
Exemplificando a taxa de natalidade absoluta e específica, considere que uma população de 20 protozoários aumente por divisão para 60 protozoários em uma hora. A natalidade bruta é 40 por hora, enquanto que a natalidade específica é 2 por hora por indivíduo (dos 20 originais).
Para a espécie humana, a taxa de natalidade é expressa como o número de crianças nascidas no período de um ano para cada 1.000 habitantes da população (AMABIS e MARTHO, 2006).
Caro(a) aluno(a), no contexto da natalidade é importante diferenciar dois termos: fertilidade e fecundidade. A fertilidade refere-se ao potencial fisiológico de reprodução de uma dada população e a fecundidade representa o número de nascimentos por fêmea. No caso da população humana, esta apresenta fecundidade igual a 1 nascimento/11 meses.fêmea (ou seja, 1 nascimento a cada 11 meses por fêmea em idade reprodutiva) e uma fertilidade média de 1 nascimento/8 anos.fêmea (ou seja, 1 nascimento a cada 8 anos por fêmea em idade reprodutiva (PINTO-COELHO, 2000).
A mortalidade representa a quantificação de mortes dos indivíduos da população. Assim como a natalidade, a mortalidade pode ser expressa pelo número de indivíduos que morrem em um determinado período de tempo
A mortalidade mínima representa a perda mínima sob condições ideais ou não limitantes. Já a mortalidade ecológica diz respeito à perda de indivíduos sob uma determinada condição ambiental. Sabe-se que, mesmo sob as melhores condições, os indivíduos morreriam de velhice, determinada pela longevidade fisiológica, que é muitas vezes maior que a longevidade ecológica média. Além disso, Odum e Barret (2007) destacam que a taxa de sobrevivência costuma ser de maior interesse do que a taxa de morte, e, neste sentido, se a taxa de morte for expressa como uma fração, M, então a taxa de sobrevivência será 1-M.
Para a espécie humana, a taxa de mortalidade é expressa pelo número de mortes ocorridas no período de um ano para cada 1.000 habitantes da população (AMABIS e MARTHO, 2006).
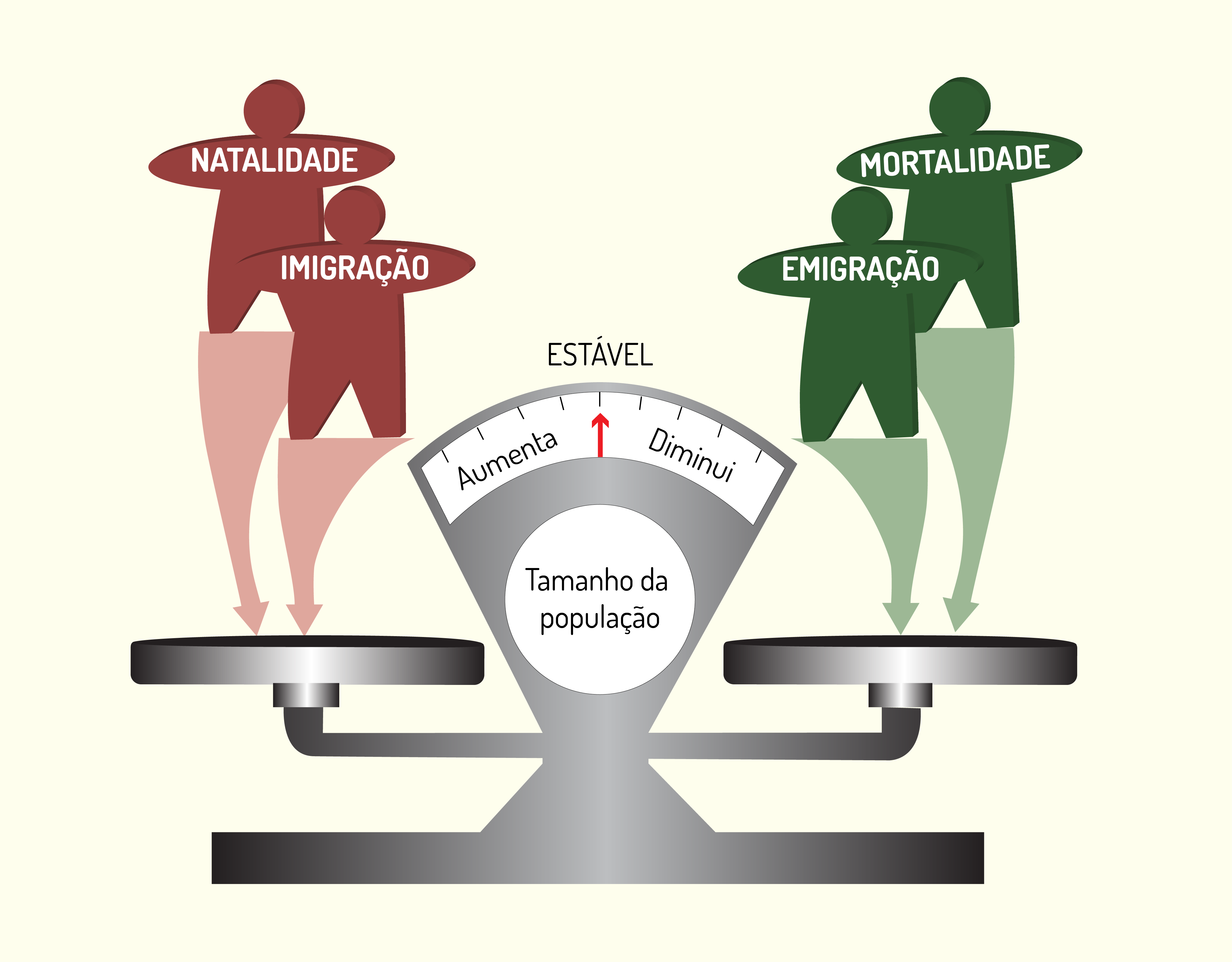
Caro(a) aluno(a), no contexto da natalidade e mortalidade, a migração que representa a entrada e saída periódica dos indivíduos pode suplementar ambas.
A emigração representa a saída dos indivíduos, afetando a forma de crescimento da mesma forma que a mortalidade. Já a imigração representa a entrada de indivíduos, agindo da mesma forma que a natalidade.
Neste sentido, caro(a) aluno(a), por meio dos conceitos de natalidade (B), mortalidade (M), imigração (I) e emigração (E), que estudamos até agora, é possível estimar se a população está aumentando, diminuindo ou se está em equilíbrio. Observe:
\[N+I=M+E→ população\ em\ equilíbrio\]
\[N+I>M+E → população\ aumenta\]
\[N+I<M+E→ população\ diminui\]
A Figura 3.1a seguir ilustra essa influência no contexto do crescimento populacional.
A emigração e imigração, assim como natalidade e mortalidade, são considerados determinantes populacionais, visto que determinam a variação do número de indivíduos de qualquer população.
Fonte: A autora.

No contexto do crescimento populacional, assinale a alternativa que diz respeito a fatores que contribuem para aumento da densidade populacional:
Natalidade e imigração.
Correta: uma vez que natalidade e imigração contribuem para aumento populacional.
Natalidade e emigração.
Incorreta: pois natalidade contribui para aumento populacional e imigração contribui para diminuição populacional.
Mortalidade e imigração.
Incorreta: pois imigração contribui para aumento populacional e mortalidade contribui para diminuição populacional.
Mortalidade e emigração.
Incorreta: pois mortalidade e emigração contribuem para a diminuição populacional.
Natalidade e mortalidade.
Incorreta: pois natalidade contribui para aumento populacional e mortalidade contribui para diminuição populacional.
Caro(a) aluno(a), agora que você já conhece os significados de densidade populacional, natalidade, mortalidade e migração é importante que tenha conhecimento de que é possível realizar estimativas do tamanho populacional em um momento futuro (Nt+1) a partir do tamanho populacional presente (Nt) bem como dos valores de nascimentos, óbitos, imigrações e emigrações.
Para essa estimativa, utiliza-se a seguinte equação:
\[{{N}_{t+1}}={{N}_{t}}+B-M+I-E\]
Em que:
\({{N}_{t+1}}\)= número de indivíduos no futuro (t+1)
\({{N}_{t}}\)= número de indivíduos no tempo presente (t)
\(B\) = número de nascimentos
\(M\)= número de óbitos
\(I\)= número de indivíduos que imigram para a população
\(E\)= número de indivíduos que emigram da população
Caro(a) aluno(a), vimos que a distribuição da população influencia tanto a natalidade quanto a mortalidade e que a razão entre os vários grupos etários em uma população determina seu estado reprodutivo, bem como o que se esperar no futuro.
Odum e Barrett (2007) explicam que, geralmente: uma população que se expande rapidamente contará com uma grande proporção de indivíduos jovens; uma população pulsante, estável, terá uma distribuição mais uniforme das classes etárias; e, por fim, uma população em declínio terá uma grande proporção de indivíduos velhos. Dessa forma, resumidamente, pode-se dizer que existem três tipos de pirâmides: em expansão, estável e em declínio.
Observe a Figura 3.2 a seguir que ilustra essas diferentes situações de distribuição etária no Brasil:
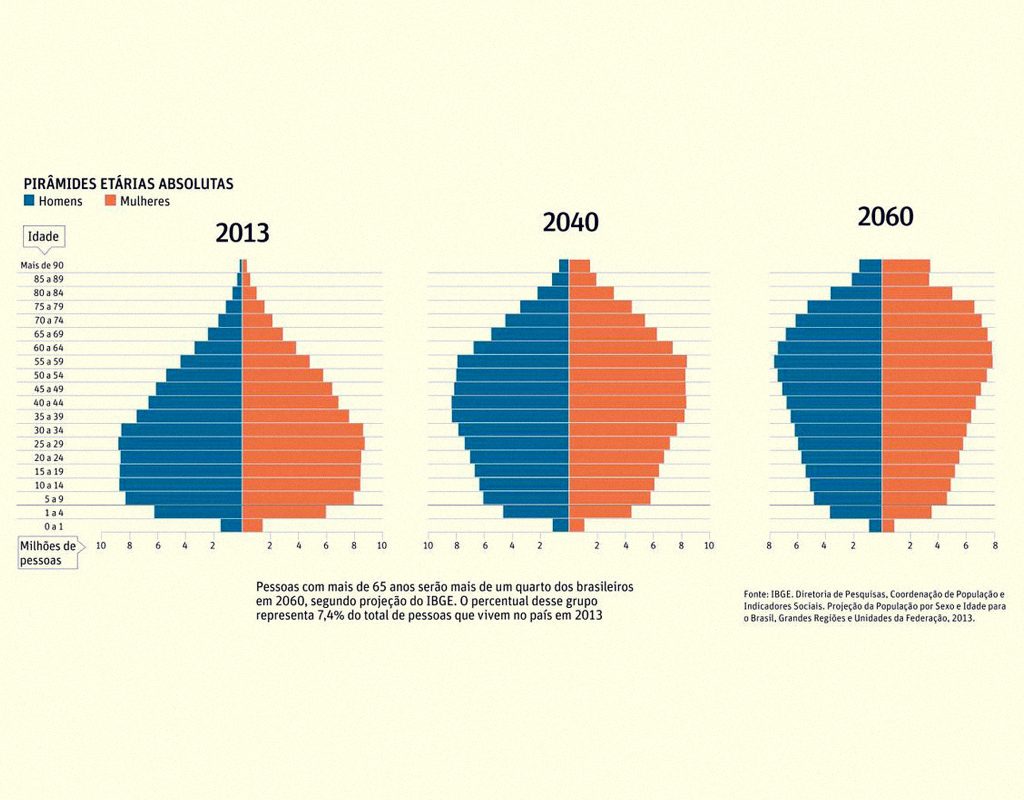
Segundo Peroni e Hernández (2011), a estrutura etária pode ser expressa com base em três idades ecológicas: pré-reprodutiva, reprodutiva e pós-reprodutiva, de modo que a duração relativa dessas idades em proporção ao tempo de vida varia com os organismos e influencia as taxas de natalidade e mortalidade na população. No caso dos seres humanos, as três idades são relativamente iguais em comprimento, com cerca de um terço de uma vida humana caindo em cada classe.
Caro(a) aluno(a), observe que não é simples estimar a idade dos diferentes organismos. No geral, para essa tarefa é possível contar os anéis de crescimento dos indivíduos. Para plantas, como ilustra a Figura 3.3 a seguir, contamos os anéis ou as cicatrizes. Já para os animais, pode-se contar os anéis de crescimento presentes em chifres (para cabras e carneiros), nos otólitos (para peixes) ou sobre a carapaça de tartarugas, as linhas de interrupção de crescimento de escamas de peixes e os pesos dos dentes de elefantes.

As tabelas de vida são uma descrição da forma como as taxas de mortalidade atuam sobre uma determinada população. Por meio delas, é possível calcular as probabilidades de sobrevivência dos indivíduos em uma determinada idade.
Neste estudo discutiremos sobre dois tipos de tabela de vida: a tabela de vida de coorte fixa e a tabela de vida estática. Segundo Begon et al. (2010), na primeira, uma única coorte de vida de indivíduos (ou seja, um grupo de indivíduos que nascem dentro de um mesmo intervalo de tempo) é acompanhada do nascimento até a morte do último sobrevivente. Esse tipo de tabela pode ser aplicada a espécies que completam seu ciclo anualmente, como as da família Poaceae.
Já na tabela estática acompanha-se ao longo do tempo todos os indivíduos que nascem e morrem em uma determinada população, de modo que é necessário definir claramente a idade de cada um deles (PERONI e HERNÁNDEZ, 2011).
A Tabela 3.1 seguir ilustra um exemplo de tabela de vida de coorte para uma espécie fictícia de planta. Observe:
Tabela 3.1: Tabela de vida de uma espécie de planta fictícia
Fonte: Peroni e Hernández (2011, p. 50).
De acordo com a Tabela 3.1, a coluna “\(x\)” fornece a idade dos indivíduos, desde o nascimento até a morte. As colunas \({{a}_{x}}\) e \({{B}_{x}}\), segundo Peroni e Hernández (2011), contêm dados coletados em campo, de forma que as demais derivam da coluna \({{a}_{x}}\).
A coluna \({{a}_{x}}\) resume os dados coletados por meio do mapeamento das posições de 800 plantas germinadas de sementes disseminadas em uma determinada área. A partir dessa coluna, os valores “\({{I}_{x}}\)” são calculados com base no número de plantas que sobrevivem até o intervalo \(x\), por meio da fórmula \({{I}_{x}}=~{{a}_{x}}/{{a}_{o}}\). Assim, podemos definir “\({{I}_{x}}\)” como o perfil de sobrevivência, ou a proporção da coorte original sobrevivente no intervalo de vida considerado.
O cálculo de “\({{d}_{x}}\)” é feito por meio da diferença entre \({{a}_{x}}\) e \({{a}_{x+1}}\). Assim, podemos definir “\({{d}_{x}}\)” como o número de indivíduos que morrem entre um intervalo e outro de tempo.
A porcentagem de mortalidade para cada idade específica, “\({{q}_{x}}\)”, é calculada por meio da fórmula \({{q}_{x}}=~{{a}_{x}}-{{a}_{x+1}}/{{a}_{x}}\).
A coluna “\({{B}_{x}}\)” indica a fecundidade para cada idade específica, que no exemplo da Tabela 3.1 indica o número médio de sementes por idade individual.
A coluna “\({{m}_{x}}\)” representa a taxa de nascimento, sendo definida como a fertilidade individual ou número médio de prole produzida por indivíduo. Calcula-se por meio da fórmula \({{m}_{x}}={{B}_{x}}/{{a}_{x}}\).
Segundo Peroni e Hernández (2011), o parâmetro \({{m}_{x}}\) é importante para se analisar o crescimento ou não de uma população. Do somatório da multiplicação de \({{I}_{x}}{{m}_{x}}\left( \mathop{\sum }_{{}}^{{}}{{I}_{x}}{{m}_{x}} \right)\) obtém-se o valor de \({{R}_{o}}\) (taxa de reprodução líquida). Assim, sabendo-se a taxa de sobrevivência das classes etárias (\({{I}_{x}}\)) e as proporções de quantos indivíduos nascem em média por indivíduo (\({{m}_{x}}\)), é possível estimar uma taxa que expressa a reprodução dessa população ao longo do tempo.
Quando sabemos os valores de \({{R}_{o}}\), pode-se analisar se a população está crescendo ou diminuindo. Com \({{R}_{o}}\)>1 há aumento por geração de população; com \({{R}_{o}}=1\) há uma tendência de estabilidade, ou seja, cada indivíduo morto é reposto por apenas um na próxima geração; e para \({{R}_{o}}<1\) há tendência de redução ou declínio da população, uma vez que as taxas de fertilidade combinadas às taxas de sobrevivência não são capazes de fazer com que a população cresça e nem se mantenha com o mesmo número de indivíduos. No exemplo ilustrado pela Tabela 3.1, o valor de \({{R}_{o}}=1,4\), ou seja, cada indivíduo produz em média 1,4 indivíduos ao longo de uma geração.
Já a Tabela 3.2 a seguir ilustra uma tabela de vida estática fictícia. A idade é determinada pelo peso e coloração da pelagem. Os valores de sobrevivência (\({{I}_{x}}\)) e mortalidade (\({{d}_{x}}\) e \({{q}_{x}}\)) são facilmente calculados. Caso a fecundidade (\({{B}_{x}}\)) seja conhecida, também é possível o cálculo da fertilidade individual (\({{m}_{x}}\)) e a taxa de reprodução líquida (\({{R}_{o}}\)).
Tabela 3.2: Tabela de vida de uma espécie fictícia de roedor
Fonte: Peroni e Hernández (2011, p. 53).
Segundo Peroni e Hernández (2011), a tabela de vida estática pode ser vista como uma “foto instantânea da população”, em que os dados são similares aos de uma tabela de vida de coorte: uma série de diferentes números de indivíduos em diferentes classes etárias. No entanto, caro(a) aluno(a), na utilização desse modelo há uma restrição: deve-se assumir que os padrões de mortalidade (ou sobrevivência) e natalidade específicos por idade permanecem constantes entre o nascimento dos indivíduos mais velhos e os dois mais novos, o que raramente acontece.
Segundo Peroni e Hernández (2011), por meio de parâmetros das tabelas de vida é possível produzir gráficos de curvas de sobrevivência. Para isso, utiliza-se a coluna dos valores da taxa de sobrevivência das classes etárias \((I_{x})\) no eixo y, em uma escala logarítmica, e as classes etárias no eixo x.
Um conjunto útil de curvas de sobrevivência foi desenvolvido por Pearl em 1928, generalizando que poderia haver três tipos básicos, nos quais os riscos de mortalidade, de acordo com a idade, poderiam estar distribuídos entre os mais diferentes organismos (BEGON et al., 2007). Observe a Figura 4:.
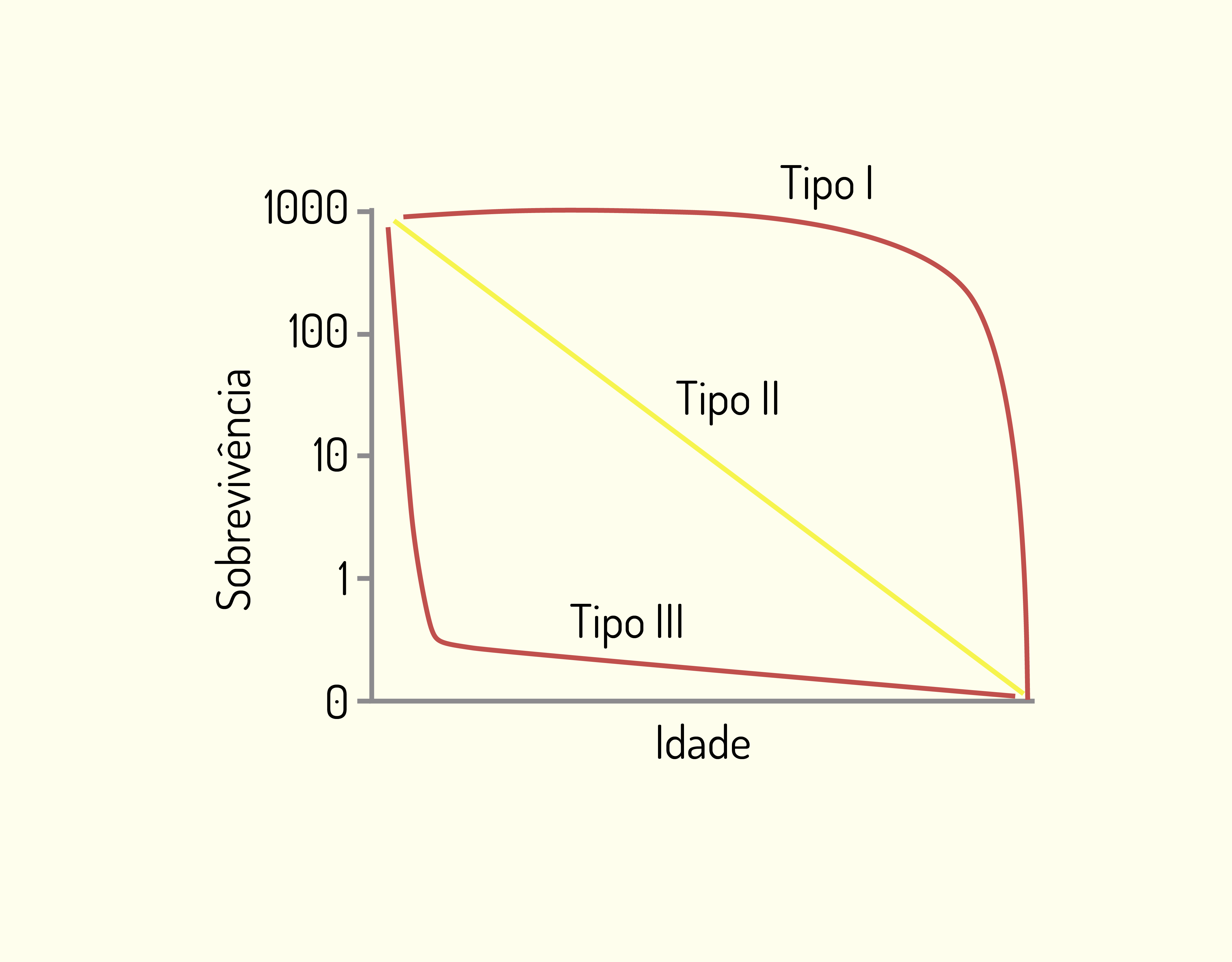
A curva do tipo I descreve situações na qual a mortalidade é concentrada no final da vida. A proporção de sobreviventes é constante durante quase todas as etapas do ciclo de vida. Esse tipo de sobrevivência pode ser observado nas populações humanas de países desenvolvidos e de mamíferos bem cuidados em zoológico e em casa, que investem em cuidados parentais, de modo a assegurar alta sobrevivência para as classes etárias jovens.
Na curva do tipo II a taxa de mortalidade é constante com a idade, conduzindo a uma curva de sobrevivência que se aproxima de uma reta diagonal, com um declínio linear. Esse exemplo pode ser aplicado a sementes de plantas enterradas no solo, de forma que a viabilidade das sementes vai caindo de maneira constante.
Por fim, na curva do tipo III há uma alta mortalidade no início, de modo que a sobrevivência é baixa para as classes etárias jovens e alta para indivíduos mais velhos. Este exemplo aplica-se a insetos, peixes invertebrados e plantas perenes, os quais podem produzir centenas de ovos, larvas ou sementes, cuja maioria acaba por morrer.
Caro(a) aluno(a), ressaltamos que determinadas espécies podem apresentar mais de uma curva, como espécies de gramíneas que apresentam a curva de sobrevivência do tipo III no estádio de plântulas, e estas, quando se desenvolvem e se transformam em plantas adultas, passam a apresentam a curva do tipo II (PERONI e HERNÁNDEZ, 2011).
Nós vimos que existem três tipos de curvas de sobrevivência que representam o número de sobreviventes num determinado período de tempo. Sobre as curvas de sobrevivência, assinale a alternativa correta:
Na curva de sobrevivência do tipo I a taxa de mortalidade é representada por uma curva de sobrevivência que se aproxima de uma reta diagonal.
Incorreta: pois na curva de sobrevivência do tipo II a taxa de mortalidade é representada por uma curva de sobrevivência que se aproxima de uma reta diagonal.
Na curva do tipo III a mortalidade é concentrada no final da vida.
Incorreta: pois na curva do tipo I a mortalidade é concentrada no final da vida.
Na curva do tipo I há uma elevada mortalidade durante os primeiros tempos de vida.
Incorreta: pois na curva do tipo III há uma elevada mortalidade durante os primeiros tempos de vida.
A curva do tipo III aplica-se aos peixes que podem produzir centenas de ovos, dos quais a maioria acaba por morrer.
Correta: uma vez que na curva do tipo III a sobrevivência é muito baixa para as classes etárias mais jovens.
A curva do tipo II aplica-se aos mamíferos que investem em cuidados parentais.
Incorreta: pois a curva do tipo I aplica-se aos mamíferos que investem em cuidados parentais.
Caro(a) aluno(a), a população está sempre em mudança, assim como a densidade, natalidade, sobrevivência, taxa de crescimento, estrutura etária etc., uma vez que as espécies se ajustam constantemente às estações, às forças e umas às outras.
A dinâmica de populações diz respeito ao estudo das mudanças no número relativo de organismos em populações e dos fatores que explicam essas mudanças (ODUM e BARRETT, 2007). Assim, os ecólogos interessam-se mais em como e a qual taxa a população está mudando do que em seu tamanho absoluto e composição.
No estudo das populações, é importante compreendermos alguns conceitos básicos de taxa. O termo taxa diz respeito à divisão da mudança em alguma quantidade pelo período de tempo que se passou durante essa mudança.
A mudança em alguma quantidade é abreviada usando-se o símbolo \(\Delta \) (delta) na frente da letra que representa a entidade em mudança. Assim, se N representa o número de organismos e t representa o tempo, temos que (ODUM e BARRETT, 2007):
\(\Delta N\)= mudança no número de organismos.
\(\frac{\Delta N}{\Delta t}=\)taxa média de mudança no número de organismos por tempo, ou seja, taxa de crescimento da população.
\(\frac{\Delta N}{N\Delta t}=\)taxa média de mudança do número de organismos por tempo por organismo, ou seja, taxa de crescimento específico.
Além da taxa média, também podemos estar interessados na taxa instantânea teórica em intervalos de tempo particulares, ou seja, quanto a taxa de mudança \(\Delta t\) se aproxima de zero. Em cálculo, a letra d (de derivada) substitui o \(\Delta \) quando se consideram as taxas instantâneas. Nesse caso, as notações anteriores tornam-se:
\(\frac{dN}{dt}=\) taxa de mudança no número de organismos por tempo em um determinado instante.
\(\frac{dN}{Ndt}=\) taxa de mudança no número de organismos por tempo por indivíduo em um determinado instante.
A Figura 3.5 a seguir ilustra a diferença entre uma curva de crescimento e uma curva de taxa de crescimento. Observe que a curva A mostra a densidade populacional (número de indivíduos por unidade de área) contra o tempo e a curva B demonstra a taxa de mudança (número de indivíduos adicionados por unidade de tempo) contra o tempo para a mesma população:
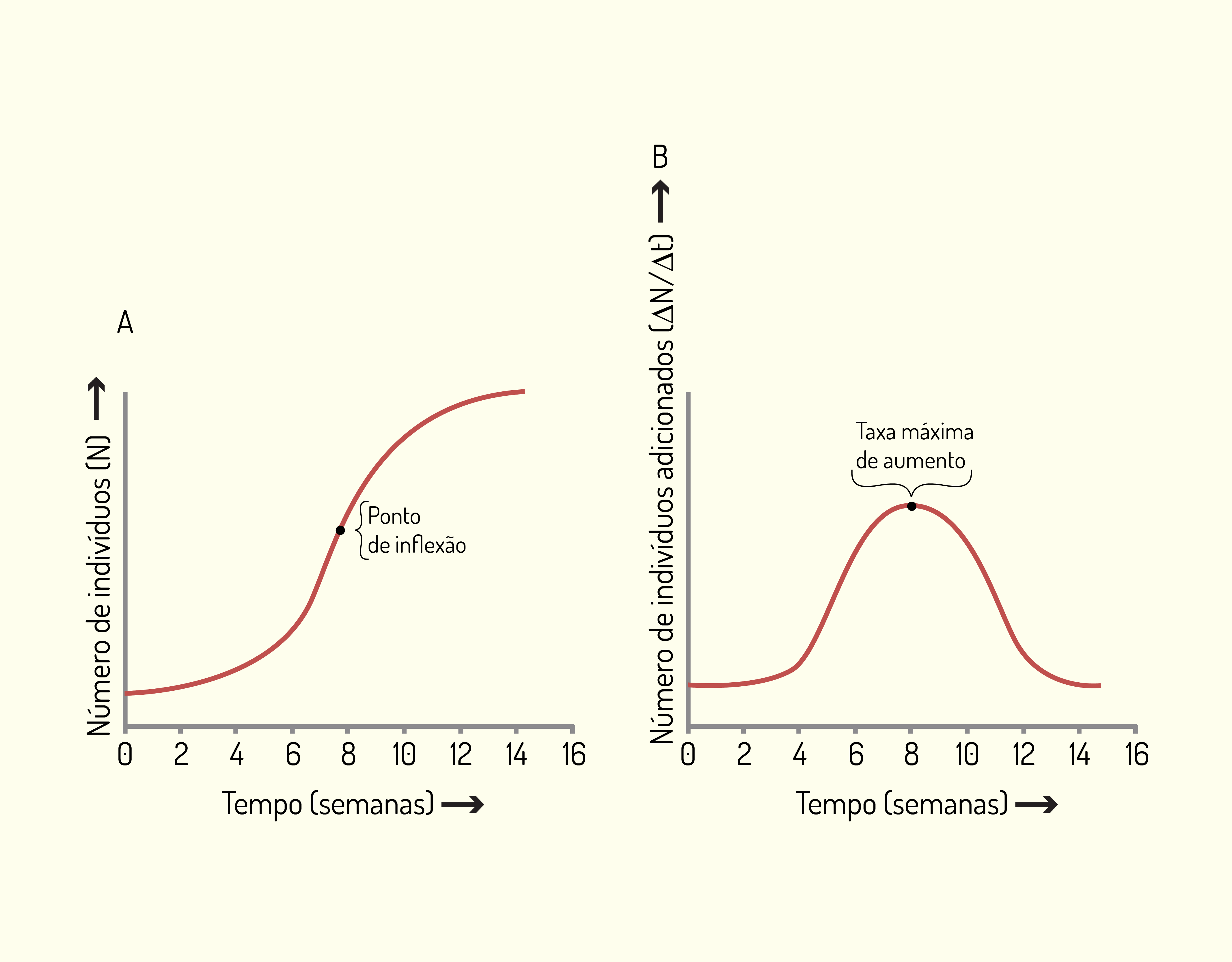
Conhecer o crescimento populacional é importante para compreender o comportamento das populações de um ecossistema. Medidas do tamanho de uma população, tomadas em diferentes intervalos de tempo, informam se a população está em expansão, estável ou em declínio, de modo a possibilitar fazer correlações com o clima, disponibilidade de alimento etc.
Fonte: Amabis e Martho (2006).

As curvas de crescimento, ilustradas na Figura 3.5, em formato de S e as curvas da taxa de crescimento em corcova são geralmente características de populações em estágios pioneiros ou em início de crescimento. Por meio da Figura 3.5 (B) observa-se que a taxa de crescimento foi máxima na oitava semana e caiu para zero após 16 semanas. O ponto em que a taxa de crescimento é máxima é denominado de ponto de inflexão.
Caro(a) aluno(a), vimos que as populações mostram padrões de crescimento e, ao admitirem a mortalidade nula, Amabis e Martho (2006) trazem um exemplo que ilustra essa situação: uma única bactéria que se reproduza a cada 20 minutos levaria apenas 36 horas para produzir descendentes suficientes para cobrir a superfície da Terra. No entanto, sabemos que essa situação fictícia não ocorre na prática, de modo que o crescimento da população torna-se limitado devido a alguns fatores, como disponibilidade de recursos, alimento, espaço, abrigo, quando a geada ou outro fator sazonal interfere, ou quando a estação reprodutiva termina, bem como por doenças, predadores, interações sociais etc.
Neste contexto, o crescimento populacional pode ser em forma de J e em forma de S, conforme demonstra a Figura 3.6 a seguir:
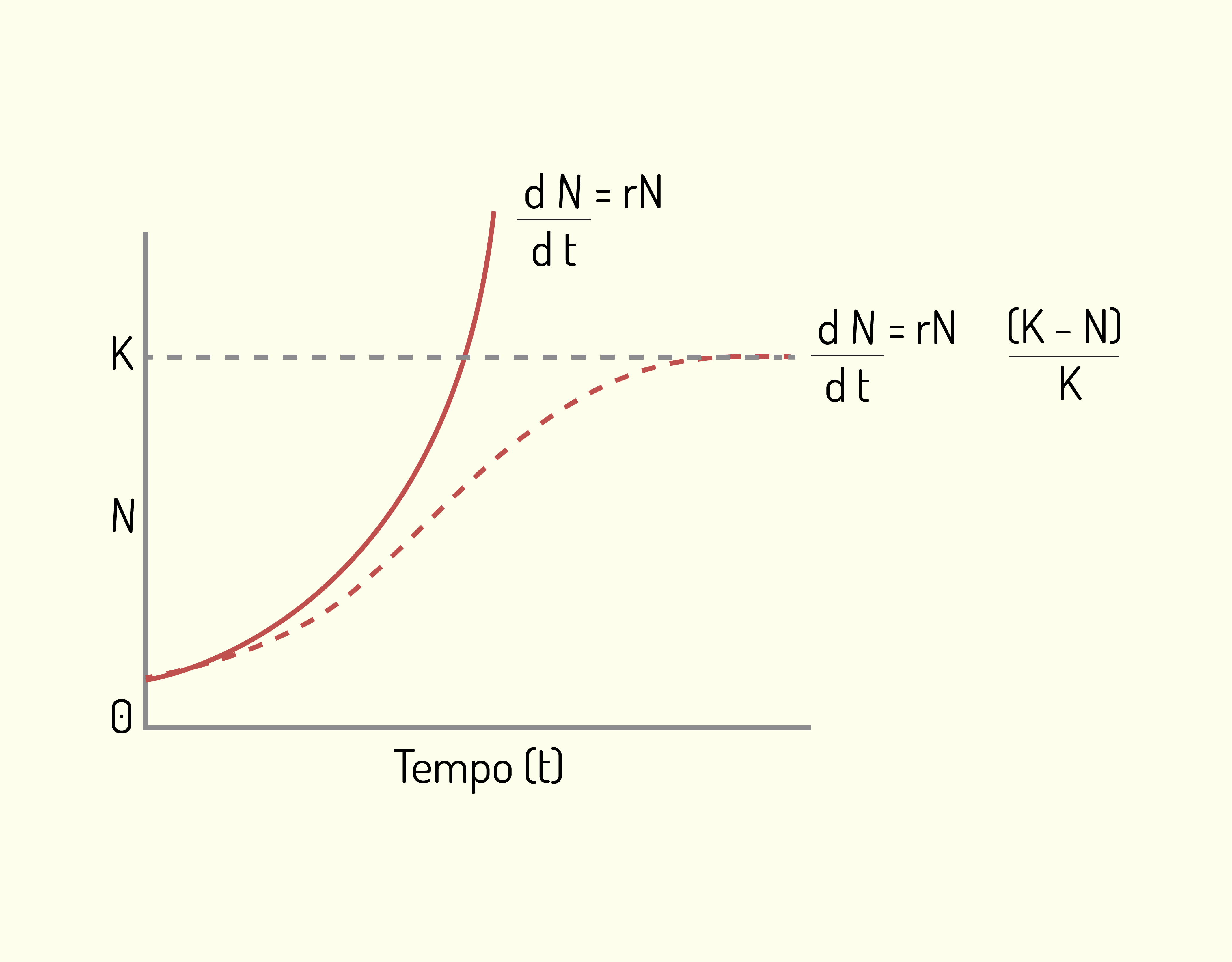
No crescimento em forma de J, a densidade aumenta rapidamente de forma exponencial, e então para abruptamente quando a resistência ambiental, ou outro fator limitante, torna-se efetivo. O modelo de crescimento em forma de J pode ser representado por meio da equação:
\[\frac{dN}{dt}=rN\]
Em que o parâmetro \(r\) é conhecido como taxa de crescimento instantânea, ou taxa intrínseca de crescimento, e pode ser calculado por meio da taxa de natalidade instantânea \((b)\) e da taxa de mortalidade instantânea \((m)\), ou seja:
\[r=b-m\]
O valor de r determina se a população vai crescer exponencialmente \((r > 0)\), se vai permanecer constante \((r = 0)\) ou se vai diminuir até a extinção \((r < 0)\).
Segundo Peroni e Hernandez (2011), a equação descrita para o crescimento em forma de J permite medir a taxa de crescimento populacional, mas não o tamanho da população. Utilizando o cálculo diferencial e integral é possível expressar a equação de crescimento populacional pela seguinte relação:
\[{{N}_{t}}={{N}_{0}}{{e}^{rt}}\]
Em que:
\({{N}_{t}}\)= tamanho da população no tempo t
\({{N}_{0}}\)= tamanho da população inicial
\({{e}^{{}}}\)= constante, base do logaritmo neperiano (aproximadamente 2,717).
Nesse modelo a população cresce indefinidamente pois não há efeito de dependência da densidade, ou seja, não há limites de recursos para o crescimento da população, e não está ocorrendo competição entre indivíduos da mesma espécie.
Quando há uma constante redução na taxa intrínseca de aumento, enquanto a densidade aproxima-se da capacidade de suporte, a população deixa de exibir um crescimento exponencial (TOWNSEND et al., 2010), e este passa a ser em forma de S, de modo que a população aumenta devagar no início, depois com rapidez e então desacelera quando a resistência do ambiente aumenta em porcentagem até que o equilíbrio seja alcançado e mantido. O modelo de crescimento em forma de S pode ser representado por meio da equação:
\[\frac{dN}{dt}=rN~\left( 1-\frac{N}{K} \right)~~\]
Nessa equação a população para de crescer quando \(r = 0\), \(N = 0\), ou também quando \(N = K\).
Assim, o tamanho populacional aumenta até alcançar a estabilidade, um limite máximo, conhecido como capacidade de suporte \((K)\), que representa o tamanho de uma população que os recursos do ambiente podem suportar. Assim, segundo Townsend et al. (2010), em densidades abaixo de \(K\) os nascimentos excedem as mortes, de modo que a população aumenta. Já em densidades acima de \(K\) as mortes excedem os nascimentos, e a população diminui em número de indivíduos. Dessa forma, existe uma tendência para que a densidade flutue em torno do valor de \(K\), por influência da competição intraespecífica (entre indivíduos da mesma espécie).
Barrett e Odum (2000) apresentaram os dois tipos de crescimento que estudamos, levando à capacidade de suporte máxima ou à capacidade de suporte ótima, conforme demonstra a Figura 3.7 a seguir:
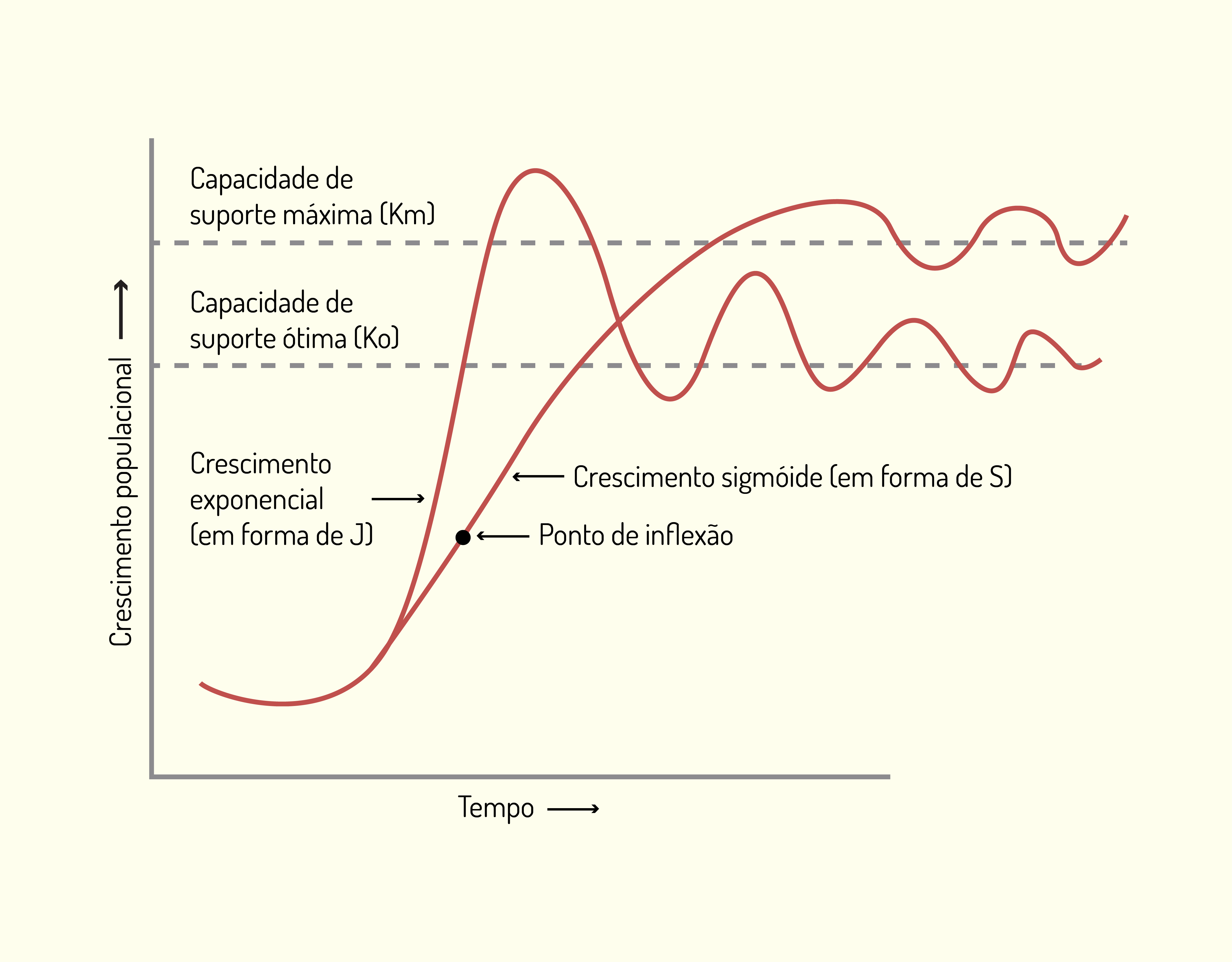
Por meio da Figura 3.7 observa-se que a capacidade de suporte máxima \((K_{m})\) é a densidade máxima que os recursos em um certo habitat podem suportar. Já a capacidade de suporte ótima \((K_{o})\) é a densidade de nível mais baixo que pode ser sustentada em um certo habitat sem “viver no limiar” aos recursos como alimento ou espaço (ODUM e BARRETT, 2007).
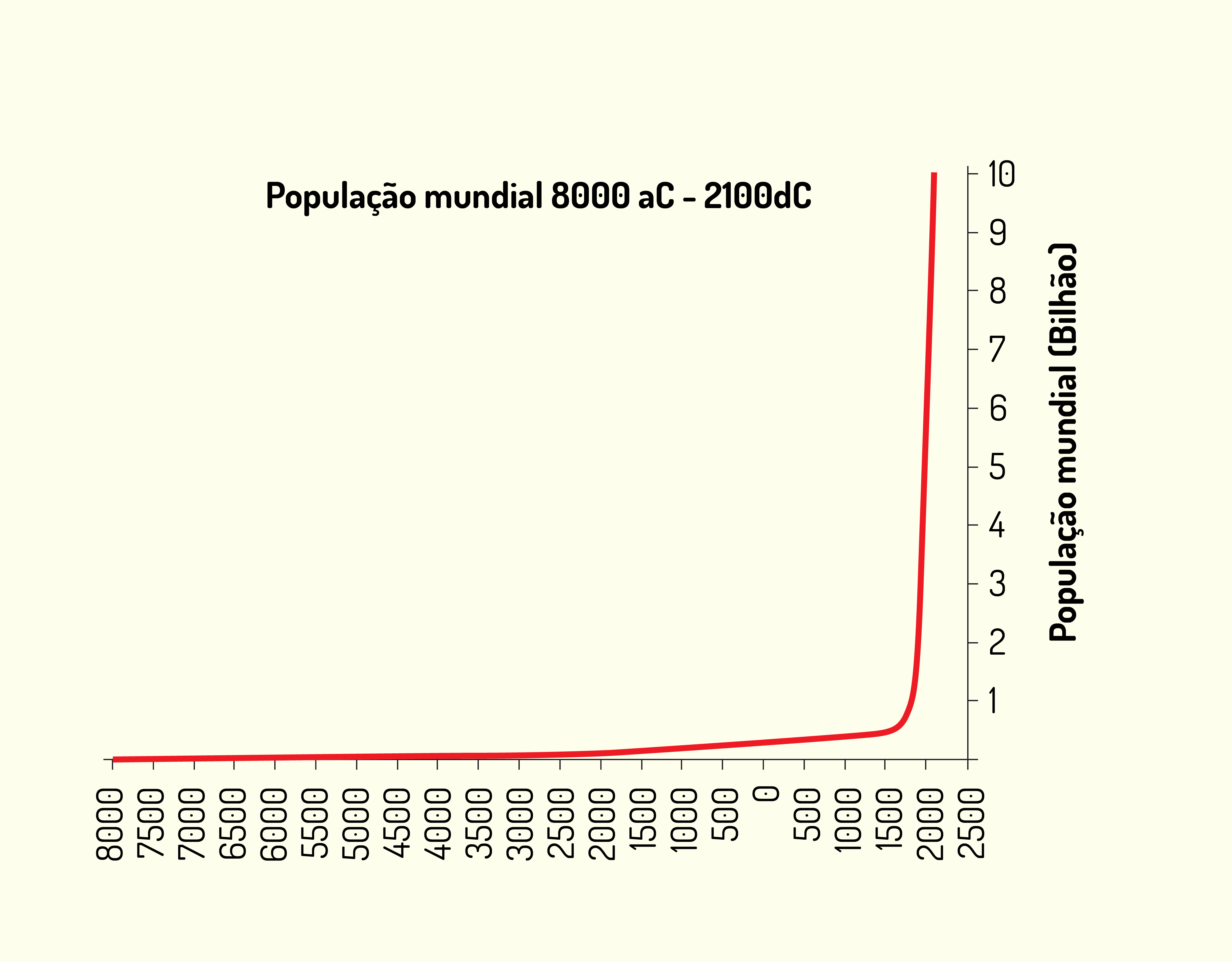
Caro(a) aluno(a), no contexto do crescimento da população humana mundial, observa-se por meio da Figura 3.8 que este vem aumentando. Calcula-se que em 8000 a. C. a população humana era de aproximadamente 5 milhões de pessoas; na época de Cristo foi de 300 milhões; 1650 saltou para 500 milhões; em 1850 era de aproximadamente 1 bilhão de pessoas, passando a 2 bilhões de pessoas em 1930 (AMABIS e MARTHO, 2006).
Esse crescimento acelerado, segundo Amabis e Martho (2006), deve-se principalmente à diminuição da taxa de mortalidade, decorrente de avanços tecnológicos, entre eles agrícolas, médicos e sanitários.
Quanto às estratégias de crescimento populacional, é possível classificar as populações de duas formas: r-estrategistas e k-estrategistas.
As espécies r-estrategistas possuem potencial de se multiplicar rapidamente favorecido pela seleção natural em ambientes efêmeros, de modo a capacitar os organismos a colonizar novos habitats e explorar novos recursos. Em geral, produzem descendentes de tamanho pequeno, mas numerosos. O tempo de vida dessas espécies é curto e não há cuidados com a prole. Como exemplos desse tipo de espécie citamos insetos e a maioria dos peixes.
Já as espécies k-estrategistas são aquelas que conseguem deixar descendentes pois capturam uma maior quantidade de recursos, muitas vezes porque nascem maiores e/ou crescem mais rápido. Em geral, apresentam tempo de vida mais longo e os pais cuidam da prole. Como exemplos desse tipo de espécie citamos grandes felinos, elefantes e os seres humanos.
Segundo Odum e Barrett (2007), quando as populações completam seu crescimento e a média de \(\Delta N/\Delta t\) permanece em zero por um período longo de tempo, a densidade da população tende a pulsar ou flutuar tanto acima como abaixo do nível de capacidade de suporte, uma vez que as populações estão sujeitas a várias formas de controle por retroalimentação em vez de controles de pontos de ajuste.
Assim, algumas populações podem ser irruptivas, ou seja, explodem em números em um padrão de ascensão-e-queda. Já outras podem ser cíclicas, populações que oscilam regularmente, de modo que quanto mais organizada e madura a comunidade estiver, ou mais estável o ambiente físico, menor será a amplitude das flutuações na densidade populacional com o passar do tempo.
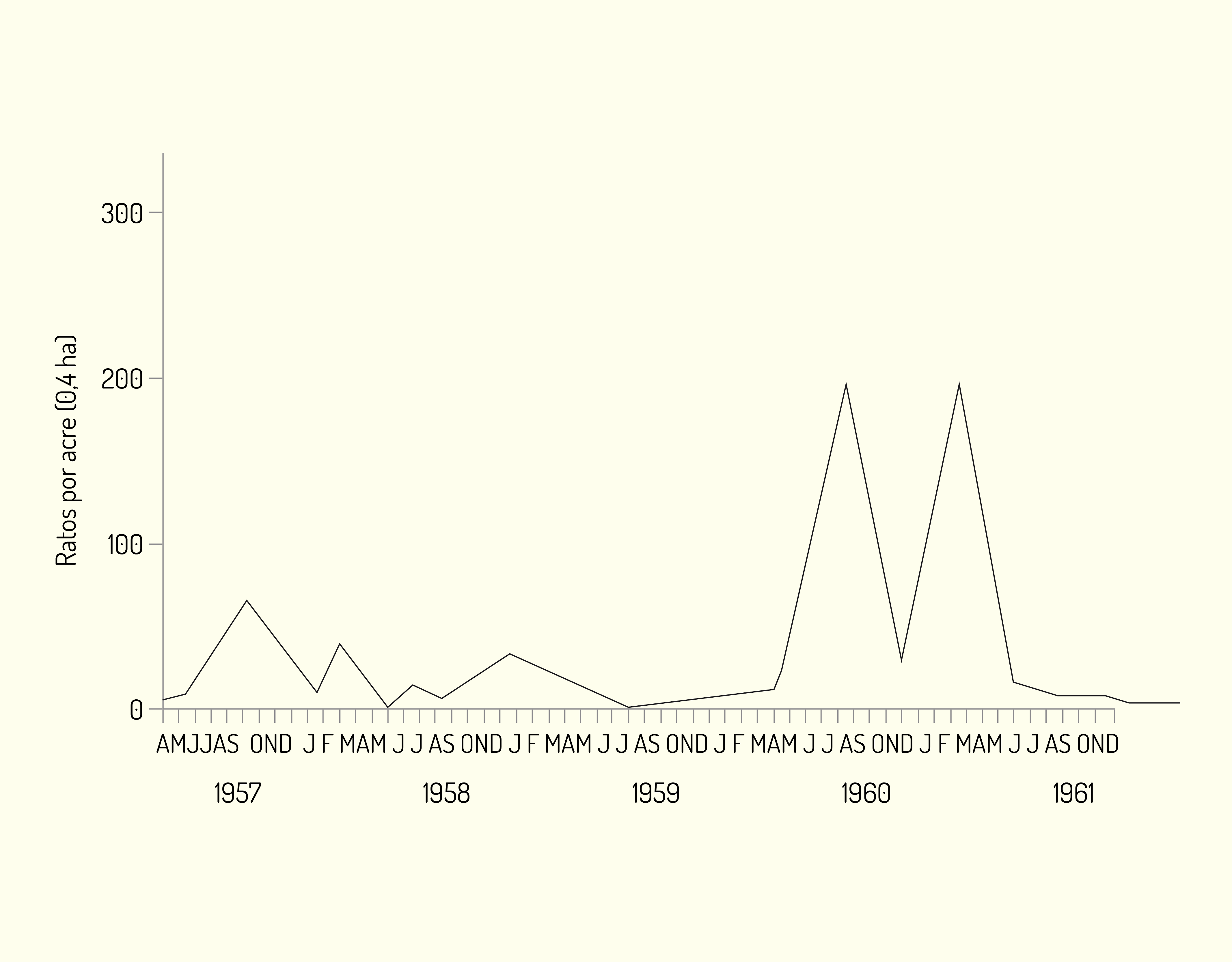
Como exemplo de padrão irruptivo de flutuação da densidade populacional citamos o que ocorreu com ratos domésticos ferais (Mus musculus) na Califórnia entre 1959 e 1960, cuja população explodiu duas vezes, provavelmente devido a condições favoráveis do ambiente, incluindo temperatura, alimento, cobertura vegetal para reduzir a predação etc. Observe a Figura 3.9 a seguir:
Já como exemplo de padrão cíclico citamos as oscilações da população de lebre americana (Lepus americanus) e do lince (Felis lynx) que ocorre de 9 a 10 anos. Observe por meio da Figura 3.10 a seguir que os picos de abundância são seguidos por declínios rápidos de modo que lince e lebres tornavam-se escassos em períodos próximos, uma vez que, como o lince depende da lebre como alimento, o ciclo predador-presa está relacionado.
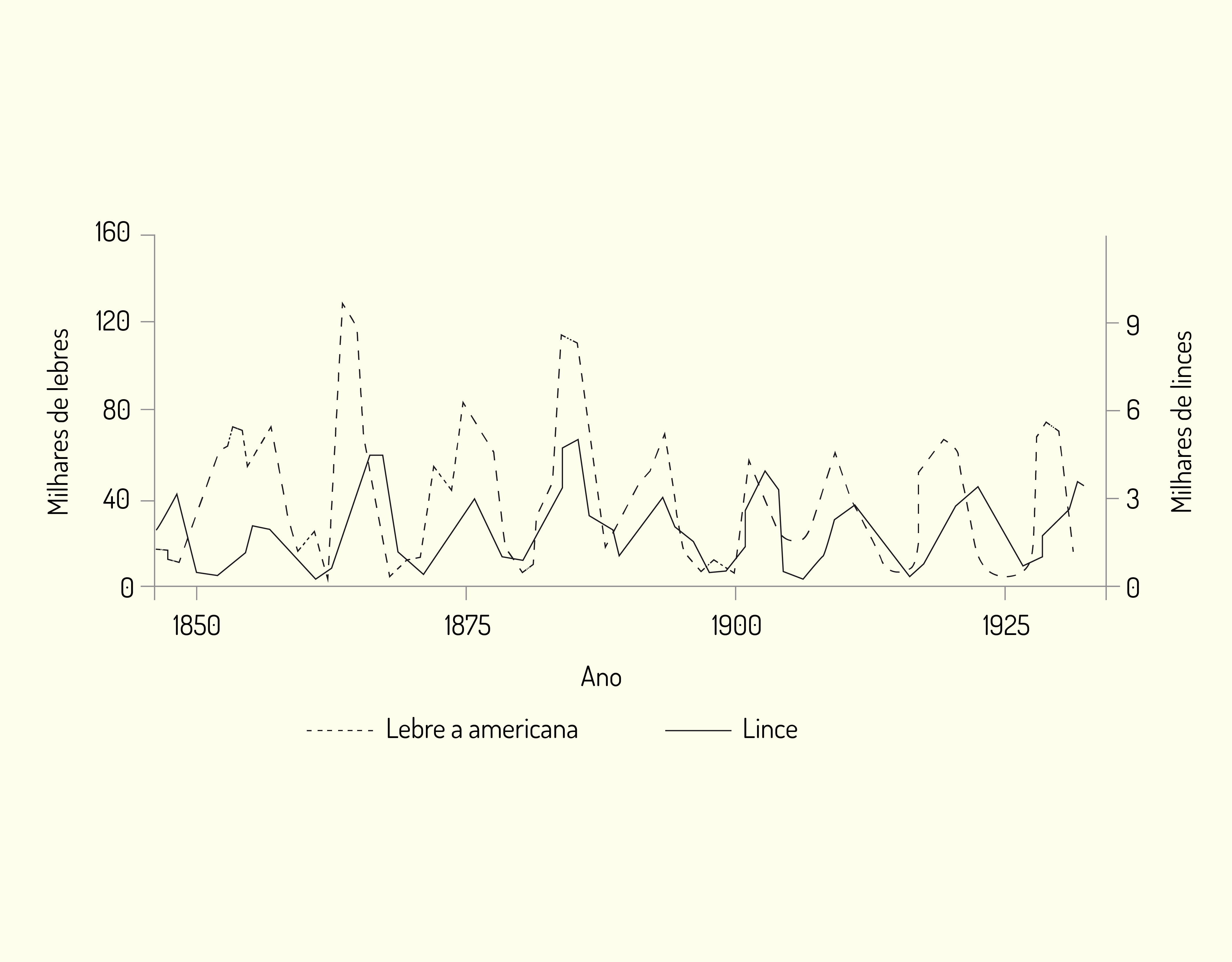
As flutuações podem ser consideradas por meio de fatores extrínsecos e intrínsecos. As flutuações controladas por fatores extrínsecos, como temperatura e chuva, estão fora da esfera das interações da população. Já as oscilações sujeitas a fatores intrínsecos, a exemplo dos fatores bióticos, como disponibilidade de alimento e energia, doenças ou predação, são controladas pela dinâmica populacional.
Caro(a) aluno(a), atente-se para o fato de que, em geral, as populações mais estáveis ocorrem em espécies com indivíduos de vida longa e taxas reprodutivas baixas, uma vez que os indivíduos pequenos e de vida curta são geralmente mais vulneráveis às alterações ambientais. Neste sentido, as densidades populacionais de insetos tendem a flutuar muito mais do que as de aves e mamíferos (SADAVA et al., 2009).
Caro(a) aluno(a), em ecossistemas de baixa diversidade, fisicamente estressados (como tempestades e fogo) ou sujeitos a perturbações extrínsecas irregulares ou imprevisíveis, o tamanho da população tende a ser influenciado por fatores físicos, como clima, correntes de água, condições químicas limitantes e poluição. Já em ecossistemas de alta diversidade em ambientes com baixa probabilidade de estresse físico as populações tendem a ser controladas biologicamente, de modo que sua densidade seja autorregulada (ODUM e BARRETT, 2007).
Assim, os fatores limitantes ou favoráveis para uma população serão independentes de densidade se seu efeito for independente do tamanho da população, ou dependentes de densidade se seu efeito na população for uma função da densidade populacional. Normalmente, fatores climáticos, como um período muito frio ou um furacão, agem de maneira independente de densidade, enquanto que fatores bióticos, como competição, parasitas ou patógenos, agem de maneira dependente de densidade.
As taxas de natalidade e mortalidade podem ser dependentes da densidade por alguns motivos (SADAVA et al. (2009):
Segundo Odum e Barrett (2007), a teoria geral da regulação de população é resultado da discussão sobre o potencial biótico, formas de crescimento e variação em torno do nível da capacidade de suporte. Nesse contexto, o crescimento em forma de J tende a ocorrer quando fatores extrínsecos ou independentes de densidade determinam em que ponto o crescimento para ou desacelera. Por outro lado, a forma de crescimento em forma de \(S\) é dependente da densidade, porque os efeitos intrínsecos controlam o crescimento da população.
Ainda de acordo com os referidos autores, os fatores independentes de densidade do ambiente, como fatores climáticos, tendem a causar variações na densidade populacional e também deslocamento nos níveis da assíntota superior ou da capacidade de suporte. Já os fatores dependentes de densidade, como a competição, tendem a manter a população em estado de pulsação estável ou apressar o retorno a esse nível.
“Os fatores ambientais independentes de densidade têm um papel mais importante nos ecossistemas fisicamente estressados; a mortalidade e a natalidade dependentes da densidade se tornam mais importantes em ambientes benignos nos quais o estresse extrínseco é reduzido.”
Fonte: Odum e Barrett (2007, p. 257).

As plantas possuem mecanismos de regulação de população dependentes de densidade. Dessa forma, as populações vegetais em altas densidades passam por um processo chamado de autodesbaste, o qual tende a regular e controlar as densidades das populações para permanecer dentro ou perto da capacidade de suporte estabelecida pela disponibilidade de recursos e condições do ambiente.
Quando a semeadura dá-se em altas densidades, as plantas emergentes ou plântulas competem vigorosamente. Durante o crescimento, muitas mudas morrem, reduzindo a densidade das mudas sobreviventes. O aumento da taxa de crescimento das plantas individuais sobreviventes resulta em competição contínua, levando a uma diminuição do número de plantas sobreviventes. Lançando o logaritmo do peso médio da planta em um gráfico como função do logaritmo da densidade populacional, os pontos dos dados ao longo da estação de crescimento geram uma linha com uma inclinação de aproximadamente -3/2. Essa regularidade também é conhecida como lei da potência -3/2 (ODUM e BARRETT, 2007), conforme demonstra a Figura 3.11 a seguir.

A distribuição de indivíduos em uma população descreve a distância relativa entre um e outro (RICKLEFS, 2010). Quanto ao padrão de dispersão, os indivíduos de uma população podem ser dispersos em quatro tipos gerais de padrões: aleatório, regular, agregado e agregado regular, conforme ilustra a Figura 3.12 a seguir:

A distribuição aleatória ocorre quando o ambiente é uniforme e não há tendência a se agregar. A dispersão regular ocorre quando a competição entre indivíduos é severa, ou quando há antagonismo positivo que promove espaçamento uniforme (esse padrão é frequente em plantações e florestas de monocultura). A distribuição de agregados representa o padrão mais comum, em que os indivíduos de uma população formam grupos de certos tamanhos, podendo ser aleatório ou em padrão regular.
Na natureza, a forma como os padrões se manifestam a um observador e sua relevância para a vida de outros organismos depende da escala espacial na qual estamos trabalhando (BEGON et al., 2010). Consideremos a distribuição de um afídeo (pulgão) que vive em uma determinada espécie de árvore em uma floresta. Se pensarmos na floresta como um todo, os afídeos pareceriam estar agregados em manchas florestais e inexistentes em áreas mais abertas. Mas se pensarmos nas amostragens retiradas de áreas menores somente florestadas, os afídeos ainda poderiam estar agregados, mas apenas em torno de sua própria planta hospedeira. Entretanto, se pensarmos em amostragens ao nível da folha da árvore, os afídeos poderiam aparecer estar aleatoriamente distribuídos sobre a árvore como um todo.
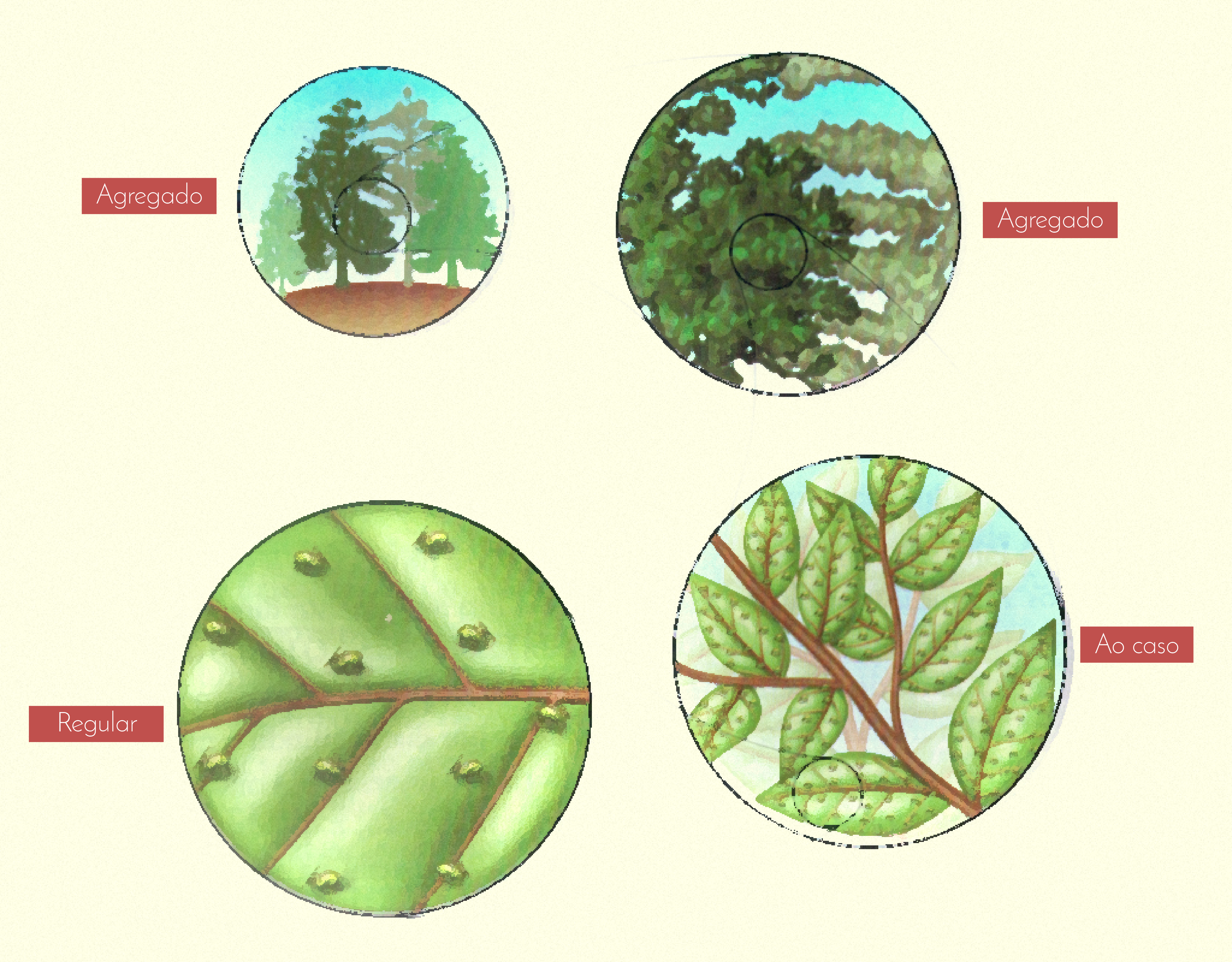
Quanto ao padrão de dispersão, os indivíduos de uma população podem ser dispersos em alguns tipos gerais de padrões. Sobre esses padrões, assinale a alternativa correta:
Na distribuição regular, os indivíduos formam grupos.
Incorreta: pois na distribuição agregada os indivíduos encontram-se agrupados.
Quando agregados, os grupos de indivíduos podem estar distribuídos de modo aleatório ou regular.
Correta: uma vez que a dispersão do agregado pode ser regular ou aleatória.
Na distribuição aleatória, os indivíduos mantêm uma distância mínima entre si e seus vizinhos.
Incorreta: pois na distribuição regular os indivíduos mantêm uma distância mínima entre si e seus vizinhos.
Na distribuição regular, os indivíduos estão distribuídos randomicamente.
Incorreta: pois na distribuição regular os indivíduos mantêm uma distância mínima entre si e seus vizinhos, uniformemente espaçados.
A dispersão aleatória pode ocorrer quando há antagonismo positivo que promove espaçamento uniforme.
Incorreta: pois a dispersão regular pode ocorrer quando há antagonismo positivo que promove espaçamento uniforme.
Caro(a) aluno(a), nesta unidade nós discutimos algumas propriedades das populações, como elas crescem e por que flutuam em tamanho. No entanto, ainda nos resta um questionamento: Por que algumas espécies são mais comuns do que outras?
A abundância das espécies, ou seja, o número de indivíduos, está relacionada a diversos fatores, entre eles destacam-se: a história da espécie, a disponibilidade dos recursos que ela necessita para sobreviver e se reproduzir, bem como as taxas de natalidade, mortalidade e migração.
Os autores Sadava et al. (2009) relacionam a densidade populacional com quatro fatores: disponibilidade de recursos, tamanho corporal, tempo que a espécie viveu na área e organização social. Observe:
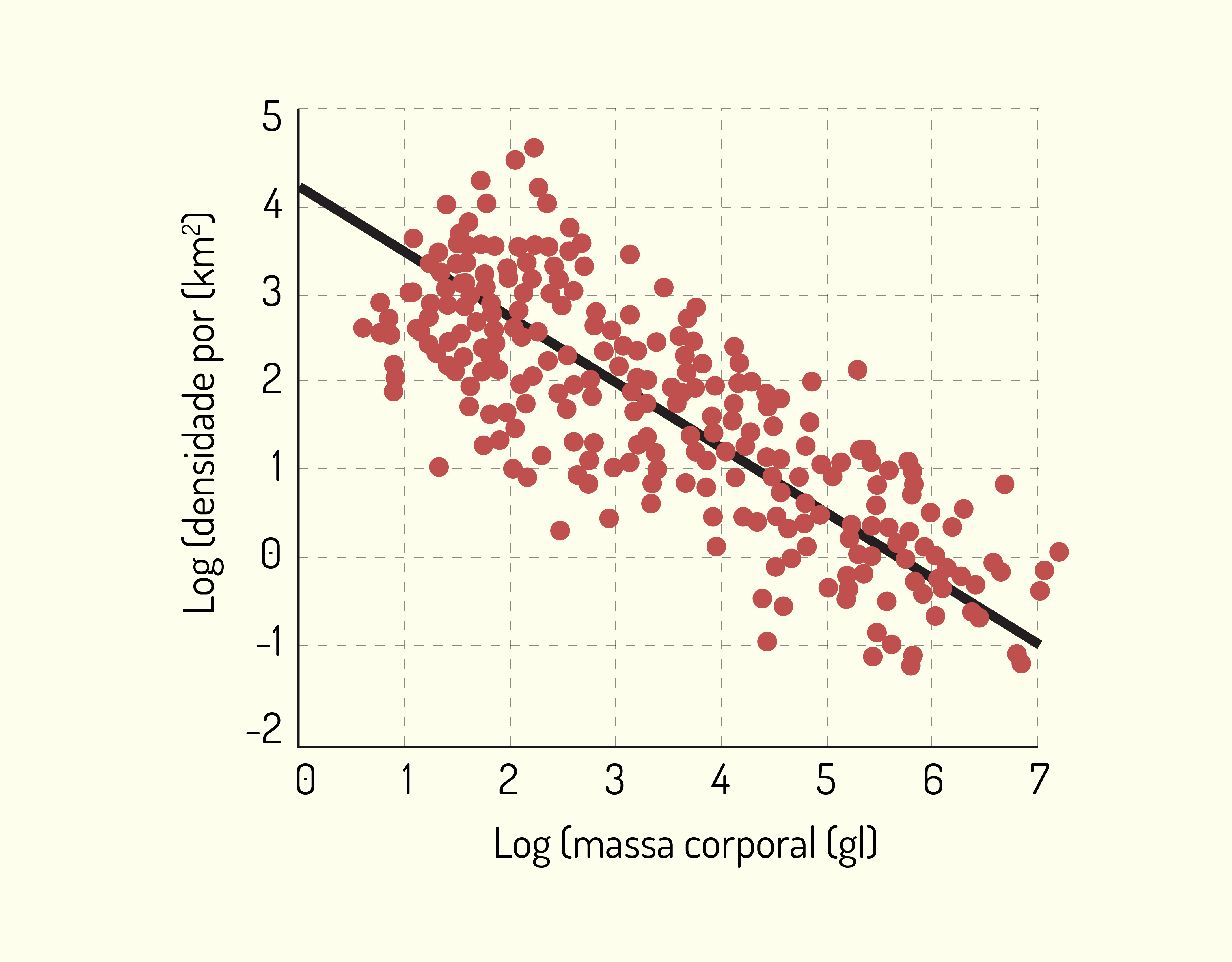
Quanto à distribuição das espécies, Peroni e Hernandez (2011) utilizam-se da Figura 3.15 a seguir para explicá-la. Observe:
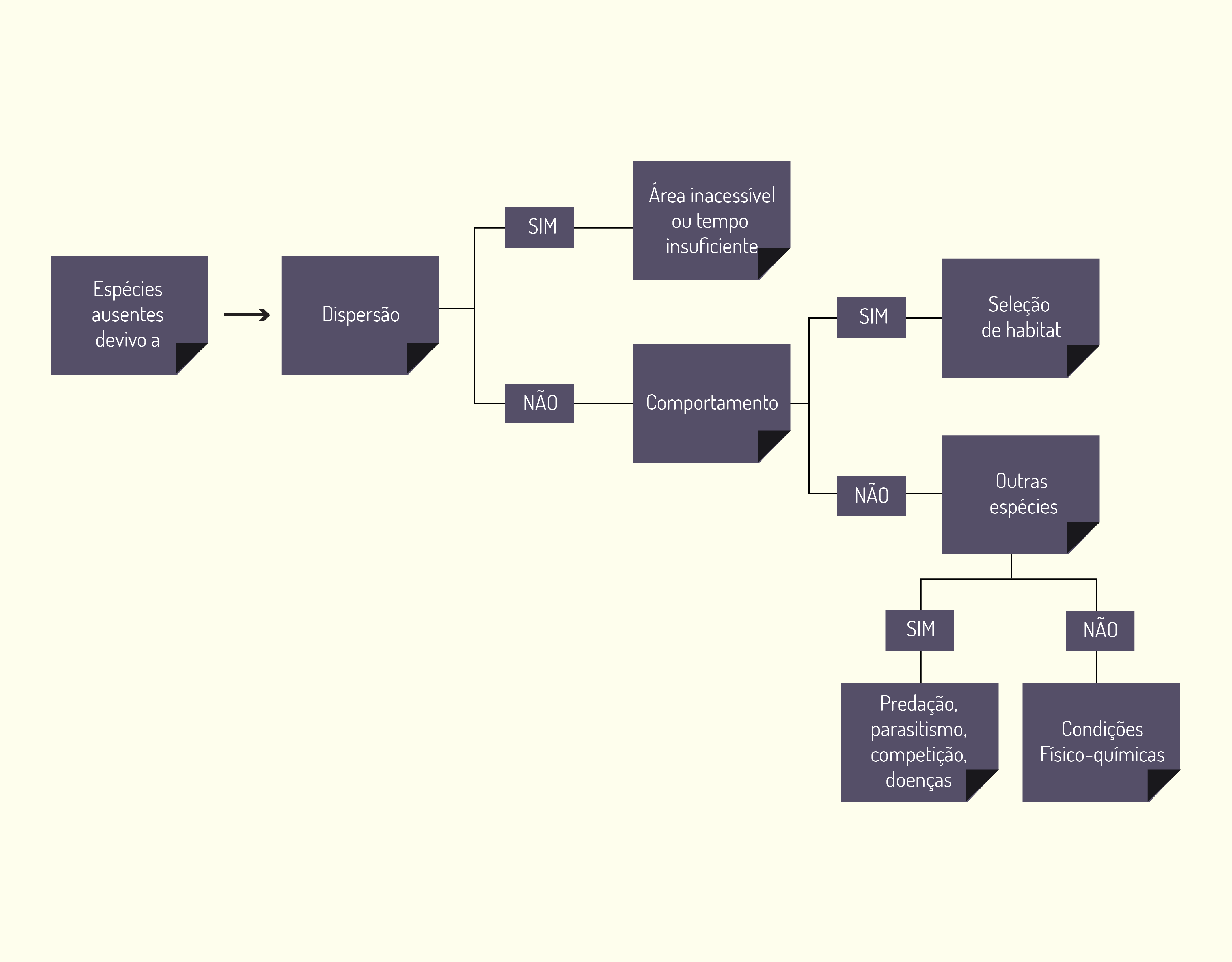
Por meio da Figura 3.15, pode-se dizer que o comportamento de uma espécie em escolher uma área para viver e se reproduzir pode ser a causa de estar ausente pela sua incapacidade de dispersar. Mas, se esta não for sua limitação, talvez as limitações sejam as interações com outras espécies, as condições físico-químicas e assim por diante.
Caro(a) aluno(a), para finalizarmos esta unidade, o controle ou manejo das populações deve ser baseado no conhecimento de como as populações crescem e o que determina suas densidades.
Populações com alta capacidade reprodutiva podem persistir mesmo com altas taxas de exploração. É o caso das populações de peixes, em que cada fêmea é capaz de produzir milhões de ovos. Nessas populações de reprodução rápida, se os indivíduos pré-reprodutivos são retirados da população a uma taxa alta, os indivíduos que permanecem podem crescer mais rapidamente. Assim, algumas populações de peixes podem ser exploradas intensivamente, em uma base sustentável, porque um pequeno número de fêmeas produzem ovos suficientes para manter a população (SADAVA et al., 2009).
Analogamente ocorre quando queremos reduzir o tamanho de espécies indesejadas, mantendo-as em baixas densidades. De acordo com Sadava et al. (2009), normalmente as populações apresentam altas taxas de nascimento sob densidade abaixo da capacidade de suporte, e assim podem resistir a taxas de mortalidade mais altas do que quando estão próximas à capacidade de suporte. Dessa forma, quando a dinâmica populacional é influenciada principalmente por fatores dependentes da densidade, matar parte da população geralmente a reduz para uma densidade na qual ela se reproduzirá a uma taxa maior. Neste sentido, a maneira mais efetiva para reduzir essa população consiste em remover seus recursos, diminuindo a capacidade de suporte de seu ambiente (SADAVA et al., 2009).
Os referidos autores também citam que introduzir um predador ou parasito para controlar populações de espécies indesejadas nem sempre faz com que o objetivo final seja alcançado, uma vez que pode acontecer da espécie introduzida, além de atacar a praga, destruir também espécies valiosas.
É possível acabar com os camundongos presentes nos lixões retirando o resíduo disponível, ou seja, retirando seus recursos de modo a reduzir a capacidade de suporte do ambiente, ao invés de envenená-lo, o que aumentaria sua taxa reprodutiva.

Assinale a alternativa que diz respeito à melhor alternativa para reduzir a população de uma espécie indesejada a longo prazo:
Esterilizar os indivíduos.
Incorreta: pois a melhor alternativa é diminuir a capacidade de suporte do meio.
Matar adultos reprodutivos.
Incorreta: pois a melhor alternativa é diminuir a capacidade de suporte do meio.
Matar indivíduos pré-reprodutivos.
Incorreta: pois a melhor alternativa é diminuir a capacidade de suporte do meio.
Tentar matar todos os indivíduos da população.
Incorreta: pois a melhor alternativa é diminuir a capacidade de suporte do meio.
Diminuir a capacidade de suporte do ambiente para a espécie.
Correta: uma vez que diminuir a capacidade de suporte do ambiente, a longo prazo, pode reduzir a população de uma espécie indesejada.
Editora: Artmed
Autor: Michael Begon, Colin R. Townsend e John L. Harper
ISBN: 8536308842
Comentário: O livro trata da distribuição e abundância dos diferentes organismos existentes, de características físicas, químicas e biológicas, bem como das interações que determinam essas distribuições e abundância. O livro também traz uma abordagem das comunidades e ecossistemas.
