Olá, seja bem-vindo(a)!
Nesta quarta e última Unidade da disciplina Expressão Gráfica, iremos trabalhar com os diferentes tipos de projeção que podemos aplicar dentro do desenho técnico. Os sistemas sobre os quais iremos conversar já foram previamente apresentados no decorrer da disciplina, porém de uma forma superficial. Neste momento, iremos aprofundar nossos conhecimentos, com o objetivo de compreendermos as particularidades de cada um desses sistemas e o produto obtido em cada uma das formas de representação.
Quando falamos sobre sistemas de projeções, como isométrica, dimétrica, cavaleira, dentre outras, você pode até imaginar que esse tema é complexo. Porém, no decorrer desta Unidade, você irá perceber que a criação dos desenhos dentro desses sistemas é muito simples e, em alguns casos, até mesmo intuitivo. Para conseguir identificar corretamente cada tipo de projeção, lembre-se, sempre, dos elementos que compõem cada sistema estudado, assim como suas relações.
Iniciamos esta Unidade retomando o conceito de projeções e discutindo as principais diferenças entre projeções cônicas e projeções cilíndricas. Na sequência, iremos abordar as projeções cilíndricas ortogonais, focando no método de construção das figuras.
Após essa exposição, trabalharemos as projeções cilíndricas oblíquas e o método de construção das figuras nesses sistemas. Para finalizarmos esta quarta Unidade, apresentaremos a representação de poliedros.
O conteúdo que iremos debater tem, como objetivo, reunir os diversos conceitos que foram apresentados até aqui e apresentar com eles estão relacionados e irão impactar na produção e representação de projetos.
Bons estudos!
Para a representação de objetos e situações que estamos projetando, iremos fazer uso do desenho projetivo para transmitir nossas ideias e permitir a sua execução. O desenho técnico é um tipo de desenho operativo, o que significa que, após a sua confecção, será dada uma operação de fabricação, execução e montagem do projeto. As projeções são classificadas em diversas categorias, porém todos os tipos de projeção têm, como objetivo geral, representar um objeto tridimensional de forma bidimensional sobre um plano. Dessa forma, é possível resolvermos problemas sobre qualquer tipo de poliedro e simplificamos o seu processo de compreensão e leitura.
Imagine os seguintes exemplos: um projeto executivo de uma residência e um projeto executivo de uma peça mecânica. Os dois projetos encontram-se na mesma etapa e devem conter todas as informações necessárias à execução do produto final, seja em um canteiro de obras ou em uma indústria. Apesar de estarmos tratando de dois projetos de nível executivo, isso não significa que eles deverão conter os mesmos tipos de peças gráficas.
O projeto executivo da residência, por exemplo, será composto por planta baixa, cortes, elevações e desenhos executados a partir de vistas ortográficas. Já para a produção de uma peça, além das vistas ortográficas, certamente, será necessária uma visualização por meio de axonométricas, para registrar sua tridimensionalidade. Para cada tipo de problema, iremos avaliar que tipo de projeção consegue solucioná-lo da forma mais adequada.
A projeção consiste na representação gráfica, em um plano, de uma figura localizada no espaço (MICELI; FERREIRA, 2010). Quando trabalhamos com projeções, o objeto representado não precisa, necessariamente, ser uma forma tridimensional. Como vimos anteriormente, no estudo do Método Mongeano, planos e pontos também podem ser reproduzidos por meio das projeções.
Um sistema de projeção é composto, basicamente, por um plano de projeção (ou conjunto de planos de projeção), o objeto a ser representado, os raios projetantes e o centro de projeção. Vamos relembrar o que significa cada um deles!
O plano de projeção pode ser comparado a uma folha de papel. Essa superfície plana é a área na qual o modelo será registrado. Os raios projetantes, provenientes de um centro de projeção, irão passar pelo objeto e, em seguida, tocar no plano de projeção como se fossem raios visuais que tocam no modelo a ser representado. Independente do tipo de objeto que você está retratando, se ele estiver disposto no espaço, será possível representar a sua projeção sobre um plano.
Ao fazermos uma analogia, o centro de projeção seria o correspondente ao observador. Um ponto irá ser projetado quando a reta projetante (aquela referente ao raio projetante, que passa por um ponto do objeto) intersectar o plano de projeção. Observe no exemplo a seguir.
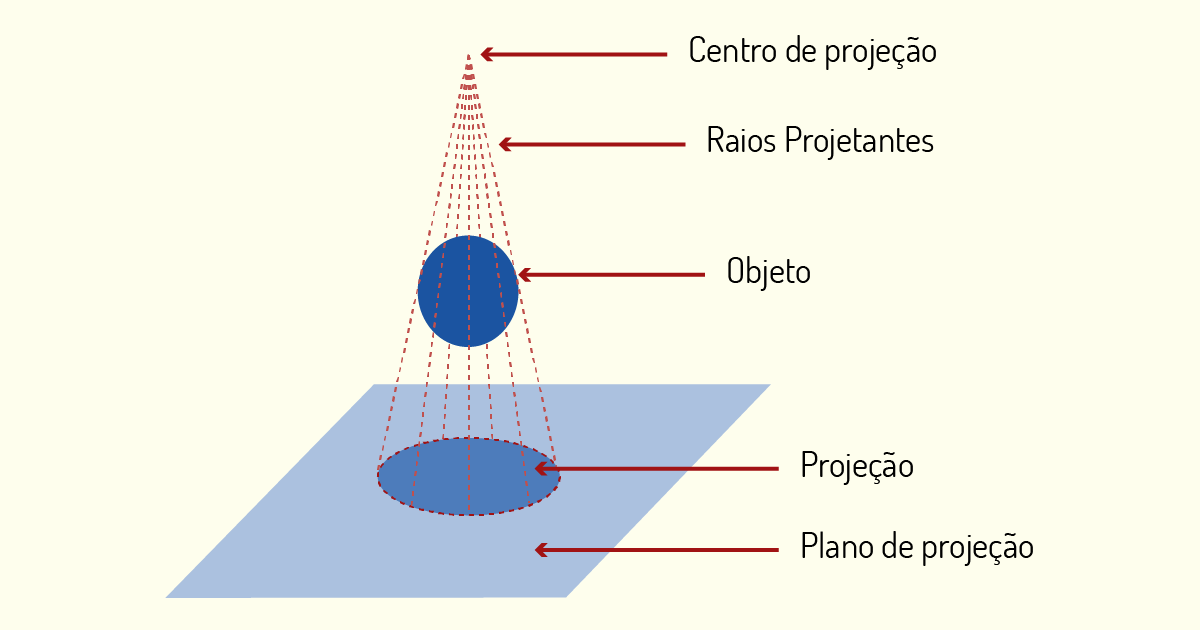
Analisando os componentes necessários para a representação de projeções, iremos notar que um deles será determinante para o tipo de registro gerado: o centro de projeção. Iremos classificar os sistemas de projeções de acordo com a posição ocupada pelo centro de projeção, determinando dois sistemas, o sistema de projeções cônicas e o sistema de projeções cilíndricas.
As projeções cônicas são caracterizadas por apresentar o centro de projeção finito, sendo conhecida, também, como projeção central. Nesta situação, os raios projetantes partem de um único ponto, dando origem a um cone de projeção, que é perpendicular ao plano de projeção.
Nesse sistema, as formas desenhadas apresentam deformações e medidas diferentes do modelo real. Devido a essas alterações, as projeções cônicas não retratam faces e arestas em Verdadeira Grandeza, o que as torna inadequadas como sistema de projeção para criação de projetos executivos.
Você pode estar se perguntando, mas, então, por que utilizar o sistema de projeção cônica? Qual a função desse tipo de representação? Embora, em um primeiro momento, possa parecer que as projeções cônicas sejam dispensáveis para a prática projetual, elas são essenciais para a compreensão global do projeto.
As perspectivas geradas a partir de projeções cônicas dão ideia de profundidade e realismo para os desenhos. Tal fator ocorre, pois o princípio dessa representação é o mesmo utilizado pela nossa visão. Por exemplo, quando observamos uma paisagem com diversos prédios, podemos notar que, à medida que estes distanciam-se de nosso olhar, “ficam” menores. Sabemos que o tamanho das edificações não se altera, mas sim o modo como os enxergamos! Quanto mais próximo, maior o objeto, assim como quanto mais distante, menor ele parecerá. É importante lembrarmos que esse aumento e diminuição não ocorrem de modo aleatório, mas sim seguindo proporções.

Para a representação do objeto por meio do sistema de projeção cônica, são necessários dois elementos essenciais: a Linha do Horizonte e o Ponto de Fuga. A Linha do Horizonte (LH) é um elemento de construção representado por uma linha paralela à linha de terra. A LH deve ser uma reta indicada na altura dos olhos do observador em relação à cena. Nessa linha, estará localizado o Ponto de Fuga, um ente do plano de visão para o qual convergem as linhas paralelas do desenho, quando este está representado em perspectiva.
Isso significa que não serão todas as linhas que irão convergir para um ponto de fuga! As linhas verticais do objeto, por exemplo, serão mantidas na vertical, enquanto as linhas horizontais do modelo, paralelas à linha de terra, serão representadas como feixes de linhas que irão convergir para o ponto indicado sobre a LH. Observe o exemplo na figura a seguir.
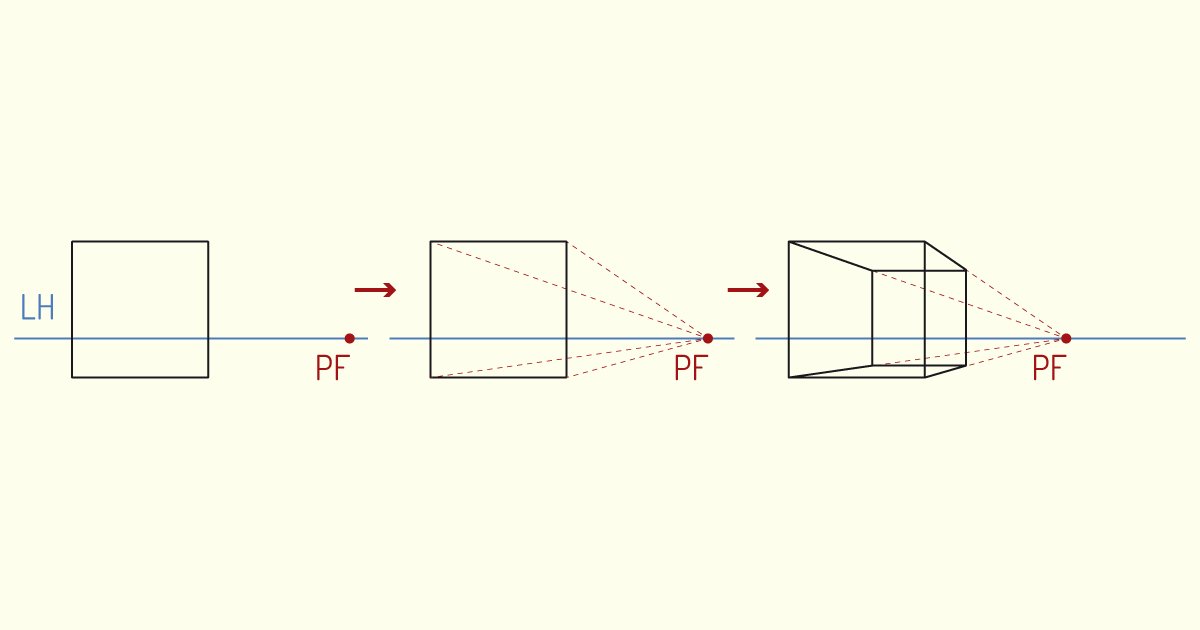
Embora, em nosso exemplo, exista um único Ponto de Fuga, é possível, também, criar perspectivas de projeção cônica com dois ou três Pontos de Fuga. A perspectiva com um Ponto de Fuga também é conhecida como perspectiva paralela, pois, nessa representação, a face frontal do objeto encontra-se disposta de forma paralela ao observador.
A perspectiva com dois Pontos de Fuga é comumente utilizada para representação externa de edificações. Nesse tipo de desenho, os dois Pontos de Fuga estão dispostos sobre a LH. Observe o exemplo na figura a seguir.
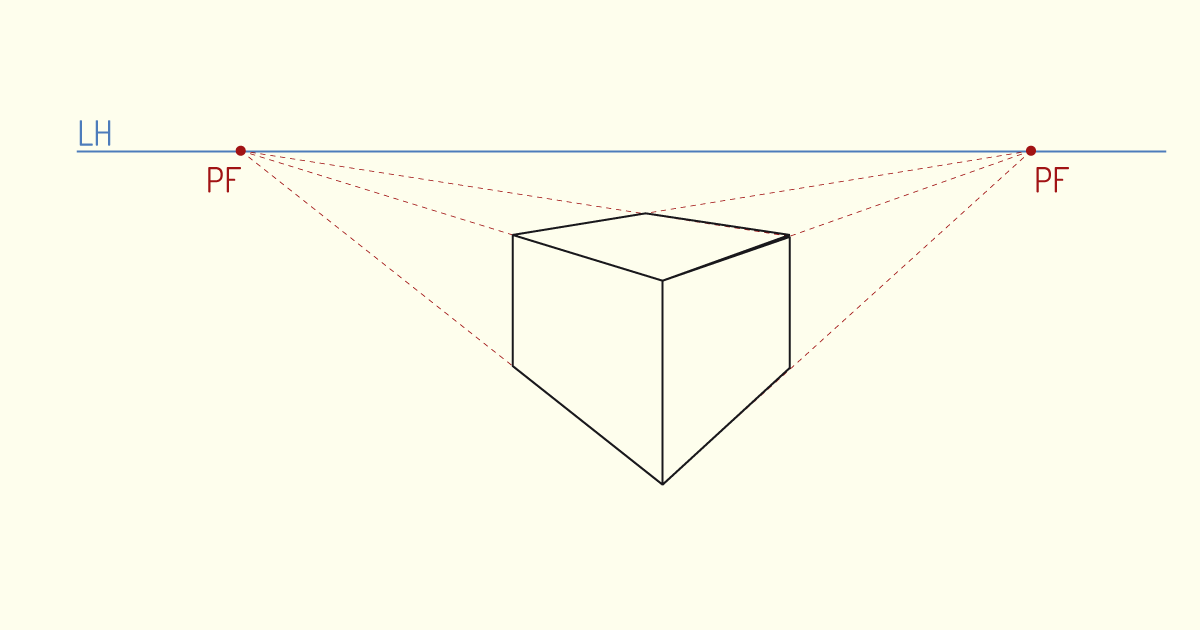
A perspectiva com três Pontos de Fuga, também conhecida como vista aérea, é utilizada quando deseja-se evidenciar a sensação de altura e profundidade da cena, por exemplo, ao representar prédios com altura acentuada. Nesse tipo de desenho, o observador está localizado muito acima ou muito abaixo da LH, dessa forma, dois dos Pontos de Fuga são representados sobre a LH e um deles é indicado fora da LH. O terceiro Ponto de Fuga estará, então, localizado sobre uma linha vertical, que é gerada a partir da convergência dos outros dois Pontos de Fuga. Observe o exemplo na figura a seguir.

Cada um desses tipos de perspectivas com ponto de fuga irá atender a uma finalidade. Para identificar qual a melhor opção ao seu desenho, se um, dois ou três pontos de fuga, é preciso considerar o que você deseja evidenciar, bem como o que não é primordial no desenho.
As projeções cilíndricas são caracterizadas por apresentar o centro de projeção infinito, sendo conhecidas, também, como projeções paralelas. Nesse caso, os raios projetantes partem de uma distância infinita em relação ao objeto e são representados de forma paralela entre si. Nesse tipo de projeção, iremos notar que o feixe de projetantes tem aspecto de um cilindro, e não de um cone, como ocorria na situação que analisamos anteriormente.
Esse sistema de projeção pode, ainda, ser dividido em duas categorias: projeção cilíndrica ortogonal e projeção cilíndrica oblíqua. A projeção ortogonal ocorre quando as projetantes partem do infinito e incidem de forma ortogonal em relação ao plano de projeção, enquanto a projeção oblíqua ocorre quando as projetantes partem do infinito e incidem de forma oblíqua em relação ao plano de projeção, ou seja, formando um ângulo diferente de 90° com o plano.
Em decorrência dessa diferença de ângulo de incidência dos raios projetantes, existirá, também, uma diferença na representação das formas dentro de cada um desses sistemas. No sistema de projeção cilíndrico ortogonal, encontraremos as vistas ortográficas e as axonométricas. A categoria das vistas ortográficas é formada pelas representações em Diedros, por meio do método mongeano, que discutimos na Unidade anterior. Já no grupo das axonométricas, estão as projeções isométrica, dimétrica e trimétrica, as quais abordaremos de modo mais detalhado na próxima aula!
Axonometria é um vocábulo formado pelos termos axon e metreo, que, em grego, significam, respectivamente, eixo e medida. Segundo o Dicionário Online Michaelis (2018), a axonometria é um processo da geometria em que das coordenadas de um objeto obtém-se sua projeção paralela sobre um plano. Nesse tipo de projeção, é utilizado um sistema ortogonal, com três eixos e que geram um triedro.

No sistema de projeção cilíndrico oblíquo, encontraremos a perspectiva cavaleira e perspectiva militar, que também terão seu modo de execução analisado passo a passo em nossas próximas aulas. Observe, na figura a seguir, a sistematização dos tipos de projeção.
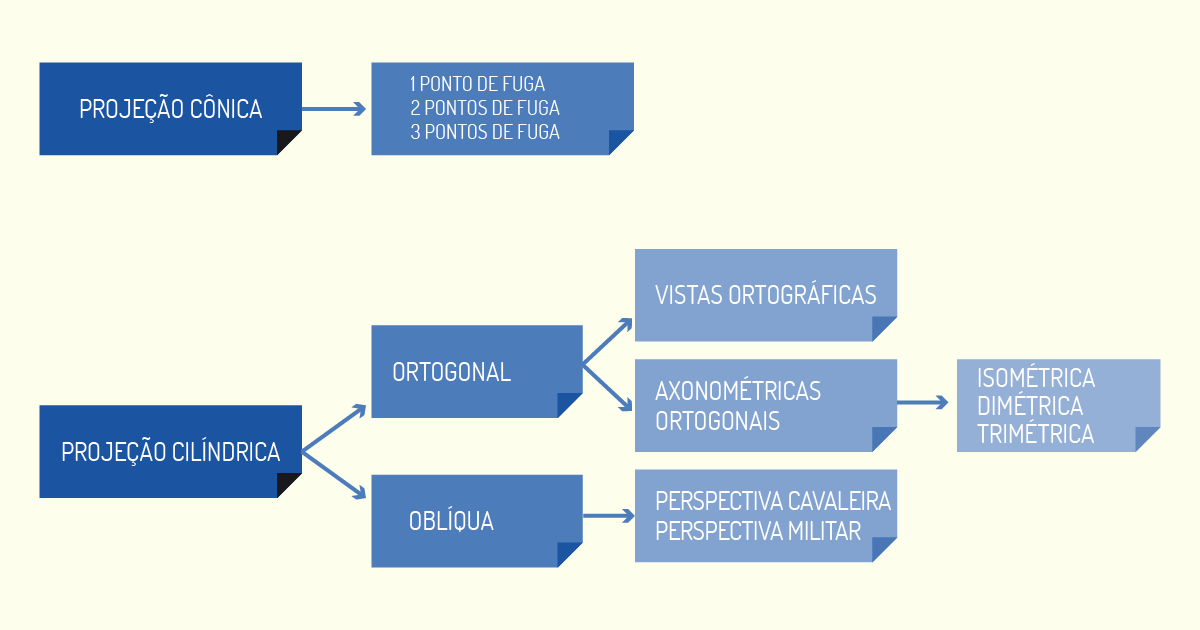
Nesta aula, você teve a oportunidade de conhecer as diferentes formas de projeções que serão utilizadas para a representação de objetos. O desenho técnico nada mais é do que a linguagem gráfica utilizada na indústria, seja ela da construção civil ou de outros setores, como as fábricas de montagem de peças.
1) Para a representação de formas no desenho projetivo, encontramos dois principais sistemas: projeções cônicas e cilíndricas. Sobre as projeções cônicas, assinale a alternativa correta.
a) O objeto é representado em Verdadeira Grandeza.
Justificativa: nas projeções cônicas, os objetos não são representados em VG.
b) O Ponto de Fuga é um lugar geométrico para o qual convergem linhas paralelas do objeto.
Justificativa correta: o(s) ponto(s) de fuga é o local para o qual as retas paralelas seguem, quando em perspectiva.
c) Quanto mais perto do observador, menor será o objeto.
Justificativa: o que ocorre é a situação contrária: quanto mais distante do objeto, menor será o seu tamanho de representação.
d) São exemplos de projeções cônicas as perspectivas militar e cavaleira.
Justificativa: as perspectivas militar e cavaleira são projeções cilíndricas.
e) A Linha do Horizonte deve ser traçada na altura do objeto a ser desenhado.
Justificativa: a Linha do Horizonte determina a altura da visão do observador; o objeto pode estar disposto abaixo, acima ou sobre a LH.
Você acredita que existem sistemas de projeções que sejam mais adequados para um tipo ou outro de especificação? Ou você acha que o desenho operativo, utilizado para a confecção de peças gráficas, não influencia no resultado final de execução do projeto?

As projeções cilíndricas ortogonais são amplamente utilizadas para representações de projetos. As vistas ortográficas, como já discutimos anteriormente, são peças gráficas fundamentais para a elaboração de projetos e indicações de cotas e especificações técnicas no desenho. Por meio de tais representações, conseguimos ter uma ideia geral de cada uma das faces do modelo a ser construído.
Porém, muitas vezes, apenas esse registro de vistas do objeto não é o suficiente para o entendimento do projeto, o que faz com que as projeções axonométricas sejam grandes aliadas para complementar o projeto. Esse tipo de projeção também é conhecido como perspectiva axonométrica ou axonometria.
As vistas ortográficas, as quais estudamos de modo detalhado na unidade anterior, são vistas criadas a partir do método mongeano. Segundo a Geometria Descritiva, os planos de projeção são perpendiculares entre si e são sobre esses planos que são realizadas as projeções dos objetos, seus planos, retas e pontos.
Para a representação das vistas ortográficas de um objeto, a situação mais usual é desenharmos suas três vistas principais: a projeção no plano vertical, que corresponde à vista frontal; a projeção no plano horizontal, que corresponde à vista superior; a projeção no plano de perfil, que corresponde à vista lateral esquerda (MICELI; FERREIRA, 2010). Lembre-se, ainda, que, para situações mais complexas, será necessária a criação de mais vistas para a representação correta do objeto, podendo aumentar o número de vistas para seis.
Para detalhar um projeto de interiores de um banheiro, por exemplo, você acredita que apenas três vistas são suficientes? Se o projeto a ser detalhado for um projeto executivo, provavelmente, você irá precisar de mais do que três imagens para conseguir registrar toda a sua ideia. Nessa situação, o ideal seria registrar as quatro paredes, o piso e o teto, ou seja, as seis faces do poliedro que esse ambiente forma.
Por outro lado, imagine que você está fazendo o detalhamento do projeto do armário desse banheiro, para que seja encaminhado a execução na marcenaria. Na maioria das vezes, esse tipo de projeto demandará apenas uma vista frontal, vista lateral e vista superior, não havendo necessidade de especificar o fundo do móvel, a outra vista lateral e a vista inferior. Lembre-se que o ideal é registrar apenas os desenhos necessários ao entendimento do projeto, pois devemos evitar representações desnecessárias.
Quando um objeto tiver formas simples e poucos detalhes, podemos, também, reduzir sua representação de três para apenas duas vistas. Tal supressão de vista deve obedecer aos seguintes critérios:
Outro ponto importante a ser relembrado é o posicionamento das vistas, que não pode ser arbitrário. Observe, na figura a seguir, o posicionamento das vistas ortográficas, quando representadas no 1° e no 3° Diedros.
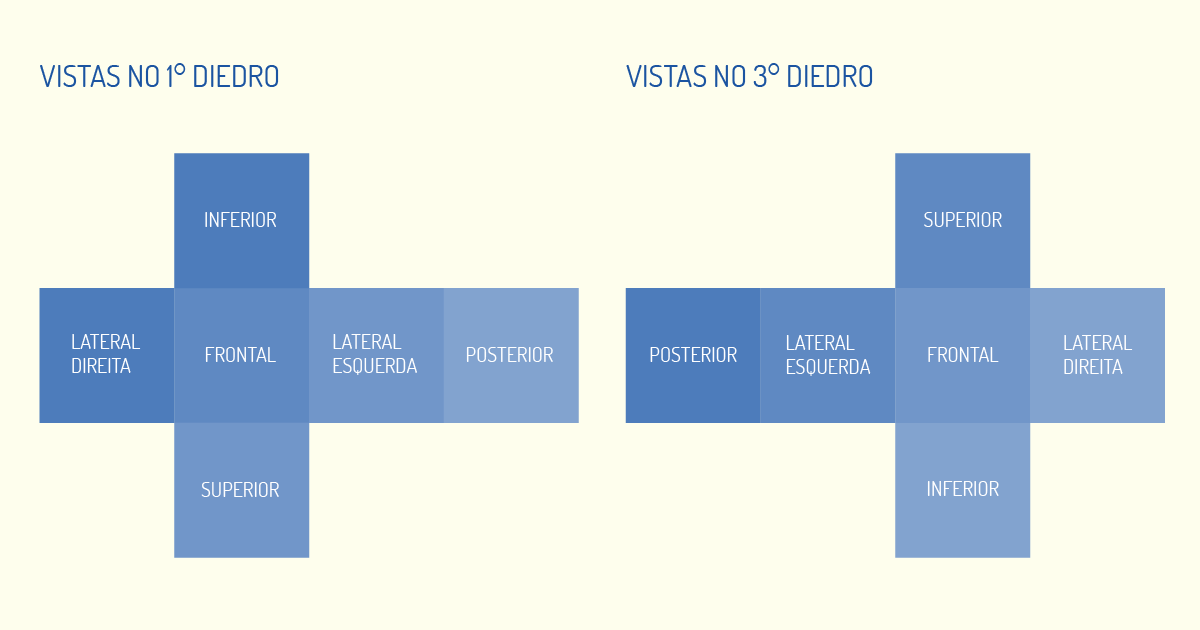
Enquanto, na Geometria Descritiva, as figuras são construídas por meio de coordenadas de abscissa, afastamento e cota, no Desenho Técnico, iremos utilizar as próprias dimensões do objeto tomadas paralelamente aos eixos de projeção.
Para a leitura das vistas ortográficas, devemos lembrar de três regras gerais. A primeira delas é a regra do alinhamento, em que a projeção de um mesmo ponto em vistas adjacentes deve estar sobre o mesmo alinhamento. A segunda regra é a das figuras contíguas, na qual figuras adjacentes representadas em uma mesma vista não estarão em um mesmo plano, ou seja, estão em níveis distintos. Por fim, a última regra é a da configuração, em que uma face plana do objeto projeta-se com a sua configuração ou como um segmento de reta e isso irá variar conforme a posição dessa face em relação ao plano de projeção.
As projeções axonométricas apresentam execução simplificada e rápida, o que as torna um método prático para a representação de modelos. Sua aplicação mais usual é na perspectiva de peças mecânicas e instalações hidráulicas, porém também pode ser empregada para detalhamentos construtivos e estudos volumétricos das edificações.
Imagine que você está apresentando um projeto para um cliente e, no meio da apresentação, surge uma nova ideia! Em uma situação real, você não iria interromper a apresentação, iniciar um programa de modelagem 3D e criar a nova volumetria para que seu cliente avalie. A representação gráfica manual, embora venha caindo em desuso, é muito prática para essas situações.
Com um lápis e um papel, é possível, enquanto você conversa com o seu cliente, construir uma perspectiva por meio das projeções axonométricas. Para a elaboração de croquis, não será necessário empregar os ângulos e proporções exatos. Apenas com o conhecimento do processo de construção já será possível desenvolver um desenho proporcional, o qual ilustre sua proposta de maneira adequada.

Diferente do que ocorre nas projeções cônicas, as projeções axonométricas não apresentam uma redução gradual do tamanho do objeto conforme aumenta a distância em relação ao observador. Outro ponto de divergência com a projeção cônica é o fato de as retas paralelas do objeto, quando representadas na axonometria, não convergirem para um Ponto de Fuga, mas, sim, serem mantidas de forma paralela.
Embora não exista essa relação com um Ponto de Fuga, nas projeções axonométricas, existe a percepção de profundidade do objeto, o qual é possível representar reproduzindo suas três dimensões. Esse sistema de representação rigoroso é baseado na reprodução de três eixos em um mesmo plano. Para a construção dos desenhos, iremos trabalhar com o comprimento, a altura e a largura do objeto. Observe o exemplo na figura a seguir.
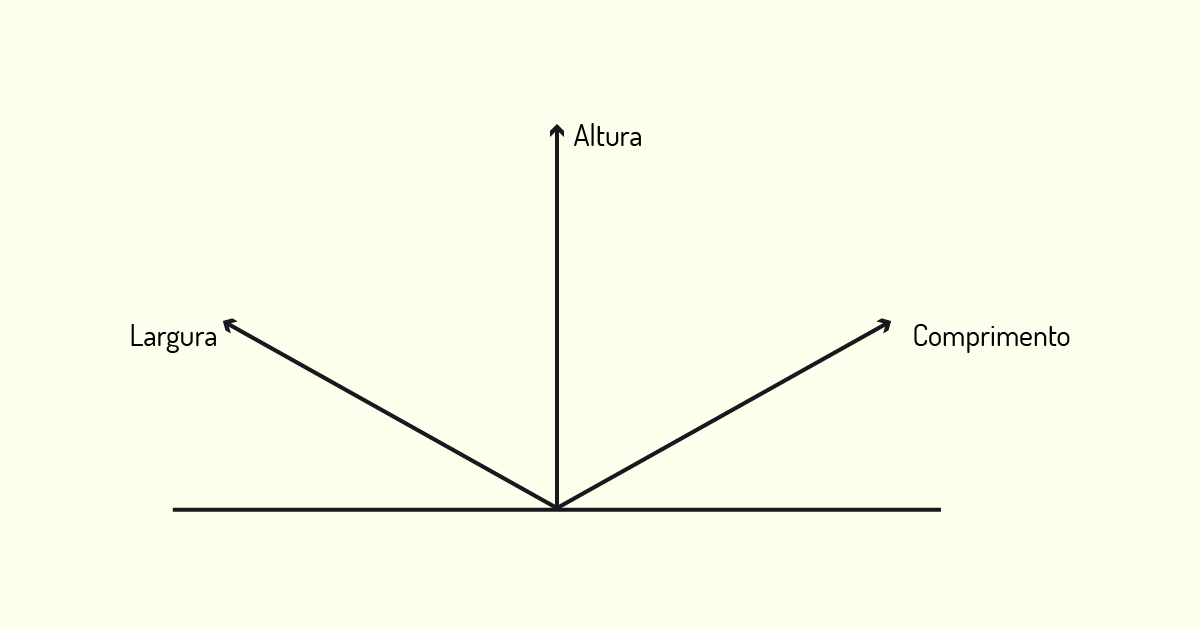
Na categoria de projeções axonométricas ortogonais, encontraremos a perspectiva isométrica, a perspectiva dimétrica e a perspectiva trimétrica. O princípio de representação em cada um desses sistemas é semelhante e segue a mesma base; o que irá variar em cada um deles é a inclinação dos eixos x, y e z. Vamos, agora, analisar cada um desses casos!
A perspectiva isométrica é a mais usual e caracteriza-se por apresentar os três eixos axonométricos com a mesma inclinação, sendo que cada um deles irá corresponder a uma das dimensões do objeto.
Na perspectiva isométrica, as medidas são representadas em Verdadeira Grandeza e o coeficiente de redução de escala é igual nos três eixos. Nessa representação, os eixos apresentam inclinação de 120° entre si. Observe o exemplo na figura a seguir.
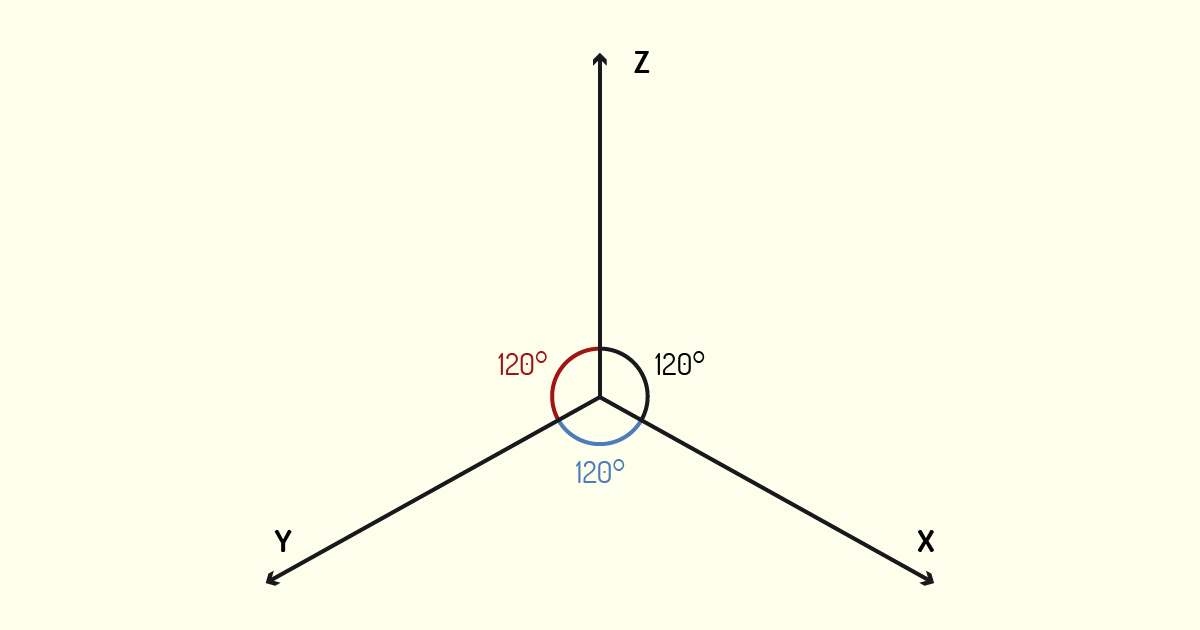
Para a construção das perspectivas, iremos trabalhar com o prolongamento dos eixos x e y, que irão formar ângulos de 30° em relação a uma linha horizontal. Já o eixo z permanece inalterado. Observe o exemplo na figura a seguir.

Uma vez desenhados os eixos isométricos, o próximo passo é marcar as dimensões gerais do objeto sobre os mesmos. Como o coeficiente de redução de escala é proporcional nos três eixos, não há a necessidade de reduzir ou ampliar as dimensões de altura, largura e profundidade do objeto; podemos utilizar a Verdadeira Grandeza para realizar essas marcações nos eixos.
Em seguida, devemos traçar retas paralelas aos eixos, unindo os pontos marcados para fechar o volume do objeto. Após ligar todos os vértices por meio das linhas guia, basta reforçar o contorno do volume final e eliminar as linhas de apoio. Observe o exemplo na figura a seguir, que ilustra a sequência de passos.
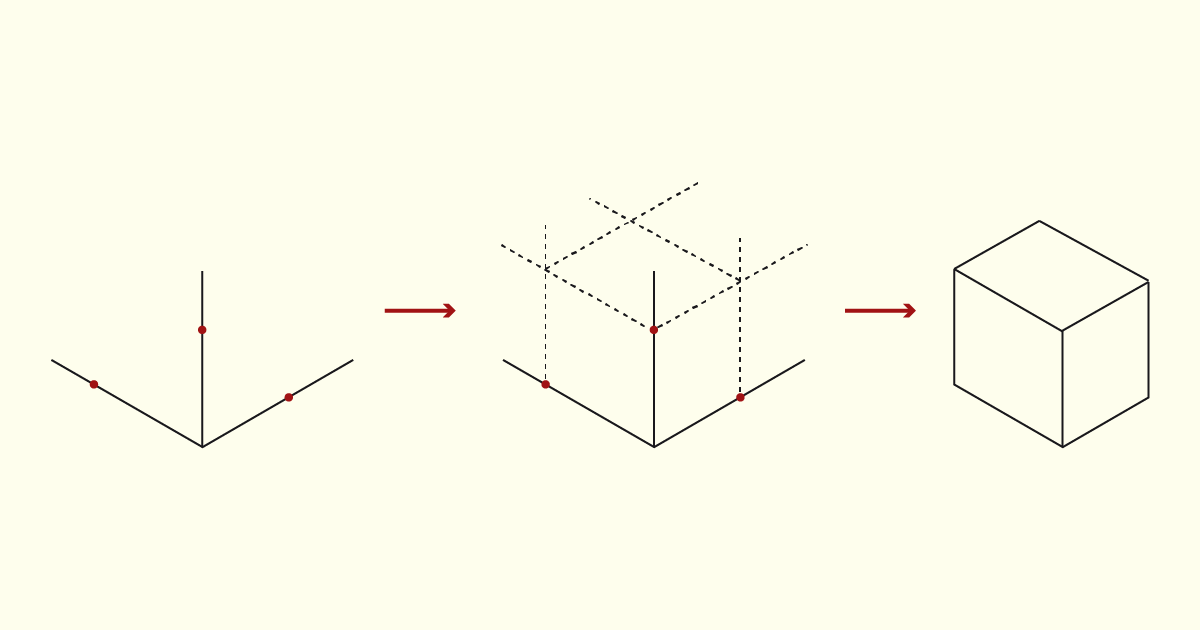
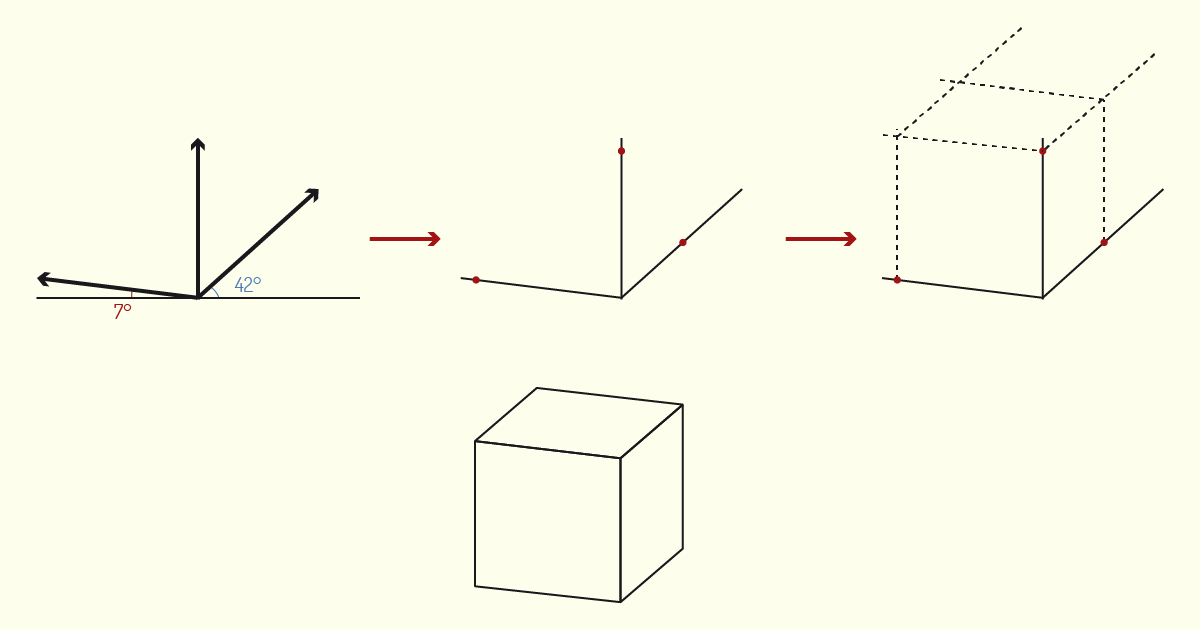
Na perspectiva dimétrica, apenas dois eixos formam ângulos iguais. Nessa situação, as medidas de dois dos eixos serão marcadas em Verdadeira Grandeza e, no terceiro eixo, será aplicada uma escala de redução para determinar o valor adotado. Segundo a Norma ISO 5456-3, que determina os princípios para a representação axonométrica, na perspectiva dimétrica, recomenda-se adotar os ângulos de 7° e 42° e aplicar a proporção 0,5/1/1 entre os coeficientes de redução para x, y e z, respectivamente.
Imagine o seguinte exemplo: vamos representar, na perspectiva dimétrica, um cubo com altura, largura e profundidade de mesmas dimensões, 5 cm cada. O primeiro passo é desenharmos os eixos. Em nosso exemplo, iremos adotar a inclinação de 7° para o eixo y e 42° para o eixo x. Em seguida, devemos marcar os valores nos eixos x, y e z, que corresponderão a 2,5 cm, 5 cm e 5 cm, respectivamente.
Após realizada a marcação de pontos, o processo é semelhante ao da construção da perspectiva isométrica. Por meio de linhas guia, traçaremos retas paralelas aos eixos, até concluir o fechamento do volume. Quando todas as arestas estiverem unidas, basta reforçarmos o traçado do objeto final e eliminarmos as linhas de apoio. Observe o exemplo na figura a seguir.
Na perspectiva trimétrica, os três eixos irão formar ângulos diferentes com o plano de projeção. Nesse caso, as medidas dos três eixos serão representadas em grandezas diferentes; em decorrência deste fator, a perspectiva trimétrica não é muito utilizada. Para a construção da perspectiva, iremos representar a altura em Verdadeira Grandeza e aplicar coeficientes de redução para determinar a largura e profundidade do objeto.
Utilizando o mesmo exemplo anterior, para construirmos um cubo na perspectiva trimétrica, iremos, primeiramente, traçar os eixos. Para cada inclinação de eixo, será atribuído um valor de escala de redução para as dimensões marcadas. Como esse tipo de perspectiva é pouco usual, não entraremos em detalhes em relação a essa escala de redução, porém é importante que você compreenda que as medidas marcadas nos eixos x e y não são arbitrárias.
Após marcar os valores em x, y e z, sendo que apenas o eixo z é em Verdadeira Grandeza, basta criarmos linhas guias, paralelas aos eixos, partindo dos pontos estabelecidos. Em seguida, com a volumetria já fechada, iremos reforçar o volume final e eliminar as linhas de apoio. Observe o exemplo, na figura a seguir, que ilustra a sequência de etapas.
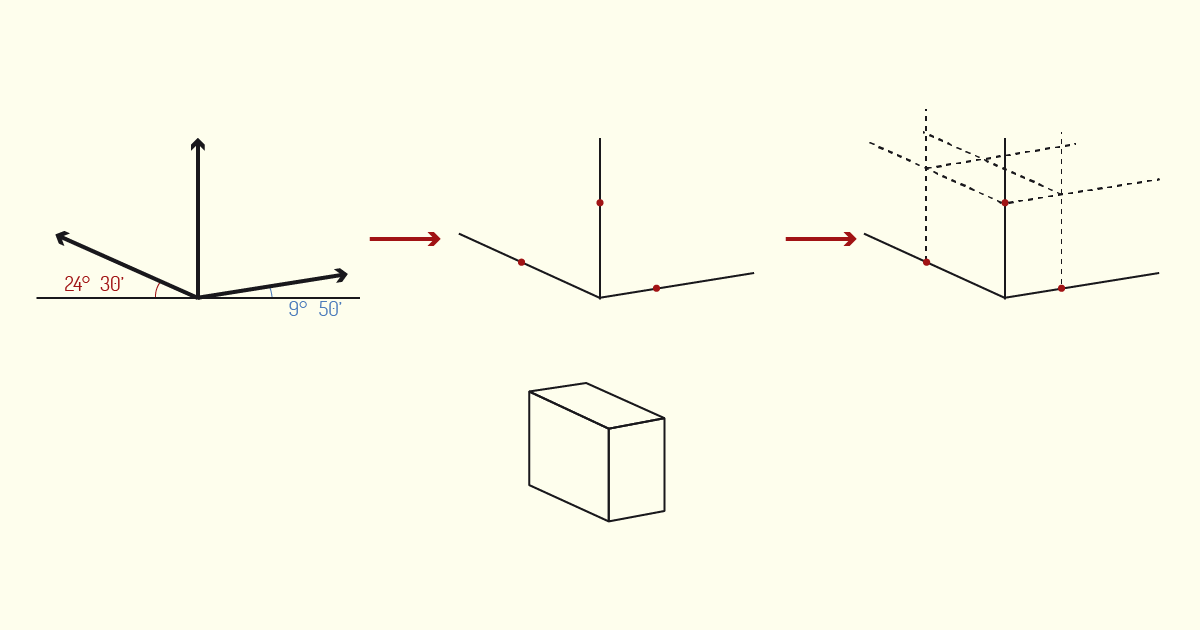
Observe os três exemplos que criamos nesta aula, representando um mesmo objeto em perspectiva isométrica, dimétrica e trimétrica. Você notou que, apesar de todos os desenhos terem sido construídos por meio de projeções cilíndricas ortogonais, cada uma delas teve um efeito diferente?
Em alguns desenhos, o modelo sofre maiores distorções do que em outros, chegando, até mesmo, a perder o seu aspecto de cubo. Esse fator deve ser considerado no momento que você escolher qual tipo de perspectiva criará. Como mencionamos, a perspectiva trimétrica é pouco aplicada no dia a dia, mas, entre a isométrica e dimétrica, você precisará avaliar o que é mais relevante ao desenho que você irá construir!
2) Assinale a alternativa que apresenta corretamente uma perspectiva isométrica.
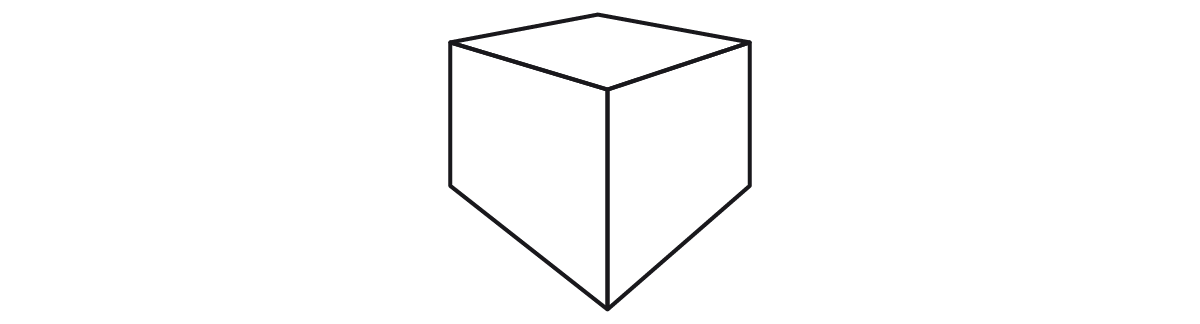
Justificativa: a imagem representa uma perspectiva com dois pontos de fuga.
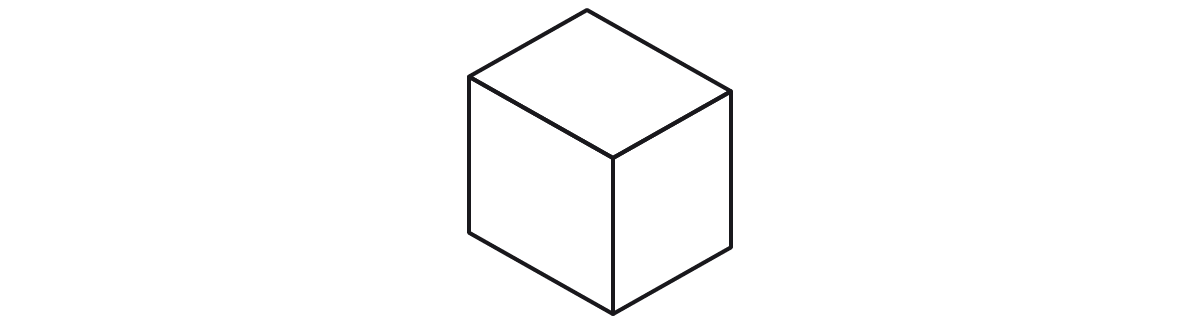
Justificativa correta: a imagem representa uma isométrica, pois é possível notar que as retas do objeto formam um ângulo de 30°, se traçarmos uma linha horizontal.
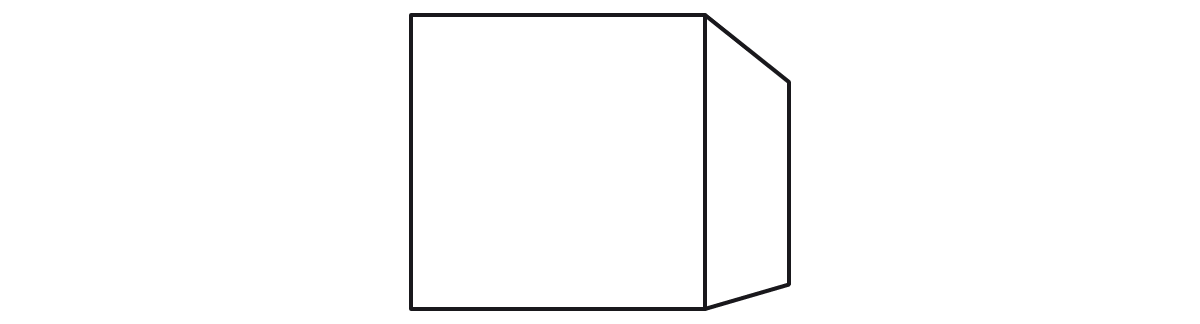
Justificativa: a imagem representa uma perspectiva com um ponto de fuga.
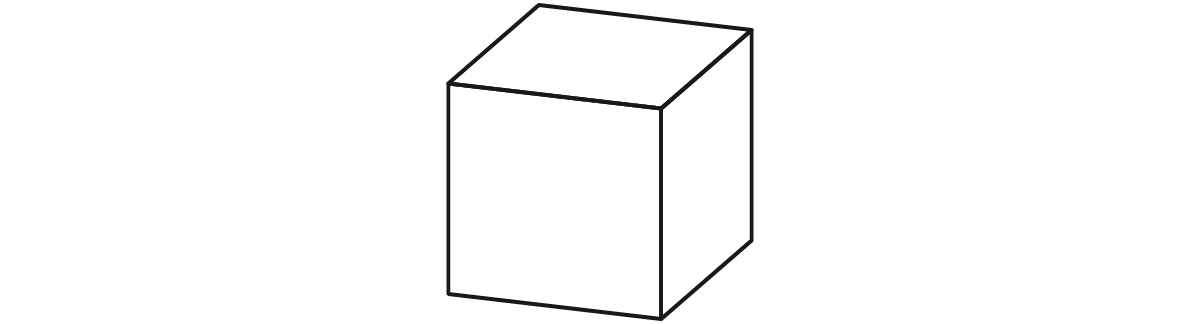
Justificativa: a imagem representa uma perspectiva dimétrica.
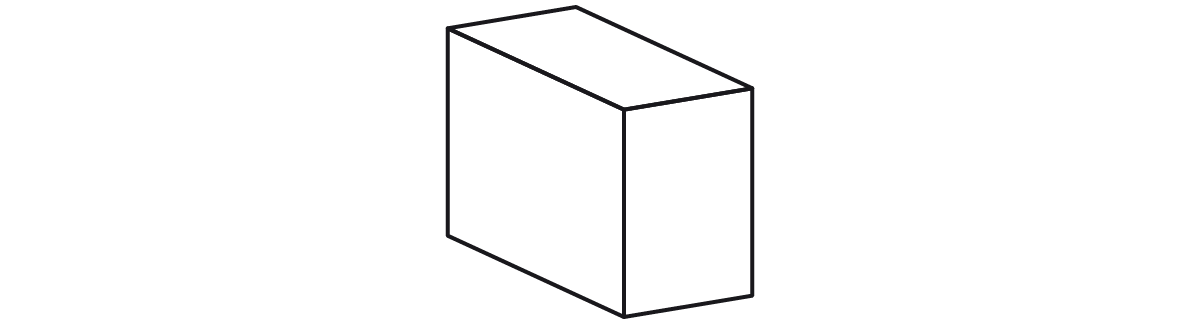
Justificativa: a imagem representa uma perspectiva trimétrica.
A perspectiva isométrica, além de ser muito utilizada para a representação de projetos, também pode ser encontrada na indústria de games. É provável que você esteja familiarizado com o aspecto que a representação isométrica dá aos objetos e cenas. Grande parte dos games de décadas anteriores fazia uso de composições de cenários por meio da perspectiva isométrica, que não exige grandes recursos e permite que o usuário tenha um amplo campo de visão no jogo. Se, por um lado, a representação isométrica foi deixada de lado nos games tradicionais, ela vem tornando-se uma tendência para os jogos disponíveis em smartphone, graças ao minimalismo desse tipo de representação. Para saber mais sobre essa tendência digital, acesse: <https://medium.com/tend%C3%AAncias-digitais/a-perspectiva-isom%C3%A9trica-no-mundo-digital-b9f83225ede>. Acesso em: 22 fev. 2019.

Nesta aula, você teve a oportunidade de conhecer mais sobre as projeções cilíndricas ortogonais e suas formas de representação. Além do mais, viu que o modo como se relaciona o modelo a ser representado e os planos de projeção, assim como a relação estabelecida entre os próprios planos, irão influenciar no resultado final do desenho.
A partir do que discutimos até o momento, qual tipo de representação gráfica você acredita que será mais utilizada em sua vida acadêmica e futura vida profissional? A quais motivos você atribui a predominância desse sistema de representação?

Os raios projetantes nas projeções cilíndrica oblíquas, ao contrário da situação que ocorre nas projeções cilíndricas ortogonais, não formam um ângulo de 90° sobre o plano de projeção. É importante destacar que, independe do valor que este ângulo de incidência de raios assuma, eles sempre serão paralelos entre si.
Muitas vezes, é comum os estudantes confundirem projeções cônicas e projeções cilíndricas oblíquas, pois, nos dois casos, os feixes projetantes incidem de forma não perpendicular ao plano. Para não ter dúvidas, lembre-se, sempre, da relação:
Para a construção das perspectivas oblíquas, assim como na elaboração de perspectivas ortogonais, você pode operar manualmente ou por meio de recursos digitais. Como o processo de visualização e compreensão de perspectivas é um feito gradual, nesse primeiro momento, recomendamos que você trabalhe de forma manual, utilizando régua paralela e esquadros.
Dessa maneira, será mais fácil compreender o passo a passo dessa construção por meio da criação de linhas guia, funcionando como uma espécie de “esqueleto”, para dar forma ao objeto representado.
A partir do momento em que você tiver o domínio do método de construção dessas perspectivas, você poderá, então, passar para a produção em meios digitais. O desenho auxiliado por computador 2D, através do software AutoCAD, é um meio largamente utilizado para produzir desenhos técnicos em perspectiva, graças ao nível de precisão desse programa, que permite que o usuário determine o comprimento e o ângulo exato que deseja criar seus segmentos de reta.
A perspectiva cavaleira é obtida por meio da projeção cilíndrica oblíqua, isso significa que o feixe de projetantes, que apresenta o formato cilíndrico, incide sobre o plano de projeção, formando um ângulo diferente de 90°.
A origem do nome dessa perspectiva não é certa. Enquanto alguns autores defendem que o termo cavaleira deriva de cavalier, um tipo de fortificação militar utilizada no século XVI, outros afirmam que o nome apresenta relação com o matemático italiano Francesco Bonaventura Cavalieri. É muito provável que você já tenha deparado-se com a imagem de uma perspectiva cavaleira. A construção desse tipo de perspectiva é rápida, o que a tornou muito popular e faz com que fosse largamente utilizada, inclusive para criação de desenhos esquemáticos à mão livre.
Na construção desse tipo de perspectiva, uma das faces do modelo é representada frontalmente, conservando sua forma e dimensões de altura e largura, enquanto o comprimento do objeto é marcado em uma única direção, representando a profundidade. Como na perspectiva cavaleira uma das faces do objeto aparece em vista, esse tipo de desenho facilita a representação de círculos e curvas, o que faz com ele seja muito empregado para o registro de peças mecânicas.
Para representar uma peça com um furo, por exemplo, por meio da perspectiva cavaleira, é possível registrar a face com o furo em vista frontal. Dessa forma, conseguimos indicar, na perspectiva, o raio ou o diâmetro da abertura, pois ela estará representada em Verdadeira Grandeza.
Todas as faces do objeto dispostas paralelas ao plano de projeção irão permanecer em Verdadeira Grandeza, enquanto as arestas perpendiculares a esse plano serão projetadas inclinadas, sofrendo deformação. A redução do comprimento dessas retas é feita de modo proporcional, conforme o ângulo de inclinação, que determina a profundidade do desenho.
As retas perpendiculares ao plano são denominadas Fugitivas e o ângulo que estas formam com a direção horizontal quando em perspectiva é chamado Ângulo das Fugitivas. Os ângulos mais adotados para a criação da perspectiva cavaleira são 30°, 45° e 60°. A redução da dimensão das Fugitivas é feita proporcionalmente a tal ângulo, pois, quanto maior a inclinação, menor será o segmento de reta. A razão entre o comprimento do segmento em perspectiva e seu comprimento real no modelo é denominada Coeficiente de Alteração ou Fator de Conversão (K). Para os Ângulos das Fugitivas mencionados, iremos adotar os seguintes Fatores de Conversão:
1. Cavaleira 30°
2. Cavaleira 45°
3. Cavaleira 60°
Para que você consiga compreender melhor esse tipo de perspectiva, vamos construir um exemplo com um passo a passo! Imagine que dispomos de um cubo com altura, largura e profundidade equivalente a 6 cm cada. Iremos, agora, representá-lo em perspectivas cavaleira de 30°, 45° e 60°. O primeiro passo é a construção dos eixos. Lembre-se que os eixos da altura e largura serão mantidos de forma ortogonal. Observe na figura a seguir.

Na sequência, devemos desenhar a vista principal de nosso objeto. Como, em nosso exemplo, estamos trabalhando com um cubo, todas as suas faces serão idênticas. A vista representada deve ser desenhada em Verdadeira Grandeza, ou seja, iremos desenhá-la com 6 cm de altura e 6 cm de largura. Observe na figura a seguir.
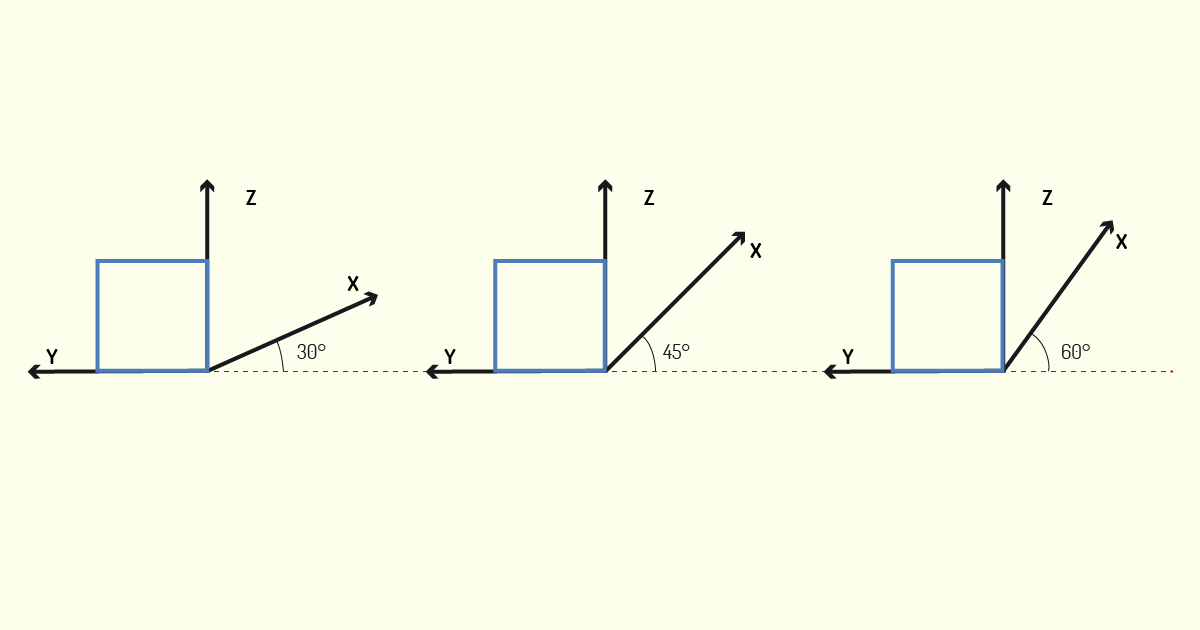
O próximo passo é determinar a profundidade do objeto. É nesse momento que iremos aplicar o Fator de Conversão. A profundidade de nosso objeto é equivalente a 6 cm. Convertendo esse valor, de acordo com os Ângulos das Fugitivas, iremos obter, para a cavaleira 30°, profundidade igual a 4 cm, para a cavaleira 45°, profundidade igual a 3 cm e, para a cavaleira 60°, profundidade igual a 2 cm. Observe a figura a seguir.
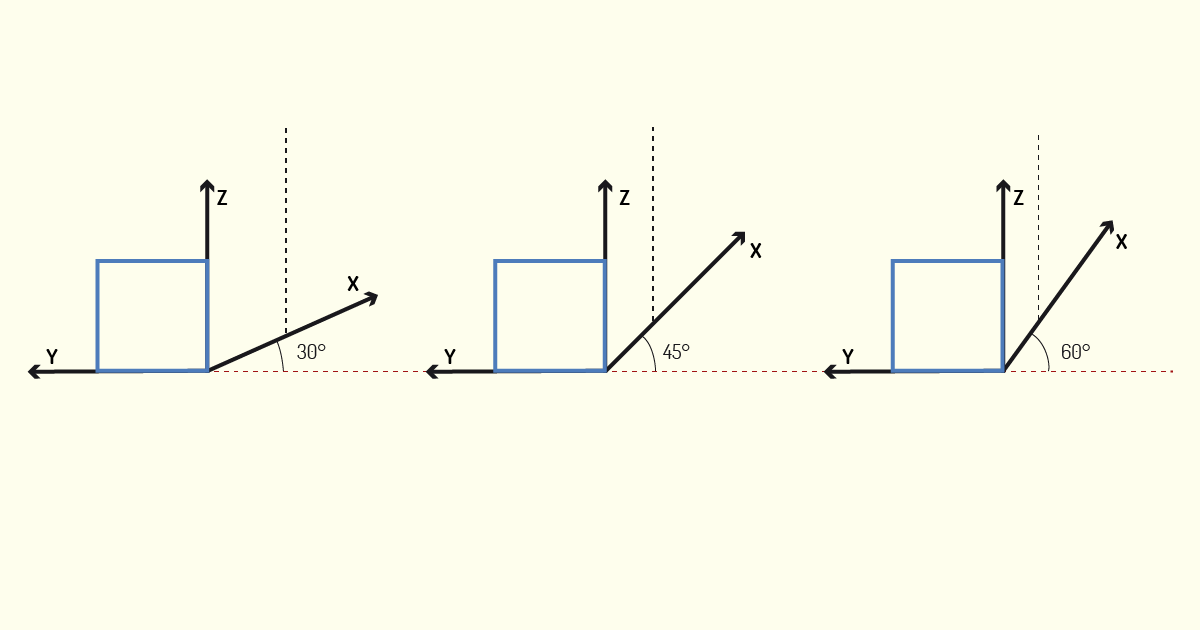
Para finalizar a construção do objeto, basta fecharmos o volume, traçando as linhas, partindo de todos os vértices do modelo, lembrando, sempre, de manter a angulação das Fugitivas, assim como sua dimensão. Observe, na figura a seguir, a construção dessas perspectivas.
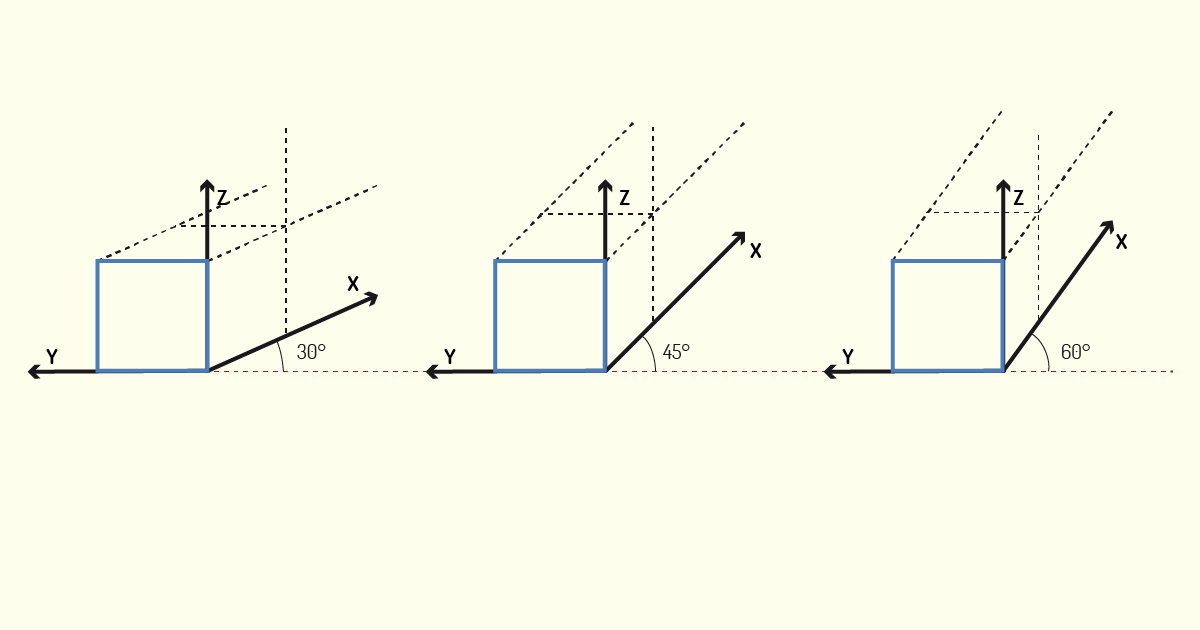
Em seguida, o próximo passo consiste em reforçar as linhas que compõem o desenho final e eliminar as linhas guias, assim como os eixos tridimensionais. Observe o resultado final na figura a seguir.
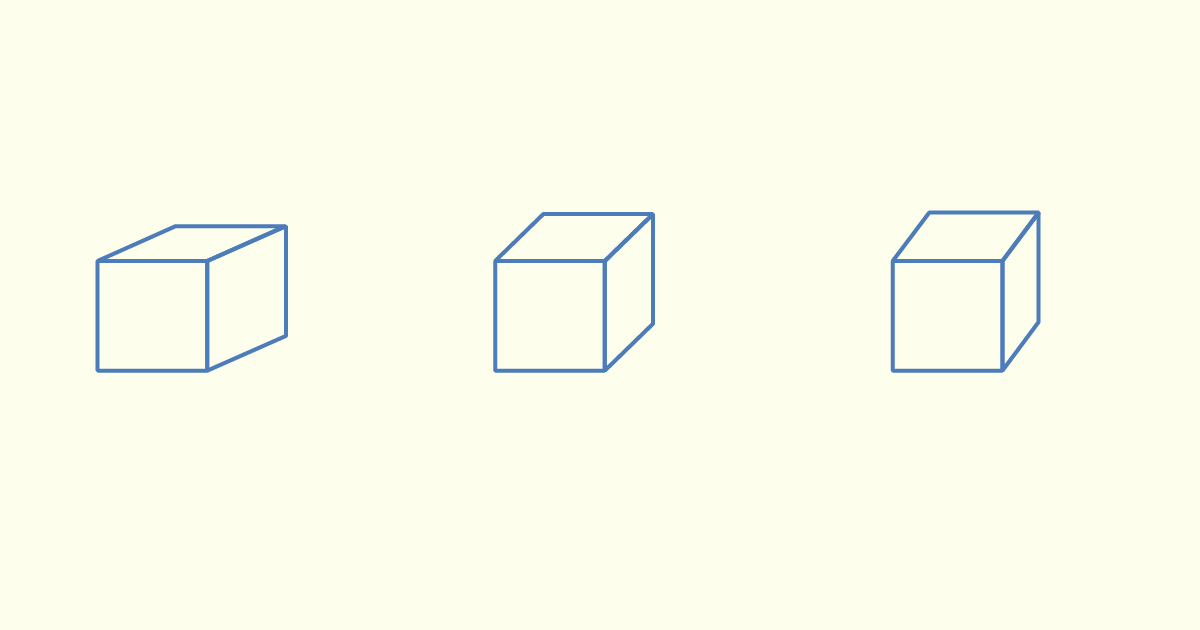
Ao compararmos cada uma das perspectivas, teremos a impressão de que o modelo representado encontra-se mais ou menos voltado para o observador. A determinação do ângulo da perspectiva deve levar em conta qual a intenção projetual, se o ponto de destaque da representação é a face frontal ou as relações estabelecidas pelas faces do objeto como um todo.
A perspectiva militar é uma variação da perspectiva cavaleira. Ela também é configurada como resultado de uma projeção cilíndrica oblíqua, porém, enquanto na cavaleira o plano de projeção é disposto de forma vertical, na militar, esse plano está localizado na horizontal. Isso significa que, nesse tipo de perspectiva, o topo e a base do objeto são vistos como o modelo, enquanto sua altura sofre deformações.
Devido a essa configuração, a perspectiva militar também é conhecida como perspectiva aérea ou vôo de pássaro. Nesse tipo de desenho, o observador encontra-se muito acima da linha do horizonte, como se sobrevoasse o objeto projetado. Acredita-se que o nome “perspectiva militar” seja em decorrência da popularização de seu uso para a criação de estratégias militares de guerra.
Na construção dessa perspectiva, os eixos x e y devem formar, entre si, um ângulo de 90°. É possível adotar qualquer inclinação para esses eixos, respeitando esse valor de 90°, mas as mais adotadas são de 45° e 45° com o plano horizontal ou, ainda, 60° e 30° com o plano horizontal. Observe o exemplo na figura a seguir.
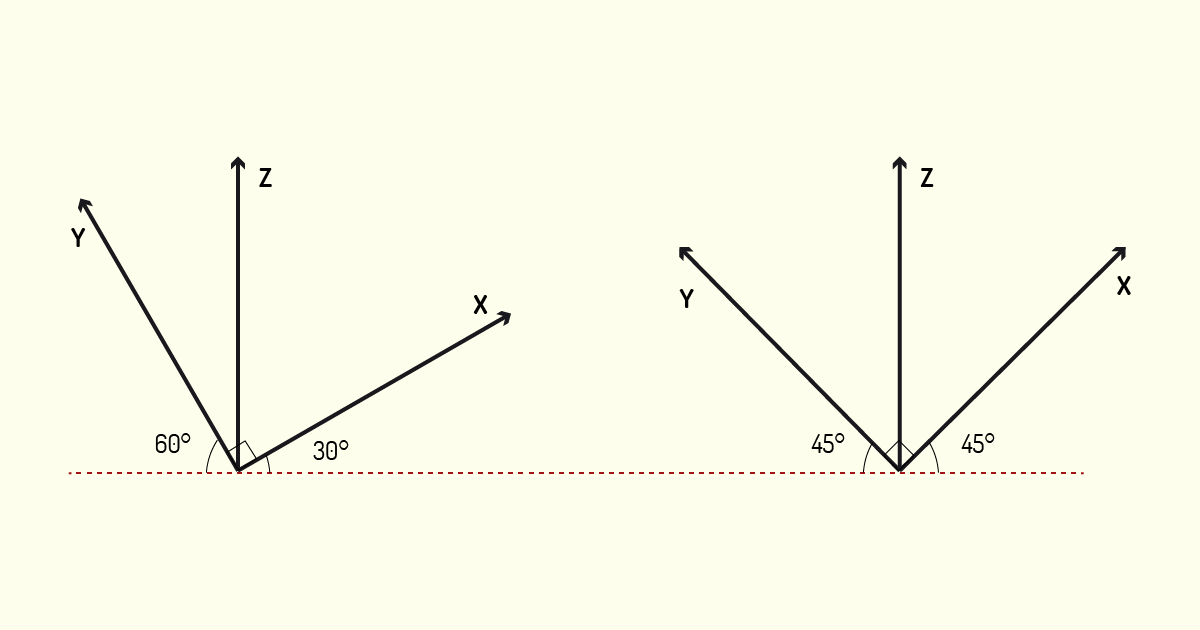
As medidas nos eixos x e y serão representadas em Verdadeira Grandeza, enquanto as medidas do eixo z, ou seja, a altura, será reduzida em 2/3. Para que você consiga compreender melhor esse tipo de perspectiva, vamos construir um exemplo em passo a passo, utilizando o mesmo modelo que aplicamos no exemplo da perspectiva cavaleira.
Primeiramente, devemos construir os eixos. Iremos adotar as inclinações de 60° e 30° para os eixos x e y. Em seguida, devemos desenhar a base do objeto em Verdadeira Grandeza. Em nosso exemplo, a base é representada como um quadrado de dimensão 6 cm. Observe na figura a seguir.
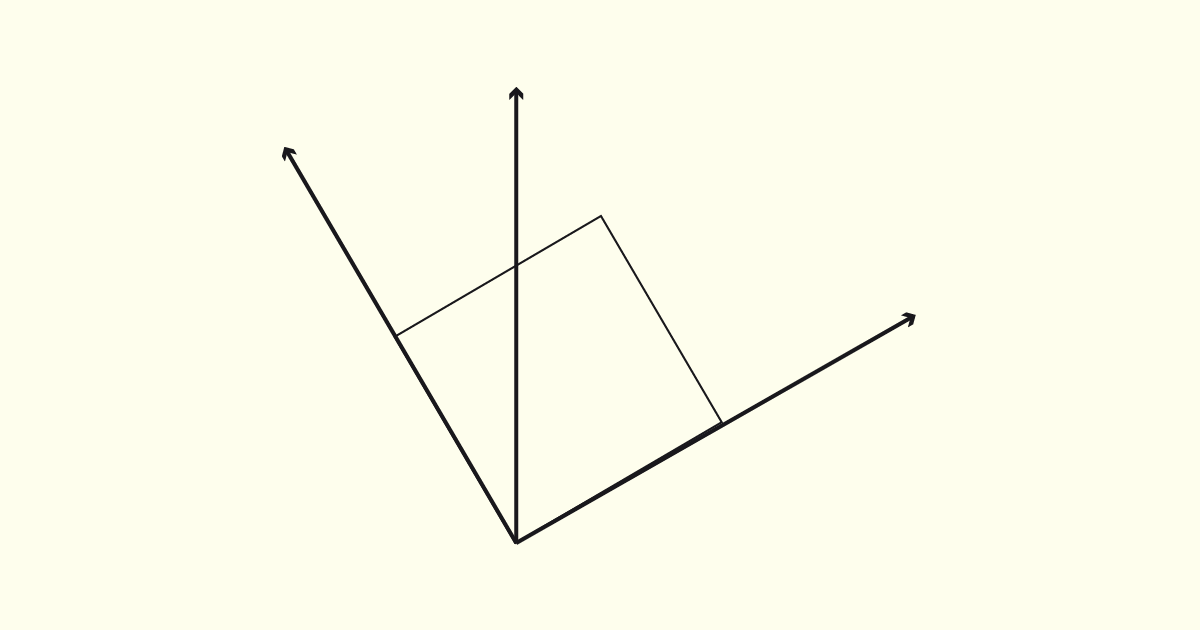
O próximo passo é determinar a altura do objeto. Nosso modelo apresenta altura equivalente a 6 cm, porém é necessário aplicar a escala de redução de 2/3. Isso significa que, na perspectiva, a altura do cubo será equivalente a 4 cm. Observe na figura a seguir.
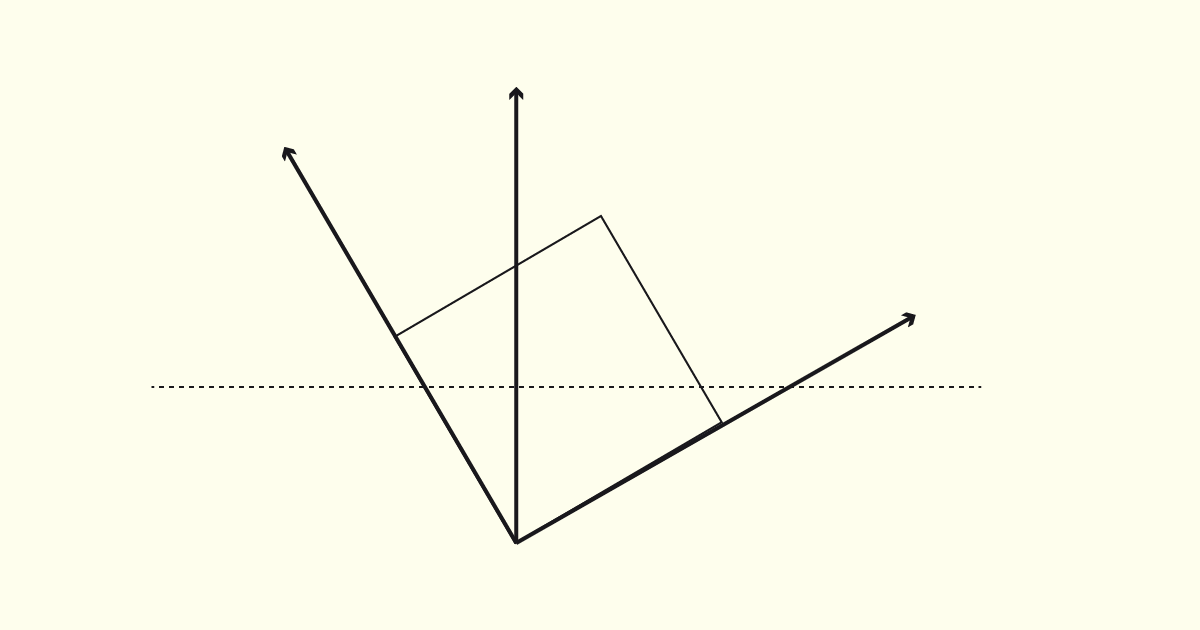
Para finalizarmos a construção da nossa perspectiva, iremos traçar linhas guias, a partir de cada vértice do objeto, lembrando-nos, sempre, de manter as inclinações, bem como respeitando a escala de redução para os segmentos na vertical. Por fim, basta reforçarmos as linhas do volume e eliminarmos as linhas auxiliares. Observe a sequência na figura a seguir.
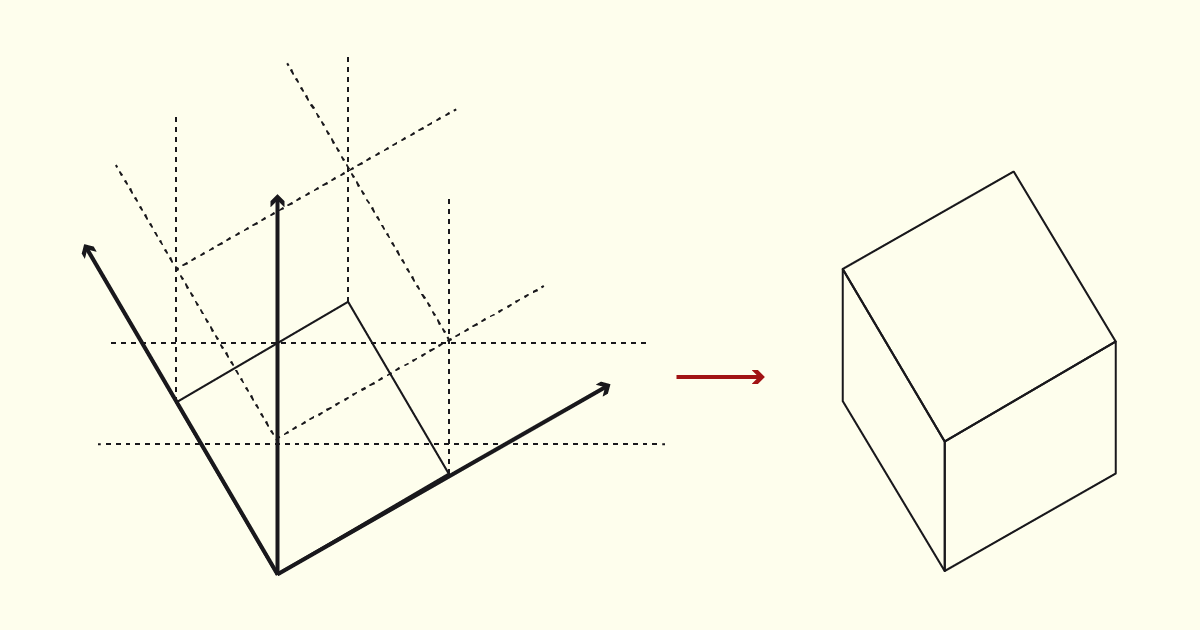
Observe que, no resultado final, a impressão que temos é de que estamos observando o objeto como se estivéssemos acima dele, enquanto que, na perspectiva cavaleira, o objeto está disposto a nossa frente. Esse fator irá te ajudar a determinar qual tipo de perspectiva utilizar, cavaleira ou militar, em seus desenhos.
Devemos aplicar a perspectiva cavaleira quando desejamos evidenciar a vista frontal do objeto ou ambiente. Como discutimos anteriormente, para representar uma peça mecânica, por exemplo, a região que merece destaque não é a vista superior da peça, mas, sim, sua vista frontal.
Porém, para criar a perspectiva rápida de um ambiente a partir, apenas, de sua planta baixa, a perspectiva militar é mais conveniente. Como nesse tipo de desenho a base e o topo são mantidos em Verdadeira Grandeza, não é necessário aplicar escala de redução aos elementos da planta baixa do projeto.
Nesse caso, basta reproduzirmos a planta baixa em sua Verdadeira Grandeza, nos eixos x e y, e, em seguida, “erguermos as paredes” no eixo z, aplicando a escala de redução adequada ao ângulo de inclinação dos eixos.
3) Tanto a perspectiva cavaleira quanto a perspectiva militar são projeções do tipo cilíndrico. Sobre a diferença entre essas duas formas de representação, assinale a alternativa correta.
a) A perspectiva militar é uma projeção cilíndrica ortogonal, enquanto a perspectiva cavaleira é uma projeção cilíndrica oblíqua.
Justificativa: tanto a perspectiva militar quanto a cavaleira são projeções cilíndricas oblíquas.
b) Na perspectiva cavaleira, a profundidade do objeto recebe uma escala de redução, enquanto que, na perspectiva militar, essa escala é aplicada para determinar a altura do objeto.
Justificativa correta: na perspectiva cavaleira, altura e comprimento são representados em VG, enquanto profundidade sofre redução. Já na perspectiva militar, comprimento e profundidade são representados em VG e a altura sofre redução.
c) Na perspectiva militar, a altura do objeto permanece em Verdadeira Grandeza, enquanto, na perspectiva cavaleira, ela é reduzida a sua metade.
Justificativa: na perspectiva militar, a altura do objeto é reduzida em 2/3 do original; já na perspectiva cavaleira, ela é mantida como no modelo.
d) Na perspectiva militar, são adotados ângulos de inclinação de eixo de largura do objeto 30°, 45° e 60°, enquanto, na perspectiva cavaleira, eixos de largura e profundidade do objeto são mantidos formando um ângulo de 30° com a horizontal.
Justificativa: na perspectiva militar, é possível adotar qualquer angulação dos eixos de comprimento e profundidade do objeto, desde que, entre estes dois eixos, seja mantido um ângulo de 90°. Já na perspectiva cavaleira, o eixo do comprimento do objeto é mantido e apenas o eixo de profundidade recebe inclinação.
e) Na perspectiva militar, o observador está localizado muito abaixo da linha do horizonte, enquanto, na perspectiva cavaleira, o observador está localizado muito acima dela.
Justificativa: na perspectiva militar, o observador está localizado muito acima da linha do horizonte, enquanto, na perspectiva cavaleira, o observador está localizado de forma frontal à vista principal do objeto.
Para finalizarmos nossa disciplina, discutiremos, agora, a representação de poliedros. Mas, antes de iniciarmos esse estudo, precisamos compreender os elementos que os compõem e suas possíveis classificações.
Para começarmos, você sabe o que é um poliedro? Esta palavra é composta por dois termos gregos, poli, que significa muitos, e hedra, que significa faces. O poliedro é uma figura volumétrica, isto é, um sólido geométrico formado por polígonos planos. Nesta aula, iremos investigar como realizar a representação de tais volumes sobre os planos bidimensionais.
Com a finalidade de facilitar a compreensão e tornar mais didático o processo de aprendizagem, iremos representar poliedros simples, ou seja, sólidos geométricos pouco trabalhados. Entretanto, em uma situação real, muitas vezes, iremos deparar-nos com objetos mais complexos. Nesses casos, antes de iniciar a representação, devemos fazer uma leitura do modelo. Muitas vezes, basta decompô-lo em volumes para encontrarmos uma solução simples de registro da forma.
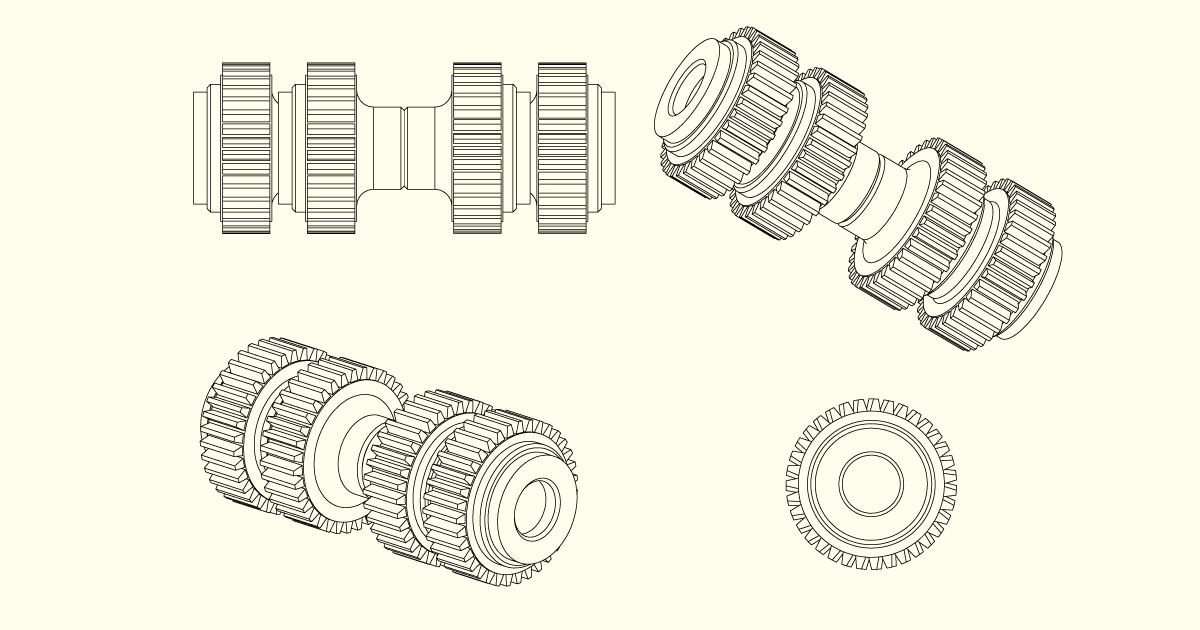
Alguns objetos podem ser compreendidos como a soma de formas volumétricas simples, enquanto outros configuram-se como volumes obtidos a partir da subtração da forma. O ideal é que, antes de iniciar a representação, façamos esta reflexão para compreender como melhor construir o modelo.
Os poliedros, independente de sua classificação, apresentam elementos em comum em sua formação. Todos os poliedros são compostos pelos seguintes elementos geométricos primitivos: vértice, aresta e face.
O vértice é um ponto resultante do encontro de duas ou mais arestas do poliedro que, por sua vez, são segmentos de retas geradas a partir do encontro de duas faces no objeto. As faces de um poliedro consistem nos polígonos que delimitam a volumetria, sendo o equivalente aos “lados” do poliedro. Tais elementos podem ser identificados mais facilmente analisando diretamente no modelo. Observe o exemplo na figura a seguir.
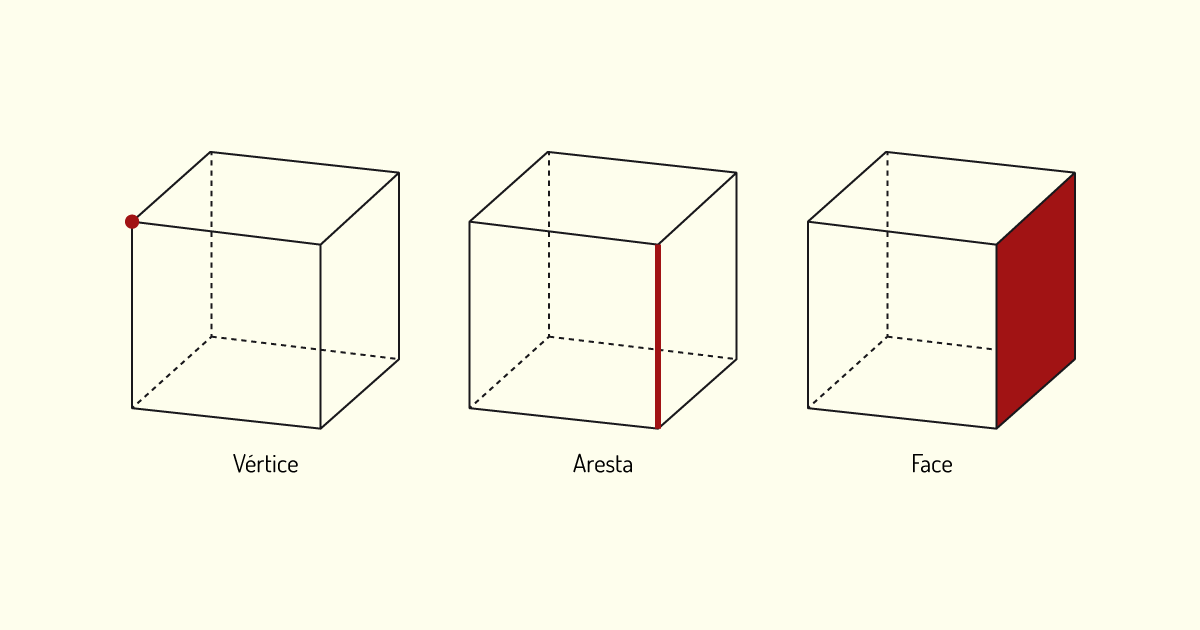
No exemplo apresentado, o cubo é formado por um total de oito vértices, doze arestas e seis faces.
Os poliedros podem ser classificados de acordo com duas principais categorias. A primeira diz respeito aos polígonos que formam o sólido, enquanto a segunda classificação analisa a convexidade do poliedro.
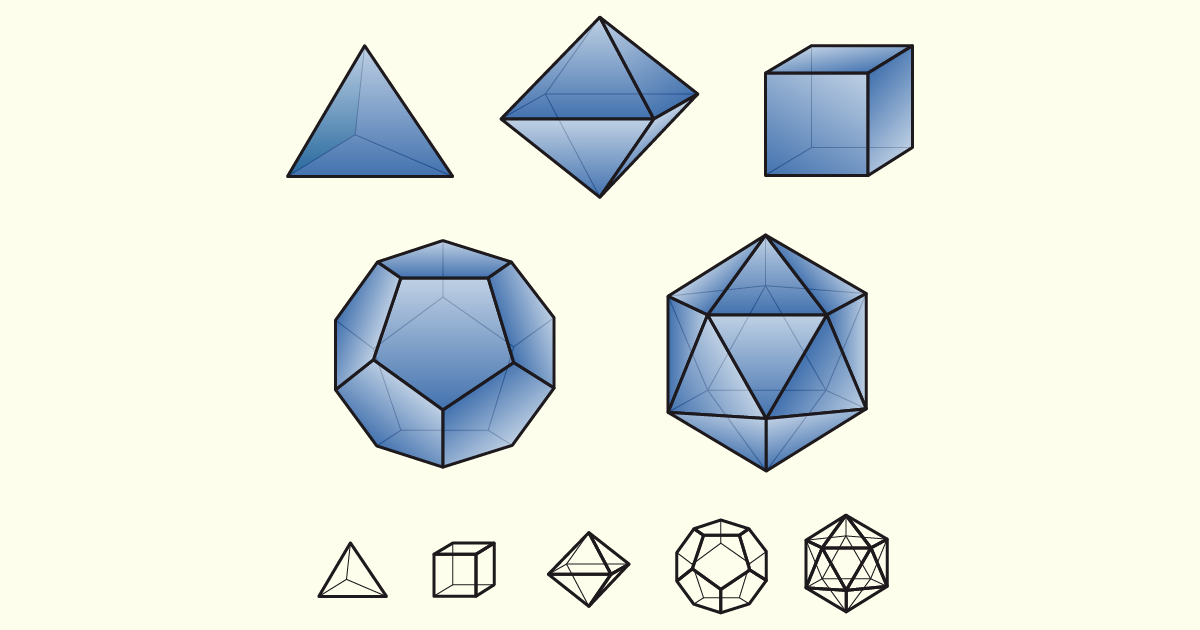
Dentro da primeira classificação, podemos dizer que um poliedro é regular ou irregular. Os poliedros regulares são aqueles que suas faces são polígonos regulares e idênticos entre si. Como exemplo de poliedro regular, iremos encontrar o tetraedro, formado por quatro faces triangulares; o hexaedro, formado por seis faces quadrangulares; o octaedro, formado por oito faces triangulares e, assim, por diante.
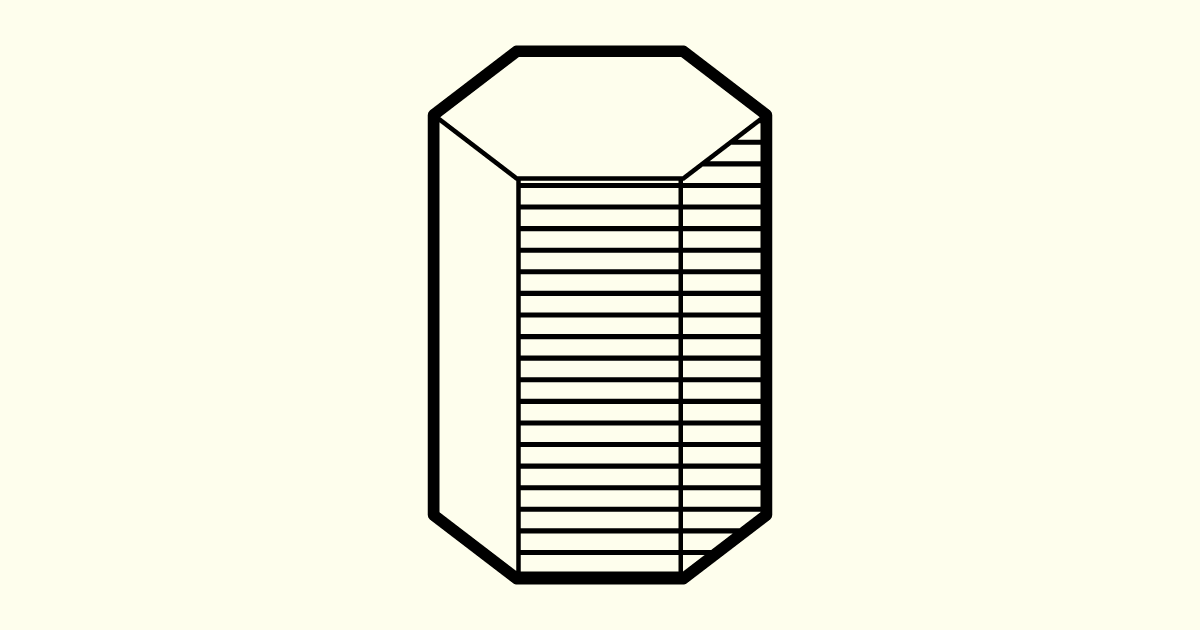
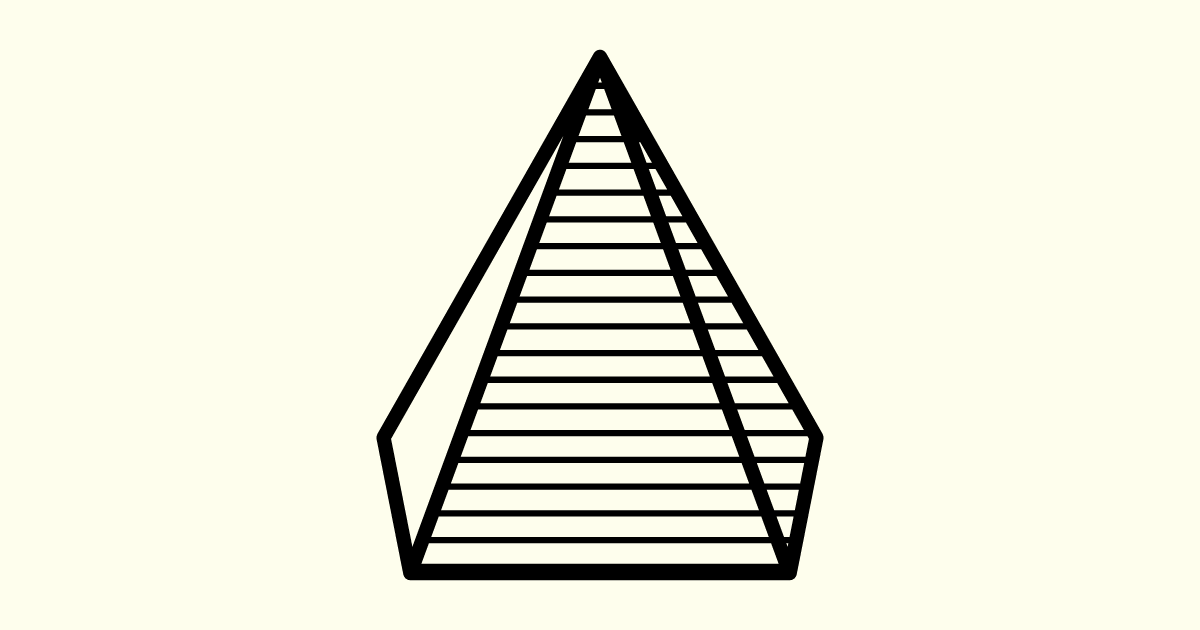
Já os poliedros irregulares são aqueles formados por polígonos regulares e irregulares. Nessa situação, ao menos uma das faces não é idêntica às demais. Os poliedros irregulares mais conhecidos são a pirâmide e o prisma. A pirâmide configura-se como um sólido geométrico, com uma base poligonal e um vértice, que irá unir as demais faces de formato triangular. O prisma, por sua vez, irá apresentar base e face superior planas e congruentes e as laterais deste sólido geométrico são compostas por quadriláteros. Observe o exemplo nas figuras a seguir.
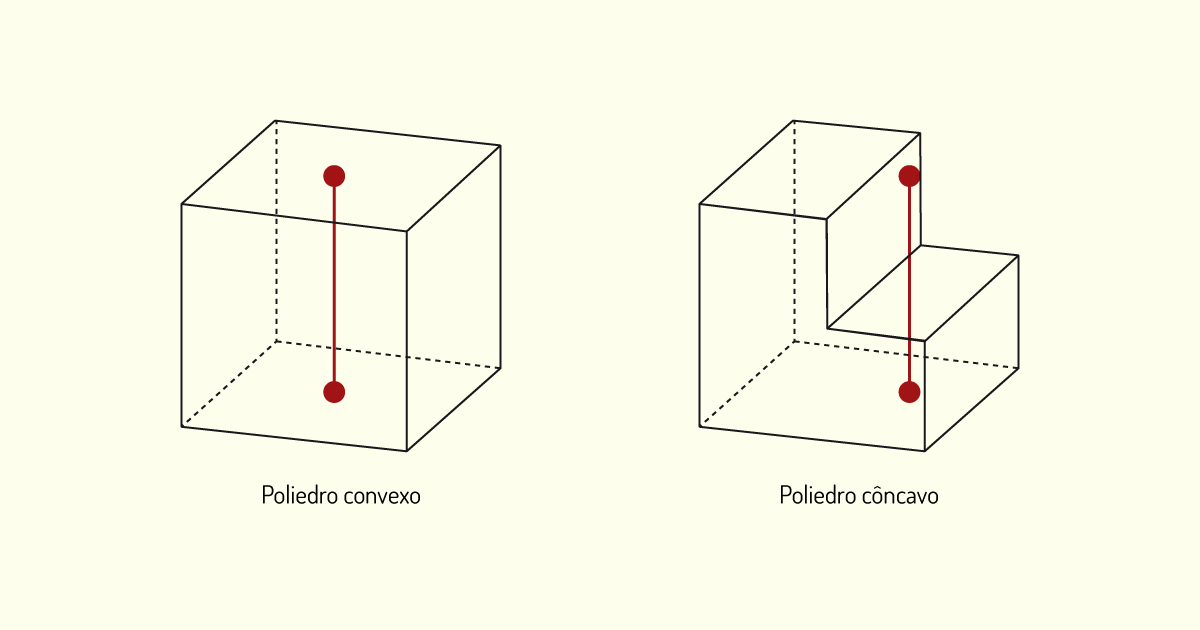
No segundo tipo de classificação, iremos determinar se o poliedro é côncavo ou convexo. Para realizar essa análise, imagine a seguinte situação: selecionamos dois pontos em diferentes faces do poliedro e traçamos um segmento de reta que une tais pontos. Caso algum trecho desse segmento fique do lado “de fora” do poliedro, ele será côncavo, enquanto que, se todo o segmento estiver contido no poliedro, será convexo. Observe o exemplo na figura a seguir.
As classificações apresentadas irão ajudar na compreensão das formas. Cada tipo de poliedro irá possuir suas características de representação e de relações matemáticas, como área, volume, dentre outros.
Para a representação dos poliedros de forma bidimensional, iremos fazer uso do método mongeano, que discutimos na Unidade anterior. As projeções estarão concentradas em dois planos, o plano vertical e o plano horizontal, nos quais as faces, arestas e vértices dos poliedros serão registrados. Consideraremos as projeções sempre no 1° Diedro e, em decorrência disso, os planos de projeção serão representados de modo simplificado nas figuras que ilustram cada caso.
O primeiro aspecto que devemos analisar é em relação à visibilidade do poliedro. As projeções horizontal e vertical irão mostrar vistas diferentes do objeto, algumas faces, vértices e arestas estarão visíveis em uma projeção e podem estar ocultas em outras. Os poliedros são considerados sempre opacos, dessa forma, as arestas que estiverem ocultas por estarem atrás de uma face serão representadas em projeção.
Quando um raio projetante atinge um elemento sem antes ter atravessado um objeto, esse elemento será visível na projeção. Tanto na projeção horizontal quanto na projeção vertical sempre haverá um conjunto de arestas e vértices visíveis, os quais são denominados Contorno Aparente da Projeção.
Existem diversas possibilidades de posição do poliedro em relação aos planos de projeção. Iremos, a seguir, analisar duas das principais situações.
A primeira etapa consiste em determinar a projeção da base do poliedro, que será representada em Verdadeira Grandeza, já que o poliedro está localizado apoiado sobre o plano horizontal ou de nível.
Em seguida, após a construção da projeção horizontal, iremos realizar as marcações no plano de projeção vertical. A base do poliedro será visualizada como uma reta paralela ou sobre a Linha de Terra, enquanto as arestas laterais serão retas perpendiculares ao plano horizontal.
A altura do poliedro pode ser marcada em Verdadeira Grandeza sobre uma das arestas laterais. Assim como a base do poliedro, o topo dele também é representado como uma reta. Observe o exemplo na figura a seguir.
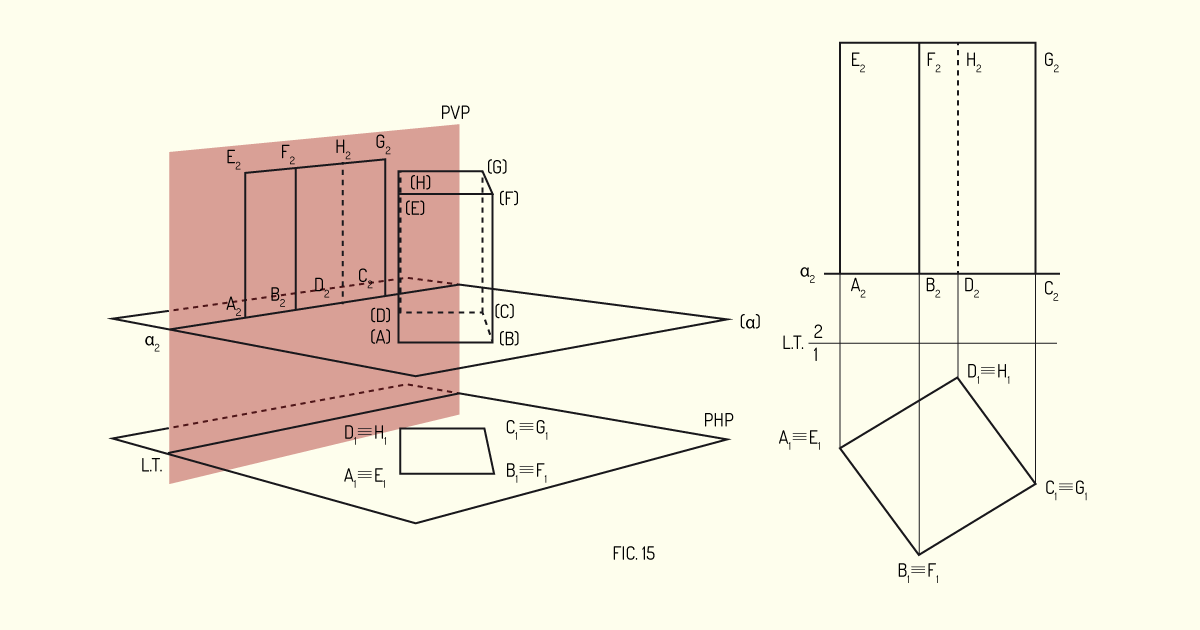
Para objetos apoiados no plano frontal, a sua representação terá características semelhantes a dos objetos apoiados em plano de nível, porém de forma paralela ao plano de projeção vertical. Observe o exemplo na figura a seguir.
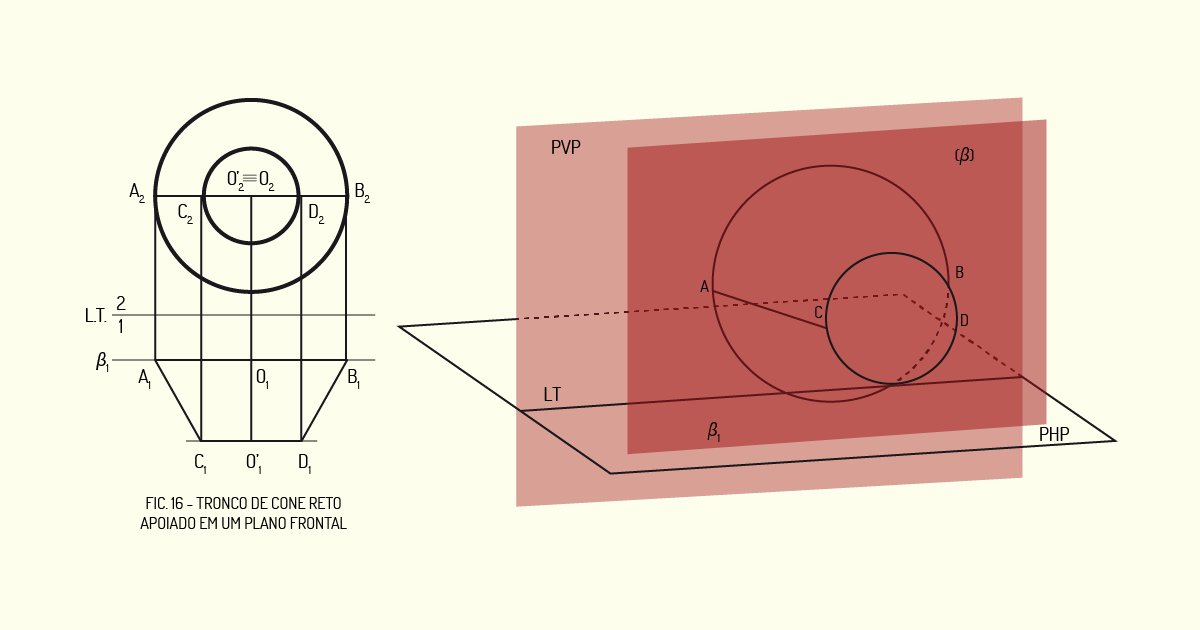
O diâmetro da figura é representado em Verdadeira Grandeza, tanto em projeção vertical quanto em projeção horizontal. A projeção horizontal da base do poliedro é representada como uma reta paralela à Linha de Terra. O contorno do sólido é determinado pelas geratrizes (AC) e (BD) e pelas semi-circunferências que retratam as circunferências de base e de topo.
Para situações nas quais o poliedro não estiver apoiado no plano horizontal, de nível ou frontal, ou seja, não esteja paralelo a um plano de projeção, será necessário utilizar um dos métodos descritivos que analisamos na Unidade anterior. Para cada caso, é importante analisar qual a melhor solução adotada, se será a rotação do objeto, o rebatimento de planos ou, ainda, a mudança de plano de projeção. Para cada tipo de problema, um método descritivo será mais adequado que o outro.
4) Observe os poliedros a seguir e assinale a alternativa que relacione corretamente as classificações dos sólidos indicados.
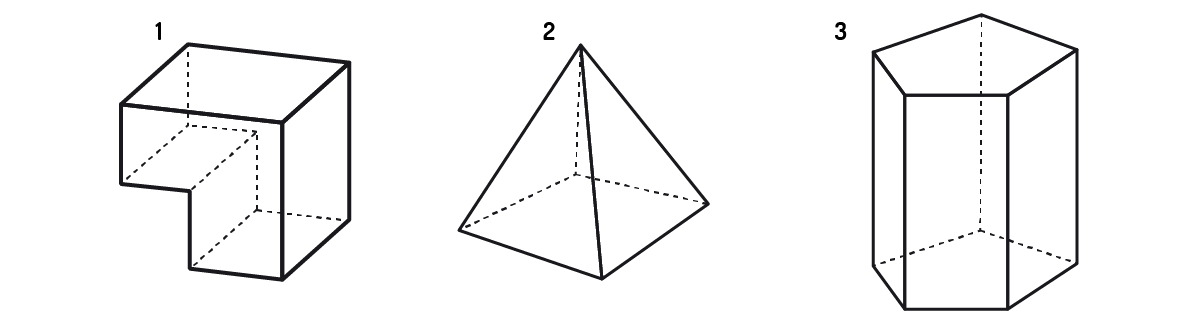
Fonte: Elaborada pela autora.
a)
1: poliedro regular e côncavo.
2: poliedro irregular e convexo.
3: poliedro regular e convexo.
Justificativa: o poliedro 1 não é regular. A descrição do poliedro 2 está correta. O poliedro 3 não é regular.
b)
1: poliedro irregular e côncavo.
2: poliedro irregular e convexo.
3: poliedro irregular e convexo.
Justificativa correta: os três poliedros são considerados irregulares, pois os polígonos que formam suas faces não são idênticos entre si. Apenas o poliedro 1 é côncavo, enquanto os poliedros 2 e 3 são convexos. Se passarmos uma reta na região esquerda do poliedro 1, iremos perceber que parte dela ficará externa ao objeto.
c)
1: poliedro irregular e côncavo.
2: poliedro regular e convexo.
3: poliedro regular e côncavo.
Justificativa: a descrição do poliedro 1 está correta. O poliedro 2 não é regular. O poliedro 3 não é regular e não é côncavo.
d)
1: poliedro irregular e convexo.
2: poliedro irregular e convexo.
3: poliedro regular e côncavo.
Justificativa: o poliedro 1 não é convexo. A descrição do poliedro 2 está correta. O poliedro 3 não é regular e não é côncavo.
e)
1: poliedro irregular e convexo.
2: poliedro regular e côncavo.
3: poliedro irregular e convexo.
Justificativa: o poliedro 1 não é convexo. O poliedro 2 não é regular e não é côncavo. A descrição do poliedro 3 está correta.
Nome do livro: A perspectiva dos profissionais - Sombras, Insolação, Axonometria
Editora: Blucher
Autor: Gildo Montenegro
ISBN: 9788521205425
Na leitura sugerida, você irá encontrar, de forma detalhada, as técnicas de perspectiva. Nesta obra, o autor foca na representação gráfica, contando com textos de apoio apenas para explicações adicionais. Por meio dessa leitura, seu conhecimento sobre o desenho projetivo será ampliado e será possível, também, relacionar a criação de perspectivas com seu futuro cenário profissional.

Nome do filme: Mestre dos mares - o lado mais distante do mundo
Gênero: Histórico, Guerra
Ano: 2004
Elenco principal: Russell Crowe, Paul Bettany, Billy Boyd
O filme sugerido traz a história de um capitão da marinha britânica durante o período em que o país esteve em conflito com a França de Napoleão. Por meio da reconstrução desse período histórico, você poderá compreender melhor o cenário no qual foram desenvolvidas e aprimoradas técnicas de representação de perspectivas, sobretudo, com finalidades bélicas.

Nome do livro: Manual básico de desenho técnico
Editora: Editora UFSC
Autor: Henderson José Speck e Virgílio Vieira Peixoto
ISBN: 978.85.328.0650-5
Na leitura indicada, você terá a oportunidade de analisar a representação de poliedros mais complexos do que aqueles que analisamos nesta disciplina! Embora o método de projeção seja empregado seguindo os mesmos princípios, para representar poliedros complexos, é necessária uma maior atenção e familiaridade com esse tipo de exibição das formas.

Nome do filme: The infinite happiness
Gênero: Documentário
Ano: 2015
Elenco principal: Ila Bêka e Louise Lemoine
No filme sugerido, Ila Bêka e Louise Lemoine contam sobre a experiência de morar durante um mês na vila vertical “8 house”, projetada pelo escritório BIG. Através deste documentário, você poderá perceber como as composições volumétricas, por meio de poliedros, fazem-se presentes na prática projetual. Deixamos, também, a seguinte reflexão: até que ponto a forma pode impactar na usabilidade do projeto? No final, qual fator tem maior peso, forma ou função?
