Olá, seja bem-vindo(a)!
Nesta terceira Unidade da disciplina Expressão Gráfica, iremos aprofundar nossos conhecimentos sobre a representação gráfica dentro da Geometria Descritiva.
A Geometria consiste em um dos campos de estudo da matemática. Em sua análise, podemos calcular as mais variadas dimensões e propriedades dos modelos representados. Em nossa disciplina, o objetivo não será voltar nosso olhar para essa questão analítica, mas sim ao aspecto de representação das formas.
Imagine a seguinte situação: após realizar a modelagem em 3D de uma residência, você precisa representar todos os elementos dessa construção de forma bidimensional, para criar um projeto executivo e encaminhá-lo à obra. Alguns elementos construtivos são muito elementares e fáceis de representar, por exemplo, as paredes e demais superfícies planas. Porém, como representar, de forma bidimensional, o telhado inclinado de uma residência? Você já parou para pensar a respeito disso? De maneira geral, as superfícies inclinadas são aquelas que geram maior dificuldade no momento de representação.
O nosso olhar não é treinado para imaginar, de modo automático, a planificação dos objetos, por isso, é importante adquirir esse hábito, para que o processo de representação das formas fique cada vez mais simples e intuitivo a você!
Iniciamos esta Unidade discutindo algumas noções básicas da Geometria e da Geometria Descritiva. Nesse primeiro momento, é essencial que você familiarize-se com os termos e definições que, no decorrer da Unidade, serão trabalhados.
Na sequência, compreenderemos o método mongeano para a projeção das figuras, bem como discutiremos sobre as vistas ortográficas e a norma brasileira que orienta em relação a esse tipo de representação gráfica.
Após levantarmos esses princípios básicos, concentraremo-nos no estudo dos elementos primitivos da Geometria e sua relação na Geometria Descritiva. Analisaremos o comportamento de ponto, reta e plano quando representados segundo o método mongeano.
Finalizando a nossa terceira Unidade, conheceremos os métodos descritivos. Esses métodos nos auxiliarão a criar projeções de elementos, sejam eles ponto, reta ou plano. Por meio deles, será possível simplificar situações complexas, como quando um objeto não se encontra disposto de modo paralelo ao plano de projeção.
O conteúdo que debateremos nesta Unidade tem, como propósito, apresentar os principais conceitos envolvidos no método de projeção da Geometria Descritiva. Analise, com atenção, cada um dos elementos que iremos abordar, conforme eles vão sendo exibidos, para que você consiga acompanhar o processo de representação das formas dos modelos.
Bons estudos!
Em nossa disciplina, iremos focar no estudo de desenhos projetivos, dessa forma, objetos com três dimensões serão registrados de forma bidimensional. Para compreendermos o modo de execução de tais representações, precisamos, primeiramente, conhecer e analisar quais elementos irão compor nossos desenhos! Os elementos básicos que iremos abordar na aula de hoje serão essenciais para que possamos construir as representações de modo correto.
A Geometria, assim como o Cálculo e a Álgebra, é um dos campos de estudos da matemática. Se analisarmos a etimologia da palavra, veremos que a Geometria significa, de modo literal, medir a terra. Carvalho (2001) aponta que a área de atuação da Geometria é a investigação das formas e dimensões dos elementos matemáticos. Isso significa que, nessa esfera, são abordados sistemas matemáticos que resultam nas representações em forma de figuras geométricas.
A Geometria apresenta diversos axiomas que traduzem conceitos matemáticos para a construção de teoremas. Esse campo de estudo pode ser dividido em dois principais grupos: a geometria métrica e a de posição.
A geometria métrica, como o próprio nome sugere, é um campo de estudo que analisa as medidas das figuras geométricas. Nela, são trabalhadas informações como as dimensões gerais das formas, a área de uma superfície, seu perímetro, o volume de um sólido geométrico e a distância entre pontos. É por meio da geometria métrica que conseguimos relacionar um objeto a suas dimensões.
Já a geometria de posição busca analisar a posição que um ponto, uma reta ou um plano ocupa no espaço. Por meio desse campo de estudo, é possível determinar a posição relativa entre duas retas, entre um ponto e uma reta, entre um ponto e um plano, dentre outros.
Os conceitos de geometria podem ser amplamente utilizados em nosso dia a dia. Para analisar a melhor rota para uma viagem, por exemplo, iremos verificar quais são os caminhos existententes entre a partida (ponto inicial) e o destino (ponto final), além de avaliar qual apresenta uma menor distância.
A representação das formas é um meio de comunicação que irá auxiliar na transmissão de ideias e na correta execução de projetos. Por meio da Geometria, é possível retratar um objeto de modo que este seja interpretado precisamente pelos envolvidos no processo de execução.
Você já ouviu falar no termo “Geometria Descritiva”? Esse campo da Geometria foi desenvolvido por um matemático francês, chamado Gaspard Monge, como uma forma de padronizar a confecção de projetos, no processo industrial, dentro do cenário francês, em meados do século XVIII (CARVALHO, 2001).
A Geometria Descritiva, a qual trataremos como GD, também é conhecida como sistema mongeano ou método diédrico. Esse sistema tem, como objetivo, representar figuras do espaço para estudar sua forma, dimensão e posição por meio desse registro.
Gaspard Monge foi o responsável por sistematizar processos construtivos para trabalhar elementos tridimensionais de forma bidimensional. A partir disso, é possível resolver problemas em que são consideradas as três dimensões do objeto, porém, por meio da geometria plana, o que torna a sua análise mais clara e descomplicada.
Imagine que você está projetando uma cadeira. Após a concepção da ideia, você precisa registrar o que imaginou, para que ela possa ser executada, não é mesmo? Embora um desenho tridimensional permita que o executor tenha uma visão global de como a cadeira deve ficar depois de pronta, essa representação não é a mais adequada para inserirmos indicações, cotas e demais elementos, os quais permitirão a sua construção.
A GD, por meio da geometria plana, como o seu próprio nome indica, é composta por métodos que irão descrever o objeto. Nessas representações, o objetivo não é explicar ou investigar a natureza do objeto, mas sim retratar de modo estritamente descritivo. No exemplo apresentado, para registrar uma cadeira, seria necessária a construção de vistas ortogonais a cada face do objeto, para a sua apresentação, de forma a permitir sua execução.
A Geometria faz uso de entes primitivos para a representação dos objetos. Iniciando pelo elemento mais simples, o ponto é adimensional e sem forma, por isso, não apresenta largura ou altura. Por não possuir tamanho e forma, o ponto é responsável por determinar o lugar exato no espaço. Sua representação gráfica é feita como um “pingo” e sua designação é dada por letras maiúsculas, por exemplo, (A), (B), (C).
A reta, por sua vez, é formada por um conjunto de pontos que se mantém em uma mesma direção, ou seja, não faz curva. A representação gráfica da reta é feita como um traçado e sua designação é dada por letras minúsculas, por exemplo, r, s, t.
O plano é formado pelo enfileiramento de retas. Sua representação gráfica é feita pelo desenho de uma superfície e sua designação é dada por letras gregas, por exemplo, α, β.
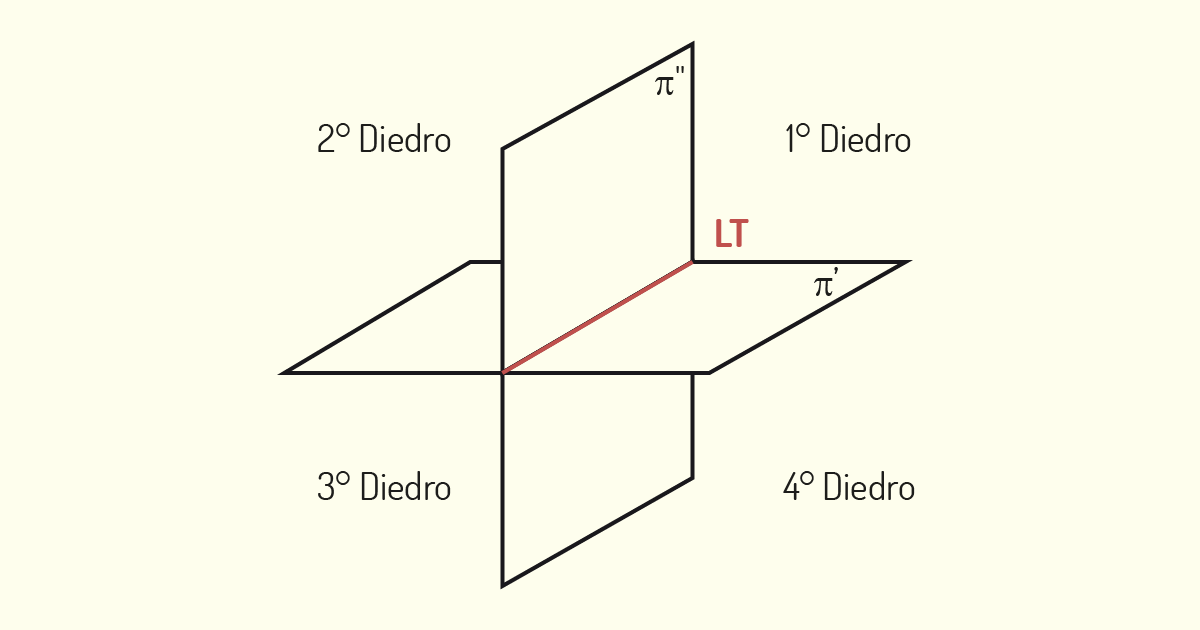
A Geometria Descritiva, por sua vez, compreenderá, além dos entes primitivos apresentados, elementos característicos para a representação das formas. Ao trabalharmos com a GD, iremos deparar-nos com a Linha de Terra, Linha de Chamada e os Diedros. Para compreendermos, melhor, o papel de cada um desses itens, vamos, primeiramente, conceituá-los!
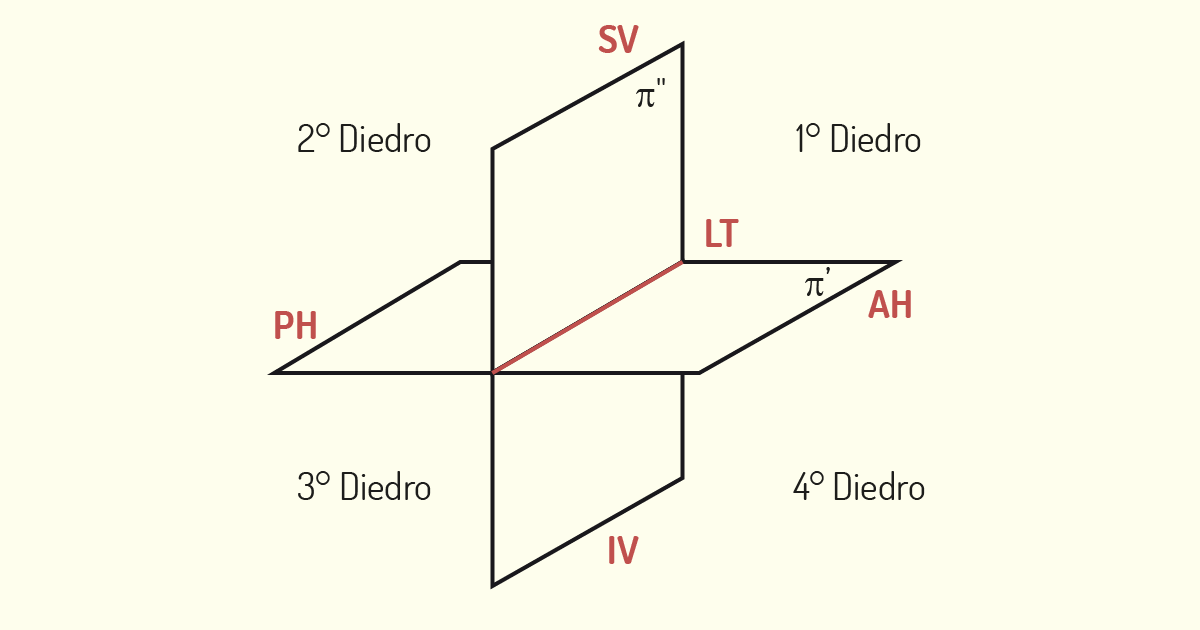
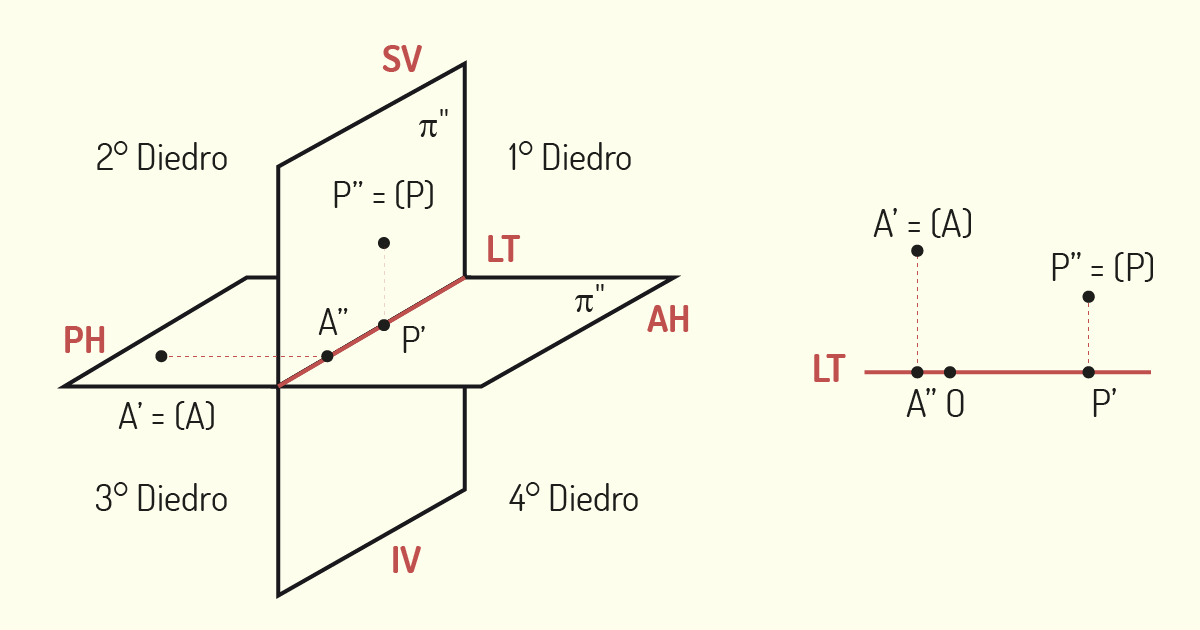
Na GD, os objetos serão representados em planos de projeção perpendiculares entre si. A Linha de Terra ou LT corresponde à reta que representa a interseção entre tais planos de projeção (CARVALHO, 2001). A Linha de Chamada é a representação da projeção das projetantes, feita de modo perpendicular à LT.
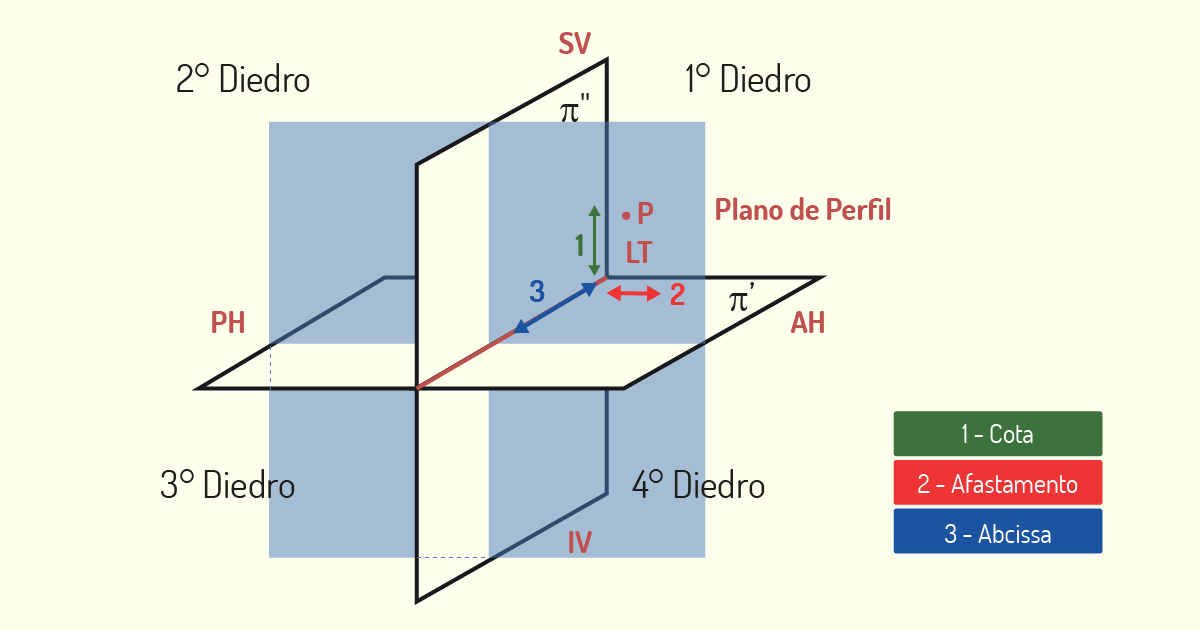
Os Diedros são os espaços formados entre os dois planos de projeção (CARVALHO, 2001). O plano horizontal, representado como π’, e o plano vertical, representado como π”, estruturam o Diedro.
Considerando o método mongeano, o plano vertical e o plano horizontal podem dividir o espaço em quatro Diedros. A denominação de tais Diedros é feita conforme o sentido trigonométrico, ou seja, seguindo o sentido anti-horário, considerando o 1° Diedro o superior à direita.
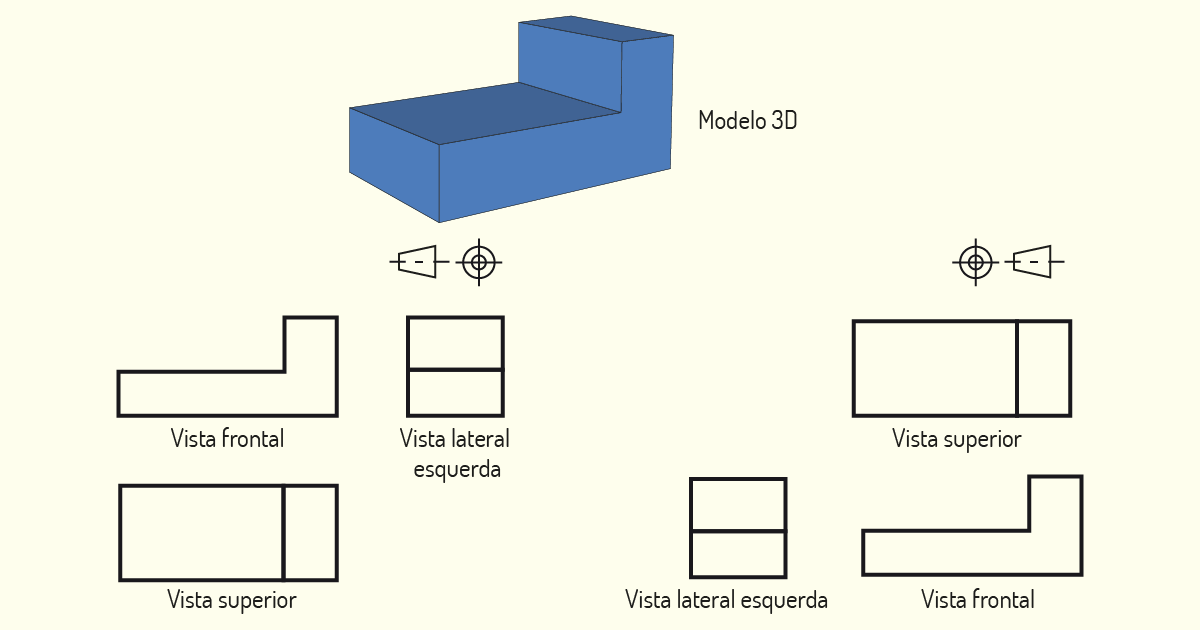
Cada um desses Diedros fornece um tipo de projeção diferente. No Brasil, a Associação Brasileira de Normas Técnicas orienta que a representação de desenhos técnicos seja feita no 1° Diedro. Já em países como Estados Unidos e Canadá, o mais usual é a representação no 3° Diedro. Quando trabalhamos com no 1° Diedro, o modelo a ser representado está localizado entre o observador e o plano de projeção. Em uma representação no 3° Diedro, o plano de projeção está situado entre o modelo e o observador. Observe, no exemplo a seguir, a diferença de representação de um mesmo modelo.
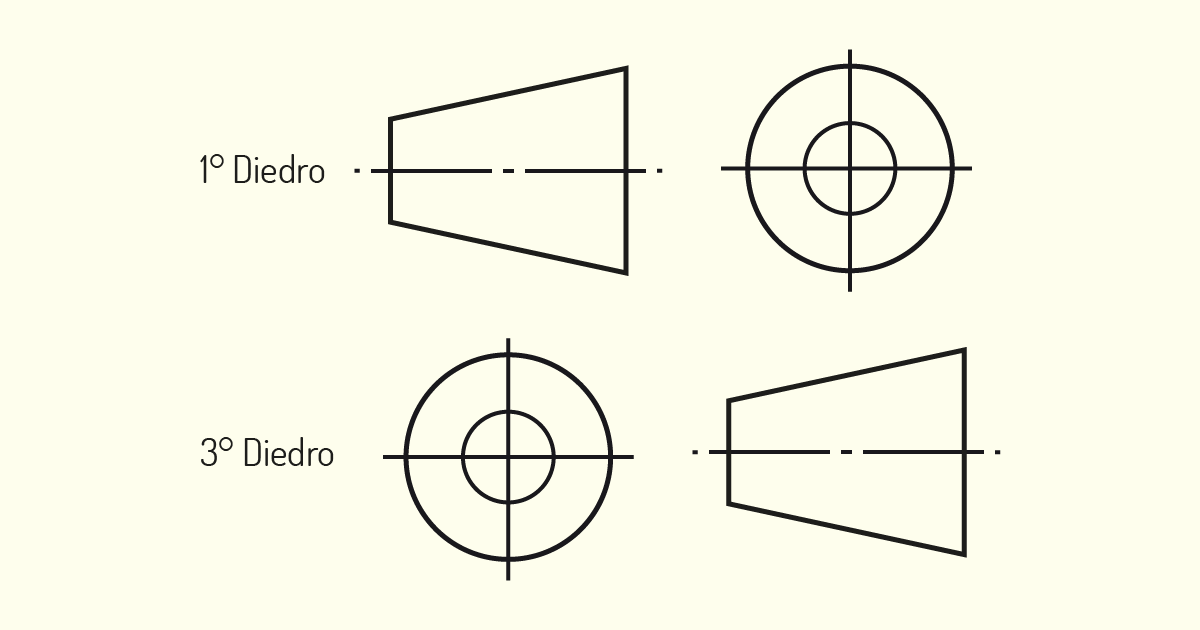
Para indicar em qual Diedro o objeto está sendo representado, é necessário apontar seu respectivo símbolo, no canto inferior direito da prancha, dentro da legenda. Observe, na figura a seguir, como representar nas duas situações mais usuais.
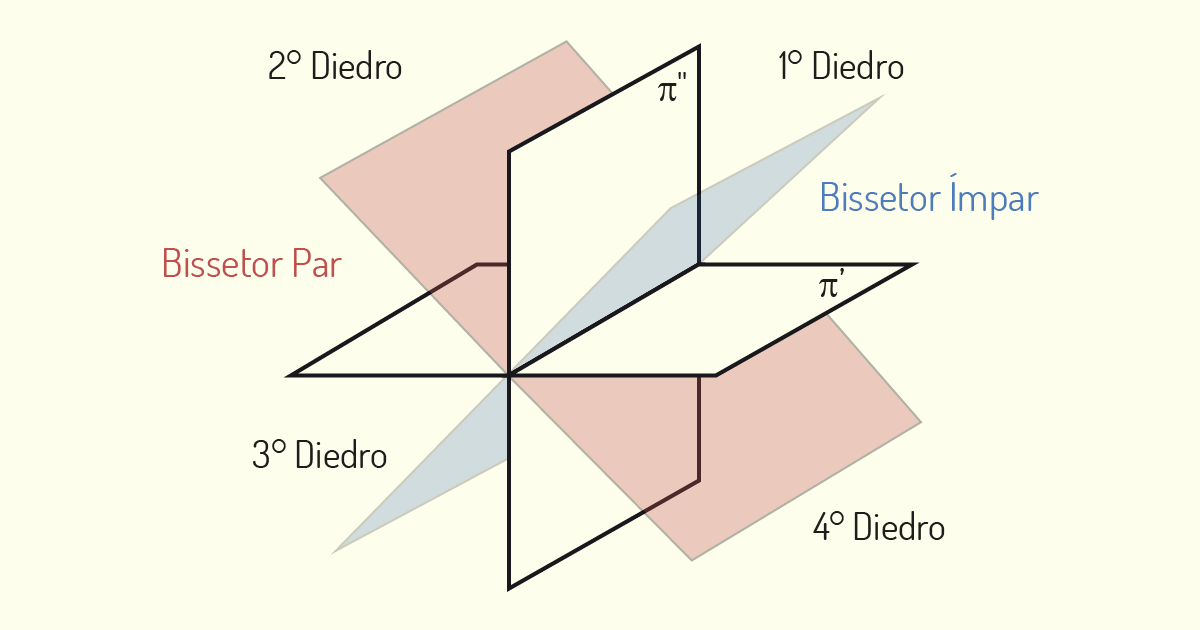
Além dos planos de projeção, existem, ainda, os planos bissetores. Uma superfície é considerada um plano bissetor quando contém a LT e divide, de modo simétrico, um Diedro, formando um ângulo de 45° com os planos de projeção. Existem dois planos bissetores, o primeiro deles, denominado Bissetor Ímpar, divide o primeiro e terceiro Diedros; o segundo, chamado Bissetor Par, divide o segundo e o quarto Diedros. Observe o exemplo na figura a seguir.
Na Geometria Descritiva, trabalhamos com o rebatimento do modelo no plano de projeção. Embora, em português, a palavra “rebatimento” esteja relacionada a repelir, jogar para longe, devemos compreender essa expressão como uma derivação do termo francês “rabattemant”, que vem do verbo “rabattre”, que significa baixar, fazer cair (MONTENEGRO, 1991).

1) Sobre a definição de elementos básicos da Geometria Descritiva, assinale a alternativa correta.
a) Os diedros são espaços caracterizados por um plano horizontal e uma Linha de Terra.
Justificativa: os diedros são configurados como espaços formados por um plano de projeção horizontal e um plano de projeção vertical.
b) O método mongeano é formado por um sistema com quatro diedros.
Justificativa correta: para representação no método mongeano, são utilizados quatro diedros que, quando rebatidos, são representados em épura.
c) A Linha de Terra corresponde ao encontro do plano horizontal e o modelo a ser representado.
Justificativa: a Linha de Terra é o encontro de plano horizontal de projeção e plano vertical de projeção. O modelo não precisa, necessariamente, estar disposto sobre a Linha de Terra.
d) No Brasil, a Norma Técnica determina que as representações sejam feitas no 3° Diedro.
Justificativa: segundo a ABNT, no Brasil, devemos utilizar o 1° Diedro para representar as projeções.
e) Os Diedros são numerados no sentido horário, sendo que o primeiro deles encontra-se localizado na parte superior esquerda do sistema.
Justificativa: os diedros são numerados no sentido anti-horário e o 1° Diedro está localizado na parte superior direita do sistema.
A projeção ortogonal é um modo de representação diferente de nossa visão, que é feita de forma tridimensional e com perspectiva. Logo, o sistema da Geometria Descritiva não é um método intuitivo de registro de objetos. Para alcançarmos o domínio dessa técnica, é necessária muita prática do raciocínio e expressão da forma que a visão espacial envolve!

A representação das figuras, segundo o método mongeano, pode ser realizada tanto em meio digital, por meio de softwares, como o AutoCAD, quanto manualmente, por meio de ferramentas, como o esquadro e a régua paralela.
Independente do meio de representação escolhido, para a criação dessas formas, seja através do uso de comandos de criação de linhas no AutoCAD ou do manejo de esquadros, será necessária a criação das Linhas de Chamadas.
Essas linhas, representadas de forma paralela entre si e perpendiculares aos planos de projeção, servirão de guia para a criação das projeções e, na representação final, tais linhas serão suprimidas do desenho. Na sequência, vamos analisar quais elementos e fatores são essenciais para a representação de modelos dentro da geometria descritiva.
A Geometria Descritiva surgiu entre 1766 e 1784, porém só veio a ser amplamente divulgada em 1794, quando Gaspard Monge ensinou a técnica aos seus alunos da Escola Politécnica da França. Apesar da divulgação científica e do desenvolvimento teórico terem sido realizados apenas a partir do século XVIII, a utilização da técnica de rebatimento para representação das formas foi utilizada de modo empírico durante milênios, desde o princípio das civilizações (MONTENEGRO, 1991).
Quando posicionamos o modelo que desejamos reproduzir em um dos Diedros, iremos trabalhar com a projeção do objeto sobre os planos. Como vimos anteriormente, os planos de projeção são divididos em planos horizontal e vertical, os quais criam uma intersecção denominada Linha de Terra. Esses planos são subdivididos, formando quatro semi-planos. Na horizontal, teremos o Semi-Plano Horizontal Posterior (SPHP ou PH) e o Semi-Plano Horizontal Anterior (SPHA ou AH). Já na vertical, serão encontrados o Semi-Plano Vertical Superior (SPVS ou SV) e o Semi-Plano Vertical Inferior (SPVI ou IV) (CARVALHO, 2001). Observe, na figura a seguir, cada um desses semi-planos.
Os Diedros configuram-se, então, como espaços tridimensionais, nos quais iremos posicionar um ponto, uma reta, uma face ou, até mesmo, um volume. Uma vez que o elemento estiver posicionado no espaço em um dos Diedros, conseguimos determinar a sua projeção sobre os planos.
Para que o modelo seja representado em duas dimensões, devemos transformar os Diedros, que são tridimensionais, em uma estrutura plana. Imagine que os planos vertical e horizontal são como folhas móveis que rotacionam e têm, como eixo de rotação, a Linha de Terra. Para tornar os Diedros bidimensionais, realizaremos um movimento de giro do plano horizontal no sentido horário, de modo que ele coincida com a posição do plano vertical. Como resultado, iremos obter a épura, a planificação do Diedro. Observe o exemplo na figura a seguir.
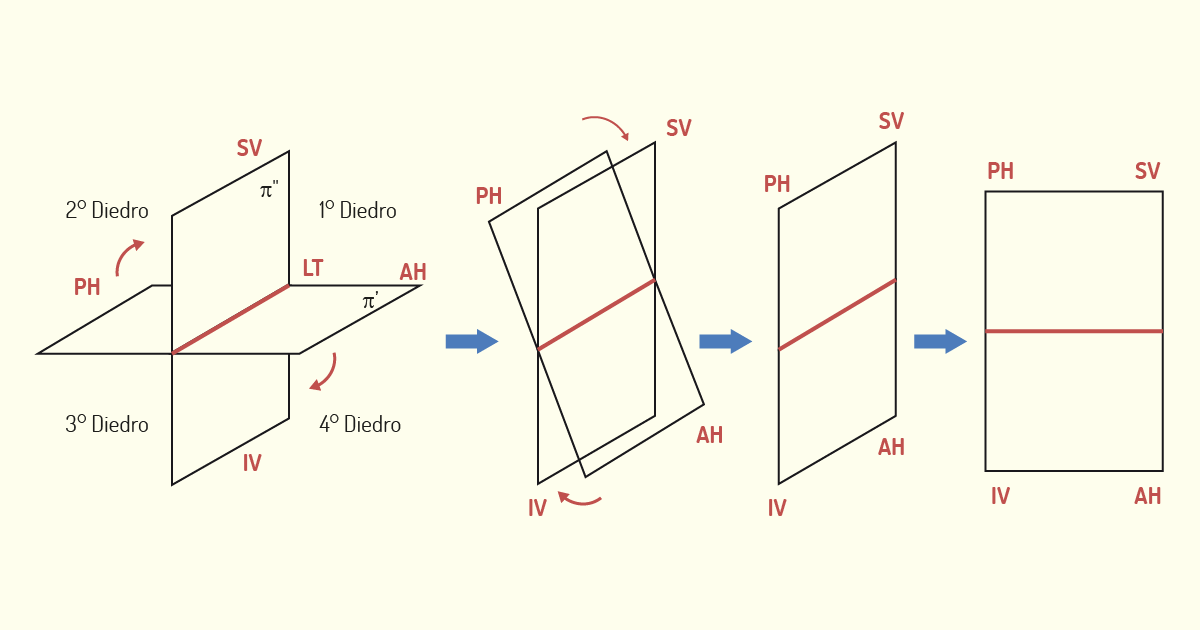
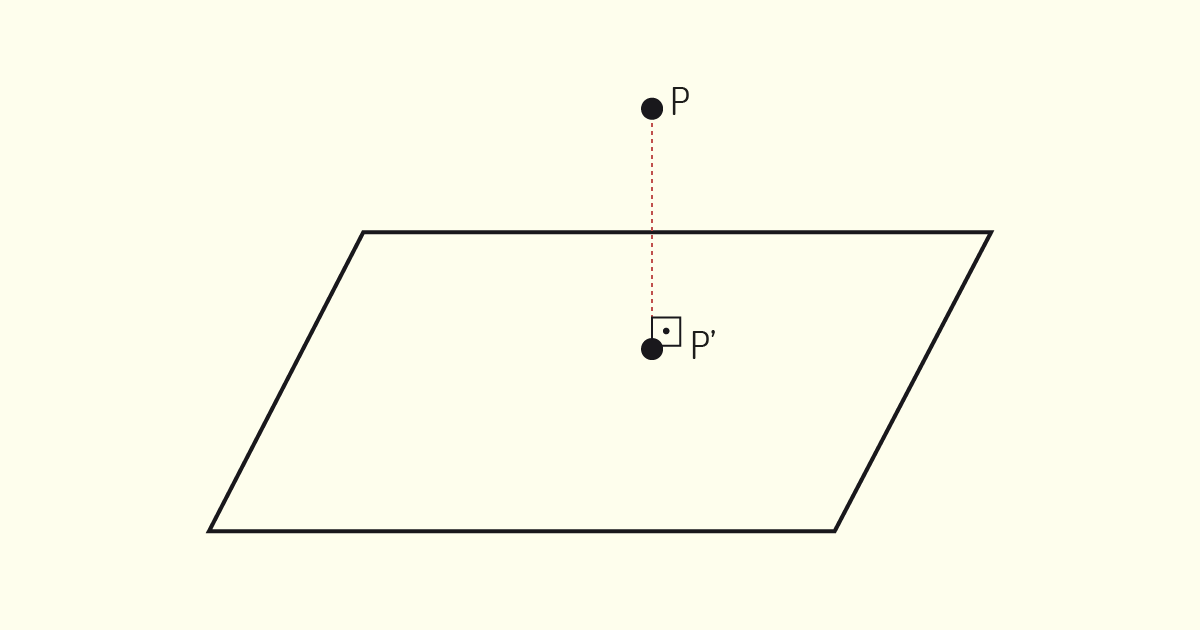
Cada ponto representado no método mongeano terá, então, ao menos duas projeções nesta épura, uma sobre o Plano Horizontal e outra sobre o Plano Vertical. Apesar de o método utilizar dois planos de projeção, ambas as figuras geradas são representadas em uma mesma folha de desenho. Essa forma de representação utiliza a projeção ortogonal, na qual os raios projetantes ou Linhas de Chamadas são perpendiculares ao plano. A projeção ortogonal de um ponto será o pé da perpendicular entre o ponto e o plano de projeção (RICCA, 2011). Observe o exemplo na figura a seguir.
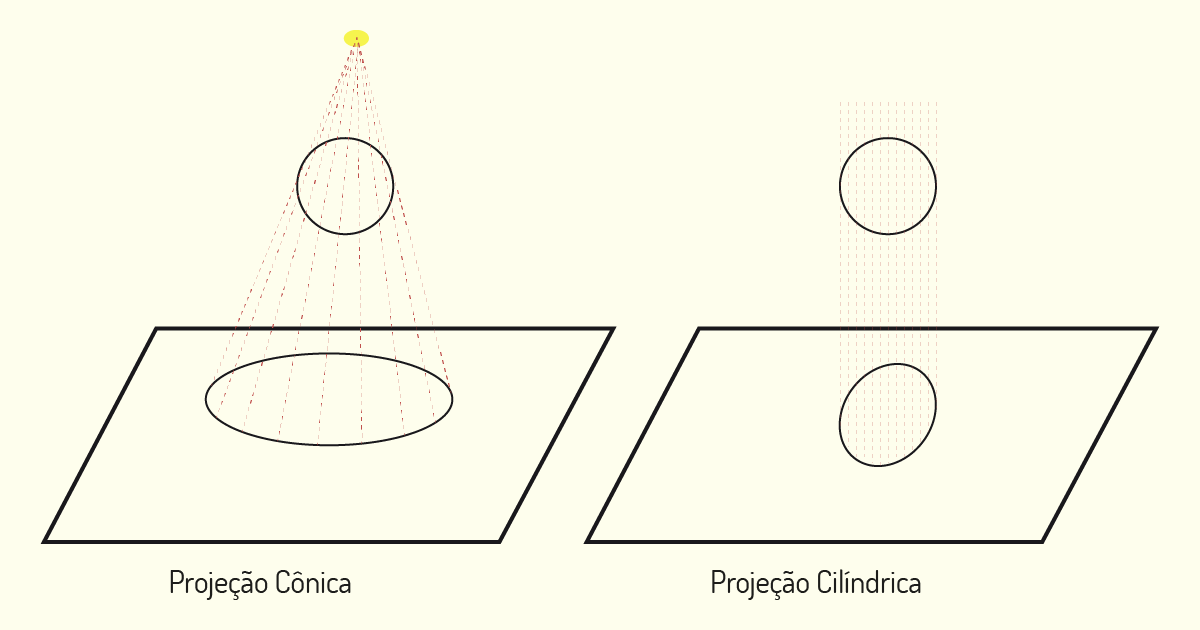
Imagine a seguinte situação: com uma lanterna apontada para um objeto, você irá criar sua sombra sobre uma parede. A sombra gerada é uma figura plana, sem profundidade e que nem sempre mantém a forma da figura original. Por exemplo, caso existam, no objeto, superfícies inclinadas em relação ao plano de projeção, no caso, a parede, elas não serão representadas de forma fiel ao real.
A projeção ortogonal que iremos realizar para a representação do modelo funciona como se fosse uma sombra, porém com raios projetantes paralelos. No exemplo da lanterna, temos apenas um centro de projeção que emite os raios projetantes. Para a projeção ortogonal, teremos os raios sendo emitidos de forma paralela, o que assegurará que as dimensões registradas sejam iguais as do modelo, sem distorções, sempre que a face representada estiver paralela ao plano de projeção. Observe, no exemplo a seguir, a diferença entre uma projeção cônica, com um centro de projeção, e uma projeção cilíndrica, com raios projetantes paralelos entre si.
Devemos estar atentos ao tipo de projeção com a qual estamos trabalhando. Um mesmo objeto pode ser representado de diversas formas, variando conforme o método de projeção que escolhemos. Para definir qual projeção é a mais adequada, precisamos compreender qual é o objetivo de nosso desenho: representar o objeto de forma técnica para a sua execução?; ilustrar o máximo de faces do objeto?; conhecer a finalidade do desenho e orientar a nossa escolha?
Em nossa atividade projetual, iremos trabalhar com a reprodução de vistas ortográficas. Seja em um projeto arquitetônico para a criação de uma edificação, um detalhamento de um móvel ou de um ambiente ou, ainda, para elaboração de um projeto mecânico, com detalhamento e especificações de peças, sempre incluiremos as vistas ortográficas no projeto.
Quando estamos desenhando uma fachada de um prédio, por exemplo, estamos trabalhando com vistas ortográficas; é como se o observador estivesse disposto de modo frontal à edificação. As linhas que “puxamos” do corte e planta baixa do projeto para a criação da fachada correspondem às Linhas de Chamada na Geometria Descritiva. Essas linhas servem de base para a criação do desenho de fachada, assim como as Linhas de Chamada ou Raios Projetantes são as guias para a criação das formas em GD.
Como já apontamos anteriormente, são essas vistas que permitirão a correta leitura e identificação do projeto como um todo, seja para sua análise, criação de orçamento ou execução. Na Geometria Descritiva, utilizamos duas projeções para a representação do modelo, no plano vertical e no plano horizontal, registradas na épura. No desenho técnico, iremos perceber que, na maioria das vezes, apenas duas projeções não são o suficiente para o registro e interpretação do objeto. Nesses casos, o mais usual é utilizarmos ao menos três projeções, a vertical, a horizontal e a de perfil, que darão a noção de profundidade do modelo representado.
Em situações mais complexas, como no registro de peças mecânicas, por exemplo, é comum trabalharmos com mais vistas, como se estivéssemos inserindo o objeto registrado no interior de um paralelepípedo, resultando, então, em um total de seis vistas. As faces do objeto são projetadas em cada uma das faces desse cubo imaginário; quando “abrimos” essa figura, os resultados serão as vistas ortogonais.
A organização do desenho é feita a partir da vista principal. Quando a representação for realizada no 1° Diedro, em relação à projeção da vista frontal (VF), iremos encontrar: vista superior (VS) abaixo, vista inferior (VI) acima, vista lateral esquerda (VLE) à direita, vista lateral direita (VLD) à esquerda e vista posterior (VP) ao lado da VLE ou da VLD, conforme a conveniência. Observe o exemplo na figura a seguir.
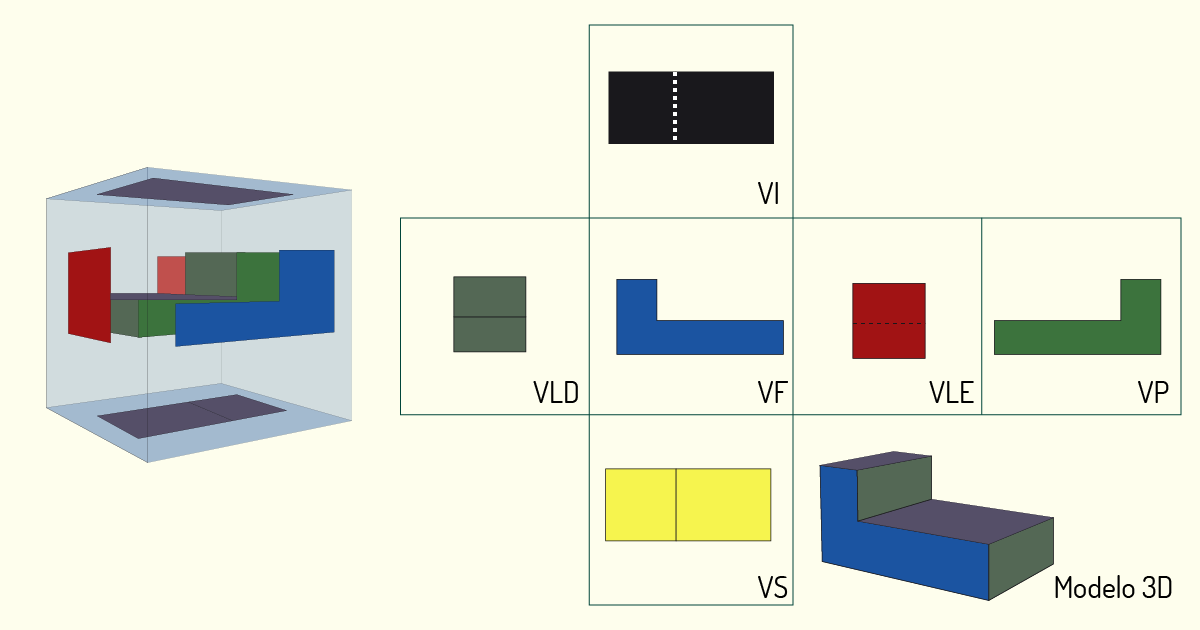
No Desenho Técnico, as faces principais do objeto a ser retratado devem estar posicionadas de forma paralela ao plano de projeção, para que as dimensões sejam representadas de acordo com a sua verdadeira grandeza (VG). Em casos que existam faces inclinadas nos objetos, é indicado criar planos de projeções auxiliares para seus registros.
Outra particularidade a qual devemos estar atentos no Desenho Técnico é que, usualmente, não se representa a LT, assim como o traço do plano de projeção em perfil. Apesar disso, é necessário manter as distâncias e regras de posicionamento da Geometria Descritiva, resultado da dupla projeção ortogonal e o rebatimento dos planos.
A representação de contornos e arestas visíveis na face projetada deve ser realizada com linha de traçado contínuo, enquanto contornos e arestas não visíveis por estarem ocultos por uma das faces devem ser realizados em linha tracejada.
No Brasil, a Associação Brasileira de Normas Técnicas - ABNT apresenta determinações para a realização de Desenho Técnico por meio da NBR 10067/1995 - Princípios Gerais de Representação em Desenho Técnico.
De acordo com tal Norma, a vista mais importante de uma peça deve ser utilizada como vista frontal. Na maioria das vezes, tal vista corresponde à representação da peça em sua posição de utilização. A vista frontal irá ilustrar a forma mais característica do objeto, preferencialmente, ilustrando-o em sua maior dimensão. Por exemplo, para desenharmos um sofá, a vista frontal será aquela que corresponde à visão que o usuário tem quando vai sentar-se nele, registrando seu assento e encosto.

A Norma também orienta que, ao representar um objeto, é necessário evitar a repetição de detalhes, assim como linhas de projeção desnecessárias. Esse excesso de informações pode prejudicar a legibilidade do projeto. Também devemos estar atentos para que todas as informações necessárias estejam contidas nos desenhos criados, pois tanto o excesso quanto a escassez de vistas podem ser prejudiciais.
O número de vistas representadas irá variar conforme a necessidade de cada caso, devendo ser utilizado o menor número possível de vistas. Elementos repetitivos podem ser simplificados e peças que apresentam simetria podem ser representadas apenas por uma parte do todo. Para isso, devemos criar uma linha de simetria, na qual, em suas extremidades, haverá a representação de dois traços curtos e paralelos para indicar essa condição de simetria.
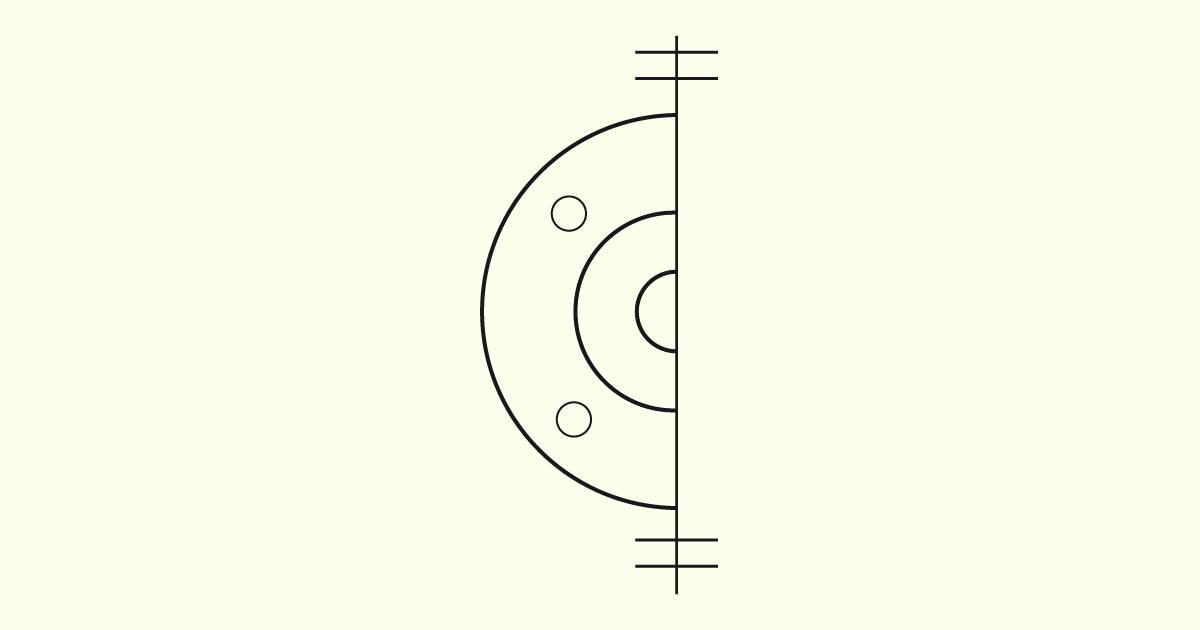
Para realizarmos a leitura das vistas ortográficas, devemos analisar todas as projeções de um modelo de forma conjunta, e não cada projeção de forma isolada. O Diedro no qual o objeto está representado também deve ser verificado para a correta leitura do desenho.
As projeções de um mesmo elemento do modelo estarão sempre sobre o mesmo alinhamento, ou seja, sobre a mesma Linha de Chamada. Isso significa que dois pontos, quando retratados em vista frontal, vista superior e vista lateral, por exemplo, irão manter o mesmo alinhamento em todas elas.
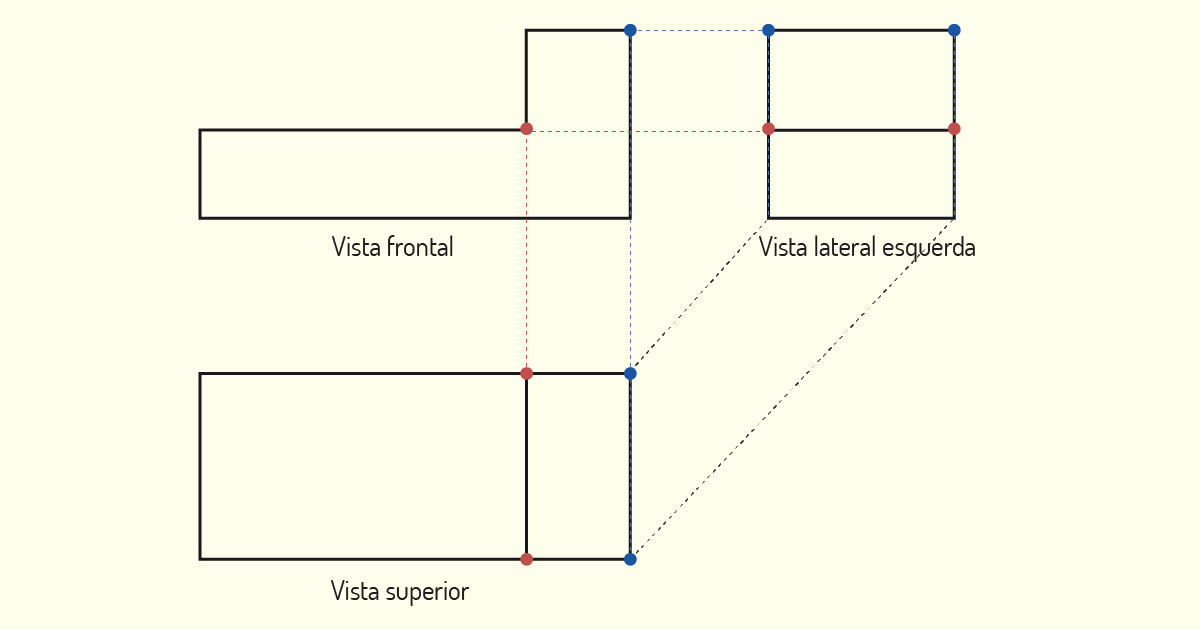
Outro ponto importante para a leitura das formas é lembrarmos que uma linha que separa duas áreas vizinhas em uma vista indica que tais áreas não estão no mesmo plano, isto é, existe um desnível entre elas. Por fim, também devemos estar atentos para as propriedades de projeção de reta e faces, assunto que iremos abordar de modo mais detalhado nas próximas aulas.
Uma face, quando projetada, será representada como aresta, se estiver perpendicular ao plano de projeção, ou como face, quando estiver paralela ou inclinada ao plano de projeção. Já a reta será representada como ponto, quando estiver perpendicular ao plano de projeção, ou como aresta, se estiver paralela ou inclinada ao plano de projeção.
O desenho técnico é um instrumento utilizado pelo projetista para comunicar-se com os demais sujeitos de um projeto. É por meio das peças gráficas que uma ideia é representada e pode ser comunicada ao cliente, ao executor e aos fornecedores. Apesar desse papel significativo, alguns projetistas encontram dificuldade no processo de representar o desenho técnico. Para aprimorar esses atributos, confira: <https://www.archdaily.com.br/br/889405/20-dicas-de-desenho-tecnico-para-arquitetura>. Acesso em: 22 fev. 2019.
Você encontrará, no link, 20 dicas que podem te ajudar na elaboração de desenhos mais claros e com qualidade estética!

2) A épura consiste na planificação dos diedros e é por meio dela que podemos registrar objetos tridimensionais de modo bidimensional. Sobre a épura, assinale a alternativa correta.
a) Na épura, o Semi-Plano Horizontal Posterior é rebatido sobre o Semi-Plano Horizontal Anterior.
Justificativa: em épura, o PH é rebatido sobre o SV (semi plano vertical superior).
b) A projeção vertical de um objeto, no terceiro diedro, será representada abaixo da Linha de Terra.
Justificativa correta: a partir do rebatimento dos planos, um objeto no terceiro diedro será representado: projeção horizontal = acima da LT e projeção vertical = abaixo da LT.
c) A épura é representada por projeções nos planos verticais, enquanto as projeções nos planos horizontais são representadas em planos bissetores.
Justificativa: na épura, são registradas tanto as projeções nos planos horizontais quanto nos planos verticais.
d) Quando em épura, a Linha de Terra passa a ser representada no sentido vertical.
Justificativa: a Linha de Terra é representada de modo horizontal tanto nos diedros quanto em épura.
e) A projeção de um objeto, no quarto diedro, será representada acima da Linha de Terra, quando em épura.
Justificativa: um objeto no quarto diedro será representado em épura apenas com projeções abaixo da Linha de Terra, devido ao rebatimento dos planos.
Enquanto a projeção cilíndrica considera raios projetantes paralelos, a projeção cônica leva em consideração raios projetantes que partem de uma única fonte. Essa diferença gerará resultados distintos, quando trabalhamos com a projeção de um mesmo objeto, sobre uma mesma superfície. Diante disso, você acredita que existe um modo de representação melhor ou pior para o registro de projetos? Você acha que o tipo de projeção adotada pode influenciar na leitura e entendimento do projeto?

Uma vez compreendidos os fundamentos básicos para a representação de objetos de acordo com a Geometria Descritiva, iremos, agora, analisar a relação dos elementos geométricos nesse tipo de representação. Iniciamos o nosso estudo pelo elemento mais básico, que é o ponto, e iremos, gradativamente, aumentando o nível de complexidade das formas.
O estudo do ponto irá concentrar-se na posição em que ele é encontrado no espaço e como isso influenciará em sua projeção sobre os planos. Um ponto pode apresentar as seguintes posições, em relação aos planos ortogonais de projeção:
Para assegurar que o sistema possua precisão na representação das formas, cada ponto do modelo apresentado irá dispor de coordenadas que o fixam no espaço. A partir dessas coordenadas, conseguimos determinar, de forma exata, qual a localização dos pontos retratados.
Os pontos que não estiverem locados sobre a Linha de Terra ou sobre um dos planos de projeção estarão localizados em um dos quatro Diedros e apresentarão projeções horizontais e verticais, que ocorrem quando o raio projetante, que passa pelo ponto, intercepta o plano de projeção.
As distâncias do ponto ao plano de projeção horizontal denominam-se Cota. As cotas podem apresentar valor positivo (+) ou negativo (-), dependendo de sua localização no espaço. Quando o ponto estiver acima do plano de projeção horizontal, ou seja, no 1° ou 2° Diedro, o valor da cota será positivo. Caso o ponto esteja abaixo do plano de projeção horizontal, seja no 3° ou 4° Diedro, o valor da cota será negativo.
As distâncias do ponto ao plano de projeção vertical denominam-se Afastamento. Os afastamentos também são representados por valores positivos (+) ou negativos (-), variando conforme a sua localização. Quando o ponto estiver a direita do plano de projeção vertical, no 1° ou 4° Diedro, o valor do afastamento será positivo. Caso o ponto esteja a esquerda do plano de projeção vertical, no 2° ou 3° Diedro, o valor do afastamento será negativo.
Essas duas coordenadas, Cota e Afastamento, ajudam a localizar o ponto no espaço, porém, como estamos trabalhando com elementos tridimensionais, é necessário, ainda, determinar a distância do ponto em relação seu sentido longitudinal. Com essas três coordenadas, é possível fixar, totalmente, o ponto no espaço.
Para determinarmos a distância do ponto em seu sentido longitudinal, será necessária a criação de mais um plano, além dos planos horizontais e verticais existentes. Esse novo plano, denominado Plano de Perfil, deve ser perpendicular aos planos de projeção, bem como determinará a coordenada das Abscissas. Quando um ponto estiver à direita do Plano de Perfil, o valor da abscissa será positivo, enquanto que, se o ponto estiver à esquerda do Plano de Perfil, o valor da abscissa será negativo.
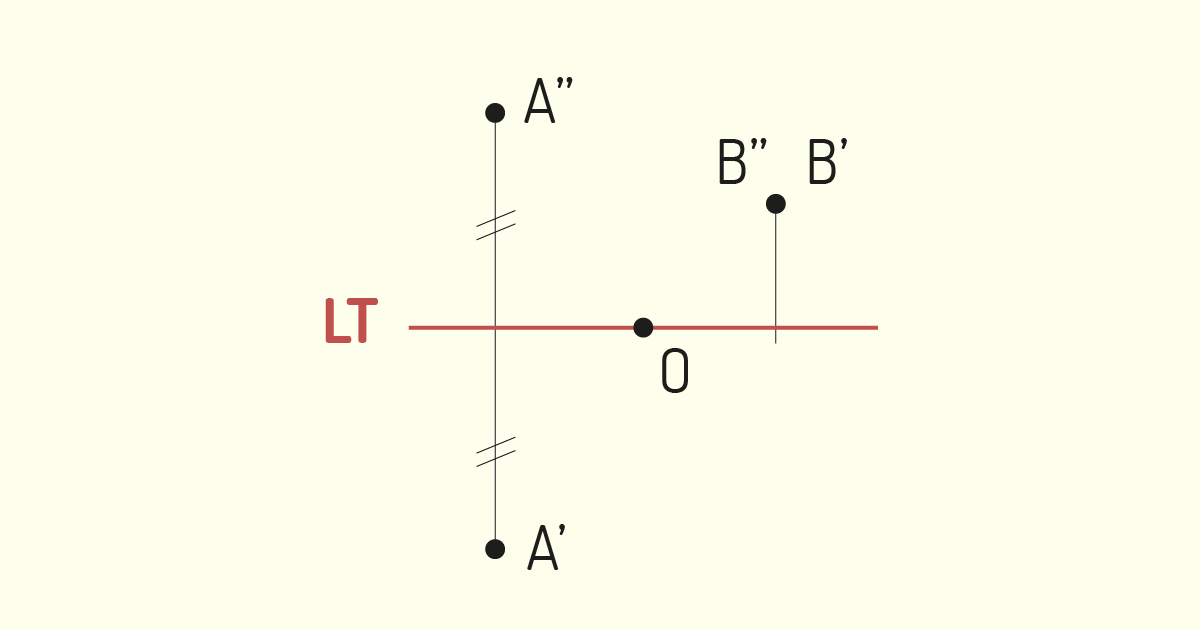
A representação de tais coordenadas deve ser feita seguindo a ordem: abscissa, afastamento e cota. Por exemplo, se dissermos que (A) (2,3,4), significa que um ponto (A) tem abscissa 2, afastamento 3 e cota 4, todos os valores de forma positiva. Com isso, podemos concluir que o ponto está localizado no 1° Diedro, pois tanto afastamento quanto cota são positivos. Observe a representação desse ponto na figura a seguir.
Fique atento à representação da épura de um ponto! Você se lembra que a épura consiste no rebatimento do plano de projeção horizontal sobre o plano de projeção vertical? Em decorrência disso, devemos tomar cuidado na leitura dessas coordenadas. O Afastamento é medido positivamente, quando abaixo da Linha de Terra, e negativamente, quando acima dessa mesma linha. Isso ocorre, pois, com o rebatimento dos planos de projeção, o Semi-Plano Horizontal Posterior (PH), localizado à esquerda do plano de projeção vertical (-), é rebatido para a região acima da Linha de Terra, enquanto o Semi-Plano Horizontal Anterior (AH), localizado à direita do plano de projeção vertical (+), é rebatido para a região abaixo da Linha de Terra.
Como na formação, na épura, o plano de projeção vertical não muda, os valores de cota são os mesmos, quando representados nos Diedros, além de as distâncias acima da Linha de Terra serem positivas, enquanto as distâncias abaixo da Linha de Terra são negativas. Com relação às abscissas em épura, devemos considerar que as medidas positivas estarão à direita da Origem das Abscissas, enquanto as medidas negativas estarão à esquerda de tal origem.
Os pontos pertencentes ao plano de projeção horizontal apresentarão cota nula e afastamento positivo, caso estejam no semi-plano horizontal anterior, ou afastamento negativo, se estiverem no semi-plano horizontal posterior. Já os pontos pertencentes ao plano de projeção vertical irão possuir afastamento nulo. Sua cota será positiva, caso estejam localizados no semi-plano vertical superior, ou negativa, caso estejam no semi-plano vertical inferior.
Os pontos pertencentes aos bissectores apresentam valor absoluto igual para cota e afastamento. Isso significa que suas projeções apresentam simetria em relação à Linha de Terra. Embora o valor absoluto seja igual para as duas coordenadas, estas podem apresentar sinal contrário. Quando o ponto está localizado sobre o bissetor ímpar, cota e afastamento serão iguais em valor e em sinais, sendo os dois positivos ou negativos.
Já quando o ponto está localizado sobre o bissetor par, cota e afastamento serão iguais em valor, porém com sinais opostos; uma das coordenadas será positiva, enquanto a outra será negativa. Isso irá resultar em pontos de projeção coincidentes em épura.
A partir do estudo do comportamento de um ponto em épura, podemos desenvolver o mesmo raciocínio para situações mais complexas, como a reta, um plano e um volume. Por esse motivo, é necessário que o conceito de épura e diedros esteja claro, uma vez que são essas definições que irão guiar-nos no estudo da representação no desenho técnico.
A reta configura-se como um ente primitivo, de maior complexidade que o ponto, porém mais simples do que um plano. A projeção ortogonal de uma linha sobre um plano de projeção corresponde à projeção ortogonal de todos os pontos que a compõem sobre tal plano. Isso significa que o modo de projeção de uma linha é semelhante ao que discutimos no estudo do ponto.
Se a linha considerada for uma reta, na maioria das vezes, a sua projeção sobre o plano também será uma reta. Perceba que não estamos afirmando que todas as projeções serão retas! Não podemos declarar tal fato, pois, quando a linha encontra-se de modo perpendicular ao plano, a projeção de seus diferentes pontos estarão coincidindo em um único ponto.
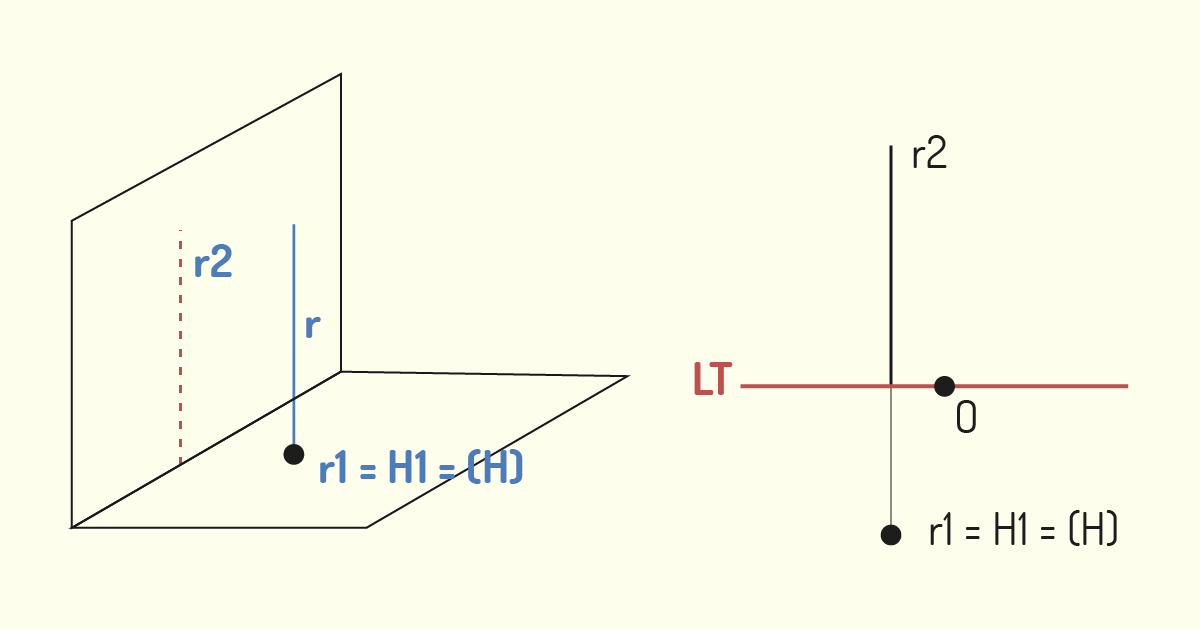
O comprimento total da projeção da reta sobre o plano também irá variar em função de sua inclinação, em relação ao plano de projeção. O menor comprimento apresentado pela projeção de uma reta é quando esta está disposta de modo perpendicular ao plano, resultando, assim, em um ponto. Já o maior comprimento apresentado por sua projeção é quando a reta está ordenada de modo paralelo ao plano e é representada em Verdadeira Grandeza, refletindo o tamanho real da reta.
Quando trabalhamos com um segmento de reta, com início e fim, para realizarmos a sua representação, devemos marcar a projeção de seu ponto inicial e de seu ponto final e, em seguida, uni-los com um traçado. A representação do segmento de reta, assim como ocorre na representação de pontos, é feita no plano de projeção horizontal e no vertical, que são rebatidos para gerar a épura.
Uma reta pode, ainda, atravessar um dos planos de projeção. O ponto da reta que toca um desses planos recebe o nome de Traço de Reta. Quando o ponto pertence a uma reta que atravessa o plano de projeção horizontal, ele é denominado Traço Horizontal da Reta e tal ponto terá a Cota nula. Já quando o ponto faz parte de uma reta que atravessa o plano de projeção vertical é denominado Traço Vertical da Reta e conta com Afastamento nulo. Para determinarmos o Traço da Reta em épura, devemos prolongar as projeções da reta até a Linha de Terra.
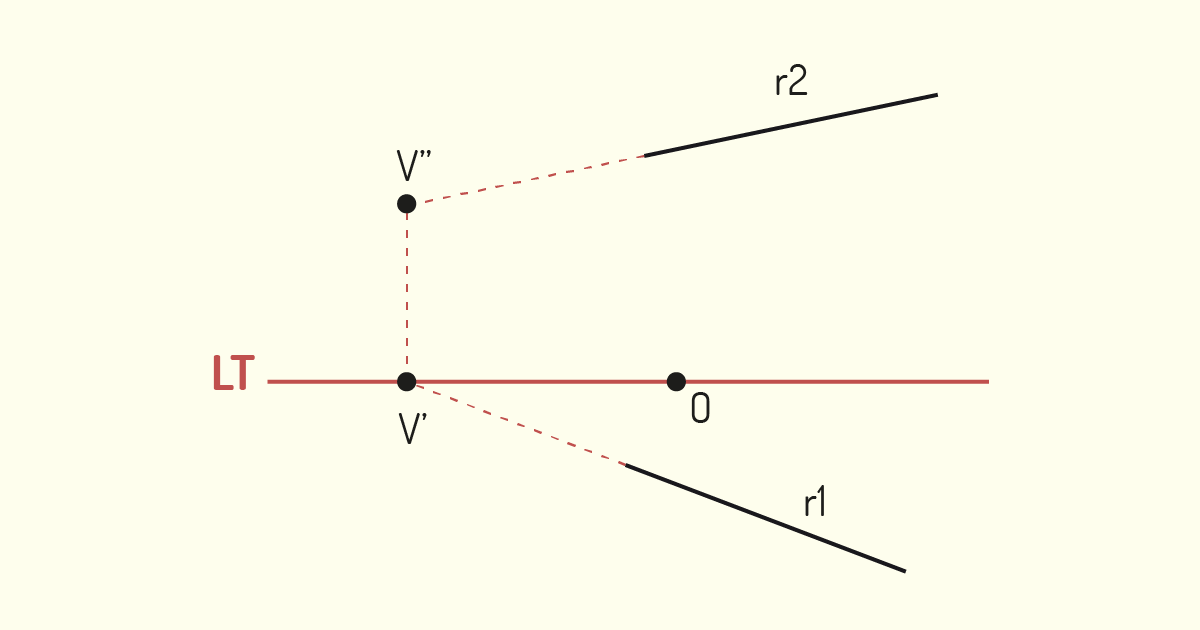
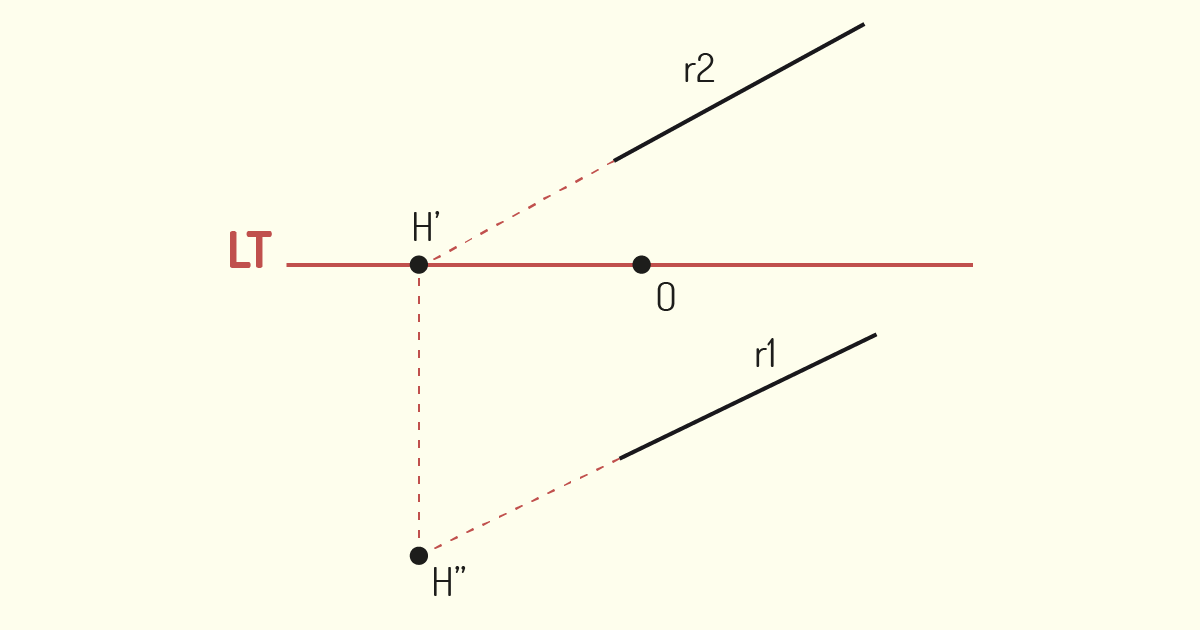
No estudo de representação das retas, notaremos que suas posições particulares irão influenciar em suas projeções. Segundo Ricca (2011), as retas podem adotar as seguintes posições:
Outra análise que devemos realizar, no estudo das retas, é a posição relativa em situações em que há mais de uma reta. De acordo com Ricca (2011), duas retas no espaço podem ser coplanares, se estiverem situadas em um mesmo plano ou, então, não coplanares, quando não estiverem contidas em um mesmo plano. As retas coplanares podem ser paralelas ou concorrentes, enquanto as não coplanares serão reversas. Vamos analisar cada uma dessas situações.
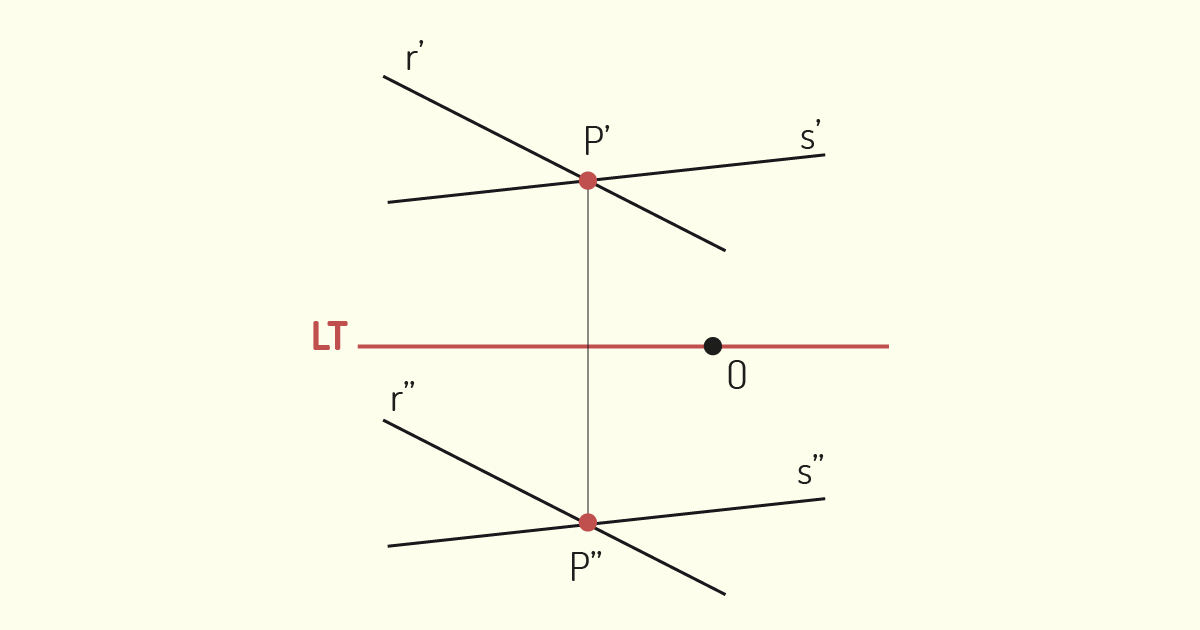
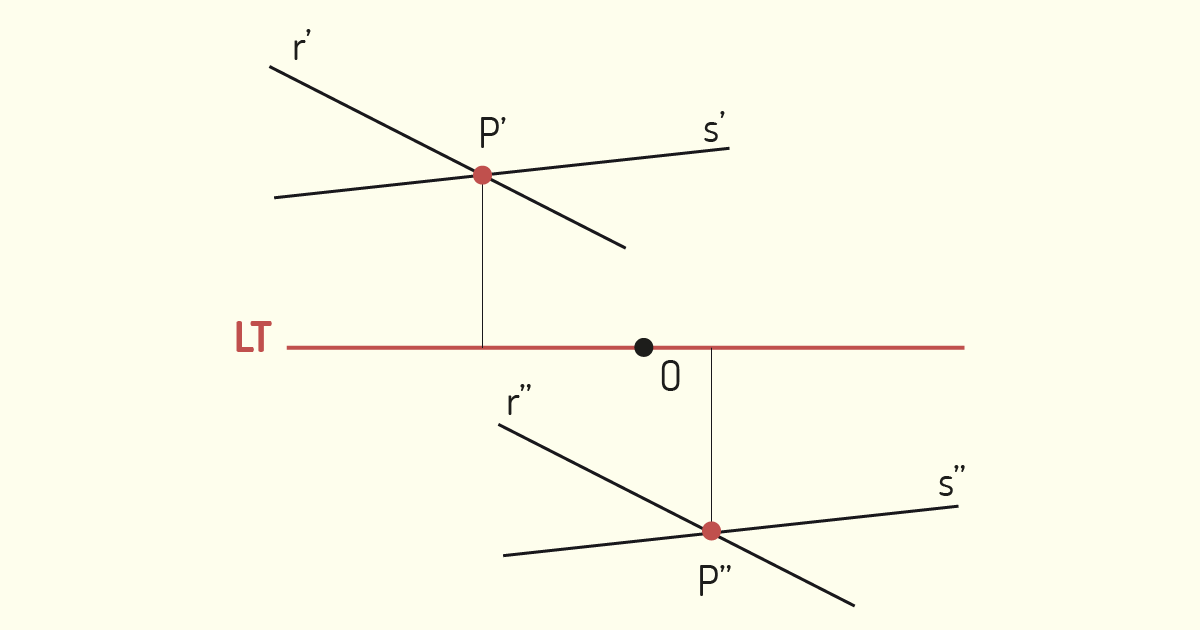
3) Sobre o estudo de ponto e de reta, na Geometria Descritiva, assinale a alternativa correta.
a) Quando um ponto está localizado sobre um plano bissetor par, cota e afastamento são iguais em sinal e em módulo.
Justificativa: quando um plano está sobre um plano bissetor par, sua cota e afastamento serão de mesmo valor, porém de sinais opostos.
b) Reta frontal e reta horizontal são tipos de retas que estão respectivamente paralelas ao plano de projeção vertical e plano de projeção horizontal.
Justificativa correta: as retas, quando nessas posições, encontram-se de modo paralelo aos planos de projeção.
c) O traço de uma reta é o local em que ela cruza um plano bissetor.
Justificativa: o traço da reta é o local em que ela cruza um plano de projeção, podendo ser traço horizontal da reta ou traço vertical da reta.
d) Retas coplanares, quando paralelas, apresentam um ponto de intersecção.
Justificativa: retas coplanares paralelas não apresentam ponto de intersecção.
e) Quando uma reta é oblíqua ao plano de projeção, é representada em sua Verdadeira Grandeza.
Justificativa: a reta é representada em sua Verdadeira Grandeza quando está paralela a um plano de projeção.
Dando continuidade ao estudo da Geometria Descritiva, iremos abordar a representação do plano segundo o método mongeano e conheceremos os métodos descritivos. Para representarmos um plano, será necessário resgatar as definições e o método de projeção que realizamos em pontos e em retas.
Já os métodos descritivos, como você pode imaginar, não são métodos restritos à projeção. Iremos perceber que estes tratam da movimentação de elementos para a representação das formas, seja por meio da movimentação do modelo retratado ou dos planos de projeção.
Para representarmos a projeção de um plano na Geometria Descritiva, devemos retratar a projeção dos elementos que o determinam, ou seja, os pontos e retas que delimitam tal plano. Quando trabalhamos com a Geometria Descritiva, o plano comumente é representado por meio de seus traços. O Traço da Reta será o ponto onde esta “fura” o plano de projeção vertical ou o plano de projeção horizontal, como vimos na aula anterior.
No estudo do plano, perceberemos que o Traço do Plano age de modo similar. A reta interseção de dois planos irá ser denominada como o Traço do Plano. Quando tal encontro se der com um dos planos de projeção, ela passa a ser denominada Traço Horizontal do Plano e Traço Vertical do Plano, de acordo com o plano de projeção em que ela intersectar.
O Traço Horizontal do Plano é uma reta horizontal de cota nula, enquanto o Traço Vertical do Plano é uma reta vertical de afastamento nulo. O traço de um plano tem sua projeção de nome contrário na Linha de Terra, ou seja, o Traço Horizontal do Plano terá a projeção vertical na Linha de Terra. Outra característica do Traço do Plano é que, em épura, eles serão paralelos à Linha de Terra ou concorrentes a ela.
Para verificarmos se uma reta ou um ponto são pertencentes a um plano, devemos considerar os seguintes aspectos:
Dentre as retas pertencentes a um plano, aquelas que se encontram localizadas de modo paralelo aos planos de projeção são chamadas de Retas Principais do plano. Tais retas irão corresponder a duas direções distintas, uma referente ao plano de projeção horizontal e outra ao plano de projeção vertical. Segundo a Geometria Elementar, as retas de um plano podem, ainda, ser classificadas como Reta de Máximo Declive (RMD) e Reta de Máxima Inclinação (RMI).
As Retas de Máximo Declive são retas do plano que são perpendiculares à intersecção do plano dado com o plano de projeção horizontal. A projeção horizontal da RMD é perpendicular ao Traço Horizontal do Plano e a RMD é perpendicular a toda horizontal do plano.
As Retas de Máxima Inclinação são retas do plano que são perpendiculares à interseção do plano dado com o plano de projeção vertical. A projeção vertical da RMI é perpendicular ao Traço Vertical do Plano e a RMI é perpendicular a toda vertical do plano.
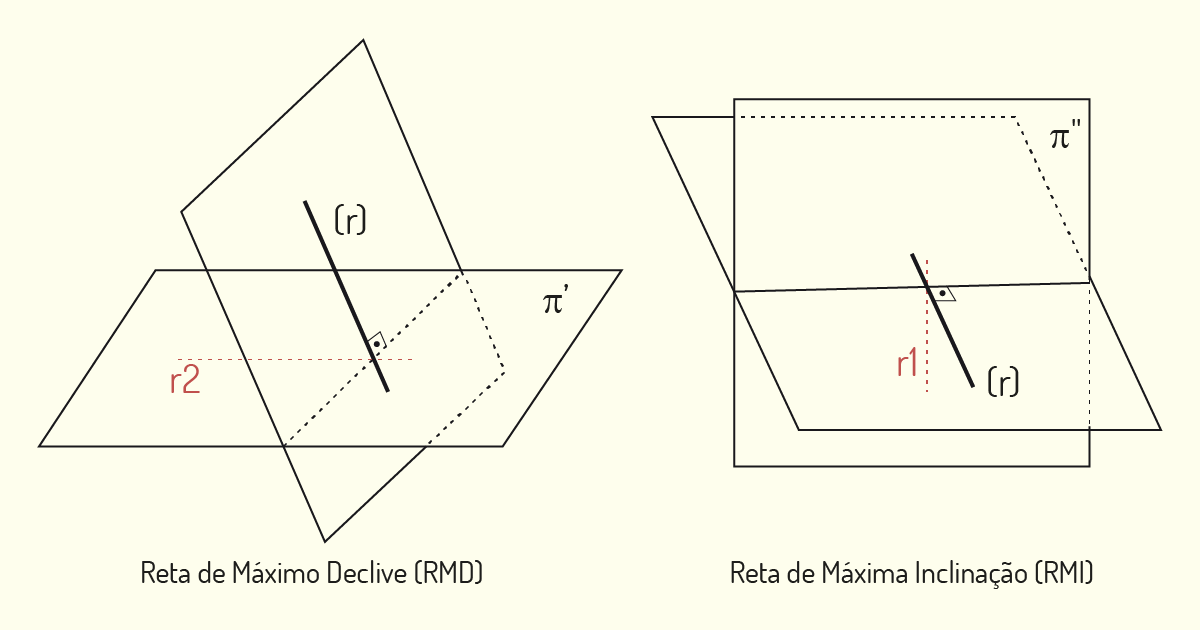
Assim como as retas, os planos ocupam uma região no espaço. A maneira como eles são dispostos irá influenciar na forma de suas projeções. Vamos analisar as posições particulares que o plano pode adotar:
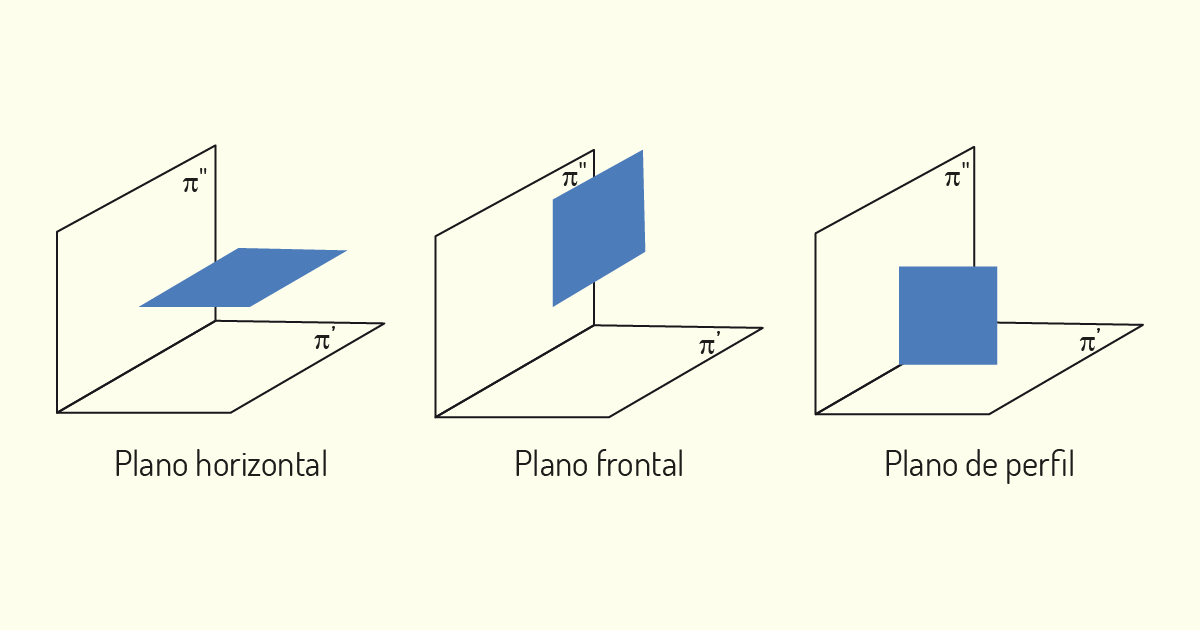
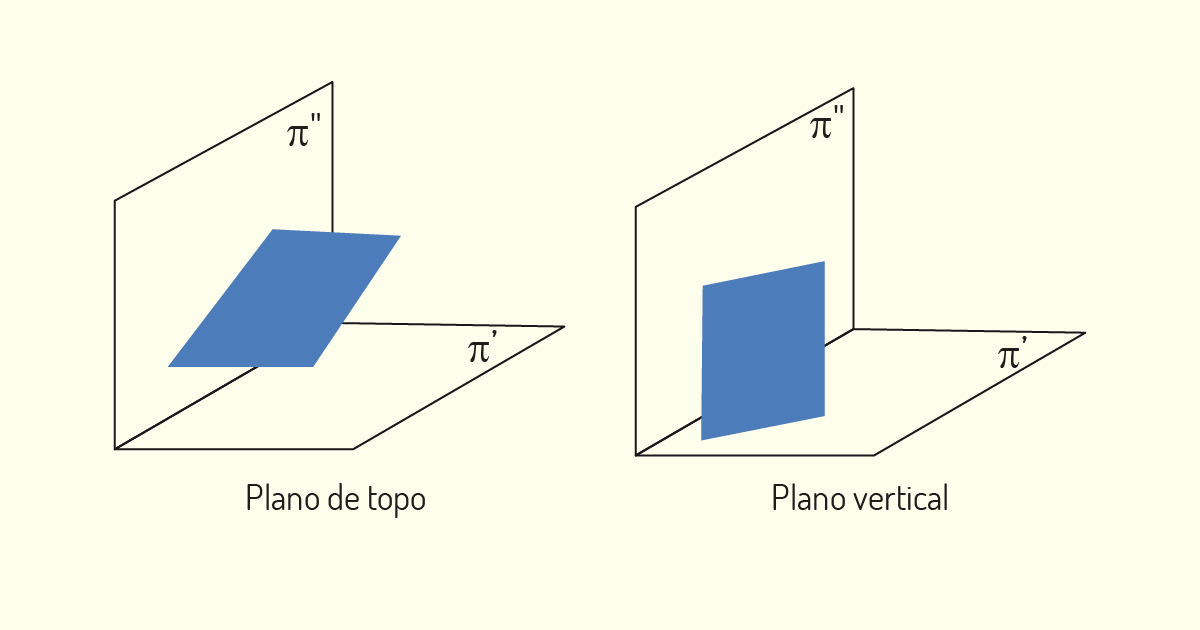
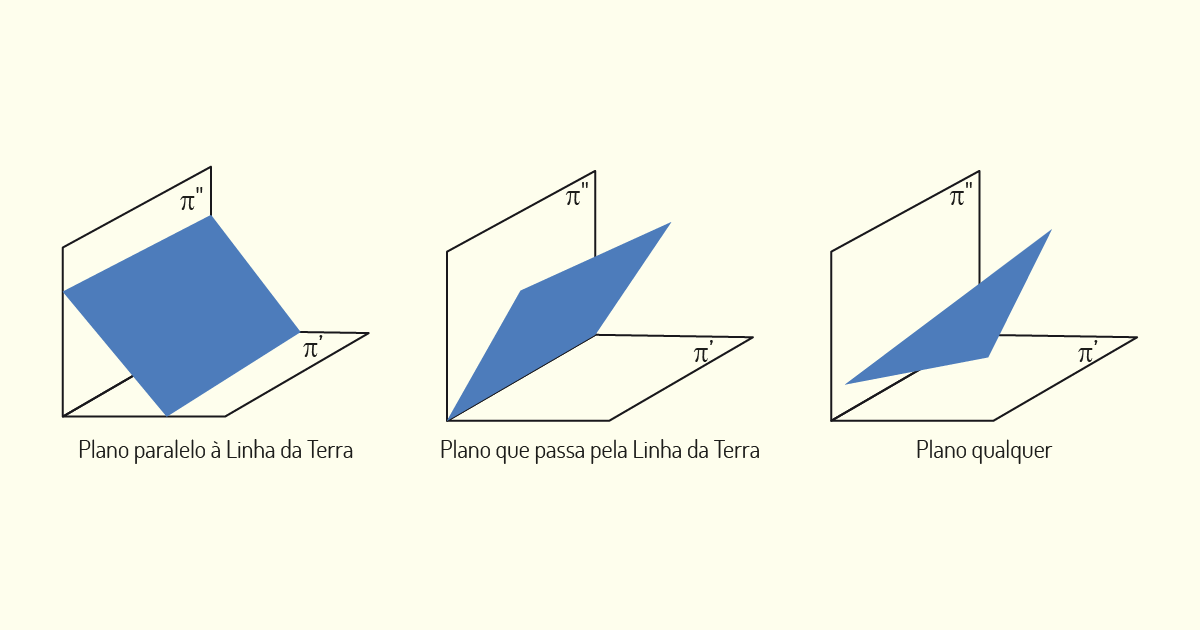
Os planos podem apresentar os mais diversos posicionamentos no diedro, e as situações indicadas são os principais casos com os quais iremos deparar-nos. É importante conseguirmos identificar qual a posição do plano, para orientar a nossa compreensão de como será a sua representação em épura.
Ao trabalharmos com a Geometria Descritiva, iremos deparar-nos com situações complexas, que podem ser simplificadas quando alteramos as posições particulares de seus elementos. Um exemplo de aplicação dessa modificação de posição é quando queremos descobrir a Verdadeira Grandeza de uma das faces do objeto, porém ela encontra-se posicionada de modo não paralelo ao plano de projeção.
Essa modificação da posição não pode ser feita de maneira arbitrária; é necessário seguirmos métodos para que a mudança mantenha as relações espaciais estabelecidas pelo modelo e suas projeções. Iremos conhecer três métodos descritivos que irão nos auxiliar nesse processo: método de rotação, rebatimento e mudança de plano de projeção. A escolha de um dos métodos deve ser feita a partir do objetivo pretendido. Devemos optar por seguir a opção que irá simplificar os problemas, utilizando do menor número de traçados.
O método de rotação consiste em rotacionar sobre um eixo fixo o objeto, uma face, uma aresta ou, ainda, um vértice do objeto. O eixo fixo de rotação sempre é uma reta perpendicular a um dos planos de projeção, podendo ser uma reta vertical ou uma reta de topo. Nesse tipo de modificação de posição, os planos de projeção continuam fixos em seu posicionamento original.
Quando rotacionamos um ponto ou uma reta, tendo, como eixo, uma reta vertical, o deslocamento será percebido no plano de projeção horizontal, enquanto que, quando assumimos, como eixo, uma reta de topo, o deslocamento será dado no plano de projeção vertical.
O método de rebatimento pode ser considerado um caso particular do método de rotação. Nessa situação, o plano é rotacionado ao redor de uma de suas retas, até que ele coincida com um dos planos de projeção ou a um plano paralelo a estes.
O método de mudança de plano baseia-se em manter a figura imóvel e alterar o plano de projeção, seja ele o vertical ou o horizontal. Nesse método, o modelo irá manter-se estático, enquanto o sistema de representação será modificado. Observe na figura a seguir.
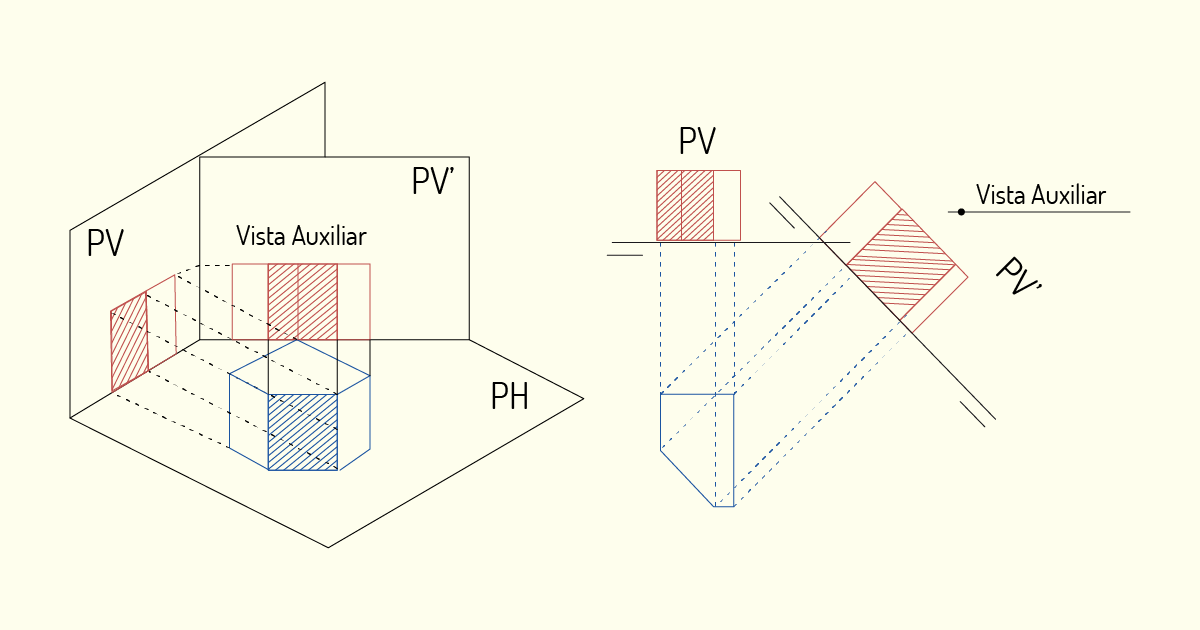
Quando realizamos a mudança no plano de projeção vertical (MPV), ele é substituído por um plano qualquer na vertical e perpendicular ao plano de projeção horizontal. Nesse caso, quando representamos um ponto, a sua projeção horizontal continua a mesma, pois não houve modificação nesse plano de projeção.
Para determinarmos a projeção com a mudança no plano de projeção vertical, devemos representar a nova Linha de Terra estabelecida entre os planos horizontal e vertical e, em seguida, traçar uma Linha de Chamada a partir da projeção horizontal, de modo perpendicular a nova Linha de Terra. Nessa Linha de Chamada, podemos marcar a nova projeção vertical, que terá o mesmo módulo e sinal do sistema inicial.
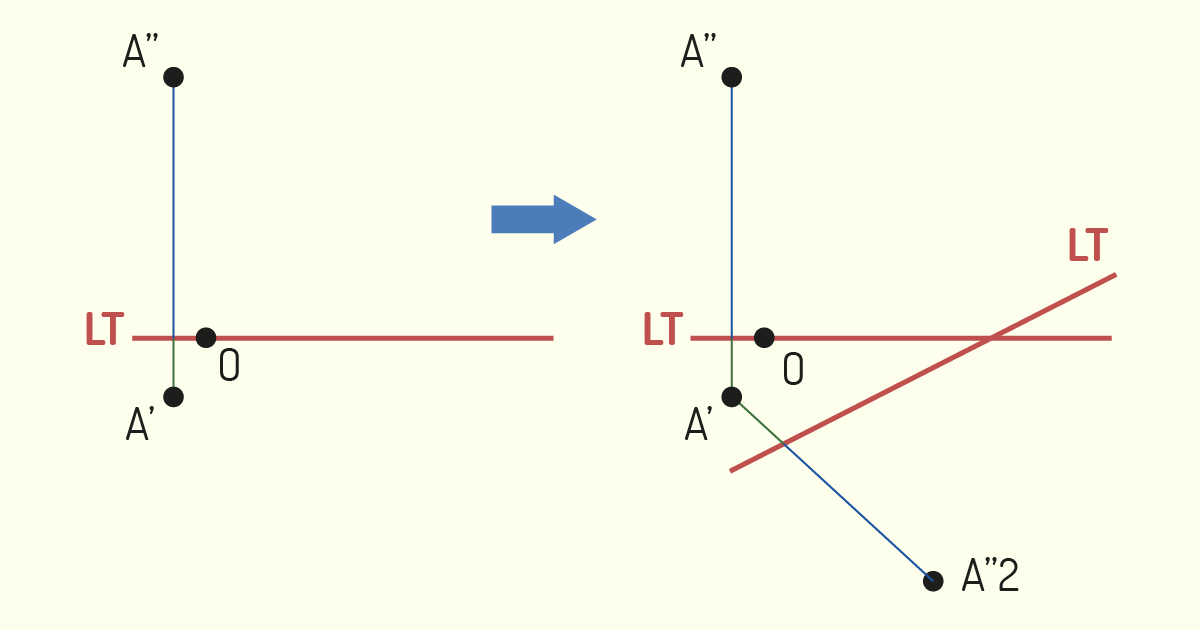
Quando realizamos a mudança no plano de projeção horizontal (MPH), ele é substituído por um plano qualquer na horizontal e perpendicular ao plano de projeção vertical. Nesse caso, quando representamos um ponto, a sua projeção vertical continua a mesma, pois não houve modificação nesse plano de projeção.
Para determinarmos a projeção com a mudança no plano de projeção horizontal, deveremos proceder de forma semelhante ao que realizamos anteriormente com o plano vertical, porém, nesse caso, a Linha de Chamada deverá ser traçada a partir do ponto de projeção vertical.
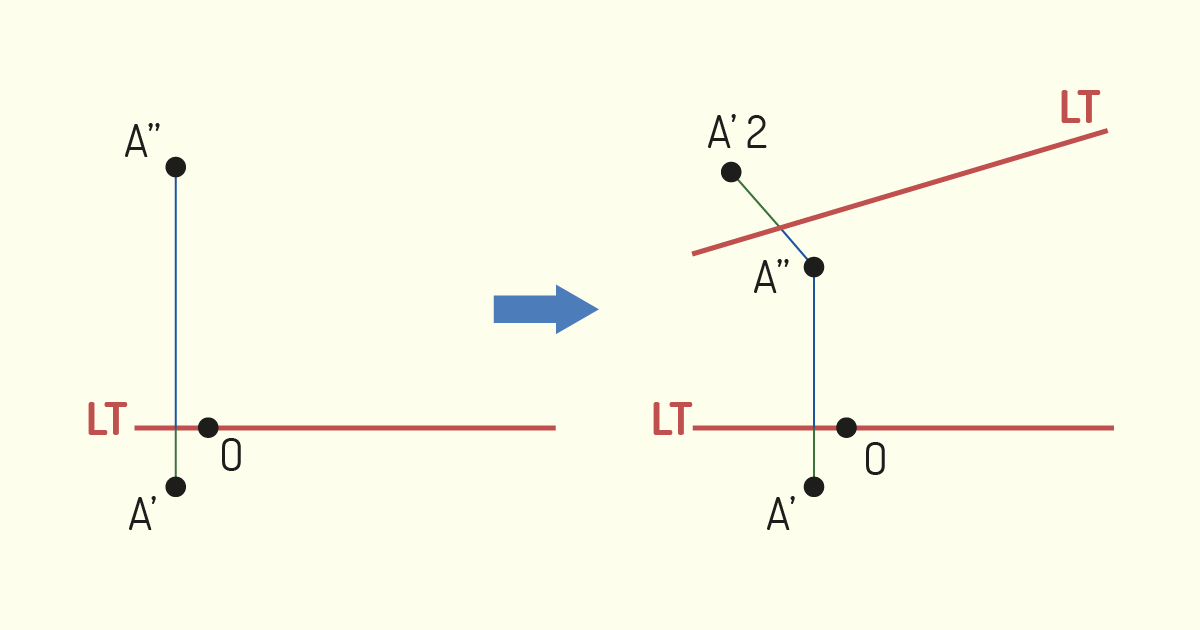
O estudo de retas com mudança no plano de projeção deve seguir o mesmo princípio para a criação de projeções de pontos. Para determinar a projeção de uma reta com mudança no plano de projeção, iremos definir dois pontos dessa reta, realizar a sua projeção, conforme apresentado anteriormente, e, em seguida, unir a projeção dos dois pontos por meio de uma reta. Lembre-se, sempre, de estar atento se a alteração de plano será MPH ou MPV, pois isso irá determinar o modo de aplicação do método.
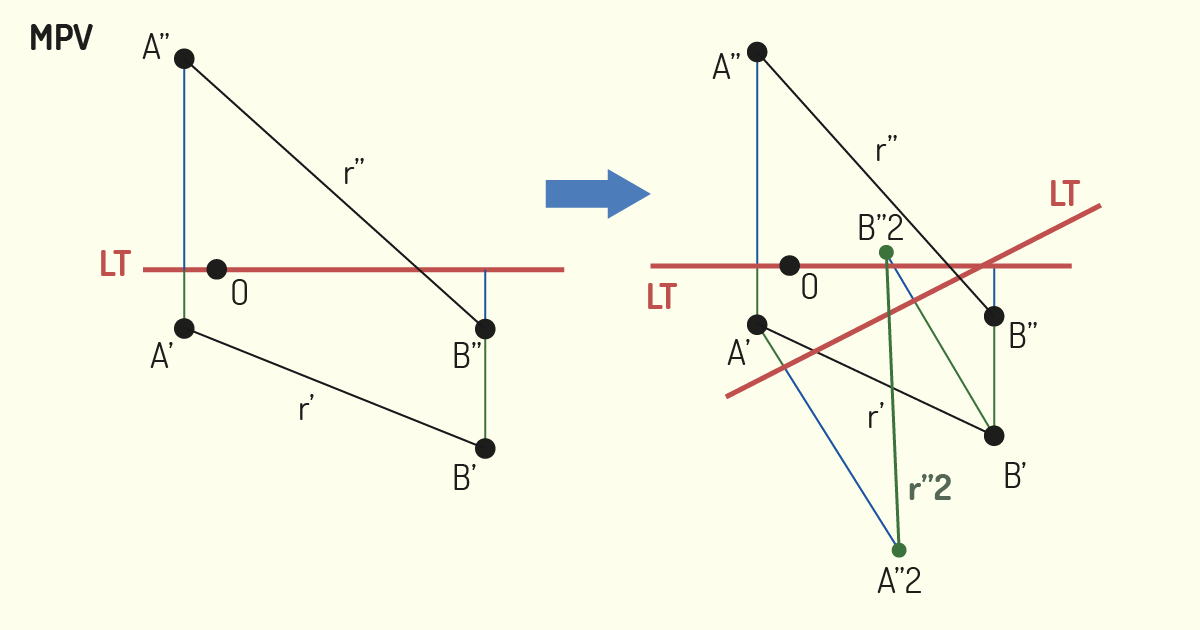
Para realizarmos o estudo de planos com mudança no plano de projeção, devemos decompor o plano a ser projetado em seus elementos primitivos, para tornar mais simples a sua representação.
Quando o plano é definido por duas retas, iremos utilizar uma reta do plano (Reta Principal do plano) e um ponto do plano, desde que ele não pertença a essa reta. Realizamos a projeção desses elementos de forma tradicional e, em seguida, utilizamos o método de mudança no plano de projeção, para encontrar a projeção final de tais elementos. Para traçar as novas projeções, devemos lembrar que o módulo e o sinal (positivo e negativo) desses distanciamentos devem ser mantidos.
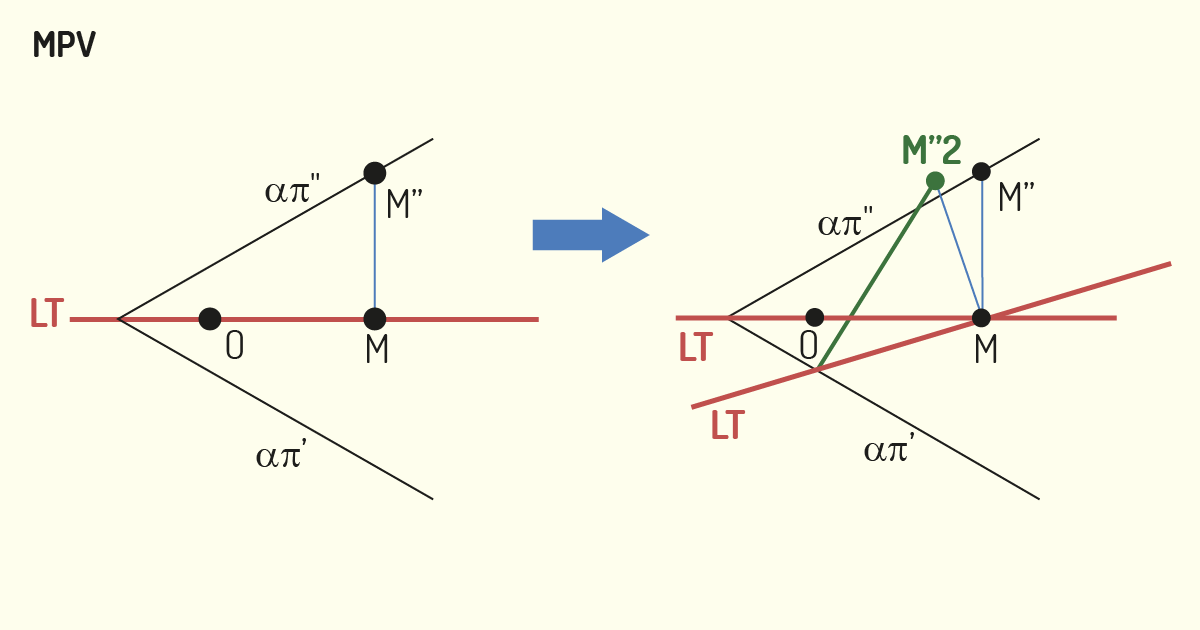
Quando o plano é definido por seus traços, iremos trabalhar com um ponto qualquer, localizado no traço vertical, para mudança de plano de projeção vertical, e um ponto localizado no traço horizontal, para a mudança de plano de projeção horizontal.
Em um caso de MPV, a nova Linha de Terra determinada deverá passar pela projeção horizontal de tal ponto. Em seguida, iremos transportar a cota do ponto de modo perpendicular à nova Linha de Terra, sempre mantendo seu módulo e sinal. Para finalizar a projeção, devemos criar um segmento de reta que passe por essa nova projeção vertical do ponto e o local de interseção entre a projeção horizontal e a nova Linha de Terra. Para realizarmos uma MPH, o processo é o mesmo, apenas devemos inverter os planos trabalhados.
A partir dos métodos apresentados, conseguimos resolver problemas de maior complexidade, sobretudo, aqueles nos quais não conhecemos a real dimensão de algum dos elementos representados. Lembre-se que os métodos que analisamos têm, como objetivo, simplificar o estudo das formas, e não torná-los mais complexas! Grande parte das situações com as quais iremos deparar-nos no desenho técnico não irá demandar a aplicação de um método descritivo.
4) Os métodos descritivos são aplicados para simplificar situações complexas. Sobre os métodos estudados, assinale a alternativa correta.
a) O método de rotação consiste em rotacionar o plano de projeção, de modo que este fique paralelo ao objeto.
Justificativa: no método de rotação, o objeto será rotacionado.
b) Por meio dos métodos descritivos, é possível descobrir a Verdadeira Grandeza de planos e retas.
Justificativa correta: por meio dos métodos descritivos, é possível deixar faces e arestas paralelas aos planos de projeção e, assim, determinar a sua Verdadeira Grandeza.
c) O método de rotação é um tipo específico de método de rebatimento.
Justificativa: o rebatimento é um tipo específico de método de rotação.
d) A mudança de plano de projeção horizontal consiste na criação de um novo plano, oblíquo ao plano de projeção vertical.
Justificativa: o novo plano de projeção deve ser ortogonal ao plano de projeção vertical.
e) É possível realizar, de forma simultânea, a mudança de plano na vertical e na horizontal.
Justificativa: não é possível realizar, em um único processo, a mudança de plano vertical e horizontal, pois é necessário sempre manter um dos planos como referência.
Nome do livro: Noções e Fundamentos de Geometria Descritiva
Editora: LTC
Autora: Helena Lacourt
ISBN: 978-85-277-0340-6
A obra indicada trabalha a representação de pontos, retas e planos em épura. A partir da leitura desse material, você poderá compreender, de forma detalhada, o passo a passo para a representação dos mais variados elementos em seus diversos posicionamentos possíveis.

Nome do filme: Cruzada
Gênero: Histórico, Ação.
Ano: 2005.
Elenco principal: Orlando Bloom, Liam Neeson, David Thewlis.
O filme traz a história de Balian, que herda terras e um título de nobreza. Além de fazer um retrato histórico do período do surgimento das cruzadas religiosas, o filme indicado também demonstra como o sistema de coordenadas, ainda que de modo rudimentar, era utilizado para questões bélicas, permitindo maior precisão e otimização dos recursos disponíveis.

Nome do livro: Geometria Descritiva
Editora: Edgard Blücher LTDA.
Autor: Gildo A. Montenegro
ISBN: 978-85-212-0192-2
Na leitura sugerida, o autor aborda diversas questões relativas à Geometria Descritiva. Nesta obra, você irá encontrar não apenas conceitos sobre os métodos de representação, mas também sobre o exercício de visualização, que é necessário para a maior compreensão no momento de representação das formas e estudo do espaço.

Nome do filme: Moebius
Gênero: Ficção científica
Ano: 1996
Elenco principal: Guillermo Angelelli, Roberto Carnaghi, Anabella Levy, Jorge Petraglia
O filme indicado explora o paradoxo espacial da fita de Möbius, na qual as propriedades de orientação são abolidas. Não existe lado de dentro e não existe lado de fora. A trama se passa na rede de metrôs de Buenos Aires, quando um dos trens desaparece de modo inesperado. Por meio desse filme, você é convidado a refletir sobre as figuras paradoxais na Geometria.
