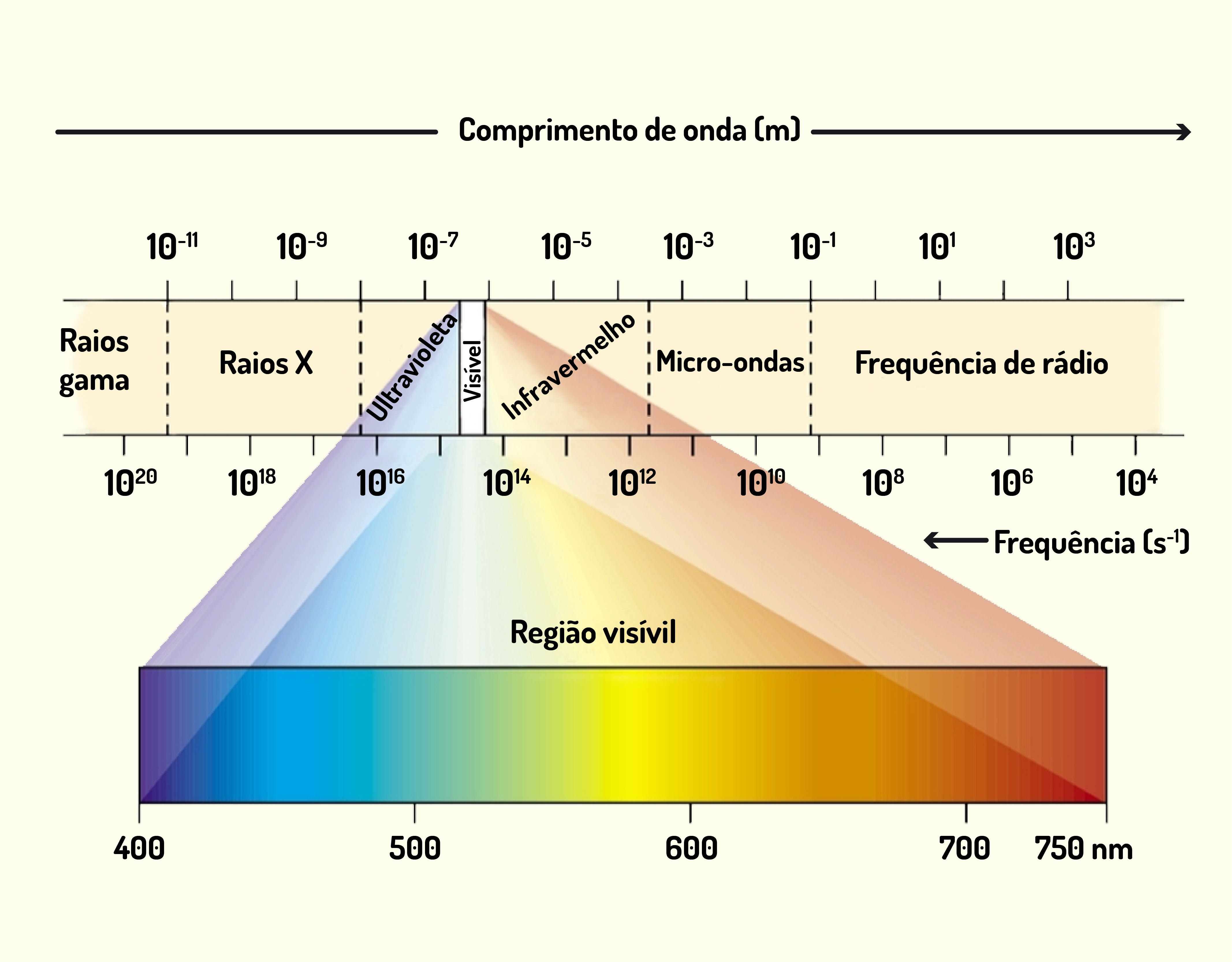
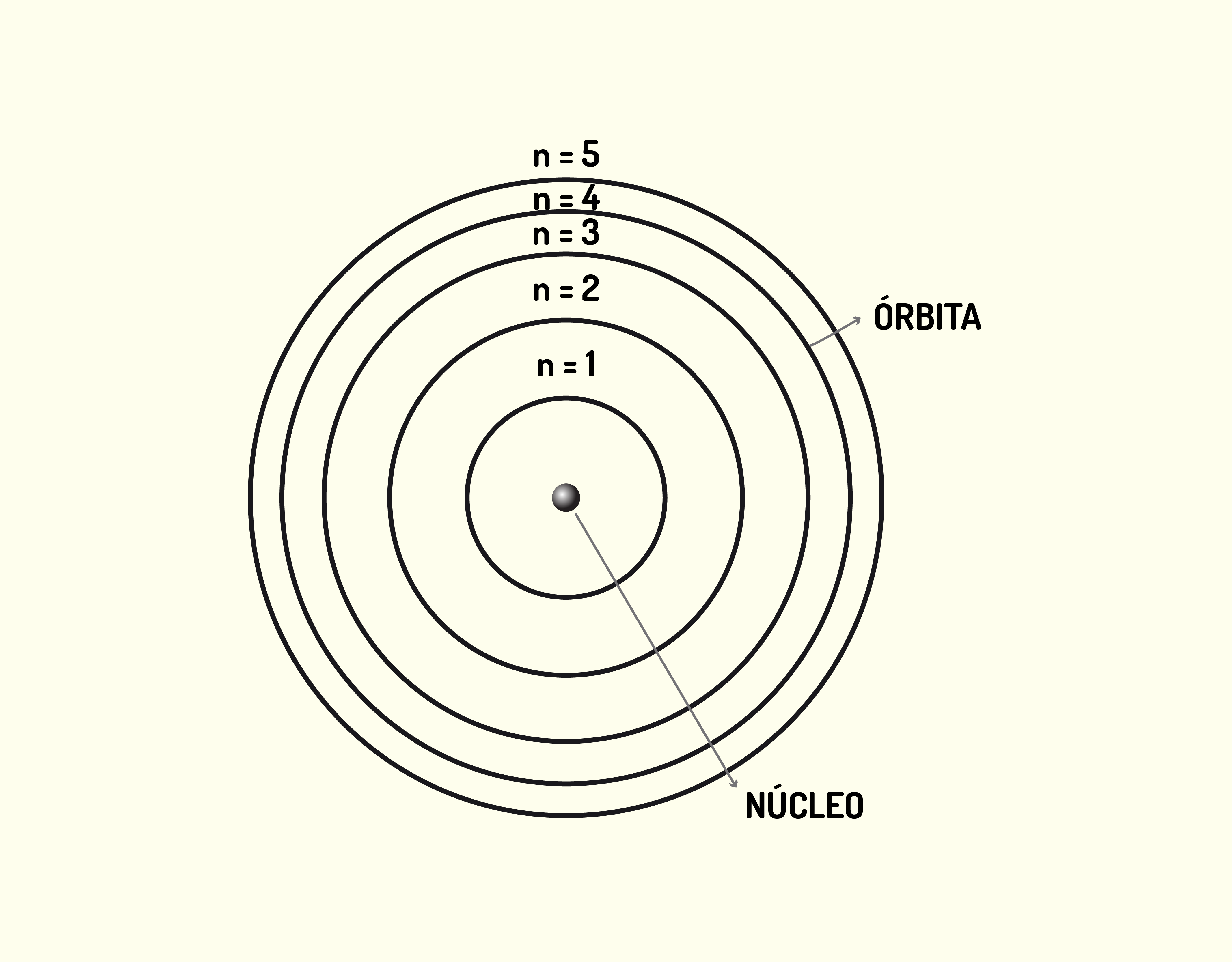
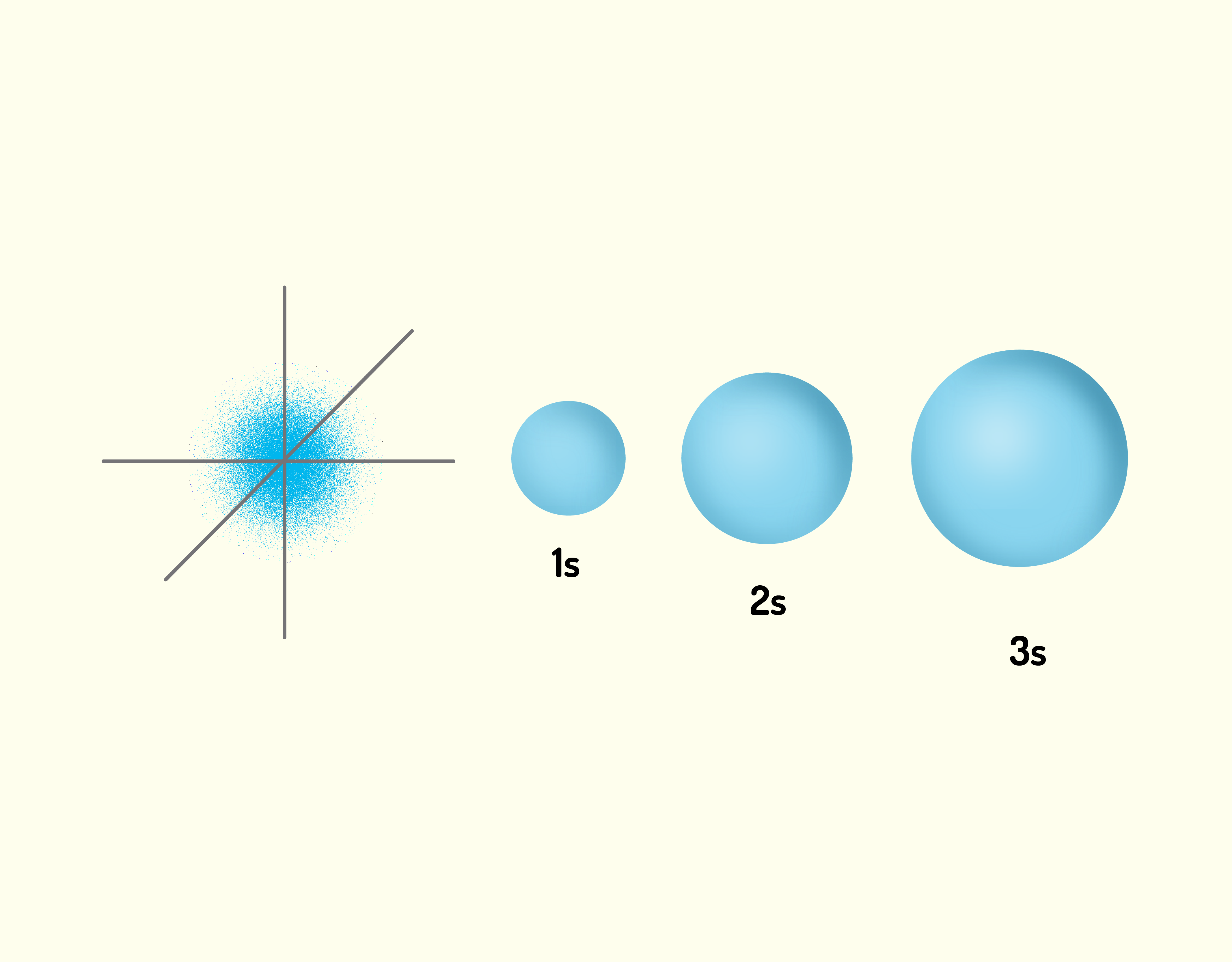
Introdução ao estudo da Química
Caro(a) aluno(a), antes de começarmos as discussões acerca da Química propriamente dita, faremos uma breve introdução que apresenta o que é preciso para que você aproveite ao máximo este livro. Assim, discutiremos, brevemente, os conceitos relacionados às medidas, às unidades e às bases matemáticas, necessários para o desenvolvimento do conteúdo.
Medidas
A Química, como uma ciência exata, precisa de observações quantitativas para progredir, ou seja, de valores sendo medidos, para que as teorias e ideias sejam validadas. Essas medidas, geralmente, são feitas em equipamentos adequados, mas que sempre apresentam alguma limitação quanto ao valor da leitura. Em outras palavras, diferentes objetos usados para mensurar valores podem apresentar diferentes escalas.
Para compreender melhor as escalas, considere que você deve medir a largura de um lápis e, para isso, possui duas réguas, uma com escala tradicional, dividida em milímetros, e outra com escala dividida em centímetros, como mostra a Figura 1.2. Ao utilizar a régua de menor escala, ou seja, a de milímetros, você constata que o lápis tem largura, ligeiramente, maior que 0,7 centímetros (ou 0,7 cm), mas menor que 0,8 cm. Desse modo, você determina que a largura do objeto é 0,72 cm. Com a outra régua, porém, você verifica que a largura do lápis é de cerca de 0,8 cm, pois essa largura encontra-se entre 0 e 1 cm, certamente, sendo maior que a metade dessa distância, aproximando-se, de modo considerável, de 1 cm.
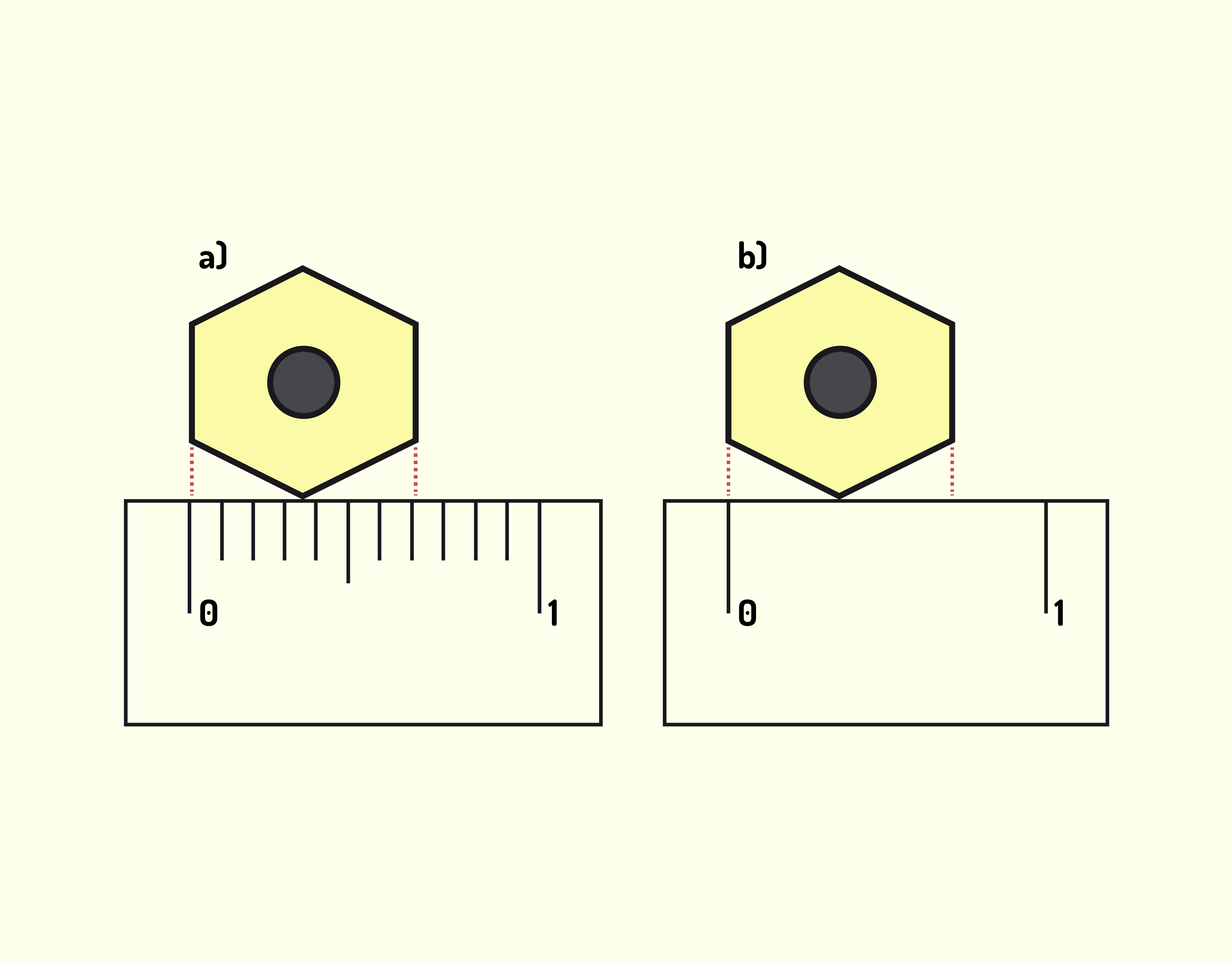
Com base nessa figura, é mais fácil perceber a diferença entre os valores medidos pelas diferentes réguas. Na régua de milímetros, a medida gerou um resultado com três algarismos (0, 7 e 2), sendo que 0 e 7 são valores corretos e 2 é incerto. Na régua de centímetros, a medida apresenta apenas dois algarismos, 0 e 8, nesse caso, somente o primeiro é um valor correto.
Sempre que você trabalhar com instrumentos analógicos de medida, estará sujeito a estimar algum algarismo ao realizar a medida, isto é, ao usar um instrumento analógico para aferir uma medida, você pode estimar um algarismo além do permitido pela escala do instrumento. Normalmente, essas estimativas são, ligeiramente, diferentes, quando avaliadas por diferentes pessoas, mas fique tranquilo, pois essas pequenas diferenças são esperadas e não causam tantos problemas quando esses valores são utilizados nos cálculos.
Os algarismos (ou dígitos) obtidos, ao se realizar uma medida, são chamados de algarismos significativos. Como exposto anteriormente, ao se escrever um número que representa uma medida, o algarismo mais à direita será sempre incerto (ou impreciso), a menos que o contrário seja informado de modo explícito. Devemos salientar que esses algarismos são importantes para mostrar quão precisa é uma medida: quanto mais algarismos significativos uma medida possuir, mais precisa ela será.
No meio acadêmico, muitas vezes, você irá se deparar com os termos “precisão” e “exatidão”. Muitas pessoas consideram que esses termos são sinônimos, mas será que elas estão corretas? O que você entende como “precisão”? E “exatidão”?
Sabendo da importância dos algarismos significativos, você deve compreender, então, como contar quantos números significativos uma medida possui. Para isso, caro(a) aluno(a), basta seguir as seguintes regras:
- Todos os números diferentes de zero são significativos.
- Todos os zeros que se encontram entre outros dois números são significativos. Por exemplo, os números 30409 e 60.1 possuem cinco e três algarismos significativos, respectivamente.
- Zeros à direita de números diferentes de zero, antes ou após a vírgula, são significativos. Por exemplo, ambos os números 2,50 e 70,0 possuem três algarismos significativos.
- Zeros à esquerda do primeiro número diferente de zero não são significativos. Por exemplo, os números 0,004 e 0,000000079 possuem um e dois algarismos significativos, respectivamente.
- Quando há valores indicados em notação científica, de modo geral, há uma quantidade ambígua de algarismos significativos. O excesso de zeros inseridos na notação científica não deve ser considerado significativo. Por exemplo, em 250, há três algarismos significativos, mas 2,5 ⋅ 102 possui apenas dois algarismos significativos.
Também existem os números exatos, os quais possuem uma quantidade infinita de algarismos significativos. Esses números exatos podem se originar de três formas:
- contagem exata de objetos. Por exemplo, o número de laranjas em uma caixa, o número de átomos em uma amostra, etc.;
- quantidades definidas, como as que definem unidades, são números exatos.
- números inteiros em equações. Por exemplo, o diâmetro de um círculo é igual ao dobro do raio desse mesmo círculo, então, o número 2, que multiplica o valor do raio, é um número exato.
Exemplo 1
determine quantos algarismos significativos possuem os números apresentados a seguir.
|
(a) 0,025. |
(b) 1060. |
(c) 30,400 ⋅ 103. |
(d) Uma dúzia. |
Solução:
- 0,025 possui dois algarismos significativos, 2 e 5. Os zeros não são considerados significativos, porque se encontram à esquerda do primeiro número diferente de zero (conforme a regra 4 dos algarismos significativos).
- 1060 possui quatro algarismos significativos, 1, 0, 6 e 0. Esses zeros são significativos, porque estão entre números e à direita de números diferentes de zero antes da vírgula (de acordo com as regras 2 e 3 dos algarismos significativos).
- 30,400 ⋅ 103 possui cinco algarismos significativos, pois os zeros estão entre números e à direita de números diferentes de zero após a vírgula (segundo as regras 2, 3 e 5 dos algarismos significativos).
- Uma dúzia equivale a 12 unidades. Nesse caso, há um número exato, ou seja, uma dúzia possui infinitos algarismos significativos.
Cálculos com algarismos significativos
Os algarismos significativos obtidos das medidas são importantes em operações matemáticas, pois não é adequado realizar as operações se houver a possibilidade de ganhar ou perder informações devido ao mau uso dos valores.
Nessa perspectiva, em cálculos de adição e subtração, há uma situação mais simples: o resultado deve sempre possuir o mesmo número de casas decimais que o valor com menos casas decimais utilizado no cálculo. Quando, no resultado, houver mais casas decimais do que o valor com menos casas decimais, é necessário arredondar o valor obtido, para ajustar o resultado. Observe a seguinte soma:

O arredondamento de um número também exige um pouco de cuidado, porque, caso o número mais à esquerda (que deve ser removido pelo arredondamento) for inferior a 5, o número anterior a ele não se altera. Caso seja o número mais à esquerda a ser removido e se ele for igual ou superior a 5, acrescenta-se 1 (uma) unidade ao número anterior a ele.
Assim, no exemplo de soma apresentado anteriormente, o número mais à esquerda, que foi removido, era 0. Logo, 5, que é o número anterior ao 0, deve ser mantido. Por sua vez, para arredondar o número 2,535 para duas casas decimais, o número mais à esquerda precisa ser removido: 5. Portanto, o resultado é 2,54.
Agora, para operações de multiplicação e divisão, o resultado deverá apresentar o mesmo número de algarismos significativos que o valor com menor quantidade de algarismos significativos. Para compreender melhor essas informações, analise a seguinte multiplicação:
|
4,30 |
x |
50,245 |
x |
0,100 |
= |
21,60535 |
= |
21,6 |
|
3 alg. sign. |
|
5 alg. sign. |
|
3 alg. sign. |
|
7 alg. sign. |
|
3 alg. sign. |
Nesse exemplo, o resultado foi arredondado para três algarismos significativos, porque essa é a menor quantidade de números significativos entre os números presentes na multiplicação.
Ademais, quando os cálculos envolvem uma série de operações diferentes, primeiro, devem ser realizadas as operações presentes dentro dos parênteses. Nessa primeira etapa, é preciso gerar uma resposta que contenha a quantidade correta de algarismos significativos e, em seguida, dar sequência aos cálculos.
Exemplo 2
Avalie a sequência de operações:
5,299 ✕ (3,67 − 1,4)
Solução: primeiramente, é necessário resolver o que há dentro dos parênteses e ajustar o valor ao número correto de algarismos significativos. Como é uma operação de subtração, o resultado deve apresentar tantas casas decimais quanto o valor com menos casas decimais. Então, como há uma subtração entre um valor com duas casas decimais e um valor com uma casa decimal, a resposta deverá apresentar apenas uma casa decimal:
(3,67 − 1,4) = 2,27 = 2,3
Agora, basta resolver a multiplicação:
5,299 ✕ (2,3) = 12,1877
Esse resultado precisa ser ajustado para a quantidade correta de algarismos significativos. Como se trata de uma multiplicação, o resultado precisa ter tantos algarismos significativos quanto o valor com menos algarismos significativos envolvido na multiplicação, ou seja, dois. Logo, a resposta é
5,299 ✕ (2,3) = 12
Unidades de medida
Nas ciências, caro(a) aluno(a), inúmeras características são quantitativas, ou seja, podem ser quantificadas numericamente, como o exemplo de como medir a largura de um lápis. Agora que você já sabe ler e utilizar, de modo matemático, valores medidos, precisa entender como caracterizar esses valores medidos, a fim de que eles não sejam apenas números sem significado.
Como você já deve imaginar, podemos dar mais significado para um número utilizando uma unidade. Por exemplo, anteriormente, verificamos que a largura de um lápis é 0,72 cm. Portanto, essa caracterização dos números é feita por meio de algum sistema de unidades. Na década atual, dois dos sistemas mais comuns, usados cientificamente, são: o Sistema Internacional de Unidades e o Sistema Inglês.
O Sistema Internacional de Unidades, conhecido simplesmente como SI, tem como base um sistema métrico. No presente livro, a maioria das unidades é fornecida no SI. Esse sistema foi divulgado em 1960, resultando de um conceito iniciado em 1948, que pretendia padronizar as medidas utilizadas mundialmente, visto que cada país tinha seus próprios costumes acerca do uso de unidades, o que tornava a divulgação científica complexa.
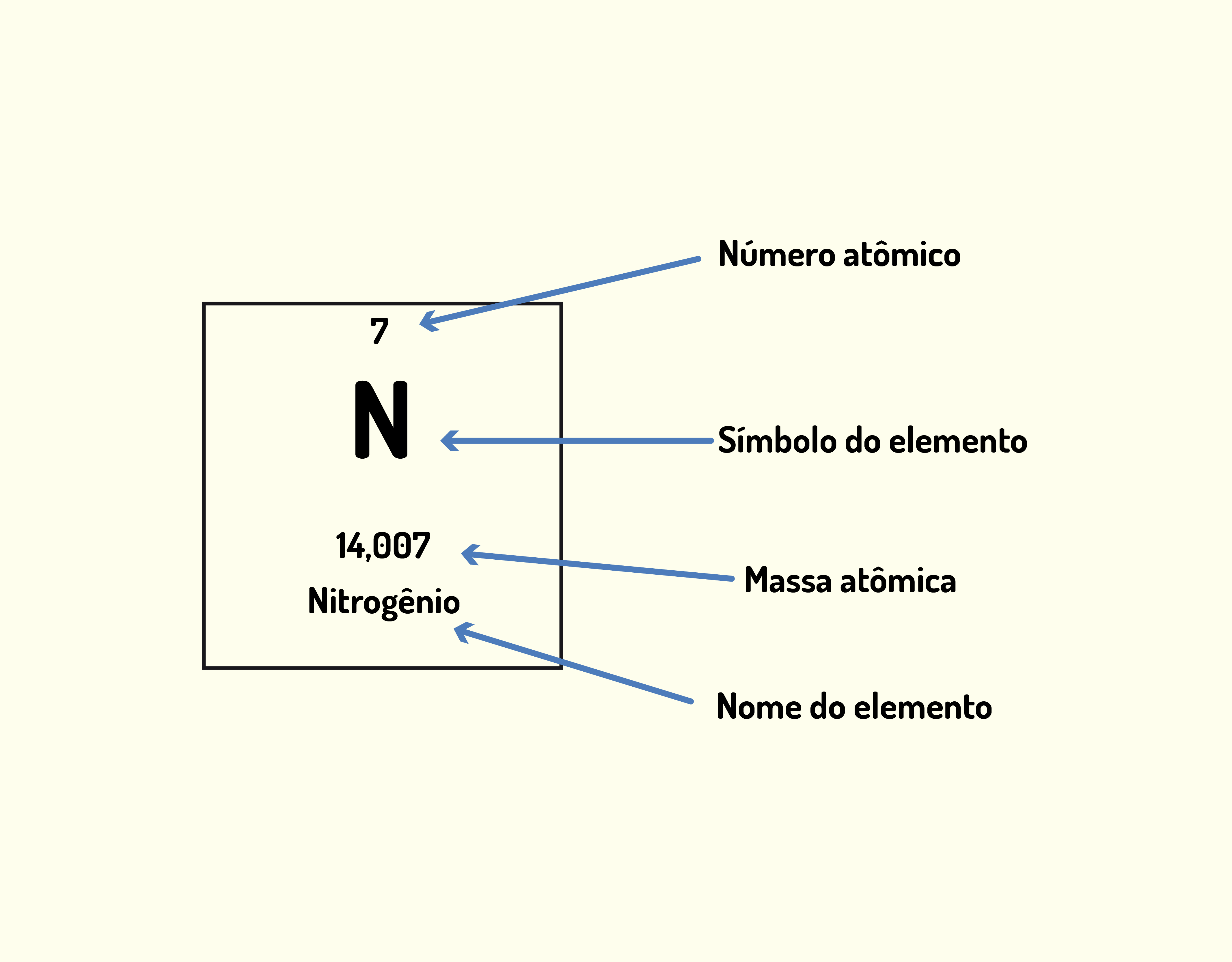
Atualmente, esse sistema de unidades foi adotado por quase todos os países, sendo os Estados Unidos uma exceção. A seguir, a Tabela 1.1 indica algumas unidades básicas do SI e seus símbolos dimensionais, que são úteis na análise dimensional de grandezas.
|
Dimensão |
Nome da unidade |
Símbolo |
Símbolo dimensional |
|
Massa |
Quilograma |
kg |
M |
|
Comprimento |
Metro |
m |
L |
|
Tempo |
Segundo |
s |
T |
|
Temperatura |
Kelvin |
K |
Θ |
|
Quantidade de matéria |
Mol |
mol |
N |
|
Corrente elétrica |
Ampère |
A |
I |
Ao escrever unidades, fique sempre atento ao símbolo e à grafia correta. Caso você tenha que digitar algum trabalho contendo unidades, sempre insira um espaço entre o valor numérico e a unidade que o caracteriza. Além disso, atente-se ao uso do símbolo de Kelvin, visto que não existe a unidade graus Kelvin (ºK), ou seja, é Kelvin (K), simplesmente! Muitos se confundem pelo fato de estarem acostumados ao uso de graus Celsius (ºC) ou de graus Fahrenheit (ºF).
O SI também utiliza prefixos multiplicadores para as suas unidades, os quais indicam que alguma multiplicação está sendo aplicada ao valor. Um dos prefixos mais comuns é o quilo, como em quilômetro, que indica a multiplicação entre o número e a unidade metro por 1000 (ou 103). Assim, em vez de escrevermos 1000 m, podemos escrever 1 km, o que equivale a 1 ⋅ 103 m. A seguir, Tabela 1.2 evidencia os principais prefixos utilizados em unidades e qual multiplicação eles representam.
|
Prefixo |
Símbolo |
Multiplicador |
Notação científica |
|
Tera- |
T |
1.000.000.000.000 |
1012 |
|
Giga- |
G |
1.000.000.000 |
109 |
|
Mega- |
M |
1.000.000 |
106 |
|
Quilo- |
k |
1.000 |
103 |
|
Deci- |
d |
0,1 |
10-1 |
|
Centi- |
c |
0,01 |
10-2 |
|
Mili- |
m |
0,001 |
10-3 |
|
Micro- |
µ |
0,000001 |
10-6 |
|
Nano- |
n |
0,000000001 |
10-9 |
|
Pico- |
p |
0,000000000001 |
10-12 |
|
Femto- |
f |
0,000000000000001 |
10-15 |
O uso desses prefixos permite expressar, com facilidade, inúmeros valores extremos e, sem eles, seria necessário trabalhar com valores gigantescos, algo que polui, visualmente, um texto e dificulta a leitura dos valores. A seguir, há a exemplificação de alguns usos desses prefixos.
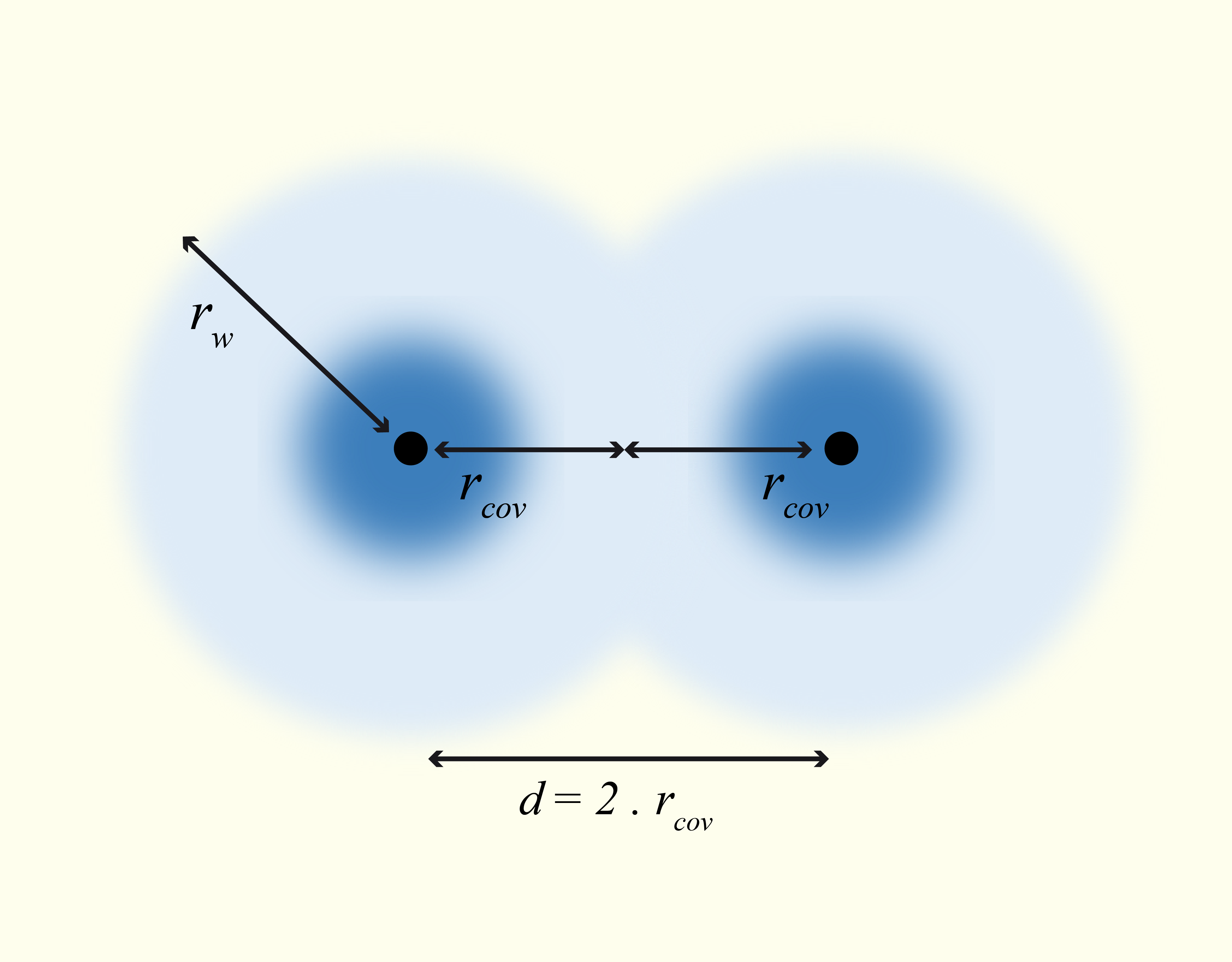
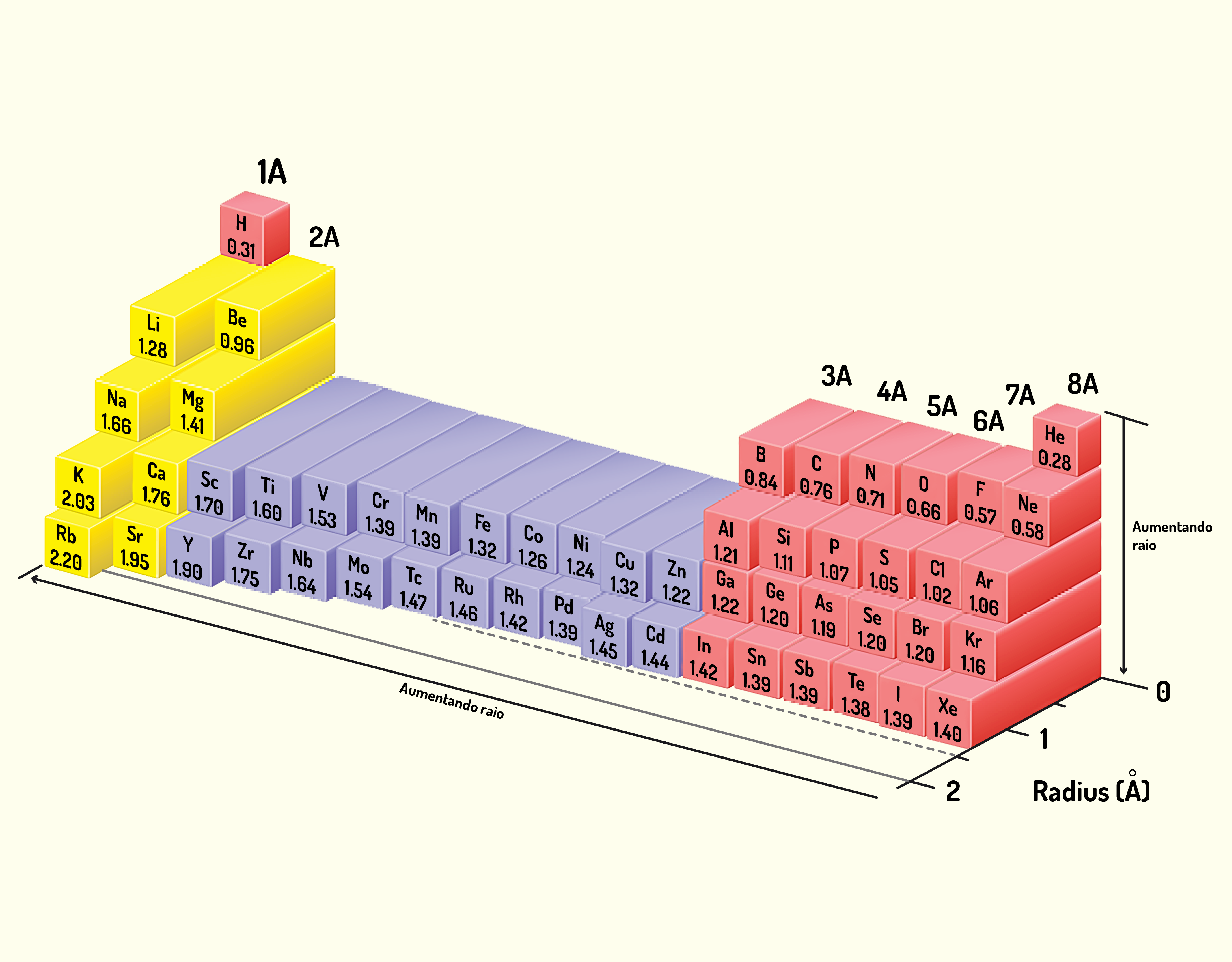
- O raio covalente do hidrogênio é igual a, aproximadamente, 31 pm (picômetros) ou 0,000000000031 m.
- O raio do planeta Terra é, aproximadamente, 6.378.100 m ou 6,3781 Mm (megametros).
- Um dia possui 86.400 s ou 86,4 ks (quilossegundos).
Veja que, partindo das unidades básicas do SI, podemos encontrar outras unidades: as derivadas. Um exemplo muito comum dessas unidades derivadas é o volume, uma medida de espaço em três dimensões. O volume é uma unidade composta pelo produto comprimento x comprimento x comprimento, ou seja, L x L x L = L3. Portanto, para o SI, a unidade de volume deve ser m3. Como você já deve saber, a unidade mais usada como medida de volume é o litro, cujo símbolo é L. Desse modo, em relação ao valor do SI, 1 L equivale a 0,001 m3.
Outro exemplo comum de unidade derivada é a unidade de massa específica, que não possui um nome exclusivo. Essa unidade é, simplesmente, a razão entre massa e volume, ou seja, M ⋅ L-3 ou M/L3. Em unidades do SI, a massa específica será representada por kg ⋅ m-3 ou kg/m3. Note que a análise dimensional pode ajudar a encontrar equações para uma grandeza: a massa específica, “[math]\rho [/math]”, de uma substância pode ser calculada pela razão entre sua massa, “m”, e o volume, “V”, ocupado por essa substância. Desse modo,
[math]\rho =\frac{m}{V}[/math]
Também devemos salientar que é possível converter unidades equivalentes livremente. Em sua vida acadêmica, caro(a) aluno(a), não será incomum você se deparar com as medidas do sistema inglês, como pé (cujo símbolo é ft) e polegada (cujo símbolo é in). Caso isso aconteça, basta que você tenha uma tabela de conversão, como a Tabela 1.3, que apresenta algumas unidades do sistema inglês e seus fatores de conversão para unidades do SI.
|
Dimensão |
Nome da unidade |
Símbolo |
Fator de conversão |
|
Massa |
libra massa |
lbm |
0,45359237 kg |
|
Comprimento |
pé |
ft |
0,3048 m |
|
Comprimento |
polegadas |
in |
0,0254 m |
O uso desses fatores de conversão é simples e indica que:
- 1 lbm = 0,45359237 kg.
- 1 ft = 0,3048 m.
- 1 in = 0,0254 m = 2,54 cm.
Assim, basta utilizar a regra de três simples para converter valores ou fazer uma sequência de multiplicações que retorne à unidade desejada. Para essa sequência, você pode gerar uma razão de unidades a partir dos fatores de conversão. Observe o exemplo a seguir.
Exemplo 3
converta 3,400 ft para unidades do SI.
Solução: para encontrar a resposta para essa conversão, você precisa se lembrar do fator de conversão de pés para metros, ou seja, você já sabe que 1 ft = 0,3048 m, o que pode ser utilizado como uma razão, conforme exposto a seguir.
[math]3,400~ft~~\frac{0,3048~m}{1~ft}[/math]
Veja, caro(a) aluno(a), que a razão foi adicionada para “cancelar” a unidade pés, que aparece tanto em cima, no numerador, quanto no denominador da multiplicação. Logo,
[math]3,400~ft=3,400~~\frac{0,3048~m}{1}=1,03632~m[/math]
Esse resultado só precisa ser ajustado para a quantidade correta de algarismos significativos. Como se trata de uma multiplicação, ele precisa ter tantos algarismos significativos quanto o valor com menos algarismos significativos envolvidos na multiplicação, ou seja, quatro. Então, a resposta é:
[math]3,400~ft=3,400~~\frac{0,3048~m}{1}=1,03632~m[/math]
Para um teste de velocidade de dissolução em seu laboratório, você deve utilizar um cubo de certo material, cuja massa é 19,00 g. Assim que o cubo é adicionado ao béquer graduado, antes da dissolução começar, você nota que 7,500 mL de líquido são deslocados. Sabendo que, para eventos futuros, a massa específica desse material será útil, qual é a massa específica do material usado?
- [math]\rho =2533,33~kg/{{m}^{3}}[/math]. Como sabemos, a massa específica é calculada pela razão entre a massa e o volume. Logo, para obtermos o valor de [math]\rho[/math], basta fazermos tal razão. Devemos nos lembrar, porém, de que é útil ter os cálculos feitos com unidades do SI. Assim, ^p^19,00 g = 19,00 ⋅ 10-3 kg e 7,500 mL = 7,500 ⋅ 10-3 L = 7,500 ⋅ 10-6 m3^p^Agora, basta realizar a divisão.^p^[math]\rho =\frac{m}{V}=\frac{19,00~\cdot ~{{10}^{-3}}~kg}{7,500~\cdot ~{{10}^{-6}}~{{m}^{3}}}=2533,333\frac{kg}{{{m}^{3}}}[/math]^p^Falta apenas ajustar os algarismos significativos. Por ser uma divisão, o resultado deve ter tantos algarismos significativos quanto o valor com menos algarismos significativos, ou seja, 4. Logo, a massa específica desse material é:^p^[math]\rho =2533~kg/{{m}^{3}}[/math]
- [math]\rho =2533~kg/{{m}^{3}}[/math]. Como sabemos, a massa específica é calculada pela razão entre a massa e o volume. Logo, para obtermos o valor de [math]\rho[/math], basta fazermos tal razão. Devemos nos lembrar, porém, de que é útil ter os cálculos feitos com unidades do SI. Assim,^p^19,00 g = 19,00 ⋅ 10-3 kg e 7,500 mL = 7,500 ⋅ 10-3 L = 7,500 ⋅ 10-6 m3^p^Agora, basta realizar a divisão.^p^[math]\rho =\frac{m}{V}=\frac{19,00~\cdot ~{{10}^{-3}}~kg}{7,500~\cdot ~{{10}^{-6}}~{{m}^{3}}}=2533,333\frac{kg}{{{m}^{3}}}[/math]^p^Falta apenas ajustar os algarismos significativos. Por ser uma divisão, o resultado deve ter tantos algarismos significativos quanto o valor com menos algarismos significativos, ou seja, 4. Logo, a massa específica desse material é:^p^[math]\rho =2533~kg/{{m}^{3}}[/math]
- [math]\rho =2,53~g/mL.[/math] Como sabemos, a massa específica é calculada pela razão entre a massa e o volume. Logo, para obtermos o valor de [math]\rho[/math], basta fazermos tal razão. Para isso, basta realizar a divisão:^p^[math]\rho =\frac{m}{V}=\frac{19,00~g}{7,500~mL}=2,533333\frac{g}{mL}[/math]^p^Falta apenas ajustar os algarismos significativos. Por ser uma divisão, nosso resultado deve ter tantos algarismos significativos quanto o valor com menos algarismos significativos, ou seja, 4. Logo, a massa específica desse material é:^p^[math]\rho =2,533~g/mL[/math]
- [math]\rho =2533,33~g/L.[/math] Como sabemos, a massa específica é calculada pela razão entre a massa e o volume. Logo, para obtermos o valor de [math]\rho[/math], basta fazermos tal razão. Vamos, então, converter mL para L:^p^7,500 mL = 7,500 ⋅ 10-3 L^p^Agora, basta realizar a divisão.^p^[math]\rho =\frac{m}{V}=\frac{19,00~g}{7,500~\cdot ~{{10}^{-3}}~L}=2533,333\frac{g}{L}[/math]^p^Falta apenas ajustar os algarismos significativos. Por ser uma divisão, o resultado deve ter tantos algarismos significativos quanto o valor com menos algarismos significativos, ou seja, 4. Logo, a massa específica desse material é:^p^[math]\rho =2533~g/L[/math]
- [math]\rho =2500~kg/{{m}^{3}}[/math]. Como sabemos, a massa específica é calculada pela razão entre a massa e o volume. Logo, para obtermos o valor de [math]\rho[/math], basta fazermos tal razão. Você deve se lembrar, porém, de que é útil ter os cálculos feitos com unidades do SI. Assim, ^p^19,00 g = 19,00 ⋅ 10-3 kg e 7,500 mL = 7,500 ⋅ 10-3 L = 7,500 ⋅ 10-6 m3^p^Agora, basta realizar a divisão.^p^[math]\rho =\frac{m}{V}=\frac{19,00~\cdot ~{{10}^{-3}}~kg}{7,500~\cdot ~{{10}^{-6}}~{{m}^{3}}}=2533,333\frac{kg}{{{m}^{3}}}[/math]^p^Falta apenas ajustar os algarismos significativos. Por ser uma divisão, o resultado deve ter tantos algarismos significativos quanto o valor com menos algarismos significativos, ou seja, 4. Logo, a massa específica desse material é:^p^[math]\rho =2533~kg/{{m}^{3}}[/math]



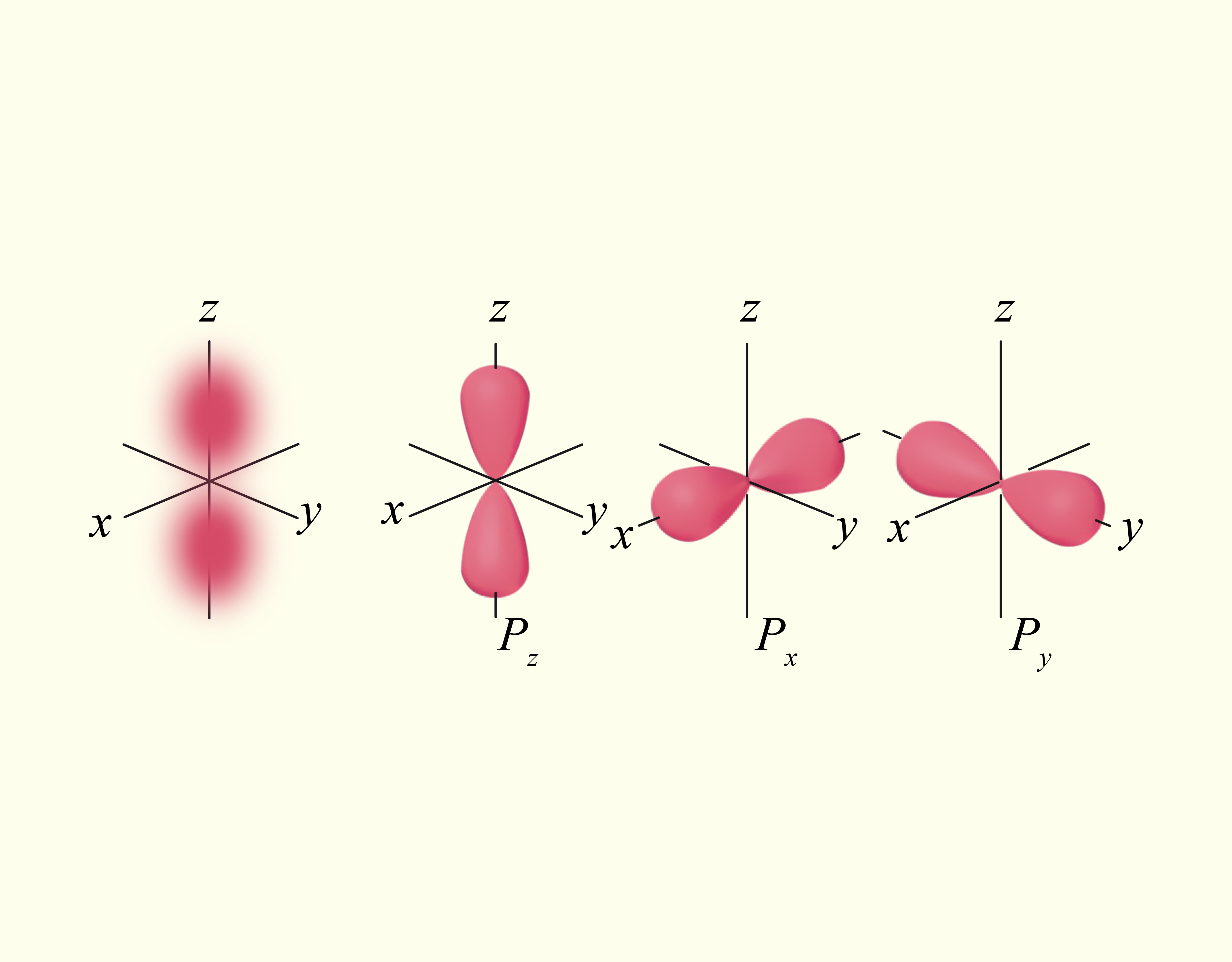




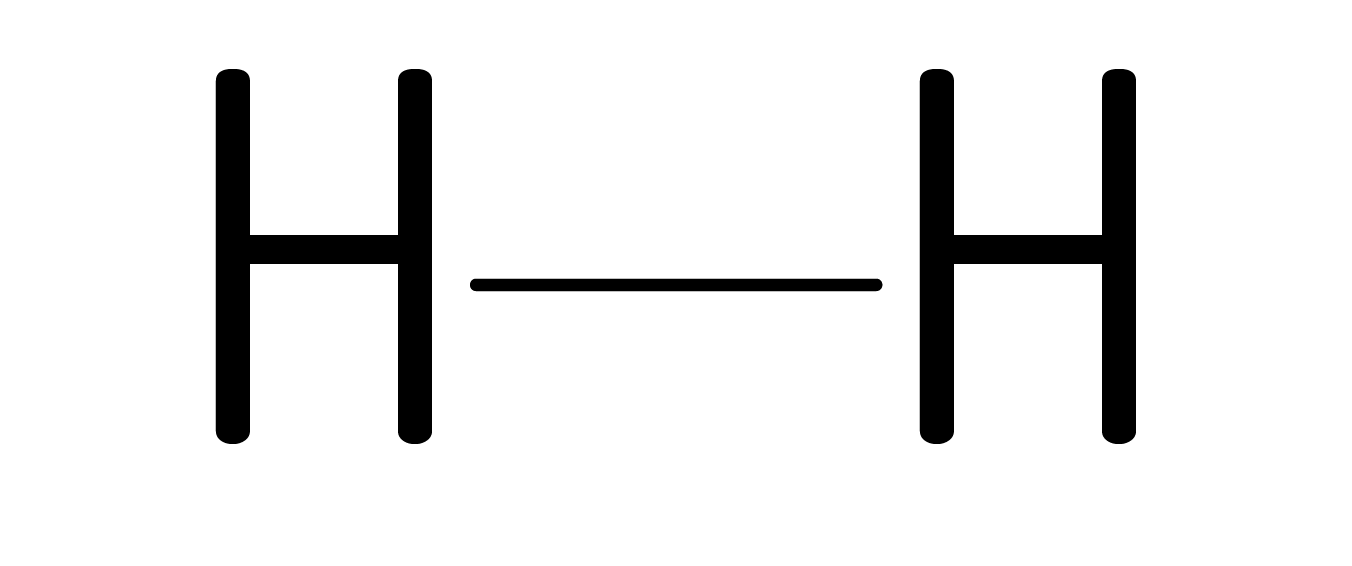
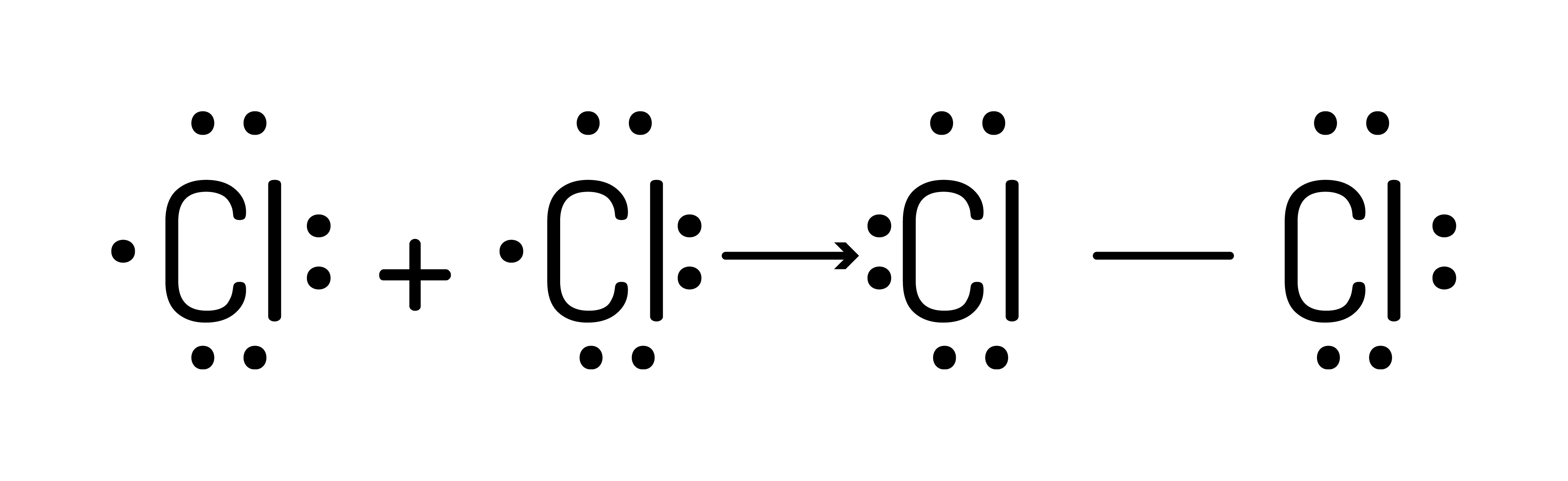
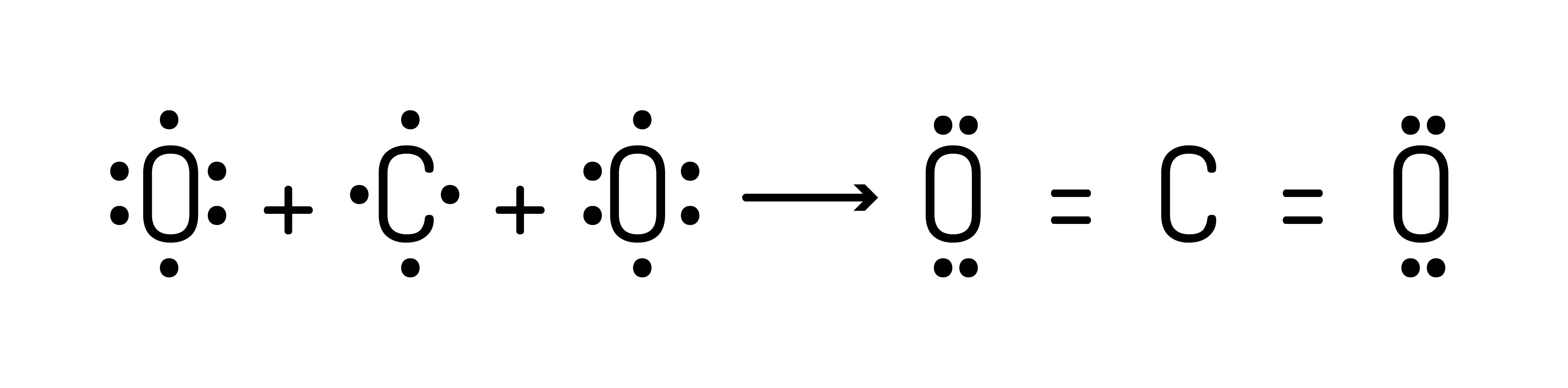
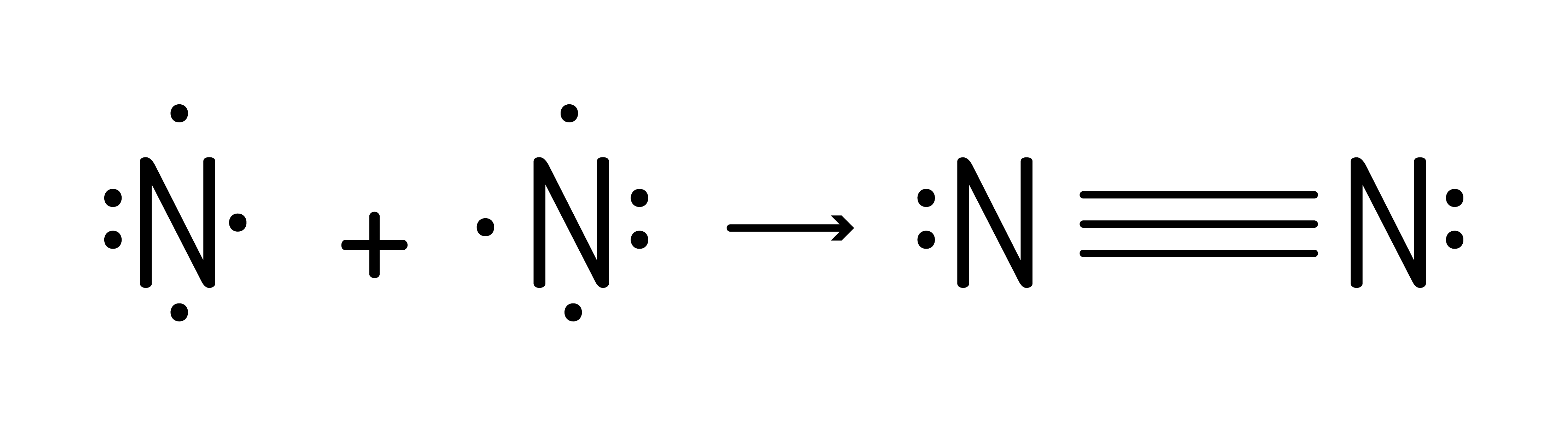
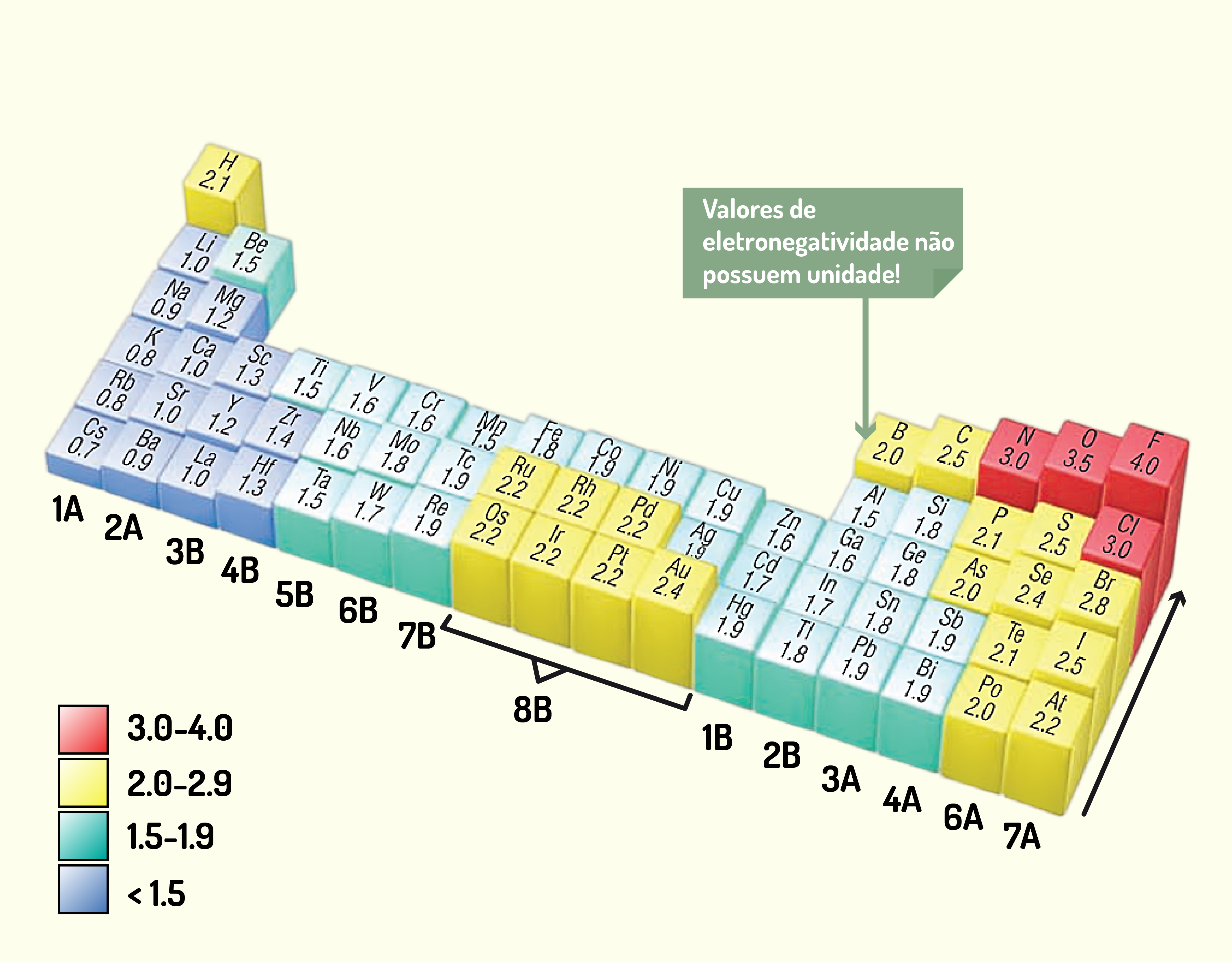
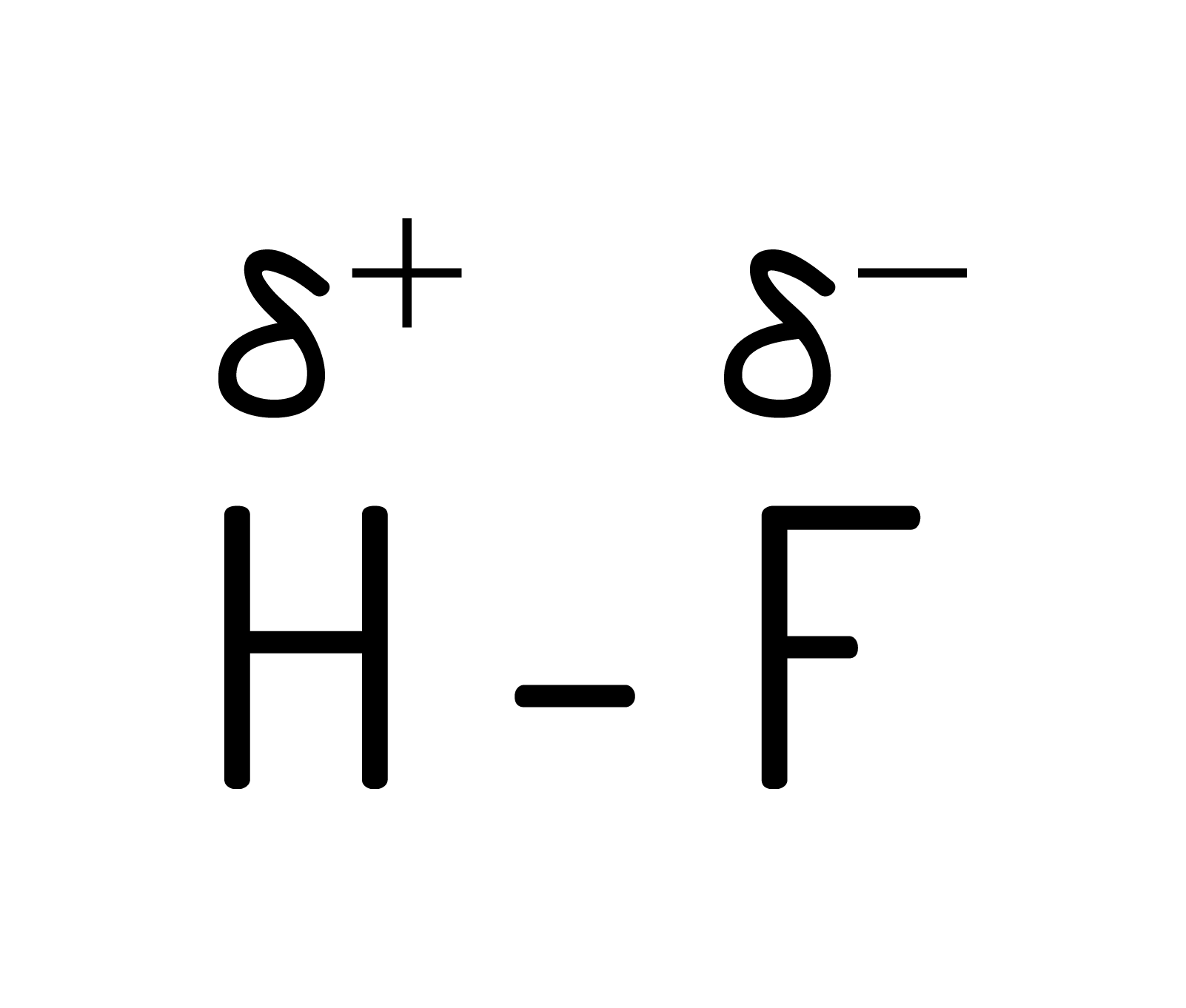 ou
ou