Teorema do trabalho e da energia cinética
O trabalho realizado (_math_W_math_) sobre um corpo é definido como o produto escalar da força (_math_\vec{F}_math_) pelo deslocamento (_math_\vec{d}_math_) da partícula. O trabalho é uma grandeza escalar, ele é positivo quando a componente da força _math_(\vec{F}_math_) é exercida no mesmo sentido do movimento do corpo; negativo nos casos em que as componentes de _math_\vec{F}_math_ e _math_\vec{d}_math_ estão em sentidos opostos; nulo quando a componente da força é perpendicular, _math_\Phi =90~_math_°, ao deslocamento. A dimensão de trabalho é Newton metro (Nm) ou Joule (1 J = 1 Nm). Na equação (24), _math_\Phi _math_ representa o ângulo entre as componentes da força e do deslocamento.
_math_W=\vec{F}.\vec{d}=Fd~cos~\Phi ~~\left( 24 \right)_math_
Para a aplicação da equação (24), duas condições são impostas. A primeira condição é que _math_\vec{F}_math_ precisa ser constante, ou seja, nem o módulo, direção ou sentido de nenhuma componente da força pode variar em função de nenhuma grandeza física durante o movimento do corpo, e a segunda condição é que o corpo porte-se como uma partícula (corpo com pequenas dimensões no sistema) rígida.
Há uma notável relação entre o trabalho realizado sobre a partícula e as velocidades inicial e final dela (HALLIDAY et al., 2008). Observe que _math_{{F}_{x}}_math_ é o módulo da força que opera sobre a partícula na direção do eixo _math_x_math_, de acordo com a 2ª Lei de Newton, _math_{{F}_{x}}=m{{a}_{x}}_math_. Quando a partícula sofre um deslocamento com módulo _math_d_math_, a força atuando sobre a partícula altera a velocidade inicial (_math_{{v}_{1}}_math_) dela para outra velocidade (_math_{{v}_{2}}_math_) até que o movimento cesse. A relação entre as velocidades e a aceleração pode ser descrita por meio da equação do movimento para aceleração constante:
_math_{{v}_{2}}^{2}={{v}_{1}}^{2}+2{{a}_{x}}d~~~\left( 25 \right)_math_
O trabalho realizado sobre a partícula é:
_math_W={{F}_{x}}d=m{{a}_{x}}x~~~\left( 26 \right)~_math_
Isolando a aceleração _math_{{a}_{x}}_math_ da equação (25), obtemos _math_{{a}_{x}}=\frac{{{v}_{2}}^{2}-{{v}_{1}}^{2}}{2d}_math_, e, a substituindo na equação (26), encontramos:
_math_W=\frac{m{{v}_{2}}^{2}}{2}-~\frac{m{{v}_{1}}^{2}}{2}~~~~\left( 27 \right)~_math_
Qualquer partícula que se mova em qualquer direção possui energia cinética. Na natureza, existem muitas formas de energia cinética: energia cinética rotacional (produzida pelo movimento de rotação da partícula), a energia cinética vibracional (provocada pelo movimento de vibração) e a energia cinética de translação (a energia correspondente ao movimento de um ponto ao outro). As energias cinéticas de rotação e vibração são mais atuantes se as observarmos em um sistema microscópico de energia, no entanto, nesta unidade, nosso objetivo é compreender como a energia cinética é descrita nos sistemas macroscópicos e, por essa razão, trabalharemos apenas com a energia cinética de translação, a qual passaremos a denominar daqui em diante somente como energia cinética. A energia cinética da partícula é _math_K=\frac{m{{v}^{2}}}{2}_math_, ela é uma grandeza escalar e sua unidade de medida é Joule (J). Fisicamente, a energia cinética é conhecida como a energia do movimento. Desse modo, a equação (27) é conhecida como o teorema do trabalho e da energia cinética, demostrando que o trabalho é a variação da energia cinética cedida ou liberada de uma partícula por via da força resultante exercida sobre esse corpo. Podemos equiparar o trabalho com a variação da energia cinética, reescrevendo a equação (27) como:
_math_W=K\left( {{x}_{2}} \right)-K\left( {{x}_{1}} \right)=\Delta K~~~\left( 28 \right)~_math_
Quando o trabalho é positivo, (_math_{{v}_{2}}>{{v}_{1}}_math_), a energia do sistema é transferida para a partícula, caso contrário, (_math_{{v}_{2}}<{{v}_{1}}_math_), a energia é liberada da partícula para o sistema.
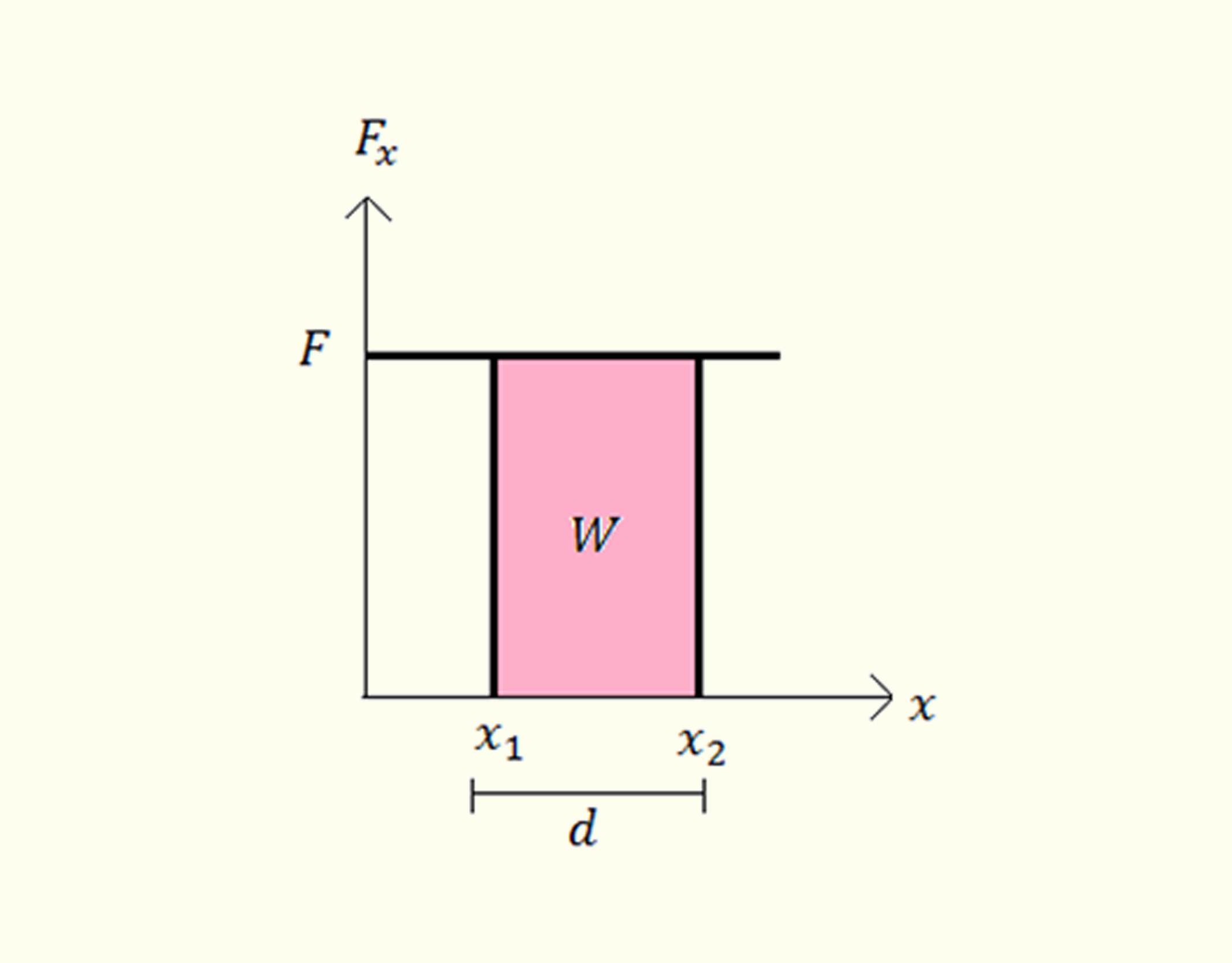
O teorema do trabalho e da energia cinética é válido para as forças constantes ou variáveis. O gráfico que descreve o trabalho realizado a partir da ação de uma força constante é exibido na Figura 3.1. A área rosa refere-se ao trabalho realizado por uma partícula, que se deslocou da posição _math_{{x}_{1}}_math_ até _math_{{x}_{2}}_math_.
317 Gráfico da força constante em função da posição. O retângulo rosa embaixo da linha é descrito como o trabalho que a partícula realiza quando submetido sobre a ação de _math_{{F}_{x}}_math_ para deslocar a partícula. Fonte: a autora.
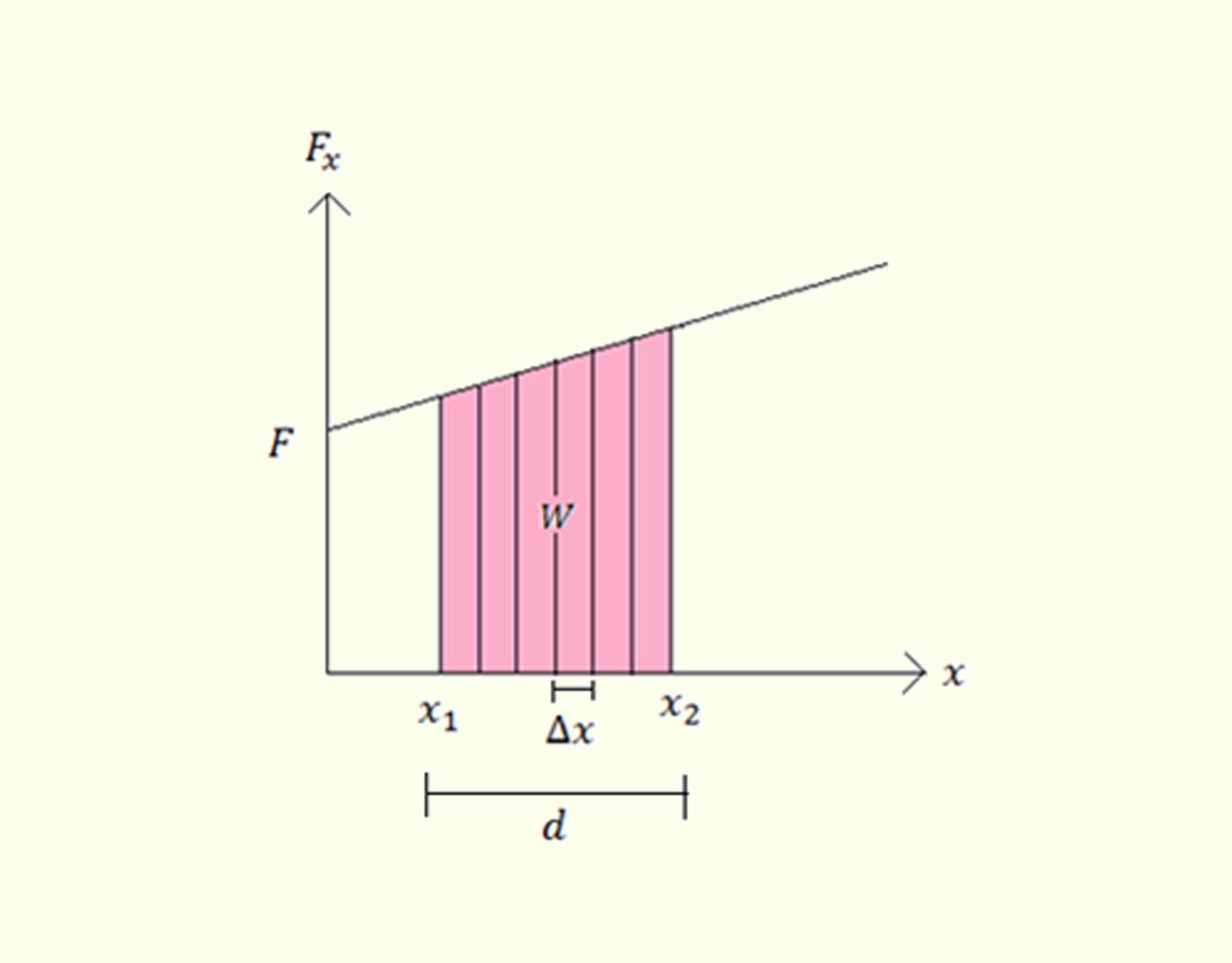
Entretanto nem todas as forças da natureza são constantes, mas variam com a posição (NUSSENZVEIG, 2002), como a força gravitacional na escala astronômica,_math_~{{\vec{F}}_{g}}_math_, a força elétrica, _math_{{\vec{F}}_{ele}}_math_, ou a força elástica, _math_{{\vec{F}}_{e}}_math_, citada na Unidade II. No caso das forças que são função da posição, podemos utilizar a representação gráfica do trabalho como a área em baixo da linha da força pelo deslocamento, como apresentado na Figura 3.2:
327 Gráfico do trabalho de uma força variável. Cada retângulo abaixo da linha representa o trabalho que um conjunto de forças aproximadamente constantes realiza para deslocar a partícula em um intervalo _math_\Delta x._math_ Fonte: a autora.
Esse gráfico indica que podemos calcular o trabalho realizado em um intervalo finito, entre _math_{{x}_{1}}_math_ e _math_{{x}_{2}}_math_, dividindo-o em um conjunto de subintervalos menores, _math_\Delta {{x}_{i}}\to 0~_math_(NUSSENZVEIG, 2002, p. 111-113) suficientemente pequenos para associar a força variável com um conjunto de forças constantes. Em cada subintervalo, o trabalho é a área do retângulo embaixo da linha e a soma de todas essas áreas expressa todo o trabalho realizado no sistema por uma série de forças constantes que se aproximam das forças variáveis:
_math_{{W}_{{{x}_{1}}\to {{x}_{2}}}}=\underset{\Delta {{x}_{i}}\to 0}{\mathop{\lim }}\,\sum {{F}_{x}}\Delta {{x}_{i}}~~~\left( 29 \right)_math_
O limite da equação (29) é conhecido como a integral definida de _math_{{F}_{x}}_math_ nos limites de _math_{{x}_{1}}_math_ e _math_{{x}_{2}}_math_, e pode ser descrito como:
_math_W=\underset{{{x}_{1}}}{\overset{{{x}_{2}}}{\mathop \int }}\,{{F}_{x}}dx~~~\left( 30 \right)_math_
A segunda Lei de Newton relaciona a força resultante com a aceleração, e a aceleração é a taxa de variação da velocidade em relação ao tempo, _math_{{a}_{x}}=\frac{d{{v}_{x}}}{dt}_math_, logo:
_math_W=\underset{{{x}_{1}}}{\overset{{{x}_{2}}}{\mathop \int }}\,m\frac{d{{v}_{x}}}{dt}dx~~~\left( 31 \right)~~~_math_
Utilizando a regra da cadeia para derivadas, _math_\frac{d{{v}_{x}}}{dt}=\frac{d{{v}_{x}}}{dx}\frac{dx}{dt}=\frac{d{{v}_{x}}}{dx}{{v}_{x}}_math_ e substituindo na equação (31), temos:
_math_W=\underset{{{v}_{1}}}{\overset{{{v}_{2}}}{\mathop \int }}\,m{{v}_{x}}d{{v}_{x}}=\frac{m{{v}_{2}}^{2}}{2}-~\frac{m{{v}_{1}}^{2}}{2}~~\left( 32 \right)~~~_math_
Em cada subintervalo, o trabalho é igual à variação da energia cinética no retângulo abaixo da linha, logo, o trabalho total realizado em todos os subintervalos por uma força em função da posição é igual à variação da energia cinética, _math_\Delta K=~\frac{m{{v}_{2}}^{2}}{2}-~\frac{m{{v}_{1}}^{2}}{2}_math_.
Reflita
Energia Eólica: Transformação da energia mecânica em energia elétrica
As correntes de ar são geradas essencialmente por causa do aquecimento da superfície da Terra nas vizinhanças da Linha do Equador e do resfriamento dos Polos do planeta. A rotação da Terra faz as massas circularem entre a Linha do Equador e os Polos. A intensidade e velocidade das correntes de ar são mensuradas por anemômetros posicionados em diferentes altitudes e analisadas por meio do ajuste da curva da potência, lida como (W/m2), em função da velocidade média dos ventos. Essas medidas são necessárias para monitorar o movimento dos aerogeradores. Durante o funcionamento dos aerogeradores, a energia cinética do deslocamento do ar aciona o rotor de uma turbina eólica, convertendo a energia cinética em energia elétrica por um gerador conectado à turbina.
FonteRecorte textual extraído da obra: RIBEIRO, V. D. ANÁLISE TÉCNICO-ECONÔMICA DE UM SISTEMA HÍBRIDO DE GERAÇÃO NA REDE ELÉTRICA DA ILHA DO FUNDÃO. 130 f. 2014. (Dissertação) Programa de Pós-Graduação em Engenharia Elétrica, COPPE - Universidade Federal do Rio de Janeiro, 2014.
Para melhor entendermos o conceito de trabalho, apresentaremos dois exemplos, envolvendo a aplicação das forças constante e variável, que demostraram a relação do trabalho com a variação da energia cinética.
Exemplo 3.1
Imagine dois transportadores levando uma caixa para dentro do caminhão. Para mover a caixa na rampa até o caminhão, por 12 m, o transportador 1 exerce uma força de 25 N sobre a caixa, com um ângulo de 45 graus abaixo da horizontal, e o carregador 2 realiza uma força de 15 N, com um ângulo de 60 graus acima da horizontal. Qual foi o trabalho total realizado por esses dois trabalhadores para mover a caixa até o caminhão?
O trabalho total é a soma do trabalho realizado pelos transportadores 1 e 2. O trabalhador 1 realizou um trabalho _math_{{W}_{1}}=\overrightarrow{{{F}_{1}}}.\vec{d}=25~N.12m.\cos 45{}^\circ =212,13~_math_J, enquanto que o trabalhador 2 realizou um trabalho _math_{{W}_{2}}=\overrightarrow{{{F}_{2}}}.\vec{d}=15~N.12m.\cos 60{}^\circ =90~_math_J. Somando o trabalho efetuado pelos dois trabalhadores, obtemos _math_W={{W}_{1}}+{{W}_{2}}=302,13~N._math_
Exemplo 3.2
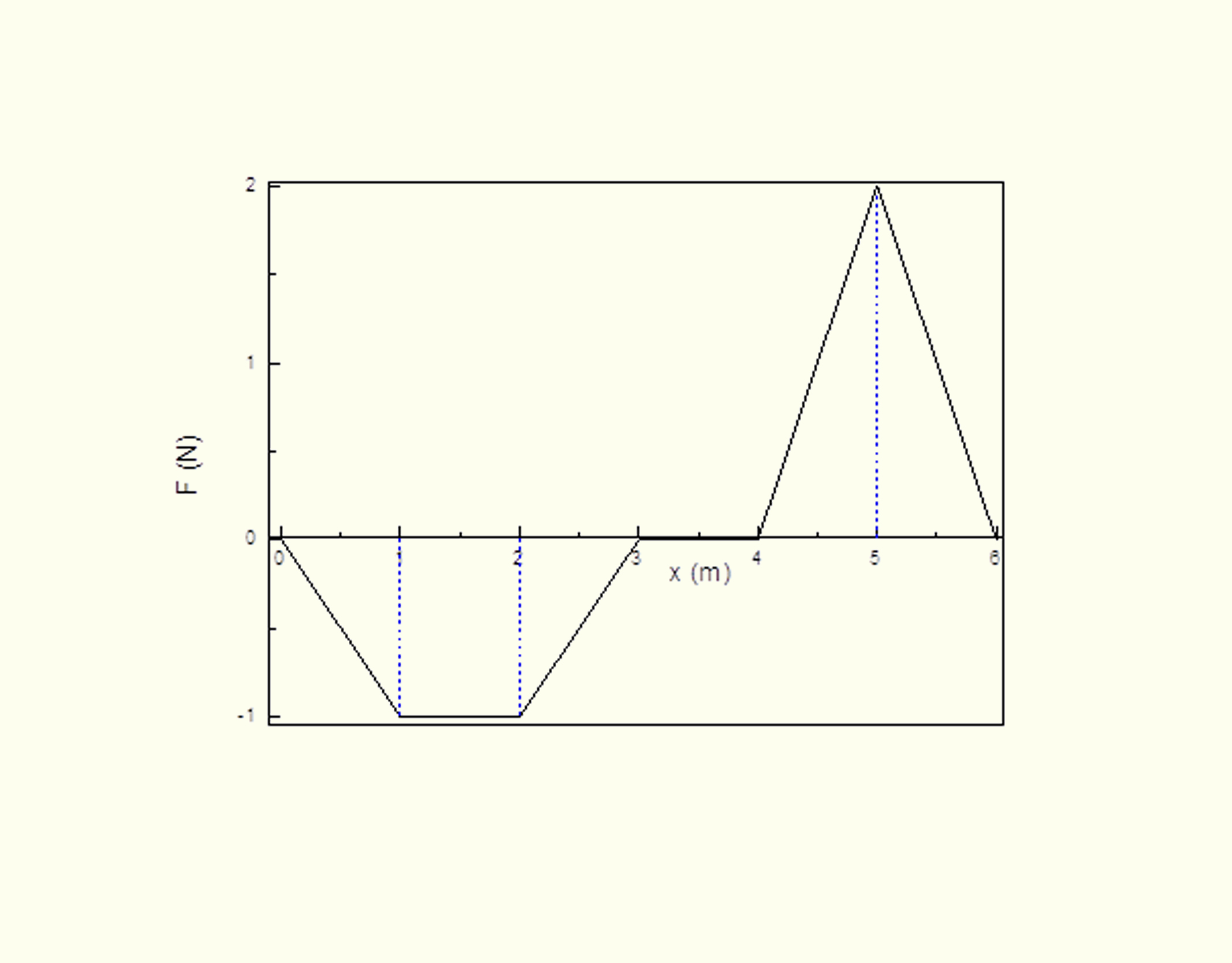
Um bloco de 5 Kg se desloca horizontalmente em uma mesa lisa, sobre a ação de uma força variável, que atua na mesma direção do movimento, de acordo com o gráfico apresentado na Figura 3.3. Qual é o trabalho total realizado para deslocar esse bloco por 6 m?
337 Gráfico da força variável em função da posição Fonte: a autora.
No gráfico, o trabalho representa a área embaixo da curva. Esse gráfico apresenta 3 geometrias diferentes.
Entre as posições de 0 até 3 m, a área em baixo da curva apresenta a geometria de um trapézio, logo,_math_~{{W}_{1}}=\left( \frac{B+b}{2} \right)h=\left( \frac{3+1}{2} \right)\left( -1 \right)=-2_math_ J. Aqui, _math_B_math_ é a base maior do trapézio, _math_b_math_ é a base menor e _math_h~_math_é a altura, que é negativa nesse caso, porque está abaixo do eixo horizontal.
Entre 3 e 4 m, a força resultante é nula e, por consequência, _math_{{W}_{2}}=0_math_ J.
No intervalo de 4 até 6 m, o trabalho é a área do triângulo embaixo da curva, _math_{{W}_{3}}=\left( \frac{bh}{2} \right)=\left( \frac{2.2}{2} \right)=2~_math_J. O trabalho resultante para mover o bloco sobre a mesa é nulo, _math_W={{W}_{1}}+{{W}_{2}}+{{W}_{3}}=0_math_ J.
314 Teorema do Trabalho e da energia cinética
Trabalho realizado por forças conservativas e variação da energia potencial
Outra forma de energia é a energia potencial, _math_U=U\left( x \right)_math_. A energia potencial é a energia correspondente à posição que uma partícula ocupa no espaço. Ela funciona como uma energia de armazenamento da partícula. Dois exemplos dessa energia são as energias potencial gravitacional (_math_{{U}_{p}}_math_), que é a energia armazenada em um corpo que se encontra a uma altura específica do solo antes de ser solto; a energia potencial elástica (_math_{{U}_{elas}}_math_), que é a energia necessária para uma partícula deformada elasticamente retornar a sua forma original.
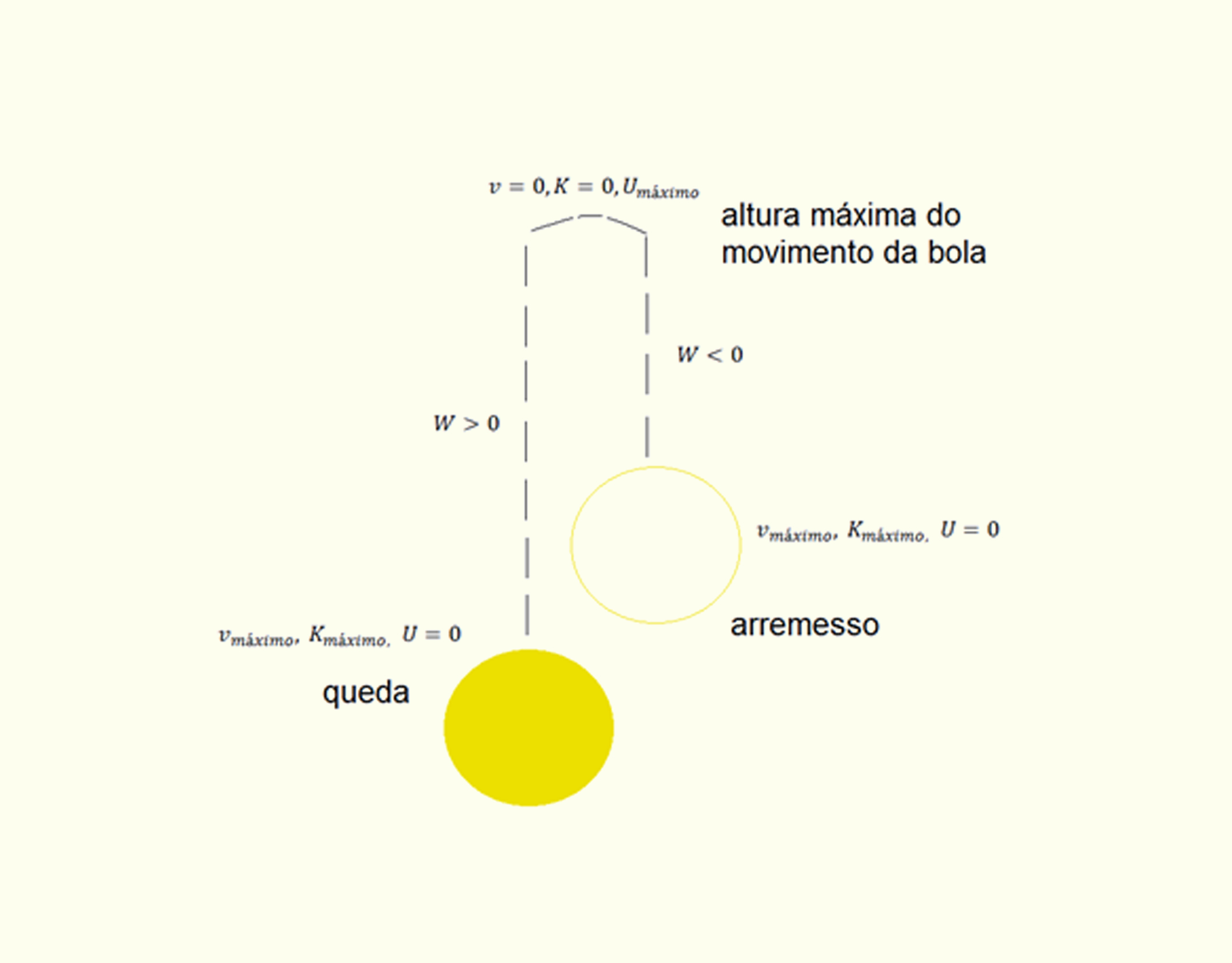
Estudaremos aqui a relação entre trabalho e energia potencial. Suponha que uma bola seja arremessada para cima e logo depois retorne ao chão devido à força gravitacional (Figura 3.4). Durante o movimento de subida da bola, a força gravitacional retira energia cinética da bola, por causa da redução da velocidade do movimento, e, portanto, o trabalho realizado pela força gravitacional é negativo, (_math_W<0_math_). Quando a bola chega ao topo da sua trajetória, toda a energia cinética da bola é transferida com o movimento, nesse momento, a bola possui apenas a energia potencial, mas, logo depois, a bola retorna ao chão, transferindo a energia potencial para a energia cinética, aumentando a velocidade do movimento, onde o trabalho torna-se positivo (_math_W>0_math_). Dessa forma, a variação da energia potencial (HALLIDAY et al., 2008, p. 181) é descrita como:
_math_W=-\Delta U~~\left( 33 \right)_math_
347 Projeção do movimento da bola. Quando a energia cinética é máxima, a energia potencial é nula, e na situação contrária, onde a energia potencial é máxima, a energia cinética é nula. Fonte: a autora.
O sinal negativo explica que energia potencial sempre terá uma tendência de comportamento oposta ao da energia cinética. Quando a partícula está perdendo energia cinética, sua energia potencial está aumentando, e, em situação oposta, com a partícula ganhando energia cinética durante seu movimento, a energia potencial diminui. Nessa situação, no instante em que a energia cinética é máxima (maior velocidade), a energia potencial é nula, e quando a energia potencial é máxima, a energia cinética (velocidade zero do movimento) é nula.
O trabalho realizado por uma força para deslocar uma partícula no intervalo entre duas posições, _math_{{x}_{1}}_math_ e _math_{{x}_{2}}_math_, resulta em uma integral de caminho (TIPLER; MOSCA, 2006):
_math_\Delta U=U\left( {{x}_{1}} \right)-U\left( {{x}_{2}} \right)=-W=-\underset{{{x}_{1}}}{\overset{{{x}_{2}}}{\mathop \int }}\,{{F}_{x}}dx~~~\left( 34 \right)_math_
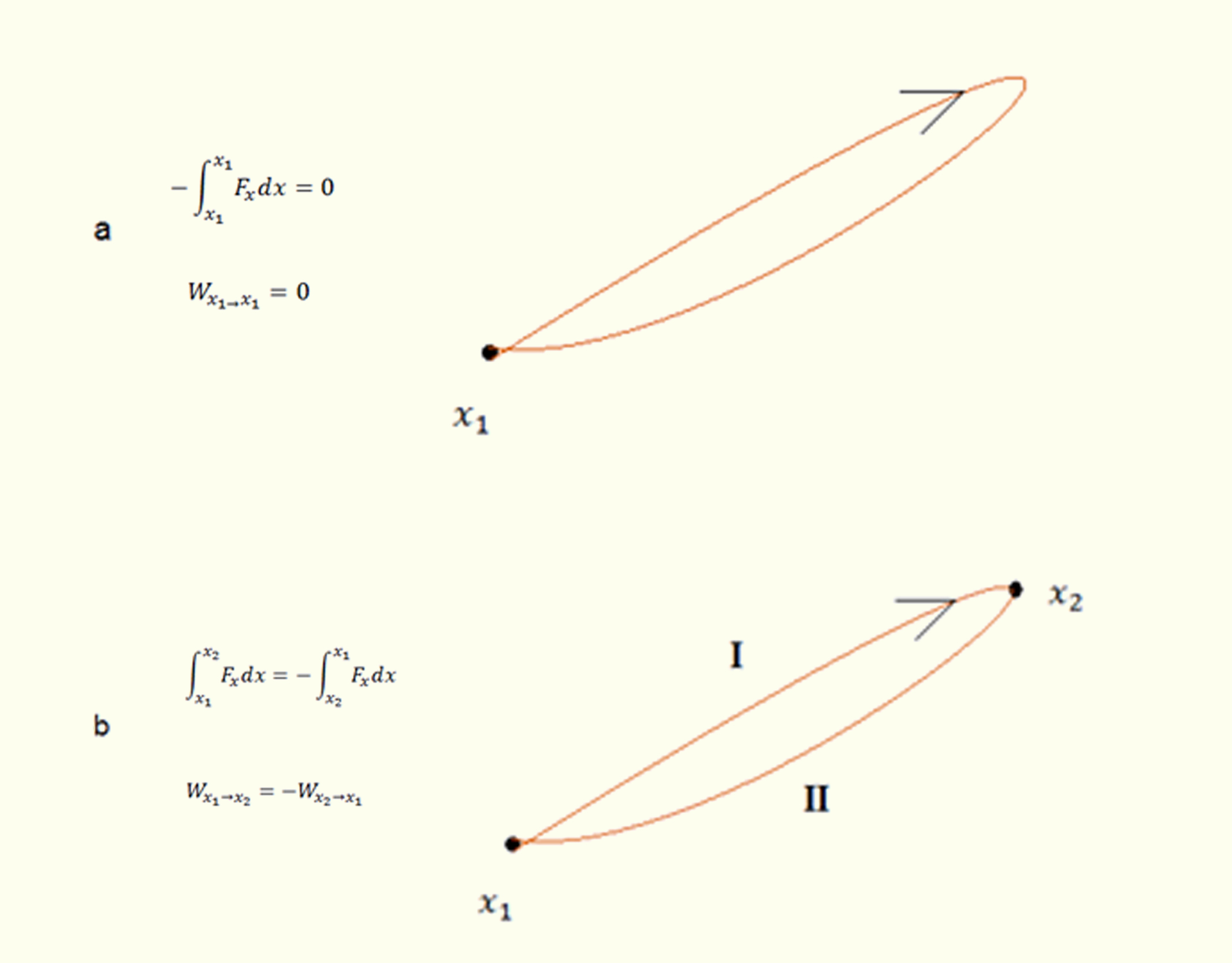
Quando a curva é fechada (Figura 3.5, item A), isto é, quando o deslocamento retorna ao mesmo ponto, a integral de caminho é nula e, dessa maneira, não há variação da energia potencial na partícula. Mas dois pontos, _math_{{x}_{1}}_math_ e _math_{{x}_{2}}_math_, também podem se encontrar ligados por inúmeros caminhos (Figura 3.5, item b). Se o trabalho efetuado por uma força é independente da trajetória e depende meramente das posições inicial e final da partícula, dizemos que essa força é conservativa. A energia potencial sempre surge da interação das forças conservativas (por exemplo, força gravitacional, força peso gravitacional e força elástica). As forças dissipativas (por exemplo, forças de atrito e de arraste) não produzem energia potencial, porque dissipam a energia cinética na forma de energia térmica.
357 a) O trabalho realizado por uma força conservativa em um caminho fechado se anula. b) A quantidade necessária de trabalho para a partícula se deslocar do ponto _math_{{x}_{1}}_math_ até o ponto _math_{{x}_{2}}_math_ é o mesmo que a partícula precisa para se deslocar de _math_{{x}_{2}}_math_ até _math_{{x}_{1}}_math_. Os sinais negativos nas equações dessa figura indicam que os sentidos dos movimentos são opostos. Fonte: Tipler e Mosca (2006, p. 185).
Toda força conservativa obedece a dois critérios: primeiro, o rotacional é nulo, _math_\vec{\nabla }X\vec{F}=0_math_, segundo, a força conservativa é equivalente ao gradiente negativo da energia potencial,_math_~\vec{F}=-\overrightarrow{\nabla .}\text{U}_math_.
Podemos encontrar a expressão para a energia potencial gravitacional. Imagine que uma partícula de massa _math_m_math_ esteja dentro da Terra na presença de um campo gravitacional uniforme (_math_\vec{g}_math_), seja lançada da posição inicial _math_{{y}_{1}}_math_ e chegue até a posição final _math_{{y}_{2}}_math_, assumindo o eixo y positivo para cima. A força peso gravitacional faz com que a partícula seja atraída para a terra, na forma, _math_\vec{F}=-m\vec{g}_math_, em que a aceleração da gravidade terá um sinal negativo na queda livre. Substituindo na equação (34) _math_{{x}_{1}}_math_ e _math_{{x}_{2}}_math_ por _math_{{y}_{1}}_math_ e _math_{{y}_{2}}_math_, e _math_dx_math_ por _math_dy_math_, determinamos a variação da energia potencial, _math_\Delta {{U}_{p}}~=-\underset{{{y}_{1}}}{\overset{{{y}_{2}}}{\mathop \int }}\,\left( -mg \right)dy=mg\left( {{y}_{2}}-{{y}_{1}} \right)=mg\Delta y_math_. A energia potencial gravitacional do sistema partícula-Terra depende somente da variação da altura (_math_\Delta y_math_) e da massa da partícula. Para garantir que a força peso gravitacional seja uma força conservativa, testamos o divergente da energia potencial, associado com a variação da altura _math_\Delta y_math_ com um deslocamento _math_y_math_ qualquer, chamando _math_{{U}_{p}}=mgy_math_, temos:
_math_\vec{\nabla }.{{U}_{p}}=\overrightarrow{\nabla .}\text{mgy}=\left( \frac{\partial \left( mgy \right)}{\partial x}\hat{i}+\frac{\partial \left( mgy~ \right)}{\partial y}\hat{j}+\frac{\partial \left( mgy~ \right)}{\partial z}\hat{k} \right)=mg\hat{j}_math_
Confirmando que a força peso gravitacional é _math_\vec{F}=-\overrightarrow{\nabla .}\text{U}_math_. A outra forma de verificar se a força peso gravitacional é conservativa é calculando o seu rotacional:
_math_\vec{\nabla }X\vec{F}=\left( \frac{\partial }{\partial x}\hat{i}+\frac{\partial }{\partial y}\hat{j}+\frac{\partial }{\partial z}\hat{k} \right)~X~\left( -mg\hat{j} \right)=\left| \\begin{matrix} {\hat{i}} & {\hat{j}} & k \\\\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\\\ 0 & -mg & 0 \\\\ \end{matrix} \right|=0_math_
_math_\vec{\nabla }X\vec{F}=\left( \frac{\partial }{\partial x}\hat{i}+\frac{\partial }{\partial y}\hat{j}+\frac{\partial }{\partial z}\hat{k} \right)~X~\left( -mg\hat{j} \right)=\left| \begin{matrix} {\hat{i}} & {\hat{j}} & k \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ 0 & -mg & 0 \\\end{matrix} \right|=0_math_
Procuramos agora uma expressão que represente o comportamento da energia potencial elástica. Considere o sistema massa-mola. Um bloco de massa m move-se da posição inicial (_math_{{x}_{i}}_math_) até a posição (_math_{{x}_{f}}_math_) submetida à ação de uma mola. A força elástica aplicada nesse deslocamento é a mesma descrita pela Lei de Hooke, cujo módulo é _math_{{F}_{e}}=-kx_math_. Calculamos a variação da energia potencial elástica utilizando a equação (34):
Chamando a posição inicial e , encontramos a expressão para energia potencial elástica, , mostrando que essa energia é proporcional ao quadrado do deslocamento do sistema preso à mola.
A verificação para constatar se a força elástica é conservativa procede do mesmo modo, calculando o gradiente da energia potencial e o rotacional da força elástica. O gradiente da energia potencial é:
_math_\vec{\nabla }.{{U}_{elas}}=\overrightarrow{\nabla .}\frac{k{{x}^{2}}}{2}=\left( \frac{\partial \left( \frac{k{{x}^{2}}}{2} \right)}{\partial x}\hat{i}+\frac{\partial \left( \frac{k{{x}^{2}}}{2} \right)}{\partial y}\hat{j}+\frac{\partial \left( \frac{k{{x}^{2}}}{2} \right)}{\partial z}\hat{k} \right)=kx\hat{i}_math_
A força elástica é conservativa, _math_\overrightarrow{{{F}_{e}}}=\vec{\nabla }.{{U}_{elas}}=-kx\hat{i}_math_. O rotacional da força elástica é:
_math_\vec{\nabla }X\overrightarrow{{{F}_{e}}}=\left( \frac{\partial }{\partial x}\hat{i}+\frac{\partial }{\partial y}\hat{j}+\frac{\partial }{\partial z}\hat{k} \right)~X~\left( -kx\vec{i} \right)=\left| \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ -kx & 0 & 0 \\\end{matrix} \right|=0_math_
Na escala astronômica, o módulo da força gravitacional é _math_\overrightarrow{{{F}_{g}}}=-G\frac{Mm}{{{r}^{2}}}\hat{r}_math_. Aqui, G = 6,67 x 10-11 Nm2/Kg2 é a constante gravitacional. Imagine um foguete em queda livre na direção radial do campo gravitacional da Terra (NUSSENZVEIG, 2002, p. 138), se aproximando a partir de uma posição do espaço muito distante do nosso planeta (_math_{{r}_{o}}\to \infty _math_) até o centro da Terra (_math_{{r}_{f~}}=r_math_). A massa do foguete é _math_m_math_ e a massa concentrada no centro da Terra é _math_M_math_. A distância entre o foguete em queda livre e o centro da Terra é _math_r={{r}_{f}}-{{r}_{o}}._math_ Estamos em busca da variação da energia potencial quando o foguete cai dentro da Terra. Trocando os termos _math_{{x}_{1}}_math_ e _math_{{x}_{2}}_math_ por _math_{{r}_{o}}_math_ e _math_{{r}_{f}}_math_ na equação (34), podemos calcular a variação da energia potencial para a queda livre do foguete:
_math_\Delta {{U}_{g}}=-\underset{\infty }{\overset{r}{\mathop \int }}\,\left( -G\frac{Mm}{{{r}^{2}}} \right)dr=-G\frac{Mm}{r}_math_
Usando coordenadas esféricas, calculamos o divergente da energia potencial gravitacional:
_math_\vec{\nabla }.{{U}_{g}}=\overrightarrow{\nabla .}\left( -G\frac{Mm}{r} \right)=\left( \frac{\partial \left( -G\frac{Mm}{r}~ \right)}{~\partial r}\hat{r}+\frac{\partial \left( -G\frac{Mm}{r}~ \right)}{r\partial \theta }\mathbf{\hat{\theta }}+\frac{\partial \left( -G\frac{Mm}{r}~ \right)}{r\sin \theta \partial \varphi }\hat{\varphi } \right)=G\frac{Mm}{{{r}^{2}}}_math_
Confirmando que a força gravitacional é uma força conservativa _math_\overrightarrow{{{F}_{g}}}=-\vec{\nabla }.{{U}_{g}}_math_. O rotacional para a força gravitacional é calculado em coordenadas esféricas:
_math_\vec{\nabla }X\overrightarrow{{{F}_{g}}}=\frac{1}{{{r}^{2}}\sin \theta }\left| \begin{matrix} {\hat{r}} & r\sin \theta \hat{\varphi } & r\mathbf{\hat{\theta }} \\ \frac{\partial }{\partial r} & \frac{\partial }{\partial \varphi } & \frac{\partial }{\partial \text{ }\!\!\theta\!\!\text{ }} \\ -G\frac{Mm}{{{r}^{2}}} & 0 & 0 \\\end{matrix} \right|=0_math_
324 Trabalho realizado por forças conservativas e variação da energia potencial
Conservação da energia mecânica
Uma partícula tem energia mecânica devido ao seu movimento e/ou à sua posição. Uma bola de vôlei, por exemplo, possui energia mecânica por causa da sua elevada velocidade ao ser arremessada (energia cinética) e da sua posição vertical acima do solo (energia potencial gravitacional); uma calculdora em repouso em cima da mesa tem energia mecânica por causa da sua posição vertical acima do solo (energia potencial gravitacional); um carro contém energia mecânica correspondente à velocidade (energia cinética) do seu movimento. Quando nenhuma força externa é aplicada ao sistema, a variação da energia mecânica é nula (_math_\Delta E=0_math_). Nas duas primeiras seções desta unidade, aprendemos que os conceitos de variação da energia cinética e potencial estão relacionados com o trabalho. Igualando as equações (28) e (34), obtemos:
_math_K\left( {{x}_{2}} \right)-K\left( {{x}_{1}} \right)=U\left( {{x}_{1}} \right)-U\left( {{x}_{2}} \right)~~\left( 35 \right)_math_
Reagrupando os termos da equação (35), encontramos:
_math_K\left( {{x}_{2}} \right)+~U\left( {{x}_{2}} \right)~=~K\left( {{x}_{1}} \right)+~U\left( {{x}_{1}} \right)~~~\left( 36 \right)_math_
A equação (36) demonstra o princípio da conservação da energia mecânica, ou seja, a energia mecânica de uma partícula sob influência de uma força conservativa em qualquer posição durante seu deslocamento é conservada. A energia mecânica é descrita como a soma da energia cinética com a energia potencial:
_math_E=K+U~~~\left( 37 \right)_math_
Fique por dentro
A física da Montanha Russa
Observe o movimento dos carrinhos da montanha russa. Mesmo no topo, o carrinho ainda tem energia cinética suficiente para completar o looping. A energia que desloca o carrinho é fornecida por um sistema de trilhos chamado de colina de elevação, o qual empurra o carrinho para cima, cedendo uma certa quantidade de energia potencial. Ao passo que o carrinho ganha altitude, passa a armazenar mais energia potencial. Essa energia armazenada gera uma acumulação da energia mecânica, que é convertida na forma de energia cinética, viabilizando o movimento. No decorrer do looping, a altitude das colinas diminui, reduzindo o armazenamento da energia mecânica, que gradualmente perderá energia por causa da força de atrito nos trilhos e da resistência do ar.
FonteRecorte textual extraído da obra:TORRES, C. M. A.; FERRARO, N. G.; SOARES, P. A. T. Física: Ciência e Tecnologia-Mecânica, v. 1. São Paulo: Editora Moderna, 2012, p. 220-223.
A equação (37) pode ser reescrita como:
_math_E=\frac{m{{v}^{2}}}{2}+U\left( x \right)~~~\left( 38 \right)_math_
Isolando a velocidade da equação (38), encontramos:
_math_v=\pm \sqrt{\frac{2}{m}\left[ E-U\left( x \right) \right]~}~~~~~~\left( 39 \right)_math_
O sinal _math_\pm _math_ representa os dois sentidos das velocidades (aclive ou declive, direita ou esquerda) no sistema. A velocidade de uma partícula deslocada no eixo horizontal pode ser reescrita como _math_v=\frac{dx}{dt}_math_, sendo assim:
_math_\frac{dx}{dt}=\pm \sqrt{\frac{2}{m}\left[ E-U\left( x \right) \right]~}~~~~~\left( 40 \right)~~~~_math_
Integrando a equação (40) desde _math_t\grave{\ }={{t}_{o}}_math_ até _math_t\grave{\ }=t_math_, no lado direito da igualdade, e _math_x\grave{\ }={{x}_{o}}_math_ até _math_x\grave{\ }=x_math_ no lado esquerdo da igualdade, temos:
_math_t-{{t}_{o}}=\pm \underset{{{x}_{o}}}{\overset{x}{\mathop \int }}\,\frac{dx}{\sqrt{\frac{2}{m}\left[ E-U\left( x \right) \right]}}~~~\left( 41 \right)_math_
Que é a solução da equação diferencial de primeiro grau para o movimento, em termos da energia mecânica e potencial.
Reflita
O pêndulo de Newton
Um equipamento encontrado para ensinar o conceito de conservação da energia mecânica é o pêndulo de Newton. Nesse equipamento, no mínimo 5 bolas de mesmo tamanho e massa são amarradas por fios de mesmo comprimento e espessura em um suporte. Inicialmente, levanta-se a bola de uma extremidade até uma determinada altura. Neste momento, essa bola tem energia potencial máxima. Em seguida, a bola é solta, colidindo nas outras, convertendo a energia potencial em energia cinética para todas as bolas. O conjunto se moverá como um pêndulo e, durante uma oscilação, a energia mecânica é completamente conservada. Posteriormente, por causa do atrito das colisões e da resistência do ar, a energia mecânica diminuirá gradualmente, até que o movimento do pêndulo cesse.
FonteRecorte textual extraído da obra: SILVA, M. C. O pêndulo de Newton: Uma abordagem desafiadora para alunos do Ensino Médio, Física da Escola, v. 11, n. 1, p. 45-46, abr. 2010.
334 Conservação da energia mecânica
Atividades
Um satélite de massa _math_m_math_ está localizado na órbita da Terra a uma distância _math_r_math_ do centro da Terra. Um corpo com massa _math_{{m}_{1}}_math_ e velocidade _math_{{v}_{1}}_math_ deixa a Terra. Assinale a alternativa que mostre qual é a expressão da velocidade do corpo ao abandonar o campo gravitacional terrestre. Admita que a massa da Terra é _math_M_math_ e o raio da Terra é _math_R._math_
Observação: Fisicamente, a velocidade na qual um objeto abandona o campo gravitacional e não retorne mais é conhecida como velocidade de escape.
- Enquanto o corpo está na Terra, a energia mecânica é_math_~{{E}_{Terra}}=\frac{{{m}_{1}}{{v}_{1}}^{2}}{2}-\frac{GM{{m}_{1}}}{r}_math_. No infinito, a energia mecânica no corpo é nula, _math_{{E}_{\infty }}=0_math_, porque a velocidade na qual o corpo atinge a órbita do satélite é zero e a energia potencial na referência infinita também é zero. Dentro do campo gravitacional, a energia mecânica é conservada, _math_{{E}_{Terra}}={{E}_{\infty }}_math_. Resolvendo a igualdade, obtemos a velocidade de escape do corpo, _math_{{v}_{1}}=\sqrt{\frac{2GM}{r}}_math_.
A energia mecânica da Terra é função do raio da Terra _math_R_math_ e não de _math_r._math_
- Enquanto o corpo está na Terra, a energia mecânica é_math_~{{E}_{Terra}}=\frac{{{m}_{1}}{{v}_{1}}^{2}}{2}-\frac{GM{{m}_{1}}}{R}_math_. No infinito, a energia mecânica no corpo é _math_{{E}_{\infty }}=-\frac{GM{{m}_{1}}}{r}_math_, porque a velocidade na qual o corpo atinge a órbita do satélite é zero e a energia potencial na referência_math_~U=-\frac{GM{{m}_{1}}}{r}_math_. Dentro do campo gravitacional, a energia mecânica é conservada, _math_{{E}_{Terra}}={{E}_{\infty }}_math_. Resolvendo a igualdade, obtemos a velocidade de escape do corpo, _math_{{v}_{1}}=\sqrt{2GM\left( \frac{1}{R}-\frac{1}{r} \right)}_math_.
O objeto deixa a Terra em direção ao espaço, portanto, no infinito, a distância do objeto é muito grande, dessa forma, a energia potencial no infinito tende a zero, _math_{{U}_{\infty }}\to 0._math_
- Enquanto o corpo está na Terra, a energia mecânica é_math_~{{E}_{Terra}}=\frac{{{m}_{1}}{{v}_{1}}^{2}}{2}-\frac{GM{{m}_{1}}}{R}_math_. No infinito, a energia mecânica no corpo é _math_{{E}_{\infty }}=-\frac{GMm}{r}_math_, porque a velocidade na qual o corpo atinge a órbita do satélite é zero e a energia potencial na referência_math_~U=-\frac{GMm}{r}_math_. Dentro do campo gravitacional, a energia mecânica é conservada, _math_{{E}_{Terra}}={{E}_{\infty }}_math_. Resolvendo a igualdade, obtemos a velocidade de escape do corpo, _math_{{v}_{1}}=\sqrt{\frac{2GM}{{{m}_{1}}}\left( \frac{{{m}_{1}}}{R}-\frac{m}{r} \right)}_math_.
Dois erros no enunciado: Primeiro, o objeto deixa a Terra em direção ao espaço, portanto, no infinito, a distância do objeto é muito grande, dessa forma, a energia potencial no infinito tende a zero, _math_{{U}_{\infty }}\to 0._math_ Segundo, o objeto continuará possuindo a massa _math_{{m}_{1}}_math_.
- Enquanto o corpo está na Terra, a energia mecânica é_math_~{{E}_{Terra}}=\frac{{{m}_{1}}{{v}_{1}}^{2}}{2}-\frac{GM{{m}_{1}}}{r}_math_. No infinito, a energia mecânica no corpo é _math_{{E}_{\infty }}=-\frac{GM{{m}_{1}}}{r}_math_, porque a velocidade na qual o corpo na qual o corpo atinge a órbita do satélite é zero e a energia potencial na referência_math_~U=-\frac{GM{{m}_{1}}}{r}_math_. Dentro do campo gravitacional, a energia mecânica é conservada, _math_{{E}_{Terra}}={{E}_{\infty }}_math_. Resolvendo a igualdade, obtemos a velocidade de escape do corpo, _math_{{v}_{1}}=0_math_.
A energia mecânica da Terra é função do raio da Terra _math_R_math_ e não de _math_r._math_ O objeto deixa a Terra em direção ao espaço, portanto, no infinito, a distância do objeto é muito grande, dessa forma, a energia potencial no infinito tende a zero, _math_{{U}_{\infty }}\to 0._math_
- Enquanto o corpo está na Terra, a energia mecânica é_math_~{{E}_{Terra}}=\frac{{{m}_{1}}{{v}_{1}}^{2}}{2}-\frac{GM{{m}_{1}}}{R}_math_. No infinito, a energia mecânica no corpo é nula, _math_{{E}_{\infty }}=0_math_, porque a velocidade na qual o corpo atinge a órbita do satélite é zero e a energia potencial na referência infinita também é zero. Dentro do campo gravitacional, a energia mecânica é conservada, _math_{{E}_{Terra}}={{E}_{\infty }}_math_. Resolvendo a igualdade, obtemos a velocidade de escape do corpo, _math_{{v}_{1}}=\sqrt{\frac{2GM}{R}}_math_.
A energia mecânica que o satélite deixa na Terra é a soma da energia cinética necessária para impulsionar o satélite e da energia potencial gravitacional.
_math_~{{E}_{Terra}}=\frac{{{m}_{1}}{{v}_{1}}^{2}}{2}-\frac{GM{{m}_{1}}}{R}_math_.
Em que _math_{{m}_{1}}_math_ é a massa do satélite, _math_M_math_ é a massa da Terra, _math_R_math_ é a distância entre o centro da Terra e o satélite e _math_{{v}_{1}}_math_ é a distância a qual que o satélite deixou a Terra.
O princípio da conservação da energia garante que ela é a mesma para o satélite, ou seja, a energia mecânica para o satélite entrar em órbita é a mesma, antes, durante e depois que o satélite deixou a Terra.
No infinito, a energia potencial é usada como a referência nula e quando o satélite entra em órbita, a velocidade do satélite também é nula. A energia mecânica resultante é zero.
Dessa forma, _math_\frac{{{m}_{1}}{{v}_{1}}^{2}}{2}=\frac{GM{{m}_{1}}}{R}_math_, o que implica em _math_{{v}_{1}}=\sqrt{\frac{2GM}{R}}._math_
Atividades
Uma bola de 500g é solta sobre uma mola, comprimindo-a em 10 cm. Assinale a alternativa que indique qual é a velocidade da bola antes de atingir a mola. A constante da mola é _math_K=200\frac{N}{m}._math_
- Duas forças atuam sobre a bola comprimindo a mola: a força peso, _math_\vec{P}=m\vec{g}_math_, e a força elástica, _math_{{\vec{F}}_{e}}=-K\vec{y}._math_ O trabalho realizado para comprimir a mola está submetido à ação das forças, _math_W={{W}_{p}}+{{W}_{e}}_math_. O trabalho feito pela força peso é _math_{{W}_{p}}=\underset{{{y}_{i}}}{\overset{{{y}_{f}}}{\mathop \int }}\,\vec{P}.dy=0,49J_math_ e o trabalho efetuado pela força elástica é _math_{{W}_{e}}=\underset{{{y}_{i}}}{\overset{{{y}_{f}}}{\mathop \int }}\,{{\vec{F}}_{e}}.dy=-2J_math_. O teorema do trabalho e da energia cinética garante que _math_W=\Delta K=\frac{m{{\overrightarrow{{{v}_{f}}}}^{2}}}{2}-\frac{m{{\overrightarrow{{{v}_{i}}}}^{2}}}{2}_math_. No final da compressão, _math_\overrightarrow{{{v}_{f}}}=0,_math_ logo, a velocidade da bola antes de atingir a mola é _math_\overrightarrow{{{v}_{i}}}=1,43\frac{m}{s}_math_ _math_\hat{j}_math_.
A velocidade é negativa porque a compressão da mola parte da marca zero até o espaço de -10 cm.
- Duas forças atuam sobre a bola comprimindo a mola: a força peso, _math_\vec{P}=m\vec{g},_math_ e a força elástica, _math_{{\vec{F}}_{e}}=-K\vec{y}._math_ O trabalho realizado para comprimir a mola está submetido à ação das forças, _math_W={{W}_{p}}+{{W}_{e}}_math_. O trabalho feito pela força peso é _math_{{W}_{p}}=\underset{{{y}_{i}}}{\overset{{{y}_{f}}}{\mathop \int }}\,\vec{P}.dy=0,49J_math_ e o trabalho efetuado pela força elástica é _math_{{W}_{e}}=\underset{{{y}_{i}}}{\overset{{{y}_{f}}}{\mathop \int }}\,{{\vec{F}}_{e}}.dy=1~J_math_. O teorema do trabalho e da energia cinética garante que _math_W=\Delta K=\frac{m{{\overrightarrow{{{v}_{f}}}}^{2}}}{2}-\frac{m{{\overrightarrow{{{v}_{i}}}}^{2}}}{2}_math_. No final da compressão, _math_\overrightarrow{{{v}_{f}}}=0,_math_ logo, a velocidade da bola antes de atingir a mola é _math_\overrightarrow{{{v}_{i}}}=2,44\frac{m}{s}_math_ _math_\hat{j}_math_.
As forças que agem sobre a bola, comprimindo a mola, são as forças peso, _math_\vec{P}=m\vec{g},_math_ e a força elástica, _math_{{\vec{F}}_{e}}=-K\vec{y}._math_
O trabalho realizado para comprimir a mola está submetido à ação das forças, que é:
_math_W={{W}_{p}}+{{W}_{e}}_math_.
O trabalho feito pela força peso é _math_{{W}_{p}}=\underset{{{y}_{i}}}{\overset{{{y}_{f}}}{\mathop \int }}\,\vec{P}.dy=0,49J_math_
O trabalho efetuado pela força elástica é _math_{{W}_{e}}=\underset{{{y}_{i}}}{\overset{{{y}_{f}}}{\mathop \int }}\,{{\vec{F}}_{e}}.dy=1~J_math_.
Portanto o trabalho resultante é _math_W={{W}_{p}}+{{W}_{e}}=0,49J+1J=1,49~J_math_
O teorema do trabalho e da energia cinética garante que
_math_W=\Delta K=\frac{m{{\overrightarrow{{{v}_{f}}}}^{2}}}{2}-\frac{m{{\overrightarrow{{{v}_{i}}}}^{2}}}{2}_math_.
No final da compressão, _math_\overrightarrow{{{v}_{f}}}=0._math_
Logo, a velocidade da bola antes de atingir a mola é:
_math_\overrightarrow{{{v}_{i}}}=\sqrt{\frac{2W}{m}}=2,44\frac{m}{s}_math_ _math_\hat{j}_math_
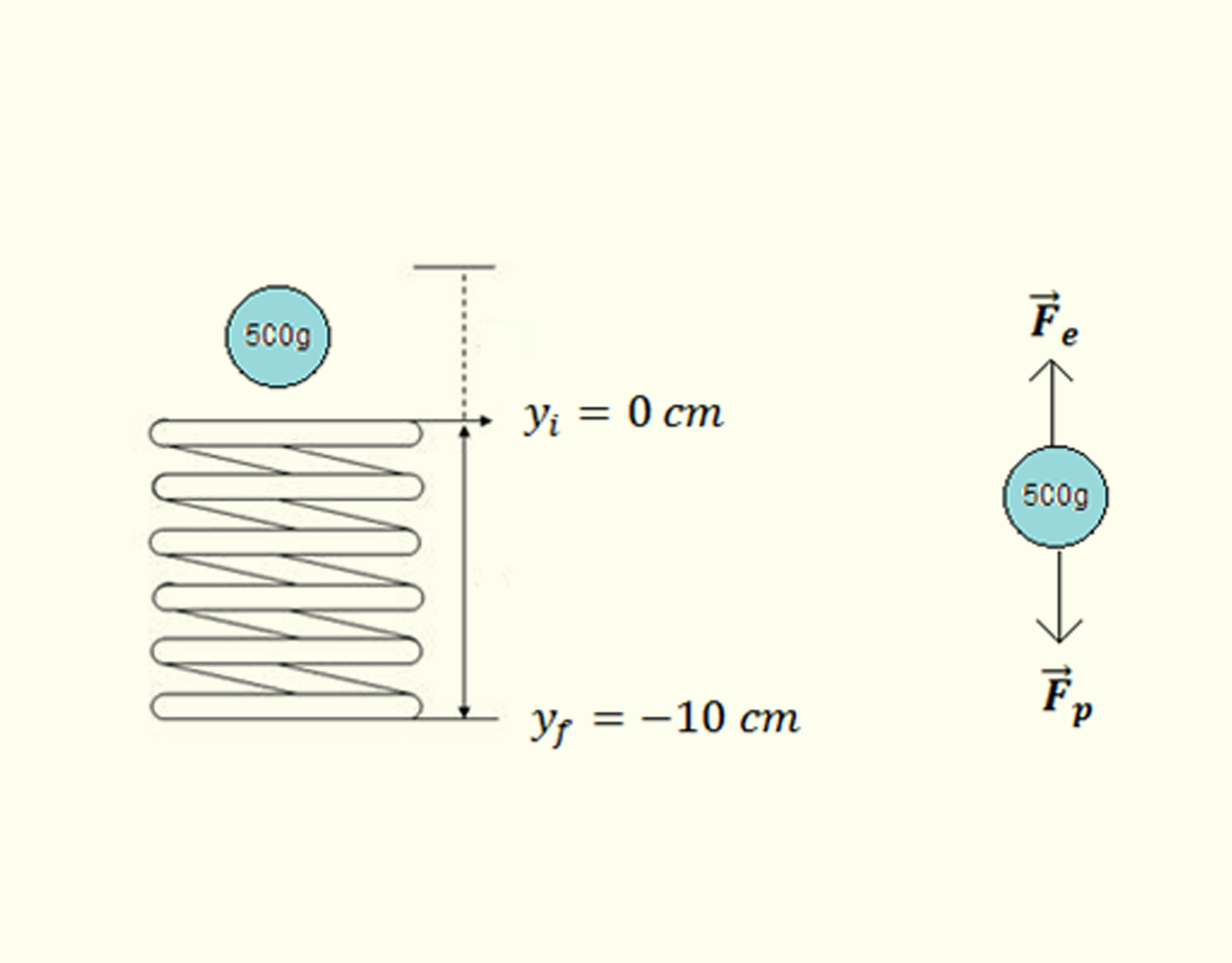
- O trabalho realizado para comprimir a mola está submetido à ação da força, _math_W={{W}_{e}}_math_. O trabalho efetuado pela força elástica é _math_{{W}_{e}}=\underset{{{y}_{i}}}{\overset{{{y}_{f}}}{\mathop \int }}\,{{\vec{F}}_{e}}.dy=1J_math_. O teorema do trabalho e da energia cinética garante que _math_W=\Delta K=\frac{m{{\overrightarrow{{{v}_{f}}}}^{2}}}{2}-\frac{m{{\overrightarrow{{{v}_{i}}}}^{2}}}{2}_math_. No final da compressão, _math_\overrightarrow{{{v}_{f}}}=0,_math_ logo, a velocidade da bola antes de atingir a mola é _math_\overrightarrow{{{v}_{i}}}=2\frac{m}{s}_math_ _math_\hat{j}_math_.
A força gravitacional também contribui com o deslocamento da mola.
- Duas forças atuam sobre a bola comprimindo a mola: a força peso, _math_\vec{P}=m\overrightarrow{g,}_math_ e a força elástica, _math_{{\vec{F}}_{e}}=-K\vec{y}._math_ O trabalho realizado para comprimir a mola está submetido à ação das forças, _math_W={{W}_{p}}+{{W}_{e}}_math_. O trabalho feito pela força peso é _math_{{W}_{p}}=\underset{{{y}_{i}}}{\overset{{{y}_{f}}}{\mathop \int }}\,\vec{P}.dy=0,49J_math_, e o trabalho efetuado pela força elástica é _math_{{W}_{e}}=\underset{{{y}_{i}}}{\overset{{{y}_{f}}}{\mathop \int }}\,{{\vec{F}}_{e}}.dy=-1J_math_. O teorema do trabalho e da energia cinética garante que _math_W=\Delta K=\frac{m{{\overrightarrow{{{v}_{f}}}}^{2}}}{2}-\frac{m{{\overrightarrow{{{v}_{i}}}}^{2}}}{2}_math_. No final da compressão, _math_\overrightarrow{{{v}_{i}}}=0,_math_ logo, a velocidade da bola antes de atingir a mola é _math_\overrightarrow{{{v}_{f}}}=-1,43\frac{m}{s}_math_ _math_\hat{j}_math_.
O trabalho da força elástica é negativo, e a bola só ficará em repouso sobre a mola depois de comprimi-la.
- O trabalho realizado para comprimir a mola está submetido à ação da força, _math_W={{W}_{e}}_math_. O trabalho efetuado pela força elástica é _math_{{W}_{e}}=\underset{{{y}_{i}}}{\overset{{{y}_{f}}}{\mathop \int }}\,{{\vec{F}}_{e}}.dy=-2J_math_. O teorema do trabalho e da energia cinética garante que _math_W=\Delta K=\frac{m{{\overrightarrow{{{v}_{f}}}}^{2}}}{2}-\frac{m{{\overrightarrow{{{v}_{i}}}}^{2}}}{2}_math_. No final da compressão, _math_\overrightarrow{{{v}_{i}}}=0,_math_ logo, a velocidade da bola antes de atingir a mola é _math_\overrightarrow{{{v}_{i}}}=2,83\frac{m}{s}_math_ _math_\hat{j}_math_.
A bola só ficará em repouso sobre a mola depois de comprimi-la.
Atividades
A figura a seguir mostra um carrinho de massa _math_m_math_ em uma montanha russa realizando um looping. Assinale a alternativa correta que informe qual é a altura mínima de _math_{{h}_{A}}_math_ para que o carrinho complete o looping. Considere o atrito desprezível e assuma que a aceleração centrípeta é _math_\overrightarrow{{{a}_{c}}}=\frac{{{{\vec{v}}}^{2}}}{R}._math_
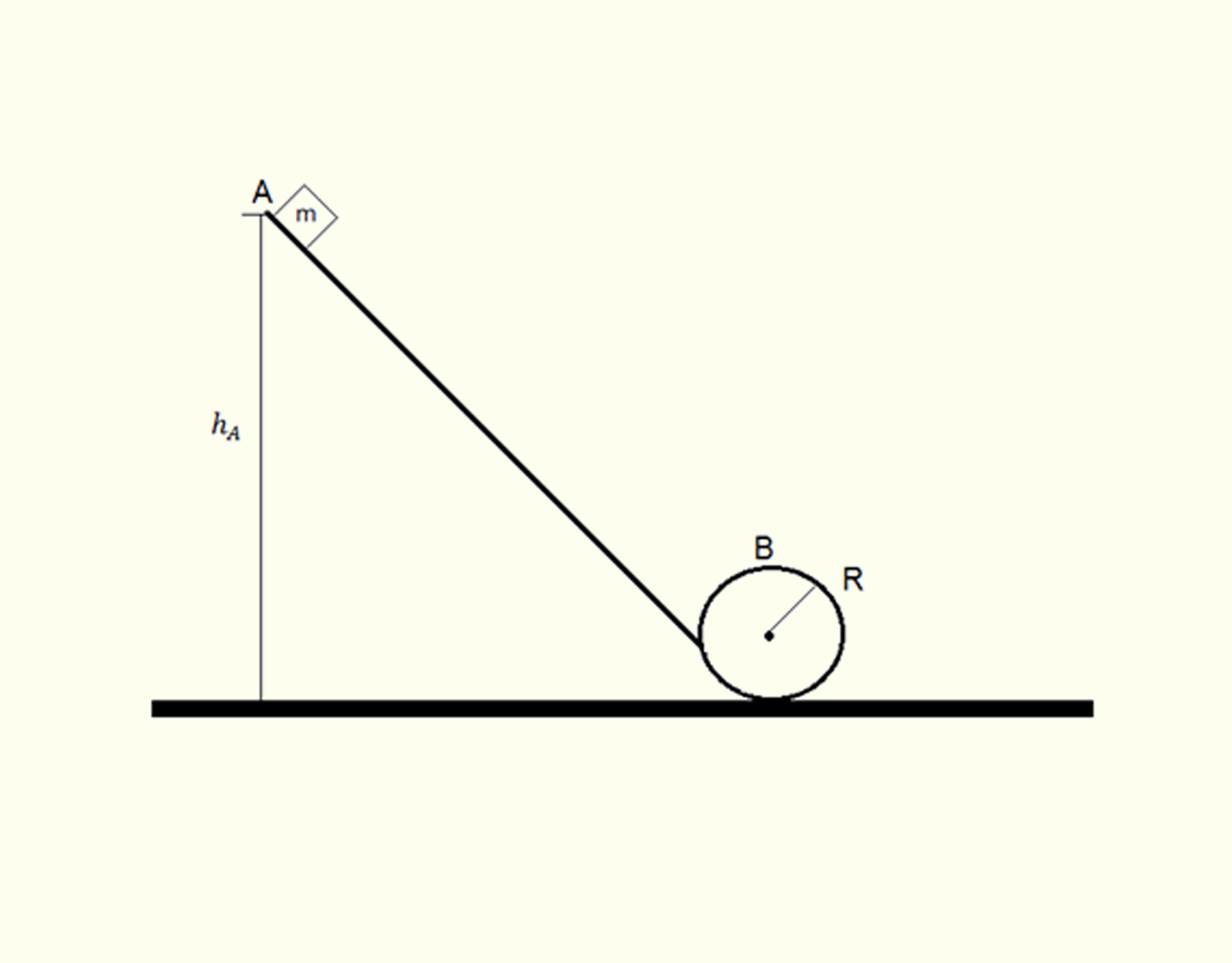
- No ponto A, a energia mecânica corresponde à energia potencial, _math_{{W}_{A}}={{U}_{A}}=mg{{h}_{A}}._math_ Para o carrinho chegar ao ponto B, o contato do carrinho no trilho circular deve ser mínimo ou, em outras palavras, _math_\vec{N}\to 0._math_ Por meio da somatória das forças, encontramos que o módulo da velocidade é _math_{{v}^{2}}=gR._math_ A energia mecânica é _math_{{W}_{B}}=\frac{5}{2}mgR._math_ De acordo com o princípio da conservação da energia _math_{{W}_{A}}={{W}_{B}}_math_, a altura mínima para o carrinho completar o looping é _math_{{h}_{A}}=\frac{5}{2}R._math_
No ponto A, o trabalho é igual à energia potencial, _math_{{W}_{A}}={{U}_{A}}=mg{{h}_{A}}._math_
No ponto B, para o carrinho chegar ao ponto B, o contato do carrinho no trilho circular deve ser mínimo ou, em outras palavras, _math_\vec{N}\to 0._math_ As forças atuantes sobre o carrinho são representadas na figura abaixo:
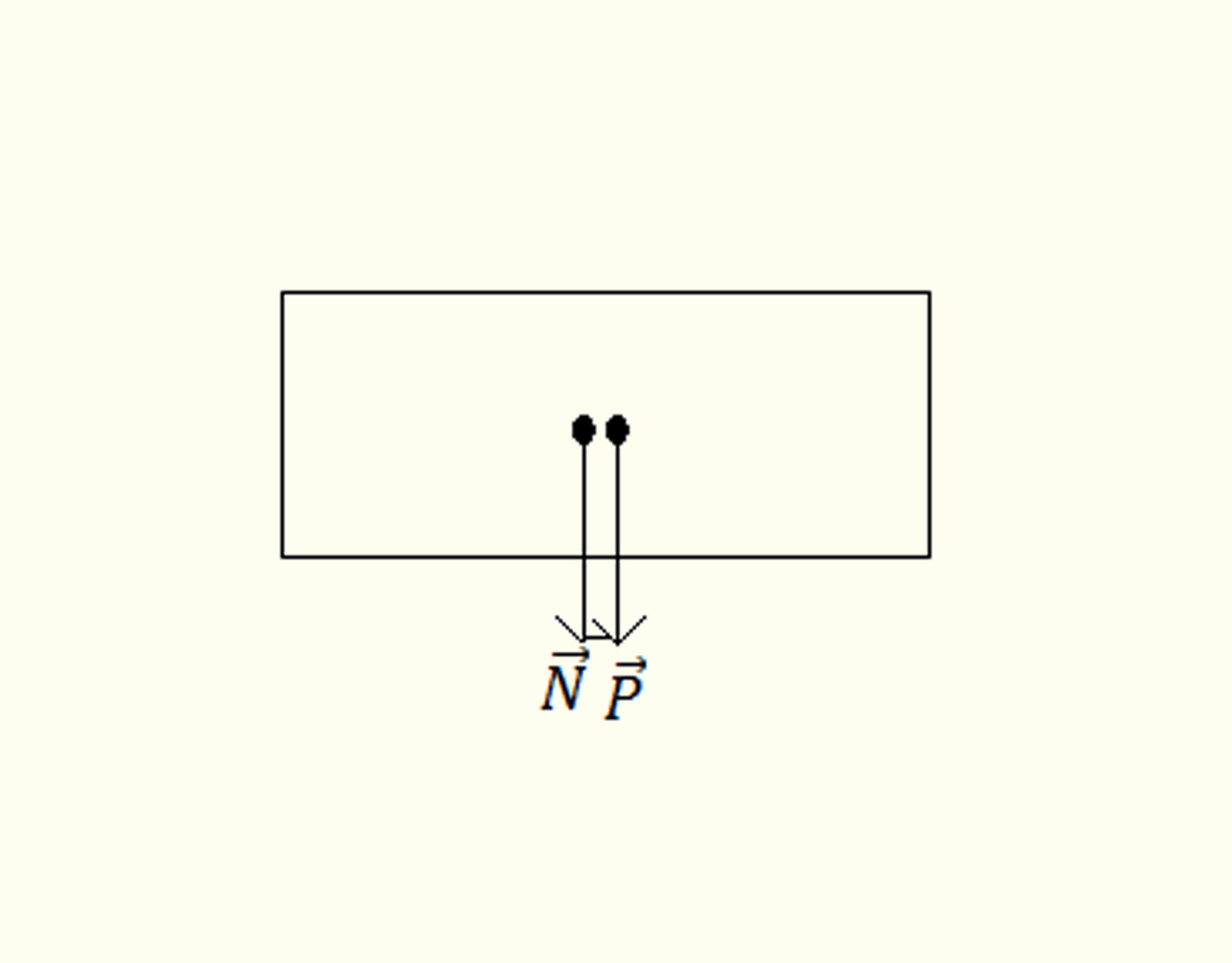
Fonte: a autora.
A segunda Lei de Newton diz que a somatória das forças é:
_math_\vec{F}=\vec{N}+\vec{P}=m\overrightarrow{{{a}_{c}}}_math_
_math_m\vec{g}=\frac{m{{{\vec{v}}}^{2}}}{R}_math_
_math_{{\vec{v}}^{2}}=\vec{g}R_math_
A energia mecânica no ponto B é:
_math_{{W}_{B}}=\frac{m{{v}^{2}}}{2}+mg{{h}_{B}}_math_
A altura no looping circular é _math_{{h}_{B}}=2R_math_.
_math_{{W}_{B}}=\frac{m{{v}^{2}}}{2}+mg2R=\frac{5}{2}mgR_math_
Segundo, o princípio da conservação da energia, _math_{{W}_{A}}={{W}_{B}}_math_.
_math_mg{{h}_{A}}=\frac{5}{2}mgR_math_
_math_{{h}_{A}}=\frac{5}{2}R_math_
- No ponto A, a energia mecânica corresponde à energia potencial, _math_{{W}_{A}}={{U}_{A}}=mg{{h}_{A}}._math_ Para o carrinho chegar ao ponto B, o contato do carrinho no trilho circular é nulo ou, em outras palavras, _math_\vec{N}=0._math_ Por meio da somatória das forças, encontramos que o módulo da velocidade é _math_{{v}^{2}}=gR._math_ A energia mecânica é _math_{{W}_{B}}=\frac{5}{2}mgR._math_ De acordo com o princípio da conservação da energia, _math_{{W}_{A}}={{W}_{B}}_math_, a altura mínima para o carrinho completar o looping é _math_{{h}_{A}}=\frac{5}{2}R._math_
A força normal tende a zero, mas não é nula, caso contrário, não haveria contato entre o carrinho e os trilhos, e o carrinho se soltaria da montanha russa.
- No ponto A, a energia mecânica corresponde à energia potencial, _math_{{W}_{A}}={{U}_{A}}=mg{{h}_{A}}._math_ No looping circular, _math_\vec{v}=0._math_ A energia mecânica é _math_{{W}_{B}}=2mgR._math_ De acordo com o princípio da conservação da energia, _math_{{W}_{A}}={{W}_{B}}_math_. A altura mínima para o carrinho completar o looping é _math_{{h}_{A}}=2R._math_
A força de contato entre o carrinho e os trilhos tem o mesmo sentido da força peso.
- No ponto A, a energia mecânica corresponde à energia potencial, _math_{{W}_{A}}={{U}_{A}}=mg{{h}_{A}}._math_ Para o carrinho chegar ao ponto B, o contato do carrinho no trilho circular deve ser mínimo ou, em outras palavras, _math_\vec{N}\to 0._math_ Por meio da somatória das forças, encontramos que o módulo da velocidade é _math_{{v}^{2}}=gR._math_ A energia mecânica é _math_{{W}_{B}}=\frac{3}{2}mgR._math_ De acordo com o princípio da conservação da energia _math_{{W}_{A}}={{W}_{B}}_math_, a altura mínima para o carrinho completar o looping é _math_{{h}_{A}}=\frac{3}{2}R._math_
A altura _math_{{h}_{B}}=2R_math_, no lopping circular e não R.
- No ponto A, a energia mecânica corresponde à energia potencial, _math_{{W}_{A}}={{U}_{A}}=mg{{h}_{A}}._math_ Para o carrinho chegar ao ponto B, o contato do carrinho no trilho circular deve ser mínimo ou, em outras palavras, _math_\vec{N}\to 0._math_ Por meio da somatória das forças, encontramos que o módulo da velocidade é _math_{{v}^{2}}=2gR._math_ A energia mecânica é _math_{{W}_{B}}=\frac{5}{2}mgR._math_ De acordo com o princípio da conservação da energia _math_{{W}_{A}}={{W}_{B}},_math_ a altura mínima para o carrinho completar o looping é _math_{{h}_{A}}=4R._math_
A velocidade é _math_{{v}^{2}}=gR_math_.
Atividades
Poliana brinca com uma pistola de brinquedo sobre uma mesa. O objetivo da garota é acertar uma bolinha em uma caixa distante 1,8 m da mesa. Na primeira tentativa, Poliana comprime a mola da pistola em 0,9 cm, mas a bola cai 15 cm antes da caixa. Assinale a alternativa que indique quanto a mola deve ser comprimida na próxima tentativa para que a bola caia dentro da caixa. A constante da mola é _math_{{K}_{m}}._math_
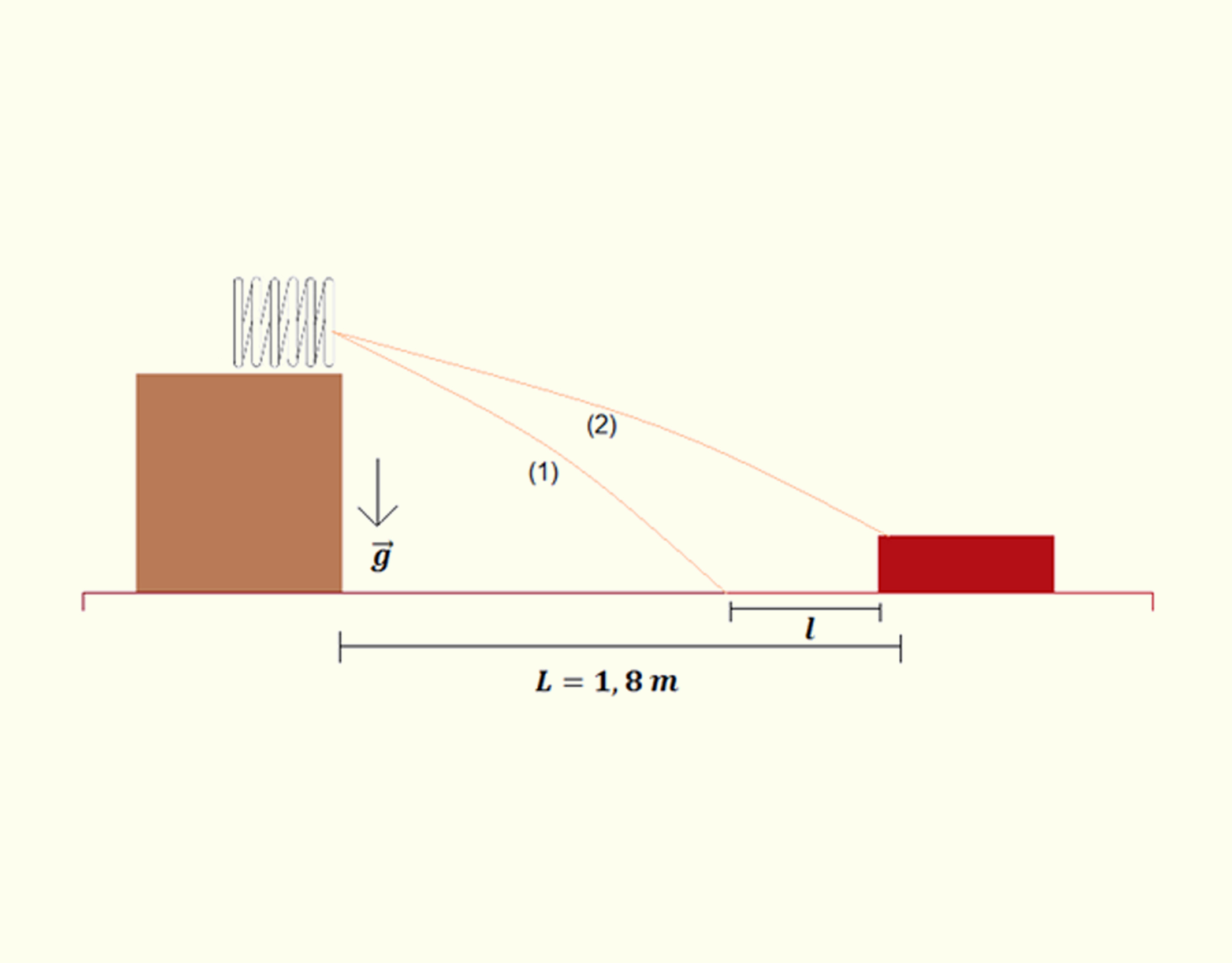
- Aplicando o princípio da conservação da energia no lançamento horizontal da bola, temos que _math_\Delta {{U}_{e}}=\Delta K_math_. Ao atingir o alvo _math_{{v}_{f}}=0_math_ e, nesse problema, isso implica em _math_{{K}_{m}}{{x}^{2}}=m{{v}_{o}}^{2}_math_. Na primeira tentativa, _math_{{K}_{m}}{{x}_{1}}^{2}=m{{v}_{o1}}^{2}~_math_e, na segunda tentativa, _math_{{K}_{m}}{{x}_{2}}^{2}=m{{v}_{o2}}^{2}_math_. A razão de proporção da compressão da mola e da velocidade da mola é _math_\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{v}_{o1}}}{{{v}_{02}}}._math_ Observando os lançamentos horizontais, na primeira tentativa encontramos _math_L-l={{v}_{o1}}t_math_ e, na segunda tentativa,_math_~~L={{v}_{o2}}t_math_. Isolando _math_{{v}_{o1}}_math_ e _math_{{v}_{o2}}_math_ das equações da trajetória e substituindo na expressão da razão _math_\frac{{{v}_{o1}}}{{{v}_{02}}}_math_, chegamos a _math_{{x}_{2}}=\frac{L}{L-l}{{x}_{1}}=0,98~cm._math_
Princípio da conservação da energia mecânica no lançamento horizontal da bolinha.
_math_\frac{m{{v}_{o}}^{2}}{2}+\frac{{{K}_{m}}{{x}_{o}}^{2}}{2}=\frac{m{{v}_{f}}^{2}}{2}+\frac{{{K}_{m}}{{x}_{f}}^{2}}{2}_math_
No final, quando a bolinha atinge o alvo, _math_{{v}_{f}}=0_math_. Antes da compressão da mola, _math_{{x}_{o}}=0_math_.
_math_\frac{m{{v}_{o}}^{2}}{2}=\frac{m{{v}_{f}}^{2}}{2}_math_
Na primeira tentativa,
_math_{{K}_{m}}{{x}_{1}}^{2}=m{{v}_{o1}}^{2}_math_
_math_{{x}_{1}}=0,9~cm_math_, a compressão na mola
Na segunda tentativa,
_math_{{K}_{m}}{{x}_{2}}^{2}=m{{v}_{o2}}^{2}_math_
_math_{{x}_{2}}=?_math_
A razão
_math_\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{v}_{o1}}}{{{v}_{02}}}_math_
A equação do lançamento horizontal é _math_x={{x}_{o}}+vt_math_
O deslocamento horizontal na primeira tentativa é:
_math_L-l={{v}_{o1}}t_math_
E, na segunda tentativa, é:
_math_L={{v}_{o2}}t_math_
Isolando, _math_{{v}_{o1}}=\frac{L-l}{t}_math_ e _math_{{v}_{o2}}=\frac{L}{t}_math_
_math_\frac{{{v}_{o1}}}{{{v}_{02}}}=\frac{L-l}{L}=\frac{{{x}_{1}}}{{{x}_{2}}}_math_
_math_{{x}_{2}}=\frac{L}{L-l}{{x}_{1}}=\frac{1,8}{1,65}0,009=0,0098~m_math_
- Aplicando o princípio da conservação da energia no lançamento horizontal da bola, temos que _math_\Delta {{U}_{e}}=\Delta K_math_. Ao atingir o alvo, _math_{{v}_{f}}=0_math_, e, nesse problema, isso implica em _math_{{K}_{m}}{{x}^{2}}=m{{v}_{o}}^{2}_math_. Na primeira tentativa, _math_{{K}_{m}}{{x}_{1}}^{2}=m{{v}_{o1}}^{2}~_math_e, na segunda tentativa, _math_{{K}_{m}}{{x}_{2}}^{2}=m{{v}_{o2}}^{2}_math_. A razão de proporção da compressão da mola e da velocidade da mola é _math_\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{v}_{o2}}}{{{v}_{01}}}._math_ Observando os lançamentos horizontais, na primeira tentativa, encontramos _math_L-l={{v}_{o1}}t_math_ e, na segunda tentativa,_math_~L={{v}_{o2}}t_math_. Isolando _math_{{v}_{o1}}_math_ e _math_{{v}_{o2}}_math_ das equações da trajetória, e substituindo na expressão da razão, _math_\frac{{{v}_{o2}}}{{{v}_{01}}}_math_, chegamos a _math_{{x}_{2}}=\frac{L-l}{L}{{x}_{1}}=0,83~cm._math_
Aplicando o princípio da conservação da energia no lançamento horizontal da bola, temos que _math_\Delta {{U}_{e}}=\Delta K_math_. Ao atingir o alvo, _math_{{v}_{f}}=0_math_, e, nesse problema, isso implica em _math_{{K}_{m}}{{x}^{2}}=m{{v}_{o}}^{2}_math_. Na primeira tentativa, _math_{{K}_{m}}{{x}_{1}}^{2}=m{{v}_{o1}}^{2}~_math_e, na segunda tentativa, _math_{{K}_{m}}{{x}_{2}}^{2}=m{{v}_{o2}}^{2}_math_. A razão de proporção da compressão da mola e da velocidade da mola é _math_\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{v}_{o1}}}{{{v}_{02}}}._math_ Observando os lançamentos horizontais, na primeira tentativa, encontramos _math_L={{v}_{o1}}t_math_ e, na segunda tentativa,_math_~L-l={{v}_{o2}}t_math_. Isolando _math_{{v}_{o1}}_math_ e _math_{{v}_{o2}}_math_ das equações da trajetória, e substituindo na expressão da razão, _math_\frac{{{v}_{o1}}}{{{v}_{02}}}_math_, chegamos a _math_{{x}_{2}}=\frac{L-l}{L}{{x}_{1}}=0,83~cm._math_
- Aplicando o princípio da conservação da energia no lançamento horizontal da bola, temos que _math_\Delta {{U}_{e}}=\Delta K_math_. Ao atingir o alvo, _math_{{v}_{i}}=0_math_, e, nesse problema, isso implica em _math_m{{v}_{f}}^{2}+{{K}_{m}}{{x}^{2}}=0_math_. Na primeira tentativa, _math_{{K}_{m}}{{x}_{1}}^{2}=-m{{v}_{f1}}^{2}~_math_e, na segunda tentativa, _math_{{K}_{m}}{{x}_{2}}^{2}=m{{v}_{f2}}^{2}_math_. A razão de proporção da compressão da mola e da velocidade da mola é _math_\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{v}_{f1}}}{{{v}_{f2}}}._math_ Observando os lançamentos horizontais, na primeira tentativa, encontramos _math_L-l={{v}_{f1}}t_math_ e, na segunda tentativa,_math_~L={{v}_{f2}}t_math_. Isolando _math_{{v}_{f1}}_math_ e _math_{{v}_{f2}}_math_ das equações da trajetória, e substituindo na expressão da razão, _math_\frac{{{v}_{f1}}}{{{v}_{f2}}}_math_, chegamos a _math_{{x}_{2}}=\frac{L}{L-l}{{x}_{1}}=0,98~cm._math_
Aplicando o princípio da conservação da energia no lançamento horizontal da bola, temos que _math_\Delta {{U}_{e}}=\Delta K_math_. Ao atingir o alvo, _math_{{v}_{i}}=0_math_, e, nesse problema, isso implica em _math_m{{v}_{f}}^{2}+{{K}_{m}}{{x}^{2}}=0_math_. Na primeira tentativa, _math_{{K}_{m}}{{x}_{1}}^{2}=-m{{v}_{f1}}^{2}~_math_e, na segunda tentativa, _math_{{K}_{m}}{{x}_{2}}^{2}=m{{v}_{f2}}^{2}_math_. A razão de proporção da compressão da mola e da velocidade da mola é _math_\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{v}_{f2}}}{{{v}_{f1}}}._math_ Observando os lançamentos horizontais, na primeira tentativa, encontramos _math_L-l={{v}_{o1}}t_math_ e, na segunda tentativa,_math_~L={{v}_{o2}}t_math_. Isolando _math_{{v}_{f1}}_math_ e _math_{{v}_{f2}}_math_ das equações da trajetória, e substituindo na expressão da razão, _math_\frac{{{v}_{f2}}}{{{v}_{f1}}}_math_, chegamos a _math_{{x}_{2}}=\frac{L-l}{L}{{x}_{1}}=0,83~cm._math_
Atividades
A velocidade rasante é a velocidade de partida necessária para que um corpo permaneça em órbita, próxima à superfície da Terra, conhecida como órbita rasante. Assinale a alternativa que determine qual é o módulo da velocidade rasante de um satélite lançado em uma estação na Terra.
Considerações: A massa da Terra é _math_M~_math_= 5,97 x 1024 Kg, a massa do satélite é _math_m=_math_ 1000 Kg, a constante gravitacional é _math_G=6,67.~{{10}^{-11}}\frac{{{m}^{3}}}{Kg{{s}^{2}}}_math_ e o raio da Terra é _math_R=~_math_6,4 x 106 m.
- Próximo da superfície da Terra, _math_\vec{P}=\overrightarrow{{{F}_{g}}}_math_. O satélite na órbita rasante possui uma aceleração centrípeta, _math_\overrightarrow{{{a}_{c}}}=\vec{g}_math_. Após as manipulações algébricas necessárias, obtemos o módulo da velocidade, que é _math_{{v}_{r}}=\sqrt{\frac{GM}{R}}\approx {{2,844.10}^{4}}\frac{Km}{h}._math_
Na superfície da Terra, existem duas forças:
i) A força peso que atua sobre os corpos.
ii) A força gravitacional, devido à Lei da Gravitação Universal.
_math_\vec{P}=\overrightarrow{{{F}_{g}}}_math_
Em módulo:
_math_mg=\frac{GMm}{{{R}^{2}}}_math_
_math_Logo:~_math_ _math_g=\frac{GM}{{{R}^{2}}}_math_
Próximo à superfície da Terra, a aceleração centrípeta de um corpo em órbita aproximadamente circular é igual à aceleração da gravidade na Terra:
_math_{{a}_{c}}=g_math_
A aceleração centrípeta é _math_{{a}_{c}}=\frac{{{v}^{2}}}{R}_math_
Igualando:
_math_\frac{{{v}^{2}}}{R}=\frac{GMm}{{{R}^{2}}}_math_
Encontramos:
_math_v=\sqrt{\frac{GM}{R}}_math_
E _math_v_math_ é chamada de velocidade rasante para o satélite se manter em órbita próxima a Terra.
Substituindo os valores numéricos, encontramos _math_v\approx 7900m/s_math_.
Convertendo, 1m/s=3,6 Km/h, temos _math_v={{2,844.10}^{4}}\frac{Km}{h}_math_.
- Enquanto o corpo está na Terra a energia mecânica é,_math_~{{E}_{Terra}}=\frac{m{{v}_{r}}^{2}}{2}-\frac{GMm}{R}_math_. Na órbita rasante, a energia mecânica no corpo é nula, _math_{{E}_{orbita}}=0_math_, porque a velocidade na qual o corpo atinge a órbita do satélite é zero e a energia potencial na referência também é zero. Dentro do campo gravitacional, a energia mecânica é conservada, _math_{{E}_{Terra}}={{E}_{orbita}}_math_. Resolvendo a igualdade, obtemos a velocidade de escape do corpo, _math_{{v}_{r}}=\sqrt{\frac{2GM}{R}}_math_.
Enquanto o corpo está na Terra a energia mecânica é,_math_~{{E}_{Terra}}=\frac{m{{v}_{r}}^{2}}{2}-\frac{GMm}{R}_math_. Na órbita rasante, a energia mecânica no corpo é, _math_{{E}_{orbita}}=-\frac{GMm}{r}_math_, porque a velocidade na qual o corpo atinge a órbita do satélite é zero e a energia potencial na referência_math_~\acute{e}~~U=-\frac{GMm}{r}_math_. Dentro do campo gravitacional, a energia mecânica é conservada, _math_{{E}_{Terra}}={{E}_{\infty }}_math_. Resolvendo a igualdade, obtemos a velocidade de escape do corpo, _math_{{v}_{r}}=\sqrt{\frac{2GM}{m}\left( \frac{M}{R}-\frac{m}{r} \right)}_math_
- Próximo da superfície da Terra, _math_\vec{P}=\overrightarrow{{{F}_{g}}}_math_. O satélite na órbita rasante possui uma aceleração centrípeta, _math_\overrightarrow{{{a}_{c}}}=\vec{g}_math_. Após as manipulações algébricas necessárias, obtemos o módulo da, _math_{{v}_{r}}=\sqrt{\frac{GM}{R}}\approx {{7,9.10}^{3}}\frac{Km}{h}._math_
Próximo da superfície da Terra, _math_\vec{P}=\overrightarrow{{{F}_{g}}}_math_. O satélite na órbita rasante possui uma aceleração centrípeta, _math_\overrightarrow{{{a}_{c}}}=2\vec{g}_math_. Após as manipulações algébricas necessárias, obtemos o módulo da, _math_{{v}_{r}}=\sqrt{2\frac{GM}{R}}\approx {{4.10}^{4}}\frac{Km}{h}._math_
Atividades
Assinale a alternativa correta que mostre qual é o módulo da velocidade rasante necessária para que o satélite citado no exercício anterior permaneça em órbita circular a uma distância _math_R/2_math_ da superfície terrestre.
- A Terra exerce a força peso e a força gravitacional sobre o satélite, _math_\overrightarrow{{{P}_{R/2}}}=\overrightarrow{{{F}_{gR/2}}}_math_. Desta igualdade encontramos o módulo do campo gravitacional à distância _math_R/2_math_ longe da superfície terrestre, igual à, _math_{{g}_{R/2}}=G\frac{M}{{{\left( \frac{1}{2}R \right)}^{2}}}=39,2\frac{m}{{{s}^{2}}}._math_ Nesta órbita a aceleração centrípeta é igual ao campo gravitacional, _math_{{a}_{c}}={{g}_{R/2}}_math_. Por meio de manipulações algébricas, obtemos, _math_{{v}_{r~R/2}}=\sqrt{\frac{GM}{R}}={{0,95.10}^{4}}~Km/h_math_.
A Terra exerce a força peso e a força gravitacional sobre o satélite, _math_\overrightarrow{{{P}_{R/2}}}=\overrightarrow{{{F}_{gR/2}}}_math_. Desta igualdade encontramos o módulo do campo gravitacional à distância _math_R/2_math_ longe da superfície terrestre, igual à, _math_{{g}_{R/2}}=G\frac{M}{{{\left( \frac{1}{2}R \right)}^{2}}}=39,2\frac{m}{{{s}^{2}}}._math_ Nesta órbita a aceleração centrípeta é igual ao campo gravitacional, _math_{{a}_{c}}={{g}_{R/2}}_math_. Por meio de manipulações algébricas, obtemos, _math_{{v}_{r~R/2}}=\sqrt{\frac{GM}{R}}={{0,26.10}^{4}}~Km/h_math_.
- A Terra exerce a força peso e a força gravitacional sobre o satélite, _math_\overrightarrow{{{P}_{R/2}}}=\overrightarrow{{{F}_{gR/2}}}_math_. Desta igualdade encontramos o módulo do campo gravitacional à distância _math_R/2_math_ longe da superfície terrestre, igual à, _math_{{g}_{R/2}}=G\frac{M}{{{\left( \frac{3}{2}R \right)}^{2}}}=4,3\frac{m}{{{s}^{2}}}._math_ Nesta órbita a aceleração centrípeta é igual ao campo gravitacional, _math_{{a}_{c}}={{g}_{R/2}}_math_. Por meio de manipulações algébricas, obtemos, _math_{{v}_{r~R/2}}=\sqrt{\frac{GM}{R}}={{1,9.10}^{4}}~Km/h_math_.
Para um satélite, em órbita à distância _math_R/2_math_ da superfície da Terra, existem duas forças atuantes:
i) a força peso que atua sobre os corpos
ii) A força gravitacional, devido a Lei da Gravitação Universal.
_math_\overrightarrow{{{P}_{R/2}}}=\overrightarrow{{{F}_{g~R/2}}}_math_
Em módulo:
_math_m{{g}_{R/2}}=\frac{GMm}{{{\left( R+\frac{R}{2} \right)}^{2}}}=\frac{GMm}{{{\left( 3\frac{R}{2} \right)}^{2}}}_math_
_math_Logo:~_math_ _math_{{g}_{R/2}}=\frac{4}{9}\frac{GM}{{{R}^{2}}}=\frac{4}{9}g=4,33~m/{{s}^{2}}_math_
A aceleração centrípeta do satélite em órbita aproximadamente circular é igual a aceleração da gravidade nesta órbita:
_math_{{a}_{c}}={{g}_{R/2}}_math_
A aceleração centrípeta é _math_{{a}_{c}}=\frac{{{v}^{2}}}{R}_math_
Igualando:
_math_\frac{{{v}^{2}}}{R}=\frac{GMm}{{{R}^{2}}}_math_
Encontramos:
_math_v=\frac{2}{3}\sqrt{\frac{GM}{R}}_math_
E _math_v_math_ é chamada de velocidade rasante para o satélite se manter em órbita próxima a Terra.
Substituindo os valores numéricos, encontramos _math_v\approx 5300~m/s_math_.
Convertendo, 1m/s=3,6 Km/h, temos _math_v={{1,9.10}^{4}}\frac{Km}{h}_math_.
- A Terra exerce a força peso e a força gravitacional sobre o satélite, _math_\overrightarrow{{{P}_{R/2}}}=\overrightarrow{{{F}_{gR/2}}}_math_. Desta igualdade encontramos o módulo do campo gravitacional à distância _math_R/2_math_ longe da superfície terrestre, igual à, _math_{{g}_{R/2}}=G\frac{M}{{{\left( \frac{3}{2}R \right)}^{2}}}=4\frac{m}{{{s}^{2}}}._math_ Nesta órbita a aceleração centrípeta é igual ao campo gravitacional, _math_{{a}_{c}}={{g}_{R/2}}_math_. Por meio de manipulações algébricas, obtemos, _math_{{v}_{r~R/2}}=\sqrt{\frac{GM}{R}}={{0,52.10}^{4}}~Km/h_math_.
Próximo da superfície da Terra, _math_\vec{P}=\overrightarrow{{{F}_{g}}}_math_. O satélite na órbita rasante possui uma aceleração centrípeta, _math_\overrightarrow{{{a}_{c}}}=\vec{g}_math_. Após as manipulações algébricas necessárias, obtemos o módulo da velocidade, que é _math_{{v}_{r}}=\sqrt{\frac{GM}{R}}\approx {{2,844.10}^{4}}\frac{Km}{h}._math_
Atividades
Uma caixa encontra-se assentada no topo de um hemisfério gelado. Assinale a alternativa que aponte a altura correta na qual a caixa perde contato e cai do bloco de gelo, após ser empurrada.
- A força peso é a única força conservativa que atua sobre a caixa. A energia mecânica da posição que a caixa estava assentada equivale à energia mecânica da altura que a caixa caiu, _math_{{E}_{A}}={{E}_{B}}._math_ Resolvendo a igualdade, obtemos a relação _math_h=R-\frac{{{v}_{B}}^{2}}{2g}_math_. No ponto B, a caixa perde contato com a superfície semiesférica, o que significa que o módulo da normal é zero. As forças que atuam em B são a força centrípeta do movimento circular da caixa, _math_{{F}_{c}}=m{{a}_{c,~}}_math_ e a força peso, P = mg. Igualando, _math_{{F}_{c}}=P_math_, encontramos _math_{{v}_{B}}^{2}=gh._math_ Substituindo _math_{{v}_{B}}^{2}_math_ na expressão _math_h_math_, determinamos a altura da qual a caixa cai do hemisfério _math_h=\frac{2}{3}R._math_
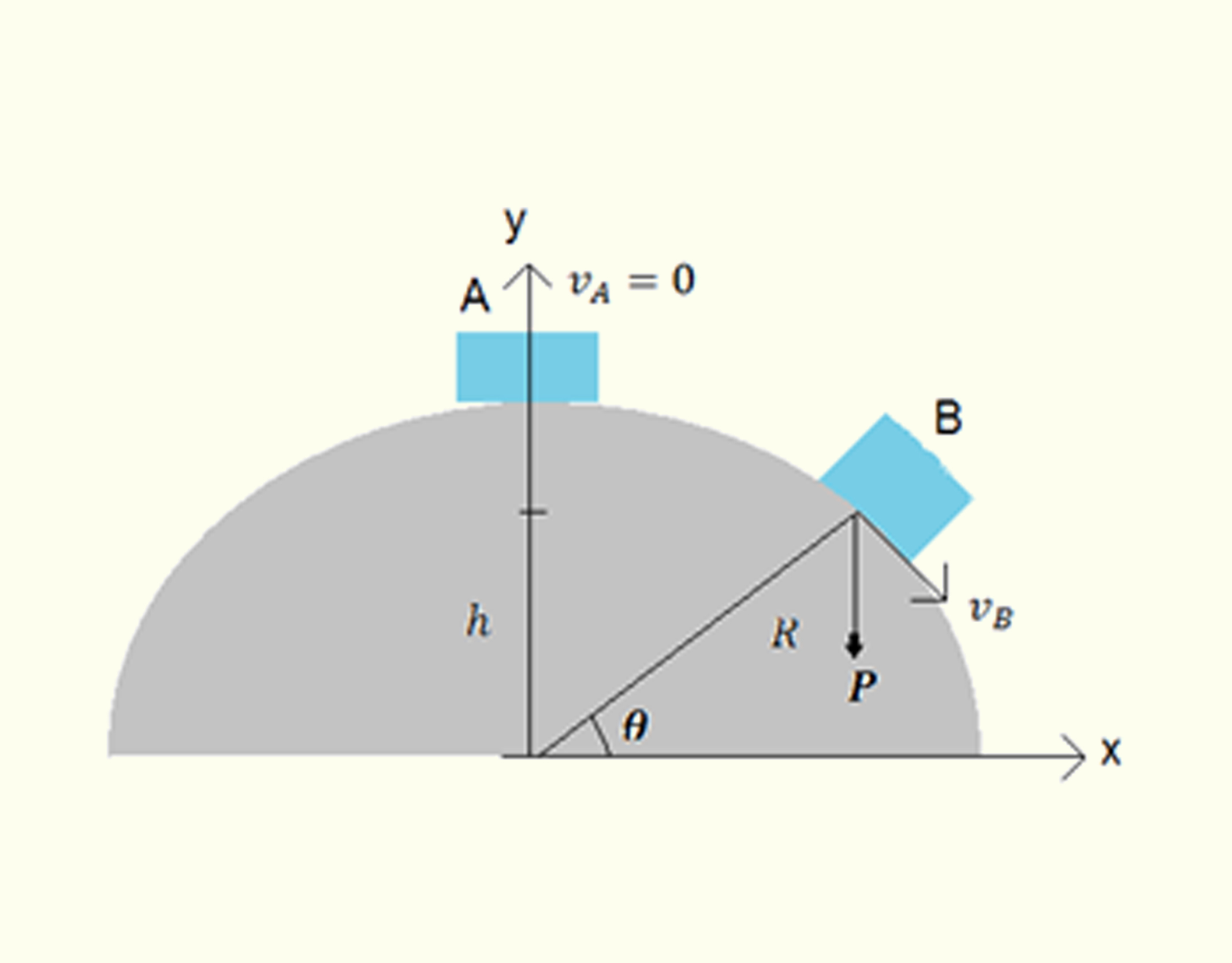
A energia em A corresponde à energia em B:
_math_{{E}_{A}}={{E}_{B}}_math_
_math_\frac{m{{v}_{A}}^{2}}{2}+mg{{h}_{A}}=\frac{m{{v}_{B}}^{2}}{2}+mg{{h}_{B}}_math_
_math_{{v}_{A}}=0_math_ (caixa está em repouso no ponto A)
_math_{{h}_{A}}=R_math_
_math_{{h}_{B}}=h_math_
Isolando a altura _math_h_math_ da equação acima:
_math_h=R-\frac{{{v}_{B}}^{2}}{2g}_math_
Em B, a caixa perde contato com o hemisfério, o que significa que a força normal é nula.
A força centrípeta é igual à força peso:
_math_m{{a}_{c}}=mg\sin \theta _math_
_math_{{a}_{c}}=\frac{{{v}_{B}}^{2}}{R}_math_ e _math_\sin \theta =\frac{h}{R}_math_
_math_m\frac{{{v}_{B}}^{2}}{R}=mg\frac{h}{R}_math_
_math_{{v}_{B}}^{2}=gh_math_
Substituindo _math_{{v}_{B}}^{2}_math_ na equação _math_h,~_math_encontramos:
_math_h=~R-\frac{gh}{2g}_math_
_math_h=\frac{2}{3}R._math_
- A força peso é a única força conservativa que atua sobre a caixa. A energia mecânica da posição que a caixa estava assentada equivale à energia mecânica da altura que a caixa caiu, _math_{{E}_{A}}=-{{E}_{B}}._math_ Resolvendo a igualdade, obtemos a relação _math_h=\frac{{{v}_{B}}^{2}}{2g}-R_math_. No ponto B, a caixa perde contato com a superfície semiesférica, o que significa que o módulo da normal é zero. As forças que atuam em B são a força centrípeta do movimento circular da caixa, _math_{{F}_{c}}=m{{a}_{c,~}}_math_ e a força peso, P = mg. Igualando, _math_{{F}_{c}}=P_math_, encontramos _math_{{v}_{B}}^{2}=gh._math_ Substituindo _math_{{v}_{B}}^{2}_math_ na expressão _math_h_math_, determinamos a altura da qual a caixa cai do hemisfério _math_h=2R._math_
A lei da conservação da energia diz que _math_{{E}_{A}}={{E}_{B}}._math_
- A força peso é a única força conservativa que atua sobre a caixa. A energia mecânica da posição que a caixa estava assentada equivale à energia mecânica da altura que a caixa caiu, _math_{{E}_{A}}={{E}_{B}}._math_ Resolvendo a igualdade, obtemos a relação _math_h=R-\frac{{{v}_{B}}^{2}}{2g}_math_. No ponto B, a caixa perde contato com a superfície semiesférica, o que significa que o módulo da normal é zero. As forças que atuam em B são a força centrípeta do movimento circular da caixa, _math_{{F}_{c}}=m{{a}_{c,~}}_math_ e a força peso, P = mg. Igualando, _math_{{F}_{c}}=-P_math_, encontramos _math_{{v}_{B}}^{2}=-gh._math_ Substituindo _math_{{v}_{B}}^{2}_math_ na expressão _math_h_math_, determinamos a altura da qual a caixa cai do hemisfério _math_h=2R._math_
A força centrípeta atua na mesma direção e sentido de _math_{{v}_{B}}._math_
- A força peso é a única força conservativa que atua sobre a caixa. A energia mecânica da posição que a caixa estava assentada equivale à energia mecânica da altura que a caixa caiu, _math_{{E}_{A}}=-{{E}_{B}}._math_ Resolvendo a igualdade, obtemos a relação _math_h=R-\frac{{{v}_{B}}^{2}}{2g}_math_. No ponto B, a caixa perde contato com a superfície semiesférica, o que significa que o módulo da normal é zero. As forças que atuam em B são a força centrípeta do movimento circular da caixa, _math_{{F}_{c}}=m{{a}_{c,~}}_math_ e a força peso, P = mg. Igualando, _math_{{F}_{c}}=-P_math_, encontramos _math_{{v}_{B}}^{2}=gh._math_ Substituindo _math_{{v}_{B}}^{2}_math_ na expressão _math_h_math_, determinamos a altura da qual a caixa cai do hemisfério, _math_h=\frac{2}{3}R._math_
A lei da conservação da energia diz que _math_{{E}_{A}}={{E}_{B}}~_math_e a força centrípeta atua na mesma direção e sentido de _math_{{v}_{B}}._math_
- A força peso é a única força dissipativa que atua sobre a caixa. A energia mecânica da posição na qual que a caixa estava assentada equivale à energia mecânica da altura da qual a caixa caiu, _math_{{E}_{A}}={{E}_{B}}._math_ Resolvendo a igualdade, obtemos a relação _math_h=R-\frac{{{v}_{B}}^{2}}{2g}_math_. No ponto B, a caixa perde contato com a superfície semiesférica, o que significa que o módulo da normal é zero. As forças que atuam em B são a força centrípeta do movimento circular da caixa, _math_{{F}_{c}}=m{{a}_{c,~}}_math_ e a força peso, P = mg. Igualando, _math_{{F}_{c}}=P_math_, encontramos _math_{{v}_{B}}^{2}=gh._math_ Substituindo _math_{{v}_{B}}^{2}_math_ na expressão _math_h_math_, determinamos a altura da qual a caixa cai do hemisfério, _math_h=\frac{2}{3}R._math_
A força peso é conservativa.
Pontos de retorno e pontos de equilíbrio da energia potencial
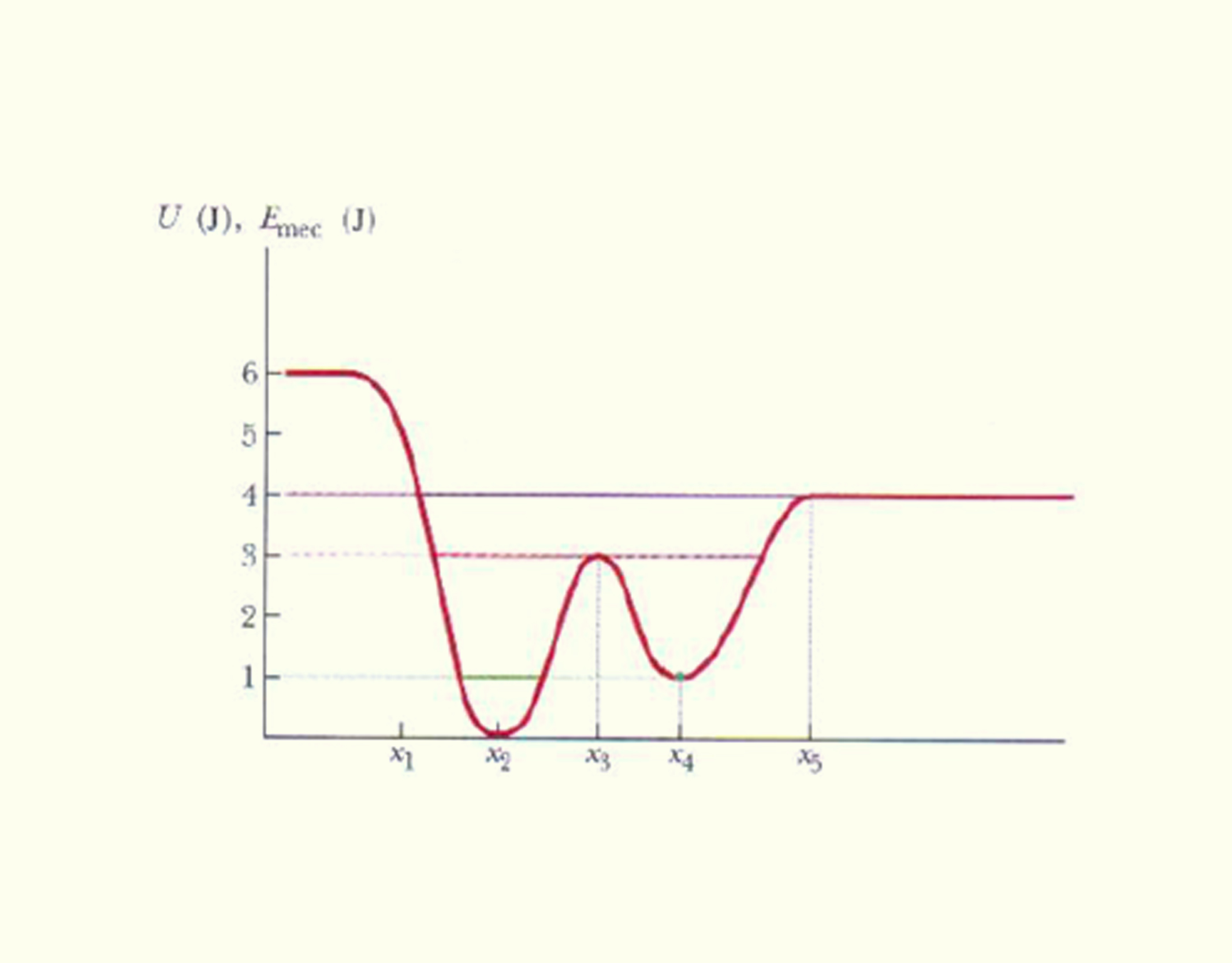
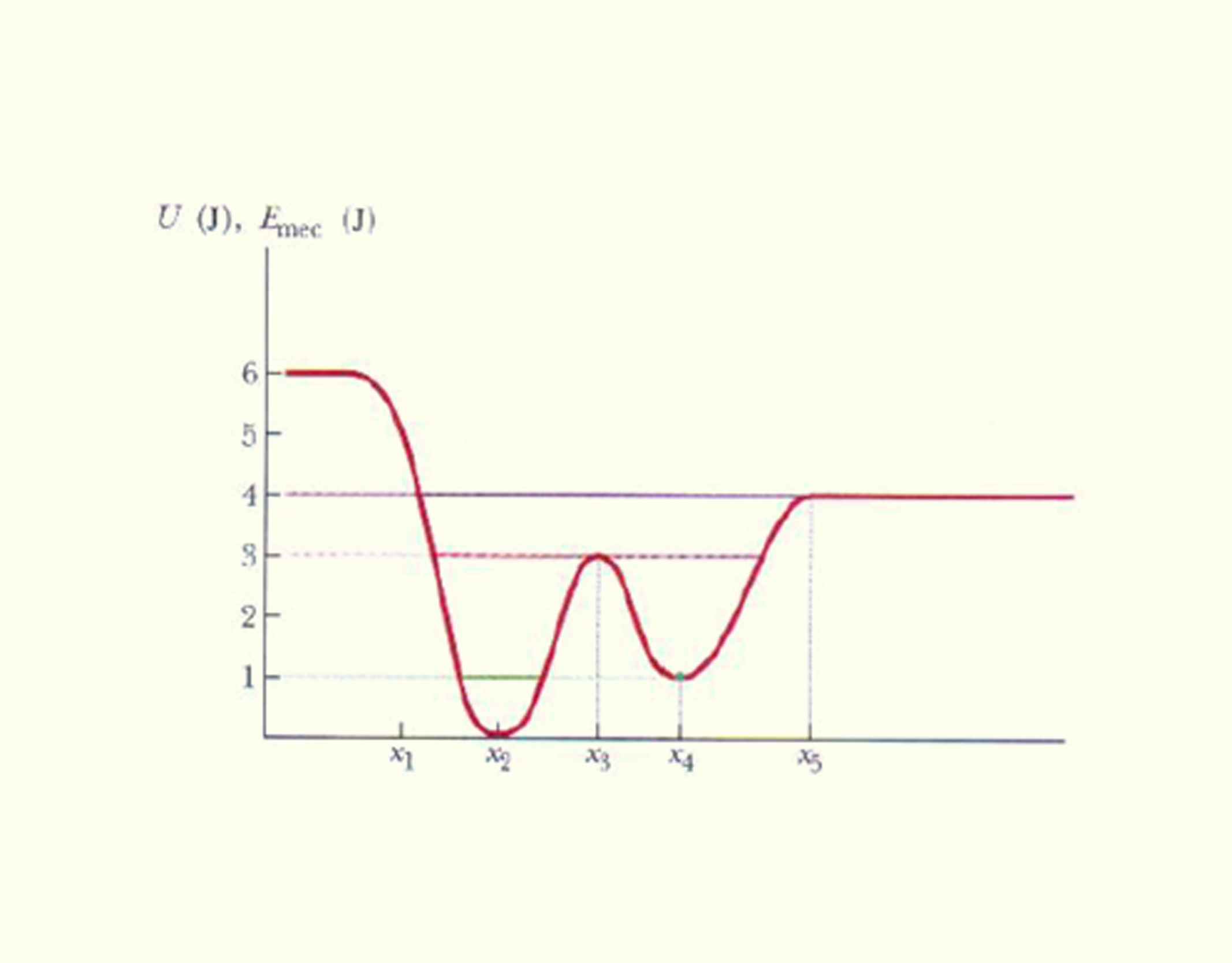
O movimento unidimensional de uma partícula pode ser analisado qualitativamente por meio do gráfico da energia potencial (Figura 3.6).
367 Curva das energias potencial e mecânica em função da posição Fonte: Halliday et al. (2008, p. 191).
Sobre a influência de uma força conservativa, a energia cinética da partícula que se move no eixo horizontal é descrita como _math_K=E-U\left( x \right)_math_. Sabemos que a energia potencial depende diretamente do quadrado da velocidade, logo, essa energia é necessariamente positiva. Na região esquerda do ponto _math_{{x}_{1}}_math_, _math_E-U\left( x \right)<0_math_, a partícula não pode se deslocar, sendo conhecida por região proibida da energia.
A partícula parte inicialmente da posição _math_{{x}_{2}}_math_, viajando até o ponto _math_{{x}_{1}}_math_, onde a energia mecânica é equivalente à energia potencial _math_E=U\left( x \right)_math_. Nessa posição, _math_K=0_math_, e a partícula estabelece uma velocidade nula, invertendo o sentido do seu movimento, da esquerda para a direita. O ponto _math_{{x}_{1}}_math_ é então chamado de ponto de retorno. Entre os pontos_math_~{{x}_{1}}_math_ e _math_{{x}_{2}},~_math_a taxa de variação _math_\frac{dU\left( x \right)}{dx}_math_ é negativa. A partir da posição _math_{{x}_{5}}_math_, a energia mecânica se torna equivalente à energia potencial, mas, aqui, a curva da energia potencial não possui inclinação, o que significa que a taxa de variação da energia potencial com a posição é nula, indicando que não há mais a ação da força na partícula, desse modo, o movimento se estenderá à direita infinitamente, sem que haja qualquer possibilidade de volta, e, portanto, _math_{{x}_{5}}_math_ não é um ponto de retorno.
Nos pontos _math_{{x}_{2}}_math_, _math_{{x}_{3}}_math_ e _math_{{x}_{4}},_math_ a inclinação da curva é zero e esses são conhecidos como pontos de equilíbrio estáveis da energia potencial. Em _math_{{x}_{2}}_math_, _math_F\left( x \right)=0_math_, _math_U\left( x \right)=0_math_ e só há energia cinética na partícula (_math_K={{K}_{m\acute{a}ximo}}_math_). Enquanto está na posição _math_{{x}_{4}}_math_, a energia potencial está em um ponto de mínimo local, onde a energia cinética é maior do que a energia potencial na região acessível da energia (U3, temos um ponto de máximo local para a energia potencial, em que a energia potencial é maior do que a energia cinética na partícula (U>k. Em X5, _math_\frac{dU\left( x \right)}{dx}=0_math_. porém essa posição é chamada de ponto de equilíbrio indiferente, porque não é nem um ponto de máximo e mínimo da energia potencial. A energia cinética faz com que a partícula continue o seu movimento à direita das posições _math_{{x}_{2}}_math_, _math_{{x}_{3}}_math_ e _math_{{x}_{4}}_math_, mesmo quando a força é nula. Entre as posições _math_{{x}_{2}}_math_ e _math_{{x}_{3}}_math_ e os pontos _math_{{x}_{4}}_math_ e _math_{{x}_{5}}_math_, a inclinação da curva é positiva,_math_~\frac{dU\left( x \right)}{dx}>0_math_ e, no intervalo de _math_{{x}_{3}}_math_ e _math_{{x}_{4}}_math_, essa inclinação é negativa. A partir do comportamento do gráfico da energia potencial, podemos traçar um gráfico da força conservativa, apresentado na Figura 3.7.
377 Curva da força obtida qualitativamente por meio dos gráficos das energias potencial e mecânica Fonte: Haliday et al. (2008, p. 191).
Atividades
Na região _math_-a
i) Qual é a força associada a essa energia potencial?
ii) Essa força é conservativa?
iii) O equilíbrio é estável na posição _math_x,_math_ na qual, _math_{{F}_{x}}=0?_math_
- Calculando a derivada da energia potencial, encontramos _math_{{F}_{x}}=\frac{\mathbf{d}U}{\mathbf{dx}}_math_, _math_{{F}_{x}}=b\left[ \frac{1}{{{\left( x-a \right)}^{2}}}-\frac{1}{{{\left( x+a \right)}^{2}}} \right]._math_ Aplicando o rotacional, concluímos que _math_\nabla x{{F}_{x}}=0_math_, portanto a força é conservativa. A derivada segunda da energia, _math_\frac{{{d}^{2}}U}{d{{x}^{2}}}<0_math_, em _math_x=0_math_, indicando que o equilíbrio é instável nesse ponto.
Para a força ser conservativa, duas condições precisam ser satisfeitas, _math_{{F}_{x}}=-\frac{\mathbf{d}U}{\mathbf{dx}}_math_ e _math_\nabla x{{F}_{x}}=0_math_. A primeira condição não está correta nesta sentença.
- Calculando a derivada da energia potencial, encontramos _math_{{F}_{x}}=-\frac{\mathbf{d}U}{\mathbf{dx}}_math_, _math_{{F}_{x}}=b\left[ \frac{1}{{{\left( x+a \right)}^{2}}}-\frac{1}{{{\left( x-a \right)}^{2}}} \right]._math_ Aplicando o rotacional, concluímos que _math_\nabla x{{F}_{x}}\ne 0_math_, portanto a força não é conservativa e não há pontos de equilíbrio para esta energia.
_math_\nabla x{{F}_{x}}=0_math_
- Calculando a derivada da energia potencial, encontramos _math_{{F}_{x}}=-\frac{\mathbf{d}U}{\mathbf{dx}}_math_, _math_{{F}_{x}}=b\left[ \frac{1}{{{\left( x+a \right)}^{2}}}-\frac{1}{{{\left( x-a \right)}^{2}}} \right]._math_ Aplicando o rotacional, concluímos que _math_\nabla x{{F}_{x}}=0_math_, portanto a força é conservativa. A derivada segunda da energia, _math_\frac{{{d}^{2}}U}{d{{x}^{2}}}<0_math_, em _math_x=0_math_, indicando que o equilíbrio é instável neste ponto.
_math_\frac{{{d}^{2}}U}{d{{x}^{2}}}>0_math_
- Calculando a derivada da energia potencial, encontramos _math_{{F}_{x}}=-\frac{\mathbf{d}U}{\mathbf{dx}}_math_, _math_{{F}_{x}}=b\left[ \frac{1}{{{\left( x+a \right)}^{2}}}-\frac{1}{{{\left( x-a \right)}^{2}}} \right]._math_ Aplicando o rotacional, concluímos que _math_\nabla x{{F}_{x}}=0_math_, portanto a força é conservativa. A derivada segunda da energia, _math_\frac{{{d}^{2}}U}{d{{x}^{2}}}=0_math_, em _math_x=0_math_, indicando que o equilíbrio é estável neste ponto.
_math_\frac{{{d}^{2}}U}{d{{x}^{2}}}>0_math_
- Calculando a derivada da energia potencial, encontramos _math_{{F}_{x}}=-\frac{\mathbf{d}U}{\mathbf{dx}}_math_, _math_{{F}_{x}}=b\left[ \frac{1}{{{\left( x+a \right)}^{2}}}-\frac{1}{{{\left( x-a \right)}^{2}}} \right]._math_ Aplicando o rotacional, concluímos que _math_\nabla x{{F}_{x}}=0_math_, portanto a força é conservativa. A derivada segunda da energia, _math_\frac{{{d}^{2}}U}{d{{x}^{2}}}>0_math_, em _math_x=0_math_, indicando que o equilíbrio é estável neste ponto.
Cálculo da derivada, _math_\frac{dU}{dx}_math_
_math_\frac{dU}{dx}=b\left[ -\frac{1}{{{\left( x+a \right)}^{2}}}+\frac{1}{{{\left( x-a \right)}^{2}}} \right]_math_
Para a força ser conservativa,
_math_{{F}_{x}}=-\frac{\mathbf{d}U}{\mathbf{dx}}_math_
_math_\nabla x{{F}_{x}}=\left[ \begin{matrix} {\hat{i}} & {\hat{j}} & {\hat{k}} \\ \frac{d}{dx} & \frac{d}{dy} & \frac{d}{dz} \\ b\left[ \frac{1}{{{\left( x+a \right)}^{2}}}-\frac{1}{{{\left( x-a \right)}^{2}}} \right] & 0 & 0 \\\end{matrix} \right]=0_math_
_math_{{F}_{x}}=0_math_ quando _math_x=0_math_
Calculando a derivada segunda da energia em x=0, obtemos _math_\frac{{{d}^{2}}U}{d{{x}^{2}}}=\frac{4b}{{{a}^{3}}}_math_.
Se _math_\frac{{{d}^{2}}U\left( x=0 \right)}{d{{x}^{2}}}>0_math_, então, _math_U\left( x=0 \right)_math_ é um ponto de mínimo e o equilíbrio é estável.
Potência média e potência instantânea
A potência é uma grandeza escalar, conceituada como a capacidade que um sistema tem para gerar ou receber energia. Em um intervalo de tempo (_math_\Delta t_math_), podemos definir a potência média como:
_math_{{P}_{m\acute{e}d}}=\frac{\text{ }\!\!\Delta\!\!\text{ }W}{\text{ }\!\!\Delta\!\!\text{ }t}~~~\left( 42 \right)_math_
No sistema internacional (Si), sua unidade de medida é definida como watt (_math_W=\frac{J}{s}_math_). Porém a taxa de variação do trabalho pode se alterar no tempo e, então, consideramos que a potência instantânea do sistema é:
_math_{{P}_{inst}}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\text{ }\!\!\Delta\!\!\text{ }W}{\text{ }\!\!\Delta\!\!\text{ }t}=\frac{dW}{dt}~~\left( 43 \right)_math_
Podemos reescrever a potência em relação à velocidade. De acordo com a equação (24), o trabalho para mover uma partícula horizontalmente sobre a ação de uma força constante, sem nenhuma inclinação, é _math_W={{F}_{x}}x_math_, derivando o trabalho em função do tempo (TIPLER; MOSCA, 2006, p. 180), chegamos a:
_math_\frac{dW}{dt}={{F}_{x}}\frac{dx}{dt}={{F}_{x}}v~~~\left( 44 \right)_math_
E, consequentemente, _math_{{P}_{inst}}={{F}_{x}}v_math_. Com um pouco mais de formalismo matemático, chamado a força constante de _math_\vec{F}_math_:
_math_{{P}_{inst}}=\vec{F}.\frac{d\vec{x}}{dt}=\vec{F}.\vec{v}~~~\left( 45 \right)_math_
Fique por dentro
Como um automóvel trabalha?
Um caminhão sem cargas sobe a ladeira mais rapidamente do que um caminhão cheio de cargas. Trafegar no aclive corresponde a elevar a energia potencial do automóvel e, para isso acontecer, o motor do automóvel realiza mais força ao longo do percurso. No topo do aclive, o caminhão sem cargas terá realizado o mesmo trabalho mecânico que o caminhão cheio de cargas, a diferença entre eles estará na taxa da realização do trabalho por esses caminhões. Essa taxa de variação é conhecida na física como potência mecânica. Usualmente, quando nos referimos a potências de automóveis, usamos a unidade de medida, cavalo-vapor (cv). Um cv equivale a 735W.
FonteRecorte textual extraído da obra: YOUNG, H. D.; FREEDMAN, R. A. Física 1: Mecânica. 10. ed. São Paulo: Pearson Education do Brasil, 2003, p.176-179.
344 Potência média e instântanea
Atividades
Um bloco de 3 Kg é puxado por um guincho no aclive, conforme exibido na Figura 3.9, por uma velocidade constante de 2 m/s. O coeficiente de atrito cinético é _math_{{\mu }_{c}}=0,3._math_ Assinale a alternativa que mostre qual é a potência fornecida pelo guincho.
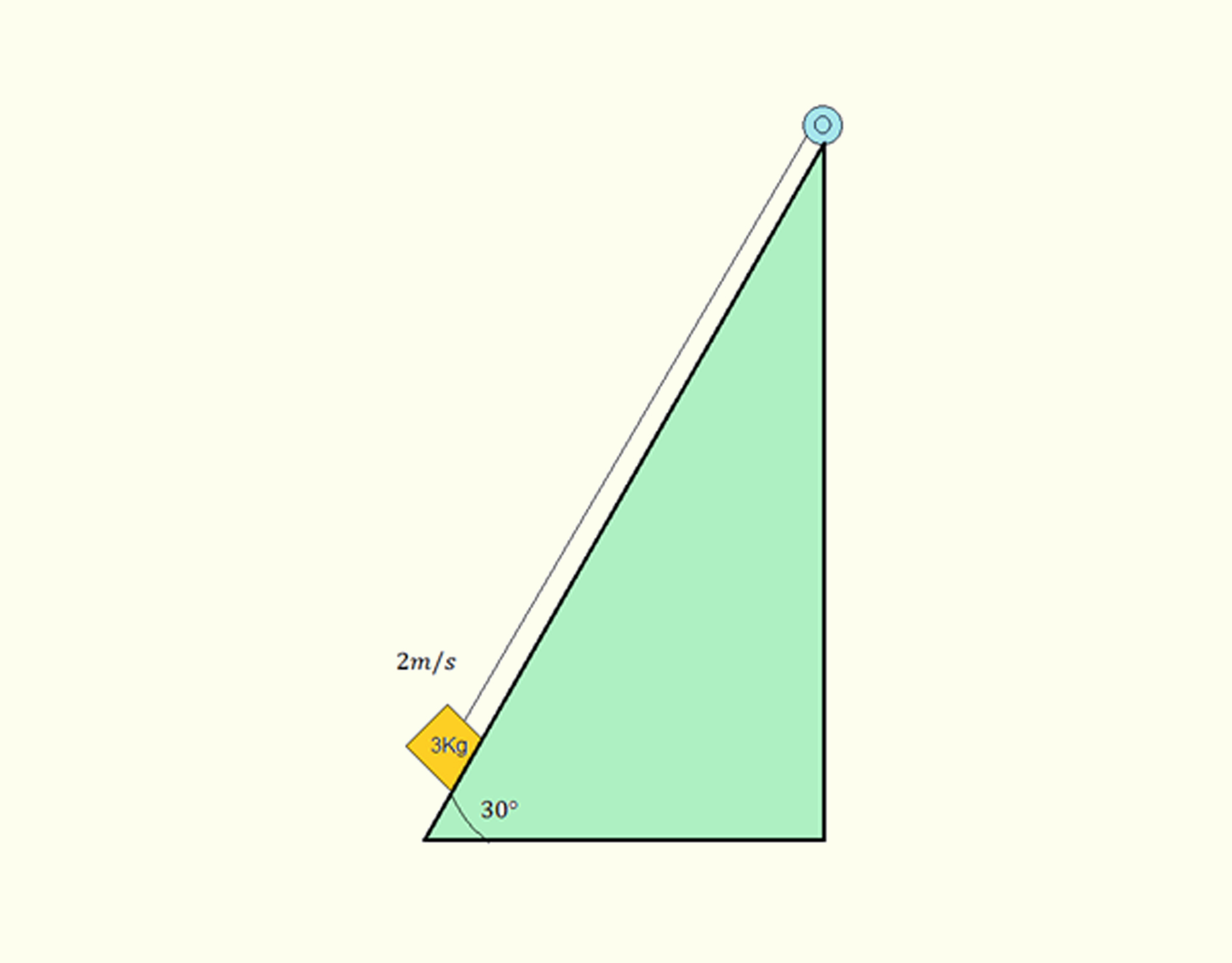
- Por meio da somatória das forças nos eixos x e y, obtemos _math_N=mg\cos \theta _math_ e _math_T={{\mu }_{c}}N+mg\sin \theta _math_. A força que realiza o trabalho para mover o bloco pelo guincho é a força tração, _math_T._math_ A potência gerada pelo guincho e transferida para a corda é _math_P=Tv\cos 30{}^\circ =38,69~W._math_
O ângulo entre a força tração e a velocidade é zero, _math_\cos 0{}^\circ =1._math_
- Por meio da somatória das forças nos eixos x e y, obtemos _math_N=mg\cos \theta _math_ e _math_T={{\mu }_{c}}N+mg\sin \theta _math_. A força que realiza o trabalho para mover o bloco pelo guincho é a força tração, _math_T._math_ A potência gerada pelo guincho e transferida para a corda é _math_P=Tv=44,67~W._math_
As forças que atuam sobre o bloco são:
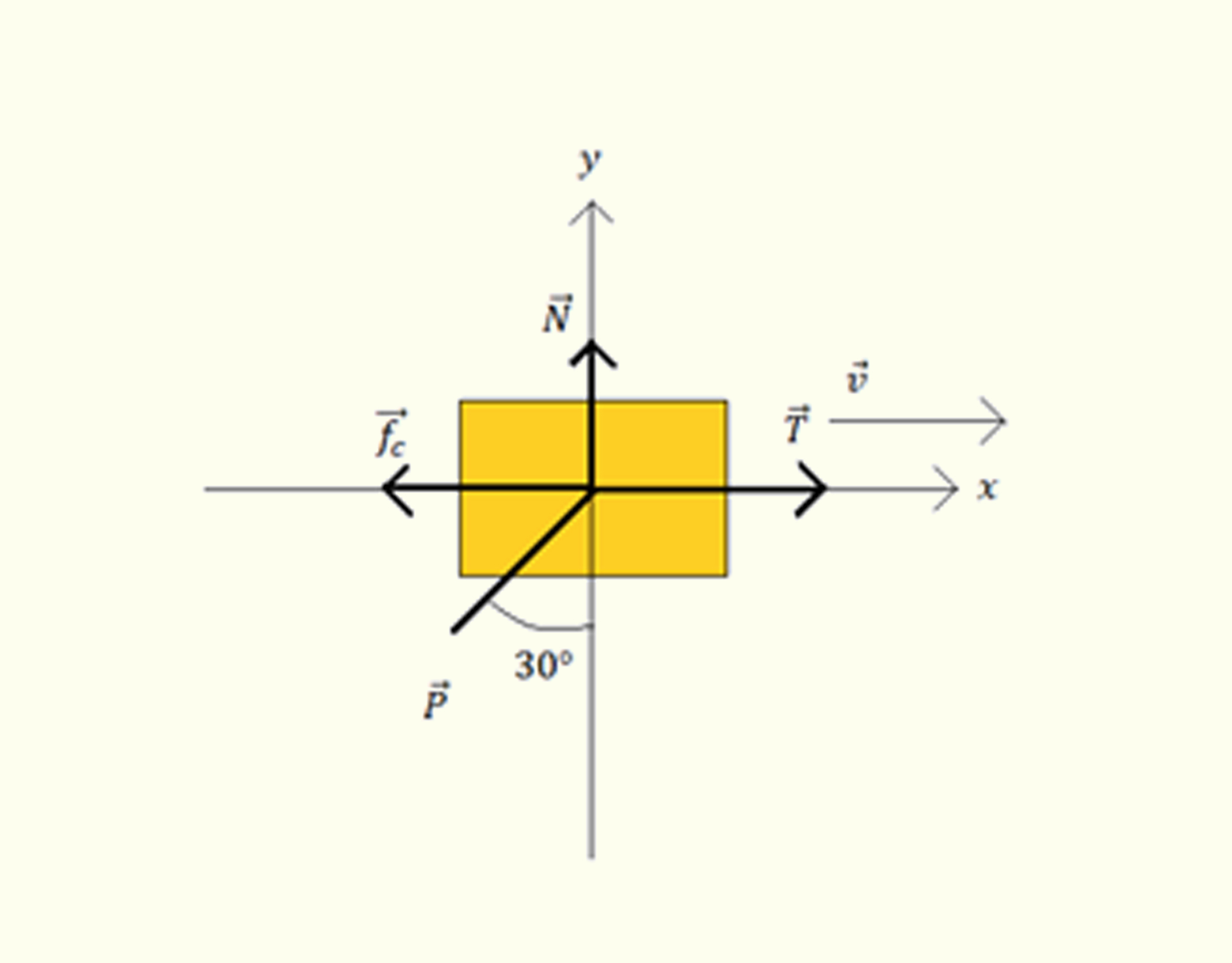
_math_\sum {{F}_{y}}=N-P\cos 30{}^\circ =0_math_
_math_N=~mg\cos 30{}^\circ =0_math_
A velocidade do deslocamento é constante, portanto _math_a=\frac{dv}{dt}=0_math_
_math_\sum {{F}_{x}}=T-{{f}_{c}}-P\sin 30{}^\circ =0_math_
_math_T=~{{f}_{c}}+mg\sin 30{}^\circ _math_
_math_T=mg\left( {{\mu }_{c}}\cos 30{}^\circ +\sin 30{}^\circ \right)_math_
A potência gerada pelo guincho é a taxa do trabalho realizado pela tração para mover a corda. O ângulo entre a tração e a velocidade é de _math_30{}^\circ _math_.
_math_P=Tv=mg\left( {{\mu }_{c}}\cos 30{}^\circ +\sin 30{}^\circ \right)v_math_
_math_P=Tv=3Kg~9,8\frac{m}{s}\left( 0,3\cos 30{}^\circ +\sin 30{}^\circ \right)2\frac{m}{s}=44,67W._math_
- Por meio da somatória das forças nos eixos x e y, obtemos _math_N=mg\sin \theta _math_ e _math_T={{\mu }_{c}}N+mg\cos \theta _math_. A força que realiza o trabalho para mover o bloco pelo guincho é a força tração, _math_T._math_ A potência gerada pelo guincho e transferida para a corda é _math_P=Tv=59,75~W._math_
_math_\sum {{F}_{y}}=N-P\cos 30{}^\circ =0_math_
_math_\sum {{F}_{x}}=T-{{f}_{c}}-P\sin 30{}^\circ =0_math_
- Por meio da somatória das forças nos eixos x e y, obtemos _math_N=mg\cos \theta _math_ e _math_T={{\mu }_{c}}N-mg\sin \theta _math_. A força que realiza o trabalho para mover o bloco pelo guincho é a força tração, _math_T._math_ A potência gerada pelo guincho e transferida para a corda é _math_P=Tv=-14,12~W._math_
_math_\sum {{F}_{x}}=T-{{f}_{c}}-P\sin 30{}^\circ =0_math_
- Por meio da somatória das forças nos eixos x e y, obtemos _math_N=mg\cos \theta _math_ e _math_T={{\mu }_{c}}N+mg\sin \theta _math_. A força que realiza o trabalho para mover o bloco pelo guincho é a força tração, _math_T._math_ A potência gerada pelo guincho e transferida para a corda é _math_P=Tv\sin 30{}^\circ =22,34~W._math_
O ângulo entre a força tração e a velocidade é zero, _math_\cos 0{}^\circ =1._math_
Atividades
Um guincho demora 5 minutos para erguer um piano de 0,25 tonelada até a sacada de um prédio à altura de 30 m. Assinale a alternativa que indique qual é a potência dissipada pelo guincho.
Considerações: A massa da Terra é _math_M~_math_= 5,97 x 1024 Kg, e a constante gravitacional é _math_G=6,67.~{{10}^{-11}}\frac{{{m}^{3}}}{Kg{{s}^{2}}}_math_.
- O único trabalho realizado para mover o piano é o trabalho da sua força peso_math_,~~W={{U}_{p}}=mgh~_math_= 7,35.10-4 J. A potência dissipada pelo guincho é _math_P=\frac{W}{\Delta t}_math_ = 1,47 .10-4 W.
Faltou converter 5min = 300 s.
- O trabalho força peso é_math_~~W={{U}_{p}}=mgh_math_= 7,35.10-4 J. O teorema do trabalho e da energia cinética é _math_W=\Delta K=\frac{m{{v}_{f}}^{2}}{2}-\frac{m{{.0}^{2}}}{2}_math_, logo, _math_{{v}_{f}}=24,25\frac{m}{s}._math_ O módulo da força peso é _math_mg=2450~N_math_. A potência dissipada pelo guincho é _math_P=mgv_math_ = 5,95.10-4 W.
Existe apenas a energia potencial da força peso, não há outra força externa contribuindo para o deslocamento do piano.
- O único trabalho realizado para mover o piano é o trabalho da sua força peso_math_,~~W={{U}_{p}}=-G\frac{Mm}{h}~_math_= 3,31.10-5 J. A potência dissipada pelo guincho é \[P=\frac{W}{\Delta t}\] = 1, 1.10-7 W.
A energia gravitacional é aplicada na escala astronômica.
- O único trabalho realizado para mover o piano é o trabalho da sua força peso_math_,~~W={{U}_{p}}=mgh_math_= 7,35.10-4 J. A potência dissipada pelo guincho é _math_P=\frac{W}{\Delta t}_math_ = 245 W.
O trabalho para erguer o piano é o trabalho da energia gravitacional:
_math_W=mgh=_math_7,35.10-4 J
A potência média é _math_P=\frac{W}{\Delta t}_math_ . Substituindo 5 min = 300 s, encontramos:
_math_P=\frac{W}{\Delta t}_math_ = 245 W.
- O único trabalho realizado para mover o piano é o trabalho da sua força peso_math_,~W={{U}_{p}}=mgh_math_= 73,5 J. A potência dissipada pelo guincho é _math_P=\frac{W}{\Delta t}_math_ = 0,245 W.
0,25 tonelada corresponde à 250 Kg.
Indicação de leitura
Nome do livro: Física 1: Mecânica
Editora: Pearson Education do Brasil
Autor: Hugh David Young e Roger A. Freedman
ISBN: 85-88639-01-7
É um livro-texto, destinado aos alunos do primeiro ano dos cursos de Física, Engenharias, Informática e Ciências da Computação. O livro oferece conceitos essenciais de cinemática, estática, dinâmica, Leis de Newton, conservação de energia e do momento, e rotação dos corpos rígidos. O primeiro capítulo apresenta uma metodologia algébrica para o tratamento vetorial. Além disso, o livro conta com exercícios resolvidos que fornecem aos estudantes, em etapas estratégicas, métodos para compreensão e resolução dos sistemas físicos. No final de cada capítulo são propostos problemas, objetivando o desenvolvimento do raciocínio físico e metódico para a descrição e resolução dos problemas físicos.
Indicação de leitura
Nome do livro: Galileu na sala de aula
Editora: Livraria da Física
Autor: Francisco Caruso, Adílio Jorge e Vitor Oguri
ISBN: 978-85786-123-06
O livro Galileu na sala de aula oferece aos estudantes do Ensino Médio e cursos acadêmicos de licenciatura em Física e Ciências Naturais algumas tirinhas, figuras, gráficos e tabelas que tornam mais fácil e prazeroso o raciocínio intuitivo sobre a física do movimento, conservação do trabalho e momento, e noções básicas de astronomia e óptica dos telescópios. Diversas atividades dinâmicas são propostas aos professores para a aplicação prática nas salas de aula.
Indicação de filme
Nome do filme: Soluções energéticas (Dublado)
Gênero: Documentário. 2007. Produção: Discovery Science Channel.
Três diferentes formas renováveis de energia são apresentadas neste documentário: o hidrato de gás, que é o metano comprimido pela pressão da água a baixas temperaturas, a fusão nuclear que aquece os átomos de hidrogênio a elevadas temperaturas, fundindo os átomos que já estão na fase de plasma, e a energia eólica, armazenando e transformando a energia cinética do deslocamento das massas de ar em energia elétrica. A duração do documentário é de 46 minutos.
Indicação de filme
Nome do filme: Se não existisse a lua (Dublado)
Gênero: Documentário. 2013. Produção: Discovery Science Channel
A teoria mais aceita é que lua se formou por meio de colisões da Terra com Orfeu, há aproximadamente 4,5 bilhões de anos. O impacto dos planetas em um ângulo descentralizado contribuiu para que a lua fosse formada por meio dos fragmentos dos planetas colididos, e empurrada para longe da órbita da Terra. A lua é a grande reguladora climática da Terra. Simulações mostram que, por causa da influência da lua, a Terra gira constantemente em seu eixo com 23°, e, sem ela, a rotação nesse eixo seria instável, variando até 50°, causando mudanças bruscas na temperatura e nas altitudes das marés.