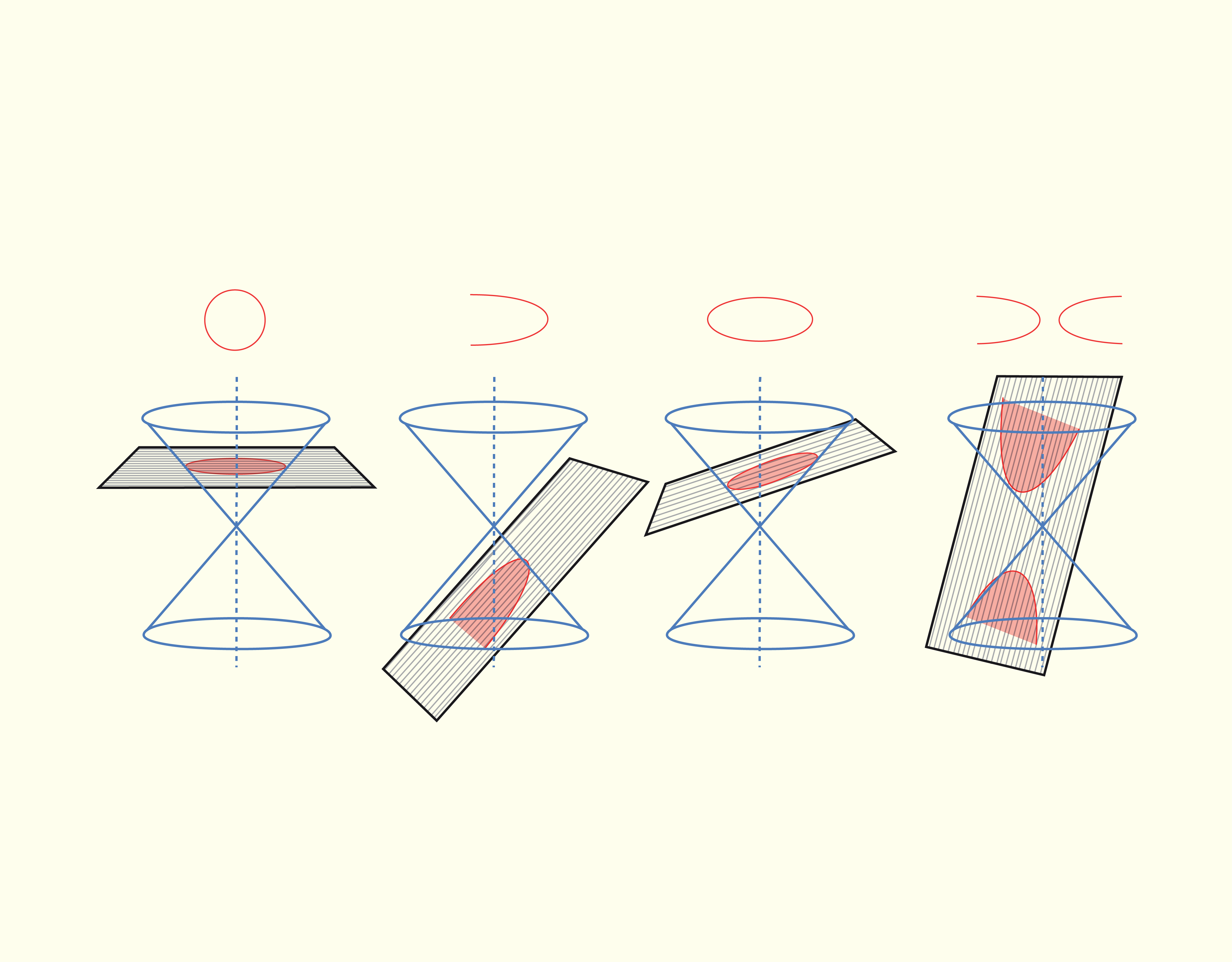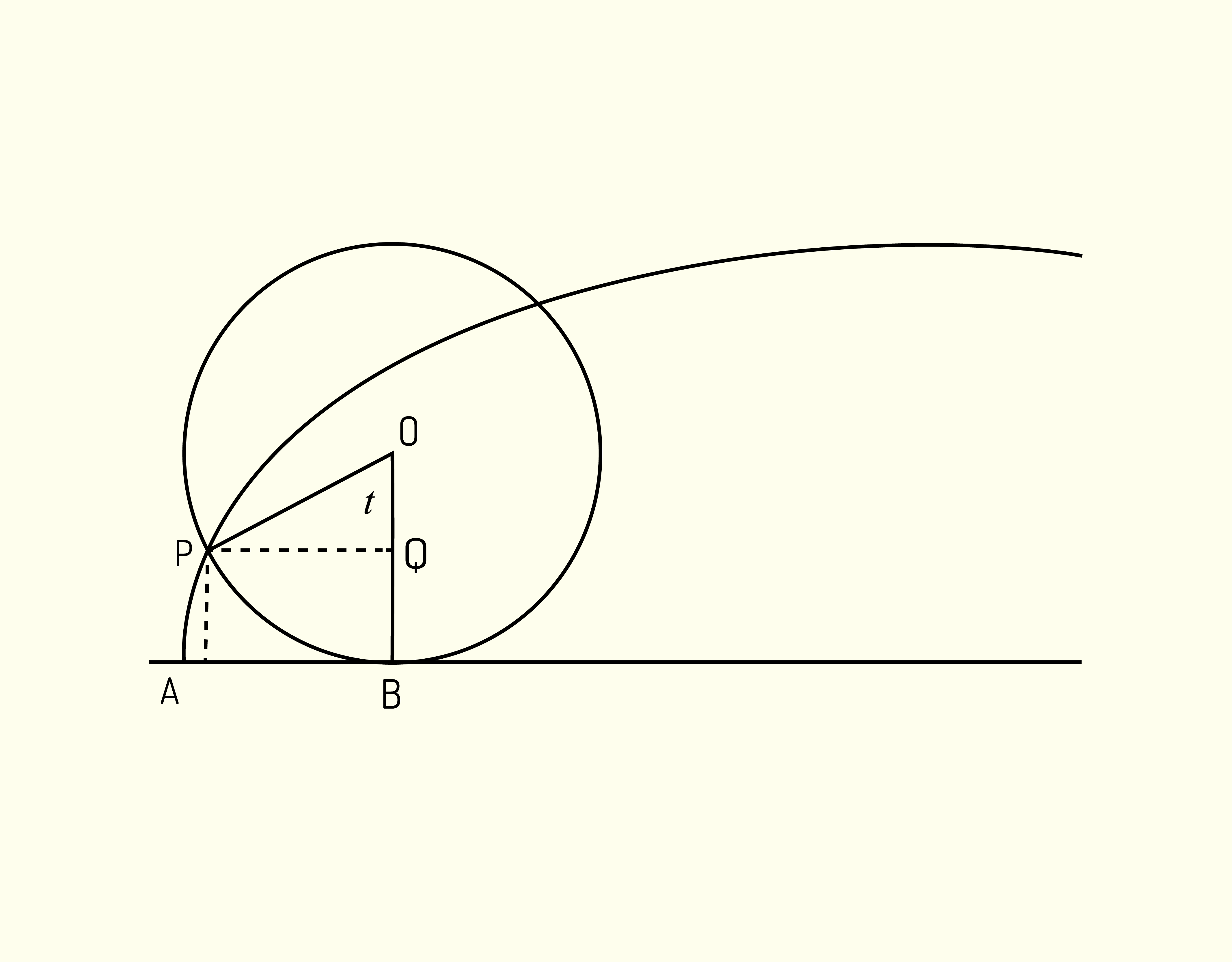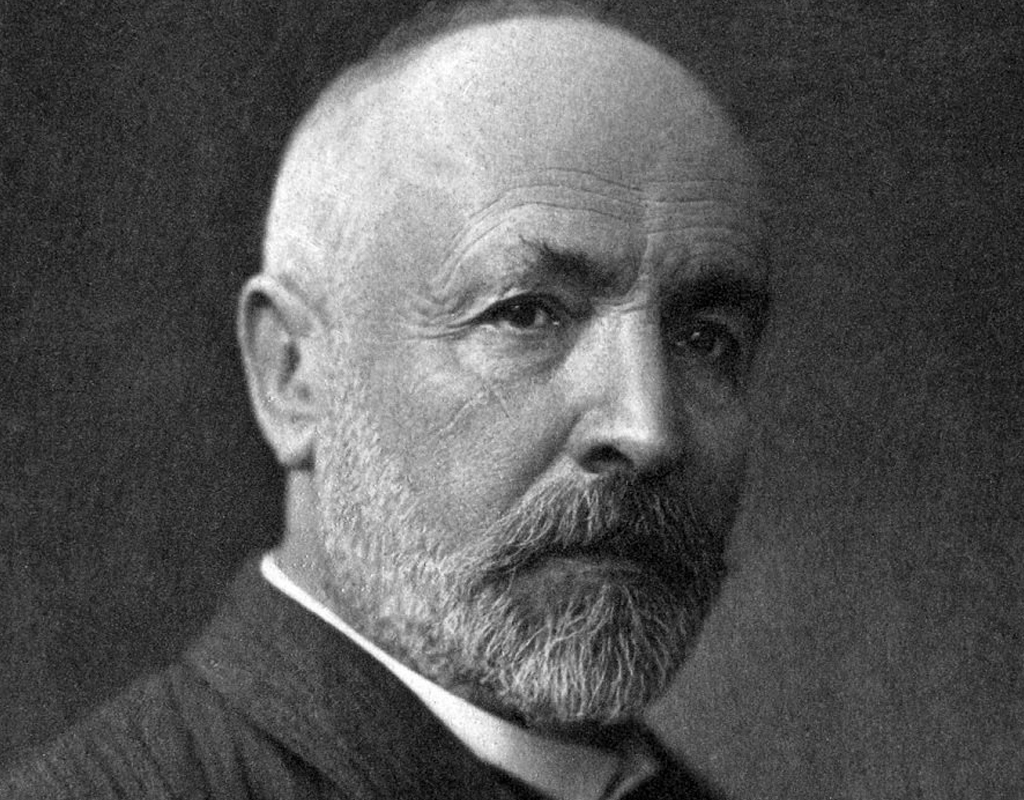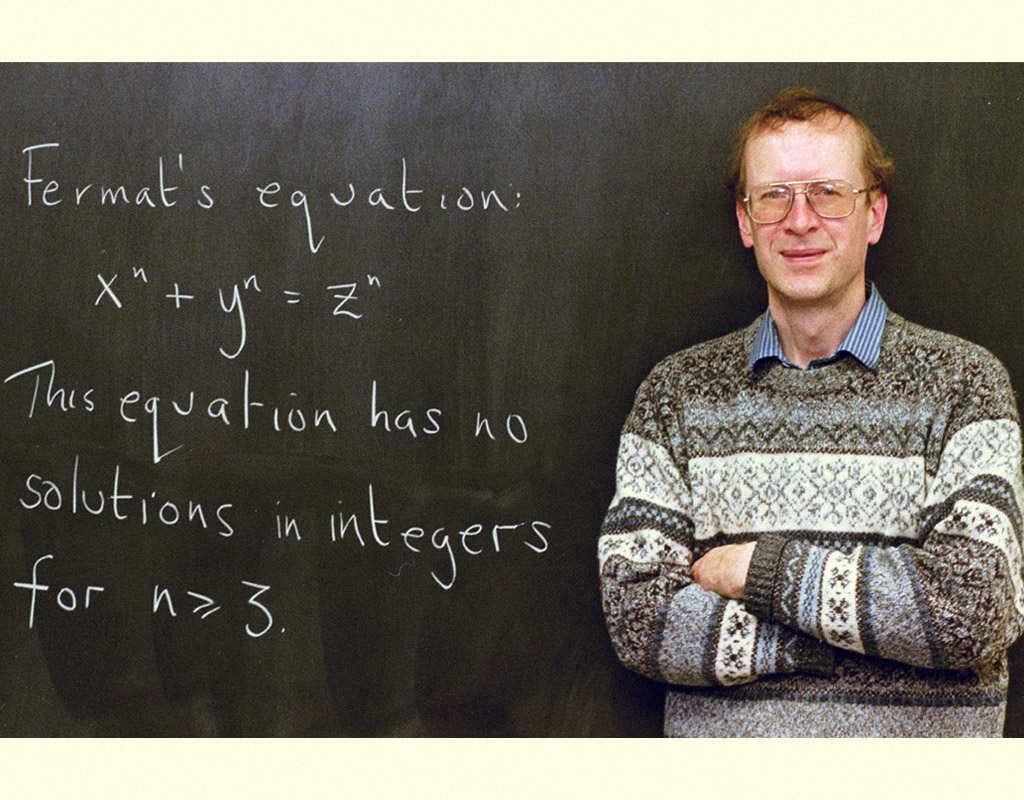Os primeiros números

Desde muito cedo, o homem já utilizava a matemática, mesmo sem ela ser organizada e estruturada como nos dias atuais, a exemplo dos homens da idade de pedra, que utilizavam formas geométricas em suas pinturas rupestres. “Porém a idade da pedra não foi estática, a sociedade foi modificando para adaptar-se a um mundo em transição” (EVES, 2011. p. 24).

O senso numérico de contagem é nato da espécie humana. Portanto, pode-se afirmar que desde a Pré-História o homem utilizava-se desse processo de acordo com a complexidade das suas necessidades, como em alguns registros arqueológicos como as artes rupestres, ou seja, representações artísticas pré-históricas, realizadas nas paredes e em tetos das cavernas, trazendo sinais gráficos abstratos. Pode-se dizer que ali deu-se início à primeira forma rudimentar de contar elementos e até mesmo à geometria. Na obra Caverna de Altamira (Espanha), é possível perceber imagens que representam as mãos, provavelmente seria uma forma de contar de cinco em cinco; nela, também eram possíveis de observar círculos concêntricos.

1112 Caverna de Altamira (Espanha) Fonte: fmanha.com.br.Último acesso: Acesso em: 23 dez. 2016.

Variados sistemas de numeração surgiram ao longo dos séculos; cada sociedade criava formas de representar os números, formalizando seu processo de contagem. Sabe-se que os primeiros achados têm em torno de 8.000 anos de idade, mas existem registros arqueológicos de que o homem já seria capaz de contar há cerca de 50.000 anos (EVES, 2011).

O primeiro material arqueológico com esse tipo de contagem recebeu a nomenclatura de Osso de Ishango, o qual tem por data aproximada 8.000 a.C., encontrado às margens do lago Edward, no Zaire (atual República Democrática do Congo), no continente africano. Essa data é atualmente questionada por arqueólogos e historiadores, contudo, para este compêndio, tomamos por referência Eves (2011). No Osso de Ishango, os números foram registrados em cinco grupos de ranhuras, supostamente relacionados aos dedos das mãos.

1212 Osso de Ishango Fonte: www.taneter.org.Último acesso: Acesso em: 23 dez. 2016.

Apesar de fontes inseguras para afirmações assertivas acerca dos primeiros processos de contagem, teóricos defendem que o procedimento de correspondência biunívoca era utilizado na contagem para controle do tamanho de grupo (rebanho ou pessoas). Utilizavam os dedos ou outras partes do corpo que correspondiam a cada elemento do grupo. Os registros numéricos dessa época se limitavam a ranhuras em ossos, pedras, madeiras ou nós em uma corda. O processo para contagem dos rebanhos ocorria duas vezes ao dia com pedrinhas postas em um saco: pela manhã, ao soltar o rebanho, colocavam no saco pedrinhas correspondendo uma para cada animal; ao recolhê-lo, faziam o processo inverso, se sobrasse pedrinhas, faltava um animal no rebanho e, se sobrasse animais, tinha nascido ou se juntado ao rebanho.
Os objetos de argilas chamados de tokens eram utilizados para efetuar o controle econômico de produtos comercializados por meio de trocas. Os tokens tinham vários formatos, cones, esferas, discos, cilindros e cada um era relacionado a um tipo de insumo e quantidade. Na Figura 1.3, temos exemplos de tokens 4.000 a.C.; o cone, as esferas e o disco plano eram utilizados para medidas de cereais: menor, maior e maior. O tetraedro era unidade padrão de trabalho, supõe-se um dia de trabalho, ou a quantidade de trabalho realizado por um homem em um dia.

1312 Alguns tipos de tokens Fonte: www.maa.org.Último acesso: Acesso em: 23 dez. 2016.

Na Figura 1.4, temos exemplos de tokens mais complexos, com marcações de estiletes que representam na primeira fileira: o comprimento de matéria têxtil, um frasco de óleo, a medida de trigo; na fileira inferior, da esquerda para a direita: uma ovelha, um comprimento de corda, um lingote de metal e uma peça de vestuário.

1412 Alguns tipos de tokens Fonte: www.maa.org.Último acesso: Acesso em: 23 dez. 2016.

Conforme Roque e Pitombeira (2012), esses tokens eram envolvidos por uma bola oca de argila que era fechada e em seu exterior eram impressas com um token a forma e a quantidade que aquela bola representava. Por exemplo, uma bola contendo 6 discos teria 6 marcas dessas na sua superfície.

1512 Bola de tokens e sua marcação externa Fonte: www.maa.org.Último acesso: Acesso em: 23 dez. 2016.

Essa forma de contagem se baseava na correspondência de um a um para compor uma bola de tokens, portanto ainda não se identificava uma base numérica. Gradativamente, percebeu-se que somente o registro na parte externa na bola era suficiente para o registro da quantidade sem a necessidade de guardar os tokens em seu interior. E progressivamente os registros passaram a ser feitos em tabletes de argila planos. Esse foi o primeiro passo para a escrita defendido por muitos historiadores.

Vale destacar neste estudo um pouco sobre os povos ágrafos (sem grafia, sem escrita) que possuíam um sistema de contagem bem organizado. São exemplos de povos ágrafos os indígenas do Estreito de Torres, localizado nas Ilhas Murray, Oceania. Esses povos faziam a seguinte relação de números com seus vocábulos: urapun (um) e okosa (dois) e a partir desses o três seria okosa urapun; o quatro, okosa okosa; o cinco, okosa okosa urapun; o seis, okosa okosa okosa. A partir do seis, utilizavam-se dos dedos e de outras partes do corpo para representação numérica.

Ainda sobre povos ágrafos, não podemos deixar de citar a civilização Inca com seu elegante e sofisticado sistema de contagem. Eles usavam um instrumento chamado Quipo (idioma aymará) ou Quipu (idioma quenchua), para registro contábil em diferentes áreas, como agricultura, exército, engenharia, recenseamento, estocagem. Os Quipos consistiam em cordas amarradas verticalmente à outra horizontal com nós, que eram dispostos com diferentes significados conforme sua posição na corda e cor. Eram confeccionados pelos quipocamayocs, que eram os responsáveis pelos registros de tudo o que ocorria nas aldeias.

Profundos estudos que perduram atualmente foram realizados para compreender a lógica do registro dos nós. Segundo Mangin (2009), o valor do número dependia da sua posição (espaçamento) nas cordas dispostas; cada corda do quipo possui três grupos de nós inferior, central e superior correspondendo às unidades, dezenas, centenas e milhares, respectivamente. Nota-se similaridade ao nosso sistema de base 10 ao serem estudados os diferentes tipos de nós, o simples, o longo e em forma de oito. Cada um dos três grupos na corda possuía até nove nós e o zero era representado pela ausência de nó. Essa interpretação do quipo, ainda segundo o mesmo autor, foi estabelecida em 1912 por um estudo de antropologia.

1612 Sistema de contagem de um quipo Fonte: Ifrah (1997, p. 100).

1712 Exemplo de um quipo Fonte: www.computer.org.Último acesso: Acesso em: 23 dez. 2016.

E, novamente, com o evoluir da sociedade, outras demandas exigiram contagens mais complexas e o processo de contar foi sendo aprimorado. Surgiram as bases de contagem, que se caracterizam por grupos de elementos aos quais são atribuídos nomes e números maiores, recebendo nomes derivados desse grupo originário. Essa ideia de contagem é bem exemplificada em Eves (2011, p. 27), ao apresentar as origens das palavras-números no idioma inglês que têm 10 como base de contagem:

one (um), two (dois), ..., ten (dez) para os números 1, 2, 10. Quando se chega a 11 a palavra usada é eleven [...] que [...] deriva de ein lifon, cujo significado é “um acima de dez”. Analogamente, twelve (doze) provém de twe lif (“dois acima de dez”), [...] thirteen (“três e dez”) para 13, [...] até nineteen (“nove e dez”) para 19. Chega-se então a twenty (twe-tig, ou “dois dez”), twenty-one (“dois dez e um”) e assim por diante. A palavra hundred (cem), segundo parece, deriva originalmente de uma outra que significa “dez vezes” (dez). .(EVES, 2011. p. 27)

Vamos tratar brevemente sobre as principais bases para contagem e as evidências para sua utilização.

Sistema de numeração de base 5, ou base quinária, tem origem na constituição anatômica de nossas mãos, com cinco dedos. Para representar qualquer número na base 5, se utilizam os números de 0 a 4. Assim, o número cinco corresponde ao 10; o número 25, ao 100, e 60 corresponde ao 20. Eves (2011) afirma que algumas tribos da América do Sul e da Sibéria utilizam essa base para contagem. Esse sistema também se fazia presente em calendários germânicos no início do século XX. A base vigesimal (20) tem referência também nos nossos dedos e remota ao tempo que o homem passava maior tempo descalço.

Para a base 12, há evidências de sua utilização desde a Pré-História. Trata-se de uma base que ainda é utilizada ao relacionar o número de lunações anuais, quantidade de meses do ano, horas de um relógio e o emprego usual da palavra dúzia. Já a base 60 foi amplamente utilizada pelos babilônicos e é ainda muito utilizada, especialmente nas operações de ângulos, minutos e segundos.

Os relatos supracitados são baseados em fontes identificadas na literatura de história e história da matemática. Tratam-se dos procedimentos de contagem utilizados para registrar as atividades administrativas da sociedade que foram sendo aprimoradas conforme a evolução da organização da sociedade. A partir dos registros em tabletes planos e do interesse pelas propriedades representativas dos números, se desenvolve a escrita cuneiforme (em forma de cunha) e, daí, o sistema de contagem posicional em que um mesmo símbolo serve para representar diferentes quantidades de acordo com sua posição.

Embora as evidências históricas não nos permitam contar a história da matemática de forma linear, procuraremos apresentar a evolução dos sistemas de contagem com alguma evolução consecutiva partindo do estudo dos sistemas numéricos posicionais e não posicionais.

Sistemas numéricos posicionais e não posicionais

Os sistemas de contagem que conhecemos hoje derivaram de procedimentos de agrupamentos cujos dígitos organizados em grupos representam distintas quantidades de acordo com uma base estabelecida. Começamos falando de dois processos de contagem na Mesopotâmia Antiga. Ouvimos dizer que os processos de contagem iniciaram-se contando animais, rebanhos de ovelhas, aos quais se associavam traços marcados na argila, na areia; houve os processos de contagem feitos de modo mais sofisticado, por meios de tokens, que eram pequenas esculturas de argilas que serviam para contar por meios de figuras diferentes: um cone servia para contar ovelhas; entre outras esculturas e coisas. A contagem era feita de maneira muito interessante e cada objeto contado era armazenado em invólucros de argila que continham tokens de processos diferentes, isso por volta de 4.000 a.C., mas perceberam que eram desnecessários quando constataram que os objetos poderiam ser contados mediante marcas em tabletes. Esse processo de contagem está relacionado ao processo de escritas, que eram geradas pela impressão desses tokens na argila molhada. Em um estágio posterior, foi se uniformizando esse processo de contagem, pois, conforme a sociedade se aperfeiçoou, passou a ter necessidade de muitos objetos para representar numericamente.

O fato em que ao iniciar uma utilização de símbolos iguais para seres de naturezas distintas torna-se uma etapa para abstração em que os números estão associados. Ao pegar duas reuniões de seres, em que os seres que compõem os agregados têm naturezas distintas, por exemplo, latas de grãos e homens, usando o mesmo símbolo para contar seres de números diferentes, está sendo isolado uma propriedade desse agregado de seres, pois contém dois elementos; em ambos os casos, não me preocupo com a qualidade dos objetos e me preocupo somente com a quantidade. Inicia assim o processo de numeração.

A contagem inicialmente limitava-se a simplesmente comparar, uma comparação por correspondência, ou seja, termo a termo, entre duas coleções, exemplos, rebanhos e pedras. Nessa etapa, o conceito de números não avançava, mas, com a criação de símbolos para simbolizar coleções, permitiu-se a passagem de números relativos para absolutos, “[...] uma vez criada e adotada a palavra numérica, ela se torna um modelo tão bom quanto o objeto que representava anteriormente” (DANTZIG, 1970, p. 20).

Com o passar do tempo, o homem passou a confiar em sua linguagem, o que possibilitou a formação de palavras numéricas (um, dois, três...) e só então se construíram a memória e o uso da palavra números, passando a significar medidas de pluralidade. Após admitir a possibilidade de comparação entre duas coleções, estabelecendo correspondência, as civilizações alcançaram o conceito de número cardinal, por exemplo, “existem tantas ovelhas quanto os dedos das mãos”, porém as ordens heterogêneas de modelos dos tipos asas de pássaros, trevos, entre outros, tornam-se insuficientes para determinar o processo de contagem, necessitando arranjar modelos em uma sequência ordenada e crescente. Segundo Dantzig (1970, p. 21), “[...] uma vez criado esse sistema, contar uma coleção significa designar a cada número um termo na sequência natural em sucessão ordenada até que a coleção esteja esgotada.”.

Por sua vez, o último termo da sequência natural pronunciado e que designa o último membro da coleção (após todos terem sido contados) é chamado de número ordinal da coleção. Além disso, a comparação, sozinha, não possibilita o estabelecimento das operações aritméticas, uma vez que estas se baseiam na pressuposição tácita de que todo número possui um sucessor, ou seja, a ordinalidade, em sua essência.

Nos dedos, o homem possui um artifício que lhe permite passar imperceptivelmente dos números cardinais para o ordinal: se quiser indicar que certa coleção tem quatro elementos (cardinal), ele abaixará ou erguerá quatro dedos simultaneamente e, se quiser contar a mesma coleção (ordinal), ele erguerá ou abaixará os dedos em sucessão .(DANTZIG, 1970, p. 70)

A partir dos números cardinais é que se estabeleceu a base para os sistemas de numeração, então sinais gráficos e palavras deram origem à forma concreta da escrita e oralidade da enumeração, possibilitando a numeração ser escrita como aditiva, em que se adiciona para formar o número, ou as numerações de posição, em que são ligadas à posição da escrita propriamente dita, será a posição que determinará o seu valor.

A numeração de posição escapou à maioria dos povos da história. Essa regra essencial só foi imaginada quatro vezes no curso da história. Apareceu pela primeira vez no início do segundo milênio antes de nossa era, entre os sábios da Babilônia. Foi redescoberta, em seguida, pelos matemáticos chineses, um pouco antes do início da era cristã, depois, entre os séculos III e V d.C., pelos astrônomos maias e, enfim, pelos matemáticos da Índia, por volta do séc. V. .(IFRAH, 1997, p. xxii)

Um número pequeno de civilizações utilizava o sistema de numeração posicional, pois apresentavam muitas dificuldades em perceber a necessidade de um símbolo que representa a posição vazia, ou seja, o zero, cuja função é norteadora para o princípio posicional. Vale destacar que somente a representação indiana para o zero foi concebida como número, os demais indicavam apenas uma coluna vazia. Cada uma das antigas civilizações construiu sua linguagem, sua escrita e seu sistema de numeração, do qual se origina a aritmética e, embora os registros de quantidade sejam anteriores à própria escrita, a aritmética foi, dentre as três (aritmética, linguagem e escrita), a que mais tempo e esforço exigiu para ser assimilada pela humanidade. Entretanto, apesar das diferenças inerentes ao sistema de numeração adotado, que interferem nos procedimentos, as operações, as regras e as leis aritméticas são idênticas e obedecem a uma mesma sequência de construção, independentemente das diferentes culturas. Segundo Eves (2011, p. 19),

Esse sistema de numeração posicional ressentiu-se, até depois do ano 300 a.C., da falta de um símbolo para o zero que representasse as potências ausentes de 60, levando assim a possíveis mal-entendidos na expressão de um número dado. Finalmente introduziu-se um símbolo, consistindo em duas cunhas pequenas, inclinadas, mas esse símbolo só era usado para indicar uma potência ausente de 60 dentro de um número, nunca quando ela ocorresse no seu final. Esse símbolo era, portanto, apenas um zero parcial, pois um zero verdadeiro serve para indicar as potências ausentes da base tanto no meio como no final dos números, como é o caso de nossos 304 e 340.

De acordo com a história, o sistema numérico é dividido em dois grupos, o grupo dos sistemas posicionais e o dos não posicionais. No dos sistemas posicionais, o valor depende da posição que o número ocupa, já no dos não posicionais, não depende da posição, possuem valores definidos e imutáveis.

Nosso próprio sistema de numeração é um exemplo de um sistema de numeração posicional. Para esse sistema, depois de se escolher uma base b, adotam-se símbolos para 0, 1, 2, ..., b 1. Assim, há no sistema b símbolos básicos, no caso de nosso sistema, frequentemente chamados dígitos (EVES, 2011).

Para o processo de organização humana, torna-se indispensável o uso dos números, mesmo sendo um conceito abstrato. Desde a antiguidade, no tempo em que os homens habitavam em cavernas, existia a necessidade de contar, eles contavam as caças, as plantações, os rebanhos, as luas, entre outros; inclusive na sociedade contemporânea há necessidade de contar, é claro que na sociedade moderna desenvolveram-se práticas tecnológicas, como o sistema binário computacional, que se utiliza dos números.

Há aproximadamente cem mil anos que o homem habita na terra, nesse tempo, o homem se transformou e evoluiu, ocorreram inúmeras mudanças de hábitos, principalmente mudanças nos costumes e crenças, mas em cada geração as heranças culturais são repassadas, mas sempre com alguma evolução. Durante todos esses anos, a maneira mais eficaz de registrar as informações foi por meio da escrita. Desde o tempo das cavernas que o homem se comunica mediante a escrita, mesmo que seja por desenhos em cavernas até a escrita atual, independente do modo, ela serve para registrar as transformações culturais.

O processo para desenvolver o número propriamente dito partiu do próprio desenvolvimento da escrita. Vale ressaltar algumas escritas, como os hieróglifos, que eram uma espécie de símbolos, que são utilizados até hoje em países como Japão e China. Os números surgiram da necessidade que o homem possuía de contar várias formas; esse processo de contagem era relacionado às relações biunívocas, utilizando pedras, trações, desenhos, entre outros, mas o processo de contagem estava inserido, então era necessário desenvolver métodos precisos para os sistemas de numeração.

O sistema de numeração propriamente dito foi surgindo há mais de 3.000 a.C. na Mesopotâmia, porém o sistema que gerou a contagem atual foi o sistema de numeração indo-arábico. A partir dos árabes, com seu sistema de numeração decimal, é que chegamos aos sistemas atuais. Sabe-se que cada sistema tem os seus símbolos para representar quantidades, operações numéricas, entre outros, dessa forma, é possível classificar os sistemas como posicionais e não posicionais.

Um bom exemplo desses símbolos trata-se do sistema de numeração decimal, que é utilizado em quase todo mundo. Nesse sistema, estabelecemos que a base de contagem seja a base 10, pois o sistema decimal possui um alfabeto de 10 símbolos, chamados de algarismos, são eles: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Esse é um sistema posicional, pois as operações básicas passam pelo posicionamento da ordem dos números.

O sistema de numeração surgiu da necessidade de contar, pois desde a antiguidade as civilizações sentem necessidade de uma civilização com uma variável quantitativa. Árabes e indianos criaram o sistema decimal, surgindo como base os 10 dedos da mão, é o sistema decimal que contribuirá para o domínio das quatro operações. Já os povos egípcios utilizavam desenhos para representar o seu sistema de numeração, porém a posição dos números não era significativa, embora muitos dos sistemas numéricos implantados deixaram de existir o sistema sexagesimal permanece como herança até os dias atuais.

O processo de contar parte da essência de comparação. O homem desenvolveu ao longo do tempo métodos para a quantificação, originados de sua própria curiosidade. O maior despertar do sistema numérico ainda é a abstração, pois é o início do processo de contagem de qualquer civilização que tenha desenvolvido o sistema de numeração. De acordo com Eves (2011, p. 27), temos que,

quando se tornou necessário efetuar contagens mais extensas, o processo de contar teve de ser sistematizado. Isso foi feito dispondo-se os números em grupos básicos convenientes, sendo a ordem de grandeza desses grupos determinada em grande parte pelo processo de correspondência empregado. Esquematizando- se as ideias, o método consistia em escolher um certo número b como base e atribuir nomes aos números 1, 2, ..., b. Para os números maiores do que b os nomes eram essencialmente combinações dos nomes dos números já escolhidos.

Ao longo da história, foram desenvolvidos sistemas numéricos posicionais e não posicionais. No sistema posicional, os números eram escritos seguindo a ordem, seguiam o processo de correspondência empregada; o princípio de escrita do número dependia da escolha de sua base. Um exemplo foi desenvolvido na Babilônia, entre 2500 a.C., quando desenvolveu o sistema sexagesimal. Esse sistema tinha a base 60 e o princípio posicional de representação. Na Grécia antiga, usava-se a representação algébrica. O sistema utilizado na Índia era o decimal, lá representavam o zero e outros dígitos. Segundo Eves (2011), dependendo de cada povo, a base era significativa, cada um com sua forma de contagem.

1812 Sistema de contagem sexagesimal Fonte: adaptado de qualeoxisdaquestao.files.wordpress.com.Último acesso: Acesso em: 8 dez. 2016.

Sistemas numéricos não posicionais

O sistema de numeração não posicional foi o pontapé inicial para o sistema de numeração posicional. No sistema de numeração não posicional, eram escolhidos símbolos simples para representar números e se formavam numerais a partir da repetição dos símbolos. A operação utilizada era basicamente adição e multiplicação, com símbolos de valor fixo independentes da posição relativa do número. Um exemplo desse tipo de sistema eram os mesmos utilizados pelas civilizações grega, romana e egípcia, os povos egípcios utilizaram a escrita hieroglífica e utilizavam a linguagem pictórica, e os símbolos representavam números. Esse processo de escrita predominou desde o terceiro milênio a.C. até os primeiros séculos da era cristã.

Os hieróglifos eram desenhos de seres vivos e de objetos diversos, e cada figura significava a palavra correspondente ao objeto representado. Os sons eram representados por hieróglifos que reproduziam nomes de objetos com esse som. .(BOYER, 1996, p. 55)

 

No sistema de numeração hieroglífico egípcio, a base utilizada era a 10, herança adquirida pelo sistema de numeração decimal. Existiam símbolos para os números 1, 10, 100, 1000, 10000 e 100000.

 

1912 Símbolos do sistema hieroglífico Fonte: Gullberg (1997, p. 34).

 

O sistema de numeração não posicional foi importante e deixou um legado para os sistemas posicionais, pois foi um processo de ideias aproveitadas, mas o sistema de numeração não posicional não era tão simples, tinha inúmeros problemas em relação à grandeza dos números, o que levou à utilização de objetos que ajudariam na resolução dos cálculos dentro do sistema posicional.

O primeiro instrumento inventado para auxiliar e facilitar os cálculos foi o ábaco, trata-se de um objeto originário do Oriente Médio, por volta do século III a.C., cuja função era auxiliar na resolução das quatro operações. A contagem era feita seguindo o princípio do sistema decimal. Seguindo esse raciocínio, fez com que na Índia criasse o sistema de numeração decimal, ou seja, numeração posicional de base 10. Enfim, outros sistemas foram criados ao longo do tempo.

Há algumas aplicações do sistema não posicional que, apesar de ser pouco utilizado atualmente, é de grande importância dentro da história. Veja alguns exemplos:

Era utilizado entre os egípcios em suas operações, como na multiplicação egípcia, em que usavam multiplicação por 2 e, em seguida, somas, esse método é conhecida como regra do dobro; na multiplicação Russa; na divisão Suméria, em que faziam seus cálculos por meio da base sexagesimal, entre tantas outras.

 

Atividades

Sobre os sistemas numéricos posicionais e não posicionais, é correto o que se afirma em:

• Os sistemas de contagem que conhecemos hoje derivaram de procedimentos de agrupamentos cujos dígitos organizados em grupos representam distintas quantidades de acordo com uma base estabelecida.

  Os sistemas de contagem que conhecemos hoje derivaram de procedimentos de agrupamentos cujos dígitos organizados em grupos representam distintas quantidades de acordo com uma base estabelecida.

• Os sistemas de contagem que conhecemos hoje derivaram de procedimentos de exclusão de dígitos distribuídos em grupos representando iguais quantidades de acordo com uma base estabelecida.

  Os sistemas de contagem que conhecemos hoje derivaram de procedimentos de agrupamentos cujos dígitos organizados em grupos representam distintas quantidades de acordo com uma base estabelecida.

• Iniciou o processo de abstração ao utilizarem símbolos diferentes para seres de naturezas iguais.

  Começo da utilização de símbolos iguais para seres de naturezas distintas é uma etapa para abstração.

• O processo para desenvolver o número partiu do próprio desenvolvimento humano.

  O processo para desenvolver o número propriamente dito partiu do próprio desenvolvimento da escrita.

• O sistema de numeração propriamente dito foi surgindo há mais de 5000 a.C. na Babilônia, porém o sistema que gerou a contagem atual foi o sistema de numeração indo-arábico.

  O sistema de numeração propriamente dito foi surgindo há mais de 3000 a.C. na Mesopotâmia, porém o sistema que gerou a contagem atual foi o sistema de numeração indo-arábico.

A matemática no Egito, na Mesopotâmia e na Grécia

As civilizações iniciam-se na mesma região que cultiva a agricultura, nas bacias dos rios Tigre e Eufrates, ao mesmo tempo, a civilização Egípcia na Mesopotâmia começa a se desenvolver nas margens do rio Nilo, concomitante com a civilização hindu, no centro sul da Ásia, nas bacias dos rios Indo e Ganges; sem esquecer-se da civilização chinesa, que surge na bacia dos rios Huang Ho e Yang Tsé, na Ásia Oriental, onde surgem as civilizações Hindu e Chinesa, sobre as quais abordaremos e discutiremos na próxima unidade deste material. O foco desta unidade serão as civilizações do Egito, Mesopotâmia e Grécia.

A expansão dessas civilizações à margem dos rios se justifica por estarem inseridas em terrenos férteis, onde se possibilitavam colheitas abundantes, proporcionando condições dos primeiros vilarejos se instalarem, consequentemente, dando origem às sociedades evoluídas nos milênios III, IV e V a.C. Objetivando compreender a origem da Matemática, torna-se necessário realizar uma leitura dos registros da origem das civilizações antigas, como Egito, Mesopotâmia e Grécia, civilizações que são consideradas referências na História da Matemática.

A civilização egípcia e a matemática

 

11012 Pedra de roseta Fonte: portalpesquisa.com.Último acesso: Acesso em: 23 dez. 2016.

 

A origem da civilização egípcia é desconhecida, provavelmente por volta do IV milênio a.C., podendo considerar o início da civilização por volta de 4000 a.C. O Egito foi uma das grandes civilizações do passado, cujo maior legado foi a matemática, região onde ocorreram diversos fatores que influenciaram a sociedade moderna, por conta disso, o Egito é considerado o berço da Matemática. A civilização egípcia formou-se e desenvolveu-se no vale do Rio Nilo, aproximadamente 3200 a.C. até o início da era cristã. Por conta da sua localização geográfica, manteve-se protegida de invasões estrangeiras; possuíam um governo pacífico e com sucessão de dinastias. Entre as escritas utilizadas pelos povos egípcios, destaca-se a hieroglífica, muito usada nos papiros, que mais tarde resultaria em escrita demótica, porém, para a História da Matemática, tudo começou por volta de 1799, quando as tropas do exército de Napoleão vão ao Egito e encontram, às margens do Rio Nilo, a pedra de Roseta, a qual trata-se de um fragmento basáltico polido. Nessa pedra estavam gravados escritos em egípcio, ou seja, nela continha mensagem repetida em hieroglíficos, em caracteres demóticos e em grego, e foi a partir da escrita grega uma possibilidade de decifrar a escrita egípcia.

Com a decifração das escritas da pedra de Roseta, possibilitou-se abrir uma grande porta para o conhecimento, em que, por meio dessa descoberta, permitiu-se revelar muitos segredos, entre eles, o sistema de numeração usado pelos egípcios, que consideravam agrupamento simples na base dez, assim cada figura representava um múltiplo de 10. O sistema de multiplicação e divisão usado pelos egípcios era simples, por exemplo, na multiplicação duplicava-se o número pelo valor que era dividido, assim, se quiser dividir 12 por 27, dobrava o 12 por 27 vezes, no entanto os egípcios também tinham fórmulas de calcular bem mais complexas, como a chamada regra da falsa posição.

O sistema de numeração era decimal, ou seja, de base 10, de modo que o mesmo símbolo podia ser repetido nove vezes, depois era substituído por outro que podia ser repetido até nove vezes e, assim, sucessivamente. Dez símbolos iguais eram trocados por um novo símbolo de um agrupamento superior. O valor do número escrito é a soma dos valores dos símbolos utilizados. Esse sistema de numeração possui mais de cinco mil anos.

Por meio das descobertas foi possível perceber que tratava-se de um resultado concreto de enumeração, assim os números são representados por alinhamento, por meio de uma associação ordenando as unidades, por exemplo, utilizando pedras para as unidades, conchas para as dezenas e bolinhas para as centenas, pauzinhos para os milhares e assim sucessivamente. A numeração hieroglífica já continha sinais específicos para representar as diversas ordens, assim, um traço vertical representava a unidade; um sinal em forma de alça indicava a dezena; um sinal parecido com um pedaço de corda enrolada valia cem; uma flor de lótus, com seu talo, para representar mil; um dedo humano, dobrado, representava dez mil; com um girino representava cem mil; uma figura humana ajoelhada representava um milhão.

A Aritmética dos egípcios apresentava símbolos hieróglifos para alguns números, que eram combinados para formar números intermediários e, como na maioria das escritas orientais, o sentido era da esquerda para a direita. Essencialmente aditiva, a aritmética egípcia determinava os resultados das adições e subtrações mediante simples combinação de símbolos; as multiplicações e divisões eram reduzidas a processos aditivos.

No Egito antigo, o homem foi capaz de diversos feitos que continuam a influenciar em nosso cotidiano até os dias atuais, como o sistema de numeração da base 10, multiplicação e divisão. As descobertas egípcias influenciam, inclusive, assuntos Matemáticos, como a Álgebra, com o sistema de numeração, frações unitárias, equações lineares, progressões aritméticas e geométricas; influenciam a Geometria, mediante as construções das pirâmides, com seus triângulos e retângulos, área de um círculo, sem deixar de elencar a Matemática aplicada com o calendário solar.

Decifrar a Pedra de Roseta foi possível graças à dedicação e sabedoria do francês Jean-Françoies Champollion (1790-1832), linguista e egiptólogo, considerado o pai da egiptologia, pois a ele se deve a decifração dos hieróglifos egípcios. Em 1809, se torna professor de História em Grenoble, sua paixão pela língua oriental o conduziu ao trabalho de decifrar a Pedra de Roseta, um trabalho intenso que o levou a dedicar 2 anos de sua vida para esse trabalho, então, de 1822 a 1824, Jean expandiu os trabalhos de egiptologia do físico inglês Thomas Young (1773-1829) e decifra essa nova descoberta. Esse trabalho importante de Jean só foi possível devido à pedra conter inscrições de mensagens idênticas em hieroglíficos, caracteres demóticos em grego. Partindo da base grega foi possível decifrar a escrita egípcia, porém demorou algum tempo até que outros estudiosos realizassem as leituras de outros textos egípcios com propriedade e confiança.

Boyer (1974, p. 9) chama atenção para o fato de que “[...] há um limite para a quantidade de informação que se pode retirar de calendários e pedras tumulares”, o que restringiria muito o conhecimento da contribuição egípcia para a Matemática, caso não existissem outras fontes, as quais, felizmente, existem. “Um certo número de papiros egípcios de algum modo resistiu ao desgaste do tempo por mais de três e meio milênios”. (BOYER, 1974, p. 9).

Impossível escrever sobre a História da Matemática na civilização egípcia sem registrar dois importantes papiros, cujos registros da matemática egípcia antiga encontram-se neles. O papiro Golonishev, ou de Moscou, datado aproximadamente no ano de 1850 a.C., contém registrados 25 problemas, e o papiro Rhind, ou Ahmes, datado aproximadamente no ano de 1650 a.C., em que são possíveis de encontrar 85 problemas em escrita hierática.

 

11112 Papiro Rhind Fonte: progettomatematica.dm.unibo.it.Último acesso: Acesso em: 23 dez. 2016.

 

Nesses registros importantes encontra-se a descrição de métodos de multiplicação e divisão dos egípcios, demonstra o uso das frações unitárias, a regra da falsa posição e como eram empregadas soluções para problemas que envolviam a determinação da área do círculo, entre outros problemas práticos que eram apresentados no Papiro Rhind. Como o sistema de numeração utilizado pelos egípcios era o agrupamento simples de base 10, todos os problemas apresentados no papiro Rhind e Moscou são numéricos, a maioria com aplicações práticas, com questões que envolviam afazeres diários, como a distribuição de pão e cerveja, divisão e balanceamento de rações animais e principalmente sobre armazenamento de grãos. Esses problemas aparentemente foram produzidos para os estudantes, sem finalidade utilitária, pois para muitos desses problemas apresentados a resolução era uma simples equação linear, porém, entre eles, há problemas que envolvem questões teóricas, como progressão aritmética e geométrica; mostravam também conhecimento em cálculos de áreas de triângulos e retângulos, inclusive volume cilíndrico, entre outros.

Há um certo simbolismo na álgebra egípcia. No papiro Rhind, encontram-se símbolos para mais e menos. O primeiro deles representa um par de pernas caminhando da esquerda para a direita, o sentido normal da escrita egípcia, e o outro representa um par de pernas caminhando da direita para a esquerda, em sentido contrário à escrita egípcia. Empregavam-se também símbolos, ou ideogramas, para igual e para a incógnita. (EVES, 2011, p. 75).

 

Alguns dos problemas apresentados nos papiros apresentam, ainda que entre linhas de forma tímida, as equações do primeiro grau, as quais eram resolvidas com o uso de processos puramente aritméticos, sem atingir a ideia de resolução de equações; não adotavam nenhuma simbologia simplificadora, porém utilizavam um artifício bastante engenhoso e que ficou conhecido como a regra da falsa posição ou a regra do falso.

Por exemplo: qual o número que somado à sua terça parte dá oito? Pela Regra da Falsa Posição, fazia-se uma hipótese inicial qualquer a respeito do número e verificava-se o que ocorria. Suponhamos, em nosso caso, que tal número fosse 3. Ora, 3 somado com sua terça parte dá 3+1=4, exatamente a metade dos 8 que deveria dar. Portanto, o número procurado é o dobro de 3, ou seja, 6. .(GARBI, 1997, p. 13)

 

O modo como foram escritos os papiros, particularmente os papiros de Ahmes e de Moscou, indica terem sido destinados a estudantes e apresentam, hoje, a “[...] direção e as tendências do ensino de Matemática no antigo Egito” (quase todo prático e com ênfase nos cálculos, deixando claro que o principal objetivo era o domínio da técnica e não a compreensão). Entretanto, tais informações, reunidas a “[...] outras evidências fornecidas por inscrições sobre monumentos”, demonstram que os egípcios pouco aproveitaram de seus conhecimentos geométricos e deixam claro, também, que a Aritmética de Ahmes era a de seus antepassados e, portanto, bem mais antiga (BOYER, 1974, p. 16).

Entre as inúmeras crenças da civilização egípcia, podemos destacar a crença na vida após a morte, em que era comum conservar os corpos embalsamados e guardados em túmulos em formato de grandes pirâmides. Nas construções das pirâmides é possível notar aplicações de engenharia, inclusive o forte interesse pela astronomia, pois dependiam do sistema solar para prevenir e se preservar das inundações anuais do rio Nilo, então, partindo da astronomia, sabiam com exatidão o início e o final da inundação, estabelecendo assim um calendário solar que é a base da Matemática Aplicada. Todavia, as comparações geométricas utilizadas para justificar os cálculos realizados para estabelecer determinados perímetros ou áreas podem ser consideradas “[...] entre as primeiras afirmações precisas da história referentes a figuras não curvilíneas” (BOYER, 1974, p. 13).

Para Cajori (2007), é estranho e curioso que os egípcios tenham alcançado resultados tão avançados em período tão remoto, “mas é estranho, na verdade, o fato de que durante os seguintes dois mil anos não fizeram, em absoluto, progresso algum neste campo”. O autor considera que a antiga civilização do vale do rio Nilo era estática, tanto para assuntos que envolviam aprendizagem quanto para assuntos governamentais. Isso fica demonstrado pelas pesquisas realizadas pelos estudiosos gregos, que os visitaram seis séculos antes de Cristo e verificaram que o conhecimento de Geometria que os egípcios possuíam naquela época era o mesmo já dominado por eles, “[...] desde dois mil anos antes, quando construíram aquelas estupendas e gigantescas estruturas – as pirâmides” (CAJORI, 2007, p. 42).

 

A matemática na mesopotâmia

Às margens dos rios Eufrates e Tigre, por volta do IV milênio a.C., ocorreu um notável progresso cultural, período em que se desenvolve a escrita, passam a dominar metais e usar a roda, podendo assim ser considerada como uma civilização avançada. Sua origem veio de antigas civilizações, entre eles, os caldeus, assírios e sumérios, assim a Babilônia ia florescendo e surgia a região da Mesopotâmia. Devido ao material utilizado nesse período para registros, torna-se difícil datar com precisão os conhecimentos daquele período, o material utilizado para registros eram placas de barro cozido, indestrutíveis, diferente dos escritos egípcios, deixaram de ser um enigma a partir século XVIII, ou seja, demoraram séculos para chegarem à compreensão. Sabia-se bem pouco sobre a Matemática babilônica, pois as informações estavam restritas à literatura grega e aos registros dos matemáticos caldeus, fator que ocasionou muitos equívocos, como, por exemplo, supor que existia algum tipo de misticismo numérico ou numerologia na Mesopotâmia, o que demonstrou ser falso em virtude de descobertas mais recentes.

Isso justifica as informações sobre a civilização e sobre a Matemática babilônia estar dividida em dois períodos, uns datam cerca de 2000 a.C. e outros por volta de 600 a 300 a.C. Ao contrário do Egito, a Mesopotâmia possuía uma localização privilegiada, o que facilitava a rota de caravanas, isso gerou o desenvolvimento superior das demais sociedades da região, além disso, as inundações dos rios Tigre e Eufrates eram imprevisíveis, e o aproveitamento das áreas férteis necessitava de mais “[...] perícia técnica e administração do que o Nilo”, exigindo maiores estudos matemáticos, levando, consequentemente, também a Matemática a maiores desenvolvimentos (STRUICK, 1992, p. 52).

Em meados do século XX, o conhecimento matemático dos babilônios foi ampliado, graças à dedicação de O. Neugebauer e F. ThureauDangin, que conseguiram decifrar inúmeras placas de argila, deixando claro que a matemática babilônica atingiu um nível mais elevado do que o obtido pela matemática egípcia, com evidências de grande habilidade para o cálculo. Tinham uma tendência e, de certa forma, uma predominância ao caráter aritmético-algébrico, mesmo quando se trata de geometria, surgindo, inclusive, problemas que se relacionavam com medição, cuja forma geométrica de um determinado problema também servia para apresentar uma questão algébrica; utilizavam o sistema sexagesimal, o que supostamente tenha possibilitado a divisão das horas em 60 minutos e a cada 1 minuto em 60 segundos, inclusive o cálculo de 360 graus, porém não representavam o “0” com nenhum símbolo especial.

Essa base de notação posicional era utilizada inclusive para representar frações, porém a base 60 não era absoluta, surgindo também textos com sistemas numéricos que utilizavam múltiplos e submúltiplos de 60, 24, 12, 10, 6 e 2, para calcular área, medidas de peso, datas e cunhagem de moedas, inclusive o uso do numeral 12 como base para horas e polegadas 10 para contagem usual.

 

11212 Sistema de numeração da Babilônia Fonte: www.educarhojeonline.com.Último acesso: Acesso em: 23 dez. 2016.

 

A Babilônia utilizava o sistema aditivo de numeração base 10 e continha símbolos especiais para Um, Dez, Cem, Mil e Dez Mil; a base 60 possuía apenas dois símbolos representados em pedaços de argila, continham aspectos semelhantes à cunha, assim surge a nomenclatura da escrita “cuneiforme”. Já para a unidade, sua representação era um símbolo mais fino, na posição vertical, que seguia uma sequência de repetição até nove, o símbolo mais largo que aparece na imagem na posição vertical representava o valor de dez, utilizado e repetido junto ao símbolo de unidade conforme a necessidade; a representação dos números era de 11 até 59, de 60 em diante, era utilizado o princípio da posição para indicar potências de 60. O sistema funcionava de seguinte maneira: na segunda posição, o símbolo deixava de valer um pra valer 60, na terceira posição valia 60 vezes 60, e assim por diante. Assim, a partir de 60, o sistema se tornava complexo e utilizavam o princípio da posição para indicar múltiplos de potências de 60, como 600, 3 600 e 36 000.

Esse sistema de numeração da Babilônia foi encontrado nas escavações arqueológicas na Mesopotâmia, esse mesmo sistema foi criado há aproximadamente 4 mil anos. Sabe-se que entre 1600 a 1800 a.C. nenhum símbolo representava o zero, ou seja, não existia nenhuma representação, então um espaço em branco era deixado para representar qualquer potência de 60, isso causava falha na interpretação, pois o valor do número só ficaria claro de acordo com o contexto, gerando muita confusão.

Os Babilônios nos últimos três séculos a.C. criaram em seus escritos cuneiformes o símbolo para representar a posição vazia, ou seja, criaram o zero em seu sistema de numeração. A eles inclusive se deve a invenção do sistema posicional, utilizando apenas símbolos representando as unidades e as dezenas, conseguiam representar qualquer número por repetição e mudança de posição, sem importar-se com a grandeza desse número, é essa mudança de posição que caracteriza um sistema posicional.

Criaram tábuas para expressar multiplicação, demonstrando claramente que os povos da mesopotâmia conheciam e utilizavam com precisão as quatro operações aritméticas fundamentais, que podemos dizer que foi o pontapé inicial para as tabuadas, além da demonstração de domínio em raízes quadradas, cubos e raízes cúbicas. Para Aaboe (1984), uma enorme desvantagem de uma base grande, como 60, é o tamanho desconfortável de uma tábua (tabela) de multiplicação que mostra o produto de dois números quaisquer de um algarismo.

Treme-se ao imaginar os pobres alunos babilônios tentando memorizar uma tal tábua de dimensões 59 por 59, e sentimos alívio de saber que havia grande quantidade de tábuas de vários tipos, incluindo as de multiplicação; de maneira que se torna clara que uma tal memorização era desnecessária .(AABOE, 1984, p. 28)

 

Enquanto os egípcios apresentavam alguns trabalhos relacionados a equações lineares, os babilônios já demonstravam interesse e trabalhavam com equações de 2º graus, utilizando o método fundado no complemento do quadrado, princípio que foi utilizado por Bhaskara quase três milênios depois, embora resultados fossem corretos, a exemplo dos papiros egípcios, os tabletes que tratam de “soluções de equações do 2º grau apresentam apenas sequências do tipo ‘faça isto’, ‘faça aquilo’, ‘este é o resultado’, sem qualquer justificativa lógica sobre o caminho seguido” (GARBI, 1997, p. 13).

Por não conhecerem números negativos, os mesopotâmios ignoravam as raízes negativas das equações. Nos registros, demonstram conhecer as triplas pitagóricas, um pouco de teoria dos números, além de serem os primeiros a utilizarem uma indicação especial para as incógnitas, que atualmente são representadas por letras, mas naquela época não eram conhecidas, portanto eram representadas por palavras, comprimento, largura, área e volume, não porque as incógnitas representassem essas medidas geométricas, mas em sentido realmente abstrato, visto que eles operavam com essas palavras, ou seja, não hesitavam “em somar um ‘comprimento’ com uma ‘área’, ou uma ‘área’ com um ‘volume’. Tais problemas tomados literalmente não podiam ter base em mensuração”, fazendo crer que pelo fato de muitos problemas algébricos derivarem de problemas geométricos a utilização da terminologia geométrica se tornasse padrão (BOYER, 1974, p. 23).

Os Babilônios iniciaram o estudo da álgebra, com o uso especial de termos para representar incógnitas, com a solução de determinadas equações, em especial, as quadráticas, que envolviam uma ou mais incógnitas, principalmente ao apresentar um leve envolvimento com a matemática abstrata, porém, seguindo o exemplo dos egípcios, os babilônios não registraram nenhum emprego a demonstrações matemáticas, a processos algébricos e aritméticos. Quanto à Geometria, alguns autores estabelecem que se a Matemática da Mesopotâmia superou a dos egípcios na Aritmética e na Álgebra, o mesmo não aconteceu em relação à Geometria devido ao fato de que esta última era tratada como um assunto à parte da Matemática, isto é, não como uma disciplina ou tópico integrante do corpo de conhecimento matemático, mas como uma espécie de Álgebra ou Aritmética aplicada que relacionava números e figuras. Todavia, o principal argumento utilizado para confirmar tal assertiva se prende, “[...] em geral, à medida do círculo ou ao volume do tronco de pirâmide”, uma vez que os babilônios determinavam a área do círculo “[...] tomando três vezes o quadrado do raio e, em precisão, isso é bem inferior à medida egípcia”, que apresentava uma melhor aproximação para o valor de π (BOYER, 1974, p. 28).

 

Atividades

Entre os registros importantes da Matemática na civilização egípcia, podemos destacar:

• Carapaças de tartarugas e Tokens.

  Carapaças de tartarugas e Tokens são do período da pré- história.

• Pedra de roseta e os papiros.

  Dois marcos importantes para a matemática são a pedra de roseta e os papiros Golonishev e Rhind.

• Papirus Moskovs.

  O nome do Papiro está incorreto, um Papiro importante na história egípcia é conhecido como Papiro Golonishev ou Moscou.

• Pedra Rosácea.

  O nome Pedra de Rosácea está incorreto o correto é Pedra de Roseta, trata-se de um fragmento basáltico polido, nessa pedra estava gravado escritos em egípcio.

• Problemas registrados nas cavernas em escrita árabe.

  Os egípcios utilizavam a Escrita hierática, não a Escrita árabe.

Início do período helênico: Pitágoras, Tales de Mileto, Apolônio de Perga

Por volta de 600 a.C. até 300 a.C. inicia-se o período helênico, após a morte de Alexandre, o Grande, e de Aristóteles. O período helenístico chega até os princípios da era cristã; esse período também é considerado o período de ouro para a Matemática grega, nele a matemática se desenvolve em comum acordo com as escolas filosóficas, retirando alguns de seus fundamentos, que passaram a ser permanentes e outros transitórios. Nesse período, a Matemática se torna autônoma e atinge consideradas realizações por meio de Euclides, Arquimedes e Apolônio.

No período helênico, também conhecido como matemática clássica, apesar de ser mais recente que as descobertas conquistadas pelos povos dos vales dos rios Nilo, Tigre e Eufrates, as produções matemáticas gregas que resistiram até os tempos atuais são muito mais escassas e, basicamente, compilações tardias, na maioria das vezes, realizadas muitos séculos após os escritos originais, ou então simples traduções, particularmente, as árabes.

Uma das fontes que contribuíram nesse período, podemos colocar como fonte indireta, é o livro Sumário Eudemiano, de Proclus (410-485), um filósofo neo-platônico; trata-se de um breve esboço de desenvolvimento da Geometria grega, desde os tempos primitivos até Euclides e, embora Proclus tenha vivido no século V d.C., mais de um milênio depois do advento da Geometria grega, teve acesso a numerosos trabalhos históricos que se perderam, exceções feitas a alguns fragmentos e alusões preservadas por ele e outros. Um trabalho aparentemente completo da Geometria Grega, foi escrito por Eudemo (Séc. IV a.C.), discípulo de Aristóteles.

Um dos responsáveis por traduzir o trabalho de Eudemo foram os povos árabes, cujas versões traduzidas em latim foram derivadas dos textos árabes, o que gerou dúvidas sobre a fidedignidade dos resultados apresentados, pois podem ter sofrido alterações pelos tradutores, por consequência de interpretações equivocadas. Nem mesmo as compilações preservam a autenticidade dos textos originais, como no caso célebre de Os Elementos de Euclides em que, no texto Os elementos de Euclides, embora o Manifesto de Heron (séc. II ou III a.C.) não tenha se conservado até a atualidade, é sabido que Euclides realizou provas diferentes e adicionou novos casos aos teoremas, além de recíprocas. Da mesma forma, Teon de Alexandria, no final do século IV da era cristã, altera noções de os Elementos em sua edição.

Nesse período clássico, os gregos utilizavam o sistema de numeração decimal e não posicional, utilizando o sistema alfabeto ordinal, e por inúmeras vezes também utilizavam a função da letra, ou seja, a letra assume uma dupla função: hora é letra, hora é numeral. Os gregos também utilizavam apóstrofes para indicar que a função da letra em determinado momento era a de numeral, os dois sistemas mais importantes utilizados pelos gregos foram o Ático (usado pelos atenienses), o mais antigo, que já era usado por volta de 600 a.C.; e o jônico (por volta de 200 a.C.), possivelmente chegou à Grécia pelos fenícios. Herdamos muito do sistema grego, como os prefixos pentas, deca, hecto e quilo. Esse sistema usava o princípio aditivo e não posicional.

Já o sistema jônico usava o princípio aditivo, de base dez e não posicional; utilizava o alfabeto grego empregando as 24 letras do alfabeto e mais três letras do alfabeto que desapareceram, exemplo: 1, 2, 3 ... e [math]\alpha =1,\beta =2,\gamma =3[math]... As cidades que surgiram ao longo da costa da Ásia eram menores e no continente grego eram comerciais, portanto eram cidades de negócio, onde os senhores feudais tinham que lutar contra uma classe de mercadores e política.

Mais ainda, segundo Caraça (1984) e Struick (1992), os gregos podiam usufruir de lazer, resultado da abundância do trabalho escravo; podiam filosofar sobre seu mundo. A ausência de uma religião instituída levou muitos habitantes das cidades costeiras ao misticismo, porém também estimulou o oposto, o crescimento do racionalismo e da visão científica de mundo. Essa estrutura social, com o trabalho escravo possibilitando à elite dirigente um alienamento da realidade concreta, imprimiu um caráter original à matemática grega, em que não existia nenhum tipo de preocupação com as aplicações práticas. A pergunta “como?” é substituída pela questão “por quê?”, e não seria estranho que um grego da classe dirigente se dedicasse a especulações intelectuais e, motivado unicamente por questões estéticas, se dedicasse a abstrações (MACHADO, 1987).

Refletindo as contextualizações dos autores como Machado (1987), Struick (1992) e Caraça (1984), entendemos que os gregos edificaram um sistema científico sobre os primeiros materiais de Geometria e Astronomia coletados pelos babilônios e egípcios, e, além da sistematização desses conhecimentos, os primeiros estudos de Matemática grega tinham um objetivo principal: compreender o lugar do homem no universo de acordo com um esquema racional, de consequência direta da inexistência de explicações religiosas.

O desenvolvimento da Matemática Grega ocorreu em diversos centros, cada um deles construído sobre o trabalho de seus predecessores. Por muitos séculos, os centros se situavam entre os mares Egeu e Jônio, inclusive a civilização helênica se situava ao longo da costa do Mediterrâneo e do Mar Negro, nessas regiões afastadas, a Matemática ganhou um forte impulso, com os habitantes da orla marítima, particularmente os da Jônia, que se sobressaíam dos demais por duas vantagens: “[...] tinham o espírito ousado e imaginativo típico de pioneiros e estavam mais próximos dos dois principais vales de rios de onde podiam extrair conhecimentos” (BOYER, 1974, p. 34).

Tales de Mileto - fundador da escola jônica ou joniana

Tales de Mileto (640-564 a.C.), segundo Eves (2011, p. 94), é “um dos “sete sábios” da Antiguidade, durante a primeira metade do sexto século a.C.”. Foi o fundador da escola Jônica, ou Joniana, onde entre seus principais seguidores destacam-se Anaximandro (500-418 a.C.) e Anaxímenes (c.585-525 a.C.). Existem rumores de que Pitágoras tenha aprendido Matemática com Tales, porém, quando a civilização Persa dominou a região, a escola Jônica perde gradualmente a sua importância. “A matemática grega se inicia com o mesmo nome com que se inicia a filosofia grega: o de Tales de Mileto, um dos ‘sete sábios’, e o primeiro também entre os membros da chamada escola jônica” (BABINI, 1969, p. 18).

Porém não existe nenhum registro de Tales, inclusive não constam fontes contemporâneas a seu respeito. Como todo elemento da escola jônica, Tales foi um “filósofo da natureza” e mediante “[...] observações empíricas sobre os seres, sobre as coisas e sobre os fenômenos, especialmente meteorológicos, chegou a uma concepção de que todo o universo estava submetido a um processo de transformação contínua” e, segundo Aristóteles, foi o primeiro a afirmar que a água era a substância fundamental do universo e de toda matéria (BABINI, 1969, p. 18). Tales representa fundamentos da Matemática, da ciência, inclusive da filosofia, sempre procurava responder o “por quê”.

Assim, os resultados geométricos de Tales eram baseados em raciocínios lógicos, e não em intuição ou experimentação, tendo introduzido o conceito, revolucionário à época, mas até hoje fundamental da Matemática, de que as verdades matemáticas precisam ser demonstradas. No século VI a.C., das ruínas do que outrora havia sido o Império Assírio, surgiu a Pérsia de Aquemênides. Os persas conquistaram as cidades da Anatólia, foram repelidos nas batalhas históricas de Maratona, Salamina e Plateia. A hegemonia de Atenas é expandida, e a segunda metade do século VI a.C. é considerada o início da idade do ouro da Grécia, período em que a Matemática é parte integrante de uma investigação mais ampla do mundo moral e natural.

Fim do período helênico: Euclides e os elementos

Diofanto de alexandria

Diofanto de Alexandria (201 – 298 d.C.), nascido provavelmente no séc. III, foi um matemático grego, considerado por muitos como “o pai da álgebra”, pouco se conhece sobre a vida de Diofanto, então, para situar sobre a vida desse matemático, optou-se em marcar limites temporais que permitem situar a vida de Diofanto, um dos seus feitos foi desempenhar um papel semelhante ao de Euclides na Geometria e de Ptolomeu na Astronomia. Dentre os matemáticos que estudaram teoria dos números, Diofanto, sem dúvidas, foi um dos mais importantes, entre suas obras, a Arithmetica escrita por volta de 250 d.C. aborda principalmente a solução de equações indeterminadas com coeficientes inteiros. Ele estudou e trabalhou na Escola de Alexandria, e deixou um enigmático verso em Antologia escrito em sua tumba:

Aqui jaz Diofanto. Maravilhosa habilidade. Pela arte da álgebra a lápide nos diz sua idade: Deus deu um sexto da vida como infante, um duodécimo mais como jovem, de barba abundante; e ainda uma sétima parte antes do casamento; em cinco anos nasce-lhe o rebento. Lástima! O filho do mestre e sábio do mundo se vai. Morreu quando da metade da idade final do pai. Quatro anos a mais de estudos consolam-no do pesar; para então, deixando a terra, também ele alívio encontrar. .(AGUIAR, 2004. p. 120)

 

Daí, poderemos representar como uma equação algébrica e descobrirmos sua idade:

Logo, x representa a idade de Diofanto resultando em 84 anos.

Mais do que um grande estudioso de Aritmética e de Geometria, como o foram todos os seus precursores gregos, aparece de forma isolada no conjunto da Matemática grega por estar mais próximo da Matemática dos povos orientais, podendo, portanto, ser considerado um dos principais precursores da moderna Álgebra, tendo exercido enorme influência sobre os europeus, que posteriormente se dedicaram à Teoria dos Números.

Por conter poucas informações sobre a época em que viveu Diofanto e sobre sua nacionalidade, a maioria dos historiadores costuma situá-lo no século III da era cristã. É certo, porém, que sua carreira floresceu em Alexandria, onde estudou e trabalhou na Universidade local (o mesmo Museu onde Euclides havia ensinado).

Diofanto de Alexandria teve uma importância enorme para o desenvolvimento da álgebra e uma grande influência sobre os europeus, que posteriormente se dedicaram à teoria dos números. Tal como no caso de Herão, nada se sabe com certeza acerca da nacionalidade de Diofanto e da época exata em que viveu. Apesar de haver algumas evidências tênues de que possa ter sido contemporâneo de Herão, a maioria dos historiadores tende a situá-lo no século III de nossa era (EVES, 2011, p. 207).

Seguindo os antigos métodos babilônicos, Diofanto deu um novo impulso à Álgebra (deve-se a ele o estilo sincopado de escrever equações). Diofanto escreveu três trabalhos: Aritmética, o mais importante deles, do qual sobreviveram apenas seis dos treze livros e que se destaca por sua novidade e originalidade única na literatura matemática grega, “[...] pois, ao invés de apresentar teoremas e proposições, traz apenas problemas, em sua maioria, com números abstratos” (BABINI, 1969, p. 44); de sua outra obra, Sobre Números Poligonais, restou apenas um fragmento; e Porismas, a última, se perdeu.

Na resolução dos 130 problemas do Aritmética, alguns dos quais muito difíceis e que pertenceriam ao domínio da hoje denominada “análise indeterminada”, Diofante emprega um simbolismo semelhante ao que atualmente se aplica a polinômios de uma variável, utilizando métodos diferentes para cada caso em particular, “[...] porém esses métodos e os recursos auxiliares de que Diofanto lança mão são tão engenhosos e fecundos que conferem a toda obra uma peculiar fisionomia algébrica que a caracteriza e distingue dos demais escritos gregos” (BABINI, 1969, p. 44).

Dentre os trabalhos de Diofanto, podemos destacar três já citados: Aritmética, composto de 13 livros, porém foram resgatados apenas 6; Sobre Números Poligonais, do qual restou apenas um fragmento; e Porismas, que se perdeu.

 

A Aritmética teve muitos comentadores, mas a primeira voz a clamar por uma tradução do original grego foi a de Regiomontanus, isso em 1463, ao descobrir em Pádua um exemplar da obra. Uma tradução de muitos méritos, com comentários, foi feita em 1575 por Xilander (nome grego adotado por Wilhelm Holzmann, um professor da Universidade de Heidelberg). Essa tradução, por sua vez, foi usada pelo francês Bachet de Méziriac que, em 1621, publicou a primeira edição do texto em grego juntamente com uma tradução latina acompanhada de notas .(EVES, 2011, p. 207)

 

Por volta de 1670 surge a segunda edição da obra de Diofante, porém com alguns problemas de impressão, mesmo assim, foi importante historicamente por conter as famosas notas marginais de Fermat, que estimulava as pesquisas em teoria dos números. Na obra Aritmética, aborda-se de forma analítica sobre a teoria algébrica dos números, elevando Diofante a gênio nesse campo. Segundo Eves (2011, p. 207):

A parte remanescente do trabalho se dedica à resolução de 130 problemas, numa variedade considerável, que levam a equações do primeiro e do segundo graus. Só uma cúbica muito particular é resolvida. O primeiro livro se ocupa de equações determinadas em uma incógnita e os demais de equações indeterminadas de segundo grau, e às vezes de grau maior, em duas ou três incógnitas. É notável a falta de métodos gerais e a aplicação repetida de artifícios engenhosos ideados para as necessidades de cada problema específico. Diofanto só admitia respostas entre os números racionais positivos e, na maioria dos casos, satisfazia-se com uma resposta apenas do problema.

 

Nos teoremas apresentados na obra Aritmética de Diofante, cujos enunciados indicam sem prova, mas com uma alusão de Porismas, que a diferença entre dois cubos racionais sempre será a soma de dois cubos racionais, este tema chamou atenção posteriormente de Viète, Bachet e Fermat. Há muitas proposições relativas à representação de números como soma de dois, três ou quatro quadrados, um campo de investigações que iria ser completado mais tarde por Fermat, Euler e Lagrange. Talvez seja interessante enunciar alguns poucos problemas que se encontram na Aritmética; todos eles são atraentes e alguns são instigantes. Deve-se ter em mente que “número” significa “número racional positivo” (EVES, 2011, p. 207).

Dessa forma, os problemas algébricos indeterminados, em que se procura apenas as soluções racionais, ficaram conhecidos como problemas Diofantinos. Porém não foi Diofanto o primeiro a trabalhar com equações indeterminadas, também não foi ele o primeiro a resolver equações quadráticas de maneira não geométrica, porém pode ter sido o pioneiro nas descobertas rumo a uma notação algébrica. Diofanto tinha abreviações para a incógnita, potências da incógnita até a de expoente seis, subtração, igualdade e inversos. Foi assim que a álgebra retórica se tornou álgebra sincopada.

 

A matemática chinesa, hindu e árabe

É impossível contextualizar sobre a História da Matemática sem abordar culturas como a dos Chineses, Hindus e Árabes. Isso se justifica por optarmos em iniciar nossas reflexões abordando sobre os chineses. Os primeiros numerais de que se tem história dentro da civilização chinesa ocorreram em meados do 3º milênio a.C., quando os chineses fixavam a sua civilização às margens dos rios Huang-Ho e Yang Tsé (rios Amarelo e Azul), na dinastia Hsia, iniciada pelo imperador Yu.

Nesse período, foi possível perceber registros numéricos em carcaças de tartarugas e em ossos de animais, os chamados ossos oraculares que eram utilizados para adivinhações, mas isso ocorreu por volta de 1500 a.C. com a dinastia Shang, que governou e dominou até 1027 a.C. e só então tornou-se um Estado Feudal, governado pela dinastia Chou.

Segundo Nogueira (2015, p. 25):

O início da civilização acontece na mesma região onde aparece a agricultura, nas bacias dos rios Tigre e Eufrates, na Mesopotâmia, concomitantemente com o surgimento, no vale do rio Nilo, da civilização egípcia, com os hindus, no centro-sul da Ásia, nas bacias dos rios Indo e Ganges e os chineses, aglutinados nas regiões dos rios Huang Ho e Yang Tsé, na Ásia Oriental.

Após o grande império se dividir, isso por volta de 700 a 400 a.C., é que surgem os primeiros registros da Matemática, as primeiras obras. O Chou Pei Suan Ching - que contém um diálogo sobre as propriedades dos triângulos retângulos e no qual o teorema de Pitágoras é enunciado; nele é dada sua demonstração geométrica. Nessa obra é possível perceber que existe uma breve explicação sobre o cálculo aritmético.

De acordo com Struick (1992), os chineses começam a utilizar o papel em torno do século I a.C., porém poucos escritos anteriores a 700 a.C. foram conservados. Finalmente, e talvez seja essa a principal razão para a falta de informação acerca da China antiga, grande parte dos registros de caráter técnico foi destruída por mudanças dinásticas, guerras ou inundações.

Até onde se relata sobre a história, afirma-se que existem relatos de que por volta de 200 a.C. a China teve que conviver com um déspota chamado Shi Huang-ti. Este mandou que eliminasse todo e qualquer tipo de material voltado ao estudo, isso obrigou muitos estudiosos a possuírem obras na íntegra em sua memória. Nesse período, muitos conhecimentos eram compartilhados oralmente de geração para geração. Esse compartilhamento possibilitou a codificação do conhecimento chinês, pois, após longos anos, alguns desses materiais destruídos foram reconstruídos, porém, historicamente, dificulta a identificação e a catalogação das datas.

Na antiga matemática chinesa, algumas das obras relevantes de que se tem registro são os Chiu chang suan shu, ou Nove Capítulos da Arte Matemática, e o Chou Pei Suang Ching, que estão pautadas na época da dinastia Han (206 a.C. – 220 d.C.). Os Nove Capítulos são inteiramente dedicados à matemática chinesa e tratam de cálculo aritmético, raiz cúbica, sistemas de equações utilizando matrizes e números negativos, que aparecem pela primeira vez na história apresentando, enfim, as características gerais da Matemática chinesa que perduraram por milhares de anos.

É impossível abordar a Matemática chinesa sem relatar uma das obras mais perfeitas da China, que são as muralhas chinesas. Essa grande muralha se estende por milhões de quilômetros. A construção, por volta de 200 a.C., que se estendeu por muitos anos, foi efetuada com o objetivo de proteger o império chinês crescente. Construída em um local de difícil acesso, os construtores observaram que precisavam fazer cálculos com ângulos de distância, gasto de materiais, ângulos de elevação, provavelmente isso possa justificar a importância e a evolução da matemática chinesa.

Na China, quando o matemático queria somar, ele usava pequenos gravetos de bambus, mas os antigos chineses só usavam o sistema de casas decimais quando iriam realizar operações utilizando gravetos; quando iriam escrever, utilizavam a escrita. Eles usavam um sistema bem mais trabalhoso no qual símbolos especiais representavam dezenas, centenas e milhar. O único problema dos chineses é que não utilizavam o zero, não conheciam o zero, isso deixaria o número escrito extremamente limitado.

Mas, na verdade, havia uma enorme admiração por números na antiga China. De acordo com a lenda, o imperador ordenou para sua divindade criar a Matemática, acreditando no poder de influência dos números, no poder cósmico e, até hoje, os chineses acreditam no poder dos números, por exemplo, o número 4 deveria ser evitado e o 8 representa boa sorte.

Numa tal atmosfera cultural estagnada, as novas descobertas tornavam-se exceções, o que garantia mais uma vez a invariabilidade da tradição matemática. Tal tradição podia ser transmitida através de milênios, sendo somente abalada ocasionalmente por grandes catástrofes históricas .(STRUICK, 1992, p. 67)

Dessa forma, a civilização chinesa vai surgindo e, juntamente, a História da Matemática. Então, às margens do Huang-Ho e do Yang Tsé, lutavam contra secas e enchentes, drenando pântanos, canalizando a água em canais e “construindo dia a dia, durante séculos, cabanas e casas, templos e escolas, aldeias, cidades e Estados” (DURANT, 1957, v. III, p. 91).

De acordo com Nogueira (2015, p. 42):

Enquanto os mesopotâmicos usavam placas de barro cozido, que são praticamente indestrutíveis, e os egípcios usavam o papiro, que se conservou graças ao clima seco, os chineses (assim como os hindus) utilizavam cascas de árvore e bambu, materiais de fácil deterioração.

Vale lembrar que os chineses começaram a utilizar o papel por volta do século I a.C., e que, por ordem do imperador, muitas obras foram destruídas, então era comum pesquisadores possuírem o livro completo em suas memórias e isso acaba dificultando a identificação das datas.

Mas a matemática também tinha um papel vital para o imperador, pois o calendário e o movimento dos planetas eram de grande importância na vida do imperador, influenciando diretamente em suas decisões. Logo, os astrônomos eram pessoas próximas do imperador e todos os astrônomos eram matemáticos. Tudo na vida do imperador era governado pelo calendário, ele cumpria as suas tarefas com precisão matemática.

A antiga China era um império vasto em crescimento, com código legal escrito com um sistema de peso, medidas e sistema monetário padronizado, então precisava de um serviço civil altamente treinado que dominava a matemática. Havia um livro de matemática com 9 capítulos escrito cerca de 200 a.C. O livro é uma compilação de 246 problemas de áreas práticas como comércio, pagamento de salário e impostos, e no centro desse problemas estava o foco principal da matemática, como resolver as equações, ou seja, você recebe uma informação de determinado número desconhecido e com essas informações você tem que descobrir o valor desconhecido.

Os antigos chineses aplicavam números cada vez maiores em situações cada vez mais complicadas, mas isso só apareceu no ocidente no início do século XIV, em 1809, por meio de Gauss, também conhecido como príncipe da matemática, ou seja, ele redescobriu esse método, e, mais uma vez, a China chegou na frente da Europa. Os chineses continuaram a desenvolver a Matemática, resolvendo equações ainda mais complicadas, o que ficou conhecido como teorema chinês do resto. Os chineses criaram um novo tipo de problema, nesse sabemos o número que resta quando o número desconhecido na equação é dividido por um dado número como 3,5 ou 7; claro que é um problema matemático bastante abstrato, mas os chineses conseguiram sustentá-lo em termos práticos.

No século VI d.C., o sistema do resto era utilizado na astronomia, e até hoje é utilizado, como, por exemplo, a criptografia. No século XIII, a era de ouro da matemática havia chegado, e o seu Matemático mais importante era um administrador imperial que cruzou a China se apropriando do dinheiro do governo e envenenando todo mundo que cruzasse o seu caminho; ele se tornou um guerreiro implacável lutando contra os mongóis.

Então, surgem as equações de segundo grau, pois envolviam números ao quadrado ou a segunda potência, equações perfeitas para medir figuras planas ou tridimensionais. Mas não pararam por aqui e foram resolver equações cúbicas; o poder dessa técnica é que ela pode ser aplicada ainda em situações mais complicadas em matemáticas altamente complexas, porém foram aperfeiçoadas por Isaac Newton.

Um dos principais registros de que se tem história da Matemática no período Chinês ficou conhecido como Chiu chang suan shu, ou Nove Capítulos da Arte Matemática, e o Chou Pei Suang Ching, que datam, na sua forma atual, da época da dinastia Han 206 a.C. – 220 d.C.

De acordo com Eves (2011, p. 244):

Um acontecimento interessante ocorrido em janeiro de 1984 foi a descoberta de um livro de aritmética escrito em tiras de bambu, desenterrado de túmulos que remontam à dinastia Han. O trabalho, transcrito por volta do século II a.C., é uma coleção de mais de 90 problemas envolvendo as quatro operações matemáticas fundamentais, tanto com inteiros como com frações, proporções, áreas e volumes. Atualmente é o trabalho matemático chinês mais antigo de que se tem notícia.

Um dos mais antigos clássicos Matemáticos, o Chou Pei Suang Ching, tratava de cálculos astronômicos, mas com dedicação parcial à Matemática, pois abordava o Teorema de Pitágoras, uma discussão algébrica entre os chineses, inclusive nesse clássico existiam pequenos registros sobre frações. Até o segundo milênio a.C., os números eram expressos utilizando nove símbolos diferentes do sistema utilizado pelo período de Han. Para realizar operações recorria-se a tabuleiros parecidos com ábacos; a diferença eram os espaços em branco para representar o zero, pois seu registro só veio a ocorrer no século XIII d.C. Nesse período, o sistema decimal não era absoluto e, para calcular o calendário, utilizava um sistema sexagesimal “[...] um tanto comparável à combinação de duas rodas dentadas ligadas, uma com 12 outra com 10 dentes, de modo que 60 se tornasse uma unidade mais elevada” (STRUICK, 1992, p. 66).

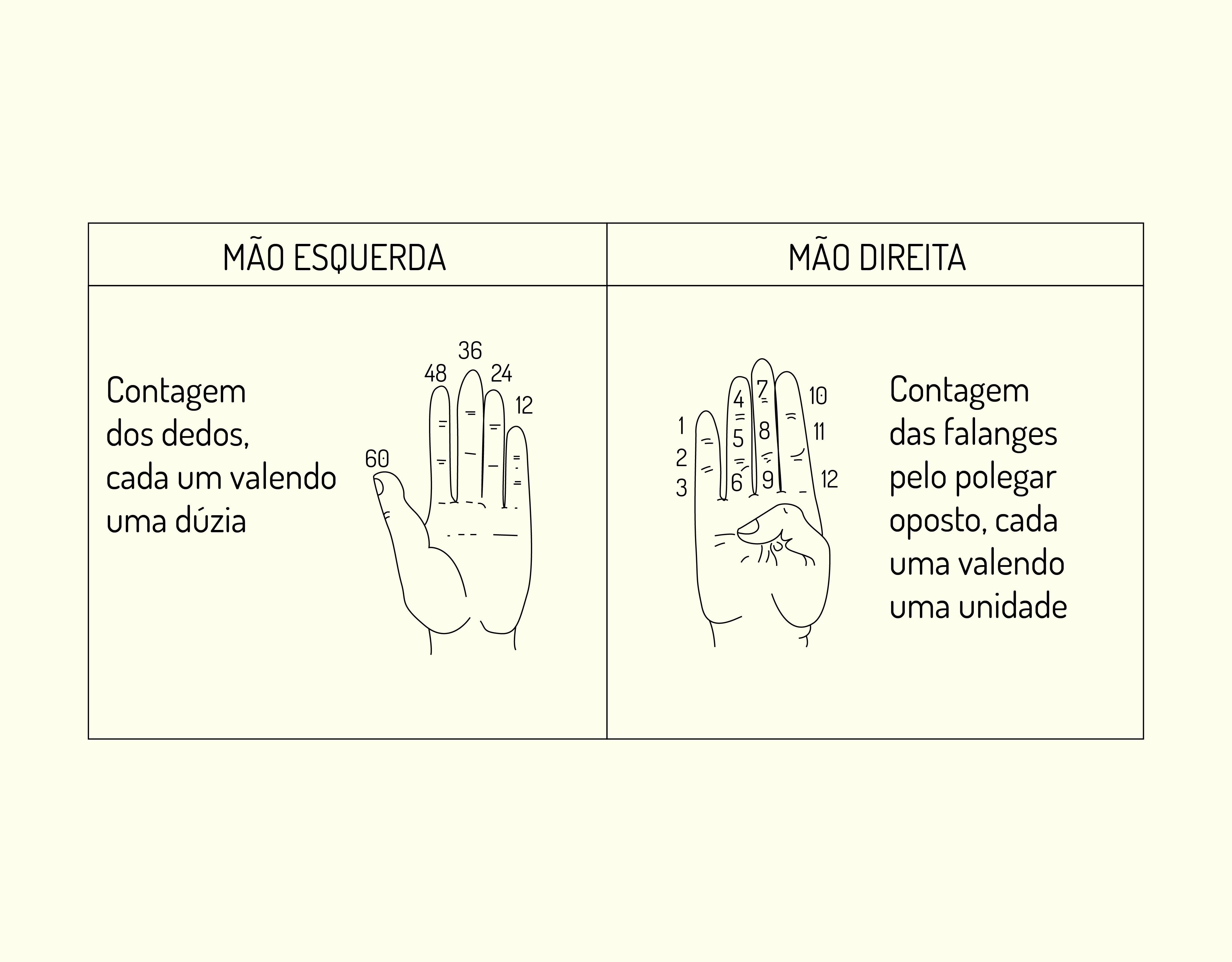
Os chineses faziam uso do sistema posicional utilizando símbolos diferentes para representar os números, conforme (Figura 2.1):

2118 Sistema de numeração chinesa Suan Zí Fonte: Nogueira (2016. p. 44).

As próximas descobertas matemáticas aconteceriam em um país a sudoeste da China, um país que tinha uma rica tradição matemática que mudaria sua história para sempre, assim começam a Matemática entre os indianos. Foram os indianos que criaram a palavra números e classificaram o sistema de contagem, o sistema de valor posicional decimal. Supõe-se que os indianos aprenderam o sistema com mercadores que viajavam pela Índia com suas varas de contar, então, eles se aperfeiçoaram e refinaram, criando os ancestrais dos nove numerais que utilizamos até hoje, se desenvolvendo o mais próximo do que podemos chamar de uma linguagem universal.

Por ora, deixando os Chineses, mas sem desprezar a importância dessa civilização para a História da Matemática, passamos a estudar sobre os Hindus, uma civilização que surgiu às margens dos rios Indo e Ganges, que, como as demais civilizações, vários documentos e obras importantes encontram-se soterrados, prejudicando a descoberta da história por completa, pois jamais serão desenterrados. As cidades da Índia que merecem destaque são: Calcutá, Bombaim e Madrasta, pois nelas há museus que guardam grande parte da história; trata-se de uma região muito rica em vestígios históricos e até hoje é possível encontrar objetos neolíticos em todo país.

Sabe-se que a fonte histórica mais antiga são ruínas de uma cidade de 5000 anos localizada em Mohenio Daro, trata-se de um sítio localizado na cidade de Karachi no Paquistão. Entre as ruínas, é possível encontrar piscinas públicas, pisos ladrilhados, ruas largas, casas de tijolos, até mesmo rede de esgotos, isso vem comprovar que naquele período histórico a civilização que ali habitava tratava de uma cultura avançada diferente de qualquer outra do oriente antigo, eles possuíam sistema de escrita, contagem, pesos e medidas, inclusive dominavam as técnicas de canais de irrigação; note que apresentavam requisitos básicos para qualquer engenharia e Matemática.

2218 Aryabhatas Fonte: www.apprendre-math.info.Último acesso: Acesso em: 24 dez. 2016.

Até próximo ao final do século XV, a Índia sofreu com inúmeras invasões estrangeiras, como os Hunos, depois Árabes e também os Persas, mas esse período de invasão fez despertar diversos matemáticos, como Aryabhatas, Brahmagupta, Mahavira e Bhaskara. Eles destacaram-se por produzir obras como o Livro de Astronomia, escrito em verso, intitulado como Aryabhatiya. O que chama atenção nessa obra escrita por Aryabhatas é que o autor destinou um capítulo a abordar assuntos matemáticos Hindus do século VII. O Matemático Mahavira destacou-se em meados de 850, após escrever sobre Matemática elementar. Por fim, surge Bhaskara, que em seu trabalho Siddhanta S’iromani (“diadema de um sistema astronômico”), escrito em 1150, mostrou pouco progresso em relação a Brahmagupta, ou seja, mesmo após cinco séculos, pouca coisa foi aprimorada e descoberta, porém as duas descobertas e obras mais importantes de Bhaskara são Lilavati (“bela”) e Vijaganita (“extração de raízes”), que tratam de aritmética e álgebra.

Após esse período, a Matemática Hindu teve pouco progresso ou podemos dizer que teve progressos irregulares até os tempos modernos. Podemos destacar que a Sociedade Matemática Indiana foi fundada em 1907 e dois anos depois apareceu em Madras, o Journal of the Indian Mathematical Society. O matemático indiano mais brilhante de todos os tempos modernos talvez tenha sido o Srinivasa Ramanujan (1887-1920), pois possuía uma espantosa capacidade de percepção rápida das relações numéricas intrincadas, mas iremos destacar a matemática moderna ao longo de nossos estudos.

Por ora, voltamos nossas reflexões ao ano de 1924, período em que o mundo passou a conhecer a cultura indiana. Nesse período existia uma suposta convicção de que a Índia era povoada por bárbaros e que somente com a vinda dos europeus que os indianos tiveram contato com a arte e ciências. O fator norteador da vida indiana sempre foi ligado à religião, então as primeiras ciências desenvolvidas na Índia eram ligadas à religião, por exemplo, a astronomia, a astrologia, a matemática, pois nesse período existia a necessidade de construir o calendário religioso e, principalmente, as construções dos templos; a gramática, pois havia a necessidade de catalogar e registrar as ideias que iam nascendo, pois toda prece deveria ser textual e foneticamente correta; por fim, a Filosofia; nesse período todo cientista da Índia era sacerdote. De acordo com Cajori (2007), os hindus foram o primeiro povo que produziram de forma significativa a influência no que diz respeito ao progresso mundial da matemática, após a contribuição dos gregos.

Voltando a nossas reflexões sobre a influência dos gregos nessa civilização, pode-se perceber claramente nos escritos de Siddanthas e Varahamihira, o Sistema Completo de Astrologia Natural e redes de cordas, escritos durante o último milênio a.C., os conteúdos matemáticos que eram dominados pelos Hindus, formados basicamente por regras e métodos para a construção religiosa de altares; utilizavam como instrumentos cordas, palitos de bambu, em que é possível encontrar figuras geométricas, como triângulo, retângulo quadrado e trapézio, polígonos.

Os Sulvasutras eram compostos por um apêndice de Vedas, o livro Sagrado das Escrituras, os principais Sulvasutras escritos em versos por Baudahayana; em algum deles aparecem procedimentos para calcular raízes quadradas com alto grau de precisão. No de Apastamba, podem-se encontrar “[...] regras para a construção de ângulos retos por meio de ternas de cordas cujos comprimentos formem tríades pitagóricas como 3, 4 e 5; 5, 12 e 13; 8, 15 e 17 ou 12, 35 e 37” (BOYER, 1974, p. 153). Essas tríades eram facilmente encontradas pelas antigas regras dos babilônios, o que pode indicar ser provável a influência da Matemática da Mesopotâmia nos Sulvasutras. Nos três Sulvasutras, existem construções (para a quadratura do círculo) que fornecem aproximações para π, de 3,0044 e 3,0088 (BOYER, 1974, p. 153).

Nos Sulvasutras, há expressões apontando a relação entre a diagonal e os lados de um quadrado, ou seja, a base de conhecimento para o Teorema de Pitágoras, porém os registros chamam atenção para o fato de que os conhecimentos dos Sulvasutras não constam nos trabalhos posteriores dos indianos, o que nos leva a crer a ausência da continuidade da tradição Matemática hindu. Para o autor Struick (1992), duas podem ser as razões para tal descontinuidade: uma seria a grande extensão territorial da Índia e a outra a existência de várias escolas, de tradições diferentes – nem mesmo Buda foi unanimidade na Índia – com o jainismo, outro forte ramo do pensamento indiano, cujo líder espiritual era Jaina, e tão antigo quanto o budismo (c. 500 a.C.). O jainismo também apresenta estudos matemáticos em seus textos sagrados. Por volta do ano 300 a.C., os indianos usavam um sistema de numeração decimal, não posicional, chamado numerais brahmi, que utilizava um sinal especial para cada número, com a maior parte dos historiadores situando “[...] o final do desenvolvimento do sistema, com uso pleno e sistemático do zero e do princípio do valor relativo, provavelmente em alguma época entre o século IV d.C. e o século VII” (GUNDLACH, 1992, p. 32).

Então, dentro da civilização hindu, chegamos à criação do zero, ou seja, seu objetivo era marcar uma posição vazia, inclusive a variação do valor de um algarismo em função de sua posição numeral, relacionando a escrita do número com a possibilidade de estabelecer diversos algoritmos das operações. Na Índia, encontram-se registros de símbolos numéricos parecidos com os utilizados atualmente, os registros mais antigos foram localizados em colunas de pedras de um templo que foi construído por volta de 250 a.C., na época do rei Asoka, mas o uso do zero, segundo os historiadores, só surgiria entre os séculos IV d.C e VII d.C., quando por volta de 800 d.C. esse sistema teria sido adotado pelos árabes em Bagdá, assim os árabes passam a registrar um importante papel na história matemática.

2318 Al-Khwārizmī Fonte: mateeduc.blogspot.com.br.Último acesso: Acesso em: 24 dez. 2016.

Dentro da cultura árabe, sempre houve o reconhecimento desse sistema atrelado à cultura hindu. Em meados de 825 d.C., Al-Khwārizmī reconhece e atribui o sistema e suas formas computacionais aos hindus. Em suas viagens pela África e Espanha, os árabes divulgaram esse trabalho para o mundo ocidental, mas, infelizmente, todo o trabalho de Al-Khwārizmī se perdeu e o conhecimento que temos hoje a respeito desse trabalho provém da tradução latina do século XII, intitulada como Liber algoritmi de numero indorum, e geralmente citada como Liber algorismi, provavelmente feita por Adelardo de Bath, um monge inglês. Nessa obra, surge o nome de algoritmo para representar inúmeros processos computacionais.

Veja na Figura 2.4 as diversas mudanças que o sistema numeração decimal passou ao longo dos tempos:

2418 As principais mudanças nos símbolos indo-arábicos Fonte: Pimentel e Andrade (2010b).

Os primeiros textos matemáticos da civilização hindu de que se tem registro estão datados no primeiro século da era Cristã, com o primeiro grande matemático Aryabhata, autor do antigo texto hindu Aryabhatiya, datado em 499, um texto de pouco volume e escrito em versos, que trata inclusive de astronomia, cálculos, trazendo pela primeira vez o nome das potências de dez. Possui também instruções da determinação de raízes quadradas e cúbicas de números inteiros; também apresenta regras de mensuração, porém metade delas erradas; apresenta cálculo de área de um triângulo, do círculo e do trapézio. Em seus textos possui a afirmação: some-se 4 a 100, multiplique-se por 8, e some-se 62000. O resultado é aproximadamente a circunferência de um círculo cujo diâmetro é 20 000. É possível verificar que sua aproximação para π é 3,1416, número este exatamente igual ao valor usado por Ptolomeu. A probabilidade de Aryabhata ter sido influenciado pelos gregos é reforçada pela “[...] adoção da miríade, 10 000, como número de unidades do raio” (BOYER, 1974, p. 154).

A parte mais importante da obra de Aryabhatiya aborda a medida do tempo e a trigonometria esférica, apresenta inclusive primeiros vestígios do que seria o atual Sistema de Numeração Decimal. Na segunda parte dessa obra, Arybhata escreveu o princípio de aplicação do valor posicional. Seu sucessor nessa obra foi Brahmagupta, quando, em sua obra de maior relevância, expressa a generalização da fórmula de Heron, em que era possível achar a área de uma equação linear diofantina, apontando um avanço relevante à libertação do real, ou seja, os estudos apontam para interesses matemáticos, deixando os interesses empíricos. Tanto as obras de Diofante como de Brahmagupta apresentam fortes indícios de influência grega, ambos podem até mesmo ter utilizado fontes comuns, possivelmente a Álgebra mesopotâmica.

Mas o foco principal da matemática na Índia, sem sombra de dúvidas, é atrelado à Bhaskara. Ele foi considerado o matemático mais importante do século XII, pois considerava o problema da divisão por zero. Nos registros de Bhaskara, surge a afirmação de que o quociente entre um número diferente de zero e zero é infinito; sua obra mais conhecida recebe o título de Lilayati, na qual aparecem também as compilações “[...] equações lineares e quadráticas, tanto determinadas quanto indeterminadas, simples mensuração, progressões aritméticas e geométricas, radicais, tríades pitagóricas e outros” (BOYER, 1974, p. 162).

Bhaskara morreu pelo fim do século doze e, por vários séculos, houve poucos matemáticos na Índia de importância comparável. É interessante notar, no entanto, que Srinivasa Ramanujan (1887-1920), o gênio hindu do século vinte, tinha a mesma habilidade manipulativa em aritmética e álgebra que se encontrava em Bhaskara. ...Na obra de Ramanujan também observamos o caráter desorganizado, a força do raciocínio intuitivo, e o pouco caso pela geometria que eram tão evidentes em seus predecessores .(BOYER, 1974, p. 163)

Esses registros só comprovam que existem lacunas entre o crescimento matemático hindu e grego. A civilização hindu era encantada pelos cálculos, eram extremamente calculistas; em contrapartida, os gregos eram fascinados pela geometria, isso pouco contribuiu para o desenvolvimento matemático.

De um certo ponto de vista foi uma infelicidade que o seu primeiro amor fosse a teoria dos números em geral, e a análise indeterminada em particular, pois não foi desses temas que veio o posterior desenvolvimento da matemática. A geometria analítica e o cálculo tiveram raízes gregas, não hindus, e a álgebra européia não veio da Índia, mas dos países islâmicos .(BOYER, 1974, p. 163)

Esse fato pode se atribuir à estrutura social de cada uma dessas civilizações serem diferentes umas das outras, até mesmo suas atividades econômicas eram diferentes. Segundo Machado (1987), esse fato, aliado às constantes invasões de migrantes, às frequentes alterações político-sociais, exigiam uma comunicação escrita mais eficiente e alguma mobilidade social. Por outro lado, ainda de acordo com Machado (1987), ao serem constantemente pressionados por uma necessidade imediata de adaptação a novas situações, os hindus se sentiam livres de preocupações em relação à lógica, à estética e ao rigor formal dos gregos e, portanto, levaram em consideração os números irracionais, resultando que a Álgebra indiana possuísse resultados bem mais interessantes do que a grega, embora não sistematizados nem formalizados.

Europa de 500 a 1600: Fibonacci, Ferrari, Tartaglia, Cardamo e Viéte

E assim inicia a Matemática na Idade Média, período no qual deixaram a Matemática pura e passaram para assuntos ligados à religião, “Intelectuais e inventores deixaram de se interessar pela ciência pura e a matemática e voltaram suas energias mais e mais para a engenharia e a religião” (EVES, 1995, p. 283).

Nesse período, a Europa dividiu-se em duas áreas distintas, o mundo árabe iraniano e o mundo europeu. Isso foi consequência da transformação europeia de antiga para medieval, permitindo à própria Europa se subdividir em duas regiões, onde a cultura norteadora era a germânico-latina em uma região e na outra a greco-eslávica; essas separações são notadas no século XXI.

Assim, em meados do século V, o cartaginês Marciano Capella escreve uma enciclopédia sobre as sete Artes Liberais, isto é, gramática, dialética e retórica (trivium), geometria, aritmética, astronomia e música (quadrivium), que gozou de grande apreço e difusão durante a Idade Média. Nela, a geometria se reduz às definições dos Elementos, com o enunciado do primeiro problema; e a aritmética a algumas noções de caráter neopitagórico (BABINI, 1969, p. 45-46).

Considerando que se destacam as sínteses ou cópias dos escritos gregos, é possível entender porque esse período da história da humanidade, a Idade Média ou Medieval, é conhecido como a Idade das Trevas para a ciência, pois muitos que viviam nessa época optaram por esconder seus conhecimentos a serem considerados pagãos. Nesse período, apenas alguns trabalhos são produzidos na Europa, como o trabalho do inglês Beda (c. 673-735), o início dos trabalhos eruditos dos países do Norte, no final do século VII. Foi o primeiro a escrever sobre elementos de cálculo numérico, pois naquele momento precisavam elaborar o calendário religioso. Nesse período também surge Alcuin de York (c. 735-804), nascido no período em que Beda morreu, mas, mesmo assim, foi influenciado pelas pesquisas e conhecimentos de Beda. Desenvolveu o renascimento carolingiano, pois foi um dos poucos mestres convidados por Carlos Magno para revitalizar a instrução na França, é responsável pelos textos que despertam o raciocínio, com problemas que envolvem aritmética e geometria, envolvido com questões místicas e recreativas, exigindo pouco conhecimento matemático, pois na época existia um baixo nível de desenvolvimento da matemática. Após a morte do imperador, a matemática entra em declínio, perdendo toda a importância.

Ainda sobre os marcos importantes da Idade Média, temos o francês Gerbert (c. 950-1003), famoso pelo seu talento incomum e precoce, foi um dos primeiros cristãos a se interessar pelas escolas muçulmanas da Espanha, onde teve contato com a Matemática grega. Seus trabalhos mais relevantes foram de astrologia, aritmética e geometria; suas obras eram síntese ou abreviações dos escritos gregos, material importante para a retomada das pesquisas matemáticas pela Europa Ocidental. Como as civilizações eram muito ligadas a religiosidades e os trabalhos eram de autoria do rei da igreja, despertou o interesse externo e a matemática começa a avançar, depois de longos séculos de estagnação. De acordo com Boyer (1974), os cristãos foram tão radicais quanto os islâmicos quando destruíram a Biblioteca de Alexandria: “A pesquisa científica, escreveu Tertuliano, se tornará supérflua desde que fora recebido o Evangelho de Jesus Cristo” (BOYER, 1974, p. 182).

Nesse período, predominava a mesma numeração que utilizamos hoje em representações de século, que é a numeração romana. Os povos romanos utilizavam letras para a representação de números. Ao contrário dos gregos, os romanos utilizavam letras específicas, usavam o sistema decimal, aditivo e não posicional. Os cálculos eram realizados com a ajuda de ábacos, cujos resultados seriam apresentados em algarismos romanos, até o início do século XI, na Idade Média, período em que a matemática fica restrita às contribuições dos povos hindus, árabes e chineses.

Os povos gregos no século XI começaram a traduzir textos em latim e assim se aproximaram da Europa Ocidental. Assim, no século seguinte, foi o período marcado pelos tradutores, pois era impossível estudar matemática ou astronomia sem um bom conhecimento da língua árabe, pois até o século XII todos os matemáticos eram mouros, judeus ou gregos. Esse período foi muito marcante para os gregos, período de grandes ocupações, como as cruzadas. “[...] finalmente absorvidos pelo que restou da cultura greco-romana, o comércio liderado por Veneza e outras cidades italianas floresceu, começaram as construções das grandes catedrais, Marco Polo chegou ao Extremo Oriente” (GARBI, 1997, p. 27) e os estudos reassumem a importância merecida, com o surgimento da escolástica e de diversas universidades: Bologna (1088), Paris (1200), Oxford (1214), Pádua (1222), Nápoles (1224) e a de Cambridge (1231).

O comércio na Itália foi restabelecido, oportunizando aos comerciantes visitar o Oriente e estudar as civilizações, com o objetivo de reproduzir, mas também de assimilar sua ciência e sua arte, favorecendo assim a sociedade mercantil e a expansão do comércio bancário e a indústria capitalista. Nesse período se destaca o maior matemático europeu, o italiano Leonardo de Pisa (Leonardo Pisano), nascido em Pisa, provavelmente no ano de 1175, e que morreu em 1250, mais conhecido por Fibonacci.

A primeira instrução de Fibonacci veio de seu pai, pois era alfandegário, assim permitiu para Fibonacci percorrer toda a costa mediterrânea, tendo contato com locais influenciados pela culturas árabes e assim chegou ao conhecimento Matemático, após o domínio da língua Árabe, uma vez que a maioria dos textos eram traduzidos pelos árabes. Fibonacci foi o responsável pelo sistema indo-arábico, importantíssimo para a difusão do sistema de numeração decimal, ou seja, em um livro apresentou o estudo detalhado sobre métodos e problemas algébricos, divulgando e mostrando as vantagens de utilizar o modo usual do cálculo, o ábaco e os algarismos romanos. O Liber abacci foi a primeira produção científica escrita por um europeu (branco) considerando o conhecimento matemático produzido pelos hindus e divulgado pelos árabes.

Porém a oposição entre ábaco e algoritmos persistia mesmo com a introdução de algoritmos, pois a sua aceitação ocorreu de forma lenda e gradativa, reconhecendo assim que algarismo árabe é mais simples e fácil que os algarismos romanos. Em seu livro Lider abacci, posicionavam em defesa da numeração com dígitos de 0-9, estabelecendo um sistema de posição e incluindo o zero.

A sequência de Fibonacci

Trata-se de uma sucessão de algarismos, tais que, determinando os dois primeiros 0 e 1, os algarismos seguintes serão obtidos por meio da adição dos seus dois antecessores, veja:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

Vivendo no mesmo século de Fibonaci e destacando-se entre outros matemáticos, Giovanni Campanus foi responsável pelas primeiras traduções em latim, também pela primeira versão impressa da obra de Euclides. De acordo com suas traduções, percebe-se que Campanus tinha propriedade sobre o tema abordado: “[...] fundar a aritmética dos números naturais sobre um sistema de axiomas e de postulados”, tarefa posteriormente efetivada por Peano (BABINI, 1969, p. 58).

Outros estudiosos contribuíram para a expansão do conhecimento matemático, como o estudioso Sacrobosco, que contribuiu para a divulgação do sistema de numeração decimal, escreveu uma coleção de regras de Aritmética e foi o responsável, inclusive, por uma compilação do Almagesto de Ptolomeu. Além de trabalhos de alguns astrônomos árabes, a sua produção teve importância significativa para a difusão dos símbolos arábicos e da numeração decimal.

Mais de 1/3 da população Europeia foi dizimada pela Peste Negra e por consequência da Guerra de Cem Anos, trazendo transformações políticas e econômicas para todo o norte da Europa. Mas no século XIII ocorreu um avanço imenso se comparado ao século passado. Porém foi no século XIV que destacou-se o matemático Nicole Oresme (1323-1382), que exerceu a carreira de magistério até bispado, escrevendo cinco obras matemáticas. Também foi responsável pela tradução do trabalho de Aristóteles. Foi em suas obras registrado pela primeira vez os expoentes fracionários. Utiliza pontos e coordenadas, permitindo o pontapé inicial para a Geometria Analítica. Seu último trabalho provavelmente influenciou vários matemáticos durante o renascimento, inclusive Descartes. Não pode-se deixar de registrar que nos trabalhos de Oresme também aparecem noções da representação gráfica de fenômenos variáveis, inclusive estabelecimento de uma série infinita, permitindo mostrar que a série harmônica é divergente.

Os filósofos da escolástica conduziam suas produções e relatos para as teorizações sobre o movimento infinito e contínuo, que posteriormente seriam conceitos norteadores para a Matemática Moderna. Nesse período, São Tomás de Aquino (1226-1274) assume um papel importante para o desenvolvimento da Matemática, “[...] além de especulações sobre os conceitos básicos de contínuo e discreto infinitamente grande e infinitamente pequeno”, escreveu quatro pequenos trabalhos sobre Aritmética e Geometria (EVES, 1995, p. 296).

No século XV, a Matemática começa a prosperar, recuperando-se da decadência e improdutividade que foi no século XIV. No mesmo período em que acontece o Renascimento Europeu, surge a imprensa e a conjunção entre a Arte e as Ciências, ramificada com Leonardo da Vinci, esses acontecimentos favoreceram o desenvolvimento da Matemática, pois, com a imprensa, permitiu-se acessibilidade a clássicos da Antiguidade, bem como a transmissão e difusão de trabalhos científicos. Com o acesso a imagens e obras artísticas da antiguidade grega e árabe, possibilitou-se acesso à ótica geométrica e, consequentemente, à retomada aos estudos da Geometria, Astronomia, aumentando o interesse das civilizações pela aritmética, contagem e computação.

No século XV, destaca-se o matemático Regiomontanus, mais conhecido como Johann Muller (1436-1476), que foi responsável por traduzir a obra de Almagesto de Ptolomeu, inclusive trabalhos, de Herão, Apolonio e Arquimedes, destacando o seu trabalho intitulado de triangulis omnimodis, escrito por volta de 1464, mas publicado apenas em 1533, após a sua morte, “[...] é a primeira exposição europeia sistemática de trigonometria plana e esférica, num tratamento independente da astronomia” (EVES, 1995, p. 296).

A maioria dos matemáticos do século XV eram de origem italiana ou alemã, mas, entre eles, destaca-se o francês Nicolas Chuquet, que produziu o manuscrito Triparty en la sciense des nombres, que possui relevância comparada com Liber abaci. “A primeira das três partes desse trabalho se ocupa do cálculo com números racionais, a segunda com números irracionais e a terceira aborda a teoria das equações” (EVES, 1995, p. 297-298). A maior parte da Álgebra de Chuquet é sincopada e ele admitia expoentes inteiros, positivos e negativos. “Seu trabalho era demasiado avançado para a época, razão pela qual acabou não exercendo praticamente nenhuma influência sobre os contemporâneos do autor” (EVES, 1995, p. 297-298).

Após a imprensa, as produções matemáticas eram voltadas para aplicações na prática, principalmente aplicações comerciais, e “[...] o mais impressionante livro de matemática desses primeiros tempos de imprensa foi escrito pelo franciscano Luca Paciolli” (c. 1445-1509), intitulado Summa de Arithmetica, Geometrica, proportioni et proportionalita. Escrito em um italiano bastante agradável, este trabalho é uma compilação livre de muitas fontes e pretendia ser um sumário da Aritmética, da Álgebra, da Geometria e da Trigonometria até então existente e, se não apresenta muitas novidades em termos de conteúdos, inova essencialmente nas notações, superiores a todas de então (STRUICK, 1992, p. 145).

Nas produções escolares, destaca-se Robert Recorde (1510-1558), no século XVI, “Recorde escreveu em inglês e seus trabalhos tinham a forma de diálogos entre um mestre e um estudante”, e é devido a ele o símbolo = para designar a expressão “é igual a” (EVES, 1995, p. 301). Mesmo diante de toda importância desses trabalhos, ainda não havia nada de inovador, ou nada de novidade ao conhecimento acumulado pelos gregos e árabes, sendo assim, os clássicos matemáticos continuam a ser atrelados aos italianos no século XVI, quando desenvolveram uma teoria matemática “[...] que conduziu às soluções algébricas gerais de equações cúbicas, foi descoberta por Scipione Del Ferro e pelos seus alunos na Universidade de Bologna”, nessa época, uma das maiores e mais famosas da Europa e onde estudaram, entre outros, Paccioli e Copérnico (STRUICK, 1992, p. 144).

Era costume esconder as descobertas, e muitas produções nunca foram publicadas. Era comum guardar segredo das soluções e comentar os resultados apenas para poucos amigos, por exemplo, os resultados de alguns problemas só foram revelados trinta anos após suas descobertas, isso só ocorre com a disputa entre os Matemáticos Cardano, Tartaglia e Ferrari. Nesse período, os calculistas e algebristas começam a disputa pelo domínio da ciência, então, publicamente, começam a solucionar problemas que utilizavam em suas resoluções equações de terceiro grau (cúbicas); essas disputam eram vinculadas aos problemas propostos pelos discípulos de Del Ferro.

 

2518 Nicolo Fontana Fonte: images.fineartamerica.com.Último acesso: Acesso em: 25 dez. 2016.

 

Nessas disputas, destaca-se Nicolo Fontana (1500-1557), natural da Brescia, na Itália, matemático, popularmente conhecido como o Tartaglia, porém não publicou seus resultados, nem revelou os métodos utilizados, mas comentou o caminho utilizado com Gerome Cardano (1501-1576), que, mesmo prometendo segredo, publica a descoberta de Tartaglia em 1545, no livro intitulado de Ars Magna, mas, antes de publicar, aperfeiçoou os métodos de Tartaglia e reconhece os méritos ao verdadeiro autor.

O livro Ars Magna aborda as equações cúbicas, a resolução das equações quárticas, e teve a contribuição nas equações quárticas de seu aluno Ludovico Ferrari (1522-1565). Junto com Cardano, Tartaglia e Ferrari ocorreu o avanço significativo da Álgebra, mas, em 1572, com a publicação de Rafael Bombelli, em seu livro intitulado de Álgebra, Bombelli contribui para a solução de um caso especial de equações cúbicas, que, embora possuam três raízes reais, se expressam como a diferença entre duas raízes cúbicas de números complexos imaginários, hoje chamamos casos como esse de irredutível. Em sua obra, define que as raízes são apenas aparentemente imagináveis, mas, com a introdução de recursos algébricos, consegue resolver o enigma que tanto atormentou os algebristas.

 

2618 Françõies Viete Fonte: pt.wikipedia.org.Último acesso: Acesso em: 25 dez. 2016.

 

Bombelli escreveu a teoria sobre os números imaginários, porém nunca foi publicado, mas a sistematização sobre os números imaginários se formaliza no século XIV. Nas publicações posteriores sobre aritméticas e algébricas é que a álgebra simbólica vai se formalizando, mas a álgebra simbólica só ganha destaque com o francês François Viéte (1540-1603), natural de Fontenay-le-Comte de Paris, advogado e matemático, dedicava-se à matemática apenas em momentos de lazer, pois sua formação original era advogado, mesmo assim, Viéte contribuiu para a aritmética, álgebra, geometria e trigonometria, “[...] relações fundamentais entre as funções circulares dos ângulos e de seus múltiplos, como também os principais teoremas, ainda que de forma distinta da atual”, tanto da trigonometria plana, como da esférica (BABINI, 1969, p. 69).

 

Atividades

Sobre Fibonacci e seus estudos, analise as alternativas e assinale a alternativa correta:

• O conhecimento de Fibonacci teve pouca influência pela cultura árabe.

  A alternativa está incorreta, pois, pela profissão do pai, Fibonacci pode percorrer toda a costa mediterrânea tendo contato com locais influenciados pela cultura árabe.

• A sequência de Fibonacci é iniciada por 0 e 1, e os algarismos seguintes são obtidos pela subtração de seus dois elementos antecessores.

  A alternativa está incorreta, pois a sequência é obtida pela soma de seus dois elementos antecessores.

• Fibonacci não colaborou para difusão do sistema de numeração decimal.

  A alternativa está incorreta, pois Fibonacci foi importantíssimo para a difusão do sistema de numeração decimal.

• Fibonacci foi responsável pelo sistema indo-arábico.

  A alternativa está correta, pois Fibonacci foi responsável pelo sistema indo-arábico.

• Em seu livro, Fibonacci apresenta superficialmente métodos e problemas algébricos.

  A alternativa está incorreta, pois em seu livro é apresentado um estudo detalhado sobre métodos e problemas algébricos.

 

Gênese da matemática moderna (1600 – 1614): Galileu, Kepler e Napier

No século XVI, a Geometria não alcançou muito progresso, na verdade, ficou estagnada apenas nas traduções de Clássicos Gregos, porém esse período foi marcado pelos avanças na Trigonometria, na Álgebra e na Aritmética. Vale atentar-se para que esse século foi marcado por um período em que despertaram e avançaram os estudos voltados aos infinitésimos, estudos esses que abriram o caminho para estudiosos do século seguinte chegarem à análise infinitesimal. O século XVI foi o período de passagem no qual se encerra um período para iniciar outro, ou seja, encerra o período da História da Matemática, pois iniciou-se a decadência grega e junto com a decadência inicia um novo período para a ciência, que foi nomeado como período da ciência moderna, das criações constantes, do progresso.

Partimos para o século XVII. Podemos dizer que foi um período muito produtivo para a matemática, utilizando a geometria dos séculos passados, com sua estrutura ampla, rígida e com caminhos pré-estabelecidos, com a álgebra com suas regras flexíveis, tendendo ao algoritmo. No século XVII, podemos destacar o estudo da Geometria Analítica por meio de Descartes. Seguindo essa era triunfal da matemática, alguns matemáticos e seus feitos se destacaram, sendo que o primeiro matemático do século XVII a se destacar foi John Napier (1550-1617), natural de Edimburgo na Escócia, físico, astrônomo e teólogo, que seguiu a linha de Viéte, que também não era um matemático de formação, mas, sim, era o barão de Murchiston, administrador de suas propriedades e escritor nato, interessado por diversos assuntos matemáticos, o computacional e o trigonométrico.

2718 John Napier Fonte: www.maa.org.Último acesso: Acesso em: 26 dez. 2016.

Provavelmente, Napier, em 1614, tenha descoberto os logaritmos naturalmente, após tentar simplificar cálculos aritméticos e, consequentemente, facilitar as atividades ligadas à astronomia e nas orientações para as navegações, pois, no século XVII, os cálculos envolvendo navegação e astronomia eram longos e trabalhosos. Os logaritmos como instrumentos de calcular surgiram para realizar a simplificação, uma vez que transformam multiplicações e divisões em operações mais simples de soma e de subtração. Napier realizou essas descobertas quase que simultaneamente com Jobst Burgi, em 1620. Mesmo que os processos de descoberta tenham sido distintos, ambos são responsáveis pelos logaritmos, porém Henry Briggs aperfeiçoou essas técnicas, apresentando os logaritmos decimais.

A ideia de Napier é inspirada na trigonometria e no produto de potência de base comum que transformavam as multiplicações em adições e subtrações, consistia em elaborar tabelas com termos de progressão geométrica que pudessem ser um auxiliar de cálculo, mas Briggs foi o responsável pela aceitação dos logaritmos pelos cientistas, ele propôs os logaritmos na base dez e construiu uma tabela de logaritmos que foi usada até o século XIX.

2818 Bastões de Napier Fonte: www.fisica-interessante.com.Último acesso: Acesso em: 26 dez. 2016.

Uma das descobertas de Napier eram os bastões de Napier. Tratava-se de um conjunto de nove bastões, um para cada dígito, que transformavam a multiplicação de dois números em uma soma das tábuas de cada dígito. Esse dispositivo originou a conhecida régua de cálculos, que mais tarde foi considerada o primeiro computador analógico. Com o desenvolvimento da ciência, pode-se perceber que muitos fenômenos, físicos, biológicos e econômicos, podem ser representados por funções logarítmicas.

2918 Galileu Galilei Fonte: pt.wikipedia.org.Último acesso: Acesso em: 26 dez. 2016.

O século XVI e XVII foi marcado pelas grandes contribuições matemáticas. Nesse século, dois astrônomos se destacaram, Galileu Galilei (1564-1642) e Johan Kepler (1571-1630). Galileu, devido à pressão de seu pai, teve que desistir da faculdade de Matemática e acabou se formando em Medicina, porém sua paixão pela matemática o levou até Florenza, local onde, para sobreviver, teve que lecionar aulas particulares de Matemática, possibilitando a descoberta e o início da ideia de equipotência dos conjuntos infinitos, ponto norteador para a Teoria dos Conjuntos, desenvolvida posteriormente por Cantor. Impulsionando assim o desenvolvimento da análise moderna, descobriu o isocronismo do pêndulo determinando que o seu período não depende da massa, mas apenas do comprimento dos fios, despertando o interesse e a curiosidade que isso o permitiria construir relógios mais precisos. Em 1588, com o apoio de um Matemático, Galilei foi nomeado para a cátedra de matemática na universidade de Pisa, fazendo a sua famosa experiência de quedas de corpos inclinados, nesta, demonstra que a velocidade de queda não depende de peso, aproximando para o que seria a primeira lei de Newton. Galileu demonstra inclusive o conhecido como princípio da inércia, e suas experiências sobre o movimento tiveram um significado especial, levando à abordagem matemática usada para analisá-las. Se tornaria mais tarde como o pai da física matemática. Galilei foi o primeiro a fazer uso do telescópio, o primeiro a analisar as manchas solares, descobriu que a via láctea é composta por diversas estrelas, inclusive as crateras da lua. Seguindo o exemplo de Galileu, destaca-se Kepler, ao buscar soluções aos problemas de astronomia, ganhando, ao contrário de Galileu, liberdade para estudar a trajetória dos planetas ao redor do sol.

21018 Johannes Kepler Fonte: Shutterstock.

Johannes Kepler (1571-1630) foi um astrônomo, nasceu em Weil der Stadt, no sul da Alemanha, exímio matemático, dedicou-se 21 anos de sua vida a definir as três leis do movimento planetário que imortalizaram seu nome. Desde muito jovem ele já considerava o heliocentrismo, pois considerava o sol o centro da vida. Também acreditava que Deus havia planejado o planeta de modo racional, fazendo uso da matemática. Uma de suas ideias resultou na tentativa de encaixar os movimentos dos planetas em uma associação de sólidos platônicos e esferas perfeitas, mas, no fim, percebeu que não havia nenhuma evidência para sustentar essa proposta, essas comprovações só vieram a se sustentar quando Kepler se uniu com um astrônomo em um observatório chamado Uranienborg. Assim Kleper concluiu que os planetas andam de forma elíptica e o sol é um dos focos dessa elíptica, sendo assim, essa descoberta passou a ser conhecida como a 1ª Lei de Kepler.

As leis de Kepler servem para quaisquer sistemas binários, veja a definição e a importância das descobertas de Kepler, “[...] são marcos fundamentais da História da Astronomia e da Matemática; pois num esforço para justificá-las, Isaac Newton foi levado a criar a mecânica celeste moderna”, além do que a descoberta empírica dessas leis, a partir de dados deixados pelo dinamarquês-sueco Tycho Brahe, de quem havia sido assistente, “[...] constitui um dos mais notáveis trabalhos de indução jamais feitos na ciência” (EVES, 1995, p. 357).

Kepler não apresentou nenhuma novidade ao conhecimento matemático, pois suas pesquisas eram pautadas nos estudos gregos, porém agregou com suas descobertas sobre as secções cônicas, chamando atenção para as pesquisas matemáticas com um caráter inteiramente dedutivo e aplicável no real. Suas pesquisas eram voltadas para matemática pura, o que impossibilita se afirmar que poderá ser aplicada no real, pois “[...] se os gregos não tivessem estudado as secções cônicas, Kepler jamais teria superado Ptolomeu” (WHEWELL apud EVES, 1995, p. 357). Assim Kepler passa a ser considerado um dos pioneiros do cálculo, esse atributo só é possível graças ao cálculo de áreas que utilizava, em que envolvia a segunda lei dos movimentos Planetários, “[...] volumes de noventa e três sólidos obtidos pela rotação de segmentos de secções cônicas em torno de um eixo de seu plano”, sendo possível que tivesse influenciado Cavalieri, que também impulsionou o cálculo infinitesimal com o seu método dos indivisíveis (EVES, 1995, p. 358).

O astrônomo alemão também deixou notáveis contribuições à Geometria, como o estudo dos poliedros; a palavra foco na Geometria das cônicas; e estabeleceu uma aproximação para o perímetro da elipse. Na análise, foi o principal responsável pela extensão dos logaritmos de Napier por todo o continente europeu.

Geometria Analítica (1635 – 1640): Fermat, Descartes, Torricelli e Roberval

A matemática no século XVII, com o conhecimento acumulado durante séculos sobre a Geometria desde o período Helenístico, com seu desenvolvimento rígido disseminado em boa parte do mundo, juntamente com o aprimoramento da Álgebra com o seu forte rigor em seus algoritmos e linguagem simbólica, foi o estopim para o início da evolução da Geometria Analítica que conhecemos hoje, ou seja, foi o princípio da união da ciência das formas (Geometria) com a ciência dos números (Álgebra).

Já foram realizadas tentativas para unir esses dois ramos da matemática, mas somente no século XVII que foi possível realizar um grande avanço nessa área e finalmente unir a área da Álgebra com a Geometria.

No século III a.C., Apolônio de Perga empregava sistemas de coordenadas para definir pontos no plano ou no espaço, o que já constitui uma boa aproximação de números e formas. Bem posterior, do século X, é a confecção de gráficos para ilustrar o relacionamento entre grandezas variáveis [...] .(NOGUEIRA, 2016, p. 130)

Neste tópico, iremos abordar as contribuições de René Descartes, Pierre de Fermat, Evangelista Torricelli e Gilles Personne de Roberval. Na França, a partir da segunda metade do século XVII, Descartes e Fermat deram início à elaboração da Geometria Analítica paralelamente, mas com visões distintas sobre ela.

Descartes (1596 – 1650) nasceu em uma boa família e teve bons estudos no colégio La Flèche, de origem jesuíta. Formou-se em Direito na Universidade de Poitier e, posteriormente, viajou para Holanda, onde permaneceu por vários anos acompanhando campanhas militares. Em suas viagens pela Europa, entrou em contato com grandes matemáticos como Faulhaber, o qual escreveu sobre as soluções das equações quárticas. Conheceu também Desargues na França, que foi um dos precursores da Geometria Projetiva, e Mersenne, um teólogo e matemático lembrado pelos estudos de números primos que poderiam ser escritos da forma 2ⁿ - 1, com n natural, conhecidos futuramente como primos de Mersenne.

21118 René Descartes Fonte: pt.wikipedia.org.Último acesso: Acesso em: 26 dez. 2016.

René Descartes foi um grande matemático e filósofo, e, em 1637, é publicada a sua obra intitulada como Discurso sobre o método para bem utilizar a razão e de encontrar a verdade nas ciências, na qual é abordada de forma sistemática como definir fontes claras e necessárias para obter conclusões de maneira verdadeira para supostas dúvidas.

Nessa obra, Descartes possuía uma filosofia visionária para a época, em oposição ao seu trabalho relacionado com a Geometria nessa obra, talvez a matemática realmente é acumulada de forma progressiva comparada com as outras ciências, ou seja, ela possui um desenvolvimento mais gradativo do que um desenvolvimento brusco.

O livro citado anteriormente possui um apêndice denominado de A Geometria, em que o autor trabalhava primeiramente o lugar geométrico para encontrar a equação que define esse lugar geométrico. Com relação à parte algébrica, a notação progrediu, sendo pouca a diferença que encontramos em nossas notações atuais. Por exemplo, a equação:

y³ - - byy - - cdy + bcd + dxy α 0

É equivalente a equação, a qual conhecemos como:

y3 - by2 - cdy + bcd + dxy = 0

Com variáveis x, y e parâmetros b, c e d.

Descartes também passou a considerar os valores de x² e x3 como comprimentos de seguimento de reta e substituindo a visão de que essas respectivas quantidades representam quadrados e cubos. O fato mais relevante trabalhado por ele é que equações com duas variáveis coincidem com um lugar geométrico no plano, ou seja, equações do tipo y² = ax - bxy + cx - dx² que correspondem a um lugar geométrico. Essa mesma equação corresponde à equação geral de uma cônica que passa pela origem, mas isso é muito distante do que conhecemos atualmente por seções cônicas. Observe na Figura 2.12, em que imaginamos um plano cortando um cone circular reto de duas folhas em várias cônicas como a circunferência, a parábola, a elipse e a hipérbole.

21218 Seções Cônicas Fonte: pensevestibular.com.br.Último acesso: Acesso em: 11 nov. 2016.

Na mesma época, Pierre de Fermat (1601 – 1665) contribui imensamente não só com a Geometria Analítica, mas em áreas como o Cálculo e os princípios elementares da teoria das probabilidades. Fermat atuava como advogado no parlamento francês e, posteriormente, se tornou conselheiro, praticava a matemática por hobby. Apesar de nunca ter exercido a matemática profissionalmente, foi um dos grandes gênios de seu tempo.

21318 Pierre de Fermat Fonte: pt.wikipedia.org.Último acesso: Acesso em: 20 dez. 2016.

Fermat também gostava de tentar reconstruir obras perdidas da antiguidade fundamentado em informações encontradas nas escritas clássicas ainda preservadas e, como consequência, Fermat passou a reconstruir a obra Lugares Planos,da autoria de Apolônio, que mais tarde o levaria à descoberta de um valoroso enunciado para a Geometria Analítica.

[...] Um subconjunto desse esforço foi a descoberta, não mais tarde que 1636, do princípio fundamental da geometria analítica:
Sempre que numa equação final encontram-se duas quantidades incógnitas, temos um lugar, a extremidade delas descrevendo uma, linha reta ou curva. [...] .(BOYER, 1974, p. 253)

Esse princípio foi escrito por Fermat, previamente à geometria de Descartes, além de outros estudos relacionados à geometria. Fermat não publicou quase nada em vida, por muito tempo a Geometria Analítica ficou conhecida como Geometria Cartesiana. Diferentemente de Descartes, Fermat utilizava as equações primeiramente para depois determinar o seu lugar geométrico.

Os estudos de Fermat foram publicados após sua morte na obra Introdução aos Lugares Planos e Sólidos. Nessa obra, o autor trata das equações gerais das cônicas. Fermat estipulou que a equação xy = k² define uma hipérbole, mostrou também que as equações da forma a⁴± x² = by, x²+y²+2ax+2by=c² e a²-x²=ky² são uma parábola, uma circunferência e uma elipse.

Pierre também estudou as quádricas, que seriam as superfícies que podem ser esboçadas em três dimensões, cuja equação algébrica seria de segunda ordem em três variáveis. Ele notou que equações quádricas e cúbicas poderiam ser solucionadas utilizando as cônicas. Para os estudos em geometria, é relevante que Fermat utilizava eixos coordenados ortogonais, o que foi um enorme progresso, que foi essencial à matemática.

Pela sua grande dedicação à matemática por deleite, Fermat colaborou com outros vários campos da área como o Cálculo e a Teoria dos Números. O mesmo teoriza sobre as curvas da forma y = xⁿ com n pertencente aos inteiros e estuda um método de determinar máximos e mínimos de curvas polinomiais. A expressão para determinar esses máximos e mínimos é bem parecida com a fórmula da derivada que conhecemos hoje.

Entre todos os seus estudos, nenhum teve maior repercussão que sua conjectura, conhecida como “o último teorema de Fermat”. A suposição era de que, para n > 2, não é possível determinar números inteiros x, y e z, tais que a equação xⁿ + yⁿ = zⁿ seja satisfeita. Essa conjectura foi demonstrada três séculos mais tarde pelo matemático Andrew Wiles.

[...] os matemáticos não conseguiram encontrar uma demonstração absoluta para o “último teorema de Fermat”, incluídos os gênios Euler e Gauss, o que fez com que se colocasse em dúvida o fato de que Fermat descobrira uma “prova admirável desse fato”. A demonstração do teorema se transformou então num desafio, com prêmios sendo oferecidos e despertando rivalidades até ser conseguida pelo notável matemático inglês Andrew Wiles, em 1993 [...] .(NOGUEIRA, 2016, p. 133)

Fermat realizou avanços fantásticos na matemática, mas, como sabemos, quase não publicou nada em vida e se contentava a escrever para o seu amigo Mersenne sobre suas reflexões em assuntos matemáticos. Esse último, em 1615, levou em consideração a curva denominada cicloide para os matemáticos, talvez por influência de Galileu. O cicloide consiste no arco formado a partir de um ponto em uma circunferência, quando rola em um plano, representado pela (Figura 2.14).

21418 Cicloide Fonte: php.math.unifi.it.Último acesso: Acesso em: 12 nov. 2016.

Em 1628, Mersenne recomendou à Roberval (1602 – 1675) que estudasse a curva cicloide. Roberval era um matemático profissional e professor em Collège Royal, ele também pertencia ao “grupo de Mersenne”. No ano de 1638, Roberval descobriu como traçar a reta tangente à curva por um ponto pertencente a ela, mas esse problema já havia sido resolvido por Descartes e Fermat. Posteriormente, também conseguiu determinar os volumes gerados pela revolução da área em torno de seu eixo de simetria ou em torno da tangente no ponto de vértice.

Mas Roberval não teve interesse em publicar seus achados sobre a curva cicloide. Porém quem mostrou interesse em estudar essa curva foi Evangelista Torricelli (1608 – 1647) quase na mesma época que Roberval. Torricelli se envolveu nesse estudo por estímulo de Mersenne ou até mesmo influenciado por Galileu. No ano de 1644, publicou a obra De parabole, na qual divulgava seus resultados sobre a quadratura da cicloide, operação que define um quadrado de área de mesmo valor da área delimitada pela curva, e ainda como construir a tangente a essa curva.

Os trabalhos de Torricelli e Roberval são distintos, mas seguem uma linha de pesquisa similar. Em meados de 1640 e 1650, compreenderam e mostraram a análise de Cavalieri a respeito da parábola e a espiral. Esses estudos levaram Torricelli a vários resultados, inclusive à descoberta da curva que hoje conhecemos como x = log y. Também determinou a sua assíntota, a área delimitada pela curva e ainda o volume do sólido rotacionando à curva em torno do eixo x.

Nos anos de 1634 a 1642, Torricelli trabalhou com Galileu e, com isso, despertou seu interesse pela área da Física, tanto que Torricelli é conhecido pela invenção do barômetro e por seus estudos referentes às trajetórias parabólicas de projéteis do que como matemático em si. Em seus estudos referentes a equações que relacionam a distância, tempo e velocidade, Torricelli notou que os problemas de quadraturas eram inversos aos problemas com relação à tangente e, talvez, se sua morte não fosse prematura, aos 39 ano, se tornaria o precursor do Cálculo.

Geometria Analítica (1650 – 1670): Pascal, Barrow e Huygens

Um dos grandes gênios matemáticos foi Blaise Pascal (1623 – 1662). Seu pai também foi um grande matemático, o qual estudou a curva denominada limaçon ou caracol de Pascal, como hoje é conhecida. Veja a Figura 2.15. O pai de Pascal, Etienne Pascal, a princípio, não influenciou o filho com a matemática, deixando-o livre para desenvolver os seus próprios interesses. Mas, com apenas 12 anos, mostrou seu gosto pela matemática e uma grande habilidade com geometria, então, a partir daí, o seu talento matemático foi encorajado.

21518 Caracol de Pascal Fonte: opticalengineering.spiedigitallibrary.org.Último acesso: Acesso em: 20 dez. 2016.

Foi publicada uma obra de Blaise Pascal, com apenas 16 anos de idade, um texto de uma única página no qual estaria o que hoje conhecemos como Teorema de Pascal. Nesse trabalho, Pascal apresenta a teoria de que os lados opostos de um hexágono inscrito em uma cônica se interceptam em três pontos pertencentes a uma mesma reta. Mas esse resultado só é válido se utilizar um hexágono regular inscrito em uma circunferência ou se ainda utilizar conceitos da geometria projetiva.

Com 19 anos, Pascal inventou uma calculadora para auxiliar no trabalho de seu pai e chegou a construir e vender cerca de 50 exemplares, algumas ainda existentes e à mostra em alguns museus da França, veja a Figura 2.16. O interesse de estudos de Pascal mudava da água para o vinho e, em 1648, ele inicia os seus estudos em Hidrostática e, por meio dele, conseguiu comprovar o peso do ar e também conseguiu solucionar o paradoxo hidrostático, ou seja, a pressão e a força são independentes do formato do reservatório e da quantidade de fluido. Pascal volta a trabalhar em matemática em 1954 e o seu foco de trabalho é voltado para o estudo das cônicas, dando continuidade ao seu primeiro trabalho publicado aos 16 anos.

21618 Calculadora de Pascal Fonte: 2.bp.blogspot.com.Último acesso: Acesso em: 20 dez. 2016.

Durante o seu trabalho com as cônicas, um amigo lhe propôs um problema relacionado à probabilidade. O problema era a respeito dos lances de dado de um jogador. Para resolver o problema, Pascal começa a trocar correspondências com Fermat sobre o assunto. Segundo Nogueira (2016, p. 132), temos que:

Em suas trocas de correspondência com Blaise Pascal, em que discutiam questões referentes aos jogos de azar, surgiram os princípios básicos da teoria das probabilidades, ramo que posteriormente recebe grandes estímulos de crescimento, em função de suas aplicações tanto na Física teórica quanto na vida prática.

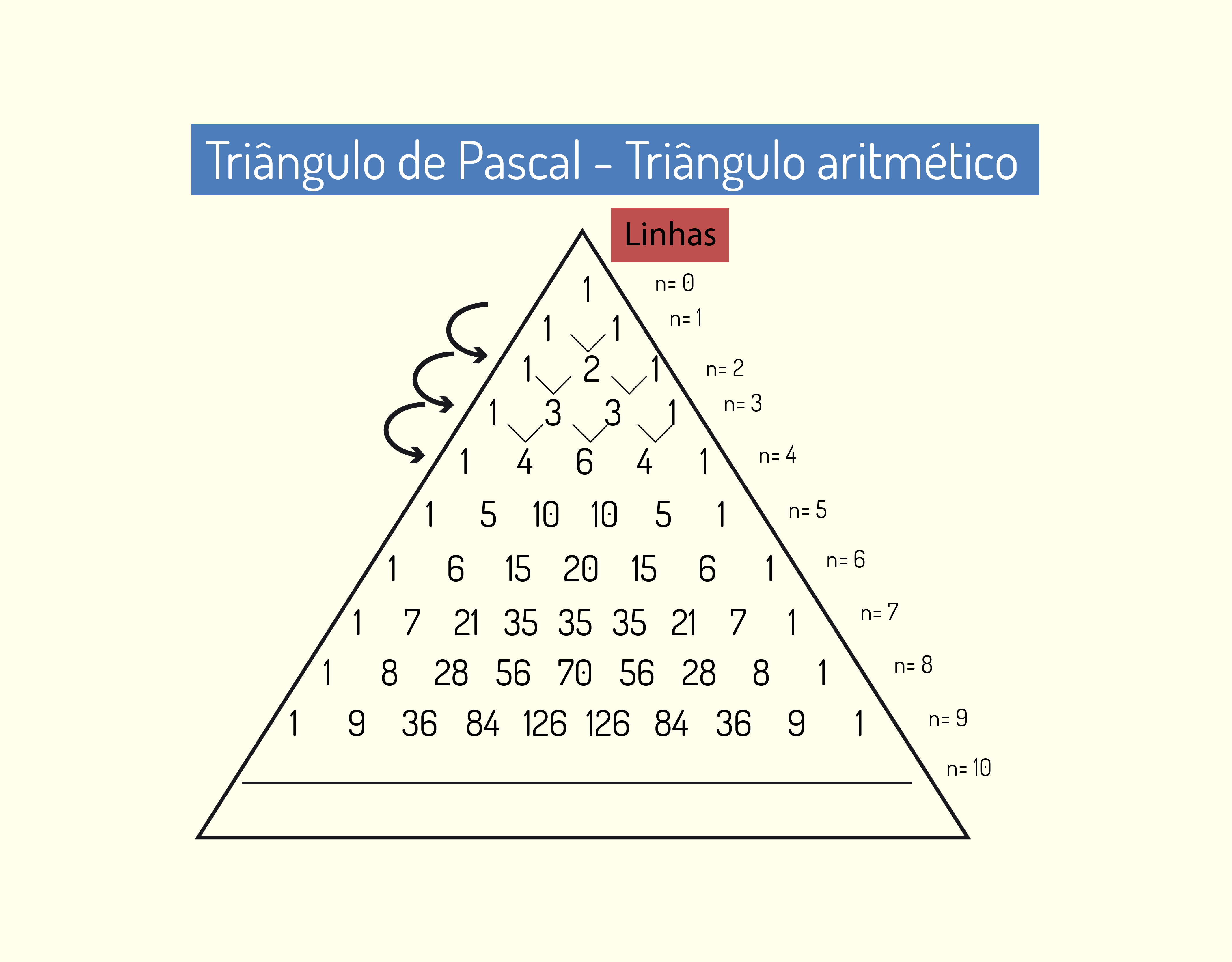
Por meio desses estudos, Pascal conseguiu relacionar a probabilidade com triângulo aritmético, hoje conhecido como triângulo de Pascal. Esse triângulo já era conhecido há mais de seis séculos, mas Pascal enunciou propriedades inéditas sobre esse.

21718 Triângulo de Pascal Fonte: images.slideplayer.com.br.Último acesso: Acesso em: 20 dez. 2016.

No mês de novembro de 1654, Pascal decide trocar a matemática pela teologia e filosofia. Ele só retorna aos seus estudos relacionados à matemática em 1658, quando em uma noite em que não conseguia dormir, pois sentia muita dor, resolveu estudar a cicloide para se distrair e então essa dor passou e ele melhorou. Pascal entendeu isso como uma aprovação divina aos seus estudos, consequentemente, surgiram resultados novos, como a fórmula generalizada do comprimento de arco da cicloide e a fórmula da semicircunferência da elipse.

Pascal se aproximou da descoberta do Cálculo em seu trabalho Tratado sobre senos num quadrante de um círculo, em que realiza estudos relacionados às integrais da função seno. Leibniz, um dos criadores da teoria do cálculo, reconhece esse trabalho de Pascal e afirma que esse trabalho foi uma luz e uma inspiração em seus estudos. Pascal foi um grande matemático sem sombra de dúvidas, além dele, outros matemáticos como Hyugens e Barrow foram essenciais no desenvolvimento dessa ciência.

Vamos falar um pouco agora sobre o cientista Cristiann Huygens (1629 – 1695), conhecido pelos seus estudos na teoria ondulatória da luz e a invenção do relógio de pêndulo. Huygens pôde perceber com o seu invento que, quando o pêndulo é solto, o tempo que o mesmo leva para atingir o ponto mais baixo será quase indiferente dependendo da altura em que ele foi solto. Nesse mesmo período em que o cientista inventou o relógio de pêndulo, ele participava do concurso que Pascal promoveu sobre alguns problemas relacionados à cicloide. Esse fato o levou a estudar o pêndulo de maneira que descrevesse um arco de cicloide invertido.

21818 Huygens e seu pêndulo Fonte: k60.kn3.net.Último acesso: Acesso em: 15 nov. 2016.

A Geometria Analítica era essencialmente pura, sem aplicações práticas, até a chegada do pêndulo cicloidal de Huygens, isso o levou a escrever sobre as evolutas e involutas, ou seja, curvas arranjadas a partir de uma curva dada. Seu trabalho escrito em 1673 serviu de inspiração para Newton dez anos mais tarde. Esse trabalho englobava resultados relevantes sobre a mecânica, incluindo a força centrípeta para movimentos circulares, o princípio da conservação da energia cinética, entre outros resultados.

Outro matemático significativo foi Isaac Barrow (1630 – 1677), que foi professor de geometria em Gresham College e depois professor de geometria em Cambrige. Era um conservador, acreditava que a álgebra deveria ser parte da lógica e também não gostava de seu formalismo. Barrow era um grande apreciador dos antigos, ele editou as obras de Arquimedes, Apolônio e Euclides. Publicou também suas obras com a ajuda de Newton nas edições, Lectiones optícae (1669) e Lectiones geometriae (1970).

Como Barrow, em sua obra Lectiones geometiae, queria que a obra descrevesse a situação em que a geometria se encontrava na época. Ele conseguiu expor em seu trabalho de forma completa as novas descobertas sobre quadraturas e tangentes, que estavam em alta na época. Barrow também descobriu um método para calcular tangente bem similar ao método que usamos hoje em cálculo. Diferentemente de Fermat, Barrow utilizava duas variáveis em seu cálculo da tangente, o que utilizamos hoje como ∆x e ∆y.

Barrow foi um matemático que realmente antecipou partes do cálculo diferencial e integral, e tinha pleno conhecimento de problemas de quadraturas e tangentes. Infelizmente, seu ponto de vista conservador o impediu que realizasse mais avanços relevantes. Ainda bem que Newton, seu pupilo, estava estudando os mesmos problemas que ele, assim Barrow o induziu que publicasse seus resultados.

O nascimento do cálculo

O cálculo diferencial e integral que conhecemos hoje, existente nos cálculos de fenômenos mensuráveis em economia, estatística, física, química, entre outras tantas áreas, é basicamente definido pela derivação e pela integração. Enquanto a derivação está relacionada a descrever e medir a variação dos fenômenos, ou seja, como eles se movem ou crescem, a integração está relacionada à soma das áreas sob curvas ou figuras.

Mas, de acordo com os livros que tratam atualmente do assunto, o desenvolvimento do cálculo se deu de maneira contrária, pois primeiro nasceu o cálculo integral para depois surgir o cálculo diferencial.

Para a discussão do surgimento do cálculo, vamos retomar um pouco a história da Grécia no período do século V a.C. O filósofo Zenão de Eleia (c. 490 - 430 a.C.) ficou conhecido pelos seus famosos paradoxos, como o paradoxo da flecha ou da corrida entre Aquiles e a tartaruga. Esse último paradoxo consiste na corrida em que Aquiles dá uma vantagem inicial à tartaruga e, após iniciar a corrida, ele não consegue alcançar a tartaruga, pois, quando Aquiles se move, a tartaruga também já percorreu certa distância, ou seja, sempre haverá um espaço entre Aquiles e a tartaruga, por menor que seja esse espaço.

3122 Zenão de Eleia Fonte: fisikanarede.blogspot.com.br.Último acesso: Acesso em: 30/11/2016.

Com a visão de Zenão, a matemática teve de ser repensada a respeito dos conceitos de infinito, contínuo, tempo e movimento.

Os argumentos de Zenão, juntamente com a descoberta dos incomensuráveis, desencadearam entre os matemáticos de então uma “crise” advinda da incerteza sobre a matemática ser possível como ciência exata [...] .(NOGUEIRA, 2016, p. 76)

Outro filósofo que contribuiu para o desenvolvimento do cálculo foi Eudoxo (408 - 355 a.C.). O método da exaustão desenvolvido por Eudoxo e criado com o intuito de resolver os paradoxos de Zenão consiste em considerar uma grandeza que pode ser dividida indefinidamente. Esse método é justamente o princípio do cálculo integral. Um outro método para calcular área e volume foi mais tarde aperfeiçoado por Arquimedes (287 - 212 a.C.).

Vejamos qual é a ideia fundamental do método de Arquimedes. Para determinar uma área ou um volume, corte a região correspondente num número muito grande de tiras planas ou de fatias paralelas finas e (mentalmente) pendure esses pedaços numa das extremidades de uma alavanca dada, de tal maneira a estabelecer o equilíbrio com uma figura de área ou volume e centroide conhecidos .(EVES, 2011, p. 422)

3222 Cálculo da área do círculo pelo método de Arquimedes Fonte: tananyag.geomatech.hu.Último acesso: Acesso em: 01 dez. 2016.

Avançando no tempo para o século XVII, Johann Kepler (1571 - 1630), astrônomo e matemático alemão, utiliza os métodos de integração para desenvolver a segunda lei do movimento planetário, a qual define que o segmento que liga o ponto central do sol e um planeta descreve áreas iguais em tempos equivalentes. Kepler não era muito paciente com a matemática rigorosa e gostava de trabalhar com os seus cálculos sem muito rigor.

3322 Estudos de Kepler Fonte: ventosdouniverso.blogspot.com.br.Último acesso: Acesso em: 01 dez. 2016.

Nesse período, temos outro grande matemático que estudou o cálculo integral. Bonaventura Cavalieri (1598 - 1647), originário da Itália, trabalhou com a indivisibilidade. Seu trabalho consistia em tomar uma figura plana e dizer que sua área é formada por infinitas cordas, ou seções retangulares, dispostas de tal forma que cordas tenham o mesmo formato da figura.

3422 Estátua de Cavalieri em Milão na Itália Fonte: Shutterstock.

Cavalieri aplicava uma teoria semelhante para sólidos, tomando-se infinitas seções planas e paralelas ao sólido de forma que essas seções tivessem o mesmo formato.

Esses resultados, ligeiramente generalizados, fornecem os chamados princípios de Cavalieri:
1. Se duas porções planas são tais que toda reta secante a elas e paralela a uma reta dada determina nas porções segmentos de reta cuja razão é constante, então a razão entre as áreas dessas porções é a mesma constante.
2. Se dois sólidos são tais que todo plano secante a eles e paralelo a um plano dado determina nos sólidos secções cuja razão é constante, então a razão entre os volumes desses sólidos é a mesma constante .(EVES, 2011, p. 426)

Com o segundo princípio de Cavalieri, é possível mostrar a generalização da fórmula do cálculo do volume da esfera. Tome uma esfera de raio r e um cilindro de altura 2r e raio da base r. Desse cilindro, subtraímos dois cones retos opostos pelo vértice de altura r e raio da base igual à r; esse sólido é conhecido como anticlepsidra. Cortando ambos os sólidos paralelamente, temos que as secções dos sólidos possuem a mesma área igual à [math]\pi \left( {{r}^{2}}-{{h}^{2}} \right)[math]. De fato, com a matemática elementar, conseguimos mostrar que a área da seção da esfera mais a seção do cone é igual à seção da área do cilindro. Assim,

[math]{{V}_{esfera}}={{V}_{cilindro}}-2{{V}_{cone}}[math]

[math]{{V}_{esfera}}=\pi {{r}^{2}}\cdot 2r-\frac{2\left( \pi {{r}^{2}}\cdot r \right)}{3}[math]

[math]{{V}_{esfera}}=2\pi {{r}^{3}}-\frac{2\pi {{r}^{3}}}{3}[math]

[math]{{V}_{esfera}}=\frac{6\pi {{r}^{3}}-2\pi {{r}^{3}}}{3}[math]

[math]{{V}_{esfera}}=\frac{4\pi {{r}^{3}}}{3}[math]

3522 Esfera e Anticlepsidra Fonte: obaricentrodamente.blogspot.com.br.Último acesso: Acesso em: 02 dez. 2016.

Assim, com Cavalieri, foi estabelecida uma forma mais simples para o cálculo. Na concepção de sua teoria dos indivisíveis, a soma infinita das partes de uma dimensão inferior forma o todo, ou seja, a soma infinita das retas forma as figuras planas, e a soma infinita das seções planas forma o sólido. Esse método dos indivisíveis foi utilizado por outros matemáticos, como Torricelli, Pascal e Barrow. No desenvolvimento de seus trabalhos foi possível chegar aos resultados da integração das expressões de [math]{{x}^{n}},~sen~\theta ,~se{{n}^{2}}~\theta ~e~\theta ~sen~\theta [math]. (EVES, 2011).

Um pouco mais à frente no tempo, na Inglaterra, os matemáticos John Wallis (1616 - 1703) e Isaac Barrow (1630 - 1677), antecessores a Newton, contribuíram muito em seu tempo para o desenvolvimento do cálculo. As contribuições de Wallis estão na análise infinitesimal em sua obra Arithmetica infinitorum (1655). Nessa obra, o autor dispõe de forma sistematizada os métodos de Descartes e Cavalieri; estudou também a integral que representa a área sob o semicírculo [math]y=\sqrt{x-{{x}^{2}}}[math].

Wallis se dedicou a calcular π pela expressão da área de um quadrante de um círculo de raio um e centro na origem, equivalente a calcular [math]\underset{~~0}{\overset{~~1}{\mathop \int }}\,{{\left( 1-{{x}^{2}} \right)}^{\frac{1}{2}}}~dx[math]. Como na época era desconhecido o teorema geral do binômio, calculou então a sequência:

[math]\underset{~~0}{\overset{~~1}{\mathop \int }}\,{{\left( 1-{{x}^{2}} \right)}^{0}}dx,\underset{~~0}{\overset{~~1}{\mathop \int }}\,{{\left( 1-{{x}^{2}} \right)}^{1}}dx,~\underset{~~0}{\overset{~~1}{\mathop \int }}\,{{\left( 1-{{x}^{2}} \right)}^{2}}dx,\ldots ,\underset{~~0}{\overset{~~1}{\mathop \int }}\,{{\left( 1-{{x}^{2}} \right)}^{n}}dx~[math]

Considerando essa sequência para n = 0, 1, 2, 3, ..., Wallis conseguiu determinar o valor de [math]n=\frac{1}{2}[math] por meio de interpolação (processo matemático que determina valores dos extremos de uma sequência numérica). As contribuições de Wallis não param por aí. Em sua obra, é introduzida a notação de infinito ([math]\infty [math]) e também considera potências de expoentes diferentes dos naturais.

3622 John Wallis Fonte: upload.wikimedia.org.Último acesso: Acesso em: 02 dez. 2016.

Enquanto Wallis fez um grande avanço no cálculo integral, Isaac Barrow, nascido em Londres, fez mais progressos nos estudos sobre o cálculo diferencial. Barrow foi um grande matemático, físico, astrônomo e estudante de teologia, ocupou a cátedra de Cambrige, que mais tarde seria ocupada por Newton. O seu trabalho mais importante está na obra Lectiones opticae et geometricae (1669). Nessa obra encontramos seus estudos sobre o cálculo diferencial, em que aborda o assunto de uma maneira muito semelhante de como é estudado cálculo diferencial atualmente.

Barrow utilizou o triângulo diferencial no seu trabalho, o qual consiste em determinar a tangente a uma curva por um ponto dado utilizando um triângulo indefinidamente pequeno. A razão do cateto oposto e do cateto adjacente desse triângulo diferencial é o que hoje conhecemos por [math]\frac{dx}{dy}[math].

3722 Triângulo Diferencial Fonte: Eves (2011).

John Barrow foi precursor ao notar que a diferenciação e a integração são, na verdade, operações inversas. Esse fato é conhecido hoje como o teorema fundamental do cálculo. Esse teorema aparece na obra Lectiones, de Barrow.

Newton e Leibniz 

Newton e Leibniz se destacam na história do cálculo por relacionarem o problema da tangente e da quadratura, ou seja, o problema de calcular a área no interior de uma curva. Eles estabeleceram uma nova simbologia e unificaram os métodos de cálculo diferencial e integral, os quais são hoje uma ferramenta poderosa na matemática.

Isaac Newton (1642 - 1727) nasceu em Woolsthorpe, no Reino Unido. Quando jovem, projetava engenhosidades mecânicas, o que levou a sua permanência prolongada na escola. O interesse de Newton por matemática foi despertado por volta dos 18 anos, quando estudava no Trinity College, Cambridge. Foi um livro de astrologia que desencadeou o seu gosto de matemática, esse livro despertou o interesse em ler outros livros, como os Elementos, de Euclides; Clavis, de Oughtred; Arithmetica infinitorum, de Wallis e ainda trabalhos de Kleper e Viète.

[...] começou a ler um livro sobre Astrologia que continha algumas passagens envolvendo Trigonometria que ele não conseguiu entender. Comprou então um livro de Trigonometria, mas dependia de pré-requisitos para compreendê-lo, portanto começou a ler Euclides, cuja parte inicial lhe pareceu tão simples que o entediava e só teve seu interesse desperto a partir do Teorema de Pitágoras .(NOGUEIRA, 2016, p. 135)

Assim, Newton começou a produzir seus próprios estudos e, posteriormente, conseguiu desenvolver o teorema do binômio na sua forma geral. Aos 24 anos, Newton deixou Cambridge e foi se refugiar em sua terra natal, pois existia um surto de peste bubônica, e a Universidade de Cambridge, entre os anos de 1665 e 1667, esteve praticamente fora de funcionamento. Newton desenvolveu seu cálculo em Cambridge a partir de sua reabertura em 1666, depois mostrou interesse pelo estudo da óptica e, posteriormente, desenvolveu a teoria das cores, em que estudou a dispersão da luz branca por meio de um prisma.

3822 Isaac Newton estudando a natureza da luz Fonte: Shutterstock.

Em 1675, Newton informou à Royal Society sobre sua teoria corpuscular da luz. Logo, Newton ganhava confiança e reputação no meio científico. Começou a lecionar álgebra e teoria das equações nos anos de 1673 a 1683. No ano de 1679, conseguiu averiguar a teoria da gravitação, ou seja, que dois corpos se atraem com uma força diretamente proporcional ao produto de suas massas e inversamente à distância entre elas ao quadrado.

Por pressão de seu colega Halley, Newton enviou seu manuscrito Principia à Royal Society. A obra trata da mecânica celeste e do teorema que justificava as leis dos movimentos dos planetas de Kepler. Como Newton demorava a publicar seus estudos, por volta de 1689 recebe acusações de Hooke sobre seu trabalho, o que quase o levou a abandonar o terceiro livro de Principia. Dedicou sua vida estudando química, alquimia e teologia. Posteriormente, trabalhou na casa da moeda e, em 1703, foi presidente da Royal Society e se reelegeu todos os anos até a sua morte, aos 84 anos. Suas obras mais importantes eram geralmente publicadas por influência e insistência dos amigos.

Todas as importantes publicações de Newton, exceto os Principia, só apare­ceram anos depois de o autor descobrir seus conteúdos e quase sempre por pressões de amigos. As datas de publicação dessas obras, em ordem cronológica, são: Principia, 1687; Opticks, com dois apêndices, Cubic Curves e Quadrature and Rectification of Curves by the Use of Infinite Series, 1704; Arithmetica universalis, 1707; Analysis per series, Fluxiones, etc. e Methodus differentialis, 1711; Lectiones opticae, 1729; e The Method of Fluxions and Infinite Series, traduzido do original latino de Newton por J. Colson em 1736 .(EVES, 2011, p. 438)

Com relação aos seus estudos matemáticos, Newton criou o método das séries infinitas e seus primeiros resultados sobre o cálculo apareceram na obra Philosopgiae naturalidade principia Mathematica. Estudando o cálculo, Newton foi capaz de consolidar os algoritmos para a diferenciação e a integração aplicável a praticamente todas as funções, seja ela algébrica ou transcendente. Na obra Aritmética universalismo, podemos encontrar a teoria que relaciona as equações reais e suas raízes complexas, em que essas raízes aparecem em pares de números complexos conjugados. Nessa obra, também são apresentadas regras de limites superiores para determinar raízes de uma equação real. Newton também consegue estabelecer o número de raízes imaginárias de uma equação real.

Em sua outra obra intitulada de Cubic Curves, Isaac trabalha com as propriedades das curvas dadas por equações cúbicas utilizando geometria analítica e enuncia vários teoremas, mas não chega a demonstrá-los. Um desses teoremas é que qualquer cúbica pode ser obtida por meio de projeções centrais de curvas.

[math]{{y}^{2}}=a{{x}^{3}}+b{{x}^{2~}}+cx+d[math]

Em suma, Newton, com suas habilidades fora do comum, se tornou um dos maiores cientistas que o mundo já viu, segundo o depoimento de Leibniz:

[...] o Leibniz, que nobremente lhe prestou um tributo dizendo: “Tomando a matemática desde o início do mundo até a época em que Newton viveu, o que ele fez foi, em grande escala, a metade melhor” .(EVES, 2011, p. 441)

Segundo Newton, se ele pode ir mais longe que os outros é porque pode subir nos ombros de gigantes. Existem relatos de que Isaac Newton passava entre 18 e 19 horas escrevendo. Entre as descobertas mais importantes realizadas por Newton, podemos destacar o cálculo, o teorema binomial, a lei da gravidade e a teoria da natureza das cores. Mas outro matemático que se destaca por trabalhar no cálculo diferencial e integral é Leibniz.

3922 Gottfried Leibniz Fonte: Shutterstock.

O alemão Gottfried Wilhelm Leibniz (1646 - 1716) nasceu em Leipzig. Quando era criança já se fazia notar sua peculiaridade, pois aprendeu latim e grego sozinho. Leibniz, aos 12 anos de idade, já apresentava um vasto conhecimento de filosofia, teologia e matemática. Realmente a genialidade de Leibniz era notória. Com quinze anos ingressou na universidade e se formou aos dezessete anos. Na universidade estudou as áreas de seu interesse, filosofia, matemática e direito. Dizem que é um dos poucos que conseguiu um conhecimento de modo universal.

Com vinte anos de idade estava se preparando para o doutorado em direito, mas o grau de doutor foi recusado pela pouca idade. Assim, saiu de sua cidade natal e foi obter o seu grau de doutorado na Universidade de Altdorf. Depois, ingressou no serviço diplomático, ao qual esteve ligado no decorrer de sua vida. Quando estava em uma missão diplomática em Paris, no ano de 1672, conheceu o grande cientista e matemático Hyugens. Leibniz convenceu Hyugens a dar aulas para ele, seu professor o influenciou a ler os tratados de Pascal. Conheceu também Oldenburg, secretário da Royal Society. Assim Leibniz teve a oportunidade de mostrar a sua máquina de calcular para a instituição.

A carreira diplomática de Leibniz proporcionava tempo para poder estudar os seus assuntos favoritos e também publicar artigos sobre variados temas. No ano de 1682, juntamente com Otto Mencke, Leibniz fundou a revista Act Editorum; muitos dos seus artigos matemáticos foram publicados na própria revista. No ano de 1700, Leibniz originou a Academia de Ciências em Berlim, depois se empenhou em criar outras academias. Os últimos anos do matemático foram marcados pela polêmica criada por terceiros a respeito da criação do cálculo, com Isaac Newton. Em 1714, foi marginalizado devido ao seu eleitor ser o primeiro rei alemão na Inglaterra.

Com relação ao cálculo, Leibniz o inventou, separadamente de Newton, entre os anos de 1673 e 1676, e foi o primeiro a estabelecer a simbologia S para o símbolo da integral, em que o S tem origem da palavra latina summa, a qual significa soma. Leibniz define várias simbologias que utilizamos hoje em cálculo, inclusive a notação dy/dx.

O alemão Gottfried Whilhelm Leibniz (1646-1716) inventou o seu cálculo entre 1673 e 1676, posteriormente, portanto, a Newton, mas não se pode esquecer que Newton havia comunicado seus resultados apenas aos mais íntimos, sendo, portanto, impossível que o sábio alemão pudesse ter tido conhecimento do trabalho do inglês. Devido a sua grande sensibilidade para a forma matemática, compreendia a importância de um simbolismo adequado e sua notação para o cálculo e bem mais engendrada, apropriada e flexível que a de Newton .(NOGUEIRA, 2016, p. 136)

O matemático se preocupava muito com a nitidez dos conceitos matemáticos e com sua simbologia, de modo que ela fosse universal. O que levou Liebniz a se preocupar com sua characterística generalis, a qual abrange o conceito da matemática de modo genérico e da lógica matemática. A maior parte do cálculo que vemos hoje nos cursos de graduação já tinha uma boa porção escrita em meados de 1700. Em 1969, Guillaume François Antonie, conhecido como marquês de L’Hospital, publicou um texto sobre cálculo, o qual tratava do método de calcular o limite de uma razão quando o limite de seu numerador e denominador tendem a zero.

31022 Marquês de L’ Hospital Fonte: pbs.twimg.com.Último acesso: Acesso em: 02 dez. 2016.

Indubitavelmente, porém, a realização matemática mais notável do período foi a invenção do cálculo, perto do final do século, por Isaac Newton e Gottfried Wilhelm Leibniz. Com essa invenção a matemática criativa passou a um plano superior e a história da matemática elementar essencialmente terminou .
Assim, podemos destacar que o século XVII foi muito produtivo com relação ao cálculo e à matemática em si, e que as contribuições de Newton e Leibniz, praticamente simultâneas e independentes, foram indispensáveis para a história do cálculo diferencial e integral. Muito da simbologia do cálculo e sua estrutura sistemática foi pensado nessa época. Os problemas de cálculo consistiam em determinar áreas, volumes e determinação do comprimento de arcos, que deram origem ao que chamamos atualmente de Análise Infinitesimal.(EVES, 2011, p. 417)

Exploração do Cálculo

31122 Queda da Bastilha Fonte: sensoincomum.org.Último acesso: Acesso em: 10 dez. 2016.

O século XVIII foi marcado por revoltas tanto na Europa como na América. Foi uma época de agitação, em que a transição do feudalismo para o capitalismo com a ascensão da burguesia era evidente. Assim, houve um grande êxodo rural, muitas pessoas estavam migrando para as cidades. Tanto a burguesia como a nova filosofia do liberalismo tomavam cada vez mais espaço na sociedade. A classe burguesa toma o poder na Inglaterra, França e em várias localidades na América nos anos entre 1688 e 1825, de maneira pacífica ou não. Grande parte da população camponesa e a classe baixa urbana estavam descontentes com a estrutura governamental antiga.

Com relação ao panorama matemático, o cálculo descoberto no século XVIII se mostrou uma ferramenta de extrema importância para solucionar problemas matemáticos que pareciam invencíveis. O cálculo atraiu muitos pesquisadores pelo seu vasto leque de aplicabilidade. Podemos notar isso pelo aumento do número de periódicos publicados. Anterior ao ano de 1700, haviam sido publicados 17 periódicos; no século XVIII, esse número aumentou para 210, chegando ao século XX com cerca de 2600.

Podemos destacar que o século XVIII foi marcado por explorar ferramentas poderosas no cálculo. Com o decorrer dos anos, assuntos como integrabilidade, convergência, dimensão e espaço passaram a se apresentar de forma mais abstrata, pois esses conceitos foram ganhando uma forma mais genérica. Os principais matemáticos a contribuir com a matemática no século XVIII foram os matemáticos da família Bernoulli, Leonhard Euler, Joseph Louis Lagrange, Pierre-Simon Laplace, Adrien-Marie Legendre.

A família Bernoulli teve lugar na história por mais de um século, originária da Holanda, porém residente na Suíça, produziu matemáticos entre os séculos XVII e XIX, dos quais se destacam os irmãos Jakob e Johann; e Daniel filho de Johann (NOGUEIRA, 2016). Jakob Bernoulli (1645 - 1705) e Johann Bernoulli (1667 - 1748) se interessaram mais pela matemática do que por outras carreiras e ambos foram aprendizes de Leibniz.

31222 Jakob Bernoulli Fonte: www.thefamouspeople.com.Último acesso: Acesso em: 10 dez. 2016.

Os irmãos Bernoulli notaram como o cálculo poderia ser aplicado a uma infinidade de problemas com a revista Acta eruditorum, dos artigos de Leibniz. Jakob trabalhou na Universidade de Basileia entre 1687 até o ano de sua morte; já o seu irmão Johann foi professor da Universidade de Gröninger e, após a morte de seu irmão, o sucedeu na Universidade que seu irmão trabalhava. Apesar dos atritos, os irmãos Bernoulli trabalharam muito juntos em questões científicas e trocavam ideias com Leibniz. Jakob e Johann resolveram muitos problemas que envolviam métodos infinitesimais da Mecânica e Geometria. Jakob Bernoulli foi um dos primeiros a utilizar coordenadas polares em cálculo, é um sistema de duas dimensões em que a distância do ponto de um plano é relacionada a um ponto fixo e ao ângulo relacionado a uma direção fixa. Estudou o uso de coordenadas retangulares, estudou também a curva conhecida como catenária com fios de várias densidades e sob a ação da força no centro da curva. Trabalhou com figuras isoperimétricas, ou seja, figuras com o mesmo perímetro. Jakob também estudou probabilidade, tanto que seu nome aparece em teoremas ou cálculos como a distribuição de Bernoulli e o teorema de Bernoulli. Jakob também contribuiu com o cálculo integral.

Na resolução de Jakob Bernoulli do problema da curva isócrona, publicada na Acta eruditorum em 1690, encontra-se pela primeira vez a palavra integral com um sentido ligado ao cálculo. Leibniz havia chamado o cálculo integral de calculus summatorius; em 1696 Leibniz e Johann Bernoulli acordaram em chamá-lo de calculus integralis .(EVES, 2011, p. 464)

O irmão de Jakob, Johann Bernoulli, contribui ainda mais para a matemática de seu tempo. Johann trabalhou com fenômenos da óptica como a refração e a reflexão, também trabalhou com família de curvas, quadraturas de áreas utilizando séries, estudou cálculo exponencial, trigonometria analítica e uma série de outros assuntos.

31322 Johann Bernoulli Fonte: images.fineartamerica.com.Último acesso: Acesso em: 10 dez. 2016.

Segundo Nogueira, Johann tinha ligações com o marquês de L’Hospital. Como sabemos, L’Hospital publicou um tratado sobre o cálculo, mas nessa obra continha as lições de Bernoulli e também correspondências que trocaram, inclusive após a morte do marquês, Johann reivindicou os direitos autorais da regra hoje conhecida como regra de L’Hospital. Posteriormente, os três filhos de Johann Bernoulli seguiram também a carreira na matemática, Nicolaus (1695 - 1726), Daniel (1700 - 1783) e Johann (II) (1719 - 1790), mas o filho que obteve mais destaque foi Daniel.

Daniel se dedicou aos estudos de probabilidade, à astronomia, à hidrodinâmica e à física. Foi pioneiro na área das equações diferenciais parciais, criou a teoria cinética dos gases e ainda estudou o princípio da hidrodinâmica, que hoje é conhecido pelo seu nome em livros de física elementar.

Tratando agora de outro matemático, um dos mais famosos do século XVIII, Leonhard Euler (1707 - 1783), de origem suíça, foi um dos matemáticos que mais produziu e publicou trabalhos. Euler seguiu o caminho da matemática após ter tentado seguir o caminho da teologia, seu pai estudou com Jakob Bernoulli e, por meio desse contato, o pai conseguiu que Euler estudasse com Johann Bernoulli.

Com 20 anos, Euler foi indicado para membro da instituição da Academia de São Petersburgo por Daniel e Nicolaus Bernoulli. Euler permaneceu em São Petersburgo por 14 anos, depois aceitou o cargo de chefia da seção de matemática da Academia de Berlim, o qual exerceu por 25 anos e, por um convite de Catarina, retornou à Academia de São Petersburgo até o final de sua vida. O mais interessante é que Euler nunca exerceu o cargo de professor.

Euler foi um escritor muito produtivo, apesar de ter ficado cego após o seu retorno a São Petersburgo, mas esse empecilho não o impediu de escrever. Por possuir uma memória impecável, Euler produziu ainda diversos trabalhos com a ajuda de um secretário. Ele publicou cerca de 530 trabalhos enquanto viveu e, ao morrer, deixou um legado de uma série de manuscritos. O matemático contribuiu com trabalhos relacionados ao cálculo, teoria dos números, probabilidade, óptica e mecânica. A principal contribuição de Euler é a respeito de números primos, que os relaciona com séries de potências dando origem à teoria analítica de primos. Sistematizou os números complexos e estabeleceu a famosa fórmula:

[math]{{e}^{ix}}=cos~x~+i~sen~x[math]

Escreveu sobre análise infinitesimal em sua obra Introductio in analysis infinitorum (1748), em que trabalha com o conceito de função e utiliza a notação f(x) para representar a função na variável x. Euler também fez sua contribuição em Álgebra escrevendo sobre equações biquadradas e cúbicas, e ainda consegue demonstrar o Último Teorema de Fermat para os casos em que n = 3 e n = 4. No campo da geometria, Euler cria a famosa expressão entre o número de vértices (V), faces (F) e arestas (A) de um poliedro convexo, em que V - A + F = 2.

Sem sombra de dúvidas, Euler foi o maior gênio de seu tempo. Não tinha interesse apenas por matemática, também era um sábio com relação à física, botânica, química, teologia e às línguas orientais. Diziam que Euler fazia cálculos, assim como nós respiramos. Outro matemático notável junto ao Euler foi Joseph Louis Lagrange (1736 - 1813), de origem italiana. Ainda jovem, se tornou professor de matemática da academia militar. Posteriormente, após a saída de Euler de Berlim, ocupou o seu lugar por 20 anos a convite de Frederico, o Grande.

31422 Joseph Louis Lagrange Fonte: images.fineartamerica.com.Último acesso: Acesso em: 12 dez. 2016.

Após sua estadia em Berlim, Lagrange foi convidado a ocupar a cátedra na Escola Normal e depois na Escola Politécnica em Paris. Durante o Regime do Terror na França, Lagrange sentia uma grande indignação com a crueldade instalada na época.

Quando o grande químico Lavoisier foi executado na guilhotina, ele expressou sua indignação nos seguintes termos: “Bastou à turba um momento apenas para decepar-lhe a cabeça; um século não será suficiente para que surja outra igual” .(EVES, 2011, p. 484)

Sua contribuição matemática foi muito relevante para os conceitos e estudos matemáticos que estavam por vir. Lagrange se preocupou em elaborar com rigor matemático os fundamentos de análise. Em sua obra Théorie des Fonctions Analytiques Contenant les Principes du Calcul Différentiel, trabalhou com a ideia de expressar uma função utilizando a série de Taylor. Trabalhou também com um método de aproximação de raízes reais por meio de funções que sejam contínuas, estimulou o desenvolvimento das equações diferenciais parciais. Lagrange tinha um gosto para a área de Teoria dos Números, seus trabalhos a respeito influenciaram Galois no desenvolvimento da teoria dos grupos, inclusive, atualmente, existe um teorema conhecido como teorema de Lagrange na teoria dos grupos.

Outros grandes matemáticos contemporâneos a Lagrange foram Laplace e Legendre. Pierre - Simon Laplace (1749 - 1827), com sua habilidade matemática e na política, conseguiu boas oportunidades no ensino e meios de se locomover entre as facções durante a Revolução Francesa (EVES, 2011). Suas obras mais importantes foram Traité de Mécanique Céleste (1799 – 1825), publicada em cinco volumes, e Théorie Analytique des Probabilités (1812). A primeira obra trata da mecânica celeste na época, a qual Laplace também inclui suas considerações, e a segunda, sobre probabilidades.

31522 Pierre - Simon Laplace Fonte: Shutterstock.

Sua contribuição na matemática com a transformada de Laplace e o teorema de Laplace ajudou no desenvolvimento do cálculo operacional e na teoria dos determinantes, respectivamente. O matemático não era muito rigoroso no quesito das demonstrações em si, para ele, a matemática era uma ferramenta que era utilizada para desvendar os fenômenos da natureza. Laplace era muito generoso com seus alunos, muitas das vezes deixava de publicar uma descoberta matemática para que seu pupilo o fizesse primeiro.

Vamos agora tratar de um outro matemático contemporâneo a Lagrange e a Laplace, Adrien-Marie Legendre (1752-1833), seu trabalho foi voltado para a teoria dos números, integrais, o método dos mínimos quadrados e funções elípticas. Em sua principal obra, Éléments de Géométrie (1794), Legendre reescreve a obra Elementos de Euclides de uma forma mais didática, reordenando e simplificando os teoremas e proposições.

31622 Adrien-Marie Legendre Fonte: divisbyzero.files.wordpress.com.Último acesso: Acesso em: 14 dez. 2016.

Posteriormente, publicou Essai sur la Théorie des Nombres (1797-1798), em que trata sobre teoria dos números, e também publicou Traité des Fonctions Elliptiques et des Intégrals Eulériennes (1825-1832). Nessa obra, Legendre trabalha com integrais eulerianas, são integrais que provém do estudo do problema de interpolação, para funções denominadas beta e gama. Legendre tentou provar o postulado das paralelas de Euler, trabalhou também com equações diferenciais, as soluções das equações do tipo:

[math]\left( 1-{{x}^{2}} \right)y’’-~2xy’~+~n\left( n~+~1 \right)y~=~0[math]

São conhecidas como funções Legendre. O matemático obteve uma certa fama pelo seu estudo em geodésia e sua triangulação.

A Matemática na Revolução Industrial 

A Revolução Industrial do século XIX é um marco na história mundial. Grande parte da população agrária vai para as cidades, surgindo assim a mão de obra operária. Nos grandes centros urbanos, surge a classe do proletariado e acontecem avanços tecnológicos mais fantásticos. A Revolução iniciou no século XVIII e durante o século XIX proliferou na Europa e na América. O avanço tecnológico também desencadeou o avanço na ciência, principalmente na mecânica e na química.

Justamente nas primeiras décadas do século XIX surge o matemático conhecido como o príncipe da matemática, Carl Friedrich Gauss (1777 - 1855). De origem alemã, Gauss já mostrava os seus dotes desde pequeno, ele é um daqueles casos raros de criança com uma genialidade fora do comum. Com três anos, dizem que identificou um erro no borrador de seu pai. Outra história famosa é de quando Gauss tinha apenas dez anos e o seu professor na escola propôs para a sua turma somar todos números de 1 a 100, o professor ficou surpreso pois Gauss apresentou a solução exata em pouco tempo, na verdade, o menino havia calculado a soma da progressão aritmética, ou seja, ele notou que na soma de 1 + 2 + 3 + ... + 100 há um padrão em que 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, e assim por diante, então a soma poderia ser calculada como 50×101.

Impressionado pela genialidade precoce de Gauss, o duque de Brunswick o apadrinhou e acompanhou sua entrada no colégio Brunswick com 15 anos e depois seu ingresso na Universidade de Göttingen, aos 18 anos de idade. Seu gosto por matemática se torna evidente aos 19 anos, quando descobre que um polígono regular de 17 lados pode ser construído com régua e compasso. O matemático sentia tanto orgulho dessa descoberta que pediu para gravar o desenho em seu túmulo, apesar de seu pedido não ter sido atendido, há um memorial em sua homenagem em sua cidade natal que possui o heptadodecágono.

31722 As fábricas químicas da BASF em Ludwigshafen, Alemanha (1881) Fonte: upload.wikimedia.org.Último acesso: Acesso em: 14 dez. 2016.

31822 Karl Friedrich Gauss Fonte: Shutterstock.

Gauss, assim como Newton, era relutante e lento para publicar suas descobertas. Por sorte, Gauss mantinha um diário com suas anotações e registros matemáticos. Quase todo seu diário foi decifrado, nesses registros, é encontrada a demonstração de que qualquer número inteiro positivo é a soma de três números triangulares. Havia registrado a descoberta para a periodicidade dupla de algumas funções elípticas, depois descobriu isso para o caso geral. Com apenas 20 anos, escreveu sua tese de doutorado na Universidade de Helmstädt e provou, satisfatoriamente, o teorema fundamental da álgebra, a qual afirma que uma equação polinomial com coeficientes complexos com o grau maior que zero possui pelo menos uma raiz complexa. Matemáticos como Euler, Newton, Lagrange e D´Alembert tentaram demonstrar esse teorema, mas sem sucesso.

Sua publicação de maior importância é a obra Disquisitiones arithmeticae. Essa obra trata da teoria dos números e de suas descobertas de construções de polígonos regulares. Gauss também contribuiu para a astronomia, física e eletricidade. Gauss ainda fez a primeira investigação sobre convergência de séries e o estudo sobre geometria intrínseca de superfícies. Em 1807, ele ingressou no observatório Göttingen como professor de matemática e diretor do observatório, posto que ocupou até a sua morte. No ano de sua morte, o rei de Hanover pediu para fazer uma medalha em sua homenagem com as seguintes inscrições: “Jorge V rei de Hanover ao Príncipe dos Matemáticos”. A partir daí, Gauss fica conhecido como o príncipe dos matemáticos.

O rigor da análise matemática teve início com Lagrange, Gauss e também com outro matemático do qual que vamos discutir a respeito. Augustin-Louis Cauchy (1789 – 1857), nascido em Paris, chamou a atenção de Lagrange e Laplace em 1805, os quais persuadiram-no a seguir a carreira da matemática pura ao invés da engenharia. Posteriormente, assumiu como professor na Escola Politécnica. Cauchy, ao contrário de Newton e Gauss, era bastante produtivo, sua obra se reúne em vários livros e em 789 artigos. Sua colaboração em relação à matemática está relacionada às convergências e divergências de séries infinitas, equações diferenciais, determinantes, probabilidade e teoria das funções.

Grande parte do cálculo apresentado hoje nos livros universitários é consequência da abordagem trabalhada pelo matemático. Cauchy define a derivada de uma função em relação a x muito parecida como definimos hoje, assim como a integral também. O matemático trabalha com a equação característica envolvendo determinantes e matrizes. Seu trabalho serviu de inspiração para outros matemáticos devido ao seu rigor. Adepto ao partido dos Bourbons, foi forçado a se afastar do cargo de professor por 18 anos depois da Revolução de 1830. Após esse período, Cauchy conseguiu retornar para a Escola Politécnica. Cauchy veio a falecer em 1857 de maneira súbita, foi para o campo descansar, mas foi acometido por uma febre que seria fatal.

31922 Augustin-Louis Cauchy Fonte: upload.wikimedia.org.Último acesso: Acesso em: 14 dez. 2016.

Dois outros grandes personagens na história da matemática são Abel e Galois. Ambos deixaram contribuições de um brilhantismo intenso que infelizmente terminou na morte prematura desses dois matemáticos. Abel faleceu aos 26 anos de idade de tuberculose e subnutrição, e Galois perdeu em um duelo aos 21 anos. Niels Henrik Abel (1802 - 1829), de origem norueguesa, já em 1824 publicou um artigo em que demonstrava a impossibilidade de determinar a solução geral das equações quínticas por meio de radicais. Assim, Abel obteve uma bolsa que lhe permitiu viajar para Itália, Alemanha e França. Durante esse tempo, desenvolveu seus estudos e publicou artigos a respeito das funções elípticas, convergência de séries infinitas e das integrais abelianas como conhecemos hoje.

Todo aluno de análise encontra a equação integral de Abel e o teorema de Abel sobre a soma das integrais das funções algébricas que leva às funções abelianas. No capítulo das séries infinitas, há o teste de convergência de Abel e o teorema de Abel sobre séries de potências. .(EVES, 2011, p. 534)

Abel viveu sua vida na pobreza e nunca conseguiu um cargo como professor em uma universidade, infelizmente, após sua morte em Froland, lhe foi enviado um convite para trabalhar na Universidade de Berlim. Hermite alegava que Abel deixou um trabalho para que os matemáticos se ocupassem por mais de 500 anos.

Foi trágica também a vida de Évariste Galois (1811 - 1832), nascido na França, em uma pequena cidade, seu talento para a matemática começou a despertar com apenas 15 anos de idade. Tentou ingressar na Escola Politécnica, mas foi recusado, pois não tinha o preparo para cumprir as exigências formais da escola, por outro lado, a escola falhou por não notar a sua genialidade. Em 1829, ingressou na Escola Normal, mas na época se envolveu na Revolução de 1830, o que resultou em sua expulsão da escola e meses na prisão. Após sua saída da prisão, se envolveu em um caso amoroso, o qual levou a duelar e perder sua vida aos 21 anos.

Galois fez grandes contribuições à matemática. Em 1830, publicou um artigo sobre equações. Na noite anterior ao duelo, escreveu um testamento com as suas descobertas ainda não publicadas, para serem trabalhadas por outros grandes matemáticos. Esse testamento, na verdade, continha a teoria dos grupos e a teoria de Galois, como é conhecida agora. Posteriormente, sua teoria foi utilizada de maneira genial na geometria por Saphus Lie (1842 - 1899) e Felix Klein (1849 - 1925). A teoria dos grupos se desenvolveu adiante por cauchy e outros que sucederam o matemático.

Com relação à teoria que ficaria conhecida como geometria não euclidiana atualmente, essa se deu ao fato de o postulado das paralelas ser independente dos demais postulados da geometria euclidiana. Os matemáticos precursores a essa teoria foram Gauss, o russo Nicolai Ivanovitch Lobachevsky (1793-1856) e o matemático Janos Bolyai (1802-1860), de origem húngara. Provavelmente, Gauss foi precursor à geometria não euclidiana, pois já havia levantado questões relevantes a ela, mas nunca publicou nada a respeito, ao contrário de Lobachevsky e Bolyai.

Janos Bolyai era um oficial e seu pai era professor de matemática e amigo de Gauss. Bolyai recebeu estímulos de seu pai nos estudos sobre o postulado das paralelas e, em 1832, seu ensaio sobre o tema apareceu como um apêndice no trabalho de seu pai, depois disso não publicou mais nada. O seu interesse estava voltado às proposições que não dependiam do postulado das paralelas, assim essas proposições eram válidas tanto na geometria euclidiana como na não euclidiana.

Por outro lado, Lobachevsky passou a maior parte de seu tempo em vida como aluno, depois professor e, finalmente, reitor da Universidade de Kazan. Entre os anos de 1829 e 1830, publicou seu artigo sobre geometria não euclidiana. Publicou, posteriormente, Geometrische Untersuchungen Zur Theorie der Parallellinien (Investigações Geométricas sobre a Teoria das Paralelas) e Pangéométrie (Pangeometria). A geometria não euclidiana ganharia forma com o matemático Georg Friedrich Bernhard Riemann (1826-1866). Ele mostrou que eliminando a infinitude da reta e tomando ela como ilimitada e reajustando os postulados de Euclides pode-se ter uma geometria não euclidiana consistente. Hoje, as geometrias não euclidianas são conhecidas como geometria parabólica, geometria elíptica e geometria hiperbólica.

Os séculos XIX e XX

No século XIX, é notável o desenvolvimento da geometria do triângulo e círculo, aparecendo inúmeros artigos sobre o assunto. Muito do material produzido na época foi organizado em textos com o título de Geometria Moderna. No século XIX, foi possível demonstrar que não é possível resolver os três problemas famosos da antiguidade, o problema da quadratura do círculo, da duplicação do cubo e o da trissecção do ângulo utilizando instrumentos euclidianos. A estrutura lógica simbólica da matemática e seus fundamentos se desenvolvem no século XX. Muitos conceitos passam por generalizações e evoluções notáveis. Nesse período, a lógica matemática se desenvolve e o grande avanço computacional interfere na matemática.

Um grande matemático do século XIX foi alemão Georg Friedrich Bernhard Riemann, o qual já havíamos citado no tópico anterior, nasceu em Berlim, em 1826, veio de uma família modesta, mas o pai conseguiu lhe dar estudos apropriados. Riemann se formou na Universidade de Berlim e realizou o seu doutorado na Universidade de Göttingen. Os estudos matemáticos de Riemann estavam voltados para as equações diferenciais e, mais tarde, se voltou à geometria. Riemann deixou várias contribuições para a matemática, como a teoria da integração e seus estudos sobre funções de variáveis complexas.

O caminho métrico-diferencial foi estabelecido por um dos grandes matemáticos do século XIX, o alemão Georg Friedrich Bernhard Riemann (1826-1866), discípulo de Gauss que, em 1854, provou ser possível o desenvolvimento de uma nova Geometria não euclidiana, além da hiperbólica, a hoje denominada Geometria elíptica, na qual, por um ponto exterior a uma reta dada, não passa nenhuma paralela à mesma .(NOGUEIRA, 2016, p. 164)

Dois outros importantes matemáticos do século XIX e XX são Georg Cantor e Henri Poincaré. O dinamarquês Georg Ferdinand Ludwig Philip Cantor (1845 - 1918) estudou em Zurique, Göttingen e Berlim, e, posteriormente, na Universidade de Halle, desenvolveu a sua carreira profissional. Os estudos de Cantor influenciaram o desenvolvimento da teoria dos números, séries trigonométricas e equações indeterminadas. O matemático criou uma base para depois Dedekind desenvolver seu trabalho em teoria dos conjuntos e teoria do infinito. A teoria de conjuntos de Cantor é de tamanha importância que ela praticamente tem risco em quase todos os compostos de matemática atualmente. Em seus artigos, trabalhou com a teoria dos números transfinitos de maneira semelhante aos números finitos.

32022 Georg Ferdinand Ludwig Philip Cantor Fonte: www.thefamouspeople.com.Último acesso: Acesso em: 20 dez. 2016.

Outro importante matemático desse período é Jules Henri Poincaré (1854 - 1912). Nascido na França, o matemático foi um dos poucos universalistas a respeito de seus estudos, ou seja, um dos poucos a entender praticamente todos os ramos da matemática. Poincaré tem origem em uma família influente, com estadistas e cientistas, inclusive seu primo foi presidente da França durante o período da Primeira Guerra Mundial, e um de seus irmãos teve uma carreira de destaque na Física. Poincaré se formou na Escola Politécnica e também se formou na École des Mines como engenheiro; fez o doutorado na Universidade de Paris e, posteriormente, trabalhou como professor na Universidade de Caen e depois foi para Universidade de Paris, ocupando várias cadeiras.

32122 Jules Henri Poincaré Fonte: p2.trrsf.com.Último acesso: Acesso em: 20 dez. 2016.

Poincaré lecionava diversos assuntos de matemática aplicada e matemática pura. Sua produção matemática era bem fértil, resultando em mais de 30 livros e 500 artigos. Poincaré era um cientista bem versátil, contribuindo para várias áreas da ciência. Na matemática, contribuiu na área de equações diferenciais, topologia, teoria dos grupos e teoria das probabilidades.

Poincaré nunca se preocupou em permanecer num campo por muito tempo, antes preferia pular lepidamente duma área para outra. Foi descrito por um de seus contemporâ­neos como “um conquistador, não um colonizador” .(EVES, 2011, p. 617)

O cientista era dotado de uma genialidade incrível, e ele podia reter grande parte de um conteúdo caso lesse. Dizem que o matemático criava enquanto caminhava de maneira intranquila e fazia suas anotações de maneira rápida e precisa, que não necessitava de observações posteriores. Atualmente, o campo da matemática é tão vasto e se encontra em constante crescimento que será muito difícil surgir um matemático que, de maneira universal, consiga trabalhar a matemática da maneira que Poincaré trabalhou.

O século XX é marcado pelos fundamentos, lógica matemática, sistematização e estudo sobre postulados e suas propriedades. Na parte axiomática, temos pesquisas modernas que envolveram os estudos das propriedades e postulados da geometria euclidiana. Os conceitos básicos relacionados aos estudos de análise matemática e cálculo diferencial e integral foram reformulados a partir da teoria de Cantor.

Um grande feito recente na história da matemática foi a prova do Teorema de Fermat pelo matemático inglês Andrew Wiles, em 1994. O teorema de Fermat afirma que não existe solução para a equação da forma [math]{{x}^{n}}+{{y}^{n}}={{z}^{n}}[math], com x, y e z inteiros positivos e n maior que 2. Wiles trabalha como professor na Universidade de Oxford, e a demonstração de um teorema de mais de 300 anos lhe rendeu vários prêmios, inclusive o prêmio Abel da matemática. De acordo com o matemático, para poder resolver esse teorema, foi necessário o uso de curvas elípticas, formas modulares e representações de Galois. O problema de 358 anos passou por vários matemáticos até a sua solução final com Wiles.

32222 Andrew Wiles Fonte: static.independent.co.uk.Último acesso: Acesso em: 20 dez. 2016.

Outro grande feito foi realizado por Gregori Perelman. O matemático russo resolveu um dos sete problemas do milênio, são problemas elencados que ainda não possuem solução e o Instituto Clay de Matemática dá um milhão de dólares para quem resolver um desses sete problemas, que na atualidade são seis sem resolução até agora. O problema resolvido pelo matemático se trata da conjectura de Poincaré, que afirma que uma toda variedade tridimensional fechada juntamente com um grupo fundamental trivial é equivalente a uma esfera tridimensional. Perelman foi indicado a receber o prêmio da medalha Fields, que corresponde ao prêmio Nobel da matemática, mas o ele recusou. Ele afirmou que a medalha era irrelevante comparada ao resultado correto que obteve, que pra ele já era um prêmio.

Período Colonial e Brasil Império

Para compreender esse período, torna-se necessário partirmos de uma divisão histórica que inicia uma viagem cultural pelos registros dos acontecimentos desde o período colonial, cuja colonização do Brasil ocorreu no período entre os séculos XVI e XIX, em que o território brasileiro era uma colônia de Portugal. Nesse período, há poucos relatos sobre a História da Matemática, isto é explicável, pois, nessa época, os colonizadores não tinham interesse nem estrutura para ensinar a Matemática, a sua maior preocupação era catequizar os povos indígenas e aprender a língua materna. Nesse período, quem eram os responsáveis por ensinar eram os jesuítas, que defendiam exclusivamente os interesses da Igreja. Aos jesuítas, atribui-se o título de responsáveis por criar as primeiras escolas brasileiras.

Em 1549, o Padre Manuel de Nóbrega (1517- 1570) chegou ao Brasil e, nesse mesmo ano, tomou a iniciativa de criar um escola de primeiras letras, então, em 15 de abril de 1549, foi fundada, na cidade de Salvador, Bahia, a primeira escola primária no Brasil, na qual ensinava exclusivamente a ler e escrever, tendo como primeiro professor o jesuíta Vicente Rijo Rodrigues (1528-1600). A Companhia de Jesus deixa claro que o ensino não era um de seus objetivos principais e imediatos. Veja:

Quando Inácio de Loyola e seus companheiros fundaram a Companhia de Jesus, parece não haver nenhuma intenção de que um de seus objetivos seria o ensino, e até mesmo a Bula Papal que aprova esta Ordem não se refere a isso. No entanto, vamos encontrá-la nas “Constituições” da Companhia que, apesar de terem começado a ser escrita por Inácio de Loyola em 1539, só foram aprovadas em 1558 [...] (Ana I. Rodrigues da Silva Rosendo, in “Inácio Monteiro e o Ensino da Matemática em Portugal no Século XVIII”, Dissertação de Mestrado, Departamento de Matemática Univ. do Minho, Braga, 1996, p. 20-21)

4114 Padre Leonardo Nunes Fonte: 1.bp.blogspot.com.Último acesso: Acesso em: 20 dez. 2016.

No ano de 1550, com a chegada do jesuíta Leonardo Nunes (1940-1554), português, natural de Vila de São Vicente Guarda, foi fundada em São Vicente, São Paulo, a segunda escola primária do Brasil. Porém, nas duas primeiras escolas, não existia o ensino da matemática. Somente em 1572 foi proporcionado pelos jesuítas um curso mais avançado. Naquela época, os jesuítas eram chamados de inicianos. O primeiro curso de Artes ofertado no Brasil foi pelo Colégio de Salvador, tinha duração de três anos, no qual se estudava: matemáticas, lógicas, físicas, metafísicas e ética. Esse curso proporcionava aos alunos a titulação de bacharelado ou licenciado, sendo o pontapé inicial para os cursos de bacharelados e licenciaturas no Brasil.

O ensino da Matemática no Brasil iniciou com o ensino de algarismos ou aritmética, sendo os responsáveis por esse ensino os jesuítas, cujos alguns nomes podem ser elencados: o jesuíta Valentim Estancel, Aluízio Conrado Pfiel, Manual Amaral, Inácio Stafforo, Felipe Bourel, Jacobo Cocleo ou Jacques Cocler, Diogo Soares, Domingos Capassi e João Brewer. Esses eram responsáveis por lecionar no Colégio de Salvador, em que o principal objetivo da ordem dos jesuítas era: além da educação cultural, proporcionar a educação cristã e formação religiosa, mas o colégio era frequentado também por alunos que não tinham nenhum interesse em seguir essa formação religiosa.

No ano de 1573, na cidade do Rio de Janeiro, foi fundado um colégio de ordem jesuítas, que ofertava o curso de Artes, que em seu currículo continha o estudo sistemático das matemáticas. Então, em 1575, possibilitou conceder os primeiros títulos de bacharelado e licenciados aos alunos, e, em 1578, surgiram os primeiros títulos de mestres em Artes; em 1581, os primeiros títulos de doutores em Teologia. Nessa primeira fase, a oferta era para os meninos, que, posteriormente, foi expandida às meninas.

Somente em 1578, na cidade do Rio de Janeiro, com o escrivão Francisco Lopes, surgem os primeiros indícios do ensino da aritmética para turmas particulares, pois, naquele período, nas escolas elementares, não existia o ensino da matemática e, quando existia, eram apenas as quatro operações elementares, que não passavam de operações algébricas. Os jesuítas utilizavam em suas escolas livros didáticos produzidos pelos próprios jesuítas, como os Elementos Matemáticos, produzido em Lisboa no ano de 1634, e Teoremas Matemáticos, também produzido em Lisboa no ano de 1636, produzido pelo jesuíta Inácio Stafford.

O início do ensino da Matemática no Brasil atribui-se aos jesuítas, que, em algumas escolas elementares, ensinavam as quatro operações algébricas, inclusive a geometria elementar, ministrada nos cursos de Artes pelo grau de complexidade e avanço. Somente em 1605, nas cidades de Salvador, Rio de Janeiro e Recife, alguns tópicos elementares de aritmética eram ensinados, como razões, proporções e geometria euclidiana, e é por meio dessa influência dos jesuítas no ensino da matemática que possibilitou-se a criação, no colégio de Salvador, da Faculdade de Matemática em 1757.

O matemático José Monteiro Rocha (1734-1819), figura importante na Matemática do século XVIII e XIX, foi para o Brasil ainda criança, levado pela Companhia de Jesus, frequentando em Salvador o Colégio dos Jesuítas, de onde entrou para a Companhia de Jesus; estaria no colégio de Todos os Santos, quando, em 1759, o Marquês de Pombal decretou a retirada da Companhia de Jesus do país. Isso fez com que, em 1760, se desligasse da Ordem dos Jesuítas. Essa opção de abandonar proporcionava a possibilidade de continuar a residir nos domínios da coroa, caso contrário, se permanecessem na companhia, seriam exilados, assim, ao abandonar a companhia, passou ao clero secular. Dessa forma, permaneceu na cidade de Salvador a ensinar os filhos do governador. Com a expulsão dos jesuítas, gerou-se como consequência a desorganização do sistema de ensino em Portugal e, principalmente, nas colônias portuguesas, obrigando o governo a elaborar um plano alternativo, criando um quadro de professores públicos, financiados pelo Estado. Foi, então, a oportunidade de Monteiro da Rocha candidatar-se a esse cargo, realizando o primeiro exame exigido pelo Estado. Nesse período, percebeu-se que os conhecimentos adquiridos no Colégio Jesuíta de Salvador contribuíram bastante para sua aprovação; sendo aprovado, tornou-se professor de Gramática Latina e de Retórica.

4214 Marques de Pombal Fonte: ummarderecordacoes.blogs.sapo.pt.Último acesso: Acesso em: 20 dez. 2016.

No século XVIII, Monteiro Rocha foi convocado por Sebastião José de Carvalho e Melo (1699-1782), conhecido como Marquês de Pombal, para integrar e compor a comissão responsável em reformar a Universidade de Coimbra, criando inclusive a Faculdade de Matemática, em 1772. O que era ensinado na faculdade de Matemática de Salvador era praticamente a mesma matemática ensinada na Universidade de Coimbra, mas, durante algum tempo, não era reconhecida pela metrópole a titulação concedida pelos jesuítas no Brasil aos acadêmicos; em consequência, os graduados no Brasil que queriam continuar seus estudos deveriam ir para Coimbra, chegando em Coimbra, eram obrigados a repetir tudo aquilo que haviam estudado no Brasil, assim, após a expulsão dos jesuítas, o ensino brasileiro ficou estagnado apenas ao ensino primário.

Com a vinda de Monteiro Rocha para Coimbra, ele se matriculou na Faculdade de Canones, frequentando-a por três anos (1767-1770). Destacou-se nas cadeiras de direito canônico, recebeu, em 1772, o título de Doutor em Matemática pelas mãos do Marquês de Pombal, e foi nomeado à cadeira de Phoronomia (Ciências Físico- Matemáticas), abrindo nesse mesmo ano a Faculdade de Matemática.

Destacou-se por dois feitos fundamentais, primeiramente por reorganizar os estudos matemáticos na Universidade de Coimbra e, segundo, por suas produções e obras científicas de valor imensurável.

4314 Matemáticos Portugueses na Universidade de Coimbra Fonte: www.mat.uc.pt.Último acesso: Acesso em: 20 dez. 2016.

Após esse período, outras ordens religiosas tentaram abrir instituições de ensino, porém o estudo da Matemática ficou de fora e a faculdade Franciscana acabou não sendo fundada. No século XVII e XVIII, alguns matemáticos estiveram no Brasil:

Diogo Soares (1684-1748) e Domenico Capassi (1694-1733) renovaram a cartografia brasileira, promovendo uma grande renovação. Juntos foram os responsáveis por fazer o primeiro levantamento cartográfico de todo território brasileiro, cartografando pela primeira vez e fazendo um levantamento das latitudes e longitudes do território brasileiro.

João Brewer (1718 - 1789), professor da Faculdade de Matemática no Colégio Salvador. Os professores jesuítas não possuíam, naquela época, um conhecimento matemático elevado como os outros matemáticos contemporâneos, mas ministravam matemática na Universidade Portuguesa Pré-Pombalina.

Alguns fatos que ocorreram em Portugal nesse período marcaram e afetaram a educação brasileira, pois pertencíamos a Portugal. Então, a reforma do ensino da Universidade de Coimbra, executada pelo Marquês de Pombal, afetou a cultura científica e comercial da colônia Brasil, assim Portugal proíbe a língua nativa e atrasa ainda mais a cultura brasileira, assim, várias escolas são fechadas, pois o objetivo do Marquês era fechar as escolas para a fé e torná-las escolas para o Estado. Essa reforma potencializou em 1772, quando atingiu a Universidade de Coimbra por meios de estatutos. Pombal esperava preparar os homens para a Revolução Industrial que se processava na Europa.

A chegada da família real ao Brasil, por volta de 1808, que trouxe mais de 60 mil livros entre seus pertences, afetou diretamente o ensino brasileiro, com a reforma do ensino português, que atingiu diretamente os jovens brasileiros que foram a Portugal estudar e regressaram sem estudo algum.

4414 Família Real no Brasil Fonte: Disponível em: trilhahistorica.Último acesso: Acesso em: 20 dez. 2016.

Vale ressaltar que a Universidade de Coimbra não buscava investigar ramos das ciências e restringia a conservação e transmissão de conhecimentos já construídos. Como o conhecimento não era repassado, ficaram apenas entre os “muros” de Coimbra e não puderam contribuir para a evolução dela. Somente com a criação da Universidade de Berlim que passou a ter como objetivo as pesquisas.

Academia Real Militar e o cenário da pesquisa Matemática no Brasil

Portugal não se preocupou em contratar profissionais que avançassem e impulsionassem o conhecimento Matemático, automaticamente, o cenário não foi favorável para as pesquisas matemáticas. Os engenheiros italianos contratados não tinham nenhum interesse em pesquisas básicas de Matemática, tampouco em fazer escola. Mas, mesmo diante dessa situação, a elite portuguesa sentiu um forte impacto com a Faculdade de Matemática, pois foi o início de algo inovador em Portugal, onde podem ser concedidos títulos de doutores aos especialistas em Matemática.

4514 José Anastácio de Cunha Fonte: donamariaprimeira.blogspot.com.br.Último acesso: Acesso em: 20 dez. 2016.

É claro que alguns jovens se destacaram naquela época, como José Monteiro Rocha (1734-1819) e José Anastácio de Cunha (1744-1787). Ambos não se preocupavam em fazer educação, formar escola, porém seus sucessores se tornaram exímios matemáticos. Esses acontecimentos refletiriam negativamente no desenvolvimento matemático no Brasil, pois, dos brasileiros que foram estudar matemática em Portugal na Universidade de Coimbra, inclusive em Escolas Militares, cinco deles interromperam seus estudos, sendo obrigados a voltar ao Brasil, com a Família Real no século XVIII. Chegando ao Brasil, fizeram parte do primeiro corpo docente da Academia Real Militar.

Poucos brasileiros passaram pela Faculdade de Matemática em Portugal e, a partir de 1772, apenas alguns conseguiram o título de doutor em Ciências Matemáticas, justificando a decadência das pesquisas no Brasil, dentre eles, podemos destacar: Antônio Pires da Silva (1750-1805), natural da Bahia; Francisco José de Lacerda e Almeida (1753-1802), natural de São Paulo; Antônio Francisco Bastos, natural de Pernambuco; Thomás Antônio de Oliveira Lobo, natural do Rio de Janeiro; com exceção de João Antônio Coqueiro (1837-1910), natural de São Luís, que antes de ser graduado publicou o livro O Tratado de Aritmética. Este, após frequentar aulas da faculdade de Ciências, recebeu o título de bacharel e doutor em Ciências Físicas pela Universidade de Bruxelas, na Bélgica.

4614 Academia Real Militar Fonte: Google/imagensÚltimo acesso: Acesso em: 20 dez. 2016.

No final de 1807, a família real foge para o Brasil e, com a sua fuga, foi autorizada a criação da Academia Real Militar na corte do Rio de Janeiro em 1808, em sua composição, constava o curso de Matemática com duração de quatro anos e o curso militar de três anos, porém o ensino superior no Brasil iniciou em 1810, sendo optativo.

A Academia Real Militar iniciou suas atividades em 23 de abril de 1811, tendo em sua oferta inicial as disciplinas:

• No 1º ano, proporcionava a seus alunos as disciplinas de Aritmética, Álgebra, Geometria Trigonometria e Desenho;
• Para complementar a grade curricular, no 2º ano, ofertava Álgebra, Geometria Analítica, Cálculo Diferencial e Integral, Geometria Descritiva e Desenho;
• Mecânica, Balística e Desenho eram ministradas no 3º ano;
• Ficando para o 4º ano Trigonometria Esférica, Física, Astronomia, Geodésia, Geografia Geral e Desenho;
• No 5º ano, eram ministradas as disciplinas de Tática, Estratégia, Castrametração (arte de assentar equipamentos), Fortificação de Companhia e Reconhecimento de Terreno e Química;
• No 6º ano: Fortificação Regular e Irregular, Ataque e Defesa de Práticas, Mineralogia e Desenho;
• No 7º ano: Artilharia, Minas e História Natural.

Somente com a Proclamação da República inicia uma nova fase do ponto de vista matemático, porém ainda não trouxe muitas inovações ao Brasil com relação ao ensino superior. Com o período republicano, foi promulgado o Decreto 2221, que possibilitou abrir as Escolas Politécnicas. Nesse período, o ensino da matemática estava nas mãos dos engenheiros (eram formados engenheiros-matemáticos), talvez isso justifique a carência de pesquisas e o retardo no desenvolvimento das matemáticas no Brasil.

Em 1934, surge a Fundação da Universidade de São Paulo – USP, com a criação da Faculdade de Filosofia, Ciências e Letras, possibilitando o desenvolvimento do ensino da Matemática no país, pois, até o momento, o ensino da matemática era voltado às necessidades das engenharias, com objetivos específicos da área, desses engenheiros matemáticos que dedicavam-se a pesquisas. Destacam-se dois deles:

4714 Joaquim Gomes de Souza Fonte: www.dec.ufcg.edu.br.Último acesso: Acesso em: 20 dez. 2016.

Joaquim Gomes de Souza (1829-1864), natural de Itapecuru - Mirim, conhecido como Souzinha, matemático, astrônomo, filósofo, parlamentar brasileiro, autodidata, considerado um dos pioneiros no ensino da matemática no Brasil, deixou como legado uma obra impressionante; publicou trabalhos sobre Física, Matemática, Integração de Equações Diferenciais Parciais, Equações Integrais, entre outros. Entre suas obras, destacaram-se Resoluções das Equações Numéricas (1850), conhecida como uma dos mais importantes na história científica do Brasil.

4814 Oto de Alencar Silva Fonte: www.dec.ufcg.edu.br.Último acesso: Acesso em: 20 dez. 2016.

Otto de Alencar Silva (1874-1912), natural de Fortaleza – CE, físico, astrônomo, topógrafo, considerado um dos pioneiros nas pesquisas matemáticas brasileiras, graduou-se nas escolas politécnicas, sendo influenciado pelas ideias de Auguste Comte (1798-1857). Autodidata, deu continuidade em seus estudos, dedicando-se à astronomia, à matemática e à física. Ministrou na escola politécnica cursos de Geometria Analítica, Cálculo Diferencial e Integral, Mecânica Racional, entre outros.

A Universidade de São Paulo – USP foi o princípio do processo de pesquisa Matemática, na formação de pesquisadores antes da institucionalização do governo federal para os programas de pós-graduação e stricto sensu. Desde o início da criação da USP, as autoridades, devido à necessidade de amparo e fomento a pesquisas científicas, passou a priorizar o regime de trabalho integral dos professores, que, posteriormente, criou a Fundação de Amparo à Pesquisa do Estado de São Paulo - FAPESP.

Até a década de 1940, várias tentativas para criar universidades foram realizadas. Durante a fase imperial, 42 anteprojetos foram apresentados, mas ficaram apenas em tentativas de criar uma universidade. Porém alguns registros históricos marcam o ano de 1538 como sendo o marco inicial das discussões para criar uma universidade no país, mas nenhuma dessas tentativas se preocupava com a necessidade de criar uma universidade voltada ao ensino da matemática, pois, até o século XVII, os jesuítas (inicianos) mantinham no Colégio da Bahia uma Faculdade de Matemática.

O Príncipe João Maurício de Nassau (1604-1679) mandou instalar um observatório astronômico na torre de seu palácio em Friburgo, em 1820. José Bonifácio de Andrade e Silva (1763 - 1838) esboçou um projeto visando criar universidades no Brasil, incluindo a ciência matemática, nesse pré-projeto, surge o que é considerado o primeiro registro para a criação de um curso de Matemática no país. Após a extinção da Faculdade de Matemática dos inicianos, somente em 1842 que elaborou-se um projeto que visava à criação de uma universidade no país, que contemplasse os cursos de Teologia, Direito, Filosofia, Medicina e Matemática, tendo como modelo a faculdade de Coimbra.

Com a Lei Orgânica do Ensino Superior e do Ensino Fundamental, em 1911, o Decreto n.º 8659 – Lei Rivadávia permitia a criação de universidades particulares, surgindo várias instituições de ensino superior. A pesquisa matemática no Brasil só se concretizou graças à dedicação e ao empenho de um pequeno grupo de pessoas que haviam estudado fora do país e possuíam um grau elevado de cultura; mas, acima de tudo, pessoas dotadas das qualidades universais necessárias ao pesquisador, pessoas levadas pela dedicação e força de vontade de serem cientistas, movidas pela necessidade interior.

O Movimento da Educação Matemática no Brasil

O movimento da Educação Matemática no Brasil ficou marcado por quatro períodos distribuídos ao longo de cinco séculos, períodos políticos e administrativos que caracterizam-se dentro da história pela disposição dos dados ao longo dos cinco séculos (BURKE, 1992, p. 29). Essa história, por tomar como referência o próprio conhecimento matemático, pode ser agrupada em quatro períodos: a matemática jesuíta; a matemática militar; a matemática positivista; a matemática institucionalizada. Diferentemente daquela periodização que toma como marco os eventos político-administrativos, a periodização do conhecimento matemático é relativa no sentido de que os períodos não são rígidos na sua delimitação.

A matemática jesuíta foi marcada pela expulsão dos jesuítas do Brasil em 1759, quando o Primeiro Ministro Marquês de Pombal (1699-1782) ordenou a retirada de todos os jesuítas, pois, naquele momento, a educação era voltada para a igreja e não era interesse do Estado manter a educação dessa forma. Então, a partir do século XVII, bons matemáticos jesuítas estiveram no Brasil, uns lecionavam, outros não. Nesse período, foi mantida no Colégio de Salvador a Faculdade de Matemática, mesmo não sendo reconhecida pela metrópole. Pelos corredores do Colégio de Salvador muitos passaram, entre eles, o matemático e jesuíta José Monteiro da Rocha.

Após a descoberta do Brasil, era proibida a criação de escolas superiores, a circulação e a impressão de livros, jornais, panfletos e qualquer tipo de tipografia, o que, de certa forma, atrasou o avanço do ensino da matemática no país. A única circulação clandestina que circulava no Brasil era do jornal Correio Brasiliense, produzido por Hipólito José da Costa Pereira Furtado de Mendonça (1774 - 1823), brasileiro refugiado em Londres que, após fugir para Portugal, edita e publica o jornal, cuja matéria é subversiva pelas autoridades portuguesas.

A criação das escolas jesuítas partiu dos interesses missionários da Companhia de Jesus e da política colonizadora, porém a primeira escola criada no Brasil visava à leitura e à escrita, conhecida como Escola Primária de Letras, idealizada em 1549, por Padre Manuel da Nóbrega (1517-1570), tendo como primeiro mestre-escola o jesuíta Vicente Rijo Rodrigues (1528-1600).

Em 1550, com a chegada do jesuíta Leonardo Nunes em São Vicente-SP, foi construída a segunda escola primária do país, porém não havia o ensino da Matemática. Com o primeiro curso de Artes criado em 1572, no colégio Salvador-BA, estudava Matemática, Lógica, Física, Metafísica e Ética. A base do ensino da matemática naquele momento era algarismo ou aritmética, seguindo até o conteúdo matemático da faculdade de matemática, onde era possível estudar Geometria Euclidiana, trigonometria, equações algébricas, juros, razão e proporção. As aulas eram ministradas pelos jesuítas, dentre eles: Inácio Stafford, Aloísio Conrado Pfeil, Manuel do Amaral, Valentim Estancel, Filipe Bourel, Jacobo Cocleo ou Jacques Cocle, Diogo Soares, Domingos Capassi e João Brewer.

Foram fundados pelos jesuítas dezessete colégios, desses dezessete, apenas oito ofertavam os cursos de Artes ou Filosofia, a maioria tinha como objetivo interesses de ordem religiosa, formar religiosos. Em 1573, fundou-se o Colégio na cidade do Rio de Janeiro, fundado pelos jesuítas, que, posteriormente, ofertariam o curso de Artes, que continha em seu currículo o estudo da Matemática. No ano de 1575, são concedidos os primeiros títulos de bacharéis e licenciados aos alunos do Colégio da Bahia. Nesse mesmo colégio, no ano de 1578, formam-se as primeiras turmas de mestres em Artes, e, em 1581, os primeiros títulos de doutores aos alunos de Teologia. Assim, podemos conceder aos jesuítas o título de pioneiros no ensino da Matemática no Brasil.

Nos Colégios da Bahia, Recife, Pernambuco e Rio de Janeiro, em 1605, iniciaram aulas de aritmética e, entre seus tópicos, eram abordados Razões e Proporções, Geometria Euclidiana Elementar, marcando um avanço gradativo e positivo no ensino da Matemática, esse caminho percorrido pelo ensino da matemática possibilitou, em 1757, a criação no Colégio de Salvador da Faculdade de Matemática.

Para os jesuítas, a Matemática é organizada como um recurso auxiliar no processo educacional de Física e de Geografia, e apenas em 1757 se torna um ensino separado. De acordo com Valente (2007, p. 32), apesar de existirem entre os jesuítas alguns homens que se dedicavam ao desenvolvimento da Matemática enquanto Ciência, “a generalização dos estudos matemáticos como cultura escolar dos colégios Jesuítas parece ter fracassado ou, no mínimo, não ganhou destaque como Ciência, nem entre os professores e nem como disciplina” (VALENTE, 2007, p. 32).

Porém, enquanto o Brasil estava estagnado no ensino da matemática, nesse mesmo período a Europa avançava consideravelmente no ensino de Matemática. De acordo com Morales, Ambrósio, Magalhães e Pedrassoli (2003, p. 27-28), cria-se o Método Científico por Galileu; desenvolve-se o simbolismo da Álgebra Clássica por Recorde, Viete, Bombelli, Oughtred e Harriot; já se resolvem equações de 3º e 4º graus, com Cardano e Tartáglia; criam-se as frações decimais por Stevin, e os logaritmos com Napier e Briggs; desenvolve-se a Teoria dos Números com Fermat; ocorrem avanços na Geometria Analítica com Fermat e Descartes, e na Geometria Projetiva com Descartes e Pascal; desenvolve-se o Cálculo Diferencial e Integral com Fermat, Cavalieri, Barrow, Leibniz e Newton. Também estão se dando aplicações do Cálculo Diferencial e Integral em todas as Ciências e os embriões da Topologia e das Geometrias não Euclidianas.

Apesar da grande expansão e do avanço no ensino da Matemática, no Brasil, o retardo deve-se ao fato de os ingressantes nos cursos superiores da companhia de Jesus serem padres ou teólogos, não tendo interesse nessa área de formação científica, fazendo com que se distanciassem as concepções e a produção da Matemática europeia. Essa desvalorização leva a lacunas entre a produção e o aprendizado, consequentemente, levando a um retardo no ensino da matemática como ciência.

Com a expulsão dos jesuítas em 1759, o ensino da Matemática tomou novos caminhos, o que fez muitos jesuítas se desligarem da ordem e muitos permaneceram no Brasil, recebendo o título de bacharel em Canônes pela Universidade de Coimbra. Dessa forma, em 1772, foi a Faculdade de Matemática, cuja proposta metodológica era pautada na Universidade de Coimbra. Mesmo assim, durante muitos anos, a metrópole não considerava os títulos de graduados concedidos aos acadêmicos dos colégios jesuítas no Brasil, isso impedia os graduandos de prosseguirem seus estudos na Universidade de Coimbra, pois eram obrigados a repetir em Coimbra todo o curso realizado no Brasil. Somente no ano de 1689, o reino concedeu aos colégios dos jesuítas um estatuto civil, esse fato foi importante, pois aqueles estudantes que queriam estudar fora do país não precisavam passar por exame de equivalência ou repetirem o curso em Coimbra.

[...] Foi assim dado o primeiro passo para a intervenção da ordem de Santo Inácio de Loyola na instrução pública portuguesa. Depois esta Ordem, lutando com a pertinácia que a caracteriza contra as resistências que se lhe opunham, subiu pouco a pouco em influência até conquistar o domínio completo da instrução universitária e depois o de toda a instrução nacional. Decaíram todos os ensinos, exceto o da Filosofia racional e o da Teologia, únicas ciências que mereceram a atenção dos invasores do ensino português [...]” .(TEIXEIRA apud OLIVEIRA, 1989, p. 17)

Vale atentar-se a que, com a expulsão dos jesuítas, ficou uma lacuna enorme na instrução primária. Outras ordens religiosas tentaram se estabelecer no Brasil, abrindo suas escolas de primeiras letras com autorização da metrópole, ordens como: Beneditinos, Franciscanos, Carmelitas.

A ordem franciscana montou um projeto para instalação de uma faculdade, porém a matemática ficaria de fora. A proposta era estudar hebraico, grego, filosofia, eclesiástica, entre outros, chegando a ser aprovada pela metrópole, em 1776, cujo estatuto seguia o de Coimbra, porém não aconteceu a fundação da faculdade. Nessa fase de escolas elementares, as aulas eram frequentadas apenas pelos meninos e, posteriormente, para as meninas.

Em meados do século XVI, entre as classes existentes no país, estavam as classes que eram conduzidas por não religiosos. No ano de 1578, no Rio de Janeiro, o professor de Aritmética, o escrivão Francisco Lopes, ministrava suas aulas para classes particulares. O ensino da matemática, principalmente nas escolas elementares, eram apenas as quatro operações algébricas, não prosseguia além disso. Dentro das salas de aula, nas escolas dos jesuítas, utilizavam-se livros que eram produzidos por inicianos, tais como: Elementos Matemáticos e Teoremas Matemáticos, ambos escritos pelo jesuíta Inácio Stafford (1599-1642). Livros que foram impressos em Lisboa no ano de 1636.

Em 1772, acontece a reforma da Universidade de Coimbra, considerada como a reforma do ensino público português, período anterior a Marquês de Pombal, que refletiu até D. João V. Os envolvidos não percebiam o atraso cultural, apenas os diplomatas de outros países europeus é que percebiam o atraso científico e cultural em que se encontrava Portugal e suas províncias. Nesse período, inicia uma nova fase dentro da educação, inicia-se a Matemática Militar, pois uma parte da elite cultural do país permaneceu aberta ao desenvolvimento cultural e científico. Surge, então, a Academia Militar, em respeito à qualidade do ensino jesuíta da época. O matemático F. Gomes Teixeira argumenta:

[...] Mas, depois que no século XVII a Astronomia e a Física helénicas caíram, os jesuítas portugueses ficavam como estonteados diante das novas ciências que as substituíram, como se ameaçassem a própria igreja católica, e continuavam a ensinar as velhas doutrinas astronómicas e físicas dos antigos mestres, convencidos certamente de que estavam apenas diante de uma crise das doutrinas escolásticas, diante de uma vaga destruidora que passasse [...]” .(TEIXEIRA apud OLIVEIRA, 1986, p. 84)

Nesse período, surgem duas fases no desenvolvimento do Positivismo: o pré-positivismo, século XVIII; o positivismo de Comte, início do século XIX, refletindo de formas diferentes no ensino da matemática no Brasil. O pré- positivismo tinha aversão à religiosidade e à metafísica, buscava a simplicidade, clareza, possuía representações exatas e precisas, possuía uma metodologia uniforme a todas as ciências. Para Silva (1999), durante o período colonial e no início do Império, a influência marcante no Brasil é a do pré-positivismo propagado em Portugal por um pedagogo e um político. A proposta educacional foi ampla e atingiu a Universidade de Coimbra, com o reconhecimento da profissão de professor de matemática, em 1772, assim a Matemática passa a ser obrigatória em todos os cursos de graduação da Universidade de Coimbra. Seguindo essa linha, é criada a Academia Militar do Rio de Janeiro, em 1810, sem fugir da concepção da Universidade de Coimbra, em que a Matemática ganha destaque e é reconhecida e aplicada como a disciplina principal e voltada para as ciências experimentais, que se tornaria mais tarde uma fonte de difusão do positivismo de Comte no Brasil.

4914 Auguste Comte Fonte: pt.wikipedia.org.Último acesso: Acesso em: 20 dez. 2016.

Auguste Comte (1798-1857), natural de Montipellier - França, filósofo de formação politécnica, escritor e professor de Matemática, que havia sido secretário de Henri de Saint-Simon (1760-1825), autor, positivista, defendia e ajudou a fundar o Socialismo. Tendo entre suas obras a de maior relevância, intitulada de “Curso de Filosofia Positiva”, em seis volumes publicados entre 1830 e 1842. Em sua Filosofia Positiva, Comte aplica às ciências sociais os métodos racionais utilizados na Matemática para extrair as leis que regem o desenvolvimento da sociedade, atribuindo um papel social à ciência. Assim, o positivismo busca classificar todos os fenômenos por meio de um reduzido número de leis naturais e invariáveis, sendo que o estudo dos fenômenos deve começar dos mais gerais ou mais simples e, a partir deles, conseguir a ordenação nas ciências, até alcançar os mais complicados ou particulares.

A partir das ideias de Comte, o qual ordenava as ciências, que a Matemática passou a ser vista como educação científica, passou a ser a primeira ciência a atingir o estado positivo devido às leis com aplicações universais, mesmo sendo a mais simples de todas as ciências. O método experimental da Matemática é, inclusive, o único aceito pelas pesquisas positivistas, garantindo a neutralidade e a objetividade do conhecimento, sem descartar o rigor do conhecimento e a racionalidade técnica.

As principais características da filosofia positivista são:

1. O estudo da ciência positiva fornece-nos o único meio racional de pôr em evidência as leis lógicas do espírito;
2. a filosofia positiva deve conduzir a uma transformação do nosso sistema de educação;
3. o ensino científico pode ser considerado como a base da educação geral, verdadeiramente racional;
4. a filosofia positiva pode ser considerada como a única base sólida da reorganização da sociedade .(SILVA, 1999, p. 39)

Essas características fizeram com que o positivismo de Comte exercesse influência no Brasil após o início do Império, encontrando uma forte adesão entre os docentes de Matemática e engenheiros da Academia Militar, iniciando no Rio de Janeiro e se espalhando por todo o território nacional:

Muitos historiadores consideram a influência do positivismo no Brasil como um fenômeno único e afirmam inclusive que a Matemática desempenhou um papel essencial na introdução e divulgação do positivismo no país. O motivo disso é que houve no Brasil uma instituição que desempenhou um papel decisivo para isso – a Escola Militar do Rio de Janeiro. Lá, a ideologia positivista encontrou uma forte sustentação e pôde, então, atingir a vida social, política, pedagógica e ideológica brasileira. Os docentes de Matemática desempenharam um papel muito importante na propagação das idéias positivistas. Nessa escola, a Matemática era, inclusive, a disciplina principal. Durante um período de mais de cem anos (1810-1920), a Academia Militar do Rio de Janeiro (e todas as suas ramificações: Escola Central, Escola Militar, Escola Politécnica, Escolas preparatórias) foi praticamente a única instituição onde os brasileiros poderiam adquirir conhecimentos matemáticos sistemáticos de nível superior e obter um diploma de bacharel e doutorado em ciências físicas e Matemáticas .(SILVA, 1999, p. 13)

No Brasil, o positivismo encontrou condições para sua propagação, em meio a um momento polÍtico, uma nova burguesia sendo formada com pessoas intelectuais e com militares que lutavam contra a monarquia

Segundo Silva (1999), uma das prováveis razões para o grande sucesso dessa filosofia entre os meios acadêmicos militares é que não havia no país uma tradição em pesquisa científica, e o modelo da ciência construída como uma prática técnica estava de acordo com as aspirações dos alunos e docentes.

Em meados do século XX, a década de 50 fica marcada por transformações internacionais, período pós-guerra, muito confronto polÍtico e ideológico. O Brasil passava por um período democrático e de expansão econômica. A matemática passava por um período de estruturação, pois, até o momento, o ensino tradicional prevalecia.

Nesse período, ocorre a Matemática institucionalizada. Trata-se do período no qual ocorre a expansão das instituições que ofertam cursos com Matemática e que trabalham com a matemática, como, por exemplo: Institutos de Pesquisas, Universidades, Escolas e Sociedades Científicas. Mesmo com cursos superiores já abertos, é somente em meados do século que ocorre a expansão dos cursos, período em que será definido o que será trabalhado, aumentando e incentivando o intercâmbio entre outros países, como França e Estados Unidos.

As sociedades do Brasil: SBEM, SBM, IMPA, entre outras

A partir da década de 1920, a sociedade intelectual brasileira passou a se mobilizar para ações que se voltassem a pesquisas e publicações científicas, iniciando um trabalho para conscientizar a nação das necessidades em buscar grandes soluções aos problemas da época que envolviam educação, saúde, economia, entre outros.

Surgem então movimentos voltados a interesses comuns, um dos movimentos foi intitulado de Semana da Arte Moderna, em 1922, realizado na cidade de São Paulo, envolvendo escritores e artistas.

41014 Semana da Arte Moderna em 1922 Fonte: saopaulonaoquersercinza.wordpress.com.Último acesso: Acesso em: 20 dez. 2016.

Com a Semana da Arte Moderna, possibilitou-se o intercâmbio entre países, abrindo as portas para o conhecimento. A Sociedade Brasileira de Ciências, criada em 03 de maio de 1916, que passou a ser chamada de Academia Brasileira de Ciências ( ABC), trata-se de uma associação de direito privado, sem fins lucrativos, com sede na cidade do Rio de Janeiro, tendo por objetivo contribuir para o desenvolvimento da ciência e da tecnologia, da educação e do bem-estar social do País, inicialmente direcionava suas produções para três áreas: Ciências Matemáticas, Ciências Físico-Químicas e Ciências Biológicas, cujo foco era estimular o trabalho científico e o desenvolvimento da pesquisa brasileira, pois tratava-se de fator fundamental para o desenvolvimento tecnológico do Brasil.

Em 1920, a ABC ativa o programa de intercâmbio com cientistas de instituições estrangeiras, onde vários cientistas vieram ao Brasil para realizar cursos e conferências, entre eles: Jacques Hadamard (1865-1963), Emile Borel (1871-1956) e Albert Einstein (1879-1955).

Em 1948, surge a Sociedade Brasileira para o Progresso da Ciência – SBPC. Trata-se de uma associação civil, de direito privado, sem fins lucrativos, laica e sem caráter político partidário, situada na cidade de São Paulo, tem como objetivo contribuir para o desenvolvimento científico e tecnológico do país. Sua primeira reunião ocorreu em 1951 na cidade de Belo Horizonte, passando a integrar a sociedade científica, inclusive a tratar de conhecimentos matemáticos, um dos seus posicionamentos mais relevantes refere-se à defesa da pesquisa e da Universidade Pública. Após 1940, foram fundadas as primeiras sociedades científicas do Brasil.

Fundada em 1945, a primeira Sociedade de Matemática de São Paulo, que acabou sendo extinta em 1969, deu continuidade aos trabalhos fundando a segunda Sociedade de Matemática Brasileira, que foi a Sociedade Paranaense de Matemática - SPM, criada em 1953. Trata-se de uma associação civil de caráter educacional, com sede em Curitiba-PR, porém deslocou sua sede para Maringá-PR. A SPM tem por fim congregar todos os cultores da Matemática e ciências afins do Paraná, estimular e manter um interesse ativo pela Matemática e suas aplicações, incentivar a pesquisa e contribuir para o aperfeiçoamento desse ramo das ciências.

Instituto Nacional de Matemática Pura e Aplicada - IMPA foi a primeira unidade de pesquisas criada pelo Conselho Nacional de Pesquisas - CNPq, fundada em 1951, seu interesse sempre foi voltado à pesquisa científica. Localizada na cidade do Rio de Janeiro, seu intercâmbio era estimulado e conta com uma das melhores bibliotecas do país.

41114 IMPA Fonte: www.impa.br.Último acesso: Acesso em: 20 dez. 2016.

Outras sociedades foram fundadas posteriormente e merecem ser destacadas:

Sociedade Brasileira de Matemática – SBM, fundada em 1969 com sede no Rio de Janeiro, trata-se de uma associação civil, com direito privado, sem fins lucrativos. De acordo com o seu Estatuto (SOCIEDADE BRASILEIRA DE MATEMÁTICA, 2015. Disponível em: www.sbm.org.br. Acesso em: 20 dez. 2016), estabelece como finalidade:

A SBM tem por finalidades:
I. congregar os matemáticos e professores de Matemática do Brasil;
II. estimular a pesquisa de alto nível em Matemática e assegurar sua divulgação através de publicações próprias;
III. estimular a melhoria do ensino de Matemática em todos os níveis;
IV. promover a divulgação de conhecimentos de Matemática;
V. incentivar e promover o intercâmbio entre os profissionais de Matemática do Brasil e do exterior;
VI. zelar pela liberdade de ensino e pesquisa, bem como pelos interesses científicos e profissionais dos matemáticos e professores de Matemática no Brasil;
VII. promover a implantação e zelar pelo constante aprimoramento de altos padrões de trabalho e formação científica em Matemática no Brasil;
VIII. oferecer assessoria e colaboração, no campo da Matemática, visando o desenvolvimento do país; e
IX. oferecer assessoria, colaboração, divulgação, distribuição e outras atividades relativas à produção de livros e periódicos didático-científicos, especialmente no tocante aos assuntos correlatos às finalidades da SBM descrita nos incisos anteriores.

A partir disso foram criadas outras sociedades, entre elas:

• A Sociedade de Matemática Aplicada e Computacional - SBMAC, fundada em 1978, trata-se de uma sociedade civil e cultural aberta de caráter não lucrativo, com sede em São Carlos-SP. Seu principal objetivo é congregar profissionais, estudantes e instituições que tenham interesse pela computação aplicada e computacional.
• Sociedade Brasileira de Educação Matemática – SBEM, criada em 27 de janeiro de 1988, é uma associação civil, sem fins lucrativos, de direito privado, de âmbito nacional, sem qualquer vinculação política ou religiosa, tem como objetivo promover o desenvolvimento da área da educação matemática, e a sua implementação na práxis educativa, tendo como missão:
• A SBEM tem como objetivo buscar condições para o desenvolvimento propício da formação matemática de todo cidadão de nosso país. Para que isso seja colocado em prática, ela conta com a colaboração de profissionais e alunos envolvidos com a área de Educação Matemática e com áreas afins, e procura promover o desenvolvimento desse ramo do conhecimento científico por meio do estímulo às atividades de pesquisa e de estudos acadêmicos. É também objetivo da SBEM a difusão ampla de informações e de conhecimentos nas inúmeras vertentes da Educação Matemática.

Além das sociedades, outras associações e iniciativas ocorreram e influenciaram diretamente o Ensino da Matemática. Em 1924, foi fundada a Associação Brasileira de Educação - ABE, sua maior preocupação era a qualidade da educação. Em 1932, ocorreu o Manifesto dos Pioneiros, marco importante na educação nova, tendo como precursor Anísio Teixeira. A Associação Brasileira de Educação passou a estimular a publicação de jornais e artigos científicos.

Em 1930, foram criadas revistas periódicas com intuito de absorver temas de matemática pura e aplicada:

1. Jornal da Matemática Pura e Aplicada. Essa foi a primeira revista dedicada a trabalhos de pesquisa Matemática publicada no Brasil;
2. Summa Brasiliensis Matemática, fundada em 1945, revista de nível internacional financiada pelo Instituto Brasileiro de Educação Ciência e Cultura do Rio de Janeiro. Em 1968, foi publicado o seu último fascículo;
3. Boletim da Sociedade de Matemática de São Paulo. Seu primeiro volume foi publicado em 1946 e seu último volume foi publicado em 1966.
4. Revista Científica, essa publicação era da responsabilidade do Departamento de Matemática, Física, Química e História Natural da Faculdade Nacional de Filosofia;
5. Anuário da Sociedade Paranaense de Matemática, revista fundada em 1950 e interrompida em 1960;
6. Boletim da Sociedade Paranaense de Matemática, fundada em 1958;
7. Revista do Professor de Matemática e Matemática Universitária. Publicações da SBM. Ambas fundadas em 1969 no VII Colóquio Brasileiro de Matemática;
8. Matemática Aplicada e Computacional, uma revista da SBMAC, fundada em 1978.

História da Matemática como Tendência de Ensino

Como vimos, a ênfase inicial da matemática ocorreu na aritmética e na mensuração prática; uma arte especial começou a tomar corpo para o cultivo, aplicação e ensino dessa ciência prática. Nesse contexto, todavia, desenvolvem-se tendências no sentido da abstração e, até certo ponto, passou-se então a estudar a ciência por si mesma.

Atualmente, as pesquisas voltadas à educação matemática vêm ganhando espaço e crescendo em grande escala, porém ainda não alcançou a unanimidade entre os pesquisadores. O que se observa é que cada pesquisador possui e desenvolve uma metodologia, mas essa diversidade nos conduz a interpretações e análises para entender a Matemática como uma ciência. Ao longo de nossas leituras e reflexões, identificamos que a Matemática precisa de uma reestruturação, devido à complexidade, à visão única que os envolvidos possuem para essa ciência.

O grande problema enfrentado na educação Matemática é devido à falta de interpretação e organização, pois a maioria das aulas de matemática segue o ensino mecanizado, e os envolvidos seguem modelos prontos e ensino mecânico; não se envolvem com a construção do seu próprio conhecimento.

Os registros nos mostram a evolução e a linha do tempo traçada pela Matemática, construindo e registrando a sua história, com as mudanças acontecendo de forma gradativa na maneira de ensinar. Com o passar do tempo, torna-se necessária uma atenção especial ao ensino da matemática, pois as mudanças acontecem em todo o momento, a evolução da espécie em todo instante. e o ensino da matemática precisa acompanhar essas mudanças. Podemos dizer que a sociedade passa por transformações profundas, decorrentes do ritmo acelerado dos avanços científicos e tecnológicos.

E, diante dessas transformações, o professor de Matemática está sendo desafiado constantemente e passa a trabalhar com um campo investigativo, onde o professor passa a construir seus próprios métodos, até mesmo dentro das academias, as literaturas são voltadas para a necessidade de uma abordagem metodológica diferenciada. Assim, surgem as Tendências educacionais no ensino da Matemática, construindo um novo processo de ensino e de aprendizagem.

As novas metodologias e abordagens pedagógicas levam ao uso de materiais concretos, jogos e atividades lúdicas nas aulas de Matemática. As atividades despertam o interesse do ser humano tornando as aulas atrativas e significativas, levando o ser humano a resolver problemas, em diversas situações, utilizando movimentos cotidianos para problematizar, produzindo conhecimento partindo desses métodos.

Com isso, apresentamos a seguir as tendências metodológicas que integram e agregam o ensino da Matemática na atualidade, são elas:

Etnomatemática, Modelagem Matemática, Mídias Tecnológicas, História da Matemática, Investigação Matemática e Resolução de Problemas.

Etnomatemática

os primeiros rumores sobre Etnomatemática surgiram na década de 1970, pautados nas críticas sobre o ensino tradicional da Matemática, fazendo uma análise sobre as práticas matemáticas e considerando seus diferentes contextos culturais de conhecimento. É também considerada como uma interdisciplinaridade entre a cognição, a epistemologia, a história, a sociologia e a difusão.

 

41214 Ubiratan D’Ambrosio Fonte: historiadamatematica.webnode.com.Último acesso: Acesso em: 22 dez. 2016.

 

Seu pioneiro foi Ubiratan D’Ambrósio, nascido em 1932, na cidade de São Paulo. Em 2016 completou 84 anos. Doutor em matemática, é um teórico da educação Matemática e um dos pioneiros no estudo da etnomatemática, aliás termo que foi proposto pelo próprio Ubiratan, com intuito de descrever as práticas matemáticas dos grupos culturais em que estão inseridos, seja em uma comunidade, um grupo religioso, entre outros. Etnomatemática, cujo significado é:

• ETNO = ambiente natural, social, cultural e imaginário;
• MATEMA = explicar, aprender, conhecer, lidar com;
• TICA = modos, estilos, artes, técnicas.

 

Então, Etnomatemática é a arte ou técnica de explicar, de entender, de desempenhar na realidade dentro de um conceito cultural próprio. A Etnomatemática possibilita um campo de informações claras e evidentes para a educação Matemática, transformando a sala de aula em uma microcultura, considerando os aspectos sociológicos e cognitivos prévios que o aluno carrega consigo.

São várias as atividades pedagógicas que envolvem as diversas culturas, ou seja, são várias atividades com as quais pode-se trabalhar com a etnomatemática, atividades como exploração de figuras geométricas, atividades com tapeçarias, entre outras atividades artísticas.

Para a aplicar em sala de aula, sabemos que cada indivíduo carrega consigo conhecimentos prévios e pré-estabelecidos, sua própria cultura, entre outros fatores. Em uma sala de aula, existe o encontro de culturas que devem ser consideradas e respeitadas, porém, mesmo diante da diversidades em sala de aula, é possível notar algo em comum entre eles, é em cima desse ponto comum que o professor trabalhará, aplicando a etnomatemática, partindo do senso comum e aplicando o conhecimento acadêmico.

Trabalhando com os conceitos prévios dos alunos, o professor se interage dos costumes, possibilitando ao aluno perceber se os conceitos que ele tem são válidos ou não e assim estabelecer mudanças. Isso exige muita disponibilidade do professor. Os principais trabalhos nessa linha são: D’Ambrosio (1986); Carraher, Carraher e Schlieman (1988), entre outros.

 

Modelagem matemática

É defendida e conceituada por diversos pesquisadores e autores. Mesmo sendo conceituada por diversos autores, todos acordam que a modelagem matemática se trata de uma arte de transformar problemas da realidade em problemas que possam ser resolvidos na sala de aula, por meio da análise de resultados.

A modelagem Matemática é uma parceira da Etnomatemática e caminham juntas, mesmo defendendo ideias diferentes. A modelagem Matemática iniciou no Brasil por volta de 1960, com o Professor Ubiratan D`Ambrosio, tendo contribuição e destaque dos matemáticos Aristides Camargos, Rodney Carlos Bassanezi.

 

41314 Aristides Carmargo Barreto Fonte: www.furb.br. Último acesso: Acesso em: 22 dez. 2016.

 

Aristides Camargos Barreto, um dos precursores da modelagem matemática, teve seu primeiro contato com a modelagem matemática na década de 1960, quando cursava Engenharia. Isso fez com que, em 1970, amadurecesse a ideia de usar a modelagem em Educação Matemática. Então, em meados desse mesmo ano, inicia um trabalho na PUC-Rio, pois, nesse período, Barreto passou a atuar como professor nessa mesma Instituição. Na PUC-Rio, Barreto sempre foi um homem curioso e que gostava de inovar, tornar suas aulas agradáveis e atrativas, sendo assim, sempre procurava utilizar-se de modelos como estratégia de ensino nas disciplinas de Fundamentos da Matemática, Prática de Ensino e Cálculo Diferencial Integral. Em 1976, realizou a primeira experiência pedagógica com 212 alunos de um Curso de Engenharia. Conjuntamente com os alunos, elaborou vários modelos em áreas específicas, como Linguística, Ecologia, Biologia, dentre outras.

 

41414 Rodney Carlos Bassanezi Fonte: www.furb.br.Último acesso: Acesso em: 22 dez. 2016.

 

Nos anos 80, mais precisamente na década de 1980, eis que começa a despertar outros matemáticos com interesses comuns sobre a Modelagem Matemática, então começa a se destacar Rodney Carlos Bassanezi, que, naquele período, coordenava outro curso. Também com o apoio da OEA- Organização dos Estados Americanos e promovido na IMECC-UNICAMP, esse curso foi ministrado para 30 professores da disciplina de Cálculo Diferencial Integral, de diversas Instituições de Educação Superior da região sul do Brasil, com duração de uma semana. Nesse curso, não havia método pré-estabelecido, ou melhor, não se pretendia fazer uso do método tradicional de ensino. Assim, em primeiro momento, após ‘bate-papo’ com os participantes, foi proposto a eles que se reunissem por 2h e apresentassem um problema que envolvesse o Cálculo Diferencial e Integral para a solução. Então, depois de duas horas de discussões, percebeu-se que a maioria dos problemas propostos era igual aos que se apresentavam nos livros-texto, sem criatividade. Foi quando Bassanezi, com sua percepção dinâmica, viu nessa situação o momento exato para propor a modelagem matemática, em particular, na resolução de problemas de biologia aplicados ao Cálculo Diferencial Integral (biomatemática).

Para desenvolver um trabalho pautado na modelagem matemática, é necessário estabelecer um tema, explorar esse tema, levantar os problemas diante desse tema, resolver esses problemas levantados; em seguida, uma análise das resoluções. Muitas vezes, para atender e trabalhar dentro da Modelagem, é necessário romper sequências estabelecidas. A modelagem Matemática passa a ser uma alternativa metodológica que contribui para o ensino da Matemática, principalmente em turmas de Educação Básica, tornando-se uma estratégia desafiadora, capaz de romper barreiras tão rígidas que o ensino tradicional construiu, onde espera um ensino no qual o aluno participa da construção dos conceitos e dos conhecimentos matemáticos.

 

Mídias tecnológicas

Para ser professor no século XXI, é necessário dominar as mídias, ou elementos, conhecer as máfias, pois o uso das novas tecnologias está sendo implantado nas escolas. A tecnologia não pode ser usada apenas como pretexto de modernização, mas também como ferramenta que auxilia o trabalho do professor, com intuito de aprimorar as práticas pedagógicas.

As questões tecnológicas inovam as aulas de Matemática e, quando o professor insere a tecnologia em suas aula, é capaz de torná-la significativa. Vieira Pinto cita que: “A escolha das técnicas a utilizar e o sentido que lhes dará depende da atitude de cada um, no 3 cultivo de finalidades verdadeiramente humanas, no esforço pela eliminação das circunstâncias naturais e sociais nocivas.” (PINTO, 2006, p. 746).

O professor é o precursor da aprendizagem, o mediador do processo de ensino e aprendizagem, em uma abordagem didático-dialética com os alunos; as mídias e o estudo do conhecimento matemático, no contexto social, é possível para estabelecer defesa e produção de vida digna.

A sociedade está envolvida com a tecnologia e se estrutura a partir dela, cabe ao professor fazer com que os envolvidos reconheçam a matemática como uma atividade social, “[...] o conhecer reflexivo tem de ser desenvolvido para dar à alfabetização matemática uma dimensão crítica” (SKOVSMOSE, 2006, p. 118).

Infelizmente, em algumas escolas, as mídias tecnológicas são pouco utilizadas, isso deve-se ao fato dos profissionais não estarem preparados para atuar com esses recursos tecnológicos, ou seja, mesmo com escolas equipadas, o problema vai além da dedicação e vontade do professor ou do sistema educacional.

 

História da matemática

Entre as tendências educacionais, destaca-se a História da Matemática, visto que conhecer e resgatar conhecimentos vivenciados é um passo para aulas significativas e codificar conhecimento, pois, ao ler a História da matemática, ela nos mostra que as grandes descobertas matemáticas surgiram pela curiosidade do homem.

 

Investigação matemática

De acordo com as Diretrizes Curriculares do Estado do Paraná (2009), a prática pedagógica da investigação matemática vem despontando como um caminho aceito e recomendado por muitos estudiosos como forma de proporcionar ao aluno uma melhor compreensão da disciplina. As atividades investigativas devem ser desafiadoras e preparadas com antecedência pelo professor, que poderá usar um mesmo texto com questões diferentes aos grupos participantes. Podemos dividir em três etapas a atividade de investigação: a introdução da tarefa, a sua realização pelos alunos com acompanhamento do professor e a discussão/reflexão entre alunos de grupos diferentes com a participação do professor.

O conceito de investigação matemática, como atividade de ensino-aprendizagem, ajuda a trazer para a sala de aula o espírito de atividade matemática genuína, constituindo, por isso, uma poderosa metáfora educativa. O aluno é chamado a agir como um matemático, não só na formulação de questões e conjecturas e na realização de provas e refutações, mas também na apresentação de resultados e na discussão e argumentação com seus colegas e o professor .(PONTE; BROCARDO; OLIVEIRA, 2009, p. 23)

 

Essa metodologia foi uma estratégia de superar o ensino tradicional, meramente repetitivo, mecanizado e técnico da Matemática, em que a investigação matemática considera que o aluno é capaz de resolver as atividades propostas a partir do momento que ele percebe que faz parte do processo, que a sua presença é útil para solucionar desafios e, consequentemente, navegar em descobertas.

Essa tendência de aprendizagem é favorável, pois incentiva a socialização, o compartilhamento de opiniões e ideias, favorecendo um ambiente democrático, no qual é permitida a exposição de ideias, representando significativamente uma mudança nas aulas tradicionais de matemática.

 

Resolução de problemas

é por meio dessa tendência que se mantém alinhado com as demais tendências, dessa forma, entendemos que a resolução de problemas é a tendência com que a matemática mais se envolve, pois os problemas são importantes por envolver novas ideias.

De acordo com Polya (2006), à medida do possível, é importante que os problemas sejam provocativos, pois, quando o aluno é desafiado, suas emoções de entusiasmo na busca de solução são despertadas. Em seus textos, o professor deve instigar a curiosidade mediante problemas, gerando uma satisfação com a descoberta do resultado, podendo ativar talentos, porém devemos atentar-se para que os problemas devem ser de acordo com a faixa etária do aluno.

Outro fator importante é a explicação e a contextualização que o professor fará ao propor a resolução de problemas, é preciso deixar claro aos alunos que não será uma tarefa fácil e que poderemos chegar ao resultado de diversas maneiras, e que a leitura flutuante não agrega no aprendizado e tampouco contribuirá na resolução do problema. Então, para resolver problemas, é preciso compreendê-los, elaborar um plano de ação, executá-lo e, por fim, verificá-lo.

 

Reflita

Como as Tendências educacionais estão influenciando e contribuindo com as aulas de matemática?

 

Fique por dentro

Você pode conhecer mais sobre o ensino de Matemática no Brasil consultando o site a seguir: repositorio.ufsc.br.