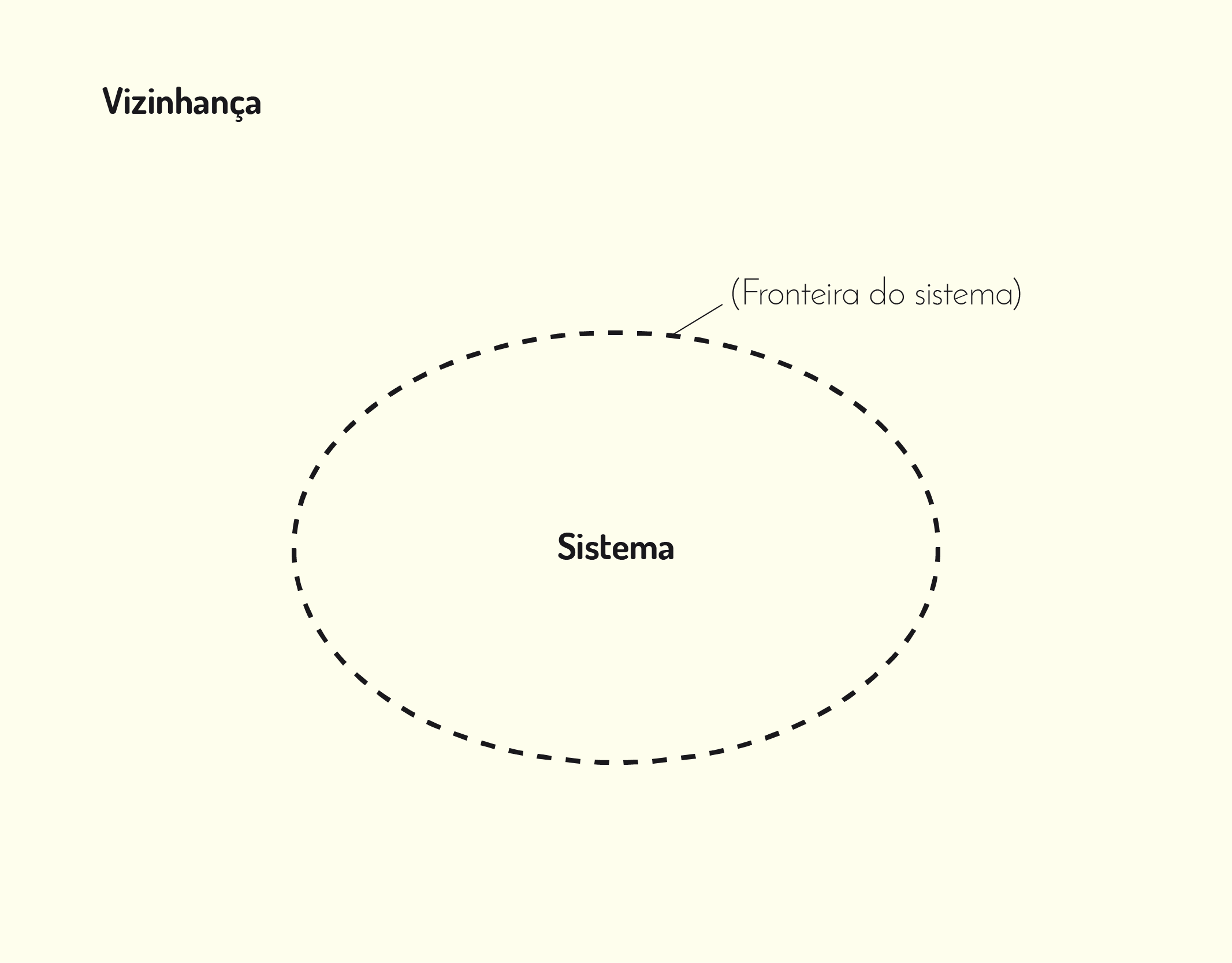
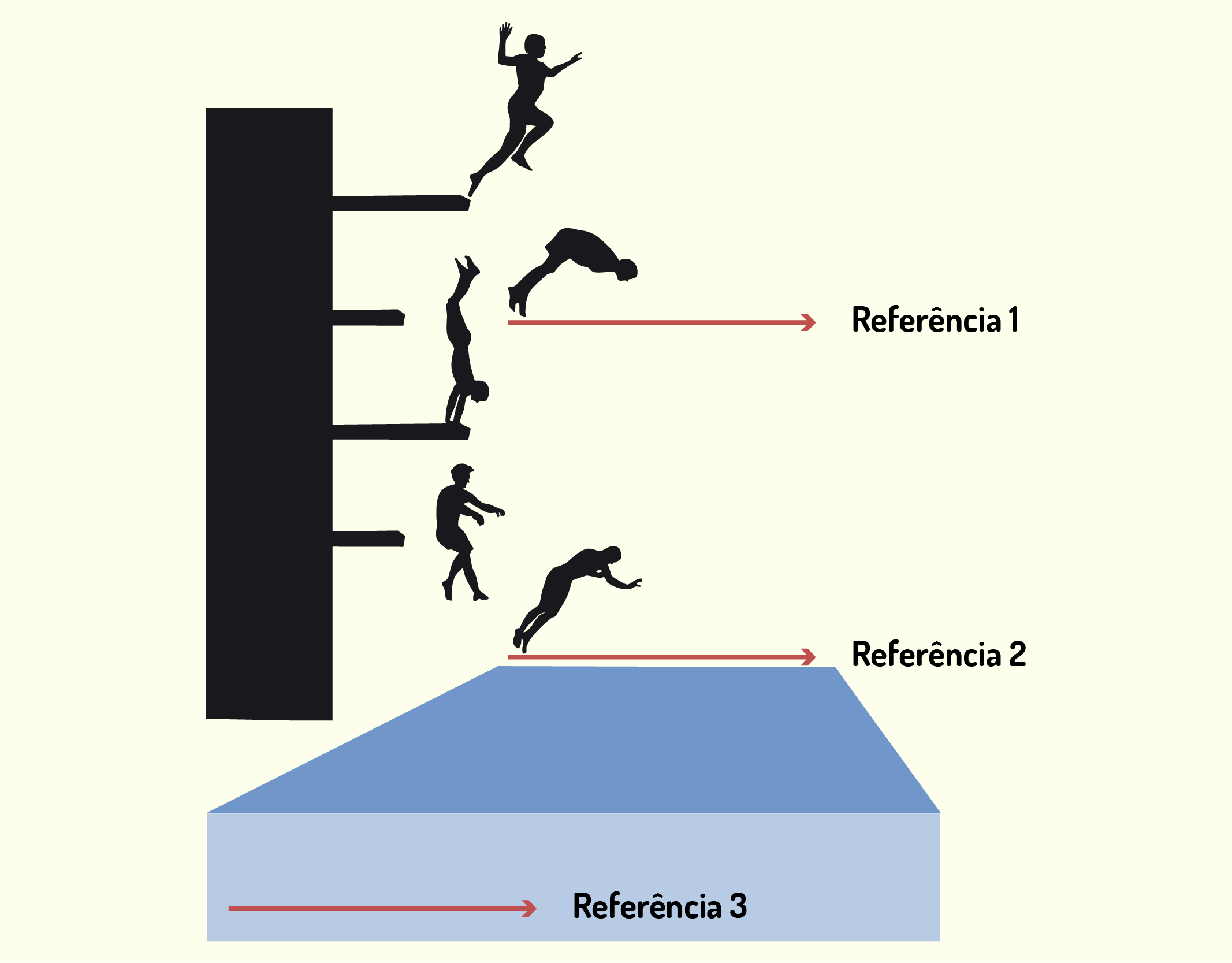
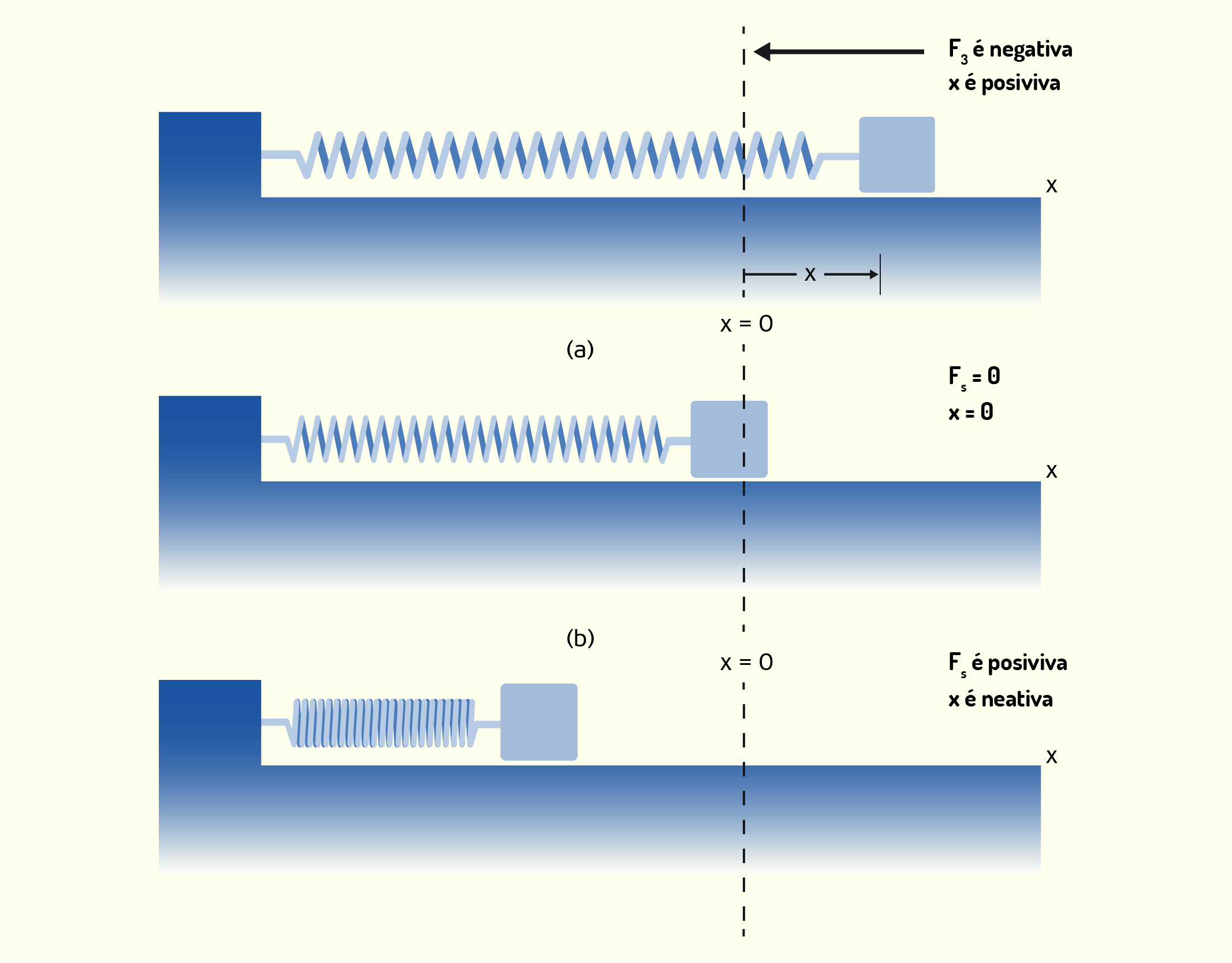
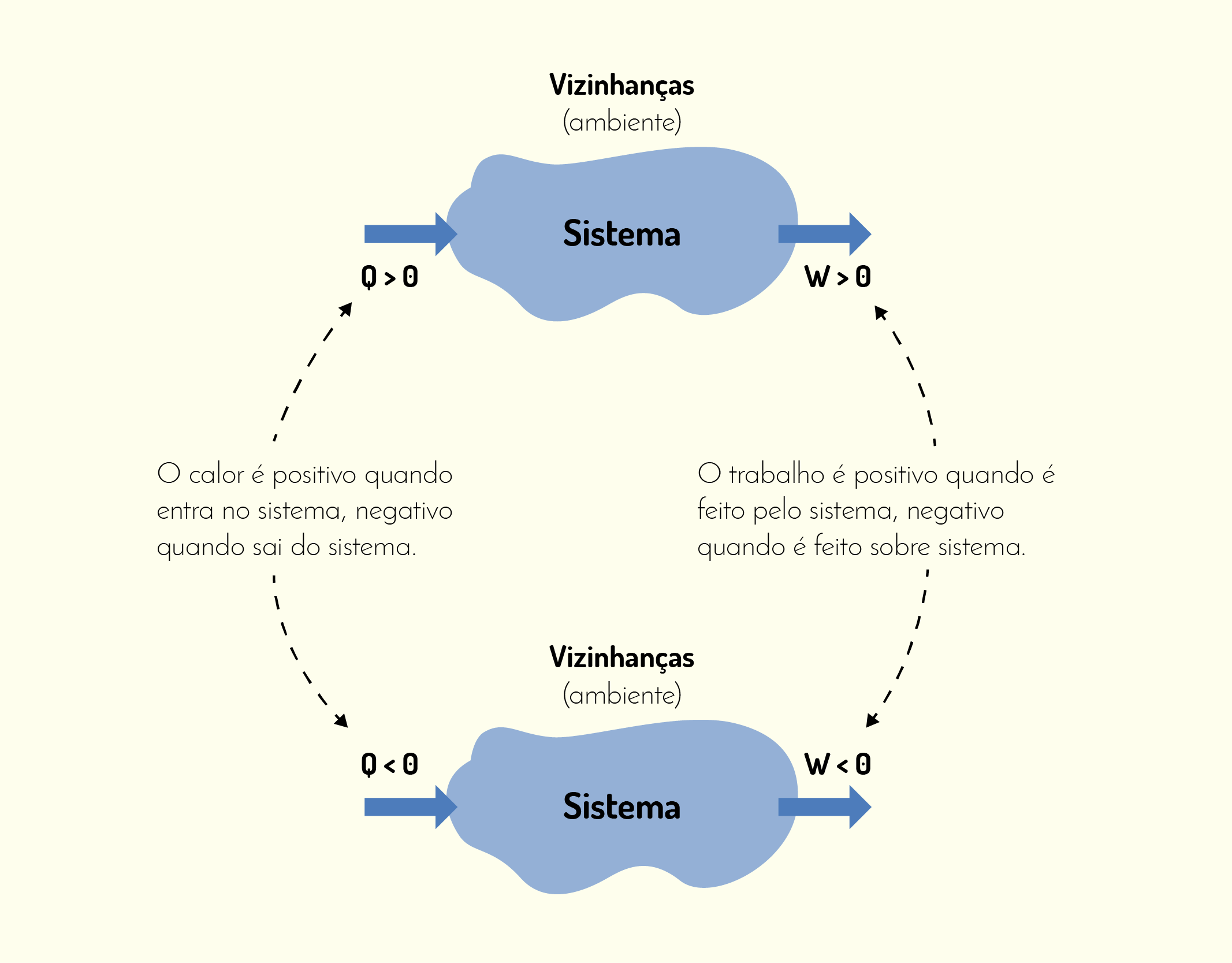
Sobre Ciência
Então a Física serve somente para explicar os movimentos naturais? Não. A física da natureza está presente em diversas áreas do conhecimento. Nas áreas de estudo da química, você sabe quem explica a estrutura das moléculas de qualquer elemento natural? A Física, a partir da análise das forças que atraem as partículas, consegue estabelecer uma explicação para isso. Além disso, a Física está presente também em todas as construções de engenharia, pois o engenheiro, ao projetar a estrutura, deve entender os princípios físicos presentes em sua construção.
A seguir, nós aprenderemos e veremos alguns exemplos de como algumas teorias físicas foram criadas, ou seja, vamos observar qual é a natureza das teorias e grandezas físicas.
Natureza da Física
Caro(a) aluno(a), você já ouviu alguém comentando sobre a famosa história de que Isaac Newton, que, quando estava sentado à sombra de uma árvore, viu uma maçã caindo e pensou: “Por que a maçã está caindo, ao invés de flutuar? ”. A partir disso, ele desenvolveu inúmeros cálculos e teorias para explicar o porquê de a maçã ter caído.
Essa e diversas outras histórias mostram que a física é uma ciência experimental, ou seja, através da observação de fenômenos naturais, busca explicação para fatos cotidianos, sejam eles simples como o cair de um objeto ou complexos como o movimento dos planetas.
Porém, se desejarmos desenvolver uma teoria física, alguns passos precisam ser bem definidos: primeiro devemos formular perguntas específicas sobre o fenômeno que estamos observando, para então sermos capazes de criar experimentos que nos auxiliem na busca das respostas, assim, finalmente seremos capazes de chegar às conclusões pertinentes aos resultados obtidos.
Um exemplo clássico de montagem de experimentos para validação de teorias é o caso de Galileu (Galileo Galilei – 1564-1642). O filósofo queria comprovar a afirmação de Aristóteles (384 a.C. – 322 a.C.), que dizia que se duas pedras, uma mais pesada do que a outra, fossem jogadas ao mesmo tempo de uma certa altura, a mais pesada cairia primeiro. Galileu então subiu na Torre de Pisa e, ao mesmo tempo, abandonou duas esferas com pesos diferentes, observando que as duas levavam o mesmo tempo para atingir o solo. Esse experimento então serviu para invalidar a teoria de Aristóteles.
Outro experimento foi abandonar objetos bastante diferentes e com pesos muito distintos, observou então que o mais pesado atingia o solo primeiro. A partir dessa observação, ele criou uma hipótese de que a força exercida pelo ar era a responsável por retardar a queda do objeto mais leve.
Anos mais tarde, de posse de uma tecnologia mais avançada, cientistas puderam comprovar a hipótese de Galileu e ainda verificaram que, quando os corpos são abandonados de uma mesma altura no vácuo, eles demoram exatamente o mesmo tempo para cair. Isso mostra que realmente o ar era o responsável pela diferença no tempo de queda dos objetos, pois, em um ambiente com completo vácuo, não há ar nenhum exercendo forças contra os corpos.
Com esse exemplo, podemos observar que a física é originada da natureza, ou seja, ela está presente em nosso dia a dia e nas mais variadas ocasiões.
Solução de problemas de física
Provavelmente, ao estudar algum tópico de física, você deve ter se feito a seguinte pergunta: “Por que eu consigo entender os conceitos, mas não consigo aplicá-los na resolução de problemas?”. Como vimos anteriormente, a física é uma ciência experimental, então, nós só saberemos e entenderemos física se formos capazes de fazer física. Mas como assim? Para fazer física, nós estudaremos a seguir alguns métodos, por exemplo, a criação de modelos que ilustram nosso problema e o seu cenário de aplicação.
Uma estratégia bastante eficiente é a identificação de conceitos e variáveis relevantes. Ao fazer essa análise, você pode não precisar fazer nenhum cálculo, porém essa tarefa pode ser bastante desafiadora. Primeiramente, você deve conseguir identificar claramente a variável-alvo do seu problema. Por exemplo: eu quero saber qual a velocidade de uma bola de futebol que é chutada em uma cobrança de pênalti, ou então a força do soco de um lutador de boxe. Após isso, é aconselhável que você siga alguns outros passos:
- Preparação do problema: a partir da identificação feita, aconselhamos que você escolha as equações que considera mais úteis para a resolução e tente representar graficamente o problema.
- Execução: nessa etapa, você vai precisar colocar em prática todas suas habilidades com números. A partir das equações escolhidas, vamos observar quais são as variáveis conhecidas e utilizar as equações para encontrar as desconhecidas, chegando então à resposta final.
- Avaliação da resposta: com o valor encontrado, você deve observar suas grandezas, unidades. Pergunte-se também: “esse resultado faz sentido? “. Se você queria saber qual a velocidade com que a tartaruga anda, sua resposta não pode ser 150km/h, por exemplo.
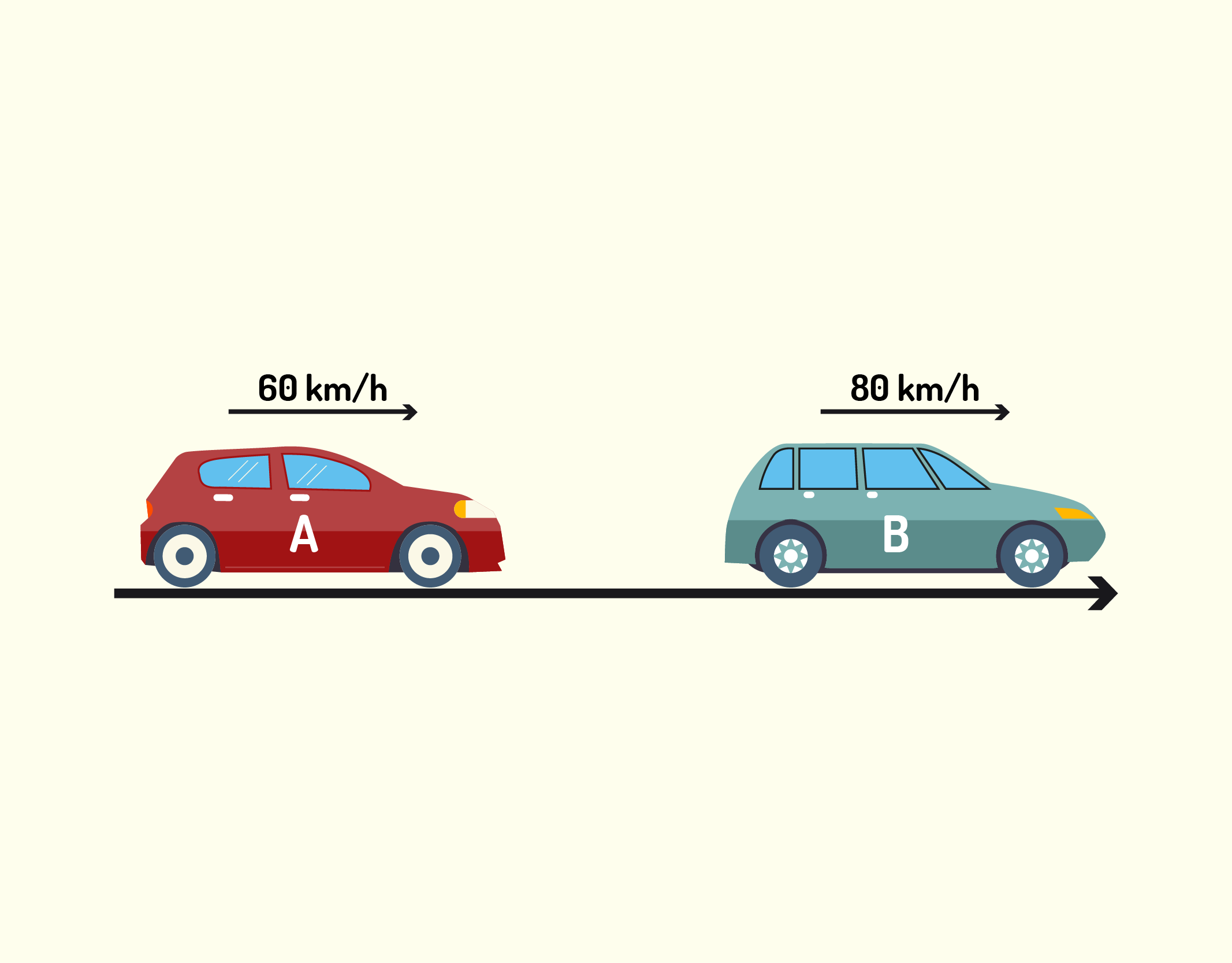
Vamos então estudar um exemplo: considere dois carros lado a lado, um a 60km/h e outro a 80km/h, sendo que o carro da frente está mais rápido do que o de trás. Qual será a distância entre eles após uma hora de movimento?
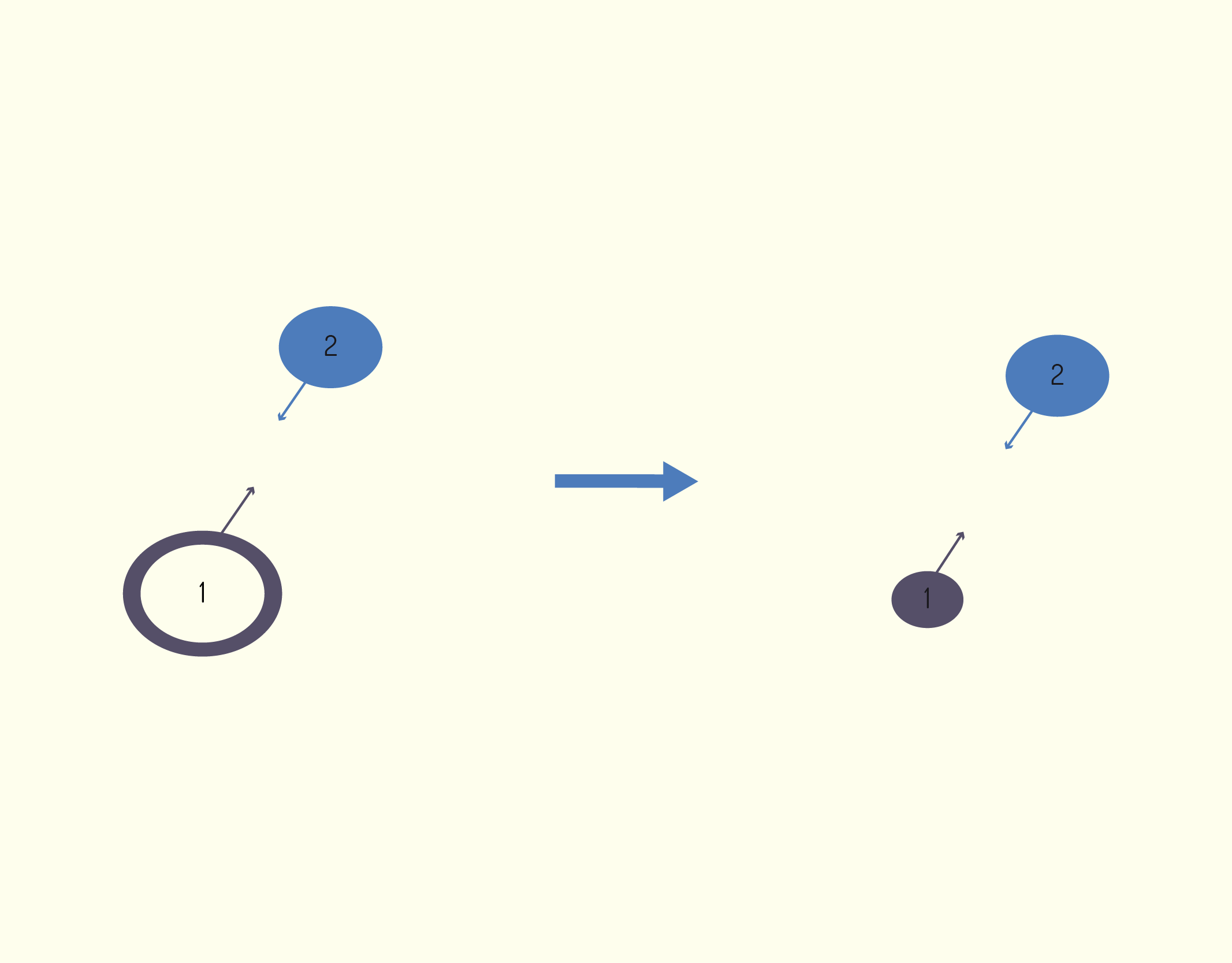
Como vimos, primeiramente, devemos identificar a variável-alvo. Nesse caso, queremos encontrar a distância (dada em metros). Como preparação, você poderá fazer um esquema semelhante ao apresentado na Figura 1, em que desenhamos o carro e escrevemos a velocidade de cada um deles.
1137 Representação da etapa de preparação de um problema Fonte: os autores.
Após isso, você deve escolher as equações aplicáveis a esse caso, analisar a velocidade relativa entre os veículos e depois chegar à resposta da distância percorrida ao longo de uma hora (considerando a velocidade relativa encontrada). Como resposta, você deveria encontrar 20km. A etapa de validação serve para você observar a realidade do problema. Se, por um acaso, você encontrar 2000km como resposta, pode pensar que é um resultado não realístico e, então, deve rever as contas feitas.
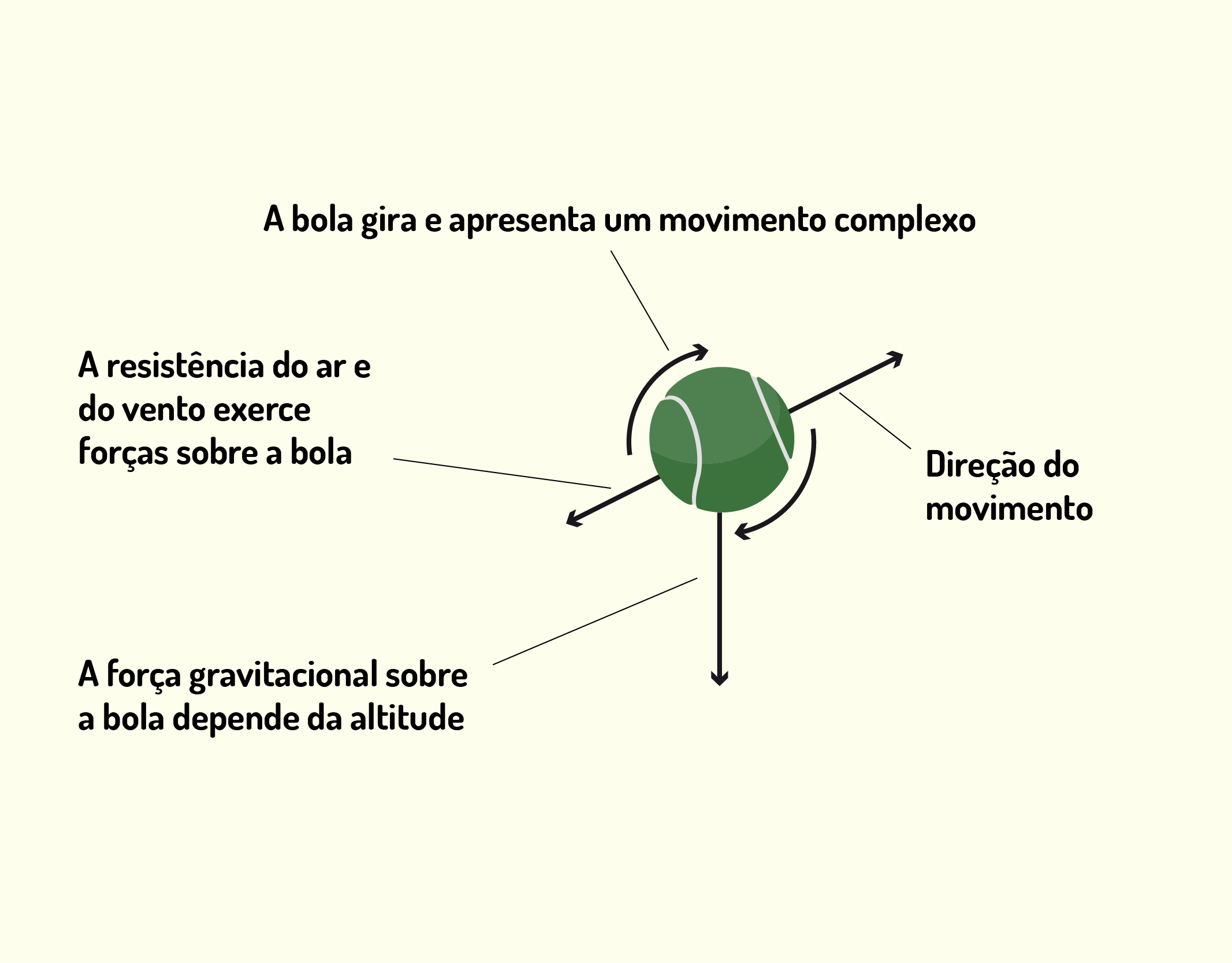
Uma outra estratégia é a criação de modelos, em que você deve tentar criar uma versão simplificada de um cenário ou sistema físico que, se observado por completo ou como é na realidade, seria complicado demais. Imagine uma bola de beisebol em movimento no ar (Figura 1.2). Isso é um sistema complicado? Na verdade, sim. A bola não é uma esfera perfeita, possui rugosidades e gira quando está no ar. A resistência do ar influencia em seu movimento e também existe a força do peso da bola. Todos esses fatores podem tornar o problema bastante complicado de ser analisado.
1237 Possíveis forças atuantes em um arremesso real de uma bola de beisebol Fonte: Young e Freedman ( 2010, p. 03).
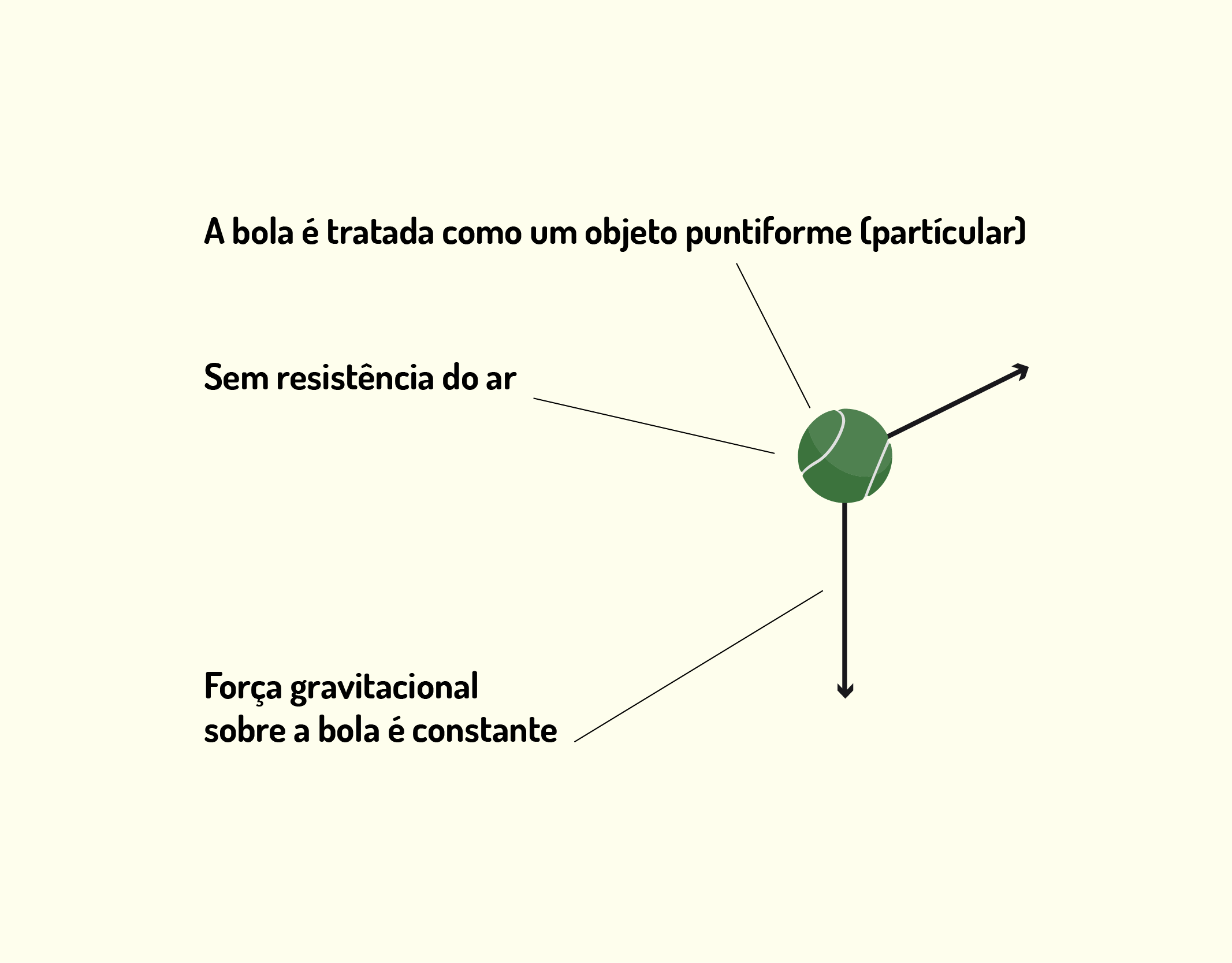
Se você for capaz de simplificar algumas interferências, é possível criar um modelo bastante simples para o movimento dessa bola. Lembra do experimento de Galileu? Então, suponha que a bola esteja no vácuo e despreze o tamanho e peso da bola, como ilustrado na Figura 1.3. Isso sim é uma versão bem mais simplificada e fácil de ser analisada.
1337 Modelização do problema do movimento de uma bola de beisebol Fonte: Young e Freedman (2010, p. 03).
Portanto, caro(a) aluno(a), se você deseja criar um modelo para seu problema, lembre-se de que será necessário fazer algumas considerações, desprezar certas forças e interferências. Porém, não podemos ser exagerados na hora de desprezar as coisas, caso contrário nosso modelo será muito distante da realidade que queremos representar.
Vetores e suas representações
Como você representa a temperatura de um forno? Podemos simplesmente falar a quantos graus Celsius (oC) ele está. Mas como você representa o movimento de um avião? Não podemos simplesmente falar a quantos quilômetros por hora ele voa. Devemos especificar também em qual direção e sentido ele está indo. Para essa segunda representação, nós utilizamos os vetores, que possuem módulo, direção e sentido.
Os cálculos feitos com grandezas escalares utilizam as operações básicas que aprendemos em matemática (soma, subtração, divisão e multiplicação). Porém, quando observamos uma grandeza vetorial, é necessário utilizar cálculos específicos.
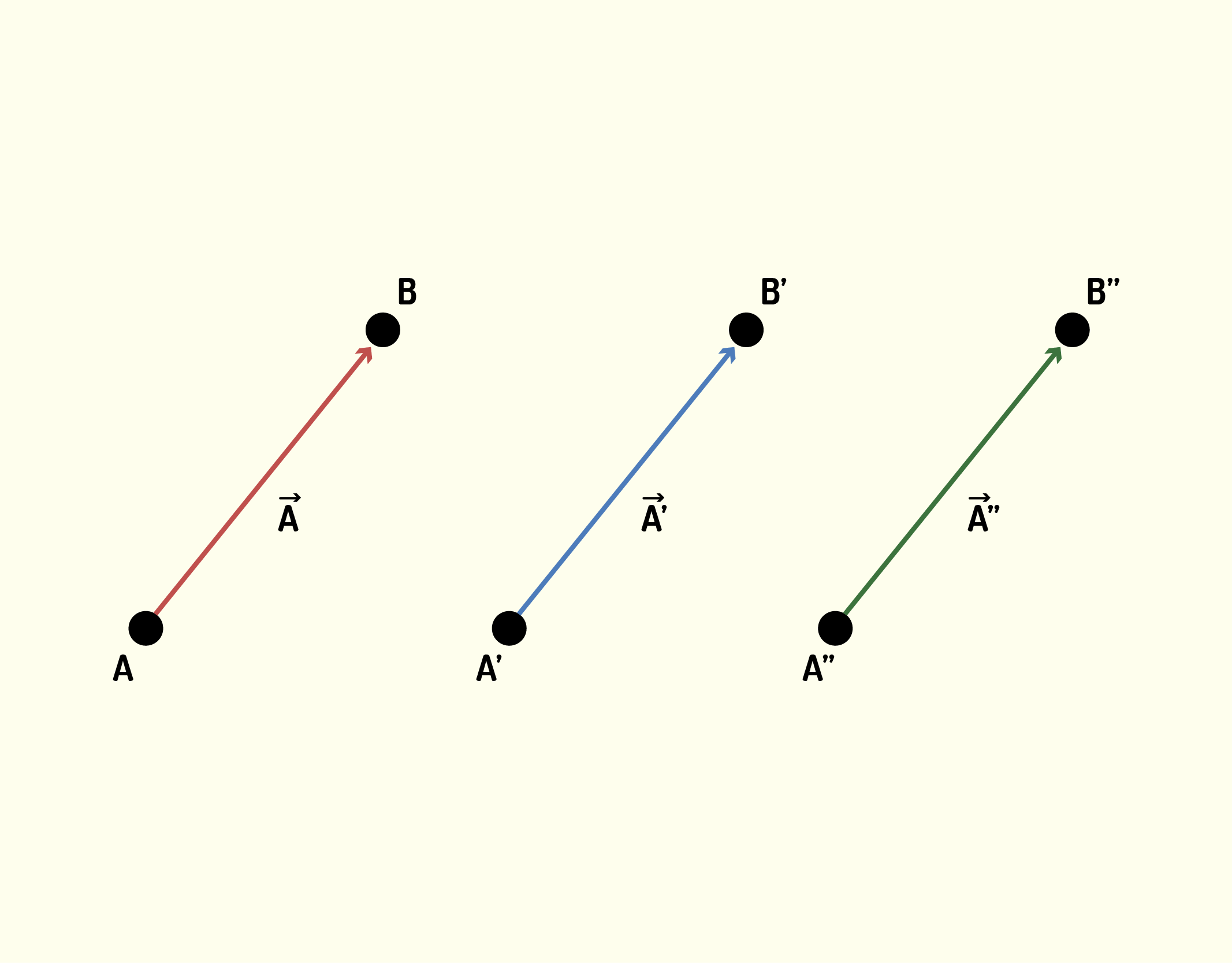
Então, como caracterizamos uma mudança de posição? É através do chamado vetor deslocamento. Observando a Figura 1.4, podemos identificar uma partícula que se moveu do ponto A para B. A seta entre os pontos é a representação gráfica do deslocamento, que é o vetor deslocamento [math]\vec{A}[/math]. Você pode observar também outros dois vetores [math]\overrightarrow{A’}[/math] e[math]~\overrightarrow{A’’}[/math] que possuem mesmo módulo e orientação e, portanto, representam a mesma variação de posição da partícula. Com isso, você já pode verificar que, na representação gráfica do vetor, o tamanho da seta indica seu módulo. Além disso, a partir de agora, um vetor será representado por uma letra em itálico e negrito com uma seta em cima.
1437 Representação gráfica de três vetores com mesmo módulo, direção e sentido Fonte: os autores.
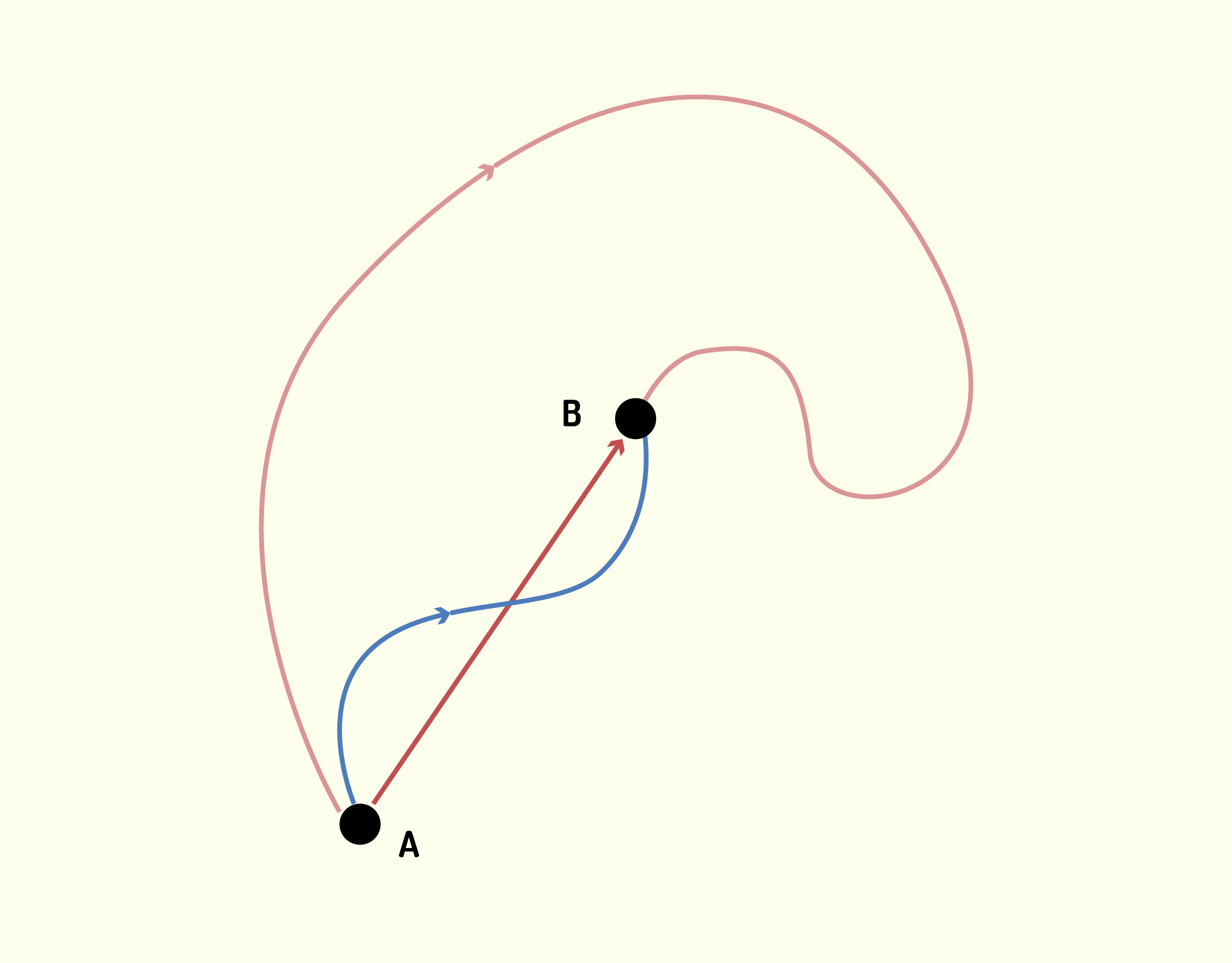
Mas o que aconteceu com a partícula durante o caminho feito entre os dois pontos? Boa pergunta. Isso nós não podemos representar apenas desenhando a flecha indicativa do vetor. Se observarmos a Figura 1.5, podemos verificar que há inúmeras alternativas para descrever a trajetória feita pela partícula.
1537 Representação gráfica de possíveis trajetórias para deslocamento entre dois pontos. Fonte: Halliday e Resnick (2012, p. 40).
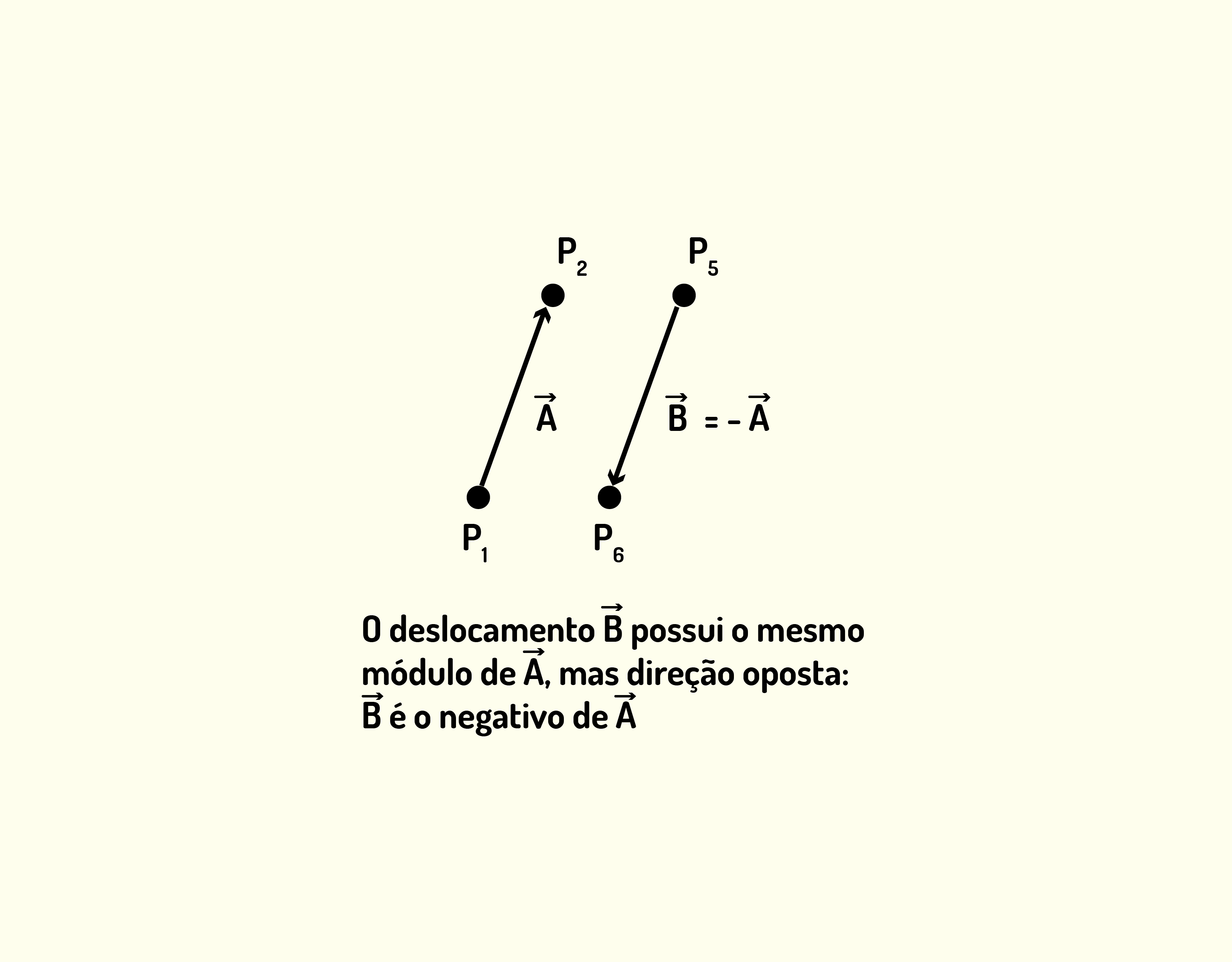
E quando os vetores estão em sentidos opostos? Neste caso, você pode dizer que um vetor é negativo (ou contrário ao outro). A Figura 1.6 ilustra esse caso, em que o vetor [math]\vec{B}[/math] possui o mesmo módulo, porém sentido contrário ao vetor [math]\vec{A}[/math]. Matematicamente, podemos expressar esses vetores como [math]\vec{A}=-\vec{B}[/math].
E se os vetores tiverem sentido contrário e módulos diferentes? Neste caso, quando dois vetores [math]\vec{A}[/math] e [math]\vec{C}[/math] possuem mesma direção, sentidos contrários e módulos diferentes, você dirá que eles são vetores antiparalelos.
Você pode estar se perguntando o que é esse “módulo” do vetor que nós tanto estamos discutindo. Basicamente é a representação da intensidade de um vetor. Sendo assim, é uma grandeza escalar sempre positiva. Matematicamente, nós representamos o módulo pela mesma letra em itálico (sem negrito) de seu respectivo vetor ou pela notação de barras verticais laterais: [math]\left( M\acute{o}dulo~de~\vec{A} \right)=A=~\left| {\vec{A}} \right|[/math].
1637 Representação gráfica de vetores negativos. Fonte: Young e Freedman (2010, p. 11).
Soma vetorial
E como representamos um deslocamento com mais de um caminho? Suponha que uma partícula faça dois deslocamentos: passe de A para B e depois para C. Como ilustrado na Figura 1.7, a representação gráfica é da mesma forma que já vimos: você deve desenhar uma seta ligando os pontos A e B e outra ligando B e C, de modo que o início da segunda seta coincida com o final da primeira, representando assim os dois deslocamentos feitos pela partícula. O deslocamento total resultante será o vetor que liga os pontos A e C.
1737 Representação gráfica da soma de vetores, desenhando a extremidade de um com o início de outro. Fonte: Young e Freedman (2010, p.12).
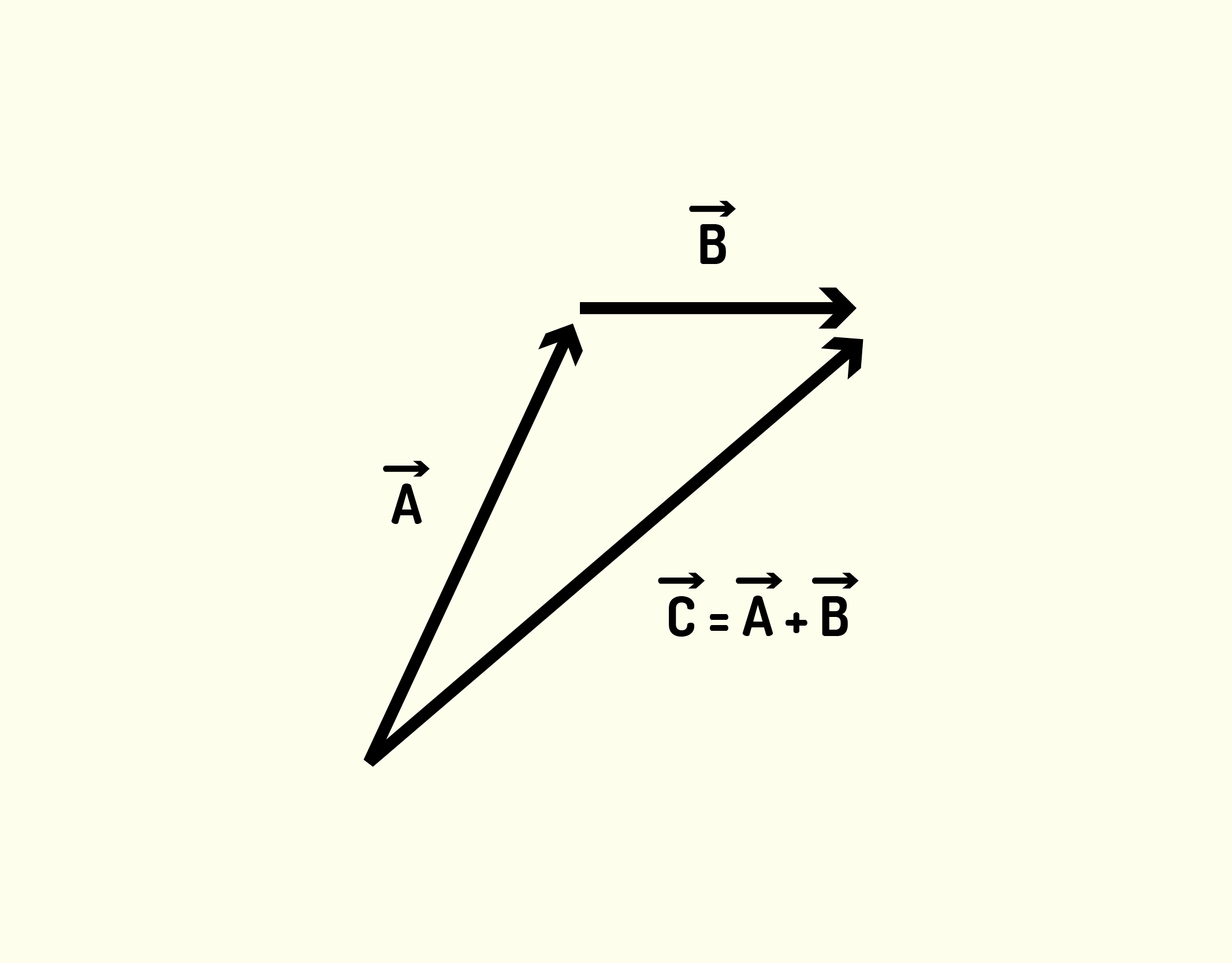
Mas como eu posso escrever matematicamente essa relação? Essa ligação é a soma vetorial expressa da seguinte forma:
[math]\vec{C}=~\vec{A}+\vec{B}[/math] (1.1)
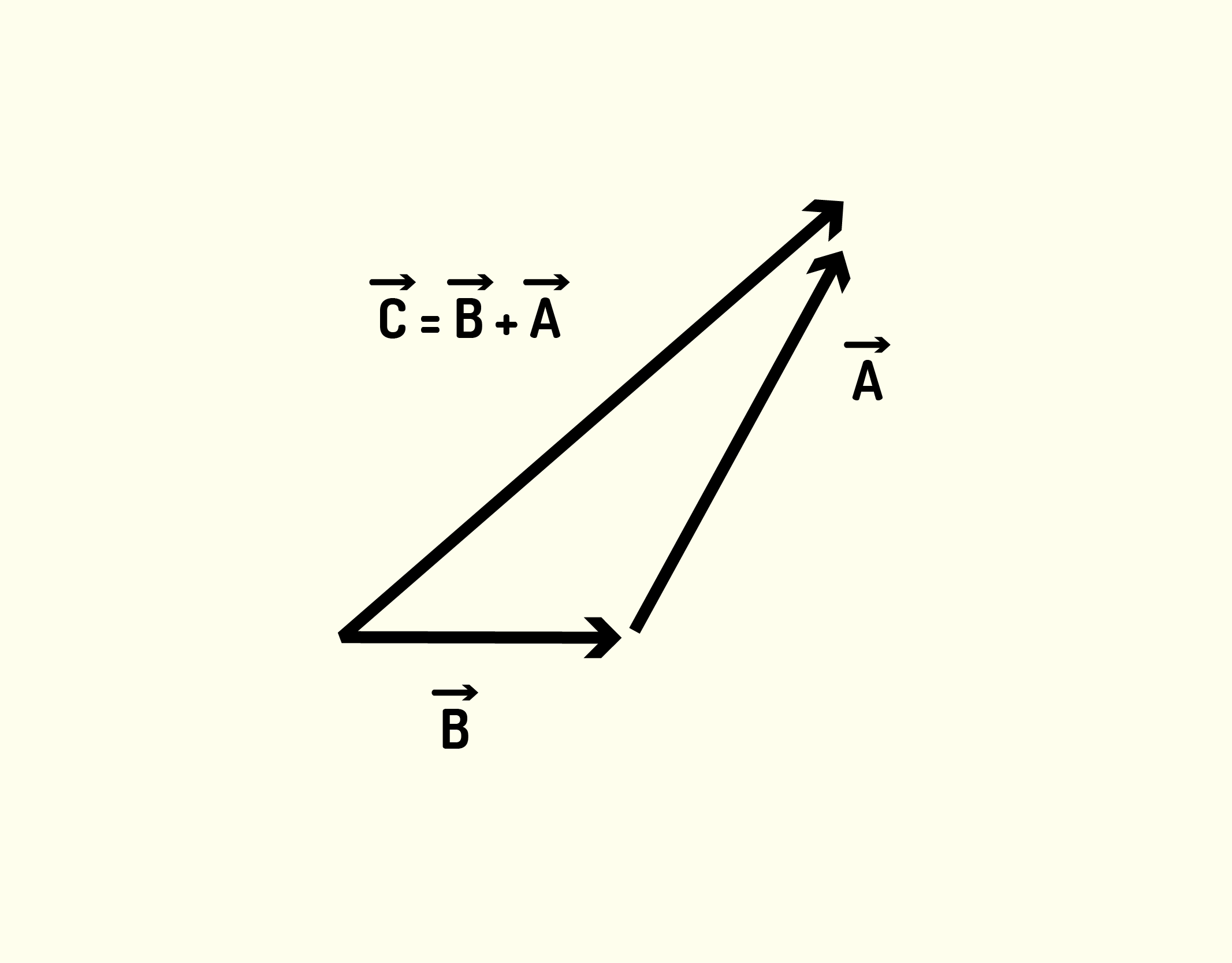
Você pode estar neste momento se perguntando se, na soma vetorial, podemos também inverter a ordem dos operandos. Se observarmos a Figura 1.8, veremos que isso é permitido, ou seja, a ordem da soma vetorial não importa. Isso é uma propriedade básica da soma vetorial, que é a comutatividade. Matematicamente, podemos então escrever:
[math]\vec{C}=~\vec{A}+\vec{B}=~\vec{B}+\vec{A}[/math] (1.2)
1837 Representação gráfica comutatividade na soma de vetores Fonte: Young e Freedman (2010, p.12).
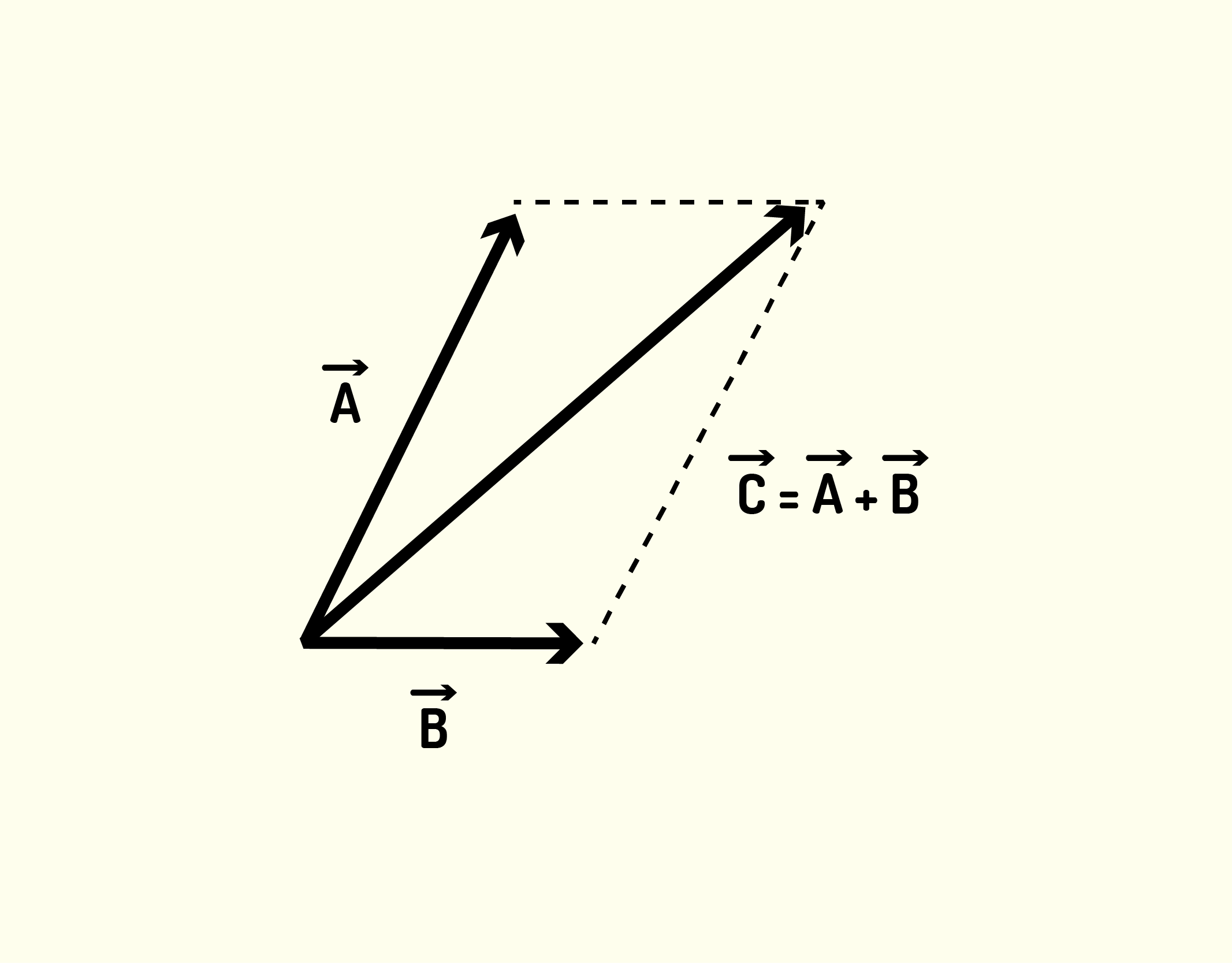
Ou então podemos fazer a soma de uma terceira forma: desenhamos uma projeção do vetor [math]\vec{A}[/math] no início de [math]\vec{B}[/math] e fazemos o mesmo para o vetor [math]\vec{B}[/math], formando assim um paralelogramo. O vetor [math]\vec{C}[/math] resultante é a ligação do ponto de origem até a extremidade oposta do paralelogramo, assim como ilustrado na Figura 1.9.
1937 Representação gráfica da soma de vetores, desenhando-se um paralelogramo Fonte: Young e Freedman (2010, p.12).
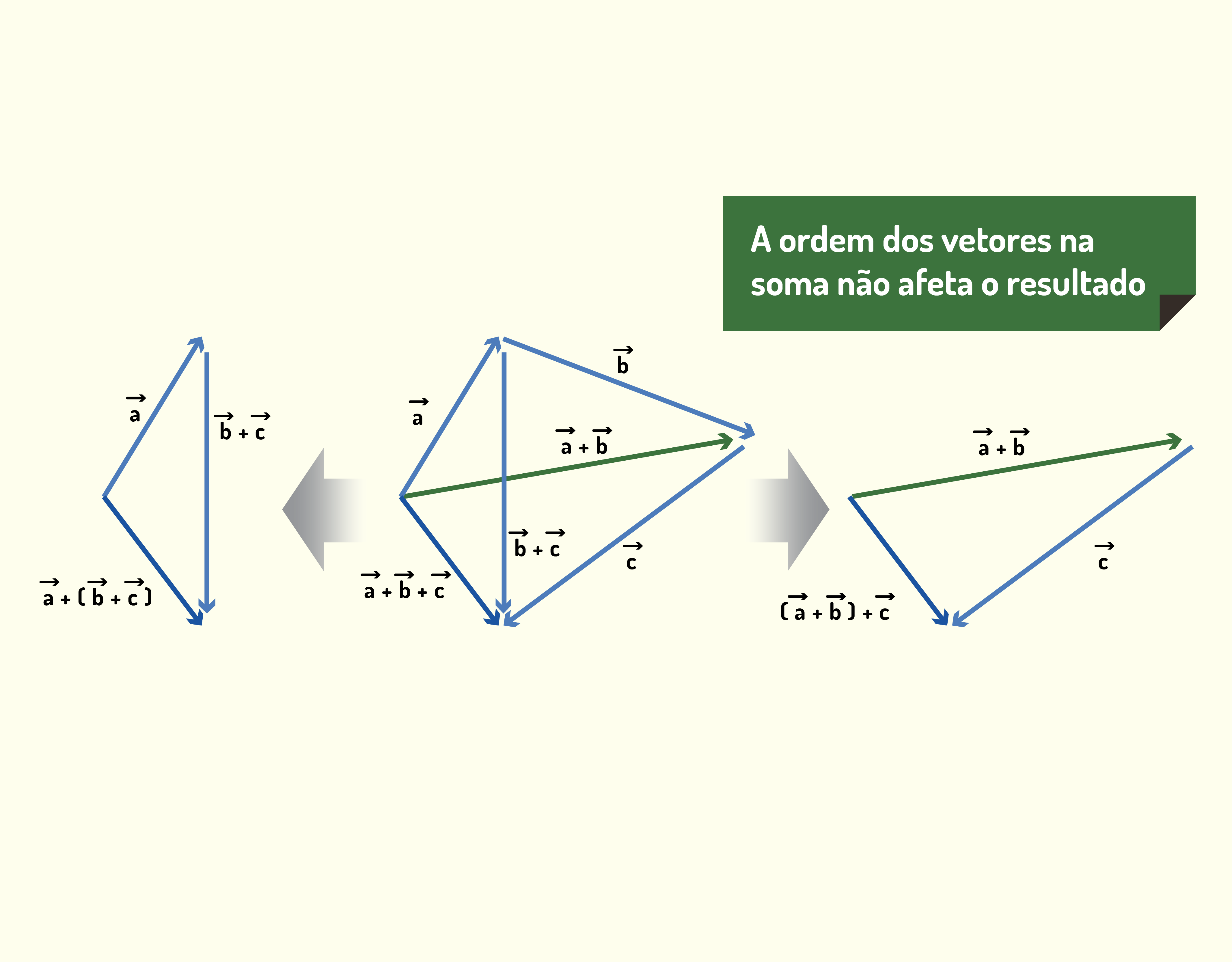
E se quisermos somar mais do que dois vetores? Primeiramente, devido à lei associativa, podemos associar a soma de qualquer forma que desejarmos, assim como descrito na Equação (1.3).
[math]\left( \vec{A}+\vec{B} \right)+\vec{C}=~\vec{A}+\left( \vec{B}+\vec{C} \right)[/math] (1.3)
Sendo que a correspondência gráfica para a Equação (1.3) é que nós podemos agrupar os vetores (coincidindo o início de um com o final de outro) de qualquer forma e o resultado será o mesmo, assim como ilustrado na Figura 1.10.
11037 Representação gráfica da soma de três vetores Fonte: Halliday e Resnick (2012, p.41).
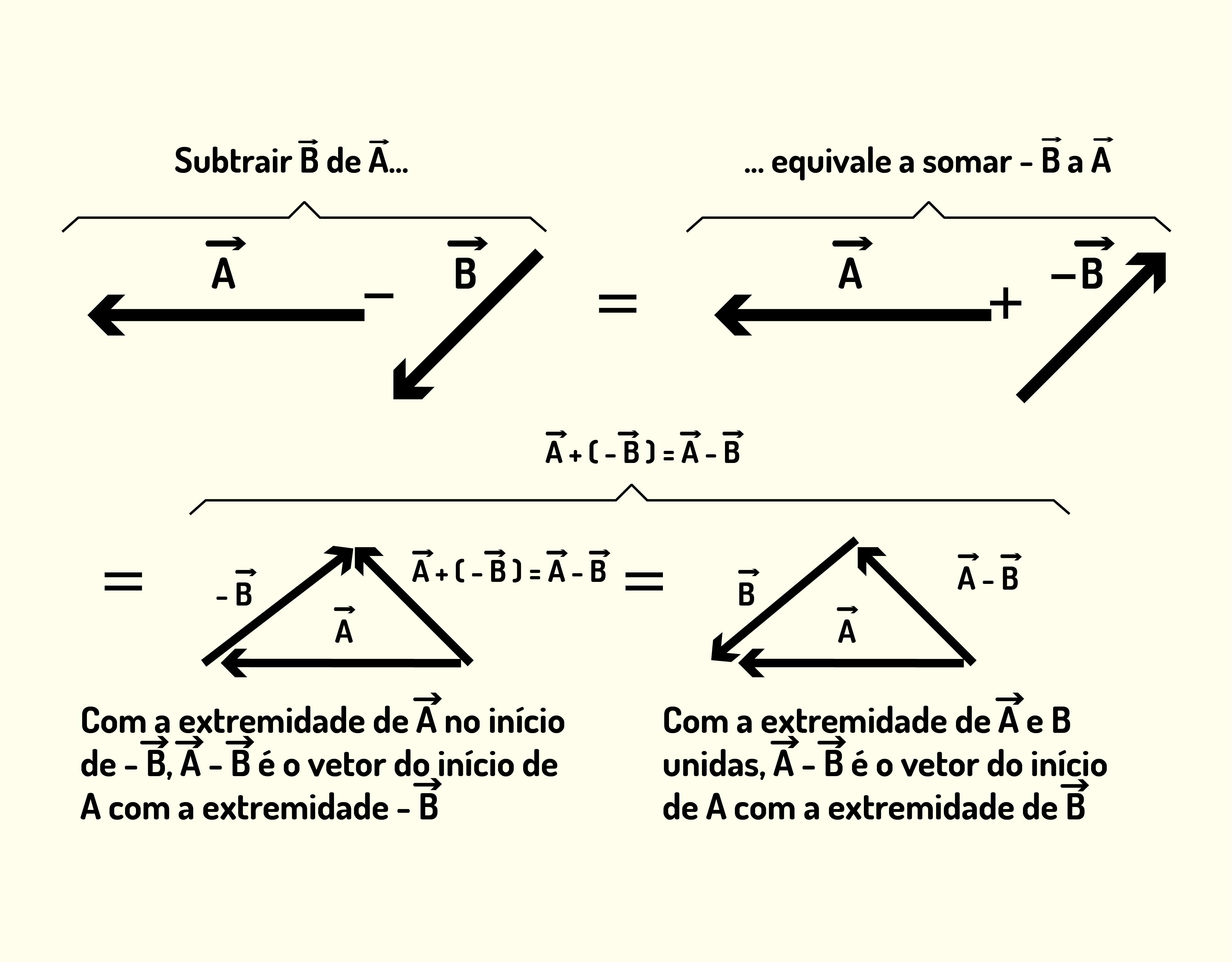
Da mesma forma que você aprendeu a fazer soma de vetores, podemos também executar operações de subtração. Por exemplo, se desejarmos fazer [math]\vec{A}-\vec{B}[/math], podemos utilizar as propriedades aprendidas para manipular a operação da seguinte forma:
[math]\vec{A}-\vec{B}=\vec{A}+\left( -\vec{B} \right)[/math] (1.4)
Sendo [math]-\vec{B}[/math] o vetor negativo de [math]\overrightarrow{B,}[/math] que, graficamente, podemos representar como descrito na Figura 1.11.
11137 Representação gráfica da subtração de dois vetores Fonte: Young e Freedman (2012, p.13).
Componentes de vetores
Caro(a) aluno(a), na seção anterior você aprendeu como fazer operações com vetores de forma gráfica. Porém, essa pode não ser a maneira mais prática e precisa, pois seria sempre necessário ter consigo réguas e esquadros para auxiliarem no desenho. Uma forma mais simples é o uso de uma representação dos vetores em um sistema de coordenadas retangulares (cartesianas). Os eixos desse sistema de coordenadas são chamados de eixos [math]{{O}_{x}}[/math] e [math]{{O}_{y}}[/math], sendo O a origem desse sistema. Para o caso de vetores tridimensionais ainda existirá o eixo [math]{{O}_{z}}[/math], mas, para simplificar, trabalharemos somente com o sistema bidimensional.
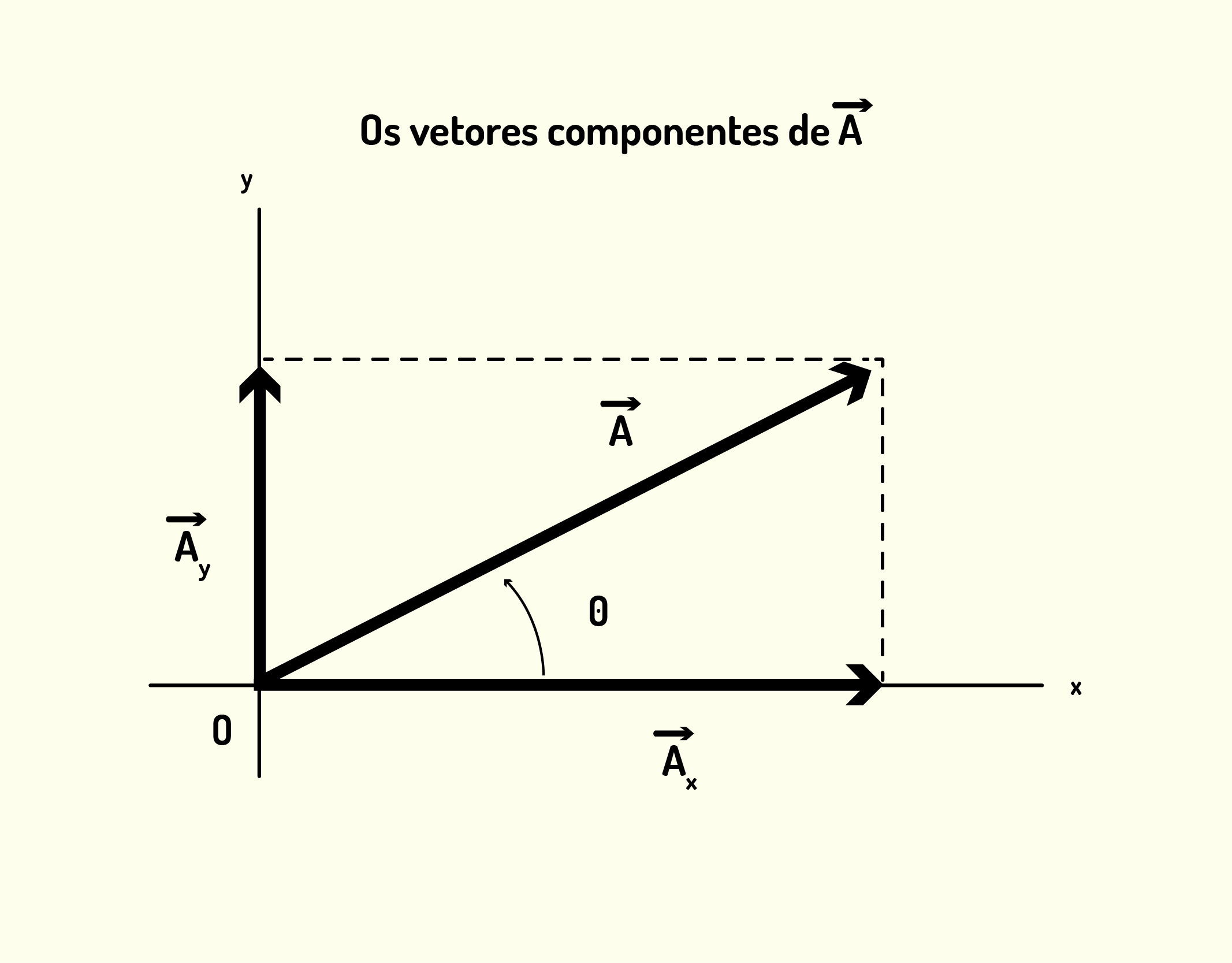
A ideia é que qualquer vetor no plano [math]xy[/math] pode ser representado como a soma de dois vetores, sendo um vetor [math]{{\vec{A}}_{x}}[/math] paralelo ao eixo [math]{{0}_{x}}[/math], e outro [math]{{\vec{A}}_{y}}[/math], paralelo ao eixo [math]{{O}_{y}}[/math]. Esses vetores paralelos são chamados de vetores componentes do vetor [math]\vec{A}[/math], que pode ser escrito como:
[math]\vec{A}={{\vec{A}}_{x}}+{{\vec{A}}_{y}}[/math] (1.4)
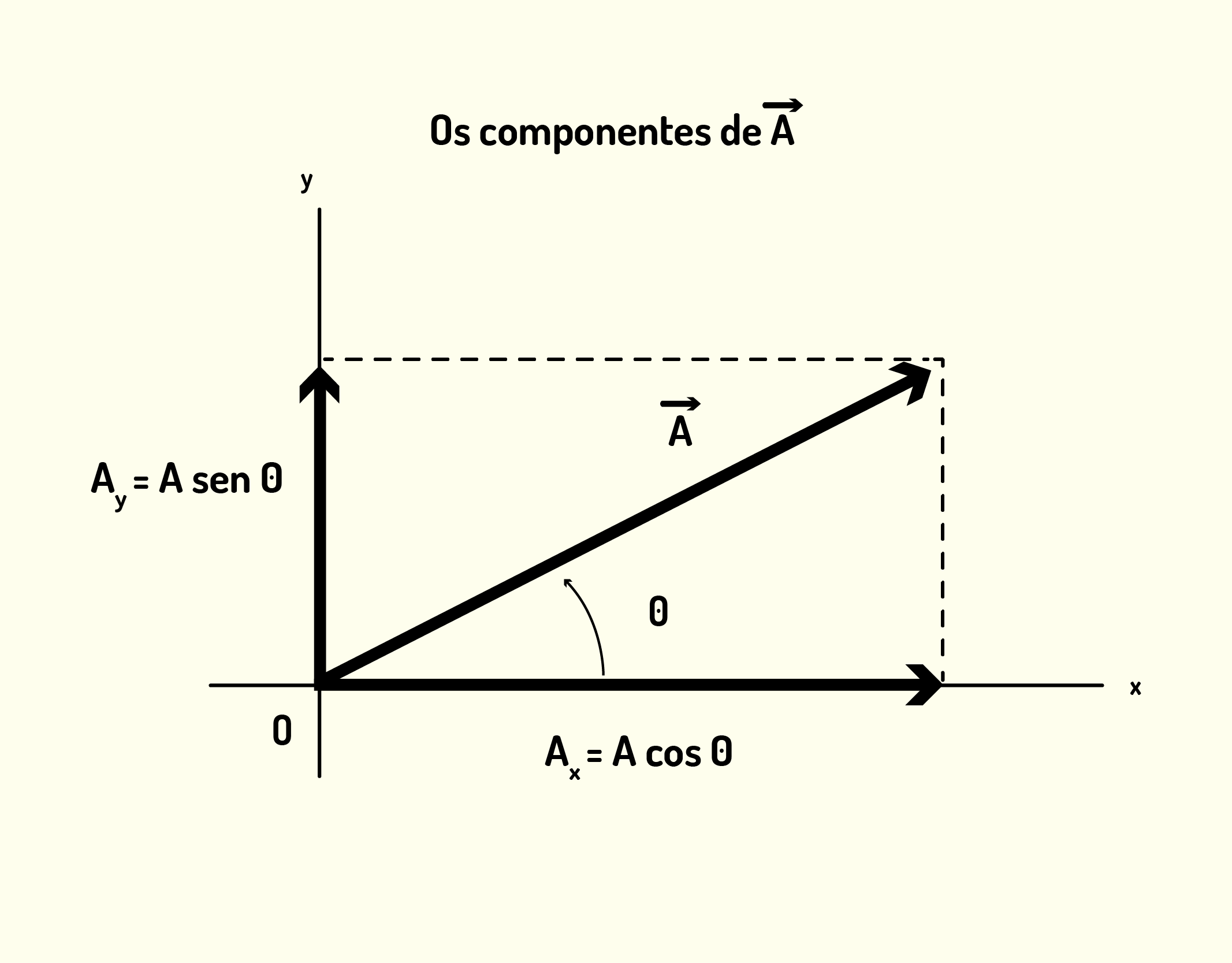
O módulo de cada vetor componente é chamado de componente (falamos componente [math]{{A}_{x}}[/math] para o vetor [math]{{\vec{A}}_{x}}[/math] e componente [math]{{A}_{y}}[/math] para o vetor [math]{{\vec{A}}_{y}}[/math]), e é um número escalar que pode ser positivo ou negativo, dependendo do sentido do vetor componente. Na Figura 1.12, podemos identificar a localização dos vetores componentes, que são a projeção do vetor principal [math]\vec{A}[/math] em cada um dos eixos do sistema de coordenadas. Já na Figura 1.13, observamos como relacionar os componentes do vetor com o vetor [math]\vec{A}[/math]. Essa relação é feita se estabelecendo um ângulo entre esse vetor e alguma referência (na figura, a referência é o eixo [math]{{O}_{x}})[/math]
11237 Representação do vetor [math]\vec{A}[/math] em vetores componentes [math]{{\vec{A}}_{x}}[/math] e [math]{{\vec{A}}_{y}}[/math] Fonte: Young e Freedman (2012, p.15).
11337 Representação do vetor [math]\vec{A}[/math] em componentes [math]{{A}_{x}}[/math] e [math]{{A}_{y}}[/math] Fonte: Young e Freedman ( 2012, p.15).
O cálculo das componentes, como citado acima e ilustrado na Figura 1.13, é feito a partir da identificação do ângulo θ formado entre o vetor e uma determinada referência, do cálculo das funções seno e cosseno (sen(θ) e cos(θ) respectivamente) e do conhecimento do módulo do vetor principal:
[math]\frac{{{A}_{x}}}{A}=cos~\theta ~[/math] e [math]\frac{{{A}_{y}}}{A}=sen~\theta ~ [/math] (1.5)
Caro(a) aluno(a), é importante notar que as relações na Equação (1.5) são válidas somente quando o ângulo θ for medido quando consideramos uma rotação no sentido +[math]{{O}_{x}}[/math].
Sabia que podemos também obter as informações de um vetor a partir de seus componentes? Sim, isso é possível. Se aplicarmos o teorema de Pitágoras no triângulo da Figura 1.13, em que o módulo de [math]\vec{A}[/math] é obtido da seguinte forma:
[math]A=~\sqrt{{{A}_{x}}^{2}+{{A}_{y}}^{2}~}[/math] (1.6)
Podemos também encontrar o valor do ângulo θ a partir da seguinte análise trigonométrica:
[math]tg~\theta =~\frac{{{A}_{y}}}{{{A}_{x}}}[/math] e [math]~\theta =~arctg\frac{{{A}_{y}}}{{{A}_{x}}} [/math] (1.7)
Sendo que “arctg” representa a função inversa da tangente, ou seja, o ângulo cuja tangente possui valor [math]\frac{{{A}_{y}}}{{{A}_{x}}}[/math].
Multiplicação de uma grandeza escalar por uma vetorial
Caso você encontre alguma ocasião em que há um número escalar multiplicando um vetor, esse escalar positivo irá apenas multiplicar o módulo do vetor. Caso o valor seja negativo, seu modo será multiplicado e seu sentido será invertido. Porém, podemos também utilizar a propriedade distributiva da multiplicação por escalar para calcular essa multiplicação através do uso das componentes do vetor:
[math]\vec{D}=c\left( ~\vec{A}~ \right)=c\left( ~\overrightarrow{{{A}_{x}}}+\overrightarrow{{{A}_{y}}~} \right)=c\overrightarrow{{{A}_{x}}}+c\overrightarrow{{{A}_{y}}}=~\overrightarrow{{{D}_{x}}}+\overrightarrow{{{D}_{y}}}[/math] (1.8)
Soma vetorial através do uso das componentes
De uma forma bem simples, podemos falar que o cálculo do vetor resultante é a soma das componentes de cada eixo de todos os vetores a serem somados. Sendo que o componente [math]{{O}_{x}}[/math] de um vetor só pode ser somado com os componentes [math]{{O}_{x}}[/math] dos outros vetores, e o mesmo vale para componentes referentes a outros eixos. Ou seja, se desejamos encontrar o vetor [math]\vec{R}~[/math]resultante da soma entre três vetores [math]\vec{A}[/math], [math]\vec{B}[/math] e [math]\vec{C}[/math], é necessário fazer as seguintes operações:
[math]{{R}_{x}}={{A}_{x}}+{{B}_{x}}+{{C}_{x}}[/math] e [math]{{R}_{y}}={{A}_{y}}+{{B}_{y}}+{{C}_{y}} [/math] (1.9)
Extensão para vetores tridimensionais
Caso você deseje trabalhar com vetores tridimensionais, o cálculo do seu módulo é facilmente obtido através da inserção da componente [math]{{O}_{z}}~[/math]na Equação (1.6) da seguinte forma:
[math]A=~\sqrt{{{A}_{x}}^{2}+{{A}_{y}}^{2}+{{A}_{z}}^{2}} [/math] (1.10)
E se for necessário somar dois ou mais vetores tridimensionais, faz-se a soma dos componentes [math]{{O}_{z}}[/math] de forma similar ao procedido com os componentes dos outros eixos:
[math]{{R}_{x}}={{A}_{x}}+{{B}_{x}}+{{C}_{x}}[/math] e [math]{{R}_{y}}={{A}_{y}}+{{B}_{y}}+{{C}_{y}}[/math] e [math]{{R}_{z}}={{A}_{z}}+{{B}_{z}}+{{C}_{z}} [/math] (1.11)
Vetores unitários
Os vetores unitários são aqueles que possuem módulo igual a 1 (um), cujo objetivo principal é apontar a direção e o sentido dos eixos das coordenadas. Os vetores unitários possuem sinal positivo e apontam no mesmo sentido dos eixos[math]~{{O}_{x}}[/math], [math]{{O}_{y}}[/math] e [math]{{O}_{z}}[/math]. Por definição, o vetor unitário [math]\hat{i}[/math] aponta para o sentido positivo de [math]{{O}_{x}}[/math], [math]\hat{j}[/math] aponta para [math]+{{O}_{y}},[/math] e o vetor unitário [math]\hat{k}[/math] representa o sentido positivo do eixo [math]{{O}_{z}}[/math].
Além de apontar o sentido positivo, os vetores unitários também são úteis na representação matemática dos vetores, auxiliando também na escrita das operações com vetores:
[math]\vec{A}~={{A}_{x}}\hat{i}+{{A}_{y}}\hat{j}[/math]
[math]\vec{B}~={{B}_{x}}\hat{i}+{{B}_{y}}\hat{j}[/math]
[math]\vec{R}~=\vec{A}+\vec{B}[/math]
[math]=\left( {{A}_{x}}\hat{i}+{{A}_{y}}\hat{j} \right)+~\left( {{B}_{x}}\hat{i}+{{B}_{y}}\hat{j} \right) [/math] (1.12)
[math]=\left( {{A}_{x}}+{{B}_{x}} \right)\hat{i}+~\left( {{A}_{y}}+{{B}_{y}} \right)\hat{j}[/math]
[math]={{R}_{x}}\hat{i}+{{R}_{y}}\hat{j}[/math]
Produtos de vetores
Neste momento, você já deve estar apto para executar somas de vetores através de vários métodos, além de saber representá-los gráfica e matematicamente. Porém, ainda precisamos aprender a lidar com produtos de vetores. Lembra-se de que um vetor é completamente diferente de um escalar? Sendo assim, o produto comum não pode ser aplicado. Existem dois tipos de produtores de vetores: i) produto escalar terá como resultado uma grandeza escalar, ao passo que o ii) produto vetorial irá gerar uma grandeza vetorial.
Produto escalar
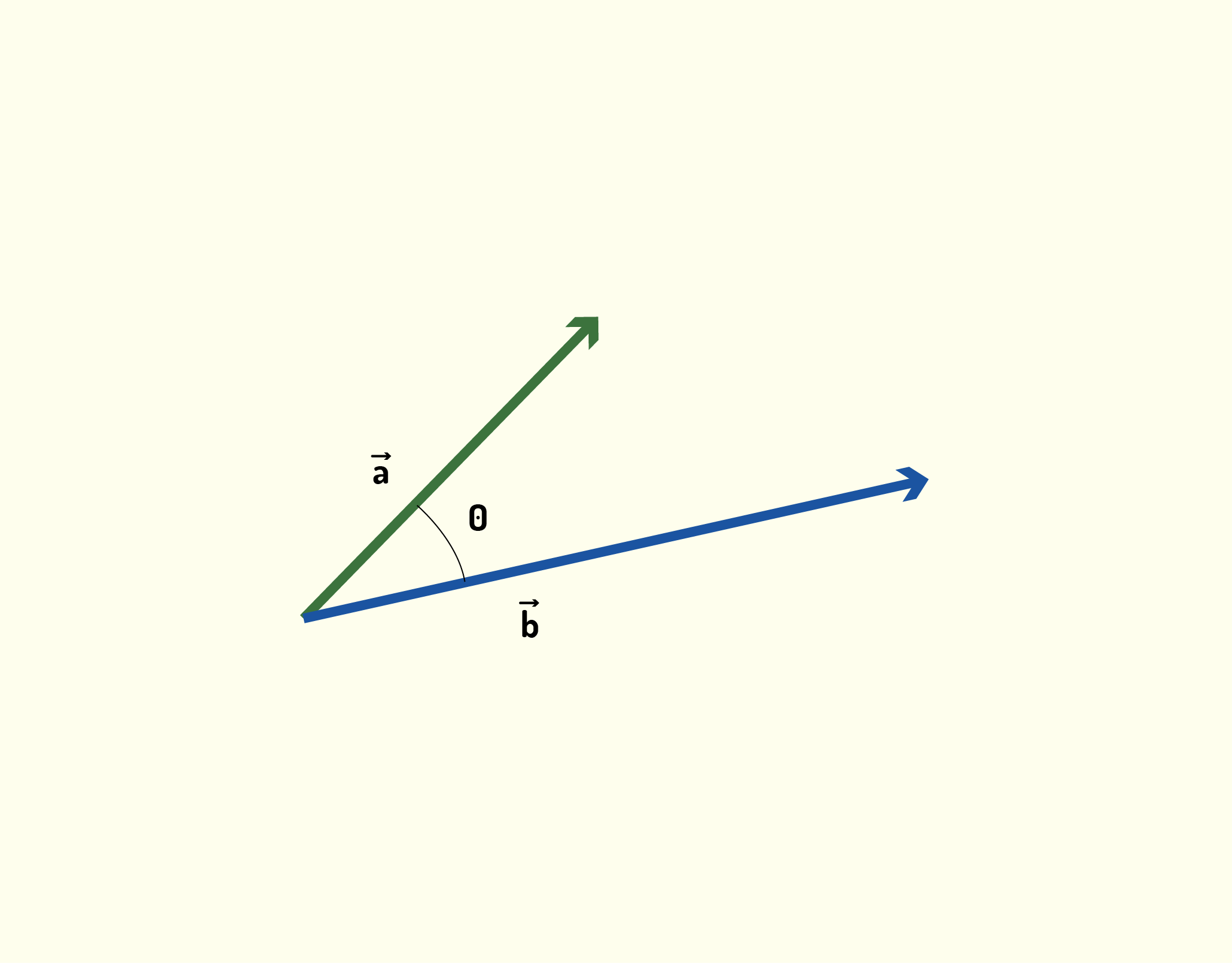
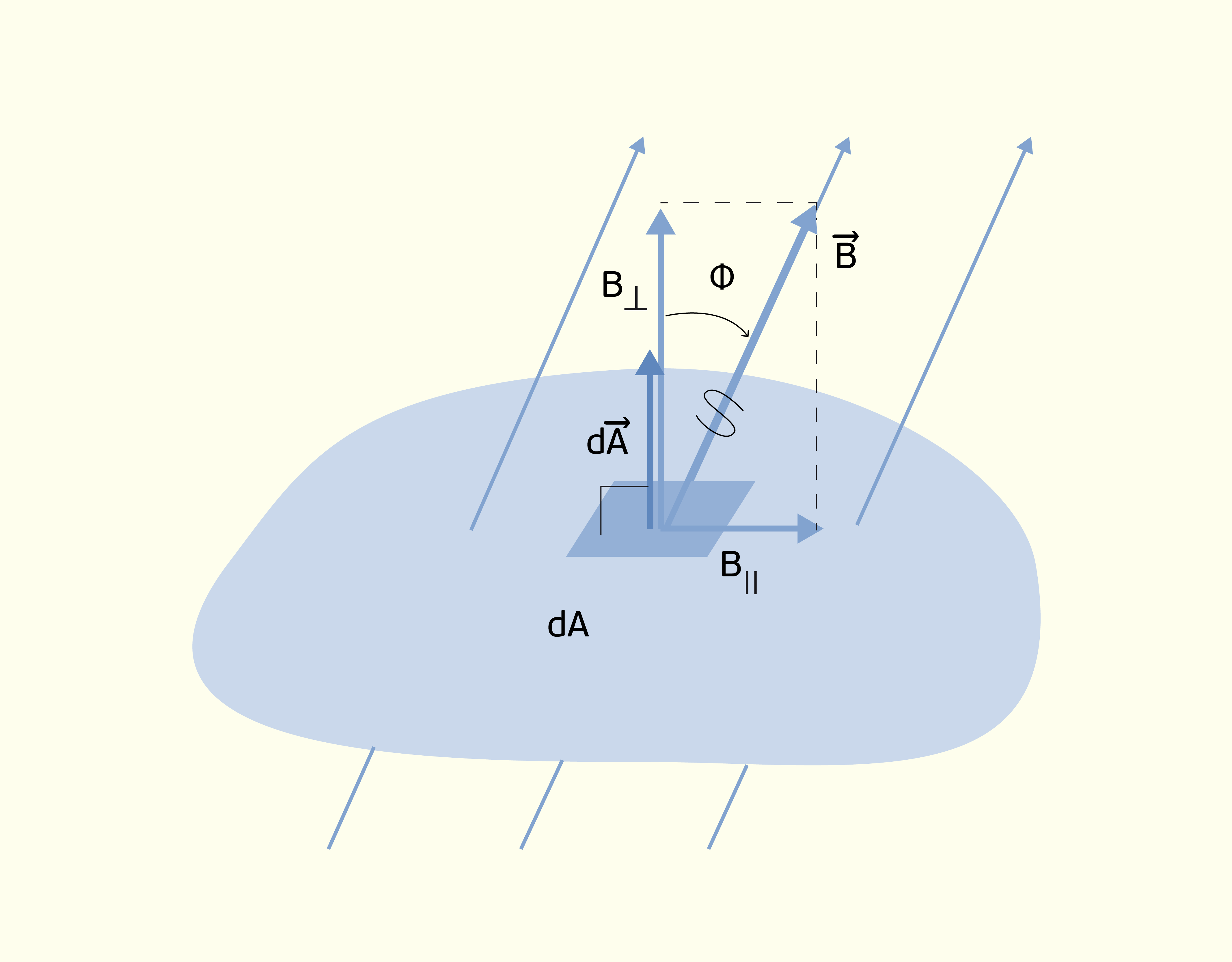
O produto escalar entre dois vetores [math]\vec{A}[/math] e [math]\vec{B}[/math], cuja notação é [math]\left( \vec{A}\vec{B} \right)[/math], está relacionado ao ângulo [math]\phi [/math], que é o menor ângulo formado entre esses dois vetores, assim como ilustrado na Figura 1.14, e é obtido matematicamente através da seguinte relação matemática:
[math]\left( \vec{A}\vec{B} \right)=AB~cos\phi[/math] (1.13)
Ou então, quando você estiver trabalhando com a notação de vetores unitários, poderá calcular o produto escalar da seguinte forma:
[math]\left( \vec{A}\vec{B} \right)=\left( {{A}_{x}}\hat{i}+{{A}_{y}}\hat{j} \right)\left( {{B}_{x}}\hat{i}+{{B}_{y}}\hat{j} \right)[/math] [math]={{A}_{x}}{{B}_{x}}+{{A}_{y}}{{B}_{y}} [/math] (1.14)
Sendo que, para chegar à Equação (1.14), foi preciso utilizar a propriedade distributiva e também a Equação (1.13) para calcular o produto escalar entre os vetores unitários:
[math]\hat{i}\hat{i}=~\hat{j}\hat{j}=\left( 1 \right)\left( 1 \right)cos~0{}^\circ ~=1[/math]
[math]\hat{i}\hat{j}=~\left( 1 \right)\left( 1 \right)cos~90{}^\circ ~=0 [/math] (1.15)
11437 Representação gráfica do produto escalar entre dois vetores Fonte: Halliday e Resnick (2012, p.50).
Produto vetorial
Como você leu anteriormente que o resultado do produto vetorial entre dois vetores [math]\vec{A}[/math] e [math]\vec{B}[/math], que é escrito como [math]\vec{C}=\vec{A}\times \vec{B}[/math], é também um vetor. O módulo desse vetor resultante é dado por:
[math]C=\left| \vec{A}\times \vec{B} \right|=AB~cos\phi [/math] (1.16)
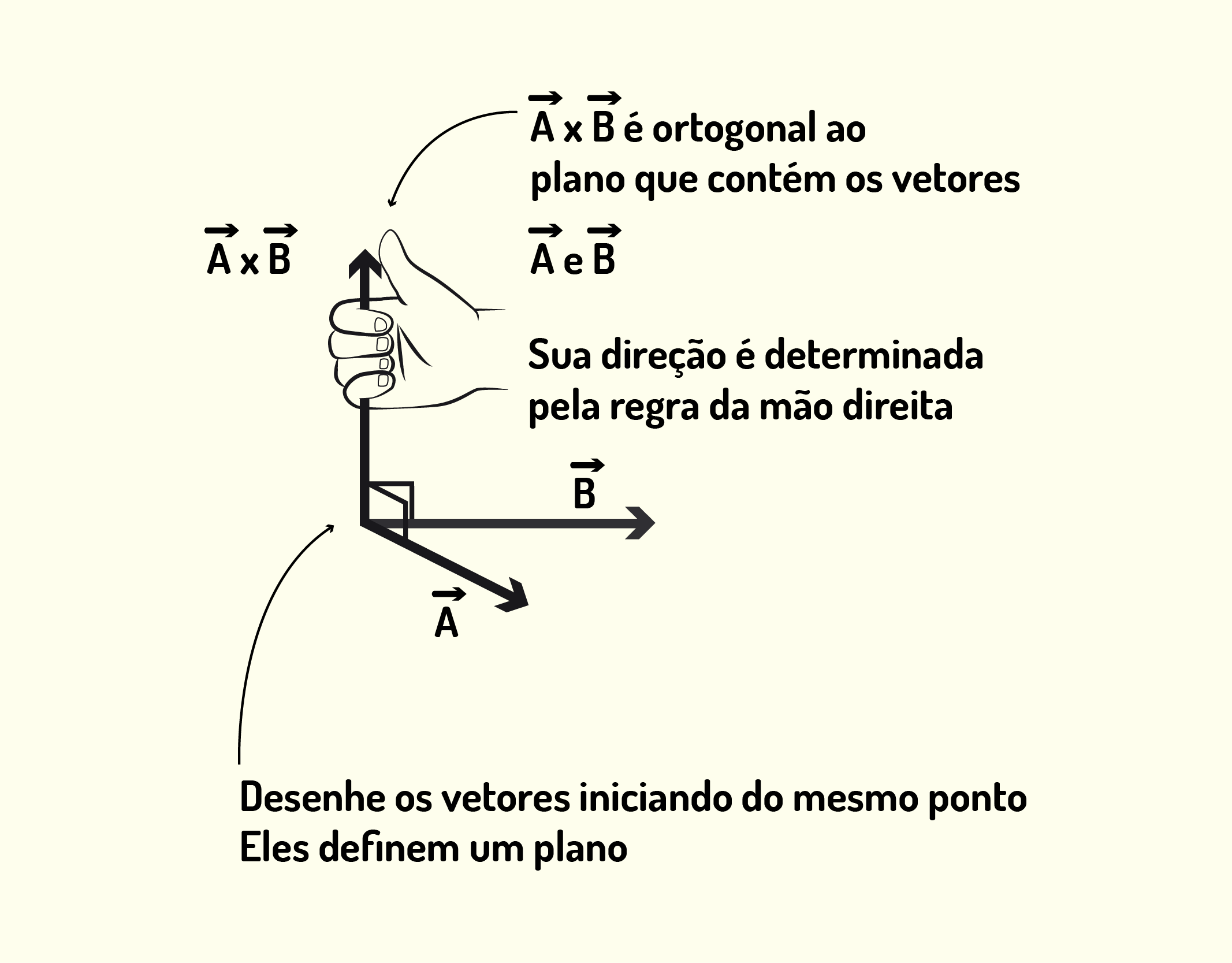
A direção do produto vetorial é sempre ortogonal ao plano que contém os vetores [math]\vec{A}[/math] e [math]\vec{B}[/math]. Porém, sempre existirá dois sentidos para essa direção ortogonal. Para saber qual o sentido certo, devemos utilizar a regra da mão direita. Imagine os dois vetores no mesmo plano e que o vetor [math]\vec{A}[/math] deve girar no sentido do menor ângulo entre os dois vetores. Essa regra diz que, se os quatro dedos da sua mão direita estiverem apontando no mesmo sentido do movimento desse giro, o seu polegar estará apontando para o sentido da resultante do produto vetorial. Para entendermos melhor, observe as ilustrações das Figuras 1.15 e 1.16.
11537 Regra da mão direita para [math]\vec{C}=\vec{A}\times \vec{B}[/math] Fonte: Young e Freedman (2012, p.23).
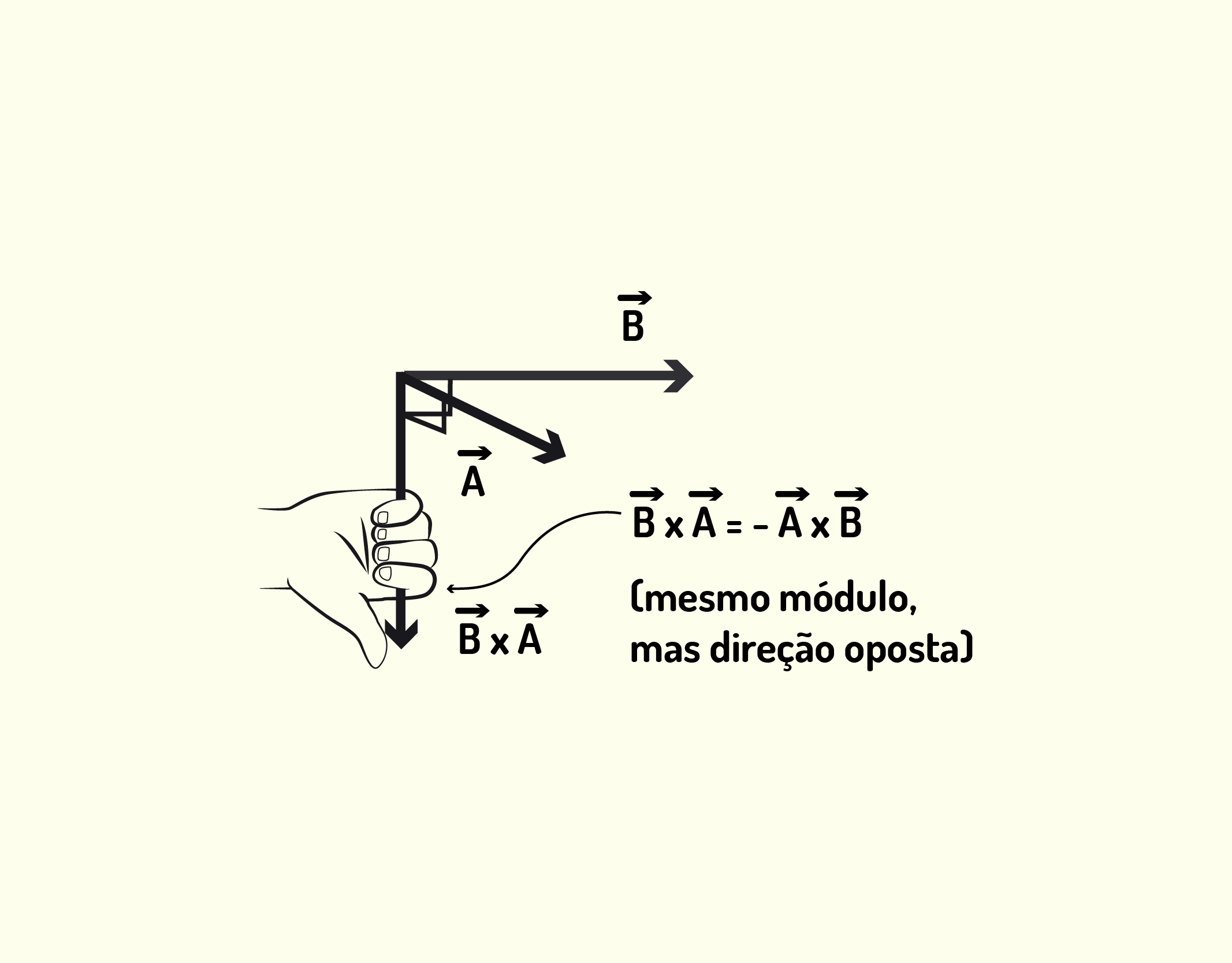
Analogamente, podemos verificar que [math]\vec{C}=\vec{B}\times \vec{A}=-\vec{A}\times \vec{B}[/math] se observarmos a regra da mão direita ilustrada na Figura 1.16.
11637 Regra da mão direita para [math]\vec{C}=\vec{B}\times \vec{A}=-\vec{A}\times \vec{B}[/math] Fonte: Young e Freedman (2010, p.23).
Porém, caro(a) aluno(a), se você está preferindo trabalhar com as componentes dos vetores, vamos agora entender como encontrar o resultado do produto vetorial a partir da notação de vetores unitários. Primeiramente, vamos analisar a multiplicação vetorial entre cada um dos vetores unitários para o caso tridimensional. Como o ângulo entre um vetor consigo mesmo é zero, podemos afirmar que o produto vetorial dele com ele mesmo também é zero:
[math]\hat{i}\times \hat{i}=\hat{j}\times \hat{j}=\hat{k}\times \hat{k}=0 [/math] (1.17)
Utilizando a Equação (1.17) e a regra da mão direita, o produto vetorial entre os outros vetores unitários pode ser encontrado:
[math]\hat{i}\times \hat{j}=-\hat{j}\times \hat{i}=\hat{k}[/math]
[math]\hat{j}\times \hat{k}=-\hat{k}\times \hat{j}=\hat{i} [/math] (1.18)
[math]\hat{k}\times \hat{i}=-\hat{i}\times \hat{k}=\hat{j}[/math]
Aplicando então a propriedade distributiva no produto vetorial escrito com suas componentes e vetores unitários, podemos chegar à solução simplificada (é interessante que você tente expandir a equação e chegar ao resultado a seguir):
[math]\vec{A}\times \vec{B}=\left( {{A}_{y}}{{B}_{z}}-{{A}_{z}}{{B}_{y}} \right)\hat{i}+~\left( {{A}_{z}}{{B}_{x}}-{{A}_{x}}{{A}_{z}} \right)\hat{j}+\left( {{A}_{x}}{{B}_{y}}-{{A}_{y}}{{B}_{x}} \right)\hat{k}[/math] (1.19)
Como você viu, na parte introdutória desta unidade, a Física é uma ciência experimental. Sendo assim, que tal exercitarmos o conhecimento adquirido até agora com um pequeno exercício?
Os deslocamentos que nós fazemos quando viajamos de uma cidade para outra podem também ser representados por vetores. Quando queremos apenas mostrar as distâncias percorridas, é mais conveniente utilizarmos vetores bidimensionais, mesmo que a viagem seja feita de avião. Para você entender melhor como isso é feito, vamos analisar o caso de um avião que precisou fazer um pouso de emergência.
Atividades
Considere que um avião tenha saído do aeroporto de Congonhas e viajado por 150km, a 60o de leste para norte. De repente, foi necessário mudar a rota, e o avião voou 200km a 50o de sul para leste, onde fez um pouso de emergência. Quando o aeroporto enviar uma equipe de resgate, em que direção e qual a distância que eles deverão percorrer? Sugestão: desenhe os vetores e utilize notação em vetores unitários, como ilustrado na Figura.
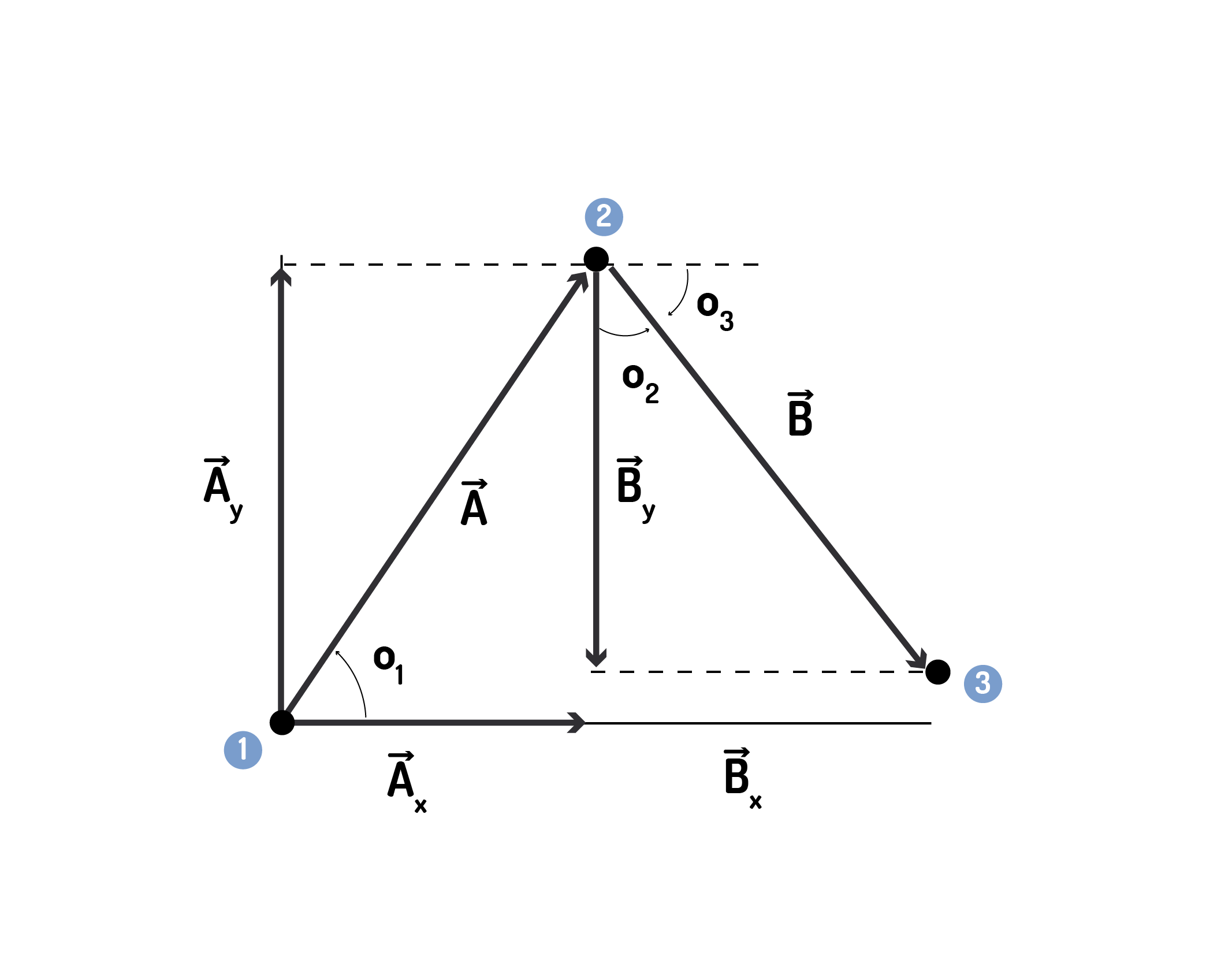
Trajeto feito pela aeronave.
Fonte: os autores.
- A equipe deverá percorrer 150km ao norte.
Essa resposta está completamente errada. Caso seja escolhida, a interpretação do problema não foi feita corretamente.
- A equipe deverá viajar 200km a 45o de leste para norte.
Essa resposta está completamente errada. Caso seja escolhida, a interpretação do problema não foi feita corretamente.
- A equipe deverá viajar 348km a 54o de leste para norte.
Essa resposta será encontrada caso o aluno não consiga interpretar corretamente o ângulo do vetor [math]\vec{B}[/math]. Se utilizarmos o valor fornecido (50o), ao invés de 270o+[math]{{\theta }_{2}}[/math] (equivalente a -(90o-[math]{{\theta }_{2}})[/math]), e fizermos todas as contas abaixo com [math]{{\theta }_{3}}=[/math]-(90o-[math]{{\theta }_{2}})[/math].
[math]\vec{A}~=150cos~{{\theta }_{1}}~\hat{i}+150sin~{{\theta }_{1}}~\hat{j}=75\hat{i}+129,9038\hat{j}[/math] e [math]\vec{B}~=200cos~{{\theta }_{3}}~\hat{i}+200sin~{{\theta }_{3}}~\hat{j}=128,5575\hat{i}+153,2089\hat{j}[/math]. Encontramos: [math]\vec{R}~={{R}_{x}}\hat{i}+{{R}_{y}}\hat{j}=\left( {{A}_{x+}}{{B}_{x}} \right)\hat{i}+({{A}_{y}}+{{B}_{y}})\hat{j}=203,5574+283,1128\hat{j}[/math] , com [math]\left| {\vec{R}} \right|=348,6954[/math] e [math]{{\theta }_{R}}=54,2839{}^\circ [/math]
- A equipe deverá viajar 228km a -0,34o de leste para norte.
Fazendo-se as seguintes decomposições [math]\vec{A}~=150cos~{{\theta }_{1}}~\hat{i}+150sin~{{\theta }_{1}}~\hat{j}=75\hat{i}+129,9038\hat{j}[/math] e [math]\vec{B}~=200cos~{{\theta }_{3}}~\hat{i}+200sin~{{\theta }_{3}}~\hat{j}=153,2089\hat{i}-128,5575\hat{j}[/math]. Encontramos: [math]\vec{R}~={{R}_{x}}\hat{i}+{{R}_{y}}\hat{j}=\left( {{A}_{x+}}{{B}_{x}} \right)\hat{i}+({{A}_{y}}+{{B}_{y}})\hat{j}=228,2089\hat{i}+1,3463\hat{j}[/math] , com [math]\left| {\vec{R}} \right|=228,2129[/math] e [math]{{\theta }_{R}}=0,3381{}^\circ [/math]. Como o módulo e o ângulo do vetor resultante representam a distância e a direção, respectivamente, podemos dizer que a equipe deverá viajar aproximadamente 228km a 0,34o de leste para norte.
Grandezas básicas: deslocamento, velocidade e aceleração
Você já se perguntou como e por que uma bola, ao ser jogada para cima, atinge uma determinada altura e depois começa a cair? Ou então, quando você deixa um objeto cair de sua mão, qual o tempo que você tem para recuperá-lo antes dele chegar ao solo? Essas e diversas outras situações são explicadas pela cinética, que é a parte da física mecânica que estuda os diversos tipos de movimentos.
Portanto, caro(a) aluno(a), agora nós aprenderemos as características de um dos tipos mais simples de movimento, que é o de uma partícula que se move em linha reta, possuindo ou não algum tipo de aceleração. Então você deve estar se perguntando por que no tópico anterior você estudou os vetores? É que tanto a velocidade quanto a aceleração são grandezas vetoriais.
Estudaremos também casos em que a aceleração do objeto não é constante. Um exemplo clássico é a queda livre de uma bola de boliche. Ao soltarmos essa bola de uma determinada altura, a força de seu peso fará com que, gradativamente, a aceleração do corpo aumente.
Deslocamento, tempo e velocidade média
Imagine o simples movimento de um carro em uma pista reta. Para podermos descrever esse movimento, o primeiro passo é estabelecer um sistema de coordenadas que possa nos orientar. Para isso, vamos escolher o eixo Ox. A posição do carro é descrita em função do tempo, ou seja, em cada instante (dependendo de sua velocidade e aceleração), o carro estará em um ponto. Se considerarmos sempre onde a extremidade dianteira do carro está, poderemos reduzir a representação do carro a uma simples partícula.
Para facilitar o entendimento, vamos observar a Figura 1.17. Considere que inicialmente a dianteira do carro estava na origem e, após 1 segundo, o carro percorreu 19 metros (ponto [math]{{P}_{1}})~[/math]e, após 4s de movimento, a partícula já tenha chegado ao ponto [math]{{P}_{2}}[/math], que fica a 277m da origem. Portanto, o carro sofreu um certo deslocamento em um intervalo de tempo específico. O deslocamento do carro entre [math]{{P}_{1}}[/math] e [math]{{P}_{2}}[/math] foi de (277 – 19) = 258m em um intervalo de tempo [math]({{t}_{2}}-{{t}_{1}})=4-1=3[/math] segundos. Com isso, você já é capaz de calcular a velocidade média em relação ao [math]x~[/math]([math]{{v}_{mx}}[/math]) da partícula nesse período, que é a variação de distância ([math]\Delta x[/math]) dividida pelo intervalo de tempo ([math]\Delta t[/math]):
[math]{{v}_{mx}}=~\frac{\Delta x}{\Delta t}=~\frac{{{x}_{2}}-{{x}_{1}}}{{{t}_{2}}-{{t}_{1}}}=\frac{277-19}{4-1}=\frac{258~m}{3,0~s}=86~m/s [/math] (1.19)
11737 Posição, deslocamento e velocidade média de um carro. Fonte: Young e Freedman (2010, p.36).
Nesse caso, a velocidade média é positiva, significando que, durante o intervalo de tempo em questão, o valor da posição do carro no eixo [math]x[/math] cresce (movimento da esquerda para a direita na Figura 1.17). Então, quando a velocidade média será negativa? Velocidade média negativa não significa que estamos perdendo velocidade. Como a velocidade é uma grandeza vetorial, o caso em que ela é negativa representa um movimento no sentido [math]-{{O}_{x}}[/math], que é quando o valor de [math]x[/math] se torna cada vez menor (ou mais negativo).
Por isso, é muito importante que você tenha cuidado ao analisar as posições e observe a orientação e a origem do sistema de coordenadas adotado. Por exemplo, no caso do carro, escolhemos a origem à esquerda da figura, e o carro se movimentou para a direita. Porém, se a origem fosse admitida como sendo na extremidade direita, o sentido positivo de [math]x[/math] seria da direita para a esquerda e, consequentemente, a velocidade média do móvel seria negativa. Agora você viu como é importante prestar atenção na origem do sistema de coordenadas, não é mesmo?!
Velocidade instantânea
Como vimos anteriormente, a velocidade média relaciona um determinado deslocamento a um intervalo de tempo. E como encontramos a velocidade de uma partícula em um tempo específico? Para isso, devemos analisar a fórmula da velocidade média quando o intervalo de tempo tende a zero, ou seja:
[math]{{v}_{x}}=~li{{m}_{\Delta t\to 0}}~\frac{\Delta x}{\Delta t}=~\frac{dx}{dt} [/math] (1.20)
Conseguiu observar que a velocidade instantânea [math]{{v}_{x}}[/math] é a taxa na qual a posição da partícula varia em um instante de tempo específico? Assim como [math]{{v}_{mx}}[/math], a velocidade instantânea é também um vetor. Sendo assim, você pode também querer encontrar a velocidade escalar instantânea, ou somente velocidade escalar, que é o módulo de [math]{{v}_{x}}[/math]. Note que a velocidade escalar de dois objetos pode ser a mesma, embora eles estejam com velocidades bastante diferentes. Por exemplo, a velocidade escalar de duas pessoas correndo a [math]+5m/s~[/math]e [math]-5m/s~[/math]é a mesma, embora elas estejam em direções opostas.
Você sabe dizer qual tipo de velocidade está sendo marcada no velocímetro do seu carro? É a velocidade escalar, pois ele não indica o sentido nem a direção para onde você está indo.
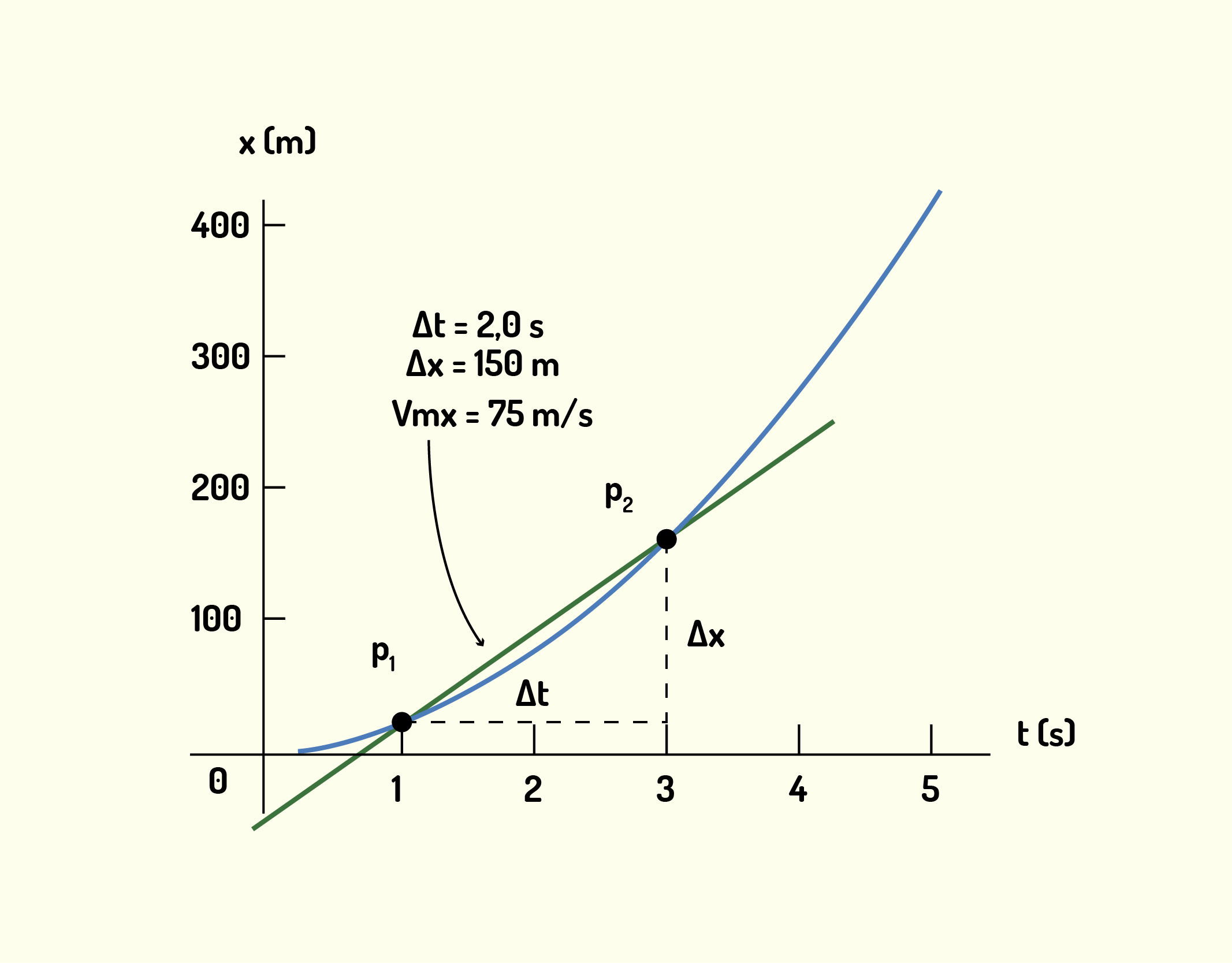
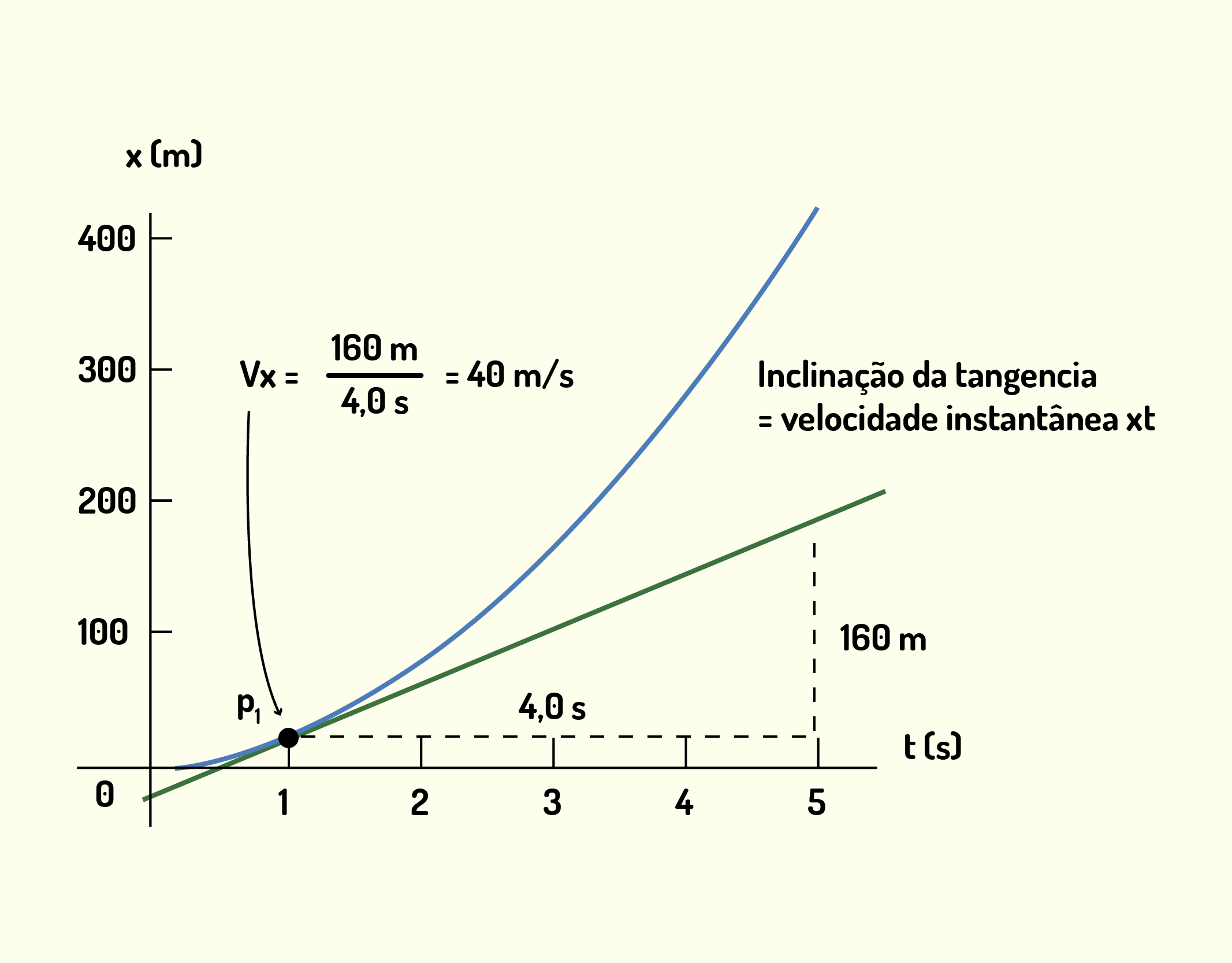
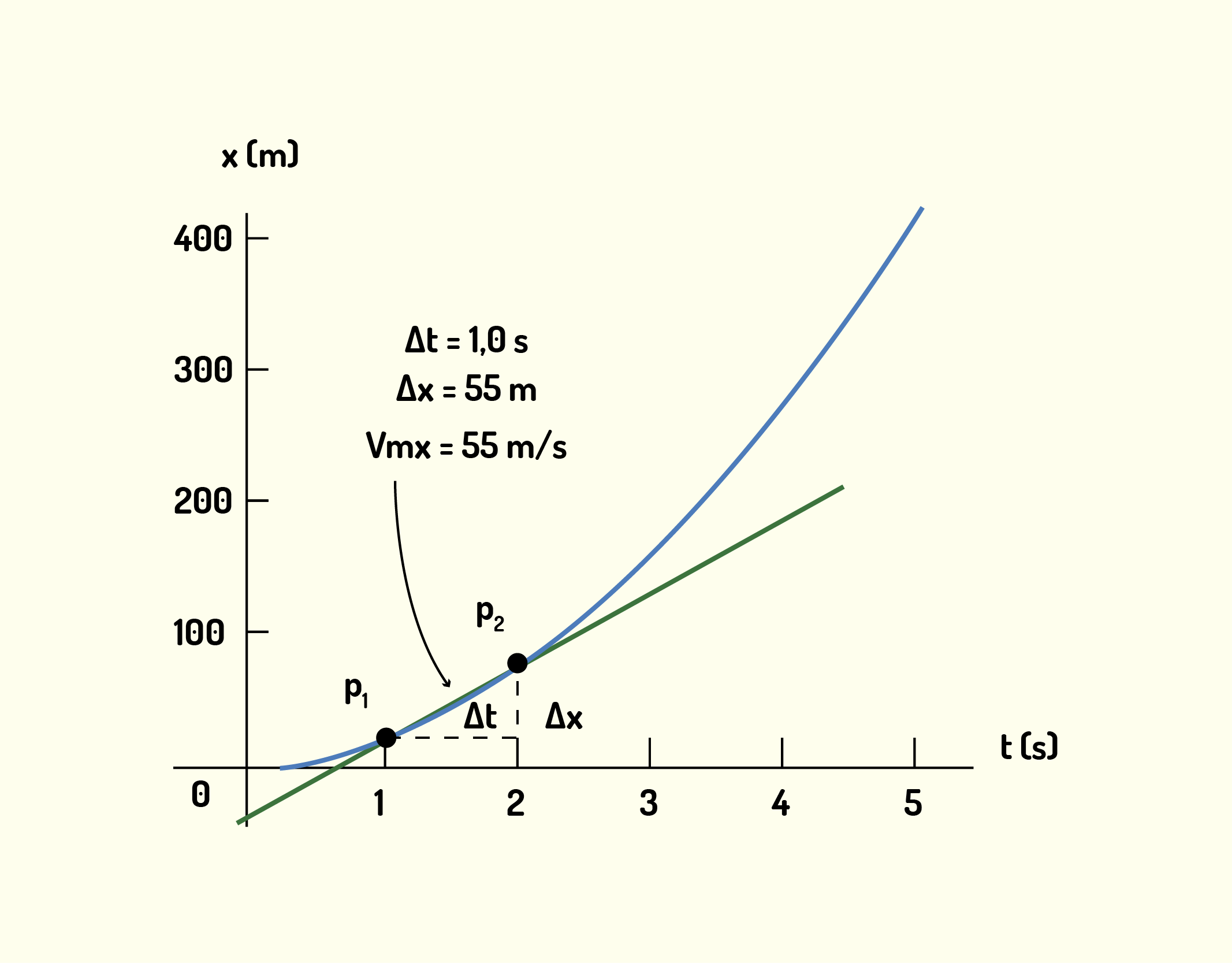
Na física, é extremamente importante que você saiba interpretar os diversos tipos de gráficos. Então, por que não utilizarmos agora um exemplo de como calcular velocidades média e instantânea a partir de gráficos? Considere as figuras de 1.18 a 1.20, nas quais temos um gráfico da posição de um objeto em função do tempo. Considere a Figura 1.18 a em que calculamos a velocidade média do móvel entre os instantes 1s e 3s. Agora, a partir do momento em que começamos a diminuir o intervalo de tempo (Figura 1.19) avaliado em [math]{{v}_{mx}}[/math], seu valor tende para a velocidade instantânea, até que [math]\Delta t[/math] se torna tão pequeno ao ponto de representar a inclinação da tangente da curva de deslocamento, representando então a velocidade instantânea [math]{{v}_{x}}[/math] (Figura 1.20).
11837 Uso do gráfico de deslocamento em função de tempo para o cálculo da velocidade média Fonte: Young e Freedman ( 2010, p.41).
11937 Diminuição do intervalo de tempo para o cálculo da velocidade média Fonte: Young e Freedman (2010, p.41).
12037 Velocidade instantânea do móvel. Fonte: Young e Freedman (2010, p.41).
Aceleração instantânea e aceleração média
Vimos que a velocidade média descreve a taxa de variação de posição em função de um intervalo de tempo. Similarmente, a aceleração média descreve uma taxa de variação de velocidade em um determinado intervalo de tempo.
Vamos observar mais uma vez um objeto que se move ao longo do eixo [math]Ox[/math]. Além disso, considere que, no instante [math]{{t}_{1}}[/math], ela apresenta uma velocidade instantânea [math]{{v}_{1x}}[/math] e que, no instante [math]{{t}_{2}}[/math] , sua velocidade é [math]{{v}_{2x}}[/math]. Portanto, você pode agora calcular a variação de velocidade [math]\Delta {{v}_{x}}={{v}_{2x}}-{{v}_{1x}}~[/math]que ocorreu no intervalo de tempo [math]\Delta t={{t}_{2}}-{{t}_{1}}[/math]. Sendo assim, a aceleração média [math]{{a}_{mx}}[/math] é definida como:
[math]{{a}_{mx}}=\frac{\Delta {{v}_{x}}}{\Delta t}=\frac{{{v}_{2x}}-{{v}_{1x}}}{{{t}_{2}}-{{t}_{1}}} [/math] (1.21)
E como definimos a unidade de aceleração? A forma mais comum é quando relacionamos as velocidades em m/s e o tempo em segundos, obtendo então: [math]m/s/s=m/{{s}^{2}}[/math] (metros por segundo ao quadrado).
Agora, através do mesmo raciocínio utilizado para definir a velocidade instantânea, vamos encontrar a aceleração instantânea calculando o limite da variação de velocidade quando o intervalo de tempo considerado tende a zero (um intervalo [math]\Delta t[/math] infinitesimal):
[math]{{a}_{x}}=~li{{m}_{\Delta t\to 0}}~\frac{\Delta {{v}_{x}}}{\Delta t}=~\frac{d{{v}_{x}}}{dt} [/math] (1.22)
Ou ainda, se você preferir, pode encontrar a aceleração instantânea através da variação de posição. Basta substituir a Equação (1.20) em (1.21):
[math]{{a}_{x}}=~\frac{d{{v}_{x}}}{dt}=\frac{d}{dt}\left( \frac{dx}{dt} \right)=\frac{{{d}^{2}}x}{d{{t}^{2}}} [/math] (1.22)
Vetores posição, velocidade e aceleração
Agora, nós conhecemos todos os conceitos básicos para estudar o movimento de uma partícula. Porém, você consegue descrever o movimento feito por uma bola que foi lançada da janela de um prédio? Para responder a essa pergunta, é necessário saber unir os conceitos vetoriais aprendidos na Seção 1 à descrição cinemática estudada até aqui. Para isso, passaremos a representar a posição das partículas também no sistema tridimensional de coordenadas, onde utilizamos os eixos [math]x[/math], [math]y[/math] e [math]z[/math].
Vetores posição e velocidade
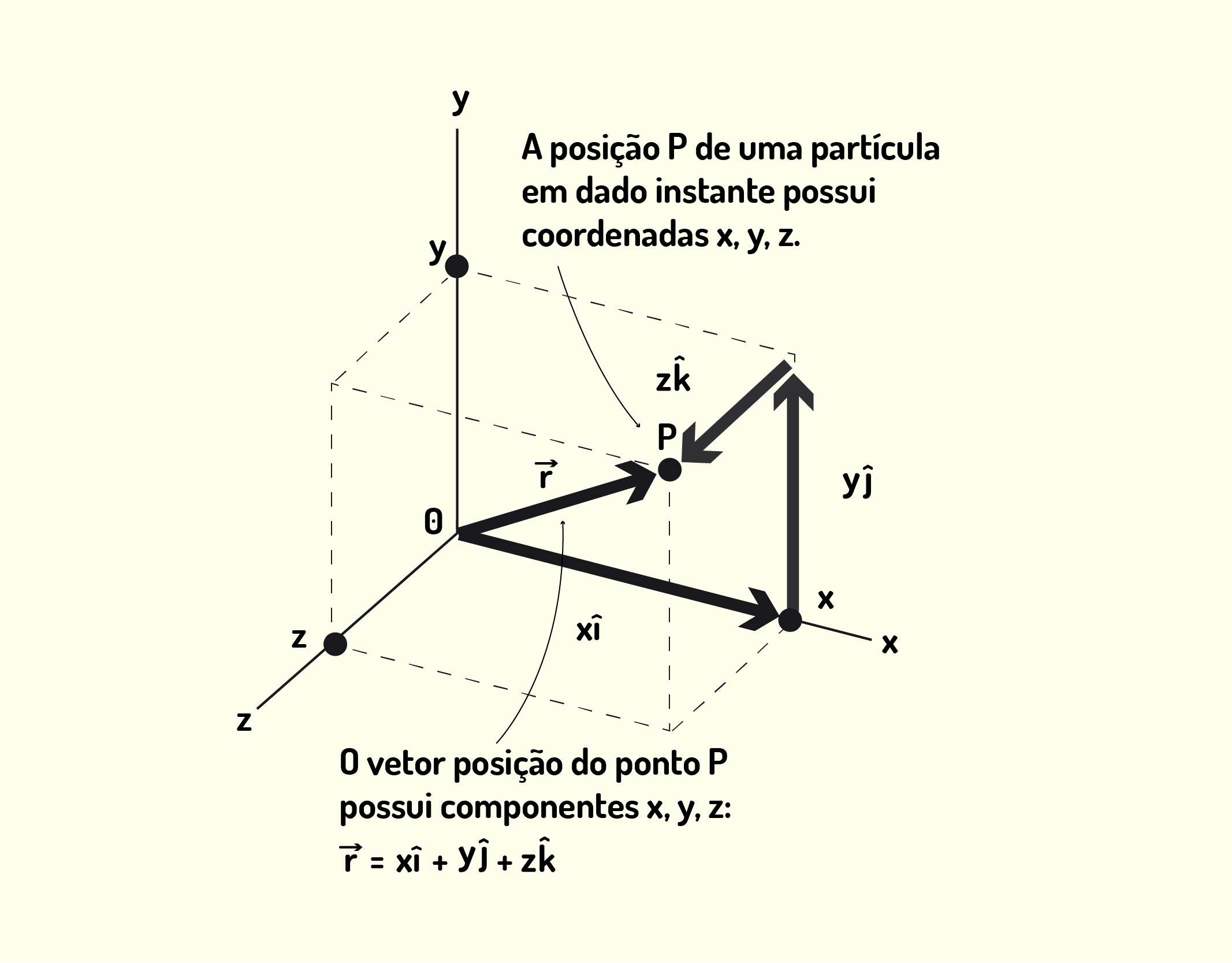
Imagine que há uma partícula em um ponto P e em um determinado instante. Como representamos a posição dela? Isso é feito através de um vetor posição [math]\vec{r}[/math]que começa na origem do sistema de coordenadas e termina no ponto P (Figura 1.21). Esse vetor terá sua representação utilizando os vetores unitários dos três eixos:
[math]\vec{r}=x\hat{i}+y\hat{j}+z\hat{k} [/math] (1.31)
Quando a partícula se mover de uma posição [math]{{P}_{1}}[/math] para [math]{{P}_{2}}[/math], cujos vetores posição que representam esses pontos são respectivamente [math]{{\vec{r}}_{1}}[/math] e [math]{{\vec{r}}_{2}}[/math], haverá então um vetor deslocamento resultante, dado por [math]\Delta \vec{r}[/math]:
[math]\Delta \vec{r}=~{{\vec{r}}_{2}}-{{\vec{r}}_{1}}=\left( {{x}_{2}}-{{x}_{1}} \right)\hat{i}+\left( {{y}_{2}}-{{y}_{1}} \right)\hat{j}+\left( {{z}_{2}}-{{z}_{1}} \right)\hat{k}~[/math] (1.32)
12137 Vetor posição [math]\hat{r}[/math] e suas componentes Fonte: Young e Freedman (2010, p.70).
Nesse caso, como houve um deslocamento, podemos também definir uma velocidade média vetorial [math]{{\vec{v}}_{m}}[/math] de forma similar ao que foi feito no movimento retilíneo, ou seja:
[math]{{\vec{v}}_{m}}={{v}_{mx}}\hat{i}+{{v}_{my}}\hat{j}+{{v}_{mz}}\hat{k}=\frac{\Delta \vec{r}}{\Delta t}=\frac{{{{\vec{r}}}_{2}}-{{{\vec{r}}}_{1}}}{{{t}_{2}}-{{t}_{1}}} [/math] (1.33)
Observe que [math]{{v}_{mx}}=\left( {{x}_{2}}-{{x}_{1}} \right)/\left( {{t}_{2}}-{{t}_{1}} \right)=\Delta x/\Delta t[/math] é o mesmo apresentado na Equação (1.19), ou seja, podemos falar que, em cada uma das dimensões, ocorre um movimento retilíneo acelerado unidimensional.
Mais uma vez, assim como você já fez anteriormente, podemos encontrar a velocidade instantânea apenas aplicando o limite quando o intervalo de tempo tende a zero. A diferença essencial é que agora o deslocamento é vetorial, o que vai gerar uma velocidade instantânea também vetorial:
[math]\vec{v}=li{{m}_{\Delta t\to 0}}~\frac{\Delta \vec{r}}{\Delta t}=\frac{d\vec{r}}{dt}~=\frac{dx}{dt}\hat{i}+\frac{dy}{dt}\hat{j}+\frac{dz}{dt}\hat{k}={{v}_{x}}\hat{i}+{{v}_{y}}\hat{j}+{{v}_{z}}\hat{k} [/math] (1.34)
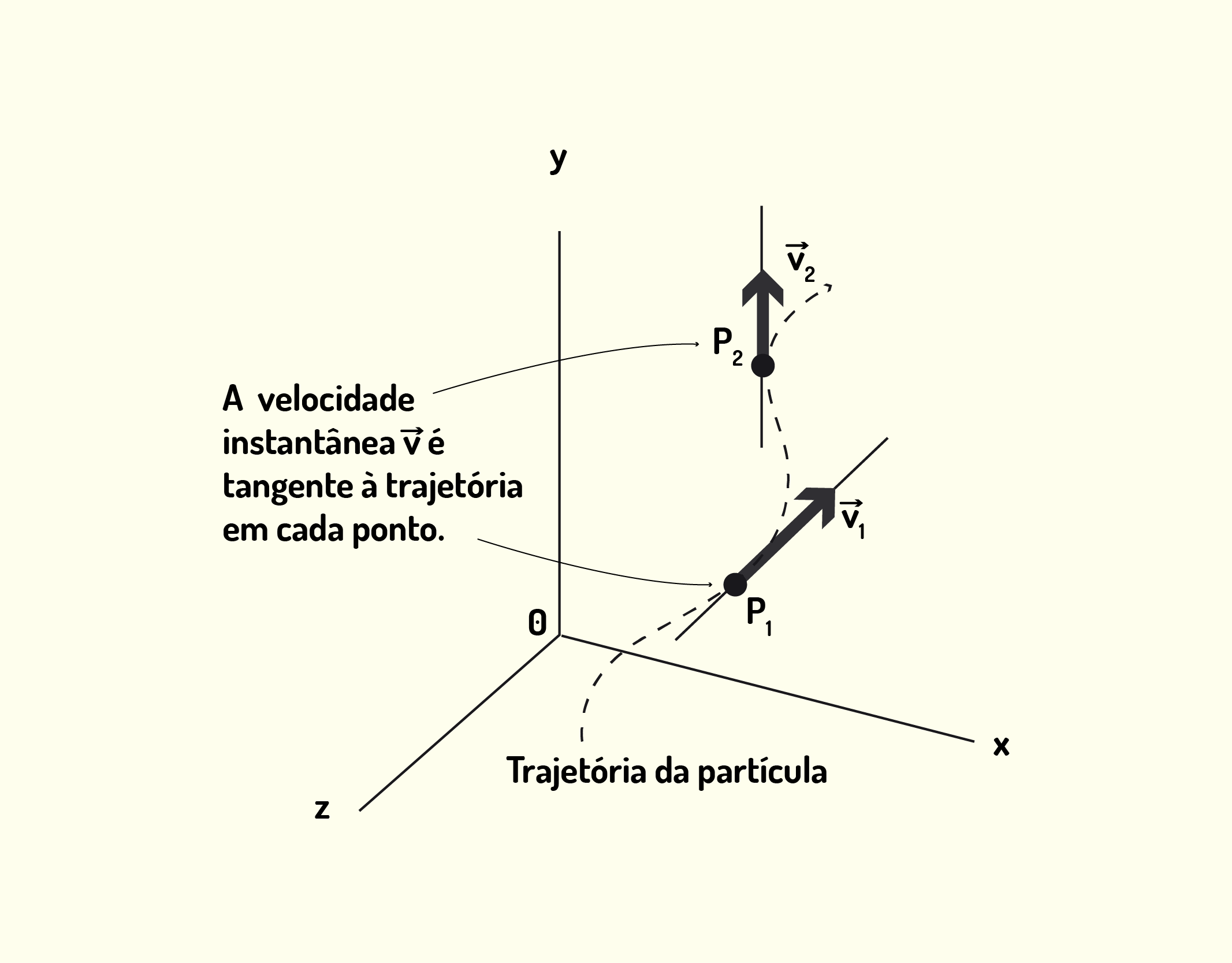
O vetor [math]\Delta \vec{r}~[/math] representa o deslocamento entre dois pontos [math]{{P}_{1}}[/math] e [math]{{P}_{2}}[/math] que são coincidentes. Logo, a velocidade instantânea assumirá a mesma direção e sentido de [math]\Delta \vec{r}[/math]. Nesse limite, o vetor [math]\Delta \vec{r}[/math] é tangente à trajetória feita pela partícula. Logo, podemos afirmar que a velocidade instantânea de uma partícula é tangente à trajetória em todo e qualquer ponto percorrido. Para melhor entender como isso acontece, a Figura 1.22 ilustra uma trajetória qualquer e dois vetores de velocidade instantânea tangentes à trajetória.
12237 Vetores de velocidade instantânea [math]{{\vec{v}}_{1}}[/math] e [math]{{\vec{v}}_{2}}[/math] tangentes à trajetória nos pontos [math]{{P}_{1}}[/math] e [math]{{P}_{2}}~[/math] Fonte: Young e Freedman (2010, p.70).
Vetores de aceleração média e instantânea
Da mesma forma que a velocidade de uma partícula podia variar quando estudamos o movimento retilíneo com aceleração constante, ela pode variar também no caso com posição e velocidade vetoriais. Portanto, imagine que a velocidade de um objeto está variando de [math]{{\vec{v}}_{1}}[/math] para [math]{{\vec{v}}_{2}}[/math] ao longo de um intervalo de tempo [math]\Delta t[/math]. Assim como calculado em (1.21), para encontrar a aceleração média, você deve dividir a variação de velocidade pelo intervalo de tempo em que essa variação ocorreu:
[math]{{\vec{a}}_{m}}=\frac{{{{\vec{v}}}_{2}}-{{{\vec{v}}}_{1}}}{\Delta t}=\frac{\Delta \vec{v}}{\Delta t} [/math] (1.35)
E como você já deve ter observado, para encontrarmos a aceleração instantânea, é necessário fazer o intervalo [math]\Delta t[/math] em (1.35) tender a zero:
[math]\vec{a}=li{{m}_{\Delta t\to 0}}~\frac{\Delta \vec{v}}{\Delta t}=\frac{d\vec{v}}{dt}~=\frac{d{{v}_{x}}}{dt}\hat{i}+\frac{d{{v}_{y}}}{dt}\hat{j}+\frac{d{{v}_{z}}}{dt}\hat{k}={{a}_{x}}\hat{i}+{{a}_{y}}\hat{j}+{{a}_{z}}\hat{k} [/math] (1.36)
Ou seja, os componentes escalares de [math]\vec{a}[/math] são obtidos através da derivada dos componentes escalares de [math]\vec{v}[/math] em relação ao tempo. Ou ainda, utilizando o fato de que os componentes escalares de [math]\vec{v}[/math] são os derivados dos componentes escalares de [math]\vec{r}[/math], podemos escrever:
[math]\vec{a}=\frac{{{d}^{2}}x}{d{{t}^{2}}}\hat{i}+\frac{{{d}^{2}}y}{d{{t}^{2}}}\hat{j}+\frac{{{d}^{2}}z}{d{{t}^{2}}}\hat{k} [/math] (1.37)
Atividades
Dado que nós acabamos de aprender, não somente as propriedades dos vetores deslocamento, velocidade e aceleração, mas também suas características principais e dimensões, encontre a alternativa que esteja correta dentre as opções a seguir:
- Um vetor aceleração paralelo e com mesmo sentido da velocidade da partícula provoca variações em módulo e direção.
Se a aceleração da partícula é paralela e possui mesmo sentido do que a velocidade, haverá mudança somente no módulo da velocidade, e não em sua direção.
- Se o vetor aceleração for ortogonal à velocidade, haverá drástica mudança no módulo da velocidade.
Uma aceleração ortogonal à velocidade provoca somente mudança de direção e não afeta de forma alguma o módulo da velocidade.
- A velocidade instantânea é tangente à trajetória da partícula em cada ponto da trajetória.
Como a velocidade instantânea é a derivada da trajetória em relação ao tempo em um ponto específico, o resultado é sempre tangente à trajetória.
- Quando uma partícula está com velocidade constante ao longo de uma trajetória curva, sua aceleração é nula.
A equação que define a aceleração mostra que há uma aceleração quando ocorre qualquer variação no vetor velocidade, mesmo que essa variação seja somente em ângulo (que é o que ocorre quando uma partícula apresenta velocidade constante ao longo de uma trajetória curva).
Movimento uniforme variado
Movimento com aceleração constante
Existem vários tipos de movimentos com aceleração. Como, por exemplo, um carro de fórmula 1, que fica constantemente acelerando e desacelerando, ou então movimentos em que há uma aceleração inicial e, ao atingir-se uma velocidade determinada, para-se de acelerar. Nesta seção, vamos estudar o movimento retilíneo acelerado constante, que pode ser considerado o mais simples dos movimentos acelerados.
Quando falamos que a aceleração é constante, podemos inferir que a aceleração instantânea, em qualquer instante, é a mesma. Consequentemente, a aceleração média torna-se igual à aceleração instantânea. A partir dessa constatação, você vai ser capaz de deduzir as equações básicas do movimento com aceleração constante.
Como dissemos, [math]{{a}_{mx}}={{a}_{x}}=\frac{v-{{v}_{0}}}{t-{{t}_{0}}}[/math]. Assumindo que [math]{{v}_{0}}[/math] é a velocidade no instante [math]t=0[/math], podemos rearranjar os termos e encontrar a equação da velocidade em um determinado instante de tempo [math]t[/math]:
[math]v=~{{v}_{0}}+{{a}_{x}}t [/math] (1.23)
Para confirmar a validade de (1.23), você pode calcular a derivada da velocidade, que deve ser igual à aceleração: [math]\frac{dv}{dt}={{a}_{x}}[/math].
Lembra-se da equação (1.19) que definia a velocidade média? Fazendo de forma similar a (1.23), podemos chegar a [math]{{v}_{mx}}=\frac{x-{{x}_{0}}}{t-0}[/math] e, rearranjando a expressão, você chegará na equação para a posição do objeto em um determinado instante de tempo:
[math]x={{x}_{0}}+{{v}_{mx}}t [/math] (1.24)
Você deve saber também que, como [math]{{v}_{mx}}[/math] é a velocidade média, podemos encontrá-la através da média aritmética entre a velocidade inicial [math]{{v}_{0}}[/math] e a velocidade final [math]v[/math]:
[math]{{v}_{mx}}=\frac{1}{2}\left( {{v}_{0}}+v \right) [/math] (1.25)
E, substituindo (1.23) em (1.25), pode-se chegar a:
[math]{{v}_{mx}}={{v}_{0}}+\frac{1}{2}{{a}_{x}}t [/math] (1.27)
Finalmente, substituindo (1.26) em (1.24) e manipulando os termos, obtemos:
[math]x-{{x}_{0}}={{v}_{0}}t+\frac{1}{2}{{a}_{x}}{{t}^{2}} [/math] (1.27)
Essas são as principais equações para o movimento retilíneo com aceleração constante. Porém, algumas outras podem também ser úteis na resolução de problemas. Elas serão apresentadas aqui, mas fica como DESAFIO para você deduzi-las. Isso pode ser feito apenas com a substituição das equações básicas, assim como acabamos de fazer.
[math]{{v}^{2}}=v_{0}^{2}+2{{a}_{x}}\left( x-{{x}_{0}} \right) [/math] (1.28)
[math]x-{{x}_{0}}=\frac{1}{2}\left( {{v}_{0}}+v \right)t [/math] (1.29)
[math]x-{{x}_{0}}=vt-\frac{1}{2}a{{t}^{2}} [/math] (1.30)
Queda livre
E quando que o movimento retilíneo com aceleração constante acontece? Provavelmente, o exemplo mais clássico e que está presente em inúmeras situações de seu cotidiano é a queda livre dos corpos. Quando qualquer objeto é abandonado no ar, além da resistência do ar (que pode ser desprezada quando criamos um modelo), temos a força da gravidade. E o que seria essa força? É basicamente uma força exercida pela Terra para atrair os objetos para seu centro (caso contrário, os objetos poderiam sair flutuando).
Essa força faz com que, quando os objetos são abandonados, haja uma aceleração constante, cujo módulo é popularmente representado pela letra g. Perto da superfície da Terra, temos que [math]g=9,8m/{{s}^{2}}[/math] é a aceleração em queda livre. Sendo assim, todas as equações que você deduziu na seção anterior valem também para o movimento de queda livre, sendo que [math]{{a}_{x}}=-g=-9,8m/{{s}^{2}}[/math].
Porém, há uma diferença grande nos eixos de referência: i) por convenção, o movimento de queda livre acontece ao longo do eixo [math]y[/math] (vertical), e não no eixo [math]x[/math] como estávamos estudando, sendo que o sentido crescente (movimento positivo) é para cima no eixo [math]y[/math]; ii) a aceleração no movimento de queda livre acontece em direção ao centro da Terra, que é para baixo no eixo [math]y[/math], portanto a aceleração é negativa e, nas equações, deve ser substituída por [math]-g[/math].
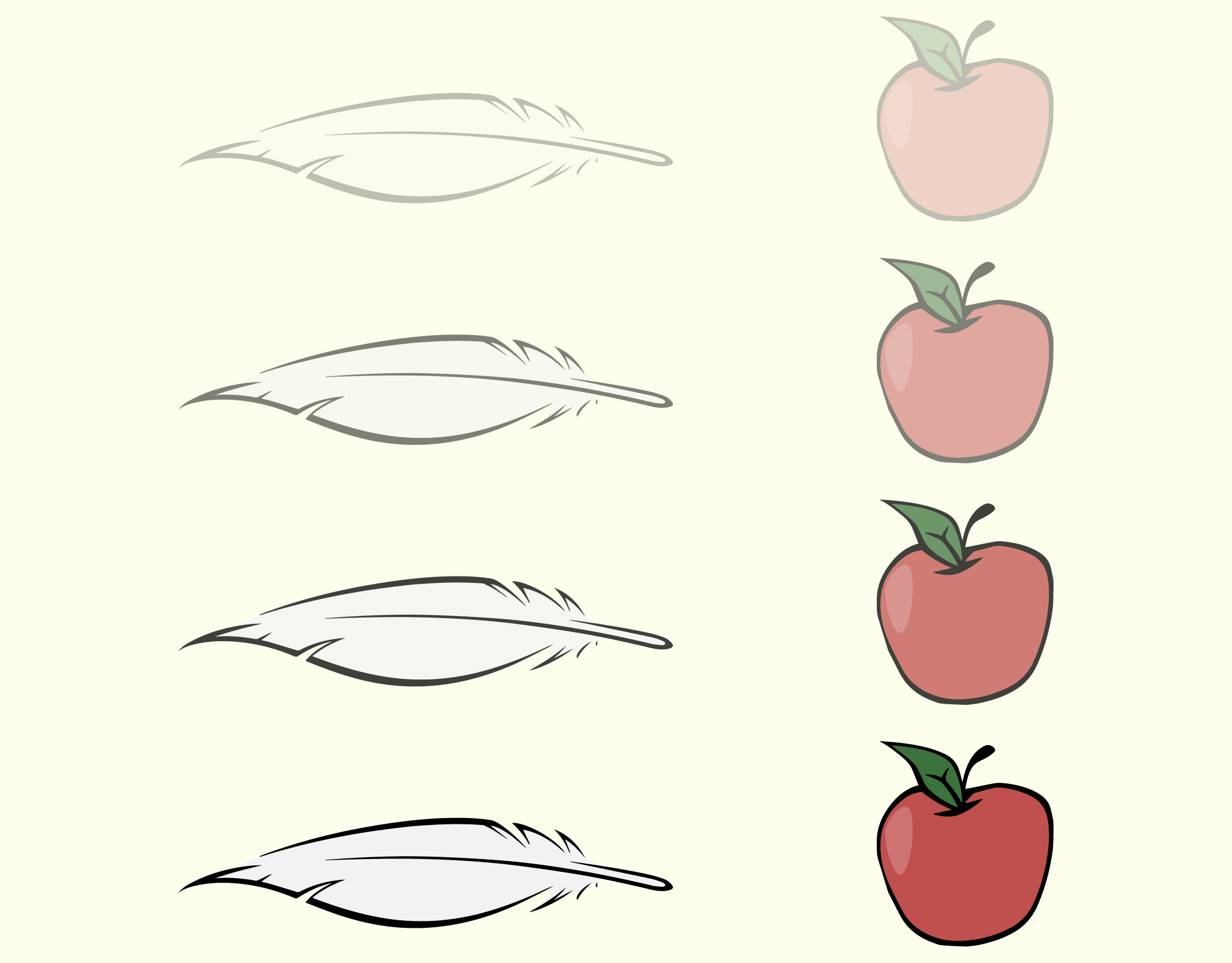
Para ilustrar esse movimento, observe a Figura 1.23, em que dois objetos (uma maçã e uma pena) estão em queda livre em um ambiente com completo vácuo (não há resistência do ar) para que a única força presente seja a gravidade. Observe que, no início, o deslocamento é pequeno, mas à medida que o tempo passa, a velocidade aumenta e a distância percorrida em um mesmo espaço de tempo também (isso acontece porque há uma aceleração de [math]g=-9,8m/{{s}^{2}}[/math] agindo sobre ambos os corpos.
12337 Queda livre de dois objetos no vácuo Fonte: Halliday e Resnick (2012, p.26).
Movimento de um projétil
O que é um projétil? No contexto de física, não é somente a munição de uma arma de fogo. Um projétil pode ser qualquer objeto lançado e que irá, ao longo de seu percurso, sofrer ação determinada somente pela força gravitacional e pela resistência do ar. O lance de uma bola de basquete, uma pedra arremessada pela janela e um pacote largado de um avião são alguns exemplos do que chamamos de projétil. Note que a curva feita pelo objeto (projétil) é chamada de trajetória.
A análise do movimento de um projétil é bastante facilitada quando você conseguir tratar as coordenadas [math]x[/math] e [math]y[/math] isoladamente (isso para o caso bidimensional). Como dito anteriormente, a única aceleração agindo sobre o projétil é a da gravidade. Portanto, se você isolar os dois eixos, o componente [math]x[/math] da aceleração será nulo, pois, como já estudamos, a gravidade atua somente no eixo [math]y[/math] e é constante igual a [math]-g[/math].
Assim, caso a velocidade e a aceleração sejam corretamente decompostas em [math]x[/math] e [math]y[/math], você poderá dizer que um projétil se movimenta verticalmente com aceleração constante igual a [math]-g[/math] e horizontalmente com velocidade constante. Ou seja, você pode escrever a seguinte relação:
[math]\vec{a}={{a}_{x}}\hat{i}+{{a}_{y}}\hat{j}=0-g\hat{j} [/math] (1.38)
A partir de (1.38) (que nos mostra como os componentes [math]{{a}_{x}}[/math] e [math]{{a}_{y}}[/math] são constantes), você pode usar as equações obtidas anteriormente, pois todas elas também lidam com movimentos com aceleração constante. Por exemplo, considerando o movimento em [math]x[/math], sabendo que [math]{{a}_{x}}=0[/math], as equações (1.23) e (1.27) são reduzidas a:
[math]{{v}_{x}}={{v}_{0x}} [/math] (1.39)
[math]x={{x}_{0}}+{{v}_{0x}}t [/math] (1.40)
Já o movimento em [math]y[/math], por possuir aceleração constante [math]{{a}_{y}}=-g[/math], pode ser descrito como:
[math]{{v}_{y}}={{v}_{0y}}-gt [/math] (1.41)
[math]y={{y}_{0}}+{{v}_{0y}}t-\frac{1}{2}g{{t}^{2}} [/math] (1.42)
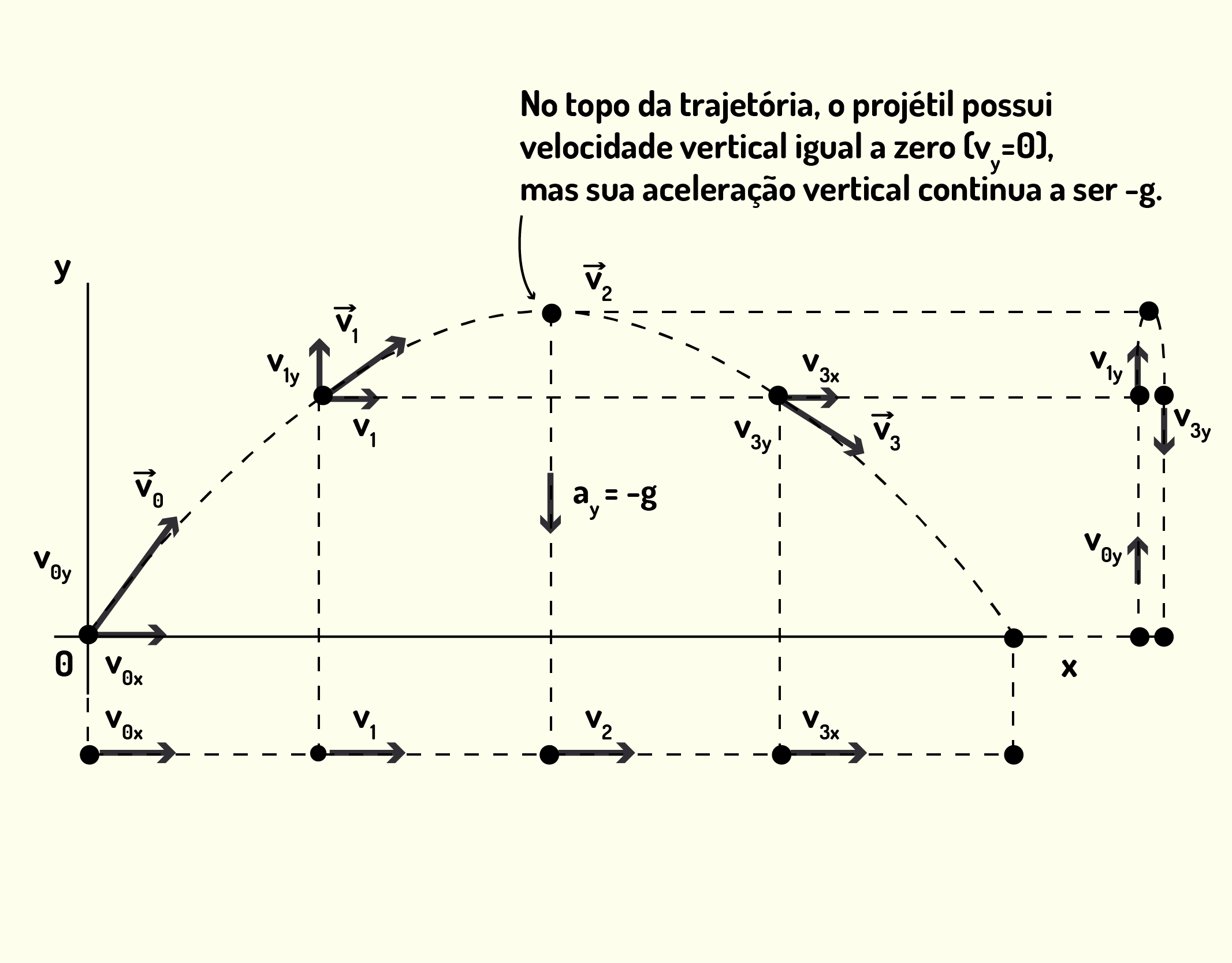
A Figura 1.24 apresenta a trajetória de um projétil que começou seu movimento na origem. Em diversos pontos, a velocidade é decomposta nos planos [math]x[/math] e [math]y[/math], assim como orientamos para você. Um ponto importante que você deve conhecer é o topo da trajetória do projétil, pois é onde a velocidade vertical [math]{{v}_{y}}[/math] é nula. Porém, a aceleração gravitacional ainda continua agindo, somente a velocidade vertical é igual a zero.
12437 Trajetória de um projétil com [math]\vec{v}[/math] em alguns pontos importantes[math]~[/math] Fonte: Young e Freedman (2010, p.78).
Movimento circular uniforme
O próprio nome já diz bastante sobre esse tipo de movimento, não é mesmo? Quando uma partícula está em movimento circular uniforme, ela percorre uma trajetória em formato de circunferência com uma velocidade escalar constante, por isso o movimento é chamado uniforme.
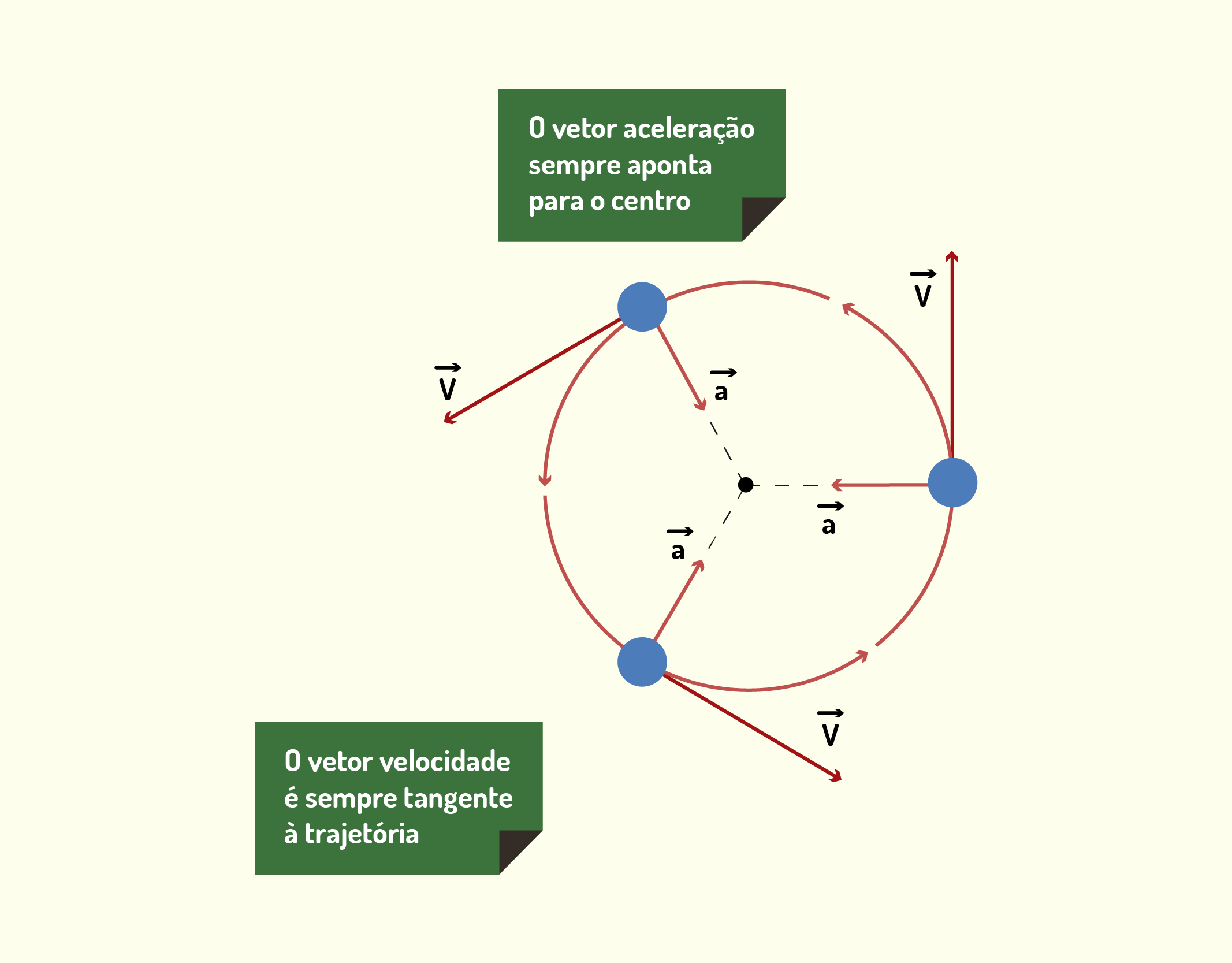
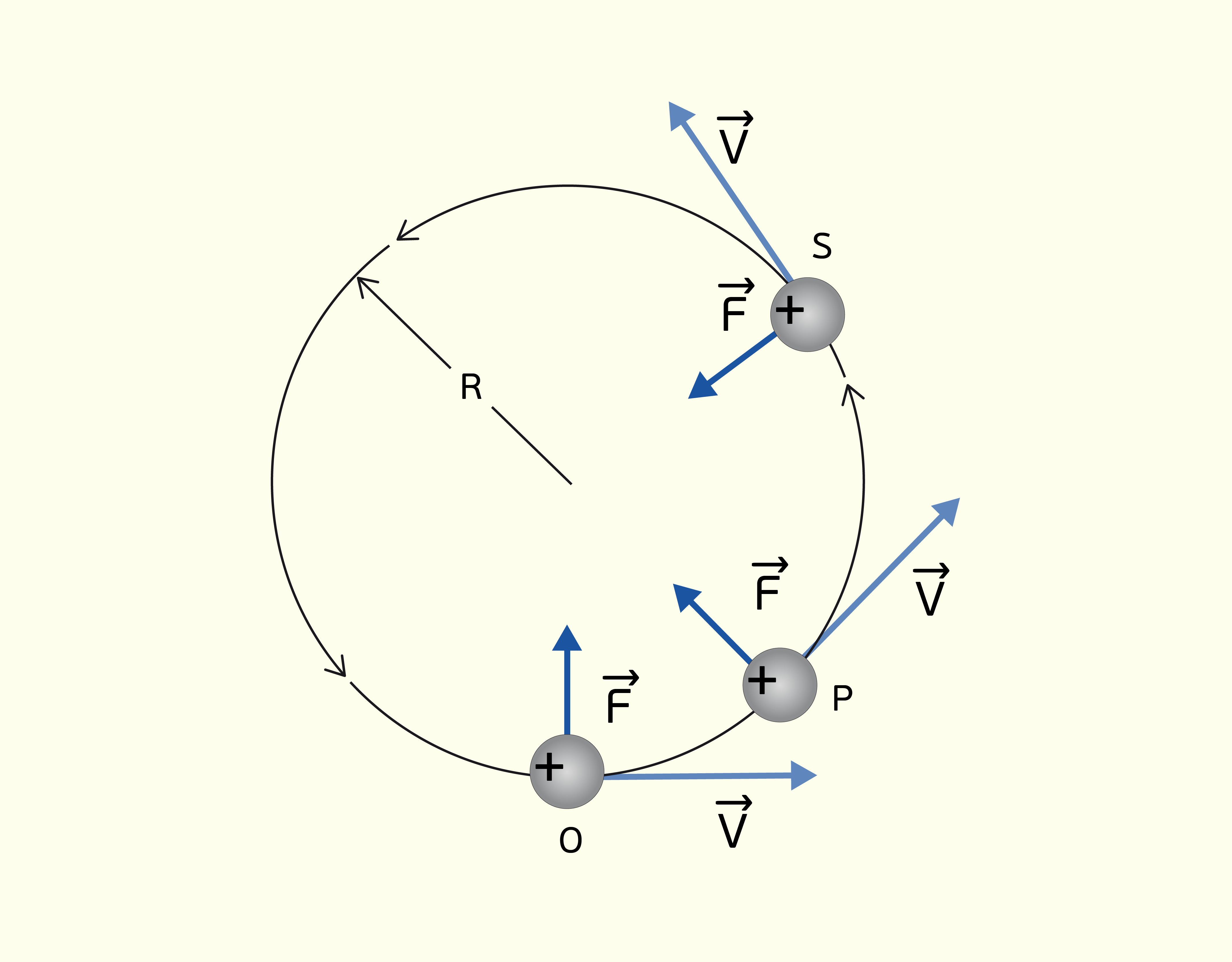
Se você observar a Figura 1.25, poderá notar que o vetor de velocidade é sempre tangente à circunferência de trajetória da partícula, além de possuir o mesmo módulo ao longo de todo o percurso. Porém, você deve ter observado que há um vetor de aceleração. Mas o movimento não é uniforme com velocidade constante? Sim. Esse vetor de aceleração é um pouco diferente, por isso está apontando para o centro da circunferência. Essa aceleração é chamada centrípeta e é resultante da força exercida sobre a partícula quando ela tenta manter o movimento circular.
O módulo dessa aceleração centrípeta está relacionado ao módulo da velocidade do objeto e ao raio da circunferência pela seguinte equação:
[math]{{a}_{rad}}=\frac{{{v}^{2}}}{r} [/math] (1.43)
Caro(a) aluno(a), é interessante, para você estudar como fizemos para deduzir a Equação (1.48):
12537 Ilustração dos vetores velocidade e aceleração centrípeta em um movimento circular uniforme Fonte: Halliday e Resnick (2012, p.73).
Além disso, seria interessante se você aprendesse como expressar o módulo dessa aceleração em termos de [math]T[/math], que é o período que o corpo leva para dar uma volta completa na circunferência de raio [math]r[/math]. Lembrando que o perímetro de uma circunferência é dado por [math]p=2\pi r[/math], podemos afirmar que é essa a distância percorrida durante o período [math]T[/math]. Logo, a velocidade pode ser definida como:
[math]v=\frac{2\pi r}{T} [/math] (1.44)
Se você substituir (1.44) em (1.43), chegará ao seguinte resultado para a aceleração centrípeta:
[math]{{a}_{rad}}=\frac{4\pi {{r}^{2}}r}{{{T}^{2}}} [/math] (1.45)
Velocidade relativa
Você certamente já deve ter se deparado com uma situação em que, ao tentar ultrapassar um carro na estrada, ficou em dúvida se o tempo seria suficiente. Você sabe por que essa dúvida existe? Devido à velocidade relativa entre os dois veículos. Isso acontece porque, quando há dois corpos em movimentos (estejam eles na mesma direção ou em sentidos opostos), a velocidade observada por um dos corpos é diferente da sua própria velocidade.
Se há uma pessoa no interior de um trem caminhando para ir ao banheiro a uma velocidade de 2m/s, sendo que o trem está andando a 5m/s, qual é a velocidade da pessoa? Essa pergunta não possui apenas uma resposta, pois não especificamos qual o ponto de referência para medição da velocidade. A velocidade da pessoa, em relação a outro passageiro, é 2m/s; porém, se há uma terceira pessoa parada fora do trem, então a velocidade relativa entre o passageiro do trem e a pessoa parada ao lado de fora é 2+5=7m/s.
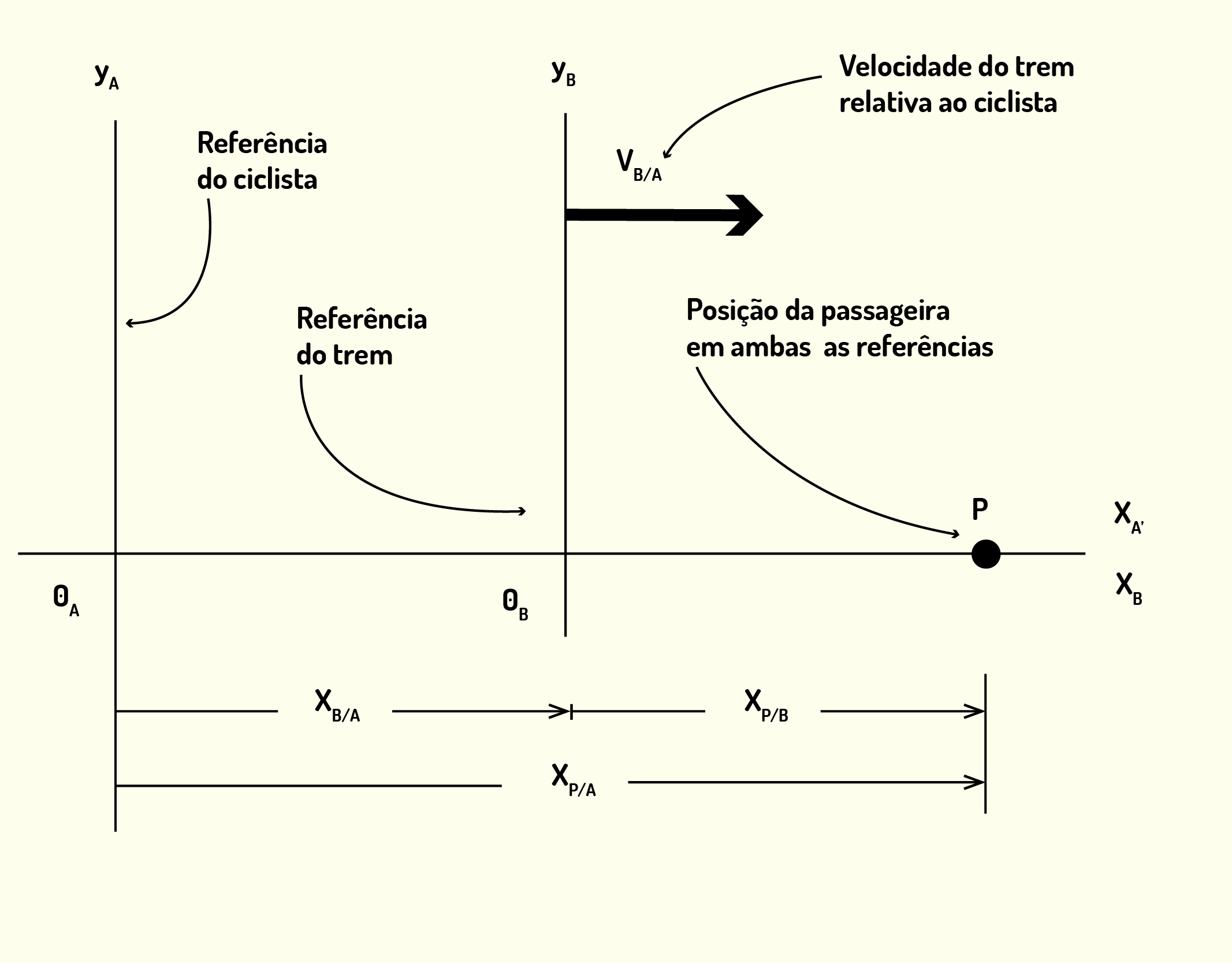
Que tal se nós definirmos matematicamente o que acabamos de falar? Vamos assumir que o ciclista parado do lado de fora do trem é a referência A, e o trem é o sistema B de referência, assim como descrito na Figura 1.26. Se você desejar descrever a posição de um ponto P em relação ao sistema B, deve escrever [math]{{x}_{P|B}}[/math]. Da mesma forma, [math]{{x}_{B|A}}[/math] é a distância entre a origem do sistema A e a origem de B. Portanto, se você observar a Figura 1.26, vai ser capaz de deduzir que:
[math]{{x}_{P|A}}={{x}_{P|B}}+{{x}_{B|A}} [/math] (1.46)
Agora, você vai poder entender mais facilmente a velocidade relativa. Lembra-se de que a velocidade é encontrada a partir da derivada do deslocamento em relação ao tempo? Então, podemos derivar [math]{{x}_{P|A}}[/math] para encontrar [math]{{v}_{P|A}}[/math]. Derivando (1.46):
[math]~\frac{d{{x}_{P|A}}}{dt}=\frac{d{{x}_{P|B}}}{dt}+\frac{d{{x}_{B|A}}}{dt}[/math] ou
[math]{{v}_{P|Ax}}={{v}_{P|Bx}}+{{v}_{B|Ax}} [/math] (1.47)
Vamos, então, voltar ao exemplo do passageiro no trem. Usando a notação anterior e o sistema de referências admitido na Figura 1.26, podemos escrever:
[math]{{v}_{P|Bx}}=~+2,0~m/s~~~~~~~~~~~~~~~~{{v}_{B|Ax}}=+5,0~m/s[/math]
E através de (1.47), a velocidade do passageiro relativa ao observador externo [math]{{v}_{P|A}}[/math] é escrita como:
[math]{{v}_{P|Ax}}=+2,0+5,0=7~m/s[/math]
Observe também que, caso o passageiro olhe através da janela do trem, ele verá o ciclista se movendo para trás com velocidade [math]{{v}_{A|Px}}[/math], que é igual e contrária a [math]{{v}_{P|Ax}}[/math].
12637 Sistema de referências adotado para expressar as velocidades e deslocamentos relativos no exemplo do passageiro caminhando no trem Fonte: Young e Freedman (2010, p.89).
Como você deve ter percebido, neste capítulo, nós aprendemos diversos tópicos diferentes, por isso, é recomendável que você procure aprofundar seu conhecimento em cada um dos temas através da literatura de referência que é apresentada ao final da unidade. Agora nós teremos somente um exercício para ser resolvido, no qual você precisará recapitular o aprendizado sobre vetores, velocidade e aceleração.
Atividades
O conteúdo estudado até agora nos proporcionou identificar e analisar alguns tipos de movimento uniformemente acelerado. Esse movimento pode estar presente em diversas situações, então faça a análise do caso em que um coelho corre com aceleração constante em um campo, sendo que suas coordenadas nos eixos [math]x[/math] e [math]y[/math] em função do tempo [math]t~[/math]podem ser descritas a partir das seguintes equações:
[math]x\left( t \right)=~-0,32{{t}^{2}}+7,2t+28[/math]
[math]y\left( t \right)=0,22{{t}^{2}}-9,1t+30[/math]
No instante [math]t=20s[/math], qual é o valor dos vetores posição [math]\vec{r}[/math], velocidade [math]\vec{v}[/math] e aceleração [math]\vec{a}[/math].
Dica: note que o vetor posição pode ser escrito como [math]\vec{r}=x\left( t \right)\hat{i}+y\left( t \right)\hat{j}[/math] e lembre-se das equações (1.34) e (1.36).
- [math]\vec{r}=~44\hat{i}-64\hat{j}~m[/math]; [math]\vec{v}=-5,6\hat{i}-0,3\hat{j}~m/s[/math]; [math]\vec{a}=\frac{d\vec{v}}{dt}=-0,64\hat{i}+0,44\hat{j}~m/{{s}^{2}}.[/math]
Caso o aluno tenha feito as contas corretas, essa deverá ser a resposta certa.
Encontrando [math]\vec{r}[/math] em [math]t=20s[/math], temos que [math]x\left( 20 \right)=-0,32{{\left( 20 \right)}^{2}}+7,2\cdot 20+28=44~m[/math]; [math]y\left( 20 \right)=0,22{{\left( 20 \right)}^{2}}-9,1\cdot 20+30=-64~m[/math] e [math]\vec{r}\left( 20 \right)=~44\hat{i}-64\hat{j}~m[/math]. A partir de (1.34) podemos encontrar:
[math]\vec{v}=\frac{d\vec{r}}{dt}=\frac{d}{dt}\left( -0,32{{t}^{2}}+7,2t+28 \right)\hat{i}+\frac{d}{dt}\left( 0,22{{t}^{2}}-9,1t+30 \right)\hat{j}=\left( -0,64t+7,2 \right)\hat{i}+\left( 0,44t-9,1 \right)\hat{j}~[/math]
[math]\vec{v}\left( 20 \right)=-5,6\hat{i}-0,3\hat{j}~m/s[/math]
A partir de (1.36) encontraremos finalmente o valor da aceleração como sendo[math]\vec{a}=\frac{d\vec{v}}{dt}=-0,64\hat{i}+0,44\hat{j}~m/{{s}^{2}}[/math]. Ou seja, a aceleração do coelho é constante em ambos os eixos.
- [math]\vec{r}=~44\hat{i}-64\hat{j}~m[/math]; [math]\vec{v}=5,6\hat{i}+0,3\hat{j}~m/s[/math]; [math]\vec{a}=\frac{d\vec{v}}{dt}=0,64\hat{i}-0,44\hat{j}~m/{{s}^{2}}.[/math]
Caso haja uma confusão na direção do vetor velocidade, haverá troca de sinal, e o aluno chegará a essa resposta.
- [math]\vec{r}=~44\hat{i}-64\hat{j}~m[/math]; [math]\vec{v}=0.8\hat{i}-4,7\hat{j}~m/s[/math]; [math]\vec{a}=\frac{d\vec{v}}{dt}=-0,32\hat{i}+0,22\hat{j}~m/{{s}^{2}}.[/math]
Essa resposta está errada, pois o valor das equações obtidas não confere com a realidade.
- [math]\vec{r}=~44\hat{i}-64\hat{j}~m[/math]; [math]\vec{v}=-0.8\hat{i}+4,7\hat{j}~m/s[/math]; [math]\vec{a}=\frac{d\vec{v}}{dt}=0,32\hat{i}-0,22\hat{j}~m/{{s}^{2}}.[/math]
Essa resposta está errada, pois o valor das equações obtidas não confere com a realidade.
Leis de Newton
Você já tentou entender qual o motivo de um objeto se movimentar quando alguém o empurra? Ou então por que é mais difícil controlar um carro sobre uma pista de gelo do que sobre uma estrada? As respostas para essas indagações devem ser baseadas na análise das forças que estão agindo sobre os corpos para produzir movimentos.
Para que você consiga ser capaz de responder a essas e outras perguntas, será preciso entender bem os conceitos de força e massa, que faremos neste capítulo. As relações entre força, massa e movimento foram teorizadas primeiramente por Isaac Newton (1642-1727) em sua obra “Princípios Matemáticos da Filosofia Natural” (Philosophiae Naturalis Principia Mathematica) e são denominadas Leis de Newton do movimento. Como dito no início da matéria, a física é uma ciência experimental. Logo, essas Leis não são simplesmente deduções matemáticas; elas são uma síntese, normatização e fundamentação do que diversos físicos vinham observando.
As Leis de Newton, embora sejam bastante simples, são fundamentais para o entendimento da dinâmica do movimento dos corpos. Porém, em seu dia a dia, você deve já ter criado um pensamento sobre como o movimento ocorre, por exemplo, quando você empurra ou puxa uma caixa. Por isso, em alguns momentos, teremos que deixar nosso senso comum de lado e tentar entender o que a física está querendo nos dizer.
Força e interações
Quando falamos em força, você provavelmente pensa em quão forte uma pessoa é, ou então em quanta força é preciso fazer para levantar uma pedra, por exemplo. Uma definição mais precisa para força é a interação entre dois objetos/corpos ou entre o ambiente e um corpo inserido nele. Quando você empurra um sofá, está exercendo uma força sobre ele; uma viga de concreto exerce uma força sobre a estrutura que está sendo sustentada.
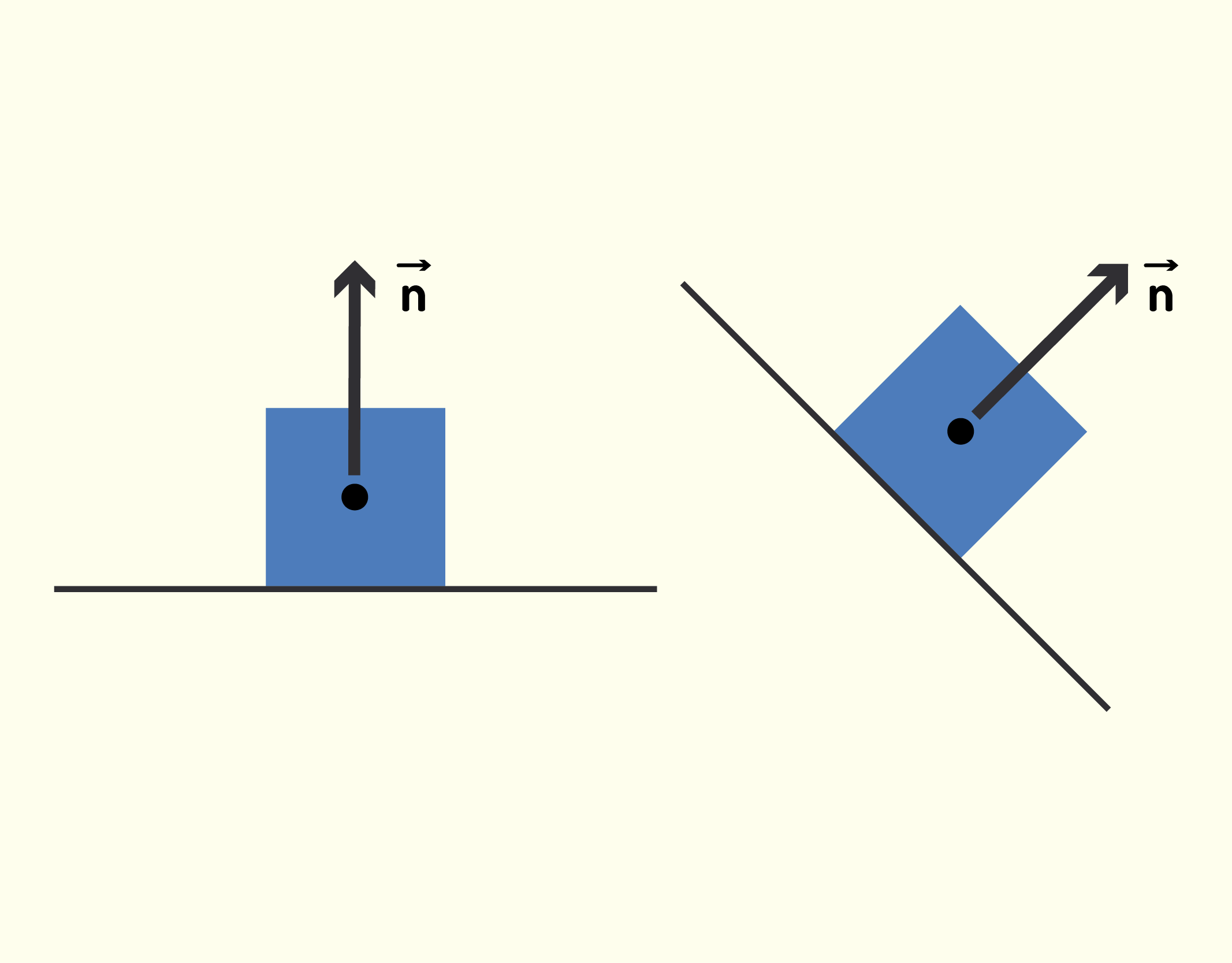
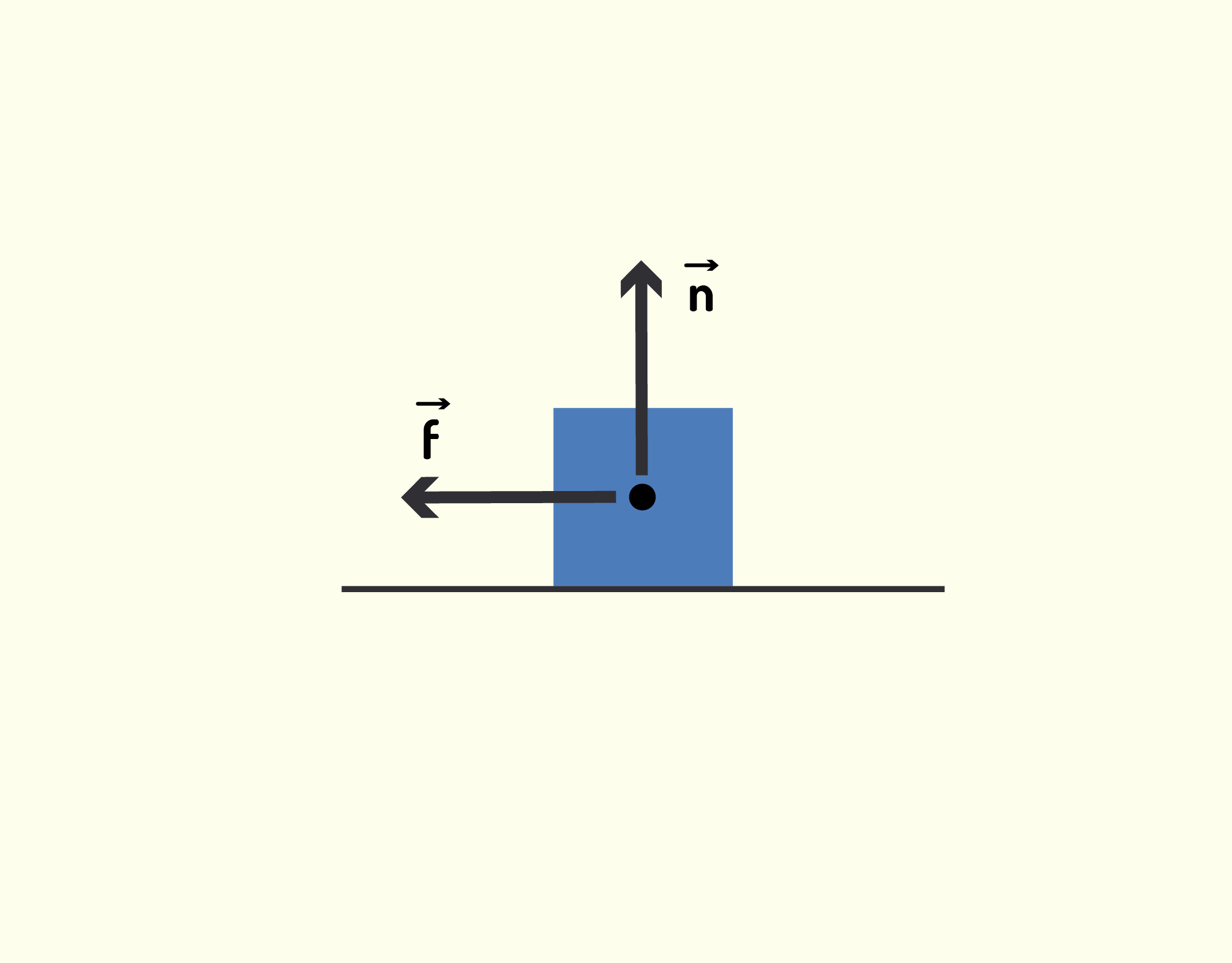
Das Figura 1.27 a 1.30 estão exemplificados quatro tipos de força para mostrar que uma força é uma grandeza vetorial. Algumas forças típicas presentes em diversas ocasiões do nosso cotidiano estão também ilustradas. Você pode observar a força normal [math]\vec{n}[/math] na Figura 1.27, que é a força perpendicular à superfície sobre a qual o objeto repousa (daí vem o nome normal), e está presente em todo corpo que está sobre alguma superfície. A força de atrito [math]\vec{f}[/math](Figura 1.28) é paralela à superfície sobre a qual o objeto se movimenta e possui direção oposta ao deslizamento
12737 Força normal [math]\vec{n}[/math] é sempre perpendicular à superfície Fonte: Young e Freedman (2010, p.106).
12837 Forças normal [math]\vec{n}[/math] de atrito [math]\vec{f}[/math] Fonte: Young e Freedman (2010, p.106).
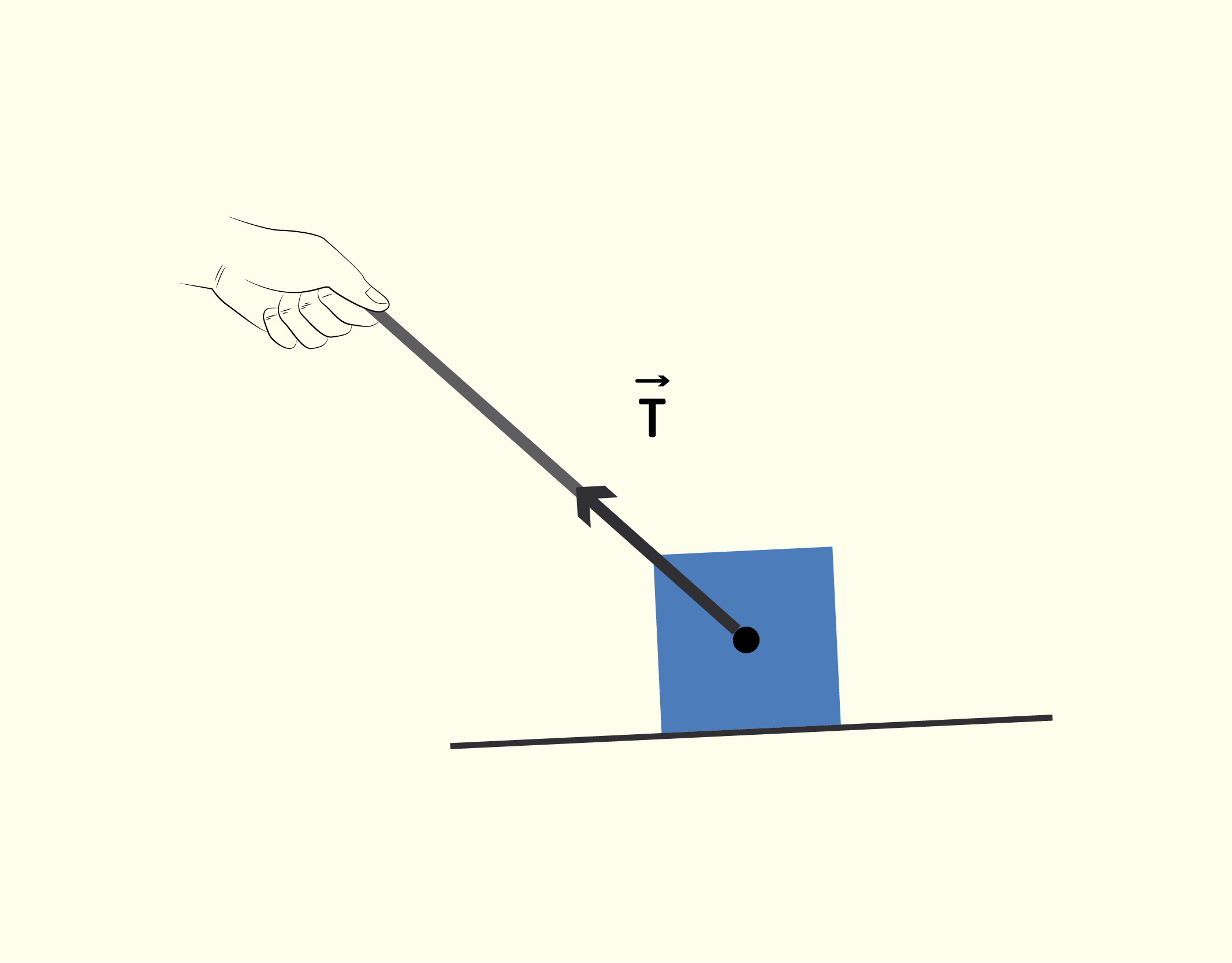
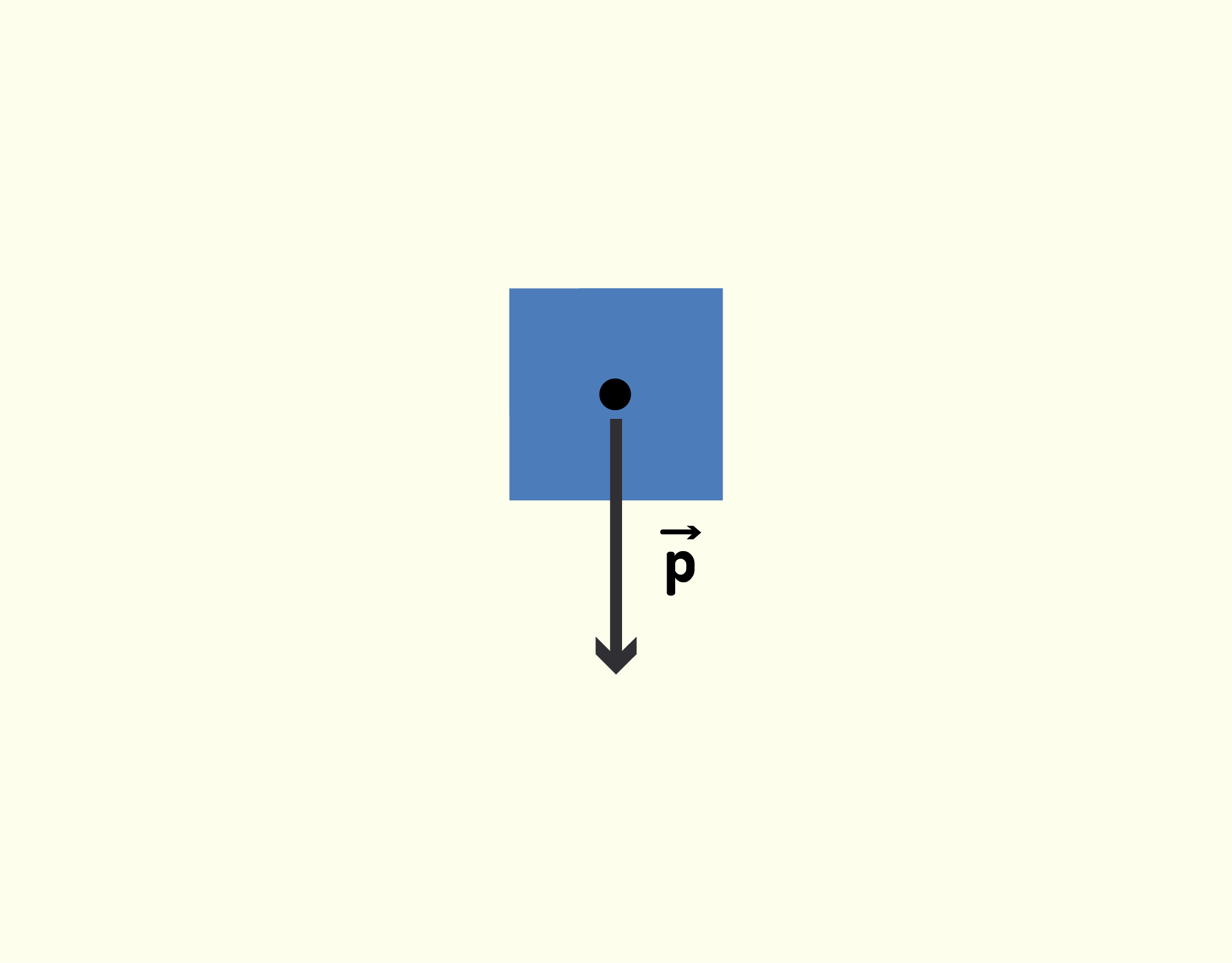
Quando puxamos um objeto através de uma corda esticada, cabo ou haste, há a força de tensão [math]\vec{T}[/math] (Figura 1.29), que possui a mesma direção do cabo que está esticado. Um exemplo comum ocorre quando você vai passear com seu cachorro e o puxa pela coleira. A força peso [math]\vec{p}[/math] (Figura 1.30) é exercida pela atração gravitacional da Terra (mesmo que a Terra e o objeto não estejam em contato) e está sempre direcionada a puxar o objeto para o centro da Terra.
Por definição, a unidade de força é o newton (N) e 1 N (um newton) é a força produzida que gera uma aceleração de [math]1m/{{s}^{2}}[/math] em um objeto de um quilograma (1kg).
12937 Força de tensão [math]\vec{T}[/math] Fonte: Young e Freedman (2010, p.106).
13037 Força peso [math]\vec{p}[/math] Fonte: Young e Freedman (2010, p.106).
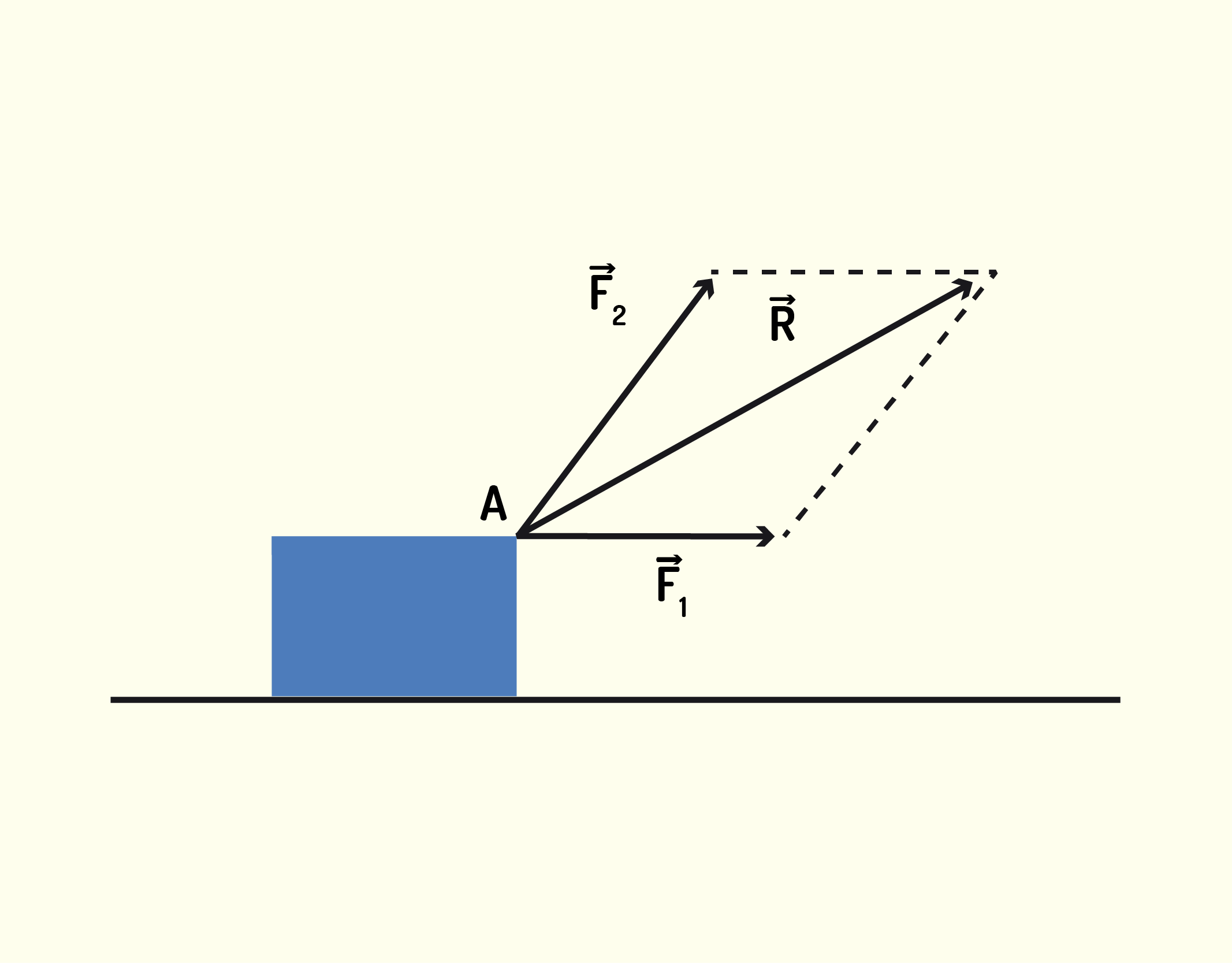
A partir disso, você consegue perceber que, em um único corpo em movimento, pode haver mais de uma força agindo ao mesmo tempo? É por isso que, para resolver um problema, será preciso encontrar o vetor resultante de todas as forças que atuam no movimento do objeto. Para isso, usaremos a letra grega [math]\Sigma [/math], que corresponde à operação de soma. Por exemplo, se em um corpo há duas forças [math]{{\vec{F}}_{1}}[/math] e [math]{{\vec{F}}_{2}}[/math], como mostra a Figura 1.31, então a força resultante é:
[math]\vec{R}=\sum \vec{F}=~{{\vec{F}}_{1}}+{{\vec{F}}_{2}} [/math] (1.48)
13137 Duas forças agindo sobre um objeto e sua respectiva força resultante Fonte: Young e Freedman (2010, p.107).
Lembre-se de que toda a matemática vetorial, assim como decomposição em componentes, soma, módulo e ângulo estão valendo e deverão ser utilizadas para manipular as forças e encontrar a resultante.
Primeira Lei de Newton
Vamos pensar em um exemplo bastante simples: imagine um disco de hóquei que, ao invés de estar sendo usado em uma pista de gelo, foi lançado sobre uma mesa de madeira. Ao fazer isso, quando lançamos o disco, ele rapidamente vai parar. Se utilizarmos o mesmo disco em uma quadra de hóquei (pista de gelo), ele conseguirá percorrer uma distância bem maior antes de parar completamente. Você sabe explicar por que isso acontece? A resposta é simples. Na mesa de madeira, o atrito que a superfície exerce sobre o disco é muito grande, o que provoca uma rápida parada. Já na pista de gelo, o atrito é muito menor, ou seja, a força que tenta fazer o disco parar é muito pequena.
O que vai acontecer com o disco se ele for lançado em um local sem atrito? Se isso for possível, ao empurrarmos o disco, ele vai entrar em movimento e nunca mais irá parar.
É a partir dessa observação que podemos extrair a Primeira Lei de Newton: Se não há nenhuma força sendo exercida sobre um corpo, sua velocidade não irá mudar, ou seja, o corpo não vai sofrer aceleração. De uma maneira mais simples, podemos dizer que, se um corpo está em repouso, ele vai continuar repousado; se ele está se movimento, irá continuar com o exato mesmo movimento (velocidade com mesmo módulo e orientação). Essa tendência de o corpo permanecer com o mesmo movimento é denominada inércia.
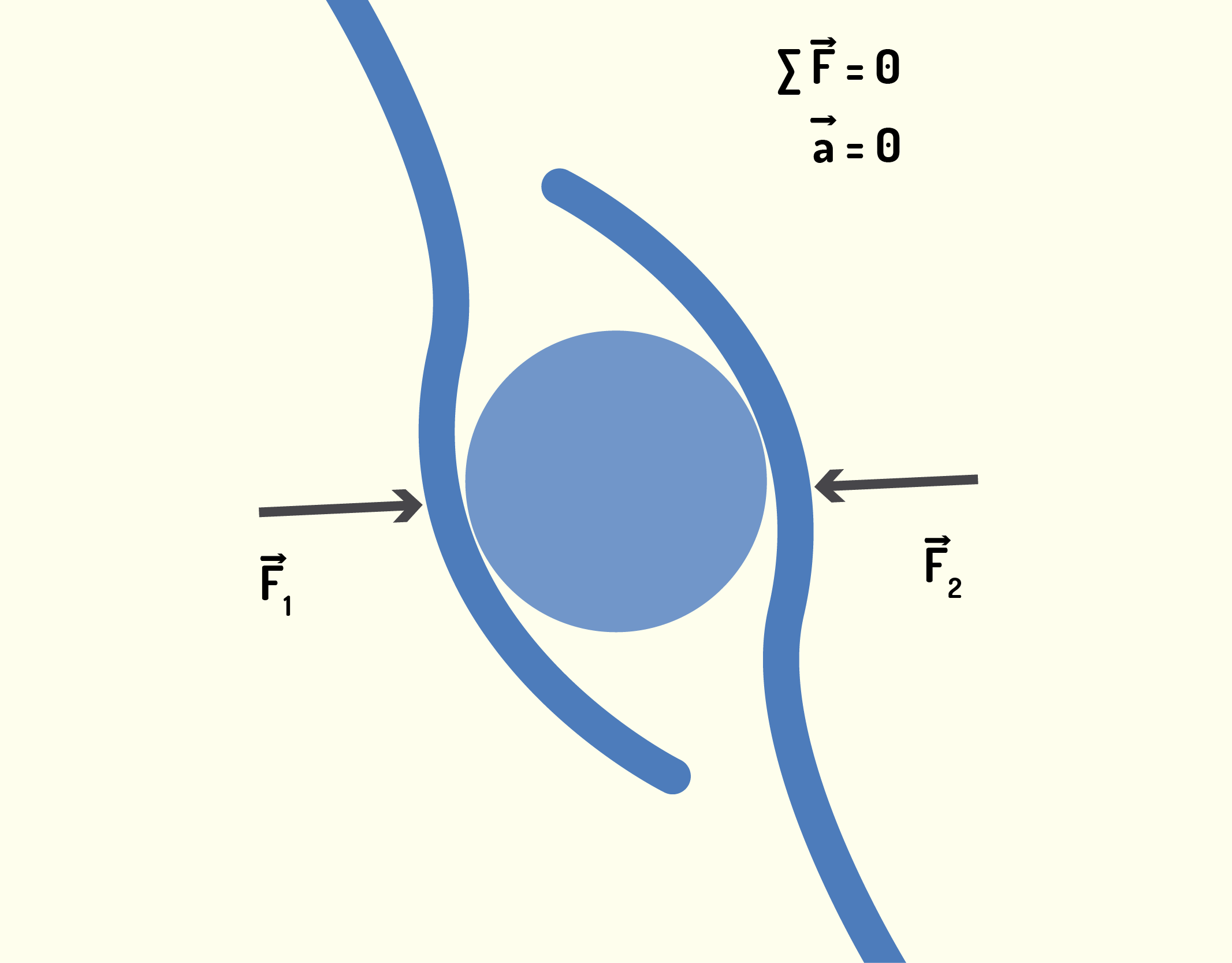
Por isso que, para estudar e aplicar essa lei, você deve saber calcular corretamente a força resultante que age sobre o corpo. Por exemplo, se em um mesmo objeto há duas forças antiparalelas e de mesmo módulo (Figura 1.32), ou seja, [math]{{\vec{F}}_{1}}=-{{\vec{F}}_{2}}[/math], a resultante é nula, pois [math]\underset{{}}{\overset{{}}{\mathop \sum }}\,\vec{F}={{\vec{F}}_{1}}-{{\vec{F}}_{2}}=0[/math]. Nesse caso, dizemos também que o corpo está em equilíbrio (a soma de todas as forças que atuam sobre ele é nula).
13237 Corpo em equilíbrio, em que a soma das forças que agem sobre ele é nula, ou seja, [math]\underset{{}}{\overset{{}}{\mathop \sum }}\,\vec{F}=0[/math] Fonte: Young e Freedman (2010, p.111).
Segunda Lei de Newton
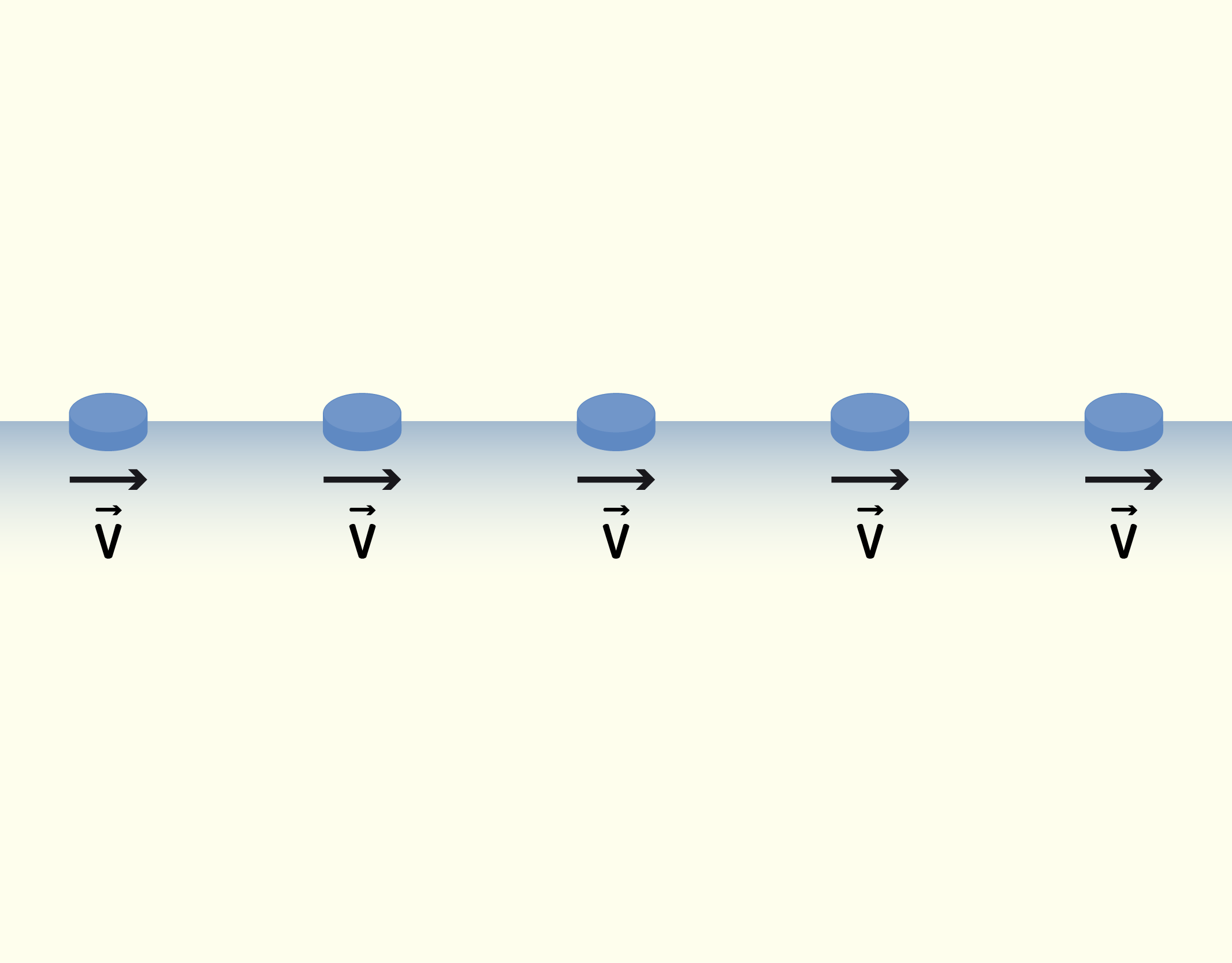
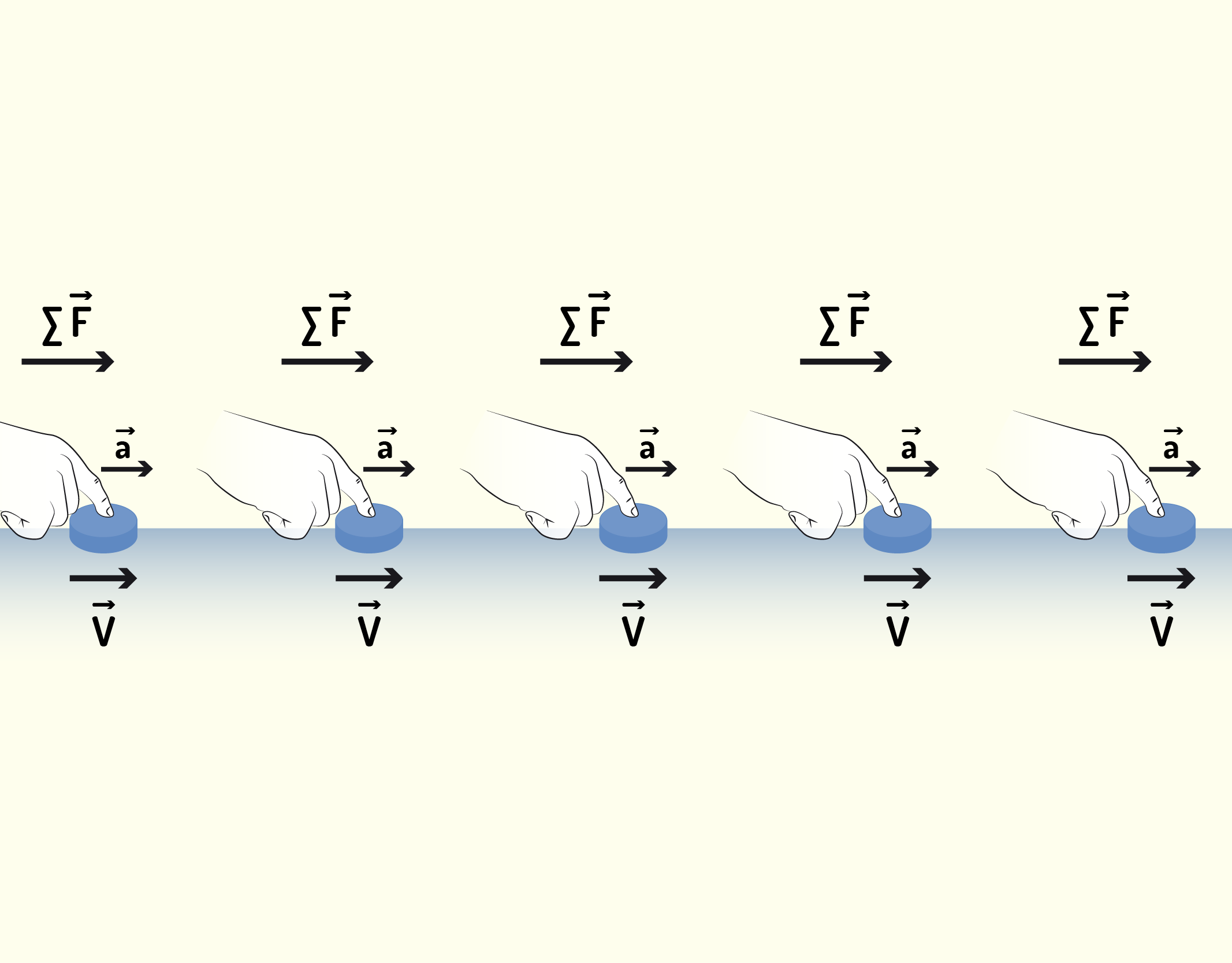
A Primeira Lei de Newton nos mostrou o que acontece quando a resultante das forças atuantes em um corpo é nula. Mas e quando isso não acontece? E quando a resultante aponta para alguma direção? As Figuras de 1.33 a 1.35 nos mostram três casos possível de resultante das forças. O caso da Figura 1.33 é o mesmo estudado anteriormente, em que a resultante é nula. Já na Figura 1.34, a resultante não é nula e provoca uma aceleração constante no mesmo sentido do movimento do disco, veja que a intensidade do vetor [math]\vec{v}[/math] está gradativamente aumentando.
13337 Disco de hóquei em velocidade constante, ou seja, [math]\vec{R}=\sum \vec{F}=0;\overrightarrow{a=0}[/math] Fonte: Young e Freedman (2010, p.114).
13437 Força resultante no mesmo sentido do movimento provoca aceleração constante no mesmo sentido Fonte: Young e Freedman (2010, p.114).
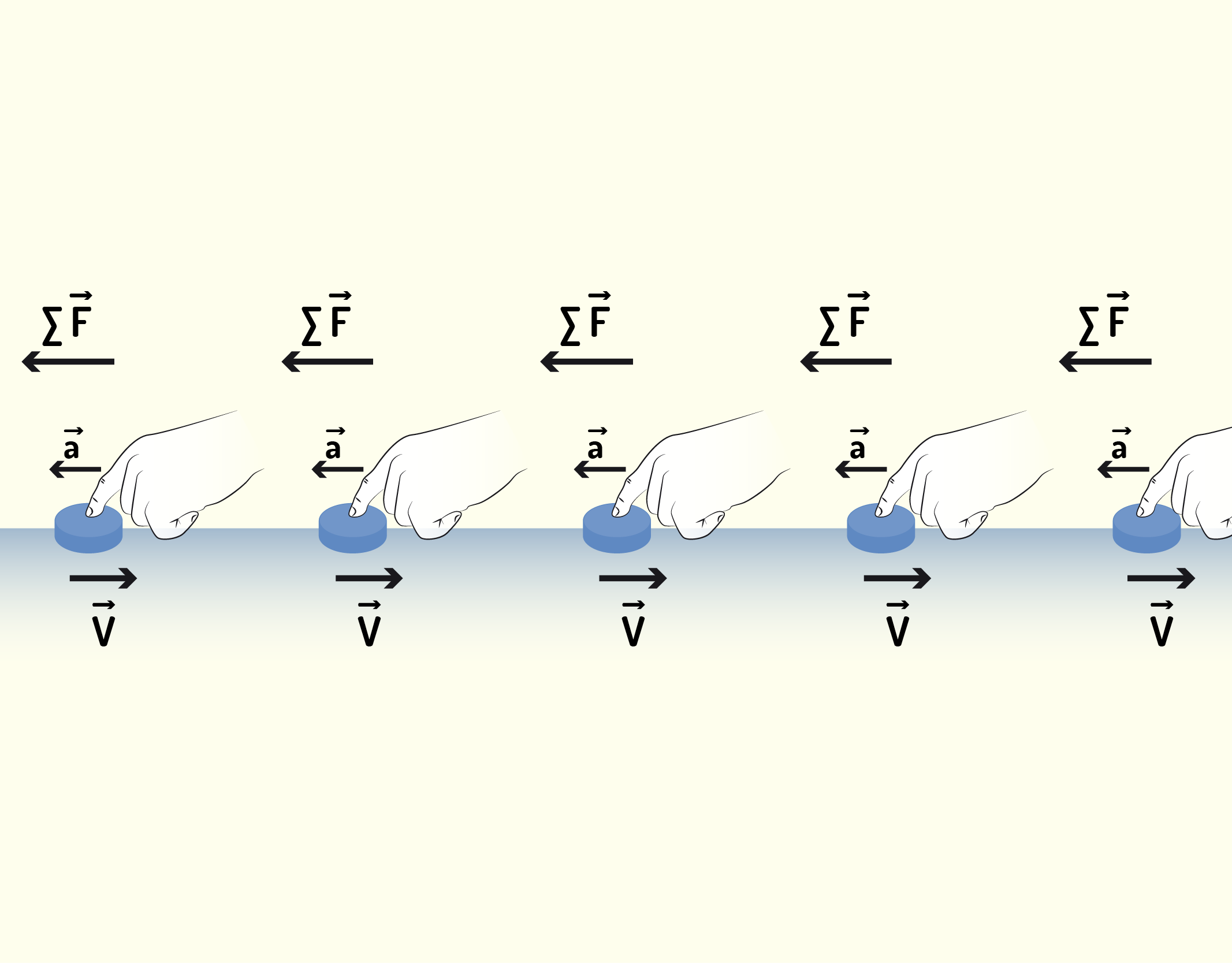
A Figura 1.35 mostra o caso oposto, em que a resultante das forças causa uma aceleração na direção oposta ao movimento do disco, fazendo com que o módulo de [math]\vec{v}[/math] diminua e, caso o movimento continue, [math]\vec{v}[/math] acabará mudando de sentido.
13537 Força resultante no sentido oposto do movimento provoca aceleração constante no sentido da força resultante Fonte: Young e Freedman (2010, p.114).
A Segunda Lei de Newton relaciona essa força resultante à massa e à aceleração do corpo pela seguinte equação:
[math]\vec{R}=\sum \vec{F}=m\vec{a} [/math] (1.49)
Sendo [math]m[/math] a massa do corpo e [math]\vec{a}[/math] a aceleração resultante.
Apesar de (1.49) ser bastante simples, você deve tomar bastante cuidado como e onde usá-la. Primeiramente você deve definir em qual corpo a equação será aplicada. Para então poder analisar todas as forças atuantes sobre ele. Somente assim será possível calcular a resultante e utilizar a segunda Lei de Newton.
Assim como todos os outros cálculos vetoriais, também existe a independência dos componentes para a resultante vetorial. Logo, pode-se analisar três diferentes equações, uma em cada eixo do sistema de coordenadas [math]xyz[/math]:
[math]{{R}_{x}}=m{{a}_{x}};~~~~~{{R}_{y}}=m{{a}_{y}};~~~~~{{R}_{z}}=m{{a}_{z}} [/math] (1.50)
A partir da definição na segunda Lei de Newton, você pode também observar a dimensão das unidades de força, relacionando a massa e a aceleração dos corpos:
[math]1~N=\left( 1kg \right)\left( 1m/{{s}^{2}} \right)=1kg\cdot m/{{s}^{2}} [/math] (1.51)
A análise de sistemas com mais de um corpo pode se tornar um pouco mais complexa, por isso não serão consideradas neste momento. Porém, caso esses diversos corpos estejam rigidamente ligados, de modo que as forças exercidas não alterem a posição e características dos corpos, então o sistema poderá ser tratado como um único corpo. Um exemplo é o sistema formado por uma locomotiva e um vagão. Caso a locomotiva estrague e necessite ser rebocada, o reboque irá puxar a locomotiva, porém a força exercida pelo reboque atuará sobre o sistema, puxando também o vagão. Sendo assim, quando os corpos estiverem rigidamente ligados, você poderá considerar todas as forças externas atuantes no sistema para encontrar a força resultante e aplicar a segunda Lei de Newton.
Massa e peso
Os termos massa e peso são comumente confundidos ou utilizados como sinônimos. A massa de um objeto é a responsável por caracterizar sua inércia. Pense em um exemplo famoso: o ato de puxar uma toalha muito rapidamente para que a louça continue praticamente parada sobre a mesa. É a massa da louça que tenta mantê-la parada no lugar. Pensando na segunda Lei de Newton, [math]\sum \vec{F}=m\vec{a}[/math], podemos verificar que quanto maior a massa do corpo, maior a força necessária para produzir uma certa aceleração.
Viu só como muitas vezes nós confundimos o peso com a massa? Na verdade, o peso é a força que a Terra exerce para tentar atrair os corpos para ela. Massa e peso são relacionados, mas não são sinônimos. Quanto maior a massa, maior o peso.
Para entender melhor, você deve pensar no exemplo da queda livre de um corpo. Quando um corpo com massa igual a 1kg cai próximo à superfície da Terra, com aceleração da gravidade [math]g=9,8m/{{s}^{2}}[/math], a força resultante é
[math]F=ma=\left( 1kg \right)\left( 9,8m/{{s}^{2}} \right)=9,8kg\cdot m/{{s}^{2}}=9,8N [/math] (1.52)
Em outras palavras, podemos dizer que a força que faz um corpo acelerar em direção ao centro da Terra é o peso. Então, qualquer objeto com massa [math]m[/math] possui um peso [math]p[/math] dado por:
[math]p=mg \text{ (1.53)}[/math]
Sendo que, para as proximidades da Terra, já vimos que [math]g=9,8m/{{s}^{2}}[/math]. Porém, se você um dia resolver ir para a Lua, irá se deparar com uma aceleração gravitacional bem diferente, pois lá [math]g=1,62m/{{s}^{2}}[/math].
Terceira lei de Newton
Você provavelmente já deve ter ouvido o ditado que toda ação tem uma reação. Sabia que isso é baseado na terceira lei de Newton? Quando você chuta uma bola de futebol, além dela mover-se para frente, você também sente a força exercida pela bola em seu pé. Ou quando você bate em um saco de areia e sente sua mão dolorida, isso é causado pela força de reação que foi exercida em sua mão.
Mais formalmente, a terceira lei de Newton diz que, quando um determinado corpo A exerce uma força sobre um corpo B, então, o corpo B também exerce uma força sobre A (o corpo A praticou uma “ação” e B reagiu). Essas duas forças têm a mesma intensidade (mesmo módulo), sentidos contrários e atuam em corpos diferentes. Ou seja, matematicamente, você pode definir essa lei como sendo:
[math]{{\vec{F}}_{A~em~B}}=-{{\vec{F}}_{B~em~A}}[/math]
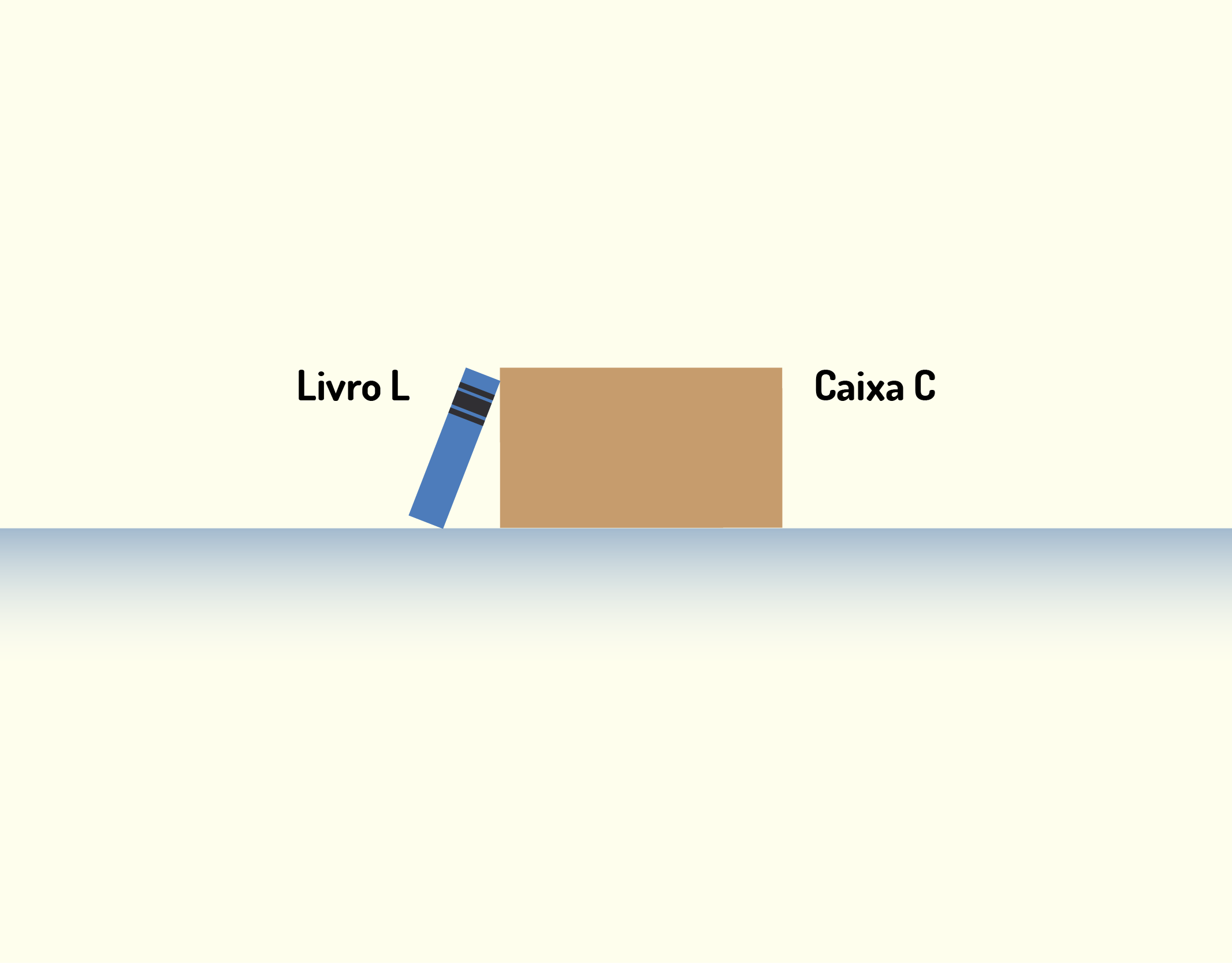
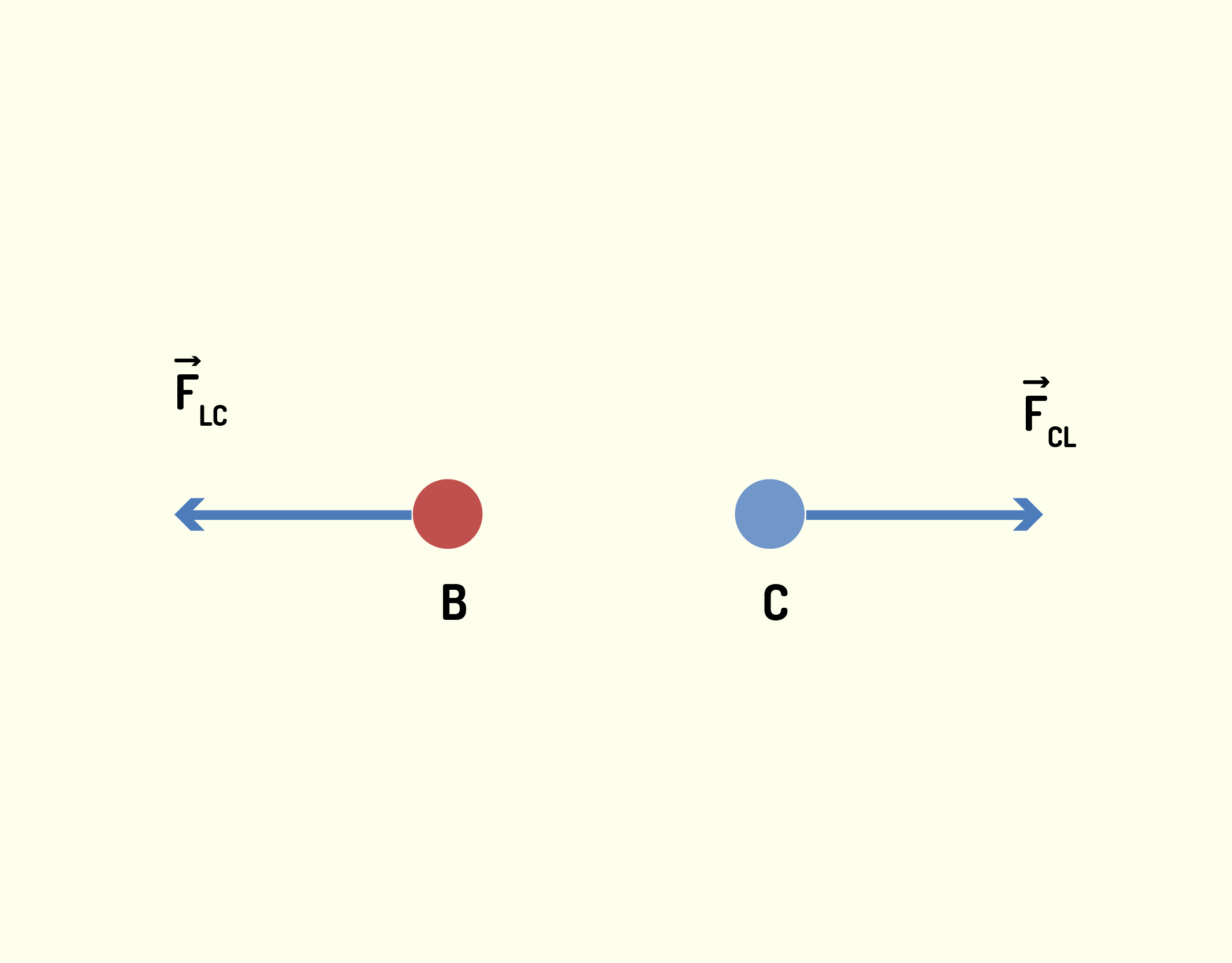
Note que não importa a natureza do corpo, ele exercerá uma força mesmo sendo inanimado (como o saco de pancadas). Vamos observar um exemplo. Considere um livro encostado em um caixa, como ilustrado na Figura 1.36. Como o livro está um pouco tombado e apoiado na caixa, ele está exercendo uma força [math]{{\vec{F}}_{LC}}[/math] sobre a caixa. Porém, como dissemos, a caixa tem uma reação e exerce uma força [math]{{\vec{F}}_{CL}}[/math] no livro. A Figura 1.37 mostra essas duas forças e suas direções contrárias, sendo elas [math]{{\vec{F}}_{LC}}=-{{\vec{F}}_{CL}}[/math], que estão sendo aplicadas em corpos distintos.
13637 Ilustração de como o livro está apoiado na caixa Fonte: Halliday e Resnick (2012, p.102).
13737 Esquema das forças [math]{{\vec{F}}_{LC}}[/math] e [math]{{\vec{F}}_{CL}}[/math] no livro apoiado na caixa Fonte: Halliday e Resnick (2012, p.102).
Agora você já deve estar bem preparado para resolver problemas envolvendo corpos em movimentos. Portanto, para verificar se você realmente aprendeu os conceitos básicos sobre as leis de Newton e as relações entre peso e massa, vamos responder a uma questão conceitual!
Atividades
Você estudou a diferença entre peso e massa, além de ter conhecido as leis de Newton, que analisam objetos em inércia, com força resultante nula ou não e as forças de ação e reação. A partir do conhecimento adquirido, encontre a alternativa verdadeira.
- Quando aplicamos uma força de mesmo módulo, direção e sentido em corpos diferentes, a aceleração gerada será sempre a mesma.
Como estudado anteriormente, a partir da segunda lei de Newton, nós vimos que a força resultante em um corpo produz uma aceleração que é proporcional à massa do objeto. Se uma força com intensidade de 10 N for aplicada em um objeto com massa igual a 100g, a aceleração será diferente do que se a mesma força for aplicada em um corpo de 50kg.
- Se um corpo em equilíbrio que possui aceleração nula estiver em movimento em um local sem atrito, ele irá parar em um tempo proporcional às forças aplicadas nele.
Se um corpo está em equilíbrio e movimenta-se em um lugar sem atrito, ele nunca irá parar, pois a resultante das forças exercidas sobre ele é nula. Isso é o que nos diz a primeira lei de Newton.
- Uma balança mede o peso de um objeto, mostra em seu display a massa desse corpo e consegue efetuar a medida sem erros inclusive quando inserida em referenciais não inerciais.
A balança realmente utiliza o peso e mostra o valor da massa do objeto. Porém se o referencial não é inercial, há outras forças atuando sobre o objeto a ser medido, o que pode acabar (dependendo da direção e sentido) anulando (ou aumentando) completa ou parcialmente a força peso do objeto.
- Quando uma laranja está em queda livre, ela também possui um par de forças, sendo uma a força que a Terra exerce na laranja e a outra a força de reação que a laranja exerce na Terra.
Através da Terceira Lei de Newton, aprendemos que toda força de ação acarreta uma reação. Com um corpo em queda livre não é diferente. Ele irá possuir a força devido à aceleração da gravidade, cujo par de reação está na superfície da Terra.
Querido(a) aluno(a), creio que agora você tenha entendido um pouco mais que as Leis de Newton estão presentes em praticamente todas as nossas atividades diárias. Desde o simples digitar em um teclado, em que você aplica uma força e o teclado reage com uma força aplicada em seu dedo, até as estrelas em órbita ao redor da Terra, que são atraídas para o centro a fim de não saírem flutuando pelo espaço. Agora, para que você possa pensar mais um pouco sobre, vamos observar uma questão mais ampla e refletir sobre sua resposta.
Reflita
Você, com certeza, já deve ter assistido a filmes que contenham algum tipo de batida de carro. Então já viu exemplo clássico usado para análise das leis de Newton. Sabia que os equipamentos de proteção (cinto de segurança e airbag) estão lá para tentar aliviar o efeito da primeira lei de Newton?
Fique por dentro
Você sabia que o efeito das marés é causado por uma das forças que estudamos nesta unidade? Exatamente. A força responsável por isso é a força da gravidade. A aceleração gravitacional provoca uma atração entre a Terra e a Lua (chegando até a modificar a geometria esférica da Terra). Essa atração age sobre todos os pontos da Terra, inclusive os oceanos e rios. A atração não ocorre somente entre Terra e Lua. Ela acontece também entre a Terra e o Sol. Sendo assim, quando a direção das duas atrações está alinhada, o mar é atraído mais fortemente, provocando as marés altas. Quando as duas forças de atração são ortogonais, a resultante é drasticamente reduzida, provocando as marés baixas.
FonteExplicações mais detalhadas e dinâmicas estão www.youtube.com.