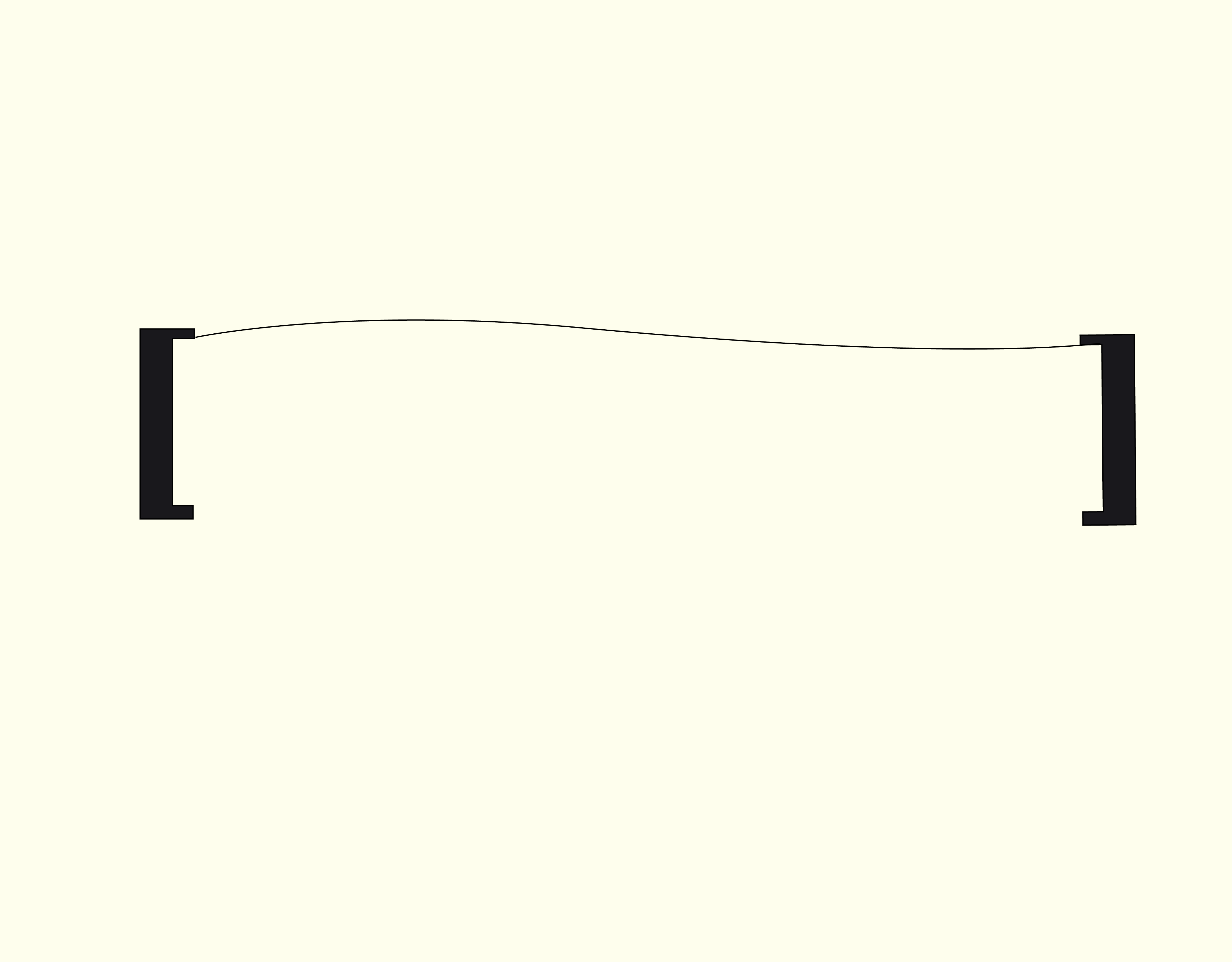Conceitos básicos
A humanidade, desde seus primórdios, possui uma necessidade muito grande de contar.
Segundo Ramos (2011), civilizações muito antigas já sentiam necessidade de quantificar e de expressar quantitativamente seu cotidiano. Os primeiros registros de quantificação não numérica foram entalhes em ossos, de aproximadamente 30000 a 20000 a.C. Muitas civilizações usaram objetos para auxiliar suas contagens, fazendo marcas e registros no chão, nas paredes ou em ossos; muitos desses instrumentos ou registros utilizavam a contagem um a um.
Nos dias de hoje, temos os computadores, que resolvem de uma maneira muito mais fácil essa necessidade da sociedade, realizando não só cálculos extremamente complexos, como também atividades que não possuem, aparentemente, nenhuma relação com números, como editores de texto, softwares de apresentação, programas para manipulação de imagens, entre outros.
O sistema computacional é formado pela combinação do hardware e do software. O hardware é a máquina em si, com seus circuitos digitais, ou seja, o equipamento. O software são os programas que comandam a máquina ou fazem com que o computador execute a tarefa a que se propõe, resolvendo problemas de naturezas diversas.
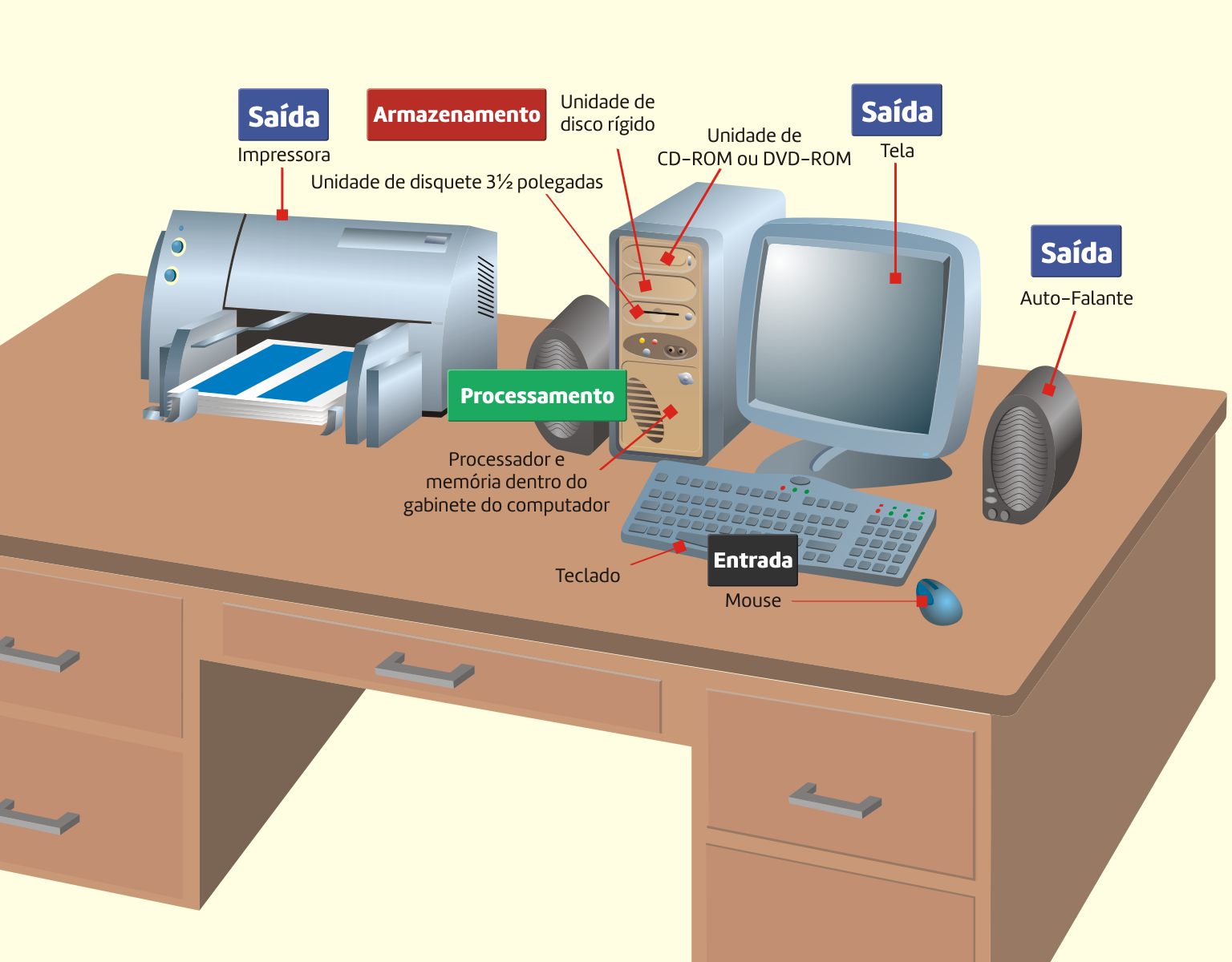
A Figura 3.1 apresenta um sistema computacional com seus principais componentes.
3119 Sistema computacional Fonte: Capron (2004).
Weber (2012, p.27) acrescenta que:
cada computador tem um conjunto de operações e convenções único para determinar as posições dos dados com os quais a operação será realizada. Os vários computadores diferem nas operações específicas que fornecem e nos métodos que usam para referenciar os dados que serão manipulados por uma operação.
As funções básicas que um computador pode realizar são: processamento de dados, armazenamento de dados, movimentação de dados e controle.
a. Processamento de Dados
Monteiro (2012, p.1) caracteriza que “processamento de Dados (Data Processing) consiste, então, em uma série de atividades ordenadamente realizadas, com o objetivo de produzir um arranjo determinado de informações a partir de outras obtidas inicialmente”.
O mesmo autor complementa que processar o dado é executar com ele uma ação que produza algum tipo de resultado” (MONTEIRO, 2012, p.173).
Uma instrução é a responsável pela codificação de uma determinada operação.
Quando se tem um conjunto de instruções, colocadas de forma adequada (em sequência) forma-se um programa.
Weber (2012, p.27) define isso de uma maneira muito clara:
um programa é constituído por uma sequência pré-determinada de instruções, que deve ser seguida para que seja atingido o objetivo computacional. Este programa e os dados correspondentes estão armazenados na memória da máquina; o conjunto de instruções (ou programa) deve ser interpretado para realização do processamento, isto é, a informação codificada correspondente às ações e aos operandos deve ser entendida e então processada.
b. Armazenamento de Dados
O armazenamento de dados e instruções é realizado pela memória de um sistema computacional. Essa memória é organizada em posições, cada uma com seu endereço específico.
c. Movimentação de Dados
A movimentação de dados diz respeito à comunicação do computador com o mundo exterior, o processo de entrada e saída.
Essa comunicação é realizada pelos dispositivos de entrada e saída, como mouses, monitores de vídeo e impressoras.
Exemplo: uma pessoa fornece o número do CEP da sua residência por meio do teclado e o programa, no monitor de vídeo, mostra o nome da rua e o bairro.
d. Controle
O controle é necessário para que se possa gerenciar as funções anteriores e é realizado pela Unidade de Controle, existente dentro do computador. Na seção sobre a Unidade Central de Processamento, detalharemos um pouco mais essa função.
Quando desenvolvemos um programa, geralmente ele é codificado utilizando linguagens chamadas de alto nível, como C, C++, C# ou Java. Todas essas linguagens possuem uma sintaxe específica, com definições e bibliotecas básicas e são mais simples para o programador, pois ele pode utilizar seu raciocínio de forma mais clara. Além disso, elas são independentes do computador para o qual são desenvolvidas. Assim, o mesmo programa pode ser utilizado em máquinas diferentes.
Mas o computador não é projetado para trabalhar com esse tipo de linguagem (lembre-se: ele trabalha somente com 0s e 1s) e sim com a chamada linguagem de máquina, que contém instruções de máquina, muito mais simples do que as utilizadas no alto nível.
As principais atividades que podem ser realizadas por uma instrução de máquina são:
- Operações aritméticas e lógicas;
- Movimentação de bits;
- Controle;
- Desvios na sequência do programa; e
- Comunicação com dispositivos de entrada e saída.
A linguagem de máquina utiliza mnemônicos para indicar a instrução ou operação que será executada, facilitando a programação. Mas esse programa precisa ser traduzido para a linguagem de máquina para ser executado pelo computador. O programa que realiza essa tradução é chamado de montador.
Um montador realiza praticamente apenas uma tradução “um para um” das instruções da linguagem simbólica para instruções de máquina (ao contrário de um compilador, que gera rotinas em linguagem de máquina para cada instrução da linguagem de alto nível e depois otimiza código e alocação de variáveis) (WEBER, 2012).
Existe, também, um outro método para se executar um programa, chamado interpretação que, segundo Monteiro (2012), se caracteriza por realizar as três fases (compilação, ligação e execução), comando a comando, do programa-fonte. Não há, pois, um processo explícito de compilação e ligação. Na realidade, um programa-fonte é diretamente executado (interpretado) por outro programa (o interpretador) e produz o resultado.
Funcionamento básico de um computador
Complementando as informações anteriores, o computador é uma máquina que pode ser programada para aceitar dados (entrada), transformá-los em informações (saída) útil e armazená-los (em um dispositivo de saída secundário) para proteção ou reutilização. O processamento da entrada para a saída é conduzido pelo software, mas realizado pelo hardware (CAPRON, 2008).
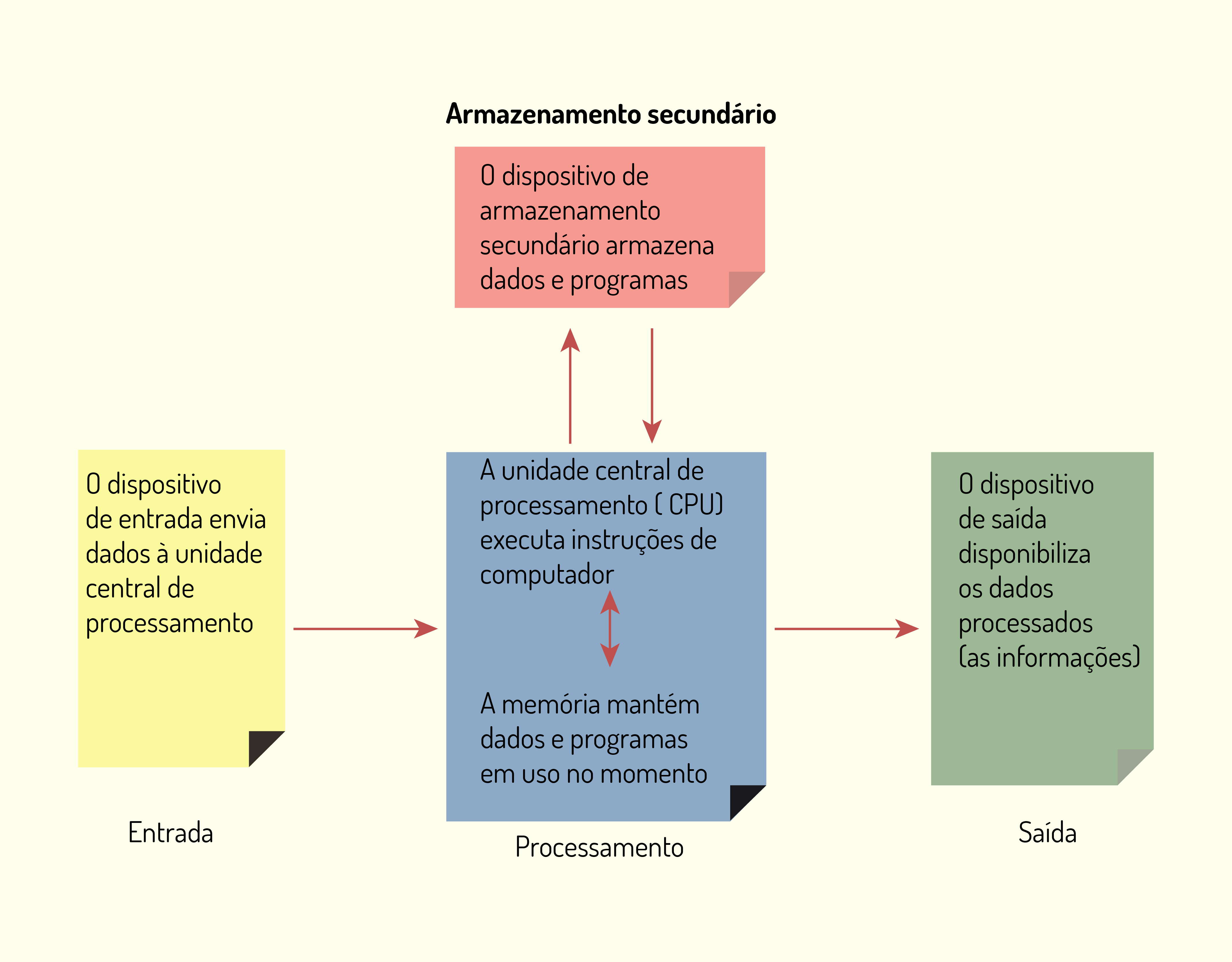
A Figura 3.2 ilustra os quatro componentes principais de um computador.
3219 Componentes principais de um computador Fonte: Capron (2004).
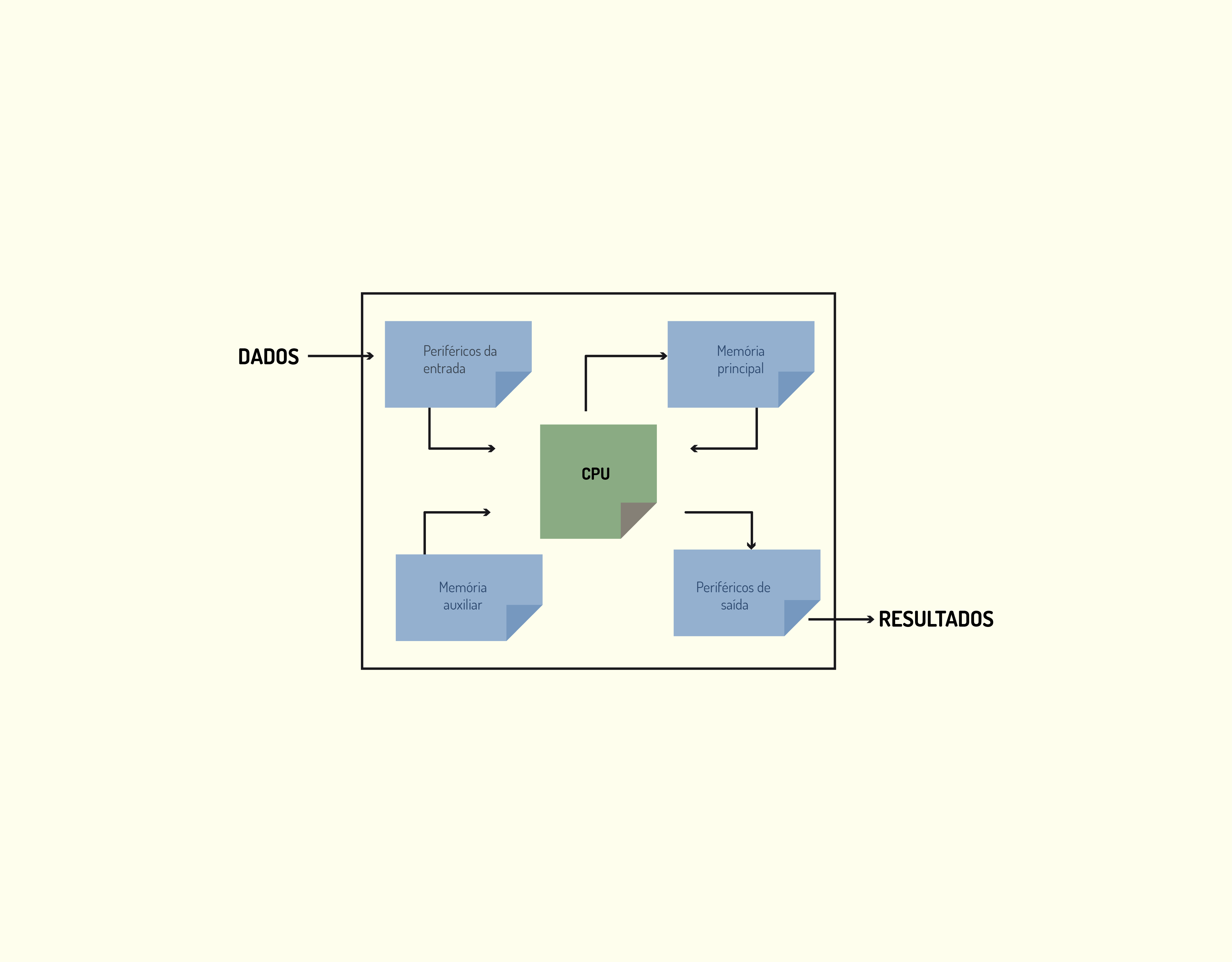
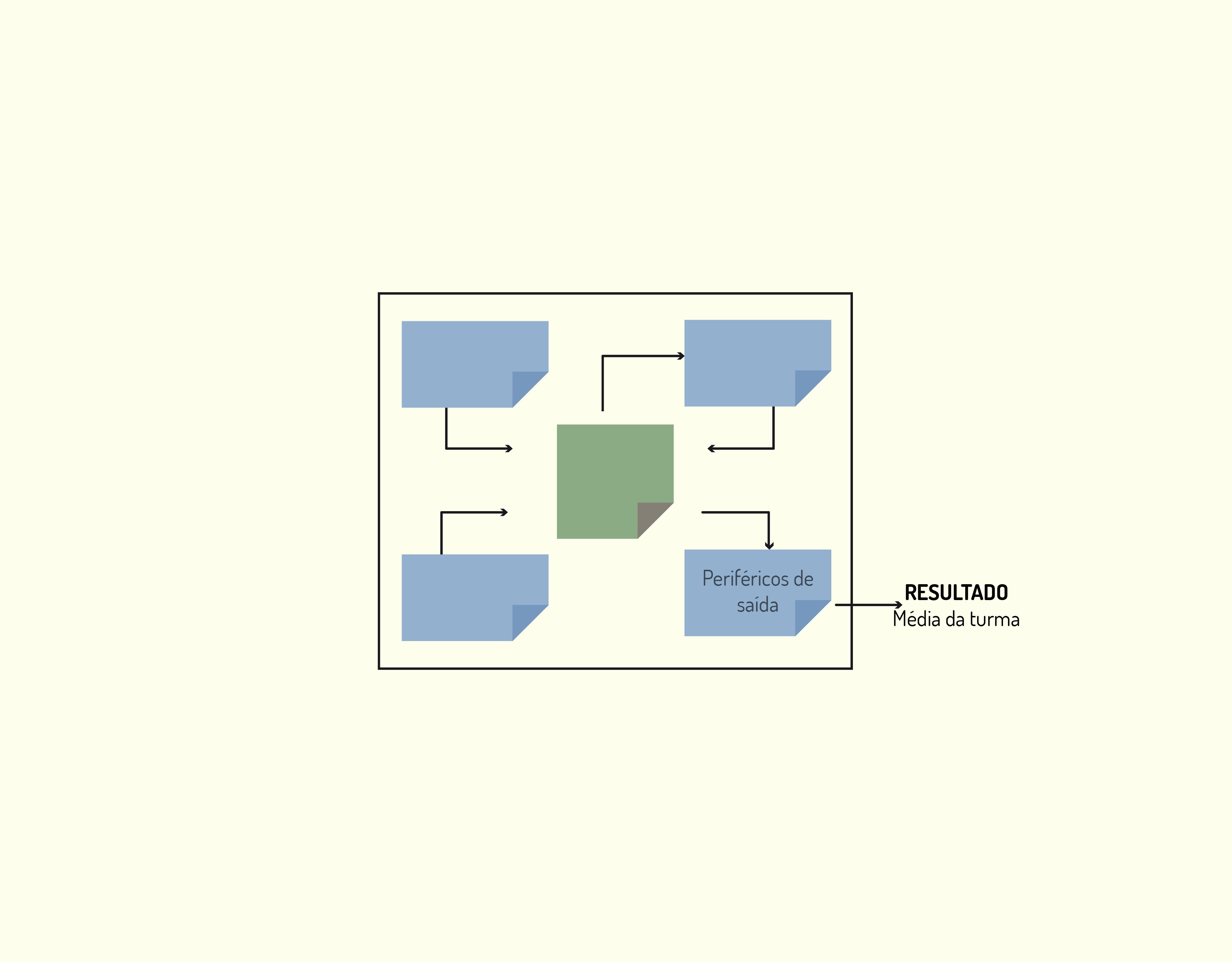
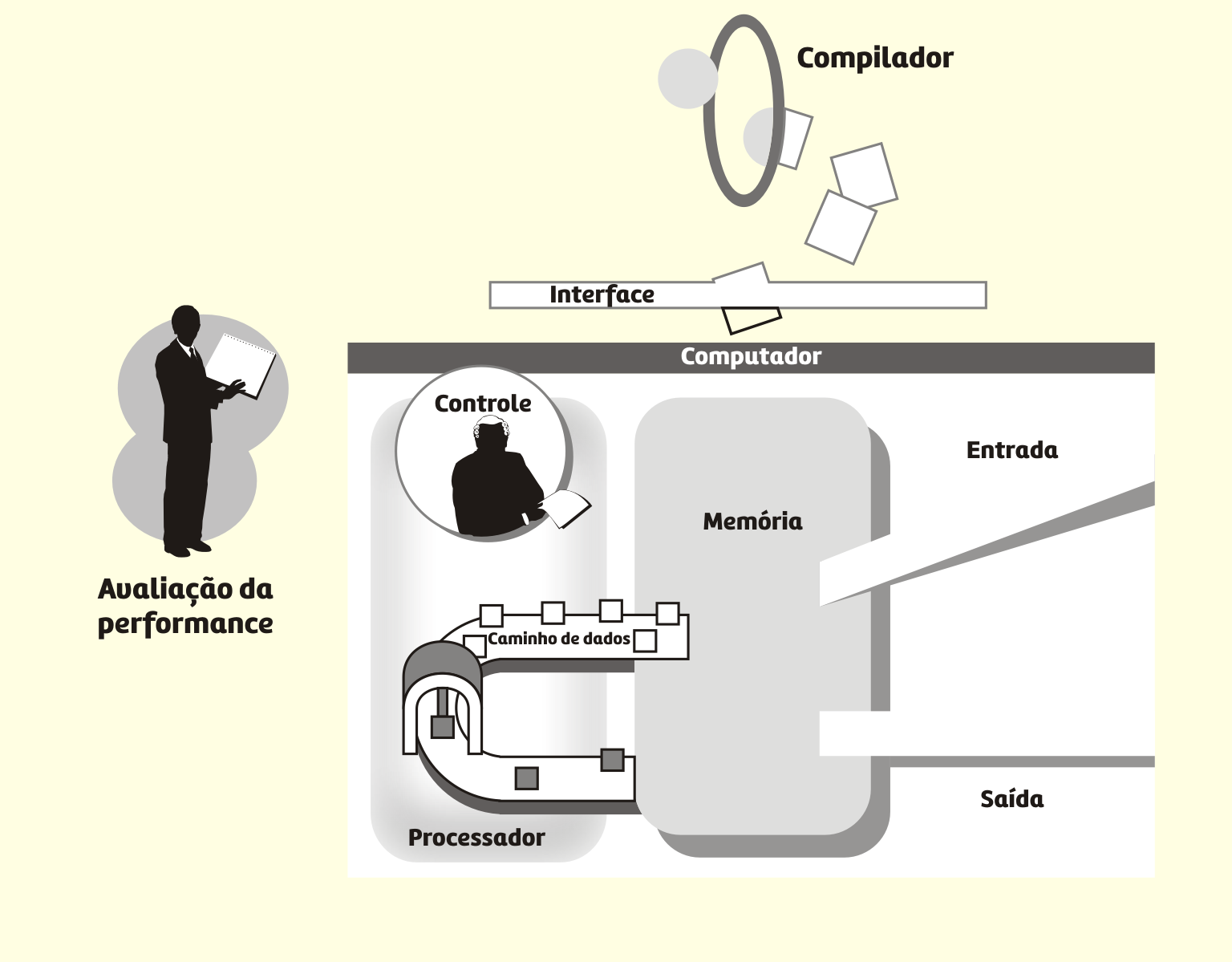
Para mostrar o funcionamento geral de um computador, vamos utilizar o esquema apresentado na Figura 3.3.
3319 Esquema geral de um computador Fonte: A autora.
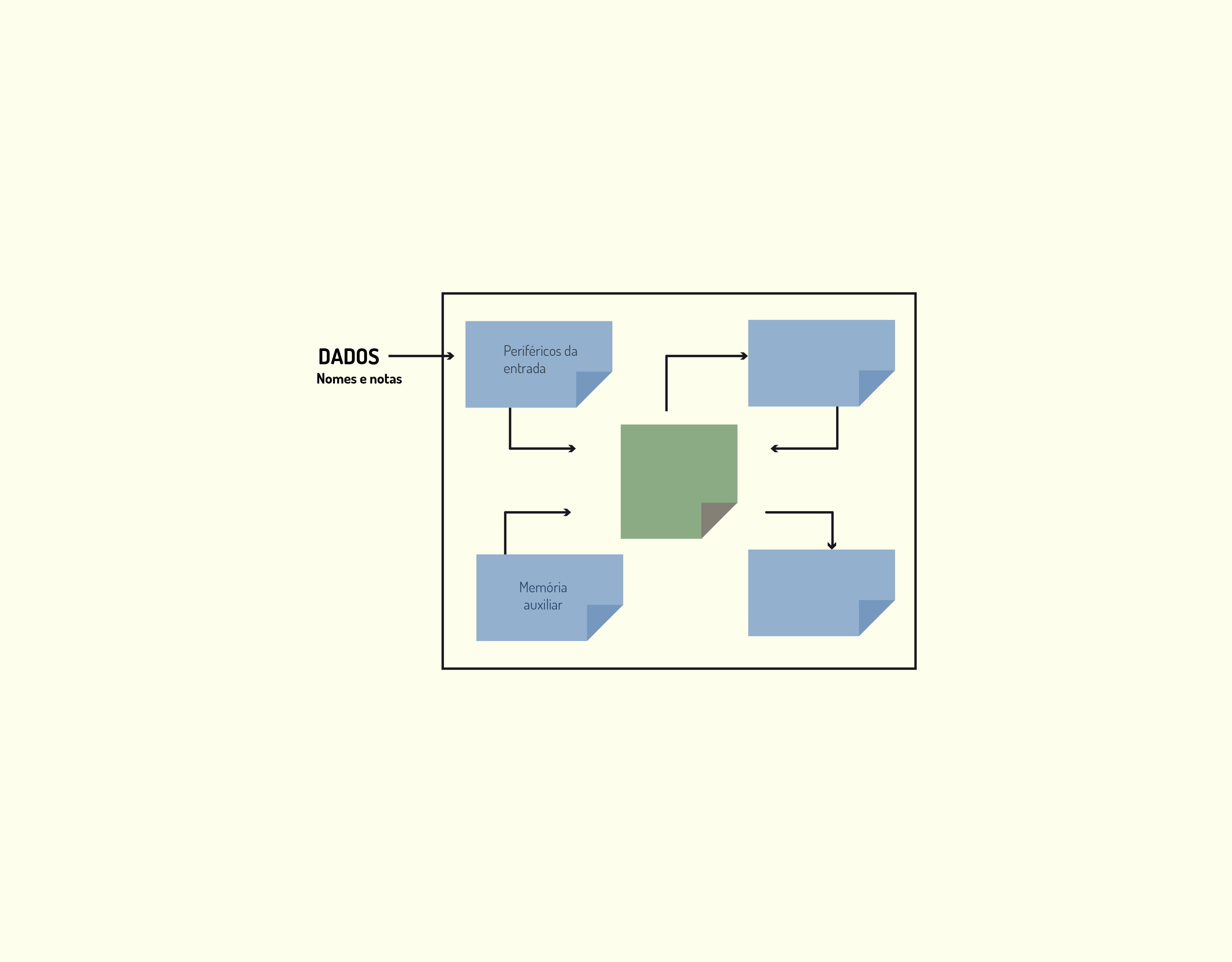
Vamos utilizar como exemplo o cálculo da média de notas de uma turma. Os passos necessários para esse cálculo podem ser divididos em:
- Os periféricos de entrada do computador recebem o nome e a média de cada um dos alunos da turma, conforme visto na Figura 3.4. Os dados podem vir também da memória auxiliar, onde estão armazenados.
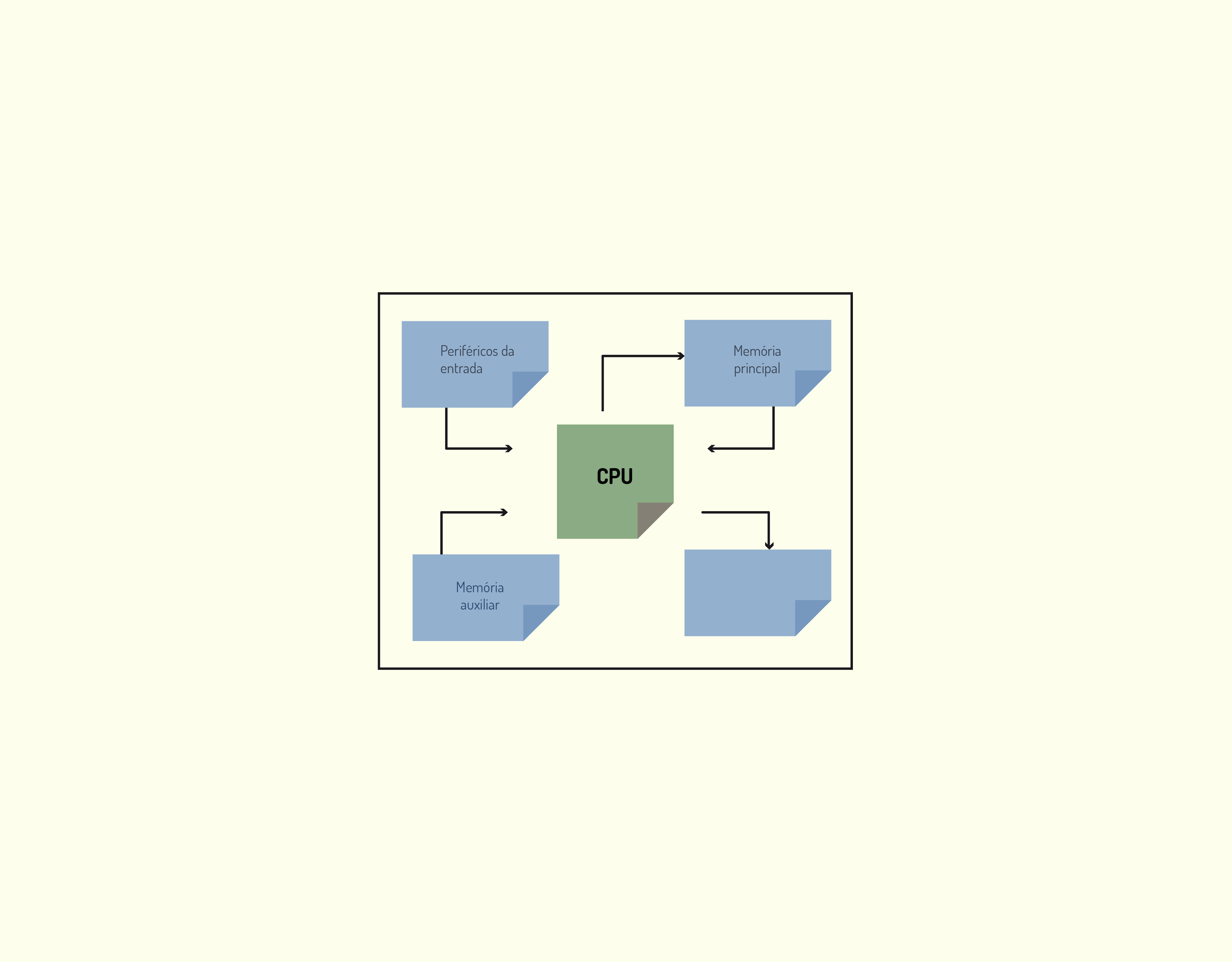
- A UCP transfere as informações recebidas no periférico de entrada para a memória principal, processo ilustrado na Figura 3.5.
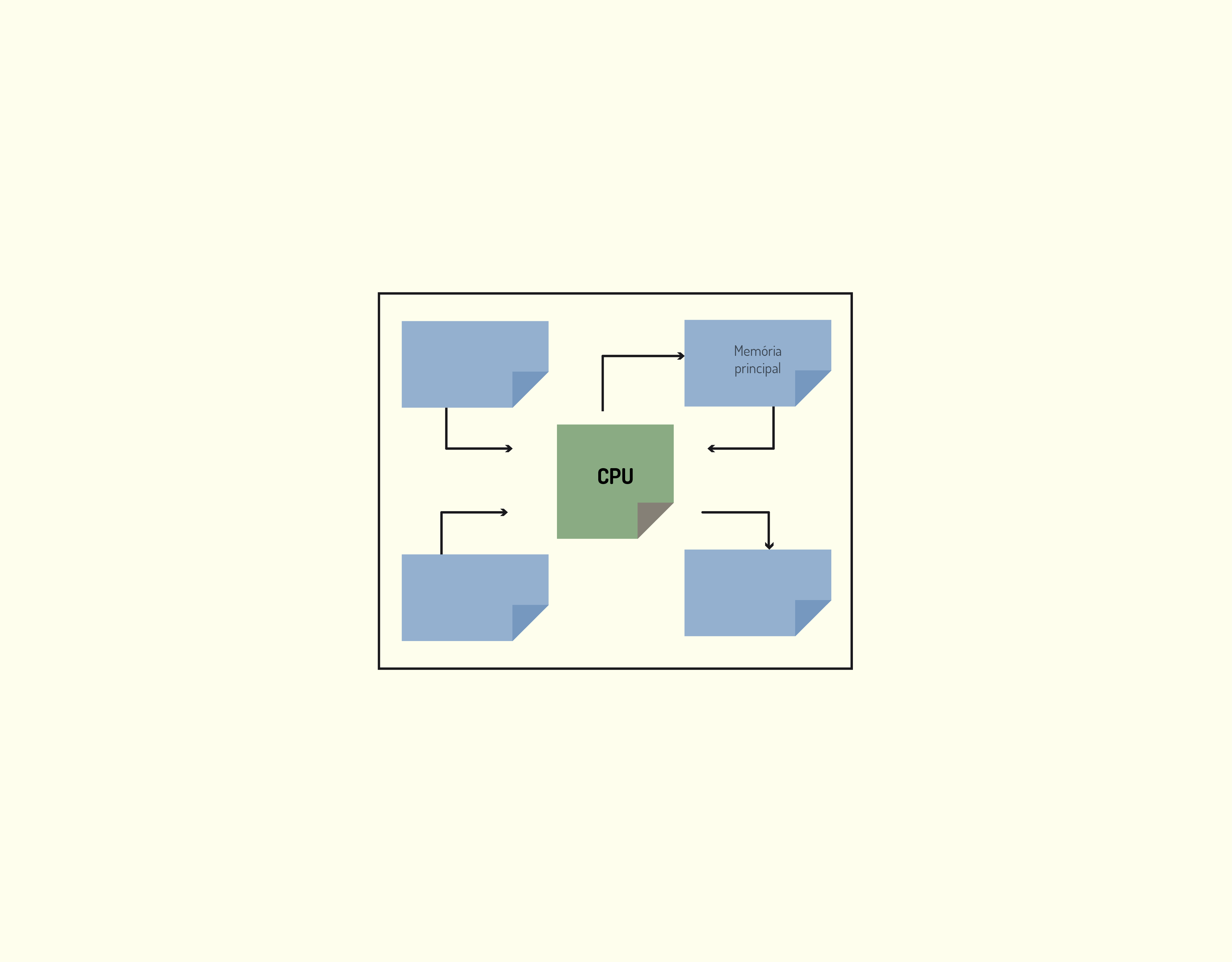
- A UCP trabalha com os dados armazenados na memória principal, neste caso calculando a média da turma, conforme mostra a Figura 3.6. Todos os valores intermediários de cálculo vão sendo armazenados na memória principal.
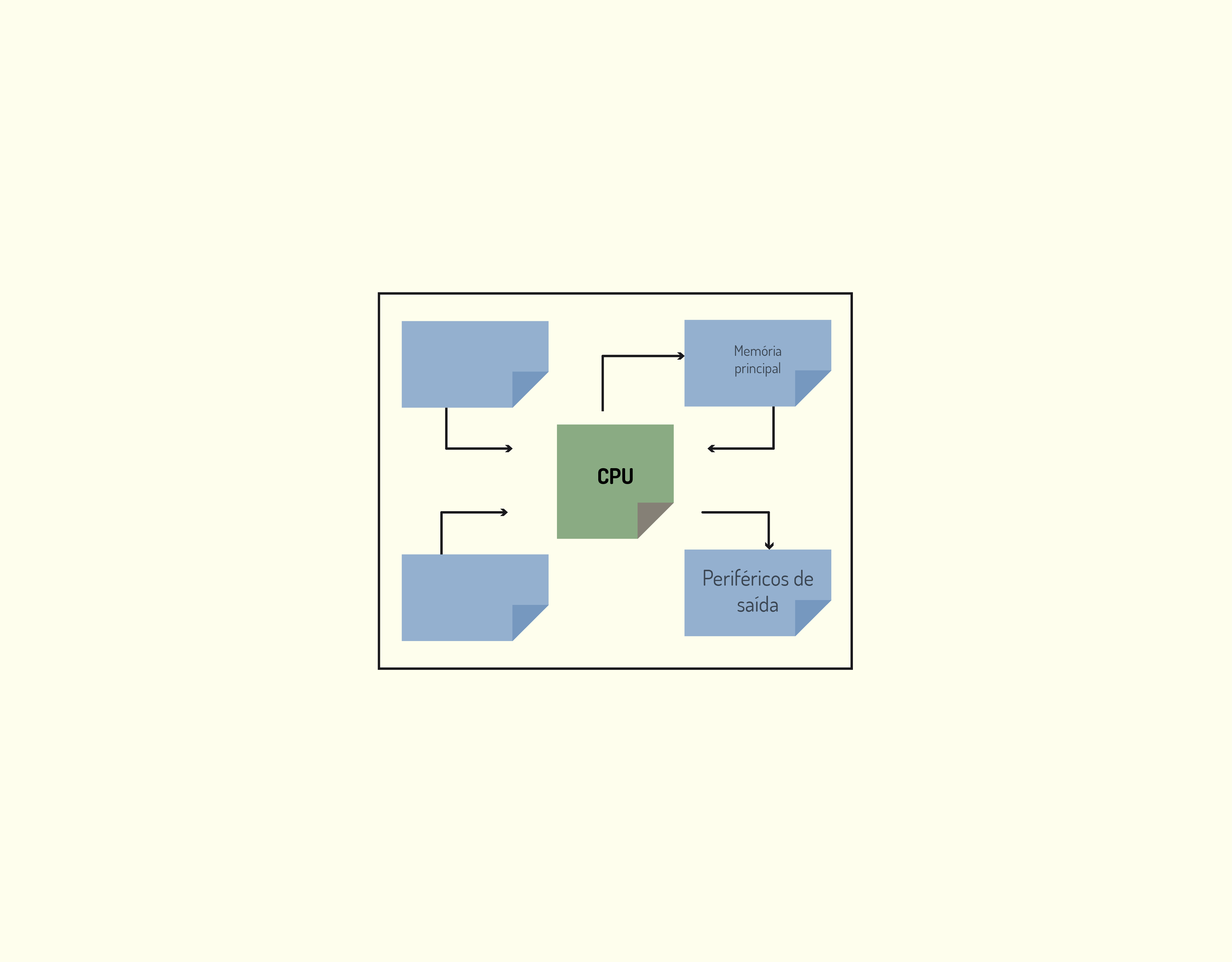
- Quando os cálculos foram todos realizados, a UCP transfere o valor final para os periféricos de saída, representada na Figura 3.7.
- E, por último, por meio do periférico de saída é mostrado o resultado final (neste caso, a média da turma) ao usuário, o que pode ser visto na Figura 3.8.
3419 Processo de entrada Fonte: A autora.
3519 Transferência das informações Fonte: A autora.
3619 Etapa de cálculos Fonte: A autora.
3719 Transferência para os periféricos de saída Fonte: A autora.
3819 Apresentação do resultado final Fonte: A autora.
Atividades
Conceitos básicos
O computador não trabalha com programas codificados em linguagem de alto nível, como C, C++, C#, Java, entre outras, e sim com a chamada linguagem de máquina, composta por instruções simples que executam pequenas atividades no computador. Assinale a alternativa que não contém uma operação que pode ser realizada por uma instrução de máquina:
- Cálculos aritméticos.
Essa é uma das operações que pode ser realizada via instrução de máquina.
- Comunicação com a internet.
A comunicação com a internet não é uma atividade simples, ela necessita da execução de várias operações, não podendo ser executada por uma simples instrução de máquina.
- Desvios na sequência do programa.
Essa é uma das operações que pode ser realizada via instrução de máquina.
- Movimentação de bits.
Essa é uma das operações que pode ser realizada via instrução de máquina.
- Operações lógicas.
Essa é uma das operações que pode ser realizada via instrução de máquina.
Evolução Histórica dos Computadores
Atualmente, temos os computadores sendo utilizados nas mais diversas aplicações, seja na educação, no comércio, nos transportes, em controles financeiros, na agricultura, na medicina, dentre vários outros usos.
Mas a maior evolução pode ser observada na utilização de computadores por pessoas comuns, na realização de tarefas triviais do seu dia a dia. Como escrever um texto, comunicar-se com nossos amigos ou realizar uma pesquisa sobre um determinado assunto? Até quando precisamos de uma nova receita de doce consultamos a internet, que nos traz inúmeras opções.
Não podemos nos esquecer, também, que os celulares modernos também são um tipo de computador. Como viver sem eles?
Pode-se caracterizar as principais evoluções dos computadores pensando em seu aumento de velocidade, diminuição do tamanho dos componentes, aumento da capacidade de memória e capacidade e velocidade do sistema de entrada e saída.
O aumento da velocidade está diretamente ligado à diminuição do tamanho dos componentes, pois isso reduz a distância entre eles e aumenta a velocidade.
O que há de notável a respeito da era da computação é que grande parte ocorreu em um tempo muito curto. Demos um salto ao longo de quatro gerações de tecnologia em aproximadamente 55 anos – um intervalo de tempo cujos eventos ainda estão na memória de muitas pessoas. As três primeiras “gerações” de computadores estão intimamente ligadas a três desenvolvimentos tecnológicos: a válvula a vácuo, o transistor e o circuito integrado. Cada um modificou drasticamente a natureza dos computadores. Definimos o tempo de ocorrência de cada geração de acordo com o início do fornecimento comercial da tecnologia de hardware. Definir as gerações seguintes não foi fácil, pois a indústria inteira tornou-se mais complexa (CAPRON, 2008).
Antes de falarmos das gerações de computadores, vamos relembrar a época dos dispositivos mecânicos e eletromecânicos. Pode-se falar que o primeiro computador inventado foi o ábaco, que é uma máquina de cálculo utilizada até os dias de hoje, principalmente no desenvolvimento do raciocínio matemático. Nele, os números são representados por símbolos de madeira que mudam de valor conforme a posição que ocupam no instrumento.
A Figura 3.9 mostra um ábaco.
3919 O ábaco Fonte: Google imagens
Em 1642, o filósofo e matemático francês Blaise Pascal inventou a chamada primeira calculadora do mundo: a Pascaline, que foi uma evolução do ábaco. Essa calculadora era um contador mecânico formado por rodas e engrenagens (daí também vem o nome de rodas dentadas de Pascal) e realiza operações de soma e subtração.
A máquina, embora rudimentar, era eficaz para sua época, sendo inteiramente mecânica e não automática (funcionava por comando de uma manivela acionada manualmente). A linguagem de programação PASCAL foi assim chamada em homenagem a esse cientista pelo seu trabalho pioneiro em matemática e também devido a sua invenção (MONTEIRO, 2012).
Após algum tempo, Gottfried Leibniz construiu uma calculadora mais avançada que a de Pascal, que realizava, além das operações de soma e subtração, também as de multiplicação e divisão. O filósofo e matemático alemão introduziu mais dois conjuntos de rodas ao dispositivo de Pascal.
Em 1823, Charles Babbage passou a desenvolver sua máquina analítica. Sua intenção era de que ela possuísse a capacidade de modificar suas operações e realizasse diferentes cálculos, ou seja, possuísse um programa que pudesse ser alterado. O projeto da máquina de Babbage previa os mesmos elementos que um computador atual: memória, processador e entrada/saída.
Infelizmente, essa máquina nunca foi colocada em prática, por ser muito avançada para a época.
Herman Hollerith, em 1889, criou o cartão perfurado, utilizado para guardar dados, juntamente com uma máquina tabuladora mecânica. Essa máquina era acionada por um motor elétrico, que era capaz de contar, classificar e ordenar as informações do cartão perfurado. Portanto, essa já era uma máquina eletromecânica. O sucesso foi tanto que o Bureau of Census dos EUA contratou o cientista para apurar os dados do censo de 1890. Essa apuração demorou dois anos e meio, mas foi uma grande inovação.
Segundo Monteiro (2012), o problema dos computadores mecânicos e eletromecânicos residia em dois fatos: baixa velocidade de processamento, devido à parte mecânica de seus elementos, e falta de confiabilidade dos resultados, já que seu armazenamento e movimento interno eram realizados por engrenagens, incapazes de realizar sempre o mesmo tipo de movimento, principalmente com o desgaste causado pelo tempo.
Em 1937, o matemático inglês Alan Turing desenvolveu a máquina de Turing, que possuía componentes eletrônicos. De acordo com o matemático, se essa máquina fosse adequadamente instruída, poderia simular qualquer comportamento. Esse é um dos princípios da Inteligência Artificial, área na qual Turing foi um dos grandes precursores.
Recentemente, com a divulgação de documentos militares do governo britânico, antes sigilosos, é que se tomou conhecimento de que o primeiro computador verdadeiramente eletrônico foi colocado em operação em 1943, com o propósito de quebrar códigos militares secretos de comunicação dos alemães. Esta máquina, construída por Alan Turing com válvulas eletrônicas, foi denominada Colossus, provavelmente devido a seu tamanho. Sua grande desvantagem residia no fato de não ser uma máquina de emprego geral, pois não podia resolver outros problemas a não ser a quebra de códigos militares. Ela era, então, um sistema de computação com programa único (MONTEIRO, 2012).
Reflita
A guerra é péssima para a humanidade, mas excelente para o desenvolvimento da tecnologia. Assim, a partir da Segunda Guerra Mundial, começou o desenvolvimento dos computadores eletrônicos.
A evolução desses computadores pode ser dividida em gerações, de acordo com as inovações que trouxeram.
Primeira geração – Válvulas (1945-1955)
Os computadores dessa geração funcionavam com válvulas a vácuo, aproximadamente com o tamanho de uma lâmpada, e que eram utilizadas como componentes internos do computador e que permitiam ou não a passagem de corrente elétrica.
Segundo Souza Filho (2014), as instruções eram programadas diretamente em linguagem de máquina e gravadas em cartões perfurados, o que tornava o seu funcionamento lento e sua programação difícil de ser executada.
Um dos exemplos de máquina dessa geração é o ENIAC, que era uma máquina decimal, em vez de binária. Ele foi concluído em 1946 e, como não pôde mais ser utilizado na Segunda Guerra, ajudou a determinar a viabilidade da bomba de hidrogênio.
Essa máquina, de acordo com Stallings (2010), era enorme, pesava 30 toneladas, ocupando 1500 pés quadrados de superfície e contendo mais de 18000 válvulas. Quando estava em operação, ela consumia 140 kilowatts de potência. Ela também era mais rápida que qualquer computador eletromecânico, capaz de realizar 5000 adições por segundo.
A Figura 3.10 mostra o processo de programação do ENIAC.
Essa geração também marcou o surgimento da máquina de Von Neumann, que será discutida mais a seguir.
Segunda geração – Transistores (1955-1965)
A segunda geração de computadores é caracterizada pela substituição das válvulas pelos transistores. Segundo Stallings (2010), o transistor é menor, mais barato e dissipa menos calor que uma válvula, mas pode ser usado da mesma forma que uma válvula para construir computadores. Diferente da válvula, que exige fios, placas de metal, uma cápsula de vidro e um vácuo, o transistor é um dispositivo de estado sólido, feito de silício.
Também fazem parte das evoluções dessa geração o surgimento das unidades aritméticas e lógicas mais complexas e da unidade de controle, além do armazenamento em disco e fita magnética.
Como se não bastassem todas essas inovações, a linguagem Assembly passou a substituir a linguagem de máquina e iniciou-se o uso de linguagens de programação de alto nível, como o FORTRAN.
Terceira geração – Circuitos integrados (1965-1980)
A invenção do circuito integrado de silício por Robert Noyce em 1958 permitiu que dezenas de transistores fossem colocados em um único chip. Esse empacotamento possibilitava a construção de computadores menores, mais rápidos e mais baratos do que seus precursores transistorizados (TANENBAUM, 2007).
Monteiro (2012) também cita outras evoluções dessa geração:
- O conceito de família de computadores, em vez de máquina individual, como até então. Este conceito permite que o fabricante ofereça o mesmo tipo de máquina (arquitetura igual, linguagem de máquina semelhante etc.) com diferentes capacidades e preços, o que garante uma maior quantidade de clientes;
- A utilização de unidade de controle com microprogramação em vez das tradicionais unidades de controle no hardware;
- O emprego de uma técnica chamada multiprogramação, pela qual vários programas compartilham a mesma memória principal e dividem o uso da UCP, dando a impressão ao usuário de que estão sendo executados simultaneamente;
- A elevada capacidade de processamento (para a época), com palavra de 32 bits e ciclo de instrução de até 250 nanossegundos, bem como a grande capacidade de armazenamento na memória principal, 16 Mbytes;
- Memória principal orientada a byte, isto é, cada célula de MP armazena oito bits de informação, independentemente do tamanho de bits definido para a palavra de dados, característica utilizada até hoje;
- O lançamento de um programa (conjunto de programas é o melhor termo) gerenciador dos recursos de hardware, de modo mais integrado e eficaz, o sistema operacional OS/360.
Além disso, os computadores também passaram a utilizar linguagens de alto nível, como FORTRAN e Cobol.
Quarta geração – Integração em escala muito grande (1980-dias atuais)
A quarta geração de computadores é caracterizada, principalmente, pelo surgimento do microprocessador, o que proporcionou o desenvolvimento dos computadores pessoais.
O termo VLSI (Very Large Scale Integration), integração em larga escala, caracteriza uma classe de dispositivos eletrônicos capazes de armazenar, em um único invólucro, milhares e até milhões de diminutos componentes. Este dispositivo, denominado pastilha (chip), vem constituindo a base da estrutura de todos os principais sistemas de computação modernos (MONTEIRO, 2012).
A Tabela 3.1 apresenta os principais marcos no desenvolvimento dos computadores modernos.
Ano | Nome | Construído por | Comentários |
1834 | Máquina analítica | Babbage | Primeira tentativa de construir um computador digital |
1936 | Z1 | Zuse | Primeira máquina de calcular com relés |
1943 | COLOSSUS | Governo britânico | Primeiro computador eletrônico |
1944 | MarkI | Aiken | Primeiro computador norte-americano de uso geral |
1946 | ENIAC | Eckert/Mauchley | A história moderna dos computadores começa aqui |
1949 | EDSAC | Wilkes | Primeiro computador com programa armazenado |
1951 | Whirlwind I | M.I.T. | Primeiro computador de tempo real |
1952 | IAS | von Neumann | A maioria das máquinas atuais usa esse projeto |
1960 | PDP-l | DEC | Primeiro minicomputador (50 vendidos) |
1961 | 1401 | IBM | Máquina para pequenos negócios de enorme popularidade |
1962 | 7094 | IBM | Dominou a computação científica no início da década de 1960 |
1963 | B5000 | Burroughs | Primeira máquina projetada para uma linguagem de alto nível |
1964 | 360 | IBM | Primeira linha de produto projetada como uma família |
1964 | 6600 | CDC | Primeiro supercomputador científico |
1965 | PDP-8 | DEC | Primeiro minicomputador de mercado de massa (50 mil vendidos) |
1970 | PDP- 11 | DEC | Dominou os minicomputadores na década de 1970 |
1974 | 8080 | Intel | Primeiro computador de uso geral de 8 bits em um chip |
1974 | CRAY-I | Cray | Primeiro supercomputador vetorial |
1978 | VAX | DEC | Primeiro superminicomputador de 32 bits |
1981 | IBM PC | IBM | Deu início à era moderna do computador pessoal |
1981 | Osborne-l | Osborne | Primeiro computador portátil |
1983 | Lisa | Apple | Primeiro computador pessoal com uma GUI |
1985 | 386 | Intel | Primeiro ancestral de 32-bits da linha Pentium |
1985 | MIPS | MIPS | Primeira máquina comercial RISC |
1987 | SPARC | Sun | Primeira estação de trabalho RISC baseada em SPARC |
1990 | RS6000 | IBM | Primeira máquina superescalar |
1992 | Alpha | DEC | Primeiro computador pessoal de 64 bits |
1993 | Newton | Apple | Primeiro computador palmtop |
312 Alguns marcos do desenvolvimento do computador digital moderno Fonte: Tanenbaum (2007).
Máquina de Von Neumann
A máquina de Von Neumann foi concebida durante a primeira geração de computadores, em 1946, mas sua arquitetura continua sendo usada até hoje.
John Von Neumann, segundo Tanenbaum (2007), era um gênio, da mesma estirpe de Leonardo da Vinci. Falava muitos idiomas, era especialista em ciências físicas e matemática e guardava na memória tudo que já ouvira, vira ou lera. Conseguia citar, sem consulta, palavra por palavra, o texto de livros que tinha lido havia anos. Na época em que se interessou por computadores, já era o mais eminente matemático do mundo.
O autor complementa que:
uma das coisas que ficou óbvia para ele foi que programar computadores com quantidades imensas de interruptores e cabos era uma tarefa lenta, tediosa e mecânica. Ele percebeu que o programa podia ser representado em forma digital na memória do computador, junto com os dados. Também viu que a desajeitada aritmética decimal usada pelo ENIAC, com cada dígito representado por 10 válvulas (1 acesa e 9 apagadas), podia ser substituída usando aritmética binária paralela .(TANENBAUM, 2007, p.10)
A arquitetura concebida por Von Neumann era composta por:
- A UCP, formada pela Unidade Aritmética e Lógica e a Unidade de Controle.
Esses componentes possuíam a mesma função utilizada até hoje: a unidade aritmética e lógica era responsável por realizar operações sobre dados agora binários e a unidade de controle por interpretar e executar as instruções armazenadas na memória. - A Memória Principal, responsável por armazenar dados e instruções (essa foi uma grande inovação para a época).
- O equipamento de entrada e saída, controlado pela unidade de controle.
- O acumulador, que é um registrador interno especial.
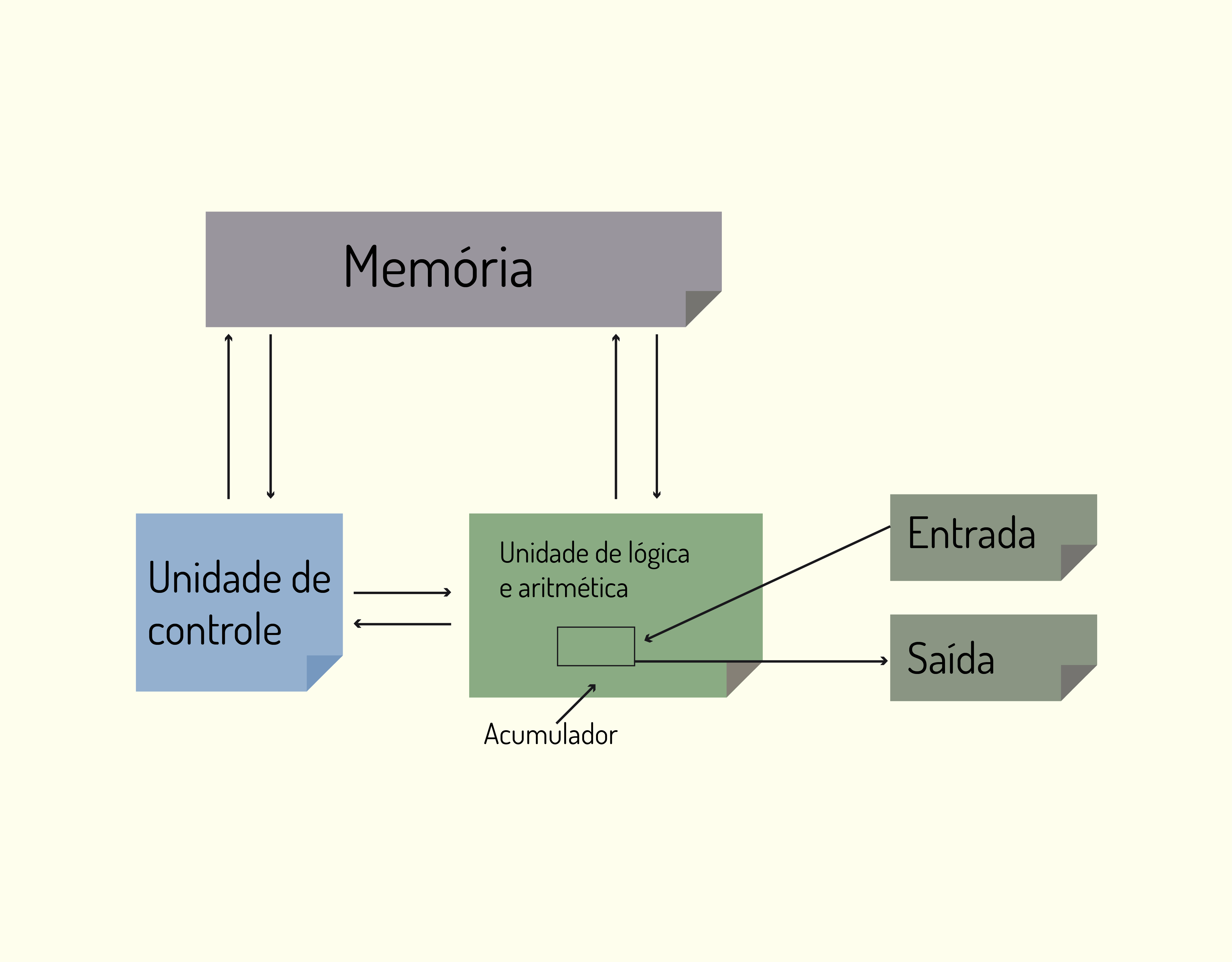
A Figura 3.11 mostra um esboço da arquitetura de Von Neumann.
31119 Máquina original de Von Neumann Fonte: Tanenbaum (2007).
Atividades
Evolução histórica dos computadores
Os computadores modernos foram classificados em gerações, de acordo com sua tecnologia e desempenho. Cada uma dessas gerações foi marcada por inovações diferentes. Assinale a alternativa que apresenta as inovações da segunda e quarta gerações:
- Válvulas e circuitos integrados.
As válvulas são uma inovação da primeira geração e os circuitos integrados da terceira.
- Transistores e microprocessadores.
A segunda geração é marcada justamente pela substituição das válvulas pelos transistores e a quarta pelo surgimento do microprocessador.
- Microprocessador e dispositivos multimídia.
O microprocessador é uma inovação da quarta geração e os dispositivos multimídia não fazem parte de nenhuma das gerações estudadas.
- Transistores e circuitos integrados.
Os transistores são uma inovação da segunda geração e os circuitos integrados da terceira.
- Circuitos integrados e internet.
Os circuitos integrados são uma inovação da terceira geração e a internet não faz parte de nenhuma das gerações estudadas.
Componentes de um Sistema de Computação
Como foi dito no início da nossa unidade, os computadores funcionam utilizando programas, que são um conjunto de instruções que efetuam ações ou operações visando a um objetivo comum.
Eles são formados por vários elementos acoplados, chamados componentes que, juntos, funcionam como um sistema só.
Os componentes principais de um sistema computacional são:
- A Unidade Central de Processamento (UCP);
- A Memória;
- Os dispositivos de entrada; e
- Os dispositivos de saída.
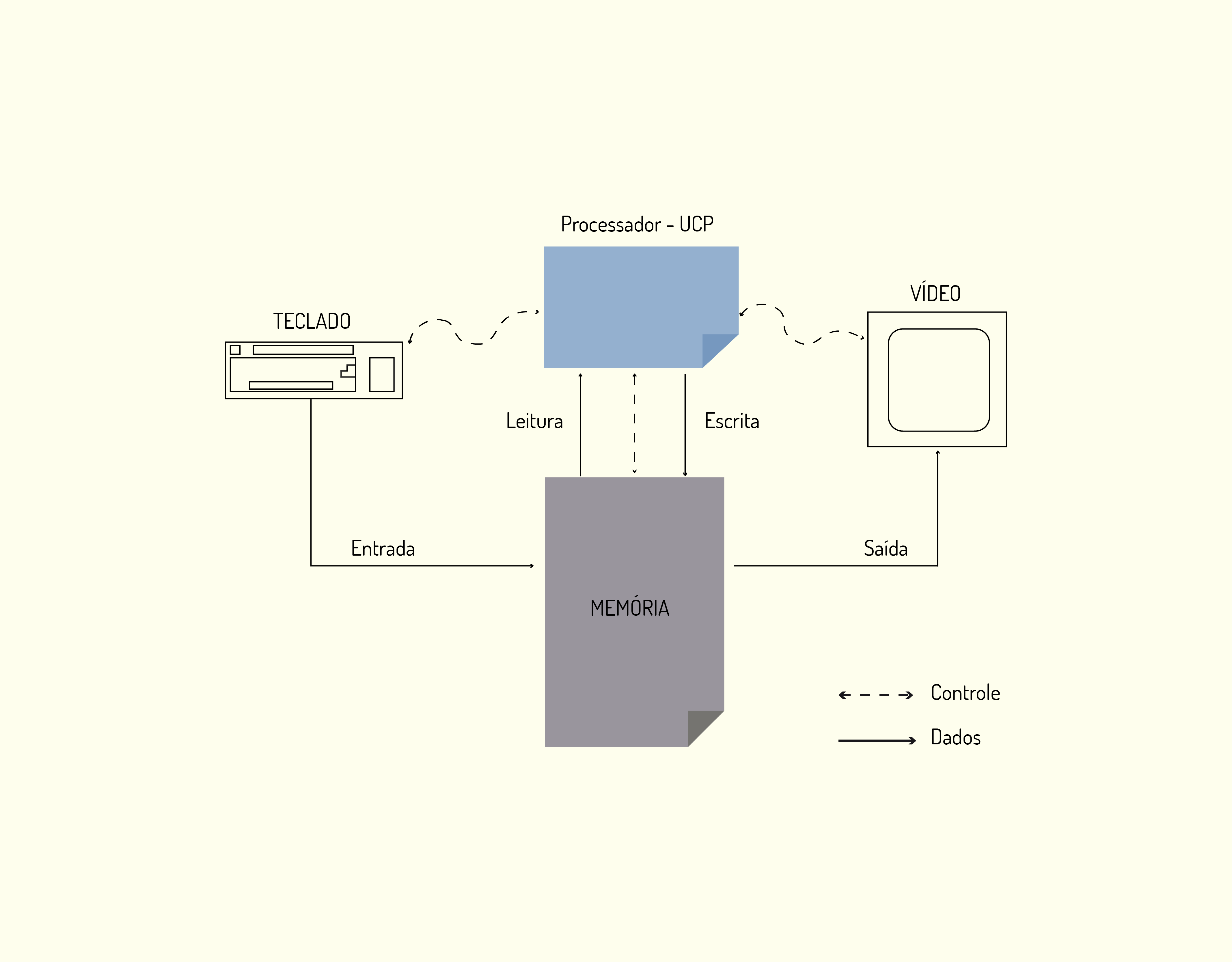
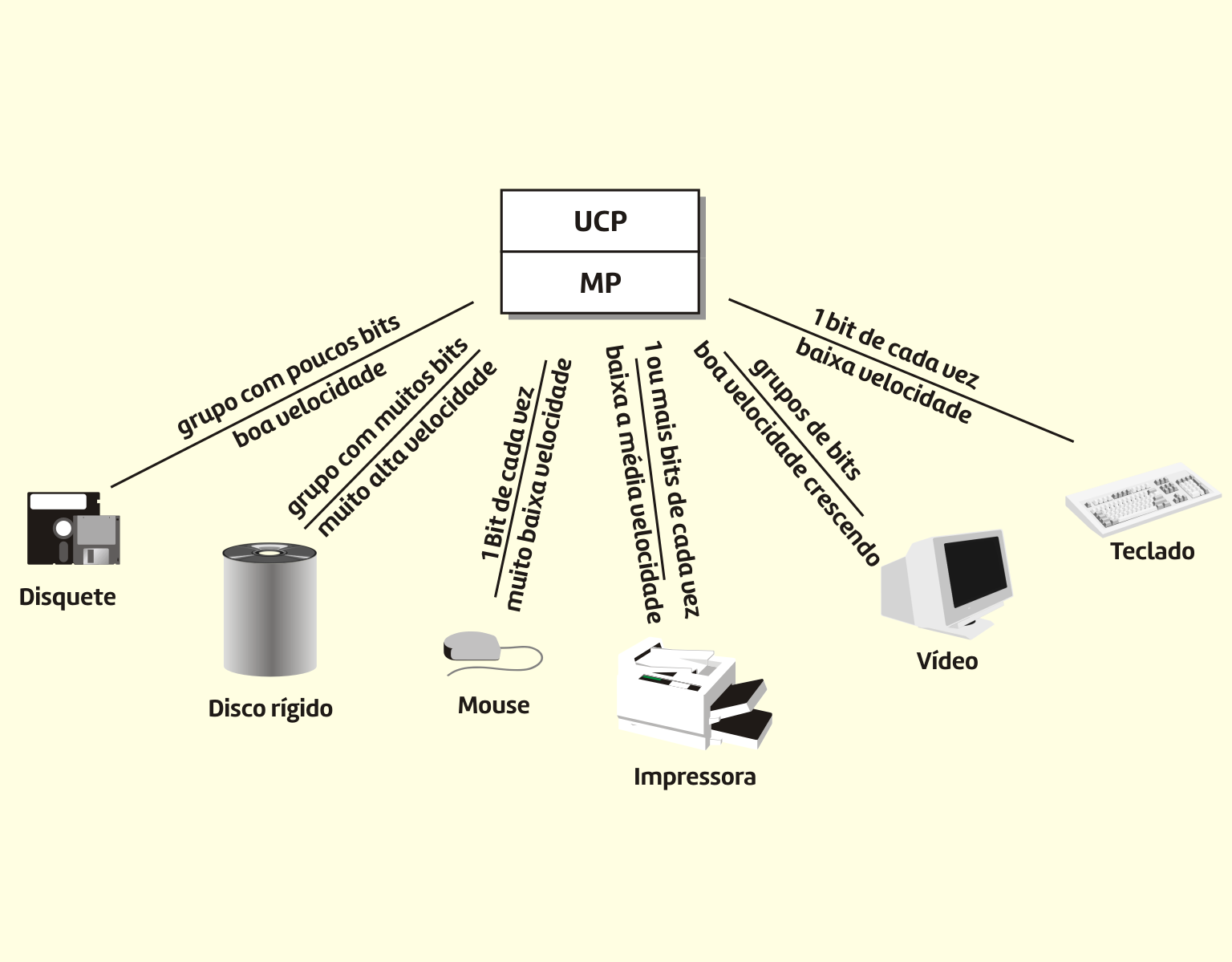
A Figura 3.12 mostra estes componentes e sua interligação.
31219 Componentes de um sistema de computação Fonte: Monteiro (2012).
Unidade Central de Processamento
A Unidade Central de Processamento (UCP) ou, em inglês, Central Processing Unit (CPU) ou processador, é o “cérebro” do sistema computacional.
Para Monteiro (2012), uma UCP ou processador é constituída de milhões de minúsculos circuitos e componentes eletrônicos (transistores, resistores etc.), cujas funções básicas são ler e interpretar instruções de máquina e realizar as operações matemáticas (ou outras) definidas após a interpretação de uma determinada instrução.
Por ser um componente tão importante, teremos, logo a seguir, um item dedicado somente a ela.
Memória
Segundo Souza Filho (2014), um espaço de memória pode conter uma instrução de um programa ou um dado qualquer, que serão endereçados na memória pela unidade de controle da UCP. Os dados que serão processados pela ULA ficam na memória e a unidade de controle endereça estes dados. Isto permite que a ULA identifique onde estão os dados a serem processados, execute as operações necessárias, e a unidade de controle pode definir onde armazenar os dados resultantes do processamento. A memória que recebe esse endereçamento é usada para receber as informações da unidade de entrada e as processadas pelo computador é a memória RAM.
A ULA (Arithmetic Logic Unit) ou ULA (Unidade Aritmética e Lógica) é a responsável, dentro do processador, pelas operações matemáticas e lógicas.
Reflita
A arquitetura de Von Neumann prevê a possibilidade de uma máquina digital armazenar os programas e os dados no mesmo espaço de memória, e estes serão processados por uma unidade de processamento central (CPU) composta por uma unidade controle e uma unidade aritmética e lógica (ULA). Os dados são fornecidos mediante dispositivos de entrada e retornados por meio dos dispositivos de saída (RAINER, 2012).
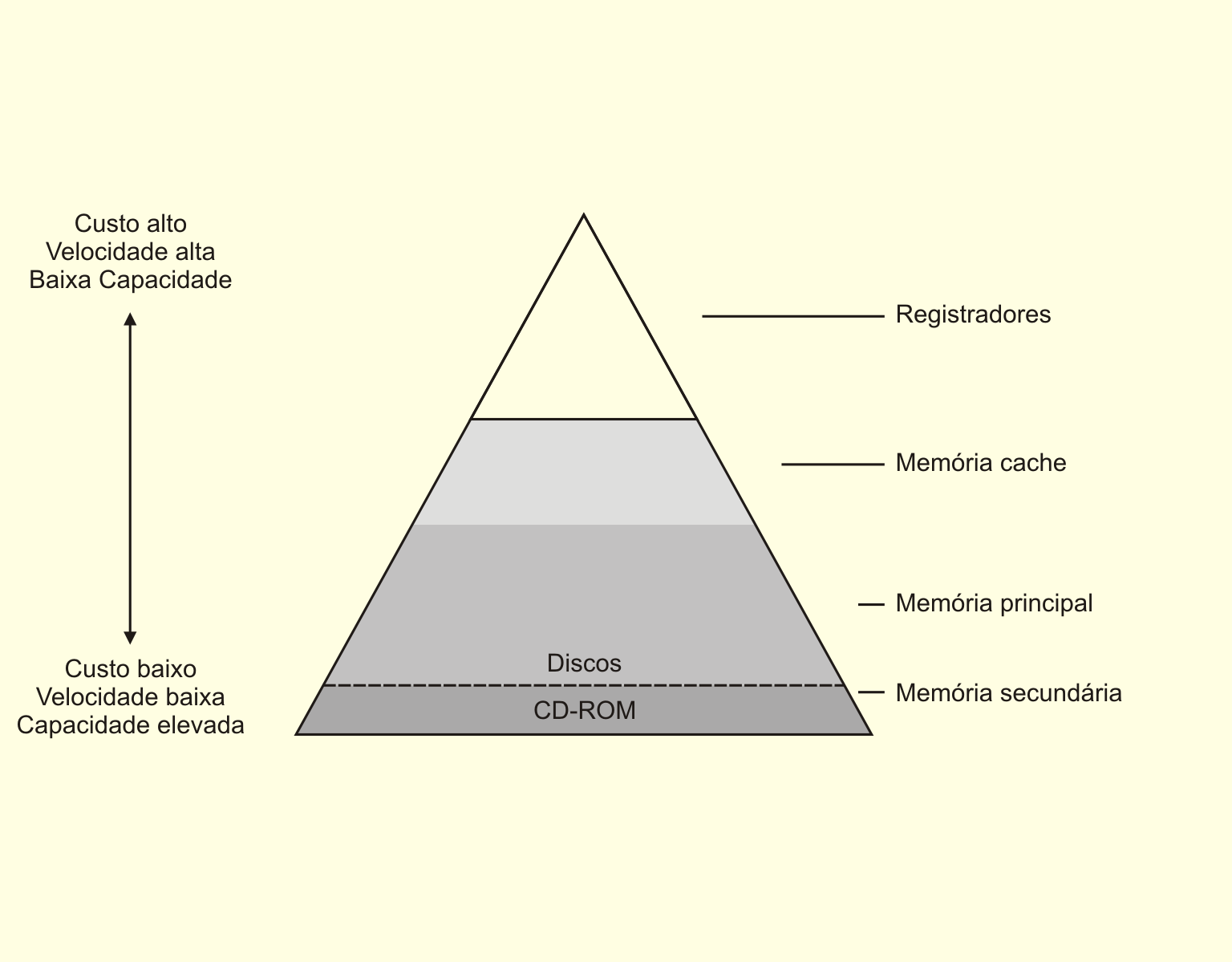
Os dispositivos de memória podem ser de quatro tipos: registradores, memória cache, memória principal e memória secundária. Eles serão estudados com mais detalhes na nossa próxima unidade.
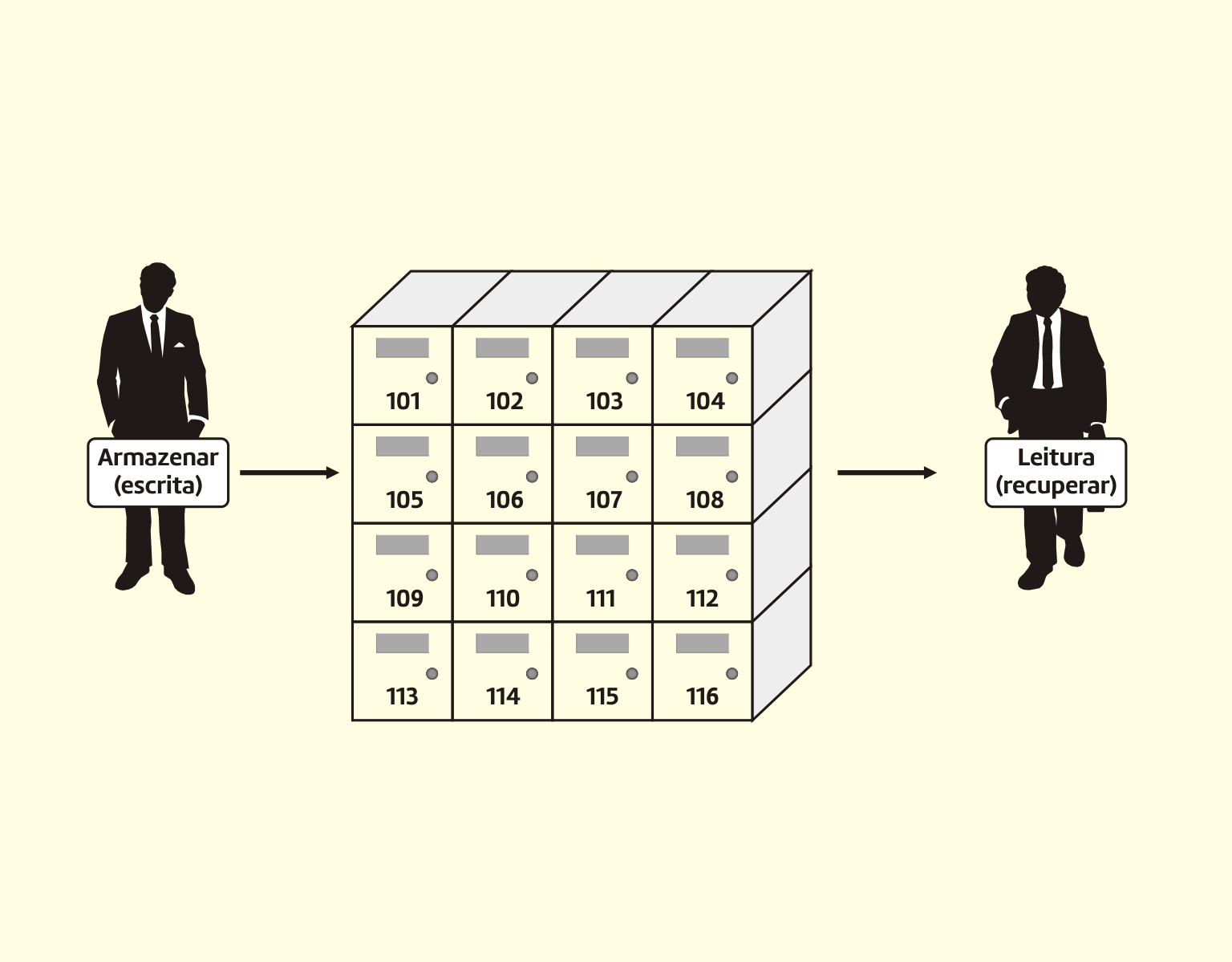
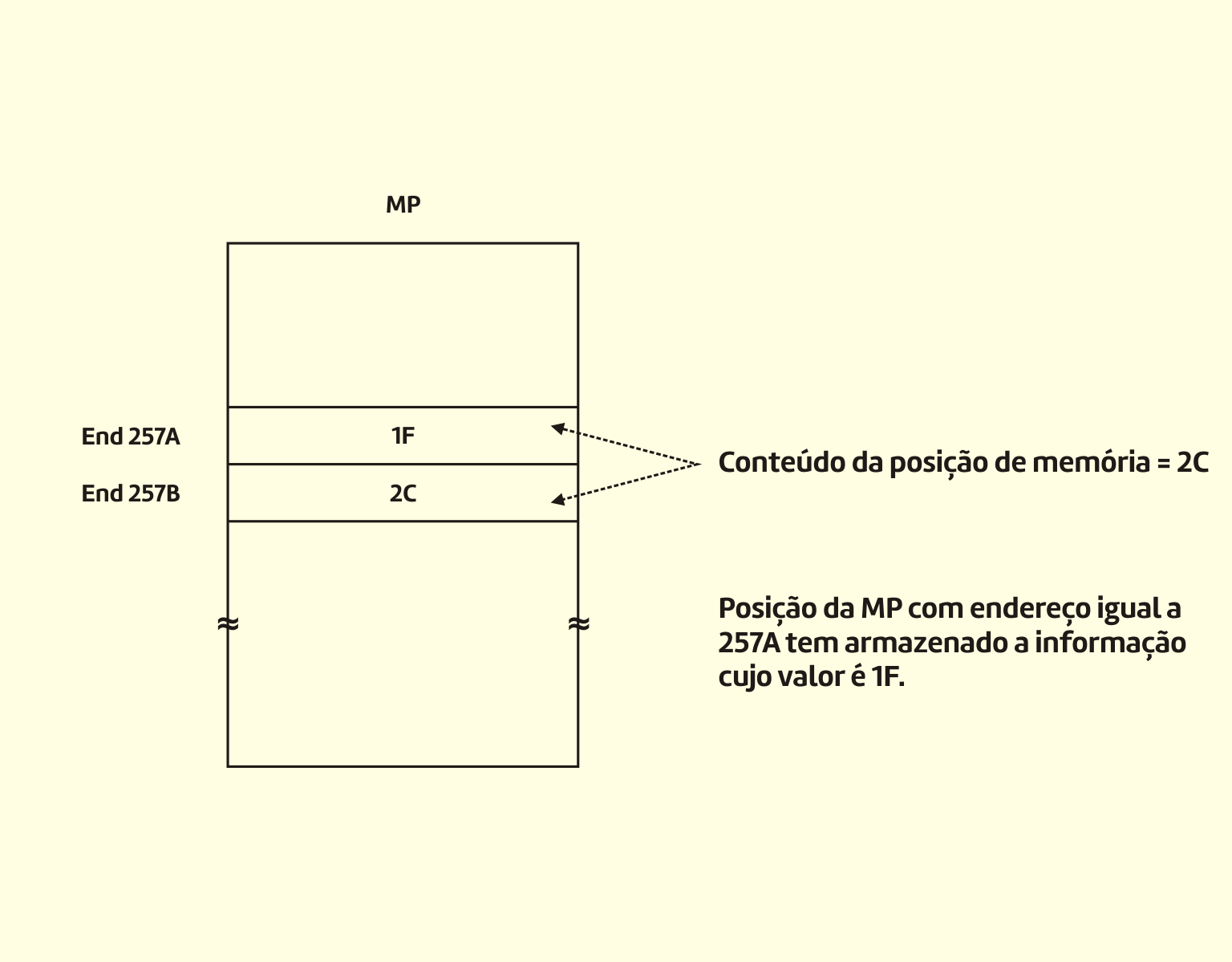
A memória é formada por elementos armazenadores de informação. Uma memória está dividida em palavras. Cada palavra é identificada por um endereço. O conteúdo armazenado nas palavras da memória tanto pode representar dados como instruções (WEBER, 2012).
Ou seja, para que se possa armazenar ou localizar uma informação na memória, precisamos de um endereço, que define um local de forma precisa e única.
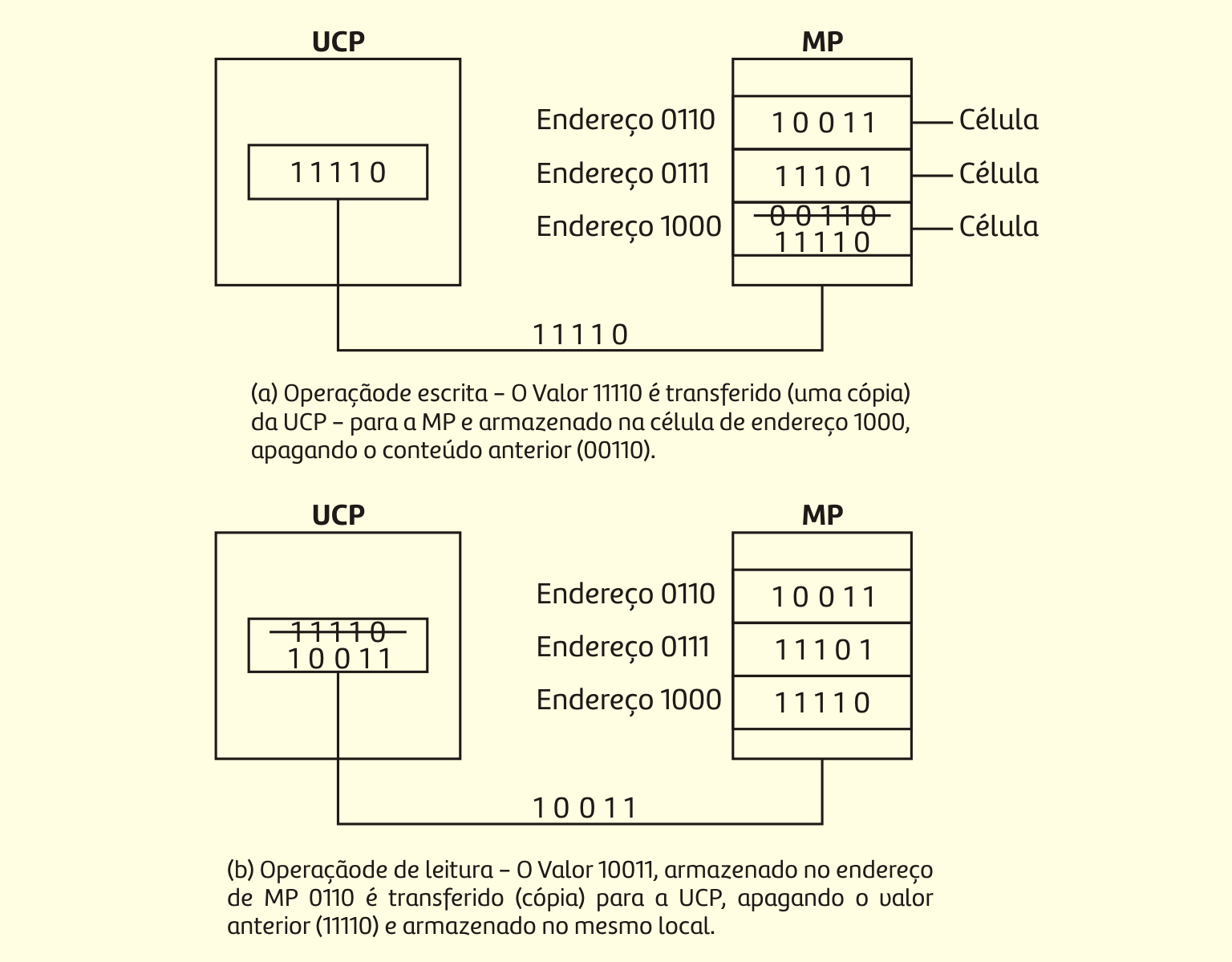
Existem dois tipos de ações que podem ser realizadas na memória:
- Armazenamento de informações, que é a operação de escrita e gravação; e
- Recuperação de informação, que consiste na operação de leitura.
Assim, podemos definir os princípios de operação da memória como sendo:
- Selecionar o endereço de memória que está sendo acessado por uma operação de leitura ou escrita;
- Selecionar uma operação de escrita ou de leitura para ser executada;
- Fornecer os dados de entrada para serem armazenados na memória durante a operação de escrita;
- Manter os dados de saída vindos da memória durante uma operação de leitura;
- Habilitar (ou desabilitar) a memória de modo que ela responda (ou não) às entradas de endereço e ao comando de leitura e escrita.
As memórias diferem pela sua tecnologia de fabricação.
Tipos de memória RAM (Random Access Memory)
- Estáticas (SRAM – static RAM): são formadas por flip-flops, que permanecem em um determinado estado indefinidamente, desde que a alimentação do circuito seja mantida.
- Dinâmicas (DRAM – dynamic RAM): armazenam os sinais em capacitores, possuindo alta capacidade e baixo consumo. Como os capacitores possuem uma fuga de carga, há a necessidade de recargas periódicas das células de memória (refresh). Este é o tipo de memória utilizada nos computadores atuais.
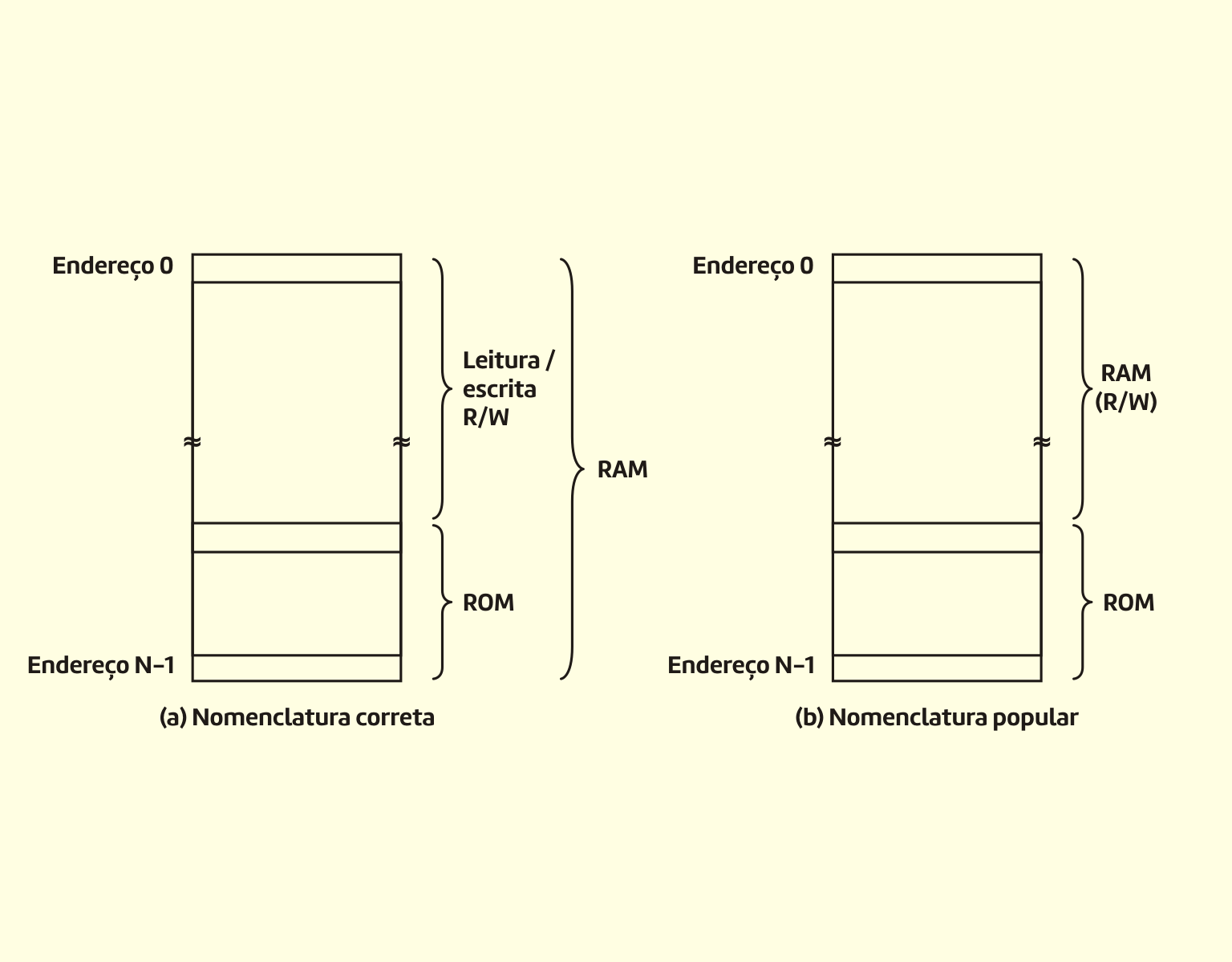
Tipos de memória ROM (Read Only Memory)
A ROM é programada pelo fabricante, mas pode ser alterada, podendo ser classificada em:
a. PROM (ROMs programáveis)
A PROM pode ser programada pelo usuário, mas somente uma vez. O processo geralmente é realizado por um programador de PROM, que também verifica se os dados armazenados estão corretos.
b. EPROM (ROM programável e apagável – Erable Programable ROM)
Uma EPROM pode ser programada pelo usuário e também ser apagada e reprogramada quantas vezes for desejado. Uma vez programada, a EPROM é uma memória não volátil que mantém indefinidamente os dados armazenados (TOCCI, 2011).
A EPROM pode ser apagada mediante a exposição à luz ultravioleta, que apaga todas as células ao mesmo tempo.
c. EEPROM (PROM apagável eletricamente – Eletrically Erasable PROM)
A EEPROM pode ser apagada eletricamente no próprio circuito, permitindo que se apague e reescreva bytes individualmente.
d. Flash
A memória Flash também pode ser apagada eletricamente, sem a remoção do circuito. Seu nome é derivado do tempo curto de apagamento e escrita. Oferecem um modo de apagamento por setor, no qual setores específicos podem ser apagados de cada vez.
Dispositivos de entrada e saída
Os dispositivos de entrada e saída são utilizados para permitir a comunicação entre o computador e o mundo externo. Esses dispositivos são também chamados de dispositivos de I/O ou dispositivos periféricos. Podem ser divididos em duas categorias: dispositivos que são utilizados como memória secundária e dispositivos que servem para interface homem-máquina.
Os dispositivos utilizados como memória secundária, como discos rígidos e pen drives, se caracterizam por um custo relativamente baixo, porém o tempo de acesso à memória secundária é bem maior que o acesso à memória principal.
Os dispositivos que servem de comunicação homem-máquina são os que realmente conhecemos como sendo de entrada e saída, que realizam a interface entre as pessoas e o sistema computacional, podendo ser chamados também de periféricos.
Dispositivos de entrada
Como o próprio nome diz, os dispositivos de entrada são responsáveis pela inserção de dados no sistema para que possam ser processados.
Os principais periféricos de entrada que encontramos comercialmente são:
- O teclado, que é o meio mais comum de comunicação entre o homem e a máquina;
- O mouse, que é um dispositivo utilizado para apontar e selecionar informações no vídeo.
Atualmente, podemos citar, também, o joystick, a caneta ótica, scanners, leitores de código de barras e as telas sensíveis ao toque.
A Figura 3.13 mostra alguns dispositivos de entrada, como o teclado, mouse e um leitor de código de barras.
31319 Dispositivos de entrada Fonte: Capron (2004).
Dispositivos de saída
O monitor de vídeo é um dispositivo utilizado para mostrar ao usuário os dados por ele digitados e os resultantes das operações da UCP. É o meio mais utilizado para a saída dos dados.
Já as impressoras são os dispositivos mais usados para apresentar os resultados das operações do computador no papel.
Podemos ter, também, como periférico de saída, as caixas de som.
Interconexão entre os componentes
Mas para que todos os componentes de um sistema de computação trabalhem corretamente, é necessário uma ligação entre eles, o chamado barramento.
Um barramento é um caminho de comunicação que conecta dois ou mais dispositivos. Uma característica-chave de um barramento é que ele é um meio de transmissão compartilhado. Múltiplos dispositivos se conectam ao barramento, e um sinal transmitido por qualquer dispositivo está disponível para recepção por todos os outros dispositivos conectados ao barramento. Se dois dispositivos transmitirem durante o mesmo período, seus sinais serão sobrepostos e ficarão distorcidos. Assim, somente um dispositivo de cada vez pode transmitir com sucesso (STALLINGS, 2010).
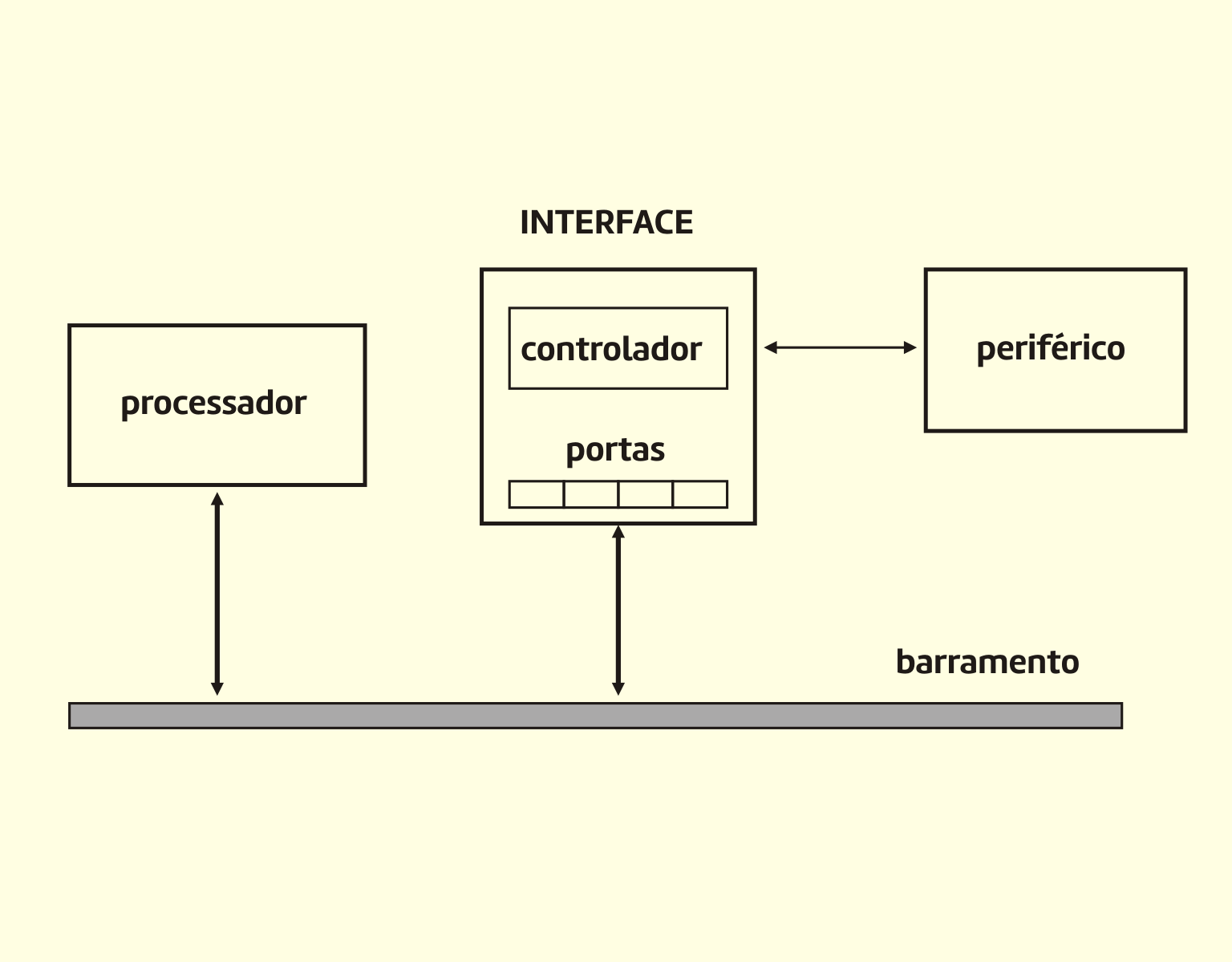
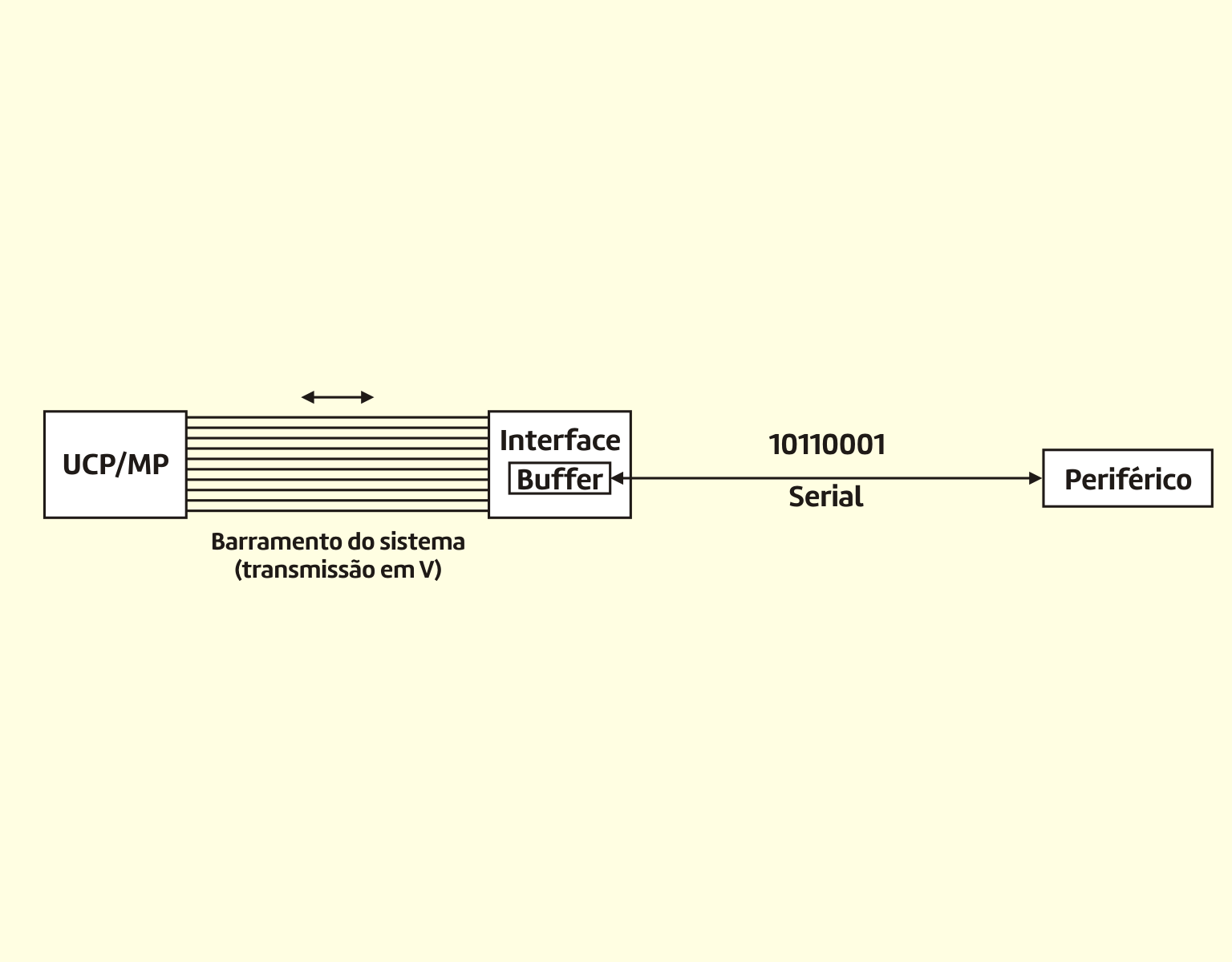
Monteiro (2012) apresenta, na Figura 3.14, o exemplo de um cabo de ligação (apresentação física de um barramento) entre um periférico e um processador, constituído de diversos fios paralelos bem próximos um dos outros, cada um conduzindo um bit da informação que está sendo transferida (ou um sinal de controle diferente).
31419 Exemplo de um barramento Fonte: Monteiro (2012).
Os barramentos podem ser classificados em:
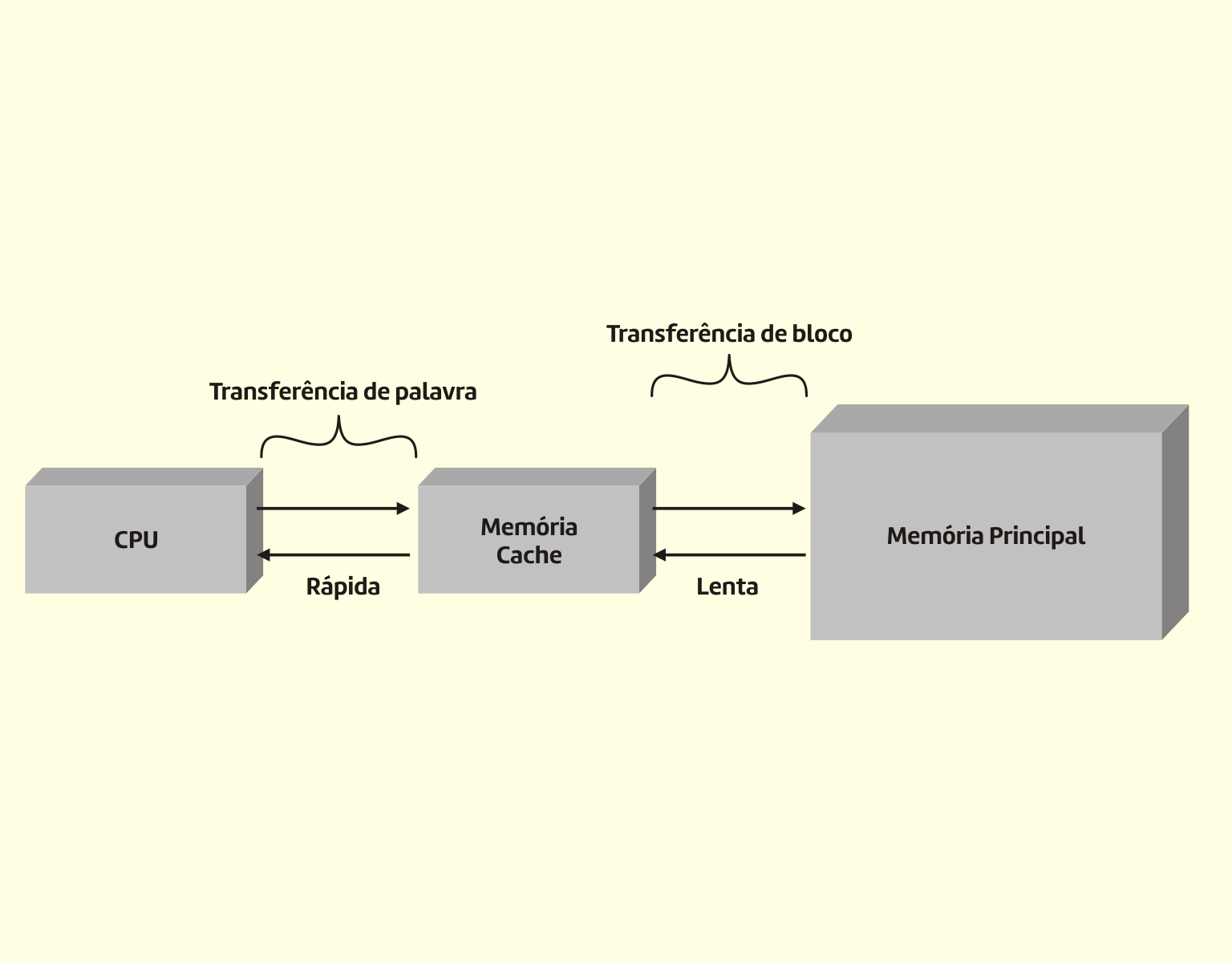
- Barramento local: interliga a UCP aos dispositivos de maior velocidade, como a memória cache e a memória principal. Esse barramento geralmente funciona na mesma frequência da UCP, sendo o de maior velocidade de transferência de dados;
- Barramento do sistema: em alguns modelos de computador, a UCP não acessa diretamente a memória principal e sim a memória cache. O barramento do sistema realiza a ligação entre a memória cache e a memória principal;
- Barramento de expansão: é utilizado para interligar os dispositivos de entrada e saída.
Representação das informações
Toda informação introduzida em um computador (sejam dados que serão processados ou instruções de um programa) precisa ser entendida pela máquina, para que possa corretamente interpretá-la e processá-la (MONTEIRO, 2012).
Como discutimos em nossa Unidade II, o computador não “pensa”. Ele apenas realiza operações com os sinais recebidos e armazenados, que podem ser representados por sinais elétricos.
A partir desses conhecimentos, conseguimos entender por que o sistema computacional trabalha com o sistema binário e não o decimal. Isso ficou bem claro quando falamos do ENIAC em nosso histórico. Ele utilizava o sistema decimal. Veja o tamanho dele e a potência que era consumida.
O sistema binário é composto por somente dois dígitos, 0 e 1, chamados bits (binary digit). O bit é a menor quantidade de informação que podemos ter (lembra das palavras cruzadas? Isso sempre aparece).
Mas somente um bit não representa praticamente nada. Assim, utilizamos agrupamentos deles para poder representar as informações. Assim, temos, primeiramente, o byte, que é composto por 8 bits.
Como os principais códigos de representação de caracteres utilizam grupos de oito bits por caractere, os conceitos de byte e caractere tornam-se semelhantes, e as palavras, quase sinônimas. O termo caractere é mais empregado para fins comerciais (propaganda, apresentações a pessoas não familiarizadas com o jargão de computação), enquanto o termo byte é empregado mais na linguagem técnica dos profissionais da área (MONTEIRO, 2012).
Pensando bem, 8 bits também é muito pouco para expressarmos quantidades de informação, somente um caractere.
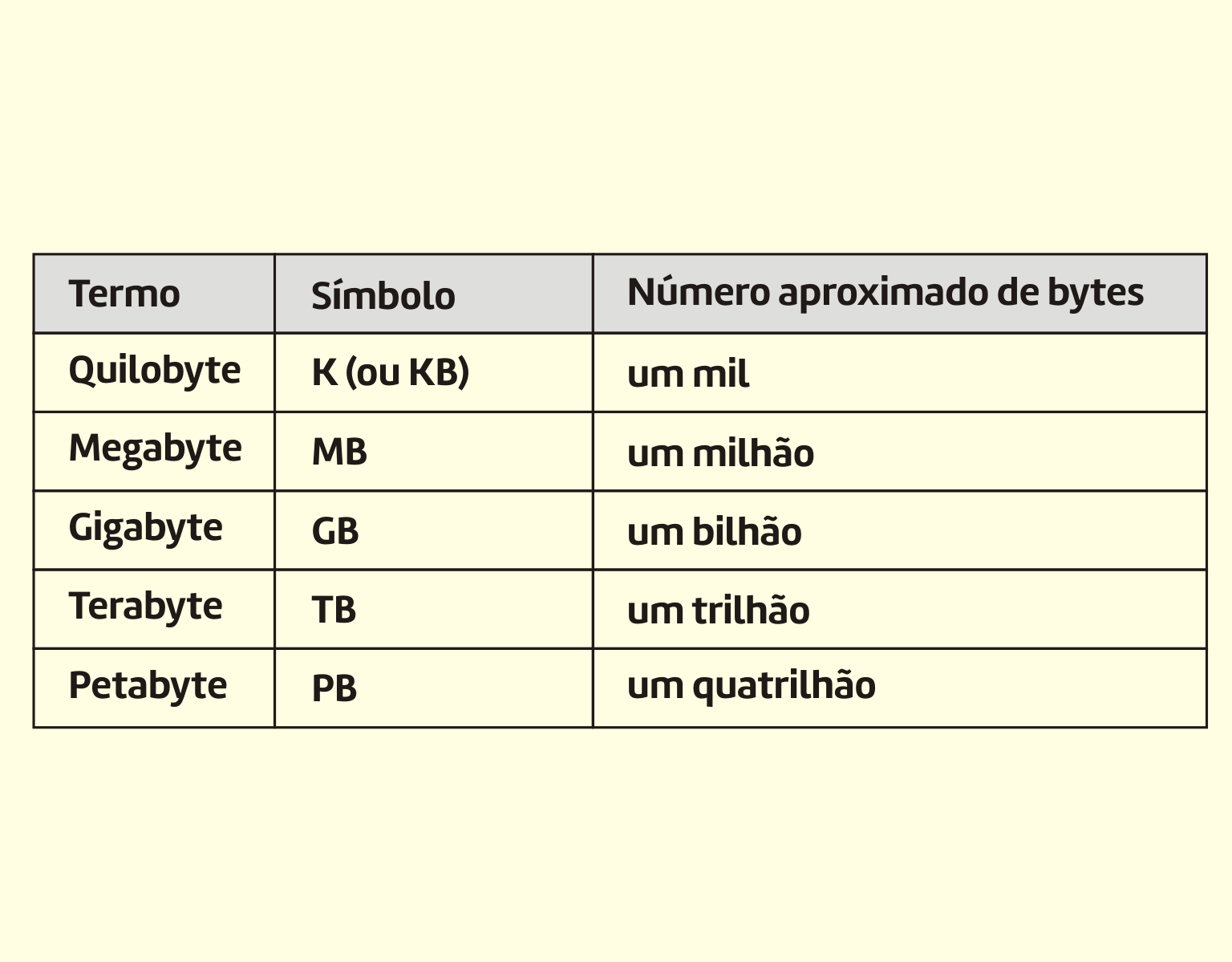
Assim, surgiram os múltiplos dos bytes, que podem ser vistos na Tabela 3.2.
Termo | Símbolo | Número aproximado de bytes |
Quilobyte | K (ou KB) | um mil |
Megabyte | MB | um milhão |
Gigabyte | GB | um bilhão |
Terabyte | TB | um trilhão |
Petabyte | PB | um quatrilhão |
322 Capacidades de armazenamento Fonte: Capron (2004).
Reflita
Os múltiplos utilizados na informática são praticamente iguais aos do sistema métrico, mas existe uma diferença fundamental. Quando falamos em 1 Kg, estamos falando em 103 gramas, ou mil gramas. No sistema binário, como trabalhamos com potências de 2 (essa é a base nesse sistema), passamos a ter, em 1 KB, 210 bytes, o equivalente a 1024 bytes.
Classificação de sistemas de computação
Os sistemas computacionais podem ser classificados em: microcomputadores, estações de trabalho, minicomputadores, computadores de grande porte e supercomputadores.
a. Microcomputadores (desktops, laptops, notebooks, palmtops)
Os microcomputadores são também chamados de computadores pessoais, ou PCs. É o tipo de sistema de computação mais difundido no mercado, possuindo, inclusive, a possibilidade de serem ligados em rede.
Temos várias categorias de microcomputadores, que variam de acordo com seu tamanho e portabilidade, como os desktops (computadores de mesa), laptops (portáteis de tamanho razoável), notebooks (portáteis de tamanho menor) e os palmtops, que são quase do tamanho de uma palma da mão (vem daí o seu nome).
A Figura 3.15 ilustra o desktop e o notebook.
31519 Microcomputadores Fonte: Google imagens.
Os Tablets, iPads e Smartphones também se enquadram nesta categoria de computadores pessoais.
b. Estações de trabalho (workstations)
As estações de trabalho são pequenas o bastante para caberem em uma escrivaninha e contam com grande capacidade de processamento de dados, superior a muitos computadores de grande porte (CAPRON, 2008).
Elas são utilizadas para fins específicos, como na área científica ou industrial, geralmente para se trabalhar com programas de imagem e projeto.
c. Minicomputadores
Segundo Capron (2004), os computadores midrange (anteriormente chamados de minicomputadores) são computadores multiusuário projetados para atender às necessidades das organizações de porte médio. Centenas ou, às vezes, milhares de usuários podem estabelecer conexão com um computador midrange por meio de terminais ou PCs ligados em rede para acessar aplicativos em toda a empresa, como entrada de pedidos e controle de estoque.
d. Computadores de grande porte (mainframes)
Monteiro (2012, p.35) explica que:
os computadores de grande porte são sistemas projetados para manusear considerável volume de dados e executar simultaneamente programas de uma grande quantidade de usuários. Essas máquinas podem interagir com centenas de usuários em um dado instante, como, por exemplo, um sistema de reserva de passagens aéreas, onde há necessidade de armazenamento em grande escala (todos os dados de vôos e das reservas realizadas), bem como uma contínua solicitação de processamento por parte dos incontáveis terminais conectados diretamente ao sistema, aos quais o computador tem que atender e responder em poucos segundos.
A Figura 3.16 mostra um mainframe fabricado pela IBM.
31619 Mainframe Fonte: Google imagens
e. Supercomputadores
É o tipo de computador mais poderoso e rápido.
Segundo Capron (2004), podem ser encontrados em aplicações prevalecentes tão variadas quanto análise de ações, design de automóveis, efeitos especiais cinematográficos e até mesmo ilustrações gráficas sofisticadas. Entretanto, durante muitos anos, seus clientes foram um grupo exclusivo – órgãos do Governo Federal -, que os utilizavam para tarefas que requerem uma gigantesca manipulação de dados, como a previsão meteorológica que engloba o mundo inteiro e pesquisas de armamento.
Desempenho dos computadores
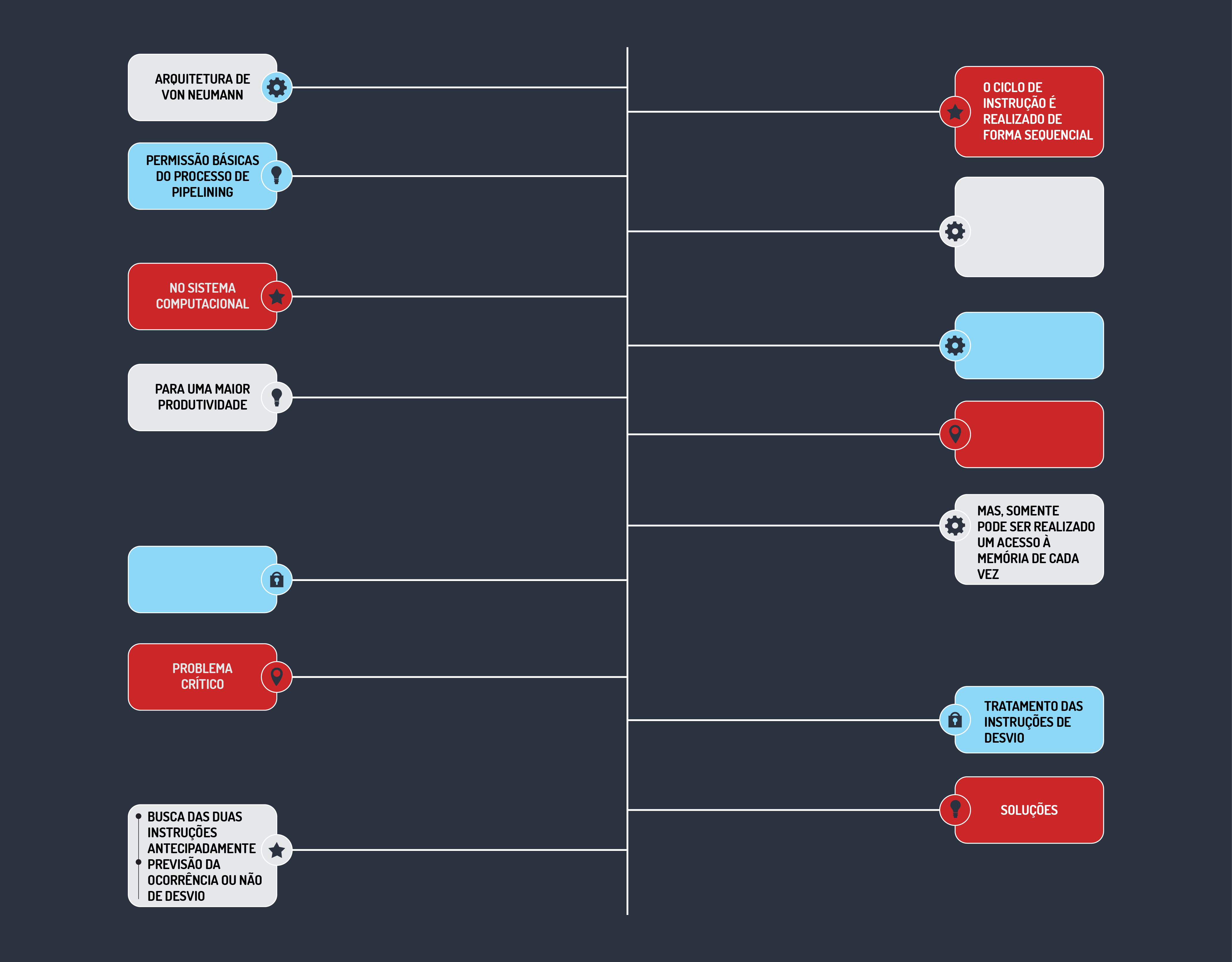
Os computadores têm se desenvolvido cada vez mais rapidamente, seja com a utilização de novas tecnologias para a fabricação de seus componentes ou modificações na forma como o ciclo de instruções é realizado. Mas ainda temos os mesmos princípios básicos de arquitetura concebidos por Von Neumann.
Na busca do aumento de desempenho, verifica-se que a medida geral deste desempenho depende fundamentalmente da capacidade e velocidade de seus diferentes componentes, da velocidade com que estes componentes se comunicam entre si e do grau de compatibilidade que possa existir entre eles (por exemplo, se a velocidade da UCP de um sistema é muito maior que a da memória, então esse sistema tem um desempenho inferior ao de um outro em que a UCP e a memória têm velocidades mais próximas) (MONTEIRO, 2012).
Isto significa que o computador deve se desenvolver como um todo, pois as diferentes velocidades existentes nele afetam o desempenho global do sistema.
Segundo Ricarte (2016), como há um grande número de alternativas para a organização de um computador, é preciso ter mecanismos que permitam realizar a avaliação de cada arquitetura. Algumas medidas básicas de avaliação são necessárias para tanto. O desempenho está usualmente associado à velocidade de execução de instruções básicas (taxas MIPS e FLOPS) ou à velocidade de execução de programas representativos das aplicações (benchmarks). Lembrando que MIPS significa milhões de instruções por segundo e FLOPS, operações de ponto flutuante por segundo.
Em essência, o termo benchmark utilizado na computação tem o mesmo significado do benchmark utilizado no mundo corporativo, por exemplo, já que visa a comparação de mecanismos, processos, objetos e resultados. Geralmente, na computação, o termo “benchmarking” é associado com avaliação de características de desempenho de um hardware, mas também pode ser aplicado a software, desde que se leve em consideração dados apenas técnicos (CANALTECH, 2016).
Fique por dentro
Medidas de desempenhoMedidas de desempenho dependem do ponto de vista individual. Um usuário de computador está mais preocupado com o tempo de resposta: o tempo total para o sistema realizar uma tarefa. Administradores de sistema estão mais preocupados com vazão: quantas tarefas concorrentes o sistema pode realizar sem afetar de forma adversa seu tempo de resposta. Estes dois pontos de vista são inversamente relacionados (ANDRADE, 2016).
Temos várias medidas de desempenho:
- Tempo de resposta: é o intervalo de tempo entre a requisição do usuário e a resposta do sistema. É uma medida relacionada ao desempenho do sistema como um todo e não de seus componentes individuais.
- Tempo de acesso: é relativo ao uso da memória, quando são realizadas operações com a mesma (escrita e leitura). Este tempo depende da velocidade da UCP, da memória e da interligação entre elas.
- Vazão (throughput), ou taxa de processamento, ou ainda taxa de serviço: é a quantidade executada de serviço por unidade de tempo.
Almeida (2009) apresenta mais algumas métricas para o desempenho:
- Eficiência: capacidade útil/capacidade nominal;
- Utilização: porcentagem de tempo que o recurso está executando o serviço;
- Custo‐benefício = custo/desempenho;
- Métricas específicas: porcentagem de perda de pacotes, qualidade do sinal.
Atividades
Componentes de um sistema de computação
Para cada função que o computador executa existe uma série de placas e equipamentos que a torna possível. Cada função básica também pode ser chamada de Unidade, assim temos: Unidade de Entrada, Unidade de Saída, Unidade de Processamento e Unidade de Armazenamento, cada unidade com seus respectivos equipamentos e placas (OLIVEIRA, 2007). Levando esses dados em consideração, principalmente a questão dos equipamentos, assinale a alternativa que contém elementos correspondentes, respectivamente, à Unidade de Entrada, Unidade de Saída, Unidade de Processamento e Unidade de Armazenamento:
- Caixa de som; Processador; HDs; Tela sensível ao toque.
Cuidado! A Caixa de som é uma Unidade de Saída, o Processador é uma Unidade de Processamento, os HDs são Unidades de Armazenamento e a Tela sensível ao toque, nesse caso, é uma Unidade de Entrada.
- Tela sensível ao toque; Caixa de som; Processador; HDs.
Esses elementos correspondem exatamente às unidades na ordem apresentada.
- HDs; Processador; Caixa de som; Tela sensível ao toque.
Cuidado! Os HDs são Unidades de Armazenamento, o Processador é uma Unidade de Processamento, a Caixa de som é uma Unidade de Saída e a Tela sensível ao toque, nesse caso, é uma Unidade de Entrada.
- Tela sensível ao toque; HDs; Processador; Caixas de som.
Cuidado! Os HDs são Unidades de Armazenamento e a Caixa de som é uma Unidade de Saída.
- Processador; Tela sensível ao toque; HDs; Caixa de som.
Cuidado! O Processador é uma Unidade de Processamento, a Tela sensível ao toque, nesse caso, é uma Unidade de Entrada, os HDs são Unidades de Armazenamento e a Caixa de som é uma Unidade de Saída.
Unidade Central de Processamento (UCP) e Linguagem de Montagem
Tanenbaum (2007, p.29) define:
a CPU (Central Processing Unit – unidade central de processamento) é o “cérebro” do computador. Sua função é executar programas armazenados na memória principal buscando suas instruções, examinando-as e então executando-as uma após a outra. Os componentes são conectados por um barramento, que é um conjunto de fios paralelos que transmitem endereços, dados e sinais de controle. Barramentos podem ser externos à CPU, conectando-a à memória e aos dispositivos de E/S, mas também podem ser internos à CPU.
Na realidade, a UCP é responsável pela realização de qualquer operação realizada por um computador. Isto quer dizer que a UCP comanda não somente as ações efetuadas internamente, como também, em decorrência da interpretação de uma determinada instrução, ela emite os sinais de controle para os demais componentes do computador agirem e realizarem alguma tarefa (MONTEIRO, 2012).
Como acabamos de ver, a UCP é responsável por uma grande quantidade de atividades. Elas podem ser divididas em duas categorias: função processamento e função controle.
Função processamento
A função processamento se encarrega de realizar as atividades relacionadas com a efetiva execução de uma operação, ou seja, processar (MONTEIRO, 2012).
Algumas das operações que podem ser realizadas por essa parte da UCP são:
- Aritméticas (soma, subtração, multiplicação e divisão);
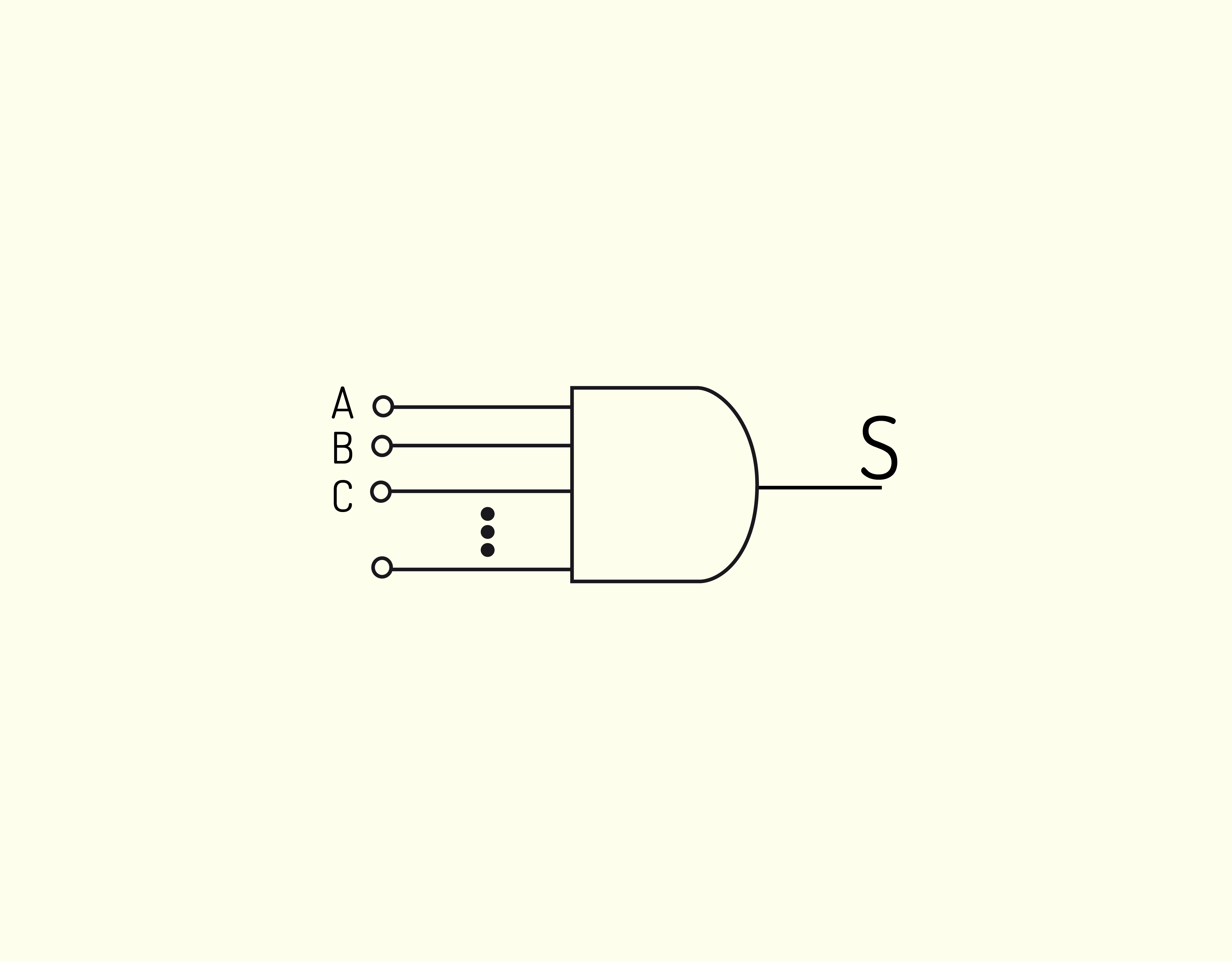
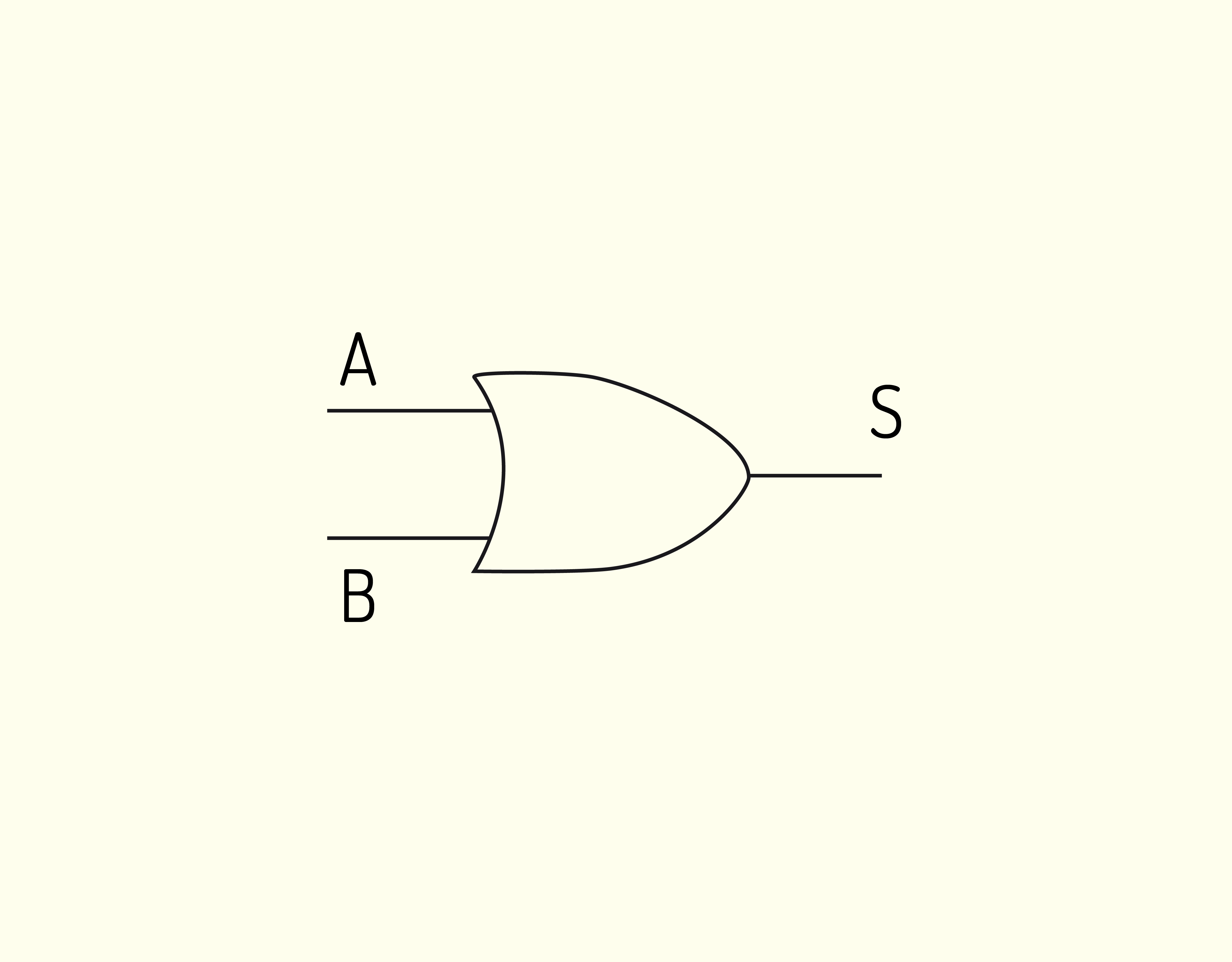
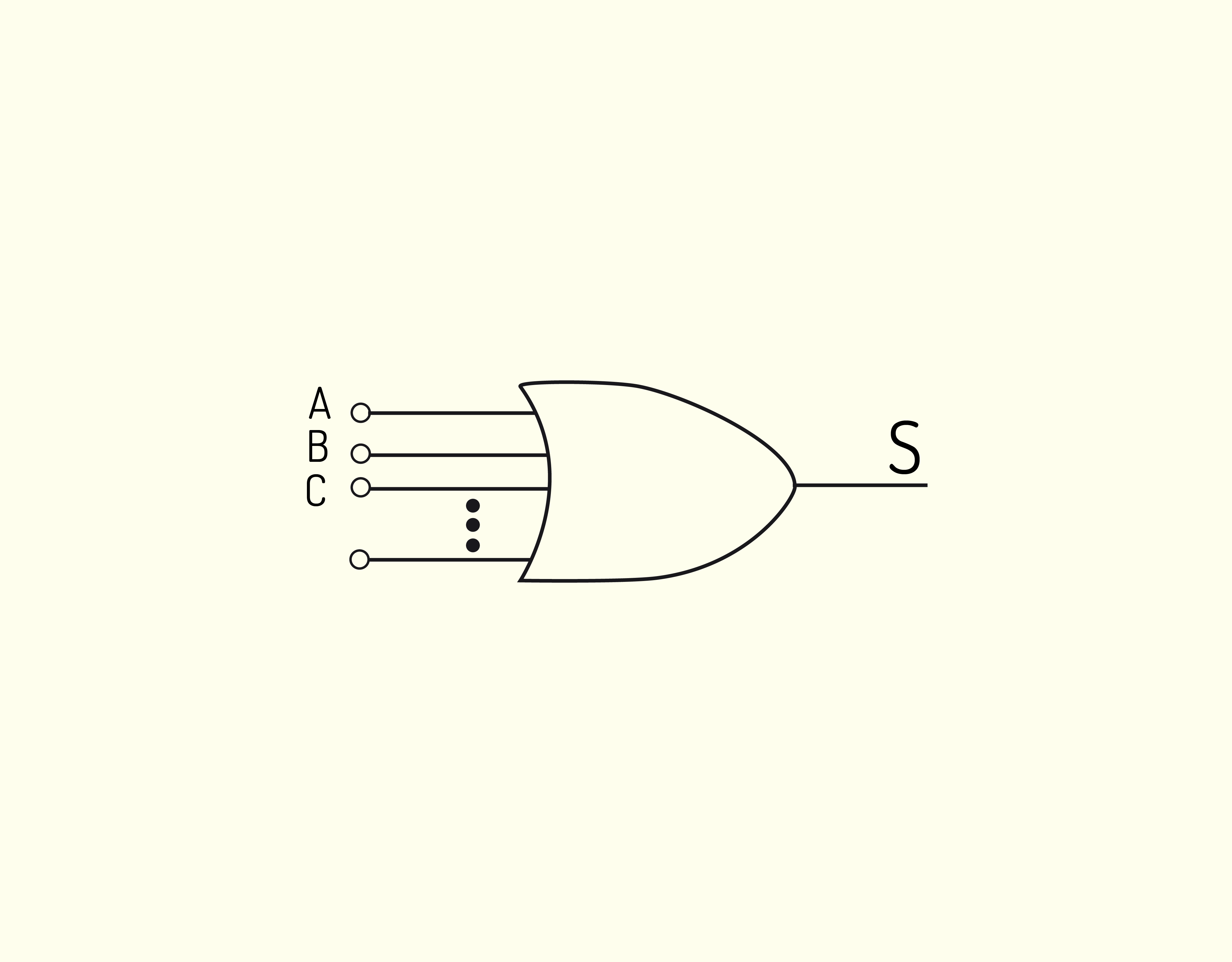
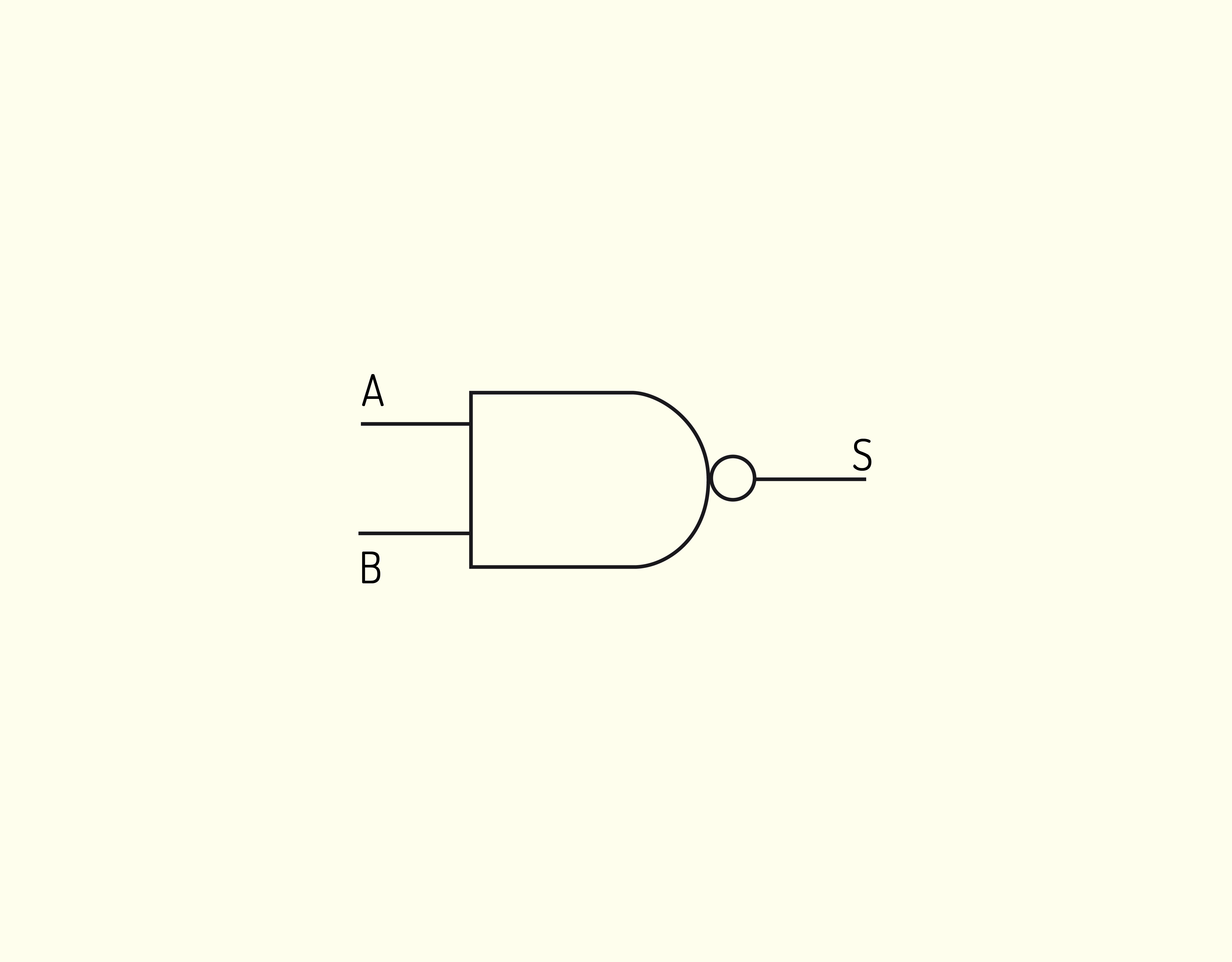
- Lógicas (as mesmas realizadas pelas portas lógicas);
- Movimentação de dados (por exemplo, entre memória e UCP);
- Desvios (alterações na sequência normal do programa);
- Entrada e saída.
A parte da UCP que realiza a função processamento é formada pela UAL (Unidade Aritmética e Lógica) ou ULA (Unidade Lógica e Aritmética) ou, ainda, em inglês, ALU (Arithmetic Logic Unit) e pelos registradores, interligados pelo barramento interno.
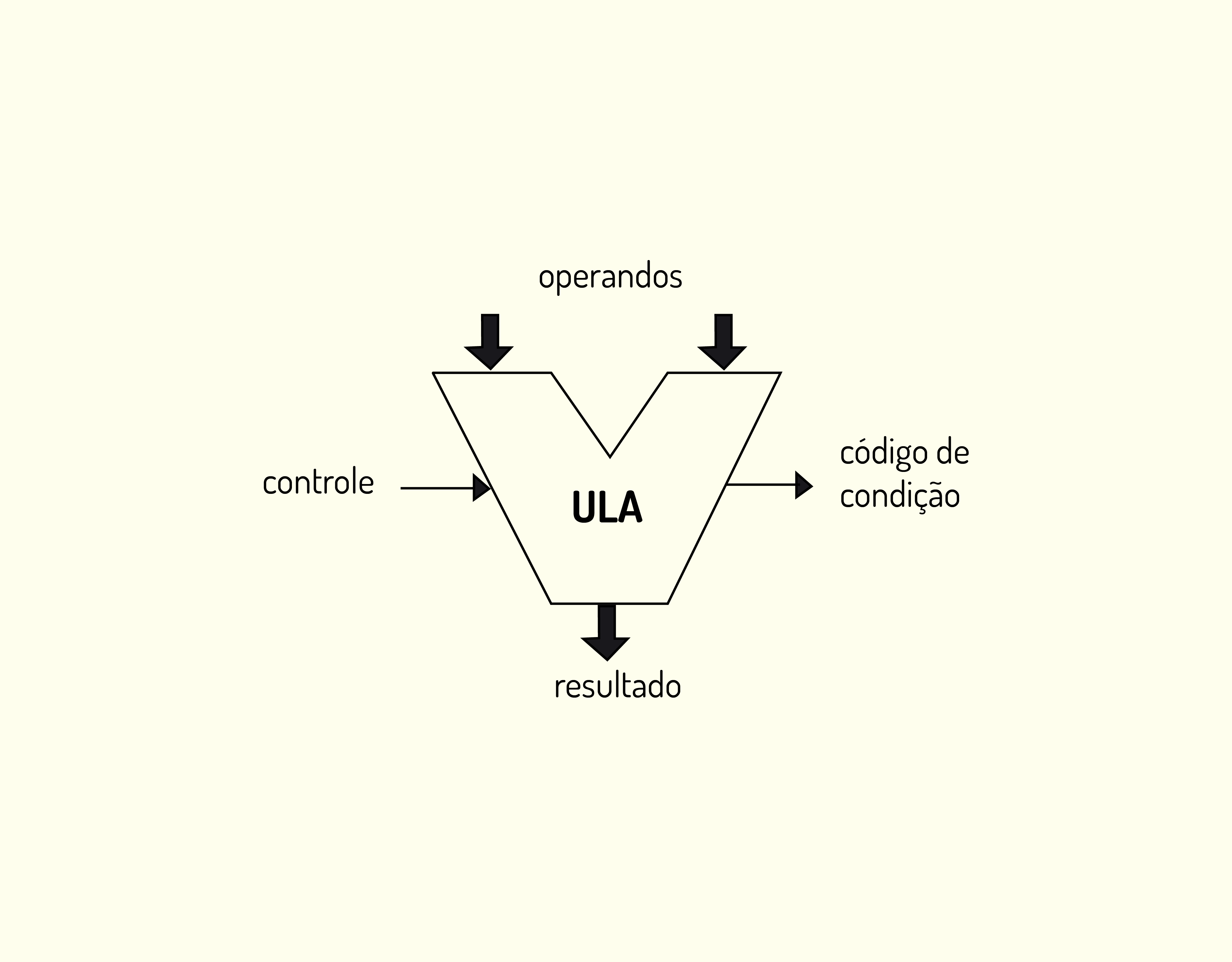
Unidade Aritmética e Lógica
Como o próprio nome diz, a Unidade Aritmética e Lógica é responsável pelas operações matemáticas e lógicas que podem ser realizadas pelo computador, citadas anteriormente.
A UAL possui duas entradas, pois pode realizar operações com um ou dois valores. Por exemplo, as operações de soma e subtração necessitam de dois valores na entrada, mas a de complemento somente um.
Quando o resultado é obtido, por meio da passagem dos sinais pelos circuitos lógicos que compõem a UAL, estes dados são repassados à saída pelo barramento interno de dados.
A Figura 3.17 apresenta o desenho esquemático de uma UAL.
31719 Modelo estrutural da UAL Fonte: Weber (2012).
Registradores
Os registradores são um tipo de memória interna à UCP, extremamente rápidos, mas presentes em pequena quantidade. São áreas de armazenamento temporário, para guardar dados, instruções e endereços, que estão sendo utilizados na operação que está sendo executada.
Os principais registradores presentes na UCP são:
- ACC (Acumulador): serve de ligação entre a UCP e os outros dispositivos dela. É quem armazena os resultados obtidos na UAL.
- RDM (Registrador de Dados da Memória): contém o dado lido da memória ou que deverá ser escrito nela. Em inglês é chamado de Memory Buffer Register (MBR).
- REM (Registrador de Endereços da Memória): contém o endereço do dado que deverá ser lido ou escrito na memória. Em inglês é chamado de Memory Address Register (MAR).
- RI (Registrador de Instrução): contém a instrução que foi lida mais recentemente. Em inglês, é chamado de Instruction Register (IR).
- CI (Contador de Instrução): contém o endereço da próxima instrução que será lida. Em inglês, é chamado de Program Counter (PC).
- RST (Registrador de Estado): armazena os bits de estado, referentes ao resultado de operações realizadas, como os de sinal, overflow, zero, vai 1 e paridade. Seu nome, em inglês, é Program Status Word (PSW), ou palavra de estado.
- Registradores de uso geral: registradores genéricos presentes na UCP que a auxiliam em suas atividades.
Função controle
A função controle é exercida pelos componentes da UCP que se encarregam das atividades de busca, interpretação e controle da execução das instruções, bem como do controle da ação dos demais componentes do sistema de computação (memória, entrada/saída) (MONTEIRO, 2012).
O principal elemento da função controle é a Unidade de Controle, que é considerado o dispositivo mais complexo da UCP.
Unidade de Controle
Capron (2008, p.94) define:
a unidade de controle contém circuitos que usam sinais elétricos para coordenar o computador inteiro para realizar ou executar instruções armazenadas de um programa. Como um maestro de orquestra, a unidade de controle não executa instruções de programa: ao contrário, ela comanda outras partes do sistema para isso. A unidade de controle deve comunicar-se tanto com a unidade lógica e aritmética quanto com a memória.
Assim, a unidade de controle gera todos os sinais de controle para comandar a máquina (microeventos ou micro-operações), emitidos de tempos em tempos, coordenados pelo relógio (clock).
Os sinais para estes microeventos ou micro-operações podem ser gerados de duas formas: programados no hardware (hardwired control) ou por microprogramação.
A diferença básica entre os dois métodos, segundo Monteiro (2012), está no processo de controle da realização do ciclo de instrução. No primeiro caso (hardwired), cada etapa é realizada segundo uma lógica preestabelecida, implementada fisicamente no hardware da área de controle. No caso de controle microprogramado, a interpretação e as consequentes etapas do ciclo de instrução são realizadas passo a passo por um programa, denominado microprograma.
Fique por dentro
Funções processamento e controlePodemos fazer uma analogia com os seres humanos, imaginando que a área de controle é o cérebro que comanda o ato de andar, e a área de processamento são os músculos e ossos das pessoas que realizam efetivamente o ato. Os nervos são análogos ao barramento de interligação entre os diversos elementos (MONTEIRO, 2012).
Ciclo de instrução
Conforme vimos anteriormente, a UCP é responsável por executar os programas, que são compostos de instruções. Agora, veremos como isto é feito, o que chamamos de ciclo de instrução. Cada uma destas instruções é dividida em etapas.
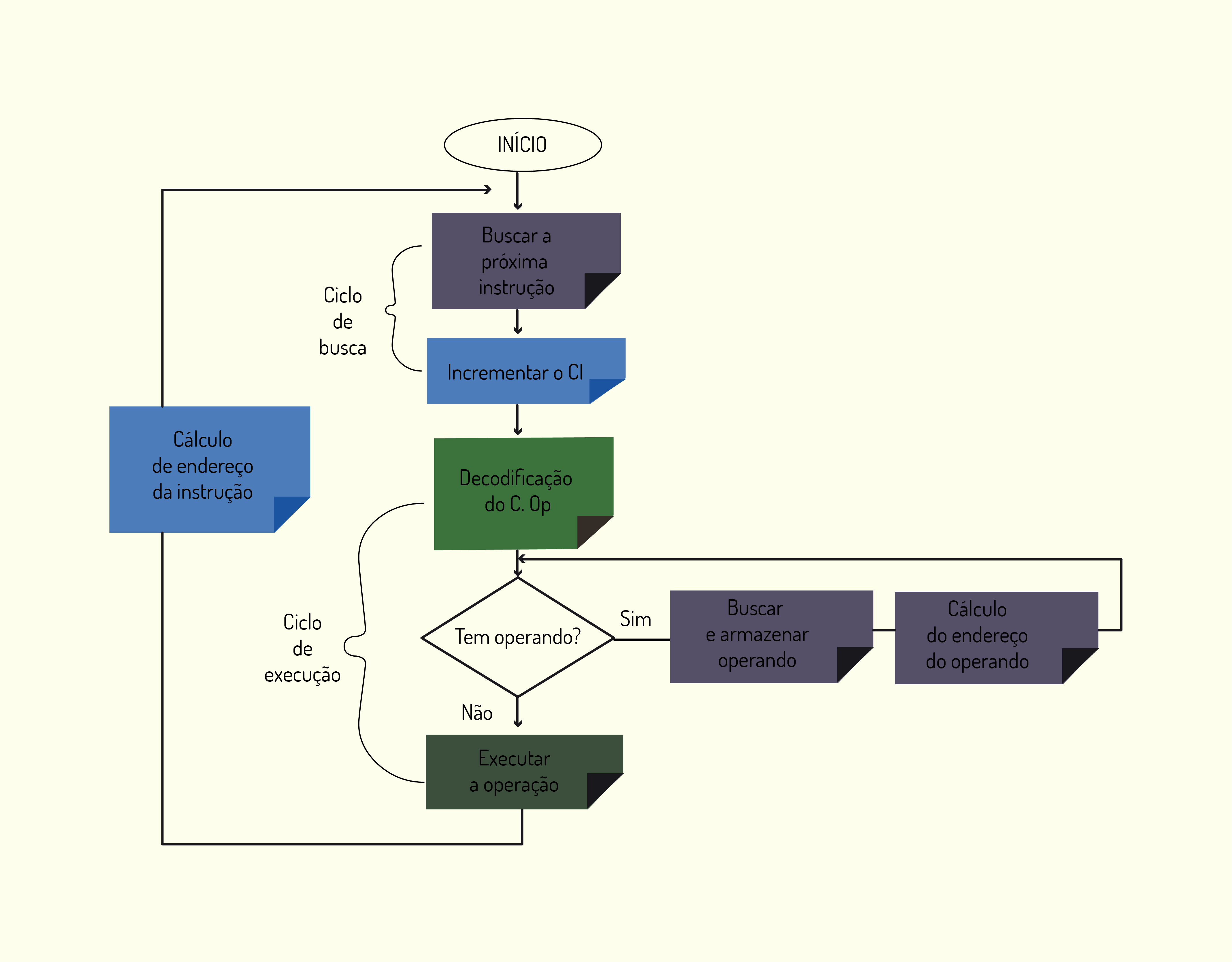
Tanenbaum (2007) define as seguintes etapas, chamadas de ciclo buscar-decodificar-executar:
- Trazer a próxima instrução da memória até o registrador;
- Alterar o contador de programa para indicar a próxima instrução;
- Determinar o tipo de instrução trazida;
- Se a instrução usar uma palavra na memória, determinar onde esta palavra está;
- Trazer a palavra para dentro de um registrador da CPU, se necessário;
- Voltar à etapa 1 para iniciar a execução da instrução seguinte.
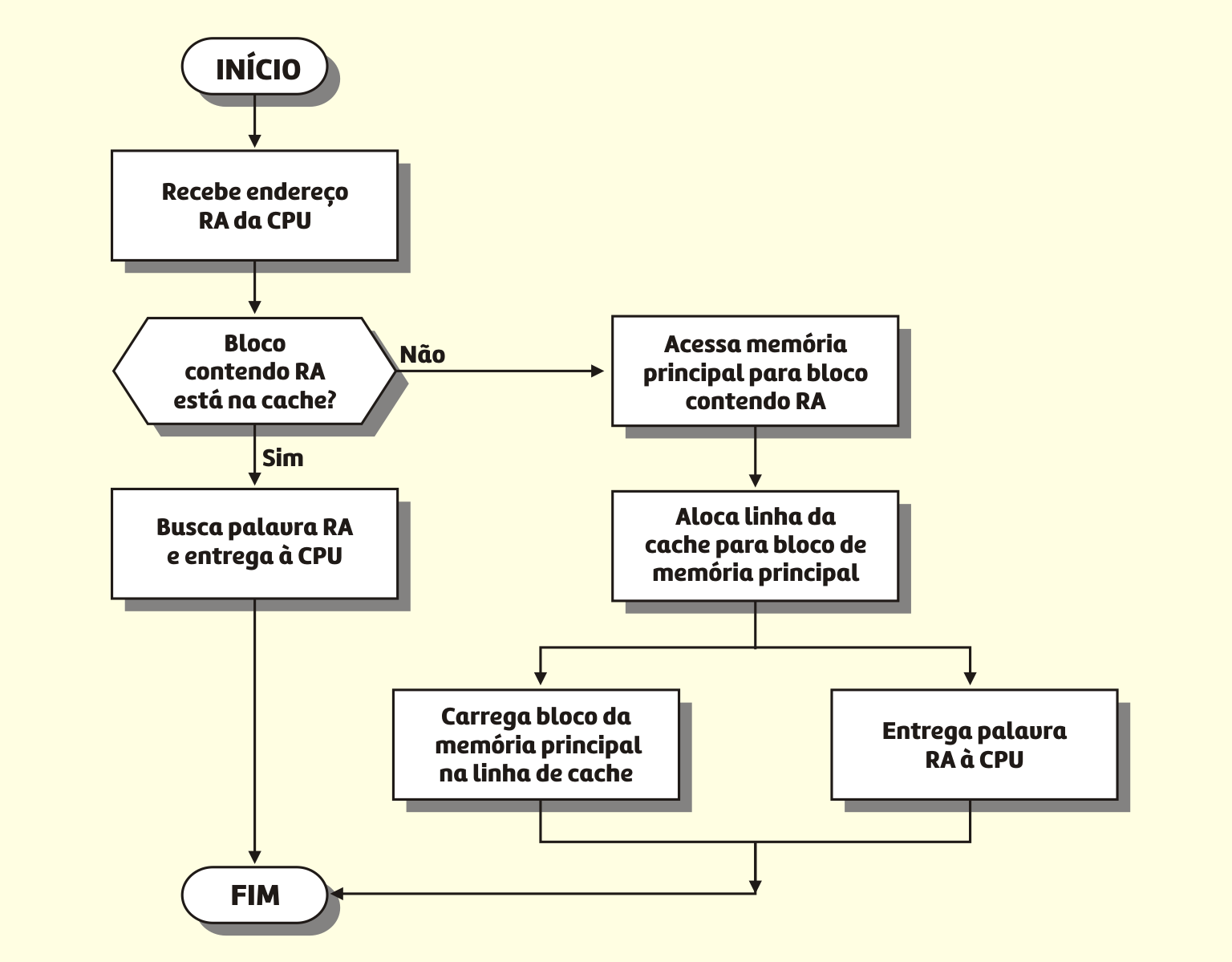
A Figura 3.18 ilustra essas etapas.
31819 Fluxograma de um ciclo de instrução Fonte: Monteiro (2012).
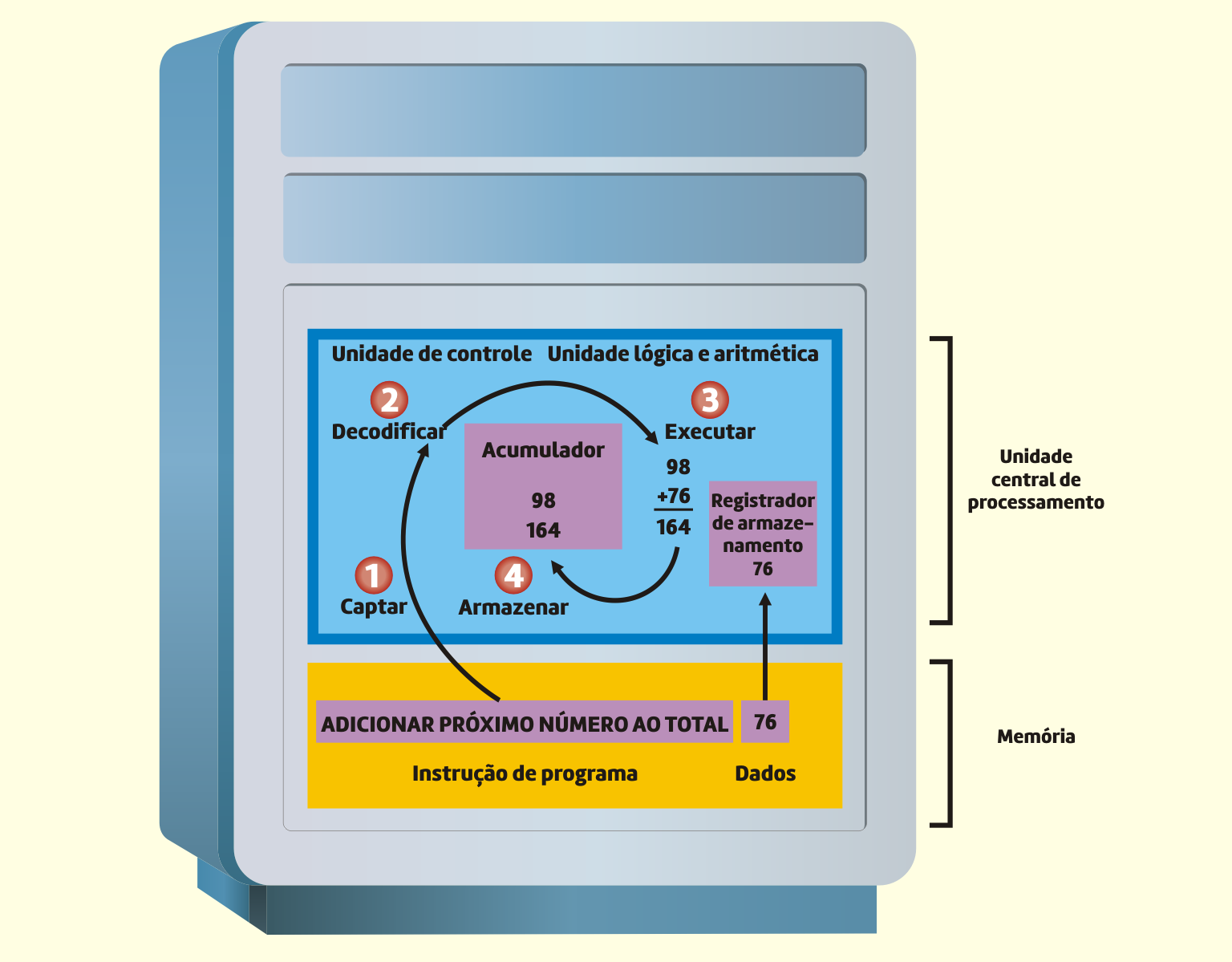
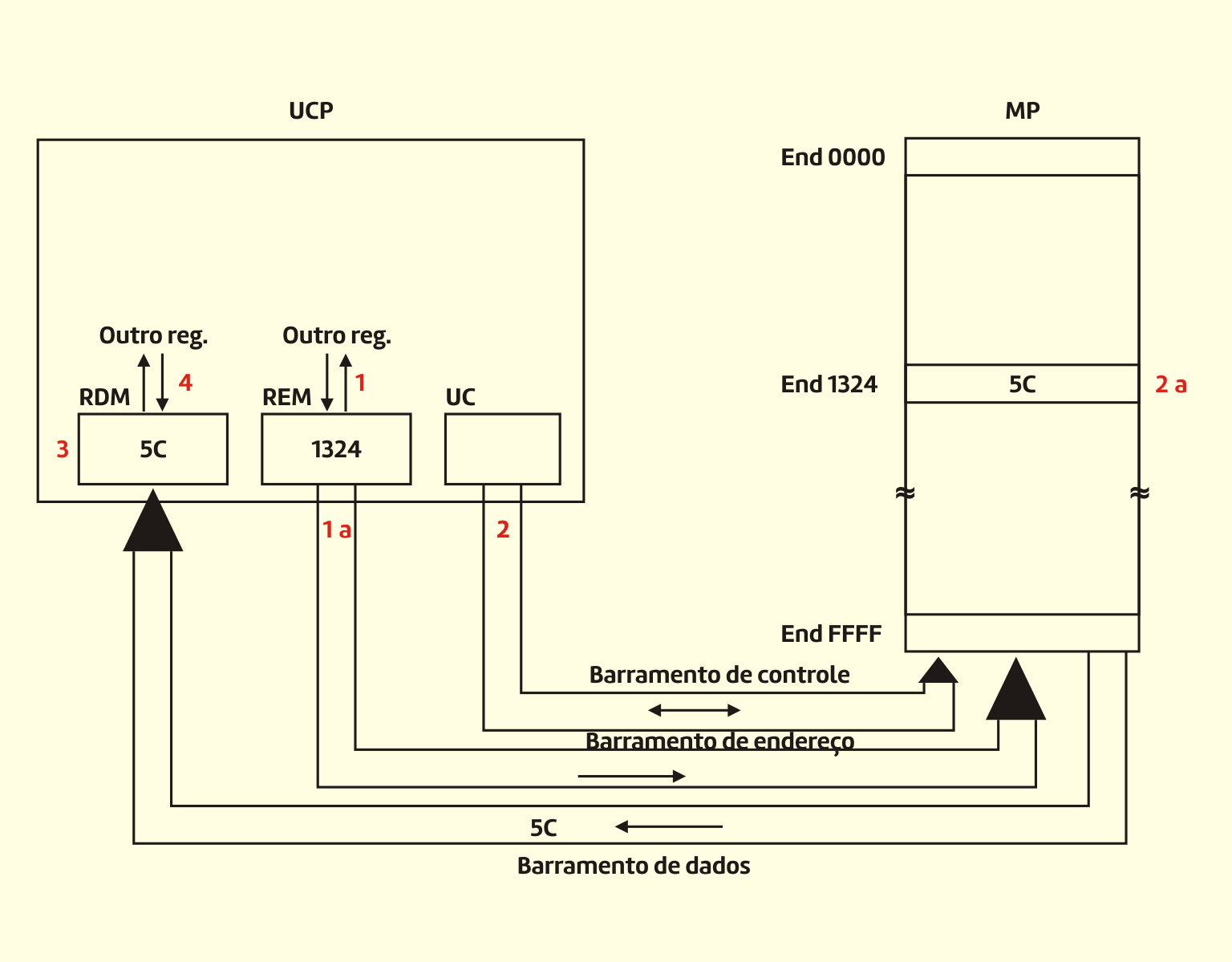
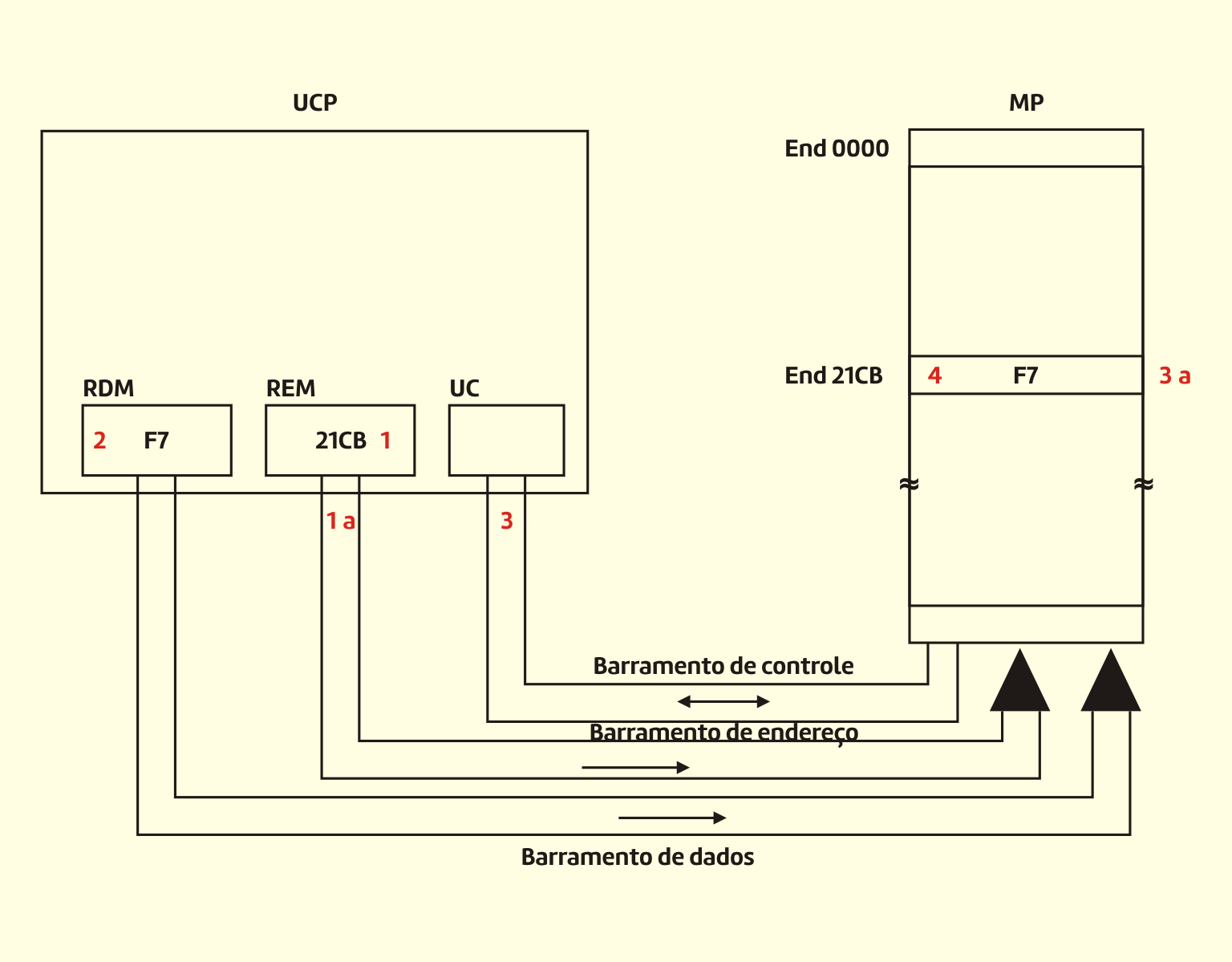
Capron (2008, p.98) apresenta um exemplo simples do ciclo de instrução:
suponhamos que um programa queira encontrar a média de cinco pontuações de exame. Para isso, deve totalizar as cinco pontuações e depois dividir o resultado por cinco. O programa inicia fixando o total em 0. Depois, adiciona cada um dos cinco números, um por vez, ao total. Suponhamos que as pontuações sejam 88, 76, 91, 83 e 87. Nesse cálculo, o total foi fixado em 0 e, depois, 88, a primeira pontuação do exame, foi adicionada. Examine agora o ciclo de máquina quando ele adiciona a pontuação seguinte, 76, ao total. Siga as etapas do ciclo de máquina. (1) Captar: a unidade de controle capta a instrução ADD da memória. (2) Decodificar: a unidade de controle decodifica a instrução ADD. Ela determina que a adição deve ser efetuada e fornece instruções para que o número seguinte, 76, seja colocado em um registrador para esse propósito. O total atual, 88, já está no acumulador. (3) Executar: o número seguinte, 76, é colocado no registrador. A ALU faz a adição, aumentando o valor para 164. (4) Armazenar: nesse caso, a ALU armazena o resultado no acumulador, em vez de na memória, porque ainda é necessário adicionar mais números a ela. O novo total, 164, substitui o total anterior, 88 e o processo continua.
Esse exemplo é ilustrado na Figura 3.19.
31919 O ciclo de máquina em ação Fonte: Capron (2004)
Introdução à linguagem de montagem
Conforme falamos anteriormente, o computador é projetado para trabalhar com a linguagem de máquina, que utiliza mnemônicos para indicar a instrução ou operação que será executada.
O projeto de um processador é centrado no conjunto de instruções de máquina que se deseja que ele execute (na realidade, do conjunto de operações primitivas que ele poderá executar). Uma das mais fundamentais análises e decisões do projeto envolve o tamanho e a complexidade do conjunto de instruções. Quanto menor e mais simples o conjunto de instruções, mais rápido é o ciclo de tempo do processador (MONTEIRO, 2012).
Representação de instruções
O formato geral de uma instrução de máquina é:
C. Op. | Op. |
Código de operação | Operando |
Em que:
Código de operação: identifica a operação que será realizada. Temos um código para cada instrução que pode ser realizada pelo computador.
Operando: indica a localização do dado que será usado durante a operação. Esse campo pode conter mais de um operando.
Exemplos de instruções:
a. Com um operando:
- LDA Op., fornece o resultado Acc ⃪ (Op.)
O acumulador recebe o conteúdo do operando.
- ADD Op., fornece o resultado Acc ⃪ Acc + (Op.)
O acumulador recebe o seu valor anterior acrescido do conteúdo do operando.
b. Com dois operandos:
- MOVE Op.1, Op.2, fornece o resultado (Op.1) ⃪ (Op.2)
O operando 1 recebe o conteúdo do operando 2.
- SUB Op.1, Op.2, fornece o resultado (Op.1) ⃪ (Op.1) – (Op.2)
O operando 1 recebe o seu valor anterior subtraído do conteúdo do operando 2.
c. Com três operandos:
- ADD Op.1, Op.2, Op.3, fornece o resultado (Op. 3) ⃪ (Op.1) + (Op.2)
O operando 3 recebe a soma entre o conteúdo dos operando 1 e 2.
O campo operando não precisa, necessariamente, indicar o endereço do dado. O modo de endereçamento é que define como este dado será localizado, o que varia de instrução para instrução.
Os modos de endereçamento principais, segundo Tanenbaum (2007), são:
a. Endereçamento imediato
O modo mais simples de uma instrução especificar um operando é a parte da instrução referente ao endereço realmente conter o operando em si em vez de um endereço ou outra informação que descreva onde o operando está. Tal operando é denominado operando imediato porque ele é automaticamente buscado na memória, ao mesmo tempo que a própria instrução; por conseguinte, ele está imediatamente disponível para uso. O endereçamento imediato tem a virtude de não exigir uma referência extra à memória para buscar o operando. A desvantagem é que somente uma constante pode ser fornecida desse modo.
Exemplo: a instrução MOV B, 22H, que move o valor hexadecimal 22 para o registrador B, utiliza o endereçamento imediato.
b. Endereçamento direto
Um método para especificar um operando na memória é dar seu endereço completo. Esse modo é denominado endereçamento direto. Assim como o endereçamento imediato, o endereçamento direto tem uso restrito: a instrução sempre acessará exatamente a mesma localização de memória. Portanto, embora o valor possa mudar, a localização não pode. Assim, o endereçamento direto só pode ser usado para acessar variáveis globais cujos endereços são conhecidos no momento da compilação. Não obstante, muitos programas têm variáveis globais, portanto, esse modo é amplamente usado.
Exemplo: a instrução ADD A, que soma o valor do endereço A ao acumulador utiliza o endereçamento direto.
c. Endereçamento de registrador
Endereçamento de registrador é conceitualmente o mesmo que endereçamento direto, mas especifica um registrador em vez de uma localização de memória. Como os registradores são tão importantes (devido ao acesso rápido e endereços curtos), esse modo de endereçamento é o mais comum na maioria dos computadores.
Exemplo: a instrução ADD A, B, soma o conteúdo do registrador B ao conteúdo do acumulador, armazenando o resultado no acumulador. Essa instrução utiliza o endereçamento de registrador.
d. Endereçamento indireto de registrador
Nesse modo, o operando que está sendo especificado vem da memória ou vai para a memória, mas seu endereço não está ligado à instrução, como no endereçamento direto. Em vez disso, o endereço está contido em um registrador. Quando um endereço é usado dessa maneira, ele é denominado ponteiro. Uma grande vantagem do endereçamento indireto de registrador é que ele pode referenciar memória sem pagar o preço de ter um endereço de memória completo na instrução.
Exemplo: a instrução ADD (A), que soma ao acumulador do conteúdo de memória apontado pelo endereço representado por A, utiliza o endereçamento indireto de registrador.
e. Endereçamento indexado.
Muitas vezes é útil poder referenciar palavras de memória cujo deslocamento em relação a um registrador é conhecido. Endereçamento indexado é o nome que se dá ao endereçamento de memória que fornece um registrador (explícito ou implícito) mais um deslocamento constante.
Atividades
Unidade Central de Processamento (UCP) e Linguagem de Montagem
A quantidade e o uso dos registradores variam bastante de modelo para modelo de UCP. Além dos registradores de dados, a UCP possui sempre outros registradores que não participam diretamente da função processamento, com funções específicas ou que funcionam para a área de controle. Entre estes registradores, pode-se citar o Registrador de Instrução (RI) e o Contador de Instrução (CI), além do Registrador de Endereços de Memória (REM) e o Registrador de Dados de Memória (RDM). Levando isso em consideração, é correto afirmar que:
- O registrador de dados armazena a próxima instrução a ser executada pela UCP.
O registrador de dados contém o dado lido da memória ou que deverá ser gravado nela.
- O registrador de instrução armazena a instrução que está sendo executada no momento.
O registrador de instrução guarda a instrução que foi lida mais recentemente, ou seja, a que está sendo executada.
- O registrador de endereços da memória é utilizado pela UCP e dispositivos de entrada e saída para comunicação e transferência de informações.
O registrador de endereços da memória é utilizado para comunicação entre UCP e memória.
- O contador de instrução armazena a quantidade de operações que foram realizadas.
O contador de instruções armazena o endereço da próxima instrução a ser lida.
- O registrador de endereços, juntamente com o registrador de dados, é responsável pelo envio de sinais de controle para a UCP.
Tanto o registrador de endereços quanto o de dados são responsáveis pela comunicação entre UCP e memória.
Indicação de leitura
Nome do livro: Turing e o computador em 90 minutos
Editora: Le Livros
Autor: Paul Strathern
ISBN: não tem
O livro apresenta um histórico bem completo da evolução das máquinas, desde a era a.C., quando ainda nem se pensava em computadores da maneira que temos hoje. Também contém uma biografia bem completa de Alan Turing, mostrando, também, curiosidades de sua vida até chegar no momento do desenvolvimento da máquina que viria a decifrar a Enigma, responsável pela codificação das mensagens alemãs. Finaliza com algumas datas significativas no desenvolvimento do computador e sugestões de leitura. É um livro curto e fácil de ler, ideal para quem quer saber um pouco mais sobre a história do computador.
O livro está disponível em: Le Livro - Turing e o Computador em 90 minutos – Paul Strathern.
Indicação de leitura
Nome do livro: Introdução à Organização de Computadores
Editora: LTC – Livros Técnicos e Científicos
Autor: Mário Antonio Monteiro
ISBN: 9788521615439
O livro é bastante didático e contém todos os conteúdos estudados nesta unidade, como o funcionamento do computador, seu histórico, componentes e uma explicação bem completa sobre a Unidade Central de Processamento. Apresenta exemplos práticos, comparando a máquina com situações da vida real. É um livro muito indicado para fixar e conhecer mais profundamente os conceitos trabalhados.
Indicação de filme
Nome do filme: O jogo da imitação
Gênero: Biografia, Drama
Ano: 2015
Elenco: Benedict Cumberbatch, Keira Knightley, Matthew Goode
O filme conta a história de Alan Turing que, durante a Segunda Guerra Mundial, foi contratado pelo governo britânico para decifrar a máquina Enigma, utilizada pelos alemães para trocar mensagens codificadas. Ele deverá, junto com sua equipe, construir uma máquina que consiga analisar todas as possibilidades de codificação da Enigma em apenas 18 horas, para que os ingleses possam entender as comunicações alemãs e ter acesso as suas estratégias com antecedência. É uma maneira agradável de conhecer os primórdios da computação, compreendendo como Turing conseguiu chegar a seus projetos e visualizar os “computadores” da época.